BÀI 8 LÝ THUYẾT ƯỚC LƯỢNG (Có bổ xung). Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

lOMoAR cPSD| 59285474
BÀI 8 LÝ THUYẾT ƯỚC LƯỢNG
8.1 MỘT SỐ PHƯƠNG PHÁP TÌM HÀM ƯỚC LƯỢNG ĐIỂM CHO THAM SỐ
• Định nghĩa 8.1 Cho X f ( x ;θ) , và X1 , X2 ,…, Xn, là mẫu ngẫu nhiên từ X. Mọi hàm thống
kê ta có thể sử dụng để dự báo về tham số θ, được gọi là một ước lượng của θ. Ta
thường ký hiệu ước lượng của θbởi θ^. Ví dụ:
Phân phối chuẩn N (μ;σ2)có các tham số cần ước lượng là μ=θ1;σ2=θ2 ;
Phân phối mũcó tham số cần ước lượng là λ=θ;
Để tìm hàm ước lượng cho tham số θ, có nhiều phương pháp khác nhau như
1) Phương pháp momen (Moment Method)
2) Phương pháp hợp lý cực đại (Maximum Likelihood Method)
3) Phương pháp Bayes (Bayes Method)
4) Phương pháp bình phương tối thiểu (Least Squares Method)
5) Phương pháp cực tiểu Chi-bình phương (Minimum Chi-Squares Method)
Dưới đây ta sẽ làm quen với 02 phương pháp thông dụng nhất trong các phương pháp liệt kê trên
• Phương pháp momen
Cho X1 , X2 ,…, Xn, là mẫu ngẫu nhiên từ X f (x ;θ1 ,θ2,…,θm), trong đó θ1 ,θ2 ,…,θm là m tham
số chưa biết. Với momen gốc bậc k E . (8.1)
Mặt khác ta có momen mẫu bậc k là n M kxki . (8.2) =1
Trong phương pháp momen ta sẽ tìm ước lượng cho các tham số θ1 ,θ2 ,…,θm bởi hệ phương
trình từ m momen mẫu (8.2) đối chứng với các dạng (8.1), nghĩa là từ hê 1 lOMoAR cPSD| 59285474
E ( X )=M1
E (X2)=M 2
E (X3)=M 3 ⋮
E (Xm)=M m
Phương pháp momen là một trong những phương pháp thống kê kinh điển do Karl Pearson đưa ra năm 1902.
Ví dụ 8.1 Giả sử X1, X2,…, Xn là mẫu từ biến X, với phân phối có hàm mật độ , f
Ta sẽ tìm ước lượng cho α và β theo phương pháp momen.
Về lý thuyết ta biết rằng X có phân phối đều trên đoạn [ α, β ] , do đó nó có 2 E ( ( β−α)
X )=;Var ( X )= ; 12
Mặt khác từ cách xác định các momen mẫu ta có n M . M ¿ .¿ Từ đó suy ra ¿ . Vì vậy: .
Kết hợp với giá trị của kỳ vọng ta thu được 2 lOMoAR cPSD| 59285474 . Từ đó sẽ suy ra .
Mặt khác vì α<β , nên các hàm ước lượng cho α ,β sẽ là 2 ; i
Ví dụ 8.2 Cho X1 , X2 ,…, Xn là mẫu từ biến ngẫu nhiên X, với phân phối có hàm mật độ −x f { ( x ;θ)= e
β ;nếu x∈ (0,∞) , 0;nếu
x∉ (0,∞) .
Ta sẽ tìm ước lượng cho tham số θ, bằng phương pháp momen.
Trong trường hợp này chỉ có một tham số nên ta chỉ cần sử dụng momen bậc nhất là kỳ vọng: −x EXe β dx ¿ .
Vì EX=M1=X, nên ta có phương trình: 7 β=X
Do đó ước lượng của θ, xác định theo phương pháp momen là: ^β= X.
• Phương pháp hợp lý cực đại (Maximum likelihood method)
Phương pháp hợp lý cực đại được R. Fisher sử dụng từ năm 1912, để tìm hàm ước
lượng cho các tham số chưa biết. Tuy nhiên, phương pháp này phát triển từ các công
trình của Gauss và Bernuolli. Tiếp theo chúng ta sẽ làm quen chi tiết về phương pháp 3 lOMoAR cPSD| 59285474
này. Định nghĩa 8.2 Cho mẫu ngẫu nhiên X1 , X2 ,…, Xn với hàm mật độ f ( x ;θ) , trong
đó θ là tham số chưa biết. Hàm hợp lý L (θ) là phân phối của mẫu, xác định bởi n
L (θ)=∏ f (xi ;θ ). (8.3) i=1
Định nghĩa này cho ta thấy rằng hàm hợp lý của mẫu ngẫu nhiênX1, X2,…, Xn là mật độ đồng
thời của các biến ngẫu nhiên X1 , X2 ,…, Xn.
Khi θ tối đa hóa hàm hợp lý L (θ) , nó được gọi là ước lượng hợp lý cực đại của θ, và được
ký hiệu là θ^. Do đó
θ^=Arg¿θ∈ΩL (θ) , trong đó Ω là không gian tham số của θ, sao cho L (θ) là
mật độ đồng thời của mẫu.
Phương pháp hợp lý cực đại được tóm tắt như sau:
1) Lấy một mẫu ngẫu nhiên x1, x2,…, xn từ phân phối của X với hàm mật độ f ( x ;θ) ;
2) Xác định hàm hợp lý từ mẫu x1, x2,…, xn bởi hệ thức
L (θ)=f (x1 ;θ) f (x2 ;θ)…f (xn ;θ );
3) Tìm cực trị của hàm hợp lý L (θ) , theo biến θ.
4) Thay θ bởi θ^ để thu được biểu thức ước lượng hợp lý cực đại cho θ;
Ví dụ 8.3 Cho X1, X2,…, Xn là mẫu từ biến ngẫu nhiên X, với phân phối có hàm mật độ f ,
Trước hết ta xét hàm hợp lý xác định bởi n n n
L (θ)=∏ f (xi ;θ )⇒ln L (θ )=ln∏ f (xi ;θ )=∑ lnf (xi;θ )⇒ i=1 i=1 i=1 n n
ln L (θ)=∑ ln ((1−θ ) x−θ)=nln(1−θ )−θ∑ lnxi ; i=1 i=1
Để tìm cực đại của ln L (θ) ta xét đạo hàm 4 lOMoAR cPSD| 59285474 d xi i=1 i=1
Đạo hàm nói trên triệt tiêu (= 0), khi n i = 1−θ lnX ; 1−θ n i 1
Vậy ước lượng hợp lý cực đại của θ sẽ là θ^=1+ 1 ; lnX
Ví dụ 8.4 Cho X1 , X2 ,…, Xn là mẫu từ biến ngẫu nhiên X, có phân phối chuẩn
N (μ,σ2) f
Hàm hợp lý L (μ ,σ )sẽ xác định bởi n L =1 Từ đó ta có −n 1 n 2 lnLln
(2π )−nln(σ )− 2 ∑ 2σ i
Lấy đạo hàm riêng của ln L (μ ,σ ) theo μ và σ ta sẽ thu được n n lnL (xi−μ) 2σ i=1 σ i=1 n lnL σ σ3 i . 5 lOMoAR cPSD| 59285474
Thiết lập hệ phương trình , 0.
Giải hệ phương trình trên ta thu được các ước lượng hợp lý cực đại cho các tham số là n xi, i=1
(xi−μ)2 .
8.2 PHÂN LOẠI VÀ SO SÁNH CÁC ƯỚC LƯỢNG ĐIỂM
Trong phần này ta thấy rằng vấn đề đặt ra khá tự nhiên là với các con đường khác nhau sẽ
đi đến các ước lượng khác nhau thì đánh giá chúng thế nào? Cần so sánh và phân loại
chúng ra sao ? Loại nào là tốt hơn với những yêu cầu khác nhau và có loại nào tốt nhất không!
Một số tiêu chí thường dùng để đánh giá mức độ tốt của một hàm ước lượng là:
1) Không lệch (hay còn gọi là ước lượng không chệch - unbiasedness).
2) Hiệu quả và hiệu quả tương đối (efficiency and relative efficiency).
3) Không chệch với phương sai tối thiểu đều (Uniform minimum variance unbiasedness). 4) Tính đủ (Sufficiency).
5) Tính vững (Consistency).
Ta sẽ lần lượt xét các đặc tính đó cùa các hàm ước lượng tham số.
• Ước lượng không chệch (The unbiased estimator)
Định nghĩa 8.9 Cho mẫu ngẫu nhiên X1 , X2 ,…, Xn với hàm mật độ f ( x ;θ) , trong đó θ là
tham số chưa biết cần ước lượng. Với θ^ là hàm của các biến ngẫu nhiên X1 , X2 ,…, Xn
không chứa tham số θ. Ước lượng θ^ được gọi là không chệch khi và chỉ khi
E (θ^ )=θ. 6 lOMoAR cPSD| 59285474
Ví dụ 8.14 Cho mẫu ngẫu nhiên X1, X2,…, Xn của phân phối chuẩn với kỳ vọng μ, và phương
sai σ 2. Nghĩa là ta có Xi N (μ ,σ2), khi đó
. ⇒ E ( X )=μ.
Vậy theo định nghĩa 8.9,
Xi là ước lượng không chệch của μ.
Nếu ta dùng phương pháp hợp lý cực đại để ước lượng σ 2 ta sẽ thu được hàm ước lượng là
, với ước lượng này ta sẽ có:
E (σ^2)=E n = i
n n−1 i=1 i n , i 1 ∞ trong đó:S2
; và như vậy . Do đó E .
Vậy σ^2 là ước lượng chệch (chứ không phải không chệch) của σ2, theo định nghĩa 8.9.
• Ước lượng hiệu quả tương đối (The relatively efficient estimator)
Nếu ta có hai ước lượng đều là không chệch cho một tham số, khi đó ước lượng nào có
phương sai nhỏ hơn được coi là có hiệu quả hơn, do đó ta đi đến định nghĩa sau. Định
nghĩa 8.10 Cho θ^1 và θ^2 là hai ước lượng không lệch của θ. Ước lượng θ^1 được gọi là
có hiệu quả hơn θ^2 nếu
Var (θ^1)<Var(θ^2).
Tỷ số η xác định bởi
η(θ^1,θ^2)=
được gọi là hiệu quả tương đối của θ^1 với θ^2 .
Ví dụ 8.15 Cho mẫu ngẫu nhiên X1 , X2 ,…, Xn của một phân phối xác suất với kỳ vọng μ 7 lOMoAR cPSD| 59285474
, phương sai σ2đều hữu hạn và đều chưa biết. Nếu xét hai ước lượng n
X1+2 X2+…+n X n 1 n i=1 i 2 1+2+…+n ; Ta sẽ có
Eθ^1=1n nμ=μ; n Eθ^2= 2∑= iEXi=
n (n2+1) μ n (n2+1) =μ.
n (n+1) i 1
Vậy θ^1 và θ^2 đều là những ước lượng không chệch của kỳ vọng μ.
Nếu xét phương sai của chúng ta sẽ thu được: n 2 ; n i=1 n Var Var ^ 4 n 4 n i2 Var (X i) (n+1) =1 4 n 2 2 4σ 2
n (n+1) (2n+1) ¿
n2( n+1)2 σ ∑i=1 i = n2 2 6 (n+1 ) ¿ ;
Mặt khác ta có nhận xét:
>1;(khin≥2) .
Từ đó suy ra: Var (θ^1)<Var(θ^2), hay nói cách khác ước lượng θ^1 hiệu quả hơn ước
lượng θ^2 . Hiệu quả tương đối của θ^1 với θ^2trong trường hợp này bằng: 8 lOMoAR cPSD| 59285474
^ ,θ^2)=VarVar ((θθ^^21))=23
(2(nn++11) ) ; η(θ1
Ước lượng không chệch với phương sai tối thiểu đều và ước lượng hiệu quả
(The uniform minimum variance unbiased estimator and efficient estimator)
Cho mẫu ngẫu nhiên X1 , X2 ,…, Xn với hàm mật độ f ( x ;θ) , trong đó θ là tham số chưa biết
cần ước lượng, với θ^ là ước lượng không chệch của θ. Ta thường quan tâm đến các ước
lượng không chệch θ^ với phương sai nhỏ nhất, nghĩa là
Var (θ^ )≤Var (T^ ) , với mọi ước lượng không chệch T^ của θ, ước lượng như vậy
ta gọi là tối thiểu đều. Cần chú ý rằng nếu θ^ là ước lượng không chệch của θ, nghĩa là E
(θ^ )=θ, ta sẽ có
Var (θ^ )=E[(θ^−E (θ^ ))2]=E [(θ^−θ)2].
Phương sai này, nếu tồn tại, nó sẽ có giá trị tối thiểu trong tất cả các ước lượng không
chệch của θ. Do đó, ta có thể định nghĩa về ước lượng không chệch với phương sai tối
thiểu đều như sau.
Định nghĩa 8.11 Cho θ^ là ước lượng không chệch của θ, ta nói rằng nó là ước lượng
không chệch với phương sai tối thiểu đều của θ nếu nó cực tiểu phương sai E [(θ^−θ)2].
Một cách để tìm ước lượng không chệch với phương sai tối thiểu đều cho tham số là sử
dụng giới hạn dưới Cramer-Rao hoặc bất đẳng thức thông tin Fisher theo định lý sau.
Định lý 8.5 (Cramer-Rao) Cho mẫu ngẫu nhiên X1, X2,…, Xn cỡ n từ biến ngẫu nhiên X với
hàm mật độ f ( x ;θ) , trong đó θ là một tham số vô hướng. Cho θ^ là một ước lượng không
chệch tùy ý của θ. Giả định hàm hợp lý L (θ) là khả vi theo θ và thỏa điều kiện d ∞ ∞
dθ −∫∞ …−∫∞ h(x1,…, xn) L (θ) dx1…d xn ∞ ∞ d , (8.7) ¿
∫ …∫ h(x ,…,xn) dθ L (θ) dx1…d xn 9 lOMoAR cPSD| 59285474
với mọi h(x1 ,…, xn) có E (h( X1, X2 ,…, Xn))<∞. Khi đó
Var (θ^ )≥ 1 ; 2 E (8.8)
Từ đặc tính nêu trong định lý 8.5 ta xét một loại ước lượng là ước lượng hiệu quả mà định
nghĩa của nó dựa vào bất đẳng thức Cramer – Rao nêu trên.
Định nghĩa 8.12 Ước lượng không chệch θ^ được gọi là ước lượng hiệu quả nếu nó thỏa
cận dưới Cramer – Rao, nghĩa là
Var (θ^ )= 1 dlnL (θ) 2 E[( ) ] dθ
Ví dụ 8.16 Cho mẫu ngẫu nhiên X1, X2,…, Xn có phân phối chuẩn với kỳ vọng μchưa biết và
phương sai σ 2,đã biết. Ta sẽ tìm ước lượng không chệch hiệu quả của kỳ vọng μ. Trước hết
ta tìm ước lượng không chệch của μ bằng phương pháp hợp lý cực đại. Với hàm mật độ f . Ta sẽ có lnf .
Từ đó suy ra hàm hợp lý L (μ ) và ln L (μ ) sẽ là −n n ln L (μ )= 2 2σ 2 i .
Lấy đạo hàm của ln L (μ ) , theo μ ta thu
được d lnL ( μ) 1 n dμ ∑=1 x μ .
Theo phương pháp hợp lý cực đại, cần cho đạo hàm trên bằng 0, và giải cho μ, ta sẽ có 10 lOMoAR cPSD| 59285474 1 n ∑ .
Mặt khác ta thấy rằng ;
Tiếp theo, ta xác định cận dưới Cramer - Rao cho ước lượng X . Trước hết ta tính các đạo
hàm của ln L (μ ) , ta có
d lnL ( μ) 1 n
d2 ln L (μ ) −n dμ
σ2 ∑i=1 (xi−μ)⇒ d μ2 = σ 2 ; = Vì vậy
d2 ln L( μ ) −n 1 σ 2 −1 ( Ed μ ) 2 = σ2 ;⇒−
2 = n ;⇒Var ( X )=
d2 ln L( μ) ;
d ln L( μ) ( E ) ) 2 E( 2 d μ d μ
8.2.4 Ước lượng đủ (Sufficient estimator)
Trong nhiều trường hợp ta thấy rằng không thể dễ dàng tìm được sự phân bố của ước lượng
θ^cho tham số θ, mặc dù chúng ta biết sự phân bố của dân số. Do đó, chúng ta khó biết
liệu ước lượng θ^ của chúng ta chệch hay không chệch. Do đó, chúng ta cần một số tiêu
chí khác để đánh giá chất lượng của một ước lượng. Tính đủ là một trong những tiêu chí
để đánh giá chất lượng của một ước lượng. Cần nhớ rằng ước lượng của một tham số
về tổng thể là một hàm của các giá trị trong mẫu và không chứa tham số. Ước lượng sẽ
tóm tắt thông tin tìm thấy trong mẫu về tham số.
Định nghĩa 8.13 Cho X
f ( x ;θ) và mẫu ngẫu nhiên X1 , X2 ,…, Xn có cỡ n từ X. Ước lượng
θ^của tham số θ được gọi là ước lượng đủ của tham số θ nếu phân phối có điều kiện của
mẫu cho bởi ước lượng θ^không phụ thuộc vào tham số θ.
Ví dụ 8.17 Cho mẫu ngẫu nhiên X1, X2,…, Xn với hàm mật độ 11 lOMoAR cPSD| 59285474
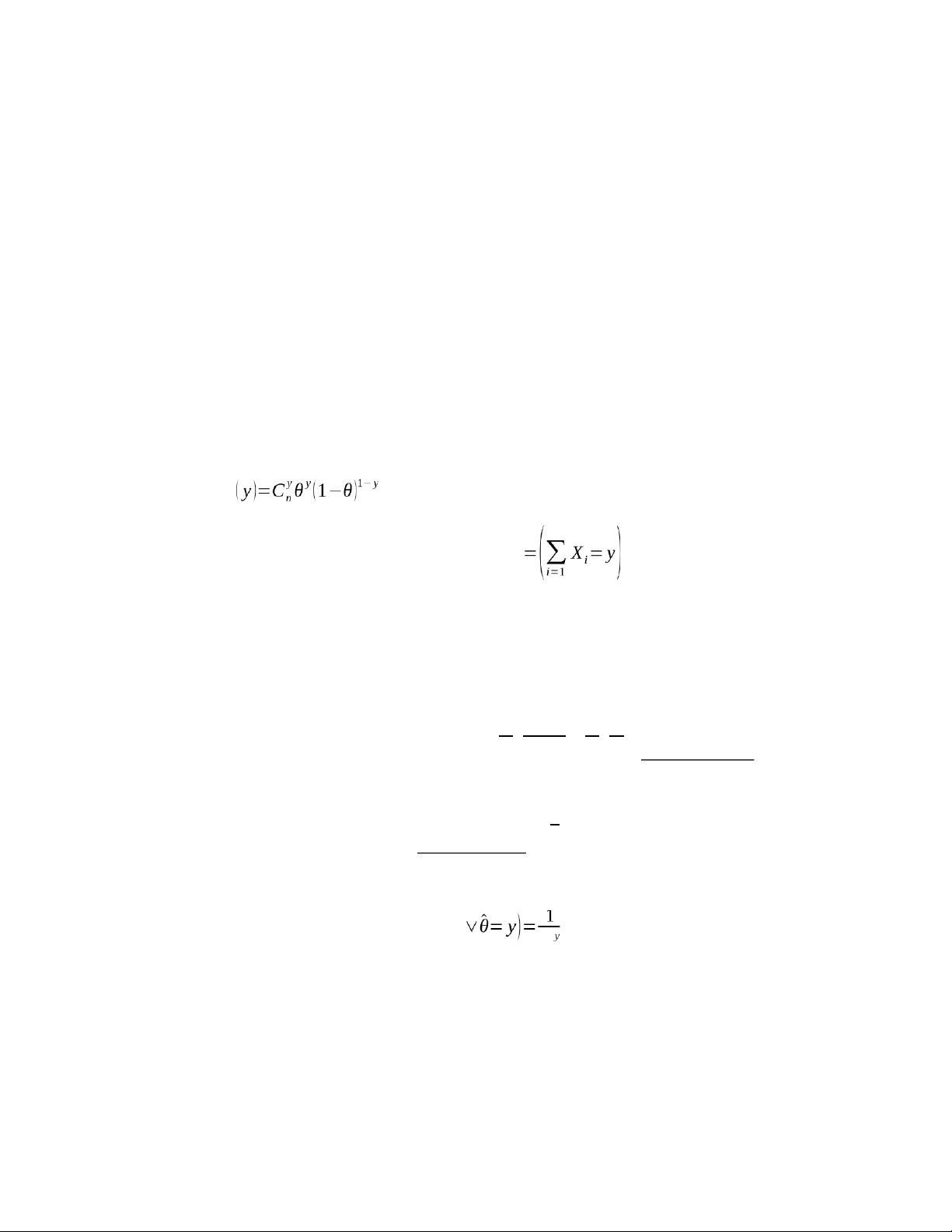
f ( x ;θ)={θx (1−θ)1−x ;nếu x=0;1; 0;nếu x≠0;1; n
trong đó θ∈(0,1 ). Ta xét xem thống kê θ^=∑ Xi có phải là ước lượng đủ không ? i=1
Trước tiên ta thấy rằng Xi ;i=1,…,n có phân phối Bernoulli với tham số θ, do đó n
θ^=∑ Xi B (n,θ) , i=1
nghĩa là θ^ có phân phối nhị thức B (n,θ ). Vậy hàm mật độ của θ^ sẽ xác định bởi g . n
Nếu ta đặt A=(X1=x1 , X2=x2 ,…, Xn=xn∨θ^=y) và B , ta sẽ có
A⊂B⇒ A∩B=A .
Với nhận xet trên ta xác định mật độ có điều kiện
f ( x1 , x2,…, xn∨θ^= y)=P ( X1=x1, X2=x2 ,…, Xn=xn∨θ^=y)
P ( A ∩B ) P ( A ) f (x1, x2 ,…, xn)
¿ P ( A∨B)= = = P ( B) P (B) g ( y )
θ y (1−θ )1−y 1
¿ Cny θy (1−θ)1−y =Cny ;
Vậy xác suất có diều kiện f ( x1 , x2,…, xn
, không phụ thuộc vào tham số θ. Cn n
Do đó θ^=∑ Xi là ước lượng đủ. i=1 12 lOMoAR cPSD| 59285474
• Định lý 8.9 (Factorization theorem – Fisher- Neyman) Cho mẫu ngẫu nhiên X1, X2,…, Xn
có hàm mật độ f (x1 ,x2 ,…,xn ;θ), phụ thuộc vào tham số θ. Ước lượng θ^ sẽ là đủ cho θ,
khi và chỉ khi f (x1 ,x2 ,…,xn ;θ)=ф(θ^ ,θ)φ (x1 , x2 ,…, xn)
ф (θ^ ,θ) phụ thuộc vào x1, x2,…, xn chỉ qua θ^ ,và φ (x1 ,x2 ,…,xn) không phụ thuộc vàoθ.
Định lý 8.9 đôi khi được gọi là tiêu chuẩn tách Fisher-Neyman.
Ví dụ 8.18 Cho mẫu ngẫu nhiên X1 , X2 ,…, Xn có phân phối Poisson với hàm mật độ λx e−λ f ( x ;λ)=
x !;nếu x=0,1,2,…,∞,
0;trong cáctrườnghợpkhác.
Trong ví dụ này khi sử dụng phương pháp hợp lý cực đại ta sẽ thu được ước lượng ^λ=x ,
với hàm ước lượng là n
L ( λ)=f (x1, x2,…, xn;λ )=∏ f (xi ;λ)=λn x e−nλ i=1 i
¿ф (^λ, λ)φ(x1 ,x2 ,…,xn), 1
trong đó: φ(x1 ,x2 ,…,xn)=¿ n ; ∏ (x !) i
Vậy theo Định lý 8.9, ước lượng ^λ=x là ước lượng đủ cho λ.
• Ước lượng vững (Consistent estimator).
Định nghĩa 8.14 Cho mẫu ngẫu nhiên X1, X2,…, Xn từ biến ngẫu nhiên X với hàm mật độ f
( x ;θ) . Dãy các ước lượng {θ^n}của θ, được gọi là vững khi và chỉ khi dãy {θ^n} hội tụ
theo xác suất đến θ, nghĩa là với mọi ε>0 ta sẽ có lim P(|θ^n−θ|≥ε)=0. n→∞
Lưu ý rằng tính vững thực sự là một khái niệm liên quan đến một dãy ước lượng
Định lý sau đây phát biểu rằng nếu sai số bình phương trung bình bằng 0 khi n tiến đến vô
cùng, thì {θ^n} hội tụ theo xác suất đến θ. 13 lOMoAR cPSD| 59285474
• Định lý 8.10 Cho mẫu ngẫu nhiên X1 , X2 ,…, Xn từ biến ngẫu nhiên X với hàm mật độ f
( x ;θ) , và {θ^n} là dãy các ước lượng của θ. Nếu phương sai của θ^n tồn tại, hữu hạn và thỏa điều kiện
lim E((θ^n−θ)2)=0, n→∞
khi đó, với mọi ε>0 ta sẽ có lim
P(|θ^n−θ|≥ε)=0. n→∞
. ƯỚC LƯỢNG KHOẢNG VÀ KHOẢNG TIN CẬY CHO CÁC THAM SỐ
8.3.1 Khái niệm về ước lượng khoảng.
Cần nhớ rằng mẫu là một phần của dân số thường được chọn bởi phương pháp chọn mẫu
ngẫu nhiên và như vậy nó là một tập hợp các biến ngẫu nhiên X1, X2,…, Xnvới cùng một hàm
mật độ xác suất f (x; θ). Sau khi lấy mẫu xong, ta nhận được
X1=x1 , X2=x2 ,…,X n=xn ,
trong đó x1, x2,…, xnlà dữ liệu mẫu.
Bài toán ước lượng khoảng có thể được phát biểu như sau: Với mẫu X1 , X2 ,…, Xnvà giá trị
xác suất 1−α, tìm một cặp thống kê
θi (X1 , X2 ,…,X n);i=1,2;θ1 ≤θ2
sao cho xác suất của θ trên khoảng ngẫu nhiên (θ1 ,θ2) là 1−α, nghĩa là
P (θ1 (X1 , X2 ,…, X n)≤θ≤θ2( X1, X2 ,…, Xn))=1−α.
Biến ngẫu nhiên θ1 được gọi là giới hạn tin cậy dưới và θ2được gọi là giới hạn tin
cậy trên. Số (1 − α) được gọi là hệ số tin cậy hoặc mức tin cậy. Khoảng tin cậy cho một mẫu
• Khoảng tin cậy cho giá trị trung bình μ, đã biết phương sai
của phân phối chuẩn, đã biết phương sai, hoặc
của phân phối với cỡ mẫu lớn, đã biết phương sai. 14 lOMoAR cPSD| 59285474
Tìm khoảng tin cậy (1 − α) cho trung bình µ của một phân phối chuẩn với phương sai đã
biếtσ 2 hoặc: Tìm khoảng tin cậy (1 - α) cho giá trị trung bình µ của một dân số có phương
sai đã biết σ2,trong đó cỡ mẫu n lớn.
a) Tính giá trị trung bình của mẫux.
b) Xác định giá trị tới hạn z sao cho Φ
, trong đó Φ( z)là hàm
phân phối chuẩn tắc. Nghĩa là, z được xác định để: ; c) Tính hằng số k= ; √n
d) Khoảng tin cậy (1 - α) đối với µ được cho bởi [ x−k , x+k ] . Tóm lại
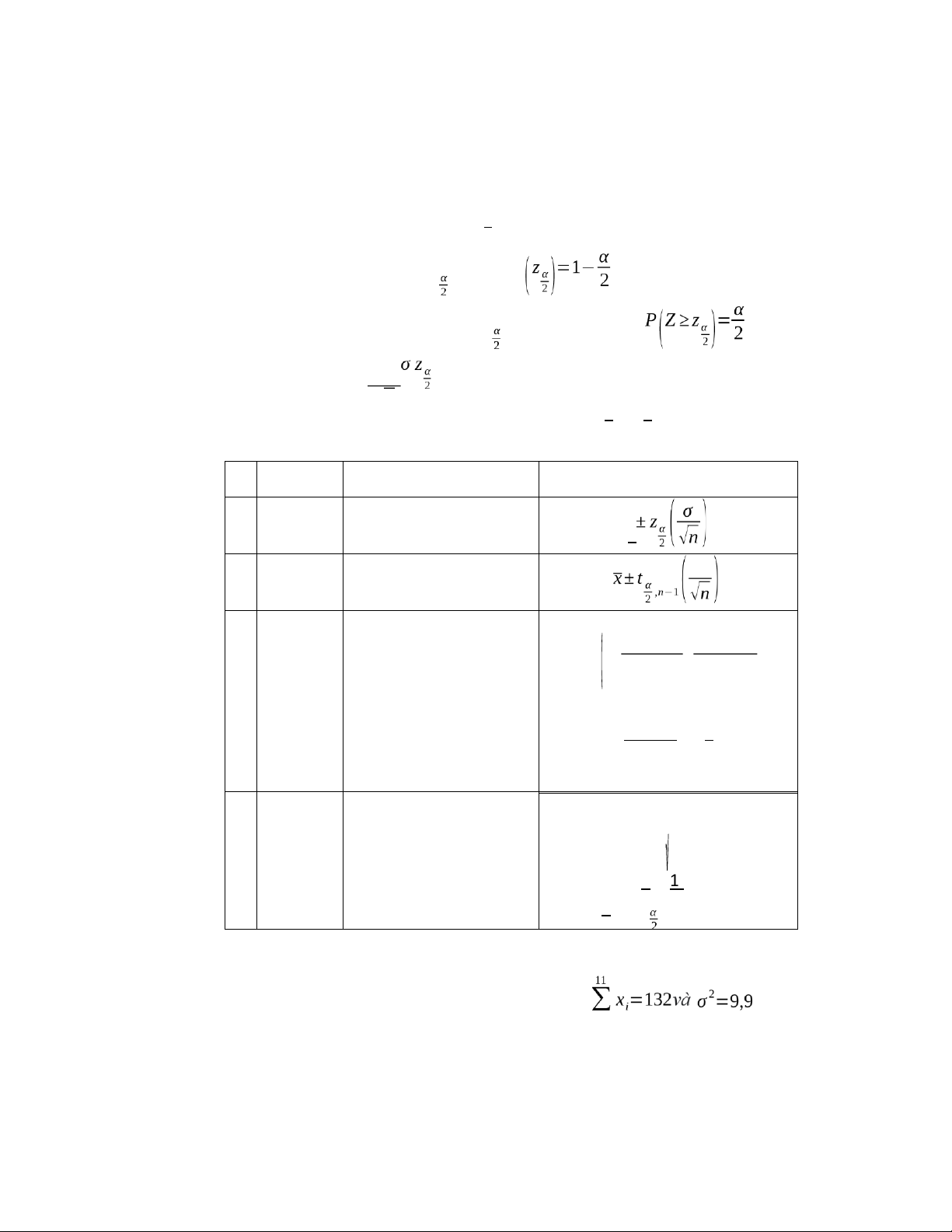
cần xem cách tìm trong phần a) bảng 8.1. Tham số Giả định
Khoảng tin cậy (1−α) a) μ
n lớn,σ 2đã biết, hoặc
p.p chuẩn,σ 2đã biết, x b μ
p.p chuẩn,σ 2chưa biết ) s c) σ 2 p.p chuẩn,
(n−1) s2(n−1) s2 , ) χ 2α χ2 α − ,n 1 1 ,n 1 2 − −2 d p p.p nhị thức, ) n lớn p^ (1 n ^p±z.−p^ )
Bảng 8.1: Tóm tắt các khoảng tin cậy phổ biến: một mẫu
Ví dụ 8.22 Cho mẫu X1, X2,…, X11; có phân phối chuẩn với ; Ta i=1
cần tính khoảng tin cậy 95%¿ (1−α) cho tham số μ. Trước hết ta có 15 lOMoAR cPSD| 59285474 .
Dùng bảng giá trị của phân phối chính tắc N (0,1) , ta sẽ thu được: z =z0,025=1.96.
Sử dụng trường hợp a) (trong Bảng 8.1) ta có khoảng tin cậy cho tham số μ, sẽ là . 40
Ví dụ 8.23 Cho mẫu X1, X2,…, X40;với ∑ xi=286,56 ,và phương sai σ 2=10. i=1
Ta cần tính khoảng tin cậy 90%¿ (1−α) cho tham số μ. Ta coi n=40>30làlớn. Theo giả
thuyết ta có (1−α)=0,9⇒ =0,05⇒z0,05=1,64 ,(Theo bảng giá trị N (0,1) ¿.
Mặt khác ta có giá trị của trung bình mẫu là: x=
=7,164. Sử dụng trường hợp a)
(trong bảng A), ta có khoảng tin cậy sẽ là .
• Khoảng tin cậy cho giá trị trung bình μ, của phân phối chuần khi chưa biết phương sai.
(Xem cách tính theo phần b) trong Bảng 8.1).
Ví dụ 8.24 Một công ty phần mềm đã tiến hành một cuộc khảo sát về kích thước của một
loại tập tin văn bản. Với n = 23 tập tin được chọn ngẫu nhiên, x=4822(kb) và s=127.
Tìm khoảng tin cậy 95% cho kích thước trung bình của loại tập tin văn bản đó.
Theo cách tính trong phần b) bảng 8.1, và từ giả định đã cho ta có: ⇒t ⇒t
Vậy khoảng tin cậy 95% cho kích thước trung bình của loại tập tin văn bản đó sẽ là .
• Khoảng tin cậy cho phương sai của phân phối chuẩn.
(Xem cách tính theo phần c) trong bảng 8.1). 16 lOMoAR cPSD| 59285474
Ví dụ 8.25 Cho mẫu X1, X2, …, X13;có phân phối chuẩn N (μ,σ2)với 13 13
x =∑ x ≈246,61; ∑ x2=4806,61. =1
Ta cần tính khoảng tin cậy 90%¿(1−α) cho tham số σ2.
Trước hết ta tính s2 n−1 1 = i 12 i=1 i i 1
⇒ 12.s2=128,41.
Theo giả thuyết ta có
; Từ bảng giá trị của phân phối
chi bình phương ta sẽ thu được: ;
Sử dụng trường hợp c) (trong bảng A) ta có khoảng tin cậy cho tham sốσ 2 sẽ là .
• Khoảng tin cậy cho tham số p của phân phối nhị thức.
(Xem cách tính theo phần d) trong bảng 8.1).
Ví dụ 8.26 Khi khảo sát ý kiến về một vấn đề, người ta đã lấy ý kiến của 78 người, và thu
nhận được 33 ý kiến đồng ý (về vấn đề đó). Cần tìm khoảng tin cậy 95% cho tham số p (tỉ
lệ đồng ý) cho bài toán ước lượng khoảng.
Trước hết ta thấy rằng: ^p
Áp dụng cách tính theo phần d) trong bảng 8.1, với khoảng tin cậy 95%, ta có z
(Dùng bảng chuẩn N (0,1)). Từ đó suy ra: ^p
Tương tự ta tính được: ^p+z ,
Vậy khoảng tin cậy cho p sẽ là: [ 0,3135;0,5237] . 17