Bài 8: Phân Tích Dãy Số Thời Gian và Dự Báo Kết Quả môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 8
PHÂN TÍCH DÃY SỐ THỜI GIAN 1 NỘI DUNG CHÍNH I II III Một số vấn đề Phân tích đặc Dự báo chung về dãy điểm biến động số thời gian của hiện tượng qua thời gian 2 1 2025-06-02 1. NHỮNG VẤN ĐỀ CHUNG Khái niệm DSTG Cấu tạo DSTG Các loại DSTG Các thành phần của DSTG Tác dụng của DSTG
Yêu cầu khi xây dựng DSTG 3 1. NHỮNG VẤN ĐỀ CHUNG Khái niệm
Dãy số thời gian là một dãy các chỉ tiêu thống kê được sắp xếp theo một thứ tự thời gian
Ví dụ: Giá trị sản xuất của doanh nghiệp A qua các năm Năm 2003 2004 2005 2006 GTSX (trđ) 2500 2900 3600 5000 4 2 2025-06-02 1. NHỮNG VẤN ĐỀ CHUNG Cấu tạo DSTG
•Thời gian: ngày, tháng, quý, năm,…
Độ dài giữa hai thời gian được gọi là khoảng cách thời gian
•Chỉ tiêu thống kê về hiện tượng nghiên cứu: tên chỉ tiêu, đơn vị tính
và trị số của chỉ tiêu – các mức độ của dãy số thời gian, y (i = 1,n). i
Ví dụ: Giá trị sản xuất của doanh nghiệp A qua các năm Năm 2003 2004 2005 2006 GTSX (trđ) 2500 2900 3600 5000 5 1. NHỮNG VẤN ĐỀ CHUNG Các loại DSTG
•Căn cứ vào đặc điểm của hiện tượng qua thời gian
-Dãy số thời kỳ: biểu hiện mặt lượng của hiện tượng trong từng khoảng thời gian nhất định
-Dãy số thời điểm: biểu hiện mặt lượng của hiện tượng tại những thời điểm nhất định
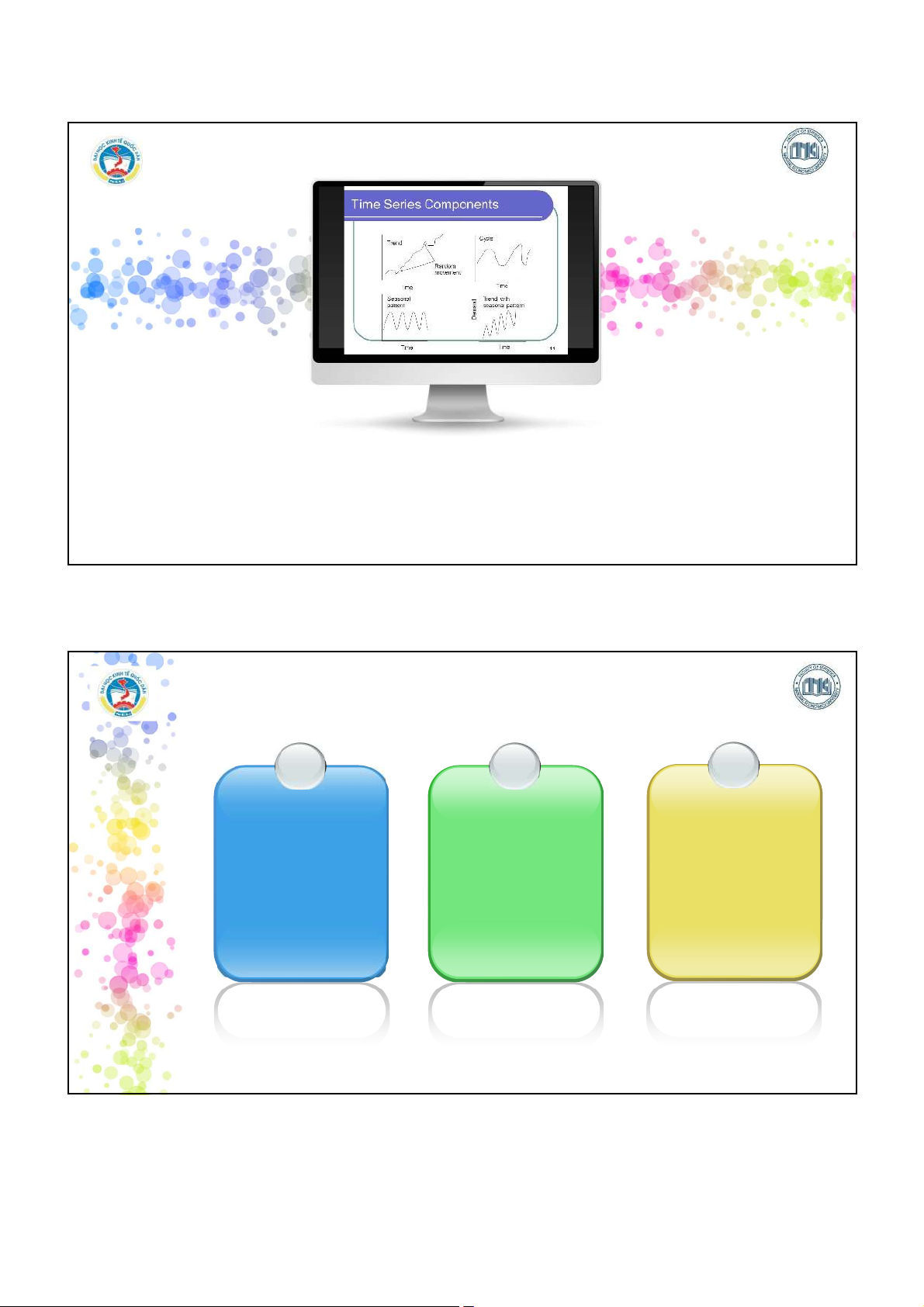
•Căn cứ vào loại chỉ tiêu -Dãy số tuyệt đối -Dãy số tương đối -Dãy số bình quân 6 3 2025-06-02 1. NHỮNG VẤN ĐỀ CHUNG Các thành phần của DSTG Xu thế Dãy số Ngẫu thời Mùa nhiên vụ gian Chu kỳ 7
Các thành phần của dãy số thời gian
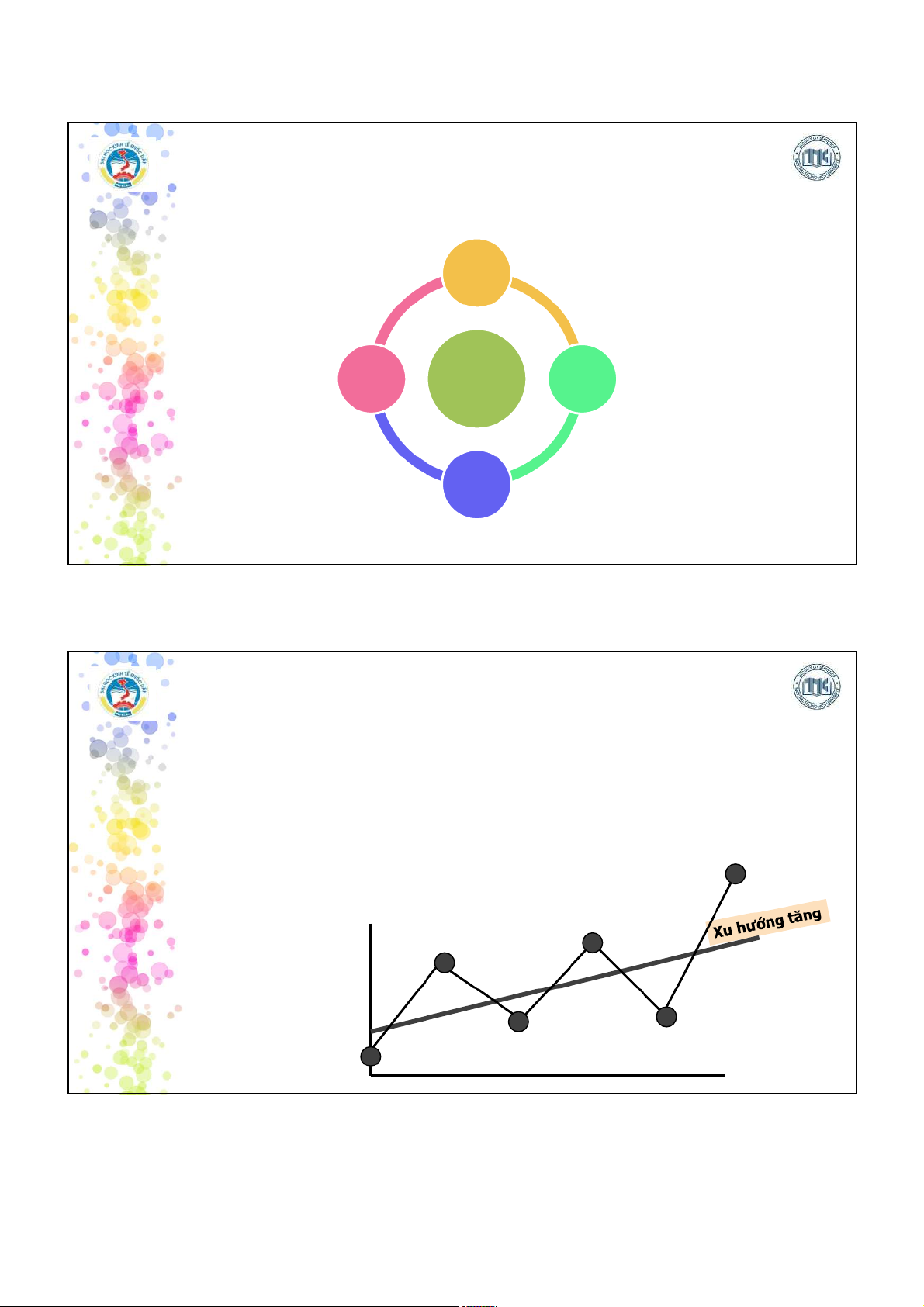
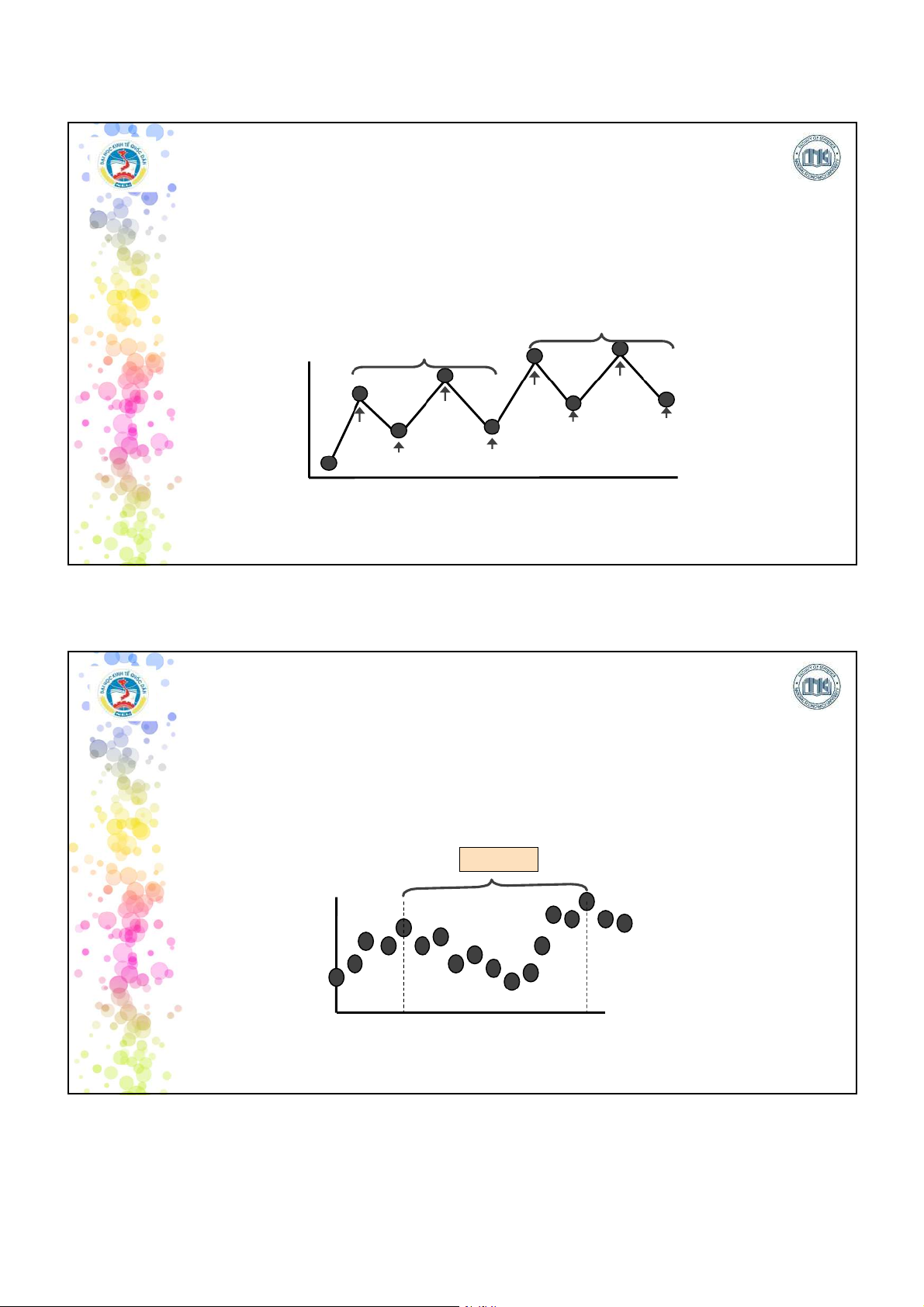
Xu thế: cho thấy xu hướng biến động của các giá trị quan sát qua thời gian
– Xu thế có thể là tăng hoặc giảm
– Xu thế có thể là tuyến tính hay phi tuyến GDP Thời gian 8 4 2025-06-02
Các thành phần của dãy số thời gian
Mùa vụ: là những biến động của hiện tượng có tính chất lặp đi
lặp lại trong từng thời gian nhất định của năm. Năm thứ n+1 Doanh thu Năm thứ n Hè Đông Hè Đông Xuân Thu Xuân Thu Thời gian (Quý) 9
Các thành phần của dãy số thời gian
Chu kỳ: là những biến động lặp lại trong một khoảng thời gian nhất
định, thường là nhiều năm. 1 chu kỳ Doanh thu Năm 10 5 2025-06-02
Các thành phần của dãy số thời gian
Ngẫu nhiên: là những biến động ngẫu nhiên (bất quy tắc) trong một chuỗi thời gian. 11
Các thành phần của dãy số thời gian
Các thành phần của dãy số thời gian có thể kết hợp với nhau theo: – Mô hình cộng: Yt= Tt+ St+ Ct+ It – Mô hình nhân: Yt= Ttx Stx Ctx It Trong đó:
Yt= Số liệu thực tế của hiện tượng ở thời gian t
Tt= Xu thế ở thời gian t
St= Thành phần mùa vụ ở thời gian t
Ct= Thành phần chu kỳ ở thời gian t
It= Thành phần ngẫu nhiên ở thời gian t 12 6 2025-06-02 1. NHỮNG VẤN ĐỀ CHUNG Tác dụng của DSTG
- Phân tích đặc điểm về sự biến động qua thời gian, qua đó xác
định xu hướng và tính quy luật phát triển của hiện tượng qua thời gian
- Trên cơ sở dãy số thời gian có thể dự báo các mức độ của
hiện tượng trong tương lai 13 1. NHỮNG VẤN ĐỀ CHUNG Yêu cầu khi DSTG
Yêu cầu cơ bản khi xây dựng DSTG là phải đảm bảo tính chất có thể so sánh
được giữa các mức độ trong dãy số nhằm phản ánh đúng biến động của hiện tượng qua thời gian Cụ thể:
- Phải thống nhất về nội dung và phương pháp tính chỉ tiêu qua thời gian
- Phải thống nhất về phạm vi tính chỉ tiêu qua thời gian
- Các khoảng cách thời gian trong dãy số nên bằng nhau, đặc biệt đối với dãy
số tuyệt đối thời kỳ thì phải bằng nhau. 14 7 2025-06-02 NỘI DUNG CHÍNH I II III Một số vấn đề Phân tích đặc Dự báo chung về dãy điểm biến động số thời gian của hiện tượng qua thời gian 15
2. Phân tích Đặc điểm biến động của hiện tượng
Mức độ trung bình qua thời gian
Lượng tăng (giảm) tuyệt đối Tốc độ phát triển Tốc độ tăng (giảm)
Giá trị tuyệt đối của 1% tốc độ tăng (giảm) liên hoàn Chỉ số mùa vụ 16 8 2025-06-02
2. Phân tích Đặc điểm biến động của hiện tượng
2.1. Mức độ trung bình qua thời gian (𝒚 )
Phản ánh mức độ đại biểu cho tất cả các mức độ của dãy số. Cách tính:
Đối với dãy số thời kỳ = 
Dãy số tuyệt đối: 𝑦 = ⋯   ∑      
Dãy số tương đối/bình quân: căn cứ vào chỉ tiêu đang phân tích và
đặc điểm về tài liệu để xác định công thức tính cho phù hợp lý
thuyết tính số bình quân 17
2. Phân tích Đặc điểm biến động của hiện tượng
2.1. Mức độ bình quân qua thời gian (𝒚 )
Đối với dãy số thời điểm 𝑦 = Đ
Dãy số biến động đều: 
Dãy số biến động không đều và có khoảng cách thời gian bằng nhau 𝑦 +𝑦 2+ 𝑦   + ⋯ + 𝑦 𝑦 = 2 𝑛 − 1
Dãy số biến động không đều và có khoảng cách thời gian không bằng nhau ∑𝑦 𝑦 = 𝑡 ∑ 𝑡 18 9 2025-06-02
2. Phân tích Đặc điểm biến động của hiện tượng
2.2. Lượng tăng (giảm) tuyệt đối
Phản ánh sự biến động về tuyệt đối của chỉ tiêu qua thời gian Các loại:
Lượng tăng (giảm) tuyệt đối liên hoàn (𝛿𝑖)𝛿𝑖= 𝑦  − 𝑦
Lượng tăng (giảm) tuyệt đối định gốc (∆𝑖)∆𝑖= 𝑦  − 𝑦
Lưu ý: Mối liên hệ giữa 𝛿  
𝑖 và ∆𝑖:∆𝑖=∑𝛿𝑖 hay ∆  𝑛=∑𝛿𝑖 
Lượng tăng (giảm) tuyệt đối bình quân: là trung bình cộng của các
lượng tăng (giảm) tuyệt đối liên hoàn 𝛿=∑𝛿 𝑖 𝑛  − 1 =∆𝑛 𝑛 − 1 =𝑦𝑛− 𝑦1 𝑛 − 1
ĐKVD: Chỉ nên tính lượng tăng (giảm) tuyệt đối bình quân khi dãy số
có lượng tăng (giảm) tuyệt đối liên hoàn xấp xỉ nhau 19
2. Phân tích Đặc điểm biến động của hiện tượng 2.3. Tốc độ phát triển
Phản ánh xu hướng phát triển chỉ tiêu qua thời gian Các loại 
Tốc độ phát triển liên hoàn (𝑡  𝑖) 𝑡𝑖=  
Tốc độ phát triển định gốc (𝑇  𝑖) 𝑇𝑖= 
Lưu ý: Mối liên hệ giữa 𝑡 =∏𝑡 =∏𝑡 𝑖 và 𝑇𝑖 :𝑇 𝑖 hay  𝑖 𝑇 𝑛  𝑖
Tốc độ phát triển bình quân: là trung bình nhân của các Tốc độ phát triển liên hoàn 𝑡=∏𝑡     𝑖    = 𝑇𝑛 =  
ĐKVD: chỉ nên tính tốc độ phát triển bình quân khi dãy số có các tốc độ phát
triển liên hoàn xấp xỉ nhau 20 10 2025-06-02
2. Phân tích Đặc điểm biến động của hiện tượng
2.4. Tốc độ tăng (giảm)
Phản ánh mức độ của hiện tượng đã tăng (giảm) bao nhiêu lần (hay %) qua thời gian Các loại  -
Tốc độ tăng (giảm) liên hoàn (𝑎 =  =  − 1 = 𝑡 𝑖) 𝑎𝑖=      − 1    ∆    -
Tốc độ tăng (giảm) định gốc (𝐴     𝑖) 𝐴𝑖= = = − 1 = 𝑇     − 1   
Lưu ý: KHÔNG có mối liên hệ giữa𝑖 𝑎và A𝑖 -
Tốc độ tăng (giảm) bình quân: 𝑎 = 𝑡− 1
ĐKVD: chỉ nên tính tốc độ phát triển bình quân khi dãy số có các tốc độ tăng (giảm) (tốc
độ phát triển) liên hoàn xấp xỉ nhau 21
2. Phân tích Đặc điểm biến động của hiện tượng
2.5. Giá trị tuyệt đối của 1% tốc độ tăng (giảm) liên hoàn
Phản ánh cứ 1% tốc độ tăng (giảm) liên hoàn thì tương ứng với 1 số tuyệt đối là bao nhiêu.
Là sự kết hợp giữa số tương đối và số tuyệt đối trong thống kê. Công thức
𝑔𝑖=𝛿𝑖𝑎𝑖(%) =𝛿𝑖 =𝑦𝑖−1 𝛿𝑖 100 𝑦 100 𝑖−1
Lưu ý: Thực tế, thường không tính chỉ tiêu Giá trị tuyệt đối của 1% tốc độ tăng (giảm) định
gốc vì nó luôn là 1 số không đổi
𝐺𝑖=∆𝑖𝐴𝑖(%) =∆𝑖 =𝑦1 100 = ℎằ𝑛𝑔 𝑠ố ∆𝑖 𝑦 100 1 22 11 2025-06-02 2.6. Chỉ số mùa vụ
Áp dụng khi dãy số thời gian có mùa vụ nhưng không có xu thế.
Chỉ số mùa vụ ở thời kỳ (tháng/quý) j (j = 1, m) được xác định như sau:  S   =  Trong đó: 
•Y = ∑  
là trung bình của thời kỳ thứ j trong n năm.  ∑ ∑   
•Y =    là trung bình của tất cả các thời kỳ trong n năm.    23 NỘI DUNG CHÍNH I II III Một số vấn đề Phân tích đặc Dự báo chung về dãy điểm biến động số thời gian của hiện tượng qua thời gian 24 12 2025-06-02 3. Dự báo Khái niệm dự báo Dự báo cho chuỗi dừng
Dự báo cho chuỗi không dừng
Các thước đo đo độ chính xác của dự báo 25 3.1. Khái niệm dự báo
Dự báo là việc đưa ra các mức độ của hiện tượng trong tương lai với
giả định quy luật biến động trong quá khứ là không thay đổi.
Tùy thuộc vào đặc điểm của dãy số thời gian mà lựa chọn mô hình dự báo cho phù hợp.
Có thể sử dụng các thước đo đo độ chính xác của dự báo để đánh
giá và lựa chọn mô hình dự báo. 26 13 2025-06-02 Chuỗi dừng
Chuỗi thời gian dừng: Chuỗi Y  được gọi là một chuỗi dừng nếu quy luật
phân phối xác suất không thay đổi theo thời gian. –Trung bình của chuỗi: E Y  = μ ∀t –Phương sai của chuỗi:
Var Y  = E Y − μ  = σ  ∀t
–Hiệp phương sai giữa Y  và Y chỉ phụ thuộc vào độ dài (s) về thời
gian giữa t và t-s, không phụ thuộc vào thời điểm t.
Cov Y, Y = E[ Y − μ Y − μ ] = γ ∀t
Chuỗi thời gian không dừng: nếu chuỗi Y
 không thỏa mãn một trong ba điều kiện trên. 27
3.2. Dự báo cho chuỗi dừng
Áp dụng cho các chuỗi thời gian dừng. Các phương pháp:
• Trung bình trượt giản đơn
• San bằng mũ giản đơn 28 14 2025-06-02
3.2.1. Phương pháp trung bình trượt giản đơn
Dãy số thời gian: Y1, Y2, Y3, …, Yn
Sử dụng giá trị trung bình của k thời kỳ gần nhất trong dãy số thời gian
để dự báo cho thời kỳ tiếp theo. =Y F
 + Y + ⋯ + Y  k
• Áp dụng quyền số như nhau cho các mức độ.
Chỉ dự báo được cho một thời kỳ tiếp theo. 29
3.2.1. Phương pháp trung bình trượt giản đơn
Việc lựa chọn k có thể ảnh hưởng đến kết quả dự báo.
– k lớn, dãy số trơn hơn, dự báo ổn định hơn nhưng chậm phản ứng
với những biến động trong dãy số thời gian.
– k nhỏ, dự báo sẽ phản ứng nhanh hơn với các biến động của dãy
số nhưng kết quả dự báo có thể bị ảnh hưởng bởi các biến động
ngẫu nhiên hoặc tạm thời nên không ổn định hoặc kém chính xác.
Để lựa chọn k phù hợp, có thể căn cứ vào độ chính xác của dự báo. 30 15 2025-06-02
3.2.2. Phương pháp san bằng mũ giản đơn
Phương trình san bằng mũ giản đơn dự báo giá trị ở thời kỳ t+1:
F = αY + 1 − α F
α: hệ số san bằng mũ, 0    1
Y: giá trị thực tế ở thời kỳ t
F: giá trị dự báo (san bằng mũ) ở thời kỳ t •
Áp dụng quyền số không bằng nhau cho các mức độ trong quá khứ 31
3.2.2. Phương pháp san bằng mũ giản đơn
Không thể dự báo cho kỳ đầu tiên vì không có dữ liệu ở kỳ trước đó.
Để bắt đầu tính các giá trị dự báo, cần phải gán giá trị cho kết quả dự báo của kỳ thứ hai.
– Cách phổ biến: đặt giá trị dự báo của kỳ thứ hai bằng với giá trị
quan sát thực tế của kỳ đầu tiên, tức F = Y
Chỉ dự báo được cho một thời kỳ tiếp theo. 32 16 2025-06-02
3.2.2. Phương pháp san bằng mũ giản đơn
Giá trị của hệ số san bằng mũ có ảnh hưởng đến kết quả dự báo.
–càng gần 1, dự báo phản ứng nhanh với những thay đổi mới
nhất trong dữ liệu nhưng có thể không ổn định và dễ bị ảnh
hưởng bởi những biến động nhỏ, không liên quan đến xu hướng dài hạn.
–càng gần 0, dự báo trơn mượt, ổn định hơn và ít bị ảnh hưởng
bởi các biến động ngắn hạn nhưng khó bắt kịp với những thay
đổi quan trọng hoặc xu hướng mới của dãy số thời gian.
Có thể thử nghiệm nhiều giá trị khác nhau và lựa chọn dựa trên độ chính xác của dự báo. 33
3.3. Dự báo cho chuỗi không dừng
Áp dụng cho các chuỗi thời gian không dừng: có xu thế và không có mùa vụ. Các phương pháp:
– Dự báo dựa vào lượng tăng (giảm) tuyệt đối bình quân
– Dự báo dựa vào tốc độ phát triển bình quân
– Dự báo dựa vào ngoại suy hàm xu thế 34 17 2025-06-02
3.3.1. Dự báo dựa vào lượng tăng (giảm) tuyệt đối bình quân
Công thức dự đoán: 𝑦
= 𝑦+ 𝛿ℎh: tầm xa của dự đoán 𝑛+ℎ
Ví dụ: Dự đoán doanh thu của cửa hàng nói trên năm 2012 và năm 2013 𝛿=𝑦𝑛− 𝑛 𝑦 −11 =22,9 − 10 6 − 1 = 2,58
Năm 2012 h = 1 𝑦2012 = 22,9 + 2,58𝑥1 = 25,48 (tỷ đồng)
Năm 2013 h = 2 𝑦2013 = 22,9 + 2,58𝑥2 = 28,06 (tỷ đồng)
ĐKVD: Chỉ nên dự đoán dựa vào lượng tăng (giảm) tuyệt đối bình quân khi
dãy số có các lượng tăng (giảm) tuyệt đối liên hoàn xấp xỉ nhau 35
3.3.2. Dự báo dựa vào tốc độ phát triển bình quân
Công thức dự báo: 𝑦 = 𝑦 𝑛+ℎ 𝑡 ℎ h: tầm xa của dự báo
Ví dụ: Dự báo doanh thu của cửa hàng nói trên năm 2012 và năm 2013 𝑡=𝑦𝑛 =22  ,  9  = 1,18 𝑦1 10
Năm 2012 h = 1 𝑦2012 = 22,9𝑥1,18  = 27,022 (tỷ đồng)
Năm 2013 h = 2 𝑦2013 = 22,9𝑥1,18  = 31,89 (tỷ đồng)
ĐKVD: Chỉ nên dự báo dựa vào tốc độ phát triển bình quân khi dãy số có
các tốc độ phát triển liên hoàn xấp xỉ nhau 36 18 2025-06-02
3.3.3. Dự báo dựa vào ngoại suy hàm xu thế
Xây dựng hàm xu thế phản ánh xu hướng biến động của hiện tượng qua thời gian: Y  = f(t)
– Hàm xu thế tuyến tính – Hàm xu thế phi tuyến
Sử dụng hàm xu thế để dự báo cho các thời kỳ tiếp theo: F  = Y 37
3.3.3. Dự báo dựa vào ngoại suy hàm xu thế
Hàm xu thế tuyến tính: Y  = a + bt
Trong đó: Y là giá trị dự báo theo xu thế tuyến tính ở thời gian t a là hệ số chặn b là hệ số góc t là thứ tự thời gian 38 19 2025-06-02
3.3.3. Dự báo dựa vào ngoại suy hàm xu thế
Hàm xu thế tuyến tính: Y  = a + bt
Ước lượng a, b theo phương pháp bình phương nhỏ nhất ∑ 
b =     a = Y− b t ∑    
Trong đó: Y là giá trị quan sát thực tế ở kỳ t
n là số thời kỳ trong dãy số thời gian Y
là giá trị trung bình của dãy số thời gian
tlà giá trị trung bình của t 39
3.3.3. Dự báo dựa vào ngoại suy hàm xu thế Hàm xu thế phi tuyến • Nghịch đảo: Y  = a + b  • Bậc 2: Y  = a + bt + b t • Mũ: Y = ab • Tuyến tính – log: Y  = a + bln (t) • Log – tuyến tính: ln Y = a + bt 40 20