Bài 8: Phân Tích Dãy Số Thời Gian và Dự Báo môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 8
PHÂN TÍCH DÃY SỐ THỜI GIAN VÀ DỰ BÁO 1 Nội dung I II III Một số vấn đề Phân tích đặc Dự báo chung về dãy số điểm biến động thời gian của hiện tượng qua thời gian 2 1 3/3/2025
Một số vấn đề chung về dãy số thời gian
Khái niệm dãy số thời gian
Phân loại dãy số thời gian
Yêu cầu của phân tích dãy số thời gian
Ý nghĩa của phân tích dãy số thời gian
Các thành phần của dãy số thời gian 3
Khái niệm dãy số thời gian
Dãy số thời gian (chuỗi thời gian) là tập hợp các giá trị của biến nghiên cứu
được sắp xếp theo thứ tự thời gian. Ví dụ • Chuỗi GDP qua các năm
• Chuỗi CPI qua các tháng
• Chuỗi giá vàng theo ngày… 4 2 3/3/2025
Khái niệm dãy số thời gian
Cấu tạo của dãy số thời gian
Thời gian: ngày, tháng, quý, năm,… Độ dài giữa hai thời gian gọi là khoảng cách thời gian.
Giá trị của biến: gọi là mức độ của dãy số thời gian, ký hiệu Yi (i=1, n). 5
Phân loại dãy số thời gian
Dãy số số tuyệt đối Thời điểm Thời kỳ
Dãy số số tương đối Dãy số số bình quân 6 3 3/3/2025
Phân loại dãy số thời gian
Chuỗi thời gian dừng (Stationary): Chuỗi Yđược gọi là một chuỗi dừng
nếu quy luật phân phối xác suất không thay đổi theo thời gian. • Trung bình của chuỗi: EY= μ ∀t
• Phương sai của chuỗi:
Var Y= E Y− μ = σ∀t
• Hiệp phương sai giữa Y và Y chỉ phụ thuộc vào độ dài (s) về thời gian
giữa t và t-s, không phụ thuộc vào thời điểm t.
Cov Y, Y = E[ Y− μ Y − μ ] = γ∀t
Chuỗi thời gian không dừng (Non-Stationary): nếu chuỗi Ykhông thỏa
mãn một trong ba điều kiện trên. 7
Yêu cầu của phân tích dãy số thời gian
Đảm bảo tính chất có thể so sánh được giữa các mức độ của DSTG
• Thống nhất về nội dung, phương pháp và phạm vi tính
• Thống nhất về thời gian tương ứng với mỗi lần quan sát: ngày, tuần, tháng, quý, năm, … 8 4 3/3/2025
Ý nghĩa của phân tích dãy số thời gian
Nắm được quy luật biến động của hiện tượng qua thời gian.
Dự báo cho các mức độ của hiện tượng trong tương lai. 9
Các thành phần của dãy số thời gian
Phân rã các thành phần của DSTG là một phương pháp mô tả DSTG.
Mục tiêu chính của phân tích DSTG là để dự báo.
• Càng hiểu nhiều về DSTG và các thành phần của nó, cách thức các
thành phần trong dãy số được kết hợp như thế nào
→ dự báo đưa ra càng chính xác. 10 5 3/3/2025
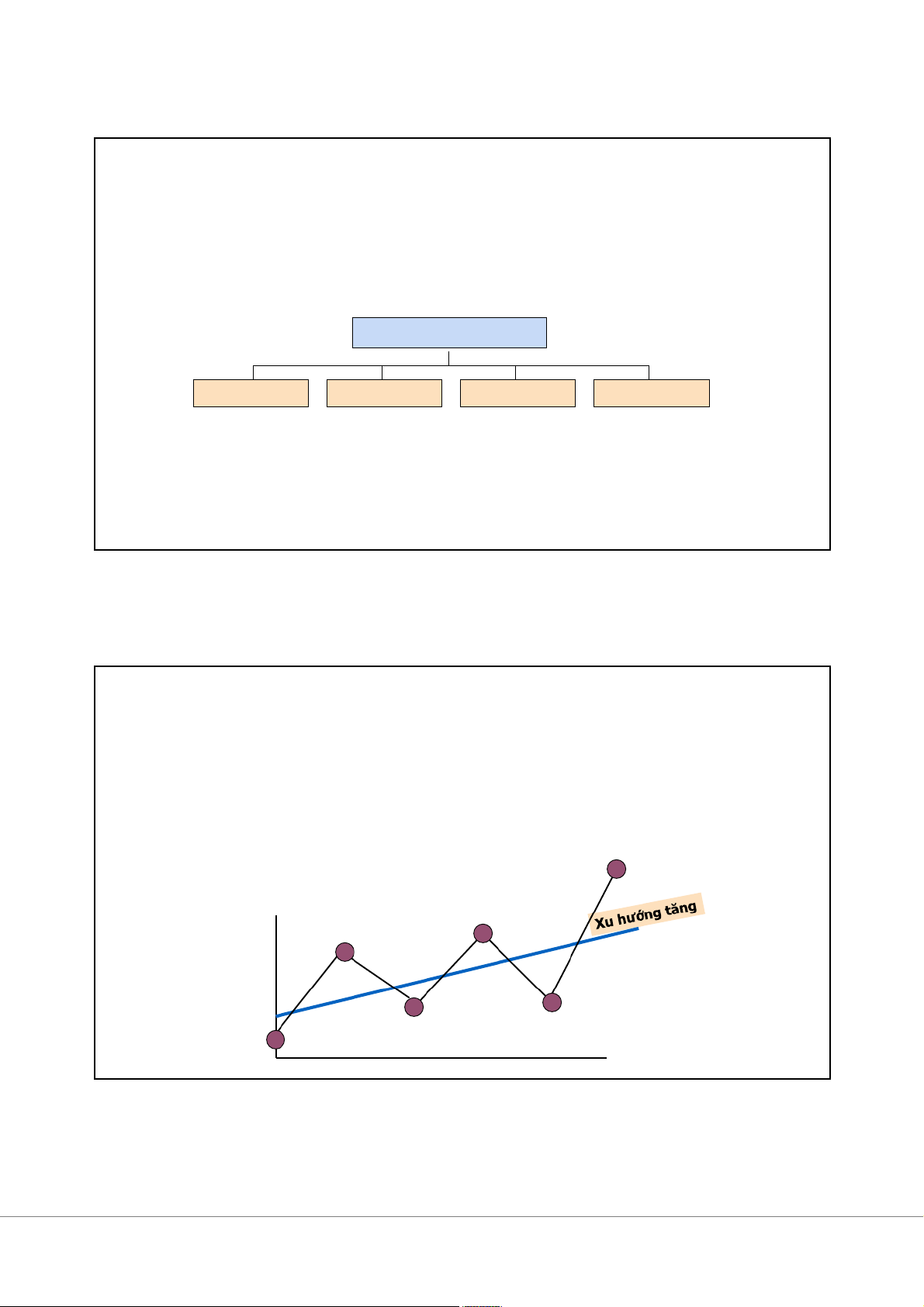
Các thành phần của dãy số thời gian Dãy số thời gian Xu thế Mùa vụ Chu kỳ Bất quy tắc 11 Xu thế (Trend)
Cho thấy xu hướng biến động của hiện tượng qua thời gian
Nguyên nhân: do sự biến động, ví dụ về dân số, sự phát triển của khoa học
kỹ thuật, thay đổi công nghệ… GDP Thời gian 12 6 3/3/2025 Xu thế (Trend)
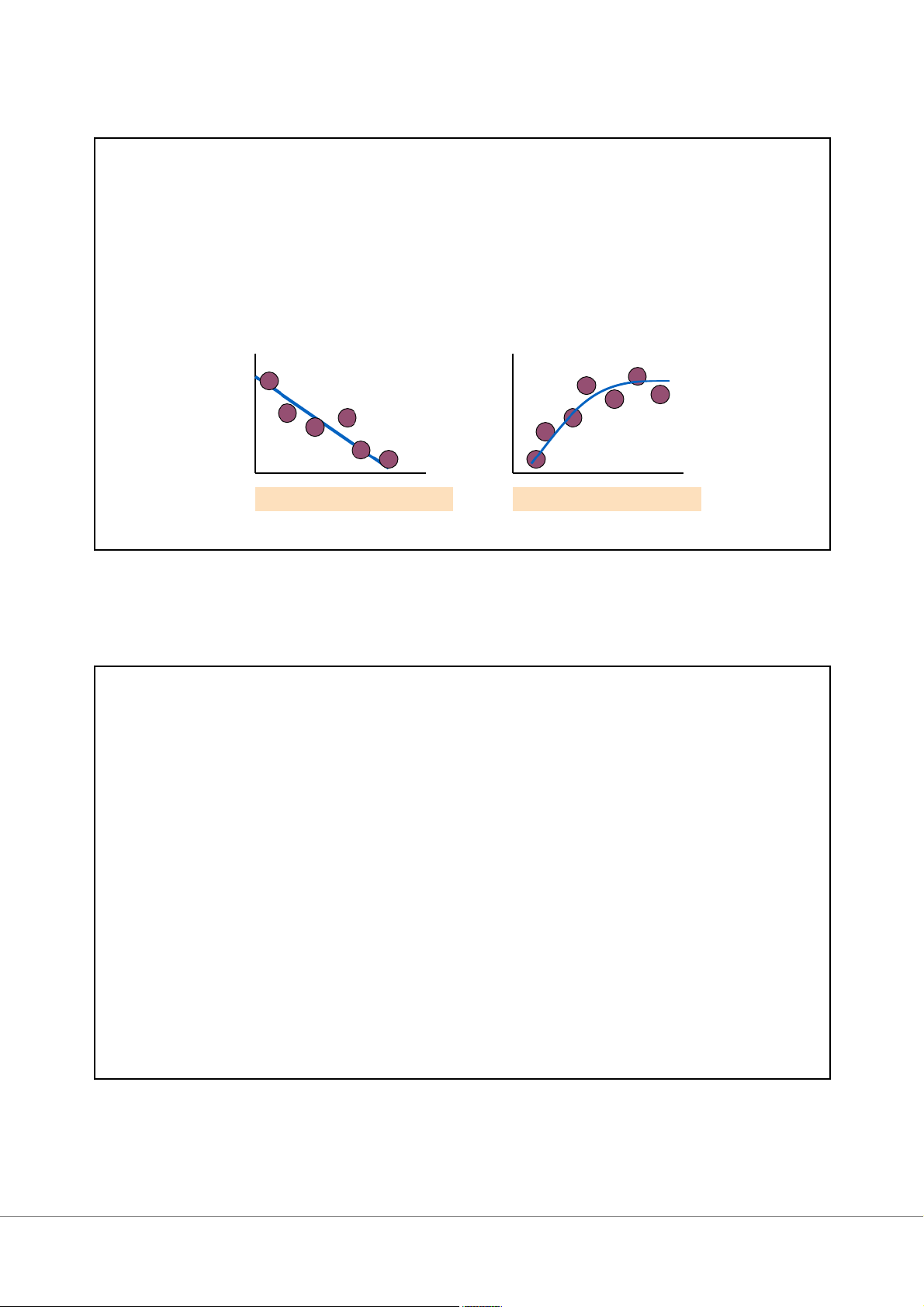
Xu hướng có thể là tăng hoặc giảm
Xu hướng có thể là tuyến tính hay phi tuyến GDP GDP Thời gian Thời gian
Xu hướng tuyến tính giảm Xu hướng phi tuyến tăng 13 Mùa vụ (Seasonality)
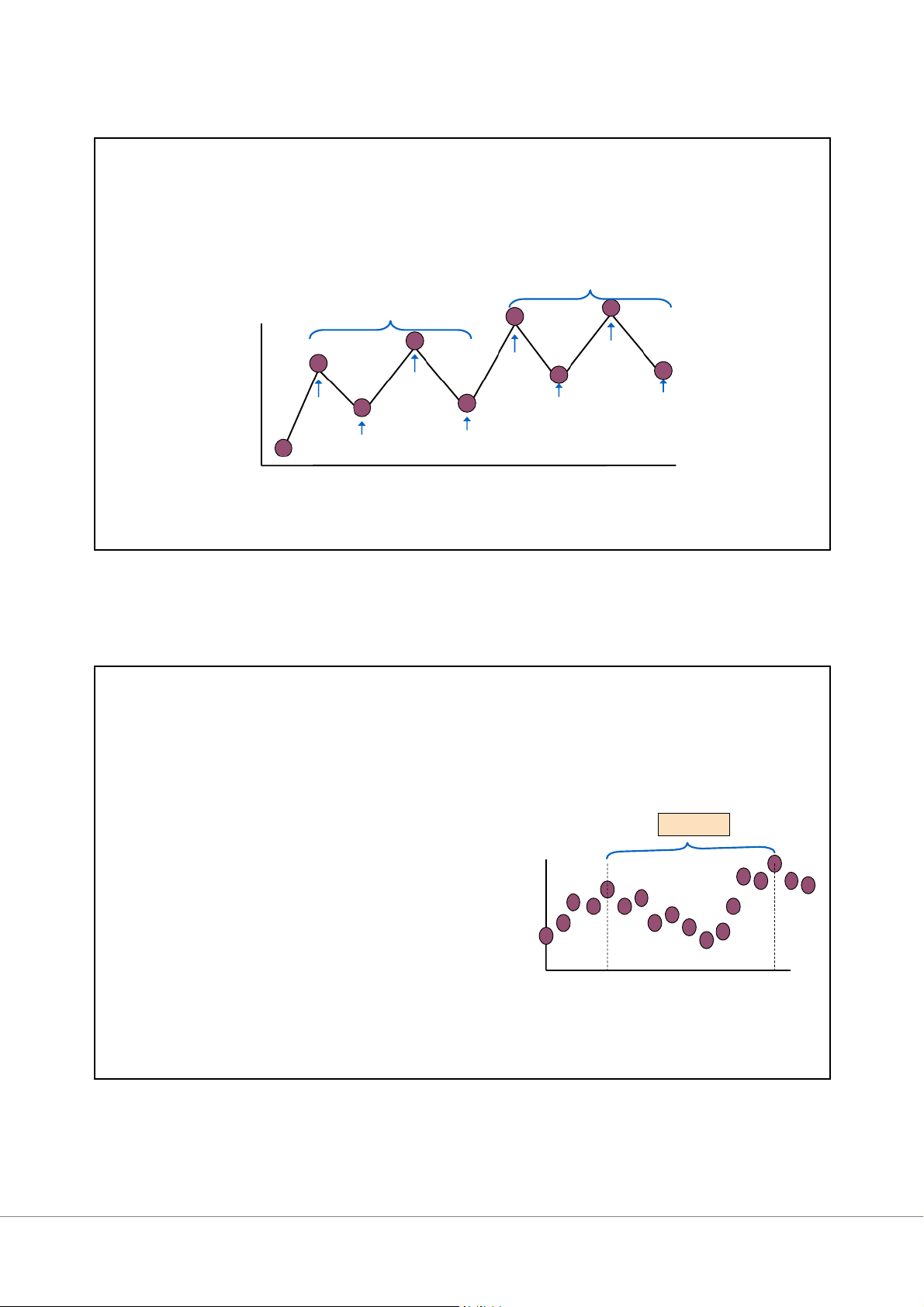
Là những biến động của hiện tượng có tính chất lặp đi lặp lại trong từng
thời gian nhất định của năm.
Mô hình có dạng sóng thường xuyên trong ngắn hạn
Thường được quan sát trong 1 năm, theo tuần, tháng hoặc quý…
Nguyên nhân: do thời tiết, phong tục tập quán sinh hoạt, mùa màng trong
năm hoặc các đặc điểm riêng theo tháng, tuần hoặc ngày. 14 7 3/3/2025 Mùa vụ (Seasonality) Năm thứ n+1 Doanh thu Năm thứ n Hè Đông Hè Đông Xuân Thu Xuân Thu Quý 15 Chu kỳ (Cyclical)
Là những biến động lặp lại trong một
khoảng thời gian nhất định, thường là 1 chu kỳ nhiều năm. Doanh thu
Mô hình dạng sóng trong dài hạn (lặp lại
trong thời gian dài hơn 1 năm)
Thường xuyên xảy ra nhưng có thể thay đổi độ dài Năm
Nguyên nhân: do tương tác của các yếu
tố có ảnh hưởng đến nền kinh tế 16 8 3/3/2025 Bất quy tắc (Irregular)
Là những biến động xảy ra ngẫu nhiên, không thể đoán trước
Thường xảy ra trong thời gian ngắn và không lặp lại
Nguyên nhân: do sự biến động ngẫu nhiên của tự nhiên (động đất, sóng
thần…), tai nạn hoặc các sự kiện bất thường (đình công…)
Làm cho việc phát hiện mô hình biểu diễn các thành phần của DSTG khó
khăn hơn (nhiễu trong DSTG) 17
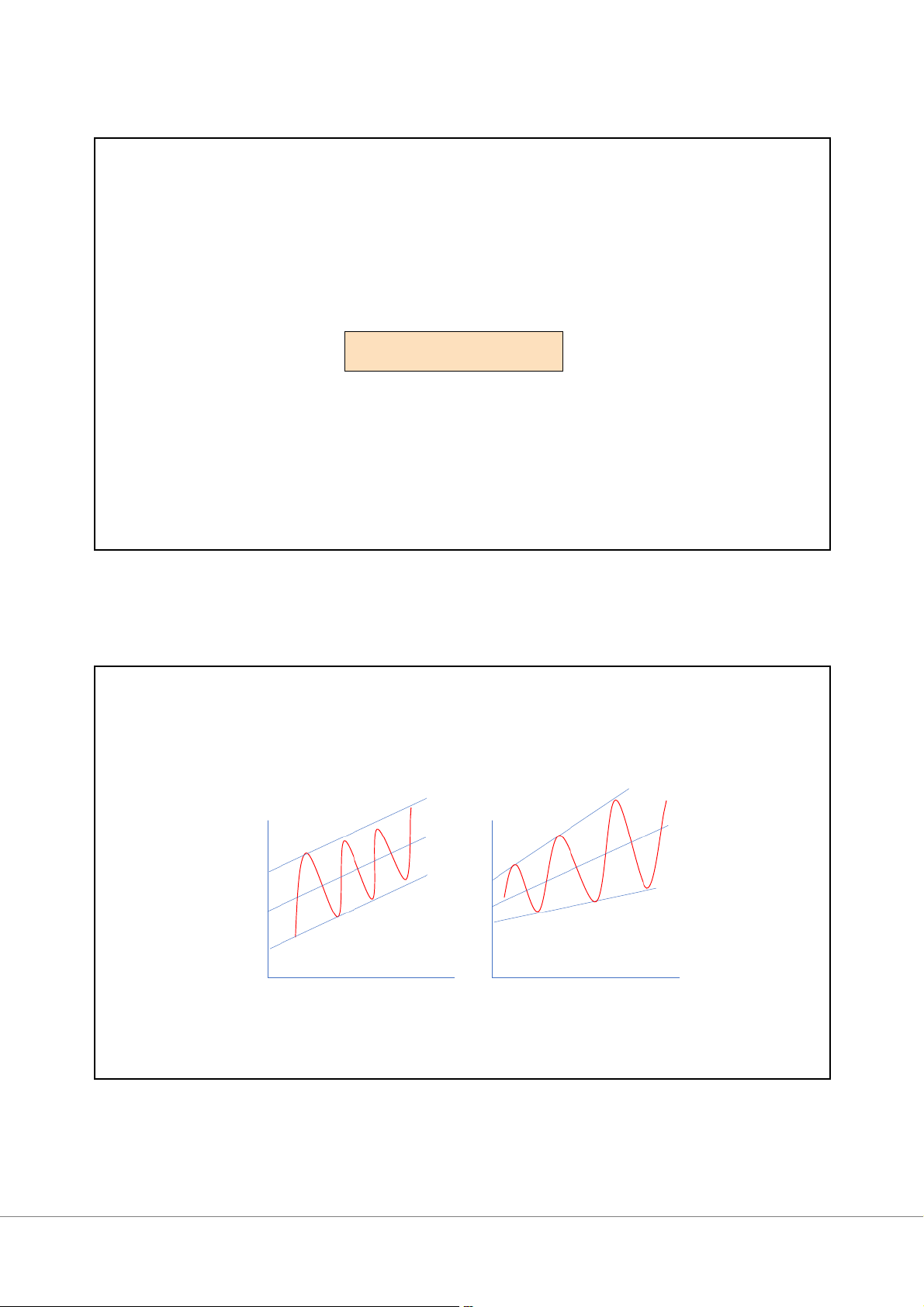
Mô hình kết hợp các thành phần của DSTG
Mô hình cộng (Additive model): phù hợp khi các biến động theo mùa vụ
không phụ thuộc vào mức độ của chuỗi thời gian. Yt= Tt+ St+ Ct+ It Trong đó:
Yt= Số liệu thực tế của hiện tượng ở thời gian t
Tt= Xu hướng ở thời gian t
St= Thành phần mùa vụ ở thời gian t
Ct= Thành phần chu kỳ ở thời gian t
It= Thành phần bất quy tắc ở thời gian t 18 9 3/3/2025
Mô hình kết hợp các thành phần của DSTG
Mô hình nhân (Multiplicative model): phù hợp khi biến động theo mùa vụ
dao động mạnh qua thời gian, phụ thuộc vào yếu tố xu thế và chu kỳ.
𝐘𝐭= 𝐓𝐭 𝐱 𝐒𝐭 𝐱 𝐂𝐭 𝐱 𝐈𝐭 Trong đó:
Yt= Số liệu thực tế của hiện tượng ở thời gian t
Tt= Xu hướng ở thời gian t
St= Thành phần mùa vụ ở thời gian t
Ct= Thành phần chu kỳ ở thời gian t
It= Thành phần bất quy tắc ở thời gian t 19
Mô hình kết hợp các thành phần của DSTG Y Y tt Mô hình cộng Mô hình nhân 20 10 3/3/2025
Các dạng chuỗi thời gian • Gồm có:
• Chuỗi thời gian không có xu thế, không có mùa vụ
• Chuỗi thời gian có xu thế, không có mùa vụ
• Chuỗi thời gian không có xu thế, có mùa vụ
• Chuỗi thời gian có xu thế và mùa vụ
→ Tùy thuộc vào đặc điểm của chuỗi thời gian để lựa chọn mô hình và
phương pháp phân tích, dự báo cho phù hợp
Lưu ý: Nội dung học phần không xem xét ảnh hưởng chu kỳ do thường không có số liệu phù hợp 21
Phân tích đặc điểm biến động của hiện tượng qua thời gian
Mức độ bình quân qua thời gian
Lượng tăng (giảm) tuyệt đối Tốc độ phát triển Tốc độ tăng (giảm)
Giá trị tuyệt đối của 1% tốc độ tăng (giảm) Chỉ số mùa vụ 22 11 3/3/2025
Mức độ bình quân qua thời gian
Là trung bình của các mức độ trong dãy số thời gian. Cách tính Dãy số thời kỳ: 󰆽=Y+ Y+. . . +Y n  =  ∑ + Y Y  Y  n 23
Mức độ bình quân qua thời gian Dãy số thời điểm:
• Biến động đều, có số liệu ở đầu và cuối kỳ Y=Yđ + Y 2
• Biến động không đều, có số liệu tại thời điểm có khoảng cách thời gian bằng nhau 
... Y=  
• Biến động không đều, có số liệu tại thời điểm có khoảng cách thời gian không bằng nhau ΣYt Y = Σt 24 12 3/3/2025
Mức độ bình quân qua thời gian
Ví dụ: Có số liệu lao động của DN A vào các ngày dưới đây trong năm 2024 Ngày 1/1 1/4 1/7 1/10 31/12 Số LĐ (người) 300 320 360 340 380
• Tính số lao động bình quân của từng quý trong năm
• Tính số lao động bình quân của một quý trong năm 25
Mức độ bình quân qua thời gian
Ví dụ: Có biến động về số lao động của DN A trong tháng 4/2024 như sau. • Ngày 1/4 DN có 150 LĐ Ngày yi ti yiti
• Ngày 6/4 DN tuyển thêm 5 LĐ 1.4 150 5 750
• Ngày 15/4 DN tuyển thêm 10 LĐ 6.4 155 9 1395
• Ngày 21/4 DN cho thôi việc 8 LĐ 15.4 165 6 990
Tính số lao động bình quân trong tháng 4. 21.4 157 10 1570 Tổng 30 4705 ΣYt 4705 Y = = = 156,83 Σt 30 26 13 3/3/2025
Lượng tăng (giảm) tuyệt đối
Phản ánh biến động tăng (giảm) tuyệt đối của hiện tượng qua thời gian. • Liên hoàn: δ= Y− Y • Định gốc: Δ= Y− Y • Mối liên hệ: Δ  =∑δ • Bình quân:  δ=∑ 
 = =  27 Tốc độ phát triển
Phản ánh xu hướng biến động của hiện tượng qua thời gian. • Liên hoàn: t= x100 • Định gốc: T=x100 • Mối liên hệ: T  =∏t • Bình quân: t=∏t     =  T  =   28 14 3/3/2025 Tốc độ tăng (giảm)
Phản ánh biến động tăng (giảm) tương đối của hiện tượng qua thời gian. • Liên hoàn:
a= x100 = 
 x100 = t− 100 • Định gốc:
A=x100 =  x100 = T− 100 • Mối liên hệ: Không có mối liên hệ • Bình quân: a = t− 100 29
Giá trị tuyệt đối của 1% tốc độ tăng (giảm)
Phản ánh lượng tuyệt đối tương ứng với 1% tốc độ tăng (giảm) • Liên hoàn:
g=(%) = =   • Định gốc:
G=(%) = = Không tính   = const • Mối liên hệ: Không xem xét • Bình quân: Không tính 30 15 3/3/2025 Ví dụ Năm 2020 2021 2022 2023 2024 =δ+ δ+ δ 4+ = δ ∆   δ Lợi nhuận (Tỷ đ) 1040 1264 1455 1915 2200 4 =  = 290 (tỷ đồng) I (Tỷ đ) - 224 191 460 285 I (Tỷ đ) - 224 415 875 1160 ti(%) - 121,54 115,11 131,62 114,88 t=1,2  1  54x1,1511x1,3162x1,1488 Ti (%) - 121,54 139,90 184,13 211,54 = = 1,206 lần. a =2,1154 i(%) - 21,54 15,11 31,62 14,88  Ai (%) - 21,54 39,90 84,13 111,54 gi(Tỷ đ) - 10,40 12,64 14,55 19,15
a = t-1= 1,206 – 1 = 0,206 lần 31 Chỉ số mùa vụ
Áp dụng khi dãy số thời gian có mùa vụ nhưng không có xu thế.
Chỉ số mùa vụ ở thời kỳ (tháng/quý) j (j = 1, m) được xác định như sau: S=   Trong đó:  • =∑ Y  
là trung bình của thời kỳ thứ j trong n năm. ∑ ∑   • Y  =     
là trung bình của tất cả các thời kỳ trong n năm. 32 16 3/3/2025 Chỉ số mùa vụ
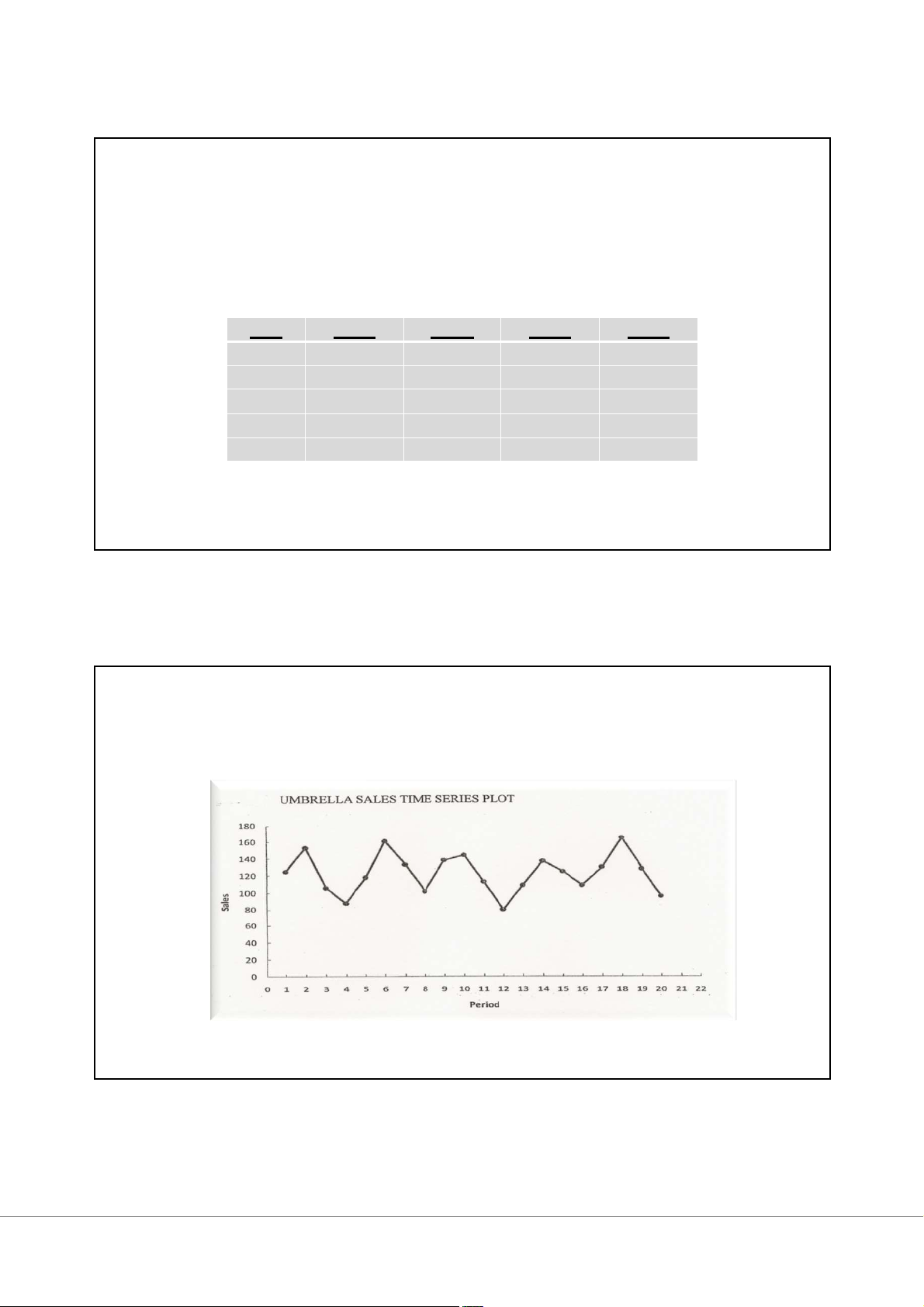
Ví dụ: Tính chỉ số mùa vụ cho chuỗi dữ liệu về doanh số bán ô của một cửa hàng trong 5 năm. Năm Quý 1 Quý 2 Quý 3 Quý 4 1 125 153 106 88 2 118 161 133 102 3 138 144 113 80 4 109 137 125 109 5 130 165 128 96 33 Chỉ số mùa vụ 34 17 3/3/2025 Chỉ số mùa vụ Trung Chỉ số Năm 1 Năm 2 Năm 3 Năm 4 Năm 5 Tổng bình quý mùa vụ Quý 1 125 118 138 109 130 620 124 1.008 Quý 2 153 161 144 137 165 760 152 1.236 Quý 3 106 133 113 125 128 605 121 0.984 Quý 4 88 102 80 109 96 475 95 0.772 Chung 472 514 475 480 519 2460 123 35 Dự báo Khái niệm dự báo
Độ chính xác của dự báo
Dự báo cho chuỗi dừng
Dự báo cho chuỗi không dừng 36 18 3/3/2025 Khái niệm dự báo
Dự báo là việc xác định các mức độ của hiện tượng trong tương lai bằng các phương pháp phù hợp
Thường dùng để dự báo trong kinh tế
Có 2 nhóm phương pháp dự báo chính:
• Phương pháp dự báo định tính
• Phương pháp dự báo định lượng 37 Khái niệm dự báo
Phương pháp dự báo định tính: thường sử dụng các đánh giá chuyên gia để thực hiện dự báo.
• Phù hợp khi không có hoặc không thu thập được dữ liệu trong quá khứ.
• Ví dụ: Dự báo về các sản phẩm mới, công nghệ mới… 38 19 3/3/2025 Khái niệm dự báo
Phương pháp dự báo định lượng: áp dụng khi
• Thu thập được dữ liệu trong quá khứ về hiện tượng nghiên cứu,
• Thông tin có thể định lượng được, và
• Có cơ sở để giả định rằng quy luật biến động của hiện tượng trong quá
khứ không thay đổi ở hiện tại và tương lai
• Dự báo có thể được thực hiện bằng cách sử dụng phương pháp chuỗi thời
gian hoặc phương pháp nhân quả.
→Tập trung chủ yếu vào phương pháp dự báo định lượng dựa vào phân tích chuỗi thời gian 39 Khái niệm dự báo
Tùy theo đặc điểm của dãy số thời gian mà lựa chọn mô hình dự báo khác nhau.
Sử dụng các thước đo đo độ chính xác của dự báo để đánh giá và lựa
chọn mô hình dự báo phù hợp. 40 20