lOMoARcPSD| 36625228
Downloaded by Jin Dian (dianjin008@gmail.com) lOMoARcPSD| 36625228
Phần I (5 điểm)
Một công ty cần thực hiện một dự án lắp đặt hệ thống nhà xưởng bao gồm các công việc với các yêu
cầu đặt ra cho trong bảng sau đây. Trong đó, a là thời gian ước tính hoàn thành công việc một cách lạc
quan, m là thời gian ước tính hoàn thành công việc trong điều kiện bình thường, b là thời gian ước tính
hoàn thành công việc một cách bi quan. Công việc Thời gian cần (ngày) Thời gian tiến hành a m b A 2 3 5 , 4 Bắt đầu ngay B 2 3 , 3 5 Bắt đầu ngay C 1 , 5 2 5 , 7 Bắt đầu ngay D 6 6 5 , 10 Sau A hoàn thành E 4 6 8 Sau B,C,D hoàn thành F 6 7 , 5 10 Sau A hoàn thành G 2, 5 3 , 5 5 , 5 Sau B,C,D hoàn thành H 1 ,5 2 2 , 5 Sau C hoàn thành I 3 5 5 , 6 Sau C hoàn thành J 3 3 5 , 7 Sau E,F,G,H hoàn thành K 6 6 5 , 10 Sau E,F hoàn thành L 3 , 5 5 5 , 6 Sau E,F hoàn thành M 4 5 6 Sau B,D,H hoàn thành N 5 6 7 Sau J,K,M hoàn thành O 1 ,5 2 , 2 5 Sau B,D,H hoàn thành
a) Hãy tính kỳ vọng và phương sai cho các đại lượng ngẫu nhiên biểu thị thời gian hoàn thànhcông
việc. Khi tính kỳ vọng làm tròn số phần thập phân như sau: Khoảng (0; 0,125] (0 ,125; 0,25] (0 ,25; 0,375] (0 ,375,0, 5] (0 ,5; 0,625] (0 ,625; 0,75] (0 ,75; 0,875] (0 ,875, 1) Làm tròn thành 0,125 0 , 25 0,375 0 , 5 0.625 0 , 75 0,875 1
b) Lập sơ đồ PERT, xác định đường găng, ước tính thời gian trung bình để hoàn thành dự án. Tínhxác
suất để toàn bộ dự án được hoàn thành với thời gian không quá 33 ngày (bỏ qua sai số do việc làm
tròn số). Lập bảng chỉ tiêu thời gian cho các công việc. Dựng sơ đồ PERT ngang với điều kiện
công việc H và I không thể thực hiện trong cùng một thời điểm. Dựng sơ đồ PERT ngang với điều
kiện nguồn lực của công ty không thể thực hiện 4 công việc cùng một thời điểm.
c) Giả sử chi phí để rút ngắn thời gian hoàn thành mỗi công việc theo quy luật ( là hệ số tỷ lệ được
cho trong bảng, Ck là chi phí rút ngắn ngày thứ k ứng với mỗi công việc và có đơn vị tính là triệu đồng) C. A B C D E F G H I J K L M N O vieäc Heä soá 5 6 3 5 4 9 4 6 5 7 6 5 6 5 8 lOMoARcPSD| 36625228
Hãy rút ngắn thời gian trung bình hoàn thành dự án không quá 25 ngày với chi phí thấp nhất và tính
chi phí tăng thêm đó. Lập bảng chỉ tiêu thời gian cho các công việc và dựng sơ đồ PERT ngang đối
với kế hoạch sau khi rút ngắn thời gian trung bình hoàn thành dự án không quá 25 ngày.
d) Dự án đang thực hiện theo kế hoạch đang lập ở (c) thì vào đầu ngày 6 có một sự cố xảy
ralàm toàn bộ công việc của công ty phải ngưng thực hiện 01 ngày . Hy điều chỉnh kế
hoạch sao cho thời gian trung bình hoàn thành dự án không quá 25 ngày với chi phí thấp nhất.
e) Trình bày chi tiết mỗi kế hoạch ở (c) và (d) trên 1 trang giấy A3 biết: Dự án bắt đầu ngày sáng
thứ hai ngày 04/07/2022, mỗi tuần làm việc 5 ngày (thứ hai đến thứ sáu), sáng từ 7 giờ đến 11 giờ
và chiều từ 13 giờ đến 17 giờ.(phần này giáo viên sẽ hướng dẫn chi tiết)
Yêu cầu tiến độ thực hiện phần I
Từ lúc nhận đề đến 12/5/2022
Làm xong câu (a), (b) và báo cáo kết quả với giáo viên
hướng dẫn. (chưa đánh máy)
Từ 12/5/2022đến 14/5/2022
Làm xong câu (c) và báo cáo kết quả với giáo viên hướng dẫn. (chưa đánh máy)
Từ 14/5/2022đến 16/5/2022
Làm xong câu (d) và báo cáo kết quả với giáo viên hướng dẫn. (chưa đánh máy)
Từ 16/5/2022đến 19/5/2022 Kiểm tra một lần nữa kết quả câu (c), (d) chính xác & giáo
viên hướng dẫn chi tiết làm câu (e).
Từ 19/5/2022đến 21/5/2022
Đánh máy, vẽ hình, trình bày đầy đủ bài thu hoạch.
Kiểm tra và sửa (làm lại) những chỗ còn sai sót (nếu có).
Từ 21/5/2022đến 23/5/2022 Cả nhóm kiểm tra toàn bộ kết quả chính xác và trình bày đầy đủ
rồi thì mới nộp bài cho giáo viên. là các ngày dự trữ & nộp bài.
Phần II (3,5 điểm)
Tìm hiểu cách sử dụng một trong các phần mềm Excel, Maple, Matlab,…để giải bài toán quy hoạch
tuyến tính, bài toán vận tải. Trình bày cách giải, nhập số liệu, giải và in kết quả đối với các bài toán
(đối với bài 3, bài 4 phải lập mô hình toán học) sau:
Bài 1 Giải bài toán QHTT f(x) = 4x1+8x2+5x3 max (2) (3) tuøy yù, ,
Bài 2 Một công ty cần sản xuất 45 đơn vị sản phẩm loại A , 85 đơn vị sản phẩm loại A 120 đơn vị 1 2,
sản phẩm A trong vòng 3 tháng. Công ty có 4 xí nghiệp B 3
1, B2, B3, B4 với khả năng sản xuất (số đơn
vị sản phẩm loại A hay sản phẩm loại A
sản phẩm loại A ) trong 3 tháng lần lượt là 90, 70, 60, 1 2 hay 3
50 đơn vị sản phẩm. Lợi nhuận (đơn vị tính 1.000.000 đồng/1 sản phẩm và tính bằng giá bán trừ chi
phí cho mỗi sản phẩm) của mỗi sản phẩm khi sản xuất tại các xí nghiệp được cho trong bảng sau lOMoARcPSD| 36625228 B 1 B 2 B 3 B 4 Sản phẩm 90 70 60 50 A 1 :45 6 5 4 7 A 2 :85 6 7 6 8 A 3 :120 4 9 5 6 Đại lý
Vì chiến lược phát triển chung của công ty, nên xí nghiệp B3 phải sản xuất đủ 60 đơn vị sản phẩm. Hỏi
phải phân phối cho các xí nghiệp sản xuất số lượng các sản phẩm như thế nào để tổng lợi nhuận lớn
nhất và tính tổng lợi nhuận lớn nhất đó Bài 3
The National Credit Union has $250,000 available to invest in a 12-month commitment. The money
can be placed in Treasury notes yielding an 8% return or in municipal bonds at an average rate of return
of 9%. Credit union regulations require diversification to the extent that at least 50% of the investment
be placed in Treasury notes. Because of defaults in such municipalities as Cleveland and New York, it
is decided that no more than 40% of the investment be placed in bonds. How much should the National
Credit Union invest in each security so as to maximize its return on investment? Bài 4
Wilson Creek Farm has 200 acres of land available for planting. The owner is considering planting
three crops: corn, soybeans, and wheat. The production yield, water requirements, and labor
requirements for a salable crop are given here. The owner expects to have only 35,000 gallons of water
available per week to use for the crops, and during the growing season he will only have 8000 person-
hours of labor available. The expected profit per bushel of each crop is $1.50 for corn, $1.90
for soybeans, and $3.60 for wheat. The
owner can use any mix of crops (i.e., he can plant the same crop on all 200 acres or he
can plant all three crops in different proportions).
a) Formulate the problem as a linear program to find the profit-maximizing planting strategy.
b) Solve the problem using a computer. lOMoARcPSD| 36625228
Phần III (1,5 điểm) DESIGNING YOUR LIFE
How to Build a Well-Lived, Joyful Life?
Designing/Planning/Programming YOUR LIFE lOMoARcPSD| 36625228
CUỘC ĐỜI CỦA BẠN như thế nào là TỐI ƯU?
3.1) CUỘC ĐỜI CỦA BẠN như thế nào là TỐI ƯU?
Nếu bạn có được một đời Bình an-Hạnh phúc-Cân bằng-Viên mãn là tối ưu chưa? Hay bạn cần
phải Giàu sang-Thành đạt có đầy đủ Của cải vật chất và Địa vị xã hội thì mới tối ưu? Hay bạn
chỉ cần một cuộc sống đạt ở mức cơ bản về vật chất-không mất nhiều thời gian công sức học
tập làm việc phục vụ cho nhu cầu vật chất- dành thời gian và nguồn lực đời người để tạo dựng
một đời sống thật khỏe mạnh về thể chất, phong phú về tinh thần, thăng hoa tâm thức, …? Hãy
suy ngẫm về tính tương đối&tính tuyệt đối của hệ thống các giá trị trong cộng đồng, xã hội, đời sống, nhân sinh,…
3.2) Bạn có những thiết kế/quy hoạch dài hạn, trung hạn, ngắn hạn như thế nào và
ước tính cách thực hiện ra sao để được một cuộc đời tối ưu hoặc gần tối
ưu? (khi quy hoạch/thiết kế cần chú ý đến các giới hạn về mặt sinh học của chính bản thân bạn, các ràng
buộc mối quan hệ của bạn với gia đình, cộng đồng, các điều kiện tự nhiên-xã hội,…..)
Hãy nêu trả lời cơ bản ngắn gọn các câu hỏi trên trong một hoặc vài trang giấy. Mỗi người có
điều kiện, hoàn cảnh, trải nghiệm, nhân sinh quan, thế giới quan,… khác nhau có thể trả lời
khác nhau nhưng phù hợp cho cùng một câu hỏi (nếu người trả lời yêu cầu giữ bí mật các thông tin
rieâng tư có trong câu trả lời thì giáo viên sẽ tuyệt đối thực hiện). ***
Các bạn SINH VIÊN thân mến,
Đây là câu hỏi mở về vấn đề quá rộng và còn rất nhiều bất định nên không thể có câu trả lời xác định.
Trong câu hỏi ẩn chứa nhiều điều không tường minh. Tuy nhiên, giáo viên mong muốn hỏi để học từ
các bạn sinh viên và để các bạn sinh viên thực sự áp dụng những kiến thức và kỹ năng đã học được
vào trong công việc và cuộc sống để thành công và hạnh phúc hơn. Khi trả lời các câu hỏi này sẽ giúp
người trả lời hiểu rõ hơn bản chất và ý nghĩa cuộc sống, có các hoạch định/thiết kế và thực hiện các kế
hoạch tương lai tốt hơn nhờ đó tăng khả năng thành công, thích ứng tốt hơn và vững vàng hơn với các
khó khăn và biến động trong đời sống xã hội, từ đó giúp bạn có được một đời sống sáng tạo-phong
phú-biến đổi tiến triển-đầy thú vị- cân bằng-viên mãn.
Giáo viên tin và ủng hộ quan điểm: “Người học thật nhiều kiến thức mà không biết ứng dụng gì cho
cuộc sống được hạnh phúc thì giống như con lừa thồ sách”
Chúc Bạn và Gia đình KHỎE MẠNH-BÌNH AN-HẠNH PHÚC! Ngô Hữu Tâm
…………………………………………………………………………………………………
Có thể tìm trên Internet (nên làm theo cách này) hay tham khảo các tài liệu sau:
[1] Nguyễn Đình Tê, EXCELL XP quyển 2, nhà xuất bản Lao động Xã hội – 2007.
[2] Trần Trí Dũng, EXCELL Solver cho kỹ sư, NXB Khoa học Kỹ thuật – 2005.
[3]Phạm Minh Hoàng, MAPLE &các bài toán ứng dụng, NXB Khoa học Kỹ thuật–2005.
[4] Phạm Trí Cao, Tối Ưu hóa Ứng dụng, NXB Lao động Xã hội -2014. lOMoARcPSD| 36625228
Một số yêu cầu đối với bài thu hoạch:
Bài làm được đánh máy trên giấy A , các hình vẽ thì vẽ bằng tay hay vẽ bằng máy cũng được 4
miễn sao đạt yêu cầu rõ ràng chính xác. (kỹ năng vẽ bằng máy hiện chưa cần nên vẽ tay thì tốt hơn)
Ghi đầy đủ họ tên, mã số sinh viên các thành viên trong nhóm và ít nhất một số điện thoại để
liên lạc khi cần. Tự nhận xét và đánh giá nhóm của các bạn.
Thời gian nộp bài: Từ 21/5/2022 đến 23/5/2022. Nộp lại đề bài này chung với bài làm– Đề
bài ghép chung ngay trước phần bài làm ( không nhận bài nộp mà không có đề ).
Mục tiêu đánh giá
Phần I Sử dụng sơ đồ PERT-CPM để: Lập kế hoạch cho dự án có thời gian ngẫu nhiên và biết cách sử dụng
thời gian dữ trữ các công việc không găng để điều chỉnh tối ưu kế hoạch sao cho thuận tiện trong việc thực hiện
và quản lý (câu a&b). Điều chỉnh tối ưu hóa về mặt tài chính với quy định thời gian cho trước (câu c). Khắc
phục sự cố dự án sao cho tối ưu hóa về mặt tài chính với thời gian quy định cho trước (câu d). Biết cách lập kế
hoạch ngắn gọn chi tiết triển khai thực hiện kế hoạch dự án với thời gian thực (câu e).
Phần II Nhận dạng được bài toán thực tế dưới dạng ngôn ngữ thông thường (tiếng Việt hoặc tiếng Anh), lập
được mô hình toán học, sử dụng máy tính và phần mềm thích hợp để giải tìm lời giải tối ưu rồi suy ra kết quả bài toán thực tế.
Phần III Hoạch định cuộc đời bạn phù hợp nhất/tốt nhất với các điều kiện/ràng buộc của chính bạn, luôn vững
vàng và an lạc trước vạn biến/vô thường của cuộc đời.
Phát triển kỹ năng phối hợp làm việc nhóm, tìm kiếm tài liệu, trình bày, tranh
luận & phản biện,… Bài làm: *Phần 1:
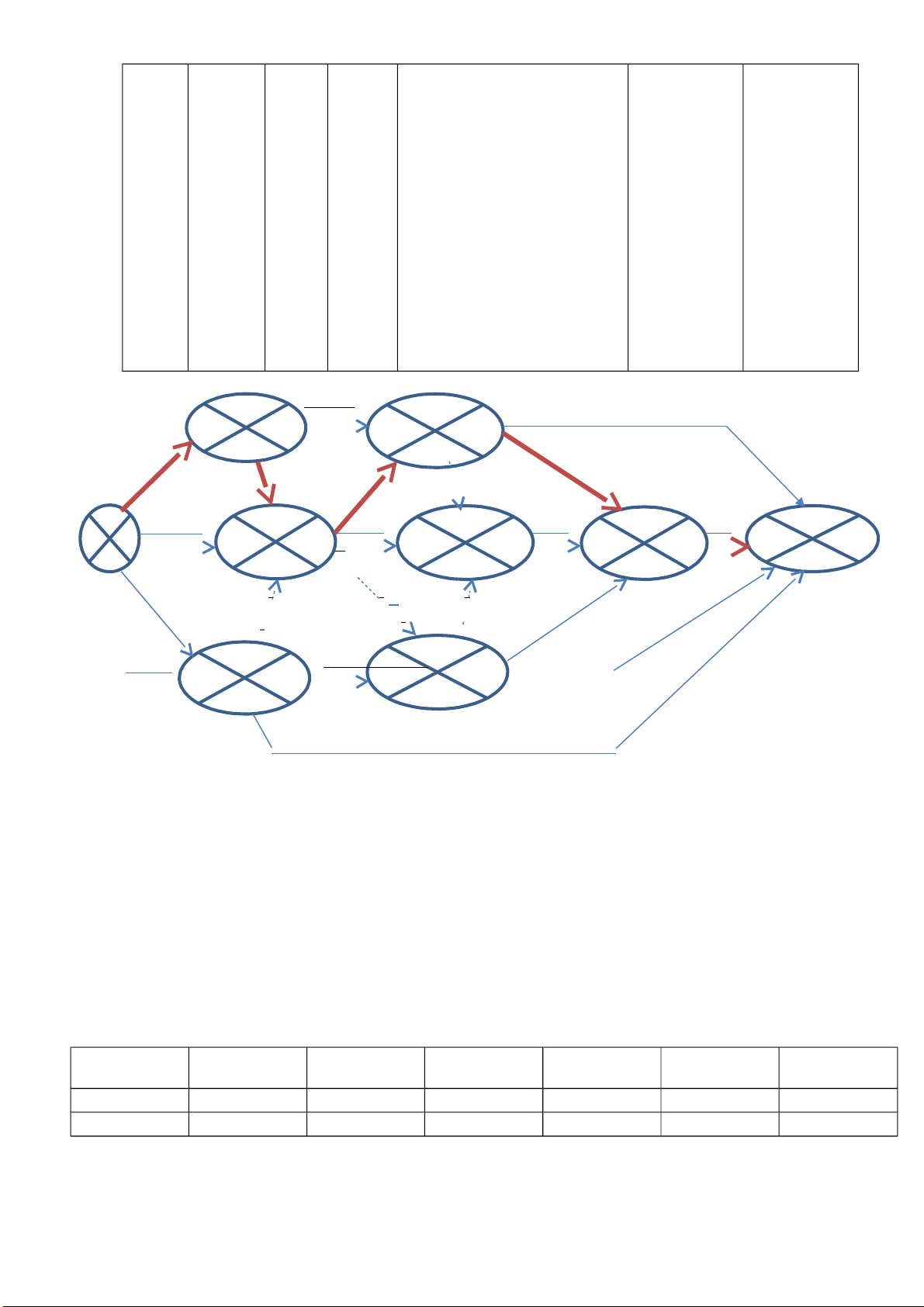
a) Bảng tính kì vọng và phương sai: Công Thời gian cần (ngày) Thời gian tiến hành Công việc Thời gian việc a cần (ngày) a m b A 2 , 3 5 A 2 3,375 / 1 9 B 2 3 B 2 3 1 16 / C 1 5 , 2 5 , C 1 , 5 3,125 121/144 D 6 6 , 5 D 6 7 4 / 9 lOMoARcPSD| 36625228 E 4 6 E 4 6 4/9 F 6 7,5 F 6 7,75 4/9 G 2,5 3,5 G 2,5 3,75 1/4 H 1,5 2 H 1,5 2 1/36 I 3 5,5 I 3 5,25 1/4 J 3 3,5 J 3 4 4/9 K 6 6,5 K 6 7 4/9 L 3,5 5,5 L 3,5 5,25 25/144 M 4 5 M 4 5 1/9 N 5 6 N 5 6 1/9 O 1,5 2 O 1,5 2 1/36 b) 2 F 5 L 3,375 3,375 16,375 16,375 0 7,75 0 K 5,25 A 7 3,375 7 D E 6 1 4 7 8 9
0 0 B 10,375 10,375 G 16,375 19,375 J 23,375 23,375 N 29.375 29.375 0 3 0 3,75 3 4 0 6 0 C 3,125 M 5 3 6 O 3,125 10,375 H 10,375 18,375 2 7,25 2 8 I 5,25
Đường găng: (1,A, 2, D, 4, E, 5, K, 8, N, 9.)
Thời gian trung bình hoàn thành dự án: E(T)=29,375 Var=14/9 => 1,25
Xác suất để toàn bộ dự án được hoàn thành với thời gian không quá 33 ngày: P(T33)= 0() + 0() = 0(2,9) + 0(23,5) Với 0(z) =
Bảng chỉ tiêu thời gian công việc: Công việc t ks hs km hm c dl ij t ij t ij t ij d ij d ij A(1,2) 0 3,375 0 3,375 0 0 B(1,4) 0 3 7,375 10,375 7,375 7,375 lOMoARcPSD| 36625228 C(1,3) 0 3,125 7,25 10,375 7,25 0 D(2,4) 3,375 10,375 3,375 10,375 0 0
E(4,5) 10,375 16,375 10,375 16,375 0 0 F(2,5) 3,375 11,125 8,625 16,375 5,25 5,25 G(4,7) 10,375 14,125 15,625 19,375 5,25 2,25
H(3,6) 3,125 5,125 16,375 18,375 13,25 0 I(3,9) 3,125 8,375 24.125 29.375 21 13.75 J(7,8) 16,375 20,375 19,375 23,375 3 0
K(5,8) 16,375 23,375 16,375 23,375 0 0 L(5,9) 16,375 21,625 24.125 29.375 7.75 7.75 M(6,8) 10,375 15,375 18,375 23,375 8 0 N(8,9) 23,375 29,375 23.375 29.375 0 0 O(6,9) 10,375 12,375 27.375 29.375 17 9
Ta thấy thời gian dự trữ của I là 13.75 ngày nên ta dời I thêm 2 ngày. Ta có sơ đồ PERT ngang với
điều kiện H và I không thể thực hiện trong cùng một thời điểm như sau:
Vì công ty không thể làm 4 việc cùng 1 lúc nên - Dời O thêm 13 ngày - Dời G thêm 0.75 ngày
Ta được như sơ đồ PERT ngang với điều kiện nguồn lực công ty không thể thực hiện 4 công
việc cùng một thời điểm như sau:
c) Chi phí rút ngắn ngày thứ k với công việc găng C=5αk-4 Công việc Chi phí ngày Chi phí ngày thứ nhất thứ hai ( triệu đồng ) ( triệu đồng ) A 21 46 D 21 46 E 16 36 K 26 56 N 21 46 lOMoARcPSD| 36625228
Cần phải rút 5 ngày để thời gian hoàn thành trung bình dự án không quá 25 ngày
Để chi phí thấp nhất ta sẽ rút E,A,D,N,K mỗi việc 1 ngày:
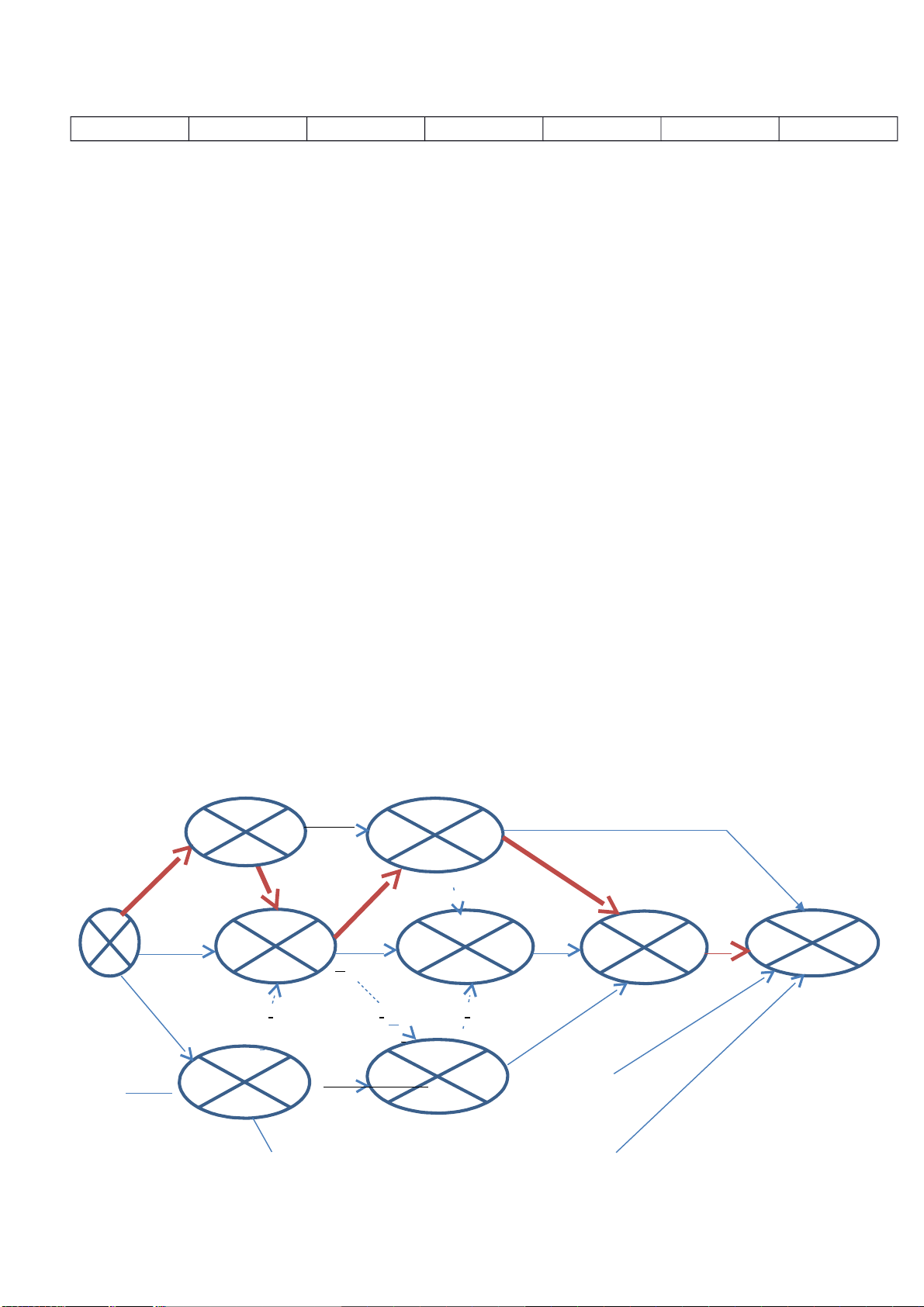
Chi phí tăng thêm là : 21+21+16+26+21=105 (triệu đồng) Rút E: 2 F 5 L 3,375 3,375 15,375 15,375 0 7,75 0 K 5,25 A 7 3,375 7 D E 5 1 4 7 8 9 0
0 B 10,375 10,375 G 15,375 18,375 J 22,375 22,375 N 28.375 28.375 0 3 0 3,75 3 4 0 6 0 C 3,125 M 5 3 6 O 3,125 10,375 H 10,375 17,375 2 7,25 2 7 I 5,25 Rút A: 2 F 5 L 2,375 2,375 14,375 14,375 0 7,75 0 K 5,25 A 7 2,375 7 D E 5 1 4 7 8 9 0
0 B 9,375 9,375 G 14,375 17,375 J 21,375 21,375 N 27.375 27.375 0 3 0 3,75 3 4 0 6 0 C 3,125 M lOMoARcPSD| 36625228 5 3 6 O 3,125 9,375 H 9,375 16,375 2 6,25 2 7 I 5,25 Rút D: 2 F 5 L 2,375 2,375 13,375 13,375 0 7,75 0 K 5,25 A 7 2,375 6 D E 5 1 4 7 8 9 0
0 B 8,375 8,375 G 13,375 16,375 J 20,375 20,375 N 26.375 26.375 0 3 0 3,75 3 4 0 6 0 C 3,125 M 5 3 6 O 3,125 8,375 H 8,375 15,375 2 5,25 2 7 I 5,25 Rút N: 2 F 5 L 2,375 2,375 13,375 13,375 0 7,75 0 K 5,25 A 7 2,375 6 D E 5 1 4 7 8 9 0
0 B 8,375 8,375 G 13,375 16,375 J 20,375 20,375 N 25.375 25.375 0 3 0 3,75 3 4 0 5 0 lOMoARcPSD| 36625228 C 3,125 M 5 3 6 O 3,125 8,375 H 8,375 15,375 2 5,25 2 7 I 5,25 Rút K: 2 F 5 L 2,375 2,375 13,375 13,375 0 7,75 0 K 5,25 A 6 2,375 6 D E 5 1 4 7 8 9
0 0 B 8,375 8,375 G 13,375 15,375 J 19,375 19,375 N 24.375 24.375 0 3 0 3,75 2 4 0 5 0 C 3,125 M 5 3 6 O 3,125 8,375 H 8,375 14,375 2 5,25 2 6 I 5,25
*Bảng chỉ tiêu thời gian công việc: Công việc tijks tijhs tijkm tijhm dijc dijdl A(1,2) 0 2,375 0 2,375 0 0 B(1,4) 0 3 5,375 8,375 5,375 5,375 C(1,3) 0 3,125 5,25 8,375 5,25 0 D(2,4) 2,375 8,375 2,375 8,375 0 0
E(4,5) 8,375 13,375 8,375 13,375 0 0 F(2,5) 2,375 10,125 5,625 13,375 3,25 3,25 G(4,7) 8,375 12,125 11,625 15,375 3,25 1,25 H(3,6)
3,125 5,125 12,375 14,375 9,25 0 I(3,9) 3,125 8,375 19,125 24,375 16 10,75 J(7,8) 13,375 17,375 15,375 19,375 2 0 lOMoARcPSD| 36625228
K(5,8) 13,375 19,375 13,375 19,375 0 0 L(5,9) 13,375 18,625 19,125 24,375 5,75 5,75
M(6,8) 8,375 13,375 15,375 19,375 9,25 0 N(8,9) 19,375 24,375 19,375 24,375 0 0 O(6,9)
8,375 10,375 22,375 24,375 17,25 8
d) Do đầu ngày 6 có một sự cố xảy ra nên các công việc D, F, I bị trì hoãn 1 ngày nên thời gian hoàn
thành tăng thêm 1 ngày. Để dự án không vượt quá 25 ngày với chi phí thấp nhất thì ta rút E đi 1 ngày. Sơ đồ PERT: 2 F 5 L 2,375 2,375 13,375 13,375 0 8,75 0 K 5,25 A 6 2,375 7 D E 4 1 4 7 8 9
0 0 B 9,375 9,375 G 13,375 15,375 J 19,375 19,375 N 24,375 24,375 0 3 0 3,75 2 4 0 5 0 C 3,125 M 5 3 6 O 3,125 9,375 H 9,375 14,375 2 6,25 2 5 lOMoARcPSD| 36625228 I 6,25
Bảng chỉ tiêu thời gian công việc: Công việc tijks tijhs tijkm tijhm dijc dijdl A(1,2) 0 2,375 0 2,375 0 0 B(1,4) 0 3 6,375 9,375 6,375 6,375 C(1,3) 0 3,125 6,25 9,375 6,25 0 D(2,4) 2,375 9,375 2,375 9,375 0 0
E(4,5) 9,375 13,375 9,375 13,375 0 0 F(2,5) 2,375 11,125 4,625 13,375 3,25 3,25 G(4,7) 9,375 13,125 11,625 15,375 3,25 1,25
H(3,6) 3,125 5,125 12,375 14,375 10,25 0 I(3,9) 3,125 9,375 18,125 24,375 17 9,75 J(7,8) 13,375 17,375 15,375 19,375 2 0
K(5,8) 13,375 19,375 13,375 19,375 0 0 L(5,9) 13,375 18,625 19,125 24,375 5,75 5,75
M(6,8) 9,375 14,375 14,375 19,375 9,25 0 N(8,9) 19,375 24,375 19,375 24,375 0 0 O(6,9) 9,375 11,375 22,375 24,375 17,25 8 Phần II Câu 1:
Bước 1: Vào File => Options. Tại hộp thoại Excel Options chọn Add-ins, tại dòng Manage chọn Go… Hộp
thoại Add-ins xuất hiện: lOMoARcPSD| 36625228 Nháy chọn Solver Add-ins và nháy Oke
Lúc này, nháy vào hộp thoại Data ta thấy tại Analysis xuất hiện lệnh Solver.
Bước 2: Nhập vào Excel cám hàm mục tiêu, các giá trị ràng buộc
Hàm mục tiêu: f(x)=4x1+8x2+5x3→max. Công thức tính hàm mục tiêu cho bài toán ta sử dụng hàm
SUMPRODUCT: =SUMPRODUCT(C4:E4,C3:E3)
Công thức ràng buộc thứ nhất: =SUMPRODUCT(C5:E5,$C$3:$E$3)
Công thức ràng buộc thứ hai: =SUMPRODUCT(C6:E6,$C$3:$E$3)
Công thức ràng buộc thứ ba: =SUMPRODUCT(C7:E7,$C$3:$E$3)
Công thức ràng buộc thứ tư: =SUMPRODUCT(C8:E8,$C$3:$E$3) lOMoARcPSD| 36625228
Bước 3: Tiến hành giải bài toán
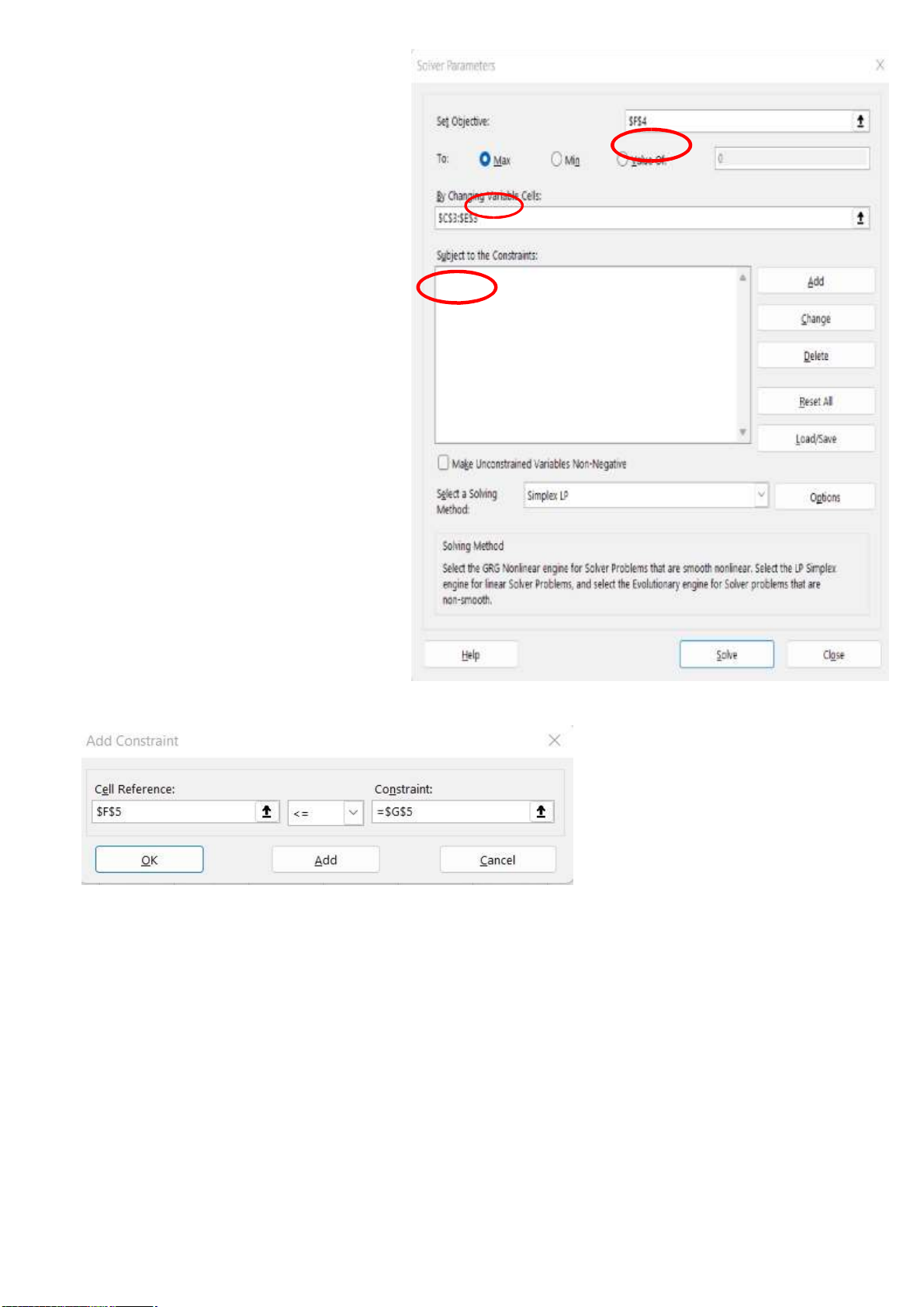
Vào Data, chọn Solver lúc này màn hình xuất hiện hộp thoại Solver Pramateres
Set Objective: Ô chứa hàm mục tiêu lOMoARcPSD| 36625228
To: là giá trị tối ưu của hàm mục tiêu
By changing variable cells: Địa chỉ
của các ô chứa thành phần phương án nghiệm
Subject to the Constraints: Các ràng buộc của bài toán
Set Objective: Ô chứa hàm mục tiêu là ô F4
Trong bài toán này hàm mục tiêu
hướng về Min do đó trong hộp thoại
Solver Pramateres, ở hàng To ta chọn Max.
By changing variable cells: Nhập C3:E3
Subject to the Constraints: Các ràng buộc của bài toán
Bấm nút Add để nhập ràng buộc thứ
nhất, trên màng hình xuất hiện hộp
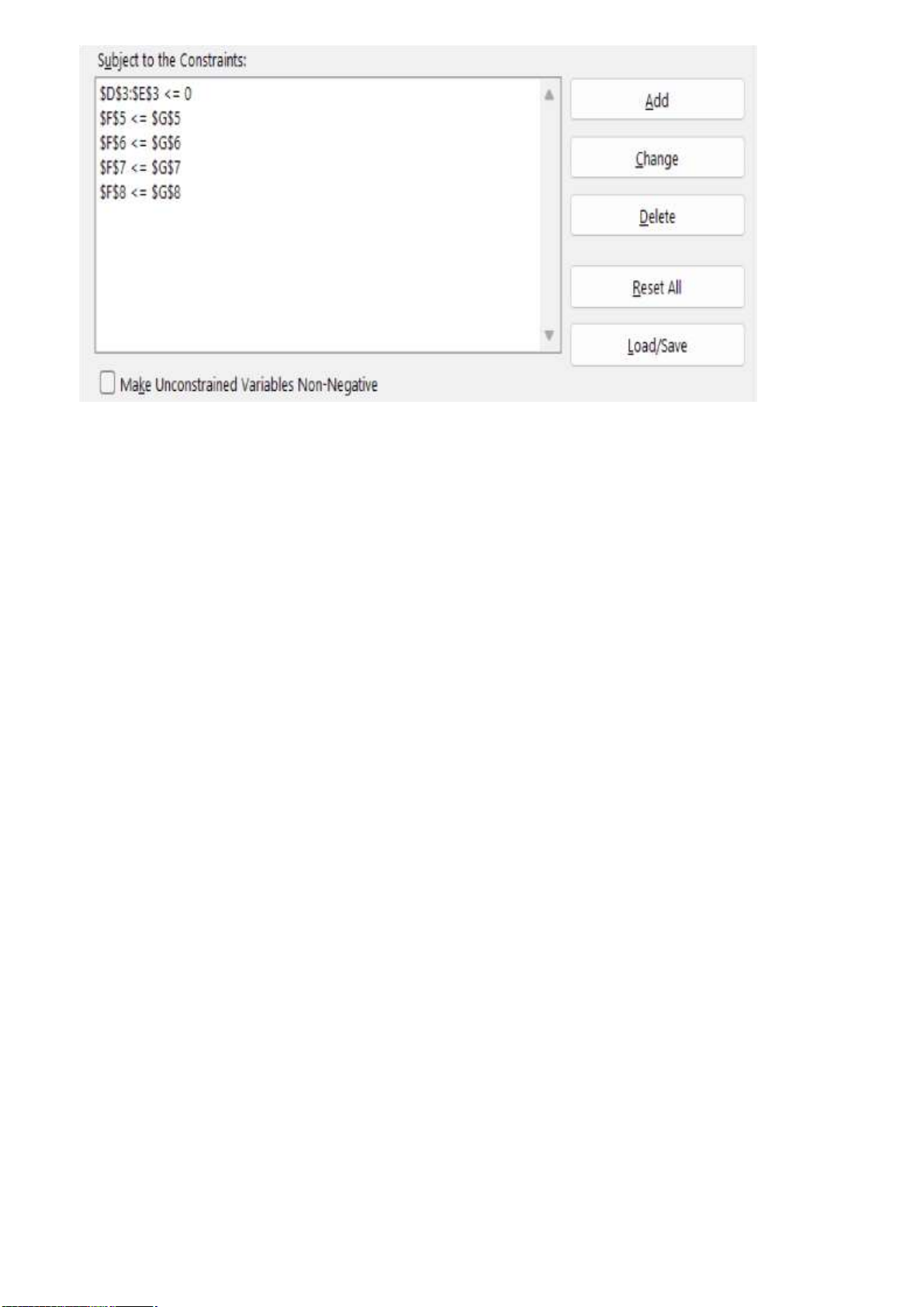
thoại Add Constraint như sau.
Với ràng buộc 2X1 + 4X2 – X3 ≤ -2 nhập theo thứ tự như sau: $F$5 <= =$G$5
Sau đó bấm Add để nhập tiếp các ràng buộc còn lại
Với ràng buộc 2X1+4X2+X3 ≤ 7 ta nhập $F$6 <= =$G$6
Với ràng buộc X1 + X2 + X3 ≤ 2 ta nhập $F$7 <= =$G$7
Với ràng buộc -3X1 + X2 + 2X3 ≤ 10 ta nhập $F$8 <= =$G$8
Với Ràng buộc ẩn ta nhập $D$3:$E$3 <= 0
Sau khi nhập xong các ràng buộc nháy Ok để quay lại hộp thoại Solver Parameteres, lúc này tại
ô Subject to the Constraints ta hoàn thành được bản điều kiện như hình bên. lOMoARcPSD| 36625228 lOMoARcPSD| 36625228
Tuy nhiên muốn thêm ràng buộc
ta chọn Add, hiệu chỉnh ràng buộc
ta chọn Change, xóa ràng buộc ta
chọn ràng buộc từ danh sách
Subject to the Constraints và
nhấn Delete Tại Select a Solving
Method chọn một phương pháp
giải ta chọn Simplex LP là giải
theo phương pháp đơn hình Sau
khi kết thúc bước nhập dữ liệu
bấm Solve để chương trình bắt đầu chạy.
Ta thấy sau khi nhấp vào Solve,
hộp thoại Solver Results xuất
hiện: Keep Solver Solution: Giữ lại lời bài toán
Restore Original Values: Phục
hồi lại giá trị ban đầu
Save Scenario…: Lưu kết quả
vừa tìm được thành một tình
huống có thể xem lại sau này
Bài toán trên ta chọn Keep Solver
Solution và nháy Ok, ta thu được kết quả như sau: lOMoARcPSD| 36625228
Từ bảng kết quả trên ta tính đc X1=-1, X2=0, X3=0 và fmax=-4
Câu 2: Đây là bài toán không cân bằng thu phát (Tổng thu lớn hơn tổng phát) với lượng phát ít hơn
thu một lượng là (90+70+60+50) – ( 45+85+120) = 20 đơn vị sản phẩm. Ta lập một trạm sản xuất giả
A4 với lượng phát cần là α4 = 20 đơn vị sản phẩm. Để trạm B3 thu đủ hàng thì lượng hàng giả trạm A4
không được phát vào trạm B3 nên ô và (4,3) là ô cấm, vì cần tổng lợi nhuận cao nhất nên đây là bài
toán f => Max do đó cước phí ô (4,3) là -M (số dương lớn tùy ý).
Gọi Xij là lượng sản phẩm vận chuyển từ nhà máy i đến điểm tiêu thụ j nên Xij ≥ 0, i=(1,4), j=(1,4) Hàm mục tiêu: F(X) = lOMoARcPSD| 36625228
6X11+5X12+4X13+7X14+6X21+7X22+6X23+8X24+4X31+9X32+5X33+6X34+MX41+0X42+0X43+MX44 => Max Các ràng buộc: X11 + X12 + X13 + X14 = 45 X21 + X22 + X23 + X24 = 85 X31 + X32 + X33 + X34 = 120 X41 + X42 + X43 + X44 = 20 X11 + X21 + X31 + X41 = 50 X12 + X22 + X32 + X42 = 50 X13 + X23 + X33 + X43 = 70 X14 + X24 + X34 + X44 = 100
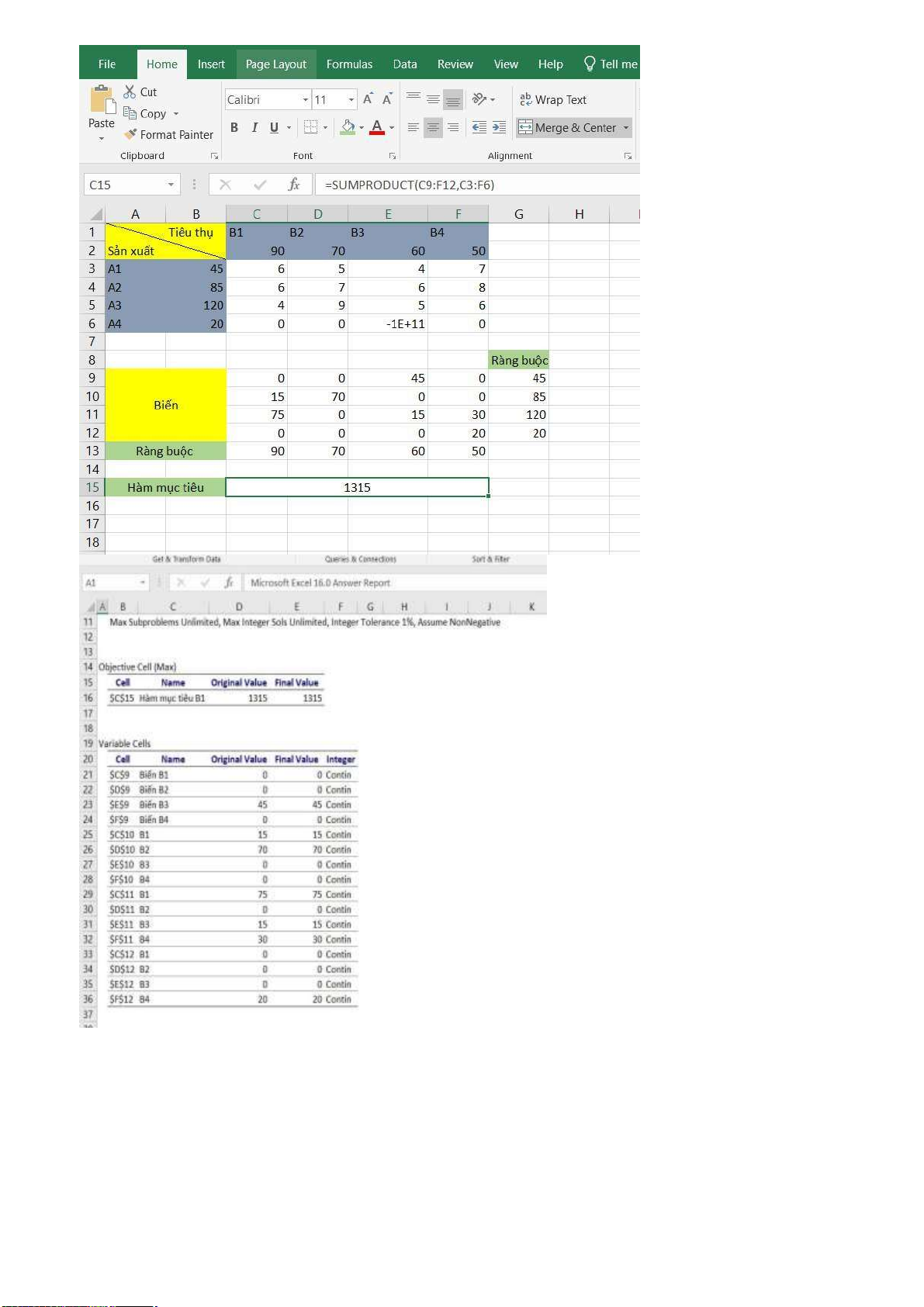
Tổ chức dữ liệu trên bảng tính như sau:
Khởi tạo giá trị ban đầu của các biến Xij = 0; với i=(1,4); j=(1,4)
Sau đó ta lập công thức tính hàm mục tiêu tại ô C15 = SUMPRODUCT(C9:F12,C3:F6)
Số lượng sản phẩm A1, A2, A3, A4 sản xuất tiêu thụ ở các cửa hàng B1, B2, B3, B4 đúng bằng lượng sản phẩm yêu cầu X11 + X12 + X13 + X14 = 45 X21 + X22 + X23 + X24 = 85 X31 + X32 + X33 + X34 = 120 X41 + X42 + X43 + X44 = 20 lOMoARcPSD| 36625228
Số lượng sản phẩm phân phối cho các cửa hàng bằng với khả năng tiêu thụ mà công ty yêu cầu X11 + X21 + X31 + X41 = 90 X12 + X22 + X32 + X42 = 70 X13 + X23 + X33 + X43 = 60 X14 + X24 + X34 + X44 = 50
Dựa vào các ràng buộc trên ta nhập vào ô tính như sau: Bên phía A:
Tại ô G9 nhập: =SUM(C9:F9)
Tại ô G10 nhập: =SUM(C10:F10)
Tại ô G11 nhập: =SUM(C11:F11)
Tại ô G12 nhập: =SUM(C12:F12) Bên phía B:
Tại ô C13 nhập: =SUM(C9:C12)
Tại ô D13 nhập: =SUM(D9:D12)
Tại ô E13 nhập: =SUM(E9:E12)
Tại ô F13 nhập: =SUM(F9:F12)
Tiến hành giải bài toán:
Vào Data chọn Solver để mở hộp thoại Solver Parameters Set Objective: $C$15 To: Min
By Changing Variable Cells: $C$9:$F$12
Click Add để mở hộp thoại Add Constraints sau đó nhập lần lượt các ràng buộc:
Với X11 + X12 + X13 + X14 = 45 ta nhập $G$9 = $B$3
Với X21 + X22 + X23 + X24 = 85 ta nhập $G$10 = $B$4 Với X = 120 ta nhập $G$11 = $B$5 31 + X32 + X33 + X34
Với X41 + X42 + X43 + X44 = 20 ta nhập $G$12 = $B$6
Với X11 + X21 + X31 + X41 = 90 ta nhập $C$13 = $C$2
Với X12 + X22 + X32 + X42 = 70 ta nhập $D$13 = $D$2
Với X13 + X23 + X33 + X43 = 60 ta nhập $E$13 = $E$2
Với X14 + X24 + X34 + X44 = 50 nha nhập $F$13 = $F$2
Sau khi nhập xong các ràng buộc ở dòng Select a Solving Methods chọn Simples LP lOMoARcPSD| 36625228
Sau đó nhấn Solve để mở hộp thoại Solver Results,
Chọn Keep Solver Solutions và nhấn OK ta được kết quả lOMoARcPSD| 36625228 lOMoARcPSD| 36625228
Vậy số sản phẩm phân phối cho các cửa hàng là như sau: Tiêu thụ B1 B2 B3 B4 Sản phẩm 50 50 70 100 6 5 4 7 A1 : 70 0 0 45 0 6 7 6 8 A2 : 80 15 70 0 0 4 9 5 6 A3 : 60 75 0 15 30
Vậy chi phí thấp nhất là f min = 1315 Câu 3:
1. Lập mô hình bài toán khoa học:
Gọi X,Y lần lượt là lượng đầu tư vào trái phiếu Kho bạc và trái phiếu đô thị ($)
Tổng số tiền đầu tư là 250000: X + Y = 250000
Ít nhất 50% khoản đầu tư được đặt trong các kỳ phiếu Kho bạc: X ≥ 125000
Người ta quyết định rằng không quá 40% đầu tư vào trái phiếu đô thị: Y ≤ 100000 Tối đa hoá lợi nhuận: 0,08X + 0,09Y -> max
Vì số tiền đầu tư là không âm nên: X ≥ 0, Y ≥ 0
Ta có mô hình bài toán quy hoạch tuyến tính: (1) 0,08X + 0,09Y → max lOMoARcPSD| 36625228 (2) X + Y = 250000 X ≥ 125000 Y ≤ 100000 (3) X ≥ 0, Y ≥ 0
2 . Trình bày bài giải bằng Excel :
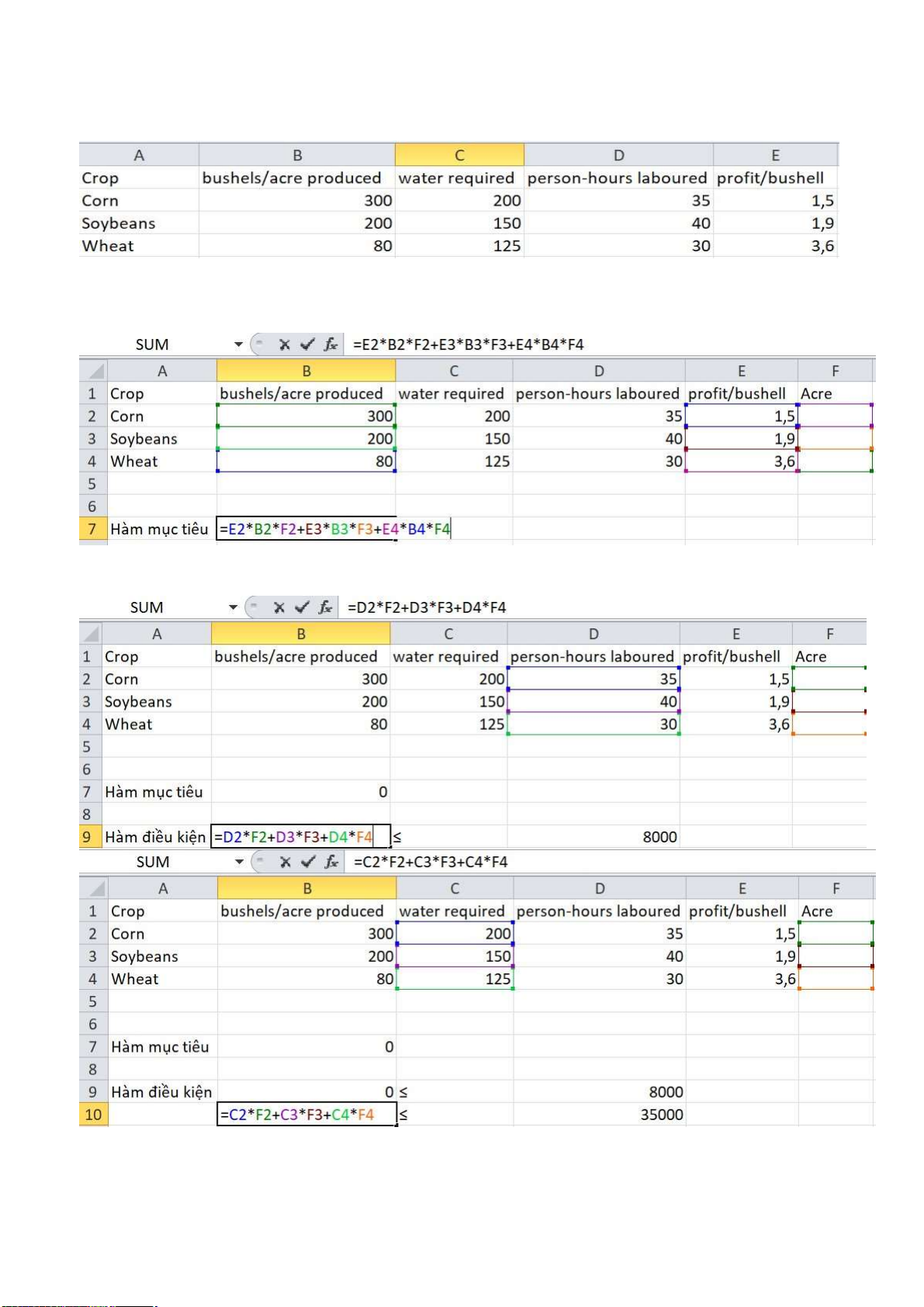
Bước 1 : Nhập dữ liệu bài toán vào Excel theo bảng sau :
Bước 2: Tìm giá trị hàm mục tiêu và các ràng buộc:
Để tính hàm mục tiêu cho bài toán, ta sử dụng công thức hàm tại ô D2: =SUMPRODUCT(B2:C2,B6:C6)
Tiếp theo sử dụng công thức hàm tương tự với các ô E3:E5 để tính các giá trị vế trái và thu được kết quả như sau:
Bước 3: Trên tab Data→Solver, màn hình xuất hiện hộp thoại Solver Parameters lOMoARcPSD| 36625228
Nhập ô chứa giá trị hàm mục tiêu cho Set Objective: D2
Nhập giá trị tối ưu hóa bài toán tại To: Max
Nhập các ô để chứa giá trị thành phần của phương án tối ưu vào By Changing Variable Cells: B6:C6 lOMoARcPSD| 36625228
Subject to the Constraints: Để nhập các ràng buộc của bài toán ta thực hiện như sau:
1. Để thêm các ràng buộc, chọn Add, xuất hiện hộp thoại Add Constraint:
Nhập lần lượt các ràng buộc: X + Y = 250000 như sau X ≥ 125000 Y ≤ 100000
Nhập điều kiện của biến X ≥ 0, Y ≥ 0 lOMoARcPSD| 36625228
Sau khi nhập dữ liệu vào ta nhấn Add để thêm, khi thêm đủ tất cả các ràng buộc và điều kiện ta nhấn
OK để quay lại hộp thoại Solver Pramateres.
Tại ô Select a Solving Method chọn phương pháp giải “Simplex LP” sau đó nháy Solve để tiến hành giải.
Sau khi nháy Solve, hộp thoại Solver Results xuất hiện: lOMoARcPSD| 36625228
Chọn Keep Solver Solution để giữ lại lời bài toán và nháy OK, kết quả thu được như sau:
Từ bảng trên ta có được kết quả của bài toán tối ưu là (150000, 100000) với lợi nhuận đạt được cao nhất là 21000$
Câu 4: Gọi f(x) là hàm mục tiêu max
Gọi x1, x2, x3 lần lượt là số lượng mẫu ngô, đậu tương và lúa mì cần sản xuất sao cho lợi
nhuận thu được là lớn nhất.
- Lợi nhuận lớn nhất: f(x) = 1,5.300.x1 + 1,9.200.x2 + 3,6.80.x3 = 450x1 + 380x2 + 288x3 max
- Có sẵn 200 mẫu đất để trồng trọt : x1 + x2 + x3 ≤ 200
- Chỉ có 35000 gallon nước mỗi tuần : 200x1 + 150x2 + 125x3 ≤ 35000
- Chỉ có 8000 giờ lao động : 35x1 + 40x2 + 30x3 ≤ 8000 - x1, x2, x3 ≥ 0
Vậy ta có mô hình bài toán:
(1) f(x) = 450x1 + 380x2 + 288x3 max (2) lOMoARcPSD| 36625228 (3) x1, x2, x3 ≥ 0
* Giải bằng Excel (Web)
Bước 1: Nhập dữ liệu bài toán vào Excel.
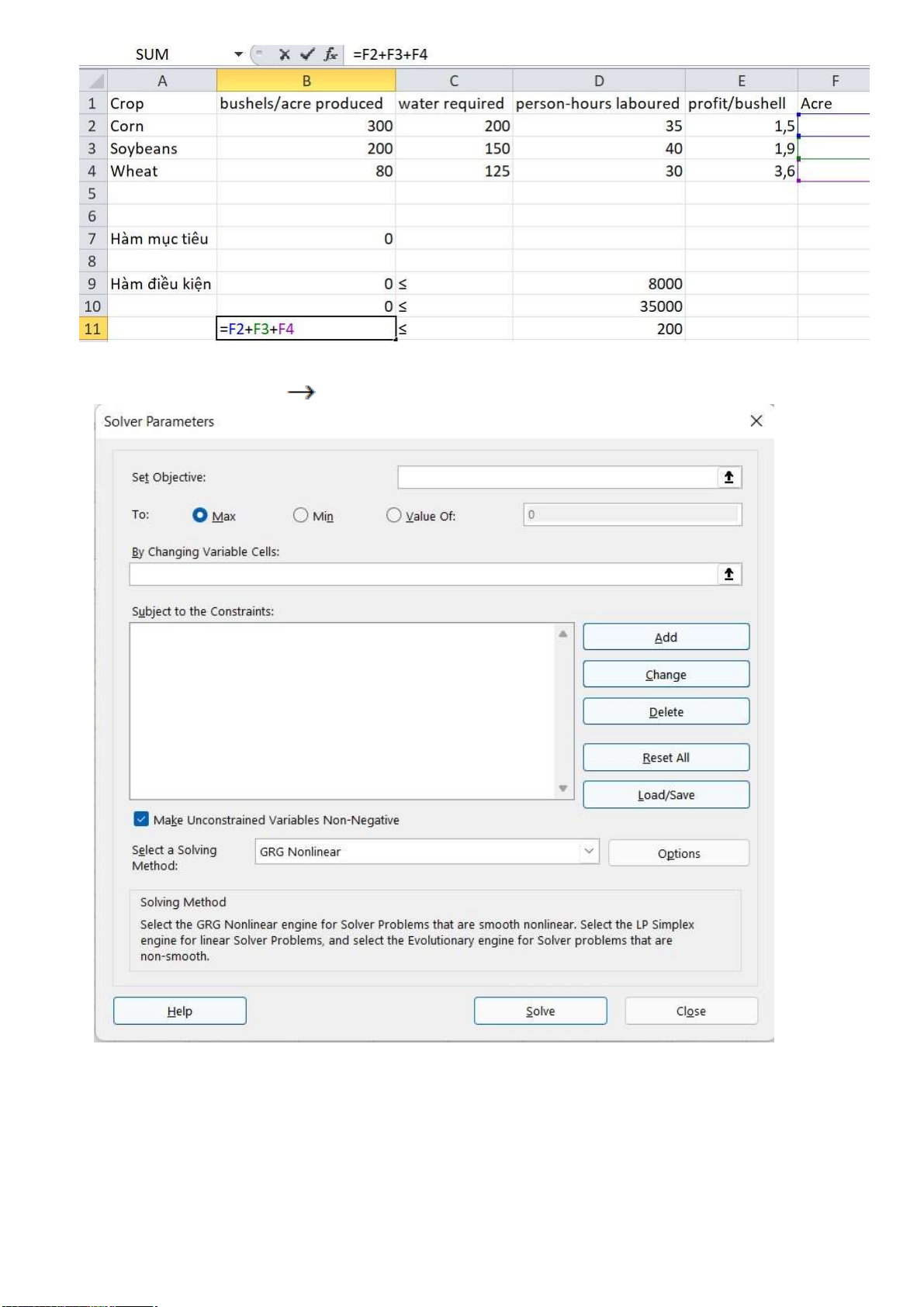
Bước 2: Nhập vào Excel các hàm mục tiêu và các giá trị rang buộc rồi tiến hành giải bài toán:
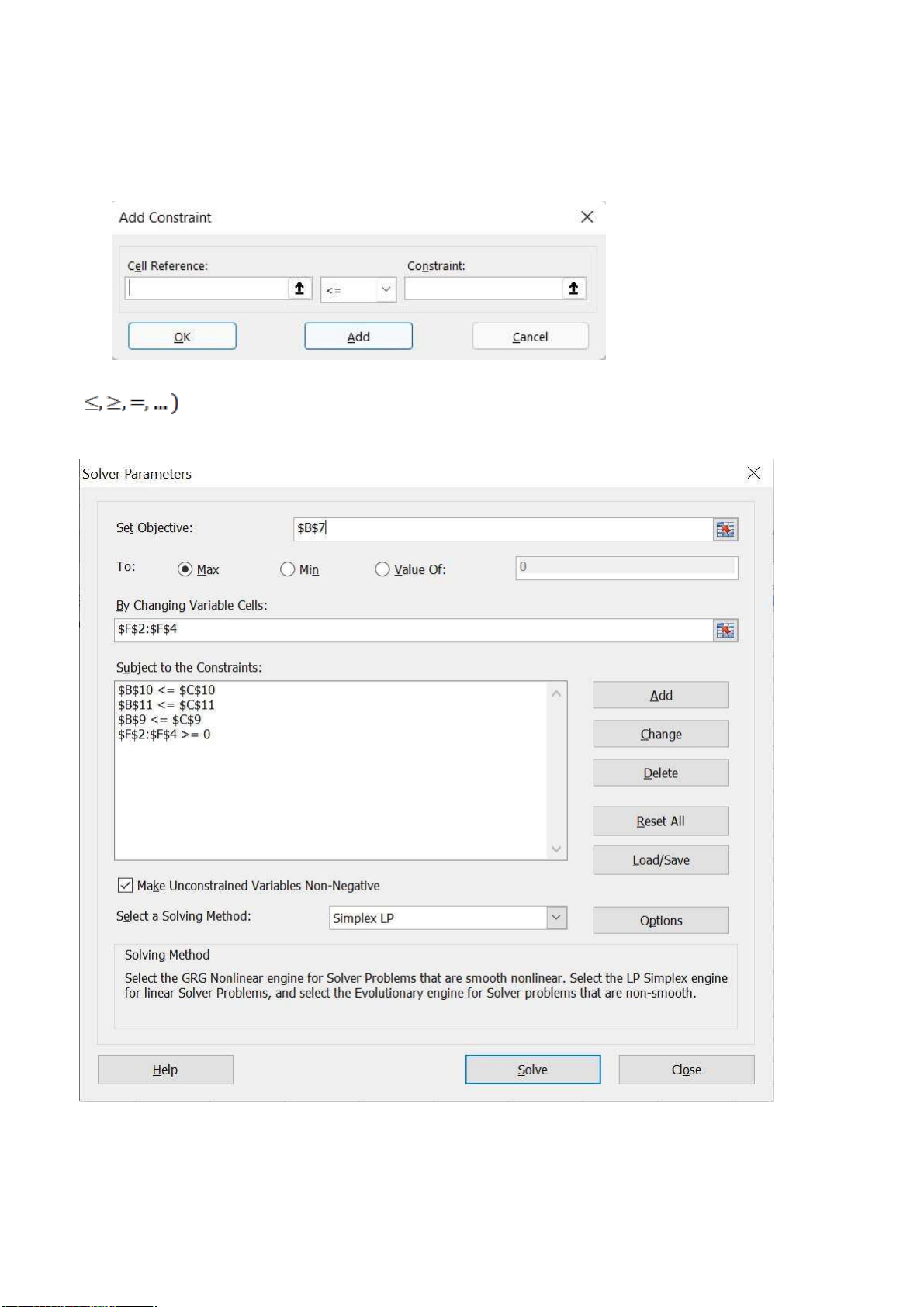
Hàm mục tiêu là hàm f(x) = 450x1 + 380x2 + 288x3 max Ta nhập như sau:
Các giá trị ràng buộc ta nhập như sau: lOMoARcPSD| 36625228
Bước 3: Chọn lệnh Data Solvers, xuất hiện hộp thoại Solver Parameter.
Tại ô Set Objective: Chọn ô chứa giá trị hàm mục tiêu là ô B7.
To: Tối ưu hóa bài toán Max hay Min. Bài toán này ta chọn Max. lOMoARcPSD| 36625228
By Changing Valuable Cells: Chọn hàng để nhập các giá trị tối ưu khi giải xong bài
toán, ta quét chọn hàng F2:F4
Subjects to the Constraints: Khoảng trống này để chúng ta tiến hành nhập các ràng buộc
của bài toán. Để tiến hành nhập ràng buộc ta thực hiện như sau:
1. Chọn Add để thêm các ràng buộc, khi nháy chọn sẽ xuất hiện hộp thoại Add Constrait.
2. Tại dòng Cell Reference: quét chọn các hàng có chứa tham số trước biến. Chọn đẳng thức (
phù hợp bài toán. Constrait là tham số ứng với ràng buộc. Sau khi nhập từng ràng
buộc, nháy Add. Nhập xong tất cả các ràng buộc, nháy chọn OK. Ta được hình như sau: lOMoARcPSD| 36625228
Chọn phương pháp giải “Simplex LP” tại dòng Select a Solving Method. Nháy chọn
Solve để tiến hành giải. Tùy theo bài toán có phương án tối ưu hay không sẽ được hiển thị
đáp án tại dòng ban đầu đã chọn. Đối với bài toán này, kết quả bài toán như ảnh:
Nháy OK để quay lại trang tính đầu để xem kết quả:
Vậy để lợi nhuận thu được lớn nhất là 83000$ thì cần sản xuất 100 mẫu ngô (corn), 100 mẫu
đậu tương (soybeans) và không sản xuất đậu tương (wheat).