Bài giải xác suất thống kê | Trường đại học Công Nghệ Sài Gòn

Bài giải xác suất thống kê | Trường đại học Công Nghệ Sài Gòn được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

62 31 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Xác suất thống kê(CNSG)

Trường: Đại học Công nghệ Sài Gòn

Thông tin:

53 trang 5 tháng trước

Tác giả:

Profile Kim Oanh
1
BAØI GIAÛI
XAÙC SUAÁT THOÁNG KEÂ
(GV: Traàn Ngoïc Hoäi – 2009)
CHÖÔNG 1
NHÖÕNG ÑÒNH LYÙ CÔ BAÛN TRONG
LYÙ THUYEÁT XAÙC SUAÁT
Baøi 1.1: Coù ba khaåu suùng I, II vaø III baén ñoäc laäp vaøo moät muïc tieâu. Moãi
khaåu baén 1 vieân. Xaùc suaát baén truùng muïc tieâu cuaû ba khaåu I, II vaø III laàn
löôït laø 0,7; 0,8 vaø 0,5. Tính xaùc suaát ñeå
a) coù 1 khaåu baén truùng.
b) coù 2 khaåu baén truùng.
c) coù 3 khaåu baén truùng.
d) ít nhaát 1 khaåu baén truùng.
e) khaåu thöù 2 baén truùng bieát raèng coù 2 khaåu truùng.
Lôøi giaûi
Toùm taét:
Khaåu suùng I IIù III
Xaùc suaát truùng 0,7 0,8 0,5
Goïi A
j
(j = 1, 2, 3) laø bieán coá khaåu thöù j baén truùng. Khi ñoù A
1
, A , A
2 3
ñoäc
laäp vaø giaû thieát cho ta:
1 1
2 2
3 3
P(A ) 0,7; P(A ) 0,3;
P(A ) 0, 8;P(A ) 0, 2;
P(A ) 0,5; P(A ) 0,5.
= =
= =
= =
a) Goïi A laø bieán coá coù 1 khaåu truùng. Ta coù
1 2 3 1 2 3 1 2 3
A
A A A A A A A A A= + +
Vì caùc bieán coá
1 2 3 1 2 3 1 2 3
A
A A , A A A , A A A xung khaéc töøng ñoâi, neân
theo coâng thöùc Coäng xaùc suaát ta coù
1 2 3 1 2 3 1 2 3
1 2 3 1 2 3 1 2 3
P(A) P(A A A A A A A A A )
P(A A A ) P(A A A ) P(A A A )
= + +
= + +
Vì caùc bieán coá A
1
, A
2
, A
3
ñoäc laäp neân theo coâng thöùc Nhaân xaùc suaát ta
coù
2
1 2 3 1 2 3
1 2 3 1 2 3
1 2 3 1 23 3
P(A A A ) P(A )P(A )P(A ) 0,7.0, 2.0, 5 0, 07;
P(A A A ) P(A )P(A )P(A ) 0, 3.0, 8.0, 5 0,12;
P(A A A ) P(A )P(A )P(A ) 0, 3.0, 2.0, 5 0,03.
= = =
= = =
= = =
Suy ra P(A) = 0,22.
b) Goïi B laø bieán coá coù 2 khaåu truùng. Ta coù
1 2 3 1 2 3 1 2 3
B A A A A A A A A A= + +
Tính toaùn töông töï caâu a) ta ñöôïc P(B) = 0,47.
c) Goïi C laø bieán coá coù 3 khaåu truùng. Ta coù
1 2 3
C A A A .
=
Tính toaùn töông töï caâu a) ta ñöôïc P(C) = 0,28.
d) Goïi D laø bieán coá coù ít nhaát 1 khaåu truùng. Ta coù
D A B C.
=
+ +
Chuù yù raèng do A, B, C xung khaéc töøng ñoâi, neân theo coâng thöùc Coäng xaùc
suaát ta coù:
P(D) = P(A) + P(B) + P(C) = 0,22 + 0,47 + 0,28 = 0,97.
e) Gæa söû coù 2 khaåu truùng. Khi ñoù bieán coá B ñaõ xaûy ra. Do ñoù xaùc suaát
ñeå khaåu thöù 2 truùng trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän
P(A
2
/B).
Theo coâng thöùc Nhaân xaùc suaát ta coù:
P(A
2
B) = P(B)P(A
2
/B)
Suy ra
2
2
P(A B)
P(A /B) .
P(B)
=
Maø
2 1 2 3 1 2 3
A
B A A A A A A= + neân lyù luaän töông töï nhö treân ta ñöôïc
P(A
2
B)=0,4
Suy ra P(A
2
/B) =0,851.
Baøi 1.2: Coù hai hoäp I vaø II moãi hoäp chöùa 10 bi, trong ñoù hoäp I goàm 9 bi
ñoû, 1 bi traéng; hoäp II goàm 6 bi ñoû, 4 bi traéng. Laáy ngaãu nhieân töø moãi hoäp
2 bi.
a) Tính xaùc suaát ñeå ñöôïc 4 bi ñoû.
b) Tính xaùc suaát ñeå ñöôïc 2 bi ñoû vaø 2 bi traéng.
c) Tính xaùc suaát ñeå ñöôïc 3 bi ñoû vaø 1 bi traéng.
d) Giaû söû ñaõ laáy ñöôïc 3 bi ñoû vaø 1 bi traéng. Haõy tìm xaùc suaát ñeå bi traéng
coù ñöôïc cuûa hoäp I.
3
Lôøi giaûi
Goïi A
i
, B
i
(i = 0, 1, 2) laàn löôït laø caùc bieán coá coù i bi ñoû vaø (2 - i) bi
traéng coù trong 2 bi ñöôïc choïn ra töø hoäp I, hoäp II.
Khi ñoù
- A
0
, A
1
, A
2
xung khaéc töøng ñoâi vaø ta coù:
0
1 1
9 1
1
2
10
2 0
9 1
2
2
10
P(A ) 0;
9
P(A ) ;
45
36
P(A ) .
45
C C
C
C C
C
=
= =
= =
- B
0
, B
1
, B
2
xung khaéc töøng ñoâi vaø ta coù:
0 2
6 4
0
2
10
1 1
6 4
1
2
10
2 0
6 4
2
2
10
6
P(B ) ;
45
24
P(B ) ;
45
15
P(B ) .
45
C C
C
C C
C
C C
C
= =
= =
= =
- A
i
vaø B
j
ñoäc laäp.
- Toång soá bi ñoû coù trong 4 bi choïn ra phuï thuoäc vaøo caùc bieán coá A
i
vaø
B
j
theo baûng sau:
B B B
0 1 2
A
0
0 1 2
A
1
1 2 3
A
2
2 3 4
a) Goïi A laø bieán coá choïn ñöôïc 4 bi ñoû. Ta coù:
A = A
2
B .
2
Töø ñaây, do tính ñoäc laäp , Coâng thöùc nhaân xaùc suaát thöù nhaát cho ta:
2 2
36 15
P(A) P(A )P(B ) . 0,2667.
45 45
= = =
b) Goïi B laø bieán coá choïn ñöôïc 2 bi ñoû vaø 2 bi traéng. Ta coù:
4
B = A
0
B
2
+ A
1
B
1
+ A
2
B
0
Do tính xung khaéc töøng ñoâi cuûa caùc bieán coá A
0
B B
2
, A
1
B
1
, A
2 0
, coâng
thöùc Coäng xaùc suaát cho ta:
P(B) = P(A
0
B
2
+ A
1
B
1
+ A
2
B
0
) = P(A
0
B
2
) + P(A
1
B
1 2 0
) + P(A B )
Töø ñaây, do tính ñoäc laäp , Coâng thöùc nhaân xaùc suaát thöù nhaát cho ta:
P(B) = P(A
0
)P(B )P(B )P(B
2
) + P(A
1 1
) + P(A
2 0
) = 0,2133.
c) Goïi C laø bieán coá choïn ñöôïc 3 bi ñoû vaø 1 bi traéng. Ta coù:
C = A
1
B B
2
+ A
2 1
.
Lyù luaän töông töï nhö treân ta ñöôïc
P(C) = P(A
1
)P(B )P(B
2
) + P(A
2 1
) = 0,4933.
d) Giaû söû ñaõ choïn ñöôïc 3 bi ñoû vaø 1 bi traéng. Khi ñoù bieán coá C ñaõ
xaûy ra. Do ñoù xaùc suaát ñeå bi traéng coù ñöôïc thuoäc hoäp I trong tröôøng hôïp
naøy chính laø xaùc suaát coù ñieàu kieän P(A
1
/C). Theo Coâng thöùc nhaân xaùc
suaát , ta coù
1 1
P(A C) P(C)P(A /C)
=
.
Suy ra
1
1
P(A C)
P(A /C)
P(C)
= .
Maø A
1 1
C = A B
2
neân
1 1 2 1 2
9 15
P(A C) P(A B ) P(A )P(B ) . 0, 0667.
45 45
= = = =
Do ñoù xaùc suaát caàn tìm laø: P(A
1
/C) = 0,1352.
Baøi 1.3: Moät loâ haøng chöùa 10 saûn phaåm goàm 6 saûn phaåm toát vaø 4 saûn
phaåm xaáu. Khaùch haøng kieåm tra baèng caùch laáy ra töøng saûn phaåm cho
ñeán khi naøo ñöôïc 3 saûn phaåm toát thì döøng laïi.
a) Tính xaùc suaát ñeå khaùch haøng döøng laïi ôû laàn kieåm tra thöù 3.
b) Tính xaùc suaát ñeå khaùch haøng döøng laïi ôû laàn kieåm tra thöù 4.
b) Giaû söû khaùch haøng ñaõ döøng laïi ôû laàn kieåm tra thöù 4. Tính xaùc suaát ñeå
ôû laàn kieåm tra thöù 3 khaùch haøng gaëp saûn phaåm xaáu.
Lôøi giaûi
Goïi T
i
, X
i
laàn löôït laø caùc bieán coá choïn ñöôïc saûn phaåm toát, xaáu ôû laàn kieåm
tra thöù i.
a) Goïi A laø bieán coá khaùch haøng döøng laïi ôû laàn kieåm tra thöù 3. Ta coù:
5
A = T
1
T T
2 3
.
Suy ra P(A) = P(T
1
T
2
T
3
) = P(T
1
) P(T
2
/T
1
) P(T
3
/ T
1
T
2
)
= (6/10)(5/9)(4/8) = 0,1667.
b) Goïi B laø bieán coá khaùch haøng döøng laïi ôû laàn kieåm tra thöù 4. Ta coù:
B = X
1
T T
2 3
T
4
+ T
1
X
2
T T
3 4 4
+ T
1
T
2 3
X T .
Suy ra
P(B) = P(X
1
T T
2 3
T
4
) + P(T
1
X
2
T T
3 4
) + P(T
1
T
2
X
3
T
4
)
= P(X
1
) P(T
2
/X /X /X
1
) P(T
3 1
T
2
) P(T
4 1
T
2
T
3
)
+ P(T
1
) P(X
2
/T /T
1
) P(T
3 1
X
2
) P(T
4
/T
1
X
2
T
3
)
+ P(T
1
) P(T
2
/T
1
) P(X
3
/ T
1
T
2
) P(T
4
/ T
1
T
2
X )
3
= (4/10)(6/9)(5/8)(4/7) + (6/10)(4/9)(5/8)(4/7)+(6/10)(5/9)(4/8)(4/7)
= 3(4/10)(6/9)(5/8)(4/7) = 0,2857.
c) Giaû söû khaùch haøng ñaõ döøng laïi ôû laàn kieåm tra thöù 4. Khi ñoù bieán
coá B ñaõ xaûy ra. Do ñoù xaùc suaát ñeå ôû laàn kieåm tra thöù 3 khaùch haøng
gaëp saûn phaåm xaáu trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän
P(X
3
/B).
Theo Coâng thöùc nhaân xaùc suaát , ta coù
3 3
P(X B) P(B)P(X /B)= .
Suy ra
3
3
P(X B)
P(X /B)
P(B)
= .
Maø X
3
B = T
1
T
2
X
3
T
4
neân
P(X
3
B) = P(T
1
T
2
X
3
T
4
) = P(T
1
) P(T
2 3 1 4
/T
1
) P(X / T T
2
) P(T / T
1
T
2 3
X )
= (6/10)(5/9)(4/8)(4/7) = 0,0952.
Suy ra P(X
3
/B) = 0,3333.
Baøi 1.4: Moät hoäp bi goàm 5 bi ñoû, 4 bi traéng vaø 3 bi xanh coù cuøng côõ. Töø
hoäp ta ruùt ngaãu nhieân khoâng hoøan laïi töøng bi moät cho ñeán khi ñöôïc bi ñoû
thì döøng laïi. Tính xaùc suaát ñeå
a) ñöôïc 2 bi traéng, 1 bi xanh vaø 1 bi ñoû.
b) khoâng coù bi traéng naøo ñöôïc ruùt ra.
6
Lôøi giaûi
Goïi D
i
, T
i
, X
i
laàn löôït laø caùc bieán coá choïn ñöôïc bi ñoû, bi traéng, bi xanh ôû
laàn ruùt thöù i.
a) Goïi A laø bieán coá ruùt ñöôïc 2 bi traéng, 1 bi xanh vaø 1 bi ñoû. Ta coù:
A xaûy ra ⇔ Ruùt ñöôïc
T T X D
T X T D
X T T D
− − −
⎡
⎢
− − −
⎢
⎢
− − −
⎣
Suy ra
A = T
1
T
2
X
3
D D
4
+ T
1
X
2
T
3 4
+ X
1
T T
2 3
D
4
Töø ñaây, do tính xung khaéc töøng ñoâi cuûa caùc bieán coá thaønh phaàn, ta coù:
P(A) = P(T
1
T
2
X
3
D
4
)+ P(T
1
X
2
T
3
D
4
) + P(X
1
T
2
T
3
D
4
)
Theo Coâng thöùc Nhaân xaùc suaát, ta coù
P(T
1
T
2
X
3
D
4
) = P(T
1
)P(T /T )P(X /T T )P(D /T
2 1 3 1 2 4 1
T
2
X
3
)
= (4/12)(3/11)(3/10)(5/9) = 1/66;
P(T
1
X X
2
T
3
D
4
) = P(T
1
)P(X /T )P(T /T
2 1 3 1 2
)P(D /T X
4 1 2
T
3
)
= (4/12)(3/11)(3/10)(5/9) = 1/66;
P(X
1
T T
2 3
D
4
) = P(X
1
)P(T /X )P(T /X )P(D /X
2 1 3 1
T
2 4 1
T
2
T
3
)
= (3/12)(4/11)(3/10)(5/9) = 1/66.
Suy ra P(A) = 3/66 = 1/22 = 0,0455.
b) Goïi B laø bieán coá khoâng coù bi traéng naøo ñöôïc ruùt ra. Ta coù:
B xaûy ra ⇔ Ruùt ñöôïc
D
X D
X X D
X
X X D
⎡
⎢
−
⎢
⎢
− −
⎢
− − −
⎣
Suy ra
B = D
1
+ X + X
1
D
2 1
X
2
D
3
+ X
1
X
2
X
3
D
4
Töø ñaây, do tính xung khaéc töøng ñoâi cuûa caùc bieán coá thaønh phaàn, ta coù:
P(B) = P(D
1
)+ P(X
1
D
2
) + P(X
1
X
2
D
3
) + P(X
1
X
2
X
3
D
4
)
Theo Coâng thöùc Nhaân xaùc suaát, ta coù
7
P(B) = P(D
1
) + P(X
1
)P(D /X )P(X /X )P(D /X
2 1
) + P(X
1 2 1 3 1
X
2
)
+ P(X
1
)P(X /X )P(X /X )P(D /X
2 1 3 1
X
2 4 1
X
2
X
3
)
= 5/12+ (3/12)(5/11) + (3/12)(2/11)(5/10) + (3/12)(2/11)(1/10)(5/9)
= 5/9
Baøi 1.5: Saûn phaåm X baùn ra ôû thò tröôøng do moät nhaø maùy goàm ba phaân
xöôûng I, II vaø III saûn xuaát, trong ñoù phaân xöôûng I chieám 30%; phaân
xöôûng II chieám 45% vaø phaân xöôûng III chieám 25%. Tæ leä saûn phaåm loaïi
A do ba phaân xöôûng I, II vaø III saûn xuaát laàn löôït laø 70%, 50% vaø 90%.
a) Tính tæ leä saûn phaåm loïai A noùi chung do nhaø maùy saûn xuaát.
b) Choïn mua ngaãu nhieân moät saûn phaåm X ôû thò tröôøng. Giaû söû ñaõ mua
ñöôïc saûn phaåm loaïi A. Theo baïn, saûn phaåm aáy coù khaû naêng do phaân
xöôûng naøo saûn xuaát ra nhieàu nhaát?
c) Choïn mua ngaãu nhieân 121 saûn phaåm X (trong raát nhieàu saûn phaåm X)
ôû thò tröôøng.
1) Tính xaùc suaát ñeå coù 80 saûn phaåm loaïi A.
2) Tính xaùc suaát ñeå coù töø 80 ñeán 85 saûn phaåm loaïi A.
Lôøi giaûi
Toùm taét:
Phaân xöôûng I II III
Tæ leä saûn löôïng 30% 45% 25%
Tæ leä loaïi A 70% 50% 90%
a) Ñeå tính tæ leä saûn phaåm loaïi A noùi chung do nhaø maùy saûn xuaát ta
choïn mua ngaãu nhieân moät saûn phaåm ôû thò tröôøng. Khi ñoù tæ leä saûn phaåm
loaïi A chính laø xaùc suaát ñeå saûn phaåm ñoù thuoäc loaïi A.
Goïi B laø bieán coá saûn phaåm choïn mua thuoäc loaïi A.
A
1
, A , A
2 3
laàn löôït laø caùc bieán coá saûn phaåm do phaân xöôûng I, II, III saûn
xuaát. Khi ñoù A
1
, A
2
, A
3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
P(A
1
) = 30% = 0,3; P(A
2
) = 45% = 0,45; P(A
3
) = 25% = 0,25.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(B) = P(A
1
)P(B/A )P(B/A )P(B/A
1
) + P(A
2 2
) + P(A
3 3
)
Theo giaû thieát,
P(B/A
1
) = 70% = 0,7; P(B/A
2
) = 50% = 0,5; P(B/A
3
) = 90% = 0,9.
8
Suy ra P(B) = 0,66 = 66%. Vaäy tæ leä saûn phaåm loaïi A noùi chung do nhaø
maùy saûn xuaát laø 66%.
b) Choïn mua ngaãu nhieân moät saûn phaåm X ôû thò tröôøng. Giaû söû ñaõ mua
ñöôïc saûn phaåm loaïi A. Theo baïn, saûn phaåm aáy coù khaû naêng do phaân
xöôûng naøo saûn xuaát ra nhieàu nhaát?
Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Khi ñoù bieán coá B ñaõ xaûy ra. Do ñoù,
ñeå bieát saûn phaåm loaïi A ñoù coù khaû naêng do phaân xöôûng naøo saûn xuaát ra
nhieàu nhaát ta caàn so saùnh caùc xaùc suaát coù ñieàu kieän P(A
1
/B), P(A
2
/B) vaø
P(A
3
/B). Neáu P(A
i
/B) laø lôùn nhaát thì saûn phaåm aáy coù khaû naêng do phaân
xöôûng thöù i saûn xuaát ra laø nhieàu nhaát. Theo coâng thöùc Bayes ta coù:
1 1
1
2 2
2
3 3
3
P(A )P(B/A ) 0, 3.0, 7 21
P(A /B) ;
P(B) 0,66 66
P(A )P(B/A ) 0,45.0, 5 22,5
P(A /B) ;
P(B) 0, 66 66
P(A )P(B/A ) 0, 25.0, 9 22, 5
P(A /B) .
P(B) 0, 66 66
= = =
= = =
= = =
Vì P(A
2
/B) = P(A
3
/B) > P(A
1
/B) neân saûn phaåm loaïi A aáy coù khaû naêng
do phaân xöôûng II hoaëc III saûn xuaát ra laø nhieàu nhaát.
c) Choïn mua ngaãu nhieân 121 saûn phaåm X (trong raát nhieàu saûn phaåm X)
ôû thò tröôøng.
1) Tính xaùc suaát ñeå coù 80 saûn phaåm loaïi A.
2) Tính xaùc suaát ñeå coù töø 80 ñeán 85 saûn phaåm loaïi A.
Aùp duïng coâng thöùc Bernoulli vôùi n = 121, p = 0,66, ta coù:
1) Xaùc suaát ñeå coù 80 saûn phaåm loaïi A laø
80 80 41 80 80 41
121 121 121
P (80) C p q C (0,66) (0,34) 0, 076.= = =
2) Xaùc suaát ñeå coù töø 80 ñeán 85 saûn phaåm loaïi A laø
85 85 85
k k 121 k k k 121 k
121 121 121
k 80 k 80 k 80
P (k) C p q C (0,66) (0,34) 0,3925.
− −
= = =
= = =
∑ ∑ ∑
9
Baøi 1.6: Coù ba cöûa haøng I, II vaø III cuøng kinh doanh saûn phaåm Y. Tæ leä
saûn phaåm loaïi A trong ba cöûa haøng I, II vaø III laàn löôït laø 70%, 75% vaø
50%. Moät khaùch haøng choïn nhaãu nhieân moät cöûa haøng vaø töø ñoù mua moät
saûn phaåm
a) Tính xaùc suaát ñeå khaùch haøng mua ñöôïc saûn phaåm loaïi A.
b) Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Theo baïn, khaû naêng ngöôøi
khaùch haøng aáy ñaõ choïn cöûa haøng naøo laø nhieàu nhaát?
Lôøi giaûi
Toùm taét:
Cöûa haøng I II III
Tæ leä loaïi A 70% 75% 50%
Choïn nhaãu nhieân moät cöûa haøng vaø töø ñoù mua moät saûn phaåm.
a) Tính xaùc suaát ñeå khaùch haøng mua ñöôïc saûn phaåm loaïi A.
Goïi B laø bieán coá saûn phaåm choïn mua thuoäc loaïi A.
A
1
, A , A
2 3
laàn löôït laø caùc bieán coá choïn cöûa haøng I, II, III. Khi ñoù A
1
, A
2
,
A
3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
P(A
1
) = P(A
2
) = P(A
3
) = 1/3.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(B) = P(A
1
)P(B/A
1
) + P(A
2
)P(B/ A
2
)+ P(A
3
)P(B/A
3
)
Theo giaû thieát,
P(B/A
1
) = 70% = 0,7;
P(B/A
2
) = 75% = 0,75;
P(B/A
3
= 50% = 0,5.
Suy ra P(B) = 0,65 = 65%. Vaäy xaùc suaát ñeå khaùch haøng mua ñöôïc saûn
phaåm loaïi A laø 65%.
b) Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Theo baïn, khaû naêng ngöôøi
khaùch haøng aáy ñaõ choïn cöûa haøng naøo laø nhieàu nhaát?
Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Khi ñoù bieán coá B ñaõ xaûy ra. Do ñoù,
ñeå bieát saûn phaåm loaïi A ñoù coù khaû naêng khaùch haøng aáy ñaõ choïn cöûa
haøng naøo laø nhieàu nhaát ta caàn so saùnh caùc xaùc suaát coù ñieàu kieän P(A
1
/B),
10
P(A
2
/B) vaø P(A
3
/B). Neáu P(A
i
/B) laø lôùn nhaát thì cöûa haøng thöù i coù nhieàu
khaû naêng ñöôïc choïn nhaát.
Theo coâng thöùc Bayes ta coù:
1 1
1
2 2
2
3 3
3
P(A )P(B/A ) (1 / 3).0,7 70
P(A /B) ;
P(B) 0, 65 195
P(A )P(B/A ) (1 / 3).0,75 75
P(A /B) ;
P(B) 0,65 195
P(A )P(B/A ) (1 / 3).0,5 50
P(A /B) .
P(B) 0, 65 195
= = =
= = =
= = =
Vì P(A
2
/B) > P(A
1
/B) > P(A
3
/B) neân cöûa haøng II coù nhieàu khaû naêng ñöôïc
choïn nhaát.
Baøi 1.7: Coù hai hoäp I vaø II moãi hoäp chöùa 12 bi, trong ñoù hoäp I goàm 8 bi
ñoû, 4 bi traéng; hoäp II goàm 5 bi ñoû, 7 bi traéng. Laáy ngaãu nhieân töø hoäp I
ba bi roài boû sang hoäp II; sau ñoù laáy ngaãu nhieân töø hoäp II boán bi.
a) Tính xaùc suaát ñeå laáy ñöôïc ba bi ñoû vaø moät bi traéng töø hoäp II.
b) Giaû söû ñaõ laáy ñöôïc ba bi ñoû vaø moät bi traéng töø hoäp II. Tìm xaùc suaát
ñeå trong ba bi laáy ñöôïc töø hoäp I coù hai bi ñoû vaø moät bi traéng.
Lôøi giaûi
Goïi A laø bieán coá choïn ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II.
A
i
(i = 0, 1, 2, 3) laø bieán coá coù i bi ñoû vaø (3-i) bi traéng coù trong 3 bi choïn
ra töø hoäp I. Khi ñoù A
0
, A , A
1
, A
2 3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
ta coù:
0 3
8 4
0
3
12
1 2
8 4
1
3
12
2 1
8 4
2
3
12
3 0
8 4
3
3
12
4
P(A ) ;
220
48
P(A ) ;
220
112
P(A ) ;
220
56
P(A ) .
220
C C
C
C C
C
C C
C
C C
C
= =
= =
= =
= =
a) Tính xaùc suaát ñeå laáy ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II.
11
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(A)=P(A
0
)P(A/A )P(A/A )+P(A )P(A/A )+P(A )P(A/A
0
)+P(A
1 1 2 2 3 3
)
Theo coâng thöùc tính xaùc suaát löïa choïn, ta coù
3 1
5 10
0
4
15
3 1
6 9
1
4
15
3 1
7 8
2
4
15
3 1
8 7
3
4
15
100
P(A / A ) ;
1365
180
P(A / A ) ;
1365
280
P(A / A ) ;
1365
392
P(A / A ) .
1365
C C
C
C C
C
C C
C
C C
C
= =
= =
= =
= =
Suy ra xaùc suaát caàn tìm laø P(A) = 0,2076.
b) Giaû söû ñaõ laáy ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II. Tìm xaùc suaát ñeå
trong 3 bi laáy ñöôïc töø hoäp I coù 2 bi ñoû vaø 1 bi traéng.
Giaû söû ñaõ laáy ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II. Khi ñoù bieán coá A ñaõ
xaûy ra. Do doù xaùc suaát ñeå trong 3 bi laáy ñöôïc töø hoäp I coù 2 bi ñoû vaø 1 bi
traéng trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän P(A
2
/A). Aùp
duïng coâng thöùc Bayes, ta coù:
2 2
2
112 280
.
P(A )P(A/A )
220 1365
P(A /A) 0,5030.
P(A) 0,2076
= = =
Vaäy xaùc suaát caàn tìm laø P(A
2
/A) = 0,5030.
Baøi 1.8: Coù ba hoäp moãi hoäp ñöïng 5 vieân bi trong ñoù hoäp thöù nhaát coù 1 bi
traéng, 4 bi ñen; hoäp thöù hai coù 2 bi traéng, 3 bi ñen; hoäp thöù ba coù 3 bi
traéng, 2 bi ñen.
a) Laáy ngaãu nhieân töø moãi hoäp moät bi.
1) Tính xaùc suaát ñeå ñöôïc caû 3 bi traéng.
2) Tính xaùc suaát ñöôïc 2 bi ñen, 1 bi traéng.
3) Giaû söû trong 3 vieân laáy ra coù ñuùng 1 bi traéng.Tính xaùc suaát ñeå bi
traéng ñoù laø cuûa hoäp thöù nhaát.
b) Choïn ngaãu nhieân moät hoäp roài töø hoäp ñoù laáy ngaãu nhieân ra 3 bi.
Tính xaùc suaát ñöôïc caû 3 bi ñen.
12
Lôøi giaûi
a) Goïi A
j
(j = 1, 2, 3) laø bieán coá laáy ñöôïc bi traéng töø hoäp thöù j. Khi ñoù A
1
,
A
2
, A
3
ñoäc laäp vaø
1 1
2 2
3 3
1 4
P(A ) ; P(A ) ;
5 5
2 3
P(A ) ; P(A ) ;
5 5
3 2
P(A ) ; P(A ) .
5 5
= =
= =
= =
1) Goïi A laø bieán coá laáy ñöôïc caû 3 bi traéng. Ta coù
1 2 3
A
A A A .
=
Suy ra P(A) = P(A
1
) P(A
2
) P(A
3
) = 0,048.
2) Goïi B laø bieán coá laáy 2 bi ñen, 1 bi traéng. Ta coù
1 2 3 1 2 3 1 2 3
B A A A A A A A A A= + +
Suy ra P(B) =0,464 .
3) Giaû söû trong 3 vieân laáy ra coù ñuùng 1 bi traéng. Khi ñoù bieán coá B
ñaõ xaûy ra. Do ñoù xaùc suaát ñeå bi traéng ñoù laø cuûa hoäp thöù nhaát trong tröôøng
hôïp naøy chính laø xaùc suaát coù ñieàu kieän P(A
1
/B). Theo coâng thöùc Nhaân xaùc
suaát ta coù:
P(A
1
B) = P(B)P(A
1
/B)
Suy ra
1
1
P(A B)
P(A /B) .
P(B)
=
Maø
1 1 2 3
B A A A= neân lyù luaän töông töï nhö treân ta ñöôïc P(A
1
B) = 0,048.
Suy ra
P(A
1
/B) =0,1034 .
b) Choïn ngaãu nhieân moät hoäp roài töø hoäp ñoù laáy ngaãu nhieân ra 3 bi.
Tính xaùc suaát ñöôïc caû 3 bi ñen.
Goïi A laø bieán coá laáy ñöôïc caû 3 bi ñen.
A
1
, A , A , A
2 3
laàn löôït laø caùc bieán coá choïn ñöôïc hoäp I, II, III. Khi ñoù A
1 2
,
A
3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
P(A
1
) = P(A
2
) = P(A
3
) = 1/3.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(A) = P(A
1
)P(A/A )P(A/A
1
) + P(A
2
)P(A/ A
2
)+ P(A
3 3
)
Theo coâng thöùc xaùc suaát löïa choïn, ta coù:
13
0 30 3
2 3
1 4
1 2 3
3 3
5 5
C CC C 4 1
P(A/A ) = ;P(A/A ) = ; P(A/A ) =0.
10 10
C C
= =
Suy ra P(A) = 0,1667.
Baøi 1.9: Coù 20 hoäp saûn phaåm cuøng loïai, moãi hoäp chöùa raát nhieàu saûn
phaåm, trong ñoù coù 10 hoäp cuûa xí nghieäp I, 6 hoäp cuûa xí nghieäp II vaø
4 hoäp cuûa xí nghieäp III. Tæ leä saûn phaåm toát cuûa caùc xí nghieäp laàn
löôït laø 50%, 65% vaø 75%. Laáy ngaãu nhieân ra moät hoäp vaø choïn ngaãu
nhieân ra 3 saûn phaåm töø hoäp ñoù.
a) Tính xaùc suaát ñeå trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaåm
toát.
b) Giaû söû trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaååm toát. Tính
xaùc suaát ñeå 2 saûn phaåm toát ñoù cuûa xí nghieäp I.
Lôøi giaûi
Goïi A laø bieán coá trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaåm toát.
A
j
(j = 1, 2, 3) laø bieán coá choïn ñöôïc hoäp cuûa xí nghieäp thöù j.
Khi ñoù A
1
, A , A
2 3
laø moät ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
1
10
1
1
20
1
6
2
1
20
1
4
3
1
20
10
P(A ) ;
20
6
P(A ) ;
20
4
P(A ) .
20
C
C
C
C
C
C
= =
= =
= =
Maët khaùc, töø giaû thieát, theo coâng thöùc Bernoulli, ta coù
2 2
1 3
2 2
2 3
2 2
3 3
P(A / A ) C (0,5) (1 0,5) 0, 375
P(A / A ) C (0,65) (1 0,65) 0, 443625
P(A / A ) C (0,75) (1 0,25) 0,421875
= − =
= − =
= − =
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(A) = P(A
1
)P(A/A )P(A/A )P(A/A
1
) + P(A
2 2
) + P(A
3 3
)
= (10/20).0,375 + (6/20). 0,443625 + (4/20). 0,421875 = 0,4050.
b) Giaû söû trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaååm toát. Khi ñoù,
bieán coá A ñaõ xaûy ra. Do ñoù, xaùc suaát ñeå 2 saûn phaåm toát ñoù cuûa xí
nghieäp I chính laø xaùc suaát coù ñieàu kieän P(A
1
/A).
14
Aùp duïng Coâng thöùc Bayes vaø söû duïng keát quaû vöøa tìm ñöôïc ôû caâu a) ta
coù
1 1
1
P(A )P(A/A ) (10/20).0,375
P(A /A) 0, 4630.
P(A) 0,4050
= = =
Baøi 1.10: Coù 10 sinh vieân ñi thi, trong ñoù coù 3 thuoäc loaïi gioûi, 4 khaù vaø 3
trung bình. Trong soá 20 caâu hoûi thi qui ñònh thì sinh vieân loïai gioûi traû lôøi
ñöôïc taát caû, sinh vieân khaù traû lôøi ñöôïc 16 caâu coøn sinh vieân trung bình
ñöôïc 10 caâu. Goïi ngaãu nhieân moät sinh vieân vaø phaùt moät phieáu thi goàm
4 caâu hoûi thì anh ta traû lôøi ñöôïc caû 4 caâu hoûi. Tính xaùc suaát ñeå sinh vieân
ñoù thuoäc loaïi khaù.
Lôøi giaûi
Toùm taét:
Xeáp loaïi sinh vieân Gioûi Khaù Trung bình
Soá löôïng 3 4 3
Soá caâu traû lôøi ñöôïc/20 20 16 10
Goïi A laø bieán coá sinh vieân traû lôøi ñöôïc caû 3 caâu hoûi.
A
1
, A , A
2 3
laàn löôït laø caùc bieán coá sinh vieân thuoäc loaïi Gioûi, Khaù;
Trung bình.
Yeâu caàu cuûa baøi toaùn laø tính xaùc suaát coù ñieàu kieän P(A
2
/A).
Caùc bieán coá A
1
, A
2
, A
3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi, vaø ta coù:
P(A
1
) = 3/10; P(A
2
) = 4/10; P(A
3
) = 3/10.
Theo coâng thöùc Bayes, ta coù
2 2
2
P(A )P(A/A )
P(A /A) .
P(A)
=
Maët khaùc, theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(A) = P(A
1
)P(A/A )P(A/A )P(A/A ).
1
) + P(A
2 2
) + P(A
3 3
Theo coâng thöùc tính xaùc suaát löïa choïn, ta coù:
4
20
1
4
20
4 0
16 4
2
4
20
4 0
10 10
3
4
20
C
P(A / A ) 1;
C
C C 1820
P(A / A ) ;
C 4845
C C 210
P(A / A ) .
C 4845
= =
= =
= =
15
Suy ra P(A
2
/A) = 0,3243.
Baøi 1.11: Coù hai hoäp I vaø II, trong ñoù hoäp I chöùa 10 bi traéng vaø 8 bi ñen;
hoäp II chöùa 8 bi traéng vaø 6 bi ñen. Töø moãi hoäp ruùt ngaãu nhieân 2 bi boû ñi,
sau ñoù boû taát caû caùc bi coøn laïi cuûa hai hoäp vaøo hoäp III (roãng). Laáy ngaãu
nhieân 2 bi töø hoäp III. Tính xaùc suaát ñeå trong 2 bi laáy töø hoäp III coù 1
traéng, 1 ñen.
Lôøi giaûi
Goïi A laø bieán coá bi laáy ñöôïc 1 traéng, 1 ñen.
A
j
(j = 0, 1, 2, 3, 4) laø bieán coá coù j bi traéng vaø (4-j) bi ñen coù trong 4
bi boû ñi (töø caû hai hoäp I vaø II). Khi ñoù A
0
, A , A , A
1 2 3
, A
4
laø moät heä ñaày ñuû,
xung khaéc töøng ñoâi.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(A) = P(A
0
)P(A/A )P(A/A )P(A/A )P(A/A
0
) + P(A
1 1
) + P(A
2 2
)+ P(A
3 3
) +
P(A
4
)P(A/A
4
).
trong ñoù
1 1
18 10
0
2
28
C C
10
P(A/A ) =
21
C
= (Vì khi A
0
ñaõ xaûy ra thì trong hoäp III coù 28 bi goàm
18 traéng , 10 ñen).
Töông töï,
1 1 1 1
17 11 16 12
1 2
2 2
28 28
1 1
1 1
15 13
14 14
3 4
2 2
28 28
C C C C187 32
P(A/A ) = ;P(A/A ) = ;
378 63
C C
C C C C65 14
P(A/A ) = ;P(A/A ) = .
126 27
C C
= =
= =
Baây giôø ta tính P(A
0
); P(A
1
); P(A
2
); P(A
3
); P(A
4
).
Goïi B
i
, C
i
(i = 0, 1, 2) laàn löôït laø caùc bieán coá coù i bi traéng vaø (2 - i) bi
ñen coù trong 2 bi ñöôïc choïn ra töø hoäp I, hoäp II. Khi ñoù
- B
0
, B
1
, B
2
xung khaéc vaø ta coù:
0 2 1 1 2 0
10 8 10 8 10 8
0 1 22 2 2
18 18 18
28 80 5
P(B ) ; P(B ) ;P(B ) .
153 153 17
C C C C C C
C C C
= = = = = =
- C
0
, C
1
, C
2
xung khaéc vaø ta coù:
0 2 1 1 2 0
8 6 8 6 8 6
0 1 22 2 2
14 14 14
15 48 28
P(C ) ; P(C ) ; P(C ) .
91 91 91
C C C C C C
C C C
= = = = = =
16
- B
i
vaø C
j
ñoäc laäp.
- Toång soá bi traéng coù trong 4 bi choïn ra phuï thuoäc vaøo caùc bieán coá B
i
vaø
C
j
theo baûng sau:
C
0
C C
1 2
B
0
0 1 2
B
1
1 2 3
B
2
2 3 4
A
0
= B
0
C
0
⇒ P(A
0
) = P(B
0
)P(C
0
) = 20/663.
A C )P(C )P(C
1
= B
0 1
+ B
1
C
0
⇒ P(A
1
) = P(B
0 1
) + P(B
1 0
) = 848/4641.
A
2
= B
0
C C )P(C )+P(B )P(C )+P(B )P(C
2
+ B
1
C
1
+ B
2 0
⇒ P(A
2
) = P(B
0 2 1 1 2 0
)
=757/1989.
A
3
= B + B
1
C
2 2
C
1
⇒ P(A
3
) = P(B
1
)P(C )P(C
2
)+P(B
2 1
) = 4400/13923.
A C )P(C
4
= B
2 2
⇒ P(A
4
) = P(B
2 2
) = 20/221.
Töø ñoù suy ra P(A) = 0,5080.
Baøi 1.12: Coù hai hoäp cuøng côõ. Hoäp thöù nhaát chöùa 4 bi traéng 6 bi xanh,
hoäp thöù hai chöùa 5 bi traéng vaø 7 bi xanh. Choïn ngaãu nhieân moät hoäp roài
töø hoäp ñoù laáy ra 2 bi thì ñöôïc 2 bi traéng. Tính xaùc suaát ñeå vieân bi tieáp
theo cuõng laáy töø hoäp treân ra laïi laø bi traéng.
Lôøi giaûi
Goïi A
1
laø bieán coá 2 bi laáy ñaàu tieân laø bi traéng.
A
2
laø bieán coá bi laáy laàn sau laø bi traéng.
Baøi toùan yeâu caàu tính P(A
2
/A
1
).
Theo coâng thöùc nhaân xaùc suaát, ta coù P(A
1
A
2
) = P(A
1
) P(A
2
/A
1
). Suy ra
1 2
2 1
1
P(A A )
P(A / A )
P(A )
= .
Baây giôø ta tính caùc xaùc suaát P(A
1
) vaø P(A
1
A
2
).
Goïi B
1
, B
2
laàn löôït laø caùc bieán coá choïn ñöôïc hoäp I, hoäp II. Khi ñoù B
1
, B
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù: P(B
1
) = P(B
2
) = 0,5.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(A
1
) = P(B
1
) P(A
1
/ B / B
1
) + P(B
2
) P(A
1 2
)
17
Maø
2 0
4 6
1 1
2
10
2 0
5 7
1 2
2
12
6
P(A / B ) ;
45
10
P(A / B ) .
66
C C
C
C C
C
= =
= =
neân P(A
1
) = 47/330.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(A
1
A
2
) = P(B
1
) P(A
1
A
2
/ B
1
) + P(B
2
) P(A
1
A
2
/ B
2
).
Maø
1 2 1 1 1 2 1 1
1 2 2 1 2 2 1 2
6 2 1
P(A A / B ) P(A / B )P(A / A B ) ;
45 8 30
10 3 1
P(A A / B ) P(A / B )P(A / A B ) .
66 10 22
= = =
= = =
neân P(A
1
A
2
) = 13/330. Suy ra xaùc suaát caàn tìm laø P(A
2
/A
1
) =13/47= 0,2766.
Baøi 1.13: Moät loâ haøng goàm a saûn phaåm loaïi I vaø b saûn phaåm loaïi II ñöôïc
ñoùng gôùi ñeå göûi cho khaùch haøng. Nôi nhaän kieåm tra laïi thaáy thaát laïc 1
saûn phaåm. Choïn ngaãu nhieân ra 1 saûn phaåm thì thaáy ñoù laø saûn phaåm loaïi
I. Tính xaùc suaát ñeå saûn phaåm thaát laïc cuõng thuoäc loaïi I.
Lôøi giaûi
Goïi A laø bieán coá saûn phaåm ñöôïc choïn ra thuoäc loïai I.
A
1
, A
2
laàn löôït laø caùc bieán coá saûn phaåm thaát laïc thuoäc loaïi I, loaïi II.
Yeâu caàu cuûa baøi toaùn laø tính xaùc suaát coù ñieàu kieän P(A
1
/A).
Ta thaáy A
1
, A
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
1 0 0 1
a b a b
1 2
1 1
a b a b
C C C C
a b
P(A ) ; P(A ) .
C a b C a b
+ +
= = = =
+ +
Theo coâng thöùc Bayes, ta coù
1 1 1 1
1
1 1 2 2
P(A )P(A / A ) P(A )P(A / A )
P(A / A)
P(A) P(A )P(A / A ) P(A )P(A / A )
= =
+
Maø
1 0 1 0
a 1 b a b 1
1 21 1
a b 1 a b 1
C C C Ca 1 a
P(A / A ) ; P(A / A ) .
C a b 1 C a b 1
− −
+ − + −
−
= = = =
+ − + −
neân
18
1
a a 1
.
a 1
a b a b 1
P(A / A)
a a 1 b a
a b 1
. . .
a b a b 1 a b a b 1
−
−
+ + −
= =
−
+ −
+
+
+ − + + −
Baøi 1.14: Coù 3 hoäp phaán, trong ñoù hoäp I chöùa 15 vieân toát vaø 5 vieân xaáu,
hoäp II chöùa 10 vieân toát vaø 4 vieân xaáu, hoäp III chöùa 20 vieân toát vaø 10 vieân
xaáu. Ta gieo moät con xuùc xaéc caân ñoái. Neáu thaáy xuaát hieän maët 1 chaám thì
ta choïn hoäp I; neáu xuaát hieän maët 2 hoaëc 3 chaám thì choïn hoäp II, coøn xuaát
hieän caùc maët coøn laïi thì choïn hoäp III. Töø hoäp ñöôïc choïn laáy ngaãu nhieân
ra 4 vieân phaán. Tìm xaùc suaát ñeå laáy ñöôïc ít nhaát 2 vieân toát.
Lôøi giaûi
Goïi A laø bieán coá choïn ñöôïc ít nhaát 2 vieân phaán toát.
A
j
(j =1,2, 3) laø bieán coá choïn ñöôïc hoäp thöù j. Khi ñoù A
1
, A , A
2 3
laø heä
ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
- A
1
xaûy ra khi vaø chæ khi thaûy con xuùc xaéc, xuaát hieän maët 1 chaám, do
ñoù P(A
1
) = 1/6.
- Töông töï, P(A
2
) = 2/6; P(A
3
) = 3/6.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(A) = P(A
1
)P(A/A )P(A/A )P(A/A
1
) + P(A
2 2
) + P(A
3 3
).
Töø giaû thieát ta coù:
2 2 3 1 4 0
15 5 15 5 15 5
1
4 4 4
20 20 20
2 2 3 1 4 0
10 4 10 4 10 4
2
4 4 4
14 14 14
2 2 3 1 4 0
20 10 20 10 20 10
3
4 4 4
30 30 30
C C C C C C 4690
P(A / A ) ;
C C C 4845
C C C C C C 960
P(A / A ) ;
C C C 1001
C C C C C C 24795
P(A / A ) .
C C C 27405
= + + =
= + + =
= + + =
Suy ra P(A) =0,9334.
Baøi 1.15: Coù hai kieän haøng I vaø II. Kieän thöù nhaát chöùa 10 saûn phaåm,
trong ñoù coù 8 saûn phaåm loaïi A. Kieän thöù hai chöùa 20 saûn phaåm, trong ñoù
coù 4 saûn phaåm loaïi A. Laáy töø moãi kieän 2 saûn phaåm. Sau ñoù, trong 4 saûn
phaåm thu ñöôïc choïn ngaãu nhieân 2 saûn phaåm. Tính xaùc suaát ñeå trong 2
saûn phaåm choïn ra sau cuøng coù ñuùng 1 saûn phaåm loaïi A.
Lôøi giaûi
19
Goïi C laø bieán coá trong 2 saûn phaåm choïn ra sau cuøng coù ñuùng 1 saûn
phaåm loaïi A.
A
j
(j = 0, 1, 2, 3, 4 ) laø bieán coá coù j saûn phaåm loïai A vaø (4-j) saûn
phaåm loïai B coù trong 4 saûn phaåm laáy töø hai kieän I vaø II. Khi ñoù A
0
, A
1
,
A
2
, A , A
3 4
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi. Theo coâng thöùc xaùc suaát
ñaày ñuû, ta coù
P(C) = P(A
0
)P(C/A )P(C/A )P(C/A )P(C/A
0
) + P(A
1 1
) + P(A
2 2
) + P(A
3 3
)
+ P(A
4
)P(C/A
4
).
Ta coù:
0
1 1
1 3
1
2
4
1 1
2 2
2
2
4
1 1
3 1
3
2
4
4
P(C/A ) = 0;
C C
3
P(C/A ) =
6
C
C C 4
P(C/A ) =
6
C
C C
3
P(C/A ) =
6
C
P(C/A ) =0.
=
=
=
Baây giôø ta tính P(A
1
); P(A
2
); P(A
3
).
Goïi B
i
, C
i
(i = 0, 1, 2) laàn löôït laø caùc bieán coá coù i sp A vaø (2 - i) sp B
coù trong 2 sp ñöôïc choïn ra töø kieän I, kieän II. Khi ñoù
- B
0
, B
1
, B
2
xung khaéc töøng ñoâi vaø ta coù:
0 2
8 2
0
2
10
1 1
8 2
1
2
10
2 0
8 2
2
2
10
1
P(B ) ;
45
16
P(B ) ;
45
28
P(B ) .
45
C C
C
C C
C
C C
C
= =
= =
= =
- C
0
, C
1
, C
2
xung khaéc töøng ñoâi vaø ta coù:
20
0 2
4 16
0
2
20
1 1
4 16
1
2
20
2 0
4 16
2
2
20
120
P(C ) ;
190
64
P(C ) ;
190
6
P(C ) ;
190
C C
C
C C
C
C C
C
= =
= =
= =
- B
i
vaø C
j
ñoäc laäp.
- Toång soá sp A coù trong 4 sp choïn ra phuï thuoäc vaøo caùc bieán coá B
i
vaø
C
j
theo baûng sau:
C
0
C C
1 2
B
0
0 1 2
B
1
1 2 3
B
2
2 3 4
Ta coù:
A
1
= B + B
0
C
1 1
C
0
.
A
2
= B + B
0
C
2 1
C
1
+ B
2
C
0
.
A
3
= B + B
1
C
2 2
C
1
.
Töø ñaây, nhôø caùc coâng thöcù coäng vaø nhaân xaùc suaát ta tính ñöôïc:
P(A
1
) = 0,2320 ; P(A
2
) = 0,5135 ; P(A
3
) = 0,2208 .
Suy ra xaùc suaát caàn tìm laø P(C) = 0,5687.
Baøi 1.16: Moät xaï thuû baén 10 vieân ñaïn vaøo moät muïc tieâu. Xaùc suaát ñeå 1
vieân ñaïn baén ra truùng muïc tieâu laø 0,8 . Bieát raèng: Neáu coù 10 vieân truùng
thì muïc tieâu chaéc chaén bò dieät. Neáu coù töø 2 ñeán 9 vieân truùng thì muïc tieâu
bò dieät vôiù xaùc suaát 80%. Neáu coù 1 vieân truùng thì muïc tieâu bò dieät vôùi xaùc
suaát 20%.
a) Tính xaùc suaát ñeå muïc tieâu bò dieät.
b) Giaû söû muïc tieâu ñaõ bò dieät. Tính xaùc suaát coù 10 vieân truùng.
Lôøi giaûi
Toùm taét:
- Soá vieân baén ra: 10 vieân.
- Xaùc suaát truùng cuûa moãi vieân: 0,8.
21
Soá vieân truùng 1 2-9 10
Xaùc suaát muïc tieâu bò dieät 20% 80% 100%
a) Goïi A laø bieán coá muïc tieâu bò dieät.
A
0
, A , A
1
, A
2 3
laàn löôït laø caùc bieán coá coù 0; 1; 2-9; 10 vieân truùng. Khi
ñoù, A
0
, A , A
1 2
, A
3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø giaû thieát cho
ta:
P(A/A
0
) = 0; P(A/A
1
) = 20% = 0,2;
P(A/A
2
) = 80%= 0,8; P(A/A
3
) = 100% = 1.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(A) = P(A
0
)P(A/A )P(A/A )P(A/A )P(A/A
0
) + P(A
1 1
) + P(A
2 2
) + P(A
3 3
).
Theo coâng thöùc Bernoulli vôùi n =10; p = 0,8, q = 0,2, ta coù
10 10
0
1 9 9
1 10
10 10
3
10 9 10
2 0 1 3
P(A ) q (0,2) ;
P(A ) C pq 10(0,8)(0,2) ;
P(A ) p (0,8) ;
P(A ) 1 P(A ) P(A ) P(A ) 1 (0, 2) 10(0,8)(0,2) (0,8) .
= =
= =
= =
= − − − = − − −
Suy ra P(A) = 0,8215.
b) Giaû söû muïc tieâu ñaõ bò dieät. Khi ñoù bieán coá A ñaõ xaûy ra. Do ñoù xaùc
suaát coù 10 vieân truùng trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän
P(A
3
/A).
Theo coâng thöùc Bayes, ta coù:
3 3
3
P(A )P(A / A )
P(A / A)
P(A)
=
Töø ñaây ta tính ñöôïc P(A
3
/A) = 0,1307.
Baøi 1.17: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä saûn phaåm loaïi A laø 60%.
Moät loâ haøng goàm 10 saûn phaåm vôùi tæ leä saûn phaåm loaïi A laø 60%. Cho maùy
saûn xuaát 2 saûn phaåm vaø töø loâ haøng laáy ra 3 saûn phaåm.
a) Tính xaùc suaát ñeå soá saûn phaåm loaïi A coù trong 2 saûn phaåm do maùy saûn
xuaát baèng soá saûn phaåm loaïi A coù trong 3 saûn phaåm ñöôïc laáy ra töø loâ haøng.
b) Giaû söû trong 5 saûn phaåm thu ñöôïc coù 2 saûn phaåm loaïi A. Tính xaùc suaát
ñeå 2 saûn phaåm loaïi A ñoù ñeàu do maùy saûn xuaát.
22
Lôøi giaûi
Goïi A
j
(j = 0, 1, 2) laø caùc bieán coá coù j saûn phaåm loaïi A vaø (2-j) saûn
phaåm khoâng thuoäc loaïi A coù trong 2 saûn phaåm do maùy saûn xuaát.
Goïi B
j
(j = 0, 1, 2, 3) laø caùc bieán coá coù j saûn phaåm loaïi A vaø (3-j) saûn
phaåm khoâng thuoäc loaïi A coù trong 3 saûn phaåm laáy töø loâ haøng.
Khi ñoù
- A
0
, A , A
1 2
xung khaéc töøng ñoâi vaø theo coâng thöùc Bernoulli vôùi n = 2; p
= 0,6; q = 0,4 ta coù:
0
0 2 2
0
2
1
1 1
1
2
2
2 0 2
2
2
P(A ) p q (0,4) 0,16;
P(A ) p q 2(0, 6)(0, 4) 0,48;
P(A ) p q (0,6) 0,36.
C
C
C
= = =
= = =
= = =
- B
0
, B
1
, B
2
, B
3
xung khaéc töøng ñoâi vaø theo coâng thöùc tính xaùc suaát löïa
choïn vôùi N = 10, N
A
= 6, n= 3 ta coù (vì loâ haøng goàm 10 saûn phaåm vôùi tæ
leä saûn phaåm loaïi A laø 60%, nghóa laø loâ haøng goàm 6 saûn phaåm loaïi A vaø 4
saûn phaåm khoâng thuoäc loaïi A):
0 3
6 4
0
3
10
1 2
6 4
1
3
10
2 1
6 4
2
3
10
3 0
6 4
3
3
10
4
P(B ) ;
120
36
P(B ) ;
120
60
P(B ) ;
120
20
P(B ) .
120
C C
C
C C
C
C C
C
C C
C
= =
= =
= =
= =
- A
i
vaø B
j
ñoäc laäp.
a) Goïi C laø bieán coá soá saûn phaåm loaïi A coù trong 2 saûn phaåm do maùy saûn
xuaát baèng soá saûn phaåm loaïi A coù trong 2 saûn phaåm ñöôïc laáy ra töø loâ haøng.
Ta coù:
C = A
0
B B
0
+ A
1 1
+ A
2
B
2
.
Töø ñaây, do tính xung khaéc vaø ñoäc laäp, caùc coâng thöùc coäng vaø nhaân xaùc
suaát cho ta:
P(C) = P(A
0
)P(B )P(B )P(B
0
)+ P(A
1 1
)+ P(A
2 2
) = 0,3293.
23
b) Goïi D laø bieán coá coù 2 saûn phaåm loaïi A trong 5 saûn phaåm coù ñöôïc.
Giaû söû trong 5 saûn phaåm treân coù 2 saûn phaåm loaïi A. Khi ñoù bieán coá D ñaõ
xaûy ra. Do ñoù, xaùc suaát ñeå 2 saûn phaåm loaïi A ñoù ñeàu do maùy saûn xuaát
chính laø xaùc suaát coù ñieàu kieän P(A
2
/D).
Theo coâng thöùc nhaân xaùc suaát ta coù:
2
2
P(A D)
P(A /D) .
P(D)
=
Nhaän xeùt raèng toång soá saûn phaåm loaïi A coù trong 5 saûn phaåm thu ñöôïc
phuï thuoäc vaøo caùc bieán coá A
i
vaø B
j
theo baûng sau:
B
0
B B B
1 2 3
A
0
0 1 2 3
A
1
1 2 3 4
A
2
2 3 4 5
Suy ra
D = A
0
B
2
+ A
1
B
1
+ A
2
B B
0
vaø A
2
D = A
2 0
.
Töø ñaây, ta tính ñöôïc P(D) = 0,236 ; P(A
2
D) = 0,012. Suy ra xaùc suaát caàn
tìm laø
P(A
2
/D) = 0,0508.
Baøi 1.18: Coù hai loâ haøng, moãi loâ chöùa 60% saûn phaåm toát, trong ñoù loâ I
chöùa 15 saûn phaåm, loâ II chöùa raát nhieàu saûn phaåm. Töø loâ II laáy ra 3 saûn
phaåm boû vaøo loâ I, sau ñoù töø loâ I laáy ra 2 saûn phaåm.
a) Tính xaùc suaát laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I.
b) Tính xaùc suaát laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I, trong ñoù sp toát coù
trong loâ I töø tröôùc.
c) Giaû söû ñaõ laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I. Tính xaùc suaát ñaõ laáy
ñöôïc 2sp toát, 1sp xaáu töø loâ II.
Lôøi giaûi
Goïi A
j
(j = 0,1, 2, 3) laø bieán coá coù j saûn phaåm toát vaø (3-j) saûn phaåm xaáu coù
trong 3 saûn phaåm ñöôïc choïn ra töø loâ II. Khi ñoù A
0
, A
1 2 3
, A , A laø moät heä
ñaày ñuû, xung khaéc töøng ñoâi. Theo coâng thöùc Bernoulli ta coù:
0 0 3 3
0 3
1 1 2 1 2
1 3
2 2 1 2 1
2 3
3 3 0 3
3 3
P(A ) C p q (0,4) 0,064;
P(A ) C p q 3(0, 6) (0,4) 0,288;
P(A ) C p q 3(0, 6) (0,4) 0,432;
P(A ) C p q (0,6) 0,216.
= = =
= = =
= = =
= = =
24
a) Goïi A laø bieán coá laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(A) = P(A
0
)P(A/A )P(A/A )P(A/A )P(A/A
0
) + P(A
1 1
) + P(A
2 2
) + P(A
3 3
).
Töø giaû thieát ta suy ra trong loâ I coù 15.60% = 9 sp toát vaø 6 sp xaáu. Do ñoù
theo coâng thöùc tính xaùc suaát löïa choïn, ta coù:
1 1
9 9
0
2
18
1 1
10 8
1
2
18
1 1
11 7
2
2
18
1 1
12 6
3
2
18
C C 81
P(A / A ) ;
C 153
C C 80
P(A / A ) ;
C 153
C C 77
P(A / A ) ;
C 153
C C 72
P(A / A ) .
C 153
= =
= =
= =
= =
Suy ra xaùc suaát caàn tìm laø: P(A) = 0,5035
b) Goïi B laø bieán coá laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I, trong ñoù sp toát coù
trong loâ I töø tröôùc. Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(B) = P(A
0
)P(B/A )P(B/A )P(B/A )P(B/A
0
) + P(A
1 1
) + P(A
2 2
) + P(A
3 3
).
Ta coù:
1 1
9 9
0
2
18
1 1
9 8
1
2
18
1 1
9 7
2
2
18
1 1
9 6
3
2
18
C C 81
P(B / A ) ;
C 153
C C 72
P(B / A ) ;
C 153
C C 63
P(B / A ) ;
C 153
C C 54
P(B / A ) .
C 153
= =
= =
= =
= =
Suy ra xaùc suaát caàn tìm laø: P(B) = 0,4235.
c) Giaû söû ñaõ laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I. Khi ñoù bieán coá A ñaõ xaûy ra.
Do ñoù xaùc suaát ñaõ laáy ñöôïc 2sp toát, 1sp xaáu töø loâ II trong tröôøng hôïp naøy
chính laø XS coù ñieàu kieän P(A
2
/A). Theo coâng thöùc Bayes, ta coù:
25
2 2
2
77
0, 432.
P(A )P(A / A )
153
P(A / A) 0, 4318.
P(A) 0, 5035
= = =
--------------
*
-------------
7
1 42 1 42 40,56 1
P (X 42) f ( ) f ( ) f(0, 29)
4, 9101 4, 9101 4, 9101
0, 3825
0, 0779 7,79%.
4, 9101
− μ −
= = = =
σ σ
= = =
(Tra baûng giaù trò haøm Gauss ta ñöôïc f(0,29) = 0,3825).
b) Xaùc suaát ñeå coù töø 40 ñeán 45 kieän ñöôïc nhaän laøø
45 40 45 40,56 40 40,56
P (40 X 45) ( ) ( ) ( ) ( )
4,9101 4, 9101
(0, 90) ( 0,11) (0,90) (0,11) 0,3159 0,0438 0,3597 35,97%.
−
μ
−
μ
− −
≤ ≤ = ϕ − ϕ = ϕ − ϕ
σ σ
= ϕ − ϕ − = ϕ + ϕ = + = =
(Tra baûng giaù trò haøm Laplace ta ñöôïc ϕ (0,9) = 0,3519; ϕ (0,11) =
0,0438).
c) Xaùc suaát ñeå coù ít nhaát 42 kieän ñöôïc nhaän laøø
100 42 100 40,56 42 40,56
P (42 X 100) ( ) ( ) ( ) ( )
4,9101 4, 9101
(12) (0, 29) 0,50 0,1141 0,3859 38,59%.
−
μ
−
μ
− −
≤ ≤ = ϕ − ϕ = ϕ − ϕ
σ σ
= ϕ − ϕ = − = =
(Tra baûng giaù trò haøm Laplace ta ñöôïc ϕ(12) = ϕ(5) = 0,5; ϕ(0,29) =
0,1141).
Baøi 2.5: Saûn phaåm trong moät nhaø maùy ñöôïc ñoùng thaønh töøng kieän, moãi
kieän goàm 10 saûn phaåm Soá saûn phaåm loaïi A trong caùc hoäp laø X coù phaân
phoái nhö sau:
X 6 8
P 0,9 0,1
Khaùch haøng choïn caùch kieåm tra nhö sau: töø moãi kieän laáy ra 2 saûn phaåm;
neáu thaáy caû 2 saûn phaåm ñeàu loaïi A thì môùi nhaän kieän ñoù; ngöôïc laïi thì
loaïi kieän ñoù. Kieåm tra 144 kieän (trong raát nhieàu kieän).
a) Tính xaùc suaát ñeå coù 53 kieän ñöôïc nhaän.
b) Tính xaùc suaát ñeå coù töø 52 ñeán 56 kieän ñöôïc nhaän.
c) Phaûi kieåm tra ít nhaát bao nhieâu kieän ñeå xaùc suaát coù ít nhaát 1 kieän
ñöôïc nhaän khoâng nhoû hôn 95%?
8
Lôøi giaûi
Tröôùc heát ta tìm xaùc suaát p ñeå moät kieän ñöôïc nhaän.
Goïi C laø bieán coá kieän haøng ñöôïc nhaän. Ta caàn tìm p = P(C).
Töø giaû thieát ta suy ra coù hai loaïi kieän haøng:
Loaïi I: goàm 6A, 4B chieám 0,9 = 90%.
Loaïi II: goàm 8A, 2B chieám 0,1 = 10%.
Goïi A
1
, A
2
laàn löôït laø caùc bieán coá kieän haøng thuoäc loaïi I, II. Khi ñoù A
1
,
A
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù
P(A
1
) = 0,9; P(A
2
) = 0,1.
Theo coâng thöùc xaùc suaát ñaày ñuû ta coù:
P(C) = P(A
1
) P(C/A
1
) + P(A
2
) P(C/A
2
).
Theo giaû thieát, töø moãi kieän laáy ra 2 saûn phaåm; neáu caû 2 saûn phaåm thuoäc
loaïi A thì môùi nhaän kieän ñoù. Do ñoù:
2 0
6 4
1 2
2
10
C C 1
P(C / A ) P (2) ;
C 3
= = =
2 0
8 2
2 2
2
10
C C 28
P(C / A ) P (2) .
C 45
= = =
Suy ra P(C) = 0,9. (1/3) + 0,1.(28/45) = 0,3622.
Vaäy xaùc suaát ñeå moät kieän ñöôïc nhaän laø p = 0,3622.
Baây giôø, kieåm tra 144 kieän. Goïi X laø soá kieän ñöôïc nhaän trong 144 kieän
ñöôïc kieåm tra, thì X coù phaân phoái nhò thöùc X ∼ B(n,p) vôùi n = 144, p =
0,3622. Vì n = 144 khaù lôùn vaø p = 0,3622 khoâng quaù gaàn 0 cuõng khoâng
quaù gaàn 1 neân ta coù theå xem X coù phaân phoái chuaån nhö sau:
X ,
∼ N(μ σ
2
)
vôùi μ = np = 144.0,3622 = 52,1568;
npq 144.0,3622.(1 0, 3622) 5,7676.
σ = = − =
a) Xaùc suaát ñeå coù 53 kieän ñöôïc nhaän laø P(X=53) = 6,84% (Töông töï Baøi
21).
b) Xaùc suaát ñeå coù töø 52 ñeán 56 kieän ñöôïc nhaän laø P(52 ≤ X ≤ 56) =
26,05% (Töông töï Baøi 21).
c) Phaûi kieåm tra ít nhaát bao nhieâu kieän ñeå xaùc suaát coù ít nhaát 1 kieän
ñöôïc nhaän khoâng nhoû hôn 95%?
Goïi n laø soá kieän caàn kieåm tra vaø D laø bieán coá coù ít nhaát 1 kieän ñöôïc nhaän.
Yeâu caàu baøi toaùn laø xaùc ñònh n nhoû nhaát sao cho P(D) ≥ 0,95.
9
Bieán coá ñoái laäp cuûa D laø D: khoâng coù kieän naøo ñöôïc nhaän.
Theo chöùng minh treân, xaùc suaát ñeå moät kieän ñöôïc nhaän laø p = 0,3622.
Do ñoù
Theo coâng thöùc Bernoulli ta coù:
n n n
P(D) 1 P(D) 1 q 1 (1 0, 3622) 1 (0, 6378) .= − = − = − − = −
Suy ra
n
n
P(D) 0, 95 1 (0, 6378) 0, 95
(0, 6378) 0, 05
n ln(0, 6378) ln 0, 05
ln 0, 05
n 6, 6612
ln(0, 6378)
n 7.
≥ ⇔ − ≥
⇔ ≤
⇔ ≤
⇔ ≥ ≈
⇔ ≥
Vaäy phaûi kieåm tra ít nhaát 7 kieän.
Baøi 2.6: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä saûn phaåm ñaït tieâu chuaån
laø 80% vaø moät maùy khaùc cuõng saûn xuaát loaïi saûn phaåm naøy vôùi tæ leä saûn
phaåm ñaït tieâu chuaån laø 60%. Choïn ngaãu nhieân moät maùy vaø cho saûn xuaát
100 saûn phaåm. Tính xaùc suaát ñeå
a) coù 70 saûn phaåm ñaït tieâu chuaån.
b) coù töø 70 ñeán 90 saûn phaåm ñaït tieâu chuaån.
c) coù khoâng ít hôn 70 saûn phaåm ñaït tieâu chuaån.
Lôøi giaûi
Goïi X laø ÑLNN chæ soá saûn phaåm ñaït tieâu chuaån trong 100 saûn phaåm.
A
1
, A
2
laàn löôït laø caùc bieán coá choïn ñöôïc maùy 1, maùy 2.
Khi ñoù A
1
, A
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
P(A
1
) = P(A
2
) = 0,5.
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù:
1 1 2 2
1 2
P(X = k) = P(A )P(X=k/A ) + P(A )P(X= k/A )
1 1
= P(X=k/A )+ P(X=k/A )
2 2
(1)
Nhö vaäy, goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá saûn phaåm ñaït tieâu
chuaån trong tröôøng hôïp choïn ñöôïc maùy 1, maùy 2. Khi ñoù:
• (1) cho ta
1 2
1 1
P(X = k) = P(X =k)+ P(X =k)
2 2
10
• X
1
coù phaân phoái nhò thöùc X
1
∼ B(n
1
,p
1
) vôùi n
1
= 100, p
1
= 80% =
0,8. Vì n
1
= 100 khaù lôùn vaø p
1
= 0,8 khoâng quaù gaàn 0 cuõng khoâng
quaù gaàn 1 neân ta coù theå xem X
1
coù phaân phoái chuaån nhö sau:
X
1
∼ N(μ
1
, σ
1
2
)
vôùi μ
1
= n
1
p
1
= 100.0,8 = 80;
1 1 1 1
n p q 100.0, 8.0, 2 4.σ = = =
• X
2
coù phaân phoái nhò thöùc X
2
∼ B(n
2
,p
2
) vôùi n
2
= 100, p
2
= 60% =
0,60. Vì n
2
= 100 khaù lôùn vaø p
2
= 0,60 khoâng quaù gaàn 0 cuõng
khoâng quaù gaàn 1 neân ta coù theå xem X
2
coù phaân phoái chuaån nhö
sau:
X
2
∼ N(μ
2
, ) σ
2
2
vôùi μ
2
= n
2
p
2
= 100.0,60 = 60;
2 2 2 2
n p q 100.0, 60.0, 40 4, 8990.σ = = =
a) Xaùc suaát ñeå coù 70 saûn phaåm ñaït tieâu chuaån laø:
1 2
1 2
1 1 2 2
70 701 1 1 1 1 1
P(X = 80) = P(X =70)+ P(X =70) = f( ) f ( )
2 2 2 2
1 1 70 80 1 1 70 60 1 1 1 1
= . f ( ) . f ( )= . f ( 2,5) . f (2,04)
2 4 4 2 4, 8990 4,8990 2 4 2 4,8990
1 1 1 1
= . 0,0175 . 0, 0498 0,000727
2 4 2 4, 8990
−
μ − μ
+
σ σ σ σ
− −
+ − +
+ =
b) Xaùc suaát ñeå coù töø 70 ñeán 90 saûn phaåm ñaït tieâu chuaån laø:
1 2
1 1 2 2
1 1 2 2
1 1
P(70 X 90) = P(70 X 90)+ P(70 X 90)
2 2
90 70 90 701 1
= [ ( ) ( )] [ ( ) ( )]
2 2
1 90 80 70 80 1 90 60 70 60
= [ ( ) ( )] [ ( ) ( )]
2 4 4 2 4,899 4,899
1
= [ (2,5) ( 2,5) (6,12) (2,04)]
2
1
= (0,49379 0,
2
≤ ≤ ≤ ≤ ≤ ≤
− μ − μ − μ − μ
ϕ − ϕ + ϕ − ϕ
σ σ σ σ
− − − −
ϕ − ϕ + ϕ − ϕ
ϕ − ϕ − + ϕ − ϕ
+ 49379 0,5 0, 47932)
0,50413
+ −
=
c) Xaùc suaát coù khoâng ít hôn 70 saûn phaåm ñaït tieâu chuaån laø
P(70 X 100) =0,5072
≤
≤
(Töông töï caâu b)
Baøi 2.7: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä pheá phaåm laø 1% vaø moät
maùy khaùc cuõng saûn xuaát loaïi saûn phaåm naøy vôùi tæ leä pheá phaåm laø 2%.
11
Choïn ngaãu nhieân moät maùy vaø cho saûn xuaát 1000 saûn phaåm. Tính xaùc
suaát ñeå
a) coù 14 pheá phaåm.
b) coù töø 14 ñeán 20 pheá phaåm.
Lôøi giaûi
Goïi X laø ÑLNN chæ soá pheá phaåm trong 1000 saûn phaåm.
A
1
, A
2
laàn löôït laø caùc bieán coá choïn ñöôïc maùy 1, maùy 2.
Khi ñoù A
1
, A
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
P(A
1
) = P(A
2
) = 0,5.
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù:
1 1 2 2
1 2
P(X = k) = P(A )P(X=k/A ) + P(A )P(X= k/A )
1 1
= P(X=k/A )+ P(X=k/A )
2 2
(1)
Nhö vaäy, goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá pheá phaåm trong tröôøng
hôïp choïn ñöôïc maùy 1, maùy 2. Khi ñoù:
• (1) cho ta
1 2
1 1
P(X = k) = P(X =k)+ P(X =k)
2 2
• X
1
coù phaân phoái nhò thöùc X
1
∼ B(n
1
,p
1
) vôùi n
1
= 1000 vaø p
1
= 1% =
0,001. Vì n
1
khaù lôùn vaø p
1
khaù beù neân ta coù theå xem X
1
coù phaân
phaân phoái Poisson:
X
1
∼ P(a
1
) vôùi a
1
= n
1
p
1
= 1000.0,01 = 10, nghóa laø X
2
∼ P(10).
• X
2
coù phaân phoái nhò thöùc X
2
∼ B(n
2
,p
2
) vôùi n
2
= 1000 vaø p
2
= 2% =
0,002. Vì n
2
khaù lôùn vaø p
2
khaù beù neân ta coù theå xem X
2
coù phaân
phaân phoái Poisson:
X
1
∼ P(a
2
) vôùi a
2
= n
2
p
2
= 1000.0,02 = 20, nghóa laø X
2
∼ P(20).
a) Xaùc suaát ñeå coù 14 pheá phaåm laø:
10 14 20 14
1 2
1 1 1 e 10 1 e 20
P(X = 14) = P(X =14)+ P(X =14) = 0,0454
2 2 2 14! 2 14!
− −
+ =
b) Xaùc suaát ñeå coù töø 14 ñeán 20 pheá phaåm laø:
1 2
20 20
10 k 20 k
k 14 k 14
1 1
P(14 X 20) = P(14 X 20)+ P(14 X 20)
2 2
1 e 10 1 e 20
= 31, 35%
2 k ! 2 k !
− −
= =
≤ ≤ ≤ ≤ ≤ ≤
+ =
∑ ∑
12
Baøi 2.8: Moät xí nghieäp coù hai maùy I vaø II. Trong ngaøy hoäi thi, moãi coâng
nhaân döï thi ñöôïc phaân moät maùy vaø vôùi maùy ñoù seõ saûn xuaát 100 saûn
phaåm. Neáu soá saûn phaåm loaïi A khoâng ít hôn 70 thì coâng nhaân ñoù seõ ñöôïc
thöôûng. Giaû söû ñoái vôùi coâng nhaân X, xaùc suaát saûn xuaát ñöôïc 1 saûn phaåm
loaïi A vôùi caùc maùy I vaø II laàn löôït laø 0,6 vaø 0,7.
a) Tính xaùc suaát ñeå coâng nhaân X ñöôïc thöôûng.
b) Giaû söû coâng nhaân X döï thi 50 laàn. Soá laàn ñöôïc thöôûng tin chaéc nhaát laø
bao nhieâu?
Lôøi giaûi
Goïi Y laø ÑLNN chæ soá saûn phaåm loaïi A coù trong 100 saûn phaåm ñöôïc saûn
xuaát.
A
1
, A
2
laàn löôït laø caùc bieán coá choïn ñöôïc maùy I, maùy II.
Khi ñoù A
1
, A
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
P(A
1
) = P(A
2
) = 0,5.
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù:
1 1 2 2
1 2
P(Y = k) = P(A )P(Y=k/A ) + P(A )P(Y= k/A )
1 1
= P(Y=k/A )+ P(Y=k/A )
2 2
(1)
Nhö vaäy, goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá saûn phaåm loaïi A coù
trong 100 saûn phaåm ñöôïc saûn xuaát trong tröôøng hôïp choïn ñöôïc maùy I,
maùy II. Khi ñoù:
• (1) cho ta
1 2
1 1
P(Y = k) = P(X =k)+ P(X =k)
2 2
• X
1
coù phaân phoái nhò thöùc X
1
∼ B(n
1
,p
1
) vôùi n
1
= 100, p
1
= 0,6. Vì
n
1
= 100 khaù lôùn vaø p
1
= 0,6 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn
1 neân ta coù theå xem X
1
coù phaân phoái chuaån nhö sau:
X
1
∼ N(μ
1
, ) σ
1
2
vôùi μ
1
= n
1
p
1
= 100.0,6 = 60;
1 1 1 1
n p q 100.0, 6.0, 4 4, 8990.σ = = =
• X
2
coù phaân phoái nhò thöùc X
2
∼ B(n
2
,p
2
) vôùi n
2
= 100, p
2
= 0,7. Vì n
2
= 100 khaù lôùn vaø p
2
= 0,7 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn 1
neân ta coù theå xem X
2
coù phaân phoái chuaån nhö sau:
X
2
∼ N(μ
2
, σ
2
2
)
vôùi μ
1
= n
2
p
2
= 100.0,7 = 70;
2 2 2 2
n p q 100.0, 7.0, 3 4, 5826.σ = = =
a) Xaùc suaát ñeå coâng nhaân X ñöôïc thöôûng laø:
13
1 2
1 1 2 2
1 1 2 2
1 1
P(70 Y 100) = P(70 X 100)+ P(70 X 100)
2 2
100 70 100 701 1
= [ ( ) ( )] [ ( ) ( )]
2 2
1 100 60 70 60 1 100 70 70 70
= [ ( ) ( )] [ ( ) ( )]
2 4, 899 4, 899 2 4,5826 4, 5826
1
= [ (8,16) (2,04) (6, 55) (0)
2
≤ ≤ ≤ ≤ ≤ ≤
− μ − μ − μ − μ
ϕ − ϕ + ϕ − ϕ
σ σ σ σ
− − − −
ϕ − ϕ + ϕ − ϕ
ϕ − ϕ + ϕ − ϕ
1
]= (0,5 0, 47932 0,5) 0,2603
2
− + =
b) Giaû söû coâng nhaân X döï thi 50 laàn. Soá laàn ñöôïc thöôûng tin chaéc nhaát laø
bao nhieâu?
Goïi Z laø ÑLNN chæ soá laàn coâng nhaân X ñöôïc thöôûng. Khi ñoù Z coù
phaân phoái nhò thöùc Z ∼ B(n,p) vôùi n = 50, p = 0,2603. Soá laàn ñöôïc
thöôûng tin chaéc nhaát chính laø Mod(Z). Ta coù:
Mod(Z) k np q k np q 1
50.0, 2603 0,7397 k 50.0,2603 0,7397 1
12, 2753 k 13, 2753 k 13
= ⇔ − ≤ ≤ − +
⇔ − ≤ ≤ − +
⇔ ≤ ≤ ⇔ =
Vaäy soá laàn ñöôïc thöôûng tin chaéc nhaát cuûa coâng nhaân X laø 13 laàn.
Baøi 2.9: Trong ngaøy hoäi thi, moãi chieán só seõ choïn ngaãu nhieân moät trong
hai loaïi suùng vaø vôùi khaåu suùng choïn ñöôïc seõ baén 100vieân ñaïn. Neáu coù töø
65 vieân trôû leân truùng bia thì ñöôïc thöôûng. Giaû söû ñoái vôùi chieán só A, xaùc
suaát baén 1 vieân truùng bia baèng khaåu suùng loaïi I laø 60% vaø baèng khaåu
suùng loaïi II laø 50%.
a) Tính xaùc suaát ñeå chieán só A ñöôïc thöôûng.
b) Giaû söû chieán só A döï thi 10 laàn. Hoûi soá laàn ñöôïc thöôûng tin chaéc nhaát
laø bao nhieâu?
c) Chieán só A phaûi tham gia hoäi thi ít nhaát bao nhieâu laàn ñeå xaùc suaát coù
ít nhaát moät laàn ñöôïc thöôûng khoâng nhoû hôn 98%?
Lôøi giaûi
Goïi X laø ÑLNN chæ soá vieân truùng trong 100 vieân ñöôïc baén ra.
Goïi A
1
, A
2
laàn löôït laø caùc bieán coá choïn ñöôïc khaåu suùng loaïi I, II.
Khi ñoù A
1
, A
2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
P(A
1
) = P(A
2
) = 0,5.
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù:
14
1 1 2 2
1 2
P(X = k) = P(A )P(X=k/A ) + P(A )P(X= k/A )
1 1
= P(X=k/A )+ P(X=k/A )
2 2
(1)
Nhö vaäy, goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá vieân truùng trong 100
vieân ñöôïc baén ra trong tröôøng hôïp choïn ñöôïc khaåu loaïi I, II. Khi ñoù:
• (1) cho ta
1 2
1 1
P(X = k) = P(X =k)+ P(X =k)
2 2
• X
1
coù phaân phoái nhò thöùc X
1
∼ B(n
1
,p
1
) vôùi n
1
= 100, p
1
= 0,6. Vì n
1
= 100 khaù lôùn vaø p
1
= 0,6 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn 1
neân ta coù theå xem X
1
coù phaân phoái chuaån nhö sau:
X
1
∼ N(μ
1
, ) σ
1
2
vôùi μ
1
= n
1
p
1
= 100.0,6 = 60;
1 1 1 1
n p q 100.0, 6.0, 4 4, 8990.σ = = =
• X
2
coù phaân phoái nhò thöùc X
2
∼ B(n
2
,p
2
) vôùi n
2
= 100, p
2
= 0,5. Vì n
2
= 100 khaù lôùn vaø p
2
= 0,5 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn 1
neân ta coù theå xem X
2
coù phaân phoái chuaån nhö sau:
X
2
∼ N(μ
2
, ) σ
2
2
vôùi μ
1
= n
2
p
2
= 100.0,5 = 50;
2 2 2 2
n p q 100.0, 5.0, 5 5.σ = = =
a) Xaùc suaát ñeå chieán só A ñöôïc thöôûng laø:
1 2
1 1 2 2
1 1 2 2
1 1
P(65 X 100) = P(65 X 100)+ P(65 X 100)
2 2
100 65 100 651 1
= [ ( ) ( )] [ ( ) ( )]
2 2
1 100 60 65 60 1 100 50 65 50
= [ ( ) ( )] [ ( ) ( )]
2 4,899 4,899 2 5 5
1 1
= [ (8,16) (1, 02) (10) (3)]= (0,5 0,3
2 2
≤ ≤ ≤ ≤ ≤ ≤
− μ − μ − μ − μ
ϕ − ϕ + ϕ − ϕ
σ σ σ σ
− − − −
ϕ − ϕ + ϕ − ϕ
ϕ − ϕ + ϕ − ϕ − 4614 0,5 0, 49865) 0,0776.+ − =
b) Giaû söû chieán só A döï thi 10 laàn. Soá laàn ñöôïc thöôûng tin chaéc nhaát laø
bao nhieâu?
Goïi Y laø ÑLNN chæ soá laàn chieán só A ñöôïc thöôûng. Khi ñoù Y coù phaân
phoái nhò thöùc Y ∼ B(n,p) vôùi n = 10, p = 0,0776. Soá laàn ñöôïc thöôûng tin
chaéc nhaát chính laø mod(Y). Ta coù:
mod(Y) k np q k np q 1
10.0, 0776 0,9224 k 10.0,0776 0, 9224 1
0,1464 k 0,8536 k 0
= ⇔ − ≤ ≤ − +
⇔ − ≤ ≤ − +
⇔ − ≤ ≤ ⇔ =
15
Vaäy soá laàn ñöôïc thöôûng tin chaéc nhaát cuûa chieán só A laø 0 laàn, noùi caùch
khaùc, thöôøng laø chieán só A khoâng ñöôïc thöôûng laàn naøo trong 10 laàn tham
gia.
c) Chieán só A phaûi tham gia hoäi thi ít nhaát bao nhieâu laàn ñeå xaùc suaát coù
ít nhaát moät laàn ñöôïc thöôûng khoâng nhoû hôn 98%?
Goïi n laø soá laàn tham gia hoäi thi vaø D laø bieán coá coù ít nhaát 1 laàn ñöôïc
thöôûng. Yeâu caàu baøi toaùn laø xaùc ñònh n nhoû nhaát sao cho P(D) ≥ 0,98.
Bieán coá ñoái laäp cuûa D laø D: khoâng coù laàn naøo ñöôïc thöôûng.
Theo chöùng minh treân, xaùc suaát ñeå moät laàn ñöôïc thöôûng laø p = 0,0776.
Do ñoù
Theo coâng thöùc Bernoulli ta coù:
n n n
P(D) 1 P(D) 1 q 1 (1 0, 0776) 1 (0, 9224) .= − = − = − − = −
Suy ra
n
n
P(D) 0, 98 1 (0, 9224) 0, 98
(0, 9224) 0, 02
n ln 0, 9224 ln 0, 02
ln 0, 02
n 48, 43
ln 0, 9224
n 49.
≥ ⇔ − ≥
⇔ ≤
⇔ ≤
⇔ ≥ ≈
⇔ ≥
Vaäy chieán só A phaûi tham gia hoäi thi ít nhaát laø 49 laàn.
Baøi 2.10: Moät ngöôøi thôï saên baén 4 vieân ñaïn. Bieát xaùc suaát truùng ñích
cuûa moãi vieân ñaïn baén ra laø 0,8. Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá vieân
ñaïn truùng ñích.
a) Tìm luaät phaân phoái cuûa X.
b) Tìm kyø voïng vaø phöông sai cuûa X.
Lôøi giaûi
a) Ta thaáy X coù phaân phoái nhò thöùc X∼ B(n,p) vôùi n = 4, p = 0,8. X laø
ÑLNN rôøi raïc nhaän 5 giaù trò: 0, 1, 2, 3 , 4. Luaät phaân phoái cuûa X coù daïng:
X 0 1 2 3 4
P p
0
p p p p
1 2 3 4
16
Theo coâng thöùc Bernoulli ta coù:
0
0 4
4
1
1 3
4
2
2 2
4
3
3 1
4
4
4 0
4
P(X 0) (0, 8) (0,2) 0, 0016;
P(X 1) (0, 8) (0,2) 0,0256;
P(X 2) (0, 8) (0, 2) 0,1536;
P(X 3) (0,8) (0,2) 0, 4096;
P(X 4) (0, 8) (0,2) 0, 4096.
C
C
C
C
C
= = =
= = =
= = =
= = =
= = =
Vaäy luaät phaân phoái cuûa X laø:
X 0 1 2 3 4
P 0,0016 0,0256 0,1536 0,4096 0,4096
b) Tìm kyø voïng vaø phöông sai cuûa X.
- Kyø voïng: M(X) = np = 3,2.
- Phöông sai: D(X) = npq = 0,64.
Baøi 2.11: Coù hai loâ haøng I vaø II, moãi loâ chöùa raát nhieàu saûn phaåm. Tæ leä
saûn phaåm loaïi A coù trong hai loâ I vaø II laàn löôït laø 70% vaø 80%. Laáy
ngaãu nhieân töø moãi loâ 2 saûn phaåm.
a) Tính xaùc suaát ñeå soá saûn phaåm loaïi A laáy töø loâ I lôùn hôn soá saûn phaåm
loaïi A laáy töø loâ II.
b) Goïi X laø soá saûn phaåm loaïi A coù trong 4 saûn phaåm ñöôïc laáy ra. Tìm kyø
voïng vaø phöông sai cuûa X.
Lôøi giaûi
Goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá sp loaïi A coù trong 2 sp ñöôïc
choïn ra töø loâ I, II. Khi ñoù
• X
1
coù phaân phoái nhò thöùc X
1
∼ B(n
1
, p
1
); n
1
= 2; p
1
= 70% = 0,7
vôùi caùc xaùc suaát ñònh bôûi:
k
k 2 k
1
2
P(X k) (0, 7) (0, 3)
C
−
= =
Cuï theå
X
1
0 1 2
P 0,09 0,42 0,49
• X
2
coù phaân phoái nhò thöùc X
2
∼ B(n
2
, p
2
); n
2
= 2; p
2
= 80% = 0,8
vôùi caùc xaùc suaát ñònh bôûi:
k
k 2 k
2
2
P(X k) (0, 8) (0, 2)
C
−
= =
Cuï theå
X
2
0 1 2
P 0,04 0,32 0,64
17
a) Xaùc suaát ñeå soá saûn phaåm loaïi A laáy töø loâ I lôùn hôn soá saûn phaåm loaïi A
laáy töø loâ II laø:
P(X
1
≥ X =0)]
2
) = P[(X
1
=2)(X
2
=0)+ (X
1
=2)(X
2
=1)+ (X
1
=1)(X
2
= P(X
1
=2)P(X
2
=0)+ P(X
1
=2)P(X
2
=1)+ P(X
1
=1)P(X
2
=0) =
0,1932.
b) Goïi X laø soá sp loaïi A coù trong 4 sp choïn ra . Khi ñoù
X = X
1
+ X
2
Vì X
1
, X
2
ñoäc laäp neân ta coù:
- Kyø voïng cuûa X laø M(X) = M(X
1
) + M(X
2
) = n
1
p
1
+ n
2
p
2
= 3
- Phöông sai cuûa X laø D(X) = D(X
1
) + D(X
2
) = n
1
p
1
q
1
+ n
2
p
2
q
2
= 0,74.
Baøi 2.12: Cho hai hoäp I vaø II, moãi hoäp coù 10 bi; trong ñoù hoäp I goàm 6 bi
ñoû, 4 bi traéng vaø hoäp II goàm 7 bi ñoû, 3 bi traéng. Ruùt ngaãu nhieân töø moãi
hoäp hai bi.
a) Tính xaùc suaát ñeå ñöôïc hai bi ñoû vaø hai bi traéng.
b) Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá bi ñoû coù trong 4 bi ñöôïc ruùt ra.
Tìm luaät phaân phoái cuûa X.
Lôøi giaûi
Goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá bi ñoû coù trong 2 bi ñöôïc choïn
ra töø hoäp I, hoäp II. Khi ñoù
- X
1
coù phaân phoái sieâu boäi X
1
∼ H(N
1
, N
1A
, n
1
); N
1
= 10; N
1A
= 6; n
1
=
2 vôùi caùc xaùc suaát ñònh bôûi:
k 2 k
6 4
1
2
10
P(X k) .
C C
C
−
= =
Cuï theå
X
1
0 1 2
P 6/45 24/45 15/45
- X
2
coù phaân phoái sieâu boäi X
2
∼ H(N
2
, N
2A
, n
2
); N
2
= 10; N
2A
= 7; n
2
= 2
vôùi caùc xaùc suaát ñònh bôûi:
k 2 k
7 3
2
2
10
P(X k) .
C C
C
−
= =
Cuï theå
18
X
2
0 1 2
P 3/45 21/45 21/45
Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá bi ñoû coù trong 4 bi ñöôïc ruùt ra. Khi
ñoù
X = X
1
+ X
2
Baûng giaù trò cuûa X döïa vaøo X
1
, X
2
nhö sau:
X X
2
X
1
0 1 2
0 0 1 2
1 1 2 3
2 2 3 4
a) Xaùc suaát ñeå ñöôïc 2 bi ñoû vaø 2 bi traéng laø:
P(X = 2) = P[(X
1
=0) (X
2
=2)+ (X =2) (X
1
=1) (X
2
=1)+ (X
1 2
=0)]
= P(X
1
=0) P(X
2
=2)+ P(X
1
=1)P(X
2
=1)+ P(X
1
=2)P(X
2
=0)]
= (6/45)(21/45) + (24/45)(21/45) + (15/45)(3/45) = 1/3.
b) Luaät phaân phoái cuûa X coù daïng:
X 0 1 2 3 4
P p
0
p p p p
1 2 3 4
trong ñoù:
p
0
= P(X = 0)= P(X
1
=0) P(X
2
= 0) = 2/225;
p
1
= P(X = 1)= P(X
1
=0) P(X
2
= 1) + P(X
1
=1) P(X
2
= 0)= 22/225;
p
2
= P(X = 2) = 1/3;
p
3
= P(X = 3)= P(X
1
=1) P(X
2
= 2) + P(X
1
=2) P(X
2
= 1)= 91/225;
p
4
= P(X = 4)= P(X
1
=2) P(X
2
= 2) = 7/45.
Vaäy luaät phaân phoái cuûa X laø :
X 0 1 2 3 4
P 2/225 22/225 1/3 91/225 7/45
19
Baøi 2.13: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä pheá phaåm 10%. Moät loâ
haøng goàm 10 saûn phaåm vôùi tæ leä pheá phaåm 30%. Cho maùy saûn xuaát 3 saûn
phaåm vaø töø loâ haøng laáy ra 3 saûn phaåm. Goïi X laø soá saûn phaåm toát coù trong
6 saûn phaåm naøy.
a) Tìm luaät phaân phoái cuûa X.
b) Khoâng duøng luaät phaân phoái cuûa X, haõy tính M(X), D(X).
Lôøi giaûi
Goïi X
1
, X
2
laàn löôït laø caùc ÑLNN chæ soá sp toát coù trong 3 saûn phaåm do
maùy saûn xuaát; do laáy töø loâ haøng. Khi ñoù X
1
, X
2
ñoäc laäp vaø ta coù:
- X
1
coù phaân phoái nhò thöùc X
1
∼ B(n
1
, p
1
); n
1
= 3; p
1
= 0,9. Cuï theå
ta coù:
0
0 2 3
1
3
1
1 2 2
1
3
2
2 1 2
1
3
3
3 0 3
1
3
P(X 0) p q (0,1) 0,001;
P(X 1) p q 3(0,9)(0,1) 0, 027;
P(X 2) p q 3(0, 9) (0,1) 0, 243;
P(X 3) p q (0, 9) 0, 729.
C
C
C
C
= = = =
= = = =
= = = =
= = = =
- X
2
coù phaân phoái sieâu boäi X
2
∼ H(N
2
, N
2A
, n
2
); N
2
= 10; N
2A
= 7; n
2
= 3 (vì loâ haøng goàm 10 saûn phaåm vôùi tæ leä pheá phaåm laø 30%, nghóa laø loâ
haøng goàm 7 saûn phaåm toát vaø 3 saûn phaåm xaáu). Cuï theå ta coù:
0 3
7 3
2
3
10
1 2
7 3
2
3
10
2 1
7 3
2
3
10
3 0
7 3
2
3
10
1
P(X 0) ;
120
21
P(X 1) ;
120
63
P(X 2) ;
120
35
P(X 3) .
120
C C
C
C C
C
C C
C
C C
C
= = =
= = =
= = =
= = =
a) Ta coù X = X
1
+ X
2
. Luaät phaân phoái cuûa X coù daïng:
X 0 1 2 3 4 5 6
P p
0
p p p p p p
1 2 3 4 5 6
20
trong ñoù:
p
0
= P(X = 0)= P(X
1
= 0)P(X
2
= 0) = 1/120000;
p
1
= P(X = 1)= P(X
1
= 0)P(X
2
= 1) + P(X
1
= 1)P(X
2
= 0) = 1/2500;
p
2
= P(X = 2) = P(X
1
= 0)P(X
2
= 2) + P(X
1
= 1)P(X
2
= 1) + P(X
1
= 2)P(X
2
=0)
= 291/40000
p
3
= P(X = 3) = P(X
1
= 0)P(X
2
= 3) + P(X
1
= 1)P(X
2
= 2) + P(X
1
= 2)P(X
2
=1)
+ P(X
1
= 3)P(X
2
=0) = 473/7500
p
4
= P(X = 4) = P(X
1
= 1)P(X
2
= 3) + P(X
1
= 2)P(X
2
= 2) + P(X
1
= 3)P(X
2
= 1)
= 10521/40000
p
5
= P(X = 5) = P(X
1
= 2) P(X
2
= 3) + P(X
1
= 3)P(X
2
= 2) = 567/1250
p
6
= P(X = 6) = P(X
1
= 3)P(X
2
= 3) = 1701/8000.
Vaäy luaät phaân phoái cuûa X laø:
X 0 1 2 3 4 5 6
P 1/120000 1/2500 291/40000 473/7500 10521/40000 576/1250 1701/8000
b) Vì X = X
1
+ X
2
vaø X
1
, X
2
ñoäc laäp neân ta coù:
- Kyø voïng cuûa X laø
M(X) = M(X
1
) + M(X
2
) = n p )
1
p
1
+ n
2 2
= 4,8 (vôùi p
2
=
N /N
2A 2
- Phöông sai cuûa X laø
D(X) = D(X
1
) + D(X
2
) = n
1
p q (N -n )/(N
1
q
1
+ n
2
p
2 2 2 2 2
-1)= 0,76.
Baøi 2.14: Cho hai hoäp I vaø II, moãi hoäp coù 10 bi; trong ñoù hoäp I goàm 8 bi
ñoû, 2 bi traéng vaø hoäp II goàm 6 bi ñoû, 4 bi traéng. Ruùt ngaãu nhieân töø hoäp I
hai bi boû sang hoäp II, sau ñoù ruùt ngaãu nhieân töø hoäp II ba bi.
a) Tính xaùc suaát ñeå ñöôïc caû 3 bi traéng.
b) Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá bi traéng coù trong ba bi ñöôïc ruùt
ra töø hoäp II. Tìm luaät phaân phoái cuûa X. Xaùc ñònh kyø voïng vaø phöông sai
cuûa X.
Lôøi giaûi
Goïi X laø ÑLNN chæ soá bi traéng coù trong 3 bi ruùt ra töø hoäp II.
A
i
(i = 0, 1, 2) laø bieán coá coù i bi traéng vaø (2-i) bi ñoû coù trong 2 bi laáy ra töø
hoäp I. Khi ñoù A
0
, A , A
1 2
laø heä bieán coá ñaày ñuû, xung khaéc töøng ñoâi vaø ta
coù:
21
0 2
2 8
0
2
10
1 1
2 8
1
2
10
2 0
2 8
2
2
10
28
P(A ) ;
45
16
P(A ) ;
45
1
P(A ) .
45
C C
C
C C
C
C C
C
= =
= =
= =
Vôùi moãi k = 0, 1, 2, 3 theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
P(X = k) = P(A
0
)P(X = k/A )P(X = k/A
0
) + P(A
1 1
) + P(A
2
)P(X = k/A
2
)
a) Xaùc suaát ñeå ñöôïc caû ba bi traéng laø:
P(X = 3) = P(A
0
)P(X = 3/A )P(X = 3/A
0
) + P(A
1 1
) + P(A
2
)P(X = 3/A
2
)
Maø
3 0
4 8
0
3
12
3 0
5 7
1
3
12
3 0
6 6
2
3
12
4
P(X 3 / A ) ;
220
10
P(X 3 / A ) ;
220
20
P(X 3 / A ) .
220
C C
C
C C
C
C C
C
= = =
= = =
= = =
neân P(X= 3) = 73/2475.
b) Luaät phaân phoái cuûa X coù daïng:
X 0 1 2 3
P p
0
p p p
1 2 3
trong ñoù, töông töï nhö treân ta coù:
22
0 3 0 3 0 3
4 8 5 7 6 6
0
3 3 3
12 12 12
1 2 1 2 1 2
4 8 5 7 6 6
1
3 3 3
12 12 12
2 1 2 1 2 1
4 8 5 7 6 6
2
3 3 3
12 12 12
28 16 1
p P(X 0) . . . 179 / 825;
45 45 45
28 16 1
p P(X 1) . . . 223 / 450;
45 45 45
28 16 1
p P(X 2) . . . 1277 / 4950;
45 45 45
C C C C C C
C C C
C C C C C C
C C C
C C C C C C
C C C
= = = + + =
= = = + + =
= = = + + =
p
3
= P(X= 3) = 73/2475.
Suy ra luaät phaân phoái cuûa X laø:
X 0 1 2 3
P 179/825 223/450 1277/4950 73/2475
Töø ñoù suy ra kyø voïng cuûa X laø M(X) = 1,1 vaø phöông sai cuûa X laø
D(X) = 0,5829.
Baøi 2.15: Coù ba loâ saûn phaåm, moãi loâ coù 20 saûn phaåm. Loâ thöù i coù i+4 saûn
phaåm loaïi A (i = 1, 2, 3).
a) Choïn ngaãu nhieân moät loâ roài töø loâ ñoù laáy ra 3 saûn phaåm. Tính xaùc
suaát ñeå trong 3 saûn phaåm ñöôïc laáy ra coù ñuùng 1 saûn phaåm loaïi A.
b) Töø moãi loâ laáy ra 1 saûn phaåm. Goïi X laø toång soá saûn phaåm loaïi A coù
trong 3 saûn phaåm ñöôïc laáy ra. Tìm luaät phaân phoái cuûa X vaø tính Mod(X),
M(X), D(X).
Lôøi giaûi
a) Goïi C laø bieán coá trong 3 saûn phaåm ñöôïc laáy ra coù ñuùng 1 saûn phaåm
loaïi A.
Goïi A
1
, A , A
2 3
laàn löôït laø caùc bieán coá choïn ñöôïc loâ I, II, III. Khi ñoù A
1
, A
2
,
A
3
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø P(A
1
) = P(A
2
) = P(A
3
) = 1/3.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(C) = P(A
1
)P(C/A
1
) + P(A
2
)P(C/ A
2
)+ P(A
3
)P(C/A
3
)
Theo Coâng thöùc xaùc suaát löïa choïn:
23
1 2
5 15
1
3
20
1 2
6 14
2
3
20
1 2
7 13
3
3
20
525
P(C / A ) ;
1140
546
P(C / A ) ;
1140
546
P(C / A ) .
1140
C C
C
C C
C
C C
C
= =
= =
= =
Suy ra P(C)= 0,4728.
b) Luaät phaân phoái cuûa X coù daïng:
X 0 1 2 3
P p
0
p p p
1 2 3
Goïi B
j
(j = 1, 2, 3) laø bieán coá laáy ñöôïc sp loaïi A töø loâ thöù j. Khi ñoù B
1
, B
2
,
B
3
ñoäc laäp vaø
1 1
2 2
3 3
5 15
P(B ) ; P(B ) ;
20 20
6 14
P(B ) ; P(B ) ;
20 20
7 13
P(B ) ; P(B ) .
20 20
= =
= =
= =
Ta coù
1 2 3 1 2 3
1 2 3 1 2 3 1 2 3
1 2 3 1 2 3 1 2 3
1 2 3 1 2 3 1 2 3
1 2 3 1 2 3
" X 0" B B B P(X 0) P(B )P(B )p(B ) 273 / 800
" X 1" B B B B B B B B B
P(X 1) P(B )P(B )P(B ) P(B )P(B )P(B ) P(B )P(B )P(B ) 71 / 160
" X 2" B B B B B B B B B
P(X 2) P(B )P(B )P(B ) P(B )P(B )P(B )
− = = ⇒ = = =
− = = + + ⇒
= = + + =
− = = + + ⇒
= = + +
1 2 3
1 2 3 1 2 3
P(B )P(B )P(B ) 151 / 800
" X 3" B B B P(X 3) P(B )P(B )P(B ) 21 / 800
=
− = = ⇒ = = =
Vaäy luaät phaân phoái cuûa X laø
X 0 1 2 3
P 273/800 71/160 151/800 21/800
Töø luaät phaânphoái cuûa X ta suy ra mode, kyø voïng vaø phöông sai cuûa X :
- Mode: Mod(X) = 1.
- Kyø voïng: M(X) = 0,9.
- Phöông sai: D(X) = 0,625.
24
2.16: Moät ngöôøi coù 5 chìa khoùa beà ngoaøi raát gioáng nhau, trong ñoù chæ coù 2
chìa môû ñöôïc cöûa. Ngöôøi ñoù tìm caùch môû cöûa baèng caùch thöû töøng chìa moät
cho ñeán khi môû ñöôïc cöûa thì thoâi (taát nhieân, chìa naøo khoâng môû ñöôïc thì
loaïi ra). Goïi X laø soá chìa khoùa ngöôøi ñoù söû duïng. Tìm luaät phaân phoái cuûa
X. Hoûi ngöôøi ñoù thöôøng phaûi thöû bao nhieâu chìa môùi môû ñöôïc cöûa? Trung
bình ngöôøi ñoù phaûi thöû bao nhieâu chìa môùi môû ñöôïc cöûa?
Lôøi giaûi
Ta thaáy X laø ÑLNN rôøi raïc nhaän 4 giaù trò: 1, 2, 3, 4. Luaät phaân phoái cuûa
X coù daïng:
X 1 2 3 4
P p
1
p p p
2 3 4
Goïi A
j
(j = 1,2, 3, 4) laø bieán coá chìa khoùa choïn laàn thöù j môû ñöôïc cöûa. Khi
ñoù:
P(X=1) = P(A
1
) = 2/5.
1 2 1 2 1
1 2 3 1 2 1 3 1 2
1 2 3 4 1 2 1 3 1 2 4 1 2 3
P(X 2) P(A A ) P(A )P(A / A ) (3 / 5)(2/ 4) 3 / 10;
P(X 3) P(A A A ) P(A )P(A / A )P(A / A A ) (3 / 5)(2 / 4)(2/ 3) 1 / 5
P(X 4) P(A A A A ) P(A )P(A / A )P(A / A A )P(A / A A A )
(3 / 5)(2 / 4)(1/ 3)(2 / 2) 1 / 10
= = = = =
= = = = =
= = =
= =
Vaäy luaät phaân phoái cuûa X laø:
X 1 2 3 4
P 2/5 3/10 1/5 1/10
Töø luaät phaân phoái treân ta suy ra:
- Mode cuûa X laø Mod(X) = 1.
- Kyø voïng cuûa X laø
i i
M(X) x p 2
=
=
∑
.
Vaäy ngöôøi ñoù thöôøng phaûi thöû 1 chiaø thì môû ñöôïc cöûa. Trung bình ngöôøi
ñoù phaûi thöû 2 chìa môùi môû ñöôïc cöûa.
Baøi 2.17: Moät ngöôøi thôï saên coù 5 vieân ñaïn. Ngöôøi ñoù ñi saên vôùi nguyeân
taéc: neáu baén truùng muïc tieâu thì veà ngay, khoâng ñi saên nöõa. Bieát xaùc suaát
25
truùng ñích cuûa moãi vieân ñaïn baén ra laø 0,8. Goïi X laø ñaïi löôïng ngaãu nhieân
chæ soá vieân ñaïn ngöôøi aáy söû duïng trong cuoäc saên.
a) Tìm luaät phaân phoái cuûa X.
b) Tìm kyø voïng vaø phöông sai cuûa X.
Lôøi giaûi
a) Ta thaáy X laø ÑLNN rôøi raïc nhaän 5 giaù trò: 1, 2,..., 5. Luaät phaân phoái
cuûa X coù daïng:
X 1 2 3 4 5
P p
1
p p p p
2 3 4 5
Goïi A
j
(j = 1,2,..., 5) laø bieán coá vieân ñaïn thöù j truùng ñích. Khi ñoù:
j j
P(A ) 0,8;P(A ) 0,2= =
Ta coù:
P(X=1) = P(A
1
) = 0,8.
1 2 1 2
1 2 3 1 2 3
1 2 3 4 1 2 3 4
1 2 3 4 1 2 3 4
P(X 2) P(A A ) P(A )P(A ) 0,2.0, 8 0,16;
P(X 3) P(A A A ) P(A )P(A )P(A ) 0,2.0,2.0,8 0,032;
P(X 4) P(A A A A ) P(A )P(A )P(A )P(A ) 0,2.0,2.0,2.0, 8 0,0064;
P(X 5) P(A A A A ) P(A )P(A )P(A )P(A ) 0,2.0,2
= = = = =
= = = = =
= = = = =
= = = = .0,2.0,2 0,0016.=
Vaäy luaät phaân phoái cuûa X laø:
X 1 2 3 4 5
P 0,8 0,16 0,032 0,0064 0,0016
b) Töø luaät phaân phoái cuûa X ta suy ra:
- Kyø voïng cuûa X laø M(X) = 1,2496.
- Phöông sai cuûa X laø D(X) = 0,3089.
Baøi 2.18: Moät ngöôøi thôï saên coù 4 vieân ñaïn. Ngöôøi ñoù ñi saên vôùi nguyeân
taéc: neáu baén 2 vieân truùng muïc tieâu thì veà ngay, khoâng ñi saên nöõa. Bieát
xaùc suaát truùng ñích cuûa moãi vieân ñaïn baén ra laø 0,8. Goïi X laø ñaïi löôïng
ngaãu nhieân chæ soá vieân ñaïn ngöôøi aáy söû duïng trong cuoäc saên.
a) Tìm luaät phaân phoái cuûa X.
b) Tìm kyø voïng vaø phöông sai cuûa X.
Lôøi giaûi
a) Ta thaáy X laø ÑLNN rôøi raïc nhaän 3 giaù trò: 2, 3, 4. Luaät phaân phoái cuûa
X coù daïng:
26
X 2 3 4
P p
2
p p
3 4
Goïi A
j
(j = 1,2, 3, 4) laø bieán coá vieân ñaïn thöù j truùng ñích. Khi ñoù:
j j
P(A ) 0,8;P(A ) 0,2= =
Ta coù:
1 2 1 2
1 2 3 1 2 3 1 2 3 1 2 3
1 2 3 1 2 3
1 2 3 1 2 3 1 2 3 1 2 3
1 2 3
P(X 2) P(A A ) P(A )P(A ) 0,8.0,8 0,64;
P(X 3) P(A A A A A A ) P(A A A ) P(A A A )
= P(A )P(A )P(A ) P(A )P(A )P(A ) 0,2.0,8.0,8 0, 8.0, 2.0, 8 0,256
P(X 4) P(A A A A A A A A A A A A )
P(A )P(A )P(A ) P
= = = = =
= = + = +
+ = + =
= = + + +
= +
1 2 3 1 2 3 1 2 3
(A )P(A )P(A ) P(A )P(A )P(A ) P(A )P(A )P(A )
0, 2.0, 2.0,2 0,8.0,2.0,2 0, 2.0, 8.0, 2 0,2.0,2.0, 8 0,104
+ +
= + + + =
Vaäy luaät phaân phoái cuûa X laø:
X 2 3 4
P 0,64 0,256 0,104
b) Töø luaät phaân phoái cuûa X ta suy ra:
- Kyø voïng cuûa X laø M(X) = 2,464.
- Phöông sai cuûa X laø D(X) = 0,456704.
--------------------------------
1
BAØI GIAÛI
XAÙC SUAÁT THOÁNG KEÂ
(GV: Traàn Ngoïc Hoäi – 2009)
CHÖÔNG 3
LYÙ THUYEÁT MAÃU VAØ ÖÔÙC LÖÔÏNG
Baøi 3.1. Ñeå khaûo saùt troïng luôïng X cuûa moät loaïi vaät nuoâi trong noâng traïi,
ngöôøi ta quan saùt moät maãu vaø coù keát quûa sau:
X(kg) 36 42 48 54 60 66 72
Soá con 15 12 25 18 10 10 10
a) Öôùc löôïng troïng löôïng trung bình cuûa loaïi vaät nuoâi treân vôùi ñoä tin caäy
96%.
b) Vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi
treân laø bao nhieâu? Toái thieåu laø bao nhieâu?
c) Nhöõng con vaät coù troïng löôïng töø 60kg trôû leân ñöôïc goïi laø nhöõng con
“ñaït tieâu chuaån”. Haõy öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy
95%.
d) Neáu muoán öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy 99% vaø ñoä
chính xaùc 10% thì caàn phaûi ñieàu tra theâm bao nhieâu con vaät nöõa?
e) Vôùi ñoä tin caäy 90%, tæ leä con ñaït tieâu chuaån toái ña cuûa loaïi vaät nuoâi
treân laø bao nhieâu? Toái thieåu laø bao nhieâu?
Lôøi giaûi
Ta coù:
n 100;=
i i
X n 5196;=
∑
2
i i
X n 282096.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X
X n 51, 96(kg).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (11, 0054) (kg ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2 2
n
S S (11, 0608) (kg ).
n 1
= =
−
• Tæ leä maãu con ñaït tieâu chuaån laø
n
m 30
F 0,3
n 100
= = =
2
vì trong n = 100 con coù m = 10 + 10 + 10 = 30 con coù troïng löôïng töø
60kg trôû leân, nghóa laø coù 30 con ñaït tieâu chuaån.
a) Öôùc löôïng troïng löôïng trung bình cuûa loaïi vaät nuoâi treân vôùi ñoä tin caäy
96%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
γ α = 1- = 96% = 0,96.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
cho kyø voïng:
S S
(X z ; X z )
n n
α α
− + ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,06. Vaäy öôùc löôïng khoaûng laø:
11, 0608 11,0608
(51, 96 2, 06 ; 51, 96 2, 06 ) (49, 68; 54, 24).
100 100
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 96%, troïng löôïng trung bình cuûa moät con
naèm trong khoaûng töø 49,68kg ñeán 54,24kg.
b) Vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi
treân laø bao nhieâu? Toái thieåu laø bao nhieâu?
Ta coù ñoä tin caäy γ = 1 - α α = 95% = 0,95 ( = 0,05).
- Ñeå bieát troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi treân laø bao
nhieâu ta caàn öôùc löôïng khoaûng beân traùi cho kyø voïng μ = M(X).
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng
khoaûng beân traùi cho kyø voïng:
2
S
( ; X z )
n
α
−∞ + ,
trong ñoù ϕ(z
2α
) = (1- 2α)/2 = (1- 2.0,05)/2 = 0,90/2 = 0,45. Tra baûng giaù
trò haøm Laplace ta ñöôïc z
2α
= 1,65. Suy ra troïng löôïng trung bình toái ña
laø:
2
S 11, 0608
X
z 51, 96 1,65 53,7850(kg)
n 100
α
+ = + =
.
Vaäy vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi
treân laø 53,7850kg.
- Ñeå bieát troïng löôïng trung bình toái thieåu cuûa loaïi vaät nuoâi treân laø bao
nhieâu ta caàn öôùc löôïng khoaûng beân phaûi cho kyø voïng μ = M(X).
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng
khoaûng beân traùi cho kyø voïng:
2
S
(X z ; )
n
α
− +∞ ,
trong ñoù z
2α
= 1,65. Suy ra troïng löôïng trung bình toái thieåu laø:
3
2
S 11,0608
X
z 51, 96 1, 65 50,1350(kg)
n 100
α
− = − =
.
Vaäy vôùi ñoä tin caäy 95%, tr ieåu cuûa loaïi vaät nuoâi oïng löôïng trung bình toái th
treân laø 50,1350kg.
c) Nhöõng con vaät coù troïng löôïng töø 60kg trôû leân ñöôïc goïi laø nhöõng con
“ñaït tieâu chuaån”. Haõy öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy
95%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p con ñaït tieâu chuaån vôùi ñoä
tin caäy γ = 1- α = 95% = 0,95. Ta coù coâng thöùc öôùc löôïng khoaûng :
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− + ,
trong ñoù ϕ (z
α
) = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
0, 3(1 0, 3) 0,3(1 0, 3)
(0, 3 1,96 ; 0,3 1, 96 ) (21, 02%; 38, 98%).
100 100
− −
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä con ñaït tieâu chuaån naèm trong
khoaûng töø 21,02% ñeán 38,98%.
d) Neáu muoán öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy 99% vaø ñoä
chính xaùc 10% thì caàn phaûi ñieàu tra theâm bao nhieâu con vaät nöõa?
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng tæ leä con ñaït tieâu
chuaån vôùi ñoä chính xaùc ε = 10% = 0,1 vaø ñoä tin caäy γ = 1- α = 99% = 0,99.
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
−
ε = ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,99/2 = 0,495. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,58. Suy ra
2
n n
2
z F (1 F )
n
α
−
=
ε
Thöïc teá yeâu caàu:
2
2
n n
2 2
z F (1 F )
2,58 .0,3(1 0,3)
n 139,7844.
0,1
α
−
−
≥ = ≈
ε
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n
1
= 140. Vì n
1
=
140 > 100 (100 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm ít nhaát laø
140 -100 = 40 con vaät nöõa.
e) Vôùi ñoä tin caäy 90%, tæ leä con ñaït tieâu chuaån toái ña cuûa loaïi vaät nuoâi
treân laø bao nhieâu? Toái thieåu laø bao nhieâu?
4
Ta coù ñoä tin caäy γ = 1 - α α = 90% = 0,90 ( = 0,1).
- Ñeå bieát tæ leä toái ña con ñaït tieâu chuaån cuûa loaïi vaät nuoâi treân laø bao
nhieâu ta caàn öôùc löôïng khoaûng beân traùi cho tæ leä p con ñaït tieâu chuaån.
Ta coù coâng thöùc öôùc löôïng khoaûng beân traùi cho tæ leä p :
n n
n 2
F (1 F )
( ;F z )
n
α
−
−∞ + ,
trong ñoù ϕ(z
2α
) = (1- 2α)/2 = 0,80/2 = 0,40. Tra baûng giaù trò haøm Laplace
ta ñöôïc z
2α
= 1,28. Suy ra tæ leä toái ña con ñaït tieâu chuaån laø:
n n
n 2
F (1 F ) 0,3(1 0,3)
F z 0,3 1, 28 0,3587
n 100
α
− −
+ = + = .
Vaäy vôùi ñoä tin caäy 90%, tæ leä toái ña con ñaït tieâu chuaån cuûa loaïi vaät nuoâi
treân laø 35,87%.
- Ñeå bieát tæ leä toái thieåu con ñaït tieâu chuaån cuûa loaïi vaät nuoâi treân laø bao
nhieâu ta caàn öôùc löôïng khoaûng beân phaûi cho tæ leä p con ñaït tieâu chuaån.
Ta coù coâng thöùc öôùc löôïng khoaûng beân phaûi cho tæ leä p:
n n
n 2
F (1 F )
(F z ; )
n
α
−
− +∞ ,
trong ñoù z
2α
= 1,28. Suy ra tæ leä toái thieåu con ñaït tieâu chuaån laø:
n n
n 2
F (1 F ) 0,3(1 0,3)
F z 0,3 1,28 0,2413.
n 100
α
− −
− = − =
Vaäy vôùi ñoä tin caäy 90%, tæ leä toái thieåu con ñaït tieâu chuaån cuûa loaïi vaät nuoâi
treân laø 24,13%.
Baøi 3.2. Caân thöû 100 traùi quít cuûa moät vöôøn, ta coù baûng keát quaû sau:
X(g) 40 50 60 70 80 90 100 110
Soá traùi 3 10 12 15 28 16 11 5
trong ñoù X chæ troïng löôïng (ñôn vò tính gam).
a) Haõy öôùc löôïng troïng löôïng trung bình cuûa moät traùi quít trong vöôøn quít
treân vôùi ñoä tin caäy 94%.
b) Nhöõng traùi quít coù troïng löôïng X > 75g laø traùi loaïi I. Haõy öôùc löôïng tæ
leä traùi loaïi I trong vöôøn quít treân vôùi ñoä tin caäy 95%.
c) Nhöõng traùi quít coù troïng löôïng X < 65g laø traùi loaïi III. Haõy öôùc löôïng
troïng luôïng trung bình cuûa moät traùi quít loaïi III trong vöôøn quít treân vôùi
ñoä tin caäy 99% (Giaû söû X coù phaân phoái chuaån).
Lôøi giaûi
Ta coù:
n 100;
=
i i
X n 7720;=
∑
2
i i
X n 625800.=
∑
• Kyø voïng maãu cuûa X laø
5
i i
1
X X n 77, 2(g).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (17, 2673) (g ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2 2
n
S S (17,3543) (kg ).
n 1
= =
−
• Tæ leä maãu traùi loaïi I laø
n
m 60
F 0, 6.
n 100
= = =
vì trong n = 100 traùi coù m = 28 + 16 + 11 + 5 = 60 traùi coù troïng löôïng
töø 75g trôû leân, nghóa laø coù 60 traùi loaïi I.
a) Haõy öôùc löôïng troïng löôïng trung bình cuûa moät traùi quít trong vöôøn
quít treân vôùi ñoä tin caäy 94%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin
caäy γ = 1- α = 94% = 0,94.
Vì n = 100
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng
khoaûng cho kyø voïng:
S S
(X z ; X z )
n n
α α
− +
trong ñoù ϕ(z
α
) = γ/2 = 0,94/2 = 0,47. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,88. Vaäy öôùc löôïng khoaûng laø:
17,3543 17,3543
(77, 2 1,88 ; 77, 2 1,88 ) (73,94; 80,46).
100 100
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 94%, troïng löôïng trung bình cuûa moät traùi
quyùt töø 73,94g ñeán 80,46g.
b) Nhöõng traùi quít coù troïng löôïng X > 75g laø traùi loaïi I. Haõy öôùc löôïng tæ
leä traùi loaïi I trong vöôøn quít treân vôùi ñoä tin caäy 95%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc traùi loaïi I vôùi ñoä tin
caäy γ = 1- α = 95% = 0,95.
Ta coù coâng thöùc öôùc löôïng khoaûng:
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− +
trong ñoù ϕ(z
α
) = (1- α)/2 = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm
Laplace ta ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
0, 6(1 0, 6) 0,6(1 0, 6)
(0, 60 1,96 ; 0, 60 1, 96 ) (50, 40%; 69,60%)
100 100
− −
− + =
6
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä traùi loaïi I töø 50,40% ñeán 69,60%.
c) Nhöõng traùi quít coù troïng löôïng X < 65g laø traùi loaïi III. Haõy öôùc löôïng
troïng luôïng trung bình cuûa moät traùi quít loaïi III trong vöôøn quít treân vôùi
ñoä tin caäy 99% (Giaû söû X coù phaân phoái chuaån).
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ
III
= M(X
III
) cuûa chæ
tieâu X = X
III
cuûa nhöõng traùi quít loaïi III vôùi ñoä tin caäy γ = 1- α = 99% =
0,99.
Ta laäp baûng soá lieäu cuûa X
III
:
X
IIIi
40 50 60
n
IIIi
3 10 12
Töø baûng treân ta tính ñöôïc:
III
n 25;=
IIIi IIIi
X n 1340;=
∑
2
IIIi IIIi
X n 73000.=
∑
• Kyø voïng maãu cuûa X
III
laø
III IIIi IIIi
III
1
X
X n 53, 6 (g).
n
= =
∑
• Phöông sai maãu cuûa X
III
laø:
2
2 2 2 2
III
IIIi IIIi III
III
1
S X n X (6,8586) (g ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X
III
laø:
2
2 2 2
III
III
III
III
n
S S 7 (g ).
n 1
= =
−
Vì n
III
< 30, X
III
coù phaân phoái chuaån, σ
III
2
= D(X
III
) chöa bieát, neân ta coù
coâng thöùc öôùc löôïng khoaûng cho kyø voïng:
k k
III III
III α III α
III III
S S
(X -t ;X +t )
n n
,
trong ñoù
k
α
t
ñöôïc xaùc ñònh töø baûng phaân phoái Student vôùi k = n
III
–1= 24
vaø α = 1 - γ = 1 – 0,99 = 0,01. Tra baûng phaân phoái Student ta ñöôïc
k
t 2, 797
α
= . Vaäy öôùc löôïng khoaûng laø:
7 7
(53, 6 2,797 ; 53,6 2,797 ) (49,68; 57,52).
25 25
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 99%, troïng löôïng trung bình cuûa moät traùi
quít loaïi III töø 49,68g ñeán 57,52g.
Baøi 3.3. Ñeå khaûo saùt chæ tieâu X cuûa moät loaïi saûn phaåm cuûa xí nghieäp I,
ngöôøi ta quan saùt moät maãu trong kho vaø coù keát quûa sau:
X(cm) 11-15 15-19 19-23 23-27 27-31 31-35 35-39
Soá sphaåm 8 9 20 16 16 13 18
7
a) Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa loaïi saûn phaåm treân
vôùi ñoä tin caäy 96%.
b) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,8cm thì seõ ñaït ñöôïc
ñoä tin caäy laø bao nhieâu?
c) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,5cm vaø ñoä tin caäy
99% thì phaûi ñieàu tra theâm ít nhaát bao nhieâu saûn phaåm nöõa?
d) Nhöõng saûn phaåm coù chæ tieâu X töø 19cm trôû xuoáng ñöôïc goïi laø nhöõng
saûn phaåm loaïi B. Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa nhöõng
saûn phaåm loaïi B vôùi ñoä tin caäy 98% (GS X coù phaân phoái chuaån).
e) Haõy öôùc löôïng tæ leä saûn phaåm loaïi B vôùi ñoä tin caäy 92%. Baûng soá lieäu
treân ñöôïc choïn ngaãu nhieân töø moät kho trong ñoù coù 1000 saûn phaåm loaïi B.
Haõy öôùc löôïng soá saûn phaåm trong kho vôùi ñoä tin caäy 92%.
f) Neáu öôùc löôïng tæ leä nhöõng sp loaïi B vôùi ñoä chính xaùc 6% thì seõ ñaït
ñöôïc ñoä tin caäy laø bao nhieâu?
g) Neáu öôùc löôïng tæ leä nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy 96% vaø ñoä
chính xaùc 8% thì caàn phaûi ñieàu tra theâm bao nhieâu saûn phaåm nöõa?
h) Giaû söû trong kho ñeå laãn 1000 saûn phaåm cuûa xí nghieäp II vaø trong 100
saûn phaåm laáy töø kho coù 9 saûn phaåm cuûa xí nghieäp II. Haõy öôùc löôïng soá
saûn phaåm cuûa xí nghieäp I coù trong kho vôùi ñoä tin caäy 82%.
Lôøi giaûi
Laäp baûng
X
i
13 17 21 25 29 33 37
n
i
8 9 20 16 16 13 18
Ta coù:
;100=n
i i
X n 2636;=
∑
2
i i
X n 75028.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 26,36(cm).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (7, 4452) (cm ).
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa X laø:
2
2 2 2
n
S S (7,4827) (cm ).
n 1
= =
−
8
a) Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa loaïi saûn phaåm treân
vôùi ñoä tin caäy 96%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
γ α = 1- = 96% = 0,96.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
cho kyø voïng:
S S
(X z ; X z )
n n
α α
− +
trong ñoù ϕ(z
α
) = γ
/2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,06. Vaäy öôùc löôïng khoaûng laø:
7,4827 7,4827
(26, 36 2, 06 ; 26, 36 2, 06 ) (24, 82; 27, 90).
100 100
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 96%, giaù trò trung bình cuûa chæ tieâu X naèm
trong khoaûng töø 24,82cm ñeán 27,93 cm.
b) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,8cm thì seõ ñaït ñöôïc ñoä
tin caäy laø bao nhieâu?
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi öôùc löôïng kyø voïng cuûa
chæ tieâu X vôùi ñoä chính xaùc ε = 1,8cm.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc
cuûa öôùc löôïng:
S
z
n
α
ε =
trong ñoù ϕ(z
α
) = γ
/2. Suy ra
n 1,8. 100
z 2, 41.
S 7,4827
α
ε
= = =
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø
2 (z ) 2 (2, 41) 2.0,4920 98, 40%.
α
γ
= ϕ = ϕ = =
Vaäy ñoä tin caäy ñaït ñöôïc laø 98,40%.
c) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,5cm vaø ñoä tin caäy 99%
thì phaûi ñieàu tra theâm ít nhaát bao nhieâu saûn phaåm nöõa?
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng kyø voïng cuûa chæ tieâu X
vôùi ñoä chính xaùc ε = 1,5cm vaø ñoä tin caäy γ = 1- α = 99% = 0,99. Vì n ≥ 30,
σ
2
= D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
S
z
n
α
ε
= ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,99/2 = 0,495. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,58. Suy ra
9
2
z S
n
α
ε
⎛ ⎞
=
⎜ ⎟
⎝ ⎠
Thöïc teá yeâu caàu:
2
2
z S
2,58.7,4827
n 165,64.
1,5
α
ε
⎛ ⎞⎛ ⎞
≥ = ≈
⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
Giaù trò n nguyeân nhoû nhaát thoûa baát ñaúng thöùc treân laø n
1
= 166. Vì n
1
=
166 > 100 (100 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm ít nhaát laø
166 – 100 = 66 saûn phaåm nöõa.
d) Nhöõng saûn phaåm coù chæ tieâu X töø 19cm trôû xuoáng ñöôïc goïi laø nhöõng
saûn phaåm loaïi B. Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa nhöõng
saûn phaåm loaïi B vôùi ñoä tin caäy 98% (GS X coù phaân phoái chuaån).
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ
B
= M(X
B
) cuûa chæ tieâu
X = X
B
cuûa nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy γ = 1- α = 98% = 0,98.
Ta laäp baûng soá lieäu cuûa X
B
:
X
Bi
13 17
n
Bi
8 9
Töø baûng treân ta tính ñöôïc:
;17=
B
n ;257
∑
=
BiBi
nX
2
Bi Bi
X n 3, 953.=
∑
• Kyø voïng maãu cuûa X
B
laø
∑
== ).(1176,15
1
cmnX
n
X
BiBiB
• Phöông sai maãu cuûa X
B
laø:
2
2 2 2 2
B
Bi Bi B
ˆ
1
S X n X (1,9965) (cm ).
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa X
B
laø:
2
2 2 2
B
B
B
B
n
S S (2,0580) (cm ).
n 1
= =
−
Vì n
B
< 30, X
B
coù phaân phoái chuaån, σ
2
B
= D(X
B
) chöa bieát, neân ta coù coâng
thöùc öôùc löôïng khoaûng cho kyø voïng:
);(
B
B
k
B
B
B
k
B
n
S
tX
n
S
tX
αα
+− ,
10
trong ñoù
k
t
α
ñöôïc xaùc ñònh töø baûng phaân phoái Student vôùi k = n
B
–1=16
vaø α = 1 - γ = 1 – 0,98 = 0,02. Tra baûng phaân phoái Student ta ñöôïc
k
t 2, 583
α
= . Vaäy öôùc löôïng khoaûng laø:
2,0580 2,0580
(15,1176 2,583 ; 15,1176 2,583 ) (13,83; 16,41).
17 17
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 98%, giaù trò trung bình cuûa chæ tieâu X cuûa
nhöõng saûn phaåm loaïi B naèm trong khoaûng töø 13,83cm ñeán 16,41cm.
e) Haõy öôùc löôïng tæ leä nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy 92%. Baûng
soá lieäu treân ñöôïc choïn ngaãu nhieân töø moät kho trong ñoù coù 1000 saûn phaåm
loaïi B. Haõy öôùc löôïng soá saûn phaåm trong kho vôùi ñoä tin caäy 92%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc saûn phaåm loaïi B vôùi
ñoä tin caäy γ = 1- α = 92% = 0,92. Ta coù coâng thöùc öôùc löôïng khoaûng :
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− + ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,92/2 = 0,46. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,75. Maët khaùc, trong n =100 saûn phaåm coù m = 17 saûn phaåm
loaïi B neân tæ leä maãu saûn phaåm loaïi B laø F
n
= 0,17. Vaäy öôùc löôïng khoaûng
laø:
0,17(1 0,17) 0,17(1 0,17)
(0,17 1,75 ; 0,17 1,75 ) (10, 43%; 23,57%).
100 100
− −
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 92%, tæ leä saûn phaåm loaïi B naèm trong
khoaûng töø 10,43% ñeán 23,57%.
Khi trong kho coù 1000 saûn phaåm loaïi B, goïi N laø soá saûn phaåm coù trong
kho, ta coù tæ leä saûn phaåm loaïi B laø 1000/N. Theo keát quaû treân, vôùi ñoä tin
caäy 92%, tæ leä caùc saûn phaåm loïai B töø 10,43% ñeán 23,57%, do ñoùù:
1000 10,43 1000 23,57
10,43% 23,57%
N 100 N 100
100.1000 100.1000
N
23,57 10, 430
4242, 68 N 9587,73
≤ ≤ ⇔ ≤ ≤
⇔ ≤ ≤
⇔ ≤ ≤
4243 N 9587
⇔
≤ ≤
Vaäy vôùi ñoä tin caäy 92%, ta öôùc löôïng trong kho coù töø 4243 ñeán 9587 saûn
phaåm.
f) Neáu öôùc löôïng tæ leä nhöõng sp loaïi B vôùi ñoä chính xaùc 6% thì seõ ñaït
ñöôïc ñoä tin caäy laø bao nhieâu?
11
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi löôïng tæ leä caùc saûn
phaåm loaïi B vôùi ñoä chính xaùc ε = 6% = 0,06. Ta coù coâng thöùc tính ñoä
chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
−
ε = ,
trong ñoù ϕ(z
α
) = γ
/2. Suy ra:
n n
n 100
z 0,06. 1, 60.
F (1 F ) 0,17(1 0,17)
α
= ε = =
− −
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø
2 (z ) 2 (1,60) 2.0, 4452 89,04%.
α
γ
= ϕ = ϕ = =
g) Neáu öôùc löôïng tæ leä nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy 96% vaø ñoä
chính xaùc 8% thì caàn phaûi ñieàu tra theâm bao nhieâu saûn phaåm nöõa?
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng tæ leä caùc saûn phaåm loaïi
B vôùi ñoä chính xaùc ε = 8% = 0,08 vaø ñoä tin caäy γ = 1- α = 96% = 0,96. Ta
coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
−
ε = ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,06. Suy ra
2
n n
2
z F (1 F )
n
α
−
=
ε
Thöïc teá yeâu caàu:
2
2
n n
2 2
z F (1 F )
2, 06 .0,17(1 0,17)
n 93,56.
0,08
α
−
−
≥ = ≈
ε
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n
1
= 94. Vì n
1
=
94 < 100 (100 laø côõ maãu ñang coù) neân ta khoâng caàn ñieàu tra theâm saûn
phaåm nöõa.
h) Giaû söû trong kho ñeå laãn 1000 saûn phaåm cuûa xí nghieäp II vaø trong 100
saûn phaåm laáy töø kho coù 9 saûn phaåm cuûa xí nghieäp II. Haõy öôùc löôïng soá
saûn phaåm cuûa xí nghieäp I coù trong kho vôùi ñoä tin caäy 82%.
Tröôùc heát ta öôùc löôïng tæ leä saûn phaåm cuûa xí nghieäp I coù trong kho vôùi
ñoä tin caäy 82%. Ta coù coâng thöùc öôùc löôïng khoaûng :
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− +
12
trong ñoù ϕ(z
α
) = γ
/2 = 0,82/2 = 0,41. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,34. Maët khaùc, theo giaû thieát, trong n =100 saûn phaåm coù 9
saûn phaåm cuûa xí nghieäp II töùc laø coù 91 saûn phaåm cuûa xí nghieäp I, neân tæ
leä maãu saûn phaåm cuûa xí nghieäp I laø F
n
= 91/100 = 0,91. Vaäy öôùc löôïng
khoaûng laø:
0, 91(1 0,91) 0, 91(1 0,91)
(0, 91 1,34 ; 0, 91 1, 34 ) (87,17%; 94, 83%).
100 100
− −
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 92%, tæ leä saûn phaåm cuûa xí nghieäp I naèm
trong khoaûng töø 87,17% ñeán 94,83%.
Baây giôø goïi N laø soá saûn phaåm cuûa xí nghieäp I coù trong kho. Khi ñoù:
- Toång soá saûn phaåm coù trong kho laø N + 1000ø.
- Tæ leä saûn phaåm cuûa xí nghieäp I coù trong kho laø N/(N+1000).
Theo keát quaû treân, vôùi ñoä tin caäy 82%, tæ leä saûn phaåm cuûa xí nghieäp I
coù trong kho naèm trong khoaûng töø 87,17% ñeán 94,83%, do ñoùù:
N N
87,17% 94,83% 87,17% 94,83%
N 1000 N 1000
1000
87,17% 1 94,83%
N 1000
1000
5,17% 12,83%
N 1000
≤ ≤ ⇔ ≤ ≤
+ +
⇔ ≤ − ≤
+
⇔ ≤ ≤
+
1000 1000
-1000 N -1000
12,83% 5,17%
6794,23 N 18342,36
6795 N 18342
⇔ ≤ ≤
⇔ ≤ ≤
⇔ ≤ ≤
Vaäy vôùi ñoä tin caäy 82%, ta öôùc löôïng soá saûn phaåm cuûa xí nghieäp I coù
trong kho naèm trong khoaûng töø 6795 ñeán 18342.
Baøi 3.4. Ñeå khaûo saùt chieàu cao X cuûa moät gioáng caây troàng, ngöôøi ta quan
saùt moät maãu vaø coù keát quûa sau:
X(cm) 95-105 105-115 115-125 125-135 135-145 145-155 155-165
Soá caây 10 10 15 30 10 10 15
a) Öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä tin
caäy 96%.
b) Neáu muoán öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi
ñoä tin caäy 99% vaø ñoä chính xaùc 4 cm thì caàn phaûi ñieàu tra theâm bao
nhieâu caây nöõa?
c) Neáu öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä
chính xaùc 4,58cm thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
13
d) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
“cao”. Haõy öôùc löôïng tæ leä nhöõng caây “cao”vôùi ñoä tin caäy 95%.
e) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä chính xaùc 10% thì
seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
f) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä tin caäy 95% vaø ñoä
chính xaùc 11% thì caàn phaûi ñieàu tra theâm bao nhieâu caây nöõa?
g) Öôùc löôïng chieàu cao trung bình cuûa caùc caây cao cuûa gioáng caây troàng
treân vôùi ñoä tin caäy 94%.
Lôøi giaûi
Ta coù:
;100=n
i i
X n 13100;=
∑
2
i i
X n 1749000.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 131(cm).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
ˆ
1
S X n X (18,1384) (cm ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2 2
ˆ
n
S S (18,2297) (cm ).
n 1
= =
−
a) Öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä tin
caäy 96%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
γ α = 1- = 96% = 0,96.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
cho kyø voïng:
S S
(X z ; X z )
n n
α α
− + ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,06. Vaäy öôùc löôïng khoaûng laø:
18, 2297 18, 2297
(131 2, 06 ; 131 2, 06 ) (127, 2447; 134, 7553).
100 100
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 96%, chieàu cao trung bình cuûa moät caây naèm
trong khoaûng töø 127,2447cm ñeán 134,7553cm.
14
b) Neáu muoán öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi
ñoä tin caäy 99% vaø ñoä chính xaùc 4cm thì caàn phaûi ñieàu tra theâm bao nhieâu
caây nöõa?
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng kyø voïng cuûa chæ tieâu X
vôùi ñoä chính xaùc ε = 4cm vaø ñoä tin caäy γ = 99% = 0,99.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc
cuûa öôùc löôïng:
S
z
n
α
ε
= ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,99/2 = 0, 495. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,58. Suy ra
2
z S
n
α
ε
⎛ ⎞
=
⎜ ⎟
⎝ ⎠
.
Thöïc teá yeâu caàu:
2
2
z S 2,58.18,2297
n 138, 254.
4
α
⎛ ⎞ ⎛ ⎞
≥ = ≈
⎜ ⎟⎜ ⎟
ε
⎝ ⎠
⎝ ⎠
Giaù trò n nguyeân nhoû nhaát thoûa baát ñaúng thöùc treân laø n
1
= 139. Vì n
1
=
139 > 100 (100 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm ít nhaát laø
139 – 100 = 39 caây nöõa.
c) Neáu öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä
chính xaùc 4,58cm thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi öôùc löôïng kyø voïng cuûa
chæ tieâu X vôùi ñoä chính xaùc ε = 4,58cm.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc
cuûa öôùc löôïng:
S
z
n
α
ε
= ,
trong ñoù ϕ(z
α
) = γ
/2 . Suy ra
n 4,58. 100
z 2,5123.
S 18, 2297
α
ε
= = =
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø
2 (z ) 2 (2,5123) 2 (2, 52) 2.0,4941 98, 82%.
γ
γ
= ϕ = ϕ = ϕ = =
d) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
“cao”. Haõy öôùc löôïng tæ leä nhöõng caây “cao”vôùi ñoä tin caäy 95%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc caây cao vôùi ñoä tin caäy
γ α = 1- = 95% = 0,95. Ta coù coâng thöùc öôùc löôïng khoaûng :
15
n n n n
n n
F (1 F ) F (1 F )
(F z ; F z )
n n
α α
− −
− + ,
trong ñoù ϕ (z
α
) = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,96. Trong n = 100 caây coù m = 10 + 10 + 15 = 35 caây coù
chieàu cao töø 135cm trôû leân neân tæ leä maãu caùc caây cao laø F
n
= 35/100 =
0,35. Vaäy öôùc löôïng khoaûng laø:
0, 35(1 0,35) 0, 35(1 0,35)
(0, 35 1,96 ; 0,35 1, 96 ) (25,65%; 44,35%).
100 100
− −
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä caây cao naèm trong khoaûng töø
25,65% ñeán 44,35%.
e) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä chính xaùc 10% thì seõ
ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy khi löôïng tæ leä caây cao vôùi ñoä
chính xaùc ε = 10% = 0,1.
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
ε
−
= ,
trong ñoù ϕ (z
α
) = γ
/2 . Ta coù tæ leä maãu caây cao laø: F
n
= 0,35. Suy ra
n n
n 100
z 0,1. 2,0966.
F (1 F ) 0, 35(1 0,35)
α
= ε = =
− −
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø
2 (z ) 2 (2, 0966) 2 (2,1) 2.0,4821 96,42%.
α
γ
=
ϕ
=
ϕ
=
ϕ
= =
f) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä tin caäy 95% vaø ñoä
chính xaùc 11% thì caàn phaûi ñieàu tra theâm bao nhieâu caây nöõa?
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng tæ leä caây cao vôùi ñoä
chính xaùc ε = 11% = 0,11 vaø ñoä tin caäy γ = 1- α = 95% = 0,95.
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
ε
−
= ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,96. Suy ra
2
n n
2
z F (1 F )
n
α
ε
−
= .
Thöïc teá yeâu caàu:
2 2
n n
2 2
z F (1 F ) 1,96 .0, 35(1 0, 35)
n 72, 23.
0,11
α
− −
≥ = ≈
ε
16
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n
1
= 73. Vì n
1
=
73 < 100 (100 laø côõ maãu ñang coù) neân ta khoâng caàn ñieàu tra theâm caây
naøo nöõa.
g) Öôùc löôïng chieàu cao trung bình cuûa caùc caây cao cuûa gioáng caây troàng
treân vôùi ñoä tin caäy 94%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ
C
= M(X
C
) cuûa chæ
tieâu X = X
C
cuûa nhöõng caây cao vôùi ñoä tin caäy γ = 1- α = 94% = 0,94. Ta
laäp baûng soá lieäu cuûa X
C
:
X
Ci
140 150 160
n
Ci
10 10 15
Töø baûng treân ta tính ñöôïc:
C
n 35;=
Ci Ci
X
n 5300;=
∑
2
Ci Ci
X
n 805000.=
∑
• Kyø voïng maãu cuûa X
C
laø:
C Ci Ci
1
X
X n 151, 4286(cm).
n
= =
∑
• Phöông sai maãu cuûa X
C
laø:
2
2 2 2 2
C
Ci Ci C
1
S X n X (8,3299) (cm ).
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa X
C
laø:
2
2 2 2
C
C
C
C
n
S S (8,4515) (cm ).
n 1
= =
−
Vì n
C
= 35 > 30, σ
2
C
= D(X
C
) chöa bieát, neân ta coù coâng thöùc öôùc löôïng
khoaûng cho kyø voïng:
C C
C C
C C
S S
(X z ; X z )
n n
α α
− + ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,94/2 = 0,47. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,88. Vaäy öôùc löôïng khoaûng laø:
8,4515 8, 4515
(151,4286 1,88 ; 151,4286 1, 88 ) (148,74; 154,11).
35 35
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 94%, chieàu cao trung bình cuûa caây cao naèm
trong khoaûng töø 148,74cm ñeán 154,11cm.
Baøi 3.5. Traùi caây cuûa moät chuû haøng ñöôïc ñöïng trong caùc soït, moãi soït 100
traùi. Ngöôøi ta kieåm tra 50 soït thì thaáy coù 450 traùi khoâng ñaït tieâu chuaån.
a) Öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån cuûa loâ haøng treân vôùi ñoä tin
caäy 95%.
b) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc
0,5% thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
17
c) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc
1% vaø ñoä tin caäy 99% thì phaûi ñieàu tra theâm ít nhaát bao nhieâu soït nöõa?
Lôøi giaûi
Soá traùi trong 100 soït laø 50×100 = 5000. Do ñoù:
• Côõ maãu n = 5000.
• Soá traùi khoâng ñaït tieâu chuaån laø: m = 450.
• Tæ leä maãu caùc traùi khoâng ñaït tieâu chuaån laø:
F
n
= m/n = 450/5000 = 0,09.
a) Öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån cuûa loâ haøng treân vôùi ñoä tin
caäy 95%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc traùi khoâng ñaït tieâu
chuaån vôùi ñoä tin caäy γ = 1- α = 95% = 0,95.
Ta coù coâng thöùc öôùc löôïng khoaûng:
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− +
trong ñoù ϕ (z
α
) = (1- α)/2 = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm
Laplace ta ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
0,09(1 0,09) 0, 09(1 0,09)
(0, 09 1,96 ; 0, 09 1, 96 ) (8,21%; 9,79%)
5000 5000
− −
− + =
.
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä traùi khoâng ñaït tieâu chuaån töø
8,21% ñeán 9,79%.
b) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc
0,5% thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
Yeâu caàu cuûa baøi toùan: Xaùc ñònh ñoä tin caäy γ = 1- α.
Giaû thieát: - Öôùc khoûang cho tæ leä traùi khoâng ñaït tieâu chuaån.
- Ñoä chính xaùc ε = 0,5% = 0,005.
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
−
ε =
trong ñoù ϕ (z
α
) = γ
/2 . Suy ra
n n
n 5000
z 0, 005. 1,24.
F (1 F ) 0,09(1 0, 09)
α
= ε = =
− −
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø:
2 (z ) 2 (1,24) 2.0, 3925 79, 5%.
α
γ
= ϕ = ϕ = =
Vaäy ñoä tin caäy ñaït ñöôïc laø 79,5%.
18
c) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc
1% vaø ñoä tin caäy 99% thì phaûi ñieàu tra theâm ít nhaát bao nhieâu soït nöõa?
Yeâu caàu cuûa baøi toùan: Xaùc ñònh côõ maãu.
Giaû thieát: - Öôùc khoûang cho tæ leä traùi khoâng ñaït tieâu chuaån.
- Ñoä chính xaùc ε = 1% = 0,01.
- Ñoä tin caäy γ = 1- α = 99% = 0,99.
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
n n
F (1 F )
z
n
α
−
ε =
trong ñoù ϕ(z
α
) = (1- α)
/2 = 0,99/2 = 0,495. Tra baûng giaù trò haøm Laplace
ta ñöôïc z
α
= 2,58. Suy ra
2
n n
2
z F (1 F )
n
α
−
=
ε
Thöïc teá yeâu caàu:
2
2
n n
2 2
z F (1 F )
2, 58 .0,09(1 0,09)
n 5451,6.
0, 01
α
−
−
≥ = ≈
ε
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n
1
= 5452.
Vì n
1
= 5452 > 5000 (5000 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm
ít nhaát laø 5452 – 5000 = 452 traùi, nghóa laø khoaûng 5 soït nöõa.
Baøi 3.6. Ñeå nghieân cöùu nhu caàu cuûa moät loaïi haøng ôû moät khu vöïc, ngöôøi
ta khaûo saùt 400 hoä gia ñình. Keát quaû nhö sau:
Nhu caàu (kg/thaùng/hoä) 0-1 1-2 2-3 3-4 4-5 5-6 6-7 7-8
Soá hoä 10 35 86 132 78 31 18 10
Cho bieát trong khu vöïc coù 4000 hoä.
a) Öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc trong
moät naêm vôùi ñoä tin caäy 95%.
b) Khi öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc
trong moät naêm, neáu ta muoán ñaït ñöôïc ñoä tin caäy 99% vaø ñoä chính xaùc laø
4,8taán thì caàn khaûo saùt ôû ít nhaát bao nhieâu hoä gia ñình?
Lôøi giaûi
Goïi X(kg) laø nhu caàu cuûa moät hoä veà loaïi haøng treân trong moät thaùng. Ta coù:
Xi 0,5 1,5 2,5 3,5 4,5 5,5 6,5 7,5
ni 10 35 86 132 78 31 18 10
19
n 400;=
i i
X
n 1448;=
∑
2
i i
X n 6076.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 3, 62.
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2
i i
ˆ
1
S X n X (1, 4442) .
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2
ˆ
n
S S (1,4460) .
n 1
= =
−
a) Öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc trong
moät naêm vôùi ñoä tin caäy 95%.
Tröôùc heát ta öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa moät
hoä trong khu vöïc trong moät thaùng vôùi ñoä tin caäy 95%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
γ α = 1- = 95% = 0,95.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
cho kyø voïng:
S S
(X z ; X z )
n n
α α
− + ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
1, 4460 1, 4460
(3, 62 1, 96 ; 3,62 1, 96 ) (3, 4783; 3,7617).
400 400
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, nhu caàu trung bình veà maët haøng naøy
cuûa moät hoä trong khu vöïc trong moät thaùng naèm trong khoaûng töø
3,4783kg ñeán 3,7617kg. Xeùt 4000 hoä trong moät naêm 12 thaùng, ta coù caùc
nhu caàu töông öùng laø:
3,4783 4000× ×12 = 166958,4kg = 166,9584taán;
3,7617 4000× ×12 = 180561,6kg = 180,5616taán.
Keát luaän: Vôùi ñoä tin caäy 95%, nhu caàu trung bình veà maët haøng naøy cuûa
toaøn khu vöïc trong moät naêm naèm trong khoaûng töø 166,9584taán ñeán
180,5616taán.
b) Khi öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc
trong moät naêm, neáu ta muoán ñaït ñöôïc ñoä tin caäy 99% vaø ñoä chính xaùc
laø 4,8taán thì caàn khaûo saùt ôû ít nhaát bao nhieâu hoä gia ñình?
Khi öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc
trong moät naêm vôùi ñoä tin caäy 99% vaø ñoä chính xaùc laø 4,8 taán= 4800kg,
nghóa laø ta öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa moät hoä
20
trong moät thaùng vôùi ñoä tin caäy γ = 1- α = 0,99 vaø ñoä chính xaùc ε =
4800/(4000×12) = 0,1kg. Nhö vaäy, ta ñöa veà baøi toaùn xaùc ñònh côõ maãu
khi öôùc löôïng kyø voïng cuûa chæ tieâu X vôùi ñoä chính xaùc ε = 0,1 vaø ñoä tin
caäy γ = 1- α = 99% = 0,99.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc
cuûa öôùc löôïng:
S
z
n
α
ε
= ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,99/2 = 0, 495. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 2,58. Suy ra
2
z S
n
α
ε
⎛ ⎞
=
⎜ ⎟
⎝ ⎠
.
Thöïc teá yeâu caàu:
22
z S
2, 58 1,4460
n 1391,8.
0,1
α
×
⎛ ⎞
⎛ ⎞
≥ = ≈
⎜ ⎟
⎜ ⎟
ε
⎝ ⎠
⎝ ⎠
Giaù trò n nguyeân nhoû nhaát thoûa baát ñaúng thöùc treân laø n
1
= 1392. Vaäy
caàn khaûo saùt ít nhaát laø 1392 hoä gia ñình.
Baøi 3.7. Ñeå bieát soá löôïng caù trong hoà lôùn ngöôøi ta baét leân 2000 con ñaùnh
daáu xong roài thaû chuùng xuoáng hoà. Sau ñoù ngöôøi ta baét leân 400 con vaø thaáy
coù 80 con ñöôïc ñaùnh daáu.
a) Vôùi ñoä tin caäy 95%, haõy öôùc löôïng soá caù coù trong hoà.
b) Öôùc löôïng soá caù toái ña coù trong hoà vôùi ñoä tin caäy 96%.
c) Öôùc löôïng soá caù toái thieåu coù trong hoà vôùi ñoä tin caäy 94%.
Lôøi giaûi
Goïi N laø soá caù coù trong hoà. Khi ñoù tæ leä caù ñöôïc ñaùnh daáu coù trong hoà
laø p = 2000/N.
Vôùi maãu thu ñöôïc, ta coù:
• Côõ maãu n = 400.
• Soá con ñöôïc ñaùnh daáu trong maãu laø: m = 80.
• Tæ leä maãu con ñöôïc ñaùnh daáu laø:
F
n
= m/n = 80/400 = 0,2.
a) Vôùi ñoä tin caäy 95%, haõy öôùc löôïng soá caù coù trong hoà.
Tröôùc heát ta öôùc löôïng khoaûng cho tæ leä p caùc con ñöôïc ñaùnh daáu vôùi
ñoä tin caäy γ = 1- α = 95% = 0,95.
Ta coù coâng thöùc öôùc löôïng khoaûng:
21
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− + ,
trong ñoù ϕ(z
α
) = (1- α)/2 = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm
Laplace ta ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
0, 2(1 0, 2) 0, 2(1 0, 2)
(0, 2 1,96 ; 0,2 1, 96 ) (16, 08%; 23, 92%)
400 400
− −
− + =
Nhö vaäy, vôùi ñoä tin caäy 95%, tæ leä con ñöôïc ñaùnh daáu naèm trong khoaûng
töø 16,08% ñeán 23,92%, do ñoùù:
2000 2000 2000
16,08% 23,92% N
N 23,92% 16,08%
8361,20 N 12437,81
8362 N 12437
≤ ≤ ⇔ ≤ ≤
⇔ ≤ ≤
⇔ ≤ ≤
Vaäy vôùi ñoä tin caäy 95%, ta öôùc löôïng soá caù coù trong hoà khoaûng töø 8362
ñeán 12437 con.
b) Öôùc löôïng soá caù toái ña coù trong hoà vôùi ñoä tin caäy 96%.
Soá caù toái ña coù trong hoà töôg öùng vôùi giaù trò toái thieåu cuûa tæ leä con ñöôïc
ñaùnh daáu. Do ñoù tröôùc heát ta öôùc löôïng khoaûng beân phaûi cho tæ leä p caùc
con ñöôïc ñaùnh daáu vôùi ñoä tin caäy γ = 1- α = 96% = 0,96 (α = 0,04).
Ta coù coâng thöùc öôùc löôïng khoaûng beân phaûi:
n n
n 2
F (1 F )
(F z ; )
n
α
−
− +∞
trong ñoù ϕ(z
2α
) = (1- 2α)/2 = γ
/2 = 0,92/2 = 0,46. Tra baûng giaù trò haøm
Laplace ta ñöôïc z
2α
= 1,75. Suy ra giaù trò toái thieåu cuûa tæ leä con ñöôïc ñaùnh
daáu laø:
n n
n 2
F (1 F ) 0,2(1 0,2)
F z 0,2 1,75 0,165.
n 400
α
− −
− = − =
Nhö vaäy, vôùi ñoä tin caäy 96%, ta coù
2000 2000
0,165 N 12121,2
N 0,165
≥ ⇔ ≤ =
Vaäy vôùi ñoä tin caäy 96%, soá caù toái ña coù trong hoà laø 12121.
c) Öôùc löôïng soá caù toái thieåu coù trong hoà vôùi ñoä tin caäy 94%.
Soá caù toái thieåu coù trong hoà töông öùng vôùi giaù trò toái ña cuûa tæ leä con
ñöôïc ñaùnh daáu. Do ñoù tröôùc heát ta öôùc löôïng khoaûng beân traùi cho tæ leä p
caùc con ñöôïc ñaùnh daáu vôùi ñoä tin caäy γ = 1- α = 94% = 0,94 (α = 0,06).
Ta coù coâng thöùc öôùc löôïng khoaûng beân traùi:
n n
n 2
F (1 F )
( ;F z )
n
α
−
−∞ + ,
22
trong ñoù ϕ(z
2α
) = (1- 2α)/2 = γ/2 = 0,88/2 = 0,44. Tra baûng giaù trò haøm
Laplace ta ñöôïc z
2α
= 1,56. Suy ra giaù trò toái ña cuûa tæ leä con ñöôïc ñaùnh
daáu laø:
n n
n 2
F (1 F ) 0,2(1 0,2)
F z 0,2 1,56 0, 2312.
n 400
α
− −
+ = + =
Nhö vaäy, vôùi ñoä tin caäy 94%, ta coù
2000 2000
0,2312 N 8650,5
N 0,2312
≤ ⇔ ≥ =
Vaäy vôùi ñoä tin caäy 94%, soá caù toái thieåu coù trong hoà laø 8651.
Baøi 3.8. Tröôùc kyø baàu cöû toång thoáng ngöôøi ta phoûng vaán ngaãu nhieân 1800
cöû tri thì thaáy coù 1180 ngöôøi uûng hoä cöû tri A. Vôùi ñoä tin caäy 99%, hoûi öùng
cöû vieân A coù theå thu ñöôïc toái thieåu bao nhieâu phaàn traêm soá phieáu baàu? Vaø
toái ña laø bao nhieâu?
Lôøi giaûi
Vôùi maãu thu ñöôïc, ta coù:
• Côõ maãu n = 1800.
• Soá ngöôøi uûng hoä öùng cöû vieân A laø m = 1180.
• Tæ leä maãu soá ngöôøi uûng hoä laø:
F
n
= m/n = 1180/1800 = 0.6556.
Vôùi ñoä tin caäy 99%, ñeå bieát öùng cöû vieân A coù theå thu ñöôïc toái thieåu bao
nhieâu phaàn traêm soá phieáu baàu ta caàn öôùc löôïng khoaûng beân phaûi cho tæ leä
p nhöõng ngöôøi uûng hoä vôùi ñoä tin caäy γ = 1- α = 99% = 0,99 (α = 0,01).
Ta coù coâng thöùc öôùc löôïng khoaûng beân phaûi:
n n
n 2
F (1 F )
(F z ; )
n
α
−
− +∞
trong ñoù ϕ(z
2α
) = (1- 2α)/2 = γ
/2 = 0,98/2 = 0,49. Tra baûng giaù trò haøm
Laplace ta ñöôïc z
2α
= 2,33. Suy ra giaù trò toái thieåu cuûa tæ leä ngöôøi uûng hoä
laø:
n n
n 2
F (1 F ) 0,6556(1 0, 6556)
F z 0,6556 2,33 0,6295.
n 1800
α
− −
− = − =
Nhö vaäy, vôùi ñoä tin caäy 99%, öùng cöû vieân A coù theå thu ñöôïc toái thieåu laø
62,95% soá phieáu baàu.
Vôùi ñoä tin caäy 99%, ñeå bieát öùng cöû vieân A coù theå thu ñöôïc toái ña bao
nhieâu phaàn traêm soá phieáu baàu ta caàn öôùc löôïng khoaûng beân traùi cho tæ leä
p nhöõng ngöôøi uûng hoä vôùi ñoä tin caäy γ = 1- α = 99% = 0,99 (α = 0,01).
Ta coù coâng thöùc öôùc löôïng khoaûng beân traùi:
23
n n
n 2
F (1 F )
( ;F z )
n
α
−
−∞ + ,
trong ñoù z
2α
= 2,33. Suy ra giaù trò toái ña cuûa tæ leä ngöôøi uûng hoä laø:
n n
n 2
F (1 F ) 0,6556(1 0,6556)
F z 0,6556 2,33 0,6817.
n 1800
α
− −
+ = + =
Nhö vaäy, vôùi ñoä tin caäy 99%, öùng cöû vieân A coù theå thu ñöôïc toái ña laø
68,17% soá phieáu baàu.
Baøi 3.9. Khaûo saùt thu nhaäp vaø tyû leä thu nhaäp chi cho giaùo duïc ôû 350 hoä
gia ñình, ta thu ñöôïc caùc soá lieäu ôû baûng sau:
X
Y
10 20 30 40 50
150 - 250 10 40 20
250 - 350 40 60 20
350 - 450 20 30 40
450 - 550 30 30 10
trong ñoù : X laø tyû leä thu nhaäp chi cho giaùo duïc (tính theo %)
Y laø thu nhaäp bình quaân 1 ngöôøi/thaùng cuûa moät hoä (ñôn vò tính
ngaøn ñoàng).
a) Öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc cuûa
moät hoä gia ñình vôùi ñoä tin caäy 95% .
b) Nhöõng gia ñình coù thu nhaäp bình quaân ngöôøi treân 450 laø hoä coù thu
nhaäp cao. Öôùc löôïng tyû leä hoä coù thu nhaäp cao vôùi ñoä tin caäy 97%.
c) Ñeå öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc vôùi
ñoä chính xaùc ε = 0,8% thì ñaûm baûo ñoä tin caäy laø bao nhieâu?
Lôøi giaûi
• Côõ maãu: n = 350.
• Kyø voïng maãu cuûa X laø
i Xi
1
X
X n 29,7143.
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2
X
i Xi
1
S X n X (8,7785) .
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa X laø:
2
2 2
X
X
n
S S (8,7910) .
n 1
= =
−
24
a) Öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc cuûa
moät hoä gia ñình vôùi ñoä tin caäy 95% .
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
γ α = 1- = 95% = 0,95.
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
cho kyø voïng:
X X
S S
(X z ; X z )
n n
α α
− + ,
trong ñoù ϕ(z
α
) = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
8,7910 8, 7910
(29, 7143 1, 96 ; 29,7143 1,96 ) (28,7933;30,6353).
350 350
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, giaù trò trung bình cuûa tyû leä thu nhaäp
chi cho giaùo duïc cuûa moät hoä gia ñình töø 28,7933% ñeán 30,6353%.
b) Nhöõng gia ñình coù thu nhaäp bình quaân ngöôøi treân 450 laø hoä coù thu
nhaäp cao. Öôùc löôïng tyû leä hoä coù thu nhaäp cao vôùi ñoä tin caäy 97%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc hoä coù thu nhaäp cao
vôùi ñoä tin caäy γ = 1- α = 97% = 0,97.
Ta coù coâng thöùc öôùc löôïng khoaûng :
n n n n
n n
F (1 F ) F (1 F )
(F z ;F z )
n n
α α
− −
− +
trong ñoù ϕ(z
α
) = (1- α)/2 = γ
/2 = 0,97/2 = 0,485.
• Tra baûng giaù trò haøm Laplace ta ñöôïc z
α
= 2,17.
• Côõ maãu n = 350.
• Trong n = 350 hoä coù m = 30 + 30 + 10 = 70 hoä coù thu nhaäp bình
quaân ngöôøi treân 450 neân coù m = 70 hoä coù thu nhaäp cao. Do ñoù tæ leä maãu
hoä coù thu nhaäp cao laø:
F
n
= m/n = 70/350 = 0,2.
Vaäy öôùc löôïng khoaûng laø:
0,2(1 0,2) 0, 2(1 0, 2)
(0, 2 2,17 ; 0, 2 2,17 ) (15, 36%; 24, 64%).
350 350
− −
− + =
.
Noùi caùch khaùc, vôùi ñoä tin caäy 97%, tæ leä hoä coù thu nhaäp cao töø 15,36% ñeán
24,64%.
c) Ñeå öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc vôùi
ñoä chính xaùc ε = 0,8% thì ñaûm baûo ñoä tin caäy laø bao nhieâu?
Yeâu caàu cuûa baøi toùan: Xaùc ñònh ñoä tin caäy γ = 1- α.
25
Giaû thieát: - Öôùc khoûang cho kyø voïng cuûa X.
- Ñoä chính xaùc ε = 0,8 (%).
Vì n
≥ 30, σ
2
= D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc cuûa
öôùc löôïng:
S
z
n
α
ε =
,
trong ñoù ϕ (z
α
) = (1- α)/2 = γ
/2 . Suy ra
n 0, 8. 350
z 1,70
S 8,7910
α
ε
= = =
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø:
2 (z ) 2 (1,70) 2.0,4554 91, 08%.
α
γ
= ϕ = ϕ = =
Vaäy ñoä tin caäy ñaït ñöôïc laø 91,08%.
Baøi 3.10. X(%) vaø Y(kg/mm
2
) laø hai chæ tieâu chaát löôïng cuûa moät loaïi saûn
phaåm. Quan saùt moät soá saûn phaåm ta coù baûng soá lieäu nhö sau:
X
Y
0-5 5-10 10-15 15-20 20-25
120 7
130 12 8 10
140 20 15 2
150 19 16 9 5
160 8 3
Saûn phaåm coù chæ tieâu X ≥ 15% laø loaïi A.
a) Öôùc löôïng tæ leä saûn phaåm loaïi A ñoä tin caäy 95%.
b) Öôùc löôïng giaù trò trung bình chæ tieâu Y cuûa nhöõng saûn phaåm loaïi A
vôùi ñoä tin caäy 95% (Giaû söû Y coù phaân phoái chuaån).
c) Neáu muoán öôùc löôïng giaù trò trung bình cuûa chæ tieâu Y vôùi ñoä chính
xaùc 1,6 kg/mm
2
thì seõ ñaûm baûo ñöôïc ñoä tin caäy laø bao nhieâu?
Lôøi giaûi
a) Öôùc löôïng tæ leä saûn phaåm loaïi A ñoä tin caäy 95%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc saûn phaåm loaïi A vôùi
ñoä tin caäy γ = 1- α = 95% = 0,95.
Töø baûng soá lieäu ñaõ cho ta tính ñöôïc:
• Côõ maãu: n = 134.
• Trong n = 134 saûn phaåm coù m = 2 + 9 + 8 + 5 + 3 = 27 saûn phaåm
coù chæ tieâu X ≥ 15% neân coù m = 27 saûn phaåm loaïi A. Do ñoù tæ leä maãu
saûn phaåm loaïi A laø:
26
F
n
= m/n = 27/134 = 0,2015.
Ta coù coâng thöùc öôùc löôïng khoaûng:
n n n n
n n
F (1 F ) F (1 F )
(F z ; F z )
n n
α α
− −
− +
trong ñoù ϕ(z
α
) = γ
/2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
ñöôïc z
α
= 1,96. Vaäy öôùc löôïng khoaûng laø:
0, 2015(1 0,2015) 0,2015(1 0, 2015)
(0, 2015 1,96 ; 0,2015 1,96 )
134 134
(0,1336; 0, 2694) (13,36%; 26, 94%).
− −
− +
= =
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä saûn phaåm loaïi A töø 13,36% ñeán
26,94%.
b) Öôùc löôïng giaù trò trung bình chæ tieâu Y cuûa nhöõng saûn phaåm loaïi A vôùi
ñoä tin caäy 95% (Giaû söû Y coù phaân phoái chuaån).
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ
YA
= M(Y
A
) cuûa chæ
tieâu Y = Y
A
cuûa nhöõng saûn phaåm loaïi A vôùi ñoä tin caäy γ = 1- = 95% = α
0,95.
Ta laäp baûng soá lieäu cuûa Y
A
:
Y
Ai
140 150 160
n
Ai
2 14 11
Töø baûng treân ta tính ñöôïc:
A
n 27;
=
Ai Ai
Y
n 4140;=
∑
2
Ai Ai
Y
n 635800.=
∑
• Kyø voïng maãu cuûa Y
A
laø
A
Ai Ai
1
Y
Y n 153,3333.
n
= =
∑
• Phöông sai maãu cuûa Y
A
laø:
2
2
2 2
AYA
Ai Ai
1
S Y n Y (6, 0858) .
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa Y
A
laø:
2
2 2
A
YA
YA
A
n
S S (6,2017) .
n 1
= =
−
Vì n
A
< 30, Y
A
coù phaân phoái chuaån, σ
2
YA
= D(X
A
) chöa bieát, neân ta coù coâng
thöùc öôùc löôïng khoaûng cho kyø voïng:
27
k k
YA YA
A A
A A
S S
(Y t ; Y t )
n n
α α
− +
,
trong ñoù
k
t
α
ñöôïc xaùc ñònh töø baûng phaân phoái Student vôùi k = n
A
–1=26
vaø α = 1- γ = 1–0,95 = 0,05. Tra baûng phaân phoái Student ta ñöôïc
k
t 2, 056
α
= . Vaäy öôùc löôïng khoaûng laø:
6, 2017 6,2017
(153, 3333 2,056 ; 153,3333 2,056 ) (150, 8794; 155,7872).
27 27
− + =
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, giaù trò trung bình cuûa chæ tieâu Y cuûa
nhöõng saûn phaåm loaï
i A töø 150,8794kg/mm
2
ñeán 155,7872kg/mm
2
.
c) Neáu muoán öôùc löôïng giaù trò trung bình cuûa chæ tieâu Y vôùi ñoä chính
xaùc 1,6 kg/mm
2
thì seõ ñaûm baûo ñöôïc ñoä tin caäy laø bao nhieâu?
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi öôùc löôïng kyø voïng cuûa
chæ tieâu Y vôùi ñoä chính xaùc
ε = 1,6kg/mm
2
.
Töø baûng soá lieäu ñaõ cho ta tính ñöôïc:
• Côõ maãu: n = 134.
• Kyø voïng maãu cuûa Y laø
j Yj
1
Y Y n 142, 0149.
n
= =
∑
• Phöông sai maãu cuûa Y laø:
2
2 2 2
Y
i Yi
1
S Y n Y (10,4224) .
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa Y laø:
2
2 2
Y
Y
n
S S (10,4615) .
n 1
= =
−
Vì n
≥ 30, σ
2
Y
= D(Y) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc
cuûa öôùc löôïng:
Y
S
z
n
α
ε = ,
trong ñoù ϕ(z
α
) = γ
/2. Suy ra
Y
n 1,6. 134
z 1,77
S 10, 4615
α
ε
= = =
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø:
2 (z ) 2 (1, 77) 2.0, 4646 92,92%.
α
γ
= ϕ = ϕ ≈ =
Vaäy ñoä tin caäy ñaït ñöôïc laø 92,92%.
-----------------------------------------
1
BAØI GIAÛI
XAÙC SUAÁT THOÁNG KEÂ
(GV: Traàn Ngoïc Hoäi – 2009)
CHÖÔNG 4
KIEÅM ÑÒNH GIAÛ THIEÁT
Baøi 4.1. Troïng löôïng cuûa moät saûn phaåm theo qui ñònh laø 6kg. Sau moät
thôøi gian saûn xuaát, ngöôøi ta tieán haønh kieåm tra 121 saûn phaåm vaø tính
ñöôïc trung bình maãu laø 5,975kg vaø phöông sai maãu hieäu chænh 5,7596kg
2
.
Saûn xuaát ñöôïc xem laø bình thöôøng neáu caùc saûn phaåm coù troïng löôïng
trung bình baèng troïng löôïng qui ñònh. Vôùi möùc yù nghóa 5%, haõy keát luaän
veà tình hình saûn xuaát.
Lôøi giaûi
Goïi X laø troïng löôïng cuûa moät saûn phaåm. Giaû thieát cho ta:
• Côõ maãu n = 121.
• Kyø voïng maãu cuûa X laø
X 5,975 (kg)=
.
•
Phöông sai maãu hieäu chænh cuûa X laø S
2
= 5,7596(kg
2
).
•
Ñoä leäch maãu hieäu chænh cuûa X laø S
= 2,3999(kg).
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 5% = 0,05:
H
0
: μ = 6 vôùi giaû thieát ñoái H
1
: μ ≠ 6.
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n
(5,975 6) 121
z 0.1146.
S 2, 3999
− μ
−
= = = −
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1- α)/2 = 0,95/2 = 0,475
ta ñöôïc z
α
= 1,96.
Böôùc 3: Kieåm ñònh. Vì |z|= 0,1146 < 1,96 = z
α
neân ta chaáp nhaän
giaû thieát H
0
: μ = 6.
Keát luaän: Vôùi möùc yù nghóa 5%, tình hình saûn xuaát ñöôïc xem laø bình
thöôøng.
2
Baøi 4.2. Troïng löôïng cuûa moät saûn phaåm coù phaân phoái chuaån vôùi troïng
löôïng trung bình laø 500g. Sau moät thôøi gian saûn xuaát, ngöôøi ta nghi ngôø
troïng löôïng trung bình cuûa loaïi saûn phaåm naøy coù xu höôùng giaûm neân tieán
haønh kieåm tra 25 saûn phaåm vaø thu ñöôïc keát quaû sau:
Troïng löôïng (g) 480 485 490 495 500 510
Soá saûn phaåm 2 3 8 5 3 4
Vôùi möùc yù nghóa 3%, haõy keát luaän ñieàu nghi ngôø treân coù ñuùng hay khoâng.
Lôøi giaûi
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 3% = 0,03:
H
0
: μ = 500 vôùi giaû thieát ñoái H
1
: μ < 500.
Ta coù:
Xi 480 485 490 495 500 510
ni 2 3 8 5 3 4
n 25;
=
i i
X n 12350;=
∑
2
i i
X n 6102800.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 494(g).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (8,7178) (g ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2 2
n
S S (8, 8976) (g ).
n 1
= =
−
Vì n < 30;
σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (494 500) 25
z 3,3717.
S 8,8976
− μ −
= = = −
Böôùc 2: Ñaët k = n - 1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø 2α = 0,06 ta ñöôïc
2
t
α
= 1,974.
Böôùc 3: Kieåm ñònh. Vì -z = 3,3717 > 1,974 =
2
t
α
neân ta baùc boû giaû
thieát H
0
: : μ = 500, nghóa laø chaáp nhaän H
1
μ < 500.
Keát luaän: Vôùi möùc yù nghóa 3%, ñieàu nghi ngôø troïng löôïng trung bình
cuûa loaïi saûn phaåm naøy coù xu höôùng giaûm laø ñuùng.
Baøi 4.3. Naêng suaát luùa trung bình cuûa nhöõng vuï tröôùc laø 5,5taán/ha. Vuï
luùa naêm nay ngöôøi ta aùp duïng moät phöông phaùp kyõ thuaät môùi cho toaøn boä
3
dieän tích troàng luùa trong vuøng. Ñieàu tra naêng suaát 100ha luùa, ta coù baûng
soá lieäu sau:
Naêngsuaát (taï/ha) 40-45 45-50 50-55 55-60 60-65 65-70 70-75 75-80
Dieän tích (ha) 7 12 18 27 20 8 5 3
Vôùi möùc yù nghóa 1%, haõy keát luaän xem phöông phaùp kyõ thuaät môùi coù laøm
taêng naêng suaát luùa trung bình cuûa vuøng naøy hay khoâng?
Lôøi giaûi
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 1% = 0,01:
H
0
: μ = 55 vôùi giaû thieát ñoái H
1
: μ > 55.
(5,5taán = 55taï).
Ta coù:
X
i
42,5 47,5 52,5 57,5 62,5 67,5 72,5 77,5
n
i
7 12 18 27 20 8 5 3
n 100;=
i i
X n 5750;=
∑
2
i i
X
n 337475.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 57, 5(taï).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (8,2765) (taï ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2 2
n
S S (8,3182) (taï ).
n 1
= =
−
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n
(57,5 55) 100
z 3,0055.
S 8, 3182
− μ
−
= = =
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1- 2α)/2 = 0,98/2 = 0,49
ta ñöôïc z
2α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì z = 3,0055 > 2,33 = z
2α
neân ta baùc boû giaû thieát
H
0
: : μ = 55, nghóa laø chaáp nhaän H
1
μ > 55.
Keát luaän: Vôùi möùc yù nghóa 1%, phöông phaùp kyõ thuaät môùi laøm taêng
naêng suaát luùa trung bình cuûa vuøng naøy.
Baøi 4.4. Moät coâng ty döï ñònh môû moät sieâu thò taïi moät khu daân cö. Ñeå
ñaùnh giaù khaû naêng mua haøng cuûa daân cö trong khu vöïc, ngöôøi ta tieán
4
haønh ñieàu tra veà thu nhaäp cuûa 100 hoä trong khu vöïc vaø coù baûng soá lieäu
sau:
Thu nhaäp bình quaân
(ngaøn/ngöôøi/thaùng)
150 200 250 300 350
Soá hoä 8 15 38 22 17
Theo boä phaän tieáp thò thì sieâu thò chæ hoaït ñoäng coù hieäu quaû taïi khu vöïc
naøy khi thu nhaäp bình quaân haøng thaùng cuûa caùc hoä toái thieåu laø vaøo
khoaûng 250ngaøn/ngöôøi/thaùng. Vaäy theo keát quaû ñieàu tra treân, coâng ty coù
neân quyeát ñònh môû sieâu thò taïi khu vöïc naøy hay khoâng vôùi möùc yù nghóa
5%?
Lôøi giaûi
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 5% = 0,05:
H
0
: μ = 250 vôùi giaû thieát ñoái H
1
: μ > 250.
Ta coù:
Xi 150 200 250 300 350
ni 8 15 38 22 17
n 100;
=
i i
X
n 26250;=
∑
2
i i
X n 7217500.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 262, 5.
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2
i i
1
S X n X (57,1730) .
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2
n
S S (57,4610) .
n 1
= =
−
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (262,5 250) 100
z 2,1754.
S 57,4610
− μ −
= = =
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1- 2α)/2 = 0,90/2 = 0,45
ta ñöôïc z
2α
= 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 2,1754 > 1,65 = z
2α
neân ta baùc boû giaû thieát
H
0
: : μ = 250, chaáp nhaän giaû thieát H
1
μ > 250, nghóa laø thu nhaäp bình
quaân cuûa caùc hoä cao hôn 250ngaøn/ngöôøi/thaùng.
Keát luaän: Vôùi möùc yù nghóa 5%, coâng ty neân quyeát ñònh môû sieâu thò taïi
khu vöïc naøy.
5
Baøi 4.5. Ñeå nghieân cöùu nhu caàu cuûa moät loaïi haøng, ngöôøi ta tieán haønh
khaûo saùt nhu caàu cuûa maët haøng naøy ôû 400 hoä. Keát quaû nhö sau:
Nhu caàu (kgï/thaùng) 0 0-1 1-2 2-3 3-4 4-5 5-6 6-7
Soá hoä 10 35 86 132 78 31 18 10
Giaû söû khu vöïc ñoù coù 4000 hoä. Neáu cho raèng nhu caàu trung bình veà maët
haøng naøy cuûa toaøn khu vöïc laø 14taán/thaùng thì coù chaáp nhaän ñöôïc khoâng
vôùi möùc yù nghóa 2%?
Lôøi giaûi
Khi cho raèng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc laø
14taán/thaùng, nghóa laø nhu caàu trung bình veà maët haøng naøy cuûa moät hoä
trong moät thaùng laø
14taán 14000kg
3,5kg.
4000 4000
= =
Do ñoù ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi
möùc yù nghóa α = 2% = 0,02:
H
0
: μ = 3,5 vôùi giaû thieát ñoái H
1
: μ ≠ 3,5.
Ta coù:
Xi 0 0,5 1,5 2,5 3,5 4,5 5,5 6,5
ni 10 35 86 132 78 31 18 10
n 400;=
i i
X n 1053;=
∑
2
i i
X
n 3577,5.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 2, 6325.
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2
i i
1
S X n X (1, 4190) .
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2
n
S S (1,4208) .
n 1
= =
−
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (2, 6325 3,5) 400
z 12, 2114.
S 1,4208
− μ −
= = = −
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1- α)/2 = 0,98/2 = 0,49
ta ñöôïc z
α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì |z| = 12,2114 > 2,33 = z
α
neân ta baùc boû giaû
thieát H
0
: : μ = 3,5, chaáp nhaän giaû thieát H
1
μ ≠ 3,5.
6
Keát luaän: Vôùi möùc yù nghóa 5%, khoâng theå cho raèng nhu caàu trung bình
veà maët haøng naøy cuûa toaøn khu vöïc laø 14taán/thaùng.
Baøi 4.6. Troïng löôïng cuûa moät loaïi gaøø coâng nghieäp ôû moät traïi chaên nuoâi coù
phaân phoái chuaån. Troïng löôïng trung bình khi xuaát chuoàng naêm tröôùc laø
2,8kg/con. Naêm nay, ngöôøi ta söû duïng moät loaïi thöùc aên môùi. Caân thöû 25
con khi xuaát chuoàng ngöôøi ta tính ñöôïc trung bình maãu laø 3,2kg vaø
phöông sai maãu hieäu chænh 0,25kg
2
.
a) Vôùi möùc yù nghóa 5%, haõy keát luaän xem loaïi thöùc aên môùi coù thöïc söï
laøm taêng troïng löôïng trung bình cuûa ñaøn gaø hay khoâng?
b) Neáu traïi chaên nuoâi baùo caùo troïng löôïng trung bình khi xuaát chuoàng
laø 3,3kg/con thì coù chaáp nhaän ñöôïc khoâng vôùi möùc yù nghóa 5%?
Lôøi giaûi
Goïi X laø troïng löôïng cuûa moät con gaø sau khi söû duïng loaïi thöùc aên môùi.
Giaû thieát cho ta:
• X coù phaân phoái chuaån.
• Côõ maãu n = 25.
• Kyø voïng maãu cuûa X laø
X 3,2(kg)=
.
•
Phöông sai maãu hieäu chænh cuûa X laø S
2
= 0,25(kg ).
2
•
Ñoä leäch maãu hieäu chænh cuûa X laø S
= 0,5(kg).
a) Vôùi möùc yù nghóa 5%, haõy keát luaän xem loaïi thöùc aên môùi coù thöïc söï laøm
taêng troïng löôïng trung bình cuûa ñaøn gaø hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 5% = 0,05:
H
0
: μ = 2,8 vôùi giaû thieát ñoái H
1
: μ > 2,8.
Vì n < 30; X coù phaân phoái chuaån;
σ
2
= D(X) chöa bieát, neân ta kieåm ñònh
nhö sau:
Böôùc 1: Ta coù
0
(X ) n (3,2 2,8) 25
z 4.
S 0,5
− μ −
= = =
Böôùc 2: Ñaët k = n
-1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø 2
α = 0,1 ta ñöôïc
k
2 2
t t 1,711.
α α
= =
Böôùc 3: Kieåm ñònh. Vì z = 4 > 1,711 = t
2α
neân ta baùc boû giaû thieát
H
0
: μ = 2,8, ghóa laø chaáp nhaän giaû thieát H
1
: μ > 2,8.
Keát luaän: Vôùi möùc yù nghóa 5%, loaïi thöùc aên môùi thöïc söï laøm taêng
troïng löôïng trung bình cuûa ñaøn gaø.
7
b) Neáu traïi chaên nuoâi baùo caùo troïng löôïng trung bình khi xuaát chuoàng laø
3,3kg/con thì coù chaáp nhaän ñöôïc khoâng vôùi möùc yù nghóa 5%?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 5% = 0,05:
H
0
: μ = 3,3 vôùi giaû thieát ñoái H
1
: μ ≠ 3,3.
Vì n < 30; X coù phaân phoái chuaån;
σ
2
= D(X) chöa bieát, neân ta kieåm ñònh
nhö sau:
Böôùc 1: Ta coù
0
(X ) n
(3, 2 3, 3) 25
z 1.
S 0,5
− μ
−
= = = −
Böôùc 2: Ñaët k = n
-1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø
α = 0,05 ta ñöôïc
k
t t 2,064.
α α
= =
Böôùc 3: Kieåm ñònh. Vì |z| = 1 < 2,064 = t
α
neân ta chaáp nhaän giaû thieát
H
0
: μ = 3,3.
Keát luaän: Vôùi möùc yù nghóa 5%, baùo caùo troïng löôïng trung bình khi
xuaát chuoàng laø 3,3kg/con laø chaáp nhaän ñöôïc.
Baøi 4.7. Chieàu cao trung bình cuûa 100 nam sinh lôùp 12 ôû moät tröôøng
trung hoïc noäi thaønh laø 1,68m vôùi ñoä leäch maãu hieäu chænh 6cm. Trong khi
kieåm tra 120 nam sinh lôùp 12 ôû moät huyeän ngoaïi thaønh thì chieàu cao
trung bình laø 1,64m vôùi ñoä leäch maãu hieäu chænh 5cm. Vôùi möùc yù nghóa 1%,
coù theå keát luaän raèng nam sinh noäi thaønh thöïc söï cao hôn nam sinh ngoaïi
thaønh hay khoâng?
Lôøi giaûi
Goïi X, Y (cm) laàn löôït laø chiều cao cuûa nam sinh noäi thaønh vaø nam
sinh ngoaïi thaønh. Baøi toaùn treân chính laø baøi toaùn kieåm ñònh so saùnh hai
kyø voïng vôùi möùc yù nghóa α = 1% = 0,01:
H
0
: μ
X
= μ
Y
vôùi giaû thieát ñoái H
1
: μ
X
> μ
Y
.
1) Ñoái vôùi X, giaû thieát cho ta:
• Côõ maãu n
X
= 100.
• Kyø voïng maãu cuûa X laø
X 168(cm)= .
•
Ñoä leäch maãu hieäu chænh cuûa X laø S
X
= 6(cm).
2) Ñoái vôùi Y, giaû thieát cho ta:
• Côõ maãu n
Y
= 120
• Kyø voïng maãu cuûa Y laø
Y 164(cm)=
.
•
Ñoä leäch maãu hieäu chænh cuûa Y laø S
Y
= 5(cm).
8
Vì n
X
> 30; n
Y
> 30 neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù:
2 2 2 2
X Y
X Y
X Y 168 164
z 5,3059.
S S 6 5
100 120n n
− −
= = =
++
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,98/2 = 0,49
ta ñöôïc z
2α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì z = 5,3059 > 2,33 = z
2α
neân ta baùc boû giaû
thieát : H
0
μ
X
= μ
Y
, nghóa laø chaáp nhaän H
1
: μ
X
> μ
Y
.
Keát luaän: Vôùi möùc yù nghóa 1%, coù theå keát luaän raèng nam sinh noäi
thaønh thöïc söï cao hôn nam sinh ngoaïi thaønh.
Baøi 4.8. Moät hôïp taùc xaõ troàng thöû hai gioáng luùa, moãi gioáng treân 30 thöûa
ruoäng vaø ñöôïc chaêm soùc nhö nhau. Cuoái vuï thu hoaïch ta ñöôïc soá lieäu nhö
sau:
Naêng suaát trung bình (taï/ha) Ñoä leäch maãu hieäu chænh
Gioáng luùa 1 45 2,5
Gioáng luùa 2 46,5 4,0
a) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa hai gioáng luùa treân
laø nhö nhau hay khoâng?
b) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa gioáng luùa 2 cao
hôn cuûa gioáng luùa 1 hay khoâng?
Lôøi giaûi
Goïi X, Y (taï/ha) laàn löôït laø naêng suaát cuûa gioáng luùa 1 vaø 2. Khi ñoù:
1) Ñoái vôùi X, giaû thieát cho ta:
• Côõ maãu n
X
= 30.
• Kyø voïng maãu cuûa X laø
X
= 45.
•
Ñoä leäch maãu hieäu chænh cuûa X laø S
X
= 2,5.
2) Ñoái vôùi Y, giaû thieát cho ta:
• Côõ maãu n
Y
= 30.
• Kyø voïng maãu cuûa Y laø
Y
= 46,5.
•
Ñoä leäch maãu hieäu chænh cuûa Y laø S
Y
= 4.
a) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa hai gioáng luùa treân laø
nhö nhau hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa
2% = 0,02:
H
0
: μ
X
= μ
Y
vôùi giaû thieát ñoái H
1
: μ
X
≠ μ
Y
.
Vì n
X
= n
Y
= 30 neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù:
9
2 2 2 2
X Y
X Y
X Y 45 46,5
z 1,7418.
S S 2, 5 4
30 30n n
− −
= = = −
++
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1 - α)/2 = 0,98/2 = 0,49
ta ñöôïc z
α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,7418 < 2,33 = z
α
neân ta chaáp nhaänû
giaû thieát H
0
: μ
X
= μ
Y
.
Keát luaän: Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa hai gioáng
luùa treân laø nhö nhau.
b) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa gioáng luùa 2 cao hôn
cuûa gioáng luùa 1 hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa α =
2% = 0,02:
H
0
: μ
X
= μ
Y
vôùi giaû thieát ñoái H
1
: μ
X
< μ
Y
.
Vì n
X
= n
Y
= 30 neân ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu a), ta coù:
2 2
X Y
X Y
X Y
z 1,7418.
S S
n n
−
= = −
+
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,96/2 = 0,48
ta ñöôïc z
2α
= 2,06.
Böôùc 3: Kieåm ñònh. Vì -z = 1,7418 < 2,06 = z
2α
neân ta chaáp nhaänûû
giaû thieát H
0
: μ
X
= μ
Y
.
Keát luaän: Vôùi möùc yù nghóa 2%, chöa theå xem naêng suaát cuûa gioáng
luùa 2 cao hôn cuûa gioáng luùa 1.
Baøi 4.9. Moät maùy saûn xuaát töï ñoäng, luùc ñaàu tæ leä saûn phaåm loaïi A laø 45%.
Sau khi aùp duïng moät phöông phaùp saûn xuaát môùi, ngöôøi ta laáy ra 400 saûn
phaåm ñeå kieåm tra thì thaáy coù 215 saûn phaåm loaïi A. Vôùi möùc yù nghóa 5%,
haõy keát luaän xem phöông phaùp môùi coù thöïc söï laøm taêng tæ leä saûn phaåm
loaïi A hay khoâng?
Lôøi giaûi
Töø giaû thieát ta suy ra:
• Côõ maãu n = 400.
• Soá saûn phaåm loaïi A coù trong maãu laø m = 215.
• Tæ leä maãu saûn phaåm loaïi A laø F
n
= m/n = 215/400 = 0,5375.
10
Ta ñöa baøi toaùn veà baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn
phaåm loaïi A vôùi möùc yù nghóa α = 5% = 0,05:
H
0
: p = 45% = 0,45 vôùi giaû thieát ñoái H
1
: p > 0,45.
Ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
n 0
0 0
(F p ) n (0,5375 0,45) 400
z 3,5176.
p (1 p ) 0,45(1 0,45)
− −
= = =
− −
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,90/2 = 0,45
ta ñöôïc z
2α
= 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 3,5176 > 1,65= z
2α
neân ta baùc boû giaû thieát
H
0
: p = 0,45, nghóa laø chaáp nhaän H
1
: p > 0,45.
Keát luaän: Vôùi möùc yù nghóa 5%, phöông phaùp môùi thöïc söï laøm taêng tæ leä
saûn phaåm loaïi A.
Baøi 4.10. Thoáng keâ 10650 treû sô sinh ôû moät ñòa phöông ngöôøi ta thaáy coù
5410 beù trai.
a) Vôùi möùc yù nghóa 3%, hoûi coù söï khaùc bieät veà tæ leä sinh beù trai vaø beù
gaùi hay khoâng?
b) Vôùi möùc yù nghóa 1%, hoûi tæ leä sinh beù trai coù thöïc söï cao hôn tæ leä
sinh beù gaùi hay khoâng?
Lôøi giaûi
Töø caùc giaû thieát cuûa baøi toaùn ta suy ra:
1) Khi khaûo saùt tæ leä beù trai p
1
:
• Côõ maãu n
1
= 10650.
• Soá beù trai laø m
1
= 5410.
• Tæ leä beù trai F
n1
= 5410/10650.
2) Khi khaûo saùt tæ leä beù gaùi p
2
:
• Côõ maãu n
2
= 10650.
• Soá beù gaùi laø m
2
= 10650 – 5410 = 5240.
• Tæ leä beù gaùi F
n2
= 5240/10650.
3) p
0
= 0,5.
a) Vôùi möùc yù nghóa 3%, hoûi coù söï khaùc bieät veà tæ leä sinh beù trai vaø beù gaùi
hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
α = 3% = 0,03:
H
0
: p
1
= p
2
(= p
0
) vôùi giaû thieát ñoái H
1
: p
1
≠ p
2
11
Ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù:
n1 n2
0 0
1 2
5410 5240
F F
10650 10650
z 2, 3296.
1 1
1 1
0,5(1 0,5)
p (1 p )
10650 10650
n n
−
−
= = =
⎛ ⎞ ⎛ ⎞
− +
− +
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1 - α)/2 = 0,97/2 = 0,485
ta ñöôïc z
α
= 2,17.
Böôùc 3: Kieåm ñònh. Vì |z| = 2,3296 > 2,17 = z
α
neân ta baùc boû giaû
thieát H
0
: p
1
= p
2
, nghóa laø chaáp nhaän H
1
: p
1
≠ p .
2
Keát luaän: Vôùi möùc yù nghóa 3%, coù söï khaùc bieät veà tæ leä sinh beù trai vaø
beù gaùi.
b) Vôùi möùc yù nghóa 1%, hoûi tæ leä sinh beù trai coù thöïc söï cao hôn tæ leä sinh
beù gaùi hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
α = 1% = 0,01:
H
0
: p
1
= p
2
vôùi giaû thieát ñoái H
1
: p
1
> p
2
Ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu a), ta coù:
n1 n2
0 0
1 2
F F
z 2, 3296.
1 1
p (1 p )
n n
−
= =
⎛ ⎞
− +
⎜ ⎟
⎝ ⎠
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,98/2 = 0,49
ta ñöôïc z
2α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì z = 2,3296 < 2,33 = z
2α
neân ta chaáp nhaän giaû
thieát H
0
: p
1
= p
2
.
Keát luaän: Vôùi möùc yù nghóa 1%, chöa theå noùi tæ leä sinh beù trai thöïc söï
cao hôn tæ leä sinh beù gaùi.
Baøi 4.11. Beänh A coù theå chöõa baèng hai loaïi thuoác H vaø K. Coâng ty saûn
xuaát thuoác H tuyeân boá tæ leä beänh nhaân khoûi beänh do duøng thuoác cuûa hoï laø
85%. Ngöôøi ta duøng thöû thuoác H chöõa cho 250 beänh nhaân thì thaáy coù 210
ngöôøi khoûi beänh, duøng thöû thuoác K cho 200 beänh nhaân thì thaáy coù 175
ngöôøi khoûi beänh.
a) Vôùi möùc yù nghóa 1% coù theå keát luaän thuoác K coù khaû naêng chöõa beänh
A toát hôn thuoác H hay khoâng?
b) Xeùt xem hieäu quaû chöõa beänh cuûa thuoác H coù ñuùng nhö coâng ty
quaûng caùo vôùi möùc yù nghóa 5% hay khoâng.
12
Lôøi giaûi
Töø caùc giaû thieát cuûa baøi toaùn ta suy ra:
1) Ñoái vôùi loaïi thuoác H:
• Côõ maãu n
1
= 250.
• Soá beänh nhaân khoûi beänh: 210.
• Tæ leä maãu beänh nhaân khoûi beänh F
n1
= 210/250 = 0,84.
2) Ñoái vôùi loaïi thuoác K:
• Côõ maãu n
2
= 200.
• Soá beänh nhaân khoûi beänh: 175.
• Tæ leä maãu beänh nhaân khoûi beänh F
n2
= 175/200 = 0,875.
1 n1 2 n2
0
1 2
n F n F 250.0,84 200.0,875 385
3) p .
n n 250 200 450
+
+
= = =
+ +
a) Vôùi möùc yù nghóa 1% coù theå keát luaän thuoác K coù khaû naêng chöõa beänh A
toát hôn thuoác H hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
α = 1% = 0,01:
H
0
: p
1
= p
2
vôùi giaû thieát ñoái H
1
: p
1
< p
2
Ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù:
n1 n2
0 0
1 2
F F 0,84 0,875
z 1,0495.
385 385 1 1
1 1
1
p (1 p )
450 450 250 200
n n
−
−
= = = −
⎛ ⎞ ⎛ ⎞ ⎛ ⎞
− +
− +
⎜ ⎟⎜ ⎟
⎜ ⎟
⎝ ⎠⎝ ⎠
⎝ ⎠
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,98/2 = 0,49
ta ñöôïc z
2α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì -z = 1,0495 < 2,33 = z
2α
neân ta chaáp nhaän giaû
thieát H
0
: p
1
= p
2
.
Keát luaän: Vôùi möùc yù nghóa 1%, khoâng theå keát luaän thuoác K coù khaû
naêng chöõa beänh A toát hôn thuoác H.
b) Xeùt xem hieäu quaû chöõa beänh cuûa thuoác H coù ñuùng nhö coâng ty quaûng
caùo vôùi möùc yù nghóa 5% hay khoâng.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p
1
caùc beänh nhaân khoûi
beänh A khi ñöôïc ñieàu trò baèng thuoác H vôùi möùc yù nghóa α = 5% = 0,05:
H
0
: p
1
= 85% = 0,85 vôùi giaû thieát ñoái H
1
: p
1
< 0,85.
Ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
13
n1 01 1
01 01
(F p ) n
(0, 84 0,85) 250
z 0,4428.
p q 0,85(1 0, 85)
−
−
= = = −
−
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,90/2 = 0,45
ta ñöôïc z
2α
= 1,65.
Böôùc 3: Kieåm ñònh. Vì - z = 0,4428 < 1,65 = z
2α
neân ta chaáp nhaän
giaû thieát H
0
: p
1
= 0,85.
Keát luaän: Vôùi möùc yù nghóa 5%, hieäu quaû chöõa beänh cuûa thuoác H ñuùng
nhö coâng ty quaûng caùo.
Baøi 4.12. Ñeå khaûo saùt chæ tieâu X cuûa moät loaïi saûn phaåm, ngöôøi ta quan
saùt moät maãu vaø coù keát quûa sau:
X(cm) 11-15 15-19 19-23 23-27 27-31 31-35 35-39
Soásaûn phaåm 8 9 20 16 16 13 18
Nhöõng saûn phaåm coù chæ tieâu X töø 19cm trôû xuoáng ñöôïc goïi laø nhöõng saûn
phaåm loaïi B.
a) Giaû söû trung bình tieâu chuaån cuûa chæ tieâu X laø 29cm. Haõy cho nhaän xeùt
veà tình hình saûn xuaát vôùi möùc yù nghóa 2%.
b) Baèng phöông phaùp saûn xuaát môùi, sau moät thôøi gian ngöôøi ta thaáy giaù
trò trung bình cuûa chæ tieâu X cuûa nhöõng saûn phaåm loaïi B laø 16cm. Haõy
cho keát luaän veà phöông phaùp saûn xuaát môùi vôùi möùc yù nghóa 1% (GS X
coù phaân phoái chuaån).
c) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä nhöõng saûn phaåm loaïi B laø
12%. Haõy nhaän ñònh veà taøi lieäu naøy vôùi möùc yù nghóa 5%.
Lôøi giaûi
Laäp baûng:
X
i
13 17 21 25 29 33 37
n
i
8 9 20 16 16 13 18
Ta coù:
;100=n
i i
X n 2636;=
∑
2
i i
X n 75028.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 26, 36(cm).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (7,4452) (cm ).
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa X laø:
14
2
2 2 2
n
S S (7,4827) (cm ).
n 1
= =
−
a) Giaû söû trung bình tieâu chuaån cuûa chæ tieâu X laø 29cm. Haõy cho nhaän
xeùt veà tình hình saûn xuaát vôùi möùc yù nghóa 2%.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 2% = 0,02:
H
0
: μ = 29 vôùi giaû thieát ñoái H
1
: μ ≠ 29.
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (26,36 29) 100
z 3, 5281.
S 7,4827
− μ −
= = = −
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1- α)/2 = 0,98/2 = 0,49
ta ñöôïc z
α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì |z|= 3,5281 > 2,33 = z
α
neân ta baùc boû giaû thieát
H
0
: : μ=29, nghóa laø chaáp nhaän H
1
μ ≠ 29.
Keát luaän: Vôùi möùc yù nghóa 1%, tình hình saûn xuaát khoâng bình thöôøng
vì giaù trò trung bình cuûa chæ tieâu X khoâng ñuùng tieâu chuaån.
b) Baèng phöông phaùp saûn xuaát môùi, sau moät thôøi gian ngöôøi ta thaáy giaù
trò trung bình cuûa chæ tieâu X cuûa nhöõng saûn phaåm loaïi B laø 16cm. Haõy
cho keát luaän veà phöông phaùp saûn xuaát môùi vôùi möùc yù nghóa 1% (GS X
coù phaân phoái chuaån).
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
B
= M(X
B
) cuûa chæ tieâu
X = X
B
cuûa nhöõng saûn phaåm loaïi B vôùi möùc yù nghóa α = 1% = 0,01:
H
0
: μ
B
= 16 vôùi giaû thieát ñoái H
1
: μ
B
≠ 16.
Ta laäp baûng soá lieäu cuûa X
B
:
X
Bi
13 17
n
Bi
8 9
Töø baûng treân ta tính ñöôïc:
;17
=
B
n ;257
∑
=
BiBi
nX
2
Bi Bi
X n 3, 953.=
∑
• Kyø voïng maãu cuûa X
B
laø
∑
== ).(1176,15
1
cmnX
n
X
BiBiB
• Phöông sai maãu cuûa X
B
laø:
2
2 2 2 2
B
Bi Bi B
1
S X n X (1,9965) (cm ).
n
= − =
∑
• Phöông sai maãu ñaõ hieäu chænh cuûa X
B
laø:
2
2 2 2
B
B
B
B
n
S S (2,0580) (cm ).
n 1
= =
−
15
Vì n
B
< 30, X
B
coù phaân phoái chuaån, σ
2
B
= D(X
B
) chöa bieát, neân ta kieåm
ñònh nhö sau:
Böôùc 1: Ta coù
B 0 B
B
(X ) n
(15,1176 16) 17
z 1,7678.
S 2, 0580
− μ
−
= = = −
Böôùc 2: Ñaët k = n
B
-1 = 16. Tra baûng phaân phoái Student öùng vôùi k =
16 vaø α = 0,01 ta ñöôïc
t
α
= 2,921.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,7678 < 2,921= t
α
neân ta chaáp nhaän giaû
thieát H
0
: μ
B
= 16.
Keát luaän: Vôùi möùc yù nghóa 2%, phöông phaùp môùi khoâng coù taùc duïng
laøm thay ñoåi giaù trò trung bình cuûa chæ tieâu X
B
cuûa caùc saûn phaåm loaïi B.
c) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä saûn phaåm loaïi B laø 12%. Haõy
nhaän ñònh veà taøi lieäu naøy vôùi möùc yù nghóa 5%.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn phaåm loaïi B
vôùi möùc yù nghóa α = 5% = 0,05:
H
0
: p = 12% = 0,12 vôùi giaû thieát ñoái H
1
: p ≠ 0,12.
Ta coù qui taéc kieåm ñònh nhö sau:
Böôùc 1: Ta coù
n 0
0 0
(F p ) n (0,17 0,12) 100
z 1,5386.
p q 0,12(1 0,12)
− −
= = =
−
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1- α)/2 = 0,95/2 = 0,475
ta ñöôïc z
α
= 1,96.
Böôùc 3: Kieåm ñònh.
Vì |z| = 1,5386 < 1,96 = z
α
neân ta chaáp nhaän giaû
thieát H
0
: p = 0,12.
Keát luaän:
Vôùi möùc yù nghóa 5%, taøi lieäu cuõ veà tæ leä saûn phaåm loaïi B coøn
phuø hôïp.
Baøi 4.13. Ñeå khaûo saùt chieàu cao X cuûa moät gioáng caây troàng, ngöôøi ta quan
saùt moät maãu vaø coù keát quûa sau:
X(cm) 95-105 105-115 115-125 125-135 135-145 145-155 155-165
Soá caây 10 10 15 30 10 10 15
a) Moät taøi lieäu thoáng keâ cuõ cho raèng chieàu cao trung bình cuûa gioáng caây
troàng treân laø 127cm. Haõy cho keát luaän veà taøi lieäu ñoù vôùi möùc yù nghóa
1%.
b) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
“cao”. Tröôùc ñaây, tæ leä nhöõng caây “cao” cuûa loaïi caây troàng treân laø 40%.
Caùc soá lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi.
Haõy cho keát luaän veà kyõ thuaät môùi vôùi möùc yù nghóa 5%.
16
c) Nhöõng caây troàng coù chieàu cao töø 105cm ñeán 125cm ñöôïc goïi laø nhöõng
caây loaïi A. Baèng phöông phaùp môùi, sau moät thôøi gian ngöôøi ta thaáy
chieàu cao trung bình cuûa nhöõng caây loaïi A laø 119,5cm. Haõy cho keát
luaän veà phöông phaùp môùi vôùi möùc yù nghóa 1% (GS X coù phaân phoái
chuaån).
Lôøi giaûi
X
i
100 110 120 130 140 150 160
n
i
10 10 15 30 10 10 15
Ta coù:
;100
=
n
i i
X n 13100;=
∑
2
i i
X n 1749000.=
∑
• Kyø voïng maãu cuûa X laø
i i
1
X X n 131(cm).
n
= =
∑
• Phöông sai maãu cuûa X laø:
2
2 2 2 2
i i
1
S X n X (18,1384) (cm ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø:
2
2 2 2
n
S S (18,2297) (cm ).
n 1
= =
−
a) Moät taøi lieäu thoáng keâ cuõ cho raèng chieàu cao trung bình cuûa gioáng caây
troàng treân laø 127cm. Haõy cho keát luaän veà taøi lieäu ñoù vôùi möùc yù nghóa
1%.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 1% = 0,01:
H
0
: μ = 127 vôùi giaû thieát ñoái H
1
: μ ≠ 127
Vì n
≥ 30; σ
2
chöa bieát, neân ta coù qui taéc kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (131 127) 100
z 2,1942.
S 18, 2297
− μ −
= = =
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1 - α)/2 = 0,99/2 = 0,495
ta ñöôïc z
α
= 2,58.
Böôùc 3: Kieåm ñònh. Vì |z| = 2,1942 < 2,58 = z
α
neân ta chaáp nhaän
H
0
: μ = 127.
Keát luaän: Vôùi möùc yù nghóa 1%, taøi lieäu cuõ veà chieàu cao trung bình cuûa
gioáng caây troàng treân coøn phuø hôïp vôùi thöïc teá.
b) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
“cao”. Tröôùc ñaây, tæ leä nhöõng caây “cao” cuûa loaïi caây troàng treân laø 40%.
17
Caùc soá lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi.
Haõy cho keát luaän veà kyõ thuaät môùi vôùi möùc yù nghóa 5%.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc caây cao vôùi möùc yù
nghóa α = 5% = 0,05:
H
0
: p = 40% = 0,4 vôùi giaû thieát ñoái H
1
: p ≠ 0,4
Ta coù qui taéc kieåm ñònh nhö sau:
Böôùc 1: Ta coù
n 0
0 0
(F p ) n (0,35 0, 4) 100
z 1, 0206.
p q 0,4(1 0,4)
− −
= = = −
−
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ( z
α
) = (1 - α)/2 = 0,95/2 = 0,475
ta ñöôïc z
α
= 1,96.
Böôùc 3: Kieåm ñònh.
Vì|z| = 1,0206 < 1,96 = z
α
neân ta chaáp nhaän giaû
thieát H
0
: p = 0,4.
Keát luaän: Vôùi möùc yù nghóa 5%, phöông phaùp môùi khoâng coù taùc duïng
laøm thay ñoåi tæ leä caùc caây cao.
c) Nhöõng caây troàng coù chieàu cao töø 105cm ñeán 125cm ñöôïc goïi laø nhöõng
caây loaïi A. Baèng phöông phaùp môùi, sau moät thôøi gian ngöôøi ta thaáy
chieàu cao trung bình cuûa nhöõng caây loaïi A laø 119,5cm. Haõy cho keát
luaän veà phöông phaùp môùi vôùi möùc yù nghóa 1% (GS X coù phaân phoái
chuaån).
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
A
= M(X
A
) cuûa chieàu
cao X = X
A
cuûa caùc caây loaïi A vôùi möùc yù nghóa α = 1% = 0,01:
H
0
: μ
A
= 119,5 vôùi giaû thieát ñoái H
1
: μ
A
≠ 119,5.
Ta laäp baûng soá lieäu cuûa X
A
:
X
Ai
110 120
N
Ai
10 15
Töø baûng treân ta tính ñöôïc:
A
n 25;=
Ai Ai
X
n 2900;=
∑
2
Ai Ai
X n 337000.=
∑
- Kyø voïng maãu cuûa X
A
laø
A Ai Ai
1
X X n 116(cm).
n
= =
∑
- Phöông sai maãu cuûa X
A
laø:
2
2 2 2 2
A
Ai Ai A
1
S X n X (4, 8990) (cm ).
n
= − =
∑
- Phöông sai maãu hieäu chænh cuûa X
A
laø:
2
2 2 2A
A
A
A
n
S S 5 (cm ).
n 1
= =
−
18
Vì n
A
= 25 < 30, X
A
coù phaân phoái chuaån, σ
2
A
= D(X
A
) chöa bieát, neân ta
kieåm ñònh nhö sau:
Böôùc 1: Ta coù
A 0 A
A
(X ) n
(116 119,5) 25
z 3, 5.
S 5
− μ
−
= = = −
Böôùc 2: Ñaët k = n
A
- 1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø
α = 0,01 ta ñöôïc
k
t t
α
α
= = 2,797.
Böôùc 3: Kieåm ñònh. Vì |z| = 3,5 > 2,797 = t
α
neân ta baùc boû giaû thieát
H
0
: μ
A
= 119,5, nghóa laø chaáp nhaän H
1
: μ
A
≠ 119,5. Cuï theå, ta nhaän ñònh
μ
A
< 119,5 (vì
A
X 116 119,5= <
).
Keát luaän: Vôùi möùc yù nghóa 1%, phöông phaùp môùi coù taùc duïng laøm thay
ñoåi chieàu cao trung bình cuûa caùc caây loaïi A, theo höôùng laøm taêng chieàu
cao trung bình cuûa caùc caây loaïi naøy.
Baøi 4.14. Cho caùc soá lieäu nhö Baøi 4.13.
a) Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 125cm. Coù theå khaúng
ñònh raèng vieäc canh taùc laøm taêng chieàu cao trung bình cuûa gioáng caây
troàng treân vôùi möùc yù nghóa 1% hay khoâng?
b) Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 134cm. Coù theå khaúng
ñònh raèng vieäc canh taùc laøm giaûm chieàu cao trung bình cuûa gioáng caây
troàng treân vôùi möùc yù nghóa 2% hay khoâng?
c) Sau khi aùp duïng phöông phaùp canh taùc môùi, ngöôøi ta thaáy chieàu cao
trung bình cuûa caùc caây loaïi A laø 114cm. Haõy keát luaän xem phöông phaùp
môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây loaïi A hay khoâng
vôùi möùc yù nghóa 3% (Giaû söû X coù phaân phoái chuaån).
d) Tröôùc ñaây, chieàu cao trung bình cuûa caùc caây loaïi A laø 120cm. Caùc soá
lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi. Haõy keát
luaän xem kyõ thuaät môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây
loaïi A hay khoâng vôùi möùc yù nghóa 2% (Giaû söû X coù phaân phoái chuaån).
e) Sau khi aùp duïng moät phöông phaùp saûn xuaát, ngöôøi ta thaáy tæ leä caây loaïi
A laø 35%. Haõy keát luaän xem phöông phaùp môùi coù laøm taêng tæ leä caây
loaïi A leân hay khoâng vôùi möùc yù nghóa 2% .
f) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä caây loaïi A laø 20%. Haõy xeùt xem
vieäc canh taùc coù laøm taêng tæ leä caây loaïi A hay khoâng vôùi möùc yù nghóa
5%?
Lôøi giaûi
Ta coù:
• Côõ maãu laø n = 100.
• Kyø voïng maãu cuûa X laø
19
i i
1
X X n 131(cm).
n
= =
∑
• Phöông sai maãu cuûa X laø
2
2 2 2 2
i i
1
S X n X (18, 1384) (cm ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø
2
2 2 2
n
S S (18,2297) (cm ).
n 1
= =
−
a) Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 125cm. Coù theå khaúng
ñònh raèng vieäc canh taùc laøm taêng chieàu cao trung bình cuûa gioáng caây
troàng treân vôùi möùc yù nghóa 1% hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 1% = 0,01:
H
0
: μ = 125 vôùi giaû thieát ñoái H
1
: μ > 125.
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (131 125) 100
z 3, 2913.
S 18,2297
− μ −
= = =
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2 2α
thoaû ϕ(z
α
) = (1- 2α)/2
= 0,98/2 = 0,49 ta ñöôïc z
2α
= 2,33.
Böôùc 3: Kieåm ñònh. Vì z = 3,2913 > 2,33 = z
2α
neân ta baùc boû giaû thieát
H
0
: μ=125, nghóa laø chaáp nhaän H
1
: μ > 125.
Keát luaän: Vôùi möùc yù nghóa 1%, coù theå keát luaän raèng vieäc canh taùc laøm
taêng chieàu cao trung bình cuûa gioáng caây troàng treân.
b) Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 134cm. Coù theå khaúng
ñònh raèng vieäc canh taùc laøm giaûm chieàu cao trung bình cuûa gioáng caây
troàng treân vôùi möùc yù nghóa 2% hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
nghóa α = 2% = 0,02:
H
0
: μ = 134 vôùi giaû thieát ñoái H
1
: μ < 134.
Vì n
≥ 30; σ
2
= D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
0
(X ) n (131 134) 100
z 1,6457.
S 18,2297
− μ −
= = = −
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû )/2 ϕ(z
2α
) = (1- 2α
= 0,96/2 = 0,48 ta ñöôïc z
2α
= 2,06.
Böôùc 3: Kieåm ñònh. Vì –z = 1,6457 < 2,06 = z
2α
neân ta chaáp nhaän
giaû thieát H
0
: μ = 134.
20
Keát luaän: Vôùi möùc yù nghóa 2%, khoâng theå keát luaän raèng vieäc canh taùc
laøm giaûm chieàu cao trung bình cuûa gioáng caây troàng treân.
c) Sau khi aùp duïng phöông phaùp canh taùc môùi, ngöôøi ta thaáy chieàu cao
trung bình cuûa caùc caây loaïi A laø 114cm. Haõy keát luaän xem phöông
phaùp môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây loaïi A hay
khoâng vôùi möùc yù nghóa 3% (Giaû söû X coù phaân phoái chuaån).
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
A
= M(X
A
) cuûa chæ
tieâu X = X
A
cuûa caùc caây loaïi A vôùi möùc yù nghóa α = 3% = 0,03:
H H
0
: μ
A
= 114 vôùi giaû thieát ñoái
1
: μ
A
> 114.
Ta laäp baûng soá lieäu cuûa X
A
:
X
Ai
110 120
N
Ai
10 15
Töø baûng treân ta tính ñöôïc:
A
n 25;
=
Ai Ai
X n 2900;=
∑
2
Ai Ai
X
n 337000.=
∑
- Kyø voïng maãu cuûa X
A
laø
A Ai Ai
1
X X n 116(cm).
n
= =
∑
- Phöông sai maãu cuûa X
A
laø:
2
2 2 2 2
A
Ai Ai A
1
S X n X (4, 8990) (cm ).
n
= − =
∑
- Phöông sai maãu hieäu chænh cuûa X
A
laø:
2
2 2 2A
A
A
A
n
S S 5 (cm ).
n 1
= =
−
Vì n
A
< 30, X
A
coù phaân phoái chuaån, σ
2
A
= D(X
A
) chöa bieát, neân ta kieåm
ñònh nhö sau:
Böôùc 1: Ta coù
A 0 A
A
(X ) n
(116 114) 25
z 2.
S 5
− μ
−
= = =
Böôùc 2: Ñaët k = n
A
- 1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø 2α = 0,06 ta ñöôïc
2
t
α
= 1,974.
Böôùc 3: Kieåm ñònh. Vì z = 2 > 1,974 =
2
t
α
neân ta baùc boû giaû thieát
H
0
: μ
A
= 114, nghóa laø chaáp nhaän H
1
: μ
A
> 114.
Keát luaän: Vôùi möùc yù nghóa 3%, phöông phaùp môùi laøm giaûm chieàu cao
trung bình cuûa caùc caây loaïi A.
d) Tröôùc ñaây, chieàu cao trung bình cuûa caùc caây loaïi A laø 120cm. Caùc soá
lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi. Haõy keát
21
luaän xem kyõ thuaät môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây
loaïi A hay khoâng vôùi möùc yù nghóa 2% (Giaû söû X coù phaân phoái chuaån).
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
A
= M(X
A
) cuûa chæ
tieâu X = X
A
cuûa caùc caây loaïi A vôùi möùc yù nghóa α = 2% = 0,02:
H H
0
: μ
A
= 120 vôùi giaû thieát ñoái
1
: μ
A
< 120.
Vì n
A
< 30, X
A
coù phaân phoái chuaån, σ
2
A
= D(X
A
) chöa bieát, neân ta kieåm
ñònh nhö sau:
Böôùc 1: Ta coù
A 0 A
A
(X ) n
(116 120) 25
z 4.
S 5
− μ
−
= = = −
Böôùc 2: Ñaët k = n
A
- 1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø 2α = 0,04 ta ñöôïc
2
t
α
= 2,1715.
Böôùc 3: Kieåm ñònh. Vì - z = 4 > 2,1715 =
2
t
α
neân ta baùc boû giaû thieát
H
0
: μ
A
= 120, nghóa laø chaáp nhaän H
1
: μ
A
< 120.
Keát luaän: Vôùi möùc yù nghóa 2%, kyõ thuaät môùi laøm giaûm chieàu cao
trung bình cuûa caùc caây loaïi A.
e) Sau khi aùp duïng moät phöông phaùp saûn xuaát, ngöôøi ta thaáy tæ leä caây
loaïi A laø 35%. Haõy keát luaän xem phöông phaùp môùi coù laøm taêng tæ leä
caây loaïi A leân hay khoâng vôùi möùc yù nghóa 2% .
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn phaåm loaïi A
vôùi möùc yù nghóa α = 2% = 0,02:
H
0
: p = 35% = 0,35 vôùi giaû thieát ñoái H
1
: p < 0,35.
Ta coù tæ leä maãu caùc caây loaïi A laø F
n
= 25/100 = 0,25. Ta kieåm ñònh
nhö sau:
Böôùc 1: Ta coù
n 0
0 0
(F p ) n (0,25 0, 35) 100
z 2, 0966.
p q 0,35(1 0, 35)
− −
= = = −
−
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,96/2 = 0,48
ta ñöôïc z
2α
= 2,06.
Böôùc 3: Kieåm ñònh. Vì -z= 2,0966 > 2,06 = z
2α
neân ta baùc boû giaû thieát
H
0
: p = 0,35, nghóa laø chaáp nhaän H
1
: p < 0,35.
Keát luaän: Vôùi möùc yù nghóa 2%, phöông phaùp môùi laøm taêng tæ leä caây
loaïi A.
f) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä caây loaïi A laø 20%. Haõy xeùt xem
vieäc canh taùc coù laøm taêng tæ leä caây loaïi A hay khoâng vôùi möùc yù nghóa
5%?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn phaåm loaïi A vôùi
möùc yù nghóa α = 5% = 0,05:
22
H
0
: p = 20% = 0,20 vôùi giaû thieát ñoái H
1
: p > 0,20.
Ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù
n 0
0 0
(F p ) n (0, 25 0,20) 100
z 1, 25.
p q 0, 20(1 0,20)
− −
= = =
−
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,90/2 = 0,45
ta ñöôïc z
2α
= 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 1,25 < 1,65 = z
2α
neân ta chaáp nhaän giaû
thieát H
0
: p = 0,20.
Keát luaän: Vôùi möùc yù nghóa 5%, vieäc canh taùc khoâng laøm taêng tæ leä caùc
caây loaïi A.
Baøi 4.15. Ñeå khaûo saùt ñöôøng kính cuûa moät chi tieát maùy ngöôøi ta kieåm tra
moät soá saûn phaåm cuûa hai nhaø maùy. Trong keát quaû sau ñaây, X laø ñöôøng
kính cuûa chi tieát maùy do nhaø maùy 1 saûn xuaát coøn Y laø ñöôøng kính cuûa chi
tieát maùy do nhaø maùy 2 saûn xuaát. Nhöõng saûn phaåm coù chi tieát maùy nhoû
hôn 19cm ñöôïc xeáp vaøo loaïi C.
X(cm) 11-15 15-19 19-23 23-27 27-31 31-35 35-39
Soá saûn phaåm 9 19 20 26 16 13 18
Y(cm) 13-16 16-19 19-22 22-25 25-28 28-31 31-34
Soá saûn phaåm 7 9 25 26 18 15 11
a) Coù theå keát luaän raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do
hai nhaø maùy saûn xuaát baèng nhau hay khoâng vôùi möùc yù nghóa 1%?
b) Coù theå cho raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø
maùy thöù 1 saûn xuaát lôùn hôn ñöôøng kính trung bình cuûa moät chi tieát
maùy do nhaø maùy thöù 2 saûn xuaát hay khoâng vôùi möùc yù nghóa 5%?
c) Xeùt xem ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø maùy
thöù 2 saûn xuaát coù nhoû hôn ñöôøng kính trung bình cuûa moät chi tieát
maùy do nhaø maùy thöù 1 saûn xuaát hay khoâng vôùi möùc yù nghóa 2%?
d) Vôùi möùc yù nghóa 4%, tæ leä saûn phaåm loaïi C do hai nhaø maùy saûn xuaát
coù nhö nhau khoâng?
e) Vôùi möùc yù nghóa 3%, coù theå cho raèng tæ leä saûn phaåm loaïi C do nhaø
maùy thöù 1 saûn xuaát lôùn hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 2
saûn xuaát hay khoâng?
23
f) Haõy nhaän xeùt veà yù kieán cho raèng tæ leä saûn phaåm loaïi C do nhaø maùy
thöù 2 saûn xuaát nhoû hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 1
saûn xuaát vôùi möùc yù nghóa 5%?
Lôøi giaûi
1) Ñoái vôùi X ta coù baûng soá lieäu:
Xi 13 17 21 25 29 33 37
ni 9 19 20 26 16 13 18
Ta coù:
X
n 121;=
i Xi
X n 3069;=
∑
2
i Xi
X n 84337.=
∑
• Kyø voïng maãu cuûa X laø
i Xi
X
1
X X n 25, 3636(cm).
n
= =
∑
• Phöông sai maãu cuûa X laø
2
2 2 2 2
X
i Xi
X
1
S X n X (7, 3271) (cm ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa X laø
2
2 2 2
X
X
X
X
n
S S (7,3575) (cm ).
n 1
= =
−
• Tæ leä saûn phaåm loaïi C laø
X
Xn
X
m 9 19
F 0, 2314.
n 121
+
= = =
2) Ñoái vôùi Y ta coù baûng soá lieäu:
Yi 14,5 17,5 20,5 23,5 26,5 29,5 32,5
ni 7 9 25 26 18 15 11
Ta coù:
Y
n 111;=
i Yi
Y n 2659, 5;=
∑
2
i Yi
Y n 66405,75.=
∑
• Kyø voïng maãu cuûa Y laø
i Yi
Y
1
Y Yn 23, 9595(cm).
n
= =
∑
• Phöông sai maãu cuûa Y laø
2
2
2 2 2
Y
i Yi
Y
1
S Y n Y (4, 9188) (cm ).
n
= − =
∑
• Phöông sai maãu hieäu chænh cuûa Y laø
2
2 2 2Y
Y
Y
Y
n
S S (4, 9411) (cm ).
n 1
= =
−
• Tæ leä saûn phaåm loaïi C laø
24
Y
Yn
Y
m 7 9
F 0,1441.
n 111
+
= = =
a) Coù theå keát luaän raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do
hai nhaø maùy saûn xuaát baèng nhau hay khoâng vôùi möùc yù nghóa 1%?
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa
α = 1% = 0,01:
H
0
: μ
X
= μ
Y
vôùi giaû thieát ñoái H
1
: μ
X
≠ μ
Y
.
Vì n
X
> 30; n
Y
> 30 neân ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù:
2 2 2 2
X Y
X Y
X Y 25,3636 23,9595
z 1,7188.
S S (7,3575) (4,9411)
121 111n n
− −
= = =
++
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1 - α)/2 = 0,99/2 = 0,495
ta ñöôïc z
α
= 2,58.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,7188 < 2,58 = z
α
neân ta chaáp nhaänû
giaû thieát H
0
: μ
X
= μ
Y
.
Keát luaän: Vôùi möùc yù nghóa 1%, coù theå xem ñöôøng kính trung bình cuûa
moät chi tieát maùy do hai nhaø maùy saûn xuaát laø baèng nhau.
b) Coù theå cho raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø
maùy thöù 1 saûn xuaát lôùn hôn ñöôøng kính trung bình cuûa moät chi tieát
maùy do nhaø maùy thöù 2 saûn xuaát hay khoâng vôùi möùc yù nghóa 5%?
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa
α = 5% = 0,05:
H
0
: μ
X
= μ
Y
vôùi giaû thieát ñoái H
1
: μ
X
> μ
Y
.
Vì n
X
> 30; n
Y
> 30 neân ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu a), ta coù:
2 2
X Y
X Y
X Y
z 1,7188.
S S
n n
−
= =
+
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,90/2 = 0,45
ta ñöôïc z
2α
= 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 1,7188 > 1,65 = z
2α
neân ta baùc boûû giaû thieát
H
0
: μ
X
= μ
Y,
nghóa laø chaáp nhaän H
1
: . μ
X
> μ
Y
Keát luaän: Vôùi möùc yù nghóa 5%, coù theå xem ñöôøng kính trung bình cuûa
moät chi tieát maùy do nhaø maùy thöù 1 saûn xuaát lôùn hôn ñöôøng kính trung
bình cuûa moät chi tieát maùy do nhaø maùy thöù 2 saûn xuaát.
25
c) Xeùt xem ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø maùy thöù
2 saûn xuaát coù nhoû hôn ñöôøng kính trung bình cuûa moät chi tieát maùy do
nhaø maùy thöù 1 saûn xuaát hay khoâng vôùi möùc yù nghóa 2%?
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa
α = 2% = 0,02:
H
0
: μ
X
= μ
Y
vôùi giaû thieát ñoái H
1
: μ
X
> μ
Y
.
Vì n
X
> 30; n
Y
> 30 neân ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu a), ta coù:
2 2
X Y
X Y
X Y
z 1,7188.
S S
n n
−
= =
+
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,96/2 = 0,48
ta ñöôïc z
2α
= 2,06.
Böôùc 3: Kieåm ñònh. Vì z = 1,7188 < 2,06 = z
2α
neân ta chaáp nhaän giaû
thieát : H
0
μ
X
= μ
Y
.
Keát luaän: Vôùi möùc yù nghóa 2%, chöa theå xem ñöôøng kính trung bình
cuûa moät chi tieát maùy do nhaø maùy thöù 2 saûn xuaát nhoû hôn ñöôøng kính
trung bình cuûa moät chi tieát maùy do nhaø maùy thöù 1 saûn xuaát.
d) Vôùi möùc yù nghóa 4%, tæ leä saûn phaåm loaïi C do hai nhaø maùy saûn xuaát coù
nhö nhau khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
α = 4% = 0,04:
H
0
: p
1
= p
2
vôùi giaû thieát ñoái H
1
: p
1
≠ p
2
Ta kieåm ñònh nhö sau:
Böôùc 1: Ta coù:
1 n1 2 n2
0
1 2
n F n F 28 16
p 0,1897.
n n 121 111
+ +
= = =
+ +
n1 n2
0 0
1 2
F F 0,2314 0,1441
z 1,6942.
1 1
1 1
0,1897(1 0,1897)
p (1 p )
121 111
n n
− −
= = =
⎛ ⎞ ⎛ ⎞
− +
− +
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
α
thoaû
ϕ(z
α
) = (1 - α)/2 = 0,96/2 = 0,48
ta ñöôïc z
α
= 2,06.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,6942 < 2,06 = z
α
neân ta chaáp nhaän giaû
thieát H
0
: p
1
= p
2
.
Keát luaän: Vôùi möùc yù nghóa 4%, coù theå xem tæ leä saûn phaåm loaïi C do hai
nhaø maùy saûn xuaát laø nhö nhau.
26
e) Vôùi möùc yù nghóa 3%, coù theå cho raèng tæ leä saûn phaåm loaïi C do nhaø
maùy thöù 1 saûn xuaát lôùn hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 2
saûn xuaát hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
α = 3% = 0,03:
H
0
: p
1
= p
2
vôùi giaû thieát ñoái H
1
: p
1
> p
2
Ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu d), ta coù:
n1 n2
0 0
1 2
F F
z 1,6942.
1 1
p (1 p )
n n
−
= =
⎛ ⎞
− +
⎜ ⎟
⎝ ⎠
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,94/2 = 0,47
ta ñöôïc z
2α
= 1,88.
Böôùc 3: Kieåm ñònh. Vì z = 1,6942 < 1,88 = z
2α
neân ta chaáp nhaän giaû
thieát H
0
: p
1
= p
2
.
Keát luaän: Vôùi möùc yù nghóa 3%, chöa theå cho raèng tæ leä saûn phaåm loaïi
C do nhaø maùy thöù 1 saûn xuaát lôùn hôn tæ leä saûn phaåm loaïi C do nhaø maùy
thöù 2 saûn xuaát.
f) Haõy nhaän xeùt veà yù kieán cho raèng tæ leä saûn phaåm loaïi C do nhaø maùy
thöù 2 saûn xuaát nhoû hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 1 saûn
xuaát vôùi möùc yù nghóa 5%?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
α = 5% = 0,05:
H
0
: p
1
= p
2
vôùi giaû thieát ñoái H
1
: p
1
> p
2
Ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu d), ta coù:
n1 n2
0 0
1 2
F F
z 1,6942.
1 1
p (1 p )
n n
−
= =
⎛ ⎞
− +
⎜ ⎟
⎝ ⎠
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
2α
thoaû
ϕ(z
2α
) = (1 - 2α)/2 = 0,90/2 = 0,45
ta ñöôïc z
2α
= 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 1,6942 > 1,65 = z
2α
neân ta baùc boû giaû thieát
H
0
: p
1
= p
2
, nghóa laø chaáp nhaän H
1
: p
1
> p
2
.
Keát luaän: Vôùi möùc yù nghóa 5%, coù theå chaáp nhaän yù kieán cho raèng tæ leä
saûn phaåm loaïi C do nhaø maùy thöù 2 saûn xuaát nhoû hôn tæ leä saûn phaåm loaïi
C do nhaø maùy thöù 1 saûn xuaát.
------------------------------------------------------------------
| 1/53
| | Tải xuống

Có thể bạn quan tâm:

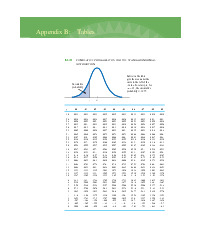
Preview text:

BAØI GIAÛI
P(A A A ) = P(A )P(A )P(A ) = 0, 7.0, 2.0, 5 = 0, 07; 1 2 3 1 2 3
P(A A A ) = P(A )P(A )P(A ) = 0, 3.0, 8.0, 5 = 0,12;
XAÙC SUAÁT THOÁNG KEÂ 1 2 3 1 2 3
P(A A A ) = P(A )P(A )P(A ) = 0, 3.0, 2.0, 5 = 0, 03.
(GV: Traàn Ngoïc Hoäi – 2009) 1 2 3 1 2 3 3 Suy ra P(A) = 0,22.
b) Goïi B laø bieán coá coù 2 khaåu truùng. Ta coù CHÖÔNG 1 B = A + + 1A 2A 3 A 1A 2A 3 A 1A 2A 3
NHÖÕNG ÑÒNH LYÙ CÔ BAÛN TRONG
Tính toaùn töông töï caâu a) ta ñöôïc P(B) = 0,47.
c) Goïi C laø bieán coá coù 3 khaåu truùng. Ta coù
LYÙ THUYEÁT XAÙC SUAÁT C = A A A . 1 2 3
Tính toaùn töông töï caâu a) ta ñöôïc P(C) = 0,28.
Baøi 1.1: Coù ba khaåu suùng I, II vaø III baén ñoäc laäp vaøo moät muïc tieâu. Moãi
d) Goïi D laø bieán coá coù ít nhaát 1 khaåu truùng. Ta coù D = A + B + C.
khaåu baén 1 vieân. Xaùc suaát baén truùng muïc tieâu cuaû ba khaåu I, II vaø III laàn
Chuù yù raèng do A, B, C xung khaéc töøng ñoâi, neân theo coâng thöùc Coäng xaùc
löôït laø 0,7; 0,8 vaø 0,5. Tính xaùc suaát ñeå suaát ta coù:
a) coù 1 khaåu baén truùng.
P(D) = P(A) + P(B) + P(C) = 0,22 + 0,47 + 0,28 = 0,97.
b) coù 2 khaåu baén truùng. e) c)
Gæa söû coù 2 khaåu truùng. Khi ñoù bieán coá B ñaõ xaûy ra. Do ñoù xaùc suaát coù 3 khaåu baén truùng.
ñeå khaåu thöù 2 truùng trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän
d) ít nhaát 1 khaåu baén truùng. P(A
e) khaåu thöù 2 baén truùng bieát raèng coù 2 khaåu truùng. 2/B).
Theo coâng thöùc Nhaân xaùc suaát ta coù: Lôøi giaûi P(A2B) = P(B)P(A2/B) Suy ra Toùm taét: P(A B) Khaåu suùng I IIù III 2 P(A /B) = . 2 P(B) Xaùc suaát truùng 0,7 0,8 0,5
Maø A B = A A A + A A A neân lyù luaän töông töï nhö treân ta ñöôïc Goïi A 2 1 2 3 1 2 3
j (j = 1, 2, 3) laø bieán coá khaåu thöù j baén truùng. Khi ñoù A1, A2, A3 ñoäc
laäp vaø giaû thieát cho ta: P(A2B)=0,4 P(A ) = 0,7; P(A ) = 0,3; Suy ra P(A2/B) =0,851. 1 1 P(A ) = 0, 8; P(A ) = 0, 2; 2 2
Baøi 1.2: Coù hai hoäp I vaø II moãi hoäp chöùa 10 bi, trong ñoù hoäp I goàm 9 bi P(A ) = 0,5; P(A ) = 0,5. 3 3
ñoû, 1 bi traéng; hoäp II goàm 6 bi ñoû, 4 bi traéng. Laáy ngaãu nhieân töø moãi hoäp
a) Goïi A laø bieán coá coù 1 khaåu truùng. Ta coù 2 bi. A = A A A + A A A + A A A
a) Tính xaùc suaát ñeå ñöôïc 4 bi ñoû. 1 2 3 1 2 3 1 2 3
Vì caùc bieán coá A A A , A A A , A A A xung khaéc töøng ñoâi, neân
b) Tính xaùc suaát ñeå ñöôïc 2 bi ñoû vaø 2 bi traéng. 1 2 3 1 2 3 1 2 3
c) Tính xaùc suaát ñeå ñöôïc 3 bi ñoû vaø 1 bi traéng.
theo coâng thöùc Coäng xaùc suaát ta coù
d) Giaû söû ñaõ laáy ñöôïc 3 bi ñoû vaø 1 bi traéng. Haõy tìm xaùc suaát ñeå bi traéng
P(A) = P(A A A + A A A + A A A ) 1 2 3 1 2 3 1 2 3 coù ñöôïc cuûa hoäp I.
= P(A A A ) + P(A A A ) + P(A A A ) 1 2 3 1 2 3 1 2 3 Vì caùc bieán coá A
1, A2, A3 ñoäc laäp neân theo coâng thöùc Nhaân xaùc suaát ta coù 1 2 Lôøi giaûi B = A0B2 + A1B1 + A2B0
Do tính xung khaéc töøng ñoâi cuûa caùc bieán coá A0B2 , A1B1 , A2B0, coâng
Goïi Ai , Bi (i = 0, 1, 2) laàn löôït laø caùc bieán coá coù i bi ñoû vaø (2 - i) bi
thöùc Coäng xaùc suaát cho ta:
traéng coù trong 2 bi ñöôïc choïn ra töø hoäp I, hoäp II.
P(B) = P(A0B2 + A1B1 + A2B0) = P(A0B2 ) + P(A1B1) + P(A2B0) Khi ñoù
Töø ñaây, do tính ñoäc laäp , Coâng thöùc nhaân xaùc suaát thöù nhaát cho ta:
- A0, A1, A2 xung khaéc töøng ñoâi vaø ta coù:
P(B) = P(A0)P(B2 ) + P(A1)P(B1) + P(A2)P(B0) = 0,2133. P(A ) = 0; 0 1 1 c) 9 C C
Goïi C laø bieán coá choïn ñöôïc 3 bi ñoû vaø 1 bi traéng. Ta coù: 9 1 P(A ) = = ; C = A 1 2 45 C 1B2 + A2B1. 10
Lyù luaän töông töï nhö treân ta ñöôïc 2 0 C C 36
P(C) = P(A1)P(B2 ) + P(A2)P(B1) = 0,4933. 9 1 P(A ) = = . 2 2 45 C10
d) Giaû söû ñaõ choïn ñöôïc 3 bi ñoû vaø 1 bi traéng. Khi ñoù bieán coá C ñaõ
- B0, B1, B2 xung khaéc töøng ñoâi vaø ta coù:
xaûy ra. Do ñoù xaùc suaát ñeå bi traéng coù ñöôïc thuoäc hoäp I trong tröôøng hôïp
naøy chính laø xaùc suaát coù ñieàu kieän P(A1/C). Theo Coâng thöùc nhaân xaùc 0 2 6 suaát , ta coù = C6C4 P(B ) = ; 0 2 45 C P(A C) = P(C)P(A /C) . 1 1 10 1 1 Suy ra 24 C C 6 4 P(B ) = = ; P(A C) 1 1 2 P(A /C) = 45 C . 1 P(C) 10 2 0 Maø A C = A B neân 15 1 1 2 = C6C4 P(B ) = . 2 2 45 C 10 9 15
P(A C) = P(A B ) = P(A )P(B ) = . = 0, 0667. - A 1 1 2 1 2 i vaø Bj ñoäc laäp. 45 45
- Toång soá bi ñoû coù trong 4 bi choïn ra phuï thuoäc vaøo caùc bieán coá Ai vaø
Do ñoù xaùc suaát caàn tìm laø: P(A1/C) = 0,1352. Bj theo baûng sau: B0 B1 B2
Baøi 1.3: Moät loâ haøng chöùa 10 saûn phaåm goàm 6 saûn phaåm toát vaø 4 saûn A0 0 1 2
phaåm xaáu. Khaùch haøng kieåm tra baèng caùch laáy ra töøng saûn phaåm cho A1 1 2 3
ñeán khi naøo ñöôïc 3 saûn phaåm toát thì döøng laïi. A2 2 3 4
a) Tính xaùc suaát ñeå khaùch haøng döøng laïi ôû laàn kieåm tra thöù 3.
b) Tính xaùc suaát ñeå khaùch haøng döøng laïi ôû laàn kieåm tra thöù 4.
a) Goïi A laø bieán coá choïn ñöôïc 4 bi ñoû. Ta coù:
b) Giaû söû khaùch haøng ñaõ döøng laïi ôû laàn kieåm tra thöù 4. Tính xaùc suaát ñeå A = A2 B2 .
ôû laàn kieåm tra thöù 3 khaùch haøng gaëp saûn phaåm xaáu.
Töø ñaây, do tính ñoäc laäp , Coâng thöùc nhaân xaùc suaát thöù nhaát cho ta: Lôøi giaûi 36 15 P(A) = P(A )P(B ) = . = 0, 2667. 2 2 45 45
Goïi Ti, Xi laàn löôït laø caùc bieán coá choïn ñöôïc saûn phaåm toát, xaáu ôû laàn kieåm tra thöù i.
a) Goïi A laø bieán coá khaùch haøng döøng laïi ôû laàn kieåm tra thöù 3. Ta coù:
b) Goïi B laø bieán coá choïn ñöôïc 2 bi ñoû vaø 2 bi traéng. Ta coù: 3 4 A = T Lôøi giaûi 1T2T3.
Suy ra P(A) = P(T1T2T3) = P(T1) P(T2/T1) P(T3/ T1T2)
Goïi Di, Ti, Xi laàn löôït laø caùc bieán coá choïn ñöôïc bi ñoû, bi traéng, bi xanh ôû = (6/10)(5/9)(4/8) = 0,1667. laàn ruùt thöù i.
b) Goïi B laø bieán coá khaùch haøng döøng laïi ôû laàn kieåm tra thöù 4. Ta coù:
a) Goïi A laø bieán coá ruùt ñöôïc 2 bi traéng, 1 bi xanh vaø 1 bi ñoû. Ta coù: B = X ⎡ − − −
1T2T3T4 + T1X2T3T4 + T1T2X3T4 . T T X D
A xaûy ra ⇔ Ruùt ñöôïc T ⎢ − X − T − D ⎢ Suy ra X ⎢ − T − T − ⎣ D
P(B) = P(X1T2T3T4 ) + P(T1X2T3T4 ) + P(T1T2X3T4 ) = P(X Suy ra
1) P(T2/X1) P(T3/X1T2) P(T4/X1T2T3) + P(T
A = T1T2X3D4 + T1X2T3D4 + X1T2T3D4
1) P(X2/T1) P(T3/T1X2) P(T4/T1X2T3) + P(T
Töø ñaây, do tính xung khaéc töøng ñoâi cuûa caùc bieán coá thaønh phaàn, ta coù:
1) P(T2/T1) P(X3/ T1T2) P(T4/ T1T2 X3)
= (4/10)(6/9)(5/8)(4/7) + (6/10)(4/9)(5/8)(4/7)+(6/10)(5/9)(4/8)(4/7)
P(A) = P(T1T2X3D4)+ P(T1X2T3D4) + P(X1T2T3D4 )
= 3(4/10)(6/9)(5/8)(4/7) = 0,2857.
Theo Coâng thöùc Nhaân xaùc suaát, ta coù
P(T1T2X3D4) = P(T1)P(T2/T1)P(X3/T1T2)P(D4/T1T2X3)
c) Giaû söû khaùch haøng ñaõ döøng laïi ôû laàn kieåm tra thöù 4. Khi ñoù bieán
= (4/12)(3/11)(3/10)(5/9) = 1/66;
coá B ñaõ xaûy ra. Do ñoù xaùc suaát ñeå ôû laàn kieåm tra thöù 3 khaùch haøng
gaëp saûn phaåm xaáu trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän
P(T1X2T3D4) = P(T1)P(X2/T1)P(T3/T1X2)P(D4/T1X2T3) P(X
= (4/12)(3/11)(3/10)(5/9) = 1/66; 3/B).
Theo Coâng thöùc nhaân xaùc suaát , ta coù P(X B) = P(B)P(X /B) .
P(X1T2T3D4) = P(X1)P(T2/X1)P(T3/X1T2)P(D4/X1T2T3) 3 3
= (3/12)(4/11)(3/10)(5/9) = 1/66. Suy ra P(X B) 3 P(X /B) = . 3
Suy ra P(A) = 3/66 = 1/22 = 0,0455. P(B) Maø X3B = T1T2X3T4 neân
b) Goïi B laø bieán coá khoâng coù bi traéng naøo ñöôïc ruùt ra. Ta coù:
P(X3B) = P(T1T2X3T4 ) = P(T1) P(T2/T1) P(X3/ T1T2) P(T4/ T1T2 X3)
= (6/10)(5/9)(4/8)(4/7) = 0,0952. D ⎡ X ⎢ −D Suy ra P(X ⎢ 3/B) = 0,3333.
B xaûy ra ⇔ Ruùt ñöôïc X ⎢ −X −D ⎢
Baøi 1.4: Moät hoäp bi goàm 5 bi ñoû, 4 bi traéng vaø 3 bi xanh coù cuøng côõ. Töø X X − X − D − ⎣
hoäp ta ruùt ngaãu nhieân khoâng hoøan laïi töøng bi moät cho ñeán khi ñöôïc bi ñoû
thì döøng laïi. Tính xaùc suaát ñeå Suy ra
a) ñöôïc 2 bi traéng, 1 bi xanh vaø 1 bi ñoû.
B = D1 + X1D2 + X1X2D3+ X1X2X3 D4
b) khoâng coù bi traéng naøo ñöôïc ruùt ra.
Töø ñaây, do tính xung khaéc töøng ñoâi cuûa caùc bieán coá thaønh phaàn, ta coù:
P(B) = P(D1)+ P(X1D2) + P(X1X2D3 ) + P(X1X2X3 D4)
Theo Coâng thöùc Nhaân xaùc suaát, ta coù 5 6
P(B) = P(D1) + P(X1)P(D2/X1) + P(X1)P(X2/X1)P(D3/X1X2)
Suy ra P(B) = 0,66 = 66%. Vaäy tæ leä saûn phaåm loaïi A noùi chung do nhaø maùy saûn xuaát laø 66%.
+ P(X1)P(X2/X1)P(X3/X1X2)P(D4/X1X2X3)
= 5/12+ (3/12)(5/11) + (3/12)(2/11)(5/10) + (3/12)(2/11)(1/10)(5/9)
b) Choïn mua ngaãu nhieân moät saûn phaåm X ôû thò tröôøng. Giaû söû ñaõ mua
ñöôïc saûn phaåm loaïi A. Theo baïn, saûn phaåm aáy coù khaû naêng do phaân = 5/9
xöôûng naøo saûn xuaát ra nhieàu nhaát?
Baøi 1.5: Saûn phaåm X baùn ra ôû thò tröôøng do moät nhaø maùy goàm ba phaân
Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Khi ñoù bieán coá B ñaõ xaûy ra. Do ñoù,
xöôûng I, II vaø III saûn xuaát, trong ñoù phaân xöôûng I chieám 30%; phaân
ñeå bieát saûn phaåm loaïi A ñoù coù khaû naêng do phaân xöôûng naøo saûn xuaát ra
xöôûng II chieám 45% vaø phaân xöôûng III chieám 25%. Tæ leä saûn phaåm loaïi
nhieàu nhaát ta caàn so saùnh caùc xaùc suaát coù ñieàu kieän P(A1/B), P(A2/B) vaø
A do ba phaân xöôûng I, II vaø III saûn xuaát laàn löôït laø 70%, 50% vaø 90%.
P(A3/B). Neáu P(Ai/B) laø lôùn nhaát thì saûn phaåm aáy coù khaû naêng do phaân
a) Tính tæ leä saûn phaåm loïai A noùi chung do nhaø maùy saûn xuaát.
xöôûng thöù i saûn xuaát ra laø nhieàu nhaát. Theo coâng thöùc Bayes ta coù:
b) Choïn mua ngaãu nhieân moät saûn phaåm X ôû thò tröôøng. Giaû söû ñaõ mua
ñöôïc saûn phaåm loaïi A. Theo baïn, saûn phaåm aáy coù khaû naêng do phaân P(A )P(B/A ) 0, 3.0, 7 21 1 1 P(A /B) = = = ; 1
xöôûng naøo saûn xuaát ra nhieàu nhaát? P(B) 0, 66 66
c) Choïn mua ngaãu nhieân 121 saûn phaåm X (trong raát nhieàu saûn phaåm X) P(A )P(B/A ) 0, 45.0, 5 22,5 2 2 P(A /B) = = = ; ôû thò tröôøng. 2 P(B) 0, 66 66
1) Tính xaùc suaát ñeå coù 80 saûn phaåm loaïi A. P(A )P(B/A ) 0, 25.0, 9 22, 5 2) 3 3
Tính xaùc suaát ñeå coù töø 80 ñeán 85 saûn phaåm loaïi A. P(A /B) = = = . 3 P(B) 0, 66 66 Lôøi giaûi Vì P(A
2/B) = P(A3/B) > P(A1/B) neân saûn phaåm loaïi A aáy coù khaû naêng
do phaân xöôûng II hoaëc III saûn xuaát ra laø nhieàu nhaát. Toùm taét: Phaân xöôûng I II III
c) Choïn mua ngaãu nhieân 121 saûn phaåm X (trong raát nhieàu saûn phaåm X)
Tæ leä saûn löôïng 30% 45% 25% ôû thò tröôøng. Tæ leä loaïi A 70% 50% 90%
1) Tính xaùc suaát ñeå coù 80 saûn phaåm loaïi A.
2) Tính xaùc suaát ñeå coù töø 80 ñeán 85 saûn phaåm loaïi A.
a) Ñeå tính tæ leä saûn phaåm loaïi A noùi chung do nhaø maùy saûn xuaát ta
choïn mua ngaãu nhieân moät saûn phaåm ôû thò tröôøng. Khi ñoù tæ leä saûn phaåm
Aùp duïng coâng thöùc Bernoulli vôùi n = 121, p = 0,66, ta coù:
loaïi A chính laø xaùc suaát ñeå saûn phaåm ñoù thuoäc loaïi A.
1) Xaùc suaát ñeå coù 80 saûn phaåm loaïi A laø
Goïi B laø bieán coá saûn phaåm choïn mua thuoäc loaïi A.
A1, A2, A3 laàn löôït laø caùc bieán coá saûn phaåm do phaân xöôûng I, II, III saûn 80 80 41 80 80 41 = = = 1 P 21(80) C121p q C121(0, 66) (0, 34) 0, 076.
xuaát. Khi ñoù A1, A2, A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
P(A1) = 30% = 0,3; P(A2) = 45% = 0,45; P(A3) = 25% = 0,25.
2) Xaùc suaát ñeå coù töø 80 ñeán 85 saûn phaåm loaïi A laø
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(B) = P(A1)P(B/A1) + P(A2)P(B/A2) + P(A3)P(B/A3) 85 85 85 k k 121−k k k 121−k ∑ P (k) = ∑ C p q = ∑ C (0,66) (0, 34) = 0, 3925. 121 121 121 k =80 k =80 k=80 Theo giaû thieát,
P(B/A1) = 70% = 0,7; P(B/A2) = 50% = 0,5; P(B/A3) = 90% = 0,9. 7 8
Baøi 1.6: Coù ba cöûa haøng I, II vaø III cuøng kinh doanh saûn phaåm Y. Tæ leä
P(A2/B) vaø P(A3/B). Neáu P(Ai/B) laø lôùn nhaát thì cöûa haøng thöù i coù nhieàu
saûn phaåm loaïi A trong ba cöûa haøng I, II vaø III laàn löôït laø 70%, 75% vaø
khaû naêng ñöôïc choïn nhaát.
50%. Moät khaùch haøng choïn nhaãu nhieân moät cöûa haøng vaø töø ñoù mua moät
Theo coâng thöùc Bayes ta coù: saûn phaåm
a) Tính xaùc suaát ñeå khaùch haøng mua ñöôïc saûn phaåm loaïi A. P(A )P(B/A ) (1 / 3).0, 7 70 1 1 P(A /B) = = = ; 1
b) Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Theo baïn, khaû naêng ngöôøi P(B) 0, 65 195
khaùch haøng aáy ñaõ choïn cöûa haøng naøo laø nhieàu nhaát? P(A )P(B/A ) (1 / 3).0,75 75 2 2 P(A /B) = = = ; 2 P(B) 0, 65 195 Lôøi giaûi P(A )P(B/A ) (1 / 3).0, 5 50 3 3 P(A /B) = = = . 3 P(B) 0, 65 195 Toùm taét: Cöûa haøng I II III Vì P(A Tæ leä loaïi A 70% 75% 50%
2/B) > P(A1/B) > P(A3/B) neân cöûa haøng II coù nhieàu khaû naêng ñöôïc choïn nhaát.
Choïn nhaãu nhieân moät cöûa haøng vaø töø ñoù mua moät saûn phaåm.
Baøi 1.7: Coù hai hoäp I vaø II moãi hoäp chöùa 12 bi, trong ñoù hoäp I goàm 8 bi
ñoû, 4 bi traéng; hoäp II goàm 5 bi ñoû, 7 bi traéng. Laáy ngaãu nhieân töø hoäp I
a) Tính xaùc suaát ñeå khaùch haøng mua ñöôïc saûn phaåm loaïi A.
ba bi roài boû sang hoäp II; sau ñoù laáy ngaãu nhieân töø hoäp II boán bi.
Goïi B laø bieán coá saûn phaåm choïn mua thuoäc loaïi A.
a) Tính xaùc suaát ñeå laáy ñöôïc ba bi ñoû vaø moät bi traéng töø hoäp II. A
b) Giaû söû ñaõ laáy ñöôïc ba bi ñoû vaø moät bi traéng töø hoäp II. Tìm xaùc suaát
1, A2, A3 laàn löôït laø caùc bieán coá choïn cöûa haøng I, II, III. Khi ñoù A1, A2,
ñeå trong ba bi laáy ñöôïc töø hoäp I coù hai bi ñoû vaø moät bi traéng.
A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø P(A Lôøi giaûi 1) = P(A2) = P(A3) = 1/3.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
Goïi A laø bieán coá choïn ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II.
P(B) = P(A1)P(B/A1) + P(A2)P(B/ A2)+ P(A3)P(B/A3) A Theo giaû thieát,
i (i = 0, 1, 2, 3) laø bieán coá coù i bi ñoû vaø (3-i) bi traéng coù trong 3 bi choïn ra töø hoäp I. Khi ñoù A P(B/A
0, A1, A2, A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø 1) = 70% = 0,7; ta coù: P(B/A2) = 75% = 0,75; 0 3 P(B/A 4 C C 3 = 50% = 0,5. 8 4 P(A ) = = ; 0 3 220 C12
Suy ra P(B) = 0,65 = 65%. Vaäy xaùc suaát ñeå khaùch haøng mua ñöôïc saûn 1 2 C C phaåm loaïi A laø 65%. 48 8 4 P(A ) = = ; 1 3 220 C12
b) Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Theo baïn, khaû naêng ngöôøi 2 1 112 C C
khaùch haøng aáy ñaõ choïn cöûa haøng naøo laø nhieàu nhaát? 8 4 P(A ) = = ; 2 3 220 C12
Giaû söû ñaõ mua ñöôïc saûn phaåm loaïi A. Khi ñoù bieán coá B ñaõ xaûy ra. Do ñoù, 3 0 56 C C
ñeå bieát saûn phaåm loaïi A ñoù coù khaû naêng khaùch haøng aáy ñaõ choïn cöûa 8 4 P(A ) = = . 3 3 220 C
haøng naøo laø nhieàu nhaát ta caàn so saùnh caùc xaùc suaát coù ñieàu kieän P(A 12 1/B),
a) Tính xaùc suaát ñeå laáy ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II. 9 10
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù: Lôøi giaûi
P(A)=P(A0)P(A/A0)+P(A1)P(A/A1)+P(A2)P(A/A2)+P(A3)P(A/A3)
Theo coâng thöùc tính xaùc suaát löïa choïn, ta coù
a) Goïi Aj (j = 1, 2, 3) laø bieán coá laáy ñöôïc bi traéng töø hoäp thöù j. Khi ñoù A1, 3 1 100 C C A2, A3 ñoäc laäp vaø 5 10 P(A / A ) = = ; 0 4 1365 C 1 4 P(A ) = ; P(A ) = ; 15 1 1 5 5 3 1 C C 180 2 3 6 9 P(A / A ) = = ; P(A ) = ; P(A ) = ; 1 4 1365 C 2 2 5 5 15 3 1 3 2 280 C C P(A ) = ; P(A ) = . 7 8 P(A / A ) = = ; 3 3 5 5 2 4 1365 C15
1) Goïi A laø bieán coá laáy ñöôïc caû 3 bi traéng. Ta coù 3 1 C C A = A A A . 392 1 2 3 8 7 P(A / A ) = = . 3 4 Suy ra P(A) = P(A 1365 C 1) P(A2) P(A3) = 0,048. 15
2) Goïi B laø bieán coá laáy 2 bi ñen, 1 bi traéng. Ta coù
Suy ra xaùc suaát caàn tìm laø P(A) = 0,2076. B = A A A + A A A + A A A 1 2 3 1 2 3 1 2 3 Suy ra P(B) =0,464 .
b) Giaû söû ñaõ laáy ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II. Tìm xaùc suaát ñeå
trong 3 bi laáy ñöôïc töø hoäp I coù 2 bi ñoû vaø 1 bi traéng.
3) Giaû söû trong 3 vieân laáy ra coù ñuùng 1 bi traéng. Khi ñoù bieán coá B
ñaõ xaûy ra. Do ñoù xaùc suaát ñeå bi traéng ñoù laø cuûa hoäp thöù nhaát trong tröôøng
Giaû söû ñaõ laáy ñöôïc 3 bi ñoû vaø 1 bi traéng töø hoäp II. Khi ñoù bieán coá A ñaõ
hôïp naøy chính laø xaùc suaát coù ñieàu kieän P(A
xaûy ra. Do doù xaùc suaát ñeå trong 3 bi laáy ñöôïc töø hoäp I coù 2 bi ñoû vaø 1 bi
1/B). Theo coâng thöùc Nhaân xaùc suaát ta coù:
traéng trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän P(A2/A). Aùp P(A
duïng coâng thöùc Bayes, ta coù: 1B) = P(B)P(A1/B) 112 280 Suy ra . P(A )P(A/A ) P(A B) 1 2 2 220 1365 P(A /A) = = = 0, 5030. P(A /B) = . 1 2 P(A) 0, 2076 P(B) Maø A B = A A A
Vaäy xaùc suaát caàn tìm laø P(A
neân lyù luaän töông töï nhö treân ta ñöôïc P(A 1 1 2 3 1B) = 0,048. 2/A) = 0,5030. Suy ra
Baøi 1.8: Coù ba hoäp moãi hoäp ñöïng 5 vieân bi trong ñoù hoäp thöù nhaát coù 1 bi P(A1/B) =0,1034 .
traéng, 4 bi ñen; hoäp thöù hai coù 2 bi traéng, 3 bi ñen; hoäp thöù ba coù 3 bi
b) Choïn ngaãu nhieân moät hoäp roài töø hoäp ñoù laáy ngaãu nhieân ra 3 bi. traéng, 2 bi ñen.
Tính xaùc suaát ñöôïc caû 3 bi ñen.
a) Laáy ngaãu nhieân töø moãi hoäp moät bi.
1) Tính xaùc suaát ñeå ñöôïc caû 3 bi traéng.
Goïi A laø bieán coá laáy ñöôïc caû 3 bi ñen.
2) Tính xaùc suaát ñöôïc 2 bi ñen, 1 bi traéng.
A1, A2, A3 laàn löôït laø caùc bieán coá choïn ñöôïc hoäp I, II, III. Khi ñoù A1, A2,
3) Giaû söû trong 3 vieân laáy ra coù ñuùng 1 bi traéng.Tính xaùc suaát ñeå bi
A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø
traéng ñoù laø cuûa hoäp thöù nhaát. P(A1) = P(A2) = P(A3) = 1/3.
b) Choïn ngaãu nhieân moät hoäp roài töø hoäp ñoù laáy ngaãu nhieân ra 3 bi.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
Tính xaùc suaát ñöôïc caû 3 bi ñen.
P(A) = P(A1)P(A/A1) + P(A2)P(A/ A2)+ P(A3)P(A/A3)
Theo coâng thöùc xaùc suaát löïa choïn, ta coù: 11 12
Aùp duïng Coâng thöùc Bayes vaø söû duïng keát quaû vöøa tìm ñöôïc ôû caâu a) ta 0 3 0 3 1 C 4 C 4 C C 1 coù 2 3 P(A/A ) = = ; P(A/A ) = = ; P(A/A ) =0. 1 3 2 3 3 C 10 C 10 P(A )P(A/A ) (10/20).0,375 5 5 1 1 P(A /A) = = = 0, 4630. Suy ra P(A) = 0,1667. 1 P(A) 0,4050
Baøi 1.9: Coù 20 hoäp saûn phaåm cuøng loïai, moãi hoäp chöùa raát nhieàu saûn
Baøi 1.10: Coù 10 sinh vieân ñi thi, trong ñoù coù 3 thuoäc loaïi gioûi, 4 khaù vaø 3
phaåm, trong ñoù coù 10 hoäp cuûa xí nghieäp I, 6 hoäp cuûa xí nghieäp II vaø
trung bình. Trong soá 20 caâu hoûi thi qui ñònh thì sinh vieân loïai gioûi traû lôøi
4 hoäp cuûa xí nghieäp III. Tæ leä saûn phaåm toát cuûa caùc xí nghieäp laàn
ñöôïc taát caû, sinh vieân khaù traû lôøi ñöôïc 16 caâu coøn sinh vieân trung bình
löôït laø 50%, 65% vaø 75%. Laáy ngaãu nhieân ra moät hoäp vaø choïn ngaãu
ñöôïc 10 caâu. Goïi ngaãu nhieân moät sinh vieân vaø phaùt moät phieáu thi goàm
nhieân ra 3 saûn phaåm töø hoäp ñoù.
4 caâu hoûi thì anh ta traû lôøi ñöôïc caû 4 caâu hoûi. Tính xaùc suaát ñeå sinh vieân
a) Tính xaùc suaát ñeå trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaåm ñoù thuoäc loaïi khaù. toát. Lôøi giaûi
b) Giaû söû trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaåm toát. Tính Toùm taét:
xaùc suaát ñeå 2 saûn phaåm toát ñoù cuûa xí nghieäp I. Xeáp loaïi sinh vieân Gioûi Khaù Trung bình Lôøi giaûi Soá löôïng 3 4 3
Soá caâu traû lôøi ñöôïc/20 20 16 10
Goïi A laø bieán coá trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaåm toát.
Aj (j = 1, 2, 3) laø bieán coá choïn ñöôïc hoäp cuûa xí nghieäp thöù j.
Goïi A laø bieán coá sinh vieân traû lôøi ñöôïc caû 3 caâu hoûi.
Khi ñoù A1, A2, A3 laø moät ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù: A 1
1, A2, A3 laàn löôït laø caùc bieán coá sinh vieân thuoäc loaïi Gioûi, Khaù; 10 C10 P(A ) = = ; Trung bình. 1 1 20 C 20 1 C
Yeâu caàu cuûa baøi toaùn laø tính xaùc suaát coù ñieàu kieän P(A2/A). 6 6 P(A ) = = ; 2 1 20 C20
Caùc bieán coá A1, A2, A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi, vaø ta coù: 1 P(A 4 C
1) = 3/10; P(A2) = 4/10; P(A3) = 3/10. 4 P(A ) = = .
Theo coâng thöùc Bayes, ta coù 3 1 20 C20 P(A )P(A/A ) 2 2 P(A /A) = .
Maët khaùc, töø giaû thieát, theo coâng thöùc Bernoulli, ta coù 2 P(A) 2 2
P(A / A ) = C (0, 5) (1 − 0,5) = 0, 375 1 3
Maët khaùc, theo coâng thöùc xaùc suaát ñaày ñuû, ta coù 2 2
P(A / A ) = C (0, 65) (1 − 0, 65) = 0, 443625 P(A) = P(A 2 3
1)P(A/A1) + P(A2)P(A/A2) + P(A3)P(A/A3). 2 2
Theo coâng thöùc tính xaùc suaát löïa choïn, ta coù:
P(A / A ) = C (0,75) (1 − 0, 25) = 0, 421875 3 3 4 C
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù 20 P(A / A ) = = 1; 1 4 C P(A) = P(A 20
1)P(A/A1) + P(A2)P(A/A2) + P(A3)P(A/A3)
= (10/20).0,375 + (6/20). 0,443625 + (4/20). 0,421875 = 0,4050. 4 0 C C 1820 16 4 P(A / A ) = = ; 2
b) Giaû söû trong 3 saûn phaåm choïn ra coù ñuùng 2 saûn phaåm toát. Khi ñoù, 4 C 4845 20
bieán coá A ñaõ xaûy ra. Do ñoù, xaùc suaát ñeå 2 saûn phaåm toát ñoù cuûa xí 4 0 C C 210 10 10 P(A / A ) = = .
nghieäp I chính laø xaùc suaát coù ñieàu kieän P(A 3 4 1/A). C 4845 20 13 14 Suy ra P(A2/A) = 0,3243. - Bi vaø Cj ñoäc laäp.
Baøi 1.11: Coù hai hoäp I vaø II, trong ñoù hoäp I chöùa 10 bi traéng vaø 8 bi ñen;
hoäp II chöùa 8 bi traéng vaø 6 bi ñen. Töø moãi hoäp ruùt ngaãu nhieân 2 bi boû ñi,
- Toång soá bi traéng coù trong 4 bi choïn ra phuï thuoäc vaøo caùc bieán coá Bi vaø
sau ñoù boû taát caû caùc bi coøn laïi cuûa hai hoäp vaøo hoäp III (roãng). Laáy ngaãu Cj theo baûng sau:
nhieân 2 bi töø hoäp III. Tính xaùc suaát ñeå trong 2 bi laáy töø hoäp III coù 1 traéng, 1 ñen. C0 C1 C2 B0 0 1 2 Lôøi giaûi B1 1 2 3 B2 2 3 4
Goïi A laø bieán coá bi laáy ñöôïc 1 traéng, 1 ñen.
Aj (j = 0, 1, 2, 3, 4) laø bieán coá coù j bi traéng vaø (4-j) bi ñen coù trong 4 A0 = B0C0
⇒ P(A0) = P(B0)P(C0) = 20/663.
bi boû ñi (töø caû hai hoäp I vaø II). Khi ñoù A0, A1, A2 , A3, A4 laø moät heä ñaày ñuû, A1 = B0C1 + B1C0
⇒ P(A1) = P(B0)P(C1 ) + P(B1)P(C0) = 848/4641. xung khaéc töøng ñoâi.
A2 = B0C2 + B1C1 + B2C0 ⇒ P(A2) = P(B0)P(C2)+P(B1)P(C1)+P(B2)P(C0)
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù =757/1989.
P(A) = P(A0)P(A/A0) + P(A1)P(A/A1) + P(A2)P(A/A2)+ P(A3)P(A/A3) + A3 = B1C2 + B2C1
⇒ P(A3) = P(B1)P(C2)+P(B2)P(C1) = 4400/13923. P(A4)P(A/A4). A4 = B2C2
⇒ P(A4) = P(B2)P(C2) = 20/221. trong ñoù 1 1 C C 10 18 10
Töø ñoù suy ra P(A) = 0,5080. P(A/A = 0 ) = (Vì khi A 2
0 ñaõ xaûy ra thì trong hoäp III coù 28 bi goàm C 21 28 18 traéng , 10 ñen). Töông töï,
Baøi 1.12: Coù hai hoäp cuøng côõ. Hoäp thöù nhaát chöùa 4 bi traéng 6 bi xanh, 1 1 1 1 C C 187 C C 32
hoäp thöù hai chöùa 5 bi traéng vaø 7 bi xanh. Choïn ngaãu nhieân moät hoäp roài 17 11 16 12 P(A/A1) = = ; P(A/A ) = = ; 2 2 2 C 378 C 63
töø hoäp ñoù laáy ra 2 bi thì ñöôïc 2 bi traéng. Tính xaùc suaát ñeå vieân bi tieáp 28 28 1 1 1 1 C
theo cuõng laáy töø hoäp treân ra laïi laø bi traéng. 15C13 65 C14C14 14 P(A/A ) = = ; P(A/A ) = = . 3 2 4 2 C 126 C 27 28 28 Lôøi giaûi
Baây giôø ta tính P(A0); P(A1); P(A2); P(A3); P(A4).
Goïi Bi , Ci (i = 0, 1, 2) laàn löôït laø caùc bieán coá coù i bi traéng vaø (2 - i) bi Goïi A
ñen coù trong 2 bi ñöôïc choïn ra töø hoäp I, hoäp II. Khi ñoù
1 laø bieán coá 2 bi laáy ñaàu tieân laø bi traéng. A
2 laø bieán coá bi laáy laàn sau laø bi traéng.
Baøi toùan yeâu caàu tính P(A - B 2/A1).
0, B1, B2 xung khaéc vaø ta coù:
Theo coâng thöùc nhaân xaùc suaát, ta coù P(A 1A2) = P(A1) P(A2/A1). Suy ra 0 2 1 1 2 0 C C 28 C C 80 C C 5 10 8 10 8 10 8 P(B ) = = ; P(B ) = = ; P(B ) = = . P(A A ) 0 2 1 2 2 2 1 2 153 153 17 C C C P(A / A ) = . 2 1 18 18 18 P(A ) 1
Baây giôø ta tính caùc xaùc suaát P(A1) vaø P(A1A2).
- C0, C1, C2 xung khaéc vaø ta coù:
Goïi B1, B2 laàn löôït laø caùc bieán coá choïn ñöôïc hoäp I, hoäp II. Khi ñoù B1, B2
laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù: P(B1) = P(B2) = 0,5. 0 2 1 1 2 0 15 48 28 C C C C C C
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù 8 6 8 6 8 6 P(C ) = = ; P(C ) = = ; P(C ) = = . 0 2 1 2 2 2 91 91 91 C C C
P(A1) = P(B1) P(A1/ B1) + P(B2) P(A1/ B2) 14 14 14 15 16 Maø a a − 1 . 2 0 a −1 + + − 6 C C = a b a b 1 P(A / A) = 1 4 6 P(A / B ) = = ; a a 1 − b a a b + 1 − 1 1 + 2 45 . . . C a +b a+ b− 1 a+ b a+ b− 1 10 2 0 C C 10 5 7 P(A / B ) = = .
Baøi 1.14: Coù 3 hoäp phaán, trong ñoù hoäp I chöùa 15 vieân toát vaø 5 vieân xaáu, 1 2 2 66 C12
hoäp II chöùa 10 vieân toát vaø 4 vieân xaáu, hoäp III chöùa 20 vieân toát vaø 10 vieân neân P(A
xaáu. Ta gieo moät con xuùc xaéc caân ñoái. Neáu thaáy xuaát hieän maët 1 chaám thì 1) = 47/330.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù
ta choïn hoäp I; neáu xuaát hieän maët 2 hoaëc 3 chaám thì choïn hoäp II, coøn xuaát P(A
hieän caùc maët coøn laïi thì choïn hoäp III. Töø hoäp ñöôïc choïn laáy ngaãu nhieân
1A2) = P(B1) P(A1A2/ B1) + P(B2) P(A1A2/ B2). Maø
ra 4 vieân phaán. Tìm xaùc suaát ñeå laáy ñöôïc ít nhaát 2 vieân toát. 6 2 1
P(A A / B ) = P(A / B )P(A / A B ) = = ; 1 2 1 1 1 2 1 1 45 8 30 Lôøi giaûi 10 3 1
P(A A / B ) = P(A / B )P(A / A B ) = = . 1 2 2 1 2 2 1 2 66 10 22
Goïi A laø bieán coá choïn ñöôïc ít nhaát 2 vieân phaán toát. neân P(A A
1A2) = 13/330. Suy ra xaùc suaát caàn tìm laø P(A2/A1) =13/47= 0,2766.
j (j =1,2, 3) laø bieán coá choïn ñöôïc hoäp thöù j. Khi ñoù A1, A2, A3 laø heä
ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
Baøi 1.13: Moät loâ haøng goàm a saûn phaåm loaïi I vaø b saûn phaåm loaïi II ñöôïc
- A1 xaûy ra khi vaø chæ khi thaûy con xuùc xaéc, xuaát hieän maët 1 chaám, do
ñoùng gôùi ñeå göûi cho khaùch haøng. Nôi nhaän kieåm tra laïi thaáy thaát laïc 1 ñoù P(A1) = 1/6.
saûn phaåm. Choïn ngaãu nhieân ra 1 saûn phaåm thì thaáy ñoù laø saûn phaåm loaïi - Töông töï, P(A2) = 2/6; P(A3) = 3/6.
I. Tính xaùc suaát ñeå saûn phaåm thaát laïc cuõng thuoäc loaïi I.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù Lôøi giaûi
P(A) = P(A1)P(A/A1) + P(A2)P(A/A2) + P(A3)P(A/A3). Töø giaû thieát ta coù: 2 2 3 1 4 0
Goïi A laø bieán coá saûn phaåm ñöôïc choïn ra thuoäc loïai I. C C C C C C 4690 15 5 15 5 15 5 P(A / A ) = + + = ; 1 4 4 4 A C C C 4845
1, A2 laàn löôït laø caùc bieán coá saûn phaåm thaát laïc thuoäc loaïi I, loaïi II. 20 20 20
Yeâu caàu cuûa baøi toaùn laø tính xaùc suaát coù ñieàu kieän P(A 2 2 3 1 4 0 1/A). C C C C C C 960 10 4 10 4 10 4 = + + = Ta thaáy A P(A / A ) ; 2
1, A2 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø 4 4 4 C C C 1001 1 0 0 1 C C 14 14 14 a C C b a b a b P(A ) = = ; P(A ) = = . 2 2 3 1 4 0 C C C C C C 24795 1 1 2 1 C + + 20 10 20 10 20 10 P(A / A ) = + + = . + a b C + a b a b a b 3 4 4 4 C C C 27405
Theo coâng thöùc Bayes, ta coù 30 30 30 P(A )P(A / A ) P(A )P(A / A ) 1 1 1 1 P(A / A) = = 1 P(A)
P(A )P(A / A ) + P(A )P(A / A ) Suy ra P(A) =0,9334. 1 1 2 2 Maø
Baøi 1.15: Coù hai kieän haøng I vaø II. Kieän thöù nhaát chöùa 10 saûn phaåm, 1 0 1 0 C C a −1 C C a
trong ñoù coù 8 saûn phaåm loaïi A. Kieän thöù hai chöùa 20 saûn phaåm, trong ñoù a− 1 b a b− 1 P(A / A ) = = ; P(A / A ) = = . 1 1 2 1 C a + b − 1 C a + b − 1
coù 4 saûn phaåm loaïi A. Laáy töø moãi kieän 2 saûn phaåm. Sau ñoù, trong 4 saûn a +b 1 − a +b 1 −
phaåm thu ñöôïc choïn ngaãu nhieân 2 saûn phaåm. Tính xaùc suaát ñeå trong 2 neân
saûn phaåm choïn ra sau cuøng coù ñuùng 1 saûn phaåm loaïi A. Lôøi giaûi 17 18 0 2 120 C 4C16
Goïi C laø bieán coá trong 2 saûn phaåm choïn ra sau cuøng coù ñuùng 1 saûn P(C ) = = ; 0 2 190 C phaåm loaïi A. 20 1 1
Aj (j = 0, 1, 2, 3, 4 ) laø bieán coá coù j saûn phaåm loïai A vaø (4-j) saûn C C 64 4 16 P(C ) = = ;
phaåm loïai B coù trong 4 saûn phaåm laáy töø hai kieän I vaø II. Khi ñoù A 1 2 0, A1, 190 C A 20
2, A3, A4 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi. Theo coâng thöùc xaùc suaát 2 0 ñaày ñuû, ta coù 6 C 4C16 P(C ) = = ; 2 2 190 C20
P(C) = P(A0)P(C/A0) + P(A1)P(C/A1) + P(A2)P(C/A2) + P(A3)P(C/A3) - Bi vaø Cj ñoäc laäp. + P(A4)P(C/A4).
- Toång soá sp A coù trong 4 sp choïn ra phuï thuoäc vaøo caùc bieán coá Bi vaø Ta coù: C P(C/A ) = 0; j theo baûng sau: 0 1 1 C C 3 1 3 C P(C/ = 0 C1 C2 1 A ) = 2 C 6 B 4 0 0 1 2 1 1 B C 1 1 2 3 2C2 4 P(C/A = 2 ) = B 2 2 2 3 4 C 6 4 1 1 C C 3 Ta coù: 3 1 P(C/A ) = = 3 2 C 6 A1 = B0C1 + B1C0 . 4 A P(C/A 2 = B0C2 + B1C1 + B2C0 . 4 ) =0. A3 = B1C2 + B2C1 .
Baây giôø ta tính P(A1); P(A2); P(A3).
Töø ñaây, nhôø caùc coâng thöcù coäng vaø nhaân xaùc suaát ta tính ñöôïc:
Goïi Bi , Ci (i = 0, 1, 2) laàn löôït laø caùc bieán coá coù i sp A vaø (2 - i) sp B
coù trong 2 sp ñöôïc choïn ra töø kieän I, kieän II. Khi ñoù
P(A1) = 0,2320 ; P(A2) = 0,5135 ; P(A3) = 0,2208 .
- B0, B1, B2 xung khaéc töøng ñoâi vaø ta coù: 0 2 1 = C8C2
Suy ra xaùc suaát caàn tìm laø P(C) = 0,5687. P(B ) = ; 0 2 45 C 10 Baøi 1.16 1 1
: Moät xaï thuû baén 10 vieân ñaïn vaøo moät muïc tieâu. Xaùc suaát ñeå 1 16 C C 8 2 P(B ) = = ;
vieân ñaïn baén ra truùng muïc tieâu laø 0,8 . Bieát raèng: Neáu coù 10 vieân truùng 1 2 45 C
thì muïc tieâu chaéc chaén bò dieät. Neáu coù töø 2 ñeán 9 vieân truùng thì muïc tieâu 10 2 0
bò dieät vôiù xaùc suaát 80%. Neáu coù 1 vieân truùng thì muïc tieâu bò dieät vôùi xaùc 28 C8C2 P(B ) = = . suaát 20%. 2 2 45 C10
a) Tính xaùc suaát ñeå muïc tieâu bò dieät. - C
b) Giaû söû muïc tieâu ñaõ bò dieät. Tính xaùc suaát coù 10 vieân truùng.
0, C1, C2 xung khaéc töøng ñoâi vaø ta coù: Lôøi giaûi Toùm taét:
- Soá vieân baén ra: 10 vieân.
- Xaùc suaát truùng cuûa moãi vieân: 0,8. 19 20 Lôøi giaûi Soá vieân truùng 1 2-9 10
Xaùc suaát muïc tieâu bò dieät 20% 80% 100%
Goïi Aj (j = 0, 1, 2) laø caùc bieán coá coù j saûn phaåm loaïi A vaø (2-j) saûn
phaåm khoâng thuoäc loaïi A coù trong 2 saûn phaåm do maùy saûn xuaát.
a) Goïi A laø bieán coá muïc tieâu bò dieät.
Goïi Bj (j = 0, 1, 2, 3) laø caùc bieán coá coù j saûn phaåm loaïi A vaø (3-j) saûn
A0, A1, A2, A3 laàn löôït laø caùc bieán coá coù 0; 1; 2-9; 10 vieân truùng. Khi
phaåm khoâng thuoäc loaïi A coù trong 3 saûn phaåm laáy töø loâ haøng.
ñoù, A0, A1, A2, A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø giaû thieát cho Khi ñoù ta:
- A0, A1, A2 xung khaéc töøng ñoâi vaø theo coâng thöùc Bernoulli vôùi n = 2; p
P(A/A0) = 0; P(A/A1) = 20% = 0,2; = 0,6; q = 0,4 ta coù: P(A/A 0 0 2 2
2) = 80%= 0,8; P(A/A3) = 100% = 1. P(A ) = p q = (0, 4) = 0,16; 0 C2 1 1 1 = = =
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù: P(A ) p q 2(0, 6)(0, 4) 0, 48; 1 C 2 2 2 0 2 P(A ) = p q = (0, 6) = 0, 36. 2 C P(A) = P(A 2
0)P(A/A0) + P(A1)P(A/A1) + P(A2)P(A/A2) + P(A3)P(A/A3). - B
0, B1, B2 , B3 xung khaéc töøng ñoâi vaø theo coâng thöùc tính xaùc suaát löïa choïn vôùi N = 10, N
Theo coâng thöùc Bernoulli vôùi n =10; p = 0,8, q = 0,2, ta coù
A = 6, n= 3 ta coù (vì loâ haøng goàm 10 saûn phaåm vôùi tæ 10 10
leä saûn phaåm loaïi A laø 60%, nghóa laø loâ haøng goàm 6 saûn phaåm loaïi A vaø 4 P(A ) = q = (0,2) ; 0
saûn phaåm khoâng thuoäc loaïi A): 1 9 9 P(A ) = C pq = 10(0,8)(0,2) ; 0 3 1 10 4 C C 6 4 P(B ) = = ; 10 10 P(A ) = p = (0,8) ; 0 3 3 120 C10 10 9 10
P(A ) = 1 − P(A ) − P(A ) − P(A ) = 1− (0, 2) − 10(0,8)(0,2) − (0,8) . 1 2 2 0 1 3 36 6 C 4 C Suy ra P(A) = 0,8215. P(B ) = = ; 1 3 120 C 10 2 1
b) Giaû söû muïc tieâu ñaõ bò dieät. Khi ñoù bieán coá A ñaõ xaûy ra. Do ñoù xaùc 60 C C 6 4 P(B ) = = ;
suaát coù 10 vieân truùng trong tröôøng hôïp naøy chính laø xaùc suaát coù ñieàu kieän 2 3 120 C P(A 10 3/A). 3 0
Theo coâng thöùc Bayes, ta coù: 20 C6C4 P(B ) = = . 3 3 120 C P(A )P(A / A ) 10 3 3 P(A / A) = 3 P(A) - Ai vaø Bj ñoäc laäp.
Töø ñaây ta tính ñöôïc P(A3/A) = 0,1307. a)
Goïi C laø bieán coá soá saûn phaåm loaïi A coù trong 2 saûn phaåm do maùy saûn Baøi 1.17
xuaát baèng soá saûn phaåm loaïi A coù trong 2 saûn phaåm ñöôïc laáy ra töø loâ haøng.
: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä saûn phaåm loaïi A laø 60%. Ta coù:
Moät loâ haøng goàm 10 saûn phaåm vôùi tæ leä saûn phaåm loaïi A laø 60%. Cho maùy C = A
saûn xuaát 2 saûn phaåm vaø töø loâ haøng laáy ra 3 saûn phaåm. 0B0 + A1B1 + A2B2.
a) Tính xaùc suaát ñeå soá saûn phaåm loaïi A coù trong 2 saûn phaåm do maùy saûn
Töø ñaây, do tính xung khaéc vaø ñoäc laäp, caùc coâng thöùc coäng vaø nhaân xaùc
xuaát baèng soá saûn phaåm loaïi A coù trong 3 saûn phaåm ñöôïc laáy ra töø loâ haøng. suaát cho ta:
b) Giaû söû trong 5 saûn phaåm thu ñöôïc coù 2 saûn phaåm loaïi A. Tính xaùc suaát
ñeå 2 saûn phaåm loaïi A ñoù ñeàu do maùy saûn xuaát.
P(C) = P(A0)P(B0)+ P(A1)P(B1)+ P(A2)P(B2) = 0,3293. 21 22
b) Goïi D laø bieán coá coù 2 saûn phaåm loaïi A trong 5 saûn phaåm coù ñöôïc.
a) Goïi A laø bieán coá laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I.
Giaû söû trong 5 saûn phaåm treân coù 2 saûn phaåm loaïi A. Khi ñoù bieán coá D ñaõ
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
xaûy ra. Do ñoù, xaùc suaát ñeå 2 saûn phaåm loaïi A ñoù ñeàu do maùy saûn xuaát
chính laø xaùc suaát coù ñieàu kieän P(A2/D).
P(A) = P(A0)P(A/A0) + P(A1)P(A/A1) + P(A2)P(A/A2) + P(A3)P(A/A3).
Theo coâng thöùc nhaân xaùc suaát ta coù: P(A D) 2 P(A /D) = .
Töø giaû thieát ta suy ra trong loâ I coù 15.60% = 9 sp toát vaø 6 sp xaáu. Do ñoù 2 P(D)
theo coâng thöùc tính xaùc suaát löïa choïn, ta coù:
Nhaän xeùt raèng toång soá saûn phaåm loaïi A coù trong 5 saûn phaåm thu ñöôïc 1 1 C C 81 9 9 P(A / A ) = = ;
phuï thuoäc vaøo caùc bieán coá A 0 2 C 153 i vaø Bj theo baûng sau: 18 1 1 C C 80 B 10 8 P(A / A ) = = ; 0 B1 B2 B3 1 2 C 153 A 18 0 0 1 2 3 1 1 A C C 77 1 1 2 3 4 11 7 P(A / A ) = = ; 2 2 A C 153 2 2 3 4 5 18 Suy ra 1 1 C C 72 12 6 P(A / A ) = = . D = A 3 2 0 B2 + A1B1 + A2B0 vaø A2D = A2B0 . C 153 18
Töø ñaây, ta tính ñöôïc P(D) = 0,236 ; P(A2D) = 0,012. Suy ra xaùc suaát caàn
Suy ra xaùc suaát caàn tìm laø: P(A) = 0,5035 tìm laø
b) Goïi B laø bieán coá laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I, trong ñoù sp toát coù P(A2/D) = 0,0508.
trong loâ I töø tröôùc. Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
Baøi 1.18: Coù hai loâ haøng, moãi loâ chöùa 60% saûn phaåm toát, trong ñoù loâ I
P(B) = P(A0)P(B/A0) + P(A1)P(B/A1) + P(A2)P(B/A2) + P(A3)P(B/A3).
chöùa 15 saûn phaåm, loâ II chöùa raát nhieàu saûn phaåm. Töø loâ II laáy ra 3 saûn
phaåm boû vaøo loâ I, sau ñoù töø loâ I laáy ra 2 saûn phaåm. Ta coù: a)
Tính xaùc suaát laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I. 1 1 C C 81 b) 9 9
Tính xaùc suaát laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I, trong ñoù sp toát coù P(B / A ) = = ; 0 2 C 153 trong loâ I töø tröôùc. 18 1 1 c) C C 72
Giaû söû ñaõ laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I. Tính xaùc suaát ñaõ laáy 9 8 P(B / A ) = = ; 1 2
ñöôïc 2sp toát, 1sp xaáu töø loâ II. C 153 18 Lôøi giaûi 1 1 C C 63 9 7 P(B / A ) = = ; 2 2 C 153 18
Goïi Aj (j = 0,1, 2, 3) laø bieán coá coù j saûn phaåm toát vaø (3-j) saûn phaåm xaáu coù 1 1 C C 54
trong 3 saûn phaåm ñöôïc choïn ra töø loâ II. Khi ñoù A 9 6 = = 0, A1, A2, A3 laø moät heä P(B / A ) . 3 2
ñaày ñuû, xung khaéc töøng ñoâi. Theo coâng thöùc Bernoulli ta coù: C 153 18 0 0 3 3
P(A ) = C p q = (0,4) = 0, 064;
Suy ra xaùc suaát caàn tìm laø: P(B) = 0,4235. 0 3 1 1 2 1 2
P(A ) = C p q = 3(0, 6) (0, 4) = 0, 288; 1 3
c) Giaû söû ñaõ laáy ñöôïc 1sp toát, 1sp xaáu töø loâ I. Khi ñoù bieán coá A ñaõ xaûy ra. 2 2 1 2 1
P(A ) = C p q = 3(0, 6) (0, 4) = 0, 432; 2 3
Do ñoù xaùc suaát ñaõ laáy ñöôïc 2sp toát, 1sp xaáu töø loâ II trong tröôøng hôïp naøy 3 3 0 3
P(A ) = C p q = (0, 6) = 0, 216. 3 3
chính laø XS coù ñieàu kieän P(A2/A). Theo coâng thöùc Bayes, ta coù: 23 24 77 0, 432. P(A )P(A / A ) 2 2 153 P(A / A) = = = 0, 4318. 2 P(A) 0, 5035
-------------- * ------------- 25 1 42 − μ 1 42 − 40,56 1 Lôøi giaûi P (X = 42) = f ( ) = f ( ) = f (0, 29) σ σ 4, 9101 4, 9101 4, 9101 0, 3825
Tröôùc heát ta tìm xaùc suaát p ñeå moät kieän ñöôïc nhaän. = = 0, 0779 = 7,79%. 4, 9101
Goïi C laø bieán coá kieän haøng ñöôïc nhaän. Ta caàn tìm p = P(C).
Töø giaû thieát ta suy ra coù hai loaïi kieän haøng:
Loaïi I: goàm 6A, 4B chieám 0,9 = 90%.
(Tra baûng giaù trò haøm Gauss ta ñöôïc f(0,29) = 0,3825).
Loaïi II: goàm 8A, 2B chieám 0,1 = 10%. Goïi A
b) Xaùc suaát ñeå coù töø 40 ñeán 45 kieän ñöôïc nhaän laø
1, A2 laàn löôït laø caùc bieán coá kieän haøng thuoäc loaïi I, II. Khi ñoù A1, 45 − μ 40 − μ 45 − 40,56 40 − 40, 56
A2 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù P (40 ≤ X ≤ 45) = ϕ ( ) − ϕ( ) = ϕ( ) − ϕ( ) σ σ 4, 9101 4, 9101 P(A1) = 0,9; P(A2) = 0,1.
= ϕ (0, 90)− ϕ (− 0,11) = ϕ (0, 90)+ ϕ (0,11) = 0, 3159+ 0,0438 = 0,3597 = 35, 97%.
Theo coâng thöùc xaùc suaát ñaày ñuû ta coù:
P(C) = P(A1) P(C/A1) + P(A2) P(C/A2).
(Tra baûng giaù trò haøm Laplace ta ñöôïc ϕ (0,9) = 0,3519; ϕ (0,11) = 0,0438).
Theo giaû thieát, töø moãi kieän laáy ra 2 saûn phaåm; neáu caû 2 saûn phaåm thuoäc
loaïi A thì môùi nhaän kieän ñoù. Do ñoù:
c) Xaùc suaát ñeå coù ít nhaát 42 kieän ñöôïc nhaän laø 2 0 C C 1 6 4 P(C / A ) = P (2) = = ; 100 − μ 42 − μ 100 −40,56 42 −40,56 1 2 2 P (42 ≤ X ≤ 100) = ( ϕ ) − ( ϕ ) = ( ϕ ) − ( ϕ ) C 3 10 σ σ 4, 9101 4, 9101
= ϕ(12) − ϕ(0, 29) = 0,50 − 0,1141 = 0, 3859 = 38,59%. 2 0 C C 28 8 2 P(C / A ) = P (2) = = . 2 2 2 C 45
(Tra baûng giaù trò haøm Laplace ta ñöôïc ϕ(12) = ϕ(5) = 0,5; ϕ(0,29) = 10 0,1141). Suy ra
P(C) = 0,9. (1/3) + 0,1.(28/45) = 0,3622.
Vaäy xaùc suaát ñeå moät kieän ñöôïc nhaän laø p = 0,3622.
Baøi 2.5: Saûn phaåm trong moät nhaø maùy ñöôïc ñoùng thaønh töøng kieän, moãi
Baây giôø, kieåm tra 144 kieän. Goïi X laø soá kieän ñöôïc nhaän trong 144 kieän
ñöôïc kieåm tra, thì X coù phaân phoái nhò thöùc X
kieän goàm 10 saûn phaåm Soá saûn phaåm loaïi A trong caùc hoäp laø X coù phaân
∼ B(n,p) vôùi n = 144, p =
0,3622. Vì n = 144 khaù lôùn vaø p = 0,3622 khoâng quaù gaàn 0 cuõng khoâng phoái nhö sau:
quaù gaàn 1 neân ta coù theå xem X coù phaân phoái chuaån nhö sau: X ∼ N(μ, X 6 8 σ2) vôùi
μ = np = 144.0,3622 = 52,1568; P 0,9 0,1 σ =
npq = 144.0, 3622.(1 − 0, 3622) = 5, 7676.
a) Xaùc suaát ñeå coù 53 kieän ñöôïc nhaän laø P(X=53) = 6,84% (Töông töï Baøi
Khaùch haøng choïn caùch kieåm tra nhö sau: töø moãi kieän laáy ra 2 saûn phaåm; 21).
neáu thaáy caû 2 saûn phaåm ñeàu loaïi A thì môùi nhaän kieän ñoù; ngöôïc laïi thì
b) Xaùc suaát ñeå coù töø 52 ñeán 56 kieän ñöôïc nhaän laø P(52 ≤ X ≤ 56) =
loaïi kieän ñoù. Kieåm tra 144 kieän (trong raát nhieàu kieän).
26,05% (Töông töï Baøi 21).
a) Tính xaùc suaát ñeå coù 53 kieän ñöôïc nhaän.
c) Phaûi kieåm tra ít nhaát bao nhieâu kieän ñeå xaùc suaát coù ít nhaát 1 kieän
b) Tính xaùc suaát ñeå coù töø 52 ñeán 56 kieän ñöôïc nhaän.
ñöôïc nhaän khoâng nhoû hôn 95%?
c) Phaûi kieåm tra ít nhaát bao nhieâu kieän ñeå xaùc suaát coù ít nhaát 1 kieän
ñöôïc nhaän khoâng nhoû hôn 95%?
Goïi n laø soá kieän caàn kieåm tra vaø D laø bieán coá coù ít nhaát 1 kieän ñöôïc nhaän.
Yeâu caàu baøi toaùn laø xaùc ñònh n nhoû nhaát sao cho P(D) ≥ 0,95. 7 8
Bieán coá ñoái laäp cuûa D laø D : khoâng coù kieän naøo ñöôïc nhaän.
• X1 coù phaân phoái nhò thöùc X1 ∼ B(n1,p1) vôùi n1 = 100, p1 = 80% =
Theo chöùng minh treân, xaùc suaát ñeå moät kieän ñöôïc nhaän laø p = 0,3622.
0,8. Vì n1 = 100 khaù lôùn vaø p1 = 0,8 khoâng quaù gaàn 0 cuõng khoâng Do ñoù
quaù gaàn 1 neân ta coù theå xem X1 coù phaân phoái chuaån nhö sau:
Theo coâng thöùc Bernoulli ta coù: X 2 1 ∼ N(μ1, σ1 ) n n n
P(D) = 1 − P(D) = 1 − q = 1 − (1 − 0, 3622) = 1 − (0, 6378) .
vôùi μ1 = n1p1 = 100.0,8 = 80; σ = n p q = 100.0, 8.0, 2 = 4. 1 1 1 1 Suy ra
• X2 coù phaân phoái nhò thöùc X2 ∼ B(n2,p2) vôùi n2 = 100, p2 = 60% = n
P(D) ≥ 0, 95 ⇔ 1 − (0, 6378) ≥ 0, 95
0,60. Vì n2 = 100 khaù lôùn vaø p2 = 0,60 khoâng quaù gaàn 0 cuõng n ⇔ (0, 6378) ≤ 0, 05
khoâng quaù gaàn 1 neân ta coù theå xem X2 coù phaân phoái chuaån nhö sau: ⇔ n ln(0, 6378) ≤ ln 0, 05 X 2 2 ∼ N(μ2, σ2 ) ln 0, 05 ⇔ n ≥ ≈ 6, 6612
vôùi μ2 = n2p2 = 100.0,60 = 60; ln(0, 6378) σ =
n p q = 100.0, 60.0, 40 = 4, 8990. 2 2 2 2 ⇔ n ≥ 7.
a) Xaùc suaát ñeå coù 70 saûn phaåm ñaït tieâu chuaån laø: 1 1 1 1 70 − μ 1 1 70 1 − μ2
P(X = 80) = P(X =70)+ P(X =70) = f( ) + f ( )
Vaäy phaûi kieåm tra ít nhaát 7 kieän. 1 2 2 2 2 σ σ 2 1 1 σ 2 σ 2 1 1 70 − 80 1 1 70 − 60 1 1 1 1 Baøi 2.6 = . f ( ) + . f ( )= . f ( 2 − , 5) + . f (2, 04)
: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä saûn phaåm ñaït tieâu chuaån 2 4 4 2 4,8990 4,8990 2 4 2 4,8990
laø 80% vaø moät maùy khaùc cuõng saûn xuaát loaïi saûn phaåm naøy vôùi tæ leä saûn 1 1 1 1
phaåm ñaït tieâu chuaån laø 60%. Choïn ngaãu nhieân moät maùy vaø cho saûn xuaát = . 0,0175 + . 0, 0498 = 0,000727 2 4 2 4,8990
100 saûn phaåm. Tính xaùc suaát ñeå
a) coù 70 saûn phaåm ñaït tieâu chuaån.
b) Xaùc suaát ñeå coù töø 70 ñeán 90 saûn phaåm ñaït tieâu chuaån laø:
b) coù töø 70 ñeán 90 saûn phaåm ñaït tieâu chuaån. 1 1 c)
P(70 ≤ X ≤ 90) = P(70 ≤ X ≤ 90)+ P(70 ≤ X ≤ 90)
coù khoâng ít hôn 70 saûn phaåm ñaït tieâu chuaån. 1 2 2 2 1 90− μ1 70− μ1 1 90− μ 2 70− μ 2 Lôøi giaûi = [ ( ϕ ) − ( ϕ )] + [ ( ϕ ) − ( ϕ )] 2 σ σ 2 1 1 σ 2 σ 2 1 90 − 80 70 − 80 1 90 − 60 70 − 60
Goïi X laø ÑLNN chæ soá saûn phaåm ñaït tieâu chuaån trong 100 saûn phaåm. = [ ( ϕ ) − ( ϕ )] + [ ( ϕ ) − ( ϕ )] 2 4 4 2 4,899 4,899 A
1, A2 laàn löôït laø caùc bieán coá choïn ñöôïc maùy 1, maùy 2. 1
Khi ñoù A1, A2 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù: = [ ( ϕ 2, 5) − ( ϕ 2 − , 5) + ( ϕ 6,12) − ( ϕ 2, 04)] 2 P(A1) = P(A2) = 0,5. 1
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù:
= (0, 49379 + 0,49379 + 0, 5 − 0, 47932) 2 = P(X = k) = P( 0,50413 1 A )P(X=k/ 1 A ) + P( 2 A )P(X= k/A2 ) 1 1 c) (1)
Xaùc suaát coù khoâng ít hôn 70 saûn phaåm ñaït tieâu chuaån laø = P(X=k/A )+ P(X=k/A ) 1 2 P(70 ≤ X ≤ 100) =0,5072 2 2 (Töông töï caâu b)
Nhö vaäy, goïi X1, X2 laàn löôït laø caùc ÑLNN chæ soá saûn phaåm ñaït tieâu
chuaån trong tröôøng hôïp choïn ñöôïc maùy 1, maùy 2. Khi ñoù: 1 1
Baøi 2.7: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä pheá phaåm laø 1% vaø moät • (1) cho ta P(X = k) = P(X =k)+ P(X =k) 1 2 2 2
maùy khaùc cuõng saûn xuaát loaïi saûn phaåm naøy vôùi tæ leä pheá phaåm laø 2%. 9 10
Choïn ngaãu nhieân moät maùy vaø cho saûn xuaát 1000 saûn phaåm. Tính xaùc
Baøi 2.8: Moät xí nghieäp coù hai maùy I vaø II. Trong ngaøy hoäi thi, moãi coâng suaát ñeå
nhaân döï thi ñöôïc phaân moät maùy vaø vôùi maùy ñoù seõ saûn xuaát 100 saûn a) coù 14 pheá phaåm.
phaåm. Neáu soá saûn phaåm loaïi A khoâng ít hôn 70 thì coâng nhaân ñoù seõ ñöôïc
b) coù töø 14 ñeán 20 pheá phaåm.
thöôûng. Giaû söû ñoái vôùi coâng nhaân X, xaùc suaát saûn xuaát ñöôïc 1 saûn phaåm Lôøi giaûi
loaïi A vôùi caùc maùy I vaø II laàn löôït laø 0,6 vaø 0,7.
a) Tính xaùc suaát ñeå coâng nhaân X ñöôïc thöôûng.
Goïi X laø ÑLNN chæ soá pheá phaåm trong 1000 saûn phaåm.
b) Giaû söû coâng nhaân X döï thi 50 laàn. Soá laàn ñöôïc thöôûng tin chaéc nhaát laø A bao nhieâu?
1, A2 laàn löôït laø caùc bieán coá choïn ñöôïc maùy 1, maùy 2. Khi ñoù A
1, A2 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù: P(A Lôøi giaûi 1) = P(A2) = 0,5.
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù:
Goïi Y laø ÑLNN chæ soá saûn phaåm loaïi A coù trong 100 saûn phaåm ñöôïc saûn P(X = k) = P( 1 A )P(X=k/ 1 A ) + P( 2 A )P(X= k/A2 ) xuaát. 1 1 (1) A = P(X=k/A )+ P(X=k/A )
1, A2 laàn löôït laø caùc bieán coá choïn ñöôïc maùy I, maùy II. 1 2 2 2
Khi ñoù A1, A2 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
Nhö vaäy, goïi X1, X2 laàn löôït laø caùc ÑLNN chæ soá pheá phaåm trong tröôøng P(A1) = P(A2) = 0,5.
hôïp choïn ñöôïc maùy 1, maùy 2. Khi ñoù:
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù: 1 1 • (1) cho ta P(X = k) = P(X =k)+ P(X =k) 1 2 2 2
P(Y = k) = P(A )P(Y=k/A ) + P(A )P(Y= k/A ) 1 1 2 2
• X1 coù phaân phoái nhò thöùc X1 ∼ B(n1,p1) vôùi n1 = 1000 vaø p1 = 1% = 1 1 (1) = P(Y=k/A )+ P(Y=k/A ) 0,001. Vì n 1 2
1 khaù lôùn vaø p1 khaù beù neân ta coù theå xem X1 coù phaân 2 2 phaân phoái Poisson:
Nhö vaäy, goïi X1, X2 laàn löôït laø caùc ÑLNN chæ soá saûn phaåm loaïi A coù
X1 ∼ P(a1) vôùi a1 = n1p1 = 1000.0,01 = 10, nghóa laø X2 ∼ P(10).
trong 100 saûn phaåm ñöôïc saûn xuaát trong tröôøng hôïp choïn ñöôïc maùy I, maùy II. Khi ñoù:
• X2 coù phaân phoái nhò thöùc X2 ∼ B(n2,p2) vôùi n2 = 1000 vaø p2 = 2% = 1 1 P(Y = k) = P(X =k)+ P(X =k) 0,002. Vì n • (1) cho ta 1 2
2 khaù lôùn vaø p2 khaù beù neân ta coù theå xem X2 coù phaân 2 2 phaân phoái Poisson:
• X1 coù phaân phoái nhò thöùc X1 ∼ B(n1,p1) vôùi n1 = 100, p1 = 0,6. Vì
X1 ∼ P(a2) vôùi a2 = n2p2 = 1000.0,02 = 20, nghóa laø X2 ∼ P(20).
n1 = 100 khaù lôùn vaø p1 = 0,6 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn
1 neân ta coù theå xem X1 coù phaân phoái chuaån nhö sau:
a) Xaùc suaát ñeå coù 14 pheá phaåm laø: X 2 1 ∼ N(μ1, σ1 ) 1 − 0 14 2 − 0 14 1 1 1 e 10 1 e 20 vôùi μ
P(X = 14) = P(X =14)+ P(X =14) = + = 0, 0454 1 = n1p1 = 100.0,6 = 60; 1 2 2 2 2 14! 2 14 ! σ =
n p q = 100.0, 6.0, 4 = 4, 8990. 1 1 1 1
• X2 coù phaân phoái nhò thöùc X2 ∼ B(n2,p2) vôùi n2 = 100, p2 = 0,7. Vì n2
b) Xaùc suaát ñeå coù töø 14 ñeán 20 pheá phaåm laø:
= 100 khaù lôùn vaø p2 = 0,7 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn 1 1 1
P(14 ≤ X ≤ 20) = P(14 ≤ X ≤ 20)+ P(14 ≤ X ≤ 20)
neân ta coù theå xem X2 coù phaân phoái chuaån nhö sau: 1 2 2 2 X 2 2 ∼ N(μ2, σ2 ) 20 20 1 − 0 k 2 − 0 k 1 e 10 1 e 20 vôùi μ = + = 31, 35% ∑ ∑ 1 = n2p2 = 100.0,7 = 70; 2 k ! 2 k ! σ =
n p q = 100.0, 7.0, 3 = 4, 5826. k 1 2 2 2 2 = 4 k 1 = 4
a) Xaùc suaát ñeå coâng nhaân X ñöôïc thöôûng laø: 11 12 1 1
P(70 ≤ Y ≤ 100) = P(70 ≤ X ≤ 100)+ P(70 ≤ X ≤ 100) 1 2 2 2
P(X = k) = P(A )P(X=k/A ) + P(A )P(X= k/A ) 1 1 2 2 1 100 − μ 70 − μ 1 100 − μ 70 1 1 2 − μ2 = [ϕ( ) − ϕ( )] + [ϕ( ) − ϕ( )] 1 1 (1) 2 = P(X=k/A )+ P(X=k/A ) σ σ 2 σ σ 1 2 1 1 2 2 2 2 1 100 − 60 70 − 60 1 100 −70 70 −70 Nhö vaäy, goïi X = [ϕ( ) − ϕ( )] + [ϕ( ) − ϕ( )]
1, X2 laàn löôït laø caùc ÑLNN chæ soá vieân truùng trong 100 2 4, 899 4,899 2 4,5826 4,5826
vieân ñöôïc baén ra trong tröôøng hôïp choïn ñöôïc khaåu loaïi I, II. Khi ñoù: 1 1 1 1
= [ϕ(8,16) − ϕ(2,04) + ϕ(6, 55) − ϕ(0)]= (0, 5 − 0, 47932 + 0,5) = 0,2603 • (1) cho ta P(X = k) = P(X =k)+ P(X =k) 1 2 2 2 2 2
• X1 coù phaân phoái nhò thöùc X1 ∼ B(n1,p1) vôùi n1 = 100, p1 = 0,6. Vì n1
b) Giaû söû coâng nhaân X döï thi 50 laàn. Soá laàn ñöôïc thöôûng tin chaéc nhaát laø
= 100 khaù lôùn vaø p1 = 0,6 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn 1 bao nhieâu?
neân ta coù theå xem X1 coù phaân phoái chuaån nhö sau: 2 X1 ∼ N(μ1, σ1 )
Goïi Z laø ÑLNN chæ soá laàn coâng nhaân X ñöôïc thöôûng. Khi ñoù Z coù
vôùi μ1 = n1p1 = 100.0,6 = 60;
phaân phoái nhò thöùc Z ∼ B(n,p) vôùi n = 50, p = 0,2603. Soá laàn ñöôïc σ =
n p q = 100.0, 6.0, 4 = 4, 8990. 1 1 1 1
thöôûng tin chaéc nhaát chính laø Mod(Z). Ta coù:
• X2 coù phaân phoái nhò thöùc X2 ∼ B(n2,p2) vôùi n2 = 100, p2 = 0,5. Vì n2
= 100 khaù lôùn vaø p2 = 0,5 khoâng quaù gaàn 0 cuõng khoâng quaù gaàn 1
Mod(Z) = k ⇔ np − q ≤ k ≤ np − q + 1
neân ta coù theå xem X2 coù phaân phoái chuaån nhö sau:
⇔ 50.0, 2603− 0, 7397 ≤ k ≤ 50.0,2603 − 0,7397 + 1 X 2 2 ∼ N(μ2, σ2 )
⇔ 12, 2753 ≤ k ≤ 13, 2753 ⇔ k = 13
vôùi μ1 = n2p2 = 100.0,5 = 50; σ = n p q = 100.0, 5.0, 5 = 5. 2 2 2 2
Vaäy soá laàn ñöôïc thöôûng tin chaéc nhaát cuûa coâng nhaân X laø 13 laàn.
a) Xaùc suaát ñeå chieán só A ñöôïc thöôûng laø:
Baøi 2.9: Trong ngaøy hoäi thi, moãi chieán só seõ choïn ngaãu nhieân moät trong 1 1
P(65 ≤ X ≤ 100) = P(65 ≤ X ≤ 100)+ P(65 ≤ X ≤ 100)
hai loaïi suùng vaø vôùi khaåu suùng choïn ñöôïc seõ baén 100vieân ñaïn. Neáu coù töø 1 2 2 2
65 vieân trôû leân truùng bia thì ñöôïc thöôûng. Giaû söû ñoái vôùi chieán só A, xaùc 1 100 − μ 65 − μ 1 100 − μ 65 − μ 1 1 2 2 = [ ( ϕ ) − ϕ( )] + [ ( ϕ ) − ϕ( )]
suaát baén 1 vieân truùng bia baèng khaåu suùng loaïi I laø 60% vaø baèng khaåu 2 σ σ 2 1 1 σ 2 σ 2 suùng loaïi II laø 50%. 1 100 − 60 65 − 60 1 100 − 50 65 − 50 = [ ( ϕ ) − ϕ( )] + [ϕ( ) − ( ϕ )]
a) Tính xaùc suaát ñeå chieán só A ñöôïc thöôûng. 2 4, 899 4, 899 2 5 5
b) Giaû söû chieán só A döï thi 10 laàn. Hoûi soá laàn ñöôïc thöôûng tin chaéc nhaát 1 1 = [ ( ϕ 8,16) − ϕ(1, 02) + ( ϕ 10) − ϕ(3)]=
(0, 5 − 0,34614 + 0,5 − 0, 49865) = 0, 0776. laø bao nhieâu? 2 2
c) Chieán só A phaûi tham gia hoäi thi ít nhaát bao nhieâu laàn ñeå xaùc suaát coù
ít nhaát moät laàn ñöôïc thöôûng khoâng nhoû hôn 98%?
b) Giaû söû chieán só A döï thi 10 laàn. Soá laàn ñöôïc thöôûng tin chaéc nhaát laø bao nhieâu? Lôøi giaûi
Goïi Y laø ÑLNN chæ soá laàn chieán só A ñöôïc thöôûng. Khi ñoù Y coù phaân
phoái nhò thöùc Y ∼ B(n,p) vôùi n = 10, p = 0,0776. Soá laàn ñöôïc thöôûng tin
Goïi X laø ÑLNN chæ soá vieân truùng trong 100 vieân ñöôïc baén ra.
chaéc nhaát chính laø mod(Y). Ta coù: Goïi A
1, A2 laàn löôït laø caùc bieán coá choïn ñöôïc khaåu suùng loaïi I, II.
mod(Y) = k ⇔ np − q ≤ k ≤ np −q +1
Khi ñoù A1, A2 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø ta coù:
⇔ 10.0, 0776 − 0,9224 ≤ k ≤ 10.0, 0776 − 0, 9224 + 1 P(A1) = P(A2) = 0,5. ⇔ 0
− ,1464 ≤ k ≤ 0, 8536 ⇔ k = 0
Theo coâng thöùc xaùc xuaát ñaày ñuû, vôùi moãi 0 ≤ k ≤ 100, ta coù: 13 14
Theo coâng thöùc Bernoulli ta coù:
Vaäy soá laàn ñöôïc thöôûng tin chaéc nhaát cuûa chieán só A laø 0 laàn, noùi caùch 0 0 4 P(X = 0) = (0, 8) (0, 2) = 0, 0016; C4
khaùc, thöôøng laø chieán só A khoâng ñöôïc thöôûng laàn naøo trong 10 laàn tham 1 1 3 gia. P(X = 1) = (0, 8) (0, 2) = 0, 0256; C 4 2 2 2 P(X = 2) = (0, 8) (0, 2) = 0,1536; C
c) Chieán só A phaûi tham gia hoäi thi ít nhaát bao nhieâu laàn ñeå xaùc suaát coù 4 3 3 1
ít nhaát moät laàn ñöôïc thöôûng khoâng nhoû hôn 98%? P(X = 3) = (0, 8) (0, 2) = 0, 4096; C4 4 4 0 P(X = 4) = (0, 8) (0, 2) = 0, 4096. C
Goïi n laø soá laàn tham gia hoäi thi vaø D laø bieán coá coù ít nhaát 1 laàn ñöôïc 4
Vaäy luaät phaân phoái cuûa X laø:
thöôûng. Yeâu caàu baøi toaùn laø xaùc ñònh n nhoû nhaát sao cho P(D) ≥ 0,98.
Bieán coá ñoái laäp cuûa D laø D : khoâng coù laàn naøo ñöôïc thöôûng. X 0 1 2 3 4
Theo chöùng minh treân, xaùc suaát ñeå moät laàn ñöôïc thöôûng laø p = 0,0776. P
0,0016 0,0256 0,1536 0,4096 0,4096 Do ñoù
b) Tìm kyø voïng vaø phöông sai cuûa X.
Theo coâng thöùc Bernoulli ta coù: n n n
- Kyø voïng: M(X) = np = 3,2.
P(D) = 1 − P(D) = 1 − q = 1 − (1 − 0, 0776) = 1 − (0, 9224) .
- Phöông sai: D(X) = npq = 0,64. Suy ra
Baøi 2.11: Coù hai loâ haøng I vaø II, moãi loâ chöùa raát nhieàu saûn phaåm. Tæ leä n
P(D) ≥ 0, 98 ⇔ 1 − (0, 9224) ≥ 0, 98
saûn phaåm loaïi A coù trong hai loâ I vaø II laàn löôït laø 70% vaø 80%. Laáy n ⇔ (0, 9224) ≤ 0, 02
ngaãu nhieân töø moãi loâ 2 saûn phaåm. ⇔ n ln 0, 9224 ≤ ln 0, 02
a) Tính xaùc suaát ñeå soá saûn phaåm loaïi A laáy töø loâ I lôùn hôn soá saûn phaåm ln 0, 02 loaïi A laáy töø loâ II. ⇔ n ≥ ≈ 48, 43 ln 0, 9224
b) Goïi X laø soá saûn phaåm loaïi A coù trong 4 saûn phaåm ñöôïc laáy ra. Tìm kyø
voïng vaø phöông sai cuûa X. ⇔ n ≥ 49. Lôøi giaûi
Vaäy chieán só A phaûi tham gia hoäi thi ít nhaát laø 49 laàn.
Goïi X1, X2 laàn löôït laø caùc ÑLNN chæ soá sp loaïi A coù trong 2 sp ñöôïc
choïn ra töø loâ I, II. Khi ñoù
Baøi 2.10: Moät ngöôøi thôï saên baén 4 vieân ñaïn. Bieát xaùc suaát truùng ñích
• X1 coù phaân phoái nhò thöùc X1 ∼ B(n1, p1); n1 = 2; p1 = 70% = 0,7
cuûa moãi vieân ñaïn baén ra laø 0,8. Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá vieân
vôùi caùc xaùc suaát ñònh bôûi: ñaïn truùng ñích. k k 2 k P(X k) (0, 7) (0, 3) C − = =
a) Tìm luaät phaân phoái cuûa X. 1 2
b) Tìm kyø voïng vaø phöông sai cuûa X. Cuï theå X1 0 1 2 Lôøi giaûi P 0,09 0,42 0,49
• X2 coù phaân phoái nhò thöùc X2 ∼ B(n2, p2); n2 = 2; p2 = 80% = 0,8
a) Ta thaáy X coù phaân phoái nhò thöùc X∼ B(n,p) vôùi n = 4, p = 0,8. X laø
vôùi caùc xaùc suaát ñònh bôûi: k k 2 k
ÑLNN rôøi raïc nhaän 5 giaù trò: 0, 1, 2, 3 , 4. Luaät phaân phoái cuûa X coù daïng: P(X k) (0, 8) (0, 2) 2 C − = = 2 Cuï theå X 0 1 2 3 4 X2 0 1 2 P p0 p1 p2 p3 p4 P 0,04 0,32 0,64 15 16
a) Xaùc suaát ñeå soá saûn phaåm loaïi A laáy töø loâ I lôùn hôn soá saûn phaåm loaïi A X2 0 1 2 laáy töø loâ II laø: P 3/45 21/45 21/45
P(X1 ≥ X2) = P[(X1 =2)(X2 =0)+ (X1 =2)(X2 =1)+ (X1 =1)(X2 =0)]
= P(X1 =2)P(X2 =0)+ P(X1 =2)P(X2 =1)+ P(X1 =1)P(X2 =0) =
Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá bi ñoû coù trong 4 bi ñöôïc ruùt ra. Khi 0,1932. ñoù X = X1 + X2
b) Goïi X laø soá sp loaïi A coù trong 4 sp choïn ra . Khi ñoù
Baûng giaù trò cuûa X döïa vaøo X1, X2 nhö sau: X = X1 + X2
Vì X1 , X2 ñoäc laäp neân ta coù: X X2 0 1 2
- Kyø voïng cuûa X laø M(X) = M(X1) + M(X2) = n1p1 + n2p2 = 3 X1
- Phöông sai cuûa X laø D(X) = D(X1) + D(X2) = n1p1q1 + n2p2q2 = 0,74. 0 0 1 2 1 1 2 3
Baøi 2.12: Cho hai hoäp I vaø II, moãi hoäp coù 10 bi; trong ñoù hoäp I goàm 6 bi 2 2 3 4
ñoû, 4 bi traéng vaø hoäp II goàm 7 bi ñoû, 3 bi traéng. Ruùt ngaãu nhieân töø moãi hoäp hai bi.
a) Xaùc suaát ñeå ñöôïc 2 bi ñoû vaø 2 bi traéng laø:
a) Tính xaùc suaát ñeå ñöôïc hai bi ñoû vaø hai bi traéng.
b) Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá bi ñoû coù trong 4 bi ñöôïc ruùt ra.
P(X = 2) = P[(X1=0) (X2=2)+ (X1=1) (X2=1)+ (X1=2) (X2=0)]
Tìm luaät phaân phoái cuûa X.
= P(X1=0) P(X2=2)+ P(X1=1)P(X2=1)+ P(X1=2)P(X2=0)]
= (6/45)(21/45) + (24/45)(21/45) + (15/45)(3/45) = 1/3. Lôøi giaûi
b) Luaät phaân phoái cuûa X coù daïng:
Goïi X1, X2 laàn löôït laø caùc ÑLNN chæ soá bi ñoû coù trong 2 bi ñöôïc choïn
ra töø hoäp I, hoäp II. Khi ñoù
- X1 coù phaân phoái sieâu boäi X1 ∼ H(N1, N1A, n1); N1 = 10; N1A= 6; n1 = X 0 1 2 3 4
2 vôùi caùc xaùc suaát ñònh bôûi: P p0 p1 p2 p3 p4 k 2 −k C C 6 4 P(X = k) = . 1 2 C trong ñoù: 10
p0 = P(X = 0)= P(X1 =0) P(X2 = 0) = 2/225; Cuï theå
p1 = P(X = 1)= P(X1 =0) P(X2 = 1) + P(X1 =1) P(X2 = 0)= 22/225; p2 = P(X = 2) = 1/3; X1 0 1 2
p3 = P(X = 3)= P(X1 =1) P(X2 = 2) + P(X1 =2) P(X2 = 1)= 91/225; P 6/45 24/45 15/45
p4 = P(X = 4)= P(X1 =2) P(X2 = 2) = 7/45.
- X2 coù phaân phoái sieâu boäi X2 ∼ H(N2, N2A, n2); N2 = 10; N2A = 7; n2
Vaäy luaät phaân phoái cuûa X laø : = 2
vôùi caùc xaùc suaát ñònh bôûi: X 0 1 2 3 4 k 2 −k C7C3 P(X P 2/225 22/225 1/3 91/225 7/45 = k) = . 2 2 C 10 Cuï theå 17 18
Baøi 2.13: Moät maùy saûn xuaát saûn phaåm vôùi tæ leä pheá phaåm 10%. Moät loâ
haøng goàm 10 saûn phaåm vôùi tæ leä pheá phaåm 30%. Cho maùy saûn xuaát 3 saûn trong ñoù:
phaåm vaø töø loâ haøng laáy ra 3 saûn phaåm. Goïi X laø soá saûn phaåm toát coù trong
p0 = P(X = 0)= P(X1 = 0)P(X2 = 0) = 1/120000; 6 saûn phaåm naøy.
p1 = P(X = 1)= P(X1 = 0)P(X2 = 1) + P(X1 = 1)P(X2 = 0) = 1/2500;
a) Tìm luaät phaân phoái cuûa X.
p2 = P(X = 2) = P(X1 = 0)P(X2 = 2) + P(X1 = 1)P(X2 = 1) + P(X1 = 2)P(X2 =0)
b) Khoâng duøng luaät phaân phoái cuûa X, haõy tính M(X), D(X). = 291/40000
p3 = P(X = 3) = P(X1 = 0)P(X2 = 3) + P(X1 = 1)P(X2 = 2) + P(X1 = 2)P(X2 =1) Lôøi giaûi + P(X1 = 3)P(X2=0) = 473/7500
p4 = P(X = 4) = P(X1 = 1)P(X2 = 3) + P(X1 = 2)P(X2 = 2) + P(X1 = 3)P(X2 = 1) Goïi X = 10521/40000
1, X2 laàn löôït laø caùc ÑLNN chæ soá sp toát coù trong 3 saûn phaåm do
maùy saûn xuaát; do laáy töø loâ haøng. Khi ñoù X p
1, X2 ñoäc laäp vaø ta coù:
5 = P(X = 5) = P(X1 = 2) P(X2 = 3) + P(X1 = 3)P(X2 = 2) = 567/1250 - X p
1 coù phaân phoái nhò thöùc X1 ∼ B(n1, p1); n1 = 3; p1 = 0,9. Cuï theå
6 = P(X = 6) = P(X1 = 3)P(X2 = 3) = 1701/8000. ta coù: 0 0 2 3 P(X = 0) = p q = (0,1) = 0, 001;
Vaäy luaät phaân phoái cuûa X laø: 1 C3 1 1 2 2 P(X = 1) = p q = 3(0, 9)(0,1) = 0, 027; 1 C X 0 1 2 3 4 5 6 3 2
P 1/120000 1/2500 291/40000 473/7500 10521/40000 576/1250 1701/8000 2 1 2 P(X = 2) = p q = 3(0, 9) (0,1) = 0, 243; 1 C3 3 3 0 3 P(X = 3) = p q = (0, 9) = 0, 729. b) Vì X = X 1 C
1 + X2 vaø X1 , X2 ñoäc laäp neân ta coù: 3 - Kyø voïng cuûa X laø M(X) = M(X - X
1) + M(X2) = n1p1 + n2 p2 = 4,8 (vôùi p2 = N2A/N2)
2 coù phaân phoái sieâu boäi X2 ∼ H(N2, N2A, n2); N2 = 10; N2A = 7; n2
= 3 (vì loâ haøng goàm 10 saûn phaåm vôùi tæ leä pheá phaåm laø 30%, nghóa laø loâ - Phöông sai cuûa X laø D(X) = D(X
haøng goàm 7 saûn phaåm toát vaø 3 saûn phaåm xaáu). Cuï theå ta coù:
1) + D(X2) = n1p1q1 + n2 p2q2(N2-n2)/(N2-1)= 0,76. 0 3
Baøi 2.14: Cho hai hoäp I vaø II, moãi hoäp coù 10 bi; trong ñoù hoäp I goàm 8 bi 1 C C 7 3 P(X = 0) = = ;
ñoû, 2 bi traéng vaø hoäp II goàm 6 bi ñoû, 4 bi traéng. Ruùt ngaãu nhieân töø hoäp I 2 3 120 C10
hai bi boû sang hoäp II, sau ñoù ruùt ngaãu nhieân töø hoäp II ba bi. 1 2 21 C
a) Tính xaùc suaát ñeå ñöôïc caû 3 bi traéng. 7C3 P(X = 1) = = ; 2 3 120 C
b) Goïi X laø ñaïi löôïng ngaãu nhieân chæ soá bi traéng coù trong ba bi ñöôïc ruùt 10
ra töø hoäp II. Tìm luaät phaân phoái cuûa X. Xaùc ñònh kyø voïng vaø phöông sai 2 1 63 C C cuûa X. 7 3 P(X = 2) = = ; 2 3 120 C 10 Lôøi giaûi 3 0 35 C7C3 P(X = 3) = = . 2 3 120 C
Goïi X laø ÑLNN chæ soá bi traéng coù trong 3 bi ruùt ra töø hoäp II. 10 A
i (i = 0, 1, 2) laø bieán coá coù i bi traéng vaø (2-i) bi ñoû coù trong 2 bi laáy ra töø hoäp I. Khi ñoù A a) Ta coù X = X
0, A1, A2 laø heä bieán coá ñaày ñuû, xung khaéc töøng ñoâi vaø ta
1 + X2. Luaät phaân phoái cuûa X coù daïng: coù: X 0 1 2 3 4 5 6 P p0 p1 p2 p3 p4 p5 p6 19 20 0 2 0 3 0 3 0 3 28 C 28 16 1 2C8 C C C C C C P(A ) = = ; 4 8 5 7 6 6 p = P(X = 0) = . + . + . = 179 / 825; 0 2 45 C 0 3 3 3 45 45 45 C C C 10 12 12 12 1 1 C C 1 2 1 2 1 2 16 28 C C 16 C C 1 C C 2 8 P(A ) = = ; 4 8 5 7 6 6 p = P(X = 1) = . + . + . = 223 / 450; 1 2 45 C 1 3 3 3 45 45 45 C C C 10 12 12 12 2 0 2 1 2 1 2 1 1 C 28 16 1 2C8 C C C C C C P(A ) = = . 4 8 5 7 6 6 p = P(X = 2) = . + . + . = 1277 / 4950; 2 2 45 C 2 3 3 3 45 45 45 C C C 10 12 12 12
Vôùi moãi k = 0, 1, 2, 3 theo coâng thöùc xaùc suaát ñaày ñuû, ta coù p3 = P(X= 3) = 73/2475.
Suy ra luaät phaân phoái cuûa X laø:
P(X = k) = P(A0)P(X = k/A0) + P(A1)P(X = k/A1) + P(A2)P(X = k/A2) X 0 1 2 3
a) Xaùc suaát ñeå ñöôïc caû ba bi traéng laø: P
179/825 223/450 1277/4950 73/2475
P(X = 3) = P(A0)P(X = 3/A0) + P(A1)P(X = 3/A1) + P(A2)P(X = 3/A2)
Töø ñoù suy ra kyø voïng cuûa X laø M(X) = 1,1 vaø phöông sai cuûa X laø Maø D(X) = 0,5829. 3 0 4 C C 4 8 P(X = 3 / A ) = = ; 0 3 220 C
Baøi 2.15: Coù ba loâ saûn phaåm, moãi loâ coù 20 saûn phaåm. Loâ thöù i coù i+4 saûn 12
phaåm loaïi A (i = 1, 2, 3). 3 0 10 C C
a) Choïn ngaãu nhieân moät loâ roài töø loâ ñoù laáy ra 3 saûn phaåm. Tính xaùc 5 7 P(X = 3 / A ) = = ; 1 3 220 C
suaát ñeå trong 3 saûn phaåm ñöôïc laáy ra coù ñuùng 1 saûn phaåm loaïi A. 12
b) Töø moãi loâ laáy ra 1 saûn phaåm. Goïi X laø toång soá saûn phaåm loaïi A coù 3 0 20 C C 6 6 P(X = 3 / A ) = = .
trong 3 saûn phaåm ñöôïc laáy ra. Tìm luaät phaân phoái cuûa X vaø tính Mod(X), 2 3 220 C M(X), D(X). 12 neân P(X= 3) = 73/2475.
b) Luaät phaân phoái cuûa X coù daïng: Lôøi giaûi X 0 1 2 3
a) Goïi C laø bieán coá trong 3 saûn phaåm ñöôïc laáy ra coù ñuùng 1 saûn phaåm P p loaïi A. 0 p1 p2 p3
Goïi A1, A2, A3 laàn löôït laø caùc bieán coá choïn ñöôïc loâ I, II, III. Khi ñoù A1, A2,
trong ñoù, töông töï nhö treân ta coù:
A3 laø moät heä ñaày ñuû, xung khaéc töøng ñoâi vaø P(A1) = P(A2) = P(A3) = 1/3.
Theo coâng thöùc xaùc suaát ñaày ñuû, ta coù:
P(C) = P(A1)P(C/A1) + P(A2)P(C/ A2)+ P(A3)P(C/A3)
Theo Coâng thöùc xaùc suaát löïa choïn: 21 22 1 2 C C 525
2.16: Moät ngöôøi coù 5 chìa khoùa beà ngoaøi raát gioáng nhau, trong ñoù chæ coù 2 5 15 P(C / A1) = = ; 3 1140 C
chìa môû ñöôïc cöûa. Ngöôøi ñoù tìm caùch môû cöûa baèng caùch thöû töøng chìa moät 20
cho ñeán khi môû ñöôïc cöûa thì thoâi (taát nhieân, chìa naøo khoâng môû ñöôïc thì 1 2 C C 546 6 14 P(C / A ) = = ;
loaïi ra). Goïi X laø soá chìa khoùa ngöôøi ñoù söû duïng. Tìm luaät phaân phoái cuûa 2 3 1140 C
X. Hoûi ngöôøi ñoù thöôøng phaûi thöû bao nhieâu chìa môùi môû ñöôïc cöûa? Trung 20 1 2 C C
bình ngöôøi ñoù phaûi thöû bao nhieâu chìa môùi môû ñöôïc cöûa? 7 13 546 P(C / A ) = = . 3 3 1140 C20 Lôøi giaûi Suy ra P(C)= 0,4728.
Ta thaáy X laø ÑLNN rôøi raïc nhaän 4 giaù trò: 1, 2, 3, 4. Luaät phaân phoái cuûa
b) Luaät phaân phoái cuûa X coù daïng: X coù daïng: X 0 1 2 3 X 1 2 3 4 P p0 p1 p2 p3 P p1 p2 p3 p4
Goïi Bj (j = 1, 2, 3) laø bieán coá laáy ñöôïc sp loaïi A töø loâ thöù j. Khi ñoù B1, B2,
Goïi Aj (j = 1,2, 3, 4) laø bieán coá chìa khoùa choïn laàn thöù j môû ñöôïc cöûa. Khi B3 ñoäc laäp vaø ñoù: 5 15 P(B ) = ; P(B ) = ; 1 1 20 20 P(X=1) = P(A1) = 2/5. 6 14 P(B )
P(X = 2) = P(A A ) = P(A )P(A / A ) = (3 / 5)(2 / 4) = 3 / 10; = ; P(B ) = ; 1 2 1 2 1 2 2 20 20 P(X = 3) = P( 1 A A2 3 A ) = P( 1 A )P( 2 A / 1 A )P(A3 / 1 A 2
A ) = (3 / 5)(2 / 4)(2 / 3) = 1 / 5 7 13 P(B ) = ; P(B ) = .
P(X = 4) = P(A A A A ) = P(A )P(A / A )P(A / A A )P(A / A A A ) 3 3 1 2 3 4 1 2 1 3 1 2 4 1 2 3 20 20
= (3 / 5)(2 / 4)(1 / 3)(2 / 2) = 1 / 10 Ta coù "
− X = 0" = B B B ⇒ P(X = 0) = P(B )P(B )p(B ) = 273 / 800 1 2 3 1 2 3
Vaäy luaät phaân phoái cuûa X laø: "
− X =1 " = B B B + B B B + B B B ⇒ 1 2 3 1 2 3 1 2 3
P(X = 1) = P(B )P(B )P(B ) + P(B )P(B )P(B ) + P(B )P(B )P(B ) = 71 / 160 1 2 3 1 2 3 1 2 3 X 1 2 3 4 "
− X = 2" = B B B + B B B + B B B P 2/5 3/10 1/5 1/10 1 2 3 1 2 3 1 2 3 ⇒
P(X = 2) = P(B )P(B )P(B ) + P(B )P(B )P(B ) P(B )P(B )P(B ) = 151 / 800 1 2 3 1 2 3 + 1 2 3 "
− X = 3" = B B B ⇒ P(X = 3) = P(B )P(B )P(B ) = 21 / 800
Töø luaät phaân phoái treân ta suy ra: 1 2 3 1 2 3
Vaäy luaät phaân phoái cuûa X laø
- Mode cuûa X laø Mod(X) = 1. X 0 1 2 3
- Kyø voïng cuûa X laø M(X) = x p = 2 ∑ i i . P 273/800 71/160 151/800 21/800
Vaäy ngöôøi ñoù thöôøng phaûi thöû 1 chiaø thì môû ñöôïc cöûa. Trung bình ngöôøi
Töø luaät phaânphoái cuûa X ta suy ra mode, kyø voïng vaø phöông sai cuûa X :
ñoù phaûi thöû 2 chìa môùi môû ñöôïc cöûa. - Mode: Mod(X) = 1. Baøi 2.17 - Kyø voïng: M(X) = 0,9.
: Moät ngöôøi thôï saên coù 5 vieân ñaïn. Ngöôøi ñoù ñi saên vôùi nguyeân - Phöông sai: D(X) = 0,625.
taéc: neáu baén truùng muïc tieâu thì veà ngay, khoâng ñi saên nöõa. Bieát xaùc suaát 23 24
truùng ñích cuûa moãi vieân ñaïn baén ra laø 0,8. Goïi X laø ñaïi löôïng ngaãu nhieân
chæ soá vieân ñaïn ngöôøi aáy söû duïng trong cuoäc saên. X 2 3 4
a) Tìm luaät phaân phoái cuûa X. P p2 p3 p4
b) Tìm kyø voïng vaø phöông sai cuûa X.
Goïi Aj (j = 1,2, 3, 4) laø bieán coá vieân ñaïn thöù j truùng ñích. Khi ñoù: Lôøi giaûi P(A ) = 0, 8;P(A ) = 0, 2 j j
a) Ta thaáy X laø ÑLNN rôøi raïc nhaän 5 giaù trò: 1, 2,..., 5. Luaät phaân phoái Ta coù: cuûa X coù daïng: P(X = 2) = P( 1 A 2 A ) = P( 1 A )P( 2 A ) = 0,8.0, 8 = 0, 64; X 1 2 3 4 5
P(X = 3) = P(A A A + A A A ) = P(A A A ) + P(A A A ) 1 2 3 1 2 3 1 2 3 1 2 3 P p1 p2 p3 p4 p5
= P(A )P(A )P(A ) + P(A )P(A )P(A ) = 0,2.0, 8.0, 8 + 0, 8.0, 2.0, 8 = 0,256 Goïi A 1 2 3 1 2 3
j (j = 1,2,..., 5) laø bieán coá vieân ñaïn thöù j truùng ñích. Khi ñoù: P(A )
P(X = 4) = P(A A A + A A A + A A A + A A A ) = 0,8; P(A ) = 0, 2 j j 1 2 3 1 2 3 1 2 3 1 2 3 Ta coù:
= P(A )P(A )P(A ) + P(A )P(A )P(A ) + P(A )P(A )P(A ) + P(A )P(A )P(A ) 1 2 3 1 2 3 1 2 3 1 2 3 P(X=1) = P(A
= 0, 2.0, 2.0, 2 + 0, 8.0, 2.0, 2 + 0, 2.0, 8.0, 2 + 0, 2.0, 2.0, 8 = 0,104 1) = 0,8.
P(X = 2) = P(A A ) = P(A )P(A ) = 0, 2.0, 8 = 0,16; 1 2 1 2
P(X = 3) = P(A A A ) = P(A )P(A )P(A ) = 0,2.0, 2.0, 8 = 0,032;
Vaäy luaät phaân phoái cuûa X laø: 1 2 3 1 2 3 P(X
= 4) = P(A A A A ) = P(A )P(A )P(A )P(A ) = 0, 2.0,2.0,2.0, 8 = 0, 0064; 1 2 3 4 1 2 3 4 X 2 3 4 P(X = 5) = P( 1 A 2 A 3 A 4 A ) = P( 1 A )P( 2 A )P( 3 A )P( 4
A ) = 0,2.0,2.0, 2.0, 2 = 0, 0016. P 0,64 0,256 0,104
Vaäy luaät phaân phoái cuûa X laø:
b) Töø luaät phaân phoái cuûa X ta suy ra: X 1 2 3 4 5
- Kyø voïng cuûa X laø M(X) = 2,464. P 0,8 0,16 0,032 0,0064 0,0016
- Phöông sai cuûa X laø D(X) = 0,456704.
b) Töø luaät phaân phoái cuûa X ta suy ra:
--------------------------------
- Kyø voïng cuûa X laø M(X) = 1,2496.
- Phöông sai cuûa X laø D(X) = 0,3089.
Baøi 2.18: Moät ngöôøi thôï saên coù 4 vieân ñaïn. Ngöôøi ñoù ñi saên vôùi nguyeân
taéc: neáu baén 2 vieân truùng muïc tieâu thì veà ngay, khoâng ñi saên nöõa. Bieát
xaùc suaát truùng ñích cuûa moãi vieân ñaïn baén ra laø 0,8. Goïi X laø ñaïi löôïng
ngaãu nhieân chæ soá vieân ñaïn ngöôøi aáy söû duïng trong cuoäc saên.
a) Tìm luaät phaân phoái cuûa X.
b) Tìm kyø voïng vaø phöông sai cuûa X. Lôøi giaûi
a) Ta thaáy X laø ÑLNN rôøi raïc nhaän 3 giaù trò: 2, 3, 4. Luaät phaân phoái cuûa X coù daïng: 25 26 BAØI GIAÛI
vì trong n = 100 con coù m = 10 + 10 + 10 = 30 con coù troïng löôïng töø
XAÙC SUAÁT THOÁNG KEÂ
60kg trôû leân, nghóa laø coù 30 con ñaït tieâu chuaån.
(GV: Traàn Ngoïc Hoäi – 2009)
a) Öôùc löôïng troïng löôïng trung bình cuûa loaïi vaät nuoâi treân vôùi ñoä tin caäy 96%. CHÖÔNG 3
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy γ = 1- α = 96% = 0,96.
LYÙ THUYEÁT MAÃU VAØ ÖÔÙC LÖÔÏNG
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng cho kyø voïng: S S
Baøi 3.1. Ñeå khaûo saùt troïng luôïng X cuûa moät loaïi vaät nuoâi trong noâng traïi, (X − z ; X + z ) α α , n n
ngöôøi ta quan saùt moät maãu vaø coù keát quûa sau:
trong ñoù ϕ(zα) = γ /2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta X(kg) 36 42 48 54 60 66 72
ñöôïc zα = 2,06. Vaäy öôùc löôïng khoaûng laø: Soá con 15 12 25 18 10 10 10 11, 0608 11, 0608 (51, 96 − 2, 06 ; 51, 96 + 2, 06 ) = (49, 68; 54, 24).
a) Öôùc löôïng troïng löôïng trung bình cuûa loaïi vaät nuoâi treân vôùi ñoä tin caäy 100 100 96%.
Noùi caùch khaùc, vôùi ñoä tin caäy 96%, troïng löôïng trung bình cuûa moät con
b) Vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi
naèm trong khoaûng töø 49,68kg ñeán 54,24kg.
treân laø bao nhieâu? Toái thieåu laø bao nhieâu?
c) Nhöõng con vaät coù troïng löôïng töø 60kg trôû leân ñöôïc goïi laø nhöõng con
b) Vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi
“ñaït tieâu chuaån”. Haõy öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy
treân laø bao nhieâu? Toái thieåu laø bao nhieâu? 95%.
Ta coù ñoä tin caäy γ = 1 - α = 95% = 0,95 (α = 0,05).
d) Neáu muoán öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy 99% vaø ñoä
- Ñeå bieát troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi treân laø bao
chính xaùc 10% thì caàn phaûi ñieàu tra theâm bao nhieâu con vaät nöõa?
nhieâu ta caàn öôùc löôïng khoaûng beân traùi cho kyø voïng μ = M(X).
e) Vôùi ñoä tin caäy 90%, tæ leä con ñaït tieâu chuaån toái ña cuûa loaïi vaät nuoâi
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng
treân laø bao nhieâu? Toái thieåu laø bao nhieâu?
khoaûng beân traùi cho kyø voïng: S Lôøi giaûi (− ; ∞ X + z , 2 ) α n Ta coù: trong ñoù ϕ(z n = 100; ∑ 2 ∑
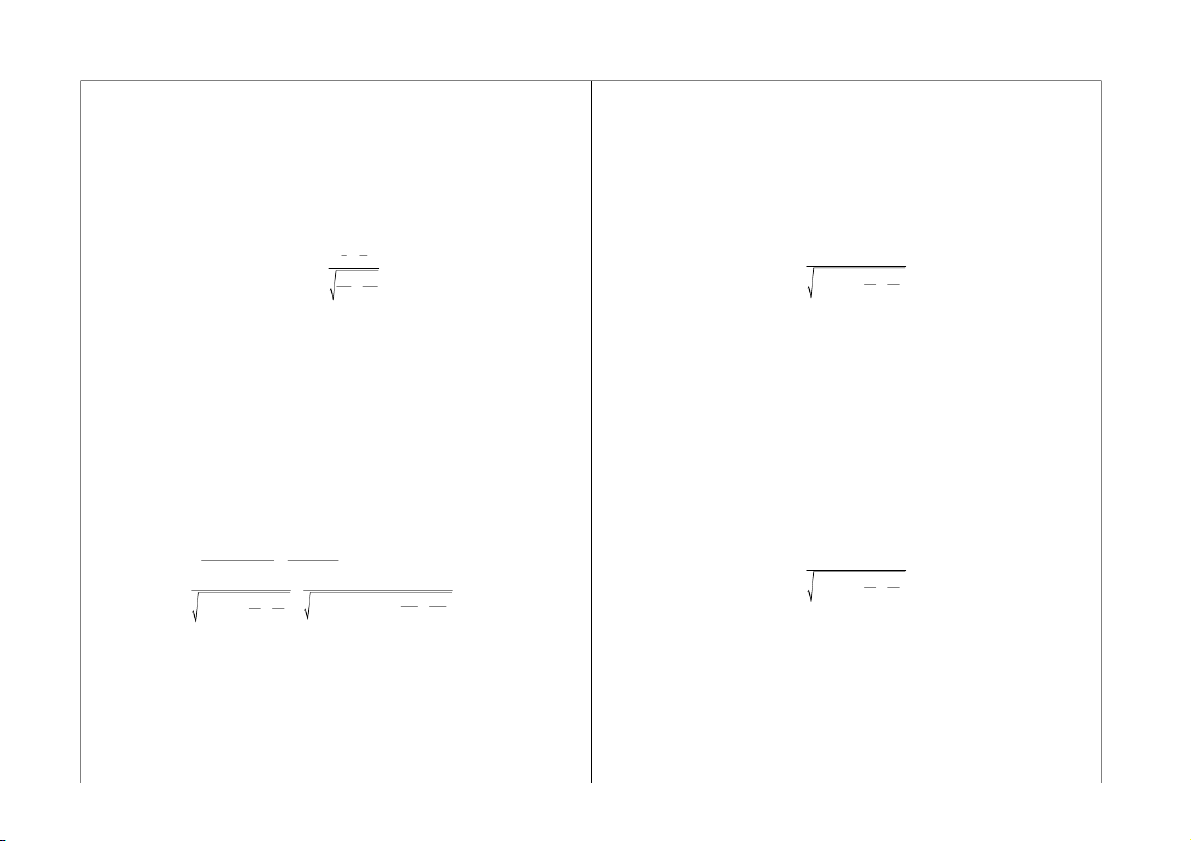
2α) = (1- 2α)/2 = (1- 2.0,05)/2 = 0,90/2 = 0,45. Tra baûng giaù i X i n =5196; X n 2 = 82096. i i
trò haøm Laplace ta ñöôïc z2α = 1,65. Suy ra troïng löôïng trung bình toái ña
• Kyø voïng maãu cuûa X laø laø: 1 X = X n ∑ =51, 96(kg). S 11, 0608 i i X + z α = 51, 96 + 1, 65 = 53,7850(kg). n 2 n 100
• Phöông sai maãu cuûa X laø:
Vaäy vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái ña cuûa loaïi vaät nuoâi 2 1 2 2 2 2 S = ∑ X treân laø 53,7850kg. i n i − X ( = 11, 0054) (kg ). n
- Ñeå bieát troïng löôïng trung bình toái thieåu cuûa loaïi vaät nuoâi treân laø bao
• Phöông sai maãu hieäu chænh cuûa X laø:
nhieâu ta caàn öôùc löôïng khoaûng beân phaûi cho kyø voïng μ = M(X). n S =  2 2 2 2 S = (11, 0608) (kg ).
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng n − 1
khoaûng beân traùi cho kyø voïng:
• Tæ leä maãu con ñaït tieâu chuaån laø S m 30 (X − z ; + ) ∞ , F = = = 0, 3 2α n n n 100
trong ñoù z2α = 1,65. Suy ra troïng löôïng trung bình toái thieåu laø: 1 2 S 11,0608 X − = − =
Ta coù ñoä tin caäy γ = 1 - α = 90% = 0,90 (α = 0,1). 2 z α 51, 96 1, 65 50,1350(kg) . n 100
- Ñeå bieát tæ leä toái ña con ñaït tieâu chuaån cuûa loaïi vaät nuoâi treân laø bao
Vaäy vôùi ñoä tin caäy 95%, troïng löôïng trung bình toái thieåu cuûa loaïi vaät nuoâi
nhieâu ta caàn öôùc löôïng khoaûng beân traùi cho tæ leä p con ñaït tieâu chuaån. treân laø 50,1350kg.
Ta coù coâng thöùc öôùc löôïng khoaûng beân traùi cho tæ leä p : n F (1 − n F ) (− ; ∞ n F + z2 ) α ,
c) Nhöõng con vaät coù troïng löôïng töø 60kg trôû leân ñöôïc goïi laø nhöõng con n
“ñaït tieâu chuaån”. Haõy öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy
trong ñoù ϕ(z2α) = (1- 2α)/2 = 0,80/2 = 0,40. Tra baûng giaù trò haøm Laplace 95%.
ta ñöôïc z2α = 1,28. Suy ra tæ leä toái ña con ñaït tieâu chuaån laø:
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p con ñaït tieâu chuaån vôùi ñoä n F (1 − n F ) 0,3(1 − 0, 3) n F + 2 z = 0, 3 + 1, 28 = 0,3587 .
tin caäy γ = 1- α = 95% = 0,95. Ta coù coâng thöùc öôùc löôïng khoaûng : α n 100
Vaäy vôùi ñoä tin caäy 90%, tæ leä toái ña con ñaït tieâu chuaån cuûa loaïi vaät nuoâi treân laø 35,87%. n F (1− n F ) n F (1 − n F ) ( n F − z ; + , α n F z ) n α n
- Ñeå bieát tæ leä toái thieåu con ñaït tieâu chuaån cuûa loaïi vaät nuoâi treân laø bao trong ñoù ϕ (z
nhieâu ta caàn öôùc löôïng khoaûng beân phaûi cho tæ leä p con ñaït tieâu chuaån.
α) = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta ñöôïc z
Ta coù coâng thöùc öôùc löôïng khoaûng beân phaûi cho tæ leä p:
α = 1,96. Vaäy öôùc löôïng khoaûng laø: 0, 3(1 − 0, 3) 0, 3(1 − 0, 3) n F (1− n F ) (0, 3 − 1, 96 ; 0, 3+ 1, 96 ) = (21, 02%; 38, 98%). ( n F − 2 z ; + ) ∞ , α 100 100 n
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä con ñaït tieâu chuaån naèm trong
trong ñoù z2α = 1,28. Suy ra tæ leä toái thieåu con ñaït tieâu chuaån laø:
khoaûng töø 21,02% ñeán 38,98%. n F (1 − n F ) 0,3(1 − 0,3) F − z = 0,3 −1,28 = 0,2413. n 2α n 100
d) Neáu muoán öôùc löôïng tæ leä con ñaït tieâu chuaån vôùi ñoä tin caäy 99% vaø ñoä
Vaäy vôùi ñoä tin caäy 90%, tæ leä toái thieåu con ñaït tieâu chuaån cuûa loaïi vaät nuoâi
chính xaùc 10% thì caàn phaûi ñieàu tra theâm bao nhieâu con vaät nöõa? treân laø 24,13%.
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng tæ leä con ñaït tieâu
chuaån vôùi ñoä chính xaùc ε = 10% = 0,1 vaø ñoä tin caäy γ = 1- α = 99% = 0,99.
Baøi 3.2. Caân thöû 100 traùi quít cuûa moät vöôøn, ta coù baûng keát quaû sau:
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: X(g) 40 50 60 70 80 90 100 110 Soá traùi 3 10 12 15 28 16 11 5 n F (1 − n F ) ε = zα , n
trong ñoù X chæ troïng löôïng (ñôn vò tính gam). trong ñoù ϕ(z
a) Haõy öôùc löôïng troïng löôïng trung bình cuûa moät traùi quít trong vöôøn quít
α) = γ /2 = 0,99/2 = 0,495. Tra baûng giaù trò haøm Laplace ta ñöôïc z
treân vôùi ñoä tin caäy 94%. α = 2,58. Suy ra 2 z F (1 −F )
b) Nhöõng traùi quít coù troïng löôïng X > 75g laø traùi loaïi I. Haõy öôùc löôïng tæ n n n α = 2
leä traùi loaïi I trong vöôøn quít treân vôùi ñoä tin caäy 95%. ε Thöïc teá yeâu caàu:
c) Nhöõng traùi quít coù troïng löôïng X < 65g laø traùi loaïi III. Haõy öôùc löôïng 2 2 z F (1 −F ) −
troïng luôïng trung bình cuûa moät traùi quít loaïi III trong vöôøn quít treân vôùi α 2,58 .0,3(1 0,3) n n n ≥ = ≈ 139,7844. 2 2 ε 0,1
ñoä tin caäy 99% (Giaû söû X coù phaân phoái chuaån).
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n 1 = 140. Vì n1 =
140 > 100 (100 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm ít nhaát laø Lôøi giaûi
140 -100 = 40 con vaät nöõa. Ta coù: = n 100; ∑X 2 ∑ in i 7 = 720; Xi i n 6 = 25800.
e) Vôùi ñoä tin caäy 90%, tæ leä con ñaït tieâu chuaån toái ña cuûa loaïi vaät nuoâi
• Kyø voïng maãu cuûa X laø
treân laø bao nhieâu? Toái thieåu laø bao nhieâu? 3 4 1
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä traùi loaïi I töø 50,40% ñeán 69,60%. X = X n = 77, 2(g). ∑ i i n
• Phöông sai maãu cuûa X laø:
c) Nhöõng traùi quít coù troïng löôïng X < 65g laø traùi loaïi III. Haõy öôùc löôïng 2 1 2 2 2 2 S = X n − X =(17, 2673) (g ). ∑
troïng luôïng trung bình cuûa moät traùi quít loaïi III trong vöôøn quít treân vôùi i i n
ñoä tin caäy 99% (Giaû söû X coù phaân phoái chuaån).
• Phöông sai maãu hieäu chænh cuûa X laø:
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μIII = M(XIII) cuûa chæ 2 n 2 S =  2 2 S = (17,3543) (kg ). tieâu X = X
III cuûa nhöõng traùi quít loaïi III vôùi ñoä tin caäy γ = 1- α = 99% = n − 1 0,99.
• Tæ leä maãu traùi loaïi I laø
Ta laäp baûng soá lieäu cuûa XIII: m 60 F = = = 0, 6. XIIIi 40 50 60 n n 100 nIIIi 3 10 12
vì trong n = 100 traùi coù m = 28 + 16 + 11 + 5 = 60 traùi coù troïng löôïng
Töø baûng treân ta tính ñöôïc:
töø 75g trôû leân, nghóa laø coù 60 traùi loaïi I. n III = 25; ∑X 2 IIIin IIIi 1 = 340; X ∑ IIIinIIIi =73000.
• Kyø voïng maãu cuûa XIII laø
a) Haõy öôùc löôïng troïng löôïng trung bình cuûa moät traùi quít trong vöôøn 1 X = X n = 53, 6 (g).
quít treân vôùi ñoä tin caäy 94%. III ∑ IIIi IIIi I n II
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin
• Phöông sai maãu cuûa XIII laø:
caäy γ = 1- α = 94% = 0,94. 1
Vì n = 100 ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng  2 2 2 2 2 SIII = X n ∑ − X =(6, 8586) (g ). IIIi IIIi III n khoaûng cho kyø voïng: III S S
• Phöông sai maãu hieäu chænh cuûa XIII laø: (X − z ; X+ z ) α n α n n III 2 2 2 2 I S II = I S II = 7 (g ). trong ñoù ϕ(z n − 1
α) = γ/2 = 0,94/2 = 0,47. Tra baûng giaù trò haøm Laplace ta III ñöôïc z 2
α = 1,88. Vaäy öôùc löôïng khoaûng laø:
Vì nIII < 30, XIII coù phaân phoái chuaån, σIII = D(XIII) chöa bieát, neân ta coù 17, 3543 17, 3543 (77, 2 − 1, 88 ; 77, 2 + 1, 88 ) = (73, 94; 80, 46).
coâng thöùc öôùc löôïng khoaûng cho kyø voïng: 100 100 k S S III k III (X -t ;X +t )
Noùi caùch khaùc, vôùi ñoä tin caäy 94%, troïng löôïng trung bình cuûa moät traùi III α III α , I n II nIII
quyùt töø 73,94g ñeán 80,46g. trong ñoù kα
t ñöôïc xaùc ñònh töø baûng phaân phoái Student vôùi k = nIII –1= 24
b) Nhöõng traùi quít coù troïng löôïng X > 75g laø traùi loaïi I. Haõy öôùc löôïng tæ
vaø α = 1 - γ = 1 – 0,99 = 0,01. Tra baûng phaân phoái Student ta ñöôïc
leä traùi loaïi I trong vöôøn quít treân vôùi ñoä tin caäy 95%. k t 2,797 α =
. Vaäy öôùc löôïng khoaûng laø:
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc traùi loaïi I vôùi ñoä tin 7 7 (53, 6 − 2, 797 ; 53, 6 + 2, 797 ) = (49, 68; 57,52).
caäy γ = 1- α = 95% = 0,95. 25 25
Ta coù coâng thöùc öôùc löôïng khoaûng:
Noùi caùch khaùc, vôùi ñoä tin caäy 99%, troïng löôïng trung bình cuûa moät traùi n F (1 − n F ) n F (1 − n F )
quít loaïi III töø 49,68g ñeán 57,52g. ( n F − z ; α n F + z ) n α n
trong ñoù ϕ(zα) = (1- α)/2 = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm
Baøi 3.3. Ñeå khaûo saùt chæ tieâu X cuûa moät loaïi saûn phaåm cuûa xí nghieäp I,
Laplace ta ñöôïc zα = 1,96. Vaäy öôùc löôïng khoaûng laø:
ngöôøi ta quan saùt moät maãu trong kho vaø coù keát quûa sau: X(cm)
11-15 15-19 19-23 23-27 27-31 31-35 35-39 0, 6(1 − 0, 6) 0, 6(1 − 0, 6) (0, 60 − 1, 96 ; 0, 60 + 1, 96 ) = (50, 40%; 69, 60%) Soá sphaåm 8 9 20 16 16 13 18 100 100 5 6
a) Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa loaïi saûn phaåm treân
a) Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa loaïi saûn phaåm treân vôùi ñoä tin caäy 96%. vôùi ñoä tin caäy 96%.
b) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,8cm thì seõ ñaït ñöôïc
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
ñoä tin caäy laø bao nhieâu? γ = 1- α = 96% = 0,96.
c) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,5cm vaø ñoä tin caäy
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
99% thì phaûi ñieàu tra theâm ít nhaát bao nhieâu saûn phaåm nöõa? cho kyø voïng:
d) Nhöõng saûn phaåm coù chæ tieâu X töø 19cm trôû xuoáng ñöôïc goïi laø nhöõng S S (X − z ; X + z ) α α
saûn phaåm loaïi B. Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa nhöõng n n
saûn phaåm loaïi B vôùi ñoä tin caäy 98% (GS X coù phaân phoái chuaån).
trong ñoù ϕ(zα) = γ /2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta
e) Haõy öôùc löôïng tæ leä saûn phaåm loaïi B vôùi ñoä tin caäy 92%. Baûng soá lieäu
ñöôïc zα = 2,06. Vaäy öôùc löôïng khoaûng laø:
treân ñöôïc choïn ngaãu nhieân töø moät kho trong ñoù coù 1000 saûn phaåm loaïi B. 7, 4827 7, 4827 (26, 36 − 2, 06 ; 26, 36 + 2, 06 ) = (24, 82; 27, 90).
Haõy öôùc löôïng soá saûn phaåm trong kho vôùi ñoä tin caäy 92%. 100 100
f) Neáu öôùc löôïng tæ leä nhöõng sp loaïi B vôùi ñoä chính xaùc 6% thì seõ ñaït
Noùi caùch khaùc, vôùi ñoä tin caäy 96%, giaù trò trung bình cuûa chæ tieâu X naèm
ñöôïc ñoä tin caäy laø bao nhieâu?
trong khoaûng töø 24,82cm ñeán 27,93 cm.
g) Neáu öôùc löôïng tæ leä nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy 96% vaø ñoä
chính xaùc 8% thì caàn phaûi ñieàu tra theâm bao nhieâu saûn phaåm nöõa?
b) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,8cm thì seõ ñaït ñöôïc ñoä
h) Giaû söû trong kho ñeå laãn 1000 saûn phaåm cuûa xí nghieäp II vaø trong 100 tin caäy laø bao nhieâu?
saûn phaåm laáy töø kho coù 9 saûn phaåm cuûa xí nghieäp II. Haõy öôùc löôïng soá
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi öôùc löôïng kyø voïng cuûa
saûn phaåm cuûa xí nghieäp I coù trong kho vôùi ñoä tin caäy 82%.
chæ tieâu X vôùi ñoä chính xaùc ε = 1,8cm.
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc Lôøi giaûi cuûa öôùc löôïng: Laäp baûng S ε = zα n Xi 13 17 21 25 29 33 37
trong ñoù ϕ(zα) = γ /2. Suy ra ni 8 9 20 16 16 13 18 ε n 1,8. 100 z = = = 2, 41. α S 7,4827 Ta coù:
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø n = ; 100 X n =2636; ∑ 2 X n 7 = 5028. ∑ i i i i γ = 2 (
ϕ zα ) = 2ϕ(2, 41) = 2.0, 4920 = 98, 40%.
• Kyø voïng maãu cuûa X laø
Vaäy ñoä tin caäy ñaït ñöôïc laø 98,40%. 1 X = X n = 26, 36(cm). ∑ i i n
c) Neáu öôùc löôïng GTTB cuûa X vôùi ñoä chính xaùc 1,5cm vaø ñoä tin caäy 99%
• Phöông sai maãu cuûa X laø:
thì phaûi ñieàu tra theâm ít nhaát bao nhieâu saûn phaåm nöõa? 2 1 2 2 2 2 S = X n − X ( = 7, 4452) (cm ). ∑
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng kyø voïng cuûa chæ tieâu X i i n
vôùi ñoä chính xaùc ε = 1,5cm vaø ñoä tin caäy γ = 1- α = 99% = 0,99. Vì n ≥ 30,
• Phöông sai maãu ñaõ hieäu chænh cuûa X laø:
σ2 = D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: S ε = z , 2 n α 2 S =  2 2 S = (7,4827) (cm ). n n− 1 trong ñoù ϕ(z
α) = γ /2 = 0,99/2 = 0,495. Tra baûng giaù trò haøm Laplace ta ñöôïc zα = 2,58. Suy ra 7 8 2 ⎛ z S⎞ n α = trong ñoù k t ⎜
α ñöôïc xaùc ñònh töø baûng phaân phoái Student vôùi k = nB–1=16 ε ⎟ ⎝ ⎠
vaø α = 1 - γ = 1 – 0,98 = 0,02. Tra baûng phaân phoái Student ta ñöôïc Thöïc teá yeâu caàu: k
t = 2, 583 . Vaäy öôùc löôïng khoaûng laø: 2 2 α ⎛ z S⎞ ⎛ 2,58.7,4827⎞ n α ≥ = ≈ 165, 64. 2, 0580 2, 0580 ⎜ ε ⎟ ⎜ 1,5 ⎟ (15,1176 − 2,583 ; 15,1176 + 2,583 ) = (13, 83; 16,41). ⎝ ⎠ ⎝ ⎠ 17 17
Giaù trò n nguyeân nhoû nhaát thoûa baát ñaúng thöùc treân laø n1 = 166. Vì n1 =
Noùi caùch khaùc, vôùi ñoä tin caäy 98%, giaù trò trung bình cuûa chæ tieâu X cuûa
166 > 100 (100 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm ít nhaát laø
nhöõng saûn phaåm loaïi B naèm trong khoaûng töø 13,83cm ñeán 16,41cm.
166 – 100 = 66 saûn phaåm nöõa.
e) Haõy öôùc löôïng tæ leä nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy 92%. Baûng
d) Nhöõng saûn phaåm coù chæ tieâu X töø 19cm trôû xuoáng ñöôïc goïi laø nhöõng
soá lieäu treân ñöôïc choïn ngaãu nhieân töø moät kho trong ñoù coù 1000 saûn phaåm
saûn phaåm loaïi B. Öôùc löôïng giaù trò trung bình cuûa chæ tieâu X cuûa nhöõng
loaïi B. Haõy öôùc löôïng soá saûn phaåm trong kho vôùi ñoä tin caäy 92%.
saûn phaåm loaïi B vôùi ñoä tin caäy 98% (GS X coù phaân phoái chuaån).
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc saûn phaåm loaïi B vôùi
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μB = M(XB) cuûa chæ tieâu
ñoä tin caäy γ = 1- α = 92% = 0,92. Ta coù coâng thöùc öôùc löôïng khoaûng :
X = XB cuûa nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy γ = 1- α = 98% = 0,98.
Ta laäp baûng soá lieäu cuûa XB: n F (1− n F ) n F (1 − n F ) (Fn − z ;F α n + z ) , n α n XBi 13 17
trong ñoù ϕ(zα) = γ /2 = 0,92/2 = 0,46. Tra baûng giaù trò haøm Laplace ta nBi 8 9
ñöôïc zα = 1,75. Maët khaùc, trong n =100 saûn phaåm coù m = 17 saûn phaåm
Töø baûng treân ta tính ñöôïc:
loaïi B neân tæ leä maãu saûn phaåm loaïi B laø Fn = 0,17. Vaäy öôùc löôïng khoaûng laø: n = ; 17 ∑ X n 2 X n =3, 953. ∑ 0,17(1 0 − ,17) 0,17(1 −0,17) Bi Bi = ; 257 B Bi Bi (0,17 − 1, 75 ; 0, 17 + 1, 75 ) = (10, 43%; 23, 57%). 100 100 • Kyø voïng maãu cuûa X
Noùi caùch khaùc, vôùi ñoä tin caäy 92%, tæ leä saûn phaåm loaïi B naèm trong B laø 1
khoaûng töø 10,43% ñeán 23,57%. X B = ∑X n Bi Bi = 1176 , 15 (cm). n •
Khi trong kho coù 1000 saûn phaåm loaïi B, goïi N laø soá saûn phaåm coù trong
Phöông sai maãu cuûa XB laø:
kho, ta coù tæ leä saûn phaåm loaïi B laø 1000/N. Theo keát quaû treân, vôùi ñoä tin ˆ
caäy 92%, tæ leä caùc saûn phaåm loïai B töø 10,43% ñeán 23,57%, do ñoù:  2 1 2 2 2 2 SB = X n − X = (1, 9965) (cm ). ∑ Bi Bi B n • 1000 10,43 1000 23,57
Phöông sai maãu ñaõ hieäu chænh cuûa XB laø: 10,43% ≤ ≤ 23,57% ⇔ ≤ ≤ N 100 N 100 100.1000 100.1000 2 2 B n ⇔ ≤ N ≤ S =  2 2 B S B =(2, 0580) (cm ). − 23,57 10, 430 B n 1 ⇔ 4242, 68 ≤ N ≤ 9587,73
Vì nB < 30, XB coù phaân phoái chuaån, σ2B= D(XB) chöa bieát, neân ta coù coâng ⇔ 4243 ≤ N ≤ 9587
thöùc öôùc löôïng khoaûng cho kyø voïng:
Vaäy vôùi ñoä tin caäy 92%, ta öôùc löôïng trong kho coù töø 4243 ñeán 9587 saûn S S ( k B X −t + phaåm. α ; k B X tα ) , B B n n B B
f) Neáu öôùc löôïng tæ leä nhöõng sp loaïi B vôùi ñoä chính xaùc 6% thì seõ ñaït
ñöôïc ñoä tin caäy laø bao nhieâu? 9 10
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi löôïng tæ leä caùc saûn
trong ñoù ϕ(zα) = γ /2 = 0,82/2 = 0,41. Tra baûng giaù trò haøm Laplace ta
phaåm loaïi B vôùi ñoä chính xaùc ε = 6% = 0,06. Ta coù coâng thöùc tính ñoä
ñöôïc zα = 1,34. Maët khaùc, theo giaû thieát, trong n =100 saûn phaåm coù 9
chính xaùc cuûa öôùc löôïng:
saûn phaåm cuûa xí nghieäp II töùc laø coù 91 saûn phaåm cuûa xí nghieäp I, neân tæ n F (1 − n F )
leä maãu saûn phaåm cuûa xí nghieäp I laø F ε = z
n = 91/100 = 0,91. Vaäy öôùc löôïng α , n khoaûng laø:
trong ñoù ϕ(zα) = γ /2. Suy ra: 0, 91(1 − 0, 91) 0, 91(1 − 0, 91) (0, 91 − 1, 34 ; 0, 91 + 1, 34 ) = (87,17%; 94, 83%). n 100 100 100 z = ε = = α 0, 06. 1, 60. F (1 − F ) 0,17(1 − 0,17)
Noùi caùch khaùc, vôùi ñoä tin caäy 92%, tæ leä saûn phaåm cuûa xí nghieäp I naèm n n
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø
trong khoaûng töø 87,17% ñeán 94,83%.
γ = 2ϕ (z )= 2ϕ (1, 60)= 2.0, 4452= 89, 04%.
Baây giôø goïi N laø soá saûn phaåm cuûa xí nghieäp I coù trong kho. Khi ñoù: α
- Toång soá saûn phaåm coù trong kho laø N + 1000ø. g)
- Tæ leä saûn phaåm cuûa xí nghieäp I coù trong kho laø N/(N+1000).
Neáu öôùc löôïng tæ leä nhöõng saûn phaåm loaïi B vôùi ñoä tin caäy 96% vaø ñoä
chính xaùc 8% thì caàn phaûi ñieàu tra theâm bao nhieâu saûn phaåm nöõa?
Theo keát quaû treân, vôùi ñoä tin caäy 82%, tæ leä saûn phaåm cuûa xí nghieäp I
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng tæ leä caùc saûn phaåm loaïi
coù trong kho naèm trong khoaûng töø 87,17% ñeán 94,83%, do ñoù:
B vôùi ñoä chính xaùc ε = 8% = 0,08 vaø ñoä tin caäy γ = 1- α = 96% = 0,96. Ta N N
coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: 87,17% ≤ ≤ 94,83% ⇔ 87,17% ≤ ≤ 94,83% N + 1000 N + 1000 1000 F (1 −F ) ⇔ 87,17% ≤ 1 − ≤ 94,83% n n ε = z N + 1000 α , n 1000 trong ñoù ϕ(z ⇔ 5,17% ≤ ≤ 12,83%
α) = γ /2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta N + 1000 ñöôïc zα = 2,06. Suy ra 1000 1000 ⇔ -1000 ≤ N ≤ -1000 2 z F − 12,83% 5,17% n(1 Fn) n α = 2 ε
⇔ 6794,23 ≤ N ≤ 18342,36 Thöïc teá yeâu caàu: ⇔ 6795 ≤ N ≤ 18342 2 2 z F (1 − F ) −
Vaäy vôùi ñoä tin caäy 82%, ta öôùc löôïng soá saûn phaåm cuûa xí nghieäp I coù α 2, 06 .0,17(1 0,17) n n n ≥ = ≈ 93,56. 2 2 ε 0, 08
trong kho naèm trong khoaûng töø 6795 ñeán 18342.
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n1 = 94. Vì n1 =
Baøi 3.4. Ñeå khaûo saùt chieàu cao X cuûa moät gioáng caây troàng, ngöôøi ta quan
94 < 100 (100 laø côõ maãu ñang coù) neân ta khoâng caàn ñieàu tra theâm saûn phaåm nöõa.
saùt moät maãu vaø coù keát quûa sau: X(cm) 95-105
105-115 115-125 125-135 135-145 145-155 155-165 Soá caây 10 10 15 30 10 10 15
h) Giaû söû trong kho ñeå laãn 1000 saûn phaåm cuûa xí nghieäp II vaø trong 100
a) Öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä tin
saûn phaåm laáy töø kho coù 9 saûn phaåm cuûa xí nghieäp II. Haõy öôùc löôïng soá caäy 96%.
saûn phaåm cuûa xí nghieäp I coù trong kho vôùi ñoä tin caäy 82%.
b) Neáu muoán öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi
Tröôùc heát ta öôùc löôïng tæ leä saûn phaåm cuûa xí nghieäp I coù trong kho vôùi
ñoä tin caäy 99% vaø ñoä chính xaùc 4 cm thì caàn phaûi ñieàu tra theâm bao
ñoä tin caäy 82%. Ta coù coâng thöùc öôùc löôïng khoaûng : nhieâu caây nöõa?
c) Neáu öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä n F (1− n F ) n F (1 − n F ) (F − z ;F + z )
chính xaùc 4,58cm thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu? n α n n α n 11 12
d) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
b) Neáu muoán öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi
“cao”. Haõy öôùc löôïng tæ leä nhöõng caây “cao”vôùi ñoä tin caäy 95%.
ñoä tin caäy 99% vaø ñoä chính xaùc 4cm thì caàn phaûi ñieàu tra theâm bao nhieâu
e) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä chính xaùc 10% thì caây nöõa?
seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng kyø voïng cuûa chæ tieâu X
f) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä tin caäy 95% vaø ñoä
vôùi ñoä chính xaùc ε = 4cm vaø ñoä tin caäy γ = 99% = 0,99.
chính xaùc 11% thì caàn phaûi ñieàu tra theâm bao nhieâu caây nöõa?
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc
g) Öôùc löôïng chieàu cao trung bình cuûa caùc caây cao cuûa gioáng caây troàng cuûa öôùc löôïng:
treân vôùi ñoä tin caäy 94%. S ε = z , α n Lôøi giaûi
trong ñoù ϕ(zα) = γ /2 = 0,99/2 = 0, 495. Tra baûng giaù trò haøm Laplace ta Ta coù: ñöôïc zα = 2,58. Suy ra 2 n = ; 100 X n 13 = 100; ∑ ∑X n 1 = 749000. ⎛z S ⎞ i i 2 i i n α = ⎜ . ε ⎟ ⎝ ⎠ 1 Thöïc teá yeâu caàu:
• Kyø voïng maãu cuûa X laø X = X n = 131(cm). ∑ 2 2 i i n ⎛z S ⎞ ⎛2, 58.18, 2297 n α ⎞ ≥ = ≈ 138, 254. ⎜ ⎟ ⎜ ⎟ • ⎝ ε ⎠ ⎝ 4 ⎠
Phöông sai maãu cuûa X laø: ˆ
Giaù trò n nguyeân nhoû nhaát thoûa baát ñaúng thöùc treân laø n  2 1 2 2 2 2 S = X n − X ( = 18,1384) (cm ). ∑ 1 = 139. Vì n1 = i i n
139 > 100 (100 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm ít nhaát laø
• Phöông sai maãu hieäu chænh cuûa X laø:
139 – 100 = 39 caây nöõa. ˆ n  2 2 2 2 S = S = (18,2297) (cm ). n − 1
c) Neáu öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä
chính xaùc 4,58cm thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
a) Öôùc löôïng chieàu cao trung bình cuûa gioáng caây troàng treân vôùi ñoä tin
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi öôùc löôïng kyø voïng cuûa caäy 96%.
chæ tieâu X vôùi ñoä chính xaùc ε = 4,58cm.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc γ = 1- α = 96% = 0,96. cuûa öôùc löôïng:
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng S ε = z , cho kyø voïng: α n S S (X − z ; X + z ) trong ñoù ϕ(z α α , α) = γ /2 . Suy ra n n ε n 4,58. 100 trong ñoù ϕ(z z = = = 2, 5123.
α) = γ /2 = 0,96/2 = 0,48. Tra baûng giaù trò haøm Laplace ta α S 18, 2297
ñöôïc zα = 2,06. Vaäy öôùc löôïng khoaûng laø:
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø γ =2 ( ϕz ) =2 ( ϕ2, 5123) =2 ( ϕ2, 52) =2.0, 4941 =98, 82%. 18, 2297 18, 2297 γ (131 − 2, 06 ; 131 + 2, 06 ) = (127, 2447; 134, 7553). 100 100
d) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
Noùi caùch khaùc, vôùi ñoä tin caäy 96%, chieàu cao trung bình cuûa moät caây naèm
“cao”. Haõy öôùc löôïng tæ leä nhöõng caây “cao”vôùi ñoä tin caäy 95%.
trong khoaûng töø 127,2447cm ñeán 134,7553cm.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc caây cao vôùi ñoä tin caäy
γ = 1- α = 95% = 0,95. Ta coù coâng thöùc öôùc löôïng khoaûng : 13 14
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n n F (1 − n F ) n F (1 − n F ) ( 1 = 73. Vì n1 = n F − z ; α n F + z ) , n α n
73 < 100 (100 laø côõ maãu ñang coù) neân ta khoâng caàn ñieàu tra theâm caây
trong ñoù ϕ (zα) = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta naøo nöõa.
ñöôïc zα = 1,96. Trong n = 100 caây coù m = 10 + 10 + 15 = 35 caây coù
chieàu cao töø 135cm trôû leân neân tæ leä maãu caùc caây cao laø Fn = 35/100 =
g) Öôùc löôïng chieàu cao trung bình cuûa caùc caây cao cuûa gioáng caây troàng
0,35. Vaäy öôùc löôïng khoaûng laø:
treân vôùi ñoä tin caäy 94%.
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μC = M(XC) cuûa chæ 0, 35(1 − 0, 35) 0, 35(1 − 0, 35) (0, 35− 1, 96 ; 0, 35+ 1, 96 )= (25, 65%; 44, 35%).
tieâu X = XC cuûa nhöõng caây cao vôùi ñoä tin caäy γ = 1- α = 94% = 0,94. Ta 100 100
laäp baûng soá lieäu cuûa XC:
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä caây cao naèm trong khoaûng töø 25,65% ñeán 44,35%. XCi 140 150 160 nCi 10 10 15
e) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä chính xaùc 10% thì seõ
Töø baûng treân ta tính ñöôïc:
ñaït ñöôïc ñoä tin caäy laø bao nhieâu? C n = 35; X ∑ 2 X Cin Ci = 5300; ∑ Ci C n i = 805000.
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy khi löôïng tæ leä caây cao vôùi ñoä
• Kyø voïng maãu cuûa XC laø: chính xaùc ε = 10% = 0,1. 1 X = ∑X n =151,4286(cm).
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: C Ci Ci n Fn(1 − Fn) ε • = z
Phöông sai maãu cuûa XC laø: α , n 1  2 2 2 2 2 SC = X n − X ( = 8,3299) (cm ). ∑ Ci Ci C trong ñoù ϕ (z n
α) = γ /2 . Ta coù tæ leä maãu caây cao laø: Fn = 0,35. Suy ra n 100
• Phöông sai maãu ñaõ hieäu chænh cuûa XC laø: z = ε = 0,1. = 2, 0966. 2 α n F (1 − F ) 0, 35(1 − 0, 35) 2 C S =  2 2 C C S = (8,4515) (cm ). n n − C n 1
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø
Vì nC = 35 > 30, σ2C = D(XC) chöa bieát, neân ta coù coâng thöùc öôùc löôïng khoaûng cho kyø voïng: γ = 2ϕ (z = ϕ = ϕ = = α ) 2 (2, 0966) 2 (2,1) 2.0,4821 96, 42%. C S C S (X − z ; X + z ) C α C α , C n C n
f) Neáu öôùc löôïng tæ leä nhöõng nhöõng caây “cao” vôùi ñoä tin caäy 95% vaø ñoä
trong ñoù ϕ(zα) = γ /2 = 0,94/2 = 0,47. Tra baûng giaù trò haøm Laplace ta
chính xaùc 11% thì caàn phaûi ñieàu tra theâm bao nhieâu caây nöõa? ñöôïc z
Ñaây laø baøi toaùn xaùc ñònh côõ maãu khi öôùc löôïng tæ leä caây cao vôùi ñoä
α = 1,88. Vaäy öôùc löôïng khoaûng laø: 8, 4515 8, 4515
chính xaùc ε = 11% = 0,11 vaø ñoä tin caäy γ = 1- α = 95% = 0,95. (151, 4286 −1, 88 ; 151, 4286 +1, 88 ) = (148,74; 154,11). 35 35
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
Noùi caùch khaùc, vôùi ñoä tin caäy 94%, chieàu cao trung bình cuûa caây cao naèm Fn(1 − Fn) ε = z
trong khoaûng töø 148,74cm ñeán 154,11cm. α , n
trong ñoù ϕ(zα) = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
Baøi 3.5. Traùi caây cuûa moät chuû haøng ñöôïc ñöïng trong caùc soït, moãi soït 100 ñöôïc zα = 1,96. Suy ra
traùi. Ngöôøi ta kieåm tra 50 soït thì thaáy coù 450 traùi khoâng ñaït tieâu chuaån. 2 z F (1 − F ) n n n α = .
a) Öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån cuûa loâ haøng treân vôùi ñoä tin 2 ε caäy 95%. Thöïc teá yeâu caàu: 2 2
b) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc z F (1 − F ) 1, 96 .0, 35(1 − 0, 35) α n n n ≥ = ≈ 72, 23.
0,5% thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu? 2 2 ε 0,11 15 16
c) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc
1% vaø ñoä tin caäy 99% thì phaûi ñieàu tra theâm ít nhaát bao nhieâu soït nöõa?
c) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc
1% vaø ñoä tin caäy 99% thì phaûi ñieàu tra theâm ít nhaát bao nhieâu soït nöõa? Lôøi giaûi
Yeâu caàu cuûa baøi toùan: Xaùc ñònh côõ maãu.
Giaû thieát: - Öôùc khoûang cho tæ leä traùi khoâng ñaït tieâu chuaån.
Soá traùi trong 100 soït laø 50×100 = 5000. Do ñoù:
- Ñoä chính xaùc ε = 1% = 0,01. • Côõ maãu n = 5000.
- Ñoä tin caäy γ = 1- α = 99% = 0,99.
• Soá traùi khoâng ñaït tieâu chuaån laø: m = 450.
• Tæ leä maãu caùc traùi khoâng ñaït tieâu chuaån laø:
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: F F (1 − F ) n = m/n = 450/5000 = 0,09. n n ε = z α n
a) Öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån cuûa loâ haøng treân vôùi ñoä tin
trong ñoù ϕ(zα) = (1- α) /2 = 0,99/2 = 0,495. Tra baûng giaù trò haøm Laplace caäy 95%.
ta ñöôïc zα = 2,58. Suy ra
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc traùi khoâng ñaït tieâu 2 z n F (1 − n F ) n α =
chuaån vôùi ñoä tin caäy γ = 1- α = 95% = 0,95. 2 ε
Ta coù coâng thöùc öôùc löôïng khoaûng: Thöïc teá yeâu caàu: 2 2 zα n F (1 − n F ) 2, 58 .0, 09(1 − 0,09) n ≥ = ≈ 5451,6. 2 2 ε 0, 01 n F (1 − n F ) n F (1 − n F ) ( n F − z ; α n F + z ) n α n
Giaù trò n nguyeân nhoû nhaát thoaû baát ñaúng thöùc treân laø n1 = 5452.
trong ñoù ϕ (zα) = (1- α)/2 = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm
Vì n1 = 5452 > 5000 (5000 laø côõ maãu ñang coù) neân ta caàn ñieàu tra theâm
Laplace ta ñöôïc zα = 1,96. Vaäy öôùc löôïng khoaûng laø:
ít nhaát laø 5452 – 5000 = 452 traùi, nghóa laø khoaûng 5 soït nöõa. 0, 09(1 − 0, 09) 0, 09(1 − 0, 09) (0, 09 − 1, 96 ; 0, 09 + 1, 96 ) = (8, 21%; 9,79%) . 5000 5000
Baøi 3.6. Ñeå nghieân cöùu nhu caàu cuûa moät loaïi haøng ôû moät khu vöïc, ngöôøi
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä traùi khoâng ñaït tieâu chuaån töø
ta khaûo saùt 400 hoä gia ñình. Keát quaû nhö sau: 8,21% ñeán 9,79%.
Nhu caàu (kg/thaùng/hoä) 0-1 1-2 2-3 3-4 4-5 5-6 6-7 7-8
b) Neáu muoán öôùc löôïng tæ leä traùi khoâng ñaït tieâu chuaån vôùi ñoä chính xaùc Soá hoä 10 35 86 132 78 31 18 10
0,5% thì seõ ñaït ñöôïc ñoä tin caäy laø bao nhieâu?
Cho bieát trong khu vöïc coù 4000 hoä.
a) Öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc trong
Yeâu caàu cuûa baøi toùan: Xaùc ñònh ñoä tin caäy γ = 1- α.
moät naêm vôùi ñoä tin caäy 95%.
Giaû thieát: - Öôùc khoûang cho tæ leä traùi khoâng ñaït tieâu chuaån.
b) Khi öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc
- Ñoä chính xaùc ε = 0,5% = 0,005.
trong moät naêm, neáu ta muoán ñaït ñöôïc ñoä tin caäy 99% vaø ñoä chính xaùc laø
Ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng:
4,8taán thì caàn khaûo saùt ôû ít nhaát bao nhieâu hoä gia ñình? Fn(1 − Fn) ε = z α n Lôøi giaûi
trong ñoù ϕ (zα) = γ /2 . Suy ra n 5000 z = ε = 0, 005. = 1, 24.
Goïi X(kg) laø nhu caàu cuûa moät hoä veà loaïi haøng treân trong moät thaùng. Ta coù: α F (1 − F ) 0, 09(1 − 0, 09) n n
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø: Xi 0,5 1,5 2,5 3,5 4,5 5,5 6,5 7,5 γ = 2ϕ(z = ϕ = = α ) 2 (1, 24) 2.0, 3925 79, 5%. ni 10 35 86 132 78 31 18 10
Vaäy ñoä tin caäy ñaït ñöôïc laø 79,5%. 17 18 n = 400; ∑ X n 1 = 448; 2 ∑X n =6076.
trong moät thaùng vôùi ñoä tin caäy γ = 1- α = 0,99 vaø ñoä chính xaùc ε = i i i i
4800/(4000×12) = 0,1kg. Nhö vaäy, ta ñöa veà baøi toaùn xaùc ñònh côõ maãu 1
khi öôùc löôïng kyø voïng cuûa chæ tieâu X vôùi ñoä chính xaùc ε = 0,1 vaø ñoä tin
• Kyø voïng maãu cuûa X laø X = X n = 3, 62. ∑ i i n
caäy γ = 1- α = 99% = 0,99.
• Phöông sai maãu cuûa X laø:
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc ˆ  2 1 2 2 2 S = X n − X =(1, 4442) . ∑ cuûa öôùc löôïng: i i n S ε = z , • α
Phöông sai maãu hieäu chænh cuûa X laø: n ˆ n 2 2 2 S = S = (1,4460) .
trong ñoù ϕ(zα) = γ /2 = 0,99/2 = 0, 495. Tra baûng giaù trò haøm Laplace ta n −1 ñöôïc zα = 2,58. Suy ra
a) Öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc trong 2 ⎛z S ⎞
moät naêm vôùi ñoä tin caäy 95%. n α = ⎜ . ε ⎟ ⎝ ⎠
Tröôùc heát ta öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa moät Thöïc teá yeâu caàu:
hoä trong khu vöïc trong moät thaùng vôùi ñoä tin caäy 95%. 2 2 ⎛ z S ⎞ ⎛ 2, 58 × 1,4460 ⎞
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy n α ≥ = ≈ 1391,8. ⎜ ⎟ ⎜ ⎝ ⎠ 0,1 ⎟ ε γ = 1- α = 95% = 0,95. ⎝ ⎠
Giaù trò n nguyeân nhoû nhaát thoûa baát ñaúng thöùc treân laø n
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng 1 = 1392. Vaäy cho kyø voïng:
caàn khaûo saùt ít nhaát laø 1392 hoä gia ñình. S S (X − z ; X + z ), α n α n
Baøi 3.7. Ñeå bieát soá löôïng caù trong hoà lôùn ngöôøi ta baét leân 2000 con ñaùnh trong ñoù ϕ(z
daáu xong roài thaû chuùng xuoáng hoà. Sau ñoù ngöôøi ta baét leân 400 con vaø thaáy
α) = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta ñöôïc z
coù 80 con ñöôïc ñaùnh daáu.
α = 1,96. Vaäy öôùc löôïng khoaûng laø: 1, 4460 1, 4460
a) Vôùi ñoä tin caäy 95%, haõy öôùc löôïng soá caù coù trong hoà. (3, 62 − 1, 96 ; 3, 62 + 1, 96 ) = (3, 4783; 3, 7617). 400 400
b) Öôùc löôïng soá caù toái ña coù trong hoà vôùi ñoä tin caäy 96%.
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, nhu caàu trung bình veà maët haøng naøy
c) Öôùc löôïng soá caù toái thieåu coù trong hoà vôùi ñoä tin caäy 94%.
cuûa moät hoä trong khu vöïc trong moät thaùng naèm trong khoaûng töø
3,4783kg ñeán 3,7617kg. Xeùt 4000 hoä trong moät naêm 12 thaùng, ta coù caùc Lôøi giaûi
nhu caàu töông öùng laø:
3,4783×4000×12 = 166958,4kg = 166,9584taán;
Goïi N laø soá caù coù trong hoà. Khi ñoù tæ leä caù ñöôïc ñaùnh daáu coù trong hoà
3,7617×4000×12 = 180561,6kg = 180,5616taán. laø p = 2000/N.
Keát luaän: Vôùi ñoä tin caäy 95%, nhu caàu trung bình veà maët haøng naøy cuûa
Vôùi maãu thu ñöôïc, ta coù:
toaøn khu vöïc trong moät naêm naèm trong khoaûng töø 166,9584taán ñeán • Côõ maãu n = 400. 180,5616taán.
• Soá con ñöôïc ñaùnh daáu trong maãu laø: m = 80.
• Tæ leä maãu con ñöôïc ñaùnh daáu laø:
b) Khi öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc Fn = m/n = 80/400 = 0,2.
trong moät naêm, neáu ta muoán ñaït ñöôïc ñoä tin caäy 99% vaø ñoä chính xaùc
laø 4,8taán thì caàn khaûo saùt ôû ít nhaát bao nhieâu hoä gia ñình?
a) Vôùi ñoä tin caäy 95%, haõy öôùc löôïng soá caù coù trong hoà.
Tröôùc heát ta öôùc löôïng khoaûng cho tæ leä p caùc con ñöôïc ñaùnh daáu vôùi
Khi öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc
ñoä tin caäy γ = 1- α = 95% = 0,95.
trong moät naêm vôùi ñoä tin caäy 99% vaø ñoä chính xaùc laø 4,8 taán= 4800kg,
Ta coù coâng thöùc öôùc löôïng khoaûng:
nghóa laø ta öôùc löôïng nhu caàu trung bình veà maët haøng naøy cuûa moät hoä 19 20 trong ñoù ϕ(z n F (1− n F ) n F (1 − n F ) (
2α) = (1- 2α)/2 = γ/2 = 0,88/2 = 0,44. Tra baûng giaù trò haøm n F − z ; α n F + z ) , n α n
Laplace ta ñöôïc z2α = 1,56. Suy ra giaù trò toái ña cuûa tæ leä con ñöôïc ñaùnh
trong ñoù ϕ(zα) = (1- α)/2 = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm daáu laø:
Laplace ta ñöôïc zα = 1,96. Vaäy öôùc löôïng khoaûng laø: n F (1 − n F ) 0,2(1 − 0,2) F + z = 0, 2 + 1,56 = 0, 2312. α 0, 2(1 − 0, 2) 0, 2(1 − 0, 2) n 2 n 400 (0, 2 −1, 96 ; 0, 2 +1, 96 ) = (16, 08%; 23, 92%) 400 400
Nhö vaäy, vôùi ñoä tin caäy 94%, ta coù
Nhö vaäy, vôùi ñoä tin caäy 95%, tæ leä con ñöôïc ñaùnh daáu naèm trong khoaûng 2000 2000 ≤ 0,2312 ⇔ N ≥ = 8650,5
töø 16,08% ñeán 23,92%, do ñoù: N 0,2312
Vaäy vôùi ñoä tin caäy 94%, soá caù toái thieåu coù trong hoà laø 8651. 2000 2000 2000 16,08% ≤ ≤ 23,92% ⇔ ≤ N ≤ N 23, 92% 16, 08%
Baøi 3.8. Tröôùc kyø baàu cöû toång thoáng ngöôøi ta phoûng vaán ngaãu nhieân 1800
⇔ 8361,20 ≤ N ≤ 12437,81
cöû tri thì thaáy coù 1180 ngöôøi uûng hoä cöû tri A. Vôùi ñoä tin caäy 99%, hoûi öùng ⇔ 8362 ≤ N ≤ 12437
cöû vieân A coù theå thu ñöôïc toái thieåu bao nhieâu phaàn traêm soá phieáu baàu? Vaø
Vaäy vôùi ñoä tin caäy 95%, ta öôùc löôïng soá caù coù trong hoà khoaûng töø 8362 toái ña laø bao nhieâu? ñeán 12437 con. Lôøi giaûi
b) Öôùc löôïng soá caù toái ña coù trong hoà vôùi ñoä tin caäy 96%.
Soá caù toái ña coù trong hoà töôg öùng vôùi giaù trò toái thieåu cuûa tæ leä con ñöôïc
Vôùi maãu thu ñöôïc, ta coù:
ñaùnh daáu. Do ñoù tröôùc heát ta öôùc löôïng khoaûng beân phaûi cho tæ leä p caùc • Côõ maãu n = 1800.
con ñöôïc ñaùnh daáu vôùi ñoä tin caäy γ = 1- α = 96% = 0,96 (α = 0,04).
• Soá ngöôøi uûng hoä öùng cöû vieân A laø m = 1180.
Ta coù coâng thöùc öôùc löôïng khoaûng beân phaûi:
• Tæ leä maãu soá ngöôøi uûng hoä laø:
Fn = m/n = 1180/1800 = 0.6556. n F (1− n F ) (Fn − z2 ;+∞) α n
Vôùi ñoä tin caäy 99%, ñeå bieát öùng cöû vieân A coù theå thu ñöôïc toái thieåu bao trong ñoù ϕ(z
nhieâu phaàn traêm soá phieáu baàu ta caàn öôùc löôïng khoaûng beân phaûi cho tæ leä
2α) = (1- 2α)/2 = γ /2 = 0,92/2 = 0,46. Tra baûng giaù trò haøm Laplace ta ñöôïc z
p nhöõng ngöôøi uûng hoä vôùi ñoä tin caäy γ = 1- α = 99% = 0,99 (α = 0,01).
2α = 1,75. Suy ra giaù trò toái thieåu cuûa tæ leä con ñöôïc ñaùnh daáu laø:
Ta coù coâng thöùc öôùc löôïng khoaûng beân phaûi: F (1 −F ) n F (1 − n F ) 0, 2(1 − 0,2) n n (F − z ;+∞) n F − z2 = 0,2 −1,75 = 0,165. α n 2α n 400 n
Nhö vaäy, vôùi ñoä tin caäy 96%, ta coù
trong ñoù ϕ(z2α) = (1- 2α)/2 = γ /2 = 0,98/2 = 0,49. Tra baûng giaù trò haøm 2000 2000 Laplace ta ñöôïc z ≥ 0,165 ⇔ N ≤ = 12121,2
2α = 2,33. Suy ra giaù trò toái thieåu cuûa tæ leä ngöôøi uûng hoä N 0,165 laø:
Vaäy vôùi ñoä tin caäy 96%, soá caù toái ña coù trong hoà laø 12121. n F (1 − n F ) 0, 6556(1 − 0,6556) F − z = 0,6556 − 2,33 = 0,6295. c) n 2α
Öôùc löôïng soá caù toái thieåu coù trong hoà vôùi ñoä tin caäy 94%. n 1800
Soá caù toái thieåu coù trong hoà töông öùng vôùi giaù trò toái ña cuûa tæ leä con
Nhö vaäy, vôùi ñoä tin caäy 99%, öùng cöû vieân A coù theå thu ñöôïc toái thieåu laø
ñöôïc ñaùnh daáu. Do ñoù tröôùc heát ta öôùc löôïng khoaûng beân traùi cho tæ leä p 62,95% soá phieáu baàu.
caùc con ñöôïc ñaùnh daáu vôùi ñoä tin caäy γ = 1- α = 94% = 0,94 (α = 0,06).
Ta coù coâng thöùc öôùc löôïng khoaûng beân traùi:
Vôùi ñoä tin caäy 99%, ñeå bieát öùng cöû vieân A coù theå thu ñöôïc toái ña bao
nhieâu phaàn traêm soá phieáu baàu ta caàn öôùc löôïng khoaûng beân traùi cho tæ leä n F (1 − n F ) (− ; ∞ + , n F z2 ) α n
p nhöõng ngöôøi uûng hoä vôùi ñoä tin caäy γ = 1- α = 99% = 0,99 (α = 0,01).
Ta coù coâng thöùc öôùc löôïng khoaûng beân traùi: 21 22
a) Öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc cuûa n F (1 − n F ) (− ; ∞ n F + z2 ) α , n
moät hoä gia ñình vôùi ñoä tin caäy 95% .
trong ñoù z2α = 2,33. Suy ra giaù trò toái ña cuûa tæ leä ngöôøi uûng hoä laø:
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μ = M(X) vôùi ñoä tin caäy γ = 1- α = 95% = 0,95. n F (1− n F ) 0, 6556(1− 0,6556) n F + z2 = 0, 6556 + 2, 33 = 0,6817. α n 1800
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc öôùc löôïng khoaûng
Nhö vaäy, vôùi ñoä tin caäy 99%, öùng cöû vieân A coù theå thu ñöôïc toái ña laø cho kyø voïng: 68,17% soá phieáu baàu. SX SX (X − z ; X + z ) , α α n n
Baøi 3.9. Khaûo saùt thu nhaäp vaø tyû leä thu nhaäp chi cho giaùo duïc ôû 350 hoä
trong ñoù ϕ(zα) = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta
gia ñình, ta thu ñöôïc caùc soá lieäu ôû baûng sau:
ñöôïc zα = 1,96. Vaäy öôùc löôïng khoaûng laø: X 10 20 30 40 50 8, 7910 8, 7910 (29, 7143 − 1, 96 ; 29, 7143 + 1, 96 ) = (28,7933;30,6353). Y 350 350 150 - 250 10 40 20
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, giaù trò trung bình cuûa tyû leä thu nhaäp 250 - 350 40 60 20
chi cho giaùo duïc cuûa moät hoä gia ñình töø 28,7933% ñeán 30,6353%. 350 - 450 20 30 40 450 - 550 30 30 10
b) Nhöõng gia ñình coù thu nhaäp bình quaân ngöôøi treân 450 laø hoä coù thu
trong ñoù : X laø tyû leä thu nhaäp chi cho giaùo duïc (tính theo %)
nhaäp cao. Öôùc löôïng tyû leä hoä coù thu nhaäp cao vôùi ñoä tin caäy 97%.
Y laø thu nhaäp bình quaân 1 ngöôøi/thaùng cuûa moät hoä (ñôn vò tính
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc hoä coù thu nhaäp cao ngaøn ñoàng).
vôùi ñoä tin caäy γ = 1- α = 97% = 0,97.
a) Öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc cuûa
Ta coù coâng thöùc öôùc löôïng khoaûng :
moät hoä gia ñình vôùi ñoä tin caäy 95% . F (1 − F ) F (1 − F )
b) Nhöõng gia ñình coù thu nhaäp bình quaân ngöôøi treân 450 laø hoä coù thu n n n n ( n F − z ; α n F + z ) n α n
nhaäp cao. Öôùc löôïng tyû leä hoä coù thu nhaäp cao vôùi ñoä tin caäy 97%.
c) Ñeå öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc vôùi
trong ñoù ϕ(zα) = (1- α)/2 = γ /2 = 0,97/2 = 0,485. •
ñoä chính xaùc ε = 0,8% thì ñaûm baûo ñoä tin caäy laø bao nhieâu?
Tra baûng giaù trò haøm Laplace ta ñöôïc zα = 2,17. • Côõ maãu n = 350. • Lôøi giaûi
Trong n = 350 hoä coù m = 30 + 30 + 10 = 70 hoä coù thu nhaäp bình
quaân ngöôøi treân 450 neân coù m = 70 hoä coù thu nhaäp cao. Do ñoù tæ leä maãu
hoä coù thu nhaäp cao laø: • Côõ maãu: n = 350. F • n = m/n = 70/350 = 0,2.
Kyø voïng maãu cuûa X laø 1
Vaäy öôùc löôïng khoaûng laø: X = X n ∑ = 29, 7143. i Xi n 0, 2(1 − 0, 2) 0, 2(1 − 0, 2) • .
Phöông sai maãu cuûa X laø: (0, 2 − 2,17 ; 0, 2 + 2,17 ) = (15, 36%; 24, 64%). 350 350
Noùi caùch khaùc, vôùi ñoä tin caäy 97%, tæ leä hoä coù thu nhaäp cao töø 15,36% ñeán  2 1 2 2 2 S 24,64%. X = X n ∑ − X ( = 8,7785) . i Xi n
• Phöông sai maãu ñaõ hieäu chænh cuûa X laø:
c) Ñeå öôùc löôïng giaù trò trung bình cuûa tyû leä thu nhaäp chi cho giaùo duïc vôùi
ñoä chính xaùc ε = 0,8% thì ñaûm baûo ñoä tin caäy laø bao nhieâu? n 2 2 2 S = X S = (8,7910) . X n − 1
Yeâu caàu cuûa baøi toùan: Xaùc ñònh ñoä tin caäy γ = 1- α. 23 24
Giaû thieát: - Öôùc khoûang cho kyø voïng cuûa X. Fn = m/n = 27/134 = 0,2015.
- Ñoä chính xaùc ε = 0,8 (%).
Ta coù coâng thöùc öôùc löôïng khoaûng:
Vì n ≥ 30, σ2 = D(X) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: n F (1 − n F ) n F (1 − n F ) (F − z ; F + z ) S n α n n α n ε = zα , n
trong ñoù ϕ(zα) = γ /2 = 0,95/2 = 0,475. Tra baûng giaù trò haøm Laplace ta trong ñoù ϕ (z ñöôïc z
α) = (1- α)/2 = γ /2 . Suy ra
α = 1,96. Vaäy öôùc löôïng khoaûng laø: ε n 0,8. 350 0, 2015(1− 0, 2015) 0,2015(1− 0, 2015) z = = = 1,70 (0, 2015 −1,96 ; 0,2015 +1,96 ) α S 8,7910 134 134
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø:
= (0,1336; 0, 2694) = (13, 36%; 26, 94%).
γ = 2ϕ (z )= 2ϕ (1,70)= 2.0, 4554= 91, 08%.
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, tæ leä saûn phaåm loaïi A töø 13,36% ñeán α
Vaäy ñoä tin caäy ñaït ñöôïc laø 91,08%. 26,94%.
Baøi 3.10. X(%) vaø Y(kg/mm2 ) laø hai chæ tieâu chaát löôïng cuûa moät loaïi saûn
b) Öôùc löôïng giaù trò trung bình chæ tieâu Y cuûa nhöõng saûn phaåm loaïi A vôùi
phaåm. Quan saùt moät soá saûn phaåm ta coù baûng soá lieäu nhö sau:
ñoä tin caäy 95% (Giaû söû Y coù phaân phoái chuaån). X 0-5 5-10 10-15 15-20 20-25 Y
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho kyø voïng μYA = M(YA) cuûa chæ tieâu Y = Y α 120 7
A cuûa nhöõng saûn phaåm loaïi A vôùi ñoä tin caäy γ = 1- = 95% = 0,95. 130 12 8 10
Ta laäp baûng soá lieäu cuûa Y 140 20 15 2 A: 150 19 16 9 5 Y 160 8 3 Ai 140 150 160 n
Saûn phaåm coù chæ tieâu X ≥ 15% laø loaïi A. Ai 2 14 11
Töø baûng treân ta tính ñöôïc:
a) Öôùc löôïng tæ leä saûn phaåm loaïi A ñoä tin caäy 95%.
b) Öôùc löôïng giaù trò trung bình chæ tieâu Y cuûa nhöõng saûn phaåm loaïi A n = 27; Y n =4140; ∑ 2 Y n =635800. ∑
vôùi ñoä tin caäy 95% (Giaû söû Y coù phaân phoái chuaån). A Ai Ai Ai Ai •
c) Neáu muoán öôùc löôïng giaù trò trung bình cuûa chæ tieâu Y vôùi ñoä chính
Kyø voïng maãu cuûa YA laø 1
xaùc 1,6 kg/mm2 thì seõ ñaûm baûo ñöôïc ñoä tin caäy laø bao nhieâu? Y A = ∑ Y n = 153,3333. Ai Ai n Lôøi giaûi
• Phöông sai maãu cuûa YA laø: 2 2 1 a) 2 2
Öôùc löôïng tæ leä saûn phaåm loaïi A ñoä tin caäy 95%.  S YA = Y n −Y A ( = ∑ 6, 0858) . Ai Ai n
Ñaây laø baøi toaùn öôùc löôïng khoaûng cho tæ leä p caùc saûn phaåm loaïi A vôùi
• Phöông sai maãu ñaõ hieäu chænh cuûa Y
ñoä tin caäy γ = 1- α = 95% = 0,95. A laø:
Töø baûng soá lieäu ñaõ cho ta tính ñöôïc: 2 n • 2 A 2 Côõ maãu: n = 134. S  = SYA = (6, 2017) . YA n −1
• Trong n = 134 saûn phaåm coù m = 2 + 9 + 8 + 5 + 3 = 27 saûn phaåm A
coù chæ tieâu X ≥ 15% neân coù m = 27 saûn phaåm loaïi A. Do ñoù tæ leä maãu
Vì nA < 30, YA coù phaân phoái chuaån, σ2YA= D(XA) chöa bieát, neân ta coù coâng saûn phaåm loaïi A laø:
thöùc öôùc löôïng khoaûng cho kyø voïng: 25 26 k S S YA k YA (YA − t ; YA + t ) α , n α n A A trong ñoù k
t ñöôïc xaùc ñònh töø baûng phaân phoái Student vôùi k = n α A–1=26
vaø α = 1- γ = 1–0,95 = 0,05. Tra baûng phaân phoái Student ta ñöôïc k
t = 2, 056 . Vaäy öôùc löôïng khoaûng laø: α 6, 2017 6, 2017 (153, 3333 − 2, 056 ; 153, 3333 + 2, 056 ) = (150, 8794; 155, 7872). 27 27
Noùi caùch khaùc, vôùi ñoä tin caäy 95%, giaù trò trung bình cuûa chæ tieâu Y cuûa
nhöõng saûn phaåm loaïi A töø 150,8794kg/mm2 ñeán 155,7872kg/mm2.
c) Neáu muoán öôùc löôïng giaù trò trung bình cuûa chæ tieâu Y vôùi ñoä chính
xaùc 1,6 kg/mm2 thì seõ ñaûm baûo ñöôïc ñoä tin caäy laø bao nhieâu?
Ñaây laø baøi toaùn xaùc ñònh ñoä tin caäy γ = 1- α khi öôùc löôïng kyø voïng cuûa
chæ tieâu Y vôùi ñoä chính xaùc ε = 1,6kg/mm2.
Töø baûng soá lieäu ñaõ cho ta tính ñöôïc: • Côõ maãu: n = 134.
• Kyø voïng maãu cuûa Y laø 1 Y = Y n = ∑ 142, 0149. j Yj n
• Phöông sai maãu cuûa Y laø:  2 1 2 2 2 Y S = Y n − Y ( = 10, 4224) . ∑ i Yi n
• Phöông sai maãu ñaõ hieäu chænh cuûa Y laø: n = 2 2 2 S Y S = (10, 4615) . Y n − 1
Vì n ≥ 30, σ2Y= D(Y) chöa bieát neân ta coù coâng thöùc tính ñoä chính xaùc cuûa öôùc löôïng: Y S ε = z , α n
trong ñoù ϕ(zα) = γ /2. Suy ra ε n 1,6. 134 z = = = 1,77 α Y S 10, 4615
Tra baûng giaù trò haøm Laplace ta ñöôïc ñoä tin caäy laø:
γ = 2ϕ(z )= 2ϕ(1, 77) ≈ 2.0, 4646= 92, 92%. α
Vaäy ñoä tin caäy ñaït ñöôïc laø 92,92%.
----------------------------------------- 27 BAØI GIAÛI
Baøi 4.2. Troïng löôïng cuûa moät saûn phaåm coù phaân phoái chuaån vôùi troïng
löôïng trung bình laø 500g. Sau moät thôøi gian saûn xuaát, ngöôøi ta nghi ngôø
XAÙC SUAÁT THOÁNG KEÂ
troïng löôïng trung bình cuûa loaïi saûn phaåm naøy coù xu höôùng giaûm neân tieán
(GV: Traàn Ngoïc Hoäi – 2009)
haønh kieåm tra 25 saûn phaåm vaø thu ñöôïc keát quaû sau: Troïng löôïng (g) 480 485 490 495 500 510 CHÖÔNG 4 Soá saûn phaåm 2 3 8 5 3 4
Vôùi möùc yù nghóa 3%, haõy keát luaän ñieàu nghi ngôø treân coù ñuùng hay khoâng.
KIEÅM ÑÒNH GIAÛ THIEÁT Lôøi giaûi
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
Baøi 4.1. Troïng löôïng cuûa moät saûn phaåm theo qui ñònh laø 6kg. Sau moät nghóa α = 3% = 0,03:
thôøi gian saûn xuaát, ngöôøi ta tieán haønh kieåm tra 121 saûn phaåm vaø tính
H0: μ = 500 vôùi giaû thieát ñoái H1: μ < 500.
ñöôïc trung bình maãu laø 5,975kg vaø phöông sai maãu hieäu chænh 5,7596kg2. Ta coù:
Saûn xuaát ñöôïc xem laø bình thöôøng neáu caùc saûn phaåm coù troïng löôïng Xi 480 485 490 495 500 510
trung bình baèng troïng löôïng qui ñònh. Vôùi möùc yù nghóa 5%, haõy keát luaän ni 2 3 8 5 3 4
veà tình hình saûn xuaát. Lôøi giaûi n = 25; X n 1 = 2350; ∑ 2 X n =6102800. ∑ i i i i
• Kyø voïng maãu cuûa X laø
Goïi X laø troïng löôïng cuûa moät saûn phaåm. Giaû thieát cho ta: 1 X = X n = ∑ 494(g). • Côõ maãu n = 121. i i n
• Kyø voïng maãu cuûa X laø X = 5,975 (kg) .
• Phöông sai maãu cuûa X laø:
• Phöông sai maãu hieäu chænh cuûa X laø S2 = 5,7596(kg2). 1  2 2 2 2 2 S = ∑ X n − X =(8,7178) (g ). • i i
Ñoä leäch maãu hieäu chænh cuûa X laø S = 2,3999(kg). n
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
• Phöông sai maãu hieäu chænh cuûa X laø: nghóa α = 5% = 0,05: n S  2 2 2 2 = S = (8, 8976) (g ). H n − 1
0: μ = 6 vôùi giaû thieát ñoái H1: μ ≠ 6.
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Vì n < 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau: Böôùc 1: Ta coù Böôùc 1: Ta coù (X − μ ) n (X − μ ) n (494 −500) 25 (5, 975 − 6) 121 0 = = = − 0 z = = = −0.1146. z 3,3717. S 2, 3999 S 8, 8976
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
Böôùc 2: Ñaët k = n - 1 = 24. Tra baûng phaân phoái Student öùng vôùi k = α thoaû ϕ(z
24 vaø 2α = 0,06 ta ñöôïc t 2α = 1,974.
α) = (1- α)/2 = 0,95/2 = 0,475 ta ñöôïc z
Böôùc 3: Kieåm ñònh. Vì -z = 3,3717 > 1,974 = t α = 1,96. 2α neân ta baùc boû giaû
Böôùc 3: Kieåm ñònh. Vì |z|= 0,1146 < 1,96 = zα
thieát H μ = 500, nghóa laø chaáp nhaän H μ < 500. neân ta chaáp nhaän 0: 1: giaû thieát H0: μ = 6.
Keát luaän: Vôùi möùc yù nghóa 3%, ñieàu nghi ngôø troïng löôïng trung bình
Keát luaän: Vôùi möùc yù nghóa 5%, tình hình saûn xuaát ñöôïc xem laø bình
cuûa loaïi saûn phaåm naøy coù xu höôùng giaûm laø ñuùng. thöôøng.
Baøi 4.3. Naêng suaát luùa trung bình cuûa nhöõng vuï tröôùc laø 5,5taán/ha. Vuï
luùa naêm nay ngöôøi ta aùp duïng moät phöông phaùp kyõ thuaät môùi cho toaøn boä 1 2
dieän tích troàng luùa trong vuøng. Ñieàu tra naêng suaát 100ha luùa, ta coù baûng
haønh ñieàu tra veà thu nhaäp cuûa 100 hoä trong khu vöïc vaø coù baûng soá lieäu soá lieäu sau: sau:
Naêngsuaát (taï/ha) 40-45 45-50 50-55 55-60 60-65 65-70 70-75 75-80 Thu nhaäp bình quaân 150 200 250 300 350 Dieän tích (ha) 7 12 18 27 20 8 5 3 (ngaøn/ngöôøi/thaùng)
Vôùi möùc yù nghóa 1%, haõy keát luaän xem phöông phaùp kyõ thuaät môùi coù laøm Soá hoä 8 15 38 22 17
taêng naêng suaát luùa trung bình cuûa vuøng naøy hay khoâng?
Theo boä phaän tieáp thò thì sieâu thò chæ hoaït ñoäng coù hieäu quaû taïi khu vöïc
naøy khi thu nhaäp bình quaân haøng thaùng cuûa caùc hoä toái thieåu laø vaøo Lôøi giaûi
khoaûng 250ngaøn/ngöôøi/thaùng. Vaäy theo keát quaû ñieàu tra treân, coâng ty coù
neân quyeát ñònh môû sieâu thò taïi khu vöïc naøy hay khoâng vôùi möùc yù nghóa
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù 5%? nghóa α = 1% = 0,01: Lôøi giaûi H
0: μ = 55 vôùi giaû thieát ñoái H1: μ > 55. (5,5taán = 55taï).
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù Ta coù: nghóa α = 5% = 0,05: X H
i 42,5 47,5 52,5 57,5 62,5 67,5 72,5 77,5
0: μ = 250 vôùi giaû thieát ñoái H1: μ > 250. ni 7 12 18 27 20 8 5 3 Ta coù: Xi 150 200 250 300 350 n = 100; X n =5750; ∑ 2 ∑X n =337475. ni 8 15 38 22 17 i i i i •
Kyø voïng maãu cuûa X laø 1 n =100; ∑X n =26250; 2 ∑ X n 7 = 217500. i i i i X = ∑ X n = 57,5(taï). i i n
• Kyø voïng maãu cuûa X laø
• Phöông sai maãu cuûa X laø: 1 X = X n = 262, 5. ∑ 1 i i n 2 2 2 2 2 S =
∑X n − X (=8,2765) (taï ). i i n
• Phöông sai maãu cuûa X laø:
• Phöông sai maãu hieäu chænh cuûa X laø:  2 1 2 2 2 S = ∑ X n − X (=57,1730) . n i i n S 2 2 2 2 = S = (8,3182) (taï ). n − 1
• Phöông sai maãu hieäu chænh cuûa X laø:
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau: n S  2 2 2 = S = (57,4610) . Böôùc 1: Ta coù n − 1 (X − μ ) n (57,5 − 55) 100
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau: 0 z= = = 3,0055. S 8, 3182 Böôùc 1: Ta coù
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z (X − μ ) n (262,5 − 250) 100 2α thoaû 0 z = = = 2,1754. ϕ(z S 57,4610
2α) = (1- 2α)/2 = 0,98/2 = 0,49 ta ñöôïc z
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z 2α = 2,33. 2α thoaû
Böôùc 3: Kieåm ñònh. Vì z = 3,0055 > 2,33 = z ϕ(z
2α neân ta baùc boû giaû thieát
2α) = (1- 2α)/2 = 0,90/2 = 0,45 H ta ñöôïc z
0: μ = 55, nghóa laø chaáp nhaän H1: μ > 55. 2α = 1,65.
Keát luaän: Vôùi möùc yù nghóa 1%, phöông phaùp kyõ thuaät môùi laøm taêng
Böôùc 3: Kieåm ñònh. Vì z = 2,1754 > 1,65 = z2α neân ta baùc boû giaû thieát
naêng suaát luùa trung bình cuûa vuøng naøy.
H0: μ = 250, chaáp nhaän giaû thieát H1: μ > 250, nghóa laø thu nhaäp bình
quaân cuûa caùc hoä cao hôn 250ngaøn/ngöôøi/thaùng.
Baøi 4.4. Moät coâng ty döï ñònh môû moät sieâu thò taïi moät khu daân cö. Ñeå
Keát luaän: Vôùi möùc yù nghóa 5%, coâng ty neân quyeát ñònh môû sieâu thò taïi
ñaùnh giaù khaû naêng mua haøng cuûa daân cö trong khu vöïc, ngöôøi ta tieán khu vöïc naøy. 3 4
Keát luaän: Vôùi möùc yù nghóa 5%, khoâng theå cho raèng nhu caàu trung bình
Baøi 4.5. Ñeå nghieân cöùu nhu caàu cuûa moät loaïi haøng, ngöôøi ta tieán haønh
veà maët haøng naøy cuûa toaøn khu vöïc laø 14taán/thaùng.
khaûo saùt nhu caàu cuûa maët haøng naøy ôû 400 hoä. Keát quaû nhö sau: Nhu caàu (kgï/thaùng) 0 0-1 1-2 2-3 3-4 4-5 5-6 6-7
Baøi 4.6. Troïng löôïng cuûa moät loaïi gaø coâng nghieäp ôû moät traïi chaên nuoâi coù Soá hoä 10 35 86 132 78 31 18 10
phaân phoái chuaån. Troïng löôïng trung bình khi xuaát chuoàng naêm tröôùc laø
Giaû söû khu vöïc ñoù coù 4000 hoä. Neáu cho raèng nhu caàu trung bình veà maët
2,8kg/con. Naêm nay, ngöôøi ta söû duïng moät loaïi thöùc aên môùi. Caân thöû 25
haøng naøy cuûa toaøn khu vöïc laø 14taán/thaùng thì coù chaáp nhaän ñöôïc khoâng
con khi xuaát chuoàng ngöôøi ta tính ñöôïc trung bình maãu laø 3,2kg vaø vôùi möùc yù nghóa 2%?
phöông sai maãu hieäu chænh 0,25kg2. Lôøi giaûi
a) Vôùi möùc yù nghóa 5%, haõy keát luaän xem loaïi thöùc aên môùi coù thöïc söï
laøm taêng troïng löôïng trung bình cuûa ñaøn gaø hay khoâng?
Khi cho raèng nhu caàu trung bình veà maët haøng naøy cuûa toaøn khu vöïc laø
b) Neáu traïi chaên nuoâi baùo caùo troïng löôïng trung bình khi xuaát chuoàng
14taán/thaùng, nghóa laø nhu caàu trung bình veà maët haøng naøy cuûa moät hoä
laø 3,3kg/con thì coù chaáp nhaän ñöôïc khoâng vôùi möùc yù nghóa 5%? trong moät thaùng laø 14taán 14000kg = = 3,5kg. Lôøi giaûi 4000 4000
Do ñoù ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi
Goïi X laø troïng löôïng cuûa moät con gaø sau khi söû duïng loaïi thöùc aên môùi.
möùc yù nghóa α = 2% = 0,02: Giaû thieát cho ta:
H0: μ = 3,5 vôùi giaû thieát ñoái H1: μ ≠ 3,5.
• X coù phaân phoái chuaån. Ta coù: • Côõ maãu n = 25. Xi 0 0,5 1,5 2,5 3,5 4,5 5,5 6,5
• Kyø voïng maãu cuûa X laø X = 3,2(kg). ni 10 35 86 132 78 31 18 10 2
• Phöông sai maãu hieäu chænh cuûa X laø S2 = 0,25(kg ). n = 400; X n 1 = 053; ∑ 2 X n =3577,5.
• Ñoä leäch maãu hieäu chænh cuûa X laø S = 0,5(kg). i i ∑ i i
• Kyø voïng maãu cuûa X laø 1
a) Vôùi möùc yù nghóa 5%, haõy keát luaän xem loaïi thöùc aên môùi coù thöïc söï laøm X = X n = ∑ 2, 6325. i i
taêng troïng löôïng trung bình cuûa ñaøn gaø hay khoâng? n •
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
Phöông sai maãu cuûa X laø: nghóa α = 5% = 0,05:  2 1 2 2 2 S = X n − X ( = ∑ 1, 4190) . i i n
H0: μ = 2,8 vôùi giaû thieát ñoái H1: μ > 2,8.
• Phöông sai maãu hieäu chænh cuûa X laø:
Vì n < 30; X coù phaân phoái chuaån; σ2 = D(X) chöa bieát, neân ta kieåm ñònh n 2 nhö sau: 2 S =  2 S = (1,4208) . n −1 Böôùc 1: Ta coù
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau: (X − μ ) n (3,2− 2, 8) 25 0 z = = = 4. Böôùc 1: Ta coù S 0,5 (X − μ ) n (2, 6325 − 3,5) 400 0 z = = = 12 − , 2114.
Böôùc 2: Ñaët k = n -1 = 24. Tra baûng phaân phoái Student öùng vôùi k = S 1,4208
24 vaø 2α = 0,1 ta ñöôïc k t 2 = t 2 =1,711. α α
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm zα thoaû
Böôùc 3: Kieåm ñònh. Vì z = 4 > 1,711 = t2α neân ta baùc boû giaû thieát
ϕ(zα) = (1- α)/2 = 0,98/2 = 0,49
H0: μ = 2,8, ghóa laø chaáp nhaän giaû thieát H1: μ > 2,8. ta ñöôïc zα = 2,33.
Keát luaän: Vôùi möùc yù nghóa 5%, loaïi thöùc aên môùi thöïc söï laøm taêng
Böôùc 3: Kieåm ñònh. Vì |z| = 12,2114 > 2,33 = zα neân ta baùc boû giaû
troïng löôïng trung bình cuûa ñaøn gaø.
thieát H0: μ = 3,5, chaáp nhaän giaû thieát H1: μ ≠ 3,5. 5 6
b) Neáu traïi chaên nuoâi baùo caùo troïng löôïng trung bình khi xuaát chuoàng laø
Vì nX > 30; nY > 30 neân ta kieåm ñònh nhö sau:
3,3kg/con thì coù chaáp nhaän ñöôïc khoâng vôùi möùc yù nghóa 5%? Böôùc 1: Ta coù:
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù X − Y 168 − 164 z = = = 5,3059. nghóa α = 5% = 0,05: 2 2 2 2 X S Y S 6 5 H + +
0: μ = 3,3 vôùi giaû thieát ñoái H1: μ ≠ 3,3. X n Y n 100 120
Vì n < 30; X coù phaân phoái chuaån; σ2 = D(X) chöa bieát, neân ta kieåm ñònh
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû nhö sau:
ϕ(z2α) = (1 - 2α)/2 = 0,98/2 = 0,49 Böôùc 1: Ta coù ta ñöôïc z2α = 2,33. (X − μ ) n (3, 2 − 3, 3) 25 0 z = = = 1. −
Böôùc 3: Kieåm ñònh. Vì z = 5,3059 > 2,33 = z2α neân ta baùc boû giaû S 0,5
thieát H0: μX = μY, nghóa laø chaáp nhaän H1: μX > μY.
Böôùc 2: Ñaët k = n -1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
Keát luaän: Vôùi möùc yù nghóa 1%, coù theå keát luaän raèng nam sinh noäi
24 vaø α = 0,05 ta ñöôïc k t = t = 2,064. α α
thaønh thöïc söï cao hôn nam sinh ngoaïi thaønh.
Böôùc 3: Kieåm ñònh. Vì |z| = 1 < 2,064 = t
α neân ta chaáp nhaän giaû thieát H
Baøi 4.8. Moät hôïp taùc xaõ troàng thöû hai gioáng luùa, moãi gioáng treân 30 thöûa 0: μ = 3,3.
Keát luaän: Vôùi möùc yù nghóa 5%, baùo caùo troïng löôïng trung bình khi
ruoäng vaø ñöôïc chaêm soùc nhö nhau. Cuoái vuï thu hoaïch ta ñöôïc soá lieäu nhö
xuaát chuoàng laø 3,3kg/con laø chaáp nhaän ñöôïc. sau:
Naêng suaát trung bình (taï/ha) Ñoä leäch maãu hieäu chænh
Baøi 4.7. Chieàu cao trung bình cuûa 100 nam sinh lôùp 12 ôû moät tröôøng Gioáng luùa 1 45 2,5 Gioáng luùa 2 46,5 4,0
trung hoïc noäi thaønh laø 1,68m vôùi ñoä leäch maãu hieäu chænh 6cm. Trong khi
a) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa hai gioáng luùa treân
kieåm tra 120 nam sinh lôùp 12 ôû moät huyeän ngoaïi thaønh thì chieàu cao laø nhö nhau hay khoâng?
trung bình laø 1,64m vôùi ñoä leäch maãu hieäu chænh 5cm. Vôùi möùc yù nghóa 1%,
b) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa gioáng luùa 2 cao
coù theå keát luaän raèng nam sinh noäi thaønh thöïc söï cao hôn nam sinh ngoaïi
hôn cuûa gioáng luùa 1 hay khoâng? thaønh hay khoâng? Lôøi giaûi
Goïi X, Y (taï/ha) laàn löôït laø naêng suaát cuûa gioáng luùa 1 vaø 2. Khi ñoù: Lôøi giaûi
1) Ñoái vôùi X, giaû thieát cho ta: • Côõ maãu n
Goïi X, Y (cm) laàn löôït laø chiều cao cuûa nam sinh noäi thaønh vaø nam X = 30.
• Kyø voïng maãu cuûa X laø X = 45.
sinh ngoaïi thaønh. Baøi toaùn treân chính laø baøi toaùn kieåm ñònh so saùnh hai
• Ñoä leäch maãu hieäu chænh cuûa X laø S X = 2,5.
kyø voïng vôùi möùc yù nghóa α = 1% = 0,01:
2) Ñoái vôùi Y, giaû thieát cho ta:
H0: μX = μY vôùi giaû thieát ñoái H1: μX > μY. • Côõ maãu nY = 30.
• Kyø voïng maãu cuûa Y laø Y = 46,5.
1) Ñoái vôùi X, giaû thieát cho ta:
• Ñoä leäch maãu hieäu chænh cuûa Y laø S = 4. • Y Côõ maãu nX = 100.
• Kyø voïng maãu cuûa X laø X = 168(cm) .
a) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa hai gioáng luùa treân laø
• Ñoä leäch maãu hieäu chænh cuûa X laø S X = 6(cm). nhö nhau hay khoâng?
2) Ñoái vôùi Y, giaû thieát cho ta:
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa • Côõ maãu nY = 120 2% = 0,02:
• Kyø voïng maãu cuûa Y laø Y = 164(cm) . H0: μ •
X = μY vôùi giaû thieát ñoái H1: μX ≠ μY.
Ñoä leäch maãu hieäu chænh cuûa Y laø S Y = 5(cm).
Vì nX = nY = 30 neân ta kieåm ñònh nhö sau: Böôùc 1: Ta coù: 7 8 X − Y 45 − 46,5
Ta ñöa baøi toaùn veà baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn z = = = −1,7418. 2 2 2 2 S
phaåm loaïi A vôùi möùc yù nghóa α = 5% = 0,05: X S Y 2, 5 4 + + n H X n Y 30 30
0: p = 45% = 0,45 vôùi giaû thieát ñoái H1: p > 0,45.
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z Ta kieåm ñònh nhö sau: α thoaû ϕ(z Böôùc 1: Ta coù
α) = (1 - α)/2 = 0,98/2 = 0,49 ta ñöôïc z (F − p ) n (0, 5375 − 0,45) 400 α = 2,33. n 0 z = = = 3,5176.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,7418 < 2,33 = z p (1 − p ) 0, 45(1 − 0, 45) α neân ta chaáp nhaänû 0 0
giaû thieát H0: μX = μY.
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû
Keát luaän: Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa hai gioáng
ϕ(z2α) = (1 - 2α)/2 = 0,90/2 = 0,45 luùa treân laø nhö nhau. ta ñöôïc z2α = 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 3,5176 > 1,65= z2α neân ta baùc boû giaû thieát
b) Vôùi möùc yù nghóa 2%, coù theå xem naêng suaát cuûa gioáng luùa 2 cao hôn
H0: p = 0,45, nghóa laø chaáp nhaän H1: p > 0,45.
cuûa gioáng luùa 1 hay khoâng?
Keát luaän: Vôùi möùc yù nghóa 5%, phöông phaùp môùi thöïc söï laøm taêng tæ leä
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa α = saûn phaåm loaïi A. 2% = 0,02:
H0: μX = μY vôùi giaû thieát ñoái H1: μX < μY.
Baøi 4.10. Thoáng keâ 10650 treû sô sinh ôû moät ñòa phöông ngöôøi ta thaáy coù
Vì nX = nY = 30 neân ta kieåm ñònh nhö sau: 5410 beù trai.
Böôùc 1: Töông töï caâu a), ta coù:
a) Vôùi möùc yù nghóa 3%, hoûi coù söï khaùc bieät veà tæ leä sinh beù trai vaø beù X − Y z = = 1 − ,7418. gaùi hay khoâng? 2 2 X S Y S +
b) Vôùi möùc yù nghóa 1%, hoûi tæ leä sinh beù trai coù thöïc söï cao hôn tæ leä X n Y n sinh beù gaùi hay khoâng?
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z 2α thoaû ϕ(z Lôøi giaûi
2α) = (1 - 2α)/2 = 0,96/2 = 0,48 ta ñöôïc z 2α = 2,06.
Böôùc 3: Kieåm ñònh. Vì -z = 1,7418 < 2,06 = z2α neân ta chaáp nhaänû
Töø caùc giaû thieát cuûa baøi toaùn ta suy ra:
giaû thieát H0: μX = μY.
1) Khi khaûo saùt tæ leä beù trai p1:
Keát luaän: Vôùi möùc yù nghóa 2%, chöa theå xem naêng suaát cuûa gioáng • Côõ maãu n1 = 10650.
luùa 2 cao hôn cuûa gioáng luùa 1.
• Soá beù trai laø m1 = 5410.
• Tæ leä beù trai Fn1 = 5410/10650.
Baøi 4.9. Moät maùy saûn xuaát töï ñoäng, luùc ñaàu tæ leä saûn phaåm loaïi A laø 45%.
2) Khi khaûo saùt tæ leä beù gaùi p2:
Sau khi aùp duïng moät phöông phaùp saûn xuaát môùi, ngöôøi ta laáy ra 400 saûn • Côõ maãu n2 = 10650.
phaåm ñeå kieåm tra thì thaáy coù 215 saûn phaåm loaïi A. Vôùi möùc yù nghóa 5%,
• Soá beù gaùi laø m2 = 10650 – 5410 = 5240.
haõy keát luaän xem phöông phaùp môùi coù thöïc söï laøm taêng tæ leä saûn phaåm
• Tæ leä beù gaùi Fn2 = 5240/10650. loaïi A hay khoâng? 3) p0 = 0,5. Lôøi giaûi
Töø giaû thieát ta suy ra:
a) Vôùi möùc yù nghóa 3%, hoûi coù söï khaùc bieät veà tæ leä sinh beù trai vaø beù gaùi • Côõ maãu n = 400. hay khoâng?
• Soá saûn phaåm loaïi A coù trong maãu laø m = 215.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
• Tæ leä maãu saûn phaåm loaïi A laø F α = 3% = 0,03: n = m/n = 215/400 = 0,5375.
H0: p1 = p2 (= p0) vôùi giaû thieát ñoái H1: p1 ≠ p2 9 10 Ta kieåm ñònh nhö sau: Böôùc 1: Ta coù: Lôøi giaûi 5410 5240 F F − − n1 n2 10650 10650 z = = = 2, 3296.
Töø caùc giaû thieát cuûa baøi toaùn ta suy ra: ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ p (1 − p ) ⎜ + 0,5(1 −0,5) +
1) Ñoái vôùi loaïi thuoác H: 0 0 ⎟ ⎜ ⎟ n n ⎝ 10650 10650 ⎠ ⎝ 1 2 ⎠ • Côõ maãu n1 = 250.
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm zα thoaû
• Soá beänh nhaân khoûi beänh: 210.
ϕ(zα) = (1 - α)/2 = 0,97/2 = 0,485
• Tæ leä maãu beänh nhaân khoûi beänh Fn1 = 210/250 = 0,84. ta ñöôïc zα = 2,17.
2) Ñoái vôùi loaïi thuoác K:
Böôùc 3: Kieåm ñònh. Vì |z| = 2,3296 > 2,17 = zα neân ta baùc boû giaû • Côõ maãu n2 = 200.
thieát H0: p1 = p2, nghóa laø chaáp nhaän H1: p1 ≠ p2.
• Soá beänh nhaân khoûi beänh: 175.
Keát luaän: Vôùi möùc yù nghóa 3%, coù söï khaùc bieät veà tæ leä sinh beù trai vaø
• Tæ leä maãu beänh nhaân khoûi beänh Fn2 = 175/200 = 0,875. beù gaùi. n + + 1Fn1 n 2Fn2 250.0,84 200.0,875 385 3) = = = 0 p . n + + 1 n 2 250 200 450
b) Vôùi möùc yù nghóa 1%, hoûi tæ leä sinh beù trai coù thöïc söï cao hôn tæ leä sinh
a) Vôùi möùc yù nghóa 1% coù theå keát luaän thuoác K coù khaû naêng chöõa beänh A beù gaùi hay khoâng?
toát hôn thuoác H hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa α = 1% = 0,01: α = 1% = 0,01:
H0: p1 = p2 vôùi giaû thieát ñoái H1: p1 > p2
H0: p1 = p2 vôùi giaû thieát ñoái H1: p1 < p2 Ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu a), ta coù: Ta kieåm ñònh nhö sau: F −F n1 n2 z = = 2, 3296. Böôùc 1: Ta coù: ⎛ 1 1 ⎞ p (1 − p ) F −F 0,84 −0,875 0 0 ⎜ + ⎟ n1 n2 n z = = = 1 − ,0495. ⎝ 1 n2⎠ ⎛ 1 1 385 385 1 1 ⎞ ⎛ − + 1 ⎞ ⎛ ⎞ − +
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z p0(1 p0) ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ 2α thoaû n n 450 ⎝ ⎠ ⎝ 450 ⎠⎝ 250 200 ⎠ 1 2
ϕ(z2α) = (1 - 2α)/2 = 0,98/2 = 0,49
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z ta ñöôïc z 2α thoaû 2α = 2,33. ϕ(z
Böôùc 3: Kieåm ñònh. Vì z = 2,3296 < 2,33 = z
2α) = (1 - 2α)/2 = 0,98/2 = 0,49
2α neân ta chaáp nhaän giaû ta ñöôïc z thieát H 2α = 2,33. 0: p1 = p2.
Böôùc 3: Kieåm ñònh. Vì -z = 1,0495 < 2,33 = z
Keát luaän: Vôùi möùc yù nghóa 1%, chöa theå noùi tæ leä sinh beù trai thöïc söï
2α neân ta chaáp nhaän giaû thieát H
cao hôn tæ leä sinh beù gaùi. 0: p1 = p2.
Keát luaän: Vôùi möùc yù nghóa 1%, khoâng theå keát luaän thuoác K coù khaû
naêng chöõa beänh A toát hôn thuoác H.
Baøi 4.11. Beänh A coù theå chöõa baèng hai loaïi thuoác H vaø K. Coâng ty saûn
xuaát thuoác H tuyeân boá tæ leä beänh nhaân khoûi beänh do duøng thuoác cuûa hoï laø
b) Xeùt xem hieäu quaû chöõa beänh cuûa thuoác H coù ñuùng nhö coâng ty quaûng
85%. Ngöôøi ta duøng thöû thuoác H chöõa cho 250 beänh nhaân thì thaáy coù 210
caùo vôùi möùc yù nghóa 5% hay khoâng.
ngöôøi khoûi beänh, duøng thöû thuoác K cho 200 beänh nhaân thì thaáy coù 175
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p ngöôøi khoûi beänh. 1 caùc beänh nhaân khoûi
beänh A khi ñöôïc ñieàu trò baèng thuoác H vôùi möùc yù nghóa α = 5% = 0,05:
a) Vôùi möùc yù nghóa 1% coù theå keát luaän thuoác K coù khaû naêng chöõa beänh
H0: p1 = 85% = 0,85 vôùi giaû thieát ñoái H1: p1 < 0,85.
A toát hôn thuoác H hay khoâng? Ta kieåm ñònh nhö sau:
b) Xeùt xem hieäu quaû chöõa beänh cuûa thuoác H coù ñuùng nhö coâng ty Böôùc 1: Ta coù
quaûng caùo vôùi möùc yù nghóa 5% hay khoâng. 11 12 (F − p ) n (0, 84 − 0, 85) 250 n 2 2 2 2 n1 01 1 z = = = −0, 4428. S = S = (7,4827) (cm ). n− 1 p q 0, 85(1 − 0, 85) 01 01
a) Giaû söû trung bình tieâu chuaån cuûa chæ tieâu X laø 29cm. Haõy cho nhaän
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû
xeùt veà tình hình saûn xuaát vôùi möùc yù nghóa 2%.
ϕ(z2α) = (1 - 2α)/2 = 0,90/2 = 0,45
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù ta ñöôïc z2α = 1,65. nghóa α = 2% = 0,02:
Böôùc 3: Kieåm ñònh. Vì - z = 0,4428 < 1,65 = z2α neân ta chaáp nhaän
H0: μ = 29 vôùi giaû thieát ñoái H1: μ ≠ 29. giaû thieát H0: p1 = 0,85.
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Keát luaän: Vôùi möùc yù nghóa 5%, hieäu quaû chöõa beänh cuûa thuoác H ñuùng Böôùc 1: Ta coù nhö coâng ty quaûng caùo. (X − μ ) n (26, 36 − 29) 100 0 z = = = 3 − , 5281. S 7, 4827
Baøi 4.12. Ñeå khaûo saùt chæ tieâu X cuûa moät loaïi saûn phaåm, ngöôøi ta quan
saùt moät maãu vaø coù keát quûa sau:
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm zα thoaû ϕ(z X(cm)
11-15 15-19 19-23 23-27 27-31 31-35 35-39
α) = (1- α)/2 = 0,98/2 = 0,49 Soásaûn phaåm 8 9 20 16 16 13 18 ta ñöôïc zα = 2,33.
Böôùc 3: Kieåm ñònh. Vì |z|= 3,5281 > 2,33 = z
Nhöõng saûn phaåm coù chæ tieâu X töø 19cm trôû xuoáng ñöôïc goïi laø nhöõng saûn
α neân ta baùc boû giaû thieát
H μ=29, nghóa laø chaáp nhaän H μ ≠ 29. phaåm loaïi B. 0: 1:
Keát luaän: Vôùi möùc yù nghóa 1%, tình hình saûn xuaát khoâng bình thöôøng
a) Giaû söû trung bình tieâu chuaån cuûa chæ tieâu X laø 29cm. Haõy cho nhaän xeùt
vì giaù trò trung bình cuûa chæ tieâu X khoâng ñuùng tieâu chuaån.
veà tình hình saûn xuaát vôùi möùc yù nghóa 2%.
b) Baèng phöông phaùp saûn xuaát môùi, sau moät thôøi gian ngöôøi ta thaáy giaù
b) Baèng phöông phaùp saûn xuaát môùi, sau moät thôøi gian ngöôøi ta thaáy giaù
trò trung bình cuûa chæ tieâu X cuûa nhöõng saûn phaåm loaïi B laø 16cm. Haõy
trò trung bình cuûa chæ tieâu X cuûa nhöõng saûn phaåm loaïi B laø 16cm. Haõy
cho keát luaän veà phöông phaùp saûn xuaát môùi vôùi möùc yù nghóa 1% (GS X
cho keát luaän veà phöông phaùp saûn xuaát môùi vôùi möùc yù nghóa 1% (GS X coù phaân phoái chuaån). coù phaân phoái chuaån).
c) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä nhöõng saûn phaåm loaïi B laø
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
12%. Haõy nhaän ñònh veà taøi lieäu naøy vôùi möùc yù nghóa 5%. B = M(XB) cuûa chæ tieâu
X = XB cuûa nhöõng saûn phaåm loaïi B vôùi möùc yù nghóa α = 1% = 0,01: H Lôøi giaûi
0: μB = 16 vôùi giaû thieát ñoái H1: μB ≠ 16.
Ta laäp baûng soá lieäu cuûa X Laäp baûng: B: XBi 13 17 Xi 13 17 21 25 29 33 37 nBi 8 9 ni 8 9 20 16 16 13 18
Töø baûng treân ta tính ñöôïc: Ta coù: n ∑ X n 2 ∑X n =3,953. Bi Bi = ; 257 B = ; 17 Bi Bi n = ; 100 X n =2636; ∑ 2 X n 7 = 5028. ∑ i i i i
• Kyø voïng maãu cuûa XB laø 1
• Kyø voïng maãu cuûa X laø X B = ∑ X n Bi Bi = 1176 , 15 (c ) m . n 1 X = X n = ∑ 26, 36(cm). i i n
• Phöông sai maãu cuûa XB laø:
• Phöông sai maãu cuûa X laø:  2 1 2 2 2 2 B S = X n − X ( = 1, 9965) (cm ). ∑ Bi Bi B n  2 1 2 2 2 2
S = ∑ X n − X =(7, 4452) (cm ). i i n
• Phöông sai maãu ñaõ hieäu chænh cuûa XB laø:
• Phöông sai maãu ñaõ hieäu chænh cuûa X laø: n B S  2 2 2 2 B = SB = (2, 0580) (cm ). n B −1 13 14
Vì nB < 30, XB coù phaân phoái chuaån, σ2B = D(XB) chöa bieát, neân ta kieåm
c) Nhöõng caây troàng coù chieàu cao töø 105cm ñeán 125cm ñöôïc goïi laø nhöõng ñònh nhö sau:
caây loaïi A. Baèng phöông phaùp môùi, sau moät thôøi gian ngöôøi ta thaáy Böôùc 1: Ta coù
chieàu cao trung bình cuûa nhöõng caây loaïi A laø 119,5cm. Haõy cho keát (X − μ ) n (15,1176 −16) 17
luaän veà phöông phaùp môùi vôùi möùc yù nghóa 1% (GS X coù phaân phoái B 0 B z = = = 1 − ,7678. S B 2, 0580 chuaån).
Böôùc 2: Ñaët k = nB -1 = 16. Tra baûng phaân phoái Student öùng vôùi k = Lôøi giaûi
16 vaø α = 0,01 ta ñöôïc tα = 2,921.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,7678 < 2,921= tα neân ta chaáp nhaän giaû Xi 100 110 120 130 140 150 160 thieát H ni 10 10 15 30 10 10 15 0: μB = 16.
Keát luaän: Vôùi möùc yù nghóa 2%, phöông phaùp môùi khoâng coù taùc duïng Ta coù: n =
laøm thay ñoåi giaù trò trung bình cuûa chæ tieâu X ; 100 ∑ X n 1 = 3100; 2 ∑ X n 1 = 749000.
B cuûa caùc saûn phaåm loaïi B. i i i i
• Kyø voïng maãu cuûa X laø
c) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä saûn phaåm loaïi B laø 12%. Haõy 1 X = X = ∑ i in 131(cm).
nhaän ñònh veà taøi lieäu naøy vôùi möùc yù nghóa 5%. n
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn phaåm loaïi B
• Phöông sai maãu cuûa X laø:
vôùi möùc yù nghóa α = 5% = 0,05:  2 1 2 2 2 2 S = X − = ∑ i n i X (18,1384) (cm ). H n
0: p = 12% = 0,12 vôùi giaû thieát ñoái H1: p ≠ 0,12.
Ta coù qui taéc kieåm ñònh nhö sau:
• Phöông sai maãu hieäu chænh cuûa X laø: Böôùc 1: Ta coù n S  2 2 2 2 = S = (18,2297) (cm ). (F n − 1 −p ) n (0,17 −0,12) 100 n 0 z = = = 1, 5386. p q 0,12(1 − 0,12)
a) Moät taøi lieäu thoáng keâ cuõ cho raèng chieàu cao trung bình cuûa gioáng caây 0 0
troàng treân laø 127cm. Haõy cho keát luaän veà taøi lieäu ñoù vôùi möùc yù nghóa
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm zα thoaû 1%.
ϕ(zα) = (1- α)/2 = 0,95/2 = 0,475
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù ta ñöôïc zα = 1,96. nghóa α = 1% = 0,01:
Böôùc 3: Kieåm ñònh. Vì |z| = 1,5386 < 1,96 = zα neân ta chaáp nhaän giaû H thieát H
0: μ = 127 vôùi giaû thieát ñoái H1: μ ≠ 127 0: p = 0,12.
Vì n ≥ 30; σ2 chöa bieát, neân ta coù qui taéc kieåm ñònh nhö sau:
Keát luaän: Vôùi möùc yù nghóa 5%, taøi lieäu cuõ veà tæ leä saûn phaåm loaïi B coøn Böôùc 1: Ta coù phuø hôïp. (X − μ ) n (131 − 127) 100 0 z = = = 2,1942. Baøi 4.13. S 18, 2297
Ñeå khaûo saùt chieàu cao X cuûa moät gioáng caây troàng, ngöôøi ta quan
saùt moät maãu vaø coù keát quûa sau:
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm zα thoaû ϕ(z X(cm) 95-105
105-115 115-125 125-135 135-145 145-155 155-165
α) = (1 - α)/2 = 0,99/2 = 0,495 Soá caây 10 10 15 30 10 10 15 ta ñöôïc zα = 2,58.
a) Moät taøi lieäu thoáng keâ cuõ cho raèng chieàu cao trung bình cuûa gioáng caây
Böôùc 3: Kieåm ñònh. Vì |z| = 2,1942 < 2,58 = zα neân ta chaáp nhaän
troàng treân laø 127cm. Haõy cho keát luaän veà taøi lieäu ñoù vôùi möùc yù nghóa H0: μ = 127. 1%.
Keát luaän: Vôùi möùc yù nghóa 1%, taøi lieäu cuõ veà chieàu cao trung bình cuûa b)
gioáng caây troàng treân coøn phuø hôïp vôùi thöïc teá.
Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
“cao”. Tröôùc ñaây, tæ leä nhöõng caây “cao” cuûa loaïi caây troàng treân laø 40%.
Caùc soá lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi.
b) Nhöõng caây troàng coù chieàu cao töø 135cm trôû leân ñöôïc goïi laø nhöõng caây
Haõy cho keát luaän veà kyõ thuaät môùi vôùi möùc yù nghóa 5%.
“cao”. Tröôùc ñaây, tæ leä nhöõng caây “cao” cuûa loaïi caây troàng treân laø 40%. 15 16
Caùc soá lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi.
Vì nA = 25 < 30, XA coù phaân phoái chuaån, σ2A= D(XA) chöa bieát, neân ta
Haõy cho keát luaän veà kyõ thuaät môùi vôùi möùc yù nghóa 5%. kieåm ñònh nhö sau:
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc caây cao vôùi möùc yù Böôùc 1: Ta coù nghóa α = 5% = 0,05: (X − μ ) n (116 − 119,5) 25 H A 0 A z = = = 3 − , 5.
0: p = 40% = 0,4 vôùi giaû thieát ñoái H1: p ≠ 0,4 S 5
Ta coù qui taéc kieåm ñònh nhö sau: A Böôùc 1: Ta coù
Böôùc 2: Ñaët k = nA - 1 = 24. Tra baûng phaân phoái Student öùng vôùi k =
24 vaø α = 0,01 ta ñöôïc k t = t = 2,797. (F − p ) n (0, 35 − 0, 4) 100 α α n 0 z = = = −1, 0206.
Böôùc 3: Kieåm ñònh. Vì |z| = 3,5 > 2,797 = t neân ta baùc boû giaû thieát p q 0, 4(1 − 0, 4) α 0 0 H
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
0: μA = 119,5, nghóa laø chaáp nhaän H1: μA ≠ 119,5. Cuï theå, ta nhaän ñònh α thoaû μ X = 116 < 119,5). ϕ( z A < 119,5 (vì A
α) = (1 - α)/2 = 0,95/2 = 0,475 ta ñöôïc z
Keát luaän: Vôùi möùc yù nghóa 1%, phöông phaùp môùi coù taùc duïng laøm thay α = 1,96.
ñoåi chieàu cao trung bình cuûa caùc caây loaïi A, theo höôùng laøm taêng chieàu
Böôùc 3: Kieåm ñònh. Vì|z| = 1,0206 < 1,96 = zα neân ta chaáp nhaän giaû
cao trung bình cuûa caùc caây loaïi naøy. thieát H0: p = 0,4.
Keát luaän: Vôùi möùc yù nghóa 5%, phöông phaùp môùi khoâng coù taùc duïng
Baøi 4.14. Cho caùc soá lieäu nhö Baøi 4.13.
laøm thay ñoåi tæ leä caùc caây cao.
a) Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 125cm. Coù theå khaúng c)
ñònh raèng vieäc canh taùc laøm taêng chieàu cao trung bình cuûa gioáng caây
Nhöõng caây troàng coù chieàu cao töø 105cm ñeán 125cm ñöôïc goïi laø nhöõng
caây loaïi A. Baèng phöông phaùp môùi, sau moät thôøi gian ngöôøi ta thaáy
troàng treân vôùi möùc yù nghóa 1% hay khoâng?
chieàu cao trung bình cuûa nhöõng caây loaïi A laø 119,5cm. Haõy cho keát
b) Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 134cm. Coù theå khaúng
luaän veà phöông phaùp môùi vôùi möùc yù nghóa 1% (GS X coù phaân phoái
ñònh raèng vieäc canh taùc laøm giaûm chieàu cao trung bình cuûa gioáng caây chuaån).
troàng treân vôùi möùc yù nghóa 2% hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
c) Sau khi aùp duïng phöông phaùp canh taùc môùi, ngöôøi ta thaáy chieàu cao A = M(XA) cuûa chieàu cao X = X
trung bình cuûa caùc caây loaïi A laø 114cm. Haõy keát luaän xem phöông phaùp
A cuûa caùc caây loaïi A vôùi möùc yù nghóa α = 1% = 0,01: H
môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây loaïi A hay khoâng
0: μA = 119,5 vôùi giaû thieát ñoái H1: μA ≠ 119,5.
Ta laäp baûng soá lieäu cuûa X
vôùi möùc yù nghóa 3% (Giaû söû X coù phaân phoái chuaån). A: X
d) Tröôùc ñaây, chieàu cao trung bình cuûa caùc caây loaïi A laø 120cm. Caùc soá Ai 110 120
lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi. Haõy keát NAi 10 15
luaän xem kyõ thuaät môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây
Töø baûng treân ta tính ñöôïc:
loaïi A hay khoâng vôùi möùc yù nghóa 2% (Giaû söû X coù phaân phoái chuaån). n = 25; ∑ X n =2900; 2 X n 3 ∑ = 37000. A Ai Ai Ai Ai
e) Sau khi aùp duïng moät phöông phaùp saûn xuaát, ngöôøi ta thaáy tæ leä caây loaïi
- Kyø voïng maãu cuûa XA laø
A laø 35%. Haõy keát luaän xem phöông phaùp môùi coù laøm taêng tæ leä caây 1 X = ∑ =
loaïi A leân hay khoâng vôùi möùc yù nghóa 2% . A XAinAi 116(cm). n
f) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä caây loaïi A laø 20%. Haõy xeùt xem
- Phöông sai maãu cuûa XA laø:
vieäc canh taùc coù laøm taêng tæ leä caây loaïi A hay khoâng vôùi möùc yù nghóa  2 1 2 2 2 2 S 5%? A = ∑X n − X =(4,8990) (cm ). Ai Ai A n Lôøi giaûi
- Phöông sai maãu hieäu chænh cuûa XA laø: Ta coù: nA S =  2 2 2 2 SA = 5 (cm ). A • Côõ maãu laø n = 100. n − A 1
• Kyø voïng maãu cuûa X laø 17 18 1 X = X n = ∑ 131(cm).
Keát luaän: Vôùi möùc yù nghóa 2%, khoâng theå keát luaän raèng vieäc canh taùc i i n
laøm giaûm chieàu cao trung bình cuûa gioáng caây troàng treân.
• Phöông sai maãu cuûa X laø 2  1 2 2 2 2 S = X n ∑ − X = (18,1384) (cm ).
c) Sau khi aùp duïng phöông phaùp canh taùc môùi, ngöôøi ta thaáy chieàu cao i i n
trung bình cuûa caùc caây loaïi A laø 114cm. Haõy keát luaän xem phöông
• Phöông sai maãu hieäu chænh cuûa X laø
phaùp môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây loaïi A hay n 2 2 S =  2 2 S = (18,2297) (cm ).
khoâng vôùi möùc yù nghóa 3% (Giaû söû X coù phaân phoái chuaån). n − 1 a)
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ
Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 125cm. Coù theå khaúng A = M(XA) cuûa chæ
ñònh raèng vieäc canh taùc laøm taêng chieàu cao trung bình cuûa gioáng caây
tieâu X = XA cuûa caùc caây loaïi A vôùi möùc yù nghóa α = 3% = 0,03:
H0: μA = 114 vôùi giaû thieát ñoái H
troàng treân vôùi möùc yù nghóa 1% hay khoâng? 1: μA > 114.
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù
Ta laäp baûng soá lieäu cuûa XA: nghóa α = 1% = 0,01: H XAi 110 120
0: μ = 125 vôùi giaû thieát ñoái H1: μ > 125.
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau: NAi 10 15 Böôùc 1: Ta coù
Töø baûng treân ta tính ñöôïc: (X − μ ) n (131 − 125) 100 = X n ∑ =2900; ∑ = A n 25; 2 X n 337000. Ai Ai Ai Ai 0 z = = = 3, 2913. S 18, 2297 -
Kyø voïng maãu cuûa XA laø 1
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû ϕ(z2α) = (1- 2α)/2 X = ∑ = A XAinAi 116(cm). = 0,98/2 = 0,49 ta ñöôïc z n 2α = 2,33.
Böôùc 3: Kieåm ñònh. Vì z = 3,2913 > 2,33 = z -
Phöông sai maãu cuûa XA laø:
2α neân ta baùc boû giaû thieát 1
H0: μ=125, nghóa laø chaáp nhaän H1: μ > 125. 2 2 2 2 2 A S =
∑ X n − X =(4,8990) (cm ). Ai Ai A
Keát luaän: Vôùi möùc yù nghóa 1%, coù theå keát luaän raèng vieäc canh taùc laøm n
taêng chieàu cao trung bình cuûa gioáng caây troàng treân.
- Phöông sai maãu hieäu chænh cuûa XA laø: A n S =  2 2 2 2 SA = 5 (cm ). b) A
Giaû söû trung bình tieâu chuaån cuûa chieàu cao X laø 134cm. Coù theå khaúng − A n 1
ñònh raèng vieäc canh taùc laøm giaûm chieàu cao trung bình cuûa gioáng caây
Vì nA < 30, XA coù phaân phoái chuaån, σ2A= D(XA) chöa bieát, neân ta kieåm
troàng treân vôùi möùc yù nghóa 2% hay khoâng? ñònh nhö sau:
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μ = M(X) vôùi möùc yù Böôùc 1: Ta coù nghóa α = 2% = 0,02: (X − μ A 0 ) nA (116 − 114) 25 H z = = = 2.
0: μ = 134 vôùi giaû thieát ñoái H1: μ < 134. SA 5
Vì n ≥ 30; σ2 = D(X) chöa bieát, neân ta kieåm ñònh nhö sau:
Böôùc 2: Ñaët k = nA - 1 = 24. Tra baûng phaân phoái Student öùng vôùi k = Böôùc 1: Ta coù
24 vaø 2α = 0,06 ta ñöôïc t 2α = 1,974. (X − μ ) n (131− 134) 100 0 z = = = 1 − ,6457.
Böôùc 3: Kieåm ñònh. Vì z = 2 > 1,974 = t S 18, 2297
2α neân ta baùc boû giaû thieát H
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
0: μA = 114, nghóa laø chaáp nhaän H1: μA > 114.
2α thoaû ϕ(z2α) = (1- 2α)/2
Keát luaän: Vôùi möùc yù nghóa 3%, phöông phaùp môùi laøm giaûm chieàu cao
= 0,96/2 = 0,48 ta ñöôïc z2α = 2,06.
trung bình cuûa caùc caây loaïi A.
Böôùc 3: Kieåm ñònh. Vì –z = 1,6457 < 2,06 = z2α neân ta chaáp nhaän giaû thieát H0: μ = 134.
d) Tröôùc ñaây, chieàu cao trung bình cuûa caùc caây loaïi A laø 120cm. Caùc soá
lieäu treân thu thaäp ñöôïc sau khi ñaõ aùp duïng moät kyõ thuaät môùi. Haõy keát 19 20
luaän xem kyõ thuaät môùi coù laøm giaûm chieàu cao trung bình cuûa caùc caây
H0: p = 20% = 0,20 vôùi giaû thieát ñoái H1: p > 0,20.
loaïi A hay khoâng vôùi möùc yù nghóa 2% (Giaû söû X coù phaân phoái chuaån). Ta kieåm ñònh nhö sau:
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà kyø voïng μA = M(XA) cuûa chæ Böôùc 1: Ta coù
tieâu X = XA cuûa caùc caây loaïi A vôùi möùc yù nghóa α = 2% = 0,02: (F − p ) n (0, 25 − 0, 20) 100 n 0 z = = = 1, 25.
H0: μA = 120 vôùi giaû thieát ñoái H1: μA < 120. p q 0, 20(1 − 0, 20) 0 0
Vì nA < 30, XA coù phaân phoái chuaån, σ2A= D(XA) chöa bieát, neân ta kieåm
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû ñònh nhö sau:
ϕ(z2α) = (1 - 2α)/2 = 0,90/2 = 0,45 (X − μ ) n − Böôùc 1: Ta coù A 0 A (116 120) 25 z= = = − 4. ta ñöôïc z2α = 1,65. SA 5
Böôùc 3: Kieåm ñònh. Vì z = 1,25 < 1,65 = z2α neân ta chaáp nhaän giaû
Böôùc 2: Ñaët k = nA - 1 = 24. Tra baûng phaân phoái Student öùng vôùi k = thieát H0: p = 0,20.
24 vaø 2α = 0,04 ta ñöôïc 2 t α = 2,1715.
Keát luaän: Vôùi möùc yù nghóa 5%, vieäc canh taùc khoâng laøm taêng tæ leä caùc
Böôùc 3: Kieåm ñònh. Vì - z = 4 > 2,1715 = t caây loaïi A.
2α neân ta baùc boû giaû thieát H
0: μA = 120, nghóa laø chaáp nhaän H1: μA < 120.
Keát luaän: Vôùi möùc yù nghóa 2%, kyõ thuaät môùi laøm giaûm chieàu cao
Baøi 4.15. Ñeå khaûo saùt ñöôøng kính cuûa moät chi tieát maùy ngöôøi ta kieåm tra
trung bình cuûa caùc caây loaïi A.
moät soá saûn phaåm cuûa hai nhaø maùy. Trong keát quaû sau ñaây, X laø ñöôøng
kính cuûa chi tieát maùy do nhaø maùy 1 saûn xuaát coøn Y laø ñöôøng kính cuûa chi
e) Sau khi aùp duïng moät phöông phaùp saûn xuaát, ngöôøi ta thaáy tæ leä caây
tieát maùy do nhaø maùy 2 saûn xuaát. Nhöõng saûn phaåm coù chi tieát maùy nhoû
loaïi A laø 35%. Haõy keát luaän xem phöông phaùp môùi coù laøm taêng tæ leä
hôn 19cm ñöôïc xeáp vaøo loaïi C.
caây loaïi A leân hay khoâng vôùi möùc yù nghóa 2% .
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn phaåm loaïi A X(cm)
11-15 15-19 19-23 23-27 27-31 31-35 35-39
vôùi möùc yù nghóa α = 2% = 0,02: Soá saûn phaåm 9 19 20 26 16 13 18 H
0: p = 35% = 0,35 vôùi giaû thieát ñoái H1: p < 0,35.
Ta coù tæ leä maãu caùc caây loaïi A laø F Y(cm)
13-16 16-19 19-22 22-25 25-28 28-31 31-34
n = 25/100 = 0,25. Ta kieåm ñònh nhö sau: Soá saûn phaåm 7 9 25 26 18 15 11 Böôùc 1: Ta coù a) (F − p ) n (0, 25 − 0, 35) 100
Coù theå keát luaän raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do n 0 z= = = − 2, 0966.
hai nhaø maùy saûn xuaát baèng nhau hay khoâng vôùi möùc yù nghóa 1%? p q 0, 35(1 − 0, 35) 0 0
b) Coù theå cho raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû
maùy thöù 1 saûn xuaát lôùn hôn ñöôøng kính trung bình cuûa moät chi tieát
ϕ(z2α) = (1 - 2α)/2 = 0,96/2 = 0,48
maùy do nhaø maùy thöù 2 saûn xuaát hay khoâng vôùi möùc yù nghóa 5%? ta ñöôïc z2α = 2,06.
c) Xeùt xem ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø maùy
Böôùc 3: Kieåm ñònh. Vì -z= 2,0966 > 2,06 = z2α neân ta baùc boû giaû thieát
thöù 2 saûn xuaát coù nhoû hôn ñöôøng kính trung bình cuûa moät chi tieát
H0: p = 0,35, nghóa laø chaáp nhaän H1: p < 0,35.
maùy do nhaø maùy thöù 1 saûn xuaát hay khoâng vôùi möùc yù nghóa 2%?
Keát luaän: Vôùi möùc yù nghóa 2%, phöông phaùp môùi laøm taêng tæ leä caây
d) Vôùi möùc yù nghóa 4%, tæ leä saûn phaåm loaïi C do hai nhaø maùy saûn xuaát loaïi A. coù nhö nhau khoâng?
e) Vôùi möùc yù nghóa 3%, coù theå cho raèng tæ leä saûn phaåm loaïi C do nhaø
f) Moät taøi lieäu thoáng keâ cuõ cho raèng tæ leä caây loaïi A laø 20%. Haõy xeùt xem
maùy thöù 1 saûn xuaát lôùn hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 2
vieäc canh taùc coù laøm taêng tæ leä caây loaïi A hay khoâng vôùi möùc yù nghóa saûn xuaát hay khoâng? 5%?
Ñaây laø baøi toaùn kieåm ñònh giaû thieát veà tæ leä p caùc saûn phaåm loaïi A vôùi
möùc yù nghóa α = 5% = 0,05: 21 22
f) Haõy nhaän xeùt veà yù kieán cho raèng tæ leä saûn phaåm loaïi C do nhaø maùy m 7 +9 Y F = = = 0,1441. Yn
thöù 2 saûn xuaát nhoû hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 1 n 111 Y
saûn xuaát vôùi möùc yù nghóa 5%?
a) Coù theå keát luaän raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do
hai nhaø maùy saûn xuaát baèng nhau hay khoâng vôùi möùc yù nghóa 1%? Lôøi giaûi
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa α = 1% = 0,01:
1) Ñoái vôùi X ta coù baûng soá lieäu:
H0: μX = μY vôùi giaû thieát ñoái H1: μX ≠ μY.
Vì nX > 30; nY > 30 neân ta kieåm ñònh nhö sau: Xi 13 17 21 25 29 33 37 Böôùc 1: Ta coù: ni 9 19 20 26 16 13 18 X − Y 25,3636 − 23,9595 z = = = 1,7188. Ta coù: 2 2 2 2 SX S Y (7,3575) (4,9411) + + X n = 121; ∑ X n =3069; 2 ∑X n =84337. i Xi n n 121 111 i Xi X Y
• Kyø voïng maãu cuûa X laø
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm zα thoaû 1 X = X n = 25, 3636(cm). ∑
ϕ(zα) = (1 - α)/2 = 0,99/2 = 0,495 i Xi nX ta ñöôïc zα = 2,58.
• Phöông sai maãu cuûa X laø
Böôùc 3: Kieåm ñònh. Vì |z| = 1,7188 < 2,58 = zα neân ta chaáp nhaänû 2 1 2 2 2 2 S = X n ∑ − X ( = 7, 3271) (cm ). giaû thieát H X 0: μX = μY. i Xi n X
Keát luaän: Vôùi möùc yù nghóa 1%, coù theå xem ñöôøng kính trung bình cuûa
• Phöông sai maãu hieäu chænh cuûa X laø
moät chi tieát maùy do hai nhaø maùy saûn xuaát laø baèng nhau. n 2 2 S =  2 2 X S = (7,3575) (cm ). X X n − 1 X
b) Coù theå cho raèng ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø
• Tæ leä saûn phaåm loaïi C laø
maùy thöù 1 saûn xuaát lôùn hôn ñöôøng kính trung bình cuûa moät chi tieát m 9 + 19 X F = = = 0, 2314.
maùy do nhaø maùy thöù 2 saûn xuaát hay khoâng vôùi möùc yù nghóa 5%? Xn n 121 X
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa α = 5% = 0,05:
2) Ñoái vôùi Y ta coù baûng soá lieäu:
H0: μX = μY vôùi giaû thieát ñoái H1: μX > μY.
Vì nX > 30; nY > 30 neân ta kieåm ñònh nhö sau:
Yi 14,5 17,5 20,5 23,5 26,5 29,5 32,5
Böôùc 1: Töông töï caâu a), ta coù: ni 7 9 25 26 18 15 11 X − Y Ta coù: z = = 1,7188. 2 2 S S n Y n =2659, 5; ∑ 2 Y n =66405,75. ∑ X Y + Y = 111; i Yi i Yi X n Y n
• Kyø voïng maãu cuûa Y laø 1
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z2α thoaû Y = Y n ∑ = 23, 9595(cm). i Yi ϕ(z n
2α) = (1 - 2α)/2 = 0,90/2 = 0,45 Y ta ñöôïc z
• Phöông sai maãu cuûa Y laø 2α = 1,65.
Böôùc 3: Kieåm ñònh. Vì z = 1,7188 > 1,65 = z 2 1
2α neân ta baùc boû giaû thieát  2 2 2 2 Y S = ∑ Y n − Y (=4,9188) (cm ). i Yi n
H0: μX = μY, nghóa laø chaáp nhaän H1: μX > μY. Y •
Keát luaän: Vôùi möùc yù nghóa 5%, coù theå xem ñöôøng kính trung bình cuûa
Phöông sai maãu hieäu chænh cuûa Y laø n
moät chi tieát maùy do nhaø maùy thöù 1 saûn xuaát lôùn hôn ñöôøng kính trung Y S =  2 2 2 2 SY = (4, 9411) (cm ). Y n − 1
bình cuûa moät chi tieát maùy do nhaø maùy thöù 2 saûn xuaát. Y
• Tæ leä saûn phaåm loaïi C laø 23 24
c) Xeùt xem ñöôøng kính trung bình cuûa moät chi tieát maùy do nhaø maùy thöù
e) Vôùi möùc yù nghóa 3%, coù theå cho raèng tæ leä saûn phaåm loaïi C do nhaø
2 saûn xuaát coù nhoû hôn ñöôøng kính trung bình cuûa moät chi tieát maùy do
maùy thöù 1 saûn xuaát lôùn hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 2
nhaø maùy thöù 1 saûn xuaát hay khoâng vôùi möùc yù nghóa 2%? saûn xuaát hay khoâng?
Ñaây laø baøi toaùn kieåm ñònh so saùnh hai kyø voïng vôùi möùc yù nghóa
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa α = 2% = 0,02: α = 3% = 0,03: H0: μ H
X = μY vôùi giaû thieát ñoái H1: μX > μY.
0: p1 = p2 vôùi giaû thieát ñoái H1: p1 > p2
Vì nX > 30; nY > 30 neân ta kieåm ñònh nhö sau: Ta kieåm ñònh nhö sau:
Böôùc 1: Töông töï caâu a), ta coù:
Böôùc 1: Töông töï caâu d), ta coù: X − Y F − F n1 n2 z = = 1,7188. z= = 1,6942. 2 2 S ⎛ 1 1 ⎞ X S Y + p (1 − p ) ⎜ + 0 0 ⎟ n ⎝ n n ⎠ X n Y 1 2
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z 2α thoaû 2α thoaû ϕ(z ϕ(z
2α) = (1 - 2α)/2 = 0,96/2 = 0,48
2α) = (1 - 2α)/2 = 0,94/2 = 0,47 ta ñöôïc z ta ñöôïc z 2α = 2,06. 2α = 1,88.
Böôùc 3: Kieåm ñònh. Vì z = 1,7188 < 2,06 = z
Böôùc 3: Kieåm ñònh. Vì z = 1,6942 < 1,88 = z
2α neân ta chaáp nhaän giaû
2α neân ta chaáp nhaän giaû thieát H thieát H 0: μX = μY. 0: p1 = p2.
Keát luaän: Vôùi möùc yù nghóa 2%, chöa theå xem ñöôøng kính trung bình
Keát luaän: Vôùi möùc yù nghóa 3%, chöa theå cho raèng tæ leä saûn phaåm loaïi
cuûa moät chi tieát maùy do nhaø maùy thöù 2 saûn xuaát nhoû hôn ñöôøng kính
C do nhaø maùy thöù 1 saûn xuaát lôùn hôn tæ leä saûn phaåm loaïi C do nhaø maùy
trung bình cuûa moät chi tieát maùy do nhaø maùy thöù 1 saûn xuaát. thöù 2 saûn xuaát.
d) Vôùi möùc yù nghóa 4%, tæ leä saûn phaåm loaïi C do hai nhaø maùy saûn xuaát coù
f) Haõy nhaän xeùt veà yù kieán cho raèng tæ leä saûn phaåm loaïi C do nhaø maùy nhö nhau khoâng?
thöù 2 saûn xuaát nhoû hôn tæ leä saûn phaåm loaïi C do nhaø maùy thöù 1 saûn
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa
xuaát vôùi möùc yù nghóa 5%? α = 4% = 0,04:
Ñaây laø baøi toaùn kieåm ñònh giaû thieát so saùnh hai tæ leä vôùi möùc yù nghóa H α = 5% = 0,05:
0: p1 = p2 vôùi giaû thieát ñoái H1: p1 ≠ p2 Ta kieåm ñònh nhö sau:
H0: p1 = p2 vôùi giaû thieát ñoái H1: p1 > p2 Böôùc 1: Ta coù: Ta kieåm ñònh nhö sau: n + +
Böôùc 1: Töông töï caâu d), ta coù: 1Fn1 n 2Fn2 28 16 = = = 0 p 0,1897. n + + − n F 1 n F 2 1 n 2 121 111 z= = 1,6942. F − F 0, 2314 − 0,1441 ⎛ 1 1 ⎞ n1 n2 z = = = 1,6942. p (1 − p ) ⎜ + 0 0 ⎟ n n ⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎝ 1 2 ⎠ p (1 − p ) ⎜ + 0,1897(1 − 0,1897) + 0 0 ⎟ ⎜ ⎟ n n ⎝ 121 111 ⎠ ⎝
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z 1 2 ⎠ 2α thoaû
Böôùc 2: Tra baûng giaù trò haøm Laplace ñeå tìm z
ϕ(z2α) = (1 - 2α)/2 = 0,90/2 = 0,45 α thoaû ϕ(z ta ñöôïc z2α = 1,65.
α) = (1 - α)/2 = 0,96/2 = 0,48 ta ñöôïc z
Böôùc 3: Kieåm ñònh. Vì z = 1,6942 > 1,65 = z2α neân ta baùc boû giaû thieát α = 2,06.
Böôùc 3: Kieåm ñònh. Vì |z| = 1,6942 < 2,06 = z
H0: p1 = p2, nghóa laø chaáp nhaän H1: p1 > p2 .
α neân ta chaáp nhaän giaû thieát H
Keát luaän: Vôùi möùc yù nghóa 5%, coù theå chaáp nhaän yù kieán cho raèng tæ leä 0: p1 = p2.
Keát luaän: Vôùi möùc yù nghóa 4%, coù theå xem tæ leä saûn phaåm loaïi C do hai
saûn phaåm loaïi C do nhaø maùy thöù 2 saûn xuaát nhoû hôn tæ leä saûn phaåm loaïi
nhaø maùy saûn xuaát laø nhö nhau.
C do nhaø maùy thöù 1 saûn xuaát.
------------------------------------------------------------------ 25 26