Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
CHƯƠNG 1. ĐỘNG HỌC CHẤT ĐIỂM
Nội dung giảng dạy
1.1. Những khái niệm mở đầu. 1.2. Vận tốc. 1.3. Gia tốc.
1.4. Một số dạng chuyển động cơ đặc biệt. Bài toán ứng dụng.
1.1. Những khái niệm mở đầu
1.1.1. Chuyển động và hệ quy chiếu
Chuyển động cơ học của một vật là sự chuyển dời vị trí của vật đó đối với các vật
khác trong không gian và the o thời gian.
Khái niệm chuyển động chỉ có tính chất tương đối, phụ th ộ
u c vào hệ quy chiếu ta chọn. Một vật có
thể đứng yên trong hệ quy chiếu này nhưng lại có
thể chuyển động trong hệ quy chiếu khác. Thí dụ:
ta ngồi yên trong ô tô đang chạy, so với cây bên
đường thì ta chuyển động, còn so với chính ô tô đó thì ta đang đứng yên.
Để xác định vị trí của vật trong không gian, ta cần có vật mốc (vật được quy ước là
đứng yên) và các trục tọa độ gắn với vật mốc. Để xác định thời gian chuyển động của
vật, ta cần có một mốc thời gian và một đồng hồ đo. Hệ gồm: vật mốc + các trục tọa độ
+ gốc thời gian + đồng hồ đo được gọi là hệ quy chiếu. Với một chuyển động thẳng, hệ
quy chiếu thường được chọn như sau:
➢ Trục tọa độ Ox trùng với quỹ đạo chuyển động.
➢ Gốc tọa độ gắn với vị trí ban đầu của vật.
➢ Gốc thời gian là lúc vật bắt đầu chuyển động.
➢ Chiều dương là chiều chuyển động của vật.
1.1.2. Chất điểm và hệ chất điểm
Chất điểm là một vật có kích thước nhỏ không đáng kể so với những khoảng cách,
kích thước mà ta đang khảo sát. Thí dụ như viên đạn bay trong không khí hay Trái Đất
chuyển động quanh Mặt Trời.
Khái niệm chất điểm cũng chỉ có tính chất tương đối. Thí dụ khi xét chuyển động
của Trái Đất xung quanh Mặt Trời, có thể coi Trái Đất là chất điểm, nhưng chuyển
động của một điện tử xung quanh trục của nó thì không thể coi là chất điểm. - 1 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
Hệ chất điểm là tập hợp các chất điểm. Thí dụ như hệ các hành tinh xung quanh
Mặt Trời là một hệ chất điểm. 1.1.3. Quỹ đạo
Quỹ đạo của chất điểm chuyển động là đường tạo bởi tập hợp tất cả các vị trí của
chất điểm trong không gian, trong suốt quá trình chuyển động.
1.1.4. Phương trình chuyển động của chất điểm
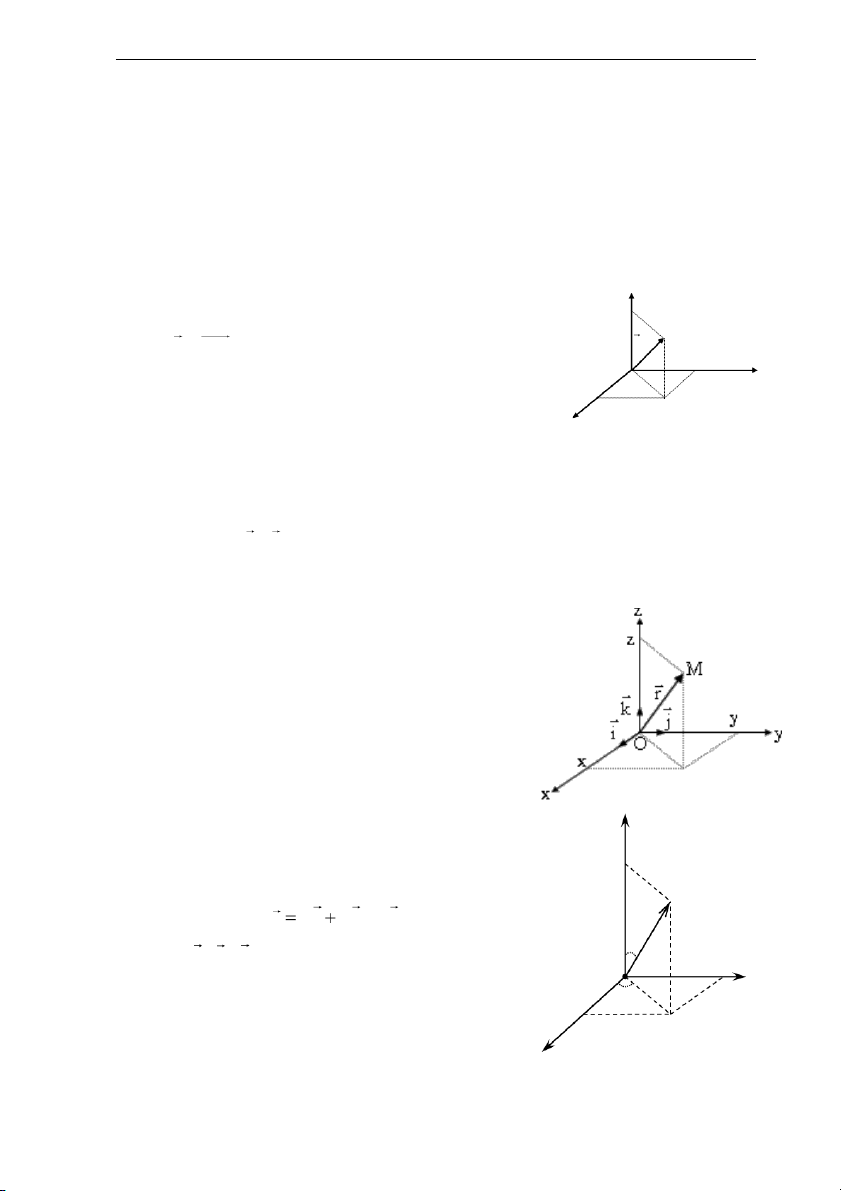
Trong hệ quy chiếu với gốc O làm vật mốc, vị trí M z
của chất điểm ở thời điểm nào đó sẽ được xác định bởi zM M
vector r = OM, vector này được gọi là vector toạ độ của r 0 chất điểm. yM y xM
Khi chất điểm chuyển động, vị trí của nó so với hệ x
quy chiếu sẽ thay đổi, vì thế vector toạ độ của chất điểm
thay đổi theo thời gian. Phương trình nêu lên sự phụ thuộc của vector toạ độ hay các
toạ độ không gian vào thời gian được gọi là phương trình chuyển động. r = r(t) hay x f = (t), y =g(t), z = h(t. (1.1) Ví dụ: y = 5t hay x 10 = cos(2 t  + /  2.
1.15. Phương trình quỹ đạo của chất điểm
Để tìm dạng quỹ đạo chuyển động, ta phải tìm
mối liên hệ giữa các toạ độ không gian của chất điểm.
Phương trình nêu lên mối liên hệ giữa các toạ độ không
gian như thế được gọi là phương trình quỹ đạo. f (x, y,z) c = ons. (1.2)
1.1.6. Một số hệ toạ độ thường gặp z
a. Hệ toạ độ Đề-các vuông góc (Oxyz)
Vector toạ độ xác định vị trí của chất điểm M: M r x.i y.j +z.k, (1.3)  r
trong đó i , j , k là ba vector đơn vị chỉ phương.  y O b. Hệ toạ độ cầu 
Hệ tọa độ cầu sử dụng các tọa độ r, , . x
Giữa các toạ độ của hệ toạ độ cầu và hệ toạ độ
vuông góc Đề-các liên hệ với nhau theo công thức: - 2 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm x  = r cos sin y   = r sin sin (1.4) z  = r cos  c. Toạ độ cong
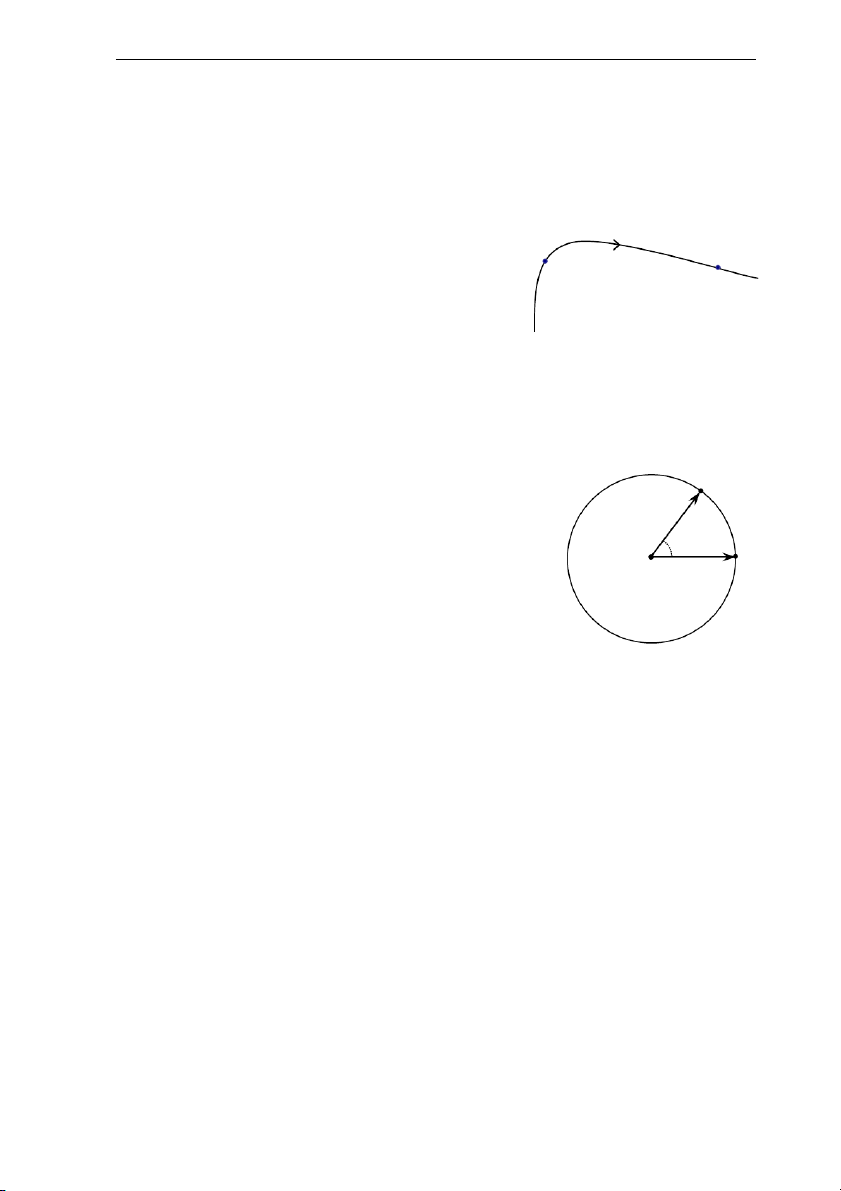
Khi chất điểm chuyển động trên một đường (+) M0
cong quỹ đạo (C), trên (C) ta chọn một điểm M M 0
làm mốc và chọn một chiều dương. Khi đó, ở (C)
mỗi thời điểm t, vị trí M của chất điểm trên
đường cong được xác định bởi độ dài đại số của cung M0M.
s = M0M gọi là hoành độ cong của M. d. Hệ toạ độ góc
Khi chất điểm M chuyển động theo một đường tròn M
tâm O bán kính không đổi thì chỉ có góc mà bán kính OM R
quét được thay đổi theo thời gian, người ta chọn đại lượng  M0
góc đó để làm toạ độ của M và được gọi là toạ độ góc. O
Giữa toạ độ góc và toạ độ cong được xác định theo
công thức: s = R., ở đây  tính theo đơn vị radian. - 3 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
1.2. Vận tốc (vận tốc dài)
Vận tốc là đại lượng vật lý đặc trưng cho phương, chiều và sự nhanh chậm của
chuyển động. Vận tốc là một đại lượng vector. Vận tốc tương đương với tốc độ và
hướng. Thí dụ: 80 km/h về hướng bắc.
1.2.1. Vận tốc trung bình và vận tốc tức thời M2 (C) a. Vận tốc trung bình r M1  
Xét chuyển động của chất điểm trên đường cong r r 1 2
(C). Giả sử tại thời điểm t1 chất điểm ở vị trí M1 có O
vector toạ độ , ở thời điểm t2 chất điểm ở vị trí M 1 2
có vector toạ độ r . Sau khoảng thời gian t = t2 - t1, vector toạ độ chất điểm biến đổi 2 một lượng r  r r
M M gọi là vector độ dời. 2 1 1 2
Vận tốc trung bình là độ biến đổi trung bình của vector tọa độ trong một đơn vị thời gian: 2 1 v . tb = = (1.5) t t − t 2 1
b. Vận tốc tức thời (gọi tắt là vận tốc)
Để tìm vận tốc tại một thời điểm, người ta có thể xem xét khoảng thời gian biến
đổi t rất nhỏ. Khi đó, vận tốc trung bình sẽ tiến đến một giới hạn xác định, đặc trưng
cho sự biến đổi của vector tọa độ tại thời điểm đang xét. Giới hạn đó được gọi là vận
tốc tức thời hay gọi tắt là vận tốc. v r dr = . (1.6) t→0  t d M1, t1 M2, t2
Vậy vận tốc được xác định bởi đạo hàm của vector tọa
độ theo thời gian. Vận tốc đặc trưng cho hướng và mức độ nhanh chậm của chuyển
động tại từng thời điểm. Phương của vận tốc luô
n trùng với phương của ti p ế tuyến
quỹ đạo chuyển động. Đơn vị vận tốc trong hệ SI là mét trên giây (m/s).
Xét trong hệ toạ độ Đề-các: v = = i + j + k. (1.7) dt dt dt dt dx dy dz Đặt: v = ,v = ,v =
. v , v ,v chính là hình chiếu của vận tốc theo x y z dt dt dt x y z
các trục tọa độ Ox, Oy, Oz tương ứng. Do đó, có thể viết lại v v = i v + j v + k. Về x y z - 4 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm độ lớn, 2 2 2 v = v v + + v. x y z
1.2.2. Tốc độ trung bình và tốc độ tức thời s 
a. Tốc độ trung bình: v = , với s
 là quãng đường đi được trong thời gian t  . tb t
Tốc độ trung bình là một vô hướng, đặc trưng M2 (C)
cho mức độ nhanh chậm của chuyển động trên cả s  quãng đường s  . r M1
Vật chuyển động thẳng, một chiều, dọc theo
trục tọa độ thì tốc độ trung bình bằng độ lớn vận tốc trung bình.
b. Tốc độ tức thời (gọi tắt là tốc độ)
Để tìm tốc độ tại một thời điểm, người ta có thể xem xét khoảng thời gian biến
đổi t rất nhỏ. Khi đó, s ds v lim  = hay v = . (1.8) t→0  t dt
Tốc độ tức thời đặc trưng cho mức độ nhanh chậm của chuyển động tại một thời
điểm. Độ lớn của vector vận tốc tức thời luôn luôn bằng tốc độ tức thời.
Đơn vị vận tốc và tốc độ (SI): m/s.
Ngoài ra: 1 km/h = 1/3,6 m/s.
dặm/giờ: 1 mph = 0,44704 m/s;
hải lý/giờ: 1 nút = 0,51444 m/s; feet/giâ : y 1 ft/s = 0,30480 m/s;
tốc độ âm thanh = 343 m/s; tốc độ ánh sáng = 2 99792.46 km/s. - 5 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
1.3. Gia tốc (gia tốc dài) 1.3.1. Gia tốc
Vận tốc có thể thay đổi cả phương, chiều, và độ lớn. Để đặc trưng cho sự thay
đổi đó, người ta đưa ra đại lượng gia tốc.
a. Gia tốc trung bình
Giả sử tại thời điểm t chất điểm có vận tốc 1 1 v , M v 2 2 v 1 ở t ờ
h i điểm t chất điểm có vận tốc v . Sau khoảng 2 2 (C) M1 thời gian t
 = t − t , vận tốc chất điểm biến đổi một 2 1 lượng v  = 2 v − . 1 v
Gia tốc trung bình được định nghĩa là độ biến đổi trung bình của vận tốc trong một đơn vị thời gian. v − v 2 1 a . tb = = (1.9) t t − t 2 1
✓ Gia tốc trung bình là một đại lượng vector. v  v − v
✓ Nếu chuyển động là thẳng và một chiều  2 1 a = = . tb t t − t 2 1
✓ Đơn vị của gia tốc trong hệ SI là mét trên giây2 (m/s2).
b. Gia tốc tức thời (gọi tắt là gia tốc)
Để tìm gia tốc tại một thời điểm bất kỳ, ta có thể xem xét khoảng thời gian biến đổi t
 rất nhỏ. Khi đó, gia tốc trung bình sẽ dần tiến đến một giới hạn xác định đặc
trưng cho sự thay đổi của vận tốc tại thời điểm đang xét. Giới hạn đó được gọi là gia
tốc tức thời hay gọi tắt là gia tốc. v dv a = lim = . (1.10) t  0 →  t dt dv Trong hệ Đề-các: x a = = i + j + k. dt dt dt dt 2 2 2 dv d x dv d y dv d z Đặt y x z a = = ,a = = ,a= =
. ax, ay, az chính là hình chiếu của x 2 y 2 z 2 dt dt dt dt dt dt
gia tốc lên các trục t ọa độ Ox, Oy, Oz tương ứng. Ta có thể viết lại: a a i a j a + k. x y z Và độ lớn: 2 2 2 a =a a + +a. x y z - 6 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
1.3.2. Gia tốc tiếp tuyến và gia tốc pháp tuyến
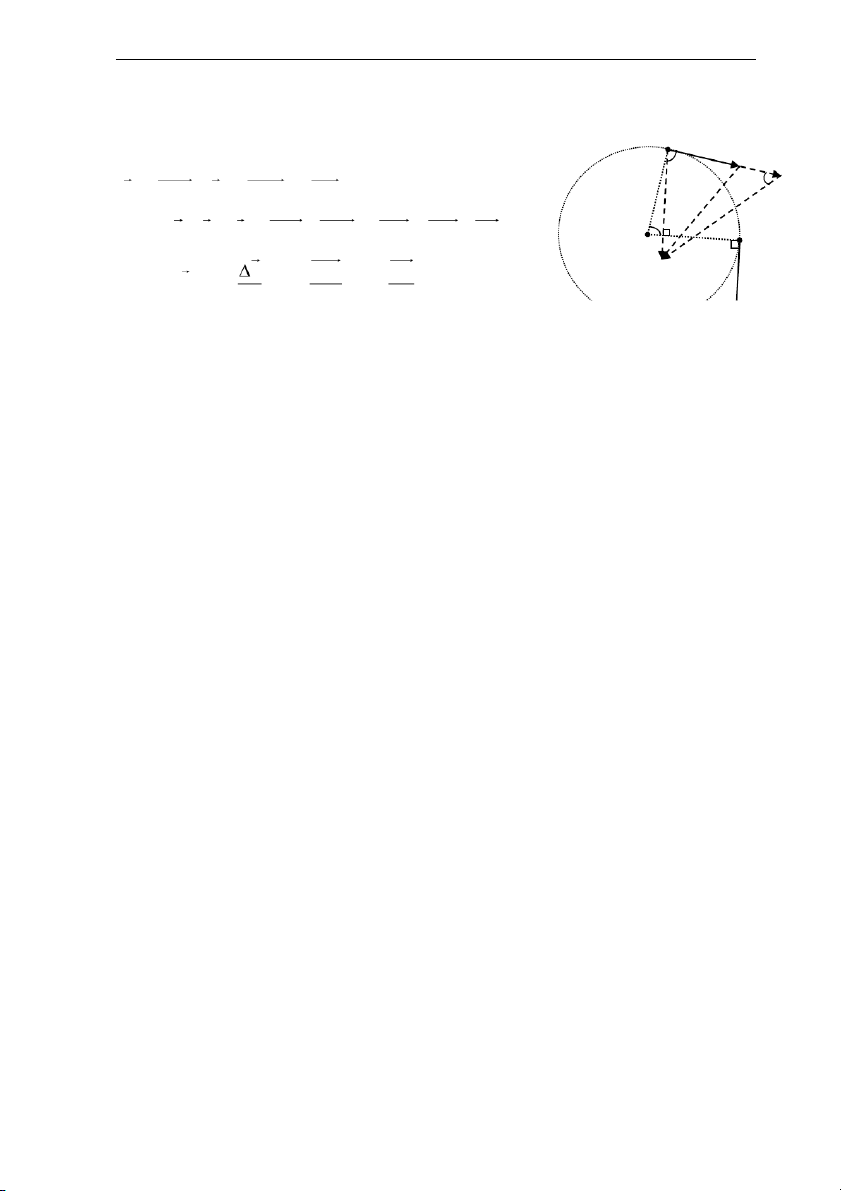
Để đơn giản, ta xét chất điểm chuyển động với quỹ M1, t1
đạo là một cung tròn. Trên hình vẽ, lưu ý rằng A1  C 1 v =M A ; v 2 M = A =MB; M A = AC. Nên 1 1 2 2 2 2 v v ,  2 = v1 − M = B M − A A = B A = C +C 1 1 1 1 1 M2, t2 O v A C CB B Vì vậy 1 a = lim = lim + lim . t  → 0t  t→ 0t  t→ 0 t A C
a. Gia tốc tiếp tuyến: 1 a = lim A t 2 t  0 →  t
✓ Phương là phương tiếp tuyến với quỹ đạo tại M1.
✓ Chiều là chiều chuyển động nếu vận tốc tăng, và ngược lại. A C M C− M A v − v  v ✓ Độ lớn: 1 1 1 1 2 1 a = lim = lim = lim = lim hay t t  → 0 t  t→ 0  t  t → 0  t  t → 0   t dv a = . (1.11) t dt
Vậy độ lớn của gia tốc tiếp tuyến bằng đạo hàm độ lớn vận tốc theo thời gian. Gia
tốc tiếp tuyến đặc trưng cho sự thay đổi của vận tốc về giá trị. CB
b. Gia tốc pháp tuyến: a = lim n  t→ 0  t   −   ✓ Phương: Vì BM  C cân đỉnh M lim C= lim = , nên phương gia tốc 1 1, t→ 0  t→ 0 2 2
pháp tuyến là phương pháp tuyến của quỹ đạo tại M1.
✓ Chiều: hướng về tâm của đường tròn hay tổng quát là bề lõm của quỹ đạo.
✓ Độ lớn: Có CB 2.M= C.sin / 2  2.v = .sin / 2 v . s  1 ( ) 2 ( ) 2 v . s  1  s 1 nên 2 a = lim = lim v .lim = v .v hay n 2 1 1  t→ 0 t  .R R t→ 0  t→ 0t R 2 v1 a = . (1.12) n R
Ta thấy nếu R càng lớn (quỹ đạo càng ít cong) thì an càng nhỏ và ngược lại. Vậy
gia tốc pháp tuyến đặc trưng cho sự thay đổi của vận tốc về hướng. * Tóm lại: a = na + ta, 2 2 a = a +a. (1.13) n t - 7 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
Nếu an = 0, vector vận tốc không thay đổi phương, chất điểm chuyển động thẳng.
Nếu at = 0, vector vận tốc không thay đổi độ lớn, chất điểm chuyển động cong đều.
Nếu a = 0, vector vận tốc không thay đổi cả phương và độ lớn, chất điểm chuyển động thẳng đều. - 8 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
1.4. Một số chuyển động cơ đặc biệt
1.4.1. Chuyển động thẳng
Chuyển động thẳng là chuyển động có quỹ đạo là đường thẳng, tức là vận tốc
không thay đổi phương. Trong chuyển động thẳng ta có: ; a a . (1.14) n t
a. Chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và vận tốc không thay đổi, a 0. s t
Để thu được phương trình chuyển động, ta lấy tích phân ds = v.dt   , ta được s t 0 0 s s = v + (t t − . (1.15) 0 0
với s , là tọa độ độ cong ứng với các thời điểm t , t. Tương tự, ta có thể thu được 0 0
phương trình chyển động viết theo tọa độ x, x x = v + (t t − ). (1.16) 0 0
b. Chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là chuyển động có quỹ đạo thẳng và giá trị vận
tốc biến đổi đều (tăng đều hoặc giảm đều), tức là gia tốc không đổi theo thời gian: a 0 =, a cons = . n t v t
Để thu được phương trình chuyển động, ta lấy tích phân dv = a.d   , ta có v0 t0 v v = a + (t t − ). (1.17) 0 0
với v , v là vận tốc ứng với các thời điểm t , t. 0 0 s t t
Tiếp tục lấy tích phân ds = v.dt = [v a + (t t − )].d    , ta thu được 0 0 s t t 0 0 0 2 a(t− t ) 0 s= s + v (t− t )+ . (1.18) 0 0 0 2 Dễ dàng suy ra 2 2 v v− 2 =a(s s − . (1.19) 0 0
Các phương trình viết theo tọa độ x: 1 2
x = x + v (t − t )+ a(t− t ); 2 2 v v − 2a( = x x − ) (1.20) o o 0 0 2 0 o - 9 -
Tài liệu lưu hành nội bộ - Chương 1: Động học chất điểm
Trong chuyển động thẳng nhanh dần đều thì a và v cùng chiều, hay a.v  0, tức
là a và v cùng dấu. Trái lại, với chuyển động thẳng chậm dần đều: a và v ngược
chiều, hay a.v  0, a và v trái dấu. * Rơi tự do
Rơi tự do là sự rơi của một vật chỉ chịu sự tác động của trọng lực.
Khi một vật rơi tự do, quỹ đạo là một đường thẳng, chyển động là một chiều từ
trên xuống dưới, không vận tốc ban đầu, rồi tăng dần với gia tốc bằng gia tốc trọng
trường g. Gia tốc trọng trường g hướng thẳng đứng từ trên xuống dưới, với giá trị
phụ thuộc vào độ cao và vị trí khác nhau trên Trái Đất: g ,8 m/s2. Ta có các phương trình: 2 v g( = t t− ); s g(t = t − ) /. (1.21) 0 0
* Chuyển động trên mặt phẳng nghiêng a = g  sin  x
1.4.2. Chuyển động tròn
Chuyển động tròn là chuyển động có quỹ đạo là một
đường tròn. Trong chuyển động tròn, vị trí của vật được xác  r
định bởi tọa độ góc  (radian: rad) M’
a. Vận tốc góc và gia tốc góc M
Tương tự như vận tốc trung bình và vận tốc tức thời, để
mô tả hướng và mức độ nhanh chậm của một vật chuyển động tròn, người ta định
nghĩa vận tốc góc trung bình và vận tốc góc tức thời:  d  = ,  = . (1.22) tb  t dt
Vận tốc góc có đơn vị theo SI là radian trên giây
(rad/s). Vận tốc góc liên hệ với thời gian để vật đi hết
một vòng tròn (gọi là chu kỳ T) và số vòng tròn vật đi
được trong một đơn vị thời gian (gọi là tần số f) như sau: 2 1  T = , f = = . (1.23)  T 2
Vector vận tốc góc  được định nghĩa là vector
có gốc tại tâm quỹ đạo tròn, có phương vuông góc - 10 -