












Preview text:
lOMoAR cPSD| 58833082
BÀI TẬP: GIẢI TÍCH I
CHƯƠNG III: GIỚI HẠN VÀ SỰ LIÊN TỤC CỦA HÀM SỐ
GIẢI BÀI TOÁN TÌM GIỚI HẠN
Bài 1: CMR khi x 0→ 1) 1−cosax a x ( 2 2 a 0) 2
2) sinax+ sin bx2 ax (a 0) 3) ax −1 xlna (1 a 0)
4) ln 1( + ax) ax a( 0) 5) (1+kx) − α 1 kαx (kα 0 ) 6) ax (
α + a x1 α 1+ + +... a xn α n+ axα
α 0,a 0)
Hướng dẫn giải
1) Ta có: 1−cosax = 2sin2 ax 2. ax 2 = a x2 2 khi x 0→ , đpcm. 2 2 2
2) limx 0 sinax+sin bx2 = limx 0 sinax + sin bx2
= limx 0→ sinaxax +limx 0→ sin bxax2 = +1 lim (
x 0→ bxax)2 = + =1 0 1 → ax → ax ax
sinax+sin bx2 ax, đpcm. 3) lim → = → → x 0
axlna 0x −1 0
L limx 0 a lnaxlna = limax 0 x =1 đpcm. 4) lim ( ) ( x 0→ =L limx 0→ a
) = limx 0→ 1+1ax = 1 đpcm. ln 1+ ax 0 a / 1+ ax ax 0
1+kx −1 5) lim ( ) ( + x 0 α 0 =L limx 0→
α 1( +kakx)α 1− k = lim 1 kxx 0→
)α 1− =1 đpcm. → kαx 0 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 0 6) lim ( ) ( ) = x 0 1 n 1 lim = n
lim 1( + o x( ))= 1 α → α1 − x0 + ax 0 a αx + ax + α
a xα 1+ + +...a xα n+ L
aαxα 1− + a α+1 xα
... a α+n xα n 1+ − → α α1 + αn + α x 0→ ax + ++ 1 ax ... n ax ax , đpcm .
Bài 2: Khi x 0→ , cặp VCB sau có tương đương không?
1) α x( )= +x x , β x( )= esinx −cosx
2) α x( )= ln cosx( ), β x( )=−
3) α x( )= arctan sin2x(
) , β x( )= etanx −cos2x
4) α x( )= 3 x− x , β x( )= cosx−1
Hướng dẫn giải
1) limx→0 esinx −cos =
x l im esinx − + −1 1 cosx = limx→0 esinx1/4−1+1−cosx1/4 = limx→0 x → 0 esinxx1/4x +
−1+lxi mx→0 1−xcosx1/4 x 2 7 / 4 sinx x/2 x x 1 /4 x x = lim x 1 + + /4 lx 0im = limx 0 1/4 lx 0im
= limxx 0 3/4 +limx 0
7/4 = 0 β
x( )= o(α( )x ) x 0→ x → x → x → 2 → → 2
ln 1 2sin 2 x 2 x ln cosx ln cosx − −2sin x/ 2 2) lim ( ) ) ( ) 2 =−2lim ( → 2
=−2limx 0 2 2 =−2limx 0 2 2 = 4limx 0 2 2 =1 x 0→ −tan x x 0
tan x → tan x → x → x 2
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 1 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ α x ~ β x( ) ( ) e −cos2x
3) lim tanx = lim etanx − + −1 1 cos2x = lim tanx +lim 2sin x2 = lim x +lim 2x2 = 1 x→0 arctan
sin2x( ) x→0 arctan sin2x( ) x→0 sin2x x→0 sin2x x→0 2x x→0 2x 2
α x ,β x( )( ) là các VCB cùng bậc =−
4) lim cosx 1− = lim 1−cosx = lim x / 22 1/3
1limxx 0 5/3 =0 β x( )= o(α( )x ) x 0→ 3 x − x x 0→ x
− 3 x x 0→ −x 2 →
Bài 3: So sánh cặp VCB sau đây:
1) Khi x 0→ +: α x( )= x− −3 x 4 x , β x( )= − −1 x 1
2) Khi x→+ : α x( )= +1 12 , β x( )= ln x2 +2 1 x x x
3) Khi x 0→ : α x( )= 3 x x2 + 3 , β x( )= esinx −1
4) Khi x 0→ : α x( )= tanx, β x( )= esinx − −x2 1
5) Khi x 0→ : α x( )= 3x3 −2x2 , β x( )= ln cos2x( )
6) Khi x 0→ +: α x( )= x x3 + 2 , β x( )= esinx −cos2x
Hướng dẫn giải (G ợ i ý: 3 4 x −− x
1) Đáp án: β x( )=o α (
x ( )) x~ x− 1/4 ) 1 ln1 + ln 2 2 x x 1 1 1 + + x2 +1 x
2) L = lim= lim x→+ 1 x→+ x x2 x2
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 2 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Đặt: 1 = t L = lim ln 1 t( ) = t2 = = + +2 2 lim+
limt+ 0 β x( )=o α( ( )x ) x t→0 t+t t→0 t t→0
3) Đáp án: β x( )=o α x( ( )) (Gợi ý: α x( )= 3 x x ~x2 + 3 2/3 )
4) Đáp án: α x ~β x( ) ( )
5) Đáp án: α x ~β x( ) ( )
6) Đáp án: α x ~ β x( ) ( )
Bài 4: Với α x ,β x ,γ x( )
( ) ( ) là các VCB trong cùng một quá
trình x → a, hãy chứng minh: a) Nếu α x β x( ) ( ) và β x γ x( ) ( ) thì α x γ x( ) ( ).
b) Nếu α x( ) β x( ) và β x( )= o γ x ( ) thì α x( )=o γ x ( ) .
Hướng dẫn giải α x( ) α x( )
a) limx a→ β x( ) =1 limx a γ x( ) =1 (Vì β x( ) γ x( )) α x( ) γ x( ) , đpcm. →
b) β x( )= o γ x ( ) limx a→ γ xβ x( )( ) =0 limx a→ α xγ x( )( ) =0 (Vì α x β x( ) ( ) )
α x( )=o γ x ( ) , đpcm.
Bài 5: Tính các giới hạn sau: ( )
1) lim x2 + + −3x 1 5x 4) limx→
x2 + 4x− −1
x2 + −x 5 x→−3 2x+1 1 2x+ −1 1 2) lim → x 0 3 x+ −1 1
5) limx→ 54xx22 + +− +xx 11 x
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 3 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
___________________________________________________________________________________________________________________________________________________________________________________________________ ______________ ( ) 3) xlim→−
x2 −2x + x
6) limx 3 1 5(− xsin x) (2 −1)
→0 tan −x ln cos3x
Hướng dẫn giải 2 + + −
(− + − + − −3)2 3. 3 1 5. 3 − 1) lim x 3x 1 5x =
= 16 x→−3 2x+1 2.− +3 1 5 )
2) lim 3 2x+ −11 = lim (2x+ −1 1)( x+ +1 1 = lim ( ) 2 x+ +1 1 = 4 ( ( ( x→0
x+ −1 1 x→0 x+ −1 1) 3 2x+1)2 + 3 2x+ +11 x→0 3 2x+1)2 + 3 2x+ +11 3 ( )
3) Đáp án: xlim x2 − + =2x x
− (Gợi ý: nhân liên hợp) →− ( ) 3 4) lim
x2 + − −4x 1 x2 + − =x 5 (Gợi ý: nhân
liên hợp) x→ 2 1
ln 5x + +x 1
5) lim 5x22 + +− +xx 11 x = exlim→ 4x22x− +x 1 = exlim→ln 5
14 1+− /x 1/x/x 1/xx ++
22 = e0 =1 (Chú ý: xlim A x→x0 ( ) ( ) ( )
B x( ) = ex xlim B x lnA x→ 0 )
___________________________________________________________________________________________________________________________________________________________________________________________________ ______________
Thầy Phạm Ngọc Lam Trường 4 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ x→ 4x − − ( 2 3 2 1 −5 xsinx 1 − )
1 5 xsinx 1 6) lim =l im x0 → tan( − ) xl nc ( os3x ) x0 → ( 2 − ) 2 3 x − 3
x.ln1 2 sin ( 2 1 −5 xsinx ) 3 2
+ 1 −5 xsinx 1 + 2 2 5 sinx =lim x0 → 2 x 3 − 3 ln12s in ( 2 2 15 − xsinx ) 3 2
+ 15 − xsinx 1 + 2 = 5x2 lim x0 → 2 3 x − 3 2 sin ( 2 2 15 − xsinx ) 3 2
+ 15 − xsinx 1 + 2 2 5 x =lim → 2 x0 x 3 − 3
2. . ( 2 2 1 −5 xs inx ) 3 2
+ 1 −5 xsinx 1 + 2 10 − 1 1 − 0 = lim = x0 9 → 27 3 ( 2 2 1 −5 xsinx ) 3 2
+ 1 −5 xsi nx +1
Bài 6: Tìm các giới hạn sau + 1) limx 0 sinx3x 7) limx 0→ ln 1 2tanx(e − x cosx ) + 13) lim )
x 0→ 3xln 1 2xx −( 2 4 sin x3 → e −1
2) limx 0 8) lim 1 2x( + )cotx 14) limx 0 →x→0 → ( 3) lim )) ) x 0 arcsinx2 9) limx 0→
arcsin x( 6 ln 1( −2x10
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 5 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ ( ) + → x+ 2x x 15) lim − x 0 16 e2x 1
e −cosx−ln 1 x → sin x 10) → 2 x0 lim x
4) lim ( ) 1 4+ −x 1 x 0→ ln
1−3x16) lim x e 1 − 11) lim + x0 → 2 x 0→ + ln 1( +3x) x x sinx −l ( 2 nsinx ++1 x ) 5) x 0lim→ + 12) lim → 2 x0 tanx −xc osx xe +− 2x2 x13 17) limx 0→ eαx −x eβx 6) limx 0
18) lim eαx −eβx =
→ x 0→ sinαx−sinβx Hướng dẫn giải sinx = 3x limx 0 x 1
1) Cách 1: Thay VCB tương đương: lim
x 0→ e −1 → 3x 3 =
Cách 2: Sử dụng quy tắc L’Hospital: lim sinx = cosx 1 3x limx 0 3x
x 0→ e −1 → 3e 3 =
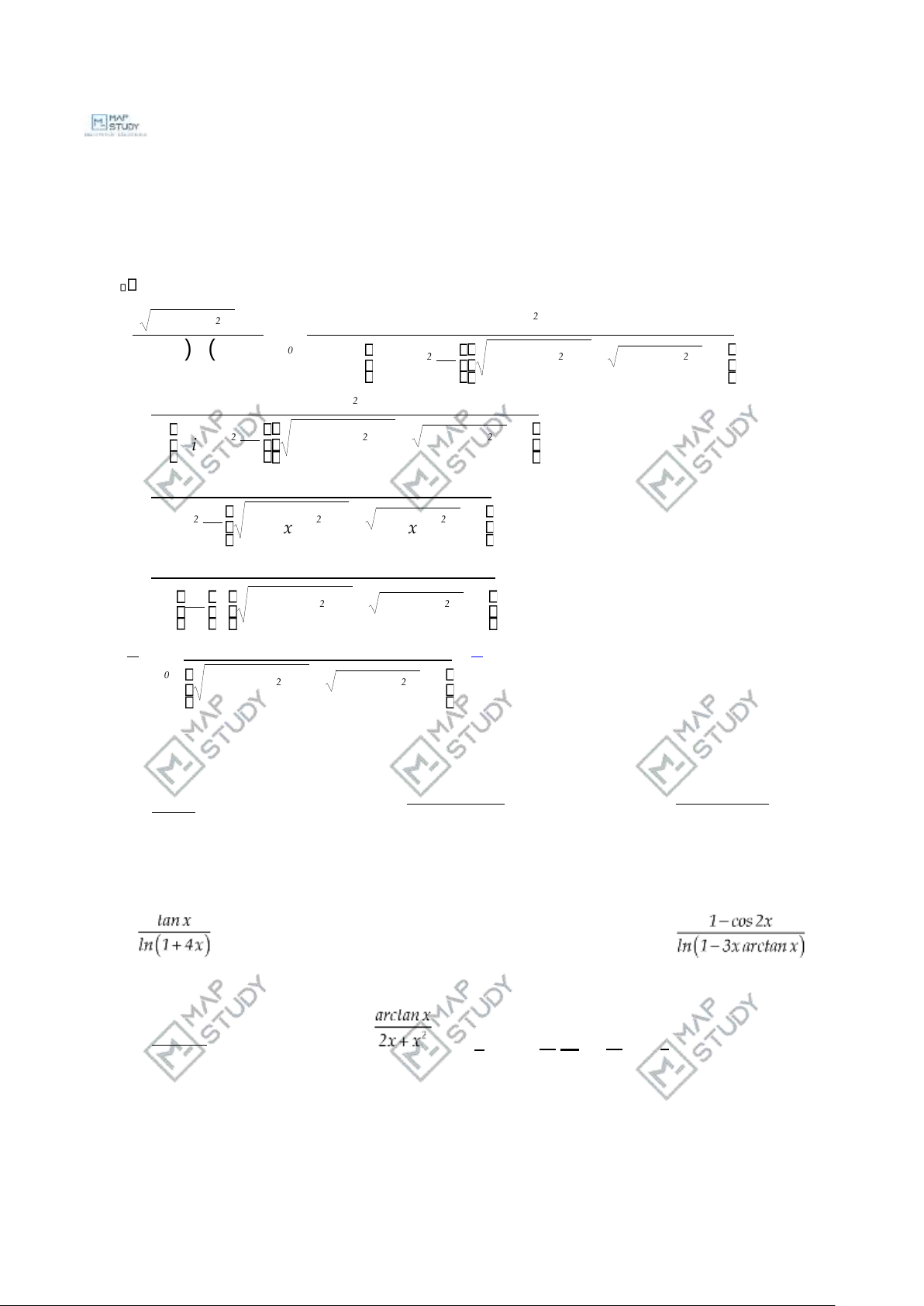
2) lim tanx 1 (Gợi ý: tương tự ý 1) x 0→ ln 1( + 4x) 4
3) lim arcsinx = lim x = 1(Ở đây đã sử dụng quy tắc ngắt bỏ VCB bậc cao: x 2x ~x+ 2 ) x 0→ x+ 2x2 x 0→ x
e2x −1 =−2 4) lim
x 0→ ln(1 3− x) 3 5) lim − = +
e2x2 13 1 x→0 x +x x
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 6 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 6) lim ) = 2(sin ) = = x 0 1(−cosx2 limx 0 2 22 limx 0 x / 22 2 1 → ln 1+x → ln 1+x → x 2 1 ln 1+ 2tanx ( ) 7) l → →
x 0im→ ex −cosx
= limx 0 ex2−tanxcosx
00 =L limx 0 e2x cos x+sinx2 = =12 2
8) lim 1( + 2x)cotx = e2(Gợi ý: Giải tương tự Bài 3, ý 5) x→0
9) limarctanx = 1 (Gợi ý: tương tự ý 3) x 0→ 2x+x2 2 ( ) + +( x → sinx− 0 x x2
00 =L limx 0 x
1+1x 0 =L l mx 0i→ ex +cosx2
1+1x)2 = 23 e
−cosx−ln 1+ x e
10) lim → 2x 0 = 11) e x x 0lim x −1 = + 2 x 0lim+ 1 → x+ x → x ( ) sinx−ln sinx + +1 x2 12) limx 0 2 → tanx− xcos x sinx = − + ) ) x x3
o x( 3 1+x2 − =1
1x2 +o x( 3 ln 1 u( + = − + +) u u2 ) u3o u( 3 6 2 2 3
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 7 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ ( ) ) ) + ) ln sinx + 1+x 1( 1( ) 2
=(sinx+ 1+x2 − −1
sinx+ 1+x2 −1 2
sinx+ 1+x2 −1 3 +o x( 3 23 = x−x ) ) ) )
3 +x2 +o x( 3 −1 x−x3 + x2 +o x( 3 2 +1 x−x3 + x2 +o x( 3 3 +o x( 3 = −x x3 +o x( ) 3 6 2 2 6 2 3 6 2 3 = + TuSo x3 o x( ) 3 6 tanx = + + ) ) x x3 o x( 3 cosx = −1
x2 +o x( 2 xcos x2 = x 1 − x ) )
2 +o x( 2 2 = −xx3 +o x( 3 3 2 2 MauSo = 4x )
3 +o x( 3 3 ( ) + +
Từ đó lim sinx−ln sinx 2 1 x2
= limx 0 x /633 = 1 x → 0
tanx− xcos x → 4x / 3 8 ) 13) lim ( + = = x xln 12 2x3 limx 0 x.2x2 2
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 8 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
→0 3x −4sin x → 3x 3
14) lim 1−cos2x = lim 2sin x = = = − 2 lim 2x2 lim 2x2
2 x 0→ ln 1( − 3xarctanx) x 0→ ln
1( −3xar tc anx) x 0→ −3xarctanx x 0→ −3x.x 3 ( arcsin x( )) ) ( ) 6 ln 1( − 2x10 x .6 −2x10 15) lx 0im = 16 limx 0 16 =−2 → sin x → x ( + + )
16) lim 1 4+ −x 1 = lim 1 4+ −x 1 = lim 1 4+ −x 1 = lim 4 = 2 → → → x 0
ln 1 3x( + ) x 0 3x x 0 3x 1 4 x 1 + + → ( ) x 0 3 1 4x 1 3 eαx −eβx 17) lim
=α−β (Tương tự ý 1) x 0→ x lim
eαx −−esinβx 0βx
0 = =L ... 1 18) x 0→ sinαx 1) limx 2 7) lim → x
Bài 7: Tìm các giới hạn sau x→+ x3 − +4x 8 ( 1)− x.cos2x x x + −1 cosx ( ) 2) + − xlim sin x 1 sin x 2 1
→+ limx 1+ sin 8)
3) xlim 3x−sin5x2x x 0→ x →+ e sin2x+cos2x 9) lim
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 9 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
4) lim x( −2)cos x 2
x→ 2x−6 + 5 x 2→ x − +5x 6
sin(2x+7).cos(x2)+cos (42 −x )3 1 10) lim
5) limx e2 sin x x→ x x→0 2 3 x (sinx+cos x) 6) lim + x
( 1)−2 x 11) xlim→− (x2 1)(x−3) → 2x +7
Hướng dẫn giải lim x→ =0 x→+ Gợi ý: 2cos
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 10 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
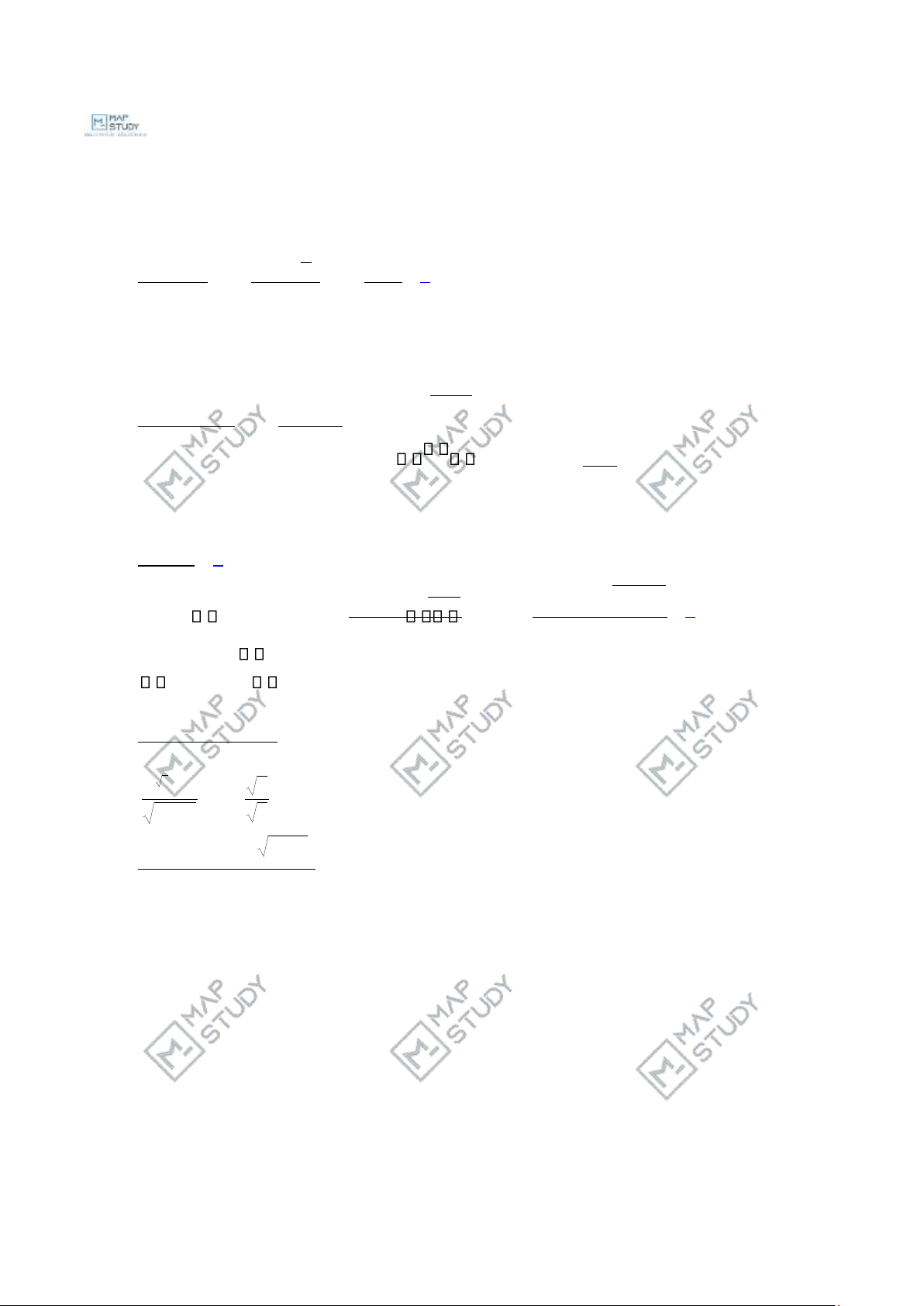
_________________________________________________________________________________________________________________________________________________________________________________________________________________ x→+ 7) lim = cosx
xlim→+ 1 4− 1 1/ x+2 +/ x8/ x3 −xlim→+ x3
−4x+8 = − =1 0 1 Ở đây, cosx xlim→+ x3
−4x+8 =0 theo nguyên lý kẹp, các bạn tự chứng minh.
Các ý 8), 9), 10), 11) giải tương tự. 8) Đáp án: 0 9) Đáp án: 5 10) Đáp án: 0 11) Đáp án: 0
Bài 8: Tính các giới hạn sau: − 1) ( )
xlim→+ π 2ln 1− arctanx+ 1 8) limx 1
−mxm 1−nxn m,n N* → 1 x
9) lim(a R ) * 2) lim (
− π 2− x)cosx x 0→ 1 ) xlim
π 2− arctanx+ x = xlim
π−2arctanxx 0 =L xlim→+ 1+−x12x2 = xlim→+
12+xx22 = xlim→+
1/ x22 +1 = 2
→+ ln 1 1 →+ 1 0
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 11 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ x→ 10) lim lnx 3) lim tanx ( )1 − cosx
x 0→ + ln sinx( ) x→ − x e−x e 4) xlim→+
(π 2− arctanx lnx) 11) limx 0→ 5) lim → x 1
xx−1− lnx1
12) limx 0→ sinx x2 1 x ) 6) lim → (
x 0 13) lim ex 0→ x + x x 7) ( ( − )) x 1lim lnxln x 1→ +
14) xlim→+ π2 arctanx x
Hướng dẫn giải −2 + x. 1 −1 1 ) lim (
− π 2− x)cosx =1 (Gợi ý: Giải tương tự Bài 3, ý 5). ( ) x→ 3) lim tanx 2cosx = −
1 (Gợi ý: Giải tương tự Bài 3, ý 5). π
x→ x→+ (π− 2arctanx lnx) = xlim→+ − 2arctanx = =
00 L ... 0 4) lim lnx
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 12 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 5) lim lnx
x 1→ x− − 1 = limx 1→ xlnx( − − +)x1 0 =L limx 1→ x− = limx 1→ lnx
0 =L limx 1→ 1/ x1+/ x1/ x2 = 12 x 1 lnx x 1 lnx
0 lnx+ x 1 lnx+
−1 1 0 x x ln sin2x 6) limx 0 ln sinx((
)) =L limx 0→= limx 0→ 2sin2x.cosxcos2x.sinx = limx 0→ 22cos2x.sinxsinxcos x2 →
= limx 0 cos2xcos x2 = 1 →
ln x( −1) 7) ( 1 ( x 1lim lnxln x+
−1))= x 1lim+ = =L ... 0 → → lnx 8) lim )( )
x 1→ −m m − −n n = limx 1→ m(1−−mxxmn
− +1n−xnxn m = limx 1→
m1−−xmxn −nx− +mn+xnxm n+m 00 1 x 1 x − = )
L limx 1n 1− −mnxmxm 1n 1−− ++nmx(m+m 1n x− m n 1+ −
00 = =L ... m2−n → −nx 9) lim → ( + ) = → − x 0 ln 1ax xax
limx 0 eax xe−ax 00 = → ( + )= L lim aex 0 ax ae−ax
2a e −e− lnx L
10) x 0lim→ + ln sinx( ) = =... 1
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 13 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 11) lim → → → x 0
sinxcosxex −e−x = 2limx 0 esin2xx −e−x = limx 0 ex −xe−x 00 =L lim e ( ) x 0→
x +e−x = 2
Các ý 12), 13), 14) giải tương tự Bài 3, ý 5 1
12) l mx 0i→ sinxx x = − 2 61 1
13) l mi (ex +x)x = e2 x 0→ 14)
xlim→+ π2 arctanx x = e−π2
Bài 9: Giải thích vì sao các giới hạn sau không dùng được quy tắc L’Hospital rồi tìm chúng bằng cách khác x−sinx x+cosx 1) lim
3) lim x→+ x+sinx x→+ x
2) limx 0→ x sin 1/ x2 sinx( ) 4) limx
0→ x+cotxsinx
Hướng dẫn giải
Không dùng được quy tắc L’Hospital vì khi x→+ các hàm sinx và cosx không tồn tại giới hạn. x− 1− sinx −sinx =1 1) lim sinx = lim x
, có lim sinx = 0 (Theo
nguyên lý kẹp) nên lim x
x→+ x+sinx
x→+ 1+ sinx x→+ x
x→+ x+sinx
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 14 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ x 2) −x ( ) = =
2 x sin 1/ x2
x2 mà lim x2 lim −x2
0 lim x sin 1/ x2 ( ) =
0 (Nguyên lý kẹp) sinx sinx sinx x→0 sinx
x→0 sinx x→0
sinx x−1 x+cosx x+1
x+1 = x 1− = x+cosx =
3) mà lim lim 1 lim x x x x→+ x x→+ x x→+
1 (Theo nguyên lý kẹp) x
4) lim x+sinx = lim(x+sinx sinx) =0 10) lim x 0→ x→0 cotx x→0 cosx
Bài 10: Tính các giới hạn sau 1) lim 11) lim x x→1/2 0→ 12) limx 0 + ( (3)x) 2) lim 2 2 x 1 sin3 πx ln 1 → x −1 sin 5) lim x→ → tan 5x x3 +8
18) lim n a+ − −x n a 6) xlim2 2 x
→− x −3x−10 x 0→ x 8) lim x 0→ 19) limx0 + x
1+tanxsinx arcsin → 1 9) lim
1−x2 x 0→ ln 1 x( − )
22) limsin2x+2arctan
3x+3x2 x 0→ ln
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 15 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
___________________________________________________________________________________________________________________________________________________________________________________________________ ______________
1( +3x+sin x ) 2 +xex
20) limx→ 2x−2
23) xlim x→+ π2 −arcsin
3 1+tan x2 − 3 1−tan x2 21) lim x x
2 +1 x 0→ x+ 3 x2 cosx−cos3x 3) limx 0→ x2 ( ) 24) lim x4/3
3 x2 + −1 3 x2 −1 4) lim x 0→ x→+ tanx−sinx 7) ( xlim 2x→−
+1) x43x++x1 25) limx 0→ sin x3
(5 1 3+ x)2 −1
13) limx 0→ sinx+2sin x2 sin 2x( 2 − −4x 6)
14) lim x 3→ ln x( 3 −26) 15) lim x 3→ 16) lim x 2→ 17) lim + x→0 x2 sin x3 2x+ 2 + 3x 2
___________________________________________________________________________________________________________________________________________________________________________________________________ ______________
Thầy Phạm Ngọc Lam Trường 16 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Hướng dẫn giải
1) limtan3x = lim 3x = 3 x 0→ tan2x x 0→ 2x 2 2) limx 1
sin3 πx 0 =L limx 1→ πcosπx3x2 = −3π
→ x −1 0
3) Cách 1: Sử dụng quy tắc L’Hospital: limx 0→
cosx−x2cos3x 0
0 =L limx 0→ −sinx+2x3sin3x 00 =L limx 0→ −cosx+29cos3x = 4
Cách 2: Thay VCB tương đương: limcosx− (− =
2cos3x = lim−2sin2xsin2
x) = limx 0 4x22 4 x 0→ x x 0→ x → x
4) limx 0→ sin5x−sin3x = limx 0→ sin5x−sin3x 0 = =L ...
2 (Có thể dùng thay VCB như ý 3) sinx x 0 5) limx 3x33 + +5x2 1 = limx
3+ 5 / x2 +1/ x33 = 3
→ 2x + −x 9
→ 2 1+ / x−9/ x 2
6) xl→−im2 2 x3 +8 0 = =L ... −12 x −3x−10 0 7 7) xlim 2x(
+1) 43x+1 = xlim 2( +1/ x) 4+1/ x2 = 4 →− x + x →− 1+1/ x 8) lim − = ( = x 12 cos3x3 4
limx 0 2sin2 2 33x / 2)4 limx
0 2. 3( x /2 2)2 = 9
→0 2x + 3x − x
→ 2x + 3x − x → 2x 4 x x arcsin −
9) lim 1−x2 = lim 1−x2 = lim 1 =−1 x 0→ ln 1 x( − ) x 0→ −x x 0→ 1−x2
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 17 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
10) lim ln 1(( + 4x ) 22 − 5x33
= lim 4x22 − 5x33 = limx 0 4x22 = 2 x 0→ ln 1+ 2x + 3x ) x 0→ 2x + 3x → 2x 11) −− xlim→1/2 arcsin 1(2
2x) = xlim→1/2
41x−22−x 0 =L xlim→1/2
8−x2 = −21 4x 1 1 0 ln 1 sin 12) lim ( ( (( (( x 0
+ 2 2 3)x) = limx 0 sin22 3x)) = limx 0 3x))22 = 9 → tan 5x → tan 5x → 5x 25 13) lim → ( → ( x 0
sinx5 1++32xsi)2n−2 x1 = limx 0 5 1+ 3xx)2 −1 00 = =L ... 65 ( ) ( ) − −
14) lim sin 2x 2 − 4x 6 = lim sin 2x 2 4x−6
2x23− 4x−6 0 = =L ... 8 → → → x 3
ln x( 3 − 26) x 3
ln 1( + x3 − 27) = limx 3
x − 27 0 27 15) l ) ) → ) → )
x 0im→ ln 1ln cos3x( (+tan x = = 2
limx 0 ln cos3xtan x( 2
limx 0 ln cos3x( x2 = = − 00 L ... 29 16) lim → →
x 2 sin 3xtan 4( (2 −−2xx2−) 8) = limx 2 3x24−−2xx2−8 0 0 = =L ... −25 17) lim ++ ) = =
x 0→ ln 1 xtx(2 sin xanx3
limx 0→ xtanxx2 1
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 18 lOMoAR cPSD| 58833082
Học online tại: https://mapstudy.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
18) lim→ n a+ −x x n a− x 00 = =L ... n2 a1/n−1 x 0 19) limx 0 + +1 tanx
1+tanxsinx = ex 0lim→ ln1sinx+sinx = =... 1 → 1 + ln + l 3 2 im → x x 1
2 x +2 + 20) 6 = 3 x 2 lim e ... == e
x → 2 x −2 3 2 + −− − 3 2 3 2 + −− 1 t anx 1 − 1 tanx 1 tanx (3 2 1 tanx ) 1 21) lim =l im → → 2 x 0 3 /3 2 x 0 + x x x 3 2 3 2 2 2 2 2 1 +t anx 1 −
1 −t anx 1 − tanx tanx tanx x =l im −l im = lim + lim = lim = lim → 2 /3 → 2 /3 → 2 /3 → 2/ 3 → 2/ 3 → 2 /3 x 0 x 0 x 0 x 0 x 0 x 0 x x 3 x 3 x 3 x 3 x 1 1 2 2 = 2limx = 4/3 0 3 x→0
22) Cách 1: Thay tương đương
Khi x → 0,sin2x + 2arctan3x + 3x ~ 8x )
2 và ln 1 3x( + +sin x2 +xe ~ 4xx (Các bạn tự chứng
minh). sin2x+2arctan3x+3x2 = lim8x = 2 Nên lim )
x 0→ ln 1 3x( + +sin x2 +xex x 0→ 4x
sin2x+2arctan3x+3x2 0 Sử dụng quy tắc L’Hospital. Cách 2: lim )
x 0→ ln 1 3x( + +sin x2 +xex 0 π− x
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 19


![[TCC] - Tóm tắt lý thuyết chương 1 dãy số - Giải tích 1. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.](https://docx.com.vn/storage/uploads/images/documents/banner/ed538236c0435a2addd79b216bf0ad19.jpg)

