






































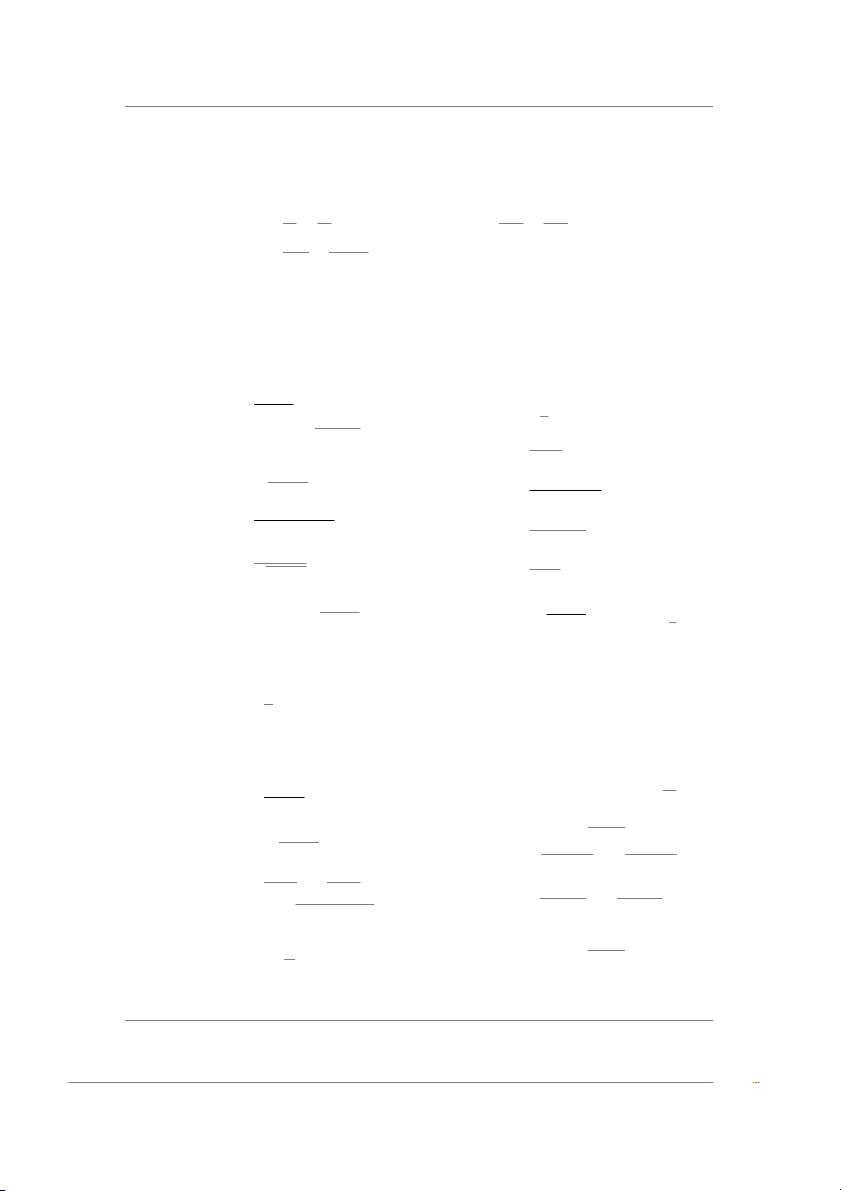











































Preview text:
Đại học Quốc gia TP.HCM
Trường Đại học Bách Khoa Bộ môn Toán Ứng dụng
. Bài Giảng Giải Tích 1
ThS.Nguyễn Hữu Hiệp
E-mail: nguyenhuuhiep@hcmut.edu.vn Ngày 8 tháng 9 năm 2014 Mục tiêu môn học
• Môn học cung cấp các kiến thức cơ bản về vi tích phân hàm một biến và phương trình vi phân.
• Giúp học viên hiễu lý thuyết, nắm vững các kỹ năng tính toán, biết vận dụng giải các bài toán cụ thể.
• Biết vận dụng các phương pháp và tư duy sáng tạo vào khoa học kỹ thuật. Tài liệu tham khảo
1) Nguyễn Đình Huy, Nguyễn Quốc Lân,. . . Phép tính vi phân hàm một biến. NXBGD, 2005
2) Ngô Thu Lương, Nguyễn Minh Hằng. Bài tập toán cao cấp 1.
3) Đỗ Công Khanh. Giải tích một biến. NXB Đại học quốc gia MỤC LỤC
1 Giới hạn và liên tục 5
1.1 Giới hạn dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.1.1 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.2 Hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.2.1 Hàm lũy thừa y = xα . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.2.2 Hàm lượng giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.2.3 Hàm mũ - Hàm logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.2.4 Hàm y = ln x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.2.5 Hàm Hyperbolic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.2.6 Các hàm lượng giác ngược . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.2.7 Hàm Hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.2.8 Hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.2.9 Hàm tham số hóa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3 Giới hạn hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.3.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.3.2 Các giới hạn cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.3.3 Vô cùng bé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.3.4 Vô cùng lớn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.4 Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2 Đạo hàm và vi phân 33
2.1 Đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.1.1 Định nghĩa và tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.1.2 Đạo hàm hàm ngược và hàm tham số hóa . . . . . . . . . . . . . . . . . 36
2.1.3 Đạo hàm cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2.2 Vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.3 Định lý giá trị trung bình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
2.4 Công thức H’Lopital . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
2.5 Công thức taylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.6 Khảo sát và vẽ đồ thị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
2.6.1 Tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
2.6.2 Chiều biến thiên và cực trị . . . . . . . . . . . . . . . . . . . . . . . . . . 54
2.6.3 Lồi, lõm và điểm uốn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
2.6.4 Khảo sát hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
2.6.5 Tìm giá trị lớn nhất - giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . 61 3 Tích phân 65
3.1 Tích phân bất định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 3 MỤC LỤC MỤC LỤC
3.1.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.1.2 Phương pháp tính tích phân bất định . . . . . . . . . . . . . . . . . . . 66
3.1.3 Nguyên hàm hàm hữu tỷ . . . . . . . . . . . . . . . . . . . . . . . . . . 68
3.1.4 Nguyên hàm hàm lượng giác . . . . . . . . . . . . . . . . . . . . . . . . 70
3.1.5 Nguyên hàm hàm vô tỷ . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
3.2 Tích phân suy rộng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.3 Ứng dụng hình học của tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . 78
3.3.1 Diện tích hình phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
3.3.2 Độ dài đường cong . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
3.3.3 Thể tích vật thể tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . 80
3.3.4 Diện tích mặt tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
4 Phương trình vi phân 83
4.1 Phương trình vi phân cấp 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
4.1.1 Phương trình vi phân tách biến . . . . . . . . . . . . . . . . . . . . . . . 83
4.1.2 Phương trình vi phân đẳng cấp . . . . . . . . . . . . . . . . . . . . . . . 85
4.1.3 Phương trình vi phân toàn phần . . . . . . . . . . . . . . . . . . . . . . 86
4.1.4 Phương trình vi phân tuyến tính . . . . . . . . . . . . . . . . . . . . . . 88
4.1.5 Phương trình vi phân Bernulli . . . . . . . . . . . . . . . . . . . . . . . 90
4.1.6 Bài tập tổng hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
4.2 Phương trình vi phân cấp 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
4.2.1 PTVP cấp 2 thuần nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
4.2.2 PTVP cấp 2 - dạng 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
4.2.3 PTVP cấp 2 - Dạng 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
4.2.4 PTVP cấp 2 - dạng 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
4.3 Hệ phương trình vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
4.3.1 Ánh xạ đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
4.3.2 Hệ phương trình vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . 98
4.4 Bài tập ôn tập cuối kỳ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
4.5 Đề thi cuối kỳ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
Đại học Bách khoa TPHCM Trang 4
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC
1.1 Giới hạn dãy số
Định nghĩa 1.1 (Sup-Inf của tập hợp) Cho tập A ⊂ R.
• Cận trên nhỏ nhất của tập A gọi là Supremum, ký hiệu sup(A).
• Cận dưới lớn nhất của A gọi là infimum, ký hiệu inf(A).
Ví dụ 1.1 a) A = [0, 1) thì sup(A) = 1 và inf(A) = 0.
Chú ý tập max(A) = 0 nhưng min(A) không tồn tại. Khái niệm sup và inf là mở rộng của max và min. 1
b) A = { |n ∈ N} thì sup(A) = 1 và inf(A) = 0. n
c) A = (−∞, 3) thì sup(A) = 3 nhưng không có inf
Định nghĩa 1.2 (Dãy số) Một dãy số là một ánh xạ từ tập số tự nhiên N vào tập số thực R. u : N −→ R n 7→ u(n) := un.
Ký hiệu 1 dãy số (u +∞ hay đơn giản (u n)n=1
n). un gọi là số hạng thứ n của dãy. √
Ví dụ 1.2 a) Cho dãy số dạng liệt kê (un) = {1; −2; 1; 4; 0; −5, 8; −3; 3, −1 , ... 3 }.
Số hạng thứ 5 là u5 = 0. (
b) Cho dãy số dạng số hạng tổng quát −1)n + n (un) : un = . n2 + 1 ( 3 Số hạng thứ 7 là −1)7 + 7 u7 = = . 72 + 1 25 ( u un+1 = 2un + 3, n ≥ 1. c) C Th a oc d ó ãy
u số dạng truy hồi 1 = 1 (un) :
2 = 2u1 + 3 = 5, u3 = 2u2 + 3 = 13, ...
Định nghĩa 1.3 (Dãy số đơn điệu) .
Dãy số (xn) gọi là tăng nếu xn ≤ xn+1, ∀n ∈ N
Dãy số (xn) gọi là giảm nếu xn ≥ xn+1, ∀n ∈ N
Bỏ dấu "=" trong đẳng thức, ta có dãy số tăng ngặt (giảm ngặt).
Dãy số tăng hoặc giảm gọi chung là đơn điệu. Ví dụ 1.3 n + 1
Xét tính đơn điệu của dãy số (xn) : xn = . n + 2 Ta có (n + 1) + 1 n + 1 (n + 2)2 − (n + 1)(n + 3) 1 xn+1 − xn = − = = > 0, ∀n. (n + 1) + 2 n + 2 (n + 3)(n + 2) (n + 3)(n + 2)
=⇒ xn+1 > xn suy ra (xn) là dãy tăng. 5 1.1. GIỚI HẠN DÃY SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC Cách khác 1 Xét x + 1 f (x) = , x ≥ 1 =⇒ f′(x) = > 0. x + 2 (x + 2)2
Vậy f(x) đồng biến nên (un) là dãy tăng.
Định nghĩa 1.4 (Dãy số bị chặn) .
Dãy (xn) gọi là bị chặn trên nếu ∃M : xn ≤ M, ∀n.
Dãy (xn) gọi là bị chặn dưới nếu ∃m : xn ≥ m, ∀n.
Dãy (xn) bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới.
Dãy (xn) bị chặn khi và chỉ khi (|xn|) bị chặn trên. Ví dụ 1.4 n
Xét tính bị chặn của dãy số (xn) : xn = . n + 1 Ta có n 0 < < 1, ∀n ∈ N. Suy ra (x n + 1
n) vừa bị chặn trên, vừa bị chặn dưới do đó bị chặn.
Định nghĩa 1.5 (Dãy con) .
Cho dãy (xn). Dãy con của (xn) là một dãy (xn )
k k mà các phần tử của nó được lấy tùy ý từ (xn) theo
thứ tự tăng dần của chỉ số. Ví dụ 1.5 2 5 3 Cho dãy n (xn) : xn = , , , 7 7 23 3 5 3 = −1, 1, , . . . . , n2 , − 2 17 23 Dãy 37 vn = −1,2n , . . . là 3 một dãy con của xn. Dãy x2n = 17 , 2 7 2n = + 1 1, . . . là
5 dãy con các chỉ số chẵn của xn. Dãy x2n+1 (2 = n)2 − 2 17 , 37 = −1, , . . .
là dãy con các chỉ số lẻ của xn. (2n + 1)2 − 2 23
Định nghĩa 1.6 (Giới hạn dãy số) Ký hiệu lim u n→+∞ n = a hay un
−−−−→ a được định nghĩa n→+∞
∀ε > 0, ∃n0 : n ≥ n0 =⇒ |un − a| < ε
Ta nói dãy (un) hội tụ về a.
Nếu (un) không hội tụ thì ta nói (un) phần kỳ.
Định nghĩa 1.7 ( dãy số dần ra vô cùng) Ký hiệu lim u n→+∞ n = +∞ hay un
−−−−→ +∞ được n→+∞ định nghĩa
∀A > 0, ∃n0 : n ≥ n0 =⇒ un > A.
Ta nói dãy (un) hội tụ về a.
Nếu (un) không hội tụ thì ta nói (un) phần kỳ.
Tượng tự cho giới hạn dần ra −∞.
Tính chất Cho xn −→ a, yn −→ b; a, b ∈ R ta có i) x a lim(x n n ± yn) = a ± b. iii) lim = , b 6= 0. n→+∞ n→+∞ yn b ii) lim(xn.yn) = ab. iv) lim |xn| = |a|. n→+∞ n→+∞
Đại học Bách khoa TPHCM Trang 6
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.1. GIỚI HẠN DÃY SỐ Định lý
1. Giới hạn dãy nếu tồn tại là duy nhất.
2. Dãy hội tụ thì bị chặn.
3. Cho xn ≤ yn ≤ zn, ∀n ≥ n0. ( =⇒ yn −→ a. xzn −→ a n −→ a
4. Mọi dãy tăng và bị chặn trên thì hội tụ.
Mọi dãy giảm và bị chặn dưới thì hội tụ. 5. ( xx2 2 n+1 → a. x n → a n → a ⇐⇒ là n Số 1 dã e y .t Ng ăngườ v i à ta bị chứ ặ n n g tr m ênin dh o đư ó ợc hộd i ã t y ụ. số Ký xhiệu n = 1 + n lim = e n 1 1 + n→∞ n
Số e là số vô tỷ có giá trị gần đúng là e = 2.718281828...
Các giới hạn cơ bản √ i) 1 n lim = 0, α > 0. iv) lim nα = 1, ∀α. n→∞ nα n→∞ ii) 1 lim = 0, α > 0. v) lim a n n→∞ lnα n 1 + = ea, ∀a. iii) lim qn = 0, |q| < 0. n→∞ n n→∞ Các dạng vô định 0 ∞ , 0
, 0.∞, ∞ − ∞, 1∞, +∞0, 00+ ∞
Khi tính giới hạn dạng vô định, ta dùng công thức hoặc biến đổi
đại số để khử dạng vô định.
Nếu giới hạn không phải dạng vô định, ta tính bình thường.
Đại học Bách khoa TPHCM Trang 7
ThS.Nguyễn Hữu Hiệp 1.1. GIỚI HẠN DÃY SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC Quy tắc 1 1 = ∞, = 0. 0 ∞
lnα n ≪ nβ(β > 0) ≪ an(a > 1) ≪ n! ≪ nn
Dấu ≪ chỉ mang tính hình thức theo nghĩa: hàm nhỏ
chia hàm lớn dần về 0 và hàm lớn chia hàm nhỏ dần về vô cùng. Ví dụ 1.6 3n 2n a) ln5 n log5 lim √ = 0. b) lim = 0. c) lim = +∞. d) lim 2 n = 0. n n! n100 n→∞ n→∞ n→∞ n→∞ 3n
Ví dụ 1.7 Tính các giới hạn sau a) 2n3 − 3n I = lim . n→∞ 4n + 3n2
Dạng ∞. Đại lượng n3 lớn nhất nên chia cả tử và mẫu cho n3. ∞ 3 2 − I = lim n2 = + 4 3
∞ (vì tử dần về 2, mẫu dần về 0). n→∞ + n2 n b) 2n3 − 4n+1 I = lim . n→∞ 3n − 22n−1 + 5n7
Dạng ∞. Đại lượng 4n = 22n lớn nhất nên chia cả tử và mẫu cho 4n. ∞ n3 2 − 4 0 − 4 I = lim 4n = 1 = 8. n→∞ 3 1 n7 ( )n − + 5 0 − + 0 4 2 4n 2 √ c) I = lim n2 + 4n − n + 1. n→∞
Dạng ∞ − ∞. Nhân lượng liên hợp. √ √ ( n2 + 4n − n)( n2 + 4n + n) 6n2 +4n− 6n2 I = lim √ + 1 lim √ + 1. Dạng ∞. n→∞ n2 + 4n + n n→∞ n2 + 4n + n ∞
Chia cả tử và mẫu cho n. 4 4 I = lim + 1 = √ + 1 = 3. n→∞ + 1 1 + 0 + 1 q n 1 + 4 √ d) √ 1 I = lim n 1 3n4 − 4n3 = lim nr
) = lim n n4(3 − 4 )n = 1.30 = 1. n→∞ n→∞ √ 1 n n→∞ n
Tương tự, ta có thể chứng m n4 in ( h3 − n 4
Pm → 1 với mọi đa thức Pm. 1 4n 4n 4n n v 2 − v 2 − 2 − e) 2 2 I = lim nr = lim n u 2n u 2n 2n u = . Vì lim n = lim = 3 u n→∞ 2n+1 3n −+4n 5n3 n→∞ 3 u 5n3 u 5n3 5n3 u 1 + n→∞ u 1 + 1 + t 3n t 3n 3n n→∞ 20 = 1.
Đại học Bách khoa TPHCM Trang 8
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.1. GIỚI HẠN DÃY SỐ 2 f) ln (2n) (ln 2 + ln n)2 I = lim = lim = lim 2 = (0 + 1)2 = 1. n→∞ ln2 n n→∞ ln2 n ln 2 + 1 √ n→∞ ln n g) n sin n! I = lim . n→∞ n + 1 √nsinn! √ . n n + 1 Ta có √ ≤ √ 0 ≤ √ n + 1 n n sin n! Vì n sin n! lim 0 = lim = 0 nên lim = 0 =⇒ lim = 0. n→+∞ n→∞ n + 1 n→∞ n + 1 n→∞ n + 1 h) 1 I = lim = lim = e−2 = . n+1 n+1 e2 n − 1 −2 1 + n→∞ n + 1 n→∞ n + 1 n2+5 i) I = lim 3n2+1 = lim (n2+5) 3n2+1 n2 + 2 −3 1 + n2 + 5 n→∞ n2 + 5 n→∞ n2+5 1 = lim # " 3n2+1 (n2+5) = (e−3)3 = e−9 = . −3 e9 1 + n2 + 5 n→∞ n+2 j) I = lim n3+1. 2n + 3 2n 3n + + 3 2 Vì 2 n3 + 1 ln i → m ∞ = , lim = +∞ nên I = 0. n→∞ 3n + 2 3 n→∞ n + 2
Chú ý bài này không phải dạng vô định. Có dạng (2/3)+∞ = 0. n √ 2+2 k) I = lim n . 2n2 + 3n √ 2n 4 2 n2 + − 3n 2n 1 n n→∞ Vì lim = , lim = 0 nên I = (1/4)0 = 1. n→∞ 4n2 − 2n 4 n→∞ n2 + 2
Chú ý bài này cũng không phải dạng vô định. n2+2 l) I = lim n . 2n3 + 3n
Bài này dạng vô định +∞0. Ta làm như sau: n→∞ 4n2 − 2n √ n2+2 n . n2 n2+2 2n3 + 3n ! n2+2 n2 1 n 1 n→∞ −−−→ (1/1) = 1. n 2n3 + 3n 2n3 + 3n n √ 4n2 − 2n = 4n2 − 2n = 4n2 − 2n
Ví dụ 1.8 Tính các giới hạn sau
a) I = lim(−1)n. Đặt xn = (−1)n n→∞
Ta có x2n = (−1)2n = 1 −→ 1, x2n+1 = (−1)2n+1 = −1 −→ −1.
Vậy không tồn tại giới hạn. b) I = lim . n n n n 1 − n . Đặt 1 − n n − 1 −2 xn = = ( 1 −1)n = (−1)n 1 + n→∞ 1 + n 1 + n 1 + n 1 + n . 2 −→ 1.e−2 = n −2 e2 x2n = (−1)2n 1 + 1 + 2n
Đại học Bách khoa TPHCM Trang 9
ThS.Nguyễn Hữu Hiệp 1.1. GIỚI HẠN DÃY SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1 . 2n+1 −→ −1.e−2 = − −2 e2 x2 V n ậ = y k (h− ô 1 n )2n+1 g tồn t 1 ại + giới hạn. 2 + 2n c) ( lim √ x q 1 = 2 p x √ n, với xn = Viết cách khác: ( n→∞ √ xn = 2 + 2 + 2 + . . . n dấu căn). xn+1 = 2 + xn, n ≥ 1.
Dùng quy nạp chứng minh được dãy xn tăng và bị chặn trên bởi 2 do đó hội tụ.
Giả sử xn → a. Từ giả thiết ta có √ √ lim xn+1 = lim
2 + xn ⇐⇒ a = 2 + a ⇐⇒ a = 2. n→∞ n→∞ Vậy lim xn = 2. n→∞ 1 1 1 d) lim xn, với xn = + + · · · + . n→∞ 1.2 2.3 n(n + 1) 1 1 1 − − − −→ 1. 1 2 1 3 n 1+ 1 Ta có 1 1 n xn = 1 − + + + · · · + = 1 − 2 3 4 n + 1 1.1.1 Bài tập Tính giới hạn n2 + 1 1 + n 1. 4n − 5−n lim 2n n √ 3n − 22n − 5n6 6. − 3 − 2 lim( ) n + 1 11. lim( ) 2 − n 2n + 5 n + 2 2. ln(3n2 − 2n) 2n − 1 lim 7. 12. lim( )n n9 + 3n2 lim np 5n + 2 n + (−1)n n sin n! n2 + 2n arctan n! 3. log210n 13. lim lim 8. lim √ 3n3 + arcsin n log2n (1 + n) n − 2 14. n − 1 lim( 1 + n )1−n 9. n2 + 1 4. 1 + n lim n lim( )2 − n2 r n10 + 2n 1 n + 2 5n + 1 15. lim √ n n! 1 n 5. 2n + 1 lim nr 10. lim( ) n − 2 16. lim √ n n2 + n 4 + n 5n n2 − 1 n! Tìm lim un biết: √ √ 17. 1 1 1 u 19. u1 = 3, u 3 + u n = + + · · · + n+1 = n 1.3 3.5 (2n − 1).(2n + 1) 18. (−1)n un = (1 + )n 20. n un = sin n 21. 1 1 1 un = √ √ + √ √ · · · + 1 1+ 3 3 + 5 √ √ √ ĐS:12 n 2n
Đại học Bách khoa TPHCM Trang − 1 + 2n + 1 10
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.2. HÀM SỐ 1 1 22. 1 u ĐS:1 n = + + · · · + 1.2.3 2.3.4 n(n + 1)(n + 2) 4 √ 23. √ u1 = 13, un+1 = 12 + un, n ≥ 1 ĐS:4 √ √ 24. √
u1 = 3 5, un+1 = 3 5un, n ≥ 1 ĐS: 5. 4 25. 1 u1 = , u u ĐS: 1. 2 n+1 = 3 n − u2n 3 √ 26. 1 5 u1 = 1, u . n+1 = 1 + , ĐS: 1 + un 2 1.2 Hàm số
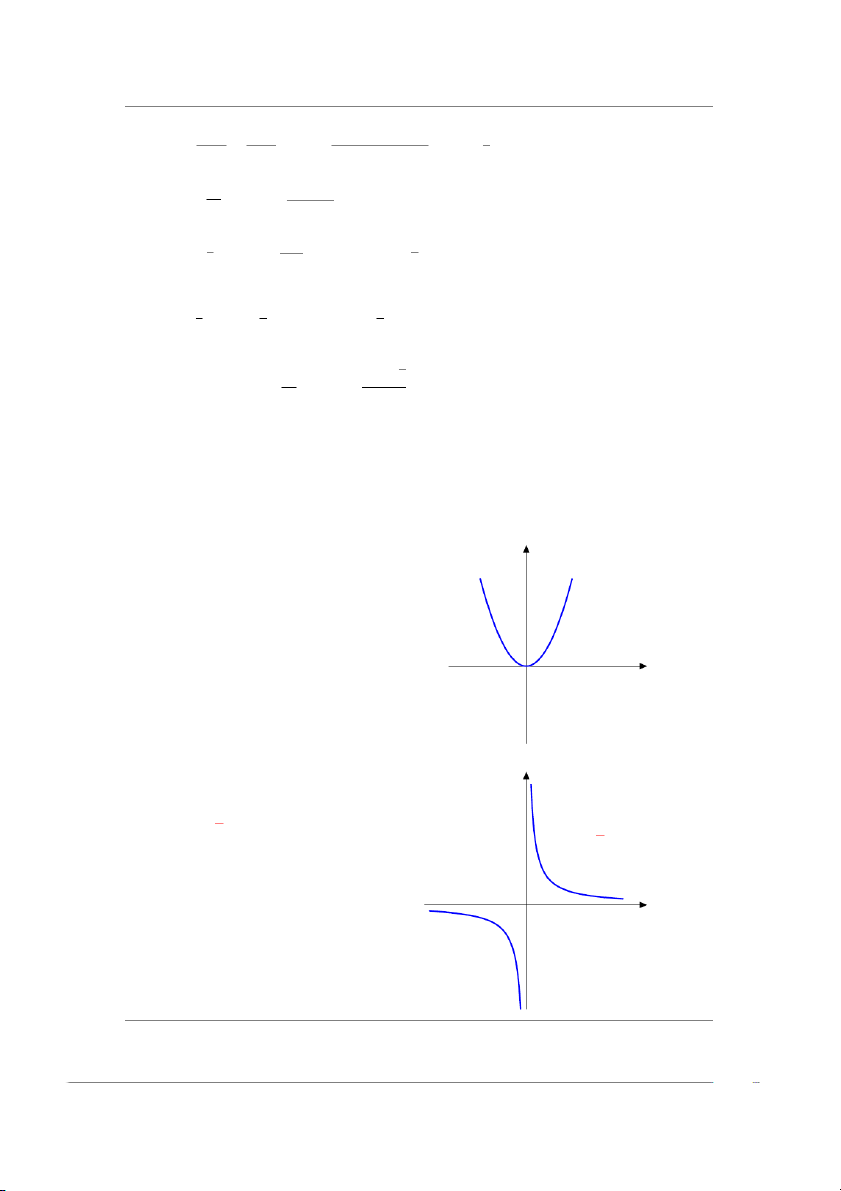
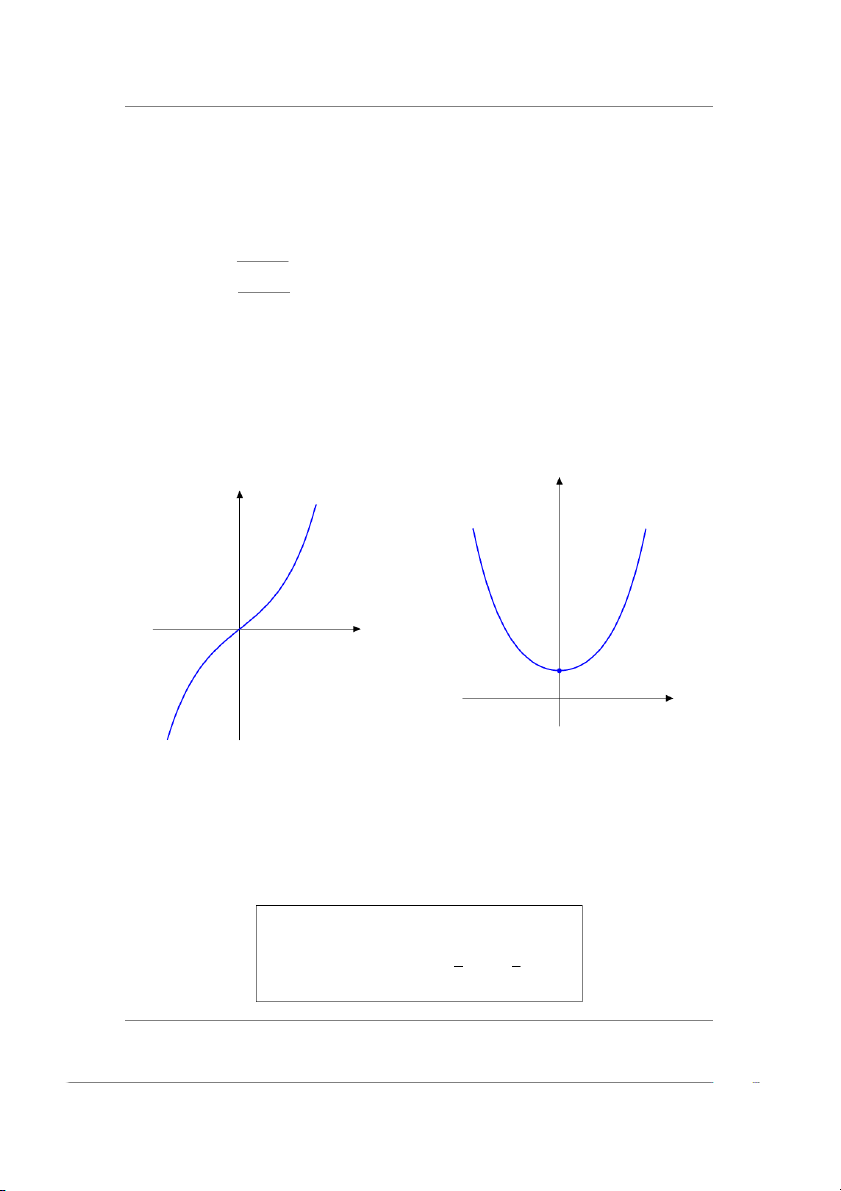
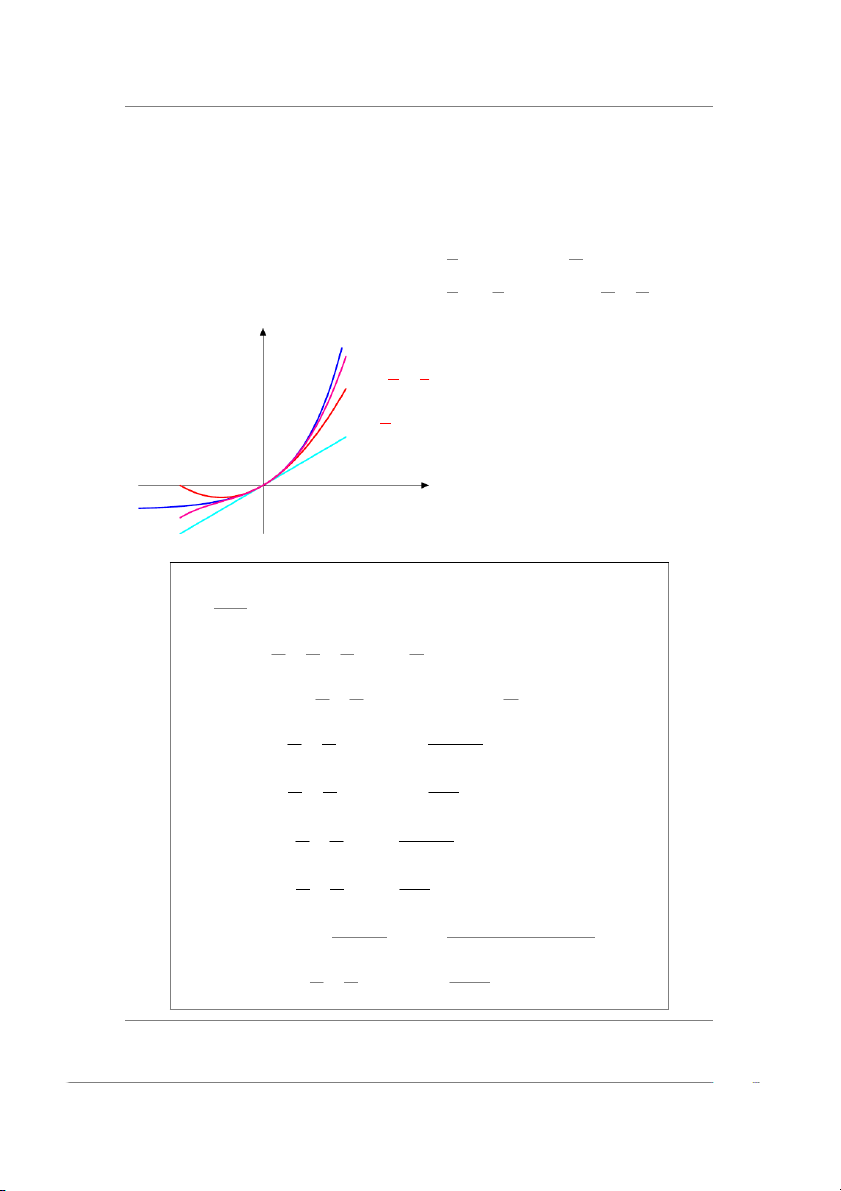
1.2.1 Hàm lũy thừa y = xα y n = 2 : y = x2 y = x2 * T XD : D = R. * T GT : T = [0, ∞).
* Hàm số tăng trên khoảng (0, ∞) và giảm 0 x trên khoảng (−∞, 0).
* Hàm chẵn, đồ thị đối xứng qua Oy. y 1 n = −1 : y = 1 x y = x * T XD : D = R \ {0}.
* T GT : T = (−∞, 0) ∪ (0, ∞).
* Hàm số giảm trên khoảng (−∞, 0) và 0 x (0, +∞)
* Hàm lẻ, đồ thị đối xứng qua O(0, 0).
Đại học Bách khoa TPHCM Trang 11
ThS.Nguyễn Hữu Hiệp 1.2. HÀM SỐ
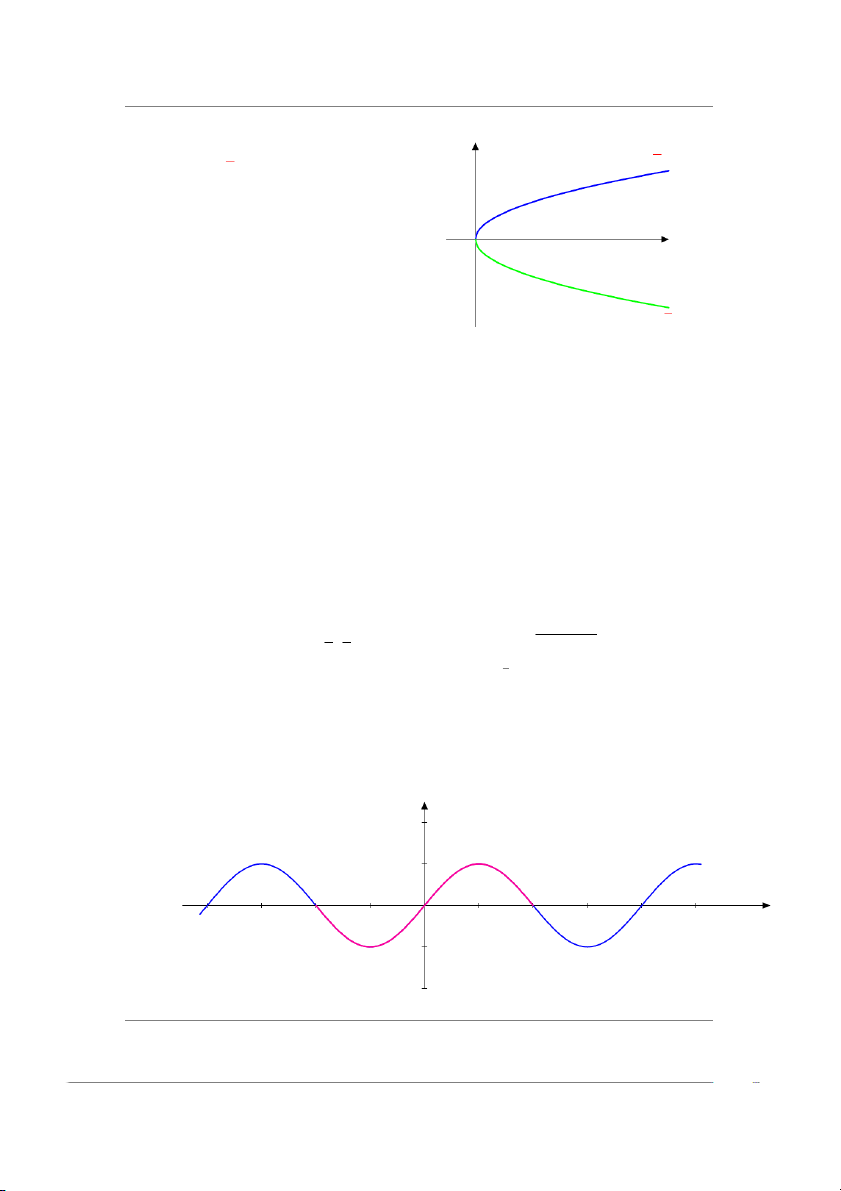
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC √ √ y n = −1 : y = x y = x * T XD : D = [0, ∞). * T GT : T = [0, ∞).
* Hàm số tăng trên khoảng (−∞, 0) và 0 x (0, +∞)
* Không có tính chẵn lẻ. √ y = − x
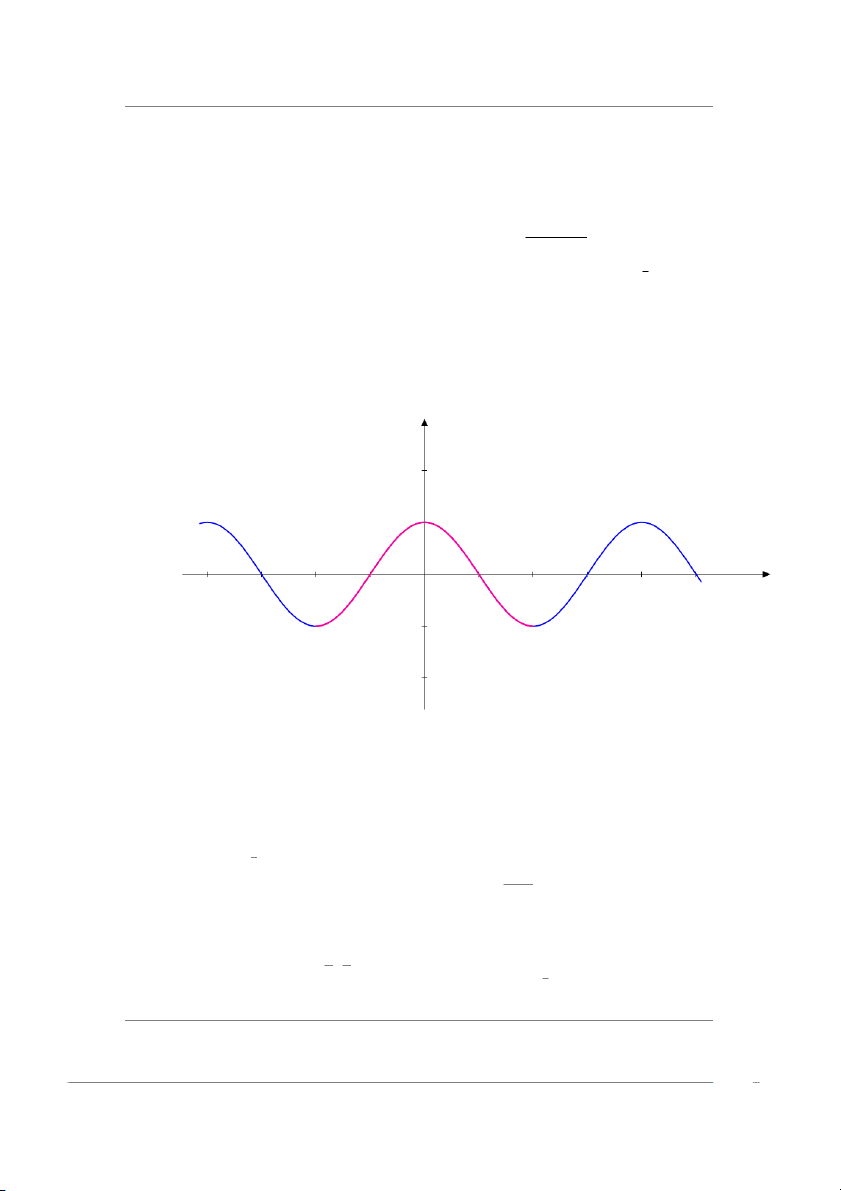
1.2.2 Hàm lượng giác Hàm số y = sin x Công thức * T XD : D = R. i) sin2 x + cos2x = 1
* Hàm số tuần hoàn với chu kỳ 2π : sin(x) = ii) sin2x = sinxcosx sin(x + 2π) iii) sin 3x = 3 sin x * − 4 sin3 x T GT : T = [−1, 1]. 1 π − cos 2x
* Hàm số tăng trên khoảng π iv) sin2 x = (− , ). 2 2 2
v) sin π = 0; sin(kπ) = 0, k ∈ Z.
* Hàm số lẻ, đồ thị đối xứng qua O(0, 0). 2 y 2 y = sin x 1 −6.28 −4.71 −3.14 −1.57 0 1.57 3.14 4.71 6.28 7.85 x −1 −2
Đại học Bách khoa TPHCM Trang 12
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.2. HÀM SỐ Hàm số y = cos x Công thức * T XD : D = R. i) cos 2x = cos2 x − sin2 x
* Hàm số tuần hoàn với chu kỳ 2π : cos(x) = ii) cos 2x = 2 cos2 x − 1 = 1 − sin2 x cos(x + 2π) iii) 1 + cos 2x * cos2 x = T GT : T = [−1, 1]. 2
* Hàm số chẵn, đồ thị đối xứng qua Oy.
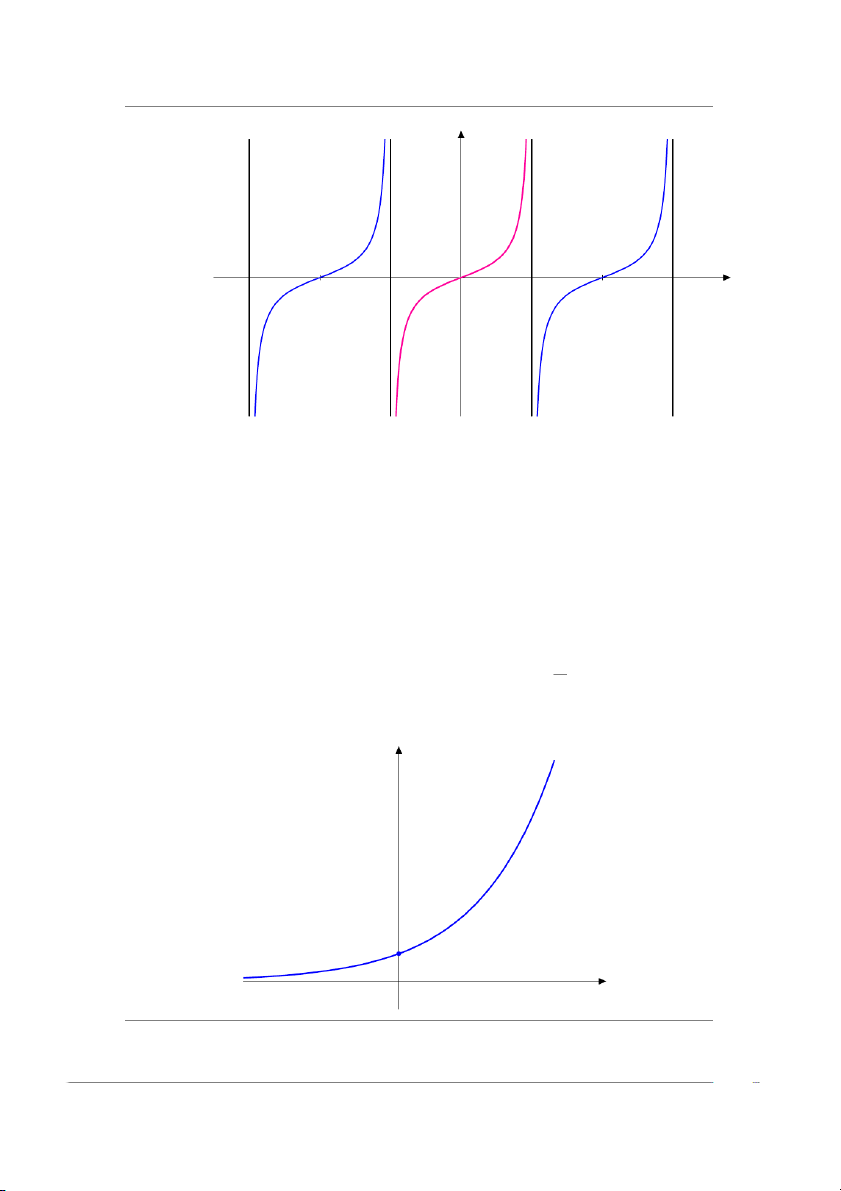
iv) cos 0 = 1; cos π = −1, cos(±π ) = 0. 2 y 2 y = cos x 1 −6.28 −4.71 −3.14 −1.57 0 1.57 3.14 4.71 6.28 7.85 x −1 −2 Hàm số y = tan x Công thức * T XD : D = R \ {π + kπ, k 2 ∈ Z}. sin x
* Hàm số tuần hoàn với chu kỳ π : tan(x) = i) tan x = cosx tan(x + π)
ii) tan(π − x) = tan(−x) = − tan x * T GT : T = R. iii) π tan(π + x) = tan(x)
* Hàm số tăng trên khoảng π (− , ). 2 2
iv) tan 0 = 0, tan(π) không xác định. 2
* Hàm số lẻ, đồ thị đối xứng qua O(0, 0).
Đại học Bách khoa TPHCM Trang 13
ThS.Nguyễn Hữu Hiệp 1.2. HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC y y = tan x x −4.71 −3.14 −1.57 0 1.57 3.14 4.71
1.2.3 Hàm mũ - Hàm logarit Công thức
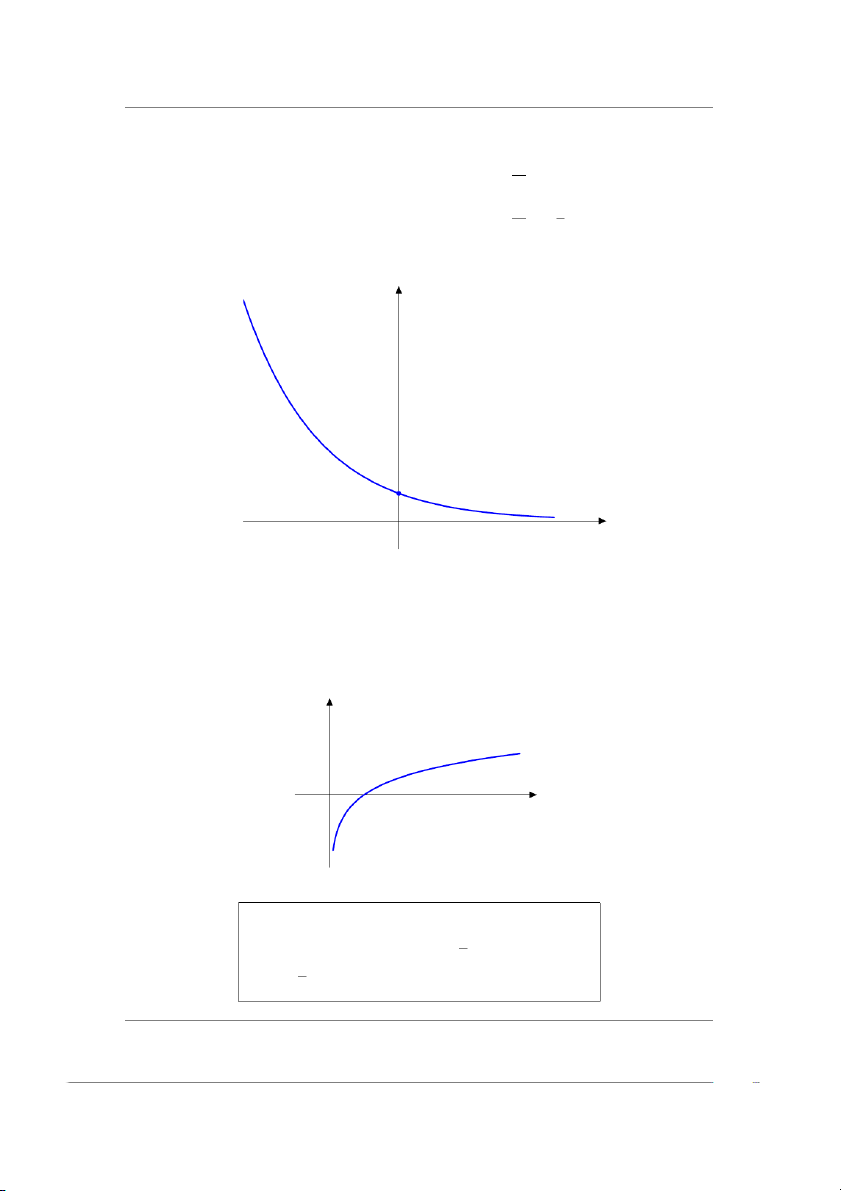
Hàm số y = ax, (a > 1) i) ax.ay = ax+y * T XD : D = R. ii) (ax)y = axy * T GT : T = (0, ∞). iii) ax.bx = (ab)x
* Hàm số tăng trên (−∞, ∞) iv) 1 a−x = ax y y = ax(a > 1) (0; 1) 0 x
Đại học Bách khoa TPHCM Trang 14
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.2. HÀM SỐ Công thức
Hàm số y = ax, (0 < a < 1) * T XD : D = R. i) ax = ax−y ay * T GT : T = (0, ∞). ii) ax x * Hàm số giảm trên a (−∞, ∞) = iii) bx a .y = (bax)y. y y = ax(0 < a < 1) (0; 1) 0 x 1.2.4 Hàm y = ln x y = ln x ⇐⇒ x = ey 0 < x < ∞ −∞ < y < ∞. y y = ln x 0 x Công thức • ln(x+y) = ln(x)+ln(y). 1 • ln = − ln x x x • ln = ln x − ln y y • ln xα = α ln x.
Đại học Bách khoa TPHCM Trang 15
ThS.Nguyễn Hữu Hiệp 1.2. HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.2.5 Hàm Hyperbolic
Hàm số y = sinh x, cosh x * Định nghĩa Công thức ex − e−x
i) Các công thức của hàm Hyperbolic được suy từ sinh x = ∈ R 2
công thức lượng giác bình thường bằng cách thay ex + e−x cosh x = ≥ 1 sin , tan , cot 2 → i sinh cos → cosh → i tanh → −i cot 2 2 * ii) cosh x − sinh x = 1 T XD : D = R. iii) * cosh2 x + sinh2 x = cosh 2x
y = sinh x là hàm lẻ và tăng trên R. * y = cosh x là hàm chẵn. y y y = cosh x y = sinh x 0 x (0; 1) 0 x
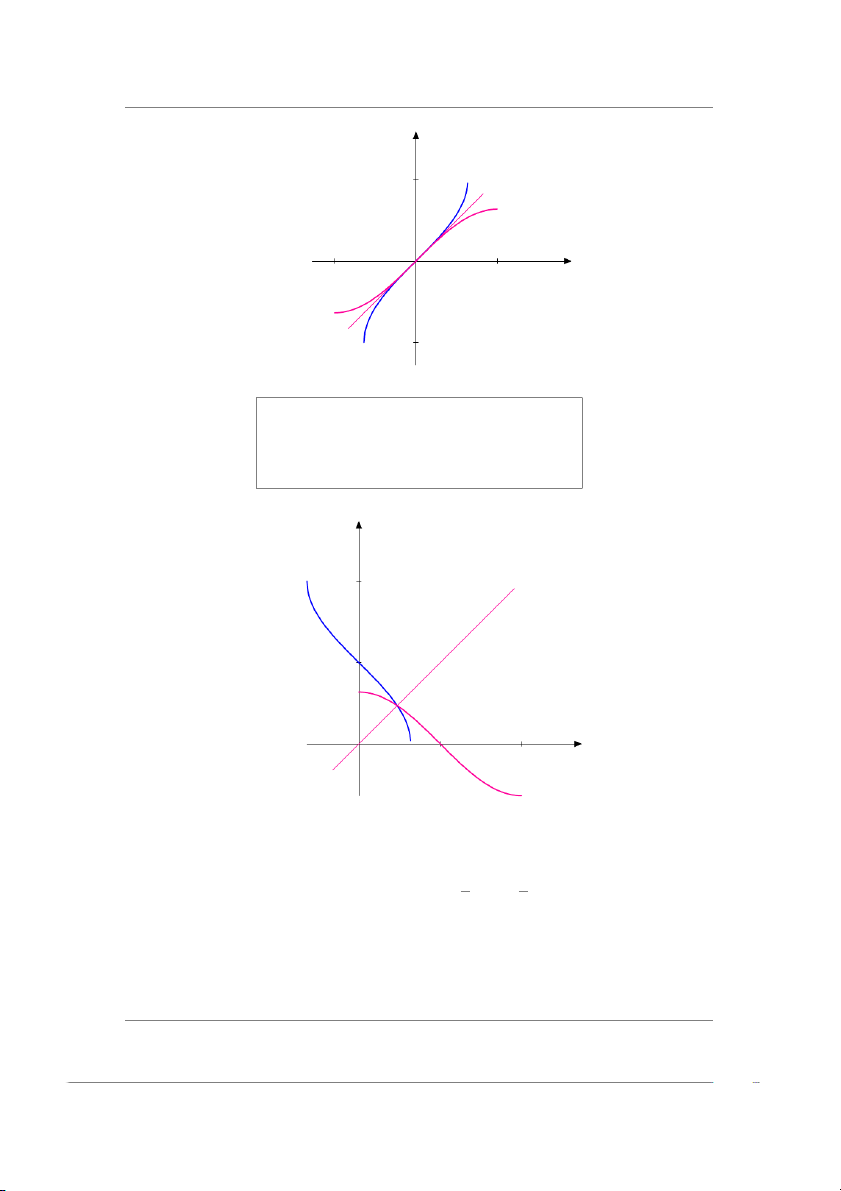
1.2.6 Các hàm lượng giác ngược Hàm y = arcsin x y = arcsin x ⇐⇒ x = sin y π π −1 ≤ x ≤ 1 − ≤ y ≤ 2 2
Đại học Bách khoa TPHCM Trang 16
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.2. HÀM SỐ y 1.57 y = arcsin x y = sin x −1.57 0 1.57 x −1.57 y = arccos x y = arccos x ⇐⇒ x = cos y −1 ≤ x ≤ 1 0 ≤ y ≤ π y 3.14 y = arccos x 1.57 0 1.57 3.14 x y = arccos x Hàm y = arctan x y = arctan x ⇐⇒ x = tan y π π −∞ ≤ x ≤ ∞ − ≤ y ≤ 2 2 1.2.7 Hàm Hợp
Định nghĩa 1.8 (Hàm Hợp) Cho 2 hàm số z = g(y) và y = f(x). Hàm số z = g(f(x)) gọi là hàm
hợp của f và g.
Đại học Bách khoa TPHCM Trang 17
ThS.Nguyễn Hữu Hiệp 1.2. HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC Ví dụ Cho √ √ z = y, y = cos x. Hàm z =
cos x là hàm hợp của 2 hàm đã cho. √ Ví dụ Cho √ z = sin u, u =
y, y = ln x. Khi đó, hàm z = sin ln x là hàm hợp của 3 hàm đã cho. 1.2.8 Hàm ngược
Cho hàm số y = f(x) : X −→ Y . Xét tập hợp
f −1(y) = {x ∈ X : f(x) = y}.
Tập này có thể có nhiều hơn một phần tử hoặc là tập rỗng.
Nếu f−1(y) luôn có đúng 1 phần tử với mọi y ∈ Y thì f−1 là một ánh xạ gọi là ánh xạ ngược của hàm số y = f(x). f −1 : Y −→ X y 7→ x = f −1(x) ⇐⇒ y = f(x) Ví dụ 1.9
a Xét hàm số y = f(x) = x2 : R −→ R.
Tập f−1(1) = {x ∈ R : x2 = 1} = {−1, 1} có 2 phần tử.
Tập f−1(−1) = {x ∈ R : x2 = ∅}.
b Xét hàm số y = f(x) = x2 : R+ −→ R+. Tập √
f −1(y) = {x ∈ R+ : x2 = y} = { y} luôn có duy nhất 1 phần tử. Do đó y 7→ f−1(y) là
ánh xạ ngược của hàm số √ √
y = f (x). Ta viết f −1(y) = y hay f −1(x) = x.
1.2.9 Hàm tham số hóa
Định nghĩa 1.9 (Hàm cho theo tham số) Cho hàm số y = y(x) qua một biến trung gian t: ( x = y x = (yt()t)
gọi là hàm cho theo tham số.
Đường cong (C) được xác đinh bởi hàm trên gọi là đường cong tham số, hay hàm trên gọi là tham số
hóa của đường cong (C). Ví dụ 1.10 (
là đường thẳng qua M(1, 0) và có véc y = 0 − t a). Cho đường cong x = 1 + 2t C có tham số hóa
tơ chỉ phương a = (2; −1): x + 2y = 1 (
là đường tròn tâm I(1; 2) bán y = 2 + 3 sin t b). Cho đường cong x = 1 + 3 cos(t) (C) 2 có tham s 2 ố hóa
kính bằng 3: (x − 1) + (y − 2) = 9
Đại học Bách khoa TPHCM Trang 18
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.3. GIỚI HẠN HÀM SỐ y2 ( là Elip x2 +
= 1 (bằng cách khử t y = b sin t a2 b2 c). Cho đường cong x = a cos t (C) có tham số hóa
từ phương trình tham số)
Ví dụ 1.11 Tìm hàm ngược của hàm số y = f(x). x √ a) − 1 f (x) = .
b) f(x) = 3 ex − 1.
c) f(ex) = 3(x + 1)3. x + 1 Bài làm y + 1 a) x − 1 y = f (x) =
⇐⇒ y(x + 1) = (x − 1) ⇐⇒ x = . x + 1 y − 1 x + 1 Vậy y + 1 f −1(y) = hay f−1(x) = . y − 1 x − 1 √
b) y = f(x) = 3 ex − 1 ⇐⇒ x = ln(y3 + 1) =⇒ f−1(x) = ln(x3 + 1).
c) f(ex) = 3(x + 1)3. Đặt t = ex ⇐⇒ x = ln t. √ √ 3 y x
f (t) = 3(ln t + 1)3 hay y = f (x) = 3(ln x + 1)3 ⇐⇒ x = e −1 3 3 =⇒ f−1(x) = e −1 3 . Bài tập
Câu 1) Tìm miền xác định của hàm số a) f(x) = ln( 1 − 1). x b) f(x) = arccos ln(1 + x) c) 1 f (x) = (1 + )x. x √x2 − 1, x > 0, 1 , x ≤ 0. d) f(x) = r + arctan x π4
Câu 2) Tìm hàm ngược của hàm số y = f(x) biết
a) f(x) = ln(x3 + 1), x > −1. b) f(x + 1) = e2x + 1. c) f(ex + 1) = 3pln(x2+1).
1.3 Giới hạn hàm số 1.3.1 Định nghĩa
Định nghĩa 1.10 (Giới hạn hàm số) cho hàm số y = f(x) xác định trên D.
Đại học Bách khoa TPHCM Trang 19
ThS.Nguyễn Hữu Hiệp 1.3. GIỚI HẠN HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC
i) lim = a ⇐⇒ (∀ε > 0, ∃δ > 0, ∀x ∈ D : 0 < |x − x0| < δ −→ |f(x) − a| < ε) x→x0
ii) lim f(x) = a ⇐⇒ (∀ε > 0, ∃N, ∀x ∈ D : x > N −→ |f(x) − a| < ε) x→+∞
iii) Tương tự cho giới hạn bằng vô cực. Định lý
lim = a ⇐⇒ ∀(xn) ⊂ D&xn 6= x0 : xn → x0 =⇒ f(xn) → a. x→x0
Định lý tương đương với định nghĩa giới hạn hàm số theo giới hạn dãy số. Do đó, những
tính chất giới hạn hàm số tương tự như giới hạn dãy số.
Ví dụ 1.12 Chứng minh giới hạn lim sin x không tồn tại. x→+∞ Bài làm
Xét dãy (xn) : xn = nπ −→ +∞ và lim sin xn = lim sin nπ = 0. n→+∞ n→+∞ Xét dãy π (yn) : yn = 2nπ + −→ +∞ và lim sin y 2 n = lim n→+∞ π
Vì tồn tại 2 dãy làm giới hạn dần về 2 giá trị khác nhau do si đn ó k 2 h n ô π n + g tồn tạ = i 1li.m sin x. n→+∞ 2 x→+∞
Định nghĩa 1.11 (Giới hạn một bên) Giới hạn trái
lim = a ⇐⇒ (∀ε > 0, ∃δ > 0, ∀x ∈ D : 0 < x0 − x < δ −→ |f (x) − a| < ε) x→x−0 Giới hạn trái
lim = a ⇐⇒ (∀ε > 0, ∃δ > 0, ∀x ∈ D : 0 < x − x0 < δ −→ |f (x) − a| < ε) x→x+0
Giới hạn trái: x < x0 và giới hạn phải:x > x0 Định lý lim f (x) = a lim x→x−0 x→x lim f (x) = a. 0 f(x) = a ⇐⇒ x→x+0
Ví dụ 1.13 Tính giới hạn |x| lim . x→0 x
Bài làm: biểu thức chứa trị tuyệt đối nên không tính trực tiếp được giới hạn. |x| −x |x| x lim x<0 ===== lim = −1. lim x>0 ===== lim = −1. x→0− x x→0− x x→0+ x x x→0+
Vậy không tồn tại giới hạn |x| lim . x→0 x
Đại học Bách khoa TPHCM Trang 20
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.3. GIỚI HẠN HÀM SỐ
1.3.2 Các giới hạn cơ bản
Giới hạn khi x → 0
1) Các hàm x, sin x, arcsin x, sinh x, tan x, arctan x, ln(x + 1), ex − 1 khi
chia cho nhau sẽ hội tụ về 1 khi x → 0 (a) sin x tan x ln(x + 1) lim = 1 (c) lim = 1 (e) lim = ex − 1 x→0 x x→0 x→0 sinh x 1 (d) sinh x lim = ln(x + 1) (b) arcsin x x lim x→0 = 1 1 (f) lim = 1 ex − 1 x→0 x x→0 2) Bốn hàm khác 1 (a) 1 − cos x 1 lim = (c) lim(1 + αx) x = eα x→0 x→0 x2 2 1 (b) cosh x − 1 (1 + x)α − 1 lim = (d) lim = α x2 x→0 2 x→0 x
Các giới hạn khi x → +∞ tương tự như giới hạn dãy số 1. lim qx = 0, |q| < 1 3. 1 lim = 0, |q| < 1 x→+∞ x→±∞ lnα |x| 2. 1 lim = 0, α > 0 4. lim x→+∞ xα a x 1 + = ea. x→±∞ x
Ví dụ 1.14 Tính giới hạn a) sin2 2x x2 I = lim = lim .4 = 1.2.4 = 8. 2 . x→0 1 − cos x sin 2x 1 − cos x x→0 2x √ √ 1 1 (1+ 3 3 t) 1 3 3 −1 b) x − 1 1 + t − 1 (1 + t) − 1 5 lim √ t=x−1→0 ===== lim √ = lim = lim t = 3 = . 5 5 1 1 1 x→1 x − 1 t→0 1 + t − 1 t→0 (1 + t) 5 − 1 t→0 (1+t) 3 5 −1 5 t ln 1 ln t t − c) t= 1 I = lim xx = lim →+∞ eln xx = lim ex ln x x ===== lim e t = lim e t = e−0 = 1. x→0+ x→0+ x→0+ t→+∞ t→+∞ x d) I = lim = lim x
x2. 1 = (e−2)0 = 1. (tương tự giới hạn dãy số). x2 − 1 −2 1 + x→∞ x2 + 1 x2 + 1 x→∞ √ e) x2 + 2x − x2 I = lim ( x2 + 2x + x) = lim √ x→−∞ x→−∞ x2 + 2x − x 2x 2x 2 2 = lim = lim = lim = = −1. x→−∞ x→−∞ x→−∞ −2 q − x − x − 1 x q x q x |x| 1 + 2 1 −x 1 + 2 1 − 1 + 2
f) I = lim (1 + sin 2x) x = lim (1 + 2 sin 2x)sin2x.sin2xx = (e2)2 = e4. x→0 x→0
Đại học Bách khoa TPHCM Trang 21
ThS.Nguyễn Hữu Hiệp 1.3. GIỚI HẠN HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC g) 1 1 x2 lim (cosh x)cot x2 = lim coshx−1
(1 + (cosh x − 1)) tanx2 = lim (1 + (cosh x − 1)) coshx−1 x2 tanx2 = x→0 x→0 x→0 √ e1. 12 .1 = e. h) x sin x I = lim √ . x→+∞ x3 + 1 arctan x x sin x √ , ∀x > 0. x3 + 1 arctan x Ta có x 0 x π lim 0 ≤ √ = lim ≤ √ = 0. = 0. Vậy I = 0. x→+∞ x3 + 1 arctan x 2 x→+∞ x3 + 1 arctan x Bài tập
11. I = lim (cos x + 5 sin x)cot x 1. I = lim 6. I = lim x→0 x2 x2 x2 + 4 2x2 + 3 x→+∞ x2 − 41 2x2 − 1 2. x→∞ 2 I = lim (1 + 2x4) 1 sin2 x 7. I = lim x2 x + 12. I = lim (1 + sin(2x2)) x→0 x x→0 1 3. e I = lim (ln(e + x))cot x 1 x→∞ x 8. x→0 I = lim(cosh x) 1−cosx 1 x→0
13. I = lim (1 + 2x4 cos x)) x4 4. 1 x→0 I = lim (1 − tan2 x) sin2 2x 9. I = lim xex+1 x x→0 x→−∞ 1 e2x + x2 5. 1 1 I = lim (cos x) x2
10. I = lim(cos 2x + sin x) sinx 14. I = lim ln x→0 x→0 x→+∞ x x2 1.3.3 Vô cùng bé
Định nghĩa 1.12 (Vô cùng bé) .
Hàm số f(x) được gọi là một vô cùng bé (VCB) khi x → x0 nếu lim f(x) = 0 x→x0 Ví dụ 1.15
a) f(x) = 2x2 − 3 sin x là VCB khi x → 0. Vì lim f(x) = lim 2x2 − 3 sin x = 0. x→0 x→0 1 b) 1 f (x) =
không phải VCB khi x → 0. Vì lim = −1 6= 0. x − 1 x→0 x − 1 Nhưng là VCB khi 1 x → ∞. Vì lim = 0. x→∞ x − 1 Tính chất
i) Tổng hữu hạn các VCB là một VCB. ii) Tích 2 VCB là một VCB.
iii) Tích của một VCB và một hàm bị chặn là một VCB.
iv) Thương 2 VCB chưa chắc là VCB.
Đại học Bách khoa TPHCM Trang 22
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.3. GIỚI HẠN HÀM SỐ
Định nghĩa 1.13 (cấp vô cùng bé) f (x)
Cho f(x), g(x) là 2 VCB khi x → x0 và lim = k x→x g(x) 0
i) Nếu k = 0 thì ta nói f(x) có bậc VCB cao hơn g(x), ta viết f(x) = o(g(x)).
ii) Nếu k hữu hạn khác 0 thì ta nói f(x) và g(x) là 2VCB cùng cấp.
iii) Nếu k = 1 thì ta nói f(x) và g(x) là 2 VCB tương đương: f(x) ∼ g(x).
iv) Nếu f(x) (x − x0)k thì ta nói f(x) là VCB bậc k.
Ví dụ 1.16 so sánh các VCB sau khi x → 0 √ √ a)
1 − x2 − 1 và tan x.
c) e3x − 1 và 1 + 6x − 1. 1
b) ln(1 − 2x2) và x4 + 3x2. d) x sin và x x Bài làm √ √ √ a) 1 − x2 − 1 1 − x2 − 1 x lim = lim . .(−x) = 0. Suy ra
1 − x2 − 1 là VCB cấp cao x→0 tan x x→0 −x2 tan x hơn tan x. b) ln(1 − 2x2) ln(1 − 2x2) −2x2 ln(1 − 2x2) −2 lim = lim = lim = 4 2 −2. x→0 x + 3x x→0 −2x2 x2(x2 + 3) x→0 −2x2 x2 + 3
Suy ra ln(1 − 2x2) và x4 + 3x2 là 2 VCB cùng cấp. c) e3x − 1 e3x − 1 6x 1 e3x − 1 1 1 1 1 lim √ = lim . √ . = lim . √ . = 1. = 1 1 x→0 1 + 6x − 1 x→0 3x 1 + 6x − 1 2 x→0 3x 1+6x−1 2 2 6x 2 √
Suy ra e3x − 1 và 1 + 6x − 1 tương đương. 1 x sin 1 d) lim
x = limsin không tồn tại nên 2 VCB này không so sánh được. x→0 x x→0 x
Các VCB thường gặp khi x → 0
⋆ x ∼ sin x ∼ arcsin x ∼ sinh x ∼ tan x ∼ arctan x ∼ ln(1 + x) ∼ ex − 1. x2 ⋆
∼ 1 − cos x ∼ cosh x − 1. 2 ⋆ (1 + x)α − 1 ∼ αx.
Đại học Bách khoa TPHCM Trang 23
ThS.Nguyễn Hữu Hiệp 1.3. GIỚI HẠN HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC
Tính chất cho các VCB tương đương khi x → x0
f (x) ∼ f1(x), g(x) ∼ g1(x) i) f(x)g(x) ∼ f1(x)g1(x)
ii) Tổng f1(x) + g1(x) gọi là dạng triệt tiêu nếu f(x) có bậc VCB thấp hơn f(x) + g(x).
Nếu không phải dạng triệt tiêu thì
f (x) + g(x) ∼ tổng bậc thấp nhất. iii) f (x) f lim 1(x) = lim x→x g(x) g 0 x→x0 1(x) Chú ý:
• Sau khi thay tương đương cộng lại mà mất đi bậc thấp nhất thì là dạng triệt tiêu.
• Thay VCB tương đương dạng tổng thì cần kiểm tra tổng không phải dạng triệt tiêu.
• Không thay tương đương cho hàm hợp.
Ví dụ 1.17 Rút gọn các VCB sau khi x → 0.
a) f(x) = 3x5 − 5x6 − 4x3 ∼ −4x3 : bậc thấp nhất là 3
b) f(x) = (e3x − 1)(sin2 2x + 3x3) ∼ 3x.((2x)2 + 3x3) ∼ 3x.x2 = 3x3. c) (2x)2
f (x) = x cos 2x − x + 3x3 = −x(1 − cos 2x) + 3x3 ∼ −x + 3x3 = x3. 2 √ d) 1 1 1 4
f (x) = 3 1 + 2x − cos 2x = [(1 + 2x) 3 − 1] + [1 − cos 2x] ∼ .2x − (2x)2 = − x2. 3 2 3
e) f(x) = (1 + 2x2 − 3x3)3 − cos(2x + x2) = [(1 + 2x2 − 3x3)3 − 1] + [1 − cos(2x + x2)] 1 1
∼ 3.(2x2 − 3x3) + (2x + x2)2 ∼ 3.2x2 + (2x)2 = 8x2. 2 2
f) f(x) = tan x − sin x ∼ x − x = 0−→ Sai.
Vì tan x và sin x đều bậc nhất. Khi thay tương đương mất đi bậc nhất do đó là dạng triệt tiêu.
Không bao giờ tương đương ra không. Ta làm lại như sau: x2 x3
f (x) = tan x − sin x = tan x(1 − cos x) ∼ x. = . 2 2 √
g) f(x) = 1 + 2x + 2x2 − 1 − x √ √ Cách 1: 1 1 f (x) =
1 + 2x + 2x2 − 1 − x ∼ 1 + 2x − 1 − x = ((1+ 2x) 2 − 1)− x ∼ 2x − x = 2 0−→ Sai.
2 chỗ: thay tương đương hàm hợp và thay tương đương dạng triệt tiêu
Đại học Bách khoa TPHCM Trang 24
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.3. GIỚI HẠN HÀM SỐ √ Cách 2: 1 f (x) =
1 + 2x + 2x2 − 1 − x ∼ (2x + 2x2) − x = x2−→ Sai. 2
Dạng triệt tiêu: mất đi bậc nhất. √ √ Cách 3: 1 + 2x − 1 f (x) =
1 + 2x + 2x2 − 1 − x ∼ 1 + 2x − 1 − x = √ − x 1 + 2x + 1 √ x(1 − 1 + 2x) x.(−1 .2x) x2 = √ ∼ 2√ = − −→ Sai. 1 + 1 + 2x 1 + 1 2
∼ đầu tiên sai vì thay tương đương hàm hợp, các ∼ sau thì đúng. √ Cách 4: 1 + 2x + 2x2 − 1 f (x) = 1 + 2x + 2x2 − 1 − x = √ − x 1 + 2x + 2x2 + 1 √ x(1 + 2x − 1 + 2x + 2x2) x.(2x − 1 .(2x + 2x2)) x2 = √ ∼ 2 √ = .−→ Đúng. 1 + 1 + 2x + 2x2 1 + 1 2
Không thay tương đương hàm hợp. Biến đổi cho đến khi hết dạng tổng triệt tiêu
rồi mới dùng tương đương.
Ví dụ 1.18 Tìm α, β sao cho f(x) ∼ α(x − x0)β khi x → x0. a) f(x) = ex − e1, x0 = 1.
f (x) = e[ex−1 − 1] ∼ e(x − 1) =⇒ α = e, β = 1.
Chú ý: x → 1 =⇒ x − 1 là VCB nên ta áp dụng công thức cho x − 1. √ b) f(x) = 3 x − x, x0 = 1 1 1 2 2
f (x) = [(1 + x − 1) 3 − 1] + 1 − x ∼ (x − 1) − (x − 1) = − (x − 1) =⇒ α = − , β = 1. 3 3 3 √ c) f(x) = 2 x − 1, x0 = 0. √ √ x √ 1
f (x) = eln 2 − 1 = e x ln 2 − 1 ∼ x ln 2 =⇒ α = ln 2, β = . 2
Ví dụ 1.19 Tính các giới hạn sau bằng cách thay VCB tương đương. a) ln(1 + x tan x) I = lim . x→0 x2 + sin3 2x
Ta có ln(1 + x tan x) ∼ x tan x ∼ x2,
x2 + sin3 2x ∼ x2 + (2x)3 ∼ x2. ln(1 + x tan x) x2 =⇒ I = lim = lim = 1 x→0 x2 + sin3 2x x→0 x2 1 − .(2x)2 b) ln cos 2x ln(1 + cos 2x − 1) cos 2x − 1 I = lim = lim = lim = lim 2 = 2. x→0 ln(1 − x2) x→0 ln(1 − x2) x→0 −x2 x→0 −x2 c) cos x − ex cos x − 1 + 1 − ex −x2 −x lim √ = lim = lim 2 − x = lim = −1. x→0 x x→0 1 + 2x − 1 x→0 2x x→0 2x. 12 √ √ √ √ d) 1 − 2x − 3 1 + 6x
1 − 2x − 1 + 1 − 3 1 + 6x −2x.1 I = lim = lim = lim 2 − 6x. 13 = 3 x→0 ln(1 − arcsin x) x→0 − arcsin x x→0 −x
Đại học Bách khoa TPHCM Trang 25
ThS.Nguyễn Hữu Hiệp 1.3. GIỚI HẠN HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC e) x2012 − 1 I = lim . x→1 ln x
Ta đặt t = x − 1 → 0(x → 0). (t + 1)2012 − 1 2012.t I = lim = lim = 2012. t→0 ln(t + 1) t→0 t f) 1 I = lim 1 (1 + 3 tan 2x) 3tan2x 3.2x sin3x = lim e ln(1+3 tan 2 sin3x
x) = lim e sin3x = lim e 3x = e2. x→0 x→0 x→0 x→0 √ 3 g) 1 + 3x2 − 1 I = lim . x→0 ecos x − 2 1 1 (1 + 3x2)3 − 1 .3x2 x2 I = lim = lim 3 = lim = −2−→ Sai. x→0 (ecos x − 1) − 1 x→0 cos x − 1 x→0 x2 − 2 Vì cos x x→0
−−→ 1 6= 0 nên áp dụng công thức ecos x − 1 ∼ cos x là sai.
Bài này không phải dạng vô định nên suy ra ngay kết quả √31 + 3x2 − 1 0 I = lim = = 0. x→0 ecos x − 2 e − 2 √ h) 1 + 2x − 1 − x I = lim
. Chú ý trên tử dạng triệt tiêu. x→0 cosh 2x − e3x2 √ (1 + 2x) − (1 + x)2 −x2 −x2 1 + 2x − 1 − x = √ = √ ∼ 1 + 2x + 1 + x 1 + 2x + 1 + x 2 1
cosh 2x − e3x2 = (cosh 2x − 1) − (e3x2 − 1) ∼ (2x)2 − 3x2 = −x2 2 x2 − 1 I = lim 2 = . x→0 −x2 2 1 1 1 i) e x2 − cos 1 e x2 − 1 + 1 − cos 1 3 I = lim x2. x = lim x2. x = lim x2 + 1 2x2 . π x2. π = x→+∞ arctan x x→+∞ π 2 x→+∞ 2 Chú ý 1 x→+∞
−−−−→ 0 nên ta áp dụng công thức cho 1 . x x
arctan x → π là hằng số nên được thế số ngay từ đầu. 2 1.3.4 Vô cùng lớn
Định nghĩa 1.14 ( Vô cùng lớn) .
Hàm số f(x) được gọi là một vô cùng lớn (VCL) khi x → x0 nếu lim |f(x)| = +∞ x→x0
Tính chất VCL tương tự VCB. Ví dụ 1.20
a) f(x) = 2x2 − 3 sin x là VCL khi x → ∞. Vì lim f(x) = lim 2x2 − 3 sin x = +∞. x→0 x→∞ b) 1 1 f (x) = là VCL khi x → 1. Vì lim = +∞. x − 1 x→1 x − 1
Đại học Bách khoa TPHCM Trang 26
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.3. GIỚI HẠN HÀM SỐ
Định nghĩa 1.15 (cấp vô cùng lớn) f (x)
Cho f(x), g(x) là 2 VCL khi x → x0 và lim = k x→x g(x) 0
i) Nếu k = ∞ thì ta nói f(x) có bậc VCL cao hơn g(x), ta viết f(x) = O(g(x)).
ii) Nếu k hữu hạn khác 0 thì ta nói f(x) và g(x) là 2VCL cùng cấp.
iii) Nếu k = 1 thì ta nói f(x) và g(x) là 2 VCL tương đương: f(x) ∼ g(x).
iv) Nếu f(x) (x − x0)k thì ta nói f(x) là VCL bậc k.
Tính chất cho các VCL tương đương khi x → x0
f (x) ∼ f1(x), g(x) ∼ g1(x) i) f(x)g(x) ∼ f1(x)g1(x)
ii) Tổng f1(x) + g1(x) gọi là dạng triệt tiêu nếu f(x) có bậc VCL cao hơn f(x) + g(x).
Nếu không phải dạng triệt tiêu thì
f (x) + g(x) ∼ tổng bậc thấp cao iii) f (x) f1(x) lim = lim x→x g(x) g 0 x→x0 1(x) Chú ý:
• Sau khi thay tương đương cộng lại mà mất đi bậc cao nhất thì là dạng triệt tiêu.
• Thay VCL tương đương dạng tổng thì cần kiểm tra tổng không phải dạng triệt tiêu.
• Các bài toán VCL có thể chuyển về VCB bằng cách đặt ẩn.
Ví dụ 1.21 Tính giới hạn a) 3x3 − 2x2 3x3 lim = lim = 3. x→∞ 1 − 2x2 + x3 x→∞ x3 √ √ √ b) 2x4 − 4x3 + 3x − 2 2x4 + 3x 2x2 lim √ = lim √ = lim = 0 3 3 x→+∞ 2x3 − 2x + x3 x→∞ 2x − x x→+∞ −2x3 √ √ c) 3x2 − 4 x6 − 3x2 3x2 − 4 x6 −4x3 lim √ = lim √ = lim = +∞ x→+∞ 1 + 2x − 5x2 x→+∞ 2x − 5x2 x→+∞ −5x2 d) x2 + ln30(x + 1) − 2x + 4x 4x 4 lim = lim = . x x x→+∞ 3 − 4x6 + 5.4 x→+∞ 5.4x 5
Đại học Bách khoa TPHCM Trang 27
ThS.Nguyễn Hữu Hiệp 1.3. GIỚI HẠN HÀM SỐ
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC √ √ e) 1 I = lim x2 + 2x − 3 x3 + x2. Đặt t = → 0. Suy ra x→+∞ x √ √ 1 + 2t − 3 1 + t I = lim q − 3 t2 + 2t q t3 + 1t2 = lim t→0+ t √ √ 1 1 1 + 2t − 1 + 1 − 3 1 + t t − t 2 = li 3 t→ m 0+ = lim = . t 3 t→0+ t→0+ t Bài tập
Bài 1) Sắp xếp các hàm số sau theo thứ tự tăng dần của bậc VCL √
(a) x → +∞ : 3x + ln3 x, x ln x, 3x, x(2 + sin4 x)
(b) x → +∞ : 2x, x2, x2 + sin4 x, x ln x √ (c) x → +∞ :
3x2 + 1 ln(2x), x ln(x2 + 3), x ln x Đáp án: √ a)
3x, x(2 + sin4 x) ≈ 3x + ln3 x, x ln x
b) x ln x, x2 ≈ x2 + sin4 x, 2x c) Bằng nhau hết.
Bài 2) Tính các giới hạn √ √ √ √ √ (a) lim x2 + 2x + x x4 + 6x3 − 3x2 + x4 2x2 + 1 − 3x + x2 x→±∞ (c) lim √ (e) lim x→−∞ x2 − 1 x→+∞ x ln(ex − x) + 3 sin 2x + 2 arcsin 3x (b) 3x2 + 1 p lim( )x2 (d) lim √ √ (f) lim x→∞ 3x2 − 1 x5 + x x x→+∞ x − x4 + 2x2
x→0 ex − ln(1 + 3x − sin(x)) Đáp án: √ √ a) lim x2 + 2x + x = +∞, lim x2 + 2x + x = −1 x→+∞ x→−∞ √ b) 3 e2 c)
Bài 3) Tính giới hạn hàm số bằng cách thay VCB tương đương (a) 2x − 1 lim e1/x2 (g) − cos 1 lim x2 x x→0 sin 3x x→+∞ arctan x (b) sin x − 1 lim 1 1 (h) 1 lim ( − ) x→ π2 tanh2(x − π2 ) x sin x tan x √ √ x→0 5 1 + 10x 1 + 3x 1 (c) − 3 (i) lim(cosh x) lim 1−cosx x→0 x→0 arcsin(3x) − tanh(x3) xx − 1 (d) 1 (j) lim lim(1 − tan2 x) sin2 x x ln x x→0 x→0+ √ √ cos x − 3 cos x (e) sin 5x − 3x2 (k) lim lim x→0 ln(cosh 2x) x→0+ x + ln x 1 (f) 1 1 lim(cos x)x2 (l) lim(e x + )x x→0 x→±∞ x
Đại học Bách khoa TPHCM Trang 28
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.4. HÀM SỐ LIÊN TỤC (m) 1 − cos x cos 2x ex − x − 1 lim (p) lim x→0 ex2 − cosh x x→0 x2 √ (n) x2 1 + x cos x 1 + 2x lim √ (q) − lim 3 x→0 1 + 3x − 1 − x √ √ x→0 x2 1 + tan x 1 + sin x (o) − lim x→0 x − x cosh x
Bài 4) Tính giới hạn hàm số bằng cách thay VCB tương đương √ √ √ 1 − n x (a) 1 + x + x2 − 7 + 2x − x2 lim (e) lim x→2 2x − x2 x→1 cosh( iπ 2 x) (b) lim x(ln(x + a) − ln x) x→+∞ (f) tan3 x − 3 tan x lim (c) xα − aα lim , α > 0 x→ π cos(x + π 3 6 ) x→a x − a (d) xa − ax xx − x lim , a > 0 (g) lim . x→a x − a x→1 ln x
1.4 Hàm số liên tục
Định nghĩa 1.16 (liên tục) Cho hàm số y = f(x).
i) f(x) gọi là liên tục tại x0 nếu lim f(x) = f(x0). x→x0
Nếu f(x) không liên tục tại x0 thì ta nói f(x) gián đoạn tại x0.
ii) f(x) gọi là liên tục trái tại x0 nếu lim f(x) = f(x0). x→x−0
iii) f(x) gọi là liên tục phải tại x0 nếu lim f(x) = f(x0). x→x+ 0
iv) f(x) gọi là liên tục trên (a, b) nếu nó liên tục tại mọi điểm x0 ∈ (a, b).
v) f(x) gọi là liên tục trên [a, b] nếu nó liên tục trên (a, b) và liên tục trái tại b, liên tục phải tại b.
Chú ý: f(x) liên tục tại x0 nếu i) f(x) xác định tại x0 ii) tồn tại lim f(x) iii) lim f(x) = f(x0). x→x0 x→x0
f (x) liên tục tại x0 nếu nó vừa liên tục trái, vừa liên tục phải tại x0.
Định nghĩa 1.17 (hàm sơ cấp) Các hàm hằng, lũy thừa, mũ, logarit, lượng giác, lượng giác ngược,
hàm hyperbolic và các hàm thu được từ các hàm này qua các phép toán cộng, trừ, nhân, chia, căn,
hợp gọi là các hàm sơ cấp. Tính chất
i) Các hàm sơ cấp liên tục trên miền xác định của nó.
ii) f(x) liên tục trên đoạn [a, b] thì đạt Max, min trên đó.
Đại học Bách khoa TPHCM Trang 29
ThS.Nguyễn Hữu Hiệp 1.4. HÀM SỐ LIÊN TỤC
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC
Ví dụ 1.22 Xét tính liên tục hàm số. √ x2 − x, x 6= 1 x − 1 . a) 1, x = 1 f (x) = √ Tại x2 − x x0 6= 1 : f(x) =
là hàm sơ cấp nên liên tục. x − 1 √ Tại x2 − x 3 x0 = 1 lim f (x) = lim =
6= f(1) = 1 =⇒ f(x) gián đoạn tại x0 = 1. x→1 x→1 x − 1 2 sin x, x 6= 0 |x| . b) 1, x = 0 f (x) = Tại sin x x0 > 0 : f (x) =
là hàm sơ cấp nên liên tục. x Tại sin x x0 < 0 : f (x) =
là hàm sơ cấp nên liên tục. −x Tại sin x sin x x0 = 0 : lim f(x) = lim = 1 = f (1), lim f (x) = lim = −1 6= f(1). x→0+ x x→0+ x→0− x→0− −x
Vậy hàm số liên tục phải tại x0 = 1 nhưng không liên tục trái tại x0 = 1 do đó không liên tục tại x0 = 1. Ví dụ 1.23 2x2 + a, x < 0 b, x = 0 liên tục trên R. 1
a) Tìm a, b để f(x) = arctan , x > 0 x
Tại x > 0 và x < 0 thì f(x) là những hàm số sơ cấp nên liên tục. π Tại 1
x0 = 0 : lim f (x) = lim 2x2 + a = a, lim f (x) = lim arctan = , f (0) = x→0− x→0− x→0+ x→0+ x 2 b. π
f liên tục trên R khi và chỉ khi a = b = . 2 ( liên tục trên R. x2 + ax + b, |x| > 1 b) Tìm x, |x| ≤ 1 a, b để f (x) =
Tại x > 1, −1 < x < 1 và x < −1 thì f(x) là những hàm số sơ cấp nên liên tục.
Ta chỉ cần xét tại x0 = ±1
Ta có f(1) = 1, f(−1) = −1. lim f (x) = lim x = 1 = f (1),
lim f (x) = lim x2 + ax + b = 1 + a + b, x→1− x→1− x→1+ x→1+
lim f (x) = lim x = −1 = f(−1),
lim f (x) = lim x2 + ax + b = 1 − a + b, x→−1+ x→−1+ x→−1− x→−1−
f liên tục trên R khi và chỉ khi ( ( 1 + a + b = 1 a = b 1 = −1. ⇐⇒ 1 − a + b = −1
Định lý giá trị trung gian
Cho f(x) liên tục trên [a, b] và f(a).f(b) < 0.
Khi đó f(x) có ít nhất một nghiệm trong (a, b).
Đại học Bách khoa TPHCM Trang 30
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC 1.4. HÀM SỐ LIÊN TỤC
Ví dụ 1.24 Phương trình xex − 1 = 0 có ít nhất một nghiệm trong (0, 1), vì f(0).f(1) = −1.(e − 1) < 0. Bài tập
Câu 1) Xét tính liên tục của hàm số
sin x − cos x + 1 nếu x 6= 0, x sin( 1) Nếu x < 0, x x a Nếu x = 0, a, nếu x = 0, a) f(x) = e2x − b c) Nếu x > 0. f (x) = ae3x − 1 x nếu x 6= 0, x nếu b) b, x = 0, β Nếu x = 0. f (x) = d) xα ln(x2) Nếu x 6= 0, f (x) =
Câu 2) Chứng minh các phương trình sau
a) x2.3x = 1 có ít nhất 1 nghiệm.
b) 2x = 4x có ít nhất 2 nghiệm.
Đại học Bách khoa TPHCM Trang 31
ThS.Nguyễn Hữu Hiệp 1.4. HÀM SỐ LIÊN TỤC
CHƯƠNG 1. GIỚI HẠN VÀ LIÊN TỤC
Đại học Bách khoa TPHCM Trang 32
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.1 Đạo hàm
2.1.1 Định nghĩa và tính chất
Định nghĩa 2.1 (Đạo hàm tại một điểm) f (x) − f(x0) ∆f f ′(x = lim 0) = lim x→x x − x ∆x 0 0 ∆x→x0
∆f = f (x) − f(x0) gọi là gia số của hàm tại x0.
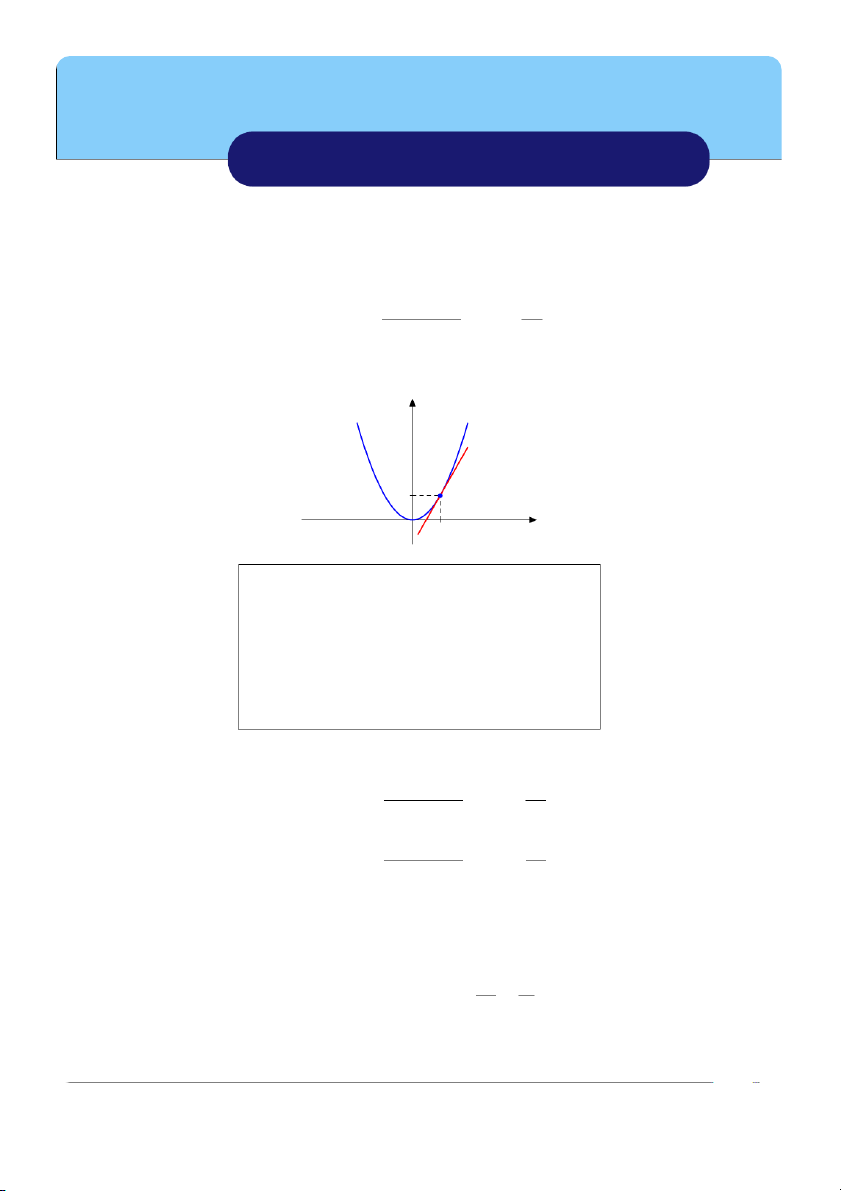
∆x = x − x0 gọi là gia số của biến tại x0. y y = f (x) 1 ϕ : tan ϕ = f ′(1) 0 1 x Tính chất
Hệ số góc của tiếp tuyến tại x0 k = f ′(x0), (k = tan ϕ)
Phương trình tiếp tuyến tại x0 y = k(x − x0) + y0.
Định nghĩa 2.2 (Đạo hàm một bên) .
Đạo hàm phải tại x0: f (x) − f(x0) ∆f f ′(x+0 ) = lim = lim x→x+ x − x ∆x 0 0 ∆x→x+0
Đạo hàm trái tại x0: f (x) − f(x0) ∆f f ′(x−0 ) = lim = lim x − x ∆x x→x−0 0 ∆x→x−0
Hàm f có đạo hàm tại x0 nếu nó có đạo hàm trái và đạo hàm phải và chúng bằng nhau.
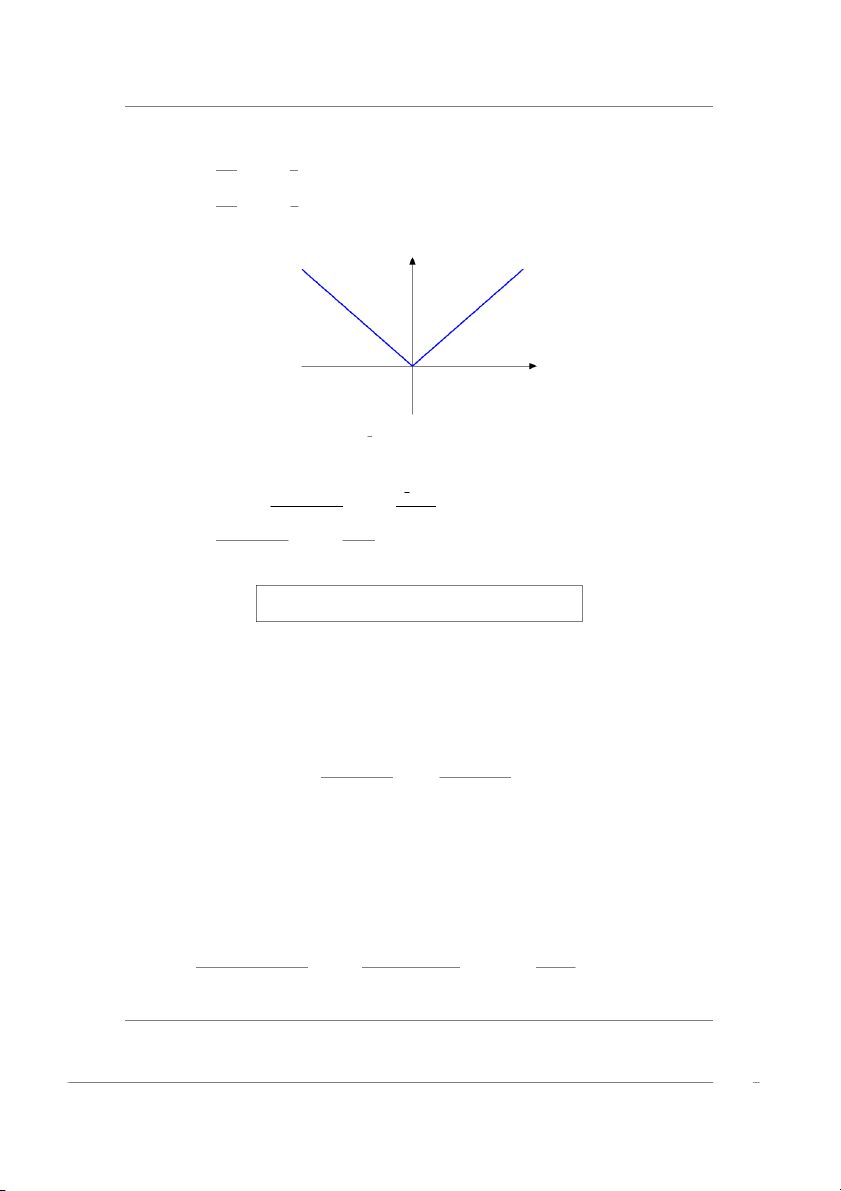
Ví dụ 2.1 Cho hàm số f(x) = |x|. Tính f′(0). Ta có ∆f |x|
∆f = f (x) − f(0) = |x| − |0| = |x| ∆x = x − 0 =⇒ = ∆x x 33 2.1. ĐẠO HÀM
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
Ta không thể tích giới hạn trực tiếp khi x → 0 mà phải tính giới hạn trái và giới hạn phải. ∆f x f ′(0+) = lim = lim = 1 ∆x x x→0+ x→0+ ∆f x f ′(0−) = lim = lim = −1 ∆x x x→0− x→0−
Vì đạo hàm trái và phải khác nhau nên hàm số không có đạo hàm tại x0 = 0. y y = |x| 0 x x , x 6= 0 ( tại x0 = 0. 1 e0, x = 0.
Ví dụ 2.2 Tính đạo hàm của f(x) = 1 f (x) − f(0) e x − 0
Bài làm f′(0+) = lim = lim = +∞. x x→0+ − 0 x→0+ x − 0 f (x) − f(0) 0 − 0 f ′(0−) = lim = lim = 0. x→0− x − 0 x→0− x − 0
Vậy hàm số không tồn tại đạo hàm tại 0. Tích nhất
Hàm số có đạo hàm tại x0 thì liên tục tại đó. (
có đạo hàm tại x0 = 0. x20, x = 0 Ví dụ 2.3 + ax + b x Tìm 6= 0 a, b để f (x) = Bài làm
f liên tục tại x0 = 0 khi và chỉ khi lim(x2 + ax + b) = 0 ⇐⇒ b = 0. x→0
f có đạo hàm tại x0 = 0 khi và chỉ khi giới hạn sau tồn tại hữu hạn f (x) − f(0) x2 + ax − 0 lim = lim = a. x→0 x − 0 x→0 x − 0 Vậy ∀a ∈ R, b = 0. (
có đạo hàm tại x0 = 0. aex x2 − a, x ≤ 0
Ví dụ 2.4 Tìm − b x > 0 a, b để f (x) = Bài làm
f liên tục tại x0 = 0 khi và chỉ khi lim (aex − b) = lim (x2 − a) ⇐⇒ a − b = −a ⇐⇒ b = 2a. x→0+ x→0−
f có đạo hàm tại x0 = 0 khi và chỉ khi (ax2 − 2a) − (−a) (x2 − a) − (−a) x2 − 1 lim = lim ⇐⇒ lim a = 0 ⇐⇒ a = 0. x x x x→0+ − 0 x→0− − 0 x→0+ Vậy a = b = 0.
Đại học Bách khoa TPHCM Trang 34
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.1. ĐẠO HÀM
Bảng công thức đạo hàm 1. C′ = 0(C = const)
3. (ex)′ = ex, (ax)′ = ax ln a
2. (xα)′ = αxα−1, α 6= 0 4. (ln |x|)′ = 1, (log x a x)′ = 1 x ln a 5. (sin x)′ = cos x. 7. (sinh x)′ = cosh x. 6. (cos x)′ = − sin x. 8. (cosh x)′ = sinh x. 9. 1 1 (tan x)′ = 10. (cot x)′ = − cos2 x sin2 x 11. 1 1 (arcsin x)′ = √ . 13. (arctan x)′ = . 1 − x2 1 + x2 12. 1 √ 1 (arccos x)′ = −√ . 14. (ln(x + x2 + k))′ = 1 − x2 x2 + k
Đạo hàm tổng, tích, thương i) (u + v)′ = u′ + v′. iii) (uv)′ = u′v + uv′ ii) (αu)′ = αu′. ′ u′v − uv′ v2 iv) u = v
Đạo hàm hàm hợp Cho hàm số y = f(u), u = u(x) f ′(x) = f ′(u).u′(x)
Ví dụ 2.5 Tính đạo hàm a) 2x
f (x) = x arcsin(x2 + 1) =⇒ f′(x) = 1. arcsin(x2 + 1) + x. p . 1 − (x2 + 1)2 √ √ b) x f (x) = arctan2
x2 + 1 =⇒ f′(x) = 2. arctan x2 + 1. x2 + 1 c) f(x) = xx.
Lấy eln: f(x) = eln xx = exln x =⇒ f′(x) = exln x.(x ln x)′ = xx.(ln x + 1). √1 + x2 d) arctan3 x. 5 f (x) = arcsin4 x √ arctan3 x. 5 1 + x2 ln Lấy eln: f(x) = e arcsin4 x = e3 ln arctan x+ 1 ln(1+ 5 x2)−4 ln arcsin x
=⇒ f′(x) = f(x).(3 ln arctan x + 15 ln(1 + x2) − 4 ln arcsin x)′ 2x 4 + − (1 + x2) 3arctan x 5(1 + x2) = f (x) √ . 1 − x2 arcsin x
Đại học Bách khoa TPHCM Trang 35
ThS.Nguyễn Hữu Hiệp 2.1. ĐẠO HÀM
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.1.2 Đạo hàm hàm ngược và hàm tham số hóa
Đạo hàm hàm ngược cho hàm số y = f(x) có hàm ngược x = g(y) 1 1 g′(y) = hay x′(y) = f ′(x) y′(x) ( xy = y(t)
Đạo hàm hàm cho bởi tham số = x(t) y = y(x) : y′(t) y′(x) = x′(t) Ví dụ 2.6 1
Chứng minh công thức đạo hàm hàm ngược (arctan x)′ = và (arcsin x)′ = 1 + x2 1 √ . 1 − x2 Bài làm
a) Xét y = arctan x ⇐⇒ x = tan y. Theo công thức 1 1 1 1 y′(x) = = = = . x′(y) tan′ y 1 + tan2 y 1 + x2
b) Xét y = arcsin x ⇐⇒ x = sin y. Theo công thức 1 1 1 1 y′(x) = = = = 1 √ . x′(y) sin′ y cos y p = 1 1 − sin2 y − x2 Ví dụ 2.7 .
a) Cho y = f(x) = x3 + x. Tính (f−1)′(2).
b) Cho y = f(x) = e3x + 2x. Tính (f−1)′(1). Bài làm 1 a) 1 y 2 ′
0 = 2 =⇒ x0 = 1, f ′(x) = 3x + 1 =⇒ (f −1) (2) = = f ′(1) 4 b) 1 1
y0 = 1 =⇒ x0 = 2, f′(x) = 3e3x + 2 =⇒ (f−1)′(1) = = . f ′(0) 5
Ví dụ 2.8 Tính đạo hàm hàm cho bởi tham số
Đại học Bách khoa TPHCM Trang 36
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.1. ĐẠO HÀM ( ( √ tại x0 = x = a cos3 t y = ln(t + t2 − 3) 1. x = t3 + 3t y = y(x) : 2. y1 = 4. y(x) : y = a sin3 t. Bài làm a.3 cos2 t(− sin t) a) y′(t) y′(x) = = = − cot t x′(t) a.3. sin2 t cos t 1 √ 1 1 b) y′(t) 1 x = t2−3 = . 0 = 14 ⇐⇒ t0 = 2. y′(x) = x′(t) =⇒ y′(x 3t2 + 3 0 = 14) = 15 15
2.1.3 Đạo hàm cấp cao
Định nghĩa 2.3 Đạo hàm cấp n của hàm số y = f(x) được định nghĩa theo truy hồi f (n)(x) = (f (n−1)(x))′. Công thức leinitz
(f.g)(n) = C0nf(0)g(n) + C1nf(1)g(n−1) 2
+ C nf(2)g(n−2) + · · · + Cnnf(n)g(0)
với quy ước f(0)(x) = f(x), g(0)(x) = g(x).
Dễ dàng kiểm tra bằng quy nạp các công thức đạo hàm cấp n của các hàm số thường gặp sau
Công thức đạo hàm cấp n
i) ((x + a)α)(n) = α(α − 1)(α − 2). . . . .(α − n + 1)(x + a)α−n. (−1)nn! = (n) 1 (x + a)n+1 =⇒ ii) (eax)(n) = x an + .ea a x. iii) (−1)n−1(n − 1)! (ln x)(n) = xn nπ iv) nπ (sin ax)(n) = an sin(ax + ) v) (cos ax)(n) = an cos(ax + ) 2 2 Chú ý: • (uv)(n) 6= u(n).v(n) • (uv)(n) 6= u(n).v + u.v(n) Ví dụ 2.9 99!2100 a) (−1)9999!.2100 (ln(2x + 3))(100) = = . (2x + 3)100 (2x + 3)100 1 (−1)n.n! 1 = ( − n) 1 x (n) 1 − 2 (x −12)n+1 − b) 1 x2 − 4 4 x + 2 4 (x + 2)n+1
Đại học Bách khoa TPHCM Trang 37
ThS.Nguyễn Hữu Hiệp 2.2. VI PHÂN
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN cos 2x 1 π π −
= 0 − 2n. cos(2x + n ). = −2n−1. cos(2x + n ). 2 (n) 2 2 2 c) ( 1 sin2 x n) = 2
d) f(x) = (3x2 + 1) ln x. Tính f(100)(1).
Áp dụng công thức leinitz với: u = 3x2 + 1, v = ln x =⇒ u′ = 6x, u′ = 6, u(k) = 0, ∀k ≥ 3.
f (100)(x) = C0100u(0)v(100) + C1100u(1)v(99) + C2100u(2)v(98) (−1)9999! (−1)9898! (−1)9797! = 1.(3x2 + 1). + 100.6x. + 4950.6. x100 x99 x98 =⇒
f (100)(1) = −4.99! + 600.98! − 29700.97! = −9708.97! ( tại x0 = −1 xy = t2 + t Ví dụ 2.10 = tet
Tính đạo hàm cấp 1 và cấp 2 của hàm số − 1 y = f (x) : Bài làm
a) x0 = −1 ⇐⇒ tet − 1 = −1 ⇐⇒ t = 0. y′(t) 2t + 1 1 f ′(x) = = =⇒ f′(x0 = −1) = = 1. x′(t) (t + 1)et 1 x = tet − 1 2t + 1 y′ = b) Ta có f′(x) : (t + 1)et (y′)′(t)
2(t + 1)et − (2t + 1)(t + 2)et 2 − 2 =⇒ f′ (x) = = =⇒ f′ (x = 0. x′(t) ((t + 1)et)3 0 = 1) = 13
Có thể áp dụng công thức sau
Đạo hàm cấp 2 hàm tham số
y′ (t)x′(t) − x′ (t)y′(t) y′ (x) = x′3(t)
Tính lại đạo hàm cấp 2
2.(t + 1)et − (t + 2)et.(2t + 1) y′ (x) = ((t + 1)et)3 2.2 Vi phân Vi phân cấp 1
f (x) khả vi tại x0 khi và chỉ khi f (x) có đạo hàm tại x0 df (x0) = f ′(x0).dx
Đại học Bách khoa TPHCM Trang 38
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.2. VI PHÂN √
Ví dụ 2.11 Tính vi phân của hàm số y = 1 + x2 tại x0 = 1. Bài làm x 1 dy = y′dx = √ dx =⇒ dy(1) = √ dx. 1 + x2 2
Tính chất của vi phân được suy trực tiếp từ tính chất của đạo hàm Tính chất i) d(α) = 0 iv) d(fg) = fdg + gdf ii) d(αf) = αdf iii) . d(f + g) = df + dg g2 v) f f dg − gdf d = g Vi phân hàm hợp Cho hàm hợp ( =⇒ y = y(u(x)) y = u y = (u u()x) dy = y′(x)dx = y′(u)du
Vi phân cấp 1 có tính bất biến ( xy = y(t) Vi phân hàm tham số = x(t) y = y(x) : y′(t) dy = y′(x)dx = dx x′(t)
Ví dụ 2.12 Tính vi phân hàm số 1
a) Cho hàm y = eu, u = arctan . Tính dy(x = 1) theo dx. x (
. Tính dy(x = 1) theo dx. x = y e = 2tt3++tt b) Cho hàm số y(x) : Bài làm
a) Ta có thể tính y′(x) = y′(u).u′(x) rồi thế x = 1 vào suy ra vi phân.
Có thể tính cách khác như sau: π x0 = 1 =⇒ u0 = 4 π
dy = y′(u)du = eudu =⇒ dy(x = 1) = e 4 du(x = 1) − 1 −1 −1 du = u′(x)dx = x2 dx = dx =⇒ du(x = 1) = dx 1 + 1 1 + x2 2 x2 Vậy 1 dy(x = 1) = − π e4 dx. 2
Đại học Bách khoa TPHCM Trang 39
ThS.Nguyễn Hữu Hiệp 2.2. VI PHÂN
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 3t2 + 1 1 b) y′(t) x = 1 ⇐⇒ t = 0. y′(x) = = =⇒ dy(x = 1) = dx. x′(t) 2e2t + 1 3
Công thức gần đúng
f (x) ≈ f(x0) + df(x0) = f(x0) + f′(x0)(x − x0)
Ví dụ 2.13 Không dùng máy tính, tính gần đúng giá trị của e0.1. Bài làm
Xét f(x) = ex =⇒ f′(x) = ex, x0 = 0, x = 0.1.
f (x) ≈ f(x0) + f′(x0)(x − x0) ⇐⇒ e0.1 ≈ e0 + e0(0.1 − 0) = 1 + 0.1 = 1.1 (giá trị gần đúng khi
dùng matlab tính là 1.1052). Vi phân cấp cao dnf (x) = f (n)(x)dx
Vi phân cấp 2 hàm hợp cho y = y(u), u = u(x)
d2y = y′ (u)du2 + y′(u)d2u.
Vi phân cấp 2 không còn tính bất biến. Tính vi phân cấp 2, cần xác định biến cần tính.
Ví dụ 2.14 Tính vi phân cấp 2 hàm số 1
a) Cho hàm y = eu, u = arctan . Tính d2y(x = 1) theo dx. x (
. Tính d2y(x = 1) theo dx. x = y e = 2t t3 + + tt b) Cho hàm số y(x) : Bài làm
a) Ta có thể thế y = earctan 1x rồi tính y′ (x) từ đó suy ra vi phân.
Có thể tính dùng công thức d2y = y′ (u)du2 + y′(u)d2u. π −1 2x x0 = 1 =⇒ u0 = .
y′(u) = y′ (u) = eu, u′(x) = , u′ (x) = . 4 1 + x2 (1 + x2)2 −1 1 =⇒ du(x = 1) = dx, d2u(x = 1) = dx2. 2 2
Thế vào công thức với x = 1, u = π ta được 4 π π 1 3 π d2y(x = 1) = e + e 4 . e4 dx2. 2 dx2 = −1 2 4 4 . dx 2 b) x = 1 ⇐⇒ t = 0.
y′ (t)x′(t) + x′ (t)y′(t) 6t.(2e2t + 1) + 4e2t.(3t2 + 1) 4 4 y′ (x) = = =⇒ y′ (x = 1) = = . (x′(t))3 (2e2t + 1)3 33 27 Vậy 4 d2y(x = 1) = dx2. 27
Đại học Bách khoa TPHCM Trang 40
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.3. ĐỊNH LÝ GIÁ TRỊ TRUNG BÌNH
2.3 Định lý giá trị trung bình
Định lý 2.4 (Fermat) Nếu hàm số y = f(x) đạt cực trị tại x0 và có đạo hàm tại x0 thì f ′(x0) = 0.
Định lý 2.5 (Rolle) Cho hàm số y = f(x) liên tục trên [a, b], khả vi trên (a, b) thỏa f(a) = f(b). Khi đó ∃c ∈ (a, b) : f′(c) = 0.
Định lý 2.6 (Lagrange) Cho hàm số y = f(x) liên tục trên [a, b], khả vi trên (a, b). Khi đó f (a) − f(b) ∃c ∈ (a, b) : = f ′(c). a − b
Định lý 2.7 (Cauchy) .
Cho 2 hàm số y = f(x), y = g(x) liên tục trên [a, b], khả vi trên (a, b) và g′(x) 6= 0∀, x ∈ (a.b). Khi đó f (a) − f(b) ∃c ∈ (a, b) : f ′(c) = g(a) − g(b) g′(c) Ví dụ 2.15 .
Cho hàm số y = f(x) khả vi trên [0, 2] thỏa f(0) = −3, f′(x) ≤ 5. Chứng minh rằng f(2) ≤ 7. Bài làm Áp dụng đính lý Lagrange
∃c ∈ (0, 2) : f(2) − f(0) = f′(c)(2 − 0) =⇒ f(2) = f(0) + 2f′(c) ≤ −3 + 2.5 = 7. 2 , π2 ].
Ví dụ 2.16 Chứng minh bất đẳng thức arctan x − arctan y ≤ x − y , ∀x, y ∈ [−π
Chứng minh. Không mất tính tổng quát, giả sử x < y. Xét 1
f (x) = arctan x =⇒ f′(x) = 1 + x2 ≤ 1. Áp dụng công thức Lagrang f (x) − f(y) ∃c ∈ (x, y) : = f ′(c) ≤ 1 =⇒ arctan x − arctan y ≤ x − y x − y
2.4 Công thức H’Lopital
Định lý 2.8 (Quy tắc L’Hopital) f (x) 0 Cho giới hạn lim dạng hoặc ∞. x→x g(x) 0 ∞ 0
Giả sử f(x), g(x) có đạo hàm tại x f ′(x) 0 và giới hạn lim
tồn tại (hữu hạn hoặc vô hạn) thì x→x g(x) 0 f (x) lim = lim f ′(x) x→x g(x) g(x) 0 x→x0
Đại học Bách khoa TPHCM Trang 41
ThS.Nguyễn Hữu Hiệp 2.4. CÔNG THỨC H’LOPITAL
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
Ví dụ 2.17 Tính giới hạn a) x2012 − 1 2012.x2011 lim √ (Dạng 0) = lim (x2012 − 1)′ √ = lim = 4024. x ( x 1 x→1 − 1 0 x→1 − 1)′ x→1 √ 2 x b) . √ √ 1 1 x + 1 − 3 3x − 1 ((x + 1) 2 − (3x − 1) lim (Dạng 0 ) = lim 3 )′ x→3 ln(x − 2) 0 x→3 (ln(x − 2))′ 1 1 √ √ 1 x − 23 .3 2 x+1 − 1 3 (3 √ x−1)2 − 13√ 1 1
= lim 2 (x + 1)− 12 − 13 (3 − 1) = lim = 2. 4 64 = = 0. 1 1 1 − x→3 x→3 4 4 x−2 x−2 1 c) . √cosx − ex −√sin x − ex 0 − 1 lim √ (Dạng 0 ) = lim 2 cos x = = 1 −1 x→0 1 + 2x − 1 0 x→0 √ .2 1 2 1+2x √ 1 1 2012 x x− 2011 2012 .1 1 d) − 1 lim (Dạng 0 ) = lim 2012 = lim 2012 = − x→1 x3 − 3x2 + 2 0 x→1 3x2 − 6x x→1 3 − 6 6036 √ √ −1 √ − − √ 7 −1 1 e) 3 − x − 3 1 − 7x 2 3− 3 3 (1−7x)2 lim (Dạng 0) = lim x 4 + 7 12 = − 2x = x→−1 − 1 0 x→−1 2x −2 6 f) . ln(cos x) − sin x − sin x.(1 − x) sin x (1 − x) lim (Dạng 0 ) = lim cos x = lim = lim . = x→0 ln(1 − x) + x 0 x→0 −1 + 1 x→0 x 1− −x. cos x cos x x x→0 1 − 0 1. = 1 1 g) 2x3 − 6x2 + 8 6x2 − 12x 12x − 12 2.12 − 12 lim (dạng 0 ) = lim (còn dạng 0) = lim = = x→2 x4 − 8x2 + 16 0 x→2 4x3 − 16x 0 x→2 12x2 − 16 12.22 − 16 12 3 = . 32 8
Dùng tương đương kết hợp với H’Lopital
i) Kiểm tra tử hoặc mẫu không phải dạng triệt tiêu thì
dùng tương đương để rút gọn.
ii) Dùng quy tắc H’Lopital để khử dạng triệt tiêu.
iii) Nếu hết dạng triệt tiêu thì có thể dùng tương đương để tính. h) x − sin x 1 − cos x lim
(dạng triệt tiêu 0 ) = lim hết dạng triệt tiêu x→0 sinh x − tan x 0 x→0 cosh x − (1 + tan2 x) tương đương x2 x2 1 ===== lim 2 = lim 2 = 2 = −1. x2 x→0 cosh x − 1 − tan2 x x→0 2 − x2 −12
Đại học Bách khoa TPHCM Trang 42
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.4. CÔNG THỨC H’LOPITAL i) cos 2x + 2x2 − 1 lim
(dạng triệt tiêu 0 ) dùng H’Lopital x→0 3x4 0 −2 sin 2x + 4x −4 cos 2x + 4 4. (2x)2 8 2 = lim = lim = lim 2 = = x→0 12x3 x→0 36x2 x→0 36x2 36 9 j) ex − x − cosh x I = lim x→0 x ln(1 + sin2 2x) x2
Trên tử là dạng triệt tiêu : x2
ex − x − cosh x = ex − 1 − x + 1 − cosh x ∼ x − x − = 0 − . 2 2
Dưới mẫu không phải dạng triệt tiêu: x ln(1 + sin2 2x) ∼ x sin2 2x ∼ x.(2x)2 = 4x3.
Ta dùng tương đương để rút gọn mẫu rồi dùng H’Lopital: ex − x − cosh x
ex − x − cosh x H’Lopital ex − 1 − sinh x I = lim = lim ===== lim x→0 x ln(1 + sin2 2x) x→0 4x3 x→0 4.3x2 ex − cosh x ex − sinh x 1 = lim = lim = . x→0 12.2x x→0 24 24 k) arctan x − sin x I = lim 2 √ . x→0 arcsin x( 1 + 2x − 1)
Dưới mẫu không phải dạng tiêu nên dùng tương đương cho mẫu trước khi dùng H’Lopital: 1 arctan x − sin x arctan x − sin x H’Lopital 1 + x2 − cos x I = lim = lim ===== lim x→0 x2. 1.2x 2 x→0 x3 x→0 3x2 −1.x2 + x2 −1 1
= lim (1 + x2)−1 − 1 + 1 − cos x = lim 2 = 2 = − x→0 3x2 x→0 3x2 3 6 l) x2 2x 2 I = lim (Dạng ∞) = lim (Dạng ∞) = lim = 0. x→+∞ ex ∞ x→+∞ ex ∞ x→+∞ ex
Các dạng vô định 0.∞, 00, ∞0, 1∞
có thể chuyển về dạng 0 và ∞ 0 ∞
Ví dụ 2.18 Tính các giới hạn sau 1 a) ln x lim x ln x (Dạng 0.∞) = lim (Dạng ∞) = lim x = lim −x = 0. x→0+ 1 x→0+ ∞ x→0+ x x→0+ − 1 x2 b) lim xx (Dạng 00) = lim exln x (Dạng 0∞) = e0 = 1 x→0+ x→0+ c) 1 1 x − sin x x − sin x 1 − cos x lim − (Dạng ∞−∞) = lim (Dạng 0) = lim = lim = x x→0 sin x x→0 x sin x 0 x→0 x2 x→0 x2 1 2 Bài tập
Câu 1) Tính đạo hàm y′(x)
Đại học Bách khoa TPHCM Trang 43
ThS.Nguyễn Hữu Hiệp 2.4. CÔNG THỨC H’LOPITAL
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN √ (a) y = (cos x)arcsin x (b) y = (2x2 + 1)arctan x 3x2 (c) sin5(2x + 1) 7 − 1 y = tanh3 x
Câu 2) Tính đạo hàm tại 1 điểm √ √ 3 (a) Cho hàm số x2 + 1. 5 x + 2 f (x) = 7 √ . Tìm f ′(0). x3 + 2 r . Tìm f ′(1). (b) Cho hàm số x x + 1 f (x) = x + √ (x − 1) arcsin
(c) Cho hàm số f(x) = 1 − e−x2. Tìm f′+(0) − f′−(0). 1 , x 6= 0, 1 + e− 1x
. Tính f′(0+) và f′(0−). (d) Cho hàm số 0 f (x) =
Câu 3) Tìm a, b để hàm số khả vi tại x0 = 0. ln(1 + x) Nếu x ≥ 0. ( (a) ax + b Nếu x < 0, cos x + β, x < 0 f (x) = (c) 2x3 + αx, x ≥ 0 f (x) = 1 , x < 0 Nếu x 6= 0, 1 1 + e x x b Nếu x = 0. x2 + αx + β, x ≥ 0. (b) xa sin 1 (d) f(x) = f (x) =
Câu 4) Tính đạo hàm hàm ngược
(a) Cho hàm số f(x) = ex + x. Tính (f−1)′(1). ĐS: 1 . 2 √ √
(b) Cho hàm số y = f(x) thỏa f(ex) = x2 + 1, x > 0. Tính (f−1)′( 2). ĐA: √ e 2.
Câu 5) Tính đạo hàm cấp cao
a) y = (2x + 3) + cos x. Tính y(100)(x).
b) y = arctan(x). Tính y(100)(0), y(101)(0).
Câu 6) Tính đạo hàm cấp 1 tại x = cấp 2 tại t = 1 y = t − arctan t. y = 3t5 − 5t3 + 1. (a) x = ln(1 + t), ln 2. (c) x = t3 − 3t + 1, cấp 2 tại π t = y = r sin t. 4
y = 4t3 − 3t2 cấp 3 tại t = 5. (b) x = r cos t, (d) x = t2 + 4
Câu 7) Tính vi phân các hàm số sau √
(a) y = 1 + u2, u = ex. Tính dy(0), dy2(0), d2y(0) theo du và dx
Tính dy(0), dy2(0), d2y(0) theo dx. x = t3 + 3t. (b) y = t2 + t, ( . Tính dy(0), d2y(0). y = arctan x (c) x = ln(x + 1), y(x)
Câu 8) Dùng quy tắc H’Lopital, tính các giới hạn sau
Đại học Bách khoa TPHCM Trang 44
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.5. CÔNG THỨC TAYLOR (a) 2x3 − 5x5 + 3x4 (m) lim lim cot 2x. cot( π4 − x) x→ π4 x→1 3x7 − 5x4 + 2 (b) 2x3 − 3x2 − 2x x arctan x2 lim (n) − 2 sin2 2x lim x→0 4x4 − x3 − 3 x→0 x cos x − sin x √ (c) ex − x − 1 lim 5 (o) 1 + 5x − x − 1 lim x→0 x2 x→0 x2 (d) ln(1 + x) − x lim (p) lim(arcsin x)tan x x→0 sinh2 x x→0+ (e) ecos x − 1 lim √ 1 (1 + x) x 1 3 (q) lim x→0 1 + 3x − 1 ( )x x→0 e √ (f) lim e−1x 1 + x cos x 1 + 2x (r) − lim x→0+ x100 x→0 x2 (g) ecos x − 1 lim √ tan x − x 3 (s) x→0 1 + 3x − 1 lim (h) x arcsin x − x ln(1 + x) lim ln x ln(1 − x) x→0 x→0+ ln(1 + sin x) − tan x (i) lim(cos x)ln sin x. (t) lim x2 x→0+ x→0 πx 1 (j) tan3 x − 3 tan x (u) lim(tan x lim ) x→+∞ 2x + 1 x→ π cos(x + π 3 6 ) 1 (k) (v) lim lnx lim ( π (tan πx x→+∞ 2 − arctan x) x→1 4 )tan πx2 b (l) lnx lim − arctan 1 (w) lim − 1 π2 a xa x x→+∞ x→1 xb 2.5 Công thức taylor
Công thức taylor của hàm y = f(x) đến cấp n tại x0 f ′(x f ′ (x0) f ′ ′(x0) f (x) = f (x 0) 2 (x 0) + .(x − x (x − x0) + − x0)3 1! 0) + 2! 3! f (n)(x + · · · + 0) (x − x n! 0)n + o(x − x0)n, Trong đó: o(x − x n
0)n là một hàm VCB cấp cao hơn (x − x0) khi x → x0.
công thức Maclaurint là công thức taylor với x0 = 0 f ′(0) f ′ (0) f ′ ′(0) f (n)(0) f (x) = f (0)+ .x+ x2 + x3 +· · ·+ xn +o(xn). 1! 2! 3! n!
Công thức taylor xấp xỉ hàm f(x) bởi một hàm đa thức bậc n Pn(x − x0):
f (x) = Pn(x − x0) + Rn(x − x0),
Rn(x − x0) = o(x − x0)n là phần dư rất bé khi x trong lân cận x0.
Xem o(x − x0)n là phần dư chứa tất cả các bậc lớn hơn n.
Đại học Bách khoa TPHCM Trang 45
ThS.Nguyễn Hữu Hiệp 2.5. CÔNG THỨC TAYLOR
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
Ví dụ 2.19 Khai triển Maclaurint hàm số f(x) = ex − 1 đến các cấp 1,2,3. Bài làm f (0) = 0. f ′(x) = ex =⇒ f′(0) = 1
f ′ (x) = ex =⇒ f′ (0) = 1.
f ′ ′(x) = ex =⇒ f′ ′(0) = 1
Khai triển Maclaurint đến cấp 1: f(x) = 0 + 1.x + o(x1) = x + o(x).
Khai triển Maclaurint đến cấp 2: 1 x2 f (x) = 0 + 1.x + x2 + o(x2) = x + + o(x2). 2! 2 1
Khai triển Maclaurint đến cấp 3: 1 x2 x3 f (x) = 0 + 1.x + x2 + + o(x3) = x + + + o(x3). 2! 3! 2 6 y y = ex − 1 y = x + x22 + x36
• Hình vẽ minh họa cho các đa thức trong khai triển
Maclaurint xấp xỉ với hàm y = x + x22 f (x) trong lân cận x0 = 0. y = x
• Cấp khai triển càng cao thì xấp xỉ càng chính xác. 0 x
Khai triển Maclaurint một số hàm số thường gặp 1. 1
= 1 − x + x2 − x3 + · · · + (−1)nxn + o(xn). 1 + x x2 x3 xn 2. x1 ex = 1 + + + + · · · + + o(xn) 1! 2! 3! n! 3. x2 x3 ln(1 + x) = x − +
− · · · + · · · + (−1)n−1 xn + o(xn) 2 3 n x5 x2n+1 4. x3 sin x = x − + − · · · + (−1)n + o(x2n+2) 3! 5! (2n + 1)! x4 x2n 5. x2 cos x = 1 − + − · · · + (−1)n + o(x2n+1) 2! 4! (2n)! 6. x3 x5 x2n+1 sinh x = x + + + · · · + + o(x2n+2) 3! 5! (2n + 1)! x4 x2n 7. x2 cosh x = 1 + + + · · · + + o(x2n+1) 2! 4! (2n)! α(α 8. α(α − 1) − 1) . . . (α − n + 1) (1+x)α = 1+αx+ x2 +· · ·+ xn +o(xn). 2! n! x5 x2n+1 9. x3 arctan x = x − + + · · · + (−1)n + o(x2n+2) 3 5 2n + 1
Đại học Bách khoa TPHCM Trang 46
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.5. CÔNG THỨC TAYLOR
Khai triển taylor bằng định nghĩa sẽ rất mất công. Ta áp dụng các công thức trên để khai triển. Ví dụ 2.20
a) Khai triển Maclaurint của hàm f(x) = sin 2x đến cấp 4.
Áp dụng công thức sin : x → 2x. (2x)3 4 sin 2x = (2x) − + o(x4) = 2x − x3 + o(x4). 3! 3
b) Tìm khai triển Maclaurint của hàm f(x) = ex+1 đến cấp 3. Vì x + 1 x→0
−−→ 1 6= 0 nên chưa thể dùng công thức cho x + 1. 1 1 e e f (x) = e.ex = e(1 + x + x2 +
x3 + o(x3)) = e + ex + x2 + x3 + o(x3). 2! 3! 2 6
Dùng công thức khai triển
Dùng công thức Maclaurint để khai triển hàm f(u), điều kiện u → 0.
c) Tìm khai triển Maclaurint của hàm 1 f (x) = đến cấp 2. 2 − x Biến đổi 1 1 f (x) = u=1−x −−−−→
= 1 − u + u2 + . . . −→ Sai . 1 + (1 − x) 1 + u Vì u = 1 − x x→0 −−→ 1 6= 0. Ta làm như sau 1 1 1 1 1 1 f (x) = = . u= −x2 −−−→ f = . = (1 − u + u2 + o(u2)) 2 − x 2 1 + −x 2 1 + u 2 2 1 1 1 = ! 2 + x + x2 + 0(x2). −x −x 12 4 8 1 − + + o(x2) = 2 2 2 √
d) Tìm khai triển taylor của hàm f(x) = 3 − 2x tại x0 = 1 đến cấp 2. Đặt t = x − 1 p √ 2 1 f (t) = 3 − 2
1 (t + 1) =1 1 − 2t = (1 − 2t)
= 1 + .(−2t) + 2.−12 .(−2t)2 + o(t2) = 1 − t − t2 + o(t2) = 1 − (x − 1) − (x − 1)2 + o(x − 1)2. 2 2!
Ví dụ 2.21 Khai triển taylor
a) Khai triển Maclautint hàm số 1 + x + x2 f (x) = đến cấp 5. 1 − x + x2 1 Cách 1: (1 + x + x2)(1 + x) f (x) = = (x3 + 2x2 + 2x + 1) = (x3 + 2x2 + 2x + 1)(1 − (1 − x + x2)(1 + x) 1 + x3 x3 + o(x5)) Khai triển 1
= 1 − x3 + (x3)2 + . . . nhưng vì ta cần đến bậc 5 nên bỏ đi bậc 6. Giờ 1 + x3
nhân vào và bỏ đi những bậc lớn hơn 5.
f (x) = 1 + 2x + 2x2 + x3 − x3 − 2x4 − 2x5− 6x6 +o(x6) = 1 + 2x + 2x2 − 2x4 − 2x5 + o(x5).
Cách 2 ta dùng phép chia đa thức theo bậc từ bé đến lớn cho đến khi phần dư có bậc lớn hơn 5.
Đại học Bách khoa TPHCM Trang 47
ThS.Nguyễn Hữu Hiệp 2.5. CÔNG THỨC TAYLOR
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 1 +x +x2 1 -x +x2 0 +2x +0x2 1 +2x +2x2 − 2x4 − 2x5 +0x +2x2 −2x3 +0x2 +0x3 −2x4 +0x4 −2x5 +0x5
Ta suy ra f(x) = 1 + 2x + 2x2 − 2x4 − 2x5 + o(x5).
Phương pháp này khá hiệu quả cho những bài dạng phân thức. Cần đi học để hiểu hơn phương pháp này.
b) Khai triển Maclaurint hàm số y = f(x) = e2x−x2 đến cấp 3. Đặt t = 2x − x2 x→0 −−→ 0. t2 t3 (2x − x2)2 (2x − x2)3 y = et = 1 + t + + + o(t3) = 1 + (2x − x2) + + + o(2x − x2)3 2! 3! 2 6 1 1 2
= 1+2x−x2+ (4x2−4x3 + x4)+ (8x3−12x4 + 6x5 − x6)+o(x3) = 1+2x+x2− x3+o(x3). 2 6 3
Ta cần khai triển đến bậc 3 nên bậc lớn hơn 3 ta bỏ. √
c) Khai triển Maclaurint hàm số y = 1 − 2x2 đến cấp 7.
Đặt t = −2x2 là một VCB bậc 2.
Ta cần khai triển theo t đến cấp 3, vì t bậc 4 tương đương với x bậc 8 > 7. √ 1 1 1 −3 y =
1 + t = 1 + t + 2 . −12 t2 + 2.−12 2 t3 + o(x7) 2 2! 3! 1 1 1 1 1 = 1 + (−2x2) − (−2x2)2 +
(−2x2)3 + o(x7) = 1 − x2 − x4 − x6 + o(x7). 2 8 16 2 2
d) Khai triển Maclaurint y = tan x đến cấp 5. x3 x5 sin x x − + + o(x5) y = = 3! 5! cos x x2 x4 1 − + + o(x4) 2! 4! Thực hiện phép chia 1 1 1 1 x − x3 + x5 1 − x2 + x4 6 120 2 16 1 1 1 2 0x + x3 − x5 x + x3 + x5. 3 30 3 15 2 +0x3 + x5 15 +0x5 2 Vậy 1 y = x + x3 + x5 + o(x5). 3 15
Trong bài này, vì sin x là VCB bậc 1 nên cos x chỉ cần khai triển đến bậc 4 là đủ.
e) Khai triển Maclaurint y = esin x đến cấp 4. 1 1 1 x3 1 1 y = 1 + sin x + sin2 x + sin3 x + sin4 x + o(sin4 x) = 1 + x − + (x − x3 (x)3 + 2! 3! 4! 6 2 6 )2 + 6 1 (x4) + o(x4) 24 x3 1 1 1 1 x2 x4 = 1 + x − + (x2 − x4) + x3 + x4 + o(x4) = 1 + x + − + o(x4). 6 2 3 6 24 2 8
Đại học Bách khoa TPHCM Trang 48
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.5. CÔNG THỨC TAYLOR
f) Khai triển Maclaurint y = ecos x đến cấp 5. 1 y = e1− x2 + x4 + + x4 2 24 o(x5) = e.e− x2 2 2 + x4 24 ) + (−x2 2 2 + x4 e 24 + o(x5) = e 1 + (−x2 x2 + x4 + o(x5) 24 )2 + o(x5) h 2 + x4 24 + x4i e2 6 = e 1 − x2 8 + o(x5) = e −
g) Khai triển Maclaurint của f(x) = ex. ln(1 + x) đến cấp 4.
Vì ln(1 + x) là VCB cấp 1 nên ta khai triển ex đến cấp 3. x3 x3 x4 + + − x2 2! x2 3 f (x) = 1 + x + + 1 o(x3 1 ) x −1 1 1 1 + o(x4) 1 1 = x + (− + 1)x2 1 + ( 3!
− + )x3 + (− + − + 4)x4 + o(x4) = x + x2 + x3 + o(x4) 2 3 2 2 4 3 4 6 2 3
h) Tìm khai triển Maclaurint của x2 f (x) = đến cấp 6. 1 + sin x
Vì trên tử bậc 2 nên ta cần khai triển 1 đến cấp 4. 1 + sin x 1
= 1 − sin x + sin2 x − sin3 x + sin4 x + o(x4) 1 + sin x 5 2 x 3 + (x 4 + o x4) = 1 x3 + x4 + o(x4). 2 − ( ) ) ( − x + x2 − x3 x3 6 3 = 1 − x − 2 2 +3 x − Vậy 5 f (x) = 3 x !− x + x4 3! − x5 + x6 + o(x6). 6 3
Tính đạo hàm cấp n tại 1 điểm bằng khai triển
Dựa vào công thức Taylor, ta suy ra f (n)(x0) = n!Tn,
với Tn là hệ số bậc n trong khai triển taylor của f(x) tại x0.
Ví dụ 2.22 Tính đạo hàm cấp cao
a) Tính y(100)(1) với y(x) = ln x.
Khai triển taylor tại x0 = 1 Đặt u = x − 1 x→1 −−→ 0. Khi đó u2 y = ln(1 + u) = u −
+ . . . + (−1)99 u100 + . . . . 2 100
Hệ số bậc 100 trong khai triển taylor tại −1 x0 = 1 là T100 = . 100 Suy ra −1 y(100)(1) = .100! = −99! 100
b) Tính y(10)(0) với y = (x2 + 1) cos x.
Khai triển Maclaurint y đến cấp 10. Chú ý ta chỉ quan tâm đến bậc 10. x8 x10 y = (x2 + 1)(· · · + − + o(x10)). 8! 10! 1
Hệ số bậc 10 trong khai triển là 1 T10 = − . 8! 10! 1 − Suy ra 1 8! y(10)(0) = 10! = 10.9 − 1 = 89. 10!
Tìm VCB tương đương
Muốn tìm một hàm lũy thừa tương đương với hàm
f (x), ta khai triển f (x) cho đến bậc đầu tiên khác 0.
Đại học Bách khoa TPHCM Trang 49
ThS.Nguyễn Hữu Hiệp 2.5. CÔNG THỨC TAYLOR
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
Ví dụ 2.23 Tìm hàm lũy thừa tương đương với các VCB sau
a) f(x) = ex − x − cos 2x khi x → 0. x2 (2x)2 5 5 f (x) = (1 + x + ) − x − (1 − ) + o(x2) = x2 + o(x2) ∼ x2. 2 2 2 2
Chú ý: o(x2) gồm những bậc lớn hơn 2. Tổng VCB ta lấy VCB bậc thấp nên bỏ đi o(x2). √
b) f(x) = 1 − 2x + x − cos x khi x → 0. 1 1 1 1
f (x) = (1 − x − x2 − x3) + x − (1 − x2 x3 + o(x3) ∼ − x3. 2 2 2 ) + o(x3) = −2 2 √ √
c) f(x) = 1 + x − 1 − x − x khi x → 0. x3 x3 f (x) = (1 + x22 − x28 + x3 16 ) − (1 − x2 2 − x2 8 − x3 + o(x3) . 16 ) − x + o(x3) = ∼ 8 8 d) x2
f (x) = ln(1 + sin x) − tan x + khi x → 0. 2 sin3 x x2 x2 x3 + ) + − + sin2 2 x x3 3 x3 6 2 f (x) =x2 sin x x3 − − (x + + o(x3) = x − − (x + ) + + o(x3) 3 2 3 3 2 x3 x3 = − + o(x3) ∼ − . 6 6
Ứng dụng khai triển Taylor để tính giới hạn dạng 00 Cho giới hạn f (x) lim dạng 0 x→x g(x) 0 0
Ta khai triển tử mẫu, tìm đại lượng tương đương và thế vào giới hạn.
Ví dụ 2.24 Tính các giới hạn sau x3 x3 x2 (x + ) − (x − ) + o(x3) 1 a) tan x − sin x lim = lim 3 6 = lim 3 = . x→0 x3 x→0 x3 x→0 x3 2 x3 x4 4 x3 − 2(x − ) + 2x(1 − ) + o(x3) x3 b)
ln(1 + x3) − 2 sin x + 2x cos x2 lim = lim 6 2 = lim 3 = x→0 x3 x→0 x3 x→0 x3 4 . 3 √ c) 1 + 2 tan x − ex + x2 I = lim . x→0 arcsin x − sin x Khai triển tử tan2 x tan3 x x2 x3 T = (1 + tan x − − ) − (1 + x + + ) + x2 2 2 2 6 x3 x2 x3 x2 x3 2 2 = (1 + x + − + ) − (1 + x + + ) + x2 = x3 + o(x3) ∼ x3. 3 2 2 2 6 3 3 x3 x3 x3 Khai triển mẫu x3 M = arcsin x − sin x = (x + ) − (x − ) + o(x3) = + o(x3) ∼ . 6 6 3 3 2 x3 Vậy I = lim 3 = 2. x→0 x3 3
Đại học Bách khoa TPHCM Trang 50
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN 2.5. CÔNG THỨC TAYLOR
Ví dụ 2.25 Tính gần đúng cos 0.1 bằng cách khai triển taylor đến cấp 4.
Chọn x0 = 0 gần giá trị x = 0.1 cần tính mà cos x0 = 0.1. Ta khai triển Taylor hàm cos x tại x0 x2 x4 0.12 0.14 cos x = 1 − + + o(x4) =⇒ cos 0.1 ≈ 1 − + đến bậc 4. 2 4! 2 24 0.01 0.0001 ≈ 1 − + ≈ 0.995004166. 2 24
Giá trị cos 0.1 theo máy tính là 0.995004165278026. Bài tập
Câu 1. Khai triển taylor f(x) đến cấp n tại x0 (a) 2x + 1 f (x) = , x (k) f(x) = ln(1 + tan x), x , n 0 = 1, n = 2. 0 = 0 = 4 x + 2 √ √ (l) f(x) = x, n = 4, x0 = 1
(b) f(x) = (x + x2) 1 − 2x2, n = 4, x0 = x 0. (m) f(x) = , n = 2, x0 = 2 x + 1 (c) 2 + 3x f (x) = ln . x2 3 + 2x (n) f(x) = , n = 4, x0 = 0 2x2 − x − 1 (d) cos 2x f (x) = , x0 = 1, n = 3 ln(1 − x) 1 + ln(1 − x) (o) f(x) = , n = 3, x0 = 0 (1 + x)2 (e) e−x tan x f (x) = √ , x0 = 1, n = 3 2x − 1 (p) f(x) = = 5 0 = 0 ex2 , n , x
(f) f(x) = sinh x ln(1−2x), x0 = 0, n = 4 (q) f(x) = arcsin2 x, n = 4 √ (g) √
f (x) = arctan x. 1 + 2x, x0 = 0, n =
(r) f(x) = ( 1 + x2 − 1) sin(x + π6), n = 3 4, x0 = 0
(h) f(x) = esin 2x, x0 = 0, n = 4
(s) f(x) = ecos x, n = 5, x0 = 0
(i) f(x) = ecos 2x, x0 = 0, n = 7
(t) f(x) = sin cosh x, x0 = 0, n = 2. (j) √ f (x) = x sin x, x0 = 1, n = 2
(u) f(x) = (1 + x2)sin x, x0 = 0, n = 3.
Câu 2. Tìm α, β để f(x) ∼ g(x) = αxβ khi x → x0:
(a) f(x) = ex − x − cos 2x, x0 = 0 x2 √
(i) f(x) = ln(1+ sin x)−tan x+ , x0 =
(b) f(x) = 1 − 2x + x − cos x, x 2 0 = 0 0.
(c) f(x) = ex − cosh x − sin x √ √
(j) f(x) = cos x − 4 cos 2x, x (d) 0 = 0 f (x) = 3 1 + 3x − cos x − ln(1 + √ √ x), x
(k) f(x) = x4 + 2x3 − 3 x6 + 3x5, x 0 = 0 0 = √ √ (e) ∞ f (x) =
x + 1 − 1 − x − x, x0 = 0 √ √ √
(f) f(x) = ex − 1 + 2x + 2x2, x
(l) f(x) = 1 − 2x2 − 3 1 − 3x2, x0 = 0 0 = 0
(g) f(x) = 1 − x + x ln x, x0 = 1
(m) f(x) = cos x2 − x sin x − e−x2, x0 = 0 √ (h) f(x) = (1 + x2 (n) 2 ) sin x − tan x, x0 = 0
f (x) = cos x − cos 2x, x0 = 0
Câu 3. Tính giới hạn cấp n tại 1 điểm
Đại học Bách khoa TPHCM Trang 51
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN √
(a) Cho f(x) = 3 2x − 1. Tính f(3)(1), f(4)(1)
(b) Cho f(x) = (1 + x2)e2x−1. Tính f(10)(0).
(c) Cho f(x) = (x2 + 1) ln x. Tính f(10)(1). (d) Cho x2 f (x) = . Tính f(10)(0), f(11)(0). 2 + x3 (e) Cho 1 + x f (x) = . Tính f(10)(0), f(11)(0). 1 − x + x2
Câu 4. Tính giới hạn bằng khai triển Maclaurint. (a) ex − 1 − x (1 + 2x)x − cosh 2x lim (g) lim x→0 1 − cosh x x→0 arctan x − arcsin x (b) arcsin x − xex lim √ ex − 1 + 2x + 2x2 x→0 x − tan x (h) lim x + tanx − sin2x (c) e2x − cos x − sin 2x lim x→0 x→0 ln(1 − x) + arcsin x 1 √ e(1 (i) − x x lim 2 ) − (1 + x) (d) 1 + 2x − cos x + x lim x→0 ln(1 − x) + sinh x x→0 2 sin x − tan 2x √ √ 1 + 2x − 1 − 2x (e) − sin 2x ex + ln(1 − sin x) − 1 lim (j) lim √3 x→0 x cos x − sin x x→0 8 − x3 − 2 √ 3 2x2 1 + 3x2 − x cot x − arcsin x − xex (f) lim 3 (k) lim √ x 1 − x2 x→0 x cos x − arcsin x x→0 − tan x
2.6 Khảo sát và vẽ đồ thị 2.6.1 Tiệm cận
Thuật toán tìm tiệm cận cho hàm số y = f(x)
i) limf(x) = ±∞ −→ tiệm cận đứng x = a. x→a
ii) lim f(x) = b −→ tiệm cận ngang y = b. x→∞
iii) Nếu lim f(x) = ∞, ta tìm tiệm cận xiên x→∞ f (x) lim = a x→∞ x −→ tiệm cận xiên lim f (x) − ax = b x→∞ y = ax + b.
Có thể tìm tiệm cận xiên y = ax+b bằng cách khai triển f (x) = ax + b + α(x)
với α(x) là 1 VCB khi x → ∞.
Đại học Bách khoa TPHCM Trang 52
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
Ví dụ 2.26 Tìm tiệm cận các hàm số sau a) arctan 2x y = . TXD: D = R ⊂ {0, 1}. x(1 − x)
Tìm tiệm cận đứng tại những điểm gián đoạn: arctan 2x lim
= 2 −→ x = 0 không là tiệm cận đứng. x→0 x(1 − x) arctan 2x lim
= ∞ −→ tiệm cận đứng x = 1. x→1 x(1 − x) arctan 2x lim
= 0 −→ tiệm cận ngang y = 0. x→∞ x(1 − x) b) ln(1 + x) y =
+ 2x. TXD: D = (−1, 0) ∩ (0 + ∞). x ln(1 + x) lim
+ 2x = +∞ −→ tiệm cận đứng x = −1. x x→−1+ ln(1 + x) lim
+ 2x = 1 −→ x = 0 không là tiệm cận đứng. x→0 x ln(1 + x) lim
+ 2x = +∞ −→ không có tiệm cận ngang. Ta tìm tiệm cận xiên. x→+∞ xln(1 + x) +2x ln(1 + x) a = lim x = 2, b = lim = x→+∞ x ln(1 + x) x→+∞ x 0,. + 2x −2x = lim x→+∞ x Tiệm cận xiên y = 2x. ln(1 + x) Cách khác ln(1 + x) y = 2x + . Vì lim
= 0 nên y = 2x là tiệm cận xiên. x x→+∞ x r
. TXD: D = (−∞, 0] ∩ (2, +∞). x − 2 c) x3 y = lim r
= +∞ −→ tiệm cận đứng x = 2. x3 x − 2
lim = +∞ −→ không có tiệm cận ngang. Ta tìm tiệm cận xiên: x x→ →2+ ∞ 2 2 r r 1 . + o( 1 x3 x 2 1 2 x − 2 x → +∞ : f(x) =2 = |x| = x 1 + = x 1 + ) . = x + 1 + x − + 2 o( 1 tiệm cận xiên y = x + 1. x−2 ) −→ x − 2 x − 2 x−2 x − 2 2 2 r r 1 . + o( 1 x3 x 2 1 2 x − 2 x → −∞ : f(x) = 2 = |x| = −x 1 + = −x 1 + x − 2 − o( 1
→ tiệm cận xiên y = −x − 1. x−2 ) − x − 2 x − 2 x−2 ) . = −x − 1 − x − 2 d) 1
y = (x + 2)e x . TXD D = R ⊂ {0}. 1
lim (x + 2)e x = +∞ −→ tiệm cận đứng (bên phải, ở trên) x = 0. x→0+ 1
lim (x + 2)e x = 2.0 = 0 −→ x = 0 không là tiệm cận đứng bên trái . x→0− + o( 1
+ (x + 2)o( 1 ) −→ y = x + 3 là tiệm cận x 1 x 2 x x xi→ ên.∞ : y = (x + 2) 1 + ) = x + 3 + x
Đại học Bách khoa TPHCM Trang 53
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6.2 Chiều biến thiên và cực trị
Chiều biến thiên cho hàm số y = f(x) có đạo hàm trên (a, b).
loại trừ tại một số hữu hạn điểm
f ′(x) > 0, ∀x ∈ (a, b) −−−−−−−−−−−−−−−−−→ f(x) tăng trong (a, b).
loại trừ tại một số hữu hạn điểm
f ′(x) < 0, ∀x ∈ (a, b) −−−−−−−−−−−−−−−−−→ f(x) giảm trong (a, b).
Trong định lý trên, tại vài điểm mà f′(x) = 0 hoặc không xác định thì vẫn khẳng định được f (x) đơn điệu. Ví dụ 2.27
Xét f(x) = x3 =⇒ f′(x) = 3x2 > 0, ∀x 6= 0.
Ngoại trừ điểm 0 thì f′(x) dương nên suy ra f(x) tăng trên R. Cực trị
i. (điều kiện cần) cho f(x) có đạo hàm tại x0.
x0 là điểm cực trị của f −→ f′(x0) = 0
ii. (điều kiện đủ 1) cho f(x) liên tục tại x0 và có đạo hàm
trong lân cận x0 (có thể loại trừ tại điểm x0).
f ′ đổi dấu từ (+) sang (−) −→ f đạt cực đại tại x0.
f ′ đổi dấu từ (−) sang (+) −→ f đạt cực tiểu tại x0.
iii. (điều kiện đủ 2) cho f có đạo hàm cấp 2 tại x0 và f′(x0) = 0.
f ′ (x0) < 0 −→ f(x) đạt cực đại tại x0.
f ′ (x0) > 0 −→ f(x) đạt cực tiểu tại x0.
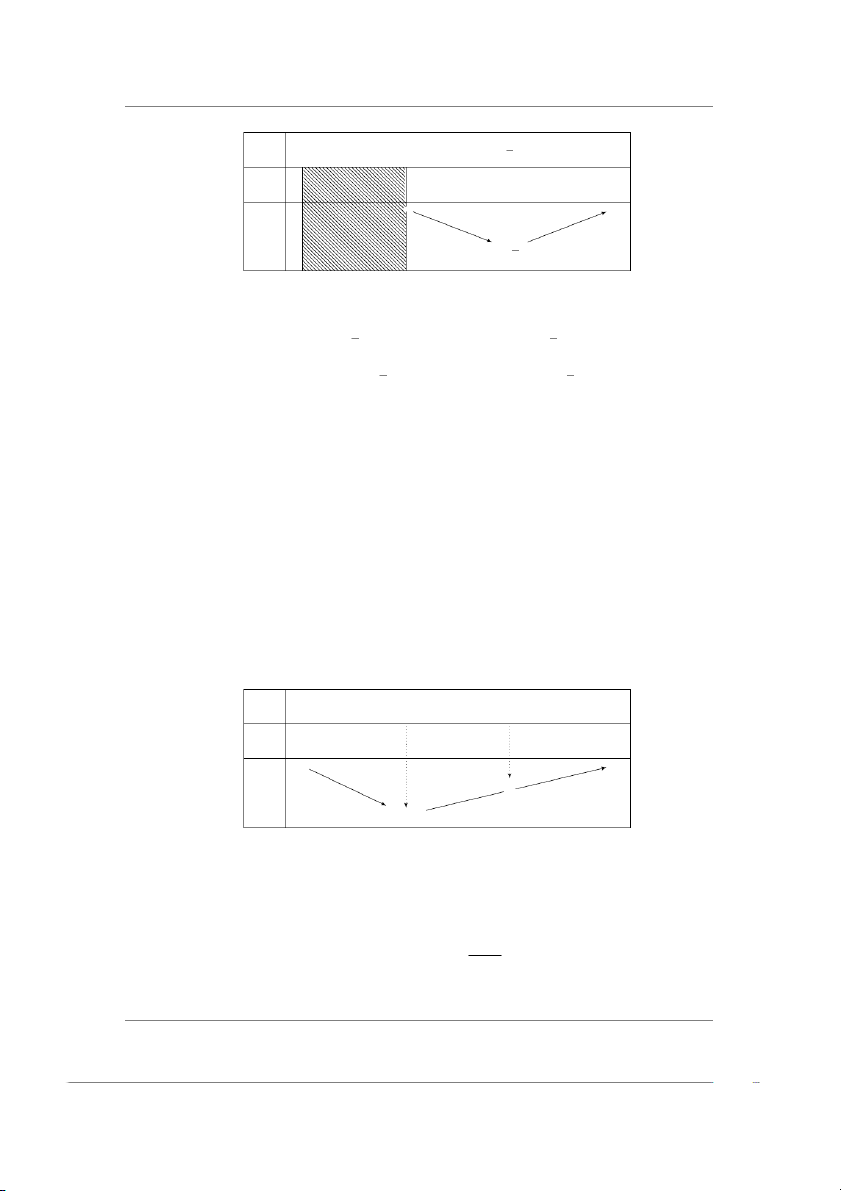
Ví dụ 2.28 Khảo sát tính đơn điệu và cực trị hàm số y = x ln x • TXD: D = (0, +∞) 1 1
• y′ = 1 + ln x. y′ = 0 ⇐⇒ ln x = −1 ⇐⇒ x = e−1 = =⇒ y = − . e e • Bảng biến thiên
Đại học Bách khoa TPHCM Trang 54
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ 1 x −∞ 0 +∞ e f ′(x) − 0 + f (x) 1 −e • Kết luận 1
– Hàm số đồng biến trên 1
( , +∞) và nghịch biến trên (0, ). e e 1
– Hàm số đạt cực tiểu tại 1 x0 =
và giá trị cực tiểu là y e 0 = − e
Ví dụ 2.29 Tìm cực trị hàm số y = −x3 + 3x.
TXD: D = R. y′ = −3x2 + 3. y′ = 0 ⇐⇒ −3x2 + 3 = 0 ⇐⇒ x = ±1.
y′ = −6x : y′ (1) = −6 < 0.y′ (−1) = 6 > 0.
Vậy hàm số đạt cực đại tại 1 và cực tiểu tại −1.
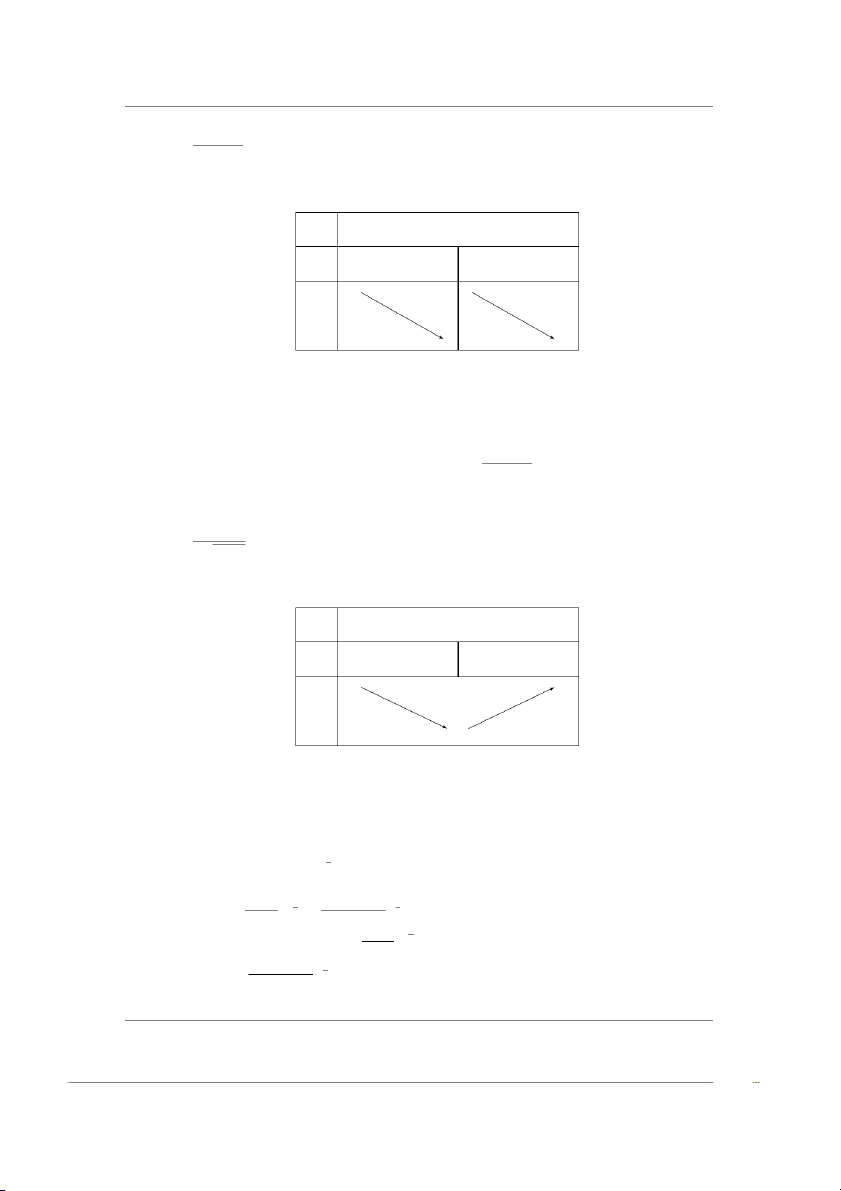
Ví dụ 2.30 Khảo sát tính đơn điệu và cực trị hàm số y = x4 + 4x3 • TXD: D = R
• y′ = 4x3 + 12x2 = 4x2(x + 3). x = 0 =⇒ y = 0 x = −3 =⇒ y = −27 y′ = 0 ⇐⇒ • Bảng biến thiên x −∞ −3 0 +∞ f ′(x) − 0 + 0 + f (x) 0 −27 • Kết luận
– Hàm số đồng biến trên (−3, +∞) và nghịch biến trên khoảng (−∞, −3).
– Hàm số đạt cực tiểu tại x0 = −3. Ví dụ 2.31 x + 1
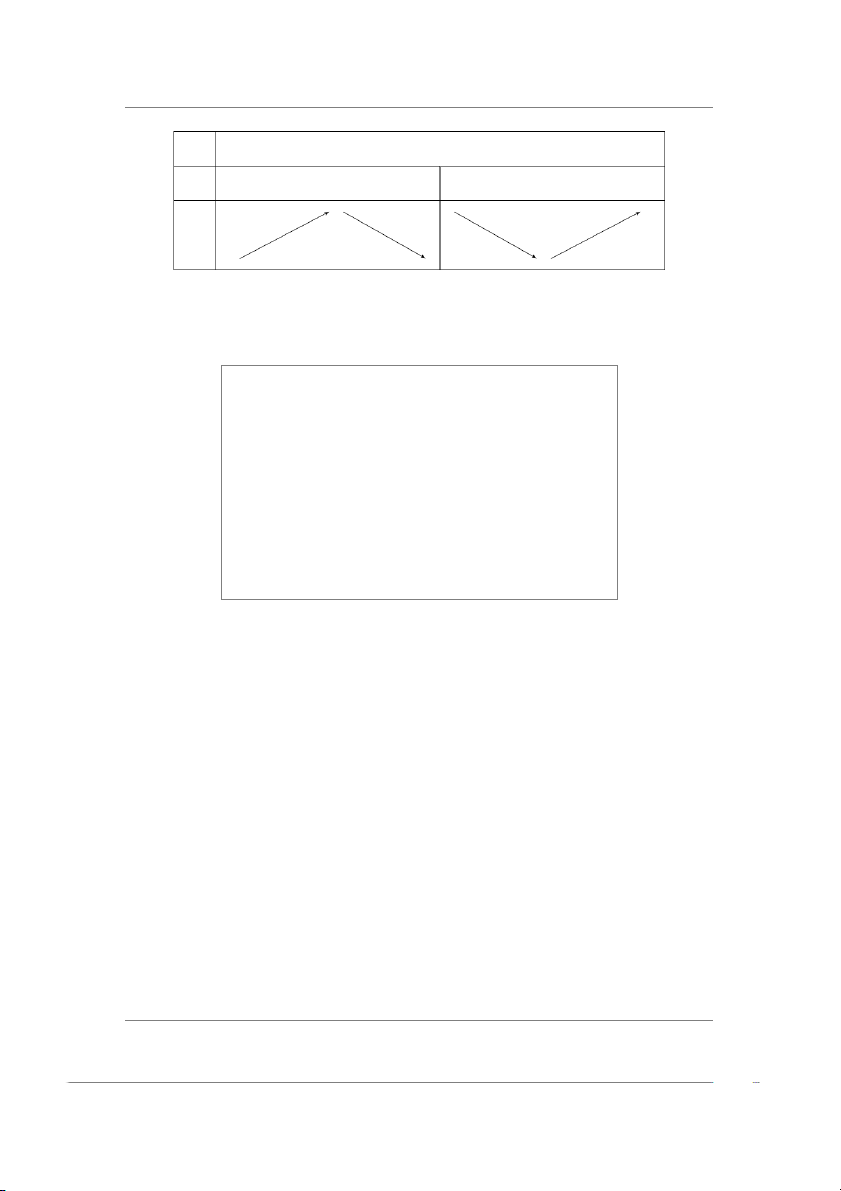
Khảo sát tính đơn điệu và cực trị hàm số y = x − 1 • TXD: D = R\{1}
Đại học Bách khoa TPHCM Trang 55
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN −2 • y′ = < 0, ∀x ∈ D. (x − 1)2 • Bảng biến thiên x −∞ 1 +∞ f ′(x) − − f (x) • Kết luận
– hàm số nghịch biến trên (−∞, 0) và (0, +∞).
– Hàm số không có cực trị
Ví dụ 2.32 Khảo sát tính đơn điệu và cực trị hàm số y = 3 p(x − 1)2 • TXD: D = R 2 • y′ = √ < 0, ∀x ∈ D. 3 3 x − 1 • Bảng biến thiên x −∞ 1 +∞ f ′(x) − + f (x) 0 • Kết luận
– hàm số nghịch biến trên (−∞, 1) và đồng biến trên (1, +∞).
– Hàm số đạt cực tiểu tại x0 = 1.
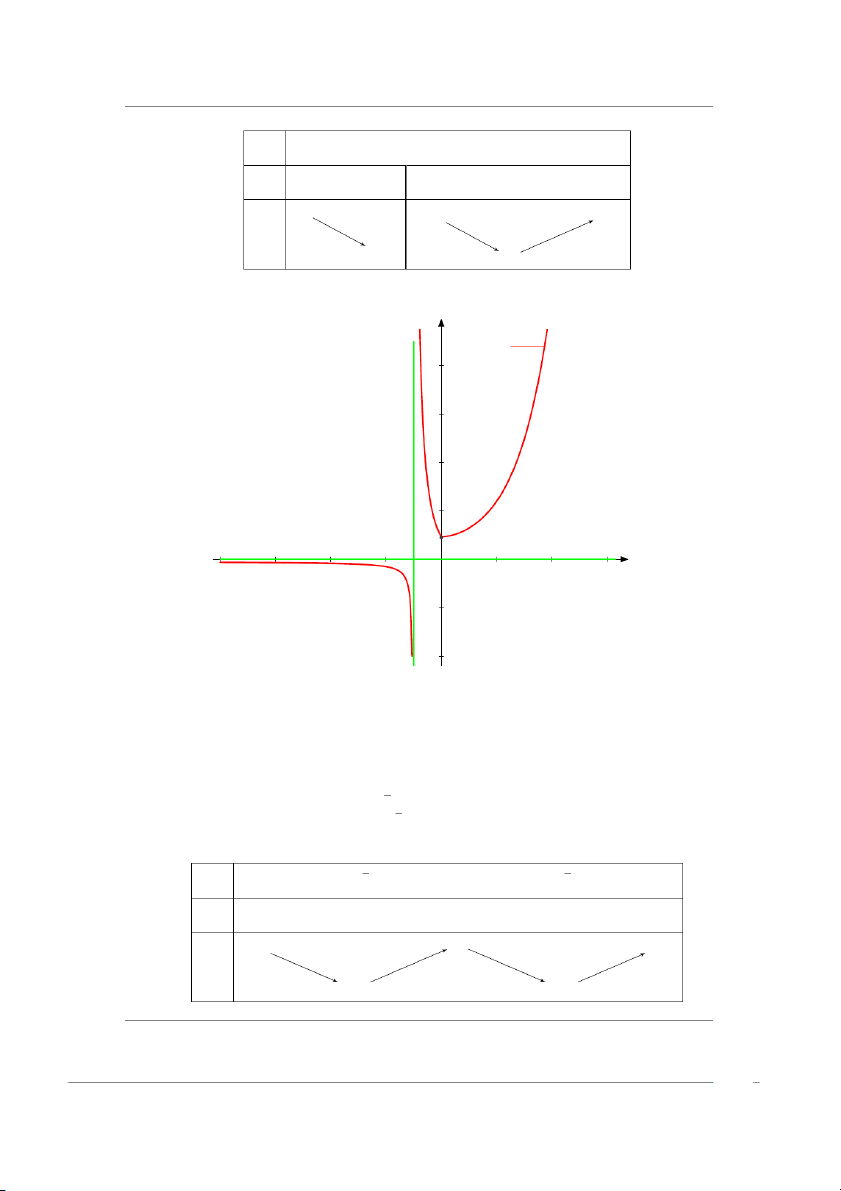
Ví dụ 2.33 Cho 1
f (x) = (x + a)ex . Tìm a để f (x) đạt cực đại tại x0 = 2. Ta có x + a x2 − x − a f ′(x) = (1 − 1 1 )ex = e x . x2 x2 2 − a√
f (x) đạt cực trị tại x ′ 0 = 2 thì f (2) = e = 0 ⇐⇒ a = 2. 4 Với x2 − x − 2 1 a = 2 : f ′(x) = ex x2 Bảng biến thiên
Đại học Bách khoa TPHCM Trang 56
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ x −∞ −1 0 2 +∞ f ′(x) + 0 − − 0 + f (x)
Vậy không tồn tại a thỏa yêu cầu bài toán.
2.6.3 Lồi, lõm và điểm uốn
Lồi, lõm và điểm uốn
Cho hàm số y = f(x) liên tục trên (a, b).
loại trừ 1 số hữu hạn điểm
f ′ (x) < 0, ∀x ∈ (a, b) −−−−−−−−−−−−−−→ f(x) lồi trên (a, b).
loại trừ 1 số hữu hạn điểm
f ′ (x) > 0, ∀x ∈ (a, b) −−−−−−−−−−−−−−→ f(x) lõm trên (a, b).
x0 ∈ (a, b) ngăn cách giữa khoảng lồi và lõm thì (x0, f(x0)) là điểm uốn.
Nếu f có đạo hàm cấp 2 tại x0 và (x0, f(x0)) là điểm uốn thì f ′ (x0) = 0.
Ví dụ 2.34 Xét tính lồi, lõm và điểm uốn của hàm số f(x) = x3 − 3x2.
TXD: D = R, f′ (x) = 6x − 1.
f ′ (x) > 0, ∀x ∈ (1, +∞) −→ f(x) lõm trên (1, +∞).
f ′ (x) < 0, ∀x ∈ (−∞, 1) −→ f(x) lồi trên (1, +∞).
Điểm (1, −2) ngăn cách giữa lồi và lõm nên là điểm uốn của đồ thị hàm số.
Ví dụ 2.35 Tìm a.b để hàm số f(x) = ax3 + 6x2 + bx đạt điểm uốn tại (1; 3).
TXD D = R, f′ (x) = 6ax + 12 xác định tại 1. ( ( ( . f ′ (1) = 0 6a + 12 = 0 a = b − = 2 −1 (1; 3) là điểm uốn thì ⇐⇒ ⇐⇒
Dễ dàng thử lại với a f = (1 − )2, = b 3 = −1 thì (1; a 3)+l 6 à + điểb =
m u3ốn của đồ thị hàm số.
Ví dụ 2.36 Tìm a.b để hàm số f(x) = x4 + ax3 + b đạt điểm uốn tại (0; 3).
f ′ (x) = 12x2 + 6ax. (0, 3) là điểm uốn nên ( ( . f ′ (0) = 0 ∀a b ∈ = R 3 ⇐⇒ Vfớ(i0b) = = 03: f′ (x) = 12x2 + 6ax.
Nếu a = 0 thì f′ (x) = 12x2 ≥ 0 không đổi dấu qua 0 nên (0, 3) không là điểm uốn.
Nếu a 6= 0 thì f′ (x) = 12x2 + 6ax đổi dấu qua 0 nên (0, 3) là điểm uốn. Vậy a 6= 0, b = 3.
Đại học Bách khoa TPHCM Trang 57
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6.4 Khảo sát hàm số
Các bước khảo sát hàm số
1. Tìm miền xác định, tính chẵn lẻ, tuần hoàn. 2. Tìm đạo hàm cấp 1.
3. Tìm đạo hàm cấp 2 (bước này có thể bỏ qua).
4. Tính các giới hạn và tìm tiệm cận. 5. Lập bảng biến thiên.
6. Tìm điểm đặc biệt và vẽ. Chú ý
• Hàm f(x) gọi là hàm số chẵn nếu ∀x ∈ D =⇒ −x ∈ D và f(−x) = f(x).
Đồ thị hàm số chẵn đối xứng qua trục Oy. Khi khảo sát hàm chẵn, ta chỉ cần khảo sát
phần x > 0, phần x < 0 được lấy đối xứng với phần x < 0 qua trục Oy.
• Hàm f(x) gọi là hàm số lẻ nếu ∀x ∈ D =⇒ −x ∈ D và f(−x) = −f(x).
Đồ thị hàm số chẵn đối xứng qua gốc O. Khi khảo sát hàm lẻ, ta chỉ cần khảo sát phần
x > 0, phần x < 0 được lấy đối xứng với phần x < 0 qua O.
• Nếu tồn tại số bé nhất T > 0 sao cho f(x + T ) = f(x) thì ta nói f(x) tuần hoàn với chu kỳ T .
Vẽ đồ thị hàm số tuần hoàn, ta chỉ cần khảo sát trên một chu kỳ rồi lấy tịnh tiến phần
vừa vẽ được theo phương ngang một khoảng kT, k ∈ Z. Ví dụ 2.37 ex
Khảo sát và vẽ đồ thị hàm số y = x + 1 • TXD: D = R\{−1}. • Tìm tiệm cận ex ⋆ lim
= ∞ : tiệm cận đứng x = −1. x→−1 x + 1 ex ⋆ lim
= 0 : tiệm cận ngang y = 0. x→−∞ x + 1 ex H’Lopital ex y ex H’Lop 2 lần ⋆ lim ===== lim = +∞ : a = lim = lim ===== +∞. x→+∞ x + 1 x→+∞ 1 x→+∞ x x→+∞ x(x + 1)
Vậy hàm số không có tiệm cận ngang. xex • y′ =
.y′ = 0 ⇐⇒ x = 0 =⇒ y = 1 (x + 1)2 Bảng biến thiên
Đại học Bách khoa TPHCM Trang 58
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ x −∞ −1 0 +∞ f ′(x) − − 0 + 0 +∞ +∞ f (x) −∞ 1 • Đồ thị y x = −1 ex y = x + 1 8 6 4 2 A y = 0 x −8 −6 −4 −2 0 2 4 6 −2 −4
Ví dụ 2.38 Khảo sát và vẽ đồ thị y = x4 − 6x2 + 3. • TXD: D = R.
• lim f(x) = +∞. Hàm đa thức bậc 3 không có tiệm cận. x→∞ x = 0 =⇒ y = 3 √ x = 3 =⇒ y = −6 √ x = 3 =
• y′ = 4x3 − 12x.y′ = 0 ⇐⇒ − ⇒ y = −6 Bảng biến thiên √ √ x −∞ − 3 0 3 +∞ f ′(x) − 0 + 0 − 0 + +∞ 3 +∞ f (x) −6 −6
Đại học Bách khoa TPHCM Trang 59
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN x = −1 =⇒ y = −2 x = 1 =⇒ y = −2
• y′ = 12x2 − 12.y′ = 0 ⇐⇒ Bảng xét dấu y′ x −∞ −1 1 +∞ f ′ (x) + 0 − 0 + Đths f(x) Lõm Lồi Lõm • Đồ thị y 6 4 2 x −4 −2 0 2 4 −2 −4 −6
Ví dụ 2.39 Khảo sát và vẽ đồ thị hàm số: y = 3p(x−1)2.(x−4) • TXD D = R. 3 2 1 ) = x−2+α(x) −→ x 1 3 4 2 4 • xti → ệm∞ cậ :n yx = iê x n y 1 = − x − 2. x 1 − x = x 1 − 1 − +xo( 1 3x 3x x − 3 • y′ = 3p . (x Bảng − 1)(x biến thiê − 4)2 n x −∞ 1 2 4 +∞ f ′(x) + − 0 + + 0 +∞ f (x) 0 √ −∞ − 3 2 • Đồ thị
Đại học Bách khoa TPHCM Trang 60
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
2.6.5 Tìm giá trị lớn nhất - giá trị nhỏ nhất Tìm max min
1. Tìm max - min trên toàn miền xác định: dựa vào bảng biến thiên
2. Tìm max - min trên đoạn [a, b].
Bước 1) Tìm điểm tới hạn trên (a, b).
Bước 2) So sánh giá trị của f(x) tại các điểm tới hạn và tại a, b suy ra Max, min.
Ví dụ 2.40 Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau
a) y = x2e−x trên đoạn [−1, 3]. x = 2 Nhận x = 0 (Nhận)
• y′ = (2x − x2)e−x. y′ = 0 ⇐⇒ 4 9
• y(0) = 0, y(2) = , y(−1) = e, y(3) = . e2 e3
Vậy: min y = 0 tại x0 = 0 và max y = e tại x0 = −1. [−1,3] [−1,3]
b) y = 3p(x−1)2.(x−4)trênđoạn[0,5].
Đại học Bách khoa TPHCM Trang 61
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN x − 3 • y′ = 3p . y′ = 0 ⇐⇒ x = 3. (x Các điể − 1)(x m tới hạ− 4)2 n: x1 = 3, x2 = 1, x3 = 4. √ √ √
• y(4) = y(1) = 0, y(3) = − 3 4, y(0) = − 3 4, y(5) = 3 16. √ √
Vậy min y = − 4 và maxy = 3 16 [0,5] [0,5] Cách khác
Đặt g = y3 = (x − 1)2.(x − 4). Vì hàm y 7→ y3 là hàm tăng nên f và g cùng cực trị.
g′(x) = 3(x − 1)(x − 3). g′(x) = 0 √ √ ⇐⇒ x = 1 √ ∨ x = 3. √ √
y(1) = 0, y(3) = − 3 4, y(0) = − 3 4, y(5) = 3 16. Vậy min y = − 4 và max y = 3 16 [0,5] [0,5]
c) f(x) = xx trên D = (0, +∞). . e 1 f ′(x) = ex ln x ′ = xx(1 + ln x). y′ = 0 ⇐⇒ x = Bảng biến thiên 1 x −∞ 0 +∞ e f ′(x) − 0 + 1 +∞ f (x) −1 e e
Dựa vào bảng biến thiên ta suy ra min −1
f (x) = e e và không tồn tại max. D Bài tập
Câu 1) Tìm cực trị của các hàm số sau: √ (a) y = 3 x2 − 2x ( (b) 1 y = xx xex, x < 0 (i) x2 − 2x, x ≥ 0 f (x) = (c) 1 y = e (j) f(x) = x |x3 + x| − 2x2 x2 (d) 1 (k) 2 y = ln(e + ) y = |x|e x (l) y = |x2 − 4x| + 3 (e) 1 y = (x + 2)ex (m) y = √ |x2 − 4x| + 2x (f) y = 3 x3 + 3x2 √
(n) f(x) = 3 x3 − x2 − x + 1 √ (g) y = x 3 4 − x (o) f(x) = x lnx (h) y = ex4−2x2+3 (p) f(x) =|x|(x + 3)
(q) f(x) = x3 + 3x2 + ax. Tìm a để hàm số có 2 cực trị.
(r) f(x) = x3 + 3x2 − ax + b. Tìm a, b để hàm số đạt cực tiểu tại (−1, 2).
(s) f(x) = x4 + 3x3 − ax + b. Tìm a, b để hàm số đạt cực đại tại (1, 2).
Câu 2) Tìm tiệm cận của các hàm số sau:
Đại học Bách khoa TPHCM Trang 62
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ (a) 1 y = xx (l) y = 3r + x − 2 (b) 1 y = e x + 2 arctan x x x3+ 2 (c) 1 3 − x2 y = ln(e + ) (m) y = x 1 + x4 (d) 1 y = (x + 2)ex (n) ln x y = (e) y = ln(1 − 1) x x √ 2x2 + ln(1 + 1)
(o) f(x) = 3 x3 − x2 − x + 1 (f) y = x x + 1 (p) x − 2 f (x) = √ (g) 1 y = 1 + x2 1 1 + e x √ (h) y = 3 x3 + 3x2 ( √ y = t3 − 3t2 (i) x = arctan t y = x2 + 2x + x (q) y(x) : √ (j) 1 t2 + 1 y = ex x2 + 4x x = t2 − t (k) x2 t3 + 1 y = √ y = x2 − 2x (r) y(x) : t − 1
Câu 3) Tìm khoảng lồi lõm và điểm uốn 1) f(x) = xe−x. ( −x2,x < 0 2) x2 − 2x, x ≥ 0 f (x) =
3) Tìm a, b để đồ thị hàm số y = x4 + 3x3 − ax2 + bx có điểm uốn là (1, 2).
4) Tìm a, b để đồ thị hàm số y = x4 − 4x3 + ax2 + bx có điểm uốn là (1, 2).
Câu 4) Khảo sát và vẽ đồ thị của các hàm số sau: (a) 1 x 2x f (x) = xx (h) f(x) = (x − 1)e x−1 (m) f(x) = e1−x2 (b) 1 f (x) = + 2 arctan x (i) f(x) = 2x + 2 − x q x−1 + x (c) 3 3 f (x) = x − 2 arctan x p (n) f(x) = x3−4x (o) x f (x) = (x − 1)ex−1 (d) f(x) = |x3 + x| − 2x2. (x + 1)2 (j) e−x f (x) = 2x (p) 1−x2 (e) 1 1 f (x) = e f (x) = e − x x 1 1 e− 1 (q) x f (x) = e (f) ex f (x) = (k) f(x) = p x − 2 1 − x x x(x + 2) ( (g) 1 f (x) = (x + 2)ex (l) f(x) = 3 xex, x < 0 p (r) x2 − 2x, x ≥ 0 f (x) = (x − 1)2(x − 3)
Câu 5) Tìm giá trị lớn nhất và nhỏ nhất: (a) x f (x) = arctan trên R 1 − x + x2 x2 + 1 (e) f(x) = trên đoạn [0, 1]. 1 + x + x2
(b) f(x) = |x2 − 3x − 4| trên đoạn [−2, 3] √ √ (f) f(x) =
100 − x2 − x2 trên đoạn
(c) f(x) = 3 x3 − 3x2 trên đoạn [−1, 2]. [−5, 5]. (d) 1 f (x) = − 2 arctan x trên R. (g) x
f (x) = |x|(x + 2) trên [−3, 2].
Đại học Bách khoa TPHCM Trang 63
ThS.Nguyễn Hữu Hiệp
2.6. KHẢO SÁT VÀ VẼ ĐỒ THỊ
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN (h) f(x) = xe−x22 trên R
(j) f(x) = |x2 − 4x| + 2x trên [1, 5] √
(i) f(x) = |x2 − 4x| + 3 trên [1, 5]
(k) f(x) = x 3 4 − x trên [0, 5].
Đại học Bách khoa TPHCM Trang 64
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN
3.1 Tích phân bất định 3.1.1 Định nghĩa
Định nghĩa 3.1 (Nguyên hàm) F (x) gọi là một nguyên hàm của f(x) nếu F ′(x) = f(x). Ký hiệu là Z f (x)dx = F (x) + C
Bảng tích phân bất định thông dụng R + C(α 6= −1). R 1) xα+1 xαdx = α + 1 3) exdx = ex + C. R = ln |x| + C. R ax + C 2) dx x 4) axdx = ln a R R = tan x + C. c d osx 2 x 5) cos xdx = sin x + C. 9) R 6) sin xdx = − cos x + C. R 7) sinh xdx = cosh x + C. R 2 = − cot x + C. R 10) sid nxx 8) cosh xdx = sinh x + C. 1 x x R = arctan + C. R √ = arcsin + C. 11) x2 dx + a2 a a 13) dx a2 − x2 a √ R √ = ln |x+ x2 + k|+C. 12) dx x2 + k Tính chất R R R • (f (x) ± g(x))dx = f (x)dx ± g(x)dx. R R • αf (x)dx = α f (x)dx. R R R • f (x).g(x)dx 6= f (x)dx. g(x)dx. 65 3.1. TÍCH PHÂN BẤT ĐỊNH CHƯƠNG 3. TÍCH PHÂN
3.1.2 Phương pháp tính tích phân bất định
Công thức đổi biến 1 Z Z x = x(t) : f (x)dx = f (x(t)).x′(t)dt
Công thức đổi biến 2 Z Z u = u(x) : f (u).u′(x)dx = f (u)du
Công thức tích phân từng phần Z Z udv = u.v − vdu
Ví dụ 3.1 Tìm nguyên hàm bằng phương pháp đổi biến. 1 cos 2x R R = .(− cos 2x) + C = − + C. a) d(2 2 x) 2 2 I = sin 2xdx = sin 2x. 1 R R = .ex2 + C. b) d(x2) xex2dx = ex2. 2 2 1 (2x + 1)2013 (2x + 1)2013 R R = + C = + C c) d(2x2 + 1) 2 4026 (2x + 1)2012dx = (2x + 1)2012. 2013 4 d(3 − 2x2) 1 (3 − 2x2)3 1 √ R 3 = − . + C = − . 3 R 1 −4 4 4 3 p d) 3 − 2x2dx = (3 − 2x2) 3 x 3 (1 − 2x2)4 + C. R R = ln d( | ln x| + C. l ln n x x ) e) dx = x ln x R R arcsin2 x + C. f) arcsin x √ dx = arcsin x.d(arcsin x) = 2 1 − x2 R R arctan2 x + C. g)
arctan xdx = arctan x.d(arctan x) = 2 1 + x2 R R + C. h) sin4 x sin3 x cos xdx = sin3 x.d(sin x) = 4 i) . R √ dx x + arcsin x R x R arcsin x I = √ dx = √ dx + 1 − x2 1 − x2d(1 − x2) 1 − x2 R √ . 1 = 1 − x2 R 1 √ arcsi + n2 x arcsin x.d(a √ rcsin x) arcsin2 x = .2 1 − x2 − + 2 + C = − 1 − x2 + + C −2 2 2
Ví dụ 3.2 Tìm nguyên hàm bằng phương pháp tích phân từng phần
Đại học Bách khoa TPHCM Trang 66
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN 3.1. TÍCH PHÂN BẤT ĐỊNH R a) I = xexdx ( ( u = x du v = = dexx =⇒ dv = exdx R R I = uv − vdu = xex − exdx = xex − ex + C. R b) I = x cos xdx ( ( u = x du v = = dsx in x =⇒ dv = cos xdx R I = x sin x − sin xdx = x sin x + cos x + C. R c) dx I = arcsin xdx du = √ ( 1 − x2 u = arcsin x v = x =⇒ dv = dx √ R √ = x arcsin x + 1 − x2 + C xdx I = x arcsin x − 1 − x2 R d) dx I = x arctan xdx du = ( 1 + x2 x2 u = arctan x v = =⇒ 2 dv = x x d 2 x x2 I = R x2 dx = R dx R 2(x d2x arctan x − 2(x2 + 1) arctan x − + + 1) 2 x2 x 1 2 2 = arctan x − + arctan x + C 2 2 2 R e) dx I = (x + 1) ln xdx du = ( x x2 u = ln x v = + x =⇒ 2 v = (xx+ 2 1)dx x2 dx I = ( R x2 + x)d(ln x) = ( R x2 + x) + x). ln x − ( 2 + x). ln x − ( 2 x 2 x2 x2 2 x2 = ( R x+ 1)dx = ( + x). ln x − − x + C + x). ln x − (2 2 4 2 R dx f) (x ln + x 1)2 I = dx u = ln x du = 1 x dv = 1 v = − =⇒ x + 1 ln x dx ln x x I = (x + 1)2 − R = − x(xdx + 1) + x + 1 + ln + C. g) . x + 1 x + 1 R R I = (x2 + 3x)exdx = (x2 + 3x)ex R − ex.(2x + 3)dx = = ((xx22 + + 3x x )e − x1 − )ex(2x + +
C 3)ex + 2ex.dx = (x2 + 3x)ex − (2x + 3)ex + 2ex + C R h) I = e2x cos xdx
Đại học Bách khoa TPHCM Trang 67
ThS.Nguyễn Hữu Hiệp 3.1. TÍCH PHÂN BẤT ĐỊNH CHƯƠNG 3. TÍCH PHÂN
3.1.3 Nguyên hàm hàm hữu tỷ
Ví dụ 3.3 Tìm nguyên hàm hàm phân thức: mẫu bậc nhất 3 R dx = ln |2x − 3| + C. a) 2x 3 − 3 2 x2 3 R R )dx = + 2x − ln |2x − 1| + C. b) 2x2 + 3x − 5 3 2 2 dx = (x + 2 −2x − 1 2x − 1 x3 2 R 3 2 R )dx =
+ x2 − x + ln |3x − 2| + C. c) 3x + 4x − 7x + 4 2 3 dx = (x2 + 2x − 1 +3x − 2 3 3x − 2 1 (2x − 1)−2 1 R R = . + C = − + C. 2 d) dx x − 2 4(2x − 1) = (2x − 1)−3 d(2 1) 2 −2 (2x − 1)3 d(5 − 3x) 1 −1 1 R R . = . + C = + C. e) dx (5 1 5 3(5 − 3x) = − 3x)2 −3 −3 − 3x (5 − 3x)2
Ví dụ 3.4 Tìm nguyên hàm hàm phân thức: R dx. 2 a) 5 x x − 1 I = − 1
Mẫu phân tích được thành tích các đa thức bậc nhất
Bước 1. Phân tích mẫu thành nhân tử: x2 − 1 = (x − 1).(x + 1).
Bước 2. Phân tich f(x) thành các phân thức đơn giản 5x − 1 A B = + x2 − 1 x − 1 x + 1
⇐⇒ 5x − 1 = A(x + 1) + B(x − 1) ⇐⇒ 5x − 1 = (A + B)x + A − B. 5x − 1 2 3 ( ( =⇒ = + . A + B = 5 A = B 2 = 3 x2 − 1 x − 1 x + 1 =⇒ ⇐⇒ A − B = −1 3 R +
)dx = 2 ln |x − 1| + 3 ln |x + 1| + C Bước 3. x 2 − 1 x + 1 I = ( R dx b) 2x2 1 − + 5 7 xx+ 2 I =
Bước 1. Phân tích mẫu thành nhân tử: 2x2 + 5x + 2 = (x + 2).(2x + 1).
Bước 2. Phân tich f(x) thành các phân thức đơn giản 1 − 7x A B = + 2x2 + 5x + 2 x + 2 2x + 1
⇐⇒ 1 − 7x = A(2x + 1) + B(x + 2) ⇐⇒ 1 − 7x = (2A + B)x + A + 2B. 1 − 7x −5 3 ( =⇒ = + . x = x − = 2 −1= 2x2 + 5x + 2 x + 2 2x + 1 2 ⇒ = A ⇒ = B − = 53 =⇒ 3 3 R +
)dx = −5 ln |x + 2| + ln |2x + 1| + C Bước 3. x 5 + 2 2x + 1 2 I = (−
Đại học Bách khoa TPHCM Trang 68
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN 3.1. TÍCH PHÂN BẤT ĐỊNH R dx c) 2x3 + 3x2 x2 + − 4x x − 7 I = − 2 2x3 + 3x2 − 4x − 7 x + 5 = 2x + 1 − x2 + x − 2 x2 + x − 2 x + 5 x + 5 A B = = + x2 + x − 2 (x − 1)(x + 2) x − 1 x + 2 ( x = x 1 = = −⇒ 2 A =⇒=B2= −1
⇐⇒ x + 5 = A(x + 2) + B(x − 1). 2x3 + 3x2 − 4x − 7 2 1 = 2x + 1 − + x2 + x − 2 x − 1 x + 2
=⇒ I = x2 + x − 2 ln |x − 1| + ln |x + 2| + C. R dx. d) 2x2 + 3x x3(x + − 1 I = 1) A B C D Phân tích 2x2 + 3x − 1 f (x) = = + + + (1) x3(x + 1) x x2 x3 x + 1
⇐⇒ 2x2 + 3x − 1 = Ax2(x + 1) + Bx(x + 1) + C(x + 1) + Dx3 (2) • x = 0 =⇒ C = −1 • x = −1 =⇒ D = 2
• Nhân x vào (1) rồi cho x → ∞ suy ra 0 = A + D =⇒ A = −D = −2 • x = 1 =⇒ B = 4. 4 1 2 1 + + + + 2 ln |x + 1| + C R − x 2 x2 − x3 x 4 2x2 I = dx = −2 ln |x| − x + 1
Ví dụ 3.5 Tìm nguyên hàm phân thức 1 x R = arctan
Mẫu bậc 2 vô nghiệm x2 dx + a2 a a √ 1 1 1 1 3 √ R = = . . arctan + C = . arctan x 3 + C. 2 R dx 1 1 1. 3x dx + 1 )2 3 3 I = x2 + ( 1 √3 √ √ 3 3 3 2. . d(2x + 1) R . dx R (2x + 1 1)2 + 16 2 I = = 1 4x 1 2 + 4x + 2x17 + 1 1 2x + 1 = . arctan + C = arctan + C 2 4 4 8 4 R dx. 3. x2 4x + − 2x 1 + 2 I = Ta phân tích: TỬ= α. (Mẫu)’ + β
4x − 1 = 2(2x + 2) − 5, ta viết lại tích phân R (2x + 2)dx R dx
= 2 ln |x2 − 2x + 2| − 5 arctan(x − 1) + C I = 2 − 5 (x − 1)2 + 1 x2 − 2x + 2
Đại học Bách khoa TPHCM Trang 69
ThS.Nguyễn Hữu Hiệp 3.1. TÍCH PHÂN BẤT ĐỊNH CHƯƠNG 3. TÍCH PHÂN 4. . R 2x3 + 5x2 − 2 R )dx 2x x2 + 7 I = 1 dx = (2x + 5 − x2 + 1 R dx 2x R x2 1+ 1 = x2 + 5x − dx − 7 = x2 + 5x − ln x2 |x2+ 1 + 1| − 7 arctan x + C R dx. 5. 5x2 + 7x I = (x − 1)2(x2 + 4x + 7) A B Cx + D Phân tích 5x2 + 7x f (x) = = + + (1) (x − 1)2(x2 + 4x + 7) x − 1 (x − 1)2 x2 + 4x + 7
⇐⇒ 5x2 + 7x = A(x − 1)(x2 + 4x + 7) + B(x2 + 4x + 7) + (Cx + D)(x − 1)2
• x = 1 =⇒ 12 = 12B =⇒ B = 1
• x = 0 : −7A + 7B + D = 0 ⇐⇒ 7A − D = 7 (2)
• Nhân x vào (1), cho x → ∞ suy ra A + C = 0 (3)
• Thế x = −1 : −2 = −8A + 4B + 4(−C + D) ⇐⇒ −8A − 4C + 4D = −6 (4) 11 7 Từ (2)-(4) suy ra 11 A = , C = − ; D = − 12 12 12 1 1 11x + 7 1 1 11 x + 4) − + ln |x−1|− − 2 (2 15 = R 2 1 x1/ −12 1 (x − 1)2 − 12 1 112 x − 1 R (x + 2) + 3 I1 = 1 1 11 2 = 15 ln |x − 1| − − ln |x x2 + + 4 4 x x + + 7 7 | + 12 12 x − 1 24 12
3.1.4 Nguyên hàm hàm lượng giác Hàm lượng giác R • Dạng sinm x. cosn xdx
i) Nếu cos bậc lẻ: đặt t = sin x.
ii) Nếu sin bậc lẻ: Đặt t = cos x.
iii) Nếu sin, cos đều chẵn: đặt t = tan x x
• Dạng bậc nhất theo sin, cos: Đặt t = tan 2
Các công thức thường gặp 2dt 2t 1 − t2 dx = , sin x = , cos x = t2 + 1 1 + t2 1 + t2
Đại học Bách khoa TPHCM Trang 70
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN 3.1. TÍCH PHÂN BẤT ĐỊNH
Ví dụ 3.6 Tìm nguyên hàm các hàm số lượng giác sau R a) s d i x n x I = R
dx. Đặt t = cos x =⇒ dt = − sin xdx. Cách 1 ssiin n2 x I = 1 1 − t 1 1 − cos x R = ln + C = ln + C. 1 −dt 2 1 + t 2 1 + cos x I = − t2 Cách 2: 2dt 1 1 R ln 1 + t2 = |t| + C = ln | tan x 2 2 | + C I = 2t 1 + t2 2 R b) dt t Đặ a t n7 t x = d t x
an x ⇐⇒ x = arctan t =⇒ dx = 1 + t2 t6 t4 t2 R t7 R )dt = − + − arctan t + C = ... 1 t I = + t2 6 4 2 dt (t5 − t3 + t − 1 + t2 R dx c) 2 s s iin n x x + − c 3 ocso x s x Phân tích T U = α.M au + β.(M au)′ −1 α = ( 13 5 2α + 3β = 1 β =
sin x + cos x = α(2 sin x −3 cos x)+β(2 cos x+ 3 sin x) ⇔ ⇔ 13 5 2 cos x + 3 sin x 5 −3α + 2β = 1 + x + ln |2 sin x − 3 cos x| + C R − 1 1 3 13 − 1 13 13 I = dx = 2 sin x − 3 cos x R dx d) sin 3 x + + cocsos x x Đặt t = tan x2. 2t 1 − t2 + 1 + t2 1 + t2 2dt R dt R 1 − t2 (t21 + + 22 ) t ( − t2 t2 + 1) = I = 3 + 1 + t2 1 + t2 At+B Ct+D Phân tích 1 + 2t − t2 = + A −2, B = 3, C = 2, D −2. (t2 + 2)(t2 + 1) 2 + t2 1 + t2 ⇐= = = Suy ra 3 t
I = − ln(2 + t) + √ arctan √ + ln(1 + t2) − 2 arctan t + C 2 2 R
dx Đặt t = sin x =⇒ dt = cos xdx e) sin2 x I = cos3 x R sin2 x R t2 dt I = cos xdx = (1 − t2)2 cos4 x A B C D 1 1 Phân tích t2 = + + + =⇒ A = − , B = C = D = . (1 − t2)2 t − 1 (t − 1)2 1 + t (1 + t)2 4 4 1 1 1 Vậy 1 t + 1 I = − + + C 4 t − 1 4 1 1+ t ln − 4 t − 1
Đại học Bách khoa TPHCM Trang 71
ThS.Nguyễn Hữu Hiệp 3.1. TÍCH PHÂN BẤT ĐỊNH CHƯƠNG 3. TÍCH PHÂN R dx f) sin2 x 1 + cos2 x 1 Đặt dt 2 + t2 t = tan x =⇒ dx = , 1 + cos2 x = 1 + = , 1 + t2 1 + tan2 x 1 + t2 t2
sin2 x = tan2 x cos2 x = 1 + t2 1 + t2 dt √ x R t2 . R t2dt = 2 arctan √ − arctan x + C I = 1 + t2 2 + t2 = (1 + t2)(2 + t2) 2 1 + t2
Ví dụ 3.7 Tìm nguyên hàm R R a) Đặt t = cos x = I = sin3 x. cos2 ⇒ dt = xdx =− sin xdx. sin2 x cos2 x. sin xdx. R R t3 cos5 x cos3 x I = (1 R − cos2 x) cos2 x. sin x + dx C = = (1 − − t2).t2.( − −dt + ) t5 C = (t4 − t2)dt = 5 3 5 3 R R sin2 x cos xdx b) sin2 x I = dx = cos2 x Đặt t c = os si x n x =⇒ dt = cos xdx R sin2 x R dt 1 t2 I = cos xdx = − t2 1 − sin2 x 1 1 R ( + 1 1 − t = ( R 1 2 1 − 1)dt = 1 1 ) + − t 1 dt = ( [ 1 − − ln t|) 1 .(1 − + t| t) + ln |1 + t|] − t + C = 1 + t 2 1 sin x + 1 . ln − t + C = 2 1 − t . ln − sin x + C 2 sin x − 1 R . c) 1 +dx sin x Đặt x 2dt t = tan =⇒ dx = 2 t2 + 1 2dt t2+1 2 2 d(t + 1) = − + C = − x + C R 1 + 2t R 2 R (t 2 + 1)2 t + 1 t2+1 = tan I = dt = t2 + 2t + 1 2 R d) dt t Đặ a t n5 t x = d t x
an x =⇒ x = arctan t =⇒ dx = t2 + 1 t2 d(t2 + 1) t4 t2 R = + dt − R 1 . − 2 I = t5. R t t 44 + 1 + t2 2 4 1 = t3 − t ta+ n2 x 1 dt = 2 t2 + 1 − 1 + t2 tan4 x + ln 1 + t2 + C =4 2 2 ln 1 + tan2 x + C 2
Đại học Bách khoa TPHCM Trang 72
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN 3.1. TÍCH PHÂN BẤT ĐỊNH
3.1.5 Nguyên hàm hàm vô tỷ √
• Biểu thức trong căn bậc nhất n ax + b √ Đặt t = n ax + b
• Biểu thức trong căn bậc hai √ i) a2 − x2 : đặt x = a sin t √ ii) a2 + x2 : đặt x = a tan t √ iii) a x2 − a2 : đặt x = sint R √ • Dạng xn ax2 + bdt √ i) n lẻ: đặt t = ax2 + b r ii) bx2 n chẵn: đặt t = a + • Dạng 1 √ (αx + β)m ax2 + bx + c Đặt 1 t = αx + β
Ví dụ 3.8 Tìm nguyên hàm R √ a) 2x + 1 I = dx. x + 1 √ Đặt t2 − 1 t = 2x + 1 =⇒ x = =⇒ dx = tdt. 2 R dt t R 2t2 t2 + 1 I = t2 − 1 + 1tdt = 2 R√ 1 √ = 2( 2 1 x − + 1 − arct d a t n = 2 2x[t − + 1 a ) rc + ta Cn t] + C t2 + 1 √3x + 1 √ dx. R 1 + 3 x2 + 2x + 1 b) 3 Đặt √ 3t2 t = 3 x − 1, I = − ln(1 + t2) + C 2 2 1 √ 3 √ R √
I = √ ln |x 2 + √ + 2x2 + 6x − 1| + C c) dx 2x2 + 6x − 1 2 2 1 2x − 10 R √ I = arcsin √ + C d) dx 3 I = 1 + 5x − 3x2 37 1(2x − 6) + 9 √ √ R √ = √
= 2 x2 − 6x − 1 + 9 ln |x − 3 + x2 − 6x − 1| + C. e) 2x + 3 x2 − 6x − 1 x2 − 6x − 1
Đại học Bách khoa TPHCM Trang 73
ThS.Nguyễn Hữu Hiệp 3.1. TÍCH PHÂN BẤT ĐỊNH CHƯƠNG 3. TÍCH PHÂN 3 R − (−1 − 10x)+ 10 R √ dx = √ = f) 3x − 1 2 − x − 5x2 2 − x − 5x2 R √ g) x2 + kdx R √ h) a2 − x2dx R √ i) x2 + 1 2x2 + x − 1 √ R j) 9 − x2 I = dx x Cách 1
Đặt x = 3 sin t =⇒ dx = 3 cos tdt √ p
9 − x2 = 9 − 9 sin2 t = 3 cos t R dt 3 cos t R co si s2 n t t I = 3 cos tdt = 3 3 sin t R 1 − sin2 t R − sin t)dt si 1 = 3 n t dt = 3 ( sin t t 3 x Các= h 3 2 (ln tan + cos t) + C, với t = arcsin √ 2
Đặt t = 9 − x2 =⇒ t2 = 9 − x2 =⇒ tdt = −xdx √ R 9 − x2 I = R (−tdt) 9 t − t2 xdx = x2 R t2 R )dt (t + 3 9 = )(t dt = (1 + − 3) t2 − 9 1 1 3 R ( − ))dt = t + 3 2 t − 3 t + 3 = (1 + √ 3 t − 3 √ ( 3 ln t9− 3x2 − − 3 ln t + 3 ) + C = t + + C = 9 − x2 +2 . ln √ + C 2 9 − x2 + 3 ln 2 t + 3 R √ 2 k) dx I = x 1 + x Cách 1 Đặt dt x = tan t =⇒ dx = cos2 t 1 r = √ √ 1 cos2 t cos t 1 + x2 = 1 + ta dtn2 t = R ta1n t 1 R dt I = cos t = t tan x Cách 2 cos2 t = ln tan + C = ln tan( sin t 2 ) + C 2 2 2
Đặt x = sinh t : tương tự như trên với chú ý cosh t − sinh t = 1 Cách 2: √
Đặt t = x2 + 1 =⇒ t2 = 1 + x2 =⇒ tdt = xdx R xdx R tdt I = √ = (1 − t2)t x2 1 + x2 1 1 R ( − )dt dt R 1 2 1 + t 1 − t = = 1 1 1 + t = − t2 + C 1 (ln 1 + t + ln 1 − t ) + C = Cách 2 3: . ln 2 1 − t
Đại học Bách khoa TPHCM Trang 74
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN 3.2. TÍCH PHÂN SUY RỘNG Đặt t = sinh x Cách 4 Đặt 1 t = Cách 5 x √ Đặt t2 − 1 t − x = x2 + 1 =⇒ x = 2t R √ . l) (4x2 + 1d ) x3 − 2x2 r x2 − 2 Đặt 3 t = R √ m) dx (x + 1) x2 + 1 Đặt 1 t = x + 1 R √ n) dx (x − 1)2 x2 + x + 1 Đặt 1 t = x − 1 R √ o) dx I = (x2 − 2x) 4x − 2x2 + 1 √ R p) x2 + x + 1 I = dx x
3.2 Tích phân suy rộng Bài tập
Bài 1. Tìm nguyên hàm 5 R √ − + 4ex)dx R R √ dx (a) 3x x x + 2 ( (f) x + 1 + 1 (2x + 1) arctan x.dx (j) dx R √ dx R 2x 7 2 x −− 7 1 x 2 + 6 R (b) 2x23 − 3x x (g) (k) dx cos4 x R . R √ x3 dx (c) R x2 sin(1 − 3x3)dx c d o x s x (l) 4 − x2 R √ (h) (d) dx x2 + 2x − 4 R R 5 + d4x (m) tan4 xdx R (i) cos x R (e) cos 2x.(x2 + 2x).dx (n) (x2 + 2).e2xdx
Bài 2. Tìm nguyên hàm hàm hữu tỷ sau R dx dx 6 R dx R (a) ( 2 5 x x + − 3 1) (c) 2x2 + 3x − 1 x4 + x (e) 4x2 2x + + 3x 3 + 5 R dx R R x2 + 1 (b) x3 4x + 3 − 2x2 + x (d) dx 2x2 − 3x + 5 (f) x2 − x + 1
Đại học Bách khoa TPHCM Trang 75
ThS.Nguyễn Hữu Hiệp 3.2. TÍCH PHÂN SUY RỘNG CHƯƠNG 3. TÍCH PHÂN R R R (g) 3 x2 + 2 1 x + 2x + 3x 4x 2x2 − 1 (j) (x2 dx + 1)2 (m) − x + 3 R dx R R x4 + 2dx (h) x4 + 1 x4 − x 2 (k) (2x + 1)dx x(x + 1)2 (n) x3 + 1 R dx R (i) x2 + 1 x4 + 1 (l) 5dx 3x2 − x + 7
Bài 3. Tìm nguyên hàm hàm lượng giác sau R R dx a) c d o x s x d) 2 sin 2x x − + c c oo s s 2 x x dx R dx R 3 sin 1 x + + si c n o xs x b) sin4 x − 2 sin2 x cos x e) R 3 sin2 x + cos 2xdx R f) sin2 x − 3 c) (tan x + 3 tan5 x)dx
Bài 4. Tìm nguyên hàm hàm vô tỷ sau √ R √ x + 1 (a) x + 1 − 2 3 dx R √ dx R √ x 2 (i) (x2 2x2 − 3x) − 5x − 1 (p) dx (2x + 1) x2 − 1 r dx R √ √ 3 R x − 1 (x + 2x) R x2 + x + 1 x2 + x + 1dx (b) x + 1 (j) (q) x x3 R √ R √ dx √ (c) dx 2x − 3x2 + 3 (k) x3 − x + 1 x2 − x + 1 R (r) x2 + x + 1dx x R √ dx √ (d) dx 5x2 − 3x − 1 R (l) dx x x2 − 4 R √ dx R √ √ (s) x3 x2 − x + 1 (e) (3x + 2)dx x − 5x2 + 1 R (m) dx (4x2 + 1) 2 − 3x2 R √ √ dx √ R x3 x2 − x + 1 (f) (2x 3x2 − 1)dx − 7x − 5 R (t) + x + 1 (n) dx (x2 − 2x) 3x2 − 6x − 2 R √ (g) 3x2 − 2x − 1dx √ R √ √ R dx R xdx (x3 − 1) x2 − 1 (h) x x2 − 2x − 3 3 − 4x − 5x2dx (o) (u)
Bài 5. Xét sự hội tụ của tích phân suy rộng +∞ 2x2 + x − ln6 x +∞ dx +∞ sin x (a) √ (g) √ (l) √ dx R 1 (x2 + 1) x3 + 3x2 R 0 x + 1 ln x R0 x x − 1 4 dx √ (b) √ +∞ 2x + x +∞ ln x − ln(x + 1) R √ dx 0 x( x − 2) (h) (m) R 0 ex − 1 R x 0 +∞ x + 1 (c) √ dx R 2 2 +∞ 1 + sin x +∞ 1 0 x x + x (i) dx ln x − 3x2 (n) − e +∞ ln2 xdx R 0 R0 √ 1 x (d) x cos x2 dx R √ 0 x + x2 + π2 tan x − x +∞ sin x 1 2x + 1 (j) dx (o) √ dx (e) √ dx R x 0 sin x R0 R0 x − x2 √x) +∞ 3x − x2 − 1 +∞ ln(1 + +∞ sin2 x − cos 1x (f) √ dx (k) dx dx ex − 1 (p) x2 R 3 R R 1 x x + 3x 0 0
Đại học Bách khoa TPHCM Trang 76
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN 3.2. TÍCH PHÂN SUY RỘNG
Bài 6. Tìm điều kiện tham số để tích phân sau hội tụ +∞ arctan 3x +∞ dx (a) dx (f) I = . R 0 xα R 0 x2 + 2xα +∞ xαdx +∞ xdx (b) (g) I = . R 0 x3 + sin x R 1 ex + xα +∞ (c) dx I = . +∞ (h) dx I = . R 0 (x3 + ln(1 + x))xα R 1 x + 2xα √ +∞ x (d) − 1 +∞ x I = ! (i) 4α I = x 3 arctan dx. R 3 1 e R 0 1 + xα ln 1 + √ dx. +∞ ln(1 + x) α +∞ (e) dx (j) I = xα|1 − x|β R 0 exα − 1 R 1
Bài 7. Tính tích phân suy rộng ∞ 1 +∞ dx (a) I = dx. (l) I = √ R e x ln2 x R 0 2e2x + 2ex + 1 +∞ √ (b) x I = dx. 1 2 − 3 x − x3 R (m) I = √ . 0 e2x R 5 0 x3 (c) +∞ 2x2 − x + 1 I = dx. 1 dx R 2 x(x − 1)3 (n) I = √ . (4 − x) 1 − x2 +∞ R −1 (d) dx I = √ R ∞ dx 1 (1 + x)2 x (o) I = √ 10 5 +∞ R x x + x + 1 (e) arctan xdx 1 I = R0 p . ∞ dx (x2 + 1)3 (p) I = √ . +∞ x2 x2 + 1 (f) (5x2 + 16x + 7)dx R 1
I = R0 (x2 + 3x + 2)(x2 + 2x + 5) +∞ (q) dx I = √ (g) +∞ 2x2 + 6 I = . R 0 (x + 1) x2 + 1 R 0 ex+1 +∞ dx +∞ (r) I = √ (h) cos xdx I = R 2 1 x x + x − 1 R 0 ex +∞ dx +∞ (i) dx (s) I = . I = √ . √ √ 3 R R x13 3 1 + x2 √ x x2 + 1 1 3 1 +∞ dx (j) dx (t) I = √ . I = √ R R 0 (4x2 + 1) x2 + 1 0 (3 + x) 1 − x 2 +∞ dx (k) x2dx I = √ (u) I = √ R 1 x2 − 1 R 0 ( x2 + 1 + x)2 dx R1 p . Tìm Bài 8. Cho tích phân +∞
α để tích phân hội tụ. Tính tích phân I = khi α = 1. (x + 1) (x2 − x)α √ ĐS: ln(3 − 2 2) 0 < α < 2, I = − √ . 2
Đại học Bách khoa TPHCM Trang 77
ThS.Nguyễn Hữu Hiệp
3.3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN CHƯƠNG 3. TÍCH PHÂN dx
. Tìm α để tích phân hội tụ. Tính tích phân khi R1 xα(x+1)(x2+x+2) Bài 9. C α ho = t1í.ch phân +∞ I = π ĐS: ln 2 1 3 α > −2, I = − √ + √ arctan √ . 2 2 7 7 7 dx R0 p . Tìm
Bài 10. Cho tích phân 2
α để tích phân hội tụ. Tính tích phân I = khi α = 1. (x2 + 1) (4 − x2)α
3.3 Ứng dụng hình học của tích phân
3.3.1 Diện tích hình phẳng
Diện tích miền phẳng D giới hạn bởi y = f(x), y = g(x), x = a, x = b là b S(D) = Z |f(x) − g(x)|dx a
Ví dụ 3.9 Tính diện tích miền D giới hạn bởi y = ln x, y = x − 1, x = e.
Phương trình hoành độ giao điểm: ln x = x − 1 ⇐⇒ x = 1. Công thức diện tích e e e x2 1 e2 + 1 S(D) = Z x ln x − − = −2e. R1 2 2 1 e2 | ln x−x+1|dx = (ln x − x + 1)dx = = 2e 2 − 1 2
Ví dụ 3.10 Tính diện tích miền D giới hạn bởi y = x2, x + y = 2, y = 0.
Cách 1 Các hoành độ giao điểm của 3 hàm số trên là x = 0, x = 1, x = 2. Ta chia miền D làm 2 phần 1 2 1 1 5
S(D) = Z x2dx + Z (2 − x)dx = + = 3 2 6 0 1
Cách 2 Ta viết hàm số theo biến √ y : x = y, x = 2 − y, y = 0.
Phương trình tung độ giao điểm √y = 2 − y ⇐⇒ y = 1.
Công thức diện tích theo biến y 1 1 5 S(D) = Z = √ R 0 √ 6 5 y − 2 + y dy =( y − 2 + y)dy = − 6 0
Ví dụ 3.11 Tính diện tích miền D giới hạn bởi y = log3x, y = 4 − x, y = 0.
Đại học Bách khoa TPHCM Trang 78
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN
3.3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN
Cách 1: Chia D làm 2 miền. 3 hoành độ giao điểm cua 3 đường là: x = 1, 3, 4. 3 4 7 2
S(D) = S(D1) + S(D2) = Z log3xdx + Z (4 − x)dx = − 2 ln 3 1 3
Cách 2: Tính theo biến y. Miền D : x = 3y, x = 4 − y, y = 0.
Phương trình tung độ giao điểm 3y = 4 − y ⇐⇒ y = 1. 1 y2 2 7 7 2 S(D) = Z − 4y + − = − . ln 3 1 2 ln 3 3y ln 3 3y − 4 + y dy = 2 = 0 2 0
3.3.2 Độ dài đường cong
Cho đường cong C : y = f(x), x ∈ [a, b]. Độ dài đường cong C là b l(C) = Z p1+f′(x)2dx a
Ví dụ 3.12 Tính độ dài đường cong C : y = x2, x ∈ [0, 1]. Công thức độ dài 1 √ 1 1 √ 1 √ l(C) = Z p 1 + 4x2 + = [ 5 + ln(2 + 5)] 1 2 1 2 2 1 + (2x)2dx = 2x √ ln 0 2x + 1 + 4x2 2 0 2
Ví dụ 3.13 Tính độ dài đường cong C : y = ln x, x ∈ [1, 3]. √x2 + 1 r = . p x √ √ Ta có 1 x2 1 + y′2 = 1 + 3 Công thức độ dài x2 + 1 x2 + 1 l(C) = dx = xdx. R 1 x x2 √
Đặt t = x2 + 1 ⇐⇒ x2 = t2 − 1 =⇒ xdx = tdt. √10 √ √ t t − 1 √ √ √ 1 10 − 1 1 2 − 1 l(C) = Z 10 = 10 − 2 + ln √ − √ . √ 2 10 + 1 2 2 + 1 √ 1 2 2 tdt = t + ln t + 1 t2 − 1 2 √ Ví dụ 3.14 x
Tính độ dài đường cong √ C : y = x x − , x ∈ [0, 1]. 3 s 1 1 1 1 + s p √ − 2 r − √ − 2 2 = Ta√có 3 x2 3 x 2 1 + y′2 = 1 + √ 9x4 = √ 3 x 1 6 x = 1 + 36x 6 x + √ . 2 6 x
Đại học Bách khoa TPHCM Trang 79
ThS.Nguyễn Hữu Hiệp
3.3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN CHƯƠNG 3. TÍCH PHÂN Công thức độ dài 1 1 4 l(C) = √ Z √ = 3 x + 2 √ x 1 √ dx = x x + 3 0 6 x 3 0
3.3.3 Thể tích vật thể tròn xoay
Cho miền D giới hạn bởi y = f(x), Ox, x = a, x = b. Thể tích vật thể tròn xoay được sinh ra
khi cho D quay quanh Ox và Oy là b VOx = π y2dx R a b VOy = 2π |xy|dx R a Chú ý
• Khi D quay quanh Ox thì không được cắt Ox. Tương tự cho Oy.
• Miền D giới hạn bởi Ox thì công thức tích phân theo x. Nếu D giới hạn bởi Oy thì ta có
công thức tương tự bằng cách đổi vai trò x,y cho nhau.
Ví dụ 3.15 Cho miền D giới hạn bởi : y = x2, y = x + 2. Tính thể tích vật thể tròn xoay khi cho D
quay quanh trục Ox và trục Oy.
Phương trình hoành độ giao điểm x2 = x + 2 ⇐⇒ x = −1 ∨ x = 2. Công thức thể tích 2 2 72 VOx = π Z π = . R 5 −1 72 x4 − (x + 2)2 dx = (x2 − x − 2)dx = − 5 −1
Vì miền D cắt trục Oy nên công thức không đúng nữa. Ta bỏ qua VOy.
Ví dụ 3.16 Cho miền D giới hạn bởi : y = x2 − 2x, y = x. Tính thể tích vật thể tròn xoay khi cho D
quay quanh trục Ox và trục Oy.
Phương trình hoành độ giao điểm x2 − 2x = x ⇐⇒ x = 0 ∨ x = 3
a) VOx. Vì miền D bị cắt bởi trục Ox nên công thức không đúng. Bài này khó, ta không tính. b) VOy. Công thức 3 3 3 27π VOy = 2π Z Z Z (3x2 − x3)dx = . 2 x(y 0 1 − y2) dx = 2π x(x2 − 2x − x) dx = 2π 0 0
Đại học Bách khoa TPHCM Trang 80
ThS.Nguyễn Hữu Hiệp CHƯƠNG 3. TÍCH PHÂN
3.3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN
3.3.4 Diện tích mặt tròn xoay
Diện tích mặt tròn xoay khi cho C : y = f(x), x ∈ [a, b] quay quanh trục Ox và Oy là b SOx = 2π R p b |y| 1 + y′2dx SOy = 2π aR p |x| 1 + y′2dx a
Ví dụ 3.17 Cho √ C : y =
x, x ∈ [0, 1]. Tính diện tích mặt tròn xoay được tạo ra cho C quay quanh trục Ox, Oy. r r . p 4x +4 1 x Ta Côcó 1 ng t1h + ứcy′2 = 1 + = 4x √ √ 1 1 √ a) 1 + 4x 5 5 − 1 SOx = 2π r dx = 2π dx = π (đặt t = 1 + 4x). R x 6 0 √ 4x +4 1 R 0 2 x b) Công thức 1 1 √ 1 1 SOy = 2π r dx = π 4x2 + xdx = π r dx 4 )2 − R 0 4x 16 4x + 1 R 0 R π x √ 1 (2x + 1 π = 4x2 + x − . ln 0 |2x + 1 = 1 √ 2x 2 32 √ √ 1 ln(9 + 4 5) + 4x2 + x 0 4 | 5 −32 2 √ 2
Ví dụ 3.18 Cho C : y = 4 − x2. Tính diện tích mặt tròn xoay khi cho C quay quanh trục Ox và Oy. √
Ví dụ 3.19 Cho đường cong C : y = 2x − x2.
1. Tính diện tích miền D giới hạn bởi C và trục Ox.
2. Tính độ dài đường cong C
3. Tính thể tích vật thể được tạo ra khi cho D quay quanh trục Ox và trục Oy.
4. Tính diện tích mặt tròn xoay khi cho C quay quanh trục Ox và trục Oy. Bài tập
1. Tính diện tích miền phẳng
(a) y = arcsin x, y = −x2, x = −1, x = 1.
(b) D : y = ln x, y = x, x = 0, x = 1. (c) 2 D : y = x2, y = 1 + x2 (d) y = x2, y = x + 2. √
(e) D : y = x − x2, y = x 1 − x
Đại học Bách khoa TPHCM Trang 81
ThS.Nguyễn Hữu Hiệp
3.3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN CHƯƠNG 3. TÍCH PHÂN (f) y = xex, y = −x, x = 1. (g) △OAB : A(2; 3), B(3; 2).
2. Tính độ dài đường cong √
(a) y = 2x − x2, 1/2 < x < 1 (b) y = ex, x = 0..1 ln x (c) x2 y = − , x = 1..3 2 4 √
(d) y = 2 1 + ex/2, x = 1.. ln 9
3. Tính thể tích vật thể tròn xoay (a) √ D : y =
xe−x, y = 0, x = 2 Tính VOx.
(b) y = x2, y = x + 2, x ≥ 0. Tính VOx, VOy. √
(c) y = 4 − x2, y = 0, y ≥ x. Tính VOx, VOy. (d) 1
y = x, y = , x = 2. Tính VOx, VOy. x
(e) y = ln x, y = 0, x = 1, x = 2. Tính VOx, VOy.
4. Tính diện tích mặt tròn xoay √
(a) C : y = 1 + x2, x = 0..1/4. Tính SOx, SOy.
(b) C : y = ln x, x = 1..e. Tính SOy. 5. Cho miền x2
D giới hạn bởi y = 2x2, y = , y = x. 2 (a) Tính diện tích D.
(b) Tính độ dài đường cong x2 C : y = , x ∈ [0, 1]. 2
(c) Tính diện tích mặt tròn xoay khi cho C quay quanh Ox và Oy.
(d) Tính thể tích vật thể tròn xoay khi cho D quay quanh Ox, Oy.
Đại học Bách khoa TPHCM Trang 82
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.1 Phương trình vi phân cấp 1
4.1.1 Phương trình vi phân tách biến
Phương trình vi phân Tách biến dạng f (x)dx = g(y)dy Nghiệm Z Z f (x)dx = g(y)dy
Ví dụ 4.1 Giải phương trình vi phân (2 + 3y2)dy − 2xdx = 0, y(0) = 0. Bài giải Lấy nguyên hàm 2 vế Z Z (2 + 3y2)dy −
2xdx = 0 ⇐⇒ 2y + y3 − x2 + C = 0 y(0) = 0 =⇒ C = 0
Vậy nghiệm là 2y + y3 − x2 = 0
Ví dụ 4.2 Giải phương trình vi phân 3y2y′ = 2x, y(0) = 1 Bài giải Phương trình trở thành √ 3y2 dy Z Z x2 + C. = 2x ⇐⇒ 3y2dy = 2xdx √ ⇐⇒ 3y2dy =
2xdx ⇐⇒ y3 = x2 + C ⇐⇒ y = 3 dx
y(0) = 1 =⇒ 1 = 3 02 + C =⇒ C = 1 √
Vậy nghiệm là y = 3 x2 + 1 √
Ví dụ 4.3 Giải phương trình vi phân x + y 1 − x2y′ = 0 Bài giải Phương trình trở thành √ dy xdx x+y 1 − x2 = 0 ⇐⇒ Z +C = 0 dx Z xdx √ y2 2 √ +ydy = 0 ⇐⇒ √ + ydy = 0 ⇐⇒ − 1 − x2+ 1 − x2 1 − x2 √
Vậy nghiệm tổng quát là y2 − 1 − x2 + + C = 0 2 √
Hay có thể viết y2 = 2 1 − x2 − 2C. 83
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
Ví dụ 4.4 Tìm nghiệm tổng quát của phương trình vi phân xy′ − y = 0 Bài giải
Phương trình được viết lại dy dx y y = y Z Z dy dx ⇐⇒ =
⇐⇒ ln |y| = ln |x| + C ⇐⇒ ln = C ⇐⇒ = eC x y x x x
Ví dụ 4.5 Tìm nghiệm của phương trình vi phân y′ = 3x2y, y(0) = 2 Bài giải
Phương trình được viết lại
dy = 3x2dx ⇐⇒ ln|y| = x3 + C ⇐⇒ |y| = ex3+C = eC.ex3 y
y(0) = 2 =⇒ |2| = eC.e0 =⇒ eC = 2
Vậy nghiệm của phương trình là |y| = 2ex3.
Ví dụ 4.6 Giải phương trình vi phân y′ + 2xy = xy2. Bài giải
Phương trình được viết lại dy dy = x(y2 − 2y) ⇐⇒ = xdx dx y2 − 2y 1 1 R ( − dy R R 1 2 y ⇐⇒ = xdx ⇐⇒ − 2 R 1 y2 −y 2y − 2 x2 y − 2 )dy = xdx ⇐⇒ = y = ex2+2C ln + C ⇐⇒ 2 y 2 y √
Ví dụ 4.7 Giải phương trình vi phân x + xy2 + y 1 − x2y′ = 0 Bài giải Viết lại phương trình √ dy xdx ydy x(1 + y2) + y 1 − x2 = 0 ⇐⇒ √ + = 0 dx 1 − x2 1 + y2 √ 1 √
⇐⇒ − 1 − x2 + ln |1 + y2| + C = 0 ⇐⇒ y2 = e2 1−x2+2C − 1 2
Ví dụ 4.8 Giải phương trình vi phân (4y − 2x)y′ = 2(x − 2y + 1)2, y(−1) = 0 (1). Bài giải
Đặt u = x − 2y + 1 =⇒ u′ = 1 − 2y′. 1 − u′ 2u2 du 2u2 + u − 1 (1) : −2(u − 1) = u2 ⇐⇒ u′ = + 1 ⇐⇒ = 2 u − 1 dx u − 1 u − 1 ⇐⇒ R u − 1 2 du = dx 1 ⇐⇒ R 2u2 + u ln |u − 1 du = dx ⇐⇒ + 1| − ln |2u − 1| 2 = u|2x|++uC 3 6 − 1 2 1 ⇐⇒
ln |x − 2y + 2| − ln |2x − 4y + 1| = |x| + C 3 6 y(−1) = 0 =⇒ C = −1. Vậy nghiệm là 2 1
ln |x − 2y + 2| − ln |2x − 4y + 1| = |x| − 1 3 6
Đại học Bách khoa TPHCM Trang 84
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
4.1.2 Phương trình vi phân đẳng cấp Dạng y y′ = f ( ) x PP: đặt y u =
⇐⇒ y = x.u =⇒ y′ = u + xu′ x Thay vào phương trình: du u + xu′ = f (u) ⇐⇒ x = f (u) − u dx
Rút gọn đưa về phương trình tách biến theo x, u du dx = f (u) − u x
Ví dụ 4.9 Giải phương trình vi phân xyy′ = x2 − xy + y2. Bài giải Chia 2 vế cho x y xy ta được y′ = − 1 + . y x Đặt y u = =⇒ y′ = u + xu′ x
Thế vào phương trình trên ta được 1 xdu 1 − u u + xu′ = − 1 + u ⇐⇒ = u dx u udu dx ⇐⇒ = 1 − u R udu R dx x ⇐⇒ = ⇐⇒ −u − ln | x 1 − u| = l 1 n | − x| u + C y x − y ⇐⇒ − y ⇐⇒ − − ln l |x − y| = = C ln |x| + C x x
Chú ý: Ta có thể xác định hàm 1 f (u) =
− 1 + u do đó phương trình đưa về dạng tách biến u du dx du dx = ⇐⇒ = f (u) − u x 1 − 1 x u
Ví dụ 4.10 Giải phương trình vi phân (y2 + 2xy)dx + xydy = 0. Bài giải
Viết lại phương trình y + 2 + y′ = 0 x Đặt y u = =⇒ f(u) = −u − 2 x dx Áp dụng công thức du = f (u) − u x
Đại học Bách khoa TPHCM Trang 85
ThS.Nguyễn Hữu Hiệp
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN Phương trình trở thành du dx −1 y 1 = ⇐⇒
ln |u+1| = ln |x|+C ⇐⇒ | +1| = −u − 2 − u Z Z e−2C. du dx x 2 x x2 ⇐⇒ = x −2u − 2
Ví dụ 4.11 Giải phương trình vi phân xy′ = x + 2y, y(1) = 3 Bài giải Chia 2 vế cho y x ta được y′ = 1 + 2x Đặt y u = =⇒ f(u) = 1 + 2u x Phương trình trở thành du dx = 1 + 2u − u R du R dx x ⇐⇒ = ⇐⇒ ln |u + 1| = ln x |x| + C ⇐ 1 ⇒+| u u + 1| = eC|x| y ⇐⇒ | + 1| = eC|x| x
y(1) = 3 =⇒ |3 + 1| = eC.|1| =⇒ eC = 4 Vậy nghiệm là y | + 1| = 4|x|. x
Ví dụ 4.12 Giải phương trình vi phân xy2y′ = x3 + y3. Bài giải y Chia 2 vế cho x2 xy2 ta được y′ = + . y2 x 1 Đặt y u = =⇒ f(u) = + u x u2
Phương trình vi phân trở thành du dx = 1 R R dxx u2 + u − u ⇐⇒ u2du = x u3 ⇐⇒ = ln |x| + C ⇐⇒ u = 3 3 p3(ln|x| + C) ⇐⇒ y = x 3p3(ln|x|+C) Ví dụ 4.13 2x
Giải phương trình vi phân − y y′ = 3x − 4y + 5
4.1.3 Phương trình vi phân toàn phần Dạng ( P ( Px′ y , y = )dx Q′ + Q(x, y)dy = 0
Nghiệm là U(x, y) = C. Trong đó Q(x, y)dy R Ry0 U (x, y) = x P (x, y y x 0)dx + Q(x 0 0, y)dy R Ry0y = xP (x, y)dx + x0
với (x0, y0) được chọn tùy ý. Thường chọn (x0, y0) = (0, 0)
Đại học Bách khoa TPHCM Trang 86
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
Ví dụ 4.14 Giải phương trình vi phân (3x + 2y)dx + (2x − 9y)dy = 0. Bài giải Ta có P ′ U (x, y) = C
y = Q′x = 2 do đó nghiệm tổng quát có dạng . (x,y) Trong đó U(x, y) = P dx + Qdy ( R 0,0)
Chọn đường đi (0, 0) −→ (x, 0) −→ (x, y) x y 3x2 9y2
U (x, y) = Z 3xdx + Z (2x − 9y)dy = + 2xy − 2 2 0 0 9y2
Nghiệm tổng quát là 3x2 + 2xy − = C 2 2
Ví dụ 4.15 Giải phương trình vi phân (3x2y2 + 7)dx + 2x3ydy = 0. Bài giải Ta có P ′ U (x, y) = C
y = Q′x = 6x2y do đó nghiệm tổng quát có dạng . (x,y) Trong đó U(x, y) = P dx + Qdy ( R 0,0)
Chọn đường đi (0, 0) −→ (x, 0) −→ (x, y) x y
U (x, y) = Z 7dx +Z 2x3ydy = 7x + x3y2. 0 0
Nghiệm tổng quát là 7x + x3y2 = C
Ví dụ 4.16 Giải phương trình vi phân (2x + yexy)dx + (1 + xexy)dy = 0, y(0) = 1. Bài giải
Ta có P ′y = Q′x = (1 + xy)exy do đó nghiệm tổng quát có dạng U(x, y) = C. (x,y) Trong đó U(x, y) = P dx + Qdy ( R 0,0)
Chọn đường đi (0, 0) −→ (x, 0) −→ (x, y) x y
U (x, y) = Z 2xdx + Z (1 + xexy)dy = x2 + y + exy − 1 0 0
Nghiệm tổng quát là x2 + y + exy = C.
y(0) = 1 =⇒ 0 + 1 + 1 = C =⇒ C = 2.
Vậy nghiệm là x2 + y + exy = 2. Ví dụ 4.17 y
Giải phương trình vi phân 1 (1 − )dx + (y2 + )dy = 0, y(1) = 0. x2 x Bài giải 1 Ta có P ′ = −
do đó nghiệm tổng quát có dạng U(x, y) = C. y = Q′x x2
Đại học Bách khoa TPHCM Trang 87
ThS.Nguyễn Hữu Hiệp
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN (x,y) Trong đó U(x, y) = P dx + Qdy ( R 1,0)
Chọn đường đi (1, 0) −→ (x, 0) −→ (x, y) x y 1 y3 y
U (x, y) = Z 1dx + Z (y2 + )dy = x − 1 + + x 3 x 1 0 y Nghiệm tổng quát là y3 x + + = C 3 x
y(1) = 0 =⇒ 1 + 0 = C =⇒ C = 1 y Vậy nghiệm là y3 x + + = 1 3 x
Ví dụ 4.18 Bài giải x x
Giải phương trình vi phân x
(x + ey )dx + e y (1 − )dy = 0, y(0) = 1. y x x Ta có P ′
= − e y do đó nghiệm tổng quát có dạng U(x, y) = C. y = Q′x y2 (x,y) Trong đó U(x, y) = P dx + Qdy ( R 0,1)
Chọn đường đi (0, 1) −→ (0, y) −→ (x, y) y x x x2 x x2 x
U (x, y) = Z 1.dy + Z (x + ey )dx = y − 1 + + y(e y − 1) = + ye y − 1 2 2 1 0 Nghiệm tổng quát là x2 x + yey = C 2
y(0) = 1 =⇒ 0 + 1.e0 = C =⇒ C = 1 Vậy nghiệm là x2 x + ye y = 1 2
4.1.4 Phương trình vi phân tuyến tính Dạng y′ + p(x)y = q(x) R • Tìm hàm h(x) = e p(x)dx • Suy ra nghiệm 1 y(x) = Z f (x)q(x)dx + C h(x)
Chú ý: có nhiều hàm h(x). Ta có thể chọn một hàm h(x) tùy ý. Ví dụ 4.19 x
Giải phương trình vi phân y′ + (3x2 + √ )y = 0 3 − x2
Đại học Bách khoa TPHCM Trang 88
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1 Bài giải x p(x) = 3x2 + √ , 1(x) = 0 3 − x2 R R √ √ (3 ) x2+ x dx 3−x2 h(x) = e p(x)dx = e 3−x2 = ex3− Nghiệm là 1 y(x) = Z Z 1 √ √ 3 2 q(x)h(x)dx + C = √ 0.ex3− 3−x2dx + C = C.e−x + 3−x h(x) ex3− 3−x2 Ví dụ 4.20 y
Giải phương trình vi phân y′ − = x2, y(1) = 1. x Bài giải 1 p(x) = − , q(x) = x2. x R R 1 1
h(x) = e p(x)dx = e − 1xdx = e− ln |x| = eln 1|x| = = ± . |x| x Chọn 1 h(x) = x 1 x3 =⇒ y(x) = Z Z + C) = + Cx 1 x2 2 2 q(x)h(x)dx + C = x x2. dx + C = x( h(x 1 ) 1 x
y(1) = 1 =⇒ 1 = + C =⇒ C = . 2 2 Vậy nghiệm là x3 + x y(x) = 2 x Ví dụ 4.21 y
Giải phương trình vi phân y′ − = . x + 1 x + 1 Bài giải 1 x p(x) = − , q(x) = . x + 1 x + 1 R 1 x+1dx h(x) = e − 1 = e− ln |x+1| = |x + 1| Chọn 1 h(x) = . x + 1 1 R . x x =⇒ y(x) = (x + 1)( + 1 R x + 1 − 1 dx1+ C) = (x + 1) dx + C x + − 1 (x + 1)2 + C) R x 1 + 1 x 1+ 1 = (x + 1) 1 ln | ( x + 1| + 1 + C(x ) +dx 1) + . C = (x + 1)(ln |x + 1| + (x + 1)2
Ví dụ 4.22 Giải phương trình vi phân y′ − y cot x = sin x. Bài giải
p(x) = − cot x, q(x) = sin x. R R 1 sinx dx = e− ln | sin x| =
h(x) = e − cot xdx = e −cosx sin x R dx + C) = sin x(x + C) si 1 n x =⇒ y(x) = sin x( sin x.
Đại học Bách khoa TPHCM Trang 89
ThS.Nguyễn Hữu Hiệp
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
Ví dụ 4.23 Giải phương trình vi phân (x2 + 1)y′ + 4xy = 3. Bài giải 3
Phương trình được viết lại 4x y′ + y = . x2 + 1 x2 + 1 4x 3 p(x) = , q(x) = . x2 + 1 x2 + 1 R 4xdx | h(x) = e x2+1 = e2 ln |x2+1 ln( = e x2+1)2 = (x2 + 1)2 1 =⇒ y(x) = R 3 .(x2 + 1)2dx + C) ( x2 + 1 (x2 + 1 1)2 = R (x3 + 3x + C) (x2 1 ( (3x2 + 3)dx + C) = + 1)2 (x2 + 1)2
Ví dụ 4.24 Giải phương trình vi phân (1 − x)(y′ + y) = e−x, y(0) = 0. Bài giải
Phương trình được viết lại e−x y′ + y = . 1 − x e−x p(x) = 1, f (x) = . 1 − x R h(x) = e 1dx = ex R .exdx + C) e−x 1 =⇒ y(x) = e−x( − x
R dx + C) = e−x(− ln |1 − x| + C). = e−x( 1 − x
y(0) = 0 =⇒ 0 = 1(0 + C) =⇒ C = 0.
Vậy nghiệm là y(x) = −e−x ln |1 − x|
4.1.5 Phương trình vi phân Bernulli
Phương trình Bernouli có dạng
y′ + p(x)y = f (x).yα, α 6= 0, 1.
Phương pháp: Đặt z = y1−α đưa về dạng tuyến tính.
Ví dụ 4.25 Giải phương trình vi phân xy′ + y = xy2 ln x, y(1) = 1. Bài giải
Ta có α = 2 nên nhân 2 vế cho y−2, ta được y−1 y−2y′ + = ln x x
Đặt z = y1−α = y−1 =⇒ z′ = −1.y−2.y′. Ta viết lại phương trình z 1 −z′ +
= ln x ⇐⇒ z′ − z = − ln x x x
Đại học Bách khoa TPHCM Trang 90
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
Giải phương trình tuyến tính R 1 −1
h(x) = e x dx = e− ln |x| = x Nghiệm tổng quát là ln2 x 1 ln2 x Z dx + C) = x(− + C) =⇒ = x(− + C) 1 x 2 y 2 z(x) = x( − ln x.
y(1) = 1 =⇒ 1 = 1(−0 + C) =⇒ C = 1
Vậy nghiệm cần tìm là 1 ln2 x = x(− + 1). y 2
Ví dụ 4.26 Giải phương trình vi phân y′ + 2xy = xex2y3 Bài giải 2x
Phương trình viết lại y′ + = xex2. y3 y2 Đặt 1 z = 2y′ =⇒ z′ = − . y2 y3
PT: −z′ + 2xz = xex2 ⇐⇒ z′ − 4xz = −2xex2 =⇒ p(x) = −4x, q(x) = −2xex2. 2 R h(x) = e (−4x)dx = e−2x2 R 1 = ex2 + Ce2x2. z(x) = e2x2
e−2x2.(−2x)ex2dx = e2x2(e−x2 + C) ⇐⇒ y2 √ Ví dụ 4.27 y
Giải phương trình vi phân 1 − 2x y′ + = . x y2 Bài giải √ PT: y3 y2y′ + = 1 − 2x. x
Đặt z = y3 =⇒ z′ = 3y2y′ z √ 3 √ 3 √ PT: z′ + = 1 − 2x ⇐⇒ z′ +
z = 3 1 − 2x =⇒ p(x) = , q(x) = 3 1 − x2. 3 x x x R 3dxx =⇒ = e3 ln x = x3. h(x) = e 1 x2 2 z(x) = y3(x) = R √ 1 − − x3. 1 − 2xdx = √ x4 5 15 x3 1 − 2x( ) + C x3 15
4.1.6 Bài tập tổng hợp
Ví dụ 4.28 Giải phương trình vi phân y′ = 2x−y, y(0) = 0. Bài giải Viết lại phương trình dy 2x =
⇐⇒ 2ydy = 2xdx (dạng tách biến) dx 2y 2y 2x ⇐⇒ = + C ⇐⇒ 2y = 2x + C. ln 2 ln 2
y(0) = 0 =⇒ 1 = 1 + C =⇒ C = 0
Vậy nghiệm là 2y = 2x =⇒ y = x.
Đại học Bách khoa TPHCM Trang 91
ThS.Nguyễn Hữu Hiệp
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
Ví dụ 4.29 Giải phương trình vi phân: y
xy′ = xex + y, y(1) = 0.. Bài giải y Viết lại phương trình y y′ = e x + (dạng đẳng cấp) x Đặt y u = , f (u) = eu + u x dx
Phương trình được viết lại theo công thức du = f (u) − u x du dx =
⇐⇒ −e−u = ln |x| + C ⇐⇒ −e−y x = ln |x| + C. eu + u − u Z Z dxx ⇐⇒ e−udu =
y(1) = 0 =⇒ −e0 x= 0 + C =⇒ C = −1
Vậy nghiệm tổng quát là −e−yx = ln |x| − 1.
Ví dụ 4.30 Giải phương trình vi phân (x4 + 6x2y2 + y4)dx + 4xy(x2 + y2)dy = 0, y(0) = 0.. Bài giải
P ′y = Q′x = 12x2y + 4y3 do đó nghiệm tổng quát có dạng U(x, y) = C. (x,y) Trong đó U(x, y) = P dx + Qdy ( R 0,0)
Chọn đường đi (0, 0) −→ (x, 0) −→ (x, y) x y x5 U (x, y) = 4 Z x4dx + Z 4xy(x2 + y2)dy = + 2x3y2 + xy . 5 0 0
Nghiệm tổng quát là x5 + 2x3y2 + xy4 = C 5 y(0) = 0 =⇒ C = 0
Vậy nghiệm là x5 + 2x3y2 + xy4 = 0 5 Ví dụ 4.31 dy
Giải phương trình vi phân e1+x2 tan ydx = . x Bài giải
Viết lại phương trình ở dạng tách biến dy 1 xex2+1dx = Z Z
dy ⇐⇒ ex2+1 = ln | sin y| + C co sisnyy 2 ⇐⇒ xex2+1dx = tan y
Ví dụ 4.32 Giải phương trình vi phân: xy′ = y + x2, y′(0) = 0. Bài giải
Viết lại phương trình y y′ − = x (dạng tuyến tính) x 1 p(x) = − , f(x) = x x R 1 −1
h(x) = e x dx = e− ln |x| = x Z + C) = x(x + C) 1 x =⇒ y(x) = x( x.
Đại học Bách khoa TPHCM Trang 92
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
y′(0) = 0 =⇒ [2x + C]x=0 = 0 =⇒ C = 0 Vậy nghiệm là y = x2. Ví dụ 4.33 1 + 2x + y
Giải phương trình vi phân y′ = . 1 − x − 2y Bài giải Viết lại phương trình dy 1 + 2x + y = dx 1 − x − 2y
⇐⇒ (1 − x − 2y)dy = (1 + 2x + y)dx
⇐⇒ (1 + 2x + y)dx + (x + 2y − 1)dy = 0 P ′ U (x, y) = C
y = Q′x = 1 (dạng toàn phần) do đó nghiệm tổng quát có dạng . (x,y) Trong đó U(x, y) = P dx + Qdy ( R 0,0)
Chọn đường đi (0, 0) −→ (x, 0) −→ (x, y) x y
U (x, y) = Z (1 + 2x)dx + Z (x + 2y − 1)dy = x + x2 + xy + y2 − y 0 0
Nghiệm tổng quát là x + x2 + xy + y2 − y = C √
Ví dụ 4.34 Giải phương trình vi phân y′ x + 1 + y ln3 y = 0, y(0) = e. Bài giải Viết lại phương trình dy√x + 1 + y ln3 y = 0 dxdy dx ⇐⇒ + √ = 0 (dạng tách biến) y ln3 y x + 1 R √ = 0 dy R dx ⇐⇒ + x + 1 y ln3 1 y √ ⇐⇒ − + 2 x + 1 + C = 0 2 ln2 y 1 3
y(0) = e =⇒ − + 2 + C = 0 =⇒ C = − 2 2 √ 3 Vậy nghiệm là 1 − + 2 x + 1 − = 0 2 ln2 y 2
Ví dụ 4.35 Giải phương trình vi phân (1 − x2)y′ + xy = (1 − x2) arcsin x, y(0) = 0. Bài giải
Viết lại phương trình x y′ +
y = arcsin x (dạng tuyến tính) 1 − x2 x p(x) = , f (x) = arcsin x 1 − x2 R 1 x ln |1−x2| − 1 h(x) = e 1−x2 dx = e−1 2
= eln |1−x2|− 1 2 = |1 − x2| 2 = √1 − x2 Z + C). √ 1 √ arcsi 2n x =⇒ y(x) = 1 − x2 arcsin x√ dx + C = 1 − x2( 1 − x2
Đại học Bách khoa TPHCM Trang 93
ThS.Nguyễn Hữu Hiệp
4.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
y(0) = 0 =⇒ 0 = 1(0 + C) =⇒ C = 0 √ Vậy nghiệm là arcsin x y(x) = 1 − x2. . 2 Ví dụ 4.36 2xy + 3
Giải phương trình vi phân y′ = , y(1) = 2. x2 Bài giải
Viết lại phương trình 2 3 y′ − y = (dạng tuyến tính) x x2 −2 3 p(x) = , f (x) = x x2 R 1 −2 −2 ln |x| ln x−2 h(x) = e x dx = e = e = x2 1 Z . + C). 3 x2 − x31 =⇒ y(x) = x2 dx + C = x2( x2
y(1) = 1 =⇒ 1 = 1(−1 + C) =⇒ C = 2 Vậy nghiệm là −1 y(x) = + Cx2 x Bài tập 1. x3y′ = y(x2 + y2). 8. ex2(y′ + 2xy) = x p √
9. xyy′ − y2 + xe−yx = 0, y(1) = 0.
2. 1 − y2dx + y 1 + x2dy = 0.
3. (xy2 + x)dx + (y − x2y)dy = 0. 10. xy′ − y = x tan y . x 4. y2 + x2y′ = xyy′. y y4 √ 11. 3y′ − √ = √ , y(0) = 1.
5. xy′ + y 1 − x2 = 0, y(1) = 1. x2 + 1 x2 + 1 √1 − x2 + 1 √ 2y − 3x + 1 = 1 − x2. 12. y′ = . 6x − 4y + 2 ĐS: ln |y| + ln √ 1 1 y y 1 2 − x2 − 1
ĐS: − (2y − 3x + 1) + ln |8y − 12x + 4| = 6. y′ − = , y(0) = 2. 4 8 x + 1 x + 1 x + C. p √
13. (2y3 − x2y)y′ = xy2 − 2x3.
7. 1 − y2dx + y 1 − x2dy = 0
Đại học Bách khoa TPHCM Trang 94
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.2. PHƯƠNG TRÌNH VI PHÂN CẤP 2
4.2 Phương trình vi phân cấp 2
4.2.1 Phương trình vi phân cấp 2 thuần nhất
Phương trình vi phân thuần nhất y′ + py′ + qy = 0.
Phương trình đặc trưng k2 + pk + q = 0(*)
• (*) có 2 nghiệm phân biệt k1 6= k2, nghiệm thuần nhất là y0 = C1ek1x + C2ek2x
• (*) có 2 nghiệm kép k1 = k2 = k0 y0 = C1ek0x + C2xek0x
• (*) có 2 nghiệm phức k = a ± bi
y0 = eax(C1 cos bx + C2 sin bx).
4.2.2 Phương trình vi phân cấp 2 không thuần nhất - dạng 1
Dạng y′ + py′ + qy = Pn(x)eαx (1). Nghiệm y = y s 0 + yr, với yr = x Qn(x)eαx
• Nếu α không là nghiệm của (*) thì s = 0
• Nếu α là nghiệm đơn của (*) thì s = 1
• Nếu α là nghiệm kép của (*) thì s = 2 Q n n−1 n(x) = Ax + Bx
+ ... là một đa thức bậc n tổng quát.
Để tính các hệ số A, B.. ta tính đạo hàm y′ thế vào (1). r, y′r
Ví dụ 4.37 Giải phương trình vi phân y′ − 3y′ − 4y = 2xe−x ĐS: 1 y = C −x 4x 1e + C2e − (5x + 2)e−x 25
Ví dụ 4.38 Giải phương trình vi phân y′ + 4y′ + 4y = (2x + 1)e−2x (*). Bài giải
a) Phương trình đặc trưng k2 + 4k + 4 = 0 ⇐⇒ k1 = k2 = −2.
Nghiệm thuần nhất y0 = C1e−2x + C2xe−2x.
b) f(x) = (2x + 1)e−2x : α = 1 =⇒ s = 1 y 3 2
r = x2(Ax + B)e−2x = (Ax + Bx )e−2x
=⇒ y′r = (−2Ax3 − 2Bx2 + 3Ax2 + 2Bx)e−2x
Đại học Bách khoa TPHCM Trang 95
ThS.Nguyễn Hữu Hiệp
4.2. PHƯƠNG TRÌNH VI PHÂN CẤP 2
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
=⇒ y′r = (4Ax3 + 4Bx2 − 12Ax2 − 8Bx + 6Ax + 2B)e−2x Thế vào (*) ta được 1 A = ( 31 −8B + 6A + 8B = 2 B =
(−8Bx + 6Ax + 2B) + 4.2Bx + 0 = 2x + 1 ⇐⇒ ⇐⇒ 2 2B = 1 1 1 Vậy nghiệm y = C−2x e + C2xe−2x + x2( x + 3 )e−2x 2
Ví dụ 4.39 Giải phương trình vi phân y′ + 4y = (2x2 + 3)e−2x (*). Bài giải
a) Phương trình đặc trưng k2 + 4 = 0 ⇐⇒ k = 0 ± 2i.
Nghiệm thuần nhất y0 = e0x(C1 cos 2x + C2 sin 2x)
b) f(x) = (2x2 + 3)e−2x : α = −2 =⇒ s = 0. yr = (Ax2 + Bx + C)e−2x
=⇒ y′r = (−2Ax2 − 2Bx − 2C + 2Ax + B)e−2x
=⇒ y′r = (4Ax2 + 4Bx + 4C − 8Ax − 4B + 2A)e−2x
Thế vào (*) (4Ax2 + 4Bx + 4C − 8Ax − 4B + 2A) + 4(Ax2 + Bx + C) = 2x2 + 3. 4A + 4A = 2 1 A = 4B − 8A + 4B = 0 41 7 . B = C = ⇐⇒ ⇐⇒ 4 16 1 7 Vậy ng 1 4C hiệ − m 4lB à y+ 2 = A C1+ c 4 osC 2 = x 3 + C2 sin 2x + ( x2 + x + 4 4 )e−2x. 16
Ví dụ 4.40 Giải phương trình vi phân y′ + 6y′ + 8y = x(e−x + e−2x) ĐS: 1 4 1 1
y = C1e−2x + C2e−4x + ( x − )e−x + ( x2 − 3 9 4 x)e−2x 4
Ví dụ 4.41 Giải phương trình vi phân y′ − 2y′ + y = e2x sin x (*)
a) Phương trình đặc trưng k2 − 2k + 1 = 0 ⇐⇒ k1 = k2 = 0
Nghiệm thuần nhất y0 = C1ex + C2xex
b) f(x) = e2x sin x : α + βi = 2 + i =⇒ s = 0 yr = e2x(A cos x + B sin x).
y′r = e2x(3A cos x + 3B sin x − A sin x + B cos x)
y′r = e2x(3A cos x + 3B sin x − 4A cos x + 4B sin x). Thế vào (*):
(3A cos x + 3B sin x − 4A cos x + 4B sin x) −2(3A cos x + 3B sin x − A sin x + B cos x) +(A cos x + B sin x) = sin x 1 A = − 2 B = 0 ⇐⇒
Đại học Bách khoa TPHCM Trang 96
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.2. PHƯƠNG TRÌNH VI PHÂN CẤP 2
4.2.3 Phương trình vi phân cấp 2 dạng 2
Dạng y′ + py′ + qy = eαx(a cos βx + b sin βx) (2).
Nghiệm y = y0 + yr, với yr = xseαx(A cos βx + B sin βx)
• Nếu α + βi là nghiệm của (*) thì s = 1
• Nếu α + βi không là nghiệm của (*) thì s = 0 Tính đạo hàm y′
thế vào (2) suy ra hệ số A, B. r, y′r
Ví dụ 4.42 Giải phương trình vi phân y′ + y = 2 sin x − cos x ĐS: 1
y = C1 cos x + C2 sin x + x(− cos x − sin x) 2
Ví dụ 4.43 Giải phương trình vi phân y′ − 6y′ + 9y = e3x(x2 + sin x)
4.2.4 Phương trình vi phân cấp 2 - dạng 3
Dạng y′ + py′ + qy = eαx(Pn(x) cos βx + Qm(x) sin βx.
Nghiệm y = y0 + yr, với yr = xseαx(Hl(x) cos βx + Kl(x) sin βx
• Nếu α + βi là nghiệm của (*) thì s = 1
• Nếu α + βi không là nghiệm của (*) thì s = 0
Trong đó, l = max m, n và Hl, Kl là các đa thức bậc l tổng quát. Tính đạo hàm y′
thế vào (2) để tìm hệ Hl và Kl. r, y′r Bài tập
Giải các phương trình vi phân sau
Bài 1. y′ + 4y′ + 3y = (2x + 1)e−3x 3 ĐS: 1 y = C1e−x + C2e−3x + x(− x − 2 )e−3x 4
Bài 2. y′ + 4y′ + 4y = 2xe−2x. ĐS: 1 y = C1e−2x + C2e−2x + x3e−2x 3
Bài 3. y′ + 4y′ + 8y = (x2 + 3x)e−2x ĐS 1 3
y = e−2x(C1 cos 2x + C2 sin 2x) + ( x2 + 4 x)e−2x 4
Bài 4. y′ + 3y′ − 4y = e2x sin x 5 cos x + ĐS: 774 y = C1ex + C2e−4x + − sin x e2x 74
Bài 5. y′ − 2y′ + y = ex cos 2x. ĐS: 1
y = C1ex + C2xex + − ex cos 2x 4
Đại học Bách khoa TPHCM Trang 97
ThS.Nguyễn Hữu Hiệp
4.3. HỆ PHƯƠNG TRÌNH VI PHÂN
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN 1 Bài 6. 1
y′ + 4y = 2 sin 2x − cos 2x ĐS: y = C1 cos 2x + C2 sin 2x + x(− cos 2x − sin 2x) 2 4
Bài 7. y′ + 5y′ + 6y = e−2x(x2 + 3x − cos x)1 1 1 ĐS: 1 y = C1e−2x + C2e−3x + x( x2 + x − 1)e−2x + e−2x( cos x − sin x). 3 2 2 2
4.3 Hệ phương trình vi phân
4.3.1 Ánh xạ đạo hàm
Định nghĩa 4.1 Cho D : C1(R) → C thỏa D(x(t)) = x′(t) gọi là ánh xạ đạo hàm Ví dụ 4.44 a) Cho x = e2t + 3t2.
4.3.2 Hệ phương trình vi phân ( x′y′ = 2x − 4y + et Ví dụ 4.45 = x
Giải hệ phương trình vi phân − 2y + 3t ( Dy = 2x − 4y + et
Ta viết lại hệ Dx = x − 2y + 3t1 1 1 x = 2C1 + C2e−3t − et + 2t2 − t − 2 3 3 2 y = C1 + C t. Nghiệm 2e−3t + t2 − 3 ( x′y′ = 2x + 4y − e−2t (2) Ví dụ 4.46 =
Giải hệ phương trình vi phân −x + 3y + 2te−2t (1) Bài giải (
2x + (D − 4)y = −e−2t (2) a) V ( iết D-4l)ạ(i1 h ) ệ (D − + 1)x − 3y = 2te−2t (1) +3(2):
(D − 4)(D + 1)x − 6x = (−4t + 2)e−2t + 2te−2t − 3e−2t
⇐⇒ (D2 − 3D − 10)x = (−12t − 1)e−2t (3)
b) Phương trình đặc trưng k2 − 3k − 10 = 0 ⇐⇒ k = −2 ∨ k = 5
Nghiệm thuần nhất y0 = C1e−2t+C2e5t
f (t) = (−12t − 1)e−2t : α = −2 =⇒ s = 1 =⇒ x 2
r = t(At + B)e−2t = (At + Bt)e−2t
=⇒ x′r = (−2At2 − 2Bt + 2At + B)e−2t
Đại học Bách khoa TPHCM Trang 98
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
4.3. HỆ PHƯƠNG TRÌNH VI PHÂN
=⇒ x′r = (4At2 + 4Bt − 8At − 4B + 2A)e−2t Thế vào (3):
(4Bt − 8At − 4B + 2A) − 3(−2Bt + 2At + B) − 10Bt = (−12t − 1)e−2t 6 19 ⇐⇒ A = , B = 7 49 19 t2 + Suy ra 67 x(t) = C1e−2t + C2e5t + e−2t c) Từ (1): 49 1 y(t) = (x′ + x − 2te−2t) 3 C 4 52 19 = − 1 e−2t + 2C t2 − t + 3 2e5t + ( 7 147 )e−2t 147 ( x′y′ = x + y + cos t (2) Ví dụ 4.47 = 3x
Giải hệ phương trình vi phân − y + t, (1) Bài giải a) Viết lại hệ ( (D − − x 3 + )x ( + D y − = 1)yt,= cos t (1) (2)
(1)+(D-3)(2): D2y − 4Dy + 4y = t − sin t − 3 cos t (3)
b) Phương trình đặc trưng k2 − 4k + 4 = 0 ⇐⇒ k1 = k2 = 2. Suy ra y0 = (C1 + C2t)e2t.
(a) Giải D2y − 4Dy + 4y = − sin t − 3 cos t (3a)
y1 = A cos t + B sin t, đạo hàm thế vào (3a)
−A cos t − B sin t + 4A sin t − 4B cos t + 4A cos t + 4B sin t = − sin t − 3 cos t 13 A = −25 9 B = ⇐⇒ 25 13 9 =⇒ y1 = − cos t + sin t 25 25
(b) Giải D2y − 4Dy + 4y = t (3b)
y1 = At + B, đạo hàm thế vào (3b) 1 A = 4 1 1 1 =⇒ y2 = t + B = 4 4 0 − 4A + 4At + 4B = t ⇐⇒ 4 9 1 1 Vậy 13 y = (C1 + C2t)e2t − cos t + sin t + t + 25 25 4 4 c) Từ (2) suy ra 4 3 t y = (C1t + C1 + C2)e2t + sin t − cos t − 25 25 4
Đại học Bách khoa TPHCM Trang 99
ThS.Nguyễn Hữu Hiệp
4.3. HỆ PHƯƠNG TRÌNH VI PHÂN
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN (
x′y′ = −x + y + e2t sin 2t Ví dụ 4.48 = 2x + y + e2t cos 2t
Giải hệ phương trình vi phân (
x′y′ = −x + 2y + cos t (2) Ví dụ 4.49 = 2x + y + t2 (1)
Giải hệ phương trình vi phân ( x + (D − 2)y = cost (2)
Viết lại hệ (D − 2)x − y = t2 (1)
(D − 2)pt(1) + pt(2) : (D2 − 4D + 5)x = 2t − 2t2 + cos t (3)
a) Phương trình đặc trưng k2 − 4k + 5 = 0 ⇐⇒ k = 2 ± i
Nghiệm thuần nhất x0 = e2t(C1 cos t + C2 sin t).
b) Giải x′ − 4x′ + 5x = 2t − 2t2 (3a)
f (t) = 2t − 2t2 : α = 0 =⇒ s = 0 2 6 4
=⇒ x1 = At2 + Bt + C. Đạo hàm thế vào (3a) suy ra A = − , B = − , C = − 5 25 125 6 4 Suy ra 2 x1 = t2 − t − . 5 25 125
c) Giải x′ − 4x′ + 5x = cos t (3b)
f (t) = cos t : α + βi = i =⇒ s = 0 =⇒ x2 = A cos t + B sin t.
Đạo hàm thế vào (3b) suy ra 3 1 x2 = − cos t + sin t 8 8 Vậy 2 6 4 3 1
x = e2t(C1 cos t + C2 sin t) + t2 − t − − cos t + sin t 5 25 125 8 8 Từ (1) suy ra y = x′ − 2x − t2 1 14 22 3 1
= e2t((C2 − 2C1) cos t(C1 − 2C2) sin t) − t2 − − − cos t + sin t. 5 25 125 8 8 Bài Tập
Giải hệ phương trình vi phân sau ( x′ Bài 1. = 3x + 2y + te2t y′ = 2x + 6y − 6e2t 8 266 118 1 32 ĐS: 1 x = −4C 2t 2t 7t 1e2t + C2e7t + (− t2 − t + )e y = C1e + C2e + (− t2 − t)e2t 2 5 25 25 5 25 ( x′ Bài 2. = 3x − y + tet y′ = 4x − y − 2et 3 2 ĐS: 1 x = (C 2 1 + tC2)et + (
t3 + t2)et, y = (2C1 + C2 + 2C2t)et + ( t3 + 2t − 2t)et. 3 2 3 (
x′y′ = 2x + 4y − e2t sin t Bài 3. = −x + 3y + e2t cos 3 5 ĐS: 1 −1 x = −3C 5t 1e−2t + C2e5t + e2t( cos t + sin t), y = C1e−2t + C + 2t( cos t + 2 17 17 2e e 17 4 sint) 17
Đại học Bách khoa TPHCM Trang 100
ThS.Nguyễn Hữu Hiệp ÔN THI CUỐI KỲ
4.4 Nội dung thi giữa kỳ
1. Khảo sát và vẽ đồ thị y = f(x).
2. Xét sự hội tụ tích phân suy rộng: Loại 1 và 2
3. Tính tích phân suy rộng
4. Ứng dụng hình học của tích phân: cho các hàm y = f(x)
5. Phương trình vi phân cấp 1: Tách biến; đẳng cấp, tuyến tính, từng phần. Chú ý điều kiện đầu
6. Phương trình vi phân cấp 2: f(x) = eαxPn(x) và f(x) = eαx(a cos βx + b sin βx)
7. Hệ Phương trình vi phân: 2 phương trình 2 ẩn giải bằng phương pháp khử.
4.5 Bài tập ôn tập cuối kỳ
Bài 1. Khảo sát và vẽ đồ thị a) x − 3 y = x2 − x − 2 b) y = (x − 2)e−1x arctan x ,x ≤ 0 x + 1 c) xe1/x, x > 0 y = +∞ dx
Bài 2. Cho tích phân I = √
. Tìm α để tích phân hội tụ. Tính tích phân khi R 0 (xα + 1) x2 + x α = 1. +∞ x Bài 3. Cho tích phân − 3 I =
dx. Tìm α để tích phân hội tụ. Tính tích phân R α 2 1 x (x − x + 1) khi α = 2.
Bài 4. Tính diện tích miền phẳng a) √ D : y = x, x + y = 2, Ox
b) D : y = x2, y = log2(x + 1), x + y = 2
Bài 5. Tính độ dài đường cong a) y = cosh x, x ∈ [0, 1] √ b) y = 1 − x2
Bài 6. Tính thể tích vật thể tròn xoay 101
4.5. BÀI TẬP ÔN TẬP CUỐI KỲ
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
a) D : y = x, y = arctan x, x = 1. Tính VOy √ √
b) D : y = x2 + 1, y = x + 1, x = 1. Tính VOx, VOy.
Bài 7. Tính diện tích mặt tròn xoay a) √ C : y =
x(x − 13), x ∈ [0, 13]. Tính SOx, SOy √
b) C : y = x − x2. Tính SOx, SOy. Bài 8. Cho miền x2
D giới hạn bởi y = 2x2, y = , y = x. 2 a) Tính diện tích D.
b) Tính độ dài đường cong x2 C : y = , x ∈ [0, 1]. 2
c) Tính diện tích mặt tròn xoay khi cho C quay quanh Ox và Oy.
d) Tính thể tích vật thể tròn xoay khi cho D quay quanh Ox, Oy.
Bài 9. Giải phương trình vi phân cấp 1 a) x3y′ = y(x2 + y2). p √
b) 1 − y2dx + y 1 + x2dy = 0, y(0) = 0.
c) (xy2 + x)dx + (y − x2y)dy = 0, y(1) = 2.
d) y2 + x2y′ = xyy′, y(1) = 1. √
e) xy′ + y 1 − x2 = 0, y(1) = 1. √1 − x2 + 1 √ = 1 − x2. ĐS: ln |y| + ln √ y y 1 2 − x2 − 1 f) y′ − = , y(0) = 2. x + 1 x + 1 p √
g) 1 − y2dx + y 1 − x2dy = 0, y(2) = 1
h) ex2(y′ + 2xy) = x, y(1) = 1
i) xyy′ − y2 + xe−yx = 0, y(1) = 0.
j) xy′ − y = x tan y , y(−1) = 1. x k) y y4 3y′ − √ = √ , y(0) = 1. x2 + 1 x2 + 1 l) 2y − 3x + 1 y′ = , y(0) = 1. 6x − 4y + 2
Bài 10. Giải phương trình vi phân cấp 2
Bài 11. Giải hệ phương trình vi phân.
Đại học Bách khoa TPHCM Trang 102
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN 4.6. ĐỀ THI CUỐI KỲ
4.6 Đề thi cuối kỳ Đề số 1 √
Câu 1. Khảo sát và vẽ đồ thị hàm số x2 + x + 2 y = . x + 1 +∞ xα
Câu 2. Tìm α để tích phân
dx hội tụ. Tính tích phân với α = 1. R 1 (x + 1)2(x2 − x + 1)
Câu 3. Tính diện tích miền phẳng giới hạn bởi √ x = y, y = 0, y = 2 − x.
Câu 4. Giải phương trình vi phân cấp 1 (ye−x + y2 + 1)dx = (e−x − 2xy)dy.
Câu 5. Giải phương trình vi phân cấp 2 y′ + 4y′ + 4y = cos 3x.
( y′(t) = x(t) + 2y(t) + cost.
Câu 6. Giải hệ phương trình vi phân x′(t) = 2x(t) − y(t) + 2 sin t, Đề số 2
Câu 1. Khảo sát và vẽ đồ thị hàm số y = xe−1x . +∞ dx
Câu 2. Tìm α để tích phân √
hội tụ. Tính tích phân với α = 1. R 1 xα x2 − x + 1
Câu 3. Tính thể tích vật thể tròn xoay khi cho miền D giới hạn bởi y = x2 và x = y2 quay quanh Ox và quay quanh Oy.
Câu 4. Giải phương trình vi phân cấp 1: y′ − 3x2y = x4ex3.
Câu 5. Giải phương trình vi phân cấp 2: y′ − 5y′ + 6y = e2x(3x − 4) + x. ( y′(t) = x(t) + 6y(t).
Câu 6. Giải hệ phương trình vi phân x′(t) = 3x(t) + 4y(t) + 3e−2t, Đề số 3
Câu 1. Giải phương trình vi phân cấp 1: (ex + 3y + 1)dx = (y3 − 3x)dx.
Câu 2. Giải phương trình vi phân cấp 2: y′ + 5y′ + 6y = (x + 1)e2x. ( y′(t) = 2x + 4y + t.
Câu 3. Giải hệ phương trình vi phân x′(t) = 3x + y + et, 3 xα
Câu 4. Tìm α để tích phân √
dx hội tụ. Tính tích phân với α = 2. R 0 9 − x2
Đại học Bách khoa TPHCM Trang 103
ThS.Nguyễn Hữu Hiệp 4.6. ĐỀ THI CUỐI KỲ
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN +∞ dx Câu 5. Tính tích phân . R 0 (x2 + x + 1)(x + 2)
Câu 6. Khảo sát và vẽ đồ thị hàm số y = x3e−x.
Câu 7. Tính diện tích miền phẳng giới hạn bởi y = −x2 và y = x2 − 2x − 4. Đề số 4
Câu 1 Giải phương trình vi phân y′ + 3x2y = 3x2 + 3x5.
Câu 2 Giải phương trình vi phân y′ + 3y′ + 2y = 2x + 3 + 6ex. 0 1
Câu 3 Tính tích phân hoặc chứng tỏ phân kỳ ex I = dx. R x3 −1 +∞ Câu 4 Tính tích phân I = e−x cos 2xdx. R 0
Câu 5 Khảo sát và vẽ đồ thị hàm số 1 y = x2ex . √
Câu 6 Tính diện tích miền phẳng giới hạn bởi x y = , y = 0, x = 1. 1 + x3 Đề số 5
Câu 1 Giải phương trình vi phân xdy − ydx = 3x2 sin xdx.
Câu 2 Giải phương trình vi phân y′ − 4y′ + 13y = (x2 + 4x)e2x. ( y′(t) = 7x −2y +3t
Câu 3 Giải hệ phương trình vi phân x′(t) = 4x + y + 2t + 1, +∞ dx
Câu 4 Tìm α để tích phân √
hội tụ. Tính Tích phân với α = 1. R √ (xα − 1) x2 − 2 2 3
Câu 5 Tính tích phân suy rộng dx I = R1 p . (4x − x2 − 3)3
Câu 6 Tính diện tích mặt tròn xoay khi cho đường cong C : y = x2, x = 0 7→ 1 quay quanh trục Ox và Oy.
Câu 7 Khảo sát và vẽ đồ thị hàm số y = x2 ln x.
Đại học Bách khoa TPHCM Trang 104
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN 4.6. ĐỀ THI CUỐI KỲ Đề số 6
Câu 1 Giải phương trình vi phân xy′ − y + ey/x = 0
Câu 2 Giải phương trình vi phân y′ + 3y′ − 4y = (x + 1)e−4x. ( y′(t) = x + 2y + 3t.
Câu 3 Giải hệ phương trình vi phân x′(t) = 3x + 2y + et, +∞ dx
Câu 4 Tìm α để tích phân √
hội tụ. Tính tích phân khi α = 1. R 2 1 xα 3x − 2x − 1
Câu 5 Khảo sát và vẽ đồ thị hàm số 2 y = e4x−x . √ √
Câu 6 Tính thể tích vật thế tròn xoay khi cho D giới hạn bởi y = x2 3 và y = 4 − x2 quay quanh trục Ox. Đề số 7
Câu 1 Khảo sát và vẽ đồ thị e−x y = . 1 − x +∞ x2 − 3
Câu 2 Tìm α để tích phân
dx hội tụ. Tính tích phân với α = 1. R α 2 1 x (x + 1)(x + 1) ln x Câu 3 Tính độ dài cung x2 y = − , 1 ≤ x ≤ 3. 2 4
Câu 4 Giải phương trình vi phân a) y y′ = + x sin x thỏa y(π) = 2π. x p b) c) x2 y′ y′ = + 6 y′ y2 + − 9y 3x2 = e + 3x(x 3 y x , x > − 2).0. ( y′ = 2x −y +e2t
Câu 5 Giải hệ phương trình vi phân x′(t) = 3x − 4y + 3t, Đề số 8
Câu 1. Khảo sát và vẽ đồ thị hàm số 8x y = √ . x2 − 4 +∞ Câu 2. Tìm 3x − 1 α để tích phân y = √ dx hội tụ. R 0 (4 + xα) 3 x4 + 5x2 +∞ dx
Câu 3. Tính tích phân suy rộng √ . R 0 (x + 1) x2 − x + 1
Đại học Bách khoa TPHCM Trang 105
ThS.Nguyễn Hữu Hiệp 4.6. ĐỀ THI CUỐI KỲ
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN √
Câu 4. Cho miền D giới hạn bởi y = x2 + 1, y = ex, x = 1. Tính thể tích vật thể tròn xoay
khi cho D quay quanh trục Ox và Oy.
Câu 5. Giải phương trình vi phân
a) (yexy + 4xy)dx + (xexy + 2x2 + 3)dy = 0. b) (x + y)y′ = (x + y)2 + 1.
c) y′ − 4y′ + 3y = cos x + xe3x. ( y′ = 3x −y −3t.
Câu 6. Giải hệ phương trình vi phân x′ = x + y + 2et,
Đề số 9: Dự thính 12/2013
Câu 1) Khảo sát và vẽ đồ thị x − 1 y = . e2x +∞ (2x + 3)dx
Câu 2) Cho tích phân I = R0 (x + 1)α(x2 + 4x + 5) (a) Tìm α để I hội tụ (b) Tính I với α = 1.
Câu 3) Tính VOx, VOy với D : y = log3 x, y = 4 − x, y = 0.
Câu 4) Giải PTVP (x2 + 4)y′ − 2xy = 6x.
Câu 5) Giải PTVP y′ − 6y′ + 8y = 6 cos 3x. ( x′y′ = 6x + 4y + 2e10t. Câu 6) Giải PTVP = 7x + 3y + e10t,
Chính quy: 2013-2014. Ca 1 p √
Câu 1 Giải PTVP x y2 + 2xy + 2x2dx = (2xy + 3x2)dy − (2y2 + 3xy)dx, y(1 + 2) = 0
Câu 2 Giải PTVP y′ − 5y′ + 6y = (x + 2)e2x. x′1 = 7x1 − 12x2 + 6x3 x′2 = 10x1 − 19x2 + 10x3
Câu 3 Giải hệ PTVP x′3 = 12x1 − 24x2 + 13x3.
Câu 4 Khảo sát và vẽ đồ thị x2 y = . |x − 2|
Câu 5 Tính diện tích miền 3 6
D : y2 − x2 = 1, y = x − 1, x = . 2 5 4 Câu 6 Tính tích phân 3 I = √ dx. R2 (x − 1) 6x − x2 − 8
Đại học Bách khoa TPHCM Trang 106
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN 4.6. ĐỀ THI CUỐI KỲ +∞
Câu 7 Tìm α để tích phân sau hội tụ I = e−x + ln(1 + 1 x2α ). R 1 xα−3(1 + xα)α−3
Chính quy: 2013-2014. Ca 2 Câu 1 Giải PTVP y y′ = + x2 cos x. x Câu 2 Giải PTVP 1
y′ + 4y = sin 2x + 1, y(0) = , y′(0) = 0. 4 ( . y′ = 2x + y − 1
Câu 3 Giải hệ PTVP x′ = x + 8y + e2t ( √
Câu 4 Khảo sát và vẽ đồ thị hàm số x + x2 2x − x − 2x, x , x > 0 ≤ 0, y =
Câu 5 Tìm thể tích vật thể tròn xoay VOy(D) biết D : xy = 1, y = x, x = 9y, x > 0, y > 0. +∞ Câu 6 Tính tích phân dx I = . R e x(ln3 x + ln2 x + ln x) 1
Câu 7 Khảo sát sự hội tụ tích phân ln xdx I = R0 px(1−x)α
Dự Thính: 2013-2014-HKII
Câu 1. Khảo sát và vẽ đồ thị hàm số f(x) = (x − 2)e−1x . +∞
Câu 2. Cho tích phân suy rộng dx I = R1 p . x2. (x − 1)α
(a) Tìm tất cả các giá trị thực α để tích phân hội tụ.
(b) Tính tích phân khi α = 1. √
Câu 3. Cho miền D giới hạn bởi y = 2x − x2 và trục Ox. Tính thể tích và diện tích xung
quanh khi cho D quay quanh trục Ox. 1
Câu 4. Giải phương trình vi phân cấp 1: y(x) y′(x) − = . x + 1 y(x).(x + 1)
Câu 5. Giải phương trình vi phân cấp 2: y′ (x) + 4y′(x) + 3y(x) = xe−3x thỏa điều kiện y(0) = y′(0) = 0.
Câu 6. Giải hệ phương trình vi phân ( x′(t) = ) − = 5 3 x x((t)) + + 3 3 y y((t)) + − t etet y′(t t t . ,
Đại học Bách khoa TPHCM Trang 107
ThS.Nguyễn Hữu Hiệp 4.6. ĐỀ THI CUỐI KỲ
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
Đề Học Lại - II/2012-2013
Câu 1. Giải phương trình vi phân
(a) y′ cos x + y = 1 − sin x (b) y′ − 3y′ + 2y = 2ex ( y′ = x + 3y + sint
Câu 2. Giải phương trình vi phân x′ = x + 3y − cos t − sin t +∞ Câu 3. Cho tích phân dx I = √
. Tìm điều kiện để tích phân hội tụ và tính tích R 2 1 xm x + 8x + 4 phân khi m = 1.
Câu 4. Tính thể tích vật thể tròn xoay khi cho miền D giới hạn bởi y = ln x, y = 0, x = 2 quay quanh trục Ox.
Câu 5. Khảo sát và vẽ đồ thị hàm số 1 y = xex .
Đề ôn tập hè 2014
Câu 1. Khảo sát và vẽ đồ thị hàm số y = (x − 1)ex Câu 2. Cho tích phân +∞ xαdx I = √ R 1 (x + 1) 2x2 − x + 3
a) Tìm α để tích phân hội tụ.
b) Tính tích phân khi α = 1
Câu 3. Cho miền D : y = x2, x = y2. Tính thể tích vật thể tròn xoay khi cho D quay quanh trục Ox và trục Oy.
Câu 4. Giải phương trình vi phân cấp 1: y2 + x2y′ = xyy′, y(1) = 1.
Câu 5. Giải phương trình vi phân cấp 2: y′ − 3y′ − 4y = 2x2e−x, y(0) = y′(0) = 0. ( y′ = 2x + 8y + tet
Câu 6. Giải hệ phương trình vi phân x′ = −x + 5y + t
Đại học Bách khoa TPHCM Trang 108
ThS.Nguyễn Hữu Hiệp ĐÁP ÁN Đề 8
a) Tiêm cận đứng x = ±2, tiệm cận ngang y = ±8. Không có cực trị. b) α > 2/3 c) Đề 8
1) Tiệm cận ngang y = 0, cực đại x = 3/2 2) 3π 1 α > 0, I = + ln 5 4 4 3) 4) y = C(x2 + 4) − 3 6 5) 108 y = C 4x 2x 1e + C2e − sin 3x − cos 3x. 325 325
6) x = −1/2C1e10t + C2et + 4/3te10t − 1/9e10t, y = C1e10t + C2et + 4/3te10t.
Chính quy: 2013-2014. Ca 1
1) Phương trình vi phân đẳng cấp y √ r r = ln |x| + 2 2. y2 + 2xy + 2x2 2 y2 + 2xy + 2x2 + ln x2 + 1 + x x2 2) 1
y = C1e2x + C2e3x + − x2 − 3x e2x. 2 x′1 = 2C1et + 3C3e−t x′2 = C1et + C2et + 5C3e−t 3) x′3 = 2C2et + 6C3e−t
4) Tiệm cận x = 2, y = x ± 2. Cực đại (0; 0) và cực tiểu (4; 8). 5) 1 24 S(D) = ln 5 + . 2 25 √ 6) I = π 3.
7) Điều kiện α2 − 3 > 1 ⇐⇒ α > 2. 109 4.6. ĐỀ THI CUỐI KỲ
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN
Chính quy: 2013-2014. Ca 2
1) y = x cos x + x2 sin x + Cx. 2) x 1 1 x 1 1
ytq = C1 cos 2x + C2 sin 2x − cos 2x + sin 2x + , y cos 2x + sin 2x + , . 4 4 4 r = −4 8 4 8 1 3) 1
x′ + 2x′ + 15x = e2t − 8, x = C1e5t + C2e−3t − e2t + , y = 15 15 (x′ − x − e2t). 8
4) Tiệm cận y = 1. Cực đại (1; 1), cực tiểu (0; 0). 5) 8π V . y = 3 √ π 3 6) ln 3 I = − . 2 18 7) α < 4 Hè :2014.
Câu 1. Khảo sát và vẽ đồ thị hàm số −x2 y = x.e 8 e Câu 2. Tìm lnα x
α để tích phân suy rộng I = R1 p dx hội tụ. x(x2 − 1)
Câu 3. Tính tích phân suy rộng +∞ dx I = . R x 2x 0 e (e + 3)
Câu 4. Tính thể tích vật thể được tạo ra khi miền phẳng giới hạn bởi các đường x2 + y =
0, x + y = 0 quay quannh trục Oy.
Câu 5. Giải phương trình (y cos x − cos 2x)dx + sin xdy = 0.
Câu 6. Tìm nghiệm của phương trình y” + 7y′ + 10y = 3xe−2x. ( x′y′(t) = −x + 3y − 1
Câu 7. Giải hệ phương trình (t) = 5x − 3y + cos 2t, Đáp án 1. Tiệm cận ngang 2 −2
y = 0. Cực đại (2; √ ), cực tiểu (−2; √ ). e e 2. 1 α > − . 2 √ π 3 3. 1 I = − . 3 27 4. π VOy = . 6
Đại học Bách khoa TPHCM Trang 110
ThS.Nguyễn Hữu Hiệp
CHƯƠNG 4. PHƯƠNG TRÌNH VI PHÂN 4.6. ĐỀ THI CUỐI KỲ sin 2x C 5. 1 y = ( + C) = cos x + . sin x 2 sin x x 6. x2
y = C1e−2x + C2e−5x + e−2x( − ). 2 3 7 1 1 x = C 2t 6t 1e − 3C2e − cos t2t + sin 2t + , 40 10 4 1 1 5 y = C1e2t + C cos 2t + sin 2t + . 7. 2e6t − 40 20 12
Đại học Bách khoa TPHCM Trang 111
ThS.Nguyễn Hữu Hiệp




