lOMoAR cPSD| 27879799 BỘ MÔN DUYỆT
BÀI GIẢNG CHI TIẾT Thay mặt nhóm
Chủ nhiệm Bộ môn (Dùng cho 75 tiết giảng) môn học Học phần: GIẢI TÍCH II
Nhóm môn học: Giải tích Bộ môn: Toán Tô Văn Ban Khoa: Công nghệ Thông tin Tô Văn Ban
Chủ biên: PGS S Tô Văn Ban
Thành viên: TS Tạ Ngọc Ánh TS Hy Đức Mạnh ThS Nguyễn Văn Hồng ThS Nguyễn Hồng Nam ThS Bùi Văn Định
Thông tin về nhóm môn học TT Họ tên giáo viên Học hàm Học vị 1 Tô Văn Ban PGS TS 2 Nguyễn Xuân Viên PGS TS 3 Nguyễn Đức Nụ Giảng viên chính TS 4 Vũ Thanh Hà Giảng viên chính TS 5 Tạ Ngọc Ánh Giảng viên TS 6 Bùi Văn Định Giảng viên ThS 7 Bùi Hoàng Yến Giảng viên ThS 8 Nguyễn Thị Thanh Hà Giảng viên chính ThS 9 Nguyễn Văn Hồng Giảng viên ThS 10 Nguyễn Thu Hương Giảng viên ThS 11 Đào Trọng Quyết Giảng viên ThS 12 Nguyễn Hồng Nam Giảng viên ThS
Địa iểm làm việc: Bộ Môn Toán, P1408, Nhà A1 (Gần ường HQ Việt) Điện
thoại, email: 069 515 330, bomontoan_hvktqs@yahoo.com
Bài giảng 1: Hàm số nhiều biến số  Chương, mục: 1 Tiết thứ: 1- 5 Tuần thứ: 1
Mục ích, yêu cầu:
• Nắm sơ lược về Học phần, các quy ịnh chung, các chính sách của giáo viên, các
ịa chỉ và thông tin cần thiết, bầu lớp trưởng Học phần.
• Nắm ược các khái niệm căn bản về các loại tập mở, óng, miền trong
n . Một số kết quả căn bản về giới hạn, liên tục của hàm nhều biến, tương
ồng với những khái niệm này ở hàm 1 biến. 1 lOMoAR cPSD| 27879799
• Nắm ược khái niệm và thuần thục tính ạo hàm riêng, vi phân của hàm nhiều biến.
- Hình thức tổ chức dạy học:
Hình thức chủ yếu: Lý thuyết, thảo luận - tự học, tự nghiên cứu - Thời gian:
Lý thuyết, thảo luận: 5t - Tự học, tự nghiên cứu: 5t - Địa iểm:
Giảng ường do P2 phân công. -
Nội dung chính:
Giới thiệu về môn học và các quy ịnh
Chương 1: Hàm số nhiều biến số
§1.1 Giới hạn – Liên tục
§1.2 Đạo hàm – Vi phân .
Giới thiệu học phần GIẢI TÍCH II (15 phút) •
Để thấy bản chất của hiện tượng cũng như mở rộng khả năng i vào
cuộc sống của toán học chúng ta cần nghiên cứu giải tích trong phạm vi nhiều biến. •
Với hàm nhiều biến, nhiều khái niệm và kết quả với hàm một biến
không còn bảo toàn mà có những biến thể tinh vi, uyển chuyển và hứa hẹn những
ứng dụng vô cùng rộng lớn. GTII - một sự tiếp tục Giải tích I - hướng chủ yếu vào
phép tính vi phân, phép tính tích phân của hàm nhiều biến. •
Chúng ta sẽ thấy rất nhiều ví dụ, bài tập liên quan ến thực tiễn cho
thấy mảng ứng dụng vô tiền khoáng hậu của lý thuyết, ảm bảo sự trường tồn của toán học. •
Các khái niệm, ịnh lý, tính chất ... thường ược phát biểu bằng lời và
kết hợp với công thức... Chính sách riêng
Mỗi lần lên bảng chữa bài tập úng ược ghi nhận, cộng vào iểm quá trình
0.5 iểm. Chữa bài tập sai không bị trừ iểm.
Sự hiện diện trên lớp: Không i học 5 buổi sẽ không ược thi.
Tài liệu tham khảo TT Tên tài liệu Tác giả Nxb Năm xb 1 Giáo trình Giải Tô Văn Ban Nxb Giáo dục 2012 tích II 2
Giải tích II & III Trần Bình KH và KT 2007 3
Toán học cao cấp Nguyễn Đình Giáo dục 2007 (T3-2) Trí và … 4
Bài tập Giải sẵn Trần Bình KH và KT 2007 giải tích 2, 3 5 Calculus: A R. Adams Addison Wesley 1991 Complete Course 2 lOMoAR cPSD| 27879799 6 Calculus
(Early Jon Rogawski W.H.Freeman and Co. 2007 Transcendentals),
Đề Bài tập về nhà GTII (trong tài liệu [1])
Ví dụ: Tự ọc; Bài tập: Chữa trên lớp CHƯƠNG I
Bổ trợ: 3(b); 4(a, b, d); 5(a); 8(c,d); 10(a); 12(b);
15; 18(b); 21(b); 22; 23(a); 24(a);
30(a); 34(c, g); 35(d, e); 37(a); 39(c); 41(a, e). Chính: 6(a, b,
c, d, e); 13(b, c); 24(c); 26(d); 33; 34(f);
35(i, j, k, l); 36(e, f, g, h, i, j, k); 37(c, d, e, f); 40( d, e, f);
VD 1.17; VD 1.26A; VD 1.27; VD 1.28;
VD 1.29 (i, ii); VD 1.30; VD 1.37; VD 1.39 CHƯƠNG II
Bổ trợ: 1(b, d); 2(b, c); 3(b); 4(a, b); 5(a, c, d); 6(b);
7(d, c); 8(a); 9(d, f); 10(c); 15; 17; 19(b); 20(a, c); 24; 27(a).
Chính: 1(e); 5(f); 6(a); 7(e, f); 8(b, d); 9(g); 10(f, g, h);
14(c, d); 19(c); 20(f); 21(c, d); 22(b, c, e); 23(a, b).
VD 2.11; VD 2.13; VD2.25 ; VD 2.26; VD 2.27;
VD 2.33; VD 2.34; VD2.37 ; VD 2.40 CHƯƠNG III
Bổ trợ: 1(d,e), 2, 4. 5(a) , 11, 14(a), 15(a, c), 17(a),
18(d), 19(a, d), 22(a, e), 26(c), 27(a); 29(a, b), 30.
Chính: 7; 8; 14(c); 16(c, d); 22(d); 24(c, d, e, f, h); 25.
VD3.16 ; VD3.23 ; VD3.23 ; VD3.25 ; VD3. 26 ; VD3.27 ;
VD3.28 ; VD3. 29 ; VD3.31 ; VD3.32 ; VD 3.33; VD3.34 . CHƯƠNG IV
Bổ trợ: 2(a); 3(a) 8; 10(e); 12(b); 15(b,c); 18(b);
20(a); 21(d); 23(a); 24(b, e); 26(a, b, d); 28(a, b); 31(c).
Chính: 3(b); 10(b, c, d, e); 12(e, f, g); 13(b); 15(f, g); 18(c, d);
19(a, b, c, d, e); 24(e); 26(f, h, i, j); 27(c, d,e);
28(d, e, f, g); 30(d, e, f); 31(b); 32; 33(a, b, c).
VD 4. 34; VD 4.35 ; VD 4.36; VD 4.48; VD 4.49;
VD 4.50; VD 4.51 ; VD 4.52; VD 4.53; VD 4.54((i), (ii)).
CẤU TRÚC ĐỀ THI, CÁCH THỨC CHO ĐIỂM Câu số Về phần Số iểm 1 Lý thuyết 2.0 2
Chương 1: Hàm số nhiều biến số 2.0 3 Chương 2: Tích phân bội 2.0 4
Chương III: Tích phân ường, tích phân mặt 2.0 5
Chương 4: phương trinh vi phân 2.0 3 lOMoAR cPSD| 27879799 Điểm bài thi 10 Điểm quá trình 10 Điểm chuyên cần 10
Tổng iểm = iểm chuyên cần x 10% + iểm 10
quá trình x 20% + iểm bài thi x 70%
Hình thức thi: Thi viết
Bầu lớp trưởng lớp học phần. Kết quả:
Số iện thoại giáo viên:
Địa chỉ Email cần: Webside cần:
Danh sách SV (Ít nhất 7 cột kiểm tra sĩ số)
Chương 1: HÀM SỐ NHIỀU BIẾN SỐ
§ 1.1. GIỚI HẠN - LIÊN TỤC 1.1.1.
Tập hợp trong n
a. Không gian n 
Xét V là tập hợp các bộ n số thực có thứ tự x (x , ... , x ), x1 n i . (Hiện thời ta
viết ậm các phần tử của V).
Trong V ưa vào phép cộng và và phép nhân với vô hướng:
x (x , ... , x ),1 n y (y ,...,y ), x , y1 n i i ,
x y (x1 y , ... , x1 n y )n , x ( x , ... ,1 x ),n .
Khi ó V trở thành không gian véc tơ trên ; phần tử của V gọi là véc tơ, ôi khi gọi là iểm.
* Tích vô hướng. Tích vô hướng của hai véc tơ x và y là một số thực, ký hiệu là
x.y , (có tài liệu viết là x,y ) xác ịnh bởi:
x.y x y1 1 ... x yn n .
* Không gian Euclide n . Không gian véc tơ V có trang bị tích vô hướng vừa nêu
gọi là không gian Euclide n chiều, ký hiệu là n .
Tích vô hướng nêu trên có các tính chất thông thường ã biết ơt phổ thông. Khi
x.y 0 ta nói hai véc tơ x và y là trực giao với nhau, và viết x y .
* Khoảng cách. Khoảng cách giữa x (x ,... ,x1 n ) và y (y ,... ,y1 n ) ký hiệu bởi
d(x, y), xác ịnh theo công thức d( ,x y) (x y x y ) ( ) . d( ,x y) (y 2 2 1 x )1 ... (yn x )n . (1.1) 4 lOMoAR cPSD| 27879799
Khoảng cách này còn gọi là khoảng cách Euclide, có các tính chất sau ây: d( , )x
y d( , )y x : tính ối xứng
d( ,x y) 0; d( ,x y) 0 x y : tính xác ịnh dương
d(x,y) d(y,z) d(x,z) : bất ẳng thức tam giác
Trong 2 , iểm hay ược ký hiệu là (x,y), trong 3 là (x,y,z).
Đồng nhất iểm M với bộ số (x,y,z) là toạ ộ của nó trong một hệ toạ ộ trức
chuẩn; thay cho iểm M, ta viết (x,y,z) hay ầy ủ hơn M(x,y,z). Khoảng cách (1.1)
chính là khoảng cách thông thường.
Trong 2 : Điểm M có thể ồng nhất với toạ ộ (x, y) của nó; thay cho iểm M ta viết
(x, y), hay ầy ủ hơn M(x, y).
Trong phần còn lại của chương này các kết quả ược trình bày chủ yếu trong 2 .
Nhiều kết quả tương tự còn úng cho n .
b. Phân loại tập hợp trong n
• Lân cận. Cho a
2; lân cận của iểm a (còn gọi là hình cầu mở tâm
a, bán kính ), kí hiệu U ( ) a , là tập hợp xác ịnh bởi: U ( ) a {x 2 :d( ,xa) }.
Điểm a ược gọi là iểm trong của tập hợp E 2 nếu E chứa một hình cầu mở
nào ó tâm a: U ( ) x E, ( 0). Đồng thời, tập E gọi là một lân cận của iểm a.
• Tập mở. Tập hợp E ược gọi là tập mở nếu mọi iểm của E ều là iểm trong của nó.
Dễ nhận thấy rằng, tập hợp U ( ) a là tập mở.
• Điểm biên. Điểm x gọi là iểm biên của E nếu trong một -lân cận bất kì
của x ều chứa ít nhất một iểm thuộc E và một iểm không thuộc E . Tập các iểm
biên của E kí hiệu là (E), gọi là biên của E.
Rõ ràng, iểm trong của E nằm trong E; iểm biên của E có thể thuộc E, có thể không thuộc E.
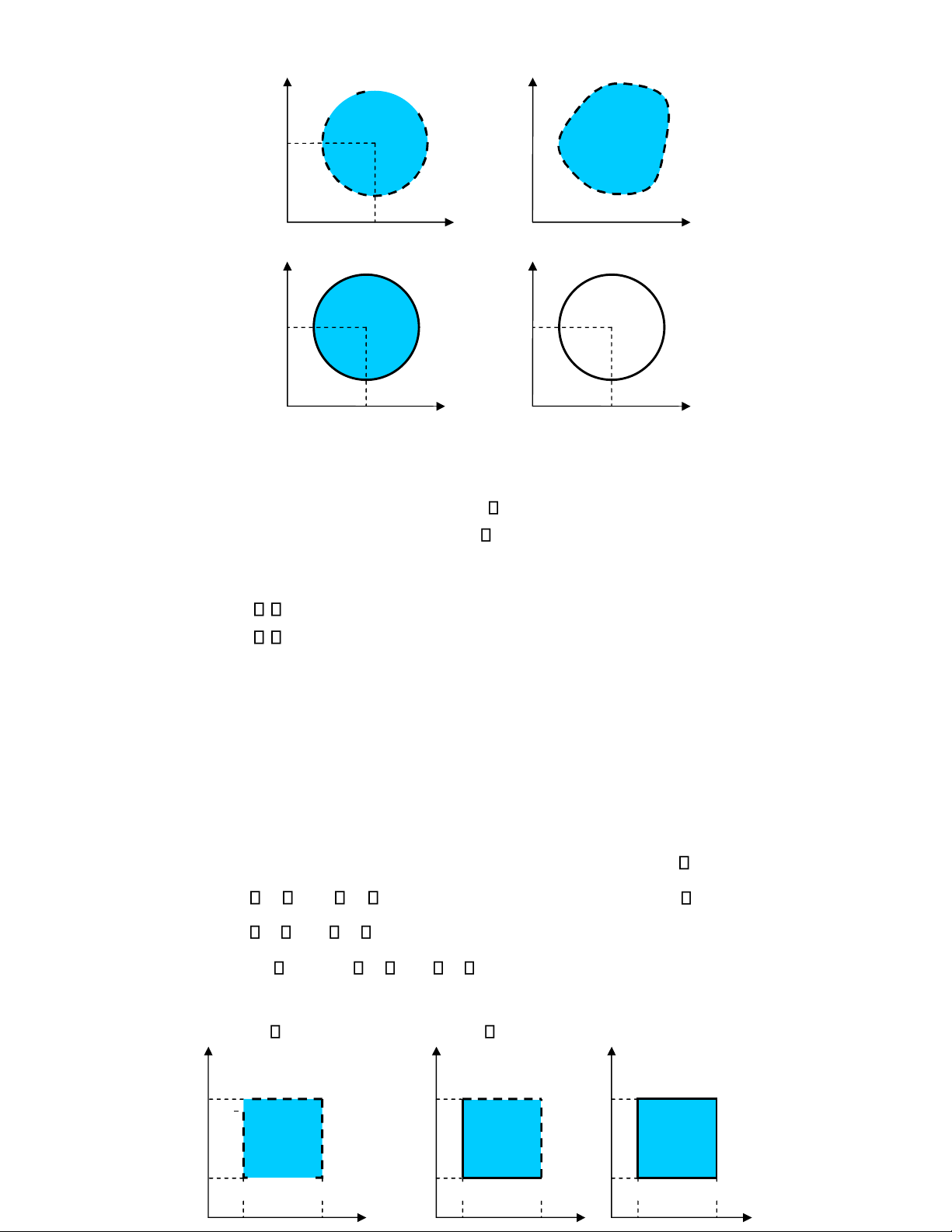
• Tập óng. E ược gọi là tập óng nếu nó chứa mọi iểm biên của nó: E óng E E E . 5 lOMoAR cPSD| 27879799 (a) (b) (c) (d)
Hình 1.1. (a) Hình cầu mở, (b) tập mở, (c) hình cầu óng,
(d) mặt cầu (tập óng) trong 2 Chẳng hạn,
các tập sau ây là óng (xem Hình 1.1):
+ Hình cầu óng tâm a, bán kính .
+ Mặt cầu óng tâm a, bán kính .
• Tập bị chặn. Tập E ược gọi là bị chặn nếu tồn tại một hình cầu mở nào ó chứa nó.
hình cầu óng nào ó chứa nó
hình cầu óng tâm O chứa nó
• Tập compắc. Tập óng và bị chặn ược gọi là tập compact.
• Miền. Mỗi tập mở là một miền mở.
Miền mở cùng với biên của nó gọi là miền óng.
Miền mở, miền óng gọi chung là miền.
Miền mà từ 2 iểm bất kỳ của nó có thể nối với nhau bởi một ường gẫy khúc nằm
hoàn toàn trong miền gọi là miền liên thông.
Sau ây, khi ã quen, ta không còn phải viết chữ ậm cho phần tử của n nữa.
Ví dụ 1.1. Cho các tập hợp sau ây trong 2 (xem Hình 1.2): D1 {(x,y): a
x b, c y d}: tập hợp mở (Không chứa biên) D2 {(x,y): a
x b, c y d}: Không mở, không óng
D3 {(x,y): a x b, c y d}: tập hợp óng (chứa biên)
Người ta còn dùng ký hiệu tích Descartes ể chỉ các hình chữ nhật ó: D1 ược ký
hiệu bởi (a, b) (c, d), ... ,D3 bởi [a, b] [c, d ]. # y y y A B A B A B d d d 6 lOMoAR cPSD| 27879799 D1 D2 D3 c c c D C D C D C a b x a b x a b x
Hình 1.2. Hình chữ nhật trong 2
1.1.2. Hàm nhiều biến số
a. Định nghĩa. Cho D n . Ánh xạ f :D
x (x ,...,x1 n ) f(x) f(x ,...,x )1 n ược gọi là hàm số trên D.
D: tập xác ịnh, f: hàm số; x: biến số (hay ối số).
Lưu ý rằng biến số có n thành phần, mỗi thành phần xem như một biến ộc lập
(cho nên hàm số trên n hay ược gọi là hàm nhiều biến).
b. Các phương pháp biểu diễn hàm số (☼) Biểu diễn bằng
biểu thức giải tích.
Biểu diễn bằng ồ thị
Sử dụng các ường ( ồng) mức Bảng dữ liệu.
1.1.3. Giới hạn của hàm nhiều biến
a. Giới hạn của dãy iểm
Ta nói dãy iểm {un} {(x ,yn
n)} 2 hội tụ ến u0 (x ,y0 0) nếu lim d(u ,u )n 0 0. (1.2) n
Khi ó ta viết lim (x ,y )n n (x ,y0
0), hay ơn giản lim un u0 hoặc n n un u0 (khi n ).
Giới hạn của dãy iểm tương ương với giới hạn của từng tọa ộ: lim (x ,y )n
n (x ,y0 0) lim xn x ;0 lim yn y .0 (1.3) n n n
* Điểm giới hạn ( iểm tụ). Điểm a ược gọi là iểm giới hạn của tập D n nếu có
một dãy {un} các phần tử khác a của D hội tụ ến a.
b. Giới hạn của hàm số
Định nghĩa. Cho hàm số f(u) xác ịnh trên D 2 và a (x ,y0 0) là một iểm
giới hạn của D. Ta nói hàm f(u) có giới hạn  khi u dần ến a nếu: 0,
0, sao cho u D, 0 d(u,u )0 f(u)  . (1.4) Khi ó ta viết lim f(u)  hay f(u) khi u a. u a
Để ầy ủ, ta còn viết lim f (x, y) (hay f (x, y) khi (x, y) (x , y0 0)) (1.5) 7 lOMoAR cPSD| 27879799 (x,y) (x ,y0 0)
Định lý 1.1. Hàm f(u) có giới hạn  khi u dần ến a khi và chỉ khi
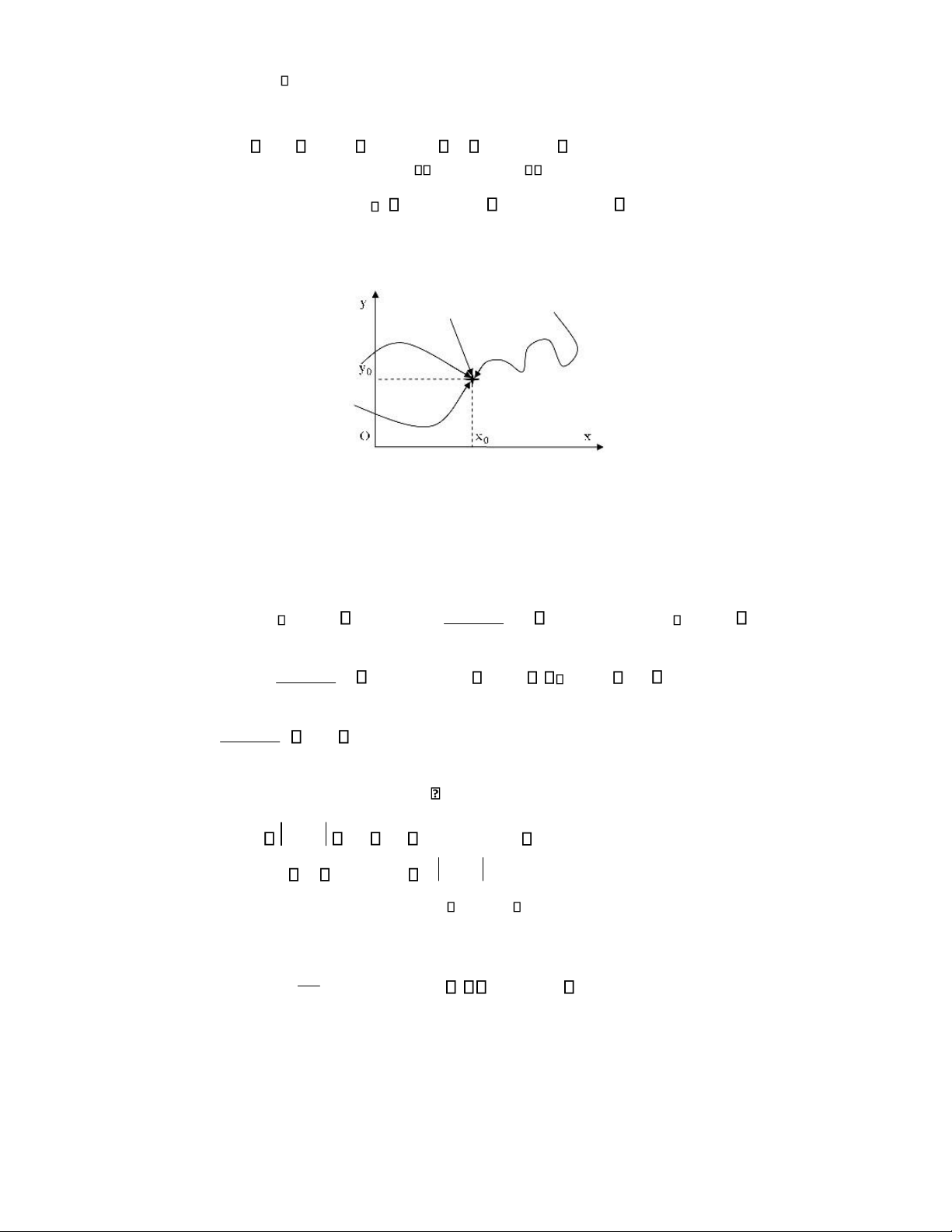
{un} D; un a; lim un a lim f(u )n . (1.6) n n
Hệ quả. Nếu lim f(u) a  thì với u (x,y) dần ến a (x ,y0 0) theo một u
ường cong tuỳ ý trong D, f(u) dần ến .
Hình 1.5. Điểm dần ến (x ,y0 0) theo những ường khác nhau
Lưu ý. Các kết quả thông thường ối với giới hạn của hàm 1 biến như giới hạn của
tổng, hiệu, ịnh lý kẹp… vẫn còn úng cho giới hạn của hàm nhiều biến.
Ví dụ 1.4. Tìm giới hạn i) (x, ylim) (1,0)(x2 y )sin2
x2 1 y2 ; ii) (x, ylim) (0,0)(x2 y )sin2
x2 1 y2 . Giải. i) lim (x2 y )sin2 2 1 y2 sin1. x,y 1,0 x ii)
Hàm số xác ịnh trên 2/{(0,0)}. Ta có
0 f(x,y) x2 y2 0 (khi (x, y) (0,0). Theo ịnh lí kẹp, lim f (x,y) 0 lim f(x,y) 0. (x, y) (0,0)(x, y) (0,0)
Định nghĩa giới hạn vô hạn tương tự như với hàm một biến. y khi (x,y) (0,3); Chẳng hạn 2 x 8 lOMoAR cPSD| 27879799 e x2 1 khi (x,y,z) (0,0,0). # y2 z2
1.1.4. Sự liên tục của hàm số
Cho hàm số f(x,y), (x,y) D , trong
ó D là tập tuỳ ý của 2 và (x ,y0
0) D là iểm giới hạn của D. Ta nói f(x, y) liên tục tại (x ,y0 0) nếu lim f(x,y) f(x ,y )0 0 . (1.7) (x,y) (x ,y0 0)
Giả sử a (x ,y0 0) D, u (x,y) (x0 x,y0 y) D .
Đặt f f(x0 x,y0 y) f(x ,y )0 0
Khi ó hàm số f(u) liên tục tại (x ,y0 0) khi và chỉ khi lim f 0. (1.8) ( x, y) (0,0)
* Hàm f(x,y) ược gọi là liên tục trên miền D nếu nó liên tục tại mọi iểm (x ,y0 0) D.
Lưu ý. Các ịnh lí về tổng, hiệu, tích, thương, luỹ thừa, hợp hàm của các hàm
liên tục, ịnh nghĩa hàm sơ cấp và tính liên tục của chúng, các khái niệm và kết quả
về sự liên tục ều ối với hàm một biến gần như vẫn còn bảo toàn cho trường hợp hàm nhiều biến. Chẳng hạn
Định lý 1.2. Hàm f(x,y) liên tục trên tập óng, giới nội D thì bị chặn trên ó và
ạt ược giá trị lớn nhất, giá trị nhỏ nhất: (x ,y ), (x ,y1 1 2 2) D ể f(x ,y )1 1 m
Min f(x,y); f(x ,y )2 2 M Max f(x,y) . (x,y) D (x,y) D
Định lý 1.3. Hàm f(x,y) liên tục trên tập óng, giới nội thì liên tục ều trên ó, tức
là với mọi 0, tìm ược số sao cho với (x,y), (x ,y ) D mà d((x,y), (x ,y )) thì f (x, y) f(x , y ) . xy (x,y)
Ví dụ 1.5. Cho hàm số u f x,y x2 y2 (0,0) (x,y) (0,0) 0
Rõ ràng hàm liên tục tại mỗi iểm (x ,y0 0) (0,0) (vì là thương hai hàm liên tục, mẫu khác 0).
Tại (x ,y0 0) (0,0), theo bất ẳng thức Cauchy. 9 lOMoAR cPSD| 27879799 0 xy x2 2 y2 2xy y2 2 (( x2x 2 y ) 2y ) 2 (x2
2y ) 2 1 . x Trường hợp 1: 1 1 (x,ylim) (0,0)f(x,y) ulim 0 2 d(u,0) ( 1)/2 0 f(0,0).
Vậy f(x,y) liên tục tại (0,0).
Trường hợp 2: 1. Xét (x,y) (0,0) theo ường y = x. 1 f x, y f x,x x2 2 2 1
0 khi x 0. Vậy f(x,y) không 2x 2x
liên tục tại (0,0). #
§ 1.2. ĐẠO HÀM - VI PHÂN
1.2.1. Đạo hàm riêng
Định nghĩa. Cho hàm số z f(x,y) xác ịnh trong tập mở D 2 , lấy iểm M
(x ,y )0 0 0 D . Cố ịnh y y0 thì f(x,y )0 là hàm một biến x. Nếu hàm này có ạo hàm
tại x x0 thì ạo hàm ó gọi là ạo hàm riêng của hàm z f(x,y) theo biến x (biến thứ
nhất) tại iểm M (x ,y )0 0 0 , kí hiệu bởi một trong các cách sau: z (x , y ), x 0 0 f (x ,y ),x 0 0 z(x , y ) 0x 0 , f (x , y ) 0x 0 .
Như vậy, cho x ủ nhỏ sao cho(x0 x,y )0 D. Đặt: xz f(x0 x,y )0 f(x ,y )0 0
gọi là số gia riêng của hàm số z f(x,y) ối với biến x tại (x ,y0 0). Khi ó f (x ,y )0 0 lim xz . x x 0 x y ( 0 x,y 0 ) ( x0 0 x,y) y 0 O x0 x0 x x 10 lOMoAR cPSD| 27879799
Hình 1.6. Cách lập số gia riêng của hàm số
Đạo hàm riêng theo biến y tại (x ,y0 0), kí hiệu là f (x ,y ), z (x ,y ),y 0 0 y 0 0 f(x ,y ) 0y 0 hay z(x ,y ) 0y 0 .
n 3: ịnh nghĩa tương tự.
Quy tắc. Khi tính ạo hàm riêng theo biến nào ó, ta chỉ việc coi các biến khác
không ổi, rồi lấy ạo hàm theo biến ó như lấy ạo hàm với hàm một biến. Ví dụ 1.7.
Tính các ạo hàm riêng của hàm số x i. z x , (xy 0). ii. z arctan , (y 0) . y z Giải. i. z yxy 1 ; x lnx.y x y ii. xz 1 x / y1 2 1y x2 y y2 ; yz 1 (x / y1 )2 yx2 x2 xy2 . # ( )
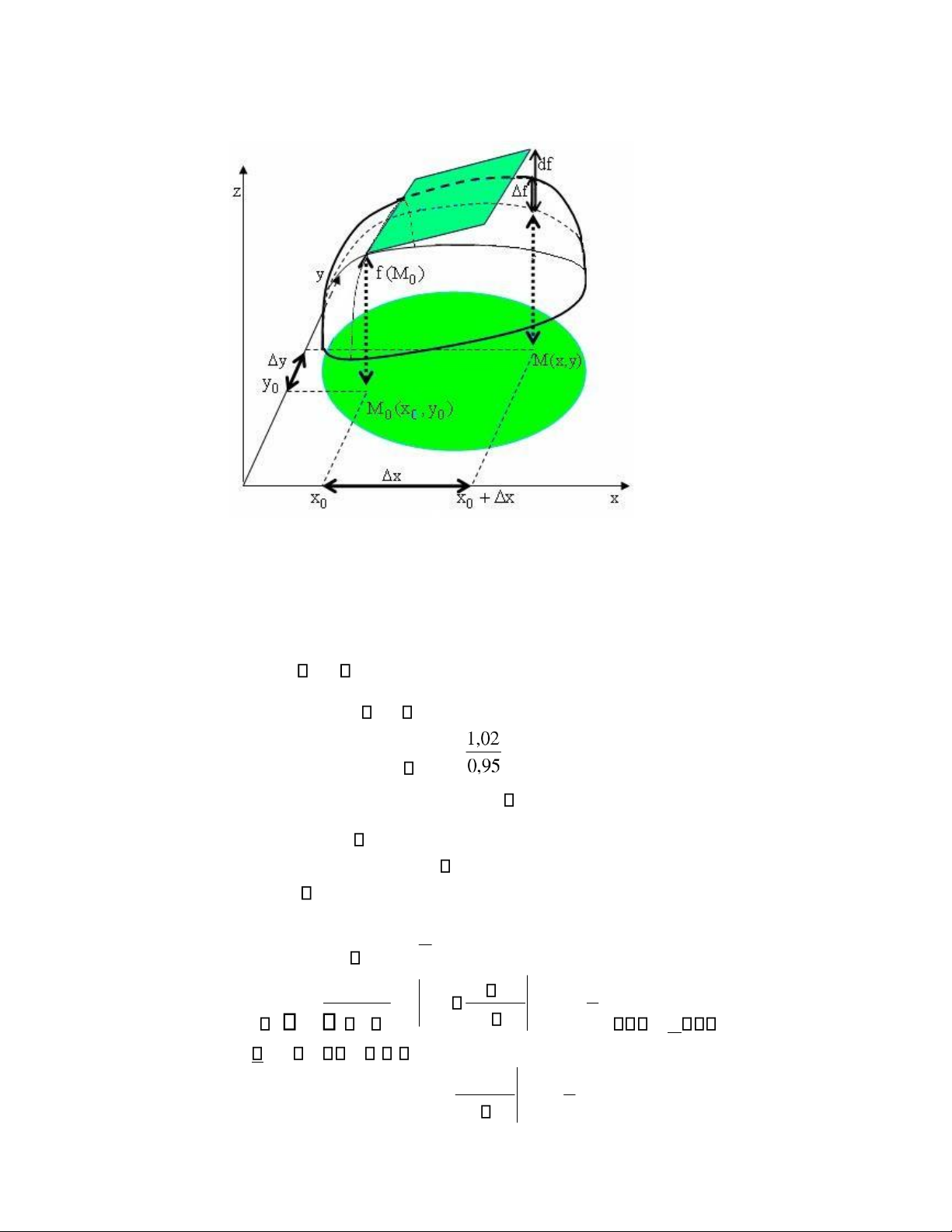
1.2.2. Vi phân của hàm nhiều biến Định nghĩa
Cho hàm số z f(x,y) xác ịnh trong tập mở D. Trong D lấy các iểm (x ,y ),
(x,y0 0 ) (x0 x,y0 y). Biểu thức
f f(x0 x,y0 y) f(x y )0 0 ược gọi là số
gia toàn phần của hàm f(x,y) tại (x ,y0 0).
Nếu số gia f có thể biểu diễn dưới dạng fA x B y x y (1.9)
trong ó A, B là những hằng số không phụ thuộc vào x, y (chỉ phụ thuộc vào (x ,y0
0)), (x,y) 0, (x,y) 0 khi x 0 vµ y 0 thì ta nói:
+ Hàm số f(x,y) khả vi tại (x ,y0 0);
+ Biểu thức A x B y gọi là vi phân toàn phần của hàm z tại (x ,y0 0) (ứng
với số gia x, y của ối số x, y tương ứng), kí hiệu là dz(x ,y )0 0 hay df(x ,y )0 0 .
Như vậy, dz(x ,y )00 A x B y .
* Hàm số z f(x,y) gọi là khả vi trên D nếu nó khả vi tại mọi iểm của D. 11 lOMoAR cPSD| 27879799
Tính chất. Nếu f(x,y) khả vi tại (x ,y0 0) thì liên tục tại ó. CM: fA x B y x y 0 khi x, y 0.
Vậy hàm liên tục tại (x ,y0 0).
Định lí 1.5. Cho hàm f(x,y) xác ịnh trong tập mở D 2 và (x ,y0 0) D. (i)
(Điều kiện cần ể hàm khả vi). Nếu f(x,y) khả vi tại iểm(x ,y0 0) thì tồn
tại các ạo hàm riêng f (x , y ), f (x , y )x 0 0 y 0 0 . Các hằng số A, B trong ịnh nghĩa
vi phân cho bởi A f (x , y ), Bx 0 0 f (x , y )y 0 0 ; nói cách khác, df(x , y )00 f (x , y )x 0 0 x f (x , y )y 0 0 y . (ii)
(Điều kiện ủ ể hàm khả vi). Nếu hàm số z f(x,y) có các ạo hàm riêng
liên tục tại lân cận của iểm (x ,y0 0) thì khả vi tại ó và dz(x , y )00 f (x , y )x 0 0 x f (x , y )y 0 0 y . (1.10) Chứng minh
(i) Từ giả thiết, f A x B y x y .
Xét y y0 const thì y 0 và f xf A x x . Do ó: 0 0 limx 0 xxf limx 0 A x x x A . f (x , y )x Tương tự, f (x ,y ) ' y 0 0 B.
(ii) Với x, y ủ nhỏ thì f f(x0 x,y0 y) f(x , y )0 0 f (x0 x, y0 y) f (x , y00 y) f (x , y00 y) f(x , y ) .0 0
Áp dụng công thức số gia giới nội cho hàm một biến dẫn ến f f (xx 0 1 x, y0 y) x f (x , yy 0 0 2 y) y trong ó 0 1 1; 0 2 1.
Vì f , fx y liên tục tại (x ,y00) nên 12 lOMoAR cPSD| 27879799 f f (x ,y )x 0 0 x f (x ,y )y 0 0
y trong ó 0, 0 khi x 0, y 0. Vậy f f (x , y )x 0 0 xf (x , y )y 0 0 y y ( pcm).
Chú ý. Giống như trường hợp một biến, nếu x, y là biến ộc lập thì dx x; dy
y. Từ ó, df (x , y )0 0 f (x ,y )dxx 0 0 f (x , y )dyy 0 0 .
Hệ quả. Nếu f (x, y), f (x,y)x y liên tục trong tập mở D thì df(x,y) f(x,y) f(x,y) dx dy . (1.11) x y
Ví dụ 1.8. Xét sự khả vi và tính vi phân dz(x,y), dz(0,1) (nếu có) của các hàm số z x3 y3 3xy. z Giải. z 3x2 3y,
3y2 3x , là những hàm liên tục trên 2 . x y
Vậy hàm số là khả vi trên 2 và dz 3[(x2 y)dx (y2 x)dy]. dz(0,1) 3dx 3dy 3( dx dy). #
Chú ý. Đối với hàm nhiều biến, sự tồn tại các ạo hàm riêng chưa ảm bảo ể hàm
số khả vi. Xét ví dụ sau.
Ví dụ 1.9. (tài liệu [1]) #
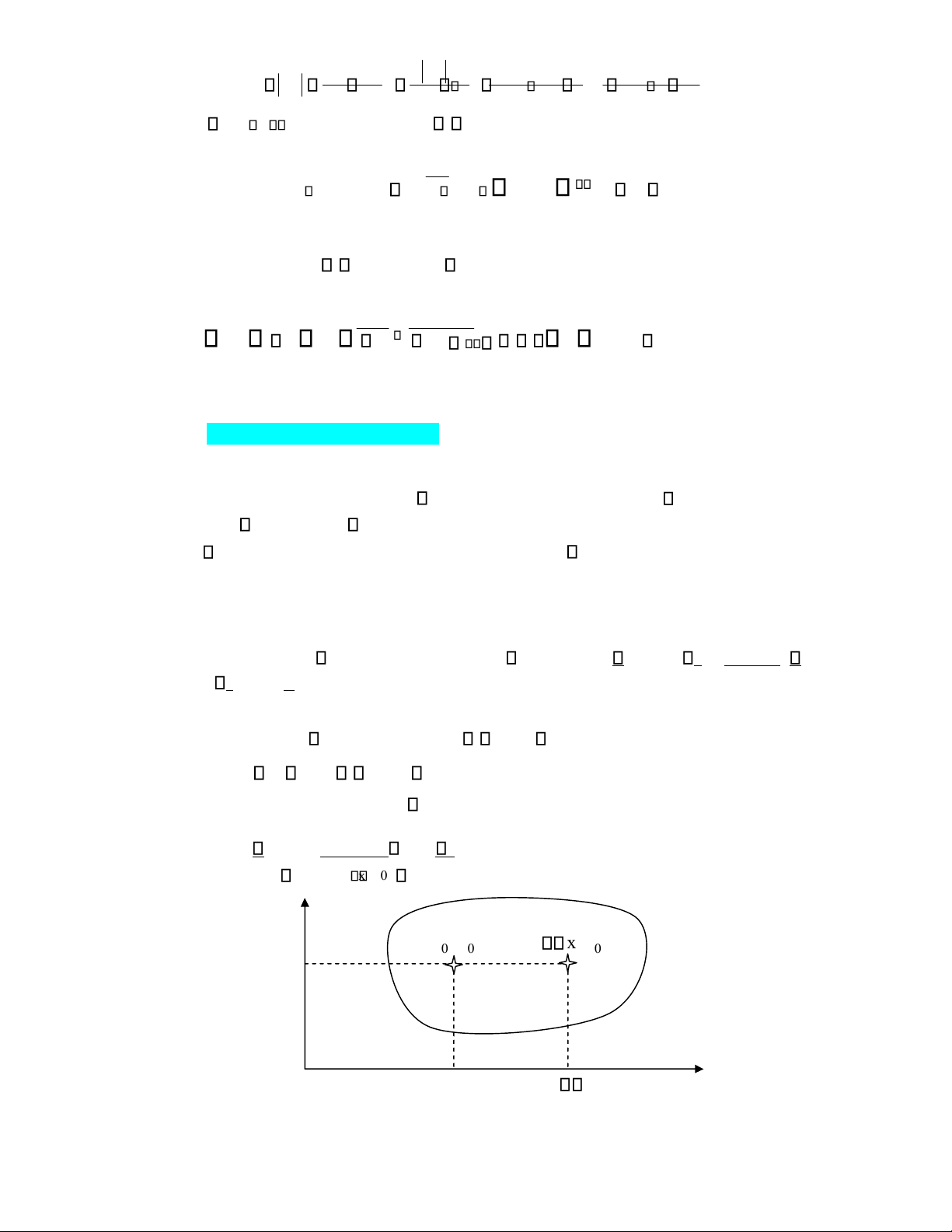
Ứng dụng vi phân ể tính gần úng. Nếu ặt
x x0 x, y y0 y (hay x x x ,0 y y y )0 , từ ịnh nghĩa vi phân ta có z f(x,y) f(x ,y )0 0 f (x ,y )(xx 0 0 x )0 f (x ,y )(yy 0 0 y )0 (x x )0 (y y )0 f (x ,y )(xx 0 0 x )0 f (x ,y )(yy 0 0 y )0 df(x ,y ).0 0
Dẫn ến công thức xấp xỉ f (x0 x, y0 y) f (x , y )0 0 f (x ,y )x 0 0 x f (x , y )y 0 0 y
( f(x ,y )00 df(x ,y )0 0 ). (1.12) 13 lOMoAR cPSD| 27879799
Công thức này cho phép tính giá trị gần úng của hàm số dùng vi phân.
Vế phải là biểu thức tuyến tính của các biến x, y nên công thức cũng có tên là
xấp xỉ tuyến tính của hàm f tại lân cận iểm (x ,y0 0).
Hình 1.7. Ý nghĩa hình học của vi phân
Giống như trường hợp một biến, khi áp dụng công thức (1.12) ể tính giá trị xấp
xỉ của biểu thức A nào ó chúng ta phải: + Xác ịnh dạng hàm f,
+ Xác ịnh iểm (x ,y0 0), ở ó dễ tính (hoặc có sẵn) f(x ,y )0 0 , các ạo hàm riêng f
(x , y ), f (x , y )x 0 0 y 0 0 ,
+ Xác ịnh các số gia x, y ; các số gia này phải ủ bé.
Ví dụ 1.10. Tính xấp xỉ A arctan .
Các bạn hãy trả lời câu hỏi “giá như?” (x ,y0 0)
Giá trị lẻ thứ nhất x
} Dạng hàm f(x,y) Giá trị lẻ thứ hai y
Giải. Xét hàm số z y
arctan tại lân cận iểm (1,1). x y 2 2 z x 1,1 1 x y 1xy 2 xy2 1,1 1,1 12, x 2 2 x y 14 lOMoAR cPSD| 27879799 z y 1,1 1 1x 2 1x 1,1 1,1 12. y
Suy ra A z 1 0,05;1 0,02 z 1,1 ( 1/ 2) 0,05 (1/ 2) 0, 02
0,035 0,785 0,035 0,820.(Giá trị úng A 0,8209). # 4
Công thức (1.12) ược áp dụng hiệu quả ể tính sai số của ại lượng o. b) Thảo luận -
Về tập mở, óng, biên, bị chặn, com pắc, liên thông,
miền mở, miền óng, miền. -
Sự giống, khác nhau của hàm 1 biến, nhiều biến. c) Tự học
- Định nghĩa giưới hạn hàm số, -
Định nghĩa liên tục, liên tục ều -
Định nghĩa vi phân theo biến x. d) Bài tập chuẩn Bài 6, (Chương I) bị tối thiểu Tài liệu Tài liệu [1], tr ....
Chú ý: Bài tập về nhà cho cả chương CHƯƠNG I 
Bổ trợ: 3(b); 4(a, b, d); 5(a); 8(c,d); 10(a); 12(b);
15; 18(b); 21(b); 22; 23(a); 24(a); 30(a);
34(c, g); 35(d, e); 37(a); 39(c); 41(a, e).
Chính: 6(a, b, c, d, e); 13(b, c); 24(c); 26(d); 33; 34(f);
35(i, j, k, l); 36(e, f, g, h, i, j, k); 37(c, d, e, f); 40( d, e, f);
VD 1.17; VD 1.26A; VD 1.27; VD 1.28; VD
1.29 (i, ii); VD 1.30; VD 1.37; VD 1.39 15 lOMoAR cPSD| 27879799
Bài giảng 2: Hàm số nhiều biến số (tiếp) Chương, mục: 1 Tiết thứ: 6-10 Tuần thứ: 2
Mục ích, yêu cầu:
• Kiểm tra kiến thức, rèn luyện kỹ năng tính Giới han và xét tính liên tục
• Nắm ược khái niệm và biết cách tính ĐH hàm hợp, ạo hàm hàm ẩn, ạo hàm theo
hướng, ý nghĩa ĐH theo hướng.
- Hình thức tổ chức dạy học:
Hình thức chủ yếu: Lý thuyết, thảo luận - tự học, tự nghiên cứu - Thời gian:
Lý thuyết, thảo luận: 5t - Tự học, tự nghiên cứu: 5t - Địa iểm:
Giảng ường do P2 phân công.
- Nội dung chính:
Chữa bài tập phần Giới han – Liên tục
§1.2 Đạo hàm – Vi phân
ĐS 6. a) Continuous , discontinuous, C; b) D; c) C; d) D; e) C.
§ 1.2. ĐẠO HÀM - VI PHÂN
1.2.3. Đạo hàm riêng của hàm hợp
F(x,y) f(u(x,y),v(x,y)), (x,y) D .
Tính chất. Hợp của các hàm liên tục là hàm liên tục. f f
Định lí 1.6. Giả sử hàm f (u,v) có các ạo hàm riêng , liên tục trong u v u u v v
, các hàm u(x,y), v(x,y) có các ạo hàm riêng , , , liên tục trong x y x y F F
D. Khi ó trong D tồn tại các ạo hàm riêng , và x y FFx FFu uxu FFv xvv., (1.13) y u y v y 16 lOMoAR cPSD| 27879799
Để tiện kí hiệu, ta không phân biệt f và F khi tính ạo hàm riêng, vậy f f u f v , f f u f v . x u x v x y u y v y Xem CM trong [1].
Chú ý. i) Trường hợp z f(u(x,y)) thì z df(u(x,y)). u(x,y); z df(u(x,y)). u(x,y). (1.14) x du x y du y
ii) Trường hợp z f(x,y), y y(x) z f(x,y(x)) (hàm một biến) thì dz f f dy . (1.15) dx x y dx
iii) Trường hợp z f(x,y), x x(t), y y(t) z f(x(t),y(t)) thì dz f dx f dy . . (1.16) dt x dt y dt
iii) Trường hợp z f(u,v,w) thì f f(u(x,y),v(x,y),w(x,y)). Lúc ó f f u f v f w , x u x v x w x f f u f v f w . (1.17) y u y v y w y u u(x, y)
iv) Cho phép ổi biến v v(x, y) biến mỗi iểm (x,y) D thành iểm (x,y) (u(x,y), v(x,y)) , ma trận u v J x x u v y y
gọi là ma trận Jacobi của phép ổi biến u u(x,y), v v(x,y).
Định thức của ma trận J gọi là ịnh thức Jacobi hay Jacobian của phép ổi D(u,v) biến, ký hiệu là : D(x,y) u u 17 lOMoAR cPSD| 27879799 D u,v x y det . (1.18) D x, y v v x y
Nhận xét ký hiệu: Các biến tham gia ở tử: Chỉ hàm số
Các biến tham gia ở mẫu: Chỉ ối số
Ví dụ 1.12. Tính ạo hàm của hàm số hợp
i) z ln(u2 v )2 với u xy, v x / y; ii) z exy ln(x2 y )2 . Giải. i) xz uz ux v xz v u22 uv2 .y u22 vv2 .1y ... x2 ; yz uz uy vz yv u22 uv2 x u22 vv2 yx2 ... 2(y(yy44 1)1) .
ii) Thực ra, khi ạo hàm ta không cần viết ra các hàm trung gian u, v, w...,
nên viết trực tiếp theo các biến cuối cùng x, y, z ... #
Sự bất biến dạng của vi phân
Xét z f(u,v), u, v là hai biến ộc lập. Khi ó f f dz du dv . (*) u v
Vẫn xét z f(u,v) nhưng với u, v là biến phụ thuộc: u u(x,y), v v(x,y).
z f(u(x,y),v(x,y)). Áp dụng (*): dz f dx f dy . x y
Từ chỗ f f u f v , ..., thay vào ược x u x v x dz uf xu v xf v dx uf uy vf yv dy 18 lOMoAR cPSD| 27879799 f ux dx fy dy vf xv dx vy dy u f f du dv. (**) u v
Như vậy công thức (**) cùng dạng với (*).
Ta nói: Vi phân cấp một bất biến dạng (có cùng dạng (*) dù là biến ộc lập hay biến phụ thuộc). Áp dụng.
Nếu u u(x,y), v v(x,y) là các hàm khả vi thì d u v du dv; d(uv) udv vdu; udv d uv vduv 2 ; df(u) f (u)du . (1.19)
Các công thức này úng cho u, v là biến ộc lập nên úng cho u, v là biến phụ thuộc.
Ví dụ 1.13. Tính vi phân của các hàm số sau i) z y arcsin 2 ; ii) z arctan(xy )2 . x Giải. i) dz 2 2 1 y x 2 xydy ydx y(ydx 2 xdy ) d 2 2 x 2 4 2 x x 4 2 y x x y y 1 x . ii) dz 1 2 2) d(xy )2 1 x y12 4 (y dx2 2xydy) . 1 (xy
1.2.4. Đạo hàm hàm số ẩn
a. Khái niệm (*). Cho trước một hệ thức giữa hai biến x và y: F(x,y) = 0. (1.20)
Nếu với mọi giá trị x0 trong một khoảng nào ó, có một (hoặc một số) giá trị y0 sao cho
F(x ,y )0 0 0 thì ta nói rằng hệ thức (1.20) xác ịnh một (hoặc một số)
hàm ẩn y theo x: y y(x) trong khoảng ấy. 19 lOMoAR cPSD| 27879799
Vậy hàm số y f(x) ược xác ịnh một cách ẩn bởi hệ thức (1.20) nếu khi thế y
f(x) vào (1.20), ta ược ồng nhất thức: f(x,y(x)) 0.
Ví dụ. x22 y22 1, y ba a2 x2 và y ba a2 x2 , a b y
x ( a, a). Ta nói hệ thức xa 2 2 2
b 2 1 xác ịnh 2 hàm ẩn trong khoảng ( a, a).
Không phải lúc nào cũng tìm ược biểu thức tường minh. Chẳng hạn, ta không
thể giải x qua y hay y qua x từ biểu thức xy yx 1 (x, y 0) , mặc dầu tồn tại mối
quan hệ hàm (ẩn) từ ràng buộc này.
Hàm ẩn vừa nói từ 1 ràng buộc, ràng buộc có 2 biến.
Mở rộng: Từ 1 (2, 3...) ràng buộc, các ràng buộc có nhiều biến. Chẳng hạn
* Hệ hai phương trình F(x, y,z,u,v) 0 G(x,y,z,u, v) 0 (1.22)
Nếu từ ây có thể giải ra ược một (hoặc một số) cặp hàm u u(x, y,z) v v(x, y,z) (1.23)
xác ịnh trong một miền G 2 nào ó, sao cho khi thay vào (1.22) ta nhận ược những
ồng nhất thức, thì ta nói (1.22) xác ịnh một (hoặc một số) cặp hàm ẩn u, v của 3 biến x, y, z .
Nói chung, khi n biến ộc lập ược liên kết với nhau bởi m ràng buộc (0 m n),
thì có nhiều nhất m biến trong chúng là hàm của các biến còn lại.
b. Cách tính ạo hàm hàm ẩn
Định lí 1.7. Định lý tồn tại và khả vi của hàm ẩn: Xem [1]
Giả sử các iều kiện của Định lí 1.7 thoả mãn, thay y = f(x) vào (1.20) thì F(x,y(x))
0 với mọi x ủ gần x0. Lấy ạo hàm 2 vế theo x: F (x,y(x)) F (x, y(x))x F (x, y(x))y (x)y 0 y x F (x,y(x))x , y 20