Đề thử giữa kỳ môn môn giải tích 2 - nn1 - học kỳ 2021.2 mã đề 1 - Giải tích II (MI1120) | Trường Đại học Bách khoa Hà Nội
Câu 1. Xác định phương trình tiếp tuyến và pháp tuyến của đường cong tại điểm A(0,4)
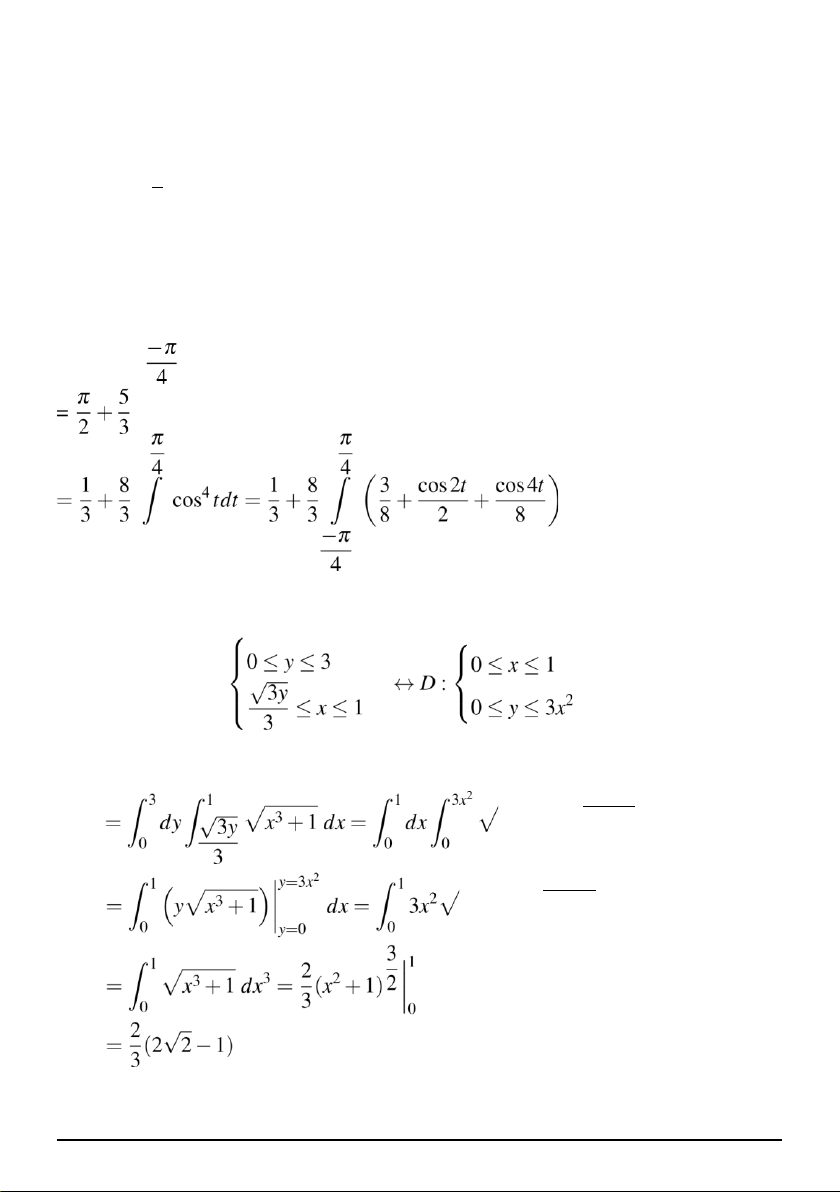
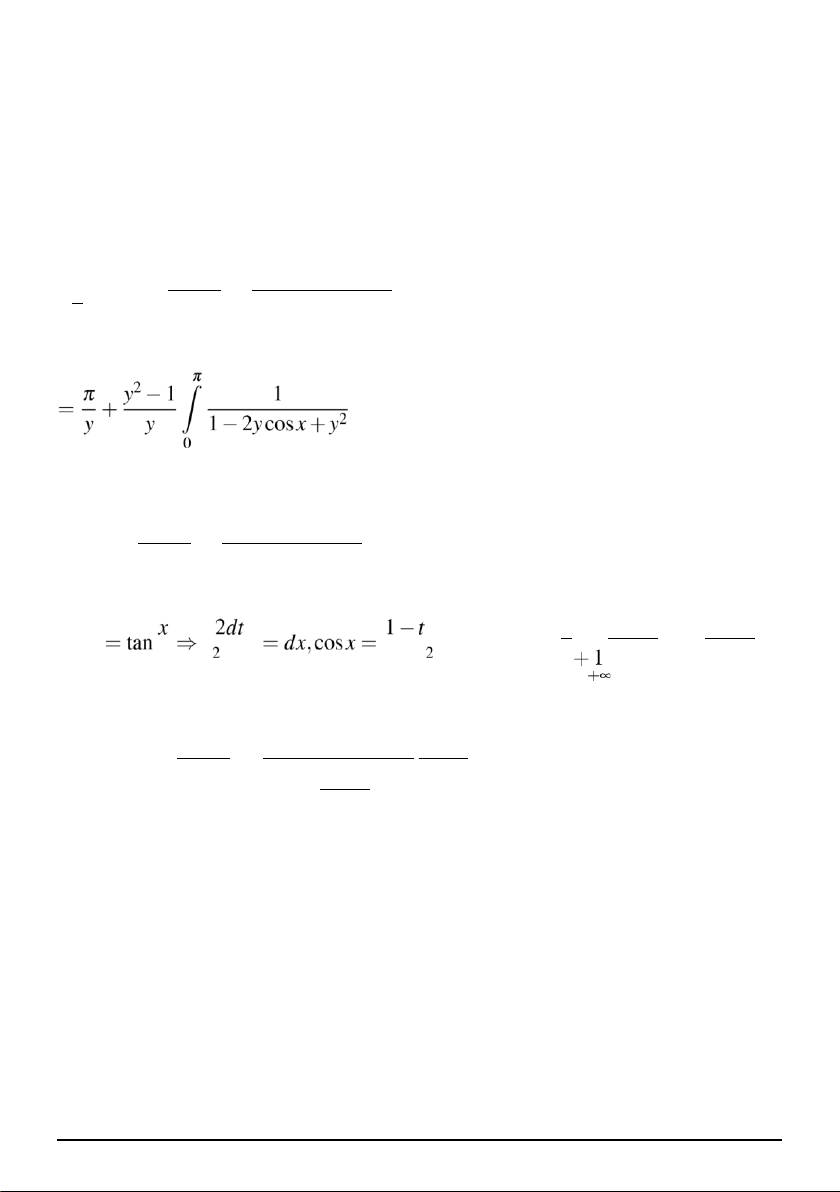
Preview text:
lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
ĐỀ THỬ GIỮA KỲ MÔN MÔN GIẢI TÍCH 2 - NN1 - HỌC KỲ 2021.2 MÃ ĐỀ 1
Đề thi gồm 2 trang
Câu 1. Xác định phương trình tiếp tuyến và pháp tuyến của đường cong tại điểm A(0,4)
x(t) = e2t −2t −1
y(t) = t +2t +4 t)
Câu 2. Tính độ cong
củatại điểm (0,;2)
y = t +1+ t2+1
Câu 3. Tìm hình bao của họ đường cong (L): x2 y2 (L) : + = 1 −
Câu 4. Tính tích phân ¨ q|y−x2|dxdy với miền D: −1 ≤ x ≤ 1,0 ≤ y ≤ 2 D
Câu 5. Tính tích phân: dx lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Câu 6. Tính thể tích vật thể giới hạn bởi z = 0,y = 0,z = 4 và mặt cong 2x = p5−2y
Câu 7. Tính ˚ zdV, trong đó E là tứ diện được giới hạn bởi bốn mặt phẳng E
x = 0,y = 0,z = 0 và x+y+z = 1.
Câu 8. Tính tích phân bội ba I
dxdydz, với V là miền xác định V
bởi −1 ≤ z ≤ 1 và 1 ≤ x2+y2 ≤ 4.
Câu 9. Tính ¨ (|x|(1+siny)−|y|)dxdy, với miền D = {(x,y)|x2+y2 ≤ 1} D Câu 10. Tính I
dx với y ∈ (−1;1). 2 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
HƯỚNG DẪN GIẢI ĐỀ THỬ GIỮA KỲ MÔN MÔN GIẢI TÍCH 2 - NN1 HỌC KỲ 2021.2 Giải câu 1.
• A(0,4) ứng với t = t0
et20 −2t0−1 = 0 ⇐⇒ t0 = 0 t0 +2t0+4 = 4
xt0(t0) = xt0(0) = −1 ⇐⇒
yt0(t0) = yt0(0) = 2 4 x
• → Tiếp tuyến: −1 = y−2 , Pháp tuyến: −x+2(y−4) = 0 Giải câu 2.
x = ln(pt2+1−t) = −ln(pt2+1+t)
→ pt2+1+t = e−x = y−1
→ Đường cong: y = f(x) = e−x +1. Tại điểm (0;2): 3 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập CM
Giải câu 3. +)Với hàm f(x,y,c) = x2 +
y2 −1 (ĐKXĐ: c =6 0,c 6= 4), xét hệ c 4−c phương trình: fx0 = 0 ⇔ 2cx2y= 0
⇒ (x,y) = (0,0) fy0 = 0 4−c = 0
Tuy nhiên (0,0) không thuộc bất kì đường nào thuộc họ đường cong (L).
⇒ Họ đường cong (L) không có điểm kì dị. +) Xét hệ phương trình: 1 = 0(1) c − y2
Từ phương trình (2) ta có: 2 c2 (2) ⇒x = − 2y2 4 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập (4 c) c 1 (4 c)2 c2 Từ đó,(1) −4 4 ⇒ ( ) ⇒ ( y = ⇒ y = = − ) + − 2 c 2 ( − ) Do x = và y =
⇒ 4 trường hợp y(x) lần lượt là: 4 4 +) y=2-x +) y=x-2 +) y=2+x +) y=-x-2
Do c =60,c =6 4 ⇒ (x,y) = (6 0;±2),(x,y) = (6 ±2;0)
Vậy hình bao (E) của họ đường cong (L) là hình gồm 4 đườngy=2-x,y=x-2,y=2+x,y=x-
2 trừ 4 điểm (0;2), (0;-2), (2;0), (-2;0).
Giải câu 4. Chia miền D thành hai miền: D1 :
2 −−1 ≤≤ x ≤≤ 1,,02≤≤y ≤≤x2 : y−−x22 ≤≤ 0 D : 1 x 1 x y 2 : y x 0 Do đó:
I = ¨ px2−ydxdy + ¨ px2−ydxdy D1 D2 y−x2dy dx 5 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Đặt: x = √2sint trong tích phân sau ta được I dt
Giải câu 5. Miền D : Ta có: I x3+1 dy x3+1 dx 6 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Giải câu 6. Ta có: 2x = p5−2y, suy ra 0 ≤ Ta có: V = ˚ dxdydz V 4
= dxdy dz với D 0 D = 4¨ dxdy D dy dx 0 ≤ x ≤
1 Giải câu 7. Từ đề bài ta xác định được miền E : 0 ≤ y ≤ 1−x 7 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
0 ≤ z ≤ 1−x−y Từ đó, ta tính được: yy 2 zdzdydx dydx x dx Giải câu 8. Ta có: 3z I 2dxdydz 2dxdydz yy V V z3+3z z +3z 8 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Vì V đối xứng qua Oxy và x
2+ 2 là hàm lẻ với z ⇒˚ y2dxdydz = 0 y Do đó: V I 2dxdydz y V x = rcosϕ 0 ≤ ϕ ≤ 2π Đặt y = rsinϕ → V’: 1 ≤ r ≤ 2 v J=r. ⇒ I
Giải câu 9. Đặt I = ¨ (|x|(1+siny)−|y|)dxdy D
Ta chia I thành hai tích phân I1 và I2:
I1 = ¨ |x|sinydxdy; I2 = ¨ (|x|−|y|)dxdy D D
Xét I1 = ¨ |x|sinydxdy 9 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập D
Đặt f(x,y) = |x|siny
Vì f(x,y) = −f(x−y)∀(x,y),(x,−y) ∈ D và D đối xứng qua trục Ox ⇒ I1 = 0
Xét I2 = ¨ (|x|−|y|)dxdy D
x = rcosϕ ⇒ | | Đặt J = r y = rsinϕ 0 r 1
Khi đó miền D trở thành D0 ≤ ≤ I
Giải câu 10. - Với mọi y0 ∈ (−1;1) luôn tồn tại đoạn [c,d] ⊂ (−1;1) sao cho y0 ∈ (c,d)
Xét f(x,y) = ln(1−2ycosx+y2) trên [0;π]×[c;d] 10 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Dễ thấy f liên tục trên [0;π]× [c;d]
Tồn tại fy0(x,y) =
−2y−2cosx 2∀y ∈ [c,d] và fy0(x,y) liên tục trên
1 2ycosx+y [0;π]×[c;d] Do đó: I
dx khả vi trên (c,d)
Mà y0 ∈ (c,d) nên I(y) khả vi tại y0
Do đó ∀y0 ∈ (−1;1),I(y) khả vi tại y0 nên I(y) khả vi trên (−1;1) π
- Từ đó ta có: I0(y) = ˆ 1−2y2−ycos2cosx+xy2dx 0 π
+ Với y = 0,I(0) = ˆ ln(1)dx = 0
+ Với y =6 0,I (y) = y ˆ 1−2−ycosx+y2dx cosx 0 π π
1 ˆ 1−2ycosx+y2 1 ˆ y2−1 − 11 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập = dx+ 2dx x+y π 1 y21 1 = y ˆ dx+ y ˆ 1− 2dx 2ycosx+y 0 0 dx π − y21 1 Đặt I1 =
yˆ 1−2 cosx 2dx y +y 0 2 Đặt t 2 t 1+t y2−1 ˆ 1 2dt Lúc này I1 = y 1− 2 t2+1 1−2y t2 2 0 +y 1+t 12 lOMoAR cPSD| 27879799
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập dt +∞ + = y − + y + y
y ( y + ) . − y . . − y − − = − = y . 0 dt y
Vậy I (y) = π +I1 = π + −π = 0 y y y
⇒ I(y) = ˆ I0(y)dy =C, do I(0) = 0 ⇒C = 0 ⇒ I(y) = 0 13