Bài giảng hàm số lượng giác

Tài liệu gồm 36 trang, tóm tắt lý thuyết trọng tâm, các dạng toán và bài tập chủ đề hàm số lượng giác, có đáp án và lời giải chi tiết, giúp học sinh lớp 11 tham khảo khi học chương trình Đại số 

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

36 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
BÀI GIẢNG HÀM SỐ LƯỢNG GIÁC
CÁC CÔNG THỨC LƯỢNG GIÁC CƠ BẢN
1. Đường tròn lượng giác và dấu của các giá trị lượng giác
Góc I II III IV
sin
x
+ + – –
cos
x
+ – – +
tan
x
+ – + –
cot
x
+ – + –
2. Công thức lượng giác cơ bản
tan .cot 1
22
sin cos 1


2
2
1
1tan
cos

2
2
1
1cot
sin

3. Cung liên kết
Cung đối nhau Cung bù nhau Cung phụ nhau

cos cosaa
sin sinaa

sin cos
2
aa




sin sinaa
cos cosaa

cos sin
2
aa




tan tanaa
tan tanaa

tan cot
2
aa





cot cotaa

cot cotaa

cot tan
2
aa




Góc hơn kém
π
Góc hơn kém
π
2
Cách nhớ:
cos đối
sin bù
phụ chéo
tang và côtang
hơn kém nhau pi
sin sin


sin cos
2




cos cos


cos sin
2




tan tan


tan cot
2





cot cot


cot tan
2




TOANMATH.co
m
Trang 2
4. Công thức cộng cung
sin sin .cos cos .sinab a b a b
cos cos .cos sin .sinab a b a b

tan tan
tan
1 tan .tan
ab
ab
ab


cot .cot 1
cot
cot cot
ab
ab
ab

5. Công thức nhân đôi, nhân ba và hạ bậc
Nhân đôi Hạ bậc
sin 2 2sin .cos

2
1cos2
sin
2
22
22
cos sin
cos 2
2cos 1 1 2sin


2
1cos2
cos
2
2
2tan
tan 2
1tan
2
1cos2
tan
1cos2
2
cot 1
cot 2
2cot
2
1cos2
cot
1cos2
Nhân ba Hạ bậc
3
sin 3 3sin 4sin


3
3sin sin3
sin
4
3
cos3 4cos 3cos


3
3cos cos3
cos
4
3
2
3tan tan
tan3
13tan
6. Góc chia đôi
Đặt
tan
2
x
t
2
2
sin
1
t
x
t
2
2
1
cos
1
t
x
t
2
2
tan
1
t
x
t
7. Công thức biến đổi tổng thành tích
cos cos 2cos cos
22
ab ab
ab


cos cos 2sin sin
22
ab ab
ab


sin sin 2sin cos
22
ab ab
ab


sin sin 2cos sin
22
ab ab
ab


sin
tan tan
cos .cos
ab
ab
ab

sin
tan tan
cos .cos
ab
ab
ab

sin
cot cot
sin .sin
ab
ab
ab

sin
cot cot
sin .sin
ba
ab
ab

TOANMATH.co
m
Trang 3
8. Công thức biến đổi tích thành tổng
 
1
cos .cos cos cos
2
ab ab ab

 
1
sin .sin cos cos
2
ab ab ab

 
1
sin .cos sin sin
2
ab ab ab

MỘT SỐ CÔNG THỨC THƯỜNG DÙNG

22
1 sin 2 sin cos ;1 sin 2 sin cos
x
xx x xx  .
22
1 sin sin cos ;1 sin sin cos
22 22
x
xxx
xx




.
22
1 cos2 2sin ;1 cos2 2cos
x
xxx .
22
1 cos 2cos ;1 cos 2sin
22
x
x
xx  .
sin cos 2 sin 2 cos
44
xx x x
 

 
 
.
sin cos 2 sin 2 cos
44
xx x x




.
sin 3 cos 2cos 2sin
63
xxx x
 

 
 
.
3 sin cos 2sin 2cos
63
xx x x




.
44 2
13cos4
sin cos 1 sin 2
24
x
xx x
 .
66 2
353cos4
sin cos 1 sin 2
48
x
xx x
 .
BẢNG GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT
0
30
45
60
90
120
135
150
180
360
0
6
4
3
2
2
3
3
4
5
6
2
sin
0
1
2
2
2
3
2
1
3
2
2
2
1
2
0 0
cos
1
3
2
2
2
1
2
0
1
2
2
2
3
2
1
1
TOANMATH.co
m
Trang 4
tan
0
3
3
1
3
||
3
1
3
3
0 0
cot
||
3
1
3
3
0
3
3
1
3
||
||
Một điểm M thuộc đường tròn lượng giác sẽ có tọa độ M
cos ;sin
HÀM SỐ LƯỢNG GIÁC
Mục tiêu
1. Nêu rõ tính chất 4 hàm lượng giác cơ bản sin,cos,tan,cot
x
xxx.
2. Phân biệt được tập xác định, tập giá trị, tính tuần hoàn và đồ thị của các hàm lượng giác.
Kiến thức
+ Tìm được tập xác định của hàm lượng giác.
+ Xác định được chu kì của các hàm lượng giác.
+ Vẽ được đồ thị của các hàm lượng giác.
+ Biết xác định giá trị lớn nhất, giá trị nhỏ nhất của một hàm lượng giác.
TOANMATH.co
m
Trang 5
I. LÍ THUYẾT TRỌNG TÂM
Hàm số
y=sinx Đồ thị hàm số sinyx
Tập xác định D .
Tập giá trị

1,1 , tức là
1sin 1,xx .
Hàm số
sinyx
là hàm số lẻ nên đồ
thị hàm số nhận gốc tọa độ O làm
tâm đối xứng.
Hàm số
sinyx
là hàm số tuần hoàn với chu kì 2T
.
Hàm số
y=cosx Đồ thị hàm số cosyx
Tập xác định
D
.
Tập giá trị

1,1
, tức là
1cos 1,xx .
Hàm số cosyx là hàm số
chẵn nên đồ thị hàm số nhận trục Oy làm trục đối xứng.
Hàm số cosyx là hàm số tuần hoàn với chu kì 2T
.
Hàm số
y=tanx Đồ thị hàm số tanyx
Tập xác định
\,
2
Dkk





.
Tập giá trị R.
Hàm số tanyx là hàm số lẻ nên
đồ thị hàm số nhận gốc tọa độ O
làm tâm đối xứng.
Hàm số tanyx là hàm số tuần
hoàn với chu kì
T
.
Hàm số y=cotx
Đồ thị hàm số cotyx
Tập xác định
\,Dkk

.
Tập giá trị
.
TOANMATH.co
m
Trang 6
Hàm số
cot
yx
là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
Hàm số cotyx là hàm số tuần hoàn với chu kì T
HÀM SỐ
LƯỢNG GIÁC
Tập xác
định
Chu kì
Tính
chẵn lẻ

2
sinyaxbT
a


2
cosyaxbT
a


tanyaxbT
a


cotyaxbT
a

sin
y
x
D
cosyx
D
tanyx
\
2
D
k



cotyx
\Dk
Hàm chẵn
Đồ thị nhận Oy làm trục đối
cứng. Hàm số chẵn khi

x
DxD
f
xfx


Hàm lẻ
Đồ thị nhận gốc tọa độ làm
tâm đối xứng. Hàm số lẻ khi

x
DxD
f
xfx


tanyx
cotyx
sin
y
x
cos
y
x
TOANMATH.co
m
Trang 7
II. CÁC DẠNG BÀI TẬP
Dạng 1: Tìm tập xác định của hàm lượng giác
Phương pháp giải
Tập xác định của các hàm phân thức, căn thức
1. Hàm số phân thức


0
DKXD
Px
yQx
Qx
.
2. Hàm số chứa căn thức
 
2
0
DKXD
n
yPx Px.
3. Hàm số chứa căn thức dưới mẫu số


2
0
DKXD
n
Px
yQx
Qx

.
Tập xác định của một số hàm lượng giác cơ bản
1.
sinyux

xác định

ux xác định.
2.

cosyux


xác định
ux xác định.
3.
tanyux


xác định

,
2
ux k k
.
4.
cotyux

xác định
,ux k k

.
Ví dụ 1: Tìm tập xác định của hàm số
23cosyx .
Hướng dẫn giải
Vì 1 cos 1,xx nên
3cos 3,xx
23cos 0,xx
.
Vậy tập xác định của hàm số là
D .
Ví dụ 2: Tìm tập xác định của hàm số
2
1
sin
4
y
x



Hướng dẫn giải
Hàm số
2
1
sin
4
y
x



xác định
2
40x
2x.
Vậy tập xác định của hàm số là
\2D  .
Ví dụ mẫu
Ví dụ.
Tìm tập xác định của hàm số
cot 2018 1yx.
Hướng dẫn giải
Hàm số
cot 2018 1yxxác định
2018 1
x
k
1
,
2018
k
xk
 .
Vậy tập xác định của hàm số
1
\,
2018
k
Dk




.
Bài tập tự luyện dạng 1
Câu 1:
Tập xác định của hàm số
1
sin 2yx
x
 là
A.
\Dk
. B.

1;1 \ 0D  . C. D . D.
\0D .
Câu 2: Tập xác định của hàm số 2cot sin3yxx là
A. \
2
Dk




. B.
\Dk
. C. D . D.
\2Dk
.
TOANMATH.co
m
Trang 8
Câu 3: Tập xác định của hàm số
cosyx
là
A.

0; 2D
. B.
0;D 
. C.
D
. D.
\0D
.
Câu 4: Tập xác định của hàm số
cos
2sin 1
x
y
x
là
A. \2
6
Dk




. B. \
2
Dk



.
C.
\
6
Dk




. D.
5
\2;2
66
Dkk





.
Câu 5: Tập xác định của hàm số
cos
2cos 3
x
y
x
là
A. \2
3
Dk




. B. \
2
Dk



.
C.
\2
6
Dk




. D.
5
\2;2
66
Dkk





.
Câu 6: Tập xác định của hàm số
cot
sin 1
x
y
x
là
A. \2
2
Dk




.
B. \
2
Dk



.
C.
\2;
2
Dkk




. D. \
22
Dk




.
Câu 7: Tập xác định của hàm số
2017
2016 tan 2yx là
A. \
2
Dk




. B. \
2
Dk



.
C.
D . D. \
42
Dk




.
Câu 8: Tập xác định của hàm số
3tan 2cotyxxx
là
A. \
2
Dk




. B. \
2
Dk



.
C. D .
D. \
42
Dk




.
Câu 9: Tập xác định của hàm số
sinx
tan 1
y
x
là
A.
\
4
Dk




.
B.
\
4
Dk



.
C.
\;
42
Dkk





. D. \2
4
Dk




.
Câu 10: Tập xác định của hàm số
22
2017 tan 2
sin cos
x
y
x
là
A. \
2
Dk




. B. \
2
Dk



.
TOANMATH.co
m
Trang 9
C.
D
. D.
\
42
Dk




.
Câu 11: Tập xác định của hàm số
tan
sin 1
x
y
x
là
A. \2
2
Dk




. B. \
2
Dk



.
C.
\
2
Dk




. D. \
42
Dk




.
Câu 12: Tập xác định của hàm số
sin
sin cos
x
y
x
x
là
A. \
4
Dk




.
B. \
4
Dk



.
C.
\;
42
Dkk





. D.
\2
4
Dk




.
Câu 13: Tập xác định của hàm số sin 2 1yxlà
A.
\Dk
. B. D .
C.
\;
42
Dkk





. D.
\2
2
Dk




.
Câu 14: Tập xác định của hàm số 1 cos 2017yx là
A.
\Dk
. B. D .
C.
\;
42
Dkk





. D. \2
2
Dk




.
Câu 15: Tập xác định của hàm số
1
1sin2
y
x
là
A.
\Dk
. B. D .
C.
\;
42
Dkk





. D. \
4
Dk




.
Câu 16: Tập xác định của hàm số
1
2cos6
y
x
là
A.
\Dk
. B. D .
C.
\;
42
Dkk





. D. \
4
Dk




.
Câu 17: Tập xác định của hàm số
tan
15 14cos13
x
y
x
là
A.
\Dk
. B. D . C. \
2
Dk




. D. \
4
Dk




.
TOANMATH.co
m
Trang 10
Câu 18: Tập xác định của hàm số
2sin
1cos
x
y
x
là
A.
\Dk
. B.
\2Dk
. C. \
2
Dk




. D. \
2
Dk



.
Câu 19: Để tìm tập xác định của hàm số tan cosyxx, một học sinh giải theo các bước sau
Bước 1. Điều kiện để hàm số có nghĩa là
sin 0
cos 0
x
x
.
Bước 2.

;
2
xk
km
xm

.
Bước 3. Vậy tập xác định của hàm số đã cho là

\,;
2
Dkmkm






.
Bài giải của bạn đó đã đúng chưa? Nếu sai, thì sai bắt đầu từ bước nào?
A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Câu 20: Hàm số nào sau đây có tập xác định là ?
A.
sinyx
.
B.
tan 2yx
. C.
cot 2yx
. D.
sinxyx
.
Dạng 2: Tính chẵn – lẻ của hàm số lượng giác
Phương pháp giải
1. Hàm số
yfx
với tập xác định
D
gọi là hàm số chẵn
nếu

x
DxD
fx fx


.
2. Hàm số
yfx với tập xác định D gọi là hàm số lẻ nếu

x
DxD
f
xfx


.
Chú ý:
+
Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị hàm số lẻ nhận gốc tọa độ
0;0O làm tâm đối
xứng.
Ví dụ: Xét tính chẵn - lẻ của hàm số
sin 2yx .
Hướng dẫn giải
Hàm số sin 2yx có tập xác định D .
Đặt
sin 2
f
xy x .
Ta có

sin 2
xD xD
f
xxfx


Suy ra hàm số sin 2yx là hàm số lẻ.
Đồ thị hàm số nhận gốc tọa độ
0;0O làm tâm đối xứng.
Ví dụ mẫu
Ví dụ 1.
Xét tính chẵn - lẻ của hàm số
tan cot .yfx x x
Hướng dẫn giải
Hàm số có nghĩa khi
cos 0
sinx 0
x
2
x
k
xl

( với ,kl ).
Tập xác định
\,|,
2
Dklkl





là tập đối xứng.
TOANMATH.co
m
Trang 11
Do đó
x
D
thì
x
D
.
Ta có
tan cot tan cot tan cot .
f
x x xxxxxfx 
Vậy

f
x là hàm số lẻ. Đồ thị hàm số nhận gốc tọa độ làm tâm đối xứng.
Ví dụ 2. Xét tính chẵn – lẻ của hàm số
2
sin 4yx
.
Hướng dẫn giải
Hàm số có nghĩa khi
2
40 ;2][2; .xx  
Tập xác định
;2] [2;D  là tập đối xứng.
Do đó
x
D
thì
x
D
Ta có
 
2
2
sin 4 sin 4 .
f
xx xfx
Vậy

f
x là hàm số chẵn. Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Ví dụ 3. Xét tính chẵn – lẻ của hàm số
2018
sin 2 cos2019yx x .
Hướng dẫn giải
Tập xác định
D
là tập đối xứng.
Do đó
x
D thì
x
D .
Ta có

2018 2018
sin 2 cos 2019 sin 2 cos 2019 .
f
xx xxxfx
Vậy
f
x
là hàm số chẵn. Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Ví dụ 4. Xét tính chẵn – lẻ của hàm số

2017
sin 5 .
2
yfx x




Hướng dẫn giải
Tập xác định D là tập đối xứng.
Do đó
x
D thì .
x
D
Ta có

2017
sin 5 sin 5 1008 sin 5 cos5 .
22 2
f
xx x x x


 


Lại có
cos 5 cos5 .
f
xxxfx
Vậy
f
x
là hàm số chẵn. Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Ví dụ 5. Xét tính chẵn – lẻ của hàm số
3
sin 4 9 cot 11 2018 .yfx x x

Hướng dẫn giải
Ta có
33
sin 4 9 cot 11 2018 sin 4 cot11yfx x x x x

 .
Hàm số có nghĩa khi
sin11 0 11 ,
11
k
xxkxk
 .
TOANMATH.co
m
Trang 12
Tập xác định
\,
11
k
Dk





là tập đối xứng.
Do đó
x
D
thì
x
D
.
Lại có
33
sin 4 cot 11 sin 4 cot11
f
xxxxx
3
sin 4 cot11
x
xfx  .
Vậy
f
x
là hàm số lẻ. Đồ thị hàm số nhận gốc tọa độ
0;0O
làm tâm đối xứng.
Bài tập tự luyện dạng 2
Câu 1:
Hàm số sin .cosyxx là
A. hàm số không lẻ. B. hàm số chẵn.
C.
hàm số không chẵn. D. hàm số lẻ.
Câu 2: Hàm số sin tan 2yx x là
A. hàm số lẻ. B. hàm số chẵn.
C.
hàm số vừa chẵn, vừa lẻ. D. hàm số không chẵn, không lẻ.
Câu 3: Hàm số sin cosyxx là
A. hàm số lẻ. B. hàm số chẵn.
C.
hàm số vừa chẵn, vừa lẻ. D. hàm số không chẵn, không lẻ.
Câu 4: Hàm số
2sin3yx x
là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số không chẵn, không lẻ.
C.
hàm số chẵn. D. hàm số lẻ.
Câu 5: Hàm số
2
12 cos3yx x là
A. hàm số lẻ. B. hàm số chẵn.
C.
hàm số không chẵn, không lẻ. D. hàm số vừa chẵn, vừa lẻ.
Câu 6: Hàm số nào là hàm số lẻ trong các hàm số sau?
A. sinyx . B.
cot
cos
x
y
x
.
C.
2
sinyx . D.
tan
sin
x
y
x
.
Câu 7: Hàm số cos 2yx x là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số không chẵn, không lẻ.
C.
hàm số chẵn. D. hàm số lẻ.
Câu 8: Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số sin .cos3yxx là hàm số lẻ.
B.
Hàm số cos 2 sinyx x là hàm số chẵn.
C.
Hàm số
2
3cot cosyxx
là hàm số lẻ.
D.
Cả 3 mệnh đề trên đều sai.
TOANMATH.co
m
Trang 13
Câu 9: Hàm số
2sin 4tan
5cos
x
x
y
x
là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số chẵn.
C.
hàm số lẻ. D. hàm số không chẵn, không lẻ.
Câu 10: Xét hai mệnh đề
(I)
Hàm số
tan cosyxx
là hàm số lẻ.
(II)
Hàm số tan sinyxx là hàm số lẻ.
Mệnh đề nào
sai?
A. Chỉ (I) sai. B. Chỉ (II) sai. C. Cả 2 sai. D. Không có mệnh đề sai.
Câu 11: Hàm số
2
sin cos tanyxxx là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số chẵn.
C. hàm số không chẵn, không lẻ. D. hàm số lẻ.
Câu 12. Hàm số
2
tan 2 cotyx x x là
A. hàm số không chẵn – lẻ. B. hàm số chẵn.
C. hàm số không lẻ. D. hàm số lẻ.
Câu 13. Hàm số
5
2 sin cos 2
2
yx x




là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số không chẵn, không lẻ.
C. hàm số chẵn. D. hàm số lẻ.
Câu 14. Cho hàm số
sin 2
f
xx và

2
tan
g
xx . Chọn mệnh đề đúng trong các mệnh đề sau:
A.
f
x là hàm số chẵn,
g
x là hàm số lẻ. B.
f
x là hàm số lẻ,
g
x là hàm số chẵn.
C.
f
x là hàm số chẵn,
g
x là hàm số chẵn. D.
f
x và
g
x đều là hàm số lẻ.
Câu 15. Hàm số
3
sin 2
cos 2
x
x
y
x
là
A. hàm số lẻ. B. hàm số chẵn.
C. hàm số vừa chẵn, vừa lẻ. D. hàm số không chẵn, không lẻ.
Câu 16. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
1sinyx . B.
2
cot .sinyxx .
C.
2
tan 2 cotyx x x. D. 1cot tanyxx .
Câu 17. Hàm số tan 2cos3yx x là
A. hàm số lẻ. B. hàm số chẵn.
C. hàm số vừa chẵn, vừa lẻ. D. hàm số không chẵn, không lẻ.
Câu 18. Hàm số
3
1 cos sin 3
2
yx x




là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số chẵn.
TOANMATH.co
m
Trang 14
C. hàm số không chẵn, không lẻ. D. hàm số lẻ.
Câu 19. Cho hai hàm số

2
cos 2
1sin3
x
fx
x
và

2
sin 2 cos3
2tan
x
x
gx
x
.
Mệnh đề nào sau đây đúng?
A.
f
x lẻ và
g
x chẵn. B.
f
x và
g
x chẵn.
C.
f
x
chẵn và
g
x
lẻ. D.
f
x
và
g
x
lẻ.
Câu 20. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
4
cos
3
yx x




.
B.
2017
cos
2
yx x




.
C.
2018
2015 cos sinyxx . D.
2017 2018
tan sinyxx.
Dạng 3. Tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác
Phương pháp giải
Sử dụng một số bất đẳng thức sau
1.
Bất đẳng thức lượng giác
1sin;cos 1,xx x
.
sin ,AB A xB AB x 
.
cos ,AB A xB AB x  .
2. Bất đẳng thức về điều kiện có nghiệm hàm số bậc
nhất.
22 22
sin cos ,AB A xB x AB x .
3. Bất đẳng thức Bunhiacopxki.
222 2
.ax by a b x y .
Dấu " " xảy ra khi và chỉ khi ay bx .
4. Sử dụng phương pháp đồ thị lượng giác.
Ví dụ: Tìm giá trị lớn nhất, giá trị nhỏ nhất của
hàm số
3cos 2yxtrên đoạn ;
22



.
Hướng dẫn giải
Xét hàm số 3cos 2yx trên đoạn ;
22



.
Khi
;
22
x




thì
0cos 1
x
.
Suy ra 2 3cos 2 5 2 5xy.
Vậy
min 2y khi
2
x

; max 5y khi
0x
.
Ví dụ mẫu
Ví dụ 1:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
66
sin cosyxx.
Hướng dẫn giải
Ta có
66 2
3
sin cos 1 sin 2
4
yxx x .
Do
2
0sin2 1
x

nên
2
33 3
.0 sin 2
44 4
x
2
331
11 sin2 1 1
444
xy .
Vậy
2
1
min khi sin 2 1 cos 2 0 ,
442
k
yxxxk
 .
TOANMATH.co
m
Trang 15
2
max 1 khi sin 2 0 sin 2 0 ,
2
k
yxxxk

.
Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
tan tan 2020yxx trên đoạn ;
44



.
Hướng dẫn giải
Ta có
2
2
1 8079
tan tan 2020 tan
24
yxx x




.
Hàm số tan
x
đồng biến và xác định trên khoảng ;
22



Mà
;;
44 22






nên hàm số
tan
x
đồng biến và xác định trên ;
44



.
Do đó
tan tan tan 1 tan 1
44
x
x





2
111311 19
1 tan 1 tan 0 tan
222222 24
xxx

  


2
8079 1 8079 9 8079 8079
tan 2022
424444
xy

 


.
Vậy
8079 1 1
min khi tan arctan
422
yxx;
max 2022 khi tan 1 ,
4
yxxkk

Chú ý:
Hàm số tan
x
luôn đồng biến trên
các khoảng xác định
của nó.
Bài tập tự luyện dạng 3
Câu 1. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số 72cos
4
yx




lần lượt là
A. -2 và 7. B. -2 và 2. C. 5 và 9. D. 4 và 7.
Câu 2. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số 4sin 31yx lần lượt là
A. 2 và 2. B. 2 và 4. C. 42và 8. D. 42 1 và 7.
Câu 3. Giá trị nhỏ nhất của hàm số
2
sin 4sin 5yxxlà
A. -20. B. -8. C. 0. D. 9.
Câu 4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2sin 3yxlà
A. max 5,min 1yy. B. max 5, min 2 5yy.
C.
max 5,min 2yy. D. max 5, min 3yy.
Câu 5. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
4
12sin
y
x
là
TOANMATH.co
m
Trang 16
A.
4
min ,max 4
3
yy
.
B.
4
min , max 3
3
yy
.
C.
4
min ,max 2
3
yy
.
D.
1
min ,max 4
2
yy
.
Câu 6. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
22
2sin cos 2yxx là
A.
3
max 4,min
4
yy.
B. max 3, min 2yy.
C. max 4, min 2yy. D.
3
max 3,min
4
yy.
Câu 7. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3sin 4cos 1yxx là
A. max 6, min 2yy. B. max 4, min 4yy.
C.
max 6, min 4yy
. D.
max 6,min 1yy
.
Câu 8. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4sin6 3cos6yxx là
A. min 5,max 5yy . B. min 4,max 4yy .
C. min 3,max 5yy . D. min 6, max 6yy .
Câu 9. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số sin 2yx trên ;
63



lần lượt là
A.
1
2
và
3
2
.
B.
3
2
và
3
2
.
C.
3
2
và
1
2
.
D.
1
2
và
1
2
.
Câu 10. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3tanyx trên ;
34



lần lượt là
A. 3và
3
3
.
B. 3và
3
3
.
C. 3và -3. D. 3và -1.
Câu 11. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
43cosyx
trên
2
0;
3



lần lượt là
A. 1 và -1. B. 11 và 5. C. 3và -3. D.
11
2
và 1.
Câu 12. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số

sin 2
4
yfx x




trên
;
44



lần lượt là
A. 1 và - 2 . B. 1 và
2
2
.
C.
2
2
và -1.
D.
2
2
và
2
2
.
Câu 13. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
sin 2 sinyx x là
A. min 0,max 3yy. B. min 0,max 4yy.
C. min 0, max 6yy. D. min 0,max 2yy.
Câu 14. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos 2sin
2sin
x
x
y
x
lần lượt là
TOANMATH.co
m
Trang 17
A.
219
3

và
219
3

.
B.
3
và
3
3
.
C.
3 và -3. D.
319
3

và
319
3

.
Câu 15. Giá trị của m để bất phương trình

2
3sin 4cos 6sin 8cos 2 1xx xxm nghiệm đúng với
mọi
x là
A. m 0. B. 0m . C. 0m . D. 1m .
Câu 16. Kết luận đúng về hàm số
22
tan cot 3 tan cot 1yxx xx
là
A. min 5y  đạt được khi
,
4
xkk

.
B. Không tồn tại giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
C. min 2y  và max 5y .
D. Tồn tại giá trị lớn nhất nhưng không tồn tại giá trị nhỏ nhất.
Câu 17. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
44
cos sinyxx trên lần lượt là
A. 2 và 0. B. 1 và
1
2
.
C. 2 và 0. D. 2 và 1.
Câu 18 . Giá trị của m để bất phương trình
2
3sin2 cos2
1
sin 2 4cos 1
xx
m
x
x


là
A.
35
4
m .
B.
35 9
4
m
.
C.
35 9
2
m
.
D.
35 9
4
m
.
Câu 19. Giá trị nhỏ nhất và lớn nhất của hàm số
2
2
cos sin .cos
1sin
x
xx
y
x
lần lượt là
A. 0 và 3. B. 2 và 4. C.
2
3
và 6.
D.
26
4
và
26
4
.
Câu 20. Cho
222
cos cos cos 1
x
yz. Giá trị lớn nhất của
222
1cos 1cos 1cosyxyz là
A. 33. B. 23. C. 43. D. 3.
Dạng 4. Tính tuần hoàn và chu kỳ hàm lượng giác
Phương pháp giải
Một số vấn đề cần chú ý
1. Tính tuần hoàn của hàm số
Định nghĩa: Hàm số
yfx xác định trên tập D
được gọi là hàm số tuần hoàn nếu có số
0T sao cho
với mọi
0x ta có
x
TD và
f
xT fx
.
Ví dụ: Tìm chu kì của hàm số
2
sin
34
x
y




.
Hướng dẫn giải
Tập xác định D .
TOANMATH.co
m
Trang 18
Số dương T nhỏ nhất thỏa mãn các điều kiện trên thì
hàm số đó được gọi là hàm số tuần hoàn với chu kỳ T.
2. Các hàm số

sin
cos
ym axb
ym axb


có chu kỳ
2
T
a
;
biên độ
m ;cực đại m ;cực tiểu - m ,
3. Hàm số
f
x
sin cosauxb vxc
(với ,uv
) là hàm số tuần hoàn với chu kì

2
,
T
uv
((u,v) là ƯCLN (u,v)).
4. Hàm số
.tan cos
f
xa uxb vxc
(với
,uv
) hàm số tuần hoàn với chu kì

2
,
T
uv
((u,v) là ƯCLN (u,v)).
Chu kì của hàm số
2
3
2
3
T

.
Ví dụ mẫu
Ví dụ 1.
Tìm chu kì cơ sở của hàm số 2sin2 3cos3yxx.
Hướng dẫn giải
Tập xác định D .
Chu kì hàm số

2
2
2,3
T
.
Ví dụ 2. Xét tính tuần hoàn và tìm chu kì của hàm số

cos cos 3
f
xx x .
Hướng dẫn giải
Giả sử hàm số đã cho tuần hoàn. Suy ra tồn tại số thực dương T thỏa mãn
  
cos cos 3 cos cos 3
f
xT fx xT xT x x



.
Chọn
0x ta được


cos 1
cos cos 3 2
cos 3 1
T
TT
T

2
3
32
m
Tn
Tm
n

(vô lí do ,mn
nên
m
n
là số hữu tỉ).
Vậy hàm số đã cho không tuần hoàn.
Bài tập tự luyện dạng 4
Câu 1.
Chu kì của hàm số
sin
36
x
y




là
A.
1
2
.
B.
3
. C.
2
3
. D. 6
.
TOANMATH.co
m
Trang 19
Câu 2. Đồ thị trong hình vẽ dưới đây là của hàm số nào?
A.
cos3yx
. B.
3cos3yx
. C.
3cos6yx
. D.
3cos3yx
.
Câu 3. Hàm số 2sin
23
x
y




là hàm số tuần hoàn với chu kì
A.
6T
.
B.
4T
.
C.
6T
. D.
2T
.
Câu 4. Khẳng định nào sau đây sai về hàm số
2sinyx
?
A. Đồ thị hàm số không đi qua gốc tọa độ.
B. Đồ thị hàm số nằm ở phía trên trục hoành.
C. Giá trị cực đại của y là 2.
D. Giá trị cực tiểu của y là 1.
Câu 5. Nếu chu kì tuần hoàn của hàm số
sin
x
y
a
là 4 thì
A. 2a  . B. 4a  . C. 2a . D. 1a  .
Câu 6. Hàm số
2
tanyx tuần hoàn với chu kì
A.
2
T
. B. T
.
C. T
. D. Hàm số không có chu kì.
Câu 7. Khẳng định nào sau đây đúng với hàm số
2cos
2
x
y
?
A. Biên độ là 2, chu kì là
. B. Biên độ là -2, chu kì là 180 .
C. Biên độ là 2, chu kì là 2
. D. Biên độ là 2, chu kì là 4
.
Câu 8. Đồ thị trong hình vẽ dưới đây là của hàm số nào?
A.
sin 2yx
. B.
sin 3yx
. C.
cos 2yx
. D.
cos3yx
.
Câu 9. Chu kì của hàm số sau
sin 3 2cos 2yx x
là
A.
0
2T
. B.
0
2
T
. C.
0
T
. D.
0
4
T
.
Câu 10. Với
0
2
x

thì hàm số

sin
3
x
fx
có giá trị cực đại là
TOANMATH.co
m
Trang 20
A. 0. B. 1. C.
1
3
.
D.
1
2
.
Câu 11. Hàm số 3cos
4
ymx




tuần hoàn có chu kì
3T
khi
A.
3
2
m  .
B. 1m  . C.
2
3
m  .
D. 2m  .
Câu 12. Xét đồ thị hàm số
sinyx
với

,2x
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có một cực đại tại
x
.
B. Đồ thị hàm số có một cực tiểu tại 2x
.
C. Đồ thị hàm số có một cực tiểu tại
3
2
x
.
D. Hàm số đồng biến trên

,2
.
Câu 13. Đồ thị trong hình vẽ dưới đây là của hàm số nào?
A. sin 2yx . B. cos 2yx . C. cos
2
x
y . D. cos3yx .
Câu 14. Chu kì của hàm số
sin 2 sinyxx
là
A. 2T
. B.
0
2
T
. C.
0
T
. D.
0
4
T
.
Câu 15. Chọn mệnh đề đúng trong các mệnh đề sau
A. Hàm số cotyx đồng biến trên khoảng ;
2



.
B. Hàm số sinyx nghịch biến trên khoảng ;
2



.
C. Hàm số
tanyx
đồng biến trên
;
22



và
cotyx
nghịch biến trên khoảng
;
22



.
D. Hàm số sinyx và cosyx cùng đồng biến trên khoảng 0;
2



.
Câu 16. Chu kì của hàm số
tan tan3yx x
là
A.
2T
. B.
T
. C.
4
T
. D.
2
T
.
Câu 17. Khẳng định nào sau đây đúng về hàm số
2sin 2017
2
x
y




?
TOANMATH.co
m
Trang 21
A. Chu kì
2
, biên độ 2. B. Chu kì
4
, biên độ 2.
C. Chu kì 2
, biên độ 1. D. Chu kì 4
, biên độ 1.
Câu 18. Chu kì của hàm số
sin 3 2017cos 2yx x
là
A. T
. B.
2
T
. C. 2T
. D.
4
T
.
Câu 19. Hình vẽ sau là đồ thị của hàm số
sin
y
ax b
. Biết 0a và b nhỏ nhất, giá trị của biểu
thức
P
ab là
A. 0. B. 1. C. 2. D. 3.
Câu 20. Chu kì cơ sở (nếu có) của hàm số sinyx là
A. hàm số không có chu kì cơ sở. B.
0
2
T
.
C.
0
T
.
D.
0
4
T
.
TOANMATH.co
m
Trang 22
ĐÁP ÁN
Dạng 1: Tìm tập xác định hàm số lượng giác
1 – D 2 – B 3 – B 4 – D 5 – C 6 – C 7 – D 8 – B 9 – C 10 – D
11 – C 12 – A 13 – B 14 – B 15 – D 16 – B 17 – C 18 – B 19 – A 20 – D
Hướng dẫn giải chi tiết
Câu 1.
Hàm số
1
sin 2yx
x
 có nghĩa
0\0xD .
Câu 2.
Hàm số 2cot sin3yxx có nghĩa

\xk D k k

 .
Câu 3:
Hàm số
cosyx có nghĩa
00;xD
.
Câu 4.
Hàm số
cos
2sin 1
x
y
x
có nghĩa

2
1
6
2sin 1 0 sin
5
2
2
6
xk
xx k
xk



.

5
\2;2
66
Dkkk






.
Câu 5.
Hàm số
cos
2cos 3
x
y
x
có nghĩa

2
3
6
2cos 3 0 cos
2
2
6
xk
xx k
xk



.

\2
6
Dkk




.
Câu 6.
Hàm số
cot
sin 1
x
y
x
có nghĩa

sin 1 0 sin 1
x
x
x
kxk



 
2
\2;
2
2
xk
kD kkk
xk






 .
Câu 7:
Hàm số
2017
2016 tan 2yx có nghĩa

cos 2 0 2
242
xxkxkk



\
42
Dkk






.
TOANMATH.co
m
Trang 23
Câu 8:
Hàm số
3tan 2cotyxxx
có nghĩa
cos 0
2
sin 0
x
xk
xxk


 
\
22
xk k D k k





 .
Câu 9: Hàm số
sin
tan 1
x
y
x
có nghĩa
tan 1
tan 1 0
2
x
x
x
k


 
4
\;
42
2
xk
kD kkk
xk









.
Câu 10:
Hàm số
22
2017 tan 2
sin cos
x
y
x
x
có nghĩa

22
cos 2 0
sin cos 0
2
42
2
x
xx
k
xk
xk










\
42 42
xkD kk
 




.
Câu 11:
Hàm số
tan
sin 1
x
y
x
có nghĩa

sin 1 0 sin 1 2
2
2
2
xxxk
xkk
xk




\
2
Dkk




.
Câu 12:
Hàm số
sin
sin cos
x
y
x
x
có nghĩa
sin cos 0 2 sin 0
4
xx x




 
\
44
xkk D kk







 .
Câu 13:
Hàm số
sin 2 1yx có nghĩa sin2 1 0 sin2 1xxxD.
Câu 14:
Hàm số
1 cos2017yx
có nghĩa
1 cos2017 0 cos 2017 1xxxD .
Câu 15:
Hàm số
1
1sin2
y
x
có nghĩa 1 sin 2 0 sin 2 1 sin 2 1
x
xx
 
22 \
24 4
xkxkk D kk







.
TOANMATH.co
m
Trang 24
Câu 16:
Hàm số
1
2cos6
y
x
có nghĩa 2cos6 0 cos6 2xxxD 
Câu 17:
Hàm số
tan
15 14cos13
x
y
x
có nghĩa
15
15 14cos13 0
cos13
14
2
2
x
x
xk
x
k






 
\
22
xkk D kk







Câu 18:
Hàm số
2sin
1cos
x
y
x
có nghĩa
1cos 0 2 \ 2xxkk Dkk

  .
Câu 19:
Hàm số
tan cotyxx
có nghĩa
 
cos 0
\
2
sin 0
2
k
xk
kD k
x
xk






Vậy bạn học sinh đó giải đúng.
Câu 20:
Hàm số
sinyx có nghĩa
00;xD .
Hàm số
tan 2yx
có nghĩa
cos 2 0 2 \
242 42
kk
xxkx D
 




.
Hàm số cot 2yx có nghĩa sin 2 0 2 \
22
kk
xxkx D




.
Hàm số
sinyx x có D .
Dạng 2: Tính chẵn – lẻ của hàm số lượng giác
1 – D 2 – A 3 – D 4 – D 5 – B 6 – B 7 - C 8 - A 9 – C 10 – A
11 – D 12 – D 13 – C 14 – B 15 – A 16 – C 17 – D 18 – B 19 – B 20 – B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1:
Hàm số
sin .cosyxx
có nghĩa
xD 
.
Ta có
sin .cos sin .cos
f
xxxxxfx   .
Vậy hàm số sin .cosyxx là hàm số lẻ.
Câu 2:
Hàm số
sin tan 2yx x
có nghĩa
cos 2 0 2 \
242 42
kk
xxkx D
 




.
Ta có
sin tan 2 sin tan 2 sin tan 2
f
xx xxxxxfx
.
TOANMATH.co
m
Trang 25
Vậy hàm số
sin tan 2yx x
là hàm số lẻ.
Câu 3:
Hàm số
sin cosyxx
có nghĩa xD .
Ta có
  

sin cos sin cos
f
xfx
fx x x x x
f
xfx

 

Vậy hàm số sin cosyxx là hàm số không chẵn, không lẻ.
Câu 4:
Hàm số
2sin3yx x
có nghĩa xD 
Ta có
2sin3 2sin3 2sin3
f
xx xx x x xfx .
Vậy hàm số 2sin3yx x là hàm số lẻ.
Câu 5:
Hàm số
2
12 cos3yx x
có nghĩa
xD 
.
Ta có
 
2
2
12 cos 3 12 cos3
f
xx xxxfx .
Vậy hàm số
2
12 cos3yx x là hàm số chẵn.
Câu 6:
Hàm số
cot
cos
x
y
x
có nghĩa
cos 0
\
2
22
sin 0
kk
xxk
xD
xxk






.
Ta có




cot
cot
cos cos
x
x
f
xfx
xx

.
Vậy hàm số
cot
cos
x
y
x
là hàm số lẻ.
Câu 7:
Hàm số
cos 2
y
xx có nghĩa xD .
Ta có
cos 2 cos 2
f
xx xx xfx
.
Vậy hàm số
cos 2
y
xx
là hàm số chẵn.
Câu 8:
Hàm số sin .cos3yxx có nghĩa xD
.
Ta có
sin .cos 3 sin .cos3
f
xxxxxfx   .
Vậy hàm số sin .cos3yxx là hàm số lẻ.
Câu 9:
Hàm số
2sin 4tan
5cos
x
x
y
x
có nghĩa

cos 0 \
22
xxkD kk






.
Ta có



2sin 4tan
2sin 4tan
5 cos 5 cos
xx
xx
f
xfx
xx




.
TOANMATH.co
m
Trang 26
Vậy hàm số
2sin 4tan
5cos
x
x
y
x
là hàm số lẻ.
Câu 10:
+ Hàm số tan cosyxx có nghĩa

cos 0 \
22
xxkD kk






.
Ta có
  

tan cos tan cos
f
xfx
fx x x x x
f
xfx

 

.
Vậy hàm số
tan cosyxx
là hàm số không chẵn, không lẻ.
+ Hàm số
tan sinyxx
có nghĩa

cos 0 \
22
xxkD kk







.
Ta có
tan sin tan sin
f
xxxxxfx  .
Vậy hàm số
tan sinyxx
là hàm số lẻ.
Câu 11:
Hàm số
2
sin cos tanyxxx có nghĩa

cos 0 \
22
xxkD kk






.
Ta có
22
sin cos tan sin cos tan
f
xxxxxxxfx  .
Vậy hàm số
2
sin cos tanyxxx là hàm số lẻ.
Câu 12:
Hàm số
2
tan 2 cotyx x x
có nghĩa

cos 2 0 2
\,
242
42
sin 0
k
k
xxkx
Dkk
xxk xk






 







.
Ta có
 
2
2
tan 2 cot tan 2 cot
f
xx x xx xxfx  .
Vậy hàm số
2
tan 2 cotyx x x là hàm số lẻ.
Câu 13:
Hàm số
5
2sincos 2
2
yx x




có nghĩa
xD .
Ta có
 
55
2sin cos 2 2sincos 2
22
f
xxxx x






33 5
2sincos 2 2sincos 2 4 2sincos 2
22 2
x
xx x x xfx


  


.
Vậy hàm số
5
2sincos 2
2
yx x




là hàm số chẵn.
Câu 14:
+ Hàm số
sin 2
f
xx có nghĩa xD .
Ta có
sin 2 sin 2
f
xxxfx .
TOANMATH.co
m
Trang 27
Vậy hàm số
sin 2
f
xx là hàm số lẻ.
+ Hàm số
2
tan
g
xx có nghĩa

cos 0 \
22
xxkD kk






.
Ta có
22
tan tan
g
xxxgx  .
Vậy hàm số
2
tan
g
xx là hàm số chẵn.
Câu 15:
Hàm số
3
sin 2
cos 2
x
x
y
x
có nghĩa

cos 2 0 2 \
242 42
kk
xxkx D k






Ta có



33
sin 2 sin 2
cos 2 cos 2
xxxx
f
xfx
xx


.
Vậy hàm số
3
sin 2
cos 2
x
x
y
x
là hàm số lẻ.
Câu 16:
Hàm số
2
tan 2 cotyx x x có nghĩa

cos 2 0 2
\,
242
42
sin 0
k
k
xxkx
Dkk
xxk xk






 







.
Ta có
 
2
2
tan 2 cot tan 2 cot
f
xx x xx xxfx  .
Vậy hàm số
2
tan 2 cotyx x x là hàm số lẻ.
Câu 17:
Hàm số
tan 2cos3yx x
có nghĩa
cos 0 \ .
22
xxkD k





Ta có
 

tan 2cos 3 tan 2cos3
f
xfx
fx x x x x
f
xfx



.
Vậy hàm số
tan 2cos3yx x là hàm số không chẵn, không lẻ.
Câu 18:
Hàm số
3
1cossin 3
2
yx x




có nghĩa
xD

.
Ta có
  
333
1cos sin 3 1cossin 3 1cossin 3
222
f
xx xxxx x






3
1cossin 3 2 1cossin 3
22
x
xxxfx


 


.
Vậy hàm số
3
1cossin 3
2
yx x




là hàm số chẵn.
Câu 19:
+ Hàm số

2
cos 2
1sin3
x
fx
x
có nghĩa
xD .
TOANMATH.co
m
Trang 28
Ta có



22
cos 2
cos 2
1sin 3 1sin3
x
x
f
xfx
xx


.
Vậy hàm số

2
cos 2
1sin3
x
fx
x
là hàm số chẵn.
+ Hàm số

2
sin 2 cos3
2tan
x
x
gx
x
có nghĩa
cos 0 \ .
22
xxkD k





Ta có



22
sin 2 cos 3
sin 2 cos3
2 tan 2 tan
xx
xx
g
xgx
xx



.
Vậy hàm số

2
sin 2 cos3
2tan
x
x
gx
x
là hàm số chẵn.
Câu 20:
Hàm số
2017
cos
2
yx x




có nghĩa
xD .
Ta có

2017
2017
cos cos
22
fx x x x x





2017 2017
cos cos
22
x
xxxfx


  


.
Vậy hàm số
2017
cos
2
yx x




là hàm số lẻ.
Dạng 3: Tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác
1 – C 2 – D 3 – B 4 – A 5 – A 6 – D 7 - C 8 - A 9 – B 10 – D
11 – D 12 – D 13 – D 14 – A 15 – B 16 – A 17 – B 18 – D 19 – D 20 – B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1:
Hàm số
72cos
4
yx




có nghĩa
xD 
.
Ta có
1 cos 1 2 2cos 2 5 7 2cos 9
44 4
xx x

  
  
  
  
.
Vậy
min 5 cos 1 2 2 ,
44 4
yxxkxkk






;
5
max 9 cos 1 2 2 ,
44 4
yx xkxkk



 


.
Câu 2:
Hàm số
4sin 3 1yx có nghĩa
sin 3 0 sin 3xxxD
.
Ta có
1sin12sin34 2 sin32xx x
TOANMATH.co
m
Trang 29
42 4sin 3 8 42 1 4sin 31 7xx
.
Vậy
min 4 2 1 sin 1 2 ,
2
yxxkk

;
max 7 sin 1 2 ,
2
yxxkk

.
Câu 3:
Hàm số
2
sin 4sin 5yxx có nghĩa xD 
Ta có

2
2
sin 4sin 5 sin 2 9yxx x .
 
22
1 sin 1 3 sin 2 1 1 sin 2 9 8 sin 2 9 0xx x x  .
Vậy
min 8 sin 2 1 sin 1 2 ,
2
yx xxkk
 
.
Câu 4:
Hàm số
2sin 3yx có nghĩa
xD 
.
Ta có
1 sin 1 2 2sin 2 1 2sin 3 5 1 2sin 3 5xxx x .
Vậy
min 1 sin 1 2 ,
2
yxxkk

;
max 5 sin 1 2 ,
2
yxxkk
 .
Câu 5:
Hàm số
2
4
12sin
y
x
có nghĩa
xD 
.
Ta có
22 2
1 sin 1 0 sin 1 0 2sin 2 1 1 2sin 3xx x x
22
11 44
14
3 1 2sin 3 1 2sin
x
x


.
Vậy
sin 1 2 ,
4
2
min , ;
32
sin 1 2 ,
2
xxkk
yxkk
xxkk



max 4 sin 0 ,yxxkk
 .
Câu 6:
Hàm số
22
2sin cos 2yxx có nghĩa xD .
Ta có
2
22 2
13
2sin cos 2 1 cos 2 cos 2 cos 2
24
yxx xxx




.
22
311 193 13
1 cos 2 1 cos2 0 cos2 cos2 3
222 244 24
xx x x
 

 
 
.
Vậy
31
min cos 2 ,
426
yxxkk
 
;
TOANMATH.co
m
Trang 30
max 3 cos 2 0 ,
42
k
yxxk

.
Câu 7:
Hàm số 3sin 4cos 1yxx có nghĩa
xD .
Ta có

34
3sin 4cos 1 5 sin cos 1 5sin 1
55
yxx x x x




với
3
arccos 2
5
k




.
5 5sin 5 4 5sin 1 6xx

  
.
Vậy

min 4 sin 1 2 2 ,
22
yx xkxkk

  
;

max 6 sin 1 2 2 ,
22
yxxkxkk

 
.
Câu 8:
Hàm số
4sin6 3cos6yxx
có nghĩa
xD

.
Ta có

43
4sin 6 3cos6 5 sin 6 cos6 5sin 6
55
yxx x x x




với
4
arccos 2
5
k




.
1 sin 6 1 5 5sin 6 5xx


.
Vậy

2
min 5 sin 6 1 6 2 ,
2123
k
yx xkx k



 
;

max 5 sin 6 1 6 2 ,
26123
k
yxxkx k


 .
Câu 9:
Hàm số sin 2yx có nghĩa
xD 
Khi
;
63
x




thì
33
sin 2
22
x .
Vậy
33
min ;max
26 23
yx yx
  .
Câu 10:
Hàm số
3tanyx có nghĩa cos 0 \
22
x
xkD k





.
Khi
;
34
x




thì hàm số tanyx luôn đồng biến.
Suy ra
3tan 1 1 3tan 3xx .
Vậy
3
min 1 ;max
324
yx y x
  .
Câu 11:
Hàm số
43cosyfx x có nghĩa xD .
TOANMATH.co
m
Trang 31
Khi
2
0;
3
x



thì
13 3 11
cos 1 3cos 3 3 3cos 1 4 3cos
22 2 2
xx x x

.
Vậy
11 2
min 1 0;max
23
yx y x

.
Câu 12:
Hàm số

sin 2
4
yfx x




có nghĩa
xD

.
Khi
;
44
x




thì
22
sin 2
242
x




.
Vậy
22
min ;max
24 24
yx yx
 .
Câu 13:
Hàm số
2
sin 2 sinyx x có nghĩa
xD 
.
Ta có
22 2 2
1 sin 1 0 sin 1 1 sin 0 1 2 sin 2 1 2 sin 2xx x x x  .
Lại có
2
1sin 1 0sin 2sin 1 2 0 1 2xxx y .
0sin 1 2
2
yxxk

.
Vậy
min 0 2
2
yx k
 .
sin 1
12
sin 0
x
y
x

(vô nghiệm).
Áp dụng bất đẳng thức Côsi ta có
22 2 2
2sin 2 sin sin 2 sin 2sin 2 sin 2xxx xxx 
22
2 2sin 2 sin 4 4 2xxyy .
Dấu “=” khi và chỉ khi
2
sin 2 sin sin 1 2 ,
2
xxxxkk
 .
Vậy
min 0 2 , ;max 2 2 ,
22
y x kk y x kk

  
.
Câu 14:
Hàm số
cos 2sin
2sin
x
x
y
x
có nghĩa
xD .
Ta có
cos 2sin
2sincos2sin
2sin
xx
yyyxxx
x

 
2
2
2 sin 2sin cos 2 2 sin cos 4 2 sin cosyy x x x y y x x y y x x  

Sử dụng bất đẳng thức Bunhiacopxki ta có
TOANMATH.co
m
Trang 32

2
22 2
219 219
214 3 450
33
yyyy y
 

.
Vậy
219 219
min ;max
33
yy
 

.
Câu 15:
Hàm số

2
3sin 4cos 6sin 8cos 2 1xx xxm có nghĩa xD .
Ta có

2 2
3sin 4cos 2 3sin 4cos 1 2 3sin 4cos 1 2
x
xxxmxxm
Để phương trình có nghiệm đúng với mọi
x
thì
20 0mm
.
Câu 16:
Hàm số
22
tan cot 3 tan cot 1yxx xx có nghĩa
cos 0
2
2
sin 0
xxk
x
k
xxk



Ta có
22
tan cot 3 tan cot 1yxx xx

2
22
tan 2 tan cot cot 3 tan cot 3 tan cot 3 tan cot 3x xx x xx xx xx
Đặt
2
tan cot 2
sin 2
xxt t
x

Ta có
2
33.yt t Cho
1
2
321
2
0
321
2
t
y
t



Vậy
2
min 5 2 sin 2 1 2 2 ;max
sin 2 2 4
yt x xkxky
x

    
Câu 17:
Hàm số
44
cos sinyxx có nghĩa xD .
Ta có
2
44 2 4 244 4 2
cos sin 1 sin sin 1 2sin sin sin 2sin 2sin 1yxx x x xxx x x .
 
2
22
22 22 2
111
2 sin 2sin 1 2 sin sin 2 sin
222
yx x xx x




.
22
22 2 2
111 11 11
1 sin 1 0 sin 1 sin 0 sin 0 2 sin
222 24 22
xx x x x
 
 
 
 
2
2
1111
2sin 1 1
2222
x
y

 


.
Vậy

2
2
sin 2
11
24
min sin
2
22
sin 2
24
xxk
yx k
xxk

 


;
TOANMATH.co
m
Trang 33
max 1 sin 0yxxkk
 .
Câu 18:
Ta có
2
1cos2
sin 2 4cos 1 sin 2 4 1 sin 2 2cos2 3 0
2
x
xx x xx

xD 

3sin2 cos2
13sin212cos23
sin 2 2cos2 3
xx
myxyxy
xx



2
2
93sin212cos2yyxyx 

Sử dụng bất đẳng thức Bunhiacopxki ta có

22
22
535 535
31292550
44
yyyyy y
 

.
Vậy
5 35 5 35 35 9
max 1
44 4
ymm
 
.
Câu 19:
Hàm số
2
2
cos sin .cos
1sin
x
xx
y
x
có nghĩa
xD 
.
2
22 2
1cos2 sin2
cos sin .cos 1 cos 2 sin 2 1 cos 2 sin 2
22
1sin 1sin 22sin 3cos2
xx
x
xx xx xx
y
xx xx



Có

1cos2 sin2
3 cos 2 1 cos 2 sin 2 1 cos 2 sin 2 3 1
3cos2
xx
yyyxxxyxxy
x



2
2
31 1 cos2sin2yyxx
Sử dụng bất đẳng thức Bunhiacopxki ta có

22
22 2
26 26
113112 19618810
44
yy yyyyyy y

 .
Vậy
26 26
min ;max
44
yy

.
Câu 20:
Theo bài ra
222
cos cos cos 1
x
yz
Áp dụng bất đẳng thức Bunhiacopxki, ta có
222222222
1cos 1cos 1cos 1 1 1.1cos 1cos 1cos
x
yz xyz
222 222
1 cos 1 cos 1 cos 3 3 cos cos cos
x
yz xyz
222
1cos 1cos 1cos 23 23xyzy   .
Vậy
max 2 3y .
TOANMATH.co
m
Trang 34
Dạng 4: Tính tuần hoàn và chu kì hàm lượng giác
1 – D 2 – D 3 – B 4 – C 5 – A 6 – D 7 – D 8 – B 9 – A 10 – D
11 – C 12 – C 13 – C 14 – A 15 – B 16 – B 17 – B 18 – C 19 – B 20 – A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1:
Hàm số
sin
36
x
y




có nghĩa
xD .
Chu kì của hàm số
2
6
1
3
T

.
Câu 2:
Tại
03xy Loại đáp án A, B.
Tại 3xy
 Loại đáp án C.
Vậy đồ thị đã cho là của hàm số 3cos3yx .
Câu 3:
Hàm số
2sin
23
x
y




có nghĩa
xD .
Chu kì của hàm số
2
4
1
2
T
.
Câu 5:
Hàm số
2sin
x
y
a
có nghĩa
xD .
Chu kì của hàm số
2
42Ta
a
.
Câu 6:
Hàm số không có chu kì cơ sở.
Câu 7:
Chu kì của hàm số
2
4.
1
2
T
 Loại đáp án A, B. Biên độ của hàm số 22A .
Câu 8:
Tại 0 0xy Loại đáp án
C, D.
Chu kì của hàm số
2
3
T
.
TOANMATH.co
m
Trang 35
Vậy đồ thị đã cho là của hàm số
sin 3yx
.
Câu 9:
Hàm số
() sin cos
f
xauxb vxc
(với
,uv
) là hàm số tuần hoàn với chu kì

2
,
T
uv
Hàm số
sin3 2cos2yx x
có nghĩa xD .
Chu kì của hàm số
2
2
1
T

.
Câu 10:
Ta có với
0
2
x
 thì hàm số

sin
3
x
fx luôn đồng biến.
Khi đó giá trị lớn nhất của hàm số là
max
1
2
y tại
2
x
.
Câu 11:
Hàm số
3cos
4
ymx




có nghĩa
xD .
Chu kì của hàm số
22
3
3
Tm
m

.
Câu 12:
Hàm số
sinyx
có nghĩa xD .
Hàm số nghịch biến trên
3
,
2



. Hàm số đồng biến trên
3
,2
2



.
Đồ thị hàm số có một cực tiểu tại
3
2
x
.
Câu 13:
Tại
01xy Loại đáp án A. Chu kì của hàm số 2.2 4T
.
Vậy đồ thị đã cho là của hàm số
cos
2
x
y .
Câu 14.
Hàm số
sin sin
f
xauxbvxc
( với
,uv ) là hàm số tuần hoàn với chu kì

2
,
T
uv
.
Hàm số sin 2 sinyxx có nghĩa
xD 
.
Chu kì của hàm số
2
2
1
T

.
Câu 15.
Ta có hàm số
sinyx
nghịch biến trên khoảng
;
2



.
TOANMATH.co
m
Trang 36
Câu 16.
Hàm số
.tan .tan
f
xa uxb vxc ( với ,uv ) là hàm số tuần hoàn với chu kì

,
T
uv
.
Hàm số
tan tan3yx x
có nghĩa
xD 
.
Chu kì của hàm số
1
T
.
Câu 17.
Hàm số 2sin 2017
2
x
y




có nghĩa
xD .
Chu kì của hàm số
2
4
1
2
T
.
Biên độ của hàm số
22A .
Câu 18.
Hàm số
sin 3 2017cos 2yx x
có nghĩa
xD 
.
Chu kì của hàm số
2
2
1
T
.
Câu 19.
Hàm số
sin
y
ax b

có nghĩa xD .
Với
0a
chu kì của hàm số
21
4
2
Ta
a
.
Tại

1
01sin1
2
xy bb
  .
Vậy
1ab.
Câu 20.
Hàm số không có chu kì cơ sở.
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

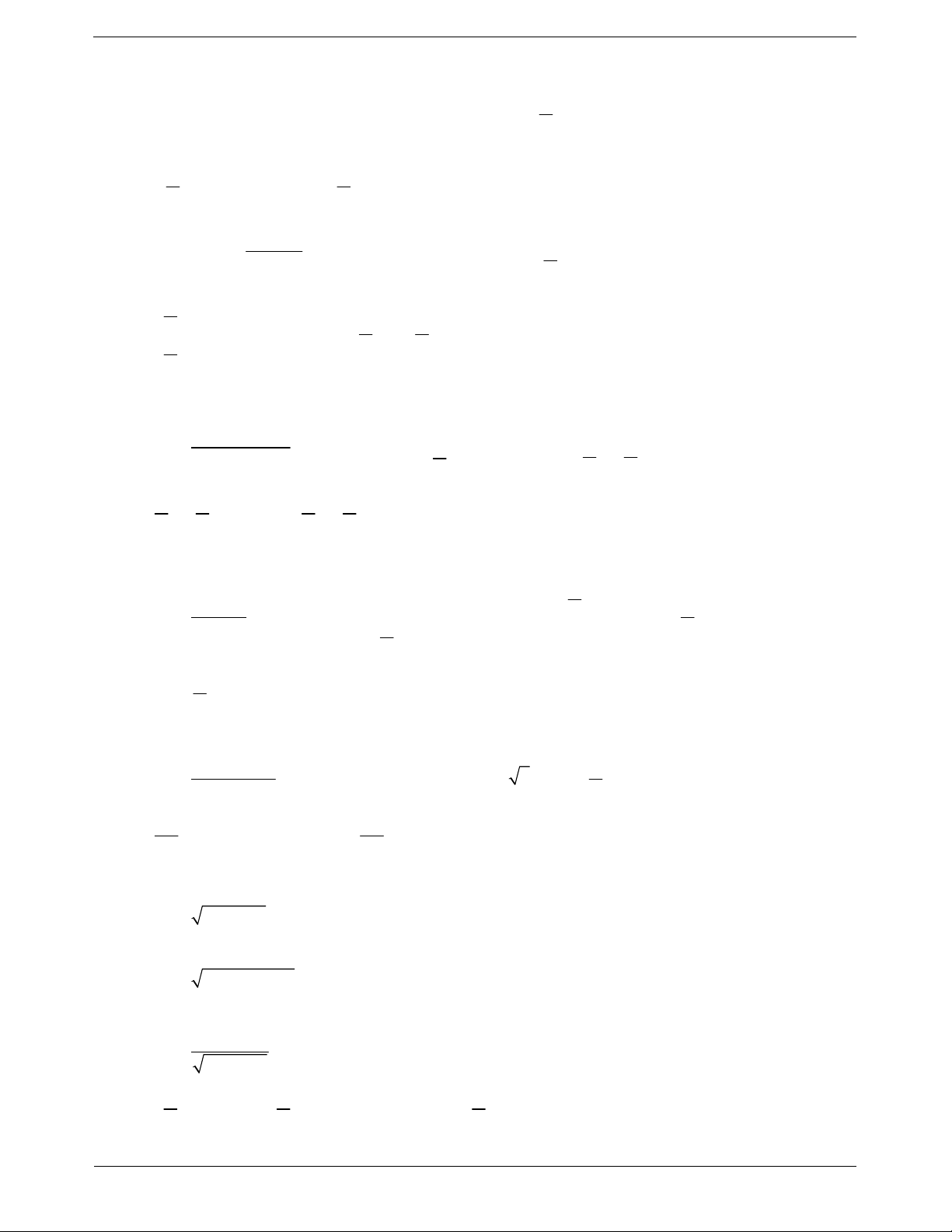
Preview text:

BÀI GIẢNG HÀM SỐ LƯỢNG GIÁC
CÁC CÔNG THỨC LƯỢNG GIÁC CƠ BẢN
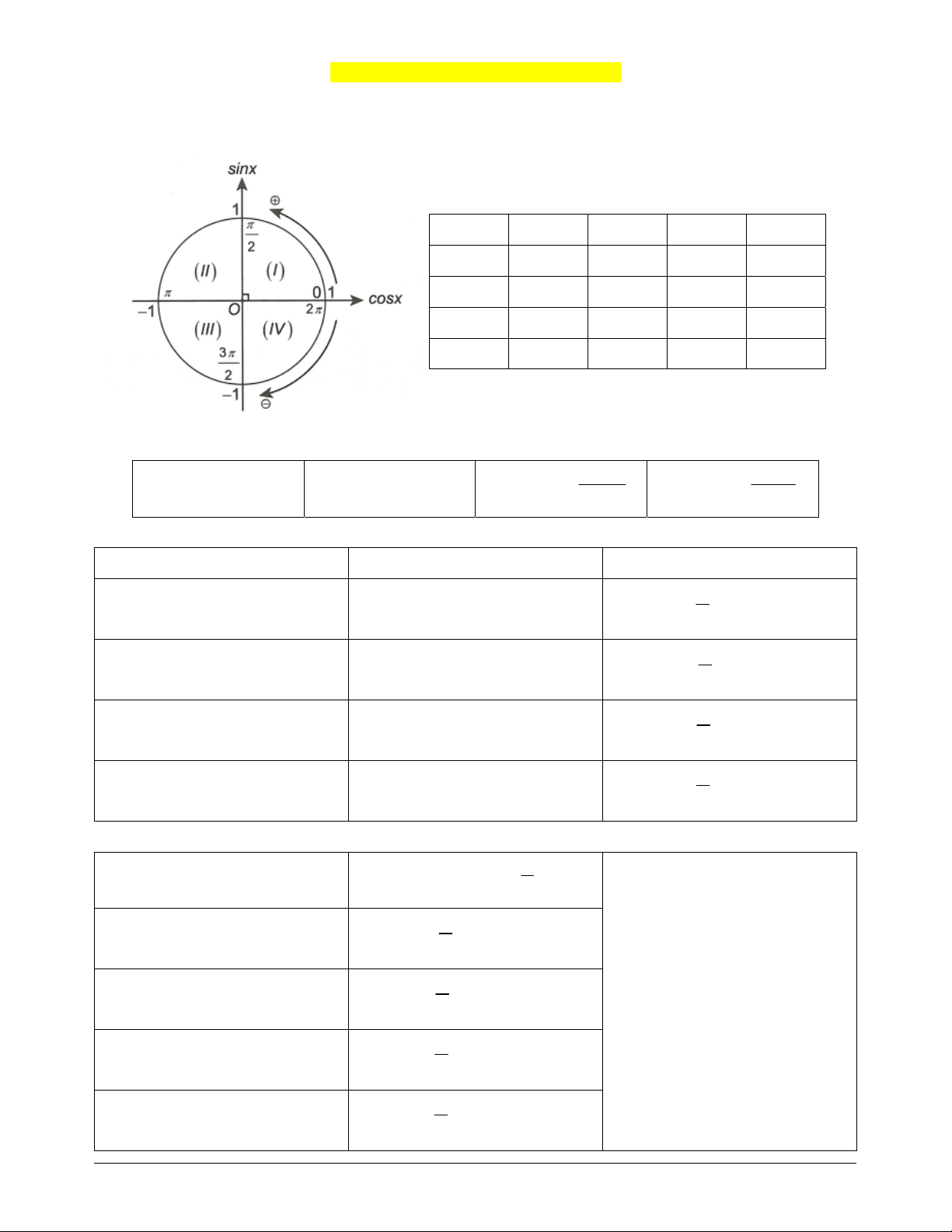
1. Đường tròn lượng giác và dấu của các giá trị lượng giác Góc I II III IV sin x + + – – cos x + – – + tan x + – + – cot x + – + –
2. Công thức lượng giác cơ bản tan.cot  1 2 2
sin   cos   1 1 1 2 1 tan   2 1 cot   2 cos  2 sin  3. Cung liên kết Cung đối nhau Cung bù nhau Cung phụ nhau
cosa  cos a
sin   a  sin a    sin  a  cos a    2 
sin a  sin a
cos   a  cos a    cos  a  sin a    2 
tan a   tan a
tan   a   tan a    tan  a  cot a    2 
cot a  cot a
cot   a  cot a    cot  a  tan a    2  Góc hơn kém π π Cách nhớ: Góc hơn kém 2 cos đối
sin     sin    sin bù sin   cos    2  phụ chéo
cos      cos    tang và côtang cos   sin    2  hơn kém nhau pi
tan     tan    tan   cot    2 
cot     cot    cot    tan    2  Trang 1
4. Công thức cộng cung
sin a b  sin .
a cos b  cos . a sin b
cos a b  cos . a cosb  sin . a sin b   a b a b tan a tan b tan 
a b cot .cot 1 cot  1 tan . a tan b cot a  cot b
5. Công thức nhân đôi, nhân ba và hạ bậc Nhân đôi Hạ bậc
sin 2  2sin.cos 1 cos 2 2 sin    2 2 2 cos   sin 1 cos 2 cos 2       2 2  2 cos
2cos  1 1 2sin  2 2 tan 1 cos 2 tan 2  2 tan   2 1 tan  1 cos 2 2 cot  1 1 cos 2 cot 2  2 cot   2cot 1 cos 2 Nhân ba Hạ bậc 3
sin 3  3sin  4sin  3sin sin 3 3 sin    4 3
cos3  4cos   3cos 3cos cos3 3 cos    4 3 3 tan  tan  tan 3  2 1 3 tan  6. Góc chia đôi x Đặt t  tan 2 2t 2 2t sin x 1 t  tan x 2 cos x 1 t 2 1 t 2 1 t
7. Công thức biến đổi tổng thành tích a b a b a b a b
cos a  cosb  2 cos cos
cos a  cosb  2sin sin 2 2 2 2 a b a b a b a b
sin a  sin b  2sin cos
sin a  sin b  2 cos sin 2 2 2 2
sin a b
sin a b
tan a  tan b
tan a  tan b  cos . a cos b cos . a cos b
sin a b
sin b a
cot a  cot b
cot a  cot b  sin . a sin b sin . a sin b TOANMATH.com Trang 2
8. Công thức biến đổi tích thành tổng 1 cos .
a cosb  cos 
a b  cosa b 2  1 sin .
a sin b  cos 
a b cosa b 2  1 sin .
a cosb  sin 
a b sina b 2 
MỘT SỐ CÔNG THỨC THƯỜNG DÙNG   x   x x2  x   x x2 1 sin 2 sin cos ;1 sin 2 sin cos . 2 2   x x   x x
1 sin x  sin  cos
;1 sin x  sin  cos     .  2 2   2 2   2 2 1 cos 2x  2sin ;
x 1 cos 2x  2cos x . x x 2 2 1 cos x  2 cos ;1 cos x  2sin . 2 2       
sin x  cos x  2 sin x   2 cos x      .  4   4        
sin x  cos x  2 sin x   2 cos x      .  4   4        
sin x  3 cos x  2cos x   2sin x      .  6   3        
3 sin x  cos x  2sin x   2cos x      .  6   3    1 3 cos 4x 4 4 2
sin x  cos x  1 sin 2x  . 2 4   3 5 3cos 4x 6 6 2
sin x  cos x  1 sin 2x  . 4 8
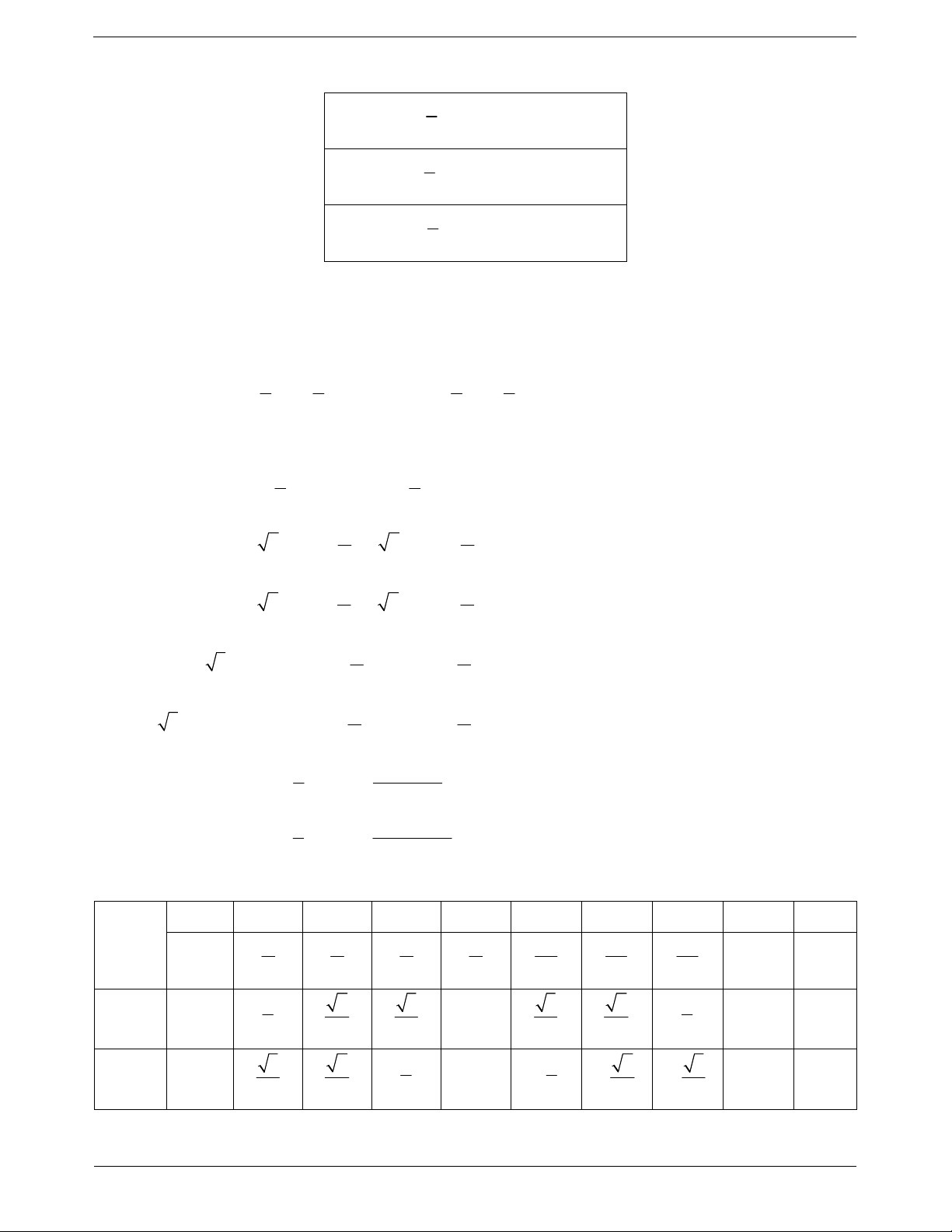
BẢNG GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT 0 30 45 60 90 120 135 150 180 360      2 3 5 0  2 6 4 3 2 3 4 6 1 1 sin 3 3 2 0 2 1 0 0 2 2 2 2 2 2 1 1 cos 3 2 3 1 0  2   1  1 2 2 2 2 2 2 TOANMATH.com Trang 3 tan 3 3 0 1 3 ||  3 1   0 0 3 3 || cot 3 3 || 3 1 0  1   3 || 3 3
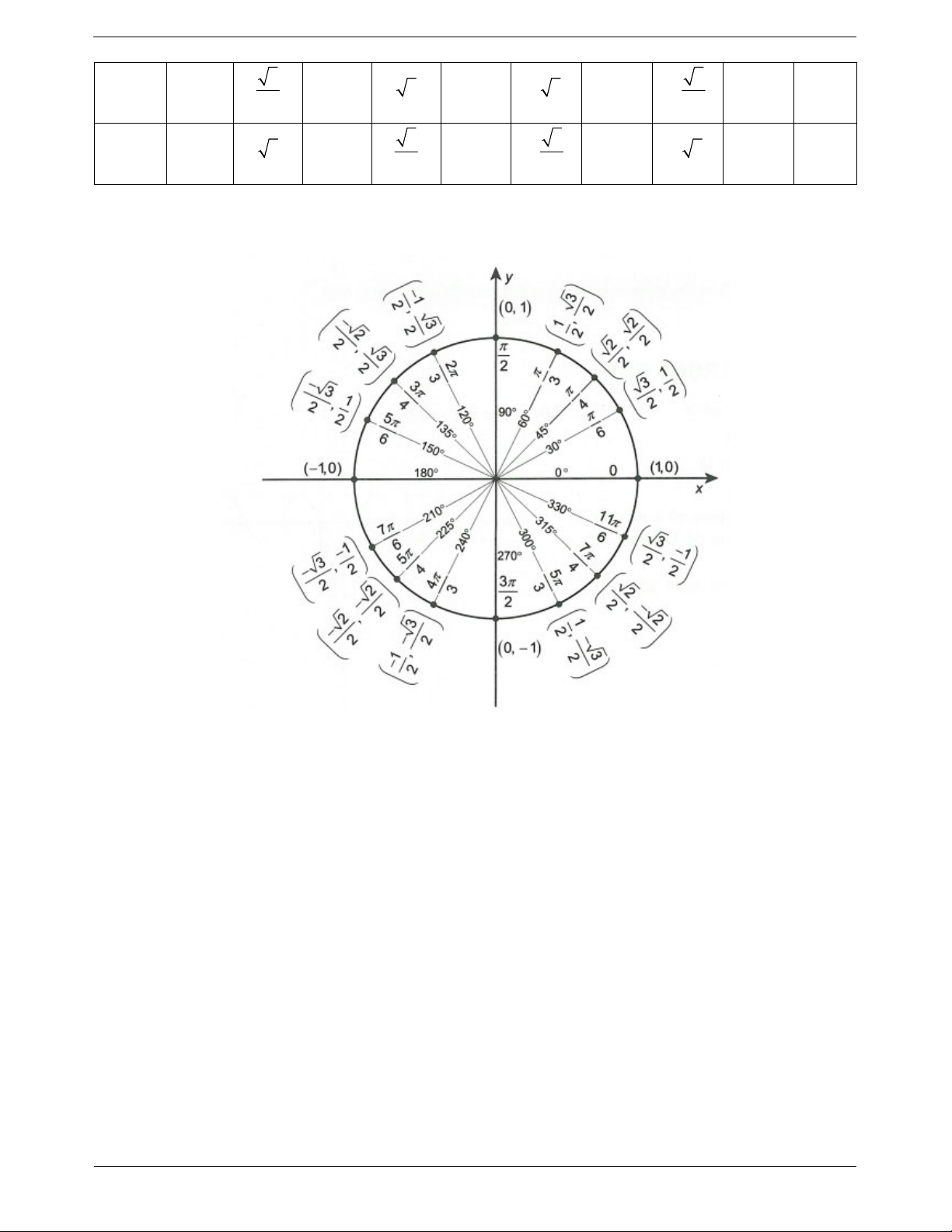
Một điểm M thuộc đường tròn lượng giác sẽ có tọa độ M cos;sin 
HÀM SỐ LƯỢNG GIÁC Mục tiêu
1. Nêu rõ tính chất 4 hàm lượng giác cơ bản sin x,cos x, tan x,cot x .
2. Phân biệt được tập xác định, tập giá trị, tính tuần hoàn và đồ thị của các hàm lượng giác.  Kiến thức
+ Tìm được tập xác định của hàm lượng giác.
+ Xác định được chu kì của các hàm lượng giác.
+ Vẽ được đồ thị của các hàm lượng giác.
+ Biết xác định giá trị lớn nhất, giá trị nhỏ nhất của một hàm lượng giác. TOANMATH.com Trang 4
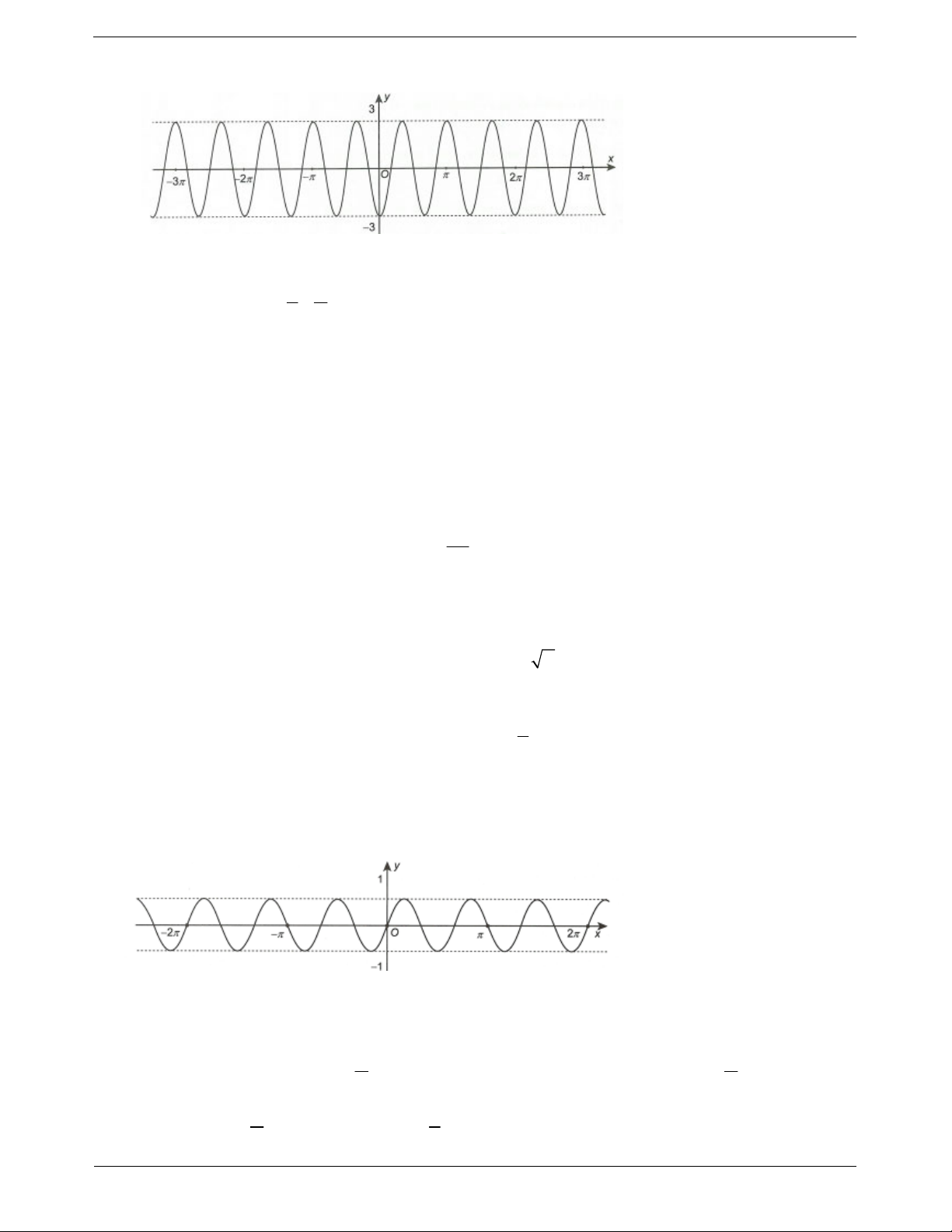
I. LÍ THUYẾT TRỌNG TÂM Hàm số y = sinx
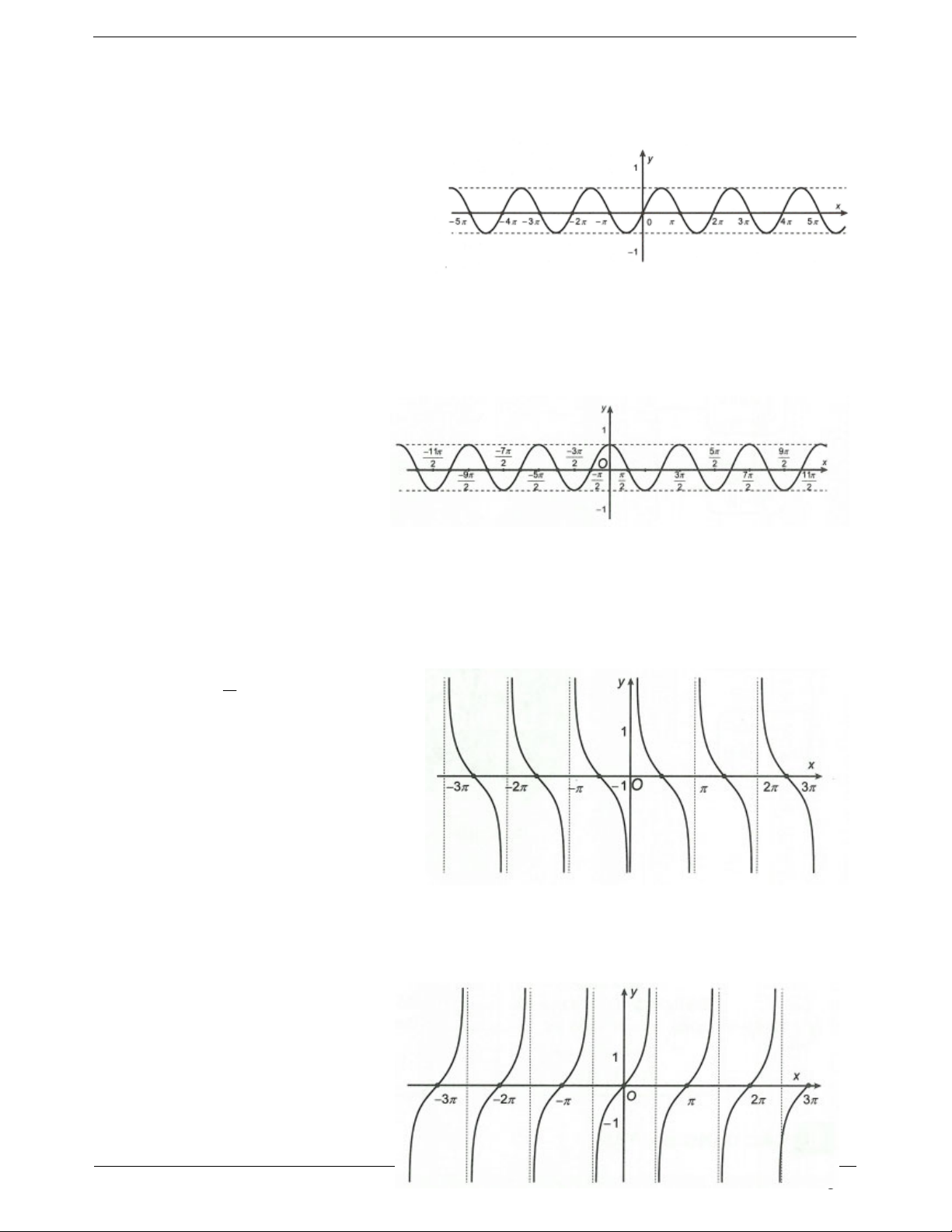
Đồ thị hàm số y  sin x
 Tập xác định D   .
 Tập giá trị 1,  1 , tức là 1
  sin x 1, x   .
 Hàm số y  sin x là hàm số lẻ nên đồ
thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
 Hàm số y  sin x là hàm số tuần hoàn với chu kì T  2 . Hàm số y = cosx
Đồ thị hàm số y  cos x
 Tập xác định D   .  Tập giá trị  1,   1 , tức là 1
  cos x  1, x    .  Hàm số cos y x là hàm số
chẵn nên đồ thị hàm số nhận trục Oy làm trục đối xứng.  Hàm số cos y
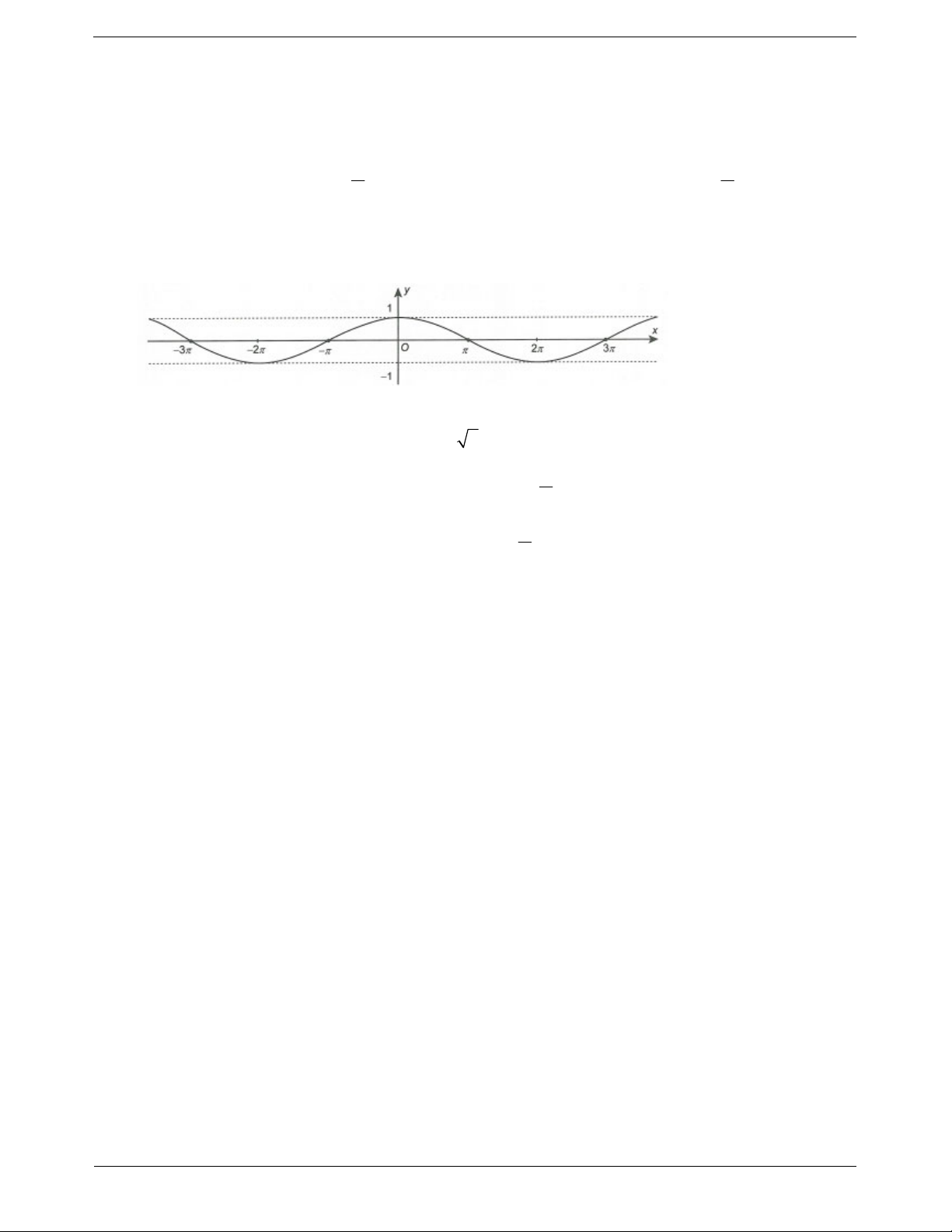
x là hàm số tuần hoàn với chu kì T  2 . Hàm số y = tanx
Đồ thị hàm số y  tan x  Tập xác định  
D   \   k ,k  .  2 
 Tập giá trị R.  Hàm số ta
y  n x là hàm số lẻ nên
đồ thị hàm số nhận gốc tọa độ O
làm tâm đối xứng.  Hàm số ta
y  n x là hàm số tuần
hoàn với chu kì T   . Hàm số y = cotx
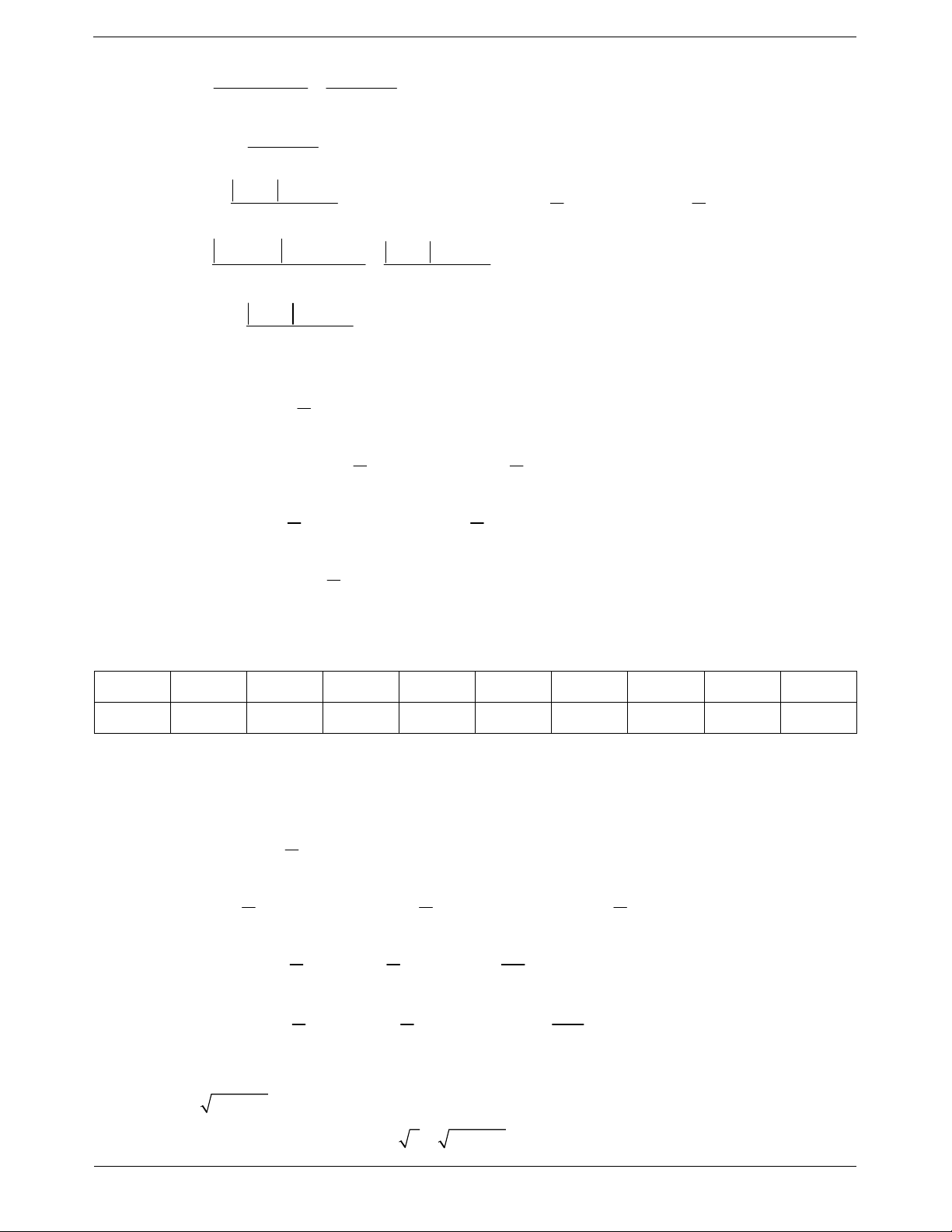
Đồ thị hàm số y  cot x  Tập xác định
D   \k ,k    .
 Tập giá trị . TOANMATH.com Trang 5
 Hàm số y  cot x là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.  Hàm số co y
t x là hàm số tuần hoàn với chu kì T   y  ax b 2 sin  T a y  sin x D    y  ax b 2 cos  T y  cos x Chu kì a Tập xác D   định y  tan x HÀM S Ố
y  tan ax b  T a   
D   \   kLƯỢNG GIÁC   2  Tính
y  cot ax b  T y  cot x a chẵn lẻ
D   \ k y  sin x Hàm chẵn Hàm lẻ
Đồ thị nhận Oy làm trục đối
Đồ thị nhận gốc tọa độ làm y  cos x cứng. Hàm số chẵn khi
tâm đối xứng. Hàm số lẻ khi y  tan x
xDxD
xDxD
f x  f x
f x   f xy  cot x TOANMATH.com Trang 6
II. CÁC DẠNG BÀI TẬP
Dạng 1: Tìm tập xác định của hàm lượng giác Phương pháp giải
Tập xác định của các hàm phân thức, căn thức
Ví dụ 1: Tìm tập xác định của hàm số 1. Hàm số phân thức
y  2  3 cos x . P xDKXD y    . Hướng dẫn giải Q xQ x 0 Vì 1
  cos x  1, x    nên
2. Hàm số chứa căn thức
 3  cos x  3, x    2    DKXD n y
P x  P x  0 .
 2  3cos x  0, x    .
3. Hàm số chứa căn thức dưới mẫu số
Vậy tập xác định của hàm số là D   . P xDKXD y
Qx  0 .
Ví dụ 2: Tìm tập xác định của hàm số 2n Q x  1  y  sin
Tập xác định của một số hàm lượng giác cơ bản  2   x  4 
1. y  sin u x 
 xác định  u x xác định. Hướng dẫn giải
2. y  cos u x  1  
 xác định  u x xác định. Hàm số y  sin  xác định 2   x  4  
3. y  tan u x 
 xác định  u x   k ,k  . 2  x  4  0 2  x  2 .
4. y  cot u x 
 xác định  u x  k , k  .
Vậy tập xác định của hàm số là D   \   2 . Ví dụ mẫu
Ví dụ. Tìm tập xác định của hàm số y  cot 2018x   1 . Hướng dẫn giải k 1
Hàm số y  cot 2018x  
1 xác định  2018x 1  k  x  , k  . 2018 k 1 
Vậy tập xác định của hàm số D   \  , k  .  2018 
Bài tập tự luyện dạng 1 1
Câu 1: Tập xác định của hàm số y  sin  2x là x
A. D   \ k . B. D  1;  1 \  
0 . C. D   . D. D   \   0 .
Câu 2: Tập xác định của hàm số 2c y
ot x  sin 3x là  
A. D   \   k  . B. D   \k . C. D   . D. D   \k2.  2  TOANMATH.com Trang 7
Câu 3: Tập xác định của hàm số y  cos x là
A. D  0;2  . B. D  0; . C. D   . D. D   \  0 . cos x
Câu 4: Tập xác định của hàm số y  là 2sin x 1     
A. D   \   k2 . B. D   \ k  .  6   2     5 
C. D   \   k  . D. D   \   k2;  k2  .  6   6 6  cos x
Câu 5: Tập xác định của hàm số y  là 2cos x  3      
A. D   \   k2  . B. D   \ k  .  3   2      5 
C. D   \   k2  . D. D   \   k2;  k2  .  6   6 6  cot x
Câu 6: Tập xác định của hàm số y  là sin x 1     
A. D   \   k2 . B. D   \ k  .  2   2      
C. D   \   k2;k  . D. D   \   k .  2   2 2 
Câu 7: Tập xác định của hàm số 2017 y  2016 tan 2x là     
A. D   \   k  . B. D   \ k  .  2   2    
C. D   .
D. D   \   k .  4 2 
Câu 8: Tập xác định của hàm số y  3tan x  2cot x x là        
A. D   \   k  . B. D   \ k  . C. D   . D. D   \   k .  2   2   4 2  sinx
Câu 9: Tập xác định của hàm số y  là tan x 1     
A. D   \   k  . B. D   \ k  .  4   4      
C. D   \   k;  k  . D. D   \   k2 .  4 2   4  2017 tan 2x
Câu 10: Tập xác định của hàm số y  là 2 2 sin  cos x     
A. D   \   k  . B. D   \ k  .  2   2  TOANMATH.com Trang 8   
C. D   .
D. D   \   k .  4 2  tan x
Câu 11: Tập xác định của hàm số y  là sin x 1     
A. D   \   k2 . B. D   \ k  .  2   2      
C. D   \   k  . D. D   \   k .  2   4 2  sin x
Câu 12: Tập xác định của hàm số y  là sin x  cos x      
A. D   \   k  . B. D   \ k  .  4   4      
C. D   \   k;  k  . D. D   \   k2 .  4 2   4 
Câu 13: Tập xác định của hàm số y  sin 2x 1 là
A. D   \ k .
B. D   .     
C. D   \   k;  k  . D. D   \   k2 .  4 2   2 
Câu 14: Tập xác định của hàm số y  1 cos 2017x là
A. D   \ k .
B. D   .     
C. D   \   k;  k  . D. D   \   k2 .  4 2   2  1
Câu 15: Tập xác định của hàm số y  là 1 sin 2x
A. D   \ k .
B. D   .     
C. D   \   k;  k  . D. D   \   k  .  4 2   4  1
Câu 16: Tập xác định của hàm số y  là 2  cos 6x
A. D   \ k .
B. D   .     
C. D   \   k;  k  . D. D   \   k  .  4 2   4  tan x
Câu 17: Tập xác định của hàm số y  là 15 14cos13x    
A. D   \ k .
B. D   .
C. D   \   k  . D. D   \   k  .  2   4  TOANMATH.com Trang 9 2  sin x
Câu 18: Tập xác định của hàm số y  là 1 cos x     
A. D   \ k . B. D   \k2 . C. D   \   k  . D. D   \ k  .  2   2 
Câu 19: Để tìm tập xác định của hàm số ta
y  n x  cos x , một học sinh giải theo các bước sau
Bước 1. Điều kiện để hàm số có nghĩa làsin x  0 cos x  0 .   
Bước 2. x   k  k; 2 m   . x m  
Bước 3. Vậy tập xác định của hàm số đã cho là D   \   k ,m k;m .  2 
Bài giải của bạn đó đã đúng chưa? Nếu sai, thì sai bắt đầu từ bước nào?
A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Câu 20: Hàm số nào sau đây có tập xác định là  ?
A. y  sin x . B. y  tan 2x . C.
y  cot 2x . D. y x  sinx .
Dạng 2: Tính chẵn – lẻ của hàm số lượng giác Phương pháp giải
1. Hàm số y f x với tập xác định D gọi là hàm số chẵn Ví dụ: Xét tính chẵn - lẻ của hàm số       y sin 2x . nếu  x D x D
f x  f x . Hướng dẫn giải
2. Hàm số y f x với tập xác định D gọi là hàm số lẻ nếu Hàm số si
y  n 2x có tập xác định D   .
xDxD
Đặt f x  y  sin 2x .
f x   f x .      Ta có  x D x D Chú ý:
f x  sin  2
x   f x
+ Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng. Suy ra hàm số si
y  n 2x là hàm số lẻ.
+ Đồ thị hàm số lẻ nhận gốc tọa độ O 0;0 làm tâm đối Đồ thị hàm số nhận gốc tọa độ xứng.
O 0;0 làm tâm đối xứng. Ví dụ mẫu
Ví dụ 1. Xét tính chẵn - lẻ của hàm số y f x  tan x  cot . x Hướng dẫn giải   
Hàm số có nghĩa khi cos x  0 x   k sinx  0   2 ( với , k l   ). x l  
Tập xác định D   \   k ,l | k,l  là tập đối xứng.  2  TOANMATH.com Trang 10 Do đó x
  D thì x D .
Ta có f x  tan x  cot x   tan x  cot x  tan x  cot x   f x.
Vậy f x là hàm số lẻ. Đồ thị hàm số nhận gốc tọa độ làm tâm đối xứng.
Ví dụ 2. Xét tính chẵn – lẻ của hàm số 2
y  sin x  4 . Hướng dẫn giải Hàm số có nghĩa khi 2
x  4  0  x  ;  2  ][2;.
Tập xác định D   ;  2
 ][2; là tập đối xứng. Do đó x
  D thì x D
Ta có f x  x2 2 sin
 4  sin x  4  f x.
Vậy f x là hàm số chẵn. Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Ví dụ 3. Xét tính chẵn – lẻ của hàm số 2018 y  sin
2x  cos 2019x . Hướng dẫn giải
Tập xác định D   là tập đối xứng. Do đó x
  D thì x D .
Ta có f  x 2018   x   x 2018 sin 2 cos 2019  sin
2x  cos 2019x f x.
Vậy f x là hàm số chẵn. Đồ thị hàm số nhận trục Oy làm trục đối xứng.   
Ví dụ 4. Xét tính chẵn – lẻ của hàm số y f x 2017  sin 5x  .    2  Hướng dẫn giải
Tập xác định D   là tập đối xứng. Do đó x
  D thì x  . D         
Ta có f x 2017  sin 5x
 sin 5x  1008  sin 5x   cos5 . x        2   2   2 
Lại có f x  cos 5
x  cos5x f x.
Vậy f x là hàm số chẵn. Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Ví dụ 5. Xét tính chẵn – lẻ của hàm số
y f x 3
 sin 4x  9   cot 11x  2018 . Hướng dẫn giải
Ta có y f x 3 
x      x    3 sin 4 9 cot 11 2018
 sin 4x  cot11x . k
Hàm số có nghĩa khi sin11x  0  11x k  x  , k  . 11 TOANMATH.com Trang 11 k 
Tập xác định D   \ 
, k  là tập đối xứng.  11  Do đó x
  D thì x D .
Lại có f x 3  
 x   x 3 sin 4
cot 11  sin 4x  cot11x   3
sin 4x  cot11x   f x .
Vậy f x là hàm số lẻ. Đồ thị hàm số nhận gốc tọa độ O0;0 làm tâm đối xứng.
Bài tập tự luyện dạng 2 Câu 1: Hàm số si y  n . x cos x là
A. hàm số không lẻ. B. hàm số chẵn.
C. hàm số không chẵn. D. hàm số lẻ.
Câu 2: Hàm số y  sin x  tan 2x là
A. hàm số lẻ.
B. hàm số chẵn.
C. hàm số vừa chẵn, vừa lẻ. D. hàm số không chẵn, không lẻ. Câu 3: Hàm số si
y  n x  cos x là
A. hàm số lẻ.
B. hàm số chẵn.
C. hàm số vừa chẵn, vừa lẻ. D. hàm số không chẵn, không lẻ.
Câu 4: Hàm số y  2x  sin 3x là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số không chẵn, không lẻ.
C. hàm số chẵn. D. hàm số lẻ. Câu 5: Hàm số 2
y  1 2x  cos3x là
A. hàm số lẻ.
B. hàm số chẵn.
C. hàm số không chẵn, không lẻ. D. hàm số vừa chẵn, vừa lẻ.
Câu 6: Hàm số nào là hàm số lẻ trong các hàm số sau? cot x
A. y  sin x . B. y  . cos x tan x C. 2
y  sin x . D. y  . sin x
Câu 7: Hàm số y x cos 2x là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số không chẵn, không lẻ.
C. hàm số chẵn. D. hàm số lẻ.
Câu 8: Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số y  sin .
x cos 3x là hàm số lẻ.
B. Hàm số y  cos x  2 sin x là hàm số chẵn.
C. Hàm số y   2
3 cot x  cos x là hàm số lẻ.
D. Cả 3 mệnh đề trên đều sai. TOANMATH.com Trang 12
2sin x  4 tan x
Câu 9: Hàm số y  là 5  cos x
A. hàm số vừa chẵn, vừa lẻ. B. hàm số chẵn.
C. hàm số lẻ.
D. hàm số không chẵn, không lẻ.
Câu 10: Xét hai mệnh đề
(I) Hàm số y  tan x  cos x là hàm số lẻ.
(II) Hàm số y  tan x  sin x là hàm số lẻ. Mệnh đề nào sai?
A. Chỉ (I) sai. B. Chỉ (II) sai. C. Cả 2 sai. D. Không có mệnh đề sai. Câu 11: Hàm số 2
y  sin x cos x  tan x là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số chẵn.
C. hàm số không chẵn, không lẻ. D. hàm số lẻ. Câu 12. Hàm số 2
y x tan 2x  cot x là
A. hàm số không chẵn – lẻ. B. hàm số chẵn.
C. hàm số không lẻ. D. hàm số lẻ.  5 
Câu 13. Hàm số y  2  sin x cos  2x   là  2 
A. hàm số vừa chẵn, vừa lẻ.
B. hàm số không chẵn, không lẻ. C. hàm số chẵn. D. hàm số lẻ.
Câu 14. Cho hàm số f x  sin 2x và g x 2
 tan x . Chọn mệnh đề đúng trong các mệnh đề sau:
A. f x là hàm số chẵn, g x là hàm số lẻ. B. f x là hàm số lẻ, g x là hàm số chẵn.
C. f x là hàm số chẵn, g x là hàm số chẵn. D. f x và g x đều là hàm số lẻ. x sin 2x
Câu 15. Hàm số y  là 3 cos 2x A. hàm số lẻ. B. hàm số chẵn.
C. hàm số vừa chẵn, vừa lẻ.
D. hàm số không chẵn, không lẻ.
Câu 16. Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2
y  1 sin x . B. 2
y  cot x .sin x . C. 2
y x tan 2x  cot x .
D. y  1 cot x  tan x . Câu 17. Hàm số tan y
x  2cos3x là A. hàm số lẻ. B. hàm số chẵn.
C. hàm số vừa chẵn, vừa lẻ.
D. hàm số không chẵn, không lẻ.  3 
Câu 18. Hàm số y  1 cos x sin  3x   là  2 
A. hàm số vừa chẵn, vừa lẻ. B. hàm số chẵn. TOANMATH.com Trang 13
C. hàm số không chẵn, không lẻ. D. hàm số lẻ. cos 2x sin 2x  cos3x
Câu 19. Cho hai hàm số f x 
và g x  . 2 1 sin 3x 2 2  tan x
Mệnh đề nào sau đây đúng?
A. f x lẻ và g x chẵn.
B. f x và g x chẵn.
C. f x chẵn và g x lẻ.
D. f x và g x lẻ.
Câu 20. Trong các hàm số sau, hàm số nào là hàm số lẻ?       A. 4
y x  cos x    . B. 2017 y x  cos x    .  3   2  C. 2018
y  2015  cos x  sin x . D. 2017 2018 y  tan x  sin x .
Dạng 3. Tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác Phương pháp giải
Sử dụng một số bất đẳng thức sau
Ví dụ: Tìm giá trị lớn nhất, giá trị nhỏ nhất của
1. Bất đẳng thức lượng giác    
hàm số y  3cos x  2 trên đoạn  ;   . 1   sin ;
x cos x  1, x    .  2 2 
A B Asin x B A B, x    . Hướng dẫn giải
A B Acos x B A B, x    .     Xét hàm số 3c y
os x  2 trên đoạn  ;  . 2 2   
2. Bất đẳng thức về điều kiện có nghiệm hàm số bậc     nhất. Khi x   ; 
thì 0  cos x  1 . 2 2    2 2 2 2
A B Asin x B cos x A B , x    .
Suy ra 2  3cos x  2  5  2  y  5 .
3. Bất đẳng thức Bunhiacopxki. 
Vậy min y  2 khi x   ; max y  5 khi x  0 . 2 2 2 2
ax by a b . x y . 2
Dấu "  " xảy ra khi và chỉ khi ay bx .
4. Sử dụng phương pháp đồ thị lượng giác. Ví dụ mẫu
Ví dụ 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 6 6
y  sin x  cos x . Hướng dẫn giải 3 Ta có 6 6 2
y  sin x  cos x  1 sin 2x . 4 3 3 3 Do 2
0  sin 2x  1 nên 2
 .0   sin 2x   4 4 4 3 3 1 2
1  1 sin 2x  1  1  y  . 4 4 4 1  k Vậy 2
min y  khi sin 2x  1  cos 2x  0  x   , k   . 4 4 2 TOANMATH.com Trang 14 k 2
max y  1 khi sin 2x  0  sin 2x  0  x  , k   . 2
Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số    2 
y  tan x  tan x  2020 trên đoạn  ;  . 4 4    Hướng dẫn giải 2  1  8079 Ta có 2
y  tan x  tan x  2020  tan x     .  2  4    
Chú ý: Hàm số tan x
Hàm số tan x đồng biến và xác định trên khoảng  ;    2 2 
luôn đồng biến trên
           
các khoảng xác định Mà  ;   ;   
 nên hàm số tan x đồng biến và xác định trên  ; .  4 4   2 2   4 4    của nó.     Do đó tan   tan x  tan  1   tan x 1    4  4 2 1 1 1 3 1 1  1  9  1
   tan x   1    tan x    0  tan x     2 2 2 2 2 2  2  4 2 8079  1  8079 9 8079 8079   tan x       y  2022   . 4  2  4 4 4 4 8079 1 1 Vậy min y
khi tan x   x  arctan ; 4 2 2 
max y  2022 khi tan x  1
  x    k ,k  4
Bài tập tự luyện dạng 3   
Câu 1. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  7  2cos x    lần lượt là  4  A. -2 và 7. B. -2 và 2. C. 5 và 9. D. 4 và 7.
Câu 2. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  4 sin x  3 1 lần lượt là A. 2 và 2. B. 2 và 4. C. 4 2 và 8. D. 4 2 1 và 7.
Câu 3. Giá trị nhỏ nhất của hàm số 2
y  sin x  4sin x  5 là A. -20. B. -8. C. 0. D. 9.
Câu 4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2sin x  3 là
A. max y  5, min y  1. B. max y  5, min y  2 5 .
C. max y  5, min y  2 . D. max y  5, min y  3 . 4
Câu 5. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  là 2 1 2sin x TOANMATH.com Trang 15 4 4
A. min y  , max y  4 .
B. min y  , max y  3. 3 3 4 1
C. min y  , max y  2 .
D. min y  , max y  4 . 3 2
Câu 6. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2
y  2sin x  cos 2x là 3
A. max y  4, min y  .
B. max y  3, min y  2 . 4 3
C. max y  4, min y  2 .
D. max y  3, min y  . 4
Câu 7. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3s y
in x  4cos x 1 là
A. max y  6, min y  2  .
B. max y  4, min y  4  .
C. max y  6, min y  4  .
D. max y  6, min y  1  .
Câu 8. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4s y
in 6x  3cos 6x là A. min y  5  ,max y  5 . B. min y  4  , max y  4 . C. min y  3  ,max y  5 . D. min y  6  , max y  6.    
Câu 9. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số sin y  2x trên  ;  lần lượt là 6 3    1 3 3 3 3 1 1 1 A. và . B. và  . C. và  . D. và  . 2 2 2 2 2 2 2 2    
Câu 10. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3 tan x trên  ;  lần lượt là 3 4    3 3 A. 3 và  . B. 3 và
. C. 3 và -3. D. 3 và -1. 3 3  2 
Câu 11. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  4  3cos x trên 0;  lần lượt là 3    11 A. 1 và -1. B. 11 và 5. C. 3 và -3. D. và 1. 2       
Câu 12. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x  sin 2x    trên  ; lần lượt là  4   4 4    2 2 2 2 A. 1 và - 2 . B. 1 và . C. và -1. D. và  . 2 2 2 2
Câu 13. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y  sin x  2  sin x là
A. min y  0, max y  3 .
B. min y  0, max y  4 .
C. min y  0, max y  6 .
D. min y  0, max y  2 . cos x  2sin x
Câu 14. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  lần lượt là 2  sin x TOANMATH.com Trang 16 2   19 2   19 3 A. và . B. 3 và . 3 3 3  3  19  3  19
C. 3 và -3. D. và . 3 3
Câu 15. Giá trị của m để bất phương trình  x x2 3sin 4cos
 6sin x  8cos x  2m 1 nghiệm đúng với mọi x   là A. m  0. B. m  0 . C. m  0 . D. m  1.
Câu 16. Kết luận đúng về hàm số 2 2
y  tan x  cot x  3tan x  cot x 1là  A. min y  5
 đạt được khi x    k , k  . 4
B. Không tồn tại giá trị lớn nhất, giá trị nhỏ nhất của hàm số. C. min y  2  và max y  5 .
D. Tồn tại giá trị lớn nhất nhưng không tồn tại giá trị nhỏ nhất.
Câu 17. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 4
y  cos x  sin x trên  lần lượt là 1 A. 2 và 0. B. 1 và . C. 2 và 0. D. 2 và 1. 2
3sin 2x  cos 2x
Câu 18 . Giá trị của m để bất phương trình  m 1là 2
sin 2x  4cos x 1 3 5 3 5  9 3 5  9 3 5  9 A. m  . B. m  . C. m  . D. m  . 4 4 2 4 2 cos x  sin . x cos x
Câu 19. Giá trị nhỏ nhất và lớn nhất của hàm số y  lần lượt là 2 1 sin x 2 2  6 2  6 A. 0 và 3. B. 2 và 4. C.  và 6. D. và . 3 4 4 Câu 20. Cho 2 2 2
cos x  cos y  cos z  1. Giá trị lớn nhất của 2 2 2
y  1 cos x  1 cos y  1 cos z là A. 3 3 . B. 2 3 . C. 4 3 . D. 3 .
Dạng 4. Tính tuần hoàn và chu kỳ hàm lượng giác Phương pháp giải
Một số vấn đề cần chú ý
1. Tính tuần hoàn của hàm số
Ví dụ: Tìm chu kì của hàm số
Định nghĩa: Hàm số y f x xác định trên tập D  2x   y  sin    .  3 4 
được gọi là hàm số tuần hoàn nếu có số T  0 sao cho Hướng dẫn giải
với mọi x  0 ta có
Tập xác định D   .
x T D và f x T   f x . TOANMATH.com Trang 17
Số dương T nhỏ nhất thỏa mãn các điều kiện trên thì 2
Chu kì của hàm số T   3 .
hàm số đó được gọi là hàm số tuần hoàn với chu kỳ T. 2 3
y msin ax b 2 2. Các hàm số   y m cos có chu kỳ T ;  ax ba
biên độ m ;cực đại m ;cực tiểu - m ,
3. Hàm số f x  a sin ux b cos vx c (với ,
u v   ) là hàm số tuần hoàn với chu kì 2 T   ((u,v) là ƯCLN (u,v)). u, v
4. Hàm số f x  .t
a an ux b cos vx c
(với u,v  ) hàm số tuần hoàn với chu kì 2 T   ((u,v) là ƯCLN (u,v)). u, vVí dụ mẫu
Ví dụ 1. Tìm chu kì cơ sở của hàm số y  2sin 2x  3cos3x . Hướng dẫn giải
Tập xác định D   . 2
Chu kì hàm số T     2 . 2,3
Ví dụ 2. Xét tính tuần hoàn và tìm chu kì của hàm số
f x  cos x  cos 3x . Hướng dẫn giải
Giả sử hàm số đã cho tuần hoàn. Suy ra tồn tại số thực dương T thỏa mãn
f x T   f x  cos x T   cos  3  x T   cos x  cos    3x. cosT  1
Chọn x  0 ta được cosT  cos  3T   2  cos   3T 1 T nm m   2  3  là số hữu tỉ). 3T  (vô lí do , m n   nên 2mn n
Vậy hàm số đã cho không tuần hoàn.
Bài tập tự luyện dạng 4 x  
Câu 1. Chu kì của hàm số y  sin    là  3 6  1  2 A. . B. . C. . D. 6 . 2 3 3 TOANMATH.com Trang 18
Câu 2. Đồ thị trong hình vẽ dưới đây là của hàm số nào?
A. y  cos3x .
B. y  3cos3x . C. y  3c  os 6x . D. y  3c  os3x .  x  
Câu 3. Hàm số y  2sin  
 là hàm số tuần hoàn với chu kì  2 3 
A. T  6 . B. T  4 . C. T  6 . D. T  2 .
Câu 4. Khẳng định nào sau đây sai về hàm số y  2  sin x ?
A. Đồ thị hàm số không đi qua gốc tọa độ.
B. Đồ thị hàm số nằm ở phía trên trục hoành.
C. Giá trị cực đại của y là 2.
D. Giá trị cực tiểu của y là 1.  x
Câu 5. Nếu chu kì tuần hoàn của hàm số y  sin là 4 thì a A. a  2  . B. a  4  . C. a  2 . D. a  1  . Câu 6. Hàm số 2
y  tan x tuần hoàn với chu kì A. 2 T   . B. T   . C. T   .
D. Hàm số không có chu kì. x
Câu 7. Khẳng định nào sau đây đúng với hàm số y  2cos ? 2
A. Biên độ là 2, chu kì là  .
B. Biên độ là -2, chu kì là 180 .
C. Biên độ là 2, chu kì là 2 .
D. Biên độ là 2, chu kì là 4 .
Câu 8. Đồ thị trong hình vẽ dưới đây là của hàm số nào?
A. y  sin 2x .
B. y  sin 3x .
C. y  cos 2x .
D. y  cos3x .
Câu 9. Chu kì của hàm số sau y  sin 3x  2cos 2x là  
A. T  2 . B. T  . C. T   . D. T  . 0 0 2 0 0 4  x
Câu 10. Với 0  x
thì hàm số f x  sin có giá trị cực đại là 2 3 TOANMATH.com Trang 19 1 1 A. 0. B. 1. C. . D. . 3 2   
Câu 11. Hàm số y  3cos  mx
 tuần hoàn có chu kì T  3 khi  4  3 2 A. m   . B. m  1. C. m   . D. m  2  . 2 3
Câu 12. Xét đồ thị hàm số y  sin x với x  , 2  . Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có một cực đại tại x   .
B. Đồ thị hàm số có một cực tiểu tại x  2 . 3
C. Đồ thị hàm số có một cực tiểu tại x  . 2
D. Hàm số đồng biến trên  ,2 .
Câu 13. Đồ thị trong hình vẽ dưới đây là của hàm số nào? x
A. y  sin 2x .
B. y  cos 2x . C. y  cos . D. cos y  3x . 2
Câu 14. Chu kì của hàm số y  sin 2x  sin x là  
A. T  2 . B. T  . C. T   . D. T  . 0 2 0 0 4
Câu 15. Chọn mệnh đề đúng trong các mệnh đề sau    A. Hàm số co y
t x đồng biến trên khoảng ;   .  2     B. Hàm số si
y  n x nghịch biến trên khoảng ;   .  2         
C. Hàm số y  tan x đồng biến trên  ; 
 và y  cot x nghịch biến trên khoảng  ;   .  2 2   2 2    
D. Hàm số y  sin x và y  cos x cùng đồng biến trên khoảng 0;   .  2 
Câu 16. Chu kì của hàm số y  tan x  tan 3x là  
A. T  2 . B. T   . C. T  . D. T  . 4 2  x
Câu 17. Khẳng định nào sau đây đúng về hàm số y  2sin  2017   ?  2  TOANMATH.com Trang 20
A. Chu kì 2 , biên độ 2.
B. Chu kì 4 , biên độ 2.
C. Chu kì 2 , biên độ 1.
D. Chu kì 4 , biên độ 1.
Câu 18. Chu kì của hàm số y  sin 3x  2017 cos 2x là   A. T   . B. T  . C. T  2 . D. T  . 2 4
Câu 19. Hình vẽ sau là đồ thị của hàm số y  sin ax b . Biết a  0 và b nhỏ nhất, giá trị của biểu
thức P a b là A. 0. B. 1. C. 2. D. 3.
Câu 20. Chu kì cơ sở (nếu có) của hàm số y  sin x là 
A. hàm số không có chu kì cơ sở. B. T  . 0 2  C. T   . D. T  . 0 0 4 TOANMATH.com Trang 21 ĐÁP ÁN
Dạng 1: Tìm tập xác định hàm số lượng giác 1 – D 2 – B 3 – B 4 – D 5 – C 6 – C 7 – D 8 – B 9 – C 10 – D
11 – C 12 – A 13 – B
14 – B 15 – D 16 – B 17 – C 18 – B 19 – A 20 – D
Hướng dẫn giải chi tiết Câu 1. 1
Hàm số y  sin  2x có nghĩa  x  0  D   \   0 . x Câu 2. Hàm số 2c y
ot x  sin 3x có nghĩa  x k  D   \kk  . Câu 3:
Hàm số y  cos x có nghĩa  x  0  D  0; . Câu 4.   cos x x   k2 1   Hàm số y  có nghĩa 6
 2sin x 1  0  sin x    k  . 2sin x 1 5 2  x   k2  6  5 
D   \   k2;
k2 k  .  6 6  Câu 5.   cos x x   k2 3   Hàm số y
có nghĩa  2 cos x  3  0  cos x   6  k  . 2 cos x  3 2 
x    k2  6   
D   \   k2 k  .  6  Câu 6. cot x Hàm số y  có nghĩa sinx10   x k   sinx 1 sin x 1 x k  
x   k2     
k    D   \   k2;k k  2 .    2 x k  Câu 7:    Hàm số 2017 y  2016 tan
2x có nghĩa  cos 2x  0  2x
k  x   k k  2 4 2   
D   \   k k .  4 2  TOANMATH.com Trang 22 Câu 8:   
Hàm số y  3tan x  2cot x x có nghĩa
cos x  0  x   k   2
sin x  0  x k    
x k k   D   \ k k  . 2  2  sin x tan x  1 
Câu 9: Hàm số y
có nghĩa  tan x 1  0    tan x 1 x   k  2   x   k  4      
k    D   \   k;  k k   .   4 2 x   k   2 Câu 10: 2 2 2017 tan 2x sin 
x  cos x  0 cos 2x  0   Hàm số y  có nghĩa        k  2 2 sin x  cos x 2x   kx   k  2  4 2       x   k
D   \   k k  . 4 2  4 2  Câu 11:   tan x
sin x 1  0  sin x  1  x   k2   Hàm số y  có nghĩa 2  
x   k k  sin x 1  2
x   k  2  
D   \   k k  .  2  Câu 12: sin x    Hàm số y
có nghĩa  sin x  cos x  0  2 sin x   0   sin x  cos x  4         x
k k   D   \ 
k k  . 4  4  Câu 13:
Hàm số y  sin 2x 1 có nghĩa  sin 2x 1  0  sin 2x  1   x
    D   . Câu 14:
Hàm số y  1 cos 2017x có nghĩa  1 cos 2017x  0  cos 2017x  1  x
    D   . Câu 15: 1 Hàm số y
có nghĩa  1 sin 2x  0  sin 2x  1  sin 2x  1 1 sin 2x    
 2x   k2  x   k k   D   \   k k  . 2 4  4  TOANMATH.com Trang 23 Câu 16: 1 Hàm số y
có nghĩa  2  cos 6x  0  cos 6x  2  x
    D   2  cos 6x Câu 17:  15 tan x 15  14cos13x  0 cos13x    Hàm số y  có nghĩa    14   15 14 cos13x x   k   2
x   k  2   
x   k k   D   \   k k  2  2  Câu 18: 2  sin x Hàm số y
có nghĩa  1 cos x  0  x k2 k   D   \k2k  . 1 cos x Câu 19:   
x   k k 
Hàm số y  tan x  cot x có nghĩa  cos 0  
k   D   \    sin x  0 2 k     2 x k 
Vậy bạn học sinh đó giải đúng. Câu 20:
Hàm số y  sin x có nghĩa  x  0  D  0; .   k  k
Hàm số y  tan 2x có nghĩa cos 2x 0 2x k         x    D   \    . 2 4 2  4 2  kk Hàm số co y  t 2x có nghĩa sin 2x 0 2x k        x
D   \  . 2  2 
Hàm số y x  sin x có D   .
Dạng 2: Tính chẵn – lẻ của hàm số lượng giác 1 – D 2 – A 3 – D 4 – D 5 – B 6 – B 7 - C 8 - A 9 – C 10 – A 11 – D 12 – D 13 – C 14 – B 15 – A 16 – C 17 – D 18 – B 19 – B 20 – B
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Hàm số y  sin .
x cos x có nghĩa x
    D   .
Ta có f x  sin x.cosx  sin .
x cos x   f x . Vậy hàm số sin y  .
x cos x là hàm số lẻ. Câu 2:   k  k
Hàm số y  sin x  tan 2x có nghĩa cos 2x 0 2x k         x    D   \    . 2 4 2  4 2 
Ta có f x  sin x  tan  2
x  sin x  tan 2x  sin x  tan 2x   f x . TOANMATH.com Trang 24
Vậy hàm số y  sin x  tan 2x là hàm số lẻ. Câu 3:
Hàm số y  sin x  cos x có nghĩa x
    D   .
f x f x
Ta có f x  sin x  cosx    
 sin x  cos x   f
 x   f x Vậy hàm số sin y
x  cos x là hàm số không chẵn, không lẻ. Câu 4:
Hàm số y  2x  sin 3x có nghĩa x
    D  
Ta có f x  2  x  sin  3  x  2
x  sin 3x  2x  sin 3x   f x .
Vậy hàm số y  2x  sin 3x là hàm số lẻ. Câu 5: Hàm số 2
y  1 2x  cos3x có nghĩa x
    D   .
Ta có f x   x2   x 2 1 2
cos 3  1 2x  cos3x  f x . Vậy hàm số 2
y  1 2x  cos3x là hàm số chẵn. Câu 6: cot x    x   x   kk k  Hàm số y  có nghĩa cos 0    x
D   \   . cos x 2 2      2 sin x 0 x k  cot x cot x
Ta có f x       f x . cosx   cos x cot x Vậy hàm số y  là hàm số lẻ. cos x Câu 7:
Hàm số y x cos 2x có nghĩa x
    D   .
Ta có f x  x cos 2
x  x cos 2x f x .
Vậy hàm số y x cos 2x là hàm số chẵn. Câu 8: Hàm số sin y  .
x cos 3x có nghĩa x
    D   .
Ta có f x  sin x.cos 3
x  sin .xcos3x   f x . Vậy hàm số si y  n .
x cos 3x là hàm số lẻ. Câu 9:
2sin x  4 tan x    Hàm số y
có nghĩa  cos x  0  x
k  D   \   k k . 5  cos x 2  2 
2sin x  4 tan x 2s
 in x  4 tan x
Ta có f x         f x . 5  cosx   5  cos x TOANMATH.com Trang 25
2sin x  4 tan x Vậy hàm số y  là hàm số lẻ. 5  cos x Câu 10:    + Hàm số ta
y  n x  cos x có nghĩa  cos x  0  x
k  D   \   k k . 2  2 
f x f x
Ta có f x  tan x  cosx    
  tan x  cos x   . f
 x   f x
Vậy hàm số y  tan x  cos x là hàm số không chẵn, không lẻ.   
+ Hàm số y  tan x  sin x có nghĩa  cos x  0  x
k  D   \   k k . 2  2 
Ta có f x  tan x  sin x   tan x  sin x   f x .
Vậy hàm số y  tan x  sin x là hàm số lẻ. Câu 11:    Hàm số 2
y  sin x cos x  tan x có nghĩa  cos x  0  x
k  D   \   k k . 2  2 
Ta có f x 
x 2 x x 2 sin cos tan
 sin x cos x  tan x   f x. Vậy hàm số 2
y  sin x cos x  tan x là hàm số lẻ. Câu 12: Hàm số 2
y x tan 2x  cot x có nghĩa     k
cos 2x  0  2x   k x    k       D   \   , 2 4 2
k k  .        4 2 sin x 0 x kx k 
Ta có f x  x2
 x  x 2 tan 2 cot
 x tan 2x  cot x   f x . Vậy hàm số 2
y x tan 2x  cot x là hàm số lẻ. Câu 13:  5 
Hàm số y  2  sin x cos  2x   có nghĩa x
    D   .  2       
Ta có f x   x 5 5 2 sin cos
 2x  2  sin x cos    2x      2   2   3   3   5   2  sin x cos 
 2x  2  sin x cos 
 2x  4  2  sin x cos  2x f       x .  2   2   2   5 
Vậy hàm số y  2  sin x cos  2x   là hàm số chẵn.  2  Câu 14:
+ Hàm số f x  sin 2x có nghĩa x
    D   .
Ta có f x  sin  2
x  sin 2x   f x. TOANMATH.com Trang 26
Vậy hàm số f x  sin 2x là hàm số lẻ.   
+ Hàm số g x 2
 tan x có nghĩa  cos x  0  x   k  D   \   k k . 2  2 
Ta có g x 2  x 2 tan
 tan x g x .
Vậy hàm số g x 2
 tan x là hàm số chẵn. Câu 15: x sin 2x   k  k Hàm số y  có nghĩa cos 2x 0 2x k         x    D   \   k  3 cos 2x 2 4 2  4 2  x sin 2  xx sin 2x
Ta có f x       f x . 3 cos  2  x 3   cos 2x x sin 2x Vậy hàm số y  là hàm số lẻ. 3 cos 2x Câu 16: Hàm số 2
y x tan 2x  cot x có nghĩa     k
cos 2x  0  2x   k x    k       D   \   , 2 4 2
k k  .        4 2 sin x 0 x kx k 
Ta có f x  x2
 x  x 2 tan 2 cot
 x tan 2x  cot x   f x . Vậy hàm số 2
y x tan 2x  cot x là hàm số lẻ. Câu 17:   
Hàm số y  tan x  2cos3x có nghĩa  cos x  0  x
k  D   \   k . 2  2 
f x f x
Ta có f x  tan x  2cos 3  x    
  tan x  2cos3x   . f
 x   f x
Vậy hàm số y  tan x  2cos3x là hàm số không chẵn, không lẻ. Câu 18:  3 
Hàm số y  1 cos x sin  3x   có nghĩa x
    D   .  2   3   3   3 
Ta có f x 1 cosxsin  3 
x 1 cos xsin
 3x 1 cos xsin    3x       2   2   2      3 
 1 cos xsin   3x  2 1 cos xsin  3x f     x.  2   2   3 
Vậy hàm số y  1 cos x sin  3x   là hàm số chẵn.  2  Câu 19: cos 2x
+ Hàm số f x  có nghĩa x
    D   . 2 1 sin 3x TOANMATH.com Trang 27 cos 2  x cos 2x
Ta có f x      f x . 2 1 sin  3  x 2   1 sin 3x cos 2x
Vậy hàm số f x  là hàm số chẵn. 2 1 sin 3x sin 2x  cos3x   
+ Hàm số g x 
có nghĩa  cos x  0  x
k  D   \   k . 2 2  tan x 2  2  sin 2  x  cos 3  x sin 2x  cos3x
Ta có g x        g x . 2 2  tan x 2   2  tan x sin 2x  cos3x
Vậy hàm số g x  là hàm số chẵn. 2 2  tan x Câu 20:    Hàm số 2017 y x  cos x    có nghĩa x
    D   .  2       
Ta có f x  x2017 2017  cos x   x  cos x       2   2       2017 2017   x
 cos x     x  cos x    f     x.  2   2     Vậy hàm số 2017 y x  cos x    là hàm số lẻ.  2 
Dạng 3: Tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác 1 – C 2 – D 3 – B 4 – A 5 – A 6 – D 7 - C 8 - A 9 – B 10 – D 11 – D 12 – D 13 – D 14 – A 15 – B 16 – A 17 – B 18 – D 19 – D 20 – B
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:   
Hàm số y  7  2cos x    có nghĩa x
    D   .  4           Ta có 1   cos x   1  2   2cos x
 2  5  7  2cos x   9       .  4   4   4       
Vậy min y  5  cos x
 1  x   k2  x   k2 ,k     ;  4  4 4     5  
max y  9  cos x   1   x   
  k2  x
k2 , k     .  4  4 4 Câu 2:
Hàm số y  4 sin x  3 1 có nghĩa  sin x  3  0  sin x  3  x
    D   . Ta có 1
  sin x 1  2  sin x  3  4  2  sin x  3  2 TOANMATH.com Trang 28
 4 2  4 sin x  3  8  4 2 1  4 sin x  3 1  7 .  
Vậy min y  4 2 1  sin x  1   x
k2 ,k  ; 2 
max y  7  sin x  1  x
k2 , k  . 2 Câu 3: Hàm số 2
y  sin x  4sin x  5 có nghĩa x
    D   Ta có y x x    x  2 2 sin 4sin 5 sin 2  9 .   x    
x      
x  2      x  2 1 sin 1 3 sin 2 1 1 sin 2 9 8 sin 2  9  0 .  Vậy min y  8
  sin x  2  1
  sin x  1  x   k2 , k  . 2 Câu 4:
Hàm số y  2sin x  3 có nghĩa x
    D   . Ta có 1
  sin x 1  2
  2sin x  2  1  2sin x  3  5  1  2sin x  3  5 .  
Vậy min y  1  sin x  1   x
k2 , k  ; 2 
max y  5  sin x  1  x
k2 ,k  . 2 Câu 5: 4 Hàm số y  có nghĩa x
    D   . 2 1 2sin x Ta có 2 2 2 1
  sin x 1  0  sin x  1  0  2sin x  2  1 1 2sin x  3 1 1 4 4   1    4 . 2 2 3 1 2sin x 3 1 2sin x    sin x  1   x   k2 , 4 k     Vậy 2 min y  
x   k , k  ;  3   2
sin x 1  x   k2 ,k   2
max y  4  sin x  0  x k , k  . Câu 6: Hàm số 2 2
y  2sin x  cos 2x có nghĩa x
    D   . 2  1  3 Ta có 2 2 2
y  2sin x  cos 2x  1 cos 2x  cos 2x  cos 2x     .  2  4 2 2 3  1 1  1  9 3  1  3 1   cos 2x 1 
 cos 2x    0  cos 2x     cos 2x    3     . 2 2 2  2  4 4  2  4 3 1 
Vậy min y   cos 2x   x    k , k   ; 4 2 6 TOANMATH.com Trang 29 k
max y  3  cos 2x  0  x   , k   . 4 2 Câu 7: Hàm số 3s y
in x  4cos x 1 có nghĩa x
    D   .  3 4   3 
Ta có y  3sin x  4cos x 1  5
sin x  cos x 1  5sin  
x   1với   arccos  k2   .  5 5   5  5
  5sin x    5  4
  5sin x   1 6.    Vậy min y  4
  sin x    1   x  
k2  x  
   k2 , k  ; 2 2  
max y  6  sin  x   1  x    k2  x  
   k2 , k  . 2 2 Câu 8:
Hàm số y  4sin 6x  3cos 6x có nghĩa x
    D   .  4 3   4 
Ta có y  4sin 6x  3cos 6x  5
sin 6x  cos 6x  5sin  
6x  với   arccos  k2   .  5 5   5 
1  sin 6x   1  5
  5sin 6x    5.      k Vậy y     x   2 min 5 sin 6  1   6x  
k2  x   , k   ; 2 12 3    k max y 5 sin 6x   1 6x k2           x    , k  . 2 6 12 3 Câu 9: Hàm số si
y  n 2x có nghĩa x
    D       3 3 Khi x   ;  thì   sin 2x  . 6 3    2 2 3  3  Vậy min y  
x   ;max y   x  . 2 6 2 3 Câu 10:   
Hàm số y  3 tan x có nghĩa  cos x  0  x
k  D   \   k  . 2  2      Khi x   ;  thì hàm số ta
y  n x luôn đồng biến. 3 4   
Suy ra  3  tan x  1  1
  3 tan x  3 .  3  Vậy min y  1
  x   ;max y   x  . 3 2 4 Câu 11:
Hàm số y f x  4  3cos x có nghĩa x
    D   . TOANMATH.com Trang 30  2  1 3  3 11 Khi x  0; 
thì   cos x  1   3cos x  3  3   3c
 os x   1 4  3cos x  . 3    2 2 2 2 11 2
Vậy min y  1  x  0;max y   x  . 2 3 Câu 12:   
Hàm số y f x  sin 2x    có nghĩa x
    D   .  4      2    2 Khi x   ;  thì   sin 2x     . 4 4    2  4  2 2   2  Vậy min y    x  ; max y   x  . 2 4 2 4 Câu 13: Hàm số 2
y  sin x  2  sin x có nghĩa x
    D   . Ta có 2 2 2 2
1  sin x  1  0  sin x  1  1
  sin x  0  1  2  sin x  2  1  2  sin x  2 . Lại có 2 1
  sin x  1 0  sin x  2  sin x  1 2  0  y 1 2 . 
y  0  sin x  1
  x    k2 . 2 
Vậy min y  0  x    k2 . 2 y    sin x 1 1 2
sin x  0 (vô nghiệm).
Áp dụng bất đẳng thức Côsi ta có 2 2 2 2
2sin x 2  sin x  sin x  2  sin x  2sin x 2  sin x  2 2 2
 2  2sin x 2  sin x  4  y  4  y  2 . 
Dấu “=” khi và chỉ khi 2
sin x  2  sin x  sin x  1  x
k2 ,k  . 2  
Vậy min y  0  x    k2 , k  ;
 max y  2  x
k2 ,k  . 2 2 Câu 14: cos x  2sin x Hàm số y  có nghĩa x
    D   . 2  sin x cos x  2sin x Ta có y
 2y y sin x  cos x  2sin x 2  sin xy y x x
x y   y   x
x y   y   2 2 2 sin 2sin cos 2 2 sin cos 4
2 sin x  cos x  
Sử dụng bất đẳng thức Bunhiacopxki ta có TOANMATH.com Trang 31      y  22 2 19 2 19 2 2 2
1  4y  3y  4y  5  0   y  . 3 3 2   19 2   19 Vậy min y  ; max y  . 3 3 Câu 15: Hàm số  x x2 3sin 4cos
 6sin x  8cos x  2m 1 có nghĩa x
    D   . Ta có  x x2   x
x   m   x x  2 3sin 4cos 2 3sin 4cos 1 2 3sin 4cos 1  2m
Để phương trình có nghiệm đúng với mọi x   thì 2m  0  m  0 . Câu 16:          Hàm số 2 2
y  tan x  cot x  3tan x  cot x 1 có nghĩa cos x 0 x k   2  x k 2 sin
 x  0  x k Ta có 2 2
y  tan x  cot x  3tan x  cot x 1  x x x x   x x    x x2 2 2 tan 2 tan cot cot 3 tan cot 3 tan cot
 3tan x  cot x 3 2
Đặt tan x  cot x t   t  2 sin 2x  3   21 t  1 Ta có 2
y t  3t  3. Cho 2 y  0   3   21 t  2  2 2    Vậy min y  5   t   2   sin 2x  1   2x
k2  x    k ;max y   sin 2x 2 4 Câu 17: Hàm số 4 4
y  cos x  sin x có nghĩa x
    D   . Ta có y x x    x2 4 4 2 4 2 4 4 4 2 cos sin 1 sin
 sin x 1 2sin x  sin x  sin x  2sin x  2sin x 1.    
y  2sin x  2sin x 1  2 sin x 2 2 2 1 1 1 2 2 2 2 2  sin x   2 sin x       .  2   2  2 2 2 1  1 1  1  1  1  1 2 2 2 2 1
  sin x  1  0  sin x  1 
 sin x    0  sin x
  0  2 sin x       2 2 2  2  4  2  2 2 1  1  1 1 2   2 sin x   1   y 1   . 2  2  2 2  2  sin x   x   k2 1 1  Vậy 2 2 4
min y   sin x    k ; 2 2  2   sin x   x   k2  2 4 TOANMATH.com Trang 32
max y  1  sin x  0  x k k  . Câu 18: 1 cos 2x Ta có 2
sin 2x  4cos x 1  sin 2x  4
1  sin 2x  2cos 2x  3  0 x
    D   2
3sin 2x  cos 2x m1 3 ysin2x12ycos2x  3y
sin 2x  2cos 2x  3
y    y
x    y 2 2 9 3 sin 2 1 2 cos 2x  
Sử dụng bất đẳng thức Bunhiacopxki ta có     
3  y2  1 2y2 5 3 5 5 3 5 2 2
 9y  2y  5y  5  0   y  . 4 4 5   3 5 5   3 5 3 5  9 Vậy max y  
m 1  m  . 4 4 4 Câu 19: 2 cos x  sin . x cos x Hàm số y  có nghĩa x
    D   . 2 1 sin x
1 cos 2x sin 2x 2  cos x  sin . x cos x
1 cos 2x  sin 2x 1 cos 2x  sin 2 2 2 x y     2 2 2 1 sin x 1 sin x 2  2sin x 3  cos 2x
1 cos 2x  sin 2x Có y
 3y y cos 2x 1 cos 2x  sin 2x  1 ycos 2x  sin 2x  3y 1 3  cos 2x   y  2 3
1  1 ycos 2x  sin 2x2
Sử dụng bất đẳng thức Bunhiacopxki ta có   
1 y2 1 3y  2 2 6 2 6 2 2 2
1  1 2 y y 1  9 y  6 y 1  8y  8y 1  0   y  . 4 4 2  6 2  6 Vậy min y  ; max y  . 4 4 Câu 20: Theo bài ra 2 2 2
cos x  cos y  cos z  1
Áp dụng bất đẳng thức Bunhiacopxki, ta có 2 2 2 2 2 2 2 2 2
1 cos x  1 cos y  1 cos z  1 1 1 . 1 cos x 1 cos y 1 cos z 2 2 2   x   y   z    2 2 2 1 cos 1 cos 1 cos 3 3
cos x  cos y  cos z 2 2 2
 1 cos x  1 cos y  1 cos z  2 3  y  2 3 . Vậy max y  2 3 . TOANMATH.com Trang 33
Dạng 4: Tính tuần hoàn và chu kì hàm lượng giác 1 – D 2 – D 3 – B 4 – C 5 – A 6 – D 7 – D 8 – B 9 – A 10 – D 11 – C 12 – C 13 – C 14 – A 15 – B 16 – B 17 – B 18 – C 19 – B 20 – A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:x   Hàm số y  sin    có nghĩa x
    D   .  3 6  2
Chu kì của hàm số T   6 . 1 3 Câu 2:
Tại x  0  y  3
  Loại đáp án A, B.
Tại x    y  3  Loại đáp án C.
Vậy đồ thị đã cho là của hàm số y  3c  os3x . Câu 3:x   Hàm số y  2sin    có nghĩa x
    D   .  2 3  2
Chu kì của hàm số T   4 . 1 2 Câu 5:x Hàm số y  2sin có nghĩa x
    D   . a 2
Chu kì của hàm số T   4  a  2   . a Câu 6:
Hàm số không có chu kì cơ sở. Câu 7: 2
Chu kì của hàm số T
 4. Loại đáp án A, B. Biên độ của hàm số A  2  2 . 1 2 Câu 8: Tại 0
x   y  0  Loại đáp án C, D. 2
Chu kì của hàm số T  . 3 TOANMATH.com Trang 34
Vậy đồ thị đã cho là của hàm số y  sin 3x . Câu 9: 2
Hàm số f (x)  a sin ux b cos vx c (với u,v  ) là hàm số tuần hoàn với chu kì T   u,v
Hàm số y  sin 3x  2cos 2x có nghĩa x
    D   . 2
Chu kì của hàm số T   2 . 1 Câu 10:x
Ta có với 0  x
thì hàm số f x  sin luôn đồng biến. 2 3 1 
Khi đó giá trị lớn nhất của hàm số là y  tại x  . max 2 2 Câu 11:    Hàm số y  3cos  mx   có nghĩa x
    D   .  4  2 2
Chu kì của hàm số T
 3  m   . m 3 Câu 12:
Hàm số y  sin x có nghĩa x
    D   . 3 3 
Hàm số nghịch biến trên    , 
. Hàm số đồng biến trên , 2 . 2     2      3
Đồ thị hàm số có một cực tiểu tại x  . 2 Câu 13:
Tại x  0  y  1 Loại đáp án A. Chu kì của hàm số T  2.2  4 . x
Vậy đồ thị đã cho là của hàm số y  cos . 2 Câu 14. 2
Hàm số f x  asin ux bsin vx c ( với u,v  ) là hàm số tuần hoàn với chu kì T   . u,v Hàm số sin y
2x  sin x có nghĩa x
    D   . 2
Chu kì của hàm số T   2 . 1 Câu 15.   
Ta có hàm số y  sin x nghịch biến trên khoảng ;   .  2  TOANMATH.com Trang 35 Câu 16.
Hàm số f x  .t a an ux  .t
b an vx c ( với u,v  ) là hàm số tuần hoàn với chu kì T   . u,v
Hàm số y  tan x  tan 3x có nghĩa x
    D   . 
Chu kì của hàm số T    . 1 Câu 17. x  Hàm số y  2sin  2017   có nghĩa x
    D   .  2  2
Chu kì của hàm số T   4 . 1 2
Biên độ của hàm số A  2  2 . Câu 18.
Hàm số y  sin 3x  2017 cos 2x có nghĩa x
    D   . 2
Chu kì của hàm số T   2 . 1 Câu 19.
Hàm số y  sin ax b có nghĩa x
    D   . 2 1
Với a  0 chu kì của hàm số T   4  a  . a 2
Tại x   y   b 1 0 1 sin 1 b  . 2
Vậy a b  1. Câu 20.
Hàm số không có chu kì cơ sở. TOANMATH.com Trang 36