Bài giảng môn Xác suất thống kê | Đại học Kiến trúc Đà Nẵng

Bài giảng môn Xác suất thống kê | Đại học Kiến trúc Đà Nẵng. Tài liệu được biên soạn dưới dạng file PDF gồm 119 trang, giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!

71 36 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Xác suất thống kê (KT1)

Trường: Đại học Kiến trúc Đà Nẵng

Thông tin:

119 trang 4 tháng trước

Tác giả:

Profile 48 Nguyễn Thị Anh Thơ
B GIÁO D O Ộ ỤC VÀ ĐÀO TẠ
I H C KI TRƯỜNG ĐẠ Ọ ẾN TRÚC ĐÀ NẴNG
----- ----- 
BÀI GI ẢNG
XÁC SU T TH NG KÊ Ấ Ố
(Tái b n l n 3) ả ầ
Giảng viên biên so n: ạ
a HThS. Vũ Hứ ạnh Nguyên
Đà Nẵng, 9/2021
Bài gi ng Xác suả ất Thống kê – i h c Ki úc à N Đạ ọ ến tr Đ ẵng
2
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
M ỤC LỤC
PHẦN I. XÁC SU T Ấ
Chương 1. PHÉP THỬ - BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ - XÁC
SUẤT CỦA BIẾN CỐ
§ 1. GIẢI TÍCH TỔ HỢP
1.1. Giai thừa
1.2. Qui t i nh ắc đếm (lố ân)
1.3. Hoán v ị
1.4. Ch nh h p ỉ ợ
1.5. T h p ổ ợ
B P ÀI TẬ
§ 2. PHÉP TH - N) LIÊN K I PHÉP TH Ử BIẾN CỐ (SỰ KIỆ ẾT VỚ Ử
2.1. Phép th ng u nhi ông gian các bi n c s p ử ẫ ên và kh ế ố ơ cấ
2.2. Bi n c ki n) li i ph ế ố (sự ệ ên kết vớ ép thử
2.3. C án v n c ác phép to ề biế ố
§ 3. XÁC SU T C A BI Ấ Ủ ẾN CỐ
3.1. C nh ngh ác su t ác đị ĩa x ấ
3.2. C ính ch n c ác su t ác t ất đơn giả ủa x ấ
§ 4. CÁC PHÉP TOÁN V XÁC SU T Ề Ấ
4.1. Phép c ng xác su t ộ ấ
4.2. Phép nhân xác su t ấ
§ 5. CÔNG TH C XÁC SU T TOÀN PH N VÀ CÔNG TH C BAYES Ứ Ấ Ầ Ứ
5.1. Công th t toàn ph n ức xác suấ ầ
5.2. Công th c Bây ét (Bayes) ứ −
§ 6. DÃY PHÉP TH BECNOULLI Ử
6.1. Dãy phép th Bernoulli ử
6.2. Công th c Bernoulli ứ
B P ÀI TẬ
Chư Ẫơng 2. BIẾ ẪU NHIÊN (ĐẠN NG I LƯỢNG NG U NHIÊN)
§ 1. BI N NG U NHI Ế Ẫ ÊN
1.1. nh ngh V Đị ĩa – í dụ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
3
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
1.2. Phân lo ác bi n ng u nhi ại c ế ẫ ên
1.3. C án trên bi n ng u nhi ác phép to ế ẫ ên
§ 2. DÃY PHÂN PH I VÀ HÀM M T Ố ẬT ĐỘ XÁC SUẤ
2.1. Hàm phân ph i xác su n ng u nhiên ố ất của biế ẫ
2.2. Dãy phân ph i xác su t c n ng u nhiên r c ố ấ ủa biế ẫ ời rạ
2.3. Hàm m xác su n ng u nhiên liên t c ật độ ất của biế ẫ ụ
2.4. Bài toán v hàm phân ph i xác su t và hàm m xác su t ề ố ấ ật độ ấ
§ 3. CÁC THAM S A BI U NHIÊN Ố ĐẶC TRƯNG CỦ ẾN NGẪ
3.1. S trung v ố ị
3.2. S MOD (Modal) ố
3.3. ng toán c a bi n ng u nhiên Kì vọ ủ ế ẫ
3.4. a bi n ng u nhiên Phương sai củ ế ẫ
3.5. l ch tiêu chu l Độ ệ ẩn (độ ệch quân phương)
3.6. Mômen
§ 4. N NG U NHIÊN n U BIẾ Ẫ − CHIỀ
4.1. Định nghĩa − Ví dụ
4.2. Hàm phân ph i xác su n ng u nhiên 2 chi u ố ất của biế ẫ − ề
4.3. B ng phân ph i xác su n ng u nhiên r c 2 chi u ả ố ất của biế ẫ ời rạ − ề
4.4. Hàm m xác su n ng u nhiên liên t c 2 u ật độ ất của biế ẫ ụ − chiề
4.5. Phân ph i xác su u ki n c n ng u nhiên 2 chi u ố ất có điề ệ ủa biế ẫ − ề
4.6. K v u ki n c n ng u nhiên 2 u ỳ ọng có điề ệ ủa biế ẫ − chiề
Ch T PHÂN PH I XÁC SU T THÔNG D ương 3. MỘT SỐ LUẬ Ố Ấ ỤNG
3.1. t phân ph i là phân ph 1) Luậ ối giản đơn (hay còn gọ ối 0 −
3.2. Lu t ph c ậ ân phối nhị thứ
3.3. Lu t ph êu b i ậ ân phối si ộ
3.4. t phân ph i chu n Luậ ố ẩ
3.5. Hàm Laplace và m k t qu ột số ế ả
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
4
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3.6. t phân ph i Poisson Luậ ố
B P ÀI TẬ
PH N II. TH Ê Ầ ỐNG K
Chư Ẫơng 4. LÝ THUYẾT M U
§ 1. LÝ THUY T M U Ế Ẫ
1.1. Đặt vấn đề
1.2. M u ng u nhiên M u th m ẫ ẫ − ẫ ực nghiệ
1.3. Hàm phân ph c nghi m Biểu đồ − ối thự ệ
§ 2. CÁC THAM S U Ố ĐẶC TRƯNG CỦA MẪ
I. Các tham s i di n cho giá tr ố đạ ệ ị trung tâm
2.1. Trung bình m u (K v ng m u) ẫ ỳ ọ ẫ
2.2. S ung v c u th m ố tr ị ủa mẫ ực nghiệ
2.3. S Mod c a m u th m ố ủ ẫ ực nghiệ
II. Các tham s i di chênh l ) ố đạ ện cho độ phân tán (độ ệch
2.4. Phương sai mẫu
2.5. u ch nh c l ch tiêu chu n l ch tiêu chu u ch nh Phương sai điề ỉ ủa mẫu − Độ ệ ẩ − Độ ệ ẩn điề ỉ
của mẫu
Chương 5. ƯỚC LƯỢNG THAM SỐ
§ 1. M ƯỚC LƯỢNG ĐIỂ
1.1. Khái ni ng tham s ệm về ước lượ ố
1.2. ng cho giá tr trung bình Ướ ợc lư ị
1.3. Ước lượng cho phương sai
2
§ 2. NG TIN C Y CHO K V KHOẢ Ậ Ỳ ỌNG
2.1. Đặt vấn đề
2.2. ng tin c y cho k v ng (tóm t t các công th Khoả ậ ỳ ọ ắ ức)
§ 3. NG KHO NG CHO T L ƯỚC LƯỢ Ả Ỉ Ệ
§ 4. M u) BÀI TOÁN XÁC ĐỊNH CỠ ẪU (kích thước mẫ
4.1. n Đặt vấ đề
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
5
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
4.2. ng h ng cho trung bình Trườ ợp ước lượ
4.3. ng h ng cho t l Trườ ợp ước lượ ỉ ệ
Chư Ảơng 6. ỂM ĐỊKI NH GI THIẾT
§ 1. V CHUNG ẤN ĐỀ
1.1. n Đặt vấ đề
1.2. n bác b Các sai l M c nh gi thi t Miề ỏ − ầm − ức ý nghĩa ủa kiểm đị ả ế
§ 2. NH GI T CHO TRUNG BÌNH KIỂM ĐỊ Ả THIẾ
2.1. ng h l ch chu n) t Trườ ợp phương sai (độ ệ ẩ
2
đã biế
2.2. ng h l ch chu n) u n 30 Trườ ợp phương sai (độ ệ ẩ
2
chưa biết, mẫ
2.3. ng h l ch chu n) m u n < 30 Trườ ợp phương sai (độ ệ ẩ 2 chưa biết, ẫ
§ 3. NH GI T CHO T L KIỂM ĐỊ Ả THIẾ Ỉ Ệ
3.1. Bài toán ki nh hai phía ểm đị
3.2. Bài toán ki nh phía ph i ểm đị ả
3.3. Bài toán ki nh phía trái ểm đị
B P ÀI TẬ
§ 4. BÀI TOÁN SO SÁNH
4.1. Đặt vấn đề
4.2. So sánh hai giá tr ị trung bình
4.3. So sánh hai t l ỉ ệ
Tài liệu tham khảo
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
6
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Phần I. XÁC SUẤT
Chương 1
PHÉP THỬ BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ - -
XÁC SUẤT CỦA BIẾN CỐ
§1. GIẢI TÍCH TỔ HỢP
Kiến thức về giải tích tổ hợp đã được học trong chương trình toán THPT, ở đây xin
được nhắc lại một số kiến thức cơ bản cùng các công thức về giai thừa, hoán vị, chỉnh hợp
không lặp, chỉnh hợp lặp, tổ hợp không lặp, tổ hợp lặp làm cơ sở để nghiên cứu xác suất −
thống kê.
1.1. Giai thừa
Định nghĩa. Cho
, ! 1.2.3 . n N n n =
Ví dụ
5! 1 2 3 4 5 120= =
Qui ước: 0! = 1.
Tính chất.
! ( 1)!. ( 2)!( 1). .n n n n n= − = − −
Ví dụ
5! = 1 3 4 5 2
= 4! 5
= 3! 5. 4
1.2. Qui tắc đếm (lối nhân)
Giả s có công vi n C , C ng: ử ệc C, được chia làm k giai đoạ
1 2
, …C
k
và tương ứ
Công việc C cách k hoàn thành,
1
có n
1
hác nhau để
Công việc C hoàn thành,
2
có n
2
cách khác nhau để
…
Công việc C hoàn thành.
k
có n
k
cách khác nhau để
Khi đó nế ệu công vi c C hoàn thành khi và ch ng thỉ khi đồ ời hoàn thành
các công vi c C thì có t t c ệ
1
;C
2
;…C
k
ấ ả
1 2 k
n n n 
cách khác nhau để hoàn thành công
vi c C. ệ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
7
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví d 1. Gi s t ng khác ụ ả ử ừ địa điểm A đến địa điểm B có 2 con đườ nhau để đi và từ địa
điểm B đến đị ểm C có 3 con đường khác nhau để đi. a đi
Khi đó có tất cả a đi ể 6 con đường khác nhau để đi từ đị ểm A đến địa đi m C.
Ví d 2. Cho t p X = 0; 1; 2; 3; 4 . T t p X l c bao nhiêu s t nhiên g m 3 ch ụ ậ ừ ậ ập đượ ố ự ồ ữ
s khác nhau. ố
Xét s c n tìm có d ng ố ầ ạ
abc
, v , 0, , , t khác nhau. ới a b, c X, a a b c đôi mộ
Khi đó: chữ s có 4 cách ch n khác nhau ố a ọ
s có 4 cách ch n khác nhau chữ ố b ọ
s có 3 cách ch n khác nhau chữ ố c ọ
KL: Có tất c 4 4 3 = 48 s các s a mãn yêu c u c ả ố ố thỏ ầ ủa bài toán.
1.3. Hoán vị
1.3.1. Định nghĩa
Cho t p X có ph n t khác nhau. M i m t cách s p x p ph n t khác nhau cậ n ầ ử ỗ ộ ắ ế n ầ ử ủa
X theo một t g i là m t hoán v c ph n t . thứ ự ọ ộ ị ủa n ầ ử
Ví d . Cho t p X = 1; 2; 3; 4 4 ph n t ụ ậ khi đó các số 1234, 3241, 4312…là các hoán vị ầ ử
của X.
1.3.2. c Công thứ
S các hoán v c n t khác nhau c a X kí hi ố ị ủa n phầ ử ủ ệu và xác định như sau:
P
n
= n!.
1.4. Chỉnh hợp
1.4.1. Ch p không l p (g t là ch nh h p) ỉnh hợ ặ ọi tắ ỉ ợ
1.4.1.1. Định nghĩa
Cho t p X có n t khác nhau. M i m t cách s p x p ph n t khác nhau cậ n phầ ử ỗ ộ ắ ế k ầ ử ủa
X (với 1 t th i là m t ch ) theo mk n ộ ứ t nh nh gự ất đị ọ ộ ỉnh h p ợ
không l p ch p c a n ph n t khác nhau. ặ ậ k ủ ầ ử
Ví dụ. Cho t p X = 0; 1; 2; 3; 4; 5 nh h p ch p ậ khi đó các số 234, 341, 412…là các chỉ ợ ậ
3 c ủa 6.
1.4.1.2. Công th c ứ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
8
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
S các ch nh h p ch c ph n t khác nhau c a X kí hiố ỉ ợ ập k ủa n ầ ử ủ ệu và xác định như
sau:
!
, 1
( )!
k
n
n
A k n
n k
=
−
.
* N u thì ch nh h p ch p c c ph n t . Chú ý. ế n = k ỉ ợ ậ k ủa n chính là hoán vị ủa n ầ ử
1.4.2. Ch p l p ỉnh hợ ặ
1.4.2.1. Định nghĩa
Cho tập X có n t khác nhau. M i m t cách s p x n phầ ử ỗ ộ ắ ếp k phần tử c X theo mủa ột
thứ t nh nh g i là m nh h p l p ch c ph n t khác nhau.ự ất đị ọ ột chỉ ợ ặ ập k ủa n ầ ử
Ví d . Cho t p X= 0; 1; 2; 3; 4; 5ụ ậ khi đó các số 22234, 10021, 32323, 44444, 33331…là
các ch a 6.ỉnh h p lợ ặp chập 5 củ
1.4.2.2. Công th c ứ
S các ch nh h p l p ch p ph n t khác nhau c a X kí hi nh ố ỉ ợ ặ ậ k của n ầ ử ủ ệu và xác đị
như sau:
k
k
n
A n=
.
1.5. Tổ hợp
1.5.1. Định nghĩa
p X có ph n t khác nhau. Cho tậ n ầ ử
M i m t t p con g ph n t khác nhau c a X (0 ) g i là m t t hỗ ộ ậ ồm k ầ ử ủ k n ọ ộ ổ ợp
không l p ch p c . ặ ậ k ủa n
Ví dụ. Cho t p X = p con , các t ậ a; b; ; c d; ; e f; g khi đó các tậ a; c; e c; g; f,…là ổ
h p ch p 3 c ợ ậ ủa 7.
1.5.2. Công th c ứ
S h p ch p c ph n t khác nhau c ố các tổ ợ ậ k ủa n ầ ử ủa X kí hiệu và xác định như sau:
.
• Chú ý. nh h p l h p l p. Tương tự như chỉ ợ ặp, ta cũng có khái niệm tổ ợ ặ
BÀI TẬP
Bài 1.1. Cho t p X = 0; 1; 2; 3; 4; 5 . ậ
1/ T t p X, có l t nhiên khác nhau g n ch s khác nhau? ừ ậ thể ập được bao nhiêu số ự ồm bố ữ ố
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
9
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2/ T t p X, có th l c bao nhiêu s t nhiên khác nhau g m b n ch s khác nhau ừ ậ ể ập đượ ố ự ồ ố ữ ố
là số n ? chẵ
3/ T t p X, có th l c bao nhiêu s t nhiên khác nhau g m b n ch s khác nhau ừ ậ ể ập đượ ố ự ồ ố ữ ố
và chia h t cho 5 ? ế
Bài 1.2. Cho t p X = 0; 1; 2; 3; 4 . ậ
1/ T t p X, ta có th l c bao nhiêu s t nhiên khác nhau g m ba ch s khác ừ ậ ể ập đượ ố ự ồ ữ ố
nhau?
2/ T t p X, ta có th l c bao nhiêu s t nhiên khác nhau g m ba s khác nhau ừ ậ ể ập đượ ố ự ồ chữ ố
và chia h t cho 3 ? ế
Bài 1.3. Cho t p X = 0; 1; 2; 3; 4 . ậ
1/ T t p X, có th l c bao nhiêu s t nhiên khác nhau g m ba ch s khác nhau và ừ ậ ể ập đượ ố ự ồ ữ ố
luôn có m t chặ ữ s 1? (ví d ố ụ 312; 104; 431; …).
2/ T t p X, có th l c bao nhiêu s t nhiên khác nhau g m ba ch s khác nhau và ừ ậ ể ập đượ ố ự ồ ữ ố
nh ỏ hơn 300 ?.
Bài 1.4. Cho t p X = 0; 1; 2; 3; 4; 5 . ậ
1/ T t p X, có th l t nhiên khác nhau g m ba ch s ừ ậ ể ập được bao nhiêu số ự ồ ữ ố?.
2/ T t p X, có th l t nhiên khác nhau g m ba ch s s n ? ừ ậ ể ập được bao nhiêu số ự ồ ữ ố là ố chẵ
3/ T t p X, có th l c bao nhiêu s t nhiên khác nhau g m ba ch s và chia hừ ậ ể ập đượ ố ự ồ ữ ố ết
cho 5 ?
Bài 1.5. 1/ M ng chéo. ột ngũ giác có bao nhiêu đườ
2/ M i có 11 c ng chéo ? ột đa giác lồ ạnh có bao nhiêu đườ
3/ M i có n c nh (n > 3) có bao ng chéo ? ột đa giác lồ ạ nhiêu đườ
Bài 1.6.
1/ Cho t p h p X là t p g m khác nhau ậ ợ ậ ồm có 4 điểm khác nhau, trong đó không có 3 điể
nào cùng n m trên m ng th ng. H i t t p X ta có th v c bao nhiêu tam giác ằ ột đườ ẳ ỏ ừ ậ ể ẽ đượ
khác nhau ?
2/ Cho t p h p X là t p g m khác nha m khác nhau ậ ợ ậ ồm có 5 điể u, trong đó không có 3 điể
nào cùng n m trên m ng th ng. H i t t p X ta có th v c bao nhiêu tam giác ằ ột đườ ẳ ỏ ừ ậ ể ẽ đượ
khác nhau ?
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
10
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3/ T ng quát cho t p h p X là t p g m khác nhau vổ ậ ợ ậ ồm có n điể ới n > 3, trong đó không có
3 điểm khác nhau nào cùng nằm trên một đường thẳng. Hỏi từ tập X ta có thể vẽ được bao
nhiêu tam giác khác nh au ?
Bài 1.7. i h c Z t c gi i th u vòng tròn mTrường đạ ọ ổ chứ ải bóng đá nam, vớ ể thức thi đấ ột
lượt. Có 5 đội u. đăng ký tham gia thi đấ
Hỏi có t t cấ ả bao nhiêu tr u ? ận đấ
Chú ý. Không có đội nào bỏ cuộc.
Bài 1.8. , m g Có 12 sinh viên được chia làm 3 tổ ỗi tổ ồm có 4 sinh viên.
Hỏi có bao nhiêu cách chia tổ ?
Bài 1.9. và 6 sinh viên n c chia làm 3 Có 18 sinh viên, trong đó có 12 sinh viên nam ữ đượ
t , m g m có 6 sinh viên. ổ ỗi tổ ồ
Hỏi có b i giao nhiêu cách chia t , vổ ớ ả thi t:ế
1/ Cách chia t là tùy ý? ổ
2/ M có 4 sinh viên nam và 2 sinh viên n ? ỗi tổ ữ
Bài 1.10. Trong m t cái h . L y ng u nhiên m t l n 2 bi ộ ộp, có 5 bi màu xanh, 1 bi màu đỏ ấ ẫ ộ ầ
t p, h ừ trong hộ ỏi:
1/ Có bao nhiêu kh y ra có cùng màu? ả năng 2 bi lấ
2/ Có bao nhiêu kh y ra khác màu? ả năng 2 bi lấ
Bài 1.11. Trong m t cái h . L y ng u nhiên m t l n 3 bi ộ ộp, có 5 bi màu xanh, 4 bi màu đỏ ấ ẫ ộ ầ
t p, h ừ trong hộ ỏi:
1/ Có bao nhiêu kh y ra có nhi u nh ả năng 3 bi lấ ề ất 1 bi xanh ?
2/ Có bao nhiêu kh 3 bi l y ra có ít nh 1 bi xanh ? ả năng ấ ất
Bài 1.12. Trong m t cái h . L y ng u nhiên m t l n 3 bi ộ ộp, có 5 bi màu xanh, 2 bi màu đỏ ấ ẫ ộ ầ
t p, h ừ trong hộ ỏi:
1/ Có bao nhiêu kh y ra có cùng màu ? ả năng 3 bi lấ
2/ Có bao nhiêu kh ả năng 3 bi lấy ra có đúng 2 bi màu xanh ?
3/ Có bao nhiêu kh y ra có ít nh t 1 bi màu xanh ? ả năng 3 bi lấ ấ
Bài 1.13. M t l p h và 18 nam). GV ch nhiộ ớ ọc có 45 sinh viên (trong đó có 27 nữ ủ ệm
muố ớ ồ ỏn thành lập một BCS l p g m 5 sinh viên; H i, có bao nhiêu cách chọn, n ếu:
1/ Ch n 5 sinh viên vào BCS là tùy ý ?. ọ
2/ Có đúng 3 nam sinh viên ?.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
11
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3/ Có ít nh sinh viên ?. ất 2 nữ
Bài 1.14. Trong m t h p có 100 s n ph m, g m 90 s n ph m t t và 10 s n ph m x u. Có ộ ộ ả ẩ ồ ả ẩ ố ả ẩ ấ
bao nhiêu cách ch n ra 10 s n ph ọ ả ẩm, trong đó:
1/ 10 s n ph c ch n ra tùy ý ? ả ẩm đượ ọ
2/ 10 s n ph c ch n ra, có 2 s n ph m x u ? ả ẩm đượ ọ ả ẩ ấ
Bài 1.15. Bài toán s p x p hành khách lên toa tàu. ắ ế
1/ H i có bao nhiêu cách s p x p m t cách ng u nhiên 4 hành khách lên 2 toa tàu khác ỏ ắ ế ộ ẫ
nhau (Chú ý r ng 4 hành khách có th lên cùng m t toa tàu). ằ ể ộ
2/ H i có bao nhiêu cách s x p m t cách ng u nhiên 3 hành khách lên 5 toa tàu khác ỏ ắp ế ộ ẫ
nhau (Chú ý r ng 3 hành khách có th lên cùng m t toa tàu) ằ ể ộ
Bài 1.16. T ng quát bài toán s p x p hành khách lên toa tàu. ổ ắ ế
Có bao nhiêu cách s p x p m t cách ng u nhiên n hành khách lên k toa tàu khác nh ắ ế ộ ẫ au
(Chú ý rằng n hành khách có th lên cùng m t toa tàu). ể ộ
§2. PHÉP THỬ BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ-
2.1. Phép thử ngẫu nhiên và không gian các biến cố sơ cấp
2.1.1. u nhiên Phép thử ngẫ
Khái niệm
Các hi c l p l i trong m t t h u kiện tượng đượ ặ ạ ộ ổ ợp các điề ện cơ bản nào đó và trong
m i l n c hi n nh ng k t qu có th x y ra khác nhau, các k t qu này x y ra m t cách ỗ ầ thự ệ ữ ế ả ể ả ế ả ả ộ
ng u nhiên không bi p h p t t c các k t qu x y ra là có th biẫ ết trước, nhưng tậ ợ ấ ả ế ả ả ể ết trước
đượ ọ ộ ọc. Các hiện tượng như vậy được g i là m t phép thử ngẫu nhiên (g i tắt là phép thử).
Ví d Gieo mụ 1. ột đồng xu.
Rõ ràng khi gieo 1 đồ ết đượng xu, ta không bi c kết quả gì có thể xảy ra khi mà
đồng xu dừng l ng xu s ng xu ng t chại (đồ ấp (S) hay đồ ữa (N)?), nhưng ta biế ắc là có 2 kết
qu x ả có thể ảy ra đó là S hoặc N.
Vậy gieo 1 đồng xu là một phép thử.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
12
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 2. Gieo m t con xúc x ng ch t phép th ộ ắc cân đối, đồ ất là mộ ử…
2.1.2. p Không gian các biến cố sơ cấ
Khái niệm
Xét m t phép th . T p h p t t c các k t qu ng kh x y ra c a mộ ử ậ ợ ấ ả ế ả đồ ả năng có thể ả ủ ột
phép th c g i là không gian các bi n c p (g i t t là không gian bi n c hay ử đó đượ ọ ế ố sơ cấ ọ ắ ế ố
còn g c kí hiọi là không gian mẫu), kí hi u là và mệ ỗi kết quả c a phép th ủ ử đượ ệu là .
Vậy là k t qu c a phép th . =  / ế ả ủ ử
Ví dụ 1. Gieo m ng xu, ; ột đồ = S, N
Ví dụ 2. ng xu, SS, SN, NS, NN ; Gieo hai đồ =
Ví dụ 3. Gieo m t con xú = {1 ch m; 2 ch m; 3 ch ộ c x c ắ = •,••,•••,… ấ ấ ấm;...}
2.2. Biến cố (sự kiện) liên kết với phép thử
2.2.1. m Khái niệ
+ Xét m t phép th , có không gian bi n c . ộ ử ế ố là
(sau đây ta viế ắt t t:Xét một phép thử / ).
Khi đó, mỗi một tậ ếp con c c gủa đượ ọi là một bi n c cố ủa phép thử đó.
M n c u b i các ch in hoa A, B, C... ột biế ố thường được kí hiệ ở ữ
Vậy A là m n c ột biế ố A .
Ở u đây, ta dùng kí hiệ thay cho phát biểu “khi và chỉ khi”.
+ Bi n c i là x y ra hay không x y ra. ế ố được gọ ả ả
M t bi n c c a m t phép th c g i là x y ra, n u khi th c hi n phép th kộ ế ố ủ ộ ử đượ ọ ả ế ự ệ ử ết
qu bi n c i, ta nói bi n c y ra. ả thuộc về ế ố đó. Ngược lạ ế ố đó không xả
Ví dụ
Gieo một con xúc x c / , xét các bi n c A = 2 ch m, 3 ch m ắ ế ố ấ ấ ;
B = 1 ch 4 ch m ; C = 1 ch m, 3 ch m, 5 ch m . ấm, ấ ấ ấ ấ
Giả s l n th nh t th c hi n phép th gieo con xúc x c ta th y k t qu x y ra là 1 ử ầ ứ ấ ự ệ ử ắ ấ ế ả ả
chấm, khi đó ta nói rằ C đã xảng biến cố B, biến cố y ra và biến cố A không xảy ra. Lần 2
thực hi n phép th gieo con xúc x c ta th y k t qu xệ ử ắ ấ ế ả ảy ra là có màu đỏ, khi đó ta nói
rằng bi n c y ra, bi n c A không x t lu n gì v bi n c C x y ế ố B đã xả ế ố ảy ra và chưa có kế ậ ề ế ố ả
ra hay không xảy ra.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
13
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2.2.2. i các bi Phân loạ ến cố
2.2.2.1. n c không th y ra) Biế ố ể (xả
Biến c c a m t phép th c g i là bi n c không th n u nó không bao gi x y ố ủ ộ ử đượ ọ ế ố ể ế ờ ả
ra ( trong m i l n th c hi n phép thọ ầ ự ệ ử biến c không th là bi n c không ch a m t kố ể ế ố ứ ộ ết
qu nào c a phép th ). Bi n c không th u là ả ủ ử ế ố ể thường được kí hiệ
.
Ví dụ. Gieo m t con xúc x . ộ ắc/
Ta có n c x y ra m c có sA: biế ố ả ặt con xúc xắ ố chấm > 7, khi đó A =
.
2.2.2.2. n c c ch n (bi n c t u) Biế ố chắ ắ ế ố ất yế
Biến c c a m t phép th c g i là bi n c c ch n n u nó luôn x y ra trong ố ủ ộ ử đượ ọ ế ố chắ ắ ế ả
m i l n th c hi n phép th bi n c c ch n là bi n c trùng v i không gian các ọ ầ ự ệ ử ( ế ố chắ ắ ế ố ớ
bi n c p). Bi n c u là ế ố sơ cấ ế ố chắc chắn thường được kí hiệ
(hay U).
Ví dụ. , Gieo một con xúc xắc/
A: biến cố xảy ra mặt con xúc xắc có số chấm < 7,
Khi đó A = .
2.2.2.3. n c u nhiên Biế ố ngẫ
Biến c c a m t phép th c g i là bi n c ng u nhiên n u bi n cố ủ ộ ử đượ ọ ế ố ẫ ế ế ố đó không là
bi n c không th và không là bi n c c ch n. ế ố ể ế ố chắ ắ
Vậy bi n c ng u nhiên là bi n c có th x y ra ho c không x y ra khi th c hiế ố ẫ ế ố ể ả ặ ả ự ện
phép th . ử
Ví dụ. , Gieo một con xúc xắc/
A: biến cố xảy ra mặt con xúc xắc có màu đỏ,
Khi đó A là một biến cố ngẫu nhiên.
2.2.2.4. n c p Biế ố sơ cấ
Biến c ng u nhiên ch g m m t và ch m t k t qu a phép th c gố ẫ ỉ ồ ộ ỉ ộ ế ả nào đó củ ử đượ ọi
là biến c p c a phép th ố sơ cấ ủ ử đó.
2.2.3. gi a các bi n c Quan hệ ữ ế ố
2.2.3.1. Quan h bao hàm ệ
Cho A, B là hai bi n c c t phép th , ế ố ủa cùng mộ ử
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
14
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Biến c c g i là bao hàm trong bi n c B n u m i k t qu c a phép th ố A đượ ọ ế ố ế ọ ế ả ủ ử ở
trong biến c trong bi n c bi n c y ra thì bi n c y ra). ố A đều ở ế ố B ( ế ố A xả ế ố B cũng xả
Kí hiệu A B.
2.2.3.2. Quan h b ng nhau ệ ằ
Cho A, B là hai bi n c c t phép th , ế ố ủa cùng mộ ử
Biến c c g i là b ng bi n c B n u m i k t qu c a phép th trong biố A đượ ọ ằ ế ố ế ọ ế ả ủ ử ở ến
cố A đều ở trong biến cố B và ngược lại ( bi ến cố A xảy ra khi và chỉ khi biến cố B
cũng xảy ra).
Kí hiệu A = B.
2.3. Các phép toán về biến cố
Nhận xét n không gian bi n c , bi n c n t p h p (t p h p các k. Nói đế ế ố ế ố là nói đế ậ ợ ậ ợ ết
qu n c c xây dả...). Do đó các phép toán trên không gian biế ố đượ ựng tương tự như trong
các phép toán trên tập h p. ợ
2.3.1. T ng hai bi p hai bi ) ổ ến cố (hợ ến cố
Đị ĩnh ngh a
Xét một phép th có không gian bi n c là và gi s A, B là hai bi n c . ử ế ố ả ử ế ố
Ta định nghĩa tổng của biến cố A và biến cố B là một biến cố C gồm mọi kế ảt qu của hai
bi n c A và B. ế ố
Kí hiệu: C = A c C = A + B (trong tài li u này ta dùng kí hi u C = A B, hoặ ệ ệ B).
• Theo định nghĩa, ta có:
Biến c C x y ra khi và ch khi ít nh t trong hai bi n c A, B x y ra. ố ả ỉ ất mộ ế ố ả
Hiển nhiên: C cũng là một biến cố của phép thử trên.
• Chú ý. n m r ng cho t ng cĐịnh nghĩa trên có thể ở ộ ổ ủa bi n c A , A ,..., A cế ố
1 2 n
ủa
cùng một phép . thử
Kí hi Aệu: X = A ...
1
A
2
n
.
Theo định nghĩa, ta có biến cố X xảy ra ít nh ất một trong các biến cố A , i = 1; 2; ...;
i
n
x y ra. ả
Ví dụ. Gieo m t con xúc x , ộ ắc/
A: bi n c x y ra m t có ch , B: bi n c x y ra m t có ch l . ế ố ả ặ ấm màu đỏ ế ố ả ặ ấm là số ẻ
Khi đó: C = AB: biế ả ặ ấ ấ ấn c xố y ra m t có chấm là 1 ch m; 3 ch m; 4 ch m; 5 chấm.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
15
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Tính chất
Xét một phép th có không gian bi n c là . ử ế ố
Ta có các tính chất:
t1/ AA = A.
t2/ A
= A.
t3/ AB = B A.
t4/ A(BC) = (A B)C.
2.3.2. Tích c a hai bi (giao c a hai bi ) ủ ến cố ủ ến cố
2.3.2.1. Định nghĩa
+ Gi s A, B là hai bi n c c xét trong cùng m t phép th có không gian bi n c ả ử ế ố đượ ộ ử ế ố là
.
Ta định nghĩa tích của biến cố A và biến cố B là một biến cố C gồm những kết
qu ng th c hai bi n c A và ả đồ ời thuộ ế ố B.
Kí hiệu C = AB hay C = A B (trong tài li u này ta dùng kí hi u C = AB). ệ ệ
• Theo định nghĩa, ta có:
Biến c C x y ra ng th hai bi n c y ra. ố ả đồ ời cả ế ố A, B xả
Hiển nhiên: C cũng là một biến cố của phép thử trên.
• Chú ý. n m r ng cho tích cĐịnh nghĩa trên có thể ở ộ ủa bi n c A , A ,..., A cế ố
1 2 n
ủa
cùng một phép th . ử
Kí hi Aệu: X = A
1 2
...A .
n
Biến c X x y ra ng th i các bi n c A , A ,..., A x y ra. ố ả đồ ờ ế ố
1 2 n
ả
Ví d Gieo mụ ột con xúc x , ắc/
A: biến c x y ra m t có ch , B: bi n c x y ra m t có ch l . ố ả ặ ấm màu đỏ ế ố ả ặ ấm là số ẻ
Khi đó: C = AB: biến cố xảy ra mặt có 1 chấm.
2.3.2.2. Tính ch t ấ
Xét một phép th có không gian bi n c là và xét các bi n c A, B, C. ử ế ố ế ố
Ta có các tính chất:
t1/ A.A = A.
t2/ A.
=
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
16
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
t3/ A.B = B.A.
t4/ A.(B.C) = (A.B).C.
2.3.2.3. Hai bi n c xung kh n bi n c xung kh ế ố ắc. Hệ − ế ố ắc từng đôi
Định nghĩa
+ Gi s n c c xét trong cùng m t phép th có không gian bi n c ả ử A, B là hai biế ố đượ ộ ử ế ố là
.
Ta nói rằng bi n c A là xung kh c bi n c ế ố ắ ế ố B AB =
+ Gi s H , H ,..., H là bi n c c xét trong cùng m t phép th ả ử
1 2 n
n − ế ố đượ ộ ử có không gian
bi n c . ế ố là
Ta nói rằng H , H ,..., H bi n c xung kh
1 2 n
là n − ế ố ắc từng đôi
H H
i j
=
, v i m i i ớ ọ j.
Ví dụ 1
Gieo một con xúc x , ta xét các bi n c sau: ắc/ ế ố
A = 1 ch m, 4 ch m ; B = 1 ch m, 3 ch m ; C = 2 ch . ấ ấ ấ ấ ấm, 6 chấm
Khi đó A và C là hai biế ắ ắn c xung khố c, B và C là hai biến c xung khố c, A
và B là hai bi n c không xung kh ế ố ắc.
Ví dụ 2
Gieo m t con xúc x , ta xét các bi n c sau: ộ ắc/ ế ố
H
1
1 ch m 5 ch m; 6 ch m 2 ch m; 4 ch m . = ấ ; H
2
= ấ ấ ; H
3
= ấ ấ
Khi đó H
1
, H , H là m
2 3
ột hệ ắ biến c xung khố c từng đôi.
2.3.3. Phép hi u c a hai bi ệ ủ ến cố
−
−
−
−−
2 bi p ến cố đối lậ
2.3.3.1. Định nghĩa
Giả s A, B là hai bi g cùng m t phép th có không gian bi n c ử ến cố được xét tron ộ ử ế ố
là .
Ta định nghĩa hiệu của biến cố A và biến cố B là một biến cố C gồm những kết
qu có trong bi n c A và không có trong bi n c ả ế ố ế ố B.
Kí hiệu C = A \ B.
• Theo định nghĩa, ta có:
Biến c C x y ra bi n c y ra và bi n c B không x y ra. ố ả ế ố A xả ế ố ả
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
17
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Hiển nhiên: C cũng là một biến cố của phép thử trên.
Ví d Gieo mụ ột con xúc x , ta xét các bi n c sau: ắc/ ế ố
A = 1 ch m, 4 ch m ; B = 1 ch m, 3 ch m; 5 ch m . ấ ấ ấ ấ ấ
Ta có A \ B = 4 ch , B \ 3 ch m; 5 ch m . ấm A = ấ ấ
2.3.3.2. Tính ch t ấ
Xét một phép th có không gian bi n c là , và xét các bi n c A, B. ử ế ố ế ố
Ta có các tính chất:
t1/ A \ A =
.
t2/ A \
= A.
t3/ A \ \ i A B B A, vớ B.
2.3.3.3. n c p Biế ố đối lậ
Đị hĩanh ng
Xét A là một biến c c t phép th có không gian bi n c là . ố ủa mộ ử ế ố
Ta định nghĩa biến cố hiệu \ A là bi ến cố đối lập của biến cố A, kí hiệu
A
.
Ví dụ
Gieo một con xúc x , ta xét các bi n c sau: ắc/ ế ố
A = 1 ch m, 4 ch m = {ch m có mà }; B = 1 ch m, 3 ch m; 5 ch m ấ ấ ấ u đỏ ấ ấ ấ
Ta có
A
2 ch m; 3 ch m; 6 ch m = {ch = ấ ấm; 5 chấ ấ ấm có màu đen}.
B
2 ch m; 4 ch m = {ch m ch n}. = ấ ấm; 6 chấ ấ ẵ
Chú ý
+ Khi th n m t phép th b , ch m t trong hai bi n c A hoực hiệ ộ ử ất kỳ ỉ có một và chỉ ộ ế ố ặc
A
x y ra. ả
+ Hai bi n c p là hai bi n c xung kh ế ố đối lậ ế ố ắc, nhưng ngược lại chưa chắc.
2.3.4. H các bi ệ đầ ủy đ ến cố
Định nghĩa
M g bi n c H , H ,..., H c a cùng m t phép có không gian ột hệ ồm có n − ế ố
1 2 n
ủ ộ thử
bi n c i là m các bi n c n u nó tho u ki n: ế ố được gọ ột hệ đầy đủ ế ố ế ả các điề ệ
(đk1) H
i
, v i i = 1, 2, ..., ới mọ n;
(đk2) Các biế ắn c H , H ,..., H xung khố
1 2 n
c t ừng đôi một;
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
18
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
(đk3) H
1
H
2
...H
n
= .
Ví dụ 1
Gieo một con xúc x c, có không gian bi n c là . Xét h n c ắ ế ố ệ các biế ố sau:
Gọi H
1
1 ch m; 4 ch m , H 2 ch , H 3 ch m; 5 ch m; 6 ch m . = ấ ấ
2
= ấm
3
= ấ ấ ấ
Khi đó H
1
, H , H
2 3
là một hệ đầy đủ các biến c . ố
Ví dụ 2
Gieo một con xúc x c, có không gian bi n c là . Xét h n c ắ ế ố ệ các biế ố sau:
Gọi H
1
= chấm có màu đỏ, H
2
= chấm có màu đen.
Khi đó H
1
, H t h
2
là mộ ệ ế các biđầy đủ n c . ố
• Chú ý
Cùng một phép th có th u h các bi n c khác nhau. ử ể có nhiề ệ ế ố đầy đủ
§3. XÁC SUẤT CỦA BIẾN CỐ
Giớ ộ ổ ội thiệu. Trong m t t h iợp các đ ều kiện nh nh, khi mất đị t phép thử được thực
hi n thì m t bi n c x y ra ho c không x y ra. Khi nghiên c u v s x y ra ệ ộ ế ố nào đó có thể ả ặ ả ứ ề ự ả
hay không x y ra c a bi n c c h t ta nghiên c u kh x y ra các ả ủ ế ố, trướ ế ứ ả năng khách quan để ả
bi n c m xác su y ra c a m n ế ố đó. Khái niệ ất dùng để đánh giá về “lượng” khả năng xả ủ ột biế
cố nào đó khi thực hiện phép th . ử
Qua quá trình phát triển của lý thuyết xác suất tùy theo đặc điểm của từng phép
thử, của các lĩnh vực nghiên cứu khác nhau, chúng ta có những cách định nghĩa khác
nha u về xác suất.
3.1. Các định nghĩa xác suất
3.1.1. Định nghĩa xác suất theo quan điểm cố điển
Xét một phép có không gian bi n c là u h n k t qu ng kh thử ế ố có hữ ạ ế ả đồ ả năng
x y ra, A là m n c . ả ột biế ố nào đó của phép th ử
Xác suất của bi n c u là P(A nh ế ố A được kí hiệ ) và được xác đị
( )
( )
( )
n A
P A
n
=
,
v ) = s t qu ng kh x y ra c a phép th , ới n( ố các kế ả đồ ả năng có thể ả ủ ử
n(A) = s các k ng kh x y ra c n c ố ết quả đồ ả năng có thể ả ủa biế ố A.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
19
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 1. Gieo m t con xúc xộ ắc/
, ta xét các bi n c ế ố sau:
A =
1 ch m, 4 ch mấ ấ
= {ch }; B = ấm có màu đỏ
1 ch m, 3 ch m; 5 ch mấ ấ ấ
.
T a bi n c a bi n c ính xác su t cấ ủ ế ố A và xác suất củ ế ố B.
Lời giải
Ta có: n() = 6, (A) = 2, (B) = 3. n n
Theo định nghĩa, xác suất của biến cố A là
( ) 2 1
( )
( ) 6 3
n A
P A
n
= = =
,
Xác su n c B là ất của biế ố
( ) 3 1
( )
( ) 6 2
n B
P B
n
= = =
.
Ví dụ 2. Trong m t cái h p có ch ) các bi này có cùng kích ộ ộ ứa (5 bi màu xanh, 3 bi màu đỏ
cỡ và tr khác nhau v các ví dọng lượng, chỉ ề u không nói gì khác thì màu sắc (sau đây nế ụ
có liên quan đến các viên bi ta thừa nh n các viên bi này có cùng kích cậ ở ng và trọng lượ
chỉ ắ khác nhau về màu s c).
L u nhiên m n 2 bi. ấy ngẫ ột lầ
a/ Tính xác su ất 2 bi được lấy ra là 2 bi xanh.
b/ Tính xác su ất 2 bi được lấy ra là 2 bi khác màu.
Lời giải
Gọi là không gian bi n c c a phép th , ta có ế ố ủ ử
2
8
( ) 28n C = =
.
a/ G c lọi A là biến cố 2 bi đượ ấy ra là 2 bi xanh, ta có
2
5
( ) 10n A C= =
,
Vậy xác su n c ất của biế ố A là
( ) 10 5
( )
( ) 28 1
n A
P A
n
= = =
.
b/ G i B là bi n c y ra là 2 bi khác màu, ta có ọ ế ố 2 bi được lấ
1 1
5 3
( ) . 15n B C C= =
,
Vậy xác su n c B là ất của biế ố
( ) 15 15
( )
( ) 28 2
n B
P B
n
= = =
.
Nhận xét
Định nghĩa xác suấ xét đốt theo cổ điển có hạn chế là chỉ i với các phép thử có
không gian các bi n c u h n các k ng kh x ế ố có hữ ạ ết đồ ả năng có thể ảy ra. Nhưng trong thực
tiễn nhi u phép th không th u ki , ch ng h là xác ề ử ỏa mãn điề ện như thế ẳ ạn như phép thử
đị ủ ộ ủ ủnh chiều dài c a m t chi tiết máy, tr ng cọng lượ a trẻ u cao csơ sinh, chiề a sinh viên...
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
20
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3.1.2. Định nghĩa xác suất theo quan điểm thống kê
Thực hiện một phép thử
n
lần với điều kiện như nhau, biến cố
A
liên kết với phép
thử xuất hiện
k
lần.
Khi đó ta gọi
( )
n
k
f A
n
=
là tần suất xuất hiện biến cố
A
trong
n
phép thử.
Khi
n
tăng lên rất lớn, dần đến vô cùng, ta thấy rằng
( )
n
f A
dao động quanh một
số
p
cố định và tiến dần về số
p
đó. T xác suất của biến cố a gọi
A
là:
( ) ( )
lim lim
n
n n
k
P A p f A
n
→+ →+
= = =
.
Trên thực tế,
( )P A
được tính xấp xỉ bởi tần suất
( )
n
f A
khi \ n đủ lớn.
Ví dụ 1 Một xạ thủ bắn 1000 viên đạn vào bia. Ta thấy có 52 viên đạn trúng bia. Khi đó,
xác suất để xạ thủ bắn trúng bia là
52
0,052
1000
=
.
Ví dụ 2
Một công ty bảo hiểm muốn xác định xác suất để một người Anh 25 tuổi
sẽ bị chết trong năm tới, người ta 100.000 thanh niên và thấy rằng có 796 người theo dõi
bị chết trong vòng 1 năm sau đó. Vậy xác suất cần tìm là:
796
0,008
100000
.
Nhận xét
Định nghĩa xác suất theo thống kê khắc phục được hạn chế của định nghĩa xác suất
theo cổ điển, nó hoàn toàn dựa trên các thí nghiệm quan sát thực tế để tìm xác suất của
biến cố, nó giải quyết được các trường hợp không gian các biến cố sơ cấp có vô hạn biến
cố sơ cấp và không cần giả thiết các biến cố đồng khả năng. Tuy nhiên, định nghĩa xác
suất theo thống kê cũng chỉ áp dụng cho các phép thử mà có thể lặp lại được nhiều lần
một cách độc lập trong những điều kiện giống hệt nhau. Ngoài ra, để xác định một cách
tương đối chính xác giá trị của xác suất thì cần tiến hành một số n đủ lớn lần các phép
thử, mà việc này đôi khi không thể làm được vì hạn chế về thời gian và kinh phí.
Ngày nay, với sự trợ giúp của công nghệ thông tin, người ta có thể mô phỏng các
phép thử ngẫu nhiên mà không cần thực hiện các phép thử trong thực tế. Điều này cho
phép tính xác suất theo phương pháp thống kê thuận tiện hơn. Và nó được ứng dụng nhiều
trong kinh tế, kĩ thuật, y học, nông lâm, sinh học …
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
21
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3.2. Các tính chất đơn giản của xác suất
Xét một phép th và A, B là hai bi n c b c a phép th ử / ế ố ất kỳ ủ ử đó, khi đó:
(tc1) 0 P(A) 1
(tc2) P(
) = 0, P() = 1
(tc3) Nếu A B thì P(A) P(B).
§4. CÁC PHÉP TOÁN VỀ XÁC SUẤT
4.1. Phép cộng xác suất
Định lý 1
Cho A, B là hai biến c c t phép th , ta có: ố ủa cùng mộ ử
P(A B) = P(A) + P(B) P(A.B) −
M h qu c suy ra t nh lý trên. ột số ệ ả đượ ừ đị
Hệ qu 1 ả
Nếu A, B là 2 bi n c xung kh c thì P(A B) = P(A) + P(B). ế ố ắ
Hệ qu 2. ả
Nếu H , H ,..., H bi n c c a cùng m t phép th và xung kh ng
1 2 n
là một hệ n − ế ố ủ ộ ử ắc từ
đôi thì P(H
1
H
2
... ) = P(H ) + P(H ) +...+ P(H H
n 1 2 n
).
Hệ qu 3. ả
Nếu H , H ,..., H h bi n c c a cùng m t phép th
1 2 n
là một ệ n − ế ố đầy đủ ủ ộ ử thì
P(H ... ) = P(H ) + P(H ) = 1.
1
H
2
H
n 1 2
) +...+ P(H
n
Hệ qu 4 ả
Nếu A, B l n c p thì P(A) = 1 P(B). à 2 biế ố đối lậ −
Hiển nhiên:
( )
( ) 1P A P A= −
.
• Chú ý
Ta có thể m r nh lý 1 ch ng h p n bi n c c a cùng m t phép th . ở ộng (mr) đị o trườ ợ − ế ố ủ ộ ử
(mr1) Cho A, B, C là ba biến c b c cùng m t phép th , ta có: ố ất kỳ ủa ộ ử
P(A B C) = P(A) + P(B) + P(C) P(A.B) P(A.C) P(B.C) + P(A.B.C). − − −
(mr2) Cho A
1
, A ,...,A n c b c ,
2 n
là n biế ố ất kỳ ủa cùng một phép thử ta có:
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
22
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Đ
1
Đ
2
?
)
( ) ( )
( )
1
1 2
, 1 , , 1
, ,
... ( 1) ...
n n
n
i i j i j nk
i j i j k
i j
i j i k k j
P A P A A P A A A P A A
−
= =
− + − + −
4.2. Phép nhân xác suất
4.2.1. Xác su ất có điều ki n ệ
Định nghĩa
Cho hai bi n c A và B. Ta g i xác su t c a bi n c A khi bi n c ế ố ọ ấ ủ ế ố ế ố B đã xảy ra
(
( )
0BP
) là xác su u ki n B.ất của A đối với điề ệ Kí hi u: ệ
( )
BAP /
.
Ví dụ 1 Một hộp có 8 viên bi, trong đó có 5 viên bi vàng, 3 viên bi đỏ ần lượ. Lấy l t ra 2
viên bi ( không hoàn lại). Tính xác suất để l n th hai l , biầ ứ ấy được bi đỏ ết rằng l n th ầ ứ
nh c bi ất lấy đượ đỏ.
Giải Gọi
i
A
n c l ng l n th (là biế ố ấy dược bi trắ ở ầ ứ i
1, 2i =
)
Ta có:
2 1
2
( / )
7
P A A =
• Chú ý:
Định nghĩa trên mang tính chất thuần túy toán học. Tuy nhiên trong thực tế, ta có
thể ng tr tính xác su t bấ ằ ực giác.
Ví dụ 2
Một b bài có 52 lá. Rút ng u nhiên 1 lá bài. Tính xác su ộ ẫ ất để rút được con Át, biết
r . ằng lá bài rút ra là lá bài màu đỏ
Giải
Gọi A là biến c ố rút được con Át
B là bi n c . ế ố rút được lá bài màu đỏ
Ta thấy trong b bài có: ộ
26 lá bài màu đỏ, nên
( )n B
= 26
2 con Át đỏ, nên
( )n AB
= 2
2 đỏ
7
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
23
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Do đó:
( )
( / )
( )
n AB
P A B
n B
=
=
2 1
26 13
=
Công thức tính xác su u ki n. ất có điề ệ
Ta xác đị điểnh công thức xác su u ki ất có điề ện theo định nghĩa cổ n.
Giả sử một phép thử đã cho có n( ) số các kết quả đồng khả năng có thể xảy ra và A, B
là hai biến cố nào đó của phép thử, khi đó ta có:
( ) ( ) (
( ) , ( ) , ( )
( ) ( ) ( )
n A n B n AB
P A P B P AB
n n n
= = =
.
Nếu có thêm điề B đã xảu kiện biến cố y ra thì tổng số các kết quả đồng kh ả năng
lúc này là n(B t qu) trong đó có n(A.B) kế ả n c rơi vào biế ố A, do đó:
( )
( )
/
( )
P AB
P A B
P B
=
(*)
(*) là công th c tính xác su t c a bi n c A khi bi n c ng cứ ấ ủ ế ố ế ố B đã xảy ra (tương ứ ủa
cùng một phép th ử).
Chứng minh
Ta chứng minh cho tr ng h p phép th có ườ ợ ử
n
ng h p cùng kh s trườ ợ ả năng. Giả ử
trong
n
ng h p này có trườ ợ
m
ng h p thu n ltrườ ợ ậ ợi cho
B
và
k
ng h p thu n l i cho trườ ợ ậ ợ
AB
. Vì
B
y ra nên s ng h p cùng khđã xả ố trườ ợ ả năng lúc này là
m
, và s ng h p ố trườ ợ
thuận l i cho ợ
A
ng h p thu n l i cho trong đó chính là số trườ ợ ậ ợ
AB
, tức là
k
. Vì v y ậ
( )
( )
( )
BP
ABP
n
m
n
k
BAP ==/
.
Ví dụ 3. Trong m t cái h p có ch ộ ộ ứa (4 bi màu xanh, 3 bi màu đỏ).
Lần th nh y ng u nhiên 1 bi không hoàn l n th hai l y ng u nhiên 1 bi. ứ ất lấ ẫ ại và lầ ứ ấ ẫ
Gọi A là bi n c bi l y l n th nh t là bi xanh, B là bi n c bi l y l n th hai là bi ế ố ấ ầ ứ ấ ế ố ấ ầ ứ
đỏ.
Khi đó A đã xả P(B/A) là xác suất của biến cố B khi biết biến cố y ra và
( )
4 3
/ .
7 6
P B A =
Ví d 4. ụ Có hai cái h p, h p I có ch ), h p II có ch a (1 bi xanh, 6 bi ộ ộ ứa (5 bi xanh, 2 bi đỏ ộ ứ
đỏ).
L u nhiên m p và t h y ng u nhiên 1 bi. ấy ngẫ ột hộ ừ ộp đó lấ ẫ
Tính xác suất bi được lấy ra là bi xanh.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
24
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Phân tích.
Ở thao tác thứ nhấ ấ ẫ ảt l y ng u nhiên một hộp có 2 kh y rnăng xả a:
+ Kh nh ả năng thứ ất:
Lấy ng c hẫu nhiên đượ ộp I, khi đó xác suất lấy được bi xanh là
5
7
.
+ Kh hai: ả năng thứ
Lấy ng u nhiê c h p IIẫ n đượ ộ , khi đó xác suất lấy được bi xanh là
1
7
.
Bây gi n u ta g i H n c l y ng p I, H n c l y ng u ờ ế ọ
1
là biế ố ấ ẫu nhiên được hộ
2
là biế ố ấ ẫ
nhiên đượ ẫu nhiên được hộp II và A là biến cố lấy ng c bi xanh.
Khi đó ta có
( ) ( )
1 2
5 1
/ , /
7 7
P A H P A H= =
.
4.2.2. Định lý nhân xác suất
4.2.2.1. Cho A, B là hai bi n c b c a cùng m t phép th , khi ế ố ất kỳ ủ ộ ử đó ta có:
(i1) P(A.B) = P(B).P(A/B) n u P(B) > 0; ế
(i2) P(A.B) = P(A).P(B/A) n u P(A) > 0. ế
4.2.2.2. Cho A , A ,..., A là n bi n c c a cùng m t phép th , th a mãn P(A .A ...A ) >
1 2 n
ế ố ủ ộ ử ỏ
1 2 n
0, khi đó, ta có:
P(A .A ...A ) = P(A ).P(A ).P(A )...P(A .A ...A )
1 2 n 1 2
/A
1 3
/A
1
A
2 n
/A
1 2 n 1−
4.2.3. Bi c l p ến cố độ ậ
4.2.3.1. Định nghĩa
Cho A, B là hai bi n c c a cùng m t phép th , n u bi n c này x y ra hay không xế ố ủ ộ ử ế ế ố ả ảy ra
không là n xác su u ki n c a bi n c kia thì ta nói hai bi n c A, m thay đổi đế ất không điề ệ ủ ế ố ế ố
B độc lập v i nhau. ớ
Hay: n u P(A/B) = P(A) ho c P(B/A) = P(B) thì ta nói A, B là hai bi n c c l p vế ặ ế ố độ ậ ới
nhau.
4.2.3.2. Cho A , A ,..., A bi n c c a cùng m t phép th , ta nói bi n c
1 2 n
là n ế ố ủ ộ ử n ế ố đó độc
l p toàn b i nhau n u m i bi n c p v i m i bi n c tích c biậ ộ vớ ế ọ ế ố trong chúng độc lậ ớ ọ ế ố ủa m ến
cố bất kỳ trong các bi n c ế ố còn lại v = 1, 2,..., 1. ới m n −
Chú ý
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
25
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
(cy1) Nếu A, B là hai bi n c p v i A, B là hai bi n c ph ế ố không độc lậ ới nhau thì ta nó ế ố ụ
thuộc nhau.
(cy2) Bi n c không th và bi n c c ch n c l p v i b t k mế ố ể ế ố chắ ắ được xem là độ ậ ớ ấ ỳ ột
bi n c ng u nhiên nào c t phép th . ế ố ẫ ủa cùng mộ ử
4.2.3.3. nh lý (v các bi n c c l p) Đị ề ế ố độ ậ
Đị ố ủ ộnh lý 1. Cho A, B là hai biến c c a cùng m t phép thử.
Điều kiệ ế ận c hai biần và đủ để n c c lố A và B độ p v i nhau là ớ
P(A.B) = P(A).P(B).
Đị ủ ộ ộnh lý 2. Nếu A , A ,..., A bi
1 2 n
là n ến cố c a cùng m t phép thử và độc lập toàn b với
nhau, thì:
P(A .A ...A ) = P(A ).P(A )... P(A
1 2 n 1 2 n
).
§5. CÔNG THỨC XÁC SUẤT TOÀN PHẦN VÀ CÔNG THỨC BAYES
5.1. Công thức xác suất toàn phần
Giả s H , H ,..., H là m các bi n c và A là m n c b cử
1 2 n
ột hệ đầy đủ ế ố ột biế ố ất kỳ ủa
cùng một phép th v biử ới n ến c ố trên, khi đó:
( ) ( )
1
( ) . /
n
i i
i
P A P H P A H
=
=
hay
P(A) = P(H ).P(A/H ) + P(H ).P( ) + P(H ).P(A/H ).P(A/H
1 1 2
A/H
2 3 3
) +...+ P(H
n n
).
5.2. ét (Bayes) Công thức Bây
−
−
−
−−
Giả s H , H ,..., H là m các bi n c và A là m n c b cử
1 2 n
ột hệ đầy đủ ế ố ột biế ố ất kỳ ủa
cùng một phép th v biử ới n ến c ố trên và có P(A) > 0, khi đó ta có:
( )
( ) ( )
. /
1, 2,..., , /
( )
j j
j
P H P A H
j n P H A
P A
= =
.
Ví dụ 1. Có hai cái h p, h p I có ch p II có ch a 2 bi xanh, 3 bi ộ ộ ứa 4 bi xanh, 1 bi đỏ và hộ ứ
đỏ.
L u nhiên m p và t h y ng u nhiên 1 bi. ấy ngẫ ột hộ ừ ộp đó lấ ẫ
a/ Tính xác su ất bi được lấy ra là bi xanh ?
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
26
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
b/ Bi ng bi l y ra là bi xanh, tìm xác su a h p II ? ết rằ ấ ất để bi đó là củ ộ thứ
Lời giải
Gọi H là bi là bi
1
ến c l p I, H ố ấy được hộ
2
ến c l p II. ố ấy được hộ
→ H , H n c và
1 2
là hệ đầy đủ các biế ố
1 2
1
( ) ( )
2
P H P H= =
.
a/ G c bi xanh , áp dọi A là biến c lố ấy đượ ụng công th c xác suứ ất toàn phần
→
( ) ( ) ( ) ( )
1 1 2 2
1 4 1 2 6 3
( ) . / . / . . 0,
2 5 2 5 10 5
P A P H P A H P H P A H= + + = = ==
.
b u c a bài toán, ta c n tính xác su/ Theo yêu cầ ủ ầ ất của
( )
2
/P H A
Áp dụng công th c Bayes ứ →
( )
( ) ( )
2 2
2
1 2
.
. /
2
2 5
/
6
( ) 3
10
P P A H
P H A
P A
H
= = =
.
Ví dụ 2. Trong một cái hộp có chứa 3 bi màu xanh, 2 bi màu đỏ.
Lần thứ nhất lấy ngẫu nhiên 1 bi và không bỏ bi đó vào lại trong hộp, lần thứ hai lấy
ngẫu nhiên 1 bi.
Tính xác suất của các biến cố sau:
a/ 2 bi l ? ấy ra đều có màu đỏ
b/ 2 bi l y ra có cùng màu ? ấ
c/ 2 bi lấy ra khác màu ?
Lời giải
Gọi X là bi i có màu xanh,
i
ến c l y l n th ố ấ ầ ứ
D n c l y l n th , v i i = 1, 2.
i
là biế ố ấ ầ ứ i có màu đỏ ớ
a/ Bi n c .D là bi n c 2 bi l u có mà n c bi l y ra l n th ế ố A = D
1 2
ế ố ấy ra đề u đỏ (biế ố ấ ầ ứ nhất
là bi đỏ và bi lấy ra lần thứ hai là bi đỏ), khi đó:
( ) ( ) ( )
1 2 1 2 1
2 1 1
. / .
5 4 10
P D D P D P D D= = =
.
b/ Bi n c B = D X n c 2 bi l y ra có cùng màu và D , X n ế ố
1
D
2
1
X
2
là biế ố ấ
1
D
2 1
X
2
là hai biế
cố xung khắc, khi đó:
( ) ( ) ( )
1 2 1 2 1 2 1 2
( )P B P D D X X P D D P X X= = +
=
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
27
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
=
( ) ( ) ( ) ( )
1 2 1 1 2 1
. / . /P D P D D P X P X X+
2 1 3 2 4
. .
5 4 5 4 10 5
= + = =
.
c/ Bi n c C = D X là bi n c 2 bi l y ra khác màu và D , X là hai bi n c ế ố
1
X
2
1
D
2
ế ố ấ
1
X
2 1
D
2
ế ố
xung kh ắc, khi đó:
( ) ( ) ( )
1 2 1 2 1 2 1 2
( )P C P D X P D P XX D X D= = +
=
=
( ) ( ) ( ) ( )
1 2 1 1 2 1
. / . /P PD P X D X P D X+
2 3 3 2 3
. .
5 4 5 4 5
= + =
.
Chú ý: Ta có th suy ra P(C) = 1 P(B) (vì B, C là hai bi n c i l p). ể − ế ố đố ậ
§6. DÃY PHÉP THỬ BECNOULLI
6.1. Dãy phép thử Bernoulli
Một dãy
n
phép thử gọi là một dãy
n
phép thử Bernoulli nếu thỏa mãn hai điều
kiện sau đây:
- Dãy
n
u. phép thử đó là độc lập với nha
- Trong mỗi phép thử chỉ xảy ra hai biến cố A hoặc
A
và xác suất xảy ra biến cố
A
trong mỗi phép thử đều là
( )
pAP =
(
0 1p
) không đổi, và xác suất xảy ra biến cố
A
là
pq −=1
.
Các bài toán thoả mãn các điều kiện trên thì được gọi là tuân theo lược đồ
Bernoulli.
Xác suất
p
gọi là , số lần xác suất thành công
A
xuất hiện trong
n
phép thử gọi là
số lần thành công trong dãy
n
phép thử Bernoulli.
Xác suất để trong phép thử Bernoulli, biến cố xuất hiện lần được kí hiệu là n A k
( )
n
P k
hay
( )
,
n
P k p
.
6.2. Công thức Bernoulli
Định lí
( )
knkk
nn
qpCpkP
−
=,
,
nk ,1=
,
pq −=1
Đẳng thức trên được gọi là công thức Bernoulli.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
28
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Chứng minh
Kí hiệu
i
A
là biến cố “phép thử thứ
i
thành công”,
ni ;1=
.
Gọi H là biến cố “có
k
lần thành công” thì H là tổng của
k
n
C
biến cố đôi một xung khắc
có dạng
nkk
iiiii
AAAAA
121 +
trong đó
niii
n
;;2;1;;;
21
=
Do tính độc lập nên ta có:
( )
( ) ( )
( )
( ) ( )
knk
iiiiiiiiii
qpAPAPAPAPAPAAAAAP
nkknkk
−
==
++
121121
Từ đó, ta suy ra:
( )
knkk
nn
qpCpkP
−
=,
(đpcm).
Hệ quả
Với lược đồ Bernoulli , xác suất để xảy ra biến cố A ít nhất lần và nhiều nhất n p, k
1
k
2
lần là:
2
1
1 2 1 1 2
( , ) ( , ) ( 1, ) ... ( , )
k k
k k n k
n n n n n
k k
P k k k p P k p P k p P k p C p
=
−
=
= + + + + =
.
Ví dụ Một lô hàng trong kho có 20% phế phẩm.
a) Lấy ngẫu nhiên sản phẩm. Tính xác suất trong sản phẩm này.5 5
i) Có 2 phế phẩm.
ii) Có ít nhất 1 phế phẩm.
b) Cần lấy ít nhất bao nhiêu sản phẩm để xác suất có ít nhất một phế phẩm không nhỏ
hơn 0,99 .
Giải
a) Bài toán trên thoả mãn lược đồ Bernoulli với
5n =
,
0, 2p =
Áp dụng công thức Bernoulli, ta có:
i) Xác suất để trong 5 sản phẩm lấy ra có 2 phế phẩm là:
( ) ( ) ( )
2048
.08,02,02,0;2
32
2
55
== CP
.
ii) Xác suất để trong 5 sản phẩm lấy ra có ít nhất 1 phế phẩm là:
( ) ( ) ( ) ( )
5
0 5
0
5 5 5 5
1
( 1;0, 2) ;0, 2 1 0; 0.2 1 0, 2 0,8 0, 6
k
P k P k P C
=
= = − = − =
.
Gọi
n
là số sản phẩm cần lấy ra. Khi đó, xác suất có ít nhất một phế phẩm là:
( ) ( ) ( )
n
n
n
k
n
PkPP 8,012,0;012,0;
1
−=−==
=
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
29
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ta cần tìm
n
nhỏ nhất sao cho
( )
99
,08,01 −
n
hay
64,20
8,0ln
01,0ln
=n
.
Vậy, ít nhất phải lấy ra
21=n
sản phẩm.
BÀI TẬP
trong h t cộp. Tính xác suấ ủa các biến c : ố
1/ 2 bi được lấy ra có cùng màu.
2/ 2 bi được lấy ra khác màu.
Bài 2.2. ong m t cái h p có ch . L y ng u nhiên m t l n 3 bi t Tr ộ ộ ứa 5 bi xanh và 2 bi đỏ ấ ẫ ộ ầ ừ
trong h t cộp. Tính xác suấ ủa các biến c : ố
1/ 3 bi được lấy ra có cùng màu.
2/ 3 bi được lấy ra có ít nhất 1 bi đỏ.
Bài 2.3. Trong m t cái h p có ch và 1 bi vàng. L y ng u nhiên mộ ộ ứa 4 bi xanh, 3 bi đỏ ấ ẫ ột
l n 2 bi t trong h p. Tính xác su t c a các bi n c : ầ ừ ộ ấ ủ ế ố
1/ 2 bi được lấy ra có cùng màu.
2/ 2 bi đượ ất 1 bi đỏc lấy ra có nhiều nh .
Bài 2.4. Trong m t cái h p có ch và 1 bi vàng. L y ng u ộ ộ ứa 3 bi xanh, 2 bi đỏ ấ ẫ
nhiên m t l n 3 bi t trong h p. Tính xác su t c n c : ộ ầ ừ ộ ấ ủa các biế ố
1/ 3 bi đượ ấy ra có đúng 2 bi xanh.c l
2/ 3 bi đượ ấy ra có đủ ba màu (xanh, đỏc l , vàng).
Bài 2.5. Trong m t cái h p có ch . L y ng u nhiên m t l n 3 bi t ộ ộ ứa 5 bi xanh và 4 bi đỏ ấ ẫ ộ ầ ừ
trong h t cộp. Tính xác suấ ủa các biến c : ố
1/ 3 bi đượ bi đỏ ấp đôi sốc lấy ra có số g bi xanh.
2/ 3 bi đượ ấy ra có đủ hai màu (xanh, đỏc l ).
Bài 2.6. Trong m t cái h p có ch và 1 bi vàng. L y ng u nhiên mộ ộ ứa 3 bi xanh, 2 bi đỏ ấ ẫ ột
l n 3 bi t trong h p. Tính xác su t c a các bi n c : ầ ừ ộ ấ ủ ế ố
1/ 3 bi được lấy ra có ít nhất 1 bi xanh.
2/ 3 bi được lấy ra có ít nhất 1 bi xanh và 1 bi đỏ.
Bài 2.7. Trong m t cái h p có ch và 1 bi vàng. L y ng u nhiên mộ ộ ứa 3 bi xanh, 2 bi đỏ ấ ẫ ột
l n 3 bi t trong h p. Tính xác su t c a các bi n c : ầ ừ ộ ấ ủ ế ố
1/ 3 bi được lấy ra có nhiều nhất 2 bi xanh.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
30
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2/ 3 bi đượ ất 1 bi đỏc lấy ra có nhiều nh .
Bài 2.8. M t nhóm g m có 10 h c sinh chuyên toán, 3 h c sinh ộ ồ ọc sinh, trong đó có 5 họ ọ
chuyên văn, 2 học sinh chuyên anh. Chọn ngẫu nhiên 4 học sinh. Tính xác suất của các
bi n c : ế ố
1/ 4 h ng. ọc sinh được chọn ra có đủ 3 đối tượ
2/ 4 h n ra có ít nh c sinh chuyên anh. ọc sinh được chọ ất 1 họ
Bài 2.9. Trong m t kho hàng có 10 s n ph m lo i I, 3 s n ph m lo i II và 2 s n ph m loộ ả ẩ ạ ả ẩ ạ ả ẩ ại
III. Chọn ng u nhiên 4 s n ph m trong kho hàng. Tính xác su a các bi n c ẫ ả ẩ ất củ ế ố:
1/ 4 s n ph c ch 3 lo n ph ả ẩm đượ ọn ra có đủ ại sả ẩm trên.
2/ 4 s n ph c ch n ra có s s n ph m lo i I b ng t ng s s n ph m lo i II và sả ẩm đượ ọ ố ả ẩ ạ ằ ổ ố ả ẩ ạ ản
ph i III . ẩm loạ
Bài 2.10. t n 25. Ch n ng u nhiên 5 t . Có 25 tấm thẻ đượ ốc đánh s ừ 1 đế ọ ẫ ấm thẻ
Tính xác suất c : ủa các bi n cế ố
1/ 5 t u mang s n. ấm thẻ được chọn ra đề ố chẵ
2/ 5 t m th có mang s t cho 3. ấm thẻ được chọn ra có đúng 3 tấ ẻ ố chia hế
Bài 2.11. t các ch s 1; 2; 3; 4; 5; 6 lên 6 t m th và s p m t cách ng u nhiên các tViế ữ ố ấ ẻ ắ ộ ẫ ấm
thẻ đó thành một hàng ngang (→ ta được một số tự nhiên gồm 6 chữ số khác nhau). Tính
xác su a các bi n c ất củ ế ố:
1/ S t nhiên nh t s n. ố ự ận được là mộ ố chẵ
2/ S t nhiên nh t s t cho 5. ố ự ận được là mộ ố chia hế
3/ S t nhiên nh c là m t s có ch s u tiên là s 1 và ch s i cùng là số ự ận đượ ộ ố ữ ố đầ ố ữ ố cuố ố 6
(chẳng h ạn như số 132546…).
Bài 2.12. Có 4 hành khách lên 2 toa tàu h a (toa I, toa II) m t cách ng u nhiên. ỏ ộ ẫ
1/ Tính xác suất mỗi toa có đúng 2 hành khách.
2/ Tính xác su t toa I có 3 hành khách và toa II có 1 hành khách. ấ
Với gi t toa tàu.ả thi t 4 hành khách có th lên cùng mế ể ộ
Bài 2.13. Có 6 hành khách lên 3 toa tàu h a (toa I, toa II, toa III) m t cách ng u nhiên. ỏ ộ ẫ
1/ Tính xác su ất mỗi toa có đúng 2 hành khách.
2/ Tính xác su t toa I có 1 hành khách, toa II có 2 hành khách, toa III có 3 hành khách. ấ
Bài 2.14. Có 4 khách hàng cùng vào mua hàng t i m t c a hàng có 5 qu y hàng. Gi s ạ ộ ử ầ ả ử
các khách hàng chọn quày hàng để hàng mmua ột cách ngẫu nhiên.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
31
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Tính xác suất của các bi n c ế ố sau:
1/ 4 khách hàng cùng vào m y hàng ?. ột quầ
2/ 4 khách hàng vào 4 qu y hàng khác nhau ?. ầ
3/ Có 3 khách hàng vào qu y s 1 ?. ầ ố
Bài 2.15. ng ch t). Tính xác su t c a n c : Gieo 2 con xúc xắc (cân đối vàg đồ ấ ấ ủ các biế ố
1/ Có ít nh t m t 1 ch ất mộ ặ ấm.
2/ Có hai m ặt 1 chấm.
3/ Không có màu đỏ nào.
Bài 2.16. ng ch t). Tính xác su n c : Gieo 2 con xúc xắc (cân đối và đồ ấ ất của các biế ố
1/ T ng s m trên hai m a hai con xúc x c b ng 10. ổ ố chấ ặt củ ắc lớn hơn hoặ ằ
2/ T ng s m trên hai m a hai con xúc x ổ ố chấ ặt củ ắc nhỏ hơn 2.
Bài 2.17. Gieo ng u nhiên 2 con xúc x ng ch t). Tính xác su t c a các ẫ ắc (cân đối và đồ ấ ấ ủ
bi n c : ế ố
1/ S m c a con xúc x a con xúc x c kia. ố chấ ủ ắc này gấp đôi số chấm củ ắ
2/ Màu s c c a hai con xúc x c là khác nhau. ắ ủ ắ
Bài 2.18. p môn xác su t và th ng kê có 12 câu h Đề cương ôn tậ ấ ố ỏi (kèm theo đáp án).
M thi g y ra m t cách ng u nhiên t ỗi đề ồm có 4 câu được lấ ộ ẫ ừ đề cương.
Giả s c thu c 4 câu. ử SV Bờm họ ộc 8 câu, SV Cu c thuội họ ộ
Tính xác suất xảy ra bi n c : ế ố
1/ SV B ờm không làm được câu nào.
2/ SV Cu 4 câu. ội làm được cả
3/ c ít nh SV Bờm làm đượ ất 3 câu.
4/ SV Cu c nhi u nh t 3 câu. ội làm đượ ề ấ
(Chú ý là B m và Cu c thu c không ờ ội rất nghiêm túc trong thi, câu nào đã họ ộc thì làm đượ
h ọc thì không làm…)
Bài 2.19. Trong m t cái h và 1 bi vàng. ộ ộp có 3 bi xanh, 4 bi đỏ
Lần th nh y ng u nhiên 1 bi và không b i vào trong h p. ứ ất lấ ẫ ỏ bi đó lạ ộ
Lần th hai l y ng u nhiên 1 bi. ứ ấ ẫ
Tính xác suất của các bi n c : ế ố
1/ 2 bi đượ ấy ra có cùng màu đỏc l .
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
32
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2/ 2 bi được lấy ra khác màu.
Bài 2.20. Trong m t cái h . ộ ộp có 3 bi xanh, 2 bi đỏ
Lần th nh y ng u nhiên 1 bi và không b l p. ứ ất lấ ẫ ỏ ại vào trong hộ
Lần th hai l y ng u nhiên 1 bi. ứ ấ ẫ
Tính xác suất của các bi n c : ế ố
1/ 2 bi được lấy ra có cùng màu.
2/ 2 bi được lấy ra khác màu.
Bài 2.21. nh gi t m nh gi y ghi ch và (Trò chơi bốc thăm) Có 4 mả ấy, trong đó có mộ ả ấ ữ có
các m nh gi y còn l i ghi ch . Có b n tham gia b n t tả ấ ạ ữ không ốn bạ ốc thăm, lầ lượ ừng người
b c trúng m nh gi y có ghi ch có thì th ng cu c. Theo các Anh (Ch ) nên ốc thăm, ai bố ả ấ ữ ắ ộ ị
b n th m y ? ốc lầ ứ ấ
Bài 2.22. M t lô hàng có 100 s n ph n ph m x u. L y ng u nhiên m ộ ả ẩm, trong đó có 5 sả ẩ ấ ấ ẫ ột
l n 4 s n ph ki u có ít nh t 1 s n ph u trong 4 s n ph c ki m tra ầ ả ẩ ểm đ ểm tra, nế ấ ả ẩm xấ ả ẩm đượ ể
thì không nhận lô hàng. Tính xác su không nh n lô hàng. ấ ểt đ ậ
Bài 2.23. Có hai cái h ng bi gi p I có ch a 4 bi xanh và 1 bi ộp đự ống như nhau, trong đó hộ ứ
đỏ ộ, h p II có ch . ứa 2 bi xanh và 3 bi đỏ
Lấy ng u nhiên m p và t h y ng u nhiên 1 bi. ẫ ột hộ ừ ộp đó lấ ẫ
1/ Tính xác su ất để bi đó là bi xanh ?
2/ Bi ng bi l y ra là bi xanh, tìm xác su p th ết rằ ấ ấ ểt đ bi đó là của hộ ứ II ?
Bài 2.24. Có ba cái h ng bi giộp đự ống như nhau, trong đó: Hộp I có 2 bi xanh và 5 bi đỏ,
h p II có 4 bi xa . L u nhiên m t h p và ộ nh và 3 bi đỏ, hộp III có 6 bi xanh và 1 bi đỏ ấy ngẫ ộ ộ
t h y ng u nhiên 1 bi. ừ ộp đó lấ ẫ
1/ Tính xác su ất để bi đó là bi xanh ?
2/ Bi ng bi l y ra là bi xanh , tìm xác su p th ết rằ ấ ất để bi đó là của hộ ứ I ?
Bài 2.25. Trong một hộp có 3 bi màu xanh, 2 bi màu đỏ. Lần thứ nhất lấy ngẫu nhiên 1 bi
và không bỏ bi đó vào lại trong hộp, lần thứ hai lấy ngẫu nhiên 1 bi.
Tính xác suất của các biến cố sau:
1/ 2 bi l u có ấy ra đề màu đỏ ?
2/ 2 bi l y ra có cùng màu ? ấ
3/ 2 bi l y ra khác màu ? ấ
Bài 2.26. Có hai cái h , h p II ộp đựng bi, trong đó hộp I có 3 bi xanh và 1 bi đỏ ộ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
33
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
có 2 bi xanh và 1 bi đỏ. Từ hộp I lấy ngẫu nhiên một bi bỏ vào hộp II, rồi từ hộp II lấy
ng u nhiên m . ẫ ột bi
1/ Tính xác su bi l y ra t h p II là bi xanh ? ất để ấ ừ ộ
2/ Bi t r ng bi l y ra t h p II là bi xanh, tìm xác su t bi l y t h p I b vào h p II là bi ế ằ ấ ừ ộ ấ ấ ừ ộ ỏ ộ
xanh.
Bài 2.27. Có ba x b n m c l p vào m t m c tiêu, xác su t b n trúng mạ thủ ắ ột cách độ ậ ộ ụ ấ ắ ục
tiêu c a x nh t là 0,7, x hai là 0,8 và x ba là 0,5. Tính xác suủ ạ thủ thứ ấ ạ thủ thứ ạ thủ thứ ất
để:
1/ Ch b n trúng m c tiêu. ỉ có đúng một xạ thủ ắ ụ
2/ Có đúng hai xạ thủ bắn trúng mục tiêu.
3/ C ba x b n không trúng m c tiêu. ả ạ thủ ắ ụ
4/ Có ít nh t x b n trúng m c tiêu. ất mộ ạ thủ ắ ụ
Bài 2.28. T l i dân t nh Q. nghi n thu c lá là 30%, t l i b b nh ph i trong s ỉ ệ ngườ ỉ ệ ố ỉ ệ ngườ ị ệ ổ ố
ngườ ố ngườ ối nghiện thuốc lá là 65%, và trong s i không nghiện thu c lá là 15%. Chọn
ng a t nh Q. ẫu nhiên 1 người củ ỉ
1/ Tính xác su b nh ph ất người đó bị ệ ổi ?
2/ Bi t b nh ph i,tính xác su i n thu c lá ? ế người đó bị ệ ổ ất để ngườ đó nghiệ ố
3/ Bi b nh ph i,tính xác su n thu ết người đó không bị ệ ổ ấ ểt đ người đó nghiệ ốc lá ?
Bài 2.29. Có hai cái h p, h p I có ch , h p II có ch a 2 bi xanh, 3 bi ộ ộ ứa 2 bi xanh, 1 bi đỏ ộ ứ
đỏ ộ ỏ ộ ộ. Từ h p I lấy ngẫu nhiên 2 bi b vào h p II (tr u), sau hộn đề đó từ p II lấy ngẫu nhiên
1 bi.
1/ Tính xác su y ra t h p II là bi xanh. ất bi được lấ ừ ộ
2/ Bi t r c l y ra t h p II là bi xanh, tính xác su t 2 bi l y t h p I b vào hế ằng bi đượ ấ ừ ộ ấ ấ ừ ộ ỏ ộp
II là cùng màu.
Bài 2.30. Có hai cái h p, h p I có ch , h p II có ch a 1 bi xanh, 1 bi ộ ộ ứa 2 bi xanh, 1 bi đỏ ộ ứ
đỏ ộ. Từ h p I lấy ngẫu nhiên 2 bi và từ hộp II lấy ngẫu nhiên 1 bi và từ 3 bi đó (trộn đều)
l y ng u nhiên 1 bi. Tính xác su l c bi xanh. ấ ẫ ất để ấy đượ
Bài 2.31. ng I có 1 con chu t tr ng và 4 con chu ng II có 2 con chuChuồ ộ ắ ột đen, chuồ ột
trắng. T ng I b t ng u nhiên 2 con chu t b vào chu ng II bừ chuồ ắ ẫ ộ ỏ ồng II, sau đó từ chuồ ắt
ra ngẫu nhiên 2 con chu ột.
1/ Tính xác su t 2 con chu chu ng II là 2 con chu t khác màu. ấ ộ ợt đư c bắt ra từ ồ ộ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
34
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2/ Bi ng 2 con chu t ra t chu ng II là 2 con chu t khác màu, tính xác su t 2 ết rằ ộ ợt đư c bắ ừ ồ ộ ấ
con chu c bột đượ ắt từ chu ng I b vào chu ng II là 2 con chu t khác màu. ồ ỏ ồ ộ
Bài 2.32. Có hai cái h ng bi giộp đự ống như nhau, trong đó: Hộp I có 2 bi xanh và 1 bi đỏ,
h p II có . T m p l y ng u nhiên ra 1 bi. ộ 3 bi xanh và 2 bi đỏ ừ ỗi hộ ấ ẫ
1/ Tính xác su y ra có cùng màu. ất để 2 bi được lấ
2/ Tính xác su y ra khác màu. ất để 2 bi được lấ
Bài 2.33. Có ba cái hộp đựng bi, trong đó hộp I có 2 bi xanh 3 bi đỏ, hộp II có 1 bi xanh 2
bi đỏ, hộp III có 1 bi xanh 1 bi đỏ. Từ hộp I và từ hộp II, mỗi hộp lấy ngẫu nhiên 1 bi đem
bỏ vào hộp III (trộn đều), sau đó từ hộp III lấy ngẫu nhiên 1 bi.
1/ Tính xác suất bi lấy ra từ hộp III là bi xanh.
2/ Biết rằng bi lấy ra từ hộp III là bi xanh, tính xác suất bi lấy từ hộp I và bi lấy từ hộp II
bỏ vào hộp III là 2 bi khác màu.
Bài 2.34. Trong m t chu ng nh t th , có 4 th ng và 2 th nâu. ộ ồ ố ỏ ỏ trắ ỏ
Lần th nh g u nhiên 2 con th ng khác. ứ ất nười ta bắt n ẫ ỏ để đưa sang chuồ
Lần th hai b t ra ng u nhiên 2 con. ứ ắ ẫ
1/ Tính xác su 2 con th l n th hai là 2 con th ng. ất để ỏ được b ắt ra ở ầ ứ ỏ trắ
2/ Bi t r ng 2 con th c b t ra l n th hai là 2 con th ng, tính xác su 2 con ế ằ ỏ đượ ắ ở ầ ứ ỏ trắ ất để
th trỏ đượ c bắt ở lần th nhứ ấ ểt đ ng khác là 2 con thđưa sang chuồ ỏ ắng.
Bài 2.35. Trong m t h ng bóng bàn, có 4 qu bóng m i và 2 quộ ộp đự ả ớ ả bóng cũ (bóng mới
là bóng chưa dùng lần nào, bóng cũ là bóng đã dùng ít nhất một lần). Lần thứ nhất lấy
m ra dùng và dùng xong b l i vào trong h p, l n th hai l y m ra dùng. ột quả ỏ ạ ộ ầ ứ ấ ột quả
1/ Tính xác su qu bóng dùng l n th ất để ả ầ ứ hai là bóng cũ.
Từ t bóng dùng l n th hai là bóng mđó suy ra xác suấ ầ ứ ới.
2/ Bi t r ng bóng dùng l n th t bóng dùng l n th nh t là ế ằ ầ ứ hai là bóng cũ, tính xác suấ ầ ứ ấ
bóng m ới.
Bài 2.36. Trong m t h ng bóng bàn, có 3 qu bóng m i và 1 qu bóng ộ ộp đự ả ớ ả cũ (bóng mới
là bóng chưa dùng lần nào, bóng cũ là bóng đã dùng ít nhất một lần). Lần thứ nhất lấy
m ra dùng và dùng xong b l i vào trong h p, l n th hai l y m ra dùng. ột quả ỏ ạ ộ ầ ứ ấ ột quả
1/ Tính xác su qu bóng dùng l n th hai là bóng m ất để ả ầ ứ ới.
2/ Bi t r ng bóng dùng l n th hai là bóng m i, tính xác su t bóng dùng l n th nh t là ế ằ ầ ứ ớ ấ ầ ứ ấ
bóng cũ.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
35
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Bài 2.37. Trong m t h ng bóng bàn, có 1 qu bóng m i và 4 qu mộ ộp đự ả ớ ả bóng cũ (bóng ới
là bóng chưa dùng lần nào, bóng cũ là bóng đã dùng ít nhất một lần). Lần thứ nhất lấy
m ra dùng và dùng xong b l i vào trong h p, l n th hai l y m ra dùng. ột quả ỏ ạ ộ ầ ứ ấ ột quả
1/ Tính xác su qu bóng dùng l n th hai là bóng m ất để ả ầ ứ ới.
2/ Bi t r ng bóng dùng l n th hai là bóng m i, tính xác su t bóng dùng l n th nh t là ế ằ ầ ứ ớ ấ ầ ứ ấ
bóng m ới.
Bài 2.38. Có hai cái h p, h p I có ch và h p II có ch ộ ộ ứa 2 bi xanh, 4 bi đỏ ộ ứa 3 bi
. xanh, 1 bi đỏ
Do sơ ý ở hộp I mất 1 bi.
Sau đó, từ hộp I lấy ngẫu nhiên ra 1 bi bỏ vào hộp II và tiếp tục từ hộp II lấy ngẫu nhiên
ra 1 bi.
1/ Tính xác su t bi l y ra t h p II là bi xanh ấ ấ ừ ộ ?.
2/ Bi t r ng bi l y ra t h p II là bi xanh, tính xác su t bi l y t h p I b vào h p II là bi ế ằ ấ ừ ộ ấ ấ ừ ộ ỏ ộ
đỏ ?.
Bài 2.39. Có hai lô hàng, lô I có ch a 6 s n ph m t t và 1 s n ph m x u và lô II có ch a 4 ứ ả ẩ ố ả ẩ ấ ứ
s n ph t và 2 s n ph u. ả ẩm tố ả ẩm xấ
Ở lô I người ta lấy ra ngẫu nhiên 2 sản phẩm.
Sau lô I l y ng u nhiên ra 2 s n ph m b vào lô II và ti p t y ng u nhiên đó, từ ấ ẫ ả ẩ ỏ ế ục từ lô II lấ ẫ
ra 2 sản ph ẩm.
1/ Tính xác su t 2 s n ph y ra t n ph m t ấ ả ẩm lấ ừ lô II là 2 sả ẩ ốt.
2/ Bi t r ng 2 s n ph c l y ra t lô II là 2 t t. Tính xác su t 2 s n ph c l y t ế ằ ả ẩm đượ ấ ừ ố ấ ả ẩm đượ ấ ừ
lô I b m tỏ vào lô II là 2 s n phả ẩ ốt.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
36
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Chương 2. BIẾN NGẪU NHIÊN (ĐẠI LƯỢNG NGẫU NHIÊN)
§1. BIẾN NGẪU NHIÊN
1.1. Định nghĩa
−
−
−
−− Ví dụ
1.1.1. Định nghĩa
Xét một phép th có không gian các bi n c là . ử ế ố
M t ánh x X: R i là m n ng u nhiên m u ( ỗi mộ ạ → (R
n
) được gọ ột biế ẫ ột chiề n
chiều) liên kết với phép th ử đó.
(+) Biến ng u nhiên m u (g t là bi n ng u bẫ ột chiề ọi tắ ế ẫu nhiên) thường được kí hiệ ởi các
chữ a X, Y, Z... in ho
(+) Giá trị c n ng c kí hi u b i các ch ng x, y, z... ủa các biế ẫu nhiên đượ ệ ở ữ thườ
(+) Cho X là một b t phép thi n ng u nhiên liên k t v i mế ẫ ế ớ ộ ử có không gian các bi n c ế ố sơ
cấp là là k =  / ết quả c a phép th , v i a, b R , ta kí hiủ ử ới mọ ệu:
(kh1) (X = a) := bi ) = aến c / X(ố 
(kh2) (X < a) := bi ) < aến c ố  / X(
(kh3) (X > a) := bi ) > aến c / X(ố 
(kh4) (a X < b) := bi n c ) < b . ế ố  / a X(
Tập t các giá tr có th a m n ng c g i là mi n giá ất cả ị ể có củ ột biế ẫu nhiên đượ ọ ề trị của
bi n ng u nhiên. ế ẫ
Ví dụ 1
Gieo một đồng xu. G i X là bi n ng u nhiên s m t N x ọ ế ẫ chỉ ố ặ ảy ra, khi đó
X: → R
N ↦ 1
S ↦ 0
X có miền giá tr {0; 1} ị
Ví dụ 2
Gieo hai đồng xu. G i X là biọ ế ẫ ặn ng u nhiên ch s mỉ ố t N x ó ảy ra, khi đ
X: → R
NN 2 ↦
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
37
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
NS 1 ↦
SN 1 ↦
0 SS ↦
X có miền giá tr {0; 1; 2} ị
Ở ví dụ ỉ ố ỉ ố 2, ta có (X < 2) ch biến c {SS; SN; NS}, (X 2) ch biến c {NN}...
1.1.2. Chú ý
(cy1)Một phép thử có thể u bicó rất nhiề ến ngẫu nhiên liên kết với phép th ử đó.
(cy2) Một bi n ng u nh u liên k t v i m bi u di n b ế ẫ iên n chiề ế ớ ột phép thử có thể ể ễ ởi một bộ
g n ng u nhiên (m u) cùng liên k i phép th ồm n biế ẫ ột chiề ết vớ ử đó.
1.2. Phân loại các biến ngẫu nhiên
1.2.1. Bi u nhiên r c ến ngẫ ời rạ
Biến ng u nhiên c g là bi n ng u nhiên r i r c n u mi n giá tr c a nó là ẫ X đượ ọi ế ẫ ờ ạ ế ề ị ủ
t p h u h n hay t p vô h c (m t dãy s vô h n). ậ ữ ạ ậ ạn đếm đượ ộ ố ạ
Miền giá tr h u h n c n ng u nhiên r i u x , x ,..., x . ị ữ ạ ủa biế ẫ ời rạc kí h ệ
0 1 n
Miền giá tr vô h n c a bi n ng u nhiên r x , x ,..., x ,... . ị ạ ủ ế ẫ ời rạc đư ệợc kí hi u
0 1 n
• Chú ý
Biến ng u nhiên r i r c X ch nh n giá tr a R v t qu c a phép th g i là ẫ ờ ạ ỉ ậ ị ới mọi kế ả ủ ử ọ
bi n ng u nhiên h ng, ta có th vi xem m t h ng sế ẫ ằ ể ết a thay cho X và do đó có thể ộ ằ ố nào đó
cũng là ế ẫ một bi n ng u nhiên.
1.2.2. Bi u nhiên c ến ngẫ liên tụ
Biến ng c g i là bi n ng u nhiên liên t c n u mi n giá tr c a nó là ẫu nhiên X đượ ọ ế ẫ ụ ế ề ị ủ
m t kho n s c, các ph n t c a mi n giá tr c a X không th t kê theo ộ ảng hay đoạ ố thự ầ ử ủ ề ị ủ ể liệ
thứ t ự được.
• Chú ý
Trong th c hành, các bi n ng u nhiên có mi n giá tr h u nh c l y mự ế ẫ ề ị ầ ư dày đặ ấp đầ ột
kho ng hay m n s c c xem là bi n ng u nhiên ả ột đoạ ố thự nào đó đượ ế ẫ
liên tục.
1.3. Các phép toán trên biến ngẫu nhiên
Nhận xét: Bi n ng u nhiên là m t ánh x , do án trên các ánh x . ế ẫ ộ ạ đó có các phép to ạ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
38
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
§2. DÃY PHÂN PHỐI VÀ HÀM MẬT ĐỘ XÁC SUẤT
2.1. Hàm ph n ân phối xác suất của biến ngẫu nhiê
Khi xét đến biến ngẫu nhiên ta không chỉ quan tâm đến giá trị của biến ngẫu nhiên
đó mà cần phải biết đến khả năng xuất hiện giá trị đó, bởi vì có nhiều biến ngẫu nhiên
khác nhau mà lại có cùng giá trị, một trong những khái niệm giúp ta phân biệt được sự
khác nhau của các biến ngẫu nhiên là khái niệm hàm phân phối xác suất.
2.1.1. Định nghĩa
Cho biến ng u nhiên X (r c hay c). ẫ ời rạ liên tụ
Hàm phân phối xác su n ng nh: ất của biế ẫu nhiên X, được kí hiệu F(x) và xác đị
xR, F(x) = P(X<x)
Ví dụ
Thực hiện phép ng xu, g i X là bithử gieo 2 đồ ọ ến ngẫu nhiên ch s mỉ ố ặt N xảy ra.
Lập hàm phân ph i xác su ố ất của X.
0 0
1
0 1
4
( )
3
1 2
4
1 2
x
x
F x
x
x
=
1/4
2
F
(
x
)
x
1
3/4
1
O
2.1.2. Tính ch t ấ
Giả s F(x) là hàm phân ph i xác su a bi n ng u nhiên X. Ta ử ố ất củ ế ẫ có:
(tc1) 0 F(x) 1, xR.
(tc2)
lim ( ) 1 , lim ( ) 0
x x
F x F x
→ →−
= =
(tc3) F(x) là hàm không gi m trên R ả
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
39
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
(tc4) F(x) liên t c bên trái t ụ ại mọi điểm.
2.1.3. H ệ quả
(hq1) a,bR, a < b, ta có: P(a X < b) = F(b) F(a). −
(hq2) Nếu X là biến ngẫu nhiên liên tục t liên tục tại hì hàm phân phối xác suất F(x) xR
và x R, ta có: P(X = x) = 0.
2.2. Dãy phân phối xác suất của biến ngẫu nhiên rời rạc
2.2.1. Định nghĩa
Giả s bi n ng u nhiên r n giá tr x , x , x ,..., x ho x , x , ử X là ế ẫ ời rạc có miề ị là
0 1 2 n
ặc
0 1
x ,..., x ,... .
2 n
Đặt p
i
= P(X = x 1, 2, ..., n ( ) , (X = x
i
), i = 0,
i
)
, khi đó dãy số:
p , p , p ,..., p i là dãy phân ph t c n u nhi c X
0 1 2 n
(...) được gọ ối xác suấ ủa biế ngẫ ên rời rạ
và b ng s ng phân ph a X hay còn g i là b ng bi u ả ố có dạng như sau gọi là bả ối xá t cc suấ ủ ọ ả ể
th luị ật phân ph i xác su X. ố ất của
X
x
1
x
2
...
x
n
p
i
p
1
p
2
...
p
n
Ví dụ
Trong một cái hộp có ch a (3 bi màu xanh, 5 bi màu ) các bi này có cùng kích ứ đỏ
cở và tr khác nhau vọng lượng, chỉ ề màu sắc. Lấy ng u nhiên m n 2 bi. G i X ẫ ột lầ ọ là biến
ng u nhiên ch s bi màu x ẫ ỉ ố anh được lấy ra.
L p b ng phân ph i xác su a X. ậ ả ố ất củ
Lời gi i ả
X có miền giá tr {0; 1; 2}, ị ta có :
0 2 1 1 2 0
3 5 3 5 3 5
2 2 2
8 8 8
. . .
10 15 3
( 0) ; ( 1) ; ( 2)
28 28 28
C C C C C C
P X P X P X
C C C
= = = = = = = = =
.
X có bảng phân ph i xác su ố ất:
X
0
1
2
p
i
10/28
15/28
3/28
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
40
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2.2.2. Tính ch t ấ
Giả s bi n ng u nhiên X có b ng phân ph i xác su ử ế ẫ ả ố ất
X
x
1
x
2
...
x
n
p
i
p
1
p
2
...
p
n
Khi đó, ta có:
1/ 0 < p < 1, i = 0, 1, 2, ... , n(
i
)
2/ p = p + p + p + ... + p
i 0 1 2 n
(+...) = 1
2.2.3. Liên h gi a hàm phân ph i xác su t và b phân ph i xác su a bi n ngệ ữ ố ấ ảng ố ất củ ế ẫu
nhiên r i r c ờ ạ
Giả s bi n ng u nhiên X có b ng phân ph i xác su ử ế ẫ ả ố ất
X
x
1
x
2
...
x
n
p
i
p
1
p
2
...
p
n
Khi đó, ta có:
1
1 1 2
1 2 2 3
0,
,
( ) ,
...
1,
n
x x
p x x x
F x p p x x x
x x
= +
Ví dụ
Cho biến ng u nhiên r ng phân ph ẫ ời rạc X có bả ối xác suất:
X
0
1
2
3
p
i
0,4
0,2
0,1
0,3
L p hàm phân ph i xác su a X. ậ ố ất củ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
41
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Lời giải
0 0
0, 4 0 1
( )
0,6 1
0,7 2 3
1 3
x
x
F x
x
x
x
=
2
x
1
F
(
x
)
0,6
0,7
0,4
1
3
O
2.3. Hàm mật độ xác suất của biến ngẫu nhiên liên tục
2.3.1. Định nghĩa
Cho X là biến ng u nhiên liên t àm m t phân ph i xác su t F(x). N u t n tẫ ục, có h ậ ố ấ ế ồ ại
hàm f(x) không âm và kh ả tích trên R, sao cho:
, ( ) ( )
x
x R F x f t d
−
=
.
thì f(x) đư t đợc gọi là hàm mậ ộ xác suất của biế ẫn ng u nhiên liên tục X.
2.3.2. Tính ch t c a hàm m ấ ủ ật độ
Giả s t x t c n ng u nhiên liên t ử f(x) là hàm mậ độ ác suấ ủa biế ẫ ục X, khi đó ta có:
(tc1)
( ) 1
+
−
=
f x dx
(tc2)
, , , ( ) ( )
=
b
a
a b R a b P a X b f x d
(tc3) Nếu f(x) liên t y F(x) kh vi t R ục tại xR, ha ả ại x , thì F’(x) = f(x).
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
42
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
F(x)
x
O
x
O
f(x)
2.4. m phâ Bài toán về hà n phối xác suất và hàm mật độ xác suất
Nội dung bài toán: Xét bi n ng u nhiên X, cho hàm phân ph i xác su t F(x) hãy tìm hàm ế ẫ ố ấ
m xác su ật độ ất và ngược lại.
Ví dụ
Cho biến ng u nhiên liên t ó hàm m ẫ ục X c ật độ xác suất f(x) xác định như sau:
3.
0 0;
2
( )
.cos 0;
2
x
f x
k x x
=
1/ Xác định k.
2/ L p hàm phân ph i xác su t F(x) c a bi n ng u nhiên X. ậ ố ấ ủ ế ẫ
3/ Tính
0
4
P X
.
Lời giải
1/ Xác định giá trị k.
+
( ) 0, .cos 0,f x x k x x k →
vì
cos 0, 0;
2
x x
+
0
2
0
2
( ) 1 ( ) ( ) ( )f x dx f x dx f x dx f x
+ +
− −
= + + =
( )
2 2
0 0
2
0
( ) 1 .cos 1 .sinx 1f x dx k xdx k k
= = = =
(thỏa mãn k 0). V ậy k = 1.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
43
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2/ L p hàm phân ph i xác su a X. ậ ố ất củ
Ta có:
( ) ( )
x
F x f t dt
−
=
; x R
+ x 0 x) = 0; → F(
+
0
0 0
0
0 ( ) ( ) ( ) cos sin sin
2
x x
x
x F x f t dt f t dt tdt t
−
→ = + = = =
;
+
0
2 2
0 0
2
2
0
( ) ( ) ( ) ( ) cos sin
2
x
x F x f t dt f t dt f t dt tdt t
−
→ = + + = = =
;
Vậy
0 0
( ) sin 0
2
1
2
x
F x x x
x
=
.
3/ Tính
2
0 (0) sin sin 0
4 4 4 2
P X F F
= − = − =
.
§ 3. CÁC THAM SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN
3.1. Số trung vị
3.1.1. Định nghĩa
Cho X là một biến ng u nhiên. ẫ
Nếu t n t i sồ ạ ố thực a sao cho
1
( )
2
P X a
và
1
( )
2
P X a
thì s c g i là ố a đượ ọ
trung v c a bi n ng u nhiên X. ị ủ ế ẫ
Kí hiệu: a = med(X).
3.1.2. H ệ quả
i/ N i rếu X là bi n ng u nhiên rế ẫ ờ ạc và có
1 1
;
2 2
i i
i i
x a x a
p p
thì med(X) = a.
ii/ Nếu X là bi n ng u nhiên liên tế ẫ ục và có
1
( )
2
F a =
hoặc
1
( )
2
a
f x dx
−
=
med(X) = a. thì
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
44
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 1
Tìm số trung v c a bi n ng u nhiên r c X có b ng phân ph i xác su ị ủ ế ẫ ời rạ ả ố ất:
X
0
1
2
3
p
i
0,2
0,1
0,4
0,3
Ta có
1
( 2) 0, 2 0,1 0,3
P X = + =
và
1
( 2) 0,3
2
P X =
, do đó med(X) = 2.
Ví dụ 2
Tìm số trung v c a bi n ng u nhi t c X có hàm phân ph i xác ị ủ ế ẫ ên liên ụ ố suất F(x) như
sau
2
0 0
( ) 0 2
8
1 2
x
x
F x x
x
=
.
Ta có
2
1 1
( ) 2
2 8 2
x
F x x= = =
,
1
(2)
2
F =
, do đó med(X) = 2.
3.1.3. Ý n ghĩa
S n ng u nhiên. ố trung vị là số đặc trưng cho giá trị trung tâm của biế ẫ
3.1.4. Chú ý
Đố ớ ờ ối v i biến ngẫu nhiên r i rạc có thể có nhiều s trung vị khác nhau,
nhưng đố ị, đười với biến ngẫu nhiên liên tục chỉ có duy nhất một số trung v ng thẳng có
phương t ởi đồ ật độrình x = a = med(X) chia hình phẳng giới hạn b thị của hàm m xác
suất f(x) thành hai ph n có di n tích b ng nhau . ầ ệ ằ
3.2. Số MOD (Modal)
3.2.1. Định nghĩa
Cho X là một biến ng u nhiên, s nh: ẫ ố Mod của X được kí hiệu Mod(X) và xác đị
i/ N t bi i rếu X là mộ ến ng u nhiên rẫ ờ ạc và n u P(X = a) = maxP(X = x , ế
i
) = p
i
i = 1, 2, ..., i là s Mod c ta vi t a = Mod(X) n thì số thực a được gọ ố ủa X và ế
ii/ Nếu X là bi n ng u nhiên liên t c có hàm m xác su t là f(x) và n u f(x) ế ẫ ụ ật độ ấ ế
đạ ị ố ọ ốt giá tr lớn nhất tại x = a thì s thực a được g i là s Mod của X và ta viết a =
Mod(X).
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
45
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 1
Tìm số Mod c a bi n ng u nhiên X có b ng phân ph i xác su ủ ế ẫ ả ố ất:
X
0
1
2
3
p
i
0,3
0,2
0,4
0,1
Ta có p
3
= P(X = 2) = 0,4 = max{0,3; 0,2; 0,1}, do đó Mod(X) = 2.
Ví dụ 2
Tìm số Mod c a n ng u nhiên liên t c X có hàm m xác su tủ biế ẫ ụ ật độ ấ
2
( ) 2 5f x x x= − + +
.
Ta dễ dàng t c GTLN c a f(x) b ng 2 t i x = ìm đượ ủ ằ − ạ −1, do đó Mod(X) = −1.
3.2.2. Chú ý
S Mod c a m t bi n ng u nhiên X có th có ho c không và có th có nhi u giá tr ố ủ ộ ế ẫ ể ặ ể ề ị
khác nhau.
S Mod là m t trong các s n ng u nhiên. ố ộ ố đặc trưng cho giá trị trung tâm của biế ẫ
3.3. Kì vọng toán của biến ngẫu nhiên
3.3.1 . Định nghĩa
Cho X là m t bi n ng u nhiên. Kì v ng toán (g i t t là k v ng) c a bi n ngộ ế ẫ ọ ọ ắ ỳ ọ ủ ế ẫu
nhiên X, kí hi nh nh ệu E(X) và xác đị ư sau:
i1/ N i r t ếu X là bi n ng u nhiên rế ẫ ờ ạc có bảng phân ph i xác suố ấ
X
x
1
x
2
x
3
…
x
n
…
p
i
p
1
p
2
p
3
…
p
n
…
và n u ế
1
i i
i
x p
=
h i t tuy ng h p X có mi n giá tr là t p vô hộ ụ ệt đối trong trườ ợ ề ị ậ ạn đếm được
thì
1
( )
n
i i
i
E X x p
=
=
.
i2/ N u X là bi n ng u nhiên liên t c có hàm m xác su t là f(x) và nế ế ẫ ụ ật độ ấ ếu
( )xf x dx
+
−
hội
t ụ tuyệt đối thì
( ) ( )E X xf x d
+
−
=
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
46
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 1
Tính kỳ v ng c a bi n ng u nhiên X có b ng phân ph i xác su ọ ủ ế ẫ ả ố ất
X
1
2
3
4
5
p
i
0,2
0,
1
0,
2
0,
4
0,
1
Ta có E(X) = 0,2 1 + 0,1 2 + 0,2 3 + 0,4 4 + 0,1 5 = 3,1.
Ví dụ 2
Tính kỳ v ng c a bi n ng u nhiên liên t c X có hàm m xác su ọ ủ ế ẫ ụ ật độ ất
2
0 nêu x [0;1]
( )
1 nêu x [0;
f x
x
=
−
Ta có
( )
0 1 1
2
0 1 0
1
( ) . ( ) . ( ) . ( ) . ( ) . 1E X x f x dx x f x dx x f x dx x f x dx x x
− −
= = + + = − =
.
3.3.2. Ý nghĩa của kỳ vọng
Kỳ v ng c a bi n ng u nhiên X là s giá trọ ủ ế ẫ ố đặc trưng về ị trung bình theo xác suất
của t a X.ất cả các giá tr cị ủ
3.3.3. Tính t chấ
(tc1) Nếu X là biến ng u nhiên hẫ ằng X = a thì E(X) = E(a) = a;
(tc2) Cho X là biến ng u nhiên có k v ng là E(X). ẫ ỳ ọ
Khi đó: kR ta có E(kX) = k.E(X).
(tc3) Cho X, Y là hai bi n ng u nhiên cùng liên k t v i m t phép th và có kì v ng E(X), ế ẫ ế ớ ộ ử ọ
E(Y).
Khi đó t trườta có: E(X Y) = E(X) E(Y) (xé ng hợp tổng quát cho bin ến ngẫu
nhiên).
(tc4) Cho X, Y là hai bi n ng u nhiên cùng liên k t v i m t phép th c l p v i nhau, ế ẫ ế ớ ộ ử và độ ậ ớ
có kì vọng ng E(X), E(Y). tương ứ
Khi đó: X.Y có kì vọng và E(X.Y) = E(X).E(Y) (xét trường hợp tổng quát cho n
bi n ng u nhiên). ế ẫ
3.4. Phương sai của biến ngẫu nhiên
3.4.1. Định nghĩa
Cho X là một biến ng u nhiên có kì v ng toán E(X) = a. ẫ ọ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
47
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Nếu bi n ng u nhiên ế ẫ X − E(X) có kì v ng thì kì v c g
2
ọ ọng đó đượ ọi là phương sai
của biến ng u nhiên X. ẫ
Kí hi u: D(X). ệ
Vậy: D(X) = E((X − E(X))
2
).
3.4.2. H ệ quả
Xét X là một biến ngẫu nhiên, khi đó ta có:
Nếu tồn tại kì vọng của biến ngẫu nhiên X và X thì tồn tại phương sa của biến
2
i
ngẫu nhiên X và ta có:
D(X) = E(X
2
) ) (X) ). − E(X)
2
= E(X
2
− E
2
(X) ( ở đây E(X)
2
= E
2
Ví dụ 1
Tính phương sai của biến ngẫu nhiên X có bảng phân phối xác suất
X
0
1
2
3
p
i
0,2
0,4
0,3
0,1
Ta có: E(X) = 0,20 + 0,4 1 + 0,3 2 + 0,1 3 = 1,3
E(X
2
) = 0,20 + 0,4 + 0,3 2 + 0,1 = 2,5
2
1
2
2
3
2
D(X) = E(X
2
) − E(X)
2
= 0,81
Ví d 2 ụ
Tính phương sai củ ẫ ụa biến ng u nhiên liên t c X có hàm mật độ ấ xác su t
2
0 nêu x [0;1]
( )
1 nêu x [0;
f x
x
=
−
Ta có:
( )
0 1 1
2
0 1 0
1
( ) . ( ) . ( ) . ( ) . ( ) . 1E X x f x dx x f x dx x f x dx x f x dx x x
− −
= = + + = − =
( ) ( )
0 1 1
2 2 2 2 2 2 2
0 1 0
2
. ( ) . ( ) . ( ) . ( ) . 1E X x f x dx x f x dx x f x dx x f x dx x x dx
− −
= = + + = − =
D(X) = E(X
2
) − E(X)
2
=
17
240
.
3.5. Độ lệch tiêu chuẩn (độ lệch quân phương)
Định nghĩa
Cho biến ngẫu nhiên X có phương sai D(X).
Khi đó
( )D X
được gọi là độ lệch tiêu chuẩn, kí hiệu
( )X
, vậy
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
48
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
( ) (X D X
=
.
3.6. Mômen
3.6.1. Định nghĩa
Cho X là một biến ngẫu nhiên và a R.
Nếu tồn tại E vọng đó được gọi là mômen cấp k (k N) của biến (X−a)
k
thì kì
ngẫu nhiên X đối với điểm a, kí hiệu m
k
(a).
+/ Nếu a = 0 thì m (0) gọi là mômen gốc cấp k của biến ngẫu nhiên X.
k
+/ Nếu a = E(X) thì m (E(X)) gọi là mômen trung tâm cấp k của biến ngẫu nhiên X và khi
k
đó kí hiệu
k
,
tức là
k
= m
k
(E(X)).
3.6.2. Ý nghĩa
Khái niệm mômen khái quát hoá các khái niệm về kì vọng toán và phương sai và
để x về hình dạng của đồ thị của hàm mật độ;ác định rõ thêm
+/ Mômen gốc cấp 1 chính là kì vọng toán của biến ngẫu nhiên X;
+/ Mômen trung tâm cấp 2 là phương sai của biến ngẫu nhiên X;
+/ Mômen trung tâm cấp 3 ( ) đặc trưng cho tính bất đối xứng của luật phân phối x
3
ác
suất của biến ngẫu nhiên X
Nếu biến ngẫu nhiên X đối xứng đối với E(X) thì
3
0. =
Nếu > 0 thì P(X>E(X)) > P(X<E
3
(X))
(phân phối xác suất của biến ngẫu nhiên X nặng về phía bên phải của E(X)).
Nếu
3
< 0 thì P(X>E(X)) < P(X<E(X))
(phân phối xác suất của biến ngẫu nhiên X nặng về phía bên trái của E(X)).
+/ Mômen trung tâm cấp 4 ( ) đặc trưng cho độ nhọn của đường cong hàm mật độ xác
4
suất của biến ngẫu nhiên X.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
49
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
§ 4. BIẾN NGẪU NHIÊN n
−
−
−
−− CHIỀU
4.1. Định nghĩa
−
−
−
−− Ví dụ
4.1.1. Định nghĩa
Xét một phép th có không gian các bi n c là . ử ế ố
M i m t ánh x R c g i là m t bi n ng u nhiên u liên k t vỗ ộ ạ X: →
n
đượ ọ ộ ế ẫ n − chiề ế ới
phép th ử đó.
Trong giáo trình này ta ch xét bi n ng u nhiên 2 n, ta kí hiỉ ế ẫ − chiều và để đơn giả ệu
(X;Y) là bi n ng u nhiên 2 u mà không c n nói rõ X; Y là hai bi n ng u nhiên cùng ế ẫ − chiề ầ ế ẫ
liên k t v i mế ớ ột phép th . ử
4.1.2. Ví d ụ
(vd1). Gieo một con xúc x ắc.
Gọi X là biến ng u nhiên ch s ẫ ỉ ố chấm xảy ra, Y là bi n ng u nhiên ch s m x y ế ẫ ỉ ố ặt màu đỏ ả
ra, khi đó ta có (X;Y): → R
2
Chẳng h n: ạ
+ N u x y ra m có 3 ch b ng 3 và y có giá tr b ng 0. ế ả ặt ấm thì X có giá trị ằ ị ằ
+ N u x y ra m t có 1 b ng 1 và y có giá tr b ng 1... ế ả ặ chấm thì X có giá trị ằ ị ằ
(vd2). Gieo hai con xúc xắc.
Gọi X là biến ng u nhiên ch t ng s ẫ ỉ ổ ố chấm x t cảy ra trên hai mặ ủa con xúc x c, Y là biắ ến
ng u nhiên ch s m x ẫ ỉ ố ặt màu đỏ ảy ra, khi đó ta có
(X;Y): → R
2
Chẳng h n: ạ
+ N u x y ra m t có 4 ch m và m t m m thì X có giá tr b ng 10 vế ả ột mặ ấ ộ ặt có 6 chấ ị ằ à Y có
giá tr b ng 1 ị ằ
+ N u x y ra m t có 2 ch m và m t m t có 5 ch m thì X có giá tr b ng 7 và Y có giá ế ả ột mặ ấ ộ ặ ấ ị ằ
trị bằng 0
+ N u x y ra m t có 1 ch m và m t m t có 1 ch m thì X có giá tr b ng 2 và Y có giá ế ả ột mặ ấ ộ ặ ấ ị ằ
trị bằng 2...
4.2. Hàm phân phối xác suất của biến ngẫu nhiên 2
−
−
−
−− chiều
4.2.1. Định nghĩa
Xét một biến ng u nhiên 2 u (X;Y). ẫ − chiề
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
50
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
x,y R, kí hi u (X < x;Y < y) = (X < x)(Y < y). ệ
Hàm phân phối xác su n ng u nhiên 2 u (X;Y c kí hi u F(x;y) và xác ất của biế ẫ − chiề ) đượ ệ
định x,y R, F(x;y) = P(X < x).P(Y < y).
4.2.2. Tính ch t ấ
Giả s F(x;y) là m t hàm phân ph i xác su n ng u nhiên 2 u (X;Y). Khử ộ ố ất của biế ẫ − chiề i
đó, ta có:
tc1/ x,y F(x;y) 1. R, 0
tc2/
lim ( ; ) 1
x
y
F x y
→
→
=
,
1
lim ( ; ) ( )
y
F x y F x
→
=
,
2
lim ( ; ) ( )
x
F x y F y
→
=
,
Trong đó F
1
(x) là hàm phân phố ủi xác suất c a biến ngẫu nhiên X, F
2
(y) là hàm
phân ph i xác su t c a bi n ng u nhiên ố ấ ủ ế ẫ Y.
tc3/ F(x;y) là hàm không giảm theo t ng bi n. ừ ế
tc4/ ta có: x , x , y , y < x , y < y ,
1 2 1 2
R, x
1 2 1 2
P(x Y < y ) = F(x ) + F(x F(x F(x
1
X < x
2
; y
1
2 1
; y
1 2
; y
2
) −
1
; y
2
) −
2
; y
1
).
4.2.3. Định lý
Điề ệ ế ếu ki n c hai biần và đủ để n ngẫu nhiên X và Y (liên k t cùng m phép thột ử)
độ ớ ốc lập v i nhau là F(x;y) = F F (x) là hàm phân ph
1
(x)
2
(y), trong đó trong đó F
1
i xác
suất c i xác suủa biến ngẫu nhiên X, F
2
(y) là hàm phân phố ất
của biến ng u nhiên Y. ẫ
4.3. Bảng phân phối xác suất của biến ngẫu nhiên rời rạc 2
−
−
−
−− chiều
4.3.1. Định nghĩa
Giả sử X, Y là hai biến ngẫu nhiên rời rạc (liên kết cùng một phép thử), X có miền
giá trị {x
0
; x ; x ; ... ; x
1 2 n
}, Y có miền giá trị {y
0
; y ; y ; ... ; y
1 2 k
}.
Đặt p
ij
= P(X = x ; Y = y
i j
), i = 0,1,2,..., n, j = 0,1,2,..., k.
Khi đó bảng số có dạng sau đây được gọi là bảng phân phối xác suất của biến ngẫu
nhiên 2 − chiều rời rạc (X; Y)
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
51
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
X
X
0
x
1
...
x
n−1
x
n
Y
y
0
p
00
p
10
p
(n−1)0
p
n0
y
1
p
01
p
11
p
(n−1)1
p
n1
y
k−1
p
0(k−1)
p
1(k−1)
P
(n−1)(k−1)
p
n(k−1)
y
k
p
0k
P
1k
p
(n−1)k
p
nk
4.3.2. Ví dụ
Trong một cái hộp có chứa (4 bi màu xanh, 2 bi màu đỏ), lấy ngẫu nhiên một lần 3
bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra, Y là biến ngẫu nhiên chỉ số bi đỏ
được lấy ra.
Lập bảng phân phối xác suất của (X;Y).
Lời giải
X có miền giá trị {1; 2; 3}, Y có miền giá trị {0; 1; 2}.
Bảng phân phối xác suất của biến ngẫu nhiên 2 chiều rời rạc (X;Y). −
X
1
2
3
Y
0
p
10
p
20
p
30
1
p
11
p
21
p
31
2
p
12
p
22
p
32
p
10
= P(X = 1;Y = 0) = 0 (biến cố này không thể xảy ra ?)
p = P(X = 2;Y = 0) = 0 ( này kh
20
biến cố ông thể xảy ra ?)
p à 3 bi xanh)
30
= P(X = 3;Y = 0) = 0,2 (xác suất của biến cố 3 bi lấy ra l
p = P(X = 1;Y = 1) =
11
0 (biến cố này không thể xảy ra ?)
p
21
= P(X = 2;Y = 1) = 0,6 (xác suất của biến cố 3 bi lấy ra có 2 bi xanh và 1 bi đỏ)
p = P(X =
31
3;Y = 1) = 0 (biến cố này không thể xảy ra ?)
p
12
= P(X = 1;Y = 2) = 0,2 (xác suất của biến cố 3 bi lấy ra có 1 bi xanh và 2 bi đỏ)
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
52
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
p
22
= P(X = 2;Y = 2) = 0 (biến cố này không thể xảy ra ?)
p
32
= P(X = 3;Y = 2) = 0 (biến cố này không thể xảy ra ?)
Thay vào bảng trên, ta có:
X
1
2
3
Y
0
0
0
0,2
1
0
0,6
0
2
0,2
0
0
4.3.3. Tính chất
Giả sử biến ngẫu nhiên 2 − chiều rời rạc (X;Y) có bảng phân phối xác suất như
trên, khi đó ta có:
tc1/ 0 i, j. p < 1,
ij
tc2/
0 0
1 , 0, , 0,
k n
ij
i j
p i k j n
= =
= = =
.
tc3/
( )
0
, 0,
k
ij j j
i
p q P Y y j n
=
= = = =
và
( )
0
, 0,
n
ij i i
j
p p P X x i k
=
= = = =
.
Nhận xét
Từ tính chất tc3/ nếu biết được bảng phân phối xác suất của biến ngẫu nhiên 2 −
chiều rời rạc (X;Y) ta có thể suy ra bảng phân phối xác suất của biến ngẫu nhiên X và
bảng phân phối xác suất của biến ngẫu nhi ên Y.
Ví dụ
Xét ví dụ 4.3.2.
Ta có bảng phân phối xác suất của biến ngẫu nhiên X như sau:
X
1
2
3
p
i
0,2
0,6
0,2
Và bảng phân phối xác suất của biến ngẫu nhiên Y như sau:
Y
0
1
2
q
i
0,2
0,6
0,2
4.3.4. Định lý
Điều kiện cần và đủ để biến hiên X là: ngẫu n và Y độc lập
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
53
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
p
ij
= P(X = x ; Y = y ) = P(X = x P(Y = y ) = p q ,
i j i
)
j i
j
i = 0, 1, 2, ..., k, j = 0, 1, 2, ..., n.
4.4. Hàm mật độ xác suất của biến ngẫu nhiên liên tục 2
−
−
−
−− chiều
4.4.1. Định nghĩa
Cho biến ngẫu nhiên liên tục 2 chiều (X;Y) hối xác suất F(x;y).− có hàm phân p
Nếu tồn tại hàm hai biến f(x;y) không âm, khả tích trên R
2
sao cho
( ; ) ( ; )
y
x
F x y f u v dud
− −
=
thì hàm f(x;y) được gọi là hàm mật độ xác suất của biến ngẫu nhiên liên tục 2 chiều −
(X;Y).
4.4.2. Tính chất
Giả sử f(x;y) là hàm mật độ xác suất của biến ngẫu nhiên liên tục 2 − chiều (X;Y).
Khi đó, ta có:
tc1/
( ; ) 1f x y dxdy
+ +
− −
=
.
tc2/ x , x , y , y < x , y < y , ta có:
1 2 1 2
R, x
1 2 1 2
( )
1 2 1 2
; ( ; )
D
P x X x y Y y f x y dxd
=
với D = {(x;y) / x
1
x < x y < y
2
; y
1
2
}.
tc3/ Nếu F(x;y) R có đạo hàm riêng cấp hai tại điểm (x;y)
2
thì
2
//
( ; ) ( ; ) ( ;
xy
F
F x y x y f x
x y
= =
.
Nhận xét
Tính chất tc3/ cho ta cách xác định hàm mật độ xác suất f(x;y) nếu biết hàm phân
phối xác suất F(x;y).
Ví dụ
Cho biến ngẫu nhiên 2
−
chiều (X;Y) có hàm phân phối xác suất
2
( ; )
y
x
F x y xe
y
= +
với y
0.
Xác định hàm mật độ xác suất của (X;Y).
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
54
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ta có:
2
2
2 2
( ; ) , ( ; ) ( ;
y y
F x F x
x y e x y e f x
x y x y y
= + = − =
.
4.4.3. Định lý
Giả sử f
1
(x) là hàm mật độ của biến ngẫu nhiên X,
f
2
(y) là hàm mật độ của biến ngẫu nhiên Y,
f(x;y) là hàm mật độ của biến ngẫu nhiên 2 − chiều (X;Y).
Điều kiện cần và đủ để X và . Y độc lập là: f(x;y) = f
1
(x)f
2
(y)
4.5. Phân phối xác suất có điều kiện của biến ngẫu nhiên 2
−
−
−
−− chiều
4.5.1. Bảng phân phối xác suất của biến ngẫu nhiên 2
−
−
−
−−
chiều rời rạc (X;Y)
Cho biến ngẫu nhiên 2 chiều rời rạc (X;Y), X có miền giá trị {x−
0
; x ; x
1 2
;...; x }, Y
k
có miền giá trị {y
0
; y ; y ..; y } và p = P(X = x ; Y = y ), i = 0, 1, 2, ..., k, j = 0, 1, 2, ...,
1 2
;.
n ij i j
n.
+ j = 0, 1, 2, ..., n, đặt P(x
i
/ y ) = P(X = x / Y = y
j i j
), i = 0, 1, 2, ..., k là xác suất có điều
kiện để X nhận giá trị x với điều kiện Y nhận giá trị y
i
j
.
+ i = 0, 1, 2, . / x ) = P(Y = y / X = x.., k, đặt P(y
j i j i
), j = 0, 1, 2, ..., n là xác suất có điều
kiện để Y nhận giá trị y với điều kiện X nhận giá
j
trị x
i
.
Khi đó các bảng có dạng như sau:
X/y
j
X
0
x
1
x
2
...
x
k
P(x )
i
/ y
j
P(x )
0
/ y
j
P(x )
1
/ y
j
P(x )
2
/ y
j
...
P(x )
k
/ y
j
j = 0,1,2,...,n
Y/x
i
Y
0
y
1
y
2
...
y
n
P(y )
j
/ x
i
P(y )
0
/ x
i
P(y )
1
/ x
i
P(y )
2
/ x
i
...
P(y )
n
/ x
i
i = 0,1,2,...,k
Theo côn / y ) và P(y / xg thức xác suất có điều kiện, các giá trị P(x
i j j i
) được tính
như sau:
( )
( )
( )
;
/ , 0, , 0,
i j
ij
i j
j
j
P X x Y y
p
P x y i k j n
q
P Y y
= =
= = = =
=
.
( )
( )
( )
;
/ , 0, , 0,
i j
ij
j i
i i
P X x Y y
p
P y x i k j n
P X x p
= =
= = = =
=
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
55
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ. Xét biến ngẫu nhiên 2
−
chiều rời rạc (X;Y) có bảng phân phối xác suất như sau:
X
x = 0
0
x = 1
1
x = 2
2
Y
y = 1
0
0,2
0,1
0
y = 2
1
0,4
0
0,3
Lập bảng phân phối xác suất có điều kiện của biến ngẫu nhiên X với các điều kiện
(Y = 1), (Y = 2).
Lời giải
Ta có:
( )
( )
( )
00
0
0
0; 1
0, 2
0 /
1 0,3
P X Y
p
P X y
P Y q
= =
= = = = =
=
,
( )
( )
( )
01
1
1
0; 2
0, 4
0 /
1 0,7
P X Y
p
P X y
P Y q
= =
= = = = =
=
,
( )
( )
( )
10
0
0
1; 1
0,1
1/
1 0,3
P X Y
p
P X y
P Y q
= =
= = = = =
=
,
( )
( )
( )
11
1
1
1; 2
0
1/ 0
2 0,7
P X Y
p
P X y
P Y q
= =
= = = = =
=
,
( )
( )
( )
20
0
0
2; 1
0
2 / 0
1 0,3
P X Y
p
P X y
P Y q
= =
= = = = =
=
,
( )
( )
( )
21
1
1
2; 2
0,3
2 /
2 0,7
P X Y
p
P X y
P Y q
= =
= = = = =
=
.
Bảng phân phối xác suất cần tìm:
X/y
0
0
1
2
P(x )
i
/ y
0
2/3
1/3
0
X/y
1
0
1
2
P(x )
i
/ y
1
4/7
0
3/7
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
56
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
4.5.2. Hàm mật độ xác suất có điều kiện của biến ngẫu nhiên liên tục (X;Y).
Xét biến ngẫu nhiên liên tục 2 − chiều (X;Y) có hàm mật độ xác suất f(x;y).
Ta có các định nghĩa:
+ Hàm mật độ xác suất của biến ngẫu nhiên Y với điều kiện (X = x), x R là một hàm một
biến được kí hiệu g(y/x) và xác định
( )
1
( ; ) ( ; )
/
( )
( ; )
f x y f x y
g y x
f x
f x y dx
+
−
= =
,
với f
1
(x) là hàm mật độ của biến ngẫu nhiên X.
+ Hàm mật độ xác suất của biến ngẫu nhiên X với điều kiện (Y = y), yR là
một hàm một bi ến được kí hiệu h(x/y) và xác định
( )
2
( ; ) ( ; )
/
( )
( ; )
f x y f x y
h x y
f y
f x y dy
+
−
= =
,
với f
2
(y) là hàm mật độ của biến ngẫu nhiên Y.
4.6. Kỳ vọng có điều kiện của biến ngẫu nhiên 2
−
−
−
−− chiều
4.6.1. Định nghĩa
4.6.1.1. Đối với biến ngẫu nhiên rời rạc 2 − chiều (X;Y)
Cho biến ngẫu nhiên rời rạc 2 chiều (X;Y), X có miền giá trị {x−
0
; x ; x ;...;
1 2
x ; y ; y ;...; y } và p = P(X = x ; Y = y ), i = 0, 1, 2, ..., k, j = 0, 1,
k
}, Y có miền giá trị {y
0 1 2 n ij i j
2, ..., n.
Ta định nghĩa:
+ Kỳ vọng có điều kiện của biến ngẫu nhiên X với điều kiện (Y = y
j
), j = 0, 1,
2, ..., n là một số được kí hiệu E(X/y
j
) và xác định:
( ) ( )
0
/ . / , 0,
k
j i i j
i
E X y x P x y j n
=
= =
.
+ Kỳ vọng có điều kiện của biến ngẫu nhiên Y với điều kiện (X = x
i
), i = 0, 1,
2,..., k là một số được kí hiệu E(Y/x
i
) và xác định:
( )
( )
0
/ . / , 0,
n
i j j i
j
E Y x y P y x i
=
= =
.
4.6.1.2. Đối với biến ngẫu nhiên liên tục 2 − chiều (X;Y)
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
57
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Cho biến ngẫu nhi tục 2 chiều (X;Y), có hàm mật độ có điều kiện là ên liên −
g(y/x), h(x/y).
Ta định nghĩa:
+ Kỳ vọng có điều kiện của biến ngẫu nhiên X với điều kiện (Y = y
j
), j = 0, 1,
2,..., n là một số được kí hiệu E(X/y) và xác định:
( ) ( )
/ / ,E X y xg x y dx y
+
−
=
.
+ Kỳ vọng có điều kiện của biến ngẫu nhiên Y với điều kiện (X = x
j
), i = 0, 1,
2,..., k là một số được kí hiệu E(Y/x) và xác định:
( ) ( )
/ / ,E Y x yh y x dy x
+
−
=
.
Chương 3. MỘT SỐ LUẬT PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
3.1. 1) Luật phân phối giản đơn (hay còn gọi là phân phối 0
−
−
−
−−
3.1.1. Định nghĩa
Biến ngẫu nhiên rời rạc X được gọi có luật phân phối xác suất giản đơn tham số p
nếu X có bảng phân phối xác suất:
X
0
1
p
i
1 p −
p
với 0 < p < 1
+ Biến ngẫu nhiên rời rạc X có luật phân phối xác suất giản đơn tham số p được kí hiệu
A(p).
Ví dụ
Thực hiện phép thử gieo một con xúc xắc. Gọi X là biến ngẫu nhiên chỉ số mặt
màu đỏ xảy ra.
Khi đó biến ngẫu nhiên X có luật phân phối giản đơn và ta cũng có:
P(X = 1) = 1/3 = p, P(X = 0) = 1 1/3 = 2/3. −
3.1.2. Các tham số đặc trưng của biến ngẫu nhiên A(p)
Nếu X là biến ngẫu nhiên A(p), thì
E(X) = p; D(X) = p(1 − p) = p.q p) (ở đây: q = 1 −
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
58
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3.2. Luật phân phối nhị thức
3.2.1. Định nghĩa
Biến ngẫu nhiên rời rạc X được gọi là có luật phân phối xác suất nhị thước kích
thước n tham số p nếu X có bảng phân phối xác suất:
X
0
1
2
...
k
...
n
p
i
p
0
p
1
p
2
...
p
k
...
p
n
Trong đó
( ) (1 ) ; 0 1; 0,
k k n k
k n
p P X k C p p p k
−
= = = − =
.
+ Biến ngẫu nhiên rời rạc X có luật phân phối xác suất nhị thức kích thước n tham số p
được kí hiệu B(n; p).
Ví dụ 1
Gieo 5 con xúc xắc.
Gọi X là biến ngẫu nhiên chỉ số mặt có màu đỏ xảy ra.
Khi đó X là biến ngẫu nhiên có luật phân phối nhị thức B(n = 5; p = 1/3).
Ở đây p = 1/3 là xác suất xảy ra mặt có màu đỏ khi gieo một con xúc xắc.
Ví dụ 2
Một thí nghiệm có xác suất thành công là p = 0,8. Thực hiện nghiệm đó 10 lần.
Gọi X là biến ngẫu nhiên chỉ số lần thành công.
Ta có X là biến ngẫu nhiên có luật phân phối xác suất B(n; p), với n =10, p = 0,8.
3.2 .2. Lược đồ Bernoulli (Dãy phép thử Bernoulli)
Xét một phép thử có hai biến cố A và B (đối lập), giả sử p = P(A) không đổi, khi
đó P(B) = 1 − p = q.
Thực hiện phép thử trên n lần độc lập với nhau.
Gọi X là biến ngẫu nhiên chỉ số lần xảy ra biến cố A.
Khi đó X có miền giá trị {0; 1; 2;...; n} và
( ) (1 ) ; 0 1; 0,
k k n k
k n
p P X k C p p p k
−
= = = − =
.
Do đó X có luật phân phối nhị thức B(n; p).
3.2.3. Các tham số đặc trưng của biến ngẫu nhiên B(n; p)
Nếu X là biến ngẫu nhiên B(n; p), thì
i/ E(X) = np; D(X) = n p (1 p) = n q. − p
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
59
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
ii/ np q Mod(X) n p q + 1. − −
3.3. Luật phân phối siêu bội
3.3.1. Định nghĩa
Biến ngẫu nhiên rời rạc X được gọi là có luật phân phối siêu bội tham số (m; n; k)
với k min{m; n} nếu miền giá trị của X là {0; 1; 2; ... ; k} và
.
( ) ; 0;
i k i
m n
i
k
m n
C C
p P X i i k
C
−
+
= = = =
.
Kí hiệu S(m; n; k).
• Chú ý
Có thể mô tả một biến ngẫu nhiên có luật phân phối siêu bội như sau:
Trong một hộp có chứa hai loại bi (giả sử có m bi đỏ và n bi không đỏ).
Lấy ngẫu nhiên một lần k bi, với k min{m; n}.
Gọi X là biến ngẫu nhiên chỉ số bi đỏ được lấy ra.
Khi đó X là một biến ngẫu nhiên có luật phân phối xác suất siêu bội.
Ví dụ
Trong một hộp có chứa (4 bi màu xanh và 6 bi màu đỏ).
Lấy ngẫu nhiên một lần 3 bi từ trong hộp.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra (trong số 3 bi được lấy ra).
Ta có X có miền giá trị {0; 1; 2 ; 3} và
0 3
4 6
0
3
10
.
( 0)
C C
p P X
C
= = =
;
1 2
4 6
1
3
10
.
( 1)
C C
p P X
C
= = =
;
2 1
4 6
2
3
10
.
( 2)
C C
p P X
C
= = =
;
3 0
4 6
3
3
10
.
( 3)
C C
p P X
C
= = =
.
Ta có X là một biến ngẫu nhiên có luật phân phối xác suất siêu bội tham số (4; 6;
3).
3.3.2. Các tha m số đặc trưng của biến ngẫu nhiên có luật phân phối S(m; n; k)
Nếu X là biến ngẫu nhiên có luật phân phối siêu bội S(m; n; k) thì
( ) . ; ( ) . . .
m m n m n
E X k D X k
m n m n m n m n
+ −
= =
+ + + + −
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
60
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
3.3.3. Quan hệ giữa biến ngẫu nhiên có luật phân phối siêu bội và phân phối nhị thức
Định lý
Nếu k cố định, m + n tăng lên vô hạn và tỉ số
m
m n+
tiến tới giới hạn p, 0 < p <1
thì phân phối siêu bội tham số (m; n; k) sẽ tiến tới phân phối nhị thức B(k; p).
Cụ thể: S(m; n; k) → B(k; p).
3.4. Luật phân phối chuẩn
3.4.1. Định nghĩa
Biến ngẫu nhiên liên tục X được gọi là có luật phân phối chuẩn tham số t và ( >
0) nếu hàm mật độ xác suất của X có dạng
( )
2
2
2
1
( ) . ,
2
x t
f x e x R
−
−
=
.
Kí hiệu: N(t; ).
+ Hàm phân phối của biến ngẫu nhiên N(t; ) là
( )
2
2
2
1
( ) . ,
2
u t
x
F x e du x R
−
−
−
=
.
+ Biến ngẫu nhiên N(t; ) còn được gọi là biến ngẫu nhiên chính qui hay biến ngẫu nhiên
Gauss.
3.4.2. Biến ngẫu nhiên chuẩn tắc
Trường hợp đặc biệt nếu t = 0, = 1 thì X được gọi là có luật phân phối chuẩn tắc
N(0; 1) và khi đó
2
2
1
( ) . ,
2
x
f x e x R
−
=
,
2
2
1
( ) . ,
2
x
u
F x e du x R
−
−
=
.
Dễ dàng ta có f(− x) = f(x) và F( x) = 1 F(x), x − − R
và
2
0
2
1 1
.
2
2
u
e du
−
−
=
.
Ta có kết quả sau:
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
61
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Nếu X có luật phân phối N(t; ) thì biến ngẫu nhiên
X t
Y
−
=
có luật phân phối
chuẩn tắc N(0; 1).
• Chú ý
Biến ngẫu nhiên N(t; ) có một ý nghĩa rất lớn trong lý thuyết cũng như thực tiễn.
3.4.3. Các tham số đặc trưng của biến ngẫu nhiên N(t;
)
3.4.3.1. Số trung vị và số Mod
Nếu X là biến ngẫu nhiên N(t; ) thì med(X) = Mod(X) = t.
3.4.3.2. Kỳ vọng toán và phương sai
Nếu X là biến ngẫu nhiên N(t; ) thì E(X) = t và D(X) = .
2
Trường hợp X là biến ngẫu nhiên chuẩn tắc N(0; 1) thì
med(X) = Mod(X) = E(X) = 0 và D(X) = 1.
3.5. Hàm Laplace và một số kết quả
3.5.1. Định nghĩa
Hàm số được kí hiệu và xác định như sau được gọi là hàm Laplace
2
2
0
1
( ) . ,
2
x
u
x e du x R
−
=
.
3.5.2. Tính c hất
i1/ ( (x), − x) = − x R ((x) là một hàm số lẻ);
i2/
1 1
lim ( ) , lim ( )
2 2
x x
x x
→− →+
= − =
;
i3/ Nếu 0 x 5 thì giá trị (x) được xác định dựa vào bảng giá trị của hàm Laplace
(xem bảng phụ lục)
và x > 5 ta có
1
( )
2
x
; và nếu x < 0 thì sử dụng tính chất (− x) = − (x).
3.5.3. Công thức liên hệ giữa hàm Laplace và hàm phân phối xác suất của biến ngẫu
nhiên chuẩn N(t;
).
Định lý
Nếu (x) là hàm Laplace và F(x) là hàm phân phối xác suất của một biến ngẫu
nhiên chuẩn N(t; ) thì:
1
( )
2
x t
F x
−
= +
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
62
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Hệ quả 1
  , R, < :
( )
t t
p X
− −
= −
.
Hệ quả 2
 R, > 0:
( )
2p X t
− =
.
3.5.4. Tính gần đúng của phân phối nhị thức B(n; p)
Định lý 1 (định lý Moivre)
Nếu xác suất P(A) = p để biến cố A xảy ra trong mỗi phép thử của dãy n phép thử
Bernoulli thỏa mãn 0 < p < 1 thì khi đó với n đủ lớn xác suất
1
( ) (1 ) . ( )
k k n k
k n
p P X k C p p f x
npq
−
= = = −
với
2
2
1
( ) . ,
2
x
k np
f x e x
npq
−
−
= =
.
Định lý 2 (định lý Moivre Laplace) −
Gọi k là số lần xảy ra biến cố A trong dãy n phép thử Bernoulli,
p = P(A), 0 < p <1 , k(xác suất để biến cố A xảy ra trong mỗi phép thử), k
1 2
là hai số
nguyên cho trước với k
1
< k .
2
Khi đó với n đủ lớn, ta có:
( )
2 1
1 2
k np k np
P k X k
npq npq
− −
= −
trong đó
2
2
1
( )
2
x
t
x e dt
−
−
=
.
Ví dụ
Gieo ngẫu nhiên n = 100 hạt giống. Tính xác suất:
1/ Có đúng 85 hạt nẩy mầm.
2/ Số hạt giống nẩy mầm từ 75 đến 85 hạt.
Cho biết hạt giống có tỉ lệ nẩy mầm là p = 0,8.
Lời giải
Mỗi một hạt giống được đem gieo là một phép thử, có xác suất nẩy mầm là p = 0,8
Gọi X là biến ngẫu nhiên chỉ số hạt giống nẩy mầm,
X có miền giá trị {0; 1; 2; ... ; k; ...; 99; 100}.
1/ Theo yêu cầu của bài toán ta tính P(X = 85).
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
63
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Áp dụng định lý 1,
1
( 85) . (1, 25
100.0,8.0, 2
P X f=
= 0,04565
với
2
2
1 85 80
( ) . , 1, 25
4
2
x
f x e x
−
−
= = =
và f(1,25) = 0,1826.
2/ Theo yêu cầu của bài toán ta tính P(75 85). X
Áp dụng định lý 2,
( ) ( ) ( )
85 80 75 80
(75 85) 1, 25 1, 25 2 1, 25 0,7
4 4
P X
− −
− = − − = =
3.6.
Luật phân phối Poisson
3.6.1. Định nghĩa
Biến ngẫu nhiên X được gọi là có luật phân phối Poisson với tham số > 0 nếu
phân phối của X có dạng
( )
.
, 0;1;2;.
!
k k
e
P X k k
k
−
= = =
.
3.6.2. Tí nh chất
+ Hàm phân phối xác suất của X là
.
( ) ,
!
k k
k x
e
F x x R
k
−
=
.
+ Kỳ vọng của X là
0
.
( ) .
!
k k
k
e
E X k
k
−
=
= =
.
BÀI TẬP
Bài 3.1. M n và b n l t m c tiêu. ột xạ thủ có 3 viên đạ ắ ần lượt vào mộ ụ
Xác su t b n trúng m c tiêu c a l n b n th nh t là 0,7, xác t b n trúng mấ ắ ụ ủ ầ ắ ứ ấ suấ ắ ục
tiêu c n b n th hai là 0,8, xác su n trúng m c tiêu c n ủa lầ ắ ứ ất bắ ụ ủa lầ
b n th ba là 0,9. ắ ứ
Gọi X là biến ng u nhiên ch s n trúng m ẫ ỉ ố đạ ục tiêu.
1/ Hãy l p b ng phân ph t c ậ ả ối xác suấ ủa X.
2/ Tính E(X), D(X).
3/ Tính P( X = 2).
Bài 3.2. M t x n và b n l t vào m t m n khi nào có ộ ạ thủ có 3 viên đạ ắ ần lượ ộ ục tiêu cho đế
m n trúng m c tiêu thì d ng b n ho c h ng b n. G i X là biột viên đạ ụ ừ ắ ặ ết đạn cũng dừ ắ ọ ến
ng u nhiên ch s n ra. ẫ ỉ ố đạn đã được bắ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
64
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Cho biết xác su n trúng m c tiêu c a m i l n b n là p = 0,7. ất bắ ụ ủ ỗ ầ ắ
1/ Hãy l p b ng phân t c ậ ả phối xác suấ ủa X.
2/ Tính E(X), D(X).
3/ Tính P( X < 3).
Bài 3.3. xây d ng th n 3 d án (d Trong năm 2011, công ty Z ự ực hiệ ự ự án I, II, III).
Xác suất thành công c án III là 0,9. ủa dự án I là 0,7, của d án II là 0,8 và cự ủa dự
Gọi X là bi ến ng u nhiên ch s d án thành công. ẫ ỉ ố ự
1/ Hãy l p b ng phân ph t c ậ ả ối xác suấ ủa X.
2/ Tính E(X), D(X).
3/ Cho bi ng n u có ít nh án thành công thì công ty thành công. ết rằ ế ất 1 dự Z
Tính xác suất công ty Z thành công.
Bài 3.4. M t lô hàng có 5 s n ph t t và 2 s n ph u. ộ ả ẩm ố ả ẩm xấ
Từ lô hàng đó lấ ần lượ ại đếy ngẫu nhiên l t từng sản phẩm không hoàn l n khi nào
đượ ốc sản phẩm t t thì dừng lại.
Gọi X là biến ng u nhiên ẫ chỉ s s n ph l y ra. ố ả ẩm đã được ấ
1/ Hãy l p b ng phân ph t c a X và l p hàm phân ph i xác ậ ả ối xác suấ ủ ậ ố suất của X.
2/ Tính E(X), D(X).
3/ Tính P(X < 3).
Bài 3.5. Trong m p có ch , 1 bi vàng. ột hộ ứa 2 bi xanh, 3 bi đỏ
Lấy ng u nhiên l t không hoàn l i t ng thì d ng ẫ ần lượ ạ ừ bi cho đến khi nào được đỏ ừ
l ại.
Gọi X là biến ng u nhiên ch s y ra. ẫ ỉ ố bi đã được lấ
Hãy lập b ng phân ph ả ối xác t csuấ ủa X.
Bài 3.6. Trong m p có ch . ột hộ ứa 6 bi xanh, 2 bi đỏ
Lấy ng u nhiên m n 3 bi. ẫ ột lầ
Gọi X là biến ng u nhiên ch s y ra. ẫ ỉ ố bi đỏ được lấ
Hãy lập b ng phân ph ả ối xác su t cấ ủa X.
Bài 3.7. Trong m p có ch , 2 bi vàng. ột hộ ứa 4 bi xanh, 3 bi đỏ
Lấy ng u nhiên m n 3 bi. ẫ ột lầ
Gọi X là biến ng u nhiên ch s c l y ra. ẫ ỉ ố bi xanh đượ ấ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
65
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Hãy lập b ng phân ph ả ối xác su t cấ ủa X.
Bài 3.8. M t xí nghi p trong m t ca s n xu t có 3 dây chuy n s n xu t ho c lộ ệ ộ ả ấ ề ả ấ ạt động độ ập
v i là dây chuy n I, II, III). ới nhau (gọ ề
Xác su t dây chuy n I b h ng trog m t ca s n xu t là 0,1, dây chuy n II b h ng trog mấ ề ị ỏ ộ ả ấ ề ị ỏ ột
ca sản xuất là 0,2, dây chuyền III b h ng trog mị ỏ ột ca sản xuất là 0,3.
Gọi X là biến ng u nhiên ch s dây chuy n b h ng trong m t ca s n xuẫ ỉ ố ề ị ỏ ộ ả ất.
1/ Hãy l p b ng phân ph t c ậ ả ối xác suấ ủa X.
2/ Bi t r ng trong m t ca s n xu t n u có ít nh t 1 dây chuy n b h ng thì xí nghiế ằ ộ ả ấ ế ấ ề ị ỏ ệp
ng ng ho ng. ừ ạt độ
Tính xác suất xí nghi p ng ng h ng (trong ca s n xu ệ ừ ọ ộat đ ả ất).
Bài 3.9. M t thi t b g m có 3 b ph n ho c l p, xác su các thi t b b hộ ế ị ồ ộ ậ ạt động độ ậ ất để ế ị ị ỏng
trong thời gian ho ng là 0,4; 0,1 và 0,2. ạt động t tương ứ
Gọi X là bi t bến ng u nhiên ch s thiẫ ỉ ố ế ị b h ng trong th i gian ho ng ị ỏ ờ ạt độ t.
1/ L p b ng phân ph i xác su a X. ậ ả ố ất củ
2/ Tính k v ỳ ọng E(X), phương sai D(X).
Bài 3.10. ng. Ch n ng u nhiên t ng bóng Trong kho có 3 bóng đèn tốt và 2 bóng đèn hỏ ọ ẫ ừ
đèn đem thử ại) cho đến khi được bóng đèn tố (thử xong không trả l t thì dừng thử. Gọi X
là bi n ng u nhiên ch s l n th . ế ẫ ỉ ố ầ ử
1/ L p b ng phân ph i xác su a X. ậ ả ố ất củ
2/ Tính trung bình c n ph bao nhiêu l n. ầ ải thử ầ
Bài 3.11. M t lô hàng có t l s n ph t là p = 0,9. ộ ỉ ệ ả ẩm tố
M y ng u nhiên 3 s n ph lô hàng. ộ ờt ngư i lấ ẫ ả ẩm từ
Gọi X là biến ng u nhiên ch s s n ph m t y ra. ẫ ỉ ố ả ẩ ốt được lấ
Lập b ng phân ph i xác su a X ả ố ất củ
Bài 3.12. M t lô hàng có 6 s n ph và 2 s n ph u. ộ ả ẩm tốt ả ẩm xấ
Lấy ng u nhiên m n 3 s n phẫ ột lầ ả ẩm.
Gọi X là biến ng u nhiên ch s s n ph m t y ra (trong s n phẫ ỉ ố ả ẩ ốt được lấ ố 3 sả ẩm).
Gọi Y là biến ng u nhiên ẫ chỉ s s n ph m x c l y ra (trong s 3 s n phố ả ẩ ấu đượ ấ ố ả ẩm).
1/ L p b ng phân ph i xác su a X và c a Y. ậ ả ố ất củ ủ
2/ Tính trung bình s s n ph y ra và tính trung bình s s n phố ả ẩm tốt được lấ ố ả ẩm xấu được
l y ra. ấ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
66
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Bài 3.13. M p có ch , 4 bi vàng. ột hộ ứa 2 bi xanh, 1 bi đỏ
Lấy ng u nhiên m n 3 b trong h p. ẫ ột lầ i từ ộ
Gọi X là biến ng u nhiên ch s c l y (trong s 3 bi). ẫ ỉ ố bi xanh đượ ấ ố
Gọi Y là biến ng u nhiên ch s y (trong s 3 bi). ẫ ỉ ố bi đỏ được lấ ố
1/ L p b ng phân ph i xác su a X và c a Y. ậ ả ố ất củ ủ
2/ Tính trung bình s y y ra. ố bi xanh được lấ ra và tính trung bình số bi đỏ được lấ
Bài 3.14. M t lô hàng có ch n ph t, 4 s n ph u. ộ ứa 7 sả ẩm tố ả ẩm xấ
Lấy ng u nhiên m n 3 s n phẫ ột lầ ả ẩm.
Gọi X là biến ng u nhiên ch s s n ph m t y (trong s 3 s n phẫ ỉ ố ả ẩ ốt được lấ ố ả ẩm).
1/ L p b ng phân ph i xác su a X. ậ ả ố ất củ
2/ Tính E(X), D(X).
Bài 3.15. Có hai cái h p, h p I có ch và h p II có ch 1 bi xanh, 3 bi ộ ộ ứa 3 bi xanh, 5 bi đỏ ộ ứa
đỏ.
Từ h p I l y ng u nhiên 2 bi b vào h h p II l y ng u nhiên 2 bi. ộ ấ ẫ ỏ ộp II, sau đó từ ộ ấ ẫ
Gọi X là biến ng u nhiên ch s c l y ra t h p II. ẫ ỉ ố bi xanh đượ ấ ừ ộ
Lập b ng phân ph i xác su a X. ả ố ất củ
Bài 3.16 Có hai cái h p, h p I có ch và h p II có ch bi xanh, 2 bi ộ ộ ứa 4 bi xanh, 1 bi đỏ ộ ứa 5
đỏ.
Từ h p I l y ng u nhiên 2 bi b vào h h p II l y ng u nhiên 3 bi. ộ ấ ẫ ỏ ộp II, sau đó từ ộ ấ ẫ
Gọi X là biến ng u nhiên ch s bi xa c l y ra t h p II. ẫ ỉ ố nh đượ ấ ừ ộ
Lập b ng phân ph i xác su a X. ả ố ất củ
Bài 3.17 Có 3 lô hàng, lô I có ch 3 s n ph m t t, 1 s n ph m x u, lô II có ch a 4 sứa ả ẩ ố ả ẩ ấ ứ ản
ph t, lô III có ch n ph t, 2 s n ph u. ẩm tố ứa 2 sả ẩm tố ả ẩm xấ
Từ m y ng u nhiên 1 s n phỗi lô hàng lấ ẫ ả ẩm.
Gọi X là bi n ng u nhiên ch s s n ph m t y ra (trong 3 s n phế ẫ ỉ ố ả ẩ ốt được lấ ả ẩm).
1/ L p b ng phân ph i xác su a X. ậ ả ố ất củ
2/ Tính trung bình s s n ph y ra. ố ả ẩm tốt được lấ
Bài 3.18 Có 3 lô hàng, lô I có ch a 3 s n ph m t t, 1 s n ph m x u, lô II có ch a 4 sứ ả ẩ ố ả ẩ ấ ứ ản
ph t, lô n ph t t, 2 s n ph u. ẩm tố III có ch ứa 2 sả ẩm ố ả ẩm xấ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
67
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Từ m i lô hàng l y ng u nhiên 1 s n ph m và t 3 s n ph y ng u nhiên ra 2 ỗ ấ ẫ ả ẩ ừ ả ẩm đó lấ ẫ
s n ph ả ẩm.
Gọi X là biến ng u nhiên ch s s n ph m t y ra trong s 2 s n phẫ ỉ ố ả ẩ ốt được lấ ố ả ẩm.
Lập b ng phân ph i xác su a X. ả ố ất củ
Bài 3.19 Có 2 h p, h p I có ch , h p II có ch a 1 bi xanh và 3 bi ộ ộ ứa 2 bi xanh và 4 bi đỏ ộ ứ
đỏ ộ ộ. Từ h p I lấy ngẫu nhiên 1 bi, từ h p II lấy ngẫu nhiên 2 bi.
Gọi X là biến ng u nhiên ch s y ra (trong s 3 bi). ẫ ỉ ố bi xanh đã được lấ ố
Lập b ng phân ph i xác su a X. ả ố ất củ
Bài 3.20 Có 2 h p, h p I có , h p II có ch a 1 bi xanh và 3 bi ộ ộ chứa 2 bi xanh và 4 bi đỏ ộ ứ
đỏ ộ ộ. Từ h p I lấy ngẫu nhiên 1 bi, từ h p II lấy ngẫu nhiên 2 bi và từ 3 bi đó lấy ngẫu
nhiên 2 bi.
Gọi X là biến ng u nhiên ch s y ra (trong s 2 bi). ẫ ỉ ố bi xanh đã được lấ ố
Lập b ng phân ph i xác su a X. ả ố ất củ
Bài 3.21. Trong m t h p có ch a 2 qu bóng bàn m i và 3 qu bó bóng ộ ộ ứ ả ớ ả ng bàn cũ ( quả
b bóng bàn s d u ít nh t m n). àn cũ là quả ử ụng thi đấ ấ ột lầ
Lần thứ nhất l y ng u nhiên 2 qu bóng bàn t trong h lấ ẫ ả ừ ộp ra thi đấu, sau đó trả ại
vào trong h p. ộ
Lần th hai l y ng u nhiên ra 2 qu u. ứ ấ ẫ ả thi đấ
Gọi X là biến ng u nhiên ch s bóng bàn m y ra l n th ẫ ỉ ố ới được lấ ở ầ ứ nhất.
và Y là bi n ng u nhiên ch s bóng bàn m y ra l n th hai. ế ẫ ỉ ố ới được lấ ở ầ ứ
Lập b ng phân ph i xác su a X và Y. ả ố ất củ
Bài 3.22. Có 2 lô hàng, lô I có a 3 s n ph m t t và 2 s n ph m x u, lô II có ch a 4 s n chứ ả ẩ ố ả ẩ ấ ứ ả
ph t và 1 s n ph u. ẩm tố ả ẩm xấ
Trong quá trình v n chuy lô I m t 1 s n ph lô I l y ngậ ển do sơ ý ở ấ ả ẩm, sau đó từ ấ ẫu
nhiên 1 s n ph m, t lô II l y ng u nhiên 2 s n ph m và t 3 s n ph y ng u nhiên ả ẩ ừ ấ ẫ ả ẩ ừ ả ẩm đó lấ ẫ
2 s n ph ả ẩm.
Gọi X là biến ng u nhiên ch s s n ph m t y ra trong s 2 s n phẫ ỉ ố ả ẩ ốt được lấ ố ả ẩm.
Lập b ng phân ph i xác su a X và Y. ả ố ất củ
Bài 3.23. n ng u nhiên liên t c X có hàm s Cho biế ẫ ụ ố f(x) xác định như sau:
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
68
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
0 0;
2
( )
.cos 0;
2
x
f x
k x x
=
1/ Xác định k.
2/ L p hàm phân ph i xác su t F(x) c n ng u nhiên X. ậ ố ấ ủa biế ẫ
3/ Tính
0
4
P X
.
Bài 3.24. n ng u nhiên liên t c X có hàm m xác su Cho biế ẫ ụ ật độ ất:
3
0 0
( )
. 0
x
x
f x
k e x
−
=
.
1/ Xác định giá trị của k.
2/ L p hàm phân ph i xác t F(x) c ậ ố suấ ủa X.
Bài 3.25. t r ng X ch i th tính = gi ) c a m t s n ph m là là bi n Giả thiế ằ ỉ tuổ ọ (đơn vị ờ ủ ộ ả ẩ ế
ng u nhiên có hàm m xác su ẫ ật độ ất f(x) xác định như sau:
2
0 0;1
( )
2 1 0;1
x
f x
kx x x
=
+ +
1/ Xác định giá trị k.
2/ Tu trung bình c n ph là bao nhiêu. ổi thọ ủa sả ẩm trên
3/ Tính t l s n ph m có tu t n 0,5 gi . ỉ ệ ả ẩ ổi thọ ừ 0,25 đế ờ
Bài 3.26. M t thí nghi ó xác su t thành công là p = 0,8. ộ ệm c ấ
Thực hi c lện thí nghi n (các lệm đó 100 lầ ần thí nghiệm là độ ập v i nhau). ớ
1/ Tính xác su t có 85 l n thì nghi m thành công. ấ ầ ệ
2 l n thí nghi m thành công t n 85 l n. / Tính xác su t sấ ố ầ ệ ừ 75 đế ầ
3/ Tính xác su t có ít nh n thí nghi m thành công. ấ ất 2 lầ ệ
Bài 3.27. Gieo ng u nhiên 400 h c nghi m), bi t r ng xác ẫ ạt đậu tương (trong phòng thự ệ ế ằ
suất n m cảy mầ ủa hạt đậu tương là p = 0,8.
1/ Tính xác su t có 340 h u y m ấ ạ ật đ tương nả ầm.
2/ Tính xác su h y m 300 h n 340 h ất số ạt đậu tương nả ầm từ ạ ết đ ạt.
3/ Tính xác su t có ít nh y m ấ ất 1 h t nạ ả ầm.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
69
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Bài 3.28. Công ty b o hi n h ng b o hi m cho n = 10.000 ả ểm AZ, trong năm 2012 nhậ ợp đồ ả ể
xe máy, v phí b o hi ng / 1x ới lệ ả ểm là 100.000 đồ e / 1năm.
Trung bình m n bù cho m t v tai n n không may x y ra là 1000.000 ức phí đề ộ ụ ạ ả
đồng.
Theo thống kê cho bi t t l i xe máy khi tham gia giao thông là 0,007. ế ỉ ệ tai nạn đối vớ
Tổng các chi phí khác (tr t b ng, thu , ho ng xã h i...) c a ả lương, thuê mặ ằ ế ạt độ ộ ủ
công ty AZ chiếm 30% t ng thu c a công ty. ổ ủ
1/ Tính xác su 12 công ty AZ phá s n. ất trong năm 20 ả
2/ Tính xác su ng. ất trong năm 2012 công ty AZ lãi ít nhất 400.000.000 đồ
Trong bài này gi t 1 xe máy n u không may b tai n n thì ch b nhi u nh t 1 ả thiế ế ị ạ ỉ ị ề ấ
l ần trong năm 2012.
Bài 3.29. t không n y m m c i X là Gieo 50 hạt đậu tương, xác suấ ả ầ ủa mỗi hạt là 0,07. Gọ
bi n ng u nhiên ch s h y m ế ẫ ỉ ố ạt đậu tương không nả ầm.
1/ L p b ng phân ph i xác su a X. ậ ả ố ất củ
2/ Trung bình có bao nhiêu h ng không n y m ạt đậu tươ ả ầm.
Tính xác suấ ểt đ có trên 48 hạ ầt đậu tương nảy m m.
3/ Tính Mod(X).
Bài 3.30. eo 100 h xác su y m a m t là 0,8. Tính xác su Gi ạt đậu tương, ất nả ầm củ ỗi hạ ất :
1/ Có hơn 75 hạt đậu tương nảy mầm .
2/ Có không quá 74 h y m ạt đậu tương nả ầm .
3/ S h y m n ng (75; 90) . ố ạt đậu tương nả ầm ằm trong khoả
Bài 3.31. t X là chi u cao c a sinh viên (cm), X có lu t phân ph n Cho biế ề ủ ậ ối chuẩ
N(155; 9). Tính xác suất khi chọn ng u nhiên mẫ ột sinh viên để u cao X: đo thì chiề
1/ Dưới 150(cm).
2/ T n 162(cm ừ 150(cm) đế ).
3/ Trên 162(cm).
Bài 3.32. M t thí nghi m có xác su t thành công là 0,9. Ph i th c hi n bao nhiêu thí ộ ệ ấ ả ự ệ
nghi nhi u kh t có 20 thí nghi ệ ểm đ ề ả năng nhấ ệm thành công.
Bài 3.33. Xác su m nh Z u ng thu c lo c kh i b nh là 0,7. Có ất để ột người đau bệ ố ố ại A đượ ỏ ệ
10 ng nh Z dùng thu c lo i X là bi n ng u nhiên ch s i khười đau bệ ố ại A đó, gọ ế ẫ ỉ ố ngườ ỏi
b nh (trong s 10 ệ ố người trên).
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
70
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Tìm k v Mod c a X, tỳ ọng, phương sai và số ủ ừ đó suy ra số người trung bình được
kh i b nh Z dùng thu c lo i A và s i c kh i b nh có ỏ ệnh khi có 10 người đau bệ ố ạ ố ngườ đượ ỏ ệ
xác su n nh ất lớ ất.
Bài 3.34. Trong m p có ch . ột hộ ứa 3 bi xanh và 2 bi đỏ
Lần th nh y ng u nhiên 2 bi t p (không hoàn lứ ất: Lấ ẫ ừ trong hộ ại).
Lần th hai: L y ng u nhiên 2 bi t p. ứ ấ ẫ ừ trong hộ
Gọi X là bi n ng u nhiên ch s c l y ra l n th nh t và g i Y là bi n ngế ẫ ỉ ố bi xanh đượ ấ ở ầ ứ ấ ọ ế ẫu
nhiên ch s y ra l n th hai. ỉ ố bi xanh được lấ ở ầ ứ
1/ L p b ng phân ph i xác su a bi n ng u nhiên 2 u r c (X; Y). ậ ả ố ất củ ế ẫ − chiề ời rạ
T ng phân ph i xác su a bi n ng u nhiên X và bi n ng u nhiên Y. ừ đó suy ra bả ố ất củ ế ẫ ế ẫ
2/ L p b ng phân ph i xác su i u ki n (X / y ậ ả ố ất có đ ề ệ
j
).
v u ki n E(X / y Tính kỳ ọng có điề ệ
j
).
Bài 3.35. hai cái h p, h p I có , h p II có ch a 3 bi xanh và 1 Có ộ ộ chứa 2 bi xanh và 1 bi đỏ ộ ứ
bi đỏ.
Lần th nh h p I l y ng u nhiên 1 bi và t h p II l y ng u nhiên 2 bi. ứ ất: Từ ộ ấ ẫ ừ ộ ấ ẫ
Lần th hai: T 3 y ra l n th nh t l y ng u nhiên 2 bi. ứ ừ bi được lấ ở ầ ứ ấ ấ ẫ
Gọi X là bi n ng u nhiên ch s c l y ra l n thế ẫ ỉ ố bi đỏ đượ ấ ở ầ ứ nhất và g i Y là bi n ngọ ế ẫu
nhiên ch s c l y ra l n th hai. ỉ ố bi đỏ đượ ấ ở ầ ứ
1/ L p b ng phân ph i xác su a bi n ng u nhi u r c (X; ậ ả ố ất củ ế ẫ ên 2− chiề ời rạ Y).
Từ ng phân ph i xác su a bi n ng u nhiên X và bi n ng u nhiên Y. đó suy ra bả ố ất củ ế ẫ ế ẫ
2/ L p b ng phân ph i xác su u ki n (X / y ậ ả ố ất có điề ệ
j
).
Tính kỳ v u ki n E(X / y ọng có điề ệ
j
).
Bài 3.36. Cho hàm m xác su t c n ng u nhiên 2 ật độ ấ ủa biế ẫ − chiều (X; Y) như sau:
( ) ( ; )
( ; )
0 ( ; )
k x y x y D
f x y
x y D
+
=
v i D = {(x; y) R x 3, 1 y 2}. ớ
2
/ 0 −
1/ Xác định giá trị của k.
2/ Tính a/ P(1 < X < 2; 0 < Y < 1). b/ P(X > 2)
3/ Tìm hàm m xác su a X và hàm m xác su t c n ng u nhiên Y. ật độ ất củ ật độ ấ ủa biế ẫ
Từ , E(Y). đó tính E(X)
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
71
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Phần II. THỐNG KÊ
Chương 4. LÝ THUYẾT MẪU
§1. LÝ TH UYẾT MẪU
1.1. Đặt vấn đề
1.1.1. Trong th c t khi ta c n tìm ki m thông tin v m t lo ng (g i chung là ự ế ầ ế ề ộ ại đối tượ ọ
ph n t ng h n: tìm hi u v ng c a m t lo i s n ph m, kh o sát thu ầ ử) nào đó, chẳ ạ ể ề chất lượ ủ ộ ạ ả ẩ ả
nh p c ng... ậ ủa người lao độ
Nếu đối tượ ừng đống cần tìm hiểu có số lượng quá lớn thì ta không thể khảo sát t i
tượng vì nh i gian, không gian, hiững lí do như là: thờ ệu quả kinh tế, biến dạng đối
tượng...
Do đó, người ta thường chọn ngẫu nhiên một số phần tử khảo sát ghi nhận kết quả,
và d g tin v ng. ựa vào các kết quả đó cho thôn ề đối tượ
Quá trình này được gọ ọi là ch n mẫu.
Đối tượng được khảo sát có số lượng rất lớn gọi là , kí hitổng thể ệu N, số phần tử
đượ ọ ọc ch n ngẫu nhiên g i là mẫu, kí hiệu . n
Ví dụ 1. o sát v chi phí ti a các h dân khu v Khả ề ền điện nước củ ộ ực Q.
Ví d 2. o sát tr ng l ng c ng... ụ Khả ọ ượ ủa một bao gạo được đóng bao tự độ
Ví dụ 3. o sát t l s n ph m là thành ph m c Khả ỉ ệ ả ẩ ẩ ủa nhà máy...
1.1.2. Các u phương pháp chọn mẫ
(1.2.1) Chọn m u có l p. ẫ ặ
(1.2.2) Chọn m u không l p. ẫ ặ
(1.2.3) Chọn m u phân lo ẫ ại...
Nhận xét
i/ Chọn m u có l p có nh m là có nh ng ph n t ng ch n r c ch n lẫ ặ ược điể ữ ầ ử, đối tượ ọ ồi đượ ọ ại
do đó thông tin bị ế...; ưu điể ẫu là độ hạn ch m là các lần chọn m c lập;
ii/ Chọn m u không l p có n m là có là các l n ch n m c l p vẫ ặ hược điể ầ ọ ẫu là không độ ậ ới
nhau...; ưu điể ử, đố ượng đã chọm là các phần t i t n rồi thì không lặp lại...
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
72
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Với nh n xét trên, trong giáo trình này, ta s d n m u có l p ậ ử ụng phương pháp chọ ẫ ặ
trong việc ch n m u. ọ ẫ
1.2. Mẫu ngẫu nhiên
−
−
−
−− Mẫu thực nghiệm
1.2.1. Định nghĩa
Giả s ng th m u n, ch n m p. ử ta xét tổ ể N, cỡ ẫ ọ ẫu theo phương pháp có lặ
Ta có m i m t l n n m u là m t l n th c hi n phép th có không gian bi n c ỗ ộ ầ chọ ẫ ộ ầ ự ệ ử ế ố
là N.
Gọi X là bi n ng u nhiên ch c tính) c ng ta c n quan tâm, ế ẫ ỉ thông tin (đặ ủa đối tượ ầ
khi đó:
Tương ứ ẫu) thu đượng với n lần thử (n lần chọn m c n biến ngẫu nhiên X ; X ; ... ;
1 2
X
n
tính v n ng u nhiên X) và các bi n ng p v i nhau. (có cùng đặc ới biế ẫ ế ẫu nhiên này độc lậ ớ
Ta có (X ; X ; ... ; X ) g i là m u ng ng v i m i bi n ng
1 2 n
ọ ẫ ẫu nhiên và tương ứ ớ ỗ ế ẫu
nhiên X , i = 1, 2,..., n có giá tr x , i = 1, 2, ..., n và (x ; x ; ... ; x ) g i là m u th
i
ị
i 1 2 n
ọ ẫ ực
nghi ệm.
Ví dụ
Khảo sát, tìm hi ểu điểm số bài thi môn Anh văn của SV trường ĐH A.
Ta chọn ng u nhiên n = 20 bài thi ( c hi n 20 phép th p). ẫ thự ệ ử độc lậ
→ Có 20 biến ngẫu nhiên (X
1
; X ; ... ; X
2 20
) gọi là mẫu ngẫu nhiên
và m có m c t dãy g ỗi m t bài thi ộ ột số (điểm số ủa bài thi đó) → mộ ồm 20 số
(7; 3; 9; 9; 5; 7; 5; 5; 6; 0; 1; 5; 8; 7; 8; 5; 4; 5; 9; 5) gọi là m u th c nghi ẫ ự ệm.
1.2.2. Cách x p x p m c nghi m ắ ế ẫu thự ệ
(1.2.2.1) Sắp tăng dần gi ( ảm dần)
Giả s u th c nghi v x ... x g i là s n. ử có mẫ ự ệm (x ; x ; ... , x
1 2 n
) ới x
1
2
n
ọ ắp tăng dầ
Và mẫu th c nghi m (x x ... x g i là s p gi n. ự ệ
1
; x ; ... , x
2 n
) với x
1
2
n
ọ ắ ảm dầ
(1.2.2.2) Sắp theo b ng phân ph i t n s ả ố ầ ố
−
t n su c nghi m không chia l p, chia lầ ất thự ệ ớ ớp
(i) Sắp theo b ng phân ph n s p: ả ối tầ ố thực nghiệm không chia lớ
x
i
x
1
x
2
...
x
k
n
i
n
1
n
2
...
n
k
v + n +.. + n = n ới n
1 2 k
(ii) Sắp theo b ng phân ph n s c nghi l p: ả ối tầ ố thự ệm chia ớ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
73
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
x
i
[x
1
) ; x
2
[x
2
; x )
3
...
[x
k−1
) ; x
k
n
i
n
1
n
2
...
n
k
v + n +.. + n = n ới n
1 2 k
Ví dụ
Khảo sát, tìm hi ểu điểm số bài thi môn Anh văn của SV trường ĐH A.
Ta chọn ng c s u ẫu nhiên n = 20 bài thi, thu đượ ố liệ
(7; 3; 9; 2; 5; 7; 4; 5; 6; 0; 1; 4; 8; 7; 8; 5; 4; 5; 9; 4)
x
i
0
1
2
3
4
5
6
7
8
9
n
i
1
1
1
1
4
4
1
3
2
2
Gọi là b i tảng phân phố ần s th c nghi m không chia l p. ố ự ệ ớ
+ Cũng vớ ớp (nhóm) dưới 5 điể 5 điểm đếi mẫu khảo sát trên, ta chia theo từng l m, từ n
dưới 8, từ ng chia l 8 điể ến 10 điểm, khi đó ta có bảm đ ớp như sau:
x
i
[0 − 5)
[5 − 8)
[8 − 10)
n
i
8
8
4
Gọi là b i tảng phân phố ần s ố thực nghiệm chia l p. ớ
+ T b ng trên, nừ các ả ếu ta đặt
, 1, 2,...,
i
i
n
i k
n
= =
ta có b ng phân phả ối t tần suấ thực
nghi m chia l p, không chia l ng. ệ ớ ớp tương ứ
1.3. Biểu đồ
−
−
−
−− Hàm phân phối thực nghiệm
1.3.1. Bi ểu đồ
Xét biến ng u nhiên X, có b ng phân ph i t n s hi m không chia l p ẫ ả ố ầ ố thực ng ệ ớ
x
i
x
1
x
2
...
x
k
n
i
n
1
n
2
...
n
k
v + n +.. + n = n ới n
1 2 k
Trên hệ c Oxy, v i Ox , Oy , n = 1, 2,..., k trụ ớ Ox
i
On
i
, đặt M
i
(x
i i
), i
Nối các điểm M
i
c bi t→ thu đượ ểu đồ ần s c u th c nghiố ủa mẫ ự ệm.
Ví dụ
L ta có các s u: ấy mẫu có kích thước n = 15, ố liệ
2 1 3 5 4 3 5 4
5 5 3 4 5 5 4
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
74
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Hãy lập b ng th ng kê, v bi hình g n s n s . ả ố ẽ ểu đồ ậy tầ ố, đa giác tầ ố
Giải
B ng th ng kê : ả ố
Biểu đồ hình gậy tần số
Đa giác tần số
1
2
3
4
5
1
3
4
6
1
2
3
4
5
1
3
4
6
1.3.2. Hàm phân ph i t c nghi m không chia l p ố ần số thự ệ ớ
Xét biến ng u nhiên X, có b ng phân ph i t n s m không chia l p ẫ ả ố ầ ố thực nghiệ ớ
x
i
x
1
x
2
...
x
k
n
i
n
1
n
2
...
n
k
v i n + n +.. + n = n. ớ
1 2 k
Hàm số c kí hi u F nh đượ ệ
n
(x) và xác đị
1
1
1 2
1 2
2 3
0,
,
( )
,
....
1,
n
k
x x
n
x x x
n
F x n n
x x x
n
x x
= +
g là hàm phân ph n s a m u th a bi n ng u nhiên X.ọi ối tầ ố thực nghiệm củ ẫ ực nghiệm củ ế ẫ
i
x
1 2 3 4 5
i
n
1 1 3 4 6
i
f
1
15
1
15
3
15
4
15
6
15
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
75
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
§2. CÁC THAM SỐ ĐẶC TRƯNG CỦA MẪU
I. Các tham số đại diện cho giá trị trung tâm
2.1. Trung bình mẫu (Kỳ vọng mẫu)
2.1.1. Định nghĩa
Xét bi n ng u nhiên X có m u ng u nhiên (X ; X ; ... ; X ) và có m u th c nghiế ẫ ẫ ẫ
1 2 n
ẫ ự ệm
(x ).
1
; x ; ... ; x
2 n
Khi đó:
+ Trung bình m u ng u nhiên c c kí hi u ẫ ẫ ủa X đượ ệ
X
nh và được xác đị
1
1
n
i
i
X X
n
=
=
+ Trung bình m u th c kí hi u ẫ ực nghiệm của X đượ ệ
x
nh và được xác đị
1
1
n
i
i
x x
n
=
=
2.1.2. Cách tính trung bình m c nghi m ẫu thự ệ
Xét biến ng u nhiên X, có b ng phân ph i t n s ghi m không chia l p ẫ ả ố ầ ố thực n ệ ớ
x
i
x
1
x
2
...
x
k
n
i
n
1
n
2
...
n
k
v + n +.. + n = n. ới n
1 2 k
Khi đó: +
1
1
k
i i
i
x n x
n
=
=
(i1)
+
( )
1
1
k
i i
i
x a n x a
n
=
= + −
, v R (i2) ới a
Trườ ợ ố ộng h p các x , i = 1, 2,..., k l
i
ập thành một cấp s c ng có công sai bằng h, thì
t tính b ng công th a có thể ằ ức:
+
1
k
i
i
i
x ah
x a n
n h
=
−
= +
, v ) ới aR (i3
2.1.3. Ý nghĩa số ung bình mtr ẫu
S trung bình m u th c nghi c làm giá tr i di n cho t t c các giá tr cố ẫ ự ệm đượ ị đạ ệ ấ ả ị ủa
m u th c nghi m c a X và n cho t ng th N n u giá tr c a các m u là ẫ ự ệ ủ nó được làm đại diệ ổ ể ế ị ủ ẫ
tương đố ồng đềi đ u.
Ngoài ra trung bình m ng cho trung bình c a bi n ngẫu được dùng để ước lượ ủ ế ẫu
nhiên X.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
76
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2.2. Số trung vị của mẫu thực nghiệm
2.2.1. Định nghĩa
Xét bi n ng u nhiên X có m u th c nghi m (x ; x ; ... ; x c s p theo th t ế ẫ ẫ ự ệ
1 2 n
) đượ ắ ứ ự
tăng dầ ặ ản (ho c gi m dần).
S trung v c a m u th c nghi m c a X là s c kí hi u med (X) và xác ố ị ủ ẫ ự ệ ủ ố thực đượ ệ
n
định:
1
, 2 1
( )
, 2
2
k
n
k k
x n k
med X
x x
n k
+
= −
=
+
=
Nhận xét
S n m gi x . ố trung vị là số ằ ữa dãy số
1
; x ; ... ; x
2 n
2.2.2. Cách tìm s trung v v i bi n ng u nhiên X có b ng phân ph i t n số ị ớ ế ẫ ả ố ầ ố thực
nghiệm
(i) Bảng phân ph i t n s không chia l p: ố ầ ố thực nghiệm ớ
1
2
,
( )
2
,
2 2
i
i k
k
in
i k
k k
i
i k
n
n
x
n
nmed X
x x
n
n
+
=
+
=
(ii) Bảng phân ph n s p:ối tầ ố thực nghiệm chia lớ
( )
( )
1 1
1 1
2
2
. ,
( )
2
1
1 ,
2 2
i
i
i k
i k
k k k
k
i
n
i k
k k k i
i k
k
n
n
n
n
x x x
n
n
n
med X
n
x x x n
n
− −
− −
−
+ −
=
+ − − =
• Chú ý. L p có ch ng v g p trung v c u ớ ứa số tru ị ọi là lớ ị ủa mẫ thực nghiệm.
2.2.3. Ý nghĩa của số trung vị
S trung v là s á tr trung tâm c a dãy các giá tr c a m u thố ị ố đặc trưng cho gi ị ủ ị ủ ẫ ực
nghi ệm.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
77
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2.3. Số Mod của mẫu thực nghiệm
2.3.1. Định nghĩa
Xét biến ng u nhiên X có m u th c nghi ẫ ẫ ự ệm ; x ; ... ; x(x
1 2 n
).
Giá tr có trong m u th c nghi m c a X có t n s l n nh c g i là s Mod cị ẫ ự ệ ủ ầ ố ớ ất đượ ọ ố ủa
m u th i c kí hi u Mod ẫ ực ngh ệm của X và đượ ệ
n
(X).
2.3.2. Cách t Mod c a X có b ng phân ph n s c nghi ìm số ủ ả ối tầ ố thự ệm.
(i) Bảng phân ph i t n s ng chia l p: ố ầ ố thực nghiệm khô ớ
Mod
n
(X) = x
i
n u n max{n ế
i
=
1
; n ; ... ; n
2 k
}.
(ii) Bảng phân ph n s p:ối tầ ố thực nghiệm chia lớ
Nếu t p th ; x n s n = max{n } thì ại lớ ứ i là [x
i−1 i
] có tầ ố
i 1
; n ; ... ; n
2 k
1
( )
2
i i
n
x x
Mod X
−
+
=
• Chú ý. L p có ch a s i là l p Mod c a m u th c nghi m. ớ ứ ố Mod gọ ớ ủ ẫ ự ệ
2.3.3. Ý nghĩa của số trung vị
S Mod cho bi c giá tr nào c a m u th c nghi m là xu t hi n nhi u nh t, nó ố ết đượ ị ủ ẫ ự ệ ấ ệ ề ấ
không ph c vào các giá tr quá l n hay quá nh c a m u th c nghi ụ thuộ ị ớ ỏ ủ ẫ ự ệm.
II. Các tham số đại diện cho độ phân tán (độ chênh lệch)
2.4. Phương sai mẫu
2 .4.1. Định nghĩa
Xét bi n ng u nhiên X có m u ng u nhiên (X ; X ; ... ; X ) và có m u th c nghi m ế ẫ ẫ ẫ
1 2 n
ẫ ự ệ
(x
1
; x ; ... ; x ) và gi s X có trung bình m u ng u nhiên là
2 n
ả ử ẫ ẫ
X
, trung bình m u thẫ ực
nghiệm
x
. Khi đó:
+ Ph u ng u nhiên c a X là m t bi n ng c kí hi u S c xác ương sai mẫ ẫ ủ ộ ế ẫu nhiên đượ ệ
2
và đượ
định
( )
2
2
1
1
n
i
i
S X X
n
=
= −
+ Phương sai mẫ và đượ
u thực nghiệm của X là một số thực được kí hiệu s
2
c xác định
( )
2
2
1
1
n
i
i
s x x
n
=
= −
2.4.2. Cách tín u c nghi m h phương sai mẫ thự ệ
Xét biến ng u nhiên X, có b ng phân ph i t n s m không chia l p ẫ ả ố ầ ố thực nghiệ ớ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
78
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
x
i
x
1
x
2
...
x
k
n
i
n
1
n
2
...
n
k
v + n +.. + n = n ới n
1 2 k
Khi đó: +
( )
2
2 2
1
1
( )
k
i i
i
s n x x
n
=
= −
(k1)
+
( )
( )
2
2
2
1
1
k
i i
i
s n x a x a
n
=
= − − −
, v R (k2) ới a
Trườ ợ ộ ố ộng h p các x , i = 1, 2,..., k l
i
ập thành m t cấp s c ng có công sai bằng h, thì ta có
th tínhể b ng công th c: ằ ứ
+
( )
2
2
2
2
1
k
i
i
i
x ah
s n x a
n h
=
−
= − −
, v R (k2) ới a
2.5. Phương sai điều chỉnh của mẫu
−
−
−
−− Độ lệch tiêu chuẩn
−
−
−
−− Độ lệch tiêu chuẩn
điều chỉnh của mẫu
2.5. 1. Định nghĩa
Xét bi n ng u nhiên X có m u ng u nhiên (X ; X ; ... ; X ) và có m u th c nghiế ẫ ẫ ẫ
1 2 n
ẫ ự ệm
(x
1
; x ; ... ; x ) và gi s u ng u nhiên là S u th
2 n
ả ử X có phương sai mẫ ẫ
2
, phương sai mẫ ực
nghi . ệm s
2
Khi đó:
+
2 2
1
.
1
n
S S
n
=
−
g u ch nh c a m u ng u nhiên c a X. ọi là phương sai điề ỉ ủ ẫ ẫ ủ
+
2 2
1
.
1
n
s s
n
=
−
g u ch nh c a m u th c nghi a X. ọi là phương sai điề ỉ ủ ẫ ự ệm củ
+
2
S S=
g l ch tiêu chu n c u ng u nhiên c ọi là độ ệ ẩ ủa mẫ ẫ ủa X.
+
2
s s=
g l ch tiêu chu n c u th ọi là độ ệ ẩ ủa mẫ ực nghiệm của X.
+
2
1 1
S S=
g l ch tiêu chu i u ch nh c a m u ng u nhiên c ọi là độ ệ ẩn đ ề ỉ ủ ẫ ẫ ủa X.
+
2
1 1
s s=
g l ch tiêu chu u ch nh c a m u th m c ọi là độ ệ ẩn điề ỉ ủ ẫ ực nghiệ ủa X.
2.5.2. Ý nghĩa
Các giá tr l tiêu chu n cho ta nh n bi t s u c a các ị phương sai hay độ ệch ẩ ậ ế ự đồng đề ủ
giá tr c a m u th c nghi ị ủ ẫ ự ệm.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
79
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 1
Tìm hi u m c thu nh p c àm thêm t i khu v c Z, v i c m u n = ể ứ ậ ủa sinh viên đi l ạ ự ớ ỡ ẫ
100, đơn vị tính 100.000 ngàn.
Ta thu được bả ố ầng phân ph i t n số thực nghi ệm như sau:
x
i
3
5
6
8
10
n
i
20
18
32
25
5
Tính các tham s ố
2 2
1 1
, , ,x s s
.
Lời gi i ả
* Cách 1
Áp dụng công thức
1
1
k
i i
i
x n x
n
=
=
,
( )
2
2 2
1
1
( )
k
i i
i
s n x x
n
=
= −
:
1 592
20 3 18 5 32 6 25 8 5 10 5
100 100
x = + + + + = =
.
( )
2
2 2 2 2 2 2
1
20 3 18 5 32 6 25 8 5 10 5,92 3,7
100
s
= + + + + − =
.
2 2
1
100
. 3,7736 3,8
1 99
n
s s
n
= = =
−
.
2
1 1
1,95s s= =
.
* Cách 2
Lập b ảng để tính các giá trị tham số như sau:
x
i
n
i
x a
i
−
n
i
(x
i
− a)
n
i
(x
i
− a)
2
3
20
−3
−60
180
5
18
−1
−18
18
a = 6
32
0
0
0
8
25
2
50
100
10
5
4
20
80
100
−8
378
( )
1
1 1
6 ( 8) 5,92
100
k
i i
i
x a n x a
n
=
= + − = + − =
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
80
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
( )
( )
( )
2
2 2
2
1
1 1
378 0,08 3,773
100
k
i i
i
s n x a x a
n
=
= − − − = − =
.
Ví dụ 2
Khả ộ ạo sát mức chi phí ti n và ti c trên mền điệ ền nướ t tháng của hộ dân t i khu vực
Z, với cỡ m tính 100.000 ngàn. ẫu n = 100, đơn vị
Ta thu được bả ống phân ph i tần số thực nghi ệm như sau:
x
i
3 7 −
7−11
11 15 −
15 19 −
n
i
45
25
20
10
Tính các tham s ố
2 2
1 1
, , ,x s s
.
Lời giải
Chuyển b ng d ng không ch p ả trên về ạ ia lớ
x
i
5
9
13
17
n
i
45
25
20
10
Tính các tham số
2 2
1 1
, , ,x s s
.
Vì các giá tr x là m t c p s c ng có công sai h = 4, d ng các công ị
i
ộ ấ ố ộ do đó ta sử ụ
thức
1
k
i
i
i
x ah
x a n
n h
=
−
= +
và
( )
2
2
2
2
1
k
i
i
i
x ah
s n x a
n h
=
−
= − −
.
Lập b ảng để tính các giá trị tham số như sau:
x
i
n
i
i
x a
h
−
i
i
x a
n
h
−
2
i
i
x a
n
h
−
5
45
−1
−45
45
a = 9
25
0
0
0
13
20
1
20
20
17
10
2
20
40
−5
105
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
81
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
1
4
9 ( 5) 8,8
100
k
i
i
i
x ah
x a n
n h
=
−
= + = + − =
( )
2
2
2
2 2
1
16
105 (0, 2) 16,7
100
k
i
i
i
x ah
s n x a
n h
=
−
= − − = − =
.
Chương 5. ƯỚC LƯỢNG THAM SỐ
§1. ƯỚC LƯỢNG ĐIỂM
1.1. Khái niệm về ước lượng tham số
Xét m t t ng th N, gi s ta c n quan n bi n ng ng (ộ ổ ể ả ử ầ tâm đế ế ẫu nhiên X đo lườ đánh
giá) m t thông tin (d u hi a cá th n t ) trong t ng th ng ộ ấ ệu) nào đó củ ể (phầ ử ổ ể N, X là đại lượ
t ph n t này n ph n t khác... hay đổi từ ầ ử đế ầ ử
Ví d xét t ng th N là SV (m i SV là m t cá th , là m t ph n t ) và gi sụ ổ ể ỗ ộ ể ộ ầ ử ả ử thông
tin ta c m s bài thi môn toán xác su t & th ng kê, n ngần quan tâm là điể ố ấ ố ở đây X là biế ẫu
nhiên ch m s bài thi c a m có giá tr i t ph n t n ph n t ỉ điể ố ủ ỗi SV → X ị thay đổ ừ ầ ử này đế ầ ử
khác (điể thay đổm số của mỗi bài thi có sự i...).
Phân ph i xác su a X t ng ta gi viố ất củ hường khó “nắm bắt” và thông thườ ới hạn ở ệc
xác đị đặc trưng của X như giá trị phương sai, nh một số các tham số trung bình (kì vọng),
trung v ta gị, mode...(các tham s ố ọi chung là tham s ố t)
Các tham s này không th nh chính xác n u không bi c phân ph i xác ố ể xác đị ế ết đượ ố
suất X, mà ph ng t c a X trên m t m n ng u nhiên ả c lưi ướ ợ ừ các giá trị ủ ộ ẫu được chọ ẫ
→ Bài toán ướ ểu như c lượng tham số được phát bi sau:
Gi s bi n ng u nhiên X có tham s t mà ta quan tâm. ả ử ế ẫ ố đặc trưng t nào đó chưa biế
Vấn đề đặt ra l trên n giá tr x , x , ... c t m t m u thà căn cứ ị
1 2
, x
n
của X (đo đượ ừ ộ ẫ ực
nghi n tìm ra m t giá tr g a t . ệm) cầ ộ ị ần đúng T củ
Ta có các định nghĩa sau:
Đị nghĩanh 1
M t hàm T = T ; x ;...; x ) c a n giá tr x ; x ;...; x c g i là mộ
n
(x
1 2 n
ủ ị
1 2 n
đượ ọ ột ước lượng
điểm cho t .
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
82
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Để ọ ộ ị khảo sát về mặt Toán h c, ta coi (x ; x ;...; x ) là m
1 2 n
t giá tr quan sát được (là
giá tr c nghi m) c a m u ng u nhiên (X ; X ;...; X ), tr n ng u nhiên Xị thự ệ ủ ẫ ẫ
1 2 n
ong đó các biế ẫ
i
;
i = 1, 2, ..., n là độc lập có cùng phân phối xác suất với X.
Như vậ ột hàm ước lượ do đó y m ng T = T là hàm n bi
n
ến ngẫu nhiên X ; X ;...; X
1 2 n
nó cũng là mộ ủa ước lượ cũng thay đổt biến ngẫu nhiên và giá trị c ng i từ mẫu quan sát
này đến mẫu quan sát khác.
Việc lựa chọn m c tiêu chu n sau: ột ước lượng nào là “tốt nhất” được căn cứ trên cá ẩ
Định nghĩa 2
Định nghĩa 2.1. Ướ ược l ng không chệch
Ướ ợ đượ ợ ủc lư ng T
n
c gọi là ước lư ng không chệch c a t nếu E(T t .
n
) =
Tính chất không ch ch c ng T không có sai s h ng. ệ ó nghĩa là ước lượ
n
ố ệ thố
Định nghĩa 2.2. Ước lượng v ngữ
Ướ ợ đượ ợ ủc lư ng T
n
c gọi là ước lư ng vững c a t n ếu:
 > 0,
lim 1
n
n
P T t
→
− =
.
Tính ch t v ng là b ng T g n t tùy ý v xác su t cao khi c ấ ữ ảo đảm cho ước lượ
n
ầ ới ấ ỡ
m u n l ẫ ớn.
Định nghĩa 2.3. Ước lượng hi u quệ ả
Ước lượ ọi là ước lượ là ước lượng T
n
được g ng hiệu quả của t n ếu T
n
ng không
chệch và phương s ấ ấ ả c lư ệai D(T nh
n
) là nhỏ t trong l p tớ t c các ướ ợng không ch ch.
1.2. Ước lượng cho giá trị trung bình
Giả s X là bi n ng u nhiên v i E(X) = t), c g i là giá tr trung ử ế ẫ ớ ( chưa biế đượ ọ ị
bình c ng th s t t ng quát trên). ủa tổ ể N ( ở đây là tham ố ổ ở
Nếu ta có m t m u th c nghi m n giá tr x ; x ;...; x c a X thì trung bình m u ộ ẫ ự ệ ị
1 2 n
ủ ẫ
x
s ng cho . ẽ được dùng làm ước lượ
Định lý
Trung bình m u ẫ
x
là ước lượng không chệch và vững cho trung bình của tổng thể
N.
1.3. ) Ước lượng cho phương sai
( hoặc kí hiệu
2
Giả s X là bi n ng u nhiên v i D(X) = c gử ế ẫ ớ
2
(
2
chưa biết),
2
đượ ọi là phương
sai c a tủ ổng thể t t ng quát trên). N (
2
ở đây là tham số ổ ở
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
83
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Nếu ta có m t m u th c nghi m n giá tr x ; x ;...; x cộ ẫ ự ệ ị
1 2 n
ủa X thì phương sai điều
chỉnh mẫu thực nghiệm s
1
2
sẽ ng cho . đượ ớ ợc dùng làm ư c lư
2
Định lý
Phương sai điều chỉnh mẫu thực nghiệm s
1
2
là ước lượng không chệch cho .
2
§2. KHOẢNG TIN CẬY CHO KỲ VỌNG
2.1. Đặt vấn đề
2.1.1. Bài toán tìm kho ảng tin cậy đặt ra như sau:
Căn cứ ) xác đị ảng (a; b) để trên mẫu thực nghiệm (x ; x ;...; x
1 2 n
nh một kho khoảng
đó chứ cho trướ ờng đượ 0, thườa tham số t với xác suất 1 - c (1 - thư c chọn 0,9 ng là
0,95).
M xác kho ng tin c ột cách chính ả ậy đượ ịnh nghĩa như sau:c đ
Định nghĩa 1
Giả s bi n ng u nhiên X có m u ng u nhiên (X ử ế ẫ ẫ ẫ
1
; X ; ...; X
2 n
).
Nếu có hai hàm f
1
(X
1
; X ; ...; X ; X ; ...; X
2 n
), f
2
(X
1 2 n
a mãn: ) thỏ
P[f (X 1 - , v 1 - g n b
1
(X
1
; ; ...; XX
2 n
) < t < f
2 1
; X ; ...; X
2 n
)] = ới ầ ằng 1, thì khi đó
Với m t m u th c nghi m (x ; x ; ...; x ) kho ng sộ ẫ ự ệ
1 2 n
ả ố thực (f
1
(x
1
; x ; ...; x ); f
2 n 2
(x
1
;
x ; ...; x c g i là kho ng tin c y hay còn g i là kho n ng c a tham s t c
2 n
)) đượ ọ ả ậ ọ ả g ước lượ ủ ố ủa
X.
Thường được viết dưới dạng f
1
(x
1
; x ; ...; x
2 n
) < t < f
2
(x
1
; x ; ...; x
2 n
).
+ 1 - tin c y và ng ch n 1 - 0,95; là độ ậ thườ ọ
+ f f dài kho ng tin c y.
2
(x
1
; x ; ...; x
2 n
) −
1
(x
1
; x ; ...; x
2 n
) = l gọi là độ ả ậ
Nhận xét:
Khoảng tin c y c a tham s t ph thu c vào các hàm f ; X ; ...; X ), f ; Xậ ủ ố ụ ộ
1
(X
1 2 n 2
(X
1 2
;
...; X tin c y
n
) và độ ậ
y càng l n thì kho ng tin c y càng r ng (l l n). và độ tin cậ ớ ả ậ ộ ớ
Ứng với một độ tin cậy
c, kho ng tin c dài l ng n nhcho trướ ả ậy nào có độ ắ ất được
xem là kho ng tin c y t a tham s ả ậ ốt nh t cấ ủ ố t của X.
Bài toán tìm kho tin c y c a tham s a X là tìm kho ng tin c y t ảng ậ ủ ố t củ ả ậ ốt nhất.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
84
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
2.1.2. Bài toán tìm kho y ảng tin cậ
+ L p m t m u ng u nhiên (X ậ ộ ẫ ẫ
1
; X ; ...; X
2 n
) của X;
+ C tin c y 1 - ho độ ậ
+ Tìm các hàm f ; X
1
(X
1
; X ; ...; X
2 n
), f
2
(X
1 2
; ...; X
n
) sao cho
P[f ) < t < f 1 -
1
(X
1
; X ; ...; X
2 n 2
(X
1
; X ; ...; X
2 n
)] = (i1)
và hi u f ; X ; ...; X f ; X ; ...; X ) nh n m i giá tr nh nh t trong các cệ
2
(X
1 2 n
) −
1
(X
1 2 n
ậ ọ ị ỏ ấ ặp
hàm th a mãn (i1). ỏ
+ L p kho ng tin c y t t nh t f ; x ; ...; x ) < t < f ; x ; ...; x ) v i (x ; x ; ...; x ) lậ ả ậ ố ấ
1
(x
1 2 n 2
(x
1 2 n
ớ
1 2 n
à
m u th a X. ẫ ực nghiệm củ
• Chú ý. Ngoài bài toán trên, ta còn có các bài toán khác:
(b1) Cho độ y 1 - dài kho ng tin c c m u n; tin cậ , cho độ ả ậy l, tìm kích thướ ẫ
(b2) Cho độ dài khoảng tin cậy l, cho kích thước mẫu n, tìm độ tin cậy 1 - .
2.2. Khoảng tin cậy cho kỳ vọng (tóm tắt các công thức)
X là biến ng u nhiên chu n N(t; ẫ ẩ ).
2.2.1. Trường hợp
t đã biế
Khoảng tin c y cho tham s ng: ậ ố t có dạ
1 1
1 1
2 2
. .x x
n n
− −
− −
− +
(i2)
với
2
2
0
1
( )
2
x
t
x e dt
−
=
e, giá tr o b ng ph l (hàm Laplac ị được ch ở ả ụ ục).
Chú ý. N u b ng tra là ế ả
2
2
1
( )
2
x
t
x e dt
−
−
=
thì
( )
1
2
u = −
.
Chú ý. Từ (i1) →
1 1 1
1 1 2 1
.
2 2 2
. .x x
nn n
− − −
− − −
+ − − =
g dài ọi là độ
kho ng tin c y và ả ậ
1
1
2
.
n
−
−
g i là sai s . ọ ố
2.2.2. Trường hợp
t chưa biế
+ Xét c m u n > 30. ỡ ẫ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
85
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Khoảng tin c y cho tham s ng: ậ ố t có dạ
1 1
1 1
1 1
. .
2 2
s s
x x
n n
− −
− −
− +
(i3)
với
2 2 2
1 1 1
, .
1
n
s s s s
n
= =
−
, u th c nghi m c ở đây s
2
là phương sai của mẫ ự ệ ủa X.
+ Xét c m u n < 30. ỡ ẫ
Khoảng tin c y cho tham s ng: ậ ố t có dạ
1 1
1; 1;
2 2
. .
n n
s s
x t x t
n n
− −
− +
(i4)
v i ớ
1;
2
n
t
−
phân ph i Student (tra b ng) : ố ả
Các ví d h a ụ minh ọ
Ví d 1. ụ Khảo sát ng u nhiên n = 36 SV c a m i h c cho th y tiẫ ủ ột trường đạ ọ ấ ền ăn trung
bình là 380 ngàn đồ ền ăn SV là biếng /1 tháng/1 SV. Giả sử ti n ngẫu nhiên X tuân theo
luậ ố ẩt phân ph i chu n N(;
),
ng. = 14 ngàn đồ
Với độ ền ăn trung bình củ ủa trườ tin cậy 1 - = 0,95, hãy tìm kho ảng tin cậy ti a SV c ng
đạ ọi h c đó.
Lời giải
Gọi t là tiền ăn trung bình của SV, t = E(X)
Khoảng tin c y cho t có d ng : ậ ạ
1 1
1 1
2 2
. .x x
n n
− −
− −
− +
(i)
Từ giả thiết
1
1
380; 14; 36; 1 0,95 1,9
2
x n
−
−
= = = − = → =
, thay vào (i) thu
được 375,4 < < 384,6.
Ví dụ 2. Trọng lượng của một loại quả là một biến ngẫu nhiên X, có luật phân phối chuẩn
N(;
).
Với mẫu n = 36, thu được bảng phân ph n s ối tầ ố thực nghi m: ệ
x
i
[0,9 − 1,3)
[1,3 − 1,7)
[1,7 − 2,1)
[2,1 − 2,5)
n
i
6
10
8
12
Hãy xác định kho ng cho trung bình, vảng ước lượ ới độ ậ tin c y 1 - = 0,97.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
86
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Lời giải
Khoảng ước lượng có dạng:
1 1
1 1
1 1
. .
2 2
s s
x x
n n
− −
− −
− +
) (1
Từ b ng b ng phân ph n s ả ả ối tầ ố thực nghi b ng thu g n: ệm → ả ọ
x
i
1,1
1,5
1,9
2,3
n
i
6
10
8
12
Tính được
1,789x =
, s = 0,445, 1 - = 0,97
1
1
1
2,17
2
−
−
→ =
.
thay vào (1), thu được: 1,628 < 1,95. <
Ví dụ 3. X là bi n ng u nhiên, có lu t phân ph n N(ế ẫ ậ ối chuẩ ;
).
Với mẫu n = 100, thu được
20,06x =
, s = 0,7890.
1
Hãy xác đị ủnh kho ng cho trung bình cảng ước lượ a X, với độ ậ tin c y 1 - = 95%.
Lời gi i ả
Khoảng ước lượng có dạng:
1 1
1 1
1 1
. .
2 2
s s
x x
n n
− −
− −
− +
(1)
20,06x =
, s = 0,7890, 1 - = 0,95
1
1
1
1,96
2
−
−
→ =
thay vào (1), thu được: 19,9054 < < 20,2196.
Ví dụ 4. X là bi n ng u nhiên, có lu t phân n N(ế ẫ ậ phối chuẩ ;
).
Với mẫu n ng phân ph n s = 25, thu được bả ối tầ ố thực nghiệm:
x
i
2,0
2,2
2,5
2,6
n
i
6
7
9
3
Hãy xác đị ủnh ng cho trung bình ckhoảng ước lượ a X, với độ ậ tin c y 1 - 95%. =
Lời giải
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
87
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Khoảng ước lượng có dạng:
1 1
1; 1;
2 2
. .
n n
s s
x t x t
n n
− −
− +
(1)
Từ bảng trên, tính được:
2,308x =
, s 0,227,
1
=
1 - = 0,95 →
1;
2
n
t
−
= t = 2,064 .
(24 ; 0,025)
Thay vào (1), thu được: 2,214 < < 2,402.
§ 3 . ƯỚC LƯỢNG KHOẢNG CHO TỈ LỆ
(Ướ ợc lư ng khoảng cho xác suất)
Xét t N, vổng th ể ớ đượi đối tượng c chia làm hai nhóm (A và
A
).
X biến ng ng lên t ng th ẫu nhiên tác độ ổ ể X, xác định như sau:
1
( )
0
A
X
A
=
Khi đó P(X ọn được đối tượ= 1) = p (ch ng A khi chọn ngẫu nhiên một phần tử từ
t ng th N) và p là t l ng A có trong t ng ổ ể ỉ ệ đối tượ ổ thể N.
Nhận xét:
+ X là bi n ng u nhiên có lu t phân ph n A(p) và E(X) = p, D(X) = p(1 p) ế ẫ ậ ối đơn giả −
+ Vì t ng th có s ng l n và ta không th kh o sát h t các ph n t c a t ng thổ ể ố lượ ớ ể ả ế ầ ử ủ ổ ể N →
ta không thể nh chính xác p. xác đị
− Ước lượ g điể ủa p là ước lượng điể ẫu nhiên đơn giản m c m của kỳ vọng của biến ng n
A(p), giá tr chính là t l ng A có trong m u v i m u n có kích ị ước lượng đó ỉ ệ đối tượ ẫ ớ ẫ
thước lớn.
Nếu đặt
k
f
n
=
a p là f. thì ước lượng điểm củ
(n càng lớn thì sai s gi ố ữa p và f càng nhỏ (?)).
− ng kho ng c ng kho v ng to Ướ ợc lư ả ủ ợa p xem như là ư c lướ ảng đối với kỳ ọ án
E(X) = p.
+ Kho ng tin c y c a p có d ng: ả ậ ủ ạ
1 1
(1 ) 1 (1 ) 1
. .
2 2
f f f f
f p f
n n
− −
− − − −
− +
Ví dụ 5. Khảo sát ng n ph a công ty Z. ẫu nhiên 200 người, có 50 người thích sả ẩm củ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
88
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Tìm khoảng tin c y cho t l p nh i thích s n ph m c a công ty Z, v ậ ỉ ệ ững ngườ ả ẩ ủ ới độ
tin cậy 1 - = 0, . 95
Lời giải
Gọi p là tỉ l nh n ph a công ty Z. ệ ững người thích sả ẩm củ
Từ gi ả thiết, ta có:
50
0, 2
200
f = =
, n.f = 50 > 10 và n(1 − f) = 150 > 10
Khoản ng cho p có d ng: g ước lượ ạ
1 1
(1 ) 1 (1 ) 1
. .
2 2
f f f f
f p f
n n
− −
− − − −
− +
(1)
v 1 - = 0,95 ới
1
1
1,96
2
−
−
→ =
.
Thay c c: 0,19 < p < 0,31.ác giá tr ị tương ứng vào vào (1), thu đượ
Ví d 6. ụ Khảo sát ng u nhiên 100 SV, có 60 SV n i không thích h c môn toán xác suẫ gườ ọ ất
& thống kê.
Tìm kho ng tin c y cho t l p nh ng SV không thích h c môn toán xác su t & ả ậ ỉ ệ ữ ọ ấ
th tinố ộng kê, với đ cậy
= 0,90.
Lời giải.
Gọi p là tỉ l nh c môn toán xác su t & th ng kê. ệ ững người không thích họ ấ ố
Từ gi ả thiết, ta có:
60
0,6
100
f = =
, n.f = 60 > 10 và n(1 − f) = 40 > 10
Khoảng ước lượng cho p có dạng:
1 1
(1 ) 1 (1 ) 1
. .
2 2
f f f f
f p f
n n
− −
− − − −
− +
(1)
v i 1 - = 0,90 ớ →
1
1
1,64
2
−
−
→ =
Thay các giá trị tương ứng vào vào (1), thu được: 0,52 < p < 0,68.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
89
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví d 7. ụ Để xác đị ột hòn đảo. Ngườnh số lượng Khỉ có trên m i ta bắt ngẫu nhiên 700 con
và làm d u trên nh ng con Kh chúng ra l i kh o. M t th i gian sau ấ ữ ỉ đó, sau đó thả ạ ắp đả ộ ờ
b u nhiên 200 con, nh n y có 50 con có làm d u. ắt ngẫ ậ thấ ấ
Hãy ước lượ có trên hòn đả ới động khoảng cho tổng số Khỉ o, v tin cậy 1 - =
0,90.
Lời giải
Gọi N là t ng sổ ố Khỉ có trên đảo và p là tỉ lệ Khỉ có làm d o, ta có: ấu ở trên đả
700
p
N
=
.
Từ gi ả thi t:ế
50
0, 2
200
f = =
, n.f = 50 > 10 và n(1 − f) = 150 > 10
Khoảng ng cho p có d ng: ước lượ ạ
1 1
(1 ) 1 (1 ) 1
. .
2 2
f f f f
f p f
n n
− −
− − − −
− +
(1)
v 1 - = 0,90 ới →
1
1
1,64
2
−
−
→ =
thay các giá trị tương ứ hu đượng vào vào (1), t c:
0,199 < p < 0,300
700
0,199 0,300 2331 350N
N
.
KL: Tổng s ố Khỉ có o n m trong kho ng [2333; 3517]. trên đả ằ ả
Ví dụ 8. Một lô hàng có 100.000 s n ph ả ẩm.
Kiểm tra ng u nhiên 400 s n ph m, có 20 s n ph u (ph ph m). ẫ ả ẩ ả ẩm xấ ế ẩ
Hãy ướ ới độc lượng khoảng cho tổng số sản phẩm xấu có trong lô hàng, v tin cậy
1 - = 0,95.
Lời giải
Gọi m là t ng s s m x u có trong lô hàng và p là t l s n ph m x u có trong ổ ố ản phẩ ấ ỉ ệ ả ẩ ấ
lô hàng đó, ta có:
100.000
m
p =
.
Từ gi ả thi t:ế
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
90
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
20
0,05
400
f = =
, n.f = 20 > 10 và n(1 − f) = 380 > 10
Khoảng ước lượng cho p có dạng:
1 1
(1 ) 1 (1 ) 1
. .
2 2
f f f f
f p f
n n
− −
− − − −
− +
(1)
v - = 0,95 ới 1
1
1
1,96
2
−
−
→ =
. Thay các giá trị tương ứng vào vào (1), thu được:
0,0285 < p < 0,0714
0,0285 0,0714 2864 71
100.000
m
m
.
KL: Tổng s s n ph m x u có trong lô hàng n ng [2850; 7140]. ố ả ẩ ấ ằm trong khoả
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
91
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Chương 6. K M ĐỊNH GIẢ THIẾTIỂ
§1. VẤN ĐỀ CHUNG
1.1. Đặt vấn đề
Khi xét m t m u ho c nhi u m c ch n ra t m t t ng th N, ta có m t nhộ ẫ ặ ề ẫu đượ ọ ừ ộ ổ ể ộ ận
đị ờ ủ ổnh tạm th i, có tính ch quan về các đặc điểm, dấu hiệu mà ta cần nghiên cứu trên t ng
th luể. N ng nh nh v tham s , vếu đó là nhữ ận đị ề các ố ề ật phân ph i c a bi n ng u nhiên X ố ủ ế ẫ
nà ng lên t ng th hay là nh ng nh n nh v s khác nhau hay gi ng nhau co đó tác độ ổ ể ữ ậ đị ề ự ố ủa
hai kì v ng c a hai bi n ng u nhiên thì ta g ng gi t th ng k ọ ủ ế ẫ ọi đó là nhữ ả thiế ố
Những gi t th c có th sai, ta c n ph i kiả thiế ống kê được đưa ra có thể đúng hoặ ể ầ ả ểm
định giả thi c là xét xem giết đó, tứ ả thiết đưa ra có được chấp nhận hay không và chấp
nh n m nào.ậ ở ức độ
Đố ớ ộ ụi v i m t giả ế thi t th sống kê được đưa ra ta có thể ử d ng nhiều phương pháp để
ki nh gi ểm đị ả thiết đó.
Các gi thi t th c kí hi u là H , các gi thi t trái v i gi t H ả ế ống kê thường đượ ệ
0
ả ế ớ ả thiế
0
(hay bác bỏ gi t Hả thiế
0
) được gọi là đối thiết, kí hiệu H
1
; H
2
;…
Câu hỏi đặt ra là: Chúng ta chấp nhận hay bác bỏ một giả thiết bằng cách nào?
Các nhà thống kê đều thống nhất với nhau một nguyên lý sau đây:
“Nếu một biến cố có xác suất rất nhỏ thì trong một phép thử hay một vài phép thử, biến
cố đó sẽ không xảy ra”.
→ Như vậy, ta bác bỏ giả thiết H
0
nếu xác suất xuất hiện (xảy ra) của một bc quan sát
được, tính trong điều k đúng là “nhỏ” iện giả thiết H
0
1.2. t Miền bác bỏ
−
−
−
−− Các sai lầm
−
−
−
−− Mức ý nghĩa của kiểm định giả thiế
1.2.1. Miền bác bỏ
Giả sử có giả thiết H
0
; Ta lập mẫu ngẫu nhiên của biến ngẫu nhiên X là
(X
1
;X ;x
2
;…;X
n
). Nếu qua một giá trị của mẫu ngẫu nhiên là mẫu thực nghiệm (x
1 2
;…;x
n
)
ta bác bỏ, không thừa nhận giả thiết H ) gọi là điểm bác bỏ của giả thiết
0
thì (x
1
;x
2
;…;x
n
H
0
.
Tập h m bác b g i là mi n bác b c ợp các điể ỏ ọ ề ỏ ủa giả thiết H .
0
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
92
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Việc ki nh gi thi t H ng là vi n bác b c a gi t H , kí ểm đị ả ế
0
thườ ệc đi tìm miề ỏ ủ ả thiế
0
hi u i là qui t nh (ho c ki nh W). ệ (hoặc W), gọ ắc kiểm đị ặ ắc qui t ểm đị
1.2.2. Các lo i sai l m c a ki t ạ ầ ủ ểm định giả thiế
i1/ Sai l m lo i 1: Gi thi nh ta bác b t H ầ ạ ả ết H
0
đúng, nhưng qua kiểm đị ỏ giả thiế
0
đó là một
sai lầm và g i là sai l m lo i 1.ọ ầ ạ
i2/ Sai l m lo i 2: Gi t H nh ta ch p nh n gi thi t Hầ ạ ả thiế
0
sai, nhưng qua kiểm đị ấ ậ ả ế
0
đó là
m và g i là sai l i ột sai l m ầ ọ ầm loạ 2.
Hai loại sai l m này có nh ng m tác h i khác nhau. ầ ữ ức độ ạ
1.2.3. M a ki nh gi thi t ức ý nghĩa củ ểm đị ả ế
Kí hiệu l = P(m = P(bác b thi
1
ắ ầc sai l m lo i 1)ạ ỏ giả thiết H
0
/ giả ết H
0
đúng).
và l = (m i 2) = P(ch p nh n gi i t H sai).
2
ắc sai lầm loạ ấ ậ ả th ết H
0
/ giả thiế
0
M t qui t c ki nh càng t t n u các l , l u cùng nh c cùng lúc ộ ắ ểm đị ố ế
1 2
đề ỏ, nhưng việ
làm cực ti c nhau. ểu l , l n vì l , l là ng
1 2
là không đơn giả
1 2
ượ
Trong th i ta xây d ng m t qui t c ki nh W sao cho khi dùng qui ực hành ngườ ự ộ ắ ểm đị
t ( c ng ch n 0,05) và l c c ti u. S c g i là mắc đó thì l
1
= ố định và thườ ọ
2
ự ể ố đượ ọ ức
ý nghĩa của kiểm định và
là miền bác bỏ.
Chú ý: n thi t, ng vi n hành m nh gi ng kê g Các bước cầ ế tro ệ ếc ti ột kiểm đị ả thiết thố ồm:
(b1) Phát biểu giả thiết H và đối thiết H
0
1
…
(b2) Định rõ mức ý nghĩa (xác suất mắc sai lầm loại 1)…
(b3) Chọn test thống kê …kí hiệu T
(b4) Chọn miền bác bỏ giả thiết H …kí hiệu
0
(b5) Tính gi á trị của test thống kê từ mẫu quan sát được…
(b6) KL bác bỏ giả thiết H
0
hay chấp nhận H
0
tùy theo giả thiết của test thống kê
có rơi vào miền bác bỏ giả thiết hay không…
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
93
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
§ 2. KIỂM ĐỊNH GIẢ THIẾT CHO TRUNG BÌNH
Xét X là biến ngẫu nhiên có luật phân phối chuẩn X N(;
2
).
Tổng thể là tập hợp các giá trị có thể có của X.
Một mẫu có cở n là một tập gồm n giá trị x ;…; x thu được từ quan sát độc lập
1
; x
2 n
về X., ( x ) là mẫu thực nghiệm…
1
; x
2
;…; x
n
Ta muốn kiểm định giả thiết về .
Xét các trường hợp:
2.1. Trường hợp phương sai (độ lệch chuẩn)
2
đã biết
Bài toán 1. Bài toán kiểm định hai phía.
Ta muốn kiểm định giả thiết H
0
: ; =
0
; đối thiết H
1
: ≠
0
với o trước.
0
là giá trị ch
Test thống kê được chọn:
( )
0
x n
T
−
=
Miền bác bỏ giả thiết H có dạng > c}, với c là hằng số phụ thuộc vào mức ý
0
= {T
nghĩa
được xác định như sau:
2
2
1
( ) 1 ; ( ) .
2
2
t
x
c x e dt
−
−
= − =
.
hoặc
2
2
0
1 1
( ) ; ( ) .
2
2
t
x
c x e d
−
−
= =
.
Bài toán 2. Bài (ph toán kiểm định một phía ía phải)
Ta muốn kiểm định giả thiết H
0
: ; =
0
: ; đối thiết H
1
>
0
với á trị cho trước.
0
là gi
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
94
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Test thống kê được chọn:
( )
0
x n
T
−
=
Miền bác bỏ giả thiết H có dạng c}, với c là hằng số phụ ộc vào mức
0
= {T > thu
ý nghĩa được xác định như sau:
2
2
1
( ) 1 ; ( ) .
2
t
x
c x e d
−
−
= − =
.
hoặc
2
2
0
1 1
( ) ; ( ) .
2
2
t
x
c x e d
−
= − =
.
Bài toán 3. Bài toán kiểm định một phía (phía trái)
Ta muốn kiểm định giả thiết H
0
: = t ;
0
; đối thiết H
1
: <
0
với
0
là giá trị cho trước.
Test thống kê được chọn:
( )
0
x n
T
−
=
Miền bác bỏ giả thiết H T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa
0
có dạng = {
được xác định như sau:
2
2
1
( ) 1 ; ( ) .
2
t
x
c x e d
−
−
= − =
.
hoặc
2
2
0
1 1
( ) ; ( ) .
2
2
t
x
c x e d
−
= − =
.
2.2. T 30. rường hợp phương sai (độ lệch chuẩn)
2
chưa biết, mẫu n
Trường hợp này ta vẫn dùng test thống kê như trên, trong đó được thay bằng độ
lệch tiêu chuẩn có điều chỉnh s
1
…
Bài toán 4. h 140 ngàn Một thông báo cho rằng trung bình một người vào siêu thị tiêu ết
đô.
Để kiểm định công bố trên. Chọn ngẫu nhiên mẫu gồm 50 người vào mua hàng
tính được số tiền trung bình họ tiêu là 154 ngàn đô, với độ lệch tiêu chuẩn có điều chỉnh
của mẫu là 62 ngàn đô và cho mức ý nghĩa Hãy kiểm định xem công bố = 0,02. của
nhóm nghiên cứu có đúng không?
Lời giải
Phát biểu giả thiết H = 140 (đơn vị tính = ngàn)
0
:
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
95
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
đối thiết H
1
: ≠ 140
(Bài toán kiểm định hai phía, với chưa biết, n > 30).
Khi đó Test thống kê
( )
( )
0
1
154 140 50
1,5
62
x t n
T
s
−
−
= = =
.
Hằng số c được xác định:
( ) 1 0,99 2,3
2
c c
= − = → =
.
( nhớ rằng
2
2
1
( )
2
x
t
x e dt
−
−
=
)
Nếu dùng bảng hàm Laplace
2
2
0
1 1
( ) ( )
2
2
x
t
x e dt c
−
−
= → =
.
Nhận xét chưa có cơ sở để bác bỏ giả thiết H Tạm thời chấp T = 1,59 < c = 2,33 →
0
→
nhận bá o của nhóm nguyên cứu là đúng.o cá
Bài toán 5. Công ty “LANHLUNG” có một hệ thống máy tính có thể xử lí 1200 hóa đơn
trong một giờ. Công ty “LANHLUNG” mới nhập về một hệ thống máy tính mới. Hệ thống
này khi chạy kiểm tra (chạy thử nghiệm) trong 40 giờ cho hấy số hóa đơn được xử lý t
trung bình trong 1 giờ là 1260, với độ lệch tiêu chuẩn của mẫu thực nghiệm là 215 và
mức ý nghĩa
= 5%.
Hãy nhận định xem hệ thống mới có tốt (về năng suất xử lí) hơn hệ thống cũ
không?
Lời giải
Phát bi = 1200 ểu giả thiết H
0
: (hệ thống mới tốt bằng hệ thống cũ)
) đối thiết H
1
: > 1200 (hệ thống mới tốt hơn hệ thống cũ
(Bài toán kiểm định một phía).
Ở đây ta tin một cách tiên quyết rằng hệ thống mới không thể tồi hơn hệ thống cũ.
Khi đó Test thống kê
( )
( )
0
1
1260 1200 40
1,7
215
x t n
T
s
−
−
= = =
.
Hằng số c được xác định: (c) = 1− = 0,95 → c = 1,64
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
96
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Nhận xét T = 1, bác bỏ giả thiết H Hệ thống mới tốt hơn hệ thống cũ 76 > c = 1,64 →
0
→
với mức ý nghĩa = 5%.
2.3. Trường hợp phương sai (độ lệch chuẩn)
2
chưa biết, mẫu n < 30.
B ài toán 6. Bài toán kiểm định hai phía.
Ta muốn kiểm định giả thiết H ;
0
: =
0
; đối thiết H
1
: ≠
0
với
0
là giá trị cho trước.
Test thống kê được chọn:
( )
0
1
x t n
T
s
−
=
Miền bác bỏ giả thiết H có dạng >c}, với c là hằng số phụ thuộc vào mức ý
0
= {T
nghĩa được xác định như sau:
1;
2
c t n
= −
.
Bài toán 7. Bài toán kiểm định một phía (phía phải).
Ta muốn kiểm định giả thiết H
0
: ; =
0
; đối thiết H
1
: >
0
với
0
là giá trị cho trước.
Test thống kê được chọn:
( )
0
1
x t n
T
s
−
=
Miền bác bỏ giả thiết H có dạng c}, với c là hằng số phụ thuộc vào mức ý
0
= { T >
nghĩa được xác định như sau:
( )
1;c t t n
= = −
.
Bài toán 8. m phía (phía trái). Bài toán kiểm định ột
Ta muốn kiểm định giả thiết H
0
: ; =
0
; đối thiết H
1
: <
0
với
0
là giá trị cho trước.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
97
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Test thống kê được chọn:
( )
0
1
t x n
T
s
−
=
Miền bác bỏ giả thiết H có dạn = { T>c}, với c là hằ ố phụ thuộc vào mức ý nghĩa
0
g ng s
được xác định như sau:
( )
1;c t t n
= = −
.
§3. KIỂM ĐỊNH GIẢ THIẾT CHO TỈ LỆ
3.1. Bài toán kiểm định hai phía
Kiểm định giả thiết H
0
: p = p
0
; ( p
0
là một số đã cho)
đối thiết H
1
: p ≠ p
0
;
Tiến hành n phép thử độc lập có k lần xảy ra biến cố A tần suất xảy ra biến cố A là → →
k
f
n
=
.
(f cho ta một “hình ảnh” của A trong tổng thể N (?))
Nhận xét: n.p
0
5 và n(1 p −
0
) 5
→ Test thống kê được chọn là
( )
( )
0
0 0
1
f p n
T
p p
−
=
−
.
Miền bác bỏ giả thiết H có dạng >c}, với c là hằng số phụ thuộc vào
0
= {T
mức ý nghĩa được xác định như sau:
2
2
1
( ) 1 ; ( ) .
2
2
t
x
c x e d
−
−
= − =
hoặc
2
2
0
1 1
( ) ; ( ) .
2
2
t
x
c x e d
−
−
= =
.
Ví dụ 1. Một đảng chính trị trong một cuộc bầu cử tổng thống tuyên bố (dự đoán) rằng
45% cử tri sẽ bỏ phiếu cho ứng cử viên A của họ.
Khảo sát 200 cử tri có 80 cử tri tuyên bố sẽ bỏ phiếu cho ông A. Với mức ý nghĩa
= 5%, hãy kiểm định xem dự đoán trên có đúng không.
Lời giải
Đây là bài toán kiểm định 2 phía.
Giả thiết H
0
: p = 0,45;
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
98
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
đối thiết H : p ≠ 0,45;
1
Tiến hành khảo sát 200 người ( thực hiện 200 phép thử độc lập)
→ có 80 cử tri bỏ phiếu cho ông A ( có 80 lần xảy ra biến cố )
→ tần suất xảy ra biến cố là
80 2
0, 4
200 5
f = = =
.
với n.p
0
= 200.(0,45) = 90 5 và n p ) = 200.(0,55) = 110 5 (1 −
0
→ test thống kê được chọn là
( )
( )
( )
0
0 0
0, 40 0, 45
1,
(0, 45).(0,55)
1
f p n
n
T
p p
−
−
= = = −
−
.
Với mức ý nghĩa = 0,05 →
( ) 1 0,975 1,9
2
c c
= − = → =
.
So sánh = 1,43 < c = 1,96 T → không có cơ sở bác bỏ giả thiết H
0
. Dự đoán của đảng
trên có thể đúng.
3.2. án ki Bài to ểm định phía phải
Kiểm định giả thiết H
0
: p = p
0
; ( p
0
là một số đã cho)
: p > p đối thiết H
1 0
;
Tiến hành n phép thử độc lập → có k lần xảy ra biến cố A → tần suất xảy ra biến cố A là
k
f
n
=
.
(f cho ta một “hình ảnh” của A trong tổng thể N (?))
Nhận xét: n.p
0
5 và n(1 p −
0
) 5
→ Test thống kê được chọn là
( )
( )
0
0 0
1
f p n
T
p p
−
=
−
.
Miền bác bỏ giả thiết H
0
có dạng = { T >c}, với c là hằng số phụ thuộc vào mức ý nghĩa
được xác định như sau:
2
1
2
( ) 1 ; ( ) .
2
t
x
c x e d
−
= − =
−
.
hoặc
2
1 1
2
( ) ; ( ) .
2
2
0
t
x
c x e d
−
= − =
.
Ví dụ 2. Một báo cáo nói rằng 18% gia đình ở thành phố T có máy tính ở nhà.
Để kiểm tra, người ta khảo sát ngẫu nhiên 80 gia đình ở thành phố T có trẻ em đang đi
học và thấy rằng có 22 gia đình ới mức ý nghĩa = 0,02, hãy kiểm định có máy tính. V
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
99
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
xem liệu trong các ga đình có trẻ em đang đi học, tỉ lệ gia đình có máy tính có hơn tỉ lệ
chung không?
Lời giải.
Đây là bài toán kiểm định 1 phía (phía phải).
Giả thiết H
0
: p = 0,18;
đối thiết H
1
: p > 0,18;
Nhận ới n.pxét v
0
= 80.(0,18) = 14,4 5 và n(1 p 6 5 −
0
) = 80.(0,82) = 65,
→ test thống kê được chọn là
( )
( )
0
0 0
1
f p n
T
p p
−
=
−
; với
0
22
0, 275 ; 80 ; 0,
80
f n p= = = =
→
( )
( )
0
0 0
2, 21
1
f p n
T
p p
−
= =
−
Với mức ý nghĩa = 0,05 →
( ) 1 0,98 2,0c c
= − = → =
So sánh T = 2,21 > c = 2,05 → Bác bỏ giả thiết H
0
→ Trong các gia đình có trẻ em đi
học, tỉ lệ gia đình có máy tính cao hơn tỉ lệ chung.
3.3. Bài toán kiểm định phía trái
Kiểm định giả thiết H
0
: p = p
0
; ( p
0
là một số đã cho)
: p < p đối thiết H
1 0
;
Tiến hành n phép thử độc lập → có k lần xảy ra biến cố A → tần suất xảy ra biến cố A là
k
f
n
=
.
(f cho ta một “hình ảnh” của A trong tổng thể N (?))
Nhận xét: n.p
0
5 và n(1 p −
0
) 5
→ Test thống kê được chọn là
( )
( )
0
0 0
1
p f n
T
p p
−
=
−
.
Miền bác bỏ giả thiết H
0
có dạng = { T >c}, với c là hằng số phụ thuộc vào mức ý nghĩa
được xác định như sau:
2
2
1
( ) 1 ; ( ) .
2
t
x
c x e d
−
−
= − =
.
hoặc
2
2
0
1 1
( ) ; ( ) .
2
2
t
x
c x e d
−
= − =
.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
100
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 3. Công ty QQ sản xuất bánh kẹo tuyên bố (dự đoán) rằng 2/3 trẻ em thích bánh
kẹo của công ty. Khảo sát 100 em có 55 em thích bánh kẹo của công ty QQ . Với mức ý
nghĩa
= 5%, hãy kiểm định xem tuyên bố của công ty QQ có nói quá không.
Lời giải
Đây là bài toán kiểm định 1 phía (phía trái).
Giả thiết H
0
: p = 2/3;
đối : p < 2/3; thiết H
1
Nhận xét với n.p
0
= 66,7 5 và n(1 p ) = 33,4 5 −
0
→ test thống kê được chọn là
( )
( )
0
0 0
2, 49
1
p f n
T
p p
−
= =
−
;
Với mức ý nghĩa = 0,05 →
( ) 1 0,95 1,6c c
= − = → =
So sánh T = 2,21 > c = 2,05 g ty → Bác bỏ giả thiết H
0
→ Công bố của côn là lớn hơn sự
thật.
Ví dụ 4. Tỉ lệ khỏi bệnh khi dùng thuốc A qua thống kê nhiều năm cho thấy là 16%. Với
một loại thuốc B mới khi dùng cho 600 bệnh nhân thì có 70 người khỏi bệnh, với không
mức ý nghĩa
hai = 5%, hãy so sánh tỉ lệ không khỏi bệnhcủa loại thuốc A và B.
Lời giải (tóm tắt)
Đây là bài toán kiểm định 2 phía.
Giả thiết H
0
: p = 0,16;
→ tần suất không khỏi bệnh khi dùng thuốc B là
70
0,116
600
f =
với n.p
0
= 600.(0,16) = 96 5 và n(1 p ) = 600.(0,84) = 504 5 −
0
→ g kê test thốn được chọn là
( )
( )
( )
0
0 0
0, 40 0, 45
2
(0, 45).(0,55)
1
f p n
n
T
p p
−
−
= = = −
−
.
Với mức ý nghĩa = 0,05 →
( ) 1 0,975 1,9
2
c c
= − = → =
.
So sánh = 2,9 > c = 1,96 T → Bác bỏ giả thiết H
0
→ Tỉ lệ không khỏi bệnh khi dùng
thuốc A và thuốc B là khác nhau một cách có ý nghĩa ở mức = 5%.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
101
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Ví dụ 5. Tỉnh Q báo cáo rằng tỉ lệ học sinh giỏi của tỉnh ít nhất là 20%. Bộ tiến hành xác
minh báo cáo này. Chọn ngẫu nhiên 400 học sinh, thấy rằng có 60 học sinh giỏi. Với mức
ý nghĩa
= 1%.
Bộ có cơ sở bác bỏ báo cáo của tỉnh Q hay không?
Lời gi (tóm tắtải )
Đây là bài toán kiểm định 1 phía (phía trái).
Gọi p là tỉ lệ học sinh . giỏi của tỉnh Q
Giả thiết H
0
: p = 0,2;
đối thiết H
1
: p < 0,2;
Nhận xét với n.p
0
= 400.(0,2) 5 và n(1 p 5 −
0
) = 400.(0,8)
với tần suất xuất hiện học sinh giỏi trong mẫu quan s át là f = 0,15
→ test thống kê được chọn là
( )
( )
0
0 0
2,5
1
p f n
T
p p
−
= =
−
;
Với mức ý nghĩa = 0,01 2,33 → c =
→ → T > c Bác bỏ giả thiết H
0
→ Bộ có cơ sở để cho rằng tỉ lệ học sinh giỏi của tỉnh Q thấp hơn 20%.
BÀI TẬP
Bài 1. X là bi n ng nhiên ch tr ng ng c a m t lo i s n ph m, X có lu t phân phế ẫu ỉ ọ lượ ủ ộ ạ ả ẩ ậ ối
chuẩn N( = 3,1. ;),
Với mẫu n = 100, thu được
26,5x =
.
Với m t ức ý nghĩa = 0,05, hãy kiểm định giả thiế
gt H i thi
0
: = 26 và đố ết đt H
1
: ≠ 26.
Lời giải.
Phát bi u bài toán: gt H = 26. ể
0
:
đt H
1
: ≠ 26.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
102
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Với m c ý = 0,05, Test th ng kê c n ứ nghĩa ố ầ chọn là:
( )
( )
0
26,5 26 100
1,6
3,1
x t n
T
−
−
= = =
.
Xác đị ỏnh miền bác b gt H , = { > c},
0
T
v = 0,05 c = 1,96 ới →
Nhận xét = 1,61 < c = 1,96 T
KL: Chưa có cơ sở bác bỏ giả thiết H m th i ch
0
, tạ ờ ấp nh n gi thi t H . ậ ả ế
0
Bài 2. X là bi n ng u nhiên ch u cao c a thi u niên, X có lu t phân ph i chu n ế ẫ ỉ chiề ủ ế ậ ố ẩ
N(; = 3,4 ),
Với mẫu n = 64, thu được
13,5x =
.
Với mức ý nghĩa = 0,01, hãy kiểm định giả thiết
gt H : > 13.
0
: = 13 và đối thiết đt H
1
Lời giải.
Phát bi u bài toán: gt H = 13. ể
0
:
: > 13. đt H
1
Với mức ý nghĩa = 0,01, Test thống kê cần chọn là:
( )
( )
0
13,5 13 64
2,6
1,5
x t n
T
−
−
= = =
.
Xác đị ỏnh miền bác b gt H , = { T > c},
0
v i = 0,01 c = 2,33 ớ →
Nhận xét T = 2,66 > c = 2,33
KL: Bác bỏ gi . ả thiết H
0
Bài 3. X là bi n ng u nhiên ch i th ng bình c a m t lo i s n ph m, X có lu t phân ế ẫ ỉ tuổ ọ tru ủ ộ ạ ả ẩ ậ
ph n N( ; = 14 ối chuẩ ),
Với mẫu n = 25, thu được
196x =
.
Với m c ý n = 0,05, hãy ki nh giứ ghĩa ểm đị ả thiết
gt H H : < 200.
0
: = 200 và đối thiết đt
1
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
103
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Lời giải.
Phát bi u bài toán: gt H = 200. ể
0
:
> 200. đt H
1
:
Với mức ý nghĩa = 0,05, Test thống kê cần chọn là:
( )
( )
0
200 196 25
1,8
11
t x n
T
−
−
= = =
.
Xác đị ỏnh miền bác b gt H , = { T > c},
0
v = 0,05 ,96 ới → c = 1
Nhận xét T = 1,81 < c = 1,96
KL: Chưa có cơ sở bác bỏ giả thiết H m th
0
, tạ ời chấp nh n gi thi t H . ậ ả ế
0
Bài 4. M t nhóm nghiên c u tuyên b r ng trung bình m t gia t 14 ) ộ ứ ố ằ ộ đình chi phí hế (m
3
nướ ộc trong m t tháng.
M u ng u nhiên n = 49 h u ột mẫ ẫ ộ thu được số liệ
15x =
, độ ẩn điề lệch tiêu chu u chỉnh
s = 5,8.
1
Hãy kiểm định tuyên b i m = 0,02. ố trên đúng hay sai vớ ức ý nghĩa
Lời giải.
Phát bi u bài toán: gt H = 14. ể
0
:
đt H
1
: ≠14.
Với m = 0,02, Test th ng kê c n ch n là: ức ý nghĩa ố ầ ọ
( )
( )
0
1
15 14 49
2,187
3, 2
x t n
T
s
−
−
= = =
.
Xác đ ềịnh mi n bác b gt H , = { > c}, ỏ
0
T
v = 0,02 c = 2,33 ới →
Nhận xét = 2,1857 < c = 2,33 T
KL: Chưa có cơ sở bác bỏ giả ế thi t H
0
, tạm thời chấp nhận giả ế thi t H T
0
ạm thời chấp
nh n tuyên b t ậ ố rên là đúng.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
104
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Bài 6. H ng dây chuy n xu c 120 s n ph m trong m t gi . C i ti n dây ệ thố ền cũ sả ất đượ ả ẩ ộ ờ ả ế
chuyền sản xu t trên, qua chấ ạy th nghi m 36 gi c s u trung bình m t gi ử ệ ờ, thu đượ ố liệ ộ ờ
s n xu c 125 s n ph l u ch nh s = 19. ả ất đượ ả ẩm, độ ệch tiêu chuẩn điề ỉ
1
Hãy ki nh h ng dây chuy n sau c i ti n có hi u qu n không, v i mểm đị ệ thố ề ả ế ệ ả hơ ớ ức ý nghĩa
= 0,05.
Lời giải.
Phát bi u bài toán: gt H = 120. ể
0
:
> 120. đt H
1
:
Với m c ý = 0,05, Test th ng kê c n ch n là: ứ nghĩa ố ầ ọ
( )
( )
0
1
125 120 36
1,7
17
x t n
T
s
−
−
= = =
.
Xác đị ỏnh miền bác b gt H , = {T > c},
0
v = 0,05 c = 1,64 ới →
Nhận xét T = 1,76 > c = 1,64
KL: Bác b t H h ng dây chuy n sau c i ti n không có hi u qu , vỏ giả thiế
0
ệ thố ề ả ế ệ ả hơn ới
m = 0,05. ức ý nghĩa
Bài 7. M t nhà máy s n xu t m t lo i s n ph m tuyên b s n ph m c a h có tu i th ộ ả ấ ộ ạ ả ẩ ố ả ẩ ủ ọ ổ ọ
trung bình là 200 gi . ờ
Nghi ng l i tuyên b i ta ti n hành ki m tra ng u nhiên n = 100 ờ ờ ố trên là đúng sự thật, ngườ ế ể ẫ
s n ph m c g bình m u ả ẩ ủa nhà máy đó, thu được trun ẫ
195x =
, độ ẩn điề lệch tiêu chu u
chỉnh s = 31.
1
Hãy kiểm định gt H = 200.
0
:
< 200. đt H
1
:
Lời giải.
Phát bi u bài toán: gt H = 200. ể
0
:
H < 200. đt
1
:
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
105
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Với m c ý = 0,05, Test th ng kê c n ch n là: ứ nghĩa ố ầ ọ
( )
( )
0
1
200 195 100
1,6
31
t x n
T
s
−
−
= = =
.
Xác đị ỏnh miền bác b gt H , = {T > c},
0
v = 0,05 c = 1,64 ới →
Nhận xét T = 1,61 < c = 1,64
KL: Chưa có cơ sở bác bỏ giả ế thi t H t
0
ạm thời chấp nhận giả ế thi t H p nh
0
chấ ận
tuyên b = 0,05. ố trên là đũng, với mức ý nghĩa
Bài 8. M t tuyên b c a u tra xã h i h c cho r ng trung bình trong m t ngày ộ ố ủ các nhà điề ộ ọ ằ ộ
SV bỏ ra 3 gi t h ờ để ự ọc.
Với một m u ng c s ẫ ẫu nhiên n = 16 SV, thu đượ ố liệu:
x
i
1
1,5
2
2,5
3
3,5
4
n
i
3
2
4
1
8
2
5
Hãy kiểm định gt H = 3.
0
:
đt H
1
: ≠ 3.
Cho m = 0,05. ức ý nghĩa
Lời giải.
Phát bi u bài toán: gt H = 3. ể
0
:
đt H
1
: ≠ 3.
Với m : ức ý nghĩa = 0,05, Test thống kê cần chọn là
( )
0
1
x t n
T
s
−
=
(1)
Xác đị ỏnh miền bác b gt H , = { > c},
0
T
v = 0,05 ới →
1; (24;0,025) 2,06
2
c t n t
= − = =
t b ng trên ừ ả →
2,7x =
, s = 1
1
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
106
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
thay vào (1) → 1,5 T = −
Nhận xét T = 1,5 < c = 2,064 −
KL: Chưa có cơ sở bác bỏ giả ế thi t H t
0
ạm thời chấp nhận giả thiết H p nh
0
chấ ận
tuyên b i mố trên là đũng, vớ ức ý nghĩa = 0,05.
Bài 9. Có m t tuyên b cho r ng thu nh p hàng tháng c a m ng ph thông là 630 ộ ố ằ ậ ủ ột lao độ ổ
đồng.
Với m u ng c sẫ ẫu nhiên n = 25, thu đượ ố liệu
650x =
và độ ẩn có điề lệch tiêu chu u chỉnh
s = 64.
1
Với mức ý nghĩa ấp hơn sự = 5%, hãy kiểm định tuyên bố trên có th thật không.
Lời giải.
Phát bi u bài toán: gt H = 630. ể
0
:
> 630. đt H
1
:
Với mức ý nghĩa = 0,05,
Test th là: ống kê c n chầ ọn
( )
( )
0
1
650 630 25
1,562
64
x t n
T
s
−
−
= = =
.
Miền bác b gt H , = {T > c}, v i c là h ng s nh c 1, ) = t(24; ỏ
0
ớ ằ ố được xác đị = t(n −
0,05) = 1,711.
Nhận xét: T = 1,5625 < c = 1,711 bác b gtH t m th i ch p nh→ Chưa có cơ sở ỏ
0
ạ ờ ấ ận
gtH p nh n tuyên b s
0
chấ ậ ố trên là đúng ự thật.
Bài 10. Có m t tuyên b cho r ng m i chi phí cho vi c khám ch a b nh c a b n ộ ố ằ ột ngườ ệ ữ ệ ủ ả
thân là 30 ngàn đồng trong một tháng.
Với mẫu ng c s ẫu nhiên n = 16, thu đượ ố liệu
25x =
và độ ẩn có điề lệch tiêu chu u chỉnh s
1
= 7,1.
Với mức ý = 0,01, hãy ki nh tuyên b trên có quá s nghĩa ểm đị ố ự thật không.
Lời giải.
Phát bi u bài toán: gt H = 30. ể
0
:
< 30. đt H
1
:
Với mức ý nghĩa = 0,01,
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
107
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Test thống kê c n ch n là: ầ ọ
( )
( )
0
1
30 25 16
2,816
7,1
t x n
T
s
−
−
= = =
.
Miền bác b gt H , = {T > c}, v i c là h ng s nh c = t(n 1, ) = t(15; ỏ
0
ớ ằ ố được xác đị −
0,01) = 2,606.
Nhận xét: T = 2,8169 < c = 2,606 Bác b . → ỏ gtH
0
Bài 11. Công ty Z nh nh r n ph m c a công ty. ận đị ằng có 40% người thích sả ẩ ủ
M t m u ng u nhiên n = c m dò ý ki i thích s n ph m cộ ẫ ẫ 100 người đượ thă ến có 45 ngườ ả ẩ ủa
công ty Z.
Với m c ý = 5%, hãy ki nh nh n nh trên c a công ty ứ nghĩa ểm đị ậ đị ủ Caqueo có đúng sự
thật không.
Lời gi i. ả
Phát bi u bài toán: gt H : p = 0,40. ể
0
0,40 đt H
1
: p
Với m ý ng , Test th n ức hĩa ống kê được chọ
( )
0
0 0
(1 )
f p n
T
p p
−
=
−
(1)
với
0
45
0, 45, 0, 40, 1
100
f p n= = = =
xé u ki n n.p = 40 5 và n.(1 p ) = 60 t điề ệ
0
−
0
5 được thỏa.
thay vào (1) → T = 1,0208
Miền bác b gt H , = { > c}, v i c là h ng s c nh ỏ
0
T ớ ằ ố đượ xác đị
như ớ sau: v i = 0,05 → c = 1,96
Nhận xét = 1,0208 < c = 1,96 bác b gtH t m th i p nhT → Chưa có cơ sở ỏ
0
ạ ờ chấ ận
gtH p nh n tuyên b
0
chấ ậ ố trên là đúng sự thật.
Bài 12. Cho r ng t l n y m a h ằ ỉ ệ ả ầm củ ạt đậu tương là 90%.
Gieo ngẫu nhiên 100 h g, k có 85 h y m ạt đậu tươn ết quả ạt nả ầm.
Với mức ý nghĩa trên có đúng không. = 5%, hãy kiểm định tuyên bố
Lời giải.
Phát bi u bài toán: gt H : p = 0,90. ể
0
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
108
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
0,90 đt H
1
: p
Với mức ý nghĩa ống kê đượ, Test th c chọn
( )
0
0 0
(1 )
f p n
T
p p
−
=
−
(1)
với
0
85
0,85, 0,90, 1
100
f p n= = = =
xét điề 5 đượu kiện n.p = 90 5 và n.(1 p ) = 10
0
−
0
c thỏa.
thay các giá trị vào (1) → T = 1,66
Miền bác b gt H , = { > c}, v i c là h ng s = 0,05 ỏ
0
T ớ ằ ố được xác định như sau: với
→ c = 1,96
Nhận x = 1,66 < c = 1,96 bác b gtH t m th i ch p nh n gtH ét T → Chưa có cơ sở ỏ
0
ạ ờ ấ ậ
0
ch p nh n tuyên b ấ ậ ố trên là đúng sự thật.
Bài 13. Có m t tuyên b r ng 25% SV thích h t & th ng kê. ộ ố ằ ọc môn toán xác suấ ố
M u ng i ý ki n có 20 SV thích h c môn toán xác su t & ột mẫ ẫu nhiên n = 100 SV được hỏ ế ọ ấ
thống kê.
Với mức ý nghĩa = 0,4, hãy kiểm định tuyên bố có quá sự thật không.
Lời gi i. ả
Phát bi u bài toán: gt H : p = 0,25. ể
0
: p < 0,25 đt H
1
Với mức ý nghĩa ống kê đượ, Test th c chọn
( )
0
0 0
(1 )
p f n
T
p p
−
=
−
(1)
với
0
20
0, 20, 0, 25, 1
100
f p n= = = =
thay vào (1) → T = 1,154
Xét các điều ki n n.p = 25 5 và n.(1 p ) = 75 ệ
0
−
0
5 được thỏa.
Miền bác b gt H , = {T > c}, v i c là h ng s = 0,4 ỏ
0
ớ ằ ố được xác định như sau: với → c
= 0,84
Nhận xét T= 1,154 > c = 0,84 Bác b gtH . → ỏ
0
Bài 14. Công ty Z cho r nh T là thích s n ph m c . ằng 75% người dân tỉ ả ẩ ủa họ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
109
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
M t m u ng i dân t c h i ý ki i thích sộ ẫ ẫu nhiên n = 160 ngườ ỉnh T đượ ỏ ến có 130 ngườ ản
ph a công ty Z. ẩm củ
Với mức ý nghĩa ơn sự = 0,01, hãy kiểm định tuyên bố có ít h thật không.
Lời gi i. ả
Phát bi u bài toán: gt H : p = 0,75. ể
0
> 0,75 đt H
1
: p
Với mức ý nghĩa c ch, Test thống kê đượ ọn
( )
0
0 0
(1 )
f p n
T
p p
−
=
−
(1)
với
0
130
0,8125, 0,75, 1
160
f p n= = = =
Xét các điề ệu ki n n.p = 120 5 và n.(1 p ) = 40
0
−
0
5 được thỏa → khi đó thay các giá trị
trên vào (1)
→ T = 1,825795416
Xét các điề ệu ki n n.p = 25 5 và n.(1 p ) = 75
0
−
0
5 được thỏa.
Miền bác b gt H , = {T > c}, v i c là h ng s nh ỏ
0
ớ ằ ố được xác đị
như sau: với = 0,05 1,96 → c =
Nhận xét T= 1,82 < c = 0,84 T m th p nh n gtH . → ạ ời chấ ậ
0
Bài 15. Cho r ng t l ph m có trong m t lô hàng là 0,02. ằ ỉ ệ phế ẩ ộ
M u ng u nhiên n = 400 s n ph ph ột mẫ ẫ ả ẩm, k t quế ả có 10 phế ẩm.
Với mức ý nghĩa = 0,01, hãy kiểm định giả thi t:ế
gt H : p = 0,02.
0
đt H
1
: p > 0,02
Lời gi ải.
Phát bi u bài toán: gt H : p = 0,02. ể
0
: p > 0,02 đt H
1
Với mức ý nghĩa ống kê đượ, Test th c chọn
( )
0
0 0
(1 )
f p n
T
p p
−
=
−
(1)
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
110
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
với
0
10
0,025, 0,02, 4
400
f p n= = = =
Xét các điề 5 đượ khi đó thay các giá trịu kiện n.p = 8 5 và n.(1 p ) = 392
0
−
0
c thỏa →
trên vào (1) → T = 0,714285.
Miền bác b gt H , = {T > c}, v i c là h ng s = 0,05 ỏ
0
ớ ằ ố được xác định như sau: với → c
= 1,65
Nhận xét T= 0,714285 < c = 1,65
→ T i ch p nh n gtH . ạm thờ ấ ậ
0
§4. BÀI TOÁ SÁNH N SO
4.1. Đặt vấn đề
Trong cuộc sống hàng ngày ta thường có thói quen so sánh, so sánh giữa người này
v kia, gi a ch ng c a s n ph m này v i ch ng c a s n ph m kia, so ới người ữ ất lượ ủ ả ẩ ớ ất lượ ủ ả ẩ
sánh gi t nhu c u. sánh là ữa phương pháp này với phương pháp kia...So sánh là mộ ầ so
động lực để ể phát tri n...
Trong lý thuy t xác su ng kê, ta s xét bài toán so sánh các tham s c a hai ế ất − thố ẽ ố ủ
hay nhi u t ng th (N). ề ổ ể
4.2. So sánh hai giá trị trung bình
Xét X, Y là hai bi n ng u nhiên có lu t phân ph i chu n X ), Y ế ẫ ậ ố ẩ N(
1
;
1
N(
2
;
2
).
Bài toán đặ uan sát đột ra là ta muốn so sánh , d
1
2
ựa trên hai mẫu q c lập của X
và c ủa Y.
Giả s u th c nghi x ), Y có m u th m (y ử X có mẫ ự ệm (
1
; x ; ... ; x
2 n
ẫ ực nghiệ
1
; y ; ... ; y
2 m
).
4.2.1. Trường hợp
1
,
2
đã biết.
Bài toán 1. nh hai ph . Kiểm đị ía
Phát bi u bài toán: gt H . ể
0
:
1
=
2
. đt H
1
:
1
2
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
111
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Với mức ý nghĩa , Test thống kê được chọn
2 2
1 2
x y
T
n m
−
=
+
.
Miền bác bỏ giả thiết H có dạng > c}, với c là hằng số phụ thuộc vào mức ý
0
= {T
nghĩa định như được xác sau:
2
2
0
1 1
( ) , ( ) .
2
2
t
x
c x e d
−
−
= =
(hàm Laplace).
Bài toán 2. nh m Kiểm đị ột phía.
Phát bi u bài toán: gt H . ể
0
:
1
=
2
. đt H
1
:
1
>
2
Với mức ý nghĩa ống kê đượ, Test th c chọn
2 2
1 2
x y
T
n m
−
=
+
.
Miền bác b H ỏ giả thiết
0
có dạng = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa
được xác định như sau:
2
2
0
1 1
( ) , ( ) .
2
2
t
x
c x e dt
−
= − =
(hàm Laplace).
4.2.2. Trường hợp
1
,
2
t chưa biế
4.2.2.1. ng h p m u n > 30, m > 30 Trườ ợ ẫ
Trong trườ ết tương tự như trên, ng hợp mẫu n > 30, m > 3 bài toán 0 được giải quy
ta thay i s
1
b i s , bở
1
2
ở
2
.
Bài toán 1. nh hai ph Kiểm đị ía.
Phát bi u bài toán: gt H . ể
0
:
1
=
2
. đt H
1
:
1
2
Với mức ý nghĩa ống kê đượ, Test th c chọn
2 2
1 2
x y
T
s s
n m
−
=
+
.
M = {iền bác bỏ giả thiết H
0
có dạng T > c}, với c là hằng số phụ thuộc vào mức ý
nghĩa xác định như sau: được
2
2
0
1 1
( ) , ( ) .
2
2
t
x
c x e d
−
−
= =
(hàm Laplace).
Bài toán 2. nh m Kiểm đị ột phía.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
112
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Phát bi u bài toán: gt H . ể
0
:
1
=
2
. đt H
1
:
1
>
2
Với mức ý nghĩa ống kê đượ, Test th c chọn
2 2
1 2
x y
T
s s
n m
−
=
+
.
Miền bác bỏ giả thiết H = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa
0
có dạng
được xác định như sau:
2
2
0
1 1
( ) , ( ) .
2
2
t
x
c x e dt
−
= − =
(hàm Laplac . e)
Ví dụ 1
Xét hai biến ngẫu nhiên độc lập X, Y có luật phân phối chuẩn với hai mẫu thực
nghiệm có kích thước mẫu n = 40, m = 50 và
2 2
1 2
130, 140, 80, 10x y
= = = =
.
Hãy kiểm định hai phía.
gt H .
0
:
1
=
2
đt H
1
:
1
.
2
Với mức ý nghĩa
= 1%,
Lời giải
Với m = 0,01, Test th n ức ý nghĩa ống kê được chọ
2 2
1 2
5
x y
T
n m
−
= =
+
Xác định c, ta có
1
( ) 0, 4950 2,5
2
c c
−
= = → =
Nhận xét: gi . T = 5 > c = 2,58 do đó ta bác bỏ ả thi tHế
0
4.2.2.2. ng h p m u nh n < 30 ho c m < 30 Trườ ợ ẫ ỏ ặ
Giả s X có m u th c nghi m (x ; x ; ... ; x ), có ử ẫ ự ệ
1 2 n
x
, s và Y có m u th nghi
1
ẫ ực ệm
(y
1
; y ; ... ; y
2 m
), có
y
, s .
2
Trước hết, ta ước lượng phương sai chung:
( ) ( )
2 2
2 2
1 1
2
1 2
( 1) ( 1)
2 2
n m
i j
i j
x x y y
n s m
s
n m n m
= =
− + −
− + −
= =
+ − + −
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
113
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Test thống kê c n ch n là ầ ọ
2 2
1 1
.
x y x y
T
s s
s
n m
n m
− −
= =
+
+
.
B . nh hai phía ài toán 1 Kiểm đị
Phát bi u bài toán: gt H . ể
0
:
1
=
2
. đt H
1
:
1
2
Với mức ý nghĩa ống kê đượ , Test th c chọn
2 2
1 1
.
x y x y
T
s s
s
n m
n m
− −
= =
+
+
.
Miền bác bỏ giả thiết H có dạng = {T > c}, với c là hằng số phụ t vào mức
0
huộc
ý nghĩa được xác định như sau:
( )
2;c t n m= + −
(phân phối Student).
Bài toán 2. nh m Kiểm đị ột phía.
Phát bi u bài toán: gt H . ể
0
:
1
=
2
. đt H
1
:
1
>
2
Với mức ý nghĩa ống kê đượ, Test th c chọn
2 2
1 1
.
x y x y
T
s s
s
n m
n m
− −
= =
+
+
.
Miền bác bỏ giả thiết H
0
có dạng = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa
được xác định như sau:
( )
2;c t n m= + −
(phân phối Student).
4.3. So sánh hai tỉ lệ
Bài toán
Xét hai t ng th N , N c tính A m m i ph n t ng) trong hai tổ ể
1 2
và đặ à ỗ ầ ử (đối tượ ổng
thể N , N có hay không.
1 2
có thể
Bài toán đặ ợng có đặt ra là so sánh tỉ lệ đối tư c tính A trong hai tổng thể N , N .
1 2
Gọi p
1
, p ng là t l
2
tương ứ ỉ ệ đối tượng có đặc tính A trong tổng thể N , N .
1 2
Chú rằng các tham s p , p ng bi ố
1 2
là có thật (ta có tham vọ ết?).
Ta muốn so sánh p , p d p c
1 2
ựa trên hai mẫu quan sát độc lậ ủa X và c a Y.ủ
Giả s X có m u c nghi m (x ; x ; ... ; x ), Y có m u th c nghi m (y ; y ; ... ; ử ẫ thự ệ
1 2 n
ẫ ự ệ
1 2
y )
m
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
114
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
1 2
1 2
,
k k
f f
n m
= =
.
+ Trướ ại và có ước lược hết ta nhập chung hai mẫu l ng cho giá trị chung p là tần suất
chung f xác định như sau:
1 2
k k
f
m n
+
=
+
.
Bài toán 1. nh hai phía. Kiểm đị
Phát bi u bài toán: gt H = p . ể
0
: p
1 2
p . đt H
1
: p
1
2
Với mức ý nghĩa , Test th n ống kê được chọ
( )
1 2
1 1
1
f f
T
f f
m n
−
=
− +
Với điều kiện (m + n)f 10 ta có miền bác bỏ giả thiết H dạng 10, (m + n)(1 − f)
0
có
= {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa được xác định như sau:
2
2
0
1 1
( ) , ( ) .
2
2
t
x
c x e d
−
−
= =
pl (hàm La ace).
Bài toán 2. nh phía ph Kiểm đị ải.
Phát bi u bài toán: gt H = p . ể
0
: p
1 2
H > p . đt
1
: p
1 2
Bài toán 3. nh phía trái. Kiểm đị
Phát bi u bài toán: gt H = p . ể
0
: p
1 2
< p . đt H
1
: p
1 2
Được giải quyết tương tự.
Ví d 1 ụ
Có hai phương pháp nuôi gà lấy trứng.
Theo phương pháp A nuôi m = 100 con có 80 con gà đẻ ứng, theo phương pháp tr
B nuôi n = 125 con có 90 con gà đẻ trứng.
Hãy so sánh hiệu qu c = 5%. ả ủa hai phương pháp với
Ví dụ 2
Để ỉ ủ so sánh t lệ thành phẩm c a một loại sản phẩ ệm do hai xí nghi p A, B sản xuất.
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
115
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Tiến hành kh o sát ng u nhiên m = 100 s n ph m do xí nghi p A s n xu có 85 ả ẫ ả ẩ ệ ả ất,
s n ph m t t (thành ph m), kh o sát ng u nhiên n = 200 s n ph m do xí nghi p B s n ả ẩ ố ẩ ả ẫ ả ẩ ệ ả
xu n ph m t ất, có 170 sả ẩ ốt.
Hãy so sánh t l ành ph a hai xí nghi p v = 1%. ỉ ệ th ẩm củ ệ ới
*****
***
*
Tài liệu tham khảo:
[1] Lý thuy t Xác su t và th ng kê; tác gi : Ph u; NXB Khoa h c và kế ấ ố ả ạm Văn Kiề ọ ỹ thuật
Hà Nội 1998.
[2] Giáo trình Xác su t th ng kê; tác gi : T gia Hà Nấ ố ả ống Đình Quỳ; NXB ĐH Quốc ội
2003.
[3] Thống kê và ng d ng; tác gi ng Hùng Th ng; NXB GD 1999. ứ ụ ả: Đặ ắ
[4] Giáo trình Xác suất th ng kê; tác gi ng Công Hanh; tài li . ố ả: Đặ ệu lưu hành nội bộ
[5] Bài giảng Xác su t th ng kê; Gi ng. ấ ố ảng viên Lê Xuân Hòa; ĐH Kiến trúc Đà Nẵ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
116
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
B I B ng giá tr hàm Laplace ảng : ả ị
2
2
0
1
( ) .
2
x
u
x e du
−
=
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
117
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
B : B giá tr hàm m c a phân ph i chu c N(0; 1) ảng II ảng ị ậ ột đ ủ ố ẩn tắ
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
118
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
Bài gi ng Xác su t Th ng k i h c Ki n trúc à N ả ấ ố ê – Đạ ọ ế Đ ẵng
119
Giảng
viên:
ThS.
Vũ
Hứa
Hạnh
Nguyên
B ân ph i Student tảng III: Bảng ph ố
(n;
)
| 1/119
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC KIẾN TRÚC ĐÀ NẴNG ---------- BÀI GIẢN G
XÁC SUẤT THỐNG KÊ (Tái b n l ả n 3) ầ
Giảng viên biên soạn:
ThS. Vũ Hứa Hạnh Nguyên Đà Nẵng, 9/2021
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g MỤC LỤC
PHẦN I. XÁC SUẤT
Chương 1. PHÉP THỬ - BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ - XÁC
SUẤT CỦA BIẾN CỐ § 1. GIẢI TÍCH TỔ HỢP 1.1. Giai thừa
1.2. Qui tắc đếm (lối nhân) 1.3. Hoán vị 1.4. Chỉnh hợp 1.5. Tổ hợp BÀI TẬP
§ 2. PHÉP THỬ - BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ
2.1. Phép thử ngẫu nhiên và không gian các biến cố sơ cấp
2.2. Biến cố (sự kiện) liên kết với phép thử
2.3. Các phép toán về biến cố
§ 3. XÁC SUẤT CỦA BIẾN CỐ
3.1. Các định nghĩa xác suất
3.2. Các tính chất đơn giản của xác suất
§ 4. CÁC PHÉP TOÁN VỀ XÁC SUẤT 4.1. Phép cộng xác suất 4.2. Phép nhân xác suất
§ 5. CÔNG THỨC XÁC SUẤT TOÀN PHẦN VÀ CÔNG THỨC BAYES
5.1. Công thức xác suất toàn phần
5.2. Công thức Bây−ét (Bayes)
§ 6. DÃY PHÉP THỬ BECNOULLI
6.1. Dãy phép thử Bernoul i 6.2. Công thức Bernoulli BÀI TẬP
Chương 2. BIẾN NGẪU NHIÊN (ĐẠI LƯỢNG NGẪU NHIÊN) § 1. BIẾN NGẪU NHIÊN
1.1. Định nghĩa – Ví dụ 2
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 1.2. Phân loại á c c biến ngẫu nhiên
1.3. Các phép toán trên biến ngẫu nhiên
§ 2. DÃY PHÂN PHỐI VÀ HÀM MẬT ĐỘ XÁC SUẤT
2.1. Hàm phân phối xác suất của biến ngẫu nhiên
2.2. Dãy phân phối xác suất của biến ngẫu nhiên rời rạc
2.3. Hàm mật độ xác suất của biến ngẫu nhiên liên tục
2.4. Bài toán về hàm phân phối xác suất và hàm mật độ xác suất
§ 3. CÁC THAM SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN 3.1. Số trung vị 3.2. Số MOD (Modal)
3.3. Kì vọng toán của biến ngẫu nhiên
3.4. Phương sai của biến ngẫu nhiên
3.5. Độ lệch tiêu chuẩn (độ lệch quân phương) 3.6. Mômen
§ 4. BIẾN NGẪU NHIÊN n − CHIỀU
4.1. Định nghĩa − Ví dụ
4.2. Hàm phân phối xác suất của biến ngẫu nhiên 2 − chiều
4.3. Bảng phân phối xác suất của biến ngẫu nhiên rời rạc 2 − chiều
4.4. Hàm mật độ xác suất của biến ngẫu nhiên liên tục 2 − chiều
4.5. Phân phối xác suất có điều kiện của biến ngẫu nhiên 2 − chiều
4.6. Kỳ vọng có điều kiện của biến ngẫu nhiên 2 − chiều
Chương 3. MỘT SỐ LUẬT PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
3.1. Luật phân phối giản đơn (hay còn gọi là phân phối 0 − 1)
3.2. Luật phân phối nhị thức 3.3. Luật phân phối s ê i u bội
3.4. Luật phân phối chuẩn
3.5. Hàm Laplace và một số kết quả 3
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3.6. Luật phân phối Poisson BÀI TẬP
PHẦN II. THỐNG KÊ
Chương 4. LÝ THUYẾT Ẫ M U § 1. LÝ THUYẾT MẪU 1.1. Đặt vấn đề
1.2. Mẫu ngẫu nhiên − Mẫu thực nghiệm
1.3. Biểu đồ − Hàm phân phối thực nghiệm
§ 2. CÁC THAM SỐ ĐẶC TRƯNG CỦA MẪU
I. Các tham số đại diện cho giá trị trung tâ m
2.1. Trung bình mẫu (Kỳ vọng mẫu)
2.2. Số trung vị của mẫu thực nghiệm
2.3. Số Mod của mẫu thực nghiệm
II. Các tham số đại diện cho độ phân tán (độ chênh lệch) 2.4. Phương sai mẫu
2.5. Phương sai điều chỉnh của mẫu − Độ lệch tiêu chuẩn − Độ lệch tiêu chuẩn điều chỉnh của mẫu
Chương 5. ƯỚC LƯỢNG THAM SỐ § 1. ƯỚC LƯỢNG ĐIỂM
1.1. Khái niệm về ước lượng tham số
1.2. Ước lượng cho giá trị trung bình
1.3. Ước lượng cho phương sai 2
§ 2. KHOẢNG TIN CẬY CHO KỲ VỌNG 2.1. Đặt vấn đề
2.2. Khoảng tin cậy cho kỳ vọng (tóm tắt các công thức)
§ 3. ƯỚC LƯỢNG KHOẢNG CHO TỈ LỆ
§ 4. BÀI TOÁN XÁC ĐỊNH CỠ MẪU (kích thước mẫu) 4.1. Đặt vấn đề 4
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
4.2. Trường hợp ước lượng cho trung bình
4.3. Trường hợp ước lượng cho tỉ lệ
Chương 6. KIỂM ĐỊNH GIẢ THIẾT § 1. VẤN ĐỀ CHUNG 1.1. Đặt vấn đề
1.2. Miền bác bỏ − Các sai lầm − Mức ý nghĩa của kiểm định giả thiết
§ 2. KIỂM ĐỊNH GIẢ THIẾT CHO TRUNG BÌNH
2.1. Trường hợp phương sai (độ lệch chuẩn) 2 đã biết
2.2. Trường hợp phương sai (độ lệch chuẩn) 2 chưa biết, mẫu n  30
2.3. Trường hợp phương sai (độ lệch chuẩn) 2 chưa biết, mẫu n < 30
§ 3. KIỂM ĐỊNH GIẢ THIẾT CHO TỈ LỆ
3.1. Bài toán kiểm định hai phía
3.2. Bài toán kiểm định phía phải
3.3. Bài toán kiểm định phía trái BÀI TẬP § 4. BÀI TOÁN SO SÁNH 4.1. Đặt vấn đề
4.2. So sánh hai giá trị trung bìn h 4.3. So sánh hai tỉ lệ Tài liệu tham khảo 5
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Phần I. XÁC SUẤT Chương 1
PHÉP THỬ - BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ -
XÁC SUẤT CỦA BIẾN CỐ
§1. GIẢI TÍCH TỔ HỢP
Kiến thức về giải tích tổ hợp đã được học trong chương trình toán THPT, ở đây xin
được nhắc lại một số kiến thức cơ bản cùng các công thức về giai thừa, hoán vị, chỉnh hợp
không lặp, chỉnh hợp lặp, tổ hợp không lặp, tổ hợp lặp làm cơ sở để nghiên cứu xác suất − thống kê. 1.1. Giai thừa Định nghĩa. Cho n , N !n 1. =2.3 .  n Ví dụ 5! 1 = 2  3  4  5  = 120 Qui ước: 0! = 1. Tính chất. ! n (= n 1)−!. n ( = n 2) − !( n1) −. . Ví dụ 5! = 12345 = 4!5 = 3!45.
1.2. Qui tắc đếm (lối nhân)
Giả sử có công việc C, được chia làm k giai đoạn C1, C2, …Ck và tương ứng:
Công việc C1 có n1 cách khác nhau để hoàn thành,
Công việc C2 có n2 cách khác nhau để hoàn thành, …
Công việc Ck có nk cách khác nhau để hoàn thành.
Khi đó nếu công việc C hoàn thành khi và chỉ khi đồng thời hoàn thành
các công việc C1;C2;…Ck thì có tất cả
n n n cách khác nhau để hoàn thành công 1 2 k việc C. 6
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ 1. Giả sử từ địa điểm A đến địa điểm B có 2 con đường khác nhau để đi và từ địa
điểm B đến địa điểm C có 3 con đường khác nhau để đi.
Khi đó có tất cả 6 con đường khác nhau để đi từ địa điểm A đến địa điểm C.
Ví dụ 2. Cho tập X = 0; 1; 2; 3; 4. Từ tập X lập được bao nhiêu số tự nhiên gồm 3 chữ số khác nhau.
Xét số cần tìm có dạng
abc, với a, b, c  X, a  0, a, b, c đôi một khác nhau.
Khi đó: chữ số a có 4 cách chọn khác nhau
chữ số b có 4 cách chọn khác nhau
chữ số c có 3 cách chọn khác nhau
KL: Có tất cả 4  4  3 = 48 số các số thỏa mãn yêu cầu của bài toán.
1.3. Hoán v ị
1.3.1. Định nghĩa
Cho tập X có n phần tử khác nhau. Mỗi một cách sắp xếp n phần tử khác nhau của
X theo một thứ tự gọi là một hoán vị của n phần tử.
Ví dụ. Cho tập X = 1; 2; 3; 4 khi đó các số 1234, 3241, 4312…là các hoán vị 4 phần tử của X.
1.3.2. Công thức
Số các hoán vị của n phần tử khác nhau của X kí hiệu và xác định như sau: Pn = n!. 1.4. Chỉnh hợp
1.4.1. Chỉnh hợp không lặp (gọi tắt là chỉnh hợp) 1.4.1.1. Định nghĩa
Cho tập X có n phần tử khác nhau. Mỗi một cách sắp xếp k phần tử khác nhau của
X (với 1  k  n) theo một thứ tự nhất định gọi là một chỉnh hợp
không lặp chập k của n phần tử khác nhau.
Ví dụ. Cho tập X = 0; 1; 2; 3; 4; 5 khi đó các số 234, 341, 412…là các chỉnh hợp chập 3 của 6. 1.4.1.2. Công thức 7
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Số các chỉnh hợp chập k của n phần tử khác nhau của X kí hiệu và xác định như ! n sau: k A = , 1 k  n. n (n − k )!
* Chú ý. Nếu n = k thì chỉnh hợp chập k của n chính là hoán vị của n phần tử.
1.4.2. Chỉnh hợp lặp 1.4.2.1. Định nghĩa
Cho tập X có n phần tử khác nhau. Mỗi một cách sắp xếp k phần tử của X theo một
thứ tự nhất định gọi là một chỉnh hợp lặp chập k của n phần tử khác nhau.
Ví dụ. Cho tập X=0; 1; 2; 3; 4; 5 khi đó các số 22234, 10021, 32323, 44444, 33331…là
các chỉnh hợp lặp chập 5 của 6. 1.4.2.2. Công thức
Số các chỉnh hợp lặp chập k của n phần tử khác nhau của X kí hiệu và xác định như sau: k k . n A = n 1.5. Tổ hợp
1.5.1. Định nghĩa
Cho tập X có n phần tử khác nhau.
Mỗi một tập con gồm k phần tử khác nhau của X (0  k  n) gọi là một tổ hợp
không lặp chập k của n.
Ví dụ. Cho tập X = a; b; c; d; e; f; g khi đó các tập con a; c; e, c; g; f,…là các tổ hợp chập 3 của 7.
1.5.2. Công thức
Số các tổ hợp chập k của n phần tử khác nhau của X kí hiệu và xác định như sau: n! k C = , 0 k n. n k!.(n − ) k !
• Chú ý. Tương tự như chỉnh hợp lặp, ta cũng có khái niệm tổ hợp lặp. BÀI TẬP
Bài 1.1. Cho tập X = 0; 1; 2; 3; 4; 5.
1/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm bốn chữ số khác nhau? 8
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm bốn chữ số khác nhau là số chẵn ?
3/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm bốn chữ số khác nhau và chia hết cho 5 ?
Bài 1.2. Cho tập X = 0; 1; 2; 3; 4.
1/ Từ tập X, ta có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số khác nhau?
2/ Từ tập X, ta có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số khác nhau và chia hết cho 3 ?
Bài 1.3. Cho tập X = 0; 1; 2; 3; 4.
1/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số khác nhau và
luôn có mặt chữ số 1? (ví dụ 312; 104; 431; …).
2/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số khác nhau và nhỏ hơn 300 ?.
Bài 1.4. Cho tập X = 0; 1; 2; 3; 4; 5.
1/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số?.
2/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số là số chẵn ?
3/ Từ tập X, có thể lập được bao nhiêu số tự nhiên khác nhau gồm ba chữ số và chia hết cho 5 ?
Bài 1.5. 1/ Một ngũ giác có bao nhiêu đường chéo.
2/ Một đa giác lồi có 11 cạnh có bao nhiêu đường chéo ?
3/ Một đa giác lồi có n cạnh (n > 3) có bao nhiêu đường chéo ? Bài 1.6.
1/ Cho tập hợp X là tập gồm có 4 điểm khác nhau, trong đó không có 3 điểm khác nhau
nào cùng nằm trên một đường thẳng. Hỏi từ tập X ta có thể vẽ được bao nhiêu tam giác khác nhau ?
2/ Cho tập hợp X là tập gồm có 5 điểm khác nhau, trong đó không có 3 điểm khác nhau
nào cùng nằm trên một đường thẳng. Hỏi từ tập X ta có thể vẽ được bao nhiêu tam giác khác nhau ? 9
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3/ Tổng quát cho tập hợp X là tập gồm có n điểm khác nhau với n > 3, trong đó không có
3 điểm khác nhau nào cùng nằm trên một đường thẳng. Hỏi từ tập X ta có thể vẽ được bao nhiêu tam giác khác nhau ?
Bài 1.7. Trường đại học Z tổ chức giải bóng đá nam, với thể thức thi đấu vòng tròn một
lượt. Có 5 đội đăng ký tham gia thi đấu.
Hỏi có tất cả bao nhiêu trận đấu ?
Chú ý. Không có đội nào bỏ cuộc.
Bài 1.8. Có 12 sinh viên được chia làm 3 tổ, mỗi tổ gồm có 4 sinh viên.
Hỏi có bao nhiêu cách chia tổ ?
Bài 1.9. Có 18 sinh viên, trong đó có 12 sinh viên nam và 6 sinh viên nữ được chia làm 3
tổ, mỗi tổ gồm có 6 sinh viên.
Hỏi có bao nhiêu cách chia tổ, với giả thiết:
1/ Cách chia tổ là tùy ý?
2/ Mỗi tổ có 4 sinh viên nam và 2 sinh viên nữ?
Bài 1.10. Trong một cái hộp, có 5 bi màu xanh, 1 bi màu đỏ. Lấy ngẫu nhiên một lần 2 bi từ trong hộp, hỏi:
1/ Có bao nhiêu khả năng 2 bi lấy ra có cùng màu?
2/ Có bao nhiêu khả năng 2 bi lấy ra khác màu?
Bài 1.11. Trong một cái hộp, có 5 bi màu xanh, 4 bi màu đỏ. Lấy ngẫu nhiên một lần 3 bi từ trong hộp, hỏi:
1/ Có bao nhiêu khả năng 3 bi lấy ra có nhiều nhất 1 bi xanh ?
2/ Có bao nhiêu khả năng 3 bi lấy ra có ít nhất 1 bi xanh ?
Bài 1.12. Trong một cái hộp, có 5 bi màu xanh, 2 bi màu đỏ. Lấy ngẫu nhiên một lần 3 bi từ trong hộp, hỏi:
1/ Có bao nhiêu khả năng 3 bi lấy ra có cùng màu ?
2/ Có bao nhiêu khả năng 3 bi lấy ra có đúng 2 bi màu xanh ?
3/ Có bao nhiêu khả năng 3 bi lấy ra có ít nhất 1 bi màu xanh ?
Bài 1.13. Một lớp học có 45 sinh viên (trong đó có 27 nữ và 18 nam). GV chủ nhiệm
muốn thành lập một BCS lớp gồm 5 sinh viên; Hỏi, có bao nhiêu cách chọn, nếu:
1/ Chọn 5 sinh viên vào BCS là tùy ý ?.
2/ Có đúng 3 nam sinh viên ?. 10
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3/ Có ít nhất 2 nữ sinh viên ?.
Bài 1.14. Trong một hộp có 100 sản phẩm, gồm 90 sản phẩm tốt và 10 sản phẩm xấu. Có
bao nhiêu cách chọn ra 10 sản phẩm, trong đó:
1/ 10 sản phẩm được chọn ra tùy ý ?
2/ 10 sản phẩm được chọn ra, có 2 sản phẩm xấu ?
Bài 1.15. Bài toán sắp xếp hành khách lên toa tàu.
1/ Hỏi có bao nhiêu cách sắp xếp một cách ngẫu nhiên 4 hành khách lên 2 toa tàu khác
nhau (Chú ý rằng 4 hành khách có thể lên cùng một toa tàu).
2/ Hỏi có bao nhiêu cách sắp xếp một cách ngẫu nhiên 3 hành khách lên 5 toa tàu khác
nhau (Chú ý rằng 3 hành khách có thể lên cùng một toa tàu)
Bài 1.16. Tổng quát bài toán sắp xếp hành khách lên toa tàu.
Có bao nhiêu cách sắp xếp một cách ngẫu nhiên n hành khách lên k toa tàu khác nhau
(Chú ý rằng n hành khách có thể lên cùng một toa tàu).
§2. PHÉP THỬ - BIẾN CỐ (SỰ KIỆN) LIÊN KẾT VỚI PHÉP THỬ
2.1. Phép thử ngẫu nhiên và không gian các biến cố sơ cấp
2.1.1. Phép thử ngẫu nhiên Khái niệm
Các hiện tượng được lặp lại trong một tổ hợp các điều kiện cơ bản nào đó và trong
mỗi lần thực hiện những kết quả có thể xảy ra khác nhau, các kết quả này xảy ra một cách
ngẫu nhiên không biết trước, nhưng tập hợp tất cả các kết quả xảy ra là có thể biết trước
được. Các hiện tượng như vậy được gọi là một phép thử ngẫu nhiên (gọi tắt là phép thử).
Ví dụ 1. Gieo một đồng xu.
Rõ ràng khi gieo 1 đồng xu, ta không biết được kết quả gì có thể xảy ra khi mà
đồng xu dừng lại (đồng xu sấp (S) hay đồng xu ngữa (N)?), nhưng ta biết chắc là có 2 kết
quả có thể xảy ra đó là S hoặc N.
Vậy gieo 1 đồng xu là một phép thử. 11
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ 2. Gieo một con xúc xắc cân đối, đồng chất là một phép thử…
2.1.2. Không gian các biến cố sơ cấp Khái niệm
Xét một phép thử. Tập hợp tất cả các kết quả đồng khả năng có thể xảy ra của một
phép thử đó được gọi là không gian các biến cố sơ cấp (gọi tắt là không gian biến cố hay
còn gọi là không gian mẫu), kí hiệu là  và mỗi kết quả của phép thử được kí hiệu là .
Vậy  =  /  là kết quả của phép thử.
Ví dụ 1. Gieo một đồng xu,  = S, N;
Ví dụ 2. Gieo hai đồng xu,  = SS, SN, NS, NN;
Ví dụ 3. Gieo một con xúc xắc  = •,••,•••,… = {1 chấm; 2 chấm; 3 chấm;...}
2.2. Biến cố (sự kiện) liên kết với phép thử
2.2.1. Khái niệm
+ Xét một phép thử, có không gian biến cố là  .
(sau đây ta viết tắt:Xét một phép thử / ).
Khi đó, mỗi một tập con của  được gọi là một b ế
i n cố của phép thử đó.
Một biến cố thường được kí hiệu bởi các chữ in hoa A, B, C...
Vậy A là một biến cố  A  .
Ở đây, ta dùng kí hiệu  thay cho phát biểu “khi và chỉ khi”.
+ Biến cố được gọi là xảy ra hay không xảy ra.
Một biến cố của một phép thử được gọi là xảy ra, nếu khi thực hiện phép thử kết
quả thuộc về biến cố đó. Ngược lại, ta nói biến cố đó không xảy ra. Ví dụ
Gieo một con xúc xắc / , xét các biến cố A = 2 chấm, 3 chấm;
B = 1 chấm, 4 chấm; C = 1 chấm, 3 chấm, 5 chấm.
Giả sử lần thứ nhất thực hiện phép thử gieo con xúc xắc ta thấy kết quả xảy ra là 1
chấm, khi đó ta nói rằng biến cố B, biến cố C đã xảy ra và biến cố A không xảy ra. Lần 2
thực hiện phép thử gieo con xúc xắc ta thấy kết quả xảy ra là có màu đỏ, khi đó ta nói
rằng biến cố B đã xảy ra, biến cố A không xảy ra và chưa có kết luận gì về biến cố C xảy ra hay không xảy ra. 12
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2.2.2. Phân loại các biến cố
2.2.2.1. Biến cố không thể (xảy ra)
Biến cố của một phép thử được gọi là biến cố không thể nếu nó không bao giờ xảy
ra trong mọi lần thực hiện phép thử ( biến cố không thể là biến cố không chứa một kết
quả nào của phép thử). Biến cố không thể thường được kí hiệu là  .
Ví dụ. Gieo một con xúc xắc/.
Ta có A: biến cố xảy ra mặt con xúc xắc có số chấm > 7, khi đó A =  .
2.2.2.2. Biến cố chắc chắn (biến cố tất yếu)
Biến cố của một phép thử được gọi là biến cố chắc chắn nếu nó luôn xảy ra trong
mọi lần thực hiện phép thử ( biến cố chắc chắn là biến cố trùng với không gian các
biến cố sơ cấp). Biến cố chắc chắn thường được kí hiệu là  (hay U).
Ví dụ. Gieo một con xúc xắc/,
A: biến cố xảy ra mặt con xúc xắc có số chấm < 7, Khi đó A = .
2.2.2.3. Biến cố ngẫu nhiên
Biến cố của một phép thử được gọi là biến cố ngẫu nhiên nếu biến cố đó không là
biến cố không thể và không là biến cố chắc chắn.
Vậy biến cố ngẫu nhiên là biến cố có thể xảy ra hoặc không xảy ra khi thực hiện phép thử.
Ví dụ. Gieo một con xúc xắc/,
A: biến cố xảy ra mặt con xúc xắc có màu đỏ,
Khi đó A là một biến cố ngẫu nhiên.
2.2.2.4. Biến cố sơ cấp
Biến cố ngẫu nhiên chỉ gồm một và chỉ một kết quả nào đó của phép thử được gọi
là biến cố sơ cấp của phép thử đó.
2.2.3. Quan hệ giữa các biến cố 2.2.3.1. Quan hệ bao hàm
Cho A, B là hai biến cố của cùng một phép thử, 13
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Biến cố A được gọi là bao hàm trong biến cố B nếu mọi kết quả của phép thử ở
trong biến cố A đều ở trong biến cố B ( biến cố A xảy ra thì biến cố B cũng xảy ra). Kí hiệu A  B .
2.2.3.2. Quan hệ bằng nhau
Cho A, B là hai biến cố của cùng một phép thử,
Biến cố A được gọi là bằng biến cố B nếu mọi kết quả của phép thử ở trong biến
cố A đều ở trong biến cố B và ngược lại ( biến cố A xảy ra khi và chỉ khi biến cố B cũng xảy ra). Kí hiệu A = B.
2.3. Các phép toán về biến cố
Nhận xét. Nói đến không gian biến cố, biến cố là nói đến tập hợp (tập hợp các kết
quả...). Do đó các phép toán trên không gian biến cố được xây dựng tương tự như trong
các phép toán trên tập hợp.
2.3.1. Tổng hai biến cố (hợp hai biến cố) Định nghĩa
Xét một phép thử có không gian biến cố là  và giả sử A, B là hai biến cố.
Ta định nghĩa tổng của biến cố A và biến cố B là một biến cố C gồm mọi kết q ả u của hai biến cố A và B.
Kí hiệu: C = A  B, hoặc C = A + B (trong tài liệu này ta dùng kí hiệu C = AB).
• Theo định nghĩa, ta có:
Biến cố C xảy ra khi và chỉ khi ít nhất một trong hai biến cố A, B xảy ra.
Hiển nhiên: C cũng là một biến cố của phép thử trên.
• Chú ý. Định nghĩa trên có thể mở rộng cho tổng của n biến cố A1, A2,..., An của cùng một phép thử.
Kí hiệu: X = A1A2...An.
Theo định nghĩa, ta có biến cố X xảy ra  ít nhất một trong các biến cố Ai, i = 1; 2; ...; n xảy ra.
Ví dụ. Gieo một con xúc xắc/,
A: biến cố xảy ra mặt có chấm màu đỏ, B: biến cố xảy ra mặt có chấm là số lẻ.
Khi đó: C = AB: biến cố xảy ra mặt có chấm là 1 chấm; 3 chấm; 4 chấm; 5 chấm. 14
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Tính chất
Xét một phép thử có không gian biến cố là . Ta có các tính chất: t1/ AA = A. t2/ A  = A. t3/ AB = BA.
t4/ A(BC) = (AB)C .
2.3.2. Tích của hai biến cố (giao của hai biến cố) 2.3.2.1. Định nghĩa
+ Giả sử A, B là hai biến cố được xét trong cùng một phép thử có không gian biến cố là .
Ta định nghĩa tích của biến cố A và biến cố B là một biến cố C gồm những kết
quả đồng thời thuộc hai biến cố A và B.
Kí hiệu C = AB hay C = AB (trong tài liệu này ta dùng kí hiệu C = AB).
• Theo định nghĩa, ta có:
Biến cố C xảy ra  đồng thời cả hai biến cố A, B xảy ra.
Hiển nhiên: C cũng là một biến cố của phép thử trên.
• Chú ý. Định nghĩa trên có thể mở rộng cho tích của n biến cố A1, A2,..., An của cùng một phép thử. Kí hiệu: X = A1A2...An.
Biến cố X xảy ra  đồng thời các biến cố A1, A2,..., An xảy ra.
Ví dụ Gieo một con xúc xắc/,
A: biến cố xảy ra mặt có chấm màu đỏ, B: biến cố xảy ra mặt có chấm là số lẻ.
Khi đó: C = AB: biến cố xảy ra mặt có 1 chấm. 2.3.2.2. Tính chất
Xét một phép thử có không gian biến cố là  và xét các biến cố A, B, C. Ta có các tính chất: t1/ A.A = A. t2/ A. = . 15
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g t3/ A.B = B.A. t4/ A.(B.C) = (A.B).C.
2.3.2.3. Hai biến cố xung khắc. Hệ n − biến cố xung khắc từng đôi Định nghĩa
+ Giả sử A, B là hai biến cố được xét trong cùng một phép thử có không gian biến cố là .
Ta nói rằng biến cố A là xung khắc biến cố B  AB = 
+ Giả sử H1, H2,..., Hn là n − biến cố được xét trong cùng một phép thử có không gian biến cố là .
Ta nói rằng H1, H2,..., Hn là n − biến cố xung khắc từng đôi  Hi Hj = , với mọi i  j. Ví dụ 1
Gieo một con xúc xắc/, ta xét các biến cố sau:
A = 1 chấm, 4 chấm; B = 1 chấm, 3 chấm; C = 2 chấm, 6 chấm.
Khi đó A và C là hai biến cố xung khắc, B và C là hai biến cố xung khắc, A
và B là hai biến cố không xung khắc. Ví dụ 2
Gieo một con xúc xắc/, ta xét các biến cố sau:
H1 = 1 chấm; H2 = 5 chấm; 6 chấm; H3 = 2 chấm; 4 chấm.
Khi đó H1 , H2 , H3 là một hệ biến cố xung khắc từng đôi.
2.3.3. Phép hiệu của hai biến cố− 2 biến cố đối lập 2.3.3.1. Định nghĩa
Giả sử A, B là hai biến cố được xét trong cùng một phép thử có không gian biến cố là .
Ta định nghĩa hiệu của biến cố A và biến cố B là một biến cố C gồm những kết
quả có trong biến cố A và không có trong biến cố B . Kí hiệu C = A \ B.
• Theo định nghĩa, ta có:
Biến cố C xảy ra  biến cố A xảy ra và biến cố B không xảy ra. 16
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Hiển nhiên: C cũng là một biến cố của phép thử trên.
Ví dụ Gieo một con xúc xắc/, ta xét các biến cố sau:
A = 1 chấm, 4 chấm; B = 1 chấm, 3 chấm; 5 chấm.
Ta có A \ B = 4 chấm, B \ A = 3 chấm; 5 chấm. 2.3.3.2. Tính chất
Xét một phép thử có không gian biến cố là , và xét các biến cố A, B. Ta có các tính chất: t1/ A \ A = . t2/ A \  = A.
t3/ A \ B  B \ A, với A  B.
2.3.3.3. Biến cố đối lập Định nghĩa
Xét A là một biến cố của một phép thử có không gian biến cố là .
Ta định nghĩa biến cố hiệu  \ A là biến cố đối lập của biến cố A, kí hiệu A . Ví dụ
Gieo một con xúc xắc/, ta xét các biến cố sau:
A = 1 chấm, 4 chấm = {chấm có màu đỏ}; B = 1 chấm, 3 chấm; 5 chấm
Ta có A = 2 chấm; 3 chấm; 5 chấm; 6 chấm = {chấm có màu đen}.
B = 2 chấm; 4 chấm; 6 chấm = {chấm chẵn}. Chú ý
+ Khi thực hiện một phép thử bất kỳ, chỉ có một và chỉ một trong hai biến cố A ho A ặ c xảy ra.
+ Hai biến cố đối lập là hai biến cố xung khắc, nhưng ngược lại chưa chắc.
2.3.4. Hệ đầy đủ các biến cố Định nghĩa
Một hệ gồm có n − biến cố H1, H2,..., Hn của cùng một phép thử có không gian
biến cố  được gọi là một hệ đầy đủ các biến cố nếu nó thoả các điều kiện:
(đk1) Hi   , với mọi i = 1, 2, ..., n;
(đk2) Các biến cố H1, H2,..., Hn xung khắc từng đôi một; 17
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
(đk3) H1H2...Hn = . Ví dụ 1
Gieo một con xúc xắc, có không gian biến cố là . Xét hệ các biến cố sau:
Gọi H1 = 1 chấm; 4 chấm, H2 = 2 chấm, H3 = 3 chấm; 5 chấm; 6 chấm.
Khi đó H1, H2, H3 là một hệ đầy đủ các biến cố. Ví dụ 2
Gieo một con xúc xắc, có không gian biến cố là . Xét hệ các biến cố sau:
Gọi H1 = chấm có màu đỏ, H2 = chấm có màu đen.
Khi đó H1, H2 là một hệ đầy đủ các biến cố. • Chú ý
Cùng một phép thử có thể có nhiều hệ các biến cố đầy đủ khác nhau.
§3. XÁC SUẤT CỦA BIẾN CỐ
Giới thiệu. Trong một tổ hợp các điều kiện nhất định, khi một phép thử được thực
hiện thì một biến cố nào đó có thể xảy ra hoặc không xảy ra. Khi nghiên cứu về sự xảy ra
hay không xảy ra của biến cố, trước hết ta nghiên cứu khả năng khách quan để xảy ra các
biến cố đó. Khái niệm xác suất dùng để đánh giá về “lượng” khả năng xảy ra của một biến
cố nào đó khi thực hiện phép thử.
Qua quá trình phát triển của lý thuyết xác suất tùy theo đặc điểm của từng phép
thử, của các lĩnh vực nghiên cứu khác nhau, chúng ta có những cách định nghĩa khác nhau về xác suất.
3.1. Các định nghĩa xác suất
3.1.1. Định nghĩa xác suất theo quan điểm cố điển
Xét một phép thử có không gian biến cố là  có hữu hạn kết quả đồng khả năng
xảy ra, A là một biến cố nào đó của phép th ử.
Xác suất của biến cố A được kí hiệu là P(A) và được xác định ( n ) ( ) A P A = , ( n )
với n() = số các kết quả đồng khả năng có thể xảy ra của phép thử,
n(A) = số các kết quả đồng khả năng có thể xảy ra của biến cố A. 18
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ 1. Gieo một con xúc xắc/
, ta xét các biến cố sau:
A = 1 chấm, 4 chấm = {chấm có màu đỏ}; B = 1 chấm, 3 chấm; 5 chấm .
Tính xác suất của biến cố A và xác suất của biến cố B. Lời giải
Ta có: n() = 6, n(A) = 2, n(B) = 3. ( n A ) 2 1
Theo định nghĩa, xác suất của biến cố A là P(A) = = = , n( ) 6 3 ( n B ) 3 1
Xác suất của biến cố B là P( B) = = = . ( n ) 6 2
Ví dụ 2. Trong một cái hộp có chứa (5 bi màu xanh, 3 bi màu đỏ) các bi này có cùng kích
cỡ và trọng lượng, chỉ khác nhau về màu sắc (sau đây nếu không nói gì khác thì các ví dụ
có liên quan đến các viên bi ta thừa nhận các viên bi này có cùng kích cở và trọng lượng
chỉ khác nhau về màu sắc).
Lấy ngẫu nhiên một lần 2 bi.
a/ Tính xác suất 2 bi được lấy ra là 2 bi xanh.
b/ Tính xác suất 2 bi được lấy ra là 2 bi khác màu. Lời giải
Gọi  là không gian biến cố của phép thử, ta có (n 2 )  =C 2 = 8. 8
a/ Gọi A là biến cố 2 bi được lấy ra là 2 bi xanh, ta có 2 (n )A =C 1 =0, 5 ( n A) 10 5
Vậy xác suất của biến cố A là P(A) = = = . n( ) 28 1
b/ Gọi B là biến cố 2 bi được lấy ra là 2 bi khác màu, ta có (n 1 1 )B = . C C 15 = , 5 3 ( n B ) 15 15
Vậy xác suất của biến cố B là P( ) B = = = . ( n ) 28 2 Nhận xét
Định nghĩa xác suất theo cổ điển có hạn chế là chỉ xét đối với các phép thử có
không gian các biến cố có hữu hạn các kết đồng khả năng có thể xảy ra. Nhưng trong thực
tiễn nhiều phép thử không thỏa mãn điều kiện như thế, chẳng hạn như phép thử là xác
định chiều dài của một chi tiết máy, trọng lượng của trẻ sơ sinh, chiều cao của sinh viên... 19
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3.1.2. Định nghĩa xác suất theo quan điểm thống kê
Thực hiện một phép thử n lần với điều kiện như nhau, biến cố A liên kết với phép thử xuất hiện k lần. k
Khi đó ta gọi f A = là tần suất xuất hiện biến cố A trong n phép thử. n ( ) n
Khi n tăng lên rất lớn, dần đến vô cùng, ta thấy rằng f A dao động quanh một n ( )
số p cố định và tiến dần về số p đó. Ta gọi xác suất của biến cố A là: k P ( )A = p= lim f( )A= lim . n n→+ n→+ n Trên thực tế, ( P )
A được tính xấp xỉ bởi tần suất f A khi n đủ lớn.\ n ( )
Ví dụ 1 Một xạ thủ bắn 1000 viên đạn vào bia. Ta thấy có 52 viên đạn trúng bia. Khi đó, 52
xác suất để xạ thủ bắn trúng bia là 0 = ,052. 1000 Ví dụ 2
Một công ty bảo hiểm muốn xác định xác suất để một người Anh 25 tuổi
sẽ bị chết trong năm tới, người ta theo dõi 100.000 thanh niên và thấy rằng có 796 người 796
bị chết trong vòng 1 năm sau đó. Vậy xác suất cần tìm là: 0  ,008. 100000 Nhận xét
Định nghĩa xác suất theo thống kê khắc phục được hạn chế của định nghĩa xác suất
theo cổ điển, nó hoàn toàn dựa trên các thí nghiệm quan sát thực tế để tìm xác suất của
biến cố, nó giải quyết được các trường hợp không gian các biến cố sơ cấp có vô hạn biến
cố sơ cấp và không cần giả thiết các biến cố đồng khả năng. Tuy nhiên, định nghĩa xác
suất theo thống kê cũng chỉ áp dụng cho các phép thử mà có thể lặp lại được nhiều lần
một cách độc lập trong những điều kiện giống hệt nhau. Ngoài ra, để xác định một cách
tương đối chính xác giá trị của xác suất thì cần tiến hành một số n đủ lớn lần các phép
thử, mà việc này đôi khi không thể làm được vì hạn chế về thời gian và kinh phí.
Ngày nay, với sự trợ giúp của công nghệ thông tin, người ta có thể mô phỏng các
phép thử ngẫu nhiên mà không cần thực hiện các phép thử trong thực tế. Điều này cho
phép tính xác suất theo phương pháp thống kê thuận tiện hơn. Và nó được ứng dụng nhiều
trong kinh tế, kĩ thuật, y học, nông lâm, sinh học … 20
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3.2. Các tính chất đơn giản của xác suất
Xét một phép thử /  và A, B là hai biến cố bất kỳ của phép thử đó, khi đó: (tc1) 0  P(A) 1 (tc2) P() = 0, P() = 1
(tc3) Nếu A  B thì P(A)  P(B).
§4. CÁC PHÉP TOÁN VỀ XÁC SUẤT
4.1. Phép cộng xác suất Định lý 1
Cho A, B là hai biến cố của cùng một phép thử, ta có:
P(AB) = P(A) + P(B) − P(A.B)
Một số hệ quả được suy ra từ định lý trên. Hệ quả 1
Nếu A, B là 2 biến cố xung khắc thì P(AB) = P(A) + P(B). Hệ quả 2.
Nếu H1, H2,..., Hn là một hệ n − biến cố của cùng một phép thử và xung khắc từng
đôi thì P(H1H2...Hn) = P(H1) + P(H2) +...+ P(Hn). Hệ quả 3.
Nếu H1, H2,..., Hn là một hệ n − biến cố đầy đủ của cùng một phép thử thì
P(H1H2...Hn) = P(H1) + P(H2) +...+ P(Hn) = 1. Hệ quả 4
Nếu A, B là 2 biến cố đối lập thì P(A) = 1 − P(B). Hiển nhiên: ( P )A 1 = ( −P )A. • Chú ý
Ta có thể mở rộng (mr) định lý 1 cho trường hợp n − biến cố của cùng một phép thử.
(mr1) Cho A, B, C là ba biến cố bất kỳ của cùng một phép thử, ta có:
P(ABC) = P(A) + P(B) + P(C) − P(A.B) − P(A.C) − P(B.C) + P(A.B.C).
(mr2) Cho A1, A2,...,An là n biến cố bất kỳ của cùng một phép thử, ta có: 21
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g P  A − P A A+ P A A A − − + − P A A    i ) n ( i j) n ( i j k) n 1 ... ( 1) ( ... 1 2 )n  i , j 1 = i, j ,k= 1 i j i j, i , k k j
4.2. Phép nhân xác suất
4.2.1. Xác suất có điều kiện Định nghĩa
Cho hai biến cố A và B. Ta gọi xác suất của biến cố A khi biến cố B đã xảy ra ( (
P B)  0) là xác suất của A đối với điều kiện B. Kí hiệu: ( P A B / ).
Ví dụ 1 Một hộp có 8 viên bi, trong đó có 5 viên bi vàng, 3 viên bi đỏ. Lấy lần lượt ra 2
viên bi ( không hoàn lại). Tính xác suất để lần thứ hai lấy được bi đỏ, biết rằng lần thứ
nhất lấy được bi đỏ.
Giải Gọi A là biến cố lấy dược bi trắng ở lần thứ i ( i 1 = , 2) i 2 đỏ 7 Đ2 ? Đ1 Ta có: 2 P( A / ) A = 2 1 7 • Chú ý:
Định nghĩa trên mang tính chất thuần túy toán học. Tuy nhiên trong thực tế, ta có
thể tính xác suất bằng trực giác. Ví dụ 2
Một bộ bài có 52 lá. Rút ngẫu nhiên 1 lá bài. Tính xác suất để rút được con Át, biết
rằng lá bài rút ra là lá bài màu đỏ. Giải
Gọi A là biến cố rút được con Át
B là biến cố rút được lá bài màu đỏ.
Ta thấy trong bộ bài có: 26 lá bài màu đỏ, nên ( n ) B = 26 2 con Át đỏ, nên ( n A ) B = 2 22
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g n( A ) B Do đó: P ( A / B )= = 2 1 = n (B ) 26 13
Công thức tính xác suất có điều kiện.
Ta xác định công thức xác suất có điều kiện theo định nghĩa cổ điển.
Giả sử một phép thử đã cho có n() số các kết quả đồng khả năng có thể xảy ra và A, B
là hai biến cố nào đó của phép thử, khi đó ta có: n( ) A ( n B ) n( AB P( ) A = , ( P B )= , P ( A ) B= . ( n  ) ( n ) n(  )
Nếu có thêm điều kiện biến cố B đã xảy ra thì tổng số các kết quả đồng khả năng P AB
lúc này là n(B) trong đó có n(A.B) kết quả rơi vào biến cố A, do đó: P( A ) ( ) / B = (*) (P )B
(*) là công thức tính xác suất của biến cố A khi biến cố B đã xảy ra (tương ứng của cùng một phép thử). Chứng minh
Ta chứng minh cho trường hợp phép thử có
n trường hợp cùng khả năng. Giả sử
trong n trường hợp này có m trường hợp thuận lợi cho B và k trường hợp thuận lợi cho
AB. Vì B đã xảy ra nên số trường hợp cùng khả năng lúc này là m , và số trường hợp
thuận lợi cho A trong đó chính là số trường hợp thuận lợi cho AB, tức là k . Vì vậy k ( P A B / ) n ( P AB) = = . m ( P B) n
Ví dụ 3. Trong một cái hộp có chứa (4 bi màu xanh, 3 bi màu đỏ).
Lần thứ nhất lấy ngẫu nhiên 1 bi không hoàn lại và lần thứ hai lấy ngẫu nhiên 1 bi.
Gọi A là biến cố bi lấy lần thứ nhất là bi xanh, B là biến cố bi lấy lần thứ hai là bi đỏ.
Khi đó P(B/A) là xác suất của biến cố B khi biết biến cố A đã xảy ra và P( B ) 4 3 / A = . 7 6
Ví dụ 4. Có hai cái hộp, hộp I có chứa (5 bi xanh, 2 bi đỏ), hộp II có chứa (1 bi xanh, 6 bi đỏ).
Lấy ngẫu nhiên một hộp và từ hộp đó lấy ngẫu nhiên 1 bi.
Tính xác suất bi được lấy ra là bi xanh. 23
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Phân tích. Ở thao tác thứ nhất ấ
l y ngẫu nhiên một hộp có 2 khả năng xảy ra: + Khả năng thứ nhất: 5
Lấy ngẫu nhiên được hộp I, khi đó xác suất lấy được bi xanh là . 7 + Khả năng thứ hai: 1
Lấy ngẫu nhiên được hộp II, khi đó xác suất lấy được bi xanh là . 7
Bây giờ nếu ta gọi H1 là biến cố lấy ngẫu nhiên được hộp I, H2 là biến cố lấy ngẫu
nhiên được hộp II và A là biến cố lấy ngẫu nhiên được bi xanh. 5 1 Khi đó ta có P( / A H) = , ( P / A ) H = . 1 2 7 7
4.2.2. Định lý nhân xác suất
4.2.2.1. Cho A, B là hai biến cố bất kỳ của cùng một phép thử, khi đó ta có:
(i1) P(A.B) = P(B).P(A/B) nếu P(B) > 0;
(i2) P(A.B) = P(A).P(B/A) nếu P(A) > 0.
4.2.2.2. Cho A1, A2,..., An là n biến cố của cùng một phép thử, thỏa mãn P(A1.A2...An) > 0, khi đó, ta có:
P(A1.A2...An) = P(A1).P(A2/A1).P(A3/A1A2)...P(An/A1.A2...An−1)
4.2.3. Biến cố độc lập 4.2.3.1. Định nghĩa
Cho A, B là hai biến cố của cùng một phép thử, nếu biến cố này xảy ra hay không xảy ra
không làm thay đổi đến xác suất không điều kiện của biến cố kia thì ta nói hai biến cố A, B độc lập với nhau.
Hay: nếu P(A/B) = P(A) hoặc P(B/A) = P(B) thì ta nói A, B là hai biến cố độc lập với nhau.
4.2.3.2. Cho A1, A2,..., An là n biến cố của cùng một phép thử, ta nói n biến cố đó độc
lập toàn bộ với nhau nếu mọi biến cố trong chúng độc lập với mọi biến cố tích của m biến
cố bất kỳ trong các biến cố còn lại với m = 1, 2,..., n −1. Chú ý 24
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
(cy1) Nếu A, B là hai biến cố không độc lập với nhau thì ta nói A, B là hai biến cố phụ thuộc nhau.
(cy2) Biến cố không thể  và biến cố chắc chắn  được xem là độc lập với bất kỳ một
biến cố ngẫu nhiên nào của cùng một phép thử .
4.2.3.3. Định lý (về các biến cố độc lập)
Định lý 1. Cho A, B là hai biến cố của cùng một phép thử.
Điều kiện cần và đủ để hai biến cố A và B độc lập với nhau là P(A.B) = P(A).P(B).
Định lý 2. Nếu A1, A2,..., An là n biến cố của cùng một phép thử và độc lập toàn bộ với nhau, thì:
P(A1.A2...An) = P(A1).P(A2)... P(An).
§5. CÔNG THỨC XÁC SUẤT TOÀN PHẦN VÀ CÔNG THỨC BAYES
5.1. Công thức xác suất toàn phần
Giả sử H1, H2,..., Hn là một hệ đầy đủ các biến cố và A là một biến cố bất kỳ của
cùng một phép thử với n biến cố trên, khi đó: n P( ) A =  (P H P A H i ) . ( / i ) i=1 hay
P(A) = P(H1).P(A/H1) + P(H2).P(A/H2) + P(H3).P(A/H3) +...+ P(Hn).P(A/Hn).
5.2. Công thức Bây−é − t (Bayes)
Giả sử H1, H2,..., Hn là một hệ đầy đủ các biến cố và A là một biến cố bất kỳ của
cùng một phép thử với n biến cố trên và có P(A) > 0, khi đó ta có: P H P A H j = 1, 2,...,n ,P( H /A = . j ) ( j ). ( / j ) P (A )
Ví dụ 1. Có hai cái hộp, hộp I có chứa 4 bi xanh, 1 bi đỏ và hộp II có chứa 2 bi xanh, 3 bi đỏ.
Lấy ngẫu nhiên một hộp và từ hộp đó lấy ngẫu nhiên 1 bi.
a/ Tính xác suất bi được lấy ra là bi xanh ? 25
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
b/ Biết rằng bi lấy ra là bi xanh, tìm xác suất để bi đó là của hộp thứ II ? Lời giải
Gọi H1 là biến cố lấy được hộp I, H2 là biến cố lấy được hộp II. 1
→ H1 , H2 là hệ đầy đủ các biến cố và P( H ) = ( P ) H = . 1 2 2
a/ Gọi A là biến cố lấy được bi xanh , áp dụng công thức xác suất toàn phần 1 4 1 2 6 3 → P (A) =( P H . P A / H P + H . P / A H = . + . = = =0,. 1) ( 1) ( )2 ( )2 2 5 2 5 10 5
b/ Theo yêu cầu của bài toán, ta cần tính xác suất c Pủ(a H / A 2 ) 1 2 . P H .P / A H 2
Áp dụng công thức Bayes → P ( 2 5 H / A = = = . 2 ) ( 2) ( 2 ) ( P ) A 6 3 10
Ví dụ 2. Trong một cái hộp có chứa 3 bi màu xanh, 2 bi màu đỏ.
Lần thứ nhất lấy ngẫu nhiên 1 bi và không bỏ bi đó vào lại trong hộp, lần thứ hai lấy ngẫu nhiên 1 bi.
Tính xác suất của các biến cố sau:
a/ 2 bi lấy ra đều có màu đỏ ?
b/ 2 bi lấy ra có cùng màu ?
c/ 2 bi lấy ra khác màu ? Lời giải
Gọi Xi là biến cố lấy lần thứ i có màu xanh,
Di là biến cố lấy lần thứ i có màu đỏ, với i = 1, 2.
a/ Biến cố A = D1.D2 là biến cố 2 bi lấy ra đều có màu đỏ (biến cố bi lấy ra lần thứ nhất
là bi đỏ và bi lấy ra lần thứ hai là bi đỏ), khi đó: P( 2 1 1 D D P = D. P / D D = . = . 1 )2 ( )1 ( 2 )1 5 4 10
b/ Biến cố B = D1D2  X1X2 là biến cố 2 bi lấy ra có cùng màu và D1D2 , X1X2 là hai biến cố xung khắc, khi đó: ( P ) B (P= D D X X P = D D P + X X = 1 2 1 )2 ( 1 )2 ( 1 )2 26
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 2 1 3 2 4 = ( P D. P / D D P + X. P / X X= . + . = = . 1 ) ( 2 )1 ( )1 ( 2 )1 5 4 5 4 10 5
c/ Biến cố C = D1X2  X1D2 là biến cố 2 bi lấy ra khác màu và D1X2 , X1D2 là hai biến cố xung khắc, khi đó: ( P ) C ( P= D X X  D P = D X P + X D = 1 2 1 )2 ( 1 )2 ( 1 )2 = ( P ) D . P X / D P + X . P / D X 1 ( 2 )1 ( )1 ( 2 )1 2 3 3 2 3 = . + . = . 5 4 5 4 5
Chú ý: Ta có thể suy ra P(C) = 1 − P(B) (vì B, C là hai biến cố đối lập).
§6. DÃY PHÉP THỬ BECNOULLI
6.1. Dãy phép thử Bernoulli
Một dãy n phép thử gọi là một dãy n phép thử Bernoulli nếu thỏa mãn hai điều kiện sau đây:
- Dãy n phép thử đó là độc lập với nhau.
- Trong mỗi phép thử chỉ xảy ra hai biến cố A hoặc A và xác suất xảy ra biến cố A
trong mỗi phép thử đều là ( P ) A p
= (0  p 1) không đổi, và xác suất xảy ra biến cố A là q = 1 p − .
Các bài toán thoả mãn các điều kiện trên thì được gọi là tuân theo lược đồ Bernoul i.
Xác suất p gọi là xác suất thành công, số lần A xuất hiện trong n phép thử gọi là
số lần thành công trong dãy n phép thử Bernoulli.
Xác suất để trong n phép thử Bernoulli, biến cố A xuất hiện k lần được kí hiệu là P k hay P (k, p . n ) n ( )
6.2. Công thức Bernoulli Định lí P k, p C p q − = n( ) k k n k n , k = n, 1 , q = 1 p −
Đẳng thức trên được gọi là công thức Bernoulli. 27
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Chứng minh
Kí hiệu A là biến cố “phép thử thứ i thành công”, i = n ; 1 . i
Gọi H là biến cố “có k lần thành công” thì H là tổng của k
C biến cố đôi một xung khắc n có dạng A A A A A trong đó i i; ; i; = ; 2 ; 1 ; 1 2 n  n i i 1 2 k i k i 1+ ni
Do tính độc lập nên ta có: (P A A A A A = P A P A P A P A P A = p q − i i i i i k k ) n ( i ) ( i ) ( i ) ( i k )k ( i ) k n k n 1 2 +1 1 2 +1
Từ đó, ta suy ra: P k, p C p q − = (đpcm). n( ) k k n k n Hệ quả
Với lược đồ Bernoulli n, p, xác suất để xảy ra biến cố A ít nhất k1 lần và nhiều nhất k2 lần là: k= 2 k P ( k k , k ) p= ( P , k ) p+ P( k + 1, + ) p . + .. P( , k= ) k k n− k p C p  n 1 2 n 1 n 1 n 2 n k k = 1 .
Ví dụ Một lô hàng trong kho có 20% phế phẩm.
a) Lấy ngẫu nhiên 5 sản phẩm. Tính xác suất trong 5 sản phẩm này. i) Có 2 phế phẩm.
ii) Có ít nhất 1 phế phẩm.
b) Cần lấy ít nhất bao nhiêu sản phẩm để xác suất có ít nhất một phế phẩm không nhỏ hơn 0,99. Giải
a) Bài toán trên thoả mãn lược đồ Bernoulli với n =5 , p 0, = 2
Áp dụng công thức Bernoulli, ta có:
i) Xác suất để trong 5 sản phẩm lấy ra có 2 phế phẩm là: ( P )2, 0 ; 2 2 = C ( )2, 0 ( 2 )8 , 0 3 = . 5 5 2 . 0 048
ii) Xác suất để trong 5 sản phẩm lấy ra có ít nhất 1 phế phẩm là: 5 P ( k 1;0, 2)=  ( P k ;0,)2= 1 − ( P 0; )0.2 = − 1C( )00 (, 2 )5 0 0,=8 0, 6 5 5 5 5 k=1 .
Gọi n là số sản phẩm cần lấy ra. Khi đó, xác suất có ít nhất một phế phẩm là: n P= P k 2 , 0 ;  = − P 1 2 , 0 ; 0 = 1− 8 , 0 . n ( ) ( ) ( )n n k 1 = 28
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g ln 0 , 0 1
Ta cần tìm n nhỏ nhất sao cho 1 (− )8 , 0 n  9 , 0 9 hay n  2 = 6 , 0 4. ln 8 , 0
Vậy, ít nhất phải lấy ra n =21 sản phẩm. BÀI TẬP
trong hộp. Tính xác suất của các biến cố:
1/ 2 bi được lấy ra có cùng màu.
2/ 2 bi được lấy ra khác màu.
Bài 2.2. Trong một cái hộp có chứa 5 bi xanh và 2 bi đỏ. Lấy ngẫu nhiên một lần 3 bi từ
trong hộp. Tính xác suất của các biến cố:
1/ 3 bi được lấy ra có cùng màu.
2/ 3 bi được lấy ra có ít nhất 1 bi đỏ.
Bài 2.3. Trong một cái hộp có chứa 4 bi xanh, 3 bi đỏ và 1 bi vàng. Lấy ngẫu nhiên một
lần 2 bi từ trong hộp. Tính xác suất của các biến cố:
1/ 2 bi được lấy ra có cùng màu.
2/ 2 bi được lấy ra có nhiều nhất 1 bi đỏ.
Bài 2.4. Trong một cái hộp có chứa 3 bi xanh, 2 bi đỏ và 1 bi vàng. Lấy ngẫu
nhiên một lần 3 bi từ trong hộp. Tính xác suất của các biến cố:
1/ 3 bi được lấy ra có đúng 2 bi xanh.
2/ 3 bi được lấy ra có đủ ba màu (xanh, đỏ, vàng).
Bài 2.5. Trong một cái hộp có chứa 5 bi xanh và 4 bi đỏ. Lấy ngẫu nhiên một lần 3 bi từ
trong hộp. Tính xác suất của các biến cố:
1/ 3 bi được lấy ra có số bi đỏ gấp đôi số bi xanh.
2/ 3 bi được lấy ra có đủ hai màu (xanh, đỏ).
Bài 2.6. Trong một cái hộp có chứa 3 bi xanh, 2 bi đỏ và 1 bi vàng. Lấy ngẫu nhiên một
lần 3 bi từ trong hộp. Tính xác suất của các biến cố:
1/ 3 bi được lấy ra có ít nhất 1 bi xanh.
2/ 3 bi được lấy ra có ít nhất 1 bi xanh và 1 bi đỏ.
Bài 2.7. Trong một cái hộp có chứa 3 bi xanh, 2 bi đỏ và 1 bi vàng. Lấy ngẫu nhiên một
lần 3 bi từ trong hộp. Tính xác suất của các biến cố:
1/ 3 bi được lấy ra có nhiều nhất 2 bi xanh. 29
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2/ 3 bi được lấy ra có nhiều nhất 1 bi đỏ.
Bài 2.8. Một nhóm gồm có 10 học sinh, trong đó có 5 học sinh chuyên toán, 3 học sinh
chuyên văn, 2 học sinh chuyên anh. Chọn ngẫu nhiên 4 học sinh. Tính xác suất của các biến cố:
1/ 4 học sinh được chọn ra có đủ 3 đối tượng.
2/ 4 học sinh được chọn ra có ít nhất 1 học sinh chuyên anh.
Bài 2.9. Trong một kho hàng có 10 sản phẩm loại I, 3 sản phẩm loại II và 2 sản phẩm loại
III. Chọn ngẫu nhiên 4 sản phẩm trong kho hàng. Tính xác suất của các biến cố:
1/ 4 sản phẩm được chọn ra có đủ 3 loại sản phẩm trên.
2/ 4 sản phẩm được chọn ra có số sản phẩm loại I bằng tổng số sản phẩm loại II và sản phẩm loại III .
Bài 2.10. Có 25 tấm thẻ được đánh số từ 1 đến 25. Chọn ngẫu nhiên 5 tấm thẻ.
Tính xác suất của các biến cố:
1/ 5 tấm thẻ được chọn ra đều mang số chẵn.
2/ 5 tấm thẻ được chọn ra có đúng 3 tấm thẻ có mang số chia hết cho 3.
Bài 2.11. Viết các chữ số 1; 2; 3; 4; 5; 6 lên 6 tấm thẻ và sắp một cách ngẫu nhiên các tấm
thẻ đó thành một hàng ngang (→ ta được một số tự nhiên gồm 6 chữ số khác nhau). Tính
xác suất của các biến cố:
1/ Số tự nhiên nhận được là một số chẵn.
2/ Số tự nhiên nhận được là một số chia hết cho 5.
3/ Số tự nhiên nhận được là một số có chữ số đầu tiên là số 1 và chữ số cuối cùng là số 6
(chẳng hạn như số 132546…).
Bài 2.12. Có 4 hành khách lên 2 toa tàu hỏa (toa I, toa II) một cách ngẫu nhiên.
1/ Tính xác suất mỗi toa có đúng 2 hành khách.
2/ Tính xác suất toa I có 3 hành khách và toa II có 1 hành khách.
Với giả thiết 4 hành khách có thể lên cùng một toa tàu.
Bài 2.13. Có 6 hành khách lên 3 toa tàu hỏa (toa I, toa II, toa III) một cách ngẫu nhiên.
1/ Tính xác suất mỗi toa có đúng 2 hành khách.
2/ Tính xác suất toa I có 1 hành khách, toa II có 2 hành khách, toa III có 3 hành khách.
Bài 2.14. Có 4 khách hàng cùng vào mua hàng tại một cửa hàng có 5 quầy hàng. Giả sử
các khách hàng chọn quày hàng để mu
a hàng một cách ngẫu nhiên. 30
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Tính xác suất của các biến cố sau:
1/ 4 khách hàng cùng vào một quầy hàng ?.
2/ 4 khách hàng vào 4 quầy hàng khác nhau ?.
3/ Có 3 khách hàng vào quầy số 1 ?.
Bài 2.15. Gieo 2 con xúc xắc (cân đối vàg đồng chất). Tính xác suất của các biến cố:
1/ Có ít nhất một mặt 1 chấm. 2/ Có hai mặt 1 chấm.
3/ Không có màu đỏ nào.
Bài 2.16. Gieo 2 con xúc xắc (cân đối và đồng chất). Tính xác suất của các biến cố:
1/ Tổng số chấm trên hai mặt của hai con xúc xắc lớn hơn hoặc bằng 10.
2/ Tổng số chấm trên hai mặt của hai con xúc xắc nhỏ hơn 2.
Bài 2.17. Gieo ngẫu nhiên 2 con xúc xắc (cân đối và đồng chất). Tính xác suất của các biến cố:
1/ Số chấm của con xúc xắc này gấp đôi số chấm của con xúc xắc kia.
2/ Màu sắc của hai con xúc xắc là khác nhau.
Bài 2.18. Đề cương ôn tập môn xác suất và thống kê có 12 câu hỏi (kèm theo đáp án).
Mỗi đề thi gồm có 4 câu được lấy ra một cách ngẫu nhiên từ đề cương.
Giả sử SV Bờm học thuộc 8 câu, SV Cuội học thuộc 4 câu.
Tính xác suất xảy ra biến cố:
1/ SV Bờm không làm được câu nào.
2/ SV Cuội làm được cả 4 câu.
3/ SV Bờm làm được ít nhất 3 câu.
4/ SV Cuội làm được nhiều nhất 3 câu.
(Chú ý là Bờm và Cuội rất nghiêm túc trong thi, câu nào đã học thuộc thì làm được không học thì không làm…)
Bài 2.19. Trong một cái hộp có 3 bi xanh, 4 bi đỏ và 1 bi vàng.
Lần thứ nhất lấy ngẫu nhiên 1 bi và không bỏ bi đó lại vào trong hộp.
Lần thứ hai lấy ngẫu nhiên 1 bi.
Tính xác suất của các biến cố:
1/ 2 bi được lấy ra có cùng màu đỏ. 31
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2/ 2 bi được lấy ra khác màu.
Bài 2.20. Trong một cái hộp có 3 bi xanh, 2 bi đỏ.
Lần thứ nhất lấy ngẫu nhiên 1 bi và không bỏ lại vào trong hộp.
Lần thứ hai lấy ngẫu nhiên 1 bi.
Tính xác suất của các biến cố:
1/ 2 bi được lấy ra có cùng màu.
2/ 2 bi được lấy ra khác màu.
Bài 2.21. (Trò chơi bốc thăm) Có 4 mảnh giấy, trong đó có một mảnh giấy ghi chữ có và
các mảnh giấy còn lại ghi chữ khôn .
g Có bốn bạn tham gia bốc thăm, lần lượt từng người
bốc thăm, ai bốc trúng mảnh giấy có ghi chữ có thì thắng cuộc. Theo các Anh (Chị) nên bốc lần thứ mấy ?
Bài 2.22. Một lô hàng có 100 sản phẩm, trong đó có 5 sản phẩm xấu. Lấy ngẫu nhiên một lần 4 sản phẩm ể
đ kiểm tra, nếu có ít nhất 1 sản phẩm xấu trong 4 sản phẩm được kiểm tra
thì không nhận lô hàng. Tính xác suất ể đ không nhận lô hàng.
Bài 2.23. Có hai cái hộp đựng bi giống như nhau, trong đó hộp I có chứa 4 bi xanh và 1 bi
đỏ, hộp II có chứa 2 bi xanh và 3 bi đỏ.
Lấy ngẫu nhiên một hộp và từ hộp đó lấy ngẫu nhiên 1 bi.
1/ Tính xác suất để bi đó là bi xanh ?
2/ Biết rằng bi lấy ra là bi xanh, tìm xác suất để bi đó là của hộp thứ II ?
Bài 2.24. Có ba cái hộp đựng bi giống như nhau, trong đó: Hộp I có 2 bi xanh và 5 bi đỏ,
hộp II có 4 bi xanh và 3 bi đỏ, hộp III có 6 bi xanh và 1 bi đỏ. Lấy ngẫu nhiên một hộp và
từ hộp đó lấy ngẫu nhiên 1 bi.
1/ Tính xác suất để bi đó là bi xanh ?
2/ Biết rằng bi lấy ra là bi xanh , tìm xác suất để bi đó là của hộp thứ I ?
Bài 2.25. Trong một hộp có 3 bi màu xanh, 2 bi màu đỏ. Lần thứ nhất lấy ngẫu nhiên 1 bi
và không bỏ bi đó vào lại trong hộp, lần thứ hai lấy ngẫu nhiên 1 bi.
Tính xác suất của các biến cố sau:
1/ 2 bi lấy ra đều có màu đỏ ?
2/ 2 bi lấy ra có cùng màu ? 3/ 2 bi lấy ra khác màu ?
Bài 2.26. Có hai cái hộp đựng bi, trong đó hộp I có 3 bi xanh và 1 bi đỏ, hộp II 32
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
có 2 bi xanh và 1 bi đỏ. Từ hộp I lấy ngẫu nhiên một bi bỏ vào hộp II, rồi từ hộp II lấy ngẫu nhiên một b .i
1/ Tính xác suất để bi lấy ra từ hộp II là bi xanh ?
2/ Biết rằng bi lấy ra từ hộp II là bi xanh, tìm xác suất bi lấy từ hộp I bỏ vào hộp II là bi xanh.
Bài 2.27. Có ba xạ thủ bắn một cách độc lập vào một mục tiêu, xác suất bắn trúng mục
tiêu của xạ thủ thứ nhất là 0,7, xạ thủ thứ hai là 0,8 và xạ thủ thứ ba là 0,5. Tính xác suất để:
1/ Chỉ có đúng một xạ thủ bắn trúng mục tiêu.
2/ Có đúng hai xạ thủ bắn trúng mục tiêu.
3/ Cả ba xạ thủ bắn không trúng mục tiêu.
4/ Có ít nhất một xạ thủ bắn trúng mục tiêu.
Bài 2.28. Tỉ lệ người dân tỉnh Q. nghiện thuốc lá là 30%, tỉ lệ người bị bệnh phổi trong số
người nghiện thuốc lá là 65%, và trong số người không nghiện thuốc lá là 15%. Chọn
ngẫu nhiên 1 người của tỉnh Q.
1/ Tính xác suất người đó bị bệnh phổi ?
2/ Biết người đó bị bệnh phổi,tính xác suất để người đó nghiện thuốc lá ?
3/ Biết người đó không bị bệnh phổi,tính xác suất ể
đ người đó nghiện thuốc lá ?
Bài 2.29. Có hai cái hộp, hộp I có chứa 2 bi xanh, 1 bi đỏ, hộp II có chứa 2 bi xanh, 3 bi
đỏ. Từ hộp I lấy ngẫu nhiên 2 bi bỏ vào hộp II (trộn đều), sau đó từ hộp II lấy ngẫu nhiên 1 bi.
1/ Tính xác suất bi được lấy ra từ hộp II là bi xanh.
2/ Biết rằng bi được lấy ra từ hộp II là bi xanh, tính xác suất 2 bi lấy từ hộp I bỏ vào hộp II là cùng màu.
Bài 2.30. Có hai cái hộp, hộp I có chứa 2 bi xanh, 1 bi đỏ, hộp II có chứa 1 bi xanh, 1 bi
đỏ. Từ hộp I lấy ngẫu nhiên 2 bi và từ hộp II lấy ngẫu nhiên 1 bi và từ 3 bi đó (trộn đều)
lấy ngẫu nhiên 1 bi. Tính xác suất để lấy được bi xanh.
Bài 2.31. Chuồng I có 1 con chuột trắng và 4 con chuột đen, chuồng II có 2 con chuột
trắng. Từ chuồng I bắt ngẫu nhiên 2 con chuột bỏ vào chuồng II, sau đó từ chuồng II bắt
ra ngẫu nhiên 2 con chuột.
1/ Tính xác suất 2 con chuột đ ợ
ư c bắt ra từ chuồng II là 2 con chuột khác màu. 33
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2/ Biết rằng 2 con chuột đ ợ
ư c bắt ra từ chuồng II là 2 con chuột khác màu, tính xác suất 2
con chuột được bắt từ chuồng I bỏ vào chuồng II là 2 con chuột khác màu.
Bài 2.32. Có hai cái hộp đựng bi giống như nhau, trong đó: Hộp I có 2 bi xanh và 1 bi đỏ,
hộp II có 3 bi xanh và 2 bi đỏ. Từ mỗi hộp lấy ngẫu nhiên ra 1 bi.
1/ Tính xác suất để 2 bi được lấy ra có cùng màu.
2/ Tính xác suất để 2 bi được lấy ra khác màu.
Bài 2.33. Có ba cái hộp đựng bi, trong đó hộp I có 2 bi xanh 3 bi đỏ, hộp II có 1 bi xanh 2
bi đỏ, hộp III có 1 bi xanh 1 bi đỏ. Từ hộp I và từ hộp II, mỗi hộp lấy ngẫu nhiên 1 bi đem
bỏ vào hộp III (trộn đều), sau đó từ hộp III lấy ngẫu nhiên 1 bi.
1/ Tính xác suất bi lấy ra từ hộp III là bi xanh.
2/ Biết rằng bi lấy ra từ hộp III là bi xanh, tính xác suất bi lấy từ hộp I và bi lấy từ hộp II
bỏ vào hộp III là 2 bi khác màu.
Bài 2.34. Trong một chuồng nhốt thỏ, có 4 thỏ trắng và 2 thỏ nâu.
Lần thứ nhất nười ta bắt g
n ẫu nhiên 2 con thỏ để đưa sang chuồng khác.
Lần thứ hai bắt ra ngẫu nhiên 2 con.
1/ Tính xác suất để 2 con thỏ được b ắt ra ở lần thứ hai là 2 con thỏ trắng.
2/ Biết rằng 2 con thỏ được bắt ra ở lần thứ hai là 2 con thỏ trắng, tính xác suất để 2 con
thỏ được bắt ở lần thứ nhất ể
đ đưa sang chuồng khác là 2 con thỏ trắng.
Bài 2.35. Trong một hộp đựng bóng bàn, có 4 quả bóng mới và 2 quả bóng cũ (bóng mới
là bóng chưa dùng lần nào, bóng cũ là bóng đã dùng ít nhất một lần). Lần thứ nhất lấy
một quả ra dùng và dùng xong bỏ lại vào trong hộp, lần thứ hai lấy một quả ra dùng.
1/ Tính xác suất để quả bóng dùng lần thứ hai là bóng cũ.
Từ đó suy ra xác suất bóng dùng lần thứ hai là bóng mới.
2/ Biết rằng bóng dùng lần thứ hai là bóng cũ, tính xác suất bóng dùng lần thứ nhất là bóng mới.
Bài 2.36. Trong một hộp đựng bóng bàn, có 3 quả bóng mới và 1 quả bóng cũ (bóng mới
là bóng chưa dùng lần nào, bóng cũ là bóng đã dùng ít nhất một lần). Lần thứ nhất lấy
một quả ra dùng và dùng xong bỏ lại vào trong hộp, lần thứ hai lấy một quả ra dùng.
1/ Tính xác suất để quả bóng dùng lần thứ hai là bóng mới.
2/ Biết rằng bóng dùng lần thứ hai là bóng mới, tính xác suất bóng dùng lần thứ nhất là bóng cũ. 34
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Bài 2.37. Trong một hộp đựng bóng bàn, có 1 quả bóng mới và 4 quả bóng cũ (bóng mới
là bóng chưa dùng lần nào, bóng cũ là bóng đã dùng ít nhất một lần). Lần thứ nhất lấy
một quả ra dùng và dùng xong bỏ lại vào trong hộp, lần thứ hai lấy một quả ra dùng.
1/ Tính xác suất để quả bóng dùng lần thứ hai là bóng mới.
2/ Biết rằng bóng dùng lần thứ hai là bóng mới, tính xác suất bóng dùng lần thứ nhất là bóng mới.
Bài 2.38. Có hai cái hộp, hộp I có chứa 2 bi xanh, 4 bi đỏ và hộp II có chứa 3 bi xanh, 1 bi đỏ.
Do sơ ý ở hộp I mất 1 bi.
Sau đó, từ hộp I lấy ngẫu nhiên ra 1 bi bỏ vào hộp II và tiếp tục từ hộp II lấy ngẫu nhiên ra 1 bi.
1/ Tính xác suất bi lấy ra từ hộp II là bi xanh ?.
2/ Biết rằng bi lấy ra từ hộp II là bi xanh, tính xác suất bi lấy từ hộp I bỏ vào hộp II là bi đỏ ?.
Bài 2.39. Có hai lô hàng, lô I có chứa 6 sản phẩm tốt và 1 sản phẩm xấu và lô II có chứa 4
sản phẩm tốt và 2 sản phẩm xấu.
Ở lô I người ta lấy ra ngẫu nhiên 2 sản phẩm.
Sau đó, từ lô I lấy ngẫu nhiên ra 2 sản phẩm bỏ vào lô II và tiếp tục từ lô II lấy ngẫu nhiên ra 2 sản phẩm.
1/ Tính xác suất 2 sản phẩm lấy ra từ lô II là 2 sản phẩm tốt.
2/ Biết rằng 2 sản phẩm được lấy ra từ lô II là 2 tốt. Tính xác suất 2 sản phẩm được lấy từ
lô I bỏ vào lô II là 2 sản phẩm tốt. 35
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Chương 2. BIẾN NGẪU NHIÊN (ĐẠI LƯỢNG NGẫU NHIÊN)
§1. BIẾN NGẪU NHIÊN
1.1. Định nghĩa − − Ví dụ
1.1.1. Định nghĩa
Xét một phép thử có không gian các biến cố là .
Mỗi một ánh xạ X:  → R (Rn) được gọi là một biến ngẫu nhiên một chiều (n
chiều) liên kết với phép thử đó.
(+) Biến ngẫu nhiên một chiều (gọi tắt là biến ngẫu nhiên) thường được kí hiệu bởi các chữ in h a o X, Y, Z...
(+) Giá trị của các biến ngẫu nhiên được kí hiệu bởi các chữ thường x, y, z...
(+) Cho X là một biến ngẫu nhiên liên kết với một phép thử có không gian các biến cố sơ
cấp là  =  /  là kết quả của phép thử , với mọi a, bR , ta kí hiệu:
(kh1) (X = a) := biến cố  / X() = a
(kh2) (X < a) := biến cố  / X() < a
(kh3) (X > a) := biến cố  / X() > a
(kh4) (a  X < b) := biến cố  / a  X() < b.
Tập tất cả các giá trị có thể có của một biến ngẫu nhiên được gọi là miền giá trị của biến ngẫu nhiên. Ví dụ 1
Gieo một đồng xu. Gọi X là biến ngẫu nhiên chỉ số mặt N xảy ra, khi đó X:  → R N ↦ 1 S ↦ 0
X có miền giá trị {0; 1} Ví dụ 2
Gieo hai đồng xu. Gọi X là biến ngẫu nhiên chỉ số mặt N xảy ra, khi đó X:  → R NN ↦ 2 36
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g NS ↦ 1 SN ↦ 1 SS ↦ 0
X có miền giá trị {0; 1; 2}
Ở ví dụ 2, ta có (X < 2) chỉ biến cố {SS; SN; NS}, (X  2) chỉ biến cố {NN}... 1.1.2. Chú ý
(cy1)Một phép thử có thể có rất nhiều biến ngẫu nhiên liên kết với phép thử đó.
(cy2) Một biến ngẫu nhiên n chiều liên kết với một phép thử có thể biểu diễn bởi một bộ
gồm n biến ngẫu nhiên (một chiều) cùng liên kết với phép thử đó.
1.2. Phân loại các biến ngẫu nhiên
1.2.1. Biến ngẫu nhiên rời rạc
Biến ngẫu nhiên X được gọi là biến ngẫu nhiên rời rạc nếu miền giá trị của nó là
tập hữu hạn hay tập vô hạn đếm được (một dãy số vô hạn).
Miền giá trị hữu hạn của biến ngẫu nhiên rời rạc kí hiệu x0, x1,..., xn.
Miền giá trị vô hạn của biến ngẫu nhiên rời rạc được kí hiệu x0, x1,..., xn,.... • Chú ý
Biến ngẫu nhiên rời rạc X chỉ nhận giá trị aR với mọi kết quả của phép thử gọi là
biến ngẫu nhiên hằng, ta có thể viết a thay cho X và do đó có thể xem một hằng số nào đó cũng là một b ế i n ngẫu nhiên.
1.2.2. Biến ngẫu nhiên liên tục
Biến ngẫu nhiên X được gọi là biến ngẫu nhiên liên tục nếu miền giá trị của nó là
một khoảng hay đoạn số thực, các phần tử của miền giá trị của X không thể liệt kê theo thứ tự được. • Chú ý
Trong thực hành, các biến ngẫu nhiên có miền giá trị hầu như dày đặc lấp đầy một
khoảng hay một đoạn số thực nào đó được xem là biến ngẫu nhiên liên tục.
1.3. Các phép toán trên biến ngẫu nhiên
Nhận xét: Biến ngẫu nhiên là một ánh xạ, do đó có các phép toán trên các ánh xạ. 37
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
§2. DÃY PHÂN PHỐI VÀ HÀM MẬT ĐỘ XÁC SUẤT
2.1. Hàm phân phối xác suất của biến ngẫu nhiên
Khi xét đến biến ngẫu nhiên ta không chỉ quan tâm đến giá trị của biến ngẫu nhiên
đó mà cần phải biết đến khả năng xuất hiện giá trị đó, bởi vì có nhiều biến ngẫu nhiên
khác nhau mà lại có cùng giá trị, một trong những khái niệm giúp ta phân biệt được sự
khác nhau của các biến ngẫu nhiên là khái niệm hàm phân phối xác suất.
2.1.1. Định nghĩa
Cho biến ngẫu nhiên X (rời rạc hay liên tục).
Hàm phân phối xác suất của biến ngẫu nhiên X, được kí hiệu F(x) và xác định: xR, F(x) = P(XVí dụ
Thực hiện phép thử gieo 2 đồng xu, gọi X là biến ngẫu nhiên chỉ số mặt N xảy ra.
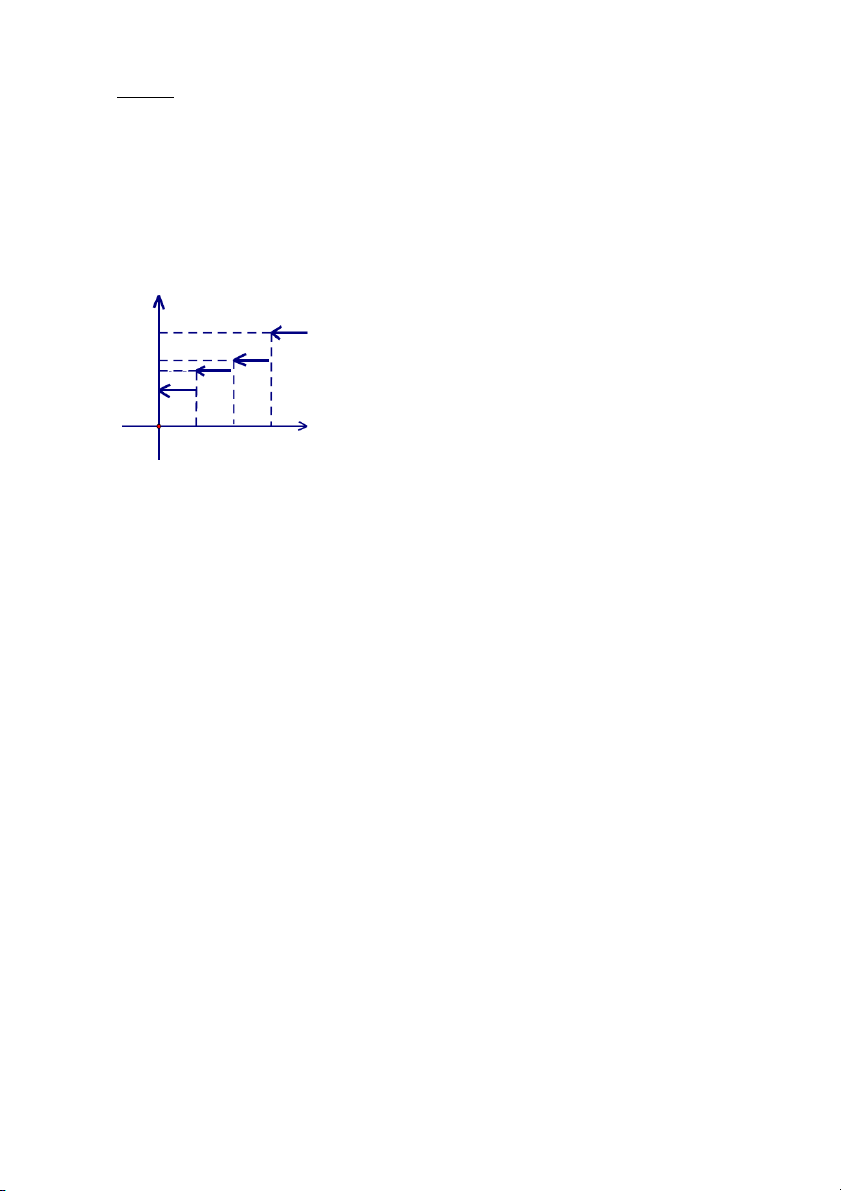
Lập hàm phân phối xác suất của X.  0 x  0  1  0 x  1  4 F (x) =  3  1 x 2  4  1 2   x F(x) 1 3/4 1/4 O 1 2 x
2.1.2. Tính chất
Giả sử F(x) là hàm phân phối xác suất của biến ngẫu nhiên X. Ta có:
(tc1) 0  F(x)  1, xR. (tc2) lim ( F ) x = 1 , lim ( F ) x= 0 x → x →−
(tc3) F(x) là hàm không giảm trên R 38
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
(tc4) F(x) liên tục bên trái tại mọi điểm. 2.1.3. Hệ quả
(hq1) a,bR, a < b, ta có: P(a  X < b) = F(b) − F(a).
(hq2) Nếu X là biến ngẫu nhiên liên tục thì hàm phân phối xác suất F(x) liên tục tại xR
và xR, ta có: P(X = x) = 0.
2.2. Dãy phân phối xác suất của biến ngẫu nhiên rời rạc
2.2.1. Định nghĩa
Giả sử X là biến ngẫu nhiên rời rạc có miền giá trị là x0, x1, x2,..., xn hoặc x0, x1, x2,..., xn,....
Đặt pi = P(X = xi), i = 0, 1, 2, ..., n () , (X = xi)  , khi đó dãy số:
p0 , p1 , p2 ,..., pn (...) được gọi là dãy phân phối xác suất của biến ngẫu nhiên rời rạc X
và bảng số có dạng như sau gọi là bảng phân phối xác suất của X hay còn gọi là bảng biểu
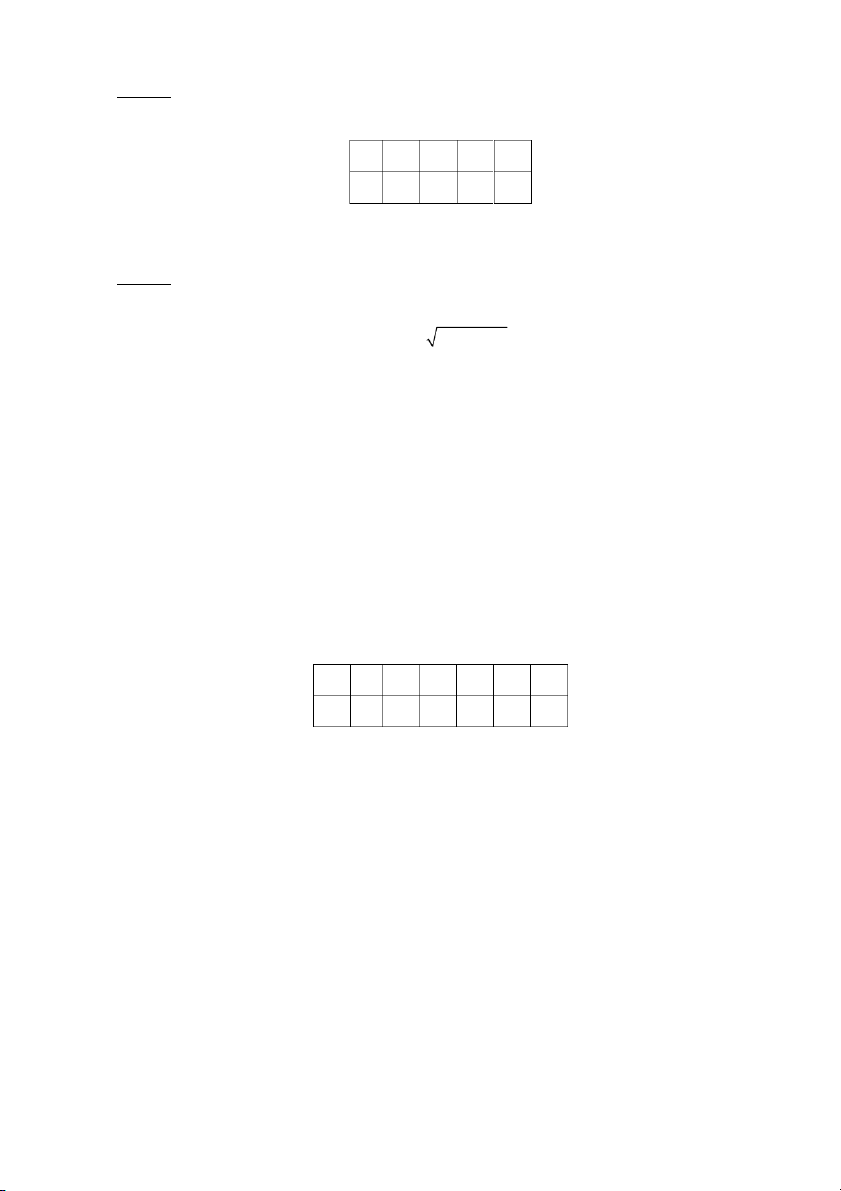
thị luật phân phối xác suất của X. X x1 x2 ... xn pi p1 p2 ... pn Ví dụ
Trong một cái hộp có chứa (3 bi màu xanh, 5 bi màu đỏ) các bi này có cùng kích
cở và trọng lượng, chỉ khác nhau về màu sắc. Lấy ngẫu nhiên một lần 2 bi. Gọi X là biến
ngẫu nhiên chỉ số bi màu xanh được lấy ra.
Lập bảng phân phối xác suất của X. Lời giải
X có miền giá trị {0; 1; 2}, ta có : 0 2 1 1 2 0 C .C 10 C .C 15 C . C 3 3 5 3 5 3 5 P( X= 0)= = ; P( X= 1)= = ; ( P X = 2) = = . 2 2 2 C 28 C 28 C 28 8 8 8
X có bảng phân phối xác suất: X 0 1 2 pi 10/28 15/28 3/28 39
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2.2.2. Tính chất
Giả sử biến ngẫu nhiên X có bảng phân phối xác suất X x1 x2 ... xn pi p1 p2 ... pn Khi đó, ta có:
1/ 0 < pi < 1, i = 0, 1, 2, ... , n()
2/ pi = p0 + p1 + p2 + ... + pn (+...) = 1
2.2.3. Liên hệ giữa hàm phân phối xác suất và bảng p
hân phối xác suất của biến ngẫu
nhiên rời rạc
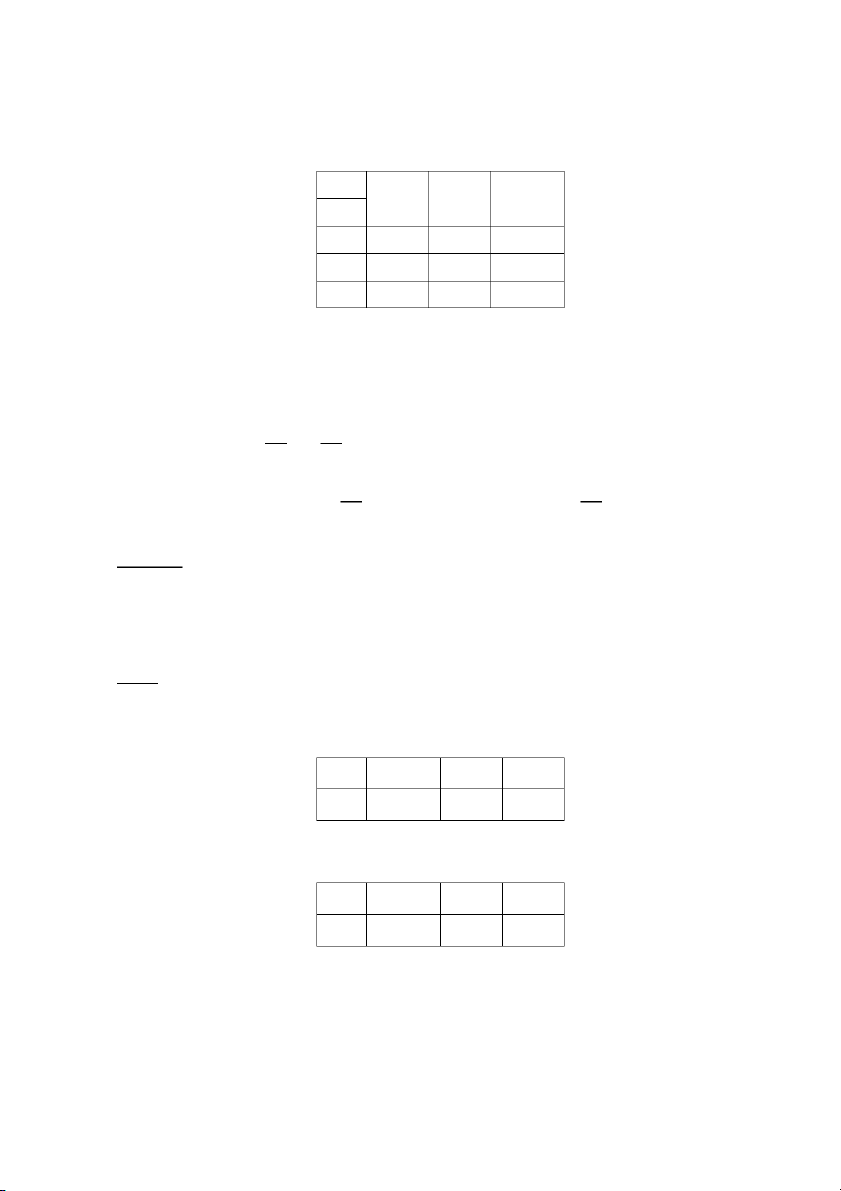
Giả sử biến ngẫu nhiên X có bảng phân phối xác suất X x1 x2 ... xn pi p1 p2 ... pn Khi đó, ta có:  0, x x1  p , x  x x 1 1 2  F ( x)  = p  + p , x  x x 1 2 2 3  ...   1, x  x  n Ví dụ
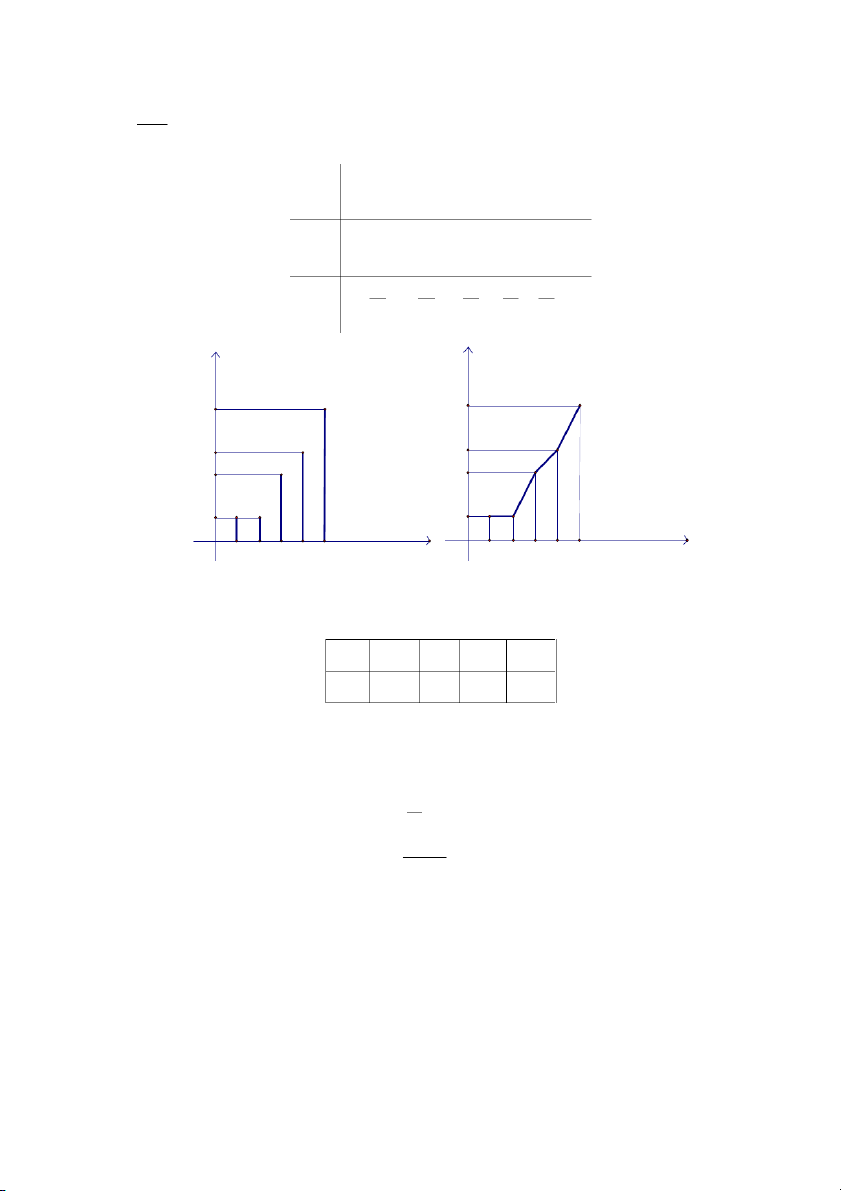
Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X 0 1 2 3 pi 0,4 0,2 0,1 0,3
Lập hàm phân phối xác suất của X. 40
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Lời giải  0 x  0 0, 4 0 x  1  F( ) x  = 0,6 1  x   0  ,7 2 x  3   1 3 x  F (x) 1 0,7 0,6 0,4 O 1 2 3 x
2.3. Hàm mật độ xá
c suất của biến ngẫu nhiên liên tục
2.3.1. Định nghĩa
Cho X là biến ngẫu nhiên liên tục, có hàm mật phân phối xác suất F(x). Nếu tồn tại
hàm f(x) không âm và khả tích trên R, sao cho: x x   , R ( F ) x = f( t ) d  . −
thì f(x) được gọi là hàm mật độ xác suất của biến ngẫu nhiên liên tục X.
2.3.2. Tính chất của hàm mật độ
Giả sử f(x) là hàm mật độ xác suất của biến ngẫu nhiên liên tục X, khi đó ta có: + (tc1) ( ) = 1  f x dx − b (tc2)  ,a  b ,R  a ,b (P  a  X ) = b (f )  x d a
(tc3) Nếu f(x) liên tục tại xR, h y
a F(x) khả vi tại xR, thì F’(x) = f(x). 41
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g F(x) f(x) O  x O  x 
2.4. Bài toán về h m
à phân phối xác suất và hàm mật độ xác suất
Nội dung bài toán: Xét biến ngẫu nhiên X, cho hàm phân phối xác suất F(x) hãy tìm hàm
mật độ xác suất và ngược lại. Ví dụ
Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất f(x) xác định như sau:    0 x 0;     2 3. f (x)    =     k.cosx x 0;   2    1/ Xác định k.
2/ Lập hàm phân phối xác suất F(x) của biến ngẫu nhiên X. 3/ Tính   P 0 X     . 4    Lời giải 1/ Xác định giá trị k. +    (f )x 0, x  . ckos x 0,  x  →k vì cosx  0, x   0;  2    + 0 2 + + ( f ) x = 1 dx ( f) x+ dx ( )f x+ dx ( )f x =     − − 0  2   2 2   (f )x d = 1 x  .co k s xd = 1 x ( .si k ) nx   2 = 1  = k 0 0 0
(thỏa mãn k  0). Vậy k = 1. 42
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2/ Lập hàm phân phối xác suất của X. x Ta có: F (x) = f (t )dt  ; xR − + x  0 → F(x) = 0; 0 x x  + 0   → ( ) = ( ) + ( ) = cos = sinx x F x f t dt f t dt tdt t = sin 2    ; 0 − 0 0   0  2 x 2 +   x → F( ) x = f (t )dt+ f (t ) dt+ f( t ) dt = cos tdt = si 2 n t=     ; 2 − 0  0 0 2   0 x  0    Vậy F ( x)= sin x 0   x . 2    1  x  2 3/ Tính       2 P 0  X = F − ( F0) = sin − sin 0=  . 4   4     4 2
§ 3. CÁC THAM SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN 3.1. Số trung vị
3.1.1. Định nghĩa
Cho X là một biến ngẫu nhiên. 1 1
Nếu tồn tại số thực a sao cho P( X  ) a  và P( X  )
a  thì số a được gọi là 2 2
trung vị của biến ngẫu nhiên X. Kí hiệu: a = med(X).
3.1.2. Hệ quả 1 1
i/ Nếu X là biến ngẫu nhiên rời rạc và có p   ; p   thì med(X) = a. i 2 i x  a x a 2 i i 1 a 1
i / Nếu X là biến ngẫu nhiên liên tục và có F (a) = hoặc f ( ) x dx=  thì m ed(X) = a. 2 2 − 43
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Ví dụ 1
Tìm số trung vị của biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X 0 1 2 3 pi 0,2 0,1 0,4 0,3 Ta có 1 P(X  2) = 0, 2+ 0,1= 0,3  và 1
P(X  2) = 0,3 , do đó med(X) = 2. 2 Ví dụ 2
Tìm số trung vị của biến ngẫu nhiên liên tục X có hàm phân phối xác suất F(x) như sau  0 x  0  2  x F ( x)= 0   x 2. 8   1 2  x  2 Ta có 1 x 1 F ( x) =  =  x = 2, 1 F (2)= , do đó med(X) = 2. 2 8 2 2
3.1.3. Ý nghĩa
Số trung vị là số đặc trưng cho giá trị trung tâm của biến ngẫu nhiên. 3.1.4. Chú ý Đối ớ
v i biến ngẫu nhiên rời rạc có thể có nhiều số trung vị khác nhau,
nhưng đối với biến ngẫu nhiên liên tục chỉ có duy nhất một số trung vị, đường thẳng có
phương trình x = a = med(X) chia hình phẳng giới hạn bởi đồ thị của hàm mật độ xác
suất f(x) thành hai phần có diện tích bằng nhau . 3.2. Số MOD (Modal)
3.2.1. Định nghĩa
Cho X là một biến ngẫu nhiên, số Mod của X được kí hiệu Mod(X) và xác định:
i/ Nếu X là một biến ngẫu nhiên rời rạc và nếu P(X = a) = maxP(X = xi) = pi ,
i = 1, 2, ..., n thì số thực a được gọi là số Mod của X và ta viết a = Mod(X)
i / Nếu X là biến ngẫu nhiên liên tục có hàm mật độ xác suất là f(x) và nếu f(x)
đạt giá trị lớn nhất tại x = a thì số thực a được gọi là số Mod của X và ta viết a = Mod(X). 44
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Ví dụ 1
Tìm số Mod của biến ngẫu nhiên X có bảng phân phối xác suất: X 0 1 2 3 pi 0,3 0,2 0,4 0,1
Ta có p3 = P(X = 2) = 0,4 = max{0,3; 0,2; 0,1}, do đó Mod(X) = 2. Ví dụ 2
Tìm số Mod của biến ngẫu nhiên liên tục X có hàm mật độ xác suất 2 (f )x = − x 2 + x 5 +.
Ta dễ dàng tìm được GTLN của f(x) bằng −2 tại x = −1, do đó Mod(X) = −1. 3.2.2. Chú ý
Số Mod của một biến ngẫu nhiên X có thể có hoặc không và có thể có nhiều giá trị khác nhau.
Số Mod là một trong các số đặc trưng cho giá trị trung tâm của biến ngẫu nhiên.
3.3. Kì vọng toán của biến ngẫu nhiên
3.3.1. Định nghĩa
Cho X là một biến ngẫu nhiên. Kì vọng toán (gọi tắt là kỳ vọng) của biến ngẫu
nhiên X, kí hiệu E(X) và xác định như sau:
i1/ Nếu X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất X x1 x2 x3 … xn … pi p1 p2 p3 … pn …  và nếu x p 
hội tụ tuyệt đối trong trường hợp X có miền giá trị là tập vô hạn đếm được i i i 1 = n thì E (X )= x p  . i i i =1 +
i2/ Nếu X là biến ngẫu nhiên liên tục có hàm mật độ xác suất là f(x) và nếu xf ( ) x dx  hội − + tụ tuyệt đối thì ( E ) X = x(f ) x d  . − 45
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Ví dụ 1
Tính kỳ vọng của biến ngẫu nhiên X có bảng phân phối xác suất X 1 2 3 4 5 pi 0,2 0, 0, 0, 0, 1 2 4 1
Ta có E(X) = 0,21 + 0,12 + 0,23 + 0,44 + 0,15 = 3,1. Ví dụ 2
Tính kỳ vọng của biến ngẫu nhiên liên tục X có hàm mật độ xác suất  0 nêu x [0;1] f ( ) x =  2 1  − x nêu x  [0;  0 1  1 Ta có E(X)= . x (f ) x dx = .x (f )x dx + . ( x f) x + dx . (x )f= x      ( 1 2 dx.− 1 )x = x . − − 0 1 0
3.3.2. Ý nghĩa của kỳ vọng
Kỳ vọng của biến ngẫu nhiên X là số đặc trưng về giá trị trung bình theo xác suất
của tất cả các giá trị của X.
3.3.3. Tính chất
(tc1) Nếu X là biến ngẫu nhiên hằng X = a thì E(X) = E(a) = a;
(tc2) Cho X là biến ngẫu nhiên có kỳ vọng là E(X).
Khi đó: kR ta có E(kX) = k.E(X).
(tc3) Cho X, Y là hai biến ngẫu nhiên cùng liên kết với một phép thử và có kì vọng E(X), E(Y).
Khi đó ta có: E(X  Y) = E(X)  E(Y) (xét trường hợp tổng quát cho n biến ngẫu nhiên).
(tc4) Cho X, Y là hai biến ngẫu nhiên cùng liên kết với một phép thử và độc lập với nhau,
có kì vọng tương ứng E(X), E(Y).
Khi đó: X.Y có kì vọng và E(X.Y) = E(X).E(Y) (xét trường hợp tổng quát cho n biến ngẫu nhiên).
3.4. Phương sai của biến ngẫu nhiên
3.4.1. Định nghĩa
Cho X là một biến ngẫu nhiên có kì vọng toán E(X) = a. 46
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Nếu biến ngẫu nhiên X − E(X)2 có kì vọng thì kì vọng đó được gọi là phương sai của biến ngẫu nhiên X. Kí hiệu: D(X). Vậy: D(X) = E((X − E(X))2 ).
3.4.2. Hệ quả
Xét X là một biến ngẫu nhiên, khi đó ta có:
Nếu tồn tại kì vọng của biến ngẫu nhiên X và X2 thì tồn tại phương sai của biến ngẫu nhiên X và ta có:
D(X) = E(X2) − E(X)2 = E(X2) − E2(X) ( ở đây E(X)2 = E2(X) ). Ví dụ 1
Tính phương sai của biến ngẫu nhiên X có bảng phân phối xác suất X 0 1 2 3 pi 0,2 0,4 0,3 0,1
Ta có: E(X) = 0,20 + 0,41 + 0,32 + 0,13 = 1,3
E(X2) = 0,202 + 0,412 + 0,322 + 0,132 = 2,5
D(X) = E(X2) − E(X)2 = 0,81 Ví dụ 2
Tính phương sai của biến ngẫu nhiên liên tục X có hàm mật độ xác suất  0 nêu x [0;1] f ( ) x =  2 1  − x nêu x  [0;  0 1  1 Ta có: E(X) = . x (f ) x dx = .x (f )x dx + . ( x f) x + dx . (x )f= x      ( 1 2 dx .− 1 )x = x − − 0 1 0   E( X ) 0 1 1 2 2 2 2 2 2 = x . f( x) dx= . x (f ) x dx + . x (f )x dx + .x (f )x= dx      (2 .x−1 )2 x= dx − − 0 1 0 17
D(X) = E(X2) − E(X)2 = . 240
3.5. Độ lệch tiêu chuẩn (độ lệch quân phương) Định nghĩa
Cho biến ngẫu nhiên X có phương sai D(X).
Khi đó D(X) được gọi là độ lệch tiêu chuẩn, kí hiệu  (X), vậy 47
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g  ( ) X= ( D X. 3.6. Mômen
3.6.1. Định nghĩa
Cho X là một biến ngẫu nhiên và a  R.
Nếu tồn tại E(X−a)k thì kì vọng đó được gọi là mômen cấp k (kN) của biến
ngẫu nhiên X đối với điểm a, kí hiệu mk(a).
+/ Nếu a = 0 thì mk(0) gọi là mômen gốc cấp k của biến ngẫu nhiên X.
+/ Nếu a = E(X) thì mk(E(X)) gọi là mômen trung tâm cấp k của biến ngẫu nhiên X và khi đó kí hiệu k, tức là k = mk(E(X)).
3.6.2. Ý nghĩa
Khái niệm mômen khái quát hoá các khái niệm về kì vọng toán và phương sai và
để xác định rõ thêm về hình dạng của đồ thị của hàm mật độ;
+/ Mômen gốc cấp 1 chính là kì vọng toán của biến ngẫu nhiên X;
+/ Mômen trung tâm cấp 2 là phương sai của biến ngẫu nhiên X;
+/ Mômen trung tâm cấp 3 (3) đặc trưng cho tính bất đối xứng của luật phân phối xác
suất của biến ngẫu nhiên X
Nếu biến ngẫu nhiên X đối xứng đối với E(X) thì 3 = 0.
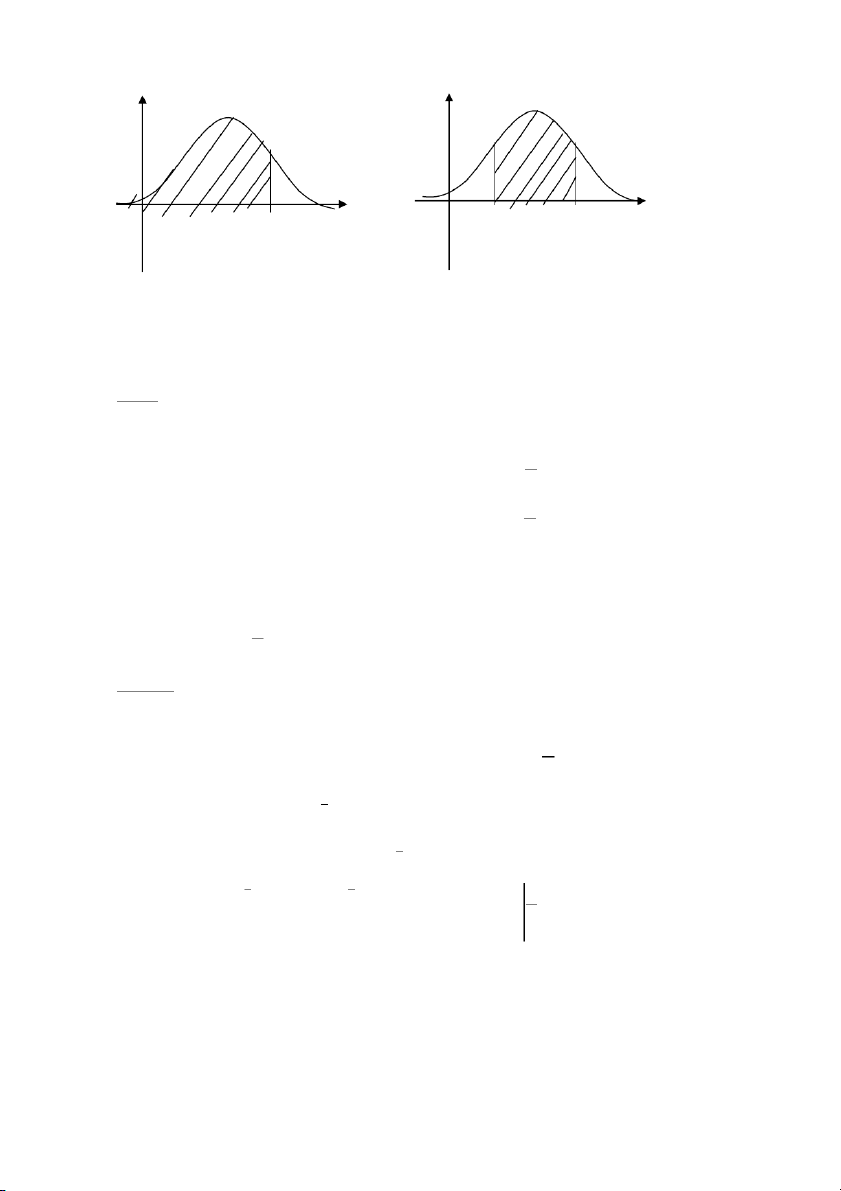
Nếu 3 > 0 thì P(X>E(X)) > P(X(phân phối xác suất của biến ngẫu nhiên X nặng về phía bên phải của E(X)).
Nếu 3 < 0 thì P(X>E(X)) < P(X(phân phối xác suất của biến ngẫu nhiên X nặng về phía bên trái của E(X)).
+/ Mômen trung tâm cấp 4 (4) đặc trưng cho độ nhọn của đường cong hàm mật độ xác
suất của biến ngẫu nhiên X. 48
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
§ 4. BIẾN NGẪU NHIÊN n − CHIỀU
4.1. Định nghĩa − − Ví dụ
4.1.1. Định nghĩa
Xét một phép thử có không gian các biến cố là .
Mỗi một ánh xạ X:  → Rn được gọi là một biến ngẫu nhiên n − chiều liên kết với phép thử đó.
Trong giáo trình này ta chỉ xét biến ngẫu nhiên 2 − chiều và để đơn giản, ta kí hiệu
(X;Y) là biến ngẫu nhiên 2 − chiều mà không cần nói rõ X; Y là hai biến ngẫu nhiên cùng
liên kết với một phép thử. 4.1.2. Ví dụ
(vd1). Gieo một con xúc xắc.
Gọi X là biến ngẫu nhiên chỉ số chấm xảy ra, Y là biến ngẫu nhiên chỉ số mặt màu đỏ xảy
ra, khi đó ta có (X;Y):  → R2 Chẳng hạn:
+ Nếu xảy ra mặt có 3 chấm thì X có giá trị bằng 3 và y có giá trị bằng 0.
+ Nếu xảy ra mặt có 1 chấm thì X có giá trị bằng 1 và y có giá trị bằng 1...
(vd2). Gieo hai con xúc xắc.
Gọi X là biến ngẫu nhiên chỉ tổng số chấm xảy ra trên hai mặt của con xúc xắc, Y là biến
ngẫu nhiên chỉ số mặt màu đỏ xảy ra, khi đó ta có (X;Y):  → R2 Chẳng hạn:
+ Nếu xảy ra một mặt có 4 chấm và một mặt có 6 chấm thì X có giá trị bằng 10 và Y có giá trị bằng 1
+ Nếu xảy ra một mặt có 2 chấm và một mặt có 5 chấm thì X có giá trị bằng 7 và Y có giá trị bằng 0
+ Nếu xảy ra một mặt có 1 chấm và một mặt có 1 chấm thì X có giá trị bằng 2 và Y có giá trị bằng 2...
4.2. Hàm phân phối xác suất của biến ngẫu nhiên 2 − − chiều
4.2.1. Định nghĩa
Xét một biến ngẫu nhiên 2 − chiều (X;Y). 49
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
x,yR, kí hiệu (X < x;Y < y) = (X < x)(Y < y).
Hàm phân phối xác suất của biến ngẫu nhiên 2 − chiều (X;Y) được kí hiệu F(x;y) và xác
định x,yR, F(x;y) = P(X < x).P(Y < y).
4.2.2. Tính chất
Giả sử F(x;y) là một hàm phân phối xác suất của biến ngẫu nhiên 2 − chiều (X;Y). Khi đó, ta có:
tc1/ x,yR, 0  F(x;y)  1. tc2/ lim ( F x; ) y = 1, lim ( F x; )y= ( F )x, lim F( x ; ) y = F ( ) y , 2 x → 1 y→ x → y→
Trong đó F1(x) là hàm phân phối xác suất của biến ngẫu nhiên X, F2(y) là hàm
phân phối xác suất của biến ngẫu nhiên Y.
tc3/ F(x;y) là hàm không giảm theo từng biến.
tc4/  x1, x2, y1, y2 R, x1 < x2, y1< y2 , ta có:
P(x1  X < x2; y1  Y < y2) = F(x1; y1) + F(x2; y2) − F(x1; y2) − F(x2; y1).
4.2.3. Định lý
Điều kiện cần và đủ để hai biến ngẫu nhiên X và Y (liên kết cùng một phép thử)
độc lập với nhau là F(x;y) = F1(x)F2(y), trong đó trong đó F1(x) là hàm phân phối xác
suất của biến ngẫu nhiên X, F2(y) là hàm phân phối xác suất của biến ngẫu nhiên Y.
4.3. Bảng phân phối xác suất của biến ngẫu nhiên rời rạc 2 − − chiều
4.3.1. Định nghĩa
Giả sử X, Y là hai biến ngẫu nhiên rời rạc (liên kết cùng một phép thử), X có miền
giá trị {x0; x1; x2; ... ; xn}, Y có miền giá trị {y0; y1; y2; ... ; yk}.
Đặt pij = P(X = xi; Y = yj), i = 0,1,2,..., n, j = 0,1,2,..., k.
Khi đó bảng số có dạng sau đây được gọi là bảng phân phối xác suất của biến ngẫu
nhiên 2 − chiều rời rạc (X; Y) 50
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g X X0 x1 ... xn−1 xn Y y0 p00 p10 p(n−1)0 pn0 y1 p01 p11 p(n−1)1 pn1 yk−1 p0(k−1) p1(k−1 ) P(n−1)(k−1) pn(k−1 ) yk p0k P1k p(n−1)k pnk 4.3.2. Ví dụ
Trong một cái hộp có chứa (4 bi màu xanh, 2 bi màu đỏ), lấy ngẫu nhiên một lần 3 bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra, Y là biến ngẫu nhiên chỉ số bi đỏ được lấy ra.
Lập bảng phân phối xác suất của (X;Y). Lời giải
X có miền giá trị {1; 2; 3}, Y có miền giá trị {0; 1; 2}.
Bảng phân phối xác suất của biến ngẫu nhiên 2 − chiều rời rạc (X;Y). X 1 2 3 Y 0 p10 p20 p30 1 p11 p21 p31 2 p12 p22 p32
p10 = P(X = 1;Y = 0) = 0 (biến cố này không thể xảy ra ?)
p20 = P(X = 2;Y = 0) = 0 (biến cố này không thể xảy ra ?)
p30 = P(X = 3;Y = 0) = 0,2 (xác suất của biến cố 3 bi lấy ra là 3 bi xanh)
p11 = P(X = 1;Y = 1) = 0 (biến cố này không thể xảy ra ?)
p21 = P(X = 2;Y = 1) = 0,6 (xác suất của biến cố 3 bi lấy ra có 2 bi xanh và 1 bi đỏ)
p31 = P(X = 3;Y = 1) = 0 (biến cố này không thể xảy ra ?)
p12 = P(X = 1;Y = 2) = 0,2 (xác suất của biến cố 3 bi lấy ra có 1 bi xanh và 2 bi đỏ) 51
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
p22 = P(X = 2;Y = 2) = 0 (biến cố này không thể xảy ra ?)
p32 = P(X = 3;Y = 2) = 0 (biến cố này không thể xảy ra ?)
Thay vào bảng trên, ta có: X 1 2 3 Y 0 0 0 0,2 1 0 0,6 0 2 0,2 0 0
4.3.3. Tính chất
Giả sử biến ngẫu nhiên 2 − chiều rời rạc (X;Y) có bảng phân phối xác suất như trên, khi đó ta có:
tc1/ 0  pij < 1, i, j. k n tc2/ p = 1 ,i= 0,k , j= 0,n  . ij i 0 = j 0 = k n tc3/ p  = q = P Y= y j= n và p  = p = P X= x i= k. ij i ( i ) , 0, ij j ( j) , 0, i 0 = j = 0 Nhận xét
Từ tính chất tc3/ nếu biết được bảng phân phối xác suất của biến ngẫu nhiên 2 −
chiều rời rạc (X;Y) ta có thể suy ra bảng phân phối xác suất của biến ngẫu nhiên X và
bảng phân phối xác suất của biến ngẫu nhiên Y. Ví dụ Xét ví dụ 4.3.2.
Ta có bảng phân phối xác suất của biến ngẫu nhiên X như sau: X 1 2 3 pi 0,2 0,6 0,2
Và bảng phân phối xác suất của biến ngẫu nhiên Y như sau: Y 0 1 2 qi 0,2 0,6 0,2
4.3.4. Định lý
Điều kiện cần và đủ để biến ngẫu nhiên X và Y độc lập là: 52
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
pij = P(X = xi; Y = yj) = P(X = xi)P(Y = yj) = pi  qj ,
i = 0, 1, 2, ..., k, j = 0, 1, 2, ..., n.
4.4. Hàm mật độ xác suất của biến ngẫu nhiên liên tục 2 − − chiều
4.4.1. Định nghĩa
Cho biến ngẫu nhiên liên tục 2 − chiều (X;Y) có hàm phân phối xác suất F(x;y).
Nếu tồn tại hàm hai biến f(x;y) không âm, khả tích trên R2 sao cho x y F (x ;y )= f (u ;v) dud   − −
thì hàm f(x;y) được gọi là hàm mật độ xác suất của biến ngẫu nhiên liên tục 2 − chiều (X;Y).
4.4.2. Tính chất
Giả sử f(x;y) là hàm mật độ xác suất của biến ngẫu nhiên liên tục 2 − chiều (X;Y). Khi đó, ta có: + + tc1/ (f ; x ) y dxdy = 1   . − −
tc2/  x1, x2, y1, y2 R, x1 < x2, y1< y2 , ta có: P( x X  x; y Y  y  = (f ; x ) y dxd  1 2 1 )2 D
với D = {(x;y) / x1  x < x2; y1  y < y2 }.
tc3/ Nếu F(x;y) có đạo hàm riêng cấp hai tại điểm (x;y)R2 thì 2  F // F (x ;y )= (x ; y)= f (x ; . xy x  y Nhận xét
Tính chất tc3/ cho ta cách xác định hàm mật độ xác suất f(x;y) nếu biết hàm phân phối xác suất F(x;y). Ví dụ
Cho biến ngẫu nhiên 2 − chiều (X;Y) có hàm phân phối xác suất 2 x F (x ; y) y = xe+ với y  0. y
Xác định hàm mật độ xác suất của (X;Y). 53
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 2 Ta có: F  2x  F 2 x (x ; ) y y = e+ , ( ; x ) y y= e− = (f ; x . 2 x y  x y y
4.4.3. Định lý
Giả sử f1(x) là hàm mật độ của biến ngẫu nhiên X,
f2(y) là hàm mật độ của biến ngẫu nhiên Y,
f(x;y) là hàm mật độ của biến ngẫu nhiên 2 − chiều (X;Y).
Điều kiện cần và đủ để X và Y độc lập là: f(x;y) = f1(x)f2(y).
4.5. Phân phối xác suất có điều kiện của biến ngẫu nhiên 2 − − chiều
4.5.1. Bảng phân phối xác suất của biến ngẫu nhiên 2 − chiều rời rạc (X;Y )
Cho biến ngẫu nhiên 2 − chiều rời rạc (X;Y), X có miền giá trị {x0; x1; x2;...; xk}, Y
có miền giá trị {y0; y1; y2;...; yn} và pij = P(X = xi; Y = yj), i = 0, 1, 2, ..., k, j = 0, 1, 2, ..., n.
+  j = 0, 1, 2, ..., n, đặt P(xi / yj) = P(X = xi/ Y = yj), i = 0, 1, 2, ..., k là xác suất có điều
kiện để X nhận giá trị xi với điều kiện Y nhận giá trị yj.
+  i = 0, 1, 2, ..., k, đặt P(yj / xi) = P(Y = yj/ X = xi), j = 0, 1, 2, ..., n là xác suất có điều
kiện để Y nhận giá trị yj với điều kiện X nhận giá trị xi.
Khi đó các bảng có dạng như sau: X/yj X0 x1 x2 ... xk
P(xi / yj) P(x0 / yj) P(x1 / yj) P(x2 / yj) ... P(xk / yj)  j = 0,1,2,...,n Y/xi Y0 y1 y2 ... yn
P(yj / xi) P(y0 / xi) P(y1 / xi) P(y2 / xi) ... P(yn / xi)  i = 0,1,2,...,k
Theo công thức xác suất có điều kiện, các giá trị P(xi / yj) và P(yj / xi) được tính như sau: ( P X = x Y= y p P / x y) ( ; i j ) ij = = i= k j= n. i j ( P Y= y q j ) , 0, , 0, j ( P X = x Y= y p P y / ) ( ; i j ) ij x = = i= k j= n. j i ( P X= ) , 0, , 0, x p i i 54
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ. Xét biến ngẫu nhiên 2 − chiều rời rạc (X;Y) có bảng phân phối xác suất như sau: X x0 = 0 x1 = 1 x2 = 2 Y y0 = 1 0,2 0,1 0 y1 = 2 0,4 0 0,3
Lập bảng phân phối xác suất có điều kiện của biến ngẫu nhiên X với các điều kiện (Y = 1), (Y = 2). Lời giải Ta có: ( P X= Y= p P X=0 / y) ( 0; )1 0, 2 00 = = = = , 0 (P Y= )1 q 0,3 0 ( P X= Y= p P X=0 / ) ( 0; )2 0, 4 01 y = = = = , 1 (P Y= )1 q 0,7 1 ( P X= Y= p P X=1/ y) ( 1; )1 0,1 10 = = = = , 0 (P Y= )1 q 0,3 0 ( P X= Y= p P X=1/ ) ( 1; )2 0 11 y = = = = 0, 1 (P Y= )2 q 0,7 1 ( P X= Y= p P X=2 / y) ( 2; )1 0 20 = = = = 0, 0 (P Y=1) q 0,3 0 ( P X= Y= p P X=2 / ) ( 2; )2 0,3 21 y = = = = . 1 (P Y= )2 q 0,7 1
Bảng phân phối xác suất cần tìm: X/y0 0 1 2 P(xi / y0) 2/3 1/3 0 X/y1 0 1 2 P(xi / y1) 4/7 0 3/7 55
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
4.5.2. Hàm mật độ xác suất có điều kiện của biến ngẫu nhiên liên tục (X;Y).
Xét biến ngẫu nhiên liên tục 2 − chiều (X;Y) có hàm mật độ xác suất f(x;y). Ta có các định nghĩa:
+ Hàm mật độ xác suất của biến ngẫu nhiên Y với điều kiện (X = x), xR là một hàm một
biến được kí hiệu g(y/x) và xác định ( y ) f (x ; ) y f ( x; ) y g / x = = , + (f )x 1 f ( x ;y ) dx −
với f1(x) là hàm mật độ của biến ngẫu nhiên X.
+ Hàm mật độ xác suất của biến ngẫu nhiên X với điều kiện (Y = y), yR là
một hàm một biến được kí hiệu h(x/y) và xác định ( x ) f (x ; ) y f (x ; ) y h / y = = , + ( f )y 2 f (x ;y )dy −
với f2(y) là hàm mật độ của biến ngẫu nhiên Y. 4.6. Kỳ vọn
g có điều kiện của biến ngẫu nhiên 2 − − chiều
4.6.1. Định nghĩa
4.6.1.1. Đối với biến ngẫu nhiên rời rạc 2 − chiều (X;Y)
Cho biến ngẫu nhiên rời rạc 2 − chiều (X;Y), X có miền giá trị {x0; x1; x2;...;
xk}, Y có miền giá trị {y0; y1; y2;...; yn} và pij = P(X = xi; Y = yj), i = 0, 1, 2, ..., k, j = 0, 1, 2, ..., n. Ta định nghĩa:
+ Kỳ vọng có điều kiện của biến ngẫu nhiên X với điều kiện (Y = yj),  j = 0, 1,
2, ..., n là một số được kí hiệu E(X/yj) và xác định: E ( k X / y = x P x y j  = n. j ) .i ( / i j ) , 0, i = 0
+ Kỳ vọng có điều kiện của biến ngẫu nhiên Y với điều kiện (X = xi),  i = 0, 1,
2,..., k là một số được kí hiệu E(Y/xi) và xác định: E( n / Y x = y P y x i  = . i ) .j ( / j i ) , 0, j=0
4.6.1.2. Đối với biến ngẫu nhiên liên tục 2 − chiều (X;Y) 56
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Cho biến ngẫu nhiên liên tục 2 − chiều (X;Y), có hàm mật độ có điều kiện là g(y/x), h(x/y). Ta định nghĩa:
+ Kỳ vọng có điều kiện của biến ngẫu nhiên X với điều kiện (Y = yj),  j = 0, 1,
2,..., n là một số được kí hiệu E(X/y) và xác định: + ( E / X )y = x (g /x )y , dx y   . −
+ Kỳ vọng có điều kiện của biến ngẫu nhiên Y với điều kiện (X = xj),  i = 0, 1,
2,..., k là một số được kí hiệu E(Y/x) và xác định: + (E /Y )x= (yh /y ) x ,dy x   . −
Chương 3. MỘT SỐ LUẬT PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
3.1. Luật phân phối giản đơn (hay còn gọi là phân phối 0 − − 1)
3.1.1. Định nghĩa
Biến ngẫu nhiên rời rạc X được gọi có luật phân phối xác suất giản đơn tham số p
nếu X có bảng phân phối xác suất: X 0 1 pi 1 − p p với 0 < p < 1
+ Biến ngẫu nhiên rời rạc X có luật phân phối xác suất giản đơn tham số p được kí hiệu A(p). Ví dụ
Thực hiện phép thử gieo một con xúc xắc. Gọi X là biến ngẫu nhiên chỉ số mặt màu đỏ xảy ra.
Khi đó biến ngẫu nhiên X có luật phân phối giản đơn và ta cũng có:
P(X = 1) = 1/3 = p, P(X = 0) = 1 − 1/3 = 2/3.
3.1.2. Các tham số đặc trưng của biến ngẫu nhiên A(p)
Nếu X là biến ngẫu nhiên A(p), thì E(X) = p; D(X) = p(1 − p) = p.q (ở đây: q = 1 − p) 57
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3.2. Luật phân phối nhị thức
3.2.1. Định nghĩa
Biến ngẫu nhiên rời rạc X được gọi là có luật phân phối xác suất nhị thước kích
thước n tham số p nếu X có bảng phân phối xác suất: X 0 1 2 ... k ... n pi p0 p1 p2 ... pk ... pn Trong đó p ( P X ) k k k C ( p1 )n p− = = = − ; k 0 p 1; k= 0, . k n
+ Biến ngẫu nhiên rời rạc X có luật phân phối xác suất nhị thức kích thước n tham số p được kí hiệu B(n; p). Ví dụ 1 Gieo 5 con xúc xắc.
Gọi X là biến ngẫu nhiên chỉ số mặt có màu đỏ xảy ra.
Khi đó X là biến ngẫu nhiên có luật phân phối nhị thức B(n = 5; p = 1/3).
Ở đây p = 1/3 là xác suất xảy ra mặt có màu đỏ khi gieo một con xúc xắc. Ví dụ 2
Một thí nghiệm có xác suất thành công là p = 0,8. Thực hiện nghiệm đó 10 lần.
Gọi X là biến ngẫu nhiên chỉ số lần thành công.
Ta có X là biến ngẫu nhiên có luật phân phối xác suất B(n; p), với n =10, p = 0,8.
3.2.2. Lược đồ Bernoulli (Dãy phép thử Bernoulli)
Xét một phép thử có hai biến cố A và B (đối lập), giả sử p = P(A) không đổi, khi đó P(B) = 1 − p = q.
Thực hiện phép thử trên n lần độc lập với nhau.
Gọi X là biến ngẫu nhiên chỉ số lần xảy ra biến cố A.
Khi đó X có miền giá trị {0; 1; 2;...; n} và p ( P X ) k k k C ( p1 )n p− = = = − ; k 0 p 1; k= 0, . k n
Do đó X có luật phân phối nhị thức B(n; p).
3.2.3. Các tham số đặc trưng của biến ngẫu nhiên B(n; p)
Nếu X là biến ngẫu nhiên B(n; p), thì
i/ E(X) = np; D(X) = np(1 − p) = npq. 58
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
i / np − q  Mod(X)  np − q + 1. 3.3. Luậ
t phân phối siêu bội
3.3.1. Định nghĩa
Biến ngẫu nhiên rời rạc X được gọi là có luật phân phối siêu bội tham số (m; n; k)
với k  min{m; n} nếu miền giá trị của X là {0; 1; 2; ... ; k} và i C . k − i C p = ( P X= ) m n i = ; i= 0; k. i k Cm+n Kí hiệu S(m; n; k). • Chú ý
Có thể mô tả một biến ngẫu nhiên có luật phân phối siêu bội như sau:
Trong một hộp có chứa hai loại bi (giả sử có m bi đỏ và n bi không đỏ).
Lấy ngẫu nhiên một lần k bi, với k  min{m; n}.
Gọi X là biến ngẫu nhiên chỉ số bi đỏ được lấy ra.
Khi đó X là một biến ngẫu nhiên có luật phân phối xác suất siêu bội. Ví dụ
Trong một hộp có chứa (4 bi màu xanh và 6 bi màu đỏ).
Lấy ngẫu nhiên một lần 3 bi từ trong hộp.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra (trong số 3 bi được lấy ra).
Ta có X có miền giá trị {0; 1; 2 ; 3} và 0 3 C. C 1 2 . C C 4 6 p = ( P X= 0) = ; 4 6 p = ( P X=1) = ; 0 3 C 1 3 C 10 10 2 1 . C C 3 0 . C C 4 6 p = ( P X= 2) = ; 4 6 p = P( X= 3)= . 2 3 C 3 3 C 10 10
Ta có X là một biến ngẫu nhiên có luật phân phối xác suất siêu bội tham số (4; 6; 3).
3.3.2. Các tham số đặc trưng của biến ngẫu nhiên có luật phân phối S(m; n; k)
Nếu X là biến ngẫu nhiên có luật phân phối siêu bội S(m; n; k) thì m m n m+ n− E(X )= . k ; ( D X )= . k . . . m+ n m+ n m + n m + − n 59
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
3.3.3. Quan hệ giữa biến ngẫu nhiên có luật phân phối siêu bội và phân phối nhị thức Định lý m
Nếu k cố định, m + n tăng lên vô hạn và tỉ số
tiến tới giới hạn p, 0 < p <1 m + n
thì phân phối siêu bội tham số (m; n; k) sẽ tiến tới phân phối nhị thức B(k; p).
Cụ thể: S(m; n; k) → B(k; p).
3.4. Luật phân phối chuẩn
3.4.1. Định nghĩa
Biến ngẫu nhiên liên tục X được gọi là có luật phân phối chuẩn tham số t và  ( >
0) nếu hàm mật độ xác suất của X có dạng (x−t) 2 1 − 2 f ( x)= .e 2 , x R.  2 Kí hiệu: N(t; ).
+ Hàm phân phối của biến ngẫu nhiên N(t; ) là x (u− )2 1 t − 2 2 F ( x)= . e d , u  x R  .  2 −
+ Biến ngẫu nhiên N(t; ) còn được gọi là biến ngẫu nhiên chính qui hay biến ngẫu nhiên Gauss.
3.4.2. Biến ngẫu nhiên chuẩn tắc
Trường hợp đặc biệt nếu t = 0,  = 1 thì X được gọi là có luật phân phối chuẩn tắc N(0; 1) và khi đó 2 1 x f ( ) x = .e−2 , x R, 2 2 1 x u − 2 F ( x)= . e du, x R  . 2 −
Dễ dàng ta có f(− x) = f(x) và F(− x) = 1 − F(x), xR 2 0 u và 1 − 1 2 . e du=  . 2 2 − Ta có kết quả sau: 60
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g X − t
Nếu X có luật phân phối N(t; ) thì biến ngẫu nhiên Y = có luật phân phối  chuẩn tắc N(0; 1). • Chú ý
Biến ngẫu nhiên N(t; ) có một ý nghĩa rất lớn trong lý thuyết cũng như thực tiễn.
3.4.3. Các tham số đặc trưng của biến ngẫu nhiên N(t; )
3.4.3.1. Số trung vị và số Mod
Nếu X là biến ngẫu nhiên N(t; ) thì med(X) = Mod(X) = t.
3.4.3.2. Kỳ vọng toán và phương sai
Nếu X là biến ngẫu nhiên N(t; ) thì E(X) = t và D(X) = 2.
Trường hợp X là biến ngẫu nhiên chuẩn tắc N(0; 1) thì
med(X) = Mod(X) = E(X) = 0 và D(X) = 1.
3.5. Hàm Laplace và một số kết quả
3.5.1. Định nghĩa
Hàm số được kí hiệu và xác định như sau được gọi là hàm Laplace 2 1 x u − 2 (  x )= . e du , x R  . 2 0
3.5.2. Tính chấ t
i1/ (− x) = − (x), xR ((x) là một hàm số lẻ); i2/ 1 1 lim (
 x ) = − , lim (x )= ; x →− 2 x→+ 2
i3/ Nếu 0  x  5 thì giá trị (x) được xác định dựa vào bảng giá trị của hàm Laplace (xem bảng phụ lục) 1
và x > 5 ta có (x)  ; và nếu x < 0 thì sử dụng tính chất (− x) = − (x). 2
3.5.3. Công thức liên hệ giữa hàm Laplace và hàm phân phối xác suất của biến ngẫu
nhiên chuẩn N(t; ). Định lý
Nếu (x) là hàm Laplace và F(x) là hàm phân phối xác suất của một biến ngẫu  x − t  1
nhiên chuẩn N(t; ) thì: F (x) =  +  .     2 61
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Hệ quả 1    −t   −t , R,  < : ( p  X )    =  −   .          Hệ quả 2   R,  > 0: p( X t  ) 2  −  =   .    
3.5.4. Tính gần đúng của phân phối nhị thức B(n; p)
Định lý 1 (định lý Moivre)
Nếu xác suất P(A) = p để biến cố A xảy ra trong mỗi phép thử của dãy n phép thử
Bernoulli thỏa mãn 0 < p < 1 thì khi đó với n đủ lớn xác suất 1 2 1 x − − p k np = ( P X= ) k k k = C ( p1− )n− k p  . (f )x với 2 f ( x)= .e , x= . k n npq 2 npq
Định lý 2 (định lý Moivre − Laplace)
Gọi k là số lần xảy ra biến cố A trong dãy n phép thử Bernoulli,
p = P(A), 0 < p <1 (xác suất để biến cố A xảy ra trong mỗi phép thử), k1, k2 là hai số
nguyên cho trước với k1 < k2 .  k − np  k − np
Khi đó với n đủ lớn, ta có: P ( k  X k) 2 1 =   −   1 2  npq  npq      2 1 x t trong đó − 2 (x) = e dt  . 2 − Ví dụ
Gieo ngẫu nhiên n = 100 hạt giống. Tính xác suất:
1/ Có đúng 85 hạt nẩy mầm.
2/ Số hạt giống nẩy mầm từ 75 đến 85 hạt.
Cho biết hạt giống có tỉ lệ nẩy mầm là p = 0,8. Lời giải
Mỗi một hạt giống được đem gieo là một phép thử, có xác suất nẩy mầm là p = 0,8
Gọi X là biến ngẫu nhiên chỉ số hạt giống nẩy mầm,
X có miền giá trị {0; 1; 2; ... ; k; ...; 99; 100}.
1/ Theo yêu cầu của bài toán ta tính P(X = 85). 62
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 1
Áp dụng định lý 1, P( X 8 = 5)  . f(1, 25= 0,04565 100.0,8.0, 2 2 1 x − 85− 80 với f ( )x = . e 2 , x= = 1, 25 và f(1,25) = 0,1826. 2 4
2/ Theo yêu cầu của bài toán ta tính P(75  X  85). Áp dụng định lý 2,  85 − 80  75− 80 P(75 X 85)      −  =     
( 1, )25−(− 1, )25= (2 )1, 2=5 0,73.6.  4   4 
Luật phân phối Poisson
3.6.1. Định nghĩa
Biến ngẫu nhiên X được gọi là có luật phân phối Poisson với tham số  > 0 nếu k − k  e
phân phối của X có dạng P( X= ) . k = , k= 0;1;2;.. k!
3.6.2. Tính chất k  . −k e
+ Hàm phân phối xác suất của X là F ( x)= , x R  . k! k x   k  . −k e
+ Kỳ vọng của X là E( X )= . k  =  . ! k k=0 BÀI TẬP
Bài 3.1. Một xạ thủ có 3 viên đạn và bắn lần lượt vào một mục tiêu.
Xác suất bắn trúng mục tiêu của lần bắn thứ nhất là 0,7, xác suất bắn trúng mục
tiêu của lần bắn thứ hai là 0,8, xác suất bắn trúng mục tiêu của lần bắn thứ ba là 0,9.
Gọi X là biến ngẫu nhiên chỉ số đạn trúng mục tiêu.
1/ Hãy lập bảng phân phối xác suất của X. 2/ Tính E(X), D(X). 3/ Tính P( X = 2).
Bài 3.2. Một xạ thủ có 3 viên đạn và bắn lần lượt vào một mục tiêu cho đến khi nào có
một viên đạn trúng mục tiêu thì dừng bắn hoặc hết đạn cũng dừng bắn. Gọi X là biến
ngẫu nhiên chỉ số đạn đã được bắn ra. 63
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Cho biết xác suất bắn trúng mục tiêu của mỗi lần bắn là p = 0,7.
1/ Hãy lập bảng phân phối xác suất của X. 2/ Tính E(X), D(X). 3/ Tính P( X < 3).
Bài 3.3. Trong năm 2011, công ty Z xây dựng thực hiện 3 dự án (dự án I, II, III).
Xác suất thành công của dự án I là 0,7, của dự án II là 0,8 và của dự án III là 0,9.
Gọi X là biến ngẫu nhiên chỉ số dự án thành công.
1/ Hãy lập bảng phân phối xác suất của X. 2/ Tính E(X), D(X).
3/ Cho biết rằng nếu có ít nhất 1 dự án thành công thì công ty Z thành công.
Tính xác suất công ty Z thành công .
Bài 3.4. Một lô hàng có 5 sản phẩm tốt và 2 sản phẩm xấu.
Từ lô hàng đó lấy ngẫu nhiên lần lượt từng sản phẩm không hoàn lại đến khi nào
được sản phẩm tốt thì dừng lại.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm đã được lấy ra.
1/ Hãy lập bảng phân phối xác suất của X và lập hàm phân phối xác suất của X. 2/ Tính E(X), D(X). 3/ Tính P(X < 3).
Bài 3.5. Trong một hộp có chứa 2 bi xanh, 3 bi đỏ, 1 bi vàng.
Lấy ngẫu nhiên lần lượt không hoàn lại từng bi cho đến khi nào được đỏ thì dừng lại .
Gọi X là biến ngẫu nhiên chỉ số bi đã được lấy ra.
Hãy lập bảng phân phối xác suất của X.
Bài 3.6. Trong một hộp có chứa 6 bi xanh, 2 bi đỏ.
Lấy ngẫu nhiên một lần 3 bi.
Gọi X là biến ngẫu nhiên chỉ số bi đỏ được lấy ra.
Hãy lập bảng phân phối xác suất của X.
Bài 3.7. Trong một hộp có chứa 4 bi xanh, 3 bi đỏ, 2 bi vàng.
Lấy ngẫu nhiên một lần 3 bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra. 64
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Hãy lập bảng phân phối xác suất của X.
Bài 3.8. Một xí nghiệp trong một ca sản xuất có 3 dây chuyền sản xuất hoạt động độc lập
với nhau (gọi là dây chuyền I, II, III).
Xác suất dây chuyền I bị hỏng trog một ca sản xuất là 0,1, dây chuyền II bị hỏng trog một
ca sản xuất là 0,2, dây chuyền III bị hỏng trog một ca sản xuất là 0,3.
Gọi X là biến ngẫu nhiên chỉ số dây chuyền bị hỏng trong một ca sản xuất.
1/ Hãy lập bảng phân phối xác suất của X.
2/ Biết rằng trong một ca sản xuất nếu có ít nhất 1 dây chuyền bị hỏng thì xí nghiệp ngừng hoạt động.
Tính xác suất xí nghiệp ngừng họat động (trong ca sản xuất).
Bài 3.9. Một thiết bị gồm có 3 bộ phận hoạt động độc lập, xác suất để các thiết bị bị hỏng
trong thời gian hoạt động t tương ứng là 0,4; 0,1 và 0,2.
Gọi X là biến ngẫu nhiên chỉ số thiết bị bị hỏng trong thời gian hoạt động t.
1/ Lập bảng phân phối xác suất của X.
2/ Tính kỳ vọng E(X), phương sai D(X).
Bài 3.10. Trong kho có 3 bóng đèn tốt và 2 bóng đèn hỏng. Chọn ngẫu nhiên từng bóng
đèn đem thử (thử xong không trả lại) cho đến khi được bóng đèn tốt thì dừng thử. Gọi X
là biến ngẫu nhiên chỉ số lần thử.
1/ Lập bảng phân phối xác suất của X.
2/ Tính trung bình cần phải thử bao nhiêu lần.
Bài 3.11. Một lô hàng có tỉ lệ sản phẩm tốt là p = 0,9. Một ng ờ
ư i lấy ngẫu nhiên 3 sản phẩm từ lô hàng.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm tốt được lấy ra.
Lập bảng phân phối xác suất của X
Bài 3.12. Một lô hàng có 6 sản phẩm tốt và 2 sản phẩm xấu.
Lấy ngẫu nhiên một lần 3 sản phẩm.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm tốt được lấy ra (trong số 3 sản phẩm).
Gọi Y là biến ngẫu nhiên chỉ số sản phẩm xấu được lấy ra (trong số 3 sản phẩm).
1/ Lập bảng phân phối xác suất của X và của Y.
2/ Tính trung bình số sản phẩm tốt được lấy ra và tính trung bình số sản phẩm xấu được lấy ra. 65
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Bài 3.13. Một hộp có chứa 2 bi xanh, 1 bi đỏ, 4 bi vàng.
Lấy ngẫu nhiên một lần 3 bi từ trong hộp.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy (trong số 3 bi).
Gọi Y là biến ngẫu nhiên chỉ số bi đỏ được lấy (trong số 3 bi).
1/ Lập bảng phân phối xác suất của X và của Y.
2/ Tính trung bình số bi xanh được lấy ra và tính trung bình số bi đỏ được lấy ra.
Bài 3.14. Một lô hàng có chứa 7 sản phẩm tốt, 4 sản phẩm xấu.
Lấy ngẫu nhiên một lần 3 sản phẩm.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm tốt được lấy (trong số 3 sản phẩm).
1/ Lập bảng phân phối xác suất của X. 2/ Tính E(X), D(X).
Bài 3.15. Có hai cái hộp, hộp I có chứa 3 bi xanh, 5 bi đỏ và hộp II có chứa 1 bi xanh, 3 bi đỏ.
Từ hộp I lấy ngẫu nhiên 2 bi bỏ vào hộp II, sau đó từ hộp II lấy ngẫu nhiên 2 bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra từ hộp II.
Lập bảng phân phối xác suất của X.
Bài 3.16 Có hai cái hộp, hộp I có chứa 4 bi xanh, 1 bi đỏ và hộp II có chứa 5 bi xanh, 2 bi đỏ.
Từ hộp I lấy ngẫu nhiên 2 bi bỏ vào hộp II, sau đó từ hộp II lấy ngẫu nhiên 3 bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra từ hộp II.
Lập bảng phân phối xác suất của X.
Bài 3.17 Có 3 lô hàng, lô I có chứa 3 sản phẩm tốt, 1 sản phẩm xấu, lô II có chứa 4 sản
phẩm tốt, lô III có chứa 2 sản phẩm tốt, 2 sản phẩm xấu.
Từ mỗi lô hàng lấy ngẫu nhiên 1 sản phẩm.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm tốt được lấy ra (trong 3 sản phẩm).
1/ Lập bảng phân phối xác suất của X.
2/ Tính trung bình số sản phẩm tốt được lấy ra.
Bài 3.18 Có 3 lô hàng, lô I có chứa 3 sản phẩm tốt, 1 sản phẩm xấu, lô II có chứa 4 sản
phẩm tốt, lô III có ch ứa 2 sản phẩm tốt, 2 sản phẩm xấu. 66
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Từ mỗi lô hàng lấy ngẫu nhiên 1 sản phẩm và từ 3 sản phẩm đó lấy ngẫu nhiên ra 2 sản phẩm.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm tốt được lấy ra trong số 2 sản phẩm.
Lập bảng phân phối xác suất của X.
Bài 3.19 Có 2 hộp, hộp I có chứa 2 bi xanh và 4 bi đỏ, hộp II có chứa 1 bi xanh và 3 bi
đỏ. Từ hộp I lấy ngẫu nhiên 1 bi, từ hộp II lấy ngẫu nhiên 2 bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh đã được lấy ra (trong số 3 bi).
Lập bảng phân phối xác suất của X.
Bài 3.20 Có 2 hộp, hộp I có chứa 2 bi xanh và 4 bi đỏ, hộp II có chứa 1 bi xanh và 3 bi
đỏ. Từ hộp I lấy ngẫu nhiên 1 bi, từ hộp II lấy ngẫu nhiên 2 bi và từ 3 bi đó lấy ngẫu nhiên 2 bi.
Gọi X là biến ngẫu nhiên chỉ số bi xanh đã được lấy ra (trong số 2 bi).
Lập bảng phân phối xác suất của X.
Bài 3.21. Trong một hộp có chứa 2 quả bóng bàn mới và 3 quả bóng bàn cũ ( quả bóng
bàn cũ là quả bóng bàn sử dụng thi đấu ít nhất một lần).
Lần thứ nhất lấy ngẫu nhiên 2 quả bóng bàn từ trong hộp ra thi đấu, sau đó trả lại vào trong hộp.
Lần thứ hai lấy ngẫu nhiên ra 2 quả thi đấu.
Gọi X là biến ngẫu nhiên chỉ số bóng bàn mới được lấy ra ở lần thứ nhất.
và Y là biến ngẫu nhiên chỉ số bóng bàn mới được lấy ra ở lần thứ hai.
Lập bảng phân phối xác suất của X và Y.
Bài 3.22. Có 2 lô hàng, lô I có chứa 3 sản phẩm tốt và 2 sản phẩm xấu, lô II có chứa 4 sản
phẩm tốt và 1 sản phẩm xấu.
Trong quá trình vận chuyển do sơ ý ở lô I mất 1 sản phẩm, sau đó từ lô I lấy ngẫu
nhiên 1 sản phẩm, từ lô II lấy ngẫu nhiên 2 sản phẩm và từ 3 sản phẩm đó lấy ngẫu nhiên 2 sản phẩm.
Gọi X là biến ngẫu nhiên chỉ số sản phẩm tốt được lấy ra trong số 2 sản phẩm.
Lập bảng phân phối xác suất của X và Y.
Bài 3.23. Cho biến ngẫu nhiên liên tục X có hàm số f(x) xác định như sau: 67
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g    0 x 0;     2 f (x)    =      k.cosx x 0;  2    1/ Xác định k.
2/ Lập hàm phân phối xác suất F(x) của biến ngẫu nhiên X. 3/ Tính   P 0 X     . 4   
Bài 3.24. Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất:  0 x 0 f (x) =  . −3 . x k e x   0
1/ Xác định giá trị của k.
2/ Lập hàm phân phối xác suất F(x) của X.
Bài 3.25. Giả thiết rằng X chỉ tuổi thọ (đơn vị tính = giờ) của một sản phẩm là là biến
ngẫu nhiên có hàm mật độ xác suất f(x) xác định như sau:  0 x    0;1 f (x) =  2 kx  + 2 x+ 1 x    0;1 1/ Xác định giá trị k.
2/ Tuổi thọ trung bình của sản phẩm trên là bao nhiêu.
3/ Tính tỉ lệ sản phẩm có tuổi thọ từ 0,25 đến 0,5 giờ.
Bài 3.26. Một thí nghiệm có xác suất thành công là p = 0,8.
Thực hiện thí nghiệm đó 100 lần (các lần thí nghiệm là độc lập với nhau).
1/ Tính xác suất có 85 lần thì nghiệm thành công.
2/ Tính xác suất số lần thí nghiệm thành công từ 75 đến 85 lần.
3/ Tính xác suất có ít nhất 2 lần thí nghiệm thành công.
Bài 3.27. Gieo ngẫu nhiên 400 hạt đậu tương (trong phòng thực nghiệm), biết rằng xác
suất nảy mầm của hạt đậu tương là p = 0,8.
1/ Tính xác suất có 340 hạt ậ đ u tương nảy mầm.
2/ Tính xác suất số hạt đậu tương nảy mầm từ 300 hạt ế đ n 340 hạt.
3/ Tính xác suất có ít nhất 1 hạt nảy mầm. 68
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Bài 3.28. Công ty bảo hiểm AZ, trong năm 2012 nhận hợp đồng bảo hiểm cho n = 10.000
xe máy, với lệ phí bảo hiểm là 100.000 đồng / 1xe / 1năm.
Trung bình mức phí đền bù cho một vụ tai nạn không may xảy ra là 1000.000 đồng.
Theo thống kê cho biết tỉ lệ tai nạn đối với xe máy khi tham gia giao thông là 0,007.
Tổng các chi phí khác (trả lương, thuê mặt bằng, thuế, hoạt động xã hội...) của
công ty AZ chiếm 30% tổng thu của công ty.
1/ Tính xác suất trong năm 2012 công ty AZ phá sản.
2/ Tính xác suất trong năm 2012 công ty AZ lãi ít nhất 400.000.000 đồng.
Trong bài này giả thiết 1 xe máy nếu không may bị tai nạn thì chỉ bị nhiều nhất 1 lần trong năm 2012.
Bài 3.29. Gieo 50 hạt đậu tương, xác suất không nảy mầm của mỗi hạt là 0,07. Gọi X là
biến ngẫu nhiên chỉ số hạt đậu tương không nảy mầm.
1/ Lập bảng phân phối xác suất của X.
2/ Trung bình có bao nhiêu hạt đậu tương không nảy mầm. Tính xác suất ể
đ có trên 48 hạt đậu tương nảy mầm. 3/ Tính Mod(X).
Bài 3.30. Gieo 100 hạt đậu tương, xác suất nảy mầm của mỗi hạt là 0,8. Tính xác suất :
1/ Có hơn 75 hạt đậu tương nảy mầm .
2/ Có không quá 74 hạt đậu tương nảy mầm .
3/ Số hạt đậu tương nảy mầm nằm trong khoảng (75; 90) .
Bài 3.31. Cho biết X là chiều cao của sinh viên (cm), X có luật phân phối chuẩn
N(155; 9). Tính xác suất khi chọn ngẫu nhiên một sinh viên để đo thì chiều cao X: 1/ Dưới 150(cm).
2/ Từ 150(cm) đến 162(cm). 3/ Trên 162(cm).
Bài 3.32. Một thí nghiệm có xác suất thành công là 0,9. Phải thực hiện bao nhiêu thí nghiệm ể
đ nhiều khả năng nhất có 20 thí nghiệm thành công.
Bài 3.33. Xác suất để một người đau bệnh Z uống thuốc loại A được khỏi bệnh là 0,7. Có
10 người đau bệnh Z dùng thuốc loại A đó, gọi X là biến ngẫu nhiên chỉ số người khỏi
bệnh (trong số 10 người trên). 69
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Tìm kỳ vọng, phương sai và số Mod của X, từ đó suy ra số người trung bình được
khỏi bệnh khi có 10 người đau bệnh Z dùng thuốc loại A và số người được khỏi bệnh có xác suất lớn nhất.
Bài 3.34. Trong một hộp có chứa 3 bi xanh và 2 bi đỏ.
Lần thứ nhất: Lấy ngẫu nhiên 2 bi từ trong hộp (không hoàn lại).
Lần thứ hai: Lấy ngẫu nhiên 2 bi từ trong hộp.
Gọi X là biến ngẫu nhiên chỉ số bi xanh được lấy ra ở lần thứ nhất và gọi Y là biến ngẫu
nhiên chỉ số bi xanh được lấy ra ở lần thứ hai.
1/ Lập bảng phân phối xác suất của biến ngẫu nhiên 2− chiều rời rạc (X; Y).
Từ đó suy ra bảng phân phối xác suất của biến ngẫu nhiên X và biến ngẫu nhiên Y.
2/ Lập bảng phân phối xác suất có điều kiện (X / yj).
Tính kỳ vọng có điều kiện E(X / yj). Bài 3.35. C
ó hai cái hộp, hộp I có chứa 2 bi xanh và 1 bi đỏ, hộp II có chứa 3 bi xanh và 1 bi đỏ.
Lần thứ nhất: Từ hộp I lấy ngẫu nhiên 1 bi và từ hộp II lấy ngẫu nhiên 2 bi.
Lần thứ hai: Từ 3 bi được lấy ra ở lần thứ nhất lấy ngẫu nhiên 2 bi.
Gọi X là biến ngẫu nhiên chỉ số bi đỏ được lấy ra ở lần thứ nhất và gọi Y là biến ngẫu
nhiên chỉ số bi đỏ được lấy ra ở lần thứ hai.
1/ Lập bảng phân phối xác suất của biến ngẫu nhiên 2− chiều rời rạc (X; Y).
Từ đó suy ra bảng phân phối xác suất của biến ngẫu nhiên X và biến ngẫu nhiên Y.
2/ Lập bảng phân phối xác suất có điều kiện (X / yj).
Tính kỳ vọng có điều kiện E(X / yj).
Bài 3.36. Cho hàm mật độ xác suất của biến ngẫu nhiên 2 − chiều (X; Y) như sau:  k( x+ )y ( ;x )y D f (x ; ) y =  0 (x ; ) y   D
với D = {(x; y)R2 / 0  x  3, −1  y  2}.
1/ Xác định giá trị của k.
2/ Tính a/ P(1 < X < 2; 0 < Y < 1). b/ P(X > 2)
3/ Tìm hàm mật độ xác suất của X và hàm mật độ xác suất của biến ngẫu nhiên Y. Từ đó tính E(X), E(Y). 70
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Phần II. THỐNG KÊ
Chương 4. LÝ THUYẾT MẪU
§1. LÝ THUYẾT MẪU
1.1. Đặt vấn đề
1.1.1. Trong thực tế khi ta cần tìm kiếm thông tin về một loại đối tượng (gọi chung là
phần tử) nào đó, chẳng hạn: tìm hiểu về chất lượng của một loại sản phẩm, khảo sát thu
nhập của người lao động...
Nếu đối tượng cần tìm hiểu có số lượng quá lớn thì ta không thể khảo sát từng đối
tượng vì những lí do như là: thời gian, không gian, hiệu quả kinh tế, biến dạng đối tượng...
Do đó, người ta thường chọn ngẫu nhiên một số phần tử khảo sát ghi nhận kết quả,
và dựa vào các kết quả đó cho thông tin về đối tượng.
Quá trình này được gọi là chọn mẫu.
Đối tượng được khảo sát có số lượng rất lớn gọi là tổng thể, kí hiệu N, số phần tử
được chọn ngẫu nhiên gọi là mẫu, kí hiệu n.
Ví dụ 1. Khảo sát về chi phí tiền điện nước của các hộ dân khu vực Q.
Ví dụ 2. Khảo sát trọng lượng của một bao gạo được đóng bao tự động...
Ví dụ 3. Khảo sát tỉ lệ sản phẩm là thành phẩm của nhà máy...
1.1.2. Các phương pháp chọn mẫu
(1.2.1) Chọn mẫu có lặp.
(1.2.2) Chọn mẫu không lặp.
(1.2.3) Chọn mẫu phân loại.. . Nhận xét
i/ Chọn mẫu có lặp có nhược điểm là có những phần tử, đối tượng chọn rồi được chọn lại
do đó thông tin bị hạn chế...; ưu điểm là các lần chọn mẫu là độc lập;
i / Chọn mẫu không lặp có nhược điểm là có là các lần chọn mẫu là không độc lập với
nhau...; ưu điểm là các phần tử, đối ư
t ợng đã chọn rồi thì không lặp lại... 71
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Với nhận xét trên, trong giáo trình này, ta sử dụng phương pháp chọn mẫu có lặp trong việc chọn mẫu.
1.2. Mẫu ngẫu nhiên −
− Mẫu thực nghiệm
1.2.1. Định nghĩa
Giả sử ta xét tổng thể N, cỡ mẫu n, chọn mẫu theo phương pháp có lặp.
Ta có mỗi một lần chọn mẫu là một lần thực hiện phép thử có không gian biến cố là N.
Gọi X là biến ngẫu nhiên chỉ thông tin (đặc tính) của đối tượng ta cần quan tâm, khi đó:
Tương ứng với n lần thử (n lần chọn mẫu) thu được n biến ngẫu nhiên X1; X2; ... ;
Xn (có cùng đặc tính với biến ngẫu nhiên X) và các biến ngẫu nhiên này độc lập với nhau.
Ta có (X1; X2; ... ; Xn ) gọi là mẫu ngẫu nhiên và tương ứng với mỗi biến ngẫu
nhiên Xi , i = 1, 2,..., n có giá trị xi , i = 1, 2, ..., n và (x1; x2; ... ; xn) gọi là mẫu thực nghiệm. Ví dụ
Khảo sát, tìm hiểu điểm số bài thi môn Anh văn của SV trường ĐH A.
Ta chọn ngẫu nhiên n = 20 bài thi (  thực hiện 20 phép thử độc lập).
→ Có 20 biến ngẫu nhiên (X1; X2; ... ; X20) gọi là mẫu ngẫu nhiên
và mỗi một bài thi có một số (điểm số của bài thi đó) → một dãy gồm 20 số
(7; 3; 9; 9; 5; 7; 5; 5; 6; 0; 1; 5; 8; 7; 8; 5; 4; 5; 9; 5) gọi là mẫu thực nghiệm.
1.2.2. Cách xắp xếp mẫu thực nghiệm
(1.2.2.1) Sắp tăng dần (giảm dần)
Giả sử có mẫu thực nghiệm (x1; x2; ... , xn) với x1  x2  ...  xn gọi là sắp tăng dần.
Và mẫu thực nghiệm (x1; x2; ... , xn) với x1  x2  ...  xn gọi là sắp giảm dần.
(1.2.2.2) Sắp theo bảng phân phối tần s
− ốt ần suất thực nghiệm không chia lớp, chia lớp
(i) Sắp theo bảng phân phối tần số thực nghiệm không chia lớp: xi x1 x2 ... xk ni n1 n2 ... nk với n1 + n2 +.. + nk = n
(i ) Sắp theo bảng phân phối tần số thực nghiệm chi a lớp: 72
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g xi [x1 ; x2) [x2 ; x3) ... [xk−1 ; xk) ni n1 n2 ... nk với n1 + n2 +.. + nk = n Ví dụ
Khảo sát, tìm hiểu điểm số bài thi môn Anh văn của SV trường ĐH A.
Ta chọn ngẫu nhiên n = 20 bài thi, thu được số liệu
(7; 3; 9; 2; 5; 7; 4; 5; 6; 0; 1; 4; 8; 7; 8; 5; 4; 5; 9; 4) xi 0 1 2 3 4 5 6 7 8 9 ni 1 1 1 1 4 4 1 3 2 2
Gọi là bảng phân phối tần số thực nghiệm không chia lớp.
+ Cũng với mẫu khảo sát trên, ta chia theo từng lớp (nhóm) dưới 5 điểm, từ 5 điểm đến dưới 8, từ 8 điểm ế
đ n 10 điểm, khi đó ta có bảng chia lớp như sau: xi [0 − 5) [5 − 8) [8 − 10) ni 8 8 4
Gọi là bảng phân phối tần số thực nghiệm chia lớp. n
+ Từ các bảng trên, nếu ta đặt i
 = , i =1, 2,...,k ta có bảng phân phối tần suất thực i n
nghiệm chia lớp, không chia lớp tương ứng. 1.3. Biểu đồ −
− Hàm phân phối thực nghiệm
1.3.1. Biểu đồ
Xét biến ngẫu nhiên X, có bảng phân phối tần số thực nghiệm không chia lớp xi x1 x2 ... xk ni n1 n2 ... nk với n1 + n2 +.. + nk = n
Trên hệ trục Oxy, với Ox  Oxi , Oy  Oni , đặt Mi (xi, ni), i = 1, 2,..., k
Nối các điểm Mi → thu được biểu đồ tần số của mẫu thực nghiệm. Ví dụ
Lấy mẫu có kích thước n = 15, ta có các số liệu: 2 1 3 5 4 3 5 4 5 5 3 4 5 5 4 73
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Hãy lập bảng thống kê, vẽ biểu đồ hình gậy tần số, đa giác tần số. Giải Bảng thống kê : x 1 2 3 4 5 i n 1 1 3 4 6 i
Biểu đồ hình gậy tần f 1 i 1 3 4 6 số Đa giác tần số 15 15 15 15 15 6 6 4 4 3 3 1 1 1 2 3 4 5 1 2 3 4 5
1.3.2. Hàm phân phối tần số thực nghiệm không chia lớp
Xét biến ngẫu nhiên X, có bảng phân phối tần số thực nghiệm không chia lớp xi x1 x2 ... xk ni n1 n2 ... nk với n1 + n2 +.. + nk = n.
Hàm số được kí hiệu Fn(x) và xác định  0, x x1  n1  , x  x x 1 2  n F ( ) x  = n  + n n 1 2 , x  x x 2 3  n ....   1, x  x  k
gọi l à hàm phân phối tần số thực nghiệm của mẫu thực nghiệm của biến ngẫu nhiên X. 74
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
§2. CÁC THAM SỐ ĐẶC TRƯNG CỦA MẪU I.
Các tham số đại diện cho giá trị trung tâm
2.1. Trung bình mẫu (Kỳ vọng mẫu)
2.1.1. Định nghĩa
Xét biến ngẫu nhiên X có mẫu ngẫu nhiên (X1; X2; ... ; Xn) và có mẫu thực nghiệm (x1; x2; ... ; xn). Khi đó:
+ Trung bình mẫu ngẫu nhiên của X được kí hiệu X và được xác định 1 n X = X  i n i 1= 1 n
+ Trung bình mẫu thực nghiệm của X được kí hiệu
x và được xác định x = x  i n i 1=
2.1.2. Cách tính trung bình mẫu thực nghiệm
Xét biến ngẫu nhiên X, có bảng phân phối tần số thực nghiệm không chia lớp xi x1 x2 ... xk ni n1 n2 ... nk với n1 + n2 +.. + nk = n. 1 k Khi đó: + x = n x  (i1) i i n i 1= + 1 k x = a + n x  − a , với aR (i2) i ( i ) n i 1=
Trường hợp các xi , i = 1, 2,..., k lập thành một cấp số cộng có công sai bằng h, thì
ta có thể tính bằng công thức: k + h  x − a i x = a+ n  , với aR (i ) 3 i n  h  i 1 = 
2.1.3. Ý nghĩa số trung bình mẫu
Số trung bình mẫu thực nghiệm được làm giá trị đại diện cho tất cả các giá trị của
mẫu thực nghiệm của X và nó được làm đại diện cho tổng thể N nếu giá trị của các mẫu là tương đối ồ đ ng đều.
Ngoài ra trung bình mẫu được dùng để ước lượng cho trung bình của biến ngẫu nhiên X. 75
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2.2. Số trung vị của mẫu thực nghiệm
2.2.1. Định nghĩa
Xét biến ngẫu nhiên X có mẫu thực nghiệm (x1; x2; ... ; xn) được sắp theo thứ tự
tăng dần (hoặc giảm dần).
Số trung vị của mẫu thực nghiệm của X là số thực được kí hiệu medn(X) và xác định:  x , n = 2 k− 1 k  med ( )X =  x+ x n k k+1 , n = 2 k  2 Nhận xét
Số trung vị là số nằm giữa dãy số x1; x2; ... ; xn .
2.2.2. Cách tìm số trung vị với biến ngẫu nhiên X có bảng phân phối tần số thực nghiệm
(i) Bảng phân phối tần số thực nghiệm không chia lớp:   n n     i  2  x , i k  k   n med ( )X  = n    n i  2 i k  x + x n k k 1 +  , n  =  2 i  2 i k
(i ) Bảng phân phối tần số thực nghiệm chia lớp:  n  n − n n      i  x + − − ( x x− ) 2 i 2 .  , ik i k  k 1 k k 1  n n med ( )  k X  n =    i n  2 i k    1  n  x + x − x 1  − , n  =  k −1 ( k k−1) 2 i n   2   k  i k
• Chú ý. Lớp có chứa số tr n
u g vị gọi là lớp trung vị của mẫu thực nghiệm.
2.2.3. Ý nghĩa của số trung vị
Số trung vị là số đặc trưng cho giá trị trung tâm của dãy các giá trị của mẫu thực nghiệm. 76
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2.3. Số Mod của mẫu thực nghiệm
2.3.1. Định nghĩa
Xét biến ngẫu nhiên X có mẫu thực nghiệm (x1; x2; ... ; xn).
Giá trị có trong mẫu thực nghiệm của X có tần số lớn nhất được gọi là số Mod của
mẫu thực nghiệm của X và được kí hiệu Modn(X).
2.3.2. Cách tìm số Mod của X có bảng phân phối tần số thực nghiệm.
(i) Bảng phân phối tần số thực nghiệm không chia lớp:
Modn(X) = xi nếu ni = max{n1; n2; ... ; nk}.
(i ) Bảng phân phối tần số thực nghiệm chia lớp:
Nếu tại lớp thứ i là [xi−1 ; xi ] có tần số ni = max{n1; n2; ... ; nk} thì x x + i 1 Mod ( ) i X − = n 2
• Chú ý. Lớp có chứa số Mod gọi là lớp Mod của mẫu thực nghiệm.
2.3.3. Ý nghĩa của số trung vị
Số Mod cho biết được giá trị nào của mẫu thực nghiệm là xuất hiện nhiều nhất, nó
không phụ thuộc vào các giá trị quá lớn hay quá nhỏ của mẫu thực nghiệm. II.
Các tham số đại diện cho độ phân tán (độ chênh lệch)
2.4. Phương sai mẫu
2.4.1. Định nghĩa
Xét biến ngẫu nhiên X có mẫu ngẫu nhiên (X1; X2; ... ; Xn) và có mẫu thực nghiệm
(x1; x2; ... ; xn) và giả sử X có trung bình mẫu ngẫu nhiên là X , trung bình mẫu thực nghiệm x . Khi đó:
+ Phương sai mẫu ngẫu nhiên của X là một biến ngẫu nhiên được kí hiệu S2 và được xác định 1 n S = ( X − X i )2 2 n i 1=
+ Phương sai mẫu thực nghiệm của X là một số thực được kí hiệu s2 và được xác định 1 n s = ( x − x i )2 2 n i 1=
2.4.2. Cách tính phương sai mẫu thực nghiệm
Xét biến ngẫu nhiên X, có bảng phân phối tần số thực nghiệm không chia lớp 77
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g xi x1 x2 ... xk ni n1 n2 ... nk với n1 + n2 +.. + nk = n 1 k Khi đó: + s = n ( ) x  − x (k1) i i ( )2 2 2 n i 1= + 1 k s = n x 
− a − x− a , với aR (k2) i ( i ) ( )2 2 2 n i 1=
Trường hợp các xi , i = 1, 2,..., k lập thành một cấp số cộng có công sai bằng h, thì ta có
thể tính bằng công thức: 2 2 k + h  x − a i s = n − x− a  , với aR (k2) i   ( )2 2 n  h i 1 = 
2.5. Phương sai điều chỉnh của mẫu −
− Độ lệch tiêu chuẩn − Độ lệch tiêu chuẩn
điều chỉnh của mẫu
2.5.1. Định nghĩa
Xét biến ngẫu nhiên X có mẫu ngẫu nhiên (X1; X2; ... ; Xn) và có mẫu thực nghiệm (x 2
1; x2; ... ; xn) và giả sử X có phương sai mẫu ngẫu nhiên là S , phương sai mẫu thực nghiệm s2. Khi đó: + n 2 2 S =
.S gọi là phương sai điều chỉnh của mẫu ngẫu nhiên của X. 1 n −1 + n 2 2 s =
.s gọi là phương sai điều chỉnh của mẫu thực nghiệm của X. 1 n −1 + 2
S = S gọi là độ lệch tiêu chuẩn của mẫu ngẫu nhiên của X. + 2
s = s gọi là độ lệch tiêu chuẩn của mẫu thực nghiệm của X. + 2
S = S gọi là độ lệch tiêu chuẩn điều chỉnh của mẫu ngẫu nhiên của X. 1 1 + 2
s = s gọi là độ lệch tiêu chuẩn điều chỉnh của mẫu thực nghiệm của X. 1 1
2.5.2. Ý nghĩa
Các giá trị phương sai hay độ lệch tiêu chuẩn cho ta nhận biết sự đồng đều của các
giá trị của mẫu thực nghiệm. 78
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Ví dụ 1
Tìm hiểu mức thu nhập của sinh viên đi làm thêm tại khu vực Z, với cỡ mẫu n =
100, đơn vị tính 100.000 ngàn.
Ta thu được bảng phân phối tần số thực nghiệm như sau: xi 3 5 6 8 10 ni 20 18 32 25 5
Tính các tham số 2 2 , x s , , s . 1 1 Lời giải * Cách 1 1 k Áp dụng công thức 1 k x = n x  , s = n ( ) x  − x : i i ( )2 2 2 i i n n i =1 i 1 = 1 x =
  +  +  +  +   592 20 3 18 5 32 6 25 8 5 10 = = 5. 100 100 1 s = 2  0 3 + 18 5 + 32  6+ 25  8+  5 10 −( )2 2 2 2 2 2 2 5,92 = 3,7 100  . n 100 2 2 s = .s = 3, 7736= 3,8. 1 n−1 99 2 s = s 1 = ,95. 1 1 * Cách 2
Lập bảng để tính các giá trị tham số như sau: xi ni xi − a ni(xi − a) ni(xi − a)2 3 20 −3 −60 180 5 18 −1 −18 18 a = 6 32 0 0 0 8 25 2 50 100 10 5 4 20 80  100 −8 378 1 k x = a + n x  − a = +  − = . i ( i ) 1 6 ( 8) 5,92 n = 100 i 1 79
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 1 k s = n x  − a − x− a =  − = . i ( i ) ( )2 2 1 378 ( 0, )2 2 08 3,773 n = 100 i 1 Ví dụ 2
Khảo sát mức chi phí tiền điện và tiền nước trên một tháng của hộ dân tại khu vực
Z, với cỡ mẫu n = 100, đơn vị tính 100.000 ngàn.
Ta thu được bảng phân phối tần số thực nghiệm như sau: xi 3−7 7−11 11−15 15−19 ni 45 25 20 10
Tính các tham số 2 2 , x s , , s . 1 1 Lời giải
Chuyển bảng trên về dạng không chia lớp xi 5 9 13 17 ni 45 25 20 10 Tính các tham số 2 2 , x s , , s . 1 1
Vì các giá trị xi là một cấp số cộng có công sai h = 4, do đó ta sử dụng các công thức k h  x − a 2 2 k h  x − a 2  i x = a+ n  và 2 i s = n  − x− a . i   ( ) i n   n  h =  h i 1  i 1 = 
Lập bảng để tính các giá trị tham số như sau: xi ni x − a  x − a  2 i n x − a  i h i i  n h    i  h    5 45 −1 −45 45 a = 9 25 0 0 0 13 20 1 20 20 17 10 2 20 40 −5 105 80
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g k h  x − a 4 i x = a+ n  = 9+  (− 5)= 8,8 i n   =  h  100 i 1 2 2 k h  x − a i s = n  − x− a =  − = . i   ( )2 16 2 2 105 (0, 2) 16,7 n  h  100 i 1 =
Chương 5. ƯỚC LƯỢNG THAM SỐ
§1. ƯỚC LƯỢNG ĐIỂM
1.1. Khái niệm về ước lượng tham số
Xét một tổng thể N, giả sử ta cần quan tâm đến biến ngẫu nhiên X đo lường (đánh
giá) một thông tin (dấu hiệu) nào đó của cá thể (phần tử) trong tổng thể N, X là đại lượng
thay đổi từ phần tử này đến phần tử khác...
Ví dụ xét tổng thể N là SV (mỗi SV là một cá thể, là một phần tử) và giả sử thông
tin ta cần quan tâm là điểm số bài thi môn toán xác suất & thống kê, ở đây X là biến ngẫu
nhiên chỉ điểm số bài thi của mỗi SV → X có giá trị thay đổi từ phần tử này đến phần tử
khác (điểm số của mỗi bài thi có sự thay đổi...).
Phân phối xác suất của X thường khó “nắm bắt” và thông thường ta giới hạn ở việc
xác định một số các tham số đặc trưng của X như giá trị trung bình (kì vọng), phương sai,
trung vị, mode...(các tham số ta gọi chung là tham số t)
Các tham số này không thể xác định chính xác nếu không biết được phân phối xác
suất X, mà phải ước lượng từ các giá trị của X trên một mẫu được chọn ngẫu nhiên
→ Bài toán ước lượng tham số được phát biểu như sau:
Giả sử biến ngẫu nhiên X có tham số đặc trưng t nào đó chưa biết mà ta quan tâm.
Vấn đề đặt ra là căn cứ trên n giá trị x1, x2, ... , xn của X (đo được từ một mẫu thực
nghiệm) cần tìm ra một giá trị gần đúng T của t .
Ta có các định nghĩa sau: Định nghĩa 1
Một hàm T = Tn(x1; x2;...; xn) của n giá trị x1; x2;...; xn được gọi là một ước lượng điểm cho t . 81
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Để khảo sát về mặt Toán học, ta coi (x1; x2;...; xn) là một giá trị quan sát được (là
giá trị thực nghiệm) của mẫu ngẫu nhiên (X1; X2;...; Xn), trong đó các biến ngẫu nhiên Xi ;
i = 1, 2, ..., n là độc lập có cùng phân phối xác suất với X.
Như vậy một hàm ước lượng T = Tn là hàm n biến ngẫu nhiên X1; X2;...; Xn do đó
nó cũng là một biến ngẫu nhiên và giá trị của ước lượng cũng thay đổi từ mẫu quan sát
này đến mẫu quan sát khác.
Việc lựa chọn một ước lượng nào là “tốt nhất” được căn cứ trên c c á tiêu chuẩn sau: Định nghĩa 2
Định nghĩa 2.1. Ước lượng không chệch
Ước lượng Tn được gọi là ước lượng không chệch của t nếu E(Tn) = t .
Tính chất không chệch có nghĩa là ước lượng Tn không có sai số hệ thống.
Định nghĩa 2.2. Ước lượng vững
Ước lượng Tn được gọi là ước lượng vững của t nếu:
 > 0, lim P  T − t   = 1  n n →  .
Tính chất vững là bảo đảm cho ước lượng Tn gần t tùy ý với xác suất cao khi cỡ mẫu n lớn.
Định nghĩa 2.3. Ước lượng hiệu quả
Ước lượng Tn được gọi là ước lượng hiệu quả của t nếu Tn là ước lượng không
chệch và phương sai D(Tn) là nhỏ nhất trong lớp tất cả các ước lượng không chệch.
1.2. Ước lượng cho giá trị trung bình
Giả sử X là biến ngẫu nhiên với E(X) =  (  chưa biết),  được gọi là giá trị trung
bình của tổng thể N ( ở đây là tham số t tổng quát ở trên).
Nếu ta có một mẫu thực nghiệm n giá trị x1; x2;...; xn của X thì trung bình m x ẫ u
sẽ được dùng làm ước lượng cho . Định lý
Trung bình mẫu x là ước lượng không chệch và vững cho trung bình của tổng thể N.
1.3. Ước lượng cho phương sai
 ( hoặc kí hiệu 2 )
Giả sử X là biến ngẫu nhiên với D(X) = 2 ( 2 chưa biết), 2 được gọi là phương
sai của tổng thể N (2 ở đây là tham số t tổng quát ở trên). 82
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Nếu ta có một mẫu thực nghiệm n giá trị x1; x2;...; xn của X thì phương sai điều
chỉnh mẫu thực nghiệm s 2
1 sẽ được dùng làm ước lượng cho 2 . Định lý
Phương sai điều chỉnh mẫu thực nghiệm s 2
1 là ước lượng không chệch cho 2 .
§2. KHOẢNG TIN CẬY CHO KỲ VỌNG
2.1. Đặt vấn đề
2.1.1. Bài toán tìm khoảng tin cậy đặt ra như sau:
Căn cứ trên mẫu thực nghiệm (x1; x2;...; xn ) xác định một khoảng (a; b) để khoảng
đó chứa tham số t với xác suất 1 -  cho trước (1 -  thường được chọn  0,90, thường là 0,95). Một cách chính x
ác khoảng tin cậy được định nghĩa như sau: Định nghĩa 1
Giả sử biến ngẫu nhiên X có mẫu ngẫu nhiên (X1; X2; ...; Xn ).
Nếu có hai hàm f1(X1; X2; ...; Xn ), f2(X1; X2; ...; Xn ) thỏa mãn:
P[f1(X1; X2; ...; Xn ) < t < f2(X1; X2; ...; Xn )] = 1 - , với 1
-  gần bằng 1, thì khi đó
Với một mẫu thực nghiệm (x1; x2; ...; xn ) khoảng số thực (f1(x1; x2; ...; xn ); f2(x1;
x2; ...; xn )) được gọi là khoảng tin cậy hay còn gọi là khoảng ước lượng của tham số t của X.
Thường được viết dưới dạng f1(x1; x2; ...; xn ) < t < f2(x1; x2; ...; xn ).
+ 1 -  là độ tin cậy và thường chọn 1 -   0,95;
+ f2(x1; x2; ...; xn ) − f1(x1; x2; ...; xn ) = l gọi là độ dài khoảng tin cậy. Nhận xét:
Khoảng tin cậy của tham số t phụ thuộc vào các hàm f1(X1; X2; ...; Xn ), f2(X1; X2;
...; Xn ) và độ tin cậy  và độ tin cậy càng lớn thì khoảng tin cậy càng rộng (l lớn).
Ứng với một độ tin cậy  cho trước, khoảng tin cậy nào có độ dài l ngắn nhất được
xem là khoảng tin cậy tốt nhất của tham số t của X.
Bài toán tìm khoảng tin cậy của tham số t của X là tìm khoảng tin cậy tốt nhất. 83
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
2.1.2. Bài toán tìm khoảng tin cậy
+ Lập một mẫu ngẫu nhiên (X1; X2; ...; Xn ) của X; + Cho độ tin cậy 1 - 
+ Tìm các hàm f1(X1; X2; ...; Xn ), f2(X1; X2; ...; Xn ) sao cho
P[f1(X1; X2; ...; Xn ) < t < f2(X1; X2; ...; Xn )] =1 -  (i1)
và hiệu f2(X1; X2; ...; Xn ) − f1(X1; X2; ...; Xn ) nhận mọi giá trị nhỏ nhất trong các cặp hàm thỏa mãn (i1).
+ Lập khoảng tin cậy tốt nhất f1(x1; x2; ...; xn ) < t < f2(x1; x2; ...; xn ) với (x1; x2; ...; xn ) là
mẫu thực nghiệm của X.
• Chú ý. Ngoài bài toán trên, ta còn có các bài toán khác:
(b1) Cho độ tin cậy 1 - , cho độ dài khoảng tin cậy l, tìm kích thước mẫu n;
(b2) Cho độ dài khoảng tin cậy l, cho kích thước mẫu n, tìm độ tin cậy 1 - .
2.2. Khoảng tin cậy cho kỳ vọng (tóm tắt các công thức)
X là biến ngẫu nhiên chuẩn N(t;).
2.2.1. Trường hợp  đã biết
Khoảng tin cậy cho tham số t có dạng:  1−   1  − −  1 −1 x− .    x+ . (i2) n  2  n  2      2 1 x t− với 2 (  x) = e dt 
(hàm Laplace, giá trị được cho ở bảng phụ lục). 2 0 2 1 x t  Chú ý. Nếu bảng tra là − 2 (  ) x = e dt  thì (u .  ) =1 − 2 2 −   1−     1−  2  1−  Chú ý. Từ (i1) → 1 − 1 − − 1 x+ . − x− . = .   gọi là độ dài  n   2     n   2     n  2    1  khoảng tin cậy và − 1 . −   gọi là sai số. n  2   
2.2.2. Trường hợp  chưa biết + Xét cỡ mẫu n > 30. 84
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g s 1−   s 1− 
Khoảng tin cậy cho tham số t có dạng x:  1 −1 1 −1 − .    x + . (i3) n  2  n  2      n với 2 2 2 s = s , s=
. s, ở đây s2 là phương sai của mẫu thực nghiệm của X. 1 1 1 n−1 + Xét cỡ mẫu n < 30. s s
Khoảng tin cậy cho tham số t có dạng x: 1 1 − . t    x+ . t (i4) n       n 1 − ; n n−    1;   2   2  với t
: phân phối Student (tra bảng)    n 1 −  ;   2 Các ví dụ minh h ọa
Ví dụ 1. Khảo sát ngẫu nhiên n = 36 SV của một trường đại học cho thấy tiền ăn trung
bình là 380 ngàn đồng /1 tháng/1 SV. Giả sử t ề
i n ăn SV là biến ngẫu nhiên X tuân theo
luật phân phối chuẩn N(;
),  = 14 ngàn đồng.
Với độ tin cậy 1 - = 0,95, hãy tìm khoảng tin cậy tiền ăn trung bình của SV của trường đại ọ h c đó. Lời giải
Gọi t là tiền ăn trung bình của SV, t = E(X)  1−   1 −
Khoảng tin cậy cho t có dạng : −  1 −1 x − .    x+ . (i) n  2  n  2       1  T − ừ giả thiết 1  x = 380; = 14;n = 36; 1 − = 0,95 − → = 1,9  , thay vào (i) thu 2    được 375,4 <  < 384,6.
Ví dụ 2. Trọng lượng của một loại quả là một biến ngẫu nhiên X, có luật phân phối chuẩn N(; ).
Với mẫu n = 36, thu được bảng phân phối tần số thực nghiệm: xi
[0,9 − 1,3) [1,3 − 1,7) [1,7 − 2,1) [2,1 − 2,5) ni 6 10 8 12
Hãy xác định khoảng ước lượng cho trung bình, với độ tin cậy 1 - = 0,97. 85
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Lời giải
Khoảng ước lượng có dạng: s 1−   s 1−   1 −1 1 −1 x − .    x + . (1) n  2  n  2     
Từ bảng bảng phân phối tần số thực nghiệm → bảng thu gọn: xi 1,1 1,5 1,9 2,3 ni 6 10 8 12 1−   Tính được x 1 = ,789, s −1 1 = 0,445, 1 -  = 0,97 →  = 2,17  . 2    thay vào (1), thu được: 1,628 <  < 1,95.
Ví dụ 3. X là biến ngẫu nhiên, có luật phân phối chuẩn N( ) ;.
Với mẫu n = 100, thu được x 2 = 0,06, s1 = 0,7890.
Hãy xác định khoảng ước lượng cho trung bình của X, với độ tin cậy 1 - = 95%. Lời giải
Khoảng ước lượng có dạng: s 1−   s 1−   1 −1 1 −1 x − .    x + .      (1) n  2  n  2   −  1−  x 2 = 0,06, s 1 1 = 0,7890, 1 -  = 0,95 →  = 1,96  2   
thay vào (1), thu được: 19,9054 <  < 20,2196.
Ví dụ 4. X là biến ngẫu nhiên, có luật phân phối chuẩn N( );.
Với mẫu n = 25, thu được bảng phân phối tần số thực nghiệm: xi 2,0 2,2 2,5 2,6 ni 6 7 9 3
Hãy xác định khoảng ước lượng cho trung bình của X, với độ tin cậy 1 - = 95%. Lời giải 86
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g s s
Khoảng ước lượng có dạng: 1 1 x − . t    x+ . t (1) n       n 1 − ; n n−    1;   2   2 
Từ bảng trên, tính được: x 2 = ,308, s1 = 0,227, 1 - = 0,95 → t = t(24 ; 0,025) = 2,064 .    n 1 −  ;   2
Thay vào (1), thu được: 2,214 <  < 2,402.
§ 3. ƯỚC LƯỢNG KHOẢNG CHO TỈ LỆ
(Ước lượng khoảng cho xác suất)
Xét tổng thể N, với đối tượng được chia làm hai nhóm (A và A ).
X biến ngẫu nhiên tác động lên tổng thể X, xác định như sau: 1   A X() =  0    A
Khi đó P(X = 1) = p (chọn được đối tượng A khi chọn ngẫu nhiên một phần tử từ
tổng thể N) và p là tỉ lệ đối tượng A có trong tổng thể N. Nhận xét:
+ X là biến ngẫu nhiên có luật phân phối đơn giản A(p) và E(X) = p, D(X) = p(1 − p)
+ Vì tổng thể có số lượng lớn và ta không thể khảo sát hết các phần tử của tổng thể N →
ta không thể xác định chính xác p.
− Ước lượng điểm của p là ước lượng điểm của kỳ vọng của biến ngẫu nhiên đơn giản
A(p), giá trị ước lượng đó chính là tỉ lệ đối tượng A có trong mẫu với mẫu n có kích thước lớn. k
Nếu đặt f = thì ước lượng điểm của p là f. n
(n càng lớn thì sai số giữa p và f càng nhỏ (?)).
− Ước lượng khoảng của p xem như là ước lượng khoảng đối với kỳ vọng toán E(X) = p. f (1− f )  1−  f (1− f )  1 − 
+ Khoảng tin cậy của p có dạng: f −1 −1 − .  p f+ . n  2  n  2     
Ví dụ 5. Khảo sát ngẫu nhiên 200 người, có 50 người thích sản phẩm của công ty Z. 87
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Tìm khoảng tin cậy cho tỉ lệ p những người thích sản phẩm của công ty Z, với độ
tin cậy 1 - = 0,95. Lời giải
Gọi p là tỉ lệ những người thích sản phẩm của công ty Z. Từ giả thiết, ta có: 50 f =
= 0, 2, n.f = 50 > 10 và n(1 − f) = 150 > 10 200
Khoảng ước lượng cho p có dạng: f (1− f )  1−  f (1− f )  1 − −   1 −1 f − .  p  f+ . (1) n  2  n  2      1  v − ới 1 -   = 0,95 −1 →  = 1,96  . 2   
Thay các giá trị tương ứng vào vào (1), thu được: 0,19 < p < 0,31.
Ví dụ 6. Khảo sát ngẫu nhiên 100 SV, có 60 SV người không thích học môn toán xác suất & thống kê.
Tìm khoảng tin cậy cho tỉ lệ p những SV không thích học môn toán xác suất &
thống kê, với ộ đ tin cậy  = 0,90. Lời giải.
Gọi p là tỉ lệ những người không thích học môn toán xác suất & thống kê. Từ giả thiết, ta có: 60 f =
= 0,6, n.f = 60 > 10 và n(1 − f) = 40 > 10 100
Khoảng ước lượng cho p có dạng: f (1− f )  1−  f (1− f )  1 − − 1 −1 f . p f .  −   +  (1) n  2  n  2      1−  với 1 - −1  = 0,90 → →  = 1,64  2   
Thay các giá trị tương ứng vào vào (1), thu được: 0,52 < p < 0,68. 88
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ 7. Để xác định số lượng Khỉ có trên một hòn đảo. Người ta bắt ngẫu nhiên 700 con
và làm dấu trên những con Khỉ đó, sau đó thả chúng ra lại khắp đảo. Một thời gian sau
bắt ngẫu nhiên 200 con, nhận thấy có 50 con có làm dấu.
Hãy ước lượng khoảng cho tổng số Khỉ có trên hòn đảo, với độ tin cậy 1 - = 0,90. Lời giải
Gọi N là tổng số Khỉ có trên đảo và p là tỉ lệ Khỉ có làm dấu ở trên đảo, ta có: 700 p = . N Từ giả thiết: 50 f =
= 0, 2, n.f = 50 > 10 và n(1 − f) = 150 > 10 200
Khoảng ước lượng cho p có dạng: f (1 − f )  1−  f (1− f )  1−  1 − 1 f − .  p  f+ . −  (1) n  2  n  2      1−  với 1 - −1  = 0,90 → →  = 1,64 
thay các giá trị tương ứng vào vào (1), thu được: 2    0,199 < p < 0,300  700 0,199  0,300 2331  N  350. N
KL: Tổng số Khỉ có trên đảo nằm trong khoảng [2333; 3517].
Ví dụ 8. Một lô hàng có 100.000 sản phẩm.
Kiểm tra ngẫu nhiên 400 sản phẩm, có 20 sản phẩm xấu (phế phẩm).
Hãy ước lượng khoảng cho tổng số sản phẩm xấu có trong lô hàng, với độ tin cậy 1 - = 0,95. Lời giải
Gọi m là tổng số sản phẩm xấu có trong lô hàng và p là tỉ lệ sản phẩm xấu có trong m lô hàng đó, ta có: p = . 100.000 Từ giả thiết: 89
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 20 f =
= 0,05, n.f = 20 > 10 và n(1 − f) = 380 > 10 400
Khoảng ước lượng cho p có dạng: f (1− f )  1−  f (1− f )  1 − −   1 −1 f − .  p  f+ . (1) n  2  n  2      1  v − ới 1 -   = 0,95 −1 →  = 1,96 
. Thay các giá trị tương ứng vào vào (1), thu được: 2    0,0285 < p < 0,0714 m  0,0285   0,0714 2864 m  71. 100.000
KL: Tổng số sản phẩm xấu có trong lô hàng nằm trong khoảng [2850; 7140]. 90
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Chương 6. KIỂM ĐỊNH GIẢ THIẾT §1. VẤN ĐỀ CHUNG
1.1. Đặt vấn đề
Khi xét một mẫu hoặc nhiều mẫu được chọn ra từ một tổng thể N, ta có một nhận
định tạm thời, có tính chủ quan về các đặc điểm, dấu hiệu mà ta cần nghiên cứu trên tổng
thể. Nếu đó là những nhận định về các tham số, về luật phân phối của biến ngẫu nhiên X
nào đó tác động lên tổng thể hay là những nhận định về sự khác nhau hay giống nhau của
hai kì vọng của hai biến ngẫu nhiên thì ta gọi đó là những giả thiết thống k
Những giả thiết thống kê được đưa ra có thể đúng hoặc có thể sai, ta cần phải kiểm
định giả thiết đó, tức là xét xem giả thiết đưa ra có được chấp nhận hay không và chấp nhận ở mức độ nào. Đối ớ v i một giả th ế
i t thống kê được đưa ra ta có thể sử dụng nhiều phương pháp để
kiểm định giả thiết đó.
Các giả thiết thống kê thường được kí hiệu là H0, các giả thiết trái với giả thiết H0
(hay bác bỏ giả thiết H0) được gọi là đối thiết, kí hiệu H1; H2;…
Câu hỏi đặt ra là: Chúng ta chấp nhận hay bác bỏ một giả thiết bằng cách nào?
Các nhà thống kê đều thống nhất với nhau một nguyên lý sau đây:
“Nếu một biến cố có xác suất rất nhỏ thì trong một phép thử hay một vài phép thử, biến
cố đó sẽ không xảy ra”.
→ Như vậy, ta bác bỏ giả thiết H0 nếu xác suất xuất hiện (xảy ra) của một bc quan sát
được, tính trong điều kiện giả thiết H0 đúng là “nhỏ”
1.2. Miền bác bỏ − − Các sai lầm −
− Mức ý nghĩa của kiểm định giả thiết
1.2.1. Miền bác bỏ
Giả sử có giả thiết H0 ; Ta lập mẫu ngẫu nhiên của biến ngẫu nhiên X là
(X1;X2;…;Xn). Nếu qua một giá trị của mẫu ngẫu nhiên là mẫu thực nghiệm (x1;x2;…;xn)
ta bác bỏ, không thừa nhận giả thiết H0 thì (x1;x2;…;xn) gọi là điểm bác bỏ của giả thiết H0.
Tập hợp các điểm bác bỏ gọi là miền bác bỏ của giả thiết H0. 91
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Việc kiểm định giả thiết H0 thường là việc đi tìm miền bác bỏ của giả thiết H0, kí
hiệu  (hoặc W), gọi là qui tắc kiểm định  (hoặc qui tắc kiểm định W).
1.2.2. Các loại sai lầm của kiểm định giả thiết
i1/ Sai lầm loại 1: Giả thiết H0 đúng, nhưng qua kiểm định ta bác bỏ giả thiết H0 đó là một
sai lầm và gọi là sai lầm loại 1.
i2/ Sai lầm loại 2: Giả thiết H0 sai, nhưng qua kiểm định ta chấp nhận giả thiết H0 đó là
một sai lầm và gọi là sai lầm loại 2.
Hai loại sai lầm này có những mức độ tác hại khác nhau.
1.2.3. Mức ý nghĩa của kiểm định giả thiết
Kí hiệu l1 = P(mắc sai lầm loại 1
) = P(bác bỏ giả thiết H0 / giả thiết H0 đúng).
và l2 = (mắc sai lầm loại 2) = P(chấp nhận giả thiết H0 / giả thiết H0 sai).
Một qui tắc kiểm định  càng tốt nếu các l1, l2 đều cùng nhỏ, nhưng việc cùng lúc
làm cực tiểu l1, l2 là không đơn giản vì l1, l2 là ngược nhau.
Trong thực hành người ta xây dựng một qui tắc kiểm định W sao cho khi dùng qui
tắc đó thì l1 =  ( cố định và thường chọn   0,05) và l2 cực tiểu. Số  được gọi là mức
ý nghĩa của kiểm định và  là miền bác bỏ.
Chú ý: Các bước cần thiết, tr n
o g việc tiến hành một kiểm định giả thiết thống kê gồm:
(b1) Phát biểu giả thiết H0 và đối thiết H1 …
(b2) Định rõ mức ý nghĩa  (xác suất mắc sai lầm loại 1)…
(b3) Chọn test thống kê …kí hiệu T
(b4) Chọn miền bác bỏ giả thiết H0…kí hiệu 
(b5) Tính giá trị của test thống kê từ mẫu quan sát được…
(b6) KL bác bỏ giả thiết H0 hay chấp nhận H0 tùy theo giả thiết của test thống kê
có rơi vào miền bác bỏ giả thiết hay không… 92
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
§ 2. KIỂM ĐỊNH GIẢ THIẾT CHO TRUNG BÌNH
Xét X là biến ngẫu nhiên có luật phân phối chuẩn X  N(;2).
Tổng thể là tập hợp các giá trị có thể có của X.
Một mẫu có cở n là một tập gồm n giá trị x1; x2;…; xn thu được từ quan sát độc lập
về X., ( x1; x2;…; xn ) là mẫu thực nghiệm…
Ta muốn kiểm định giả thiết về . Xét các trường hợp:
2.1. Trường hợp phương sai (độ lệch chuẩn) 2 đã biết
Bài toán 1. Bài toán kiểm định hai phía .
Ta muốn kiểm định giả thiết H0:  = 0 ;
đối thiết H1:  ≠ 0 ;
với 0 là giá trị cho trước. (x− n 0 )
Test thống kê được chọn: T = 
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa  2  1 t x
được xác định như sau: − 2 (  c )= 1− ;  (x )= . e dt. 2 2 − 2 1−  1 t x − hoặc (c )= ;  (x )= . e 2 d  . 2 2 0
Bài toán 2. Bài toán kiểm định một phía (phía phải)
Ta muốn kiểm định giả thiết H0:  = 0 ;
đối thiết H1:  > 0 ; với 0 là g á i trị cho trước. 93
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g (x− n 0 )
Test thống kê được chọn: T = 
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức 2 1 t x −
ý nghĩa  được xác định như sau: (c )= 1−  ; (x )= . e 2 d  . 2 − 2 1 1 t x hoặc − 2 (c )= − ;  (x )= . e d  . 2 2 0
Bài toán 3. Bài toán kiểm định một phía (phía trái)
Ta muốn kiểm định giả thiết H0:  = t0 ;
đối thiết H1:  < 0 ;
với 0 là giá trị cho trước. ( − x n 0 )
Test thống kê được chọn: T = 
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa 2 t  1 x −
được xác định như sau: (  c )= 1− ;  (x )= . e 2 d  . 2 − 2 1 1 t x hoặc − 2 (c )= − ;  (x )= . e d  . 2 2 0
2.2. Trường hợp phương sai (độ lệch chuẩn) 2 chưa biết, mẫu n   30.
Trường hợp này ta vẫn dùng test thống kê như trên, trong đó  được thay bằng độ
lệch tiêu chuẩn có điều chỉnh s1…
Bài toán 4. Một thông báo cho rằng trung bình một người vào siêu thị tiêu hết 140 ngàn đô.
Để kiểm định công bố trên. Chọn ngẫu nhiên mẫu gồm 50 người vào mua hàng
tính được số tiền trung bình họ tiêu là 154 ngàn đô, với độ lệch tiêu chuẩn có điều chỉnh
của mẫu là 62 ngàn đô và cho mức ý nghĩa  = 0,02. Hãy kiểm định xem công bố của
nhóm nghiên cứu có đúng không? Lời giải
Phát biểu giả thiết H0:  = 140 (đơn vị tính = ngàn) 94
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
đối thiết H1:  ≠ 140
(Bài toán kiểm định hai phía, với  chưa biết, n > 30). (x− t n 154− 140 50 0 ) ( ) Khi đó Test thống kê T = = = 1,5. s 62 1 
Hằng số c được xác định: (
 c )= 1− = 0,99→ c= 2,3. 2 2 1 x t − ( nhớ rằng 2 (x) = e dt  ) 2 − 2 1 x t − 1 −
Nếu dùng bảng hàm Laplace (  x) = e 2 dt → (  ) c =  . 2 2 0
Nhận xét T= 1,59 < c = 2,33 → chưa có cơ sở để bác bỏ giả thiết H0 → Tạm thời chấp
nhận báo cáo của nhóm nguyên cứu là đúng.
Bài toán 5. Công ty “LANHLUNG” có một hệ thống máy tính có thể xử lí 1200 hóa đơn
trong một giờ. Công ty “LANHLUNG” mới nhập về một hệ thống máy tính mới. Hệ thống
này khi chạy kiểm tra (chạy thử nghiệm) trong 40 giờ cho thấy số hóa đơn được xử lý
trung bình trong 1 giờ là 1260, với độ lệch tiêu chuẩn của mẫu thực nghiệm là 215 và mức ý nghĩa  = 5%.
Hãy nhận định xem hệ thống mới có tốt (về năng suất xử lí) hơn hệ thống cũ không? Lời giải
Phát biểu giả thiết H0:  = 1200 (hệ thống mới tốt bằng hệ thống cũ)
đối thiết H1:  > 1200 (hệ thống mới tốt hơn hệ thống cũ)
(Bài toán kiểm định một phía).
Ở đây ta tin một cách tiên quyết rằng hệ thống mới không thể tồi hơn hệ thống cũ. (x− t n 1260− 1200 40 0 ) ( ) Khi đó Test thống kê T = = = 1,7. s 215 1
Hằng số c được xác định: (c) = 1−  = 0,95 → c = 1,64 95
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Nhận xét T = 1,76 > c = 1,64 → bác bỏ giả thiết H0 → Hệ thống mới tốt hơn hệ thống cũ
với mức ý nghĩa  = 5%.
2.3. Trường hợp phương sai (độ lệch chuẩn) 2 chưa biết, mẫu n < 30.
Bài toán 6. Bài toán kiểm định hai phía.
Ta muốn kiểm định giả thiết H0:  = 0 ;
đối thiết H1:  ≠ 0 ;
với 0 là giá trị cho trước. (x− t n 0 )
Test thống kê được chọn: T = s1
Miền bác bỏ giả thiết H0 có dạng  = {T>c}, với c là hằng số phụ thuộc vào mức ý 
nghĩa  được xác định như sau: c t n 1;  = −  . 2  
Bài toán 7. Bài toán kiểm định một phía (phía phải).
Ta muốn kiểm định giả thiết H0:  = 0 ;
đối thiết H1:  > 0 ;
với 0 là giá trị cho trước. (x− t n 0 )
Test thống kê được chọn: T = s1
Miền bác bỏ giả thiết H0 có dạng  = { T > c}, với c là hằng số phụ thuộc vào mức ý
nghĩa  được xác định như sau: c = t = t  ( n 1 − ; )  .
Bài toán 8. Bài toán kiểm định một phía (phía trái).
Ta muốn kiểm định giả thiết H0:  = 0 ;
đối thiết H1:  < 0 ;
với 0 là giá trị cho trước. 96
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g (t −x n 0 )
Test thống kê được chọn: T = s1
Miền bác bỏ giả thiết H0 có dạng  = { T>c}, với c là hằng số phụ thuộc vào mức ý nghĩa
 được xác định như sau: c =t = t  ( n 1 − ;) .
§3. KIỂM ĐỊNH GIẢ THIẾT CHO TỈ LỆ
3.1. Bài toán kiểm định hai phía
Kiểm định giả thiết H0: p = p0; ( p0 là một số đã cho) đối thiết H1: p ≠ p0;
Tiến hành n phép thử độc lập → có k lần xảy ra biến cố A → tần suất xảy ra biến cố A là k f = . n
(f cho ta một “hình ảnh” của A trong tổng thể N (?))
Nhận xét: n.p0  5 và n(1 − p0 )  5 ( f − p n 0 )
→ Test thống kê được chọn là T = . p 1− p 0 ( 0 )
Miền bác bỏ giả thiết H0 có dạng  = {T>c}, với c là hằng số phụ thuộc vào
mức ý nghĩa  được xác định như sau: 2  1 t x − 2 (  c )= 1− ;  (x )= . e d  2 2 − 2 1  1 t x − − hoặc 2 (c )= ;  (x )= . e d. 2 2 0
Ví dụ 1. Một đảng chính trị trong một cuộc bầu cử tổng thống tuyên bố (dự đoán) rằng
45% cử tri sẽ bỏ phiếu cho ứng cử viên A của họ.
Khảo sát 200 cử tri có 80 cử tri tuyên bố sẽ bỏ phiếu cho ông A. Với mức ý nghĩa
= 5%, hãy kiểm định xem dự đoán trên có đúng không. Lời giải
Đây là bài toán kiểm định 2 phía. Giả thiết H0: p = 0,45; 97
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
đối thiết H1: p ≠ 0,45;
Tiến hành khảo sát 200 người ( thực hiện 200 phép thử độc lập)
→ có 80 cử tri bỏ phiếu cho ông A ( có 80 lần xảy ra biến cố ) → 80 2
tần suất xảy ra biến cố là f = = = 0, 4. 200 5
với n.p0 = 200.(0,45) = 90  5 và n(1 − p0 ) = 200.(0,55) = 110  5 ( f − p n 0, 40− 0, 45 n 0) ( )
→ test thống kê được chọn là T = = = − 1, . p 1− p (0, 45).(0,55) 0 ( 0 ) 
Với mức ý nghĩa  = 0,05 → (c )= 1− = 0,975→ c= 1,9. 2
So sánh T= 1,43 < c = 1,96 → không có cơ sở bác bỏ giả thiết H0. Dự đoán của đảng trên có thể đúng. 3.2. Bài t á
o n kiểm định phía phải
Kiểm định giả thiết H0: p = p0; ( p0 là một số đã cho)
đối thiết H1: p > p0;
Tiến hành n phép thử độc lập → có k lần xảy ra biến cố A → tần suất xảy ra biến cố A là k f = . n
(f cho ta một “hình ảnh” của A trong tổng thể N (?))
Nhận xét: n.p0  5 và n(1 − p0 )  5 ( f − p n 0 )
→ Test thống kê được chọn là T = . p 1− p 0 ( 0 )
Miền bác bỏ giả thiết H0 có dạng  = { T >c}, với c là hằng số phụ thuộc vào mức ý nghĩa 2 t x −  1
được xác định như sau: 2 (  c )= 1− ;  (x )= . e d  . 2 − 2 t 1 1 x − hoặc 2 (c )= −  ;  (x )= . e d 2  . 2 0
Ví dụ 2. Một báo cáo nói rằng 18% gia đình ở thành phố T có máy tính ở nhà.
Để kiểm tra, người ta khảo sát ngẫu nhiên 80 gia đình ở thành phố T có trẻ em đang đi
học và thấy rằng có 22 gia đình có máy tính. Với mức ý nghĩa  = 0,02, hãy kiểm định 98
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
xem liệu trong các ga đình có trẻ em đang đi học, tỉ lệ gia đình có máy tính có hơn tỉ lệ chung không? Lời giải.
Đây là bài toán kiểm định 1 phía (phía phải). Giả thiết H0: p = 0,18;
đối thiết H1: p > 0,18;
Nhận xét với n.p0 = 80.(0,18) = 14,4  5 và n(1 − p0 ) = 80.(0,82) = 65,6  5 ( f − p n 22 0)
→ test thống kê được chọn là T = ; với f = = 0, 275 ; n = 80 ;p = 0, p 1− p 0 80 0 ( 0 ) ( f − p n 0 ) → T = = 2, 21 p 1− p 0 ( 0 )
Với mức ý nghĩa  = 0,05 → ( )c= 1− = 0,98→ c = 2,0
So sánh T = 2,21 > c = 2,05 → Bác bỏ giả thiết H0 → Trong các gia đình có trẻ em đi
học, tỉ lệ gia đình có máy tính cao hơn tỉ lệ chung.
3.3. Bài toán kiểm định phía trái
Kiểm định giả thiết H0: p = p0; ( p0 là một số đã cho)
đối thiết H1: p < p0;
Tiến hành n phép thử độc lập → có k lần xảy ra biến cố A → tần suất xảy ra biến cố A là k f = . n
(f cho ta một “hình ảnh” của A trong tổng thể N (?))
Nhận xét: n.p0  5 và n(1 − p0 )  5 ( p − f n 0 )
→ Test thống kê được chọn là T = . p 1− p 0 ( 0 )
Miền bác bỏ giả thiết H0 có dạng  = { T >c}, với c là hằng số phụ thuộc vào mức ý nghĩa 2 1 t  x −
được xác định như sau: 2 (  c )= 1− ;  (x )= . e d. 2 − 2 1 1 t x hoặc − 2 (c )= − ;  (x )= . e d. 2 2 0 99
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ 3. Công ty QQ sản xuất bánh kẹo tuyên bố (dự đoán) rằng 2/3 trẻ em thích bánh
kẹo của công ty. Khảo sát 100 em có 55 em thích bánh kẹo của công ty QQ . Với mức ý
nghĩa = 5%, hãy kiểm định xem tuyên bố của công ty QQ có nói quá không. Lời giải
Đây là bài toán kiểm định 1 phía (phía trái). Giả thiết H0: p = 2/3;
đối thiết H1: p < 2/3;
Nhận xét với n.p0 = 66,7  5 và n(1 − p0 ) = 33,4  5 ( p − f n 0 )
→ test thống kê được chọn là T = = 2, 49 ; p 1− p 0 ( 0 )
Với mức ý nghĩa  = 0,05 → ( )c= 1−  = 0,95→ c = 1,6
So sánh T = 2,21 > c = 2,05 → Bác bỏ giả thiết H0 → Công bố của công ty là lớn hơn sự thật.
Ví dụ 4. Tỉ lệ khỏi bệnh khi dùng thuốc A qua thống kê nhiều năm cho thấy là 16%. Với
một loại thuốc B mới khi dùng cho 600 bệnh nhân thì có 70 người không khỏi bệnh, với
mức ý nghĩa = 5%, hãy so sánh tỉ lệ không khỏi bệnhcủa hai loại thuốc A và B. Lời giải (tóm tắt)
Đây là bài toán kiểm định 2 phía. Giả thiết H0: p = 0,16; → 70
tần suất không khỏi bệnh khi dùng thuốc B là f =  0,116 600
với n.p0 = 600.(0,16) = 96  5 và n(1 − p0 ) = 600.(0,84) = 504  5 ( f − p n 0, 40− 0, 45 n 0) ( ) → test thố g n kê được chọn là T = = = − 2. p 1− p (0, 45).(0,55) 0 ( 0 ) 
Với mức ý nghĩa  = 0,05 → (c )= 1− = 0,975→ c= 1,9. 2
So sánh T= 2,9 > c = 1,96 → Bác bỏ giả thiết H0 → Tỉ lệ không khỏi bệnh khi dùng
thuốc A và thuốc B là khác nhau một cách có ý nghĩa ở mức  = 5%. 100
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Ví dụ 5. Tỉnh Q báo cáo rằng tỉ lệ học sinh giỏi của tỉnh ít nhất là 20%. Bộ tiến hành xác
minh báo cáo này. Chọn ngẫu nhiên 400 học sinh, thấy rằng có 60 học sinh giỏi. Với mức ý nghĩa  = 1%.
Bộ có cơ sở bác bỏ báo cáo của tỉnh Q hay không? Lời giải (tóm tắt)
Đây là bài toán kiểm định 1 phía (phía trái).
Gọi p là tỉ lệ học sinh giỏi của tỉnh Q. Giả thiết H0: p = 0,2;
đối thiết H1: p < 0,2;
Nhận xét với n.p0 = 400.(0,2)  5 và n(1 − p0 ) = 400.(0,8)  5
với tần suất xuất hiện học sinh giỏi trong mẫu quan sát là f = 0,15 ( p − f n 0 )
→ test thống kê được chọn là T = = 2,5 ; p 1− p 0 ( 0)
Với mức ý nghĩa  = 0,01 → c = 2,33
→ T > c → Bác bỏ giả thiết H0
→ Bộ có cơ sở để cho rằng tỉ lệ học sinh giỏi của tỉnh Q thấp hơn 20%. BÀI TẬP
Bài 1. X là biến ngẫu nhiên chỉ trọng lượng của một loại sản phẩm, X có luật phân phối
chuẩn N(;),  = 3,1.
Với mẫu n = 100, thu được x 2 = 6,5.
Với mức ý nghĩa  = 0,05, hãy kiểm định giả thiết
gt H0 :  = 26 và đối thiết đt H1:  ≠ 26. Lời giải.
Phát biểu bài toán: gt H0:  = 26. đt H1:  ≠ 26. 101
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Với mức ý nghĩa  = 0,05, Test thống kê cần chọn là: (x− t n 0 ) (26,5− 2)6 100 T = = = 1,6.  3,1
Xác định miền bác bỏ gt H0,  = {T > c}, với  = 0,05 → c = 1,96
Nhận xét T= 1,61 < c = 1,96
KL: Chưa có cơ sở bác bỏ giả thiết H0, tạm thời chấp nhận giả thiết H0.
Bài 2. X là biến ngẫu nhiên chỉ chiều cao của thiếu niên, X có luật phân phối chuẩn N(;),  = 3,4
Với mẫu n = 64, thu được x 1 = 3,5.
Với mức ý nghĩa  = 0,01, hãy kiểm định giả thiết
gt H0:  = 13 và đối thiết đt H1 :  > 13. Lời giải.
Phát biểu bài toán: gt H0:  = 13. đt H1:  > 13.
Với mức ý nghĩa  = 0,01, Test thống kê cần chọn là: (x− t n 0 ) (13,5− ) 13 64 T = = = 2,6.  1,5
Xác định miền bác bỏ gt H0,  = { T > c}, với  = 0,01 → c = 2,33
Nhận xét T = 2,66 > c = 2,33
KL: Bác bỏ giả thiết H0.
Bài 3. X là biến ngẫu nhiên chỉ tuổi thọ tr n
u g bình của một loại sản phẩm, X có luật phân
phối chuẩn N(; ),  = 14
Với mẫu n = 25, thu được x 1 = 96.
Với mức ý nghĩa  = 0,05, hãy kiểm định giả thiết
gt H0:  = 200 và đối thiết đ tH1 :  < 200. 102
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Lời giải.
Phát biểu bài toán: gt H0:  = 200. đt H1:  > 200.
Với mức ý nghĩa  = 0,05, Test thống kê cần chọn là: (t − x n 0 ) (200− 1 ) 96 25 T = = = 1,8.  11
Xác định miền bác bỏ gt H0,  = { T > c}, với  = 0,05 → c = 1,96
Nhận xét T = 1,81 < c = 1,96
KL: Chưa có cơ sở bác bỏ giả thiết H0, tạm thời chấp nhận giả thiết H0.
Bài 4. Một nhóm nghiên cứu tuyên bố rằng trung bình một gia đình chi phí hết 14 (m3) nước trong một tháng.
Một mẫu ngẫu nhiên n = 49 hộ thu được số liệu x 1
= 5 , độ lệch tiêu chuẩn điều chỉnh s1 = 5,8.
Hãy kiểm định tuyên bố trên đúng hay sai với mức ý nghĩa  = 0,02. Lời giải.
Phát biểu bài toán: gt H0:  = 14. đt H1:  ≠14. Với mức ý nghĩa  = 0,02, Test thống kê cần chọn là: (x− t n 15− 14 49 0 ) ( ) T = = = 2,187. s 3, 2 1
Xác định miền bác bỏ gt H0,  = {T> c}, với  = 0,02 → c = 2,33
Nhận xét T = 2,1857 < c = 2,33
KL: Chưa có cơ sở bác bỏ giả thiết H0, tạm thời chấp nhận giả th ế
i t H0  Tạm thời chấp
nhận tuyên bố trên là đúng. 103
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Bài 6. Hệ thống dây chuyền cũ sản xuất được 120 sản phẩm trong một giờ. Cải tiến dây
chuyền sản xuất trên, qua chạy thử nghiệm 36 giờ, thu được số liệu trung bình một giờ
sản xuất được 125 sản phẩm, độ lệch tiêu chuẩn điều chỉnh s1 = 19.
Hãy kiểm định hệ thống dây chuyền sau cải tiến có hiệu quả hơn không, với mức ý nghĩa  = 0,05. Lời giải.
Phát biểu bài toán: gt H0:  = 120. đt H1:  > 120. Với mức ý nghĩa  = 0,05, Test thống kê cần chọn là: (x− t n 125− 120 36 0 ) ( ) T = = = 1,7. s 17 1
Xác định miền bác bỏ gt H0,  = {T > c}, với  = 0,05 → c = 1,64
Nhận xét T = 1,76 > c = 1,64
KL: Bác bỏ giả thiết H0  hệ thống dây chuyền sau cải tiến không có hiệu quả hơn, với mức ý nghĩa  = 0,05.
Bài 7. Một nhà máy sản xuất một loại sản phẩm tuyên bố sản phẩm của họ có tuổi thọ trung bình là 200 giờ.
Nghi ngờ lời tuyên bố trên là đúng sự thật, người ta tiến hành kiểm tra ngẫu nhiên n = 100
sản phẩm của nhà máy đó, thu được trung bình mẫu x 1
= 95, độ lệch tiêu chuẩn điều chỉnh s1 = 31.
Hãy kiểm định gt H0:  = 200. đt H1:  < 200. Lời giải.
Phát biểu bài toán: gt H0:  = 200. đt H1:  < 200. 104
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Với mức ý nghĩa  = 0,05, Test thống kê cần chọn là: (t − x n 200− 195 100 0 ) ( ) T = = = 1,6. s 31 1
Xác định miền bác bỏ gt H0,  = {T > c}, với  = 0,05 → c = 1,64
Nhận xét T = 1,61 < c = 1,64
KL: Chưa có cơ sở bác bỏ giả th ế
i t H0  tạm thời chấp nhận giả thiết H0  chấp nhận
tuyên bố trên là đũng, với mức ý nghĩa  = 0,05.
Bài 8. Một tuyên bố của các nhà điều tra xã hội học cho rằng trung bình trong một ngày
SV bỏ ra 3 giờ để tự học.
Với một mẫu ngẫu nhiên n = 16 SV, thu được số liệu: xi 1 1,5 2 2,5 3 3,5 4 ni 3 2 4 1 8 2 5
Hãy kiểm định gt H0:  = 3. đt H1:  ≠ 3.
Cho mức ý nghĩa  = 0,05. Lời giải.
Phát biểu bài toán: gt H0:  = 3. đt H1:  ≠ 3. (x− t n 0 )
Với mức ý nghĩa  = 0,05, Test thống kê cần chọn là: T = (1) s1
Xác định miền bác bỏ gt H0,  = { T > c},    với  = 0,05 → c = t n 1 − ; = (t24;0,025)= 2,06  2   
từ bảng trên → x =2,7 , s1 = 1 105
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g thay vào (1) → T = −1,5
Nhận xét T = −1,5 < c = 2,064
KL: Chưa có cơ sở bác bỏ giả thiết H0  tạm thời chấp nhận giả thiết H0  chấp nhận
tuyên bố trên là đũng, với mức ý nghĩa  = 0,05.
Bài 9. Có một tuyên bố cho rằng thu nhập hàng tháng của một lao động phổ thông là 630 đồng.
Với mẫu ngẫu nhiên n = 25, thu được số liệu x 6
= 50 và độ lệch tiêu chuẩn có điều chỉnh s1 = 64.
Với mức ý nghĩa  = 5%, hãy kiểm định tuyên bố trên có thấp hơn sự thật không. Lời giải.
Phát biểu bài toán: gt H0:  = 630. đt H1:  > 630.
Với mức ý nghĩa  = 0,05, (x− t n 650− 630 25 0 ) ( )
Test thống kê cần chọn là: T = = = 1,562. s 64 1
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định c = t(n − 1, ) = t(24; 0,05) = 1,711.
Nhận xét: T = 1,5625 < c = 1,711 → Chưa có cơ sở bác bỏ gtH0  tạm thời chấp nhận
gtH0  chấp nhận tuyên bố trên là đúng sự thật.
Bài 10. Có một tuyên bố cho rằng một người chi phí cho việc khám chữa bệnh của bản
thân là 30 ngàn đồng trong một tháng.
Với mẫu ngẫu nhiên n = 16, thu được số liệu x =25 và độ lệch tiêu chuẩn có điều chỉnh s1 = 7,1.
Với mức ý nghĩa  = 0,01, hãy kiểm định tuyên bố trên có quá sự thật không. Lời giải.
Phát biểu bài toán: gt H0:  = 30. đt H1:  < 30.
Với mức ý nghĩa  = 0,01, 106
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g (t − x n 0 ) (30− 2)5 16
Test thống kê cần chọn là: T = = = 2,816. s 7,1 1
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định c = t(n − 1, ) = t(15; 0,01) = 2,606.
Nhận xét: T = 2,8169 < c = 2,606 → Bác bỏ gtH0 .
Bài 11. Công ty Z nhận định rằng có 40% người thích sản phẩm của công ty.
Một mẫu ngẫu nhiên n = 100 người được thăm dò ý kiến có 45 người thích sản phẩm của công ty Z.
Với mức ý nghĩa  = 5%, hãy kiểm định nhận định trên của công ty Caqueo có đúng sự thật không. Lời giải.
Phát biểu bài toán: gt H0: p = 0,40. đt H1: p  0,40
Với mức ý nghĩa , Test thống kê được chọn ( f − p n 0 ) T = (1) p (1− p ) 0 0 45 với f = = 0, 45,p = 0, 40, n = 1 0 100
xét điều kiện n.p0 = 40  5 và n.(1 − p0) = 60  5 được thỏa. thay vào (1) → T = 1,0208
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định
như sau: với  = 0,05 → c = 1,96
Nhận xét T= 1,0208 < c = 1,96 → Chưa có cơ sở bác bỏ gtH0  tạm thời chấp nhận
gtH0  chấp nhận tuyên bố trên là đúng sự thật.
Bài 12. Cho rằng tỉ lệ nảy mầm của hạt đậu tương là 90%.
Gieo ngẫu nhiên 100 hạt đậu tương, kết quả có 85 hạt nảy mầm.
Với mức ý nghĩa  = 5%, hãy kiểm định tuyên bố trên có đúng không. Lời giải.
Phát biểu bài toán: gt H0: p = 0,90. 107
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g đt H1: p  0,90
Với mức ý nghĩa , Test thống kê được chọn ( f − p n 0 ) T = (1) p (1− p ) 0 0 85 với f = = 0,85,p = 0,90,n = 1 0 100
xét điều kiện n.p0 = 90  5 và n.(1 − p0) = 10  5 được thỏa.
thay các giá trị vào (1) → T = 1,66
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định như sau: với  = 0,05 → c = 1,96
Nhận xét T= 1,66 < c = 1,96 → Chưa có cơ sở bác bỏ gtH0  tạm thời chấp nhận gtH0
 chấp nhận tuyên bố trên là đúng sự thật.
Bài 13. Có một tuyên bố rằng 25% SV thích học môn toán xác suất & thống kê.
Một mẫu ngẫu nhiên n = 100 SV được hỏi ý kiến có 20 SV thích học môn toán xác suất & thống kê.
Với mức ý nghĩa  = 0,4, hãy kiểm định tuyên bố có quá sự thật không. Lời giải.
Phát biểu bài toán: gt H0: p = 0,25. đt H1: p < 0,25
Với mức ý nghĩa , Test thống kê được chọn ( p − f n 0 ) T = (1) p (1− p ) 0 0 20 với f = = 0, 20,p = 0, 25, n = 1 0 100 thay vào (1) → T = 1,154
Xét các điều kiện n.p0 = 25  5 và n.(1 − p0) = 75  5 được thỏa.
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định như sau: với  = 0,4 → c = 0,84
Nhận xét T= 1,154 > c = 0,84 → Bác bỏ gtH0.
Bài 14. Công ty Z cho rằng 75% người dân tỉnh T là thích sản phẩm của họ. 108
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Một mẫu ngẫu nhiên n = 160 người dân tỉnh T được hỏi ý kiến có 130 người thích sản phẩm của công ty Z.
Với mức ý nghĩa  = 0,01, hãy kiểm định tuyên bố có ít hơn sự thật không. Lời giải.
Phát biểu bài toán: gt H0: p = 0,75. đt H1: p > 0,75
Với mức ý nghĩa , Test thống kê được chọn ( f − p n 0 ) T = (1) p (1− p ) 0 0 130 với f = = 0,8125,p = 0,75,n = 1 0 160
Xét các điều kiện n.p0 = 120  5 và n.(1 − p0) = 40  5 được thỏa → khi đó thay các giá trị trên vào (1) → T = 1,825795416
Xét các điều kiện n.p0 = 25  5 và n.(1 − p0) = 75  5 được thỏa.
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định
như sau: với  = 0,05 → c = 1,96
Nhận xét T= 1,82 < c = 0,84 → Tạm thời chấp nhận gtH0.
Bài 15. Cho rằng tỉ lệ phế phẩm có trong một lô hàng là 0,02.
Một mẫu ngẫu nhiên n = 400 sản phẩm, kết quả có 10 phế phẩm.
Với mức ý nghĩa  = 0,01, hãy kiểm định giả thiết: gt H0: p = 0,02. đt H1: p > 0,02 Lời giải.
Phát biểu bài toán: gt H0: p = 0,02. đt H1: p > 0,02
Với mức ý nghĩa , Test thống kê được chọn ( f − p n 0 ) T = (1) p (1− p ) 0 0 109
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 10 với f = = 0,025,p = 0,02,n = 4 0 400
Xét các điều kiện n.p0 = 8  5 và n.(1 − p0) = 392  5 được thỏa → khi đó thay các giá trị
trên vào (1) → T = 0,714285.
Miền bác bỏ gt H0,  = {T > c}, với c là hằng số được xác định như sau: với  = 0,05 → c = 1,65
Nhận xét T= 0,714285 < c = 1,65
→ Tạm thời chấp nhận gtH0. §4. BÀI TOÁN SO SÁNH
4.1. Đặt vấn đề
Trong cuộc sống hàng ngày ta thường có thói quen so sánh, so sánh giữa người này
với người kia, giữa chất lượng của sản phẩm này với chất lượng của sản phẩm kia, so
sánh giữa phương pháp này với phương pháp kia...So sánh là một nhu cầu. so sánh là
động lực để phát triển...
Trong lý thuyết xác suất − thống kê, ta sẽ xét bài toán so sánh các tham số của hai hay nhiều tổng thể (N).
4.2. So sánh hai giá trị trung bìn h
Xét X, Y là hai biến ngẫu nhiên có luật phân phối chuẩn X  N(1; 1), Y  N(2; 2).
Bài toán đặt ra là ta muốn so sánh 1, 2 dựa trên hai mẫu quan sát độc lập của X và của Y.
Giả sử X có mẫu thực nghiệm (x1; x2; ... ; xn ), Y có mẫu thực nghiệm (y1; y2; ... ; ym ).
4.2.1. Trường hợp 1, 2 đã biết.
Bài toán 1. Kiểm định hai phí . a
Phát biểu bài toán: gt H0: 1 = 2. đt H1: 1  2. 110
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g x− y
Với mức ý nghĩa , Test thống kê được chọn T = . 2 2   1 2 + n m
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý 2 1− 1 t x −
nghĩa  được xác định như sau: 2 (  c )= ,  (x)= . e d (hàm Laplace). 2 2 0
Bài toán 2. Kiểm định một phía.
Phát biểu bài toán: gt H0: 1 = 2. đt H1: 1 > 2. x− y
Với mức ý nghĩa , Test thống kê được chọn T = . 2 2   1 2 + n m
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa 2 t  1 1 x −
được xác định như sau: 2 (  c )= − ,  (x )= . e dt (hàm Laplace). 2 2 0
4.2.2. Trường hợp 1, 2 chưa biết
4.2.2.1. Trường hợp mẫu n > 30, m > 30
Trong trường hợp mẫu n > 30, m > 30 bài toán được giải quyết tương tự như trên,
ta thay 1 bởi s1 , 2 bởi s2.
Bài toán 1. Kiểm định hai phía.
Phát biểu bài toán: gt H0: 1 = 2. đt H1: 1  2. x − y
Với mức ý nghĩa , Test thống kê được chọn T = . 2 2 s s 1 2 + n m
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý 2 1− 1 t x
nghĩa  được xác định như sau: − 2 (  c )= ,  (x)= . e d (hàm Laplace). 2 2 0
Bài toán 2. Kiểm định một phía. 111
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Phát biểu bài toán: gt H0: 1 = 2. đt H1: 1 > 2. x − y
Với mức ý nghĩa , Test thống kê được chọn T = . 2 2 s s 1 2 + n m
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa 2 t  1 1 x −
được xác định như sau: 2 (  c )= − ,  (x )= . e dt (hàm Laplace). 2 2 0 Ví dụ 1
Xét hai biến ngẫu nhiên độc lập X, Y có luật phân phối chuẩn với hai mẫu thực
nghiệm có kích thước mẫu n = 40, m = 50 và 2 2 =1 x 30, y = 140, = 80,  = 10. 1 2
Hãy kiểm định hai phía.
gt H0: 1 = 2.
đt H1: 1  2.
Với mức ý nghĩa  = 1%, Lời giải x− y
Với mức ý nghĩa  = 0,01, Test thống kê được chọn T = = 5 2 2   1 2 + n m 1− Xác định c, ta có ( ) c = = 0, 4950→ c= 2,5 2
Nhận xét: T = 5 > c = 2,58 do đó ta bác bỏ giả thiếtH0 .
4.2.2.2. Trường hợp mẫu nhỏ n < 30 hoặc m < 30
Giả sử X có mẫu thực nghiệm (x1; x2; ... ; xn ), có
x , s1 và Y có mẫu thực nghiệm
(y1; y2; ... ; ym ), có y , s2 .
Trước hết, ta ước lượng phương sai chung: n ( x − )2 m x + y  − y i ( j )2 2 2 = = ( n− 1) s+ ( − 1 m ) 2 i 1 j 1 1 2 s = = n + m−2 n+ − 2 m 112
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g x − y x− y
Test thống kê cần chọn là T = = . 2 2 s s 1 1 + .s + n m n m
Bài toán 1. Kiểm định hai phía
Phát biểu bài toán: gt H0: 1 = 2. đt H1: 1  2. x − y x− y
Với mức ý nghĩa , Test thống kê được chọn T = = . 2 2 s s 1 1 + .s + n m n m
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức
ý nghĩa  được xác định như sau: c (t = n +m 2
− ;) (phân phối Student).
Bài toán 2. Kiểm định một phía.
Phát biểu bài toán: gt H0: 1 = 2. đt H1: 1 > 2. x − y x− y
Với mức ý nghĩa , Test thống kê được chọn T = = . 2 2 s s 1 1 + .s + n m n m
Miền bác bỏ giả thiết H0 có dạng  = {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa
 được xác định như sau: c t=( n +m 2
− ; ) (phân phối Student).
4.3. So sánh hai tỉ lệ Bài toán
Xét hai tổng thể N1, N2 và đặc tính A mà mỗi phần tử (đối tượng) trong hai tổng
thể N1, N2 có thể có hay không.
Bài toán đặt ra là so sánh tỉ lệ đối t ợng ư
có đặc tính A trong hai tổng thể N1, N2 .
Gọi p1, p2 tương ứng là tỉ lệ đối tượng có đặc tính A trong tổng thể N1, N2 .
Chú rằng các tham số p1, p2 là c
ó thật (ta có tham vọng biết?).
Ta muốn so sánh p1, p2 dựa trên hai mẫu quan sát độc lập của X và của Y.
Giả sử X có mẫu thực nghiệm (x1; x2; ... ; xn ), Y có mẫu thực nghiệm (y1; y2; ... ; ym ) 113
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g k k 1 2 f = , f = . 1 2 n m
+ Trước hết ta nhập chung hai mẫu lại và có ước lượng cho giá trị chung p là tần suất k + k
chung f xác định như sau: 1 2 f = . m+ n
Bài toán 1. Kiểm định hai phía.
Phát biểu bài toán: gt H0: p1 = p2. đt H1: p1  p2. f − f
Với mức ý nghĩa , Test thống kê được chọn 1 2 T = f ( f ) 1 1 1  − + m n  
Với điều kiện (m + n)f  10, (m + n)(1 − f)  10 ta có miền bác bỏ giả thiết H0 có dạng 
= {T > c}, với c là hằng số phụ thuộc vào mức ý nghĩa  được xác định như sau: 2 1  1 t x − − 2 (  c )= ,  (x )= . e d (hàm Laplace). 2 2 0
Bài toán 2. Kiểm định phía phải .
Phát biểu bài toán: gt H0: p1 = p2. đt H1: p1 > p2.
Bài toán 3. Kiểm định phía trái.
Phát biểu bài toán: gt H0: p1 = p2. đt H1: p1 < p2.
Được giải quyết tương tự. Ví dụ 1
Có hai phương pháp nuôi gà lấy trứng.
Theo phương pháp A nuôi m = 100 con có 80 con gà đẻ trứng, theo phương pháp
B nuôi n = 125 con có 90 con gà đẻ trứng.
Hãy so sánh hiệu quả của hai phương pháp với  = 5%. Ví dụ 2
Để so sánh tỉ lệ thành phẩm của một loại sản phẩm do hai xí nghiệp A, B sản xuất. 114
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g
Tiến hành khảo sát ngẫu nhiên m = 100 sản phẩm do xí nghiệp A sản xuất, có 85
sản phẩm tốt (thành phẩm), khảo sát ngẫu nhiên n = 200 sản phẩm do xí nghiệp B sản
xuất, có 170 sản phẩm tốt.
Hãy so sánh tỉ lệ thành phẩm của hai xí nghiệp với  = 1%. ***** *** *
Tài liệu tham khảo:
[1] Lý thuyết Xác suất và thống kê; tác giả: Phạm Văn Kiều; NXB Khoa học và kỹ thuật Hà Nội 1998.
[2] Giáo trình Xác suất thống kê; tác giả: Tống Đình Quỳ; NXB ĐH Quốc gia Hà Nội 2003.
[3] Thống kê và ứng dụng; tác giả: Đặng Hùng Thắng; NXB GD 1999.
[4] Giáo trình Xác suất thống kê; tác giả: Đặng Công Hanh; tài liệu lưu hành nội bộ.
[5] Bài giảng Xác suất thống kê; Giảng viên Lê Xuân Hòa; ĐH Kiến trúc Đà Nẵng. 115
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 2 1 x u Bản
g I: Bảng giá trị hàm Laplace − 2 (  x )= . e du  2 0 116
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Bản g I :I Bản
g giá trị hàm mật độ của phân phối chuẩn tắc N(0; 1) 117
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g 118
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên
Bài giảng Xác suất Thống kê – Đại học Kiến trúc Đà Nẵn g Bản g III: Bản g p â
h n phối Student t(n; ) 119
Giảng viên: ThS. Vũ Hứa Hạnh Nguyên