12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TS. Nguyễn Kim Quang ĐIỆN TỪ VEC TƠ Cộng vectơ (Vector Sum) 𝐂 = 𝐀 + 𝐁 Ôn Tính chất Vectơ TRƯỜNG ĐIỆN TỪ
1. Những khái niệm mở đầu 2. Định luật Coulomb 3. Điện trường TRƯỜNG ĐIỆN TỪ ỆN 4. Định luật Gauss 5. Thế năng điện Tính chất: Hệ tọa độ Descartes: 6. Điện thế A + B = B + A
A = Ax 𝑖 + Ay 𝑗 + Az 𝑘
7. Liên hệ giữa điện trường và điện thế A + B + C = A + B + C B = Bx 𝑖 + By𝑗 + Bz 𝑘 8. Mặt đẳng thế C = A 𝑖 + Ay + By 𝑗 + A 𝑐A = A𝑐 x + Bx z + Bz 𝑘 9. Lưỡng cực điện
𝑏 𝑐A = 𝑏𝑐A = 𝑐 𝑏A = 𝑏𝑐A Tóm tắt công thức 𝑐 A + B = 𝑐A + 𝑐B 𝑏 + 𝑐A = 𝑏A + 𝑐A 2 3 ĐIỆN TỪ VEC TƠ TS. Nguyễn Kim Quang ĐIỆN TỪ VEC TƠ TS. Nguyễn Kim Quang
Tích vô hướng của hai vectơ - Scalar (dot) product
Tích vectơ (hữu hướng) của hai vectơ - Vector (cross) product + Độ lớn: C = ABsinϕ
𝐀 ∙ 𝐁 = 𝐀. 𝐁. 𝐜𝐨𝐬𝛟 = AxBx + AyBy + AzBz
𝐀 × 𝐁 = 𝐂 + Phương: C ⊥ A𝑣àC ⊥ B
+ Chiều: qui tắc bàn tay phải TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ A ∥ B ⟹ C = 0 A ⊥ B ⟹ A ∙ B = 0 A × B = −B × A A ∙ B = B ∙ A Tính chất:
cA × B = A × 𝑐B = 𝑐 A × B Tính chất:
𝑐A ∙ B = A ∙ 𝑐B = 𝑐 A ∙ B C × A + B = C × A + C × B
C ∙ A + B = C ∙ A + C ∙ B
𝑖 ∙ 𝑖 =1 ; 𝑖 ∙ 𝑗 = 0 𝑖 𝑗 𝑘 𝐀 × 𝐁 = Ax Ay Az Bx By Bz
𝐀 × 𝐁 = AyBz − AzBy 𝑖 + AZBX − AXBZ 𝑗 + AxBy − AyBx 𝑘 4 5 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
1. Những khái niệm mở đầu - Vật tích điện
Hiện tượng tĩnh điện đã được người Hy Lạp phát hiện từ nhiều thế kỷ trước CN. TRƯỜNG ĐIỆN TỪ
Sau khi cọ xát 2 vật, hỗ phách TRƯỜNG ĐIỆN T
(amber) ay nhựa ( lasti ) với da thú, thủy tinh
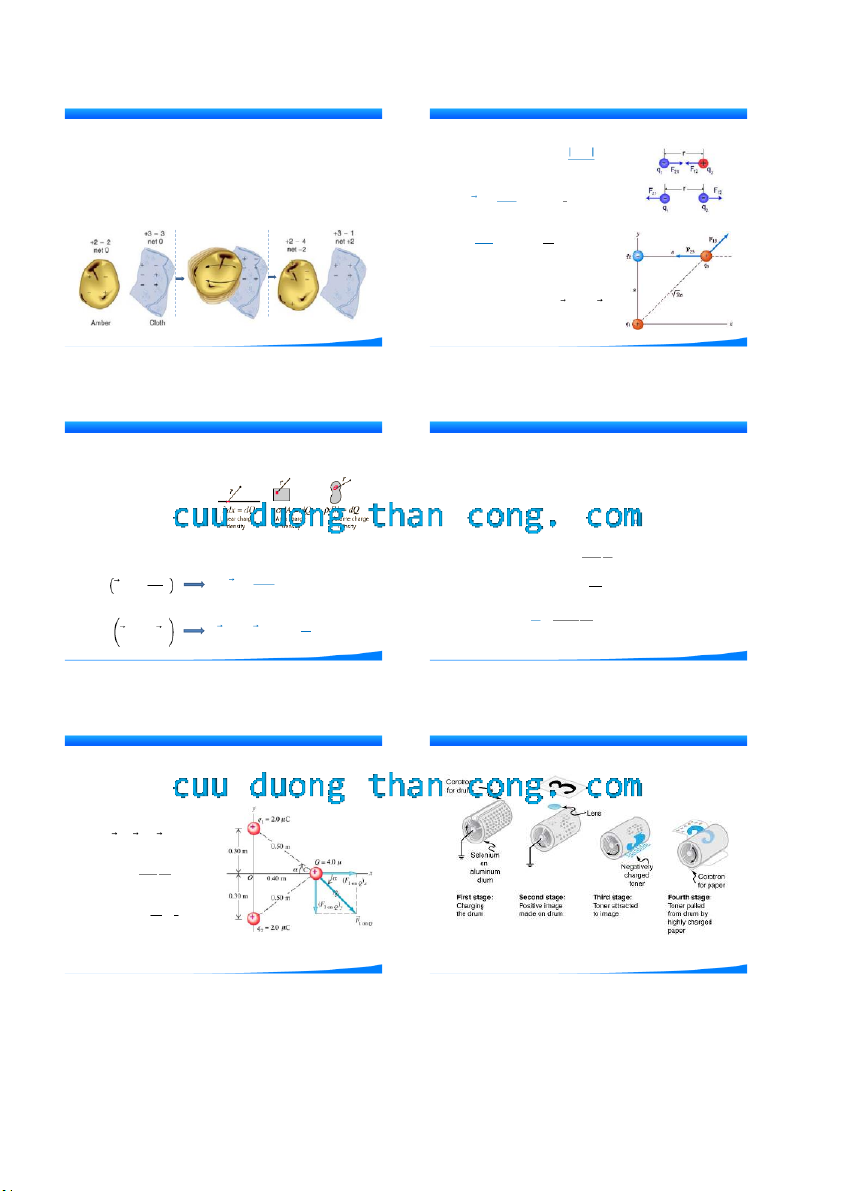
(glass) với lụa, ... Chúng trở nên nhiễm điện hay tích điện.
Hai vật tích điện cùng loại đẩy nhau và khác loại hút nhau. TRƯỜNG ĐIỆN TỪ ĐI
Tương tác giữa 2 thanh plastic Tương tác giữa 2 thanh thủy tinh
Hai vật tích điện trái dấu
Hỗ phách (Amber) – Một loại nhựa cây hóa thạch 6 7 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
1. Những khái niệm mở đầu - Vật tích điện
1. Những khái niệm mở đầu – Sét (Lightning)
Lightning - Do ma sát trong khí quyển, các đám mây có thể tích điện. Mặt đất bên dưới
đám mây cảm ứng điện tích trái chiều tạo ra điện trường mạnh giữa chúng. Điện thế có
Tóc tích điện sau khi ma sát với máng trượt plastic
thể đạt đến hàng trăm triệu Volt. Cường độ sét có thể lên đến hàng chục ngàn Ampere. 8 9 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
1. Những khái niệm mở đầu - Điện tích (Electric charge)
1. Những khái niệm mở đầu -
Vật dẫn và vật cách điện
Điện tích có cấu tạo gián đo T ạnR , ƯỜ bằn N g G mộ tĐ sIỆ ố N TỪ TRƯỜ
nguyên lần điện tích nguyên tố e.
Chất dẫn điện (Conductor) cho
Thí nghiệm giọt dầu Millikan (1909) đã chứng
điện tích di chuyển tự do trong vật. tỏ   q =ne
TD: Hầu hết kim loại dẫn điện tốt, TRƯỜNG ĐIỆN TỪ TRƯỜN
các dung dịch muối, axit, ba zờ ...
- Điện tích dương: giống điện t ch xuất hiện trên thủy tinh.
Chất cách điện (Insulator): điện
- Điện tích âm: giống điện tích xuất hiện trên
tích không thể di chuyển tự do hỗ phách, nhựa.
trong vật mà xuất hiện ở đâu thì Điện tích nguyên tố định xứ ở đó.
(elementary charge): điện tích nhỏ nhất được biết trong
tự nhiên, độ lớn bằng điện tích của electron (e, âm) hay proton (p, dương).
TD: Hầu hết phi kim, thủy tinh,
nhựa, cao su, nước nguyên chất ...
+ Điện tích của e : e  −1.6 x 10-19 C + Khối lượng: m -31 e  9,1 x 10 kg ;
Chất bán dẫn (Semiconductor): Proton: m -27 -27
có tính chất trung gian giữa chất p  1,672 x 10
kg ; Neutron: mn  1,674 x 10 kg
dẫn điện và chất cách điện.
Đơn vị điện tích (SI): Coulomb (C = A.s) TD: Silic, Germani ... (Chất cách điện) 10 11 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
1. Những khái niệm mở đầu - Vật dẫn và vật cách điện
Ứng dụng tương tác tĩnh điện - Sơn tĩnh điện TRƯỜNG ĐIỆN T Tích điện bởi ma sát TRƯỜNG ĐIỆN T (Fr ction)
Tích điện bởi cảm ứng (induction) TRƯỜNG ĐIỆN TỪ
Tích điện bởi tiếp xúc, dẫn điện (Contact, Conduction) (ma sát)
Sơn tĩnh điện – Electrostatic painting 12 13 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
1. Những khái niệm mở đầu - Nguyên lý bảo toàn điện tích
2. Định luật Coulomb (1784) - Định luật
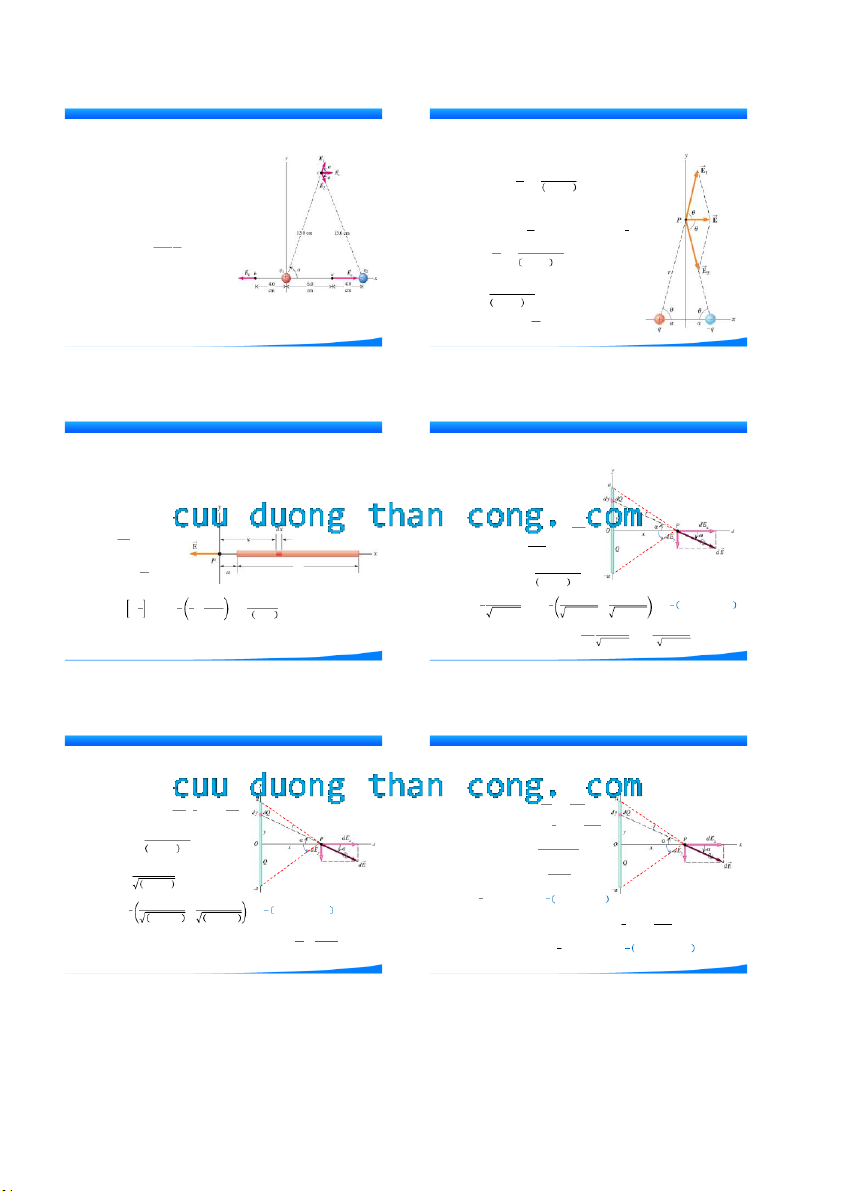
Tổng đại số điện tích trong TR mộƯỜ t hệ N c G ô lĐ ậ I p Ệ l N à hTằỪ ng số (bảo toàn). TRƯỜ q1 N q2G ĐIỆN TỪ Độ lớn lực Coulomb: F = 𝑘 Điện r2
tích không tự sinh ra hoặc mất đi mà truyền từ vật này sang vật khác.
Mọi quá trình biến đổi tự nhiên, phản ứng hóa học, phản ứng hạt nhân... đều Vectơ lực Coulomb:
bảo toàn điện tích. TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ q1q2 𝑞 F = 𝑘 𝑖 = 𝑐𝑜𝑛𝑠𝑡 r2 𝑟 , 𝑟= 𝑟𝑟 𝑖
Đơn vị SI: q (C) ; r (m) ; F (N) 1
𝑘 =4πε ≃ 9.109 (𝑁𝑚2 0 𝐶2) k: hằng số Coulomb
 : hằng số điện môi trong chân không 0 n
Nguyên lý chồng chất lực: F0 = F0i i=1 14 15 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
2. Định luật Coulomb - Phân bố điện tích liên tục
2. Định luật Coulomb - Thí dụ - Phân bố dài: dq= -27 .dl
1) Hạt  là hạt nhân của nguyên tử Heli, có khối lượng m= 6,64 x 10 kg và TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
điện tích q=2|e|=3,2 x 10-19C. So sánh lực tương tác tĩnh điện với lực hấp dẫn
: mật độ điện tích dài (C/m) giữa hai hạt .
- Phân bố mặt: dq= .dS TRƯỜN TRƯỜNG ĐIỆN TỪ
: mật độ điện tích mặt (C/m2)
Lực tĩnh điện giữa 2 hạt  là lực đẩy nhau, xuyên tâm (cùng phương)
Lực hấp dẫn giữa 2 hạt là lực hút nhau, xuyên tâ .
- Phân bố khối: dq= .dV Độ lớn của lực:
: mật độ điện tích khối (C/m3) 1 q2
Yếu tố (phần tử) điện tích dq tác dụng lên điện tích q
- tĩnh điện giữa 2 hạt: Fe = 0: 4πε0 r2 q q m2 F 0q 0dq 𝑞 = 𝑘 - hấp dẫn giữa 2 hạt: F Với G= 6,67 x 10-11 2 N.m2/kg 0 r2 𝑟 dF = 𝑘 r2 𝑟 g = G r2
Lực tĩnh điện do toàn bộ vật tích điện tác dụng lên điện tích q0: F n e 1 q2 dq So sánh độ lớn: = F Fg 4πε0Gm2 = 3,1 × 1035 0 = F0i F = dF = 𝑘q0 r2r i=1 Vật Vật 16 17 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
2. Định luật Coulomb - Thí dụ
2) Hai điện tích điểm dương q1= q2= q= 2 C tương tác với điện tích thứ ba TRƯỜNG ĐIỆN TỪ
Q=4 C (hình vẽ). Xác định độ lớn và chiều của lực tĩnh điện tác dụng lên Q.
Lực tĩnh điện tác dụng lên Q theo
phương nối liền 2 điện tích,T R đẩ ƯỜ y NG
nhau vì điện tích cùng dấu. FQ = F1Q + F2Q
- Độ lớn lực tĩnh điện tác dụng lên Q: qQ F1Q= F2Q= 14πε 2 = 0,29 N 0 r1Q
- Góc α của lực F1Q và F2Q hợp với trục x: 0,4 cos α = 0,5 = 45
- Hợp lực tác dụng lên Q theo trục x:
Ứng dụng tương tác tĩnh điện của máy photocopy (Xerography). F = F = 2.F cos = 0,46 N x 1Q  18 19 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
Ứng dụng tĩnh điện trong máy in laser.
Ứng dụng tĩnh điện của máy in phun (ink-jet printer). 20 21 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
(a) Sơ đồ thiết bị lọc khí (ngưng tụ) tĩnh điện bằng phương pháp phóng điện hoa
Ứng dụng tĩnh điện cho thiết bị lọc bụi khói thoát ra từ nhà máy. Khí thoát đi
(Corona discharge), rất hiệu quả với nhà máy đốt than sinh nhiều bụi khói. (b) và
qua các lớp lưới tích điện trái dấu.
(c) so sánh ô nhiễm không khí khi thiết bị lọc khí hoạt động và không hoạt động. 22 23 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
3. Điện trường (Electric field)
3. Điện trường - Nguyên lý chồng chất điện trường
Điện tích tạo ra xung quanh nó một điện
Vectơ cường độ điện trường tại mỗi điểm do hệ điện tích tạo ra bằng tổng TRƯỜNG ĐIỆ
trường. Một điện tích đặt tr n iện TRƯỜNG ĐIỆN T
vectơ cường độ điện trường do mỗi điện tích tạ ra tại điểm đó.
trường sẽ chịu một lực tĩnh điện.
- Phân bố điện tích r rạc:
- Phân bố điện tích liên tục: Điện trường 𝑁
là môi trường trung gian qua TRƯỜNG ĐIỆN dq
đó lực điện truyền từ điện TRƯỜNG ĐIỆN TỪ tích này đến E = E𝑖 E = dE = k r2 r điện tích khác. 𝑖=1 Q Q
Vectơ cường độ điện trường tại một điểm: F E = (N/C hay V/m) q0
Điện trường của một điện tích điểm Q: 1 E = Q 4πε0 r2 1 Q Biểu diễn vectơ: E =4πε0 r2 𝑟 24 25 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
3. Điện trường - Thí dụ
3. Điện trường - Thí dụ
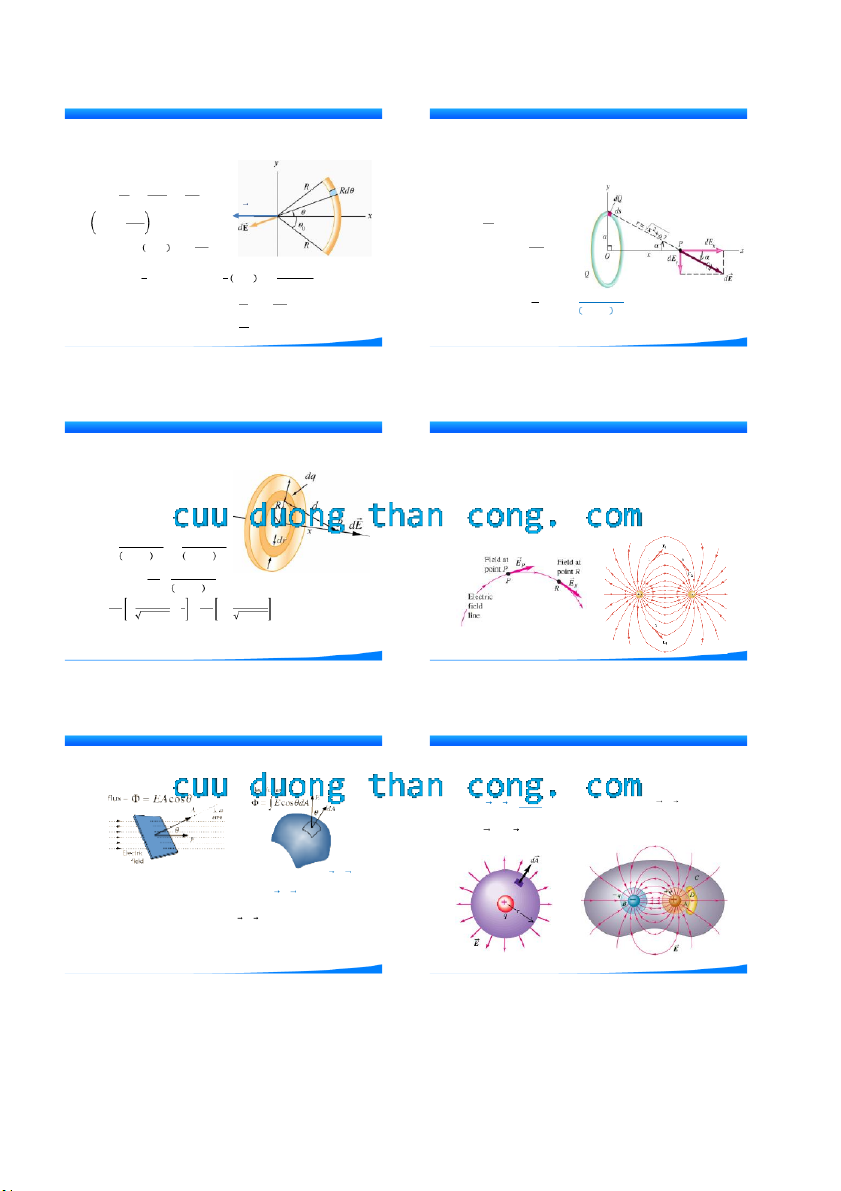
1) Điện trường của một lưỡng cực điện
2) Điện trường của một lưỡng cực điện tại 1 điểm trên trục đối xứng TRƯỜNG ĐIỆN TỪ
Hai điện tích điểm bằng nhau và trái TRƯỜNG ĐIỆN TỪ
Độ lớn điện trường do –q hay +q gây ra tại P:
dấu q =q =12 nC, đặt cách nhau một 1 2 q
khoảng d=10 cm (hình vẽ). Xác định E1 = E2 = k r2 = k q a2 + y2
điện trường sinh ra tại T cáR c ƯỜ điể N m G a, Đ b,IỆ c TRƯỜNG ĐIỆN TỪ bởi lưỡng cực điện.
Do tính đối xứng, vectơ điện trường tổng hợp E // trục
x và hướng về phía điện tích –q có độ lớn:
Điện trường theo phương xuyên tâm và
hướng ra xa điện tích dương. E = 2E1 cos θ = 2k q Q r2 cos θ Với cos θ = a r Áp dụng: E = 1 4πε0 r2 ⇒ E = 2k aq r3 = k 2aq a2 + y2 3 2
và nguyên lý chồng chất điện trường
Đặt p=q.2a : mômen lưỡng cực điện a) E = E = E + E = 9,8x104 N/C a ax 1 2 p ⇒ E = k a2 +y2 3 b) E 2 4 b= E = -E + E =6,2x10 N/C bx 1 2 Khi a << y, E ≃ kp c) E = E = E + E = 2E cos c cx 1cx 2cx 1c  , cos α =5/13 y3 26 27 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
3. Điện trường - Thí dụ
3. Điện trường - Thí dụ
3) Điện trường của một dây thẳng tích điện đều
3) Điện trường của một dây thẳng tích điện đều TRƯỜNG ĐIỆN TỪ
Điện tích dương Q phân bố đều trên dây thẳng dài L mật độ TRƯỜNG ĐIỆN TỪ . Xác định điện
Điện tích dương Q phân bố đều trên dây
trường tại P trên trục x cách đầu thanh một khoảng a.
thẳng dài. Xác định điện trường tại P cách dây khoảng x.
Phần tử điện tích: dQ = T λ R dx ƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆ
Phần tử điện tích: dQ = λdy Sinh ra điện trường dE:
Sinh ra điện trường dE: dE = 𝑘 λdy dE = 𝑘 λdx r2  x2 dE 1 () x = dE λxdy . cosα = 𝑘 r3 a+L 𝐿 𝑦2 ⇒ E= 𝑘λ dx dy x2 Ex = dEx = kλx a x2 + y2 3 2 Q 𝑦1 a+L y y2 y2 y1 ⇒ E = 𝑘λ − 1 1 Ex = k λ = k λ − = k λ α2 − α1 x = 𝑘 Q x x x2 + 𝑦 x sin sin a L a − 1 a + L = 𝑘 Q aa + L x2 + y2 x2 + 𝑦 y 22 12 1 λ2a 1 1 Với y = E = Ex = k 1 a và y =+a , 2 x = kQ x2 + a2 x x2 + a2 28 29 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
3. Điện trường - Thí dụ
3. Điện trường - Thí dụ
3) Điện trường của một dây thẳng tích điện đều
3) Điện trường của một dây thẳng tích điện đều TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆ T
Tính thành phần điện trường E : Cách tính khác: dE
Điện trường dE: dE = 𝑘 dQ y = −dE. sin λdy α = −k r2 ∙ y r2 = 𝑘 𝜆𝑑𝑦 r2 TRƯỜ r = −kλ ydy NG ĐIr3ỆN T TR x ƯỜNG ĐIỆN y ,cosα = 2 dEx = dE. cosα r ⇒ r = x cosα ⇒ E ydy y =−kλ λdy.cos3 α x2 + y2 3 2  E dE. cosα= 𝑘 1 y x = 1  () x2 1 () y L L 2 ⇒ E 1 y = −kλ
Với y = x.tg ⇒ dy = x dα x2 + y2 cos2 α y=y α 1 2 x x λ Ex = 𝑘 λ cosα.dα = k λ α2 − α1 ⇒ E x x sin sin y = −k λx − = k x2 + 𝑦 α1 22 x2 + 𝑦12 x cos α1 − cos α2
Tương tự tính E : dEy = −dE. sin α , sin α = y 2λ y r ⇒ r = y sinα α Dây rất dài (α 2 1  /2, α /2): 1   E = 0 ; E = E y x ≈ 𝑘 x = λ 2πε0x
⇒ Ey = −𝑘 λx sin𝛼.dα = kλx cos𝛼2 − cos𝛼1 α1 30 31 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
3. Điện trường - Thí dụ
3. Điện trường - Thí dụ
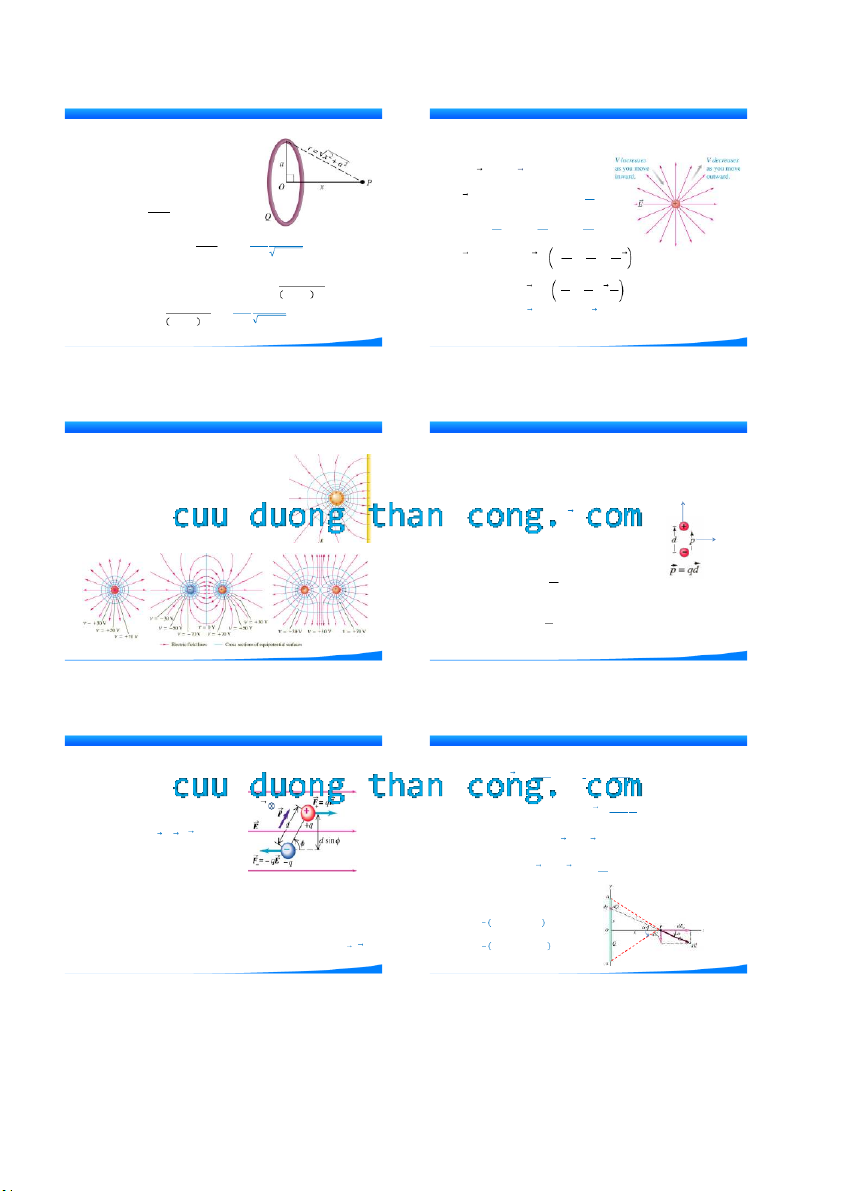
4) Điện trường của một cung tròn tích điện đều
5) Điện trường của một vòng tròn tích điện đều TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
Phần tử điện tích dQ=Rd sinh ra
Một vật dẫn hình tròn bán kính a mang điện tích Q phân bố đều (hình vẽ). Xác điện trường dE:
định điện trường ở điểm P nằm trên trục của vòng tròn, cách tâm một đoạn x. dQ TRƯỜNG ĐIỆ dE = 𝑘
Phần tử điện tích dQ sinh r T a R điƯỜ ện NG R2 = 𝑘 λRdθ R2 = 𝑘 λdθ R 𝐄 trường dE: Q với λ = dQ 2Rθ dE = 𝑘 0 r2 λdθ
dEx = dE.cosθ + π = −𝑘 R cosθ dEx = dE xdQ .cosα = 𝑘 r3 λ θ0 E = E
Điện trường tại P có phương trên
x = −𝑘 R cosθ.dθ = −2𝑘 λR sinθ0 = − Q 4π𝜀 sinθ0 0R2θ0 trục đối xứng x: −θ0 - Khi  E = E dE dQ = 𝑘 Qx
0 = /2 (Nửa vòng tròn): E = −𝑘 2λ R = −𝑘2Q πR2 x = x = 𝑘xr3 Q Q x2 + a2 3 2
- Khi 0  0 (Điện tích điểm): E = −𝑘QR2 32 33 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
3. Điện trường - Thí dụ
3. Điện trường - Đường sức điện trường (Electric field lines)
6) Điện trường của một đĩa tròn tích điện đều
Là đường (cong) tưởng tượng được vẽ ra trong không gian sao cho tiếp tuyến TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
Xét phần tử điện tích là hình vành
ở mỗi điểm trùng với vectơ điện trường tại điểm đó. Chiều đường sức theo khăn vi cấp, bán kính r: chiều vectơ E. dq=(2r.dr)= 2rdr TRƯỜNG ĐI
Đường sức điện trường là nThRƯỜ ững đ NG ườn Đ g cIỆ o N ng T h Ừ
ở (màu đỏ), xuất phát từ điện
tích dương và kết thúc ở điện tích âm, hoặc ra vô cùng.
Áp dụng kết quả điện trường s nh
bởi vòng tròn tích điện đều:
Mật độ đường sức điện trường tỉ lệ với độ lớn của điện trường tại mỗi điểm. dE dr x = 𝑘 dq.x = 𝑘 2π𝜎r .x x2 + r2 3 2 x2 + r2 3 2 R R E rdr x = dEx = σx 2ε 0 x2 + r2 3 2 r=0 0 E 1 x = σx 2ε − 1 + 1 − x 0 x2 + R2 x = σ 2ε0 x2 + R2
Khi x<(gần mặt vật dẫn): E  σ/2ε0 34 35 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
4. Định luật Gauss (1777-185 ) 5
4. Định luật Gauss - Phát biểu định luật
Thông lượng điện trường (Điện thông, Electric flux)
Thông lượng điện trường toàn phần qua một mặt kín bằng tổng điện tích chứa TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN T bên t ong chia cho 0 Q Φ trong E = E ∙ dS = Chứa điện môi: Φ ε D = D ∙ dS =Qtrong ĐIỆN 0 TRƯỜNG ĐIỆN TỪ
D = 𝜀0𝜀E (C/m2): Vectơ cảm ứng điện (Eletrical induction )
Thông lượng E qua mặt vi cấp dA:
dΦE = E⊥dA = Ecosθ.dA = E ∙ dA Thông lượng E qua mặt A: (N.m2/C) ΦE = dΦE = E ∙ dA A A
Thông lượng E qua mặt kín S: ΦE = E ∙ dS 𝑆𝑁 Thông lượng E qua N mặt: ΦE = Φ𝑖 𝑖=1 36 37 6 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
4. Định luật Gauss - Phát biểu định luật
4. Định luật Gauss Ứng dụng tính điện trường một số vật đối xứng TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
1) Trên bề mặt vật dẫn
2) Quả cầu tích điện đều (tích điện mặt) NG ĐIỆ TRƯỜNG ĐIỆN TỪ
3) Quả cầu tích điện đều (tích điện khối)
4) Dây thẳng dài tích điện đều
5) Mặt phẳng vô hạn tích điện đều
6) Giữa 2 mặt phẳng dẫn song song tích điện trái dấu
Tìm thông lượng điện trường qua 4 mặt kín S , S , S , S ? 1 2 3 4 38 39 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
4. Định luật Gauss - Ứng dụng tính điện trường
4. Định luật Gauss - Ứng dụng tính điện trường
1) Điện trường trên bề mặt vật dẫn
2) Quả cầu dẫn điện tích điện đều (Tích điện mặt) TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
Chọn mặt Gauss S kín là mặt trụ đủ nhỏ, diện tích đáy A.
Chọn mặt Gauss S kín là mặt cầu đồng tâm, bán kính r.
Điện trường bên trong vật T d R ẫnƯỜ bằ N ng G 0 ĐI TRƯ
Vectơ E có độ lớn không đổi và vuông
Vectơ E gần mặt ngoài vật dẫn có độ
góc với mặt S tạ mọi đi m trên S.
lớn không đổi và vuông góc với mặt
đáy A tại mọi điểm trên A. ΦE = E ∙ dS =E dS = E.4πr2 S ΦE = E ∙ dS =E dS = E. A - Bên ngoài vật dẫn: S đáy A q ĐL Gauss: ΦE = q Φ trong ε0 E = E. A = ε = σA 0 ε0 q ⟹ E = 1 ⇒ E =σ 4πε r2 ε 0 0
- Bên trong vật dẫn: E= 0 (q = 0) trong 40 41 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
4. Định luật Gauss - Ứng dụng tính điện trường
4. Định luật Gauss - Ứng dụng tính điện trường
3) Quả cầu cách điện tích điện đều
4) Dây thẳng dài tích điện đều TRƯỜNG Đ (Tích điện khối) TRƯỜNG ĐIỆ T
Chọn mặt Gauss S kín là mặt cầu đồng
Chọn mặt Gauss S kín là mặt trụ dài l, tâm, bán kính r
tiết diện tròn bán kính r. TRƯỜNG ĐIỆ TRƯỜNG ĐI
Vectơ E có độ lớn không đổi và vuông
Vectơ E có độ lớn không đổi và vuông
góc với mặt S tại mọi điểm trên S.
góc với mặt xung quanh tại mọi điểm. ΦE = E ∙ dS = E. 4πr2 Φ E ∙ dS =E dS = E.2πrl S E =
Điện tích phân bố trong mặt Gauss S: S 𝑋𝑞 Q 4 tr= ρVtr= Q 4 ĐL Gauss: Φ 3 πr3 = Q r3 R3 E = λl ε0 3 πR3 Qr λ - Bên trong quả cầu: Φ 2 ⇒ E = 1 E = E. 4πr = Qr3 ε 2πε r 0R3 ⇒ E = 1 4πε0 R3 ,𝑟 < 𝑅 0 Q - Bên ngoài quả cầu: Φ 2 E = E. 4πr = 𝑄 ε ⇒ E = 1 0 4πε0 r2 ,𝑟 > 𝑅 42 43 7 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
4. Định luật Gauss - Ứng dụng tính điện trường
4. Định luật Gauss - Ứng dụng tính điện trường
5) Mặt phẳng vô hạn tích điện đều
6) Hai mặt phẳng song song tích điện trái dấu TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ
Chọn mặt S (hoặc S ) là mặt trụ kín, 1 4
Chọn mặt S kín là mặt trụ diện tích đáy A. diện tích đáy A. TRƯỜNG ĐIỆ
Vectơ E có độ lớn không đổi và vuông góc TRƯỜNG
Vectơ E có độ lớn không đổi và với 2 mặt đáy.
vuông góc với mặt đáy trong vùng
giữa 2 mặt phẳng tích diện. ΦE = E ∙ dS =E dA = 2E.A S 2 đáy ΦE = E ∙ dS= E dA = E. A 𝑆1 đáy ĐL Gauss: ΦE = σA ε Φ 0 E = σA ε0 ⇒ E = σ
Điện trường giữa 2 mặt phẳng tích điện trái dấu: 2ε0 ⇒ 𝐄 =𝝈𝛆𝟎
Điện trường bên ngoài 2 mặt phẳng tích điện trái dấu: E = 0 44 45 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
5. Thế năng điện (Electric potential energy)
5. Thế năng điện (Electric potential energy)
Công của lực tĩnh điện làm dịch chuyển điện tích q từ điểm a đến b: TRƯỜNG ĐIỆN TỪ 0
Thế năng điện của điện tíc T h R đi ƯỜ ểm qNtrong trường hợp: 0 G ĐIỆN TỪ Công vi cấp:
dW = F ∙ dl = F ∙ d s =F.ds.cos F,d s =F.dr qq - Hai điện tích: U = 𝑘 0 b b r q N W 1 qi a→b= F ∙ ds = 𝑘 qq0 TRƯỜNG Đ r2 dr - Hệ điện tích điểm: UTR = ƯỜ 𝑘q0 NG ĐI + q2 ỆN T + q3 Ừ r +∙ ∙ = 𝑘q0 1 r2 r3 ri a a i=1 Wa→b= 𝑘 qq0r − 𝑘qq0 a rb
=> Công của lực tĩnh điện không
phụ thuộc quỹ đạo mà chỉ phụ
thuộc vị trí đầu và cuối. W = F ∙ ds = 0
=> Công của lực tĩnh điện làm dịch
chuyển q giữa 2 điểm bằng độ giảm 0
thế năng điện giữa 2 điểm đó: dq
- Phân bố điện tích liên tục: U = 𝑘q0 W r ab = –U= Ua – Ub Hệ 46 47 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
6. Điện thế (Electric Potential)
6. Điện thế - Thí dụ
Điện thế tại điểm đặt q là thế năng điện ứng với một đơn vị điện tích dương tại 0
1) Dây dẫn thẳng rất dài tích điện đều, mật độ . đó: TRƯỜNG ĐIỆN TỪ U TRƯỜNG ĐIỆN T
Xác định đi n thế tại đ ểm cách dây một khoảng V = (V = J/C) q0 q
Điện thế tạo bởi điện tích đi T ể R m ƯỜ q: N V G = 1 ĐIỆN TỪ 4πε TRƯỜNG ĐIỆN TỪ 0 r
Ta có điện trường tại điểm cách dây một khoảng r: q λ Do hệ điện tích điểm: V = V i i = 1 4πε r E = 2πε0r i 0 i i dq Do phân bố liên tục: V = dV = 1 N N N 4πε dr 0 r Vật V ln rN ật
VM − VN = E ∙ d r = Erdr = λ 2πε r = λ 2πε r N M M 0M 0 M
Hiệu điện thế giữa 2 điểm: VM − VN = WMN q = E ∙ d s λ 0 V = M Chọn VN= 0 ở rN= r0 : 2πε lnr0r ∞ 0 λ
Điện thế tại 1 điểm trong điện trường: E ∙ d s khi chọn V V = 0 Nếu r M = V = − lnr  0= 1 : 2πε0 M 48 49 8 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ
6. Điện thế - Thí dụ
7. Liên hệ giữa điện trường và điện thế
2) Vòng dây tròn bán kính a tích điện đều Q. Xác
Công vi cấp của lực tĩnh điện: TRƯỜNG ĐIỆN TỪ
định điện thế tại điểm P trên trục cách tâm vòng TRƯỜNG ĐIỆN TỪ tròn một khoảng x.
dW =F∙ ds = q0E ∙ ds = −dU = −q0dV
Xét phần tử dQ sinh ra điệ T n R th ƯỜ ế d N V t G ại Đ P:IỆN TỪ TRƯỜNG ĐIỆN
⇒ E ∙ d s =Esds = −dV⇒ Es = −dV dV = dQ ds 4πε0r ⇒ Ex = − 𝜕V Q 𝜕x; Ey = − 𝜕V 𝜕y;Ez = − 𝜕V𝜕z Điện thế tại P: V = dV = 1 4πε dQ = 1 0r 4πε0 x2 + a2 Q Q
⇒ E = Exi + Ejy + Ezk = −𝜕V 𝜕xi − 𝜕V𝜕yj −𝜕V𝜕z k Cách khác:
Biết điện trường sinh bởi vòng dây tròn: E = Ex = 𝑘 Qx 𝜕 x2 + a2 3 2
Biểu diễn vectơ E: E =− i j 𝜕 ∞ ∞ 𝜕x + 𝜕y + k𝜕𝜕z V V = x Q Exdx =kQ dx = 1 E = −gradV = −𝛻V x2 + a2 3 2 4πε x2 + a2 x x 0 50 51 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang
8. Mặt đẳng thế (Equipotential Surfaces)
9. Lưỡng cực điện (electric dipole)
Mặt đẳng thế là mặt trong T k R hô ƯỜ ng gN iaG n, Đ tr IỆ ên Nđ T ó Ừ điện
Là cặp điện tích bằng nhau v T à R tr ƯỜ ái dấN u G ( + Đ q IỆ và N – T q) Ừ
đặt cách nhau một khoảng d.
thế tại mọi điểm đều bằng nhau (đường màu xanh).
Tích số điện tích q và khoảng cách lưỡng cực d được gọi là moment lưỡng
 Công lực tĩnh điện dịch chuyển điện tích trên một cực: p= qd (C.m) mặt đẳng thế bằng 0. TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ x
Vectơ moment lưỡng cực điện: p = q. d
Vectơ điện trường vuông góc với mặ đ ng thế ại mọi
điểm và theo chiều giảm (mạnh nhất) của điện thế.
Điện trường do lưỡng cực là tổng vectơ điện trường do z 2 điện tích sinh ra:
- Tại điểm trên trục lưỡng cực x: Khi x>>d, 𝐸𝑥 = 2𝑘𝑝𝑥3
- Tại điểm trên trục z vuông góc với trục của lưỡng cực: Khi z>>d, 𝐸𝑧 = 𝑘𝑝𝑧3 52 53 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang TÓM TẮT CÔNG THỨC
9. Lưỡng cực điện(electric dipole) - Đặt trong điện trường
Tổng lực tĩnh điện tác dụng l
1) Lực Coulomb: F = 𝑘 q1q2 ,𝑘 = 1 ≃ 9.109 T ê R n lƯỜ ưỡn N g G c Đ ực IbỆằN n
g T0Ừnhưng momen ngẫu lực r2 𝑟 , 𝑟= 𝑟 TRƯỜN 𝑟 G ĐIỆN T 4𝜋𝜀0
(torque) τ nói chung khác 0. τ Q
τ= F.d.sin= qE.dsin =pE.
2) Điện trường của một điện tích điểm Q: E = 1 (N/C=V/m) T s R in ƯỜ  NG ĐIỆN TRƯỜNG ĐIỆN TỪ 4𝜋𝜀0r2 𝑟 𝑁 Biểu diễn vectơ: τ = p × E
3) Điện trường của hệ điện tích: E = E𝑖 𝑖=1 dq
Hệ điện tích liên tục: E = dE =k
Ngẫu lực  làm lưỡng cực quay một góc d sẽ sinh công dW tương ứng độ giảm r2 r Q Q
thế năng điện của lưỡng cực: dW = d=  pE.si  n .d =dU ϕ2
4) Điện trường của dòng điện thẳng: Công:
W = −pEsinϕ.dϕ = pEcosϕ2 − pEcosϕ1 = U1 − U2 ϕ E α α 1 x = k λx sin 2 − sin 1 W = pE(cos cos 1 1 2) ()
Thế năng điện của lưỡng cực p trong điện trường E: U = −pEcosϕ = −p ∙ E Ey = k λx cosα1 − cosα2 ( U=0 khi =/2 ) 54 55 9 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12/05/2015 TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang ĐIỆN TỪ TÓM TẮT CÔNG THỨC TÓM TẮT CÔNG THỨC
5) Điện trường của một cung tròn tích điện đều: 1 q
10) Điện trường của quả cầu tích điện đều: E = (r>R) TRƯỜNG ĐIỆN TỪ λ TRƯỜNG ĐIỆN T 4 Ừ πε0 r2 E = E 𝐄 x = −2𝑘 R sinθ0 = − Q 4π𝜀 sinθ0 0R2θ0 1 λ
11) Điện trường của dây thẳng rất dài tích điện đều: E = TRƯỜNG ĐIỆN TỪ TRƯỜNG ĐIỆN TỪ 2πε0 r
6) Điện trường của một vòng tròn tích điện đều: σ
12) Điện trường của mặt phẳng vô hạn tích điện đều: E = 2ε0 E = Ex = 𝑘 Qx 1 q x2 + a2 3 2
13) Điện thế tạo bởi điện tích điểm q: V = 4πε (V) 0 r
7) Thông lượng E qua mặt A: Φ qi E = E ∙ dA
14) Điện thế tạo bởi hệ điện tích: V= Vi = 1 r A 4πε i 0 i i Q 8) Định luật Gauss: Φ trong 2 dq E = E ∙ dS = (N.m /C) ε
Hệ điện tích liên tục: V = dV = 1 0 4πε0 r Hệ Hệ
9) Điện trường trên bề mặt vật dẫn: E =σε λ 0
15) Điện thế tạo bởi dây dẫn thẳng rất dài: V = 2πε lnr0 0 r 56 57 ĐIỆN TỪ TRƯỜNG TĨNH ĐIỆN TS. Nguyễn Kim Quang TÓM TẮT CÔNG THỨC
16) Điện thế tạo bởi vòng dây dẫn tròn tích điện đều: TRƯỜNG ĐIỆN TỪ 1 Q V =4πε0 x2 +a2 TRƯỜNG ĐIỆN TỪ N
17) Hiệu điện thế giữa 2 điểm: VM − VN = WMN q = E ∙ d s 0 ∞ M
18) Điện thế tại 1 điểm trong điện trường: VM = E ∙ d s khi chọn V = 0  M
19) Liên hệ giữa E và điện thế :
Ex = − 𝜕V𝜕x;Ey = −𝜕V𝜕y;Ez = −𝜕V𝜕z 𝜕 E =− i 𝜕
𝜕x +j 𝜕y + k 𝜕𝜕z V = −gradV 58 10 CuuDuongThanCong.com
https://fb.com/tailieudientucntt