





















































Preview text:
Bài giảng Thống kê Xã hội học Khoa Toán Tin
Trường Đại học Sư phạm Hà Nội 2020 Mục lục
1 MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 6
1.1 Định nghĩa xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.1.1
Phép thử ngẫu nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.1.2
Không gian mẫu và Biến cố sơ cấp . . . . . . . . . . . . . . . . . . . 7 1.1.3
Biến cố . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.4
Phép toán trên các biến cố . . . . . . . . . . . . . . . . . . . . . . . . 9 1.1.5
Mối quan hệ giữa các biến cố . . . . . . . . . . . . . . . . . . . . . . 9 1.1.6
Định nghĩa xác suất cổ điển . . . . . . . . . . . . . . . . . . . . . . . 10 1.1.7
Tính chất của xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.1.8
Định nghĩa xác suất theo thống kê . . . . . . . . . . . . . . . . . . . 11
1.2 Sự độc lập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.2.1
Hai biến cố độc lập . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.2.2
Dãy biến cố độc lập . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.2.3
Dãy phép thử Bernoulli . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.2.4
Công thức xác suất nhị thức . . . . . . . . . . . . . . . . . . . . . . . 13
1.3 Biến ngẫu nhiên rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.2
Phân phối của biến ngẫu nhiên . . . . . . . . . . . . . . . . . . . . . 14 1.3.3
Các số đặc trưng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.3.4
Ý nghĩa của kỳ vọng và phương sai . . . . . . . . . . . . . . . . . . . 15 1.3.5
Phân phối nhị thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.3.6
Tính chất của kỳ vọng và phương sai . . . . . . . . . . . . . . . . . . 15
1.4 Biến ngẫu nhiên liên tục và Phân phối chuẩn . . . . . . . . . . . . . . . . . 16 1.4.1
Biến ngẫu nhiên liên tục . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.4.2
Hàm mật độ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.4.3
Các số đặc trưng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.4.4
Phân phối chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 1.4.5
Tính chất của phân phối chuẩn . . . . . . . . . . . . . . . . . . . . . 18 1.4.6
Xấp xỉ phân phối nhị thức bằng phân phối chuẩn . . . . . . . . . . 19 2 MẪU NGẪU NHIÊN 21
2.1 Giới thiệu về Thống kê . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.1.1 Mẫu và quần thể
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.1.2
Quy trình nghiên cứu thống kê . . . . . . . . . . . . . . . . . . . . . 22 1 MỤC LỤC 2 2.1.3
Các bài toán thống kê sẽ học: . . . . . . . . . . . . . . . . . . . . . . 22
2.2 Thu thập dữ liệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 2.2.1
Xác định dữ liệu cần thu thập . . . . . . . . . . . . . . . . . . . . . . 23 2.2.2
Dữ liệu sơ cấp và thứ cấp . . . . . . . . . . . . . . . . . . . . . . . . . 23 2.2.3
Lấy mẫu hoàn lại và không hoàn lại . . . . . . . . . . . . . . . . . . . 24 2.2.4
Quy tắc lấy mẫu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 2.2.5
Phương pháp lấy mẫu giản đơn . . . . . . . . . . . . . . . . . . . . . 24 2.2.6
Các phương pháp lấy mẫu khác . . . . . . . . . . . . . . . . . . . . . 25
2.3 Trình bày dữ liệu bằng bảng và biểu đồ . . . . . . . . . . . . . . . . . . . . . 25 2.3.1
Biểu đồ thân-lá (stem-and-leaf diagram) . . . . . . . . . . . . . . . 25 2.3.2
Tần số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 2.3.3 Bảng tần số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.4 Biểu đồ tần số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 2.4.1
Biểu đồ tần suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.5 Số liệu và các số đặc trưng . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 2.5.1
Biến số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 2.5.2
Phân loại biến số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 2.5.3
Các số đo giá trị trung tâm . . . . . . . . . . . . . . . . . . . . . . . . 30 2.5.4
Các số đo độ phân tán . . . . . . . . . . . . . . . . . . . . . . . . . . 31 2.5.5
Thống kê . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3 KHOẢNG ƯỚC LƯỢNG 33
3.1 Khoảng ước lượng cho trung bình . . . . . . . . . . . . . . . . . . . . . . . . 33 3.1.1
Đặt vấn đề . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 3.1.2
Khoảng ước lượng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 3.1.3
KƯL cho trung bình µ khi σ2 đã biết
. . . . . . . . . . . . . . . . . . 34 3.1.4
KƯL cho trung bình µ của mẫu cỡ lớn . . . . . . . . . . . . . . . . . 37 3.1.5
KƯL cho mẫu nhỏ có phân phối chuẩn với σ2 chưa biết . . . . . . . 38 3.1.6
Vấn đề xác định cỡ mẫu . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.2 Khoảng ước lượng cho tỷ lệ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 3.2.1
Đặt vấn đề . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 3.2.2
Công thức khoảng ước lượng cho tỷ lệ . . . . . . . . . . . . . . . . . 40 3.2.3
Vấn đề xác định cỡ mẫu . . . . . . . . . . . . . . . . . . . . . . . . . 41
4 KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 43
4.1 Tình huống thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
4.2 Bài toán kiểm định giả thuyết tổng quát . . . . . . . . . . . . . . . . . . . . 44 4.2.1
Miền tiêu chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 4.2.2
Các loại sai lầm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
4.3 Bài toán kiểm định giả thuyết cho giá trị trung bình một mẫu . . . . . . . . 46 4.3.1
Bài toán 1: So sánh trung bình của mẫu có phân phối chuẩn với
phương sai σ2 đã biết . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 4.3.2
Bài toán 2: So sánh giá trị trung bình của mẫu cỡ lớn với phương
sai chưa biết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 MỤC LỤC 3 4.3.3
Bài toán 3: So sánh giá trị trung bình của mẫu có phân phối chuẩn
với phương sai chưa biết . . . . . . . . . . . . . . . . . . . . . . . . . 49
4.4 Bài toán kiểm định giả thuyết về tỉ lệ . . . . . . . . . . . . . . . . . . . . . . 52 4.4.1
Tình huống thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 4.4.2
Bài toán kiểm định giả thuyết cho tỉ lệ . . . . . . . . . . . . . . . . . 53 4.4.3
Tiêu chuẩn kiểm định . . . . . . . . . . . . . . . . . . . . . . . . . . 53
4.5 Bài toán so sánh hai giá trị trung bình
. . . . . . . . . . . . . . . . . . . . . 55 4.5.1
Tình huống thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 4.5.2
So sánh hai giá trị trung bình . . . . . . . . . . . . . . . . . . . . . . 56 4.5.3
Bài toán 1: So sánh giá trị trung bình của hai mẫu có phân phối
chuẩn với phương sai đã biết . . . . . . . . . . . . . . . . . . . . . . 56 4.5.4
Bài toán 2: So sánh hai giá trị trung bình của hai mẫu có phân phối
chuẩn với phương sai σX = σY = σ2 chưa biết . . . . . . . . . . . . . 57
4.6 Bài toán so sánh hai tỉ lệ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 4.6.1
Tình huống thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 4.6.2
So sánh hai tỉ lệ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 Giới thiệu học phần
Thống kê Xã hội học
Một số vấn đề thực tế
• Làm thế nào để biết cân nặng trung bình của trẻ sơ sinh ở một địa phương?
– Một nhà điều tra thử tính cân nặng trung bình của 50 trẻ sơ sinh ở một địa
phương thì được kết quả là 3,1kg. Có thể nói gì về cân nặng của trẻ sơ sinh toàn địa phương đó?
– Một nhà quản lý cho rằng cân nặng trung bình của tất cả các trẻ sơ sinh ở địa
phương đó là 3,3kg. Tuyên bố của nhà quản lý có đúng không?
• Làm thế nào để so sánh hiệu quả của hai phác đồ điều trị cho một bệnh nào đó?
– Có hai phác đồ điều trị cho cùng một bệnh. Trong 200 bệnh nhân điều trị theo
phác đồ 1 có 150 khỏi bệnh. Trong 50 người điều trị theo phác đồ 2 thì có 40
người khỏi bệnh. Hỏi phác đồ 2 có thực sự tốt hơn phác đồ 1 hay không?
• Con của bạn sẽ cao bao nhiêu cm?
– Chiều cao của con bị ảnh hưởng bởi chiều cao của bố hay chiều cao của mẹ?
– Chiều cao của bố/mẹ và con liên quan như thế nào đến nhau?
– Biết chiều cao của bố/mẹ thì có thể dự đoán được chiều cao của con không? 4 MỤC LỤC 5 Thống kê là gì?
Thống kê là khoa học về việc thu thập, xử lý, biểu diễn, phân tích mẫu số liệu thu thập
được từ một quần thể để rút ra được các kết luận có độ tin cậy cho toàn bộ quần thể đó.
Cơ sở khoa học của Thống kê là Lý thuyết xác suất. Nội dung học phần
1. Chương 1: Một số kiến thức xác suất cơ sở
2. Chương 2: Mẫu ngẫu nhiên
3. Chương 3: Khoảng ước lượng
4. Chương 4: Kiểm định giả thuyết thống kê 5. Chương 5: Hồi quy
Mục tiêu của học phần
1. Hiểu được ý nghĩa và tính được xác suất, kì vọng, phương sai trong một số trường hợp đơn giản.
2. Vận dụng phân phối nhị thức và phân phối chuẩn giải quyết một số bài toán thực tế.
3. Hiểu được phương pháp lấy mẫu ngẫu nhiên.
4. Biết phân loại số liệu và tính toán các đặc trưng của mẫu số liệu. Trình bày số liệu
dưới dạng biểu đồ cột, biểu đồ quạt.
5. Hiểu được ý nghĩa và tính khoảng ước lượng cho trung bình và tỉ lệ.
6. Hiểu được ý nghĩa bài toán kiểm định giả thuyết. Vận dụng để so sánh tỉ lệ và trung bình.
7. Hiểu được ý nghĩa và giải quyết được bài toán hồi quy tuyến tính đơn. Chương 1
MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ
Nội dung của chương:
1. Định nghĩa xác suất cổ điển và định nghĩa xác suất theo thống kê. 2. Sự độc lập
3. Biến ngẫu nhiên rời rạc.
4. Biến ngẫu nhiên liên tục
5. Phân phối nhị thức và Phân phối chuẩn
6. Các số đặc trưng của biến ngẫu nhiên.
Mục tiêu của chương
1. Hiểu được các khái niệm cơ bản của xác suất: phép thử ngẫu nhiên, không gian
mẫu, biến cố, mối quan hệ giữa các biến cố.
2. Hiểu được ý nghĩa của khái niệm độc lập.
3. Hiểu được ý nghĩa và tính được xác suất, kì vọng, phương sai trong một số trường hợp đơn giản.
4. Vận dụng phân phối nhị thức và phân phối chuẩn giải quyết một số bài toán thực tế. 6
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 7 1.1
Định nghĩa xác suất 1.1.1
Phép thử ngẫu nhiên
• Phép thử: việc thực hiện một tổ hợp các hành động nào đó.
• Phép thử ngẫu nhiên: phép thử mà ta không biết trước được kết quả của nó 1.1.2
Không gian mẫu và Biến cố sơ cấp
• Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử. Ta thường
kí hiệu không gian mẫu bởi Ω.
• Biến cố sơ cấp là một phần tử của không gian mẫu.
Ví dụ 1.1.1. Trong hộp có 1 bi xanh, 1 bi đỏ và 1 bi vàng. Hãy xác định không gian mẫu
và số biến cố sơ cấp của các phép thử sau:
a) Lấy ra ngẫu nhiên 1 bi từ hộp.
b) Lấy ra ngẫu nhiên đồng thời 2 bi từ hộp.
c) Lấy ra lần lượt 2 bi từ hộp.
d) Lấy ra ngẫu nhiên 1 bi từ hộp, xem màu, trả lại hộp rồi lại lấy ra ngẫu nhiên 1 bi nữa.
Lời giải. a) Lấy ra ngẫu nhiên 1 bi từ hộp n o Ω = X, Đ, V .
b) Lấy ra ngẫu nhiên đồng thời 2 bi từ hộp n o Ω = {X, Đ}, {X, V }, {Đ, V } .
c) Lấy ra lần lượt 2 bi từ hộp n o Ω = XĐ, XV, ĐX, ĐV, V X, V Đ n = (X, Đ), (X, V ), (Đ, X), o (Đ, V ), (V, X), (V, Đ)
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 8
d) Lấy ra ngẫu nhiên 1 bi từ hộp, xem màu, trả lại hộp rồi lại lấy ra ngẫu nhiên 1 bi nữa n o Ω =
XX, XĐ, XV, ĐX, ĐV, ĐĐ, V X, V Đ, V V n =
(X, X), (X, Đ), (X, V ), (Đ, X), o
(Đ, Đ), (Đ, V ), (V, X), (V, Đ), (V, V ) . 1.1.3 Biến cố
• Biến cố là một sự kiện liên quan đến phép thử. Một biến cố có thể xảy ra hoặc
không xảy ra sau khi phép thử được thực hiện. Mỗi biến cố là một tập con của không gian mẫu.
• Biến cố chắc chắn là biến cố luôn xảy ra.
• Biến cố rỗng (trống) là biến cố luôn không xảy ra.
Ví dụ 1.1.2. Xét phép thử gieo hai con xúc xắc cân đối. Hãy xác định không gian mẫu và
biểu diễn các biến cố sau dưới dạng tập hợp.
• A là b/c xuất hiện hai mặt 1 chấm.
• B là b/c xuất hiện hai mặt 4 chấm.
• C là b/c xuất hiện hai mặt cùng chấm.
• D là b/c tổng số chấm bằng 8.
• E là b/c tích số chấm xuất hiện là số lẻ. Lời giải.
Ω = {(1, 1), (1, 2), . . . , (6, 6)} = {(i, j) : 1 ≤ i, j ≤ 6}
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 9 • A = {(1, 1)}. • B = {(4, 4)}.
• C là b/c xuất hiện hai mặt cùng chấm
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}.
• D là b/c tổng số chấm bằng 8
D = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}.
• E là b/c tích số chấm xuất hiện là số lẻ
E = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}. 1.1.4
Phép toán trên các biến cố
• A ∪ B: Hợp của hai biến cố A và B.
• A ∩ B = AB: Giao của hai biến cố A và B.
• A \ B: Hiệu của hai biến cố A cho B.
Ví dụ 1.1.3. Trong phép thử gieo hai con xúc xắc, hãy xác định biến cố hợp, giao và hiệu
của các biến cố C và D. 1.1.5
Mối quan hệ giữa các biến cố
• Biến cố A được gọi là thuận lợi cho biến cố B nếu khi A xảy ra thì B cũng xảy ra. Kí hiệu là A ⊂ B.
• Biến cố A được gọi là xung khắc với biến cố B nếu khi A xảy ra thì B không xảy
ra và ngược lại. Hai biến cố xung khắc không thể đồng thời cùng xảy ra. Kí hiệu là A ∩ B = ∅.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 10
Ví dụ 1.1.4. Trong các biến cố A, B, C, D, E ở phép thử gieo hai con xúc xắc
• hãy chỉ ra biến cố nào thuận lợi cho biến cố nào;
• hãy chỉ ra các cặp biến cố xung khắc.
• Biến cố A và B là đối nhau nếu luôn chỉ có đúng một trong hai biến cố xảy ra. (A ∩ B = ∅ ⇔ A = Ω \ B. A ∪ B = Ω
Kí hiệu biến cố đối của biến cố A là ¯ A.
• Hai biến cố A và B được gọi là đồng khả năng nếu chúng có khả năng xuất hiện
như nhau trong mỗi phép thử.
Ví dụ 1.1.5. Trong phép thử gieo hai con xúc xắc, hãy xác định biến cố đối của các biến cố C, D, E. 1.1.6
Định nghĩa xác suất cổ điển
Giả sử một phép thử có n kết quả khác nhau và có cùng khả năng xảy ra, trong đó có
m kết quả thuận lợi cho biến cố A. Khi đó xác suất để biến cố A xảy ra là
Số kết quả thuận lợi cho A m P(A) = = . Tổng số kết quả n
Ví dụ 1.1.6. Giả sử hai con xúc xắc là cân đối và đồng chất.
1. Tính xác suất của các biến cố A, B, C, D, E.
2. Tính xác suất của các biến cố C ∩ D, C ∪ D, C \ D, D \ C. 1.1.7
Tính chất của xác suất • Với mọi biến cố A: 0 ≤ P(A) ≤ 1.
• Với mọi biến cố xung khắc A và B: P(A ∪ B) = P(A) + P(B). • Với mọi biến cố A: P( ¯ A) = 1 − P(A).
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 11 1.1.8
Định nghĩa xác suất theo thống kê
Thực hiện lặp đi lặp lại phép thử n lần và gọi m là số lần biến cố A xuất hiện trong n lần thử. m • Tỉ số
được gọi là xác suất thực nghiệm của biến cố A trong n lần thử. n m
• Nếu xác suất thực nghiệm
hội tụ đến một giá trị p0 nào đó thì ta nói p0 là xác suất n
của biến cố A theo nghĩa thống kê. 1.2 Sự độc lập
Tung một đồng xu hai lần. Nếu biết được kết quả lần gieo thứ nhất thì có đoán được kết
quả lần gieo thứ hai hay không? 1.2.1
Hai biến cố độc lập
Hai biến cố A và B được gọi là độc lập nếu việc A có xảy ra hay không cũng không
ảnh hưởng tới khả năng xảy ra của B và ngược lại. Theo xác suất thì P(A ∩ B) = P(A)P(B).
Ví dụ 1.2.1. Tung một đồng xu hai lần. Gọi A và B lần lượt là biến cố lần tung thứ nhất
và thứ hai xuất hiện mặt sấp thì A và B là hai biến cố độc lập.
Mệnh đề 1.2.2. Nếu A và B độc lập thì các cặp biến cố sau cũng độc lập: • ¯ A và B; • A và ¯ B; • ¯ A và ¯ B.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 12 1.2.2
Dãy biến cố độc lập
Dãy biến cố A1, A2, . . . , An được gọi là độc lập nếu việc một biến cố Ai nào đó trong
dãy có xảy ra hay không cũng không ảnh hưởng tới khả năng xảy ra của các biến cố còn
lại và ngược lại. Theo xác suất thì P(Ai ∩ A ∩ . . . ∩ A ) = ) ) . . . ), 1 i2 ik P(Ai1 P(Ai2 P(Aik
với mọi 2 ≤ k ≤ n, mọi 1 ≤ i1 < i2 < . . . < ik ≤ n.
Ví dụ 1.2.3. Gieo hú hoạ một con xúc xắc n lần, gọi Ak là biến cố lần gieo thứ k được mặt
6 chấm. Khi đó A1, A2, . . . , An là dãy các biến cố độc lập. 1.2.3
Dãy phép thử Bernoulli
Một dãy phép thử được gọi là dãy phép thử Bernoulli nếu
• Kết quả của mỗi phép thử hoặc là thành công, hoặc là thất bại.
• Xác suất thành công của mỗi lần thử đều bằng nhau.
• Kết quả của từng lần thử là dãy biến cố độc lập. Ví dụ:
• Gieo 3 hạt giống và quan sát sự nảy mầm của mỗi hạt.
• Lần lượt chọn ngẫu nhiên hồ sơ sức khoẻ của 10 trẻ 4 tuổi và kiểm tra xem trẻ có bị suy dinh dưỡng hay không?
Ví dụ 1.2.4. Gieo 3 hạt giống. Xác suất nảy mầm của mỗi hạt là 0,8. Tính xác suất để
1. Cả 3 hạt đều nảy mầm.
2. Cả 3 hạt đều không nảy mầm.
3. Có đúng 2 hạt nảy mầm.
Lời giải. Gọi Ak là biến cố hạt thứ k này mầm, k = 1, 2, 3.
1. Xác suất cả 3 hạt đều nảy mầm là
P(A1A2A3) = P(A1)P(A2)P(A3) = 0, 83.
2. Xác suất cả 3 hạt đều không nảy mầm là ¯ ¯ P( ¯ A1A2A3) = P( ¯ A1)P( ¯ A2)P( ¯ A3) = 0, 23.
3. Xác suất có đúng 2 hạt nảy mầm là ¯ ¯ P( ¯
A1A2A3) + P(A1A2A3) + P(A1A2A3) = 3 × 0, 82 × 0, 2.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 13 1.2.4
Công thức xác suất nhị thức
Gọi p là xác suất thành công trong mỗi lần thử.
Xác suất để có đúng k lần thành công trong n lần thử độc lập là Ckpk(1 − p)n−k, 0 ≤ k ≤ n. n Luyện tập
1.2.1. Tỉ lệ trẻ 4 tuổi bị suy dinh dưỡng trong một cộng đồng là 5%. Lần lượt chọn ngẫu
nhiên hồ sơ sức khoẻ của 10 trẻ 4 tuổi. Tính xác suất của các biến cố
1. Cả 10 trẻ đều không bị suy dinh dưỡng.
2. Có đúng 2 trẻ bị suy dinh dưỡng.
3. Có ít nhất 2 trẻ bị suy dinh dưỡng.
1.2.2. Trong trò chơi "Bầu, cua, cá, cọp, gà, tôm" nhà cái sẽ gieo ba con xúc xắc. Mỗi con
xúc xắc sáu mặt được dán bởi sáu hình "Bầu, cua, cá, cọp, gà, tôm". Người chơi sẽ chọn
một hình để đặt cược (chẳng hạn hình cá).
1. Tính xác suất để có 3 mặt cá xuất hiện.
2. Tính xác suất để không có mặt cá nào.
3. Tính xác suất để có ít nhất 1 mặt cá. 1.3
Biến ngẫu nhiên rời rạc 1.3.1 Định nghĩa
Biến ngẫu nhiên là một quan sát nhận giá trị bằng số kết quả của phép thử. Ví dụ 1.3.1.
1. Tung hai đồng xu, số mặt sấp xuất hiện là một biến ngẫu nhiên.
2. Gieo hai con xúc xắc, tổng số chấm xuất hiện là một biến ngẫu nhiên.
3. Gieo hai con xúc xắc, tích số chấm xuất hiện là một biến ngẫu nhiên.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 14
4. Một người đi thi cho đến khi đỗ thì số lần thi của người này cũng là biến ngẫu nhiên.
Ví dụ 1.3.2. Gieo hai đồng xu cân đối và đồng chất. Gọi X là số mặt sấp xuất hiện.
1. Biến ngẫu nhiên X nhận các giá trị nào?
2. Hãy tính xác suất để X nhận mỗi giá trị chỉ ra ở trên. Lời giải.
1. Biến ngẫu nhiên X nhận các giá 0, 1, 2 2. Không gian mẫu Ω = {SS, SN, N S, N N }. ta có 1 2 1 1 P[X = 0] = , P[X = 1] = = , P[X = 2] = . 4 4 2 4
3. Do kết quả của hai đồng xu là độc lập và xác suất để xuất hiện mặt sấp là 1/2 nên
ta cũng có thể tính các xác suất trên bằng công thức xác suất nhị thức.
Ta có bảng sau gọi là bảng phân phối xác suất của X. x 0 1 2 1 1 1 P[X = x] 4 2 4 1.3.2
Phân phối của biến ngẫu nhiên
X được gọi là bnn rời rạc nếu nó nhận các giá trị x1, x2, . . .
Kí hiệu pk = P[X = xk] với k = 1, 2, . . . Bảng phân phối của X: x x1 x2 · · · xk P[X = x] p1 p2 · · · pk Chú ý: p1 + p2 + . . . + pk = 1. 1.3.3 Các số đặc trưng
Để đánh giá biến ngẫu nhiên X, ta thường dùng các giá trị sau 1. Kỳ vọng:
E[X] = x1p1 + x2p2 + · · · + xkpk. 2. Phương sai: V ar(X) = x2p p p 1 1 + x2 2 2 + · · · + x2 k k − (E[X ])2. 3. p σ(X) =
V ar(X) là độ lệch chuẩn của X.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 15
Với mỗi hàm số ϕ : R → R ta có
E[ϕ(X)] = ϕ(x1)p1 + ϕ(x2)p2 + · · · + ϕ(xk)pk.
Ví dụ 1.3.3. Cho biến ngẫu nhiên X và Y có phân phối xác suất như sau: X -2 -1 1 2 P 0, 2 0, 3 0, 3 0, 2 Y -20 -1 1 20 P 0, 2 0, 3 0, 3 0, 2
1. Hãy tính kì vọng và phương sai của X và của Y .
2. Tính xác suất X ≥ 0 và xác suất Y ≤ 1.
Lời giải. E[X] = E[Y ] = 0, V ar(X) = 2, 2, V ar(Y ) = 320, 6. Nhận xét: X và Y có giá trị
trung bình như nhau nhưng độ phân tán của Y cao hơn so với độ phân tán của X.
P[X ≥ 0] = P[X = 1] + P[X = 2] = 0, 5.
P[Y ≤ 1] = 1 − P[Y > 1] = 1 − P[Y = 20] = 0, 8. 1.3.4
Ý nghĩa của kỳ vọng và phương sai
• Kỳ vọng đặc trưng cho giá trị trung bình mà biến ngẫu nhiên có thể nhận.
• Phương sai đặc trưng cho độ phân tán của giá trị của biến ngẫu nhiên xung quanh
giá trị trung bình của nó. Độ phân tán của biến ngẫu nhiên càng rộng thì phương sai càng lớn. 1.3.5
Phân phối nhị thức
Gọi X là số phép thử thành công trong dãy n phép thử Bernoulli. P[X = k] = Ckpk(1 − p)n−k, k = 0, 1, . . . , n. n
X có phân phối nhị thức, kí hiệu là B(n, p). E[X] = np, V ar(X) = np(1 − p). 1.3.6
Tính chất của kỳ vọng và phương sai
Với mọi số thực a, b, c và mọi bnn X và Y : • E[c] = c.
• E[aX + bY ] = aE[X] + bE[Y ].
• Nếu X ≥ Y thì E[X] ≥ E[Y ].
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 16
• V ar(X) = E[(X − E[X])2] = E[X2] − (E[X])2. • V ar(X + c) = V ar(X). • V ar(aX) = a2V ar(X). 1.4
Biến ngẫu nhiên liên tục và Phân phối chuẩn 1.4.1
Biến ngẫu nhiên liên tục
Trên thực tế có nhiều đại lượng ngẫu nhiên nhận giá trị là các số thực
• Cân nặng của một trẻ sơ sinh.
• Thời gian bạn đi từ nhà đến trường mỗi ngày.
• Chiều cao của cây bạch đàn 1 năm tuổi.
Ta gọi mỗi đại lượng trên là một biến ngẫu nhiên liên tục. 1.4.2 Hàm mật độ
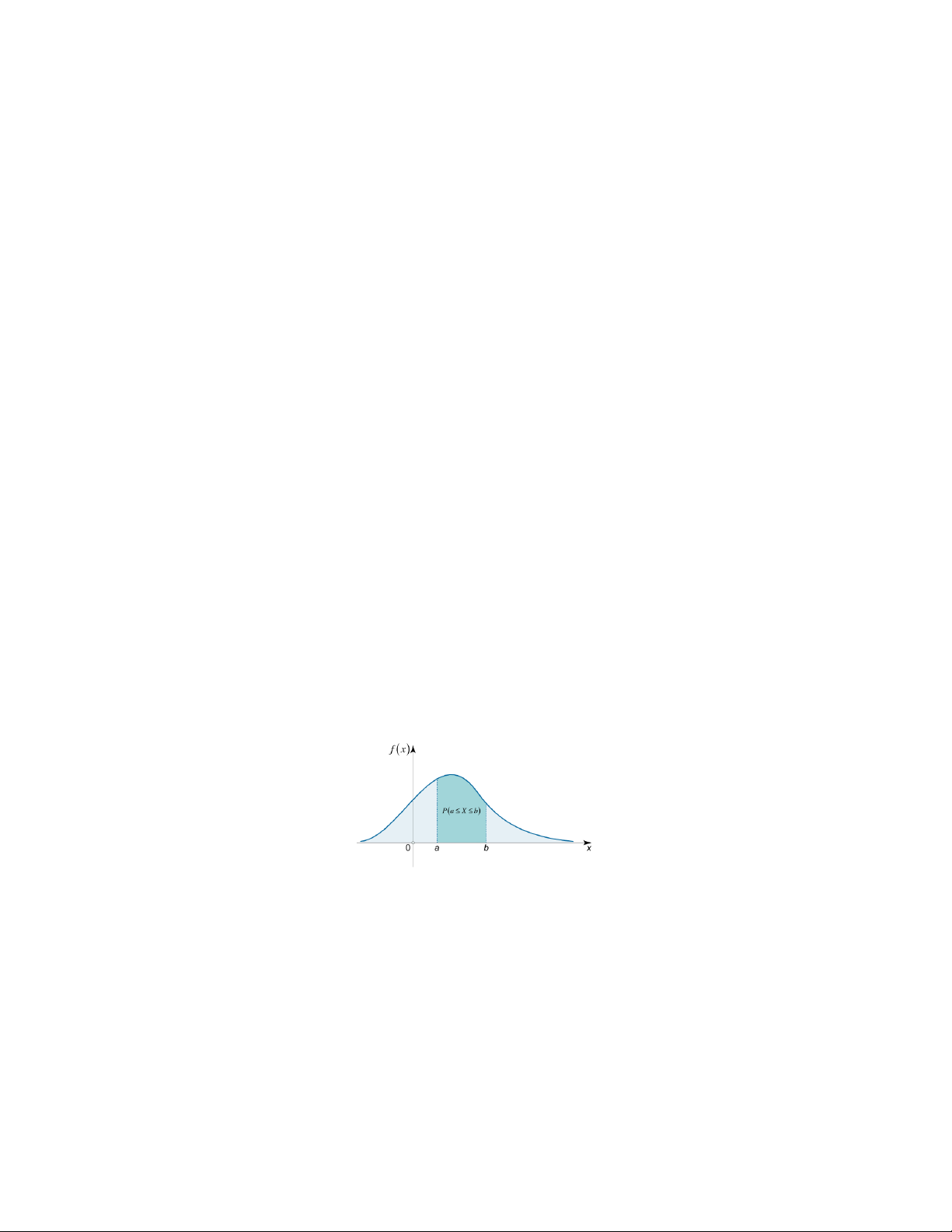
Hàm f : R → [0, ∞) được gọi là hàm mật độ của biến ngẫu nhiên liên tục X nếu Z b P[a < X < b] = f (x)dx, a
với mọi số thực a < b. Z b
P[a ≤ X ≤ b] = P[a < X ≤ b] = P[a ≤ X < b] = f (x)dx. a 1.4.3 Các số đặc trưng • Kỳ vọng Z ∞ E[X] = xf (x)dx. −∞
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 17 • Kỳ vọng của X2 Z ∞ E[X2] = x2f (x)dx. −∞ • Phương sai V ar(X) = E[X2] − (E[X])2.
Ví dụ 1.4.1. Thời gian mỗi lần Lan đi từ nhà đến quê nội (đơn vị: giờ) là một đại lượng
ngẫu nhiên X có hàm mật độ (1 nếu 1 ≤ x ≤ 2, f (x) = 0
nếu x < 1 hoặc x > 2.
1. Tính xác suất để Lan đi từ nhà đến quê nội hết hơn 90 phút.
2. Tính kì vọng và phương sai của X. 1.4.4 Phân phối chuẩn
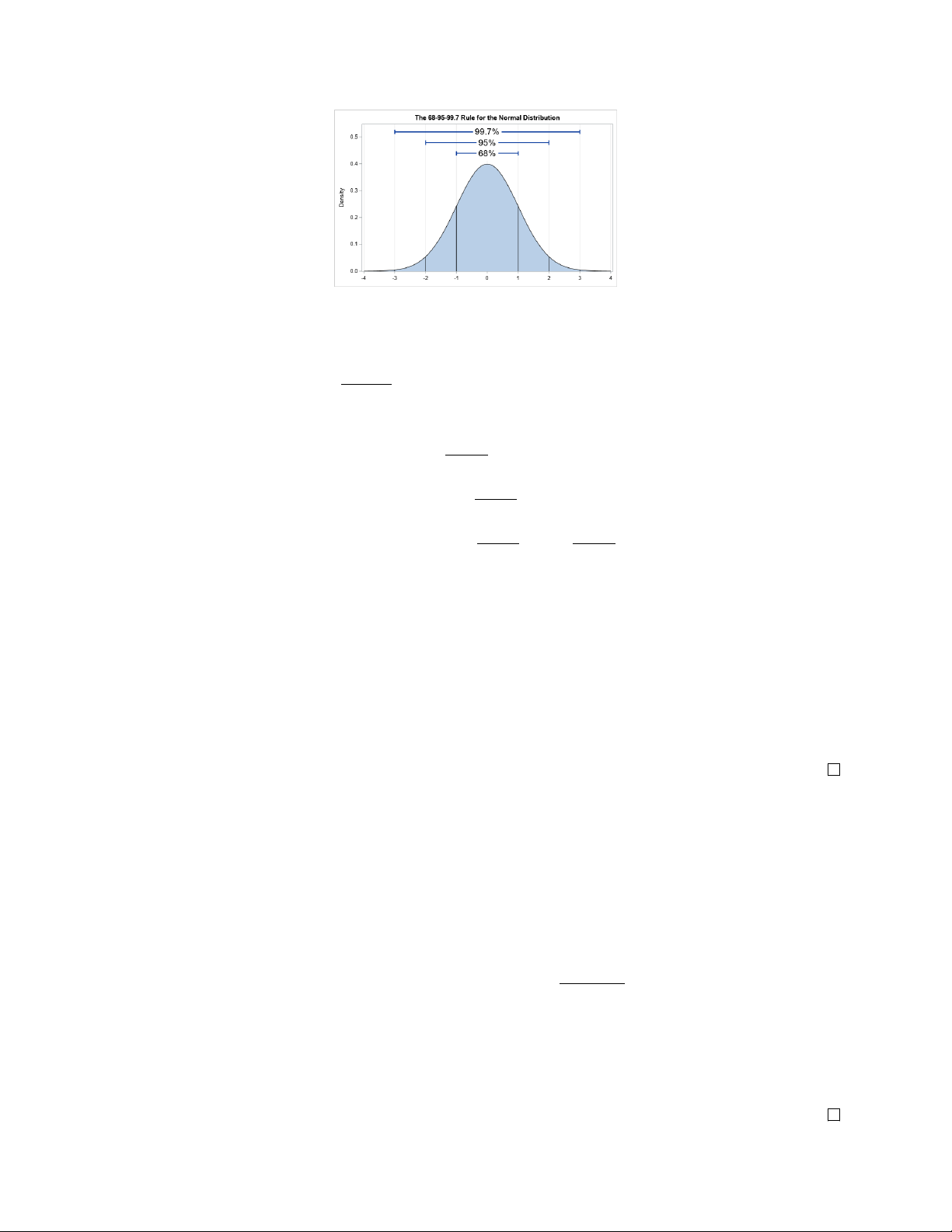
Bnn X được gọi là có phân phối chuẩn N (µ, σ2) nếu hàm mật độ của X xác định bởi 1 f (x) = √ e− x2 2σ2 . 2πσ2 Ta tính được E[X] = µ và V ar(X) = σ2.
Khi µ = 0 và σ = 1 thì ta nói X có phân phối chuẩn tắc.
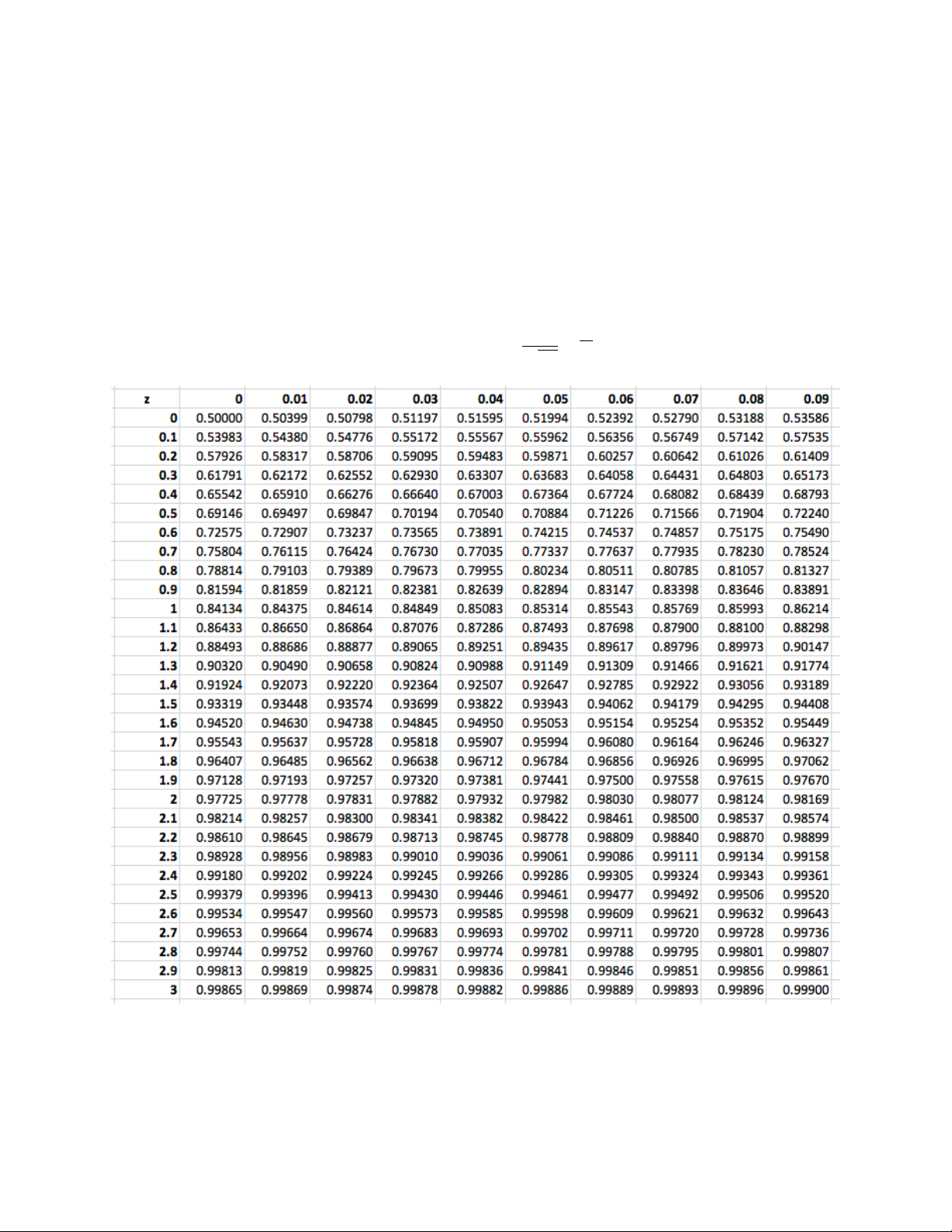
Hàm Φ xác định như sau được gọi là hàm phân phối chuẩn tắc Z z 1 Φ(z) = √ e− x2 2 dx. −∞ 2π
Hàm Φ đóng vai trò quan trọng trong thống kê. Tuy nhiên vì không tính được trực
tiếp nên ta sẽ dùng bảng để tra giá trị của nó.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 18 1.4.5
Tính chất của phân phối chuẩn X − µ
1) Nếu X ∼ N (µ, σ2) thì
sẽ có phân phối chuẩn tắc. σ Do đó a − µ P[X < a] = Φ( ) σ b − µ P[X > b] = 1 − Φ( ) σ b − µ a − µ P[a < X < b] = Φ( ) − Φ( ) σ σ 2) Φ(−x) = 1 − Φ(x).
Ví dụ 1.4.2. Cho biết Φ(1, 96) = 0, 975 và Φ(2, 58) = 0, 995, hãy tính Φ(−1, 96) và Φ(−2, 58).
Lời giải. Ta sử dụng tính chất của phân phối chuẩn tắc Φ(−x) = 1 − Φ(x) thì
• Φ(−1, 96) = 1 − Φ(1, 96) = 0, 025.
• Φ(−2, 58) = 1 − Φ(2, 58) = 0, 005.
Ví dụ 1.4.3. Trọng lượng trẻ sơ sinh là một biến ngẫu nhiên có phân phối chuẩn với trung
bình 3,2kg và độ lệch tiêu chuẩn 0,4kg. Một trẻ sơ sinh được gọi là bình thường nếu có
trọng lượng từ 2,688kg đến 3,712kg. Tính xác suất để một đứa trẻ sơ sinh có trọng lượng bình thường.
Lời giải. Gọi X là trọng lượng một trẻ sơ sinh, X ∼ N (3, 2; (0, 4)2). Xác suất để 1 trẻ bình thường là X − 3, 2
P(2, 688 < X < 3, 712) = P −1, 28 < < 1, 28 0, 4 = Φ(1, 28) − Φ(−1, 28)
= 2Φ(1, 28) − 1 = 2 × 0, 9 − 1 = 0, 8.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 19 1.4.6
Xấp xỉ phân phối nhị thức bằng phân phối chuẩn
Ví dụ 1.4.4. Trong một thành phố có 40% người dân có mức thu nhập cao. Chọn ngẫu
nhiên 300 người (chọn từng người).Tính xác xuất để trong 300 người được chọn có đúng 140 người lương cao?
Theo công thức của phân phối nhị thức, xác suất để có 140 người thu nhập cao trong 300 người là C140(0, 4)140(0, 6)160 300
Khi sử dụng máy tính bỏ túi thông thường, kết quả sẽ hiện là error! Có điều này là do
C140 là số quá lớn còn (0, 4)140 lại là số quá nhỏ nên máy tính không hiển thị được. 300
Mệnh đề 1.4.5. Giả sử X có phân phối nhị thức B(n, p). Khi n lớn thì ! ! k + 0, 5 − np k − 0, 5 − np P[X = k] ≈ Φ − Φ pnp(1 − p) pnp(1 − p) 1 (k − np)2 ≈ exp − , p2πnp(1 − p) np(1 − p) ! ! k2 + 0, 5 − np k1 − 0, 5 − np P[k1 ≤ X ≤ k2] ≈ Φ − Φ pnp(1 − p) pnp(1 − p) ! k2 + 0, 5 − np P[X ≤ k2] ≈ Φ , pnp(1 − p) ! k1 − 0, 5 − np P[X ≥ k1] ≈ 1 − Φ . pnp(1 − p)
Ví dụ 1.4.6. Gọi X là số người có mức lương cao trong 300 người được chọn. Ta coi X có
phân phối chuẩn N (µ, σ2) với µ = np = 300 × 0, 4 = 120, σ2 = np(1 − p) = 72. Xác suất để X nhận giá trị 140 là
P(X = 140) = P(139, 5 ≤ X < 140, 5) 140, 5 − 120 139, 5 − 120 ≈ Φ √ − Φ √ 72 72 ≈ Φ(2, 42) − Φ(2, 30)
≈ 0, 9920 − 0, 9893 = 0, 0027.
CHƯƠNG 1. MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ 20
Ví dụ 1.4.7. Xác suất để một hạt thóc giống bị lép là 0,006. Tìm xác suất để trong 1000 hạt thóc giống có
1. Có không quá 9 hạt lép.
2. Không ít hơn 3 hạt lép. 3. Có đúng 6 hạt lép.
Lời giải. Gọi X là số hạt lép trong 1000 hạt, X có phân phối B(n = 1000; p = 0, 006). Do n
lớn, ta coi như X có phân phối N (µ; σ2) với µ = np = 6, σ2 = np(1 − p) = 2, 4. 9, 5 − 6
1. P[X ≤ 9] = P[X < 9, 5] = Φ √ ≈ 0, 9880. 2, 4 2, 5 − 6
2. P[X ≥ 3] = 1 − P[X ≤ 2] = 1 − Φ √ ≈ 0, 9880. 2, 4 6, 5 − 6 5, 5 − 6
3. P[X = 6] = P[5.5 ≤ X < 6.5] = Φ √ − Φ √ ≈ 0, 2531. 2, 4 2, 4 Chương 2 MẪU NGẪU NHIÊN
Nội dung của chương:
1. Giới thiệu về thống kê.
2. Thu thập dữ liệu. Một số phương pháp lấy mẫu ngẫu nhiên.
3. Trình bày và mô tả dữ liệu.
4. Dữ liệu và các số đặc trưng.
Mục tiêu của chương:
1. Hiểu được các khái niệm cơ bản, quy trình nghiên cứu, mục tiêu, chức năng, nhiệm
vụ của môn Thống kê trong việc giải quyết các vấn đề thực tế của đời sống.
2. Nhận dạng được các loại dữ liệu khác nhau: dữ liệu sơ cấp, dữ liệu thứ cấp. Nắm
được các quy tắc và một số phương pháp để thu thập dữ liệu trong thực tế.
3. Nhận dạng được một số loại bảng và biểu đồ dùng để trình bày dữ liệu. Nắm được
cách vẽ và xây dựng các loại bảng và biểu đồ đó.
4. Nắm được cách xử lý dữ liệu đã thu thập được. Từ đó tính được các số đặc trưng
của mẫu dữ liệu như: trung bình mẫu, phương sai mẫu, mode, median,... cho:
• dữ liệu rời rạc được biểu diễn trong một bảng tần số
• dữ liệu rời rạc được biểu diễn theo một danh sách liệt kê
• dữ liệu liên tục được biểu diễn trong một bảng tần số theo nhóm 21
CHƯƠNG 2. MẪU NGẪU NHIÊN 22 2.1
Giới thiệu về Thống kê
Thống kê là khoa học về việc thu thập, xử lý, biểu diễn, phân tích mẫu số liệu thu thập
được từ một quần thể để rút ra được các kết luận có độ tin cậy cho toàn bộ quần thể đó. 2.1.1 Mẫu và quần thể
• Quần thể (population) là tập hợp tất cả các đối tượng mà ta cần nghiên cứu.
• Mẫu (sample) là tập hợp một số phần tử đại diện lấy từ quần thể mà ta chọn để tiến hành nghiên cứu.
Số phần tử của một mẫu được gọi là cỡ mẫu, kí hiệu là n.
• Để nghiên cứu các tính chất của một quần thể ta có thể:
– khảo sát toàn bộ các phần tử của quần thể, hoặc
– khảo sát một bộ phận của quần thể đó,
sau đó tìm cách rút ra kết luận dựa trên dữ liệu quan sát được. 2.1.2
Quy trình nghiên cứu thống kê
1. Giai đoạn 1: Thiết kế và tiến hành điều tra để thu thập dữ liệu.
2. Giai đoạn 2: Tổng hợp và trình bày kết quả điều tra thu thập được.
3. Giai đoạn 3: Phân tích đưa ra kết luận và dự báo. 2.1.3
Các bài toán thống kê sẽ học:
1. Bài toán ước lượng tham số: ước lượng điểm, ước lượng khoảng.
Một nhà điều tra thử tính cân nặng trung bình của 100 trẻ sơ sinh ở một địa phương
thì được kết quả là 3,1kg. Có thể nói gì về cân nặng của trẻ sơ sinh toàn địa phương đó?
2. Bài toán kiểm định giả thuyết.
Một nhà quản lý cho rằng cân nặng trung bình của tất cả các trẻ sơ sinh ở địa
phương đó là 3,3kg. Tuyên bố của nhà quản lý có đúng không?
CHƯƠNG 2. MẪU NGẪU NHIÊN 23
3. Bài toán hồi quy.
Chiều cao của bố/mẹ và con liên quan như thế nào đến nhau?
Biết chiều cao của bố/mẹ thì có thể dự đoán được chiều cao của con không? 2.2 Thu thập dữ liệu
Định nghĩa 2.2.1. Lấy mẫu là quá trình chọn một số lượng nhỏ những đơn vị nghiên
cứu từ một quần thể nghiên cứu xác định. Câu hỏi:
• Mẫu nghiên cứu được rút ra trên nhóm cá thể nào?
• Cần bao nhiêu cá thể trong mẫu nghiên cứu?
• Những cá thể này được chọn như thế nào? 2.2.1
Xác định dữ liệu cần thu thập
• Xác định rõ dữ liệu nào cần thu thập, thứ tự ưu tiên của các dữ liệu này. Nếu không
sẽ mất rất nhiều thời gian và chi phí cho những dữ liệu ít quan trọng hay không
liên quan đến vấn đề cần nghiên cứu.
• Xác định số các đơn vị điều tra (cỡ mẫu). 2.2.2
Dữ liệu sơ cấp và thứ cấp
Dữ liệu thứ cấp là dữ liệu đã qua tổng hợp, xử lý.
• Ưu điểm: thu thập nhanh, ít tốn kém chi phí.
• Nhược điểm: đôi khi ít chi tiết và không đáp ứng đúng nhu cầu nghiên cứu.
• Nguồn cung cấp: số liệu nội bộ, số liệu từ cơ quan thống kê nhà nước, cơ quan
chính phủ, báo, tạp chí, các tổ chức, hiệp hội, viện nghiên cứu,...
Dữ liệu sơ cấp là dữ liệu thu thập trực tiếp, ban đầu từ đối tượng nghiên cứu.
• Ưu điểm: đáp ứng tốt nhu cầu nghiên cứu.
CHƯƠNG 2. MẪU NGẪU NHIÊN 24
• Nhược điểm: tốn kém nhiều về thời gian và chi phí.
• Phương pháp thu thập: thực nghiệm, khảo sát qua điện thoại, thư hỏi, quan sát
trực tiếp và phỏng vấn cá nhân. 2.2.3
Lấy mẫu hoàn lại và không hoàn lại
• Lấy mẫu ngẫu nhiên có hoàn lại: lần lượt lấy ngẫu nhiên từ quần thể ra một phần
tử, thu thập các thông tin cần thiết từ phần tử đó rồi trả nó trở lại quần thể trước khi lấy tiếp lần sau.
• Lấy mẫu ngẫu nhiên không hoàn lại: tương tự như trên nhưng khác ở chỗ các phần
tử đã lấy ra sẽ không được chọn lại ở lần sau. 2.2.4 Quy tắc lấy mẫu
Căn cứ vào dữ liệu của mẫu mà ta thu thập được, để có thể đưa ra những kết luận
đủ chính xác về dấu hiệu nghiên cứu trong quần thể thì trước hết mẫu được chọn phải
mang tính đại diện cho quần thể.
• Mỗi phần tử được lấy vào mẫu một cách hoàn toàn ngẫu nhiên, tức là mọi phần tử
của quần thể đều có thể được lấy vào mẫu với khả năng như nhau.
• Các phần tử của mẫu được chọn lần lượt, độc lập với nhau và có hoàn lại từ quần thể.
Chú ý: Khi kích thước của tổng thể khá lớn còn kích thước của mẫu lại nhỏ thì phương
thức lấy mẫu hoàn lại và lấy mẫu không hoàn lại cho ta kết quả sai lệch không đáng kể. 2.2.5
Phương pháp lấy mẫu giản đơn
Mẫu giản đơn là mẫu được chọn trực tiếp từ danh sách đã được đánh số của tổng thể.
Từ quần thể kích thước N người ta rút ra mẫu n phần tử bằng cách bốc thăm, chọn số
ngẫu nhiên từ bảng hoặc sinh số ngẫu nhiên từ máy tính.
Phương pháp này có ưu điểm là cho phép thu được một mẫu có tính đại diện cao,
song để vận dụng phải có được toàn bộ danh sách của tổng thể nghiên cứu, và chi phí chọn mẫu sẽ khá lớn.
CHƯƠNG 2. MẪU NGẪU NHIÊN 25 2.2.6
Các phương pháp lấy mẫu khác
• Mẫu phân tầng (Stratified sampling): quần thể được chia thành nhóm và mỗi nhóm
được lấy mẫu giản đơn.
• Lấy mẫu cụm (Cluster sampling): quần thể được chia thành nhiều cụm. Đầu tiên
chọn ngẫu nhiên một số cụm, sau đó lại chọn ngẫu nhiên các phần tử từ các cụm
được chọn bằng phương pháp lấy mẫu giản đơn.
• Mẫu hệ thống (Systematic random sampling): Đánh số các phần tử của quần thể
từ 1 đến N . Chọn ngẫu nhiên ra 1 phần tử trong k phần tử đầu tiên (k < N ), từ
phần tử được chọn cứ cách k phần tử của quần thể lại lấy ra một phần tử cho vào mẫu.
• Lấy mẫu nhiều tầng (Multistage sampling): kết hợp nhiều phương pháp.
Chú ý: Để đơn giản ta chỉ xét phương pháp lấy mẫu giản đơn. 2.3
Trình bày dữ liệu bằng bảng và biểu đồ
Các phương pháp trình bày dữ liệu:
1. Đối với dữ liệu định tính
• Bảng tần số, tần suất, tần số tích lũy, tần suất tích lũy.
• Biểu đồ hình cột, hình tròn.
2. Đối với dữ liệu định lượng • Biểu đồ thân-lá.
• Bảng tần số, tần suất, tần số tích lũy, tần suất tích lũy.
• Biểu đồ hình cột, hình tròn. 2.3.1
Biểu đồ thân-lá (stem-and-leaf diagram)
Biểu đồ thân-lá là một phương pháp mô tả thông tin trực quan về mẫu x1, x2, . . . , xn,
trong đó mỗi số xi bao gồm ít nhất hai chữ số. Để xây dựng một biểu đồ thân-lá, ta thực hiện các bước như sau.
1. Bước 1: chia mỗi số xi thành hai phần: thân cây, bao gồm một hoặc nhiều chữ số
đầu và lá, bao gồm các chữ số còn lại.
2. Bước 2: liệt kê các giá trị thân thành một cột.
3. Bước 3: ghi lại lá cho mỗi quan sát bên cạnh thân cây.
4. Bước 4: đếm số lượng thân và lá.
CHƯƠNG 2. MẪU NGẪU NHIÊN 26
Ví dụ 2.3.1. Điều tra cân nặng của 20 sinh viên tại một trường ĐH, ta thu được bảng dữ liệu sau: 59.0 59.5 52.7 47.9 55.7 48.3 52.1 53.1 55.2 45.3 46.5 54.8 48.4 53.1 56.9 47.4 50.2 52.1 49.6 46.4
Xây dựng biểu đồ thân-lá cho cân nặng của 20 sinh viên như sau: Thân Lá Tần số 45 3 1 46 4 5 2 47 4 9 2 48 3 4 2 49 6 1 50 2 1 52 1 1 7 3 53 1 1 2 54 8 1 55 2 7 2 56 9 1 59 0 5 2 2.3.2 Tần số
• Tần số (frequence) là số lần biến số nhận một giá trị nào đó.
• Tỉ lệ (proportion) là tần số được diễn tả một cách tương đối, được tính bằng cách
lấy tần số chia cho tổng số quan sát.
• Tỉ lệ phần trăm (percentage) là tỉ lệ được nhân lên cho 100.
Tỉ lệ và tỉ lệ phần trăm được gọi là tần số tương đối (relative frequencies) hay tần suất.
• Bảng tần số/tần suất (frequency table) là bảng liệt kê các giá trị (hoặc khoảng giá
trị) của một biến và tần số/tần suất của chúng.
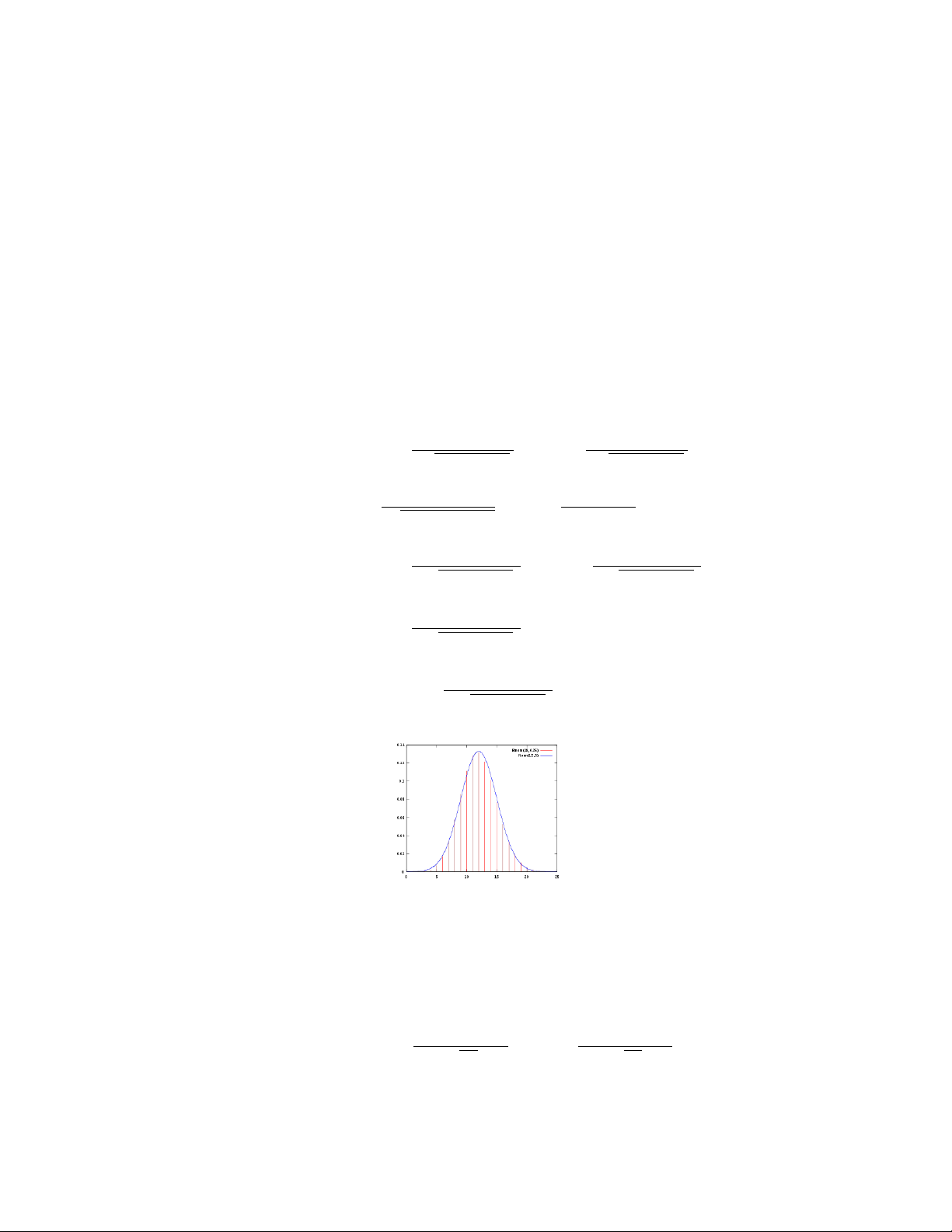
Ví dụ 2.3.2. Năm 2016, báo Tuổi trẻ Online có làm cuộc khảo sát về bình chọn Quốc hoa
Việt Nam, kết quả thu được như sau:
CHƯƠNG 2. MẪU NGẪU NHIÊN 27
Ví dụ 2.3.3. Dữ liệu về ngành học của sinh viên một trường đại học như sau: Ngành học
Tần số (số sinh viên) Tần suất (%) Quản trị kinh doanh 450 Điện tử viễn thông Công nghệ thông tin 20 Tổng 1000
? Hãy điền giá trị vào các ô trống trong bảng. 2.3.3 Bảng tần số
a) Trường hợp dữ liệu có ít giá trị:
Ví dụ: khảo sát điểm thi môn Toán của học sinh khối 12 một trường THPT như sau: Điểm thi
Tần số (số học sinh) Tần suất (%) 3 3 3,75 4 12 15 5 15 18,75 6 20 25 7 16 20 8 8 10 9 4 5 10 2 2,5 Tổng 80 100
b) Trường hợp dữ liệu có nhiều giá trị:
• Nếu dữ liệu có nhiều giá trị khác nhau, khoảng cách giữa các giá trị không đồng
đều hoặc các giá trị khác nhau rất ít thì ta sẽ biểu diễn chúng dưới dạng khoảng.
• Ví dụ: khảo sát 1200 người trong độ tuổi lao động (từ 18 đến 60 tuổi), nếu lập bảng
như ở ví dụ trên thì sẽ rất dài, làm mất đi tác dụng tóm lược thông tin. Do đó, ta
thường phân thành các nhóm, chẳng hạn: từ 18 đến 21 tuổi, từ 21 đến 30 tuổi, từ
31 đến 40 tuổi, từ 41 đến 50 tuổi, từ 51 đến 60 tuổi. • Chú ý: √ - Số khoảng tối ưu là n. x
- Độ dài mỗi khoảng xấp xỉ h = max − xmin √ . n
Ví dụ 2.3.4. Năng suất (tạ/ha) của một loại cây thu hoạch được tại 40 khu vực canh tác như sau:
CHƯƠNG 2. MẪU NGẪU NHIÊN 28 153 154 156 157 158 159 159 160 160 160 161 161 161 162 162 162 163 163 163 164 164 164 165 165 166 166 167 167 168 168 170 171 172 173 174 175 176 177 178 179
? Hãy lập bảng tần số cho mẫu số liệu trên theo mẫu. Năng suất Tần số Tần suất (%) Tổng 40 100 2.4 Biểu đồ tần số
Biểu đồ tần số là cách biểu diễn trực quan bảng tần số của số liệu.
Để xây dựng một biểu đồ tần số, ta thực hiện các bước như sau.
1. Bước 1: gắn nhãn các mốc của từng khoảng trên một thang nằm ngang.
2. Bước 2: đánh dấu và dán nhãn thang thẳng đứng theo tần số.
3. Bước 3: trên mỗi khoảng, vẽ một hình chữ nhật có chiều cao bằng với tần số tương ứng với khoảng đó. 2.4.1
Biểu đồ tần suất
Biểu đồ tần suất là cách biểu diễn trực quan bảng tần suất của số liệu.
Biều đồ tần suất thường có hình tròn, mỗi hình quạt tương ứng với một biến số hay khoảng biến số.
Chú ý: Độ lớn góc ở tâm của hình quạt = tỉ lệ ×360◦.
CHƯƠNG 2. MẪU NGẪU NHIÊN 29 2.5
Số liệu và các số đặc trưng 2.5.1 Biến số
• Biến số (variable) là khái niệm dùng để chỉ bất kỳ đặc tính nào của quần thể mà ta nghiên cứu.
• Ví dụ: Để nghiên cứu sinh viên của một trường Đại học, ta có thể nghiên cứu các biến như: – Giới tính – Tuổi – Chiều cao – Ngành học
– Số tiền chi tiêu trong một tháng,... 2.5.2
Phân loại biến số
Biến định tính (qualitative) là biến dùng để phản ánh tính chất, loại hình, không thể
hiện trực tiếp bằng các con số.
Giá trị của mỗi biến định tính có thể xếp thứ tự được (Thái độ: không hài lòng-hài
lòng-rất hài lòng), hoặc không xếp thứ tự được (Giới tính: Nam-Nữ).
Biến định lượng (quantitative) là biến dùng để diễn tả các mức độ cao, thấp của dữ
liệu, thể hiện trực tiếp bằng các con số.
Giá trị của biến định lượng có thể là đại lượng liên tục (chiều cao, cân nặng) hoặc đại
lượng rời rạc (điểm số, số ca khỏi bệnh trong một tháng).
? Hãy xác định các loại biến trong ví dụ về thống kê sinh viên.
CHƯƠNG 2. MẪU NGẪU NHIÊN 30
Ví dụ 2.5.1. Xem điểm Toán của 10 học sinh lớp A, ta thu được kết quả như sau: 10 9 5 6 1 5 7 9 5 6
? Có thể rút ra các thông tin gì từ mẫu số liệu trên? 2.5.3
Các số đo giá trị trung tâm
a) Trung bình mẫu (Sample mean)
Giả sử {x1, x2, . . . , xn} là một mẫu dữ liệu ta thu thập được. Khi đó: x x = 1 + . . . + xn . n
– Nếu mẫu dữ liệu được biểu diễn dưới dạng một bảng tần số: Giá trị x1 x2 . . . xk Tần số n1 n2 . . . nk k n 1 X Khi đó, x = 1x1 + n2x2 + . . . + nk xk = nixi. n n i=1
Trung bình mẫu ghép nhóm Nếu mẫu dữ liệu được biểu diễn dưới dạng một bảng tần số theo nhóm: Khoảng giá trị (a1; a2) (a2; a3) . . . (ak; ak+1) Tần số n1 n2 . . . nk a Gọi x i + ai+1 i =
là giá trị đại diện cho khoảng (ai; ai+1). Khi đó, 2 k n 1 X x ≈ 1x1 + n2x2 + . . . + nk xk = nixi. n n i=1
Ý nghĩa của trung bình mẫu:
• Số trung bình mẫu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số
đặc trưng quan trọng của mẫu số liệu.
• Ví dụ: nếu biết điểm trung bình môn Toán của lớp A là 6,5, của lớp C là 7,5 thì ta có
thể cho rằng sinh viên lớp C đạt điểm cao hơn sinh viên lớp A.
• Tuy nhiên, khi các số liệu trong mẫu có sự chênh lệch rất lớn đối với nhau thì số
trung bình mẫu chưa đại diện tốt cho các số liệu trong mẫu. Khi đó, ta dùng một
số đặc trưng khác thích hợp hơn là trung vị.
b) Trung vị mẫu (Median): giả sử mẫu dữ liệu {x1, . . . , xn} được sắp xếp theo thứ tự không giảm
x∗ ≤ x∗ ≤ · · · ≤ x∗ . 1 2 n
CHƯƠNG 2. MẪU NGẪU NHIÊN 31 1
- Nếu n = 2k thì trung vị mẫu là (x∗ + x∗ ). 2 k k+1
- Nếu n = 2k + 1 thì trung vị mẫu là x∗ . k+1
Chú ý: Khi các số liệu trong mẫu không có sự chênh lệch quá lớn thì trung bình
mẫu và trung vị xấp xỉ nhau.
c) Mode là giá trị của mẫu xuất hiện nhiều nhất.
Chú ý: Một mẫu số liệu có thể có một hay nhiều Mode. 2.5.4
Các số đo độ phân tán
a) Phương sai mẫu (Sample variance) n 1 X s2 = (xi − x)2. n − 1 i=1
b) Độ lệch tiêu chuẩn mẫu (Standard deviation) hay độ lệch mẫu là s.
Ý nghĩa: phương sai và độ lệch mẫu đo mức độ phân tán của các số liệu trong mẫu
quanh số trung bình mẫu. Phương sai và độ lệch mẫu càng lớn thì độ phân tán càng lớn.
c) Phạm vi mẫu (Range) là x∗ − x∗. n 1
Ví dụ 2.5.2. Theo dõi điểm Toán của 10 học sinh lớp A, ta thu được kết quả như sau: 10 9 5 6 1 5 7 9 5 6
Khi đó, các số đặc trưng của mẫu dữ liệu mà ta thu được là: • Cỡ mẫu: n = 10 • Trung bình mẫu: 1 x =
(10 + 9 + 5 + 6 + 1 + 5 + 7 + 9 + 5 + 6) = 6, 3 10 • Phương sai mẫu: 1
s2 = (10 − 6, 3)2 + (9 − 6, 3)2 + (5 − 6, 3)2 + (6 − 6, 3)2 9
+ (1 − 6, 3)2 + (5 − 6, 3)2 + 7 − 6, 3)2 + (9 − 6, 3)2 +(5 − 6, 3)2 + (6 − 6, 3)2 =6, 9
• Độ lệch mẫu: s = 2, 6268
• M ode = 5; M edian = 6; Range = 9
CHƯƠNG 2. MẪU NGẪU NHIÊN 32 2.5.5 Thống kê
Giả sử (X1, . . . , Xn) là một mẫu ngẫu nhiên.
Mỗi đại lượng được tính dựa trên các giá trị X1, . . . , Xn được gọi là một thống kê.
Ví dụ: Các số đặc trưng: trung bình mẫu, phương sai mẫu, trung vị, mode,... đều là các thống kê. Chương 3
KHOẢNG ƯỚC LƯỢNG
Nội dung của chương
1. Khoảng ước lượng của trung bình quần thể.
2. Khoảng ước lượng cho tỉ lệ.
Mục tiêu của chương
1. Hiểu được ý nghĩa của khoảng ước lượng, độ tin cậy.
2. Xác định khoảng ước lượng của trung bình với độ tin cậy cho trước.
3. Xác định khoảng ước lượng của tỉ lệ với độ tin cậy cho trước.
4. Xác định được cỡ mẫu để có khoảng ước lượng với sai số cho trước. 3.1
Khoảng ước lượng cho trung bình 3.1.1 Đặt vấn đề
Thông thường, để ước lượng trung bình µ, ta sử dụng trung bình mẫu ¯ xn.
Ví dụ 3.1.1. Để nghiên cứu trọng lượng trung bình của các sản phẩm được sản xuất bởi
một nhà máy, người ta cân 100 sản phẩm của xí nghiệp đó, dữ liệu thu được được mô tả bởi bảng sau: 33
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 34 Trọng lượng (g) 498 502 506 510 Số sản phẩm 40 20 20 20
Khi đó, trọng lượng trung bình của 100 sản phẩm là:
498 × 40 + 502 × 20 + 506 × 20 + 510 × 20 x100 = = 502, 8(g). 100
Ước lượng trọng lượng trung bình tất cả sản phẩm trong nhà máy là µ ≈ 502, 8(g).
Nếu một người khác cũng chọn ngẫu nhiên ra 100 sản phẩm và tính trọng lượng
trung bình của chúng thì có thu được đáp số là 502, 8g không? Vì ¯
xn phụ thuộc vào từng mẫu, tức là nếu ta lấy hai mẫu khác nhau thì trung bình
mẫu có thể khác nhau nên để tăng độ tin cậy của kết quả, thay vì nói µ gần bằng một số,
ta nói µ thuộc một khoảng (µ1, µ2) nào đó.
Dựa vào kết quả điều tra trên, hãy nhận xét ba phát biểu sau:
1. µ thuộc khoảng (502, 7, 502, 9).
2. µ thuộc khoảng (500, 505).
3. µ thuộc khoảng (400, 600). 3.1.2
Khoảng ước lượng
• Do ta chỉ dựa vào một mẫu nhỏ để ước lượng giá trị của µ nên ta không thể chắc
chắn 100% về kết quả thu được.
• Tuy nhiên, áp dụng các kết quả của lý thuyết xác suất, trong nhiều trường hợp ta
có thể tìm được hai thống kê µ1 và µ2 sao cho xác suất
P[µ ∈ (µ1, µ2)] = 1 − α.
Khi đó ta gọi khoảng (µ1, µ2) là khoảng ước lượng của µ với độ tin cậy 1 − α.
• Số 2ε = µ2 − µ1 được gọi là độ dài của khoảng ước lượng; số ε được gọi là sai số của ước lượng. 3.1.3
KƯL cho trung bình µ khi σ2 đã biết
Giả sử (X1, . . . , Xn) là mẫu ngẫu nhiên quan sát được từ một quần thể có phân phối
chuẩn N (µ, σ2) với phương sai σ2 đã biết.
Khoảng ước lượng (µ1, µ2) của µ với độ tin cậy 1 − α được xác định bởi σ σ µ1 = x − z √ √ α/2 , µ2 = x + z (3.1) n α/2 n
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 35 • ¯ x là trung bình mẫu
• σ là độ lệch chuẩn của X • n là kích thước mẫu α • zα/2 là phân vị mức
của phân phối chuẩn tắc. 2
Ý nghĩa của độ tin cậy
• Với mỗi mẫu ngẫu nhiên khác nhau ta sẽ thu được các khoảng ước lượng (µ1, µ2)
khác nhau. Mỗi khoảng ước lượng (µ1, µ2) có thể chứa µ hoặc không chứa µ.
• Độ tin cậy 1−α của KƯL (µ1, µ2) xác định bởi (3.1) được hiểu theo nghĩa là nếu ta sử
dụng công thức (3.1) rất nhiều lần (cho các mẫu khác nhau) để tìm ra các khoảng
ước lượng thì tỉ lệ các khoảng ước lượng thực sự chứa µ sẽ xấp xỉ (1 − α) × 100%.
• Nói cách khác, khi ta dùng công thức (3.1) để tìm một khoảng chứa µ thì xác suất
thành công (tức là tìm được khoảng thực sự chứa µ) là 1 − α.
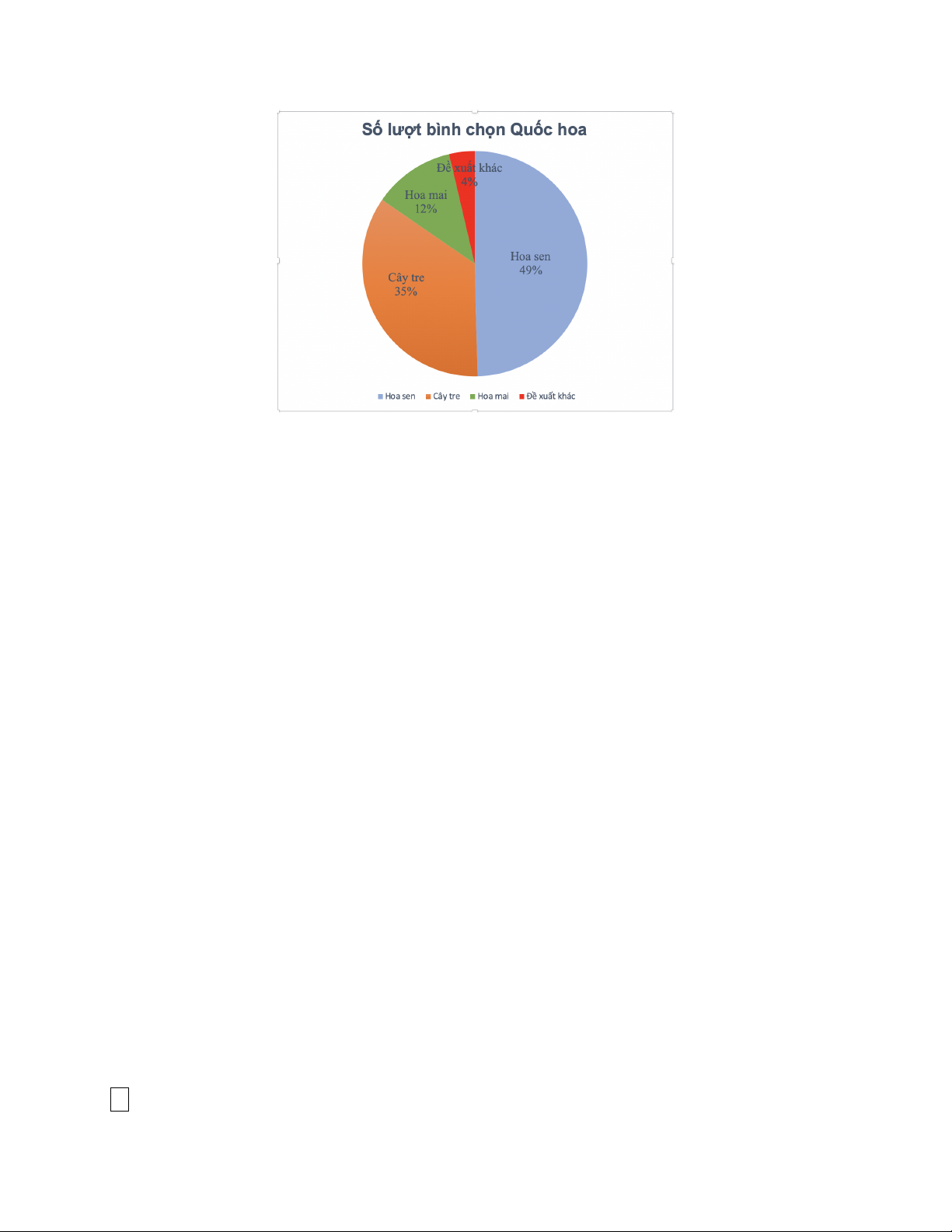
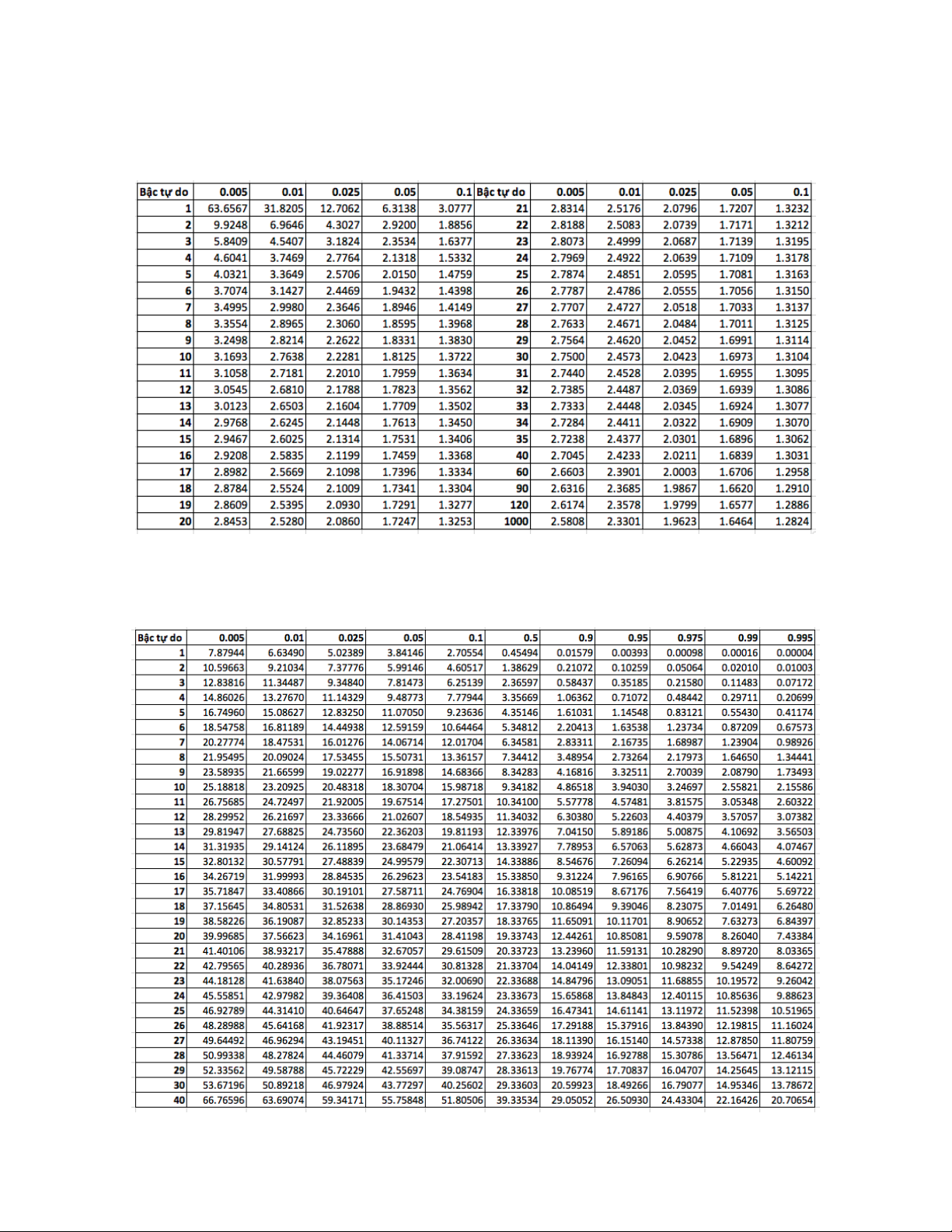
Phân vị của phân phối chuẩn tắc Phân vị mức α của phân phối chuẩn tắc Z ∼ N (0; 1)
là số thực zα thỏa mãn P(Z > zα) = α.
z0,05 = 1, 645; z0,025 = 1, 96; z0,01 = 2, 33; z0,005 = 2, 58.
Ví dụ 3.1.2. 1 Giả sử chỉ số IQ của một người là đại lượng ngẫu nhiên có phân phối chuẩn
với độ lệch chuẩn σ = 15. Để ước lượng chỉ số IQ trung bình của một cộng đồng, người
ta chọn ngẫu nhiên 200 người trong cộng đồng và tính được chỉ số IQ trung bình của 200
người này là 105. Hãy ước lượng chỉ số IQ trung bình của cộng đồng dân cư đó:
1Chỉ số IQ (TNTA: Intelligence quotient), nguồn https://vi.wikipedia.org/wiki/IQ
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 36 a) với độ tin cậy 95%. b) với độ tin cậy 99%. Lời giải. Ta có σ = 15, n = 200, ¯ x = 105.
a) Nếu 1 − α = 0, 95 thì α = 0, 05 và zα/2 = z0,025 = 1, 96. σ Tính được z √ α/2 = 2, 08. n
Vậy KƯL của chỉ số IQ trung bình µ với độ tin cậy 95% là 102, 92 < µ < 107, 08.
b) Nếu 1 − α = 0, 99 thì α = 0, 01 và zα/2 = z0,005 = 3, 87. σ Tính được z √ α/2 = 2, 08. n
Vậy KƯL của chỉ số IQ trung bình µ với độ tin cậy 99% là 101, 13 < µ < 108, 87.
Nhận xét 1. - Trên cùng một mẫu thì khoảng rộng hơn sẽ có độ tin cậy cao hơn.
- Nếu muốn tăng độ tin cậy mà không tăng sai số thì phải tăng cỡ mẫu.
? Phát biểu sau đúng hay sai: Xác suất để µ thuộc khoảng (102, 93, 107, 08) là 0, 95.
Ví dụ 3.1.3. Biết rằng chiều cao người trưởng thành là đại lượng ngẫu nhiên có phân
phối chuẩn với độ lệch chuẩn σ = 7, 62cm. Để ước lượng chiều cao nữ sinh viên một
trường đại học, người ta tiến hành khảo sát 250 nữ sinh viên và thu được trung bình mẫu ¯
x = 156, 67cm. Với độ tin cậy 90%, hãy ước lượng chiều cao trung bình của nữ sinh viên trường đại học đó. 2 Lời giải.
• Ta có σ = 7, 62, n = 250, ¯ x = 156, 67.
2Theo thống kê của Viện dinh dưỡng quốc gia năm 2019, chiều cao trung bình của người Việt Nam là
163.7 cm với nam và 153 cm với nữ (theo Vnexpress.net)
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 37
• Vì 1 − α = 0, 9 nên α = 0, 1 và zα/2 = z0,05 = 1, 64. σ • Tính được z √ α/2
= 0, 79. Vậy KƯL của chiều cao trung bình µ của nữ sinh viên với n độ tin cậy 95% là 155, 88 < µ < 157, 46. 3.1.4
KƯL cho trung bình µ của mẫu cỡ lớn
Giả sử mẫu ngẫu nhiên có cỡ mẫu n ≥ 30. Khoảng ước lượng (µ1, µ2) của trung bình
µ với độ tin cậy 1 − α được xác định bởi s s µ1 = x − z √ √ α/2 , µ2 = x + z (3.2) n α/2 n trong đó • ¯ x là trung bình mẫu • s là độ lệch mẫu • n là kích thước mẫu α • zα/2 là phân vị mức
của phân phối chuẩn tắc. 2
Ví dụ 3.1.4. Để ước lượng thu nhập trung bình trong một năm của nhân viên một tổng
công ty XYZ, người ta chọn ngẫu nhiên 150 nhân viên và tính được trung bình mẫu ¯ x =
280 (triệu đồng) với độ lệch mẫu s = 27 (triệu đồng). Hãy tìm khoảng ước lượng cho thu
nhập trung bình của nhân viên tổng công ty XYZ với độ tin cậy 95%. Lời giải. • Ta có s = 27, n = 150, ¯ x = 280.
• Vì 1 − α = 0, 95 nên α = 0, 05 và zα/2 = z0,025 = 1, 96. s • Tính được z √ α/2
= 4, 32. Vậy KƯL với độ tin cậy 95% cho thu nhập trung bình µ n
của nhân viên tổng công ty XYZ là 275, 68 < µ < 284, 32.
Ví dụ 3.1.5. Cho một loại ô tô chạy thử 40 lần từ địa điểm A tới địa điểm B, người ta ghi
nhận được lượng xăng tiêu thụ như sau.
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 38
Lượng xăng tiêu thụ (lít) Số lần chạy 9.6–9.8 5 9.8–10.0 8 10.0–10.2 11 10.2–10.4 10 10.4–10.6 6
Với độ tin cậy 99%, hãy ước lượng xăng tiêu thụ trung bình của loại ô tô này khi chạy từ A đến B. Lời giải. • Tính được n = 40, ¯ x = 10, 12, s = 0, 25.
• Vì 1 − α = 0, 99 nên α = 0, 01 và zα/2 = z0,005 = 2, 58. s • Tính được z √ α/2
= 0, 10. Vậy KƯL với độ tin cậy 95% cho lượng xăng tiêu thụ trung n
bình µ của loại ô tô đó là 10, 02 < µ < 10, 22. 3.1.5
KƯL cho mẫu nhỏ có phân phối chuẩn với σ2 chưa biết
Giả sử quần thể có phân phối chuẩn N (µ, σ2) với σ chưa biết và cỡ mẫu n ≤ 30.
Khoảng ước lượng (µ1, µ2) của µ với độ tin cậy 1 − α được xác định bởi s s µ1 = x − t √ √ α/2,n−1 , µ2 = x + t . (3.3) n α/2,n−1 n trong đó • ¯ x là trung bình mẫu • s là độ lệch mẫu • n là kích thước mẫu α
• tα/2,n−1 là phân vị mức
của phân phối Student T với n − 1 bậc tự do 2
Phân vị của phân phối Student Phân vị mức α của phân phối Student T với ν bậc tự
do được ký hiệu là tα,ν.
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 39
Ví dụ: Phân vị mức 0,025 của phân phối Student với 24 bậc tự do làt0,025,24 = 2, 064.
Chú ý Khi n đủ lớn (n ≥ 150) thì tα,n ≈ zα.
Ví dụ 3.1.6. Biết rằng trọng lượng một sản phẩm có phân phối chuẩn. Cân 25 sản phẩm
được chọn ngẫu nhiên, thu được trung bình mẫu ¯
x = 532g và độ lệch mẫu s = 12g. Với
độ tin cậy 95%, hãy tìm khoảng ước lượng cho trọng lượng trung bình của tất cả các sản phẩm. Lời giải. • Ta có n = 25, ¯ x = 532, s = 12.
• Vì 1 − α = 0, 95 nên α = 0, 05 và tα/2,n−1 = t0,025,24 = 2, 064. s • Tính được t √ α/2,n−1
= 4, 95. Vậy KƯL cho trong lượng trung bình µ của tất cả các n sản phẩm là 527, 05 < µ < 636, 95. 3.1.6
Vấn đề xác định cỡ mẫu
Với độ tin cậy cố định, kích thước mẫu càng lớn thì độ dài khoảng ước lượng càng
ngắn, nghĩa là độ chính xác của ước lượng càng cao.
Tuy nhiên kích thước mẫu càng lớn thì thời gian và công sức nghiên cứu càng nhiều.
Câu hỏi đặt ra là với độ tin cậy 1 − α cố định, cần chọn kích thước mẫu tối thiểu là
bao nhiêu để khoảng ước lượng của trung bình µ có sai số không vượt quá ε cho trước.
Công thức xác định cỡ mẫu σ
• Nếu σ đã biết. Vì ε = z √ α/2 nên chọn n zα/2σ 2 n ≈ ε
• Nếu σ chưa biết thì ta thực hiện một điều tra sơ bộ để tìm được phương sai mẫu
s2 ≈ σ2. Khi đó kích thước mẫu cần chọn là zα/2s 2 n ≈ ε 3.2
Khoảng ước lượng cho tỷ lệ 3.2.1 Đặt vấn đề
Câu hỏi: Để xác định xác suất nảy mầm của một loại hạt giống người ta phải làm thế nào?
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 40
Gieo 100 hạt giống, thấy có 80 hạt nảy mầm. Có thể nói tỉ lệ nảy mầm của tất cả các hạt giống là 80% không?
Một người khác cũng gieo 101 hạt giống. Hỏi tỉ lệ hạt nảy mầm trong 101 hạt này có thể là 80% hay không?
Để tăng độ tin cậy của kết luận, thay vì nói tỉ lệ nảy mầm p xấp xỉ một giá trị nào đó,
ta nói tỉ lệ nảy mầm p thuộc một khoảng (p1, p2) nào đó.
Xác định (p1, p2) như thế nào? 3.2.2
Công thức khoảng ước lượng cho tỷ lệ
Thực hiện một dãy phép thử độc lập n lần và gọi nA là số lần biến cố A xảy ra trong n lần thử đó. n
Tần suất xuất hiện của A trong n phép thử là f A n = . n
Khoảng ước lượng (p1, p2) cho xác suất biến cố A xuất hiện trong mỗi phép thử với độ tin cậy (1 − α) là r r fn(1 − fn) fn(1 − fn) p1 = fn − zα/2 , p2 = fn + z , (3.4) n α/2 n trong đó • n là số phép thử
• fn là tần suất xuất hiện của biến cố A trong n phép thử α • zα/2 là phân vị mức
của phân phối chuẩn tắc 2
• Nếu xác suất xuất hiện của A trong mỗi phép thử là p thì ta cũng nói rằng tỷ lệ xuất hiện của A là 100 × p%.
Ví dụ 3.2.1. Một viện nghiên cứu vừa phát triển một loại hạt giống. Để ước lượng tỷ lệ
hạt giống nẩy mầm, người ta gieo thử 100 hạt giống được chọn ngẫu nhiên và quan sát
thấy có 90 hạt nẩy mầm. Hãy tìm khoảng ước lượng cho tỷ lệ hạt nẩy mầm của loại hạt
giống đó với độ tin cậy 95% và 99%. Lời giải. • Ta có n = 100, fn = 0, 9.
(a) Độ tin cậy 95%:
• Vì 1 − α = 0, 95 nên α = 0, 05 và zα/2 = z0,025 = 1, 96. r f • z n(1 − fn) α/2 = 0, 0588. n
• Vậy KƯL cho xác suất nảy mầm của hạt giống với độ tin cậy 95% là (0, 8412, 0, 9588).
• KƯL cho tỉ lệ nảy mầm của hạt giống với độ tin cậy 95% là (84, 12%, 95, 88%).
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 41
(b) Độ tin cậy 99%:
• Vì 1 − α = 0, 99 nên α = 0, 01 và zα/2 = z0,005 = 2, 58. r f • z n(1 − fn) α/2 = 0, 0774. n
• Vậy KƯL cho xác suất nảy mầm của hạt giống với độ tin cậy 99% là (0, 8226, 0, 9774).
• KƯL cho tỉ lệ nảy mầm của hạt giống với độ tin cậy 99% là (82, 26%, 97, 74%). 3.2.3
Vấn đề xác định cỡ mẫu
Khi tăng độ tin cậy thì độ rộng của KƯL cũng tăng theo.
Câu hỏi đặt ra là với độ tin cậy 1 − α cố định, cần chọn kích thước mẫu tối thiểu là
bao nhiêu để ước lượng p với sai số không vượt quá ε cho trước? r f z2 fn(1 − fn) Vì α/2 = z n(1 − fn) α/2 nên chọn n ≈ . n ε2
Tuy nhiên ta không biết fn trước khi lấy mẫu!
Công thức xác định cỡ mẫu
Phương pháp 1: Điều tra sơ bộ
Tiến hành điều tra sơ bộ trên một mẫu cỡ vừa phải để được tần suất ˆ f ≈ fn ≈ p. Sau đó chọn z2 ˆ f (1 − ˆ f ) α/2 n ≈ . (3.5) ε2
Phương pháp 2: Không điều tra sơ bộ f 2 1 Do f n + 1 − fn n(1 − fn) ≤ =
nên để chắc chắn sai số không vượt quá ta chọn 2 4 z2α/2 n ≈ . (3.6) 4ε2 Nhận xét
• Nếu p gần với 0, 5 thì đánh giá ở hai cách trên tương đối giống nhau.
• Nhưng nếu p gần 0 hoặc gần 1, thì Phương pháp 1 thường cho cỡ mẫu nhỏ hơn Phương pháp 2.
Ví dụ 3.2.2. Với độ tin cậy 95%, xác định kích thước mẫu nhỏ nhất để sai số khi ước lượng
tỷ lệ p không vượt quá ε = 0, 01.
a. Giả sử rằng chúng ta không có thông tin gì về p.
b. Giả sử có một mẫu sơ bộ với f = 0, 9.
CHƯƠNG 3. KHOẢNG ƯỚC LƯỢNG 42 Lời giải.
• Độ tin cậy 1 − α = 0, 95 nên zα/2 = z0,025 = 1, 96.
• Khi không có thông tin gì về p, để chắc chắn chúng ta phải dùng phương pháp 2 để
xác định kích thước mẫu. Ta có z2α/2 n ≈ = 9604. 4.ε2
• Sử dụng phương pháp 1 để xác định kích thước mẫu, ta có z2 f (1 − f ) α/2 n ≈ = 3457, 4. ε2 Chương 4
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
Nội dung của chương
1. Đặt bài toán kiểm định giả thuyết.
2. So sánh trung bình, tỉ lệ cho một mẫu.
3. So sánh trung bình, tỉ lệ hai mẫu độc lập và phụ thuộc.
4. Kiểm định phân phối chuẩn.
Mục tiêu của chương
1. Hiểu được cách đặt bài toán và các khái niệm: giả thuyết, đối thuyết, sai lầm loại 1,
sai lầm loại 2, mức ý nghĩa, nguyên lý xây dựng tiêu chuẩn kiểm định.
2. Nhận biết được tình huống
• so sánh trung bình một mẫu, hai mẫu;
• so sánh tỉ lệ một mẫu, hai mẫu;
• so sánh hai mẫu độc lập và hai mẫu phụ thuộc;
• kiểm định một phía, hai phía.
3. Sử dụng quy trình 6 bước để giải bài toán kiểm định trung bình, tỉ lệ và diễn giải
chính xác kết quả thu được.
4. Nhận biết được mẫu ngẫu nhiên có phân phối chuẩn. 43
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 44 4.1
Tình huống thực tế
• Năng suất lúa trung bình của tỉnh Thái Bình năm 2015 là 66 tạ/ha.
• Khảo sát ngẫu nhiên 10 thửa ruộng ở huyện Đông Hưng thấy năng suất trung bình
của 10 thửa ruộng này là 68 tạ/ha và độ lệch mẫu s = 4 tạ/ha.
? Có thể kết luận là năng suất lúa ở Đông Hưng cao hơn năng suất trung bình của
tỉnh Thái Bình được hay không?
• Khảo sát ngẫu nhiên 50 thửa ruộng ở huyện Thái Thuỵ thấy năng suất trung bình
của 50 thửa ruộng này là 67 tạ/ha và độ lệch mẫu s = 2 tạ/ha.
? Có thể kết luận là năng suất lúa ở Thái Thuỵ cao hơn năng suất trung bình của tỉnh
Thái Bình được hay không? Mô hình hoá
• Gọi µ là năng suất lúa trung bình ở huyện.
• µ là tham số chưa biết.
• Ta muốn xem có phải µ > 66 hay không.
• Đưa về bài toán kiểm định
- giả thuyết H0 : µ = 66 với
- đối thuyết H1 : µ > 66.
• Dựa trên mẫu số liệu thu được ta cần phải chọn một trong hai quyết định:
- Bác bỏ giả thuyết H0 để ủng hộ đối thuyết H1;
- Không bác bỏ giả thuyết H0 để ủng hộ đối thuyết H1. Tức là chấp nhận H0 và không ủng hộ H1.
• Để chấp nhận hay bác bỏ H0 ta cần đưa ra một tiêu chuẩn. 4.2
Bài toán kiểm định giả thuyết tổng quát
• Giả thuyết thống kê là một phát biểu nào đó về tính chất của quần thể.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 45
• Kiểm định giả thuyết thống kê là một quy trình để xác minh xem có thể chấp nhận
giả thuyết thống kê hay không dựa trên mẫu số liệu quan sát được từ quần thể.
• Bài toán kiểm định giả thuyết cho tham số: Giả sử θ là một tham số chưa biết của
quần thể (Ví dụ: trung bình, tỉ lệ,...)
– Giả thuyết H0 : θ = θ0. – Đối thuyết 1. H1 : θ 6= θ0 2. H1 : θ > θ0 3. H1 : θ < θ0
Các loại bài toán kiểm định giả thuyết:
1. H1 : θ 6= θ0: Kiểm định hai phía
2. H1 : θ > θ0: Kiểm định một phía
3. H1 : θ < θ0: Kiểm định một phía 4.2.1 Miền tiêu chuẩn
• Kí hiệu mẫu ngẫu nhiên quan sát được là (X1, . . . , Xn).
• Miền S được gọi là miền tiêu chuẩn cho bài toán kiểm định giả thuyết H0 với đối thuyết H1 nếu
– khi (X1, . . . , Xn) ∈ S ta sẽ bác bỏ H0 để ủng hộ H1.
– khi (X1, . . . , Xn) 6∈ S ta sẽ chấp nhận H0 và không ủng hộ H1.
• Do ta đưa ra quyết định dựa trên mẫu số liệu nên có thể mắc phải sai lầm ⇒ Chọn
miền S sao cho xác suất mắc sai lầm là nhỏ nhất. 4.2.2 Các loại sai lầm Quyết định H0 đúng H1 đúng Bác bỏ giả thuyết H0 Sai lầm loại 1 Quyết định đúng
Chấp nhận giả thuyết H0 Quyết định đúng Sai lầm loại 2
• Nếu ta luôn chấp nhận H0 thì không mắc phải sai lầm loại 1 nhưng sẽ làm xác suất
mắc sai lầm loại 2 đạt cao nhất.
• Ngược lại, nếu ta luôn bác bỏ H0 thì không mắc phải sai lầm loại 2 nhưng sẽ làm
xác suất mắc sai lầm loại 1 đạt cao nhất.
• Không thể làm triệt tiêu đồng thời cả hai loại sai lầm!
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 46
Nguyên lý chung để tìm miền tiêu chuẩn:
• Trong tất cả các miền tiêu chuẩn có xác suất mắc sai lầm loại 1 không vượt quá
α ∈ (0, 1), chọn miền có xác suất mắc sai lầm loại 2 nhỏ nhất.
• α được gọi là mức ý nghĩa của tiêu chuẩn kiểm định tìm được ở trên.
• Mức ý nghĩa của một phép kiểm định là xác suất mắc sai lầm loại 1, tức là xác suất
bác bỏ giả thuyết H0 khi H0 đúng. 4.3
Bài toán kiểm định giả thuyết cho giá trị trung bình một mẫu
Ta nhắc lại vấn đề xác định năng suất lúa ở Thái Bình:
• Năng suất lúa trung bình của tỉnh Thái Bình năm 2015 là 66 tạ/ha.
• Khảo sát ngẫu nhiên 10 thửa ruộng ở huyện Đông Hưng thấy năng suất trung bình
của 10 thửa ruộng này là 68 tạ/ha và độ lệch mẫu s = 4 tạ/ha.
? Có thể kết luận là năng suất lúa ở Đông Hưng cao hơn năng suất trung bình của
tỉnh Thái Bình được hay không?
Nội dung của bài: So sánh giá trị trung bình của một quần thể với một giá trị cho
trước trong các trường hợp:
1. Mẫu có phân phối chuẩn với phương sai đã biết.
2. Mẫu cỡ lớn với phương sai chưa biết.
3. Mẫu có phân phối chuẩn với phương sai chưa biết. 4.3.1
Bài toán 1: So sánh trung bình của mẫu có phân phối chuẩn với
phương sai σ2 đã biết
Giả sử (X1, . . . , Xn) là mẫu ngẫu nhiên quan sát được từ phân phối chuẩn N (µ, σ2) với σ2 đã biết.
• Giả thuyết H0 : µ = µ0. x − µ
• Thống kê kiểm định: Z 0 0 = √ . σ/ n Đối thiết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µ 6= µ0 |Z0| > zα/2 H1 : µ > µ0 Z0 > zα H1 : µ < µ0 Z0 < −zα
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 47 Ví dụ 4.3.1.
• Năng suất lúa trung bình của tỉnh Thái Bình năm 2015 là 66 tạ/ha.
• Khảo sát ngẫu nhiên 10 thửa ruộng ở huyện Đông Hưng thấy năng suất trung bình
của 10 thửa ruộng này là 68 tạ/ha.
• Biết rằng năng suất của mỗi thửa ruộng có phân phối chuẩn với độ lệch chuẩn σ = 4 tạ/ha.
• Hãy kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất trung bình
của tỉnh Thái Bình được hay không, cho mức ý nghĩa α = 5%?
Ta áp dụng quy trình 6 bước như sau để giải bài toán kiểm định giả thuyết. Lời giải.
1. Tham số cần kiểm định là năng suất lúa trung bình của huyện Đông
Hưng, kí hiệu là µ tạ/ha.
2. Ta cần kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất trung bình
của tỉnh Thái Bình được hay không, do đó ta có bài toán kiểm định H0 : µ = 66 với H1 : µ > 66.
3. Cỡ mẫu n = 10; trung bình mẫu ¯
x = 68; độ lệch chuẩn σ = 4.
4. Mức ý nghĩa α = 5% nên zα = 1, 645. 68 − 66
5. Thống kê kiểm định Z0 = √ = 1, 5811. 4/ 10
6. Do Z0 < zα nên ta không bác bỏ H0 : µ = 66 để ủng hộ H1 : µ > 66 ở mức ý nghĩa α = 5%.
Vậy ta không có đủ căn cứ để kết luận năng suất lúa của huyện Đông Hưng cao hơn
của tỉnh Thái Bình dựa trên mẫu gồm 10 số liệu đã thu được.
? a) Với mẫu số liệu trong Ví dụ 1, hãy kiểm định xem có sự khác biệt giữa năng suất
lúa của huyện Đông Hưng và của tỉnh Thái Bình không?
b) Kết luận trong Ví dụ 1 có thay đổi không trong mỗi trường hợp sau:
(i) Độ lệch chuẩn σ = 2. (ii) Cỡ mẫu n = 50.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 48 4.3.2
Bài toán 2: So sánh giá trị trung bình của mẫu cỡ lớn với phương sai chưa biết
Giả sử (X1, . . . , Xn) là mẫu ngẫu nhiên quan sát được từ quần thể có trung bình µ và n ≥ 30.
• Giả thuyết H0 : µ = µ0. x − µ
• Thống kê kiểm định: Z 0 0 = √ . s/ n Đối thiết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µ 6= µ0 |Z0| > zα/2 H1 : µ > µ0 Z0 > zα H1 : µ < µ0 Z0 < −zα
Ví dụ 4.3.2. Trọng lượng ghi trên bao bì của mỗi gói mì chính là 2kg. Lấy mẫu ngẫu
nhiên gồm 100 gói thì thấy trọng lượng trung bình của 100 gói này là 2002g và độ lệch
mẫu s = 5g. Với mức ý nghĩa α = 0, 05 hãy cho biết trọng lượng các gói mì chính có đúng như công bố không? Lời giải.
1. Tham số cần kiểm định là trọng lượng trung bình của mỗi gói mì chính, kí hiệu là µ gam.
2. Ta cần kiểm định xem trọng lượng các gói mì chính có đúng như công bố không,
do đó ta có bài toán kiểm định H0 : µ = 2000 với H1 : µ 6= 2000.
3. Cỡ mẫu n = 100; trung bình mẫu ¯
x = 2002; độ lệch mẫu s = 5.
4. Mức ý nghĩa α = 5% nên zα/2 = 1, 96.
5. Tiêu chuẩn kiểm định: 2002 − 2000 Z0 = √ = 4. 5/ 100
6. Do |Z0| > zα/2 nên ta bác bỏ H0 : µ = 2000 để ủng hộ H1 : µ 6= 2000 ở mức ý nghĩa α = 5%.
Vậy ta có đủ căn cứ để kết luận rằng trọng lượng của mỗi gói mì chính không giống
như trong công bố của nhà sản xuất dựa trên mẫu 100 số liệu đã thu được.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 49 4.3.3
Bài toán 3: So sánh giá trị trung bình của mẫu có phân phối chuẩn
với phương sai chưa biết
Giả sử (X1, . . . , Xn) là mẫu ngẫu nhiên quan sát được từ phân phối chuẩn N (µ, σ2) với σ2 chưa biết.
• Giả thuyết H0 : µ = µ0. x − µ
• Thống kê kiểm định: T 0 0 = √ . s/ n Đối thiết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µ 6= µ0 |T0| > tα/2;n−1 H1 : µ > µ0 T0 > tα;n−1 H1 : µ < µ0 Z0 < −tα;n−1
Chú ý: Khi n > 100 thì tα;n ≈ zα. Ví dụ 4.3.3.
• Năng suất lúa trung bình của tỉnh Thái Bình năm 2015 là 66 tạ/ha.
• Khảo sát ngẫu nhiên 10 thửa ruộng ở huyện Đông Hưng thấy năng suất trung bình
của 10 thửa ruộng này là 68 tạ/ha và độ lệch mẫu s = 4 tạ/ha.
• Biết rằng năng suất của mỗi thửa ruộng có phân phối chuẩn.
• Hãy kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất trung bình
của tỉnh Thái Bình được hay không, cho mức ý nghĩa α = 5%? Lời giải.
1. Tham số cần kiểm định là năng suất lúa trung bình của huyện Đông
Hưng, kí hiệu là µ tạ/ha.
2. Ta cần kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất trung bình
của tỉnh Thái Bình được hay không, do đó ta có bài toán kiểm định H0 : µ = 66 với H1 : µ > 66.
3. Cỡ mẫu n = 10; trung bình mẫu ¯
x = 68; độ lệch mẫu s = 4.
4. Mức ý nghĩa α = 5% nên tα;n−1 = t0,05;9 = 1, 833. 68 − 66
5. Thống kê kiểm định T0 = √ = 1, 5811. 4/ 10
6. Do T0 < tα;n−1 nên ta không bác bỏ H0 : µ = 66 để ủng hộ H1 : µ > 68 ở mức ý nghĩa α = 5%.
Vậy ta không có đủ căn cứ để kết luận năng suất lúa của huyện Đông Hưng cao hơn
của tỉnh Thái Bình dựa trên mẫu gồm 10 số liệu đã thu được.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 50 Luyện tập
4.3.1. Trước đây trung bình thời gian gia công một chi tiết máy là 10 phút. Sau khi cải
tiến phương pháp, có ý kiến cho rằng, thời gian gia công một chi tiết máy có giảm xuống.
Để kết luận được vấn đề này, người ta khảo sát thời gian gia công chi tiết máy của 25 công
nhân và thu được bảng số liệu sau: X 9,3 9,5 9,7 9,8 10 10,2 10,4 10,6 Số công nhân 3 2 5 4 4 3 2 2
Với mức ý nghĩa 0, 05 hãy kiểm định xem ý kiến trên có đúng không, biết rằng thời
gian gia công có phân phối chuẩn với độ lệch chuẩn σ = 0, 2 phút. Lời giải.
1. Tham số cần kiểm định là thời gian gia công trung bình của một chi tiết máy, kí hiệu là µ phút.
2. Ta cần kiểm định xem thời gian gia công một chi tiết máy có giảm xuống được hay
không, do đó ta có bài toán kiểm định H0 : µ = 10 với H1 : µ < 10.
3. Cỡ mẫu n = 25; trung bình mẫu ¯
x = 9, 888; độ lệch chuẩn σ = 0, 04.
4. Mức ý nghĩa α = 5% nên zα = 1, 645. √ x − µ (9, 888 − 10) 25
5. Thống kê kiểm định Z 0 0 = √ = = −2, 8. σ/ n 0, 2
6. Do Z0 < −zα nên ta bác bỏ H0 : µ = 10 để ủng hộ H1 : µ < 10 ở mức ý nghĩa α = 5%.
Vậy ta có đủ căn cứ để kết luận rằng thời gian gia công một chi tiết máy có giảm
xuống dựa trên mẫu gồm 25 số liệu thu được.
4.3.2. Cự ly ném tạ trung bình của nữ sinh trường A là 12m. Khảo sát kết quả của 36 nữ
sinh trường B thu được số liệu: X (m) 11,2 11,5 11,8 12 12,3 12,6 13 13,2 Số sinh viên 5 5 5 4 4 5 4 4
Với mức ý nghĩa 5% hãy cho biết cự ly ném tạ trung bình của sinh viên hai trường có như nhau không?
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 51 Lời giải.
1. Tham số cần kiểm định là cự ly ném tạ trung bình của nữ sinh trường B, kí hiệu là µ.
2. Ta cần kiểm định xem cự ly ném tạ trung bình của nữ sinh hai trường có như nhau
không, do đó ta có bài toán kiểm định H0 : µ = 12 với H1 : µ 6= 12.
3. Cỡ mẫu n = 36; trung bình mẫu ¯
x = 12, 15; độ lệch mẫu s = 0, 7203.
4. Mức ý nghĩa α = 5% nên zα/2 = 1, 96. √ x − µ (12, 15 − 12) 36
5. Thống kê kiểm định Z 0 0 = √ = = 1, 249. σ/ n 0, 7203
6. Do |Z0| < zα nên ta không bác bỏ H0 : µ = 12 để ủng hộ H1 : µ 6= 12 ở mức ý nghĩa α = 5%.
Vậy ta không có đủ căn cứ để kết luận rằng cự ly ném tạ trung bình của nữ sinh hai
trường là khác nhau dựa trên mẫu gồm 36 số liệu thu được.
4.3.3. Năm ngoái, trọng lượng trung bình sau 4 tháng tuổi của lợn là 90kg. Năm nay,
người ta đổi mới phương pháp chăn nuôi, nên có ý kiến cho rằng trọng lượng trung bình
năm nay cao hơn năm ngoái. Để kết luận được vấn đề, người ta đem cân thử 25 con lợn
4 tháng tuổi thì thu được bảng số liệu: X (kg) 88,5 89,0 89,5 90,0 91,0 92,0 93 94 Số con 3 2 5 4 4 3 2 2
Hãy kiểm định xem ý kiến trên có đúng không, cho mức ý nghĩa α = 5%. Lời giải.
1. Tham số cần kiểm định là trọng lượng trung bình sau 4 tháng tuổi của lợn, kí hiệu là µ kg.
2. Ta cần kiểm định xem trọng lượng trung bình năm nay cao hơn năm ngoái hay
không, do đó ta có bài toán kiểm định H0 : µ = 90 với H1 : µ > 90.
3. Cỡ mẫu n = 25; trung bình mẫu ¯
x = 90, 6; độ lệch mẫu s = 1, 67.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 52
4. Mức ý nghĩa α = 5% nên tα,n−1 = t0,05;24 = 1, 71. √ (90, 6 − 90) 25
5. Thống kê kiểm định T0 = ≈ 1, 796. 1, 67
6. Do T0 > tα,n−1 nên ta bác bỏ H0 : µ = 90 để ủng hộ H1 : µ 6= 90 ở mức ý nghĩa α = 5%.
Vậy ta có đủ căn cứ để kết luận rằng trọng lượng trung bình của giống lợn đó có
tăng lên dựa trên mẫu gồm 25 số liệu thu được. 4.4
Bài toán kiểm định giả thuyết về tỉ lệ 4.4.1
Tình huống thực tế
Hỏi ngẫu nhiên 20 sinh viên năm thứ nhất của trường ĐHSP Hà Nội thấy có 12 em
đạt điểm A môn Thống kê Xã hội học.
? Tỉ lệ học sinh đạt điểm A trong mẫu là bao nhiêu?
? Tìm khoảng ước lượng với độ tin cậy 95% cho số sinh viên đạt điểm A.
? Có thể kết luận trong toàn trường tỉ lệ sinh viên năm thứ nhất đạt điểm A môn
Thống kê Xã hội học là 0,5 được không? Mô hình toán học
• Gọi p × 100% là tỉ lệ sinh viên đạt điểm A.
• p là đại lượng chưa biết.
• Ta muốn xem có phải p = 0, 5 hay không.
• Đưa về bài kiểm định
- Giả thuyết H0 : p = 0, 5 với
- Đối thuyết H1 : p 6= 0, 5.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 53 4.4.2
Bài toán kiểm định giả thuyết cho tỉ lệ
Giả sử tỉ lệ p các phần tử có tính chất A nào đó trong quần thể là chưa biết.
Ta cần so sánh p với số p0 cho trước.
Các bài toán kiểm định giả thuyết cho p như sau:
• Giả thuyết H0 : p = p0. • Đối thuyết 1. H1 : p 6= p0; 2. H1 : p > p0; 3. H1 : p < p0. 4.4.3
Tiêu chuẩn kiểm định
• Giả thuyết H0 : p = p0. (f − p √
• Thống kê kiểm định: Z 0) 0 = n. pp0(1 − p0) Đối thuyết Tiêu chuẩn bác bỏ H1 : p 6= p0 |Z0| > zα/2 H1 : p > p0 Z0 > zα H1 : p < p0 Z0 < −zα
Ví dụ 4.4.1. Những năm trước nhà máy áp dụng công nghệ A sản xuất thì có tỷ lệ phế phẩm là 6%.
Năm nay nhà máy nhập công nghệ B để sản xuất, hy vọng sẽ giảm được tỷ lệ phế
phẩm. Lấy ngẫu nhiên 100 sản phẩm để kiểm tra thì thấy có 5 phế phẩm.
Với mức ý nghĩa 5%, có thể cho rằng tỷ lệ phế phẩm của công nghệ B nhỏ hơn công nghệ A hay không. Lời giải.
1. Tham số cần kiểm định là tỉ lệ phế phẩm của nhà máy khi sản xuất theo
công nghệ B, kí hiệu là p.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 54
2. Sản xuất theo công nghệ A có tỷ lệ phế phẩm là 6%; hy vọng giảm được tỷ lệ phế
phẩm nên là bài toán kiểm định 1 phía.
Giả thuyết H0 : p = 0, 06, đối thuyết H1 : p < 0, 06. 5 3. n = 100, f = = 0, 05, p0 = 0, 06. 100
4. Mức ý nghĩa 5% nên zα = z0,05 = 1, 65. (f − p √
5. Thống kê kiểm định Z 0) 0 = n = −0, 42. pp0(1 − p0)
6. Z0 > −zα nên ta không bác bỏ giả thuyết H0 : p = 0, 06 để ủng hộ giả thuyết
H1 : p < 0, 06 ở mức ý nghĩa α = 5%.
Vậy ta không đủ căn cứ để kết luận công nghệ B giảm được tỷ lệ phế phẩm dựa trên
mẫu 100 dữ liệu cho quan sát được.
Ví dụ 4.4.2. Tổng điều tra trên một khu vực 5 năm trước cho thấy có 5% dân số ở độ tuổi
trưởng thành không biết chữ.
Năm nay điều tra ngẫu nhiên 400 người ở độ tuổi trưởng thành thì có 22 người không biết chữ.
Với mức ý nghĩa 5%, hãy cho biết tỷ lệ mù chữ năm nay có thay đổi so với 5 năm trước hay không? Lời giải.
1. Gọi p là tỉ lệ người không biết chữ năm nay.
2. 5 năm trước có 5% dân số ở độ tuổi trưởng thành không biết chữ; tỷ lệ mù chữ năm
nay có thay đổi so với 5 năm trước hay không nên là bài toán kiểm định 2 phía.
Giả thuyết H0 : p = 0, 05, đối thuyết H1 : p 6= 0, 05. 22 3. n = 400, f = = 0, 055, p0 = 0, 05. 400
4. Mức ý nghĩa 5% nên zα/2 = z0,025 = 1, 96. (f − p √
5. Thống kê kiểm định Z 0) 0 = n = 0, 4588. pp0(1 − p0)
6. |Z0| < zα/2 nên chấp nhận giả thuyết H0, bác bỏ giả thuyết H1 ở mức ý nghĩa 5%.
Vậy ta không đủ căn cứ để kết luận tỷ lệ mù chữ năm nay thay đổi so với 5 năm
trước dựa trên mẫu 400 số liệu thu được.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 55 4.5
Bài toán so sánh hai giá trị trung bình 4.5.1
Tình huống thực tế
• Một trại chăn nuôi chọn một giống gà để tiến hành nghiên cứu hiệu quả của hai
loại thức ăn A và B. Sau một thời gian nuôi thử nghiệm người ta chọn:
• 50 con gà nuôi bằng thức ăn A thì thấy khối lượng trung bình là ¯ x = 2, 2 kg, độ lệch mẫu là sX = 1, 25 kg.
• 40 con gà nuôi bằng thức ăn B thì thấy khối lượng trung bình là ¯ y = 1, 2 kg, độ lệch mẫu là sY = 1, 02 kg.
? Hãy đánh giá hiệu quả của hai loại thức ăn? Mô hình toán học
• Gọi µX, µY là trọng lượng trung bình của gà nuôi bằng thức ăn loại A, B tương ứng.
• Ta cần so sánh µX, µY ?
• Đưa về bài toán kiểm định:
- Giả thuyết H0 : µX = µY với
- Đối thuyết H1 : µX 6= µY
Nội dung của bài So sánh hai giá trị trung bình của hai quần thể trong các trường hợp sau:
1. Quần thể có phân phối chuẩn với phương sai đã biết.
2. Quần thể có phân phối chuẩn với cùng một giá trị phương sai chưa biết.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 56 4.5.2
So sánh hai giá trị trung bình
• Các cá thể của quần thể X có phân phối chuẩn N (µX, σ2 ). X
• Gọi (X1, . . . , Xn ) là mẫu ngẫu nhiên quan sát được từ quần thể X. X
• Các cá thể của quần thể Y có phân phối chuẩn N (µY , σ2 ). Y
• Gọi (Y1, . . . , Yn ) là mẫu ngẫu nhiên quan sát được từ quần thể Y . Y
• Dựa trên hai mẫu, ta muốn so sánh giá trị trung bình µX và µY .
Bài toán kiểm định
• Giả thuyết H0 : µX = µY . • Đối thuyết 1. H1 : µX 6= µY ; 2. H1 : µX > µY ; 3. H1 : µX < µY . 4.5.3
Bài toán 1: So sánh giá trị trung bình của hai mẫu có phân phối
chuẩn với phương sai đã biết
Giả sử σX, σY là đã biết.
Tiêu chuẩn kiểm định
• Giả thiết H0 : µX = µY . (x − y)
• Thống kê kiểm định: Z0 = . q σ2 σ2 X + Y nX nY Đối thuyết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µX 6= µY |Z0| > zα/2 H1 : µX > µY Z0 > zα H1 : µX < µY Z0 < −zα
trong đó x, y là trung bình của mẫu X, Y tương ứng.
Ví dụ 4.5.1. Học sinh hai trường A và B cùng học môn Toán, khảo sát kết quả thi hết môn
ta thu được kết quả như sau: • Trường A: n = 64, ¯ x = 7, 32. • Trường B: n = 68, ¯ y = 7, 66.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 57
Biết rằng điểm thi của hai trường là biến ngẫu nhiên có phân phối chuẩn với độ lệch
chuẩn tương ứng là σ1 = 1, 09; σ2 = 1, 12.
Với mức ý nghĩa 1% có thể cho rằng kết quả thi của trường B cao hơn trường A hay không? Lời giải.
1. Gọi X, Y là kết quả thi của trường A, B tương ứng. Ta có X ∼ N (µ1, σ2), Y ∼ 1 N (µ2, σ2). 2
2. Kết quả thi của trường B cao hơn trường A hay không nên ta có bài toán kiểm định 1 phía.
Giả thuyết H0 : µ1 = µ2, đối thuyết H1 : µ1 < µ2. 3. nX = 64, ¯
x = 7, 32, σ1 = 1, 09; nY = 68, ¯ y = 7, 66, σ2 = 1, 12.
4. α = 1% nên zα = z0,01 = 2, 33. 7, 32 − 7, 66 5. Thống kê Z0 = = −31, 43. r 1, 092 1, 122 + 64 68
6. Ta có Z0 < −zα nên ta bác bỏ giả thuyết H0 : µ1 = µ2 để ủng hộ đối thuyết H1 : µ1 <
µ2 ở mức ý nghĩa α = 1%.
Vậy ta có đủ căn cứ kết luận kết quả thi ở trường B cao hơn trường A dựa trên 2 mẫu thu được. 4.5.4
Bài toán 2: So sánh hai giá trị trung bình của hai mẫu có phân
phối chuẩn với phương sai σX = σY = σ2 chưa biết
Tiêu chuẩn kiểm định
• Giả thiết H0 : µX = µY . x − y
• Thống kê kiểm định: T0 = . q (n q X −1)s2 +(n X Y −1)s2 Y 1 + 1 nX +nY −2 nX nY Đối thuyết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µX 6= µY |T0| > tα/2,nX+nY −2 H1 : µX > µY T0 > tα,nX+nY −2 H1 : µX < µY T0 < −tα,nX+nY −2 trong đó:
• x, y là trung bình mẫu X, Y tương ứng.
• sX, sY là độ lệch mẫu X, Y tương ứng.
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 58
Ví dụ 4.5.2. Điều tra thu nhập (đơn vị tính $) trong một tháng của công nhân ở hai nhà
máy sản xuất thiết bị điện tử A và B ta thu được số liệu sau: • Nhà máy A: 91, 50; 94, 18; 92, 18; 95, 39; 91, 79. • Nhà máy B: 90, 46; 93, 21; 97, 19; 97, 04; 91, 07; 92, 75.
Với mức ý nghĩa 5% có thể cho rằng thu nhập trung bình của công nhân trong hai nhà
máy trên là như nhau hay không, biết rằng thu nhập trong hai nhà máy có phân phối chuẩn. Lời giải.
1. Gọi X, Y lần lượt có phân phối chuẩn N (µX, σ2 ), N (µ ) là thu nhập X Y , σ2 Y
của nhà máy A và B tương ứng. Ta cần so sánh µX và µY .
2. Thu nhập trung bình của công nhân trong hai nhà máy trên là như nhau hay không
nên có bài toán kiểm định giả thuyết H0 : µX = µY , đối thuyết H1 : µX 6= µY .
3. x = 93, 008; s2 = 2, 873; y = 93, 62; s2 = 8, 371. X Y 93, 008 − 93, 62 4. Thống kê T0 = = −0, 145. r 4.2, 873 + 5.8, 371q1 + 1 5 + 6 − 2 5 6
5. nX = 5; nY = 6; α = 5%. Tra bảng phân phối Student được tα/2,nX+nY −2 = t0,025,9 = 2, 262.
6. Ta có |T0| < tα/2,nX+nY −2 nên ta không bác bỏ H0 : µX = µY để ủng hộ H1 : µX 6= µY ở mức ý nghĩa α = 5%.
Vậy ta có đủ căn cứ để kết luận thu nhập của công nhân hai nhà máy là như nhau
dựa trên hai mẫu đã thu được. 4.6
Bài toán so sánh hai tỉ lệ 4.6.1
Tình huống thực tế
• Để so sánh chất lượng sản phẩm của hai công ty X và Y sản xuất, người ta lấy:
30 sản phẩm của công ty X thấy có 12 sản phẩm đạt loại A.
40 sản phẩm của công ty Y thấy có 14 sản phẩm đạt loại A.
? Hỏi chất lượng sản phẩm của 2 công ty có như nhau không? Mô hình toán học
• Gọi pX, pY là tỉ lệ sản phẩm loại A do công ty X, Y sản xuất tương ứng.
• Ta cần so sánh pX với pY .
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 59
• Đưa về bài toán kiểm định:
-Giả thuyết H0 : pX = pY với -Đối thuyết H1 : pX 6= pY 4.6.2 So sánh hai tỉ lệ
Ta cần so sánh pX, pY là tỉ lệ của số phần tử có cùng tính chất A nào đó của hai quần
thể X và Y tương ứng với mức ý nghĩa α.
Tiêu chuẩn kiểm định
• fX, fY là tỉ lệ số phần tử có cùng tính chất A trong mẫu X, Y tương ứng.
• nX, nY là kích thước mẫu X, Y tương ứng.
• kX, kY là số phần tử có tính chất A trong mẫu X, Y tương ứng.
• Giả thuyết H0 : pX = pY . f k
• Thống kê kiểm định: Z X − fY X + kY 0 = với f = . qf(1 − f)nX+nY nX + nY nX nY Đối thuyết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : pX 6= pY |Z0| > zα/2 H1 : pX > pY Z0 > zα H1 : pX < pY Z0 < −zα
Ví dụ 4.6.1. Điều tra hiện tượng học sinh bỏ học ở hai vùng nông thôn A và B ta thu được số liệu sau:
• Vùng A: Điều tra 1900 em có 175 em bỏ học.
• Vùng B: Điều tra 2600 em có 325 em bỏ học.
Có ý kiến cho rằng tình trạng học sinh bỏ học ở vùng A là ít phổ biến hơn vùng B. Với
mức ý nghĩa 5% hãy cho biết ý kiến đó đúng hay sai. Lời giải.
• Gọi pA, pB là tỷ lệ học sinh bỏ học ở vùng A, B tương ứng. Ta cần so sánh pA và pB.
• Tình trạng học sinh bỏ học ở vùng A là ít phổ biến hơn vùng B nên có bài toán kiểm định giả thuyết:
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 60
Giả thuyết H0 : pA = pB, đối thuyết H1 : pA < pB. 175 325 • fA = = 0, 092; fB = = 0, 125; 1900 2600 175 + 325 f = = 0, 111 1900 + 2600
• Mức ý nghĩa α = 5% nên zα = z0,05 = 1, 65. 0, 092 − 0, 125
• Thống kê kiểm định Z0 = = −3, 48 q 0, 111(1 − 0, 111) 1900+2600 1900.2600
• Ta có Z0 < −zα nên ta bác bỏ H0 : pA = pB để ủng hộ H1 : pA < pB ở mức ý nghĩa α = 5%.
Vậy có đủ căn cứ để kết luận tỉ lệ học sinh bỏ học ở vùng A là ít nghiêm trọng hơn
vùng B dựa trên 2 mẫu thu . Luyện tập
4.6.1. Đo huyết sắc tố cho 50 công nhân nông trường thấy có 30 người ở mức dưới 110g/l.
Số liệu chung của khu vực này là 30% ở mức dưới 110g/l. Với mức ý nghĩa α = 0, 05, có
thể kết luận tỉ lệ công nhân nông trường có huyết sắc tố dưới 110g/l cao hơn mức chung hay không? Lời giải.
• Tham số cần kiểm định là tỉ lệ công nhân nông trường có huyết sắc tố
dưới 110g/l, kí hiệu là p
• Tỉ lệ chung của khu vực là 30%; tỉ lệ công nhân nông trường có huyết sắc tố dưới
110g/l cao hơn mức chung nên có bài toán kiểm định giả thuyết:
Giả thuyết H0 : p = 0, 3, đối thuyết H1 : p > 0, 3. 30 • n = 50, f = = 0, 6, p0 = 0, 3. 50
• Mức ý nghĩa α = 5% nên zα = z0,05 = 1, 65. 0, 6 − 0, 3 √
• Thống kê kiểm định Z0 = 50 = 4, 629 p0, 3(1 − 0, 3)
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 61
• Ta có Z0 > zα nên ta bác bỏ H0 : p = 0, 3 để ủng hộ H1 : p > 0, 3 ở mức ý nghĩa α = 5%.
Vậy ta có đủ căn cứ để kết luận tỉ lệ công nhân nông trường có huyết sắc tố dưới
110g/l cao hơn mức chung dựa trên mẫu 50 dữ liệu thu được.
4.6.2. Điều tra tỉ lệ béo phì ở hai địa bàn A và B, người ta thu được số liệu sau:
• Địa bàn A: Điều tra 200 em thấy có 20 em béo phì.
• Địa bàn B: Điều tra 220 em thấy có 5 em béo phì.
Hãy kiểm định xem tỉ lệ trẻ em béo phì ở hai địa bàn có như nhau không với mức ý nghĩa 5% Lời giải.
• Gọi pA, pB là tỷ lệ trẻ em béo phì ở địa bàn A, B tương ứng. Ta cần so sánh pA và pB.
• Tỉ lệ trẻ em béo phì ở hai địa bàn có như nhau không nên có bài toán kiểm định giả thuyết:
Giả thuyết H0 : pA = pB, đối thuyết H1 : pA 6= pB. 20 5 20 + 5 • fA = = 0, 1; fB = = 0, 023; f = = 0, 06 200 220 200 + 220
• Mức ý nghĩa α = 5% nên zα/2 = z0,025 = 1, 96. 0, 1 − 0, 023
• Thống kê kiểm định Z0 = = 3, 319 q 0, 06(1 − 0, 06) 200+220 200.220
• Ta có |Z0| > zα/2 nên ta bác bỏ H0 : pA = pB để ủng hộ H1 : pA 6= pB ở mức ý nghĩa α = 5%.
Vậy ta có đủ căn cứ để kết luận tỉ lệ béo phì ở hai địa bàn là không như nhau dựa
trên hai mẫu dữ liệu thu được. Bảng phân phối Z z 1
Bảng giá trị phân phối chuẩn tắc Φ(z) = √ e− x2 2 dx. −∞ 2π 62
CHƯƠNG 4. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 63
Bảng giá trị phân phối student tα,n P[tn > tα,n] = α
Bảng giá trị của phân phối χ-bình phương c2α,n P[χ2 > c2 ] = α n α,n
Document Outline
- MT S KIN THC XÁC SUT C S
- Ðinh nghıa xác sut
- Phép th ngu nhiên
- Không gian mu và Bin c s cp
- Bin c
- Phép toán trên các bin c
- Mi quan h gia các bin c
- Ðinh nghıa xác sut c in
- Tính cht cua xác sut
- Ðinh nghıa xác sut theo thng kê
- S c lp
- Hai bin c c lp
- Dãy bin c c lp
- Dãy phép th Bernoulli
- Công thc xác sut nhi thc
- Bin ngu nhiên ri rac
- Ðinh nghıa
- Phân phi cua bin ngu nhiên
- Các s c trng
- Ý nghıa cua ky vong và phng sai
- Phân phi nhi thc
- Tính cht cua ky vong và phng sai
- Bin ngu nhiên liên tuc và Phân phi chun
- Bin ngu nhiên liên tuc
- Hàm mt
- Các s c trng
- Phân phi chun
- Tính cht cua phân phi chun
- Xp xi phân phi nhi thc bng phân phi chun
- Ðinh nghıa xác sut
- MU NGU NHIÊN
- Gii thiu v Thng kê
- Mu và qun th
- Quy trình nghiên cu thng kê
- Các bài toán thng kê se hoc:
- Thu thp d liu
- Xác inh d liu cn thu thp
- D liu s cp và th cp
- Ly mu hoàn lai và không hoàn lai
- Quy tc ly mu
- Phng pháp ly mu gian n
- Các phng pháp ly mu khác
- Trình bày d liu bng bang và biu
- Biu thân-lá (stem-and-leaf diagram)
- Tn s
- Bang tn s
- Biu tn s
- Biu tn sut
- S liu và các s c trng
- Bin s
- Phân loai bin s
- Các s o giá tri trung tâm
- Các s o phân tán
- Thng kê
- Gii thiu v Thng kê
- KHOANG C LNG
- Khoang c lng cho trung bình
- Ðt vn
- Khoang c lng
- KL cho trung bình khi 2 ã bit
- KL cho trung bình cua mu c ln
- KL cho mu nho có phân phi chun vi 2 cha bit
- Vn xác inh c mu
- Khoang c lng cho ty l
- Ðt vn
- Công thc khoang c lng cho ty l
- Vn xác inh c mu
- Khoang c lng cho trung bình
- KIM ÐINH GIA THUYT THNG KÊ
- Tình hung thc t
- Bài toán kim inh gia thuyt tng quát
- Min tiêu chun
- Các loai sai lm
- Bài toán kim inh gia thuyt cho giá tri trung bình mt mu
- Bài toán 1: So sánh trung bình cua mu có phân phi chun vi phng sai 2 ã bit
- Bài toán 2: So sánh giá tri trung bình cua mu c ln vi phng sai cha bit
- Bài toán 3: So sánh giá tri trung bình cua mu có phân phi chun vi phng sai cha bit
- Bài toán kim inh gia thuyt v ti l
- Tình hung thc t
- Bài toán kim inh gia thuyt cho ti l
- Tiêu chun kim inh
- Bài toán so sánh hai giá tri trung bình
- Tình hung thc t
- So sánh hai giá tri trung bình
- Bài toán 1: So sánh giá tri trung bình cua hai mu có phân phi chun vi phng sai ã bit
- Bài toán 2: So sánh hai giá tri trung bình cua hai mu có phân phi chun vi phng sai X = Y=2 cha bit
- Bài toán so sánh hai ti l
- Tình hung thc t
- So sánh hai ti l


