
























































Preview text:
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ SÀI GÒN BAN KHOA HỌC CƠ BẢN BỘ MÔN TOÁN
BÀI GIẢNG TÓM TẮT TOÁN CAO CẤP A1 TP HCM - 2022 1 Chương 1
PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN A. HÀM SỐ
§1. HÀM SỐ SƠ CẤP CƠ BẢN
1.1. Hàm lũy thừa y = xα (α : Const )
Chú ý: Miền xác định D của hàm số y = xα phụ thuộc vào α. Trường hợp α là số vô tỉ, ta có
D = [0; +∞) nếu α > 0; D = (0; +∞) nếu α < 0. 0 – 1
1.2. Hàm số mũ: y = ax (0 < a ≠ 1 : Const )
Hàm số y = ax có miền xác định D = R, miền giá trị là (0; +∞).
1.3. Hàm số logarit: y = logax (0 < a ≠ 1 : Const )
Hàm số y = logax có miền xác định D = (0; +∞), miền giá trị là R.
1.4. Hàm số lượng giác và hàm ngược:
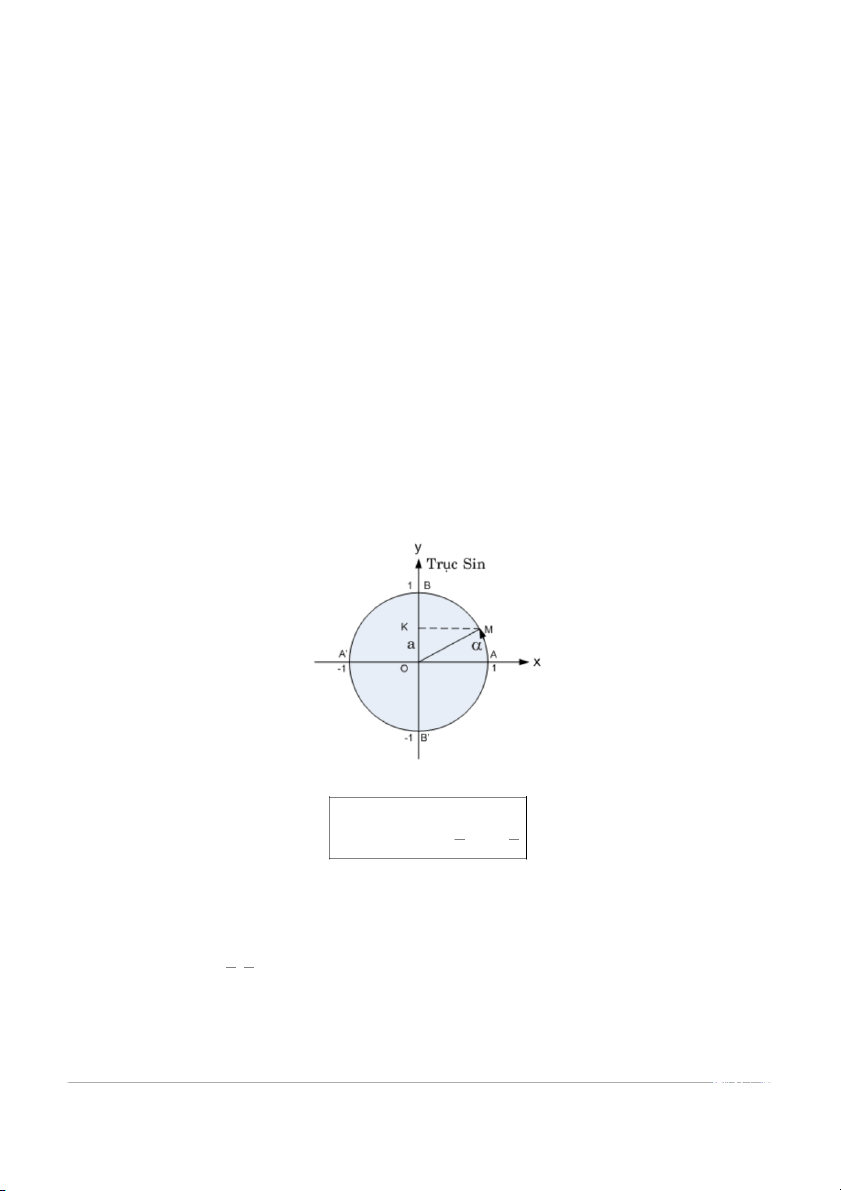
1.4.1. Hàm y = sinx và y =arcsinx:
Với –1 ≤ a ≤ 1, ta định nghĩa : s in α = a; arcsin a = α ⇔ π π − ≤ α ≤ . 2 2
Khi đó arcsina (–1 ≤ a ≤ 1) được xác định duy nhất.
Như vậy, y= arcsinx là hàm số có tính chất sau : • Miền xác định: D = – [ 1;1]. • π π Miền giá t ị r : [− ; ]. 2 2 2 • π π
∀α ∈ [− ; ],∀a ∈ [−1;1] : sinα = a ⇔ arc sin a = α. 2 2 •
y = arcsinx là hàm số lẻ, ng ĩ
h a là arcsin(–x) = – arcsinx. Ví dụ: arcsin(1/2) = π/6;
arcsin(– 3 /2) = –arcsin( 3 /2) = –π/3; arcsin(–1/2) = –π/6
arcsin(–3/4) = –arcsin(3/4)≈–0,848062079
arcsin(–4) không tồn tại.
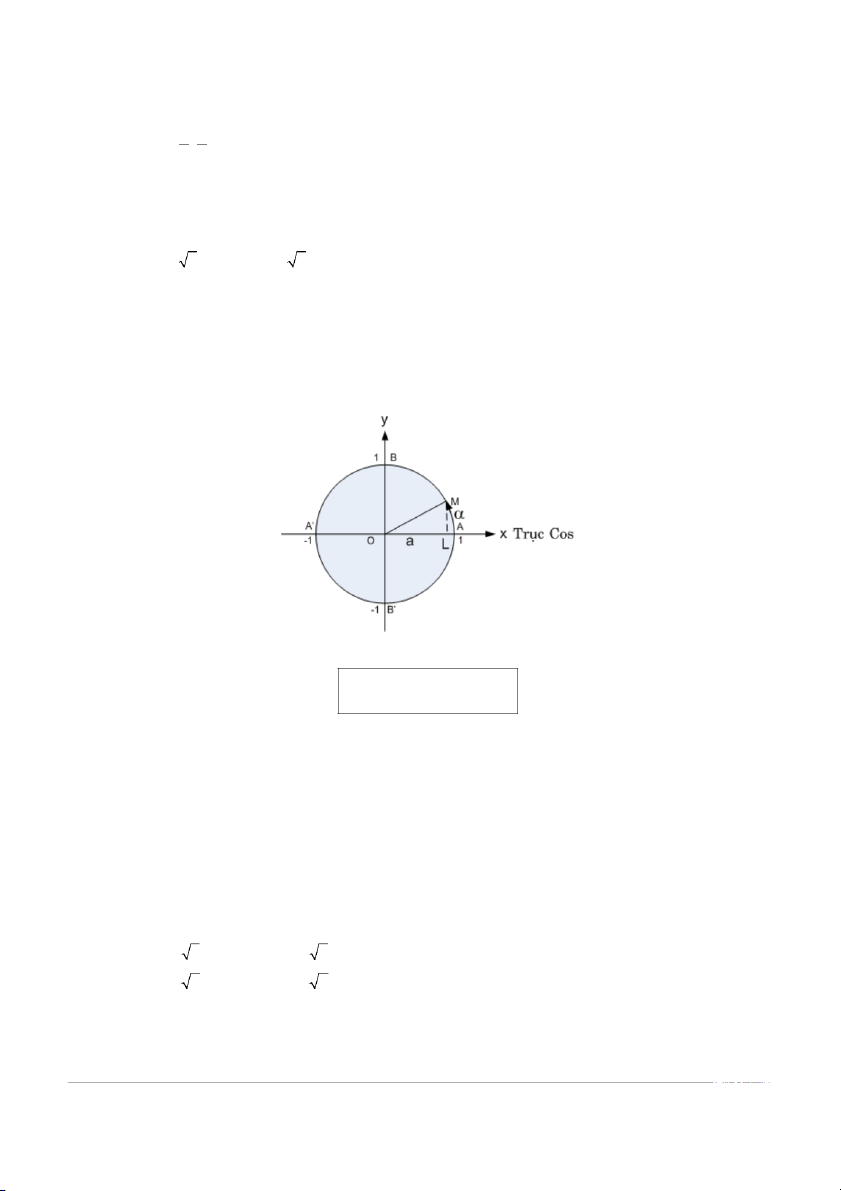
1.4.2. Hàm y = cosx và y =arccosx:
Với –1 ≤ a ≤ 1, ta định nghĩa : cos α = a; arccos a = α ⇔ 0 ≤ α ≤ . π
Khi đó arccosa (–1 ≤ a ≤ 1) đư c ợ xác định duy nhất.
Như vậy, y= arccosx là hàm số có tính chất sau : • Miền xác định: D = – [ 1;1]. • Miền giá t ị r : [0; ] π . • ∀α ∈ [0; ] π , a ∀ ∈ [ 1
− ;1] : cos α = a ⇔ arccos a = . α •
arccos(–x) = π – arccosx. Ví dụ: arccos(1/2) = π/3;
arccos(– 3 /2) = π – arccos( 3 /2) = π – π/6 = 5π/6;
arccos(– 2 /2) = π – arccos( 2 /2)= 3π/4 3
arccos(–3/4) = π – arccos(3/4)≈ 2,418858406
arccos(–4) không tồn tại.
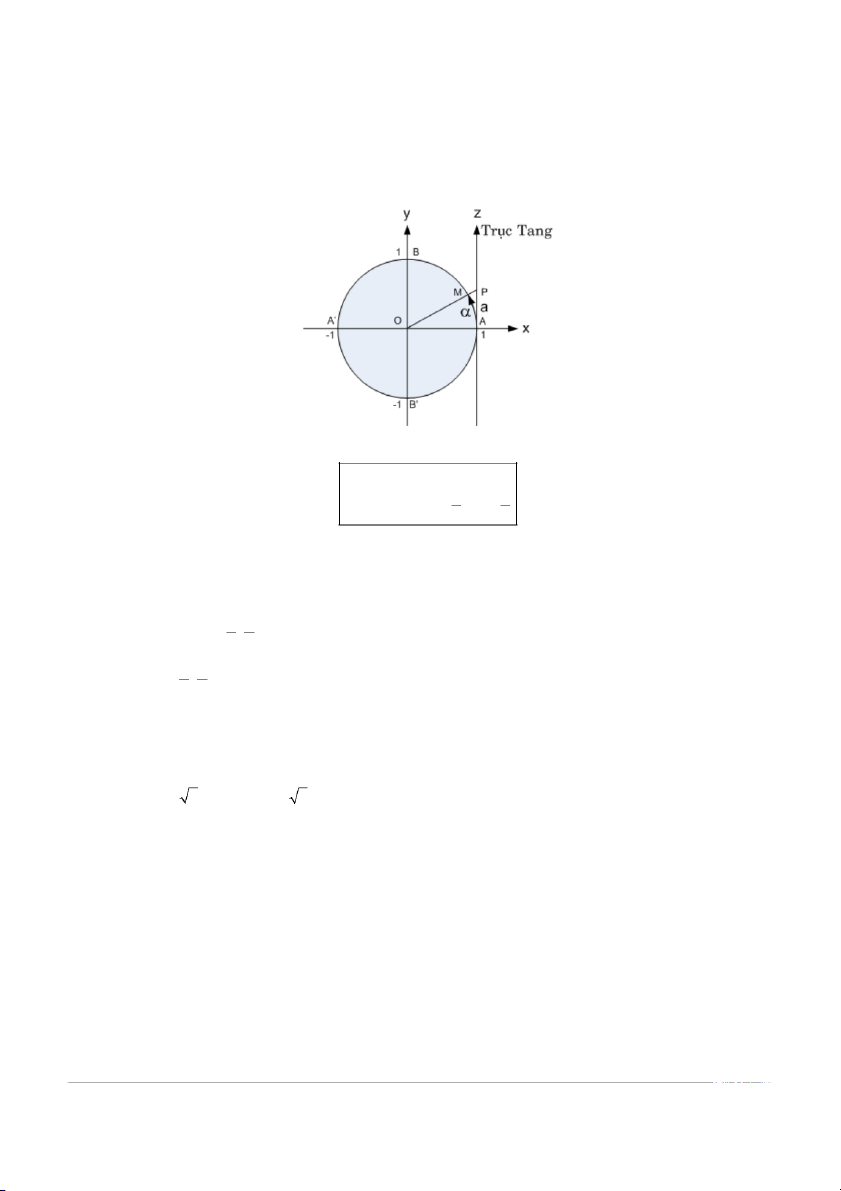
1.4.3. Hàm y = tanx và y =arctanx:
Với a∈R, ta định nghĩa: tan α = a;
arctan a = α ⇔ π π − < α < . 2 2 Khi đó arctana đư c ợ xác định duy nhất.
Như vậy, y= arctanx là hàm số có tính chất sau : •
Miền xác định: D = R. • π π Miền giá t ị r : (− ; ). 2 2 π π • ∀α ∈ (− ; ), a
∀ ∈ R : tanα = a ⇔ arctana = α. 2 2 •
y = arctanx là hàm số lẻ, ng ĩ h a là arcta ( n –x) = – arctanx. Ví dụ: arctan1 = π/4;
arctan(– 3 /3) = –arctan( 3 /3) = –π/6; arctan(–1)= –π/4 arctan(3/4) ≈ 0,643501108 arctan(–4) ≈ –1,3258.
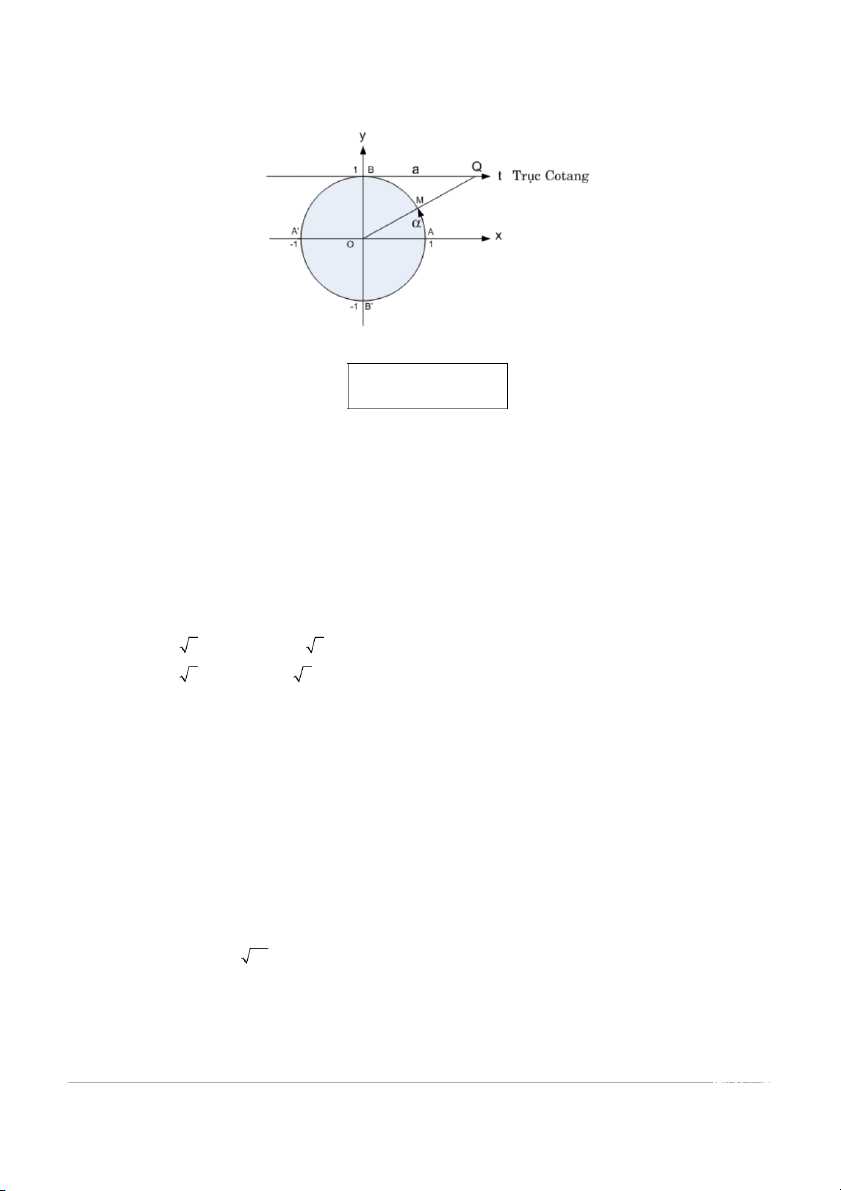
1.4.4. Hàm y = cotx và y =arccotx: 4
Với a∈R, ta định nghĩa: cotα = a; arccot a = α ⇔ 0 < α < . π Khi đó arccota đư c ợ xác định duy nhất.
Như vậy, y= arccotx là hàm số có tính chất sau : •
Miền xác định: D = R. • Miền giá t ị r : (0; ) π . •
∀α ∈ (0;π),∀a ∈ R : cot α = a ⇔ arc cot a = . α •
arccot(–x) = π – arccotx. Ví dụ: arccot1 = π/4;
arccot(– 3 /3) = π – arccot( 3 /3) = π – π/3 = 2π/3.
arccot(– 3 ) = π – arccot( 3 ) = π – π/6 = 5π/6.
arccot(3/4) = π/2 – arctan(3/4) ≈ 0,927295218
arccot(–4) = π/2 – arctan(–4) ≈ π/2 + a rctan4 ≈ 2,89661399.
trong đó ta đã sử dụng tính chất sau:
1.4.5. Tính chất:
1) Với mọi –1 ≤ x ≤ 1, arcsinx + arccosx = π/2 .
2) Với mọi x, arctanx + arccotx = π/2.
3) Với mọi x > 0, arccotx = arctan(1/x). §2. HÀM SỐ SƠ CẤP
Hàm số sơ cấp là hàm số được xây dựng từ các hàm hằng và các hàm số sơ cấp cơ bản qua
các phép toán đại số : cộng, trừ, nhân, chia và phép hợp nối ánh xạ.
Ví dụ: y = ln(1 + 2x) là một hàm số sơ cấp . 5 sin 6x neu x < 0; y = x
không là hàm số sơ cấp . cos3x neu x ≥ 0. B. GIỚI HẠN
§1. ĐỊNH NGHĨA VÀ TÍNH CHẤT.
1.1. Định nghĩa:
1) Cho hàm số f(x) xác định trên một khoảng chứa x0 ( có thể loại trừ x0). Ta nói f(x) có giới
hạn là L∈ R khi x tiến về x0, ký hiệu: lim f (x) = L hay f(x) → L khi x → x , nếu: 0 x→x 0 ∀ε > 0, ∃δ > 0, x ∀ ∈ ,0 |
< x − x |< δ ⇒|f (x) − L|< ε 0
2) Cho hàm số f(x) xác định trên một khoảng có dạng (a;x0). Ta nói f(x) có giới hạn là L∈ R khi x tiến về x −
0 bên trái, ký hiệu: lim f (x) = L hay f(x) → L khi x → x , nếu: 0 x x − → 0 ∀ε > 0, ∃δ > 0, x
∀ ∈ , 0 < x − x < δ ⇒| f (x) − L|< ε 0
3) Cho hàm số f(x) xác định trên một khoảng có dạng (x0;b). Ta nói f(x) có giới hạn là L∈ R khi x tiến về x +
0 bên phải, ký hiệu: lim f (x) = L hay f(x) → L khi x → x , nếu: 0 x x + → 0 ∀ε > 0,∃δ > 0, x
∀ ∈ , 0 < x − x < δ ⇒|f (x) − L|< ε 0 lim f (x) = L; + Như vậy, x→ x 0 lim f (x) = L ⇔ x→x lim f (x) = L. 0 x→x− 0
4) Tương tự, ta định nghĩa được các giới hạn:
lim f (x) = +∞; lim f (x) = −∞; lim f (x) = ∞;... . x→x x→x x→x 0 0 0
1.2. Định lý:
Cho các hàm số f(x), g(x) khi x→ x0. Khi đó, với a, b ∈R, ta có: 1) Nếu f(x) →a, g(x) → b thì f(x) + g(x) → a + b; f(x) – g(x) → a – b; f(x)g(x) → ab;
f(x)/g(x) → a/b ( nếu b ≠ 0).
2) Nếu f(x) →a, g(x) →∞ thì f(x) + g(x) → ∞.
3) Nếu f(x) →+∞, g(x) →+∞ thì f(x) + g(x) → +∞.
4) Nếu f(x) →a ≠ 0, g(x) →∞ thì f(x)g(x) → ∞.
5) Nếu f(x) →∞, g(x) →∞ thì f(x)g(x) →∞.
6) Nếu f(x) →a ≠ 0, g(x) →0 thì f(x)/g(x) → ∞. 6
7) Nếu f(x) →a , g(x) → ∞ thì f(x)/g(x) → 0.
8) Nếu f(x) →∞, g(x) →b thì f(x)/g(x) → ∞.
9) Nếu f(x) →a > 1, g(x) →+∞ thì f(x)g(x) → +∞.
Nếu f(x) →a với 0 < a < 1, g(x) →+∞ thì f(x)g(x) → 0.
10) Nếu f(x) →a thì |f(x)| → |a|.
11) f(x) →0 ⇔ |f(x)| → 0.
12) (Giới hạn kẹp) Giả sử f(x) ≤ h(x) ≤ g(x), ∀x khá gần x0 và f(x) → a; g(x) → a. Khi đó h(x) →a. 1.3. Định lý:
Cho f(x) là một hàm số sơ c p
ấ xác định tại x0. Khi đó
lim f (x) = f (x ). 0 x→ x0 Ví dụ: 1 − cos 2x + 1) lim = 2. 2) 1 cos 2x lim = ∞ π x→ sin x x→0 sin x 2
1.4. Các dạng vô định trong giới hạn :
Có tất cả 7 dạng vô định trong giới hạn, đó là: 0 ∞ ∞ 0 0
∞ − ∞; 0∞; ; ; 1 ; 0 ; ∞ . 0 ∞
1) Dạng ∞ − ∞ : Khi f(x) → +∞ (–∞) và g(x)→+∞ (–∞) thì ta nói lim (f(x) – g(x)) có dạng vô định ∞ − ∞ .
2) Dạng 0∞ : Khi f(x) → 0 và g(x)→∞ thì ta nói lim f(x)g(x) có dạng vô định 0∞ (Lưu ý
: f(x) → 0 không có nghĩa là f(x) ≡ 0) .
3) Tương tự cho 6 dạng còn lại.
Để tính các giới hạn có dạng vô định, ta cần biến đổi để làm mất đi dạng vô định, gọi là khử dạng vô định. §2. HÀM TƯƠNG ĐƯƠNG 2.1. Định nghĩa:
Cho các hàm số f(x), g(x) xác định và không triệt tiêu trên một khoảng chứa x0 (có thể loại
trừ x0). Ta nói f(x) tương đương với g(x) khi x →x0, ký hiệu f(x) ∼ g(x) khi x →x0, nếu f (x) lim = 1. x x → 0 g(x) Như vậy, 7 f (x) f (x) g(x) ⇔ lim = 1 x→x0 g(x) (f (x), g(x) ≠ 0)
Các tính chất sau được thỏa: 1) f(x) ∼ f(x).
2) f(x) ∼ g(x) ⇒ g(x) ∼ f(x).
3) f(x) ∼ g(x) và g(x) ∼ h(x) ⇒ f(x) ∼ h(x) .
2.2. Định lý: 1)
Nếu f(x) → L ∈ R, L ≠ 0, thì f(x) ∼ L. 2)
Nếu f(x) ∼ g(x) và g(x) → A thì f(x) → A. f (x)f (x) g (x)g (x); f (x) g (x); 1 2 1 2 3) Nếu 1 1 thì f (x) g (x) f (x) g (x). 1 1 . 2 2 f (x) g (x) 2 2 4) Nếu f(x) ∼ g(x) thì n n f (x)
g(x) (giả sử các căn có nghĩa) . 5)
2.3.Một số giới hạn và tương đương cơ bản
BẢNG GIỚI HẠN VÀ TƯƠNG ĐƯƠNG CƠ BẢN GIỚI HẠN TƯƠNG ĐƯƠNG 1 sin x sinx ∼ x khi x→0 (x: rad) lim = 1 x 0 → x 2 1 − cos x 1 lim =
1–cosx∼ 1 x2 khi x→0 (x: rad) 2 x 0 → x 2 2 3 tgx
tanx ∼ x khi x→0 (x: rad) lim = 1 x→0 x 4 arc sin x arcsinx ∼ x khi x→0 lim = 1 x→0 x 5 arctan lim x =1 arctanx ∼ x khi x→0 x→0 x 6 x e − 1
ex − 1∼ x khi x→0 lim = 1 x→0 x 7 ln(1 + x) ln(1+x) ∼ x khi x→0 lim = 1 x→0 x 8 8 (1 + x)α − 1 (1 + x)α−1 ∼
αx khi x→0 (α ≠ 0) lim = α x→0 x 9 • x x lim e = + ; ∞ lim e = 0. • Khi x→∞: x→+∞ x→−∞
anxn + an – 1xn – 1+...+amxm ∼ a • nxn lim ln x = + ; ∞ lim ln x = − . ∞ x x 0+ →+∞ → • Khi x→ 0: • lim tgx = + ; ∞ lim tgx = − . ∞ n –1 m − + π π anxn + an – 1x +...+amxm ∼ amx x→ x→ 2 2 (a ≠ 0; a 0, n > m π π n m ≠ )
• lim arctan x = ; lim arctan x = − . x →+∞ 2 x →−∞ 2 x 1 • 1 lim 1 + = e; lim (1 + x)x = e. x→∞ x→0 x
Ví dụ: Tính các giới hạn sau: ln cos 2x a) L = lim 1 2 x→0 (x + 3x) sin x 2 2 (x − 5x + 4) arcsin(x − x) b) L = lim 2 x x 1 → (e − e)(1 − 4x − 3) 8 6 3x − 5x + 4x + 2 c) L = lim . 3 8 7 4 x→∞ x − 5x + 14x + 1 2 3 Đáp số: a) L = − ; b) L =
: Đặt t = x –1 ⇔ x = t+1; c) L = 3. 1 3 2 2e 3
§3. VÔ CÙNG BÉ (VCB) – VÔ CÙNG LỚ N (VCL) 3.1. VÔ CÙNG BÉ (VCB)
1) Định nghĩa: f(x) là một VCB khi x→x0 nếu lim f (x) = 0 . x x → 0
2) Cấp của VCB: Cho f(x) là một VCB khi x→0. Ta nói VCB f(x) có cấp α khi chọn x làm VCB chính nếu: f(x)∼ axα khi x→0
trong đó a ≠ 0 và α > 0.
3) Tổng hai VCB: Cho f(x), g(x) là hai VCB khi x→0. Giả sử khi x→0: f(x)∼ axα g(x)∼ bxβ Khi đó: 9 a xα neu α < ; β f ( ) x + ( g ) x bxβ neu α > ; β ( a+b) α x neu α = ; β a+b ≠ 0.
Chú ý: Trường hợp α = β; a+b=0, VCB f(x)+g(x) sẽ có cấp lớn α, nhưng ta không có
kết luận tổng quát về cấp của VCB f(x)+g(x).
4) Qui tắc giữ lại VCB cấp bé nhất (Qui tắc ngắt ỏ b VCB cấp cao): Gi ả sử khi x→0,
VCB f(x) được phân tích thành tổng của nhiều VCB, trong đó chỉ có một VCB cấp thấp nhất là f0(x). Khi đó f(x)∼ f0(x) khi x→0. 3.2. VÔ CÙNG LỚN (VCL)
1) Định nghĩa: f(x) là một VCL khi x→x0 nếu lim f (x) = ∞ x→ 0 x
2) Cấp của VCL: Cho f(x) là một VCL khi x→∞. Ta nói VCL f(x) có cấp α khi chọn x làm VCL chính nếu: f(x)∼ axα khi x→∞
trong đó a ≠ 0 và α > 0.
3) Tổng hai VCL: Cho f(x), g(x) là hai VCL khi x→∞. Giả sử khi x→∞: f(x)∼ axα g(x)∼ bxβ Khi đó α ax neu α > ; β f ( ) x + ( g ) x bxβ neu α < ; β
(a+b)xα neu α = ;β a+b ≠ 0.
Chú ý: Trường hợp α = β; a+b=0, f(x)+ g(x) có thể không là VCL hoặc là VCL cấp bé
hơn α mà ta không có kết luận tổng quát về cấp của VCL f(x)+g(x).
4) Qui tắc giữ lại VCL cấp lớn nhất (Qui tắc ngắt bỏ VCL cấp thấp): Giả sử khi x→∞,
VCL f(x) được phân tích thành tổng của n i
h ều VCL, trong đó chỉ có một VCL cấp cao nhất là fn(x). Khi đó: f(x)∼ fn(x) khi x→∞.
Ví dụ: Tính các giới hạn sau: 10 1∞ (ln f(x))′ K = lim 00 g(x) L = lim f (x) K x→A 1 ′ x→A ∞ lim g(x) ln f (x) 0 x A L e → = g(x)
Ví dụ: Tính các giới hạn sau; π ln cos x x −x e − e − 2x 2 1 2 L = lim L = lim L = lim − cot x 1 2 3 2 x→0 x − sin x x→1 π x x 0 → tan x 2 1 3 10 L = x x lim x x e x 3 + 4 − = − 4 L = lim L lim x 2 6 + ( )ln|sin(2 x)| x→−∞ 5 x→0 2 x→2 ln(1 2 + ) L = lim (cot ) x 7 x + x 0 →
Đáp số: L1 = 2; L2 = 0; L3 = 2/3; L4 = 0; L5 = 2 3 ; L6 = 3 e ; L7 = 1. §6. KHAI TRIỂN TAYLOR
6.1. Định lý (Khai triển Taylor):
Cho hàm số f(x) có đạo hàm đến cấp n + 1 liên tục trên đoạn [a,b]. Khi đó với mỗi x0 ∈ [a,b], ta có: (n) (n 1 + ) f (′x ) f ′(′x ) f (x ) n f ( ) 0 0 2 0 c n +1
f (x ) = f (x ) + (x −x ) +
(x − x ) + . .+ (x − x ) + (x −x ) (1) 0 0 0 0 0 1! 2! n! (n+ 1)!
với mọi x ∈ [a,b], trong đó c nằm giữa x0 và x. Ta gọi (1) là khai triển Taylor đ
ến cấp n của f(x) tại
x0, trong đó phần dư của khai triển là: (n+1) f ( ) c n+1 R ( ) x = ( x− x ) n 0 ( . n +1)! Chú ý rằng R n
n(x) là một VCB cấp cao hơn VCB (x–x0)n khi x → x0, ký hiệu Rn(x) = o((x–x0) ).
Như vậy, (1) còn được viết dưới dạng: (n) f (′x ) f ′(′x ) f (x ) 0 0 2 0
f (x) = f (x )+ (x− x )+ (x− x ) + . .+
(x− x )n+ o((x− x )n) 0 0 0 0 0 1! 2! n!
6.2. Khai triển MacLaurin
Khai triển Taylor của f(x) tại x0 = 0 được gọi là khai triển MacLaurin của f(x). Như vậy, khai
triển MacLaurin đến cấp n của f(x) định bởi: 22 (n) (n 1 + ) f ′(0) f ′ (0) f (0) f (c) 2 n n+1
f (x) = f (0) + x + x + . .+ x + x (2) 1! 2! n! (n +1)! hay (n) f ( ′ 0) f ′( ′ 0) f (0) 2
f (x) = f (0)+ x + x + . . n + x + o( n x ) 1! 2! ! n
trong đó c nằm giữa 0 và x; o(xn) là một VCB cấp cao hơn VCB xn khi x → 0.
6.3. Khai triển MacLaurin của một số hàm sơ cấp 2 n n+1 x x x x x c e = 1 + + + ... + + e 1! 2! n ! (n + 1) ! 2 n x x x x n e = 1 + + + ... + + o(x ) 1! 2! n ! 3 5 2k 1 + 2k +3 x x x x π k sin x = x − + − ... + ( 1 − ) + sin[c + (2k + 3) ] 3! 5! (2k + 1)! (2k + 3)! 2 3 5 2k 1 x x x + k 2k 2 sin x = x − + − ... + ( 1 − ) + o(x + ) 3! 5! (2k + 1)! 2 4 6 2k 2k 2 x x x x x + k cos x = 1 − + − + ... + (−1) + cos[c + (k + 1)π] 2! 4 ! 6! (2k)! (2k + 2)! 2 4 6 2k x x x k x 2k 1 cos x = 1 − + − + ... + (−1) + o(x + ) 2! 4 ! 6! (2k) ! n+1 1 2 =1+ x + x +... x n + x + n+ 2 1 − x (1 −c) 1 2 =1+ x + x + ... n
+ x + o( n x ) (x <1) 1 − x n 1 1 + 2 + x n n n 1
= 1− x + x −...+ (−1) x + (−1) n+ 2 1 + x (1 +c) 1 2
= 1− x + x −...+ (−1)n n x + o( n
x ) (x > −1) 1 + x 23 2 n n 1 x x x +
ln(1 − x) = −x − −... − − n 1 2 n (n +1)(1− c) + 2 n x x
ln(1 − x) = −x − −... − + o( n x ) (x <1) 2 n 2 n n 1 x − x x + n 1 n ln(1 + x) = x − + ... + ( 1 − ) + ( 1 − ) n 1 2 n (n + 1)(1 + c) + 2 n x n 1 − x n ln(1 + x) = x − + ... + (−1) + o(x ) (x > 1 − ) 2 n 3 2k 1 x x + k 2k +2 arctan x = x − +...+ ( 1 − ) + o(x ) 3 2k +1 1 2 π π 3 5 6
tan x = x+ x + x + ( o x ) (− < x < ) 3 15 2 2
Ví dụ: Tìm khai triển Maclaurin của hàm số y= ln(1− 2x ) đến số hạng 4 x .
Giải. Cách 1. Với y = ln(1− 2x ),ta có (1) y = − 2 (2) y = − 4 (3) y = − 16 (4) y = − 96 , , , . − 1 2x ( − 2 1 2x) ( − 3 1 2x ) ( − 4 1 2x ) Do đó y = (1) y = − (2) y = − (3) y = − (4) (0) 0, (0) 2, (0) 4, (0) 16,y (0) = −96.
Suy ra khai triển Maclaurin của hàm số y= ln(1− 2x ) đến số hạng 4 x là (1) (2) (3) (4) = y y y y y y(0) + (0) x + (0) 2 x + (0) 3 x + (0) 4 x + + 4 o(x ) 1! 2! 3! 4 ! = −2x − 2 2x − 8 3 x − 4 4x + 4 o (x ). 3
Cách 2. Đặt t = 2x ,ta có
y = ln(1− 2x ) = ln(1− t). Mà 2 3 4 t t t 4 ln(1− t) = t − − − − + ( o t ) 2 3 4 nên 24 2 3 4 (2x) (2x) (2x) 4 y = 2 − x − − − + ( o (2 x) ) 2 3 4 8 2 3 4 4
= −2 x− 2 x − x − 4 x + ( o x . ) 3 6.4. Ứng dụng
1) Tính xấp xỉ: Ta thường dùng khai triển MacLaurin để tính xấp xỉ giá trị của hàm f(x) sau
khi chọn n đủ lớn để phần dư Rn(x) có trị tuyệt đối không vượt quá sai số cho phép.
Ví dụ: Tính cos25o chính xác đến 0,00001.
Giải. Xét khai triển MacLaurin của cosx: 2 4 6 2k 2k+2 cos = 1 x x x − + − + ...+ ( 1 − )k x x x + cos[c + (k +1) ] π 2! 4! 6! (2 k )! (2k + 2)!
Phần dư của khai triển là: 2k +2 ( ) x R x = cos[c + (k +1) ] π n (2 k + 2)! 5π Với x = 25o= , ta có 36 2k+ 2 2 k+2 2 k+2 x | x | 1 5π | R (x) | =
cos[c+ (k + 1)π] ≤ = n (2 k + 2)!
(2k + 2)! (2k + 2)! 36 Chọn k = 2, ta có: 2k 2 1 5 + π | R (x) |≤ < 0,00001. n 6! 36
Vậy ta có thể tính cos25o chính xác đến 0,00001 nhờ công thức: 2 4 cos 1 x x x ≈ − + 2! 4! , nghĩa là 2 4 5π 5π π o 5 36 36 cos 25 = cos ≈1 − + ≈ 0,90632. 36 2! 4!
2) Tính giới hạn dạng vô định
Ví dụ: Tính các giới hạn sau: 25 2 4
2− 2cos x − x + 2 =lim x L . 1 x 0 → ( x x −tan ) x x 3 2 6e + x − 3 x − 6 x− 6 L = lim . 2 x 0 → x − sin x 3 4 3x − 3arctan − + = lim x x x L . 3 2 3
x→ 0 6 ln(1− x) + 6x + 3x + 2x Giải. 2 4
2− 2cosx − x + 2x • L = lim . 1 x→ 0 x(x − tan x) Khi x → 0, ta c ó 2 4 2 4 x x 5 2 4
2− 2cos x− x + 2 x = 2 − 2(1− + + (
o x )) − x + 2 x 2! 4! 23 4 5 23 4 = x + ( o x ) x , 12 12 3 3 3 x 5 x 4 − tan = − ( + + ( )) = − + ( ) x x x x x o x o x − , 3 3 3 4 ( − tan ) x x x x − . 3 Suy ra 23 4 2 4 2− 2cos − + 2 x x x x 12 23 ∼ → − . 4 ( x x − tan ) x x 4 − 3 Vậy: 23 L = − . 1 4 x 3 2 6e + x − 3x − 6x − 6 • L = lim . 2 x→ 0 x − sin x Khi x → 0, ta c ó 2 3 x x x 3 2 3 3 2
6e + x − 3x − 6 x− 6 = 6(1+ x+ + + ( o x ))+ x − 3 x − 6 x− 6 2! 3! 3 3 3
= 2x + o(x ) ∼ 2x , 3 3 3 x 4 x 4 − sin = − ( − + ( )) = + ( ) x x x x x o x o x ∼ . 3! 6 6 Suy ra: 26 x 3 2 3 6e + x − 3x − 6x − 6 2x → 12 3 x − sin x x 6 Vậy: L2 = 12 . 3 4
3x −3arctan x − x + x • L = lim . 3 2 3 x 0 → 6 ln(1 − )
x + 6 x + 3 x + 2 x Khi x → 0, ta c ó 3 3 4 3 4 3 4 x 4
3x − x + x −3arctan x − x + x = 3x − x + x −3(x − + o(x )) 3 4 4 4
= x + o(x ) ∼ x , 2 3 4 2 3 x x x 4 2 3 6ln(1− )
x + 6 x+ 3x + 2 x = 6(− x− − − + (
o x ))+ 6 x+ 3x + 2 x 2 3 4 3 3 4 4 4
= − x + o(x ) ∼ − x . 2 2 Suy ra: 3 4 3 4 4
3x − x + x −3arctan x − x + x x 2 → − 2 3
6ln(1 −x) +6x +3x +2x 3 . 4 3 − x 2 2 Vậy L = − . 3 3 BÀI TẬP
Bài 1. Tính các giới hạn sau: (1− 2 3 x − − a) cos ) x (1 cos 2 ) x (e 1) lim b) lim x → 2 0 x ln(cos 4x ) 2 x→ 0 x tan 2 x −x 2 − + c) x(1 e − ) +1 − cos 4 x cos 4 x 1 2x lim d) lim 2 x 0 → x 3 x 0 → x ln(1 − sin2x ) x+ 3 + − + x 3 − + + e) 4x tan 2x 1 cos 4x x 4 ( xe 1) x tan 2x x lim f) lim x→ 0 xln(1+ 6x ) x 0 → x ln(1 + 6x )
Bài 2. Tính các giới hạn sau: a) 2 2 2 2 lim x x + x x+ x − x +x x − . x →+∞ b) 2 2 2 2 lim x x − x x + − x x− x x − . x →−∞ 27 c) lim x + x + x + − x x − + x →∞( 3 3 2 3 3 2 3 3 1 3 1 . ) d) lim x x x + + x + + x − − x x →∞ (3 3 2 3 2 3 2 2 1 1 2 . )
Bài 3. Tìm các tham số a,b để hàm số sau liên tục tại các điểm được chỉ ra: 2x e − cos2x ≠ a) khix 0; 3 y = x + 4x tại x = 0. a khi x = 0 ln(cos3x) khi x < 0; 2 x
b) y = ax b+ khi 0 x≤ ≤1; tại x = 0 và x = 1. 1 arctan khi x > 1 2 x + 2x − 3
Bài 4. Tính các giới hạn sau: x 1 − − a) 2 1+ x − ln(1 x + ) − 2 ln x e − +1 x arcsinx lim b) lim c) lim 2 x 0 → sin x 2 x 1 → (x − 1) x 0 → x − tanx 1 1 d) x 1 ln | sin 2 x | lim − e) lim f) lim − x 1 → x − 1 lnx x 0 → ln | sin 3x | x 0 → ln(1+ x ) x 2 1/x g) tan(1− ) arctan x lim (ln( x − 1)) x h) 2/lnsin lim (sin3x) x i) lim x 1+ → x 0 + → x 0 → x
Bài 5. Tìm đạo hàm của các hàm số sau: x a) sin = (cos ) x y x b) 1 y = x + . x
Bài 6. Tìm đạo hàm y (x′ ) của các hàm ẩn y= y(x ) định bởi : a) 3 2 + ln y x
y− xe = 0. Từ đó tính y (′0). b) π y cosx+ sinx+ ln y = 0. Từ đó tính y ′ . 2
Bài 7. Tìm các đạo hàm y (x′ ),y ′(x′ ) của hàm số y = y(x) được cho dưới dạng tham số: x = a cost ; π π Từ đó tính y ′ ,y ′ . y a = sint . 2 2
Bài 8. Tìm khai triển Taylor của các hàm số sau:
a) y = lnx tại x = 2 đến số hạng 3 (x − 2) . 28 b) 1 y =
tại x = 1 đến số hạng 3 (x − 1) . 1+ x
Bài 9. Tìm khai triển Maclaurin của các hàm số sau:
a) y = ln(1+ sinx ) đến số hạng 4 x .
b) y = lncosx đến số hạng 5 x . c) 1 y = đến số hạng 4 x . cosx d) 1 y = đến số hạng 4 x . 1+ sin x 29 Chương 2
PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN A. TÍCH PHÂN BẤT ĐỊNH
§1. KHÁI NIỆM TÍCH PHÂN BẤT ĐỊNH
1.1. Định nghĩa nguyên hàm
Cho hàm số f (x) xác định trong khoảng (a,b).Ta nói hàm số F(x) là một nguyên hàm của
f (x) trên (a,b) nếu: F ( ′ x) = f ( ) x ,∀x∈ ( , a ) b .
Khi nói đến nguyên hàm của f (x) mà không chỉ rõ khoảng (a,b) thì ta hiểu đó là nguyên hàm
của f (x) trên cá
c khoảng xác định của f (x). Ví dụ: 4 4 ′ a) x x
là một nguyên hàm của x3 trên R vì 3 = x . 4 4 b)
cosx là một nguyên hàm của – sinx trên R vì (cos x)′ = − sin . x
1.2. Định lý. Cho F(x) là một nguyên hàm của f (x) trên (a,b). Khi đ ó 1)
Với mọi hằng số C, F(x) + C cũng là nguyên hàm của f (x) trên (a,b). 2)
Ngược lại, mọi nguyên hàm của f (x) trên (a, b) đều có dạng F(x) + C .
1.3. Định nghĩa tích phân bất định
Tập hợp tất cả các nguyên hàm của được gọi là tích phân bất định của hàm f(x), kí hiệu là f ( ) x . dx ∫
Theo Định lý 1.2, nếu biết F(x) là một nguyên hàm của f(x) thì : f
∫ ( )x dx ={F(x)+C | C :Const} Ta viết f
∫ (x)dx = F(x) +C 4 Ví dụ: 3 x x dx = + C ∫ 4
sin xdx = −cos x +C ∫ 1.4. Tính chất. ′
1) Nếu f (x) có nguyên hàm thì ( f (x)dx ∫ ) = f (x).
2) ∫( f (x))′ dx = f (x)+ C. 30
3) Với k là hằng số, ta có :
kf (x) dx = k f (x) dx + C. ∫ ∫ 4) ∫( f ( )x + ( g ) x ) dx = ( f )x dx + (g )x . dx ∫ ∫
1.5. Bảng các tính phân cơ bản α 1 x + α dx x dx =
+ C (−1≠ α : Const) ∫ = 2 x +C ∫ α + 1 x dx 1 = − + dx C ∫ = x +C 2 ln | | ∫ x x x x x e dx = e + C ∫ x x a a dx =
+ C (0 < a ≠ 1: Const) ∫ ln a
sin xdx = − cos x + C ∫
cos xdx = sin x + C ∫ dx 2 = (1+ tan dx x)dx = tan + ∫
= (1+ cot x)dx = − cot + 2 x C ∫ 2 x C ∫ ∫ cos x 2 sin x
tan xdx = − ln | cosx | + C ∫
cot xdx =ln | sinx | + C ∫ x d = arcsin x + C ∫ dx 2 = ln + + + 2 2 x x h C ∫ a − x a 2 x + h (0 < a : Const) (0 ≠ h : Const) dx 1 + = dx 1 arctan x + x a C ∫ = ln + C ∫ 2 2 a + x a a 2 2 a − x 2a x − a (0 ≠a : Const) (0 ≠ a : Const) dx 1 − = ln x a + ∫ 2 2 C x − a 2a x + a (0 ≠ a : Const) Chú ý: Nế
u f (x)dx = F (x) + C ∫
, thì với a ≠ 0 và b là các hằng số, ta có f ( ax+ ) 1 b dx= F(ax+ ) b + C ∫ . a 3x− 4 1 3x−4 Ví dụ: e dx = e + C ∫ 3
§2. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
2.1. Phương pháp phân tích 31
Muốn tính tích phân bất định của một hàm số f (x) ta dùng các tính chất của tích phân và phân
tích f (x) để đưa tích phân cần tính về các dạng tích phân cơ bản.
Ví dụ: Tính các tích phân sau: x +1 2 1) I = dx =
x x + 2 x + C. ∫ x 3 4 3 2) x x = = − 4 + 8 arctan x I dx x + . C ∫ 2 x + 4 3 2 1 1 1 1
3) I = sin 5 xsin 3xdx = cos 2 xdx −
cos 8 xdx = sin 2 x − sin 8 x + . C ∫ ∫ ∫ 2 2 4 16 2 1 1
4) I = sin 2 x d = x
x − sin 4 x +C. ∫ 2 8 2 2 4 3 4 5
5) I = (1 + 2 x ) dx = x + x + x + . C ∫ 3 5 10 1 11 6) I = (1 + 2 ) x dx = (1 + 2 ) x + . C ∫ 22
2.2. Phương pháp đổi biến số
Trong nhiều trường hợp, khi tính f (x)dx ∫
ta không thấy được tích phân cần tính có dạng cơ bản.
Khi đó ta có thể tìm cách đổi sang một biến mới để tích phân cần tính có dạng cơ bản. Có 2 dạng đổi biến số:
1. Đổi biến số dạng 1:
Giả sử tích phân có dạng: f
∫ [u(x)]u (′x)dx , trong đó u(x)và u (′x)liên tục.
Đặt t = u(x)⇒ dt = u′(x)d . x Ta c ó f
∫ [u(x)]u'(x)dx = f (t)dt ∫ (1)
Tính tích phân sau cùng trong (1) theo t, sau đó thay t = u(x).
2. Đổi biến số dạng 2: Xét tích phân I = f ( x)dx ∫
. Đặt x = ϕ (t), trong đó ϕ (t) có đạo hàm ϕ'(t) liên tục và x = ϕ (t) có
hàm ngược t = ϕ –1(x). Khi đ ó dx = ϕ '(t)dt và ta có: I =
f ( x)dx = f ϕ ∫ ∫ (t)ϕ′ (t) dt (2 )
Tính tích phân sau cùng trong (2) theo t, sau đó thay t = ϕ –1(x).
Ví dụ: Tính các tích phân sau: 3 5 2 3 4 (3 + 2x ) 1) I = x (3 + 2x ) dx ∫ = + C 30 dt HD: Đặt 3 2 2
t =3 +2 x ⇒ dt =6 x d x ⇒ x dx = 6 32 2x + 1 2) I = dx ∫ 2 = ln x + x − 3 + C 2 x + x − 3 HD: Đặt 2
t = x + x − 3 ⇒ dt = (2x + 1)dx xdx 1 1 2 x 1 + − 13 3) I = ∫ 2
= ln | x + x − 3 | − ln + C 2 x + x − 3 2 2 13 2 x 1 + + 13 xdx 4) I = ∫ = 1 2 4 ln x + 1 + x + C 4 1 + x 2 dt HD: Đặt 2
t = x ⇒ dt = 2xdx ⇒ xdx = 2 2 ln x + 1 ln2 x 5) I = dx ∫ = + ln ln x + C x ln x 2 dx HD: Đặt t = lnx ⇒ dt = . x 3x + 5 6) I = dx ∫ = 1 3 17 (4x + 1) + 4x + 1 + C 4x + 1 8 8 2 t −1 1 HD: Đặt t = 4 x 1 + ⇒ x = ⇒ dx = tdt . 4 2
2.3. Phương pháp tích phân từng phần
Giả sử u = f(x) và v = g(x) có đạo hàm u' = f'(x) và v'= g'(x) liên tục. Khi đó: (uv)' = u'v+ v'u
Suy ra: uv 'dx = (uv) 'dx − vu 'dx = uv − vu 'dx. ∫ ∫ ∫ ∫
Ta có công thức sau, gọi là công thức tích phân từng phần: uv 'dx = uv − vu 'dx ∫ ∫
Chú ý rằng, theo nghĩa vi phân, ta có u'dx = du và v'dx = dv. Do đó ta còn viết công thức tích
phân từng phần dưới dạng sau: udv = uv − vdu ∫ ∫ Chú ý: 1) Để tính ∫ f( )
x dx bằng phương pháp tích phân từng phần ta phân tích f(x) = g(x).h(x) sau đó có 2 cách đặt: = du = g (′ ) ( ) x dx u g x ⇒ dv = ( h ) x dx v = ( h ) x d x (thuong chon C = 0) ∫ hoặc 33 = du = h( ′ ) ( ) x dx u h x ⇒ dv = ( g ) x dx v= ( g ) x d x (thuong chon C = 0) ∫
Ta chọn cách đặt nào để cho vdu ∫ tính được .
2) Đối với một số bài toán, sau khi áp dụng tích phân từng phần, ở vế phải lại xuất hiện tích phân
đã cho ban đầu tức là: ∫f( d ) x x = F( ) x + α ∫ f ( d ) x x với α ≠ 1 .
Khi đó chuyển vế ta được: f (x) 1 dx = F( ) x + C ∫ 1 − α
3) Các tích phân sau đây dược tính bằng phương pháp tích phân từng phần với cách đặt tương
ứng (ở đây p(x) là đa thức theo x): Loại 1: ∫ p(x) sin axd , x ∫ p(x) cos axd , x ∫ p(x)eaxdx Đặt u = p(x); dv = ...
Loại 2: p(x) ln axdx, p(x)arctgaxdx, p(x) arcsin axdx,... ∫ ∫ ∫ Đặt u =..., dv = p(x)dx.
Ví dụ: Tính các tích phân sau:
1) I = x cos x dx = x sin x + cos x + C ∫ = = Đặt u x du dx ⇒ dv = cos xdx v = sin x 2) x dx I =
= −xcot x + ln sin x + C ∫ 2 sin x u = x d u = dx Đặt: dx ⇒ dv = v = − cot gx 2 sin x 1 3) x = sin x I e x dx = e (sin x c − os ) x + C ∫ 2 u = sin x du = cos x dx Đặt ⇒ dv = x e dx x v = e u = cos x du = −sin x dx Tiếp theo đặt ⇒ dv = x e dx v = x e α 1 + α 1 + 4) α = ln = x = ln x I x xdx x−
+ C (−1≠ α : Const) ∫ 2 α +1 (α +1) 34 dx du = u = ln x Đặt x ⇒ α α+ 1 dv = x dx x v = α + 1 2 3x 1 3x 2 5) I = x e dx = e (9x 6 − x +2) + C ∫ 27 2 du = u = x 2xdx Đặt ⇒ 3x e3x v = dv = e dx 3 2 1 + x 1
6) I = x arctan x dx =
arctan x − x + C ∫ 2 2 dx du = = 2 u arc tan x 1+ x Đặt ⇒ 2 dv = x 1 + x v = 2
§3. TÍCH PHÂN HÀM HỮU TỈ
Hàm hữu tỉ là một hàm số có dạng: m P(x) b0 + 1 b x + ... + bm x f (x) = = (1 ) n ( Q x) a + + + 0 1 a x ... an x với ai, bi ∈
và an, bm ≠ 0 và P(x), Q(x) không có nghiệm chung .
Ta thấy nếu bậc của P(x) lớn hơn hoặc bằng bậc của Q(x) (m ≥ n) thì bằng cách chia tử cho mẫu
ta có thể biểu diễn (1) dưới dạng: P (x) 2 f (x) = P (x) + 1 Q(x)
P1(x), P2(x) là các đa thức theo x với bậc của P2(x) bé hơn n. Vì P1(x) là đa thức nên tích p â h n P1(x)
dễ dàng tính được. Vì vậy ta giả thiết rằng f(x) có dạng (1) với bậc của tử bé hơn bậc của mẫu (m < P(x) n). Khi đó
đuợc phân tích thành tổng các phân thức đơn giản như sau : Q(x)
Để minh họa, ta giả sử Q(x) có bậc 10 và được phân tích dưới dạng:
Q(x) = (x – a)(x – b)3(x2 + px + q)(x2 + rx + s)2
(p2 – 4q < 0; r2 – 4s < 0). Khi đ ó P(x) A B B B Cx + D E x + F E x + F 1 2 3 1 1 2 2 = + + + + + + 2 3 2 2 2 2 Q(x) x − a x − b (x − b) (x − b) x + px + q x + rx + s (x + rx + s)
trong đó A, B1,.., E2, F2 ∈ R. Để các định các hệ số trên ta có 2 cách như sau: 35
Cách 1 (Phương pháp hệ số bất định): Nhân hai vế cho Q(x) rồi đồng nhất hệ số của các số hạng
cùng bậc ở hai vế, đưa đến hệ phương trình tuyến tính đối với A, B1,.., E2, F2 . Giải hệ phương trình
này ta tìm được A, B1,.., E2, F2.
Cách 2 (Phương pháp giá trị riêng): Cho x nhận 10 giá trị tùy ý (số 10 ứng với số lượng các hệ số
cần xác định) rồi thế vào đẳng thức trên để được một hệ phương trình tuyến tính đối với A, B1,.., E2,
F2 . Giải hệ phương trình này ta tìm được A, B1,.., E2, F2. Ví dụ: 2x dx 1 = ln x −1 − + C ∫ . 2 2x − 4x + 2 x − 1 2 x 1 1 1 2 dx = ln | x − 2 | − − ln(x + 4) + . C ∫ 4 3 2
x − 4x + 8x − 16x + 16 4 2(x − 2) 8
§4. TÍCH PHÂN HÀM LƯỢNG GIÁC
Xét tích phân dạng I = R(sin x,cos x)dx ∫
trong đó R là một hàm hữu tỷ đối với sin x, cos x.
Dạng 1: I = R(sin x).cos xdx ∫
với R là một hàm hữu tỉ theo sinx.
Đặt t = sin x ⇒ dt = cos x d . x Khi đ
ó I = R(t)dt ∫
Dạng 2: I = R(cos x).sin xdx ∫
với R là một hàm hữu tỉ theo cosx.
Đặt t = cos x ⇒ dt = −sin x dx . Khi đó I = R(t)dt ∫
Dạng 3: I = R(tan x)dx ∫
với R là một hàm hữu t ỉtheo tanx. dt Đặt 2
t = tan x ⇒ dt = (1+ tan )
x dx hay dx = 2 1+ t ( R ) Khi đó t I = dt ∫ 2 1+ t Dạng 4: 2 2 I = R(sin ,
x cos x)dx ∫
với R là một hàm hữu tỉ . dt Đặt 2
t = tan x ⇒ dt = (1+ tan x)dx hay dx = 2 1+ t 2 t 1 Khi đó 2 2 sin x = ;cos = 2 x 2 1+ t 1+ t Dạng 5: 2 n 2 = (sin ) (cos ) m I x x dx ∫ Dùng công thức hạ bậ c 2 1 −cos 2x 2 1 +cos 2x 1 sin x = , cos x =
, sinx cosx = sin 2x 2 2 2 36 Dạng 6: sin ax cos bxd ; x sin a s x in bxd ; x cos a c x os bx dx ∫ ∫ ∫
Ta dùng công thức biến đổi tích thành tổng: 1 sin ax cosbx = [sin(ax + ) bx s + in( ax − ) bx ] 2 1 sin ax sinbx = [cos(ax −b ) x −cos(ax +b ) x ] 2 1 cos ax cosbx = [cos(ax +b ) x +cos( ax −b ) x ] 2 Ví dụ: 3 5 1) x x 2 3 sin sin sin x cos x dx = − + C ∫ 3 5 2) dx 2 1 = tan x − − +C ∫ 4 2 3 sin x cos x tan x 3 tan x 3) 1 1
sin 7 x sin 5x dx = sin 2x − sin12x + C ∫ 4 24 4) 4 2 1 1 1 1 sin xcos x dx = x − sin 4x − sin 2x + sin 6x + . C ∫ 16 64 64 192
Chú ý. Nếu I = R(sin x,cos x)dx ∫
không có các dạng trên thì ta thực hiện phép đổi biến: = tan x t , (−π < x < ) π 2 Khi đó: 2dt dx = 2 1 + t 2 2t 1 −t 2t sin x = , cos x = , tan x = 2 2 2 1+ t 1+ t 1− t
Do đó I có dạng tích phân hàm hữu tỉ đã xét ở phần trước. 3tan x +1 dx 1 2 Ví dụ: dx = arctan + C ∫
2sin x −cos x +5 5 5
§5. TÍCH PHÂN HÀM VÔ TỈ Xét tích phân dạng ax + b ax + b m n R ∫ x, ,..., dx cx d cx d + +
trong đó R(x, y, z, …) là hàm hữu tỉ; m, n, … là các số nguyên dương; a, b, c, d, là các hằng số.
Để tính tích phân này ta dùng phép đổi biến: 37 ax + b k t = cx + d
với k là bội số chung nhỏ nhất của các chỉ số căn m, n, … Ví dụ: dx 4 4
= 2x − 1+ 2 2x − 1+ 2 ln 2x − 1− 1 + C ∫ 4 2x 1 − − 2x 1 −
B. TÍCH PHÂN XÁC ĐỊNH – TÍCH PHÂN SUY RỘNG
§1. TÍCH PHÂN XÁC ĐỊNH
1.1. Định nghĩa. Xét hàm số f(x) liên tục trên đoạn [a,b]. Chia đoạn [a,b] thành các đoạn nhỏ bởi
các điểm x0, x1,..., xn như sau:
a = x < x < x < ... < x < x = b 0 1 2 n −1 n .
Trên mỗi đoạn nhỏ [xi−1, xi] lấy một điểm ε tùy ý và đặt: i x ≤ ε ≤ x (i = 1, n) i 1 − i i x ∆ = x − x = − (i 1, n) i i i 1 Lập tổng n
I = f (ε )(x − x ) + f (ε )(x − x ) + ... + f (ε )(x − x = ε ∆ − ) ∑f( ) x n 1 1 0 1 2 1 n n n 1 i i i 1 = n Xét giới hạn: lim I =
lim ∑ f (ε ) x ∆ n i i n→+∞ n→+∞ i 1 max = ∆x 0 → max ∆x 0 → i i
Nếu giới hạn trên tồn tại, h
ữu hạn và bằng I ∈ R thì ta nói f(x) khả tích trên [a,b] và I được gọi là b
tích phân xác định của f (x) trên đoạn [a,b], ký hiệu : I = f (x)dx ∫ . a Ta gọi: • a là cận dưới ; • b là cận trên ;
• f(x) là hàm số lấy tích phân;
• f(x)dx là biểu thức dưới dấu tích phân .
Nhận xét. Tích phân xác định không phụ thuộc vào ký hiệu biến số dưới dấu tích phân, nghĩa là: b b b f (x)dx = f (t)dt =
f (u )du = ... ∫ ∫ ∫ a a a 38
1.2. Ý nghĩa hình học của tích phân xác định b
Nếu y = f (x) ≥ 0,∀ x ∈ [a, b] thì f( d ) x x ∫
chính là diện tích hình thang cong giới hạn bởi các a
đường x = a, x = b, y = f (x) và trục hoành . b S = f ( d ) x . x ∫ a Chú ý: Nếu f (x) ≤ 0, x ∀ ∈[a, b] th ì b b f ( d ) x x = − [− f ( ] ) x dx = −S ∫ ∫ . a a b Do đó: S = – f (x d ) x ∫ . a
Vậy nếu f(x) không đổi dấu trên [a,b] thì b S = f ( ) x d . x ∫ a
1.3. Các tính chất của tích phân xác định a 1) f (x dx ) = 0 ∫ . a b a 2) f ( d ) x x = f ( d ) x x ∫ − ∫ . a b b b 3) k f . (x d ) x = k. f (x d ) x k ( = const) ∫ ∫ a a b b b 4) ∫[ f ( )x + ( g x ] ) dx = ( f )x dx + (g )x dx ∫ ∫ a a a b b 5) Nếu f (x) ≥ g(x) , x ∀ ∈ [a, b] , thì f x ( d ) x g(x d ) x ∫ ≥ ∫ . a a 39 b
Đặc biệt, nếu f(x) ≥ 0, ∀x∈ [a,b], thì f (x)dx ≥ 0 ∫ . a 6) Nếu m ≤ f (x) ≤ M, x ∀ ∈ [a, b] thì b ( m b − a) ≤ f ( d ) x x ≤ M(b − a) ∫ a
7) Với a, b, c bất kỳ ta có: b c b f (x d ) x = f (x d ) x + f (x d ) x ∫ ∫ ∫ a a c
(Giả sử các tích phân trên đều tồn tại).
1.4. Công thức Newton – Leibni z
1.4.1. Định lý (Tích phân xác định với cận trên biến thiên).
Giả sử hàm số f(x) liên tục trên [a, b]. Khi đó x F(x) = f (t d ) t ∫ a
là một nguyên hàm của f(x) trên [a,b], nghĩa là F′(x) = f(x), ∀x∈ [a,b].
Chú ý: Từ kết quả trên ta suy ra với ϕ(x) là hàm khả vi, ta có : ϕ(x) ′ f (t)dt = f (ϕ (x))ϕ '(x) ∫ a 1.4.2. Định l ý (Công thức Newton – Leibniz).
Nếu hàm số f(x) liên tục trên [a,b] và F(x) là một nguyên hàm của f(x) trên [a,b] thì: b b f (x)dx = F(x) = − a F(b) F(a) ∫ a Ví dụ: 1 dx π π π 1 1)
= arctan x = arctan1− arctan( 1 − ) = + = ∫ 2 −1 1 + x 4 4 2 1 − e 2 ln e x 1 e 1 2 3 2)
dx = ln x d (ln x) = ln x = ∫ ∫ 1 x 3 3 1 1 π 4 π 4 π 4 1 − cos 2x 1 1 1 π 1 π − 2 2 3) sin x dx = dx = x − sin 2x = ( − ) = . ∫ ∫ 2 2 2 2 4 2 8 0 0 0 40 4 4 4 dx 1 1 4 x − 2 4 4) = −
dx = ln x − 2 − ln x −1 = ln = ln . ∫ ∫ 2 3 x − 3 x + 2 x − 2 x −1 x −1 3 3 3 3
1.5. Các phương pháp tính tích phân xác định
1.5.1. Phương pháp đổi biến số b
Dạng 1: Xét tích phân ∫f(x d
) x với f(x) liên tục trong [a, ] b . a Đặt t = ( ϕ x) thỏa : 1) (
ϕ x) có đạo hàm liên tục trên [ , a ] b . 2) f (x d ) x trở thành g(t dt )
trong đó g(t)là một hàm liên tục trên đoạn có hai đầu mút là ϕ (a), ϕ (b). Khi đó b ϕ(b) f ( ) x dx= ( g ) t d .t ∫ ∫ a ϕ(a) b
Dạng 2: Xét tích phân f (x d ) x ∫
với f(x) liên tục trong [a, ] b . a Đặt x = ( ϕ t) thỏa: 1) (
ϕ t)có đạo hàm liên tục t o r ng [α, ] β ; 2) a = ϕ(α), b = ϕ( β) ;
3) khi t biến thiên trong [α, ] β thì (
ϕ t) biến thiên trong [a, b]. Khi đó b β f (x)dx = f ∫ ∫ [ (ϕt)] ϕ(′t)dt. a α
Ví dụ: Tính các tích phân sau: 2 1) 2 4 − x dx = π. ∫ 0 3 116
2) I = x 1+ xdx = . ∫ 15 0 π 2 cos π 3) x I = dx = . ∫ 2 1 + sin x 4 0 2 1 x e 4) I = dx = e − e ∫ 2 1 x 41
1.5.2. Phương pháp tích phân từng phần
Giả sử u(x) và v(x) là những hàm số có đạo hàm liên tục trong [a,b] khi đó:
d (uv) = vdu + udv
Lấy tích phân 2 vế trên [a,b] ta được b b b ∫ d u
( v) = ∫ udv + ∫ vdu a a a b Vì d(u ) v = (u ) b v ∫ a nên a b b b udv = (uv) − ∫ a vdu ∫ (1 ) a a
Công thức (1) được gọi là công thức tích phân từng phần.
Ví dụ: Tính các tích phân sau: e
1) ln x dx = 1. ∫ 1 2π 2) xcos x dx = 0. ∫ o π/2 π 2 e − x 1 3) e cos x dx= . ∫ 2 0 1 π 1 4) arctan x dx = − ln 2. ∫ 4 2 0 §2. TÍCH PHÂN SUY RỘNG
2.1. Tích phân suy rộng với cận vô hạn (loại I)
Giả sử hàm số f(x) xác định trên [a; + ∞), khả tích trên mỗi đoạn hữu hạn [ ; a b]. Ta định nghĩa: +∞ c
f (x )dx = lim
f (x )dx (1) ∫ ∫ c →+∞ a a
và gọi là tích phân suy rộng của hàm số f(x) trên [a; +∞). Tích phân suy rộng đó được gọi là hội
tụ (tương ứng, phân kỳ) khi giới hạn trong vế phải của (1) tồn tại và hữu hạn (tương ứng, không có
giới hạn hoặc có giới hạn vô cùng).
Tương tự, ta có định nghĩa tích phân suy rộng của hàm số f(x) trên [–∞; a): 42 a a
f (x)dx = lim f (x)dx ∫ ∫ c →−∞ −∞ c và trên(− ∞; + ∞) : +∞ a +∞ a d f (x)dx = f (x)dx +
f ( x)dx = lim
f ( x)dx + lim
f (x)dx (*) ∫ ∫ ∫ ∫ ∫ c→−∞ d →+∞ −∞ −∞ a c a
(a được chọn tùy ý). Trong (*), nếu cả hai giới hạn đều tồn tại hữu hạn thì tích phân suy rộng +∞ f (x)dx ∫ mới hội tụ . −∞
Ta thấy rằng tích phân suy rộng là giới hạn của tích phân xác định khi cho cận tích phân dần tới
vô cực. Vì vậy để tính tích phân suy rộng ta có thể dùng công thức Newton–Leibniz như sau: +∞ +∞
f (x)dx =F (x)
= F (+∞)− F (a), ∫ a a
trong đó F(x) là nguyên hàm của f(x) và F(+∞) = lim F (x) . x→+∞ Tương tự, ta có: a a f (x)dx = F(x) = F(a) − F(−∞ ∫ ) −∞ −∞ +∞ +∞ f (x)dx F( = x) = F(+∞) − F(−∞) ∫ với F(+ ) ∞ = lim F (x ) ; F(− ) ∞ = lim F (x ) . −∞ x→+∞ x→−∞ −∞ Ví dụ 1: +∞ dx π +∞ 1) = arctan x
= lim arctan x − arctan 0 = . ∫ 2 0 1 x + x →+∞ 2 0 0 0 dx π 2) = arctan x
= arctan 0− lim arctan x = . ∫ 2 1 x + x −∞ →−∞ 2 −∞ +∞ +∞ dx 0 dx dx π π 3) = + = + = π ∫ . 2 ∫ 2 ∫ 1 + x 1 + x 1 + x 2 2 2 − ∞ − ∞ 0 +∞ Ví dụ dx
2: Chứng minh rằng I = α > và phân kỳ với . α ∫ hội tụ với 1 α ≤ 1 xα 1 Giải. • Với α ≠ 1 ta c : ó b b dx −1 1 − 1 I = = = + α lim lim ∫ →+∞ xα →+∞ (α − ) lim . α− 1 1 x →+∞ (α − ) α−1 b b b 1 b α − 1 1 1 43 – Nếu α < 1 thì 1 − lim = +∞
= +∞ và tích phân phân kỳ. ( nên I α − ) 1 α b 1 bα− →+∞ – Nếu α > 1 thì 1 − lim (
= 0 nên I = 1 và tích phân hội tụ . α − ) 1 α b 1 bα− →+∞ α − 1 • Với α = 1 ta có : +∞ dx +∞ I = = nx = lim ln x − ln1 α = +∞ ∫ x 1 x→+∞ 1 Do đó tí h c phân phân kỳ.
2.2. Tích phân của hàm không bị chặn (loại II)
1) Nếu hàm số f(x) liên tục trên (a,b] và không bị chặn tại a, nghĩa là: lim f (x) = ∞ thì ta gọi x + x →a
= a là điểm bất thường của f(x) và định nghĩa tích phân suy rộng: b b f ( x)dx = lim f (x)dx (1) ∫ ∫ c a + → a c
và gọi là tích phân suy rộng của hàm số f(x) trên [a,b]. Tích phân suy rộng đó được gọi là hội tụ (tương ứng, phân k )
ỳ khi giới hạn trong vế phải của (1) tồn tại và hữu hạn (tương ứng, không có giới
hạn hoặc có giới hạn v ô cùng).
2) Nếu hàm số f (x) liên tục trên [a,b) và không bị chặn tại b, nghĩa là: lim f( ) x = ∞ ta gọi − x →b
x = b là điểm bất thường của f(x) và ta định nghĩa tích phân u s y rộng: b c f
∫ (x)dx = lim f ∫ − (x)d .x c→b a a
3) Nếu hàm số f(x) không bị chặn tại điểm c ∈ ( ,
a b) và liên tục tại mọ
i x ∈ [a,b]\{c} thì ta định
nghĩa tích phân suy rộng: b c b c1 b f
∫ (x)dx = f
∫ (x)dx + f
∫ (x)dx = lim f
∫ (x)dx + lim f ∫ (x)dx (*) − + 1 c c → c2 c → a a c a 2 c b
Trong (*), nếu cả hai giới hạn đều tồn tại hữu hạn thì tích phân suy rộng f (x)dx ∫ mới hội tụ . a
Chú ý: Nếu F(x) là một nguyên hàm của f(x) thì ta cũng có công thức Newton–Leibniz như sau:
1) Nếu hàm số f (x) liên tục trên [a, b) và không bị chặn tại b thì: b − f ( ) x dx ( F ) b x ( F b− = = ) − F( ) a ∫ a a
trong đó F(b− ) = lim F (x . − ) x→b 44
2) Nếu hàm số f (x) liên tục trên [a, b) và không bị chặn tại a thì: b f ∫ ( )xdx ( F ) b x + = = − + ( F ) b F(a ) a a
trong đó F(a+ ) = lim F(x) . x a + →
3) Nếu hàm số f(x) không bị chặn tại điểm c ∈ (a, b) và liên tục tại mọi x ∈ [a,b]\{c} thì : b c b − f ∫ (x)dx f ∫ (x)dx f ∫ (x) c b dx F(x) F(x) − + = + = + = − + − + F(c ) F(a) F(b) F(c ). a c a a c 2 Ví dụ 1 dx
: Khảo sát sự hội tụ và tính tích phân suy rộng I = ∫ . 2 0 (x − ) 1 1 Giải. Hàm số f (x) =
có điểm bất thường x = 1. Do đó ta có : (x −1)2 1 2 dx dx I = + ∫ ∫ 2 2 (x −1) (x −1) 0 1 I I 1 2 1 b dx dx −1 I = = lim = lim +1 = +∞ 1 ∫ ∫ ( x − 1)2 − (x −1)2 b 1 b 1− → → b − 1 0 0 Vậy I phân kỳ. 2 Ví dụ xdx
2: Khảo sát sự hội tụ và tính tích phân suy rộng J = ∫ x − 1 1 x Giải. Hàm số f (x) =
có điểm bất thường x = 1. Ta có: x − 1 xdx (x − 1) + 1 dx 2 = dx = x − 1 dx + = (x −1)3 + 2 x − 1 + C ∫ ∫ ∫ ∫ x − 1 (x −1) x − 1 3 Suy ra: 2 2 = ( − )3 8 2 + − = − ( − )3 8 J ( x 1 2 x 1) lim x 1 + 2 x − 1 = . 3 3 x 1+ + → 3 3 1 Vậy I hội tụ. b Ví dụ dx
3: Chứng minh rằng M = ∫
(a < b) hội tụ kh i α < 1 và phân kỳ khi α ≥ 1. (x − a)α a Giải. • Với α ≠ 1 ta có : 45 b b dx −1 −1 1 M = lim = lim = + ∫ + → (x − a)α + → (α −1) lim α 1 (x − a) − (α −1) α 1 (b − a) − + → (α −1) α 1 − c a c a c a (c − a) c c – Nếu α > 1 th ì 1 lim
= + ∞ nên M = +∞ và tích phân phân kỳ. + → (α −1) α 1 − c a (c − a) 1 −1 – Nếu α < 1 thì lim = 0 nên M = và tích phân hội tụ . + → (α −1) α 1 − c a (c − a) (α −1) 1 (b − a)α− • Với α = 1 ta có: b b dx M = lim
= lim n|x − a| = ln(b − a) − lim ln(c − a) = +∞ ∫ c a+ − c a x a + c c a+ → → → c
Do đó tích phân phân kỳ.
§3. ỨNG DỤNG CỦA TÍCH PHÂN
3.1. Tính diện tích hình phẳng
Diện tích hình hình phẳng giới hạn bởi các đường thẳng x = a, x = b, y = f1(x), y = f2(x), với
f1(x), f2(x) là các hàm số liên tục trong [a,b] thì: b S = f − ∫ (1 ) 1 ( x) f2 (x) dx a
Để tính tích phân trong (1) ta cần giải phương r
t ình hòanh độ giao điểm f1(x) = f2(x) để tìm tất cả
các nghiệm x1< x2 <...< xn thuộc [a,b]. Khi đó x x 1 2 b S = [f (x) − f (x)] dx + [f (x) − f (x)] dx + ... + [f (x) − f (x)] dx ∫ 1 2 ∫ 1 2 ∫ 1 2 a 1 x n x
Ví dụ 1: Tính diện tích S của hình phẳng giới hạn bởi các đường y = x2 + 1 và x + y=3.
Giải. Phương trình hoành độ giao điểm : x = 1 x2 + 1 = 3 – x ⇔ x = −2
Suy ra diện tích cần tìm là : 1 1 1 3 2 2 2 x x 9 9 S = [(x + 1) − (3 − x)]dx = (x + x − 2)dx = ( + − 2x) = − = . ∫ ∫ 3 2 2 2 2 − 2 − 2 −
Ví dụ 2: Tính diện tích S của hình phẳng giới hạn bởi các đường y = x3 – 2x2 + 2 x và y = x2.
Giải. Phương trình hoành độ giao điểm: 46 3 − 2 + = 2 ⇔ 2 x 2x 2x x x(x − 3x + 2) = 0 ⇔ x = 0, x = 1, x = 2.
Suy ra diện tích cần tìm là: 1 2 1 S = ∫ (x − 3x + 2x) 2 dx + ∫ (x − 3x + 2x) 4 4 3 2 3 2 x 3 2 x 3 2 dx = − x + x + − x + x 4 4 0 1 0 1 1 1 1 = + − = . 4 4 2 3.2. Tính thể tích
1) Trong không gian Oxyz với hệ tọa độ trực chuẩn cho vật thể có thể tích V. Giả sử S(x) là diện
tích của thiết diện được tạo bởi một mặt phẳng vuông góc với trục Ox tại điểm có tọa độ x (trên Ox).
Khi đó nếu vật thể giới hạn bởi hai mặt phẳng x = a và x = b (a < b) và S(x) là liên tục trên [a, b] thì: b V = S(x)dx ∫ a
2a) Thể tích vật thể tròn xoay do hình phẳng giới hạn bởi các đường y = f(x), trục hoành, x = a, x
= b (a < b) quay xung quanh Ox là: b V = π f ∫ (x) 2 dx a
2b) Thể tích vật thể tròn xoay do hình phẳng giới hạn bởi các đường x = g(y), trục tung, y = a, y
= b, quay xung quanh trục Oy là: b V = π g ∫ (y) 2 dy a
Ví dụ: Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi các đường sau:
a) y2 = 4x, y = 0, x = 0, x = 4 quay quanh Ox.
b) y2 = 4 – x, x = 0 quay quanh Oy. Giải. a) Ta có 4 2 4 V = π 4xdx = 2 x π = π ∫ 0 32 . 0 b) Ta có: 2 2 y = 4 − x ⇔ x = 4 − y
Đường cong x = 4 – y2 giao với trục tung Oy tại các điểm có tung độ là nghiệm của phương trình: 4 – y2 = 0 ⇔ y = ± 2.
Suy ra thể tích cần tìm là: 47 2 2 = π ∫ ( − ) 2 = π ∫ ( − + ) 5 2 2 2 4 8 3 y 512π V 4 y dy 16 8y y dy = ( π 16y − y + ) = . 3 5 5 2 − 2 − 2 − BÀI TẬP
1. Tính các tích phâ n a) ∫ dx b) 3 2x +8x + 4 2x − 5 dx ∫ c ) dx ∫ 1− 2 x 2 x + 4 4x − 4x − 3 2 x − 1 d) dx ∫ e) x dx ∫ f) dx ∫ 3 x + 1 4 3 2
x − 4x + 8x − 16x + 16 2 x − 4x + 6 2x − 3 g) dx ∫ h) 2 ln x tan xdx ∫ i) xdx 2 ∫ 7 + 6x − x 2 x 3 5 3 dx cos x + cos x sinx +sin x j)∫ k) dx ∫ ; l) dx ∫
4sin x + 3cos x + 5 2 4 sin x + sin x cos 2x dx sin x dx m) ∫ n) dx ∫ o) ∫ 2 2 4 sin x + 9 cos x
1+ cos x + cos 2x 3 sin x dx x x p) ∫ q) sin xsin sin dx ∫ . 4 cos x 2 3
2. Tính các tích phân : ln3 2 π /4 a) dx ∫ b) xdx ∫ c) xdx ∫ 1 x + e 1+ x − 1 2 cos 0 1 x 0 1 e 1 d) x e dx ∫ . e) | ln x | x arcsin xdx ∫ f) dx ∫ 0 1 − 1 e
3. Khảo sát sự hội tụ và tính các tích phân suy rộng sau (nếu có): +∞ 1 arctan a) dx ∫ b) xdx 2 ∫ x + x − 2 2 1+ 2 x −∞ 0 +∞ c) x xdx dx ∫ d) . ∫ x e + −∞ x 1 1
4. Khảo sát sự hội t
ụ và tính các tích phân suy rộng sau (nếu có): 0 1 x 1 a) e dx dx ∫ b)∫ 3 x (2 − x) 1− x 1 − 0 48 1 1 c) dx ∫ d) ln(1− x) . dx ∫ 2 + 0 x x 0
5. Tính diện tích các hình phẳng được giới hạn bởi các đường : 3 4x
a) y = x3 + 2x2 + x và y = 2x + 2; b) y = , y = 2x. 2 1 + x
6. Tính thể tích của các vật thể tròn xoay do hình phẳng giới hạn bởi các đường:
a) y = lnx, y = 0, x = 1, x = 2 quay quanh trục Ox;
b) x = yey, x = 0, y = 0, y = 1 quay quanh trục Oy. 49 Chương 3 PHƯƠNG TRÌNH VI PHÂN
A. PHƯƠNG TRÌNH VI PHÂN CẤP 1
§1. KHÁI NIỆM VỀ PHƯƠNG TRÌNH VI PHÂN CẤP 1
1.1. Định nghĩa. Phương trình vi phân cấp 1 là phương trình giữa biến x, hàm chưa biết
y = y(x) và đạo hàm y ′ = y ′ (x): F(x, y, y ′) = 0 (1)
Nếu từ (1) ta tính được y ′ thì (1) còn được viết dưới dạng: dy y′ = f (x, y) hay = f (x, y) (2) dx
Ta còn biến đổi (2) về dạng: P(x,y)dx + Q(x,y) dy = 0 (3)
Trong (3) ta có thể xem y là hàm, x là biến hoặc y là biến, x là hàm đều được .
1.2. Nghiệm tổng quát và nghiệm riêng.
Xét phương trình vi phân cấp 1: F(x, y, y ′) = 0 (1)
1) Nghiệm tổng quát của (1) là họ hàm y = ϕ (x,C) phụ thuộc họ hằng số C tuỳ ý, thoả (1) với mọi C.
Thông thường, nghiệm tổng quát được viết dưới dạng hàm ẩn: Φ(x,y,C) = 0.
2) Nghiệm riêng của (1) thoả điều kiện ban đầu y y |x x = = (hay y(x 0 0) = y0) là nghiệm y = 0
ϕ (x,C0) được suy từ nghiệm tổng quát y = ϕ (x,C) bằng cách xác định hằng số C dựa vào điều kiện đó.
Thông thường, nghiệm riệng được viết dưới dạng hàm ẩn: Φ(x,y,C0) = 0.
Giải một PTVP là tìm nghiệm tổng quát của nó. Nếu có kèm theo điều kiện ban đầu, thì
ta phải tìm nghiệm riêng thoả mãn điều kiện đó.
§2. PHƯƠNG TRÌNH VI PHÂN TÁCH BIẾN
2.1. Định nghĩa. Phương trình vi phân tách biến là phương trình có dạng: 50
M1(x)N1(y)dx + M2(x)N2(y)dy = 0 (1) 2.2. Cách giải. Với M2(x)N (
1 y) ≠ 0, chia hai vế của (1) cho đại lượng này, ta được: 1 M (x) N2(y) dx + dy = 0 2 M (x) 1 N (y)
Suy ra nghiệm tổn quát là: M1(x) N2(y) dx + dy = C ∫ ∫ . M2(x) N1(y)
Nếu M2(x) = 0 tại x = a thì bằng cách thử trực tiếp ta thấy x = a, y tuỳ ý thuộc miền xác
định, cũng là một nghiệm của (1).
Nếu M1(y) = 0 tại y = b thì bằng cách thử trực tiếp ta thấy y = b, x tuỳ ý thuộc miền xác
định, cũng là một nghiệm của (1).
2.3. Ví dụ. Giải phương trình vi phân: (xy2 + y2)dx + (x 2 – x2y)dy = 0 (2) ĐS: x x + y ln −
= C . Ngoài ra x = 0; y = 0 cũng là hai nghiệm của (2). y xy
§3. PHƯƠNG TRÌNH VI PHÂN TUYẾN TÍNH
3.1. Định nghĩa. Phương trình vi phân tuyến tính cấp 1 là phương trình có dạng: y′ + p(x)y = q(x) (1)
Nếu q(x) ≡ 0 thì ta có phương trình vi phân tuyến tính thuần nhất cấp 1: y′ + p(x)y = 0 (2) 3.2. Cách giải.
1) Phương trình vi phân tuyến tính thuần nhất cấp 1: y′ + p(x)y = 0 (2) − p(x)dx ∫
có nghiệm tổng quát là: y = Ce
2) Phương trình vi phân tuyến tính cấp 1: y′ + p(x)y = q(x) (1)
Dùng phương pháp biến thiên hằng số Lagrange ta tìm nghiệm tổng quát của (1) dưới dạng: 51 − p(x)dx ∫ y = C(x)e p(x)dx ∫ trong đó C′(x) = q(x)e .
Nghiệm tổng quát của (1) là − p(x)dx p(x)dx ∫ ∫ y = e q(x)e dx + C ∫
Ta có thể ghi nhớ công thức trên dưới dạng: y = u(x)v(x,C) với u(x), v(x,C) thoả: − p( ) x dx ∫ q (x ) u( ) x = e ; ( v , x ) C = dx+ C ∫ u(x)
3.3. Ví dụ. Giải phương trình vi phân: 2 xy′ + y = 3x (3) ĐS: 2 C y = x + . x
§4. PHƯƠNG TRÌNH VI PHÂN BERNOULLI
4.1. Định nghĩa. Phương trình vi phân Bernoulli là phương trình có dạng: y′ + p(x)y = q(x)yα (1)
trong đó α là hằng số khác 0 và 1. 4.2. Cách giải.
1) Nếu α > 0 thì y = 0 là một nghiệm của (1). Nếu α < 0 thì y = 0 không thoả (1).
2) Xét y ≠ 0, chia hai vế của (1) cho yα ta được :
y− αy′ + p(x)y1 − α = q(x) (2)
Đặt z = y1 − α. Ta có: z′ = (1 − α)y – αy′ và (1) trở thành: z′ + ( 1 − α)p(x)z = (1 − − α)q(x) (3)
(3) là phương trình vi phân tuyến tính cấp 1 theo hàm z biến x.
4.3. Ví dụ. Giải phương trình vi phân: 52 2 xy′ − 4y = x y (1) ĐS: 4 1 2
y = x ( ln| x| +C) . Ngoài ra y = 0 cũng là một nghiệm của (1). 2
§5. PHƯƠNG TRÌNH VI PHÂN ĐẲNG CẤP
5.1. Định nghĩa. Phương trình vi phân đẳng cấp là phương trình có dạng: y′ = f(x,y) (1)
trong đó f(x,y) có thể được biểu diễn dưới dạng một hàm của y/x, nghĩa là f(x,y) = ϕ(y/x).
Vậy (1) còn được viết dưới dạng: y y′ = ( ϕ ) (2) x 2 2 x + y
Ví dụ: Phương trình vi phân y′ = 2 là PTVP đẳng cấp. x − xy 5.2. Cách giải.
Đặt u = y/x, Ta có y = ux và y′ = u′x + u. Phương trình (2) trở thành: u′x + u = ϕ(u) nghĩa là u′x = ϕ(u) – u. hay du x = ( ϕ u) − u dx
Đây là một phương trình vi phân tách biến theo hàm u biến x.
5.3. Ví dụ. Giải phương trình vi phân: 2xy y′ = (1) 2 2 x − y ĐS: 2 2
x + y = Cy (C ≠ 0) . Ngoài ra y = 0 cũng là một nghiệm của (1).
§6. PHƯƠNG TRÌNH VI PHÂN TOÀN PHẦN
6.1. Định nghĩa. Phương trình vi phân toàn phần là phương trình có dạng: P(x,y)dx + Q(x,y)dy = 0 (1) 53 trong đó ∂Q ∂P = . x ∂ y ∂
Ví dụ: Phương trình vi phân 2 y x 2y (ln y + )dx + ( − )dy = 0 2 x ln x y ln x là PTVP toàn phần. 6.2. Cách giải. Từ điều kiện Q ∂ P ∂ =
người ta chứng minh được rằng vế phải của phượng trình (1) là ∂x ∂y
vi phân toàn phần dU của một hàm U = U(x,y) nào đó. Công thức tìm hàm U như sau: x y U =
P(x, y)dx + P(x ∫ ∫ 0, y)dy x y 0 0 hoặc x y U =
P(x, y )dx + P(x, y) ∫ 0 dy ∫ x y 0 0
trong đó x0, y0 được chọn tuỳ ý sao cho các tích phân tồn tại.
Vậy nghiệm tổng quát của (1) là: x y P(x, y)dx + P(x = ∫ ∫ 0, y)dy C x y 0 0 hay: x y P(x, y )dx + P(x, y)dy = C ∫ 0 ∫ x y 0 0
6.3. Ví dụ. Giải phương trình vi phân: (ex + y + siny)dx + (e y + x + xcosy)dy = 0 (1)
ĐS: ex + xy + xsiny + ey = C. 54
B. PHƯƠNG TRÌNH VI PHÂN CẤP 2
§1. KHÁI NIỆM VỀ PHƯƠNG TRÌNH VI PHÂN CẤP 2
1.1. Định nghĩa. Phương trình vi phân cấp 2 là phương trình giữa biến x, hàm chưa biết
y = y(x) và các đạo hàm đến cấp 2 của y:
F(x, y, y ′, y ′′′) = 0 (1)
Nếu từ (1) ta tính được y ′′′ th ì(1) còn được viết dưới dạng:
y′ = f (x, y, y′) (2)
1.2. Nghiệm tổng quát và nghiệm riêng.
Xét phương trình vi phân cấp 2:
F(x, y, y ′, y ′′′) = 0 (1)
1) Nghiệm tổng quát của (1) là họ hàm y = ϕ (x,C1,C2) phụ thuộc hai họ hằng số C1, C2
tuỳ ý, thoả (1) với mọi C1, C2 .
Thông thường, nghiệm tổng quát được viết dưới dạng hàm ẩn: Φ(x,y,C1,C2) = 0.
2) Nghiệm riêng của (1) thoả điều kiện ban đầu y = y ; y′ = y′ (hay |x = = 0 x 0 |x 0 x 0 y(x = ′ = ′ ) là nghiệm 0 0 y = ϕ(x, C , C ) đượ
c suy từ nghiệm tổng quát y = ϕ 0) y 0; y (x 0) y 0 1 2
(x,C1,C2) bằng cách xác định các hằng số C1, C2 dựa vào điều kiện đó.
Thông thường, nghiệm riệng được viết dưới dạng hàm ẩn: 0 0 Φ(x, y,C ,C ) = 0 1 2
Giải một PTVP cấp 2 là tìm nghiệm tổng quát của nó. Nếu có kèm theo điều kiện ban
đầu, thì ta phải tìm nghiệm riêng thoả mãn điều kiện đó.
§2. PHƯƠNG TRÌNH VI PHÂN CẤP 2 KHUYẾT y, y′
2.1. Định nghĩa. Phương trình vi phân cấp 2 khuyết y, y′ là phương trình có dạng: y ′′′ = f(x) (1)
2.2. Cách giải. Lấy tích phân hai vế của (1) hai lần ta được: y′ = f (x)dx + C ∫ 1 y = ( f (x)dx)dx + + ∫ ∫ 1 C x 2 C
2.3. Ví dụ. Giải phương trình vi phân: 24 y′ = (1) 5 (x + 2) 55 ĐS: 2 y = + C + 1x C2 3 (x + 2)
§3. PHƯƠNG TRÌNH VI PHÂN CẤP 2 KHUYẾT y
3.1. Định nghĩa. Phương trình vi phân cấp 2 khuyết y là phương trình có dạng: y′′′ = f(x,y′ ) (1)
2.2. Cách giải. Đặt z = y′ . Ta có z′ = y′′
′ . Phương trình (1) trở thành: z′ = f(x,z ) (2)
(2) là phương trình vi phân cấp 1 theo hàm z biến x. Giải (2) ta tìm được z = ϕ (x,C1)
nghĩa là y′ = ϕ (x,C1). Suy ra nghiệm tổng quát của (1) là y = ( ϕ x,C )dx + C ∫ 1 2
3.3. Ví dụ. Giải phương trình vi phân: y′ y′ = x − (1) x 3 ĐS: x y = + + 1 C ln| x| C2 9
§4. PHƯƠNG TRÌNH VI PHÂN TUYẾN TÍNH CẤP 2 HỆ SỐ HẰNG
4.1. Định nghĩa. Phương trình vi phân tuyến tính cấp 2 hệ số hằng ay′′ + by′ + cy = f(x) (1)
trong đó a, b, c là các hằng số thực, a ≠ 0.
Nếu f(x) ≡ 0 thì ta có phương trình vi phân tuyến tính cấp 2 thuần nhất hệ số hằng ay′′ + by′ + cy = 0 (2)
4.2. Cách giải phương trình ay′′ + by′ + cy = 0 (2)
Phương trình đặc trưng của (2) là phương trình bậc 2 định bởi: ak2 + bk + c = 0 (*)
Lập ∆ = b2 – 4ac. Ta có các trường hợp sau:
1) ∆ > 0: Khi đó (*) có 2 nghiệm thực phân biệt k1, k .
2 Nghiệm tổng quát của (2) trong
trường hợp này như sau: 56 k x k x 1 2 y = C e + C e 1 2
2) ∆ = 0: Khi đó (*) có nghiệm thực kép k0. Nghiệm tổng quát của (2) trong trường hợp này như sau: k x k x 0 0 y = C e + C xe 1 2
3) ∆ < 0: Khi đó (*) có 2 nghiệm phức phân biệt α ± iβ Nghiệm tổng quát của (2) 0 0
trong trường hợp này như sau: α x 0 y = e ( β + β 1 C cos 0x C2 sin 0x)
4.3. Ví dụ. Giải các phương trình vi phân sau: a) y′′ + y′ – 2y = 0. b) y′′ + 4y′ + 4y = 0. c) y′′ + y′ + y = 0. ĐS: a) x 2x y C e C e− = + y C e− C xe− = + 1 2 b) 2x 2x 1 2 1 − x 3 3 c) 2 y = e C cos x + C sin x 1 2 2 2
4.4. Cách giải phương trình ay′′ + by′ + cy = f(x) (1)
Ta chứng minh được rằng:
Nghiệm tổng quát của (1) = Một nghiệm riêng ủ
c a (1) + Nghiệm tổng quát của ay′′′ + by′ ′+ cy = 0 (2)
Sau đây ta chỉ ra cách tìm một nghiệm riêng của (1) trong trường hợp vế phải f(x) của (1) có dạng đặt biệt.
Nhắc lại phương trình đặc trưng của (2) là phương trình bậc 2 định bởi: ak2 + bk + c = 0 (*)
1) Trường hợp f(x) = eαxPn(x) với α là số thực; Pn(x) là một đa thức bậc n theo x:
1a) Nếu α không là nghiệm của (*) thì (1) có một nghiệm riêng dạng: y = eαxQ(x)
1b) Nếu α là nghiệm đơn của (*) thì (1) có một nghiệm riêng dạng: y = xeαxQ(x)
1c) Nếu α là nghiệm kép của (*) thì (1) có một nghiệm riêng dạng: 57 y = x2eαxQ(x)
trong đó Q(x) = anxn + ...+ a1x + a0 là đa thức tổng quát có bậc n = bậc của P ( n x). Để xác định
Q(x) ta thế y vào (1), đồng nhất các hệ số tương ứng ở hai vế để thu được một hệ phương
trình, giải hệ đó để tìm các hệ số ai.
2) Trường hợp f(x) = eαx[Pn(x)cosβx + Qm(x)sinβx] với α, β là các số thực, β ≠ 0;
Pn(x), Qm(x) là các đa thức bậc n, m theo x:
2a) Nếu α + iβ không là nghiệm của (*) thì (1) có một nghiệm riêng dạng:
y = eαx[R(x)cosβx + S(x)sinβx]
2b) Nếu α + iβ là một nghiệm của (*) thì (1) có một nghiệm riêng dạng:
y = xeαx[R(x)cosβx + S(x)sinβx]
trong đó R(x) = atxt + ...+ a1x + a ;
0 S(x) = btxt + ...+ b1x + b0 là các đa thức tổng quát có bậc t
= max{n, m}. Để xác định R(x), S(x) ta thế y vào (1), đồng nhất các hệ số tương ứng ở hai vế
để thu được một hệ phương trình, giải hệ đó để tìm các hệ số ai; bi.
3) Trường hợp f(x) = f1(x) + ... + fn(x), trong đó mỗi fi(x) có dạng thuộc một trong hai trường hợp trên.
Gọi yi là một nghiệm riêng của phương trình: ay′′ + by′ + cy = fi(x)
Khi đó y = y1+...+ yn là một nghiệm riêng của (1).
4.5. Sơ đồ giải phương trình vi phân ay′′ ′ + by′ ′+ cy = f(x) (1)
Phương trình thuần nhất tương ứng của (1) là: ay′′ + by′ + cy = 0 (2)
Phương trình đặc trưng của (2) là: ak2 + bk + c = 0 (*)
Phương trình (*) có nghiệm là ................................... Do đó nghiệm tổng quát của (2) là:
y =............................ (3)
Bây giờ ta tìm một nghiệm riêng của (1).
Vế phải của (1) là f(x) có dạng ...........................................................
Vì .................... nên (1) có một nghiệm riêng dạng:
y = .......................... (4) Từ (4) ta có:
y′ = .................; y′′ = .......................
Thế vào (1) ta được: ............................................
Đồng nhất các hệ số tương ứng ở hai vế ta được: ........................ 58
Thế vào (4) ta tìm được một nghiệm riêng của (1) là:
y = ............................ (5)
Từ (3) và (5) ta suy ra nghiệm tổng quát của (1) là:
y = ..................................
4.6. Ví dụ. Giải các phương trình vi phân sau:
a) y′′ – 5y′ + 6y = ex(2x – 1).
b) y′′ – y′ = 2(1– x).
c) y′′ – 2y′ + y = ex(x3 – 1) với y(0) = y′(0) = 1.
d) y′′ + 2y′ + 5y = 2cosx.
e) y′′ + y = 2sinx + 4cos2x. ĐS: a) x 2x 3x y = e (x + 1) + C e + C e 1 2 b) 2 x y = x + C + C e 1 2 c) 1 1 2 x 3 x x x 5 2 y =
x e (x − 10) + C e + C xe ; y = e (x − 10x + 20) 1 2 20 20 d) 2 1 − x y = cos x + sin x + e (C cos2x + C sin 2x 1 2 ) 5 5 e) 4 y = x − cos x − cos 2x + C + 1 cos x C2sin x 3 BÀI TẬP
1. Giải các phương trình vi phân sau : a) 2
1+ y dx + xy ln xdy = 0 b) 1 2 − y dx + y 1 2 − x dy = 0.
2. Giải các phương trình vi phân sau : y x a) 2 y '− = cos x tan . sin x 2 b) xy'+2y 2 = cos x.
3. Giải các phương trình vi phân sau : 2 2 4 a) y′ + y = x y . x 2 3 x 2 3 b) y′ +
y = y ( x +1) sin ; x (0 y ) =1. 3 x + 1 59
4. Giải các phương trình vi phân sau : 2 a) y y y′ = 4 + + . 2 x x
b) (x + y)dx + (x − y)dy = 0.
5. Giải các phương trình vi phân sau :
a) (2xy + 3y2)dx + (x2 + 6xy – 3y2)dy = 0.
b) (y + exsiny)dx + (x + excosy)dy = 0.
6. Giải các phương trình vi phân sau :
) ′ ′ = arctan ) ′ ′ + 2 ′ = x a y x x b xy y e
7. Giải các phương trình vi phân sau : a) y″ − 4y′ + 4y = x2. b) y″ + y′ − 6y = xe2x. c) y″ − 2y′ + y = 2xex.
d) y″ − 4y′ + 3y = excos 3x.
e) y″ − 2y′ + 5y = ex cos 2x . 60 Chương 4 LÝ THUYẾT CHUỖI §1. KHÁI NIỆM
1.1. Định nghĩa. Cho dãy số thực a1, a2,..., an,...Biểu thứ c +∞ a1 + a + 2 ...+ a + n ... hay ∑ a n n= 1
được gọi là một chuỗi số (gọi tắt là chuỗi), trong đó:
• an là số hạng tổng quát của chuỗi. • Sn = a 1 + a
2 +...+ an là tổng riêng phần thứ n của chuỗi.
Nếu giới hạn lim S tồn tại hữu hạn và bằng s∈R thì ta nói chuỗi hội tụ và có tổng là s; hki n n→+∞ +∞
đó ta viết ∑ a = s . Ngược lại, nếu giới hạn trên không tồn tại hoặc bằng vô cùng thì ta nói n n=1
chuỗi phân kỳ và không có tổng.
1.2. Chuỗi hình học: +∞
Chuỗi hình học là chuỗi có dạng n−1 ∑aq (1) n 1 =
trong đó a, q là các hằng số, a ≠ 0. Đó chính là chuỗi ứng với cấp số nhân vô hạn công bội q:
a, aq, aq2,...,aqn,... Tổng riêng phần thứ n của chuỗi hình học trên là:
na neu q = 1; n 1 −
S = a + aq + . .+ aq = a(1 n n −q ) neu q ≠1. 1− q +∞ Với chuỗi hình học n−1 ∑ aq , ta có: n 1 =
• |q|< 1: Chuỗi hội tụ và có tổng a s = . 1 − q
• |q|≥ 1: Chuỗi phân kỳ.
Ví dụ: Khảo sát sự hội tụ của các chuỗi sau: +∞ n 2.7 +∞ n+2 2.6 a) ∑ n b) ( 1 − ∑ ) 2n n n= 1 5.3 n=1 3.5 61
ĐS: a) Hội tụ và có tổng s = 7/5. b) Phân kỳ.
1.3. Tính chất: +∞ +∞
1) Từ chuỗi ∑ a , bằng cách bỏ đi k số hạng đầu ta được chuỗi ∑ a có cùng bản n n n= 1 n=k+1
chất với chuỗi ban đầu, nghĩa là chúng cùng hội tụ hoặc cùng phân kỳ. +∞ +∞
2) Xét các chuỗi ∑ a và ∑ a α
, trong đó α là hằng số, ta có: n n n= 1 n=1 +∞
• Nếu α = 0 thì chuỗi ∑ αa hội tụ và có tổng là 0. n n=1 +∞ +∞
• Nếu α ≠ 0 thì chuỗi ∑ a α
có cùng bản chất với chuỗi hội tụ ∑ a và trong trường n n n= 1 n=1 +∞ +∞
hợp hội tụ, ta có: ∑ a α = α ∑ a . n n n=1 n=1 +∞ +∞ +∞
3) Xét các chuỗi ∑ a ; ∑ b và ∑ (a + b ) ta có : n n n n n= 1 n= 1 n=1 +∞ +∞ +∞
• Nếu cả hai chuỗi ∑ a và ∑ b đều hội tụ thì chuỗi ∑ (a + b ) cũng hội tụ, hơn n n n n n=1 n=1 n=1 nữa: +∞ +∞ +∞ (a + b ) = a + b ∑ ∑ ∑ n n n n . n 1 = n 1 = n 1 = +∞ +∞ +∞
• Nếu trong hai chuỗi ∑ a và ∑ chỉ có một chuỗi hội tụ thì chuỗi + ∑ n b n (an bn) n=1 n=1 n= 1 phân kỳ. +∞ +∞ +∞
• Nếu chuỗi ∑ a hội tụ thì chuỗi +
có cùng bản chất với chuỗi . n ∑ (an bn) ∑ bn n= 1 n=1 n=1 +∞ +∞
• Chú ý: Nếu cả hai chuỗi ∑ a và
đều phân kỳ thì không có kết luận tổng n ∑ bn n= 1 n= 1 +∞
quát về bản chất của chuỗi (a + ∑ . n bn) n= 1
§2. CÁC TIÊU CHUẨN HỘI TỤ
2.1. Điều kiện cần để chuỗi hội tụ: 62 +∞
1. Định lý: Nếu chuỗi ∑ a hội tụ thì lim a = 0. n n n →+∞ n=1 +∞ 2. Hệ quả: a) Nếu lim a lim a ≠ 0 n không tồn tại hoặc n
thì chuỗi ∑ a phân kỳ. n→+∞ n→+∞ n n=1 +∞ b) Nếu lim |a | n
không tồn tại hoặc lim | ≠ n
a | 0 thì chuỗi ∑ a phân kỳ. n →+∞ n n →+∞ n=1
3. Chú ý: Nếu lim an = 0 thì không có kết luận tổng quát về bản chất của chuỗi n →+∞ +∞ ∑ a . n n= 1
Ví dụ: Khảo sát sự hội tụ của chuỗi số: +∞ n n 3 ∑ ( 1 − ) arctg n + n= 1 2 1 ĐS: Phân kỳ.
2.2. Chuỗi số dương và Tiêu chuẩn so sánh: +∞
1. Định nghĩa: Chuỗi số dương (hay chuỗi dương) là chuỗi a
∑ trong đó tất cả các số n n=1 hạng an ≥ 0. +∞
2. Nhận xét: Đối với chuỗi dương ∑ a ta thấy dãy tổng riêng phần {S n n} (Sn= a1+ n=1
a2+...+an) là dãy tăng. Do đó chuỗi hội tụ khi và chỉ khi dãy tổng riêng phần {Sn} bị chặn. +∞ +∞
3. Tiêu chuẩn So sánh: Cho các chuỗi dương ∑ a và . Khi đó: n ∑ bn n= 1 n= 1 a) Nếu an ≤ b n với mọi n thì: +∞ +∞ ∑b hoi tu ⇒ ∑ a hoi tu n n n 1 = n 1 = +∞ +∞ ∑a phan ky ⇒ ∑b phan ky n n n 1 = n 1 = +∞ +∞ b) a
Nếu an ~ bn khi n → +∞, nghĩa là n lim
= 1, thì hai chuỗi ∑ a và có cùng n ∑ bn n→+∞ bn n= 1 n=1 bản chất. 63 c) a Nếu n lim = 0 thì: n→+∞ bn +∞ +∞ b hoi tu ⇒ a hoi tu ∑ ∑ n n n 1 = n 1 = +∞ +∞ a phan ky ⇒ b phan ky ∑ ∑ n n n 1 = n 1 = d) a Nếu n lim = +∞ thì: n→+∞ bn +∞ +∞ ∑a hoi tu ⇒ ∑b hoi tu n n n 1 = n 1 = +∞ +∞ ∑b phan ky ⇒ ∑ a phan ky n n n 1 = n 1 =
Ví dụ: Khảo sát sự hội tụ của chuỗi số: +∞ n n +∞ n n 3 + 4 2 + 6 a) b) ∑ ∑ n n n n + + n 1 2 5 = n 1 3 5 = ĐS: a) Hội tụ . b) Phân kỳ. +∞ +∞
4. Hệ quả: Cho các chuỗi dương ∑ a và ∑ b . Khi đó nếu có ít nhất một trong hai n n n=1 n=1 +∞ +∞ +∞
chuỗi ∑ a ; ∑ b phân kỳ thì chuỗi ∑ (a + b ) cũng phân kỳ. n n n n n=1 n=1 n=1
2.3. Tiêu chuẩn Căn thức Cauchy: +∞
Cho chuỗi số ∑ a . Giả sử tồn tại giới hạn: n n=1 n lim | a | = λ n . n →+∞ Khi đó: +∞
1) Nếu λ < 1 thì chuỗi ∑ a hội tụ. n n= 1 +∞
2) Nếu λ > 1 thì chuỗi ∑ a phân kỳ. n n= 1 64 +∞
3) Nếu λ = 1 thì không có kết luận tổng quát về bản chất của chuỗi ∑ a . n n=1
2.4. Tiêu chuẩn Tỉ số D’Alembert: +∞
Cho chuỗi số ∑ a . Giả sử tồn tại giới hạn: n n=1 an+1 lim = λ . n →+∞ an Khi đó: +∞
1) Nếu λ < 1 thì chuỗi ∑ a hội tụ. n n= 1 +∞
2) Nếu λ > 1 thì chuỗi ∑ a phân kỳ. n n= 1 +∞
3) Nếu λ = 1 thì không có kết luận tổng quát về bản chất của chuỗi ∑ a . n n=1
2.5. Chú ý: 1) Ta thường sử dụng Tiêu chuẩn căn thức Cauchy hơn Tiêu chuẩn Tỉ số
D’Alembert. Tuy nhiên, nếu trong số hạng tổng quát của chuỗi có chứa giai thừa thì nên dùng Tiêu chuẩn D’Alembert.
2) Khi sử dụng Tiêu chuẩn Căn thức Cauchy ta cần Chú ý n lim n = 1, do đó: n →+∞ n k lim |a + + + = kn ... a1n a0 | 1 n →+∞ (k ∈ N, ak ≠ 0).
Ví dụ: Khảo sát sự hội tụ của chuỗi số: 2 +∞ n +∞ 3 n 3 n ! n + 1 (n + 1) a) b) ∑ ∑ 2 n 2 n n n 1 n = n 1 n = n 3 ĐS: a) Phân kỳ. b)Hội tụ.
2.6. Tiêu chuẩn Tích phân Cauchy: +∞
1) Định lý: Cho chuỗi dương ∑ a . Giả sử tồn tại hàm số f(x) không âm, liên tục và n n=1
giảm trên [1,+∞) sao cho an = f(n) với mọi n ≥ 1. Khi đó: 65 +∞ +∞
Chuỗi ∑ a hội tụ ⇔ Tích phân suy rộng hội tụ. n f (x)dx ∫ n=1 1 +∞ 2) Chuỗi dạng 1 ∑ (α: Const): α n= 1 n • Nếu α ≤ 0 thì 1 → / 0 nên chuỗi phân kỳ. nα • 1 Xét α > 0. Đặt 1 f (x) =
thì f(x) không âm, liên tục, giảm trên [1,+∞) và f (n) = xα nα
nên theo Tiêu chuẩn Tích phân Cauchy ta có: +∞ 1 +∞ ∑
hội tụ ⇔ Tích phân suy rộng 1 dx > 1. α ∫ hội tụ ⇔ α α n= 1 n x 1 +∞ Tóm lại, với chuỗi 1 ∑ , ta có: α n= 1 n
• α > 1: Chuỗi hội tụ.
• α ≤ 1: Chuỗi phân kỳ.
Ví dụ 1: Khảo sát sự hội tụ của chuỗi số: +∞ 3 2 +∞ 3 n + 4n +1 n +1 a)∑ b)∑ 4 3 4 3 n=1 n +2n +3n +5 n=1 n n +2n +3n +5 ĐS: a) Phân kỳ. b) Hội tụ.
Ví dụ 2: Khảo sát sự hội tụ của chuỗi số: +∞ 1 ∑ n ln n n= 2 ĐS: Phân kỳ.
2.7. Chuỗi đan dấu và Tiêu chuẩn Leibniz: +∞
1. Định nghĩa: Chuỗi đan dấu là chuỗi có dạng n ± (−
∑ 1) a trong đó a n≥ 0 với mọi n . n n=1 +∞
2. Tiêu chuẩn Leibniz: Cho chuỗi đan dấu n (−
∑ 1) a . Giả sử các điều kiện sau được n n= 1 thỏa:
• Dãy số không âm {an} là dãy giảm. 66 • lim a = . n 0 n→+∞ +∞ Khi đó chuỗi đan dấu n (− ∑ 1) a hội tụ. n n=1 +∞ n 3. Chuỗi dạng (−1) ∑ (α: Const): α n= 1 n n • (−1) Nếu α ≤ 0 thì → / 0 nên chuỗi phân kỳ. nα +∞ n +∞ • (−1) 1 Xét α > 0. Khi đó ∑
là chuỗi đan dấu có dạng n (− ∑ 1) a , trong đó a = α n n n=1 n n=1 nα
giảm và lim a = nên chuỗi hội tụ theo Tiêu chuẩn Leibniz. n 0 n→+∞ +∞ n
Tóm lại, với chuỗi đan dấu (−1) ∑ , ta có: α n=1 n
• α > 0: Chuỗi hội tụ.
• α ≤ 0: Chuỗi phân kỳ.
Ví dụ : Khảo sát sự hội tụ của chuỗi số: +∞ 3 2 n n + 4n + 1 a) (−1) ∑ 4 3 + + + n=1 n 2n 3n 5 +∞ 5 n−1 n + 1 b)∑ ( 1 − ) 4 3 + + + n=1 n n 2n 3n 5 ĐS: a) Hội tụ . b) Phân kỳ.
§3. SỰ HỘI TỤ TUYỆT ĐỐI VÀ BÁN HỘI TỤ +∞ +∞
3.1. Định lý và Định nghĩa: Cho chuỗi số ∑ a . Khi đó nếu chuỗi hội tụ thì n | ∑ an| n= 1 n=1 +∞
chuỗi ∑ a cũng hội tụ và ta có: n n=1 +∞ +∞ a ≤ ∑ . n | ∑ an | n 1 = n 1 = +∞ +∞
Tuy nhiên, nếu chuỗi ∑ a hội tụ thì chuỗi
không nhất thiết hội tụ. Ta nói: n | ∑ an| n= 1 n=1 67 +∞ +∞
• Chuỗi ∑ a hội tụ tuyệt đối nếu chuỗi hội tụ. n | ∑ an | n= 1 n= 1 +∞ +∞ • Chuỗi ∑ a hội tụ nhưng chuỗi
n bán hội tụ hay hội tụ có điều kiện nếu chuỗi ∑ an n=1 n=1 +∞ | ∑ a phân kỳ. n | n= 1 +∞ n (−1)
3.2. Chuỗi dạng ∑ (α: Const): α n= 1 n +∞ n +∞ n +∞ • (−1) ( 1 − ) 1 ∑
hội tụ tuyệt đối ⇔ ∑ = ∑ hội tụ ⇔ α > 1. α α α n=1 n n=1 n n 1 n = +∞ n − +∞ n − +∞ n +∞ • ( 1) ( 1) ( 1 − ) 1 ∑ bán hội tụ ⇔ ∑ hội tụ và ∑ = ∑ phân kỳ α α α α n=1 n n=1 n n=1 n n 1 n = ⇔ 0< α ≤ 1. +∞ n • (−1) ∑ phân kỳ ⇔ α ≤ 0. α n=1 n
Ví dụ: Khảo sát sự hội tụ tuyệt đối và bán hội tụ của các chuỗi số: +∞ 3 2 n n + 4n + 1 a) ∑ (−1) 4 3 n + 2n + 3n + 5 n= 1 +∞ 5 n 1 − n + 1 b) ( 1 − ) ∑ 6 3 + + + n= 1 n n 2n 3n 5 ĐS: a) Bán hội tụ . b) Hội tụ tuyệt đối.
3.3. Nhận xét: Trong các Tiêu chuẩn Căn thức Cauchy và Tiêu chuẩn tỉ số D’Alembert, +∞
nếu giới hạn tương ứng là λ < 1 thì thật ra chuỗi ∑ a sẽ hội tụ tuyệt đối (thay vì chỉ hội tụ như n n= 1
đã phát biểu khi trước). §4. CHUỖI LŨY THỪA
4.1. Định nghĩa: Chuỗi lũy thừa là chuỗi có dạng: +∞ n u − ∑ (1) n (x x0) n= 1 68 trong đó: • x là biến số thực;
• x0 là hằng số thực;
• {un} là dãy số thực.
Tập hợp D gồm tất cả các giá trị của biến số x sao cho chuỗi (1) hội tụ được gọi là miền hội tụ của (1).
4.2. Định lý Abel: Cho chuỗi lũy thừa: +∞ n ∑ u (x − x ) (1) n 0 n= 1
Khi đó chỉ có một trong ba trường hợp sau xảy ra:
1) Chuỗi (1) chỉ hội tụ tại x = x0.
2) Chuỗi (1) hội tụ tại mọi x ∈ R.
3) Tồn tại số thực R > 0 sao cho:
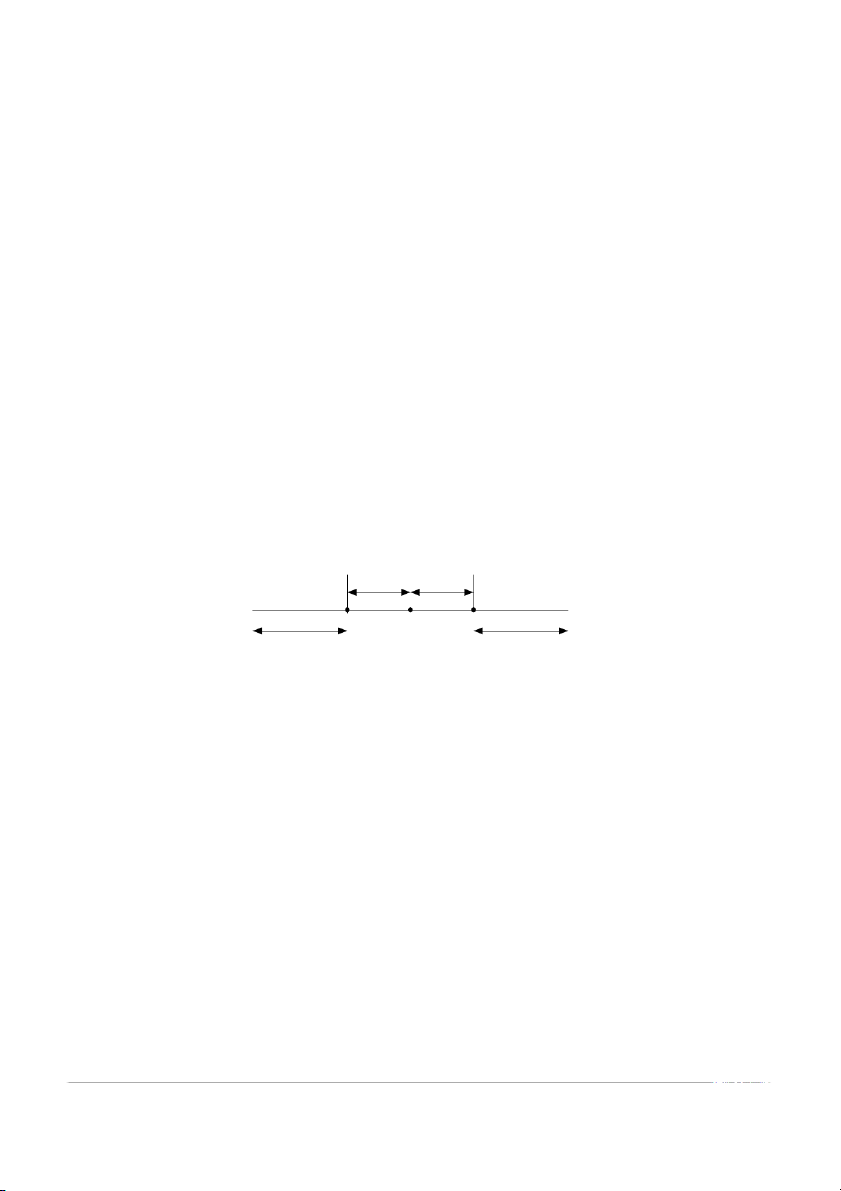
• ∀x∈ (x0 – R, x0 + R), chuỗi (1) hội tụ.
• ∀x∉ [x0 – R, x0 + R], chuỗi (1) phân kỳ. hoäi tuï hoäi tuï R R x0-R x0 x0+R phaân kyø phaân kyø
Khi đó R được gọi là bán kính hội tụ và (x0 – R, x0 + R) là khoảng hội tụ của chuỗi (1).
4.3.Chú ý: 1) Để thuận tiện khảo sát, trong Định lý Abel, nếu trường hợp 1 xảy ra, ta nói
chuỗi (1) có bán kính hội tụ R = 0, còn nếu trường hợp 2 xảy ra, ta nói chuỗi (1) có bán kính hội tụ R = +∞.
2) Trong trường hợp 3 của Định lý Abel ta không có kết luận tổng quát về bản chất của
chuỗi (1) tại x = x0 ± R .
4.4. Cách tìm bán kính hội tụ: Cho chuỗi lũy thừa: +∞ n ∑ u − (1) n (x x0) n 1 =
Để tìm bán kính hội tụ R của chuỗi (1) ta có hai cách sau: 69
1) Dùng Tiêu chuẩn Căn thức: Bước 1: Tính n lim | un |=L . n →+∞
Bước 2: Xác định bán kính hội tụ R = 1 L 1 1 (Với Qui ước = + ; ∞ = 0 0 +∞ )
2) Dùng Tiêu chuẩn Tỉ số: u Bước 1: Tính n 1 lim + = L . n →+∞ un
Bước 2: Xác định bán kính hội tụ R = 1 L (Với Qui ước 1 1 = + ; ∞ = 0 ) 0 +∞
4.5. Cách tìm miền hội tụ: Cho chuỗi lũy thừa: +∞ n u − ∑ n(x x0) (1) n 1 =
có bán kính hội tụ R. Khi đó miền hội tụ D của chuỗi (1) được xác định như sau: 1) Nếu R = 0 thì D = {x0}.
2) Nếu R = +∞ thì D = R.
3) Trường hợp 0 < R < +∞, ta có (x0 – R, x 0 + R) ⊂ D ⊂ [x – 0 R, x 0 + R] .
Như vậy, muốn xác định D trong trường hợp này ta còn phải khảo sát thêm chuỗi (1)
tại x = x0 ± R, tại giá trị nào mà chuỗi hội tụ thì giá trị đó thuộc D.
Ví dụ: Tìm miền hội tụ của các chuỗi lũy thừa sau: +∞ +∞ n +∞ n n x (x − 1) a)∑ n!(x + 2) b)∑ c)∑ n n + n= 1 n= 1 (2n) n=1 (n 1)3 ĐS: a) D = {x0} = {–2}. b) D = R. c) D = [–2,4). 70 BÀI TẬP
1) Khảo sát sự hội tụ của các chuỗi sau: ∞ ∞ n n + + n n 1 4 5 a) ∑ (−1) arctg b) ∑ n n 2n n 1 = n 2 = 3 + 6
2) Khảo sát sự hội tụ của các chuỗi sau: ∞ 2 ∞ ∞ n 2 (n !) 1 7 (n !) a) ∑ b) ∑ c) ∑ 3 (2n) ! = = ln n (2n) ! n 1 n 2 n=1 n(n−1) n ∞ n − 1 ∞ ∞ − n 3n 1 n 1 d) ∑ e) ∑ ( −1) f) ∑ ( −1) tg n + 1 2n + 1 n n= 1 n= 1 n= 1 2 ∞ ∞ n 1 (n + 1) ∞ α g) ∑ h) ∑ 2 i) ∑ n − n −1 2 3 n n n= 3 n ln n(ln ln n) n= 1 n 4 n 1 =
3) Tìm miền hội tụ của các chuỗi lũy thừa sau: ∞ 2 n ∞ 2 n ∞ n (n − 3n + 1)(x − 5) (n − 3n + 1)(x + 2) (x − 1) a) b) c) ∑ ∑ ∑ 3 n 2 n n = (n + 6n + 4)3 = (n + 6n + 4)(2 + 5 ) n ! n 1 n 1 n= 0 ∞ 2n−1 (x + 5) ∞ n ! n d) ∑ e) ∑ (x − 2) 2 n 2 n=1 n 4 n=1 n + 3n + 2 ------------------------- 71



