PHÒNG GD&ĐT PHÚC YÊN
ĐỀ THI GIAO LƯU HỌC SINH GIỎI
MÔN: TOÁN 6
Năm học 2016 - 2017
Thời gian làm bài: 120 phút, không kể thời gian giao đề.
Câu 1. (2,5 điểm) Thực hiện phép tính: a. b.
c. C = 17 + (27 – 7.6) – (94.7 – 27.99)
Câu 2. (2,0 điểm)
a. Tìm các số tự nhiên a, b, c nhỏ nhất khác 0 sao cho 16a = 25b = 30c
b. Tìm số tự nhiên x biết: 8.5 + 128 : (x - 2)2 = 42
Câu 3. (2,0 điểm)
a. Tìm các chữ số x ; y để
chia cho 2; 5 và 9 đều dư 1. b. Cho biểu thức
. Tìm tất cả các giá trị nguyên
của n để biểu thức B có giá trị là số nguyên.
Câu 4. (2,5 điểm) Cho góc
. Trên các tia Bx; By lần lượt lấy các điểm A; C
(A B ; C B ). Trên đoạn thẳng AC lấy điểm D sao cho .
a. Tính độ dài đoạn thẳng AC, biết AD = 4 cm, CD = 3 cm. b. Tính số đo của . c. Từ B vẽ tia Bz sao cho . Tính số đo .
Câu 5. (1,0 điểm)
Tìm các số tự nhiên x, y sao cho: . HẾT
Cán bộ coi thi không được giải thích gì thêm.
Họ và tên thí sinh …………………………… Số báo danh …………………
PHÒNG GD&ĐT PHÚC YÊN
HD CHẤM GIAO LƯU HỌC SINH GIỎI ————————
MÔN: TOÁN 6
Năm học 2016 - 2017 HƯỚNG DẪN CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày,
nếu học sinh giải theo cách khác mà đúng và đủ các bước thì giám khảo vẫn cho điểm tối đa.
- Trong mỗi bài, nếu ở một bước nào đó bị sai thì các bước sau có liên quan không được điểm.
- Bài hình học (ý a) bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu không có hình vẽ
đúng ở phần nào thì giám khảo không cho điểm phần lời giải liên quan đến hình của phần đó.
- Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn. BIỂU ĐIỂM VÀ ĐÁP ÁN: Câu Đáp án Điểm 1,0 a. Tính được A = b. 0.5đ = 1 0.25đ = =
c. C = 17 + (27 – 7.6) – (94.7 – 27.99) 0.25
= 17 + 27 – 7.6 - 94.7 + 27.99
= 17 + 27(1 + 99) – 7 (6 + 94) 0,25
= 17 + 27 .100 – 7 . 100 = 17 + 100.20 = 2017 0.25
Câu a. Tìm các số tự nhiên a, b, c nhỏ nhất khác 0 sao cho 16a = 25b = 30c 2 Đặt 16a = 25b = 30c = x
Mà a, b, c nhỏ nhất, khác 0 0,5
Nên x nhỏ nhất khác 0 do đó x = BCNN(16,25,30) x = 1200
Tìm được a = 75; b = 48; c = 40 0,5 0,25
b. Biến đổi được về dạng: 0,75
Vì x là số tự nhiên nên x = - 6 (loại). Vậy x = 10 Câu 3 a. Do A =
chia cho 2; 5 và 9 đều dư 1 nên y =1. Ta có A = 0,25 - Vì A = chia cho 9 dư 1 - 1 9 9 0,25
Nên x + 1 + 8 + 3 +0 9 hay x + 3 9 , mà x là chữ số nên x = 6. 0,25 Vậy x = 6; y = 1. 0,25 b. Ta có = ( , )
Để B nhận giá trị nguyên thì 5 (n – 3) Hay n - 3 phải là ước của 5. 0.5 Suy ra n – 3 Đối chiếu điều kiện , ta được 0.5 Vậy: Với
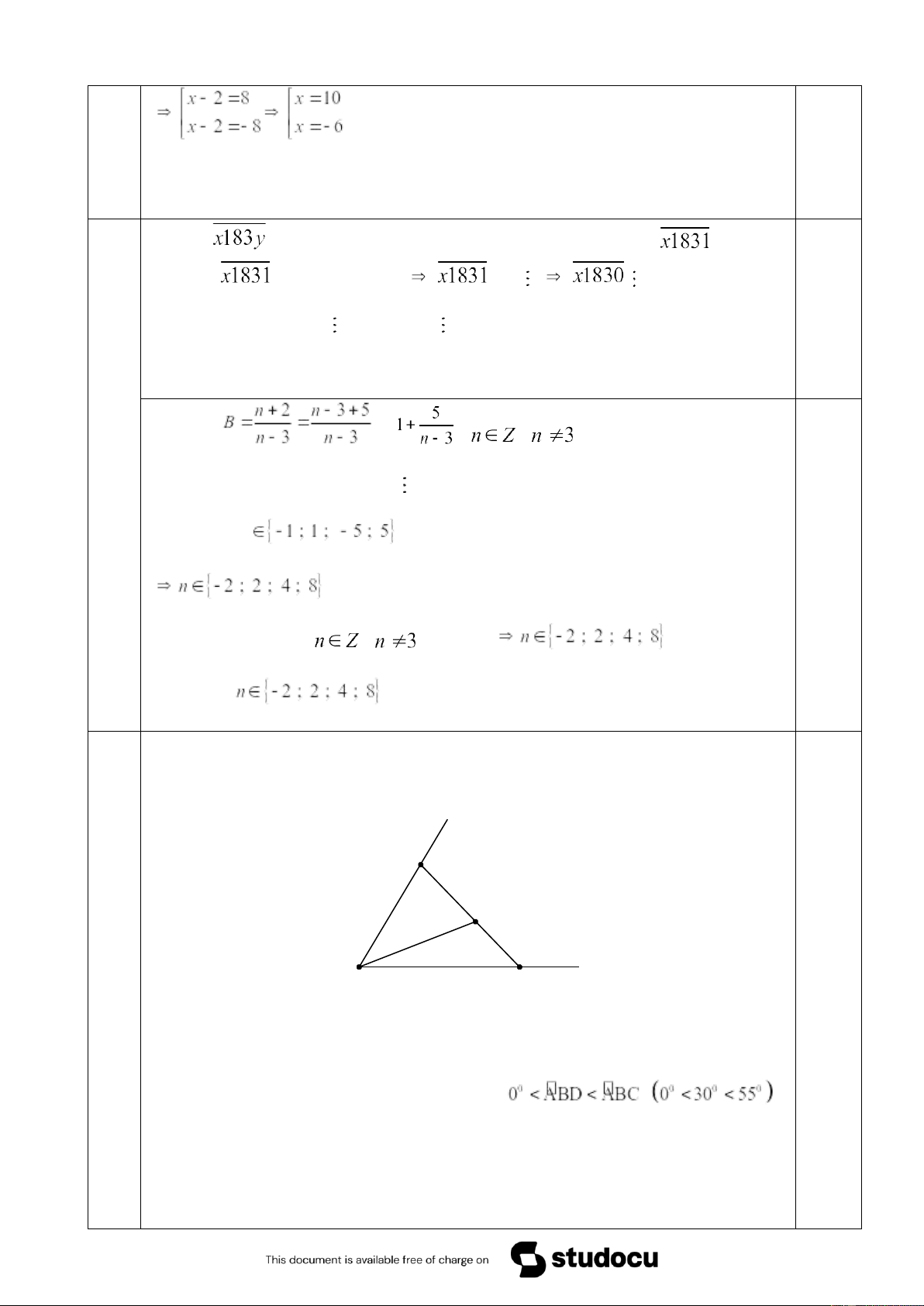
biểu thức B có giá trị nguyên. Câu a. Vẽ hình 4 x A D B C y
a. Vì điểm D thuộc đoạn thẳng AC mà
nên điểm D nằm giữa 2 điểm A và C. 0.75
Do đó AC = AD + CD = 4 + 3 = 7 (cm)
b. Điểm D nằm giữa điểm A và điểm C nên tia BD nằm giữa hai tia BA và BC ta có: 0.75 c. Xét 2 trường hợp:
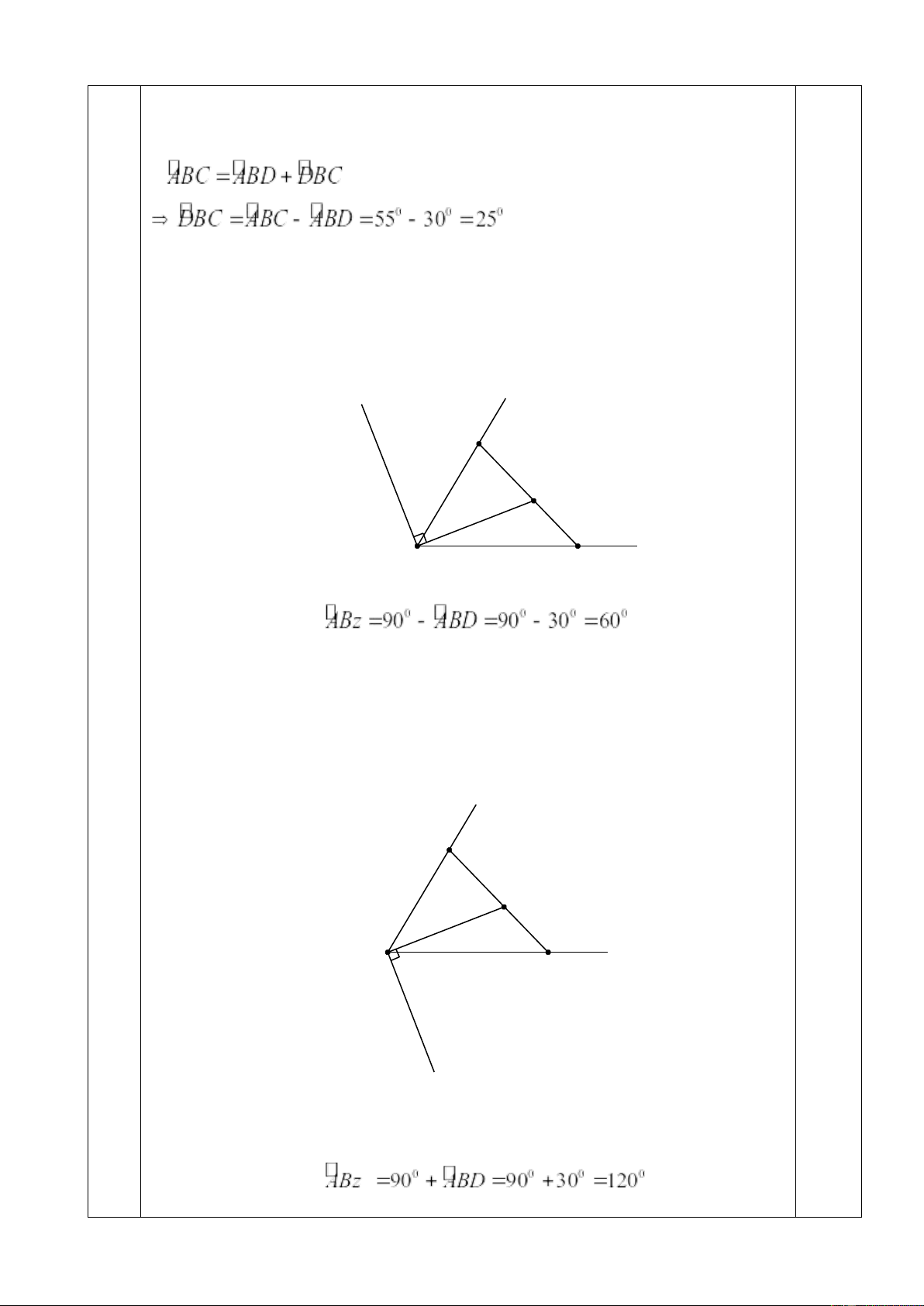
- Trường hợp 1: Tia Bz và BD nằm về hai nửa mặt phẳng có bờ là AB
nên tia BA nằm giữa hai tia Bz và BD. x z A D 0.5 B C y Tính được
- Trường hợp 2: Tia Bz và BD nằm về cùng nửa mặt phẳng có bờ là
AB nên tia BD nằm giữa hai tia Bz và BA . x A D 0.5 B C y z Tính được Từ 0,25 0,25
Vì x, y là số tự nhiên nên 2x - 1 là số tự nhiên và là ước lẻ của 54, do đó Câu 5 0,25 Ta có bảng sau: 2x - 1 1 3 9 27 x 1 2 5 14 0,25 y 54 18 6 2 Vậy:
(x; y) = (1; 54 ) ; (2; 18 ) ; (5; 6) ; (14; 2). — Hết —