












Preview text:
BÀI 4: TỔNG QUAN VỀ XÁC SUẤT
VÀ ĐỊNH LÝ GIỚI HẠN TRUNG TÂM I II Tổng quan về xác Định lý giới hạn suất trung tâm 1 I. Tổngquan vềxác suất
Khái niệm vềxác suất, biếnngẫunhiên
Phân phốixác suất củabiến ngẫunhiên liên tục 2 2 Xác suất là gì?
• X/S là khảnăngmà một sựkiệncó thểxảyra.
• X/S cung cấpmối liên hệgiữa tổng thểvà mẫu. • VD:
• Từtrung bình mẫu=> suy luậntrung bình của tổngthể
• Từ một tổngthể đã biết => tính đượckhảnăng lấy đượcmột giá trịcụthể cho mẫu. 3 3
Tại sao chúng ta cần học xác suất và phân phối xác suất? 4 4
Biến ngẫu nhiên và Xác suất
• X là biến ngẫu nhiên nếu giá trị của X=x là hoàn toàn ngẫu nhiên.
• Xác suất để X nhận giá trị x là p(x)=P(X=x).
• Nếu một biến ngẫu X nhận giá trị xi, khi đó 1. 0 p x 1 for all x i i 2. p x 1 i i x 5 5 Phân phối chuẩn 6 Phân phối chuẩn (PPC)
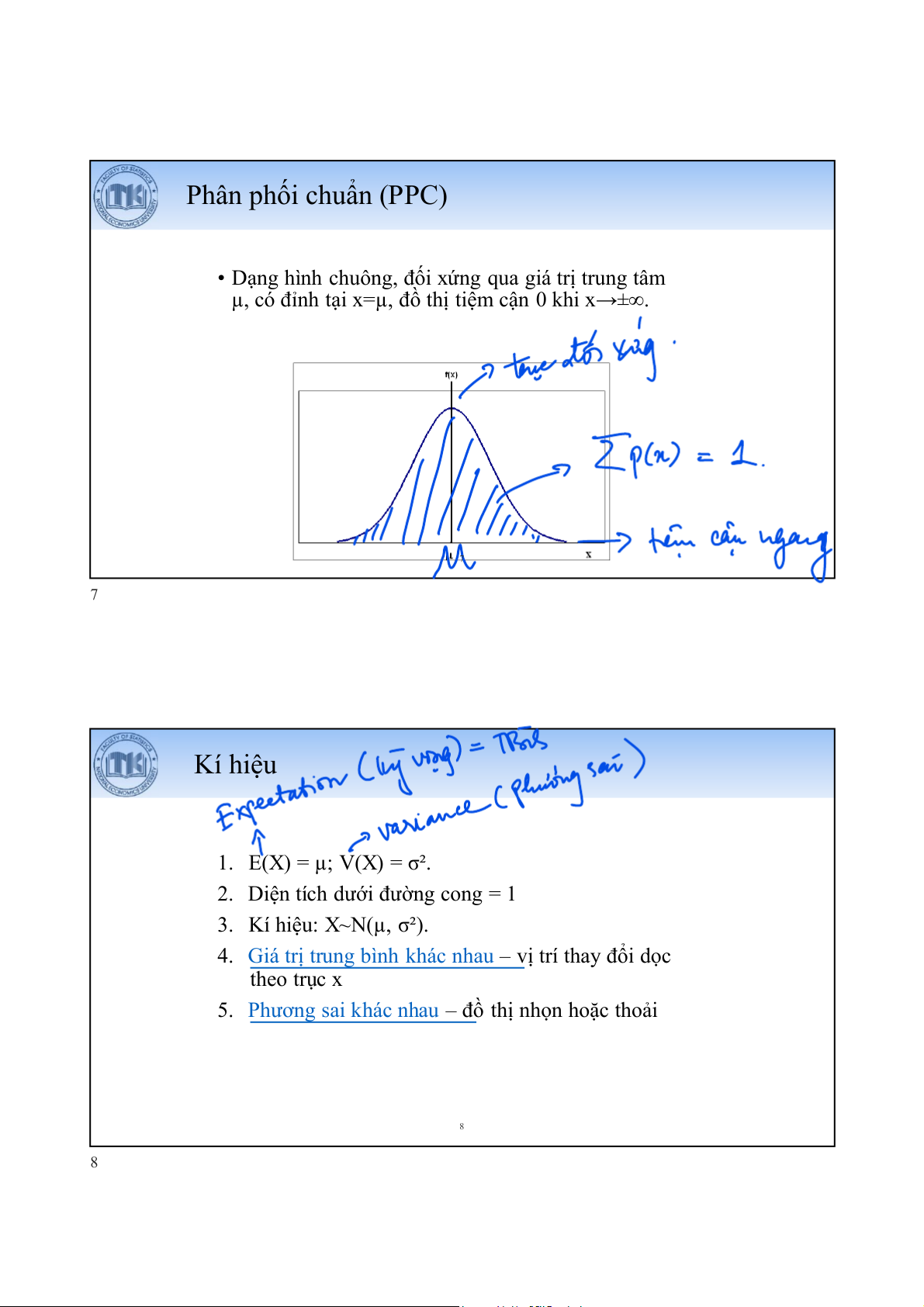
• Dạng hình chuông, đối xứng qua giá trị trung tâm
µ, có đỉnh tại x=µ, đồ thị tiệm cận 0 khi x→±∞. 7 7 Kí hiệu 1. E(X) = µ; V(X) = σ².
2. Diện tích dưới đường cong = 1 3. Kí hiệu: X~N(µ, σ²).
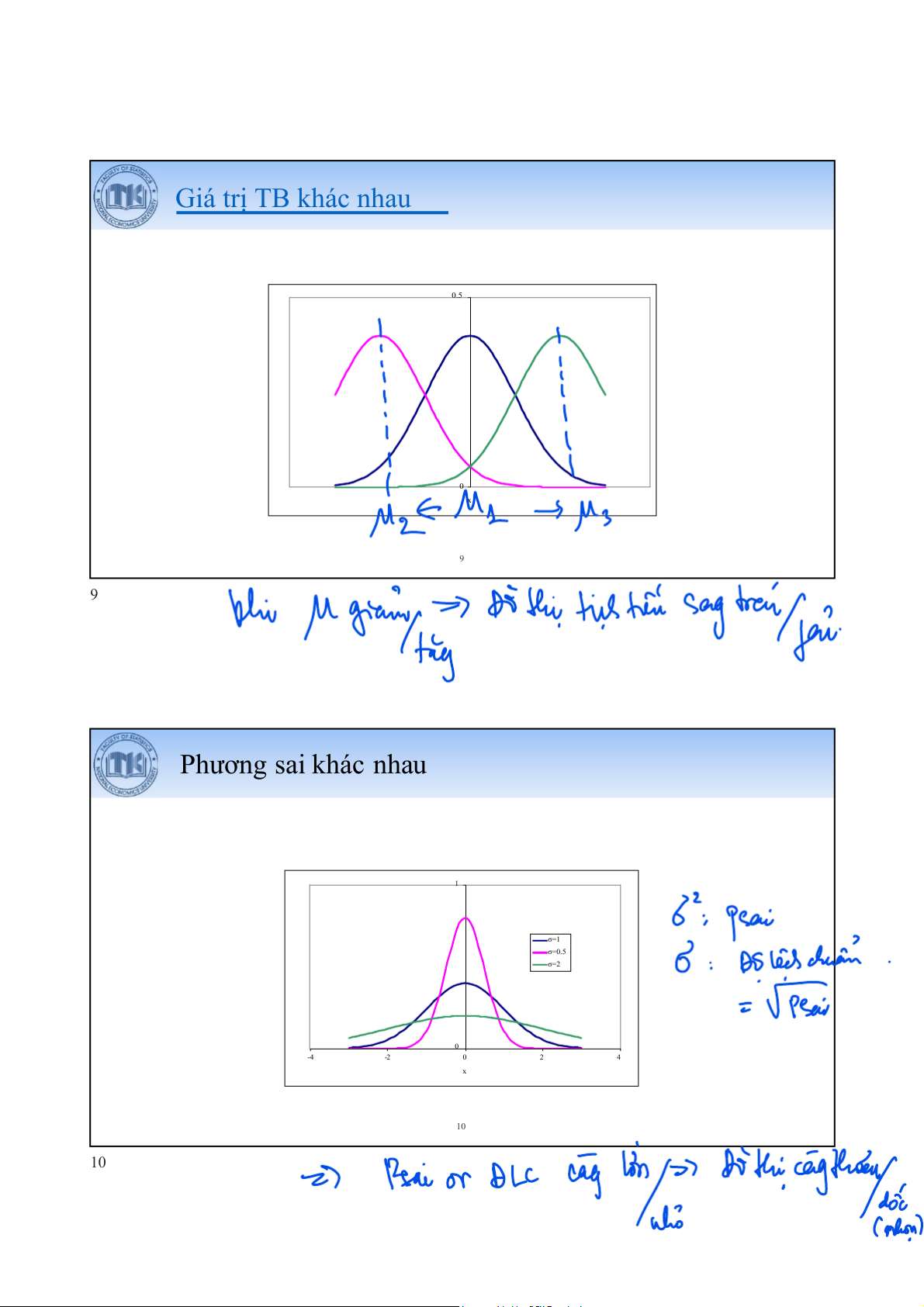
4. Giá trị trung bình khác nhau – vị trí thay đổi dọc theo trục x
5. Phương sai khác nhau – đồ thị nhọn hoặc thoải 8 8 Giá trị TB khác nhau 0.5 f(x) 0 x 9 9 Phương sai khác nhau 1 σ=1 σ=0.5 σ=2 f(x) 0 -4 -2 0 2 4 x 10 10 Tính xác suất từ PPC
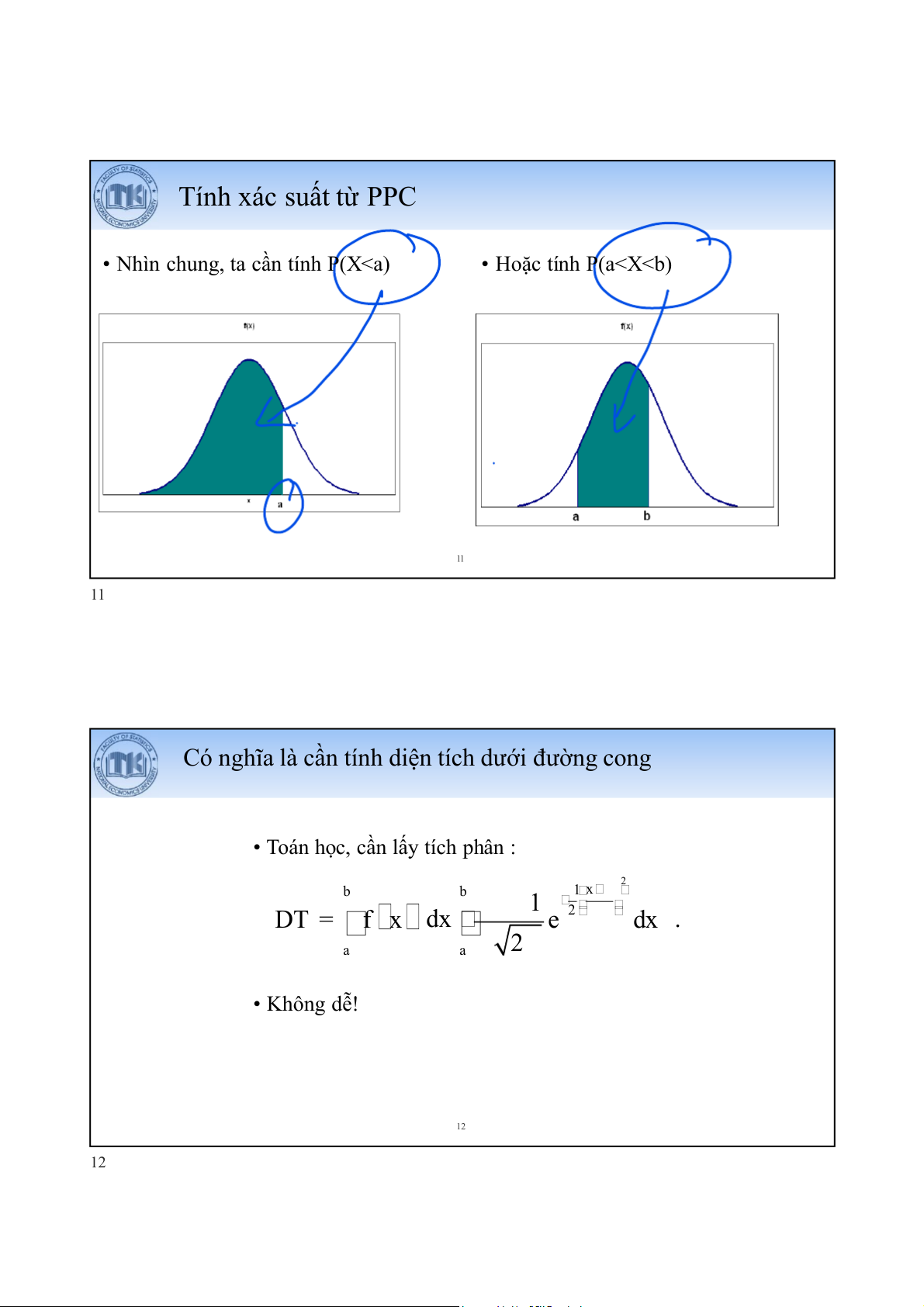
• Nhìn chung, ta cần tính P(X• Hoặc tính P(a11 11
Có nghĩa là cần tính diện tích dưới đường cong
• Toán học, cần lấy tích phân : b b 1 1 x 2 DT = f x dx e 2 dx . a a 2 • Không dễ! 12 12 Chuẩn hóa (1)
• Là quá trình chuyển một biến phân phối chuẩn về phân phối chuẩn hóa
• Nếu X~N(µ,σ²), sử dụng công thức dưới đây để chuẩn hóa: X Z ~ ( N 0,1)
Sử dụng bảng Z để tra X/S 13 13 Quy tắc tính xác suất • Quy tắc đối xứng P(Z<-a) = P(Z>a) P(Z>a) = 1 – P(Z• P(a14 14
II. Địnhlý giới hạntrung tâm Phân phốicủa mẫu
Phân phốicủa trung bình mẫu
Địnhlý giớihạn trung tâm 15 Phân phối của mẫu
• Lấy một mẫu gồm 50 quan sát (obs), đồ thị và thống kê mô tả cho dưới đây 10 5 requency F 0 10 12 14 16 18 20 22 24 26 Pizza time Variable N Mean Median SD
Pizza time 50 17.256 17.041 3.743 16 16
Một mẫu 50 obs khác; 1000 obs cũng từ tổng thể trên 100 10 50 5 requency requency F F 0 0 10 20 30 6 8 10 12 14 16 18 20 22 24 26 Pizza time Pizza time Variable N Mean Median SD
Pizza time 50 17.585 17.374 3.872
Pizza time 1000 17.934 17.627 4.009 17 17
Tăng cỡ mẫu lên đến 10,000 obs từ tổng thể đó 600 500 400 300 Frequency 200 100 0 10 20 30 40 Pizza time Variable N Mean Median SD
Pizza time 10000 18.046 17.744 4.006 18 18 Nhận xét
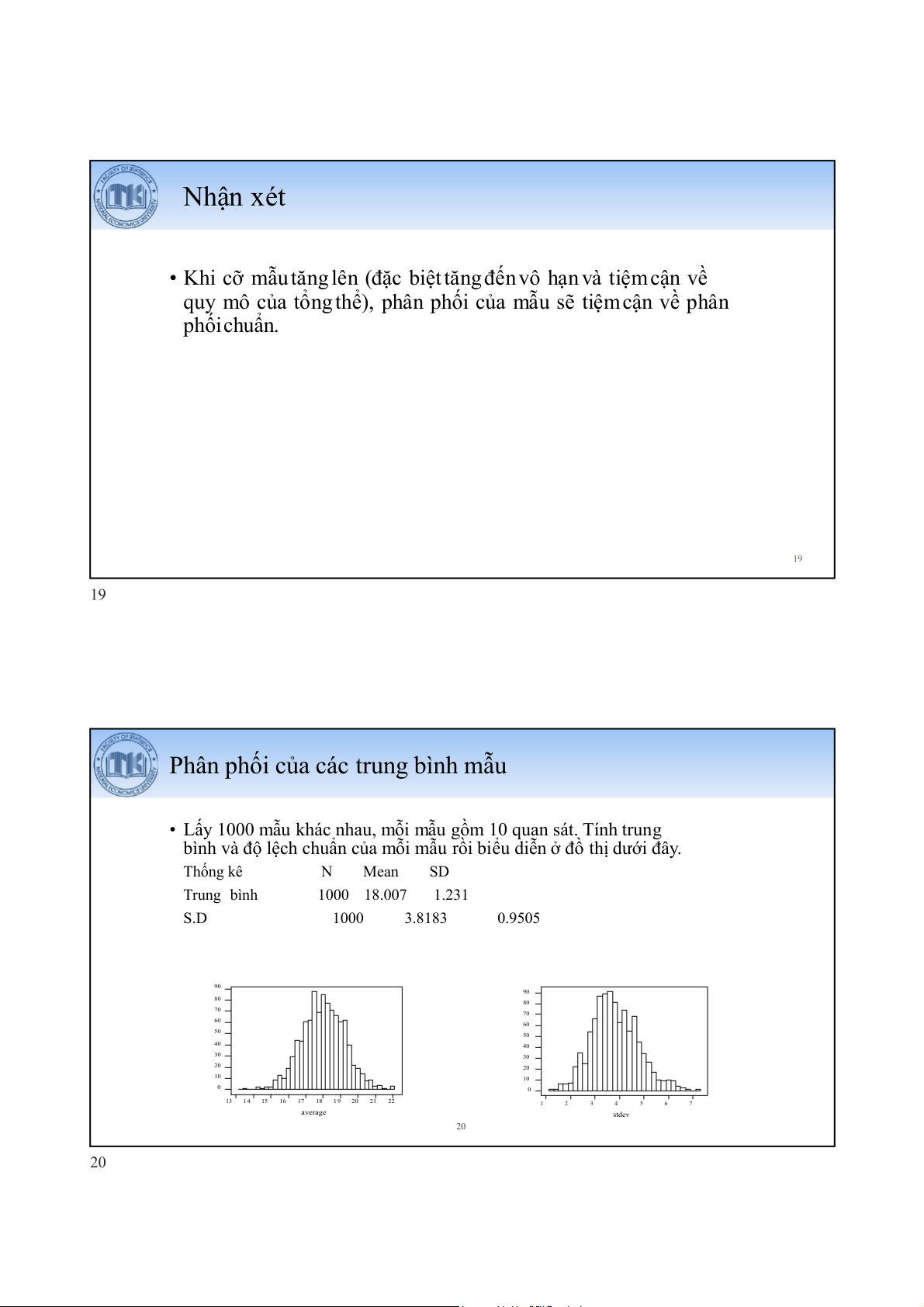
• Khi cỡ mẫu tăng lên (đặc biệt tăng đến vô hạn và tiệm cận về
quy mô của tổng thể), phân phối của mẫu sẽ tiệmcận về phân phốichuẩn. 19 19
Phân phối của các trung bình mẫu
• Lấy 1000 mẫu khác nhau, mỗi mẫu gồm 10 quan sát. Tính trung
bình và độ lệch chuẩn của mỗi mẫu rồi biểu diễn ở đồ thị dưới đây. Thống kê N Mean SD Trung bình 1000 18.007 1.231 S.D 1000 3.8183 0.9505 90 90 80 80 70 70 60 60 50 50 40 40 30 Frequency requency F 30 20 20 10 10 0 0 13 1 4 15 16 17 18 1 9 20 21 22 1 2 3 4 5 6 7 average stdev 20 20 Tăng cỡ mẫu
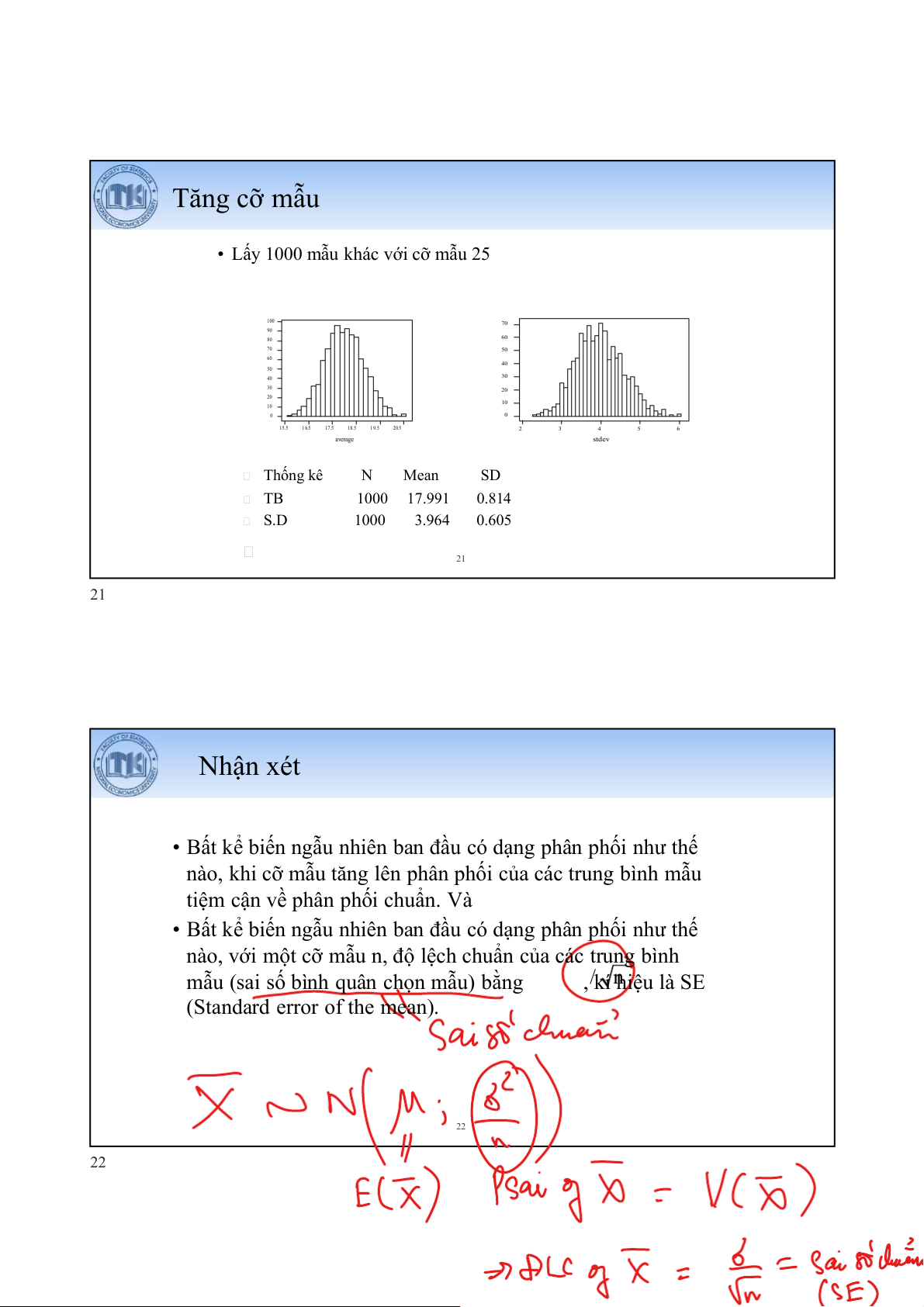
• Lấy 1000 mẫu khác với cỡ mẫu 25 100 70 90 80 60 70 50 60 40 50 40 30 requency F Frequency 30 20 20 10 10 0 0 15.5 1 6.5 17.5 18.5 1 9.5 20.5 2 3 4 5 6 average stdev Thống kê N Mean SD TB 1000 17.991 0.814 S.D 1000 3.964 0.605 21 21 Nhận xét
• Bất kể biến ngẫu nhiên ban đầu có dạng phân phối như thế
nào, khi cỡ mẫu tăng lên phân phối của các trung bình mẫu
tiệm cận về phân phối chuẩn. Và
• Bất kể biến ngẫu nhiên ban đầu có dạng phân phối như thế
nào, với một cỡ mẫu n, độ lệch chuẩn của các trung bình
mẫu (sai số bình quân chọn mẫu) bằng , k / í hniệu là SE (Standard error of the mean). 22 22 Ý nghĩa
• Bất kể tổng thể có phân phối thế nào (chuẩn hay không
chuẩn), khi cỡ mẫu đủ lớn phân phối của các trung bình
mẫu sẽ tuân theo quy luật phân phối chuẩn và chúng ta có
thể sử dụng thống kê Z để tính xác suất cho bất kỳ giá trị trung bình nào 23 23
Đây chính là định lý giới hạn trung tâm
• Nếu X là một biến ngẫu nhiên có giá trị
trung bình là µ và phương sai là σ², thì 2 X N , n X Z ~ N 0,1 as n . n 24 24
Vậy cỡ mẫu như thế nào là đủ lớn?
• Nếu tổng thể có phân phối chuẩn, quy mô mẫu có thể nhận bất kỳ giá trị nào.
• Nếu không biết hình dạng phân phối của tổng thể, quy mô mẫu
rất quan trọng. Phân phối của các trung bình mẫu sẽ tiệm cận về
phân phối chuẩn khi cỡ mẫu tăng lên vô hạn. Trên thực tế, phân
phối của các trung bình mẫu sẽ gần giống với phân phối chuẩn
khi cỡ mẫu ít nhất là 30 đơn vị.
• Xác định cỡ mẫu đề cập ở bài 5. 25 25 12/29/2024 Bài 5
ƯỚC LƯỢNG VÀ KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ I II ƯỚC LƯỢNG KIỂM ĐỊNH THỐNG KÊ GIẢ THUYẾT THỐNG KÊ 1 I. Ước lượng thống kê 1
Ước lượng (suy rộng) kết quả điều tra 2
Xác định kích thước (quy mô) mẫu 2 12/29/2024
1. Ước lượng kết quả điều tra
ƯỚC LƯỢNG BẰNG KHOẢNG TIN CẬY là khoảng giá trị được xác định từ
thống kê mẫu mà với xác suất cụ thể, tham số của tổng thể sẽ thuộc khoảng đó. 3
1. Ước lượng kết quả điều tra ' • Công thức chung
: tham số của tổng thể (parameter)
' : thống kê mẫu (statistic)
: phạm vi sai số chọn mẫu 4 12/29/2024
Ước lượng kết quả điều tra
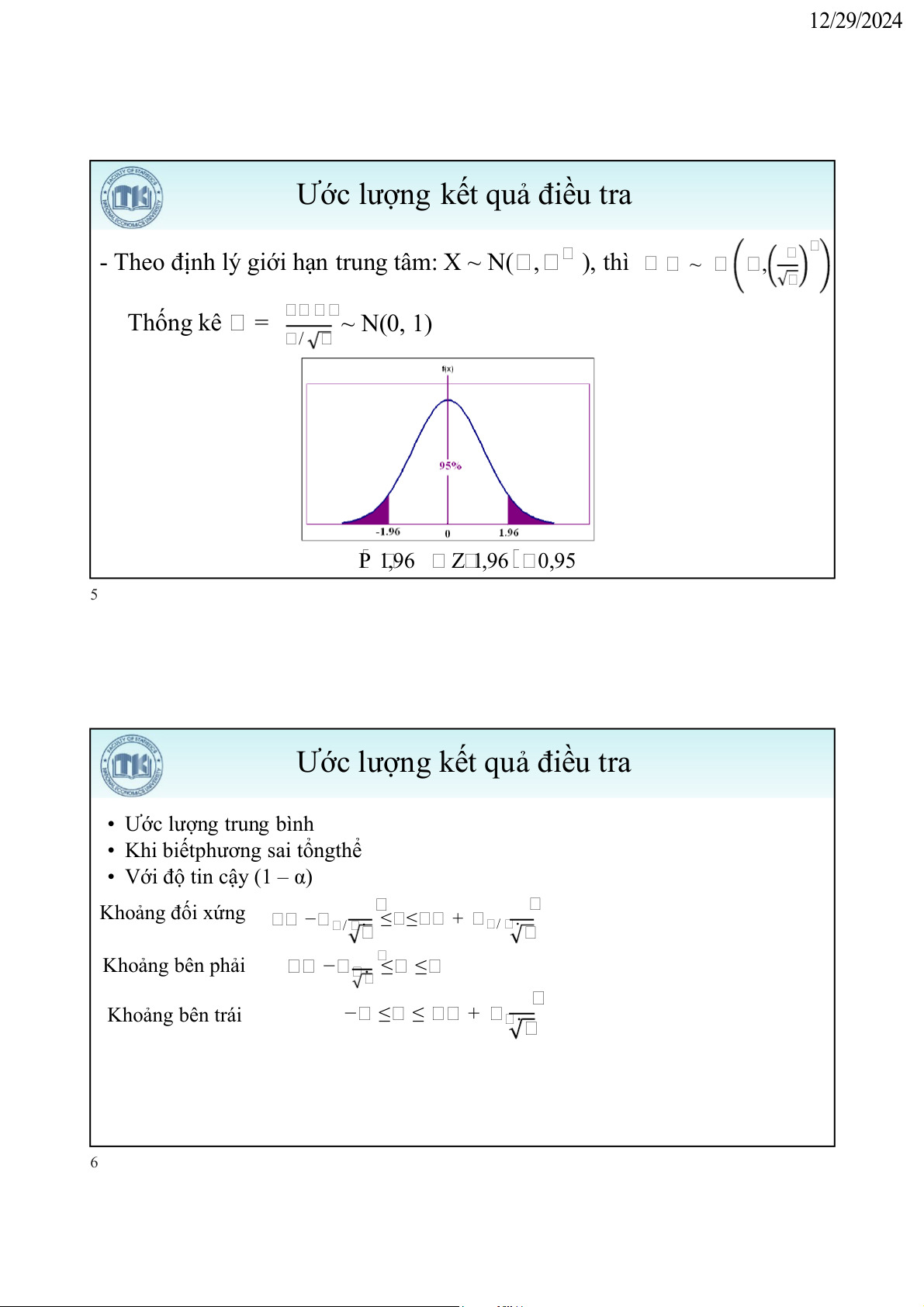
- Theo định lý giới hạn trung tâm: X ~ N( , ), thì ~ , Thống kê = ~ N(0, 1) / P 9 , 1 6 Z 9 , 1 6 0 9 , 5 5
Ước lượng kết quả điều tra
• Ước lượng trung bình
• Khi biếtphương sai tổngthể
• Với độ tin cậy (1 – α) Khoảng đối xứng − / . ≤ ≤ + / . Khoảng bên phải − . ≤ ≤ Khoảng bên trái − ≤ ≤ + . 6 12/29/2024
Ước lượng kết quả điều tra
• Ước lượng trung bình
• Với độ tin cậy (1 – α)
Khi chưabiết phươngsai tổngthể, thốngkê − ~ ( −1) / Khoảng đối xứng − . ≤ ≤ + / / . Khoảng bên phải − . ≤ ≤ Khoảng bên trái − ≤ ≤ + .
Khi cỡ mẫu lớn (n ≥ 30) có thể tra bảng z thay cho t 7
Ước lượng kết quả điều tra • Ước lượng tỷ lệ
• Với độ tin cậy (1 – α), cỡ mẫu đủ lớn [ nf ≥ 5 và n(1-f) ≥ 5 ] (1 − ) (1 − ) Khoảng đối xứng − / . ≤ ≤ + / . (1 − ) Khoảng bên phải − . ≤ ≤ (1 − ) − ≤ ≤ + . Khoảng bên trái 8 12/29/2024
Ước lượng kết quả điều tra
z , t là hệ số tin cậy (giá trị tới hạn mức α của phân phối chuẩn hoá và phân phối Student)
• α – mức ý nghĩa (xác suất mắc sai lầm)
• (1-α) là xác suất hay trình độ tin cậy 9
Hệ số điều chỉnh cho tổng thể hữu hạn
Trong trường hợp tổng thể là hữu hạn, Chúng ta điều chỉnh phạm vi sai
số trong công thức xác định khoảng tin cậy. − = −1 10 12/29/2024
2. Xác định số đơn vị mẫu điều tra
Cách chọn Tổng thể vô hạn Tổng thể hữu hạn Suy rộng . Bình quân /. = / = ( −1). + / . . (1 − ) . . (1 − ) / Tỷ lệ = / = .( −1) + / . (1 − ) 11
Các yếu tố ảnh hưởng tới kích thước mẫu
+ Hệ số tin cậy (z)/ Độ tin cậy của ước lượng
+ Phương sai (độ đồng đều) của tổng thể
+ Phạm vi sai số chọn mẫu/sai số chọn mẫu cho phép ( ) 12 12/29/2024
Một số phương pháp xác định phương sai tổng thể
+ Lấy phương sai lớn nhất hoặc tỷ lệ gần với 0,5 nhất
trong các lần điều tra trước (nếu có)
+ Sử dụng kết quả của nghiên cứu có tính chất tương tự
+ Tiến hành nghiên cứu thử nghiệm
+ Lấy tỷ lệ bằng 0,5 hoặc ước lượng phương sai dựa vào khoảng biến thiên = = 13
II. Kiểm định giả thuyết thống kê 1
Những vấn đề chung về kiểm định giả thuyết thống kê 2
Kiểm định giá trị trung bình của 1 tổng thể 3
Kiểm định tỷ lệ của 1 tổng thể 14




