



















































































































































Preview text:
lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh MỤC LỤC
LỜI NÓI ĐẦU ............................................................................................................... 1 MỤC LỤC
..................................................................................................................... 3
CHƯƠNG 1. Lý thuyết xác suất ................................................................................. 6
1.1. Bổ túc về giải tích tổ hợp ..................................................................................... 6
1.1.1. Quy tắc cộng ................................................................................................. 6
1.1.2. Quy tắc nhân ................................................................................................. 6
1.1.3. Tổ hợp ........................................................................................................... 6
1.2. Phép thử ngẫu nhiên và biến cố ........................................................................... 7
1.2.1. Phép thử ngẫu nhiên và biến cố .................................................................... 7
1.2.2. Biến cố thuận lợi, biến cố tương ương ........................................................ 8
1.2.3. Phép cộng và phép nhân các biến cố ............................................................. 8
1.2.4. Biến cố sơ cấp, biến cố ồng khả năng ......................................................... 9
1.2.5. Quan hệ giữa các biến cố ............................................................................ 10
1.3. Xác suất của biến cố .......................................................................................... 10
1.3.1. Khái niệm chung về xác suất ...................................................................... 10
1.3.2. Định nghĩa xác suất theo quan iểm cổ iển .............................................. 11
1.3.3. Định nghĩa xác suất theo quan iểm hình học ............................................ 12
1.3.4. Định nghĩa xác suất theo quan iểm thống kê ................................................ 13
1.4. Một số công thức xác suất quan trọng ............................................................... 13
1.4.1. Công thức cộng xác suất ............................................................................. 13
1.4.2. Xác suất có iều kiện .................................................................................. 14
1.4.3. Công thức nhân xác suất ............................................................................. 16
1.4.4. Công thức xác suất ầy ủ và công thức Bayes .......................................... 18
1.4.5. Công thức Bernoulli .................................................................................... 19 BÀI TẬP CHƯƠNG 1
................................................................................................ 22
CHƯƠNG 2. Biến ngẫu nhiên ................................................................................... 29
2.1. Biến ngẫu nhiên và phân phối xác suất ............................................................. 29
2.1.1. Định nghĩa biến ngẫu nhiên ........................................................................ 29
2.1.2. Luật phân phối xác suất của biến ngẫu nhiên ............................................. 30
Xác suất thống kê và Ứng dụng – 2021 3 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
2.1.3. Hàm phân phối xác suất .............................................................................. 35
2.2. Các ặc trưng số của biến ngẫu nhiên ............................................................... 37
2.2.1. Mode, med ................................................................................................... 37
2.2.2. Kỳ vọng toán ............................................................................................... 39
2.2.3. Phương sai và ộ lệch chuẩn ....................................................................... 41
2.3. Một số quy luật phân phối xác suất quan trọng ................................................ 42
2.3.1. Phân phối nhị thức ...................................................................................... 42
2.3.2. Phân phối siêu bội ....................................................................................... 44
2.3.3. Phân phối Poisson ....................................................................................... 46
2.3.4. Phân phối mũ ............................................................................................... 48
2.3.5. Phân phối ều .............................................................................................. 49
2.3.6. Phân phối chuẩn .......................................................................................... 50
2.3.7. Phân phối Chi bình phương ........................................................................ 54
2.3.8. Phân phối Student ....................................................................................... 55
2.4. Một số kết quả về luật số lớn và các ịnh lý giới hạn ....................................... 56
2.4.1. Hội tụ theo xác suất ..................................................................................... 56
2.4.2. Một số kết quả về luật số lớn và các ịnh lý giới hạn ................................. 56
2.5. Vector ngẫu nhiên và các ặc trưng ................................................................... 57
2.5.1. Khái niệm vector ngẫu nhiên ...................................................................... 57
2.5.2. Hàm phân phối xác suất của vector ngẫu nhiên .......................................... 57
2.5.3. Bảng phân phối xác suất ồng thời ............................................................. 58
2.5.4. Hàm mật ộ xác suất ồng thời ................................................................... 59
2.5.5. Các ặc trưng số của vector ngẫu nhiên...................................................... 61
BÀI TẬP CHƯƠNG 2 ................................................................................................ 65
CHƯƠNG 3. Lý thuyết mẫu và bài toán ước lượng tham số ................................. 75
3.1. Tổng thể và mẫu ................................................................................................ 75
3.1.1. Khái niệm tổng thể và mẫu ......................................................................... 75
3.1.2. Mẫu ngẫu nhiên ........................................................................................... 76
3.1.3. Các ặc trưng mẫu....................................................................................... 76
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
3.2. Ước lượng tham số............................................................................................. 79
3.2.1. Các khái niệm về ước lượng ....................................................................... 80
3.2.2. Bài toán ước lượng khoảng tin cậy cho trung bình ................................ 81
3.2.3. Bài toán ước lượng khoảng tin cậy cho tỉ lệ p ........................................... 85
3.2.4. Bài toán ước lượng phương sai 2 ............................................................. 87
BÀI TẬP CHƯƠNG 3 ................................................................................................ 89
CHƯƠNG 4. Kiểm ịnh giả thiết thống kê .............................................................. 92
4.1. Các khái niệm về kiểm ịnh giả thiết thống kê ................................................. 92
4.1.1. Giả thiết thống kê ........................................................................................ 92
4.1.2. Sai lầm loại 1 và loại 2 ................................................................................ 93
4.1.3. Mức ý nghĩa và power của kiểm ịnh ......................................................... 94
4.2. Một số bài toán kiểm ịnh thông dụng .............................................................. 94
4.2.1. Bài toán kiểm ịnh giả thuyết về giá trị trung bình ................................ 94
4.2.2. Bài toán kiểm ịnh giả thiết về tỉ lệ ............................................................ 97 4
4.2.3. Bài toán kiểm ịnh giả thiết về phương sai ................................................. 98
4.2.4. Bài toán kiểm ịnh so sánh hai giá trị trung bình ..................................... 100
4.2.5. Bài toán kiểm ịnh so sánh hai tỉ lệ .......................................................... 101
4.2.6. Kiểm ịnh giả thiết về tính ộc lập hai biến ngẫu nhiên .......................... 103
BÀI TẬP CHƯƠNG 4 .............................................................................................. 105
CHƯƠNG 5. Xử lý số liệu thực nghiệm ................................................................. 112
5.1. Sai số và khử sai số .......................................................................................... 112
5.1.1. Các loại sai số số liệu thực nghiệm thường gặp ........................................ 112
5.1.2. Biểu diễn giá trị o và sai số o ................................................................ 113
5.1.3. Một số phương pháp khử sai số thô .......................................................... 114
5.2. Xác ịnh phân phối của số liệu thực nghiệm ................................................... 118
5.2.1. Phương pháp chung ................................................................................... 118
5.2.2. Kiểm ịnh luật phân phối chuẩn, mũ, Poisson .......................................... 119
5.3. Tương quan và hồi quy ơn ............................................................................. 125
5.3.1. Một số khái niệm ....................................................................................... 125
Xác suất thống kê và Ứng dụng – 2021 5 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
5.3.2. Hệ số tương quan ...................................................................................... 126
5.3.3. Hàm hồi quy tổng thể, hàm hồi quy mẫu .................................................. 131
5.3.4. Ước lượng các hệ số hồi quy bằng phương pháp bình phương tối thiểu .. 132
5.3.5. Một số dạng hàm hồi quy tuyến tính hóa ược ......................................... 135
5.3.6. Ước lượng khoảng tin cậy và kiểm ịnh các hệ số hồi quy ...................... 137
BÀI TẬP CHƯƠNG 5 .............................................................................................. 142
CHƯƠNG 6. Xích Markov và ứng dụng ................................................................ 146
6.1. Các khái niệm cơ bản về xích Markov ............................................................ 146
6.1.1. Một số ịnh nghĩa ...................................................................................... 146
6.1.2. Xác suất chuyển trạng thái, xích Markov thuần nhất ................................ 147
6.1.3. Phân phối của hệ và ma trận xác suất chuyển ........................................... 148
6.1.4. Phân phối dừng ......................................................................................... 152
6.2. Một số ứng dụng của xích Markov rời rạc thuần nhất ..................................... 153
6.2.1. Kiểm kê hàng hóa dự trữ ........................................................................... 153
6.2.2. Tìm cân bằng thị phần ............................................................................... 155
6.2.3. Xác ịnh chính sách thay thế thiết bị ........................................................ 157
BÀI TẬP CHƯƠNG 6 .............................................................................................. 159
PHỤ LỤC 1a. Phân phối Student .............................................................................. 163
PHỤ LỤC 1b. Phân phối Student (tiếp theo) ............................................................ 164
PHỤ LỤC 2a. Phân phối Chi bình phương ............................................................... 165
PHỤ LỤC 2b. Phân phối Chi bình phương (tiếp theo) ............................................. 166
TÀI LIỆU THAM KHẢO ........................................................................................ 167
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
CHƯƠNG 1 LÝ THUYẾT XÁC SUẤT
1.1. Bổ túc về giải tích tổ hợp
1.1.1. Quy tắc cộng
Nếu có m cách chọn ối tượng x, có n cách chọn ối tượng y và nếu cách chọn x
không trùng với bất kỳ cách chọn y nào thì có m n cách chọn ối tượng “ x hoặc y”.
Tổng quát: Nếu có ni cách chọn ối tượng x ii ( 1,...,k), và nếu cách chọn xi không
trùng với bất kỳ cách chọn xj ( j i) nào thì có N n1 ... nk cách chọn ối tượng “ x1
hoặc x2 … hoặc xk ”.
1.1.2. Quy tắc nhân
Nếu một công việc ược chia thành k giai oạn, trong ó giai oạn thứ i có n ii ( 1,...,k)
cách thực hiện, thì sẽ có N n1...nk cách thực hiện xong toàn bộ công việc. 1.1.3. Tổ hợp
Một tổ hợp n chọn k là một nhóm gồm k phần tử không có thứ tự, ôi một khác nhau
ược lấy từ n phần tử ã cho. n!
Số các tổ hợp n chọn k là: C k n k n!( k)!
Ví dụ 1.1. Từ một lớp có 10 nam và 20 nữ. Hỏi có bao nhiêu cách chọn một người (nam hoặc nữ)?
Giải. Đối tượng x là “nam”: có 10 cách chọn, ối tượng y là “nữ” : có 20 cách chọn, và
chọn nam thì không chọn nữ và ngược lại. Do ó theo quy tắc cộng sẽ có: N 10 20
30 (cách chọn một người - nam hoặc nữ)
Ví dụ 1.2. Một người cần i từ thành phố A ến thành phố C, nhưng bắt buộc phải i qua
thành phố B. Có hai cách i từ A ến B và có ba cách i từ B ến C. Hỏi có tất cả bao nhiêu cách i từ A ến C? a 1 A 2 B C b 3
Hình 1.1. Sơ ồ i từ A ến C Giải. Việc di
chuyển từ A ến C ược chia làm 2 giai oạn:
Xác suất thống kê và Ứng dụng – 2021 7 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Giai oạn 1 là i từ A ến B: có 2 cách thực hiện
Giai oạn 2 là i từ B ến C: có 3 cách thực hiện
Theo quy tắc nhân sẽ có: N 2 3 6 (cách i từ A ến
C). Có thể liệt kê 6 cách này: a a1; 2; 3; 1; 2;a b b b3
Ví dụ 1.3. Có bao nhiêu tập hợp con gồm ba phần tử của tập hợp gồm năm phần tử {a,b,c,d,e}.
Giải. Một tập hợp con gồm ba phần tử từ tập gồm năm phần tử {a,b,c,d,e} là một tổ hợp 5 chọn 3.
Vậy số tập hợp con gồm ba phần tử là:C 3 5 10
1.2. Phép thử ngẫu nhiên và biến cố
1.2.1. Phép thử ngẫu nhiên và biến cố
Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thuật ngữ dùng ể chỉ một cách
thức thực hiện một số iều kiện xác ịnh nào ó (một thí nghiệm cụ thể hay quan sát một
hiện tượng nào ó), có thể cho kết cục này hoặc kết cục khác (có ít nhất 2 kết cục). Phép
thử có thể ược lặp lại nhiều lần.
Biến cố: Mỗi kết cục của phép thử ược gọi là biến cố. Biến cố ược chia thành 3
loại: Biến cố ngẫu nhiên (thường ký hiệu A B C A A, , , 1, 2,...) là biến cố có thể xảy ra
hoặc không xảy ra khi thực hiện phép thử; Biến cố chắc chắn (ký hiệu là ) là biến cố
luôn xảy ra khi thực hiện phép thử; Biến cố không thể có (ký hiệu là ) là biến cố luôn
không xảy ra khi thực hiện phép thử. Ví dụ 1.4
a) Phép thử tung một ồng xu ồng chất và cân ối lên mặt bàn. Kết qủa nhận ược sẽ là
S ( ược mặt sấp) hay N ( ược mặt ngửa). Khi ó N và S là những biến cố ngẫu nhiên.
b) Phép thử tung một con xúc xắc ồng chất và cân ối lên mặt bàn. Ký hiệu A ii (
1,...,6) là biến cố ược mặt i chấm; A là biến cố ược mặt có số chấm
6; C là biến cố ược mặt có số chấm chẵn; L là biến cố ược mặt có số chấm lẻ;
P là biến cố ược mặt có số chấm là số nguyên tố. Khi ó: A1,..., A C L P6, , , là các
biến cố ngẫu nhiên; A là biến cố chắc chắn.
c) Quá trình từ lúc ăng ký học phần “Xác suất thống kê” cho ến thi kết thúc học phần
này xong là một phép thử. Các kết cục: “qua môn”, “không qua môn”, ạt iểm 0;
0.5; 1; 1.5;...;10 là các biến cố ngẫu nhiên. 8
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1.2.2. Biến cố thuận lợi, biến cố tương ương
Biến cố A ược gọi là biến cố thuận lợi cho biến cố B, ký hiệu A B, nếu A xảy ra thì B xảy ra.
Nếu vừa có A B và B A thì ta nói A và B là hai biến cố tương ương hay biến
cố bằng nhau, ký hiệu là A B.
Lưu ý: Với mọi biến cố A, ta luôn có A , A A, A.
Ví dụ 1.5. Có 7 lá phiếu, trong ó có 2 lá phiếu trúng thưởng. Bạn An kiểm tra ngẫu
nhiên lần lượt 3 phiếu. Gọi các biến cố sau:
Ai : “lá phiếu kiểm tra lần thứ i có thưởng” (i 1,2,3) ,
B : “Bạn Nam kiểm tra ược phiếu có thưởng”,
C : “Bạn Nam kiểm tra ược 2 phiếu có thưởng”,
D : “Bạn Nam kiểm tra ược ít nhất 1 phiếu có thưởng”.
Khi ó, ta có: Ai B C;
B B; C ; B D .
1.2.3. Phép cộng và phép nhân các biến cố ➢ Phép cộng
Tổng (cộng, hợp) của hai biến cố A và B là một biến cố, ký hiệu là A B (hay A B),
nó xảy ra khi và chỉ khi trong A và B có ít nhất một biến cố xảy ra.
Tổng quát: Tổng A A1 ... An (hay A A1 A2 ... An ) xảy ra khi và chỉ khi
có ít nhất một trong n biến cố A1,..., An xảy ra. ➢ Phép nhân
Tích (nhân, giao) của hai biến cố A và B là một biến cố, ký hiệu là AB (hay AB. hay
A B), nó xảy ra khi và chỉ khi cả A và B ều xảy ra.
Tổng quát: Tích A AA1 2...An (hay A A1 A2 ... An ) xảy ra khi và chỉ khi cả
n biến cố ó cùng xảy ra. A B A AB B Hợp của A và B Giao của A và B
Hình 1.2. Minh họa phép cộng, nhân hai biến cố
➢ Các tính chất của phép cộng và phép nhân
Xác suất thống kê và Ứng dụng – 2021 9 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Với A B C, ,
là ba biến cố tùy ý, là biên cố chắc chắn, là biến cố không thể
có. Ta có các tính chất sau:
A (B C) (A B) C
A (B C) (A B) (A C)
A (B C) (A B) C
A (B C) (A B) (A C) A A A A A A A B B A A A A B B A A A A A
Ví dụ 1.6. Xét phép thử tung con xúc xắc trong ví dụ 1.4, ta có:
C A2 A4 A6
PL A3 A5
PC A2 i j , i j A A A 1 A3 A5 C L P A 2 A3 L A 1 ... A6 LC A5
Ví dụ 1.7. Một xạ thủ bắn 2 viên ạn vào một mục tiêu. Mục tiêu sẽ bị tiêu diệt nếu có
cả hai viên trúng. Gọi các biến cố :
Ai : “viên ạn thứ i trúng mục tiêu” (i 1,2) ,
A : “Mục tiêu bị trúng ạn”, B :
“Mục tiêu bị tiêu diệt”.
Khi ó, ta có: A A1 A2 ; B AA1 2
1.2.4. Biến cố sơ cấp, biến cố ồng khả năng
➢ Biến cố sơ cấp
Biến cố sơ cấp là biến cố không thể biểu diễn thành tổng của các biến cố khác.
Tập hợp tất cả các biến cố sơ cấp có thể có của một phép thử ược gọi là không gian biến
cố sơ cấp hay không gian mẫu, ký hiệu là .
➢ Biến cố ồng khả năng
Hai biến cố A và B ược gọi là ồng khả năng nếu khả năng xuất hiện của chúng là
như nhau trong cùng một phép thử. Ví dụ 1.8 10
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
a) Xét phép thử tung ồng xu. Ta có: Không gian mẫu: N S,
N S, là hai biến cố sơ cấp, ồng khả năng.
b) Xét phép thử tung con xúc xắc. Ta có: Không gian mẫu: A A A A A A1, 2, 3, 4, 5, 6 A A A A A A1, 2, 3, 4, 5, 6 là các biến
cố sơ cấp, ồng khả năng. C L P, ,
là ba biến cố không sơ cấp nhưng ồng khả năng.
A2 và C là hai biến cố không ồng khả năng.
c) Phép thử tung ồng thời hai con xúc xắc lên mặt bàn. Gọi Aij là biến cố con xúc
xắc thứ nhất xuất hiện mặt i chấm, con xúc xắc thứ hai xuất hiện mặt j chấm. Khi ó không gian mẫu là:
Aij :1 i j, 6 , bao gồm tất cả 36 biến cố sơ cấp và ồng khả năng.
1.2.5. Quan hệ giữa các biến cố
➢ Xung khắc: Hai biến cố A và B ược gọi là xung khắc nếu chúng không ồng thời
xảy ra khi thực hiện phép thử, nghĩa là AB .
➢ Xung khắc từng ôi: Nhóm n biến cố A1,..., An ược gọi là xung khắc từng ôi
(hay ôi một xung khắc) nếu hai biến cố khác nhau bất kỳ trong n biến cố ó là xung
khắc với nhau, nghĩa là AAi j , i j .
➢ Hệ ầy ủ: Hệ n biến cố A1,..., An ược gọi là hệ (nhóm) biến cố ầy ủ nếu trong phép
thử luôn có ít nhất một biến cố xảy ra.
Khi ó ta có: A1 ... An .
➢ Đối lập: Hai biến cố A và B ược gọi là ối lập nếu trong phép thử có úng một biến
cố xảy ra, nghĩa là: A B ; AB
. Biến cố ối lập của biến cố A ký hiệu là A .
Ví dụ 1.9. Xét phép thử tung con xúc xắc. Ta có:
A A1, 2 xung khắc nhau; C L L, C .
Xác suất thống kê và Ứng dụng – 2021 11 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh A A A A A A1, 2, 3, 4, 5, 6 là hệ ầy ủ và xung khắc từng ôi.
P và L là hai biến cố không xung khắc nhau. Vì P L. A3 A5 nên nếu A3 hoặc A5 xảy
ra thì cả P và L cùng xảy ra.
1.3. Xác suất của biến cố
1.3.1. Khái niệm chung về xác suất
Để so sánh hay ánh giá một hay nhiều biến cố về khả năng xuất hiện trong một
phép thử tương ứng, người ta gán cho mỗi biến cố một số thuộc oạn [0;1] sao cho với
hai biến cố bất kỳ, biến cố nào có khả năng xuất hiện nhiều hơn thì gán số lớn hơn, các
biến cố ồng khả năng xuất hiện thì gán cùng một số.
Số gán cho biến cố A, ký hiệu là P A( ), ược gọi là xác suất (Probability) của biến cố
A. Xác xuất có một số tính chất cơ bản sau:
a) 0 P A( ) 1 với mọi biến cố A.
b) P( ) 1 ( 100%): biến cố chắc chắn xảy ra.
c) P( ) 0 ( 0%): biến cố luôn không xảy ra.
d) Nếu A B thì P A( ) P B( ) .
Ví dụ 1.10. Chọn ngẫu nhiên một người từ nhóm gồm 50 người, trong ó có 10 nam và
40 nữ. Ta thấy rõ ràng rằng khả năng chọn ược 1 nữ cao hơn khả năng chọn ược 1 nam.
Các “khả năng” ó chính là xác suất xuất hiện các biến cố “chọn ược 1 nữ”, “chọn ược
1 nam”. Chúng ược tính như thế nào, chúng ta nghiên cứu các ịnh nghĩa về xác suất sau.
1.3.2. Định nghĩa xác suất theo quan iểm cổ iển
Giả sử phép thử có n biến cố sơ cấp ồng khả năng có thể xảy ra, trong số ó có mA
biến cố sơ cấp thuận lợi cho biến cố A.
Khi ó xác suất của biến cố A ược tính theo công thức sau: P A( )
mA Số biến cố sơ cấp thuận lợi cho A n
Tổng số biến cố sơ cấp ồng khả năng
Hạn chế của ịnh nghĩa cổ iển về xác suất:
1) Chỉ xét ược cho phép thử có hữu hạn các biến cố sơ cấp.
2) Không phải lúc nào ta cũng có hệ biến cố ồng khả năng. 12
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 1.11. Chọn ngẫu nhiên 3 sinh viên từ một lớp có 25 sinh viên nam và 15 sinh viên
nữ. Tính xác suất ể ược một nam và hai nữ.
Giải. Gọi A là biến cố ược một nam và hai nữ.
Số cách chọn 3 sinh viên từ lớp học là: C 3 40
Số trường hợp thuận lợi cho A ( ược 1 nam và 2 nữ): 25 C 2 15 Vậy
xác suất ể ược một nam và hai nữ là: P A() 25 2 3C15 25 105 525 0,26569 C40 9880 1976
Ví dụ 1.12. Một người gọi iện thoại quên mất 3 số cuối của số iện thoại và chỉ nhớ ược
rằng chúng khác nhau và chữ số cuối cùng là chẵn. Tìm xác suất ể quay ngẫu nhiên một
lần ược úng số cần gọi.
Giải. Gọi A là biến cố “quay ngẫu nhiên một lần ược úng số cần gọi. Số các trường
hợp có thể là các cặp ba chữ số khác nhau có thứ tự abc ược chọn từ 10 chữ số từ 0 ến
9, c là chữ số chẵn (c có 5 cách chọn, a có 9 cách chọn, b có 8 cách chọn). Theo quy tắc
nhân, số các trường hợ có thể là: n 5 9 8 360. Vậy P A( ) 0,00278 .
1.3.3. Định nghĩa xác suất theo quan iểm hình học ➢ Độ o
Ta gọi ộ o của một tập hợp trên ường thẳng là ộ dài, trong mặt phẳng là diện tích,
trong không gian là thể tích của tập ó. Trên ường thẳng thì tập hợp các iểm rời rạc có ộ
o bằng không; trong mặt phẳng, các tập hợp trên một ường cong có ộ o không; trong
không gian, các tập hợp trên một mặt cong có ộ o không.
➢ Công thức xác suất theo quan iểm hình học
Giả sử các trường hợp sơ cấp ược ặt tương ứng với các iểm của một tập hợp có ộ
o M, các trường hợp thuận lợi cho biến cố A tương ứng với các iểm của một tập hợp có ộ o m.
Khi ó, người ta ịnh nghĩa xác suất của biến cố A theo quan iểm hình học là: P A() m M
Xác suất thống kê và Ứng dụng – 2021 13 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 1.13. Hai người hẹn nhau tại một ịa iểm xác ịnh vào khoảng 19 ến 20 giờ. Người
ến trước sẽ ợi người kia 15 phút, sau ó nếu không gặp thì sẽ i khỏi iểm hẹn. Hãy tìm
xác suất ể hai người gặp nhau, nếu biết rằng mỗi người có thể ến chỗ hẹn trong khoảng
thời gian quy ịnh một cách ngẫu nhiên và không tùy thuộc vào người kia ến vào lúc nào.
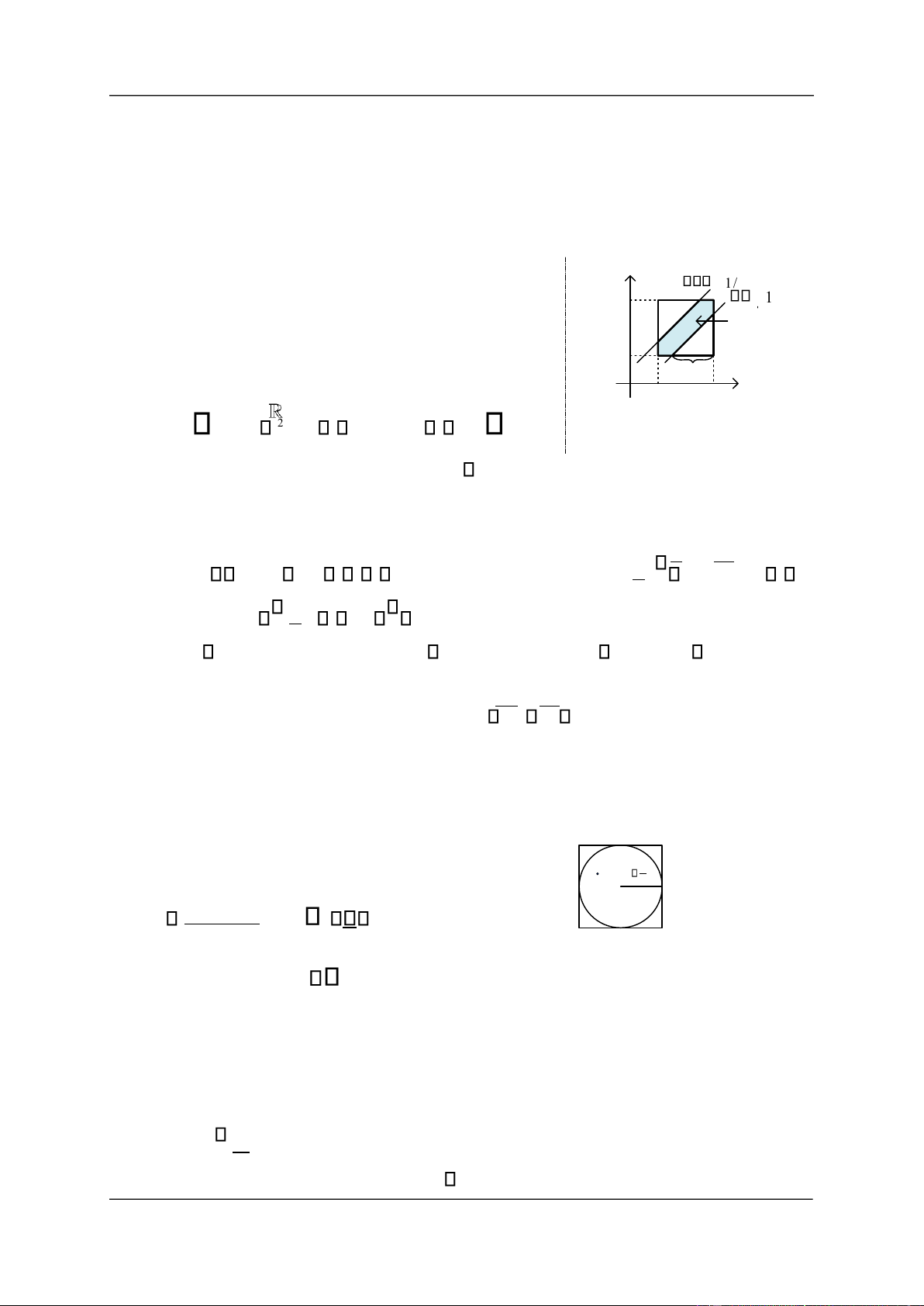
Giải. Gọi x y, tương ứng là thời iểm người thứ nhất, y xy 1 / 4
người thứ hai ến iểm hẹn. 20 xy 1 / 4 Các iểm
- Tập các iểm (biến cố) ồng khả năng là hình thuận lợi vuông ơn vị: 19 3 / 4 0 19 20 x
(x y, ) 2 :19 x 20,19 y20
Có ộ o là M 1 Hình 1.3. Hình vẽ ví dụ 1.13
- Tập các iểm thuận lợi cho biến cố A : “Hai người gặp nhau” : 1 (x y, ) M : 1 x y , có ộ o m 1 2 1 33 7 4 4 2 4 4 16
Vậy xác suất ể hai người gặp nhau là: P A( ) m 7 0,4375. M 16
Ví dụ 1.14. Chọn ngẫu nhiên một iểm A trong hình vuông cạnh a . Tính xác suất ể A
thuộc hình tròn nội tiếp hình vuông trên.
Giải. Gọi B là biến cố iểm A thuộc hình tròn nội
tiếp. Áp dụng ịnh nghĩa xác suất theo quan iểm Hình 1.4 a R hình học, ta có: 2 A P B( ) a / 22 2
0,7854 Hình vẽ ví dụ 1.14 a 4
1.3.4. Định nghĩa xác suất theo quan iểm thống kê
Giả sử trong n phép thử với iều kiện giống nhau, biến cố A xuất hiện m lần. Khi m
ó tỷ số fn (A)
ược gọi là tần suất xuất hiện biến cố A trong n lần thử. n
Xác suất của biến cố A là: P A( ) lim fn(A). 14
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh n
Trong thực tế, ta thường chọn P A( ) fn(A) khi n ủ lớn.
Ví dụ 1.15. Một công ty bảo hiểm muốn tính xác suất ể một thanh niên người Mỹ sẽ bị
chết trong năm tới, người ta theo dõi 100000 thanh niên và thấy có 798 người bị chết
trong vòng 1 năm sau ó. Vậy xác suất cần tìm xấp xỉ bằng 0,008.
Ví dụ 1.16. Để nghiên cứu khả năng xuất hiện mặt sấp (S) khi tung một ồng xu, người
ta tiến hành tung ồng xu nhiều lần và thu ược kết quả cho ở bảng sau:
Người tung ồng xu Số lần tung Số lần xuất hiện mặt S Tần suất f S( ) Buyffon 4040 2048 0.5069 Pearson 12000 6019 0.5016 Pearson 24000 12012 0.5005
Nhận xét: Khi số lần tung ồng xu tăng lên thì tần suất f S( ) cũng dần dần hội tụ về con số 0,5.
1.4. Một số công thức xác suất quan trọng
1.4.1. Công thức cộng xác suất
➢ Nhóm công thức cộng các biến cố xung khắc hoặc xung khắc từng ôi:
1) P A( B) xk P A( ) P B( ), 2) P A( ) P A(
) 1, với A là biến cố tùy ý, 3) P A( 1 ...
An) xk P A( 1) ... P A( n) .
➢ Nhóm công thức cộng các biến cố không xung khắc hoặc không xung khắc từng ôi:
4) P A( B) P A( ) P B( ) P AB( )
5) P A( B
C) P A( ) P B( ) P C( ) P AB( ) P AC( )
P BC( ) P ABC( ) 6) P n A n P A( ) P AA( ) P AA A( ) ... ( 1)n 1 P A( ...A )
i 1 i i 1 i i j i j i j k i j k 1 n
Xác suất thống kê và Ứng dụng – 2021 15 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 1.17. Một lô hàng có 10 sản phẩm, trong ó có 2 phế phẩm. Lấy ngẫu nhiên từ lô
hàng ra 6 sản phẩm. Tính xác suất ể có không quá 1 phế phẩm trong 6 sản phẩm ược lấy ra.
Giải. Gọi A là biến cố không có phế phẩm; B là biến cố có úng 1 phế phẩm; C là biến
cố có không quá 1 phế phẩm.
Ta có: A, B là hai biến cố xung khắc nhau, và C A B
P C() xk P A() P B() C866 C21 6C85 28 112 20,66667 C10 C 210 10 210 3
Ví dụ 1.18. Trong một lớp học, tỉ lệ sinh viên giỏi Toán là 15%, giỏi Lý là 8%, giỏi
Hoá là 7%, giỏi cả Toán và Lý là 6%, giỏi cả Toán và Hoá là 5%, giỏi cả Lý và Hoá là
4%, giỏi cả ba môn là 3%. Chọn ngẫu nhiên một sinh viên trong lớp. Tính xác suất ể sinh viên ó:
a) Giỏi ít nhất một môn Toán hoặc Lý,
b) Giỏi ít nhất một môn, c) Giỏi cả 3 môn.
Giải. Gọi T L H, ,
tương ứng là biến cố chọn ược sinh viên giỏi Toán, Lý,
Hóa. a) Gọi A là biến cố ược SV giỏi ít nhất một môn Toán hoặc Lý. Ta có: A T L
P A() P T( L) P T() P L() P TL() 0,17
b) Gọi B là biến cố chọn ược sinh viên giỏi ít nhất một môn. Ta có: B T L H
P B() P T( LH)
P T() P L() P H() P TL() P TH() P LH() P TLH( )
0,15 0,08 0,07 0,06 0,05 0,04 0,03 0,18
c) Gọi C là biến cố chọn ược sinh viên giỏi cả ba môn. Ta có:
C TLH ; P C() P TLH() 0,03
1.4.2. Xác suất có iều kiện
Xác suất có iều kiện của biến cố A biết biến cố B ã xảy ra (với P B( ) 0 ), ký hiệu
P A B( / ) , là xác suất của biến cố A nhưng ược tính trong trường hợp biến cố B ã xảy ra. 16
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P A B( Công thức : / ) P AB(
Ví dụ 1.19. Một lô
hàng có 100 sản phẩm, trong ó có 95 chính ) P phẩm và 5 phế B(
phẩm. Lấy ngẫu nhiên lần lượt ra 2 sản phẩm (không hoàn lại). )
Tìm xác suất ể lần thứ 2 lấy ược phế phẩm, biết
rằng lần thứ nhất lấy ược chính phẩm.
Giải. Gọi A Bi, i tương ứng là biến cố lần thứ 5 pp 5 pp
i i( 1,2) lấy ược chính phẩm, phế phẩm. 1 sp 95 cp 1 cp 94 cp Lần 1 Lần 2 P B( / A ) 0,05051 Ta có: 2 1 Hình 1.5. Hình vẽ ví dụ 1.19
Ví dụ 1.20. Có 50 câu hỏi môn xác suất thống kê ược phân bố theo bảng sau: Số lượng Câu dễ Câu khó Câu lý thuyết 12 8 Câu bài tập 20 10
Chọn ngẫu nhiên một câu trong 50 câu hỏi. Tính xác suất:
a) Được câu lý thuyết,
b) Được câu bài tập, c) Được câu dễ, d) Được câu khó,
e) Được câu khó biết rằng ó là câu lý thuyết,
f) Được câu dễ biết rằng ó là câu bài tập.
Giải. Gọi B, D, K, L tương ứng là biến cố lấy ược câu bài tập, câu dễ, câu khó, câu lý thuyết.
a) P L() 8 12 2
b) P B() 10 20 3 50 5
c) P D() 12 20 16
d) P K( ) 8 10 9 50 25 f) P D B( / ) 20
e) P K L( / ) 8 2 12 8 2 20 5 10 3
Xác suất thống kê và Ứng dụng – 2021 17 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 1.21. Xét lại ví dụ 1.18.
a) Gọi ngẫu nhiên một sinh viên thì thấy sinh viên này giỏi Toán, tính xác suất sinh viên này cũng giỏi Hóa.
b) Gọi ngẫu nhiên một sinh viên thì thấy sinh viên này giỏi Toán và Lý, tính xác suất
sinh viên này cũng giỏi cả ba môn.
Giải. a) Xác suất sinh viên giỏi Hoá khi biết sinh viên này giỏi Toán P H T( / ) P TH( ) 0,05 1 0,33333 P T( ) 0,15 3
b) Xác suất sinh viên giỏi cả ba môn biết sinh viên này giỏi cả Toán và Lý P TLH TL( / ) P TLH() 0,03 0,5 P TL() 0,06
1.4.3. Công thức nhân xác suất
➢ Công thức nhân xác suất
Từ công thức xác suất có iều kiện, ta có công thức nhân xác suất sau:
P AB( ) P B P A B( ). ( / ) (1)
(nếu biến cố B xảy ra trước) Hoặc
P AB( ) P A P B A( ). ( / ) (2)
(nếu biến cố A xảy ra trước)
Quy tắc: Biến cố nào xảy ra trước thì tính xác suất trước, và nó trở thành biến cố
iều kiện cho các biên cố sau.
P ABC( ) P A P B A P C AB( ). ( / ). ( / ) (3)
P A( 1...An) P A P A( 1).
( 2 / A P A1).( 3 / AA1 2)...P A(
n / A1...An 1) (4)
➢ Các biến cố ộc lập
Hai biến cố A và B ược gọi là ộc lập nhau nếu sự xuất hiện hay không xuất hiện
của biến cố này không phụ thuộc vào sự xuất hiện hay không xuất hiện của biến cố kia, nghĩa là: 18
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P A B( /
) P A( ) và P B A( / ) P B( )
Hệ các biến cố A1,..., An gọi là ộc lập từng ôi nếu Ai ộc lập với Aj , i j .
Hệ các biến cố A1,..., An gọi là ộc lập toàn phần nếu Ai ộc lập với A Aj1 j ...A 1 jk với mọi A
j1, Aj1,..., Ajk A1,..., An \{Ai}, i .
Từ ịnh nghĩa trên ta thấy hệ ộc lập toàn phần thì ộc lập từng ôi nhưng iều ngược
lại nói chung là không úng. Khi nói họ A A1, 2,..., An ộc lập mà không nói gì thêm
thì ta hiểu ó là ộc lập toàn phần.
➢ Xác suất của tích các biến cố ộc lập
Nếu A B, ộc lập thì:
P AB() dl P A P B(). ( ) (5)
Nếu hệ các biến cố A1,..., An ộc lập toàn phần thì ) P A A( dl 12...An
(A P A1). ( 2 )...P A( n) (6)
Ví dụ 1.22. Có ba người A, B, C cùng thi tuyển (một cách ộc lập) vào một công ty. Khả
năng thi ậu của A, B, C tương ứng là 0,7; 0,8 và 0,6.
a) Tính xác suất cả ba người cùng ậu,
b) Tính xác suất có úng hai người ậu,
c) Tính xác suất người A ậu biết rằng có hai người ậu.
Giải. Gọi A, B, C lần lượt là biến cố người A, B, C thi ậu; H là biến cố cả ba người cùng
dậu; K là biến cố có úng hai người ậu. Ta có:
P A() 0,7 ; P B() 0,8 ; P C() 0,6
P A() 0,3 ; P B() 0,2 ; P C() 0,4
a) H ABC
P H() P ABC( ) dl P A P B P C( ) ( ) ( ) 0,7 0,8 0,6 0,336
b) K ABC ABC ABC
P K( ) xk P A P B P C( ) ( ) ( ) P A P B P C( ) ( ) ( ) P A
P B P C( ) ( ) ( ) dl
Xác suất thống kê và Ứng dụng – 2021 19 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
0,7 0,8 0,4 0,7 0,2 0,6 0,3 0,8 0,6 0,452 c) P A K( / )
P AK( ) , trong ó AK ABC ABC . P K( )
Tính tương tự câu b, ta có: P AK( ) 0,308 Vậy: P A K( / ) 0,68142
Ví dụ 1.23. Một lô hàng có 100 sản phẩm, trong ó có 90 sản phẩm tốt và 10 phế phẩm.
Kiểm tra ngẫu nhiên liên tiếp không hoàn lại 4 sản phẩm. Nếu có ít nhất 1 phế phẩm
trong 4 sản phẩm kiểm tra ó thì không nhận lô hàng. Tìm xác xuất ể nhận lô hàng.
Giải. Gọi Ai là biến cố “sản phẩm kiểm tra thứ i là sản phẩm tốt”, i 1,2,3,4 ; gọi A là biến cố nhận lô hàng.
Ta có: A AA A A1 2 3 4
P A() P A A A A 1 2 34
P A P A( 1) (2 / A P A1)(3 / A A P A1 2 ) (4 / A A A1 2 3) 90 89 88 87 0,65163 100 99 98 97
Ví dụ 1.24. Tỷ lệ phế phẩm của một lô hàng là 6%. Chọn ngẫu nhiên có hoàn lại lần
lượt từng sản phẩm từ lô hàng ra kiểm tra. Phải chọn ít nhất bao nhiêu lần ể xác suất
chọn ược ít nhất một phế phẩm không nhỏ hơn 0,95?
Giải. Gọi Ai là biến cố lần thứ i chọn ược phế phẩm, i 1,2,...; Gọi B là biến cố ược ít
nhất một phế phẩm trong n lần chọn.
P B() 1P B() 1P A A( 12...An) dl1(0,94)n 0,95
(0,94)n 0,05 n 48,4156
Vậy phải chọn ít nhất là 49 lần.
1.4.4. Công thức xác suất ầy ủ và công thức Bayes
Giả sử các biến cố A1,..., An là nhóm các biến cố ầy ủ và xung khắc từng ôi. A là
một biến cố bất kỳ, ta có: 20
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
P A() P A P A A( 1)
( /1) ... P A P A A(n) ( / n) (1)
P A(k / A) P A( k ).P A A( / k ) (2) P A()
Công thức (1) gọi là công thức xác suất ầy ủ, (2) gọi là công thức Bayes.
Ví dụ 1.25. Có 3 lô sản phẩm cùng hình dáng bên ngoài, tỉ lệ phế phẩm của từng lô
tương ứng là 6%, 2%, 1%. Chọn ngẫu nhiên một lô rồi từ lô ã chọn lấy ngẫu nhiên ra một sản phẩm.
a) Tính xác suất ể lấy ược một phế phẩm,
b) Giả sử lấy ược phế phẩm. Tính xác suất ể phế phẩm ó của lô thứ ba.
Giải. Gọi A ii ( 1,2,3) là biến cố chọn ược lô hàng thứ i. Hệ A A A1, 2, 3
là ầy ủ và xung khắc từng ôi.
P A( 1) P A( 2) P A( 3) 1/ 3
a) Gọi A là biến cố lấy ược phế phẩm, ta có: P A A(
/1) 0,06;P A A( /2) 0,02;P A A( / 3) 0,01
Áp dụng công thức xác suất ầy ủ, ta có: ) ) ) P A( P A P A A( 1) ( /1 P A P A A( 2 ) ( / 2 P A P A A( 3) ( / 3) 1 0,06 1 0,02 1 0,01 0,03 3 3 3
b) Áp dụng công thức Bayes, ta có:
P A( 3 / A) P A P A A( 3 ) ( / 3) (1/ 3) 0,01 1 P A() 0,03 9
Ví dụ 1.26. Tại một bệnh viện, theo kết quả iều trị thấy rằng những người mắc bệnh B
ến khám tại bệnh viện thì tỉ lệ người mắc bệnh này trong giai oạn 1, giai oạn 2, giai oạn
3 tương ứng là 35%, 45%, 20%. Biết rằng, nếu mắc bệnh trong giai oạn 1, giai oạn 2,
giai oạn 3 thì xác suất iều trị khỏi bệnh B tương ứng là 95%, 85%, 70%. Một người vào
bệnh viện khám thì phát hiện mắc bệnh B.
a) Tính xác suất người này ược iều trị khỏi bệnh B,
Xác suất thống kê và Ứng dụng – 2021 21 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Giả sử ược iều trị khỏi bệnh B, tính xác suất người này mắc bệnh ở giai oạn 2,
c) Giả sử iều trị không khỏi bệnh B. Hỏi khả năng người ó ược phát hiện bệnh trong giai oạn nào nhất?
Giải. Gọi Ai là biến cố người ến khám mắc bệnh B ở giai oạn i i( 1,2,3). Hệ A A A1, 2, 3
là ầy ủ và xung khắc từng ôi.
P A( 1) 0,35;P A( 2) 0,45;P A( 3) 0,2
a) Gọi A là biến cố người này ược iều trị khỏi bệnh B.
Áp dụng công thức xác suất ầy ủ, ta có: ) ) P A( P A P A A( 1) ( / 1 P A P A A( 2 ) ( ) / 2 P A P A A( 3) ( / 3)
0,35 95 0,45 0,85 0,2 0,7 0,855
b) Áp dụng công thức Bayes, ta có:
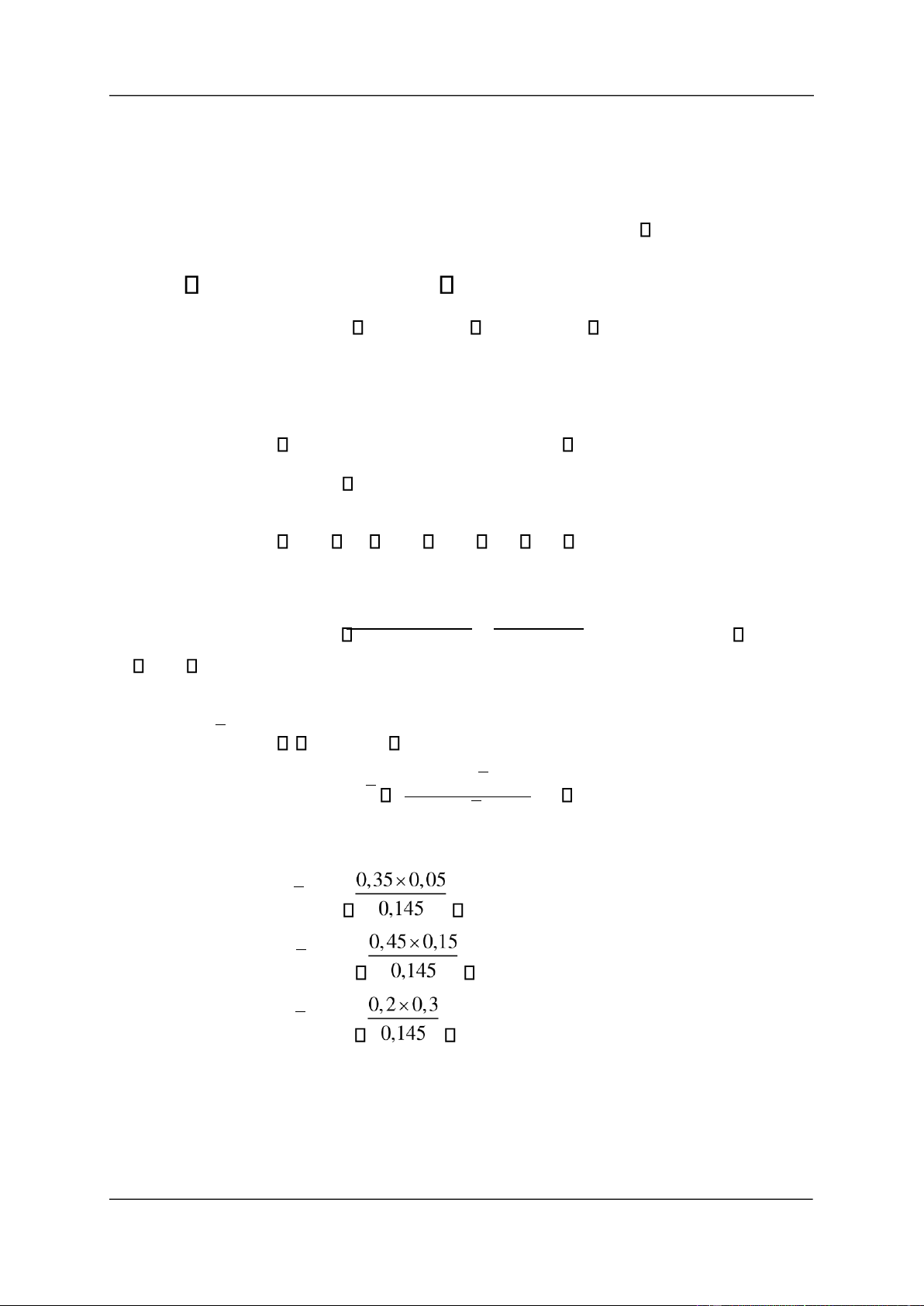
P A( 2 / A) P A P A A( 2 ) ( / 2 ) 0,45 0,85 0,44737 P A() 0,855 c) Ta có: P A(
) 1 P A( ) 0,145. Áp dụng công thức Bayes, ta có: k
P A P A( k ) (/ Ak ), k 1,2,3 P A( / A) P A( ) P A( 1 / A) 0,12069 P A( 2 / A) 0,46552 P A( 3 / A) 0,41379
Vậy có khả năng ược phát hiện bệnh trong giai oạn 2 nhất.
1.4.5. Công thức Bernoulli
➢ Dãy phép thử Bernoulli 22
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Tiến hành n phép thử ộc lập trong những iều kiện như nhau. Giả sử trong mỗi phép
thử, biến cố A xuất hiện với xác suất p không ổi, phép thử này ược gọi là phép thử
Bernoulli, và dãy gồm n phép thử như trên ược gọi là dãy phép thử Bernoulli. Xác suất
p ược gọi là xác suất thành công của biến cố A.
➢ Công thức Bernoulli
Xác suất ể biến cố A xuất hiện k lần trong n phép thử của dãy phép thử Bernoulli,
ký hiệu là P k pn( , ), ược tính theo công thức sau và gọi là công thức Bernoulli: P k p kk n( ,) C pn (1 p)n k
➢ Số có khả năng nhất
Số m0 {0,1,2,...,n} mà P m pn( 0, ) lớn nhất ược gọi là số có khả năng nhất của dãy n phép thử Bernoulli.
Định lý: Số m0 thỏa mãn iều miện sau:
(n 1) p 1m0 (n 1) p
Chứng minh: Với mỗi m {1,2,...,n 1}, ta có: P m pn ( ,
) m 1 1. p ; m 1 1. p 1 m (n 1) p 1
P mn ( 1, p) n m p n m p
P m pn ( ,) P mn( 1, p) khi m (n 1)p 1 Suy ra
P m pn ( ,) P mn( 1, p) khi m (n 1)p 1
Mặt khác do m là số nguyên nên ta có các trường hợp sau:
Nếu (n 1) p 1 thì xác suất P k pn( , ) ạt giá trị lớn nhất tại k (n 1) p 1 và
tại k 1 (n 1) p; Nếu (n 1) p 1 thì P k pn( , ) ạt giá trị lớn nhất tại một số
nguyên k nằm giữa (n 1) p 1và (n 1) p .
Vậy nếu m0 là số có khả năng cao nhất thì ta có: (n 1)p 1 m0 (n 1)p.
Ví dụ 1.27. Một bác sĩ có xác suất chữa khỏi bệnh là 0,8. Có người nói rằng cứ 10 người
ến chữa thì chắc chắn có 8 người khỏi bệnh. Điều khẳng ịnh ó có úng không?
Giải. Ta có thể xem việc chữa bệnh cho 10 người là một dãy gồm n 10 phép phép thử
Bernoulli với xác suất thành công (chữa khỏi bệnh) là p 0,8.
Áp dụng công thức Bernoulli, ta có:
Xác suất thống kê và Ứng dụng – 2021 23 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P 8 10 8;0,8
C10 (0,8) (18 0,8)10 2 0,30199
Khả năng có 8 người ược chữa khỏi bệnh trong 10 người là khoảng 30,2%. Vậy không
thể có chắc chắn 8 người khỏi bệnh. Điều khẳng ịnh trên là sai.
Ví dụ 1.28. Khả năng nảy mầm của một loại hạt giống là 0,73.
a) Tính xác suất có úng 15 hạt nảy mầm khi gieo 20 hạt giống,
b) Tính xác suất có nhiều nhất 18 hạt nảy mầm khi gieo 20 hạt giống,
c) Hỏi số hạt nảy mầm có khả năng cao nhất là bao nhiêu khi gieo 20 hạt giống?
Giải. Gọi A ii ( 0,...,20) là biến cố có i hạt giống nảy mầm, A là biến cố có nhiều nhất 18 hạt nảy mầm.
Áp dụng công thức Bernoulli với n 20 ; p 0,73, ta có: a) P A( 15
15 ) P20 (15;0,73) C20 (0,73)15 (1 0,73)5 0,198201 A ) b)
A19 A20 ; P A( ) xk P A( 19 P A( 20) P A() C 19 20 20
(0,73)19 (0,27)1 C20 (0,73)20 (0,27)0 0,01551
P A() 1P A() 0,98449
c) Ta có: n 20; p 0.73
(n 1) p 1 m0 (n 1) p 14.33 m0 15.33, m0 m0 15
Vậy số hạt giống nảy mầm có khả năng cao nhất là 15 hạt.
Ví dụ 1.29. Một xạ thủ có khả năng bắn trúng mục tiêu là 0,75. Cho xạ thủ này bắn 55
viên ạn. Tính số viên ạn trúng mục tiêu có khả năng cao nhất.
Giải. Ta có: n 55; p 0.75
(n 1) p 1 m0 (n 1) p 41 m0 42, m0 m0 41 m0 42
Vậy số viên ạn trúng mục tiêu có khả năng cao nhất là 41 hoặc 42 viên. 24
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh BÀI TẬP CHƯƠNG 1
Bổ túc giải tích tổ hợp
1.1. Một ngân hàng câu hỏi có 40 câu, trong ó có 10 câu hỏi dễ. Một ề thi gồm 3 câu
ược chọn ngẫu nhiên từ ngân hàng trên. Hỏi có bao nhiêu cách chọn một ề thi mà
trong ó có ít nhất 2 câu hỏi dễ?
1.2. Một lô sản phẩm gồm có 8 sản phẩm loại A và 12 sản phẩm loại B. Người ta lấy
ngẫu nhiên 5 sản phẩm. Hỏi có bao nhiêu cách lấy ược ít nhất 2 sản phẩm loại B?
1.3. Từ 7 chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập ược bao nhiêu
a) Số tự nhiên có 3 chữ số ?
b) Số tự nhiên chẵn có 3 chữ số khác nhau?
c) Số tự nhiên có 4 chữ số khác nhau và chia hết cho 4 ?
d) Số tự nhiên có 4 chữ số khác nhau sao cho không có hai chữ số chẵn nào ứng liền nhau ? 1.4. Cho tập A 0,1,...,9
a) Hỏi có bao nhiêu tập hợp con của A có ít nhất sáu chữ số?
b) Hỏi có bao nhiêu tập hợp con của A có sáu chữ số, trong ó có ít nhất ba chữ số nhỏ hơn 6?
1.5. Cho a giác ều gồm 2n cạnh.
a) Hỏi có tất cả bao nhiêu hình chữ nhật có bốn ỉnh là bốn ỉnh của a giác này?
b) Hỏi a giác ều nói trên có bao nhiêu ường chéo?
Xác suất thống kê và Ứng dụng – 2021 25 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1.6. Trong mặt phẳng, cho một họ gồm n n( 2) ường thẳng song song cắt một họ gồm
m m( 2) ường thẳng song song khác. Hỏi chúng tạo nên tất cả bao nhiêu hình bình hành?
1.7. Một bảng số xe gồm hai phần: phần I gồm hai ký tự lấy từ 26 ký tự và phần II gồm
bốn chữ số lấy từ 10 chữ số (0, 1, …,9). Hỏi có tất cả bao nhiêu bảng số xe có thể ược tạo ra ?
1.8. Một lớp có 30 nam và 20 nữ trong ó có cặp vợ chồng (chồng tên A vợ tên B). Hỏi
có bao nhiêu cách chọn 1 ban cán sự lớp gồm 7 người trong ó có 4 nam và 3 nữ
sao cho A và B không cùng trong ban cán sự lớp ?
Biểu diễn biến cố
1.9. Ba người cùng bắn vào bia, mỗi người bắn một viên.
Đặt Ai là biến người thứ i i( 1,2,3) bắn trúng tâm. Hãy biểu diễn các biến cố sau
theo A A A1, 2, 3 và các biến cố ối lập của nó.
1) Chỉ có người thứ nhất bắn trúng,
6) Có ít nhất một người bắn trúng,
2) Cả ba người ều bắn trúng,
7) Có úng một người bắn trúng,
3) Người thứ nhất trúng, người thứ ba trượt, 8) Có úng hai người bắn trúng,
4) Có ít nhất hai người bắn trúng,
9) Không có ai bắn trúng.
5) Có không quá hai người bắn trúng,
Định nghĩa cổ iển về xác suất
1.10. Lấy ngẫu nhiên lần lượt ba chữ số từ tập hợp {0, 1, 2, 3, 4}, xếp thành hàng ngang
từ trái qua phải. Tìm xác suất ể nhận ược một số gồm 3 chữ số.
1.11. Một lô hàng có n sản phẩm trong ó có m phế phẩm. Lấy ngẫu nhiên k sản phẩm.
Tính xác suất ể trong k sản phẩm lấy ra có 1 phế phẩm (1 k m n).
1.12. Một công ty cần tuyển 2 nhân viên. Có 4 người nữ và 2 người nam nộp ơn (khả
năng trúng tuyển là như nhau), công ty chọn ngẫu nhiên từ 6 người này. Tính xác suất ể:
a) Cả hai người trúng tuyển ều là nữ.
b) Có ít nhất một người nữ trúng tuyển.
1.13. Có 20 câu hỏi thi. Mỗi thí sinh ược rút ngẫu nhiên 3 câu và từ ó chọn một câu ể
trả lời. Một thí sinh chỉ học 12 câu, tính xác suất ể anh ta rút ược ít nhất một câu ã học. 26
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1.14. Trong 10 hạt ậu giống có 4 hạt ậu hoa vàng thuần chủng, 3 hạt ậu hoa vàng
không thuần chủng và 3 hạt ậu trắng. Chọn ngẫu nhiên 3 hạt ậu. Tính xác suất ể 3 hạt ậu ược chọn:
a) Gồm 3 loại khác nhau.
b) Là ậu cho hoa màu vàng.
c) Có ít nhất một hạt ậu cho hoa màu trắng.
Định nghĩa hình học về xác suất
1.15. Chọn ngẫu nhiên một iểm A trong hình tam giác ều cạnh a . Tính xác suất ể iểm A
thuộc hình tròn nội tiếp tam giác.
1.16. Trên oạn thẳng OA gieo ngẫu nhiên hai iểm B và C có ộ dài tương ứng OB x OC,
y y( x). Tính xác suất sao BC OB . y
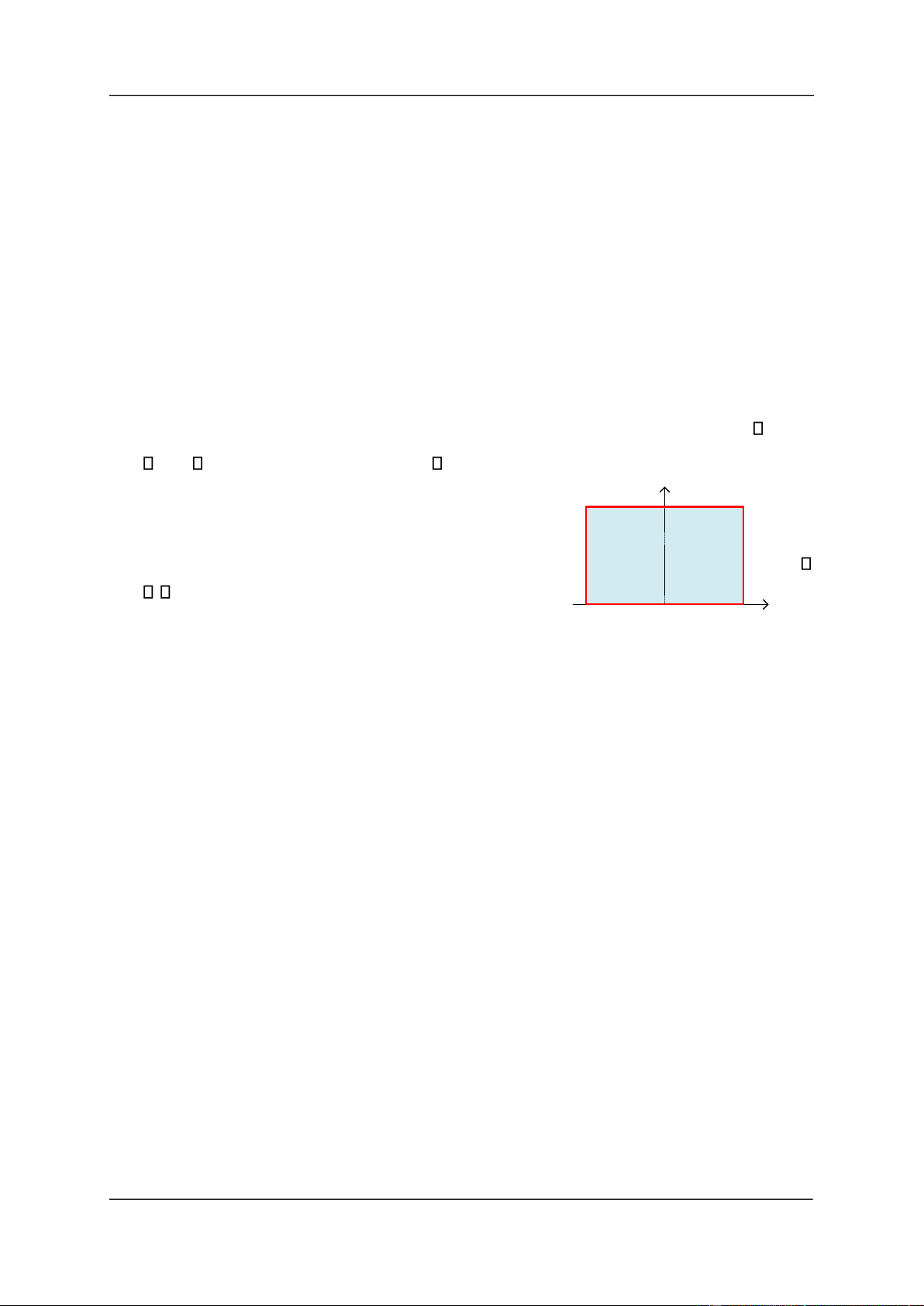
1.17. Một trò chơi iện tử ược mô tả như sau: Bắn một 5
iểm lên phạm vi hình chữ nhật (hình 1.6), nếu tọa ộ
(a,b) của iểm bắn làm cho phương trình bậc hai: x ax b2 0 có nghiệm thì ghi
ược iểm, ngược lại sẽ không ghi ược iểm. -4 0 4 x
Hình 1.6. Trò chơi, bài tập 1.17
Tìm xác suất ể khi một người chơi bắn ngẫu nhiên vào phạm vi hình chữ nhật thì ghi ược iểm.
1.18. Hai tàu thủy cập vào một cảng ể trả hàng một cách ộc lập trong vòng 24h. Biết
rằng thời gian bốc dỡ hàng của tàu thứ nhất là 2h, của tàu thứ hai là 3h. Tính xác
suất ể một trong hai tàu trên phải chờ ể cập bến.
Công thức cộng, nhân, xác suất có iều kiện
1.19. Một nhóm có 30 nhà ầu tư các loại, trong ó có 13 nhà ầu tư vàng, 17 nhà ầu tư
chứng khoán và 10 nhà ầu tư cả vàng và chứng khoáng. Một ối tác gặp ngẫu nhiên
một nhà ầu tư trong nhóm. Tìm xác suất ối tác gặp ược: a) Nhà ầu tư vàng hay chứng khoán.
b) Nhà ầu tư một loại: vàng hoặc chứng khoán.
c) Nhà ầu tư không phải vàng và cũng không phải chứng khoán.
1.20. Trong một vùng dân cư tỷ lệ người mắc bệnh tim là 8%, mắc bệnh khớp là 13%
và mắc cả hai bệnh là 7%. Chọn ngẫu nhiên một người trong vùng ó. Tính xác suất
ể người ó không mắc cả hai bệnh tim và khớp.
Xác suất thống kê và Ứng dụng – 2021 27 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1.21. Trong một hộp có 10 sản phẩm trong ó có 2 phế phẩm. Lấy ngẫu nhiên lần lượt
hai sản phẩm. Tính xác suất ể cả hai sản phẩm ều là phế phẩm trong mỗi trường hợp sau:
a) Lấy có hoàn lại.
b) Lấy không hoàn lại.
1.22. Một phân xưởng có 3 máy cùng hoạt ộng ộc lập nhau. Xác suất ể trong một ca
sản xuất các máy bị hư hỏng tương ứng là 0,1; 0,2; 0,3. Tính xác suất ể trong một ca sản xuất:
a) Cả ba máy cùng bị hư hỏng.
b) Có úng một máy bị hư hỏng.
c) Có ít nhất một máy bị hư hỏng.
d) Có không quá hai máy bị hư hỏng.
1.23. Một dây chuyền sản xuất gồm 3 bộ phận hoạt ộng ộc lập nhau. Biết rằng xác suất
ể trong một ca sản xuất các bộ phận bị hỏng là 0,08; 0,03; 0,09 và dây chuyền
ngưng hoạt ộng nếu có ít nhất một trong ba bộ phận bị hỏng. Tính xác suất ể trong
một ca sản xuất, dây chuyền bị ngưng hoạt ộng.
1.24. Xác suất ể thu ược một tín hiệu thông tin khi tín hiệu ó ược phát i là 0,65.
a) Tìm xác suất ể thu ược tín hiệu thông tin khi tín hiệu ó ược phát i 5 lần.
b) Nếu muốn thu ược tín hiệu thông tin với xác suất không dưới 99,85% thì cần
phải phát tín hiệu ó ít nhất bao nhiêu lần ?
1.25. Một lô hàng gồm 10 sản phẩm, trong ó có 3 sản phẩm lỗi. Lấy ngẫu nhiên (không
hoàn lại) từng sản phẩm ra ngoài ể kiểm tra ến khi gặp ủ 3 sản phẩm lỗi thì dừng lại.
Tính xác suất dừng lại ở lần lấy a) Thứ ba. b) Thứ tư.
c) Biết lần thứ nhất lấy ược sản phẩm lỗi, tính xác suất dừng lại ở lần lấy thứ tư.
1.26. Một cuộc thi có 3 vòng. Vòng 1 lấy 90% thí sinh; vòng 2 lấy 80% thí sinh ã qua
vòng 1; vòng 3 lấy 70% thí sinh ã qua vòng hai. a) Tính tỷ lệ thí sinh lọt qua cả 3 vòng.
b) Tính xác suất ể một thí sinh bị loại ở vòng 2 nếu biết rằng thí sinh này bị loại.
1.27. Bắn 3 viên ạn vào một cái bia một cách ộc lập. Xác suất bắn trúng bia của mỗi
viên ạn lần lượt là 0,7; 0,8; 0,9. Tính xác suất: a) Có úng một viên ạn trúng bia.
b) Bia bị trúng ạn.
c) Viên thứ nhất trúng bia, biết rằng bia bị trúng 02 viên. 28
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1.28. Có ba sinh viên cùng làm bài thi môn xác suất thống kê. Xác suất làm ược bài thi
của từng người lần lượt là 0,9; 0,8; 0,7.
a) Tìm xác suất ể có ít nhất một sinh viên làm ược bài thi.
b) Giả sử có một sinh viên làm ược bài thi. Tìm xác suất ể sinh viên thứ nhất không làm ược bài thi.
1.29. Một mạch iện với các linh kiện ược lấp ặt như hình vẽ sau. Biết rằng xác suất hỏng
hóc của các linh kiện A, B, C, D, E, F trong khoảng thời gian T tương ứng là: 0,05;
0,04; 0,06; 0,07; 0,08; 0,03 và sự hỏng hóc của chúng là ộc lập nhau. Tính xác suất
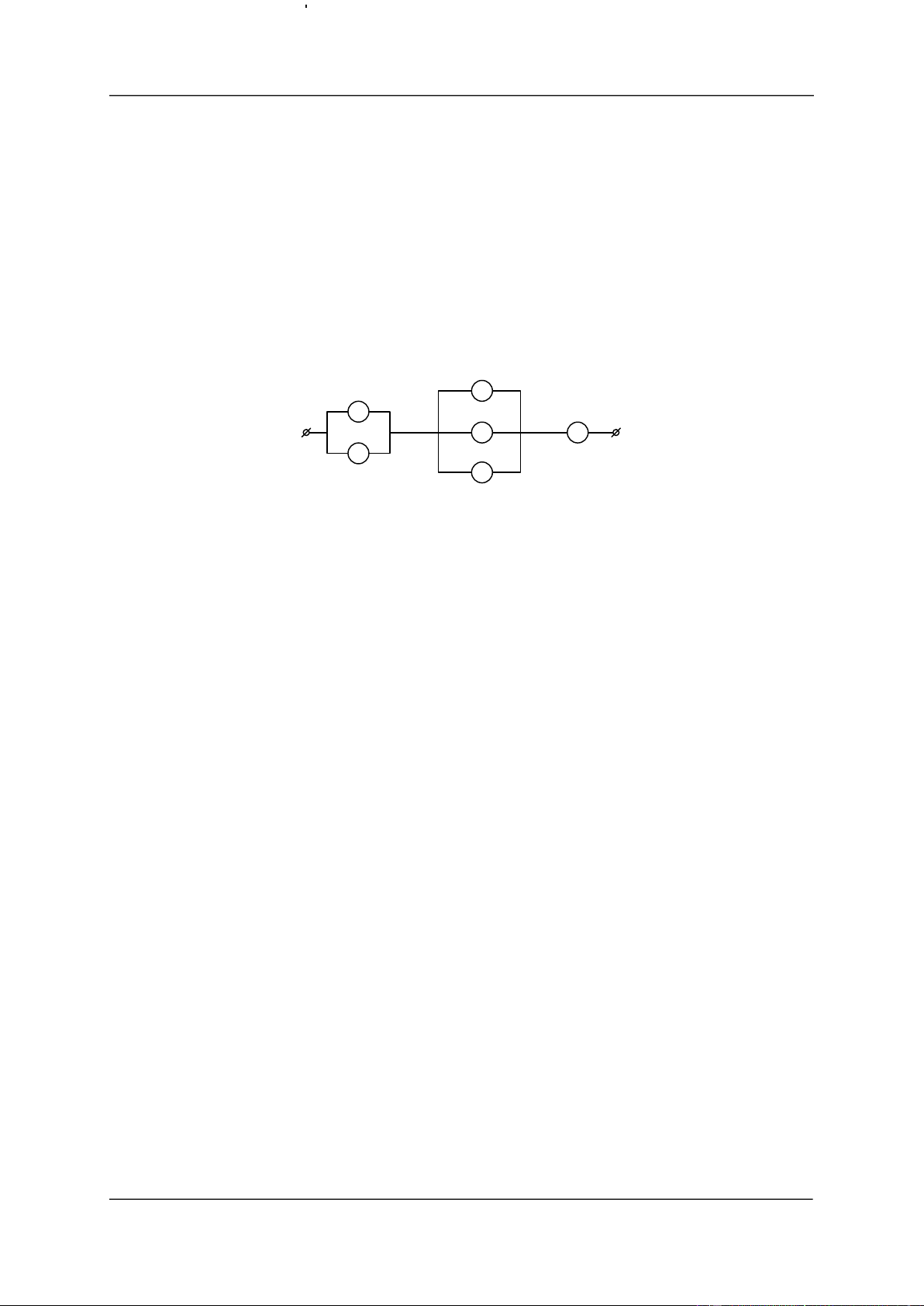
ể trong khoảng thời gian T mạch bị ngắt do sự hỏng hóc của các linh kiện này. C A D F B E
Hình 1.7. Sơ ồ mạch iện
1.30. Có ba lô sản phẩm (sp). Lô I có 15 sp trong ó có 3 sp kèm vé thưởng trị giá 20
ngàn ồng; lô II có 20 sp trong ó có 4 sp kèm vé thưởng trị giá 10 ngàn ồng và 2 sp
kèm vé thưởng trị giá 20 ngàn ồng; Lô III có 25 sp trong ó có 5 sp kèm vé thưởng
trị giá 10 ngàn ồng. Chọn ngẫu nhiên mỗi lô ra một sản phẩm. a) Tính xác suất ược
ít nhất một sp có thưởng.
b) Tính xác suất ược ít nhất hai sp không có thưởng.
c) Tính xác suất ể tổng giá trị các vé trưởng là 10 ngàn ồng.
d) Tính xác suất ể tổng giá trị các vé trưởng là 30 ngàn ồng.
Công thức xác suất ầy ủ, công thức Bayes
1.31. Trong kho có chứa 20 thùng hàng, trong ó có 12 thùng loại 1 chứa 90% sản phẩm
tốt, số thùng còn lại thuộc loại 2 chứa 60% sản phẩm tốt. Chọn ngẫu nhiên 1 thùng
và từ ó lấy ngẫu nhiên 1 sản phẩm.
a) Tính xác suất ể sản phẩm lấy ra là sản phẩm tốt.
b) Giả sử sản phẩm lấy ra là sản phẩm tốt. Tính xác suất ể thùng hàng loại 1 ược chọn.
1.32. Tỷ lệ người ến khám tại một bệnh viện mắc bệnh A là 55%, trong số những người
mắc bệnh A có 46% mắc cả bệnh B, còn trong số những người không mắc bệnh A có 73% mắc bệnh B.
a) Khám cho một người thì thấy người ó mắc bệnh B. Tính xác suất ể người ược khám cũng mắc bệnh A.
b) Nếu người ược khám không mắc bệnh B tìm xác suất ể người ó không mắc bệnh A.
Xác suất thống kê và Ứng dụng – 2021 29 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1.33. Tại một vùng dân cư, tỷ lệ người nghiện hút thuốc lá là 20%. Biết rằng tỷ lệ viêm
họng trong số người nghiện hút thuốc lá là 70% và với người không nghiện là 25%.
Khám ngẫu nhiên 1 người thì thấy người ó bị viêm họng. Tính xác suất ể người ó nghiện thuốc lá.
1.34. Một nhà máy sản xuất một chi tiết của iện thoại di ộng có tỷ lệ sản phẩm ạt tiêu
chuẩn là 87%. Trước khi xuất xưởng người ta dùng một thiết bị kiểm tra ể kết luận
sản phẩm có ạt yêu cầu chất lượng hay không. Thiết bị có khả năng phát hiện úng
sản phẩm ạt tiêu chuẩn với xác suất 0,92 và phát hiện úng sản phẩm không ạt tiêu
chuẩn với xác suất 0,96. Tìm xác suất ể 1 sản phẩm ược chọn ngẫu nhiên sau khi kiểm tra:
a) Được kết luận là ạt tiêu chuẩn
b) Được kết luận là ạt tiêu chuẩn thì lại không ạt tiêu chuẩn.
c) Được kết luận úng với thực chất của nó.
1.35. Có 20 xạ thủ tham gia bắn bia, trong ó 5 người có xác suất bắn trúng là 0,8; có 7
người bắn trúng với xác suất là 0,6; có 4 người bắn trúng là 0,7 và số còn lại có xác
suất bắn trúng là 0,5. Chọn ngẫu nhiên 1 xạ thủ và cho bắn một viên. Thấy bia không
bị trúng ạn. Hỏi xạ thủ này có khả năng thuộc nhóm nào nhất ?
1.36. Một lô hàng do 3 xí nghiệp sản xuất, trong ó xí nghiệp 1 sản xuất 50%, xí nghiệp
2 sản xuất 30%, xí nghiệp 3 sản xuất 20% số hàng hoá. Tỉ lệ phế phẩm của từng xí
nghiệp lần lượt là 1%, 2%, 3%. Lấy ngẫu nhiên một sản phẩm từ lô hàng. a) Tính
xác suất lấy ược phế phẩm.
b) Giả sử lấy ược sản phẩm tốt. Tính xác suất ể sản phẩm này do xí nghiệp 1 sản xuất.
c) Tính xác suất lấy ược phế phẩm do xí nghiệp 2 sản xuất.
1.37. Một xí nghiệp có 3 phân xưởng cùng sản xuất một loại sản phẩm A với sản lượng
tương ứng theo tỉ lệ 8:7:9. Tỉ lệ sản phẩm ạt tiêu chuẩn xuất khẩu trong phân xưởng
I là 85%, trong phân xưởng II là 75%, trong phân xưởng III là 90%. a) Tính tỉ lệ ạt
tiêu chuẩn xuất khẩu của sản phẩm A trong toàn xí nghiệp.
b) Lấy ngẫu nhiên 1 sản phẩm từ xí nghiệp thì gặp sản phẩm ạt tiêu chuẩn xuất khẩu.
Hãy cho biết khi ó sản phẩm này có khả năng nhất là của phân xưởng nào ?
1.38. Cửa hàng bán bóng èn của 3 nhà máy sản xuất. Số bóng èn của nhà máy A là 40%
của nhà máy B là 25% còn lại là của nhà máy C. Theo số liệu kiểm tra ở các nhà
máy thì tỉ lệ phế phẩm của nhà máy A là 0,1% của nhà máy B là 0,2% và của nhà
máy C là 0,3%. Mua ngẫu nhiên 1 bóng èn ở cửa hàng. a) Tính xác suất ể mua phải bóng èn hư.
b) Giả sử ta mua phải bóng èn hư, hỏi bóng ó có khả năng thuộc nhà máy nào nhất ? 30
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Công thức Bernoulli
1.39. Gieo 100 hạt ậu tương. Xác suất nảy mầm của mỗi hạt là 0,9. Tính xác suất ể trong 100 hạt:
a) Có úng 80 hạt nảy mầm.
b) Có ít nhất 1 hạt nảy mầm.
c) Có nhiều nhất 98 hạt nảy mầm.
1.40. Trong một cuộc thi bắn súng quốc tế, mỗi xạ thủ bắn 60 viên ạn vào bia. Xạ thủ
Việt Nam bắn trúng tâm với xác suất 0,92. Tính xác suất: a) Xạ thủ Việt Nam bắn trúng tâm cả 60 viên.
b) Xạ thủ Việt Nam bắn trượt ngoài tâm 2 viên.
c) Xạ thủ này bị trượt ngoài tâm ít nhất 1 viên.
d) Tìm số viên ạn trúng tâm có khả năng nhất. Tính xác suất tương ứng.
1.41. Một sọt cam rất lớn ược phân loại theo cách sau: Chọn ngẫu nhiên 20 quả cam
làm mẫu ại diện, nếu mẫu không có quả cam hỏng nào thì sọt cam ược xếp loại 1;
nếu mẫu có 1 hoặc 2 quả hỏng thì sọt cam ược xếp loại 2; trường hợp còn lại xếp loại 3.
Giả sử tỷ lệ cam hỏng của sọt cam là 3%. Hãy tính xác suất:
a) Sọt cam ược xếp loại 1.
b) Sọt cam ược xếp loại 2.
c) Sọt cam ược xếp loại 3.
1.42. Một nữ công nhân phụ trách 12 máy dệt. xác suất ể mỗi máy dệt trong khoảng
thời gian t cần ến sự chăm sóc của nữ công nhân là 0,3. Tính xác suất trong khoảng thời gian t :
a) Có 4 máy cần ến sự chăm sóc của nữ công nhân.
b) Số máy dệt cần ến sự chăm sóc của nữ công nhân không bé hơn 3 và không lớn hơn 6.
1.43. Tỷ lệ khách uống cà phê tại một quán giải khát là 65%.
a) Tính xác suất ể trong 6 khách vào quán này có ít nhất 2 khách uống cà phê.
b) Trong số 35 khách vào quán này thì số khách uống cà phê có nhiều khả năng nhất là bao nhiêu?
1.44. Bắn 6 viên ạn vào bia, xác suất trúng bia của mỗi viên ạn là 0,7. Bia sẽ bị hỏng
nếu có ít nhất 3 viên trúng. Tính xác suất ể bia không bị hỏng.
1.45. Tại một siêu thị, người ta lắp ặt một hệ thống chuông báo cháy gồm 4 chuông. Các
chuông này hoạt ộng ộc lập nhau và xác suất trong khoảng thời gian T một chuông
Xác suất thống kê và Ứng dụng – 2021 31 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
báo cháy khi khu vực có cháy là 95%. Tính xác suất ể trong khoảng thời gian T khu
vực này có chuông báo cháy khi có cháy.
1.46. Một bài thi trắc nghiệm gồm có 10 câu, mỗi câu hỏi có 5 phương án trả lời, trong
ó chỉ có 1 phương án úng. Giả sử mỗi câu trả lời úng ược 4 iểm và câu trả lời sai bị
trừ 2 iểm. Một học sinh kém làm bài bằng cách chọn hú hoạ một phương án cho mỗi
câu hỏi. Tính xác suất ể:
a) Anh ta ược 4 iểm.
b) Anh ta bị iểm âm.
Bài tập tổng hợp
1.47. Một khẩu pháo bắn vào một mục tiêu với xác suất trúng là 0,6. Tìm xác suất mục
tiêu bị tiêu diệt sau 3 lần bắn liên tiếp, biết rằng khả năng mục tiêu bị tiêu diệt khi
có 1, 2, 3 viên trúng tương ứng là 0,2; 0,5 và 0,8.
1.48. Trong 4 lần thử, mỗi lần thử biến cố A xuất hiện với xác suất là 0,6. Nếu A xuất
hiện quá 2 lần thì chắc chắn biến cố B sẽ xuất hiện, nếu A xuất hiện 1 hoặc 2 lần thì
xác suất xuất hiện của biến cố B tương ứng là 0,4 và 0,7; nếu A không xuất hiện thì
biến cố B sẽ không xuất hiện. Hãy tính xác suất xuất hiện của biến cố B.
1.49. Một hộp ậu giống gồm 2 hạt ậu trắng và 4 hạt ậu ỏ. Một hộp khác gồm 3 hạt ậu
trắng và 4 hạt ậu ỏ. Tỉ lệ nảy mầm là 0,8 ối với mỗi hạt ậu trắng, là 0,7 ối với mỗi
hạt ậu ỏ. Lấy ngẫu nhiên từ mỗi hộp ra 2 hạt em gieo. a) Tính xác suất ể cả 4 hạt ều nảy mầm.
b) Biết 4 hạt em gieo ều nảy mầm. Tính xác suất ể 4 hạt ều là hạt ậu ỏ.
CHƯƠNG 2 BIẾN NGẪU NHIÊN
2.1. Biến ngẫu nhiên và phân phối xác suất
2.1.1. Định nghĩa biến ngẫu nhiên
Đại lượng cho tương ứng mỗi kết qủa của phép thử với một số thực ược gọi là biến
ngẫu nhiên (cũng còn gọi là ại lượng ngẫu nhiên hay phần tử ngẫu nhiên) trên các
kết qủa của phép thử ó. Nói một cách khác: Biến ngẫu nhiên là một ánh xạ i từ không
gian các biến cố sơ cấp vào tập các số thực. Biến ngẫu nhiên thường ược ký hiệu bởi:
X, Y, Z, X1 ,...
Tập các giá trị của biến ngẫu nhiên X ược ký hiệu là X( ) (với là không gian các
biến cố sơ cấp). Căn cứ vào giá trị, ta chia biến ngẫu nhiên thành hai loại:
➢ Biến ngẫu nhiên rời rạc 32
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Biến ngẫu nhiên X ược gọi là biến ngẫu nhiên rời rạc nếu tập giá trị X( ) là tập
hữu hạn hoặc vô hạn ếm ược, tức là:
X ( ) x x1, 2,..., xn hoặc X ( ) x x1, 2,..., xn,...
➢ Biến ngẫu nhiên liên tục
Biến ngẫu nhiên X ược gọi là biến ngẫu nhiên liên tục nếu tập giá trị X ( ) là một
khoảng hay một số khoảng của .
Ví dụ 2.1. Các ại lượng sau là biến ngẫu nhiên, ký hiệu là X và tập giá trị tương ứng là X( ):
a) Số chấm xuất hiện khi gieo một con xúc xắc X ( ) 1,2,3,4,5,6
- Biến ngẫu nhiên rời rạc
b) Tuổi thọ của một thiết bị ang hoạt ộng. X( ) (0, )
- Biến ngẫu nhiên liên tục
c) Số khách hàng vào một hệ thống phục vụ trong một buổi sáng. X ( ) 0,1,2,...
- Biến ngẫu nhiên rời rạc
d) Số vụ tai nạn giao thông trong một ngày tại TP.HCM. X ( ) 0,1,2,...
- Biến ngẫu nhiên rời rạc
e) Sai số khi o lường một ại lượng vật lý.
X ( ) (0,b) với b 0 nào ó - Biến ngẫu nhiên liên tục
2.1.2. Luật phân phối xác suất của biến ngẫu nhiên a) Khái niệm
Luật phân phối xác suất của biến ngẫu nhiên là một quy tắc làm tương ứng mỗi
giá trị của biến ngẫu nhiên ó với một giá trị xác suất.
b) Bảng phân phối xác suất của biến ngẫu nhiên rời rạc
Xét biến ngẫu nhiên rời rạc X, có X ( ) x x1, 2,..., xn với xác suất
P X( xi ) pi .
Phân phối xác suất của X ược biểu diễn dưới dạng bảng sau, và ược gọi là bảng
phân phối xác suất:
Xác suất thống kê và Ứng dụng – 2021 33 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
X x1 x2 ... xn
P p1 p2 ... pn Trong ó, các x pi ,
i thỏa mãn ba tính chất sau: 1)
x1 x2 ... xn . 2)
0 pi 1, i 1,...,n 3)
p1 p2 ... pn 1 Lưu ý:
➢ Các biến cố {X xi}, i 1,...,n lập thành hệ ầy ủ và xung khắc từng ôi.
➢ P x( k X xm) pk pk 1 ... pm là xác suất ể X nhận giá trị trong tập xk ,..., xm , k m.
➢ Cho biến ngẫu nhiên Y
(X ) (với (X ) là một hàm số theo biến ngẫu nhiên X ).
Khi ó Y cũng là biến ngẫu nhiên rời rạc.
Các bước lập bảng phân phối xác suất của biến ngẫu nhiên Y:
- Tìm tập giá trị Y( ) .
- Tính các xác suất P Y( y j )
pi với pi P X( xi ) (xi ) yj
- Lập bảng phân phối xác suất của Y.
➢ Hai biến ngẫu nhiên rời rạc X và Y ược gọi là ộc lập nhau nếu hai biến cố {X xj}
và {Y yk} ộc lập nhau với mọi j k, .
Ví dụ 2.2. Một phòng thí nhiệm ược cấp ba triệu ồng ể tiến hành thí nghiệm tìm một
chủng vi rút trong gia cầm. Một lần thí nghiệm chi phí một triệu ồng. Nếu phát hiện ra
chủng vi rút này thì ngừng thí nghiệm. Nếu không phát hiện ra thì làm thí nghiệm cho
tới khi phát hiện ra chủng vi rút trên hoặc hết kinh phí thì dừng. Gọi X là số tiền mà
phòng thí nghiệm trên tiết kiệm ược. Biết rằng các lần thí nghiệm là ộc lập nhau và xác
suất tìm ra chủng vi rút này ở mỗi lần thí nghiệm là 0,35. Hãy lập bảng phân hối xác suất cho X.
Giải. X là biến ngẫu nhiên rời rạc có tập giá trị X ( ) {0,1,2}.
Gọi Ai là biến cố tìm ra chủng vi rút ở lần thí nghiệm thứ i.
Ta có: P A( i ) 0,35 ;P A(i ) 0,65 (i 1,2,3) 34
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
P X( 0) P A A A 1 2 3 A A A1 xk 23
dl (0,65) 0,235 (0,65)3 0,4225 P X( 1)P A A dl 12 0,35 0,65 0,2275 P X( 2) P A 1 0,35 X 0 1 2
Vậy bảng phân phối của X là: P 0,4225 0,2275 0,35
Ví dụ 2.3. Một người nhằm bắn vào một mục tiêu cho tới khi trúng mục tiêu thì dừng.
Các lần bắn ộc lập nhau. Xác suất trúng mục tiêu của mỗi lần bắn là 0,6. Gọi Y là số
viên ại phải dùng. Lập bảng phân phối xác suất của Y.
Giải. Y là biến ngẫu nhiên rời rạc có tập giá trị Y( )
{1,2,...} ( ây là tập vô hạn ếm ược).
P Y( k) (1 0,6)k 1 0,6 (0,4)k 1 0,6 (k 1 lần ầu trượt, lần thứ k bắn trúng), k 1,2,...
Vậy bảng phân phối của Y là: Y 1 2 3 ... k ...
P 0,6 0,24 0,096 ... (0,4)k 1 0,6 ...
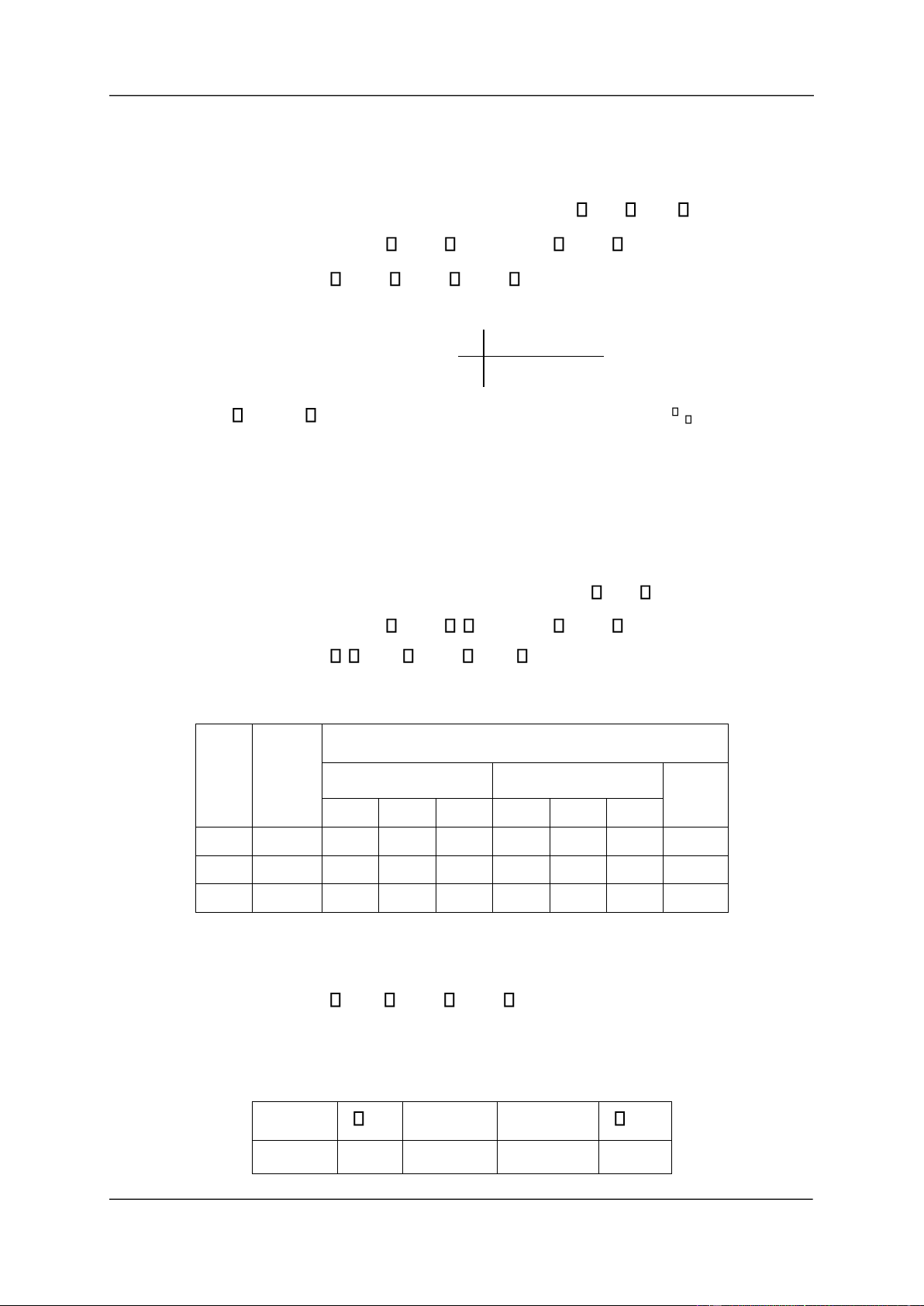
Ví dụ 2.4. Cho bnn rời rạc có bảng phân phối xác suất sau: X 1 0 1 2 3
P a 2a 0,1 2a 0,3
a) Tìm a và tính xác suất P(0 X 2).
b) Lập bảng phân phối xác suất của Y 2 | X | 3 .
Giải. a) Điều kiện 0 pi 1, i 0 a 0,5 p1
p2 ... p5 1 5a 0,4 1 a 0,12
Vậy bảng phân phối xác suất của X là: X 1 0 1 2 3
P 0,12 0,24 0,1 0,24 0,3
P(0 X 2) P {X 1}{X 2}
xk P X( 1)P X( 2) 0,1 0,24 0,34
Xác suất thống kê và Ứng dụng – 2021 35 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh X 1 0 1 2 3
b) Bảng giá trị của Y là: Y 2 | X | 3 1 3 1 1 3
Y là biến ngẫu nhiên rời rạc có tập giá trị Y( ) {1,3}.
P Y( 1) p1 p3 p4 0,46 P
Y( 2) p2 p5 0,54 Y 1 3
Bảng phân phối xác suất của Y là: P 0,46 0,54
Ví dụ 2.5. Cho hai biến ngẫu nhiên X và Y ộc lập nhau và có bảng phân phối xác suất sau: X 1 0 1 Y 1 1
P 0,2 0,5 0,3 P 0,4 0,6
Hãy lập bảng phân phối xác suất của các biến ngẫu nhiên T X Y và Z XY .
Giải. Lập các bảng cộng và bảng nhân sau:
Bảng cộng T X Y
Bảng nhân Z XY Y -1 Y 1 -1 1 X X -1 -2 0 -1 1 - 1 0 - 1 1 0 0 0 1 0 2 1 - 1 1
Các biến ngẫu nhiên T Z, là các bnn rời rạc có tập giá trị là:
T( ) 2;1;0;1 Z( ) 1;0;1
Áp dụng tính chất xung khắc, ộc lập của các biến cố, ta có: P T( 2) P X( 1).P Y( 1) 0,08 P T( 1)P X( 0).P Y( 1)0,2 P T( 0) P X(
1).P Y( 1)P X( 1).P Y( 1)0,24
P T( 1)P X( 0).P Y( 1)0,3
P T( 2) P X( 1).P Y( 1)0,18 T 2
Bảng phân phối xác suất của T : 1 0 1 2
P 0,08 0,2 0,24 0,3 0,18 36
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P Z( 1)P X(
1). (P Y 1)P X( 1). (P Y 1)0,24
P Z( 0) P X( 0).P Y(
1)P X( 0).P Y( 1)0,5 P Z( 1)P X( 1).P Y(
1)P X( 1).P Y( 1)0,26 Z 1
Bảng phân phối xác suất của Z : 0 1 P 0,24 0,5 0,26
c) Hàm mật ộ xác suất của biến ngẫu nhiên liên tục
Do biến ngẫu nhiên liên tục có vô số giá trị nên không thể liệt kê như trường hợp
rời rạc mà phải có một ại lượng khác ể thay thế, ó là: hàm mật ộ xác suất. ➢ Định nghĩa
Hàm số y f x x( ),
ược gọi là hàm mật ộ xác suất của biến ngẫu nhiên liên
tục X nếu thỏa hai iều kiện sau:
1) f x( ) 0, x y P( aXb ) = diện tích hình thang H 2) f x dx( ) 1 y () fx ➢ Hệ quả H b 0 a b x
1) P a X b f x dx( )
Hình 2.1. Minh họa ồ thị hàm mật ộ xác suất a
2) P X( a) 0, a
➢ Ý nghĩa: Hàm mật ộ xác suất f x( ) ặc trưng cho mức ộ tập trung xác suất của
biến ngẫu nhiên X trên từng khoảng giá trị của nó. 0 , x 1 x
Ví dụ 2.6. Cho bnn liên tục X có hàm mật ộ: f x( ) k x2 , 1
a) Tìm giá trị của tham số k .
b) Tính xác suất P(2 X 3) .
c) Tính xác suất ể trong 4 phép thử ộc lập thì có úng 3 lần biến ngẫu nhiên X nhận
giá trị nằm ngoài khoảng (2,3).
Giải. a) Ta có: f x( ) 0, x k 0
Xác suất thống kê và Ứng dụng – 2021 37 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 1 k 1
f x dx( ) 0dx k dx2 k 1 x x x 1 0 , x 1
Vậy k 1, ta có: f x( ) x12 , x 1
b) P 2 X 3 3 f x dx( ) 3 dx2 1 3 1 2 2 x x 2 6 1 c) 5
p P X (2,3) 1 P(2 x 3) 1 6 6
Gọi A là biến cố “có úng 3 lần X (2,3) ”. Áp dụng công thức Bernoulli với n 4;k 3; p , ta có: 5 P A() C p 33 4 (1 p)4 3 4 5 3 1 125 0,3858 6 6 324 kx , 0 x 2
Ví dụ 2.7. Cho bnn liên tục X có hàm mật ộ: f x( )
2k , 2 x 4 0 , x [0,4]
a) Tìm giá trị của tham số k và vẽ ồ thị hàm số y f x( ) .
b) Tính xác suất P( 1 X 3) .
Giải. a) Ta có:
f x( ) 0, x k 0 0 2 4 1
f x dx( ) 0dx k xdx 2k dx 0dx 0 2 4 2 2 38
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 6k k k. x 2 .k x421 2 0 6 x / 6 , 0 x 2 Khi ó: f x( ) 1/ 3 , 2 x 4 0 , x [0,4] y y 1 / 3 1 3 / Tổng diện y x /6 tích vùng S và S 2 bằng 1. S 2 S 1 y 0 y 0 0 2 4 x 1
Hình 2.2. Đồ thị hàm mật ộ xác suất y f x( )
b) P( 1 X 3) 0 0dx 1 2 xdx 1 3 dx 1. x22 1.x 32 2 0.6667 1 6 0 3 2 6 2 0 3 3
2.1.3. Hàm phân phối xác suất ➢ Định nghĩa
Hàm phân phối xác suất của biến ngẫu nhiên X, ký hiệu là F x( ) hoặc FX ( )x , là
hàm số thực xác ịnh như sau:
F x( ) P X( ➢ Ý nghĩa
Xác suất thống kê và Ứng dụng – 2021 39 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Hàm phân phối F x( ) phản ánh mức x ) , x
ộ tập trung xác suất về phía bên trái của x.
Nếu F x( ) càng lớn thì càng có nhiều giá y x () Fx f () td t = diện tích hình thang
trị của X nằm về phía bên trái của x. cong vô hạn
Lưu ý: Hàm số S x( ) P X( x) 1 F ()1 Sx () Fx
x( ) ược gọi là hàm sống sót (survival y () fx
function) nó thường ược dùng nhiều trong
kỹ thuật và y khoa, hàm S x( ) cho biết xác
suất một thiết bị, một bệnh nhân sẽ sống 0 x
sót qua một khoảng thời gian x nào ó. x () fx hàm mật ộ ➢ Hình 2.3.
Tính chất. Hàm phân phối xác suất có () Fx hàm phân phối các tính chất sau () hàm sống sót Sx
1) F x( ) không giảm trên 2) FF((
) ) limx xlim F x( )F x( ) 1 0 ➢ Hệ quả
1) 0 F x( ) 1, x
2) F x( ) liên tục trái tại mọi x thuộc .
3) P a( X b) F b( ) F a( ) .
4) Biến ngẫu nhiên liên tục X có hàm mật ộ xác suất f x( ) . Khi ó hàm phân phối
của nó ược tính theo công thức: x F x( )
f t dt( ) và F x( ) f x( )
5) Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất
X x1 x2 ... xn
P p1 p2 ... pn
Khi ó hàm phân phối của nó ược tính theo công thức: 0, x x1 40
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh F x( )
p11 , p2 , xx12 xx xx23 p ..................... ... x
p1 p2 ... pn 1, xn
Ví dụ 2.8. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X 1 2 3 1 P 0,6 0,3 0,
Hãy viết hàm phân phối xác suất F x( ) của X và vẽ ồ thị hàm số y F x( ) . Giải
Hàm phân phối xác suất: 0 ; x 1 F(x) 1 0,6 ; 1 x2 0 , 9 0 , 6 F x( ) 0,9 ; 2 x3 x 0 1 2 3
1 ; x 3Hình 2.4. Đồ thị hàm phân phối F(x)
Ví dụ 2.9. Cho X là biến ngẫu nhiên liên tục có hàm phân phối xác suất: F x( ) A
B.arctan x. Hãy tìm giá trị các tham số A, B.
Giải. Từ các tính chất của hàm F x( ), ta có: B
a) F x( ) không giảm trên F x( ) 2 0, x B 0 1 x lim F x ( ) 0 b) limxx F x ( ) 1 AA BB(( / 2)/ 2) 10 BA 11// 2
Vậy F x( ) 1 1 arctan x 2
Ví dụ 2.10. Cho biến ngẫu nhiên liên tục X có hàm mật ộ xác suất:
Xác suất thống kê và Ứng dụng – 2021 41 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
3 x x),0 x 4 32 (4 f x( ) 0 , x [0,4]
Tìm hàm phân phối xác suất F x( ) của X. x
Giải. Hàm phân phối xác suất của X là: F x( ) f t dt( ) x
c) Với x 0, ta có: F x( ) 0dt 0 d) Với 0 x 4, ta có:
F x( ) 0 0dt 3 x t(4 t dt) 3 2t 2 t3 x 3 2x2 x3 32 0 32 3 0 32 3
e) Với x 4, ta có: F x( )
0 0dt 3 4 t(4 t dt) x 0dt 1 32 0 4 0 , x 0 Vậy F x( ) 1 6x 2 x3 ,0 x 4 32 1 , x 4
2.2. Các ặc trưng số của biến ngẫu nhiên 2.2.1. Mode, med
a) Mod (mode – giá trị tin chắc nhất) 42
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Giá trị tin chắc nhất của biến ngẫn nhiên X, ký hiệu là Mod(X), là giá trị x0 X thỏa mãn:
➢ max P X( x) P X( x0) nếu X rời rạc. x X ( )
➢ max f x( ) f x( 0 ) nếu X liên tục có hàm mật ộ f x( ) . x
b) Med (median – trung vị)
Trung vị của biến ngẫu nhiên X, ký hiệu là Med(X), là giá trị x0 thỏa mãn: P X med X() x0 P X(( xx00 )) 00,,55 Lưu ý:
1) Các giá trị mod(X ),med(X) luôn tồn tại và có thể không duy nhất.
2) Đối với bnn nhiên liên tục X có hàm phân phối F x( ) và med X( ) x0 thì x0
thỏa phương trình F x( ) 0,5 .
3) Với X là bnn nhiên liên tục, người ta ịnh nghĩa các giá trị tứ phân vị (quartile)
thứ nhất, thứ nhì (median), thứ ba lần lượt là q q q1, 2, 3 ược ịnh nghĩa như sau:
F q( 1) 0,25 ; F q( 2) 0,5 ; F q( 3) 0,75.
Ví dụ 2.11. Tìm mod(X ),med(X) biết X là biến ngẫu nhiên rời rạc có bảng phân phối X 1 2 3 4
xác suất: P 0,05 0,4 0,4 0,15
Giải. Nhận thấy rằng giá trị xác suất lớn nhất bằng 0,4 tại X 2 hoặc X 3. Vậy mod(X ) 2 hoặc mod(X ) 3.
P X( 3) 0,05 0,4 0,45 0,5 Ta có: P X( 3) 0,15 0,5 med X( ) 3
Ví dụ 2.12. Tìm mod(X ),med(X), biết X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất:
Xác suất thống kê và Ứng dụng – 2021 43 lOMoAR cPSD| 15962736 Bộ môn X 1 Toán 2 – Trư 3 ờng 4 ĐH.GTV T TP. Hồ Chí Minh 1 P 0,2 0,3 0,4 0,
Giải. mod(X) 3 P X( 2) 0,2 0,5
P X( 2) 0,5 0,5 med X( ) 2 P X( 3) 0,5 0,5
P X( 3) 0,1 0,5 med X( ) 3 Với 2 m 3 P X{ m} 0,5 0,5
{ m} 0,5 0,5 med X( ) m P X
Vậy med X( ) m, m thỏa 2 m 3.
Ví dụ 2.13. Tìm mod(X ),med(X), biết X là biến ngẫu nhiên liên tục có hàm mật ộ 3 x(4 x),0 x 4 xác suất: f x( ) 32 0 , x [0,4]
Giải. a) Tìm mod(X) Với 0 x 4, ta có:
f ( )x 3 (4 2 )xBảng biến thiên x 0 2 4 32 f ( )x 0 x 2 f ( )x + 0 - Vậy Mod X( ) 2 0 f x( ) 0 3/8
b) Tìm med(X ) .
Theo ví dụ 2.10, ta có hàm phân phối của X là: 0 ,x 0 44
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh F x( ) 1 6x2 x3 ,0 x 4 32 1 ,x 4 Xét phương trình 1
F x( ) 1 1 x2(6 x) , với 0 x4 2 32 2
x3 6x2 16 0 ; 0 x4 x 2 Vậy med X( ) 2
2.2.2. Kỳ vọng toán
Kỳ vọng toán (hay ngắn gọn là kỳ vọng) của biến ngẫu nhiên X, ký hiệu là E X( ),
ược tính theo công thức sau:
E X() p x1 1 p x22 ... p xn n
nếu X rời rạc. E X( ) x f x dx.( )
nếu X liên tục có hàm mật ộ f x( ) .
➢ Ý nghĩa. E X( ) là giá trị trung bình (theo trọng số xác suất) của biến ngẫu nhiên X. ➢ Tính chất 1) E C(
) C, C là biến ngẫu nhiên hằng.
2) E k X( . ) k E X. ( ), k là hằng số.
3) E X( Y) E X( ) E Y( ).
4) E XY( ) E X E Y( ). (
), trong ó X, Y là hai biến ngẫu nhiên ộc lập nhau. 5) Nếu Y (X ) thì E Y( )
n pk. ( xk ) , nếu X rời rạc k 1
Xác suất thống kê và Ứng dụng – 2021 45 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh E Y()
( ).x f x dx( ), nếu X liên tục
Đặc biệt với Y X 2 , ta có: E X(2) p x 2 2 1 1
...p xnn , nếu X rời rạc E X( 2 ) x f x dx2. ( ) , nếu X liên tục
Ví dụ 2.14. Cho hai biến ngẫu nhiên rời rạc X Y, ộc lập nhau trong ví dụ 2.5. Tính E X(
),E Y( ), E XY( ) và cho nhận xét.
Giải. Ta có: E X( ) 0,2 0 0,3 0,1 E Y() 0,4 0,6 0,2 E XY() E Z( ) 0,24 0 0,26 0,02
Nhận xét: E XY( ) E X E Y( ). ( ) ( ây là tính chất (4))
Ví dụ 2.15. Cho bnn rời rạc X có bảng phân phối xác suất X 1 2 4 5 7
1 P a 0,2 b 0,2 0,
a) Tìm giá trị các tham số a b, , biết E X( ) 3,5.
b) Tính E X( 2);E(3X 2 5X 7) . Giải. a) Ta có: 0 a b, 1 0 a b, 1
E Xp1 p2 p3 p4 p5 1 a b0,5 ba 00,,32 ( ) 3,5 a 4b 1,4 Vậy X 1 2 4 5 7 P 0,2 0,2 0,3 0,2 0, 1
b) E X( 2 ) 10,2 4 0,2 16 0,3 25 0,2 49 0,1 15,7
E(3X 2 5X 7) 3E X(2 ) 5E X( ) E(7) 46
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 315,7 53,5 736,6
Ví dụ 2.16. Thống kê cho biết tỷ lệ tai nạn xe máy ở thành phố H trong một năm là
0,12%. Công ty bảo hiểm A ề nghị bán loại bảo hiểm này cho ông B ở thành phố H
trong một năm với số tiền chi trả là 20 triệu ồng, phí bảo hiểm là 80 ngàn ồng. Hỏi trung
bình công ty A lãi bao nhiêu khi bán bảo hiểm cho ông B?
Giải. Gọi X (triệu ồng) là tiền lãi. X nhận hai giá trị: X 0,08 20
19,92(trong năm ó ông B bị tai nạn xe máy) X
0,08 (trong năm ó ông B không bị tai nạn xe máy) X 19,92
Bảng phân phối xác suất của X là: 0,08 P 0,0012 0,9988 Kỳ vọng: E X( )
19,92 0,0012 0,08 0,9988 0,056
Vậy trung bình công ty A lãi 56 ngàn ồng khi bán bảo hiểm cho ông B.
3 (x2 2 )x , x [0,1]
Ví dụ 2.17. Cho bnn liên tục X có f x( ) 4 0 , x [0,1]
Tính E X( ),E X( 2 ),E( X ) . Giải 0 1
E X() x f x dx. ( )
0dx 3 x x( 2 2 )x dx 0dx 11 4 0 16 1 1 E X(2)
x2. ( )f x dx 3 x2(x2 2 )x dx 21 4 0 40 1
E( X ) x f x dx. ( )
3 x x( 2 2 )x dx 4 0 3 1 1 1
x5/2 2x3/2 dx 3 x7/2 2 x5/2 57
Xác suất thống kê và Ứng dụng – 2021 47 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 4 0 4 7 / 2 5 / 2 0 0 70
2.2.3. Phương sai và ộ lệch chuẩn
➢ Định nghĩa phương sai
Phương sai của bnn X, ký hiệu là D X( ) hay Var(X), ược ịnh nghĩa nnhư sau: D X() E X E X() 2
Theo các tính chất của kỳ vọng, ta biến ổi phương sai như sau: D X() E X
2 2X E X. ( ) E X( ) 2
E X( 2 ) 2E X E X( ). ( ) E X() 2 E X( 2 ) E X( ) 2
Do ó, trong thực hành người ta thường dùng công thức sau ể tính phương sai: D X() E X 2 E X( ) 2
Lưu ý. D X( ) có ơn vị o bằng bình phương ơn vị o của X. Để có một ại lượng có cùng
ơn vị o với X, người ta ưa ra khái niệm ộ lệch chuẩn như sau:
➢ Độ lệch chuẩn: (X ) D X( )
➢ Ý nghĩa của phương sai: D X( ) và (X ) phản ánh mức ộ tập trung hay phân tán
của các giá trị của X quanh giá trị trung bình E X( ) .
➢ Tính chất của phương sai 1) D X( ) 0.
2) D C( ) 0 , với C là biến ngẫu nhiên hằng.
3) D k X( . ) k D X2. (
) , với k là hằng số thực tùy ý.
4) D X( Y) D X( ) D Y( ), với X Y, ộc lập nhau.
Ví dụ 2.18. Cho bnn rời rạc X trong ví dụ 2.15. Ta có :
E X( ) 3,5 ; E X( 2) 15,7 D X( ) E X 2 E X( ) 2 15,7 (3,5)2 3,45 48
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
D(2X 7) D(2X ) D( 7) 4D X() 013,8
(X ) D X( ) 1,85742
Ví dụ 2.19. Cho bnn liên tục X trong ví dụ 2.17, và bnn rời rạc Y ( ộc lập với X ) có Y 1 bảng phân phối: 2 4 P 0,2 0,5 0,3 Ta có :
E X( ) 11 ; E X( 2 ) 21 D X( ) 21 11 2 67 16 40 40 16 1280
E Y() 2 ; E Y( 2) 7 D X( ) 7 4 3
E(16X 3 )Y 16 (E X) 3 ( )E Y 11 65
D(8X 3Y) D (8X ) ( 3Y)
D(8X ) D( 3 Y)
82 D X() ( 3)2 D Y( ) 67 9 3 607 64 1280 20
2.3. Một số quy luật phân phối xác suất quan trọng
2.3.1. Phân phối nhị thức ➢ Định nghĩa
Biến ngẫu nhiên X ược gọi là có phân phối nhị thức với hai tham số n và p, ký
hiệu X B n p( , ) , với n
, 0 p 1, nếu X rời rạc và có tập giá trị
X ( ) 0,1,...,n và xác suất ược tính theo công thức Bernoulli: P X k C p kk n
(1 p)n k , (k 0,...,n)
➢ Tínhchất. Cho X B n p( , ). Khi ó:
1) E X( ) np D X; ( ) np(1 p)
2) (n 1) p 1
mod(X ) (n 1) p
➢ Mô hình nhị thức
Xác suất thống kê và Ứng dụng – 2021 49 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Trong n lần thử ộc lập với xác suất thành công p trong mỗi lần thử (xác suất xuất
hiện biến cố A nào ó), gọi X là số lần thành công trong n lần thử thì khi ó X có phân
phối nhị thức với hai tham số n, p.
Phân phối nhị thức rất phổ biến trong thực tế, chẳng hạn: số khách hàng có ặc iểm
A nào ó trong số n khách hàng vào một hệ thống dịch vụ; số sản phẩm ạt tiêu chuẩn A
nào ó trong số n sản phẩm ược lấy ngẫu nhiên từ một cơ sở sản xuất; số tín hiệu có ặc
iểm A nào ó trong số n tín hiện nhận ược ở một máy thu; số bé gái chào ời trong n ca
sinh ở một bệnh viện,… là các biến ngẫu nhiên có phân phối nhị thức.
➢ Phân phối Bernoulli
Phân phối nhị thức trong trường hợp n 1 thì ược gọi là phân phối Bernoulli với
tham số p (0,1) (xác suất thành công), ký hiệu là X B p( ) . Bảng phân phối xác X 0 1
suất của X : P 1 p p
Ví dụ 2.20. Xác suất ể một cây sống sau một thời gian trồng là 0,8. Trồng 1000 cây.
Gọi X là số cây sống sau một thời gian trồng.
a) Tìm luật phân phối xác suất của X.
b) Tính xác suất có 750 cây sống sau một thời gian trồng.
c) Tính E X( ),D X( ) và cho biết số cây sống sau một thời gian trồng có khả năng cao nhất là bao nhiêu ?
Giải. a) Theo bài thì X có luật phân phối nhị thức với hai tham số n 1000; p 0,8. Công thức xác suất : P X k C p kk k n
(1 p)n k C1000 (0,8) (0,k2)1000 k ;k 0,1000 b) P X 750 C 750 1000 (0,8)750(0,2)250 0,000018 c)
E X( ) np 1000 0,8 800 D X(
) np(1 p) 1000 0,8 0,2 160
(n 1) p 1 mod(X ) (n 1) p 799,8 mod(X ) 800,8 mod(X ) 800
Số cây sống sau một thời gian trồng có khả năng cao nhất là 800 cây.
Ví dụ 2.21. Một lô hàng chứa rất nhiều sản phẩm, trong ó tỷ lệ sản phẩm ạt chuẩn là
70%. Chọn ngẫu nhiên từ lô hàng ra 5 sản phẩm. Gọi X là số sản phẩm ạt chuẩn có trong
5 sản phẩm chọn ra. Hãy lập bảng phân phối xác suất cho X, và tính 50
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh E X( ),D X( ).
Giải. Ta thấy rằng X có phân phối nhị thức: X B n p( ,
) với n 5; p 0,7. Xác
suất ược tính theo công thức Bernoulli:
P X( k) C p q k k n k k n
C5 (0,7) (0,k 3)5 k ; k 0,5
P X( 0) 0,00243 ; P X( 1) 0,02835
P X( 2) 0,1323 ; P X( 3) 0,3087
P X( 4) 0,36015 ; P X( 5) 0,16807
Vậy bảng phân phối xác suất của X : X 0 1 2 3 4 5
P 0,00243 0,02835 0,1323 0,3087 0,36015 0,16807 Kỳ vọng của X:
E X() np 50,7 3,5
Phương sai của X: D X( ) np(1 p) 5 0,7 0,3 1,05
2.3.2. Phân phối siêu bội ➢ Bài toán
Một tập có N phần tử, trong ó có N ( N A A
N N ) phần tử có tính chất A. Lấy ngẫu NA n
nhiên n phần tử. Gọi
X là số phần tử có tính chất A trong n phần
Hình 2.4. Mô hình phân
tử ược chọn. Khi ó X là biến ngẫu nhiên phối siêu bội
rời rạc nhận các giá trị là các số nguyên .
từ max{0,n (N N k nk C
A)} ến min{NA, }n N C A NN A n CN
Công thức xác suất: P X{ k} ➢ Định nghĩa
Biến ngẫu nhiên X ược gọi là có phân phối siêu bội, ký hiệu X H N N( , A, )n ,
trong ó N N, A,n là các số nguyên dương, thỏa mãn 0 n N, A N , nếu X rời rạc nhận
các giá trị nguyên từ max{0,n (N NA)} ến min{NA, }n và có công thức xác suất: C CNk A N Nn k P X{ k} n A CN
➢ Tính chất. Cho X H N N( , A, )n .
Xác suất thống kê và Ứng dụng – 2021 51 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh N n
Khi ó: E X( ) np ; D X( ) npq N 1
Trong ó: p N NA. 1 ,q 1 p
➢ Định lý. Cho bnn X H N N( ,
A, )n . Giả sử n rất nhỏ so với N. Khi ó X
ược xấp xỉ phân phối nhị thức X N n p( , ) , với p N NA. 1 .
Lưu ý. Cần phân biệt giữa phân phối nhị thức và phân phối siêu bội: Trong phân phối
nhị thức, n phần tử ược lấy ra từ một tập vô hạn phần tử hoặc từ một tập có số phần tử
là hữu hạn nhưng rất lớn; Trong phân phối siêu bội, n phần tử ược lấy ra từ một tập hữu
hạn. Chẳng hạn: gọi X là số sản phẩm ạt tiêu chuẩn quy ịnh trong n sản phẩm lấy ra.
Khi ó nếu n sản phẩm ược lấy ra từ một cơ sở sản xuất ( ang hoạt ộng) thì X có phân
phối nhị thức; còn nếu lấy ra từ một lô hàng (có hữu hạn sản phẩm) thì X có phân phối siêu bội.
Ví dụ 2.22. Một hộp chứa 10 viên bi, trong ó có 6 bi ỏ và 4 bi xanh. Chọn ngẫu nhiên
từ hộp ra 5 bi. Gọi X là số bi ỏ có trong 5 bi lấy ra. Hãy lập bảng phân phối xác suất cho
X, và tính kỳ vọng, phương sai của X.
Giải. Ta thấy rằng X có phân phối siêu bội X H N N( ,
A, )n với N 10,NA 6,n 5
max{0,n NA N} max{0,1} 1 A min{6,5} 5 min{N , }n
Do ó X nhận các giá trị: 1, 2, 3, 4, 5; Công thức xác suất:
P X{ k} CNk ACnN Nn k A
C C6k545 k , (k 1,2,3,4,5) CN C10 1 P X{ 1} ; P X{ 2} 5 4221 10 5 1 P X{ 3} ; P X{ 4} ; P X{ 5} 21 21 42
Vậy bảng phân phối xác suất của X là: X 1 2 3 4 5
P 1/ 42 5 / 21 10 / 21 5 / 21 1/ 42 52
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
p NA 0,6 ; q 1 p 0,4 N
Kỳ vọng của X: E X( ) np 50,6 3 N n 10 5
Phương sai của X: D X( ) npq 5 0,6 0,4 2 N 1 10 1 3
Lưu ý. Bài toán trong ví dụ này có thể làm trực tiếp theo phương pháp liệt kê các giá
trị của X, không nhất thiết phải làm theo phân phối siêu bội (phức tạp).
Ví dụ 2.23. Một lô hàng có 10000 sản phẩm, trong ó có 9000 sản phẩm loại A và 1000
sản phẩm loại B. Lấy ngẫu nhiên 12 sản phẩm từ lô hàng ể kiểm tra. Tìm xác suất lấy
ược 9 sản phẩm loại A.
Giải. Gọi X là số sản phẩm loại A có trong 12 sản phẩm lấy ra. Khi ó X có phân phối
siêu bội X H N N( , A, )n với N 10000, NA 9000, n 12. Do n 12 rất nhỏ so N
với N nên X xấp xỉ phân phối nhị thức X B n p( , ) với p A 0,9 . N
Vậy xác suất chọn ược 9 sản phẩm loại A là: P X( 9) C p 99 9
n (1 p)n 9 C12 (0,9) (0,91)3 0,085233
2.3.3. Phân phối Poisson ➢ Định nghĩa
Biến ngẫu nhiên rời rạc X ược gọi là có phân phối Poisson với tham số 0, ký
hiệu X P( ) , nếu X ( ) 0,1,2,...,n,... với xác suất ược tính theo công thức: P X k k e ; k 0,1,2,... k!
➢ Định lý Poisson
Cho bnn X có phân phối nhị thức X
B n p( , ) . Giả sử n rất lớn và p rất nhỏ
(thông thường p 0,1). Khi ó X ược xấp xỉ phân phối Poisson, X P( ) với np, ta có công thức xấp xỉ: k k k n k P X k C p (1 p ) e n k ! P( ) . Khi ó:
Xác suất thống kê và Ứng dụng – 2021 53 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
➢ Tính chất. Cho X
1) E X( ) D X( ) 2) 1 mod(X) ➢ Mô hình Poisson
Người ta chỉ ra ược rằng: số lần xuất hiện biến cố A nào ó trong khoảng thời gian
liên tục (t t1, 2) và không gian xác ịnh nào ó là biến ngẫu nhiên có phân phối Poisson.
Chẳng hạn: xét trong khoảng thời gian (t t1, 2) nào ó, số khách hàng ến một hệ thống
dịch vụ, số cuộc gọi của một mạng iện thoại di ộng, số tín hiệu nhận ược ở một máy thu
sóng, số trẻ chào ời ở một bệnh viện phụ sản, số xe qua một trạm, số xe máy ến ổ xăng
tại một trạm xăng,… là các biến ngẫu nhiên có phân phối Poisson với tham số c t( 2
t1), với c là cường ộ xuất hiện biến cố A.
Ví dụ 2.24. Một máy dệt có 5000 ống sợi, xác suất ể trong 1 phút mỗi ống sợi bị ngưng
hoạt ộng (do sợi bị ứt, bị rối,..) là 0,0004. Gọi X là số ống sợi bị ngưng hoạt ộng trong 1 phút.
a) Tìm luật phân phối xác suất của X.
b) Tính xác suất ể trong 1 phút có hơn 2 ống sợi bị ngưng hoạt ộng.
Giải. a) X có phân phối nhị thức X B n p( , ) với hai tham số n 5000 và p 0,0004. Công thức xác suất:
P X k C p kk k n
(1 p)n k C5000 (0,0004) (0,9996)k5000 k , (k 0,...,5000)
b) Do n 5000 là rất lớn và p 0,0004 rất nhỏ nên X xấp xỉ phân phối Poisson: X P( ) với np 2. P X k k e 2k e 2 k! k! Xác suất cần tìm là:
P X( 2) 1 P(0 X 2) 1 P X( 0) P X( 1) P
X( 2) 1 20 e 2 21 e 2 22 e 2 1 5e 2 54
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 0! 1! 2! Vậy
P X{ 2} 15e 2 0,323324 .
Ví dụ 2.25. Ở trạm xăng H, bình quân mỗi 10 phút có 15 xe máy ến ổ xăng. Biết rằng
số xe máy ến ổ xăng ở trạm xăng này trong khoảng thời gian t phút là biến ngẫu nhiên có phân phối Poisson.
a) Tìm xác suất ể trong khoảng thời gian 10 phút có ít nhất 4 xe máy ến ổ xăng tại trạm xăng này.
b) Tìm xác suất ể trong khoảng thời gian 15 phút có từ 20 ến 24 xe máy ến ổ xăng tại trạm xăng H.
Giải. Gọi X Y,
tương ứng là số xe máy ến ổ xăng ở trạm xăng H trong 10 phút và 15 trong phút.
Theo giả thiết, ta có: X P( ) , Y P( 1) 10c 15 c1 1,c5.15 22,5
a) Xác suất ể trong khoảng thời gian 10 phút có ít nhất 4 xe máy ến ổ xăng:
P X{ 4} 1P X{ 4}
1 P X{ 0} P X{ 1} P X{ 2} P X{ 3} 0 1 e 2 e 3 e 0,999789 1 e 0! 1! 2! 3!
b) Xác suất ể trong khoảng thời gian 15 phút có từ 20 ến 24 xe máy ến ổ xăng: 24 24
1k 1 0,403249 P{20 Y
24} P Y{ k} e k 20 k 20 k!
2.3.4. Phân phối mũ
➢ Định nghĩa. Biến ngẫu nhiên liên tục X ược gọi là có phân phối mũ với tham số
0, ký hiệu là X E( ) , nếu X có hàm mật ộ xác suất:
Xác suất thống kê và Ứng dụng – 2021 55 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh e x, x 0 f x( ) 0 , x 0
➢ Tính chất. Cho X E( ). Khi ó: E X( ) 1 ; D X( ) 12 . ➢ Mô hình mũ
Người ta chứng minh ược rằng: Nếu số lần xuất hiện của một biến cố trong một
khoảng thời gian có phân phối Poisson thì thời gian giữa hai lần xuất hiện biến cố ó có
phân phối mũ. Chẳng hạn, thời gian làm việc liên tục của một thiết bị giữa hai lần sửa
chữa, thời gian chờ của khách hàng ể ược phục vụ, tuổi thọ của một thiết bị (máy móc,
sản phẩm, một loài sinh vật),… là các biến ngẫu nhiên có phân phối mũ.
Ví dụ 2.26. Giả sử tuổi thọ X (năm) của một loại linh kiện iện tử là biến ngẫu nhiên có
phân phối mũ với tham số
0,125. Thời gian bảo hành của loại linh kiện này là 6 năm.
a) Tính tuổi thọ trung bình của loại linh kiện này.
b) Tính tỷ lệ linh kiện bán ra thị trường phải thay thế trong thời gian bảo hành.
c) Nếu muốn tỷ lệ linh kiện bán ra thị trường phải thay thế trong thời gian bảo hành
không vượt quá 15% thì cần phải ưa ra thời gian bảo hành tối a là bao nhiêu năm?
Giải. a) Tuổi thọ trung bình của loại linh kiện này bằng: E X( ) 1 1 8 (năm) 0,125 e x, x 0
b) Hàm mật ộ xác suất: f x( ) với 0,125 0 , x 0
Tỷ lệ linh kiện bán ra thị trường phải thay thế trong thời gian bảo hành là: 6 6 p P X( 6) f x dx( ) e xdx e x 60 0
1 e 6 0,527633 52,7633%
c) Gọi T là thời gian bảo hành. Khi ó tỷ lệ bảo hành là:
pT P X( T) 1 e T 56
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Theo bài, ta có: 1 e T 0,15 eT 1 1 T ln 0, 85 1,30015
Vậy thời gian bảo hành tối a khoảng 1,3 năm.
2.3.5. Phân phối ều
➢ Định nghĩa. Biến ngẫu nhiên liên tục X ược gọi là có phân phối ều trên oạn [a b, ],
ký hiệu là X U a b( , ), nếu X có hàm mật xác suất: b x ( a) 1, [a b, ] f x( ) 0 , x [a b, ]
➢ Tính chất. Cho X U a b( , ). Khi ó: a b ; D X( ) (b a)2 E X( ) 2 12
Lưu ý. Phân phối ều có nhiều ứng dụng trong thống kê, ặc biệt ối với phương pháp phi
tham số. Trong một số kết luận thống kê, người ta thường sử dụng quy tắc sau: Nếu
không biết gì về tham số cần ước lượng thì mỗi giá trị có thể của nó là ồng khả năng.
Đó chính là quan niệm coi tham số cần ước lượng như một biến ngẫu nhiên có phân phối ều.
Ví dụ 2.27. Vị trí của một người i bộ trên một oạn ường có thể ược mô hình hóa bằng
một biến ngẫu nhiên có phân phối ều, nếu như ta không có thông tin gì ngoài thông tin
người i bộ trên oạn ường ó.
Ví dụ 2.28. Lịch chạy của xe buýt tại một trạm xe buýt như sau: chiếc xe buýt ầu tiên
trong ngày sẽ khởi hành từ trạm này vào lúc 7 giờ, cứ sau mỗi 15 phút sẽ có một xe
khác ến trạm. Giả sử một hành khách ến trạm trong khoảng thời gian từ 7 giờ ến 7 giờ
30. Tìm xác suất ể hành khách này chờ:
a) Ít hơn 5 phút.
b) Ít nhất 12 phút.
Giải. Gọi X là số phút sau 7 giờ mà hành khách ến trạm. Rõ ràng ta không có thông tin
nào khác của hành khác ngoài thông tin là “hành khách ến trạm trong khoảng thời gian
từ 7 giờ ến 7 giờ 30”. Do ó bnn X ược coi là có phân phối ều trên oạn
Xác suất thống kê và Ứng dụng – 2021 57 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh [0;30]. [0,30] 30 1, x
Hàm mật ộ xác suất f x( ) 0 , x [0,30] Hành khách ến Hành khách ến Xe ến Xe ến 7h00 7h107h15 7h25 7h30 7h00 7h03 7h15 7h18 7h30
Mô hình: chờ ít hơn 5 phút
Mô hình: chờ ít nhất 12 phút
Hình 2.5. Mô hình chờ xe buýt
a) Xác suất ể hành khách ít hơn 5 phút 15 30
P(10 X 15) P(25 X 30) f x dx( ) f x dx( ) 10 25 5 5 1 0,3333 30 30 3
b) Xác suất ể hành khách ít nhất 12 phút. 3 18
P(0 X 3) P(15 X 18)
f x dx( ) f x dx( ) 0 15 3 3 1 0,2 30 30 5
2.3.6. Phân phối chuẩn a) Định nghĩa y 1
Biến ngẫu nhiên liên tục X ược gọi là có 2
phân phối chuẩn với hai tham số , 2 , ký y () fx hiệu X N(
; 2) , nếu X có hàm mật ộ xác suất: 0 x 1
Hình 2.6. Dạng ồ thị của hàm mật (x2 2)2 , x f
ộ của phân phối chuẩn x( ) e 2
b) Phân phối chuẩn chính tắc 58
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Trong trường hợp
0; 2 1 thì ta nói X có phân phối chuẩn chính tắc hay
phân phối Gauss: X N(0;1) .
Hàm mật ộ của phân phối chuẩn chính tắc: 1 f x( ) e x22 , x
(gọi là hàm Gauss ) 2
Hàm phân phối chuẩn tắc:
( )x P X( x) 1 x e t2 /2dt 0,5 ( )x 2 1 Trong ó : ( )x
x e t2/2dt (gọi là hàm Laplace ) 2 0
Lưu ý. Hàm Gauss và hàm Laplace có một số tính chất sau: 1 y Đồ thị hàm
1) f ( x) f x( ) ; ( x) ( )x 2 Gauss y () fx Giá trị của hàm Laplace () x 2) ( )( ) 0,5 ; ( ) (0) 00,5 0 , 5 0 x x
3) Giá trị của hàm Gauss và Laplace ược
Hình 2.7. Hàm Gauss, hàm Laplace
tính trực tiếp từ máy tính bỏ túi.
a) Tính chất. Cho X N(
; 2) . Khi ó: 1) Z X N(0;1) 2) E X( ) ; D X( ) 2
b) Công thức xác suất. Cho X N( ; 2) . Khi ó:
1) P a X b b a 2) P X b 0,5 b
Xác suất thống kê và Ứng dụng – 2021 59 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
3) P a X 0,5 a 4) P | X | 2 5) P | X | k 2 ( ) (k k 0)
c) Quy tắc ba xích – ma
Từ công thức 5) ở trên, nếu lấy k 3 thì thu ược: P | X | 3 2(3) 0,9973 (*) Mặt khác | X | 3 3 X 3
Ý nghĩa của quy tắc ba xích – ma như sau: Giả sử X N(
; 2) , khi ó hầu hết (với xác suất 99,73%) các giá trị của ại lượng
này sẽ rơi vào khoảng từ 3 ến
3 . Biểu thức (*) ược gọi là “quy tắc ba xích
- ma”.
d) Định lý Laplace
Cho biến ngẫn nhiên rời rạc X B n p( , ) (phân phối nhị thức). Giả sử n rất lớn và
p không quá gần 0 cũng không quá gần 1 (thường 0,1 p 0,9 ). Khi ó X ược xấp xỉ phân phối chuẩn: X N( , 2 ) với np, np(1 p) . 1 f k
Công thức xác suất: P X( k) k , ( 0,...,n)
P k( 1 X k2 ) k2 k1 1 Trong ó f x( )
e x2/2 là hàm Gauss, ( )x là hàm Laplace. 2
Lưu ý. Xác suất tại một iểm còn ược tính theo công thức sau: 60
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
P X( k) P k( 0,5 X k0,5) k 0 ,5 k 0 ,5
e) Giá trị phân vị chuẩn
Cho Z N(0;1) . Khi ó, với mỗi số thực 0
1 có duy nhất một giá trị thực z
thoả mãn: P Z( z ) .
Số thực z ược gọi là giá trị phân vị y
chuẩn mức , z ược tính theo công thức: ( PZz ) (z ) 0,5 y () fx 0 , 5 () z 0 z x
Tính z theo hai cách sau:
Hình 2.8. Giá trị phân vị chuẩn
Cách 1: Sử dụng hàm Normsinv trong Excel theo công thức sau
z Normsinv( ) với 0,5 1 z Normsinv(1 ) với 0 0,5
Cách 2: Tra bảng giá trị hàm Laplace ( )x 1 x e t2/2dt ể tìm z 2 0 x
1,645 1,751 1,881 1,960 2,054 2,170 2,326 2,576
( )x 0,45 0,46 0,47 0,475 0,48 0,485 0,49 0,495 Chẳng hạn: 0,05
(z0,05 ) 0,5 0,05 0,45 z0,05 1,645 Hoặc
z0,05 Normsinv(1 0,05) 1,645
Ví dụ 2.29. Trọng lượng của một loại sản phẩm là biến ngẫu nhiên có phân phối chuẩn N(
; 2) với trọng lượng trung bình
6,2 kg và ộ lệch chuẩn 0,2kg.
a) Tính tỷ lệ sản phẩm có trọng lượng từ 5,7 kg ến 6,8 kg.
b) Hãy so sánh tỷ lệ sản phẩm có trọng lượng nhỏ hơn 5,8 kg và sản phẩm có trọng lượng lớn hơn 6,5 kg.
Xác suất thống kê và Ứng dụng – 2021 61 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
c) Tìm a sao cho P X( a) 0,758, biết (0,7) 0,2580. Giải. Gọi X là trọng
lượng của loại sản phẩm ã cho.
Theo giả thiết, ta có: X N( ; 2) với 6,2 kg và 0,2kg. a) Tỷ
lệ những sản phẩm có trọng lượng từ 5,7 kg ến 6,8 kg:
p P(5,7 X 6,8) 6,8 5,7 6,80 ,26,2 5,70 ,26,2 (3) ( 2,5)
(3) (2,5) 0,49865 0,49379 0,99244 6,2
b) p2 P X( 6,5) 0,5 6,50 ,2 0,5 (1,5) 0,06681 6,2 6 ,2
p1 P(0 X 5,8) 5,80 ,2 0 0, 2 (2) (31) 0,02275
Vậy tỷ lệ sản phẩm có trọng lượng nhỏ hơn 5,8 kg nhỏ hơn tỷ lệ sản phẩm có trọng lượng lớn hơn 6,5 kg. 6 ,2
c) Ta có: P X( a) 0,5 a 0 , 2 0,758 a 0 ,62,2 0,258 0,7
a 6,2 0,7 a6,06 0,2
Ví dụ 2.30. Sản phẩm do một nhà máy sản xuất ược óng thành từng kiện, mỗi kiện gồm
10 sản phẩm, trong ó có 6 sản phẩm tốt và 4 sản phẩm lỗi. Khách hàng chọn cách kiểm 62
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
tra như sau: từ mỗi kiện chọn ngẫu nhiên ra 3 sản phẩm; nếu thấy có ít nhất 2 sản phẩm
tốt thì nhận kiện ó, ngược lại thì loại kiện ó. Kiểm tra 140 kiện trong rất nhiều kiện.
Tính xác suất có:
a) 93 kiện ược nhận.
b) Từ 90 ến 110 kiện ược nhận.
Giải. Gọi A là biến cố kiện hàng ược nhận khi khách hàng kiểm tra và plà xác suất nhận kiện hàng. 4 Ta có:
p P A() C62 3 C363 2 C10 C10 3
Gọi X là số kiện hàng ược nhận trong số 140 kiện hàng ược kiểm tra. Thì X có
phân phối nhị thức X B n p( , ) với n 140, p 2 / 3.
Vì n 140 là lớn, p không quá gần 0 cũng không quá gần 1 nên có xấp xỉ X N( ; 2) với np 93,33333.
np(1 p) 140.(2 / 3).(1/ 3) 2 70 5,57773 3
a) Xác suất ể có 93 kiện ược nhận là: P X( 93) 1 f 93 3 f ( 0,06) 2 70
3 f (0,06) 3 0,39822 0,071395 2 70 2 70
Sử dụng công thức khác:
P X( 93) P(93 0,5 X 93 0,5) P(92,5 X 93,5) 92, 5 93, 5 0,071301
Cũng có thể tính trực tiếp từ quy luật nhị thức:
P X( 93) C14093 .(2 / 3)93.(1 2 / 3)140 93 214093 C14093 0,071123 3
Xác suất thống kê và Ứng dụng – 2021 63 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Xác suấtcó từ 90 ến 110 kiện ược nhận là: P(90 X 110) 110 ( 90 (2,99) ( 0,6) (2,99) (0,6) 0,49861 0,22576 0,72437
2.3.7. Phân phối Chi bình phương ➢ Định nghĩa
Cho n biến ngẫu nhiên X1,..., X n ộc lập nhau và cùng có phân phối chuẩn chính tắc N(0,1).
Khi ó bnn X X 2 2 2 1
X 2 ... Xn ược gọi là có phân phối Chi bình phương với
n bậc tự do, ký hiệu là X 2 ( )n .
Hàm mật ộ tương ứng sẽ là: 1 . e x n 1 f x( ) 2n/2 n 2 x2 , khi x 2 , khi x 0 0 0 Trong ó ( )x
tx 1e dtt là hàm Gamma y 0 ➢ y () fx
Các số ặc trưng. Cho X 2 ( )n E X( ) n 0 x Khi ó: D X(
) 2n Hình 2.9. Phân phối Chi bình phương
2.3.8. Phân phối Student 64
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh ➢ Định nghĩa
Cho 2 biến ngẫu nhiên X và Y ộc lập nhau, có phân phối lần lượt là: X N(0,1); Y 2( )n .
Khi ó biến ngẫu nhiên T X
ược gọi là có phân phối Student với n bậc Y n/
tự do, ký hiệu là: T T( )n . () fx
Hàm mật ộ tương ứng sẽ là: Đồ thị hàm mật ộ của phân phối chuẩn chính tắc Đồ thị hàm mật n2 ộ của phân 1 phối Student 1 x2
n2 1 f x( ) 0 x
n . n / 2 n
Hình 2.10. Phân phối Student
➢ Các số ặc trưng. Cho X T( )n E X() 0 (n 1) Khi ó: n n D X() n 2 ( 2)
2.4. Một số kết quả về luật số lớn và các ịnh lý giới hạn
2.4.1. Hội tụ theo xác suất
➢ Dãy các biến ngẫu nhiên {Xn} gọi là hội tụ theo xác suất tới biến ngẫu nhiên X nếu
0, limn P X n X 1. Ký hiệu: X P n X n( ) .
Xác suất thống kê và Ứng dụng – 2021 65 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
➢ Ý nghĩa của sự hội tụ theo xác suất: Với mọi
0 thì xác suất ể sai khác nhau
giữa Xn và X không vượt quá càng lớn (càng gần tới 1) khi n tăng lên, hay sai
khác giữa Xn và X vượt quá ít có khả năng xảy ra.
2.4.2. Một số kết quả về luật số lớn và các ịnh lý giới hạn
Trong lý thuyết xác suất người ta gọi những ịnh lý khẳng ịnh dãy các biến ngẫu
nhiên nào ó hội tụ theo xác suất về hằng số là những ịnh lý luật số lớn, những ịnh lý
khẳng ịnh về sự hội tụ của dãy hàm phân phối của dãi biến ngẫu nhiên về hàm phân
phối của một biến ngẫu nhiên nào ó là những ịnh lý giới hạn.
➢ Bất ẳng thức Chebyshev
Cho biến ngẫu nhiên X. Với mọi 0, ta luôn có: D X( )
P | X E X() | 1 2 )
(hay P | X E X() | D X( 2 )
Ví dụ 2.31. Thu nhập bình quân hàng năm của mỗi người dân một vùng là 2000 USD
với ộ lệch tiêu chuẩn là 150 USD. Hãy xác ịnh khoảng thu nhập hàng năm quanh giá trị
trung bình của ít nhất 98% dân cư vùng ó.
Giải. Gọi X là thu nhập hàng năm của một người dân trong vùng.
Ta có: E X( ) 2000, (X) 150 . Ngoài ra chúng ta không biết thông tin về phân phối xác suất của X.
Áp dụng bất ẳng thức Chebyshev, ta có: D X( ) 150
P | X E X() | 1 2 2 1 2 0,98 1060,66 | X E X( ) | E X( ) X E X( ) 939,36 X 3060,66
Vậy ít nhất 98% dân cư của vùng có thu nhập hàng năm trong khoảng 939,36 ; 3060,66 .
➢ Định lý Khinchin (luật số lớn) 66
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Dãy các biến ngẫu nhiên {Xn} gọi là tuân theo luật số lớn nếu: 1 nk 1 n E X( k ) P 0 X n k 1 n k 1
➢ Định lý Liapounop ( ịnh lý giới hạn trung tâm)
Nếu dãy các biến ngẫu nhiên ọc lập X X1, 2,..., Xn... có cùng kỳ vọng và phương
sai 2 . Thì khi ó với mọi x , ta có giới hạn: limnP n 1n kn 1 Xk x 21 x e t2 /2dt ➢ Hệ quả 1
Nếu dãy các biến ngẫu nhiên ọc lập X X1, 2,..., Xn... có cùng kỳ vọng và phương sai 2 thì 1 n Xk P . n k 1
➢ Hệ quả 2 (luật số lớn Bernoulli)
Gọi fn(A) là tần suất xuất hiện biến cố A trong dãy n phép thử ộc lập với
P A( ) p thì fn(A) P P A() p
2.5. Vector ngẫu nhiên và các ặc trưng
2.5.1. Khái niệm vector ngẫu nhiên
Trong thực tế, trên cùng một ối tượng quan sát, nhiều trường hợp ta phải xét ồng
thời nhiều tiêu chuẩn khác nhau, chẳng hạn: ể tìm hiểu về một người, chúng ta cần biết
các thông tin về “chiều cao”, “cân nặng”, “ ộ tuổi”, “trình ộ học vấn”, “mức thu nhập”,…
Điều này có nghĩa là trong cùng một phép thử, ta thường phải xét ồng thời n biến ngẫu
nhiên khác nhau: X X1, 2,..., Xn
Ta gọi vector X (X1,..., Xn) là vector ngẫu nhiên n chiều. Nếu X k (k 1,...,n) là
các biến ngẫu nhiên rời rạc (liên tục) thì X ược gọi là vector ngẫu nhiên rời rạc (liên tục).
Xác suất thống kê và Ứng dụng – 2021 67 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 2.32. Chọn ngẫu nhiên một doanh nghiệp trong số các doanh nghiệp tại TP.
HCM, người ta quan tâm ến hai tiêu chuẩn: X1 là vốn ầu tư và X2 là doanh thu.
Khi ó ta có vector ngẫu nhiên hai chiều X (X1, X 2 ) .
2.5.2. Hàm phân phối xác suất của vector ngẫu nhiên ➢ Định nghĩa
Cho vector ngẫu nhiên vector ngẫu nhiên X (X1,..., Xn) . Ta gọi hàm n biến: n
FX (x1,..., xn ) P X 1 x1,..., X n xn , (x1,..., xn )
là hàm phân phối xác suất của vector X, hay còn gọi là hàm phân phối xác suất
ồng thời của các biến ngẫu nhiên X1,..., X n . ➢ Tính chất n
1) 0 FX (x1,..., xn) 1, (x1,..., xn)
2) FX (x1,..., xn ) ơn iệu không giảm theo từng biến 3) xxkklimlim
FFXX ((xx11,...,,..., xxnn))
0F x,Y ( k1,...,1,2,...,xk 1, xnk 1,..., xn)
Trong ó Y (X1,..., Xk 1, Xk ,..., Xn)
➢ Trường hợp vector ngẫu nhiên hai chiều: (X Y, ) 2
F x y ( ,) P X x Y, y , ( ,x y) Các tính chất: 2 1) 0 F x y ( , ) 1, (x y, )
2) F x y ( , ) không giảm theo từng biến ) ) ) 3) xlim F x y ( , 1 ; xlim F x y ( , ylim F x y ( , 0 y ) ) 4) ylim F x y ( , FX ( )x ; limx F x y ( , FY (y)
Trong ó: FX ,FY tương ứng là hàm phân phối của biến ngẫu nhiên X Y, .
2.5.3. Bảng phân phối xác suất ồng thời 68
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Cho X Y, là hai biến ngẫu nhiên rời rạc có tập giá trị X( ) {x1,..., xm}, Y( )
{y1,..., yn}. Bảng sau gọi là bảng phân phối xác suất ồng thời của (X Y, ). Trong ó:
pij P X x Yi , y j n p ij
pxi P X xi ; m pij pyj P Y y j j 1 i 1 k m pij 1 ; m pxi 1 ; n pyj 1 i 1 j 1 i 1 j 1
➢ Các phân phối biên
Từ bảng phân phối xác suất ồng thời, có thể suy ra các phân phối biên (phân phối
xác suất của từng biến) như sau: X x1 x2 ... xm Y y1 y2 ... yn
P px1 px2 ... pxm
P py1 py2 ... pyn
➢ Phân phối có iều kiện, kỳ vọng có iều kiện
- Phân phối xác suất có iều kiện của X với iều kiện Y yj X x1 x2 ... xm
P X Y( | yj ) p1|yj p2|yj ... pm y| j Trong ó: pi y| j
P X x Yi | y j
P X { x Y i, yj } y j P Y{ p ij y j}
Xác suất thống kê và Ứng dụng – 2021 69 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P Y
Kỳ vọng có iều kiên: E X Y | y m j
x pi. i y| j i 1
- Phân phối xác suất có iều kiện của Y với iều kiện X xi Y y1 y2 ... yn P Y X(
| p1|xi p2|xi ... pn x| i xi ) Trong ó: p j x| i
P Y yj | X xi
P X P X{ x Yi , xi } y j
P X{ pij xi}
Kỳ vọng có iều kiên: E Y | X x n i
y pj. j x| i j 1
2.5.4. Hàm mật ộ xác suất ồng thời
Cho vector ngẫu nhiên hai chiều (X Y,
) liên tục và có hàm phân phối xác suất F x y( , ) 2
F x y( , ) . Nếu F x y( , ) có các ạo hàm riêng cấp hai thì hàm số f x y( , )
x y ược gọi là hàm mật ộ xác suất ồng thời của (X Y, ).
Từ hàm mật ộ ồng thời có thể suy ra hàm mật ộ của từng biến:
fX ( )x f x y dy( ,
); fY ( )y f x y dx( , )
Và nếu f x y( , ) fX ( ).x fY ( )y thì X Y, ộc lập nhau. ➢ Tính chất 2
1) f x y( , ) 0, (x y, ) 70
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 2)
dx f x y dxdy( , ) 1 ➢ Hệ quả x y 1) F x y( , ) f u v dudv( , )
2) P (X Y, ) D f x y dxdy( , ) D
Ví dụ 2.33. Tại một công ty kinh doanh khoáng sản, thống kê cho thấy hàm lượng H và
giá bán G của một loại khoáng sản có bảng phân phối xác suất ồng thời sau: G 300 340 550 H 0 ,4 0 ,20 0 ,05 0 0 ,7 ,05 0 0 ,20 0 ,05 0 ,8 0 0 ,10 0 ,35
a) Có bao nhiêu phần trăm khoáng sản ược bán với giá 340?
b) Tính giá bán trung bình của công ty.
c) Tính hàm lượng trung bình của khoáng sản.
d) Tính giá bán trung bình của khoáng sản có hàm lượng 0,7. Giải. a) P G 340 0,05 0,20 0,10 0,35 35%
b) Ta có bảng phân phối của giá bán G: G 300 340 550 P 0,25 0,35 0,40
Giá bán trung bình của công ty là:
E G() 300 0,25 340 0,35 550 0,40 414
c) Ta có bảng phân phối của hàm lượng H: H 0,4 0,7 0,8 P 0,25 0,30 0,45
Hàm lượng trung bình của khoáng sản là:
E H( ) 0,4 0,25 0,7 0,3 0,8 0,4 0,63
d) Ta có: P H 0,7 0,05 0,20 0,05 0,3
Xác suất thống kê và Ứng dụng – 2021 71 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P G 300| H 0,7 P G P H 300 ,H0,7 0,7 00,,053 P G 340| H 0,7 P G 340 ,H0,7 0,7 00,,32 P H H
P G{ 550 | H 0,7} P G{ 550, 0,7} 0,05 P H{ 0,7} 0,3
Vậy giá bán trung bình của khoáng sản có hàm lượng 0,7 là E G H(/ 0,7) 300 0,5 340 2550 0,5 368,33 3 3 3
2.5.5. Các ặc trưng số của vector ngẫu nhiên n
Cho vector ngẫu nhiên X (X1,..., Xn) .
a) Vector kỳ vọng: E X( ) E X( 1),...,E X( n) b) Covariance:
Covariance hay hiệp phương sai hay mô men tương quan của hai biến ngẫu nhiên
X và Y ược ký hiệu và xác ịnh bởi: cov(X Y,) E X E X() Y E Y() E XY() E X E Y( ) ( )
Lưu ý: Nếu X Y,
ộc lập thì D X( Y) D X( ) D Y()
Vậy nếu X Y, phụ thuộc nhau thì D X( Y) tính theo công thức nào ? Ta có :
D X( Y) E X[( Y) ]2 [E X( Y)]2
E X 2 Y 2 2XY [E X() E Y( )]2
E X(2 ) E2 (X ) E Y( 2) E Y2( ) 2 E XY() E X E Y( ) ( ) 72
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
D X() D Y() 2cov(X Y, ) Vậy cov(X Y,
) ược sử dụng trong việc tính phương sai D X( Y)
D X( Y) D X() D Y() 2cov(X Y, )
Các tính chất của covariance
1) cov(X Y, ) cov(Y X, ) 2) cov(aX bY, ) abcov(X Y, )
3) cov(X X, ) D X( ) 4) cov(X Y, ) xi E X( ) yj E Y( ) pij i j
Với (X Y, ) rời rạc và pij P X( x Yi, yj ) . 5) cov(X Y, )
x E X( ) y E Y( ) f x y dxdy( , )
Với (X Y, ) liên tục có hàm mật ộ xác suất là f x y( , ) .
6) Nếu X Y, ộc lập thì cov(X Y, ) 0. Ngược lại không úng.
c) Hệ số tương quan. Hệ số tương quan giữa hai biến ngẫu nhiên X và Y là ại lượng
không có ơn vị ược xác ịnh bởi công thức: XY
cov(X Y, ) E XY( ) E X E Y( ) ( ) D X
D Y( ). ( ) D X D Y( ). ( )
Tính chất của hệ số tương quan 1)
XY YX ; XX YY 1 2) 1 XY 1 3) Nếu X Y,
ộc lập thì XY 0 . Điều ngược lại không úng
Ý nghĩa hệ số tương quan
1) Hệ số tương quan là ại lượng ặc trưng cho mối quan hệ phụ thuộc tương quan
tuyến tính giữa hai biến ngẫu nhiên.
2) Trị tuyệt ối của hệ số tương quan càng lớn thì mối quan hệ ó càng chặt chẽ, nghĩa là nếu XY 1 thì
Xác suất thống kê và Ứng dụng – 2021 73 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh E Y X(
|) AX B hoặc E X Y( | ) AY B.
3) Hệ số tương quan dương khi hai biến có quan hệ ồng biến; và âm khi hai biến có quan hệ nghịch biến.
d) Ma trận covariance
Tập tất cả các covariance: cov(X Xi,
j ) lập thành ma trận, nó ược gọi là ma
trận covariance của vector ngẫu nhiên (X1,..., X n ).
Đối với vector ngẫu nhiên hai chiều (X Y, ) thì ma trận covariance sẽ là: D X( ) cov(X Y, ) cov(X Y, ) D Y( )
Nhận xét. Ma trận covariance là ma trận vuông cấp n với các phần tử là số thực, ối
xứng, các phần tử trên ường chéo chính là phương sai của các biến ngẫu nhiên thành phần.
e) Ma trận tương quan
Tập tất cả các hệ số tương quan X Xi j lập thành ma trận, nó ược gọi là ma trận
tương quan của vector ngẫu nhiên (X1,..., X n ). 1 XY
Đối với vector hai chiều (X Y, ) thì ma trận tương quan sẽ là: XY 1 .
Ví dụ 2.34. Cho các biến ngẫu nhiên X và Y có bảng phân phối xác suất ồng thời sau: Y 1 2 3 X 1 0,12 0,15 0,03 0,3 2 0,28 0,35 0,07 0,7 0,4 0,5 0,1 1
1) Lập bảng phân phối xác suất của biến ngẫu nhiên Z X Y .
2) Lập bảng phân phối xác suất của biến ngẫu nhiên T XY .
3) Tìm vector kỳ vọng E X( ),E Y( ) của vector (X,Y). 74
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
4) Tìm bảng phân phối xác suất có iều kiện của X với iều kiện Y 2 và tính E X Y(| 2).
5) Lập ma trận covariance của vector ngẫu nhiên (X,Y).
6) Tính hệ số tương quan XY và cho nhận xét. Lập ma trận tương quan của vector
ngẫu nhiên (X,Y).
Giải.1) Lập bảng cộng của biến ngẫu nhiên Z X Y Y 1 2 3 X 1 Z 2 Z 3 Z 4 2 Z 3 Z 4 Z 5 P Z 2 P X 1,Y 1 0,12 P Z 3 P X 1,Y 2 P X 2,Y 1 0,43 P Z 4 P X 1,Y 3 P X 2,Y 2 0,38 P Z 5 P X 2,Y 3 0,07
Vậy phối xác suất của biến ngẫu nhiên Z X Y là: Z 2 3 4 5 P 0,12 0,43 0,38 0,07
2) Lập bảng nhân của biến ngẫu nhiên T XY Y 1 X 2 3 1 T 1 T 2 T 3 2 T 2 T 4 T 6
Tính tương tự câu a), ta có bảng phân phối của T XY là: T 1 2 3 4 6
P 0,12 0,43 0,03 0,35 0,07
3) Bảng phân phối riêng của X và của Y là: X 1 2 Y 1 2 3 P 0,3 0,7 P 0,4 0,5 0,1
E X( ) 1,7 ; E Y( ) 1,7
Vậy E X(),E Y() 1,7;1,7
Xác suất thống kê và Ứng dụng – 2021 75 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
4) Ta có: P Y{ 2} 0,5 p1|Y 2 P X 1|Y 2
P X P Y{ 1 ,Y2} 2 00,,155 0,3
p2|Y 2 P X 2 |Y 2 P X 2 ,Y2} 2 00,,355 0,7 P Y{
Vậy phân phối xác suất có iều kiện của X với iều kiện Y 2 là: X 1 2 P X Y( | 2) 0,3 0,7
5) Ta có: E X( ) 1,7 ; E X( 2) 3,1 D X( ) 0,21
E Y( ) 1,7 ; E Y( 2) 3,3 D X( ) 0,41 E XY( ) n m p x yij i j 2,89 i 1 j 1
Suy ra: cov(X Y, ) E XY( ) E X E Y() ( ) 0
Ma trận covariance của vector ngẫu nhiên (X,Y) là: D X( ) cov(X Y, ) 0,21 0 cov(X Y, ) D Y( ) 0 0,41
6) Ta có: XY cov(X Y, ) 0. Như vậy hai biến ngẫu nhiên X và Y không phụ D X D Y( ). ( )
thuộc tương quan tuyến tính, nhưng ta không thể kết luận chúng ộc lập nhau không. 1 XY 1 0
Ma trận tương quan của (X,Y) là: XY 1 0 1 BÀI TẬP CHƯƠNG 2
Bảng phân phối xác suất của biến ngẫu nhiên rời rạc 76
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
2.1. Một thùng hàng gồm 10 sản phẩm, trong ó có 6 sản phẩm loại A và 4 sản phẩm loại
B. Mỗi sản phẩm loại A có giá 250 ngàn ồng, mỗi sản phẩm loại B có giá 200 ngàn ồng.
Lấy ngẫu nhiên 3 sản phẩm từ thùng hàng. Gọi X là tổng trị giá 3 sản phẩm ược lấy ra.
Hãy lập bảng phân phối xác suất của X .
2.2. Một lô hàng có 7 sản phẩm ạt chuẩn và 3 sản phẩm lỗi. Chọn ngẫu nhiên từ lô hàng
ra 4 sản phẩm. Gọi X là số sản phẩm ạt chuẩn có trong 4 sản phẩm lấy ra.
Hãy lập bảng phân phối xác suất của X và của Y 5 2X .
2.3. Có 3 thùng hàng vỏ ngoài giống nhau, mỗi thùng ều chứa 10 sản phẩm. Trong ó:
thùng thứ nhất có 1 sản phẩm kèm vé thưởng trị giá 50 ngàn ồng; thùng thứ hai có 2
sản phẩm kèm vé thưởng trị giá 30 ngàn ồng cho mỗi sản phẩm; thùng thứ ba có 3 sản
phẩm kèm vé thưởng trị giá 20 ngàn ồng cho mỗi sản phẩm. Lấy ngẫu nhiên một thùng
và từ thùng ó lấy ngẫu nhiên một sản phẩm.
Gọi X là trị giá tiền thưởng có ược từ sản phẩm ược lấy ra (nếu sản phẩm lấy ra
không có vé thưởng thì X 0). Hãy lập bảng phân phối xác suất cho X.
2.4. Ba khẩu súng cùng bắn vào một mục tiêu ộc lập nhau với xác suất bắn trúng của
mỗi khẩu là 0,8; 0,6; 0,7. Gọi X là số viên ạn trúng mục tiêu. Hãy lập bảng phân phối xác suất của X.
2.5. Một phân xưởng có 4 máy hoạt ộng với xác suất ể mỗi máy bị hỏng trong một ca
sản xuất là 0,1. Gọi X là số máy bị hỏng trong một ca sản xuất. Hãy lập bảng phân phối xác suất của X.
2.6. Để thử sức chịu nén của một loại vật liệu người ta tiến hành theo ba mức sau:
Mức 1: Tiến hành thử với áp lực 200 kg/cm2. Nếu vật liệu chịu ược áp lực này
thì chuyển sang mức hai. Mức 2: Tiến hành thử với áp lực 230 kg/cm2. Nếu vật liệu
chịu ược áp lực này thì chuyển sang mức ba. Mức 3: Tiến hành thử với áp lực 250 kg/cm2.
Biết các lần thử ộc lập và xác suất ể vật liệu chịu ược các mức thử trên tương ứng
là 0,9; 0,6 và 0,4. Gọi X là số lần thử, Y là số lần thử thành công. Hãy lập bảng phân
phối xác suất của X và của Y.
2.7. Có hai vận ộng viên bắn cung A và B tập bắn. Mỗi người bắn hai lần. Xác suất bắn
trúng hồng tâm của A trong mỗi lần bắn là 0,6; của B là 0,55. Gọi X là số lần bắn trúng
hồng tâm của A trừ i số lần bắn trúng hồng tâm của B.
Hãy lập bảng phân phối xác suất của các biến ngẫu nhiên X và của | X | .
2.8. Khả năng xuất hiện một loại vi trùng (mà ta quan tâm) ở mỗi thí nghiệm là 0,1. Một
cán bộ nghiên cứu ã làm từng thí nghiệm một cho ến khi nào thành công (nhận ược loại
vi trùng trên) thì dừng. Nhưng cán bộ này chỉ ược cấp kinh phí ể làm tối a 15 thí nghiệm.
Gọi Z là số thí nghiệm không thành công mà cán bộ trên ã làm.
Xác suất thống kê và Ứng dụng – 2021 77 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
a) Tìm quy luật phân phối xác suất của Z.
b) Tính xác suất cán bộ này thành công trong 5 thí nghiệm ầu.
Các ặc trưng số của biến ngẫu nhiên rời rạc
2.9. Một cửa hàng iện máy lời 2,5 triệu ồng khi bán 1 máy giặt, nhưng nếu máy giặt
bị hỏng trước thời hạn bảo hành thì bị lỗ 4,5 triệu. Biết rằng cửa hàng lời trung
bình 1,94 triệu ồng khi bán ược 1 máy giặt. Tính tỷ lệ máy giặt phải bảo hành.
2.10. Theo thống kê dân số thì xác suất ể một người ở ộ tuổi nào ó sống thêm một năm
nữa là 98,5%. Một công ty bảo hiểm nhân thọ bán thẻ bảo hiểm một năm cho
những người ở ộ tuổi ó với giá 60 ngàn ồng. Trong trường hợp người mua bảo
hiểm bị chết thì số tiền bồi thường là 2 triệu ồng. Hỏi lợi nhuận trung bình của
công ty khi bán một thẻ bảo hiểm loại này là bao nhiêu?
2.11. Nhu cầu hàng ngày (X : kg) về một loại thực phẩm tươi sống của một khu phố có
bảng phân phối xác suất: X 35 36 37 38 P 0,15 0,25 0,45 0,15
Một cửa hàng trong khu phố nhập về mỗi ngày 38kg loại thực phẩm này với giá
30 ngàn/kg và bán ra với giá 45 ngàn/kg. Nếu bị ế, cuối này cửa hàng phải hạ giá còn
20 ngàn/kg mới bán hết. Giả sử cửa hàng luôn bán hết hàng. Tính tiền lời trung bình
của cửa hàng về loại thực phẩm trên trong một ngày.
2.12. Một người tung ồng thời 2 con xúc xắc cân ối và ồng chất. Gọi X là tổng số chấm
ở hai mặt xuất hiện. Nếu X 4 anh ta mất 10 ngàn ồng. Nếu 5 X 10 anh ta mất
5 ngàn ồng. Nếu X 10 anh ta ược 20 ngàn ồng. Gọi Y là số tiền anh ta nhận ược
sau một lần chơi. Lập bảng phân phối xác suất của Y, tính E(Y). Bạn có kết luận gì về trò chơi này?
2.13. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X 1 2 3 4 2
P 0 , 2 3 a 40 a a
a) Tìm a và tính các xác suất P(1,4 X 3), P(| 2X 1| 2)
b) Lập bảng phân phối xác suất của bnn Y X 2 4X 2
c) Viết hàm phân phối xác suất F x( ), vẽ ồ thị hàm y F x( ) .
d) Tìm E X( ),D X( ),mod(X med X), ( ).
2.14. Cho biến ngẫu nhiên X có bảng phân phối xác suất: X 0 1 2 3 4
P 0,3 3a 2a 0,25 0,05 78
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
a) Tìm a và tính các xác suất P X(| | 1), P(| 3 2X | 2)
b) Lập bảng phân phối xác suất của bnn Y 2X 2 12X 9
c) Viết hàm phân phối xác suất F x( ), vẽ ồ thị hàm y F x( ).
d) Tìm E X( ),D X( ),mod(X med X), ( ).
2.15. Biến ngẫu nhiên rời rạc X có tập giá trị X ( ) {1,2,3} và E X( ) 2,15 và E X(
2 ) 5,25. Hãy lập bảng phân phối cho X.
2.16. Biến ngẫu nhiên rời rạc X có tập giá trị X( ) {x x x1, 2, 3} ( x1 x2 x 3 ) với xác
suất tương ứng là p p1, 2, p3 .
Hãy tìm p x x3, 1, 2 . Biết x3 3; p1 0,3; p2 0,5;E X( ) 1,9;D X( ) 0,49 .
2.17. Có hai lô sản phẩm. Lô I có 7 sản phẩm A và 3 sản phẩm B; Lô II có 6 sản phẩm
A và 4 sản phẩm B. Lấy ngẫu nhiên từ lô I ra 3 sản phẩm và lô II ra 2 sản phẩm.
Bán hết 5 sản phẩm này với giá bán 30 ngàn/sản phẩm A và 15 ngàn/ sản phẩm
B. Gọi X là tổng số tiền bán ược. Tính E X( ),D X( ). 2.18. Cho X Y,
là hai biến ngẫu nhiên ộc lập có bảng phân phối xác suất sau: X 0 2 4 Y 2 4 P 0,2 0,5 0,3 P 0,6 0,4
a) Tính E X( ),E Y( ),E(3X 5Y) .
b) Tính D X( ),D Y( ),D(2X Y).
c) Lập bảng phân phối xác suất của Z X Y và của T XY .
Biến ngẫu nhiên liên tục ax bx , x [0;1]
Cho biến ngẫu nhiên liên tục X có hàm mật ộ f x( ) 2 2.19. 0 , x [0;1]
a) Tìm a b, và tính D X( ) , biết E X( ) 0,6.
b) Tìm hàm phân phối xác suất F x( ). 0 , x 2
2.20. Cho bnn liên tục X có hàm phân phối xác suất F x( )
ax3 2b x, ( 2;3] 1 , x 3
Xác suất thống kê và Ứng dụng – 2021 79 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Tìm a b, và tính xác suất P
2 Y 5 với Y 1 X 2 .
2.21. Cho biến ngẫu nhiên liên tục X có hàm mật ộ f x( ) trong mỗi trường hợp sau.
Tìm hàm phân phối xác suất F x( ) của X. 4 x a) f x( )
27 x02 (3 x,),x
[0[0;;3]3] c) f x( ) 100x02 , x , x 100100 6 x x, [0,1] ), | x | b) f x( ) 43 (1 x2 1 d) f x( ) 50 , x 0 0 , | x | 1 64 , x 1 5x
2.22. Cho bnn liên tục X có hàm mật ộ xác suất f x( ) ax(4 x) , x [0 ; 4 , x [0 ; 4] ] 0
a) Tìm a , vẽ ồ thị hàm số y f x( ) và tìm mod(X ) .
b) Tính xác suất P(1 X 3,5) .
c) Tính E X( ), D X( ) . 2 , x
Cho biến ngẫu nhiên liên tục X có hàm mật ộ: f x( ) x 2 [1;2] 2.23. 0 , x [1;2] 80
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 2
Tính E X( ),D X( ),E Y() với Y X 5 X
2.24. Cho biến ngẫu nhiên liên tục X có hàm mật ộ xác suất:
k x. 2 (2 x x), [0;2] f x( ) 0 , x [0;2]
a) Tìm giá trị của tham số k và tính xác suất P 1 X 1,5 .
b) Tính E X( ),D X( ), (X).
Cho biến ngẫu nhiên liên tục X có hàm mật ộ f x( )
k x e. 2 2x, x 0 2.25. 0 , x 0
a) Tìm giá trị của tham số k và tính mod(X ) .
b) Tìm hàm phân phối F x( ).
c) Tính E X( ),D X( ), (X ) ax, 1 x 3
2.26. Cho biến ngẫu nhiên liên tục X có hàm mật ộ f x( ) a , 3 x 7 0 , x [1,7]
a) Tìm a , vẽ ồ thị hàm số y f x( ).
b) Tìm hàm phân phối xác suất F x( ), vẽ ồ thị y F x( ).
c) Tính E X( ),D X( ),mod(X med X), ( ).
d) Tính E X( 4 ),E( X ).
e) Tính xác suất P(2,5 X 8). 2ax , x [0;1]
2.27. Cho biến ngẫu nhiên liên tục X có hàm mật ộ f x( )
a(3 x), x (1;3] 0 , x [0,3]
a) Tìm a , vẽ ồ thị hàm số y f x( ).
Xác suất thống kê và Ứng dụng – 2021 81 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Tìm hàm phân phối xác suất F x( ), vẽ ồ thị y F x( ) .
c) Tính mod(X med X), ( ) .
d) Tính E X( ),D X( ),E( X ) .
2.28. Cho hai biến ngẫu nhiên X Y, ộc lập nhau.
34 (1 x2 ), | x | 1
X có hàm mật ộ xác suất: f x( ) 0 , | x | 1 Y 3 Y 1 0 1 2
có bảng phân phối xác suất: P 0,07 0,2 0,35 0,3 0,08 a) Tính E X(
),D X( ),E Z( ) với Z 2X 2
b) Tính E Y D Y E Y( ), ( ), ( )
c) Từ kết quả câu a, b hãy tính E (3X 4Y)2 và D(3X 2Y)
d) Tính P A( B) , trong ó A [X 0,5] và B [Y 1].
e) Tính xác suất P (0,2 X 0,6) (Y 0) .
2.29. Thời gian X (phút) chờ phục vụ của khách hàng ở một hệ thống phục vụ là một
biến ngẫu nhiên liên tục có hàm mật ộ xác suất là:
12x2 2ax 3, x [0;1] f x( ) 0 , x [0,1]
a) Tìm giá trị của tham số a .
b) Thời gian chờ phục vụ của mỗi khách hàng ở hệ thống này trung bình là bao nhiêu ?
c) Tìm tỷ lệ khách hàng có thời gian chờ phục vụ không quá 1 phút ở hệ thống phục vụ này.
d) Tìm xác suất ể trong 6 khách hàng ược phục vụ, có ít nhất một khách hàng không
phải chờ phục vụ quá 1 phút.
2.30. Thu nhập hàng năm của một người dân ở ịa phương H là biến ngẫu nhiên liên 0 , x 6 82
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 1
tục X ( ơn vị: triệu ồng) có hàm mật ộ xác suất f x( )
m x . 4 , x 6 .
a) Hãy xác ịnh hằng số m.
b) Mức thu nhập bình quân của mỗi người dân ịa phương H là bao nhiêu?
c) Tính tỉ lệ người có mức thu nhập không dưới 12 triệu ồng ở ịa phương H.
Phân phối nhị thức
2.31. Ông B trồng 45 cây bạch àn với xác suất cây sống là 0,79.
a) Tính xác suất có từ 35 ến 37 cây bạch àn sống.
b) Tìm số cây bạch àn sống trung bình và số cây sống có khả năng cao nhất.
2.32. Một nhà vườn trồng 87 cây lan quý, xác suất nở hoa của mỗi cây hoa trong một
năm là 0,63. Giá bán một cây lan quý nở hoa là 5 triệu ồng.
a) Giả sử bán hết những cây lan nở hoa thì mỗi năm nhà vườn thu ược số tiền có
khả năng cao nhất là bao nhiêu?
b) Nếu muốn trung bình mỗi năm có không dưới 100 cây lan quý nở hoa thì nhà
vườn phải trồng tối thiểu bao nhiêu cây lan quý?
2.33. Một nhân viên tại một trung tâm trò chơi iện tử phụ trách 35 máy hoạt ộng ộc lập.
Xác suất ể mỗi máy cần sự giúp ỡ của nhân viên trong một giờ là 0,1.
a) Gọi X là số máy cần sự giúp ỡ của nhân viên trong một giờ. Tìm quy luật phân
phối xác suất của X.
b) Tìm xác suất ể trong một giờ làm việc có ít nhất một máy cần sự giúp ỡ của nhân viên.
2.34. Xác suất chữa khỏi bệnh B của một phương pháp iều trị là 0,8. Có 5 người ược
iều trị bằng phương pháp này. Gọi X là số người ược chữa khỏi bệnh.
a) Lập bảng phân phối xác suất của X.
b) Tính kỳ vọng và phương sai của X.
2.35. Cho X và Y là hai biến ngẫu nhiên ộc lập nhau.
Giả sử X B(1;0,4), Y B(2;0,3) .
a) Hãy lập bảng phân phối xác xuất của X Y, và X Y
b) Tính E X( Y),D X( Y) bằng hai cách.
2.36. Hai máy sản xuất tự ộng với tỷ lệ làm ra sản phẩm loại 1 lần lượt là 82% và 85%,
sản phẩm còn lại là loại 2. Cho máy thứ nhất làm ra 600 sản phẩm, máy thứ hai làm ra
400 sản phẩm. Sản phẩm làm ra của hai máy em bán với giá 50 ngàn ồng/ sản phẩm
Xác suất thống kê và Ứng dụng – 2021 83 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
loại 1 và 30 ngàn ồng/ sản phẩm loại 2. Hãy tính kỳ vọng và phương sai cho tổng số
tiền bán ược của 1000 sản phẩm này.
Phân phối Poisson, xấp xỉ Poisson
2.37. Trong một thành phố nhỏ, trung bình một tuần có 2 người chết. Biết rằng số người
chết trong một khoảng thời gian t (ngày) ở thành phố này là biến ngẫu nhiên có phân
phối Poisson. Tính xác suất ể:
a) Không có người nào chết trong vòng 1 ngày.
b) Có ít nhất 3 người chết trong vòng 2 ngày.
2.38. Tại một trạm kiểm soát giao thông trung bình một phút có 2 ô tô i qua.
a) Tính xác suất ể có úng 6 xe ô tô i qua trong vòng 3 phút.
b) Tính xác suất ể trong khoảng thời gian t phút, có ít nhất 1 xe ô tô i qua. Tìm t ể xác suất này là 0,99.
2.39. Quan sát tại siêu thị A thấy trung bình 5 phút có 18 khách ến mua hàng.
a) Tính xác suất ể trong 7 phút có 25 khách ến mua hàng.
b) Tính xác suất ể trong 2 phút có từ 3 ến 5 khách ến.
c) Tính số khách ến mua hàng tại siêu thị A trong 1 giờ có khả năng cao nhất.
2.40. Giả sử tỷ lệ ung thư gan của trẻ em Việt Nam là 0,0001. Tính xác suất ể trong 20000 có:
a) Đúng 3 em bị ung thư gan.
b) Hơn 2 em bị ung thư gan.
c) Số trẻ bị ung thư gan có khả năng cao nhất là bao nhiêu?
2.41. Ở một trường học, người ta nhận thấy rằng xác suất ể một học sinh khi i học bị
bệnh và phải nằm iều trị tại phòng y tế là 0,0006. Biết rằng trong một buổi học, trung bình có 8000 học sinh.
a) Tính xác suất trong một buổi học có 5 học sinh phải nằm iều trị tại phòng y tế.
b) Theo bạn thì phòng y tế cần trang bị khoảng bao nhiêu giường iều trị?
2.42. Xác suất bắn trúng máy bay của một viên ạn súng trường là p 0,001. Có
5000 viên ược bắn vào một chiếc máy bay. Nếu có từ ba viên trở lên trúng máy bay thì
máy bay sẽ bị hạ; còn nếu chỉ có hai viên trúng thì khả năng máy bay bị hạ là 0,8; nếu
chỉ có một viên trúng thì khả năng máy bay bị hạ là 0,4. Tính xác suất máy bay bị hạ do trúng ạn. Phân phối mũ 84
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
2.43. Cho X là biến ngẫu nhiên liên tục có hàm mật ộ xác suất f x( ) trong mỗi trường
hợp sau. Hãy tìm k , tìm hàm phân phối F(x), tính E X( ),D X( ). a) f x( )
(3 2k e2 ) k x. , x 0 b) f x( )
(3k 7)e 2x , x 0
0 , x 0 (k 0)
0 , x 0 (k 0)
2.44. Một máy tính cá nhân có thời gian sống (Life time – thời gian máy làm việc liên
tục cho ến lúc hỏng) tuân theo luật phân phối mũ với tham số 0,2 ( ơn vị tính thời gian là năm).
a) Thời gian sống trung bình của máy tính là bao nhiêu?
b) Biết thời gian bảo hành là 1,5 năm. Tính tỷ lệ máy tính phải bảo hành.
c) Tính tỷ lệ máy tính có thời gian sống từ 3 ến 6 năm.
2.45. Thời gian chờ phục vụ của một khách hàng ở một hệ dịch vụ là bnn X ( ơn vị:
phút) có phân phối mũ với với tham số 0,0513.
a) Hãy tính thời gian chờ phục vụ bình quân mỗi khách hàng ở hệ dịch vụ này.
b) Tỉ lệ khách hàng có thời gian chờ phục vụ không quá 15 phút ở hệ dịch vụ này.
2.46. Gọi Y là thời gian nói chuyện iện thoại của một khách hàng ( ơn vị: phút). Giả sử
Y có luật phân phối mũ với
0,25. Hãy tính tỷ lệ khách hàng nói chuyện iện thoại không ít hơn 10 phút.
2.47. Khoảng thời gian mà hai khách hàng kế tiếp nhau ến ngân hàng là biến ngẫu
nhiên có phân phối mũ, với
3. Giả sử vừa có một khách hàng ến. Tính xác suất ể
trong vòng ít nhất 2 phút nữa mới có người khách tiếp theo ến ngân hàng.
Phân phối chuẩn, xấp xỉ chuẩn
2.48. Cho hai bnn ộc lập X N(2;0,09) và Y E( ) , 0,2.
a) E( 3 X 2Y 7)
b) D(4X 2Y 5)
c) E 2X 2 3Y 2 5XY 7X 2Y 9
2.49. Người ta ã phát ra 480 giấy mời dự hội nghị khách hàng. Biết rằng sức chứa của
khán phòng là 400 hách và thường chỉ có 80% khách hàng ến dự. Tính xác suất tất cả
khách hàng ến dự ều có chỗ ngồi.
2.50. Lãi suất (%) của cổ phiếu của công ty A và của công ty B là các bnn có phân phối
chuẩn X1 N(11;16) , X2 N(10,7;6,95) . Một người ang cân nhắc ể mua cổ phiếu của một
Xác suất thống kê và Ứng dụng – 2021 85 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
trong hai công ty này. Vậy nếu muốn ạt lãi suất tối thiểu là 10,3% thì người ó nên mua
cổ phiếu của công ty nào?
2.51. Thu nhập hàng tháng của một lao ộng ở thành phố H là biến ngẫu nhiên X (triệu
ồng/ tháng) có phân phối chuẩn N(8,5;0,16).
a) Tính tỷ lệ người lao ộng ở thành phố này có mức thu nhập từ 7,5 ến 9,2 triệu ồng/tháng.
b) Tính tỷ lệ người lao ộng ở thành phố này có mức thu nhập chưa tới 7,4 triệu ồng/tháng.
c) Hầu hết 99,73% người lao ộng ở thành phố này có mức thu nhập vào khoảng bao nhiêu?
2.52. Đường kính của một loại trục máy do cùng một máy sản xuất là biến ngẫu nhiên
có phân phối chuẩn với ường kính trung bình (theo như thiết kế) là 20 mm và ộ lệch tiêu chuẩn
0,04 mm. Trục máy ược coi là ạt tiêu chuẩn kỹ thuật nếu ường kính của
nó sai lệch so với ường kính thiết kế không quá 0,072mm. Tìm tỉ lệ trục máy ạt tiêu
chuẩn kỹ thuật của nhà máy.
2.53. Thời gian khách phải chờ ược phụ vụ tại một cửa hàng là bnn X N(4,5;1,21) ( ơn vị: phút).
a) Tính xác suất khách phải chờ từ 3,5 phút ến 5 phút.
b) Tìm giá trị nhỏ nhất của t ể cho P X( t) 0.05.
2.54. Tuổi thọ của một sản phẩm là bnn X N(4,2;3,24) ( ơn vị: năm). Thời gian bảo
hành ược qui ịnh là 3 năm. Nếu bán một sản phẩm thì lãi 150 ngàn ồng. Nếu sản phẩm
bị hỏng trong thời gian bảo hành thì phải chi mức phí 500 ngàn ồng cho việc bảo hành.
Tính số tiền lãi trung bình khi cửa hàng bán một sản phẩm.
2.55. Thời gian i từ nhà ến trường là biến ngẫu nhiên X có phân phối chuẩn N(28; 4) .
Biết rằng thời gian vào lớp là 12h30.
a) Anh ta xuất phát từ nhà lúc 12h. Tính xác suất bị trễ học.
b) Nếu muốn xác suất không bị trễ giờ ít nhất là 0,95 thì anh ta phải xuất phát từ
nhà muộn nhất là mấy giờ?
2.56. Trong một ợt thi tuyển viên chức tại Tp.HCM có 1000 người dự thi với tỷ lệ thi
ạt là 80%. Tìm xác suất:
a) Có 172 người không ạt.
b) Có khoảng từ 170 ến 180 người không ạt.
c) Có nhiều nhất 190 người không ạt
d) Có ít nhất 780 người ạt 86
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
2.57. Trọng lượng X ( ơn vị: kg) của mỗi con bò trong một àn bò là biến ngẫu nhiên có
phân phối chuẩn N(300;50 )2 . Chọn ngẫu nhiên một con bò trong àn bò. Tính xác suất ể con bò ược chọn:
a) Có trọng lượng trên 350 kg.
b) Có trọng lượng từ 250 kg ến 350 kg.
c) Chọn ngẫu nhiên 4 con bò trong àn bò nói trên. Tính xác suất ể 2 trong 4 con bò
ược chọn có trọng lượng từ 250 kg ến 350 kg.
2.58. Trong một ngày hội, mỗi chiến sĩ sẽ chọn ngẫu nhiên một trong hai loại súng và
với khẩu súng ã chọn ược sẽ bắn 100 viên ạn. Nếu có từ 65 viên trở lên trúng bia thì
ược thưởng. Giả sử ối với chiến sĩ A, xác suất bắn 1 viên trúng bia bằng khẩu súng loại
I là 0,6 và bằng khẩu súng loại II là 0,5.
a) Tính xác suất ể chiến sĩ A ược thưởng.
b) Giả sử chiến sĩ A dự thi 10 lần. Tinh1 số lần ược thưởng tin chắc nhất.
c) Chiến sĩ A phải tham gia hội thi ít nhất bao nhiêu lần ể xác suất có ít nhất một
lần ược thưởng không nhỏ hơn 0,98? Vector ngẫu nhiên
2.59. Xác suất sinh con trai là 0,5 với mỗi người mẹ. Một gia ình dự ịnh có 3 con. Gọi
X là biến ngẫu nhiên chỉ số con trai trong gia ình có 3 con. Y là biến ngẫu nhiên chỉ dãy
các trẻ em có giới tính liền nhau, chẳng hạn nếu có 3 ứa trẻ ều là gái hoặc ều là trai thì
Y 1. Nếu ứa ầu là gái, ứa thứ 2 là trai, ứa thứ 3 là gái thì Y 3.
a) Lập bảng phân phối xs ồng thời của vector (X Y, ).
b) Lập bảng phân phối xác suất của bnn Z 3X 2Y 1.
c) Tính E X( ),D X( ).
d) Tìm phân phối xác suất của X khi Y 2.
e) Tìm hệ số tương quan XY và cho nhận xét về sự phụ thuộc tương quan tuyến
tính của X và Y.
2.60. Điều tra thu nhập hàng tháng ( ơn vị: triệu ồng) của các cặp vợ chồng ang làm
việc, với X: thu nhập của chồng, Y : thu nhập của vợ. Có bảng phân phối ồng thời như sau: Y 5 8 12 17 X 4 0,20 0,04 0,01 0,00 7 0,10 0,36 0,08 0,01
Xác suất thống kê và Ứng dụng – 2021 87 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 10 0,00 0,05 0,10 0,01 15 0,00 0,00 0,02 0,02
a) Tìm phân phối biên của X , của Y . Tính thu nhập bình quân mỗi tháng của chồng, của vợ.
b) Tìm phân phối thu nhập của vợ có chồng thu nhập 10 triệu/tháng; thu nhập trung bình của họ.
c) Tính hệ số tương quan rXY . Cho nhận xét về sự phụ thuộc tương quan tuyến tính
giữa thu nhập của vợ chồng.
d) Lập bảng phân phối xác suất của biến ngẫu nhiên Z X Y .
CHƯƠNG 3 LÝ THUYẾT MẪU VÀ BÀI TOÁN ƯỚC LƯỢNG THAM SỐ
Thống kê là một ngành của toán học, có vai trò rất quan trọng trong ời sống. Thống
kê có thể ược hiểu theo nghĩa là tập số liệu ược ghi chép lại từ những quan sát thực tế,
chẳng hạn như: giá của một loại cổ phiếu qua các lần giao dịch, số người nhiễm bệnh
sốt xuất huyết ở Việt Nam qua các tháng trong năm, số lượng du khách ến Việt Nam
qua các tháng… Bảng số liệu này mang thông tin cần thiết, trực tiếp cho người sử dụng
như giá trị trung bình của những con số hay mức ộ sai lệch giữa chúng. Ngoài ra, thống
kê còn ược hiểu là một hệ thống gồm việc thu thập số liệu, các phương pháp phân tích,
xử lý các số liệu nhằm ưa ra những thông tin bản chất hay tính quy luật của số liệu.
Thống kê hiểu theo nghĩa thứ hai rất ược quan tâm, có vai trò quan trọng trong thực tế,
bởi vì từ những gì phân tích xử lý số liệu ta có thể ưa ra những nhận xét, khẳng ịnh hay những tiên oán.
Từ ó, thống kê thường ược chia thành hai loại. Thống kê mô tả ứng với cách hiểu
theo nghĩa thứ nhất “thống kê mô tả là một ngành của thống kê bao gồm việc sắp xếp,
tổng hợp và trình bày dữ liệu”. Thống kê suy diễn ứng với cách hiểu thứ hai “thống kê
suy diễn là một ngành của thống kê bao gồm việc sử dụng mẫu từ tổng thể ể ưa ra những
kết luận về tổng thể”. Cơ sở lý thuyết của thống kê suy diễn dựa trên lý thuyết xác suất,
ặc biệt là các ịnh lý giới hạn trong xác suất. Đôi khi ta còn nghe ến thuật ngữ thống kê
ứng dụng hay thống kê Toán. Thống kê ứng dụng ược hiểu là việc sử dụng thống kê
vào thực tế, nó bao gồm cả thống kê suy diễn và thống kê mô tả. Người ta còn chia
thành các ngành riêng của thống kê ứng dụng như: thống kê bảo hiểm, thống kê dân số,
thống kê trong giáo dục, thống kê trong y học… Còn về thống kê Toán lại là lĩnh vực
nghiên cứu cơ sở lý thuyết của khoa học thống kê.
3.1. Tổng thể và mẫu
3.1.1. Khái niệm tổng thể và mẫu 88
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Giả sử ta cần nghiên cứu một tính chất nào ó của các cá thể trong một tập hợp rất
nhiều phần tử, tập này gọi là tổng thể hay ám ông. Vì một số lý do nhất ịnh nào ó mà
ta không thể khảo sát toàn bộ các phần tử của nó, nhưng lại muốn có một kết luận ủ
chính xác về tính chất của các cá thể trong tập này. Để giải quyết vấn ề này, người ta
lấy ra một tập hợp các phần tử ại diện của tập lớn. Tập các phần tử ại diện này gọi là
mẫu. Số phần tử của mẫu gọi là kích thước mẫu hay cỡ mẫu, thường ký hiệu là n.
Ví dụ 3.1. Để nghiên cứu chiều cao trung bình của người Việt Nam ở ộ tuổi từ 20 ến
30, người ta tiến hành o chiều cao của 10000 công dân ược chọn ngẫu nhiên trong ộ
tuổi ó. Khi ó, tổng thể là toàn bộ công dân Việt Nam ở ộ tuổi từ 20 ến 30 và mẫu là
10000 công dân ược chọn ra, kích thước mẫu là n 10000.
3.1.2. Mẫu ngẫu nhiên
Một mẫu ngẫu nhiên kích thước n cho dấu hiệu X của tổng thể là một vector n
chiều (X X1, 2,..., Xn), trong ó X1,..., X n là n biến ngẫu nhiên ộc lập có cùng phân phối
với X. Khi các X i nhận giá trị cụ thể x ii ( 1,...,n) , ta có mẫu cụ thể
(x x1, 2,..., xn ).
3.1.3. Các ặc trưng mẫu
Để thực hiện việc ghi lại thông tin của mẫu lấy từ tổng thể ta có thể phân chia dữ
liệu thành hai loại: dữ liệu ịnh tính và dữ liệu ịnh lượng.
✓ Dữ liệu ịnh tính là thông tin bao gồm dạng thuộc tính, tính chất, danh gọi của
ối tượng ược khảo sát.
✓ Dữ liệu ịnh lượng là thông tin ược biểu thị dưới dạng trị số, giá trị số của sự
o, ếm ối tượng ược khảo sát.
Chẳng hạn, xét giá bán của sản phẩm ược phân theo từng loại như trong bảng sau: Loại sản phẩm Loại I Loại II Loại III Giá bán(1000 /kg) 50 45 30
Thông tin về sản phẩm thuộc hai loại dữ liệu. Dữ liệu ịnh tính là thông tin sản
phẩm về phân loại: loại I, loại II, loại III. Dữ liệu ịnh lượng là thông tin về giá bán: 50, 45, 30 (nghìn ồng).
a) Mẫu ịnh tính. Đó là mẫu mà chỉ quan tâm ến các phần tử của nó có tính chất A
nào ó hay không. Các thông số của mẫu:
- Kích thước mẫu: n
- Số phần tử có tính chất A: k
Khi ó, tỷ số fn k n/ ược gọi là tỷ lệ mẫu.
Xác suất thống kê và Ứng dụng – 2021 89 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Mẫu ịnh lượng. Đó là mẫu mà ta cần quan tâm ến một yếu tố về lượng của các
phần tử. Yếu tố về lượng là yếu tố mà có thể cân, o, ong, ếm ược và có kèm theo ơn vị,
chẳng hạn như: ộ dài, khối lượng, nhiệt ộ, ộ ẩm, thời gian, thu nhập, giá bán,...
Một mẫu ịnh lượng cụ thể kích thước n có thể cho ở dạng liệt kê giá trị (về dấu
hiệu X) của tất cả các phần tử của nó (gọi là dữ liệu thô - raw data), hoặc có thể viết
dưới dạng thu gọn sau ây và gọi là bảng phân phối tần số (Frequency Table) X
x1 x2 ... xk Số phần tử ni
n1 n2 ... nk
trong ó x1 x2 ... xk ; ni (i 1,k) là số phần tử trong mẫu mà X nhận giá trị xi ;
n1 n2 ... nk n. n n p i i i
gọi là tần suất xuất hiện giá trị xi . Khi ó, bảng sau ược n1 ... nk n
gọi là bảng phân phối tần suất:
X x1 x2 ... xk
P p1 p2 ... pk
Ví dụ 3.2. Đo ường kính X ( ơn vị tính: cm) của 50 trục máy cùng loại, có kết quả ược
ghi trong bảng sau (dạng dữ liệu thô):
5,2 5,2 5,1 5,3 5,2 5,4 5,1 5,3 5,6 5,0
5,4 5,2 5,6 5,0 5,4 5,6 5,1 5,2 5,2 5,3
5,6 5,2 5,3 5,2 5,4 5,5 5,5 5,1 5,2 5,3
5,4 5,1 5,3 5,2 5,2 5,1 5,6 5,5 5,4 5,7
5,4 5,5 5,4 5,2 5,3 5,4 5,3 5,3 5,4 5,3
Kích thức mẫu: n 50 Bảng
phân phối tần số mẫu:
X cm( ) 5,0 5,1 5,2 5,3 5,4 5,5 5,6 5,7 ni 2 6 12 10 10 4 5 1
Bảng phân phối tần suất mẫu (mẫu thu gọn): X cm( ) 5,0 5,1 5,2 5,3 5,4 5,5 5,6 5,7 P
0,04 0,12 0,24 0,2 0,2 0,08 0,1 0,02
c) Các ặc trưng của mẫu ịnh lượng: › Trung bình mẫu:
x (n x1 1 ... n xk k ) n xi i n n i 1 1 1
k › Phương sai mẫu: sˆ2 1 k n xi i2 x 2 90
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh n i 1
› Phương sai mẫu hiệu chỉnh: s2 n sˆ2 n 1
› Độ lệch mẫu hiệu chỉnh: s s2
Việc tính các ặc trưng mẫu, ta có thể sử dụng các chức năng của máy tính bỏ túi
hoặc sử dụng một trong các phần mềm như: Excel, Eviews, SPSS, R, ...
Hướng dẫn sử dụng Excel trong thống kê mô tả
Bước 1: Tải file RealStats.xlam
Bước 2: Mở chương trình excel và sau ó chạy file RealStats.xlam. Khi ó trên menu của
excel xuất hiện Real Statistics. Nhấp vào Real Statistics hoặc nhấn tổ hợp phím Ctrl –
m, chọn Frequency Table. Bước 3:
InputRange: chọn vùng dữ liệu (dữ liệu dạng cột, cột giá trị ứng trước, tần số ứng sau)
Chọn Raw data nếu dữ liệu thô, Frequency Table nếu dữ liệu dạng bảng tần số.
Chọn Descriptive stats (thống kê mô tả)
OutputRange : Chọn vị trí chứa kết quả
Xác suất thống kê và Ứng dụng – 2021 91 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Kết quả như bảng sau: Descriptive Statistics Mean
5,314 Trung bình mẫu: x Standard Error
0,023906 Sai số chuẩn: s / n Median 5,3 Trung vị Mode 5,2 Mốt
Standard Deviation 0,169043 Độ lệch chuẩn (hiệu chỉnh): s Sample Variance
0,028576 Phương sai mẫu (hiệu chỉnh): s2 - Kurtosis Độ nhọn 0,507937 Skewness 0,299501 Độ nghiêng Range
0,7 Khoảng biến thiên: xmax xmin Maximum
5,7 Giá trị lớn nhất: xmax Minimum
5 Giá trị nhỏ nhất: xmin Sum 265,7 Tổng: n xi i Count
50 Kích thước mẫu: n Geometric Mean
5,311379 Trung bình nhân: n x n n 1 1...xk k Harmonic Mean
Trung bình iều hòa: n 5,308771 i i 1 (n x ) AAD 0,1368 MAD 0,1 IQR 0,2
Lưu ý: Trong trường hợp số liệu của mẫu cho bởi các lớp (a bi, i ) thì ưa mẫu này về
dạng mẫu thu gọn bằng cách lấy giá trị ại diện cho mỗi lớp là : 92
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
xi (ai bi ) / 2, (i 1,...,k)
Ví dụ 3.3. Một hãng sản xuất một loại sản phẩm công bố rằng thời gian hoạt ộng tốt X
( ơn vị : tháng) của sản phẩm của họ trong iều kiện bình thường trung bình không dưới
26,3 tháng. Một mẫu iều tra về thời gian hoạt ộng tốt của một số sản phẩm ã qua sử
dụng của hãng này ược cho trong bảng sau: X
[23-24) [24-25) [25-26) [26-27) [27-28) [28-29) [29-30] Số sản phẩm 7 25 45 60 43 16 4
Hãy tính các ặt trưng mẫu cho X.
Giải. Đặt xi (ai b
i ) / 2 . Ta có mẫu thu gọn sau : X
23,5 24,5 25,5 26,5 27,5 28,5 29,5 Số sản phẩm 7 25 45 60 43 16 4
Chạy Excel, ta có kết quả :
Kích thước mẫu: n 200
Trung bình mẫu: x 26,355
Độ lệch chuẩn (hiệu chỉnh) s 1,3201
3.2. Ước lượng tham số
Trong phần này ta sẽ tìm hiểu về các suy diễn thống kê thông qua một mô hình
thống kê. Một mô hình thống kê ược ịnh nghĩa là một cặp ( , ) , với là không
gian mẫu – tập gồm các biến quan sát, và là tập gồm các phân phối xác suất trên
. Đối với thuật ngữ suy diễn thống kê, có thể hiểu là quá trình nghiên cứu về các ặc
trưng của tổng thể từ một mẫu quan sát; ặc trưng của tổng thể ược gọi là tham số
(thường ký hiệu là , i - nếu xét nhiều tham số), ặc trưng của mẫu ược gọi là thống kê.
Có thể hiểu mục ích của việc ưa ra mô hình thống kê như sau: giả sử rằng các dữ
liệu quan sát ược tạo ra thông qua một phân phối xác suất “thực sự”. Ta chọn là tập
gồm các phân phối thích hợp ể xấp xỉ cho phân phối “thực sự” này; tuy nhiên, trường
hợp chứa phân phối “thực sự” là rất hiếm. Tập này luôn ược tham số hóa theo các i : {P i : i
}, với là tập gồm tất cả các tham số của mô hình.
Về mặt thực hành, một mô hình thống kê phải thỏa mãn các ặc tính sau:
› Chứa các công thức toán ể biểu diễn các mối quan hệ giữa biến ngẫu nhiên và các tham số.
› Có các giả thiết về bnn, hoặc thậm chí là các tham số.
› Mô hình cần diễn giải ược hầu hết các biến ộng dữ liệu
Xác suất thống kê và Ứng dụng – 2021 93 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
› Tổng quát: dữ liệu = mô hình + phần dư; trong ó phần dư chính là phần dữ liệu
mà mô hình không giải thích ược.
Trong tài liệu này, ta sẽ tìm hiểu thêm về mô hình thống kê trong chương hồi qui,
tương quan. Về phần suy diễn thống kê, sẽ ược làm rõ trong các nội dung tiếp sau, cụ thể:
Suy diễn thống kê có thể ược chia làm hai dạng: › Ước lượng
› Kiểm ịnh mức ý nghĩa cho giả thiết không.
Trong ó, ước lượng có hai dạng:
› Ước lượng iểm (giá trị hợp lí nhất cho tham số)
› Ước lượng khoảng (còn gọi là khoảng tin cậy cho tham số)
3.2.1. Các khái niệm về ước lượng
a) Khái niệm ước lượng
Ước lượng là dự oán giá trị chưa biết dựa vào quan sát (thường là quan sát lấy
mẫu). Có hai hình thức ước lượng ó là: ước lượng iểm và ước lượng khoảng tin cậy.
Trong bài này chúng ta ước lượng ba tham số ặc trưng của tổng thể ó là: trung bình
E X( ), phương sai 2 D X( ) và tỉ lệ p P A( ) (tỉ lệ các phần tử có tính chất A của tổng thể).
b) Ước lượng iểm
Cho (X1,..., X n ) là mẫu ngẫu nhiên kích thước n.
Giả sử là một tham số ặc trưng của tổng thể mà ta chưa biết, dựa vào mẫu, tìm ược số
(X1,..., Xn) gần úng với . Khi ó, số ược gọi là ước lượng iểm của .
Ước lượng này có thể tốt hoặc không tốt, tùy vào hàm mà ta chọn.
Nói chung khi mẫu ngẫu nhiên (X1,..., X n ) nhận giá trị là các mẫu cụ thể khác nhau
thì ta ược các ước lượng là khác nhau. Vì vậy ước lượng
(X1,..., Xn) của là
một biến ngẫu nhiên. Người ta gọi hàm số
(X1,..., Xn) là một thống kê của mẫu
ngẫu nhiên (X1,..., X n ). Để là ước lượng tốt cho thì phải thỏa các tính chất sau:
➢ Tính không chệch: Thống kê ược gọi là ước lượng không chệch của nếu E( )
➢ Tính vững: Thống kê ược gọi là ước lượng vững của nếu (X1,..., Xn) P .
Ý nghĩa thực hành: Khi n ủ lớn thì . 94
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
➢ Tính hiệu quả: Thống kê gọi là ước lượng hiệu quả của nếu nó là ước lượng
không chệch và có phương sai bé nhất trong các ước lượng không chệch của .
Người ta chứng minh ược rằng:
› Trung bình mẫu x , phương sai mẫu hiệu chỉnh s2 , tỷ lệ mẫu fn tương ứng là ước
lượng không chệch, vững của , 2, p.
› Phương sai mẫu sˆ2 là ước lượng chệch, vững của 2 . › Nếu X N(
, 2 ) thì trung bình mẫu x là ước lượng hiệu quả cho .
c) Ước lượng khoảng tin cậy
Giả sử tổng thể có tham số chưa biết. Ta nói có khoảng ước lượng (hay
khoảng tin cậy) là ( 1, 2 ) với ộ tin cậy 1 cho trước nếu: P 1 2 1 2 1 Khi ó số
ược gọi là ộ chính xác hay sai số của ước lượng. 2
Như vậy, ộ tin cậy chính là xác suất mà khoảng ước lượng ( 1, 2 ) chứa tham số
. Thông thường ta xét ộ tin cậy 1
khá lớn, khoảng từ 90% ến 99%.
3.2.2. Bài toán ước lượng khoảng tin cậy cho trung bình
a) Đặt bài toán: Giả sử biến quan sát X N(
, 2 ), trong ó giá trị trung bình chưa
biết. Hãy ước lượng khoảng tin cậy (KTC) cho với ộ tin cậy 1 cho trước.
b) Giải quyết bài toán: Lập mẫu cụ thể kích thước n về biến quan sát X, từ ó tính
ược trung bình mẫu x và ộ lệch mẫu hiệu chỉnh s. Khi ó khoảng tin cậy cho giá trị trung
bình ược chỉ ra tương ứng với mỗi trường hợp sau: Trường hợp
KTC ối xứng KTC bên trái KTC bên phải x 1 x x 2 x 2 1 Đã biết 2
1 z /2.; 2 z . n n x 1 x x 2 x 2 Chưa biết 2 và n 1 30 1 z /2. n s
; 2 z . n s
Xác suất thống kê và Ứng dụng – 2021 95 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh x 1 x x 2 x 2 Chưa biết 2 và n 1 30 s s 1 t /2 (n 1)
n ; 2 t (n 1) n Trong ó:
➢ z là phân vị mức của phân phối chuẩn tắc Z N(0;1) , thỏa phương trình P Z( z ) (z ) 0,5
. Giá trị z tra từ bảng sau: 1
Bảng giá trị hàm Laplace ( )x x
0 e 0,5.t2dt 2 x
1,645 1,751 1,881 1,960 2,054 2,170 2,326 2,576
( )x 0,45 0,46 0,47 0,475 0,48 0,485 0,49 0,495
Sử dụng Excel: z Normsinv(1 );
➢ t ( )n là phân mức của phân phối Student T với n bậc tự do, thỏa P T t ( )n
Giá trị t ( )n ược tra từ các phụ lục 1a và 1b cuối tài liệu; hoặc sử dụng hàm
excel: t ( )n tinv(2 , )n . Chẳng hạn: n 9,
0,025 ; t0,025 (9) Tinv(0.05,9) 2,26216 Lưu ý
➢ Bài toán ước lượng khoảng tin cậy bên trái (bên phải) của thường là bài toán ước
lượng giá trị trung bình tối a (tối thiểu) của dấu hiệu X.
➢ Bằng các phép toán giới hạn trong xác suất, có thể chứng minh ược hàm mật ộ của
phân bố student hội tụ về hàm Gauss khi bậc tự do n dần ến vô cùng, nên khi n ủ
lớn, ta xấp xỉ có xấp xỉ t ( )n z . Do ó trong trường hợp chưa biết 2 và n 30 ta
sử dụng trực tiếp phân vị z /2, z .
➢ Trong trường hợp chưa biết ược biến quan sát có phân phối chuẩn, kích thước mẫu
n cần lớn ể thỏa mãn iều kiện ịnh lý giới hạn trung tâm. Thông thường, ta có thể
chấp nhận ở mức n 30 và kết quả xem như kết quả xấp xỉ. Xấp xỉ này tốt khi phân
bố “thực sự” của tổng thể có tính ối xứng. 96
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
c) Các chỉ tiêu của bài toán khoảng tin cậy ối xứng Khoảng
tin cậy ối xứng: x ; x s Độ chính xác: z /2 (*) n Độ tin cậy: 1
, Kích thước mẫu: n Bài toán 1: Biết 1
, tìm kích thước mẫu cần iều tra m, kích thước mẫu cần iều tra
thêm là m n (với n là kích thước mẫu hiện tại)
Từ công thức (*), thu ược công thức xác ịnh m như sau: z .s m /2 2
1 (với [ ]x là phần nguyên của x)
Bài toán 2: Biết , n tìm ộ tin cậy 1 n
Từ công thức (*), ta suy ra: z /2 1 2 (z /2 ) s
Ví dụ 3.4. Lượng vitamin có trong trái cây A là bnn X (mg) có ộ lệch chuẩn 3,5 mg.
Phân tích 200 trái cây A ược lượng vitamin trung bình là 22,5 mg. Với ộ tin cậy 95%,
hãy ước lượng KTC ối xứng cho lượng vitamin trung bình có trong mỗi trái cậy A.
Giải. Ta có: X N( , 2 ) ; 3,5
Các ặc trưng mẫu: n 200 ; x 22,5
Khoảng tin cậy ối xứng cho là: (x ; x ) Độ tin cậy 1 95% 0,05 (z /2) 0,5 0,475 z /2 1,96 2
Hoặc dùng excel: z /2 normsinv(1 0,025) 1,960 Độ chính xác: z /2. 0,485 n
Xác suất thống kê và Ứng dụng – 2021 97 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Vậy: (x ; x ) 22,015 ; 22,985
Ví dụ 3.5. Năng suất X ( ơn vị: kg/ha) của một loại giống mới là biến ngẫu nhiên có phân phối chuẩn N(
, 2 ) . Gieo thử giống hạt này trên 15 mảnh vườn thí nghiệm thu
ược số liệu sau.
169, 168, 167, 170, 167, 168, 171, 169, 166, 170, 167, 169, 169, 168, 172.
a) Viết mẫu dưới dạng bảng phân phối tần số (mẫu thu gọn).
b) Với ộ tin cậy 99%, hãy ước lượng KTC ối xứng cho năng suất trung bình của loại giống này.
c) Với ộ tin cậy 96%, hãy cho biết năng suất trung bình tối a, tối thiểu của loại giống này.
Giải. a) Mẫu thu gọn: X (kg/ha) 16 167 168 169 170 171 172 Số mảnh vườn 1 3 3 4 2 1 1
b) Các ặc trưng mẫu: n 15; x 168,667; s 1,633
Cỡ mẫu n 15 30 , 2 chưa biết.
Khoảng tin cậy ối xứng cho là: (x ; x ) Độ tin cậy 1 99% 0,01
t /2 (n 1) t0,005 (14) 2,9768 (tra bảng hoặc excel) s 1,633 Độ chính xác: t /2 (n 1) 2,9768 1,255 n 15 Vậy: (x ; x ) 167,412;169,922 c) Độ tin cậy 1 96% 0,04
t (n 1) t0,04 (14) 1,8875 s 1,633 Độ chính xác: t (n 1) 1,8875 0,796 15 n
Giá trị trung bình tối a là: x 169,463
Giá trị trung bình tối thiểu là: x 167,871
Ví dụ 3.6. Trọng lượng X (kg) của một bao xi măng ở phân xưởng óng bao cho nhà máy
sản xuất vật liệu xây dựng là bnn có phân phối chuẩn. Kiểm tra 100 bao ở phân xưởng này, có kết quả sau: 98
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh X
49 49,2 49,4 49,6 49,8 50 50,2 50,4 Số bao 3 7 10 23 37 14 4 2
a) Với ộ tin cậy 97%, hãy ước lượng khoảng tin cậy ối xứng cho trọng lượng trung
bình một bao xi măng ở phân xưởng này.
b) Với ộ tin cậy 98%, hãy cho biết trọng lượng trung bình tối a, tối thiểu của một bao
xi măng ở phân xưởng này là bao nhiêu?
c) Nếu muốn ước lượng khoảng tin cậy ối xứng cho trọng lượng trung bình một bao xi
măng ảm bảo ộ tin cậy 99% và ộ chính xác 0,02 kg thì cần iều tra thêm bao nhiêu bao xi măng nữa?
d) Nếu sử dụng mẫu này và muốn ước lượng khoảng tin cậy ối xứng cho trọng lượng
trung bình một bao xi măng với ộ chính xác 0,05 kg thì ảm bảo ộ tin cậy là bao nhiêu?
Giải. Ta có: n 100; x 49,704; s 0,28353
a) Gọi là trọng lượng trung bình (thực tế) một bao xi măng ở phân xưởng này.
Cỡ mẫu n 100 30, 2 chưa biết.
Khoảng tin cậy ối xứng cho là: (x ; x ) Độ tin cậy 1 97% 0,03
z /2 normsinv(1 0.015) 2,170 s Độ chính xác: z /2 0,062 n Vậy: (x
; x ) (49,642;49,766) b) Độ tin cậy 1 98% 0,02
z normsinv(1 0.02) 2,054 s Độ chính xác: z 0,058 n
Giá trị trung bình tối a là: x 49,762
Giá trị trung bình tối thiểu là: x 49,646 c) Độ tin cậy 1 99% 0,01 z /2 2,576
Xác suất thống kê và Ứng dụng – 2021 99 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Ta có:
0,02 ; s 0,28353 Kích
thước mẫu cần iều tra là: z .s m /2 2 1 1333,61 1 1333 1 1334
Vậy cần phải iều tra thêm là: m n 1234 bao. d) Ta có:
0,05; n 100; s 0,28353 s z /2 z /2 n s. 1 1,76348 n 1 2 (z /2)
0,9222 Vậy ộ tin cậy là: 1 92,22%.
3.2.3. Bài toán ước lượng khoảng tin cậy cho tỉ lệ p
a) Đặt bài toán: Giả sử tổng thể ược chia làm hai loại phần tử: phần tử có tính chất A,
và phần tử không có tính chất A. Tỷ lệ phần tử có tính chất A trong tổng thể là p
chưa biết. Hãy ước lượng khoảng tin cậy cho p với ộ tin cậy 1 cho trước.
b) Giải quyết bài toán: Lập mẫu kích thước n về tính chất A, tính ược tỉ lệ mẫu fn .
Khi ó khoảng tin cậy cho tỉ lệ p như sau: f (1 f )
➢ Khoảng tin cậy ối xứng: f . n p fn /2 n n với n z f n (1 f ) n n
➢ Khoảng tin cậy bên trái: p fn với z . f n (1 f ) n n
➢ Khoảng tin cậy bên phải: fn p với z . Lưu ý
Bài toán ước lượng khoảng tin cậy bên trái (bên phải) của p thường là bài toán
ước lượng tỷ lệ tối a (tối thiểu) của p. n f . 5
Điều kiện cho bài toán ước lượng tỷ lệ là: n (1n f n ) 5 100
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
c) Các chỉ tiêu của bài toán khoảng tin cậy ối xứng cho tỉ lệ Khoảng
tin cậy ối xứng: fn ; fn f (1 f ) n n Độ chính xác: z /2. n (*) Độ tin cậy: 1
, Kích thước mẫu: n Bài toán 1: Biết 1
, tìm kích thước mẫu cần iều tra m. m z /2 2 fn(1 fn) 1
Bài toán 2: Biết , n tìm ộ tin cậy 1 n z f n (1 f /2 . ) n 1 2 (z /2)
Ví dụ 3.7. Để ước lượng tỉ lệ sản phẩm kém chất lượng trong một lô hàng có 10000 sản
phẩm, người ta tiến hành kiểm tra ngẫu nhiên 200 sản phẩm, thấy có 17 sản phẩm kém chất lượng.
a) Với ộ tin cậy 95%, hãy ước lượng khoảng tin cậy ối xứng cho tỷ lệ sản phẩm kém
chất lượng trong lô hàng.
b) Với ộ tin cậy 96%, hãy cho biết số lượng sản phẩm kém chất lượng tối a, tối thiểu
có trong lô hàng là bao nhiêu?
c) Nếu muốn ước lượng khoảng tin cậy ối xứng cho tỷ lệ sản phẩm kém chất lượng
trong lô hàng ảm bảo ộ tin cậy 97% và ộ chính xác 2% thì cần kiểm tra thêm bao nhiêu sản phẩm nữa?
d) Nếu sử dụng mẫu này và muốn ước lượng khoảng tin cậy ối xứng cho tỷ lệ sản phẩm
kém chất lượng với ộ chính xác 3% thì ảm bảo ộ tin cậy là bao nhiêu?
Giải. Kích thước mẫu n 200, kích thước tổng thể N 10000. Tỷ lệ mẫu: fn 0,085
a) Gọi p là tỷ lệ sản phẩm kém chất lượng của lô hàng.
Khoảng tin cậy ối xứng cho p là: fn ; fn Độ tin cậy 1 95% 0,05 z /2 1,960
Xác suất thống kê và Ứng dụng – 2021 101 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh f n (1 f ) n Độ chính xác: z /2. n 0,0387 Vậy: fn ; fn 0,0463;0,1237
b) Gọi N0 là số lượng sản phẩm kém chất lượng có trong lô hàng. Độ tin cậy 1 96% 0,04 z 1,751 f n (1 f ) n Độ chính xác: z . 0,0345 n N0
Tỷ lệ tối a là: p
fn 0,1195 max(N0) 1195 10000
Tỷ lệ tối thiểu là: p N0 fn 0,0505 min(N0) 505 10000
Vậy với ộ tin cậy 96% thì số lượng sản phẩm kém chất lượng có trong lô hàng tối a
1195 sản phẩm, tối thiểu 505 sản phẩm. c) Độ tin cậy 1 97% 0,03 z /2 2,170 Độ chính xác
0,02. Kích thước mẫu cần iều tra là: z m /2 2 fn(1 fn) 1 915,587 1915 1 916
Vậy cần phải kiểm tra thêm m n 716 sản phẩm. d) Độ chính xác
0,03; n 200; fn 0,085 n z f n (1 f /2 . ) n
1,5213 1 2 (z /2) 0,8718
Vậy ộ tin cậy cần tìm: 1 87,18%
3.2.4. Bài toán ước lượng phương sai 2
a) Đặt bài toán: Giả sử biến quan sát X N(
, 2 ), phương sai 2 chưa biết. Hãy
ước lượng khoảng tin cậy cho 2 với ộ tin cậy 1 cho trước.
b) Giải quyết bài toán: Lập mẫu kích thước n về biến quan sát X , từ ó có ược phương
sai mẫu hiệu chỉnh s2 . 102
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Khoảng tin cậy của 2 là : ( 2 2 1 ,2 )
Trường hợp ã biết trung bình E X( ):
12 n x i (2i( ) n )2 ; 22
n x1i2 ( /2i ( ) n )2 /2
Trường hợp chưa biết trung bình E X( ): 2 (n 1).s2 ; 2
(n 1).s2 1 /2 (n 1) 2 12 /2 (n 1) 2
Trong ó: s2 là phương sai mẫu hiệu chỉnh ;
2 ( )n là phân vị của phân phối Chi
bình phương với n bậc tự do thỏa mãn: P 2 2 ( )n
. Giá trị 2 ( )n ược tra
từ các phụ lục 2a và 2b cuối tài liệu; hoặc sử dụng hàm Chiinv trong Excel: 2 ( )n
Chiinv( ,n) . Chẳng hạn: 2 0 ,05(9) 16,91898.
Ví dụ 3.8. Mức hao phí nguyên liệu ể sản suất ra một sản phẩm là biến ngẫu nhiên X
(kg) có phân phối chuẩn. X 19,5 20 20,5
Một mẫu gồm 28 sản phẩm có kết quả : ni 8 18 2
Với ộ tin cậy 94%, hãy ước lượng khoảng tin cậy của phương sai 2 trong hai trường hợp sau: a) Biết trung bình
E X( ) 19,95(kg)
b) Chưa biết trung bình .
Giải. Kích thước mẫu n 28; Độ tin cậy 1 0,94 0,06 2 2 /2 ( )n 0 ,03 (28) 43,6622 2 2 1 /2 ( )n 0 ,97 (28) 15,7042
a) Ta có: n xi ( i )2
n xi ( i 19,95)2 2,27
Xác suất thống kê và Ứng dụng – 2021 103 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 12
n x i (2/2i( ) n )2 0,0520 ; 22
n x1i2 ( /2i ( ) n )2 0,1445
Vậy khoảng tin cậy của 2 là : 0,0520 ; 0,1445
b) Phương sai mẫu hiệu chỉnh s2 0,0806878 12
( n2/2 (1).n s1)2 0,0520 ; 22
(12 n /2 (1).ns 21) 0,1387
Vậy khoảng tin cậy của 2 là : 0,0520; 0,1387 BÀI TẬP CHƯƠNG 3
Bài toán ước lượng giá trị trung bình
3.1. Trọng lượng (gam) của một loại sản phẩm là bnn X N( , 2 ) với 1 (gam). Cân
thử 25 sản phẩm loại này có kết quả sau:
Trọng lượng (gam) 18 10 20 21 Số sản phẩm 3 5 15 2
Với ộ tin cậy 98% hãy tìm khoảng tin cậy ối xứng cho trọng lượng trung bình của sản phẩm trên.
3.2. Chiều cao một loại cây A là một biến ngẫu nhiên có phân phối chuẩn. Người ta o
chiều cao ngẫu nhiên 20 cây A thì thấy chiều cao trung bình 23,15m và ộ lệch mẫu chưa hiệu chỉnh là 1,24 m. Với ộ tin cậy 98%.
a) Hãy ước lượng khoảng tin cậy ối xứng cho chiều cao trung bình của cây A.
b) Hãy ước lượng chiều cao trung bình tối a, tối thiểu của cây A.
3.3. Nguyên liệu hao phí ể sản xuất một ơn vị sản phẩm K là bnn có phân phối chuẩn.
Theo dõi một số sản phẩm có kết quả sau:
Nguyên liệu hao phí (kg) [19;19,5) [19,5;20) [20;20,5) [20,5;21] Số sản phẩm 15 50 30 5
Hãy ước lượng khoảng tin cậy ối xứng cho mức hao phí nguyên liệu trung bình ể
sản xuất một ơn vị sản phẩm với ộ tin cậy 99%.
3.4. Kiểm tra tuổi thọ ( ơn vị: giờ) của 50 bóng èn do một nhà máy sản xuất, người ta thu ược kết quả sau: Tuổi thọ 3300 3500 3600 4000 Số bóng èn 10 20 12 8 104
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Giả thiết tuổi thọ của bóng èn có phân phối chuẩn.
a) Hãy ước lượng khoảng tin cậy ối xứng cho tuổi thọ trung bình của loại bóng èn này với ộ tin cậy 95%.
b) Với ộ tin cậy 98%, hãy cho biết tuổi thọ trung bình tối a, tối thiểu của loại bóng èn này là bao nhiêu?
c) Nếu yêu cầu ước lượng khoảng tin cậy cho tuổi thọ trung bình phải ạt ộ chính
xác không quá 45 giờ với ộ tin cậy 97% thì cần phải kiểm tra ít nhất bao nhiêu bóng èn?
d) Sử dụng mẫu này ể ước lượng khoảng tin cậy cho tuổi thọ trung bình. Để ộ chính
xác 50 giờ thì ộ tin cậy ạt ược là bao nhiêu?
Bài toán ước lượng tỷ lệ
3.5. Từ một àn gà cùng loại có 15000 con, kiểm tra ngẫu nhiên 100 con thấy có 18 con
có chân màu trắng. Với ộ tin cậy 99%
a) Hãy tìm khoảng tin cậy ối xứng cho tỷ lệ gà có chân màu trắng.
b) Tìm số gà có chân màu trắng tối thiểu, tối a có trong àn gà.
3.6. Theo iều tra 100 gia ình thấy có 60 gia ình có nhu cầu về loại tủ lạnh do xí nghiệp
A xản xuất. Hãy ước lượng KTC ối xứng cho tỷ lệ gia ình có nhu cầu về mặt hàng này với ộ tin cậy 95%.
3.7. Biết tỷ lệ nảy mầm của một loại hạt giống là 0,9. Với ộ tin cậy 97%, nếu muốn ước
lượng KTC cho tỷ lệ hạt nảy mầm có ộ chính xác không vượt quá 2% thì cần phải
gieo ít nhất bao nhiêu hạt?
3.8. Kiểm tra ngẫu nhiên 250 sản phẩm trong kho hàng thấy có 21 phế phẩm.
a) Hãy ước lượng khoảng tin cậy ối xứng cho tỷ lệ phế phẩm của kho hàng trên với ộ tin cậy 95%.
b) Nếu muốn ước lượng có
2% với ộ tin cậy 96% thì phải quan sát thêm ít nhất
bao nhiêu sản phẩm nữa?
c) Với mẫu ban ầu, nếu muốn ước lượng có sai số là 1,5% thì ộ tin cậy ạt ược là bao nhiêu?
3.9. Một công ty than có 10000 công nhân làm việc trực tiếp tại các hầm lò. Để xác ịnh
số công nhân mắc các bệnh về phổi, người ta tiến hành kiểm tra 820 người thấy có 120
người mắc bệnh về phổi. Với ộ tin cậy 98% hãy tìm khoảng tin cậy cho số công nhân
mắc bệnh về phổi trong tổng công ty.
3.10. Một kho hàng chứa 12000 sản phẩm. Để ước lượng số phế phẩm trong kho hàng
người ta kiểm tra 500 sản phẩm thấy có 50 phế phẩm. Với ộ tin cậy 94% hãy ước lượng
khoảng tin cậy cho số phế phẩm trong kho.
Xác suất thống kê và Ứng dụng – 2021 105 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
3.11. Để iều tra số lượng một loài cá trong hồ người ta ánh bắt 400 con cá rồi ánh dấu
mỗi con cá này bằng một vòng nhôm nhỏ sau ó thả vào hồ. Sau một thời gian người ta
bắt lại 150 con thấy trong ó có 50 con ã ược ánh dấu.
a) Với ộ tin cậy 96%, tìm KTC cho số lượng của loài cá này.
b) Với ộ tin cậy 99%, hãy cho biết số lượng cá tối a, tối thiểu có trong hồ.
Bài toán ước lượng phương sai
3.12. Biết tỷ lệ phần trăm X (%) của một nguyên tố vi lượng trong các mẫu ất thuộc châu
thổ sông Hồng có phân phối chuẩn N(
, 2 ) . Người ta tiến hành phân tích 17 mẫu ất
và tính ược s 0,3742% . Với ộ tin cậy 95%, hãy tìm KTC của 2 .
3.13. Biết khối lượng X (kg) của mỗi con gà tại một trại gà có phân phối chuẩn N( , 2
) . Cân ngẫu nhiên 20 con gà có kết quả sau: X (kg)
2,1 2,3 2,4 2,6 2,7 2,9 3,1 3,3 Số con gà 1 2 3 3 5 3 2 1
Với ộ tin cậy 96%, tìm KTC cho 2 trong hai trường hợp: a) Biết trung bình
E X( ) 2,62(kg)
b) Chưa biết trung bình .
Bài tập tổng hợp
3.14. Cân thử 100 quả trứng của một loại trứng, có kết quả sau: Trọng lượng (gam) 32 33 34 35 36 37 38 39 40 Số quả trứng 2 3 15 28 30 8 5 5 4
a) Hãy ước lượng khoảng tin cậy ối xướng cho trọng lượng trung bình của loại
trứng này với ộ tin cậy 94%.
b) Trứng có trọng lượng dưới 35 gam ược coi là trứng loại II. Tìm KTC ối xứng
cho tỉ lệ trứng loại II với ộ tin cậy 95%.
c) Hãy ước lượng khoảng tin cậy hai phía cho phương sai của trọng lượng loại trứng này với ộ tin cậy 98%.
3.15. Một kết quả iều tra về thời gian X ( ơn vị: phút) của cuộc gọi qua một mạng iện
thoại di ộng ược cho trong bảng sau:
X (phút) (0;2] (2;4] (4;6] (6;8] (8;10] (10;12] (12;14] (14,16]
Số cuộc gọi 60 180 150 230 130 70 30 10
a) Với ộ tin cậy 96%, tìm KTC ối xứng cho thời gian trung bình một cuộc gọi qua
mạng iện thoại di ộng này.
b) Với ộ tin cậy 97%, tìm KTC ối xứng cho tỷ lệ cuộc gọi có thời gian hơn 8 phút
qua mạng iện thoại di ộng nói trên. 106
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
3.16. Tuổi thọ X ( ơn vị: giờ) của bóng èn do một nhà máy sản suất là biến ngẫu nhiên
có phân phối chuẩn. Thống kê tuổi thọ của 256 bóng èn của nhà máy trên, ta có bảng thống kê sau:
Tuổi thọ (giờ ) Số bóng
Tuổi thọ (giờ) Số bóng [1000-1100) 4 [1600-1700) 42 [1100-1200) 10 [1700-1800) 32 [1200-1300) 16 [1800-1900) 26 [1300-1400) 20 [1900-2000) 14 [1400-1500) 36 [2000-2100) 8 [1500-1600) 48
a) Hãy ước lượng khoảng tin cậy ối xứng cho tuổi thọ trung bình của loại bóng èn này với ộ tin cậy 95%.
b) Những bóng có tuổi thọ từ 1800 giờ trở lên là loại bóng vượt tiêu chuẩn. Ước
lượng khoảng tin cậy ối xứng cho tỷ lệ loại bóng vượt tiêu chuẩn với ộ tin cậy 97%.
CHƯƠNG 4 KIỂM ĐỊNH GIẢ THIẾT THỐNG KÊ
Như ã trình bày trong phần trước, suy diễn thống kê gồm hai loại là: ước lượng
tham số và kiểm ịnh mức ý nghĩa, trong phần này, ta sẽ tìm hiểu về bài toán kiểm ịnh
cho tham số của tổng thể với mức ý nghĩa (significance level) cho trước. Đây là một
thủ tục quan trọng bậc nhất trong thống kê, và có ứng dụng rộng rãi trong ời sống cũng
như hầu hết các lĩnh vực khoa học. 4.1. Các khái niệm về kiểm ịnh giả thiết thống kê
4.1.1. Giả thiết thống kê
Giả thiết thống kê là những giả thiết nói về các tham số ặc trưng của tổng thể (như là:
, 2, p ), dạng quy luật phân phối, hoặc tính ộc lập của các biến ngẫu nhiên.
Việc ưa ra kết luận bác bỏ hay chấp nhận một giả thiết thống kê ược gọi là kiểm
ịnh giả thiết thống kê.
Giả thiết thống kê ưa ra kiểm ịnh ược ký hiệu H0 , giả thiết ối nghịch với
H0 gọi là giả thiết ối hay ối thiết, ký hiệu là H1 . Sau khi kiểm ịnh ta phải i ến kết luận
là chấp nhận H0 (tức bác bỏ H1 ) hoặc bác bỏ H0 (tức là chấp nhận H1 ).
Ý tưởng của bài toán kiểm ịnh tương tự như một bài toán chứng minh phản chứng.
Ta luôn giả sử H0 úng, khi ó, bằng các tiêu chuẩn thống kê từ dữ liệu mẫu, i ến kết luận
bác bỏ H0 ; tức là ta sẽ chấp nhận H1 . Như vậy chính H1 mới là giả thiết mà ta cần chứng
Xác suất thống kê và Ứng dụng – 2021 107 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
tỏ sự úng ắn. Chẳng hạn như khi cải tiến một sản phẩm, ta cần kiểm chứng rằng sau khi
cải tiến, sản phẩm có sự vượt trội “ áng kể” (hay có ý nghĩa) so với trước khi cải tiến,
như vậy iều ta mong muốn chứng minh ở ây chính là “sự khác biệt của sản phẩm sau
khi cải tiến là áng kể”, ây chính là H1 . Để ý rằng, khi ta không bác bỏ H0 không có nghĩa
là nó úng, mà có nghĩa là chưa ủ chứng cứ (từ dữ liệu mẫu) ể bác bỏ H0 , do ó, ta hạn
chế việc khẳng ịnh “chấp nhận H0 ” Ví dụ 4.1
1) Trong một báo cáo nói rằng: “Thu nhập bình quân của một người dân ở ịa phương
A là 2,75 triệu ồng/tháng”. Đây ược coi là một giả thiết thống kê, giả thiết này nói
về một tham số ặc trưng (trung bình tổng thể) của biến ngẫu nhiên X là thu nhập của
người dân ở ịa phương A. Gọi
E X( ). Đặt giả thiết thống kê H0 :
2,75; giả thiết ối H1 mang nghĩa ối
nghịch với H0 là H1 : 2,75.
2) Một nhân viên kinh doanh cho rằng: “tỉ lệ sản phẩm loại II của lô hàng là 12%”.
Đây ược coi là một giả thiết thống kê, giả thiết này nói về một tham số ặc trưng (tỉ
lệ tổng thể) của biến ngẫu nhiên biểu thị tỉ lệ sản phẩm loại II của lô hàng.
Gọi p là tỉ lệ sản phẩm loại II của lô hàng. Đặt giả thiết H0 : p 12% ; giả thiết ối là H1 : p 12%.
Nếu nhân viên kinh doanh phát biểu rằng: “ tỉ lệ sản phẩm loại II của lô hàng dưới
12%”. Khi ó giả thiết H0 : p 12% ối thiết H1 : p 12% .
Hay một khách hàng sử dụng sản phẩm nghi ngờ rằng: “tỉ lệ sản phẩm loại II lớn
hơn 12%”. Khi ó giả thiết H0 : p 12% ối thiết H1 : p 12%.
3) Một kết luận nói rằng: “chi tiêu cho tiêu dùng cá nhân không phụ thuộc vào giới
tính”. Đây là giả thiết thống kê nói về tính ộc lập của các biến ngẫu nhiên. Gọi X là
chi cho tiêu dùng cá nhân, Y là giới tính của cá nhân ó.
Giải thiết thống kê H0 : X và Y ộc lập nhau.
Giả thiết ối H1 : X và Y phụ thuộc nhau.
4.1.2. Sai lầm loại 1 và loại 2
Giả sử tổng thể có ặc trưng chưa biết. Ta cần kiểm ịnh cặp giả thiết H0 : 0 ,
ối thiết H1 là một trong các giả thiết: 0, 0, 0 .
Khi kiểm ịnh, ta có thể mắc các sai lầm sau ây:
Sai lầm loại 1: bác bỏ H0 khi H0 úng. 108
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Sai lầm loại 2: chấp nhận H0 khi H0 sai.
Khi ặt giả thiết thống kê, người ta xem xét sai lầm nào là quan trọng hơn, tức là
khi phạm phải sẽ chịu tổn thất lớn hơn, và sẽ ặt giả thiết ể sai lầm ó là loại 1.
Ví dụ 4.2. Một bác sĩ khám bệnh có thể phạm phải một trong hai tình huống sau:
1) Người có bệnh, sau khi khám ông ta kết luận không bệnh.
2) Người không bệnh, sau khi khám ông ta kết luận có bệnh.
Trong thực tế, một người i khám bệnh vì có các triệu chứng mà họ nghi ngờ là biểu
hiện bệnh lý. Do ó, iều họ cần chứng minh là H1 : “tôi bị bệnh”, ương nhiên
H0 : “tôi không bệnh”. Ở ây, có thể hiểu không bệnh tức là các chỉ số bằng với mức bình
thường và bị bệnh là khi các chỉ số của người này khác bình thường. Giả sử, thật sự H0
úng, tức là người này không bệnh mà bác sĩ lại kết luận có bệnh (dương tính giả) thì ây
là sai lầm loại I. Ngược lại, khi H0 sai, tức là người này bị bệnh mà bác sĩ lại kết luận
không bệnh (âm tính giả) thì ây là sai lầm loại II.
Một ví dụ khác về các loại sai lầm như: một chuông báo cháy lại không thể báo
cháy khi xảy ra hỏa hoạn (loại II) hoặc cứ báo cháy giả (loại I).
4.1.3. Mức ý nghĩa và power của kiểm ịnh
a) Mức ý nghĩa: Nhắc lại, việc chấp nhận H1 khi H0 úng ược gọi là sai lầm loại I.
Xác suất mắc phải sai lầm loại I ược gọi là mức ý nghĩa và ược ký hiệu là .
Nói chung, khi mức ý nghĩa càng nhỏ thì việc mắc phải sai lầm loại một cũng
giảm theo, do ó, ta thường chọn giá trị nhỏ (10%, 5% hoặc thấp hơn.)
b) Power của kiểm ịnh: Khi không thể bác bỏ H0 mặc dù H1 úng, ta mắc phải sai lầm
loại II. Xác suất mắc phải sai lầm loại II ược ký hiệu là . Mặt khác, khả năng bác bỏ
H0 khi nó sai ược gọi là “power” của kiểm ịnh và ược tính như sau: power 1 .
Trong thực tế, việc tính toán là rất khó vì nó phụ thuộc vào tham số trung bình
chưa biết. Tuy nhiên, có thể tìm ược khi cho trước , 2 ,n .
Trong kiểm ịnh, việc bác bỏ một giả thiết sai là rất quan trọng (vì ta cần chứng
minh H1 úng), do ó việc tăng power rất áng ược quan tâm. Các phương pháp làm tăng power như sau: ➢ Tăng .
➢ Dùng kiểm ịnh một phía thay vì hai phía.
➢ Giảm phương sai mẫu: tăng kích thước mẫu và dùng các phương pháp o ạc chính xác hơn.
Xác suất thống kê và Ứng dụng – 2021 109 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Giữa và có sự tương quan, khi giảm làm tăng và ngược lại. Có thể làm
giảm ồng thời cả và khi tăng cỡ mẫu n.
4.2. Một số bài toán kiểm ịnh thông dụng
4.2.1. Bài toán kiểm ịnh giả thuyết về giá trị trung bình
a) Đặt bài toán: Giả sử biến quan sát X N(
, 2 ), trong ó giá trị trung bình E
X( ) chưa biết, nhưng dựa vào những thông tin có ược, người ta có các ý kiến sau: 0 , 0 , 0 ,
0 . Với mức ý nghĩa cho trước, hãy xác minh xem ý kiến nào úng.
b) Giải quyết bài toán: Chọn giả thiết thống kê H0 :
0 và ối thiết H1 là một trong các ý kiến còn lại.
Lập mẫu kích thước n về biến quan sát X , từ ó tính ược trung bình mẫu x và ộ lệch
mẫu hiệu chỉnh s.
Bài toán ược giải quyết bằng việc chỉ ra miền bác bỏ giả thiết H0 tương ứng với
các trường hợp của giả thiết ối H1 ược cho trong bảng sau: Trường hợp Bài toán kiểm ịnh
Điều kiện bác bỏ H0 H0 : 0 ; H1 : 0 T1 z Đã biết 2 H0 : 0 ; H1 : 0 T1 z H0 : 0 ; H1 : 0 T1 z /2 H0 : 0 ; H1 : 0 T2 z Chưa biết 2 , H0 : 0 ; H1 : 0 T2 z n 30 H0 : 0 ; H1 : 0 T2 z /2 H0 : 0 ; H1 : 0
T2 t (n 1) Chưa biết 2 , H0 : 0 ; H1 : 0
T2 t (n 1) n 30 H0 : 0 ; H1 : 0
T2 t /2 (n 1) Trong ó: T1 (x
0 ) n , T2 (x 0 ) n s z normsinv(1
) là phân vị của phân phối chuẩn mức .
t ( )n Tinv(2 , )n là phân vị bậc 1
của phân phối Student với n bậc tự do. 110
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Lưu ý: Bài toán kiểm ịnh tương ứng với ối thiết H1 là 0 hoặc 0 ược gọi
là bài toán kiểm ịnh một phía; còn nếu H1 là
0 thì gọi là bài toán kiểm ịnh hai phía.
Ví dụ 4.3. Khảo sát chỉ tiêu X ( ơn vị: cm) của một loại sản phẩm, người ta quan sát
một mẫu và có kết quả sau: X
[11-15) [15-19) [19-23) [23-27) [27-31) [31-35) [35-39] Số sp 8 9 20 16 16 13 18
Những sản phẩm có chỉ tiêu X nhỏ hơn 19cm ược xếp vào loại B. Giả sử X có phân phối chuẩn.
a) Giả sử theo tiêu chuẩn, trung bình của chỉ tiêu X là 29cm. Hãy nhận ịnh về tình hình
sản xuất với mức ý nghĩa 2%.
b) Theo qui ịnh, giá trị trung bình của chỉ tiêu X là 25cm. Các số liệu trên thu thập ược
từ các sản phẩm do một máy sản xuất. Với mức ý nghĩa 5% có thể kết luận rằng các
sản phẩm do máy sản xuất có chỉ tiêu X cao hơn qui ịnh hay không? Cùng câu hỏi
nhưng ở mức ý nghĩa 3%.
c) Bằng phương pháp sản xuất mới, sau một thời gian, người ta thấy giá trị trung bình
chỉ tiêu X của những sản phẩm loại B là 16 cm. Hãy cho kết luận vềphương pháp
mới với mức ý nghĩa 1% .
d) Theo số liệu thống kê cũ, giá trị trung bình của chỉ tiêu X của những sản phẩm loại
B là 16,5cm. Các số liệu trên thu thập ược sau khi ã áp dụng một phương pháp sản
xuất mới. Hãy cho kết luận về nhận ịnh cho rằng phương pháp mới có tác dụng làm
giảm chỉ tiêu X của những sản phẩm loại B với mức ý nghĩa 4% .
Giải. Tính các ặc trưng mẫu:
n 100; x 26,36 ; s 7,483
Các ặc trưng mẫu của sản phẩm B:
nB 17; xB 15,118 ; sB 2,058
a) Gọi là giá trị trung bình của chỉ tiêu X.
Đặt giả thiết H0 :
0 29; ối thiết H1 : 0
Cỡ mẫu n 100 30, 2 chưa biết.
Tính thống kê: T (x 0 ) n (26,36 29) 100 3,528 s 7,483 Mức ý nghĩa 2% 0,02 z /2 2,326
Xác suất thống kê và Ứng dụng – 2021 111 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Điều kiện T z /2 là úng nên bác bỏ giả thiết H0 và chấp nhận ối thiết H1 .
Kết luận: với mức ý nghĩa 2%, tình hình sản xuất không bình thường vì giá trị
trung bình của chỉ tiêu X không úng tiêu chuẩn.
b) Đặt giả thiết H0 :
0 25; ối thiết H1 : 0
Cỡ mẫu n 100 30, 2 chưa biết.
Tính thống kê : T (x
0 ) n (26,36 25) 100 1,817 s 7,483
➢ Trường hợp mức ý nghĩa 5% 0,05 z 1,645
Điều kiện T z là úng nên bác bỏ giả thiết H0 và chấp nhận ối thiết H1 .
Kết luận: với mức ý nghĩa 5%, các sản phẩm do máy sản xuất có chỉ tiêu X cao hơn qui ịnh.
➢ Trường hợp mức ý nghĩa 3% 0,03 z 1,881
Điều kiện T z là sai nên chấp nhận giả thiết H0 và bác bỏ ối thiết H1 .
Kết luận: với mức ý nghĩa 3%, không thể kết luận rằng các sản phẩm do máy trên
sản xuất có chỉ tiêu X cao hơn qui ịnh.
c) Gọi B là giá trị trung bình chỉ tiêu X của những sản phẩm loại B.
Đặt giả thiết H0 : B 0 16 ; ối thiết H1 : B 0 Cỡ mẫu nB 17 30, 2 chưa biết.
Tính thống kê: TB (xB 0) nB (15,118 16) 17 1,767 sB 2,058 Mức ý nghĩa 1% 0,01
t /2(nB 1) Tinv(2 ,nB 1) Tinv(0.02,16) 2,583
Điều kiện TB t /2 (n 1) là sai nên chấp nhận giả thiết H0 và bác bỏ H1 .
Kết luận: với mức ý nghĩa 1%, phương pháp sản xuất mới không có tác dụng làm
thay ổi giá trị trung bình chỉ tiêu X của các sản phẩm loại B. d) Đặt giả thiết H0 : B 0
16,5; ối thiết H1 : B 0 Cỡ mẫu nB 17 30, 2 chưa biết. 112
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh B (xB 0) nB (15,118 16) 17 2,767 Tính thống kê : T sB 2,058 Mức ý nghĩa
4% 0,04 t (nB 1) Tinv(2 ,nB 1) Tinv(0.08,16) 1,869
Điều kiện TB t (n 1) là úng nên bác bỏ giả thiết H0 và chấp nhận ối thiết H1 .
Kết luận: với mức ý nghĩa 4%, phương pháp mới có tác dụng làm giảm giá trị
trung bình chỉ tiêu X của các sản phẩm loại B.
4.2.2. Bài toán kiểm ịnh giả thiết về tỉ lệ
a) Đặt bài toán: Giả sử p P A( ) ( p chưa biết) là tỉ lệ các phần tử có tính chất A
trong tổng thể. Dựa vào những thông tin nhất ịnh, người ta có các ý kiến sau: p p0, p
p0 , p p0 , p p0 . Với mức ý nghĩa cho trước, hãy xác minh xem ý kiến nào úng.
b) Giải quyết bài toán: Chọn giả thiết thống kê H0 : p p0 và giả thiết ối H1 là một
trong các ý kiến còn lại.
Lập mẫu kích thước n quan sát tính chất A, tính ược tỉ lệ mẫu fn . Khi ó bài toán
ược giải quyết bằng việc chỉ ra miền bác bỏ giả thiết H0 tương ứng với các trường hợp
của giả thiết ối H1 ược cho trong bảng sau: Bài toán kiểm ịnh
Điều kiện bác bỏ H0 Trong ó
H0 : p p0 ; H1 : p p0 T z
T ( fn p0 ) n
H0 : p p0 ; H1 : p p0 T z p0 (1 p0 )
H0 : p p0 ; H1 : p p0 T z /2 n p. 0 5
Lưu ý: Kích thước mẫu n phải thỏa mãn iều kiện: n.(1 p0) 5
Ví dụ 4.4. Mỗi bao xi măng ược óng tự ộng ở một phân xưởng óng bao ược coi là ạt
chuẩn nếu có trọng lượng từ 49,8kg ến 50,2kg. Kiểm tra 250 bao ở phân xưởng này,
thấy có 237 bao ạt chuẩn.
a) Với mức ý nghĩa 4% hãy kiểm ịnh giả thiết “tỉ lệ bao xi măng ạt chuẩn là 96%”.
Xác suất thống kê và Ứng dụng – 2021 113 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Tỉ lệ bao xi măng ạt chuẩn trước ây là 91%. Các số liệu trên ược kiểm tra sau khi áp
dụng công nghệ óng bao mới. Với mức ý nghĩa 3%, có thể kết luận kỹ thuật mới làm
tăng tỉ lệ bao xi măng ạt chuẩn hay không?
Giải. Cỡ mẫun 250
Tỉ lệ mẫu các bao xi măng ạt chuẩn: fn 0,948
Gọi p là tỉ lệ bao xi măng ạt chuẩn của phân xưởng.
a) Đặt giả thiết H0 : p p0 0,96 ; ối thiết H1 : p p0 p ) n
Tính thống kê: T ( fn 0 0,968 p0 (1 p0 ) Mức ý nghĩa 0,04 z /2 2,054
Điều kiện |T | z /2 là sai nên chấp nhận giả thiết H0 , bác bỏ ối thiết H1 .
Kết luận: với mức ý nghĩa 4% có thể kết luận rằng tỉ lệ bao xi măng ạt chuẩn của phân xưởng là 96%.
b) Đặt giả thiết H0 : p p0 0,91; ối thiết H 1 : p p0 p ) n
Tính thống kê T ( fn 0 2,0995 p0 (1 p0 ) Mức ý nghĩa 0,03 z 1,881
Điều kiện T z là úng nên bác bỏ giả thiết H0 , chấp nhận ối thiết H1 .
Kết luận: với mức ý nghĩa 3% có thể kết luận kỹ thuật mới làm tăng tỉ lệ bao xi măng ạt chuẩn.
4.2.3. Bài toán kiểm ịnh giả thiết về phương sai
a) Đặt bài toán: Giả sử biến quan sát X N(
, 2 ),trong ó phương sai 2 D X( )
chưa biết, nhưng dựa vào những thông tin có ược, người ta có các ý kiến: 2 2 2 2 2
0 , 2 0 , 2 0 , 2 0 . Với mức ý nghĩa
cho trước, hãy xác minh xem ý kiến nào úng. 114
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Giải quyết bài toán: Chọn giả thiết thống kê H 2 0 :
2 0 và ối thiết H1 là một
trong các ý kiến còn lại.
Lập mẫu kích thước n về biến quan sát X , từ ó tính ược ộ lệch mẫu hiệu chỉnh s. Tính thống kê 02 (n 1)02 s2 Mức ý nghĩa
0,5và n 1 bậc tự do, sử dụng hàm 2 ( )n Chiinv( ,n) trong
Excel ể tìm các phân vị Chi bình phương 12 /2 (n 1) 12
(n 1) 2 (n 1) 2/2(n 1)
Khi ó bài toán ược giải quyết bằng việc chỉ ra miền bác bỏ giả thiết H0 tương ứng
với các trường hợp của ối thiết H1 ược cho trong bảng sau: Bài toán kiểm ịnh
Điều kiện bác bỏ H0
H0 : 2 02,H1 : 2 02 02 12 (n 1) H 2 0 : 2 02,H1 : 2 02 2 (n 1) 0 02 12 /2 (n 1)
H0 : 2 02,H1 : 2 02 hoặc 2 2 /2 (n 1) 0
Ví dụ 4.5. Đường kính của một loại chi tiết máy là biến ngẫu nhiên X có phân phối
chuẩn. Người ta o ngẫu nhiên ường kính của 28 chi tiết máy do một máy sản xuất và
tìm ược phương sai mẫu hiệu chỉnh s2 (2,1053) (2 cm2).
a) Khi máy hoạt ộng bình thường thì ộ lệch chuẩn của X của các chi tiết máy do máy
sản xuất là 1,65 cm. Với mức ý nghĩa 1%, hãy xét xem máy có hoạt ộng bình thường không?
b) Theo quy ịnh, nếu ộ lệch chuẩn của X lớn hơn 1,72 cm thì phải iều chỉnh lại máy.
Với mức ý nghĩa 5%, có phải iều chỉnh lại máy không?
Giải. Đặt 2 D X( )
a) Đặt giả thiết H 2 2 0 :
2 0 (1,65)2 ; ối thiết H1 : 2 0
Kích thước mẫu n 28
Phương sai mẫu hiệu chỉnh s2 (2,1053)2 Tính thống kê 02 (n 1)02 s2 43,9566
Xác suất thống kê và Ứng dụng – 2021 115 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Mức ý nghĩa 0,01
2 (n 1) chiinv( ,n 1) 46,9629
Điều kiện 2 (n 1) 20 là sai nên chấp nhận giả thiết H0 , bác bỏ ối thiết H1 .
Kết luận: với mức ý nghĩa 1%, máy hoạt ộng bình thường.
b) Đặt giả thiết H 2 2 0 :
2 0 (1,72)2 ; ối thiết H1 : 2 0 Tính thống kê 02 (n 1)02 s2 40,4515 Mức ý nghĩa 0,05
2 (n 1) chiinv( ,n 1) 40,1133
Điều kiện 2 (n 1) 20 là úng nên bác bỏ giả thiết H0 , chấp nhận H1 .
Kết luận: với mức ý nghĩa 5%, phải iều chỉnh lại máy.
4.2.4. Bài toán kiểm ịnh so sánh hai giá trị trung bình
a) Đặt bài toán: Giả sử X và Y là hai biến quan sát ộc lập nhau, X N( 2 1, 1 ), Y N( 2
2, 2 ) , trong ó các giá trị trung bình 1
E X( ), 2 E Y( ) chưa biết. Dựa
vào những thông tin có ược, người ta có các ý kiến sau: 1 2, 1 2, 1 2, 1
2 . Với mức ý nghĩa cho trước, hãy xác minh xem ý kiến nào úng.
b) Giải quyết bài toán: Chọn giả thiết H0 : 1 2 và ối thiết H1 là một trong các ý kiến còn lại.
Lập mẫu kích thước m về biến quan sát X , tính ược x s, x . Lập mẫu kích thước n
về biến quan sát Y , tính ược y s, y .
Bài toán ược giải quyết bằng việc chỉ ra miền bác bỏ giả thiết H0 tương ứng với
các trường hợp của ối thiết H1 ược cho trong bảng sau: 116
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736 Trư Bộ môn ờng hợp Toán – Trường ĐH.GTV Bài toán kiểm ịnh T TP. Hồ Chí Minh
Điều kiện b ác bỏ H0 Trong x y ó: H ; T 0 :
1 2 ; H1 : 1 2 T1 z 1 2 2 1 2 T Đã biết 2, 2 H 2 1 2 0 :
1 2 ; H1 : 1 2 T1 z m n
H0 : 1 2 ; H1 : 1 2 T1 z /2 x Chưa biết y
H0 : 1 2 ; H1 : 1 2 T2 z 1 1 . s m n H Khi 12,22 , 0 :
1 2 ; H1 : 1 2 T2 z 1 m 30,n 30
H0 : 1 2 ; H1 : 1 2 T2 z /2 2 thì T3 Chưa biết với s
H0 : 1 2 ; H1 : 1 2 T3 t ( )k 12,22 ,
H0 : 1 2 ; H1 : 1 2
T3 t ( )k m 30, n 30
H0 : 1 2 ; H1 : 1 2
T3 t /2 ( )k Khi 1 x y 2 thì T3 T2 2 2 s s
Bậc tự do k m n x y 2 m n
Ví dụ 4.6. Theo dõi giá cổ phiếu của
hai công ty A và B 2 2
trong 31 ngày (mỗi ngày một giá trị cho ( m 1) s ( n 1) x
sy mỗi công ty), người
ta tính ược các số liệu: m n 2 Trung bình mẫu
Độ lệch mẫu hiệu chỉnh Công ty A 38,24 2,2 Công ty B 37,10 1,5
Vậy với mức ý nghĩa 1%, có thể nói rằng có sự khác biệt thực sự về giá cổ phiếu
trung bình của hai công ty A và B hay không? (Giả sử các giá cổ phiếu có phân phối chuẩn). Giải. Gọi A,
B tương ứng là giá cổ phiếu trung bình của công ty A và công ty B.
Đặt giả thiết H0 : A B ; ối thiết H1 : A B Vì n 2 2 A nB 31 30 và
A ,B chưa biết nên ta tính thống kê
T xA xB 2,3838 2 2 sA s A nA nB Mức ý nghĩa 1% z /2 2,576
Xác suất thống kê và Ứng dụng – 2021 117 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Điều kiện T z /2 là sai nên chấp nhận giả thiết H0 , bác bỏ ối thiết H1 .
Kết luận: với mức ý nghĩa 1%, có thể nói rằng giá cổ phiếu trung bình của hai công
ty A và B là như nhau.
4.2.5. Bài toán kiểm ịnh so sánh hai tỉ lệ
a) Đặt bài toán: Giả sử p1 là tỉ lệ các phần tử có tính chất A trong tổng thể 1 và p2
là tỉ lệ các phần tử có tính chất B trong tổng thể 2 . Các tỉ lệ p1 và p2 chưa biết, nhưng
dựa vào những thông tin có ược, người ta có các ý kiến sau: p1 p2 ; p1 p2 ; p1 p p2;
1 p2 . Với mức ý nghĩa
cho trước, hãy xác minh xem ý kiến nào úng.
b) Giải quyết bài toán: Chọn giả thiết H0 : p1 p2 và ối thiết H1 là một trong các ý kiến còn lại.
Lập mẫu kích thước m quan sát tính chất A, tính ược tỉ lệ mẫu fm . Lập mẫu ngẫu
nhiên kích thước n quan sát tính chất B, tính ược tỉ lệ mẫu fn .
Khi ó bài toán ược giải quyết bằng việc chỉ ra miền bác bỏ giả thiết H0 tương ứng
với các trường hợp của ối thiết H1 ược cho trong bảng sau: Bài toán kiểm ịnh
Điều kiện bác bỏ H0
H0 : p1 p H2; 1 : p1 p2 T z
H0 : p1 p H2; 1 : p1 p2 T z
H0 : p1 p H2; 1 : p1 p2 T z /2 Trong ó: T fm fn ; f
m f. m n f. n f .(1 f ) 1 1 m n m n
Lưu ý: Các cỡ mẫu m n, phải thỏa mãn các iều kiện:
m f. m 5; m.(1 fm) 5
n f. n 5 ; n.(1 fn) 5
Ví dụ 4.7. Khảo sát một số sản phẩm cùng loại ở kho I và kho II, thu ược số liệu sau: Số sản phẩm Số phế phẩm 118
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Kho I 100 7 Kho II 200 24
a) Với mức ý nghĩa 5%, có thể nói rằng chất lượng hàng (tỉ lệ phế phẩm) ở hai kho là như nhau hay không?
b) Với mức ý nghĩa 1%, có thể nói rằng chất lượng hàng ở kho I tốt hơn kho II hay không?
Giải. Gọi p p1, 2 tương ứng là tỉ lệ phế phẩm ở kho I và kho II. Kho I:
Cỡ mẫu m 100, tỉ lệ mẫu (phế phẩm) fm 0,07 Kho
II: Cỡ mẫu n 200, tỉ lệ mẫu (phế phẩm) fn 0,12
f m f. m n f. n 31 m n 300 f Tính thống kê :T fm n 1,3412 f .(1 f ) 1 1 m n
a) Đặt giả thiết H0 : p1 p2 ; ối thiết H1 : p1 p2 Mức ý nghĩa 5% z /2 1,960
Điều kiện T z /2 là sai nên chấp nhận giả thiết H0 , bác bỏ ối thiết H1 .
Kết luận: với mức ý nghĩa 5%, có thể nói rằng chất lượng hàng ở hai kho là như nhau.
b) Đặt giả thiết H0 : p1 p2 ; ối thiết ối H1 : p1 p2 Mức ý nghĩa 1% z 2,326 Điều kiện T
z là sai nên chấp nhận H0 , bác bỏ H1 .
Kết luận: với mức ý nghĩa 1%, ta chưa thể nói rằng chất lượng hàng ở kho I tốt hơn kho II.
4.2.6. Kiểm ịnh giả thiết về tính ộc lập hai biến ngẫu nhiên
a) Đặt bài toán: Giả sử X Y, là hai biến quan sát trong cùng một tổng thể. Dựa vào
những thông tin có ược, người ta có các ý kiến sau: “ X và Y ộc lập nhau”; “ X và Y phụ
thuộc nhau”. Với mức ý nghĩa cho trước, hãy xác minh xem ý kiến nào úng.
Xác suất thống kê và Ứng dụng – 2021 119 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Giải quyết bài toán: Chọn giả thiết thống kê H0 : “ X và Y ộc lập nhau ”, ối thiết
H1 : “ X và Y phụ thuộc nhau”.
Lập mẫu ngẫu nhiên kích thước n về hai biến quan sát X và Y , bảng phân phối mẫu có dạng sau:
Trong ó x1,..., xk , y1,..., yh tương ứng là tập giá trị của X và của Y ; mi là số
lần X nhận xi , nj là số lần Y nhận yj ; nij là số lần ồng thời X nhận xi và Y
nhận yj (i 1,h, j 1,k ). m h i k nij ; nj
nij ; n m1 ... mh n1 ... nk j 1 i 1 Tính thống kê 0 n 2 n
i h1 jk1 mn iij2 j n
Tính phân vị khi bình phương 2 (k 1)(h 1) . ➢ Nếu 2 0
2 (k 1)(h 1) thì chấp nhận H0 , bác bỏ H1 .
➢ Nếu 2 (k 1)(h 1) 20 thì bác bỏ H0 , chấp nhận H1 . Lưu ý: Thống kê 2
0 còn ược tính theo công thức sau: 120
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 2 k h (nij
vij )2 , vij nmi j 0 i 1 j 1 vij n
Ví dụ 4.8. Trong một tổng công ty, theo dõi số ngày nghỉ việc trong 1 năm của 1000
công nhân ược kết quả sau:
Số ngày nghỉ việc trong năm Nữ Nam [0 – 10] 300 500 (10 – 20] 80 70 > 20 20 30
Với mức ý nghĩa 5%, dựa vào kết quả trên, hãy cho biết số ngày nghỉ việc có phụ
thuộc vào giới tính hay không?
Giải. Gọi X là số ngày nghỉ việc trong năm của một công nhân và Y là giới tính của công nhân ó.
Đặt giả thiết H0 : “ X và Y ộc lập” , ối thiết H1 : “ X và Y phụ thuộc nhau”. h k n 2 ij
9 25 8 49 1 3 1,01319 i 1 j 1 mni j 32 48 75 900 50 100 2 0 1000 (1,01319 1)13,19
Tính 2 (k 1)(h 1) , với k 3,h 2, 0,05 2 (k 1)(h 1) 2
0.05 (2) Chiinv(0.05,2) 5,9915
Ta thấy 2 (k 1)(h 1) 20 nên bác bỏ giả thiết H0 , chấp nhận ối thiết H1 .
Kết luận: với mức ý nghĩa 5% thì số ngày nghỉ việc phụ thuộc vào giới tính.
Xác suất thống kê và Ứng dụng – 2021 121 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh BÀI TẬP CHƯƠNG 4
Kiểm ịnh trung bình
4.1. Giả sử biến quan sát X N( , 2 ) với
5,2 . Lấy mẫu cỡ n 120và tính ược x
27,56. Với mức ý nghĩa 5%, hãy kiểm ịnh cặp giả thiết H0 : 26 và H1 : 26 .
4.2. Một loại phương tiện vận tải ược nhận ịnh là có mức tiêu thụ nhiên liệu bình quân
trên tuyến ường CD (khi chở úng trọng tải quy ịnh) là 200 lít. Qua theo dõi 100
chuyến vận tải trên tuyến CD ối với loại phương tiện này, có bảng số liệu về mức
tiêu thụ nhiên liệu X ( ơn vị: lít) như sau: X
[188;193) [193;198) [198;203) [203;208) [208;213) [213;218] Số chuyến 3 19 42 23 11 2
Với mức ý nghĩa 4%, hãy xác minh xem nhận ịnh nói trên có phù hợp với thực tế
hay không ? (giả sử X có phân phối chuẩn)
4.3. Một hãng sản xuất một loại sản phẩm công bố rằng thời gian hoạt ộng tốt của sản
phẩm của họ trong iều kiện bình thường trung bình lớn hơn 24,5 tháng. Một mẫu iều
tra về X (tháng) là thời gian hoạt ộng tốt của một số sản phẩm ã qua sử dụng của
hãng này ược cho trong bảng sau: X
[22;23) [23;24) [24;25) [25;26) [26;27) [27;28) [28;29] Số sp 9 26 50 70 52 9 4
Với mức ý nghĩa 3%, hãy xác minh xem công bố của hãng này có chấp nhận ược
hay không? (giả sử X có phân phối chuẩn)
4.4. Tiền vé X (triệu ồng/ ngày) thu ược hàng ngày ở một iểm du lịch là biến ngẫu nhiên
có phân phối chuẩn. Chính quyền ịa phương nhận ịnh rằng trung bình mỗi ngày tiền
bán vé thu ược chưa tới 4,91 triệu ồng. Qua theo dõi tiền vé thu ược một số ngày ở
iểm du lịch này, có bảng số liệu sau: X
[4,1;4,3) [4,3;4,5) [4,5;4,7) [4,7;4,9) [4,9;5,1) [5,1;5,3) [5,3;5,5] Số ngày 6 14 23 37 19 11 5
a) Với mức ý nghĩa 4%, hãy cho nhận xét về nhận ịnh nói trên của chính quyền ịa phương.
b) Những ngày có tiền vé chưa tới 4,5 triệu ược coi là “vắng khách”. Với mức ý nghĩa
3%, hãy kiểm ịnh giả thiết “tiền vé bình quân mỗi ngày vắng khách là 4,2 triệu ồng”.
4.5. Theo dõi thời gian hoàn thành T ( ơn vị: phút) của công việc A của một số công
nhân trong một công ty, có kết quả sau: 122
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Thời gian T [24;26) [26;28) [28;30) [30;32) [32;34) [34;36) [36;38] Số công nhân 59 10 20 55 35 12 3
a) Công ty ưa ra ịnh mức thời gian hoàn thành công việc A cho mỗi công nhân bình
quân là 28 phút. Với mức ý nghĩa 5%, có thể kết luận rằng ịnh mức của công ty gây
khó khăn cho công nhân hay không?
b) Trước ây thời gian hoàn thành công việc A cho mỗi công nhân bình quân là 31,5 phút
Số liệu trên ược thu thập sau khi áp dụng công nghệ mới. Với mức ý nghĩa 4%, có
thể kết luận rằng công nghệ mới làm rút ngắn thời gian bình quân hoàn thành công việc A hay không?
4.6. Số liệu thống kê về doanh thu ( ơn vị: triệu ồng/ngày) mỗi ngày của một siêu thị như sau:
Doanh thu Số ngày Doanh số Số ngày [20;40) 2 [80;90) 15 [40;50) 3 [90;100) 10 [50;60) 6 [100;110) 8 [60;70) 8 [110;130] 3 [70;80) 10
Trước ây doanh thu trung bình 73 triệu ồng/ngày. Số liệu trên ược thu thập sau khi
siêu thị áp dụng phương thức bán hàng mới. Với mức ý nghĩa 2%, có thể kết luận rằng
phương thức bán hàng mới là tăng doanh thu mỗi ngày của siêu thị hay không?
4.7. Hãng H sản xuất một loại xe máy nhận ịnh rằng mức tiêu hao nhiên liệu X ( ơn vị:
lít/km), khi xe lưu thông bình thường trên tuyến ường AB, trung bình là 0,018
(lít/km). Theo dõi 200 xe máy của hãng H chạy trên tuyến ường AB có kết quả sau.
Giả sử X có phân phối chuẩn.
a) Với mức ý nghĩa 1%, hãy cho biết nhận ịnh của X (lít/km) Số xe
hãng H có phù hợp với thực tế hay không? [0,014 ; 0,016) 15
b) Có ý kiến cho rằng mức tiêu hao nhiên liệu trung [0,016 ; 0,018) 35
bình là hơn 0,019 (lít/km). Với mức ý nghĩa 3%, [0,018 ; 0,020) 75
hãy xác minh ý kiến trên. [0,020 ; 0,022) 45 [0,022 ; 0,024) 20
Kiểm ịnh tỷ lệ [0,024 ; 0,026] 10
4.8. Theo báo cáo, tỉ lệ phế phẩm trong kho hàng là 10%.
Kiểm tra ngẫu nhiên 250 sản phẩm thấy có 38 phế phẩm. Hỏi báo cáo trên có chấp
nhận ược ở mức ý nghĩa 5% hay không ?
Xác suất thống kê và Ứng dụng – 2021 123 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
4.9. Tỉ lệ phế phẩm trước ây là 7%. Sau khi áp dụng kỹ thuật mới, người ta chọn ngẫu
nhiên 200 sản phẩm ể kiểm tra thì thấy có 9 phế phẩm. Với mức ý nghĩa 5%, có thể
kết luận rằng việc áp dụng kỹ thuật mới có hiệu quả hơn hay không ?
4.10. Một hãng sản xuất yêu cầu các phân xưởng trực thuộc phải có tỉ lệ sản phẩm ạt
tiêu chuẩn xuất khẩu không nhỏ hơn 75%. Một mẫu ngẫu nhiên với 500 sản phẩm
của phân xưởng A ược kiểm tra cho thấy số sản phẩm ạt tiêu chuẩn xuất khẩu là 360
sản phẩm.Với mức ý nghĩa 5%, hãy xác minh xem phân xưởng A ã áp ứng ược yêu
cầu nói trên của hãng hay không?
Kiểm ịnh phương sai
4.11. Độ bền chịu nén X ( ơn vị: kg/cm2 ) của một loại bê tông K do một xưởng bê tông
sản xuất là biến ngẫu nhiên có phân phối chuẩn. Đo ộ bền chịu nén của 160 mẫu bê tông, có kết quả sau: X
[200;203) [203;206) [206;209) [209;212) [212;215) [215;218] Số mẫu 8 28 54 40 23 7
a) Xưởng bê tông nhận ịnh rằng ộ bền chịu nén của loại bê tông K có ộ lệch chuẩn
là 3,464 (kg/cm2). Với mức ý nghĩa 4%, nhận ịnh của xưởng bê tông có chấp nhận ược không?
b) Trước ây ộ lệch của ộ bền chịu nén của bê tông K là 4,1kg/cm2 (3,2 kg/cm2). Số
liệu trên thu thập ược sau khi áp dụng công nghệ sản xuất mới. Với mức ý nghĩa
3%, hãy xét xem công nghệ mới mới có làm ộ bền chịu nén của bê tông K ít biến
ộng hơn (biến ộng hơn) so với trước ây hay không?
4.12. Đem cân một số trái cây T vừa thu hoạch, có kết quả sau:
Trọng lượng (g) [200-210) [210-220) [220-230) [230-240) [240-250] Số trái 12 17 20 18 15
Trước ây trọng lượng trung bình của trái cây T là 221 (gam) và ộ lệch chuẩn là
15,1 (gam). Số liệu trên ược thu thập sau khi sử dụng một loại phân bón mới.
a) Với mức ý nghĩa 5%, có thể kết luận phân bón mới làm tăng trọng lượng trung
bình của trái cây T hay không?
b) Với mức ý nghĩa 4%, có thể kết luận phân bón mới làm cho trái cây T có trọng
lượng ồng ều hơn hay không?
Kiểm ịnh so sánh hai trung bình
4.13. Cự ly bay xa trung bình của 10 viên ạn sau khi cải tiến việc pha chế thuốc súng là 68,9 km với s 2 1
49,7 . Cự ly bay xa trung bình của 9 viên ạn cùng loại này trước
khi cải tiến việc pha chế thuốc súng là 61,52 km với s 2 2 58,8 . Hãy ánh giá hiệu 124
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
quả của việc cải tiến pha chế thuốc với mức ý nghĩa 5% (giả sử cự ly bay xa của
viên ạn trước và sau khi cải tiến thuốc súng có phân phôi chuẩn).
4.14. Điều tra về tuổi thọ trung bình của một loại linh kiện iện tử, người ta có kết quả
sau: với 248 linh kiện ã qua sử dụng do hãng A sản xuất thì tuổi thọ trung bình của
chúng là 3450 giờ, ộ lệch mẫu trên ó là 105 giờ. Với 295 linh kiện ã qua sử dụng do
hãng B sản xuất thì tuổi thọ trung bình của chúng là 3465 giờ, ộ lệch mẫu trên ó là
100 giờ. Với mức ý nghĩa 2%, hãy xác minh xem có sự khác nhau về tuổi thọ trung
bình của loại linh kiện này của hai hãng A và B hay không?
4.15. Bảng số liệu thống kê của công ty dịch vụ B&G về nhu cầu tiêu dùng (X -
kg/tháng) của sản phẩm K tại ịa phương A như sau: X (kg) 0
[1;3) [3;5) [5;7) [7;9) [9;11) [11;13) Số hộ 15 18 25 26 13 9 4
a) Hãy ước lượng khoảng tin cậy ối xứng cho tỷ lệ hộ gia ình có nhu cầu tiêu dùng sản phẩm K.
b) Công ty cũng tiến hành khảo sát nhu cầu tiêu dùng sản phẩm K trên một mẫu
gồm 200 hộ tại ịa phương B; ược các số liệu mẫu như sau: trung bình mẫu xB
6,5 kg; phương sai mẫu s 2 B
5,5, công ty ưa ra kết luận rằng nhu cầu tiêu dùng
về sản phẩm K ở hai ịa phương là khác nhau; kết luận này có chấp nhận ược
không, với mức ý nghĩa 5% ?
4.16. Một hãng hàng không giá rẻ A khẳng ịnh rằng “thời gian khởi hành bị trễ X (phút)
so với lịch bay trung bình mỗi chuyến là không quá 30 phút”. Theo dõi 200 chuyến
bay của hãng A, có kết quả cho trong bảng sau: X
[0-20) [20-30) [30-40) [40-50) [50-60) [60-90] Số chuyến 30 90 40 20 16 4
a) Với ộ tin cậy 98%, dựa vào kết quả quan sát, hãy tìm khoảng tin cậy ối xứng
cho tỷ lệ các chuyến bay của hãng A có thời gian khởi hành trễ chưa tới 40 phút.
b) Theo dõi 150 chuyến bay của hãng hàng không giá rẻ B, tính ược thời gian khởi
hành bị trễ so với lịch bay bình quân là 27,23 phút và ộ lệch mẫu hiệu chỉnh trên
ó là 12 phút. Với mức ý nghĩa 4%, hãy so sánh thời gian khởi hành bị trễ so với
lịch bay bình quân của hai hãng A và B.
Kiểm ịnh so sánh hai tỉ lệ
4.17. Kiểm tra 100 sản phẩm ở kho thứ nhất thấy có 8 phế phẩm. Kiểm tra 100 sản
phẩm ở kho thứ hai thấy có 12 phế phẩm. Hãy cho kết luận về chất lượng hàng ở hai kho ở mức ý nghĩa 5%?
4.18. Từ àn gia súc chọn ngẫu nhiên 800 con xét nghiệm thấy có 120 con mắc bệnh A.
Cũng với àn gia súc cùng loại khác, xét nghiệm 1000 con thấy có 180 con mắc bệnh
Xác suất thống kê và Ứng dụng – 2021 125 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
A. Với mức ý nghĩa 5%, có thể coi tỉ lệ mắc bệnh A của hai àn gia súc là như nhau hay không?
4.19. Theo dõi trọng lượng của một số trẻ sơ sinh tại một số nhà hộ sinh ở thành phố và
ở nông thôn, người ta thấy: trong số 150 trẻ sơ sinh ở thành phố có 100 cháu nặng
hơn 3 kg, trong số 200 trẻ sơ sinh ở nông thôn có 98 cháu nặng hơn 3 kg. Với mức
ý nghĩa 2% có thể kết luận rằng tỉ lệ trẻ sơ sinh có trọng lượng trên 3 kg ở thành phố
lớn hơn ở nông thôn hay không?
4.20. Chỉ số ường huyết X (mg/dl) trước bữa ăn của một nhóm người trong ộ tuổi từ 20 ến 30 tuổi như sau: X (mg/dl) [60,80)
[80,100) [100,120) [120,140) [140,160] Số người 20 35 66 44 35
a) Dựa vào bảng trên hãy ước lượng khoảng tin cậy ối xứng cho chỉ số ường huyết
trung bình của những người trong ộ tuổi trên với ộ tin cậy 97%.
b) Nếu chỉ số ường huyết nằm ngoài khoảng [80;140) thì sẽ có nguy cơ mắc bệnh
tiểu ường. Hãy ước lượng khoảng tin cậy ối xứng cho tỷ lệ người có nguy cơ
mắc bệnh tiểu ường trong ộ tuổi trên với ộ tin cậy 95%.
c) Khảo sát chỉ số ường huyết của một nhóm 300 người trong ộ tuổi 30 ến 40 thì
thấy có 78 người có nguy cơ mắc bệnh tiểu ường; dựa vào kết quả này, có thể
cho rằng tỉ lệ người có nguy cơ mắc bệnh tiểu ường ở hai nhóm là giống nhau không, mức ý nghĩa 5%?
Kiểm ịnh về tính ộc lập các biến ngẫu nhiên
4.21. Điều tra một số người dùng và không dùng cà phê ta có bảng kết quả sau: Có Dùng cà phê Không Có 42 68 Không 25 65 Mất ngủ
Với mức ý nghĩa 1%, xét xem cà phê có gây mất ngủ hay không?
4.22. Bảng số liệu iều tra về tình hình học tập của 10000 sinh viên của một trường ại học như sau: Giỏi Khá TB và kém Nam 1620 2680 2500 Nữ 880 1320 1000
Với mức ý nghĩa 3%, xét xem có sự khác biệt về chất lượng học tập của nam và nữ hay không?
4.23. Quan sát 100 sản phẩm ược sản xuất ở ba ca sáng, chiều, tối ta ược các số liệu cho trong bảng sau: 126
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Ca Chất lượng Sáng Chiều Tối Tốt 23 32 28 Phế phẩm 7 6 4
Với mức ý nghiã 5% có thể kết luận rằng: Chất lượng sản phẩm không phụ thuộc
vào ca sản xuất ược không ?
4.24. Khảo sát màu mắt và màu tóc của 6800 người Pháp có ta ược kết quả sau: Màu tóc Vàng Nâu Đen Hung Màu mắt Xanh 1768 807 189 47 Đen 946 1387 746 53 Nâu 115 438 288 16
Với mức ý nghĩa 5% hãy cho biết màu tóc ộc và màu mắt có ộc lập nhau không?
Bài tập tổng hợp
4.25. Thời gian chờ phục vụ (phút) của mỗi khách hàng ở hệ thống phục vụ A và hệ
thống phục vụ B tương ứng là các biến ngẫu nhiên X Y, có phân phối chuẩn. Theo
dõi thời gian chờ phục vụ của một số khách hàng của hai hệ thống phục vụ này cho kết quả sau: X (phút)
[5;10) [10;15) [15;20) [20;25) [25;30) [30;35) [35;40] Số khách 6 14 50 70 40 15 5 Y (phút)
[5;10) [10;15) [15;20) [20;25) [25;30) [30;35) [35;40) Số khách 10 25 65 75 50 20 5
a) Với mức ý nghĩa 5%, có thể kết luận rằng thời gian chờ phục vụ của mỗi khách
hàng ở hệ thống phục vụ A trung bình chưa tới 25 phút hay không?
b) Với mức ý nghĩa 3%, có thể cho rằng hệ B phục vụ nhanh hơn hệ A không?
c) Với mức ý nghĩa 4%, hãy xác minh khẳng ịnh “có hơn 60% khách hàng của hệ
thống phục vụ A có thời gian chờ phục vụ chưa tới 25 phút”.
d) Với mức ý nghĩa 2%, có thể cho rằng tỉ lệ khách hàng có thời gian chờ phục vụ
chưa tới 20 phút ở hệ B cao hơn ở hệ A hay không ?
4.26. Chiều cao của một giống cây trồng là biến ngẫu nhiên X (cm) có phân phối chuẩn.
Với phương pháp canh tác mới, người ta quan sát một mẫu và có kết quả cho bảng
sau. Những cây trồng có chiều cao 105 X 125 ược gọi là những “cây loại A”.
Xác suất thống kê và Ứng dụng – 2021 127 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
X (cm) [95;105) [105;115) [115;125) [125;135) [135;145) [145;155) [155;165] Số cây 10 10 15 30 10 10 15
a) Một báo cáo cho rằng chiều cao trung bình của giống cây trên sau khi áp dụng
phương pháp mới là 127cm (hơn 125 cm ; chưa tới 134 cm). Hãy cho kết luận về
báo cáo này với mức ý nghĩa 2%.
b) Trước ây bằng phương pháp canh tác cũ, người ta tính ược chiều cao trung bình của
những cây loại A là 114,7 cm (là 118,5 cm). Hãy kết luận xem phương pháp canh
tác mới có làm giảm tăng (làm giảm) chiều cao trung bình của cây loại A hay không với mức ý nghĩa 4%?
c) Trước ây bằng phương pháp canh tác cũ, người ta tính ược tỷ lệ cây loại A là
20,2% (28,7%). Hãy kết luận xem phương pháp mới có làm tăng (làm giảm) tỷ lệ
cây loại A hay không với mức ý nghĩa 3%?
d) Khi canh tác theo phương pháp cũ thì phương sai của chiều cao X là 300 cm2. Hãy
nhận ịnh về tình hình canh tác mới với mức ý nghĩa 4%.
e) Trước ây bằng phương pháp canh tác cũ, phương sai của chiều cao X là 350 cm2
(310 cm2). Với mức ý nghĩa 5%, hãy xét xem phương pháp canh tác mới có làm
chiều cao của giống cây trồng trên ít biến ộng hơn (biến ộng hơn) so với phương pháp cũ hay không?
4.27. Để khảo sát ường kính của một chi tiết máy, người ta kiểm tra một số sản phẩm
của hai nhà máy. Trong kết quả sau ây, X Y, (cùng ơn vị: cm) tương ứng là ường kính
của chi tiết máy do nhà máy I, nhà máy II sản xuất. Những sản phẩm có chi tiết máy
nhỏ hơn 19cm ược xếp vào loại C. X (cm)
[11;15) [15;19) [19;23) [23;27) [27;31) [31;35) [35;39] Số sản phẩm 9 19 20 26 16 13 18 Y (cm)
[13;16) [16;19) [19;22) [22;25) [25;28) [28;31) [31;34] Số sản phẩm 10 13 25 26 18 15 11
a) Có thể kết luận rằng ường kính trung bình của chi tiết máy do hai nhà máy sản xuất
bằng nhau hay không với mức ý nghĩa 2%?
b) Có thể cho rằng ường kính trung bình của chi tiết máy do nhà máy I sản xuất lớn
hơn ường kính trung bình của chi tiết máy do nhà máy II sản xuất hay không với mức ý nghĩa 3%?
c) Với mức ý nghĩa 4%, tỉ lệ sản phẩm loại C do hai nhà máy sản xuất có như nhau hay không? 128
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
d) Với mức ý nghĩa 1%, có thể cho rằng tỉ lệ sản phẩm loại C do nhà máy I sản xuất
lớn hơn tỉ lệ sản phẩm loại C do nhà máy II sản xuất hay không?
CHƯƠNG 5 XỬ LÝ SỐ LIỆU THỰC NGHIỆM
Trong thực tế, hầu hết các quy luật, các hiện tượng trong Kinh tế, Xã hội, Kỹ
thuật,… chúng ta hoàn toàn không biết một cách chính xác ược. Dựa vào các số liệu
thực nghiệm về ối tượng nghiên cứu và áp dụng các công cụ toán học, chúng ta xây
dựng các mô hình toán học phù hợp. Từ các mô hình này, sẽ ước lượng các giá trị hay
các quy luật của hiện tượng ược nghiên cứu.
Các vấn ề ược ặt ra là:
1) Số liệu thực nghiệm ã ược làm sạch chưa (có áng tin cậy không)?
2) Các mô hình ược lựa chọn có phù hợp không?
3) Các giá trị ước lượng cho ại lượng nghiên cứu có tốt nhất ứng với mô hình ược lựa
chọn không (sai số có nhỏ nhất không)?...
Giải quyết các vấn ề trên ược gọi là xử lý số liệu thực nghiệm.
5.1. Sai số và khử sai số
5.1.1. Các loại sai số số liệu thực nghiệm thường gặp
Trong thực tế, các số liệu thực nghiệm thường chứa sai số. Các sai số này thường
ược chia làm 3 loại chính sau:
a) Sai số hệ thống: là sai số do các nguyên nhân sau gây ra:
Cách sử dụng dụng cụ o không hợp lý
Bản thân dụng cụ o có khuyết iểm
Điều kiện o lường bị thay ổi (chẳng hạn: nhiệt ộ môi trường có tác ộng ến kết
quả thực nghiệm và nó biến ổi theo một quy luật nào ó)
Không hiểu biết kỹ lưỡng về tính chất của ối tượng cần o …
Trị số của sai số hệ thống thường cố ịnh hoặc là biến ổi theo quy luật vì nói chung
những nguyên nhân tạo nên nó cũng là những nguyên nhân cố ịnh hoặc biến ổi theo quy
luật. Vì vậy, thông thường các kết quả thực nghiệm ều xem như ã phát hiện sai số hệ thống và ã loại bỏ.
Xác suất thống kê và Ứng dụng – 2021 129 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Sai số ngẫu nhiên: Trong quá trình o lường, những sai số mà không thể tránh khỏi
gây bởi sự không chính xác tất yếu do các nhân tố hoàn toàn ngẫu nhiên gây ra ược
gọi là sai số ngẫu nhiên.
Sự xuất hiện mỗi sai số ngẫu nhiên là riêng biệt và không có quy luật. Nguyên
nhân gây sai số ngẫu nhiên là do những biến ổi rất nhỏ thuộc rất nhiều mặt không có
liên quan với nhau xảy ra trong khi o lường, mà ta không có cách nào tính trước ược.
Vì vậy chúng ta thừa nhận sự tồn tại của sai số ngẫu nhiên và tìm cách tính toán trị số
của nó chứ không thể tìm kiếm và khử các nhuyên nhân gây ra nó.
c) Sai số thô: Trong quá trình o lường, những sai số do vi phạm iều kiện cơ bản trong
thực nghiệm, hay do sơ xuất của người thực hiện (như: ọc sai, ghi chép sai, thao tác
sai, vô ý làm sai,…) ược gọi là sai số thô. Sai số ó làm cho số o ược khác hẳn với các
số o khác, thường có trị số rất lớn hoặc rất nhỏ (outlier) và hoàn toàn không có quy luật.
Khi phát hiện sai số thô, cần bỏ ngay kết quả và thực hiện lại công việc (nếu iều
kiện cho phép), hoặc thực hiện các phương pháp toán học loại bỏ sai số thô với ộ tin
cậy và hiệu quả nhất ịnh sao cho bảng số liệu cuối cùng ảm bảo không còn sai số thô.
5.1.2. Biểu diễn giá trị o và sai số o
Giả sử cần ước lượng iểm cho tham số của một ại lượng X , người ta tiến hành
o n lần, các giá trị thu ược ký hiệu là: x x1, 2,..., xn (các giá trị này ược ghi chép trực tiếp
từ mỗi lần o nên chúng có thể trùng nhau, và gọi là số liệu thô). Khi ó giá trị ước lượng iểm của là: x x , ta viết: x x Trong ó: 1 x
n xi là giá trị trung bình mẫu. n 1 s x
là sai số chuẩn (Standard n 1 n 2 ( x x ) n 1 i i 1
Error) s là ộ lệch mẫu hiệu chỉnh
Lưu ý: Khi o nhiều lần cho cùng một ại lượng X , ta tính trung bình của các lần o, khi ó
sai số chuẩn x chính là ộ lệch chuẩn của các trung bình. Trong khi ó s lại cho biết mức
ộ phân tán (mức ộ trải rộng) của các giá trị o trong cùng một mẫu so với giá trị trung bình x . 130
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 5.1. Đo chiều dài của một ại lượng X mười lăm lần với các kết quả o như sau: 17,62 17,62 17,615 17,62 17,61 17,61 17,62 17,625 17,62 17,6
17,61 17,615 17,61 17,605 17,61
Trung bình mẫu: x 1 n xi 17,614 n 1
Độ lệch chuẩn mẫu hiệu chỉnh: s 1 n (xi x)2 0,00687 n 1 i 1 s Sai số chuẩn: x 0,002 n
Vậy ước lượng tốt nhất cho chiều dài của ại lượng X là: x 17,614 0,002
5.1.3. Một số phương pháp khử sai số thô
Khi thu ược kết quả thực nghiệm, ta nhận ra một vài kết quả khác bất thường so
với các kết quả khác (outlier) như quá lớn hoặc quá nhỏ, khi ó các số liệu này có thể
chứa sai số thô.
Sự hiện diện của outlier có thể do lỗi trong quá trình lấy mẫu chẳng hạn như do sai
lệch của dụng cụ, do phương pháp o, hoặc một ý kiến ược ghi nhận một cách sai lệch,
hoặc khi dữ liệu không phù hợp với các giả thuyết ề ra.
Các outlier có thể ược xử lí như sau:
(1) Giữ nguyên, xem như các iểm dữ liệu bình thường.
(2) Thay ổi giá trị ể nó gần các iểm dữ liệu khác.
(3) Loại bỏ nó khỏi mẫu.
Các cách trên ều có nguy cơ làm cho ước lượng ta quan tâm bị kém chính xác,
thậm chí hoàn toàn sai lệch. Cách (2) và (3) có thể làm ước lượng bị chệch, trong khi ó,
cách (1) có thể làm cho ước lượng bị thay ổi áng kể so với giá trị tham số tổng thể. Do
ó, phải cẩn thận khi ánh giá các giá trị áng ngờ này bằng các phương pháp thống kê phù
hợp trước khi i ến quyết ịnh có loại bỏ chúng hay không.
Giả sử ta có một mẫu gồm n số liệu thực nghiệm cho một ại lượng nghiên cứu nào
ó là : x x1, 2,..., xn , trong ó có chứa số liệu bất thường xi . Có nhiều phương pháp ể xác
ịnh xem ó có phải là một outlier hay không. a) Quy tắc kinh nghiệm
Tính các ặc trưng : n x s, ,
Xác suất thống kê và Ứng dụng – 2021 131 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Nếu ộ lệch tuyệt ối giữa xi so với trung bình mẫu x mà lớn hơn 3s thì xi ược xem là
một outlier (tức là xi chứa sai số thô), nghĩa là :
| xi x | 3s
b) Phương pháp IQR (inter quartile range)
Phương pháp này sử dụng khoảng giữa tứ phân vị thứ nhất q1 và thứ ba q3 ể tìm
outlier. Khi thực hành trên mẫu, ta thường quan tâm ến năm chỉ số : min,q q q1, 2, 3,max
do ó, phương pháp này khá thông dụng. Quy tắc xác ịnh outlier như sau:
Giá trị xi là một outlier nếu thỏa:
xi [q1 1,5IQR q; 3 1,5IQR] Ngược
lại, xi không phải là một outlier. Trong ó:
IQR q3 q1
Công thức tính các tứ phân vị:
Sắp xếp các số liệu xi theo thứ tự có giá trị không giảm, giả sử:
x1 x2 ... xn Các
tứ phân vị ược tính theo công thức sau:
qi xki 1 r xi.( ki 2 xki 1) ; i 1,2,3 Trong ó:
ki [(n 1)ai ] - là phần nguyên của (n 1)ai .
ri {(n 1)ai} - là phần lẻ của (n 1)ai . a1
0,25; a2 0,5; a3 0,75.
Có thể sử dụng hàm Excel: qi quartile(array i, ) c)
Phương pháp hiệu chỉnh Thompson (tau): Các bước thực hiện:
Tính các ặc trưng : n x s, , Tính giá trị tau: (n 1).t n /22
n n 2 (t n /22 )2 132
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Tính ộ lệch tuyệt ối i | xi x |. Điểm dữ liệu có i lớn nhất là iểm áng nghi là một outlier nhất.
• Nếu i s thì iểm dữ liệu là một outlier.
• Nếu i s thì iểm dữ liệu không phải là outlier.
Trong ó: là mức ý nghĩa cho trước; t n 2
/2 là phân vị của phân phối Student, ược
tính bởi hàm Excel: t n 2 /2 tinv( ,n 2) .
Như vậy với phương pháp này, ta sẽ xét từng iểm dữ liệu. Đương nhiên khi iểm
dữ liệu có ộ lệch tuyệt ối lớn nhất không phải là outlier thì các iểm còn lại cũng không
phải. Khi có xk nào ó là outlier, ta sẽ loại bỏ nó ra khỏi mẫu, lần lượt thực hiện lại các
bước trên (tính lại x s, , ) cho tới khi tất cả outlier trong mẫu bị loại bỏ.
d) Phương pháp MAD (median absolute deviation):
Khác với những phương pháp trước thường quan tâm ộ lệch so với trung bình
mẫu, phương pháp này chỉ quan tâm ộ lệch so với giá trị trung vị q2 medX (cũng là giá
trị tứ phân vị thứ hai). Việc sử dụng trung vị giúp xử lí ược bài toán ngay cả khi mẫu có
chứa giá trị vô hạn. Do ó, giá trị MAD có tính vững (robust) tức là sẽ không bị ảnh hưởng
nhiều cho dù mẫu có chứa outlier. Giá trị MAD có công thức sau: MAD b Med. | xi q2 |
Trong ó b 1,4826 nếu mẫu ược chọn từ tổng thể có phân phối chuẩn; và b q 1 3 ,
(q3 là giá trị tứ phân vị thứ ba) nếu mẫu ược chọn từ tổng thể có phân phối khác.
Khi ó, những giá trị xi thỏa: | xi q2 | 3MAD là outlier.
Ngoài các phương pháp trên còn có rất nhiều phương pháp khác như: Dixon,
Chauvenet, Grubbs, Cochran, Brown-Forsythe,…
Ví dụ 5.2. Cho mẫu thực nghiệm có n 24 số liệu trong bảng sau.
145 155 153 158 161 148 155 154
147 146 155 159 160 172 160 156
157 153 147 154 157 158 149 152
Hãy chỉ ra các số liệu chứa sai số thô (nếu có) :
Xác suất thống kê và Ứng dụng – 2021 133 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
a) Bằng quy tắc kinh nghiệm.
b) Bằng phương pháp IQR.
c) Bằng phương pháp Thompson với mức ý nghĩa 5% .
d) Bằng phương pháp MAD, biết rằng mẫu ược chọn từ tổng thể có phân phối chuẩn.
Giải. Ta có: n 24; x 154,625; s 5,9986
a) Sắp xếp số liệu mẫu theo thứ tự có giá trị không giảm:
145 146 147 147 148 149 152 153
153 154 154 155 155 155 156 157
157 158 158 159 160 160 161 172
Khi số liệu thực nghiệm ã ược sắp thứ tự, ta lần lượt xét các số từ biên vào trong
của dãy số liệu (các số có ộ lệch tuyệt ối lớn). Số x1 145 có
| x1 x | 9,625 3s 17,9958 Số x24 172 có
| x24 x | 17,375 3s
Vậy dãy số liệu thực nghiệm không chứa outlier. b)
Tính các tứ phân vị q q1, 3 Tính q1 :
k1 [(24 1).0,25] [5,75] 5; r1 {5,75} 0,75
q1 x6 0,75(x7 x6) 149 0,75(152 149) 151,25
Tính q3 : k3 [(24 1).0,75] [17,25] 17; r3 {17,25} 0,25
q3 x18 0,25(x19 x18) 158 Ta
có: IQR q3 q1 6,75
[a b, ] [q1 1,5IQR q; 3 1,5IQR] [141,125;168,125]
Trong 24 số liệu mẫu, chỉ có số liệu 172 [a b, ] .
Vậy chỉ có 172 là một outlier.
c) n 24; x 154,625; s 5,9986
t n /22 t0.02522 tinv(0.05,22) 2,0739 (n 1).t n /22 1,899
n n 2 (t n /22 )2 134
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Xét số liệu xi 172 , ta có : i 17,375 s 11,3913.
Dó số liệu 172 là một outlier.
Ta sẽ kiểm tra tiếp giá trị có ộ lệch tuyệt ối lớn tiếp theo là 145, ể ý các ặc trưng mẫu
mới là: n 23; x 153,870; s 4,827 t n 2 21 /2 t0.025 tinv(0.05,21) 2,0796 1,896 Có i 8,87
s 9,152 nên 145 không phải là outlier; do vậy tất cả những iểm
còn lại trong mẫu ều không phải outlier. d) Tính q2 , ta có :
k2 [(24 1).0,5] [11,5] 11; r2 {11,5} 0,5
Sayra: q2 x12 0,5(x13 x12) 155 0,5(155 155) 155
| xi q2 | | xi 155 |
10;9;8;8;7;6;3;2;2;1;1;0;0;0;1;2;2;3;3;4;5;5;6;17
0;0;0;1;1;1;2;2;2;2;3;3;3;4;5;5;6;6;7;8;8;9;10;17
{y y1, 2,..., y24} Tính Med | xi q2 | : Med | xi q2 | y120,5(y 13 y12) 3 Suy ra:
3MAD 31,4826 3 13,3434
Như vậy, theo phương pháp này, giá trị 172 vẫn là một outlier vì có |172 q2 | 17
3MAD, các giá trị còn lại không phải là outlier.
5.2. Xác ịnh phân phối của số liệu thực nghiệm
Căn cứ vào kết quả thực nghiệm, ta cần xác ịnh rõ dãy số liệu này tuân theo luật
phân phối nào, thường là phân phối chuẩn, Piosson, mũ.
5.2.1. Phương pháp chung
a) Mô tả phương pháp
Giả sử dấu hiệu quan sát X của tổng thể có luật phân phối xác suất FX ( )x chưa
biết. Với mức ý nghĩa , từ mẫu quan sát (x1,..., xn) kiểm ịnh cặp giả thiết
H0 : FX ( )x F*( )x và ối thiết H1 : FX ( )x F*( )x . Trong ó F*( )x là luật phân phối xác suất ã biết.
Xác suất thống kê và Ứng dụng – 2021 135 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Để kiểm ịnh, ta dựa trên tiêu chuẩn phù hợp của Pearson. Tiêu chuẩn này ược xây
dựng dựa trên cơ sở so sánh tần số thực nghiệm và tần số lý thuyết của phân phối xác suất cần kiểm ịnh.
Xét mẫu ngẫu nhiên (X1,..., X n ), lập bảng: Lớp L L Tổng Tần số 1 k Thực nghiệm 1 N N k n Lý thuyết * * 1 N N k n Trong ó:
Ni là tần số thực nghiệm của lớp Li .
N *i là tần số lý thuyết của lớp Li khi H0 úng. N * * i
n p. *i , với pi P X( Li / H0 úng)
Xây dựng thống kê: G k
(Ni N* i*)2 i 1 Ni b) Định lý Pearson
Thống kê G có luật phân phối Chi bình phương với k r 1 bậc tự do, nghĩa là:
G 2 (k r 1).
Trong ó: r là số tham số của luật phân phối F*( )x c)
Quy tắc thực hành
Giả sử mẫu thu ược gồm k lớp có dạng:
xi x0 x1 x1 x2 ... xi 1 xi ... xk 1 xk ni n1 n2 ... ni ... nk
Kích thước mẫu: n n1 n2 ... nk .
Trường hợp biến quan sát X là rời rạc, ta thay khoảng xi 1 xi bởi giá trị
xi/ xi 1 xi . 2
Trường hợp biến quan sát X là liên tục, ta thay khoảng ầu x0 x1 bằng ( , x1) và
thay khoảng cuối xk 1 xk bằng (xk 1, ).
Dựa vào phân phối lý thuyết F*( )x , tính các xác suất sau: 136
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh p / * i*
P X xi nếu X rời rạc pi P x i 1
X xi nếu X liên tục Điều kiện ể kiểm ịnh có ý nghĩa là:
Tần số lý thuyết n * * i npi 1, i
Nếu có những lớp mà n * i
1 thì ta thực hiện ghép lớp này vào các lớp liền kề ể cho n * i 1. Tính thống kê: k (ni npi* )2 g i 1 npi*
Với mức ý nghĩa , tính giá trị phân vị 2 (k r 1) theo công thức Excel: 2 (k r
1) chiinv( ,k r 1) - Nếu g 2 (k r
1) thì bác bỏ H0 , chấp nhận H1 . - Nếu g 2 (k r
1) thì chấp nhận H0 , bác bỏ H1 .
Lưu ý: Từ các công thức n * 1
... nk n và p1 ... p*k 1, ta có: g k ni2 2nn pi i* n p2 i*2 i np k ni2 2 k k 2 ni n k pi* n i g * i 1 *
i 1 npi* i 1 i 1 n n i 1 i Suy ra:
5.2.2. Kiểm ịnh luật phân phối chuẩn, mũ, Poisson
a) Phân phối chuẩn
- Giả thiết H0 : X có phân phối chuẩn N( , 2 )
- Số tham số: r 2 - Các ước lượng: x (trung bình mẫu) 2 sˆ 2
x (phương sai mẫu)
Xác suất thống kê và Ứng dụng – 2021 137 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
- Công thức xác suất theo phân phối chuẩn N(
, 2 ) pi* P x i 1 X xi xi xi 1
Trong ó: ( )x 1 x e t2/2dt 2 0 b) Phân phối mũ
- Giả thiết H0 : X có phân phối mũ E( ) - Số tham số: r 1 - Ước lượng: n 1 n x
- Các xác suất ược tính theo phân phối mũ E( ) pi* P x i 1 X xi F*(xi ) F*(xi 1) 1 e , x 0
Trong ó F *( )x x
là hàm phân phối của phân phối mũ E( ) . 0 , x 0
c) Phân phối Poisson
- Giả thiết H0 : X có phân phối Poisson P( ) - Số tham số: r 1 - Ước lượng: x k
- Công thức xác suất: pi* P X k e k!
Ví dụ 5.3. Đo ường kính ( X : mm) của một số sản phẩm tiện cùng loại có kết quả trong bảng bên. Đường kính X Số sp ni Đường kính X Số sp ni [20,0;20,1) 9 [20,4;20,5) 27 138
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh [20,1;20,2) 18 [20,5;20,6) 11 [20,2;20,3) 40 [20,6;20,7) 6 [20,3;20,4) 55 [20,7;20,8] 2
Với mức ý nghĩa 3%, có thể coi dãy số liệu bên tuân theo luật phân phối chuẩn không?
Giải. Tính các ặc trưng mẫu:
n 168; x 1 n x 2 i 1 n x i 20,3333 ; sˆx
i ( i x)2 (0,14337)2 . n n
Kiểm ịnh cặp giả thiết:
H0 : X có phân phối chuẩn N( , 2 ) ,
H1 : X không có phân phối chuẩn N( , 2 ) . Ước lượng:
sˆx 0,14337 ; x 20,3333
Tính các xác suất lý thuyết theo phân phối chuẩn:
pi* P x i 1 X xi xi s ˆ x
xi 1sˆ x 1 ( )x x e t2/2dt ; ( ) 0,5; ( ) 0,5 2 0
Biến quan sát X là liên tục nên ghép lớp ầu tiên [20;20,1) thành lớp ( ;20,1) và
lớp cuối [20,7;20,8) thành lớp [20,7; ) . Lập bảng tính:
STT lớp Đường kính X Tần số thực Tần số lý thuyết (mm) nghiệm ni ni* npi* 1 1 ( ;20,1) 9 8.7056 2 [20,1;20,2) 18 20.8944 3 [20,2;20,3) 40 38.9569 4 [20,3;20,4) 55 45.5203 5 [20,4;20,5) 27 33.3393 6 [20,5;20,6) 11 15.3007
Xác suất thống kê và Ứng dụng – 2021 139 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 7 [20,6;20,7) 6 4.3971 8 [20,7; ) 2 0,8857
Nhận thấy rằng trong lớp thứ tám, tần số lý thuyết nhỏ hơn 1 nên ta ghép lớp thứ
tám vào lớp thứ bảy (cộng hai cột cuối). Lớp thứ bảy mới sẽ là: 7 [20,6; ) 8 5,2828
Số lớp k 7, số tham số r 2. n Tính thống kê: g k i2 n 6,2248 i 1 ni*
Giá trị phân vị 2 (k r 1) 2 0 ,03(7 2 1) 10,7119 Ta có: G 2 (k r 1)
Vậy ta chấp nhận H0 , nghĩa là dãy số liệu trên tuân theo luật phân phối chuẩn.
Sử dụng phần mềm Mathematica:
Trong oạn code sau, ta chỉ nhập vào các iểm biên xi và các tần số ni . Kết quả xuất
ra lần lượt là: số lớp k , kích thước mẫu n, trung bình mẫu x , ộ lệch mẫu sˆx , dãy tần số lý thuyết n * * i
npi ; cuối cùng là giá trị thống kê g . Kết quả
Ví dụ 5.4. Quan sát tuổi thọ (X : giờ) của một số con côn trùng cùng loại có kết quả bảng sau: X (giờ)
[1;3) [3;5) [5;7) [7;9) [9;11) [11;13) [13;15] 140
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Số côn trùng 40 19 11 7 6 4 1
Với mức ý nghĩa 5%, có thể coi dãy số liệu bên tuân theo luật phân phối mũ không?
Giải. Ta có: n 88; x 4,5455.
Kiểm ịnh cặp giả thiết:
H0 : X có phân phối mũ E( ) ,
H1 : X không có phân phối mũ E( ) . Ước lượng: n 1 0,2175 nx
Tính các xác suất lý thuyết theo phân phối mũ: p i*
P x i 1 X
xi F*(xi ) F*(xi 1) *
1 e x, x 0 Trong ó: F ( )x 0 , x 0 Lưu ý: F*( ) 1
Biến quan sát X là liên tục nên ghép lớp ầu tiên [1;3) thành lớp (0;3) và lớp cuối [13;15] thành lớp [13; ) . Lập bảng tính: STT Tuổi thọ X
Tần số thực Tần số lý thuyết lớp (giờ) nghiệm ni ni* npi* 1 1 (0;3) 40 42,1747 2 [3;5) 19 16,1642 3 [5;7) 11 10,4625 4 [7;9) 7 6,7720 5 [9;11) 6 4,3833 6 [11;13) 4 2,8372 7 [13; ) 1 5,2061
Trong bảng này, ta không cần phải hiệu chỉnh như ví dụ 5.3 vì tất cả các tần số lý
thuyết ều lớn hơn một. Số lớp k 7, số tham số r 1. k 2 n Tính thống kê: g i n 5,1160
Xác suất thống kê và Ứng dụng – 2021 141 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh i 1 ni*
Giá trị phân vị 2 (k r 1) 2 0 ,05(7 2 1) 9,4877 Ta có: g 2 (k r 1)
Vậy ta chấp nhận H0 , nghĩa là dãy số liệu trên tuân theo luật phân phối mũ.
Sử dụng phần mềm Mathematica: Kết quả: ,
nxk, , , dãy tần số lý thuyết, thống kê g.
Ví dụ 5.5. Người ta khảo sát số khách hàng (X) ến một siêu thị trong mỗi phút tại TP.
HCM. Giả sử số liệu ược ghi lại thành 500 khoảng một phút với số khách hàng tương
ứng trong mỗi khoảng như sau: Số khách hàng 0 1 2 3 4 5 6 7 8 9 Số lần lặp lại 65 93 42 98 77 54 30 24 12 5
Với mức ý nghĩa 2%, có thể coi dãy số liệu trên tuân theo luật phân phối Poisson không?
Giải. Ta có: n 500; x 3,076
Kiểm ịnh cặp giả thiết
H0 : X có phân phối Poisson P( ) ,
H1 : X không có phân phối Poisson P( ). Ước lượng: x 3,076
Tính các xác suất lý thuyết theo phân phối Poisson: 142
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
pi* P X k k e
(3,076)k e 3,076;k
0,1,2,... k! k! Lập bảng tính:
STT Số khách Tần số thực Tần số lý thuyết
lớp hàng (X) nghiệm ni ni* npi* 1 1 0 65 23.072 2 1 93 70.969 3 2 42 109.15 4 3 98 111.915 5 4 77 86.063 6 5 54 52.946 7 6 30 27.144 8 7 24 11.928 9 8 12 4.5862 10 9 5 2.2294 Lưu ý: n * * * 10 n (n1 n2 ... n *
9 ) Số lớp k 10, số tham số r 1. k ni2 Tính thống kê: g n 155 i 1 ni*
Giá trị phân vị 2 (k r1) 2 0 ,02 (10 1 1) 18,168 Ta có: g
2 (k r 1)
Vậy ta bác bỏ H0 chấp nhận H1 , nghĩa là dãy số liệu trên không theo luật phân phối Poisson.
Xác suất thống kê và Ứng dụng – 2021 143 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Sử dụng phần mềm Mathematica : Kết quả: , , knx
, dãy tần số lý thuyết, thống kê g.
5.3 . Tương quan và hồi quy ơn
5.3.1. Một số khái niệm
Trong nhiều bài toán thực tế người ta quan tâm tới mối quan hệ của hai hay nhiều
biến ngẫu nhiên, chẳng hạn: chiều cao và cân nặng của một người; lượng hàng bán ược
và giá bán; chi tiêu cho tiêu dùng cá nhân và thu nhập; năng suất tôm sú nuôi trong hệ
thống thâm canh phụ thuộc thế nào vào diện tích ao nuôi, mật ộ thả tôm giống, chi phí
hoá chất xử lý môi trường ;…
Giả sử ta cần nghiên cứu mối quan hệ giữa hai biến ngẫu nhiên X Y, . Các vần ề ược ặt ra là:
➢ X và Y có ộc lập nhau hay không? Vấn ề này ã ược kiểm ịnh trong chương 4.
Trong trường hợp chúng ộc lập nhau thì ta xét riêng từng biến.
➢ Nếu X và Y phụ thuộc thì mức ộ phụ thuộc và quy luật phụ thuộc là như thế nào?
Có ba loại phụ thuộc giữa hai biến ngẫu nhiên X và Y sau:
1) Phụ thuộc hàm số: tồn tại hàm số g x( ) sao cho Y g X( ).
2) Phụ thuộc thống kê: nếu X thay ổi thì phân phối xác suất của Y cũng thay ổi.
3) Phụ thuộc tương quan: nếu X thay ổi thì trung bình có iều kiện E Y( / X) cũng thay
ổi, nghĩa là E Y( / X ) f X( ) C (C là hằng số). Phụ thuộc tương quan là một trường
hợp riêng của phụ thuộc thống kê.
- Nếu Y phụ thuộc tương quan vào X thì phương trình sau :
E Y( / X ) f X( )
ược gọi là phương trình hồi quy của Y theo X . 144
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
- Nếu E Y( / X ) a bX ta nói Y phụ thuộc tương quan tuyến tính vào X; còn nếu
f X( ) không tuyến tính ta nói giữa Y và X có phụ thuộc tương quan phi tuyến.
Vậy bài toán phân tích tương quan là:
Xét xem có hay không sự phụ thuộc tương quan giữa giữa Y và X và ánh giá mức
ộ chặt chẽ của sự phụ thuộc tương quan (nếu có). Đặc trưng của bài toán này là hệ số tương quan.
5.3.2. Hệ số tương quan
a) Hệ số tương quan lý thuyết
Hệ số tương quan giữa hai biến ngẫu nhiên X và Y là ại lượng không có ơn vị ược
xác ịnh bởi công thức sau:
E XY( ) E X E Y( ) ( ) D X D Y( ). ( ) Tính chất 1) 1 XY 1 2) Nếu X Y, ộc lập thì
0. Điều ngược lại không úng Ý nghĩa
1) Hệ số tương quan là ại lượng ặc trưng cho mối quan hệ phụ thuộc tương quan
tuyến tính giữa hai biến ngẫu nhiên.
2) Trị tuyệt ối của hệ số tương quan càng lớn thì mối quan hệ ó càng chặt chẽ. Đặc biệt khi
1 thì X và Y có phụ thuộc tương quan tuyến tính hoàn hảo, nghĩa là : E Y X(
|) a bX hoặc E X Y( | ) a bY
3) Hệ số tương quan dương khi hai biến có quan hệ ồng biến; và âm khi hai biến có quan hệ nghịch biến.
b) Hệ số tương quan mẫu
Để xác ịnh ược ta cần biết phân phối xác suất của vector ngẫu nhiên (X Y, ),
nhưng iều này trong thực tế là khó. Vì vậy cần căn cứ vào mẫu quan sát cụ thể ể ước
lượng cho . Hệ số ược xây dựng từ một mẫu thực nghiệm và ước lượng cho ược gọi
là hệ số tương quan mẫu, ký hiệu là r .
Xi X1 X 2 ... Xn
Xét mẫu cụ thể kích thước n: (1)
Yi Y1 Y2 ... Yn
Khi ó hệ số tương quan mẫu ược tính theo công thức sau:
Xác suất thống kê và Ứng dụng – 2021 145 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
r XY X Y. ˆ ˆ s s X2 . Y2
Trong ó: X 1 n Xi ;Y 1 n Yi ; XY 1 n X Yi i n i 1 n i 1 n i 1
sˆX2 1 n (Xi X )2 1 n Xi2 (X )2
n i 1 n i 1 sˆY2 1 n (Yi Y )2 1 n Yi2 (Y )2 n i 1 n i 1
Trong mẫu (1) có thể có một số bộ số (x yi, i ) trùng nhau. Trong trường hợp mẫu
có kích thước lớn và có các bộ số (x yi, i ) trùng nhau thì ta có thể biểu diễn mẫu dưới dạng tần số: i X1 X2 Xk Y (2) i Y1 Y2 Yk Tần số ni n1 n2 nk Khi ó : n n1 ... nk
X 1 k n Xii ;Y 1 k nYi i ; XY 1 k n X Yi i i n i 1 n i 1 n i 1 sˆ 2 2 2 X 1 k n Xi (X )2 ; sˆ 1 k i Y nY 2 i i
(Y )2 n i 1 n i 1
Tính chất của hệ số tương quan mẫu: ➢ 1 r 1.
➢ r dùng ể ước lượng hướng và ộ mạnh của mối quan hệ phụ thuộc tương quan
tuyến tính giữa X và Y.
| r | 0,8 : phụ thuộc tương quan tuyến tính mạnh, 146
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 0,4 | r |
0,8: tương quan trung
bình, | r | 0,4 : tương quan yếu. 0 r
1 : tương quan tuyến tính thuận ( ồng biến), 1 r
0 : tương quan tuyến tính nghịch (nghịch biến).
➢ r là ước lượng iểm của .
Sử dụng Excel ể tìm r ( ối với mẫu (1)): r = Correl(array1,array2)
c) Kiểm ịnh giả thiết về ρ
Kiểm ịnh giả thiết về ρ là kiểm ịnh giả thiết nói về sự phụ thuộc tương quan tuyến
tính của hai biến ngẫu nhiên X và Y.
Ta cần kiểm ịnh cặp giả thiết: H0 :
0 (không có sự phụ thuộc tương quan tuyến tính) H1 : 0
(có sự phụ thuộc tương quan tuyến tính)
Lấy mẫu cụ thể có dạng (1) hoặc (2), tính ược hệ số tương quan mẫu r .
Tính thống kê: g r n 2 1 r 2
Với mức ý nghĩa , tính giá trị phân vị theo phân phối Student với n 2 bậc tự do:
t /2(n 2) (có thể tra bảng hoặc sử dụng Excel: t /2(n 2) tinv( ,n 2) ).
Nếu | g | t /2(n 2) thì bác bỏ H0 .
Ví vụ 5.6. Để nghiên cứu sự phụ thuộc tương quan giữa chiều cao X (mét) và câng nặng
Y (kg) của một người, người ta tiến hành khảo sát 10 người có số liệu trong bảng sau: X i
1 1,2 1,3 1,3 1,4 1,5 1,5 1,6 1,7 1,8
Yi 35 32 40 46 50 47 55 62 75 69
a) Hãy xác ịnh hệ số tương quan mẫu r và cho nhận xét mức ộ về mức ộ phụ thuộc
tương quan tuyến tính của X và Y.
b) Giữa X và Y có sự tương quan tuyến tính không với mức ý nghĩa 5%? Giải
a) Ta có: n 10, X 1,43; Y 51,1; XY 75,91
Xác suất thống kê và Ứng dụng – 2021 147 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
sˆX2 1 n Xi2 (X )2 20,97 (1,43)2 0,0521 n i 1 10
sˆY2 1 n Yi2 (Y )2 27929 (51,1)2 181,69 n i 1 10
r XY X Y. 75,91 1,43 51,1 0,922094 s ˆ ˆ s 2 2 X . Y 0,0521 181,69
Ta có : 0,8 r và rất gần với 1 nên X và Y có phụ thuộc tương quan tuyến tính khá
cao. Sự phụ thuộc này là ồng biến.
b) Gọi là hệ số tương quan của X và Y, ta kiểm ịnh : H0 : 0 ; H1 : 0
g r n 2 6,7398 1 r 2
t /2 (n 2) t0,025 (8) 2,306
Ta có: | g | t /2(n 2) nên bác bỏ H0 , chấp nhận H1 .
Vậy với mức ý nghĩa 5%, X và Y có phụ thuộc tương quan tuyến tính.
Vẽ ồ thị phân tán (Scatter) bằng Excel Đồ thị phântán 80 70 60 50 40 ân nặng 30 C 20 10 0
Hình 5.1. Đồ thị phân tán của dữ liệu trong ví dụ 5.6
Nhận xét: Dựa vào ồ thị phân tán, ta thấy rằng các iểm dữ liệu tập trung xung quanh
một ường thẳng ồng biến. Như vậy ta có thể dự oán rằng: chiều cao và cân nặng có phụ
thuộc tương quan tuyến tính khá cao. 148
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví vụ 5.7. Cho bảng số liệu thực nghiệm sau về hai biến ngẫu nhiên X và Y : X 1 1 2 3 3 3 4 5 6 6 i Yi 8 9 7 7 6 7 5 5 4 3 ni 4 8 15 25 12 9 7 10 5 5
a) Hãy xác ịnh hệ số tương quan mẫu.
b) Giữa X và Y có sự tương quan tuyến tính không với mức ý nghĩa 5%? Cho nhận
xét mức ộ về mức ộ phụ thuộc tương quan tuyến tính của X và Y. Giải
a) Tính các ặc trưng mẫu: n 100; X 3,18; Y 6,39 XY ˆ ˆ 18,44; s 2 2 X 1,9676 ; s Y 2,0379
r XY X Y. 18,44 3,18 6,39 0,938954 s ˆ ˆ s 2 2
X . Y 1,9676 2,0379
b) Gọi là hệ số tương quan của X và Y, ta kiểm ịnh : H0 : 0 ; H1 : 0 g r n 2 27,0175 1 r 2 n t /2 ( 2) t0,025 (98) 1,9845
Ta có: | g | t /2(n 2) nên bác bỏ H0 , chấp nhận H1 .
Vậy với mức ý nghĩa 5%, X và Y có phụ thuộc tương quan tuyến tính. Ta có : r
0,8 và rất gần với -1 nên X và Y có phụ thuộc tương quan tuyến tính
cao. Sự phụ thuộc này là nghịch biến.
Sử dụng Mathematica ể tính các ặc trưng và hệ số tương quan:
Kết quả hiển thị lần lượt là: 2 2 , ˆ ˆ , , nXYXYs , , sr, X Y XY
Xác suất thống kê và Ứng dụng – 2021 149 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví vụ 5.8. Cho bảng số liệu thực nghiệm sau về hai biến ngẫu nhiên X và Y : X i 0 1 2 3 4 Yi 6 7 8 9 4
a) Hãy xác ịnh hệ số tương quan mẫu.
b) Giữa X và Y có sự tương quan tuyến tính không với mức ý nghĩa 4%? Cho nhận
xét mức ộ về mức ộ phụ thuộc tương quan tuyến tính của X và Y. Giải
a) Tính các ặc trưng mẫu:
n 5; X 2; Y 6,8; XY 13,2; sˆ 2 2 X 2 ; sˆY 2,96 Hệ số tương quan mẫu
r XY X Y. 13,2 2 6,8 0,164399 s ˆ ˆ
s X2 . Y2 2 2,96
b) Gọi là hệ số tương quan của X và Y, ta kiểm ịnh : H0 : 0 ; H1 : 0 r n 2 0,288675 g n 1 r 2 t /2 ( 2) t0,02 (3) 3,481909
Ta có: | g | t /2(n 2) nên chấp nhận H0 , bác bỏ H1 .
Vậy với mức ý nghĩa 4%, X và Y không có phụ thuộc tương quan tuyến tính.
Ta có : | r | 0,4 và rất gần 0 nên X và Y có thể có phụ thuộc tương quan tuyến tính
nhưng rất yếu.
5.3.3. Hàm hồi quy tổng thể, hàm hồi quy mẫu
a) Khái niệm về phân tích hồi quy
Phân tích hồi quy là nghiên cứu sự phụ thuộc của một biến (gọi là biến phụ thuộc),
vào một hoặc nhiều biến khác (gọi là biến ộc lập) nhằm mục ích ước lượng hay dự oán
giá trị trung bình (của tổng thể) của biến phụ thuộc dựa trên cơ sở các giá trị biết trước 150
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
của các biến ộc lập. Nếu có một biến ộc lập thì gọi là phân tích hồi quy ơn, còn nếu có
từ hai biến ộc lập trở lên thì gọi là phân tích hồi quy bội. b) Hàm hồi quy tổng thể
Giả sử biến Y phụ thuộc tương quan vào biến X . Khi ó trung bình có iều kiện E Y(
/ X) phụ thuộc vào X theo một hàm số :
E Y( / X ) f X( ) (1)
Hàm (1) ược gọi là hàm hồi quy tổng thể (PRF – Population regression
function), dạng hàm f X( ) phụ thuộc vào các mối quan hệ kinh tế (thường ược xác ịnh
dựa vào các lý thuyết kinh tế). Để xác ịnh dạng của f X( ) người ta thường dựa vào ồ thị
biểu diễn sự biến thiên của dãy các số liệu quan sát về X và Y (gọi là ồ thị phân tán -
Scatter) kết hợp với việc phân tích bản chất của vấn ề nghiên cứu.
Người ta thường sử dụng hàm hồi quy tuyến tính: E Y( / X) 1 2X (2) Trong ó
1, 2 là các tham số chưa biết nhưng cố ịnh, và ược gọi là các hệ số hồi quy.
c) Hàm hồi quy mẫu
Trong thực tế, chúng ta không có thông tin một cách ầy ủ về mối quan hệ giữa hai biến
ngẫu nhiên X và Y , do ó chúng ta sẽ không xác ịnh ược hàm hồi quy tổng thể (PRF).
Dựa vào một mẫu thực nghiệm về hai biến X và Y , ta xây dựng ược một hàm số tương
ối “gần” với PRF. Hàm số xây dựng ược từ mẫu thực nghiệm ược gọi là hàm hồi quy
mẫu (SRF –Sample Regression Function).
Giả sử PRF có dạng tuyến tính: E Y( / X)
1 2X . Khi ó hàm hồi quy mẫu (SRF) ược ề nghị là: Yˆ ˆ1 ˆ2 X (3)
Trong ó: Yˆ là ước lượng iểm của E Y( / X)
ˆ1 là ước lượng iểm của 1
ˆ2 là ước lượng iểm của 2
5.3.4. Ước lượng các hệ số hồi quy bằng phương pháp bình phương tối thiểu
Xác suất thống kê và Ứng dụng – 2021 151 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Cần ước lượng các hệ số hồi quy
ˆ ˆ1, 2 trong trong hàm SRF: Yˆ ˆ1 ˆ2 X
, ta lấy mẫu cụ thể kích thước n: (X Y1, 1),...,(X Yn, n ) . Ứng với mỗi (X Yi, i ), ặt ei
Yi Yˆi Yi ( ˆ1 ˆ2 Xi ) thì ei ược gọi là phần dư (Residual) giữa giá trị quan ˆ
sát Yi và giá trị ước lượng Y i nhận ược từ hàm hồi quy mẫu.
Nội dung của phương pháp: ˆ ˆ Y Tìm các hệ số 1, 2 sao cho tổng
bình phương các phần dư sau ây phải ạt giá trị i Y i e ˆ nhỏ nhất i Y SRF 0 Xi X Q( ˆ ˆ 2 n 2 1,2 ) n ei Yi ˆ1 ˆ2 Xi min i 1 i 1
Hình 5.2. Đường hồi quy mẫu Theo lý thuyết hàm nhiều biến, hàm Q( ˆ ˆ1, 2 )
ạt giá trị nhỏ nhất tại iểm (
ˆ ˆ1, 2 ) là nghiệm của hệ phương trình: Qˆ1 0 2 i n1 Yi ˆ1 ˆ2 Xi 0 Qˆ2 0 2 i n1 Yi ˆ1 ˆ2 Xi Xi 0 n ˆ 1ˆ 1 Xˆi2
ˆX2 i X i2 Y i X Yi i ˆˆ12 YXY
s ˆˆX22X YX.
Vậy các hệ số của hàm hồi quy mẫu ược tính theo công thức sau: 152
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
ˆ2 XY 2 X Y. ; ˆ1 Y ˆ2 X sˆX
Ví dụ 5.9. Bảng sau cho số liệu về mức chi tiêu cho tiêu dùng (Y – usd/tuần) và thu
nhập (X – usd/tuần) của một mẫu gồm 10 gia ình. Giả sử Y và X có mối quan hệ tương quan tuyến tính.
X i 80 100 120 140 160 180 200 220 240 260
Yi 70 65 90 95 110 115 120 140 155 150
a) Hãy tìm hàm hồi quy mẫu của Y theo X và nêu ý nghĩa kinh tế của các hệ số hồi quy.
b) Từ số liệu mẫu, hãy tìm ước lượng iểm cho mức chi tiêu tiêu dùng bình quân
khi thu nhập 195 (usd/tuần). Giải
a) Hàm hồi quy tổng thể: E Y( / X) 1 2X Hàm hồi quy mẫu: Yˆ ˆ1 ˆ2 X
Các ặc trưng mẫu: n 10, X
170 ;Y 111; XY 20550 sˆ 2 2 X 1 Xi X 2 3300 n Các hệ số hồi quy
ˆ2 XY 2 X Y. 20550 170 111 0,509091 ˆ s X 3300
ˆ1 Yˆ2 X 24,4545
Vậy hàm hồi quy mẫu cần tìm là: Yˆ 24,4545 0,509091X
Ý nghĩa kinh tế của các hệ số hồi quy: ˆ E Y( / X 0) 1 24,4545 . 1
Mức chi tiêu cho tiêu dùng bình quân mỗi tuần của một hộ gia ình không có thu
nhập (giả sử các yếu tố khác không ổi) là 1 , xấp xỉ khoảng 24,455 usd/tuần. ˆ E Y( / X 1) E Y( / X ) 2 0,509091. 2
Xác suất thống kê và Ứng dụng – 2021 153 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Khi thu nhập tăng 1 usd/tuần (trong iều kiện các yếu tố khác không ổi) thì chi tiêu
cho tiêu dùng bình quân của một hộ gia ình tăng lên 2 , xấp xỉ khoảng 0,509091 usd/tuần. ˆ
b) Thay X 195 vào hàm Y
24,4545 0,509091X , thu ược: ˆ
E Y( / X 195) Y 123,727
Vậy mức chi tiêu cho tiêu dùng bình quân khi thu nhập 195 (usd/tuần) khoảng 123,727 (usd/tuần).
Sử dụng phần mềm Mathematica
Kết quả hiển thị lần lượt là: 2 ˆˆ 2 , ˆ , , nXYXYs , X , 1 , 2 , i e
Ví dụ 5.10. Một nghiên cứu khảo sát về mối quan hệ giữa lưu lượng xe giờ cao iểm
theo bề rộng mặt cắt ngang ường ược cung cấp như bảng sau: X 5,7 6,5 7,3 9,6 12,8 i Yi 3,01 4,22 4,23 6,45 7,58
X : bề rộng mặt cắt ngang ường (m), Y :
lưu lượng xe (nghìn xe q /giờ).
a) Hãy tìm hàm hồi quy mẫu Yˆ
ˆ1 ˆ2 X cho số liệu thống kê trên. Nêu ý nghĩa
kinh tế của các hệ số hồi quy ˆ ˆ1, 2 .
b) Từ dữ liệu thống kê trên, hãy tìm ước lượng cho lưu lượng xe ứng với bề mặt cắt ngang ường 10m.
Giải. a) Hàm hồi quy tổng thể: E Y( / X) 1 2X
Hàm hồi quy mẫu: Yˆ ˆ1 ˆ2 X Các ặc trưng mẫu:
n 5, X 8,38 ;Y 5,098; XY 46,882;sˆ 2 X 6,5816 154
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Các hệ số hồi quy
ˆ2 XY 2 X Y. 46,882 8,38 5,098 0,63218 ˆ s X 6,5816
ˆ1 Yˆ2 X 0,19967
Vậy hàm hồi quy mẫu cần tìm là: Yˆ
0,19967 0,63218X Ý
nghĩa kinh tế của các hệ số hồi quy: E Y( / X 0) 1 ˆ 0,19967 1
Hệ số 1 trong trường hợp này không có ý nghĩa kinh tế vì không có mặt ường
nào có bề ngang bằng không. ˆ E Y( / X 1) E Y( / X ) 2 0,63218 . 2
Khi bề rộng mặt ường tăng thêm 1m (trong iều kiện các yếu tố khác không ổi) thì
lưu lượng xe tăng bình quân là 2 , xấp xỉ khoảng 0,63218 (nghìn xe q /giờ). ˆ
b) Thay X 10 vào hàm Y
0,19967 0,63218X , thu ược: ˆ
E Y( / X 10) Y 6,12213
Vậy khi bề rộng mặt ngang ường 10m thì lưu lượng xe (giờ cao iểm) bình quân
khoảng 6,12213 (nghìn xe q /giờ).
5.3.5. Một số dạng hàm hồi quy tuyến tính hóa ược
Giả sử ta có hai biến quan sát X và Y phụ thuộc tương quan. Từ mẫu thực nghiệm,
nếu giá trị tuyệt ối của hệ số tương quan mẫu rất gần 0 thì ta không thể dùng hàm hồi
quy tuyến tính ược. Khi ó X Y, có phụ thuộc tương quan phi tuyến. Một số dạng hàm
hồi quy phi tuyến sau ây có thể tuyến tính ược. theo một hàm số :
Xét hàm hồi quy tổng thể (PRF): E Y( / X) f X( )
a) Hồi quy dạng nghịch ảo: f X( ) 1 2 1 X 1 Hồi quy mẫu: Yˆ ˆ1ˆ2 X
Xác suất thống kê và Ứng dụng – 2021 155 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Đặt Z 1 thì ta có hàm hồi quy tuyến tính mẫu: X Yˆ ˆ1 ˆ 2Z (1)
Áp dụng phương pháp bình phương tối thiểu
ối với số liệu thực nghiệm
(Z Yi , i ) (1/ X Yi, i ), i 1,n tìm ược ˆ ˆ1, 2 từ hàm
(1). b) Hồi quy dạng logarit: f X( ) 1 2 ln X Hồi quy mẫu: Yˆ ˆ1ˆ2 ln X
Đặt Z ln X , ta ược: ˆ Yˆ ˆ1 2Z (2)
c) Hồi quy dạng lũy thừa: f X( ) 1 2 X 2 Hồi quy mẫu: Yˆ ˆ1 ˆ2 X 2
Đặt Z X 2 , thu ược: Yˆ ˆ1 ˆ 2Z (3)
d) Hồi quy dạng mũ: f X( ) 1e 2.X Hồi quy mẫu: Yˆ
ˆ1e ˆ2.X lnYˆ ln ˆ1 ˆ2 X ˆ ˆ
Đặt Wˆ lnYˆ ; b 1 ln ˆ1 ; b 2 ˆ2 , thu ược:
Wˆ bˆ1b Xˆ2 (4) ˆ ˆ
Ước lượng (4) từ mẫu (X Wi ,
i ), i 1,n với Wi lnYi thu ược b b 1, 2 . Suy ra:
ˆ1 e bˆ1 ; ˆ2 bˆ2 . .X 1
e) Hồi quy dạng phân thức hữu tỉ : f X( ) X 2
Hồi quy mẫu: Yˆ ˆ1.Xˆ2 Y1ˆ 1ˆ1 ˆˆ12 X1 X 156
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 1 1 1 Đặt Wˆ ˆ ; Z bˆ 2 1 ˆ1 ; bˆ2 ˆˆ1 , thu ược: Y X
Wˆ bˆ1b Xˆ2 (5)
Ví vụ 5.11. Cho bảng số liệu thực nghiệm sau về hai biến ngẫu nhiên X và Y :
X i 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 Yi 10 7 5 3 1 4 9 13
a) Hãy xác ịnh hệ số tương quan mẫu r và cho biết giữa X và Y có sự tương quan
tuyến tính không với mức ý nghĩa 5%?
b) Từ số liệu mẫu, hãy tìm hàm hồi quy mẫu Yˆ ˆ1 ˆ 2 X 2 . Giải
a) Ta có: n 8; X 0,9; Y 6,625; XY 6,225; ˆ ˆ s 2 2 X 0,21 ; s Y 14,2344
r XY X Y. 6,225 0,9 6,625 0,15183 s ˆ ˆ s 2 2 X . Y 0,21 14,2344
Gọi là hệ số tương quan của X và Y, ta kiểm ịnh : H0 : 0 ; H1 : 0
g r n 2 0,37627 1 r 2 t /2 n (
2) t0,025 (6) 2,446912
Ta có: | g | t /2(n 2) nên chấp nhận H0 , bác bỏ H1 .
Vậy với mức ý nghĩa 5%, X và Y không có phụ thuộc tương quan tuyến tính.
b) Đặt Z X 2 , ta thu ược hàm hồi quy tuyến tính mẫu Yˆ ˆ1 ˆ2Z Số liệu thực nghiệm
Zi Xi2 0,04 1,6 3,6 6,4 1,0 1,44 1,69 2,56 Yi 10 7 5 3 1 4 9 13
Ta có: n 8;Z 1,02; Y 6,625; ZY 7,885; sˆ 2 Z 0,714
Xác suất thống kê và Ứng dụng – 2021 157 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
ˆ2 ZY 2Z Y. 7,885 1,02 6,625 1,57913 ˆ s Z 0,714
ˆ1 Yˆ2Z 5,01429
Vậy hàm hồi quy mẫu cần tìm là: Yˆ 5,01429 1,57913X 2
5.3.6. Ước lượng khoảng tin cậy và kiểm ịnh các hệ số hồi quy
a) Độ chính xác của các ước lượng ˆ ˆ
Ta thấy rằng với hai mẫu thực nghiệm khác nhau thì các ước lượng 1, 2 cũng có thể khác nhau. Do ó
ˆ ˆ1, 2 là các biến ngẫu nhiên. Vì phương sai hay sai số chuẩn ặc
trưng cho ộ phân tán của biến ngẫu nhiên nên ta dùng chúng ể o ộ chính xác của các
ước lượng. Người ta chứng minh ược các công thức sau: 2 ei2
Phương sai phần dư: ˆ var( )e n 2 Trong ó: n e 2 n 2 n i (Yi Y )2 ˆ2 (Xi X )2 i 1 i 1 i 1 var( ˆ1) ˆ 2. Xi2
i X )2 n. (X
Phương sai của các ước lượng:
var( ˆ2 ) (X ˆi 2 X )2 ˆ ˆ se( 1) var( 1)
Sai số chuẩn (Standard error): ˆ ˆ se( 2 ) var( 2 )
b) Khoảng tin cậy của các hệ số hồi quy Các tham số ˆ ˆ1,
2 tìm ược theo phương pháp OLS là ước lượng iểm của 158
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
1, 2 . Ước lượng này có nhiều khả năng khác với giá trị úng. Do ó người ta tìm khoảng
tin cậy chứa giá trị úng với ộ tin cậy 1 cho trước. Với ộ tin cậy 1
cho trước, khoảng tin cậy của j là: ˆ ˆ ˆ j j
t /2 (n 2).se( ˆj ) ; j t /2 (n 2).se( j ) , j 1,2
Trong ó: t /2(n 2) là phân vị của phân phối Student, ược tính bởi hàm Excel:
t /2(n 2) tinv( ,n 2) .
c) Kiểm ịnh giả thiết về các hệ số hồi quy
Căn cứ vào một lý thuyết kinh tế nào ó hay kinh nghiệm từ trước và dựa vào những
thông tin có ược, người ta ưa ra giả thiết H0 : j *j , ối thiết H1 là một trong các iều
kiện j *j , j *j , j *j (với j 1,2 và *j ã biết). Với mức ý nghĩa cho
trước, ta cần kiểm ịnh rằng: Kết quả tìm ược dựa trên số liệu mẫu gồm n quan sát từ
thực tế có phù hợp với giả thiết H0 hay không? Tức là cần ưa ra quyết
ịnh là chấp nhận hay bác bỏ giả thiết H0 .
Các bước thực hiện kiểm ịnh: ˆj *j
Bước 1: Tính thống kê t j ˆj ) , j 1,2. se(
Bước 2: Tính t /2(n 2) hoặc t (n 2) .
Tùy theo giả thiết H1 , ta có các iều kiện bác bỏ H0 như sau:
Cặp giả thiết kiểm ịnh
Điều kiện bác bỏ H0 H n
0 : j *j ; H1 : j *j | t j | t /2 ( 2)
H0 : j *j , H1 : j *j t j t (n 2)
H0 : j *j , H1 : j *j t j t (n 2)
Ví dụ 5.12. Xét lại ví dụ 5.9
a) Tìm khoảng tin cậy cho các hệ số hồi quy với ộ tin cậy 95%.
b) Kiểm ịnh cặp giả thiết H0 : 2 0,4 ; ối thiết H1 : 2 0,4 với mức ý nghĩa 5%.
Giải. Theo ví dụ 5.9, ta có:
Xác suất thống kê và Ứng dụng – 2021 159 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh ˆ ˆ n 10, X 2 i
322000; 1=24,4545; 2 0,509091 n (X 2 i
X )2 nsˆX 33000; n (Yi Y )2 8890 i 1 i 1 ˆ Suy ra: n e 2 n 2 n i (Yi Y )2 2
(Xi X )2 337,273 i 1 i 1 i 1
a) Ta có: ˆ 2 ei2 42,1591 n 2 . X var( ˆ ) ˆ 2 i2 i
2 41,1367 se( ˆ1) 6,41379 1 n. (X X ) ˆ ˆ var( 2 ) ˆ 2 2 0,00127754 se( 2 ) 0,03574 (Xi X ) Độ tin cậy 1 95%, n 2 8, ta có:
t /2 (n 2) t0,025 (8) 2,306 Khoảng
tin cậy của 1 là: ˆ ˆ ˆ ˆ 1
t /2 (n 2).se( 1); 1
t /2(n 2).se( 1) 9,6643; 39,2447
Khoảng tin cậy của 2 là: ˆ ˆ ˆ 2
t /2 (n 2).se( ˆ2); 2 t /2(n 2).se( 2) 0,4267; 0,5915
Từ ý nghĩa của 2 , ta có thể kết luận rằng: với ều kiện các yếu tố khác không ổi, khi
thu nhập tăng 1 usd/tuần thì chi tiêu cho tiêu dùng trung bình của một hộ gia ình tăng
trong khoảng từ 0,4267 ến 0,5915 usd/tuần. 160
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh H : * 0,4
b) Kiểm ịnh cặp giả thiết 0 2 2 H1 : 2 0,4 * 2 ˆ2 2 0,509091
0, 4 3,05235 Ta có: t se( ˆ2) 0,03574
t /2 (n 2) t0,025 (8) 2,306
Điều kiện | t2 | t /2 (n 2) là úng nên bác bỏ giả thiết H0 , chấp nhận giả thiết H1 .
Hướng dẫn sử dụng Excel cho bài toán phân tích hồi quy
Bước 1. Mở chương trình Excel và nhập dữ liệu dạng cột.
Bước 2. Mở Real Statistics (hoặc nhất tổ hợp phím Ctrl - m), sau ó chọn Linear
Regrssion (hồi quy tuyến tính). Nhấp OK.
Bước 3. Chọn vùng dữ liệu của X, Y.
Alpha (mặt ịnh của chương trình là
0.05, khi cần chúng ta thay ổi số khác).
Lưu ý: nếu chọn Column headings included with data thì việc chọn vùng dữ liệu phải
chứa ô có chữ X, Y. Kết quả như bảng sau:
Xác suất thống kê và Ứng dụng – 2021 161 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Trong bảng:
R Square : Hệ số xác ịnh R2 0,962062
Adjusted R Square : Hệ số xác ịnh iều chỉnh R2 0.957319256
Công thức tính là R2 1 (1 R2) n 1 n k
Trong ó: n là kích thước mẫu, k là số biến của mô hình.
Standard Error: Sai số chuẩn của hồi quy (Standard Error of regression) ˆ 6.493003227
Observations: số lượng quan sát (hay kích thước mẫu) n 10
Regression (SS): Tổng bình phương các sai số giữa giá trị ước lượng dựa vào hàm hồi quy và trung bình mẫu ESS
(Yˆi Y )2 8552,7
Residual (SS): Tổng bình phương các phần dư RSS
e2 i (Yi Yˆi )2 337.2727 Total (SS): TSS
(Yi Y)2 RSS ESS 8890 R
F (F-statistic): Thống kê F 2 0 (n 2).2
202.8679(dùng ể kiểm ịnh sự phù hợp 162
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 1 R
của hàm hồi quy).
p-value (probability value): Giá trị xác suất theo phân phối Fisher với hai bậc tự do 1
và n 2 (hay hai bậc tự do k 1 và n k ối với hồi quy bội k biến). Giá trị này dùng ể
kiểm ịnh sự phù hợp của hàm hồi quy theo phươg pháp giá trị xác suất.
p value P F( F0 ) FDIST F 0,1,n 2 5,75.10 7
Phần cuối của kết quả Excel: ể mô tả hàm hồi quy mẫu (SRF) Yˆ ˆ1 ˆ 2 X ˆ
Dòng Intercept (chặn, hệ số chặn) là các thông số của 1 ˆ
Dòng X là các thông số của 2
Coeff (Coefficient) : Hệ số hồi quy mẫu ˆ ˆ 1 24.45455 ; 2 0.509091
Std err (standard error): Sai số chuẩn của các hệ số hồi quy mẫu ˆ ˆ
se( 1) 6,413817; se( 2 ) 0,035743
t stat (t – Statistic) : Giá trị thống kê T có phân phối Student ˆ1 ˆ2
t1 se( ˆ1 3.812791; t2 ˆ2) 14.24317 ) se(
p-value: Giá trị xác suất theo phân phối T (Student) với n 2 bậc tự do (hay n k bậc
tự do ối với hồi quy bội k biến).
p value P T | | t j | Excel TDIST | t j |,n 2,2
Giá trị p-value dùng ể kiểm ịnh cặp giả thiết H0 : j 0 , H1 : j 0 theo phương pháp giá trị xác suất.
Lower, upper: tương ứng là cận dưới và cận trên của khoảng ước lượng của hệ số hồi quy tổng thể j
Xác suất thống kê và Ứng dụng – 2021 163 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Lower( j ) ˆj t n /22.se( ˆj )
Upper( j ) ˆj t n /22.se( ˆj )
Khoảng tin cậy của j là: j
Lower( j );Upper( j ) BÀI TẬP CHƯƠNG 5
5.1. Kết quả thí nghiệm nén ép (X, ơn vị: kN/cm2) của 12 mẫu bê tông cùng loại có kết
quả sau: 1; 1,39; 0,9; 1; 0,95; 1; 0,9; 1,1; 1,1; 0,95; 0,9; 0,9. Hãy kiểm tra và loại bỏ
(nếu có) các giá trị của X chứa sai số thô bằng mỗi phương pháp sau:
a) Quy tắc kinh nghiệm. b) Phương pháp IQR.
c) Phương pháp hiệu chỉnh Thompson (với mức ý nghĩa 4%).
d) Phương pháp MAD (giả sử mẫu ược chọn từ tổng thể có phân phối chuẩn).
5.2. Yêu cầu như câu 5.1 ối với kết quả thí nghiệm xác ịnh dung trọng tự nhiên (X -
kN/m3) của 12 mẫu ất như sau: 16,4; 16,4; 17; 16; 17,4; 17; 16; 16,5; 16,3; 18,1; 19,2; 18,1.
5.3. Quan sát năng suất X (tấn/ha) của một giống lúa thử nghiệm trên 100 thửa ruộng
(cùng diện tích) có kết quả sau: X
[8;9) [9;10) [10;11) [11;12) [12;13) [13;14) [14;15] Số thửa 8 15 21 23 16 9 8
Với mức ý nghĩa 5%, có thể xem năng suất X là biết ngẫu nhiên tuân theo luật phân phối chuẩn không?
5.4. Với mức ý nghĩa 4%, có thể coi dãy số liệu thực nghiệm sau về biến quan sát X có
tuân theo luật phân phối chuẩn không? X Số quan sát X Số quan sát [10;12) 1 [20;22) 310 [12;14) 2 [22;24) 230 [14;16) 20 [24;26) 92 [16;18) 92 [26;28) 20 [18;20) 230 [28;30] 2 164
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
5.5. Với mức ý nghĩa 5%, có thể coi dãy số liệu thực nghiệm sau về biến quan sát X có
tuân theo luật phân phối mũ không? X Số quan sát X Số quan sát [60;80) 103 [160;180) 17 [80;100) 71 [180;200) 12 [100;120) 50 [200;220) 8 [120;140) 35 [220;240) 6 [140;160) 24 [240;260] 4
5.6. Với mức ý nghĩa 2%, có thể coi dãy số liệu thực nghiệm sau về biến quan sát X có
tuân theo luật phân phối Poisson không? X 0 1 2 3 4 5 6 7 8 9 10
Số quan sát 50 149 224 224 168 101 50 22 8 3 1
5.7. Quan sát trong một số ngày về số tai nạn giao thông X xảy ra mỗi ngày ở một thành
phố ta có ược số liệu sau: Số tai nạn X 0 1 2 3 4 5 Số ngày 10 23 46 35 20 13
Với mức ý nghĩa 1%, có thể xem X là biết ngẫu nhiên có tuân theo luật phân phối Poisson không?
5.8. Để tìm hiểu lượng mũ X (gam) của cây cao su trong một ngày, ghi nhận ở 100 cây có kết quả sau: X
[200;210) [210;220) [220;230) [230;240) [240;250) [250;260) [260;270] Số cây 2 8 14 30 25 12 9
Với mức ý nghĩa 1%, có thể xem lượng mủ cao su X là biến ngẫu nhiên có tuân
theo luật phân phối chuẩn không?
5.9. Giả sử có số liệu thống kê về lãi suất ngân hàng (X – %/năm), tổng vốn ầu tư (Y –
tỷ ồng) trên ịa bàn của tỉnh A qua 10 năm liên tiếp có kết quả sau: X i 7
6,5 6,5 6,0 6,0 6,0 5,5 5,5 5,0 4,5 Yi 28 32 30 34 32 35 40 42 48 50
a) Tính hệ số tương quan mẫu.
b) Giữa X và Y có sự tương quan tuyến tính không với mức ý nghĩa 5%? Cho nhận
xét mức ộ về mức ộ phụ thuộc tương quan tuyến tính của X và Y.
c) Tìm hàm hồi quy tuyến tính mẫu Yˆ
ˆ1 ˆ2 X . Nêu ý nghĩa kinh tế của các
hệ số hồi quy. Tìm ước lượng iểm cho tổng vốn ầu tư trên ịa bàn của tỉnh A trong
năm tiếp theo khi lãi suất là 8,2%.
d) Tính tổng bình phương các phần dư.
Xác suất thống kê và Ứng dụng – 2021 165 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
e) Tìm khoảng tin cậy cho các hệ số hồi quy với ộ tin cậy 97%.
Kiểm ịnh cặp giả thiết HH 0 2 1 :: 2 1010,,55 và với mức ý nghĩa 4%. f)
5.10. Để nghiên cứu về mối quan hệ giữa thời gian tự học bình quân (X: giờ/tuần) và
iểm thi (Y) của một sinh viên ối với môn Toán chuyên ề. Khảo sát một số sinh viên
có kết quả trong bảng sau X i 0 0 1 1 1 2 3 4 5 Yi 3 6 6 5 8 7 9 8 10 Số sinh viên 7 18 25 19 30 20 15 9 3
a) Tính hệ số tương quan mẫu và kiểm ịnh sự phụ thuộc tương quan tuyến tính giữa
X và Y với mức ý nghĩa 4%.
b) Cho nhận xét mức ộ về mức ộ phụ thuộc tương quan tuyến tính của X và Y. Hãy
giải thích nguyên nhân dẫn ến sự phụ thuộc tương quan tuyến tính của X và Y là không cao.
c) Tìm hàm hồi quy tuyến tính mẫu Yˆ
ˆ1 ˆ2 X . Nêu ý nghĩa kinh tế của các hệ số hồi quy.
d) Tìm ước lượng iểm cho iểm thi trung bình của những sinh viên có thời gian tự
học bình quân là 2,5 (giờ/tuần).
e) Tìm khoảng tin cậy cho các hệ số hồi quy với ộ tin cậy 98%. Nêu ý nghĩa của các khoảng tin cậy này.
5.11. Lượng khách i xe buýt Y (triệu lượt người/năm) phụ thuộc vào tiền vé X (ngàn
ồng). Ta có bảng số liệu sau:
X i 2 3 4 2 3 3 4 3 3 2
Yi 10 6 5 8 7 8 7 7 8 9
a) Tính hệ số tương quan mẫu và kiểm ịnh sự phụ thuộc tương quan tuyến tính giữa
X và Y với mức ý nghĩa 3%. Cho nhận xét mức ộ về mức ộ phụ thuộc tương quan
tuyến tính của X và Y.
b) Tìm hàm hồi quy tuyến tính mẫu Yˆ
ˆ1 ˆ 2 X . Nêu ý nghĩa kinh tế của các
hệ số hồi quy. Hãy ước lượng số lượt khách i xe buýt bình quân khi giá vé là 5 ngàn ồng.
c) Xác ịnh khoảng tin cậy của 1, 2 với ộ tin cậy 95%.
d) Theo bạn thì tiền vé có ảnh hưởng ến lượng khách i xe buýt không, kết luận với mức ý nghĩa 3%? 166
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
e) Kiểm ịnh giả thiết H0 : 2 1,4, H1 : 2 1,4, 4%.
5.12. Tìm hiểu mối liên hệ giữa cước phí
vận chuyển Y (ngàn ồng) của một
loại hàng và giá xăng X (ngàn ồng/
lít) trong cùng thời iểm ở các ơn vị
vận tải trong thành phố A qua các
chuyến vận tải, có bảng số liệu bên:
a) Tính hệ số tương quan mẫu và
kiểm ịnh sự phụ thuộc tương quan tuyến tính giữa X và Y với mức ý nghĩa 2%.
Cho nhận xét mức ộ về mức ộ phụ thuộc tương quan tuyến tính của X và Y.
b) Tìm hàm hồi quy tuyến tính mẫu Yˆ
ˆ1 ˆ 2 X . Nêu ý nghĩa kinh tế của các
hệ số hồi quy. Hãy ước lượng cước phí vận chuyển bình quân khi giá xăng là 20 (ngàn ồng/ lít).
5.13. Theo dõi sự phụ thuộc giữa mức
suy giảm hàm lượng ường X (%)
trong nguyên liệu mía và thời gian
chờ chế biến T (ngày), có bảng số
liệu bảng bên. Giả sử T và X có sự
phụ thuộc tương quan tuyến tính.
a) Tính hệ số tương quan mẫu và
cho nhận xét mức ộ về mức ộ phụ thuộc tương quan tuyến tính của T và X.
b) Tìm hàm hồi quy tuyến tính mẫu Xˆ
ˆ1 ˆ2T . Nêu ý nghĩa kinh tế của các hệ số hồi quy.
c) Nếu thêm một ngày chờ chế biến thì bình quân hàm lượng ường giảm bao nhiêu?
5.14. Khảo sát lượng thức ăn (Y – kg/người/tháng) của một loại thức ăn A ắt tiền và thu
nhập ( X – triệu ồng/ tháng) của người ó. Bảng sau cho kết quả khảo sát của 10 người. X i 10 12 12 15 17 20 25 27 35 50 Yi
0,2 0,1 0,5 0,7 0,8 1,0 1,2 1,1 1,4 1,3
a) Tìm hàm hồi quy mẫu Yˆ ˆ1 ˆ
2 (1/ X ) . Nêu ý nghĩa kinh tế của hệ số ˆ1.
b) Hãy ước lượng lượng thức ăn trung bình của những người có thu nhập 70 (triệu ồng/ tháng).
Xác suất thống kê và Ứng dụng – 2021 167 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
5.15. Cho bảng số liệu thực nghiệm sau về hai biến ngẫu nhiên X và Y. Giả sử rằng bảng
số liệu này có hàm hồi quy tổng thể dạng f X( ) a X. b . X i
2,2 3,8 7,0 7,7 11,5 15,2 18,0 Yi 3,6 5,0 7,0 7,7 9,3 11,3 12,2
Dựa vào mẫu, hãy tìm hàm hồi quy Yˆ a Xˆ.bˆ .
5.16. Khảo sát lượng cam bán ược Y (tấn/tháng) theo giá cam X2 (ngàn ồng/kg) và giá
quýt X3 (ngàn ồng/ kg) có số liệu sau: Y 14 13 12 10 8 9 8 7 6 6 X2 2 2 3 4 5 5 6 7 8 9 X3 7 6 7 6 5 6 4 5 4 5
a) Dựa vào mẫu, hãy tìm hàm hồi quy mẫu Yˆ
ˆ1 ˆ2 X 2 ˆ3X3 . Nêu ý nghĩa
kinh tế của các hệ số hồi quy.
b) Với ộ tin cậy 96%, hãy tìm khoảng tin cậy cho 1, 2, 3 .
c) Biến X3 có ảnh hưởng ến Y hay không, với 3%?
d) Kiểm ịnh giả thiết H0 : 2 2 ; H1 : 2 2 , với 4%. CHƯƠNG 6
XÍCH MARKOV VÀ ỨNG DỤNG
6.1. Các khái niệm cơ bản về xích Markov
6.1.1. Một số ịnh nghĩa
Trong tự nhiên cũng như trong các lĩnh vực hoạt ộng của con người ta thường quan
sát sự tiến triển của các hệ theo thời gian mà tại mỗi thời iểm t là một biến ngẫu nhiên.
Ví dụ như: số khách hàng ến một dịch vụ tại thời iểm t; số tín hiệu thông tin gửi ến một
tổng ài tại thời iểm t; dân số của một quốc gia tại thời iểm t; số lượng người thất nghiệp
của một quốc gia tại thời iểm t; số lượng của một loài sinh vật tại thời iểm t; số người
chết do một loại bệnh nào ó trên thế giới tại thời iểm t,…
Trong các ví dụ trên, ta thấy rằng tại thời iểm t giá trị của mỗi dấu hiệu mà ta quan
sát là một số ngẫu nhiên. Nghĩa là tại mỗi thời iểm t ta có một biến ngẫu nhiên
X t( ) . Những hệ như vậy sẽ ược khái quát hóa trong khái niệm quá trình ngẫu nhiên sau ây.
a) Quá trình ngẫu nhiên
➢ Xét một hệ vật lý (hay một hệ sinh thái, hệ thống dịch vụ,…) tiến triển theo thời
gian t . Gọi X t( ) là vị trí (giá trị, tình trạng) của hệ tại thời iểm t , khi ó X t( ) là một 168
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
biến ngẫu nhiên. Quá trình X t( ), t T với T
ược gọi là một quá trình ngẫu . Cụ thể, thời gian rời nhiên
X t( ), t 0,1,2,... ược gọi quá trình ngẫu nhiên với
rạc và X t( ), t 0 ược gọi là quá trình ngẫu nhiên với thời gian liên tục.
➢ Tập hợp các vị trí có thể có của hệ gọi là không gian trạng thái của hệ (ký hiệu là
E ), mỗi phần tử của E ược gọi là một trạng thái của hệ.
b) Tính Markov – quá trình Markov
Nếu khi biết hiện tại mà sự tiến triển của hệ trong tương lai chỉ phụ thuộc vào hiện
tại mà không phụ thuộc vào quá khứ thì ta nói hệ có tính Markov hay tính không nhớ.
Khi ó quá trình ngẫu nhiên X t( ), t T ược gọi là quá trình Markov.
Diễn giải về mặt xác suất:
P X t ( n 1) j X t|( 0 ) i0 ,..., X t( n 1) in 1, X t( n) i
P X t ( n 1) j X t|( n) i
Xác suất ể hệ ở trạng thái j tại thời iểm tn 1 trong tương lai chỉ phụ thuộc vào
trạng thái của hệ ở thời iểm hiện tại tn mà không phụ thuộc vào các trạng thái của hệ ở
mọi thời iểm t t0, 1,...,tn 1 trong quá khứ.
Chẳng hạn: Số lượng một loài sinh vật; Số lượng các linh kiện của một hệ thống
kỹ thuật cần thay thế,… xét theo thời gian là các quá trình Markov. c) Xích Markov trạng
Nếu không gian trạng thái E gồm một số hữu hạn hoặc vô hạn ếm ược các
thái thì quá trình Markov X t( ), t T ược gọi là xích Markov. Lúc này, có thể ký hiệu E
1,2,3... , tức là các trạng thái ược ánh số. Như vậy, xích Markov chỉ là một
trường hợp riêng của quá trình Markov khi mà ta có thể ánh số ược cho các trạng thái. Hơn nữa:
Nếu tập các giá trị t là tập hợp ếm ược (chẳng hạn: t 0,1,2,...) thì ta có xích
Markov với thời gian rời rạc hay xích Markov rời rạc. Khi ó tập các giá trị t ược hiệu ngắn
ồng nhất với tập hợp {0,1,2,3,...}, và xích Markov tương ứng sẽ ược ký
gọn là X n n 0 , ở ây Xn ược hiểu là trạng thái của hệ tại thời iểm thứ n.
Nếu t [0, ) thì ta có xích Markov với thời gian liên tục, hay xích Markov liên tục.
Xác suất thống kê và Ứng dụng – 2021 169 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Ví dụ 6.1. Nghiên cứu về vấn ề nghiện hút thuốc lá của người dân ở ịa phương H theo
thời gian ( ơn vị thời gian là một quý – 3 tháng). Ký hiệu trạng thái 0 là không nghiện
và trạng thái 1 là nghiện của một người. Tại thời iểm t 0 (thời iểm hiện tại – quý 1),
người ta thống kê ược tỷ lệ người dân nghiện hút thuốc lá là 14,5%. Ký hiệu X0 là trạng
thái về hút thuốc lá của người dân ở ịa phương H tại thời iểm t 0, thì X0 là một biến
ngẫu nhiên rời rạc có thể nhận các giá trị 0 hoặc 1 với xác
suất tưởng ứng là 0,855 và 0,145.
Tại các thời iểm tiếp theo, chẳng hạn: t 1 (quý hai), t 2 (quý ba),… tình trạng
hút thuốc lá ở ịa phương H ược mô tả bởi các biến ngẫu nhiên X X1, 2,... với các bảng
phân phối xác suất tương ứng.
Khi ó, ta có một xích Markov rời rạc thời gian X n
n 0 với không gian trạng thái là E {0,1}.
6.1.2. Xác suất chuyển trạng thái, xích Markov thuần nhất Xét
xích Markov X t( ), t T .
➢ Ta nói: P X t ( ) j X s| ( ) i là xác suất chuyển trạng thái, xác suất có iều
kiện ể hệ (hay quá trình) tại thời ểm s ở trạng thái i, ến thời iểm t s chuyển sang trạng thái j. ➢ Nếu có ẳng thức:
P X t ( h) j X s|( h) i P X t ( ) j X s| ( ) i
Thì ta nói xích Markov X t( ), t T thuần nhất theo thời gian.
Do giới hạn chương trình nên trong chương này chúng ta chỉ xét xích Markov
thuần nhất và rời rạc thời gian.
6.1.3. Phân phối của hệ và ma trận xác suất chuyển Xét xích Markov X n
n 0 rời rạc thuần nhất với không gian các trạng thái E là
tập hữu hạn có d phần tử. Ký hiệu 170
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
pij P X m 1 j X| m i P X 1 j X| 0 i
p nij ( ) P X m n j X| m
i P X n j X| 0 i
U(0) (u u1, 2,...,ud ) , vơi ui P X( 0 i) U n( )
u n u n1( ), 2 ( ),...,ud ( )n , với u ni ( ) P X( n i) Ta gọi: ➢ P P(1)
pij d d là ma trận xác suất chuyển sau một bước (hoặc nói gọn là ma
trận xác suất chuyển) ➢ P n( )
p nij ( ) d d là ma trận
xác suất chuyển sau n bước.
Thỏa mãn pij 1 và p nij ( ) 1 j E j E
➢ U(0) là phân phối ban ầu của hệ, thỏa mãn ui 1 . i E
➢ U n( ) là phân phối của hệ tại thời iểm n, thỏa mãn u ni ( ) 1 . i E Định lý 6.1
Phân phối ồng thời của vector ngẫu nhiên (X0, X1,..., Xn) ược hoàn toàn xác ịnh từ
phân phối ban ầu và xác suất chuyển. Cụ thể ta có:
P X( 0 i X0, 1 i1,..., Xn in) u pi0i i01...pin 1in Chứng minh:
Theo công thức nhân xác suất, ta có:
P X(0 i X0 , 1 i1,..., Xn in)
Xác suất thống kê và Ứng dụng – 2021 171 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh P X(0 i P X0 ) (
1 i1 | X 0 i0 ) ... P X(n in | X 0 i X0 , 1
i1,..., X n 1 in 1) P X(0 i P X0 ) (
1 i1 | X 0 i0 ) ... P X( n in | X n 1 in 1)
u pi0i i01...pin 1in .
Định lý 6.2 (Phương trình Chapman - Kolmogorov) p nij ( m)
pik ( )n pkj (m) k E Chứng minh:
Hệ {Xn k k: E} là hệ ầy ủ và xung khắc từng ôi {Xn m j}
{Xn m j}{Xn k} k E
Áp dụng công thức xác suất ầy ủ và tính Markov, ta có:
p nij ( m) P X(n m j X| 0 i)
P {X n m j}.{X n k}| X 0 i k E
P X n k X|0 i P X n m j X|n k X,0 i k E
pik ( )n pkj (m) k E
Từ phương trình Chapman – Kolmogorov, xem U n( ) là một ma trận hàng, viết
dưới dạng tích các ma trận ta có hệ quả sau: Hệ quả 6.1
1) U m( 1) U m P( )
2) U m( n) U m P( ) n
3) U n( ) U(0)Pn
4) P n( ) Pn
Ví dụ 6.2. (Xét lại ví dụ 6.1) 172
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Nghiên cứu về vấn ề nghiện hút thuốc lá của người dân ở ịa phương H theo thời
gian ( ơn vị thời gian là một quý – 3 tháng). Ký hiệu trạng thái 0 là không nghiện và
trạng thái 1 là nghiện của một người. Tại thời iểm hiện tại – quý 1 năm 2018, người ta
thống kê ược tỷ lệ người dân nghiện hút thuốc lá là 14,5%. Thống kê trong nhiều năm
qua cho thấy xác suất ể một người không nghiện sau một quý vẫn không nghiện là 0,985
và xác suất ể một người nghiện sau một quý vẫn tiếp tục nghiện là 0,872.
Theo ví dụ 6.1, ta có xích Markov thuần nhất rời rạc thời gian X n n 0 với không
gian trạng thái là E {0,1}.
Phân phối ban ầu (tỷ lệ người nghiện và không nghiện trong quý 1 năm 2018): U(0) u u0, 1 0,855;0,145 Trong ó: u0 P X(
0 0) 0,855 tỷ lệ không nghiện
thuốc lá u1 P X( 0 1) 0,145 tỷ lệ nghiện thuốc lá Ma trận xác suất chuyển : p11 p 12 0,985 0,015 P p21 p 22 0,128 0,872 Trong ó:
p11 P X 1 0 | X0 0 0,985 : không nghiện kh. nghiện
p12 P X 1 1| X 0 0 0,015 : không nghiện nghiện p21
P X 1 0 | X 0 1 0,128 : nghiện không nghiện p22
P X 1 1| X 0 1 0,872 : nghiện nghiện
Theo hệ quả 5.3, ta tính ược phân phối số người không nghiệm và nghiện tương 0,985
ứng ở các quý 2, 3, 4 năm 2018 như sau: U(1) U(0)P 0,855;0,145 0,015 0,860735;0,139265 0,128 0,872
Xác suất thống kê và Ứng dụng – 2021 173 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 0,972145 U(2) U(0)P2 0,855;0,145 0,027855 0,865650;0,134350 0,237696 0,762304 0,9611280,038872
U(3) U(0)P3 0,855;0,145 0,869862;0,130138 0,331705 0,668295
Như vậy trong quý 2, quý 3, quý 4 năm 2018 tỷ lệ người nghiện thuốc lá tương
ứng sẽ là: 13,927%; 13,435% và 13,014%.
Có thể dự báo tỷ lệ người nghiện thuốc lá ở ịa phương H trong quý 3 năm 2019 (n 6) như sau:
U(6) U(0)P6 U(0)(P3 2) 0,855;0,145 0,9611280,038872 2 0,879216;0,120784 0,331705 0,668295
Vậy tỷ lệ cần tìm là: 12,078%.
Ví dụ 6.3. Cho xích Markov thuần nhất {Xn} n 0 có không gian các trạng thái là E {2,3,5}. Cho biết:
Phân phối ban ầu : U(0) (0,23;0,37;0,40) 0,2 0,5 0,3
Ma trận xác suất chuyển: P 0,3 0,4 0,3 0,5 0,3 0,2
a) Tìm các ma trận xác suất chuyển sau 2,3,4,5 bước.
b) Tìm phân phối của hệ tại thời iểm n 3 và tại n 5.
c) Tính các xác suất: P X( 4 2| X0 5) và P X( 7 3| X2 2)
d) Tính xác suất P X(
0 5, X1 3, X2 2, X5 3)
Giải. a) Ma trận xác suất chuyển sau n bước là: ( ) P n( ) p nij 3 3 Pn 174
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 0,34 0,39 0,27 P(2) P2 0,33 0,4 0,27 0,29 0,43 0,28 0,32 0,407 0,273 P(3) P3 P P2 0,321 0,406 0,273 0,327 0,401 0,272 0,3226 0,4047 0,2727
P(4) P4 P P2 2 0,3225 0,4048 0,2727 0,3217 0,4055 0,2728 0,32228 0,40499
0,27273 P(5) P5 P P3 2 0,32229 0,40498 0,27273 0,32239 0,40489 0,27272
b) Ta có: U n( ) U(0)Pn Vậy:
U(3) U(0)P3 0,3232;0,4042;0,2726
U(5) U (0)P5 0,32233;0,40494;0,27273 c) Ta có:
P X( 4 2| X0 5) p31(4) 0,3217
P X( 7 3| X2 2) P X( 2 5 3| X2 2) P X( 5 3| X0 2) p12(5) 0,40499
d) Áp dụng công thức nhân xác suất, tính Markov, tính thuần nhất, ta có:
P X( 0 5, X1 3, X 2 2, X 5 3)
P X(0 5).P X(1 3| X 0 5).P X(2 2 | X 0 5, X1 3)
P X(5 3| X 0 5, X1 3, X 2 2)
Xác suất thống kê và Ứng dụng – 2021 175 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
u p3. 32.P X( 1 2 | X 0 3).P X( 3 3| X 0
2) u p3. 32.p21.p12 (3) 0,014652
6.1.4. Phân phối dừng a) Định nghĩa Xét xích Markov X n
n 0 rời rạc thuần nhất với không gian trạng thái E có d
phần tử và P là ma trận xác suất chuyển. Phân phối U (u u1, 2,...,ud ) ược gọi là phân
phối dừng của hệ nếu thỏa mãn phương trình U P. U . b) Định lý 6.3
Giả sử U (u u1, 2,...,ud ) là phân phối của hệ ở thời iểm m và là phân phối dừng,
nghĩa là U m( ) U và U P. U . Khi ó ta có: U n( ) U, n m.
Chứng minh: Theo hệ quả 6.1, ta có:
U m( 1) U m P(). U P. U
Bằng quy nạp toán học, thu ược: U n( ) U, n m .
c) Tìm phân phối dừng
Để tìm phân phối dừng U (u u1, 2,...,ud ), ta giải hệ phương trình sau: U P. U
1 u2 ... ud 1 (thỏa iều kiện ui 0, i ) u
Ví dụ 6.4. Cho xích Markov {Xn} n 0 rời rạc thuần nhất có không gian trạng thái E
{1,2,3} với ma trận xác suất chuyển là: 1/ 3 1/ 3 1/ 3 P 1/ 4 1/ 2 1/ 4 1/ 6 1/ 3 1/ 2
Hãy tìm phân phối dừng của hệ.
Giải. Gọi U (x y z, , ) là phân phối dừng của hệ U P. U 176
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Giải hệ phương trình: x y z 1 3 x y 6 z 3x x 44y y 2 zz xzy 24 8xxx y 333yyy 622zzz 000 zxy 000,,,36244 3 2 3 x z 1 x y z 1
Vậy phân phối dừng của hệ là: U (0,24;0,4;0,36)
6.2. Một số ứng dụng của xích Markov rời rạc thuần nhất
Xích Markov rời rạc thuần nhất có nhiều ứng dụng trong Kinh tế, Kỹ thuật, Sinh
học, Xã hội học, Công nghệ thông tin,… Trong mục này, chúng ta sẽ xem xét các ứng
dụng như kiểm kê hàng hóa dự trữ, tìm cân bằng thị phần, xác ịnh chính sách thay thế vật tư thiết bị.
6.2.1. Kiểm kê hàng hóa dự trữ
Một hệ dịch vụ cần phải dự trữ trong kho một loại hàng nào ó ể áp ứng nhu cầu
liên tục của khách hàng. Hàng ược nhập kho tại cuối các chu kỳ n 0,1,2,... Tổng số
lượng hàng cần phải áp ứng nhu cầu trong chu kỳ n là biến ngẫu nhiên Yn có phân phối
ộc lập với thời gian như sau:
P Y( n k) a kk , 0,1,2,... ; ak 1 (1) k 0
Mức hàng dự trữ ược kiểm kê tại cuối mỗi chu kỳ. Nguyên tắc nhập hàng căn cứ
vào hai mức chỉ số s và S (s S ) như sau:
Nếu ở cuối mỗi chu kỳ mà lượng hàng dự trữ hiện có không vượt quá s thì phải
nhập thêm hàng ể có lượng dự trữ mới là S, nếu ở cuối mỗi chu kỳ mà lượng hàng dự
trữ hiện có vượt quá s thì không cần nhập thêm hàng.
Gọi Xn là lượng hàng hiện có vào cuối chu kỳ n khi kiểm kê (tức là trước khi ưa ra
quyết ịnh có nhập thêm hàng hay không). Khi ó tập giá trị của Xn (không gian các trạng thái) là:
Xác suất thống kê và Ứng dụng – 2021 177 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
E {..., 2, 1,0,1,2,...,S 1,S} (2)
trong ó giá trị âm là nhu cầu không ược thỏa mãn mà sẽ ược áp ứng ngay sau khi nhập hàng. Ta có: Xn 1
X n YnY n1 1,,khi Xkhi s n Xsn S (3) S
Có thể xem các biến ngẫu nhiên Y Y1, 2,... là ộc lập với nhau và có cùng phân phối (1).
Trong (3) ta thấy rằng X n 1 chỉ phụ thuộc vào Xn mà không phụ thuộc vào các chu kỳ
trong quá khứ. Vì vậy dãy {Xn} n 0 lập thành một xích Markov rời rạc và thuần nhất với
không gian trạng thái E (xác ịnh bởi (2)) và xác suất chuyển:
pij P X n 1 j X|n i
P Y n 1 ij , khi s i S (4)
P Y n 1 Sj , khi i s
Ví dụ 6.5. Cho mô hình kiểm kê hàng hóa dự trữ với các mức căn cứ nhập hàng: s
0,S 2 , và Yn là lượng hàng khách yêu cầu trong chu kỳ n có phân phối xác suất như sau: Yn 0 1 2 1 P 0,6 0,3 0,
Xét xích Markov {Xn} n 0 , trong ó Xn là số hàng hóa còn lại tại cuối chu kỳ n.
Giả sử tại cuối chu kỳ ầu tiên, số hàng hóa còn lại là một trong các trạng thái của E với xác suất như nhau.
a) Tìm không gian trạng thái E.
b) Tìm ma trận xác suất chuyển trạng thái của hệ.
c) Tìm các ma trận xác suất chuyển sau 2,3 và 4 bước.
d) Tìm phân phối ban ầu và phân phối tại các chu kỳ n 2,n 3 của hệ.
e) Tính các xác suất P X(
4 1| X0 2); P X( 5 1| X3 1) .
f) Tính xác suất P X( 0 1, X1 2, X2 0, X4 1) .
Giải. a) Gọi dn là lượng hàng dự trữ (sau khi kiểm kê và bổ sung) ở cuối chu kỳ n. Ta có bảng sau: dn Yn 1 X n 1 dn 1 178
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 0 2 2 2 1 1 1 2 0 2 0 1 1 1 1 0 2 2 -1 2
Vậy không gian trạng thái của xích Markov {Xn} n 0 là: E 1,0,1,2
b) Ma trận xác suất chuyển trạng thái của hệ: P
pij 4 4 , với các pij ược tính trong bảng sau: 0 0,1 0,3 0,6 0,1 0,3 0,6 Vậy: P 0 0,3 0,6 0 0,1 0,1 0,3 0 0,6
c) Ma trận xác suất chuyển sau 2, 3 và 4 bước lần lượt là: 0,03 0,16 0,39 0,42 P(2) P2 0,03 0,16 0,39 0,42 0,06 0,22 0,48 0,24 0,03 0,16 0,39 0,42 0,039 0,178 0,417 0,366 P(3) P3 0,039 0,178 0,417 0,366
Xác suất thống kê và Ứng dụng – 2021 179 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 0,048 0,196 0,444 0,312 0,039 0,178 0,417 0,366 0,0417 0,1834 0,4251 0,3498 P(4) P4 0,0417 0,1834 0,4251 0,3498 0,0444 0,1888 0,4332 0,3336 0,0417 0,1834 0,4251 0,3498 1
d) Theo ề cho,ta có: P X( 0 i) 1 , i E | E | 4
Vậy phân phối ban ầu của hệ: U(0) u u u u1, 2, 3, 4 0,25;0,25;0,25;0,25
Phân phối tại các chu kỳ n 2,n 3lần lượt là:
U(2) U(0)P2 0,0375;0,175;0,4125;0,375 .
U(3) U(0)P3 0,3232;0,4042;0,2726 e) Ta có:
P X( 4 1| X0 2) p41(4) 0,0417
P X( 5 1| X3 1) P X( 2 1| X0 1) p13(2) 0,39
f) Áp dụng công thức nhân xác suất, tính Markov, tính thuần nhất, ta có: P X( 0
1, X1 2, X 2 0, X 4 1) P X( 0
1).P X( 1 2 | X0
1).P X( 2 0 | X0 1, X1 2) P X( 4 1| X0 1, X1 2, X 2 0) u p P X1. 14. (
1 0 | X0 2).P X( 2 1| X0 0)
u p1. 14.p42.p23(2) 0,00585
6.2.2. Tìm cân bằng thị phần 180
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Giả sử trong một khu vực có d hệ dịch vụ cùng loại, ký hiệu là 1,2,...,d . Trong mỗi
chu kỳ thời gian, trong số N khách hàng ở khu vực, mỗi khách hàng có thể chọn một
trong d hệ dịch vụ và sang chu kỳ thời gian tiếp theo khách hàng ó có thể chọn hệ dịch
vụ khác hay vẫn ến hệ dịch vụ trước ây là tùy theo sở thích. Các hệ dịch vụ có thể cạnh
tranh nhau, tăng cường quảng cáo và nâng cao chất lượng phục vụ ể thu hút khách hàng.
Ký hiệu Xn là dịch vụ mà một khách hàng (xem như phần tử ại diện cho N khách hàng)
chọn ở chu kỳ thời gian thứ n. Khi
ó {Xn} n 0 là một xích Markov thuần nhất có không gian trạng thái
E {1,2,...,d} và phân phối ban ầu của hệ chính là tỷ lệ khách hàng vào từng hệ dịch
vụ ở chu kỳ ầu tiên (n 0).
Xác suất chuyển pij P X m 1 j X| m i chính là xác suất ể khách hàng hiện
tại ang vào hệ dịch vụ i, sang chu kỳ tiếp theo vào hệ dịch vụ j, ó là tỷ lệ khách hàng
vào hệ dịch vụ j trong chu kỳ thời gian sau trong số các khách hàng ở hệ dịch vụ i của
chu kỳ ngay trước ó. Ma trận xác suất chuyển là một ma trận vuông cấp d: P pij d d .
Ví dụ 6.6. Giả sử có 3 cửa hàng (ký hiệu là 1, 2 và 3) cùng bán một loại sản phẩm nào
ó. Khách hàng có thể chọn mua sản phẩm tại một trong 3 cửa hàng tùy theo sở thích
của họ và trong từng tháng họ không thay ổi chỗ mua hàng. Gọi Xn là cửa hàng mà
khách hàng chọn mua sản phẩm ở tháng thứ n.
Ta có xích Markov thuần nhất {Xn} n 0 có 3 trạng thái E {1,2,3}. Cho ma trận
xác suất chuyển như sau: 0,8 0,1 0,1 P 0,07 0,9 0,03 0,08 0,07 0,85
Giả sử tháng giêng cửa hàng 1 chiếm 20% khách hàng, của hàng 2 chiếm 50%
khách hàng và cửa hàng 3 chiếm 30% khách hàng.
a) Tìm phân phối khách hàng ở tháng 2, 6 và tháng 12.
b) Tìm tỷ lệ khách hàng cân bằng dừng (phân phối dừng) của hệ
Giải. a) Phân phối ban
ầu (tỷ lệ khách hàng trong tháng giêng - n 0) là:
Xác suất thống kê và Ứng dụng – 2021 181 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh U(0) 0,2;0,5;0,3 .
Phân phối khách hàng ở tháng 2 (n 1):
U(1) U(0)P 0,219;0,491;0,29 Phân
phối khách hàng ở tháng 6 (n 5):
U(5) U(0)P5 0,25525;0,47148;0,27327 Phân
phối khách hàng ở tháng 12 (n 11):
U(11) U(0)P11 0,26716;0,46254;0,27030
b) Gọi U (x y z, , ) là phân phối dừng của hệ
0,8x 0,07y 0,08z x U P. U
0,1x 0,9y 0,07z y Giải hệ: x y z 1
0,1x 0,03y 0,85z z x y z 1
0,2x 0,07y 0,08z 0 0,1x 0x, 1xy
00z,,103y1 y 0,007,15zz 00 x y 0,26931 z 0,27140 0,45929
Vậy tỷ lệ khách hàng cân bằng dừng của số khách hàng vào các cửa hàng 1,2 và 3
lần lượt là: 29,931% , 45,929% và 27,14%.
6.2.3. Xác ịnh chính sách thay thế thiết bị
Trong một hệ thống kỹ thuật, có 1500 thiết bị cùng một loại ược phân ra các tình
trạng: vừa mới thay, còn tốt, vẫn dùng ược và ã bị hỏng. Xét hai phương án thay thế thiết bị như sau:
Phương án 1: Chỉ thay mới khi thiết bị ã bị hỏng.
Phương án 2: Thay mới khi thiết bị ở trạng thái vẫn dùng ược. 182
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Theo số liệu thống kê, ta có ma trận xác suất chuyển trạng thái sau một tháng là: Mới thay Dùng ược Còn tốt Bị hỏng Mới thay 0 0 , 8 0 , 2 0 Còn tốt 0 0 , 6 0 ,4 0 Dùng ược 0 0 , 0 5 , 0 5 Bị hỏng 1 0 0 0
Giả sử rằng chi phí thay mới một thiết bị là 60 ngàn ồng và thất thu khi mỗi một
thiết bị hỏng là 45 ngàn ồng.
Hãy tính số tiền trung bình mà hệ thống phải chi cho một thiết bị trong một tháng
tương ứng với mỗi phương án thay thế thiết bị. Từ ó hãy chọn phương án thay thế thiết
bị có lợi hơn và số tiền tiết kiệm ược từ việc lựa chọn này.
Giải. Lúc ầu khi hệ thống mới i vào hoạt ộng, các thiết bị (có thể) ược trang bị mới. Sau
một thời gian nhất ịnh, tình trạng các thiết bị trong toàn hệ thống sẽ ổn ịnh, nghĩa là tình
trạng thiết bị sẽ ở trạng thái dừng. Xét phương án 1:
Gọi U (x y z t,, , ) là phân phối dừng của hệ U P. U Giải hệ: x y z t 1 t x x t 00,,82xx 00,,64yy 0y,5z z 22xx 4yy 05z 0 0,5z t z 2t 0 x y z t 1 x y z t 1 x t y 22tt txy 11z//661/ 3 U 1 1 1 16 3 3 6; ; ; z x y z t 1
Xác suất thống kê và Ứng dụng – 2021 183 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Vậy mỗi tháng hệ thống phải chi trung bình cho một thiết bị số tiền là: 60 1 45 1 17,5 (ngàn ồng). 6 6 Xét phương án 2:
Ma trận xác suất chuyển trạng thái sẽ là: Mới thay Dùng ược Còn tốt Mới thay 0 0 , 8 0 ,2 Còn tốt 0 0 , 6 , 0 4 Dùng ược 1 0 0
Gọi U (x y z, , ) là phân phối dừng của hệ U P. U Giải hệ: x y z 1 z x x z y 1 / 2 0,8x 0,6y y 2x y 0 x 1 / 4 0,2x 0,4y z x x yz 1 x 2yy z5z1 0 z 1/ 4 U 1 1 1; ; 4 2 4
Vậy mỗi tháng hệ thống phải chi trung bình cho một thiết bị số tiền là: 60 45 0 15 (ngàn ồng).
So sánh các kết quả trên, ta thấy rằng áp dụng phương án 2 sẽ có lời hơn. Khi ó
số tiền tiết kiệm ược trong một tháng của toàn hệ thống là: 1500 (17,5 15) 3750 (ngàn ồng). BÀI TẬP CHƯƠNG 6 184
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
6.1. Cho xích Markov rời rạc thuần nhất {Xn} n 0 có không gian các trạng thái là E
{1,2,3} với ma trận xác suất chuyển là: 0,1 0,2 0,7 P 0,9 0,0 0,1 0,1 0,8 0,1
Biết phân phối ban ầu của X0 là U(0) (0,3;0,4;0,3).
a) Tìm các ma trận xác suất chuyển sau 2 bước, 4 bước
b) Tìm phân phối của hệ tại các thời iểm n 2,n 4,n 10 .
c) Tính các xác suất P X( 3 1| X0 1); P X( 6 2| X2 2).
d) Tính xác suất P X( 0 1, X1 2, X2 1, X3 2) .
e) Tìm phân phối dừng của hệ.
6.2. Cho xích Markov rời rạc thuần nhất {Xn} n 0 có không gian các trạng thái là E
{1,2,3} với ma trận xác suất chuyển là: 0,1 0,5 0,4 P 0,6 0,2 0,2 0,3 0,4 0,3
Biết phân phối ban ầu của X0 là U(0) (0,1;0,6;0,3) .
a) Lập bảng phân phối xác suất của X3 .
b) Tính xác suất P X( 0 1, X1 3, X2 3, X3 2).
c) Tìm phân phối dừng.
6.3. Người ta truyền một bức iện gồm các tín hiệu 0, 1 thông qua kênh có nhiều trạm
và mỗi trạm nhận úng tín hiệu với xác suất a. Ký hiệu X0 là tín hiệu truyền i và
Xn là tín hiệu nhận ược ở trạm n. Biết rằng {Xn} n 0 lập thành xích Markov rời rạc
thuần nhất với ma trận xác suất chuyển: P 1 aa1 aa
Giả sử tín hiệu truyền i là tín hiệu 0.
Xác suất thống kê và Ứng dụng – 2021 185 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
a) Tính xác suất ể không nhận sai tín hiệu cho tới trạm n 2
b) Tính xác suất ể nhận úng tín hiệu của trạm n 2
c) Tính xác suất ể nhận úng tín hiệu của trạm n 5
6.4. Mỗi người dân của thị trấn H có 1 trong 3 nghề A, B, C. Con cái của họ nối tiếp
nghề của cha mình với xác suất tương ứng là 3/ 5,2/ 3,1/ 4 . Nếu không theo nghề
của cha mình thì chúng chọn một trong hai nghề còn lại với xác suất như nhau. Giả
sử thế hệ hiện tại có 20% theo nghề A, 30% theo nghề B và 50% theo nghề C.
a) Tìm phân phối nghề nghiệp ở thế hệ tiếp theo.
b) Tìm phân phối giới hạn theo nghề nghiệp của cư dân thị trấn H trong tương lai xa.
6.5. Tại một vùng dân cư, thời iểm hiện tại là tháng 9/2019 tỉ lệ người không có việc
làm, có việc làm tạm thời, có việc làm ổn ịnh lần lượt là 10%, 25%, 65%. Xây dụng
mô hình xích Markov {Xn} n 0 với không gian trạng thái E {0,1,2}, trạng thái 0
ứng với không việc làm, trạng thái 1 ứng với có việc làm tạm thời, trạng tháng 2
ứng với có việc làm ổn ịnh. Cho ma trận xác suất chuyển (các bước chuyển với thời
gian là một tháng, Xn là trạng thái ở tháng thứ n sau thời iểm hiện tại X0 ) 0 1 2 0 0,6 0,3 0,1 P 1 0,1 0,8 0,1 2 0 0,1 0,9
a) Hãy cho biết tình trạng việc ở tháng 1/2020.
b) Cho biết vùng dân cư này có 2 triệu dân trong ộ tuổi lao ộng, hãy ước lượng số
người không có việc làm, có việc làm tạm thời, có việc làm ổn ịnh trong tháng 3/ 2020.
c) Tìm phân phối dừng của quá trình Markov trên. Nêu ý nghĩa của phân phối dừng trong trường hợp này.
6.6. Trong phân tích thị trường, các xu hướng cơ bản bao gồm: xu hướng tăng (thị
trường bò), xu hướng giảm (thị trường gấu) và xu hướng i ngang. Xét các xu hướng
này thay ổi một cách ngẫu nhiên theo tuần và có tính Markov. Qua phân tích kỹ
thuật từ dữ liệu lịch sử cho ta xác suất chuyển ổi giữa các xu hướng ở hai tuần liên tiếp trong bảng sau: Đến Tăng Giảm Ngang 186
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh Từ Tăng 0,9 0,065 0,035 Giảm 0,15 0,75 0,1 Ngang 0,25 0,25 0,5
Đặt {Xn} n 0 là quá trình Markov với không gian trạng thái E {0,1,2}, trong ó
trạng thái 0 ứng với tăng, 1 ứng với giảm, 2 ứng với ngang. Trong ó, Xn là trạng thái ở
tuần thứ n sau tuần hiện tại X0 . Cho biết tuần hiện tại có xu hướng tăng, tức U(0) (1,0,0) .
a) Viết ma trận xác suất chuyển của quá trình Markov trên.
b) Đánh giá xu hướng thị trường (tỉ lệ của các xu hướng) ở tuần thứ 3, thứ 4 sau ó.
c) Sử dụng phần mềm Mathematica ể tìm phân phối của X100, X110, X200 . Từ ó ưa ra
nhận xét về xu hướng của thị trường này sau một thời gian xa trong tương lai.
6.7. Một hãng xe kinh doanh vận chuyển hành khách ở ba quận trong một thành phố
với nhiều xe. Thời iểm 6 giờ sáng trong ngày, tỉ lệ xe ở quận 1, quận 2, quận 3 lần
lượt là 20%, 35%, 45%. Qua thống kê trong quá khứ, hãng xe có ánh giá xác suất
chuyển ổi xe trong các quận giữa hai giờ liên tiếp nhau ược cho trong bảng sau: Đến
Quận 1 Quận 2 Quận 3 Từ Quận 1 0,7 0,2 0,1
Quận 2 0,1 0,85 0,05 Quận 3 0,1 0,15 0,75
(Giả sử sự chuyển ổi xe giữa các quận theo giờ có tính Markov).
a) Viết ma trận xác suất chuyển cho quá trình Markov trên.
b) Tính tỉ lệ xe ở các quận lúc 9 giờ, 11 giờ trong ngày.
c) Tìm phân phối dừng của quá trình Markov, nêu ý nghĩa của phân phối dừng trong trường hợp này.
6.8. Cho mô hình kiểm kê hàng hóa dự trữ với các mức căn cứ nhập hàng: s 1,S 3,
và Yn là lượng hàng khách yêu cầu trong chu kỳ n có phân phối xác suất: Yn 0 1 2
. Xét xích Markov {Xn} n 0 , trong ó Xn là số phụ tùng còn P 0.2 0.45 0.35
lại tại cuối chu kỳ n. Giả sử tại cuối chu kỳ ầu tiên, số phụ tùng còn lại là một trong
các trạng thái của E với xác suất như nhau.
a) Tìm không gian trạng thái E.
Xác suất thống kê và Ứng dụng – 2021 187 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
b) Tìm ma trận xác suất chuyển trạng thái của hệ.
c) Tìm các ma trận xác suất chuyển sau 2,3 và 4 bước.
d) Tìm phân phối ban ầu và phân phối tại các chu kỳ n 2,n 3, n 4 của hệ.
e) Tính các xác suất P X(
4 3| X0 0); P X( 5 2| X2 2).
f) Tính xác suất P X( 0 0, X1 3, X2 2, X4 1) .
6.9. Xét mô hình kiểm kê phụ tùng dự trữ có nhu cầu về số ơn vị phụ tùng thay thế là Yn 0 1 2
bnn Yn có bảng phân phối xác suất , và hai mức chỉ số tiêu P 0.4 0.3 0.3
chuẩn là s 0 và S 3. Xét xích Markov rời rạc thuần nhất {Xn} n 0 , trong ó Xn là
số phụ tùng còn lại tại cuối chu kỳ n. Giả sử tại cuối chu kỳ ầu tiên, số phụ tùng còn
lại là một trong các trạng thái của E với xác suất như nhau.
a) Tìm không gian trạng thái E.
b) Tìm ma trận xác suất chuyển trạng thái của hệ.
c) Tìm các ma trận xác suất chuyển sau 2 bước, 3 bước.
d) Tìm phân phối ban ầu và phân phối tại các chu kỳ n 2,n 3 của hệ.
e) Tính các xác suất P X( 2 2| X0 1); P X( 3 3| X1 3).
f) Tính xác suất P X( 0 1, X1 3, X2 1, X3 2) .
6.10. Xét mô hình tìm cân bằng thị phần với 3 hệ dịch vụ (DV) ở một khu vực có 1000
khách hàng cố ịnh. Kết quả iều tra như sau: Hệ Khách
Tình hình khách ở tháng hai dịch Tháng vụ Thêm từ hệ DV Mất cho hệ DV Tổng Giêng khách 1 2 3 1 2 3 1 250 0 35 25 0 45 55 210 2 350 45 0 15 35 0 25 350 3 400 55 25 0 25 15 0 440
a) Tìm ma trận xác suất chuyển.
b) Tìm phân phối khách hàng ở tháng 3, 7, 11.
c) Tính xác suất P X( 1 1, X2 2, X3 3, X4 1).
d) Tìm tỷ lệ khách hàng cân bằng dừng (phân phối dừng) của hệ
6.11. Chỉ số tiêu thụ iện năng (theo từng tháng) là biến ngẫu nhiên có phân phối tại thời iểm ban ầu như sau: X0 50 [50,100) [100,150) 150 Tỷ lệ % 5% 40% 40% 15% 188
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
Biết ma trận xác suất chuyển là 0,85 0,10 0,05 0 0,85 0,08 P 0,05 0,03 0,90 0,02 0,02 0,05 0,10 0,05 0,05 0,80
a) Hãy giải thích ý nghĩa của ma trận P.
b) Tìm phân phối lượng iện năng tiêu thụ sau tháng thứ 2, thứ 4, thứ 6.
c) Tìm phân phối dừng của xích Markov thời gian rời rạc trên ây và cho biết ý nghĩa của kết quả thu ược. PH () fx
Ụ LỤC 1a Phân phối Student t ( )n
P T{ t ( )}n , n bậc tự do 0 x t () n 0.005 0.01 0.015 0.02 0.025 0.03 0.04 0.05 n 1 63.657 31.821 21.205 15.895 12.706 10.579 7.916 6.314 2
9.925 6.965 5.643 4.849 4.303 3.896 3.320 2.920 3
5.841 4.541 3.896 3.482 3.182 2.951 2.605 2.353 4
4.604 3.747 3.298 2.999 2.776 2.601 2.333 2.132 5
4.032 3.365 3.003 2.757 2.571 2.422 2.191 2.015 6
3.707 3.143 2.829 2.612 2.447 2.313 2.104 1.943 7
3.499 2.998 2.715 2.517 2.365 2.241 2.046 1.895 8
3.355 2.896 2.634 2.449 2.306 2.189 2.004 1.860 9
3.250 2.821 2.574 2.398 2.262 2.150 1.973 1.833 10
3.169 2.764 2.527 2.359 2.228 2.120 1.948 1.812 11
3.106 2.718 2.491 2.328 2.201 2.096 1.928 1.796 12
3.055 2.681 2.461 2.303 2.179 2.076 1.912 1.782 13
3.012 2.650 2.436 2.282 2.160 2.060 1.899 1.771 14
2.977 2.624 2.415 2.264 2.145 2.046 1.887 1.761
Xác suất thống kê và Ứng dụng – 2021 189 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 15
2.954 2.602 2.397 2.249 2.131 2.034 1.878 1.753 16
2.921 2.583 2.382 2.235 2.120 2.024 1.869 1.746 17
2.898 2.567 2.368 2.224 2.110 2.015 1.862 1.740 18
2.878 2.552 2.356 2.214 2.101 2.007 1.855 1.734 19
2.861 2.539 2.346 2.205 2.093 2.000 1.850 1.729 20
2.845 2.528 2.336 2.197 2.086 1.994 1.844 1.725 21
2.831 2.518 2.328 2.189 2.080 1.988 1.840 1.721 22
2.819 2.508 2.320 2.183 2.074 1.983 1.835 1.717 23
2.807 2.500 2.313 2.177 2.069 1.978 1.832 1.714 24
2.797 2.492 2.307 2.172 2.064 1.974 1.828 1.711 25
2.787 2.485 2.301 2.167 2.060 1.970 1.825 1.708
PHỤ LỤC 1b Phân phối Student t ( )n (tiếp theo) 0.005 0.01 0.015 0.02 0.025 0.03 0.04 0.05 n 26
2.779 2.479 2.296 2.162 2.056 1.967 1.822 1.706 27
2.771 2.473 2.291 2.158 2.052 1.963 1.819 1.703 28
2.763 2.467 2.286 2.154 2.048 1.960 1.817 1.701 29
2.756 2.462 2.282 2.150 2.045 1.957 1.814 1.699 30
2.750 2.457 2.278 2.147 2.042 1.955 1.812 1.697 35 2.724 2.438 2.262 2.133 2.030 1.944 1.803 1.690 40 2.704 2.423 2.250 2.123 2.021 1.936 1.796 1.684 45 2.690 2.412 2.241 2.115 2.014 1.929 1.791 1.679 50 2.678 2.403 2.234 2.109 2.009 1.924 1.787 1.676 55 2.668 2.396 2.228 2.104 2.004 1.920 1.784 1.673 60 2.660 2.390 2.223 2.099 2.000 1.917 1.781 1.671 65 2.654 2.385 2.219 2.096 1.997 1.914 1.778 1.669 70 2.648 2.381 2.215 2.093 1.994 1.912 1.776 1.667 75 2.643 2.377 2.212 2.090 1.992 1.910 1.775 1.665 190
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 80 2.639 2.374 2.209 2.088 1.990 1.908 1.773 1.664 85 2.635 2.371 2.207 2.086 1.988 1.906 1.772 1.663 90 2.632 2.368 2.205 2.084 1.987 1.905 1.771 1.662 95 2.629 2.366 2.203 2.082 1.985 1.904 1.770 1.661 100 2.626 2.364 2.201 2.081 1.984 1.902 1.769 1.660 105 2.623 2.362 2.200 2.080 1.983 1.901 1.768 1.659 110 2.621 2.361 2.199 2.078 1.982 1.900 1.767 1.659 115 2.619 2.359 2.197 2.077 1.981 1.900 1.766 1.658 120 2.617 2.358 2.196 2.076 1.980 1.899 1.766 1.658 200 2.601 2.345 2.186 2.067 1.972 1.892 1.760 1.653 500 2.586 2.334 2.176 2.059 1.965 1.885 1.754 1.648 1000 2.581 2.330 2.173 2.056 1.962 1.883 1.752 1.646
2.576 2.326 2.170 2.054 1.960 1.881 1.751 1.645 PHỤ LỤC 2a
Phân phối Chi bình phương 2 ( )n f x( ) P 2 2 ( )n , n bậc tự do 0 2( )n x 0.995 0.990 0.975 0.950 0.900 n 1 0.000039 0.000157 0.000982 0.003932 0.015791 2 0.010025 0.020101 0.050636 0.102587 0.210721 3 0.071722 0.114832 0.215795 0.351846 0.584374 4 0.206989 0.297109 0.484419 0.710723 1.063623 5 0.411742 0.554298 0.831212 1.145476 1.610308 6 0.675727 0.872090 1.237344 1.635383 2.204131 7 0.989256 1.239042 1.689869 2.167350 2.833107 8 1.344413 1.646497 2.179731 2.732637 3.489539 9 1.734933 2.087901 2.700390 3.325113 4.168159 10 2.155856 2.558212 3.246973 3.940299 4.865182 11 2.603222 3.053484 3.815748 4.574813 5.577785 12 3.073824 3.570569 4.403789 5.226029 6.303796 13 3.565035 4.106915 5.008751 5.891864 7.041505
Xác suất thống kê và Ứng dụng – 2021 191 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 14 4.074675 4.660425 5.628726 6.570631 7.789534 15 4.600916 5.229349 6.262138 7.260944 8.546756 16 5.142205 5.812213 6.907664 7.961646 9.312236 17 5.697217 6.407760 7.564186 8.671760 10.085186 18 6.264805 7.014911 8.230746 9.390455 10.864936 19 6.843971 7.632730 8.906517 10.117013 11.650910 20 7.433844 8.260398 9.590778 10.850812 12.442609 21 8.033653 8.897198 10.282898 11.591305 13.239598 22 8.642716 9.542492 10.982321 12.338015 14.041493 23
9.260425 10.195716 11.688552 13.090514 14.847956 24
9.886234 10.856362 12.401150 13.848425 15.658684 25 10.519652
11.523975 13.119720 14.611408 16.473408 26 11.160237
12.198147 13.843905 15.379157 17.291885 27 11.807587
12.878504 14.573383 16.151396 18.113896 28 12.461336
13.564710 15.307861 16.927875 18.939243 29 13.121149
14.256455 16.047072 17.708366 19.767744 30 13.786720
14.953457 16.790772 18.492661 20.599235
PHỤ LỤC 2b Phân phối Khi bình phương 2 ( )n (tiếp theo) 0.100 0.050 0.025 0.010 0.005 n 1 2.7055 3.8415 5.0239 6.6349 7.8794
2 4.6052 5.9915 7.3778 9.2104 10.5965 3 6.2514 7.8147 9.3484 11.3449 12.8381 4 7.7794 9.4877 11.1433 13.2767 14.8602 5 9.2363 11.0705 12.8325 15.0863 16.7496 6 10.6446 12.5916 14.4494 16.8119 18.5475 7 12.0170 14.0671 16.0128 18.4753 20.2777 8 13.3616 15.5073 17.5345 20.0902 21.9549 9 14.6837 16.9190 19.0228 21.6660 23.5893 10 15.9872 18.3070 20.4832 23.2093 25.1881 11 17.2750 19.6752 21.9200 24.7250 26.7569 12 18.5493 21.0261 23.3367 26.2170 28.2997 192
Xác suất thống kê và Ứng dụng – 2021 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh 13 19.8119 22.3620 24.7356 27.6882 29.8193 14 21.0641 23.6848 26.1189 29.1412 31.3194 15 22.3071 24.9958 27.4884 30.5780 32.8016 16 23.5418 26.2962 28.8453 31.9999 34.2671 17 24.7690 27.5871 30.1910 33.4087 35.7184 18 25.9894 28.8693 31.5264 34.8052 37.1564 19 27.2036 30.1435 32.8523 36.1908 38.5821 20 28.4120 31.4104 34.1696 37.5663 39.9969 21 29.6151 32.6706 35.4789 38.9322 41.4009 22 30.8133 33.9245 36.7807 40.2894 42.7957 23 32.0069 35.1725 38.0756 41.6383 44.1814 24 33.1962 36.4150 39.3641 42.9798 45.5584 25 34.3816 37.6525 40.6465 44.3140 46.9280 26 35.5632 38.8851 41.9231 45.6416 48.2898 27 36.7412 40.1133 43.1945 46.9628 49.6450 28 37.9159 41.3372 44.4608 48.2782 50.9936 29 39.0875 42.5569 45.7223 49.5878 52.3355 30 40.2560 43.7730 46.9792 50.8922 53.6719
TÀI LIỆU THAM KHẢO
[1] Nguyễn Cao Văn, Trần Thái Ninh, Lý thuyết xác suất và Thống kê toán, NXB
Khoa học Kỹ thuật, 1996.
[2] Trần Văn Ngũ, Lý thuyết thực nghiệm, Đại học Bách Khoa TPHCM, 1997. [3]
Đặng Hùng Thắng, Thống kê và ứng dụng, NXB Giáo dục, 1999.
[4] Conover, W.J. Practical nonparametric statistics. 3rd Edn. John Wiley & Sons, New York, 1999.
[5] Nguyễn Duy Tiến, Các mô hình xác suất và ứng dụng. Phần I: Xích Markov
và ứng dụng, Nhà xuất bản Đại học Quốc gia Hà Nội 2000.
[6] Nguyễn Minh Tuyển, Quy hoạch thực nghiệm, NXB Khoa học và Kỹ thuật, 2005.
[7] Đào Hữu Hồ, Xác suất thống kê, NXB Đại học Quốc gia Hà nội, 2006.
Xác suất thống kê và Ứng dụng – 2021 193 lOMoAR cPSD| 15962736
Bộ môn Toán – Trường ĐH.GTVT TP. Hồ Chí Minh
[8] Đăng Hùng Thắng, Quá trình ngẫu nhiên và tính toán ngẫu nhiên, NXB Đại
học Quốc gia Hà nội, 2006.
[9] Lê Sĩ Đồng, Xác suất thống kê và ứng dụng, NXB Giáo dục Việt Nam, 2011.
[10] Ron Larson, Betsy Farber, Elementary Statistics, 5th ed,Prentice Hall, 2012. 194
Xác suất thống kê và Ứng dụng – 2021




