Bài Tập 21 và 52 môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

Chương 1: Bài 21:
a. Biến số trận thắng, lương, số lần ghi điểm trực tiếp trong mùa giải là: biến định lượng
Biến đội bóng và số lần thi đấu ở giải vô địch quốc gia hay giải
ngoại hàng Mỹ là: biến định tính
b. Biến số trận thắng, lương, số lần ghi điểm trực tiếp trong mùa giải
sẽ sử dụng thang đo tỷ lệ
Biến đội bóng và số lần thi đấu ở giải vô địch quốc gia hay giải
ngoại hàng Mỹ sẽ sử dụng thang đo định danh Chương 2: Bài 52:
-Bảng tần số phân phối biến tiền lương: Vì 2k > 30 nên k = 5
- Số tổ là 5 , khoảng cách mỗi tổ ≥ 227,4−68,81 = 31,718 . Ta lấy 5
khoảng cách mỗi tổ là 40 Mức lương ($ mil) Tần số 45-85 3 85-125 7 125-165 13 165-205 5 205-245 2 Tổng 30 a.
- Mức lương điển hình của một đội nằm trong khoảng từ 85 $ mil
đến 165 $ mil, thu được từ 20 đội bóng.
- Khoảng chênh lệnh giữa tiền lương lớn nhất và nhỏ nhất là: 158,59 (227,4 - 68,81)
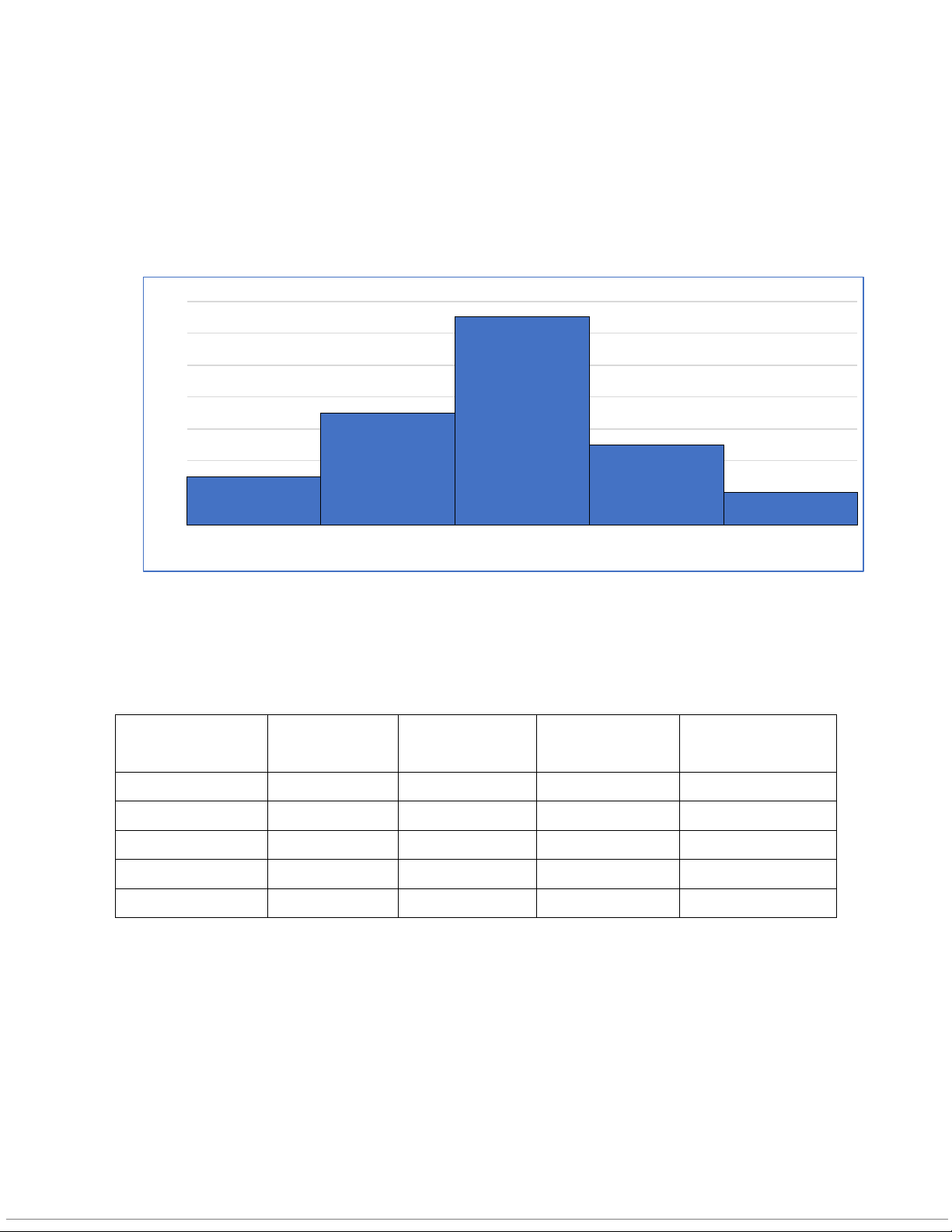
b. Ta vẽ đồ thị Histogram qua đó nhận xét hình dạng phân phối của
dữ liệu: Phân phối dữ liệu lệch phải do Skewness = 0,169815 > 0
và không có đội nào có mức lương cao hơn nhiều so với các đội còn lại. 14 12 10 8 6 Tần số 4 2 0 45-85 85-125 125-165 165-205 205-245 Tiền lương
c) Bảng tần suất tích lũy biến tiền lương: Mức lương Tần số Tần suất Tần số tích Tần suất tích ($ mil) lũy lũy Dưới 85 3 10,00% 3 10% Dưới 125 7 23,33% 10 33,33% Dưới 165 13 43,33% 23 76,67% Dưới 205 5 16,67% 28 93,33% Dưới 245 2 6,67% 30 100%
-40% số đội có mức lương nhỏ hơn 165 $ mil
-Khoảng 2 đội có lương từ 205 triệu đô-la trở lên. Chương 3: Bài 87:
a. Báo cáo tóm tắt về tiền lương của các đội: 1.
-Tiền lương của các đội có xu hướng tập trung quanh giá trị: từ 132,246- 163,964 $ mil
-Trung bình về tiền lương của các đội là: µ = ∑ x= 139,1736667 N
-Trung vị về tiền lương của các đội là:
Me = giá trị thứ 15+giá trị thứ 16 = 140,63 = 141,715 2 142,8
Nhận xét: vì phân phối bị lệch phải nên giá trị trung vị là điển hình hơn 2.
-Khoảng biến thiên là: R = 227,4 - 68,81 = 158,59 n -Độ lệch chuẩn: s = √ ∑ (x i−x )2 = 41,10117051 i=1 n−1
-Khoảng 95% lương của các đội nằm trong khoảng $56,974 đến
$221.374, được tính bằng x ± 2s = $139.174 ± 2($41.1).
Độ lệch chuẩn đại diện cho mức độ biến thiên về tiền lương
b. Tốc độ tăng trung bình về tiền lương trong giai đoạn trên là: 4,10% 1 năm
GM = 18√4,1 -1 = 0.04097571731 1,99 Chương 4: Bài 37:
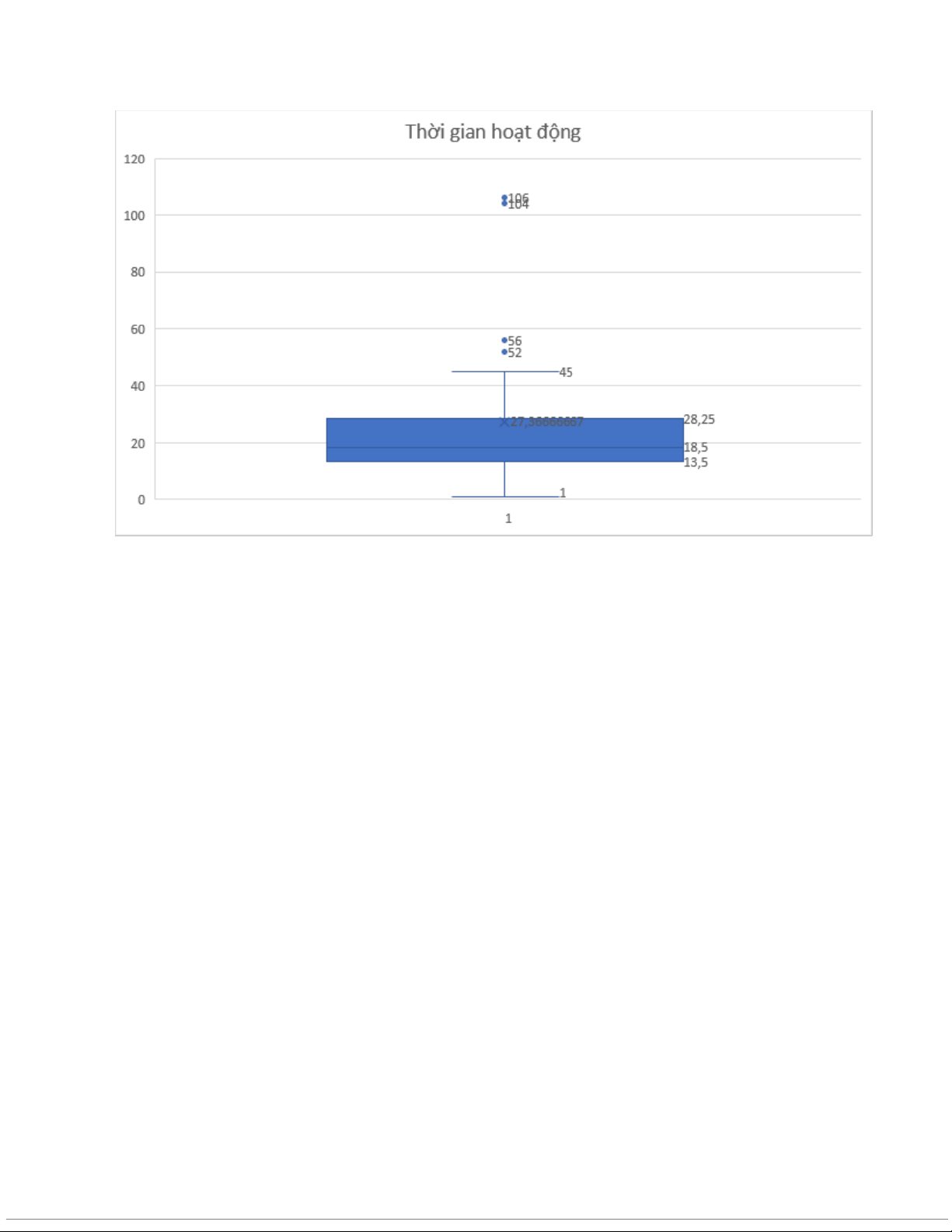
a. Biểu đồ hộp ria mèo về thời gian hoạt động của sân vận động:
Bất cứ giá trị nào lớn hơn Q3 + 1.5(Q3− Q1) = 28.25 + 1.5(28.25−13.5)
= 50.375 là giá trị đột xuất. Dãy dữ liệu có các giá trị đột xuất là
52,56,104,106. Các giá trị đột xuất có ở 5 sân vận động: Boston Red
Sox, Chicago Cubs, Los Angeles Angels, Los Angeles Dodgers, Oakland Athletics.
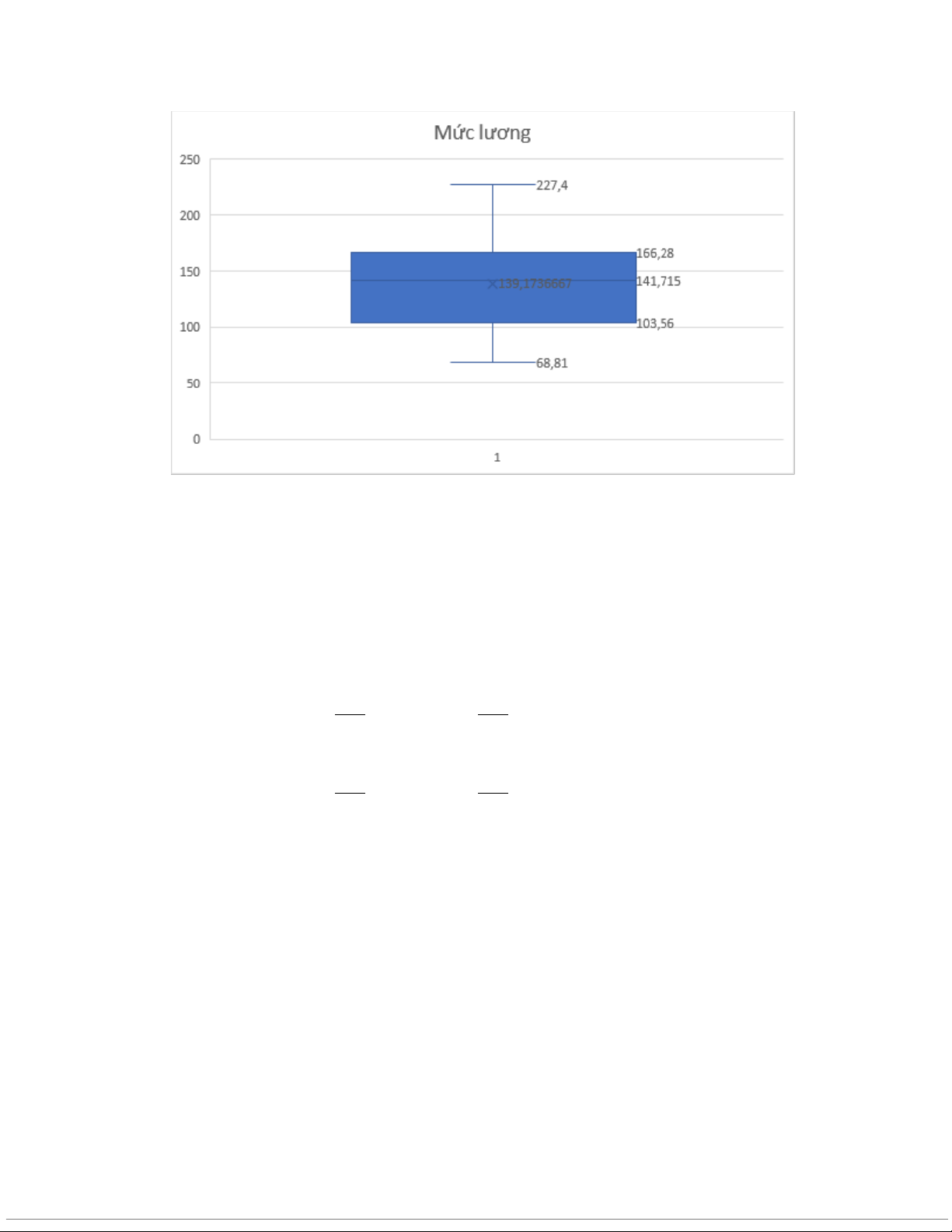
b. Biểu đồ hộp ria mèo về mức lương:
Dãy dữ liệu không có giá trị đột xuất.
Các giá trị tứ phân vị:
-Xác định vị trí tứ phân vị thứ nhất với n = 30 và P = 25 là:
L25 = (n + 1). P = (30 + 1). 25 = 7,75 100 100
-Xác định vị trí tứ phân vị thứ ba với n = 30 và P = 75 là:
L75 = (n + 1). P = (30 + 1). 75 = 23,25 100 100
Như vậy tứ phân vị thứ nhất và tứ phân vị thứ 3 được xác định lần lượt ở
các vị trí thứ 7,75 và 23,25 trong dãy. Khi đó giá trị tứ phân vị thứ nhất
và thứ 3 tương ứng là: 103,56 $ mil và 166,28 $ mil
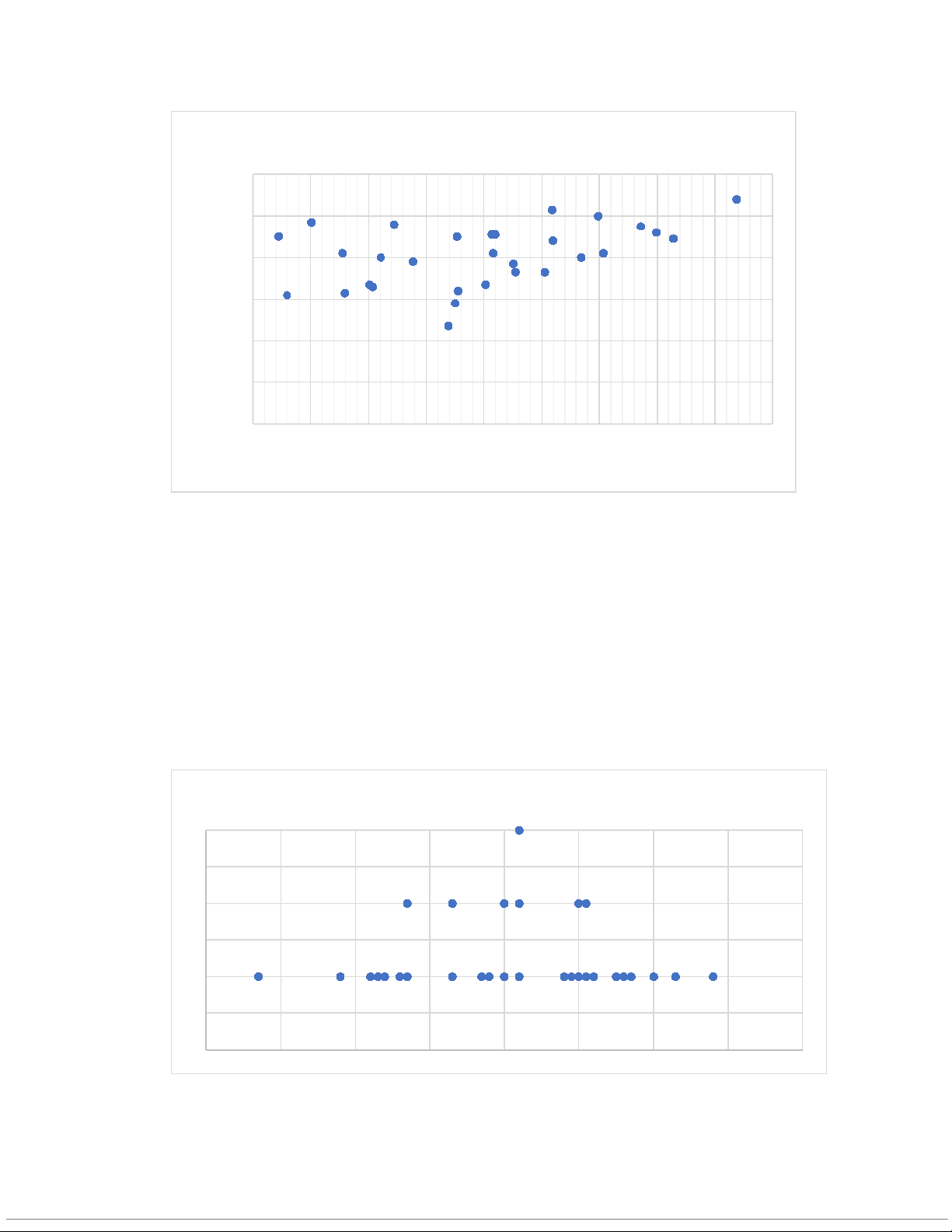
c. Biểu đồ phân tán biểu diễn mối liên hệ giữa số trận thắng với mức lương:
Số trận thắng và Mức lương 120 100 80 60 Số t40 rận thắng 20 060 80
100 120 140 160 180 200 220 240 Mức lương ($ mil)
Hệ số tương quan: 0,429212
Giữa hai biến có sự tương quan nhưng không chặt chẽ. Nhiều trận thắng
hơn không liên quan chặt chẽ tới mức lương cao hơn.
d. Đồ thị điểm về số trận thắng: Số trận thắng 3 2.5 2 1.5 1 0.5 040 50 60 70 80 90 100 110 120
Đồ thị điểm cho thấy số trận thắng của các đội rải rác từ trên 40
đến khoảng gần 110 trận. Hầu hết các đội giành chiến thắng trong
khoảng từ 65 đến 90 trận. Có 8 đội thắng dưới 70 trận. 11 đội
thắng từ 90 trận trở lên. Và 11 đội thắng từ 70 trận đến dưới 90 trận.