Bài Tập Bổ Sung môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

BÀI TẬP VẬT LÝ ĐẠI CƯƠNG 2 (BỔ SUNG) -CTTN K65
1. Ba quả cầu nhỏ như nhau, bằng kim loại, có cùng khối lượng m=10g được treo vào một
điểm O bằng ba sợi dây tơ dài bằng nhau l=50cm. Ban đầu ba quả tiếp xúc nhau. Tích
cho hệ ba quả cầu một điện tích q , người ta thấy sau đó ba quả cầu tách xa nhau và lập
thành một tam giác đều có cạnh a 0=5cm. Tính q . Lấy g=10m/s 2
ả ầu tâm O bán kính R tích điện đề 0 2. Cho qu c
u trên bề mặt với mật độ điện mặt là σ. Tính
trường tại tâm O tạo ra bởi phần mặt cầu nằm giữa hai mặt phẳng có độ cao z 1và z2 .
Từ đó suy ra trường của 1 bán cầu tại tâm
3. Một điện tích điểm q đặt tại một đỉnh của một hình lập phương cạnh a. Xác định thông
lượng vetơ cảm ứng điện gửi qua mỗi mặt hình lập phương không chứa q.
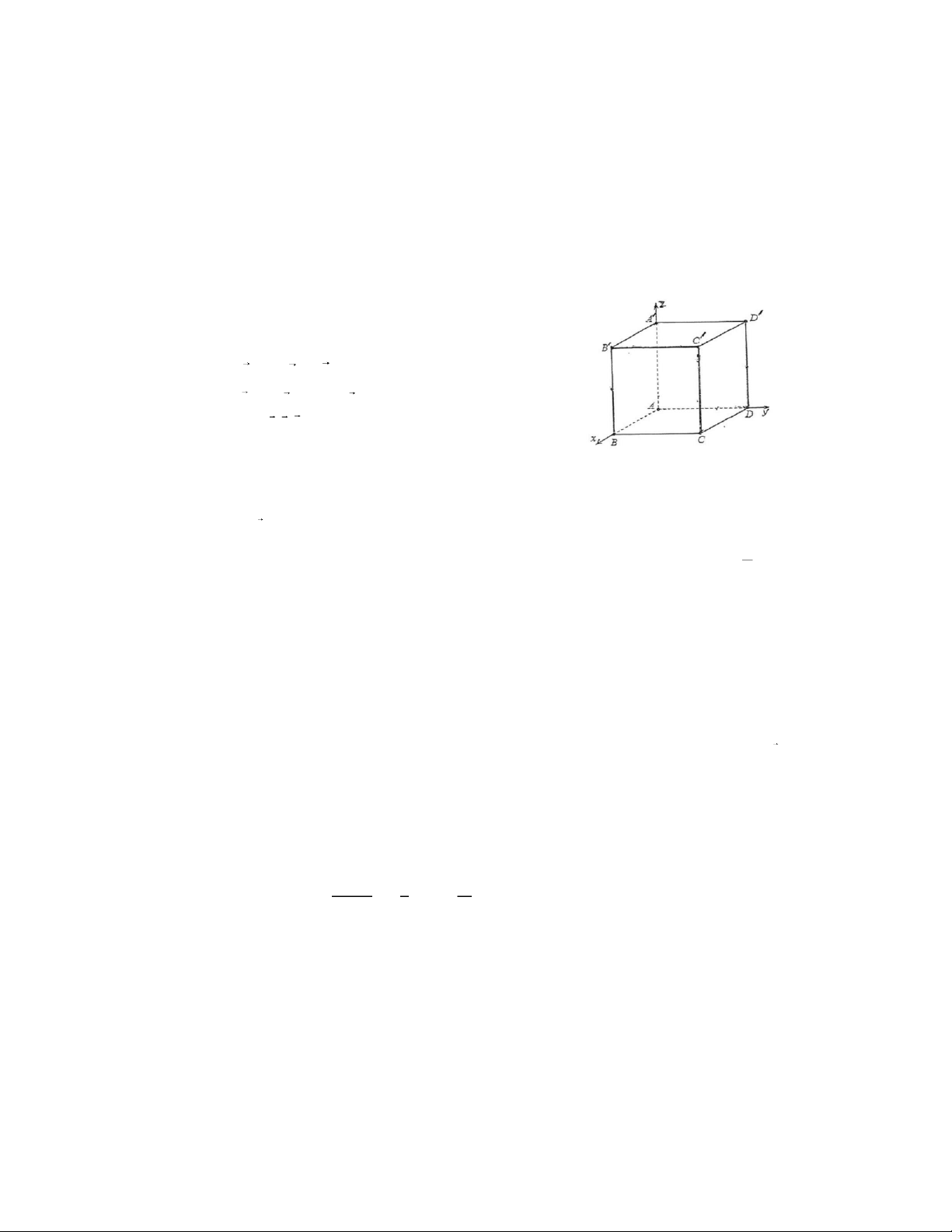
4. Một hình lập phương cạnh a nằm trong miền có điện
trường đều. Tìm điện thông qua mặt CC’D’D và điện
thông toàn phần qua khối lập phương, nếu vectơ cảm
ứng điện (tính bằng đơn vị C/m ) 2 có giá trị: D = 13 − i + 4k a)
b) D = 2−4i + (6+ 3y) j
Cho biết i , j,k là các vec tơ đơn vị hướng theo trục x, y, z
5. Cho hình lập phương ABCD A’B’C’D’. Mặt ABCD tích điện đều với mật độ điện mặt
+σ. Mặt A’B’C’D’ tích điện đều với mật độ điện mặt –σ. Tính véc tơ cường độ đi ệ v n ớ i
trường tại tâm hình lập phương. E
6. Một quả cầu điện môi bán kính R được tích điện với mật độ điện khối là r = R ảng cách tính đế
ả ầu. Tìm cường độ điện trườ 0  =const và r là kho n tâm qu c ng tại một
điểm trong quả cầu cách tâm một khoảng r (r0 7. Một vỏ
ọi cầu điện môi bán kính trong là a và bán kính ngoài là b tích điệ điể
ỏ ầu (a≤r≤b). Xác đị n với mật độ tại m m bên trong v c nh A.
điện khối 𝛒=A/r, trong đó A là hằng số và r là khoảng cách tính đến tâm của vỏ cầu. Tại
tâm vỏ cầu có một điện tích điểm q. Biết rằng cường độ điện trường có độ lớn như nhau
8. Cho khối cầu tâm O bán kính a tích điện đều với mật độ điện khối không đổi . 
Khoét lỗ hổng hình cầu tâm O’ bán kính (bE bên trong lỗ hổng.
9. Một phân bố điện tích có tính đối xứng cầu nhưng không đều tạo ra điện trường có độ
lớn E=kr4, hướng theo bán kính từ tâm của hình cầu ra ngoài, với r là khoảng cách theo
bán kính kể từ tâm đó. Xác định mật độ điện tích khối.
10. Mật độ điện tích tạo ra điện thế đối xứng cầu 2 ( ) q
1 r exp r trong đó q>0 V r  = 4 r + a −    a        0 1
a) Xác định điện tích nằm trong quả cầu bán kính r.
b) Xác định mật độ điện tích ρ.
11. Cho biết điện thế tại một điểm trên trục qua tâm một đĩa tích điện cách tâm đĩa một khoảng là z cho bởi:  V (r) =2 () 22
z +R− z . 0
Trong đó R là bán kính của đĩa. Xác định cường độ điện trường tại điểm đó.
12. Hai quả cầu nhỏ 1 và 2 dẫn điện, cùng bán kính r, đặt
cách nhau một khoảng R (R>>r). Ban đầu mỗi quả
cầu đều có điện tích q. Sau đó đóng K1, cho quả cầu 1
nối đất. Sau một thời gian trạng thái cân bằng được
thiết lập thì mở K .1 Tiếp theo đóng K2 cho quả cầu 2
nối đất. Hãy xác định điện thế cuối cùng của quả cầu 1 ( Ch
ọn mốc điện thế tại đất bằng không)
13. Một khối cầu điện môi tâm O bán kính R hằng số điện môi ε đặt trong chân không.
Điện tích Q phân bố đều trong khối cầu.Tính điện thế tại tâm khối cầu và công của lực
tĩnh điện trong dịch chuyển điện tích q từ điểm M cách tâm khối cầu một khoảng r
(r14. Một vỏ cầu dầy bán kính r1 và r2 tích điện đều với mật độ điện khối là . Tìm điện thế
V là hàm của khoảng cách r kể từ tâm cầu trong các miền (coi V(∞)=0): a) r> r 2 b) r > 2 r> r 1
c) r15. Một điện tích q được phân bố đều trong một khối cầu tâm O, bán kính R. Tìm biểu
thức của điện thế tại điểm M cách tâm cầu một khoảng r (ra) Coi V(∞)=0 b) Coi V(0)=0
16. Hai quả cầu nhỏ cùng khối lượng m, nối với nhau bằng dây dài l, nằm trên mặt phẳng
ngang có hệ số ma sát là . Điện tích mỗi quả là q. Sợi dây đang căng. Cắt đứt dây, hai
quả cầu chuyển động. Xác định vận tốc cực đại của mỗi quả cầu sau khi dây bị đứt.
17. Cho hai quả cầu dẫn điện cách xa nhau. Quả cầu hai có đường kính gấp 2 lần quả cầu 1.
Quả cầu 1 lúc đầu có điện tích dương q và quả cầu 2 lúc đầu không tích điện. Nối hai
quả cầu đó bằng sợi dây mảnh dài. a) So sánh điện thế V v 1 à V
2 của các quả cầu đó sau khi nối
b) Xác định điện tích cuối cùng q1, q 2trên 2 quả cầu
c) Xác định tỷ số mật độ điện tích mặt của 2 quả cầu sau khi nối
18. Một quả cầu dẫn có bán kính là a nằm trong quả cầu đồng tâm bán kính là b có hằng số
điện môi  . Tìm điện dung của quả cầu dẫn (cho biết môi trường xung quanh là không khí). 2
19. Một bản điện môi mỏng bề dày d, diện tích mặt bản là S,
có hằng số điện môi  , được đặt trong một điện trường
đều có cường độ E .0 Ban đầu mặt bản hợp với phương của
đường sức một góc  .
a) Tính momen lực tác dụng lên bản
b) Tính công của lực điện trường làm bản dịch chuyển
tới vị trí mặt bản vuông góc với điện trường.
20. Một sợi dây dẫn thẳng dài vô hạn tích điện đều với mật độ điện dài λ. Bao quanh sợi
dây là một lớp điện môi hình trụ có bán kính R, hằng số điện môi là ε .1 Bên ngoài lớp
đó là điện môi vô hạn đồng chất với hằng số điện môi là ε .2
a) Xác định cường độ điện trường tạo bởi sợi dậy đó
b) Xác định mật độ điện tích liên kết mặt ở mặt tiếp xúc của các lớp điện môi.
21. Hai bản kim loại được đặt thẳng đứng và song song trong một bình chứa điện môi
lỏng. Khoảng cách giữa hai bản là d và hiệu điện thế giữa chúng là U. Hỏi điện môi
lỏng giữa hai bản được nâng lên độ cao bao nhiêu. Cho biết trọng lượng riêng của điện môi lỏng là ρ.
22. Một tụ điện trụ được đặt đứng trong một chất lỏng điện môi. Lớp điện môi lỏng ở giữa
hai bản được nâng lên độ cao h. Biết bán kính của tụ điện là R1 và R2 , hiệu điện thế
giữa hai bản là U. Tính hằng số điện môi của chất lỏng nếu trọng lượng riêng của chất lỏng là . 
23. Một đĩa kim loại tâm O bán kính R mang một điện tich được phân bố đều với mật độ
điện mặt là σ. Đĩa quay với vận tốc góc không đổi ω xung quanh trục Oz của đĩa. Tính
cảm ứng từ tại một điểm M nằm trên trục của đĩa và cách tâm đĩa một khoảng bằng h.
24. Một vật dẫn hình trụ dài vô hạn có một lỗ hổng cũng hình trụ dài vô hạn (tiết diện tròn
của lỗ hổng hoàn toàn nằm trong vật dẫn). Một dòng điện không đổi, mật độ J chạy
dọc theo vật dẫn. Tìm cường độ từ trường bên trong lỗ hổng
25. Trong một từ trường đều có tính đối xứng với trục Oz, thành phần vectơ cảm ứng từ Bz
thay đổi theo quy luật tuyến tính: z B B=+ 0 h
trong đó B và h là những hằng số. Hãy z (1 ) 0
xác định góc tạo bởi vectơ cảm ứng từ với phương của trục Oz tại điểm A ở cách trục
này một khoảng R và cách mặt phẳng xOz một khoảng hA.
26. Một quả cầu kim loại tích điện đều trên bề mặt, có điện tích toàn phần q và bán kính R,
quay với tốc độ góc  không đổi quanh trục Oz. Hãy xác định môn men từ của quả cầu.
27. Hai thanh kim loại nằm trên mặt phẳng nằm ngang,
song song với nhau cách nhau một khoảng l được đặt
trong một từ trường đều có cảm ứng từ B hướng thẳng
lên phía trên; hai đầu của hai thanh nối vói một điện trở
R (hình vẽ). Một đoạn dây AB khối lượng m được đặt
vuông góc với hai thanh có thể trượt không ma sát trên
hai thanh sao cho hai đầu A, B luôn luôn tiếp xúc điện với hai thanh. Biết đoạn dây
AB trượt với vận tốc ban đầu v0như trên hình vẽ. Tìm biểu thức cường độ dòng điện I 3 qua điện trở R
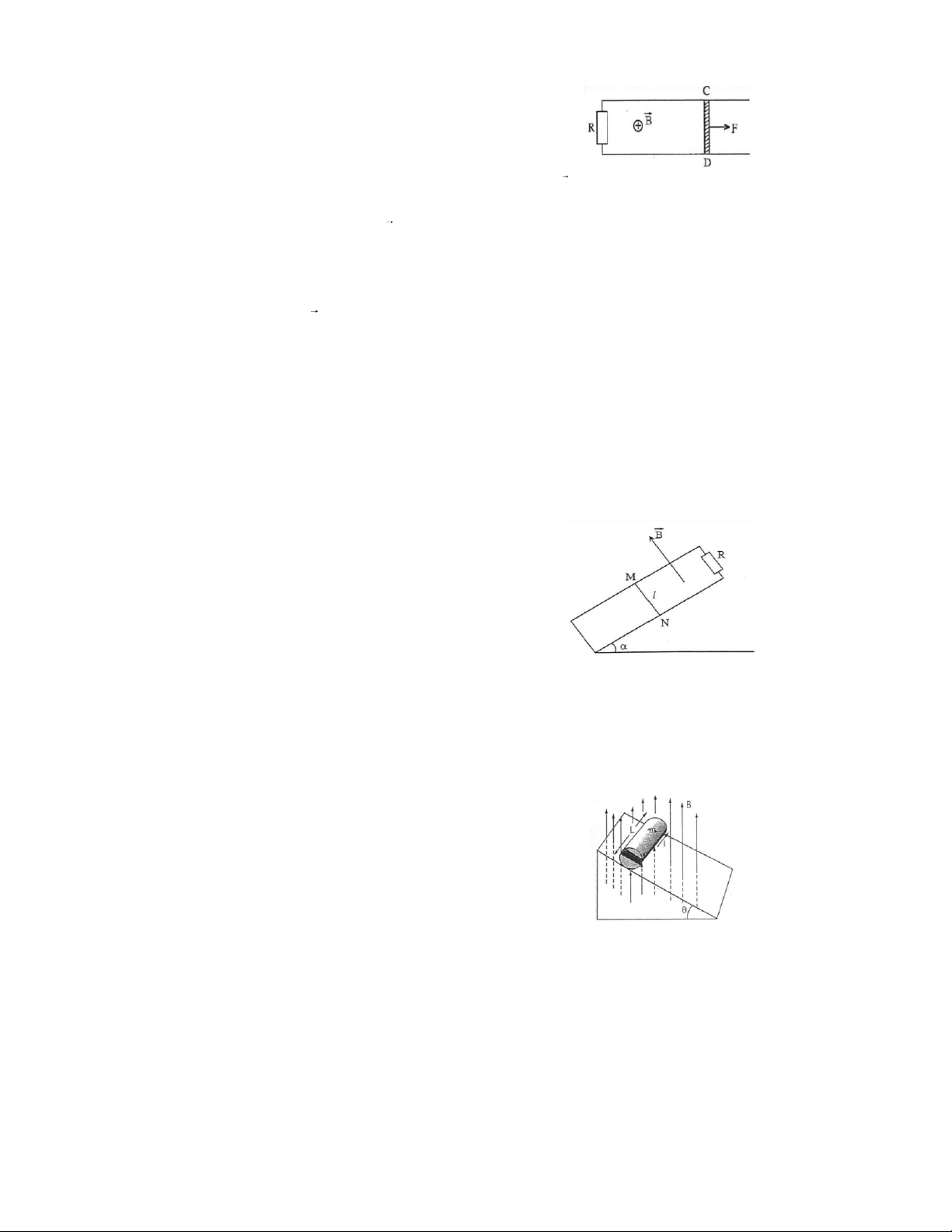
28. Hai thanh kim loại song song, cùng nằm trong mặt phẳng
ngang, cách nhau một khoảng l, điện trở không đáng kế
và có một đầu nối vào điện trở R= 0 ,5 . Một đoạn dây
dẫn CD, chiều dài l, điện trở r= 0
 ,3 , khối lượng m=0,1
kg đặt nằm trên và thẳng góc với hai thanh kim loại. Tất
cả đặt trong một từ trường đều có vectơ cảm ứng từ B
thẳng đứng, hướng xuống.
Kéo dây CD bằng một lực F không đổi để đoạn dây chuyển động về phía phải.
Khi dây CD trượt không ma sát trên hai thanh kim loại với vận tốc không đổi
v=2m/s thì hiệu điện thế giữa hai đầu điện trở R đo được là U=1V (hình vẽ).
a) Xác định độ lớn lực F
b) Bỏ lực kéo F , dây CD chuyển động chậm dẩn rồi dừng lại trên hai thanh kim
loại. Tìm quãng đường dây CD đi được.
29. Trên mặt bàn phẳng nằm ngang đặt một khung dây dẫn hình chữ nhật có các cạnh là a
và b. Khung được đặt trong một từ trường có thành phần của vec tơ cảm ứng từ dọc
theo trục z chỉ phụ thuộc vào toạn độ x theo quy luật B B=−0
x , trong đó B và z (1 ) 0 
là các hằng số (cạnh b song song trục x, trục z vuông góc với mặt khung). Truyền cho
khung một vận tốc v dọc theo trục x. Bỏ qua độ tự cảm của khung dây, hãy xác định 0
khoảng cách mà khung dây đi được cho đến khi dừng lại hoàn toàn. Cho biết điện trở
thuần của khung dây là R.
30. Trong một mặt phẳng nghiêng góc  so với mặt
phẳng nằm ngang có hai thanh kim loại cố định song
song cách nhau một khoảng l, nối với nhau bằng điện
trở R. Một thanh kim loại MN, có khối lượng m có
thể trượt không ma sát trên hai thanh kia, luôn vuông
góc và tiếp xúc với chúng (hình vẽ). Điện trở của các
thanh không đáng kế. Có một từ trường đều vuông
góc với mặt phẳng chứa các thanh và hướng lên phái
trên. Thả cho thanh MN trượt không có vận tốc ban đầu.
a) Mô tả hiện tượng và tính giá trị vmax của thanh.
b) Thay điện trở bằng một tụ điện có điện dung C. Tính gia tốc của thanh .
31. Trên hình bên vẽ một khối trụ bằng gỗ khối lượng m=0,25
kg, dài L=0,1 m, trên đó có N=10 vòng dây cuốn quanh
theo đường sinh sao cho mặt của vòng dây chứa trục của
khối trụ. Hỏi dòng điện nhỏ nhất chạy qua khung phải
bằng bao nhiêu để có thể ngăn nó không lăn xuống trên
một mặt phẳng nghiêng một góc  đối với mặt phẳng
ngang, khi có từ trường đều theo phương thẳng đứng bằng 4
0,5 T nếu mặt của vòng dây song song với mặt phẳng nghiêng ?
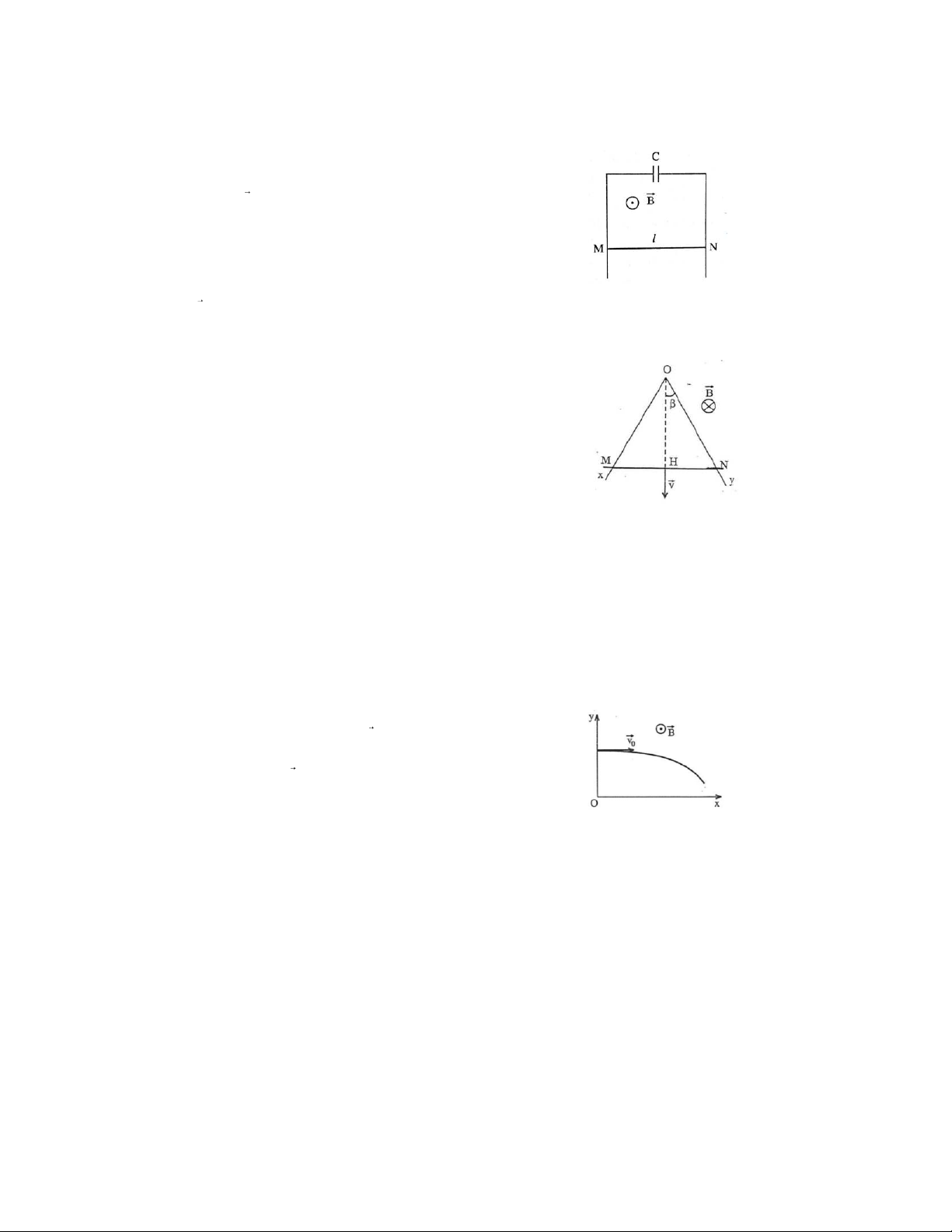
32. Hai thanh kim loại song song thẳng đứng, một đầu nối với
tụ điện C. Một đoạn dây MN, độ dài l, khối lượng m tì
vào hai thanh kim loại, tự do trượt không ma sát xuống
dưới và luôn vuông góc với hai thanh kim loại đó. Toàn
bộ hệ thống đặt trong một từ trường đều có vec tơ cảm
ứng từ B vuông góc với mặt phẳng hai thanh kim loại. Bỏ
qua điện trở của mạch. a) Tính gia tốc của MN
b) Bây giờ đặt hai thanh kim loại nghiêng với mặt ph
ẳng ngang một góc  . Độ lớn và chiều của cảm ứng từ
B vẫn như cũ. Ban đầu MN được thả từ vị trí cách đầu
dưới của thanh kim loại một đoạn a. Tìm thời gian để MN
bắ t đầu rời khỏi thanh kim loại và vận tốc của MN khi đó.
33. Một dây dẫn thẳng có điện trở là R0 ứng với một đơn vị
chiều dài. Dây được gập lại thành hai cạnh của một góc
2  . Một thanh chắn cũng bằng dây dẫn ấy đặt vuông góc
với đường phân giác của góc 2 tạo với dây dẫn gấp
khúc một chu vi tam giác kín. Chu vi này đặt trong một từ
trường đều B vuông góc với mặt phẳng của chu vi. Tìm
chiều và cường độ I của dòng điện qua chu vi khi thanh
chắn chuyển động với vận tốc v không đổi. Bỏ qua điện
trở tại các chỗ tiếp xúc.
34. Cho tụ điện trụ bán kính hai bản là R = 1 5 cm, R =
2 6 cm. Tụ điện được đặt trong từ
trường đều có cảm ứng từ B=0,2T, phương của B song song với trục của tụ điện. Một
hạt  có năng lượng W=1000eV bay vào trong tụ điện qua một khe hẹp ở cách đều hai
bản tụ điện. Khi lọt qua khe, hạt  có vận tốc vuông góc với trục và với đường kính
thiết diện của mặt trụ. Tìm hiệu điện thế giữa hai bản tụ điện, biết rằng khi chuyển
động hạt  luôn cách đều hại bản. Cho biết bản ngoài cùng của tụ điện tích điện âm,
hạt  có điện tích +2e, 27 m k − =
. Bỏ qua hiệu ứng bờ của các mép và tác dụng  g 6,64.10 của trọng lực.
35. Một hạt có khối lượng m, điện tích q dương bắt đầu
chuyển động với vận tốc v 0theo hướng song song với
trục Ox trong một từ trường đều có cảm ứng từ B=ax
(x≥0). Véc tơ Bvuông góc với mặt phẳng xOy. Hãy xác
định độ dịch chuyển cực đại của hạt theo trục Ox.
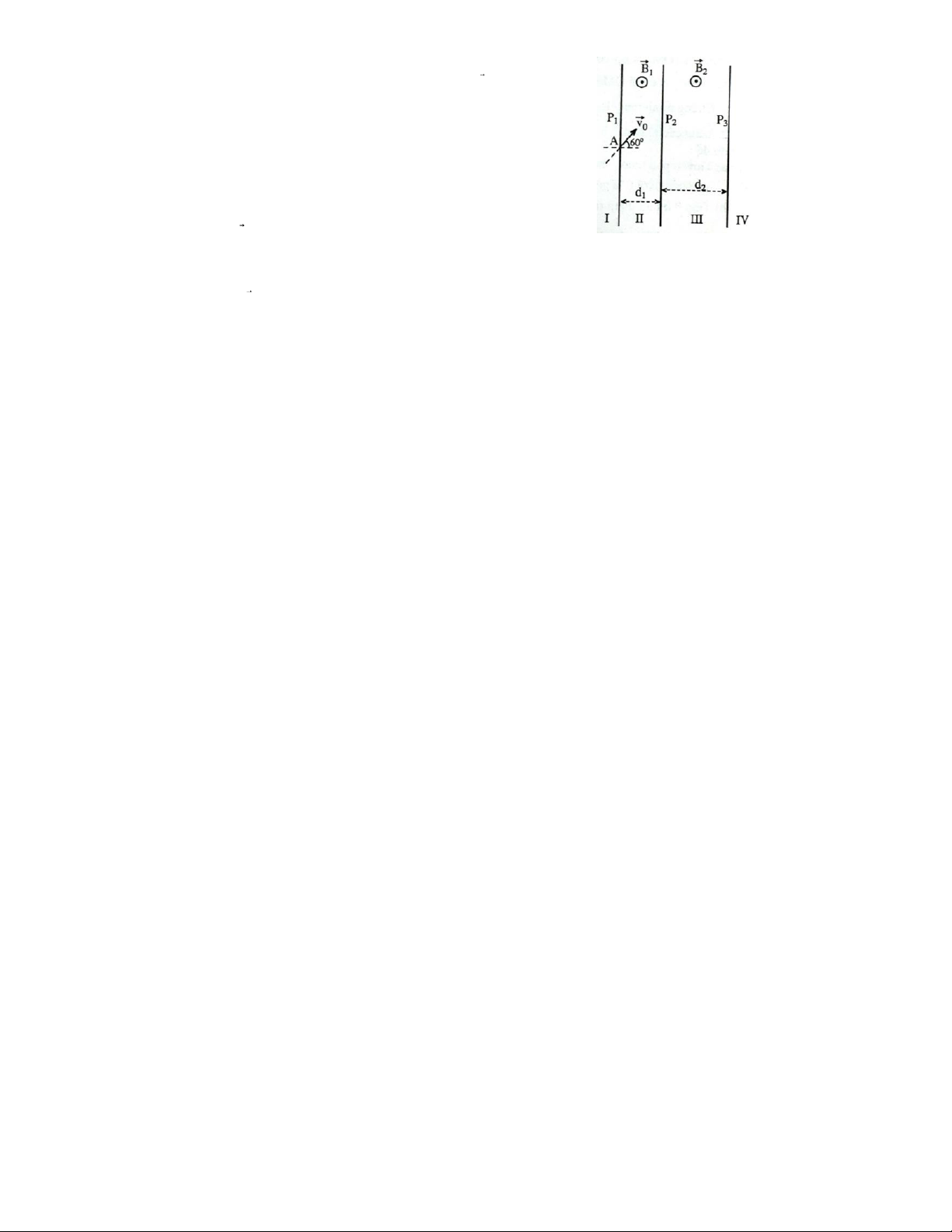
36. Ba mặt phẳng song song P P, ,P cách nhau một khoảng 1 2 3 d1=2cm và d =
2 4cm, phân không gian thành bốn vùng I, II,
III, IV. Trong vùng II và III người ta tạo ra từ trường đều
có véc tơ cảm ứng từ B 1và B 2song với ba mặt phẳng trên
và có chiều như hình vẽ. Hạt prôtôn trong vùng I được 5
tăng tốc bởi hiệu điện thế U, sau đó được đưa vào vùng II
tại điểm A trên mặt phẳng P 1với vận tốc v hợp với pháp 0
tuyến của P1 một góc 60 .0 Bỏ qua tác dụng của trọng
trường. Cho biết khối lượng và điện tích của prôtôn tương
ứng là m=1,673.10-27 kg và q=1,6.10-19C.
a) Tìm giá trị của U, biết rằng hạt đi sang vùng III với vận
tốc hướng vuông góc với P2 và cảm ứng từ B = 1 1T.
b) Cho biết hạt ra khỏi vùng III theo hướng vuông góc với
véc tơ v tại A. Tính cảm ứng từ B2. 0
37. Một ống kim loại hình trụ rỗng, tiết diện là một hình vành khăn có bán kính T Kh R 5.1 1=12cm, R =
2 14 cm và chiều cao h=10cm, được đặt trong một từ trường đều có cảm
ứng từ B hướng dọc theo trục của ống. Tìm cường độ dòng điện cảm ứng xuất hiện Có hìn
trong ống khi cảm ứng từ có độ lớn tăng tỷ lệ với thời gian t: B=kt, với k=10-3 T/s. khôn
Cho biết điện trở suất của kim loại làm ống 7  =1, 2.10 m
38. Một đĩa dẫn điện mỏng trục OZ bán kính b được đưa vào một từ trường
B B= 0cost  định xứ trong một hình trụ bán kính a và có cảm ứng từ bằng không z
ở các nơi khác. Xác định mật độ dòng điện J tại mọi điểm của đĩa. 6