Bài Tập Cảm Ứng Từ 2 môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

BÀI TẬP CẢM ỨNG TỪ 2
Bài 1. Trong khuôn khổ mẫu nguyên tử cổ điển của hiđrô, hãy đánh giá độ lớn
cảm ứng từ tại tâm quỹ đạo tròn của electron. Cho biết bán kính quĩ đạo tròn 5 , 0 1 . 3 0  này (bán kính Bohr)  r . B m 10
Gợi ý: cảm ứng từ tại tâm một dây dẫn tròn có dòng điện I chạy qua bằng μ π  H N 0m  , trong đó μ I  4 1 . 0 7 . / . B2 R 0 ĐS:   e BT  2 12, 48( ). 0 8 rm ( ) 3/ 2 5/2 1/2 Be 0 Bài 2 z
Hãy tính từ trường tạo ra tại điểm O, D
là tâm của hình chữ nhật ABCD, trong các A
trường hợp sau đây: Mỗi nửa vòng tròn có O y
bán kính a ta sẽ đặt DA = BC = 2l cường
độ dòng bằng I (hình 5). C B   ĐS:
gồm hai thành phần Bz; By. B  O Hình 5     I l   al  Bz=    2  0   a l a  a l 3 2 2 2 2  I  a  By =  3  0 l a 3 2 2 2 Bài 3
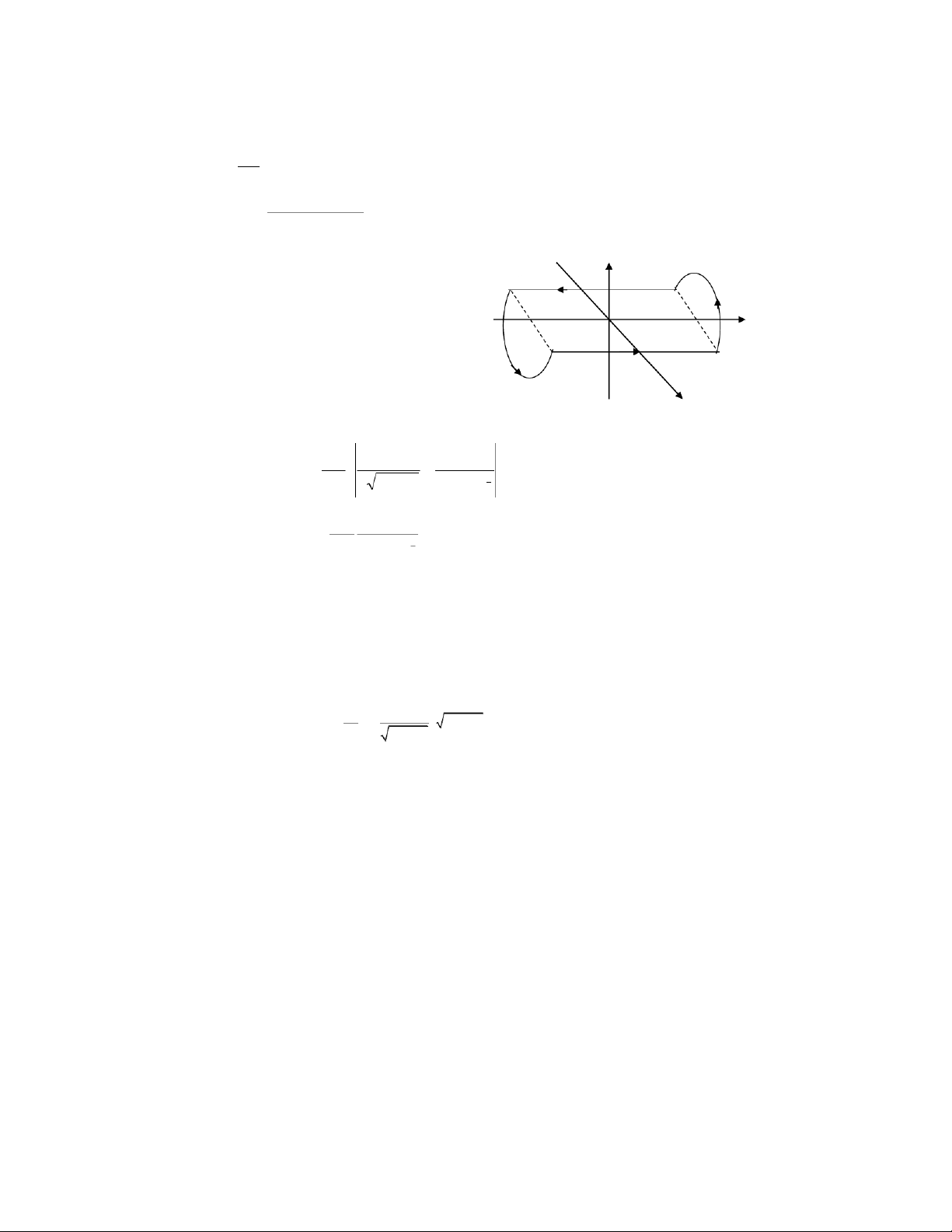
Một đĩa kim loại bán kính R, mang một điện tích được phân bố đều với mật độ
điện mặt δ (trên cả hai mặt), quay với vận tốc không đổi xung quanh trục Oz của nó.
Hãy tính trường từ tĩnh tạo ra
 bởi đĩa quay trên tại một điểm M trên trục (Oz). Đáp số:   1   B . R z z2  0 22 2 Rz M 22
Bài 4. Cuộn dây Hemhôn là một dụng cụ cho phép tạo ra từ trường đều trong
không gian hẹp. Nó gồm 2 vòng dây dẫn hình tròn cùng bán kính a được đặt đồng
trục, trong đó có dòng điện cùng chiều, cùng cường độ I chạy qua. Khoảng cách giữa hai vòng dây là L.
Tính cảm ứng từ B trên trục hai vòng dây cách trung điểm của đoạn thẳng nối
tâm hai vòng dây một khoảng x. Tìm điều kiện để B không phụ thuộc x với x nhỏ, tính B đó. ĐS: 8. I 0 Ba 55
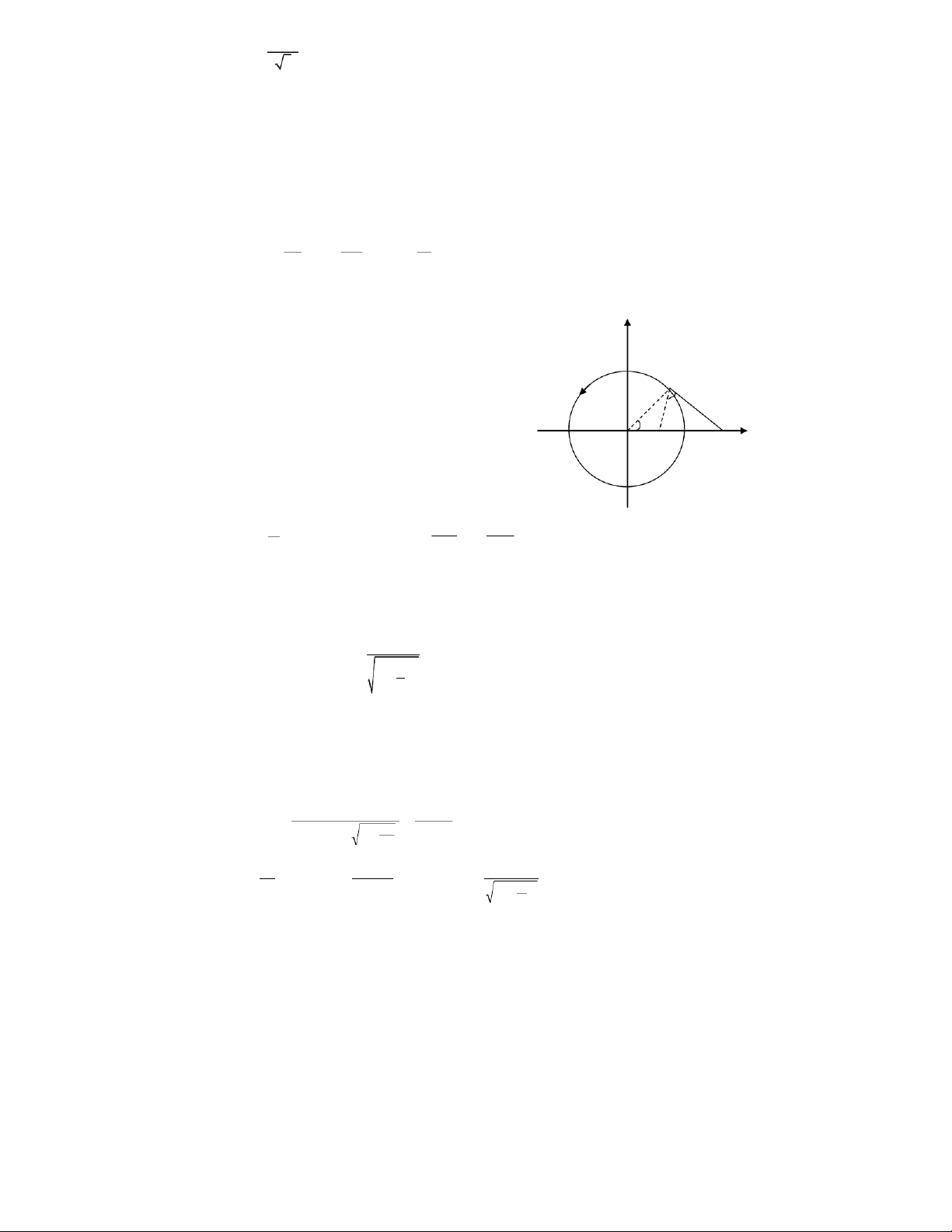
Bài 5. Một vòng tròn kim loại bán kính 𝑅 mang dòng điện 𝐼 nằm hoàn toàn
trong mặt phẳng 𝑂𝑥𝑦 tại nơi có độ từ thẩm 𝜇 = 1. Tâm của vòng tròn trùng với
gốc tọa độ 𝑂 và chiều của dòng điện trùng với chiều quay từ trục 𝑂𝑥 đến trục
𝑂𝑦. Biết vòng kim loại này ở rất xa các nguồn gây ra từ trường khác.
1. Tìm cảm ứng từ tại điểm 𝑀 trên trục 𝑂𝑥, biết 𝑂𝑀 = 𝑎 ≪ 𝑅.
2. Đường cảm ứng từ qua 𝑀 cắt 𝑂𝑥𝑦 tại 𝑁 với 𝑂𝑁 = 𝑟 ≫ 𝑅, tìm 𝑟. ĐS:1. B = μ0 2 IR(1 + 3a 2 2 R ); 2. r≈R3 a2 Bài 6 y
Một vòng tròn tâm O, bán kính R, có dòng
điện hình sợi chỉ cường độ I chạy qua (hình 4).
Người ta muốn tính từ trường tại điểm M nằm trong I P
mặt phẳng và gần tâm vòng OM = r << R. R α
1. Chứng tỏ rằng từ trường này vuông góc O θ z M x
với mặt phẳng vòng dây.
2.b Sau khi đã thiết lập công thức B dưới
dạng một tích phân có dùng góc β. Hãy chứng tỏ Hình 4  I 3 0  2 2 
rằng với r << 1 thì gần đúng: B = 1 R   4R   4  Bài 7
Một đĩa dẫn có tâm O và có bk R quay với vận tốc góc không đổi quanh trục Oz
của nó. Đĩa mang một điện tích toàn phần q được phân bố với mật độ điện mặt toàn phần ( Kể cả 2 mặt): 0   
. Trong đó r = OP là khoảng cách từ tâm tới điểm P 2 1r    R  của đĩa.
1. Tìm giá trị của  theo q và R. Tính mômen từ của đĩa. 0
2. Tìm biểu thức của từ trường tạo ra bởi 1 phân bố như thế tại 1 điểm M nằm trong mặt
phẳng đĩa và rất xa đĩa. => Q Q δ ( K = R)  R 2 0. π R 2 2 π K 1 .   2 2 1 K2  3 Rdq 2π. r.dr . π r .dr R 2  2  P ω . .π . r δ. ω . .π. r δ  .ω m    02 0 2π 2π r 0 1 R 