Bài Tập Chương 06: Trường Tĩnh Điện và Lực Tương Tác Coulomb môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Bài tập chương 6. Trường tĩnh điện
A. Phần tóm tắt lý thuyết 1. Lực tương tác Coulomb 1 q q r q q r 1 q q q q F . k . , độ lớn: F k 4 1 r 2 12r 1r 2 12 r 4 1r 2 1 r 2 12 2 2 12 2 2 0 0
8,86.10 C / Nm - hằng số điện môi (hằng số điện môi tuyệt đối của chân không), là hằng số điện 12 2 2 0
môi tỷ đối của môi trường.
2. Vectơ cường độ điện trường F E q
Cường độ điện trường gây ra bởi một điện tích điểm Q tại một điểm cách nó một khoảng r: Q r 1 Q r E k . . . | Q | , độ lớn: E k r r 4 r r r 2 2 2 0
Q>0: E hướng ra xa điện tích;
Q<0: E hướng vào điện tích.
3. Véc-tơ điện cảm (cảm ứng điện) D E 0
Véc-tơ điện cảm do một điện tích điểm gây ra: Q D . r 4 r3
4. Cường độ điện trường gây bởi một sợi dây thẳng dài vô hạn mang điện đều tại một điểm cách dây một khoảng r: E
, trong đó là mật độ điện dài của dây. 2 r
5. Cườn 0g độ điện trường gây bởi một mặt phẳng mang điện đều: E
, trong đó là mật độ điện mặt. 2
6. Địn 0h lý Ostrogradski – Gauss:
Thông lượng cảm ứng điện gửi qua một mặt kín (S) bất kỳ bằng tổng đại số các điện tích có trong mặt kín. DdS n q i i 1 S
7. Công của lực tĩnh điện khi dịch chuyển điện tích điểm q ừ điểm A đến điểm B trong điện trường: 0 A q V
V , trong đó V và V lần lượt là điện thế tại điểm A và B. A B 8. Tín0h c A hất th B
ế của trường tĩnh điện
Lưu số của véc-tơ E theo một đường cong kín bằng 0: Ed l 0
9. Hiệu điện thế giữa hai điểm A và B trong điện trường: U V V B Ed l AB A B 10. Mối liên hệ g A
iữa cường độ điện trường và điện thế V E hay E grad V s U
Trong trường hợp điện trường đều: E
, trong đó U V V là hiệu điện thế, d là khoảng cách giữa 2 d 1 2
mặt đẳng thế tương ứng.
11. Điện thế gây bở một điện tích điểm Q tại một điểm cách nó 1 khoảng r: 1 Q V 4 r 0
12. Hiệu điện thế giữa hai mặt cầu đồng tâm mang điện đều, bằng nhau, trái dấu: Q R R 2 1 V V
, trong đó R 1 là bán kính của mặt cầu trong, R2 là bán kính của mặt cầu ngoài, Q là độ 1 2 R R 0 1 2
lớn điện tích trên mỗi mặt cầu.
13. Hiệu điện thế giữa 2 mặt trụ đồng trục dài vô hạn mang điện đều bằng nhau và trái dấu: R2 V V ln , trong đó R 1 2
1 là bán kính mặt trong, R2 là bán kính mặt ngoài,
là mật độ điện dài trên 2 R0 1 mặt trụ. B. Phần bài tập
Bài 1.9. Tìm lực tác dụng lên một điện tích điểm q = (5/3).10 -9 C đặt ở tâm nửa vòng xuyến bán kính r0 = 5
cm tích điện đều với điện tích Q = 3.10-7 C (đặt trong chân không). Bài giải:
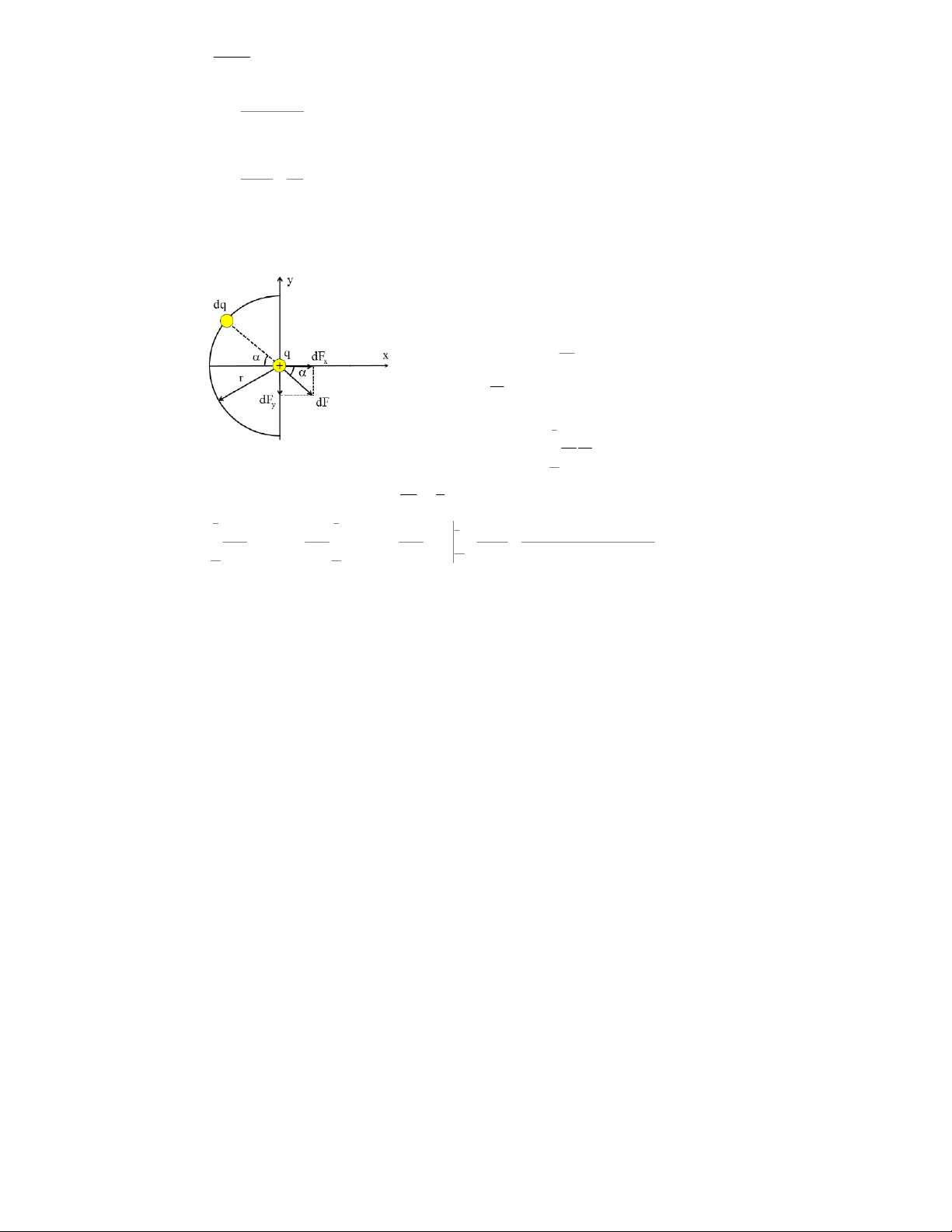
Xét một điện tích nguyên tố dq gây ra cường độ điện trường dF cho
điện tích q. Phân tích dF theo phương x và y như trên hình vẽ. Dễ
dàng thấy do tính chất đối xứng nên các thành phần dFy triệt tiêu nhau. Như vậy: kq F dF dF dQ cos x2 r Trong đó: Q dQ dl
(điện tích chia đều theo độ dài r ), dl rd r
(độ dài cung bằng bán kính nhân với góc chắn cung). 2 kq Q Thay vào trên ta được: F r cos d 2 r r 2
Từ hình vẽ dễ thấy góc biến thiên từ
khi lấy tích phân trên toàn bộ nửa vòng xuyến. 2 2 2 2kqQ kqQ kqQ 9 9 7 2 2kqQ 2.9.10 . 5 / 3 .10 .3.10 F cos d cos d sin = 3 1,1 46.10 N 2 2 2 r r r 2 2 r .0,05 2 2 2
Bài 1.10. Có hai điện tích điểm 8 q 8.10 C và 8 q
3.10 C đặt cách nhau một khoảng d = 10 cm trong 1 2 không khí. Tính:
a) Cường độ điện trường gây bởi các điện tích đó tại các điểm A, B, C. Cho biết: MN = d = 10 cm, MA = 4
cm, MB = 5 cm, MC = 9 cm, NC = 7 cm.
b) Lực tác dụng lên điện tích 10 q 5.10 C đặt tại C. Bài giải: 2
Tại điểm A: E và E cùng chiều nhau như hình vẽ: 1A 2A 8 8 q q 8.10 3.10 1 2 9 3 E E E k 9.10 . 525.10 V / m A 1A 2A 2 2 2 2 MA NA 0,04 0,06
Tại điểm B: E và E ngược chiều nhau như hình vẽ: 1B 2B 8 8 q q 8.10 3.10 1 2 9 3 E E E k 9.10 . 276.10 V / m B 1B 2B 2 2 2 2 MB NB 0,05 0,15
Tại điểm C: E và E có chiều nhau như hình vẽ. 1C 2C Ta có: 2 2 E E E 2E E cos , trong đó: C 1C 2C 1C 2C 8 q8.10 8 q3.10 19 3 E k 9.10 . 88,9.10 V / m và 29 3 E k 9.10 . 55,1.10 V / m 1C 2 2 MC 0,09 2C 2 2 NC 0,07 2 2 2 2 2 2 MC NC MN 9 7 10 5 cos , 0 76, 2 2MC.NC 2.9.7 21 Thay vào ta được: 3 2 2 3 E 10 88,9 55,1
2.88,9.55,1.(5 / 21) 92,8.10 V / m C
Cường độ điện trường tại C tạo với cạnh CN 1 góc: 0 0 90 90 76, 2 13,8 b) Lực 10 3 5 F q E 5.10 .92,8.10 4,6.10 N C C
Lực này ngược chiều với E C.
Bài 1.20. Một mặt phẳng vô hạn mang điện đều có mật độ điện tích mặt là 2.10-9 C/cm2 = 2.10-5 C/m2. Hỏi
lực tác dụng lên một đơn vị chiều dài của một sợi dây dài vô hạn mang điện đều. Cho biết mật độ điện dài của dây là 8 6 3.10 C/cm 3.10 C/m. Bài giải:
Lực tác dụng của mặt phẳng lên sợi dây bằng tổng lực tác dụng lên các phần tử của sợi dây. Ta đã biết điện
trường do 1 mặt phẳng gây ra là E2
không phụ thuộc vào khoảng cách từ mặt phẳng đến các phần tử 0
điện tích của sợi dây nên dù đặt sợi dây thế nào thì lực tác dụng lên 1 phần tử dq của sợi dây vẫn đều là dq dl dF Edq 2 , trong đó dq dl nên dF 2
. Lực tác dụng lên mỗi đơn vị chiều dài của dây là: 0 0 5 6 dF 2.10 .3.10 3, 4 N / m 12 dl 2 2.1.8,86.10 0
Bài 1.23. Cho 2 điện tích điểm 6 q 2.10 C , 6 q
10 C đặt cách nhau 10 cm. Tính công của lực tĩnh điện 1 2
khi điện tích q2 dịch chuyển trên đường thẳng nối hai điện tích đó xa thêm một đoạn 90 cm. Bài giải:
Ta coi đây là bài toán xác định công của lực tĩnh điện do điện tích q 1 tác dụng để dịch chuyển điện tích điểm
q2 dịch chuyển trong điện trường mà nó gây ra. 3 Như vậy: A q V V , trong đó V MN 2 M N
M và VN lần lượt là điện thế tại 2 điểm MN trên đường thẳng nối 2
điện tích và cách nhau 1 khoảng 90 cm. kq kq Giả sử: 1 V và 1 V M r N r r 9 6 6 kq kq kq q r 9.10 .2.10 . 10 .0,9 Suy ra: 1 1 1 2 A q 0,162 J MN 2 r r r r(r r) 1.0,1. 0,1 0,9
Dấu “-” có nghĩa là lực điện trường là lực cản, tức là ta phải thực hiện 1 công là +0,162 J để thắng lực điện
trường. Trong bài toán này, 2 điện tích là trái dấu nên hút nhau, vì thế muốn đưa 1 điện tích ra xa thêm thì
đương nhiên là phải thực hiện công thắng lại lực hút này.
Bài 1.24. Tính công cần thiết để dịch chuyển một điện tích 1 7 q
.10 C từ một điểm M cách quả cầu tích 3
điện bán kính r = 1 cm một khoảng R = 10 cm ra xa vô cực. Biết quả cầu có mật độ điện mặt là 11 2 7 2 10 C/cm 10 C/m . Bài giải:
Vẫn sử dụng công thức tính công của điện trường khi dịch chuyển điện tích từ điểm M đến N (trong trường hợp này N ở vô cực): A q V V
. Như vậy, cần phải tính điện thế tại các điểm M và N. MN M N
Nhân đây phải nói đến bài toán tính điện thế tại 1 điểm nằm bên ngoài và cách tâm quả cầu mang điện đều
1 khoảng là r>r 0 (bài mà thầy chưa có dịp tính trên lớp trong giờ lý thuyết). Ta có: dV Edr
(mối liên hệ giũa điện trường và điện thế)
Mặt khác sử dụng định lý Ostrogradski – Gauss ta dễ dàng tính được: kQ E
, trong đó Q là điện tích của 2 r quả cầu. kQ kQ kQ Thay vào ta được: dV dr V C
, chọn gốc điện thế tại vô cực ta có C = 0, suy ra: V 2 r r r
Quay trở lại bài toán của chúng ta: A q V V MN M N 2 27 9 7 7 kQ kqQ kq4 r 9.10 . 1/ 3 .10 .4 0,01 .10 V ; V 0 A 3, 42.10 J , M N MN r R r R r R 1 0,01 0,1 trong đó 2 Q 4 r .
Bài 1.25. Một vòng dây tròn bán kính 4 cm tích điện đều với điện tích Q = (1/9).10 -8 C. Tính điện thế tại: a) Tâm vòng dây;
b) Tại một điểm M trên trục vòng dây, cách tâm của vòng dây 1 đoạn là h = 3 cm.
Ta làm 1 bài tổng quát, tìm điện thế tại 1 điểm M trên trục vòng dây,
cách tâm vòng dây 1 đoạn là h. Ta có: kdQ dV 2 2 R h kdQ kQ Suy ra: V dV 2 2 2 2 R h R h
a) Điện thế tại tâm vòng dây h = 0 9 8 kQ 9.10 . 1/ 9 .10 V 250 V O R 1.0,04 9 8 kQ 9.10 . 1/ 9 .10 b) Tại điểm M: V 200 V H2 2 2 2 R h 1. 0,04 0,03
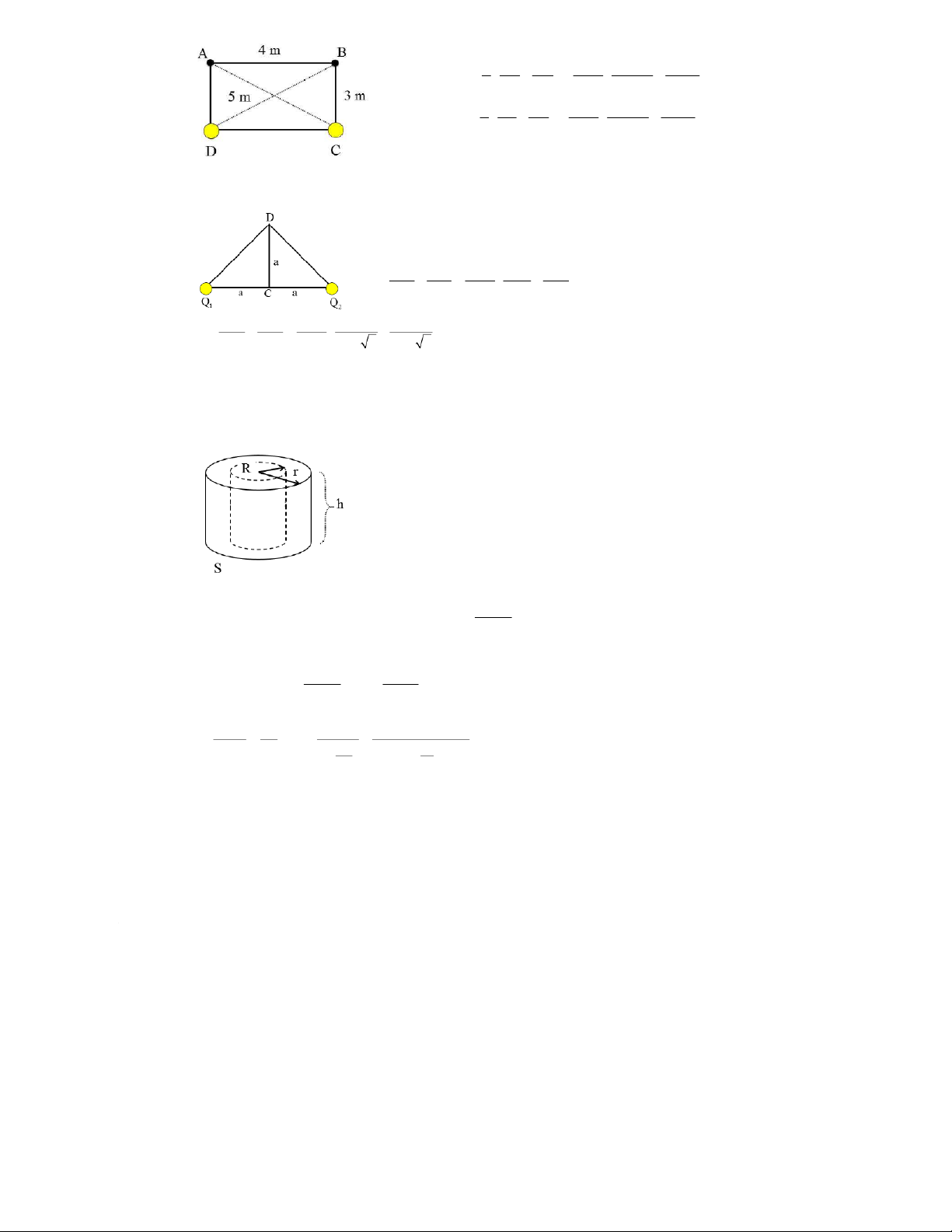
Bài 1.32. Tại hai đỉnh C, D của một hình chữ nhật ABCD (có các cạnh AB = 4 m, BC = 3 m) người ta đặt hai điện tích điểm 8 q 3.10 C (tại C) và 8 q
3.10 C (tại D). Tính hiệu điện thế giữa A và B. 1 2 Bài giải: 4 AC = BD = 5 m 9 8 8 k q q 9.10 3.10 3.10 1 2 V V V 36 V A CA DA CA DA 1 5 3 9 8 8 k q q 9.10 3.10 3.10 1 2 V V V 36 V B CB DB CB DB 1 3 5
Hiệu điện thế giữa A và B là: U V V 72 V AB A B
Bài 1.33. Tính công của lực điện trường khi chuyển dịch điện tích q = 10 -9 C từ điểm C đến điểm D nếu a = 6
cm, Q1 = (10/3).10-9 C, Q2 = 2.10-9 C. Bài giải:
Nhớ là muốn tính công của lực điện trường thì có công thức: A q V V CD C D Ta có: 99 kQ kQ 9.10 10 / 3 2 1 2 V .10 200 V C AC BC 1 0,06 0,06 99 kQ kQ 9.10 10 / 3 2 1 2 V .10 141 V D AD BD 1 0,06 2 0,06 2
Công của lực điện khi đó: 9 9 A q V V 10 200 141 59.10 J C D
Bài 1.37. Cho hai mặt trụ đồng trục mang điện đều bằng nhau và trái dấu có bán kính lần lượt là 3 cm và 10
cm, hiệu điện thế giữa chúng là 50 V. Tính mật độ điện dài trên mỗi mặt trụ và cường độ điện trường tại điểm
ở khoảng cách bằng trung bình cộng của hai bán kính. Bài giải:
Trước tiên quay trở lại bài toán tính điện trường gây ra bởi một mặt trụ dài vô hạn tích điện đều.
Xét 1 mặt Gauss có dạng mặt trụ có độ cao là h, diện tích đáy là S. Thông lượng điện: D dS D dS D dS e n n n mÆt trô mÆt bªn hai ®¸y trong đó D dS 0 vì D n n = 0 nên: hai ®¸y D dS D2 rh 2 Erh e n 0 mÆt bªn
Điện tích của khối trụ: Q h
, trong đó là mật độ điện dài của khối trụ theo chiều cao. Theo định lý O – G: Q h 2 Erh E e 0 2 r 0
Đối với những điểm nằm giữa 2 mặt trụ thì chỉ có mặt trụ ở phía trong gây ra điện trường. Ta tính điện thế tại
1 điểm cách trục của mặt trụ trong 1 khoảng là r. dr ln r dV Edr dV V C 2 r 2 0 0
Như vậy hiệu điện thế giữa 2 mặt trụ R1 = 3 cm và R 2 = 10 cm là: 12 9 R 2 V 2 1. ,86.10 .50 2 0 V ln 2,3.10 C 2 R R ln 3 R 10 2 ln 0 1 1 5