Bài tập chương 1- Điện trường Trường tĩnh điện môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Học online tại: https://tcc.mapuni.vn
BÀI TẬP: VẬT LÝ ĐẠI CƯƠNG II
_________________________________________________________________________________________________________________________________________________________________________________________________________________
CHƯƠNG I: TRƯỜNG TĨNH ĐIỆN ĐIỆN TRƯỜNG
Bài 1: Tìm lực hút giữa hạt nhân và electron trong nguyên tử Hyđrô. Biết rằng bán kính nguyên tử Hyđrô là 
, điện tích của electron = −  . 0, 5 10 − cm e 1,6 10 − C 8 19 Hướng dẫn giải
Sử dụng công thức lực tương tác giữa hai điện tích của định luật Culông (với điện tích của electron
và hạt nhân hyđrô = − = −  , khoảng cách = ): q q 1,6 10 − C r 0, 5 10 − m 19 10 e p ( )    = − = 9 ( 10 1,6 10− ) kq q 2   9 19 F 9, 23 10 − N  1 2 8 r0, 5 10 2 − 2 10
Bài 2: Có hai điện tích điểm = và = − 
đặt cách nhau một khoảng d= q 8 10− C q 3 10− C 10 cm 8 8 1 2 trong không khí. Tính:
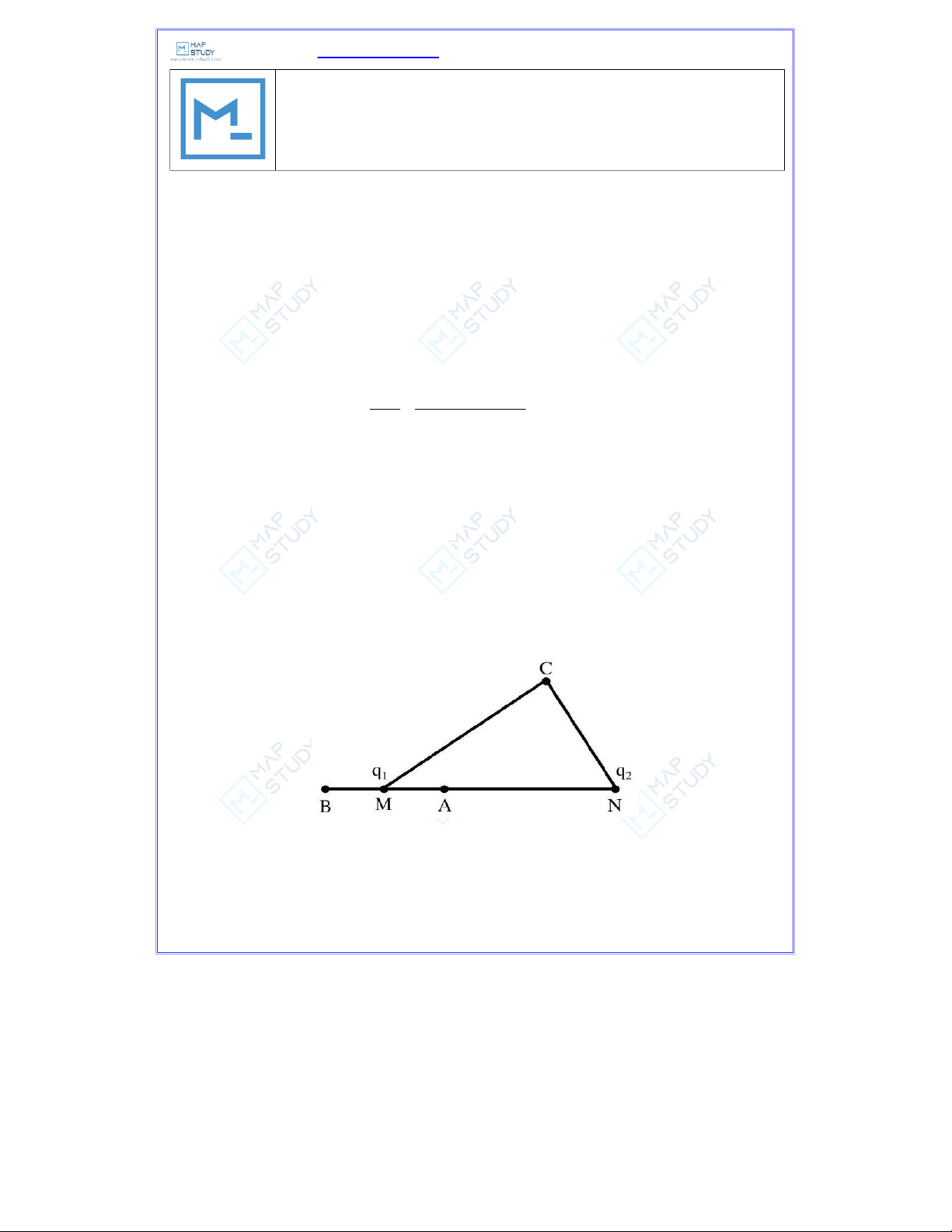
a) Cường độ điện trường gây bởi các điện tích đó tại các điểm . Cho biết: A, B,C
MN = d = 10 cm, MA = 4 cm, MB = 5 cm, MC = 9 cm ,NC = 7 cm .
b) Lực tác dụng lên điện tích = −  đặt tại . q 5 10 − C C 10 Hướng dẫn giải
a) Áp dụng nguyên lý chồng chất điện trường:
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 1
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
• Điện trường do q và q gây ra tại A cùng phương cùng chiều: 1 2 q q 1 2 E = E+ E= 4πεε ( AM) + 4πεε ( AN) A A 1 2A 2 2 0 0  −8− 8 1 8 1   0 3 10 4 E = + =  −−− 52, 5 10 V / m A12 2 2 ( ) 4π 1 8,86 10   (    
 4 10 22  )6 1 (0 )
• Điện trường do q và q gây ra tại B cùng phương ngược chiều: 1 2 q q 1 2 E E= −E
= 4πεε (BM) − 4πεε (BN) B B B 2 2 1 2 0 0  8 −−8 1 8 1   0 3 10 4 E = − =  B12 2 2 −−− 27,6 10 ( V ) 4π 1.8,86 10  ( / m   2 2  5.10 )15  (10 )
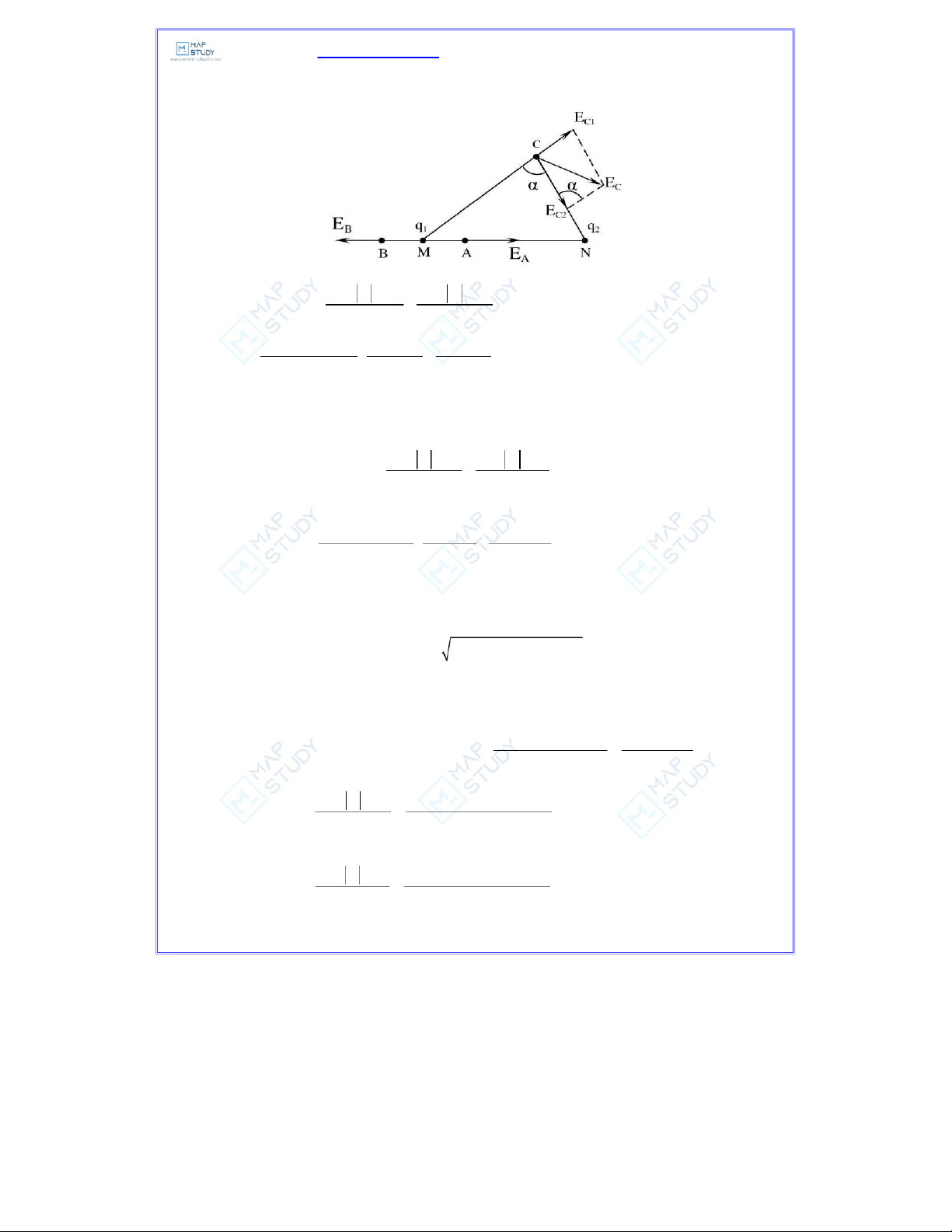
• Phương, chiều của E và E được xác định như trên hình vẽ. A B
Dùng định lý hàm số cos, ta thu được: 2 2 E= E+ E − 2E E cosα C C C C C 1 2 1 2 Ta cũng có: 2 2 2 2 2 2 + − + − 2 2 2 MC NC MN 9 7 10
MN = MC +NC −2MC NC  cosα  cosα = = = 0,23 2MC  NC 2 9  7 −8 q8 10  14 E = =
= 8,87 10 V / m C2 2 ( ) 1 1 − 2 − 2 4πεε (CM)
4π 8,86 10  9 10 0 ( ) −8 q3 10  24 E = =
= 5,50 10 V / m C2 2 ( ) 2 1 − 2 − 2 4πεε (CN ) 4π 8,86 10  7  10 0 ( )
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 2
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 2 2 Vậy: E = ( 4 8,87  10
+ 5, )50 ( 4 10
− 2 8,87 10 )44 4
5, 50 10 0=, 23 9  ,34 10 V / m C ( )
Để xác định phương của E , ta xác định góc θ là góc giữa E và CN theo định lý hàm số sin: C C E E sinθ E sinα C C 1 1 C =  = sinθ sinα E C 4 2 8,87 1
 0  1− (0,23) sinθ = =0,92 θ= 67 09 4 9,34 1  0 b) Ta có: 1 − 0 − 4 4 =  =    =  C F C q E 5 10 9,34 10 0,467 10 N ( )
Chiều của lực F ngược với chiều của điện trường E trên hình vẽ. C C
Bài 3: Xác định cường độ điện trường ở tâm một lục giác đều cạnh a , biết rằng ở sáu đỉnh của nó có đặt:
a) 6 điện tích bằng nhau và cùng dấu.
b) 3 điện tích âm và 3 điện tích dương về trị số đều bằng nhau. Hướng dẫn giải
a) Nếu ta đặt tại sáu đỉnh của lục giác đều các điện tích bằng nhau và cùng dấu, thì các cặp điện tích
ở các đỉnh đối diện sẽ tạo ra tại tâm các điện trường bằng nhau nhưng ngược chiều, nên chúng triệt
tiêu lẫn nhau. Do vậy, điện trường tổng cộng tại tâm lục giác bằng không.
E = 0 (do tính đối xứng) 0
b) Để đặt ba điện tích dương và ba điện tích âm cùng độ lớn vào sáu đỉnh của lục giác đều, ta có ba cách xếp như sau:
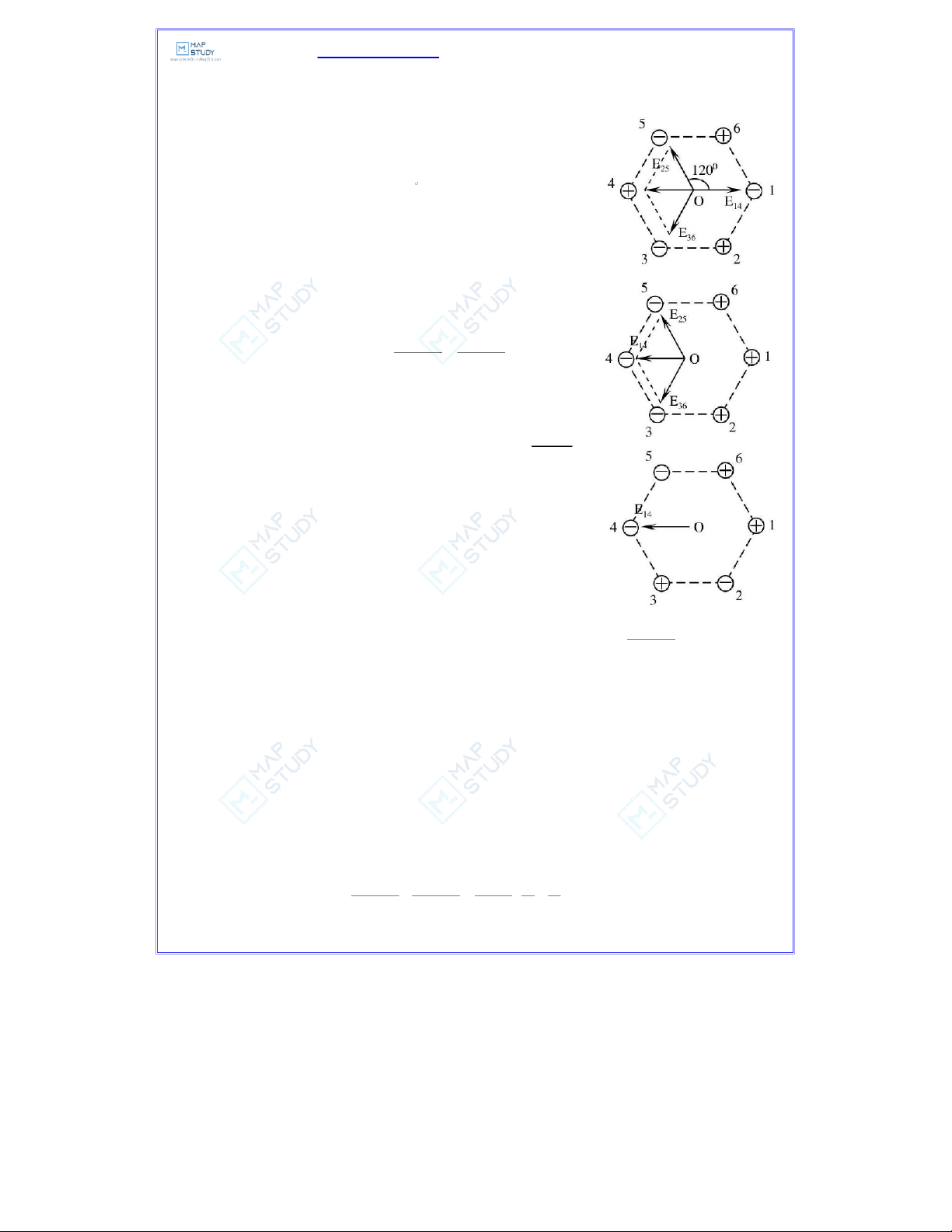
C1: Các điện tích âm và dương được đặt xen kẽ với nhau:
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 3
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Ta nhận thấy: các cặp điện trường (E ,E , E ,E và (E ,E cùng phương cùng chiều và các điện 3) 1 4 2 ) 5 ( )6
trường có cùng độ lớn.
 Các cặp điện tích 1− 4
− ,2 5 và 3 - 6 tạo ra các điện trường bằng
nhau và hợp với nhau các góc bằng 120 (Hình vẽ).
 Do tính đối xứng nên điện trường tổng hợp có giá trị bằng 0.
b) Các điện tích dương và âm đặt liên tiếp:
Các cặp điện tích 1− 4
− ,2 5 và 3−6 tạo ra các điện trường bằng nhau như hình vẽ: q q E =E= = E =2E 2 4πεε = a 2πεε a 14 25 36 1 2 2 0 0
Ta có thể dễ dàng tính được: điện trường tổng cộng E hướng theo
phương của điện trường q
E và có độ lớn bằng: E 2E == πεε a 14 14 2 0
c) Các điện tích đặt như trên hình bên:
Hai cặp điện tích cùng dấu đặt tại các đỉnh đối diện tạo ra tại O các
điện trường có cùng độ lớn nhưng ngược chiều. Do đó, điện trường
do hai cặp điện tích 2-5 và 3-6 tạo ra tại O là bằng không. Vậy, điện trường tại q
O bằng điện trường do cặp điện tích 1-4 tạo ra tại O : E E == 2πεε a 14 2 0
Bài 4: Cho hai điện tích q và 2q đặt cách nhau 10 cm. Hỏi tại điểm nào trên đường nối hai điện tích
ấy điện trường triệt tiêu. Hướng dẫn giải
Trên đường nối hai điện tích, điện trường do chúng gây ra luôn cùng phương ngược chiều nên ta có: q 2q q 1 2 E E = − = − = −  1 2E 2 2
4πεε 2 2 4πεε r 4πεε r r r 0 1 0 2 0 1 2
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 4
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Giả sử tại điểm M cách điện tích q một khoảng r , điện trường triệt tiêu. Điểm M cách điện tích
2q một khoảng là (l-r) với l là khoảng cách giữa q và 2q . q1 2 E 0= − =  2 2
4πεε r (l r)− 0 1 2 2 2  − = 0  (l − r)= 2r 2 2 r (l r−)
 l− r= 2r l 10  r = =  4,14 ( c ) m 1 ++ 2 1 2
Vậy, điện trường giữa hai điện tích q và 2q triệt tiêu tại điểm M nằm trên đường nối hai điện tích
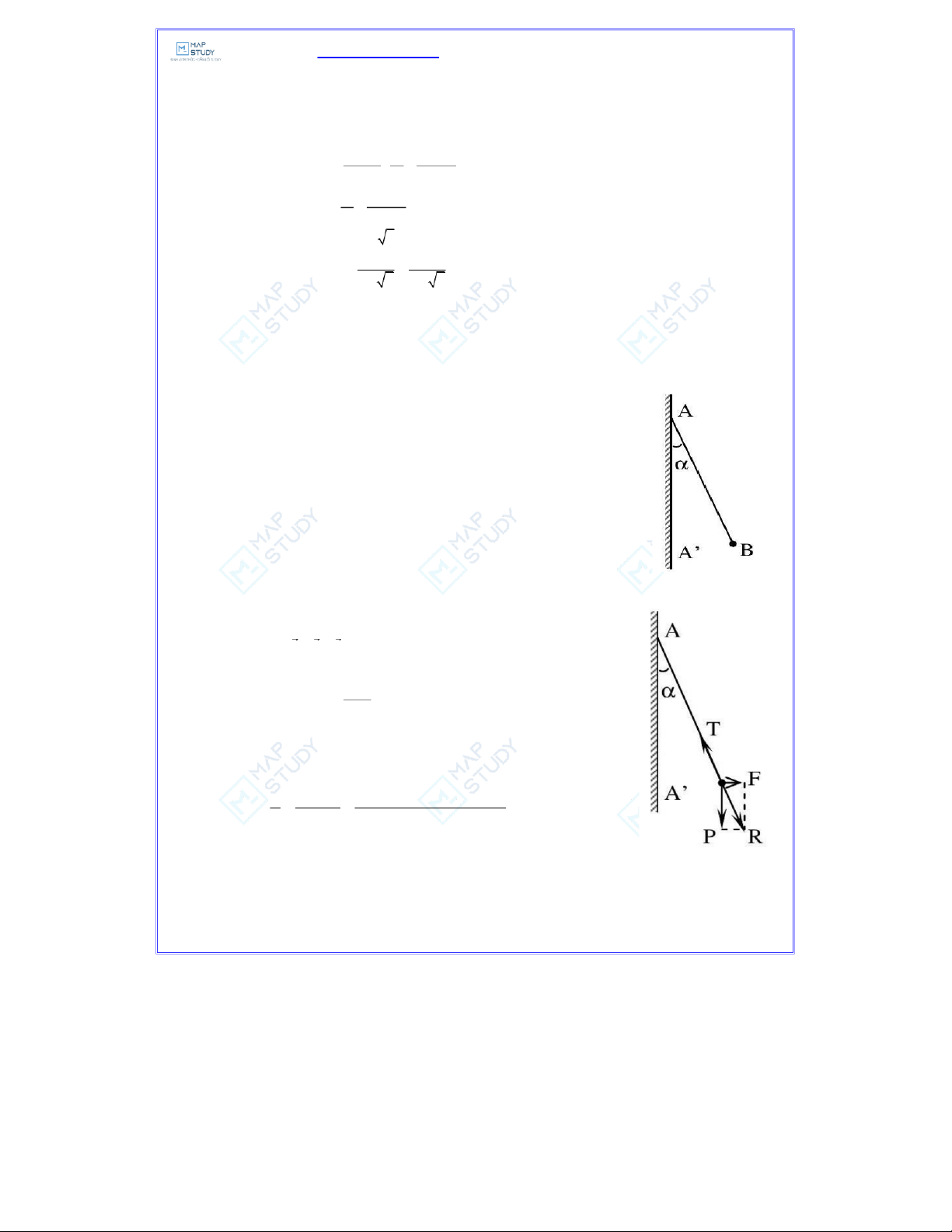
tại vị trí cách điện tích q là 4,14 (cm). Bài 5: Trên hình '
AA là một mặt phẳng vô hạn tích điện đều với mật độ điện mặt σ= −9 2
4 10 C / cm và B là một quả cầu tích điện cùng dấu với điện tích
trên mặt phẳng. Khối lượng của quả cầu bằng m = 1 g , điện tích của nó bằng 9 q 10 C − =
. Hỏi sợi dây treo quả cầu lệch đi một góc bằng bao nhiêu so với phương thẳng đứng. Hướng dẫn giải
Tại vị trí cân bằng: T + F + P= 0 Trong đó: σq
P =mg; F = Eq = 2εε 0 Từ hình vẽ ta thấy: −5− 9 F σq 4 1 0 10 0 tgα = = = = 0,2309 α= 13 −− 12 3 P 2εε mg 2 1 8  ,8  6 10 10 9,8  1 0
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 5
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Bài 6: Một thanh kim loại mảnh mang điện tích 7 −
q =2 10 C . Xác định cường độ điện trường tại một
điểm nằm cách hai đâu thanh R = 300 cm và cách trung điểm thanh R= 10 cm. Coi như điện tích 0
được phân bố đều trên thanh.
Hướng dẫn giải
Chia thanh thành những đoạn nhỏ dx . Chúng có điện tích là: q q dq dx == − dx 2 2 l2 R R 0
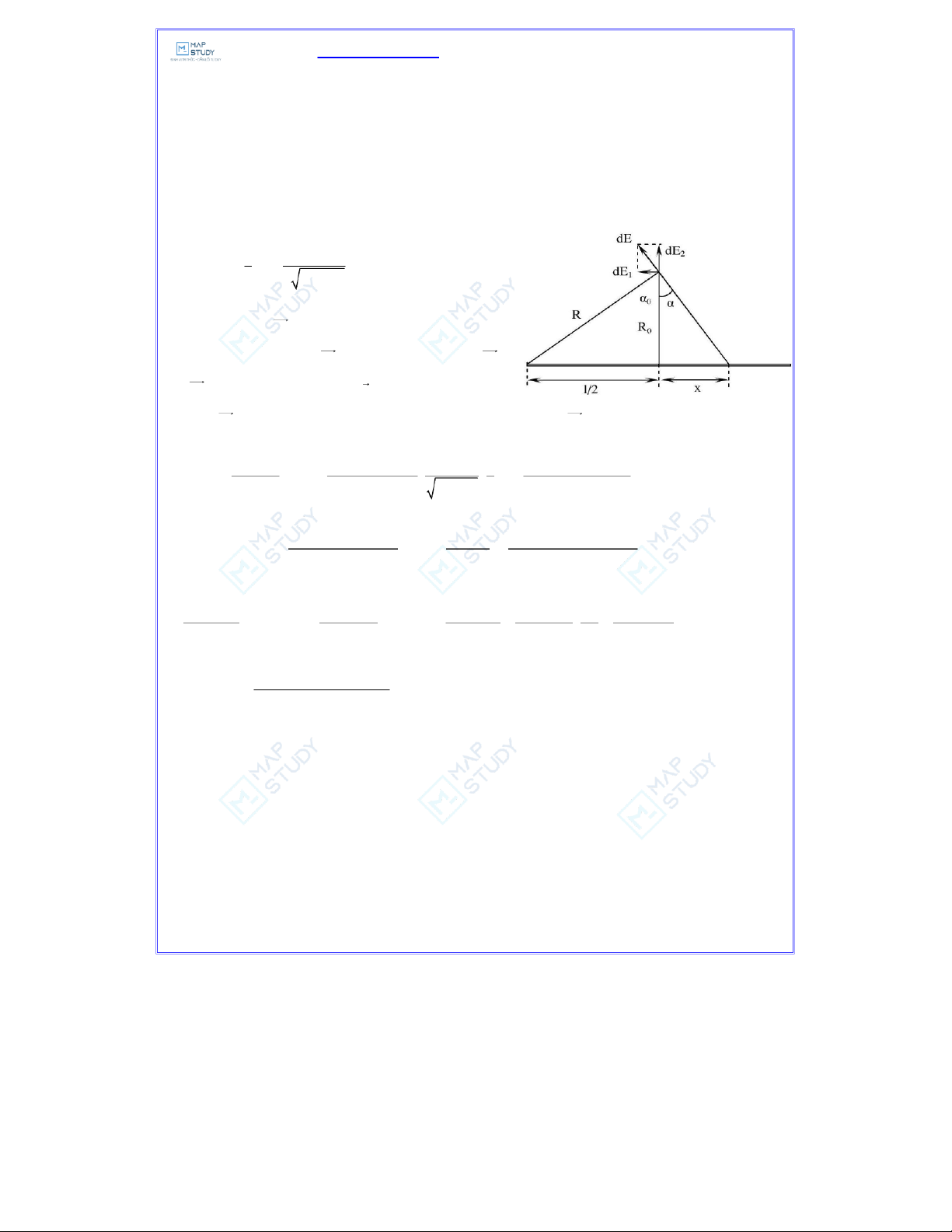
Xét điện trường dE gây ra do đoạn dx gây ra tại điểm
đang xét. Ta có thể tách dE thành hai thành phần 1 dE
và dE2 . Điện trường tổng cộng E là tổng tất cả các điện
trường dE đó. Do tính đối xứng nên tổng tất cả các thành phần d 1
E bằng không. Ta có: dq q 1 R qR 0 0 dE cos = α  = dx dx  = 22 3/24πεε r 4πεε (R ) 2 2 2 2 2 2 x +++ R x l 4πεε l R x 00 0 00 0 ( ) α 1/2 0 qR qR R 0 0 0
 E= dE= dx =  dα 23/2 3/2 = −− + 4πεε 1 4πεε 1 R x cos α R + R tg α 0 0 ( ) x R tgα 2 2 0 2 2 2 2 1/2 α 0 0 0 0 ( ) 0 α q q α0 2qsinα q q 1 0 = cosα dα = [sinα] = =  =  α − 0 4πεε IR − 4πεε 1R 4πεε lR 2πεε 1R 2R 4πεε RR 0 0 α 0 0 0 0 0 0 0 0 0 −7  Thay số: 2 10 3 E =   − 6 10 ( ) V / m 12
4π 1 8,86 10  3 0,1
Bài 7: Một đĩa tròn bán kính a = 8 cm tích điện đều với mật độ điện mặt −8 2 σ =10 C / m.
a) Xác định cường độ điện trường tại một điểm trên trục của đĩa và cách tâm đĩa một đoạn b = 6 cm
b) Chứng minh rằng nếu b → 0
thì biểu thức thu được sẽ chuyển thành biểu thức tính cường độ
điện trường gây bởi một mặt phẳng vô hạn mang điện đều.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 6
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
c) Chứng minh rằng nếu b
→ a thì biểu thức thu được chuyển thành biểu thức tính cường độ điện
trường gây bởi một điện tích điểm.
Hướng dẫn giải
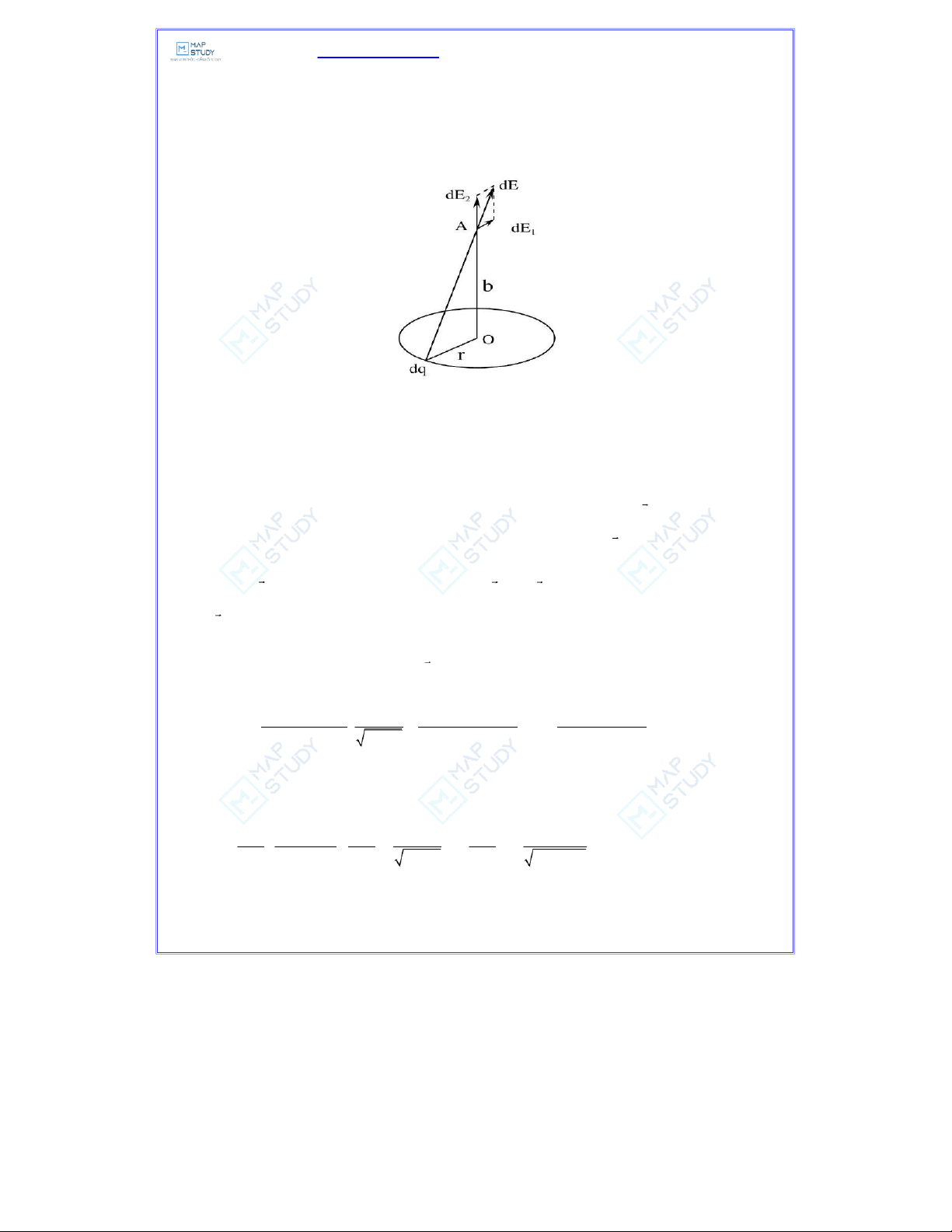
a) Chia đĩa thành từng dải vành khăn có bề rộng dr. Xét dải vành khăn có bán kính r(r a) . Vành
khăn có điện tích tổng cộng: dQ= σ.2πr.dr
Chia vành khăn thành các điện tích điểm dq . Chúng gây ra điện trường dE tại A . Theo định lý
chồng chất điện trường, điện trường tại A bằng tổng tất cả các giá trị dE đó.
Điện trường dE có thể phân thành hai thành phần dE và dE . Do tính đối xứng nên tổng các thành 1 2
phần dE bằng không. Vậy: 1 dE = = dE dEcosα, 
với α là góc giữa dE và OA r 2 dq b b bσ r dr   dE =  = dQ = 
r3/2 3/24πεε ( 2 r )2 22 2 2 b ++++ r b 4πεε r b (2 )22 εε r b 00 0 ( )
Điện trường do cả đĩa gây ra tại A là: a a bσ r dr bσ  1   σ 1  E dE = = = −  = 1−   r3/2 2 2  2εε 2εε + 2εε ++    0 0 (r b) 2 2 2 2 0 0 r b 0 1 a / b
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 7
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________  8 − 10 1  E = −  −−− 1 
226 ( V )/m 12 2 2 2.8,86.10 1 8.10  +  (/ 6.1 202 ) ( ) b) Nếu cho b →0 , ta có: σ  1 σ E lim = − 1 =  b 0 → 0 0 2 2 2εε 2ε ε 1 +a / b Điện trường khi b →0
có biểu thức giống với điện trường do mặt phẳng tích điện đều gây ra. 2 c) Nếu 1 a b
, áp dụng công thức gần đúng:  1−2b 2 2 2 1 + a / b    σ σ a σ a (πa )2 2 2 q Vậy: E = 1  1 − −  = = = 2 2 2 2 2εε 2b   4εε b 4πεε b 4πεε b 0000 Điện trường khi b
có biểu thức giống với điện trường do một điện tích điểm gây ra.
Bài 8: Trong điện trường của một mặt phẳng vô hạn tích điện đều có đặt hai thanh tích điện như
nhau. Hỏi lực tác dụng của điện trường lên hai thanh đó có như nhau không nếu một thanh nằm
song song với mặt phẳng còn thanh kia nằm vuông góc với mặt phẳng. Hướng dẫn giải
Lực tác dụng lên thanh nằm song song là: F = F  = qE  1 i i
và lực tác dụng lên thanh nằ vuông góc là: m F = F  = qE  2 k k
Do điện trường do mặt phẳng vô hạn tích điện đều gây ra là điện trường đều nên:
E = E  F= F i k 1 2
Vậy, lực tác dụng lên hai thanh là như nhau.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 8
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Bài 9: Một mặt phẳng vô hạn mang điện đều có mật độ điện tích mặt −9 2 σ = 2
 10 C / cm . Hỏi lực tác
dụng lên một đơn vị chiều dài của một sợi dây dài vô hạn mang điện đều. Cho biết mật độ điện dài của dây −8 λ = 3  10 C / cm. Hướng dẫn giải
Ta thấy, lực tác dụng lên dây không phụ thuộc vào cách đặt dây trong điện trường. Ta có:
• Điện trường do mặt phẳng gây ra là: σ E = 2εε 0
• Điện tích của dây là: q = λL
Vậy, lực tác dụng lên mỗi đơn vị chiều dài dây là: 5 −− 6 σλL 2 10  3 10  1 F = Eq = =  3, 4 N −12 ( ) 2ε    0 ε 2 1 8,86 10
Bài 10: Xác định vị trí của những điểm ở gần hai điện tích điểm q và q tại đó điện trường bằng 1 2
không trong hai trường hợp sau đây: a) q ,q cùng dấu 1 2 b) q ,q khác dấu. 1 2
Cho biết khoảng cách giữa q và q là l . 1 2 Hướng dẫn giải
Véctơ cường độ điện trường tại một điểm M bất kỳ bằng: E= E + E 1 2
với E và E là các véctơ cường độ điện trường do q , q gây ra. 1 2 1 2
Để E= 0 , thì ta phải có: E =− E 1 2
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 9
Học online tại: https://tcc.mapuni.vn
_________________________________________________________________________________________________________________________________________________________________________________________________________________
• Hai điện trường E và E cùng phương, M phải nằm trên đường thẳng đi qua điểm đặt các 1 2 điện tích.
• Hai điện trường E và E cùng độ lớn: 1 2 2 q q q x 1 2 1 E = E  =  l x =  q 1 2 2 2 4πεε x 4πεε (l− x  ) − 0 0 2 x q q 1 1  =  x  =  (l )x− l x − q q 2 2 q ∣ 1  lq q ∣2 1  x= =  l qq∣ q 11 2 1q ∣ ∣ 2
• Hai điện trường E và E ngược chiều: 1 2
a) Nếu q ,q cùng dấu thì M phải nằm giữa hai điên tích: 1 2 q1
0  x  l  x= + l q q 1 2
b) Nếu q ,q khác dấu thì M phải nằm ngoài hai điện tích: 1 2 q1
x  0, x  l  x= − l q q 1 2 __HẾT__
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Phạm Ngọc Lam Trường 10