







Preview text:
lOMoAR cPSD| 46663874 Bài 1:
a) Ta có xác suất thắng mỗi trận lần lượt là 0,4 ; 0,3 ; 0,6
Xác suất thua mỗi trận lần lượt là 0,6 ; 0,7 ; 0,4
Gọi X là là số trận thắng của đội tuyển X={0,1,2,3}
Bảng phân phối xác suất: X 0 1 2 3 P(X) 0,168 0,436 0,324 0,072
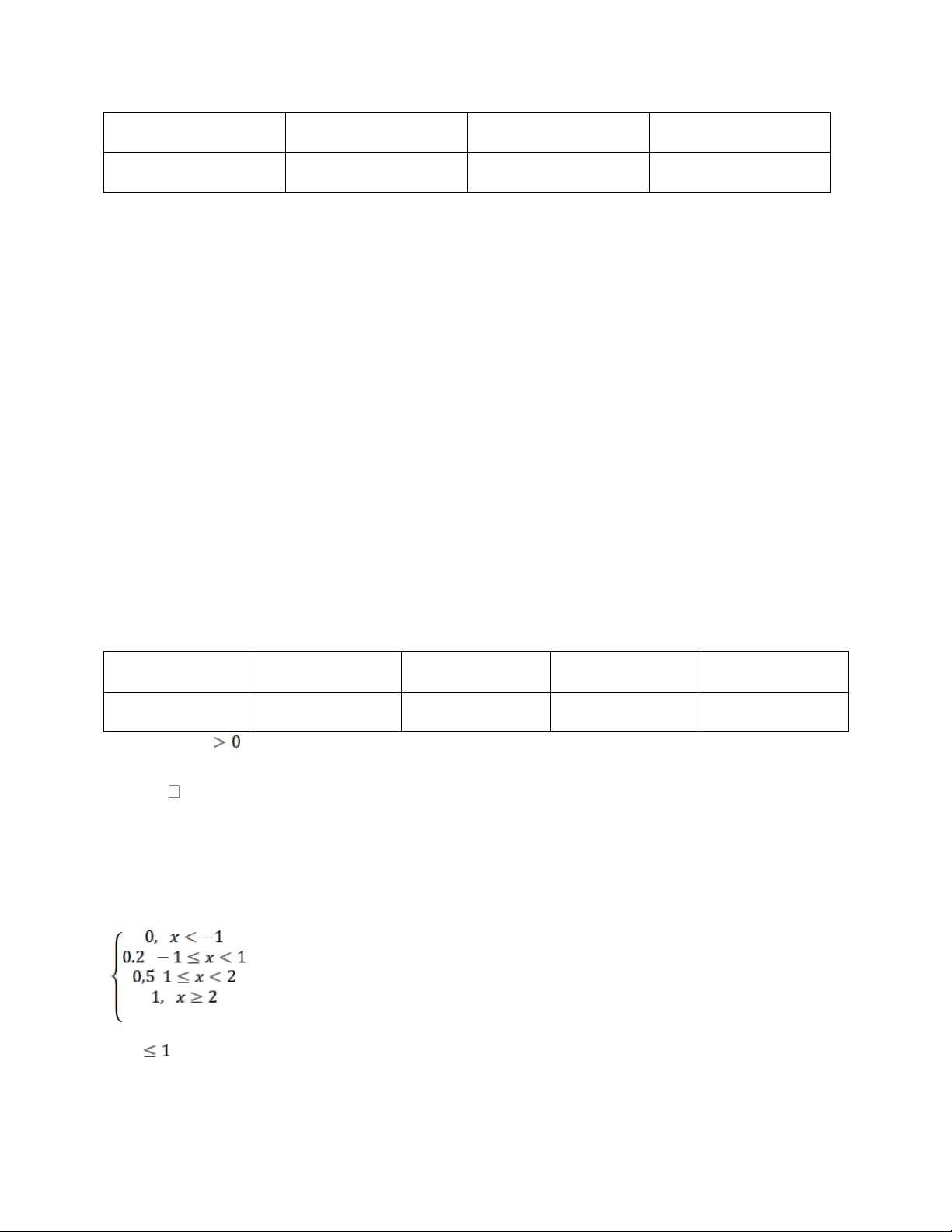
Hàm phân phối xác suất của X: F(X) =
b) Gọi B là biến cố đội tuyển thắng ít nhất 1 lần:
P(B)= 1 - P( = 1 – ( 0,6 x 0,7 x 0,4 ) = 0,832. Bài 2:
Xác suất ném trúng trong mỗi lần là 0,4 => Xác suất ném không trúng là 0,6.
Gọi X là số tiền mà An có thể nhận được:
TH1: Cả 2 lần không trúng => X= -20000.
TH2: 1 lần trúng, 1 lần không trúng => X= 10000.
TH3: Cả 2 lần trúng => X= 40000. X = { 0, 20000, 40000} lOMoAR cPSD| 46663874 X -20000 10000 40000 P 0,36 0,48 0,16
Số tiền trung bình người chơi có thể nhận được: E(X)= 0,36 x -20000 + 10000 x 0,48 + 0,16 x 40000= 4000. Bài 3:
Gọi X là số lãi A nhận được sau khi trừ chi phí và thuế:
TH1: Cả 2 công ty không nhận
X = 4 – 10 – 10% x 4 = -6,4
TH2: B nhận, C không nhận :
X = 8 – 10 – 10% x 8 = -2,8
TH3: B không nhận, C nhận:
X = 10 – 10 – 10% x 10 = -1
TH4: Cả 2 đều nhận
X = 14 – 10 – 10% x 14 = 2,6 X -6,4 -2,8 -1 2,6 P 0,06 0,14 0,24 0,56 E(X) = 0,44
A nên nhận bản thiết kế. Bài 4: Hàm phân phối xs của X: P(X ) = 0,2 + 0,3 = 0,5 Bài 5: lOMoAR cPSD| 46663874 a) X+Y -2 0 1 2 3 4 P 0,08 0,18 0,26 0,09 0,24 0,15
Vì X,Y độc lập nên ta có P(XiYj) = P(Xi) x P(Yj) XY -2 -1 1 2 4 P 0,26 0,18 0,17 0,24 0,15
b. Kỳ vọng, phương sai, độ lệch chuẩn của X + Y và XY là: E(X + Y ) = 1.68 Var(X+Y) = 2.4376 σ = 1.5612 E(XY ) = 0.55 Var(XY) = 4.4475 σ = 2.109 Bài 6: X 0 1 4 0 1 2 P 0,1 0,3 0,6 P 0,1 0,3 0,6 E(X)=2,7 E( )=1,5 Var( . Bài 7: X 0 1 2 3 P 7/24 21/40 7/40 1/120 E(X)=0,9. Bài 8: lOMoAR cPSD| 46663874 X 0 1 2 3 P 0,42 0,425 0,14 0,015 . Bài 9: X 0 1 2 3 P 0,4 0,1 0,2 0,3
Gọi A là xác suất có ít nhất 1 người chờ cắt tóc Bài 10: X 1 2 3 P 0,6 0,3 0,1 Bài 11: X 2 4 x3 P 0.2 0.4 p3
Ta có: p1 + p2 + p3 = 1 E(x) = 4.4
<=> 0.2 + 0.4 + p3 = 1 <=> x1p1 + x2p2 + x3p3 = 4.4
<=> p3 = 0.4 <=> 0.4 + 1.6 + 0.4x3 = 4.4 <=> x3 = 6 Bài 12:
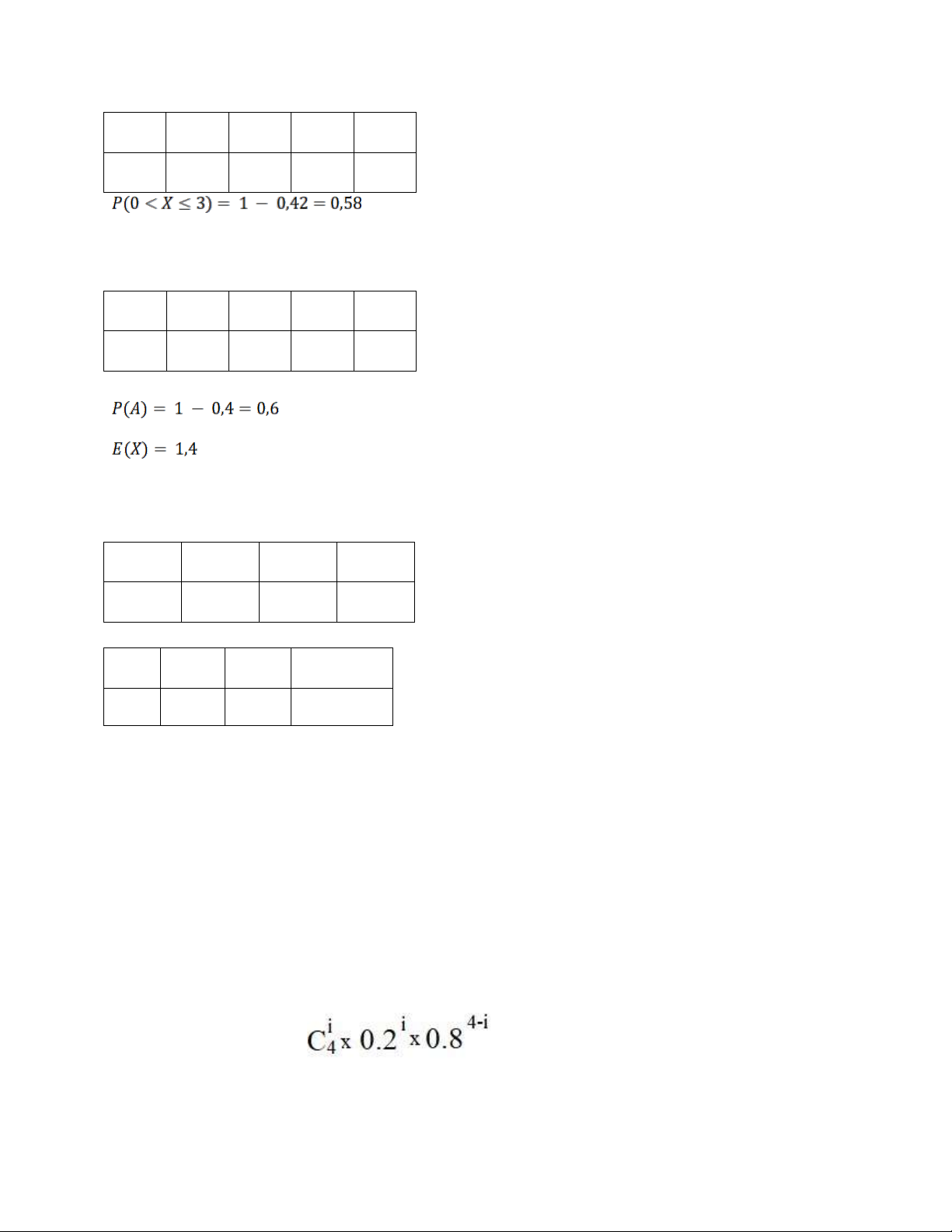
Gọi X là số lần thử thành công Ta có : P( X=xi) = Bảng ppxs lOMoAR cPSD| 46663874 X 0 1 2 3 4 P 0.4096 0.4096 0.1536 0.0256 0.0016
Vậy ta có: E(x2) = 02 0.4096 + 12 0.4096 + 22 0.1536 + 32 0.0256 + 42 0.0016 = 1,28. Bài 13:
Gọi X là số lần thử thành công Ta có: P (X=xi) = Bảng ppxs X 0 1 … n P p1 p2 …. pn
Vậy ta có: E(x) = 0×p1 + 1×p2 +….+ n×pn Bài 14:
Ta có E(x) = 1 0.6 + 2 0.3 + 3×0.1 = 1.5
E(Y) = 0 0.2 + 1 0.2 + 2 0.6 = 1.4 Do đó: E( = = 1.45. Bài 15: a. Ta có: = 1 k = lOMoAR cPSD| 46663874 b. P(0 2) = c. E(X) = . Bài 16: Ta có: a) 01ax3-3x2+2xdx = 1 a4=1 a=4
b) Thời gian xếp hàng trung bình là:
01(4x2-3x2+2x).x dx=43/60 (phút). Bài 17:
Ta có: a) 02kx2(x-2)2dx= 1 k1615 =1 k=0.9375
b) Kỳ vọng và phương sai của k là: E(x)= 02x.0,9375dx= 158.
Var(x) = 02(x-(158))2dx = 21196. Bài 18: Ta có: E(X)= = . lOMoAR cPSD| 46663874 Bài 19:
a) f(x) là hàm mật độ xác suất vì nó dương đồng thời: =1 b) P(0= Bài 20: Ta có: P( =1- P ( =1- P( =1- Bài 21: a) =1 =>k= b) x thuộc F(x)= = X không thuộc c) E(Y)=E( = = Bài 22: E(X) = lOMoAR cPSD| 46663874 Bài 23: Var(X) = Bài 24: P(X0.55)=0.551f(x) = 0.405. Bài 25:
Từ bảng phân phối xác suất đồng thời ta có: P(X=1,Y=2)=155700
P(X=1).P(Y=2)=430700 x 185700 = 15919800
Do đó, hai đại lượng ngẫu nhiên X,Y không độc lập với nhau, vì P(X=1,Y=2) P(X=1).P(Y=2)
Cov(X,Y)= 1.1.190700+ 1.2.155700 = 57 Bài 26: 1 3 4 6 P(X=xi) 2 p 0,06 0,2 0,1 p+0,36 5 0,3 0,1 0,05 q q+0,45 P(Y=yi) p+0,3 0,16 0,25 q+0,1 1 p+0,36+0,45+q=1 p+q=0,19
Từ bảng phân phối xác suất đồng thời của vectơ 2 chiều X,Y ta suy ra bảng phân phối
xác suất của X với điều kiện Y=3 : X 2 5 lOMoAR cPSD| 46663874 P(X/Y=3) 0,060,16=0,375 0,10,16=0,625 Bài 27: x1 x2 x3 P(X=xi) y1 0,1 0,3 0,2 0,6 y2 0,2 0,1 0,1 0,4 P(Y=yi) 0,3 0,4 0,3 1 Bài 28: 1 2 3 P(X=xi) 1 0,1 0,3 0,2 0,6 2 0,06 0,18 0,16 0,4 P(Y=yi) 0,16 0,48 0,36 1
Số khách trung bình: E(X)= 1.0,6 + 2.0,4 = 1,4
Số lượng hàng bán ra trung bình trong 10p: 1.0,16 + 2.0,48 + 3.0,16 = 2,2 Xác
suất có 1 người bán đến cửa hàng và có 2 sản phẩm được bán trong vòng 10p: P(X=1,Y=2) = 0,3. Bài 29: Gọi X là . số sản . phẩm cần bảo hành: a, P(X=0) = b, P(X≤5) = c, P(X≤10) = . Bài 30: lOMoAR cPSD| 46663874
Gọi X1 là tuổi thọ của bóng đèn (tháng) Xác suất
1 bóng đèn được xếp loại I là: P(X1≥11) = 1-
P(X1<11) = 1- 0,15866 = 0,84134.
a, Xác suất người đó mua 7 bóng đèn loại I trong 10 bóng đèn là: ≈ 0,143.
b, Phân phối xác suất của Y là phân phối nhị thức: P(Y≥80) = .
E(Y) = n.p = 0,84134.100= 84,134
V(X) = n.p.(1-p) = 0,84134.100.(1-0,84134) ≈ 13,35. T(X) = ≈ 3,65.




