Bài tập đại số bool - Cấu trúc rời rạc | Trường Đại học CNTT Thành Phố Hồ Chí Minh
Bài tập đại số bool - Cấu trúc rời rạc | Trường Đại học CNTT Thành Phố Hồ Chí Minh được được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Cấu trúc rời rạc
Trường: Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 40425501 Bài 1:
Tìm đối ngẫu của x.(y + 0) Giải:
Đổi chỗ các dấu . và + cho nhau, các số 0 và 1 cho nhau trong các biểu thức ta sẽ nhận được
các đối ngẫu của chúng. Đối ngẫu đó là x + (y.1) Bài 2:
Tìm đối ngẫu của .1+()
Đổi chỗ các dấu . và + cho nhau, các số 0 và 1 cho nhau trong các biểu thức ta sẽ nhận được
các đối ngẫu của chúng. Đối ngẫu đó là (x+0).(y.z) Bài 3: Chứng minh rằng:
Giải: lấy đối ngẫu 2 vế, ta được: xy x y. x x y( y) x x.1 x Bài 4 :
Chứng minh: x.y y.z z.x x.y y.z z.x Giải: -
Lấy đối ngẫu cả 2 vế
(x y).(y z).(z x)
(x y).(y z).(z x) -
Dùng tính chất phân phối
( .x y x .z y z. ).(z x)
( .x y x.z yz. ).(z x) - Rút gọn
( . . )x yz ( .z y x. ) ( . . )x yz ( .z y x. )
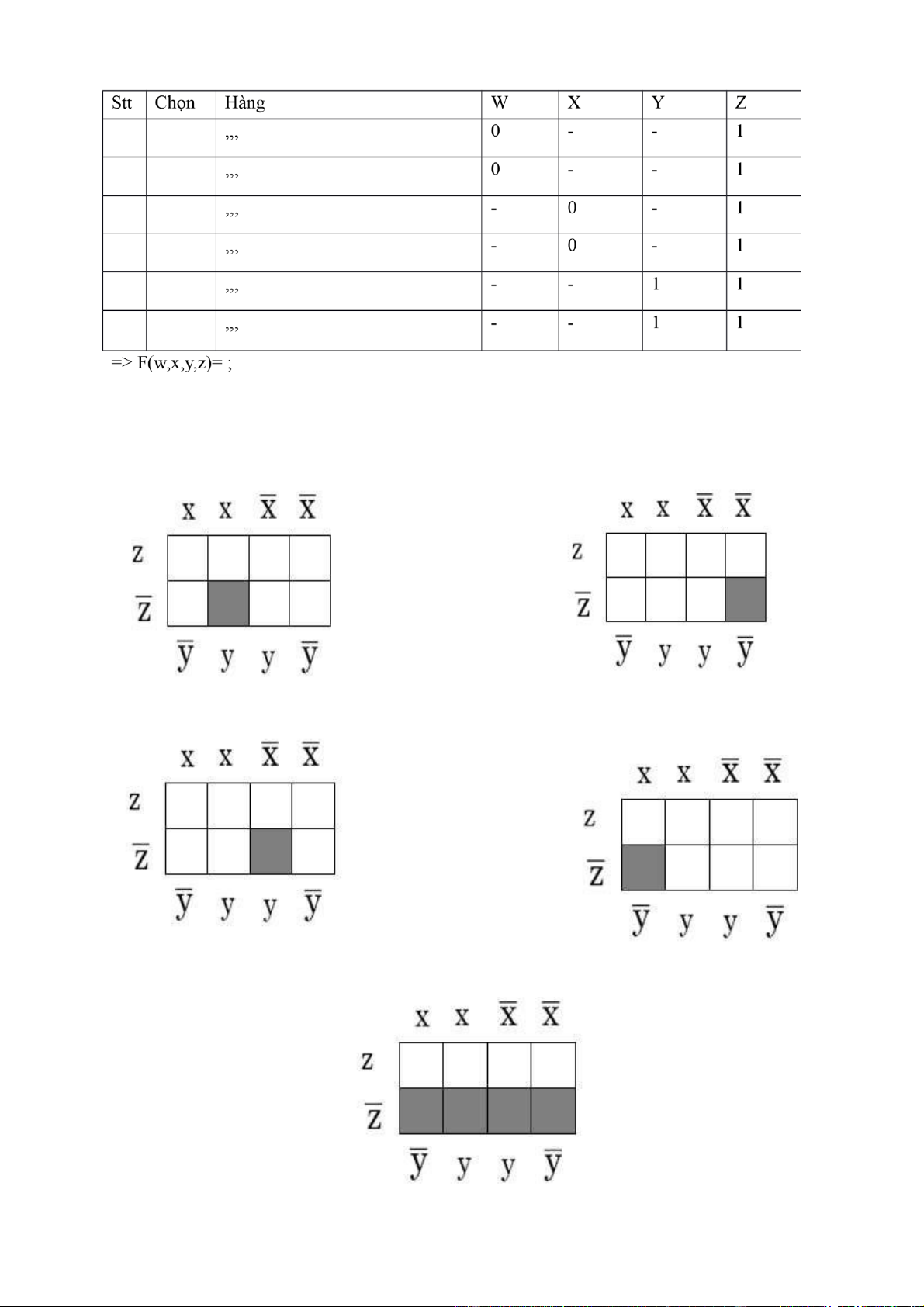
Bài 5: Tìm dạng nối rời chính tắc của hàm sau: *Cách giải 1: - Lập bảng chân trị . -
Tìm xem F(x,y,z)=1 khi nào (điều kiện của x,y,z)
=> dạng nối rời chính tắc của hàm F *Cách giải 2: -
Biến đổi thành dạng tổng các tích (nhân vào) -
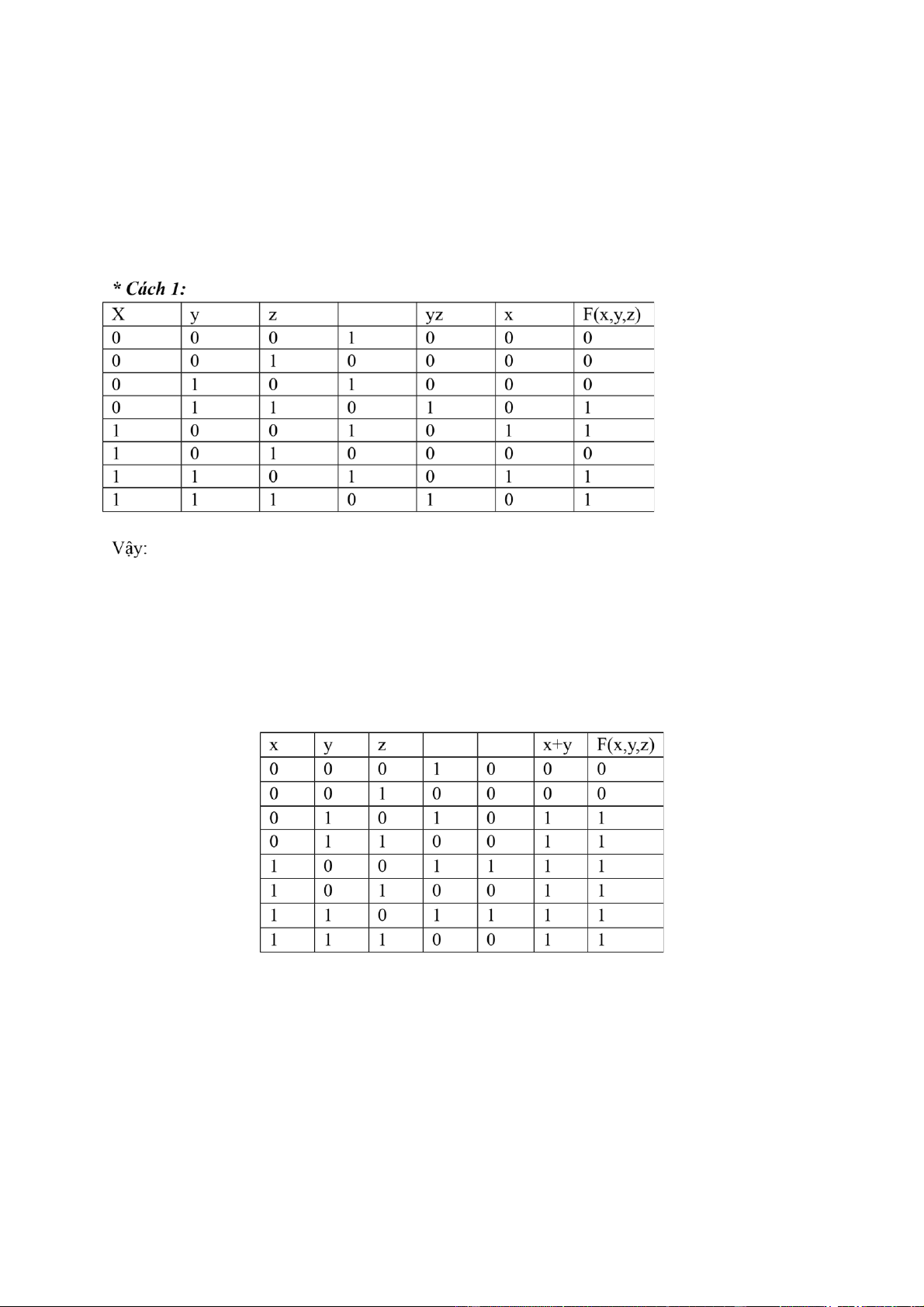
Nếu đơn thức thiếu phần tử a thì ta nhân thêm vào đơn thức đó () (vì () =1) Cách 1: lOMoAR cPSD| 40425501 Ta thấy:
F(x,y,z)=1 khi:x = 0, y = 1, z = 0 Hoặc x = 1, y = 0, z = 0
Hoặc x = 1, y = 1, z = 0 Vậy
dạng nối rời chính tắc của hàm F(x,y,z)= Cách 2: F(x,y,z) = = = = Bài 6: F(x,y,z) = yz + x Cách 2: Ta có:
Bài 7: F(x,y,z) = x + y + x * Cách 1 Vậy: F(x,y,z) = * Cách 2: Ta có:
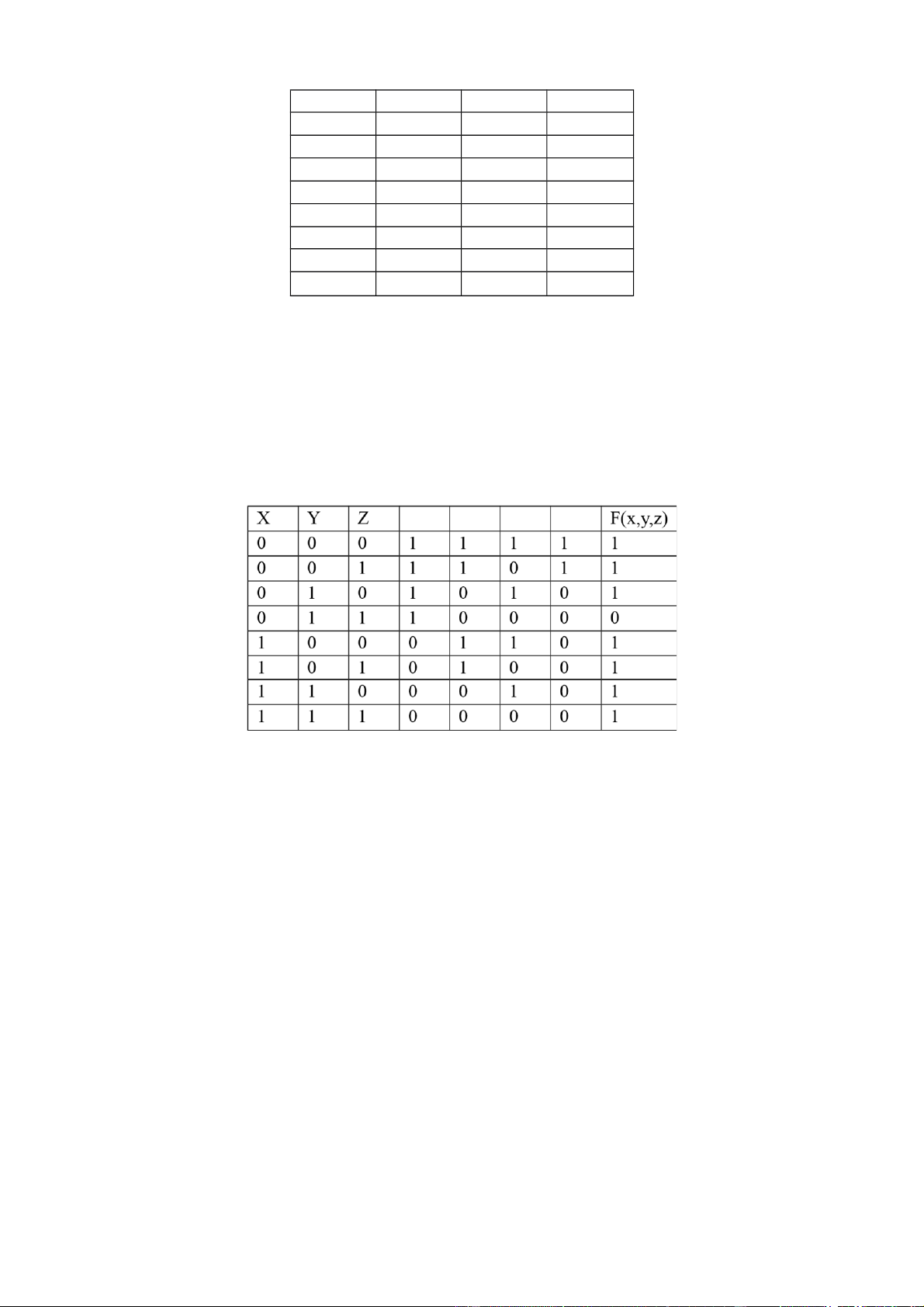
Bài 8: F(x,y,z) = x + y + z * Cách 1: lOMoAR cPSD| 40425501 x y z F(x,y,z) 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 Đ/S: F(x,y,z)= * Cách 2: Ta có: Bài 9: F(x,y,z) = Giải: Đ/S: Vậy F(x,y,z) = Bài 10: F(A,B,C,D)=
Do ở đây có 4 tham số là: A,B,C,D nên sẽ có 16 trường hợp xảy ra => Không nên sử dụng bảng chân trị. Ta có:
Bài 11. Rút gọn các hàm sau:
*Cách giải: Sử dụng các quy tắc (vd: định luật De morgan, quy luật phân phối,…) để biến đổi
hàm về dạng đơn giản. a./ F(x,y,z) = Giải:
F(x,y,z) = ) (Định lý De Morgan) = (Định lý De Morgan) = = = = b./ F(x,y,z) = Giải: lOMoAR cPSD| 40425501 F(x,y,z) = = = + + xyz = c./ F(x,y,z) = Giải: F(x,y,z) = = d./ F(w,x,y,z)= Giải: F(w,x,y,z) = ( wxz++ + e./ Ta có:
Bài 12: Đưa các biểu thức Boole sau về dạng tổng của các tích: a./ F(x, y, z, t)= F(x, y, z, t)= F(x, y, z, t)= F(x, y, z, t)= F(x, y, z, t)= b./ F(x, y, z, t)= F(x, y, z, t)= c./ F(x, y, z, t)=( F(x, y, z, t)= lOMoAR cPSD| 40425501 d./ F(x, y, z, t)=(x F(x, y, z, t)= e./ F(x, y, z, t)= F(x, y, z, t) = F(x, y, z, t) = F(x, y, z, t) =
Bài 13: Tìm dạng chính tắc nối rời của các hàm sau: a./ F(x,y,z,t) = b./ F(x, y, z, t) = F(x,y,z,t) = F(x,y,z,t) = F(x,y,z,t) = c./ F(x, y, z, t) = F(x,y,z,t) = F(x,y,z,t) = ) F(x,y,z,t) = F(x,y,z,t) = d./ F(x, y, z, t) = F(x,y,z,t) = F(x,y,z,t) = F(x,y,z,t) = F(x,y,z,t) = e./ F(x, y, z, t) = ( F(x, y, z, t) = F(x, y, z, t) = )+(x+ F(x, y, z, t) = x+ lOMoAR cPSD| 40425501 F(x, y, z, t) = + f./ F(x, y, z, t) = (x F(x, y, z, t )= F(x, y, z, t) = F(x, y, z, t) = xyzt+x F(x, y, z, t) =xyzt+x g./ F(x, y, z, t) = F(x, y, z, t) = F(x, y, z, t) = F(x, y, z, t) = F x y z( , , ) G x y z( , , )
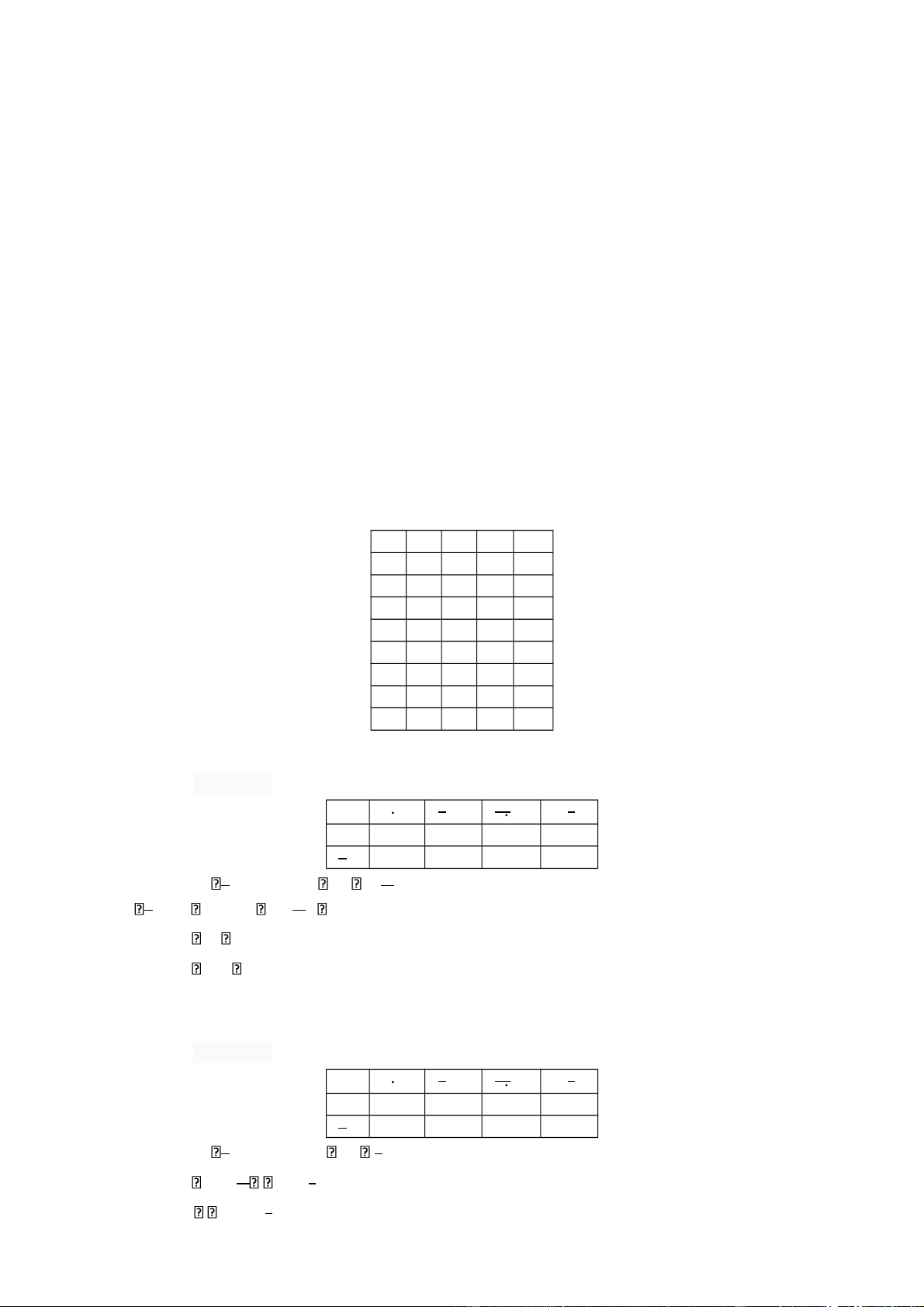
Bài 14: Tìm các biểu thức boole biểu diễn và
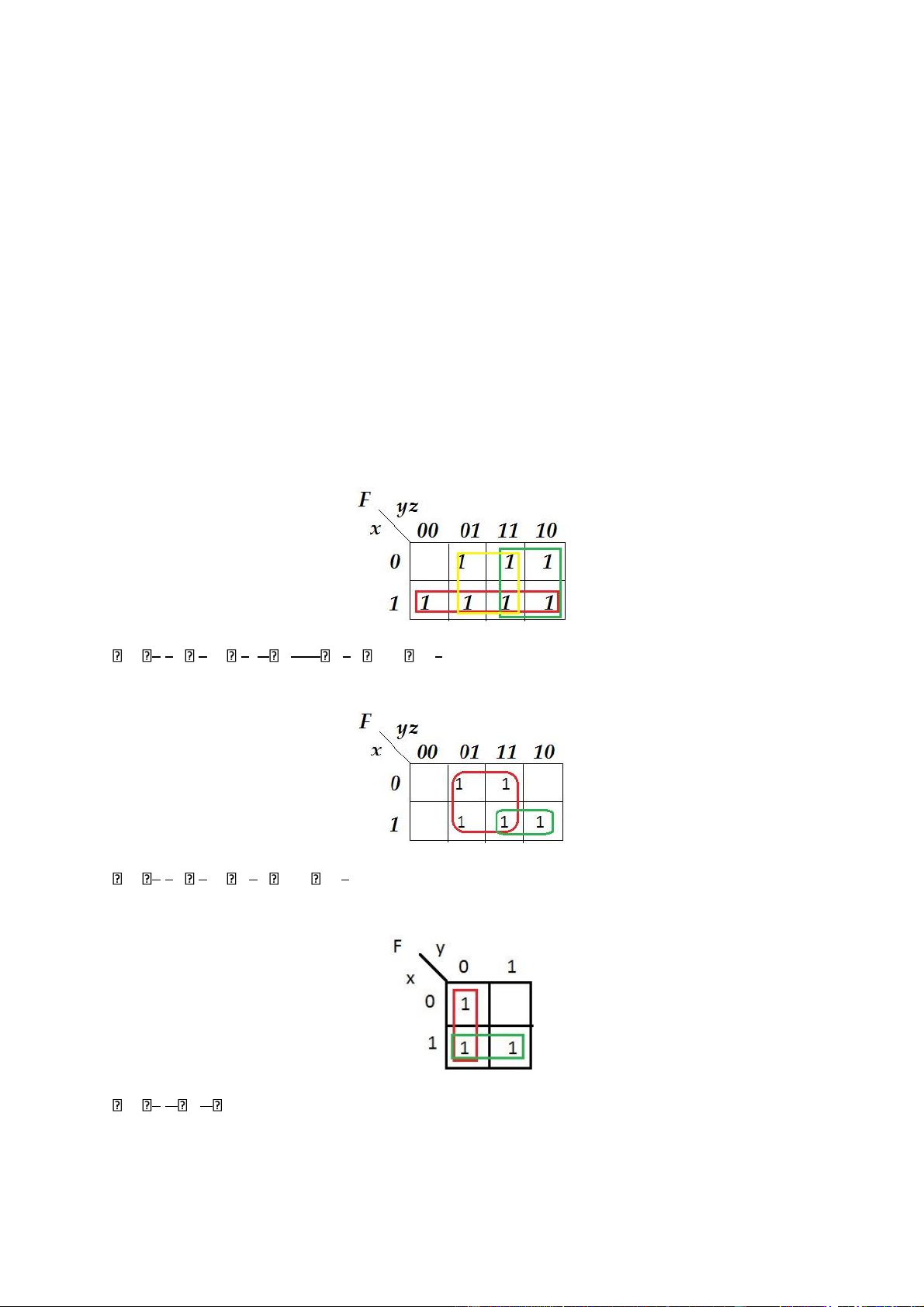
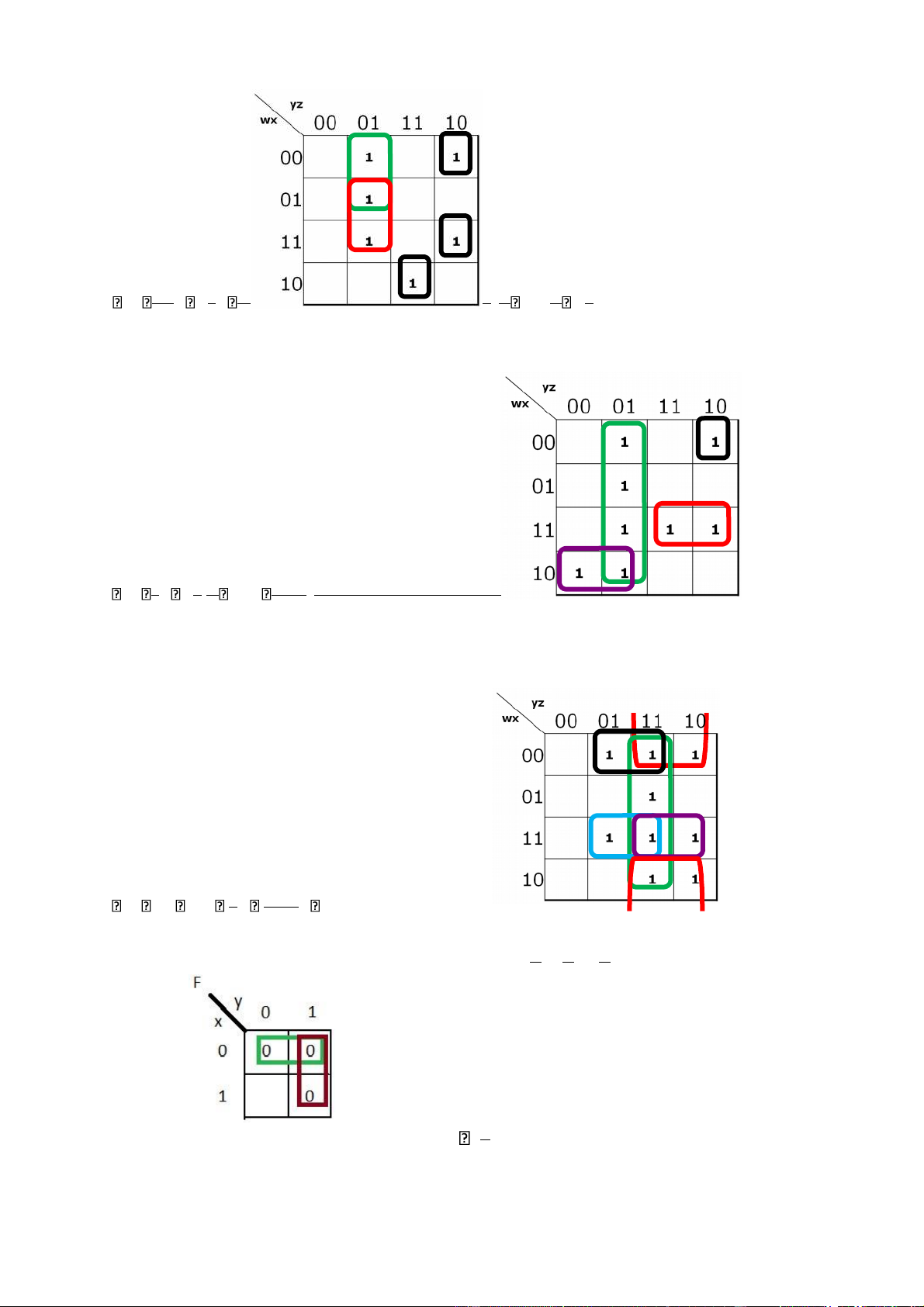
với bảng chân trị sau: x y z F G 1 1 1 0 0 1 1 0 0 1 1 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 Hàm F x y z( , , ) Vẽ bản đồ Karnaugh: . yz y. z . yz y. z x 1 1 x 1
F x y z( , , ) x. .y z x y z x . . . .y z
x. .y z x y z. . x. .y z x y z. . yz xz z x( y) Hàm G x y z( , , ) Vẽ bản đồ Karnaugh: . yz y. z . yz y. z x 1 1 x 1
G x y z( , , ) x. .y z x y z xy . . z
y z. (x x) xyz y z xy. z lOMoAR cPSD| 40425501 Bài 15:
Tìm phần bù của biều thức: * Cách giải: + Lấy phần bù F
+ Sử dụng định luật De Morgan và các quy luật thường dung cho đại số bool a./ F(y,z,t )= Ta có: = = b./ F(A,B,C,D) = Ta có: c./ F(x,y,z)= Ta có: Bài 16:
Tìm tất cả các hàm BOOL theo 4 biến sau cho:
f (x,y,z, t) = f (y,z,x, t), với mọi x, y, z, t
Để ý ta thấy : x = y, y = z, z = x
Do có tới 3 giá trị đôi một bằng nhau nên chúng có cùng một giá trị (hoặc 1 hoặc 0) và t có giá trị tùy ý.
Nên ta có hàm f (x, y, z ,t) = (xyz + x’y’z’)(t + t’) = xyzt + xyzt’ + x’y’z’t + x’y’z’t’
Bài 17: Có bao nhiêu hàm Bool 6 biến lấy giá trị 1 tại các điểm có đúng 2 thành phần có giá
trị 1 (tại các điểm khác hàm Bool có thể nhận giá trị 0 hay 1) Giải:
Xét bảng chân trị của các hàm Bool có 6 biến. Ta thấy bảng này sẽ có 26 dòng, trong đó số
dòng có đúng 2 thành phần có giá trị là 1 chính là tổ hợp chập 2 của 6:
Như vậy các thành phần của bộ giá trị tại cột f tương ứng với các dòng có đúng 2 thành phần
có giá trị 1 sẽ phải là 1. Còn lại 26 - 15 = 49 thành phần còn lại của bộ giá trị tại cột f sẽ nhận
các giá trị tùy ý của 0, 1.
Vậy số trường hợp của bộ giá trị tại cột f là 249. Đây chính là số hàm Bool 6 biến nhận giá trị
1 tại những điểm có đúng 2 biến có giá trị là 1. Bài 18:
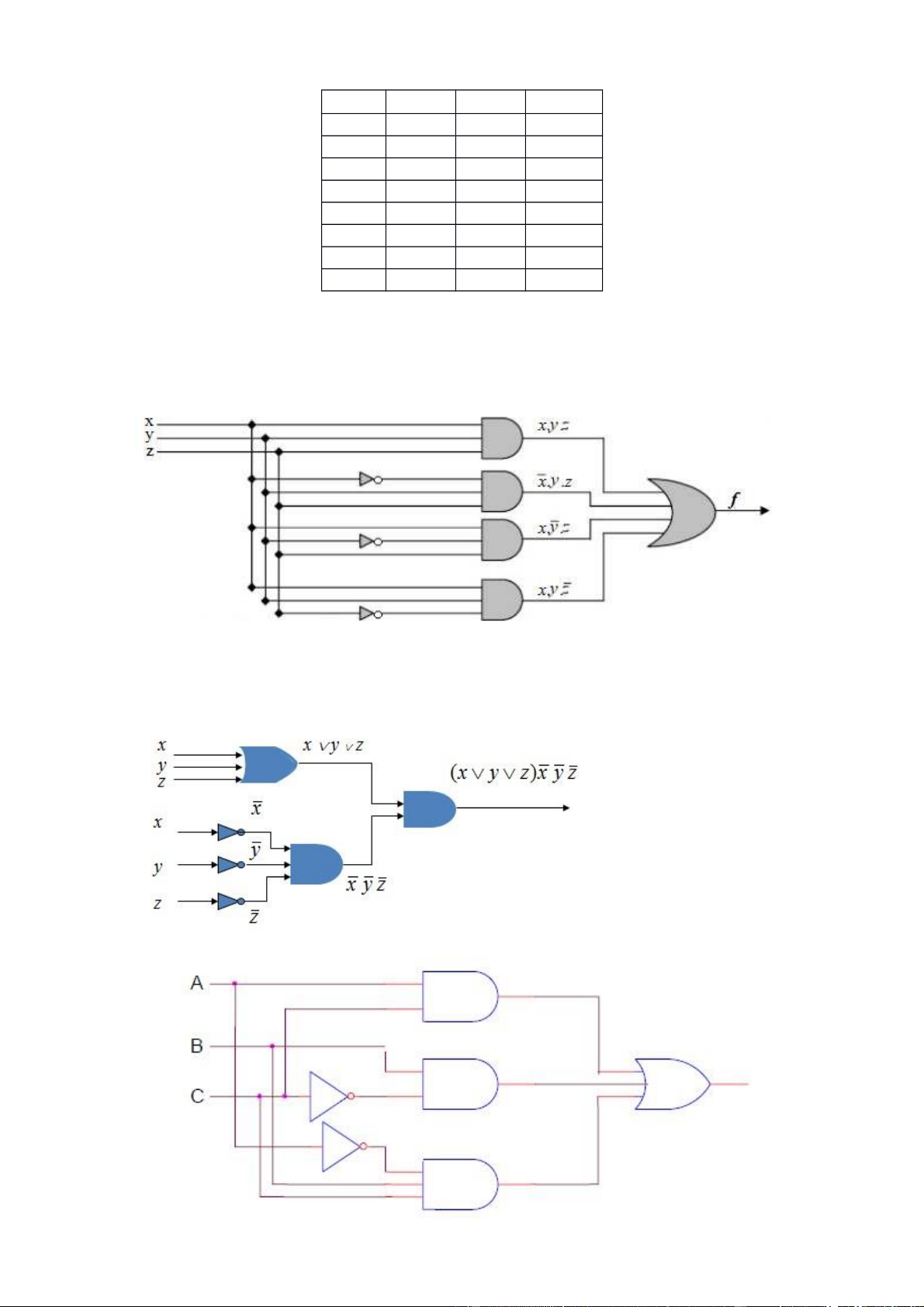
Tìm khai triển tổng các tích của hàm F(x, y, z) = (x + y) z
Bảng giá trị của hàm F: lOMoAR cPSD| 40425501 x y z x + y z x + ( y) z 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 0 0 1 1 1 0 1 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 0 0 0 0 0 1 0
F(x, y, z) = x.y.z’+ x.y’z’ + x’yz’
Bài 19: Rút gọn biểu thức: a./ F(a, b, c) = ab’c+ab’c’
Ta có: F(a, b, c) = ab’c+ab’c’= ab’(c+c’) = ab’+1 = ab’ b./ F(a, b, c, d) = abc + abd +ab
Ta có: F(a, b, c, d) = abc+abd+ab = ab(c+d+1) = ab1 = ab c./ F(a, b, c) = ab(a’+c)
Ta có: F(a, b, c) = ab(a’+c) = aa’b+abc = 0+abc = abc d./
F(a, b, c) = (a’+(bc)’)’a’
Ta có: F(a, b, c) = (a’+(bc)’)’a’ = (a’’(bc)’’)a’ = a(bc)a’=0 e./
F(a, b, c) = abc+abc’+ab’c
Ta có: F(a, b, c) = abc+abc’+ab’c = ab(a+c’) + ab’c = ab(1) + ab’c = a(a+b’c) = a(b+c)
Bài 20: Cho đại số Boole = là tập hợp các ước dương của 70. Trên ta trang bị các phép toán như sau:
a + b = LCM(a,b) : BCNN của a và b
a * b = GCD(a, b): UCLN của a và b a’=
Xét 2 tập con của X= và Y=. Xét xem X, Y có phải là các đại số con của hay không?
Ta có X đóng với các phép toán +, * nhưng 5’=14 không thuộc X. Còn Y là đóng với +, *, ‘
nên Y là một đại số con của Bài 21:
Biến đổi biểu thức sau thành tổng các tích:
F=((a.b)’.c)’.((a’+c).(b’+c’)) Ta có:
F = ((a.b)’.c)’.((a’+c).(b’+c’)) = ((a.b)’’+c’)((a’+c)’ + (b’+c’)’) = (a.b+c’)(a.c+b.c)
Áp dụng tính chất phân phối, ta có:
F = (a.b+c’)(a.c+b.c) = a.b.a.c’ +a.b.b.c + a.c’.c’ + b.c.c’
= a.b.c’ + a.b.c + a.c’ + 0 = a.c’+a.b.c lOMoAR cPSD| 40425501 Bài 22:
Biểu diễn dưới dạng tổng các tích đầy đủ : A = x(y+z’)
Ta có: A = x(y+z’) = xy + xz’ = xy(z+z’)+x(y+y’)z’
= xyz + xyz’ +xyz’ + xy’z’ = xyz+xyz’+xy’z’ Bài 23:
Biểu diễn B = x’+y dưới dạng tổng các tích đầy đủ Ta có:
B = x’+y = x’(y’+y) + (x’+x)y = x’y’+x’y+x’y+xy = x’y’+x’y+xy Bài 24:
Biểu diễn C = x+y+z dưới dạng tổng các tích đầy đủ
Ta có: C = x+y+z=x(y+y’)(z+z’) +(x+x’)y(z+z’) + (x+x’)(y+y’)z
= xyz + xy’z + xyz’+ xy’z’ +xyz + x’yz + xyz’+ x’yz’ + xyz + x’yz+ x’yz+ x’y’z
= xyz + xy’z + xyz’+ xy’z’ + x’yz + x’yz’ + x’yz+ x’y’z Bài 25:
Viết dạng đầy đủ của biểu thức: F(x,y,z) = x + y + z
F x.yz xyz xyz xy z. xyz xyz xyz Bài 26:
Viết dạng đầy đủ của biểu thức: F(x,y,z) = xy + z
F x.yz xyz xyz xyz xyz Bài 27:
Viết dạng đầy đủ của biểu thức: F(x,y) = x + y’
F x.y xy xy Bài 28: Chứng minh rằng: Ta có: Vế trái = lOMoAR cPSD| 40425501 = = = Vế phải
Bài 29: Chứng minh: (x y)(x z) xy xz Biến đổi VT:
(x y)(x z) xx xz xy yz
xz xy yz xz xy
Bài 30: Chứng minh: (xy x. )y xy xy Biến đổi VT: Bài 31: Chứng minh: Ta có: Vế trái Vế phải
Bài 32: Chứng minh: xz yz xz y z. Biến đổi VT:
xz yz xz y. z
(x z)(y z)
x.y xz y z. zz z.y zx y x. z.y zx
Bài 33: Chứng minh: (x y xy) xy xy Biến đổi VT:
(x y xy) (x y)(x y) xy xy lOMoAR cPSD| 40425501
Bài 34: Chứng minh: xyz y.z x(yz y. )z (xy xy)z xy xyz Biến đổi VT
xyz y.z x(yz y. )z xyz. .y z xyz x.yz
x(y z)(y z) xyz x.yz
xy z. xyz xyz x.yz
(xy z. xyz) (xyz x.yz)
z(xy xy) z xy( x. )y
z(xy xy) zxy xy
Bài 35: Cực tiểu hóa hàm:
F xyz xyz xyz
xyz xyz xyz xy z( z) xyz xy xyz x y( yz)
x y( y)(y z) x y( z) F x y( z)
Bài 36: Cực tiểu hóa hàm:
F xzxyk xyz.k xyz
xzxyk xyz.k xyz xz x( y k ) xyz.k xyz
xxz x.yz xzk xyz.k xyz
x.yz xzk xyz.k xyz
( .x yz xyz) (xzk xyz. )k
zy(x x) x. (k z yz)
zy x. (k z yz)
F zy x. (k z yz)
Bài 37: Cực tiểu hóa hàm:
F xyz xyz xyz xyz
xyz xyz xyz xyz xy z( z) xy z( z) xy xy y x( x) y F y
Bài 38: Cực tiểu hóa hàm: F xyz xyz xy z. xy xyz xyz xy z.
xy (xyz xy z. ) (xyz xy) lOMoAR cPSD| 40425501
xy(z z) xy(z 1) xy xy x(y y) x F x
Bài 39: Cực tiểu hóa hàm:
F xyz xyz xk xyk
xyz xyz xk xyk (xyz xyz) (xk xyk)
xz y( y) x k( yk)
xz x y( k) x y( z k) F x y( z k)
Bài 40: Cực tiểu hóa hàm:
F xy xyz xz.yk yz.k
xy xyz xz.yk yz.k y(x xz) z. (k xy y)
y(x z) z. (k x y)
xy yz xz.k yz.k
xy xz.k y z( z. )k
xy xz.k y z( k )
F xy xz.k y z( k )
Bài 41: Cực tiểu hóa hàm:
F xyz y z. x z. xyz
xyz y z. x.y z. xyz (xyz xyz) (y z. x.y z. )
xz(y y) y z. (1 x) xz y z. F xz y z.
Bài 42: Cực tiểu hóa hàm:
F xy xy xy x.y
xy xy xy x.y (xy xy) (xy x. )y
y(x x) y(x x) y y 1 F 1
Bài 43: Cực tiểu hóa hàm:
F (y z)(y z) x y z
(y z)(y z) xy
zyz y z. x y z
(yz y) x (y z. z) y x z F y x z lOMoAR cPSD| 40425501
Bài 44: cực tiểu hóa hàm: F (x
y xy)(xy xz yz)
(x y xy)(xy xz yz) (x y)(xy xz yz)
xy xyz x.yz
xy x.yz
F xy x.yz
Bài 45: Cực tiểu hàm: F(x,y,z) = F F(w,x,y,z) =
Bài 46: Cực tiểu hàm: F
Bài 47: Cực tiểu hàm: F(x,y,z) = F
Bài 48: Cực tiểu hàm: F(x,y,z) = F
Bài 49: Cực tiểu hóa hàm:
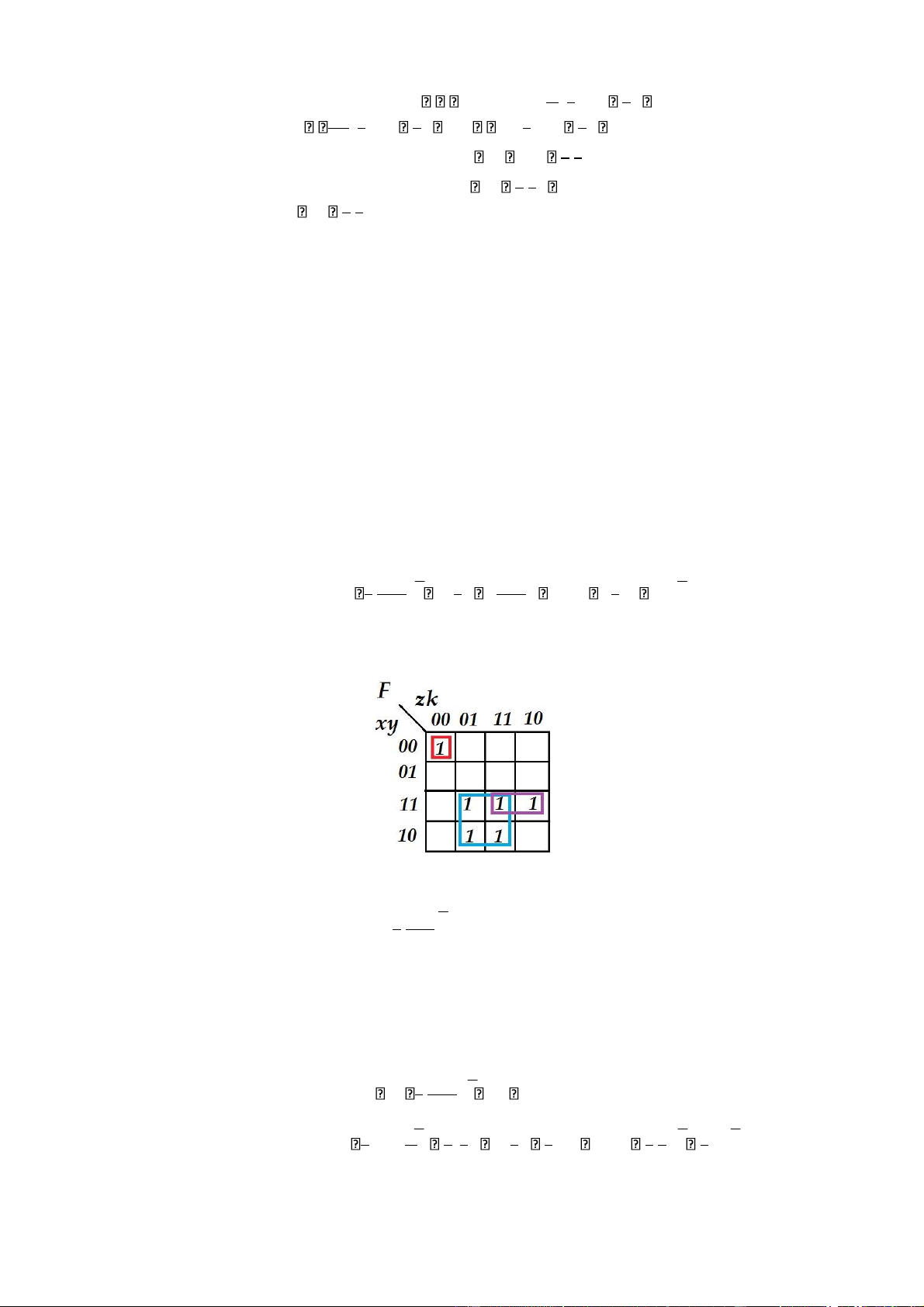
F x.y z. .k xyzk xy z. k xyzk xyzk xyzk
Hàm F theo thứ tự có dạng biểu diễn rút gọn sau:
F = ∑m(0, 13, 9, 15, 11, 14)
Gom ô màu đỏ ta được: x.y z. .k
Gom ô màu xanh dương ta được: xk xyz Gom ô màu tím ta được:
F x.y z. .k xk xyz
Bài 50: Cực tiểu hóa hàm:
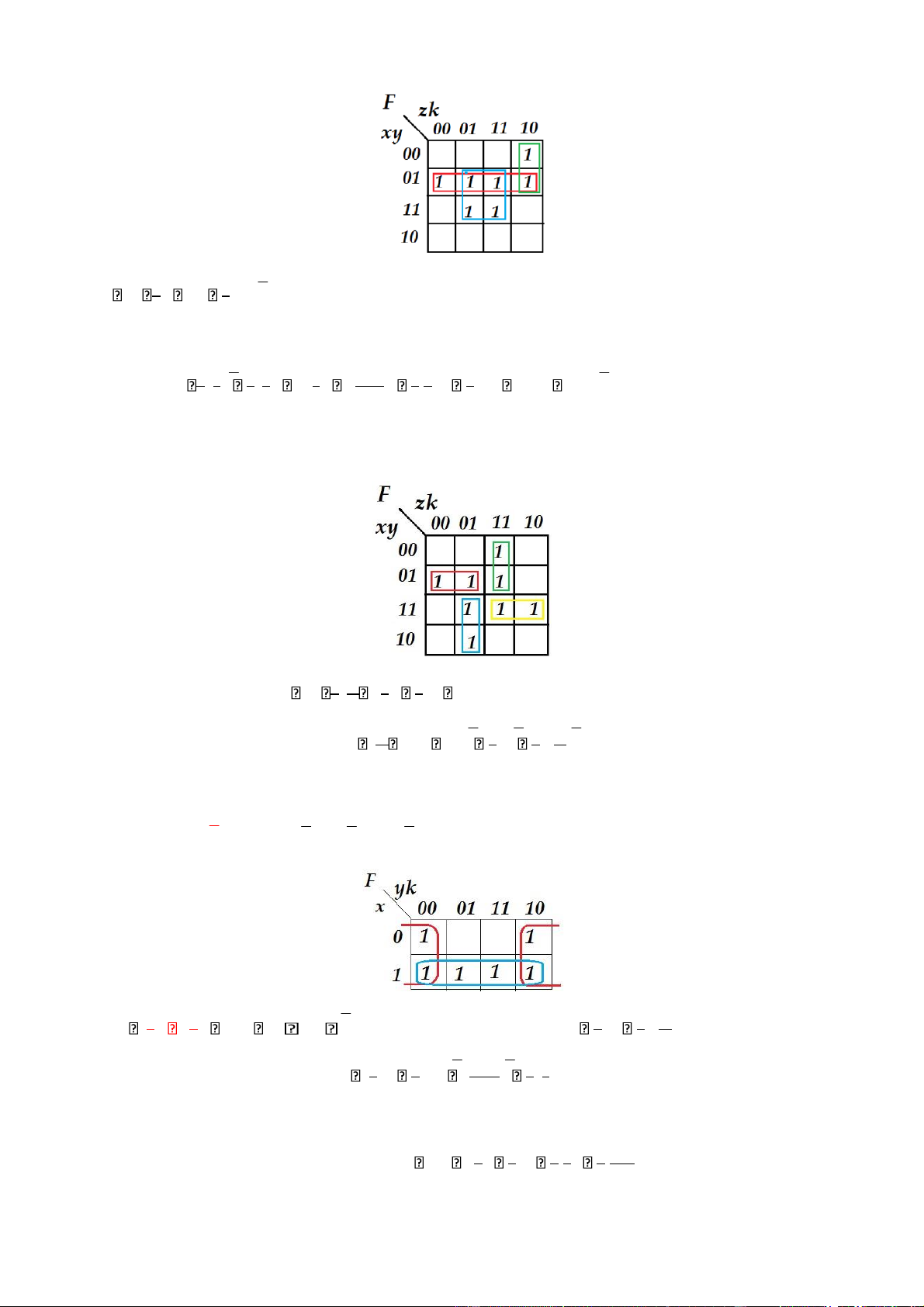
F x. . .y z k xyzk xyzk xyzk xyzk x.yzk xyzk Hàm F
theo thứ tự có dạng biểu diễn rút gọn sau:
F = ∑m(4, 5, 13, 7, 15, 2, 6) lOMoAR cPSD| 40425501
F xy yk xzk
Bài 51: Cực tiểu hóa hàm:
F xyzk zyzk xyzk xy z. k x.yzk xyzk xyzk xyzk
Hàm F theo thứ tự có dạng biểu diễn rút gọn sau:
F = ∑m(4, 5, 13, 9, 3, 7, 15, 14)
F xyz xzk xzk xyz
Bài 52: Cực tiểu hóa hàm:
F xy xyk xyk xyk x. .y k
Hàm F có thể được viết dưới dạng đầy đủ sau:
F xyk xyk xyk xy F k x
k xyk x. .y k
Bài 53: Cực tiểu hóa hàm: F xyzk xyzk xy z. k xyzk ĐS: Không tối thiểu được nữa
Bài 54: Cực tiểu hóa hàm:
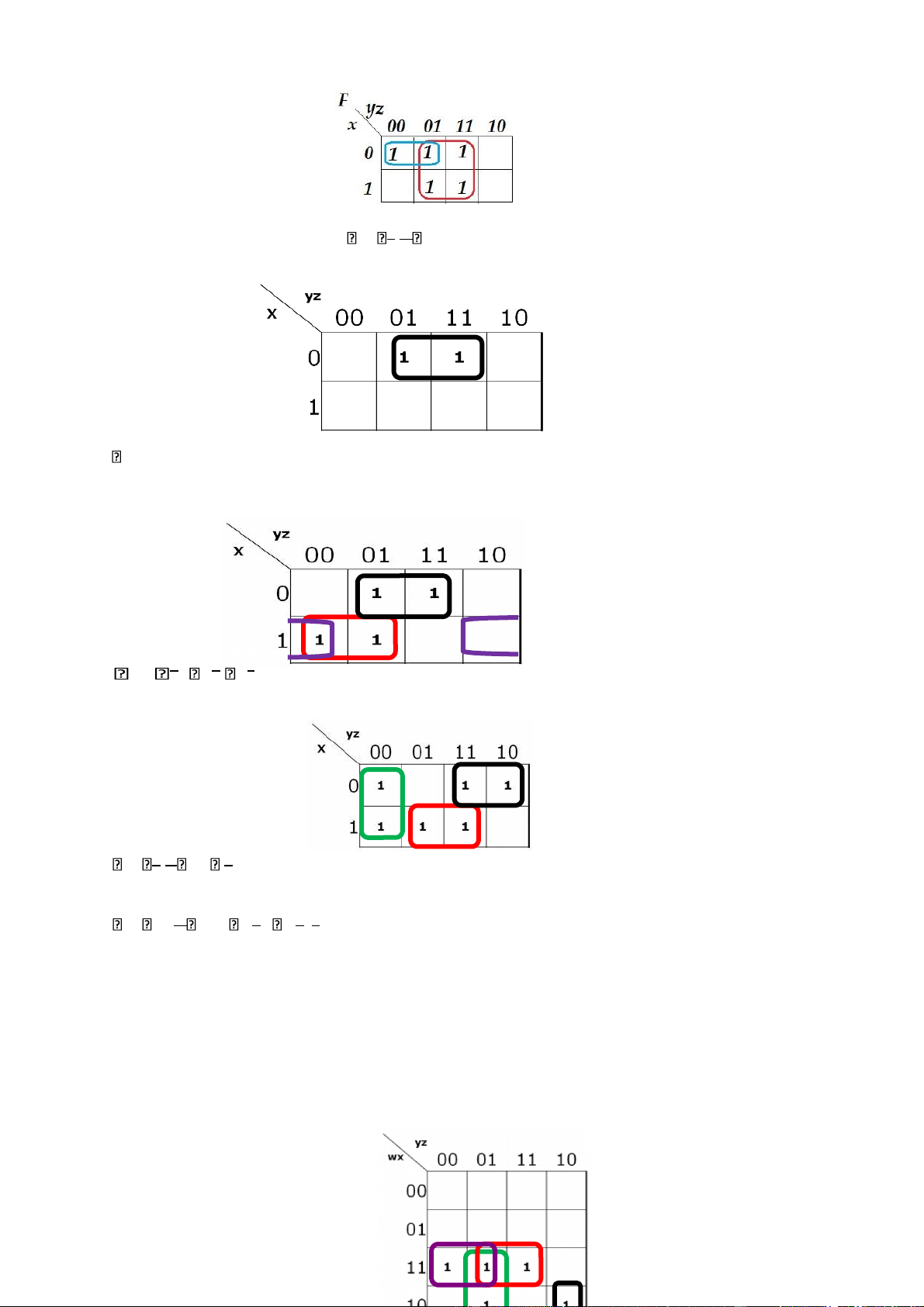
F xyz xyz xyz x.yz x.y z. lOMoAR cPSD| 40425501
F x.y z Bài 55: Rút gọn: F= Bài 56: Rút gọn: 1
F x z x y x z Bài 57: Rút gọn: .
F y.z xz xy
Bài 58: Rút gọn hàm: .
F wxy wxz wyz wxyz
Bài 59: Rút gọn hàm: lOMoAR cPSD| 40425501
F wyz xyz w
xyz wxyz wxyz
Bài 60: Rút gọn hàm: .
F yz wx.y wxy w x. yz
Bài 61: Rút gọn hàm:
F yz wy xy w x. z wxz Bài 62:
Rút gọn hàm: F(x,y) = (x + y) (x + y) (x + y) F x .y Bài 63: Rút gọn hàm: lOMoAR cPSD| 40425501
F(x,y,z) = (x + y + z) (x + y + z) (x + y + z) (x + y + z)
F (x z)(x y)(y z) Bài 64: Rút gọn hàm
F(x,y,z) = (x + y + z) (x + y + z) (x + y + z) (x + y + z) F z Bài 65: Rút gọn hàm
F(x,y,z) = (x + y + z) (x + y + z) (x + y + z) (x + y + z) (x + y + z) (x + y + z)
F x(y z)(y z) Bài 66: F x,y,z,t x y z t (x y z ( x y z t) F x z t x y z x y t x z t t) (x + y + z t) x y z t Bài 67: lOMoAR cPSD| 40425501
F x, y,z,t x y t ( x x x y + z t) ( y + z + t) ( + z y + z t)
( x + y z t) ( + y x z t)
F x z t (x y t) ( y z t) ( x z t) ( x y t) Bài 68:
F x y z t( , , , ) (x y z
t)(x y z t x)( y z t ) ( x y z
t )(x yzt )(x y z t) F (y
z t )(y z t) Bài 69:
F x y z t( , , , ) (x y z t)(x y zt x)( y z
t)(x y z t) t)(x y t )(x y
zt )(x y z t )
F (y t)(y t ) ( x y z z Bài 70:
F x y z t( , , , ) (x
y zt)(x y
zt x)( y zt)(x y z t) lOMoAR cPSD| 40425501 z (x y
zt )(x y z
t )(x y t )(x y z t ) F (x y
t)(x y t x)( y t )(x y t ) Bài 71:
F x y z t( , , , ) (x y z t)(x y zt x)( y z t x)( y z t ) t ) (x y z t )(x y z
F (x y t)(y z t)(y z t )(x y t ) Bài 72:
Tính các OR-bit, AND-bit và XOR-bit của các cặp xâu sau đây: a) 100001 và 100110 b) 111111 và 100011 c) 1111111 và 0000000
d) 000111000 và 111111111Giải 100001 và 111111 và 1111111 và 000111000 và 100110 100011 0000000 111111111 OR 100111 111111 1111111 111111111 lOMoAR cPSD| 40425501
AND 100000 100011 0000000 000111000 XOR 000111 011100 1111111 111000111 Bài 73:
Khảo sát 3 cặp các chuỗi sau đây: (i) 110001 101101 (ii) 10001111 00111100 (iii) 101100111000 000111001101
Bằng cách nào mỗi cặp trong số các chuỗi này được xử lí bởi (a) 1 Cổng OR (b) 1 cổng AND Giải :
(a) OR: 2 đầu vào đều bằng 0 (i) 110001 101101
=>Vị trí thứ 5 => đầu ra là 111101 (ii) 10001111 00111100
=>Vị trí thứ 2 => đầu ra là 10111111 (iii) 101100111000 000111001101
=>Vị trí thứ 2 và 11 => đầu ra là 1011111101
(b) AND : 2 đầu vào đều bằng 1
(i)=> vị trí thứ nhất và cuối => đầu ra là 100001
(ii)=> vị trí thứ 5 và 6 => 0000 1100
(iii)=> vị trí thứ 4 và 9 => 000100001000 Bài 73 :
1 cổng NOT sẽ xử lí chuỗi như thế nào ? (i) 110001 (ii) 10001111 (iii) 101100111000 Giải : lOMoAR cPSD| 40425501
NOT làm thay đổi 0 sang 1 và 1 sang 0 : (i) => 001110 (ii)
=> 10001111(iii)=> 010011000111 Bài 74: Cho A = 1100110110 B = 1110000111 C = 1010010110 Tìm (a) A + B + C (b) A.B.C (c) C( + B) (d) A.( Giải (a) A+B+C = 1110110111 (b) A.B.C = 1000000110 (c) = 0011001001 +B = 1111001111 C( + B) = 1010000110 (d) B+C = 1110010111 = 0001101000 A.( = 0000100000 Bài 75:
Cho 3 đầu vào A,B,C .Tìm bảng chân trị cho 8 tích căn bản A.B.C A.B. A..C A.. .B.C .B. ..C Giải :
Chuỗi đặc biệt dành cho A,B,C .Mỗi chuỗi có chứa 23 =8
Ta có : A = 00001111 => = 11110000 B = 00110011 => C = 01010101 => A.B.C=0000 0001 A.B. = 0000 0010 lOMoAR cPSD| 40425501 A..C =0000 0100 A.. =0000 1000 .B.C = 0001 0000 .B. = 0010 0000 ..C = 0100 0000 =1000 0000 Bài 76:
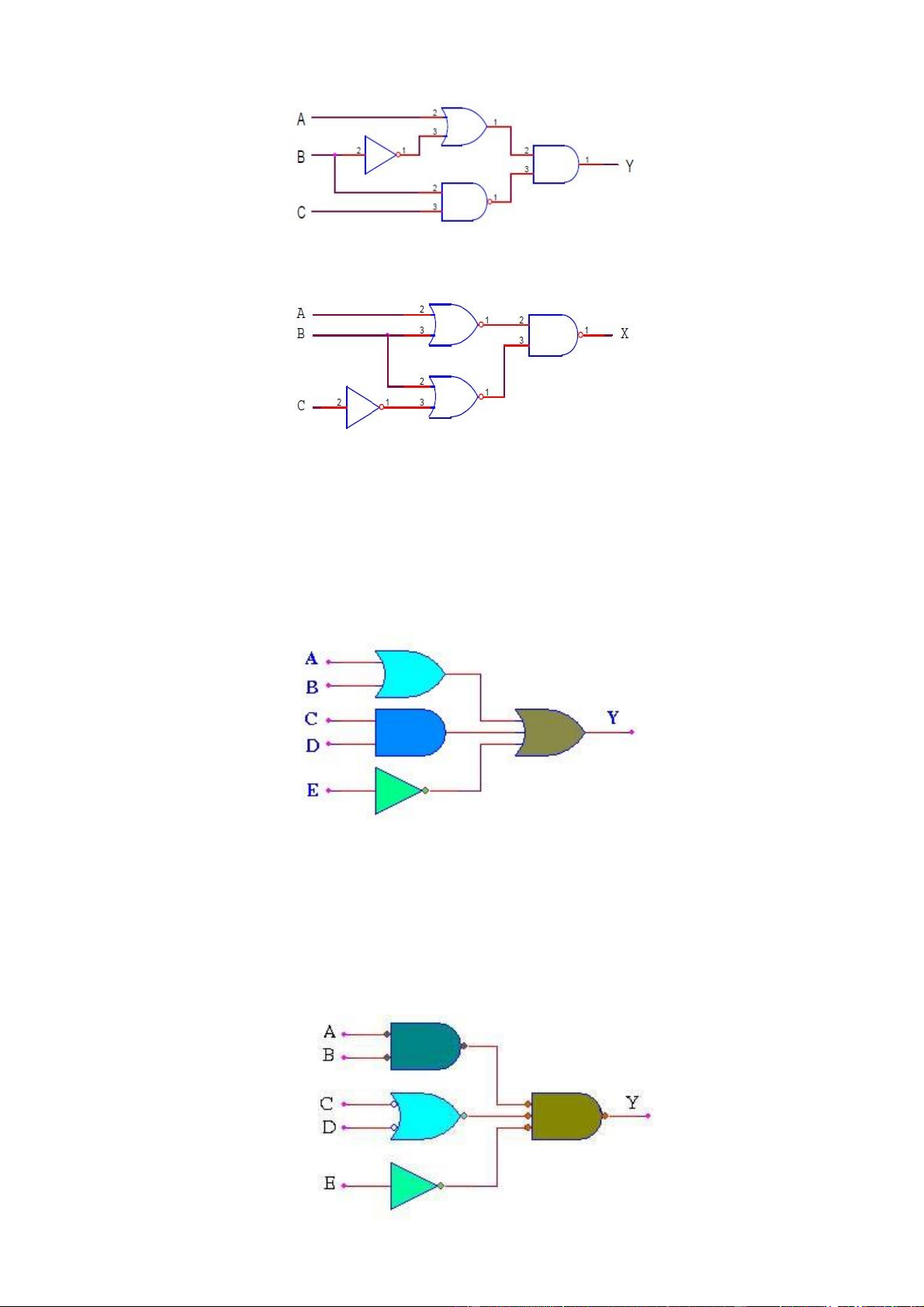
Tìm biểu thức boole và bảng chân trị dành cho mạch logic ở hình dưới đây: Giải : Y = AB + B + B Ta có : A = 0000 1111 B = 00110011 A 0000 1111 C = 01010101 = 1111 0000 B 0011 0011 = 10101010 C 0101 0101 Y 0011 0010 AB = 0000 0010 B = 00100010 B = 00110000 Y = 00110010
Bảng chân trị của mạch là : Bài 77 :
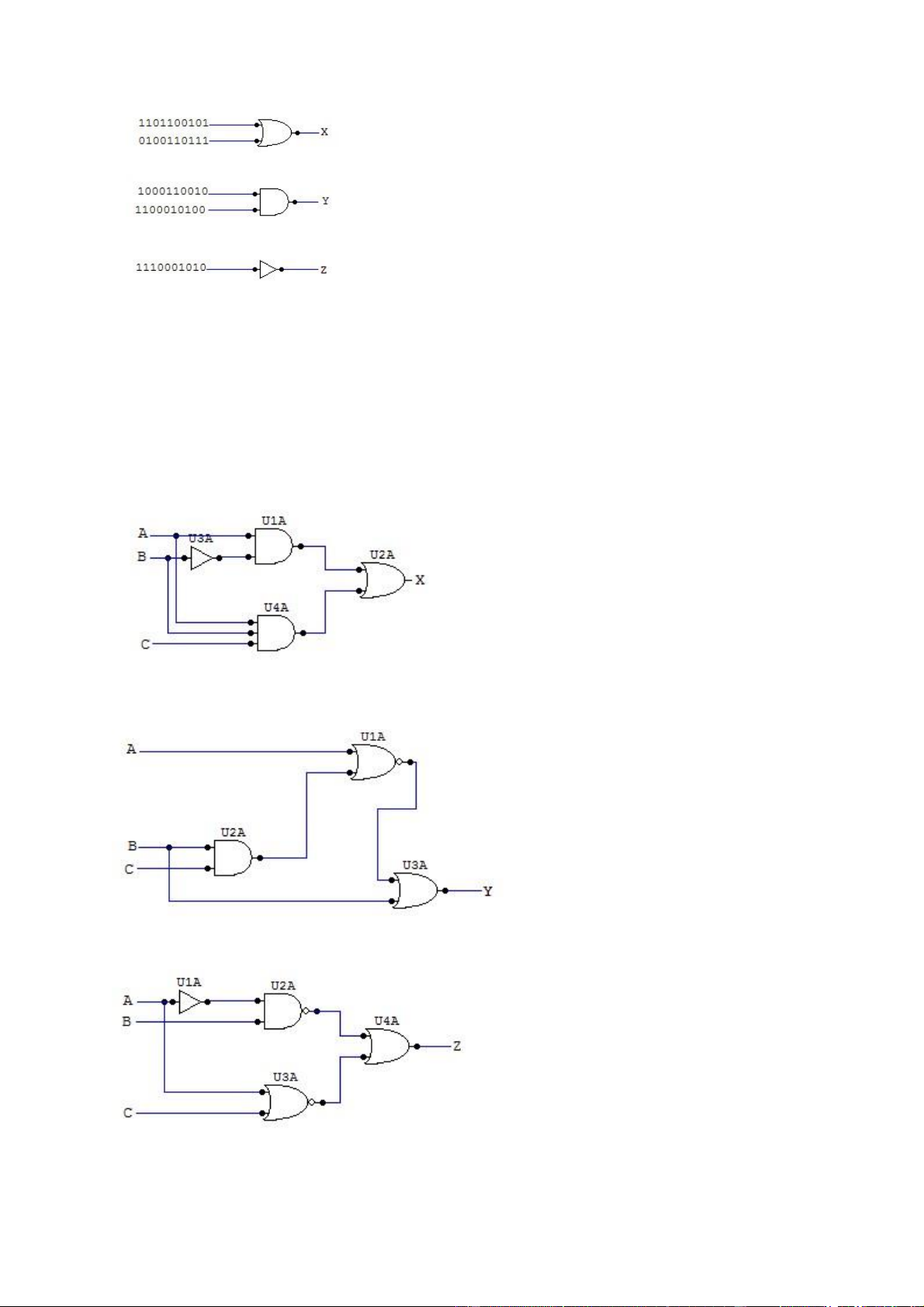
Xác định đầu ra của mỗi cổng trong hình sau : lOMoAR cPSD| 40425501 X = 1101110111 Y = 1000010000Z = 0001110101 Bài 78 :
Hãy vẽ mạch logic ứng với mỗi biểu thức bool : (a) X = A +AB (b)Y =+ B (c) Z =+ Giải (a) (b) (c) Bài 79 :
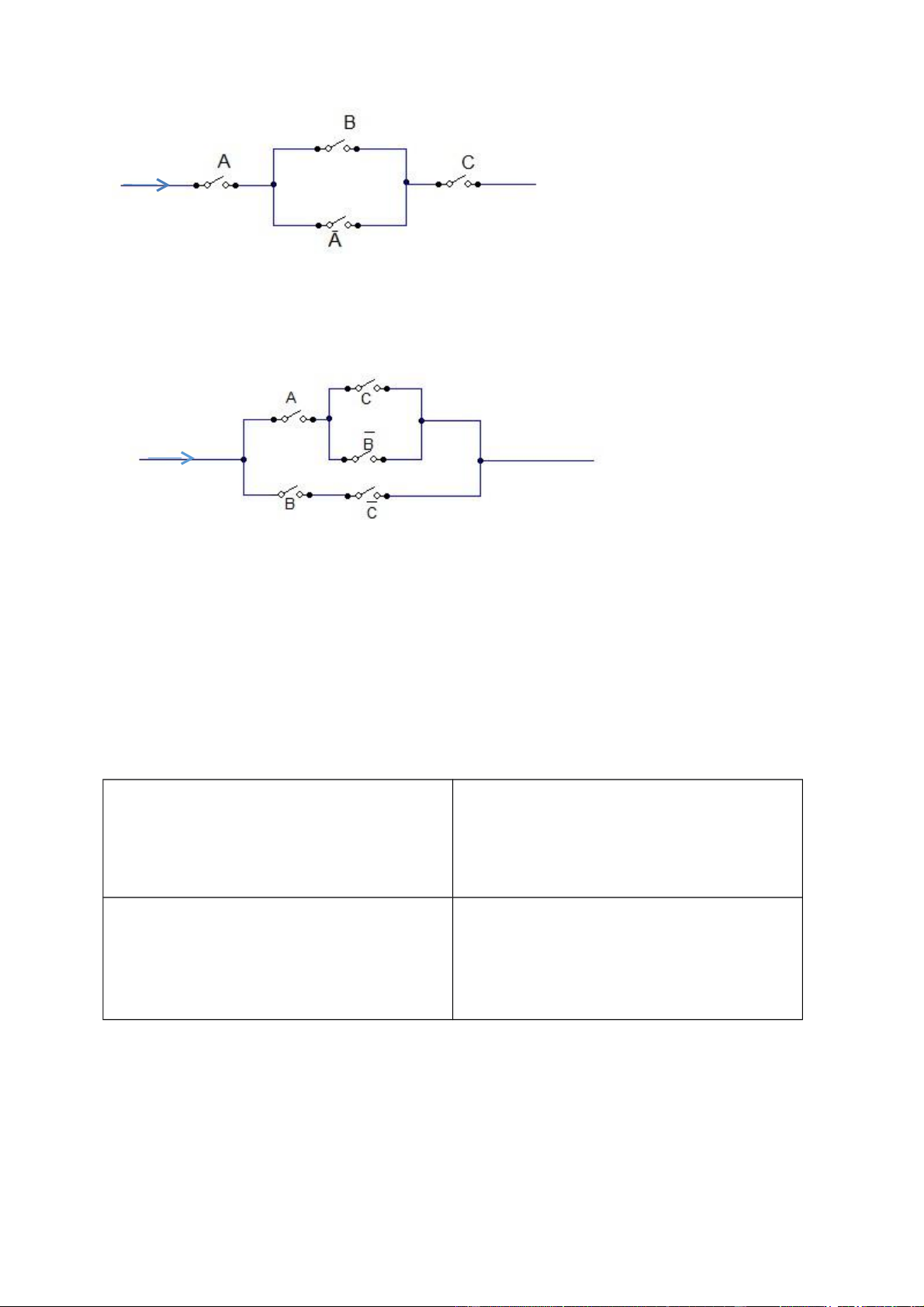
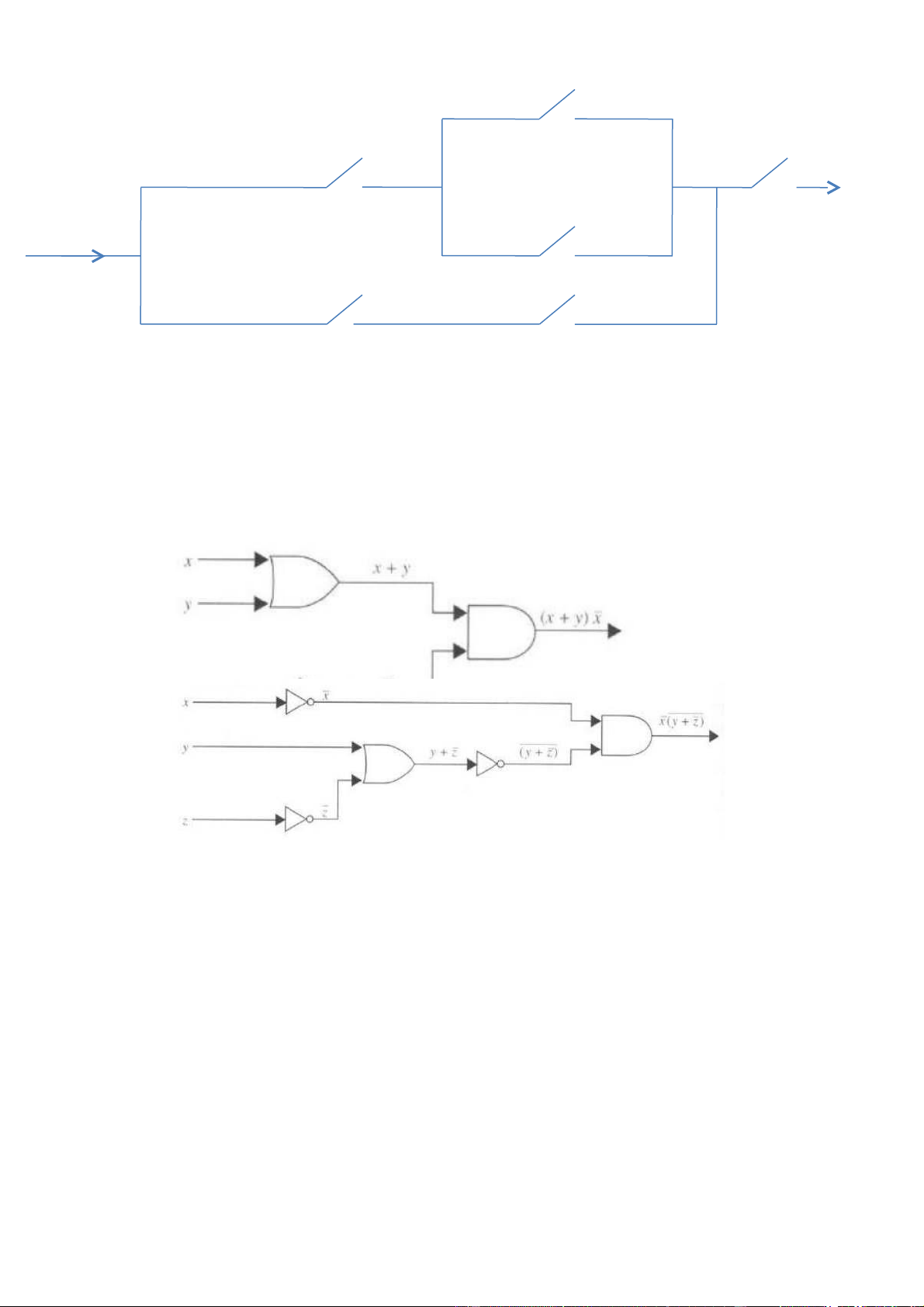
Hãy xác định biểu thức bool dành cho mỗi một mạch ngắt chuyển như hình dưới đây (a) lOMoAR cPSD| 40425501 ( b ) Giải : (a) A.(B+ ).C (b) A.(C+ ) + B. Bài 80 :
Viết các biểu thức boole cho các mạch AND-OR cực tiểu với các dữ liệu nhập A,B,C cho ra
các bảng chân trị Y1,Y2,Y3 A 1111 0000 B 11001100 C 10101010 Y 11001000 1 Y 11100011 2 Y 00111101 3 Giải : Y 1 = AB+BC Y2 = AB++C = AB+ +AC Y3 = A +B+BC Bài 81: lOMoAR cPSD| 40425501
Cho 5 đầu vào A,B,C,D và E hãy tìm các chuỗi đặc biệt,cung cấp tất cả các tổ hợp khác
nhau có thể có của các bit đầu vào Giải :
Mỗi chuỗi sẽ có chứa 25 = 32 bit
a/ Cho A được gán bằng 24 = 16 bit là các chữ số 0,theo sau là 24=16 là các chữ số 1
b/ Cho B được gán bằng 23=8 bit là các chữ số 0 theo sau là 23 = 8 bit là các chữ số 1 và sau
đó được lặp lại 1 lần
c/ Cho C được gán bằng 22=4 bit là các chữ số 0 theo sau là 23 = 8 bit là các chữ số 1 và sau
đó được lặp lại 3 lần
d/ Cho D được gán bằng 21=2 bit là các chữ số 0 theo sau là 21 = 2 bit là các chữ số 1 và sau
đó được lặp lại 7 lần
e/ Cho D được gán bằng 20=1 bit là các chữ số 0 theo sau là 20 = 1 bit là các chữ số 1 và
sau đó được lặp lại 15 lần Chuỗi đặc biệt kết quả là :
A = 0000 0000 0000 0000 1111 1111 1111 1111
B = 0000 0000 1111 1111 0000 0000 1111 1111
C = 0000 1111 0000 1111 0000 1111 0000 1111
D = 0011 0011 0011 0011 0011 0011 0011 0011
E = 0101 0101 0101 0101 0101 0101 0101 0101 Bài 82:
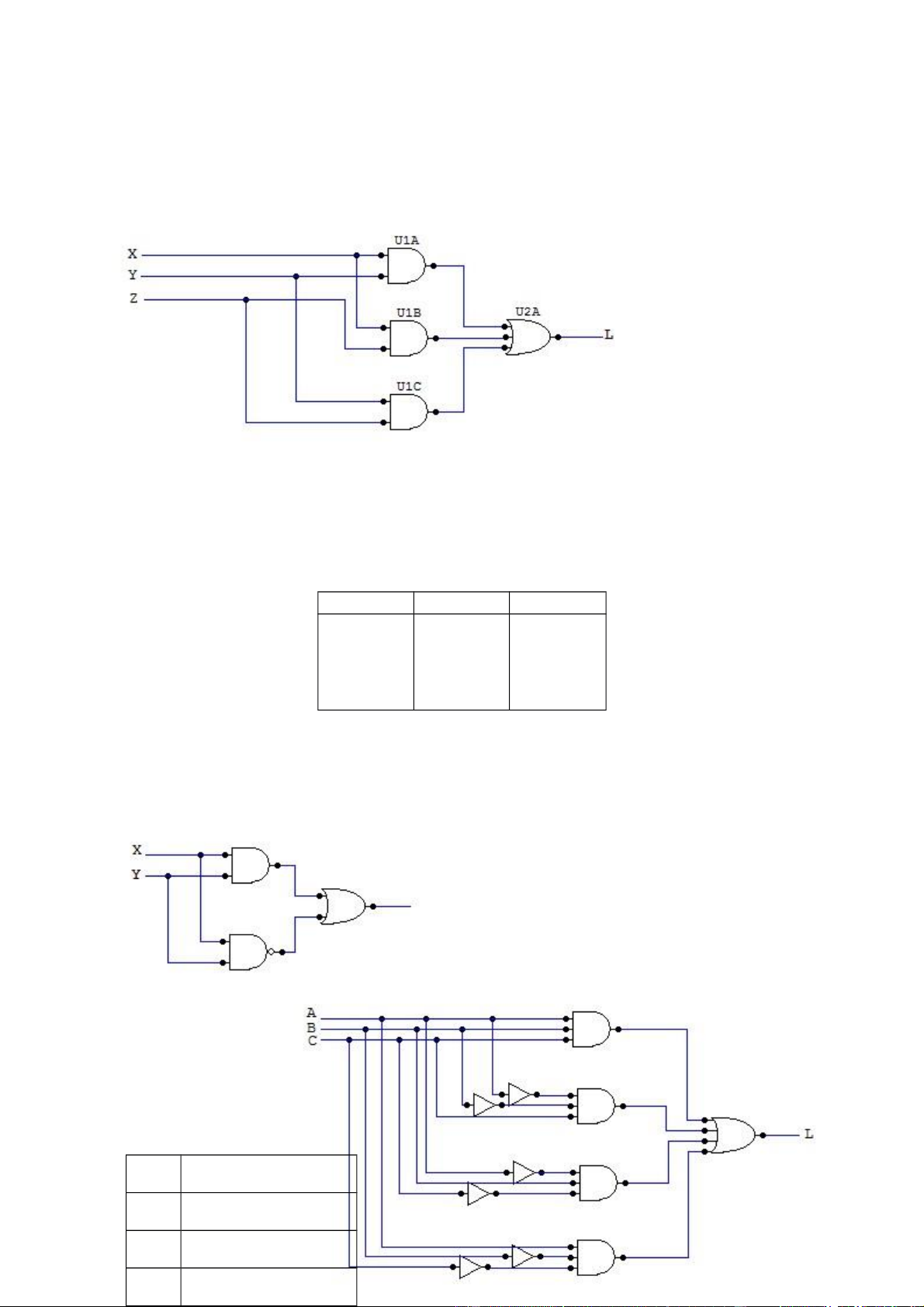
Vẽ 1 mạch AND-OR cực tiểu mà nó sẽ cho bảng chân trị sau đây : A 0000 1111 B 0011 0011 C 01010101 L 10101001 Giải :
Từ bảng chân trị, ta có : L = . + + + A.B.C BC B C A x x x x L = ABC +
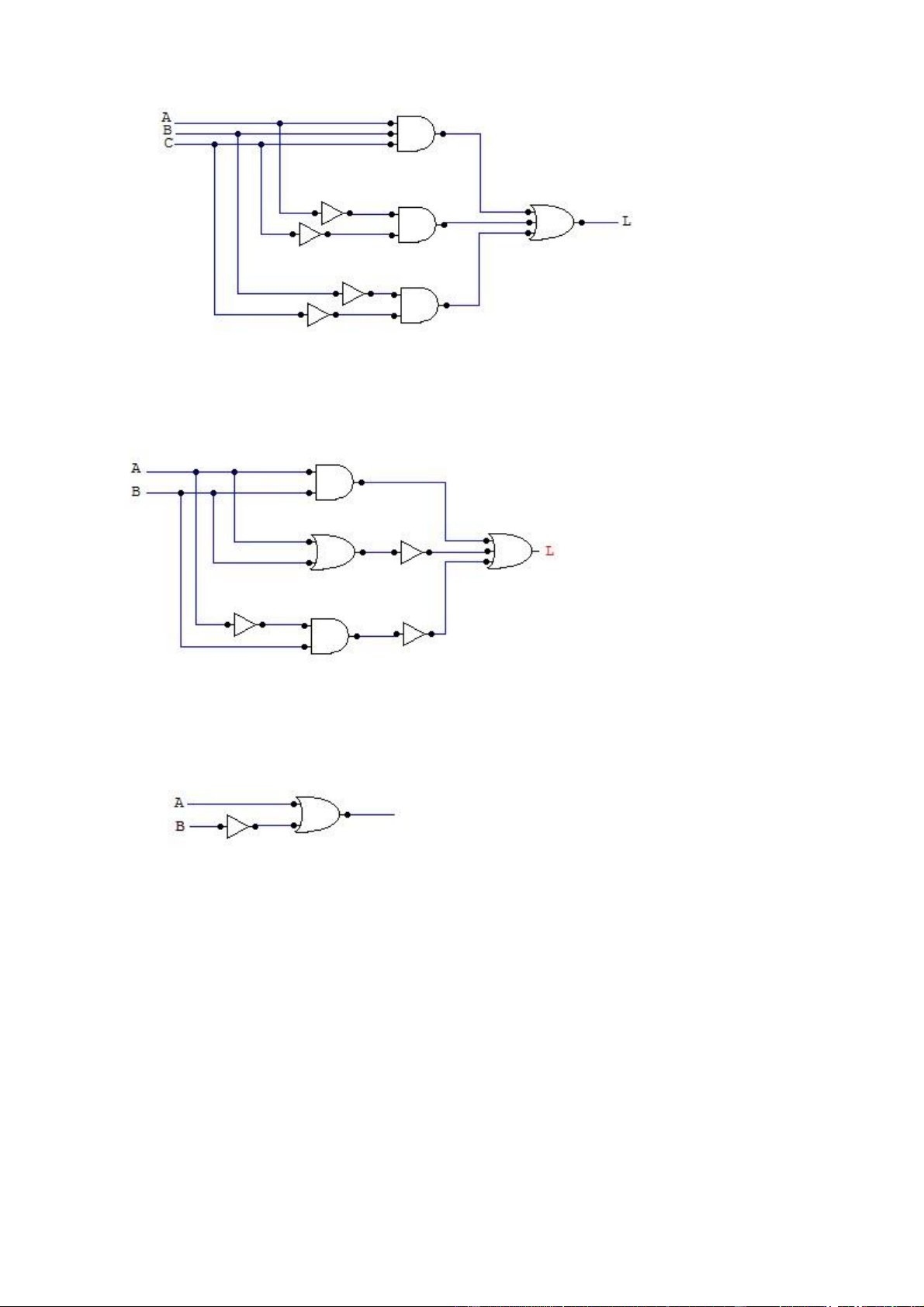
Mạch AND - OR cực tiểu tương ứng : lOMoAR cPSD| 40425501 Bài 83:
Thiết kế lại mạch L ở dưới đây thanh 1 mạch AND-OR cực tiểu Giải : Ta có : Mạch AND-OR sẽ là Bài 84:
Một ủy ban gồm 3 thành viên phải qui định các vấn đề của một tổ chức. mỗi một thành viên bỏ
phiếu tán thành hoặc không cho mỗi đề nghị được đưa ra. Mỗi đề nghị sẽ được thông qua nếu
nó nhận được ít nhất 2 phiếu tán thành. Hãy thiết kế một đoạn mạch cho phép xác định được 1
đề nghị có thông qua hay không. Giải:
Gọi x = 1 nếu thành viên thứ nhất tán thành
x = 0 nếu……………………..không tán thànhy
= 1 ………………....thứ 2 tán thành
y = 0 ………………………..không tán thànhz
= 1…………………. thứ 3 tán thành lOMoAR cPSD| 40425501
z = 0………………………...không tán thành
Khi đó mạch cần dc thiết kế sao cho nó tạo đầu ra bằng 1 từ các đầu vào x,y,z khi có 2 hoặc
nhiều hơn các biến x,y,z có giá trị là 1.
Một biểu diễn của hàm bool có giá trị đầu ra đó là L = xy + xz + yz Bài 85:
Đôi khi các hệ thống đèn cố định được điều khiển bởi nhiều công tắc, các mạch được thiết kế
sao cho khi nhấn hoặc gạt một công tắc bất kì, hệ thống đèn đang tắt sẽ bật và đang bật sẽ tắt.
hãy thiết kế một mạch thực hiện điều đó khi có 2 công tắc, khi có 3 công tắc. x y F(x,y) 1 1 1 1 0 0 0 1 0 0 0 1
Chúng ta sẽ bắt đầu bằng việc thiết kế mạch điện điều khiển hệ thống đèn khi dung 2 công tắc
khác nhau. Giả sử x=1 khi công tắc thứ nhất đóng và bằng 0 khi mở, y =1 khi công tắc thứ hai
đóng, bằng 0 khi mở. giả sử F(x,y) = 1 khi đèn sang, =0 khi đèn tắt, chúng ta hoàn toàn có thể
tùy chọn để đèn sẽ sang khi hai công tắc đều đóng, tức là F(1,1)=1. Điều này sẽ xác định các Bài 86:
Thiết kế một mạch AND-OR cực tiểu L mà qua đó công tắc A,B và C có thể điều khiển cùng
1 đèn đại sảnh.Bật-1,Tắt -0.
Cho dù 3 công tắc ở trạng thái nào thì 1 sự thay đổi trong 1 trong 3 công tắc bất kì cũng sẽ
làm thay đổi tính chẵn lẽ của số các số 1.Do đó mạch phải theo bảng chân trị sau : A 0000 1111 B 0011 0011 C 0101 0101 L 0110 1001 lOMoAR cPSD| 40425501
giá trị khác cùng hàm F. khi một trong 2 công tắc mở đèn sẽ tắt, tức F(1,0) =F(0,1)=0. Khi công
tắc còn ại cũng mở nốt thì đèn lại sáng, tức F(0,0)=1. (bảng chân trị) Chúng ta thấy rằng Giải :
Từ bảng chân trị ta có : BC B C A x x x x Mạch AND-OR sẽ là : Bài 87:
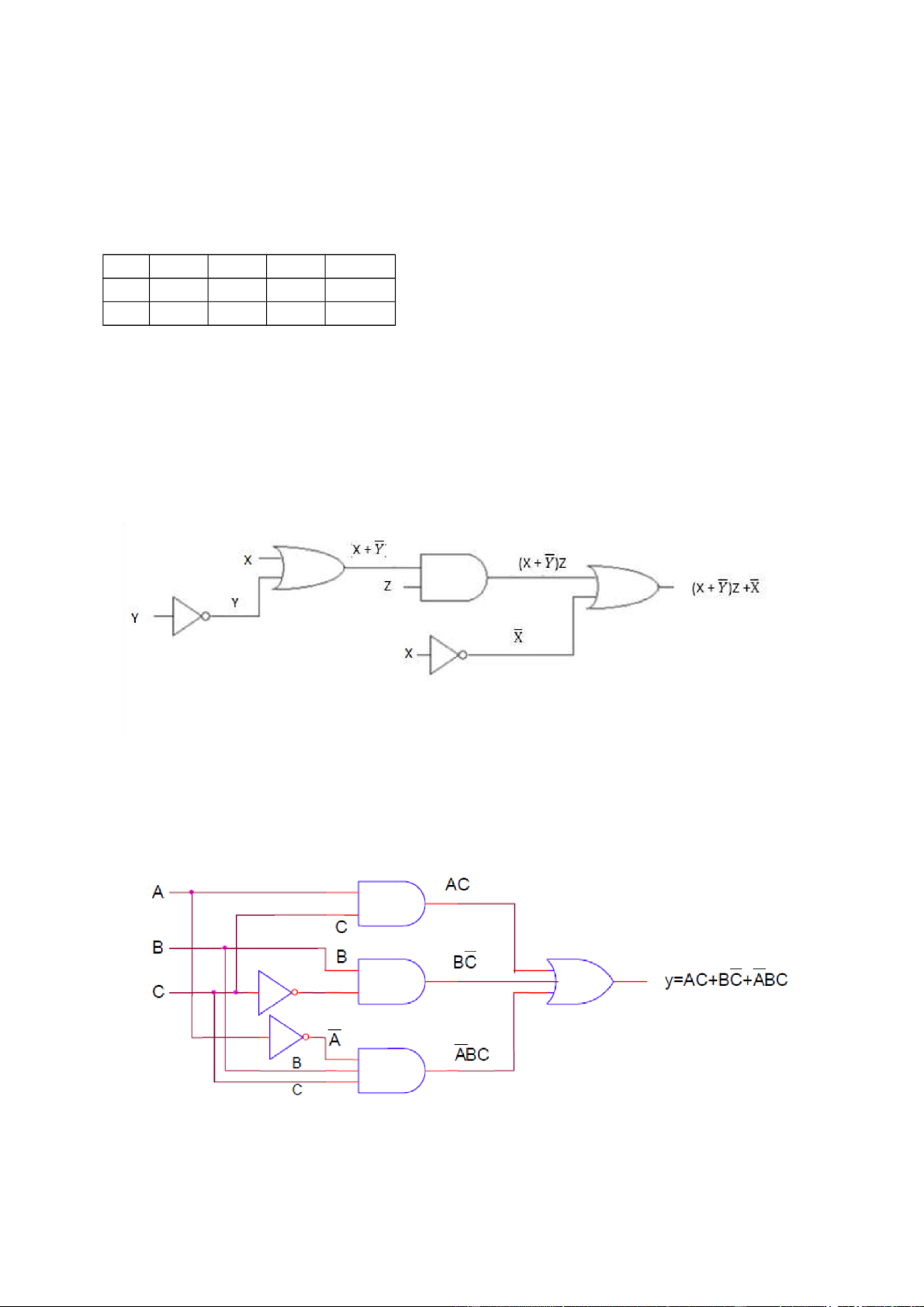
Vẽ sơ đồ mạch thực hiện biểu thức sau: (X + )Z + Giải: Bài 88:
Vẽ sơ đồ mạch thực hiện biểu thức sau: y = AC+ B + BC Giải: Bài 89:
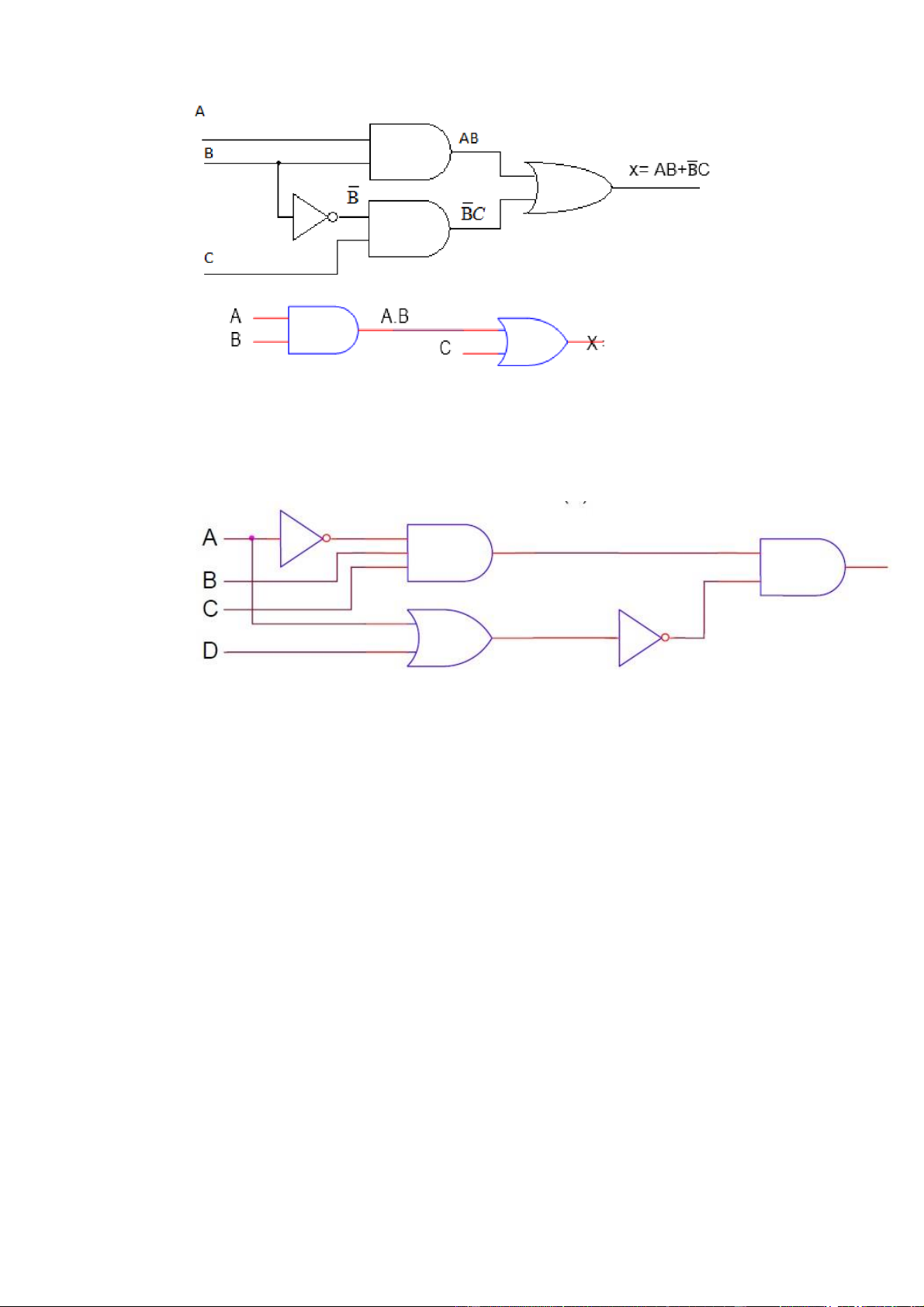
Vẽ sơ đồ mạch thực hiện biểu thức sau: x = AB+C Giải: lOMoAR cPSD| 40425501 Bài90: Mạchcó 3 ngõ vào A,B, và một ngõ ra X. Hãy sử xác định ngõ ra đó Giải: X = AB+C Bài 91:
Xác định hàm ngõ ra của mạch sau: Giải: Bài 92: Cho A=11100100 B=00110010 C=11010100 Hãy xác định: a) A+B+C b) (A+B)C c) d) Giải: a) A+B+C=11110110 b) (A+B)C=11010100 c) =11000100 d) =11111111 lOMoAR cPSD| 40425501
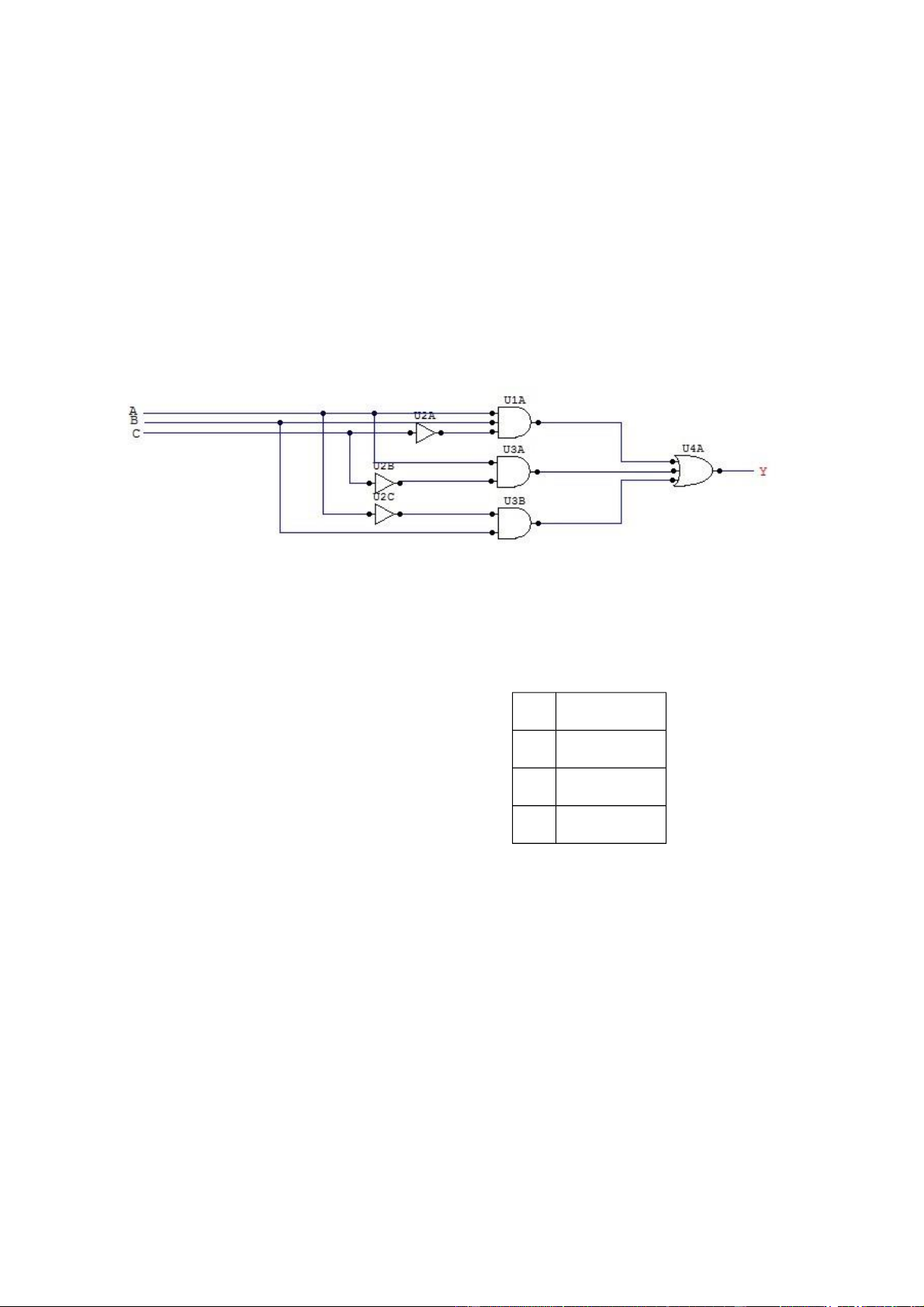
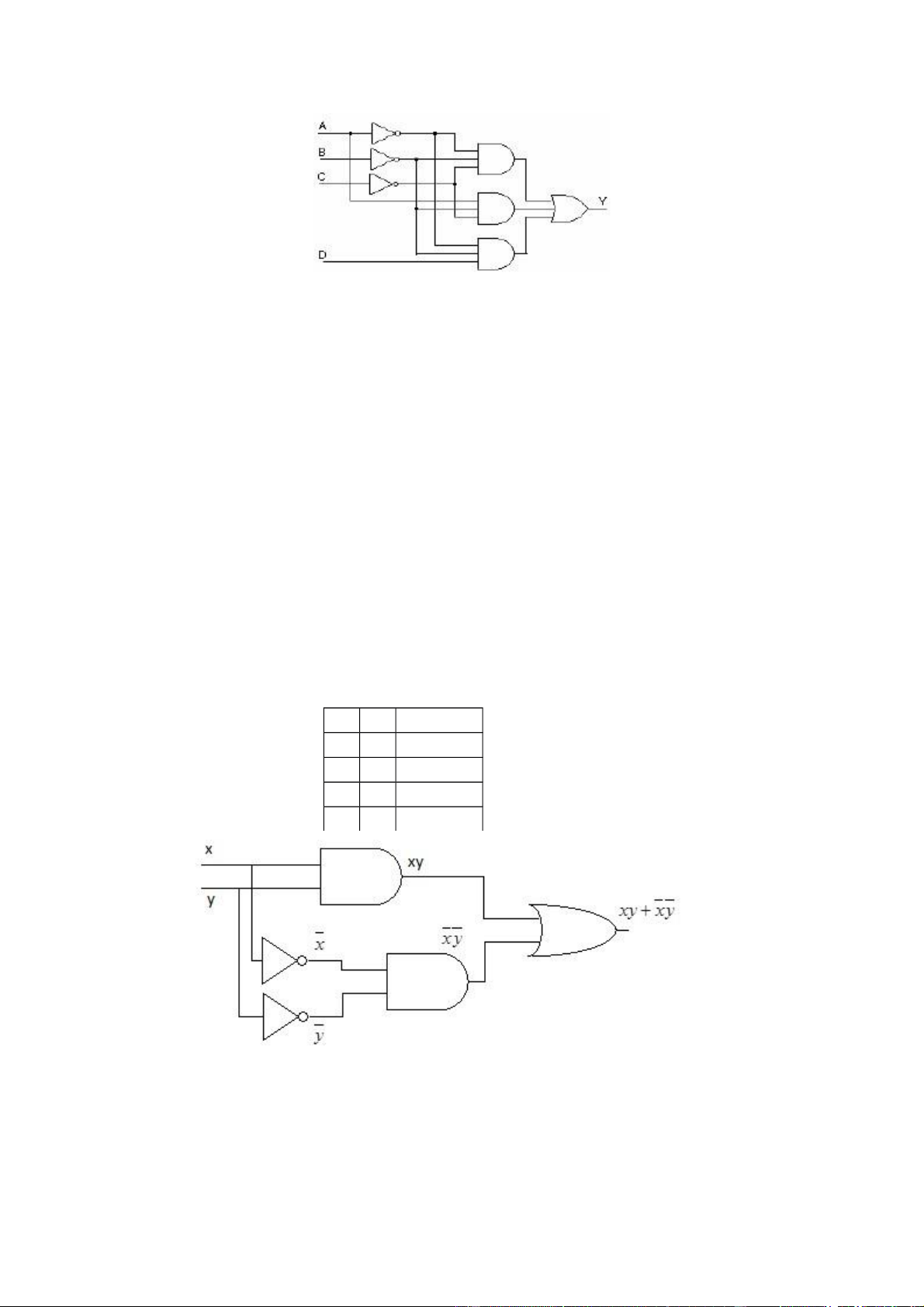
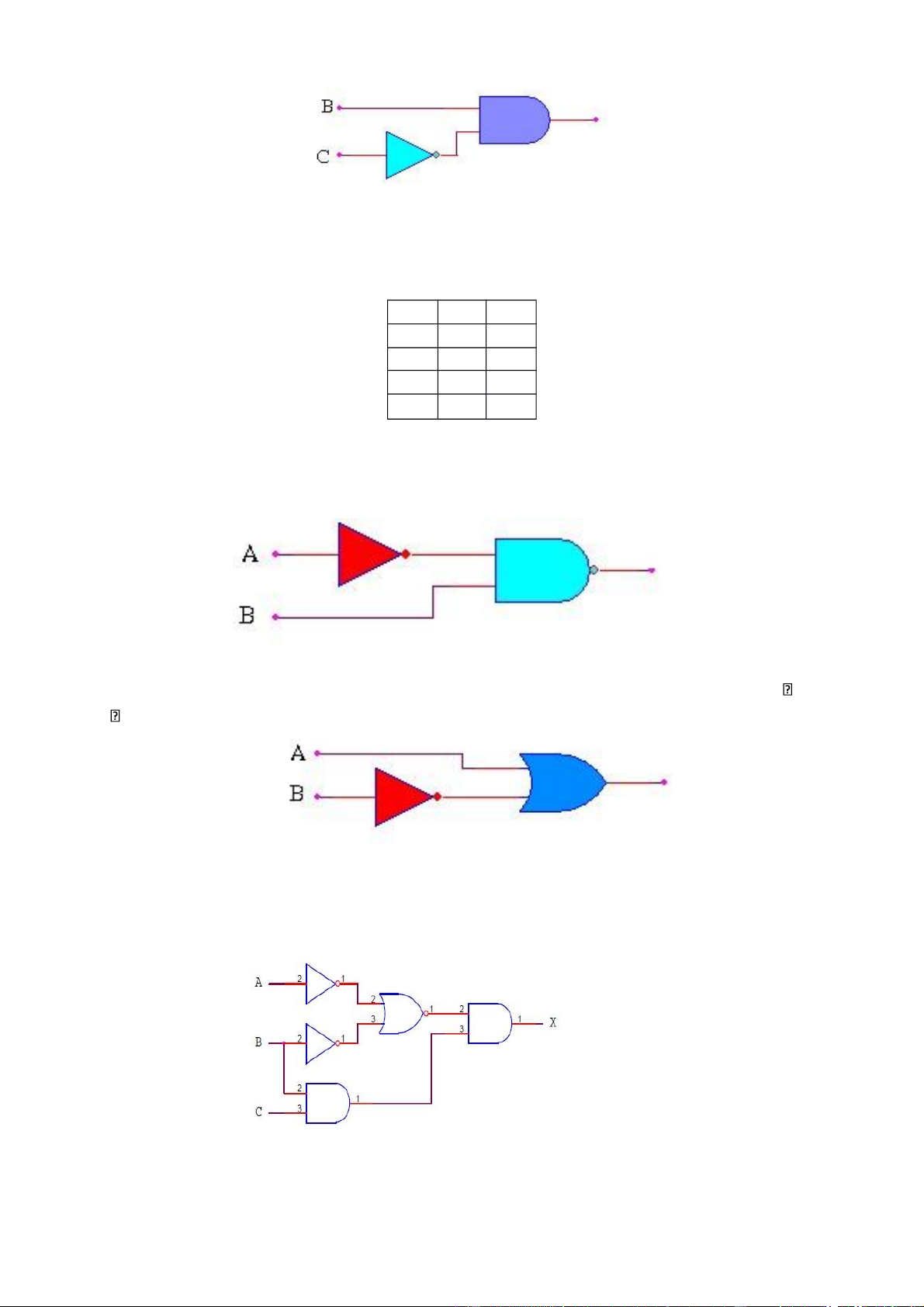
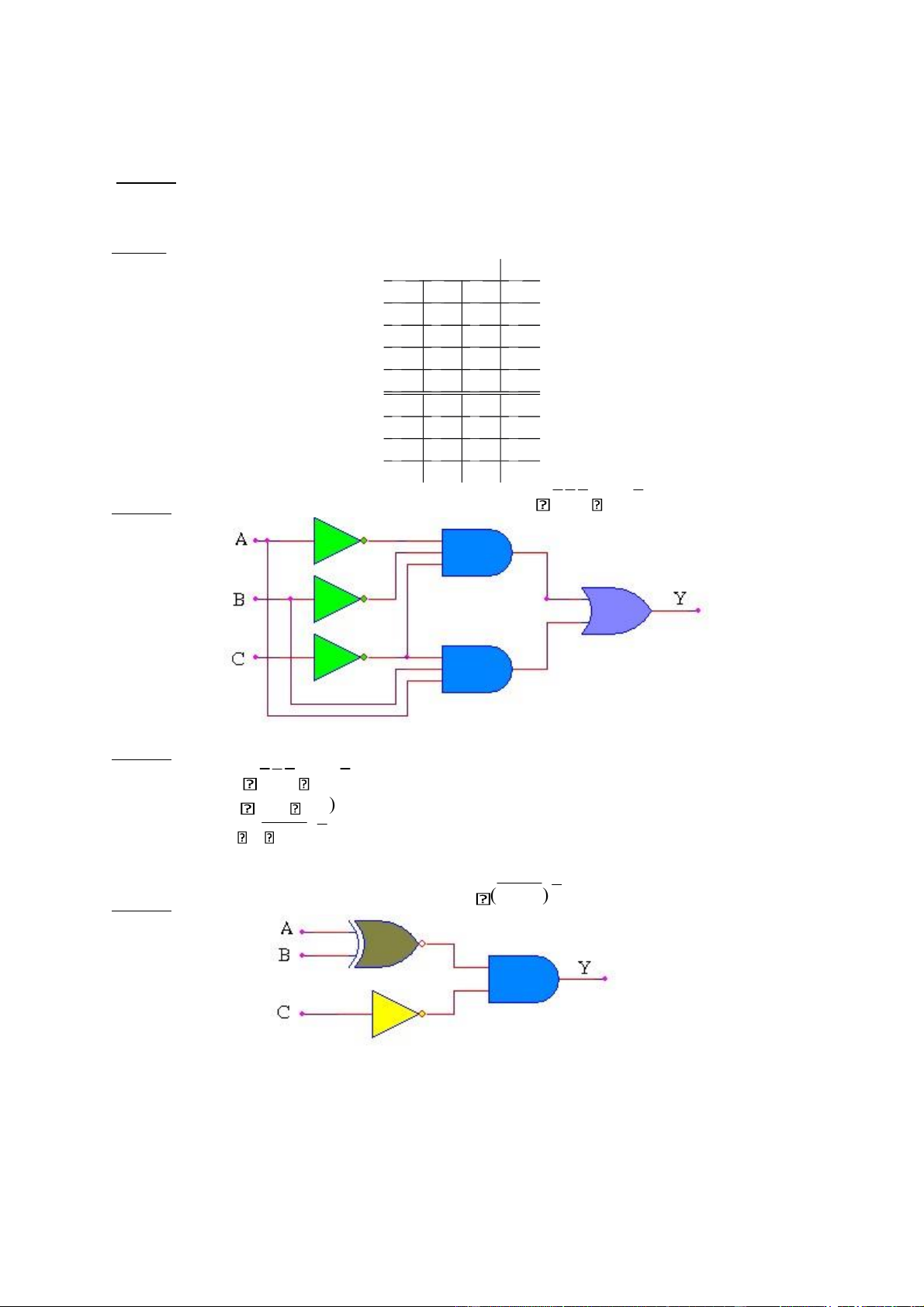
Bài 93: Cho mạch:
a./ Viết biểu thức hàm Y theo các biến A,B,C.
b./ Rút gọn hàm logic này Giải: a./ Ta có: b./ Rút gọn Bài 94:
Thiết kế một mạch điều khiển bởi 2 cầu dao với điều kiện các đèn được thiết kế sao cho khi
cả 2 cầu dao đều mở hoặc đều tắt thì đèn sáng. Giải:
Mỗi cầu dao xem như là 1 biến x,y: 1 là bật,0 là tắt
Cho F(x,y) = 1 khi đèn sáng (khi cả 2 cầu dao cùng bật hoặc cùng tắt) và 0 khi đèn tắt
Ta có bảng chân trị như sau: x y F(x,y) 1 1 1 1 0 0 0 1 0 0 0 1 Bài 95:
Hãy xác định hàm boole của mạch điện sau: lOMoAR cPSD| 40425501 B A D f(a,b,c,d) C ¬ ¬A C Giải:
Bài 96: Xây dựng mạch thể hiện các biểu thức sau: a) b) Giải a) b) Bài 97:
Trong một trận thi đấu võ thuật có 3 trọng tài sẽ cho điểm các đòn đánh được thực hiện trong
một trận đấu. Mỗi trọng tài sẽ có một nút để chấm điểm các đòn đánh. Mỗi đòn sẽ được tính
điểm nếu có từ 2 trọng tài bấm nút trở lên. Mạch điện dùng cho việc chấm điểm này sẽ gồm có
3 đầu vào tương ứng với 3 nút bấm của các trọng tài. Nếu trọng tài nào bấm nút thì tín hiệu 1
từ đường dây đó sẽ được truyền vào mạch, nếu không bấm thì tín hiệu trên đường dây vẫn là
0. Đầu ra của mạch sẽ là một tín hiệu nhị phân (0/1) thể hiện việc đòn đánh đó có được tính
điểm hay không. ( 0 – không tính điểm, 1 – tính điểm). Giải
Gọi là hàm Bool thể hiện tín hiệu đầu ra, bảng chân trị của thoe mô tả trên như sau: lOMoAR cPSD| 40425501 x y z 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1
Theo quy tắc xây dựng dạng nối rời chính tắc của hàm Bool, ta có công thức cùa hàm Bool là: v v z v
Từ đó, mạch điện được thiết kế như sau:
Bài 98: Xây dựng mạch thể hiện biểu thức: a) b) lOMoAR cPSD| 40425501
Bài 99: Xây dựng một mạch logic thực hiện hàm Bool cho bởi bảng sau: x y z 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 Giải
Theo bảng trên, hàm có dạng: Ta có: Ta có mạch sau:
Bài 100: Đơn giản mạch như hình sau: Giải Từ
hình trên ta có biểu thức logic cho đầu ra là:
Rút gọn biểu thức trên: = = = = (*)
Từ (*) ta thành lập được mạch logic mới như sau: lOMoAR cPSD| 40425501
Bài 101: Thiết kế mạch dùng hai công logic thỏa bảng sự thật sau đây: A B Y 0 0 1 0 1 0 1 0 1 1 1 1 Giải
* Vì ngõ ra bằng 0 chỏ một trường hợp nên ta viết hệ thức logic ở trường hợp này.
Y = 0 khi A = 0 và B = 1 nên => . Mạch thực hiện cổng NOT để tạo ra A đảo, tiếp
theo là cổng NAND của và B.
* Mặt khác ta có thể dựa vào bảng sự thật đề viết hàm logic cho Y và kết quả là:
Bài 102: Viết biểu thức đại số Boole cho các mạch dưới đây: a) b) lOMoAR cPSD| 40425501 c) Giải a) b) c)
Bài 103: Cho ngõ ra của mạch như hình vẽ, vẽ lại mạch để mô tả ngõ ra tác động ở mức thấp: Giải
Vì ngõ ra tác động mức thấp nên thêm vòng tròn phủ định. Do đó đổi OR thành AND
với các vòng tròn phủ định ở ngõ vào. Theo quy luật ta thêm vòng tròn phủ định cho ngõ ra
của cổng OR và NAND còn cổng NOT thì không vì đã có vòng tròn phủ định. Tiếp theo chuyển
đổi cổng OR và NAND để đảm bảo logic: lOMoAR cPSD| 40425501
Bài 104: Một ngôi nhà có 3 công tắc, người chủ nhà muốn bóng đèn sáng khi cả 3 công tắc
đều hở, hoặc khi công tắc 1 và 2 đóng còn công tắc thứ 3 hở. Hãy thiết kế mạch logic thực
hiện sao cho số cổng là ít nhất. .Bước 1:
Gọi 3 công tắc lần lượt là A, B, C. Bóng đèn là Y. Trạng thái công tắc đóng là logic 1, hở là 0.
Trạng thái đèn sáng là logic 1 và tắt là 0.
Bước 2: Từ yêu cầu bài toán ta có bảng chân trị: vào ra A B C Y 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 0
Bước 3: Từ bảng chân trị ,ta có biểu thức logic ngõ ra Y ABCABC
Bước 4: Rút gọn biểu thức logic : Y ABCABC ( AB ) ABC (A B C)
Đến đây thì ta thấy rằng biểu thức logic đã gọn và số cổng logic sử dụng là ít nhất. Bước 5: YAB(C
Mạch logic tương ứng của biểu thức: ) là Bài 105:
Một ủy ban gồm 3 thành viên phải quyết định các vấn đề của một tổ chức. Mỗi thành viên bỏ
phiếu tán thành hoặc không cho mỗi một đề nghị được đưa ra. Một đề nghị sẽ được thông
qua nếu nó nhận được ít nhất hai phiếu tán thành. Hãy thiết kế một mạch cho phép xác định
được một đề nghị có được thông qua hay không? Giải lOMoAR cPSD| 40425501
Nếu thành viên bỏ phiếu tán thành thì logic là 1, không tán thành thì logic là 0.
Khi đó mạch cần được thiết kế sao cho nó tạo đầu ra bằng 1 từ các đầu vào x, y, z có
giá trị 1. Biểu diễn hàm Boole của giá trị đầu ra là xy + yz + zx.
Mạch thực hiện hàm trên là: Bài 106:
Đôi khi các hệ thống đèn cố định được điều khiển bởi nhiều công tắc. Các mạch cần được
thiết kế sao cho khi ấn (hoặc gạt) một công tác bất kỳ, hệ thống đèn đang tắt sẽ bật và
đang bật sẽ tắt. Hãy thiết kế một mạch thực hiện điều đó khi có hai công tắc. Giải
Giả sử công tắt mở thì logic là 1, đóng là 0.
Giả sử F(x,y) = 1 khi đèn sáng và F(x,y) = 0 khi đèn tắt.
Từ yêu cầu bài toán, ta có bảng chân trị: x y F 0 0 1 0 1 0 1 0 0 1 1 1 Hàm F(x,y) cần tìm là: Do đó, ta có mạch sau: Bài 107:
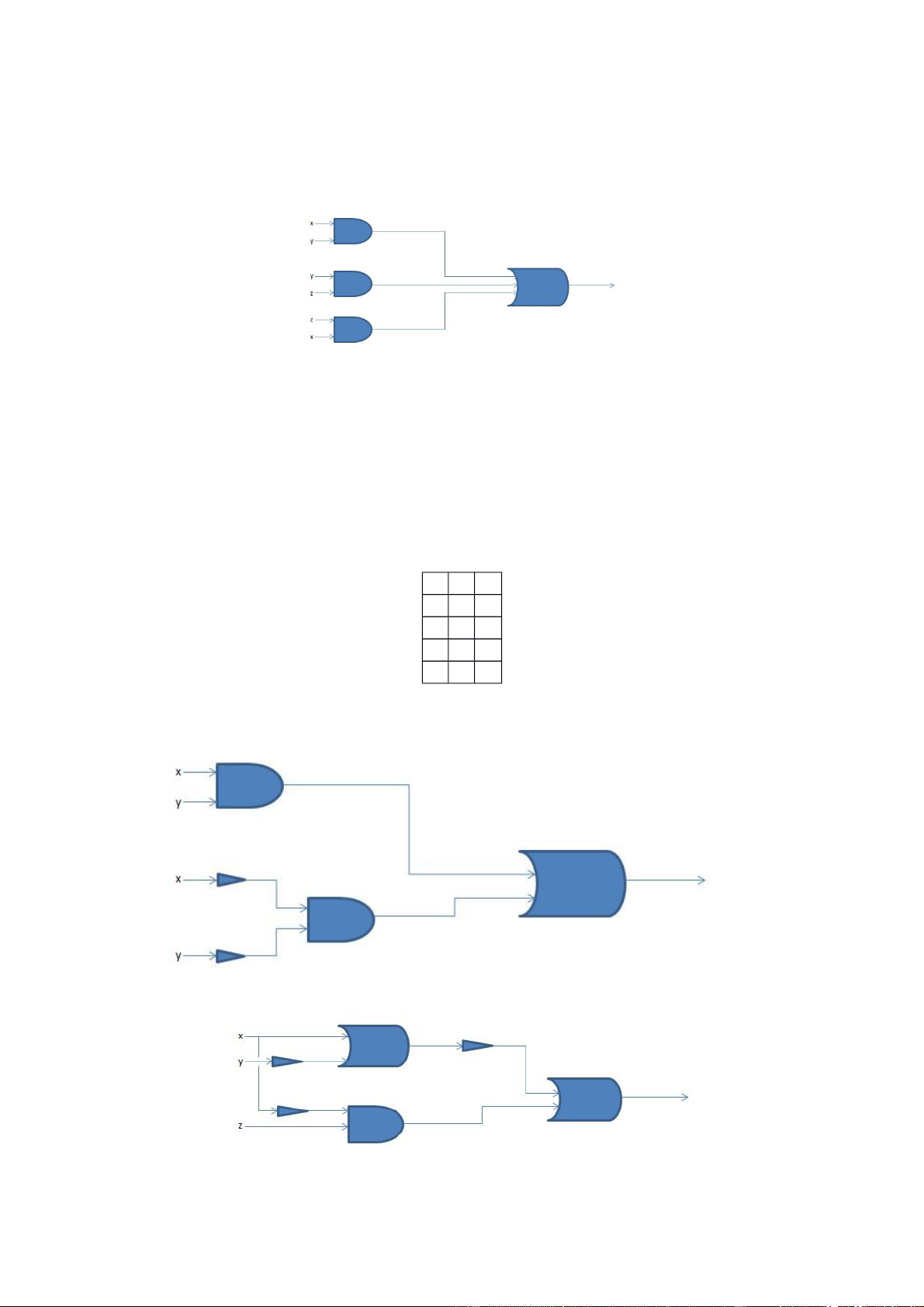
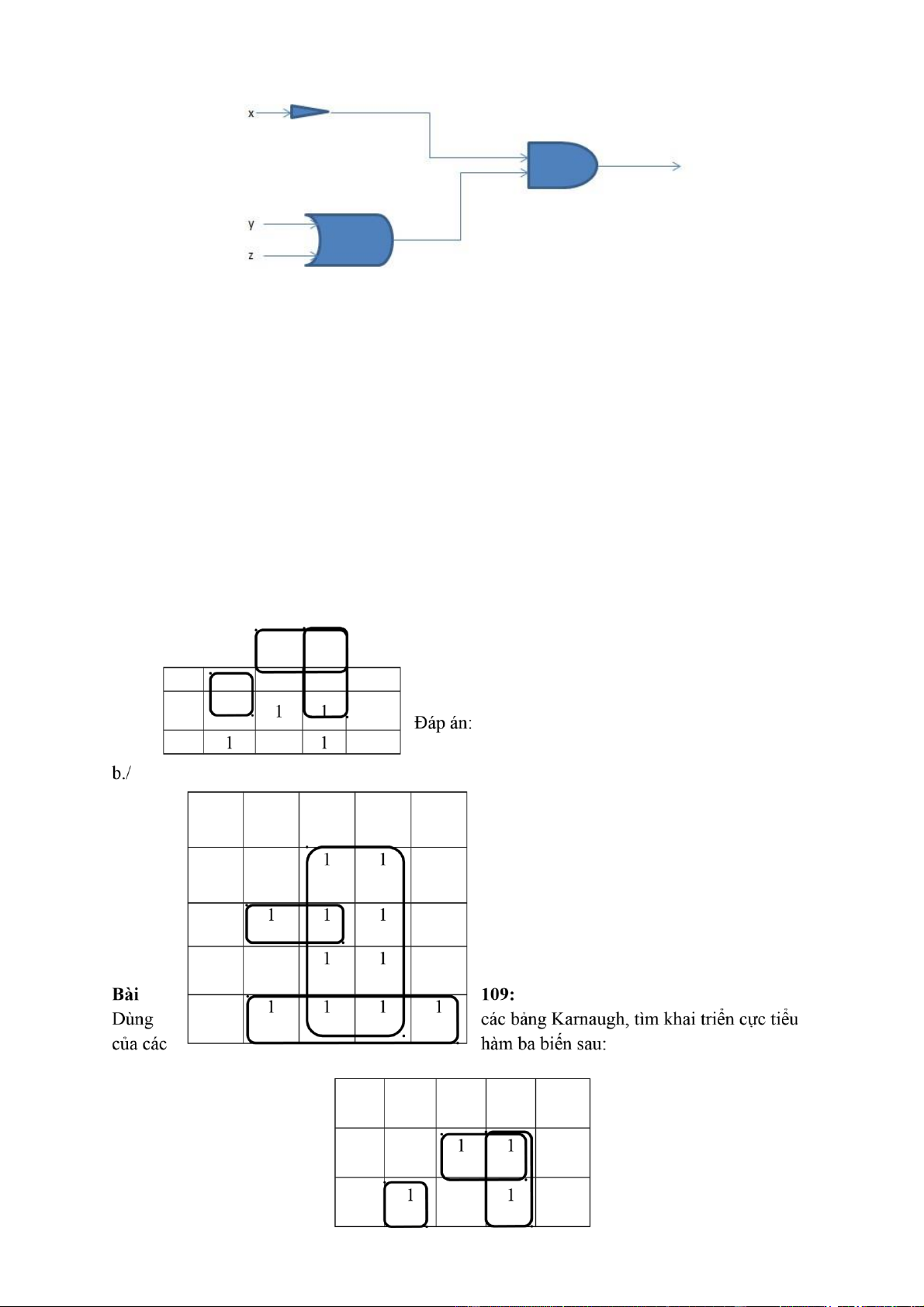
Chứng tỏ các mạch sau tương đương: lOMoAR cPSD| 40425501 Giải
Ta có biểu thức logic của từng mạch: Mạch 1: Mạch 2: (1)
Biến đổi biểu thức logic của mạch 1: = = = (2)
Từ (1) và (2), suy ra hai mạch đã cho tương đương nhau.
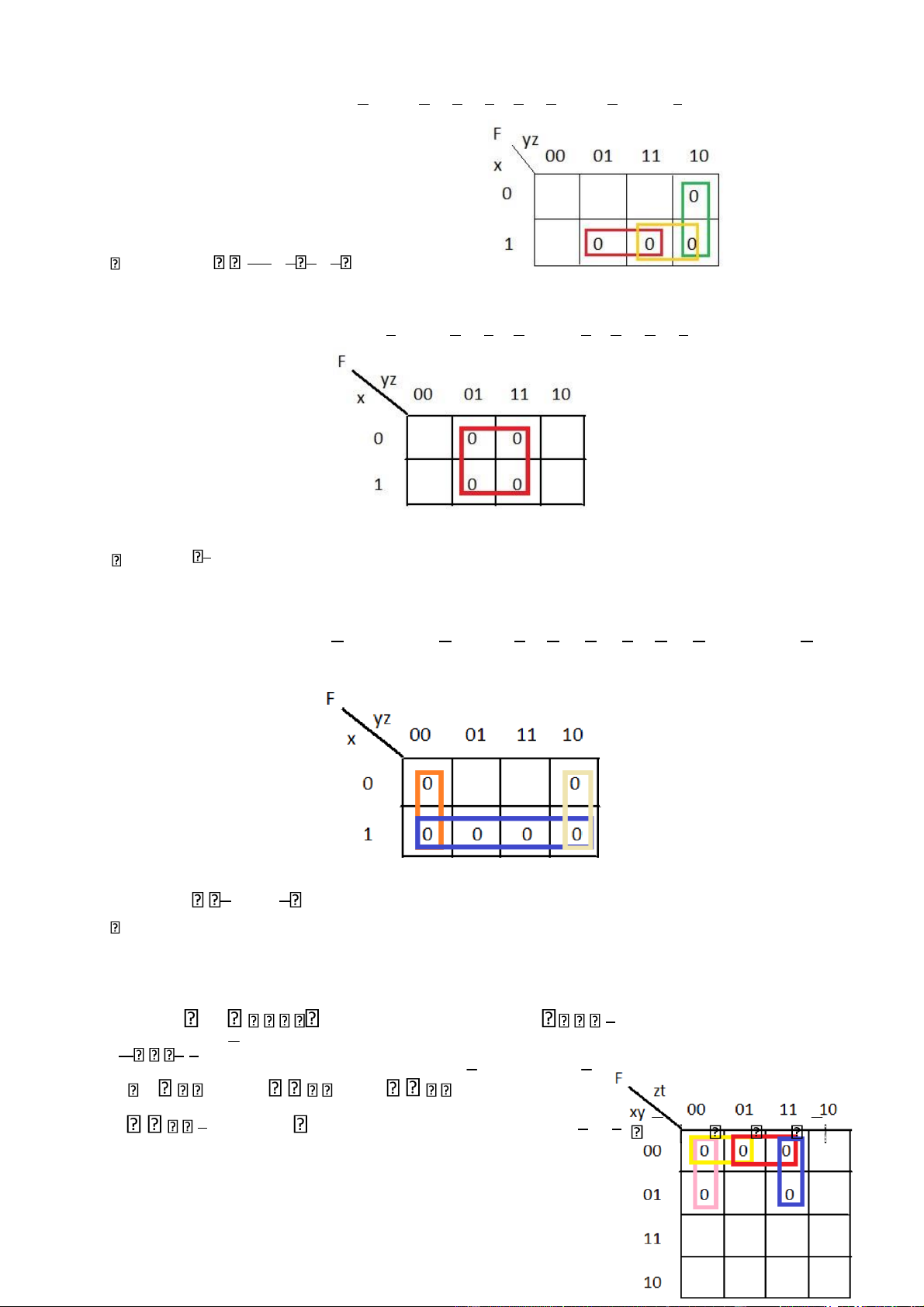
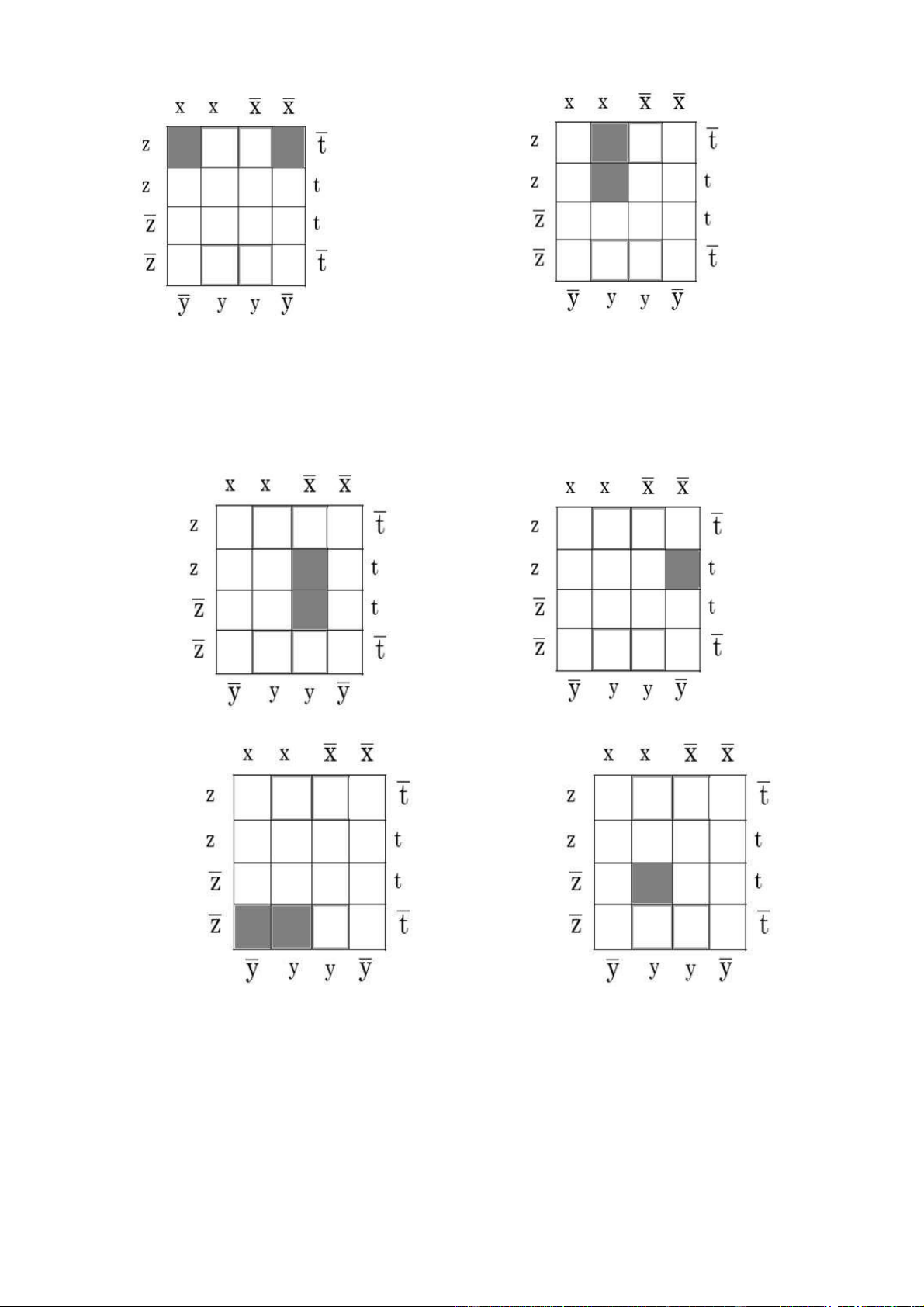
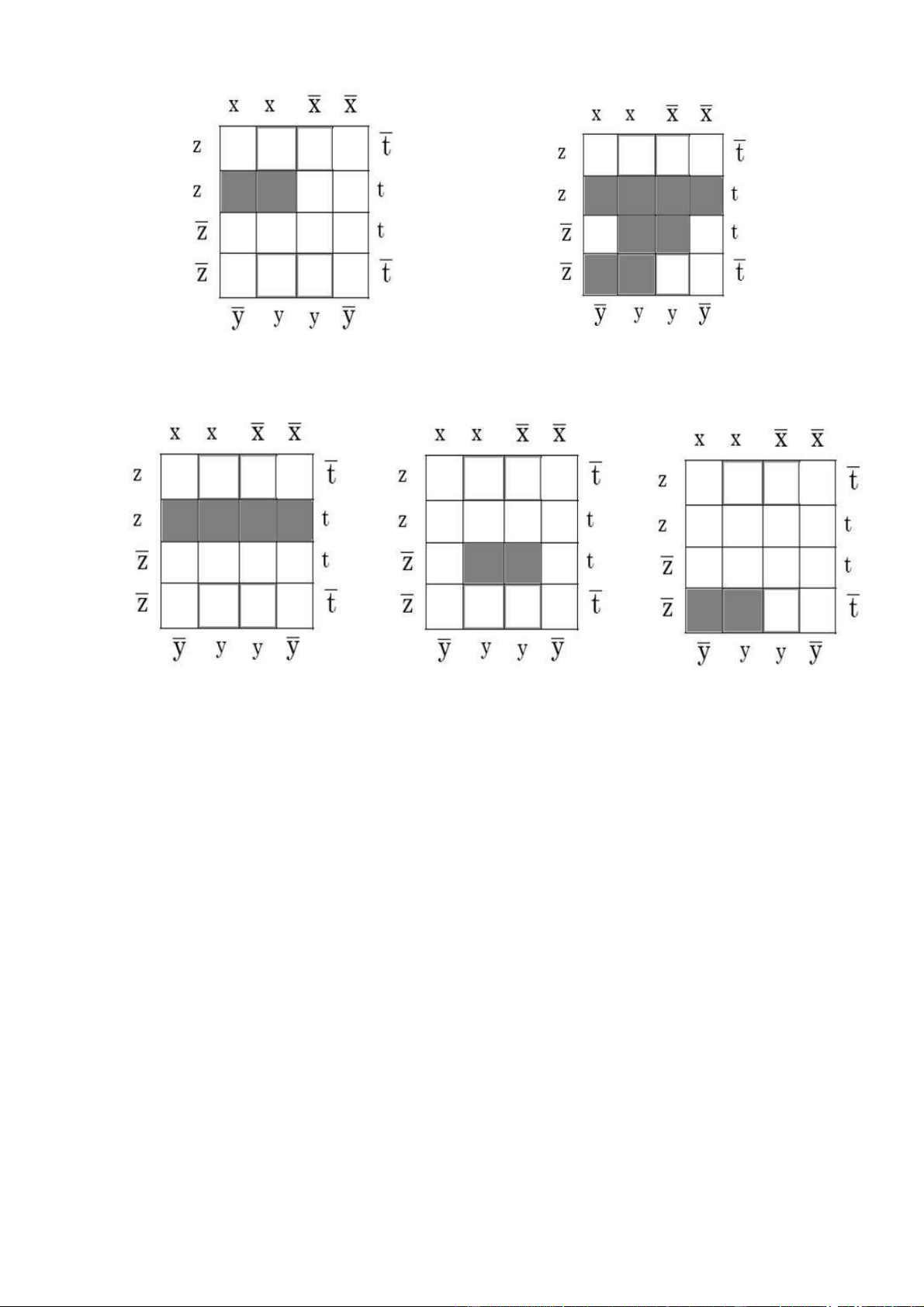
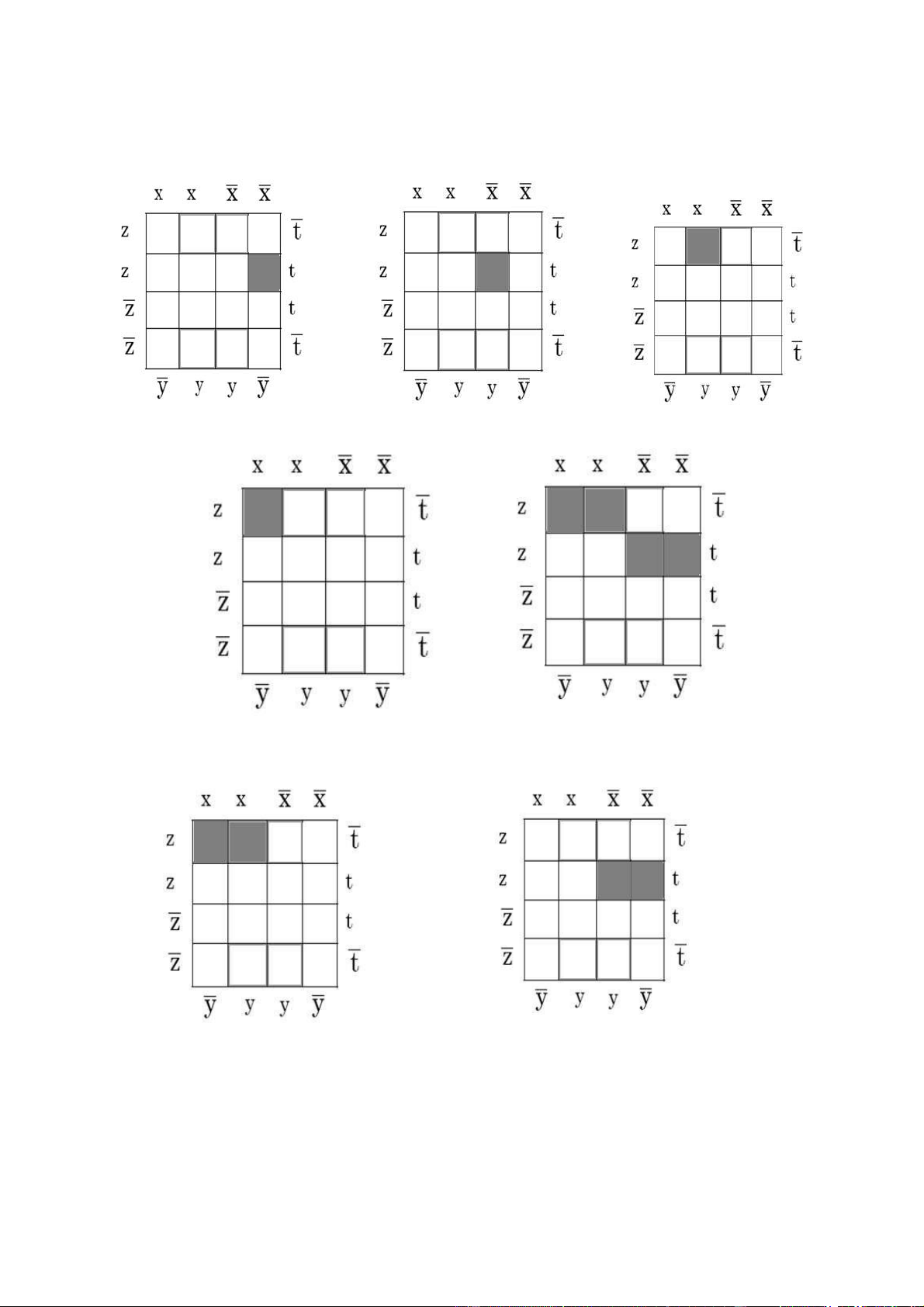
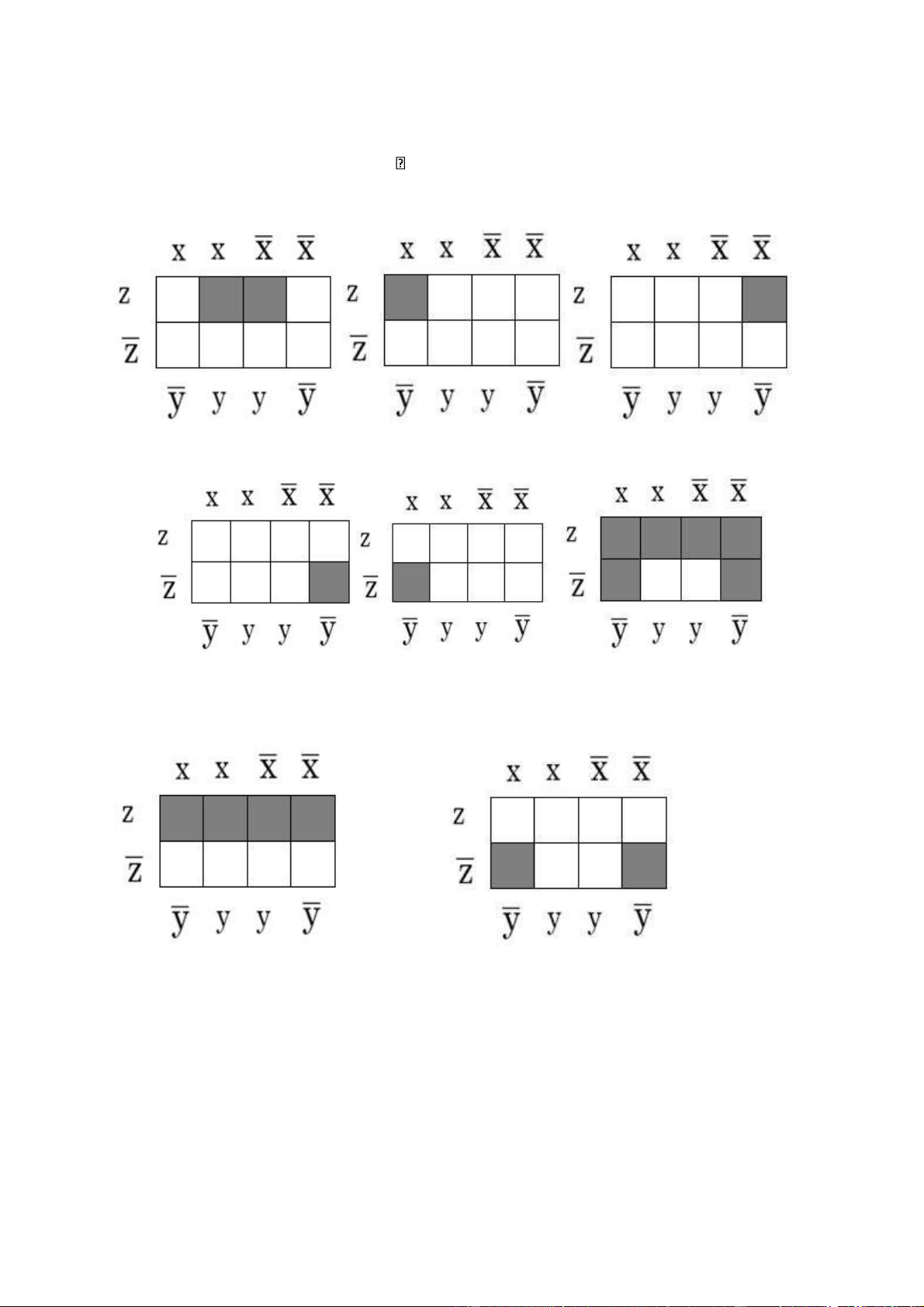
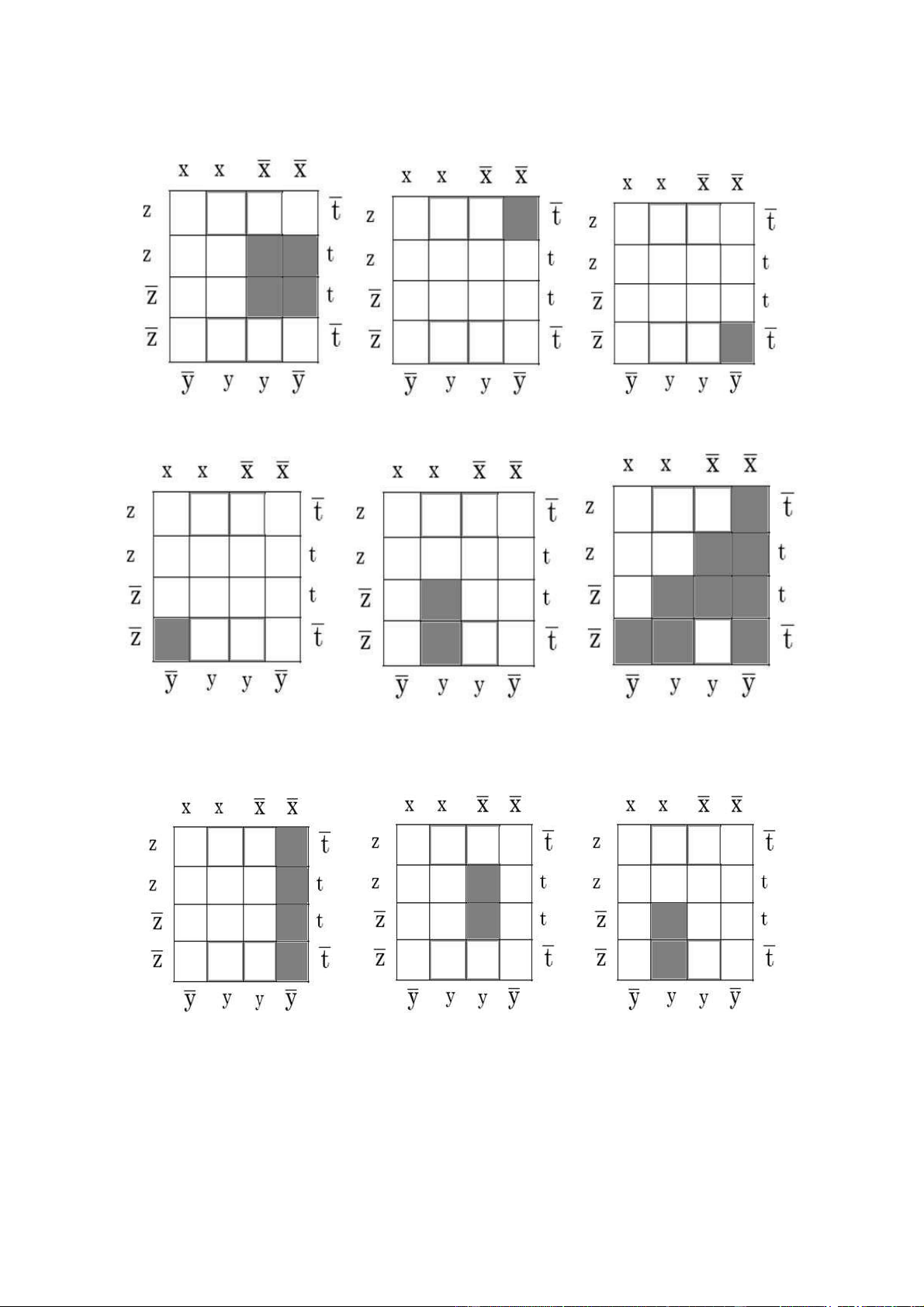
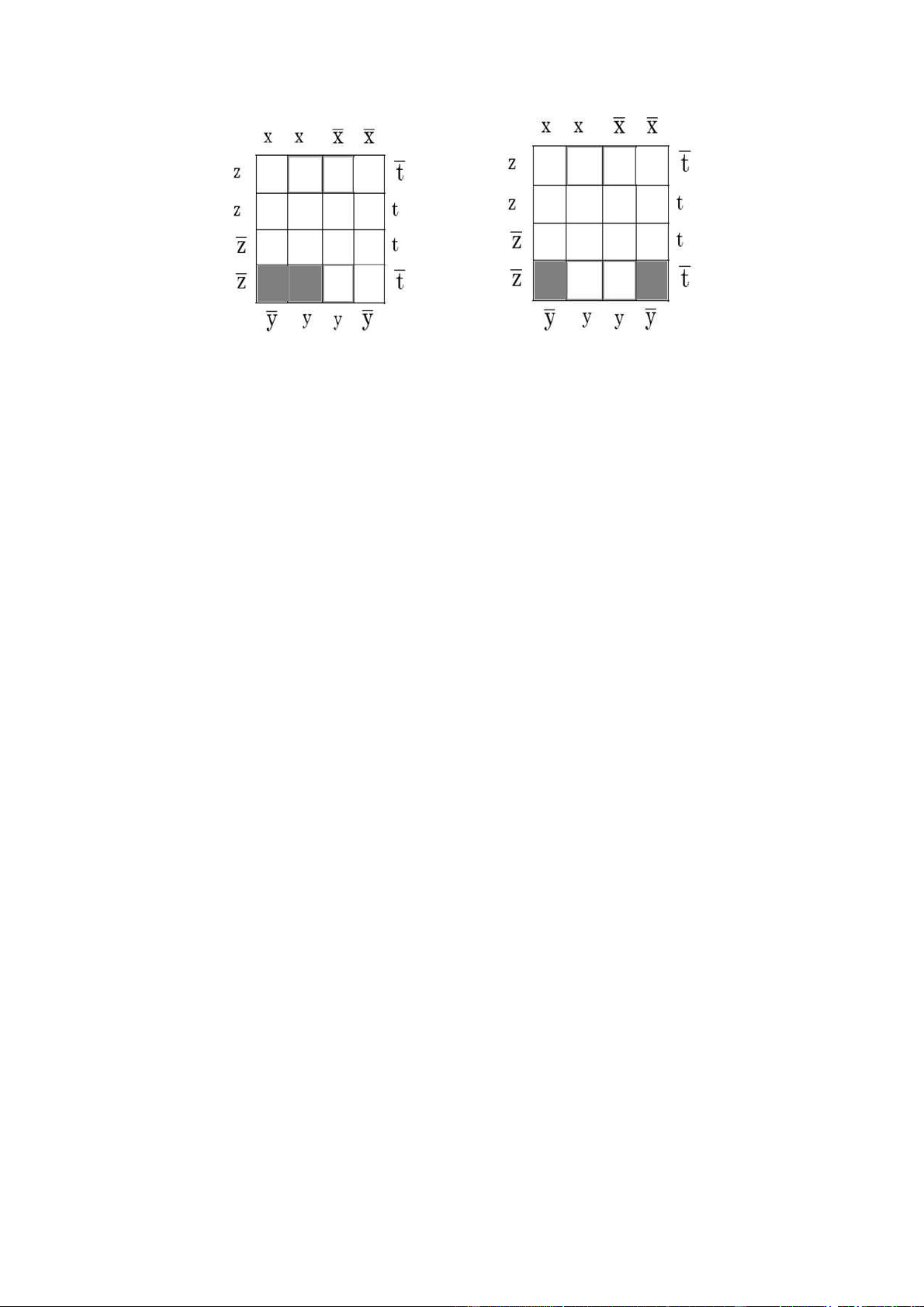
Bài 108: Tìm khai triển tổng các tích được biểu diễn bởi các bảng Karnaugh sau: a./ lOMoAR cPSD| 40425501 Đáp án: Bài của các Đáp án:
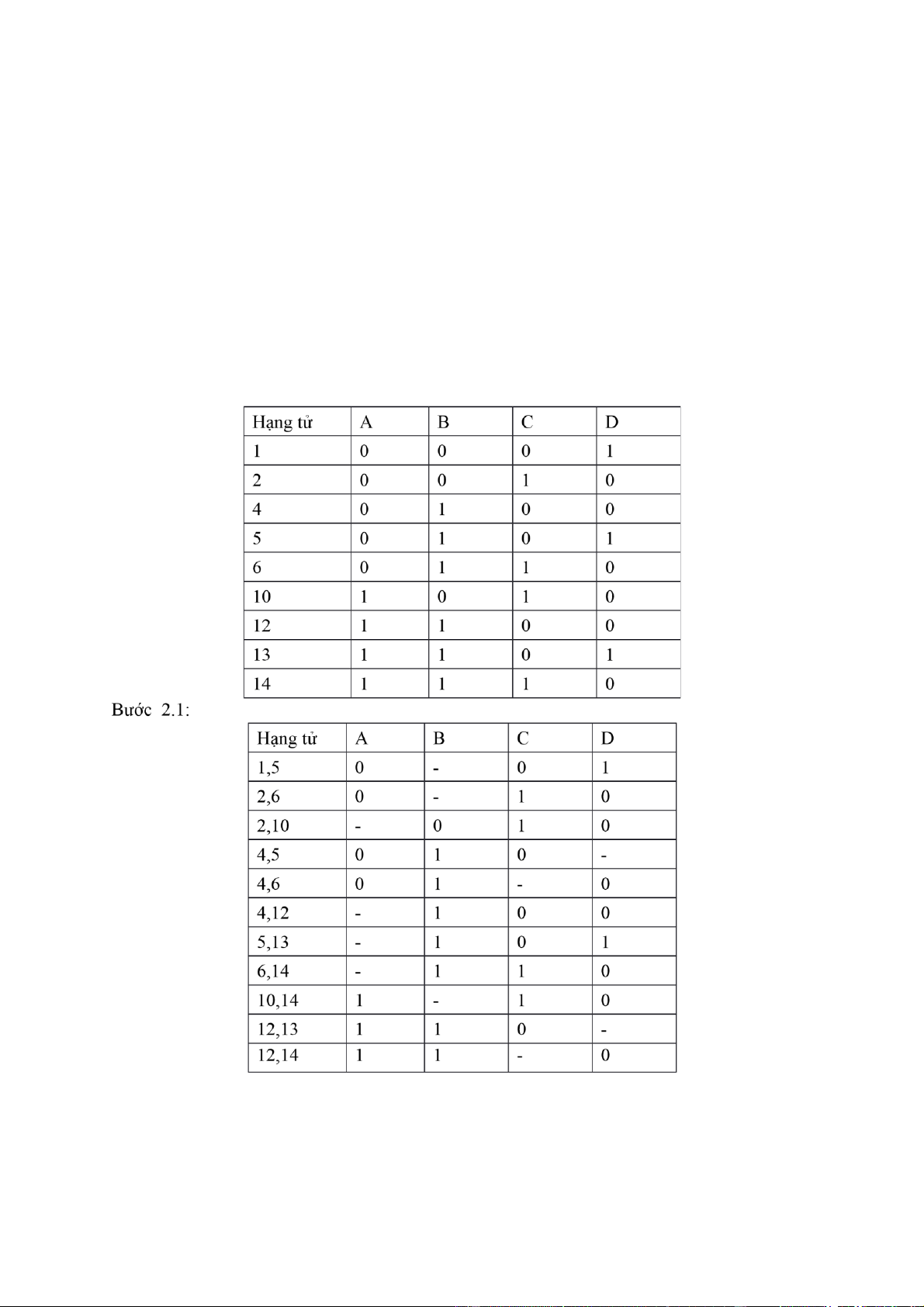
Bài 110: Rút gọn bằng Quine - McCuskey :
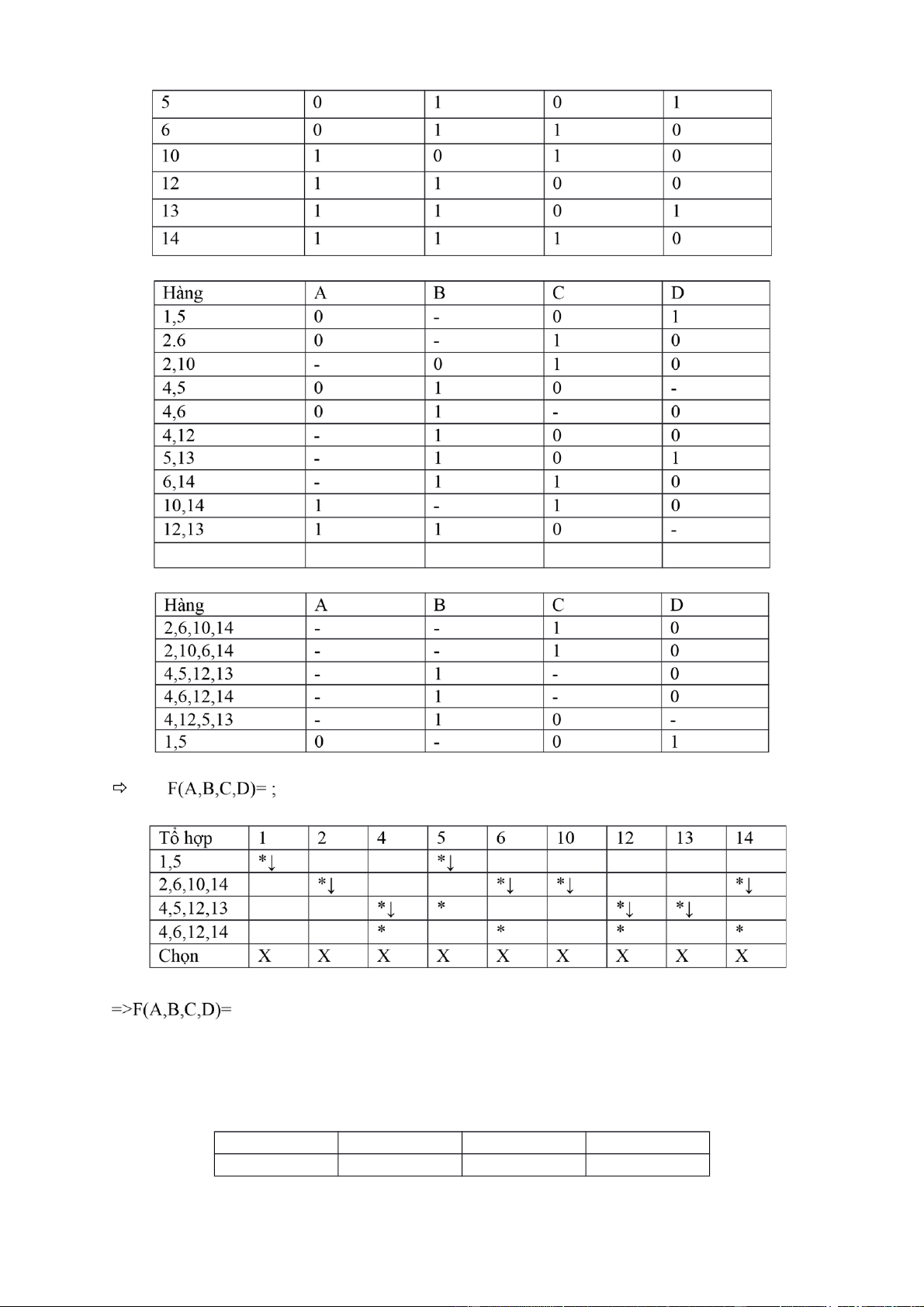
F(A,B,C,D) = (1,2,4,5,6,10,12,13,14) Bước 1: Bước 2.2: lOMoAR cPSD| 40425501 Hạng tử A B C D (2 , 6),(10,14) - - 1 0 (2 (6,14 ,10), ) - - 1 0 (4 5),( , 12,13) - 1 - 0 (4 , 6),(12,14) - 1 - 0
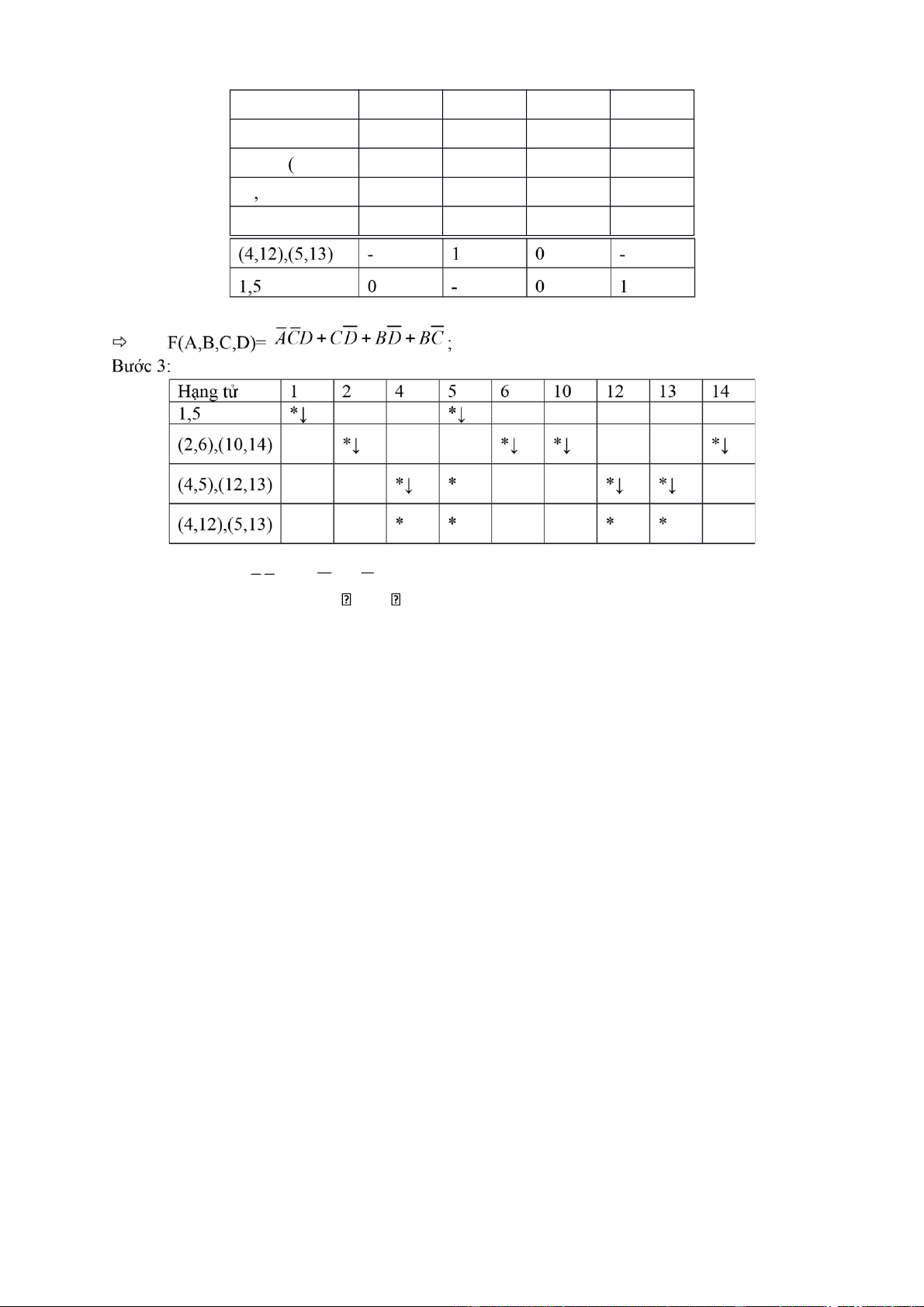
=> F(A,B,C,D) = ACD CD BC
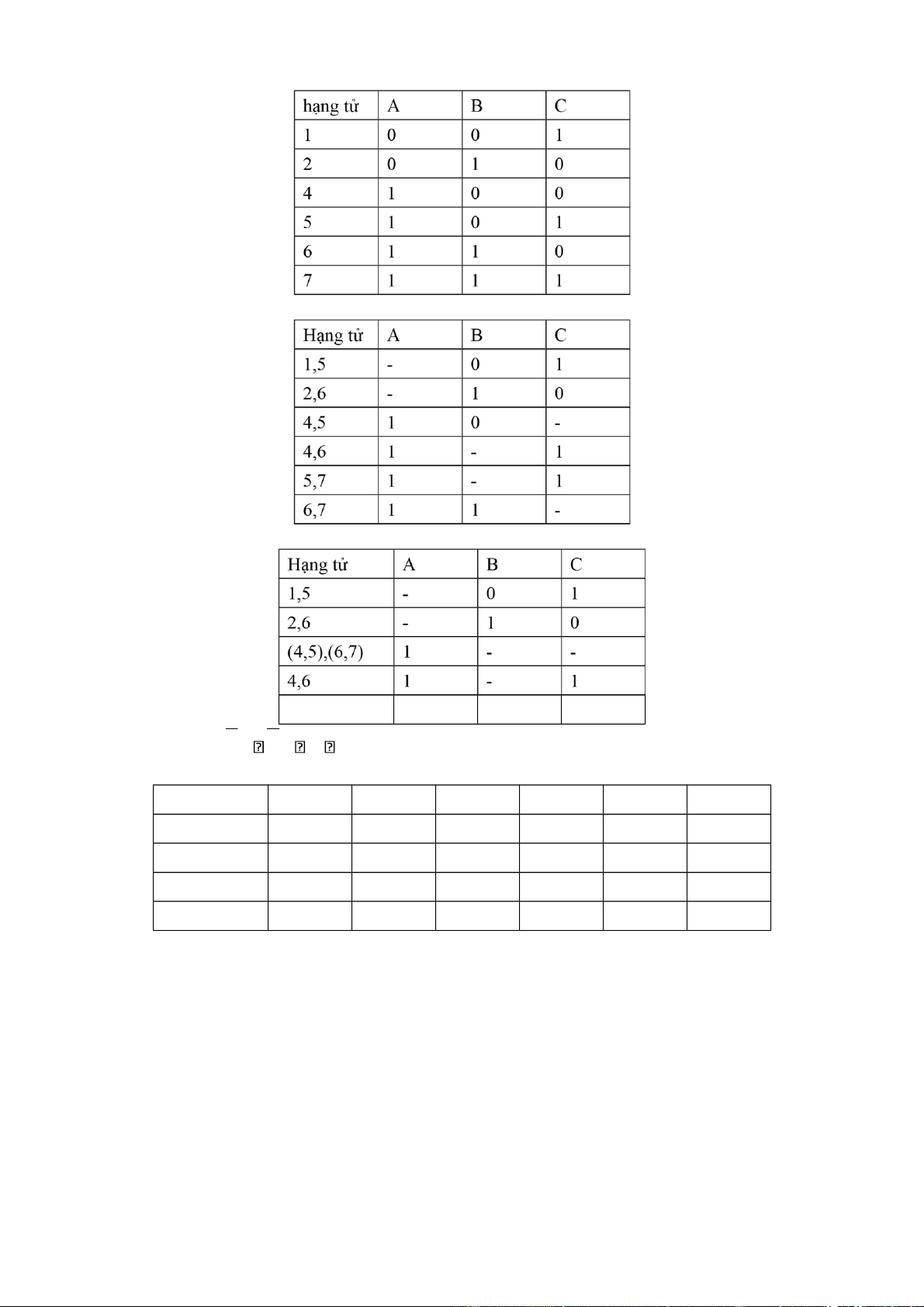
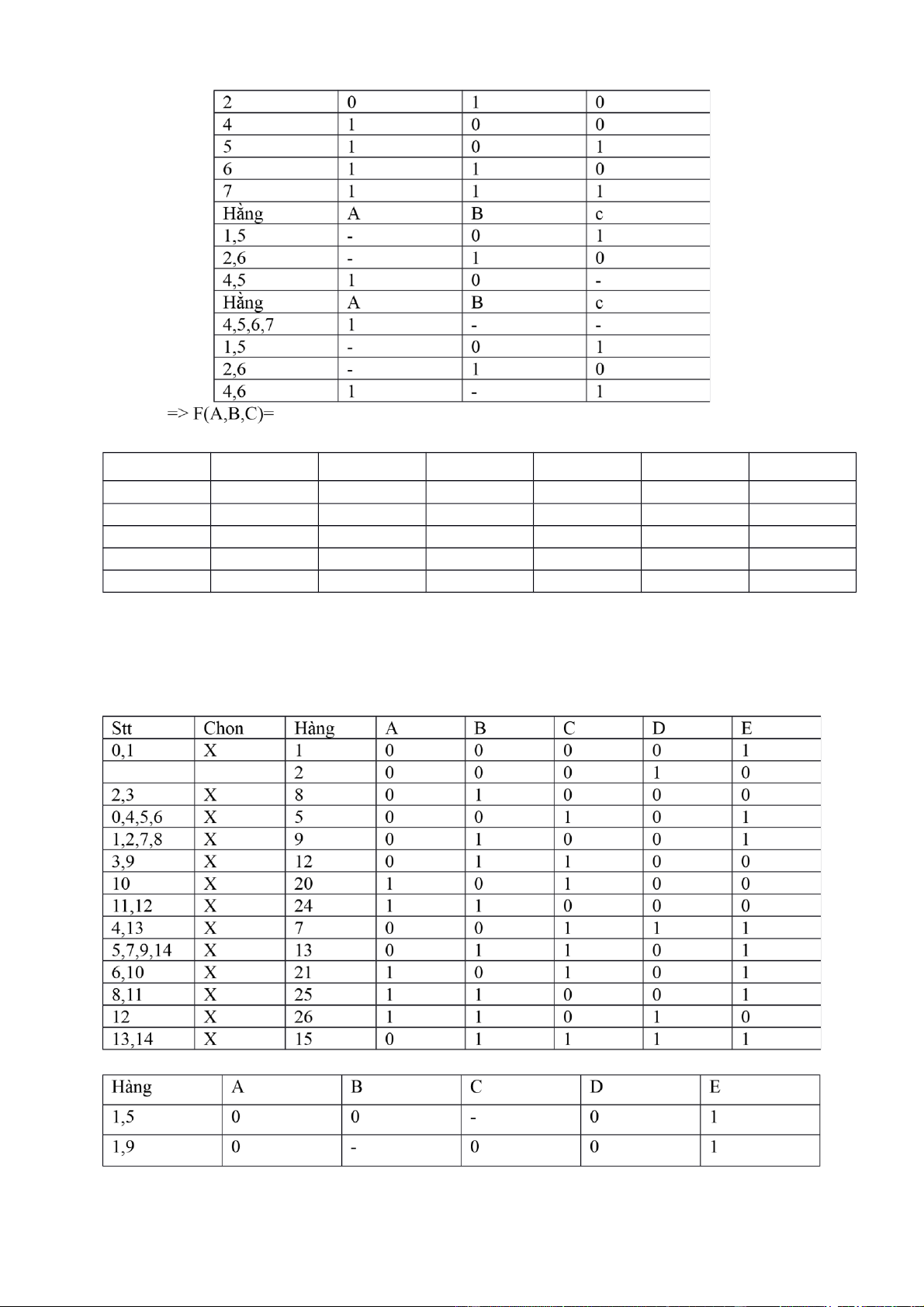
Bài 111: Rút gọn bắng Quine - McCuskey : F(A,B,C) = (1,2,4,5,6,7,8) Bước 1: lOMoAR cPSD| 40425501 Bước 2.1: Bước 2.2: 5 , 7 1 - 1
=> F(A,B,C)= BCCBAAC Bước 3: hạng tử 1 2 4 5 6 7 1 , 5 *↓ *↓ 2 , 6 *↓ *↓ (4 ,5),(6, 7) *↓ * * *↓ 4 , 6 * * => F(A,B,C) = .
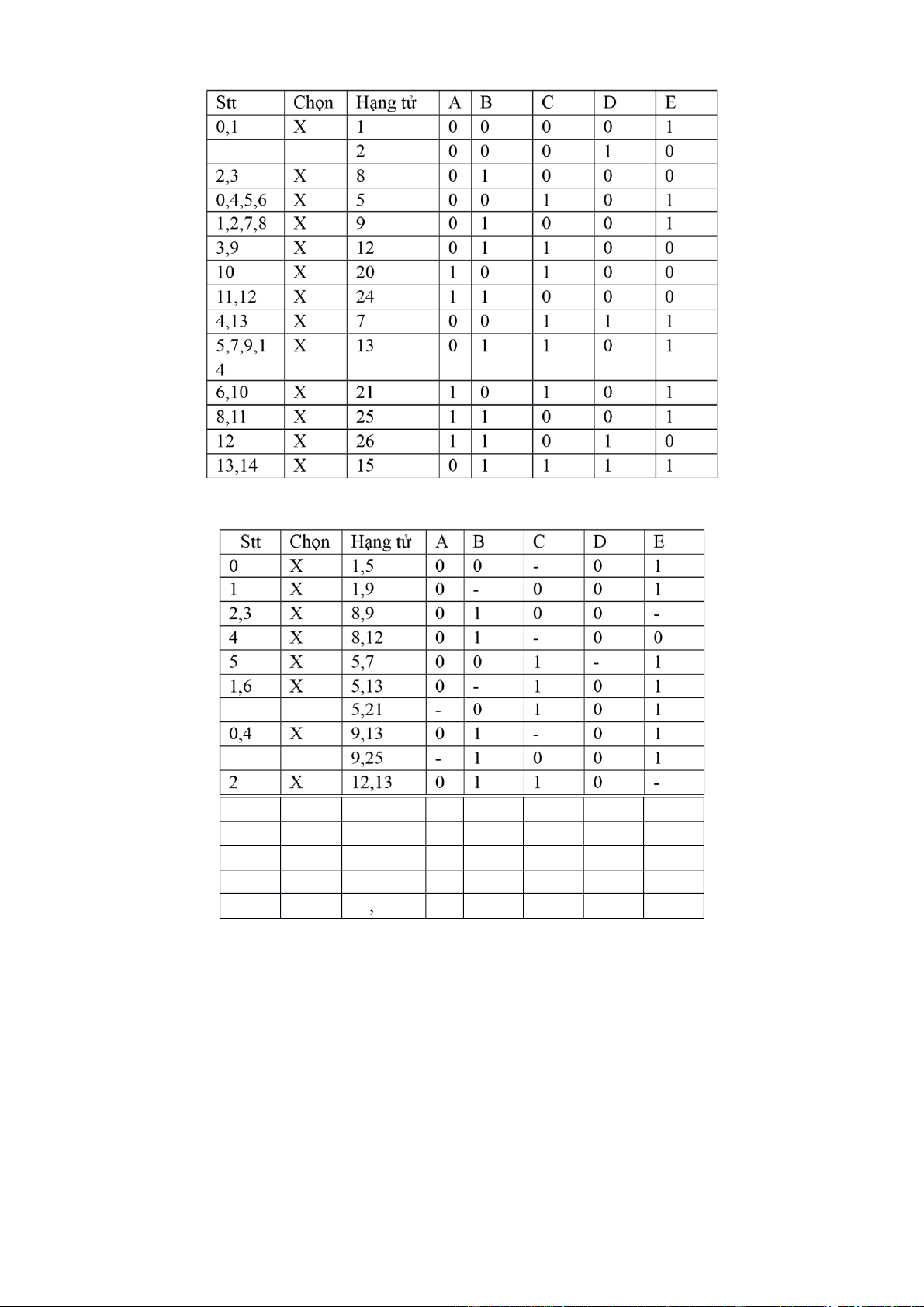
Bài 112: Rút gọn bắng Quine-McCuskey :
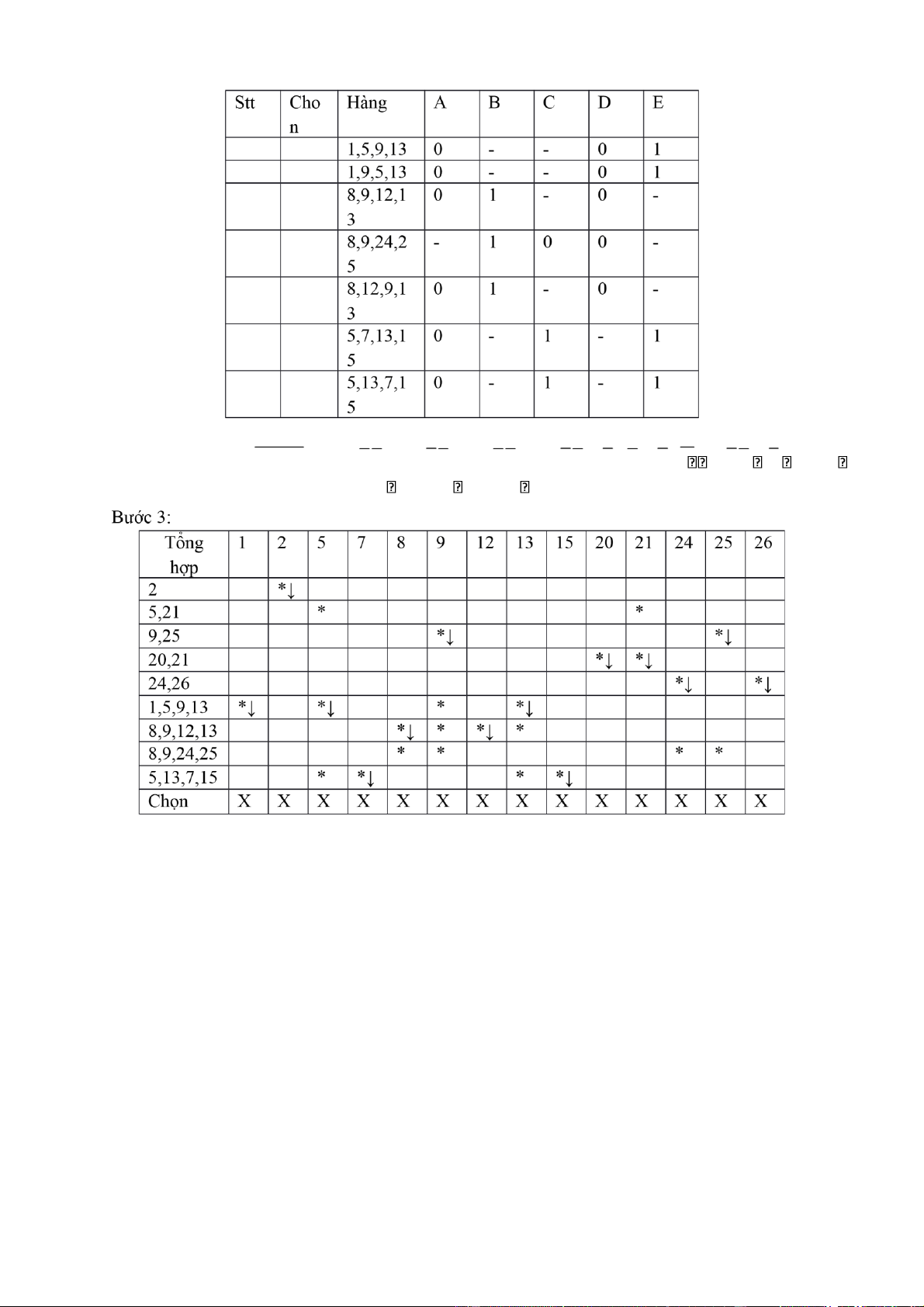
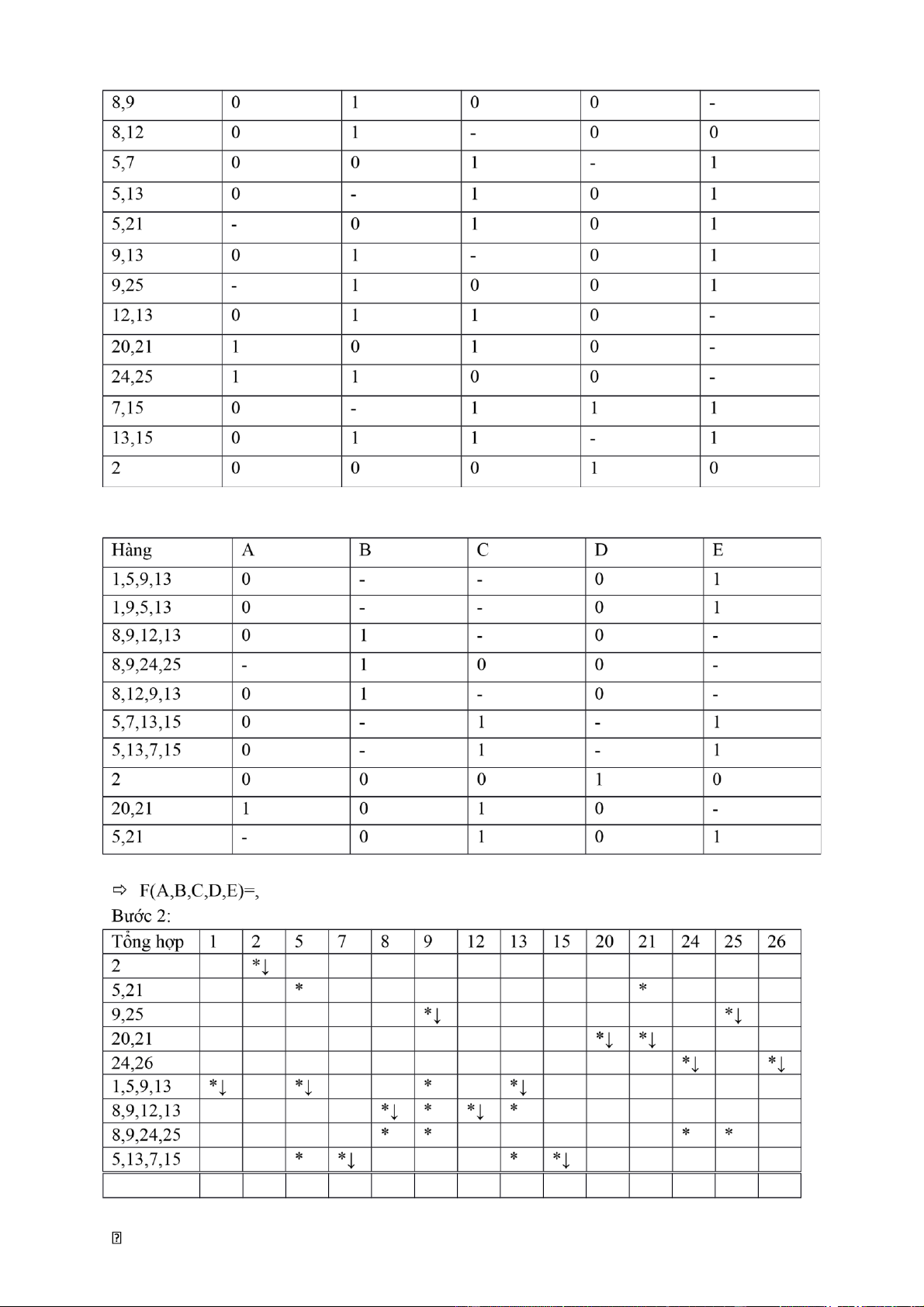
F(A,B,C,D,E) = (1,2,5,7,8,9,12,13,15,20,21,24,25,26) Bước 1: lOMoAR cPSD| 40425501 Bước 2.1: 20 , 21 1 0 1 0 - 3 X 24 , 25 1 1 0 0 - 24 26 , 1 1 0 - 0 6 X 7 , 15 0 - 1 1 1 5 X , 13 15 0 1 1 - 1 Bước 2.2: lOMoAR cPSD| 40425501
=>F(A,B,C,D,E)= ABCED CEBD BECD ACBD ABCD AED ABD BCD ACE =>F(A,B,C,E,D) = ,
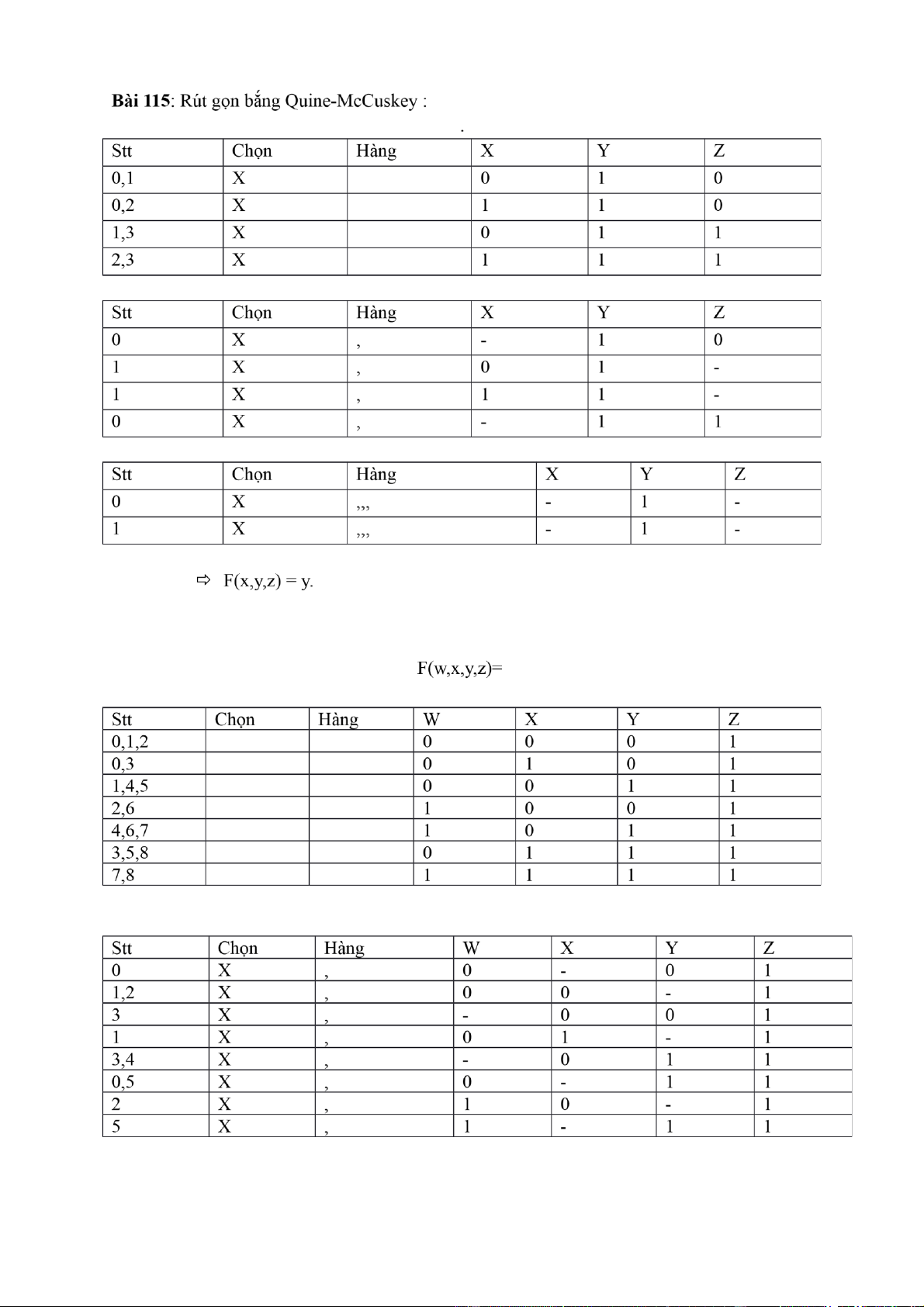
Bài 113: Rút gọn bắng Quine-McCuskey : F(x,y,z)= = lOMoAR cPSD| 40425501 => F(x,y,z) =
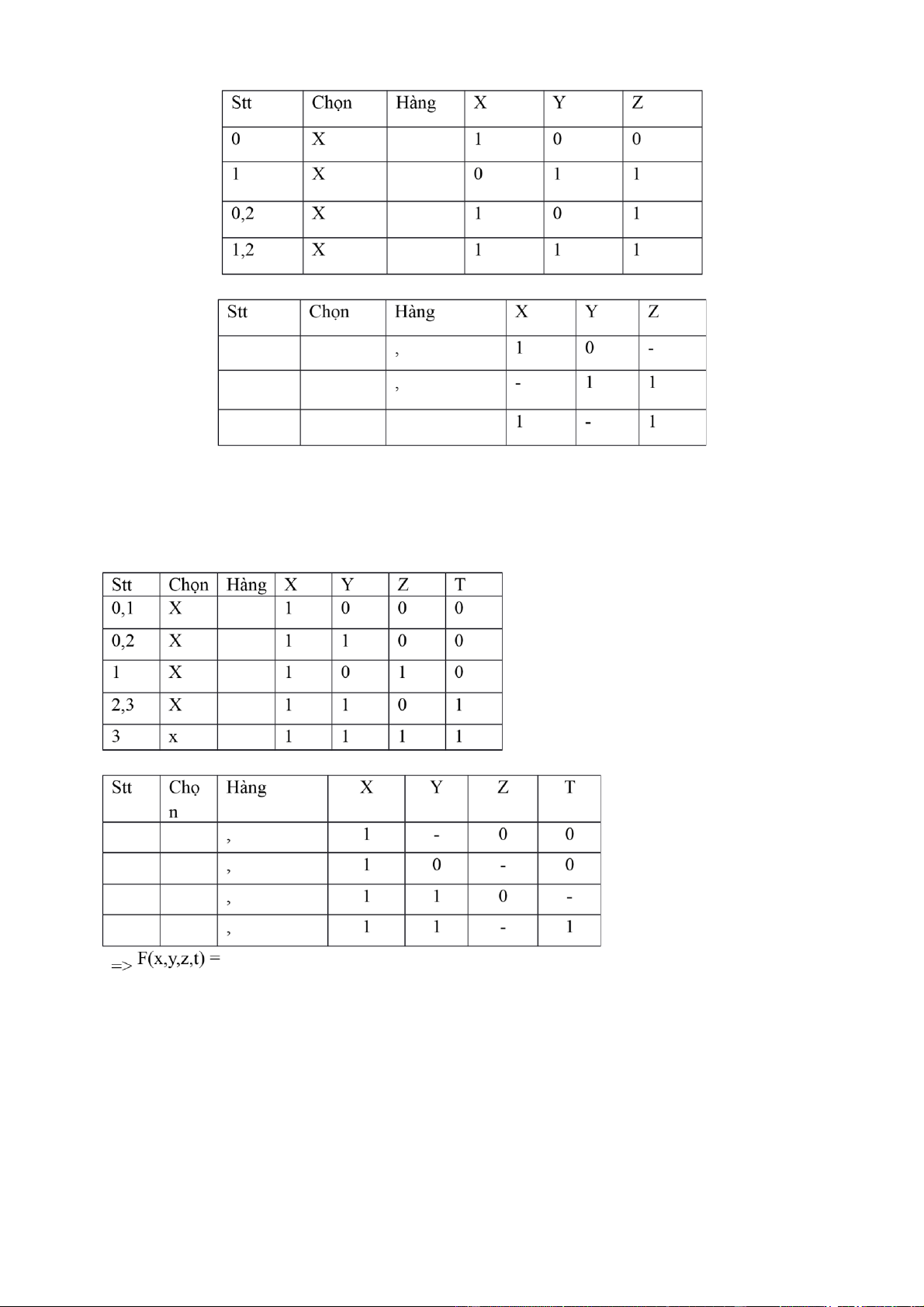
Bài 114: Rút gọn bắng Quine-McCuskey : F(x,y,z,t) = lOMoAR cPSD| 40425501
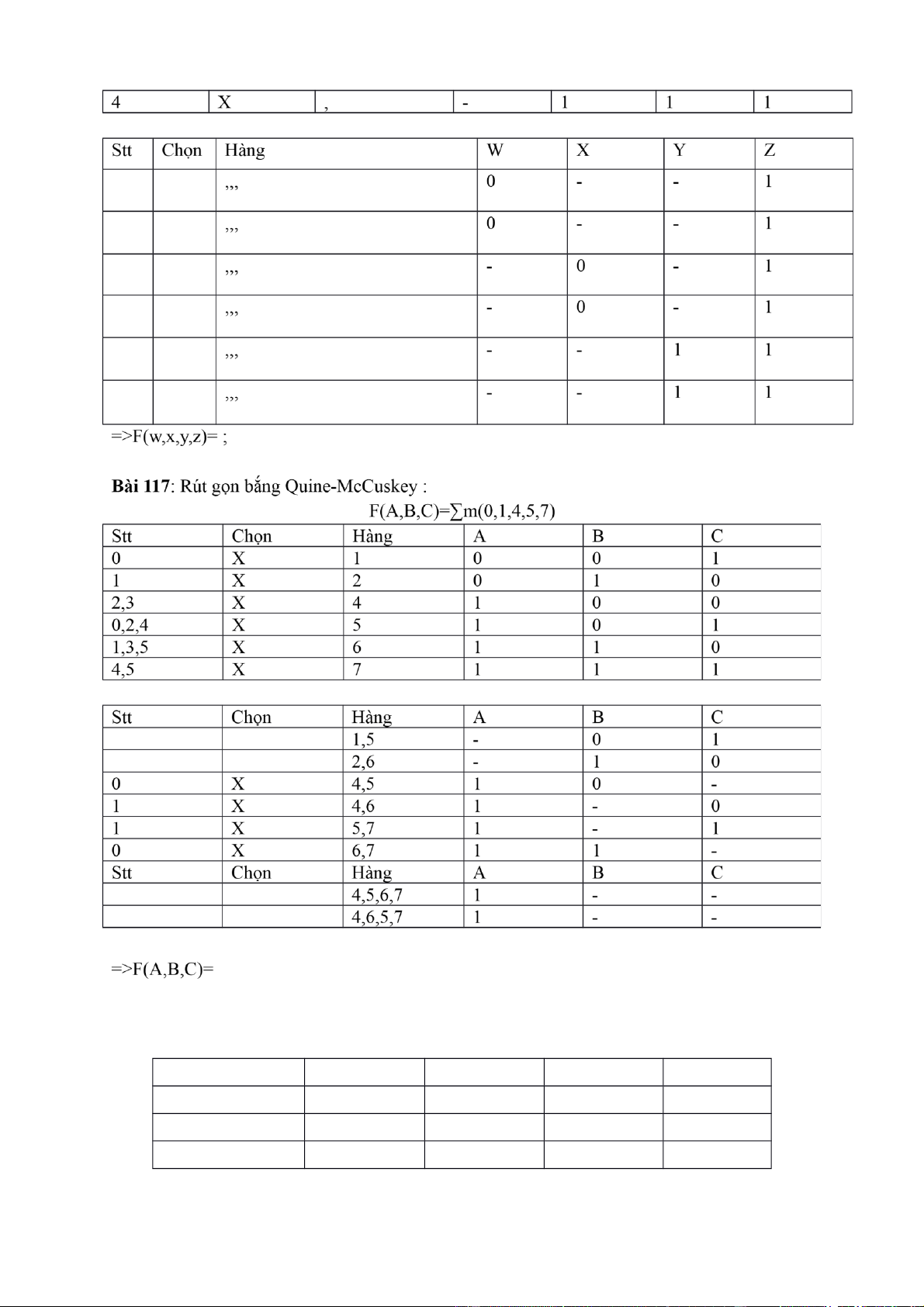
Bài 116: Rút gọn bắng Quine-McCuskey : lOMoAR cPSD| 40425501 Bài 118 : R
út gọn bắng Quine-McCuskey :
F(A,B,C,D)=(1,2,4,5,6,10,12,13,14) Hàng A B C D 1 0 0 0 1 2 0 0 1 0 4 0 1 0 0 lOMoAR cPSD| 40425501
Bài 119: Rút gọn bắng Quine-McCuskey : F(A,B,C) = (1,2,4,5,6,7,8) Bước 1: Hằng A B C 1 0 0 1 lOMoAR cPSD| 40425501 Bước 2: Tổng hợp 1 2 4 5 6 7 1 5 , *↓ *↓ , 2 6 *↓ *↓ 4 ,5,6, 7 *↓ * * *↓ 4 , 6 * * Chọn X X X X X X => F(A,B,C)= .
Bài 120: Rút gọn bắng Quine-McCuskey :
F(A,B,C,D,E)=(1,2,5,7,8,9,12,13,15,20,21,24,25,26) Bước 1: lOMoAR cPSD| 40425501 Chọn X X X X X X X X X X X X X X F(A,B,C,E,D)= lOMoAR cPSD| 40425501
Bài 121 :Rút gọn bắ ng Quine-McCuske : y F(x,y,z) = = Hàng X Y Z 1 0 0 0 1 1 1 0 1 1 1 1 Hàng X Y Z , 1 0 - , - 1 1 1 - 1 => F(x,y,z)=
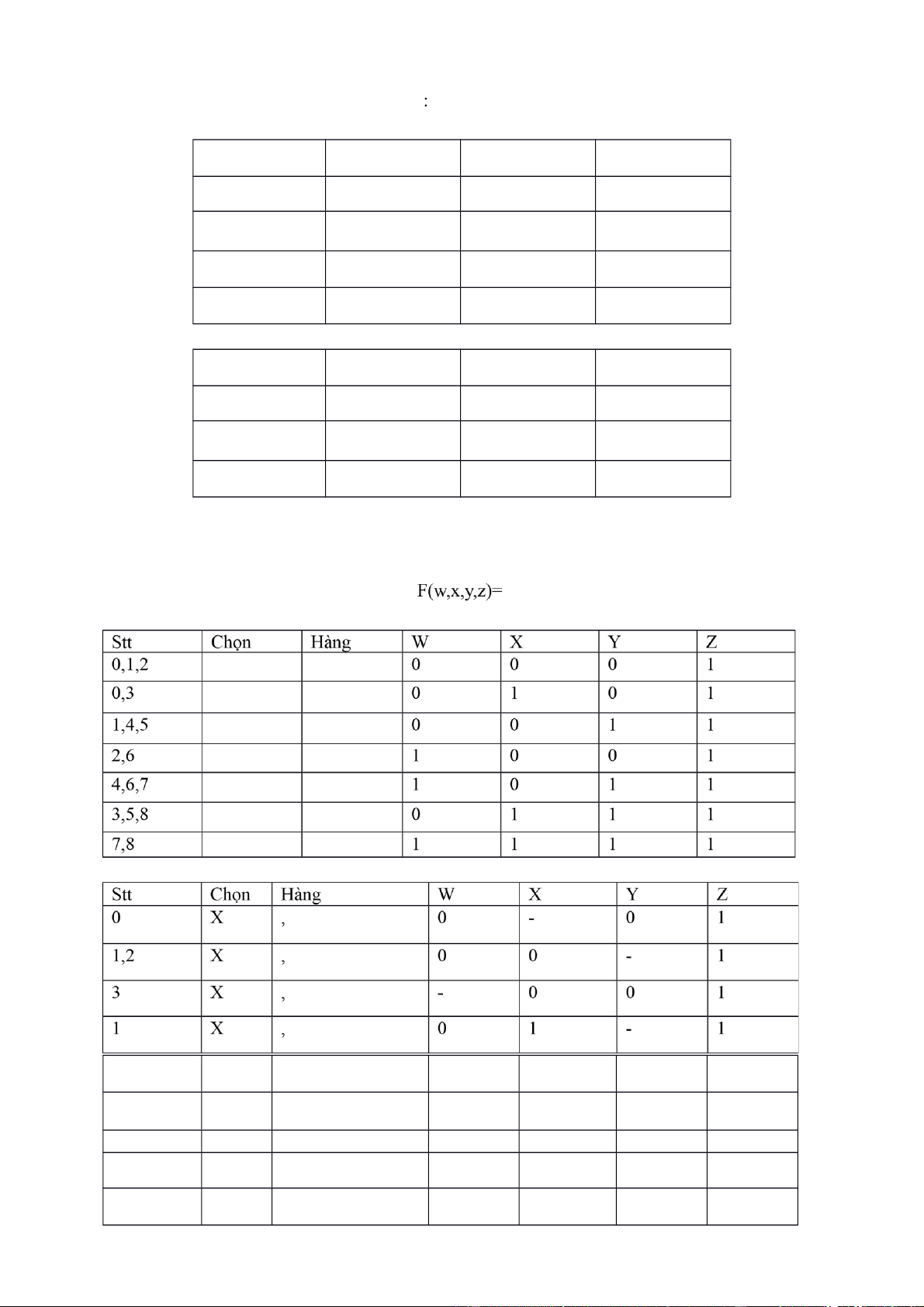
Bài 122: Rút gọn bắng Quine-McCuskey : 3 , 4 X , - 0 1 1 0 , 5 X , 0 - 1 1 2 X , 1 0 - 1 5 X , 1 - 1 1 4 X , - 1 1 1 lOMoAR cPSD| 40425501 Bài 123: Bảng kar(f)
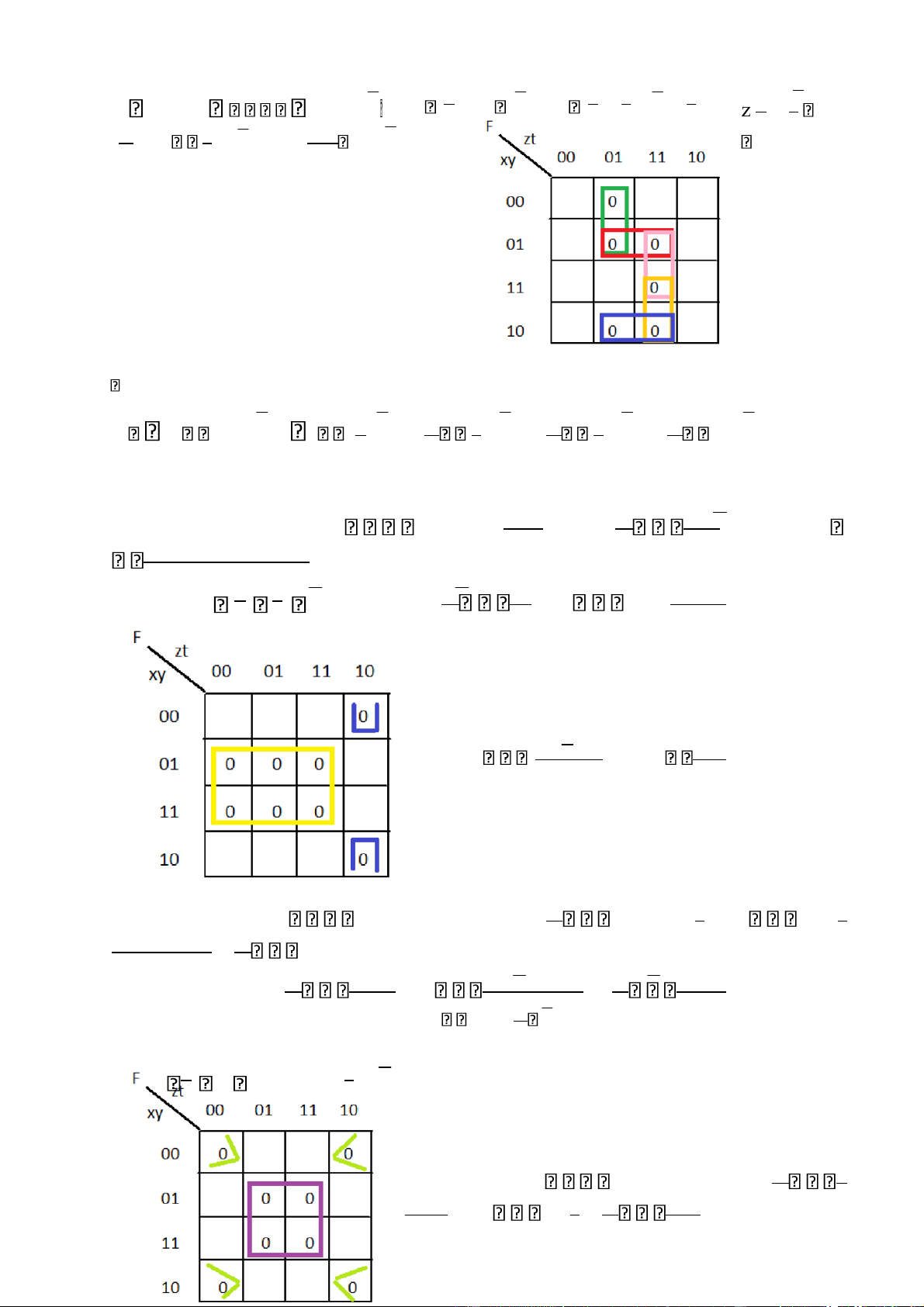
Công thức tối tiểu của f: lOMoAR cPSD| 40425501 Bài 124: Bảng kar(f) Các tế bào lớn là:
Công thức tối tiểu của f là : lOMoAR cPSD| 40425501 Bài 125: f(x,y,z,t) = Kar(f) Các tế bào lớn là :
Công thức tối tiểu của F là: Bài 126: f(x,y,z,t) = = lOMoAR cPSD| 40425501 Bảng kar (f) Các tế bào lớn là: lOMoAR cPSD| 40425501
Công thức tối tiểu của f là : Bài 127: f(x,y,z,t)= lOMoAR cPSD| 40425501 Bảng kar(f) Các tế bào lớn là:
Công thức tối tiểu của f là : lOMoAR cPSD| 40425501 Bài 128: f(x,y,z,t)= Bảng kar(f)
Các tế bào lớn là:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Bài 129:
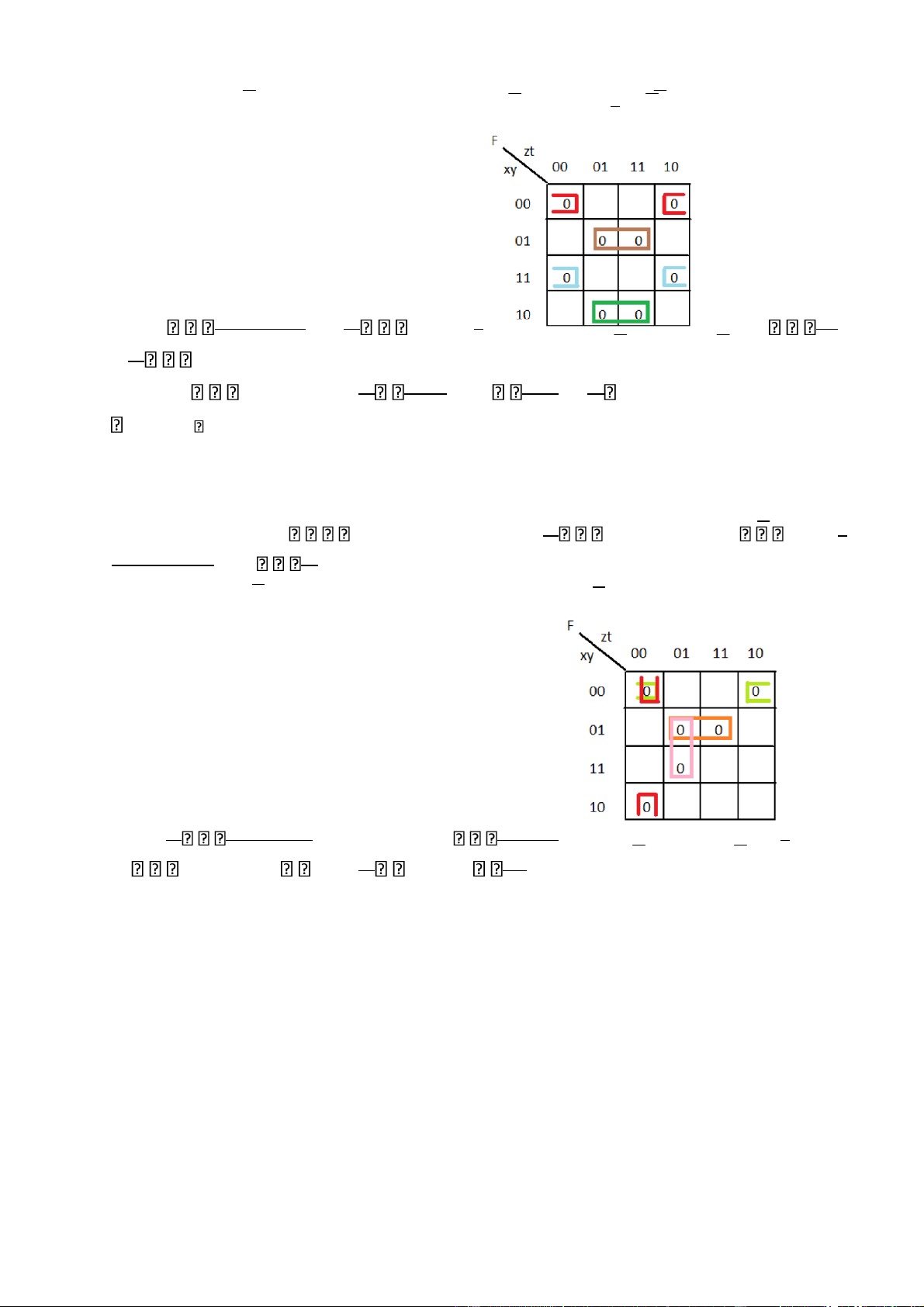
Công thức tối tiểu của f là : f(x,y,z) = = Bảng kar(f)
Các tế bào lớn là:
Công thức tối tiểu của f là : f(x,y,z,t)=
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Bài 130: Bảng kar(f)
Các tế bào lớn là:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Công thức tối tiểu của f là : (F1) (F2)
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)