Bài tập đại số tuyến tính | Học viện Kỹ thuận Quân sự

lOMoAR cPSD| 59256994
BÀI TẬP ĐẠI SỐ TUYẾN TÍNH : PHẦN SỐ PHỨC 1)
Đưa về dạng lượng giác các số phức a) b) c) . 2)
Tìm phần thực, phần ảo, căn bậc 3, bậc 4 của các số phức a) b) . 24 c) 1 3  i   d) ( 3i )  2  60 e)z  ( 2  2 )i 20 3)
Tìm căn bậc 2 của các số phức a) b) c) 4)
Tìm tất cả các số phức z thỏa mãn đẳng thức |z – 3| = |z + 2 + i|. Tìm biểu diễn
hình học của số phức đó. 5)
Tìm nghiệm dạng lượng giác của phương trình z6 + z5 + z4 + z3 + z2 + z= 0 6)
Biểu diễn hình học các số phức thỏa mãn a) 7)
Cho đa thức f(z) = z4 – 4z3 + 12z2 – 16z +32. Biết -2i là một nghiệm của đa thức.
Tìm nghiệm dưới dạng lượng giác của phương trình f(z) = 0 8)
Giải phương trình (z2  z)2 4(z2   z) 12 0 9)
Giải phương trình z6 + 2z3 + 2 = 0
10) Tìm các nghiệm dạng lượng giác của phương trình: x8 – 15x4 – 16 = 0.
11) Tìm các số phức z thỏa mãn: z6 = (-1+i)5(1+i) với i là đơn vị ảo.
12) Giải phương trình nghiệm phức a) b) c) d) e) f) lOMoAR cPSD| 59256994 g) h)
k) 𝑧3 + 3𝑧2 + 3𝑧 + 2 = 0
i) (𝑧 + 𝑖)4(1 − 𝑖) + 1 − √3𝑖 = 0 l)
𝑧3 − (2 + 𝑖)𝑧2 + (2 + 2𝑖)𝑧 − 2𝑖 = 0 m)
𝑧4 − (1 + 𝑖 + √3)𝑧2 + 𝑖 + √3 = 0.
Ma trận - Định thức - Hệ phương trình tuyến tính 1) Cho các ma trận .
a) Tính (−3𝐴) + 𝐵𝑇, 𝐵 − 2. 𝐴𝑇.
b) Cho 𝑓(𝑥) = 𝑥3 + 2𝑥2 − 3𝑥 + 2, tính 𝑓(𝐶).
c) Tính 𝐴. 𝐵và 𝐵. 𝐴.
2 1 n và tính (A)=2.I+A-3A2+A3. 2) Cho A=  . Tìm A 3 1
cosx  sinx n và (B)=2.I+B-2B2+B3. 3) Cho B=  . Tính B sinx cosx 4)
Cho ma trận 𝐴4𝑥4 thỏa mãn |𝐴| = 4. Tính |𝐴−1|và |4𝐴|. 5)
Cho ma trận 𝐴3𝑥3 thỏa mãn |𝐴| = 3. Tính |𝐴𝑇𝐴|, |𝐴3|và |3𝐴|.  a b c d    6)
Tính định thức của A2 với A= b a d c  c  d a b     d c b a  7)
Các ma trận sau có khả đảo không, nếu có, hãy tìm ma trận nghịch đảo bằng
phương pháp phần bù đại số lOMoAR cPSD| 59256994 a) . 8)
Tìm ma trận nghịch đảo bằng phương pháp Gauss-Jordan a) c) . 9) Cho ma trận
. Tìm 𝑎 để A khả nghịch. 10)
Tìm hạng của các ma trận sau : . 11)
Biện luận theo 𝑚 hạng của các ma trận sau : a) 12)
Giải các hệ phương trình 13)
Giải và biện luận hệ phương trình tuyến tính sau theo m :  x 2y 2 .mz  3  y 2 .mz  2 3x y 3z  3 2x  14)
Tìm điều kiện cần và đủ của các tham số m, n, t để hệ phương trình sau có nghiệm không tầm thường: lOMoAR cPSD| 59256994 2mx1 nx2 tx4 0  2mx 0 2 tx3  nx1 2mx  3 nx 4 0 tx nx 2mx 2 3 4 0  tx1  15)
Giải và biện luận hệ phương trình sau theo tham số a, b:  x1 3x2 x3 4x4 5  7x 2x 2x 8 2x 2 3 4 1 +(a+1)x 2b    x 4x2 3x3 4 1  16)
Giải và biện luận theo 𝑚 các hệ phương trình . 17)
Tìm hạng của ma trận theo a: a 1 1 1   a 1 1 1 
a. A=11 a1 1a 11 b. 1 a 1 a2 1 1 1 a 1 1 a a   18)
Tìm hạng của ma trận theo t t 1 1 1 3 t 1 2  t 1 1 2     a) 1 2 t
5 b. 11 1t 1t 11 c. 11 104 177 24 5 1 1 1 1 1 1 t 4 1 3 3 19)
Tính hạng của ma trận theo k lOMoAR cPSD| 59256994 1 k 1 2 1 1 1 1    
a) 2 1 k 5 b. 0 1 2 k 1 10 6 1 1 0 k 2 20)
Tìm điều kiện của 𝑎 và 𝑏 để hệ sau vô số nghiệm . (1a)x yz 1  21)
Giải và biện luận hệ x(1a)yz a  2 x y(1a)z a 22)
Tìm 𝑎 để hệ sau có nghiệm không tầm thường . KHÔNG GIAN VÉC TƠ
1.Trong không gian M2x2 các ma trận vuông cấp hai, cho tập F={ XM2:AX=}, trong đó:  1 2 A=  . 1 2
a. Chứng tỏ F là không gian con của M2x2.
b. Tìm dim(F) và một cơ sở của F. x  y z 0
2. 2. Cho F=u x y z, ,  3 :   x  y z 0 lOMoAR cPSD| 59256994
a. Chứng tỏ F là không gian con của R3.
b. Tìm một cơ sở của F.
3. Cho F=u x y z, ,  3 :x 2y 3z  0  x2y 3z  0
a. Chứng tỏ F là không gian con của R3.
b. Tìm một cơ sở của F. 
4.. Cho F=ux x1, 2,...,xn  3 :x x1    2 ... xn n 0  
x x1   2... 1 xn  0
a. Chứng tỏ F là không gian con của Rn.
b. Tìm một cơ sở và chiều của F.
5.. Trong không gian M2x2 các ma trận vuông cấp hai, cho tập  2 4 F={ XM2x2:AX= } Trong đó: A=  . 1 2
a. Chứng tỏ F là không gian con của M2x2.
b. Tìm dim(F) và một cơ sở của F.
6. Trong không gian M2x2 các ma trận vuông cấp hai, cho tập  1 2 F={ XM2x2:XA= } Trong đó: A=  . 1 2
a. Chứng tỏ F là không gian con của M2x2.
b. Tìm dim(F) và một cơ sở của F. lOMoAR cPSD| 59256994 x y z   3:1 1 1 0 
7. Cho F=u (x, y,z) R 0 1 0
a. Chứng tỏ F là một không gian của R3.
b. Biểu diễn hình học của F và tìm một cơ sở của F. x y z x y z 1 ; 0
8.. Cho F=u  (x, y,z)R  0 3 :1 11 1 0   1 1 0 1 0 1 
a. Chứng tỏ F là một không gian của R3.
b. Biểu diễn hình học của F và tìm một cơ sở của F.
9.Trong M2- không gian véc tơ các ma trận vuông cấp 2, cho tập hợp: E bao gồm các m n ma trận có dạng X   , với m, n, p  R n p
1/ Chứng minh rằng E là một không gian con của M2.
2/ Tìm một cơ sở và số chiều của E.  6 2
3/ Tìm tọa độ của B 2 8  theo cơ sở vừa tìm được ở phần 2/
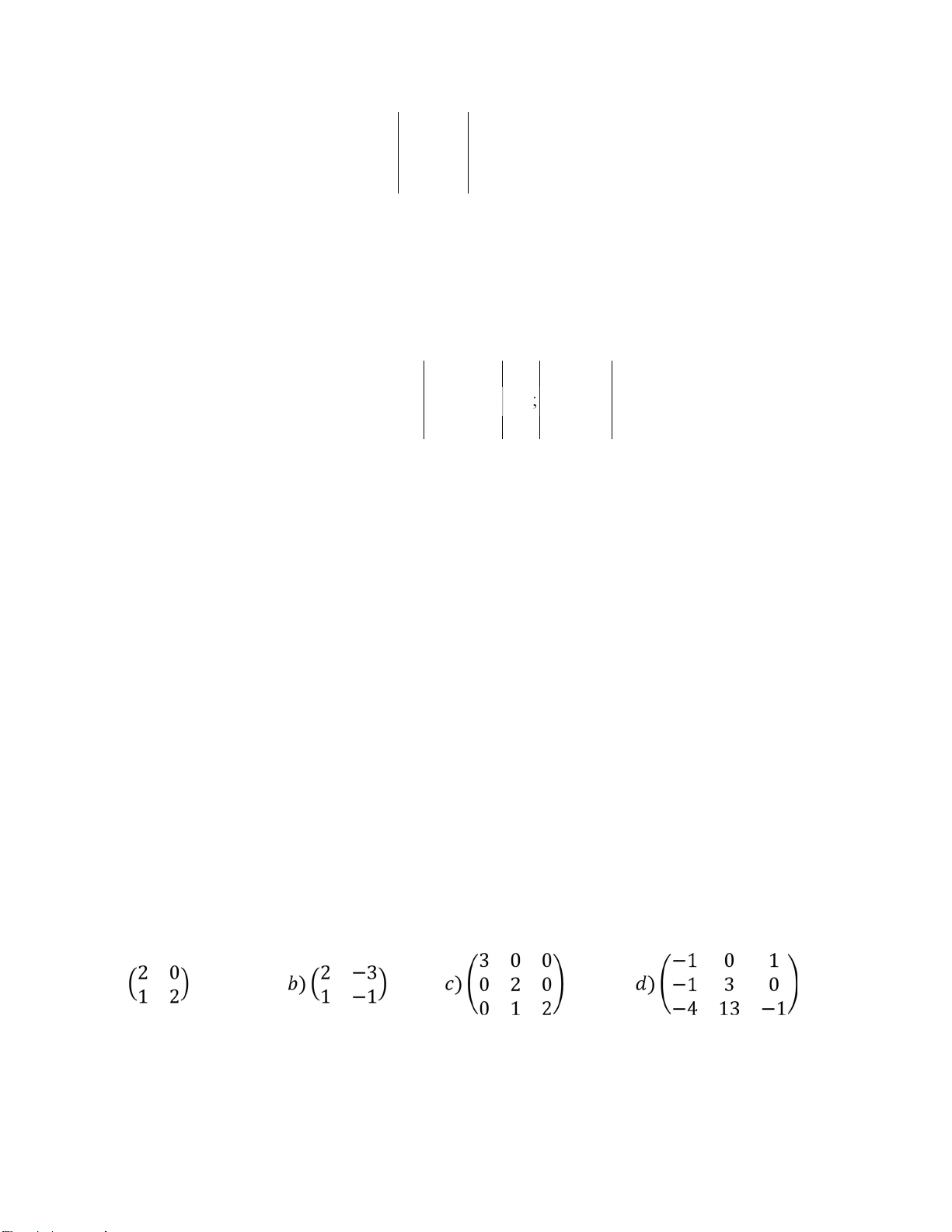
10. Chứng minh rằng các ma trận sau không chéo hoá được: a.
11.Chéo hoá các ma trận sau: lOMoAR cPSD| 59256994 a. A =
12. Tìm ma trận P làm chéo hoá A và xác định P−1AP a) A = b)A = 13.Cho A =
. CMR a)A chéo hoá được nếu (a − d)2 + 4bc > 0
b) A không chéo hoá được nếu (a − d)2 + 4bc < 0 14.Cho ma trận A =
Tìm ma trận khả nghịch T sao cho ma
trận B = T−1AT là ma trận đường chéo. ÁNH XẠ TUYẾN TÍNH
1.Gọi M2 là không gian các ma trận thực vuông cấp 2. Xét ánh xạ: f M: 2  M2 2 2 1 0
xác định bởi công thức: f(X) = AX + XB, trong đó A2 0 , B 2
1 .  1/ Chứng minh rằng f là toán tử tuyến tính.
2/ Tìm ma trận của f đối với cơ sở: S = {E1 , E2 , E3 , E4 }, với E1 10
00 , E2  00 10 , E3
10 00, E4  00 10 . 
2. Cho ánh xạ tuyến tính f: R3R2 có biểu thức: f(x,y,.z)=(2x+y+z,x-z)
a. Tìm ma trận của f trên cơ sở chính tắc của R3 và R2. 1 0 0 lOMoAR cPSD| 59256994      
b. Tìm ma trận của f trên cặp cơ sở: e1=0 e2=1 e3=0 R3
0 0 1
và 1=1 2=1 R2 0 1
c.Tìm dimImf, dimKerf, Kerf, Imf
3. Chứng tỏ các ánh xạ sau là ánh xạ tuyến tính, tìm ma trận của f trong cơ sở chính
tắc, biểu diễn f dưới dạng ma trận.
a. f(x,y,z)=(2x-y,x+3y-5z,y-z) b. f(x,y,z)=2x-3y+5z c. f(x,y)=(x+2y,2x-y,x+y)
d. f(x,y,z)=(x+2y-z,2x-y+4z,x+y)
e. f(x,y,z)=(x+2y-z,2x-y+z,x+y)
4.a. E=L[0,1]={x=x(t):x(t) hàm liên tục trên [0,1]}. Chứng tỏ: 1
f: ER: f(x)=  x(t)dt một ánh xạ tuyến tính. 0
b. Trên P3(t)}={x(t)= a0+a1t+a2t2+a3t3} tìm ma trận của ánh xạ tuyến tính f(x)= 1
 x(t)dt trên cơ sở I={1,t,t2,t3}. 0
c. Tìm dimImf, dimKerf, Kerf, Imf.
5. Chứng tỏ các ánh xạ
a. f(a+bt+ct2)=(a+b)+(a-c)t+(b+2c)t2
b. f(a+bt+ct2)=a+c+(b-a)(1+t)+(a+b-c)(1+t)2 là tự đồng cấu trên P2(t)={x(t)=a0+a1t+a2t2} lOMoAR cPSD| 59256994
Tìm ma trận của chúng trên cơ sở {1,t,t2} và trên cặp cơ sở I={1,t,t2} và W= {1,1+t,(1+t)2}.
6. Chứng tỏ các ánh xạ sau là ánh xạ tuyến tính, tìm ma trận của chúng trên các cặp cơ sở tương ứng.
a. f(a+bt)=a+b+(a-b)(1+t)+(a+2b)(1+t)2
b. f(a+bt+ct2+dt3)=a-d+(b-c)(1+t)+(a+b+c+d)(1+t)2
c. f(a+bt+ct2)=c+(a+b)t+(a+c)t2+(b+c)t3
d. f(a+bt)=a-b+(a+b)t+(2a-3b)t3
e. f(a+bt+ct2+dt3)=a+b+c+(b+c+d)t 7. Cho f : P  x y z 
3(t)={x(t)=a+bt+ct2+dt3} M2x3= A u v w    2+dt3)=ca db ac 
22db  xác định bởi: f(a+bt+ct 
Chứng tỏ f là ánh xạ tuyến tính. Tìm ma trận của f. Tìm dimImf, dimKerf, Kerf, Imf ?
8. Cho f: P2(t)={x(t)=a+bt+ct2} M2x3=A ux yv wz  b a  2b C
hứng tỏ f là ánh xạ tuyến xác định bởi: a
 tính, tìm ma trận của f, biểu  f(a+bt+ct2)=  a c c
diễn f dưới dạng ma trận.  2a
9. Cho f: M2x3=A ux yv
wz P3(t)={x(t)=a+bt+ct2}  lOMoAR cPSD| 59256994 xác định bởi:   f   x y u v z 
w  =x+y+z+(z+u)t+(u+v+w)t2 
Chứng tỏ f là ánh xạ tuyến tính, tìm ma trận của f. x y
10.Trên không gian M22 các ma trận cấp 2x2, với X=z u  , cho f(X)= 1 2 
 X . Tìm ma trận của f trên cơ sở chính tắc. 3 0
11. Cho f: M2x3=A xy z b M2x2=a  d  u v w c  xác định bởi: z x  y z u a. f y 
ux v w=z uv   w z u  v x  y b. f 
ux y w=z  yv   v w
Chứng tỏ f là ánh xạ tuyến tính, tìm ma trận của f.
12. Trong R2 chứng tỏ phép quay một góc  là một tự đồng cấu, tìm ma trận của nó. 13. Cho các ánh xạ:
f:R4R3 với f(x,y,z,u)=(x+y+u,x+y+z,y-z+u)
g:R3R2 với g(x,y,z)=(2x+z,x-y+z) tìm ma trận của gof. lOMoAR cPSD| 59256994
14. Ký hiệu Pn[x] là không gian véc tơ các đa thức một biến với hệ số thực có bậc
không quá n. Cho f là ánh xạ từ không gian véc tơ P3[x] vào không gian véc tơ
P4[x] xác định bởi quy tắc:
f(p) = (2x +1)p – (x2 – 1)p , với pP3 [x] và p , là đạo hàm của p
1/ Chứng minh rằng f là ánh xạ tuyến tính
2/ Tìm ma trận của f theo cặp cơ sở {1, x, x2 , x3 } trong P3[x] và cơ sở {1, x, x2 , x3 , x4} trong P4[x] 3/ Tìm Ker(f).
15. Cho f là ánh xạ từ không gian véc tơ thực R3 vào chính nó xác định bởi quy tắc:
f(x, y, z) = (x + 2z, z +2 y, y +2x).
1) Chứng minh rằng f là toán tử tuyến tính
2) Hãy cho biết véc tơ u = (2, 2, 2) có là véc tơ riêng của f không?
3) Viết ma trận của f theo cơ sở v1 = (1, 1, 1), v2 = (1, 1, 0), v3 = (1, 0, 0).
16. Cho f : P3[x]  P2 [x] là ánh xạ đạo hàm f(p) = p’ ,(p’ là đạo hàm của p).
1/ Chứng minh rằng f là ánh xạ tuyến tính .
2/ Tìm ma trận của f theo cơ sở S = {p1 = 3, p2 = 1 + x, p3 = x + x2 , p4 = x2 + 2x3 }
trong P3[x] và B = {q1 = 1, q2 = x, q3 = x2 } trong P2[x] . 3/ Tìm ker( f) .
17. Giả sử 𝑓: 𝐸 → 𝐹 là một ánh xạ tuyến tính. Cho A là một không gian con của E và
B là một không gian con của F. Chứng minh rằng:
1/ f(A) là một không gian con của F.
2/ f- 1(B) là một không gian con của E. a b
18. Cho M2x2={X=(xij)22} và ma trận: A=  và f :M2x2M2x2 xác định bởi: c d lOMoAR cPSD| 59256994 a. f(X)=AX b. f(X)=XA
Chứng minh rằng f là một tự đồng cấu trên M2x2 tìm điều kiện để f là một tự
đẳng cấu. Tìm ma trận của f trên cơ sở:
e1=1 0 e2=0 1 e3=0 0 e4=0 0 0 0 0 0 1 0 0 1
19. Ánh xạ f :R3  R2 được xác định như sau :
f(x,y,z) = (x + y - z , x + y + z +m) (m là tham số)
a. Xác định m để f là ánh xạ tuyến tính .
b. Với m = 0, tìm ma trận của f khi cơ sở của R3 là u1 = (-1;1;1) , u2 = (1 ;1 ;1) , u3 = (1 ;1
;1) và cơ sở của R2 là : v1 = (-1;1) và v2 = (1;1)
20. Cho các ánh xạ tuyến tính:
f: R4R3 với f(x,y,z,u)=(x+y+z,x+y+u,y+z+u) g:
R3R2 với g(x,y,z)=(x-y,y+z)
Tìm một cơ sở của Im(f)Ker(g).
CHƯƠNG VII: DẠNG SONG TUYẾN TÍNH VÀ DẠNG TOÀN PHƯƠNG. KHÔNG GIAN EUCLID 1.
Xét không gian C[0, π] là tập các hàm số liên tục trên [0, π] với tích vô hướng: =
và xét các hàm số fn(x) = cosnx, n = 0, 1, 2, ... Chứng
minh rằng fk và fl trực giao với nhau nếu k ≠ l 2.
Chứng minh rằng họ sau là một họ trực giao trong ℝ4 với tích vô hướng Euclid
u1 = (1, 0, 0, 1), u2 = (-1, 0, 2, 1), u3 = (2, 3, 2, -2), u4 = (-1, 2, -1, 1) 3.
Áp dụng trực giao hoá Gram – Schmidt để biến cơ sở sau đây thành trực chuẩn: a. u1 = (1, -3), u2 = (2, 2) b. u1 = (1, 0), u2 = (3, -5)
c. u1 = (1, 1, 1), u2 = (-1, 1, 0), u3 = (1, 2, 1) lOMoAR cPSD| 59256994
d. u1 = (1, 0, 1), u2 = (3, 7, -2), u3 = (0, 4, 1) 4.
Trong ℝ3 xét tích vô hướng Euclid. Hãy tìm một cơ sở trực chuẩn trong không
gian con sinh bởi các vectơ (0, 1, 2) và (-1, 0, 1). 5.
Trong không gian ℝ3 xét tích vô hướng = u1v1 + 2u2v2 + 3u3v3. Hãy áp
dụng trực giao hoá Gram – Schmidt để biến:
x1 = (1, 1, 1), x2 = (1, 1, 0), x3 = (1, 0, 0) thành một cơ sở trực chuẩn. 6.
Dùng phương pháp Lagrange đưa các dạng toàn phương sau về dạng chính tắc:
a. x12 + x22 + 3x32 + 4x1x2 + 2x1x3 + 2x2x3
b. x12 - 2x22 + x32 + 2x1x2 + 4x1x3 + 2x2x3
c. x12 - 3x32 - 2x1x2 + 2x1x3 - 6x2x3 7.
Tìm phép biến đổi tuyến tính để đưa mỗi dạng toàn phương dưới đây về dạng
chính tắc và cho biết dạng chính tắc đó:
a. x12 + 5x22 - 4x32 + 2x1x2 - 4x1x3
b. 4x12 + x22 + x32 - 4x1x2 + 4x1x3 - 3x2x3 c. x1x2 + x1x3 + x2x3
d. 2x12 + 18x22 + 8x32 - 12x1x2 + 8x1x3 - 27x2x3
e. −12x12 - 3x22 - 12x32 + 12x1x2 - 24x1x3 + 8x2x3 8.
Nhận dạng và vẽ đường bậc hai 5x2  4xy 8y2 8x 14y 5  0 9.
Trong không gian véc tơ thực R3 cho dạng toàn phương: Q(x, x) = 2x 2 2 2
1 – 2x1x3 + 2x2 – 2x2x3 + 3x3 . 1/ Dùng phép biến đổi trực giao
đưa dạng toàn phương trên về dạng chính tắc. 2/ Nhận dạng mặt bậc hai 4x 2 1 – 4x 2 2
1x3 + 4x2 – 4x2x3 + 6x3 = 50