Bài tập đọc kết quả SPSS: Thống kê mô tả và hồi quy tuyến tính môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

Một số dạng bài tập đọc kết quả SPSS
1. THỐNG KÊ MÔ TẢ VÀ ĐIỀU TRA CHỌN MẪU
Có số liệu ĐTCM về NSLĐ của công nhân trong 1 DN như sau: Statistics NSLD K  ý =hiệu   Cỡ mẫu Tên gọi Valid 100  N Giá trị khuyết thiếu Missing 0 
 Sai số bình quân chọn mẫu Mean 7.1600  = Trung bình √ Std. Error of Mean .32641 
(Sai số chuẩn của trung bình) Median 6.0000 Trung vị Me Mode 4.00 Mốt Mo Std. Deviation 3.26410 Độ lệch chuẩn S Variance 10.654 Phương sai S 2 Range 16.40 ế R Khoảng bi n thiên Minimum 3.60 GT nhỏ nhất (x ) min Maximum 20.00 Tổng lượng biến GT lớn nhất  =  (x   ) max Sum 716.00  
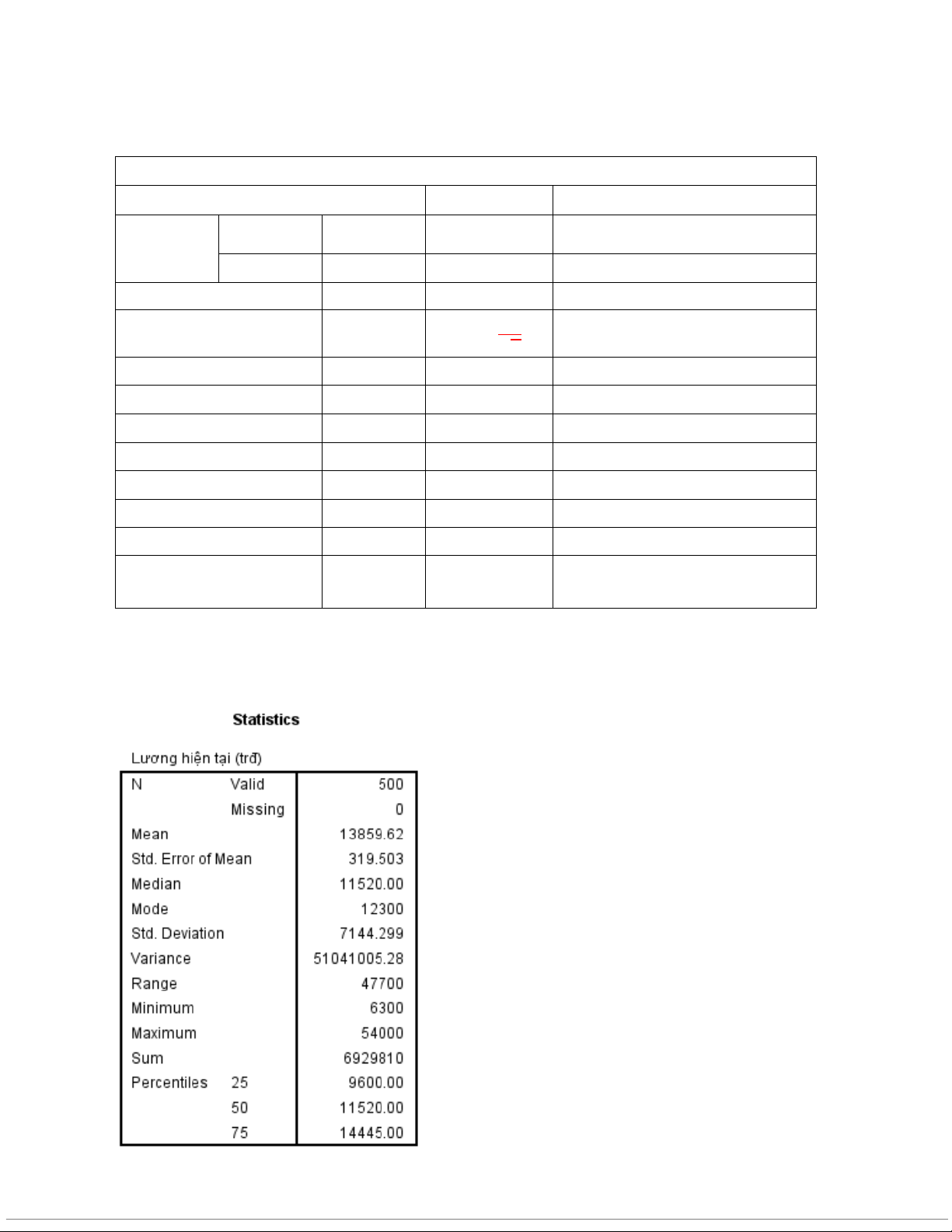
Ví dụ 1: Trong 1 doanh nghiệp, để có thông tin tiền lương người ta tiến hành ch n 500 nhâ ọ n viên
để tiến hành điều tra, sử dụng thống kê mô tả ằ
b ng SPSS có kết quả ở ả b ng sau: Yêu cầu:
1. Hãy xác định mức lương phổ biến của công nhân trong số người được điều tra. Mo = 12300(ngđ)
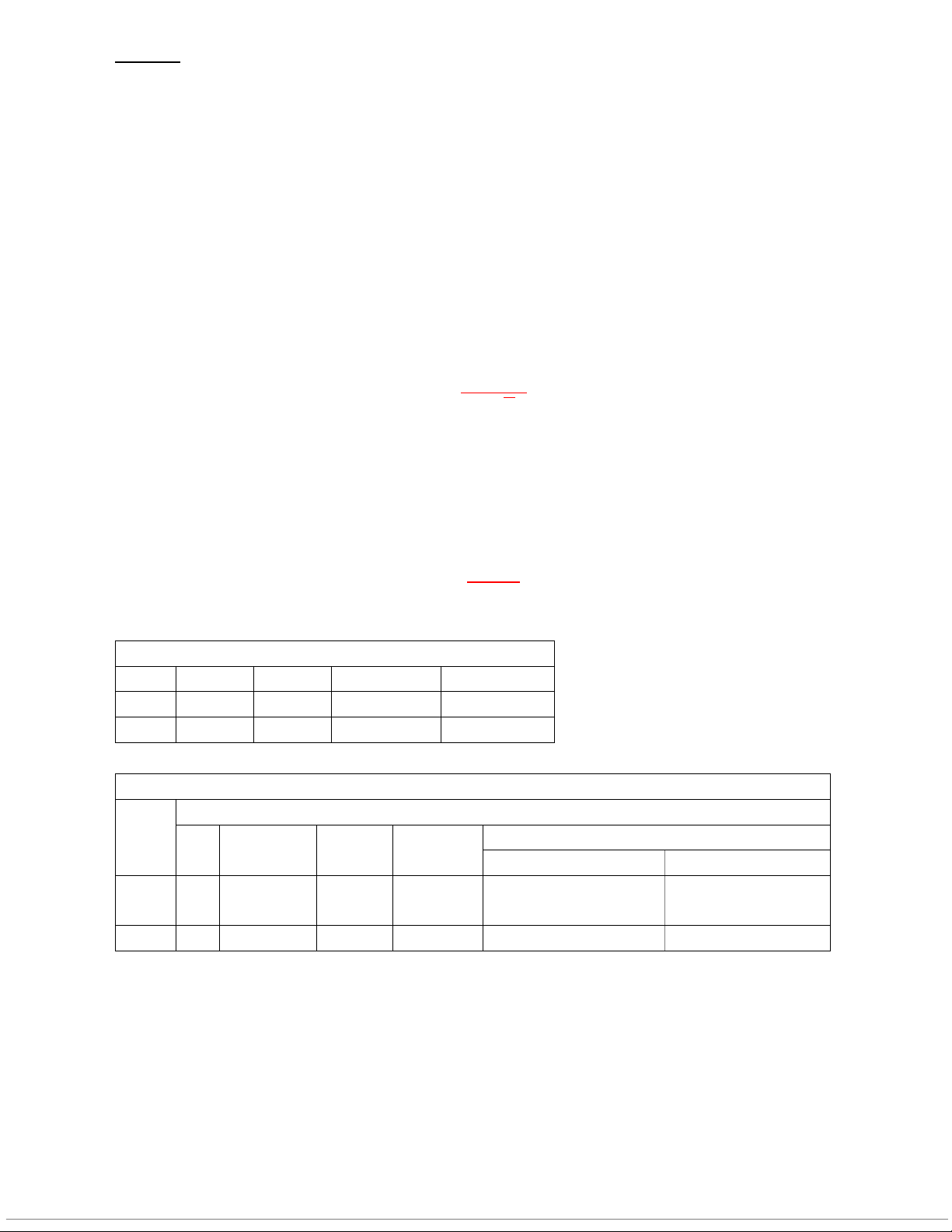
2. Với độ tin cậy 95% hãy xác định tiền lương hiện tại bình quân của công nhân toàn doanh nghiệp.  −  
/ .  ≤  ≤  +  / . 
3. Có ý kiến cho rằng, tiền lương hiện tại bình quân của nhân viên lớn hơn 12.000 (ngđ), hãy
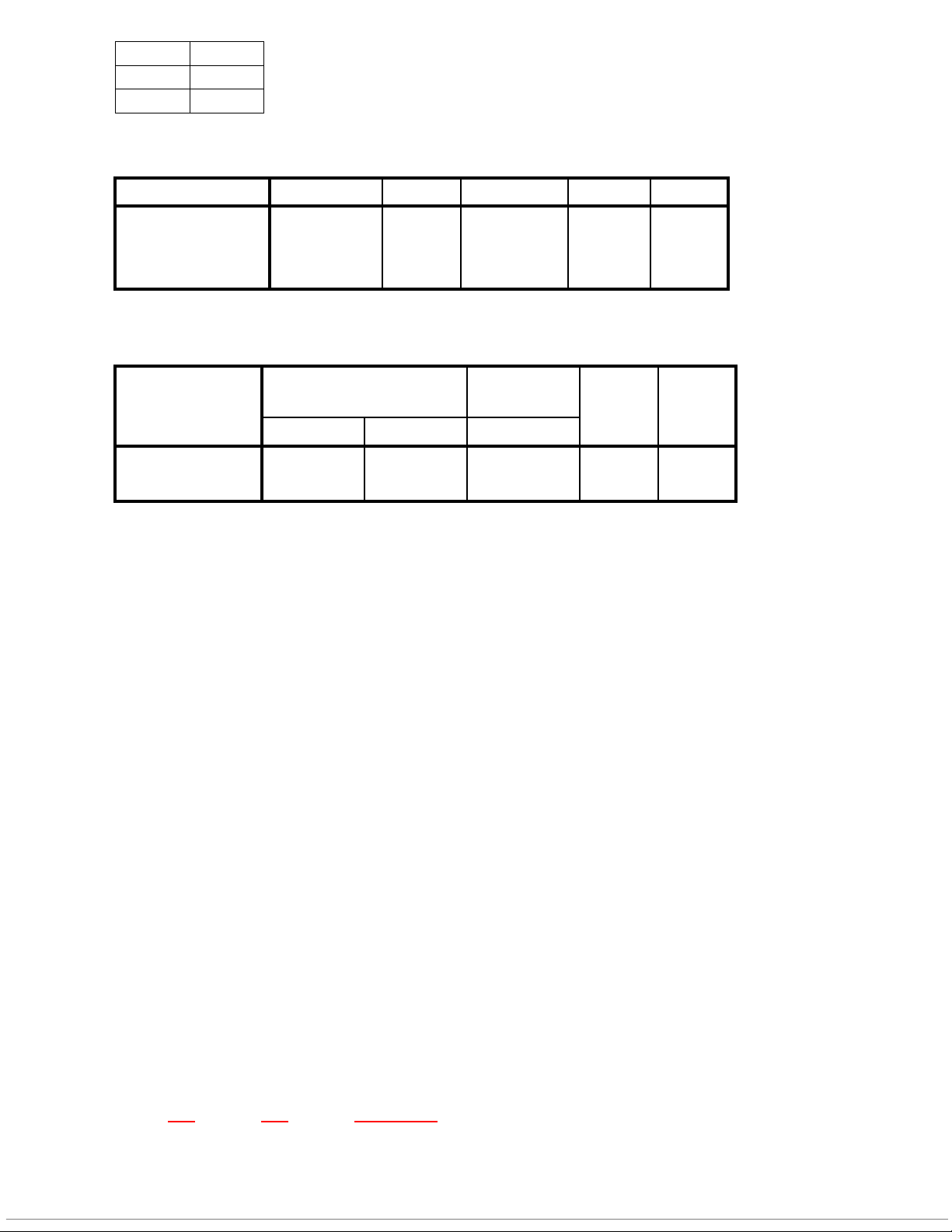
đưa ra kết luận với mức ý nghĩa 5%? :  ≤ 12000 : > 12000  = ( −  $) /√
Bác bỏ H0 khi Tqs > tα(n-1)
4. Giả sử năm tới người ta muốn điều tra để suy rộng tiền lương hiện tại bình quân, với xác suất
là 95%, phạm vi sai số chọn mẫu không vượt quá 5000 (ngđ), hãy xác định số nhân viên cần điều tra.  = &/ ' 
Ví dụ 2: Có kết qu S ả PSS như sau: One-Sample Statistics N Mean Std. Deviation Std. Error Mean  S  NSLD 70 355.00 203.511 24.324 One-Sample Test Test Value = $ t df Sig. (2- Mean
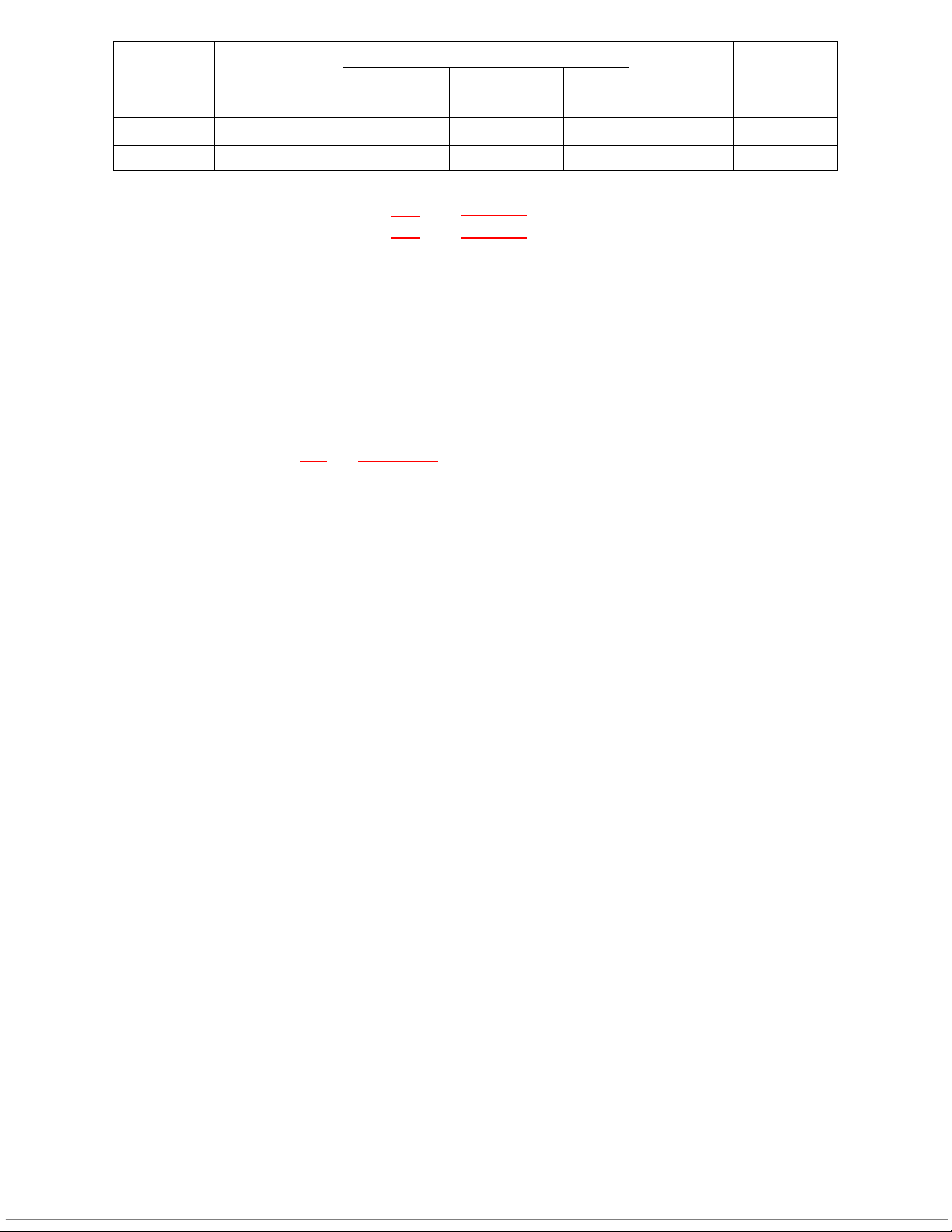
95% Confidence Interval of the Difference tailed) Difference Lower Upper Bậc tự do của +−, +−, Ký hiệu P-value  − .- .- $
( − $) − () /* ./ ( − $) + () /* ./ kiểm định NSLD .206 69 .838 5.000 -43.53 53.53 Giá trị c n k ầ
iểm định (Test Value = $) bằng bao nhiêu?: 350
2. HỒI QUY TƯƠNG QUAN Kết quả c a
ủ SPSS và giải thích các ký hiệu: Model R R Square Adjusted R Square
Std. Error of the Estimate Ký hiệu/CTT R (hoặc r) = √0  R2 = SSR/SST R2 điều chỉnh SE của mô hình ANOVAa Model Sum of Squares df Mean Square F Sig. Ký hiệu/CTT SS Bậc tự do MS Fqs P-value 0 1 = .000 Regression SSR 1 MSR=SSR/1 2 b  − 2 1 Residual SSE 12 MSE=SSE/12 Total SST 13 Tổng số quan sát: n = 14 a. Dependent Variable: DT
b. Predictors: (Constant), CPCL Coefficientsa Model Unstandardized Standardized t Sig. Coefficients Coefficients B Std. Error Beta Ký hiệu/CTT bj SE bj chuẩn hóa tqs P-value 34 = 5$ 46(5 (Constant) b0 SEb0 $) .000 5 34 =  46(5 CPCL b1 SEb1 b1 chuẩn hóa ) .000 a. Dependent Variable: DT
Ví dụ: Có số liệu về chi phí chất lượng và doanh thu của một doanh nghiệp qua các năm như sau (trđ): CPCL DT 25 500 43 536 66 580 84 618 100 650 118 690 140 728 158 760 180 800 198 836 222 870 240 902 260 940 278 980
Với số liệu trên ta có bảng kết quả SPSS dưới đây: ANOVAa Model Sum of Squares df Mean Square F Sig. Regression 1 303951.735 1 Residual 387.979 12 32.332 Total 304339.714 13 a. Dependent Variable: DT
b. Predictors: (Constant), CPCL Coefficientsa Model Unstandardized Coefficients Standardized t Sig. Coefficients B Std. Error Beta (Constant) 460.389 3.279 1 CPCL 1.868 .019 .999 a. Dependent Variable: DT Yêu cầu:
1. Viết phương trình hồi quy tuyến tính phản ánh ảnh hưởng của chi phí chất lượng đến doanh thu.
2. Xác định chiều hướng và mức độ chặt chẽ của mối liên hệ giữa chi phí chất lượng và doanh thu
3. Với độ tin cậy 95% thì khi chi phí chất lượng tăng lên 1 trđ thì doanh thu thay đổi như thế nào
4. Sự thay đổi của doanh thu do chi phí chất lượng quyết định bao nhiêu %? Với độ
tin cậy 95% mô hình có ý nghĩa không.
5. Có ý kiến cho rằng chi phí chất lượng không ảnh hưởng đến doanh thu, hãy đưa
ra kết luận với mức ý nghĩa 5%.
1. Viết phương trình hồi quy tuyến tính phản ánh ảnh hưởng của chi phí chất lượng đến doanh thu: 78 = 460.389 + 1.868x @
2. Xác định chiều hướng và mức độ chặt chẽ của mối liên hệ giữa chi phí chất lượng và doanh thu:
Chiều hướng: căn cứ vào b1 hoặc r để đưa ra kết luận.
Mức độ chặt chẽ dựa vào r để đưa ra kết luận
0 = AAB = 1 − AAD = 1 − EFG.HGH =0.998725 AAC AAC E$IEEH.GI r = 0.999362
KL: Mối liên hệ giữa CPCL và DT là MLH tương quan thuận và rất chặt chẽ
3. Với độ tin cậy 95% thì khi chi phí chất lượng tăng lên 1 trđ thì doanh thu thay đổi như
thế nào –> Ước lượng hệ số hồi quy: 5 (−2) (−2)
J − K 2⁄ 46(5J ) ≤ M ≤ 5 46(5 J J + K 2 ⁄ J) b1 = 1.868   ∝/ = $.$O = 2.179 SEb1 = .019
1.868 − 2.179 ∗ 0.019 ≤ M  ≤ 1.868 + 2.179 ∗ 0.019
1.826599 ≤ M  ≤ 1.909401
4. Sự thay đổi của doanh thu do chi phí chất lượng quyết định bao nhiêu %? Với độ tin
cậy 95% mô hình có ý nghĩa không?
Tính 0  = AAB = 1 − AAD = 1 − EFG.HGH =0.998725 (99.8725%) AAC AAC E$IEEH.GI
Kiểm định ý nghĩa của mô hình: S : 02 = 0 1 : 02 > 0 1  TU = AAB VVW = BZ( ) = 0.998725∗12 =9399.765 (BZ) (0.998725) XYZ Fα(1.n-2) = 4.75 F ỏ
qs > Fα(1.n-2) -> Bác b GT Ho
5. Có ý kiến cho rằng chi phí chất lượng không ảnh hưởng đến doanh thu, hãy đưa ra
kết luận với mức ý nghĩa 5%.
Kiểm định hệ số hồi quy: $:M = 0 :M ≠ 0 TU = 51 = 1.868 = 98.31579 46(51 ) 0.019   ∝/ = $.$O = 2.179
Vậy T qs > t α/2 ,(n-2) -> Bác bỏ GT Ho
3. DÃY SỐ THỜI GIAN Bảng kết quả SPSS
Model Summary and Parameter Estimates Dependent Variable: DT Equation Model Summary Parameter Estimates R Square F df1 df2 Sig. Constant b1 b2 Ký hiệu R 2 F ệ ố qs Bậc tự do P-value Các h s b0, b1, b2 Linear (T.tính) .992 1292.961 1 10 .000 127.030 103.175 Inverse (HPB) .534 11.447 1 10 .007 1065.641 -1036.246 Quadratic (PRB) .998 2433.715 2 9 .000 205.545 69.525 2.588
Ví dụ: Có số liệu doanh thu của 1 doanh nghiệp từ quý 1/2017 đến quý 4/2019 như sau: Năm Quý Doanh thu 2017 1 300 2 350 3 406 4 510 2018 1 630 2 740 3 812 4 928 2019 1 1040 2 1160 3 1296 4 1400
Với số liệu trên ta có bảng kết quả SPSS dưới đây: Equation
(78 − 7\) Parameter Estimates Constant b1 b2 Linear 1522241.371 127.030 103.175 Inverse 818759.433 1065.641 -1036.246 Quadratic 1531183.470 205.545 69.525 2.588
Biết ∑(7 − 7\) = 1534014.667 Yêu cầu:
1. Xác định sai số của từng mô hình hàm xu thế
2. Lựa chọn và viết phương trình hàm xu thế tốt nhất biểu diễn doanh thu qua thời gian
3. Dự đoán doanh thu của doanh nghiệp vào quý 1/2020 dựa vào HXT tốt nhất
4. Hãy xác định độ phù hợp của mô hình HXT tuyến tính (tính hệ số xác định của HXT tuyến tính) Phần tính toán thêm: Equation (78 − 7\) Parameter Estimates SSE SE Constant b1 b2 Linear 1522241.371 127.030 103.175 11773.296 76.72449 Inverse 818759.433 1065.641 -1036.246 715255.234 598.0197 Quadratic 1531183.470 205.545 69.525 2.588 2831.197 30.72023
1. Sai số của các mô hình 2 = ^ AAD = ^ ∑(`a`8a)Z _ _
2. Lựa chọn và viết phương trình hàm xu thế tốt nhất biểu diễn doanh thu qua thời gian
78 = 205.545 + 69.525 + 2.588t 2
3. Dự đoán doanh thu của doanh nghiệp vào quý 1/2020 dựa vào HXT tốt nhất
78 = 205.545 + 69.525 ∗ 13 + 2.588 ∗ 13 2 = 1546.742
4. Độ phù hợp: 02 = 0 = 1522241.371 =0.992325  1534014.667