Bài tập giao thoa - Nghiên cứu hiện tượng giao thoa ánh sáng trong thí nghiệm môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Bài t p giao thoa.
Bài 1. Trong thí nghiệm Young , khoảng cách giữa hai khe hẹp là a 1 mm , khoảng
cách từ màn quan sát đến mặt phẳng chứa hai khe là D = 2,5 m. Hệ đặt trong không khí.
Biết nguồn sáng sử dụng trong thí nghiệm phát ánh đơn sắc có bước sóng . Trên đo n
AB trên màng quan sát có độ dài AB = 6,4 mm , người ta
quan sát được 5 vân sáng ( t i
A và B cũng là các vân sáng ). a. Tính bước sóng .
b. Tìm sai số mắc phải khi đo bước sóng , biết rằng sai số trong phép đo khoảng
cách giữa hai khe và bề rộng đo n AB đều là 0,05 mm. Giải . D ai
a. Bước sóng μ từ công thức khoảng vân μ i a D
Khoảng vân i . từ đk AB = 6,4 mm có 5 vân sáng 4 AB i 6 , 1 mm 6 , 0 4 m . b. Sai số μ ai a i D Do + + D a i D với
là sai số của bước sóng
i , a và D là sai số trong các phép đo khoảng cách 0,037 m .
Bài 2. Trong thí nghiệm giao thoa khe Young , khoảng cách giữa hai khe hẹp là a
1 mm , khoảng cách từ hai khe đến màn quan sát D 2m , khoảng cách từ nguồn S
tới hai khe hẹp là d 0,5 m. Nguồn sáng S nằm trên mặt phẳng trung trực của hai
khe và phát ánh sáng đơn sắc có bước sóng 5 , 0 m.
a. Tính độ dịch chuy n của hệ vân nếu đặt bản mỏng có độ dày e 10 m , chiết suất n 5 ,
1 trước một trong hai khe sáng .
b. Cần dịch chuy n nguồn sáng S một đo n bằng bao nhiêu và theo chiều nào trên
phương vuông góc với mặt phẳng trung trực của hai khe đ đưa hệ vân về vị trí ban đầu . Giải μ a/ Ta có: Hiệu quang lộ d r r r e ne r (r r ) ( e n 1) ' ax 2 1 2 1 2 1 mà rr D 21 ax d (n 1)e D ax n e k D (n 1)eD Xét vân sáng => dk => ( 1) =>xk D aa sáng D n ( 1)eD Xét vân tối => dk (2 1) 2 => xkaa (2 1) 2 toi
Độ dịch chuy n của hệ vânμ
y x sang saudatban x sang truocdatban D n ( 1 e ) D D n ( 1)eD = kk <0 a a a a Hệ vân dịch chuy n về t b phía có đặ ản.
Bài này có 1 lưu ý là: “ Khi đặt bản mỏng thì khoảng vân i không thay đổi” b/
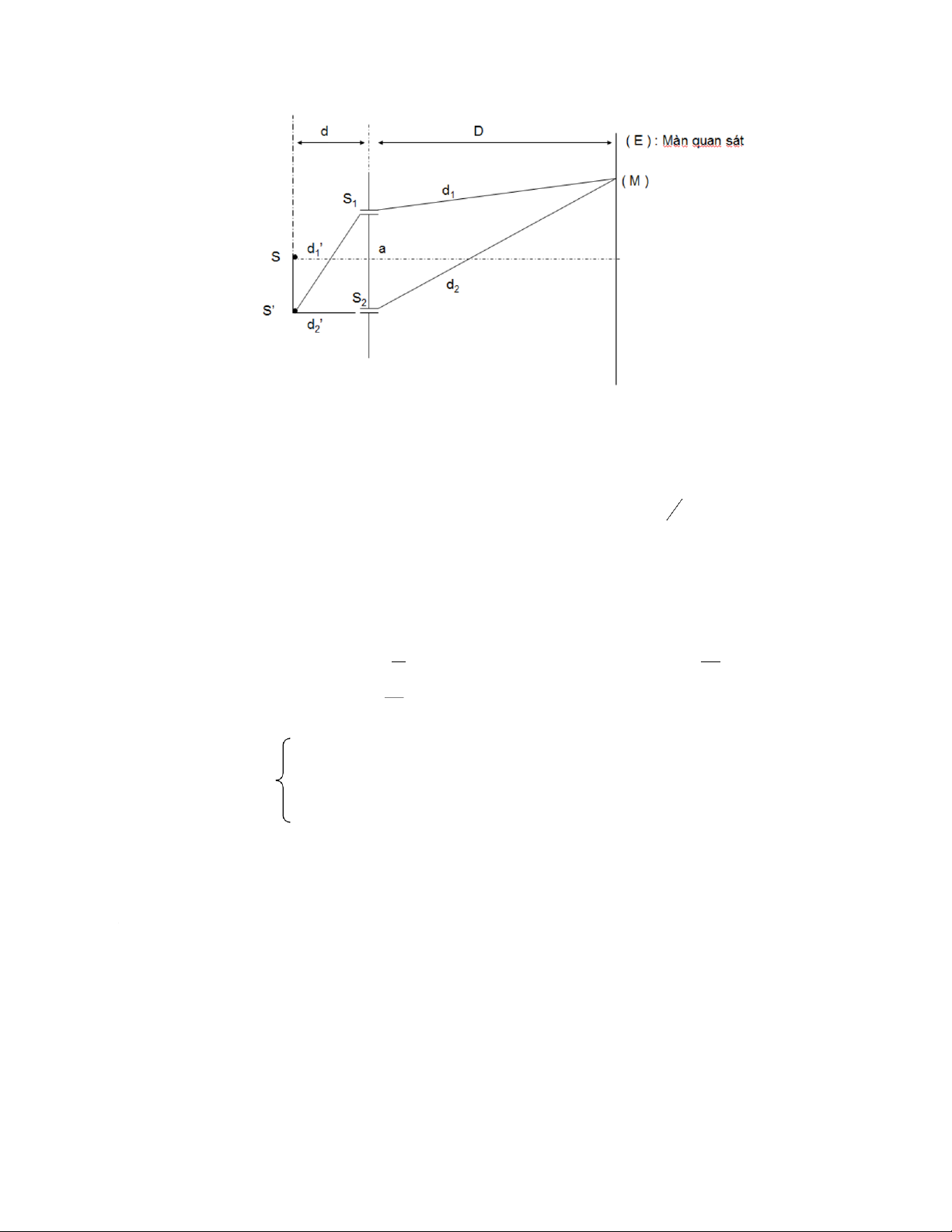
Khi nguồn sáng S dịch chuy n một đo n h ax d1 ậ d2 D a h . d1’ ậ d2’
(d là khoảng cách từ nguồn phát tới khe) d
Hiệu quang trình ( quang lộ ) ax ah
d1 + d1’ ậ ( d2 + d2’ ) ( d1 ậ d2 ) + ( d1’ ậ d2’ ) D d aX ah aX ah T i vân trung tâm μ 00 k k k D d D d ah aX dX kd 00 kh d D D a dX
Xét vân sáng trung tâm: k=0 => 0 hD
Theo câu a, ta có độ dịch chuy n <0, => h<0 => nguồn sáng sẽ dịch về phía có đặt bản.
Bài 3. Trong thí nghiệm giao thoa khe Young , hai khe nằm cách nhau a 1 mm , và
chiếu bằng ánh sáng đơn sắc có bước sóng 6 , 0
m . Màn quan sát cách mặt phẳng hai khe D 2 m .
a. Trên đo n thẳng có các đầu mút nằm
cách vân trung tâm từ 3 mm đến 7 mm , ta
quan sát được những vân giao thoa nào ?
b. Nếu thí nghiệm trên được tiến hành trong b nước có chiết suất 4 n thì kết 3
quả thay đổi như thế nào ? Giải . a. Khoảng vân i 1 m ,2 m Vân sáng: 3ki 7 2,5 k 5,8 (với k=1,2,3…)
số vân sáng μ 3 ( b c 3,4,5 ) Vân tốiμ 3 ( k 0.5i) 7 2,5 k 0.5 5,8 3 k 6.3 (với k=1,2,3…) Số vân tối μ 4 ( b c 3,4,5,6 ) D b. Khi đặt trong nước , 0n
=>bước sóng giảm n lần khoảng vân i ( i ) a D cũng giảm n lần i’ i’ m 9 , 0 m. n a . Vansang: 3,3 k 7,7 Vantoi: 3,8 k 8.2
Số vân sáng μ 4 ( 4,5,6,7 )
Số vân tối μ 5 ( 4,5,6,7,8 )
Bài 4. Trong thí nghiệm Young có khoảng cách giữa hai khe hẹp S1S2 a 1 mm,
khoảng cách từ hai khe đến màn quan sát D 2 m . Nguồn S phát ánh sáng trắng và
vân trung tâm nằm t i O . Đặt bản mỏng bề dày e16 mm trước khe S1. Bản có chiết suất n 4 , 1 .
a. Tính độ dịch chuy n của vân trung tâm.
b. Có những vân sáng và vân tối nào nằm ở vị trí vân trung tâm cũ và mới . Giải.
a. Tương tự bài ( 2 ) , tọa độ vân trung tâm sau khi đặt bản mặt ( ứng với độ dịch chuy n của hệ vân ) μ e(n 16 ) 1 D |X0| mm. a
b. Gọi k là b c của vân sáng e(n ) 1 D D X0 k. a a e(n )
1 ; với ánh sáng trắng 4, 0 m 7 , 0 6 m. k 10 5 , 3 k 20
có 10 vân sáng ứng với k 11,12,…,20. e( 1 n ) D (2 ' 1) 2 D
Gọi k’ là b c vân tối μ X0 k aa
Tương tự với ánh sáng trắng
=> có λ vân tối ứng với k=12,13,…,20.
Bài 5 μ trên đường đi của chùm sáng phát ra từ một khe của thí nghiệm young đặt ống
thủy tinh hình trụ dài e=2cm. Lúc đầu trong ống chứa không khí chiết suất n=1,0007276.
Nếu thay không khí bằng clo thì thấy hệ vân dịch chuy n một đo n bằng 20 lần khoảng vân. Toàn b
ộ thí nghiệm thực hiện trong điều kiện nhiệt độ không đ i. ổ Ánh sáng phát ra
từ nguồn sáng đơn sắc chiếu vào các khe có bước sóng , xác định chiết suất khí clo. Giải μ
Khi ống chứa không khí thì hệ vân dịch chuy n một đo n Khi ống chứa khí clo Theo đề μ
Bài 6 ( tham khảo thêm 1.22 sách Lương Duyên Bình)
Một màng nước xà phòng có chiết suất n=1,33 đặt thẳng đứng. Do trọng lực, nước xà
phòng dồn xuống dưới nên ta có th coi màng có d ng hình nêm. Quan sát vân giao
thoa của ánh sáng phản chiếu có bước sóng
0.48 m , người ta thấy vân tối thứ 6
cách giao tuyến B của nêm một đo n 1,2cm. Biết hướng quan sát vuông góc với mặt nêm.
a Tính góc nghiêng của nêm.
b Xác định vị trí vân sáng đầu tiên. Giải μ a)
Xét đi m M cách B một đo n x=BM, bề dày nêm t d xtg i M là x .. Hiệu quang lộμ d 2nd 2 .x n 22
T i vị trí vân tối μ dk (2 1) 2 =>2xnα = k + =(k+1) = k '
Vân tối đầu tiên là vân tối ở B ứng với k’=0. Vân tối thứ 6 ứng với k=5.
=>α = k /(2nx) ( với k=5 và x=1.2 cm) b)
Độ dày của màng đ có giao thoa vân sángμ d 2nd 2 .x n k 22 ( 0 k .5) xn 2
=>Vân sáng đầu tiên (k=0)μ x=0,12 cm
( Từ bài này có th tính được khoảng cách giữa 2 vân sáng liên tiếp )
Khoảng cách giữa 2 vân sáng liên tiếpμ (2 0.5) (1 0.5) i x x n n n 21 2 2 2 Bài 7:
Chiếu 1 chùm tia sáng có bước sóng vào
một nêm thủy tinh có chiết suất n=1,51. Biết số vân giao thoa trên 1cm là 8. a. Tính góc nghiêng của nêm
b. Tìm độ đơn sắc (tính bằng ) của chùm tia nếu các vân giao thoa biến mất từ đi m M cách nêm l=2,5cm. Giảiμ a. Khoảng vân i = 10/7
Từ bài 6, ta có công thức tính i . in 2
Từ đó tính được góc α b. T i M: v n giao thoa có b c
Khi hệ vân giao thoa biến mất, hai cực đ i c a các b ủ ức x và liên tiếp trùng nhau Bài 8: Hai bản th y
ủ tinh mòng, phằng t o thành nêm không khí có c nh nêm qua A. T i
đi m M cách A là l=10mm, độ dày c a
ủ nêm . Nêm được chiếu bằng ánh
sáng có bước sóng theo phương vuông góc với mặt dưới của nêm .
a. Tìm tổng số vân tối quan sát được từ A tới M.
b. Thay ánh sáng có bước sóng bằng ánh
sáng trắng chiếu vào mặt nêm. Hỏi t i N
có độ dày có vân tối nào? Giảiμ
a. Đây là nêm không khí có góc nêm , khoảng vân Hiệu quang lộμ d n 2 d ( k 2 1) 22 2nd k ( 1) k ' k ' dn 2 Ta có: 0dl
. Từ đó sẽ tìm được số vân tối.
T i Aμ d=0 => T i A là vân tối. b. Hiệu quang trình: à (ánh sáng trắng)
t i N có sự trùng nhau của 58 vân tối. Bài 9 : Khi nhìn m t
ộ váng dầu trên mặt nước theo phương làm với mặt nước m t ộ góc
, ta thấy toàn bộ váng dầu màu vàng (ứng với ). Coi chiết suất
của dầu là 1,45 và không phụ thuộc vào bước sóng.
a. Tính bề dày có th có của váng dầu.
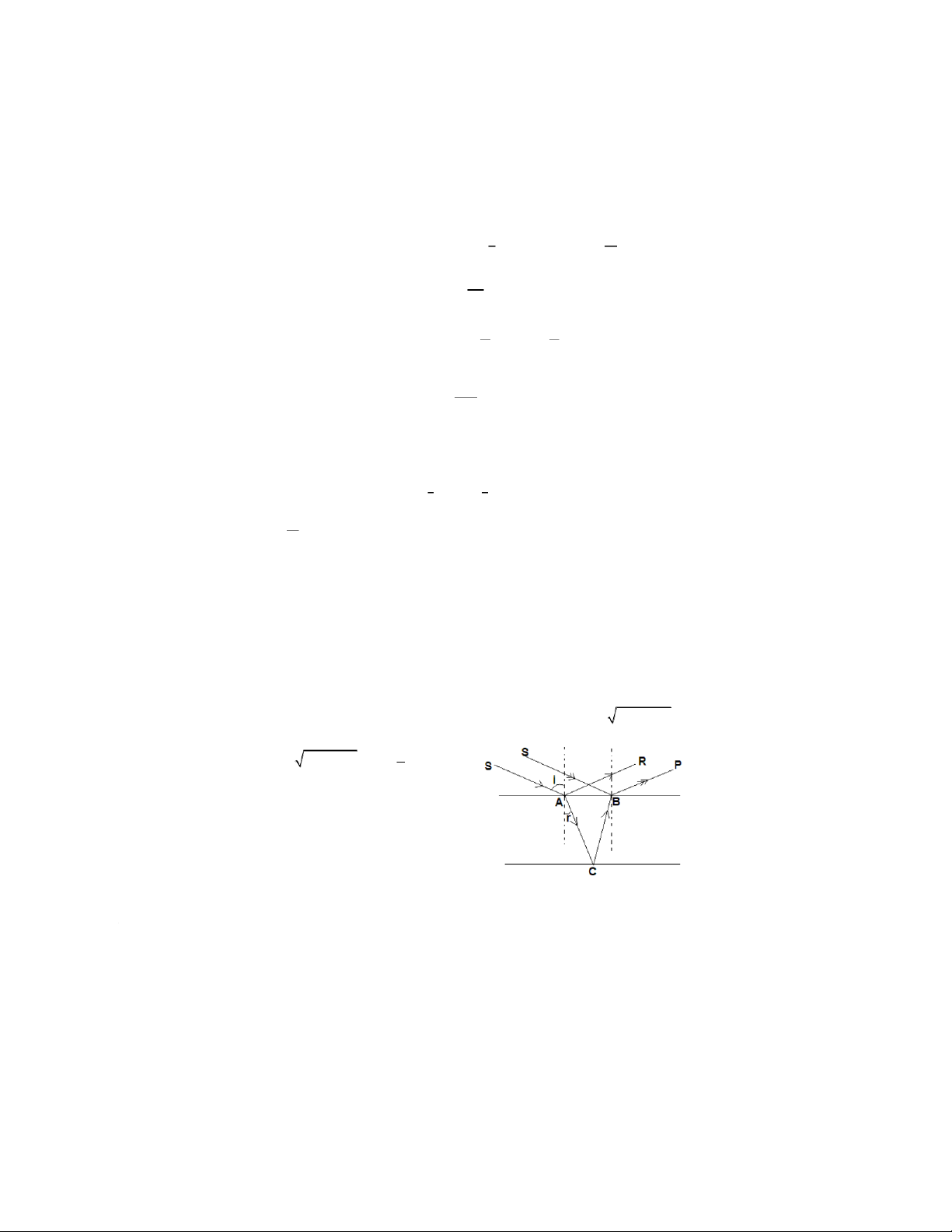
b. Nếu nhìn theo phương hợp với mặt nước một góc 300 thì váng dầu có màu gì? Giảiμ
a Hiệu quang trình giữa hai đường SACBP và SBP là μ 22 2d n sin i / 2
ứng với cực đ i giao thoa μ k 22 1 2d n sini ( k ) 2 1 ()k Bề dày lớp dầuμ 2 dni 22 2 sin 1 dmin ứng với k=0 dm . 0,13 22 4sinni b 22 1 2d n sin ( i k ) (ứng với dmin: k=0) 22 Khi i= 300 : 22 4d n sini 7,1m váng dầu màu đỏ. Bài 10:
Một hệ thống gồm 2 thấu kính mỏng giống nhau, một mặt phẳng, một mặt lồi.Đặt 2 thấu
kính tiếp xúc trực diện nhau với 2 mặt lồi. Chiếu tới hệ chùm tia đơn sắc có bước sóng
=0,5 m theo phương vuông góc với mặt phẳng.
a.Xác định bề dày của lớp không khí ở đó ta quan sát thấy vân sáng đầu tiên.
Biết vân tối thứ 5 có bán kính 2mm và thấu kính có chiết suất n=1,5. Tìm tiêu cự của hệ thấu kính trên.
b.Tìm tiêu cự của thấu kính,biết bán kính mặt cong R=0,8m. Giảiμ a.
Hiêu quang lộ ứng với vân sángμ Δ =2d + d /2=k
Với vân sáng đầu tiên k=1 =>Δ=2d+ /2= =>d= /4=1,25 m
T i đi m cách tâm r,lớp không khí có độ dày Ta có: r R 2 h 2
với h=d/2 . h là độ dày lớp không khí giữa thấu kính phẳng và lổi. =>d=r2/R =>Δ=2d+ /2 2 2 =2r 2r k 2r 2/R+ /2=(k+0.5) => => Rk R
Do t i d=0 thì có 1 vân tối => vân tối thứ 5 thì k=4 2 2r Với k=4Rk =>R=4m 1 1 1 n ( 1)( ) f R R 12 =>f=8m.
b/ Tìm tiêu cự của thấu kính,biết bán kính mặt cong R=0,8m. 1 1 1 n ( 1)( ) f R R 12 Bài 11:
Một thấu kính phẳng lồi , mặt lồi có bán kính R=cm đặt trên một bản thủy tinh phẳng.
Đỉnh mặt cầu không tiếp xúc với bản thủy phẳng bởi 1 h t bụi .
Người ta đo được bán kính các vân tối tròn Newton thứ 10 và thứ 15 là r10=5mm,
r15=7,5mm. Xác định bước sóng ánh sáng. Giảiμ
Gọi e là đường kính h t bụi 22de 2 2 r
Theo công thức vân newtonμ dR 2 Δ=r2/R + λ/ + e = k+ λ/ r102=R(k1 -2e) = R(10 -2e) r152=R(k2 -2e) = R(15 -2e) => = (r152-r102)/R(k1-k2) => = 0,5 m Bài 12:
Một thấu kính phẳng lồi L đặt trên một bản thủy tinh phẳng. Chiếu ánh sáng phản x có
bước sóng =0,546 m theo phương vuông góc và quan sát bằng ánh sáng phản x .
a.Người ta đo được đường kính vân tối thứ 5 và 15 lần lượt là λ,34mm và 16,18mm. Tính
bán kính mặt cong của L.
b.Cho một chất lỏng chiếm đầy giữa không khí và bản thủy tinh rồi lặp l i phép đo trên
ta được 8,0λmm và 14mm. Tìm chiết suất chất lỏng.
c.Trong trường hợp lớp mỏng là không khí, nếu ta tịnh tiến thấu kính lên trên thì điều gì sẽ xảy ra. Giảiμ Tương tự μ r5 =√ = 9,34mm r15 = √ =16,18mm
=>R=(r152-r52)/(15-5) = 8mm
Coi ánh sáng có ’= /n. Thay và n=1,33
T i đi m có độ dày d thì Δ=2d+ /2. Khi thấu kính dịch chuy n ra xa thì d tăng, vân phải
dịch chuy n về tâm O, các vân tròn thu
hẹp l i. Khi d khá lớn thì không quan sát được hệ vân giao thoa nữa. Bài 15:
Một thấu kính mỏng hai mặt lồi cùng bán kính R1 và
một thấu kính mỏng hai mặt lõm
cùng bán kính R2, cùng bằng thủy tinh chiết suất n1 được đặt sao cho trục chính trùng
nhau và tiếp xúc với nhau. Chiếu sáng hệ bằng một chùm sáng đơn sắc bước sóng và
quan sát hệ vân giao thoa t o thành. Vân sáng thứ 6 và vân sáng thứ 16 tính từ trong ra lần lượt là ρ1 và ρ
2. Tính tiêu cự của hệ thấu kính ghép. Giảiμ
Giữa đỉnh 2 thấu kính có 1 lớp không khí mỏng có độ dày e ở cách tâm 1 khoảng e, lớp không khí có bề dày d.
T i vị trí có vân tốiμ d = ρ2/2R1 ậ ρ2/2R2 + e = (k ậ ½)
Thay ρ=ρ1=1,855mmμ k=6μ ρ12/2(1/R1-1/R2) + e = 5,5
ρ=ρ2=3,161mmμ k=16μ ρ22/2(1/R1-1/R2) + e = 15,5
Giải hệ phương trình ta thu đượcμ
1/R1 ậ 1/R2 = 20 /(ρ22 ậ ρ12) = 1,667
Độ tụ của hệ μ D =(n-1).(1/R1 ậ 1/R2) = 0,833 dp
=>Tiêu cựμ f= 1/D = 1,2 m BÀI T P NHI U X Bài 1:
Một chùm tia sáng đơn sắc song song có bước sóng =0,6 m được rọi vuông góc với một
khe chữ nh t hẹp có bề rộng b=0,1mm. Ngay sau khe có đặt 1 thấu kính. Tìm bề rộng của
vân cực đ i chính trên màn quan sát (E) đặt t i tiêu diện của thấu kính và cách thấu kính D=1m Giảiμ
Bề rộng của vân cực đ i chính được đo bằng khoảng cách giữa 2 cực ti u nhi u x đầu
tiên ở 2 bên cực đ i chính. Góc nhi u x chính φ0 ứng
với các cực ti u nhi u x xác định bởi công thứcμ Sin φ0= /b
=>bề rộng e của cực đ i chính bằng l=2Dtg φ0=2λ /b=1,2cm Bài 2:
Một chùm tia sáng đơn sắc song song, bước sóng =0,58λ m chiếu thẳng góc với một
khe hẹp có bề rộng b=2 m . Hỏi các cực ti u nhi u x quan sát được dưới những góc
nhi u x bằng bao nhiêu? (so với phương bàn đầu) Giảiμ
Ễp dụng công thứcμ sinφ=k /b (với k=1,2,3…)
Điều kiệnμ sinφ ≤1 =>các góc nhi u x có th quan sát đượcμ φ1=1708’ φ2=3605’ φ3=620 Bài 3:
Xác định góc nhi u x ứng với các cực ti u nhi u x đầu tiên nằm ở 2 bên cực đ i giữa
trong nhi u x Fraunhofer qua một khe hẹp bề rộng b=10 m,biết chùm sáng tới hợp với
mặt phẳng khe một góc θ=300 và ánh sáng có bước sóng =0,5 m. Giảiμ
Hiệu quang trình μ Δ=b(sinθ-sinφ) (φ là góc nhi u x )
Góc nhi u x ứng với cực ti u nhi u x μ Δ=k =>sinθ-sinφ=k /b =>sinφ= -k /b + sin θ
Cực ti u nhi u x đầu tiên ứng với k= ± 1 ta cóμ φ= 330 φ=270 Bài 4:
Chiếu một chùm sáng đơn sắc song song, bước sóng =0,5 m thẳng góc với 1 cách tử
nhi u x , phía sau cách tử đặt một thấu kính hội tụ tiêu cự f=1m . Màn quan sát đặt ở tiêu
diện thấu kính. Khoảng cách giữa hai v ch cực đ i chính của quang phổ b c 1 là l= 0,202m. Xác địnhμ a.Chu kì cách tử.
b.Số v ch trên 1 cm của cách tử.
c.Số cực đ i chính tối đa có th có của cách tử.
d.Góc nhi u x ứng với v ch quang phổ ngoài cùng. Giảiμ
a.Vị trí các cực đ i chính được xác định bằng công thứcμ
sinφ=k /d=k n với n=1/d là số v
ch trên 1 đơn vị chiều dài.
Quang phổ b c 1 ứng với hai v ch cực đ i chính k=±1.
Khoảng cách giữa 2 cực đ i chính này bằngμ l = 2f.tgφ ≈ 2f.sinφ
Hay l≈2fk /d (φ nhỏ =>sinφ= tgφ và k=1) =>d=2f /l=4,λ5 m
b.Số v ch trên một cm của cách tử μ n=1/d=2020cm -1
c.Các cực đ i chính μ dsinφ =k .
=>k=dsinφ/ , với k=0,±1,±2…..
Với mỗi giá trị của k ta có một cực đ i chính, với điều kiện sinφ=1
=>Số cực đ i chính tối đa có th có ứng với kmax=d/=9,9
=>Số cực đ i chínhμ 2[kmax] + 1 = 19 với [kmax]=9 d. Góc nhi u x φmax ứng
với v ch cực đ i chính (v ch quang phổ)ngoài cùng (với kmax=9)
sin φ0=kmax /d=0,λ1=>φmax=6503’.
=>Hai v ch quang phổ ngoài cùng đối xứng nhau đối với trục chính của thấu kính và xác
định bởi các góc 6503’ và -6503’. Bài 5:
Một chùm tia sáng được rọi vuông góc với một cách tử. Biết rằng góc nhi u x ứng với
ánh sáng có bước sóng 1=0,65 m, trong quang phổ b c 2 bằng φ1=45. Xác định góc
nhi u x ứng với quang phổ =0,5 m trong quang phổ b c 3. Giảiμ Theo đề ta cóμ sinφ1=k1n 1 (k1=2) sinφ2=k2n 2 (k2=3)
=>sinφ2=k2 2sinφ1/k1 1 =>φ2≈5504’ Bài 6:
Một chùm tia sáng được phát ra từ một ống phóng điện chứa đầy khí hydro tới đ p vuông
góc với một cách tử nhi u x theo phương φ=410,người ta quan sát thấy có 2 v ch 1= 0,6563 m và
2=0,4102 m, ứng với quang phổ b c nhỏ nhất trùng nhau. Xác định chu kỳ cách tử. Giảiμ
Vì các v ch cực đ i ứng với các bước sóng 1 và 2 trùng nhau nên ta có: dsinφ=k1 1=k2 2
hay k2/k1 = 1/ 2= 0,6563/0,4102=0,16
Do k1 , k2 phải là số nguyên nên điều kiện ( 1 ) được thỏa mãn khi k1 5 , k2 8. k 6 , 0 . 5 563 1 . 0 6 Do đó μ d 1 1 m 1 . 5 0 6( ). sin 6 , 0 56 Bài 7.
Một chum sáng đơn sắc tới vuông góc với một cách tử có chu kỳ 2 , 2 m. Biết rằng giữa
các cực đ i của quang phổ b c 1 và b c 2 bằng 150 . Xác định bước sóng ánh sáng tới . Giải. Theo đềμ sin 1 d và 0 1 15 2 sin 2 . 2 d . 2 sin( Do đó μ ) sin cos sin 1 cos 1 1 d 2 Mặt khác μ cos d 1 sin 21 1 2 d sin 2 Và m sin 2 cos 1 5 , 0 4 . 5 4cos Bài 8.
Sau một cách tử nhi u x có hằng số 2 m đặt một thấu kính hội tụ và t i tiêu diện thấu
kính có một màn quan sát . Khoảng cách giữa hai v ch cực đ i của He ( ứng với các bước
sóng 4044 A0 và 4047 A0 ) trong quang phổ b c 1 trên màn quan sát bằng 1 , 0 mm .Tìm tiêu cự thấu kính . Giải. Ta có: sin k. d .
Vị trí của cực đ i trên màn μ D . f tg , với f là tiêu cự TK. D D 2 1 f . tg tg 2 1 1 , 0 ,sin Với D 1 2 2,si D n 1 mm 1 d 2 d f 6 , 0 5 . m