lOMoAR cPSD| 40342981
B I TẬP HỆ BÁNH RĂNG Bài tập 1: 2 4
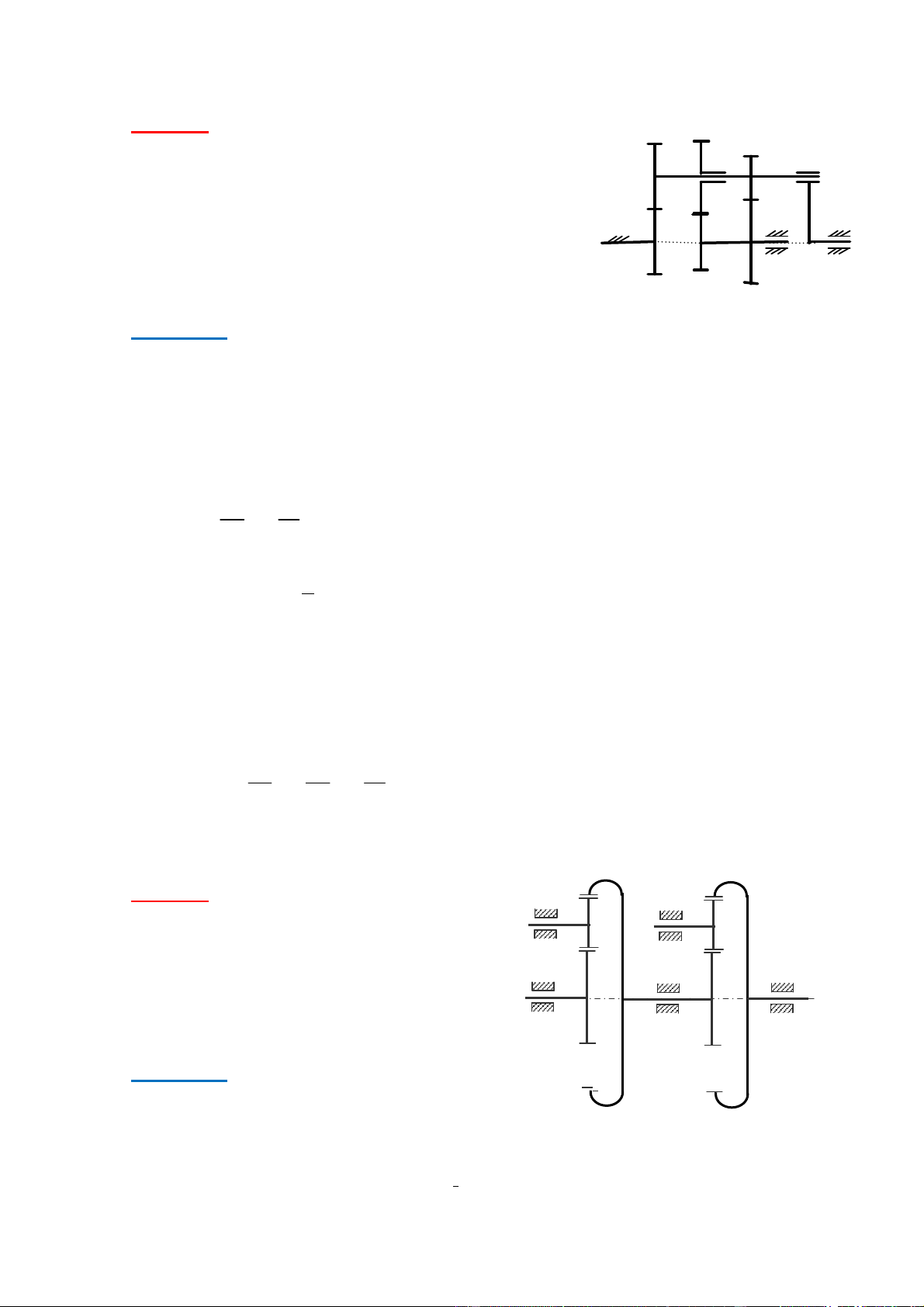
Cho hệ bánh răng như h nh vẽ. 2
Biết : Z1 = Z2 = 30; Z3 = 40; Z3 = 20; Z2 = 20; Z4 = 40. BÆnh
răng số 1 cố định. T nh : + Tỷ số truyền i3C C + Tỷ số truyền i43
+ BÆnh 2 v bÆnh 3 c quay cøng chiều hay kh ng ? 1 3 3 Hướng dẫn:
• Hệ h nh tinh - BÆnh trung t m
cố ịnh: bánh 1 • Døng c ng thức
t nh tỷ số truyền trong hệ h nh
tinh: i3C = −1 i31C Trong : i C
31 t nh như hệ thưßng với ưßng truyền: (3-2 )-(2-1)
i31C = −¼½» ZZ23’ ÀÁ¿»¼½− ZZ12 ¿ÀÁ
• T nh i43 : i43’ = i4C i3C
Døng c ng thức t nh tỷ số truyền trong hệ h nh tinh:
i4C = −1 i41C Trong : i C
41 t nh như hệ thưßng với ưßng truyền: (4-3 )-(3-2 )-(2-1)
i41C = −¼½» ZZ34’ ¿ÀÁ»¼½− ZZ23’
¿ÀÁ¼½»− ZZ12 ¿ÁÀ B i tập 2 :
Cho hệ bÆnh răng như h nh vẽ. Z2 Z Z 4
2 = Z3 = Z4 = 20; Z3 = Z5 = 60; n1 = 1800 v
ng/phœt. Cho biết ưßng t m trục cÆc bÆnh 1 v 3 thẳng h ng.
T nh n5. T nh khoảng cÆch trục A12 v A23. Cho biết Z , Z
cÆc bÆnh răng ều tiŒu chuẩn v cøng mo un m = 1 3 5. Z Hướng dẫn: 5 Z • 3
Hệ thưßng (v ưßng t m trục của cÆc bÆnh răng ều cố ịnh)
• Để t nh n5 => cần t nh i15 =¼½»nn15 ¿ÀÁ 1 lOMoAR cPSD| 40342981
• i15 = −¼½» ZZ12 ¿»Á½À¼+ ZZ23 ¿ÀÁ¼½»− ZZ34’ ¿ÀÁ¼½»+ ZZ45 ¿ÀÁ
à y chưa cho số răng Z1 => cÆch t nh Z1: A12 = + =r1
r2 A23 = −r3 r2 1 1 1 1
=> A12 = mZ1 + mZ2 = A23 = mZ3 − mZ2 2 2 2 2
=> suy ra Z1 v khoảng cÆch trục A12, A23. B i tập 3 :
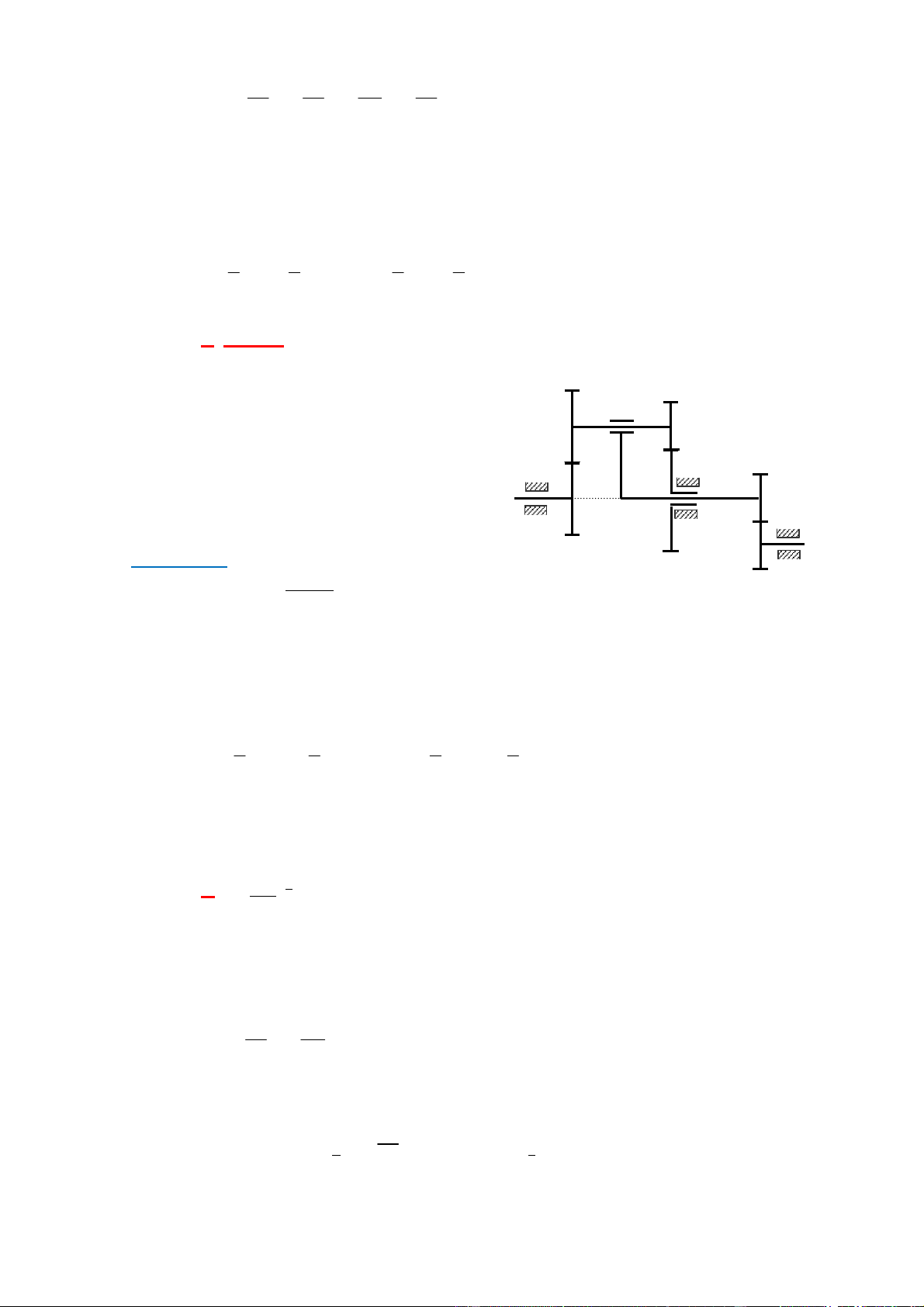
Cho hệ bÆnh răng như h nh vẽ. Cho Z1 = 35; 2 2 Z2 = 40; Z2 = 50; Z4 = Z5
+ T nh Z3. Biết rằng cÆc bÆnh răng ều tiŒu chuẩn v cøng m un. 4 + XÆc ịnh n 1 (chiều v trị số). C
Biết n5= 60 v ng/phœt; n3 = 81 v ng/phœt; n3 v n5 quay cøng chiều nhau. Hướng dẫn: 1 3 • Hệ g ? 5 Hệ thưßng : (4-5)
Hệ vi sai : (1-2) (2 -3) cần C. Hệ vi sai n y kh ng
c bÆnh trung t m n o cố ịnh
 Hệ ª cho l hệ hỗn hợp gồm hệ thưßng v hệ vi sai • T nh Z3 : Dựa v o iều
kiŒn ồng trục của hệ vi sai/h nh tinh : A12 = + =r1 r2 A2’3 = +r2’ r3
 A12 = 1 mZ1 + 1 mZ2 = A2’3 = 1 mZ2’ + 1 mZ3 2 2 2 2  Suy ra Z3
• Ta t m quan hệ n1, n3 v nC theo cÆch t nh của hệ vi sai, sau t m
quan hệ nC=n4 v n5 theo cÆch t nh của hệ thưßng
C = n1 − nC (1) Hệ vi sai: i13 n − nC 3 với i C
13 t nh như hệ thưßng với ưßng truyền (1-2)-(2 -3)
i13C = −¼½» ZZ12 ¿»À¼Á½− ZZ23’ ¿ÀÁ
Hệ thường: i45 = nn4 = −¼½» ZZ45 ¿ÀÁ = nnC5 (2) 5 2 lOMoAR cPSD| 40342981
Từ (2) suy ra: nC = X n. 5 (3) (nC bằng X lần n5)
Thay (3) v o (1) suy ra biểu thức quan hệ giữa n1, n3 v n5.
Biết n5=+60, n3=+81 => suy ược n1.
Nếu n5>0 chứng tỏ n1 cøng chiều với n5 v n3, nếu n1<0 => n1 ngược chiều với n5 v n3. B i tập 4 :
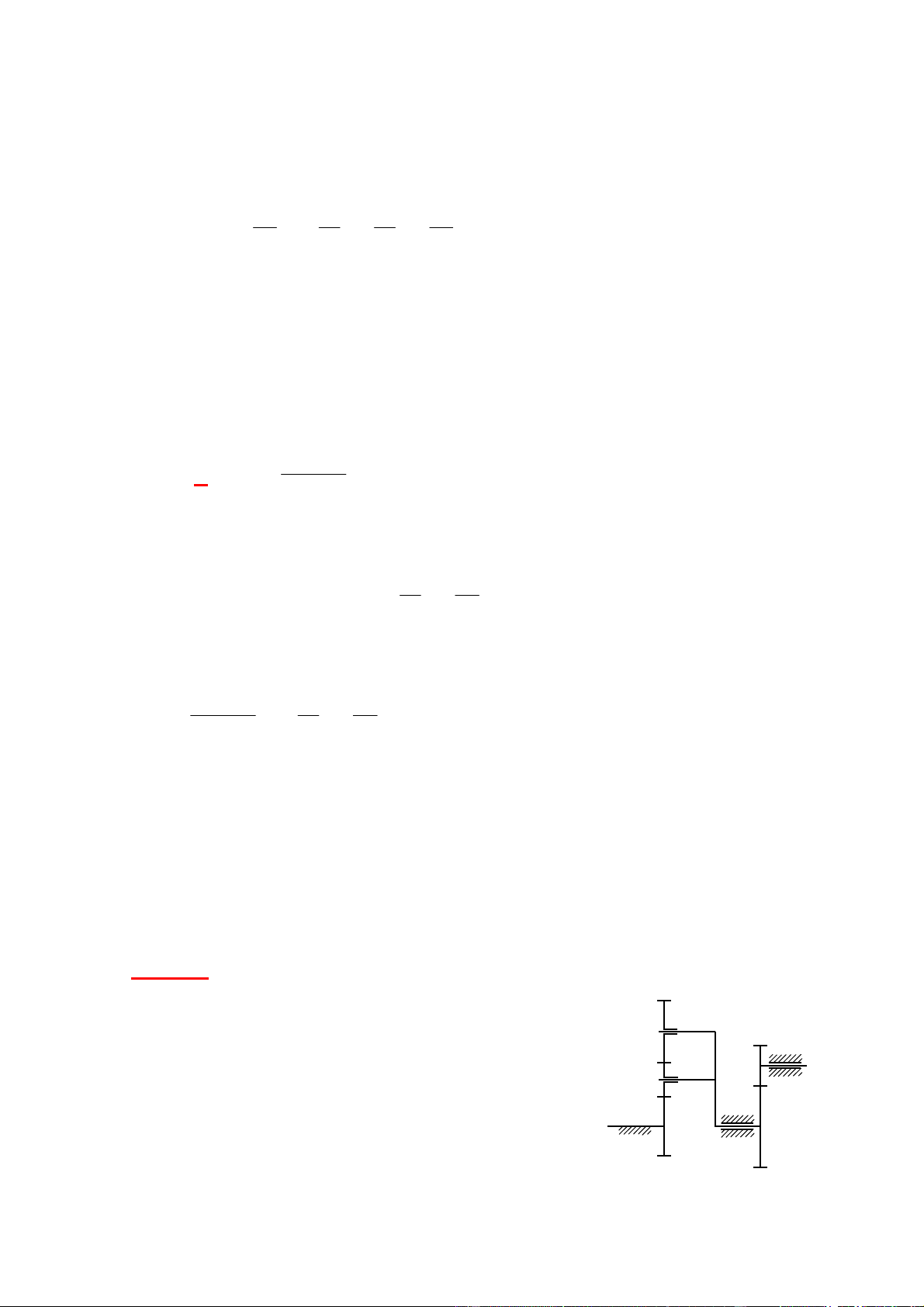
Cho hệ bÆnh răng như h nh vẽ.
Biết : Z1 = 20; Z3 = 20; Z4 = 80; Z5 = 20; Z 5= 30; Z6 = 90. 5 5
BÆnh răng số 4 cố ịnh. C 3
* Hệ bÆnh răng n y l hệ g ? V sao ?
* T nh tỷ số truyền i16. BÆnh 1 v bÆnh 6 c quay cøng 2 chiều kh ng ? V sao ? 4 6 1 Hướng dẫn: • Hệ g ?
Hệ thưßng : (1-2)-(2-3 =C)
Hệ vi sai : (4-5) (5 -6) cần C=3. Hệ vi sai n y c bÆnh trung t m 4 cố ịnh => trá th nh hệ h nh tinh
 T m lại : Hệ ª cho l hệ hỗn hợp gồm hệ thưßng v hệ h nh tinh • T nh i16: i16 = i i13.
C6 o i13 t nh theo cÆch t nh của hệ thưßng: i13 = −¼½» ZZ12 À¼Á½¿»− ZZ23 ¿ÀÁ o = i 1 C C6
với i6C t nh theo cÆch t nh của hệ h nh tinh: i6C = −1 i64 ( bÆnh 4 l i6C
bÆnh trung t m cố inh của hệ h nh tinh) i64C t nh như hệ thưßng với ưßng
truyền (6-5 )-(5-4): i64C = +½»¼ ZZ56’ ¿»À¼Á½+ ZZ45 ¿ÀÁ
• Nếu i16>0 => bÆnh 1 v bÆnh 6 quay cøng chiều. B i tập 5:
Cho hệ bÆnh răng như h nh vẽ: Z1 = Z2 = Z3 = 20 Z2 = 15 Z3 = 40 Z4 = 25 Z5 = 120
T nh cÆc tỉ số truyền i1C v i15. Biết bÆnh răng Z4 cố ịnh Hướng dẫn: • Hệ g ?
Hệ h nh tinh, bÆnh t m cố ịnh l bÆnh 4, cần C • T nh i1C: 3 lOMoAR cPSD| 40342981 i C C
1C = −1 i14 với i14 t nh như hệ thưßng với ưßng truyền (1-2) (2 -4):
i14C = −¼½» ZZ12 ¿»À¼Á½− ZZ24’ ¿ÀÁ • T nh i15:
i15 = i1C i C C 5C i5C = −1
i54 với i54 t nh như hệ thưßng với ưßng truyền (5-3 ) (3-2)-(2 -4):
i54C = +¼» ZZ35’ ¿»À¼Á½− ZZ23
Á¿À»¼½− ZZ24’ ÀÁ¿ ½ B i tập 6 :
Cho hệ bÆnh răng như h nh vẽ:
Z1 = Z2 = Z5 = 12; Z2 = Z3 = 24 Z3 = 108 Z5 = 36
T nh Z4, biết cÆc bÆnh răng ều tiŒu chuẩn v c cøng m
un. Cho biết ưßng t m bÆnh 1, bÆnh 4 v bÆnh 5 nằm
trong cøng một mặt phẳng. T nh tỉ số truyền i1C v i13 Hướng dẫn: • Hệ g :
o Hệ thưßng : (1-4), (4-5), (5 -3 =3)
o Hệ vi sai : (1-2), (2 -3), cần C
Hệ vi sai n y kh ng c bÆnh trung t m n o cố ịnh
o T m lại hệ ª cho l hệ hỗn hợp gồm
hệ vi sai v hệ thưßng. Tuy nhiŒn
c iểm ặc biệt l hệ thưßng nối bÆnh trung t m 1 v bÆnh trung t m
3=3 của hệ vi sai => hệ ª cho l hệ vi sai k n, bậc tự do W =1. • T nh Z4:
Dựa v o iều kiện ề cho v iều kiện ồng trục của hệ vi sai, ta c :
A14 + A45 = A5’3’
 Z1 + 2Z4 + Z5 = Z3’ − Z5’ 4 lOMoAR cPSD| 40342981  Suy ra Z4 • T nh i13:
o Do bÆnh 1 v bÆnh 3=3 ều thuộc hệ thưßng => t nh i13 trong hệ
thưßng với ưßng truyền (1-4) (4-5)-(5 -3 ):
i13 = ww13 = −»¼ ZZ14 ¿»À¼Á½− ZZ45
ÀÁ¿»¼½+ ZZ53’’ ¿ÀÁ (1) ½ • T nh i1C:
o Ta thấy bÆnh 1 v cần C thuộc hệ vi sai. Tuy nhiŒn trong hệ vi sai
kh ng t nh ược tỷ số truyền m chỉ t m ược quan hệ vận tốc g c. Ta ª c
quan hệ giữa w1 v w3 từ biểu thức (1), nŒn ể t m i1C (tức l quan hệ
w1 v wC), ta cần t m thŒm quan hệ w1, w3 v wC. o Với hệ vi sai, ta c : C
= w1 − wC trong : i C
13 t nh như cÆch t nh của hệ thưßng với ưßng
truyền i13 w − wC 3
(1-2)-(2 -3): i13C = −¼½» ZZ12
¿»À¼Á½− ZZ23’ ¿ÀÁ
 ww13 − wC = −»¼½ ZZ12 ¿»Á½À¼− ZZ23’ ¿ÀÁ (2) − wC
Từ (1) => rœt ra hệ thức của w3 theo w1. Thay v o (2), ta suy ược hệ thức chỉ chứa w1 v wC => suy ra i1C = (w1/wC) B i tập 7 : Z5
Cho hệ bÆnh răng như h nh vẽ: Z Z
1 = 20, Z2 = 40, Z3 = Z5 = 30 n1 = 140 v ng/phœt 1
Khoảng cÆch trục giữa bÆnh răng Z C 3 v Z5 l A35 = 180 mm. BÆnh răng Z3 cố ịnh. Z 4
T nh Z4, biết cÆc bÆnh răng ều tiŒu chuẩn v cøng m un m = 4 mm. Z
Cho biết ưßng t m bÆnh 3, bÆnh 5 v bÆnh 4 nằm trong 3 Z 2
cøng một mặt phẳng. Tinh n4, n5 v nC. 5 lOMoAR cPSD| 40342981 Hướng dẫn: • Ta c :
A35 = A34 + A45
 A35 = 1 mZ3 + 1 mZ4 + 1 mZ4 + 1 mZ5 => Suy ra ược Z4 2 2 2 2 • Hệ g : o Hệ thưßng : (1-2=C)
o Hệ vi sai : (3-4), (4-5), cần C= bÆnh 2. Hệ vi sai n y c bÆnh trung t m
3 cố ịnh => hệ trá th nh hệ h nh tinh
o T m lại hệ ª cho l hệ hỗn hợp gồm hệ h nh tinh v hệ thưßng. • T nh nC :
o Ta c bÆnh 1 v bÆnh 2 (= cần C) thuộc hệ thưßng => døng cÆch t nh ¿À
của hệ thưßng : i12 = i1C = nn1 = −»¼½ ZZ12 Á => biết n1, t m ược nC. C
• Để t nh n4 => cần t m i14 = i12. iC4 = i12/ i4C Ta c : i4C = −1 i43C với i43C = −¼½» ZZ43 ¿ÀÁ
• Để t nh i15 => cần t m i15 = i12. iC5 = i12/ i5C
Ta c : i5C = −1 i53C với i53C = −¼½» ZZ45
¿ÀÁ½»¼− ZZ43 Á¿À B i 8 : 3
Cho hệ bÆnh răng như h nh vẽ (hệ bÆnh răng n y
ược sử dụng trong cơ cấu tßi quấn cÆp). 3
Biết: Z1 = 20; Z2 = 30; Z3 = 80; Z3 = 60; Z4 = 20. 4 2
+ Hệ bÆnh răng trŒn h nh vẽ l hệ bÆnh răng g ? V sao? C
+ Cho biết cÆc bÆnh răng ều tiŒu chuẩn v cøng
mo un m. Dựa v o iều kiện ồng trục của hệ vi sai
phẳng, hªy suy ra số răng Z5. + T nh i13 v i35. 1 5
+ BÆnh 3 v bÆnh 5 quay cøng chiều hay ngược chiều? V sao? Hướng dẫn: • Hệ g :
o Hệ thưßng : (1=C-2), (2-3=3 )
o Hệ vi sai : (4-5), (4-3 =3), cần C= bÆnh 1 Hệ vi sai n y kh ng c bÆnh trung t m n o cố ịnh 6 lOMoAR cPSD| 40342981
o T m lại hệ ª cho l hệ hỗn hợp gồm hệ vi sai v hệ thưßng. Tuy nhiŒn c iểm ặc
biệt l hệ thưßng nối bÆnh cần C= bÆnh 1 v bÆnh trung t m 3 = bÆnh 3 của hệ
vi sai => hệ ª cho l hệ vi sai k n, bậc tự do W = 1. • T nh Z5:
Dựa v o iều kiện ồng trục của hệ vi sai, ta c : A54 =A3’4
 Z5 + Z4 = Z3’ − Z4  Suy ra Z5 • T nh i13:
o Do bÆnh 1 v bÆnh 3=3 ều thuộc hệ thưßng => t nh i13 trong hệ thưßng với ưßng truyền (1-2) (2-3):
i13 = w1 = −»¼½ ZZ12 ¿»À¼Á½+ ZZ23 ¿ÀÁ (1) w3
• T nh i35 = i3 5 o Ta thấy bÆnh 3 v bÆnh 5 thuộc hệ vi sai. Tuy nhiŒn trong
hệ vi sai kh ng t nh ược tỷ số truyền m chỉ t m ược quan hệ vận tốc g c. Ta ª c
quan hệ giữa w1(= wC) v w3 (= w3 ), từ biểu thức (1), nŒn ể t m i3 5 (tức l quan
hệ w3 v w5), ta cần t m thŒm quan hệ w1 = (wC), w3 v w5 theo cÆch t nh của
hệ vi sai. o Với hệ vi sai, ta c : = i w w C C C 3 ’5
w3’ −−w C trong : i3 ’5 t nh như cÆch t nh của hệ thưßng với ưßng
5 truyền (3 -4)-(4-5): i3C’5 =
+¼½» ZZ34’ ¿»À¼Á½− ZZ54 ¿ÀÁ
 ww35’ −−wwC = +¼½» ZZ34’ À¼Á½¿»− ZZ45 ÀÁ¿ (2) C
Từ (1) => suy ra hệ thức của wC (=w1) theo w3 (=w3). Thay v o (2), ta c ược hệ thức chỉ chứa
w3 v w5 => suy ra i3 5 = (w3 /w5)
• Nếu i3 5 > 0 => w3 v w5 cøng chiều nhau. Nếu i3 5 < 0 => w3 v w5 ngược chiều nhau. 7