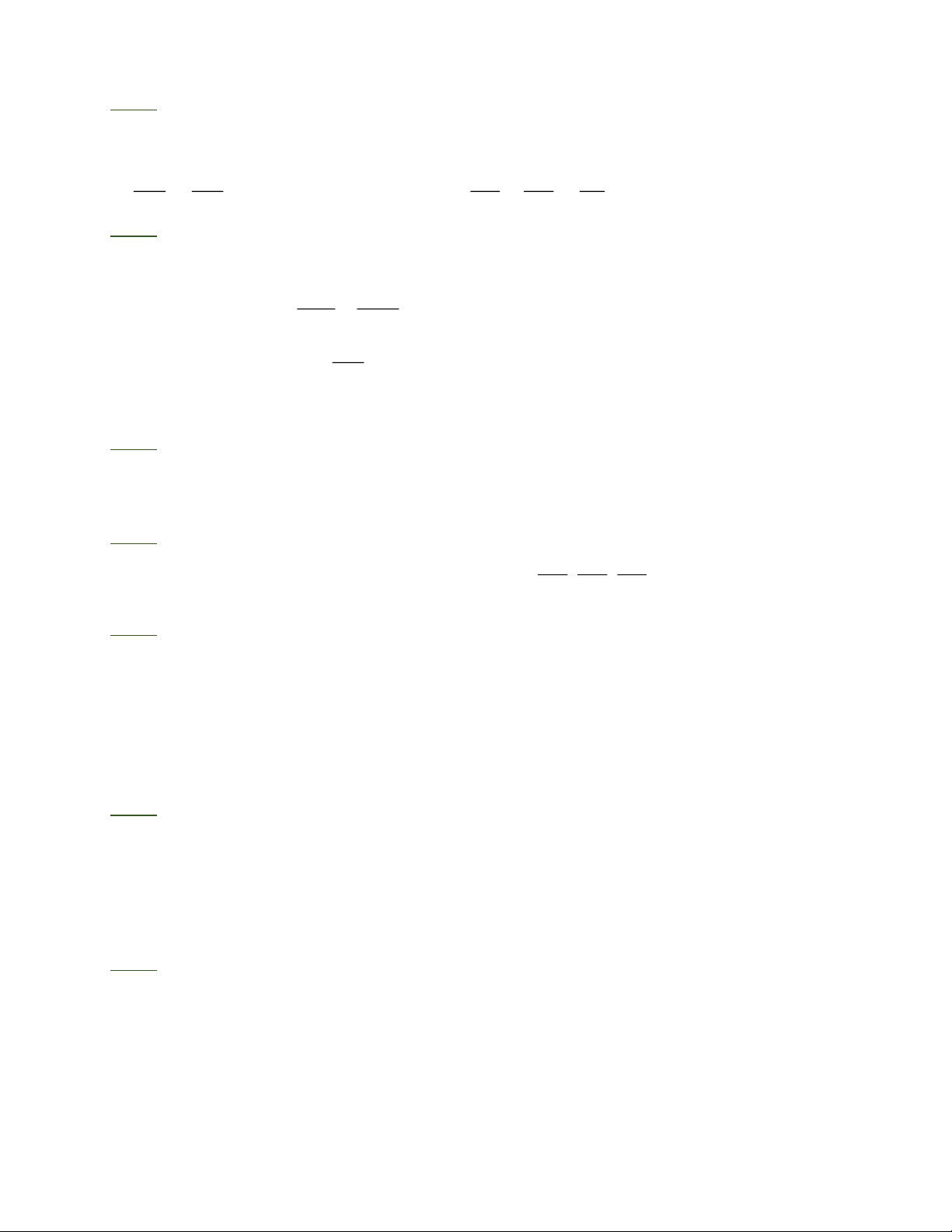

Preview text:
2. ĐỊNH LÝ TALET ĐẢO VÀ HỆ QUẢ CỦA ĐỊNH LÝ TALET
I. KIẾN THỨC CƠ BẢN
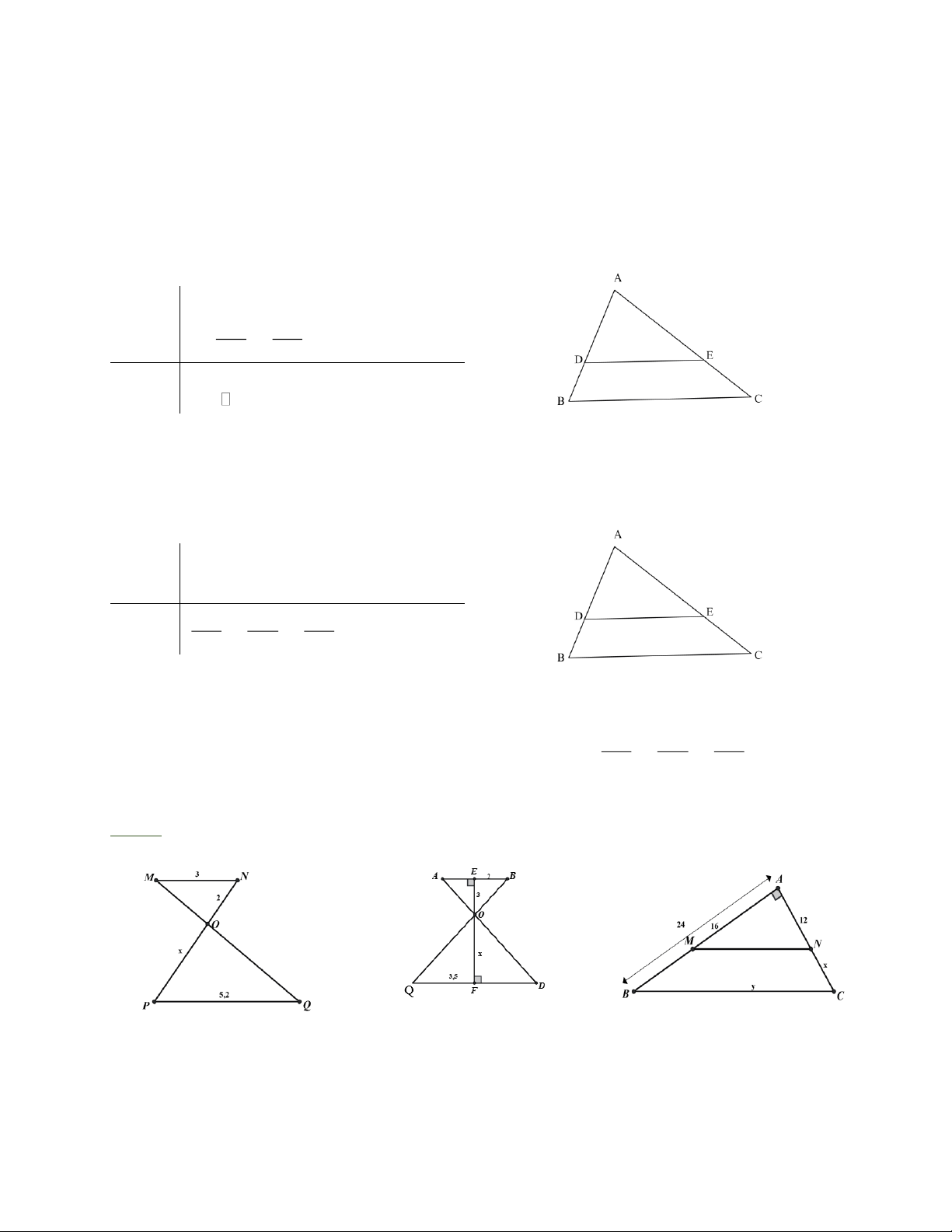
Định lý Ta – lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên
hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
DA BC : D Î A B, E Î A C GT A D A E và = BD EC KL DE BC
• Hệ quả của định lý Ta – lét: Nếu một đường thẳng cắt hai cạnh của một tam giác và
song song với cạnh còn lại thì tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba
cạnh của tam giác đã cho.
DA BC : DE / / BC GT
(D Î AB,E Î AC) A D A E DE KL = = A B A C BC
• Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng d song song với một A D A E DE
cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại: = = . A B A C BC III. BÀI TẬP
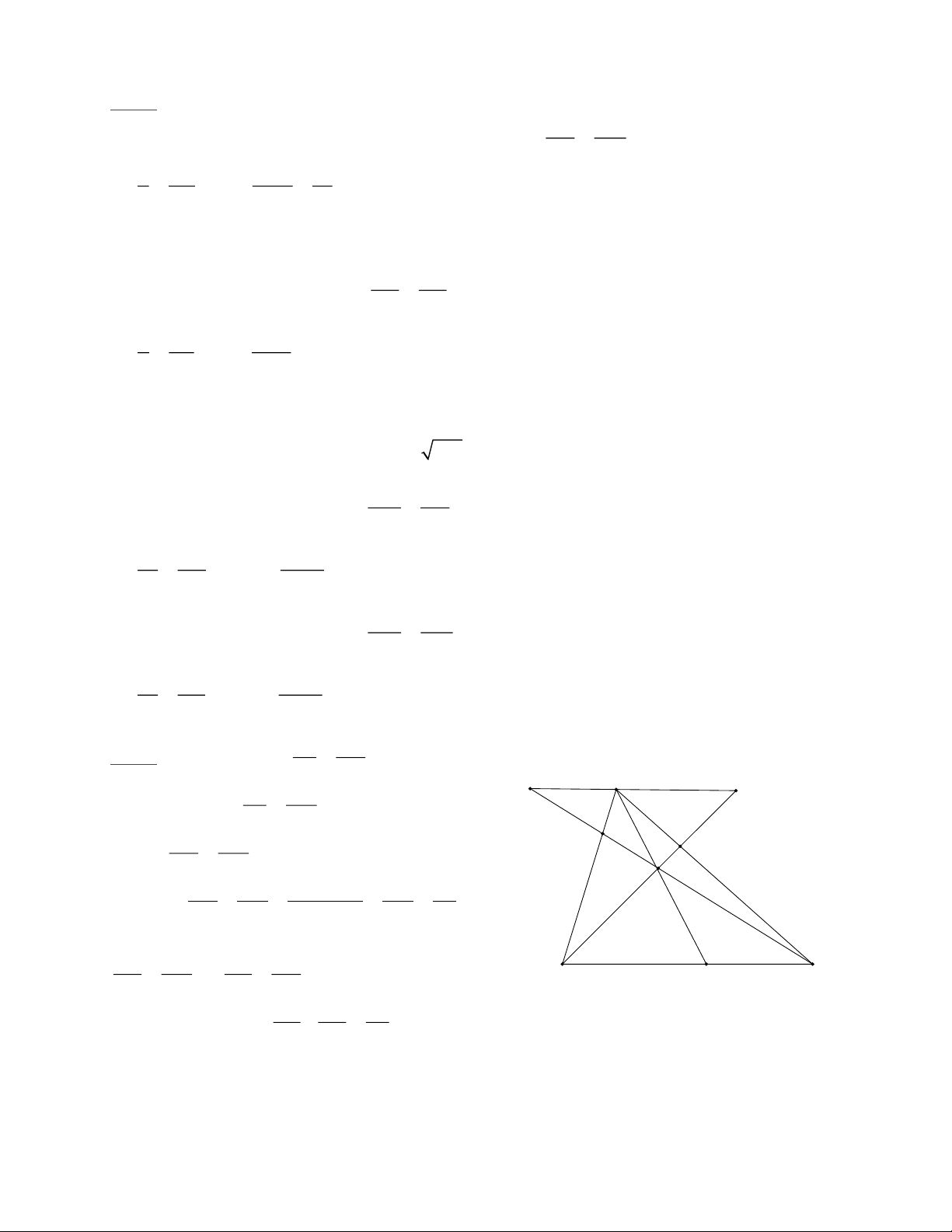
Bài 1: Tìm x trong hình
Biết MN / / PQ Hình 2 Hình 3 Hình 1 Trang 1
Bài 2: Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC,
AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh: A K HA A F A E A I a) = ; b) + = . BD DC BF CE ID
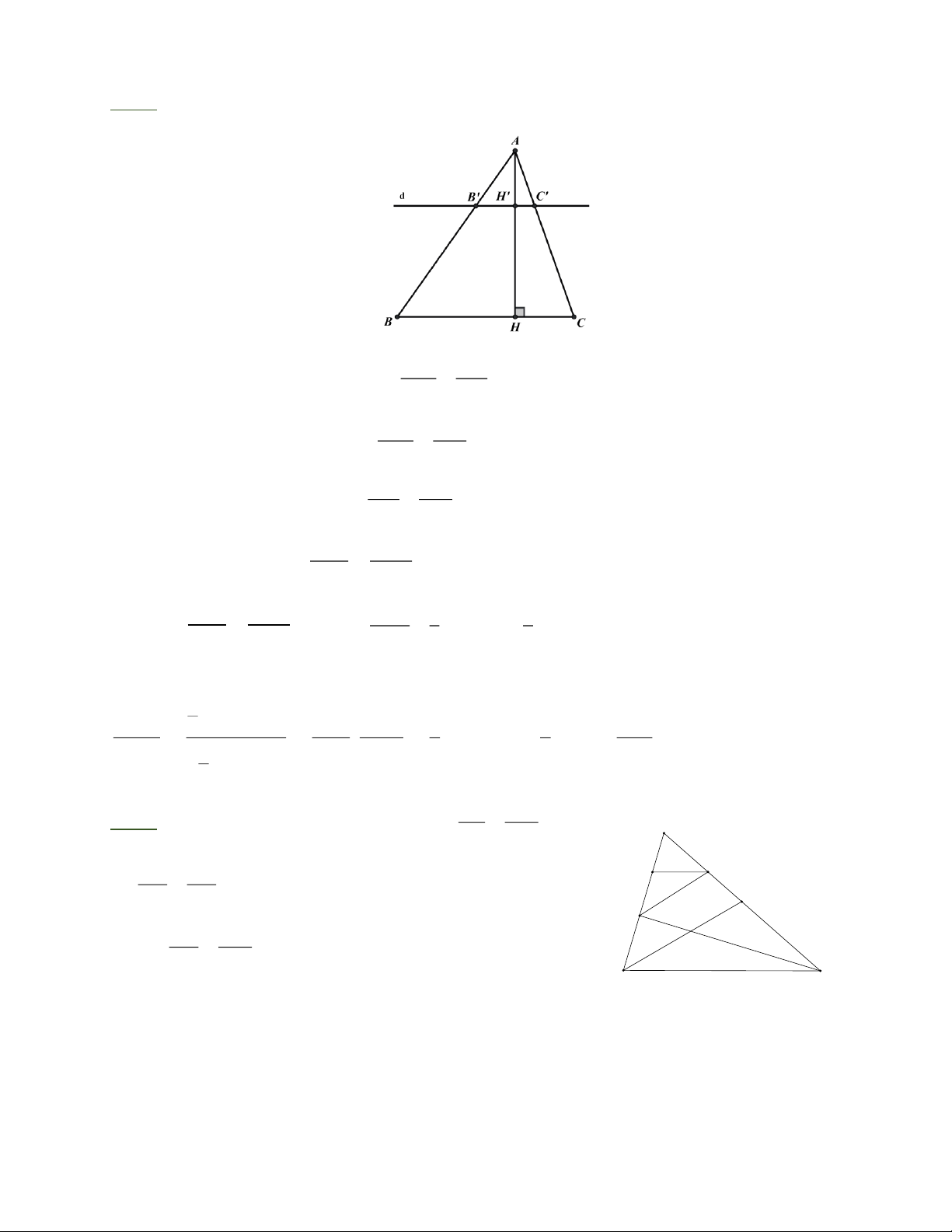
Bài 3: Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB,
AC và đường cao AH lần lượt tại B’, C’ và H’. AH ' B 'C ' a) Chứng minh rằng = AH BC A H
Áp dụng: Cho biết A H ' =
và diện tích tam giác ABC là 67,5cm2. Hãy tính diện tích 3
tam giác A B 'C ' .
Bài 4: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song
với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB).Chứng minh MN song song với BC.
Bài 5: (Định lý Céva) Trên ba cạnh BC, CA, AB của tam giác ABC lấy tương ứng ba điểm PB QC R A
P, Q, R. Chứng minh nếu AP, BQ, CR đồng quy thì . . = 1. PC QA R B
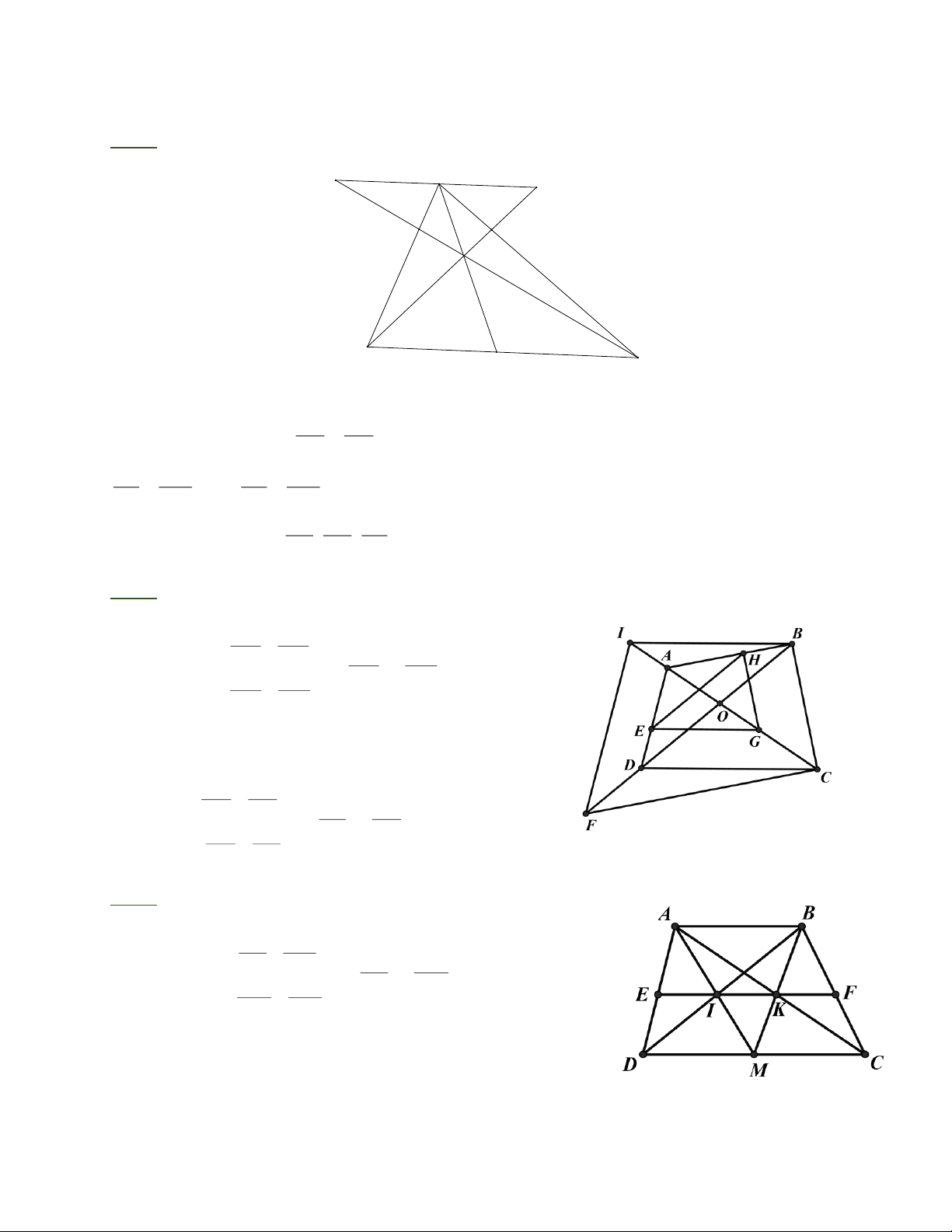
Bài 6: Cho tứ giác ABCD. Qua E AD kẻ đường thẳng song song với DC cắt AC ở G. Qua
G kẻ đường thẳng song song với CB cắt AB tại H. Chứng minh rằng: a) HE / / BD
b) Qua B kẻ đường thẳng song song với CD, cắt đường thẳng Ac tại I. Qua C kẻ đường
thẳng song song với BA, cắt BD tại F. Chứng minh IF / / A D .
Bài 7: Cho hình thang ABCD (A B / / CD). M là trung điểm của CD. Gọi I là giao điểm của
AM và BD, K là giao điểm của BM và AC.
a) Chứng minh IK / / A B
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh rằng EI = IK = K F .
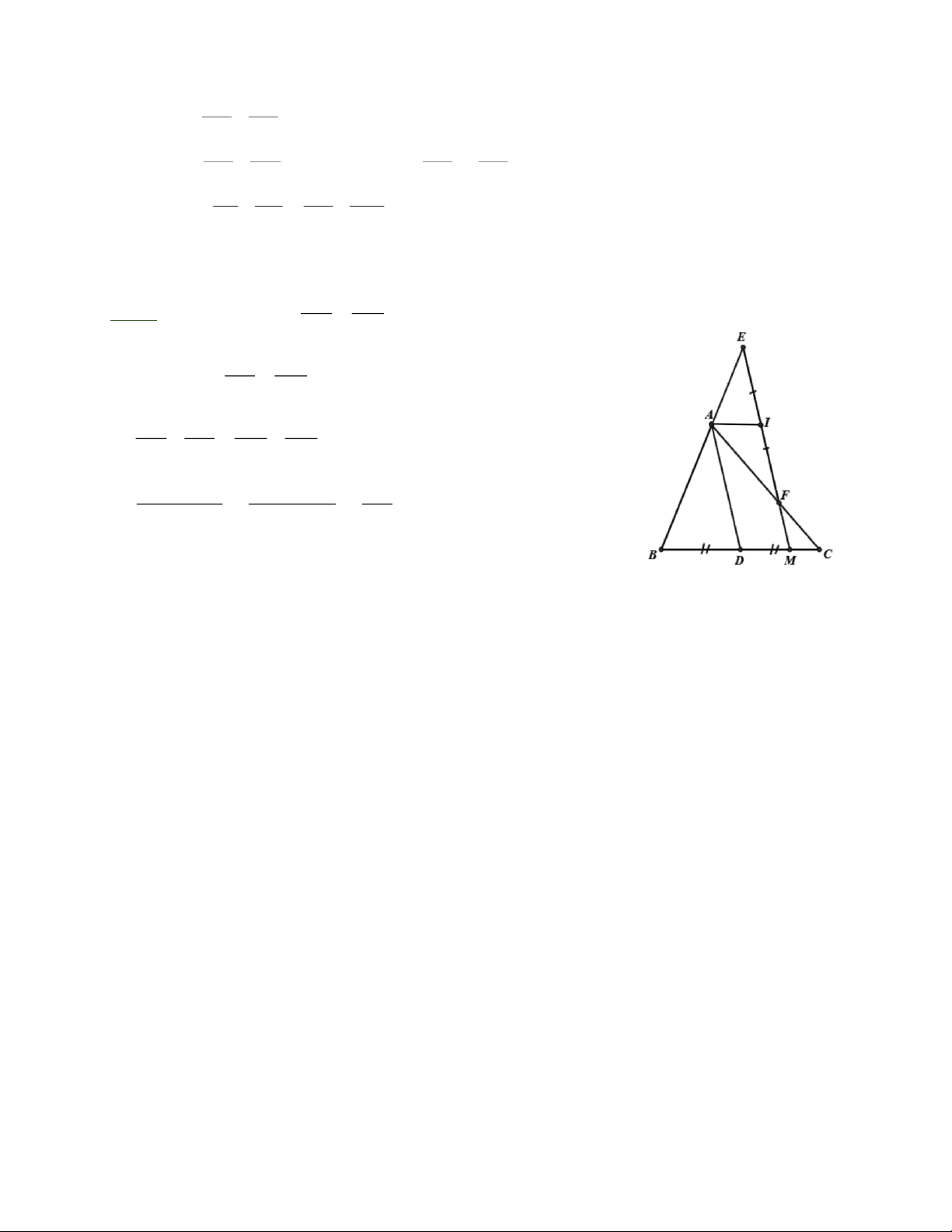
Bài 8: Cho ABC có AD là trung tuyến. Từ một điểm M bất kỳ trên cạnh BC, vẽ đường
thẳng song song với AD, cắt AB và AC lần lượt tại E và F. Gọi I là trung điểm của EF. Chứng minh :
a) ME + MF = 2A D
b) A DMI là hình hình hành Trang 2
Bài tập tự luyện
Bài 1: Cho ABC vuông ở A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE ⊥ DC
(E AC) ; DK ⊥ AC (K AC) . Chứng minh BE // HK
Bài 2: Cho tam giác ABC, trung tuyến AD có G là trọng tâm. Vẽ đường thẳng d qua G cắt
cạnh AB; AC lần lượt tại E;F. Chứng minh AB AC BE CE a) + = 3 b) + =1 AE AF AE AF
Bài 3: Cho tam giác AOB có AB = 18cm,OA = 12cm,OB = 9cm. Trên tia đối của tia OB lấy
điểm D sao cho OD = 3cm . Qua D kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F
là giao điểm của AD và BC. Tính: FD a) Độ dài OC, CD; b) Tỉ số . FA
Bài 4: Cho hình thang ABCD có hai đáy là AB và CD, M là trung điểm của AB, O là giao
điểm của AD và BC. OM cắt CD tại N. Chứng minh N là trung điểm của CD.
Bài 5: Cho tam giác nhọn ABC, hai đường cao BD và CE. Qua D kẻ DF vuông góc với AB
(F thuộc AB); qua E kẻ EG vuông góc với AC. Chứng minh: a) AD.AE = AB.AG = AC.AF; b) FG song song với BC.
KẾT QUẢ - ĐÁP SỐ Trang 3 Bài 1: OP PQ
Hình 1. Trong tam giác ABC, O
PQ, MN / /PQ ta có: =
( hệ quả của định lí Ta-let) ON MN x 5, 2 5, 2.2 52 = x = = (cm) 2 3 3 15
Hình 2. Ta có: EF ⊥ AB; EF ⊥ D
Q Suy ra AB / / D Q . OF FQ Trong O
QF,QF / /EB suy ra: =
( hệ quả của định lí Ta-let) OE EB x 3,5 3.3,5 = x = = 5,25(cm) 3 2 2
Hình 3.Áp dụng định lí Pytago trong 0 A
MN, A = 90 ta có: 2 2 2 2 2
MN = AM + AN = 16 +12 MN = 400 = 20(cm) AM AN Trong AM
N, MN / /BC suy ra: =
( hệ quả của định lí Ta-let) AB AC 16 12 24.12 = AC =
=18(cm) ; NC =18 −12 = 6(cm) 24 AC 16 AM MN Trong AM
N, MN / /BC suy ra: =
( hệ quả của định lí Ta-let) AB BC 16 20 24.20 = BC = = 30(cm) 24 BC 16 AI AK
Bài 2: a) AK / /BD = ID BD A AI AH H K
Từ AH / /DC = ID DC AK AH F Do đó = BD DC E I AK AH AK + AH HK AI b) Ta có: = = = = BD DC BD + DC BC ID Ta chứng minh AF = AH AE AK (2); = (3) B C D BF BC CE BC AE AF AI Từ (1), (2), (3) ta có + = (đpcm) CE BF ID Trang 4 Bài 3: AH ' AB ' a) Trong ABH
, B ' H '/ /BH suy ra =
(hệ quả của định lí Ta-let) (1) AH AB AH ' AC ' Trong AC
H ,C ' H '/ /CH suy ra =
( hệ quả của định lí Ta-let) (2) AH AC AB ' AC ' Trong AB
C, B 'C '/ /BC suy ra =
( hệ quả của định lí Ta-let) (3) AB AC AH ' B 'C ' Từ (1), (2) và (3) suy ra: = AH BC AH ' B 'C ' B 'C ' 1 1 b) Ta có: = ( câu a);
= B 'C ' = BC AH BC BC 3 3 Từ đó suy ra:
1 AH '.B 'C ' S
A H ' B 'C ' 1 1 67, 5 A B 'C ' 2 = = . = Þ S = S = = 9, 5 cm A B 'C ' A BC ( 2) S 1 A H BC 9 9 9 A BC A H .BC 2 AI AM
Bài 4: Từ IM / / BK và KN / / IC ta suy ra = AB AK A AN AK N M và = . AI AC K I AN AM Do đó = MN / / BC . AB AC B C Trang 5 Bài 5: M A N R Q B P C
Qua A kẻ đường thẳng song song với BC cắt BQ và CR lần lượt tại N và M. QC BC Ta chứng minh được: = (1) AQ AN RA = AM BP AN (2) ; = (3) BR BC CP AM PB QC RA Từ (1), (2), (3) suy ra =1 (đpcm) PC QA RB Bài 6: A E A G üï EG / / DC ï Þ = ïï A E A H A D A C ïý Þ = Þ EH / / BD a) A G A H ï / / A D A B GH BC Þ = ïï A C A B ïþ
b) Gọi O là giao điểm của AC và BD OI OB üï BI/ / DC ï Þ = ïï OI OF OC OD ïý Þ = Þ A D / IF OC OF ï / / OA OD A B CF Þ = ïï OA OB ïþ Bài 7: IM MD üï A B / / DM ï Þ = ïï IM MK a) IA A B ïý Þ = Þ IK / / A B MK MC ï / / IA KB A B MC Þ = ïï KB A B ïþ b) Ta có: Trang 6 IE ID üï A B / / EI ï Þ = ï A B DB ïï IK IM ïï IE IK A B / / IK ï Þ = ý Þ = Þ EI = IK A B MA ï A B A B ï DI IM DI IM ï A B / / DM ï Þ = Þ = ï BI IA BD A M ïïïþ
Tương tự IK = K F . Do đó EI = IK = KF . MF CM
Bài 8: a) MF / / A D = AD CD ME BM A D/ / ME = AD BD MF ME CM BM + = +
mà CD = BD (gt) AD AD CD BD MF + ME CM + BM BC Þ = =
= 2 Þ ME + MF = 2A D A D CD CD (đpcm)
b) ME + MF = 2A D (cmt)
Mà ME + MF = FE + MF + MF = FE + 2MF = 2IF + 2MF = 2IM
AD = IM ADIM là hình bình hành AD / /IM Trang 7