Bài Tập Hình 8 Bài Đối Xứng Tâm Có Lời Giải

8. ĐỐI XỨNG TÂM
I. KIẾN THỨC CƠ BẢN
 Hai điểm đối xứng nhau qua một điểm: Hai điểm được gọi là đối xứng nhau qua một
điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm ấy. A B O
A đối xứng với B qua O  O là trung điểm của . AB Khi đó ta còn nói:
A đối xứng với B qua O hoặc A và B đối xứng nhau qua . O
 Quy ước: Điểm đối xứng với điểm O qua điểm O là chính nó.
 Hai hình đối xứng nhau qua một điểm: Hai hình gọi là đối xứng với nhau qua điểm O
nếu một điểm bất kì thuộc hình này đối xứng với một điểm bất kì thuộc hình kia qua điểm O và ngược lại.
 Nhận xét: Nếu hai đoạn thẳng (góc, tam giác) đối xứng nhau qua một điểm thì bằng nhau.
 Hình có tâm đối xứng: Điểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với
mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
 Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó. III. BÀI TẬP
Bài 1: Cho tam giác vuông ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh BC. Gọi E là
điểm đối xứng với D qua AB, F là điểm đối xứng với D qua AC.
a) Chứng minh rằng E đối xứng với F qua A.
b) Điểm D ở vị trí nào trên cạnh BC thì EF có độ dài ngắn nhất?
Bài 2: Cho góc xOy khác góc bẹt, điểm A thuộc Ox, điểm B thuộc Oy. Gọi C là trung điểm
của AB, điểm D đối xứng với O qua A, điểm E đối xứng với O qua B, điểm F đối xứng với O qua C.
a, Chứng minh rằng D đối xứng với E qua F.
b, Các điểm A và B có vị trí như thế nào thì D đối xứng với E qua đường thẳng OF?
Bài 3: Cho tam giác ABC. Gọi M, D, E theo thứ tự là trung điểm của BC, AB, AC. Gọi I là
điểm đối xứng với M qua D, K là điểm đối xứng với M qua E. Chứng minh rằng I đối xứng với K qua A.
Bài 4: Cho tam giác ABC. Gọi D là điểm đối xứng với B qua A, E là điểm đối xứng với C
qua A. Lấy các điểm I và K theo thứ tự thuộc các đoạn thẳng DE và BC sao cho DI = BK .
Chứng minh rằng I đối xứng với K qua A. Trang 1
Bài 5: Cho tam giác ABC , trực tâm H . Gọi M là trung điểm của BC . D là điểm đối xứng với H qua M .
a, Chứng minh rằng: BD ⊥ BA, CD ⊥ CA .
b, Gọi I là trung điểm của AD . Chứng minh rằng: IM ⊥ BC .
Bài 6: Cho tam giác ABC, điểm O nằm trong tam giác. Gọi A' là điểm đối xứng với O qua
trung điểm D của BC, B' là điểm đối xứng với O qua trung điểm E của AC, C' là điểm đối
xứng với O qua trung điểm F của AB. Chứng minh rằng ΔABC = ΔAB'C'
Bài 7: Trên hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy điểm E trên
cạnh AB, lấy điểm F trên cạnh CD sao cho AE = CF .
a) Chứng minh rằng E đối xứng với F qua O.
b) Gọi I là giao điểm của AF và DE, gọi K là giao điểm của BF và CE. Chứng minh rằng I đối xứng với K qua O.
KẾT QUẢ - ĐÁP SỐ
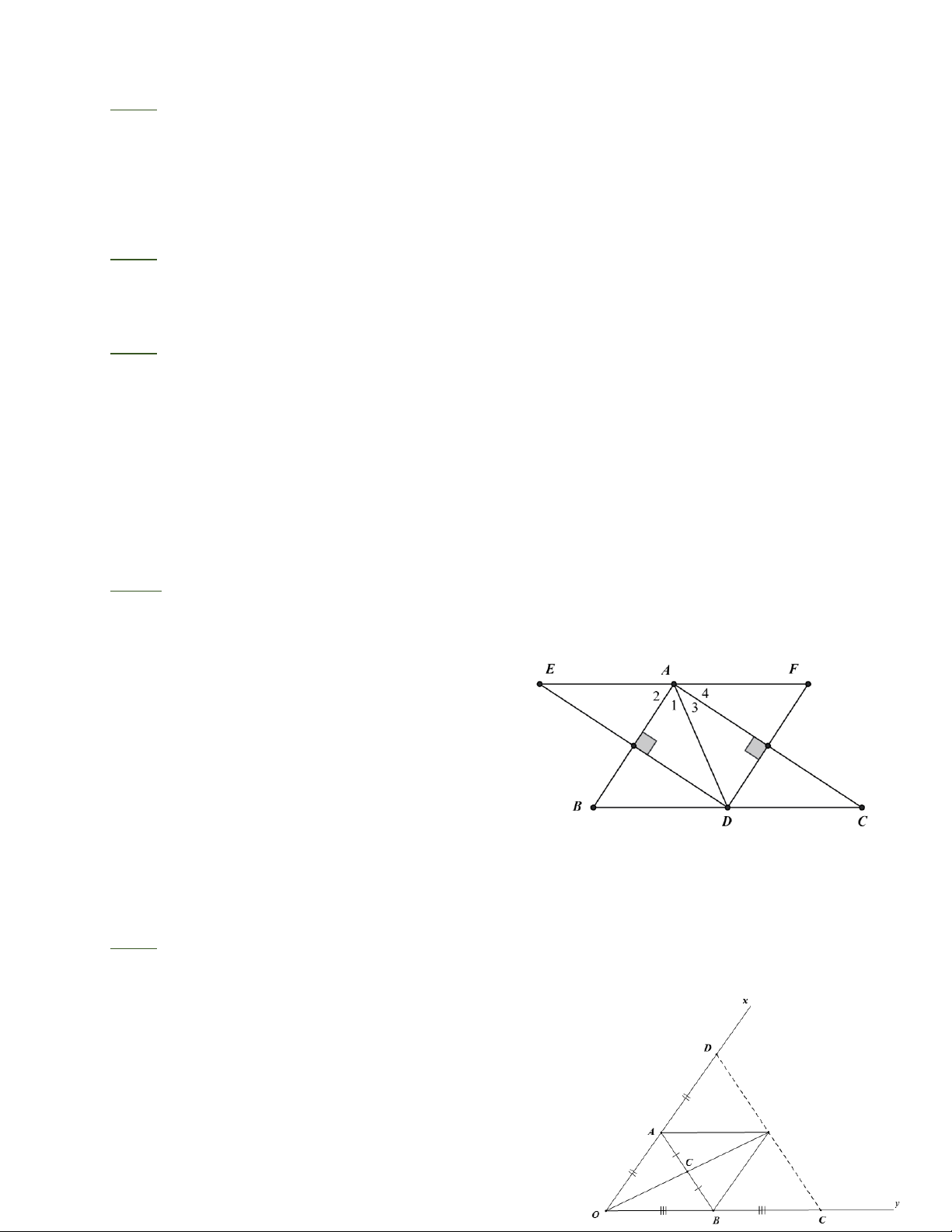
Bài 1: a) E đối xứng với D qua AB nên AD = AE và A = A . 1 2
F đối xứng với D qua AC nên AD = AF và A = A 3 4  AE = AF = AD;
DAE + DAF = 2 (A + A = 2.90 = 180 1 3 )  E,A,F thẳng hàng.
Vậy E đối xứng với F qua A.
b) Ta có: EF = 2AD nên EF nhỏ nhất  AD nhỏ nhất  D là chân đường cao kẻ từ A đến BC. Bài 2:
a, Ta có: A O = A D,CO = CF nên AC là đường trung
bình của ODF do đó FD = 2A C , FD/ / A C .
Chứng minh tương tự, CB là đường trung bình của
OEF suy ra FE = 2CB,FE / / CB . Trang 2
Ta có: FD / /CA, FE / /CB mà C nằm giữa A và B nên D, F, E thẳng hang, F nằm giữa D và E (1).
Ta có: FD = 2AC, FE = 2CB mà AC = CB  FD = FE(2)
Từ (1) và (2) suy ra F là trung điểm của DE do đó D đối xứng với E qua F.
b, D đối xứng với E qua OF  OF là đường trung trực của DE  OD = OE vì đã cso
FD = FE  OA = OB . Như vậy nếu OA = OB thì D đối xứng với E qua OF. Bài 3: · · · ·
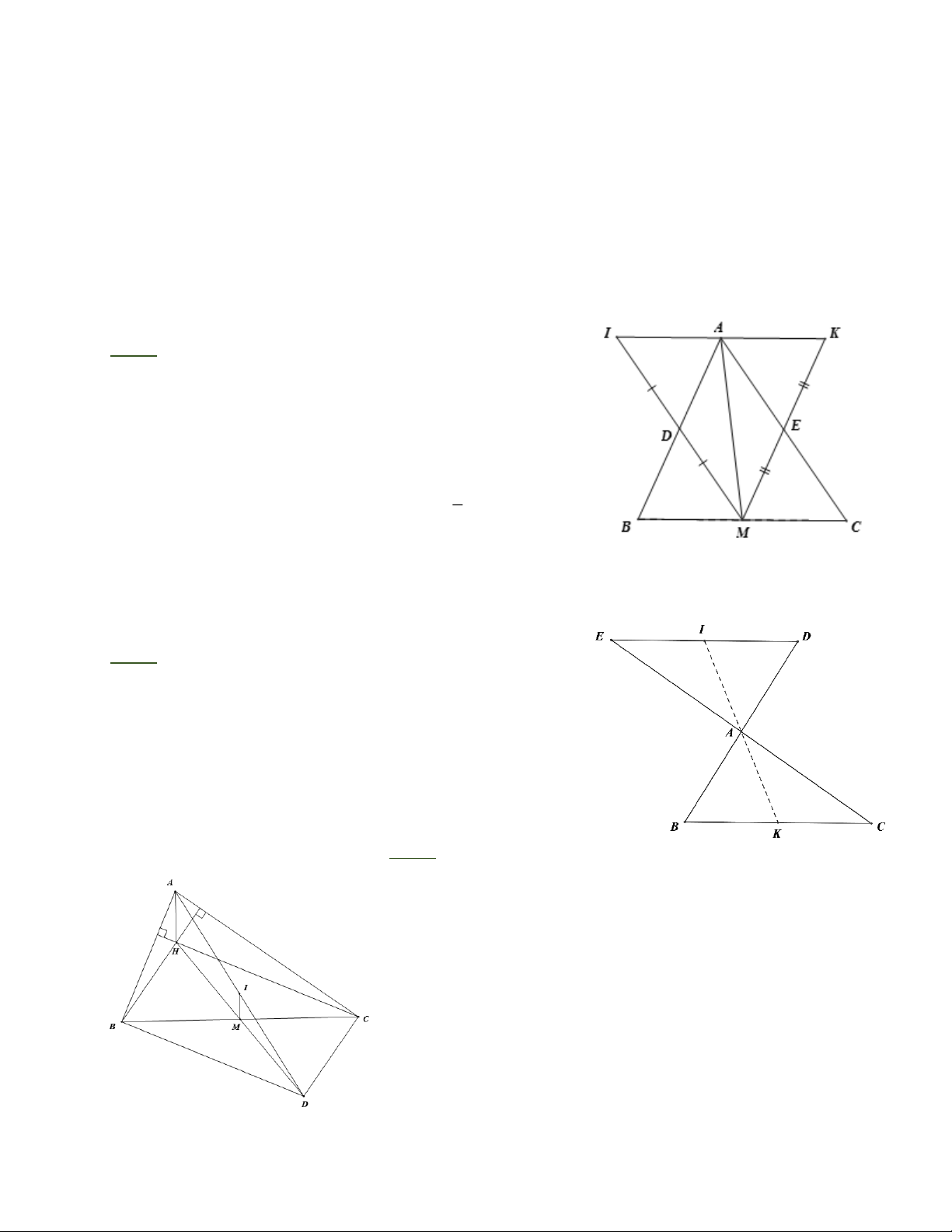
HD: Chỉ ra IA D = DBM ;KA E = ECM . Từ đó · · · · · ·
IA D + DA E + EA K = DBM + DA E + ECM = 180°
nên I , A, K thẳng hàng. 1
Dễ dàng chỉ ra IA = A K = BM = MC = BC . Từ đó 2
suy ra I đối xứng với K qua A Bài 4:
Tứ giác BEDC có AB = AD và AC = AE nên là hình
bình hành, suy ra DE//BC .
Tứ giác BIDK có DI //BK và DI = BK nên là hình bình
hành, suy ra đường chéo IK đi qua trung điểm A của
BD . Vậy I , A , K thẳng hàng. Bài 5:
a) Chứng minh được BHCD là hình bình hành suy ra
BD/ / CH ; mà CH ^ A B nên BD ^ A B
Tương tự DC / / BH ; mà BH ^ A C nên DC ^ A C
b) IM là đường trung bình của AHD nên IM / / A H ,
mà A H ^ BC nên IM ⊥ BC Trang 3 Bài 6:
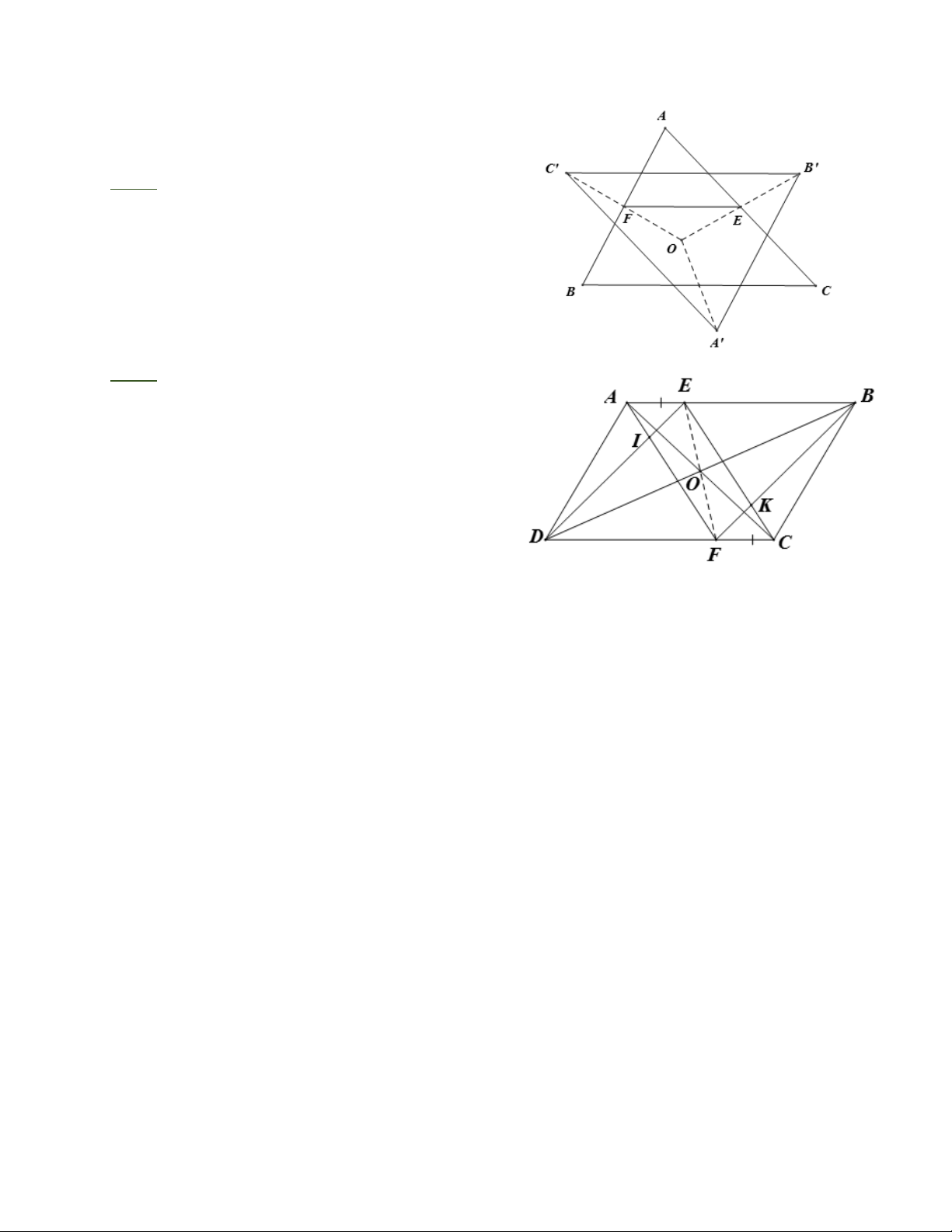
HD: Sử dụng tính chất đường trung bình trong tam giác chỉ ra 
B C = BC = 2EF . Tương tự  A  B = A ; B  A C = AC
Vậy tam giác ABC = A  B C (c.c.c). Bài 7:
HD: a. Chứng minh rằng AECF là hình bình
hành. từ đó EF đi qua trung điểm O của AC và
O là trung điểm của EF . Hay E đối xứng với F qua O.
b. Chứng minh rằng EIFK là hình bình hành
từ đó suy ra IK đi qua trung điểm của O của
EF và IO = IK từ đó suy ra I đối xứng với K qua O. Trang 4