Bài Tập Hình 8 Bài Hình Thang Có Lời Giải

2. HÌNH THANG
I. KIẾN THỨC CƠ BẢN
 Hình thang là tứ giác có một cặp cạnh đối song song với nhau.
 Hình thang có một góc vuông được gọi là hình thang vuông Nhận xét:
Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau.
Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên hai cạnh bên song song và bằng nhau. III. BÀI TẬP µ
Bài 1: Cho hình thang ABCD ( A B / / CD ) biết A = 115° Tính số đo góc D? µ µ
Bài 2: Cho hình thang ABCD ( AB // CD) có B - C = 10° Tính số đo góc B?
Bài 3: Tứ giác ABCD có BC = CD và DB là tia phân giác .
D Chứng minh rằng ABCD là
hình thang và chỉ rõ cạnh đáy và cạnh bên của hình thang.
Bài 4: Cho hình thang A B CD , đáy A B = 40cm , CD = 80cm , BC = 50cm , A D = 30cm .
Chứng minh rằng ABCD là hình thang vuông.
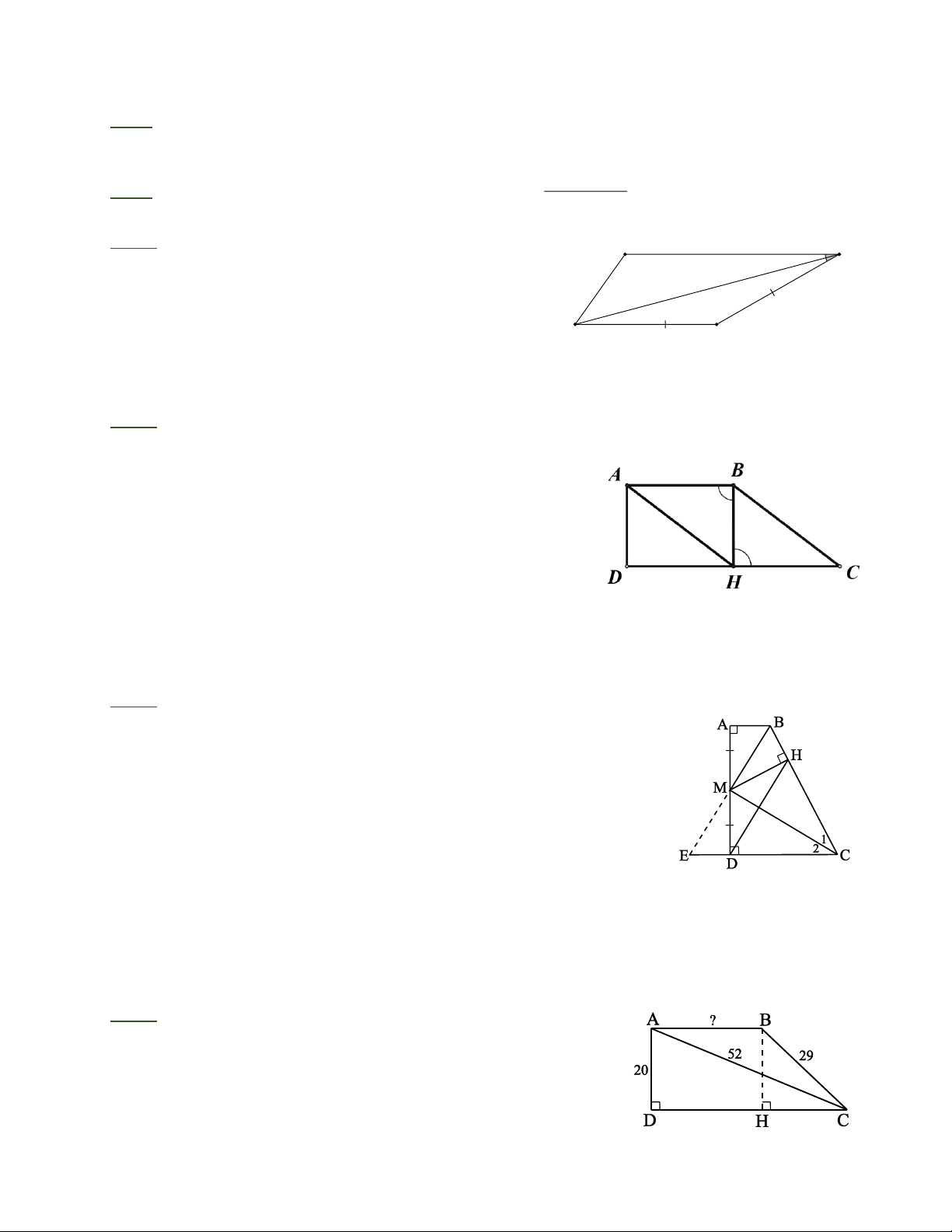
Bài 5: Cho hình thang A B CD vuông tại A và D. Gọi M là trung điểm của AD. Cho biết MB ^ MC
a) Chứng minh rằng BC = A B + CD;
b) Vẽ MH ^ BC . Chứng minh rằng tứ giác MBHD là hình thang.
Bài 6: Cho hình thang ABCD vuông tại A và D. Cho biết A D = 20 , A C = 52 và BC = 29. Tính độ dài AB.
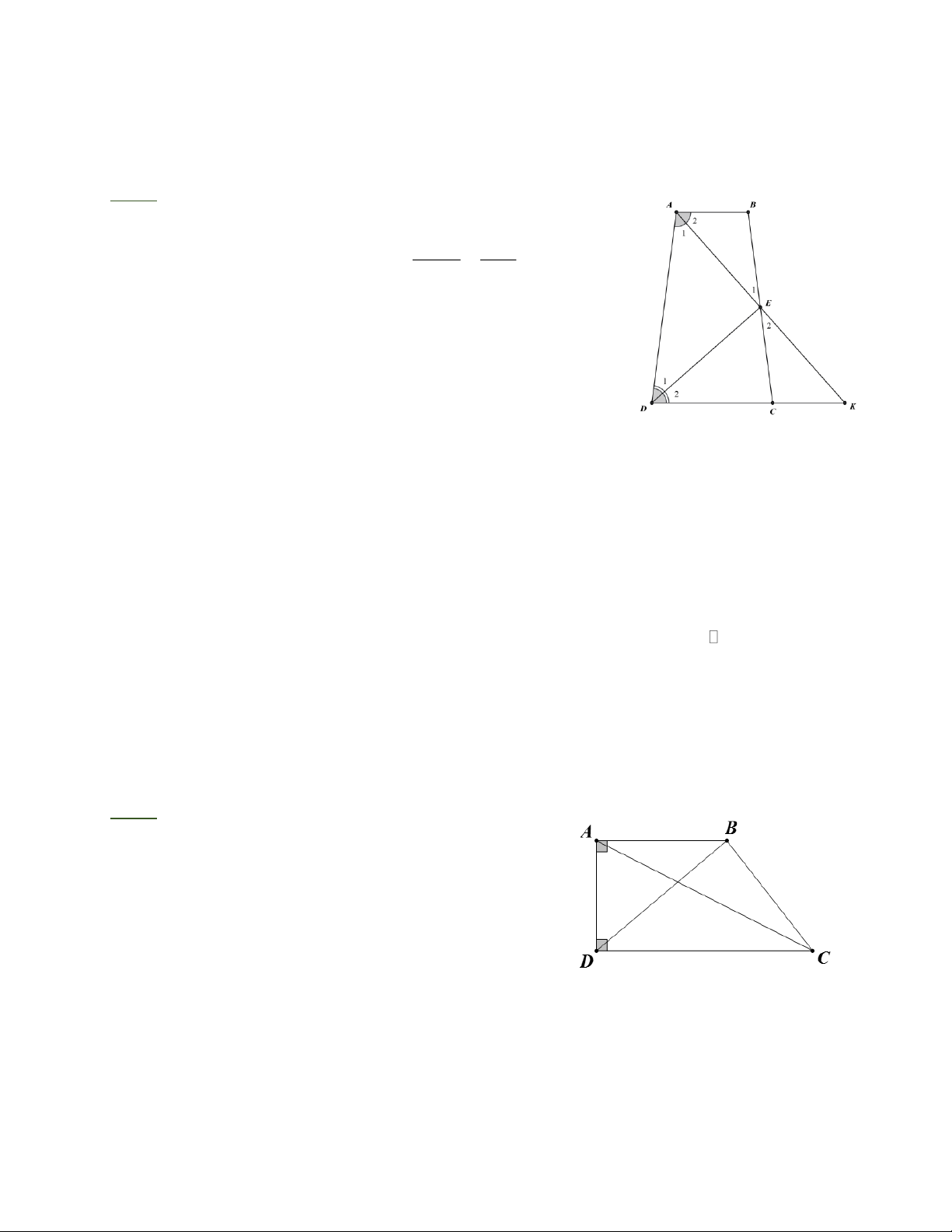
Bài 7: Hình thang ABCD (AB//CD) có các tia phân giác của các góc A và D gặp nhau tại
điểm E thuộc cạnh BC. Chứng minh rằng: a) AED =  90 . b) AD = AB + CD .
Bài 8: Một hình thang vuông có tổng hai đáy bằng a, hiệu hai đáy bằng b. Tính hiệu các
bình phương của hai đường chéo.
Bài 9: Hình thang vuông ABCD ( A D 90 = =
) có AB = BC =6cm, CD =9cm. Tính số đo các
góc B và C . (Gợi ý trong bài hình chữ nhật để khai thác) – Không chữa. (HSG7 đã học) Trang 1
KẾT QUẢ - ĐÁP SỐ µ µ µ
Bài 1: Vì A B / / CD nên A + D = 180° (hai góc trong cùng phía) Þ D = 180° - 115° = 65° µ µ µ µ µ 180° + 10°
Bài 2: B + C = 180° và B - C = 10° tính được B = = 95° 2 · ·
Bài 3: Ta có D B CD cân tại C suy ra CBD = CDB ; D A · ·
lại có A DB = CDB ( do BD là tia phân giác góc D) · ·
nên A DB = CBD mà hai góc này ở vị trí đồng vị
nên BC / / A D . B C
Tứ giác ABCD có BC / / A D nên tứ giác là hình thang. Đáy là BC ;A D , cạnh bên A B ;CD
Bài 4: Gọi H là trung điểm của CD. Ta có DH = CH = 40cm
Xét hai tam giác ABH và CHB có:
A B = CH = 40cm , ABH = CHB (so le trong), BH = HB
Suy ra D ABH = DCHB (c.g.c) Þ A H = CB = 50cm . Tam giác ADH có: 2 2 2 2 2 2
A D + DH = 40 + 30 = 50 = A H
Suy ra tam giác ADH vuông tại D. Vậy hình thang ABCD là hình thang vuông.
Bài 5: Gọi E là giao điểm của tia BM với tia CD.
DABM = DDEM(g.c.g) Þ A B = DE và MB = ME .
D CBE có CM vừa là đường trung tuyến vừa là đường cao nên là
tam giác cân Þ CB = CE
Þ CB = CD + DE Þ CB = CD + AB (vì A B = DE ).
b) D CB E cân tại C, CM ^ BM ( ) 1  = 1 C
C2 Þ MH = MD (tính chất điểm nằm trên tia phân giác).
D HCM = D DCM (cạnh huyền – góc nhọn) Þ CH = CD Þ DCHD cânÞ CM ^ DH. (2) Từ ( )
1 và (2)suy ra BM / / DH do đó tứ giác MBHD là hình thang.
Bài 6: Vẽ BH ^ CD ta được AB = DH; BH = AD = 20
 Xét D BHC vuông tại H có 2 2 2 2 2
HC = BC - BH = 29 - 20 = 441 Þ HC = 21 Trang 2
 Xét D A DC vuông tại D có 2 2 2 2 2
CD = AC - AD = 52 - 20 = 2304 Þ CD = 48
Do đó DH = CD - HC = 48 - 21 = 27 Þ AB = 27 Bài 7: a) AED = 18  0 − (A + D ( ) 1 1 1 ) A ˆ D ˆ 180 AB//CD  A ˆ +  + Dˆ =  180  A + D = = = 9  0 (2) 1 1 2 2 Từ ( ) 1 và (2)suy ra AED = 18  0 −  90 =  90 .
b) Gọi K là giao điểm của AE và DC.
Tam giác A DK có đường phân giác DE cũng là đường cao
nên là tam giác cân, suy ra: AD = DK và AE = EK (3) ΔAEB và ΔKEC có:
E = E (đối đỉnh); AE = EK (chứng minh trên); A = ˆ K (so le trong, AB DK ). 1 2 2
Do đó ΔAEB = ΔKEC (g.c.g), suy ra AB = CK (4).
Từ (3)và (4) suy ra: AD = DK = DC + CK = DC + AB .
Bài 8: Xét hình thang ABCD có A = D = 0
90 ,CD + AB = a,CD − AB = b Ta có 2 2 - = ( 2 2 + )- ( 2 2 AC BD CD AD AB + AD ) 2 2
= CD - AB = (CD + AB)(CD - AB) = ab Trang 3