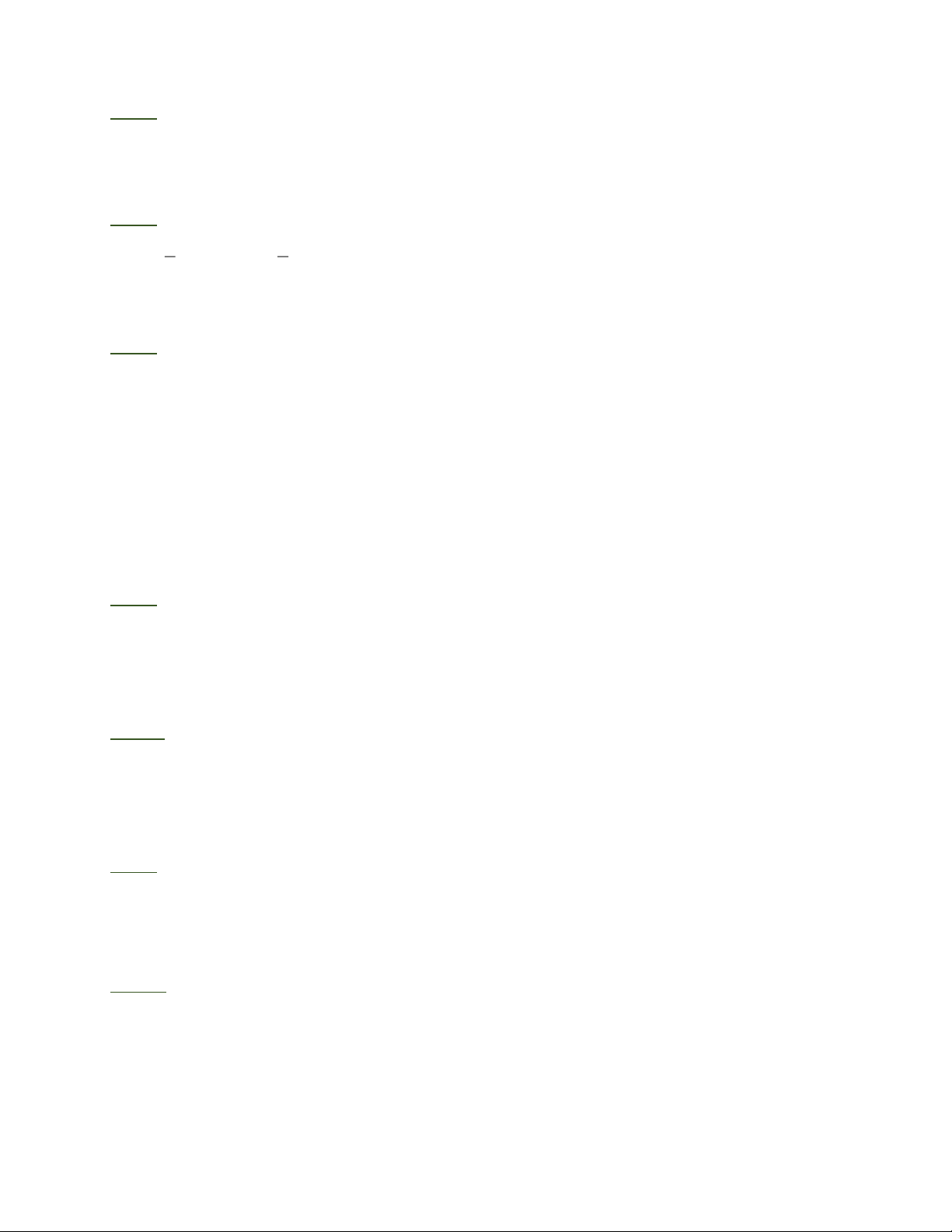

Preview text:
7. HÌNH BÌNH HÀNH
I. KIẾN THỨC CƠ BẢN
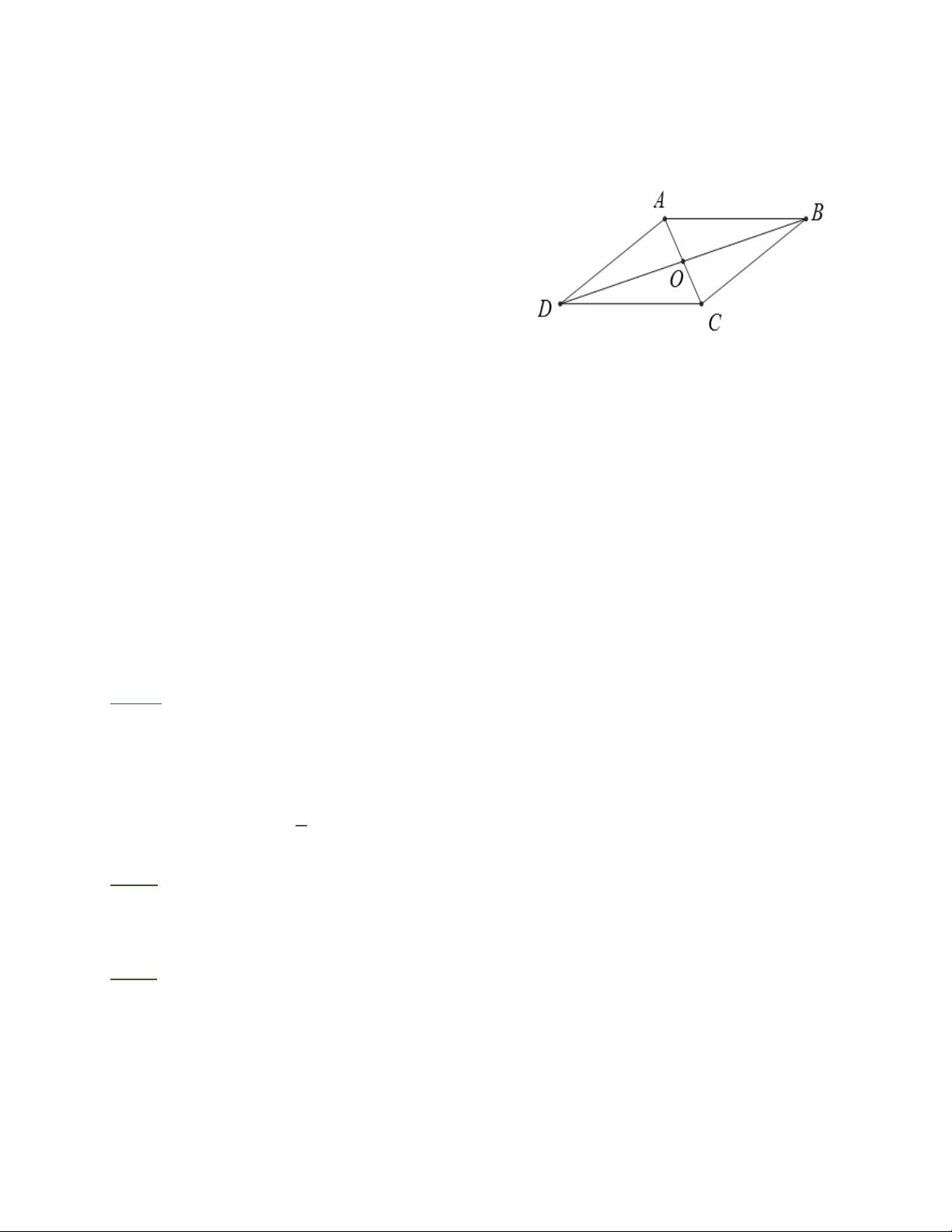
Định nghĩa: Hình bình hành là tứ giác có các cặp cạnh đối song song. AB//CD
Tứ giác ABCD là hình bình hành AD//BC
Tính chất: Trong hình bình hành:
- Các cạnh đối bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Dấu hiệu nhận biết:
- Tứ giác có các cạnh đối song song là hình bình hành.
- Tứ giác có các cạnh đối bằng nhau là hình bình hành
- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
- Tứ giác có các góc đối bằng nhau là hình bình hành.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành. III. BÀI TẬP
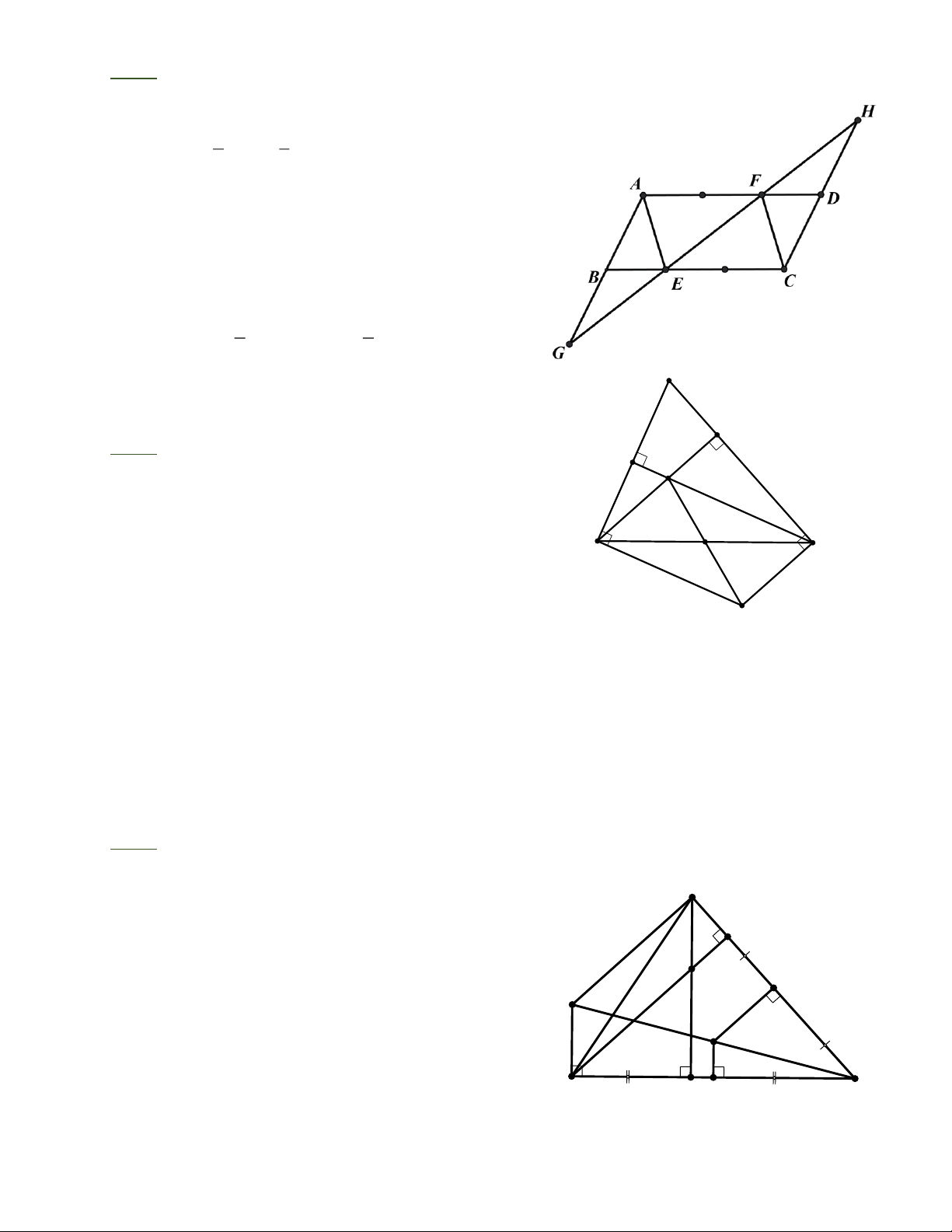
Bài 1: Cho tam giác ABC, trực tâm H. Gọi M là trung điểm của BC, N là trung điểm của
AC. Đường vuông góc với BC tại M và đường vuông góc với AC tại N cắt nhau ở O.
a) Trên tia đối của tia OC, lấy điểm K sao cho OK = OC . Chứng minh rằng AHBK là hình bình hành. b) Chứng minh = 1 OM AH . 2
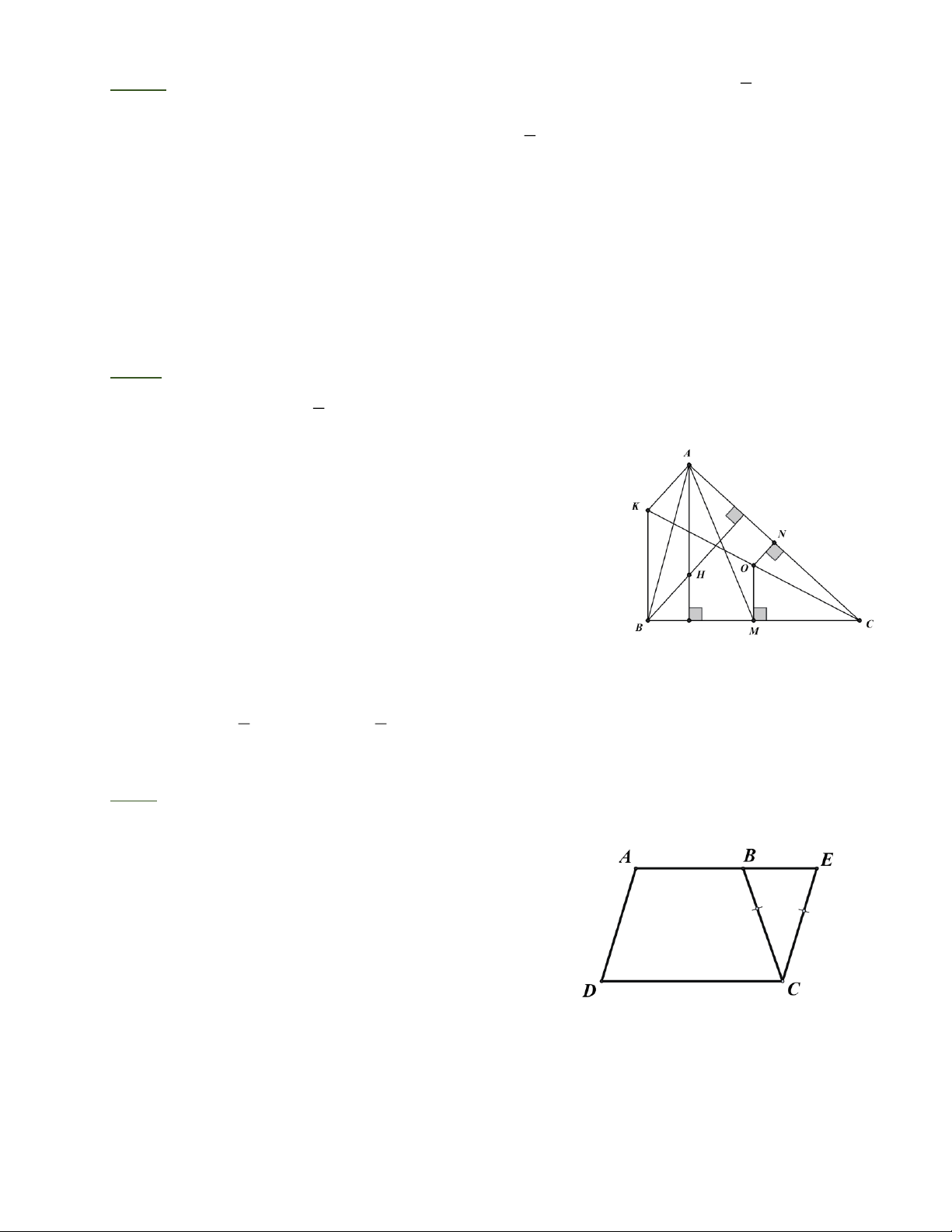
Bài 2: Cho hình thang cân ABCD (AB//CD, AB < CD). Trên tia đối của tia BA lấy điểm E
sao cho CB = CE. Chứng minh AECD là hình bình hành.
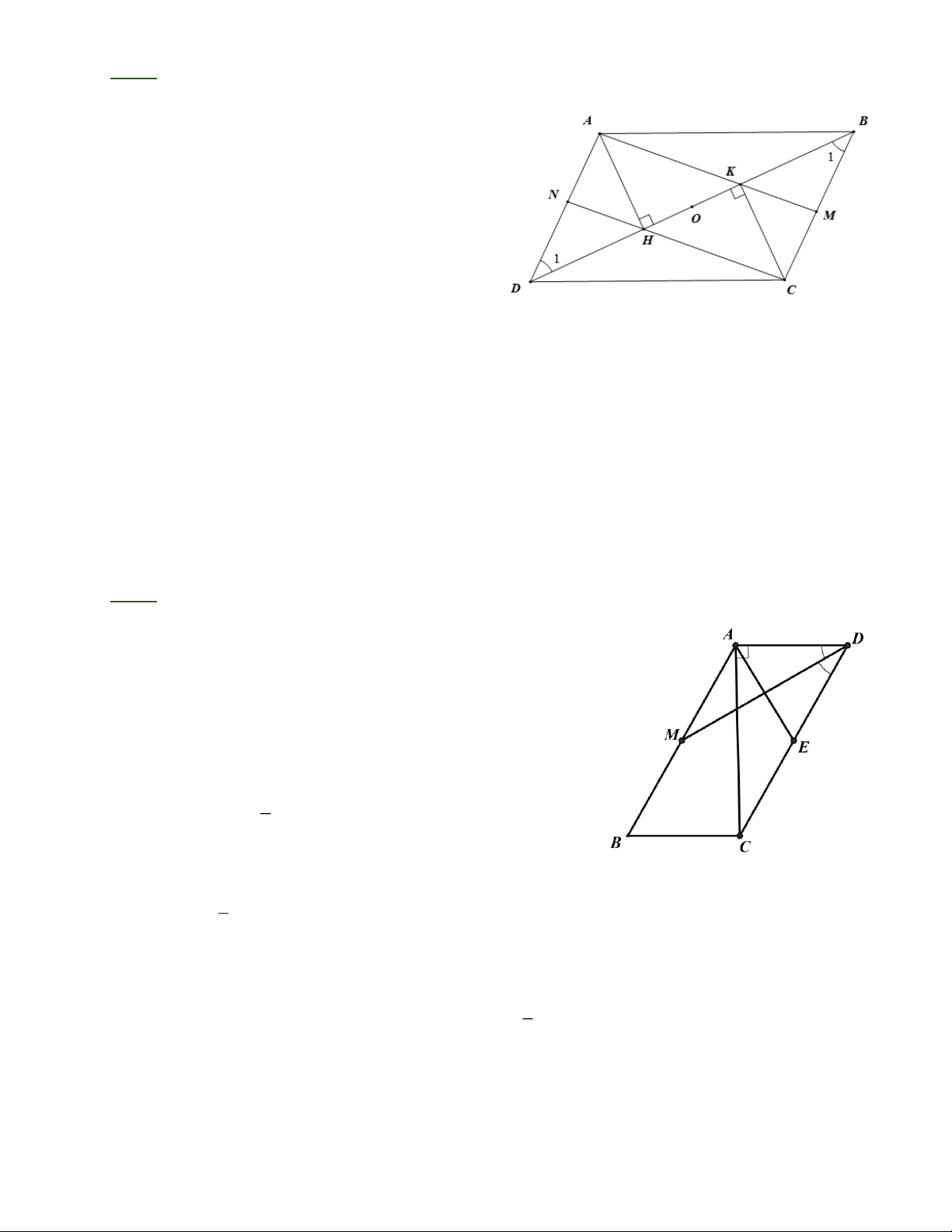
Bài 3: Cho hình bình hành ABCD . Gọi H và K theo thứ tự là chân đường vuông góc kẻ
từ A và từ C đến BD .
a) Chứng minh rằng AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC , gọi N là giao điểm của CH và AD. Chứng minh
rằng AN = CM . Trang 1
c) Gọi O là trung điểm của HK. Chứng minh rằng O, M , N thẳng hàng. µ
Bài 4: Cho hình bình hành ABCD có A = 120° , phân giác góc D đi qua trung điểm của
cạnh AB. Gọi E là trung điểm của CD. Chứng minh: a) A B = 2A D
b) D A DE đều, D A EC cân c) A C ^ A D
Bài 5: Cho hình bình hành ABCD. Hai điểm E, F lần lượt lấy trên BC, AD sao cho 1 1 BE = BC , DF =
DA và EF lần lượt cắt AB, CD tại G, H. Chứng minh rằng: 3 3
a) GE = EF = FH
b) Tứ giác A ECF là hình bình hành.
Bài 6: Cho tam giác ABC, các đường cao BH và CK cắt nhau tại E. Đường thẳng qua B
vuông góc với AB và đường thẳng qua C vuông góc với AC cắt nhau tại D. Gọi M là trung điểm của BC.
a) Tứ giác B DCE là hình gì? Vì sao?
b) Chứng minh rằng M là trung điểm của DE. Tam giác ABC thỏa mãn điều kiện gì thì DE đi qua A? · ·
c) Chứng minh rằng BAC + BDC = 180° .
Bài 7: Cho tam giác ABC, các đường cao AK và BD cắt nhau tại G. Vẽ các đường trung
trực HE, HF của các cạnh AC, BC. Đường thẳng qua A song song với BG cắt đường thẳng
qua B song song với AK tại I. Chứng minh rằng: a) BG = A I b) BG = 2HE c) A G = 2HF
Bài 8*: Cho tam giác ABC cân ở A . Lấy điểm D trên cạnh AB , điểm E trên AC sao cho
AD = CE . Gọi O là trung điểm của DE , gọi K là giao điểm của AO và BC . Chứng minh
rằng ADKE là hình bình hành. Tự luyện.
Bài 9: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD, BD.
a) Tứ giác EFGH là hình gì?
b) Tính chu vi của tứ giác EFGH biết AD = a, BC = b .
Bài 10: Cho tam giác ABC, các đường trung tuyến BD và CE. Vẽ các điểm H và K sao cho
E là trung điểm của CH, D là trung điểm của BK. Chứng minh rằng A là trung điểm của HK. Trang 2
Bài 11: Cho hình bình hành ABCD. Lấy điểm E trên cạnh CD sao cho = 1 DE DC . Gọi K là 3
giao điểm của AE và BD. Chứng minh rằng = 1 DK DB . 4
KẾT QUẢ - ĐÁP SỐ
Bài 1: a) Tam giác KBC có KO = OC, BM = MC nên OM là đường trung bình của D K B C . Suy ra = 1 OM//KB,OM
KB . Ta lại có OM//AH (cùng 2 vuông góc với BC). Suy ra KB//AH .
Chứng minh tương tự ta có: KA//BH .
Tứ giác AHBK có KB//AH,KA//BH nên là hình bình hành.
b) AHBK là hình bình hành nên KB = AH . Ta lại có = 1 OM KB nên = 1 OM AH . 2 2 · ·
Bài 2: Dễ thấy tam giác BCE cân tại C suy ra CBE = CEB · ·
Ta lại có CBA = DAB · · · ·
Mà CBA = DAB Nên CEB + DAB = 180°
Suy ra A C / / ED (2 góc trong cùng phía bù nhau)
Suy ra AECD là hình bình hành Trang 3
Bài 3: a) Cách 1 Xét A
HD và CKB (H = K = 90): AD = BC
(cạnh đối hình bình hành); D = B 1 1 (so le
trong, AD//BC ). Vậy AHD = CKB (trường
hợp cạnh huyền và góc nhọn), suy ra
AH = CK. Ta lại có AH //CK (cùng vuông góc
với BD ). Tứ giác AHCK có AH = CK, AH //CK nên là hình bình hành.
Cách 2. Chứng minh rằng tứ giác AHCK có
các đường chéo cắt nhau tại trung điểm của mỗi đường.
b) Tứ giác AHCK là hình bình hành (câu a) nên AH //CK , tức là AM //CN. Ta lại có AN //CM .
Tứ giác ANCM là hình bình hành (theo định nghĩa) nên AN = CM .
c) Hình bình hành AHCK có O là trung điểm của HK nên O là trung điểm của AC (tính
chất đường chéo hình bình hành)
Hình bình hành ANCM có O là trung điểm của AC nên O là trung điểm của MN. Vậy
M , N ,O thẳng hàng. Bài 4: · ·
a) Gọi M là trung điểm của cạnh AB, ta có AMD = CDM (1) (so le trong). · ·
Mặt khác, DM là phân giác góc D nên ADM = CDM (2) · ·
(1), (2) Þ AMD = ADM , do đó tam giác ADM cân tại A. 1 Vậy AD = AM = AB 2 µ ° µ
b) Trong hình bình hành ABCD, A 120 D 60° = Þ = và 1 AD = DE =
CD . Tam giác ADE cân và có một góc bằng 600, nên tam giác ADE đều. 2
Theo trên, tâm giác ADE đều nên A E = ED = EC , suy ra tam giác AEC cân tại E. · 1 ·
c) Vì ADE đều và ACE cân tại E nên EAC =
AED = 30° (góc ngoài của AEC) 2 · ·
Mặt khác EAD = 60° , suy ra CAD = 90° . Vậy AC ^ AD Trang 4 Bài 5:
a) Trong D A GF , B trên cạnh AG, E trên cạnh FG. 1 1 Ta có BE = BC =
AF và BE / / A F suy ra BE 3 2
là đường trung bình trong D A GF . Do đó E là trung điểm của GF (1).
Chứng minh tương tự, DF là đường trung bình
trong D CHE , nên F là trung điểm của HE (2).
Từ (1) và (2) suy ra GE = EF = FH . 2 2 b) Ta có AF = AD và EC = BC , suy ra 3 3
AF = CE . Mặt khác AF/ / CE , do vậy tứ giác A
A ECF là hình bình hành. H Bài 6: a) Ta có: K ìï BE ^ AC ï E í Þ BE/ / DC (1) ï DC ^ AC ïî M ìï CE ^ AB B C ï í Þ CE/ / BD (2) ï BC ^ AB ïî
Từ (1) và (2) suy ra BDCE là hình bình hành. D
b) Vì B DCE là hình bình hành và M là trung điểm của BC nên M là trung điểm của DE.
DE đi qua A khi và chỉ khi A, E, M thẳng hàng. Vì E là giao điểm hai đường cao BH và CK
nên AE là đường cao trong tam giác ABC. Vậy AE qua M khi và chỉ khi đường cao và
đường trung tuyến kẻ từ A trùng nhau, hay tam giác A B C cân tại A. µ µ µ µ µ µ µ µ
c) Trong tứ giác ABDC: A + B + C + D = 360° , mà B = C = 90° nên A + D = 180° . · · Vậy BAC + BDC = 180° .
Bài 7: a) Ta có A G / / BI và BG / / A I nên tứ giác AIBG là hình bình hành, suy ra BG / / A I ; BG = A I . A
b) IB / / AG Þ IB ^ BC , mà HF ^ BC , do đó IB / / HF. D
Lại có F là trung điểm của BC nên HF đi qua trung G E điểm của IC. I
Chứng minh tương tự, HE cũng đi qua trung điểm H của IC.
Từ đó ta được H là trung điểm của IC. B K F C
Trong D A IC , HE là đường trung bình, do đó Trang 5 1 1 HE = AI =
BG . Vậy BG = 2HE . 2 2
c) Theo chứng minh trên, HF là đường trung bình trong CBI. 1 1 Suy ra HF = BI =
AG (Vì A IBG là hình bình hành). Vậy A G = 2HF . 2 2 Bài 8*:
Kẻ DH / /BC , OI / /BC ta có: ADH = B , ACH = C mà
B = C nên ADH = ACH
ADH cân => AH = AD = EC . Chứng minh tiếp HI = IE để
suy ra AI = IC , AO = OK
Từ đó suy ra ADKE là hình bình hành. Trang 6



