
Preview text:
3. HÌNH THANG CÂN
I. KIẾN THỨC CƠ BẢN
Hình thang có hai góc kề một đáy bằng nhau được gọi là hình thang cân
Trong một hình thang cân: - Hai cạnh bên bằng nhau
- Hai đường chéo bằng nhau
Dấu hiệu nhận biết:
- Hình thang có hai góc kề một đáy bằng nhau được gọi là hình thang cân.
- Nếu một hình thang có hai đường chéo bằng nhau thì nó là hình thang cân.
Sai lầm cần tránh: Hình thang có 2 cạnh bên bằng nhau chưa chắc đã là hình thang cân. III. BÀI TẬP
Bài 1: Tứ giác ABCD là hình gì, biết A ˆ = 70,Bˆ = ˆC = 110 ?
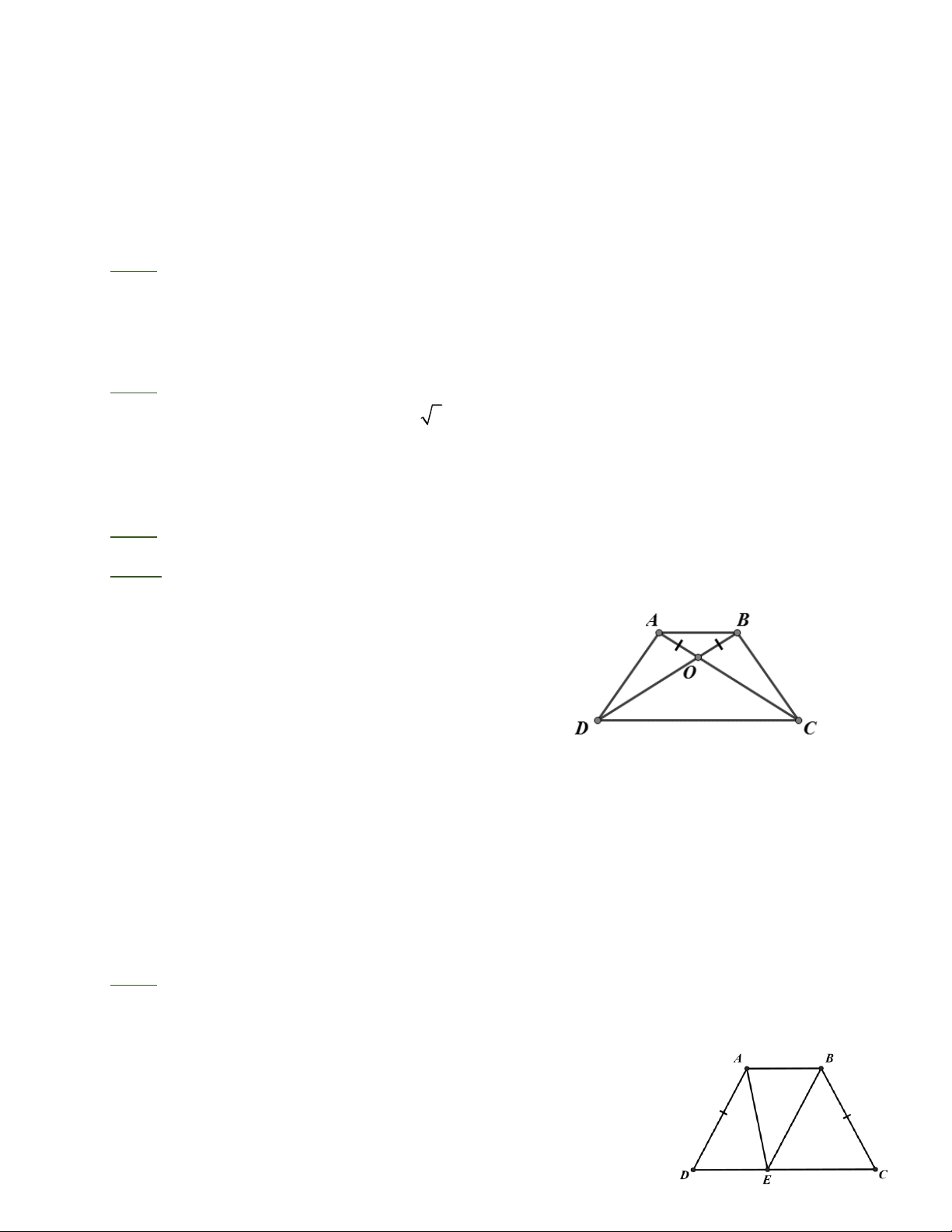
Bài 2: Cho hình thang A B CD (AB//CD) . AC cắt BD tại O. Biết OA = OB . Chứng minh
rằng: A B CD là hình thang cân.
Bài 3: Tứ giác ABCD có A B / / CD, A B < CD, A D = BC . Chứng minh ABCD là hình thang cân.
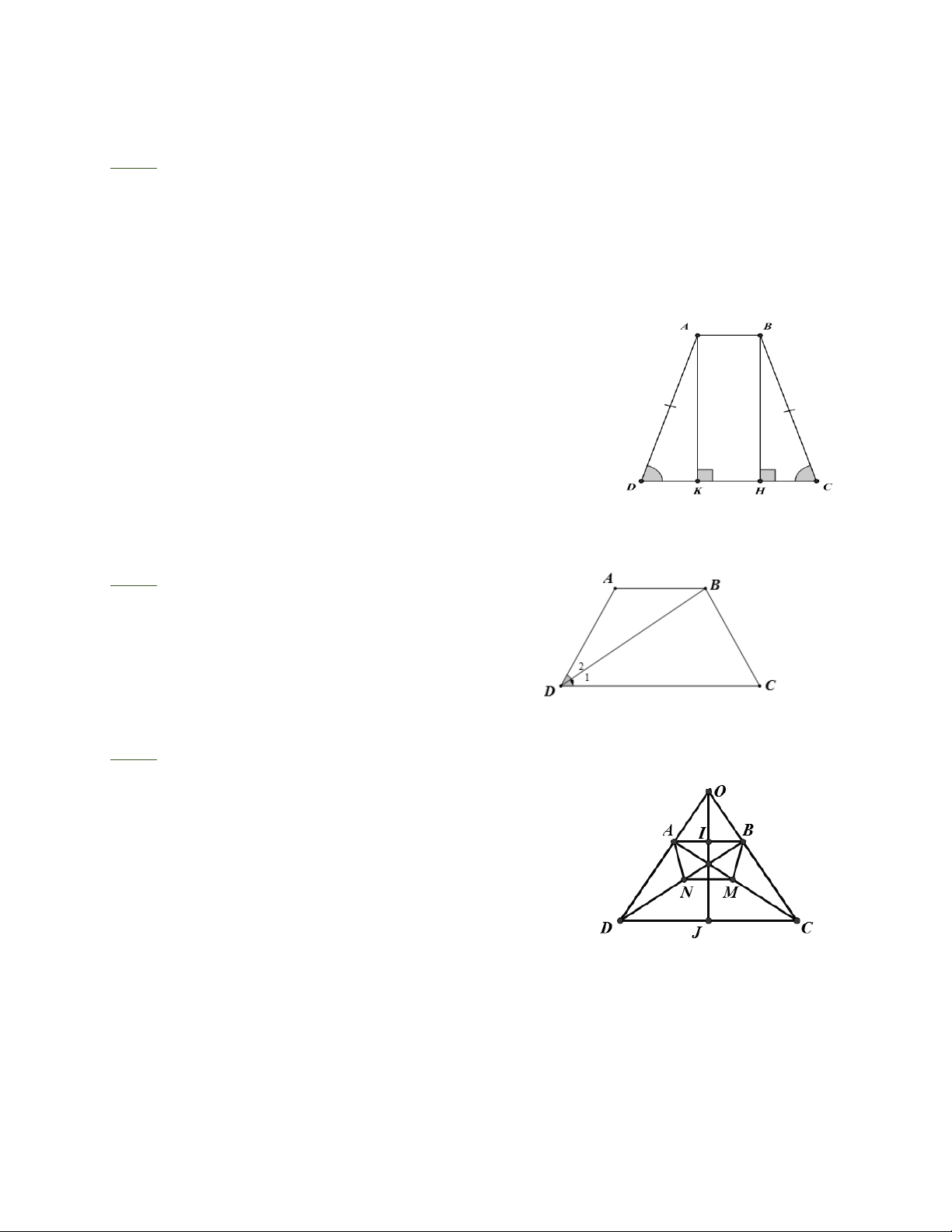
Bài 4: Cho hình thang cân ABCD (AB//CD) có AB = 3, BC = CD = 13 (cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH = DK . b) Tính độ dài BH
Bài 5: Hình thang cân ABCD(AB//CD) có ˆC = 60 , DB là tia phân giác của góc D, AB = 4 cm
a) Chứng minh rằng BD vuông góc với BC. b) Tính chu vi hình thang.
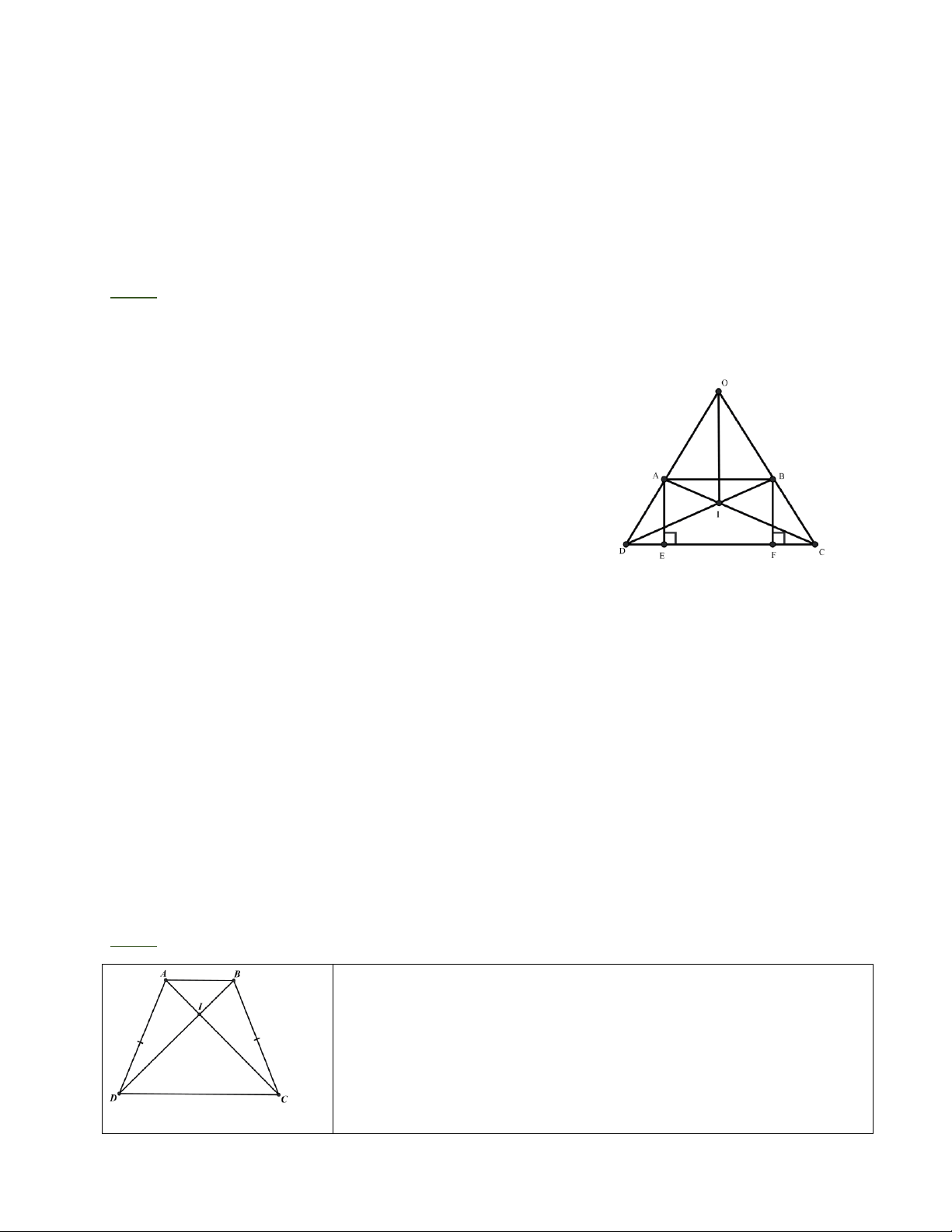
Bài 6: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng OAB cân
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng
minh rằng MNAB, MNDC là các hình thang cân.
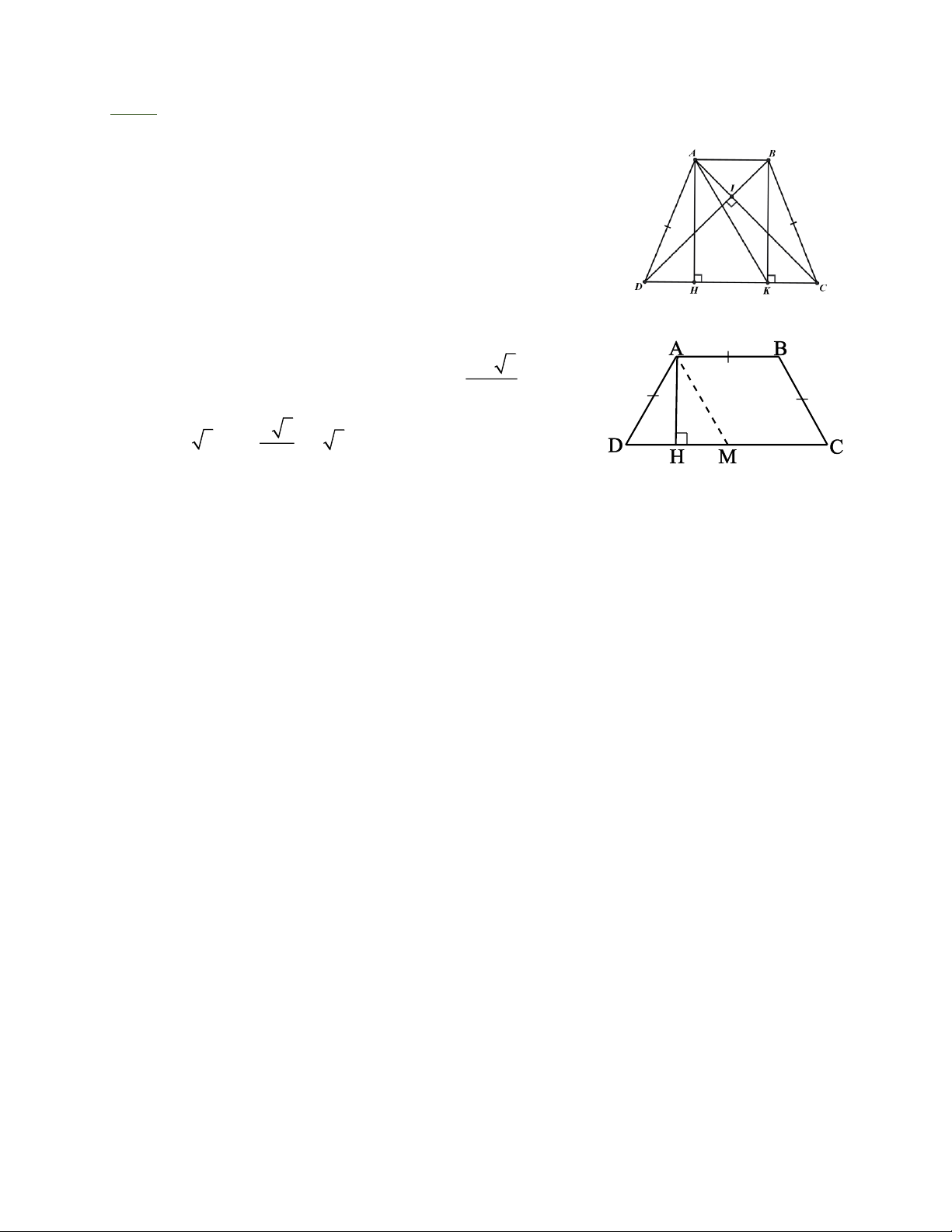
Bài 7: Cho hình thang ABCD cân có AB // CD và AB < CD. Kẻ các đường cao AE, BF. Trang 1
a. Chứng minh rằng: DE = CF.
b. Gọi I là giao điểm của 2 đường chéo hình thang ABCD. Chứng minh: IA = IB.
c. Tia DA và tia CB cắt nhau tại O. Chứng minh OI vừa là trung trực của AB vừa là trung trực của DC.
d. Tính các góc của hình thang ABCD nếu biết ABC − ADC = 80
Bài 8: Tứ giác ABCD có : A = B, BC = AD
a) Chứng minh ABCD là hình thang cân
b) Cho biết: AC ⊥ BD và đường cao AH = 4cm. Tính A B + CD.
Bài 9: Một hình thang cân có đáy nhỏ bằng cạnh bên và góc kề với đáy lớn bằng 60° . Biết
chiều cao của hình thang cân này là a 3. Tính chu vi của hình thang cân.
KẾT QUẢ - ĐÁP SỐ
Bài 1: ABCD là hình thang cân, đáy BC và AD
Bài 2: Vì OA = OB nên tam giác OAB cân tại O · · Þ OAB = OBA · · · · Ta có OCD = OAB = OBA = ODC
tam giác OCD cân tại O Þ OC = OD
Suy ra AC = OA + OC = OB + OD = BD
Hình thang ABCD có hai đường chéo AC và BD bằng nhau nên ABCD là hình thang cân. Bài 3:
Từ B kẻ BE//AD E BC . Vì AB < CD nên điểm E nằm giữa C và D.
Chứng minh DA BE = DEDA (g.c.g) Þ A D = BE
Có A D = BC Þ BE = BC Þ D BEC cân tại B BEC = C Trang 2
Mà BE//AD D = BEC ( đồng vị) D = C mà tứ giác ABCD là hình thang
Vậy tứ giác ABCD là hình thang cân.
Bài 4: a) ΔBCH và ΔADK (H = K = 90) có cạnh huyền BC = AD (cạnh bên hình thang cân), góc nhọn ˆ C = ˆ
D (góc đáy hình thang cân).
Do đó ΔBCH = ΔADK (cạnh huyền, góc nhon), suy ra CH = DK .
b) Ta có: KH = AB = 3 cm nên
CH + CK = AD − KH = 13 − 3 = 10 cm.
Do CH = DK nên CH = 10 : 2 = 5 (cm).
Áp dụng định lý Py-ta-go vào ΔBHC vuông tại H ta có: 2 = 2 − 2 = 2 − 2 = = 2 BH BC CH 13 5 144 12 Vậy BH = 12 cm.
Bài 5: D = C = 0 60 nên D = 0 30 1 Suy ra CBD = 0 90
Ta tính được AD = 4cm, BC = 4cm,
CD = 8cm. Chu vi hình thang ABCD = 20 cm µ µ
Bài 6: a) Vì ABCD là hình thang cân nên C = D suy ra OCD là tam giác cân. · µ µ ·
Ta có OAB = D = C = OBA (hai góc đồng vị)
Tam giác OAB cân tại O.
b) OI là trung tuyến của tam giác cân OAB
nên OI cũng là đường cao tam giác OAB
Þ OI ^ AB mà AB / / CD nên OI ^ CD
Tam giác OCD cân tại O có OI ^ CD nên OI cắt CD tại trung điểm J của CD.
Vậy ba điểm O, I, J thẳng hàng.
c) Xét ACD và BDC có:
A C = BD (2 đường chéo của hình thang cân)
A D = BC (2 cạnh bên của hình thang cân) Trang 3
CD = DC Do đó DACD = DBDC (c.c.c) · · · ·
Suy ra ACD = BDC hay MCD = NDC · ·
Hình thang MNDC có MCD = NDC nên MNDC là hình thang cân.
Þ MC = ND Þ AC - MC = BD - ND Þ AM = BN
Hình thang MNAB có hai đường chéo AM và BN bằng nhau nên MNAB là hình thang cân. Bài 7:
a) D A ED = D BFC (cạnh huyền – góc nhọn) DE = CF (2 cạnh tương ứng) A B chung üïï · · ïï b) DA B A BC =
ý Þ DA BD = DBA C (c. . g c) ï BD A C ï = ïïïþ · ·
Þ A BD = BA C (2 góc tương ứng)
Þ DBA I cân tại I Þ IA = IB . Có
BD = A C üïïý Þ ID = IC IA = IB ïïþ OA = OB üïï
c) D OA B cân tại O từ đó ta có
ý Þ OI là đường trung trực của AB IA = IB ïïþ OC = ODüï D ODC ï cân tại O từ đó ta có
ý Þ OI là đường trung trực của CD IA = IB ïïþ ABC = DAB =130 d) Tính được ADC = BCD = 50 Bài 8:
a) Gọi I là giao điểm của AC và BD. Chỉ ra D IA B ; D ICD cân
tại I từ đó chỉ ra A B / / CD và kết luận ABCD là hình thang cân. b) A H = HC ;
A B = HK (DA BK = DKHA);HD = KC (DAHD = DBKC ) Trang 4
Þ A B + CD = A B + HK + DH + KC = 2HK + 2KC = 2(HK + KC )= 2HC = 2AH = 8cm Bài 9: Ta đặt AD = AB = BC = x
Vẽ AM // BC (M CD), ta được
A M = BC = x và MC = A B = x. ADM cân, có o
D = 60 nên là tam giác đều,
suy ra DM = A D = x.
Vẽ AH ^ CD thì AH là đường cao của hình thang cân, AD 3
cũng là đường cao của tam giác đều: AH = . 2 x 3 Vì AH = a 3 nên
= a 3 Þ x = 2a. 2
Do đó chu vi của hình thang cân là: 2a.5 = 10a. Trang 5



