10 trang 4 lượt tải

Bài Tập Hình 8 Bài Hình Chóp Đều-Hình Chóp Cụt Đều Có Lời Giải

8

Đáy là một đa giác, các mặt bên là những tam giác có chung một đỉnh. Đường  thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao. Trong hình  trên: hình chóp S. ABCD có đỉnh là S, đáy là tứ giác ABCD, ta gọi đó là hình chóp tứ giác. Tài liệu giúp bạn tham khảo, ôn tập và đạt kêt quả cao. Mời đọc đón xem!

Chủ đề: Chương 2: Các hình khối trong thực tiễn (CTST) 8 tài liệu

Môn: Toán 8 2.2 K tài liệu

Tác giả:

Profile

Mỹ Châu

1 tuần trước
Danh sách Quiz
/10
3. HÌNH CHÓP ĐỀU. HÌNH CHÓP CỤT ĐỀU
I. KIẾN THỨC CƠ BẢN
Hình chóp c:
- Đy l mt đa gic, cc mt bên l nhng tam gic c chung
mt đnh.
- Đưng thng đi qua đnh v vuông gc vi mt phng đy gi
l đưng cao.
- Trong hình trên: hình chóp
.S A BCD
c đnh l S, đy l tứ giác
A BCD
, ta gi đ l hình chp tứ giác.
Hình chóp đều
Hình chóp
.S A BCD
trên c đy l hình vuông
A BCD
, các mt bên
SA B
,
SBC
,
SCD
và
SDA
là nhng
tam giác cân bằng nhau. Ta gi
là hình chóp
tứ gic đều
Hình chp đều l hình chp c đy l mt đa gic đều,
cc mt bên l nhng tam gic cân bằng nhau c chung
đnh.
- Chân đưng cao ca hình chp đều trng vi tâm ca đưng trn đi qua cc đnh ca
mt đy.
- Đưng cao v t đnh ca mi mt bên ca hình chp đều được gi là trung đon ca
hình chp đ.
Hình chóp cụt đều
Hình chp ct đều l phn hình chp đều nằm gia mt phng đy
ca hình chp v mt phng song song vi đy v ct hình chp.
– Mi mt bên ca hình chp ct đều l mt hình thang cân.
Din tch xung quanh của hình chóp đều.
- Diện tích xung quanh ca hình chp đều bằng na tích ca chu vi
đy vi trung đoạn.
xq
S pd=
(p là na chu vi đy; d l trung đoạn ca hình chóp)
– Diện tch ton phn ca hình chp bằng tng ca diện tch xung quanh v diện tch đy.
tp xq
S S S=+
(S: diện tch đy)
Thể tích của hình chóp đều
– Th tch ca hình chp bằng mt phn ba ca diện tch đy nhân vi chiều cao.
1
3
V S h=
(S: diện tch đy, h: chiều cao)
III. BÀI TẬP
Bài 1: Cho hình chp tam gic đều
.A BCD
. Gi H l trung đim CD. Chứng minh:
a)
CD
vuông góc vi mt phng
( )
A HB
b)
A C BD^
a) Hình chóp
.A BCD
l hình chp tam gic đều nên
tam gic CBD l tam gic đều các tam ACB, ACD,
ADB là các tam giác cân tại A. H l trung đim CD
suy ra
HB CD;A H CD^^
Vậy CD vuông góc vi hai đưng thng ct nhau
thuc mt phng
( )
A HB
nên
CD mp(AHB)^
b) Gi E l trung đim BD ta có
;A E BD CE BD^^
Vậy BD vuông góc vi hai đưng thng ct nhau
thuc mt phng
( )
A EC
nên
CD mp(AEC)^
suy ra CD vuông góc vi mi đưng thng
thuc
( )
mp A EC
Hay
A C BD^
Bài 2: Cho hình chóp tứ gic đều
. Gi O l giao đim ca AC và BD. Chứng
minh
a) SO vuông góc vi
( )
mp A BCD
b)
( )
mp SA C
vuông góc vi
( )
mp A BCD
HD:a) Hình chóp tứ gic đều
.S A BCD
nên có
A BCD
là hình vuông, các cạnh bên bằng
nhau.
Ta có
SBD
là tam giác cân tại A có
OD OB=
nên SO l đưng cao ca tam giác hay
SO BD⊥
Tương tự, ta có
SO AC⊥
SO vuông góc vi hai đưng thng ct nhau thuc
( )
mp A BCD
nên
SO ( )mp A BCD^
b) Ta có
AC ( )mp SACÎ
;
BD ( )mp SBDÎ
Mà
BD AC^
nên
( ) ( )mp SAC mp SBD⊥
Bài 3: Cho hình chóp tứ gic đều
có
2A B cm=
,
4SA cm=
. Tnh đ dài trung
đoạn và chiều cao ca hình chp đều này.
HD: Hình chóp tứ gic đều
.S A BCD
có
2A B cm=
,
4SA cm=
, nên
A BCD
là hình vuông và các cạnh bên bằng
nhau.
Ta có
2 2 2 2
2 2 2 2AC BD AD AB= = + = + =
;
2
2
AC
AO ==
Trong tam giác vuông
SOA
vuông tại O, theo Pytago ta có
2 2 4 2
4 ( 2) 3 2SO SA AO= − = − =
Vậy chiều cao hình chóp là
3 2cm
Gi H l trung đim AB, ta c SH l trung đoạn ca hình chóp
Trong tam giác
SBH
vuông tại H, theo Pytago ta có
2 2 2 1
4 1 15SH SB IB= + = − =
Vậy đ di trung đoạn là
15cm
Bài 4: Cho hình chp tam gic đều
.S A BC
có
3A B cm=
, cạnh bên
4SA cm=
. Tính
chiều cao ca hình chóp.
Hình chp tam gic đều
.S A BC
nên
A BC
l tam gic đều.
Gi H l trung đim AB, O là trong tâm tam giác ABC
Ta c CH l đưng cao tam giác ABC
Trong tam giác CHB vuông tại H ta có
2
2 2 2
3 3 3
3
22
HC CB HB

= − = − =


;
2 2 3 3
OC CH 3
3 3 2
= = × =
Trong tam giác vuông
SOC
vuông tại O ta có
2 2 2 2
4 ( 3) 13SO SC OC= − = − =
Vậy chiều cao ca hình chóp là
13cm
Bài 5: Mt hình chóp ct đều c đy ln bằng
12cm
, đy bé bằng
8cm
và cạnh bên bằng
13cm
. Tnh đ di trung đoạn và chiều cao ca hình chóp ct đ.
13cm
HD: Hình chóp ct đều ta thấy mt bên là hình
thang cân
''A A D D
. V đưng cao
'AE
và
'DF
, ta có
' 18
22
'
2'
2'
AD A D
A E D F
−−
= = = =
Vậy đ di trung đoạn là 2 cm
Khai trin hình chóp ct đều ta thấy
Trong hình thang vuông
''OBB O
v đưng cao
'BI
ta có
6 2; ' 42
2
'
BD
OB O B= = =
;
' 22'BI OB O B= − =
Vậy đưng cao hình chóp ct đều là
2 2 2
' 2' 13 (2 ) 5B I B B BI= − = − =
Bài 6: Cho hình chóp tứ gic đều c đ dài cạnh đy bằng 8cm v đ dài cạnh bên bằng
5cm. Tính diện tích toàn phn ca hình chóp.
HD: Trong tam giác vuông SHB, theo pytago ta có
2 2 2 2
5 4 3SH SB HB= − = − =
Diện tch đy l
( )
2
8.8 64 cm
d
S ==
Diện tích xung quanh hình chóp là
( )
2
(8 8).3 48 cm
xq
S pd= = + =
Diện tích toàn phn hình chóp
( )
2
64 48 112
tp xq d
S S S cm= + = + =
Bài 7: Tính diện tích toàn phn ca hình chóp tứ gic đều
.S A BCD
biết
12 2 ,BD cm=
10cmSC =
HD: Hình chóp tứ gic đều
.S A BCD
c đy
A BCD
là hình vuông nên
A D A B=
, ta có
22
2 12 2BD AD AB AB= + = =
12AB=
Trong tam giác vuông
SHB
, theo pytago ta có
2 2 2 2
10 6 8SH SB HB= − = − =
Trong tam giác
SOB
vuông tại O, theo Pytago ta có
2 2 2 2
10 (6 2) 2 7SO SB OB= − = − =
Diện tch đy l
( )
2
12.12 144
d
S cm==
Diện tích xung quanh hình chóp là
( )
2
(12 12).8 192 cm
xq
S pd= = + =
Diện tích toàn phn hình chóp
( )
2
144 192 336 cm
tp xq d
S S S= + = + =
Bài 8: Tính diện tích toàn phn ca hình chp tam gic đều biết cạnh đy bằng 10cm, cạnh
bên bằng 13cm.
Bài giải
Tam giác BCA cân tại S có
SI AB^
tại I, theo Pytago ta có
2
2 2 2
13 5 12
2
AB
ST SB

= − = − =


Tam gic ABC l tam gic đều có cạnh là
10a cm=
nên chiều cao tam gic đều là
3 10 3
53
22
a
h CI= = = =
.
.S A BC
l hình chp đều nên chân đưng cao H trùng vi giao đim ba đưng trung
tuyến ca tam giác, ta có
SH CI^
và
2 2 10 3
.5 3
3 3 3
HC CI= = =
Trong tam giác
SHC
vuông tại H, theo định lí Pytago ta có
2
2 2 2
10 3
13 11,6
3
HS SC CH

= − = −



Diện tch đy l
( )
2
11
.5 3 10 25 3 cm
22
S CIAB= = =
( )
2
10 10 10
12 180
2
xq
S pd cm
++

= = =


Vậy diện tích toàn phn ca hình chóp là
( )
2
11,6 180 191,6 cm
tp xq d
S S S= + = + =
Bài 9: Tính th tích hình chóp tứ gic đều biết đ dài
cạnh đy bằng 6cm v đ dài cạnh bên bằng
43cm
Ta có
22
6 6 6 2cmAC = + =
. Suy ra
FC 3 2cm=
Áp dng định lí pytago trong tam giác vuông EFC ta có
2
2 2 2
EF 43 (3 2) 43 18 25 5cmEC FC= − = − = − = =
Diện tích tứ gic đy
6.6 36cmS ==
Th tích hình chóp:
3
11
36.5 60cm
33
V Sh= = =
Bài 10: Tính th tch hình chp tam gic đều biết chiều cao bằng
12cm
và cạnh bên bằng
4cm.
.S A BC
l hình chp đều nên chân đưng cao H trùng vi giao đim ba đưng trung
tuyến ca tam giác, ta có
SH CI^
và
2
3
HC CI=
Trong tam giác SHC vuông tại H, theo định lí pytago ta có
2
2 2 2
4 12 2HC SC SH= − = − =
Suy ra
3CI cm=
Tam gic ABC l tam gic đều, giả sử có cạnh là a nên chiều
cao tam gic đều là
3
2
a
h =
mà CI là chiều cao tam giác ABC
nên cạnh tam gic đều là
2 2.3
23
33
h
==
hay
AB 2 3cm=
Diện tch đy l
( )
2
11
. .3.2 3 3 3 cm
22
S CI AB= = =
Th tích hình chóp là
( )
3
11
3 3 12 6
33
V Sh cm= = =
Bài 11: Tính th tích hình chóp tứ gic đều biết đ dài cạnh đy bằng 4cm v đ dài cạnh
bên bằng
Bài giải
.E A BCD
là hình chóp tứ gic đều c đy
A BCD
là hình vuông, có cạnh
4A B cm=
Ta có
22
4 4 4 2AC cm= + =
Suy ra
FC 2 2cm=
Áp dng định lí pytago trong tam giác vuông
EFC
ta có
2
2 2 2
EF 24 (2 2) 24 8 16 4cmEC FC= − = − = − = =
Chiều cao hình chóp là 4cm
Diện tích tứ gic đy
4.4 16S cm==
24cm
Th tích hình chóp
3
11
16.4 21,3cm
33
V Sh= =
Bài 12: Tính th tch hình chp tam gic đều biết đ dài cạnh bên bằng
6cm
và cạnh bên
đy 3cm.
Gi H là trng tâm tam giác
A BC
, HC ct AB tại D, ta có
3
2
AD DB==
Tam giác
CDB
vuông tại D, theo định lí Pytago, ta có
2
2 2 2
3 3 3
3
22
DC BC BD

= − = − =


và
2 2 3 3
3
3 3 2
HC CD= = =
Tam giác SHC vuông tại H, ta có
2 2 2 2
( 6) ( 3) 3SH SC HC= − = − =
Th tích ca hình chp đều là
3
1 1 1 1 1 3 3 9
. . .3 3
3 3 2 3 2 2 4
d
V S h DC AB SH cm


= = = =





Bài 13: Tính th tích hình chóp tứ gic đều c trung đoạn bằng 5cm và diện tích xung
quanh bằng
2
80cm
.
HD: Diện tích xung quanh hình chóp tứ gic đều có cạnh đy l a
cm, trung đoạn là 5cm:
2
2 .5 80
xq
S p d a cm= = =
Hay
8a cm=
Ta có
22
8 8 8 2cmAC = + =
4 2cmBF=
Ta có
4FI cm=
(vì
FI
l đưng trung bình ca tam giác ABC,
tam giác
A BC
có cạnh
8A B a cm==
)
Áp dng định lí pytago trong tam giác vuông
EFI
ta có
2 2 2 2
EF 5 4 3cmEI FI= − = − =
Th tích hình chóp
23
11
8 .3 64
33
V S h cm= = =
Bài 14: Mt hình chóp ct đều
. ' ' ' 'A BCD A B C D
có các cạnh đy bằng a v 2a, đưng cao
ca mt bên bằng a.
a) Tính diện tích xung quanh
b) Tính cạnh bên, đưng cao ca hình chóp ct đều.
Bài giải
a) Diện tích xung quanh ca hình chóp ct
đều
2
11
( ) (4.2 4 ) 6
22
xq
S p p d a a a a= + = + =
b) Khai trin hình chóp ct đều ta thấy mt
bên l hình thang cân ABA’B’. V đưng cao
A’H v B’K , ta c
2
'
2
'AB A B a
AH BK
−
= = =
Trong hình thang vuông OBB’O’ v đưng
cao
'BI
ta có
2
2; ''
22
BD a
OB a O B= = =
''
2
2
a
BI OB O B= − =
Vậy đưng cao hình chóp ct đều là
22
22
5 2 3
2 2 2
''
a a a
B I B B BI
= − = − =
Bài 15: Cho hình chp tam gic đều
.S A BC
. Gi M, N, P ln lượt l trung đim các cạnh
SA, SB, SC. Chứng minh
.A BC MNP
là hình chóp ct tam gic đều.
Ta có
/ / A B MN
;
//BC NP
nên
( ) ( )
/ / .mp MNP mp A BC
Mt khác,
.S A BC
l hình chp tam gic đều nên
SA SB SC==
Suy ra
SAB SBC=
, do đ
A MNB
là hình thang cân.
Tương tự
BNPC
;
A MPC
là các hình thang cân
Vậy
.A BC MNP
là hình chóp ct tam gic đều.
Bài 15: Cho hình chóp tứ gic đều có diện tích xung quanh bằng
1
2
diện tích toàn phn.
Chứng minh rằng các mt bên ca hình chóp là các tam giác vuông cân.
Hình chóp tứ gic đều
.S A BCD
c đy l hình vuông, cc cạnh bên là các tam giác cân tại
S (1)
Gi a l đ dài cạnh đy, d l trung đoạn ca hình chóp
Ta có
2
xq
S pd ad==
;
2
2
tp xq d
S S S ad a= + = +
Mt khác
1
2
xq tp
SS=
( )
22
11
2 2 0
22
ad ad a ad a = + − =
11
0
22
a d a d a

− = =


Gi G l trung đim AB suy ra
1
2
GB a=
Ta c SG l trung đoạn hình chóp
1
2
SG a=
Vậy trong tam giác
SGB
có
1
GB
2
SG a==
và
90G =
nên
SGB
là tam giác vuông cân
tại G
45GSB=
(2)
Tương tự, ta có
45GSA =
(3)
T (2), (3) suy ra
90BSA =
(4)
T (1), (4) suy ra
ASB
vuông cân tại S
Tương tự ta chứng minh được các cạnh bên ca hình chóp là tam giác vuông cân.
TỰ LUYỆN
Bài 1: Tính diện tích toàn phần và thể tích của hình chóp tứ giác
đều
.S A BCD
(nếu làm tròn đến chữ số thập phân thứ hai )
a) Biết AB = 6cm , SI = 5cm.
b) Biết SH = 4cm , SB = 5cm.
I
H
A
B
D
C
S
c) Biết AB = 5cm , SB = 5cm.
Bài 2: Cho hình chóp tam giác đều
S.ABC
. Gọi
O
là tâm đường tròn ngoại tiếp
ABC
và
D, E, F
lần lượt là trung điểm của các cạnh
AB, BC, CA
.
a) Chứng minh
SDO SEO SFO==
.
b) Tính diện tích xung quanh và thể tích của hình chóp.
1) Nếu biết
SO 12cm=
,
AB 10cm.=
2) Nếu biết các mặt bên là các tam giác đều,
OA 3 cm=
,
3AB cm=
3) Nếu biết
23OC cm=
và
0
SDO 60=
Bài 3: Cho hình chóp tứ giác đều
S.ABCD
. Có
SH 15=
cm,
AB 16=
cm
a) Tính trung đoạn, diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp.
b) Gọi
H'
là trung điểm của SH. Cắt hình chóp bởi 1 mặt phẳng đi qua
H'
và song song với mặt
phẳng đáy
( )
ABCD
ta được hình chóp cụt đều
ABCD.A'B'C'D'
.Tính diện tích xung quanh và thể
tich của hình chóp cụt. (làm tròn đến chữ số thập phân thứ hai).
KẾT QUẢ - ĐÁP SỐ
III. BÀI TẬP TỰ LUẬN
Bài 3:
Bài 4:
Bài 5:
Bài 8:
IV. BÀI TẬP TRẮC NGHIỆM

Tài liệu khác của Toán 8

Preview text:

3. HÌNH CHÓP ĐỀU. HÌNH CHÓP CỤT ĐỀU
I. KIẾN THỨC CƠ BẢN
Hình chóp có:
- Đáy là một đa giác, các mặt bên là những tam giác có chung một đỉnh.
- Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao.
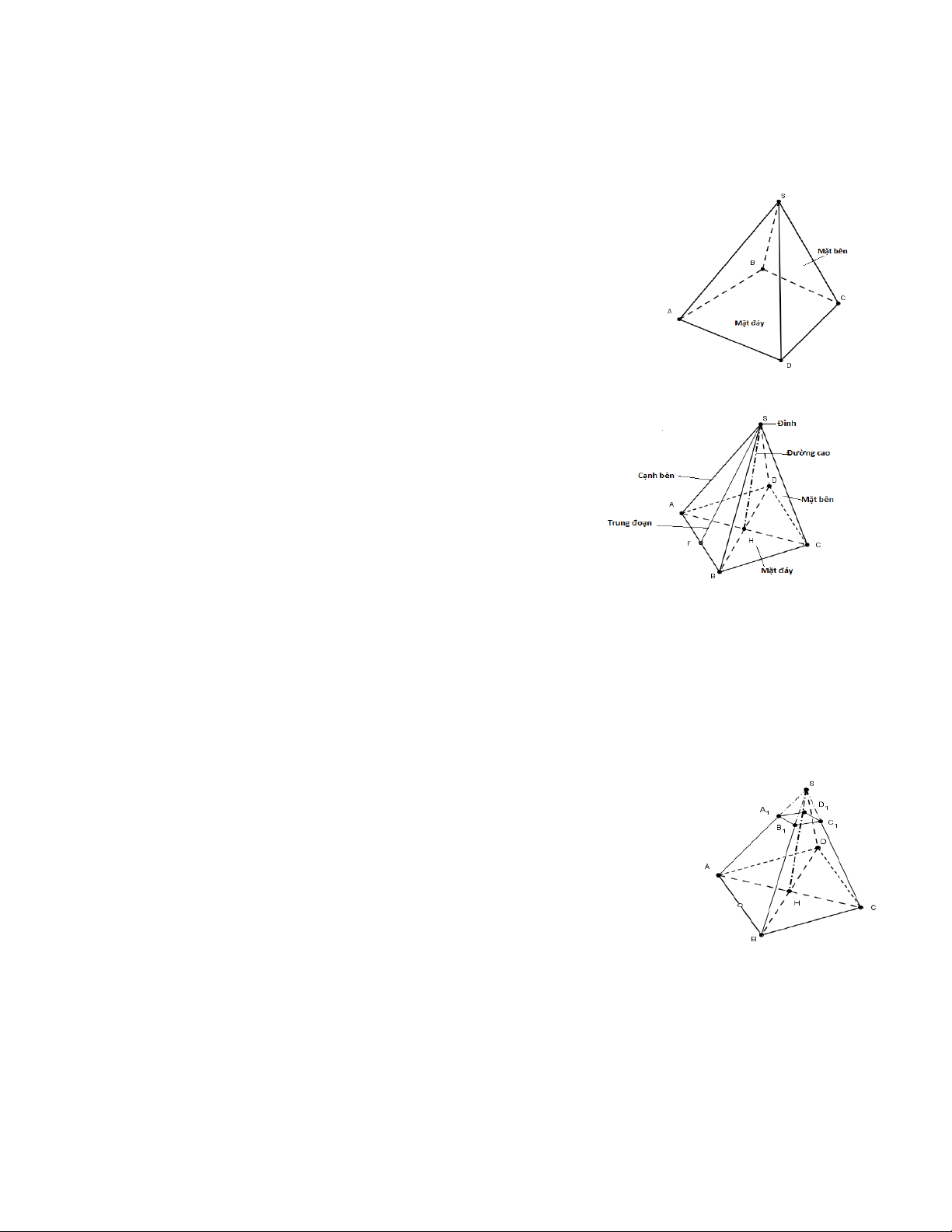
- Trong hình trên: hình chóp S .A BCD có đỉnh là S, đáy là tứ giác
A BCD , ta gọi đó là hình chóp tứ giác.  Hình chóp đều
Hình chóp S .A BCD trên có đáy là hình vuông A B CD
, các mặt bên SA B , SB C , SCD và SDA là những
tam giác cân bằng nhau. Ta gọi S .A BCD là hình chóp tứ giác đều
Hình chóp đều là hình chóp có đáy là một đa giác đều,
các mặt bên là những tam giác cân bằng nhau có chung đỉnh.
- Chân đường cao của hình chóp đều trùng với tâm của đường tròn đi qua các đỉnh của mặt đáy.
- Đường cao vẽ từ đỉnh của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
Hình chóp cụt đều
Hình chóp cụt đều là phần hình chóp đều nằm giữa mặt phẳng đáy
của hình chóp và mặt phẳng song song với đáy và cắt hình chóp.
– Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Diện tích xung quanh của hình chóp đều.
- Diện tích xung quanh của hình chóp đều bằng nữa tích của chu vi
đáy với trung đoạn. S = pd xq
(p là nữa chu vi đáy; d là trung đoạn của hình chóp)
– Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy. S = S + S tp xq (S: diện tích đáy)
Thể tích của hình chóp đều
– Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao. 1
V = S h
(S: diện tích đáy, h: chiều cao) 3 III. BÀI TẬP
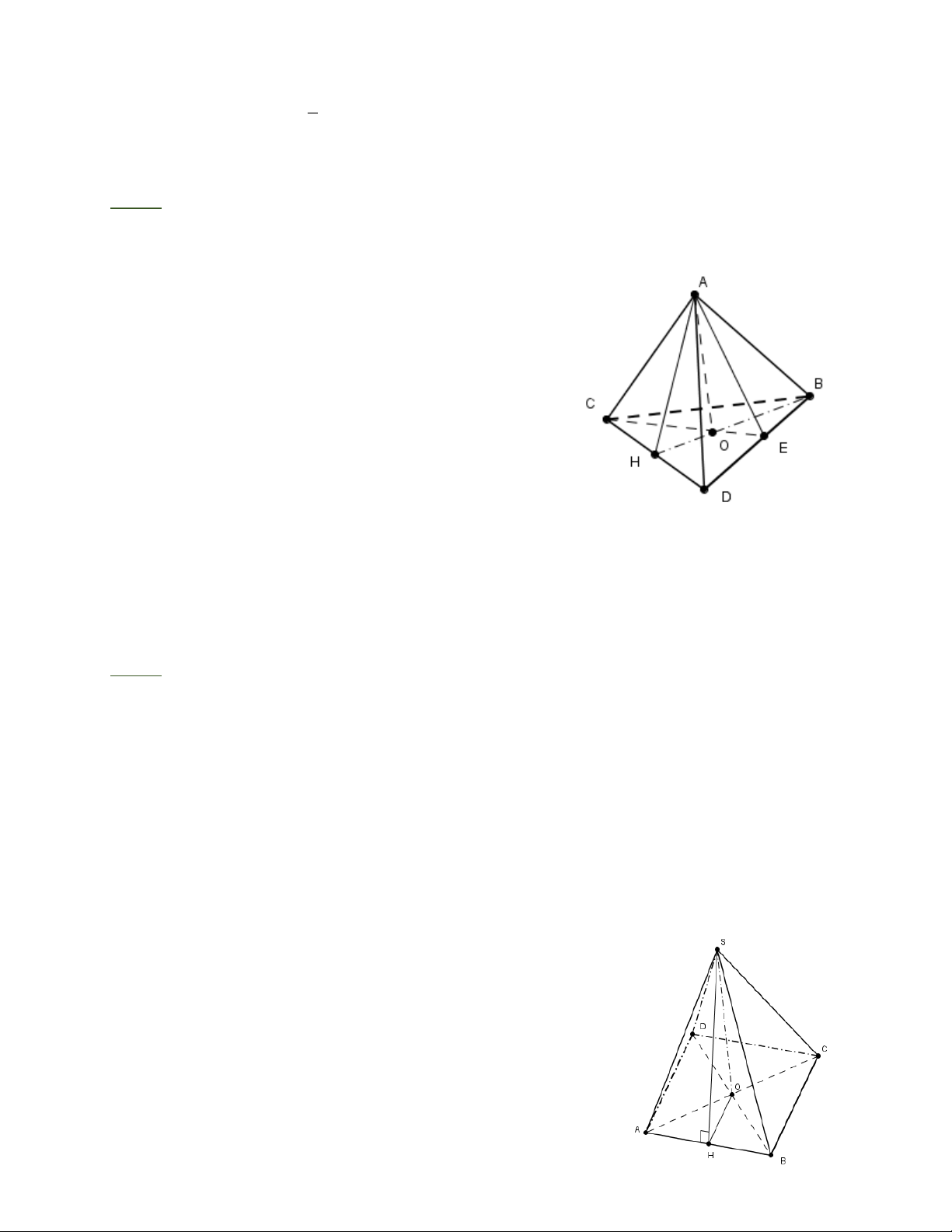
Bài 1: Cho hình chóp tam giác đều A.B CD . Gọi H là trung điểm CD. Chứng minh:
a) CD vuông góc với mặt phẳng (A HB )
b) A C ^ BD
a) Hình chóp A.B CD là hình chóp tam giác đều nên
tam giác CBD là tam giác đều các tam ACB, ACD,
ADB là các tam giác cân tại A. H là trung điểm CD suy ra HB ^ CD; AH ^ CD
Vậy CD vuông góc với hai đường thẳng cắt nhau
thuộc mặt phẳng (A HB ) nên CD ^ mp(AHB)
b) Gọi E là trung điểm BD ta có A E ^ BD;CE ^ BD
Vậy BD vuông góc với hai đường thẳng cắt nhau
thuộc mặt phẳng (A EC ) nên CD ^ mp(AEC) suy ra CD vuông góc với mọi đường thẳng
thuộc mp (A EC ) Hay A C ^ BD
Bài 2: Cho hình chóp tứ giác đều S .A BCD . Gọi O là giao điểm của AC và BD. Chứng minh
a) SO vuông góc với mp (A BCD)
b) mp (SA C ) vuông góc với mp (A BCD)
HD:a) Hình chóp tứ giác đều S .A BCD nên có A B CD là hình vuông, các cạnh bên bằng nhau.
Ta có SBD là tam giác cân tại A có OD = OB nên SO là đường cao của tam giác hay SO ⊥ BD
Tương tự, ta có SO ⊥ AC
SO vuông góc với hai đường thẳng cắt nhau thuộc
mp (A BCD) nên SO ^ m ( p A BCD) b) Ta có AC Î m (
p SA C ) ; BD Î m ( p SBD)
Mà BD ^ A C nên mp(SAC) ⊥ mp(SBD)
Bài 3: Cho hình chóp tứ giác đều S .A BCD có A B = 2cm , SA = 4cm . Tính độ dài trung
đoạn và chiều cao của hình chóp đều này.
HD: Hình chóp tứ giác đều S .A BCD có A B = 2cm ,
SA = 4cm , nên A BCD là hình vuông và các cạnh bên bằng nhau. AC Ta có 2 2 2 2
AC = BD = AD + AB = 2 + 2 = 2 2 ; AO = = 2 2
Trong tam giác vuông SOA vuông tại O, theo Pytago ta có 2 2 4 2
SO = SA − AO = 4 − ( 2) = 3 2
Vậy chiều cao hình chóp là 3 2cm
Gọi H là trung điểm AB, ta có SH là trung đoạn của hình chóp
Trong tam giác SB H vuông tại H, theo Pytago ta có 2 2 2 1
SH = SB + IB = 4 −1 = 15
Vậy độ dài trung đoạn là 15cm
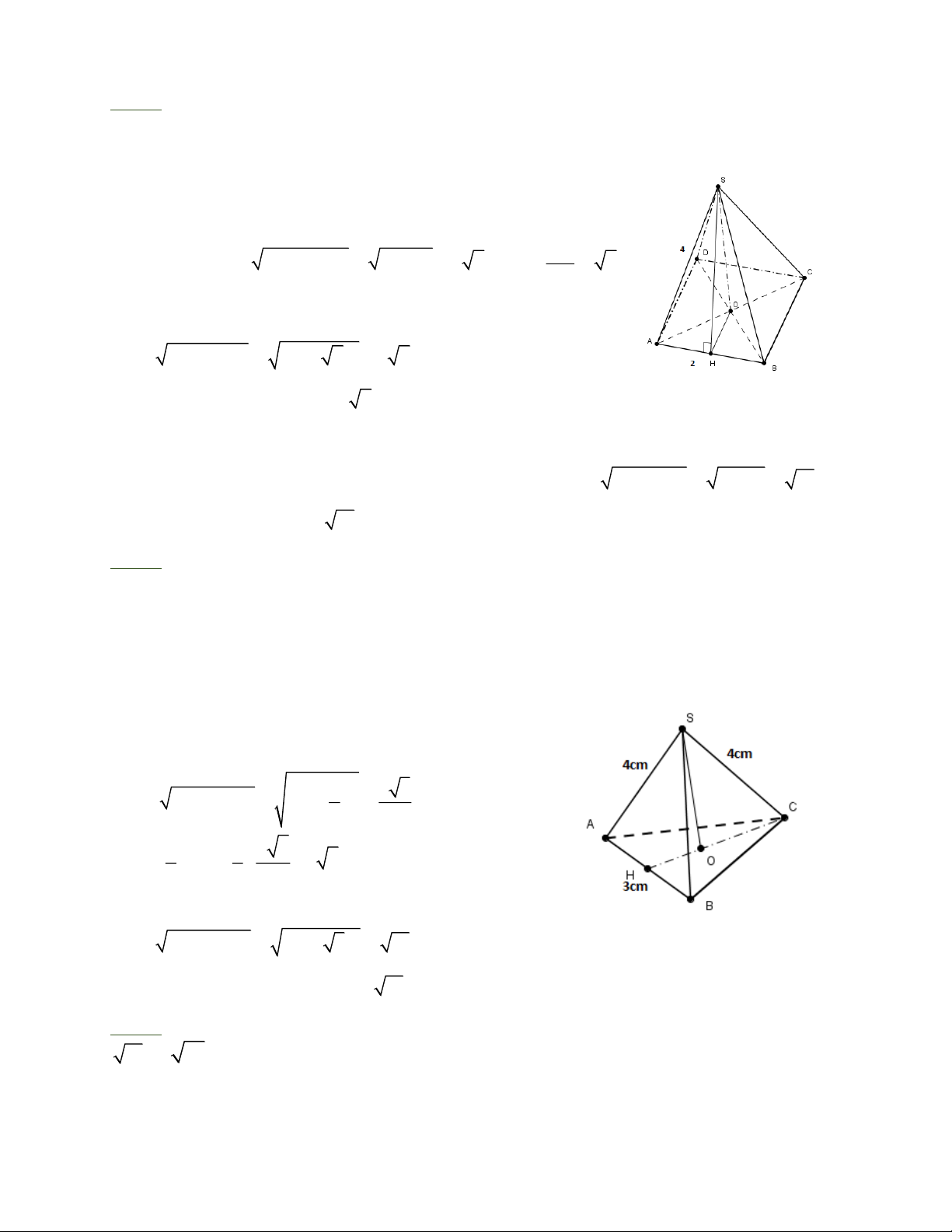
Bài 4: Cho hình chóp tam giác đều S .A B C có A B = 3cm , cạnh bên SA = 4cm . Tính
chiều cao của hình chóp.
Hình chóp tam giác đều S .A B C nên A B C là tam giác đều.
Gọi H là trung điểm AB, O là trong tâm tam giác ABC
Ta có CH là đường cao tam giác ABC
Trong tam giác CHB vuông tại H ta có 2 2 2 2  3  3 3
HC = CB − HB = 3 − =   ;  2  2 2 2 3 3 OC = CH = × = 3 3 3 2
Trong tam giác vuông SOC vuông tại O ta có 2 2 2 2
SO = SC − OC = 4 − ( 3) = 13
Vậy chiều cao của hình chóp là 13cm
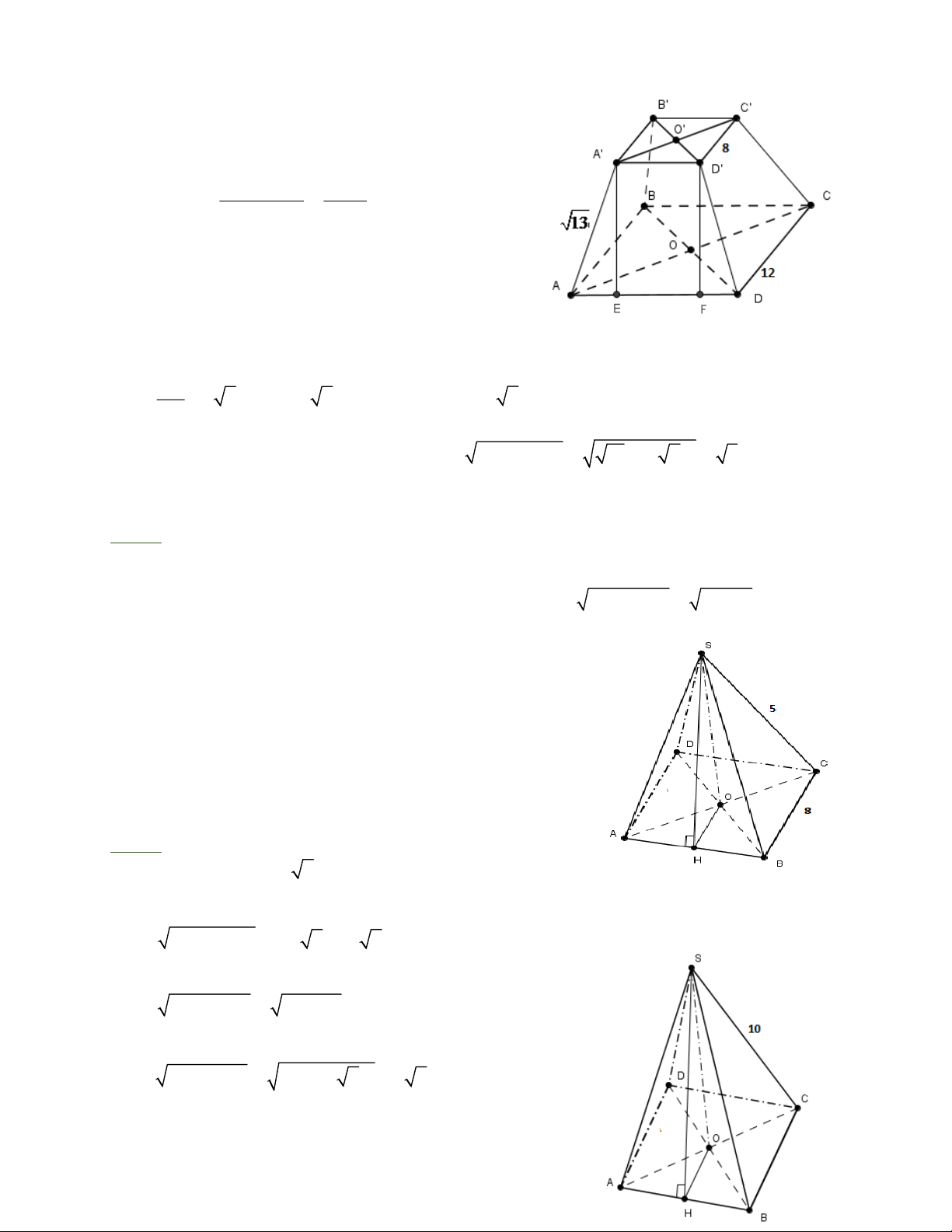
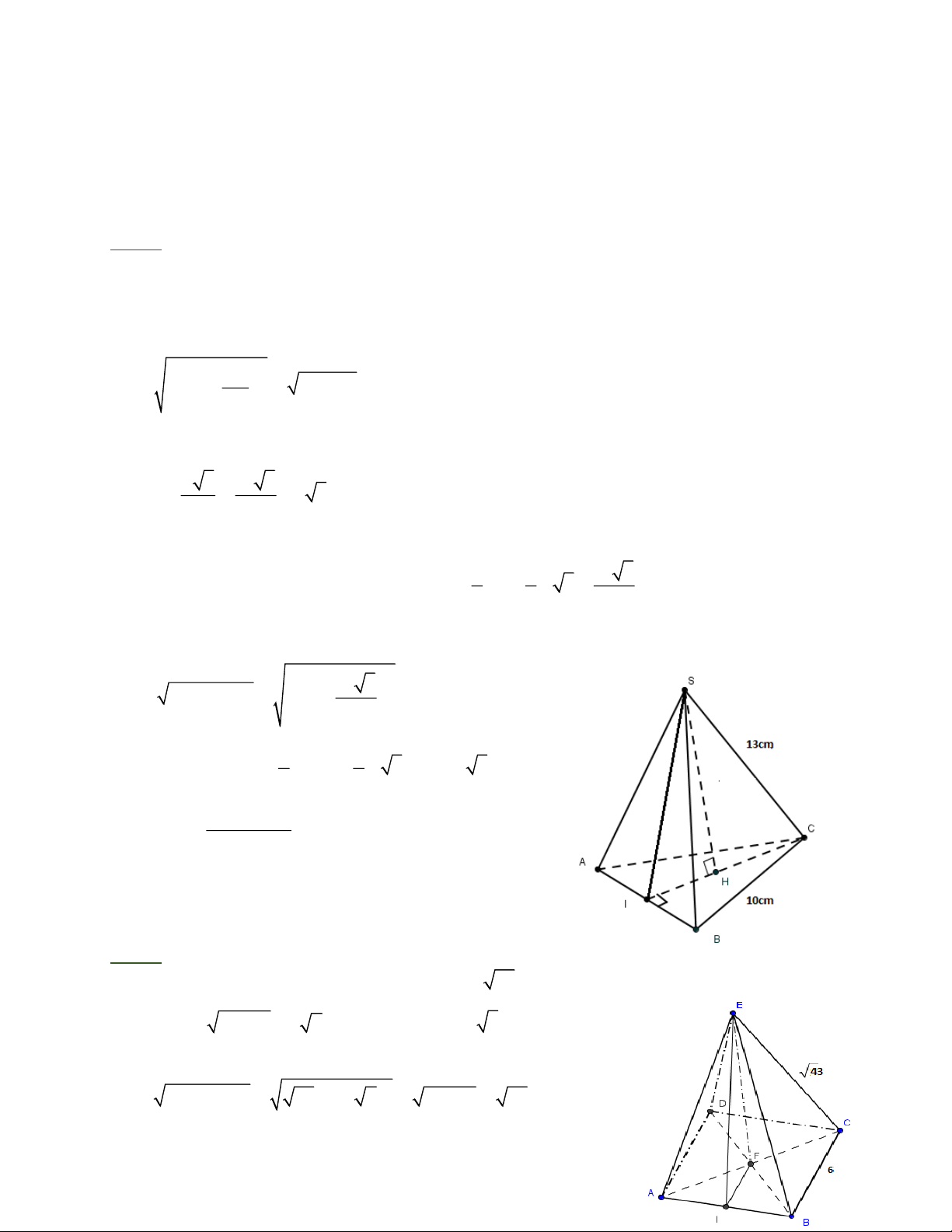
Bài 5: Một hình chóp cụt đều có đáy lớn bằng 12cm , đáy bé bằng 8cm và cạnh bên bằng
13cm 13cm . Tính độ dài trung đoạn và chiều cao của hình chóp cụt đó.
HD: Hình chóp cụt đều ta thấy mặt bên là hình
thang cân A A ' D ' D . Vẽ đường cao A ' E và D ' F , ta có
AD − A' D ' 12 − 8
A' E = D ' F = = = 2 2 2
Vậy độ dài trung đoạn là 2 cm
Khai triển hình chóp cụt đều ta thấy
Trong hình thang vuông OBB 'O ' vẽ đường cao B ' I ta có BD OB =
= 6 2;O ' B ' = 4 2 ; BI = OB − O ' B ' = 2 2 2
Vậy đường cao hình chóp cụt đều là 2 2 2
B ' I = B ' B − BI = 13 − (2 2) = 5
Bài 6: Cho hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài cạnh bên bằng
5cm. Tính diện tích toàn phần của hình chóp.
HD: Trong tam giác vuông SHB, theo pytago ta có 2 2 2 2
SH = SB − HB = 5 − 4 = 3
Diện tích đáy là S = = ( 2 8.8 64 cm d )
Diện tích xung quanh hình chóp là S = pd = + = ( 2 (8 8).3 48 cm xq )
Diện tích toàn phần hình chóp
S = S + S = + = ( 2 64 48 112 cm tp xq d )
Bài 7: Tính diện tích toàn phần của hình chóp tứ giác đều
S .A BCD biết BD = 12 2c , m SC = 10cm
HD: Hình chóp tứ giác đều S .A BCD có đáy A B CD là hình vuông nên A D = A B , ta có 2 2
BD = AD + AB = AB 2 = 12 2  AB = 12
Trong tam giác vuông SHB , theo pytago ta có 2 2 2 2
SH = SB − HB = 10 − 6 = 8
Trong tam giác SOB vuông tại O, theo Pytago ta có 2 2 2 2
SO = SB − OB = 10 − (6 2) = 2 7
Diện tích đáy là S = = ( 2 12.12 144 cm d )
Diện tích xung quanh hình chóp là S = pd = + = ( 2 (12 12).8 192 cm xq )
Diện tích toàn phần hình chóp S = S + S = + = ( 2 144 192 336 cm tp xq d )
Bài 8: Tính diện tích toàn phần của hình chóp tam giác đều biết cạnh đáy bằng 10cm, cạnh bên bằng 13cm. Bài giải
Tam giác BCA cân tại S có SI ^ A B tại I, theo Pytago ta có 2 2  AB  2 2 ST = SB − = 13 − 5 =12    2 
Tam giác ABC là tam giác đều có cạnh là a = 10cm nên chiều cao tam giác đều là a 3 10 3 h = CI = = = 5 3 . 2 2
S .A BC là hình chóp đều nên chân đường cao H trùng với giao điểm ba đường trung 2 2 10 3
tuyến của tam giác, ta có SH ^ CI và HC = CI = .5 3 = 3 3 3
Trong tam giác SHC vuông tại H, theo định lí Pytago ta có 2 10 3  2 2 2
HS = SC − CH = 13 −    11,6  3    1 1
Diện tích đáy là S = CIAB = .5 3 10 = 25 3 ( 2 cm ) 2 2 10 +10 +10  S = pd = 12 =180 cm xq   ( 2)  2 
Vậy diện tích toàn phần của hình chóp là
S = S + S = + = ( 2 11,6 180 191,6 cm tp xq d )
Bài 9: Tính thể tích hình chóp tứ giác đều biết độ dài
cạnh đáy bằng 6cm và độ dài cạnh bên bằng 43cm Ta có 2 2
AC = 6 + 6 = 6 2cm . Suy ra FC = 3 2cm
Áp dụng định lí pytago trong tam giác vuông EFC ta có 2 2 2 2 EF = EC − FC =
43 − (3 2) = 43 −18 = 25 = 5cm
Diện tích tứ giác đáy S = 6.6 = 36cm 1 1 Thể tích hình chóp: 3
V = Sh = 36.5 = 60cm 3 3
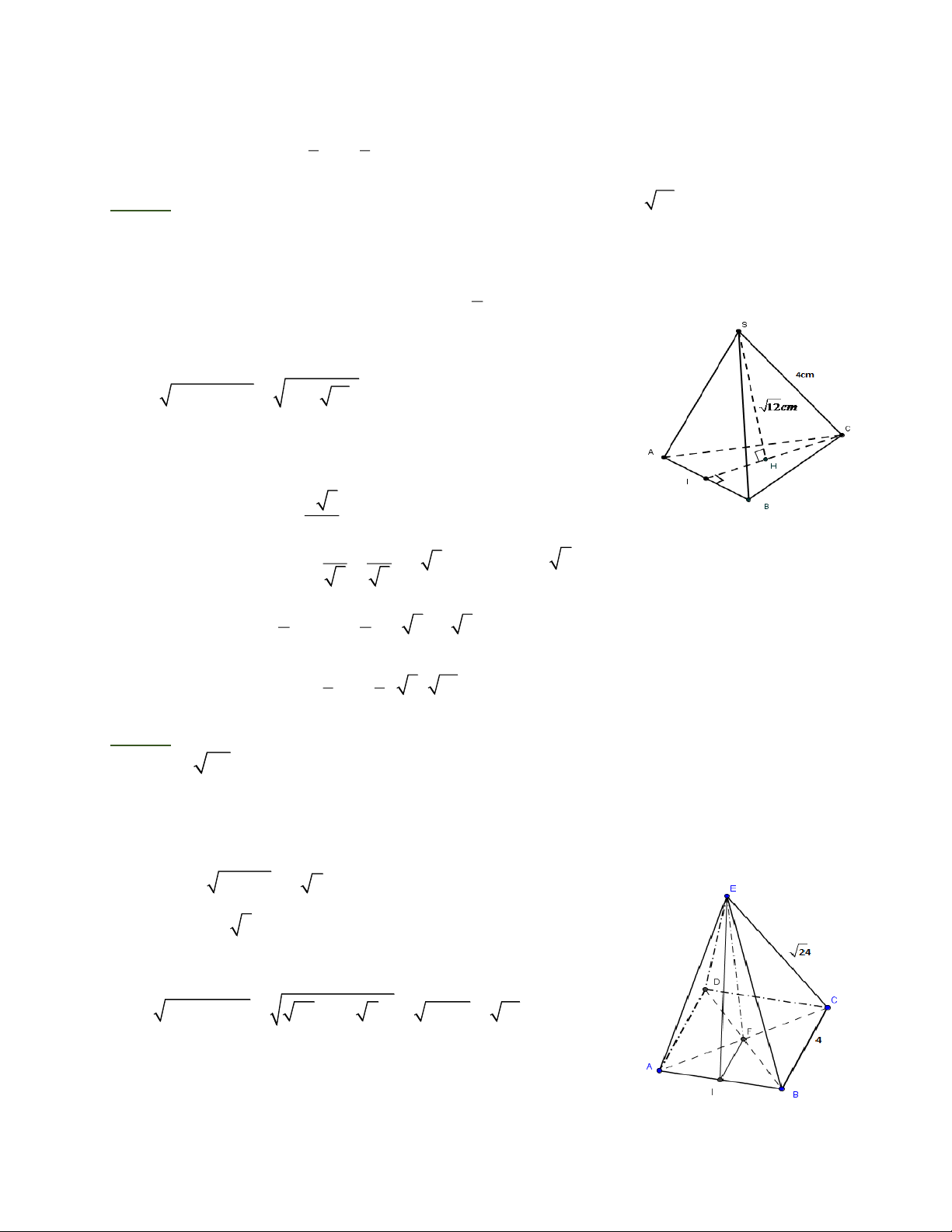
Bài 10: Tính thể tích hình chóp tam giác đều biết chiều cao bằng 12cm và cạnh bên bằng 4cm.
S .A BC là hình chóp đều nên chân đường cao H trùng với giao điểm ba đường trung 2
tuyến của tam giác, ta có SH ^ CI và HC = CI 3
Trong tam giác SHC vuông tại H, theo định lí pytago ta có 2 2 2 2
HC = SC − SH = 4 − 12 = 2
Suy ra CI = 3cm
Tam giác ABC là tam giác đều, giả sử có cạnh là a nên chiều a 3
cao tam giác đều là h =
mà CI là chiều cao tam giác ABC 2 2h 2.3
nên cạnh tam giác đều là = = 2 3 hay AB = 2 3cm 3 3 1 1
Diện tích đáy là S = CI.AB = .3.2 3 = 3 3 ( 2 cm ) 2 2 1 1
Thể tích hình chóp là V = Sh = 3 3  12 = 6 ( 3 cm ) 3 3
Bài 11: Tính thể tích hình chóp tứ giác đều biết độ dài cạnh đáy bằng 4cm và độ dài cạnh bên bằng 24cm Bài giải
E .A BCD là hình chóp tứ giác đều có đáy A BCD là hình vuông, có cạnh A B = 4cm Ta có 2 2
AC = 4 + 4 = 4 2cm Suy ra FC = 2 2cm
Áp dụng định lí pytago trong tam giác vuông EFC ta có 2 2 2 2 EF = EC − FC =
24 − (2 2) = 24 − 8 = 16 = 4cm
Chiều cao hình chóp là 4cm
Diện tích tứ giác đáy S = 4.4 = 16cm 1 1 Thể tích hình chóp 3
V = Sh = 16.4  21,3cm 3 3
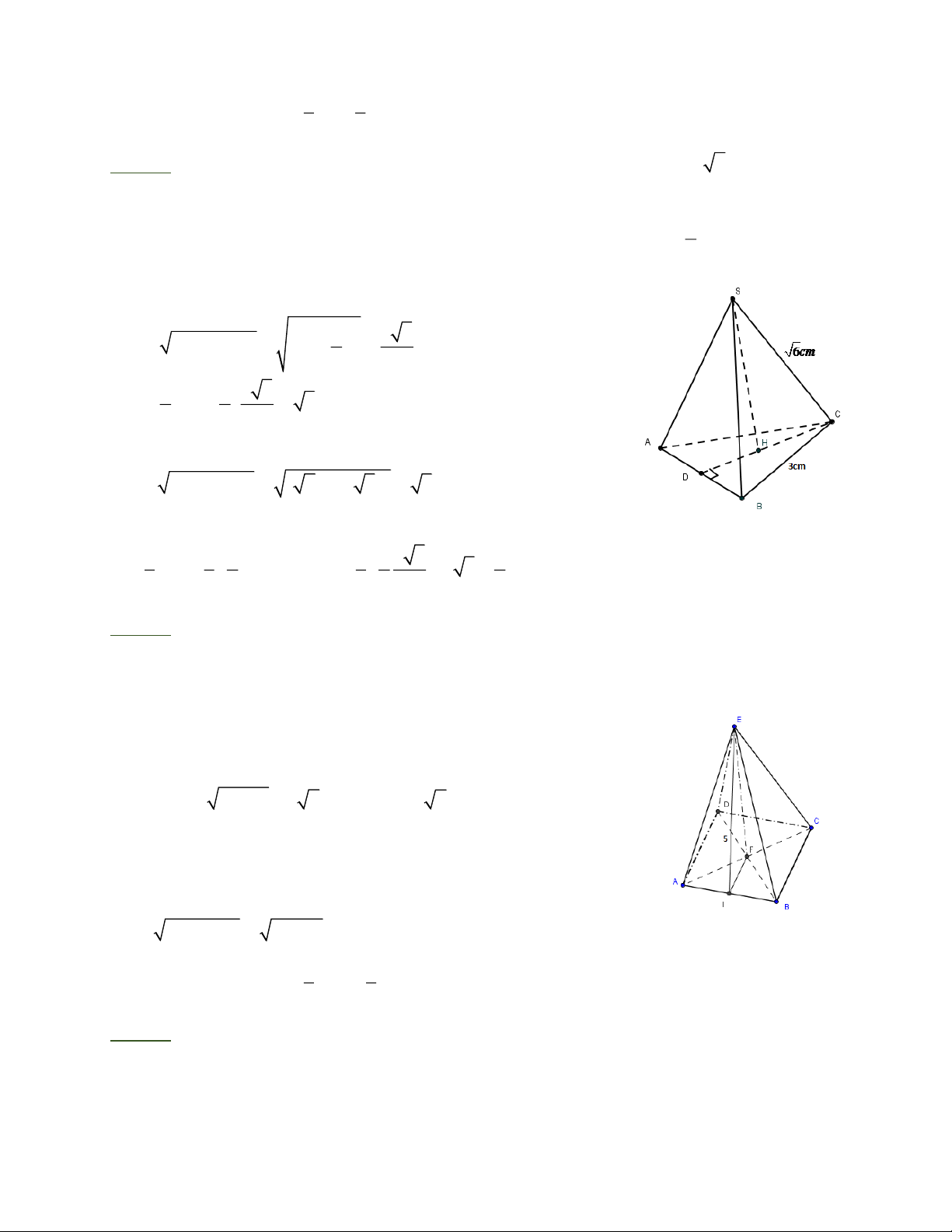
Bài 12: Tính thể tích hình chóp tam giác đều biết độ dài cạnh bên bằng 6cm và cạnh bên đáy 3cm. 3
Gọi H là trọng tâm tam giác A B C , HC cắt AB tại D, ta có AD = DB = 2
Tam giác CDB vuông tại D, theo định lí Pytago, ta có 2 2 2 2  3  3 3
DC = BC − BD = 3 − =   và  2  2 2 2 3 3 HC = CD =  = 3 3 3 2
Tam giác SHC vuông tại H, ta có 2 2 2 2
SH = SC − HC = ( 6) − ( 3) = 3
Thể tích của hình chóp đều là 1 1  1  1  1 3 3  9 3 V = S h =
DC.AB .SH =    .3 3 = cm 3 d 3 2 3  2 2    4  
Bài 13: Tính thể tích hình chóp tứ giác đều có trung đoạn bằng 5cm và diện tích xung quanh bằng 2 80cm .
HD: Diện tích xung quanh hình chóp tứ giác đều có cạnh đáy là a cm, trung đoạn là 5cm: 2
S = p d = 2 .5 a = 80cm a = cm xq Hay 8 Ta có 2 2
AC = 8 + 8 = 8 2cm  BF = 4 2cm
Ta có FI = 4cm (vì FI là đường trung bình của tam giác ABC,
tam giác A B C có cạnh A B = a = 8cm )
Áp dụng định lí pytago trong tam giác vuông EFI ta có 2 2 2 2
EF = EI − FI = 5 − 4 = 3cm 1 1 Thể tích hình chóp 2 3
V = S h = 8 .3 = 64cm 3 3
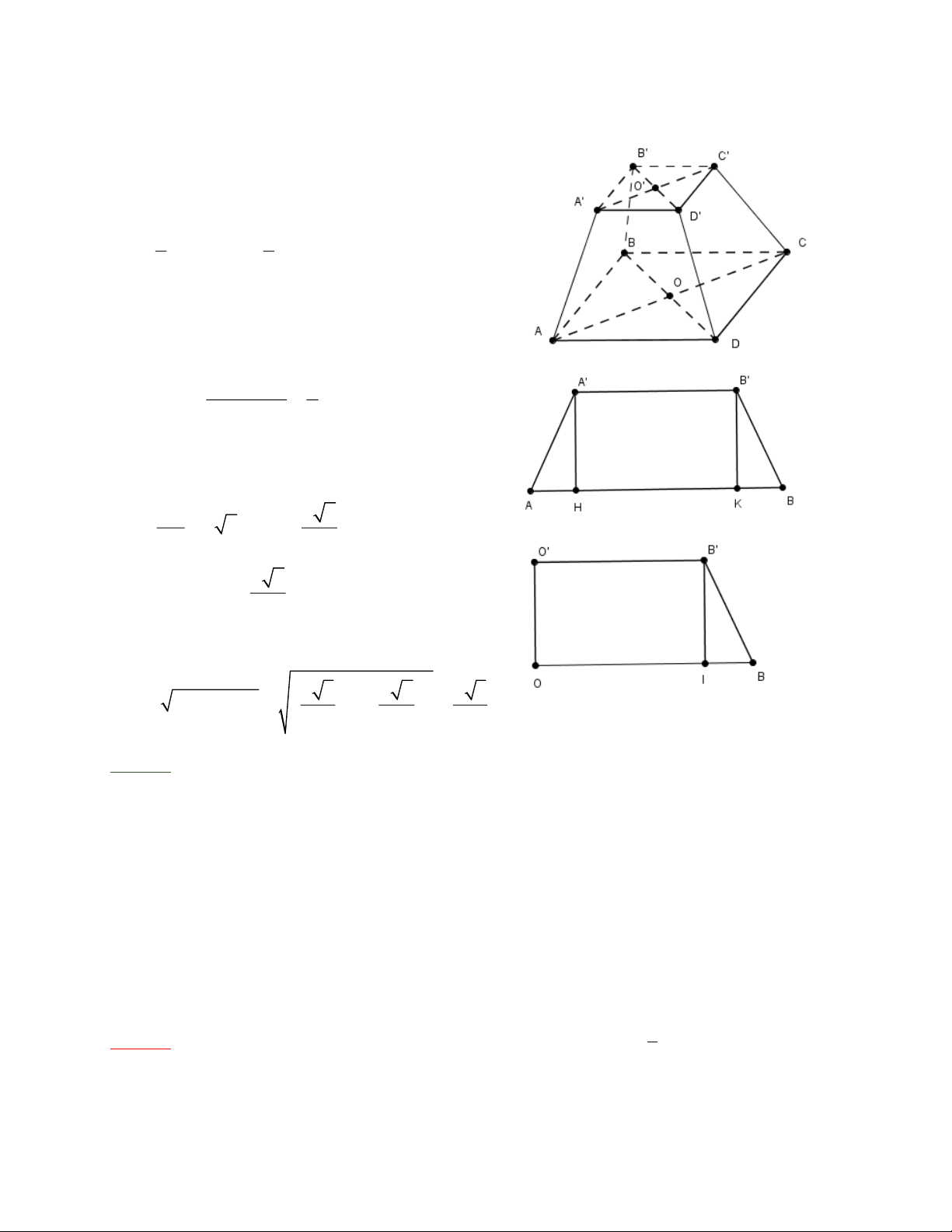
Bài 14: Một hình chóp cụt đều A BCD.A ' B 'C ' D ' có các cạnh đáy bằng a và 2a, đường cao của mặt bên bằng a.
a) Tính diện tích xung quanh
b) Tính cạnh bên, đường cao của hình chóp cụt đều. Bài giải
a) Diện tích xung quanh của hình chóp cụt đều 1 1 2
S = ( p + p)  d = (4.2a + 4a)a = 6a xq 2 2
b) Khai triển hình chóp cụt đều ta thấy mặt
bên là hình thang cân ABA’B’. Vẽ đường cao A’H và B’K , ta có
AB − A' B ' a AH = BK = = 2 2
Trong hình thang vuông OBB’O’ vẽ đường
cao B ' I ta có BD a 2 OB =
= a 2;O ' B ' = 2 2 a 2
BI = OB − O ' B ' = 2
Vậy đường cao hình chóp cụt đều là 2 2
a 5   a 2  a 3 2 2
B ' I = B ' B − BI =   −   =  2   2  2    
Bài 15: Cho hình chóp tam giác đều S .A B C . Gọi M, N, P lần lượt là trung điểm các cạnh
SA, SB, SC. Chứng minh A BC .MNP là hình chóp cụt tam giác đều.
Ta có A B / / MN ; BC / / NP nên mp (MNP )/ / mp (A BC ).
Mặt khác, S .A B C là hình chóp tam giác đều nên SA = SB = SC
Suy ra SAB = SBC , do đó A MNB là hình thang cân.
Tương tự B NPC ; A MPC là các hình thang cân
Vậy A BC .MNP là hình chóp cụt tam giác đều. 1
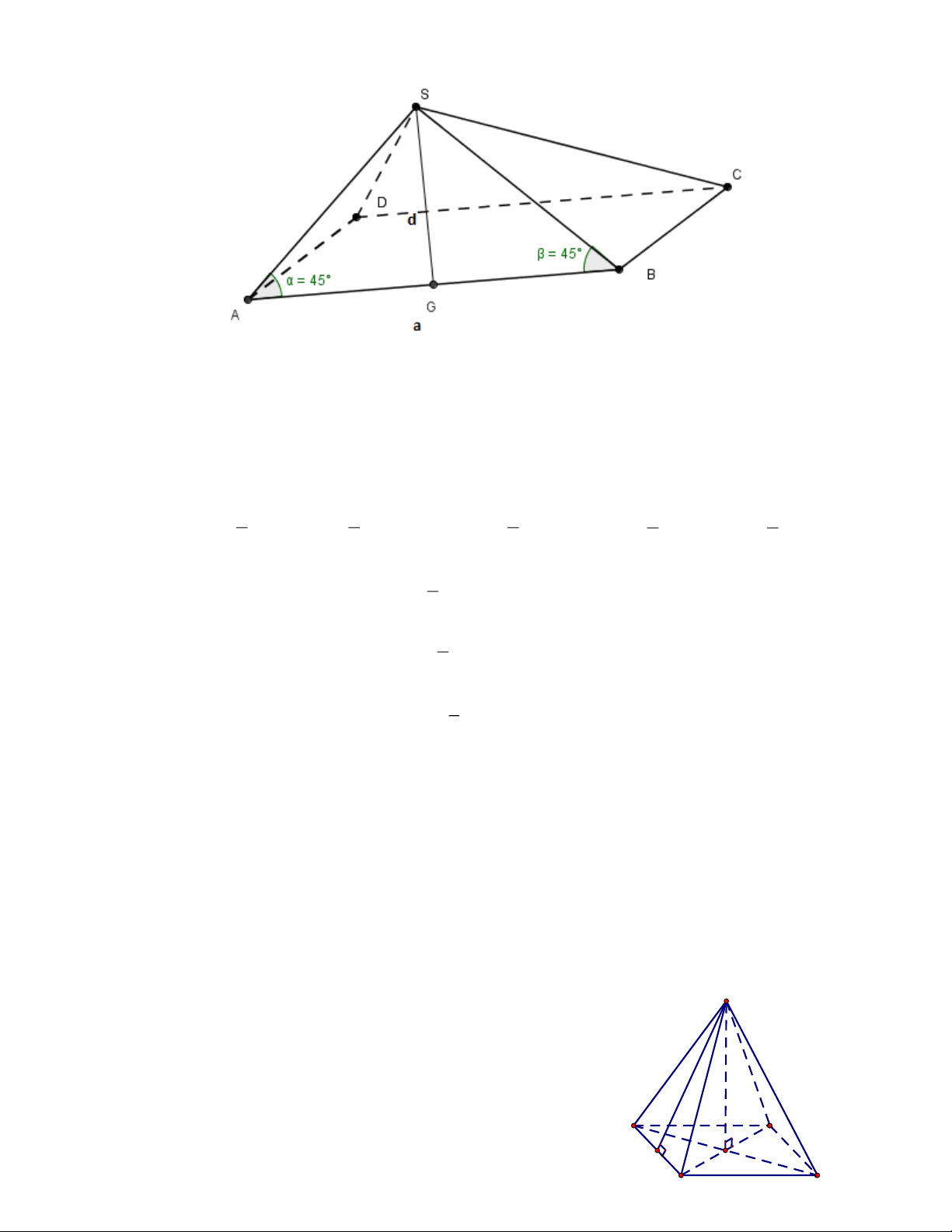
Bài 15: Cho hình chóp tứ giác đều có diện tích xung quanh bằng diện tích toàn phần. 2
Chứng minh rằng các mặt bên của hình chóp là các tam giác vuông cân.
Hình chóp tứ giác đều S .A BCD có đáy là hình vuông, các cạnh bên là các tam giác cân tại S (1)
Gọi a là độ dài cạnh đáy, d là trung đoạn của hình chóp
Ta có S = pd = 2ad S = S + S = ad + a xq ; 2 2 tp xq d 1 1 1   Mặt khác S = S  2ad = ( 2 2ad + a ) 2  ad − a = 1 1
0  a d − a = 0  d = a xq   2 tp 2 2  2  2 1
Gọi G là trung điểm AB suy ra GB = a 2 1
Ta có SG là trung đoạn hình chóp SG = a 2 1
Vậy trong tam giác SGB có GB = SG =
a và G = 90 nên SGB là tam giác vuông cân 2
tại G  GSB = 45 (2)
Tương tự, ta có GSA = 45 (3)
Từ (2), (3) suy ra BSA = 90 (4)
Từ (1), (4) suy ra ASB vuông cân tại S
Tương tự ta chứng minh được các cạnh bên của hình chóp là tam giác vuông cân. TỰ LUYỆN S
Bài 1: Tính diện tích toàn phần và thể tích của hình chóp tứ giác
đều S .A BCD (nếu làm tròn đến chữ số thập phân thứ hai )
a) Biết AB = 6cm , SI = 5cm.
b) Biết SH = 4cm , SB = 5cm. A D I H B C
c) Biết AB = 5cm , SB = 5cm.
Bài 2: Cho hình chóp tam giác đều S.ABC . Gọi O là tâm đường tròn ngoại tiếp ABC và D, E, F
lần lượt là trung điểm của các cạnh AB, BC, CA .
a) Chứng minh SDO = SEO = SFO .
b) Tính diện tích xung quanh và thể tích của hình chóp.
1) Nếu biết SO = 12cm , AB = 10cm.
2) Nếu biết các mặt bên là các tam giác đều, OA = 3 cm , AB = 3cm
3) Nếu biết OC = 2 3cm và 0 SDO = 60
Bài 3: Cho hình chóp tứ giác đều S.ABCD . Có SH = 15 cm, AB = 16 cm
a) Tính trung đoạn, diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp.
b) Gọi H' là trung điểm của SH. Cắt hình chóp bởi 1 mặt phẳng đi qua H' và song song với mặt
phẳng đáy (ABCD) ta được hình chóp cụt đều ABCD.A 'B'C'D' .Tính diện tích xung quanh và thể
tich của hình chóp cụt. (làm tròn đến chữ số thập phân thứ hai).
KẾT QUẢ - ĐÁP SỐ
III. BÀI TẬP TỰ LUẬN Bài 3: Bài 4: Bài 5: Bài 8:
IV. BÀI TẬP TRẮC NGHIỆM

Tài liệu liên quan: