Bài Tập Hình 8 Bài Tứ Giác Có Lời Giải

1. TỨ GIÁC
I. KIẾN THỨC CƠ BẢN
 Tứ giác ABCD là hình gồm bốn đoạn AB, BC, CD và ;
DA trong đó bất kì hai đoạn thẳng
nào cũng không nằm trên một đường thẳng.
 Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất
kì cạnh nào của tứ giác.
 Tổng các góc của một tứ giác luôn bằng 360° II. BÀI TẬP
Bài 1: a) Có tứ giác nào có bốn góc nhọn không?
b) Một tứ giác có nhiều nhất bao nhiêu góc nhọn, bao nhiêu góc tù, bao nhiêu góc vuông?
Bài 2: a) Cho tứ giác ABCD có µ 0 µ 0 µ 0
A = 65 ;B = 117 ;D = 70 . Tính số đo góc µ C
b) Cho tứ giác ABCD có µ µ µ A = 65 ; ° B = 117 ;
° C = 71° . Tính số đo góc ngoài tại đỉnh D
Bài 3: Tứ giác ABCD có C ˆ =  50 , D ˆ =  60 ˆ ˆ
, A : B = 3 : 2 . Tính các góc A và B. µ µ µ µ µ µ
Bài 4: Cho tứ giác ABCD biết B + C = 200° , B + D = 180°; C + D = 120°
a) Tính số đo các góc của tứ giác. µ
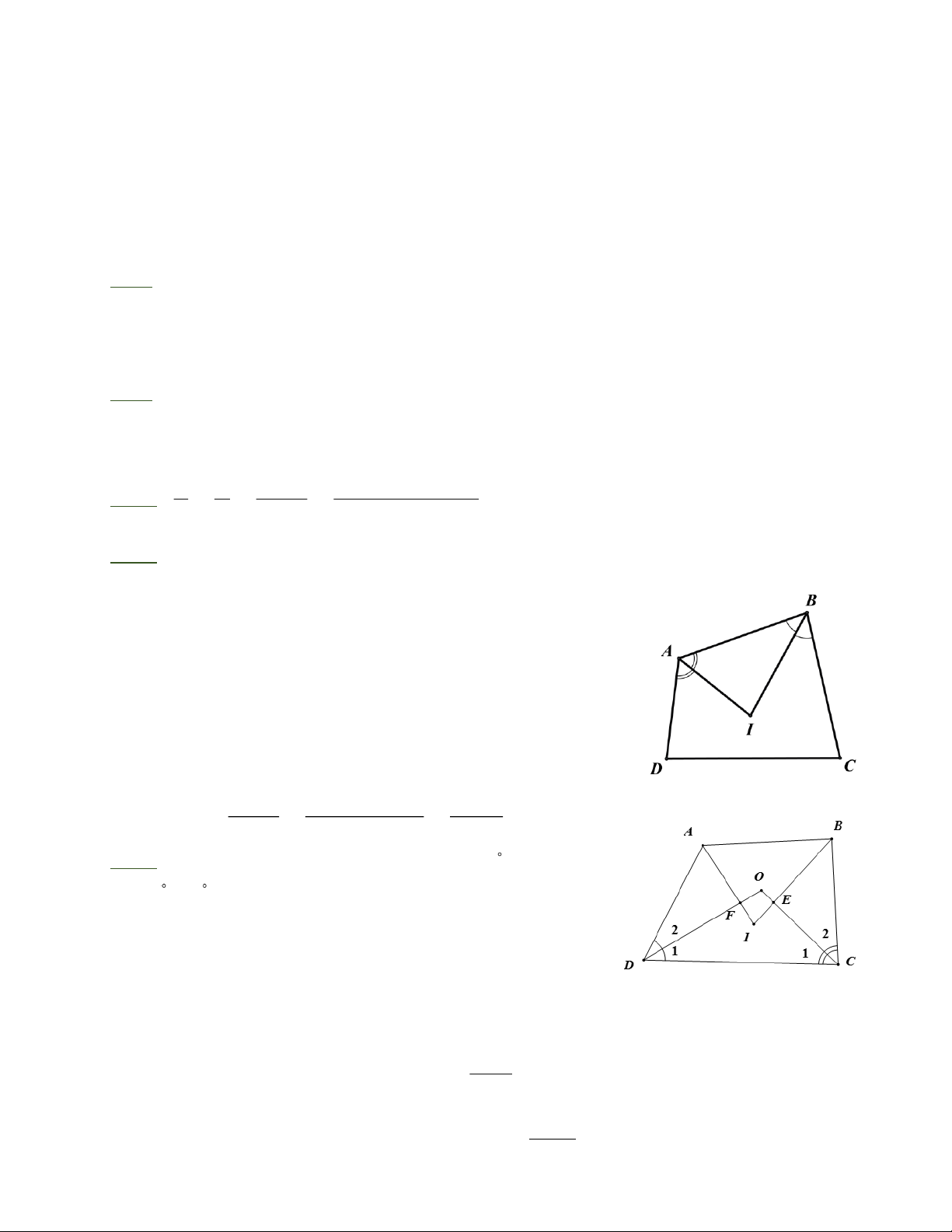
b) Gọi I là giao điểm của các tia phân giác của A và B của tứ giác. Chứng minh: µ µ · C + D AIB = 2
Bài 5: Cho tứ giác ABCD có O là giao điểm các tia phân giác của các góc C và D . a) Tính COD biết 0 0
A = 120 , B = 90 .
b) Tính COD theo A và B .
c) Các tia phân giác của góc A và B cắt nhau ở I và cắt các tia phân giác các góc C và D
thứ tự ở E và F . Chứng minh rằng tứ giác OEIF có các góc đối bù nhau.
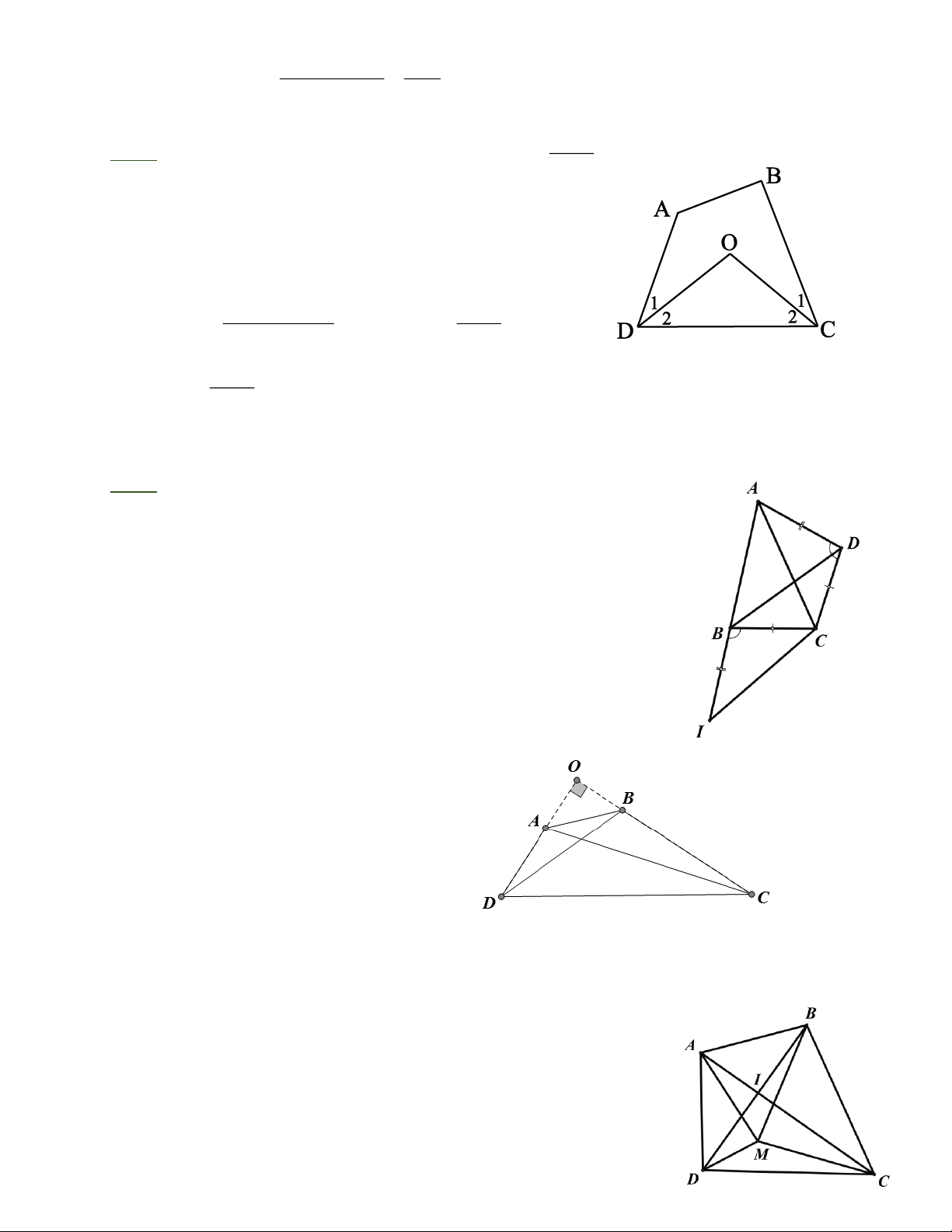
Bài 6: Cho tứ giác ABCD, o
A − B = 40 . Các tia phân giác của góc C và góc D cắt nhau tại O. Cho biết o
COD = 110 . Chứng minh rằng A B ^ BC . µ µ
Bài 7: Cho tứ giác lồi ABCD có B + D = 180° ,CB = CD . Chứng minh AC là tia phân giác của BAD .
Bài 8: Tứ giác ABCD có C ˆ + Dˆ =  90 . Chứng minh rằng 2 + 2 = 2 + 2 AC BD AB CD
Bài 9: Cho tứ giác ABCD, M là một điểm trong tứ giác đó. Xác định vị trí của M để
MA + MB + MC + MD nhỏ nhất. Trang 1
Bài 10: Cho tứ giác ABCD có góc ˆ ˆ A C 90° = =
tia phân giác góc B cắt đường thẳng AD ở E;
tia phân giác của góc D cắt đường thẳng BC ở F. Chứng minh rằng: BE // DF.
Tổng quát: Tứ giác ABCD có A = C. Chứng minh rằng các đường phân giác của góc B và
góc D song song với nhau hoặc trùng nhau.
KẾT QUẢ - ĐÁP SỐ III. BÀI TẬP
Bài 1:a) Không có tứ giác nào có 4 góc nhọn.
Tổng các góc của 1 tứ giác bằng 3600. Do đó, một tứ giác có nhiều nhất ba góc nhọn, có
nhiều nhất ba góc tù, nhiều nhất 4 góc vuông. µ µ µ µ µ
Bài 2: a) A + B + C + D = 360° Þ C = 108° µ
b) Tương tự tính được D = 107° . Vậy góc ngoài đỉnh D có số đo là 73° µ µ µ µ 360 A B A B ° - (50° + 60 ) ° + Bài 3: = = =
= 50° . Từ đó tính được A = 0 150 . B = 0 100 . 3 2 5 5
Bài 4: a) Từ giả thiết ta có: 2B + 2C + 2D = 200 +180 +120  B + C + D = 250 Vì ˆ ˆ ˆ ˆ ˆ
A + B + C + D = 360° Þ A = 110° . µ µ µ
B = 250° - (C + D) = 250° - 120° = 130° µ ° µ
C = 200 - B = 200° - 130° = 70° . 0 0 0 0
D = 120 − C = 120 − 70 = 50 . b) Trong tam giác ABI: · ˆ ˆ ° ˆ ˆ ˆ ˆ + - + + ° A B 360 (A B ) C D A IB = 180 - = = . 2 2 2
Bài 5: a) Tứ giác ABCD có A + B + C + D = 360
 120 + 90 + C + D = 360
 C + D = 150  C + D = (C + D) : 2 =150 : 2 = 75 1 1
COD có C + D = 75
COD = 180 − (C + D ) 1 1 nên 1 1
= 180° - 75° = 105° . A + B
b) Giải tương tự như câu a. Đáp số: COD = . 2 C + D
c) Chứng minh tương tự như câu b, ta được EIF = . 2 Trang 2
A + B + C + D 360
Do đó: COD + EIF = =
=180 . Suy ra: OEI + OFI = 360 −180 = 180 . 2 2 C + D
Bài 6: Xét D COD có o COD = 180 − (C + D ) o = − 2 2 180 2 (vì = = 1 C C2; 1 D D2 ). Xét tứ giác ABCD có o
C + D = 360 − (A + B), do đó o 360 − A + B o ( ) o o A + B COD = 180 − =180 −180 + . 2 2 A + B Vậy COD = . Theo đề bài o COD = 110 nên o A + B = 220 . 2 Mặt khác, o A − B = 40 nên = ( o o − ) o B 220
40 : 2 = 90 . Do đó A B ^ BC .
Bài 7: Trên tia đối tia BA lấy điểm I sao cho BI = A D.
Ta có ADC = IBC (cùng bù với góc ABC ).
A D = IB, DC = BC . Từ đó ta có ADC = IBC .
Suy ra: DAC = BIC và A C = IC .
Tam giác ACI cân tại C nên BAC = BIC = DAC .
Vậy AC là phân giác trong góc BAD .
Bài 8: Gọi O là giao điểm AD và BC. Ta có C + D = 0 90 nên O = 0 90
Áp dụng định lí Py – ta – go, Ta có 2 AC = 2 OA + 2 OC . 2 = 2 + 2 BD OB OD Nên 2 + 2 = ( 2 + 2 ) + ( 2 + 2 ) = 2 + 2 AC BD OA OB OC OD AB CD
Bài 9: Gọi I là giao điểm của AC và BD. Ta có các bất đẳng thức:
MA + MC ³ AC, MB + MD ³ BD .
Từ đó suy ra MA + MB + MC + MD ³ AC + BD
MA + MB + MC + MD = AC + BD khi M trùng với I. Trang 3
Vậy khi M là giao điểm hai đường chéo thì MA + MB + MC + MD nhỏ nhất. Bài 10: C
Xét DCF vuông tại C, có: · · 1 F 0 · 0 · 0 ·
DFC + CDF = 90 Þ DFC = 90 - CDF = 90 - CDA (1) 2 B Xét tứ giác ABCD, có: µ µ µ µ 0 A D
A + B + C + D = 360 E µ 0 µ µ
Þ B = 360 - (A + C ) µ - D 0 = 360 - ( 0 0 90 + 90 ) · 0 ·
- CDA = 180 - CDA · 1 0 · · 0 ·
Þ 2CBE = 180 - CDA Þ CBE = 90 - CDA (2) 2
Từ (1) và (2) , suy ra CBE = CFD . Mà CBE và CFD nằm ở vị trí đồng vị  BE // DF
Tổng quát: Xét tứ giác ABCD có: o + = − ( + ) o B D 360 A C = 360 − 2C. Vì = = + = − 1 B B2; 1 D D2 nên o 1 B 1 D 180 C o  + + = 1 B 1 D C 180 . (1) Xét BCM có o + + = 1 B 1 M C 180 . (2) Từ (1) và (2) suy ra = 1 D 1 M . Do đó DN // BM. Trang 4