Bài Tập Hình 8 Ôn Chương Tứ Giác Có Lời Giải

13. ÔN TẬP CHƯƠNG I I. BÀI TẬP
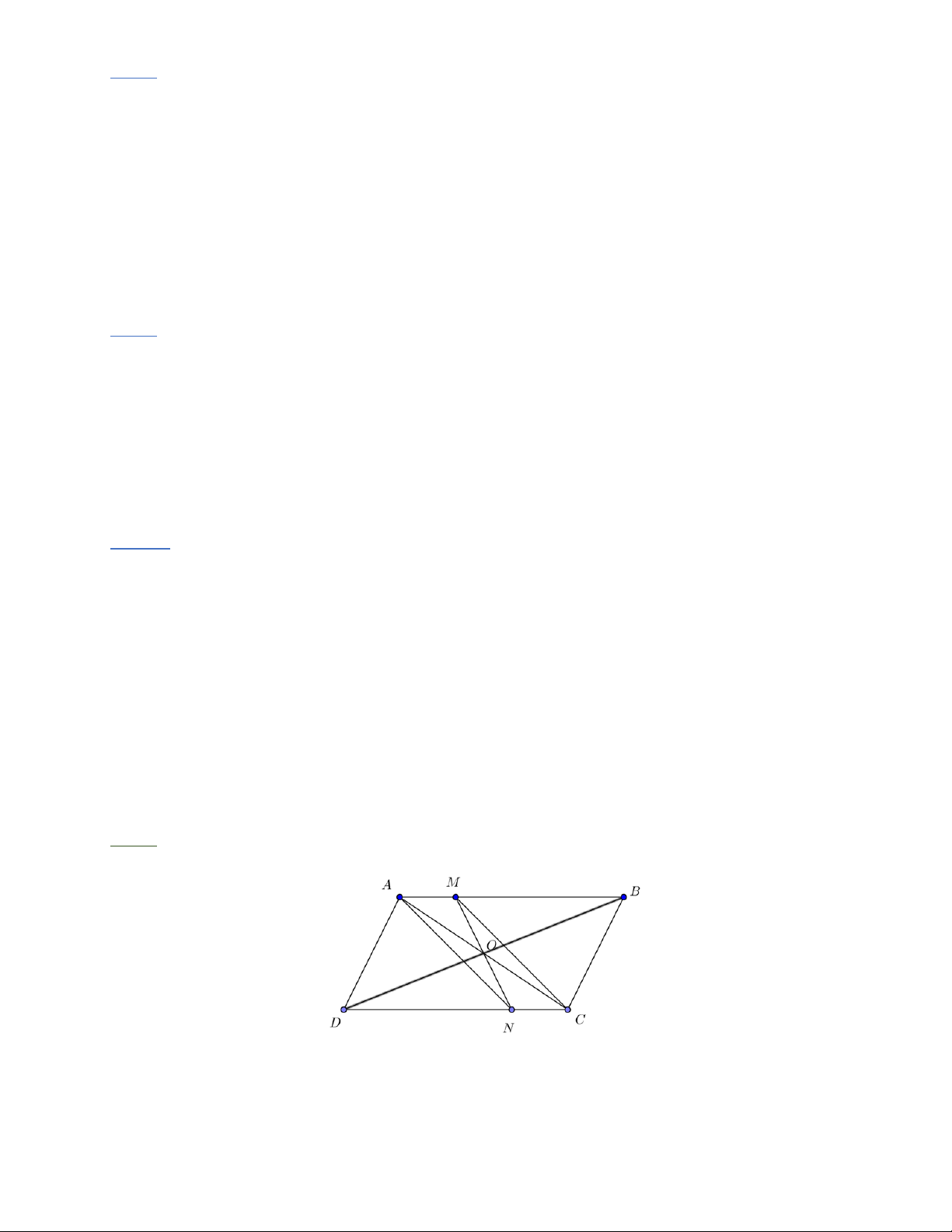
Bài 1: Cho hình bình hành ABCD . M là trung điểm AB . Nối C với M . Đường thẳng qua
A song song với CM cắt CD ở N .
a) Chứng minh rằng tứ giác AMCN là hình bình hành.
b) Gọi O là giao điểm của AC và MN . Chứng minh rằng B, O, D thẳng hàng.
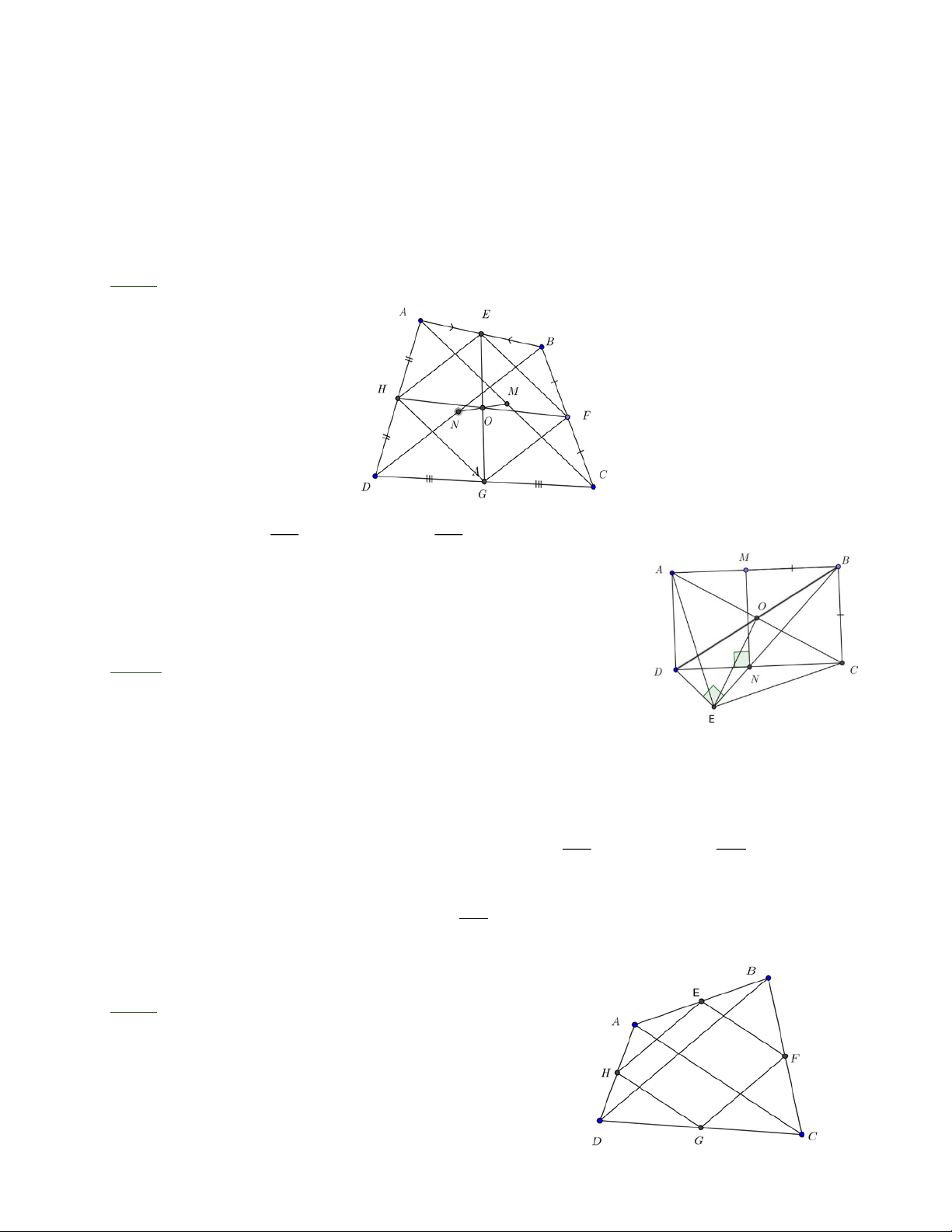
Bài 2: Cho tứ giác ABCD . Các điểm E, F, G, H, M, N lần lượt là trung điểm của các đoạn
thẳng AB, BC, CD, DA, AC, BD .
a) Chứng minh rằng EFGH là hình bình hành.
b) Gọi O là giao điểm giữa EG và HF . Chứng minh rằng M và N đối xứng nhau qua O .
Bài 3: Cho hình chữ nhật ABCD ( AB  CD ), M là điểm trên AB sao cho MB = BC. Vẽ
MN ⊥ CD tại N . Vẽ DE ⊥ BN tại E .
a) Tứ giác AMND là hình gì? Vì sao?
b) Tứ giác MBCN là hình gì? Vì sao?
c) Chứng minh rằng AEC =  90
Bài 4: Cho tứ giác ABCD . Gọi E, F, G, H lần lượt là trung điểm của các cạnh
AB, BC, CD, DA , tìm điều kiện của tứ giác ABCD để tứ giác EFGH là : a) Hình chữ nhật b) Hình thoi c) Hình vuông
Bài 5: Cho tứ giác ABCD . Gọi E, F,G, H lần lượt là trung điểm của các cạnh
AB, AC,CD, BD , tìm điều kiện của tứ giác ABCD để tứ giác EFGH là : a) Hình chữ nhật b) Hình thoi c) Hình vuông
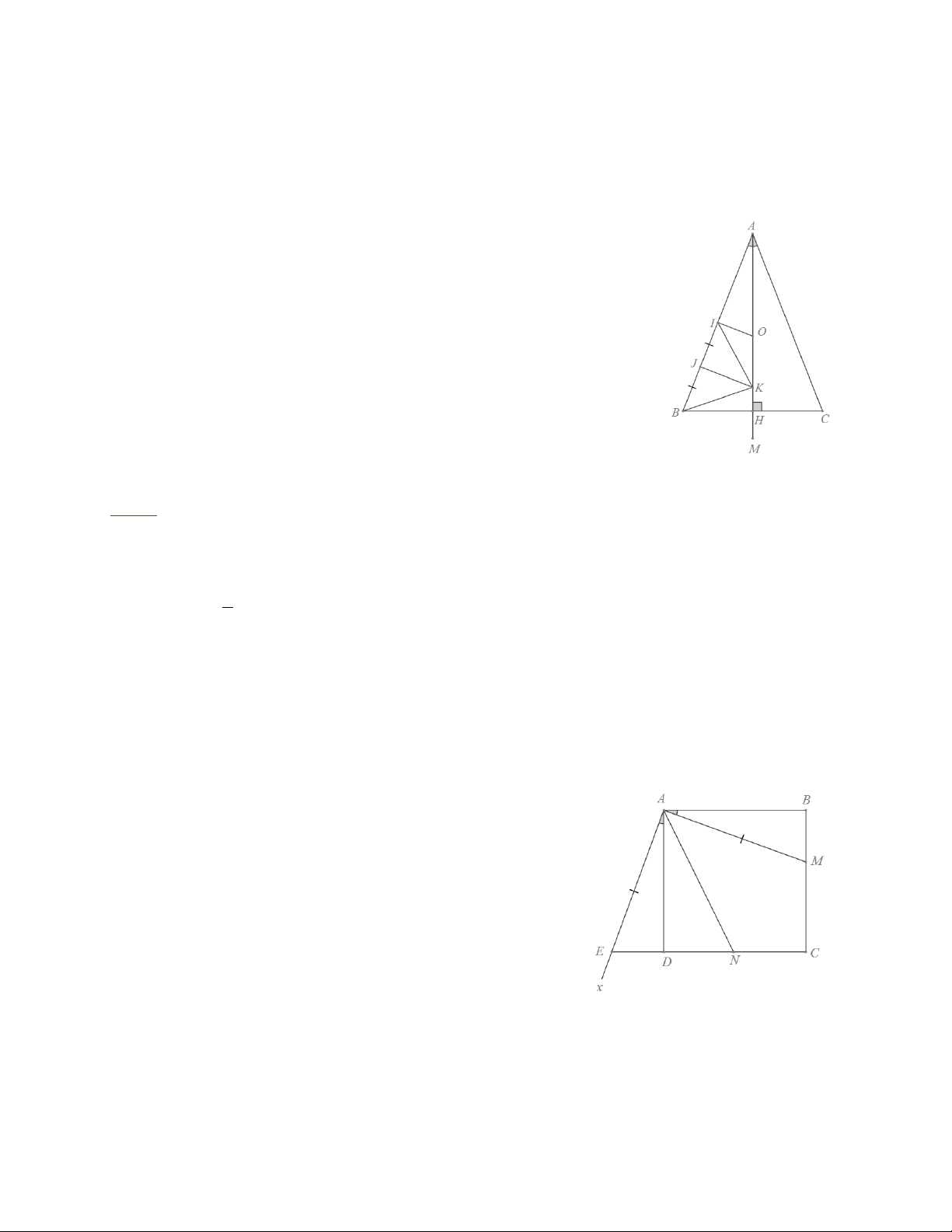
Bài 6: Cho tam giác ABC cân tại ,
A vẽ đường phân giác AH. Gọi I là trung điểm của , AB
đường vuông góc với AB ở I cắt AH tại .
O Vẽ M là điểm sao cho O là trung điểm của AM
a) Chứng minh tứ giác IOMB là hình thang vuông.
b) Gọi K là trung điểm của OM . Chứng minh tam giác IKB cân.
c) Chứng minh tứ giác AIKC có tổng các góc đối bằng 0 180 .
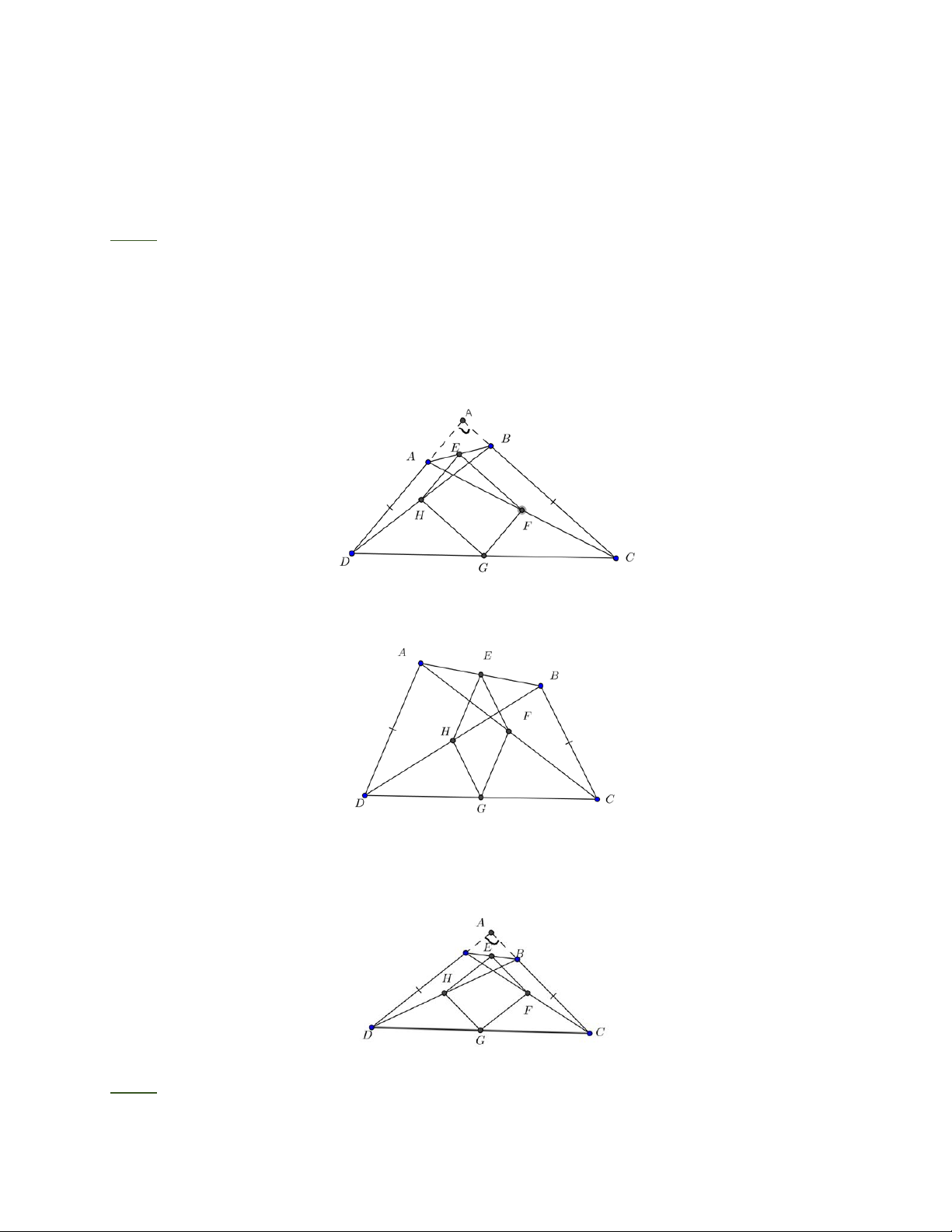
Bài 7: Cho ABCD là một hình thoi có cạnh bằng 1. Giả sử tồn tại điểm M thuộc cạnh BC
và một điểm N thuộc cạnh C sao cho tam giác CMN có chu vi bằng 2 và BAD = 2MAN.
Tính các góc của hình thoi ABCD. Bài tập tự luyện: Trang 1
Bài 8: Cho tam giác ABC vuông tại ,
A đường cao AH , trung tuyến AM .
a) Chứng minh BAH = MAC.
b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA
( D và A thuộc hai nửa mặt phẳng đối nhau bờ BC ). Chứng minh rằng AD là phân giác
chung của MAH và CA . B
c) Từ D kẻ DE, DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì? d) Chứng minh DBE  = DC  F.
Bài 9: Cho hình vuông ABC .
D Gọi E là điểm đối xứng của điểm A qua điểm . D
a) Chứng minh tam giác ACE là tam giác vuông cân.
b) Từ A hạ AH ⊥ BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng
minh tứ giác BMNC là hình bình hành.
c) Chứng minh M là trực tâm của tam giác AN . B d) Chứng minh 0 ANC = 90 .
Bài 10: Cho tam giác ABC vuông tại .
A Về phía ngoài tam giác, vẽ các hình vuông BDE, ACFG.
a) Chứng minh tứ giác BCGE là hình thang cân.
b) Gọi K là giao điểm của các tia DE và FG, M là trung điểm của đoạn thẳng EG.
Chứng minh ba điểm K, ,
A M thẳng hàng.
d) Chứng minh DC, FB và AM đồng quy.
KẾT QUẢ - ĐÁP SỐ Bài 1:
a) Tứ giác ABCD là hình bình hành
 AB//CD, AD//BC. Mà M  AB và N CD nên AM//NC Trang 2
Xét tứ giác AMCN có AM//NC (cmt) và AN//MC (gt),
Do đó AMCN là hình bình hành ( dấu hiệu nhận biết hình bình hành).
b) Tứ giác AMCN là hình bình hành ( câu a) do đó O là trung điểm của AC và MN .
Tứ giác ABCD là hình bình hành (gt) có O là trung điểm của AC nên O là trung điểm
của BD . Vậy B, O, D thẳng hàng. Bài 2: BD BD
a) EH // BD , EH =
, GF // BD , GF = 2 2
b) NGME là hình bình hành có O là trung điểm của EG. Suy
ra O là trung điểm của MN
Bài 3: a) Tứ giác AMND là hình chữ nhật.
b) Tứ giác MBCN là hình vuông.
c) Gọi O là giao điểm giữa AC và BD
Tứ giác ABCD là hình chữ nhật nên O là trung điểm AC và BD, AC = BD . BD AC
Xét ΔEBD vuông tại E có EO là trung tuyến  EO = Do vậy EO = . 2 2 AC
Xét ΔEAC có EO là trung tuyến và EO = nên 2 ΔEAC vuông tại E.
Bài 4: Tứ giác EFGH là hình bình hành
a) EFGH là hình chữ nhật  Hình bình hành EFGH có HEF = 0
90  EH ⊥ EF Trang 3 Û BD ^ A C
b) EFGH là hình thoi Û Hình bình hành EFGH có EH = EF Û BD = A C
c) EFGH là hình vuông Û Hình chữ nhật EFGH có EH = EF Û BD ^ A C và BD = A C . Bài 5:
Tứ giác EFGH là hình bình hành
a) EFGH là hình chữ nhật  Hình bình hành EFGH có HEF = 90  EH ⊥ EF  AD ⊥ BC .
b) EFGH là hình thoi  Hình bình hành EFGH có EH = EF  AD = BC
c) EFGH là hình vuông   Hình chữ nhật EFGH có EH ⊥ EF ; EH = EF  AD ⊥ BC và AD = BC Bài 6: Trang 4
a) IO là đường trung bình của tam giác A BM Þ OI / / MB . Mà AB ⊥ OI (gt) nên AB ⊥ MB ·
Tứ giác OIB M có: OI / / MB và 0
OIB = 90 suy ra OIBM là hình thang vuông.
b) Gọi J là trung điểm BI suy ra JK là đường trung bình của hình thang
OIBM Þ JK / /OI mà BI ^ OI nên JK ^ BI . Vậy JK là trung
trực của BI , K Î KJ Þ KI = KB Þ B
 KI cân tại K .
c) Do BKI cân tại K nên KBI = BIK. Trong ABC cân tại , A AH
là đường phân giác, suy ra AH là trục đối xứng  ABK = ACK
Vậy BIK = ACK Ta có 0
AIK + ACK = AIK + BIK = 180 (hai góc kề bù) 0
 IAC + IKC = 180
Bài 7: Trên nửa mặt phẳng bờ AD không chứa B vẽ tia Ax lấy điểm E sao cho AE = AM  BM = D , E ABM = ADE 1 Ta có MAN =
BAD (vì BAD = 2MAN ) 2 A  MN = A  EN ( . c . g ) c  MN = N . E
Mà CM + CN + MN = 2(gt) và có CM + CN + MB + DN = 2 (vì BC = CD = 1 )
Suy ra MN = MB + DN
Ta có NE = DE + DN  D nằm giữa , E N  D, , E N thẳng hàng.
Ta có ADN = ABC ( ABCD là hình thoi) ADE = ABC
Suy ra ADN = AD . E Hình thoi ABCD có 0
ADN = 90 nên là hình vuông Trang 5