







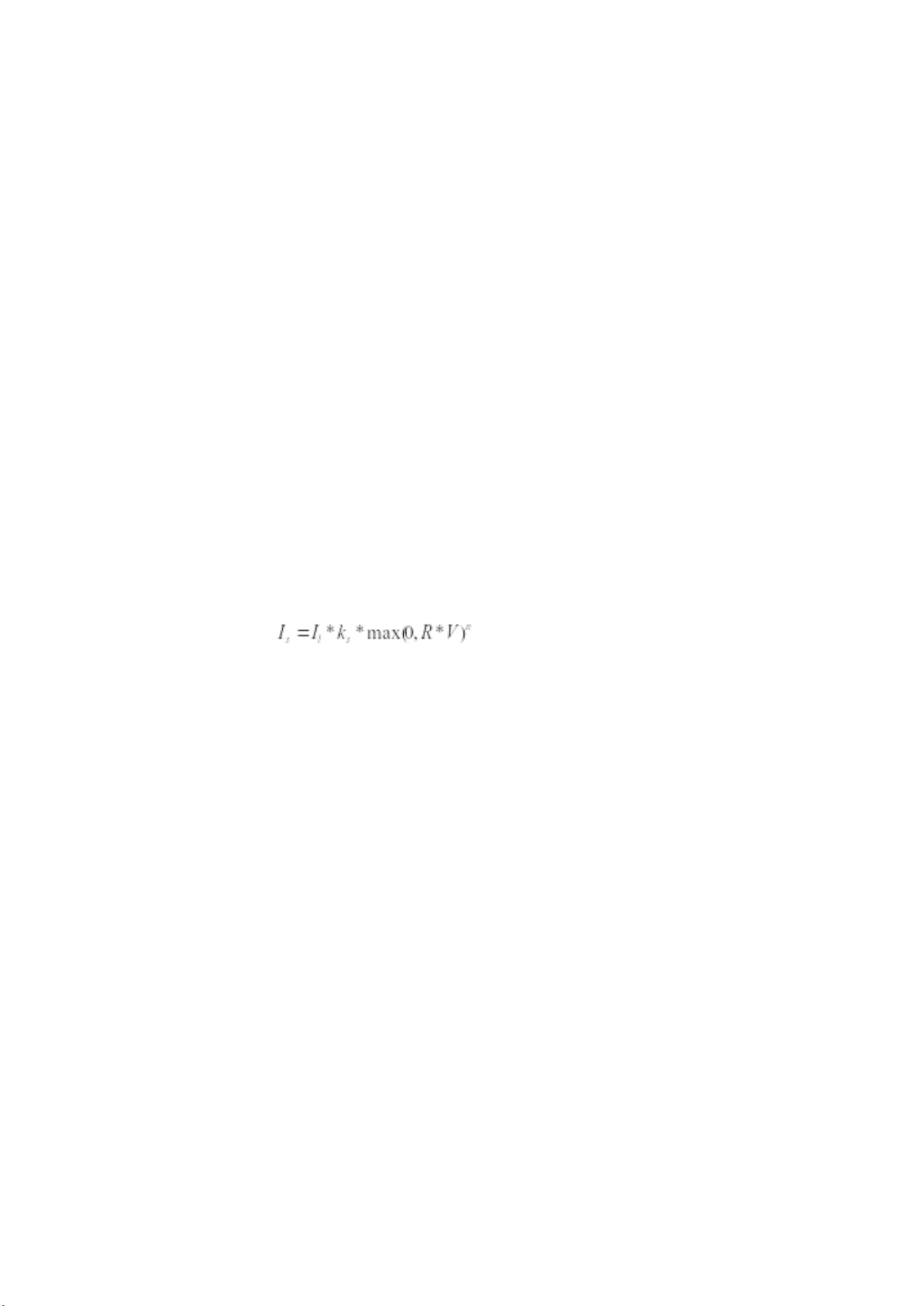











Preview text:
lOMoARcPSD| 58854646
TRƯỜNG ĐẠI HỌC KIẾN TRÚC HÀ NỘI
KHOA CÔNG NGHỆ THÔNG TIN -------------------- BÀI TẬP LỚN
MÔN: KỸ THUẬT ĐỒ HOẠ MÁY TÍNH
ĐỀ TÀI: CHIẾU SÁNG VÀ TÔ MÀU
GIẢNG VIÊN HƯỚNG DẪN:
TS. PHẠM TRỌNG TUẤN NHÓM SINH VIÊN:
NGUYỄN TRẦN BẢO KHANH VŨ VĂN HÙNG PHẠM BÌNH MINH NGUYỄN VĂN HỢP TRINH QUỐC NAM BÙI QUANG NGHỊ LỚP: 22CN3 HÀ NỘI 28- 4 - 2025 lOMoARcPSD| 58854646 Mục Lục
Mở đầu....................................................................................................................
CHỦ ĐỀ 2: CHIẾU SÁNG VÀ TÔ MÀU..............................................................
1. Giới thiệu về chiếu sáng và tô màu........................................................................2
2. Mô hình lý thuyết của chiếu sáng và khuếch tán...................................................2
3. Công thức tính các thành phần ánh sáng khuếch tán.............................................3
3.1. Công thức tính các thành phần ánh sáng khếch tán phản
chiếu”................4
3.2. Môi trường áp dụng cho các đỉnh của đối
tượng........................................5
4. Các phương pháp nội suy......................................................................................7
4.1. Phương pháp nội suy Gouraud để tô màu cho tam
giác..............................7
4.2. Phương pháp nội suy Phong để tô màu cho tam
giác.................................7
5. Sử dụng hàm gll.ighttfv() để thiết lập đặc tính vật liệu..........................................7
6. Sử dụng hmaf g.Materialf() để thiết lập đặc tính vật
liệu.......................................7
7. Công thức tính giáp tuyến của các bề mặt.............................................................8 lOMoARcPSD| 58854646
Tài liệu tham khảo................................................................................................. lOMoARcPSD| 58854646 MỞ ĐẦU
Nội dung tài liệu chủ yếu dựa trên tài liệu được cung cấp và trên mạng
Internet , dù đã cố gắng soát xét nhưng chắc hẳn còn nhiều sai sót, vì thế rất
mong nhận được ý kiến phản hồi từ bạn đọc. Mọi ý kiến xin gửi về 1303buiquanghi@gmail.com. Đồng Tác giả
Nguyễn Trần Bảo Khanh Vũ Văn Hùng Nguyễn Văn Hợp Phạm Bình Minh Bùi Quang Nghị iv lOMoARcPSD| 58854646 1 lOMoARcPSD| 58854646
CHỦ ĐỀ 2: CHIẾU SÁNG VÀ TÔ MÀU
1. Giới thiệu về chiếu sáng và tô màu
Chiếu sáng và tô màu là hai kỹ thuật quan trọng trong đồ họa máy tính nhằm
tăng tính chân thực và sinh động cho hình ảnh. Chiếu sáng (Lighting) mô phỏng
cách ánh sáng tác động đến bề mặt của vật thể, tạo ra các hiệu ứng như bóng đổ, độ
sáng tối, và sự phản xạ ánh sáng. Nhờ chiếu sáng, hình ảnh trở nên có chiều sâu và
gần gũi với thực tế hơn. Tô màu (Shading) là quá trình xác định màu sắc cuối cùng
tại mỗi điểm ảnh (pixel) trên bề mặt vật thể dựa trên ánh sáng, màu vật liệu, và các
yếu tố môi trường. Tô màu giúp vật thể thể hiện được chất liệu như bóng bẩy, nhám, mờ hay trong suốt.
Kết hợp chiếu sáng và tô màu chính là nền tảng để tạo ra những hình ảnh 3D
hoặc hình ảnh 2D sống động, chân thực trong các ứng dụng phim ảnh, game, mô phỏng khoa học...
2. Mô hình lý thuyết của chiếu sáng và khuếch tán
Trong đồ hoạ máy tính, các mô hình lý thuyết được xây dựng để mô phỏng
ánh sáng và cách nó tương tác với vật thể. Các mô hình cơ bản bao gồm: mô hình
ánh sáng và mô hình tô màu (Shading Models).
Mô hình ánh sáng gồm ánh sáng môi trường (Ambient Light) làm ánh sáng
khuếch tán đều khắp không gian, không có nguồn rõ ràng. Ánh sáng điểm (Point
Light) phát ra từ một điểm cố định và tỏa ra mọi hướng. Ánh sáng định hướng
(Directional Light) là tia sáng song song nhau như ánh sáng mặt trời.
Mô hình tô màu: Ánh sáng phóng xạ (Spot Light), tập trung vào một khu vực
giới hạn, như ánh đèn sân khấu. Flat Shading, tô màu đồng nhất cho mỗi mặt tam 2 lOMoARcPSD| 58854646
giác, phù hợp với vật thể phẳng. Gouraud Shading, tính toán màu ở các đỉnh và nội
suy màu cho các điểm bên trong tam giác, cho ra hiệu ứng mềm mại. Phong
Shading, suy vector pháp tuyến và sau đó tính màu sắc, tạo ra ánh sáng phản chiếu
mượt mà hơn. Mô hình phản xạ ánh sáng (Lighting Models). Mô hình phản xạ
Lambert, mô tả phản xạ khuếch tán (diffuse reflection), ánh sáng phản xạ đều mọi
hướng. Mô hình phản xạ phong, thêm thành phần phản xạ gương (specular
reflection) để mô phỏng độ bóng vật thể.
Phương trình ánh sáng tổng quát: Trong đó:
I là tổng cường độ ánh sáng tại một điểm trên bề mặt vật thể.
I môi trường là thành phần ánh sáng môi trường (ánh sáng toả đều, không phụ thuộc hướng chiếu).
I khuếch tán là thành phần ánh sáng khuếch tán (ánh sáng phản xạ đều khi ánh sáng
chiếu vào bề mặt vật thể).
I phản xạ gương là thành phần ánh sáng phản xạ gương (ánh sáng phản chiếu có
hướng, tạo ra độ bóng trên bề mặt).
3. Công thức tính các thành phần ánh sáng khuếch tán
Trong đồ hoạ máy tính, ánh sáng khuếch tán là một thành phần quan trọng
trong mô hình chiếu sáng (lighting model), thường được sử dụng để mô phỏng cách
ánh sáng chiếu lên một bề mặt và phân tán đều theo mọi hướng. Ánh sáng khuếch 3 lOMoARcPSD| 58854646
tán không phụ thuộc vào góc nhìn của người quan sát mà chỉ phụ thuộc vào góc
giữa nguồn sáng và bề mặt.
Công thức tổng quát cho ánh sáng khuếch tán:
Ánh sáng khuếch tán được tính theo công thức sau (dựa trên mô hình chiếu sáng Lambert):
Id=Il ∗k d ∗max(0,N ∗ L)❑ Trong đó:
Id: Cường độ ánh sáng khuếch tán tại điểm trên bề mặt.
Il: Cường độ ánh sáng từ nguồn sáng (thường là màu của ánh sáng, ví dụ: RGB).
k d : Hệ số khuếch tán của vật liệu (một giá trị màu đại diện cho khả
năng khuếch tán ánh sáng của bề mặt, cũng thường là RGB).
N: Vector pháp tuyến (normal vector) tại điểm trên bề mặt.
L: Vector hướng từ điểm trên bề mặt đến nguồn sáng.
N*L: Tích vô hướng giữa vector pháp tuyến và vector ánh sáng, biểu
thị góc giữa hai vector này.
max(0,N*L):Đảm bảo giá trị không âm (nếu góc giữa và lớn hơn 90
độ, ánh sáng không chiếu đến bề mặt, nên giá trị ánh sáng khuếch tán bằng 0). Ý nghĩa:
Ánh sáng khuếch tán mô phỏng hiện tượng ánh sáng chiếu lên một bề
mặt mờ (matte surface) như giấy hoặc vải, nơi ánh sáng bị phân tán đều theo mọi hướng. 4 lOMoARcPSD| 58854646
Khi N L=1 (ánh sáng chiếu vuông góc với bề mặt), ánh sáng khuếch ⋅
tán đạt giá trị tối đa.
Khi N L≤0 (ánh sáng chiếu từ phía sau bề mặt), ánh sáng khuếch tán ⋅ bằng 0.
3.1. Công thức tính các thành phần ánh sáng khếch tán phản chiếu”
Việc kết hợp ánh sáng khuếch tán (diffuse lighting) với ánh sáng phản chiếu
(specular lighting) trong một mô hình chiếu sáng hoàn chỉnh
Ánh sáng phản chiếu (Specular Lighting): ánh sáng phản chiếu mô phỏng
hiện tượng phản xạ ánh sáng trên các bề mặt bóng loáng (như kim loại hoặc nhựa
bóng). Không giống ánh sáng khuếch tán, ánh sáng phản chiếu phụ thuộc vào góc
nhìn của người quan sát.
Công thức ánh sáng phản chiếu (theo mô hình Phong): Trong đó:
Is : Cường độ ánh sáng phản chiếu. Il :
Cường độ ánh sáng từ nguồn sáng.
ks : Hệ số phản chiếu của vật liệu (màu specular của bề mặt).
R: Vector phản xạ của ánh sáng, được tính bằng: R=2(N*L)N−L.
V: Vector hướng từ điểm trên bề mặt đến người quan sát (camera).
R* V: Tích vô hướng giữa vector phản xạ và vector hướng nhìn.
n: Hệ số bóng loáng (shininess), quyết định độ tập trung của điểm
sáng (highlight). Giá trị nnn càng lớn, điểm sáng càng nhỏ và sắc nét. 5 lOMoARcPSD| 58854646
Kết hợp ánh sáng khuếch tán và ánh sáng phản chiếu:
Trong mô hình chiếu sáng Phong, tổng cường độ ánh sáng tại một điểm trên
bề mặt được tính bằng cách cộng ánh sáng khuếch tán, ánh sáng phản chiếu và ánh
sáng môi trường (ambient lighting):
I=Ia+Id +Is Trong đó:
Ia : Ánh sáng môi trường (ambient lighting), với a là hệ số môi trường của vật liệu.
Id,Is : Ánh sáng khuếch tán.
3.2. Môi trường áp dụng cho các đỉnh của đối tượng
Cách áp dụng các thành phần ánh sáng (như khuếch tán và phản chiếu) trong
một môi trường dựng hình, cụ thể là áp dụng tại các đỉnh (vertices) của đối tượng 3D.
Ý nghĩa trong đồ họa máy tính:
Đối tượng 3D: Một đối tượng 3D (như mô hình xe) được biểu diễn dưới
dạng lưới (mesh), gồm các đỉnh (vertices), cạnh (edges) và mặt (faces).
Áp dụng tại các đỉnh: Trong các pipeline đồ họa (như OpenGL hoặc
DirectX), ánh sáng thường được tính toán tại các đỉnh của lưới (vertex shader) trước
khi nội suy (interpolate) để áp dụng cho toàn bộ bề mặt.
Cách áp dụng ánh sáng tại các đỉnh:
1. Tính toán ánh sáng tại mỗi đỉnh:
Với mỗi đỉnh của đối tượng, bạn cần: 6 lOMoARcPSD| 58854646
Vector pháp tuyến N tại đỉnh (thường được tính bằng cách lấy trung bình
pháp tuyến của các mặt xung quanh đỉnh).
Vector ánh sáng L từ đỉnh đến nguồn sáng.
Vector nhìn V từ đỉnh đến camera.
Áp dụng công thức ánh sáng khuếch tán và phản chiếu tại mỗi đỉnh để tính màu (RGB) tại đỉnh đó.
2. Nội suy màu trên mặt (Shading):
Sau khi tính màu tại các đỉnh, pipeline đồ họa sẽ nội suy màu trên toàn bộ
mặt của đối tượng. Có hai phương pháp chính:
Flat Shading: Sử dụng một màu duy nhất (tính tại một đỉnh hoặc trung bình) cho cả mặt.
Gouraud Shading: Nội suy tuyến tính màu giữa các đỉnh để tạo hiệu ứng mượt mà hơn.
3. Môi trường (Environment):
Ánh sáng: Môi trường bao gồm các nguồn sáng (điểm, hướng, hoặc
spotlight) ảnh hưởng đến ánh sáng khuếch tán và phản chiếu.
Camera: Vị trí camera ảnh hưởng đến vector nhìn V, từ đó ảnh hưởng đến ánh sáng phản chiếu.
Hiệu ứng: Môi trường có thể bao gồm sương mù (fog), bóng (shadow), hoặc
các hiệu ứng khác làm thay đổi cách ánh sáng được áp dụng. Ví dụ thực tế:
Giả sử bạn có một mô hình xe 3D:
Mỗi đỉnh trên lưới của xe sẽ có vector pháp tuyến riêng. 7 lOMoARcPSD| 58854646
Bạn tính ánh sáng khuếch tán và phản chiếu tại mỗi đỉnh dựa trên nguồn sáng và vị trí camera.
Pipeline đồ họa (như OpenGL) sẽ nội suy màu giữa các đỉnh để tạo hiệu ứng
ánh sáng mượt mà trên bề mặt xe.
Nếu môi trường thay đổi (ví dụ: từ ban ngày sang ban đêm), ánh sáng khuếch
tán và phản chiếu tại các đỉnh sẽ thay đổi, dẫn đến sự thay đổi trong cách xe được hiển thị.
4. Các phương pháp nội suy
Nội suy (interpolation) được sử dụng để tính toán màu sắc bên trong một đa
giác dựa trên các giá trị đã biết ở một số điểm (ví dụ tại các đỉnh). Mục đích của các
phương pháp nội suy là tạo ra hiệu ứng tô màu bề mặt liên tục và mượt mà, thay vì
tô màu phẳng mỗi mặt đa giác bằng một màu duy nhất. Nhờ nội suy, ta có thể xấp
xỉ bề mặt cong một cách chân thực hơn trên mô hình lưới đa giác. Hai phương pháp
nội suy kinh điển thường được sử dụng trong kỹ thuật tô bóng bề mặt là nội suy
Gouraud và nội suy Phong. Phương pháp Gouraud tính toán ánh sáng tại các đỉnh
và nội suy màu dọc theo bề mặt đa giác, trong khi phương pháp Phong cải tiến hơn
bằng cách nội suy vectơ pháp tuyến và tính toán ánh sáng tại từng điểm ảnh (pixel)
4.1 Phương pháp nội suy Gouraud để tô màu cho tam giác
Phương pháp Gouraud (hay tô bóng Gouraud) được Henri Gouraud giới thiệu năm 1971
Đây là một trong những kỹ thuật đầu tiên để tạo bóng mịn trên mô hình đa
giác. Thay vì tô một màu đồng nhất cho toàn bộ mặt đa giác (tô màu phẳng), nội
suy Gouraud tính toán cường độ ánh sáng tại các đỉnh của đa giác dựa trên mô hình
chiếu sáng (ví dụ: mô hình Phong với thành phần khuếch tán và phản xạ gương) rồi
nội suy tuyến tính các giá trị màu hoặc độ sáng đó vào bên trong đa giác. Kết quả là
bề mặt được tô màu liên tục, các vùng chuyển tiếp màu sắc dần dần giúp giảm bớt
cảm giác “góc cạnh” giữa các đa giác liền kề. 8 lOMoARcPSD| 58854646
4.1.1) Các bước thực hiện 1.
Tính toán pháp tuyến tại các đỉnh: Xác định vectơ pháp tuyến tại mỗi
đỉnh của đa giác. Thông thường pháp tuyến đỉnh được lấy trung bình từ các
pháp tuyến mặt kề nhau (giúp bề mặt xuất hiện nhẵn hơn), hoặc nếu mô
hình đã có pháp tuyến đỉnh định sẵn thì sử dụng trực tiếp các giá trị đó. 2.
Tính màu tại các đỉnh: Áp dụng mô hình chiếu sáng (ví dụ: tính thành
phần ánh sáng môi trường, khuếch tán và phản xạ tại đỉnh) để xác định màu
hoặc cường độ sáng tại mỗi đỉnh. Mỗi đỉnh sẽ có một màu tính toán dựa
trên hướng pháp tuyến đỉnh, hướng nguồn sáng, hướng quan sát và thuộc tính vật liệu. 3.
Nội suy màu trong đa giác: Trong quá trình rasterization (quét điểm
ảnh để vẽ đa giác), thực hiện nội suy tuyến tính màu giữa các đỉnh. Ví dụ,
với tam giác, màu tại các điểm ảnh bên trong được nội suy theo tọa độ
barycentric hoặc theo từng scanline từ màu của ba đỉnh. Kết quả là mỗi
điểm ảnh bên trong đa giác được gán một giá trị màu nội suy từ các đỉnh. 4.
Hiển thị đa giác: Đặt màu vừa tính cho từng điểm ảnh của đa giác lên màn
hình. Toàn bộ đa giác sẽ có sự chuyển tiếp màu trơn tru từ màu tại các đỉnh,
tạo cảm giác bề mặt được chiếu sáng mềm mại.
4.1.2) Ưu nhược điểm Ưu điểm:
Tính toán nhanh chóng do chỉ cần áp dụng mô hình chiếu sáng tại số
lượng hữu hạn các đỉnh rồi nội suy tuyến tính cho các điểm ảnh còn lại. So
với việc tính ánh sáng tại mọi pixel, phương pháp Gouraud giúp giảm đáng
kể số phép tính, phù hợp với phần cứng đồ họa hạn chế hoặc nhu cầu thời gian thực cao.
Dễ triển khai: kỹ thuật nội suy tuyến tính màu giữa các đỉnh khá đơn
giản. Đây là phương pháp mặc định trong nhiều API đồ họa cổ điển (như
OpenGL ở chế độ GL_SMOOTH) để tạo hiệu ứng tô màu mịn mà không đòi
hỏi lập trình phức tạp. 9 lOMoARcPSD| 58854646 Nhược điểm:
Bỏ lỡ điểm sáng phản xạ (specular highlight): Phương pháp Gouraud
có thể không hiển thị đúng các điểm lóe sáng nhỏ trên bề mặt. Trường hợp tệ
nhất là khi một điểm sáng phản xạ mạnh rơi vào giữa một đa giác lớn – do
điểm sáng này không hiện diện tại các đỉnh, nội suy Gouraud sẽ không thể tái
hiện nó bên trong đa giác
Điều này dẫn đến việc các điểm sáng gương nhỏ có thể bị mất hoặc mờ nhạt hơn thực tế.
Hiệu ứng dải Mach: Nội suy tuyến tính cường độ sáng có thể gây ra
sự gián đoạn trong đạo hàm của phân bố độ sáng giữa các đa giác kề nhau,
làm xuất hiện hiệu ứng quang học Mach band – các dải sáng tối giả tạo dọc
theo ranh giới giữa các đa giác
Mắt người có xu hướng nhấn mạnh ranh giới giữa các vùng sáng tối
chuyển tiếp tuyến tính, khiến ta thấy những vệt sáng hoặc tối hơn mức có thực.
Độ chính xác hạn chế: Với các mô hình có đa giác lớn hoặc độ phản
xạ cao, Gouraud shading cho kết quả kém chính xác hơn so với phương pháp
tính toán chiếu sáng chi tiết hơn. Chất lượng hình ảnh phụ thuộc vào độ phân
chia đa giác: nếu lưới đa giác không đủ mịn, các hiệu ứng ánh sáng tinh tế có
thể không được thể hiện đầy đủ.
Không còn phù hợp cho đồ họa hiện đại: Ngày nay, với sự phát triển
của phần cứng, phương pháp Gouraud ít được sử dụng do đã có các kỹ thuật
tô bóng tiên tiến hơn cho chất lượng cao hơn. 10 lOMoARcPSD| 58854646
Tuy vẫn hữu ích trong một số trường hợp đơn giản yêu cầu tốc độ, nó
chủ yếu mang ý nghĩa lịch sử như bước đệm dẫn tới các kỹ thuật tốt hơn (ví dụ: nội suy Phong).
4.1.3) Ví dụ minh họa
Giả sử ta có một tam giác đại diện cho bề mặt một vật thể, với ba đỉnh A, B, C.
Pháp tuyến tại các đỉnh đã được tính và cho biết đỉnh A hướng gần về nguồn
sáng (nên sáng nhất), đỉnh B hướng hơi chếch (sáng vừa phải) và đỉnh C quay lưng
với nguồn sáng (nên tối nhất). Áp dụng nội suy Gouraud, ta tính được màu tại A, B,
C lần lượt là: A rất sáng, B trung bình, C tối. Khi tô màu tam giác bằng phương
pháp Gouraud, các điểm ảnh phía trong tam giác sẽ chuyển tiếp màu dần dần từ A
tới B tới C. Kết quả thu được là một bề mặt có sắc độ thay đổi mịn màng từ sáng
sang tối. Tuy nhiên, nếu trên bề mặt vật thể có một điểm lóe sáng nằm ở chính giữa
tam giác (do phản xạ gương mạnh tại điểm đó), phương pháp Gouraud sẽ không
hiển thị được điểm sáng này một cách rõ ràng, bởi vì không có đỉnh nào của tam
giác nhận được độ sáng cao bất thường đó. Điểm lóe sáng sẽ bị hòa vào nội suy
chung và có thể không được nhìn thấy, làm giảm tính chân thực của hình ảnh
4.2. Phương pháp nội suy Phong để tô màu cho tam giác
Phương pháp nội suy Phong (hay tô bóng Phong), do Bùi Tường Phong
đề xuất năm 1973, là một kỹ thuật nội suy vectơ pháp tuyến để tô màu bề mặt
vật thể một cách mượt mà và chính xác hơn. Khác với Gouraud nội suy màu,
nội suy Phong nội suy các vectơ pháp tuyến của bề mặt trong lòng mỗi đa giác
và tính màu cho từng điểm ảnh dựa trên pháp tuyến nội suy đó
Nói cách khác, phương pháp này kết hợp nội suy pháp tuyến mịn màng
trên bề mặt với việc áp dụng mô hình phản xạ ánh sáng tại mức điểm ảnh. Kỹ
thuật của Phong được xem là tiên tiến đột phá vào thời điểm giới thiệu, nhưng 11 lOMoARcPSD| 58854646
về sau đã trở thành phương pháp cơ sở trong nhiều ứng dụng kết xuất do hiệu
năng tính toán trên mỗi pixel được cải thiện đáng kể
Hiện nay, nội suy Phong (kết hợp với mô hình phản xạ Phong hoặc các
mô hình tương tự) là phương pháp tiêu chuẩn để tạo hiệu ứng tô bóng mượt cho
hầu hết các hệ thống đồ họa thời gian thực.
4.2.1 Các bước thực hiện 1.
Tính toán pháp tuyến tại các đỉnh: Tương tự Gouraud, trước hết xác
định vectơ pháp tuyến cho mỗi đỉnh của đa giác (thông qua hình học mô hình
hoặc trung bình pháp tuyến các mặt kề nhau). Những pháp tuyến đỉnh này
được dùng làm cơ sở cho nội suy tiếp theo. 2.
Nội suy pháp tuyến trong đa giác: Khi quét raster hóa đa giác, tại mỗi
điểm ảnh (pixel) nằm bên trong đa giác, tính toán vectơ pháp tuyến nội suy
từ các pháp tuyến đỉnh. Quá trình nội suy thường thực hiện tuyến tính theo
tọa độ không gian màn hình (kết hợp với kỹ thuật nội suy perspective-correct
nếu cần để chính xác trong không gian 3D). Vectơ pháp tuyến nội suy tại
mỗi pixel sau đó được chuẩn hóa (normalize) về độ dài 1, vì phép nội suy
tuyến tính có thể làm độ dài vectơ thay đổi. 3.
Tính toán màu tại mỗi điểm ảnh: Áp dụng mô hình chiếu sáng (ví dụ:
mô hình phản xạ Phong với thành phần môi trường, khuếch tán, phản xạ
gương) tại từng điểm ảnh, sử dụng vectơ pháp tuyến vừa nội suy ở bước 2.
Tức là đối với mỗi pixel, ta tính cường độ sáng dựa trên vectơ pháp tuyến đã
có, kết hợp với hướng nguồn sáng, hướng quan sát và thuộc tính vật liệu,
giống như cách tính tại đỉnh nhưng nay thực hiện cho từng điểm ảnh. Kết
quả thu được là màu sắc cuối cùng của pixel đó.
Hiển thị pixel: Gán màu tính được cho điểm ảnh tương ứng trên đa
giác. Quá trình lặp lại cho mọi pixel bên trong đa giác sẽ tô màu toàn bộ đa 12 lOMoARcPSD| 58854646
giác với mức độ chi tiết cao. Vì mỗi pixel đều được tính sáng độc lập, hiệu
quả tổng thể là bề mặt được tô bóng mịn màng, phản ánh chính xác các biến
đổi ánh sáng tinh tế trên bề mặt.
4.2.2 Ưu nhược điểm Ưu điểm:
Chất lượng hình ảnh cao: Nội suy Phong cho kết quả tô màu mượt
hơn và chính xác hơn so với Gouraud. Nhờ tính ánh sáng ở cấp độ điểm ảnh,
phương pháp này tái hiện tốt các điểm sáng nhỏ (highlight) cũng như các
thay đổi ánh sáng phức tạp trên bề mặt. Vấn đề bỏ lỡ điểm lóe sáng ở giữa đa
giác được khắc phục hoàn toàn: bất kỳ vị trí nào trên bề mặt nếu hướng phù
hợp với nguồn sáng và người quan sát sẽ hiện lên điểm sáng phản xạ rõ nét
Hình ảnh thu được vì thế chân thực hơn, đặc biệt trên các vật thể có độ bóng cao.
Giảm thiểu nhiễu thị giác: Do nội suy Phong giả lập bề mặt trơn tru
liên tục (pháp tuyến thay đổi liên tục trên bề mặt) nên hiện tượng dải Mach
giữa các đa giác gần như được loại bỏ. Ở ranh giới giữa các đa giác, nếu các
đỉnh chung có cùng pháp tuyến (trong mô hình bề mặt trơn), thì màu tính ra
tại các pixel dọc theo cạnh chung đó từ hai phía sẽ gần như giống nhau. Nhờ
đó không xuất hiện sự gián đoạn thấy rõ về độ sáng như trường hợp Gouraud.
Tiêu chuẩn hiện đại: Với sự phổ biến của phần cứng tăng tốc đồ họa
(GPU) mạnh mẽ, phương pháp Phong đã trở thành tiêu chuẩn cho tô bóng
trong thời gian thực. Các shader điểm ảnh (pixel/fragment shader) ngày nay
thường hiện thực một dạng nội suy Phong để tính ánh sáng, đảm bảo cân
bằng tốt giữa chất lượng và hiệu năng 13 lOMoARcPSD| 58854646
Khi phần cứng không còn là rào cản lớn, lợi thế về chất lượng của
Phong shading càng được phát huy, làm cho nó phù hợp trong hầu hết các
ứng dụng đồ họa interactive hiện đại. Nhược điểm:
Chi phí tính toán cao hơn: Nhược điểm chính của nội suy Phong là tốn
tài nguyên tính toán hơn Gouraud do phải thực hiện mô hình chiếu sáng cho
từng điểm ảnh thay vì chỉ vài đỉnh. Số phép toán tăng lên đáng kể, đặc biệt
đối với các cảnh độ phân giải cao. Thời gian render có thể chậm hơn nếu
phần cứng không đủ mạnh. (Trong giai đoạn những năm 1970-1980, việc
tính toán ở mức điểm ảnh bị xem là quá chậm cho thời gian thực; mãi sau
này khi GPU phát triển, phương pháp Phong mới được ứng dụng rộng rãi.)
Đòi hỏi triển khai phức tạp hơn: So với Gouraud, việc hiện thực nội
suy Phong phức tạp hơn đôi chút. Lập trình cần tính nội suy vectơ (và phải
chuẩn hóa vectơ pháp tuyến mỗi pixel), cũng như tính ánh sáng nhiều lần.
Điều này yêu cầu cẩn thận để đảm bảo hiệu suất (ví dụ: sử dụng các thuật
toán nội suy và chuẩn hóa hiệu quả). Tuy nhiên, nhược điểm này chủ yếu ảnh
hưởng ở thời kỳ đầu; ngày nay việc triển khai đã được tự động hóa qua các
API và thư viện đồ họa, do đó lập trình viên ít khi phải tự viết lại toàn bộ thuật toán Phong.
Phụ thuộc vào phần cứng: Trong quá khứ, để sử dụng nội suy Phong
trong thời gian thực, đòi hỏi phần cứng đồ họa có khả năng tính toán song
song cao. Trước khi lập trình shader trở nên phổ biến, một số hệ thống phải
đơn giản hóa hoặc sử dụng giải pháp gần đúng để đạt tốc độ. Hiện nay đây
không còn là vấn đề lớn, nhưng với các thiết bị rất hạn chế (ví dụ trên mobile
đời cũ), việc dùng Phong shading có thể bị giảm tốc độ khung hình. 14 lOMoARcPSD| 58854646 Ví dụ minh họa
Xét lại ví dụ tam giác như ở phần Gouraud: với các giá trị pháp tuyến tại A,
B, C và một điểm lóe sáng dự kiến xuất hiện ở giữa tam giác. Nếu áp dụng
nội suy Phong, tại vùng trung tâm tam giác nơi có điểm lóe, vectơ pháp
tuyến nội suy ở điểm đó sẽ hướng gần trùng với hướng tới nguồn sáng và
mắt quan sát, do đó thành phần phản xạ gương khi tính theo mô hình chiếu
sáng sẽ có cường độ cao. Kết quả là điểm lóe sáng được hiển thị rõ ràng trên
bề mặt tam giác, đúng vị trí và độ sáng cần thiết. Toàn bộ tam giác dưới
phương pháp Phong sẽ cho thấy sự biến đổi ánh sáng mượt mà: từ đỉnh A
sáng nhất, màu giảm dần qua vùng giữa (nhưng vẫn nổi bật điểm highlight
nếu có) rồi tới đỉnh C tối nhất. So sánh trực quan, hình ảnh thu được từ nội
suy Phong gần với thực tế hơn so với Gouraud – không những bề mặt trơn
tru mà các hiệu ứng phản xạ nhỏ cũng không bị bỏ sót. Bảng sau tóm tắt sự
khác biệt giữa hai phương pháp nội suy Gouraud và Phong: Tiêu chí Nội suy Gouraud Nội suy Phong
Cơ chế Nội suy màu (độ sáng) giữa các đỉnh Nội suy pháp tuyến bề mặt giữa các
nội suy của đa giác. Màu tại điểm ảnh được đỉnh. Màu tại điểm ảnh được tính
suy ra trực tiếp từ màu các đỉnh.
gián tiếp: pháp tuyến nội suy →
tính mô hình chiếu sáng để ra màu. Vị trí
Tính tại các đỉnh: mô hình chiếu
Tính tại từng điểm ảnh: mô hình
tính ánh sáng áp dụng một lần cho mỗi đỉnh. chiếu sáng áp dụng lặp lại cho mọi sáng pixel trên bề mặt.
Chi phí Thấp: Chỉ tính vài phép chiếu sáng
Cao hơn: Phải tính toán chiếu sáng tính
(theo số đỉnh) rồi nội suy (phép nội rất nhiều lần (mỗi pixel), bao gồm toán
suy tuyến tính gọn nhẹ).
thao tác chuẩn hóa pháp tuyến liên
tục, nên đòi hỏi sức mạnh tính toán lớn hơn. 15 lOMoARcPSD| 58854646 Chất
Mượt mà tương đối: Bề mặt nhìn
Rất mượt và chính xác: Bề mặt trơn lượng
chung trơn tru hơn so với tô phẳng. tru liên tục. Hiển thị đầy đủ các chi
hiển thị Tuy nhiên có thể mất chi tiết (bỏ lỡ tiết ánh sáng nhỏ như highlight.
highlight nhỏ nếu không trúng
Hầu như không bị artefact như dải
đỉnh) và đôi khi xuất hiện dải Mạch Mach, do sự thay đổi độ sáng liên
ở ranh giới đa giác gây sai lệch thị
tục và phù hợp hơn với bề mặt thật. giác. Ứng
Phù hợp khi cần tốc độ, tài nguyên
Phù hợp cho hầu hết các ứng dụng dụng
hạn chế hoặc mô hình bề mặt
đòi hỏi hình ảnh chân thực. Hiện là
không có phản xạ gương mạnh.
phương pháp chuẩn trong các game
Được dùng nhiều trong đồ họa thời 3D, mô phỏng thực tại ảo, v.v. Nhờ
kỳ đầu và trong một số ứng dụng
chất lượng cao (phần cứng hiện đại đơn giản hiện nay.
có thể đáp ứng được việc tính toán).
Tóm lại, nội suy Gouraud và Phong đều nhằm mục đích tạo ra bề mặt được
tô màu liên tục dựa trên lưới đa giác. Gouraud chú trọng vào tốc độ và tính đơn
giản, đủ tốt cho nhiều trường hợp bề mặt mờ (matte) hoặc khi phần cứng hạn chế.
Ngược lại, nội suy Phong hướng đến chất lượng hình ảnh tối ưu bằng cách tính toán
chi tiết tại từng pixel, do đó xử lý tốt hơn các hiệu ứng ánh sáng phức tạp trên bề
mặt. Trong lịch sử phát triển đồ họa, phương pháp Gouraud ra đời trước và mở
đường cho kỹ thuật tô bóng mịn, nhưng chính phương pháp Phong mới khắc phục
được các nhược điểm và đặt nền móng cho các kỹ thuật đổ bóng hiện đại. Sự lựa
chọn giữa hai phương pháp tùy thuộc vào sự đánh đổi giữa chất lượng và hiệu năng:
nếu hệ thống cho phép, nội suy Phong gần như luôn được ưa chuộng hơn nhờ ưu
thế về độ chân thực của hình ảnh
5. Sử dụng hàm gll.ighttfv() để thiết lập đặc tính vật liệu. 16




