BÀI TẬP Lý Thuyết Mạch chương 2: Phân Tích Mạch Xác Lập Điều Hòa | Đại học Điện lực

lOMoARcPSD| 59149108
MỘT SỐ BÀI TẬP PHÂN TÍCH MẠCH Ở CHẾ ĐỘ XÁC LẬP ĐIỀU HÒA Bài 1:
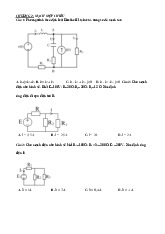
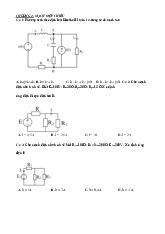
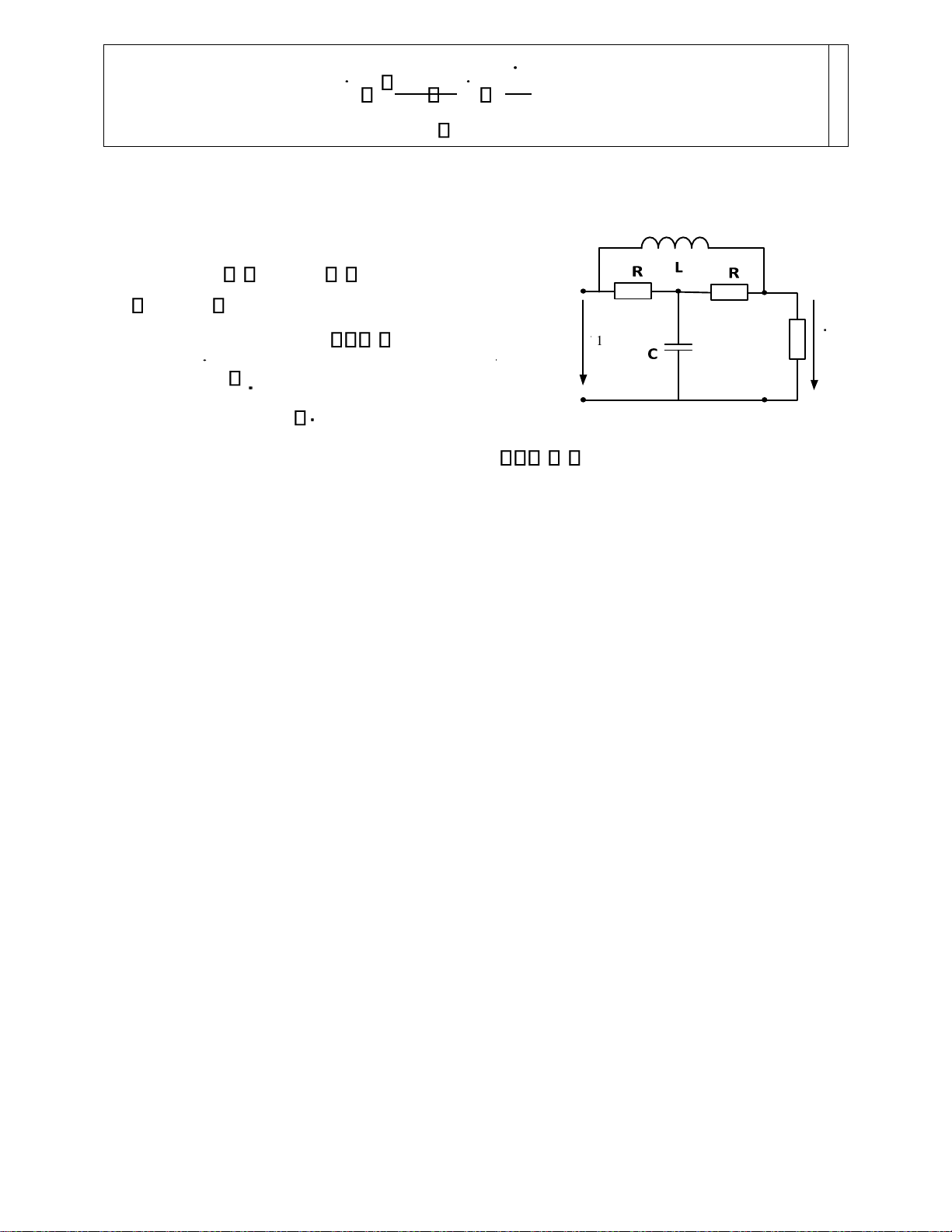
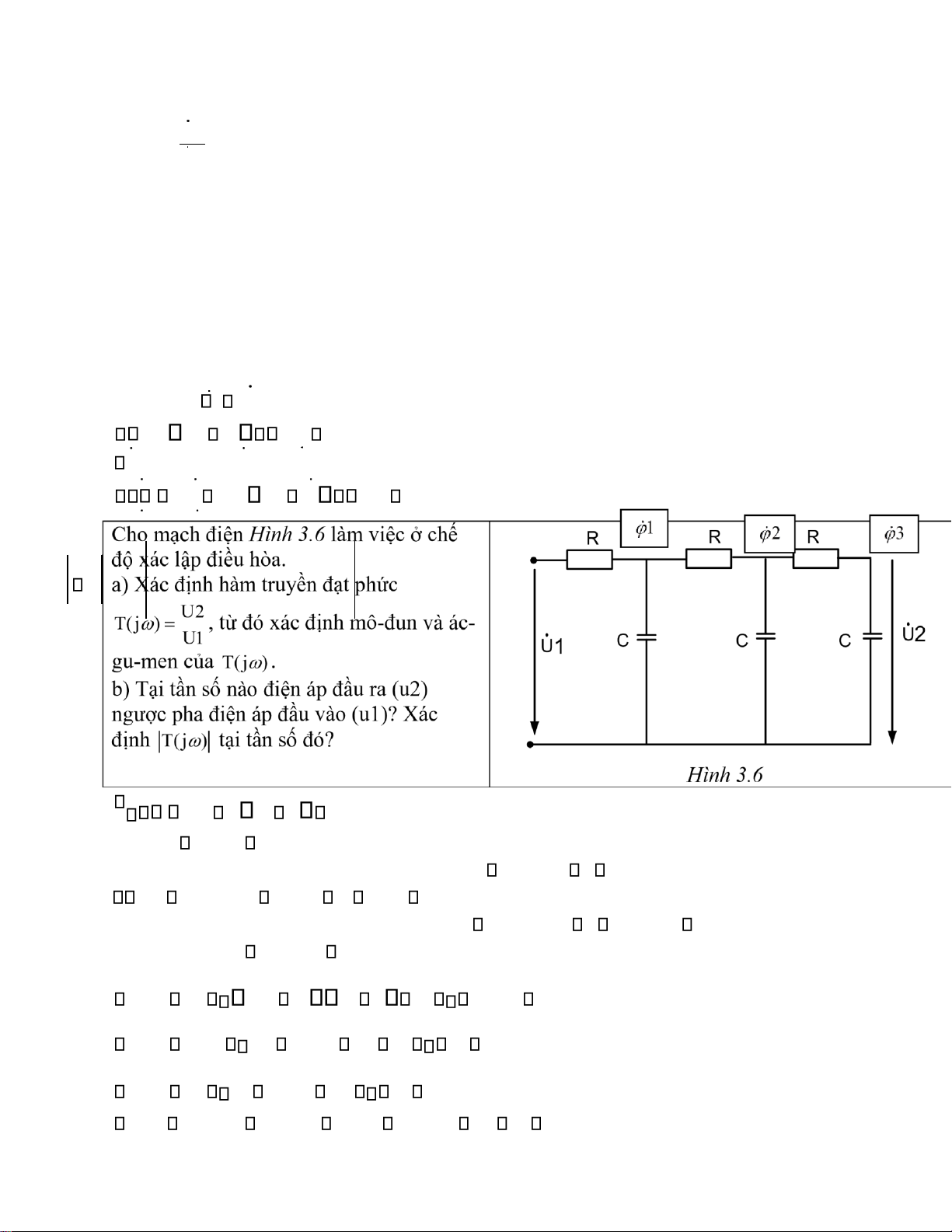
Cho mạch điện Hình 1 làm việc ở chế
độ xác L1 L2 lập điều hòa. Biết: U2 U1 R1 R2 R 100( ); L1 L2 U2 . L 0,1(H). U1 Hình 1
a) Tìm hàm truyền đạt phức T(j )
b) Xác định tần số góc V để điện áp u2
vuông pha với điện áp u1.
c) Cho U1 30ej300(V), tính U2 và UL2 tại tần số góc V .
Đáp án: (Thí sinh có thể sử dụng bất kỳ phương pháp nào) lOMoARcPSD| 59149108
a) Sử dụng phương pháp điện thế điểm nút, qui ước các nút như hình dưới: 1 2 1 2 1 U U2 1 2 0() 0 V Th ự
c hi ệ n l ậ p h ệ phương trình: Y 11 Y12 1 J11 Y 21Y22 2 J22 2 1 2R Y 11 j L; Y12 1 Y ;21 Y22 1 1 R j L j L R j LR j L j L R j LR U J 11 1 ; J22 0. j L lOMoARcPSD| 59149108 2 2 Y Y 11 12 R ( L ) j3LR YY YY 11 22 12 21 2 Y Y ( LR ) 21 22 J Y J Y U(R 11 12 11 12 jL) 1 JY 1 11 22 2 J Y 0 Y ( L)R 22 22 22 Y J Y J U 11 11 11 11 1 JY 2 11 21 2 Y J Y 0 ( L ) 12 22 12 (R jL)R 1 U 1 2 2 1 R ( L) j3LR 2 R 2 2 2 R 2 U 1 ( L) j3LR 2 jLR R U 1 2 U1; U2 2 U1 L2 2 2 2 2 R L j3LR R L j3LR 2 4 U2 R 10 T(j) 2 2 4 2 2 U1 R L j3LR 10 10 j30
b) Để u2 vuông pha với u1, hàm truyền đạt phức cần là số thuần ảo
Từ đây ta có phương trình: R 2 L 20 (1) R 100 Giải (1) ta có: V 10 (3 rad / s) L 0,1 c) Tính U2, U : Khi V 10 (3 rad / s) thì L2 R2 R 100 1 1 j900 T(j ) V j3RL. V j3L. V j3.0,1.103 j3 3e 1
Vậy U2 e j900.30ej300 10e j600 (V) 3 lOMoARcPSD| 59149108 Từ phần a) ta có: U L2 U1 U1 10ej300 (V) j LR j3 RL 3 Bài 2:
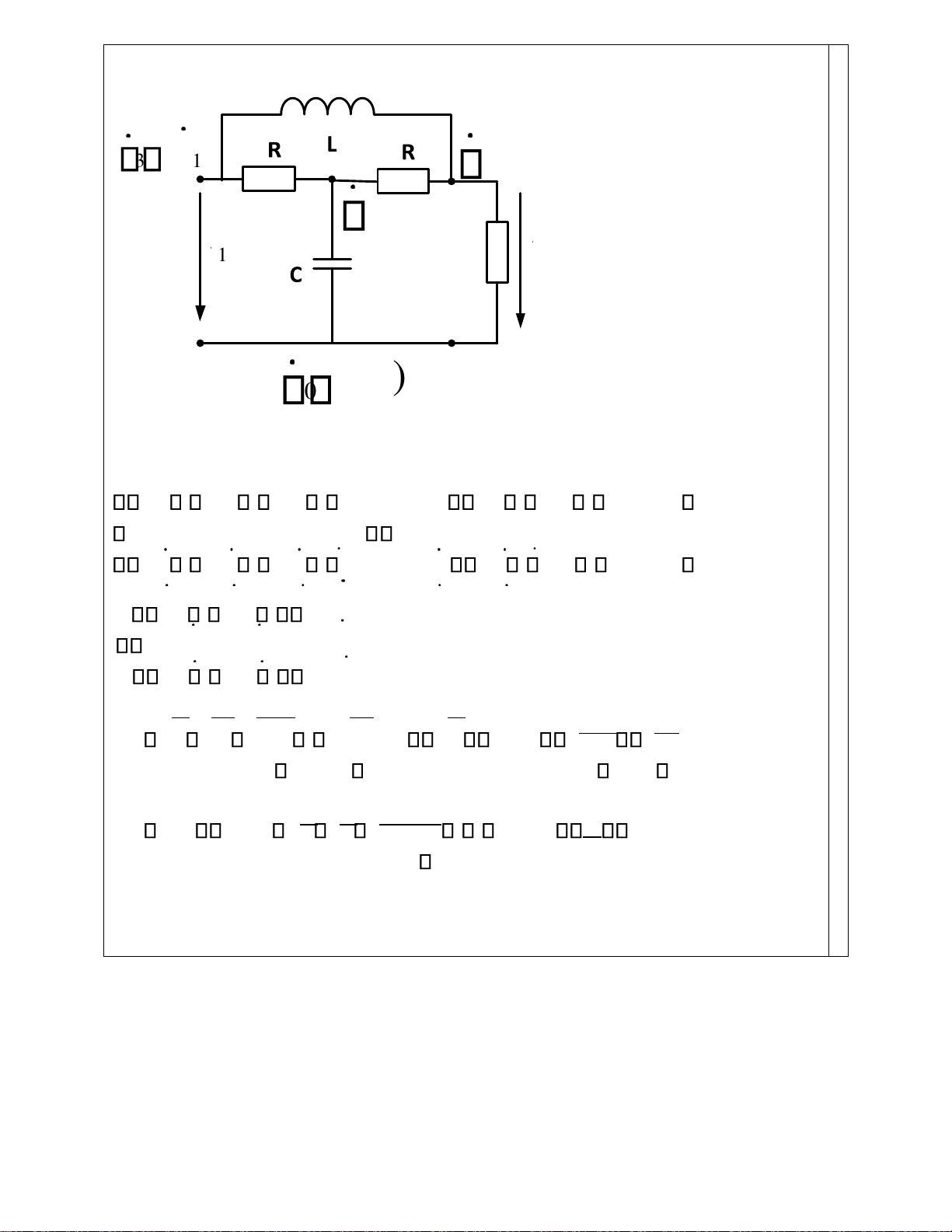
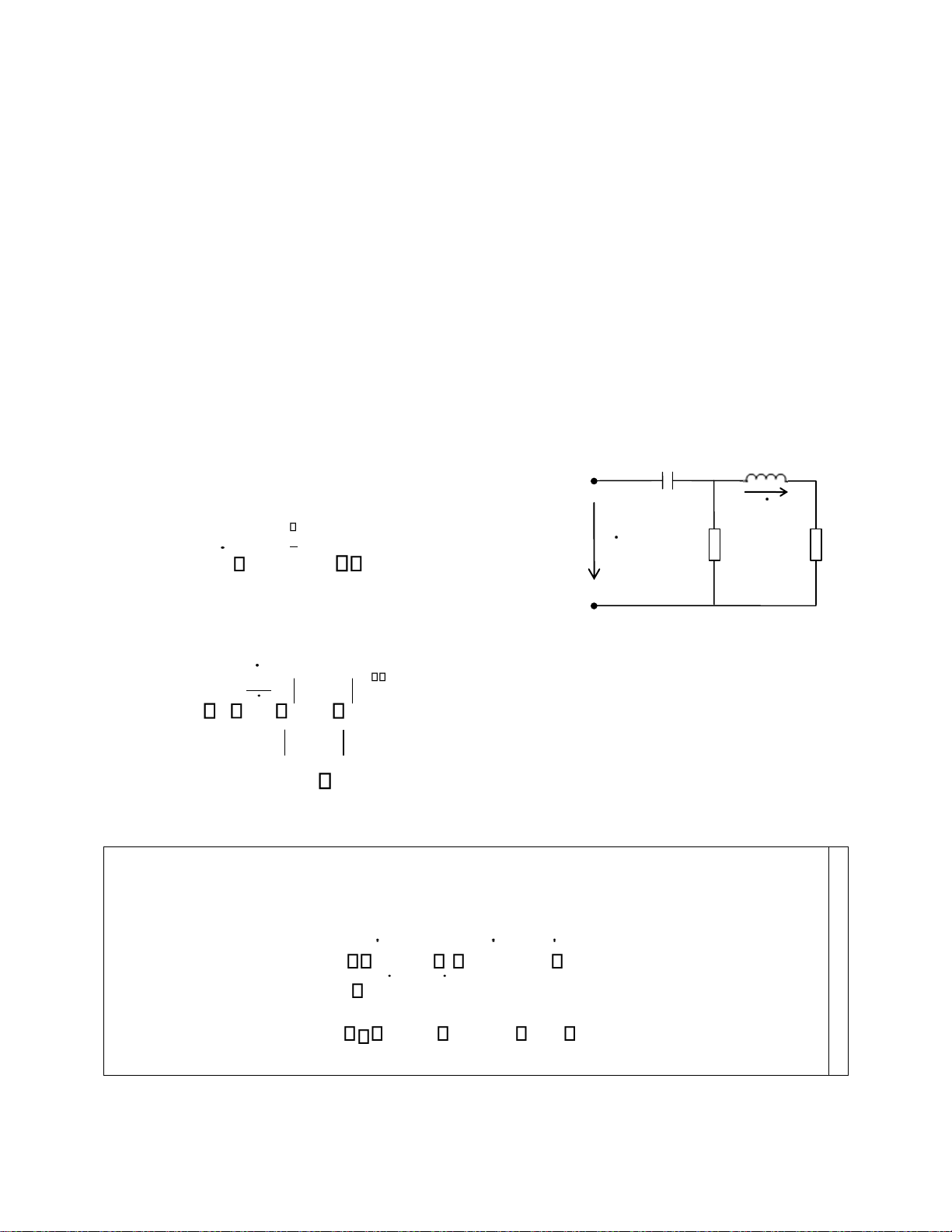
Mạch điện Hình 1 làm việc ở chế độ xác lập điều
hòa. Biết: R 1( ); Rt 1( ); L 1(H);C 1(F) a) Tại tần số góc 1(rad /s) điện áp Rt U2 1 1 U
U2 4(V), hãy xác định điện áp U1.
b) Với U1 và 1 như ở phần a), xác
định điện ápU2 tại tần số góc Hình 1 2 2 1.
Đáp án: (Thí sinh có thể giải với bất kỳ phương pháp nào) lOMoARcPSD| 59149108
Sử dụng phương pháp điện thế điểm nút, ký hiệu như hình vẽ: U 3 1 1 2 1 Rt U U2 0() 0 V Hệ phương trình: Y 11 1Y12 2Y13 3 J11 Y11 1Y12 2 Y U13 1 0 Y 21 1Y22 2Y23 3 J22 Y21 1Y22 2 Y U23 1 0 Y 11 1Y12 2Y U13 1 Y 21 1Y22 2Y U23 1 1 1 1 1 1 1 1 Y 11 2 ;Y12 1;Y13 R Rt j L j R j L j 1 1 1 1 Y 21 Y12 1;Y22 2j ;Y23 1. R R 1/ j C R lOMoARcPSD| 59149108 1 U1 1 2 j 2 j 1 2 2 j U1 j 1 2 11 4 j2 2 1j U1 1 2 j 2 j2 1 j U1 1 U1 j j U1 2 j 1 2 j2 1 j 1 U2 U1 U1 1 1 j 4 j2 j 2 j 2 j1 2 j 1 4 j2 j2 1 1 j 1 U2 1 j 2 j .U2 T(j ) U1 U1 2 j 1 1 j j j2 2 Khi 1 1(rad /s) U1 U2 U2 4 2.ej450(V) 1 j 1 j lOMoARcPSD| 59149108 Khi 2 2(rad/s) 1 U2 j U1 1 j2 U1 1 j2 U1 j 2 j 1 j2 2 j1,5 3 j4 5
.4 2.ej(a tan(2) a tan(4/3) pi/4) 2,5ej161,60 5 lOMoARcPSD| 59149108 Bài 3:
Cho mạch điện Hình 1 làm việc ở chế độ xác R 1 C 1
lập điều hòa, với U1,U2 lần lượt là tác động và
phản ứng của mạch. Biết: R1 1( ); L 1(H);C C1 1(F); 1 U j C L U2 U1 10e (V4 ). a) Cho 1 2(rad /s), tính U2.
b) Xác định tần số góc Hình 1 max để điện áp
U2 đạt cực đại. Tính U2 tại tần số max . LỜI GIẢI:
Thí sinh có thể sử dụng bất kì phương pháp nào. a) Đặt Z1 R1 Zc 1 1j j;Z2 ZL.Zc 1 1 j 2 (1) ZL Zc j 1 j Thay 2(rad/s) ta có: Z1 j 1 j0,5;Z2 j 2 3j2. 2 2 1 Z2 U2 U1 (2) Z1 Z2 j2 2 2 4,3(V). Z2 3 U1 .10 40 3 3 .10 .10 1 j Z1 Z2 1 2 1 j j 7 49 85 Suy ra 1 U2 2 3 6 36 b) Thay (1) vào (2): j 2 U2 (1 2) j(2 2 1) U1 U2 2 .10 (3) 2(1 2 2) (2 21)2 lOMoARcPSD| 59149108 Z2 2 y2 Đặt y 2 0, đặt f(y) Z2 y(1 y)2 (2y 1)2 . Khảo sát f(y) đạt max tại Z1 y 0,6 max 0,77(rad/s).
(Tính gần đúng ) – Nếu học viên tính toán gần đúng cũng đạt điểm tối đa. Thay y 2max 0,6 vào (3) ta có: U2 U2max 16,3(V). Bài 4:
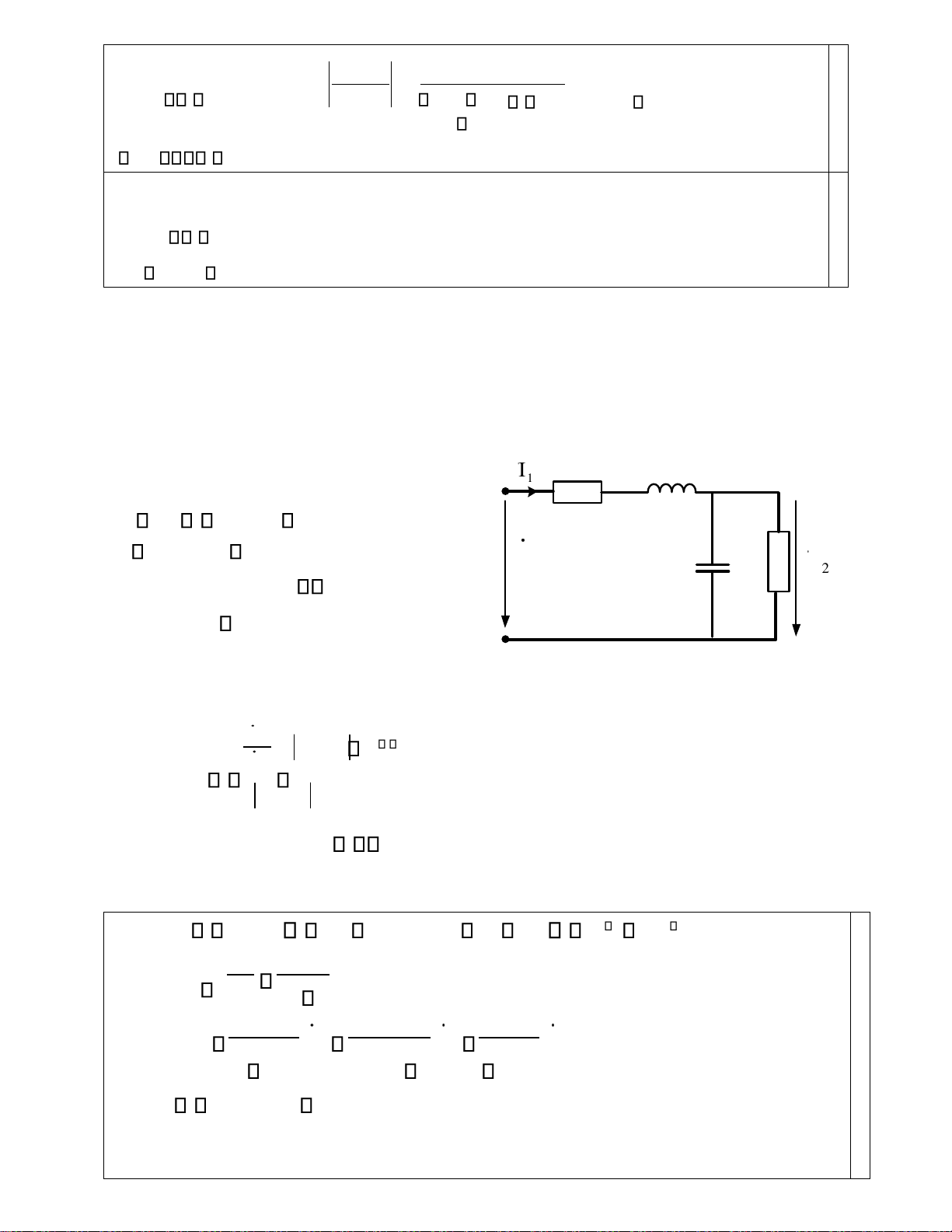
Cho mạch điện Hình 1 làm việc ở chế độ I
xác lập điều hòa. Biết: 1 L R R 1 R2 R 100( ); 1 L 1(mH);C 1(nF) U R 1 2 U 2 C a) Tại tần số góc 10 (6 rad / s) điện áp U 1(V), hãy xác định 2 I ,U11. b) Xác định Hình 1 U2 T(j ) e j ( ). Vẽ T(j ) U1 định tính T(j ) , ( ). ĐÁP ÁN:
a) Z1 R1 j L 100 j1000; 2Y G2 j C 10 2 j10 3 1103 Z2 ; Y 2 10 j Z 2 1 1 U 2 U1 U1 U1 Z1 Z2 Z Y1. 2 1 1 j10
U1 10. 2U 10( ).V lOMoARcPSD| 59149108 U1 U1 U1 (10 j) I1 3 4 Z1 Z 2 10 1000 1 j 00 10 j 1000 1000 100 1 j 000 10 j U1 (10 j) 10.1 U 2 I1 10(). A 4 1000 1 j 0000 10 b) Tính hàm truyền: Z2 1 1 T j( )
Z1 Z2 1 Z Y1. 2 1 ( 1R j L G )(2 j C ) 1 1 2 j .10 )(10 3 2 j .10 ) 9 2 2.10 12 j .10 5 1 (10 1012 12 2) j10 .7 (2.10 1012 1012 T j( ) (2.10 12 2 2) 10 .14 2 4 92.10 .12 2 4.1024 10 .7 10 .7 ( ) arctg 12 2)
arctg ( 2 2.10 )12 (2.10
Khảo sát đa thức mẫu: 4 92.10 .12 2 4.1024
Nhận thấy đa thức này đơn điệu tăng nên T j( ) đơn điệu giảm.
Vẽ đồ thị T(j ) : Khi tăng từ 0 đến , T j( ) giảm từ ½ tới 0. Đồ thị ( ): Đạt tại 2.106 2 2
 Đồ thị giảm từ 0, bằng tại
2.106 , sau đó giảm xuống 2 2 lOMoARcPSD| 59149108 Bài 5:
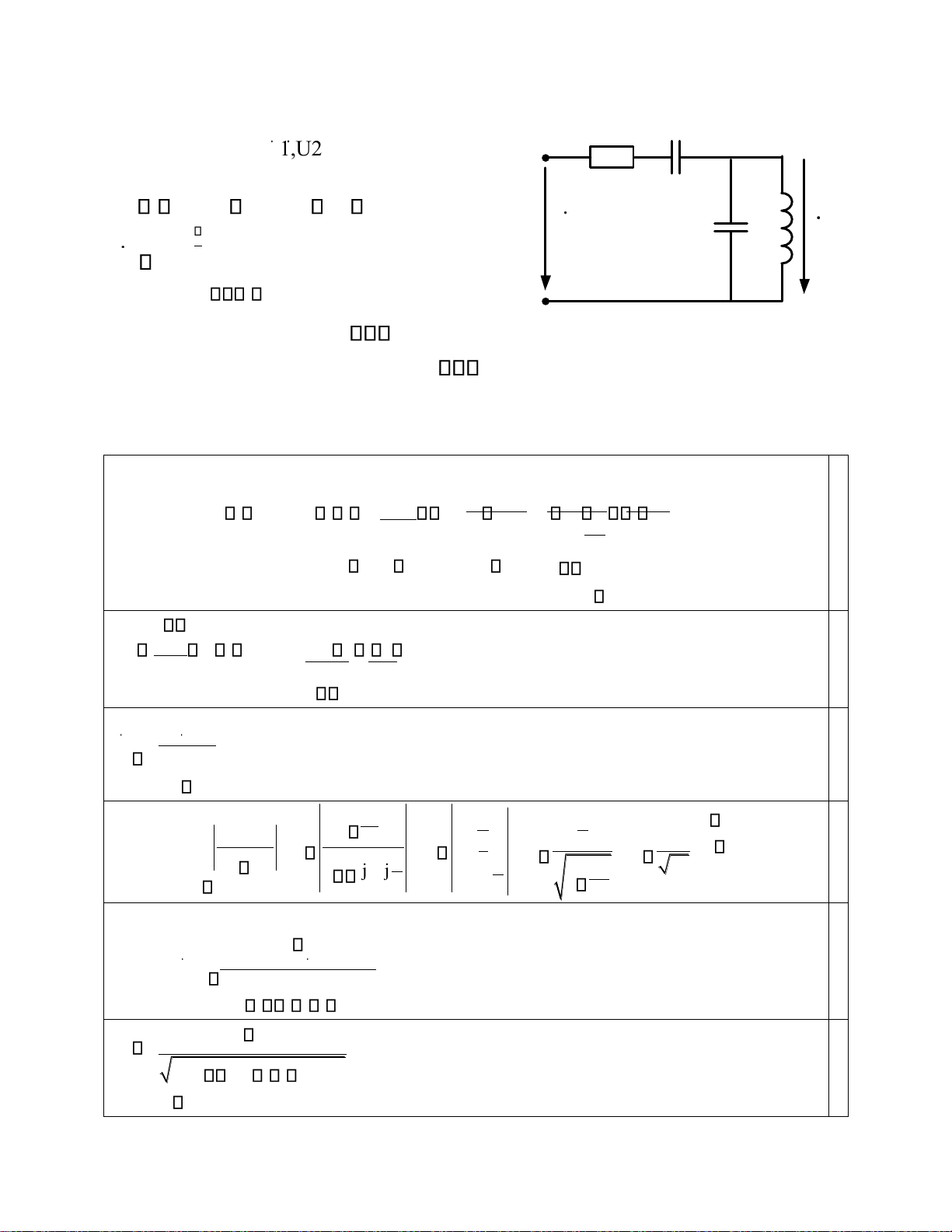
Cho mạch điện vẽ ở Hình 1 làm việc ở chế độ xác C L
lập điều hòa. Biết: R1 = R2 = R = 1(Ω), L = 1(H), C = 0.1(F). U L U a) Cho U 1 R 1 R 2 1 10e j 3 (V), 1(rad / )s ,
Hãy xác định điện áp u t ( ) trên điện cảm L L.
b) Tìm hàm truyền đạt phức UL j ( ) Hình 1 T j( ) T j( ) e . U1
c) Vẽ định tính T j( ) . Đáp án câu 1:
Thí sinh có thể sử dụng bất kỳ phương pháp nào
a) Sử dụng phương pháp dòng vòng, qui ước 2 vòng thuận chiều kim đồng hồ ta có hệ: I Z v1( C R) I R Uv2 1 (1) I R I v1 v2(2R Z L) 0 lOMoARcPSD| 59149108
Giải hệ: (nếu học viên thay số trước cũng chấm theo thang điểm này) 2 Z R R j Z R C 20 11 U C 1 ; RU 2 1 R Z 2 R j R L 0 jRU jU 2 1 1 I v2 2 2 20 11 j 20 11 j U Suy ra: U 2 1 L Iv2.ZL 2 (1) 20 j11
Thay giá trị của tần số và điện áp vào ta xác định được: j /3 e U 10 L Iv2.ZL 10
2 2 ej 4 /3 ar 11/ ctg 19
0,46ej 4 /3 ar 11/ ctg 19 19 j11 19 11
u tL( ) 0,46 2cos(t 4 / 3 arctg11/19)( )V b) Tính hàm truyền: Từ (1) rút ra: 2 T j( ) 2 j11 20 211 T j( ) ; ( ) arctg 2 20 2 2 121 2 20 lOMoARcPSD| 59149108 c) Khi 0:T j( ) 0; : T j( ) 1. 4 2 2 T j( ) 20 2 121 2 Đặt x
2, f x( ) T j( ) 2 ta có: x2 x2 f x( ) 2 2 81x 400 20 x 121x x
f ( )x 2 81x 800)400 0 x(81x x
Kết luận: f(x) và do đó T j( ) đơn điệu tăng từ 0 đến 1. Vẽ đồ thị. Bài 6: lOMoARcPSD| 59149108 Đáp án:
a) Qui ước các nút như hình vẽ, lưu ý nút thứ 3 chia đôi nhánh bên phải, như thế 3 U2 1 2. G Yc 2.G U G1. 1.G 2 2. G Yc 3.G 0 G 2.G 3 Yc G 0 2.G Yc G 0 2.G Yc G G 0 G 2.G Yc G (2.G Yc) G Yc G G Yc G 0 G Yc G (2.G Yc) 2.G Yc Yc G G2 G Yc2( G) (2.G Yc) 2.
G2 3YcG. Yc2 G2 G3 G2.Yc (2.G Yc)
G2 3YcG. Yc2 G3 G Yc2.
2.G3 6.G Yc2. 2 .GYc2 YcG. 2 3. .GYc2 Yc3 G3 G Yc2. lOMoARcPSD| 59149108
G3 6G Yc2. 5 .GYc2 Yc3 2. G Yc G 1. UG 3 3 3 G 2. G Yc 0 1. UG ;3 0 G 0 3 3 G ( Tj ) 3 2 2 3 U1 G 6 . GY c 5. GYc Yc Biến đổi tiếp: G3 G3 T j( )
G3 6G Yc2. 5 .GYc2 Yc3 G3 6 (j C G). 2 5. (G C)2 j( C)3 G3
G3 5. (G C)2 j ( C)3 6( C G). 2 G3 T j( ) G3 5. (G C)2 2
( C)3 6( C G). 2 2
( C)3 6( C G). 2
( ) arctg G3 5. (G C)2
b) Để điện áp ra ngược pha điện áp vào thì ( ) , vậy ta có:
( C)3 6( C G). 2 arctg G 3 5. (G C)2
6( C G). 2 ( C)3 0
( C)2 6G2 2 6 R C2 2 6 (rad s/ ) RC Tại
6 ( rad s/ ) , thay vào biểu thức của T j( ) ta nhận được RC T j( ) 1/29 lOMoARcPSD| 59149108 Bài 7:
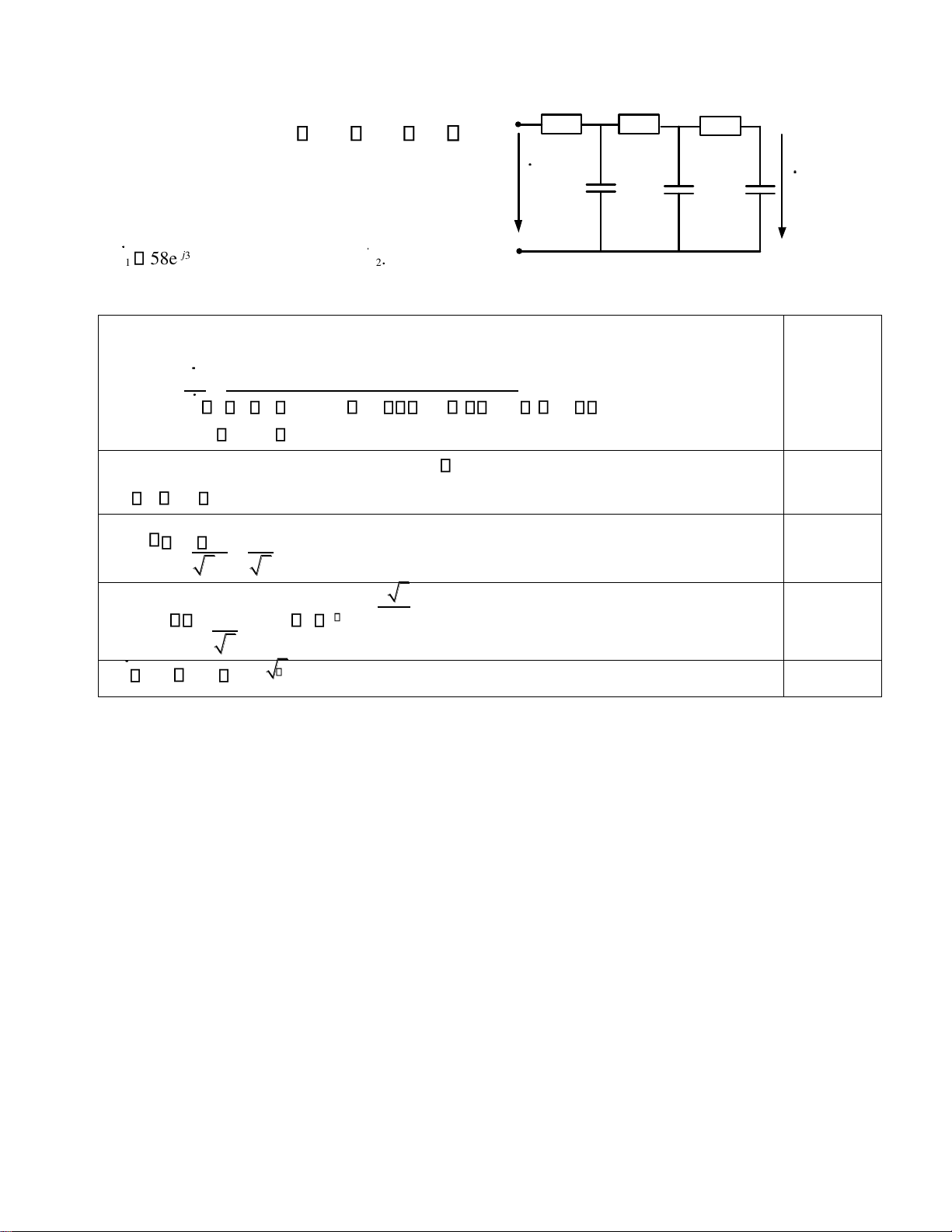
Mạch điện Hình 1 làm việc ở chế độ xác R R R
lập điều hòa. Biết: R 100( ); C 10( F).
a) Xác định tần số góc của nguồn tác động U để điện áp 1 U u vuông pha với 2 2 u1. C C C
b) Với tần số góc tìm được ở phần a), cho U 1
58e j300 ( )V , hãy xác định U2. Hình 1 ĐÁP ÁN:
a) Thí sinh có thể sử dụng bất kì phương pháp nào để nhận được: U2 G3 (1) T j( ) 1 2 5( C)2 j C 6G2 ( C)2 U G G
Để điện áp u vuông pha với 2
u1 thì T j( ) cần là số thuần ảo, dẫn tới: G2 5( C)2 0 Hay
G 103 (rad / )s 5C 5 103 5 5 b) Với
(rad / )s T j( ) e j900 ??? 5 29
U2 T j( ).U1 10. 5e j600 ( )V ???