Bài Tập Lý Thuyết Xác Suất | Môn Xác suất thống kê - Đại học Sư phạm Hà Nội 2

lOMoAR cPSD| 58950985
BÀI TẬP LÍ THUYẾT XÁC SUẤT
Chương I. Không gian xác suất
1. Không gian mẫu và biến cố
Bài 1. Cho ba biến cố A,B và C. Hãy biểu diễn các biến cố sau theo A,B và C:
a. Chỉ có A xảy ra.
b. A,B xảy ra nhưng C không xảy ra.
c. Có ít nhất 1 biến cố xảy ra.
d. Có ít nhất 2 biến cố xảy ra.
e. Tất cả đều xảy ra.
f. Không có biến cố nào xảy ra.
g. Có đúng hai biến cố xảy ra.
Bài 2. Một đồng xu được tung ba lần.
a. Xây dựng không gian mẫu khi ta muốn quan sát tình trạng sấp ngửa của các lần tung.
b. Xây dựng không gian mẫu khi ta xem xét số lần ra mặt ngửa.
Bài 3. Một xúc xắc được gieo liên tục cho tới khi xuất hiện mặt "lục" thì dừng lại.
a. Xây dựng không gian mẫu khi ta muốn quan sát các mặt xuất hiện ở mỗi lần gieo.
b. Xây dựng không gian mẫu khi ta xem xét số lần tung cho tới khi dừng lại.
Bài 4. Hai con xúc xắc được gieo đồng thời.
a. Xây dựng không gian mẫu về cặp mặt xuất hiện trong 2 tình huống: có thứ tự (xác định rõmặt xuất
hiện là của viên xúc xắc nào) và không thứ tự (không quan tâm mặt xuất hiện của viên xúc xắc nào).
b. Trong trường hợp có thứ tự, xác định các biến cố sau:
A: Các chấm xuất hiện đều là số chẵn.
B: Tổng số chấm trên hai mặt bằng 5.
C: Tổng số chấm trên hai mặt lớn hơn 10.
D: Xuất hiện mặt có 1 chấm.
E: Xuất hiện đúng 1 mặt có 1 chấm.
Bài 5. Ba bạn A,B và C lần lượt tung một đồng xu cho đến lúc có người thắng cuộc khi tung được mặt ngửa.
a. Xây dựng không gian mẫu về tình trạng sấp ngửa của đồng xu trong quá trình chơi.
b. Xác định các biến cố sau: lOMoAR cPSD| 58950985 i. A thắng. ii. B thắng. iii. A ∪ B.
Bài 6. Cho không gian mẫu có n biến cố sơ cấp. Hỏi có tất cả bao nhiêu biến cố có thể xảy ra?
Bài 7. (Mô hình cây nhị phân trong Toán tài chính) Giả sử tại thời điểm ngày hôm nay, một cổ phiếu có
giá là 100.000 đồng. Biết rằng từ ngày hôm trước sang ngày hôm sau thì giá cổ phiếu biến động theo hai
khả năng có xác suất như nhau là tăng hoặc giảm 5%.
a. Xây dựng không gian mẫu cho quá trình biến động giá cổ phiếu trong 3 ngày kể từ ngày hômnay.
b. Xây dựng không gian mẫu cho giá của cổ phiếu tại ngày thứ 3 kể từ hôm nay.
2. Định nghĩa xác suất cổ điển
Bài 8. (Trò chơi truyền hình) Một phần thưởng được giấu trong 3 ô cửa và theo luật của trò chơi thì bạn
chỉ được phép mở ra đúng 1 ô cửa. Sau khi bạn đã chọn một ô cửa, người dẫn chương trình sẽ cho mở ra
1 trong hai ô cửa còn lại, và ô cửa này không chứa phần thưởng. Sau đó, bạn có quyền giữ nguyên ô cửa
đã chọn hoặc đổi sang ô cửa còn lại. Bạn có đổi hay không? Vì sao?
Bài 9. Ta tung đồng thời một số viên xúc xắc và xét tổng số các chấm trên các mặt xuất hiện. Hãy giải
thích tại sao nếu tung 2 viên xúc xắc thì ta thường gặp tổng 9 hơn tổng 10, nhưng nếu tung 3 viên thì tổng
10 lại xuất hiện nhiều hơn?
Bài 10. Một khách sạn có 6 phòng đơn. Có 10 khách đến muốn thuê phòng trong đó có 6 nam và 4 nữ.
Người quản lí chọn ngẫu nhiên ra 6 người. Tính xác suất để: a. Cả 6 người là nam. b. Có 4 nam và 2 nữ. c. Có ít nhất 2 nữ.
Bài 11. Có 30 tấm thẻ đánh số từ 1 tới 30. Chọn ngẫu nhiên 10 tấm. Tính xác suất để:
a. Cả 10 tấm thẻ đều là số chẵn.
b. Có đúng 5 tấm thẻ mang số chia hết cho 3.
c. Có 5 tấm thẻ mang số lẻ, 5 tấm mang số chẵn trong đó có 2 tấm mang số chia hết cho 10.
Bài 12. Một lớp học có 50 bạn trong đó có 30 bạn thích học Toán và 40 bạn thích học Văn và 10 bạn
thích học cả Toán và Văn. Chọn ra ngẫu nhiên trong lớp 1 học sinh. Tính xác suất để học sinh này không thích cả Toán và Văn.
Bài 13. Trong hộp có m bóng đỏ và n bóng xanh. Ta lần lượt lấy ra ngẫu nhiên không hoàn lại mỗi lần một quả bóng.
a. Tính xác suất để lần đầu lấy được bóng đỏ.
b.* Tính xác suất để lần cuối lấy được bóng đỏ.
3. Định nghĩa tiên đề và các tính chất cơ bản
Bài 14. Cho dãy biến cố An. Đặt lOMoAR cPSD| 58950985 . Chứng minh rằng:
a. liminf An ⊂ limsupAn.
b. Nếu An là dãy giảm (An ⊃ An+1) thì .
c. Nếu An là dãy tăng (An ⊂ An+1) thì .
d. P(liminf An) ≤ liminf P(An) ≤ limsupP(An) ≤ P(limsupAn).
Bài 15. Xét hai biến cố A và B. Chứng minh rằng: P(A ∪ B)P(AB) ≤ P(A)P(B). Bài 16. Tìm cực trị của:
a. P(AB) − P(A)P(B).
b. P2(AB) − P(A)P(B).
c. P2(AB) + P2(AB) + P2(AB).
d. P2(AB) + P2(AB) + P2(AB) + P2(AB).
Bài 17. Cho P và Q là hai độ đo xác suất trên cùng một không gian (Ω,F).
a. Giả sử P(A) = Q(A) với mọi A ∈ F sao cho
. CMR: P(A) = Q(A), ∀A ∈ F.
b. Chỉ ra ví dụ cho thấy P(A) = Q(A) với mọi A ∈ F sao cho nhưng P 6= Q trên F.
Bài 18. (Nguyên lí bù trừ) Cho họ n biến cố A1,A2,. .,An. Chứng minh rằng:
a. P(A1 ∪ A2) = P(A1) + P(A2) − P(A1 ∩ A2). b. Theo quy nạp, .
Bài 19. Một người bỏ ngẫu nhiên n lá thư vào n phong bì đã ghi sẵn địa chỉ.
a. Gọi Ai là biến cố lá thư thứ i được cho vào đúng phong bì. Tính xác suất của Ai.
b. Hãy nêu ý nghĩa của biến cố A1 ∪ A2 ∪ ... ∪ An. lOMoAR cPSD| 58950985
c. Tính xác suất của biến cố ở câu b.
Bài 20. Một đoàn tàu có k toa đỗ ở sân ga. Có m hành khách bước lên tàu. Mỗi hành khách độc lập với
nhau bước lên ngẫu nhiên một toa.
a. Gọi Ai là biến cố toa thứ i không có hành khách nào bước lên. Tính xác suất của Ai.
b. Hãy nêu ý nghĩa của biến cố A = A1 ∪ A2 ∪ ... ∪ Ak.
c. Tính xác suất của biến cố A.
d. Hãy nêu ý nghĩa và tính xác suất của biến cố A.
e. * Xét r toa trong số k toa. Tính xác suất sao cho chỉ có đúng r toa này có hành khách bước lên.
f. * Tính xác suất để có đúng r toa có hành khách bước lên.
Bài 21. Chọn ngẫu nhiên 1 vé số có 5 chữ số. Tính xác suất để trong số vé: a. Có chữ số chẵn. b. Có chữ số 5.
c. Có chữ số chẵn hoặc chữ số 5.
d. Có cả chữ số chẵn và chữ số 5. 4. Xác suất độc lập
Bài 22. CMR: nếu hai biến cố A và B độc lập với nhau thì ta cũng có các cặp biến cố độc lập:
(A,B), (A,B) và (A,B).
Bài 23. Phải gieo liên tiếp ít nhất bao nhiêu lần để với xác suất không nhỏ hơn 95% có ít nhất một lần ra mặt "lục".
Bài 24. Trong một cuộc xổ số, người ta phát hành 10 vạn vé trong đó có 1 vạn vé trúng giải. Cần phải
mua ít nhất bao nhiêu vé để với xác suất không nhỏ hơn 95% ta sẽ trúng ít nhất được 1 vé?
Bài 25. Giả sử giới tính của trẻ ở mỗi lần sinh là độc lập với nhau. Tính xác suất để một cặp vợ chồng
đẻ 5 con trong đó có ít nhất 1 nam.
Bài 26. Hai người chơi A và B cùng chơi một trò chơi công bằng và người thắng cuộc là người đầu tiên
thắng được 6 ván. Tuy nhiên, vì một lí do nào đó, ở thời điểm mà người A thắng được 5
ván và người B thắng được 3 ván thì cuộc chơi bắt buộc phải dừng lại.
a. Tính xác suất thắng cuộc của từng người nếu như cuộc chơi vần được tiếp tục.
b. Từ đó hãy đề xuất cách chia tiền thưởng cho hai người chơi.
c. * Mở rộng bài toán khi người thắng cuộc là người đầu tiên thắng được m ván và cuộc chơi buộc
phải dừng lại khi người A đã thắng được n ván và người B đã thắng được k ván.
Bài 27. Một người tung liên tiếp một đồng xu cho đến khi thấy mặt ngửa thì dừng lại. Tính xác suất để:
a. Số lần tung là chẵn. lOMoAR cPSD| 58950985 b. Số lần tung là lẻ.
c. Số lần tung lớn hơn 5.
Bài 28. Ta thực hiện liên tiếp các phép thử độc lập, biết rằng xác suất thành công của phép thử thứ i là
ai. Gọi Ai là biến cố phép thử thứ i thành công.
a. Nêu ý nghĩa của biến cố A = A1 ∪ A2 ∪ ... ∪ An ∪ ....
b. CMR: A = A1 ∪ (A1 ∩ A2) ∪ (A1 ∩ A2 ∩ A3) ∪ ....
c. Tính xác suất P(A).
d. Tính xác suất P(A).
e. Từ câu c. và d. ta có thể kết luận gì.
Bài 29. Cho n đồng xu độc lập với nhau và xác suất ra mặt sấp của đồng xu thứ i là xi. Mỗi lần ta tung
đồng thời cả n đồng xu và ta thực hiện tất cả m lần tung độc lập với nhau.
a. Tính xác suất để ra ít nhất 1 mặt ngửa khi thực hiện 1 lần tung.
b. Gọi A là biến cố trong cả m lần tung thì mỗi lần đều có ít nhất 1 mặt ngửa. Tính xác suất P(A).
c. Gọi B là biến cố tồn tại một đồng xu ra mặt ngửa trong tất cả m lần tung. Nêu ý nghĩa và
tính xác suất của biến cố B.
d. CMR: P(A) + P(B) ≥ 1 và rút ra kết luận.
Bài 30.* Cho một đồ thị có n đỉnh, các cạnh được tô màu ngẫu nhiên xanh hoặc đỏ với xác suất bằng
nhau và độc lập với nhau.
a. Tính xác suất để tất cả các cạnh đều màu đỏ.
b. Cố định k đỉnh, tính xác suất để các cạnh nối 2 đỉnh trong k đỉnh này đều màu đỏ.
c. Đưa ra chặn trên cho xác suất của biến cố: tồn tại đồ thị đầy đủ con gồm k đỉnh trong n đỉnh mà các cạnh tô màu đỏ.
d. CMR: khi k ≥ 3 và n ≤ 2k/2 thì xác suất của biến cố tồn tại đồ thị đầy đủ con gồm k đỉnh trong n đỉnh
mà các cạnh tô cùng màu nhỏ hơn 1.
e. Từ câu d. ta có thể rút ra kết luận gì?
5. Xác suất điều kiện, công thức Bayes và xác suất toàn phần
Bài 31. Gieo liên tiếp một con xúc xắc.
a. Tính xác suất để lần gieo thứ k là lần đầu tiên ra mặt "bốn".
b. Tính xác suất để trong k − 1 lần gieo trước, không có lần nào ra mặt "ba". lOMoAR cPSD| 58950985
c. Tính xác suất để ra mặt "bốn" trước mặt "ba".
Bài 32. Một nhà có n người con. Tính xác suất cả n người con đều là con trai biết rằng gia đình đó có ít nhất 1 con trai.
Bài 33. Một cuộc thi có 3 vòng. Vòng 1 lấy 90% thí sinh. Vòng 2 lấy 80% thí sinh của vòng 1 và vòng 3
lấy 60% thí sinh của vòng 2.
a. Lấy ra ngẫu nhiên một thí sinh, tính xác suất thí sinh đó đỗ cả 3 vòng.
b. Tính xác suất bị loại của mỗi thí sinh.
c. Tính xác suất bị loại của thí sinh ở từng vòng.
d. Tính xác suất thí sinh bị loại ở vòng 2 biết rằng thí sinh đó bị loại.
e. Tính xác suất để thí sinh đỗ cuộc thi biết rằng thí sinh đó vượt qua vòng 1.
Bài 34. Một công ty một ngày sản xuất được 850 sản phẩm trong đó có 50 sản phẩm không đạt chất
lượng. Lần lượt lấy ra ngẫu nhiên không hoàn lại 2 sản phẩm để kiểm tra.
a. Tính xác suất để sản phẩm thứ hai không đạt chất lượng biết rằng sản phẩm thứ nhất khôngđạt chất lượng.
b. Tính xác suất để sản phẩm thứ hai không đạt chất lượng.
b. Tính xác suất để trong hai sản phẩm có ít nhất 1 sản phẩm không đạt chất lượng.
Bài 35. Trong 10 lá thăm có 1 lá trúng thưởng. 3 người lần lượt rút thăm xem ai trúng. Gọi Ai,i =
1,2,...,10 lần lượt là biến cố lá thăm trúng thưởng rút được ở lần rút thứ i.
a. Biểu diễn biến cố thắng lợi của từng người qua các biến cố Ai.
b. Tính xác suất trúng thăm của từng người.
c. Giả sử bạn là người tham gia rút thăm, bạn chọn vị trí rút thứ mấy? Tại sao?
Bài 36. Biết rằng tỉ lệ nhóm máu O,A,B và AB trong cộng đồng lần lượt là 33,7%;37,5%;20,9% và 7,9%.
Chọn ngẫu nhiên 1 người cần máu và 1 người cho máu. Tính xác suất để có thể thực hiện truyền máu.
Bài 37. Một nhà máy có hai xưởng sản xuất: xưởng I chiếm 65% tổng sản phẩm, xưởng II chiếm 35%.
Biế rằng tỉ lệ sản phẩm đạt chất lượng tốt của xưởng I là 90% và xưởng II là 85%.
a. Lấy ra ngẫu nhiên một sản phẩm của nhà máy. Tính xác suất để đó là sản phẩm chất lượngtốt.
b. Xét 1 sản phẩm không đạt chất lượng. Tính xác suất đó là sản phẩm do xưởng II sản xuất.
Bài 38. Một người chơi mong muốn có n dollars nhưng hiện tại anh ta chỉ có trong túi k dollars (k < n).
Vì thế anh ta tham gia cá cược may rủi bằng cách mỗi lần anh ta cá 1 dollar cho việc tung đồng xu ra mặt
ngửa; nếu cá thua anh ta sẽ mất tiền cá cược, còn nếu thắng thì kiếm thêm được 1 dollar. Trò chơi dừng
lại khi anh ta hết sạch tiền hoặc kiếm đủ n dollars như mong muốn. Ta sẽ tính xác suất phá sản của người
chơi. Xét pi là xác suất phá sản của người chơi khi anh ta bắt đầu với i dollars.
a. Xác định p0 và pn.
b. Giả sử đồng xu có xác suất xuất hiện mặt ngửa là p. Hãy tìm công thức liên hệ giữa pk,pk−1 và pk+1. lOMoAR cPSD| 58950985
c. Giả sử p = 1/2. Tính pk.
Chương II. Biến ngẫu nhiên
Bài 1. Cho biến ngẫu nhiên X có bảng phân phối xác suất: X 0 1 2 3 4 P 0,1 0,2 0,3 0,25 0,15
a. Tính hàm phân phối, kì vọng và phương sai của X.
b. Tính kì vọng của Y = X2 + 3.
c. Tính hàm phân phối, kì vọng và phương sai của Z = X3 − 4X2 + 10.
Bài 2. Tung liên tiếp một đồng xu cân đối cho đến khi thấy mặt ngửa thì dừng lại. Lập bảng phân phối,
tính kì vọng và phương sai của số lần tung.
Bài 3. Gieo liên tiếp một con xúc xắc cân đối cho đến khi thấy mặt "lục" thì dừng lại. Lập bảng phân
phối, tính kì vọng và phương sai của số lần gieo.
Bài 4. Một người có một chùm chìa khóa 7 chiếc giống nhau trong đó chỉ có 2 chiếc mở được cửa.
Người đó thử ngẫu nhiên từng chiếc (thử xong thì bỏ ra ngoài) cho đến khi mở được cửa. Gọi X là số lần
thử cần thiết. Lập bảng phân phối, tính kì vọng và phương sai của X.
Bài 5. Trong mô hình cây nhị thức ở bài 7 chương I, ta gọi X là giá của cổ phiếu 3 ngày sau.
a. Lập bảng phân phối, tính kì vọng và phương sai của X.
b. Một người chơi quyền chọn mua (call option) như sau: anh ta lấy một mức giá tiêu chuẩnlà 105.000
đồng; nếu giá của cổ phiếu 3 ngày sau lớn hơn giá tiêu chuẩn thì anh ta sẽ được hưởng mức chênh
lệch giữa hai loại giá, ngược lại nếu giá cổ phiếu thấp hơn hoặc bằng giá tiêu chuẩn thì anh ta không
được gì. Gọi Y là số tiền người chơi nhận được khi chơi quyền chọn này. Hãy biểu diễn Y theo X. Lập
bảng phân phối, tính kì vọng và xác suất của Y .
Bài 6. Cho một biến ngẫu nhiên nhận giá trị nguyên không âm X.
a. Viết công thức tính kì vọng của X. b. CMR: .
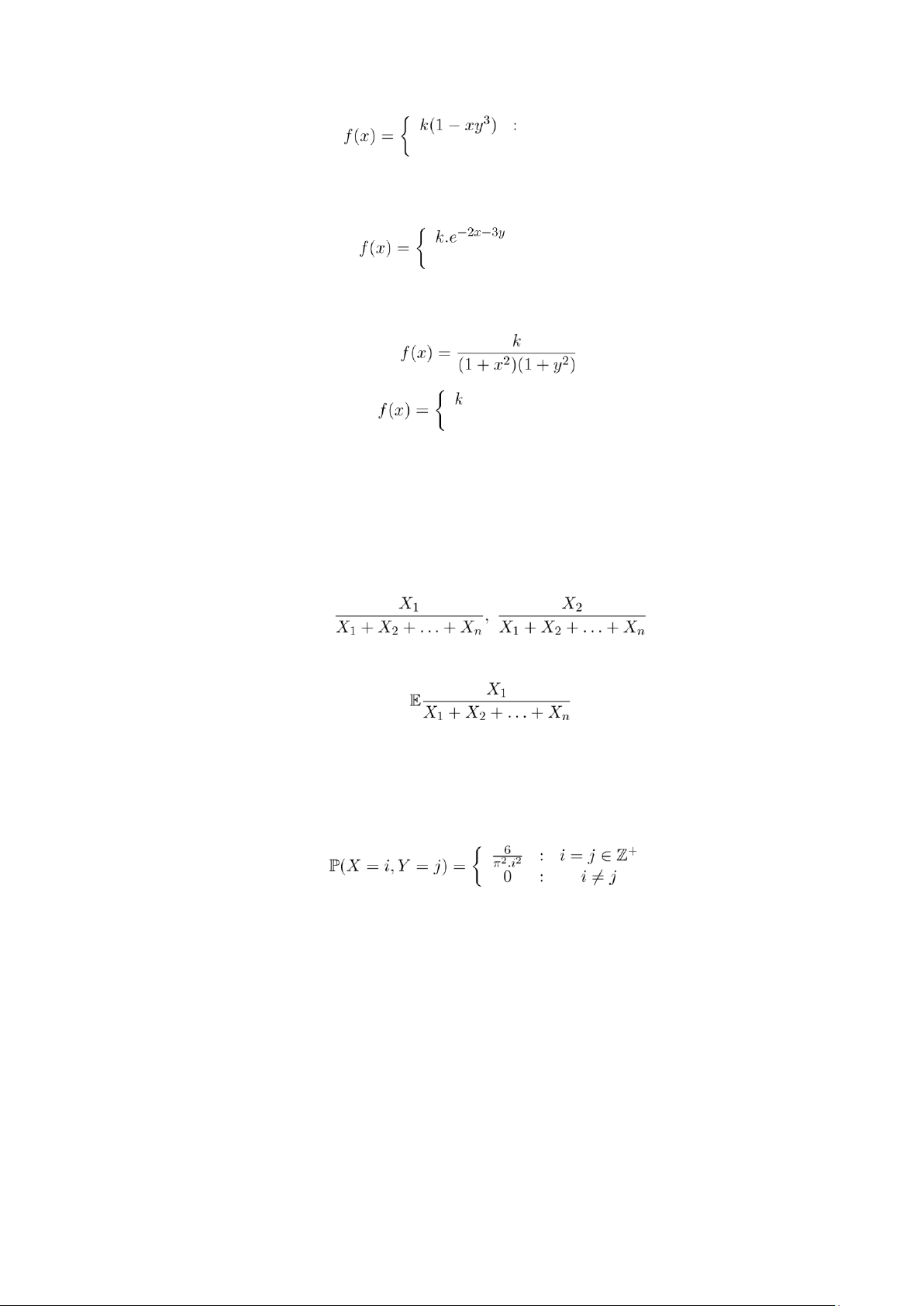
Bài 7. Cho biến ngẫu nhiên X có hàm mật độ
a. Tìm k và hàm phân phối của X.
b. Tính kì vọng và phương sai của X. c. Xét
. Tính hàm mật độ, kì vọng và phương sai của Y .
Bài 8. Cho biến ngẫu nhiên X có hàm mật độ x ∈ [0,1] 0 : ngược lại
Biết rằng kì vọng của X bằng 0,6. lOMoAR cPSD| 58950985
a. Tìm các hằng số a và b.
b. Tính phương sai của X.
c. Tính xác suất P(0,25 < X < 0,5).
d. Tính kì vọng và phương sai của Y = X2.
Bài 9.* Cho biến ngẫu nhiên không âm X thỏa mãn EXα < ∞. Chứng minh rằng: a. Nếu . b. Nếu .
Bài 10. Cho tập A gồm n phần tử. Lấy ra ngẫu nhiên một tập con của A và gọi X là số phần tử của tập
con này. Lập bảng phân phối, tính kì vọng và phương sai của X. Bài 11. Tính kì vọng và phương sai của các
phân phối quan trọng như:
a. Phân phối nhị thức B(n,p).
b. Phân phối Poisson P(λ).
c. Phân phối mũ Exp(λ).
d. Phân phối đều U(a,b).
e. Phân phối chuẩn N(a,b).
Bài 11. Cho biến ngẫu nhiên X có hàm phân phối F(x). Xét hàm quantile QX(p) xác định như sau
QX(p) = inf{x ∈ R : p ≤ F(x)}.
CMR: X và QX(U) có cùng phân bố, trong đó U là biến ngẫu nhiên phân phối đều trên đoạn [0,1]. Bài 12.
Cho biến ngẫu nhiên X và một tập Borel A. Chứng minh rằng:
a. IA(X) cũng là một biến ngẫu nhiên.
b. P(X ∈ A) = E(IA(X)).
Bài 13. Trung bình trong 100 người thì có 7 người mang nhóm máu O âm tính. Chọn ra ngẫu nhiên 6 người. Tính xác suất:
a. Có đúng 2 người mang nhóm máu O âm tính.
b. Có không ít hơn 2 người mang nhóm máu O âm tính.
Bài 14. Gieo thử nghiệm 1000 hạt giống thấy có 650 hạt nảy mầm. Chọn ra ngẫu nhiên 12 hạt giống.
Tìm số hạt nảy mầm có xác suất xảy ra cao nhất? Xác suất đó bằng bao nhiêu?
Bài 15. Trung bình một ngày có 5 vụ tai nạn giao thông xảy ra trong thành phố. Giả sử số vụ tai nạn
trong ngày tuân theo phân bố Poisson. Tính xác suất để
a. Không có vụ tai nạn nào xảy ra trong ngày.
b. Có ít nhất 3 vụ tai nạn xảy ra trong ngày.
c. Biết rằng có ngày xảy ra ít nhất 3 vụ tai nạn, tính xác suất để ngày đó xảy ra đúng 5 vụ tai nạn. lOMoAR cPSD| 58950985
d. Có đúng 20 vụ tai nạn xảy ra trong ngày. Hỏi trung bình bao nhiêu lâu mới có ngày xảy ra 20 vụ tai nạn?
Bài 16. Cho biến ngẫu nhiên X có phân phối mũ Exp(2).
a. Tính xác suất P(1 ≤ X ≤ 5).
b. Tính xác suất P(X > EX).
c. Tính giá trị các moment EXn với n tự nhiên.
d. Đặt Y = 2X. Xét phân phối của biến ngẫu nhiên Y .
Bài 17. Giả sử tuổi thọ X của một người tuân theo phân phối mũ Exp(λ). Biết rằng trung bình trong
1000 người có 500 người sống trên 60 tuổi.
a. Viết công thức tính xác suất P(X > 60). Từ đó hãy tìm tham số λ.
b. Tính tuổi thọ trung bình.
c. Tính xác suất để một người sống trên 70 tuổi.
d. Biết rằng có người sống trên 60 tuổi, tính xác suất để người này sống trên 70 tuổi.
Bài 18.* Cho biến ngẫu nhiên liên tục X. CMR: X tuân theo phân phối mũ ⇔ P(X > t+s|X >
t) = P(X > s) ∀t,s > 0.
Bài 19. Cho biến ngẫu nhiên chuẩn tắc X ∼ N(0,1). CMR
a. Với n lẻ, EXn = 0. b. Với
c. Đặt Y = µ + σX. CMR: Y ∼ N(µ,σ2).
Bài 20. Cho biến ngẫu nhiên chuẩn Y ∼ N(µ,σ2). a. Đặt
. CMR: X ∼ N(0,1).
b. Tìm α sao cho P(|Y − µ| < α) = 95%, biết rằng P(|X| < 1,96) = 95%.
c. Với α ở trên, tính xác suất P(Y < µ + α) và P(Y > µ − α).
Chương III. Vector ngẫu nhiên
Bài 1. Trong hộp có 7 bóng trắng, 6 bóng đỏ và 5 bóng xanh. Ta lấy ra ngẫu nhiên 4 quả bóng trong đó có
X bóng đỏ và Y bóng xanh.
a. Lập bảng phân phối đồng thời của X và Y .
b. Hỏi X và Y có độc lập với nhau hay không?
c. Lập bảng phân phối của Z = X.Y . lOMoAR cPSD| 58950985
Bài 2. Cho hai biến ngẫu nhiên X và Y độc lập có cùng phân phối Tính các xác suất: a. P(X = Y ). b. P(X < Y ).
c. P(max(X,Y ) ≤ k) với số nguyên dương k cho trước.
d. P(min(X,Y ) ≤ k) với số nguyên dương k cho trước.
Bài 3. Cho hai biến ngẫu nhiên độc lập X ∼ B(nX,pX) và Y ∼ B(nY ,pY ).
a. Biết rằng pX = pY = p, CMR X + Y ∼ B(nX + nY ,p).
b. Khi pX 6= pY , hãy chứng minh rằng X + Y không tuân theo phân bố nhị thức.
Bài 4. Cho hai biến ngẫu nhiên độc lập X ∼ Poi(λ) và Y ∼ Poi(µ).
a. CMR: biến ngẫu nhiên X +Y cũng tuân theo phân bố Poisson. Hãy tìm tham số của X +Y .
b. Tính xác suất P(X = k|X + Y = n).
Bài 5. Cho hai biến ngẫu nhiên độc lập X ∼ Exp(λ) và Y ∼ Exp(µ).
a. Hãy viết hàm mật độ đồng thời của (X,Y ). b. CMR: .
Bài 6. Cho hai biến ngẫu nhiên độc lập X ∼ Exp(λ) và Y ∼ Exp(µ). Xét biến ngẫu nhiên Z = min(X,Y ).
a. Tính xác suất P(Z > x) với x không âm.
b. Từ câu a. hãy suy ra phân bố của Z.
c. Cho n biến ngẫu nhiên độc lập X1,X2,. .,Xn đều tuân theo phân bố mũ với tham số tương ứng λ1,λ2,. .,λn.
Tìm phân bố của min(X1,X2,...,Xn).
d.* Tính xác suất P(X1 < min(X2,. .,Xn)).
Bài 7. Cho X1,X2,...,Xn là các biến ngẫu nhiên độc lập có cùng phân bố đều trên [0,1].
a. Tìm hàm phân phối và hàm mật độ của biến ngẫu nhiên Y = min(X1,X2,...,Xn).
b. Tìm hàm phân phối và hàm mật độ của biến ngẫu nhiên Z = max(X1,X2,...,Xn)..
c. Tìm hàm mật độ đồng thời của (Y,Z).
d. Y và Z có độc lập với nhau hay không? Tại sao?
Bài 8. Cho (X,Y ) có hàm phân phối đồng thời lOMoAR cPSD| 58950985
F(x,y) = 1 − e−λx − e−µy + e−λx−µy, với x,y > 0.
a. X và Y có độc lập với nhau hay không? Tại sao?
b. Tìm phân phối của X. Tương tự, tìm phân phối của Y .
c. Tìm hàm mật độ đồng thời của (X,Y ).
d. Tính kì vọng và phương sai của Z = X.Y .
e. Tìm hàm phân phối, tính kì vọng và phương sai của T = max(X,Y ).
Bài 9. Cho hai biến ngẫu nhiên độc lập X ∼ N(0,1) và U = ±1 với xác suất 1/2. Xét biến ngẫu nhiên Y =
U.X. Chứng minh rằng:
a. Y tuân theo phân phối chuẩn tắc N(0,1).
b. X và Y không tương quan.
c. X và Y không độc lập với nhau.
Bài 10. Cho hai biến ngẫu nhiên độc lập X và Y sao cho P(X +Y = α) = 1 với hằng số α nào đó. CMR: X
và Y là các biến ngẫu nhiên hằng số.
Bài 11. Cho X và Y là hai biến ngẫu nhiên độc lập. Tìm hàm phân phối của biến ngẫu nhiên Z = X + Y
trong các trường hợp sau:
a. X ∼ Exp(λ) và Y ∼ Exp(µ).
b. X,Y ∼ U([0,1]).
c. X ∼ Poi(λ) và Y ∼ N(0,1).
Bài 12. Xét tính độc lập, lập bảng phân phối và tính hiệp phương sai của (X,Y ) trong các trường hợp sau: a. X \ Y -1 1 -1 1/4 1/4 0 1/8 1/8 1 1/8 1/8 b. X \ Y -1 0 1 -1 4/15 1/15 4/15 0 1/15 2/15 1/15 1 0 2/15 0
Bài 13. Tìm hằng số k, xét tính độc lập và tính hiệp phương sai khi (X,Y ) có hàm mật độ đồng thời: a.
x,y ∈ [−1,1] lOMoAR cPSD| 58950985 0 : ngược lại b. : x,y ≤ 0 0 : ngược lại c. . d. : 4x2 + y2 ≤ 1 0 : ngược lại
Bài 14. Cho n biến ngẫu nhiên độc lập X1,X2,...,Xn. Chứng minh rằng:
a. Var(X1X2) ≥ Var(X1)Var(X2).
b. Var(X1.X2 ...Xn) ≥ Var(X1).Var(X2)...Var(Xn).
c. Giả sử thêm là các biến có cùng phân phối. CMR: hai biến ngẫu nhiên
có cùng phân phối. Từ đó, hãy tính kì vọng .
Bài 15. Cho hai biến ngẫu nhiên X và Y khả tích.
a. CMR: nếu X và Y độc lập thì biến ngẫu nhiên Z = X.Y cũng khả tích.
b. Xét phân phối đồng thời của (X,Y ) như sau:
Xét tính khả tích của X, xét tính độc lập của X,Y và xét tính khả tích của Z = X.Y
Bài 16. Cho n biến ngẫu nhiên độc lập X1,X2,...,Xn có cùng phân phối:
P(X1 = 1) = P(X1 = −1) = 1/2.
Xét họ biến ngẫu nhiên
Zn = X1.X2 ...Xn.
a. Tìm phân phối của Zn.
b. CMR: họ biến ngẫu nhiên {Zn, n = 1,2,. .} độc lập. lOMoAR cPSD| 58950985
Bài 17. Cho vector ngẫu nhiên Chứng minh rằng: a. |ρ| ≤ 1.
b. X + Y ∼ N(0,2 + 2ρ).
c. Ta có thể viết Y = ρX + p1 − ρ2Z trong đó Z ∼ N(0,1) và độc lập với X.
d. Emax(X,Y ) = 2E(X.IX>Y ).
e. Biểu diễn E(X.IX>Y ) qua tích phân của hàm mật độ đồng thời của X và Z. Từ đó chứng minh rằng . Bài 18.
a. CMR: ma trận covariance của một vector ngẫu nhiên là ma trận nửa xác định dương.
b. Giả sử (aij) và (bij) là ma trận covariance của hai vector ngẫu nhiên độc lập (X1,...,Xn) và (Y1,. .,Yn. Hãy
tìm ma trận covariance của vector (X1.Y1,. .,Xn.Yn). Từ đó rút ra kết luận.
Bài 19. Từ vector ngẫu nhiên
cho trước. Hãy xây dựng vector ngẫu nhiên . lOMoAR cPSD| 58950985
Chương IV. Các định lý giới hạn Các khái niệm hội tụ
Bài 1. Cho ví dụ về một dãy không hội tụ theo xác suất.
Bài 2. Cho hai dãy biến ngẫu nhiên (Xn) và (Yn). Chứng minh rằng:
a. Nếu Xn →P X và Yn →P Y thì a.Xn + b.Yn →P aX + bY với mọi a,b ∈ R. hcc hcc hcc
b. Nếu Xn → X và Yn → Y thì a.Xn + b.Yn → aX + bY với mọi a,b ∈ R. c. Nếu
với mọi a,b ∈ R.
Bài 3. Cho dãy biến ngẫu nhiên độc lập (Xn) có cùng phân phối đều U([0,1]). Đặt Yn = min(X1,X2,. .,Xn)
và Zn = max(X1,X2,...,Xn). Chứng minh rằng:
a. Yn có cùng phân bố với 1 − Zn.
b. Yn →P 0 và Zn →P 1.
c. Yn hcc→ 0 và Zn hcc→ 1. d. .
e. Tồn tại hay không số dương p sao cho Yn không hội tụ về 0 trong Lp?
Bài 4. CMR: nếu ta có Xn →P X và Xn →P Y thì X = Y hầu chắc chắn.
Bài 5. Cho dãy các biến cố (An). Ta xét họ các biến ngẫu nhiên đặc trưng {IAn}. Chứng minh rằng: P Lp
a. IAn → 0 ⇔ P(An) → 0 ⇔ IAn → 0.
b. Nếu ΣP(An) < ∞ thì IA hcc n → 0.
c. Nếu ΣP(An) = ∞ và họ {An} là họ độc lập thì .
Bài 6. Cho dãy biến ngẫu nhiên (Xn) có phân phối xác suất như sau: . Chứng minh rằng: a. Xn →P 0. b. . hcc c. Xn → 0. d. . lOMoAR cPSD| 58950985
e.* Thay số mũ 2 số mũ α, hãy biện luận theo α sự hội tụ của Xn về 0 trong các trường hợp xác suất, Lp và
hầu chắc chắn (có thể bổ sung giả thiết độc lập trong trường hợp cần thiết).
Bài 7. Cho dãy biến ngẫu nhiên (Xn) có phân phối xác suất như sau: . Chứng minh rằng: a. Xn →P 0. b. . hcc c. Xn 9 0.
Bài 8. Cho dãy biến ngẫu nhiên độc lập (Xn) có cùng phân phối xác suất như sau: .
Đặt Yn = X1.X2 ...Xn.
a. Tìm phân phối của Yn. b. CMR: . hcc c. CMR: Yn → 0.
d. Xét bài toán tương tự cho khi Xn có cùng phân phối
P(Xn = 0) = 1 − α,P(Xn = β) = α.
Bài 9. Công nhận kết quả sau đây: nếu Xn →P X thì với mọi dãy (Xnk) đều tồn tại dãy con hội tụ hầu chắc
chắn đến X. Chứng minh rằng:
a. Nếu Xn →P X thì với mọi hàm số liên tục ϕ : R → R, ta có ϕ(Xn) →P ϕ(X).
b. Nếu Xn →P X và Yn →P Y thì với mọi hàm số liên tục ϕ : R2 → R, ta có ϕ(Xn,Yn) →P ϕ(X,Y ). c. Nếu .
Bài 10. Trên không gian ([0,1],B[0,1]) với độ đo xác suất là độ đo Lebesgue, ta xét các biến ngẫu nhiên sau:
X(ω) = 2I[1/2;1](ω),
Xn(ω) = X(ω) − 2nI[1/2−n;1/2](ω).
a. Tính kì vọng của X và các Xn. hcc
b. CMR: Xn → X. lOMoAR cPSD| 58950985 Luật số lớn
Bài 11. Cho biến ngẫu nhiên X có EX = 0 và Var = σ2.
a. Tính kì vọng của biến ngẫu nhiên Yu = (X + u)2 với hằng số u cho trước.
b. Với hằng số dương a cho trước, chứng minh rằng: .
c. CMR: khi u > −a,
P(X > a) ≤ P(Yu > (a + u)2). d. CMR: .
Bài 12. Cho dãy biến ngẫu nhiên độc lập (Xn). Xét xem dãy có thỏa mãn luật số lớn hay không trong các trường hợp sau: a. . b. .
c. P(Xn = ±2n) = 2−(2n+1), P(Xn = 0) = 1 − 2−2n.
d. P(Xn = ±pln(n)) = 1/2.
Bài 13. Cho dãy biến ngẫu nhiên độc lập (Xn) có phân phối xác suất
P(Xn = ±2n) = 1/2.
a. Tính xác suất P(Xn−1 = 2n−1, Xn = 2n).
b. Chứng minh rằng khi Xn−1 = 2n−1, Xn = 2n thì tổng Sn > 2n.
c. Từ đó suy ra dãy đã cho không tuân theo luật số lớn.
Bài 14. Cho f là hàm số liên tục trên [0,1]. Tính các giới hạn sau: a. . Z 1 Z 1 √ b. lim ...
f ( n x1 ...xn)dx1 . .dxn. n→∞ 0 0
Gợi ý: viết tích phân dưới dạng kì vọng của hàm của n biến ngẫu nhiên độc lập cùng phân phối đều.
Bài 15. Cho f và g là hai hàm liên tục trên [0,1] sao cho tồn tại hằng số c > 0 thỏa mãn 0 < f(x) < c.g(x),
∀x ∈ (0,1). Chứng minh rằng: lOMoAR cPSD| 58950985 .
Bài 16. Tìm các giới hạn sau: a. . b. . c. .
Bài 17. Cho các biến ngẫu nhiên độc lập (Xn) cùng phân phối và khả tích. Đặt .
a. CMR: dãy (Yn) hội tụ hầu chắc chắn về một hằng số α. b. Tìm α.
Bài 18. Gieo một con xúc xắc cân đối n lần một cách độc lập. Gọi S là số lần mặt "lục" xuất hiện. Chứng minh rằng .
Bài 19. Cho biến ngẫu nhiên X có kì vọng EX = 5 và phương sai VarX = 0,16. Chứng minh rằng:
a. P(3 < X < 7) ≥ 0,96.
b. P(2 < X < 8) ≥ 0,98. c.
; trong đó các Xi độc lập cùng phân phối với X.
Bài 20. (Bất đẳng thức Chernoff) Cho các biến ngẫu nhiên độc lập X1,...,Xn có cùng phân phối B(1,p). Xét . a. Đặt . CMR: .
b. Tính kì vọng E(etX1). c. CMR: .
d. Xét Yn = 1 − Xn. Tìm phân bố của họ (Yn) và từ đó đưa ra chặn trên cho . lOMoAR cPSD| 58950985 e. Đánh giá .
Hàm đặc trưng, hội tụ yếu và định lý giới hạn giá trị trung tâm
Bài 21. Cho vector Gauss ngẫu nhiên (X,Y ). Chứng minh rằng: nếu hệ số tương quan của X và Y bằng 0 thì
X và Y độc lập với nhau.
Bài 22. (Xấp xỉ phân bố Bernoulli qua phân bố Poisson) Xét họ các phân bố Bernoulli Xn ∼ B(n,pn) sao
cho n.pn → λ.
a. Chứng minh rằng: với mọi số nguyên dương k, ta đều có .
Từ đó suy ra dãy (Xn) hội tụ theo phân phối về biến ngẫu nhiên có phân phối Poisson tham số λ.
b. Áp dụng: khi n > 50 và p < 0,1.
Tỉ lệ sản phẩm không đạt chất lượng là 5%. Ta lấy ra 100 sản phẩm đem đi kiểm tra. Tính xác suất để
i. Trong 100 sản phẩm có 10 sản phẩm không đạt chất lượng. ii. Có
từ 6 đến 9 sản phẩm không đạt chất lượng.
Bài 23. (Xấp xỉ phân bố Bernoulli qua phân bố chuẩn) Xét họ các phân bố Bernoulli Xn ∼ B(n,p).
a. Áp dụng định lý giới hạn trung tâm, chứng minh rằng: .
b. Áp dụng: khi n.p > 5 và n(1 − p) > 5 hoặc n.p(1 − p) > 20. i. Xấp xỉ các xác suất .
ii. Tỉ lệ sản phẩm không đạt chất lượng là 5%. Ta lấy ra 100 sản phẩm đem đi kiểm tra. Tính xác suất
để: có ít hơn 10 sản phẩm không đạt chất lượng, có từ 10 đến 30 sản phẩm không đạt chất lượng.
Bài 24. Tìm hàm đặc trưng của các biến ngẫu nhiên sau:
a. P(X = 1) = P(X = −1) = 1/2. Từ đó suy ra hàm f(t) = cosn t cũng là hàm đặc trưng.
b. P(X = 1) = P(X = 0) = P(X = −1) = 1/3
Bài 25. Chứng minh rằng hàm đặc trưng chỉ nhận giá trị thực khi và chỉ khi nó là hàm chẵn. Hãy kiểm
tra hàm f(t) = e−i|t| có phải là hàm đặc trưng hay không?
Bài 26. Cho biến ngẫu nhiên X nhận giá trị nguyên và có hàm đặc trưng ϕ(t). Chứng minh rằng:
Bài 27. Xét dãy biến ngẫu nhiên Xn ∼ N(0,n). lOMoAR cPSD| 58950985
a. Tính hàm đặc trưng ϕn(t) của Xn.
b. Với mỗi t ∈ R, tính giới hạn C(t) = lim ϕn(t). n→∞
c. Hàm số C(t) có phải là hàm đặc trưng hay không? Tại sao?
Bài 28. Chứng minh rằng một dãy biến ngẫu nhiên hội tụ yếu về một hằng số thì cũng hội tụ về hằng số ấy theo xác suất.
Bài 29. Chứng minh rằng: nếu Xn →d X và |Yn − Xn| →P 0 thì Yn →d X.
Bài 30. (Định lý Slutsky) Cho Xn →d X và Yn →P c. Chứng minh rằng:
a. Xn + Yn →d X + c.
b. Xn.Yn →d cX
c. Xn/Yn →d X/c nếu c 6= 0.
Bài 31. (Lý thuyết giá trị tối đại dạng 1: phân bố Gumbel)
Cho n biến ngẫu nhiên độc lập X1,...,Xn cùng phân phối Exp(1). Xét biến ngẫu nhiên
Yn = max(X1,...,Xn) − ln(n).
a. Cố định x ∈ R, tính xác suất P(Yn ≤ x). b. CMR: .
Bài 32. Cho biến ngẫu nhiên X có phương sai hữu hạn σ2 và thỏa mãn tính chất: nếu X và Y độc lập cùng phân bố thì a. CMR: EX = 0.
b. Nếu có X1,X2,Y1,Y2 độc lập cùng phân bố với X thì
c. CMR: X ∼ N(0,σ2).
Bài 33. Cho dãy biến ngẫu nhiên (Xn) độc lập cùng phân phối có kì vọng 0 và phương sai 1. Chứng minh rằng: a. . b. .