Bài tập môn Điện tử số ( Có lời giải) | Học viện Công Nghệ Bưu Chính Viễn Thông
Bài tập môn Điện tử số ( Có lời giải) | Học viện Công Nghệ Bưu Chính Viễn Thông. Tài liệu gồm 4 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Môn: Điện tử số
Trường: Học viện Công Nghệ Bưu Chính Viễn Thông
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Nguyễn Trọng Luật – BM Điện Tử - Khoa Điện-Điện Tử - ĐH Bách Khoa TP. HCM
BÀI T P CÓ L I GI I – PH N 1 MÔN K THU T S B môn i n t i H c Bách Khoa TP.HCM Câu 1
Cho 3 s A, B, và C trong h th ng s c s r, có các giá tr : A = 35, B = 62, C = 141.
Hãy xác nh giá tr c s r, n u ta có A + B = C.
nh ngh a giá tr : A = 3r + 5, B = 6r +2, C = r2 + 4r + 1 A + B = C
(3r + 5) + (6r + 2) = r2 + 4r + 1
PT b c 2: r2 - 5r - 6 = 0
r = 6 và r = - 1 (lo i)
H th ng c s 6 : tuy nhiên k t qu c ng không h p lý vì B = 62: không ph i s c s 6
Câu 2 S d ng tiên và nh lý:
a. Ch ng minh ng th c: A B + A C + B C + A B C = A C
VT: A B + A C + B C + A B C = B ( A + A C) + A C + B C
= B ( A + C ) + A C + B C
; x + x y = x + y
= A B + B C + A C + B C
= A B + A C + C ( B + B )
= A B + A C + C = A B + A + C
= A ( B + 1) + C
= A + C = A C : VP
b. Cho A B = 0 và A + B = 1, ch ng minh ng th c A C + A B + B C = B + C VT:
A C + A B + B C = (A + B) C + A B ; A + B = 1 = C + A B
= C + A B + A B ; A B = 0
= C + ( A + A ) B = B + C : VP 1
Nguyễn Trọng Luật – BM Điện Tử - Khoa Điện-Điện Tử - ĐH Bách Khoa TP. HCM Câu 3
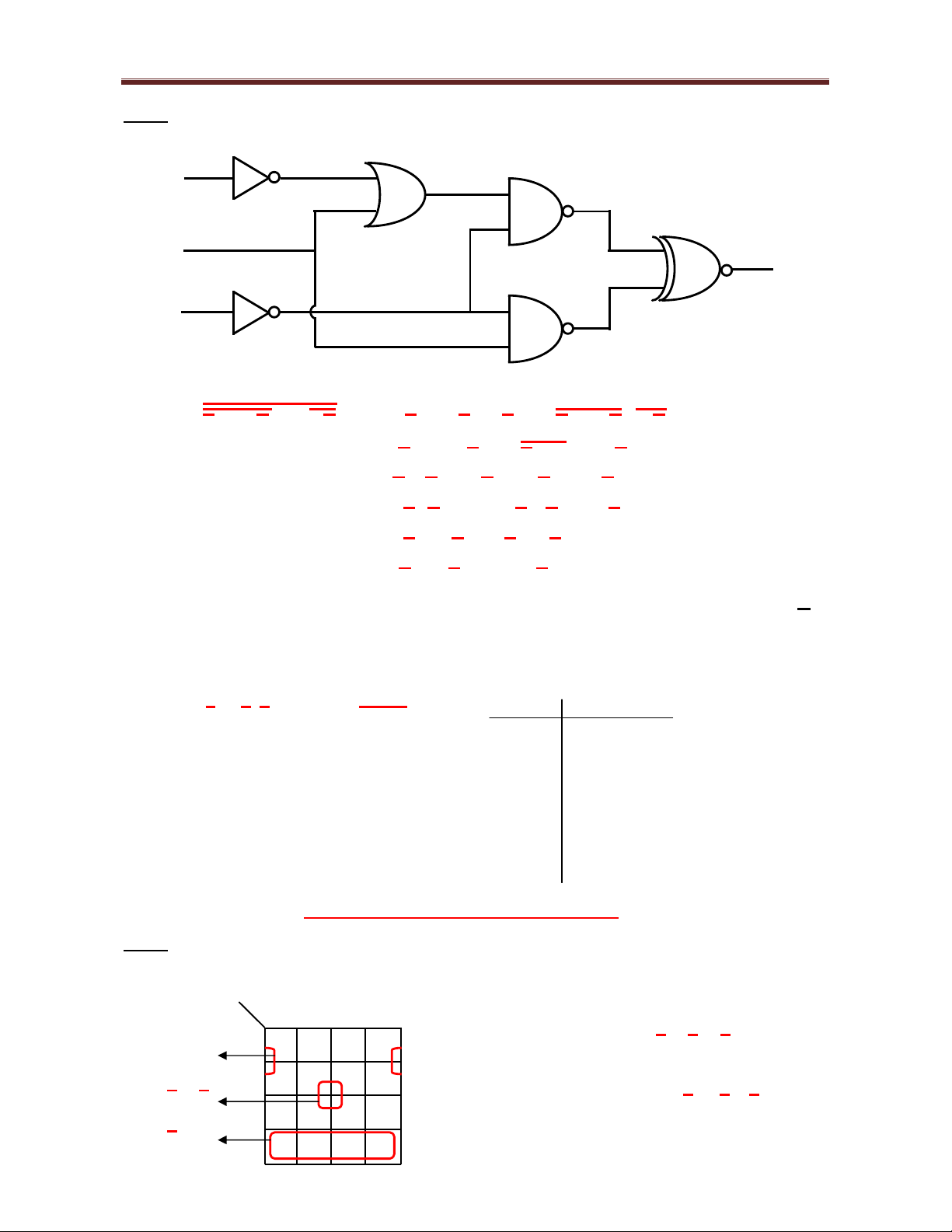
a. Cho hàm F(A, B, C) có s logic như hình v . Xác nh bi u th c c a hàm F(A, B, C). A B . F C .
Ch ng minh F có th th c hi n ch b ng 1 c ng logic duy nh t. F
= (A + B) C ⊕ B C = ((A + B) C) (B C) + ((A + B) C) (B C)
= (A + B) B C + ((A + B) + C) (B + C)
= A B C + B C + (A B + C) ( B + C)
= B C (A + 1) + A B + B C + A BC + C
= B C + A B + C (B + A B + 1)
= A B + B C + C = A B + B + C = A + B + C : C ng OR
b. Cho 3 h
à m F (A, B, C), G (A, B, C), và H (A, B, C) có quan h logic v i nhau: F = G ⊕ H
V i hàm F (A, B, C) = (0, 2, 5) và G (A, B, C)= (0, 1, 5, 7).
Hãy xác nh d ng ho c c a hàm H (A, B, C) (1,0 i m) A B C F G H
F = G ⊕ H = G H + G H = G ⊕ H 0 0 0 0 1 0
F = 1 khi G gi ng H 0 0 1 1 1 1 0 1 0 0 0 1
F = 0 khi G khác H 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1
H (A, B, C) = (1, 2, 7) = ∏ (0, 3, 4, 5, 6)
Câu 4 Rút g n các hàm sau b ng bìa Karnaugh (chú thích các liên k t)
a. F1 (W, X, Y, Z) = (3, 4, 11, 12) theo d ng P.O.S (tích các t ng) F1 WX 00 01 11 10 YZ 00 0 0
F1 = ( X + Y ) ( X + Z ) ( Y + Z ) (X + Y) 01 0 0 0 0 (X + Z)
Ho c F1 = ( X + Z ) ( Y + Z ) ( X + Y ) 11 0 0 (Y + Z) 10 0 0 0 0 2
Nguyễn Trọng Luật – BM Điện Tử - Khoa Điện-Điện Tử - ĐH Bách Khoa TP. HCM
b. F2 (A, B, C, D, E) = (1, 3, 5, 6, 7, 8, 12, 17, 18, 19, 21, 22, 24)
+ d (2, 9, 10, 11, 13, 16, 23, 28, 29) A 0 1
F2 BC 00 01 11 10 10 11 01 00 DE 00 1 1 1 X X B D E 01 1 1 X X X 1 1 B E
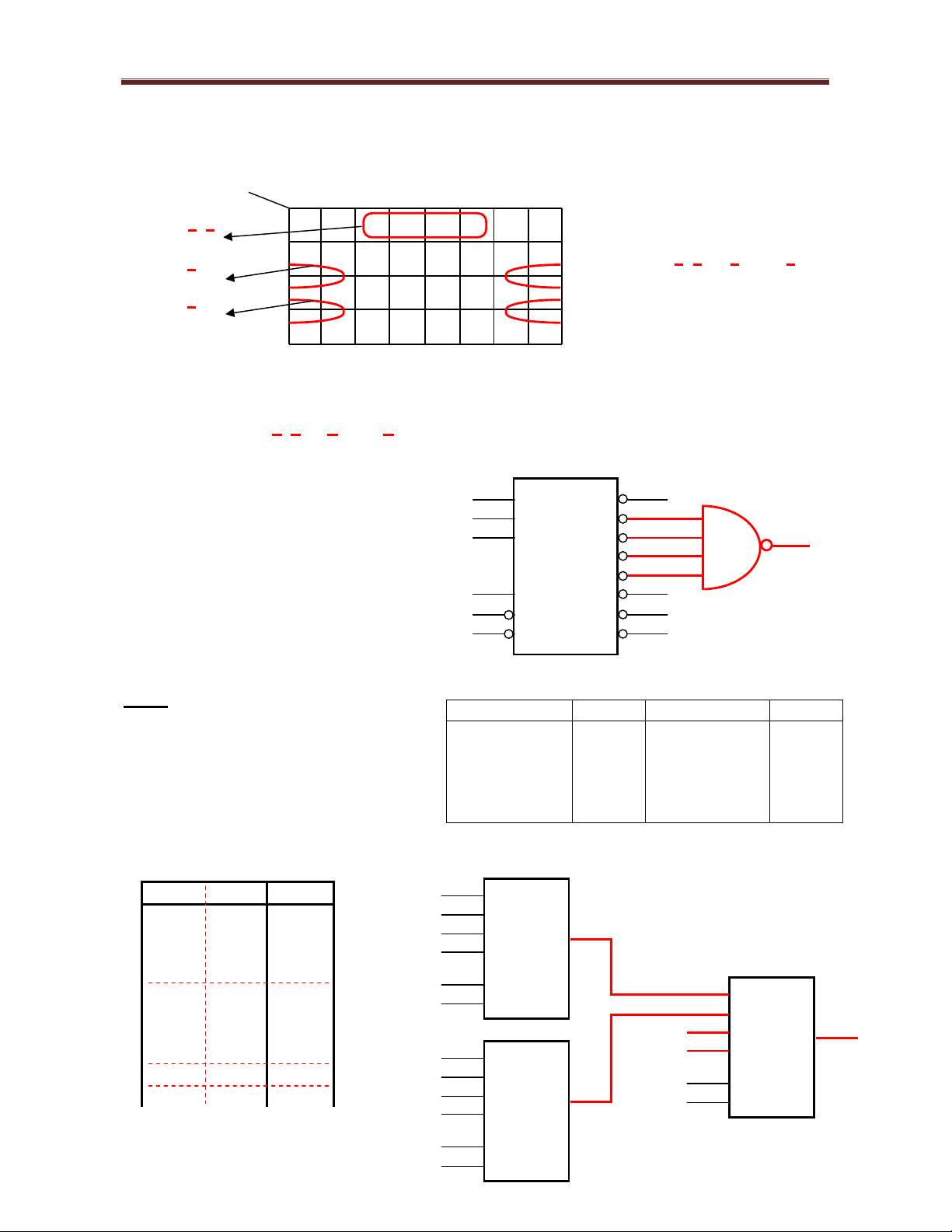
F2 = B D E + B D + B E 11 1 1 X X 1 B D 10 X 1 X 1 1
c. Th c hi n hàm F2 ã rút g n câu b ch b ng IC Decoder 74138 và 1 c ng logic
F2 (B, D, E) = B D E + B D + B E
= ( 1, 2, 3, 4) IC 74138 B C (MSB) Y0 B Y1 D A (LSB) Y2 E F2 Y3 Y4 1 G1 Y5 0 G2A Y6 0 G2B Y7 Câu 5 A B C D F A B C D F
Ch s d ng 3 b MUX 4 → 1, 0 0 0 0 IN0 0 1 0 1 IN5 IN1 IN6 hãy th c hi n b 0 0 0 1 0 1 1 0
MUX 10 → 1 0 0 1 0 IN2 0 1 1 1 IN7 có b ng ho t ng: 0 0 1 1 IN3 1 0 0 0 IN8 IN4 IN9 0 1 0 0 1 0 0 1
S p x p l i b ng ho t ng: MUX 4 1 A D B C F IN0 D0 0 0 0 0 IN0 IN2 D1 0 0 0 1 IN2 IN4 D2 Y 0 0 1 0 IN4 IN6 D3 MUX 4 1 0 0 1 1 IN6 C S0 (lsb) 0 1 0 0 IN1 D0 B S1 0 1 0 1 IN3 D1 0 1 1 0 IN5 MUX 4 1 IN8 D2 Y F 0 1 1 1 IN7 IN1 D0 IN9 D3 1 0 0 0 IN8 IN3 D1 D S0 (lsb) 1 1 0 0 IN9 IN5 D2 Y A S1 IN7 D3
Ngõ vào IN8 và IN9 c ch n C S0 (lsb)
ch ph thu c vào A và D B S1 3
Nguyễn Trọng Luật – BM Điện Tử - Khoa Điện-Điện Tử - ĐH Bách Khoa TP. HCM Câu 6
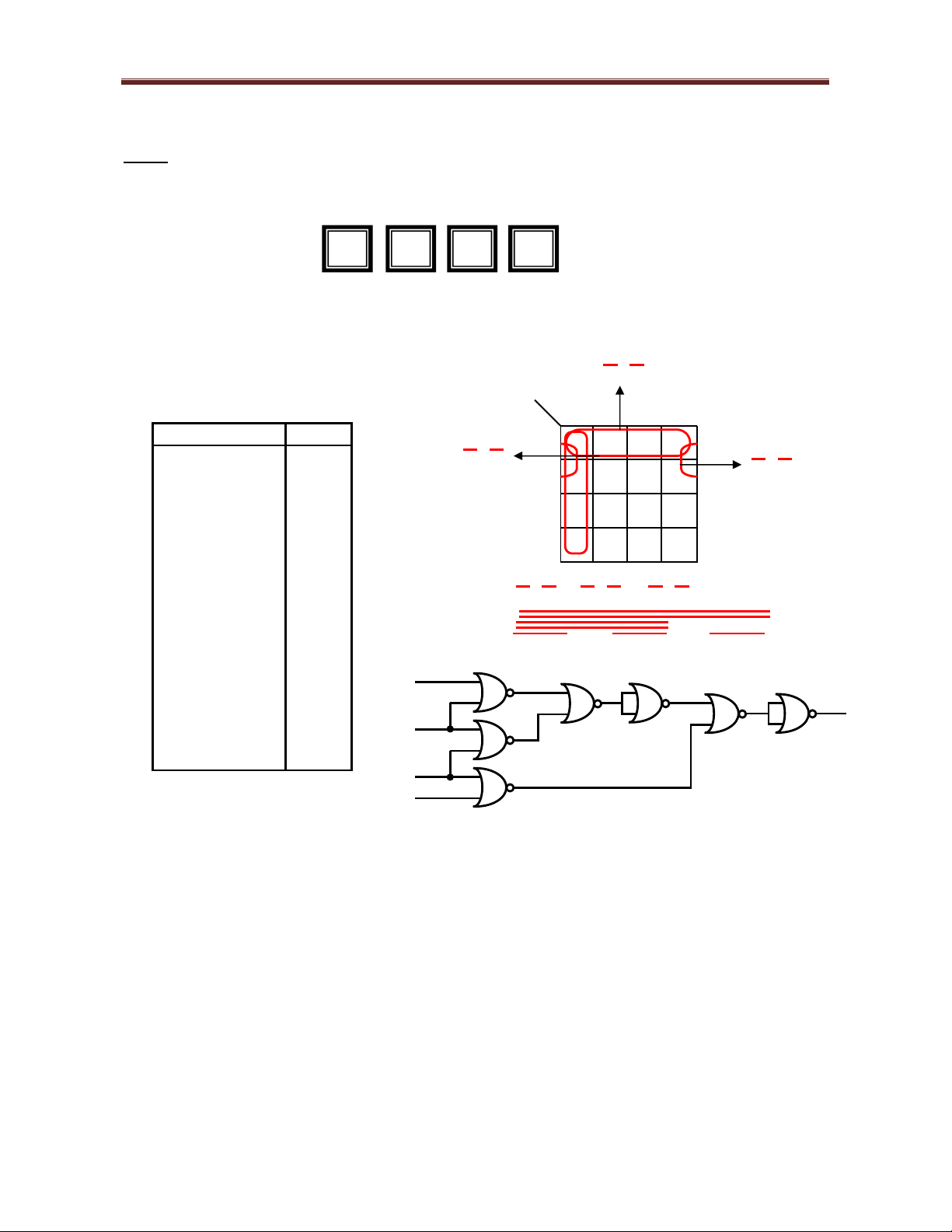
M t hàng gh g m 4 chi c gh ư!c x p theo s như hình v : G1 G2 G3 G4
N u chi c gh có ngư"i ng i thì Gi = 1, ngư!c l i n u còn tr ng thì b ng Gi = 0 (i = 1, 2, 3, 4).
Hàm F (G1, G2, G3, G4) có giá tr 1 ch khi có ít nh t 2 gh k nhau còn tr ng trong hàng.
Hãy th c hi n hàm F ch b ng các c ng NOR 2 ngõ vào. G1 G2 F G1G2 L p b ng ho t ng: G3G4 00 01 11 10 G1 G2 G3 G4 F 00 1 1 1 1 0 0 0 0 1 G3 G4 G2 G3 0 0 0 1 1 01 1 0 0 1 0 0 1 0 1 0 0 1 1 1 11 1 0 0 0 0 1 0 0 1 1 0 0 0 10 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0
F = G1 G2 + G2 G3 + G3 G4 1 0 0 0 1 1 0 0 1 1
= G1 + G2 + G2 + G3 + G3 + G4 1 0 1 0 0 1 0 1 1 0 G1 1 1 0 0 1 F 1 1 0 1 0 G2 1 1 1 0 0 1 1 1 1 0 G3 G4 4