lOMoARcPSD| 36723385
ÔN THI NGHIÊN CỨU MARKETING Câu 1:
YÊU CẦU 1: Xác ịnh danh mục thông tin
Cty sản xuất pha lê. Muốn mở rộng sp cho các phân khúc thấp hơn. Nên thu thập thông tin gì?
Phân khúc nào, ối thủ cạnh tranh có lời?
Cầu ủ chưa? Đối thủ cạnh tranh mạnh cở nào? Có sử dụng sức mạnh kênh phân phối hay không?
Dự oán sức mạnh của ối thủ nước ngoài nếu họ bước vào Pepsi
muốn mở rộng hệ thống kho?
Mức ộ hài lòng của khách hàng hài lòng với dịch vụ giao nhận hàng hay không?
Xét xem lượng cầu trong lương lai như thế nào? ổn ịnh hay mở rộng?
GĐTT cân nhắc có nên ổ thêm tiền vào quảng cáo?
Ngân sách ối thủ cạnh tranh về quảng cáo?
Có nhiều kênh marketing, nếu muốn bỏ thêm vào công cụ quảng cáo thì phải cắt i chi
phí cho công cụ khác. -> Xem các công cụ khác có hiệu quả không?
Mục tiêu của doanh nghiệp?
Hành vi người tiêu dùng? Khách hàng mục tiêu YÊU
CẦU 2: Thiết kế 1 oạn bảng câu hỏi. Câu 2: Mẫu.
YÊU CẦU 1: Xác ịnh quy trình chọn ối tượng, mẫu và giải thích
 MẪU PHI XÁC SUẤT: Áp dụng: nếu dự án nghiên cứu ặt trọng tâm về
mô tả “CHÂN DUNG”.Dùng cho Nghiên cứu Khám phá, Định tính.
1. Mẫu thuận tiện
- Dựa trên sự thuận tiện, dễ tiếp cận ối tượng, dễ lấy thông tin..
- Người nghiên cứu phải thận trọng việc tổng quát hóa từ dữ liệu
của họ khi sử dụng phương pháp này.
 Sử dụng: Nghiên cứu khám phá ( ể phỏng ịnh các trị số)/ khi bị giới hạn
về thời gian, chi phí & không có sẵn danh sách.
 ƯU: Dễ tập hợp các phần tử.
- Phải xác ịnh qui trình phỏng vấn (tránh ể phỏng vấn viên tự do chọn => sai lệch). lOMoARcPSD| 36723385
2. Mẫu theo phán oán
- Các phần tử ược chọn theo ánh giá của nhà nghiên cứu chứ
không phải phỏng vấn viên quyết ịnh ai sẽ ược chọn.
- Việc chọn mẫu dựa trên kiến thức về tổng thể nghiên cứu, những
ặc iểm của nó và mục ích của cuộc nghiên cứu.
- Nếu khả năng phán oán tốt sẽ tốt hơn là chọn mẫu thuận tiện.
- Đảm bảo sẽ chọn úng 1 số phần tử rất quan trọng của ám ông vào mẫu.
3. Mẫu theo lớp (QUOTA SAMPLING)
- Khi tổng thể nghiên cứu ược tập hợp bởi nhiều nhóm không ồng
nhất liên quan ến những ặc iểm nghiên cứu.
- Tổng thể ược chia thành các nhóm ồng nhất.
- Dùng thay cho lấy mẫu phân tầng vì không thể xác ịnh trước ai
sẽ thuộc vào nhóm nào, không có danh sách từng nhóm. Cách xác ịnh duy
nhất: hỏi trực tiếp người trả lời.
- Xác ịnh tiêu chuẩn: dựa vào 1 số ặc iểm kiểm soát xác ịnh trong tổng thể.
- Xác ịnh số phần tử của mẫu theo cùng tỉ lệ của tổng thể.
- Dừng phỏng vấn khi ã ủ số lượng ấn ịnh cho mỗi nhóm.
- Các phỏng vấn viên phải thận trọng, phải thỏa mãn các tỉ lệ 1 cách
chính xác với số người có ặc iểm ã qui ịnh.
4. Mẫu phát triển mầm.
- Chọn ngẫu nhiên những người phỏng vấn ban ầu, những người tiếp
theo ược chọn dựa trên sự giới thiệu của người i trước.
- Gây ra sai lệch vì những người ược giới thiệu tương tự nhau.
- Thà có ít dữ liệu còn hơn là không có thông tin gì?
- Vì không ai muốn trả lời phỏng vấn.
- Giảm Chi phí, Thời gian, Kích thước mẫu.
 Sử dụng: Khi tổng thể ít, khó nhận ra ối tượng cần thu thập thông tin,
khó tìm. Vd: Nghiên cứu thị trường hàng Công nghiệp /Kênh phân phối, không
dùng ể nghiên cứu hàng tiêu dùng.
 MẪU THEO XÁC SUẤT
5. Ngẫu nhiên ơn giản -
Các phần tử ược chọn theo cơ chế ngẫu nhiên. -
Các phần tử ược chọn vào mẫu có xác suất như nhau & biết trước. Việc
chọn phần tử này không ảnh hưởng ến việc chọn phần tử khác. * Yêu cầu: -
Khi ám ông có kích thước nhỏ -
Các phần tử trong tổng thể khá ồng nhất về ặc iểm muốn nghiên cứu -
Thường ược sử dụng cho việc chọn phần tử cho các phương pháp chọn mẫu khác. lOMoARcPSD| 36723385 -
Phải có danh sách ầy ủ tổng thể.
6. Mẫu theo hệ thống
-Chọn 1 iểm xuất phát ầu tiên ngẫu nhiên, dựa vào bước nhảy ể xác ịnh các phần tử tiếp theo; -Bước nhảy = N / n
 Ưu: Không cần khung mẫu hoàn chỉnh. Mẫu ược phân tán ều trên khắp tổng thể nghiên cứu.
7. Mẫu phân tầng ngẫu nhiên
- Khi tổng thể nghiên cứu ược tập hợp bởi nhiều nhóm không ồng nhất liên quan
ến những ặc iểm nghiên cứu.
- MẪU PHÂN TẦNG ngẫu nhiên khi ịa bàn chọn có qui mô nhỏ, nơi sống tập trung các nhóm ặc biệt.
- Nếu các phần tử trong cùng 1 nhóm có tính ồng nhất cao sẽ giúp cho việc chọn
các phần tử trong nhóm cho mẫu sẽ có hiệu quả thống kê.
 PHÂN TẦNG ngẫu nhiên THEO TỈ LỆ: Tổng thể ược chia thành các nhóm
ồng nhất (Phải Xác ịnh tiêu chuẩn ể chia). Sau ó trong mỗi nhóm chọn mẫu ngẫu nhiên
một số phần tử. Số phần tử trong mỗi nhóm tỷ lệ với qui mô của mỗi nhóm trong tổng thể.
- Áp dụng: Khi có 1 sự tương quan thực sự giữa các tiêu chuẩn + số liệu tìm ược. 
PHÂN TẦNG ngẫu nhiên KHÔNG THEO TỈ LỆ: Khi 1 nhóm nào ó
ít ối tượng, nhưng quan trọng phải lấy nhiều hơn cho ủ yêu cầu Ấn ịnh số lượng phần tử ở mỗi nhóm. 
Ưu: Bảo ảm thu thập ược số liệu ầy ủ trong 1 hay vài nhóm. Bảo ảm tính
ại diện => Tăng ộ tin cậy cho kết quả khảo sát 1 vài nhóm nào ó (Bằng cách tăng kích thước nhóm ó). 8. Mẫu theo nhóm -
Tổng thể có nhiều nhóm (Mỗi nhóm mang tính ại diện cho tổng thể). -
Chọn ngẫu nhiên 1 số nhóm. -
Trong mỗi nhóm chọn ngẫu nhiên các phần tử ể tạo thành mẫu. -
Trường hợp sau khi ã phân nhóm, tiếp tục chọn lựa các phần tử
trong nhóm gọi là chọn mẫu theo nhóm 2 bước. - Áp dụng:
o Khi không có khung chọn mẫu hoàn chỉnh. o Khi ịa
bàn khảo sát rộng.
o Chi phí iều tra thấp ược xem là quan trọng hơn so với
yêu cầu về sự chính xác.
 Lưu ý: Hiệu quả thống kê thấp vì việc chia nhóm thỏa mãn tính chất “Trong
nhóm dị biệt, khác nhóm ồng nhất” rất khó khăn vì các phần tử gần nhau (trong cùng
1 nhóm) thường ồng nhất cao. lOMoARcPSD| 36723385
9. Mẫu theo khu vực: Giống như chọn mẫu theo nhóm, nhưng các nhóm
ược chia theo khu vực ịa lý. BÀI TẬP MẪU: 1.
Muốn tìm hiểu hành vi lựa chọn xe gắn máy của người tiêu dùng Thảnh
phố Hồ Chí Minh. Với ngồn thống kê thương mại, biết rằng thị phần trung bình của xe
Honda là 50%, Yamaha là 30%, SYM là 15%, các nhãn hiệu khác là 5%. Với cỡ mẫu
dự tính là 300 cá nhân người tiêu dùng, công ty quyết ịnh phân bố mẫu như thế nào? Trả lời:
Phương pháp chọn mẫu ược lựa chọn là Phân tầng ngẫu nhiên theo tỉ lệ.
Số phần tử khảo sát theo tỉ lệ: 50% người tiêu dùng chọn Honda, 30% người
tiêu dùng chọn Yamaha, 15% người tiêu dùng chọn SYM, các nhãn hiệu khác là 5%.
Với cỡ mẫu dự tính là 300 cá nhân người tiêu dùng, công ty quyết ịnh phân bố mẫu như sau: + 300 x 50% = 150 NTD Honda , + 300 x 30% = 90 NTD Yamaha, + 300 x 15% = 45 NTD SYM, + 300 x 5% = 15 NTD khác. 2.
Một công ty nghiên cứu thị trường muốn khảo sát mức ộ hài lòng của
những người mới mua xe hơi. Công ty có danh sách tên của 10000 người mới mua xe,
trong ó 2500 người mua Ford, 2500 người mua Honda, 2500 người mua Toyota, 2500
người mua GM. Công ty này muốn phỏng vấn 400 chủ xe, bạn hãy trình bày cách chọn 400 chủ xe. Trả lời:
Phương pháp chọn mẫu ược lựa chọn là Phân tầng ngẫu nhiên theo tỉ lệ.
Số phần tử khảo sát theo tỉ lệ:
+ 2500/10000 = 25% người mới mua Ford,
+ 2500/10000 = 25% người mới mua Honda, +
2500/10000 = 25% người mới mua Toyota, +
2500/10000 = 25% người mới mua GM.
Với cỡ mẫu dự tính là 400 chủ xe, công ty quyết ịnh phân bố mẫu như sau:
+ 400 x 25% = 100 chủ xe Ford, lOMoARcPSD| 36723385
+ 400 x 25% = 100 chủ xe Honda,
+ 400 x 25% = 100 chủ xe Toyota,
+ 400 x 25% = 100 chủ xe GM.
3. Công ty A muốn khảo sát việc sử dụng ngân hàng iện tử của những người từ
18 trở lên. Ở gần ịa bàn của công ty A có 5 công ty khác nên công ty A ến phỏng vấn
các nhân viên của năm công ty này.
Tổng thể mà công ty A nên quan tâm là gì?
Anh chị cho rằng kết quả phân tích việc sử dụng ngân hàng iện tử của mẫu này
có phản ánh úng tổng thể không? Trả lời:
a/ Tổng thể cty nên quan tâm là người từ 18 tuổi trở lên.
b/ Theo nhóm, kết quả phân tích việc sử dụng ngân hàng iện tử của mẫu này
không phản ảnh úng tổng thể. Bởi vì: -
Tổng thể công ty muốn nhắm tới là người từ 18 tuổi trở lên. Trong ó, ta
có thể chia thành các nhóm chính theo việc làm, bao gồm: sinh viên, người ang i làm,
người ã nghỉ hưu và người thất nghiệp. -
Do ó, việc công ty phỏng vấn các nhân viên của 5 công ty khác trên cùng
ịa bàn (phương pháp chọn mẫu thuận tiện) thì không bao hàm hết các nhóm ối tượng
mà công ty cần tìm hiểu. -
Nhóm ề xuất các phương án giúp công ty có thể khảo sát việc sử dụng
ngân hàng iện tử có ối tượng mình quan tâm như sau:
+ Công ty vẫn có thể giữ phương pháp chọn mẫu thuận tiện của mình nhưng
thay vì khảo sát ở các công ty khác (chỉ kháo sát ược những người ang i làm) thì công
ty khảo sát ở ịa iểm khác tập trung các nhóm ối tượng nêu trên như công viên, siêu thị,...
+ Hoặc công ty có thể chọn mẫu theo phương pháp Phân tầng ngẫu nhiên theo
tỉ lệ. Trước tiên, công ty cần tìm hiểu số lượng người trong mỗi nhóm ối tượng ể chia tỉ
lệ. Sau ó, công ty chọn mẫu theo tỉ lệ ã tính. 4.
Cần khảo sát tình hình học tập của sv VN. Cần chọn ra 300 sv, cách chọn ntn?
Chọn mẫu theo khu vực: Chọn ngẫu nhiên n tỉnh trong các tỉnh có trường ại học.
Chọn mẫu ngẫu nhiên ơn giản: Chọn 300/n sv trong từng tỉnh ược chọn lOMoARcPSD| 36723385 5.
1 công ty tài chính, cần nhập 1 số thiết bị robot tự ộng phục vụ cho ngành
nhựa về cho thuê hoặc bán. Trước khi nhập thiết bị này cần hỏi ý kiến của KH là các
công ty nhựa. Hãy nêu cách chọn các công ty nhựa ntn ể phỏng vấn?
Chọn mẫu theo phán oán: Công ty sẽ ánh giá các công ty nhựa LỚN có thể có
nhu cầu sử dụng thiết bị robot này. PHỎNG VẤN HẾT VÌ SỐ LƯỢNG ÍT
YÊU CẦU 2: Xác ịnh cỡ mẫu
1. Tính cỡ mẫu theo Giá trị trung bình của các biến liên tục
Bước 1: Xác ịnh sai số e chấp nhận ược giữa ước lượng của mẫu & tổng thể.
Bước 2: Xác ịnh ộ tin cậy muốn có trong ước lượng mẫu nằm trong sai số e.
Bước 3: Ước tính ộ lệch chuẩn của tổng thể.
Bước 4: Tính cỡ mẫu Công thức: 𝒏 = (𝒁 ∗ 𝑺 𝟐 ) 𝑯 Nếu n ≥ 5% N
𝒏 = (𝒁 ∗ 𝑺 𝟐 ∗ √𝑵 − 𝒏 ) 𝑯 𝑵 − 𝟏
Trong ó: n: số phần tử trong mẫu.
N: số phần tử trong tổng thể.
Z: giá trị phân phối tương ứng với ộ tin cậy lựa chọn.
e: sai số tối a cho phép (Khoảng tin cậy). H: nữa khoảng tin cậy
Lưu ý: khoảng tin cậy là 10 thì H=5
nhưng khoảng tin cậy là +- 5 thì chọn H trong công thức là 5 luôn S:
ộ lệch chuẩn của mẫu.
2. Tính cỡ mẫu theo Tỉ lệ của mẫu lOMoARcPSD| 36723385
Tìm hiểu tỷ lệ biến X trong cộng ồng TP.HCM  Công thức:
𝒏 = 𝒑 ∗ 𝒒 ∗ (𝒁 𝟐 ) 𝑯 Nếu n ≥ 5% N 𝒁 𝑵 − 𝒏 𝒏 = 𝒑 ∗ 𝒒 ∗ ( )𝟐 ∗ √ 𝑯 𝑵 − 𝟏
Trong ó: n: số phần tử trong mẫu.
N: số phần tử trong tổng thể.
Z: sai số chuẩn gắn với mức tin cậy ã chọn.
p: xác suất xuất hiện dấu hiệu ang muốn nghiên cứu trong tổng thể. q: xác
suất không xuất hiện dấu hiệu ang muốn nghiên cứu trong tổng thể.
Câu 3: Phân tích dữ liệu
YÊU CẦU 1: Cho bài toán và yêu cầu tính toán + kết luận DẠNG 1:
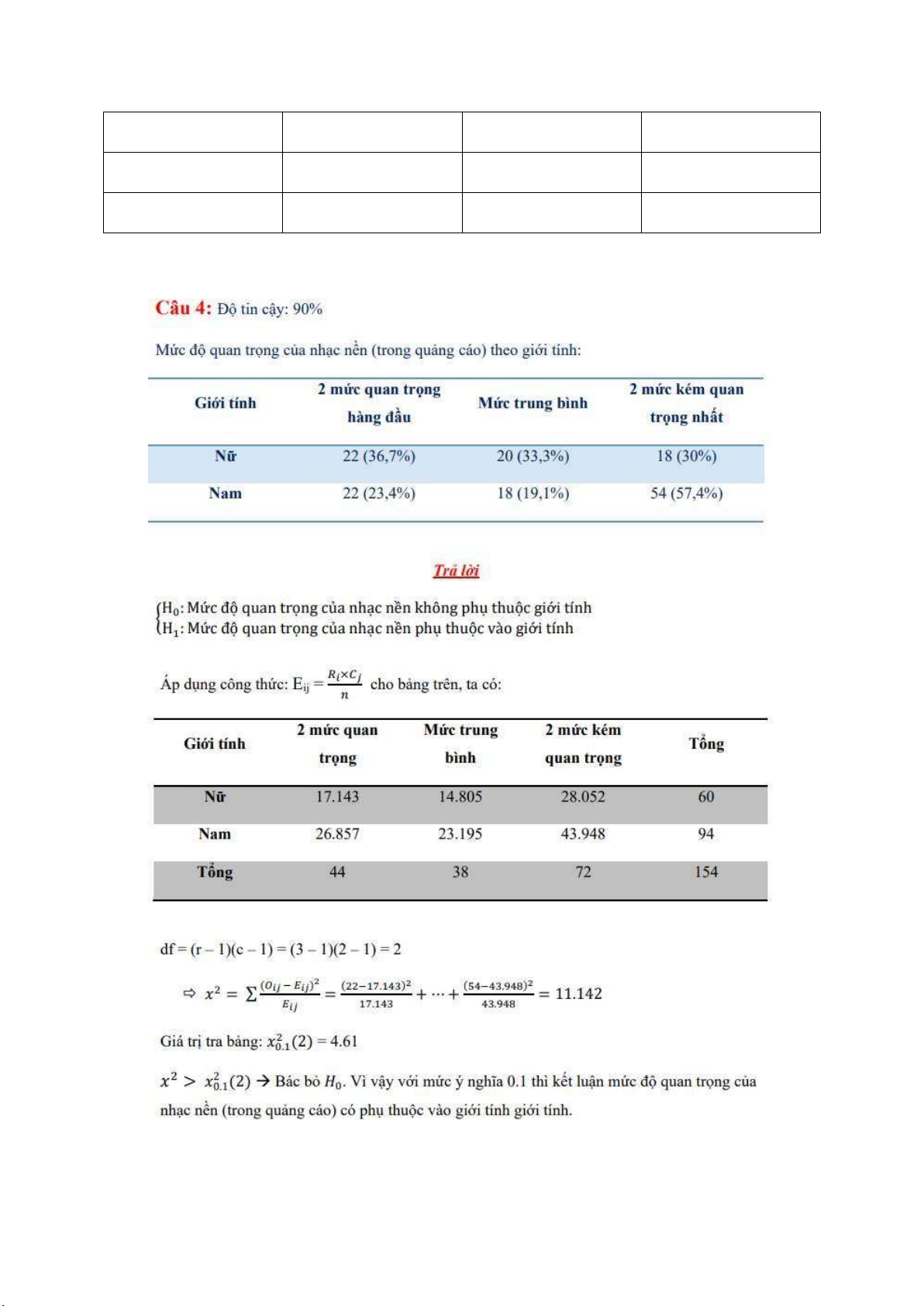
Kiểm ịnh Chi-square dùng cho THANG ĐO ĐỊNH DANH  Yêu cầu:
- Dữ liệu thu thập ược xếp theo 1 tiêu chí/ yếu tố.
- Mỗi quan sát phải và chỉ thuộc về 1 nhóm mà thôi.  Phân tích ề:
- H0: Xác suất quan sát rơi vào từng mục như nhau. (Quan sát thực tế có khác biệt
áng kể so với phân phối kì vọng).
- Oi: Số quan sát thực tế của từng hạng mục (Oi ≥ 5).
- Ei: Số quan sát của từng hạng mục theo giả thuyết H0. Công thức:
𝟐 = ∑ (𝐎𝐢 − 𝐄𝐢)𝟐 𝑿 𝐄𝐢 Hạng mục 1 2 j k Tổng
Số quan sát thực tế O1 O2 Oj Ok n Xác suất (H0) p1 p2 pj pk 1 lOMoARcPSD| 36723385 Số quan sát H0
E1= n * p1 E2= n * p2 Ej= n * pj Ek= n * pk n
 Điều kiện chấp nhận giả thuyết:
X2tính toán <= X2tra bảng
DẠNG 2: Kiểm nghiệm CHI-SQUARE ĐỂ XEM XÉT MỐI QUAN HỆ GIỮA 2
BIẾN ĐỊNH DANH/THỨ TỰ
 Mục ích: xác ịnh sự tồn tại mối quan hệ giữa 2 biến ịnh danh/ thứ tự.  Yêu cầu:
-Không có ô nào có số lần xuất hiện kì vọng < 1.
-Không quá 1/5 tổng số ô có số lần xuất hiện < 5.  Giả thuyết:
H0 : Không có mối liên hệ giữa 2 biến ( ịnh tính – ịnh tính).  Công thức df = (r -1) (c –1)
Ʃ(𝑂𝑖𝑗– 𝐸𝑖𝑗 )2 𝑋 𝐸𝑖𝑗 Điều kiện Eij ≥ 5 Eij = Ri * Cj / n
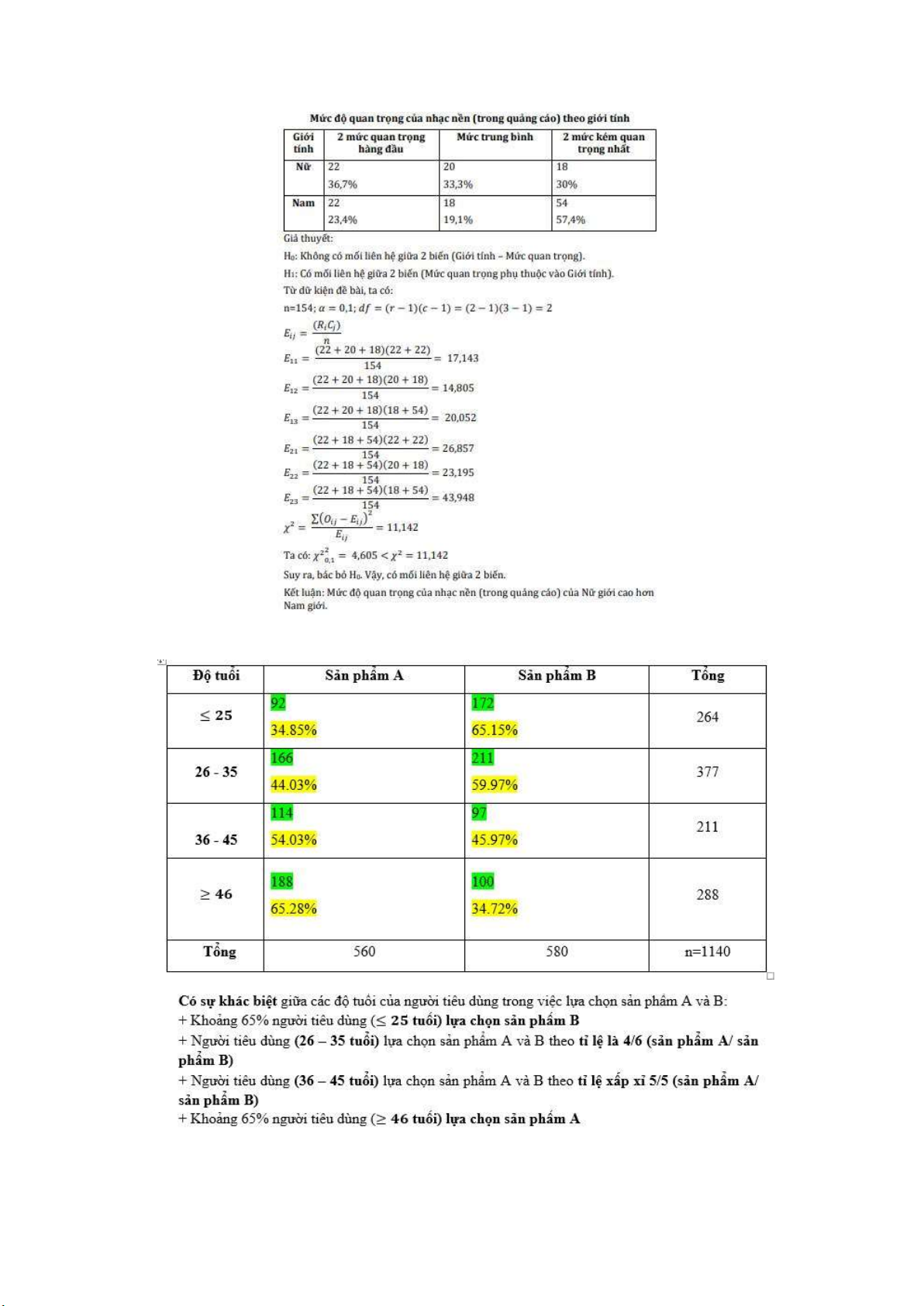
Oij : số quan sát thực tế. Độ tuổi SP A SP B Tổng lOMoARcPSD| 36723385 Ri Tổng Cj N
 Điều kiện chấp nhận giả thuyết:
X2tính toán <= X2tra bảng VD 2: lOMoARcPSD| 36723385 VD3: lOMoARcPSD| 36723385
DẠNG 3: Kiểm ịnh Kolmogorov–Smirnov dùng cho THANG ĐO THỨ TỰ -
Kiểm nghiệm tần số với thang o thứ tự.
 Đặt giả thuyết
H0: Không có sự phân biệt giữa các xử lý.  Công thức
𝑫 = 𝑴𝒂𝒙 | 𝑭(𝑶) – 𝑭(𝑯𝟎)| 𝝀𝜶 𝑫𝜶
 Điều kiện: Nếu D > Dα => Từ chối H0. Màu Tần số % % tích lũy % tích
|𝐅(𝟎) − 𝐅(𝐇𝟎)| F(0) lũy H0 F(H0) A Giả thuyết ặt, sau ó cộng dồn B C
DẠNG 4: Kiểm nghiệm GIÁ TRỊ TRUNG BÌNH ĐƠN khi giả thiết so sánh giữa
giá trị trung bình của tổng thể với giá trị ịnh trước áp dụng cho THANH ĐO
KHOẢNG HOẶC THANG ĐO TỈ LỆ (1 TỔNG THỂ)  Công thức:
Nếu n ≥ 30 => 𝒁𝒕í𝒏𝒉 𝒕𝒐á𝒏 = Ϭ
Không biết Ϭ: 𝒁𝒕í𝒏𝒉 𝒕𝒐á𝒏 = 𝑺
Nếu n < 30 => 𝒕 𝒕í𝒏𝒉 𝒕𝒐á𝒏 =
Với bậc tự do (n-1) 𝑺
 Đặt giả thuyết
H0 : μ = a0 Bác bỏ H0 nếu |𝒁| > 𝒁𝜶/𝟐 lOMoARcPSD| 36723385 H1 : μ ≠ a0
H0 : μ ≤ a0 Bác bỏ H0 nếu Z > Zα H1 : μ > a0
H0 : μ ≥ a0 Bác bỏ H0 nếu Z < -Zα H1 : μ < a0
DẠNG 5: Kiểm nghiệm 2 TRỊ TRUNG BÌNH của 2 tổng thể ộc lập áp dụng cho
THANH ĐO KHOẢNG HOẶC THANG ĐO TỈ LỆ (2 TỔNG THỂ ĐỘC LẬP)
A) Kiểm nghiệm giả thiết so sánh giá trị trung bình tổng thể của 2 tổng thể ộc lập 1. Nếu n ≥ 30:
(𝑿𝟏– 𝑿𝟐) – (𝝁𝟏– 𝝁𝟐) 𝒁𝒕𝒕 = Ϭ𝟐𝟐 √ Ϭ𝟏 𝟐 ( 𝒏𝟏 ) + ( ) 𝒏𝟐
Trường hợp: Không biết Ϭ:
(𝑿𝟏– 𝑿𝟐) – (𝝁𝟏– 𝝁𝟐) 𝒁𝒕𝒕 = 𝑺𝟐𝟐 √ 𝑺𝟏 𝟐 ( ) + ( ) 𝒏𝟏 𝒏𝟐 lOMoARcPSD| 36723385 Với:
Sd : Độ lệch chuẩn chung.
Ϭd: Độ lệch chuẩn tổng thể của các chênh lệch. n: cỡ mẫu.
2. Nếu n < 30 và Ϭ 2 2 1 = Ϭ2
Phương sai gộp: 𝑺𝒑𝟐 =
(𝒏𝟏–𝟏) 𝑺𝟏𝟐+ (𝒏𝟐–𝟏) 𝑺𝟐𝟐] (𝒏𝟏+ 𝒏𝟐–𝟐)
(𝑿𝟏– 𝑿𝟐) – (𝝁𝟏– 𝝁𝟐) 𝟏 𝟏 𝒕 = ∗ √ + . 𝑺𝒑 𝒏𝟏 𝒏𝟐
Bậc tự do df = (n1+ n2–2)
3. Nếu n < 30 và Ϭ 2 2 1 ≠ Ϭ2
(𝑿𝟏– 𝑿𝟐) – (𝝁𝟏– 𝝁𝟐) 𝒕 = 𝑺𝟐𝟐 √ 𝑺𝟏 𝟐 ( 𝒏𝟏 ) + ( ) 𝒏𝟐 Với:
Sd : Độ lệch chuẩn chung.
Ϭd: Độ lệch chuẩn tổng thể của các chênh lệch. n: cỡ mẫu Bậc tự do
[(𝑺𝟏𝟐 /𝒏𝟏) + (𝑺𝟐𝟐 /𝒏𝟐)]𝟐
𝒅𝒇 = (𝑺𝟏𝟐 /𝒏𝟏)𝟐 (𝑺𝟐𝟐 /𝒏𝟐)𝟐 +
 Đặt giả thuyết ( 𝒏𝟏–𝟏 ) ( 𝒏𝟐–𝟏 ) H0 : μ1= μ2
Bác bỏ H0 nếu |𝒁| > 𝒁𝜶/𝟐 H1 : μ1≠ μ2 H0 : μ1≤ μ2
Bác bỏ H0 nếu Z > Zα H1 : μ1> μ2 lOMoARcPSD| 36723385 H0 : μ1≥ μ2
Bác bỏ H0 nếu Z < -Zα H1 : μ1< μ2
 TRƯỜNG HỢP NHIỀU TỔNG THỂ THÌ CHIA RA NHIỀU BÀI 2
TỔNG THỂ ĐỘC LẬP MÀ LÀM lOMoARcPSD| 36723385
B) Kiểm nghiệm giả thiết so sánh giá trị trung bình tổng thể của 2 tổng thể
phụ thuộc (2 TỔNG THỂ PHỤ THUỘC)
Kiểm nghiệm giả thiết so sánh 2 trị trung bình tổng thể của cùng 1 tập ơn vị mẫu. Nếu n ≥ 30
𝑍𝑡í𝑛ℎ𝑡𝑜á𝑛 = Ϭ𝑑 Không biết Ϭd
𝑍𝑡í𝑛ℎ𝑡𝑜á𝑛 = 𝑆𝑑 Nếu n < 30
𝑡 𝑡í𝑛ℎ𝑡𝑜á𝑛 = 𝑆𝑑 Với:
Sd : Độ lệch chuẩn chung.
Ϭd: Độ lệch chuẩn tổng thể của các chênh lệch.
n: cỡ mẫu. Bậc tự do df = n -1
 Đặt giả thuyết
H0 : μd= 0 Bác bỏ H0 nếu |𝑡| > tdf, α/2 lOMoARcPSD| 36723385 H1 : μd≠ 0
H0 : μd≤ 0 Bác bỏ H0 nếu t > tdf, α/2 H1 : μd> 0
H0 : μd≥ 0 Bác bỏ H0 nếu t < - tdf, α/2 H1 : μd< 0
DẠNG 6: Kiểm ịnh TỶ LỆ ĐƠN (p) dùng cho Biến ngẫu nhiên phân phối theo qui luật 0 -1
Kiểm nghiệm giả thiết so sánh giữa tỉ lệ của tổng thể với 1 giá trị ịnh trước.
 Giả thuyết: n ≥ 40 và np, nq ≥ 5  Công thức: (𝒑𝑺– 𝒑𝟎) 𝒁𝒕𝒕 √ 𝒏 Với: -
pS: tỉ lệ thành công trong mẫu. -
p0: tỉ lệ thành công trong tổng thể.
 Đặt giả thuyết H0 : p = p0 Bác bỏ H0 nếu
|𝒁| > 𝒁𝜶/𝟐 H1 : p ≠ p0 H0 : p ≤ p0 Bác bỏ H0 nếu Z > Zα H1 : p > p0 lOMoARcPSD| 36723385 H0 : p ≥ p0 Bác bỏ H0 nếu Z < -Zα H1 : p < p0
DẠNG 7: Kiểm nghiệm 2 TỈ LỆ (Biến ngẫu nhiên phân phối theo qui luật 0-1, o
trên 2 mẫu ộc lập)
Kiểm nghiệm so sánh tỉ lệ tổng thể của 1 biến trong 2 tổng thể khác nhau.
[(𝑝𝑠1– 𝑝𝑠2 ) − (𝑝1– 𝑝2 )] 𝑍 = -
Ước lượng chung cho tỉ lệ của mẫu kết hợp 𝑝𝑠2) 𝑝𝑠 = (𝑛1 + 𝑛2) - Sai số chuẩn (p1-p2) Sp1 –p2
Điều kiện: n1*ps1, n2*ps2≥ 5
 Đặt giả thuyết H0 : p1= p2
Bác bỏ H0 nếu |𝑍| > Zα/2 H1 : p1≠ p2 H0 : p1≤ p2 Bác bỏ H0 nếu Z > Zα lOMoARcPSD| 36723385 H1 : p1> p2 H0 : p1≥ p2
Bác bỏ H0 nếu Z < -Zα H1 : p1< p2
DẠNG 8: Kiểm nghiệm 2 PHƯƠNG SAI Để kiểm ịnh 2 tổng thể có biến ộng cùng
mức ộ như nhau không? 𝑺𝟏𝟐 𝑭𝒕𝒕 = 𝑺𝟐 𝟐 Với:
Sd : Độ lệch chuẩn chung.
Ϭd: Độ lệch chuẩn tổng thể của các chênh lệch.
Giá trị phương sai lớn hơn sẽ ặt ở tử số.
df1= n1 -1 bậc tự do ở tử. (c)
df2= n2 -1 bậc tự do ở mẫu. (r)
 Đặt giả thuyết
H0 : Ϭ𝟏𝟐= Ϭ𝟐𝟐 Bác bỏ H0 nếu
H1 : Ϭ𝟏𝟐≠ Ϭ𝟐𝟐
F > Fdf1,df2,α/2 hoặc F < Fdf1,df2,1-α/2 lOMoARcPSD| 36723385
H0 : Ϭ𝟏𝟐≤ Ϭ𝟐𝟐
Bác bỏ H0 nếu F > Fdf1,df2,α
H1 : Ϭ𝟏𝟐> Ϭ𝟐𝟐
H0 : Ϭ𝟏𝟐≥ Ϭ𝟐𝟐
Bác bỏ H0 nếu F < Fdf1,df2,1-α
H1 : Ϭ𝟏𝟐< Ϭ𝟐𝟐
DẠNG 9: PHÂN TÍCH TƯƠNG QUAN
Hệ số tương quan Pearson (Pearson’s correlation coefficient -r): Để phát hiện ra mức ộ
tương quan giữa 2 biến ịnh lượng (Không có giả thuyết về nhân quả).
Hệ số tương quan cho biết biên ộ và chiều hướng biến thiên của 2 biến tương quan với nhau.
r = 0 => Không tương quan (Biết X sẽ không biết
Y). r = 0,2 => Tương quan rất yếu, không áng kể. r =
0,2 –0,4 => Tương quan yếu, thấp. r = 0,4 -0,7 =>
Tương quan vừa phải. r = 0,7 –0,9 => Tương quan
mạnh. r > 0,9 => Tương quan rất mạnh.
r = 1 => Tương quan hoàn hảo Tương
quan dương: X tăng => Y tăng.
Tương quan âm: X tăng => Y giảm.
Tương quan dương hay âm thừa nhận mối quan hệ tuyến tính.
 Kiểm nghiệm t, ể xét xem hệ số tương quan ó có thật sự là biểu hiện của
một mối tương quan nào ó. 𝑟 𝑡 =
√ [(1 − 𝑟2) / (𝑛 − 2)]
Với n: cỡ mẫu Bậc tự do df = n –2; r: hệ số tương quan mẫu
 Đặt giả thuyết
H0 : ƿ (rho) = 0 (Không có biểu hiện tương quan). H1 : ƿ ≠ 0
Bác bỏ H0 nếu |𝑡|> tn-2, α/2 hoặc p-value < α
DẠNG 10: ƯỚC LƯỢNG XÁC ĐỊNH KHOẢNG TIN CẬY lOMoARcPSD| 36723385 1) Công thức: ( 𝒑𝒔 ∗ 𝒒𝒔 )
𝒑 = 𝒑𝒔 ± 𝒁 𝜶 𝟐⁄ ∗ √ 𝒏 𝑽ớ𝒊: 𝒑𝒔
 NHỮNG GỈA ĐỊNH KHI SỬ DỤNG HỆ SỐ TƯƠNG QUAN PEARSON
- Mối quan hệ tuyến tính.
- Dữ liệu khoảng. - Mẫu ngẫu nhiên. - Phân phối chuẩn.
2) Công th ứ c: 𝒑𝒔 (𝟏− 𝒑𝒔) 𝜺=𝒁𝜶𝟐 ⁄ ∗ √ 𝒏 3) Công thức: 𝑺
𝝁 = 𝑿 ± 𝒁 𝜶⁄𝟐
• Nếu biết N lớn 𝑺 𝑵−𝒏 √ 𝑵−𝟏 lOMoARcPSD| 36723385
𝝁 = 𝑿 ± 𝒁 𝜶⁄𝟐
YÊU CẦU 2: Cho 1 oạn bảng câu hỏi rồi hỏi xem cách xử lí bằng kiểm ịnh nào (k cần tính toán)
1) Thang o khoảng và tỷ lệ dùng kiểm ịnh trung bình ơn
2) Kiểm ịnh mối quan hệ ịnh tính vs ịnh tính: chi bình phương
3) Khi có nhiều hơn 2 chọn lựa 1 trong 2 biến thì kiểm ịnh chi bình phương 4)
Nếu trong 2 biến ó chỉ có 2 chọn lựa thì kiểm ịnh tỷ lệ của 2 mẫu ộc lập
5) 1 Định tính vs 1 ịnh lượng là kiểm ịnh trung bình của 2 tổng thể ộc lập
6) 1 ịnh lượng vs 1 ịnh lượng có 2 TH
- TH1. Cái naò quan trọng hơn là trung bình
- TH2. Cái này thay ổi cái kia có thay ổi theo không: là phân tích tương quan
7) Mức ộ cạnh tranh giữa các ngành khác nhau: kiểm ịnh trung bình trên 2 tổng thể ộc lập Vd lOMoARcPSD| 36723385 2
k trung bình của các mẫu phù thuộc 3
kiểm ịnh tương qua (khoảng và khoảng) 4 kiểm ịnh phân tích tương quan