-
Thông tin
-
Quiz
Bài tập môn thống kê ứng dụng | Trường Đại học Kinh tế – Luật, Đại học Quốc gia Thành phố Hồ Chí Minh
Vì n1 và n2 <30 và phương sai hai tổng thể chưa biết nhưng bằng nhau nên. Không biết phương sai của 2 tổng thể & không có giả định phương sai 2 tổng thể bằng nhau. Ước lượng độ chênh lệch về thu nhập trung bình ở 2 công ty. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Môn: Thống kê ứng dụng (TK) 131 tài liệu
Trường: Trường Đại học Kinh Tế - Luật, Đại học Quốc gia Thành phố Hồ Chí Minh 1.4 K tài liệu
Thông tin:
Tác giả:
Preview text:
lOMoAR cPSD| 46663874 Bài 2.15
Vì n1 và n2 <30 và phương sai hai tổng thể chưa biết nhưng bằng nhau nên: ×Sp×√❑ ⇒Sp
⇒Phương sai mẫu gộp = S
→ khẳng định (i) là Sai.
Ta có, số bậc tự do của giá trị tới hạn là:
df =k=n1+n2−2=12
→ Khẳng định (ii) là Đúng.
σμ1−μ2=Sp×√❑
→ Khẳng định (iii) là Đúng.
Vậy có 2 khẳng định đúng là (ii) và (iii). Câu 3.T1: N = 40 x=42
σ2 = 9 => σ=3
Ta thấy (36;48) = (x±2σ ¿=> Có 95% trứng gà sẽ nở trong khoảng từ
36 đến 48 ngày khoảng 38 trứng âu 3.T2
Thu nhập rất cao 11 triệu đồng/tháng≧ n1=20; n2=23 < 30 không biết
phương sai của 2 tổng thể & không có giả định phương sai 2 tổng thể bằng nhau => trường hợp 3 X s ¿¿ s ¿¿ k=¿¿ t lOMoAR cPSD| 46663874 2.0345 ❑
Ước lượng độ chênh lệch về thu nhập trung bình ở 2 công ty: => Chọn A 3.T3
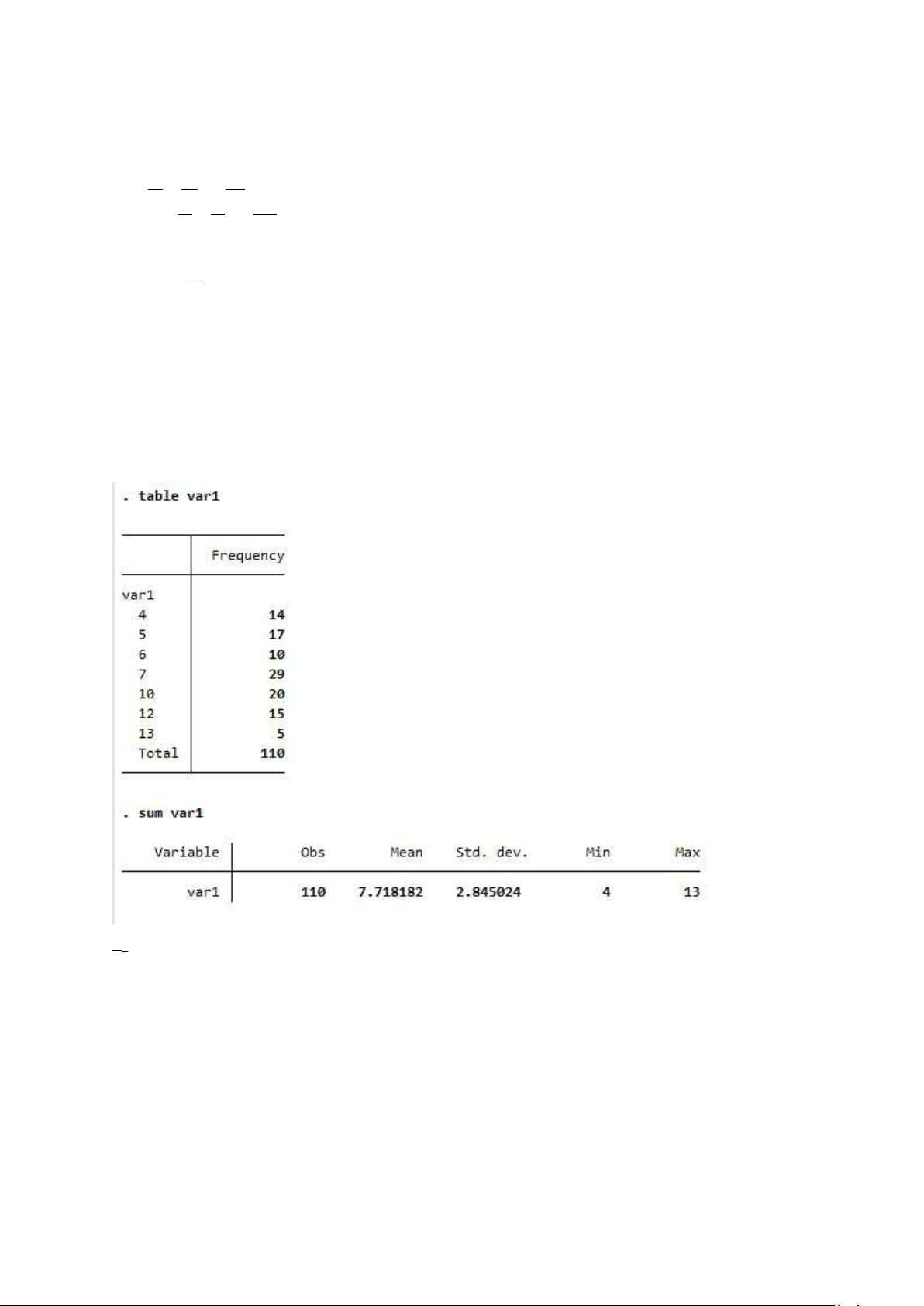
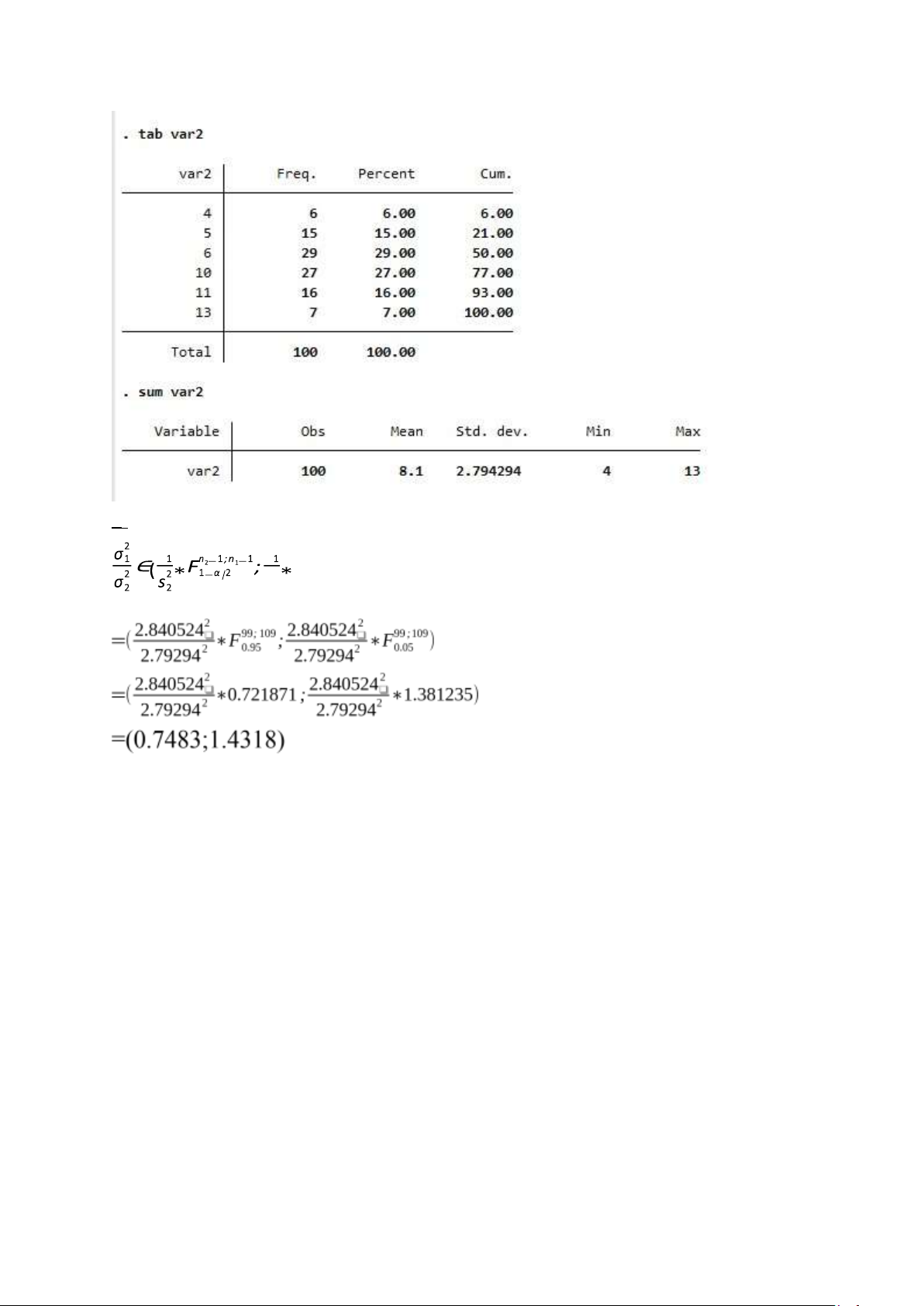
n1=110; n2=100 > 30 không biết phương sai của 2 tổng thể => trường hợp 2
Ước lượng độ chênh lệch về thu nhập trung bình ở 2 công ty: X1=7.7182; X2=8.1
s21=8.0942; s22=7.8081
Ước lượng độ khác biệt về trung bình của hai công ty:
ε=zα/2∗√❑ => Chọn B 3T4. Chọn C Ta có: m1 40
f 1= = ≈0,3636 n1 110 f Độ chính xác (sai số):
ε=zα/2×√❑
Vậy khoảng ước lượng khác biệt về tỷ lệ thu nhập rất cao giữa công ty
A và công ty B là: ( p1 ;p2)∈ (f 1−f 2)±ε=(0,3636−0,5) ±0,133=(−0,2694;−0,0034) lOMoAR cPSD| 46663874 3T5. Chọn A Ta có:
mn11 11020 f 1= =
≈0,1818 mn22 10023 23 f 2= = =0, Độ chính xác (sai số):
ε=zα/2×√❑
Vậy khoảng ước lượng khác biệt về tỷ lệ thu nhập rất cao giữa công ty
A và công ty B là: ( p1 ;p2)∈ (f 1−f 2)±ε=(0,1818−0,23)±0,1095=(−0,1577;0,0613) 3.T6 X1=7.718182 s1=2.845024 lOMoAR cPSD| 46663874
X2=8.1 s2=2.79294 s2 s2 n2−1;n1−1 2 Fα/2 ) s2 chọn B 2.18 lOMoAR cPSD| 46663874
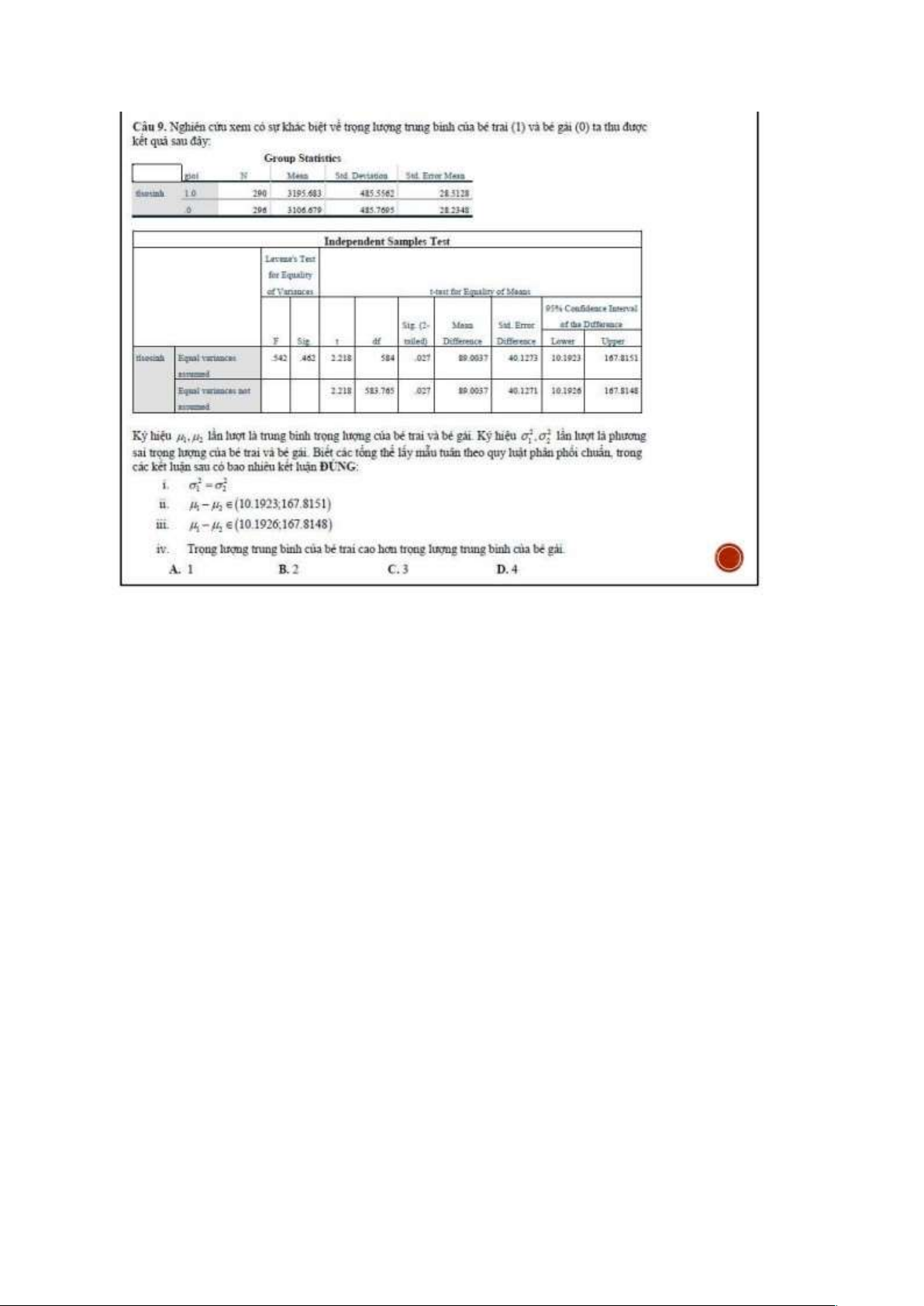
Sig. kiểm định F = 0.542 > 0.05 nên không có sự khác nhau
về phương sai của 2 tổng thể => sử dụng kết quả ở dòng
Equal variances assumed.
Sig. kiểm định t bằng 0.027 < 0.05, nghĩa là có sự khác biệt về trọng lượng trung bình i. σ1 = σ2 → Đúng
ii. µ1 − µ2 (10. 1923 ; 106. 8151) → Đúngϵ iii. µ1 - µ2 ϵ (10.1926 ; 106.8148) → Sai
iv. Đúng vì µ1 - µ2 = (+, +) thì có sự khác về trung bình về
trọng lượng trung bình vời µ1 > µ2 >>> Có 3 kết luận
đúng >>> Chọn đáp án C