Bài tập nhóm 2 môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐẠI HỌC KINH TẾ QUỐC DÂN KHOA THỐNG KÊ NHÓM 2 BÀI TẬP MÔN HỌC
THỐNG KÊ TRONG KINH TẾ VÀ KINH DOANH LỚP HỌC PHẦN: TKKD1129(224) _08 GIÁO VIÊN GIẢNG DẠY: TS. CHU THỊ BÍCH NGỌC HỌ VÀ TÊN: MÃ SINH VIÊN: Đỗ Hải Đăng 11243038 Phạm Quang Khải 11243079 Ôn Gia Bảo 11243025 Nguyễn Tuấn Mạnh 11243115 Phan Văn Như Phan 11243137 Nguyễn Hồng Đức 11243046 HÀ NỘI - 2025 MỤC LỤC Trang
GIỚI THIỆU CHUNG VỀ THỐNG KÊ 3 PHÂN TỔ THỐNG KÊ 4
CÁC MỨC ĐỘ THỐNG KÊ MÔ TẢ 6
ƯỚC LƯỢNG VÀ KHOẢNG TIN CẬY 7
KIỂM ĐỊNH GIÁ THUYẾT THỐNG KÊ 9
PHÂN PHỐI XÁC SUẤT CỦA BIẾN NGẤU NHIÊN LIÊN TỤC 10
MẪU, PHƯƠNG PHÁP CHỌN MẪU 11 CHỈ SỐ 14
PHÂN TÍCH DÃY SỐ THỜI GIAN VÀ DỰ BÁO 17 2 PHẦN BÀI 1:
Bài 13: Hãy điền mỗi biến dưới đây vào bảng và nhận xét tại sao có những biến có thể điền vào hai chỗ: a/ Lương b/ Giới tính
c/ Doanh thu từ bán thiết bị âm nhạc điện tử
d/ Sở thích về đồ uống e/ Nhiệt độ f/ Điểm SAT
g/ Xếp hạng sinh viên trong lớp học h/ Xếp hạng giảng viên
i/ Số lượng tivi trong mỗi gia đình BÀI LÀM Biến rời rạc Biến liên tục (b) Giới tính (d) Sở thích ăn uống Định tính
(g) Xếp hạng sinh viên trong lớp học
(h) Xếp hạng giảng viên
(c) Doanh thu từ bán thiết bị âm (e) Nhiệt độ Định lượng nhạc điện tử (f) Điểm SAT
(i) Số lượng tivi trong mỗi gia đình (a) Lương Rời rạc Liên tục Định danh (b) Giới tính
(g) Xếp hạng sinh viên trong lớp học Thứ bậc
(h) Xếp hạng giảng viên (d) Sở thích ăn uống (e) Nhiệt độ Khoảng (f) Điểm SAT
(i) Số lượng tivi trong mỗi gia đình (a) Lương Tỷ lệ
(c) Doanh thu từ bán thiết bị âm nhạc điện tử 3 Nhận xét:
- Lương có thể là cả biến rời rạc và biến liên tục tùy theo cách đo lường (nếu tính theo từng
bậc cố định thì là rời rạc, nếu có thể có giá trị bất kỳ trong một khoảng thì nó là liên tục)
- Doanh thu từ bán thiết bị âm nhạc điện tử: thường được đo bằng một con số cụ thể, nó có
thể là rời rạc khi tính theo từng giao dịch riêng lẻ, là liên tục nếu
xét tổng doanh thu trong một khoảng thời gian. PHẦN PTTK:
Bài 31/tr 44: Một nhà khoa học đang nghiên cứu về việc sử dụng iPod của sinh viên đại học. Khảo
sát 45 sinh viên về số bài hát họ đã nghe trong ngày và thu thập được kết quả sau: 4 6 8 7 9 6 3 7 7 6 7 1 4 7 7 4 6 4 10 2 4 6 3 4 6 8 4 3 3 6 8 8 4 6 4 6 5 5 9 6 8 8 6 5 10
Sắp xếp dữ liệu trên thành bảng tần số phân phối:
a/ Nên lựa chọn số tổ là bao nhiêu:
b/ Nên lựa chọn khoảng cách tổ bằng bao nhiêu
c/ Giới hạn dưới của tổ đầu tiên có giá trị bằng bao nhiêu
d/ Xây dụng bảng tần số phân phối
e/ Nhận xét về hình dáng phân phối của dãy số BÀI LÀM
a/ Áp dụng quy tắc: !!!"#" #$ % $ !!!"#" &'$ % ("#$" ')&* + ("#$, -
Vậy lựa chọn số tổ là 6 b/
Có khoảng cách tổ: .$/0$1 , $%!$% !"# & ! % ,'(&' ), 2)'
Vì khoảng cách tổ thường làm tròn đến số thích hợp nên 1 , !
c/ Giới hạn dưới của tổ đầu tiên có giá trị bằng 0
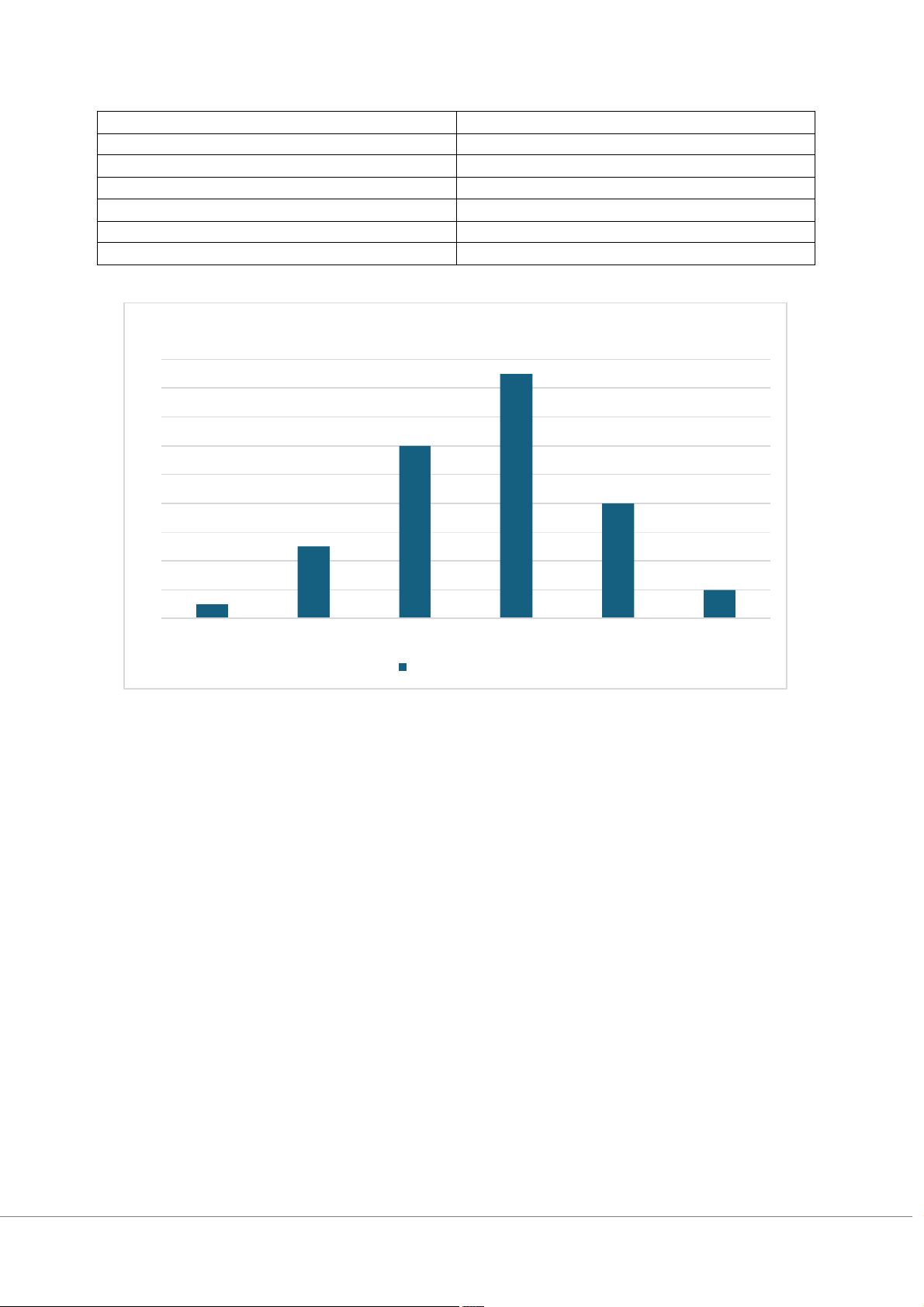
d/ Xây dựng bảng tần số phân phối 4 Số bài hát nghe Tần số Từ 0 đến 2 1 Từ 2 đến 4 5 Từ 4 đến 6 12 Từ 6 đền 8 17 Từ 8 đến 10 8 Từ 10 đến 12 2
Số bài hát đã nghe trong ngày 18 16 14 12 10 8 6 4 2 0 Từ 0 đến 2 Từ 2 đến 4 Từ 4 đến 6 Từ 6 đền 8 Từ 8 đến 10 Từ 10 đến 12 Số bài hát đã nghe e/
- Phân phối lệch trái nhẹ: vì số lượng sinh viên từ 4-8 bài nhiều nhất
- Dạng gần đối xứng nhưng có phần hơi dồn về phía mà số lượng bài hát sinh viên nghe ít bài hát hơn.
---------------------------------------------------------------------------------------------------------------------
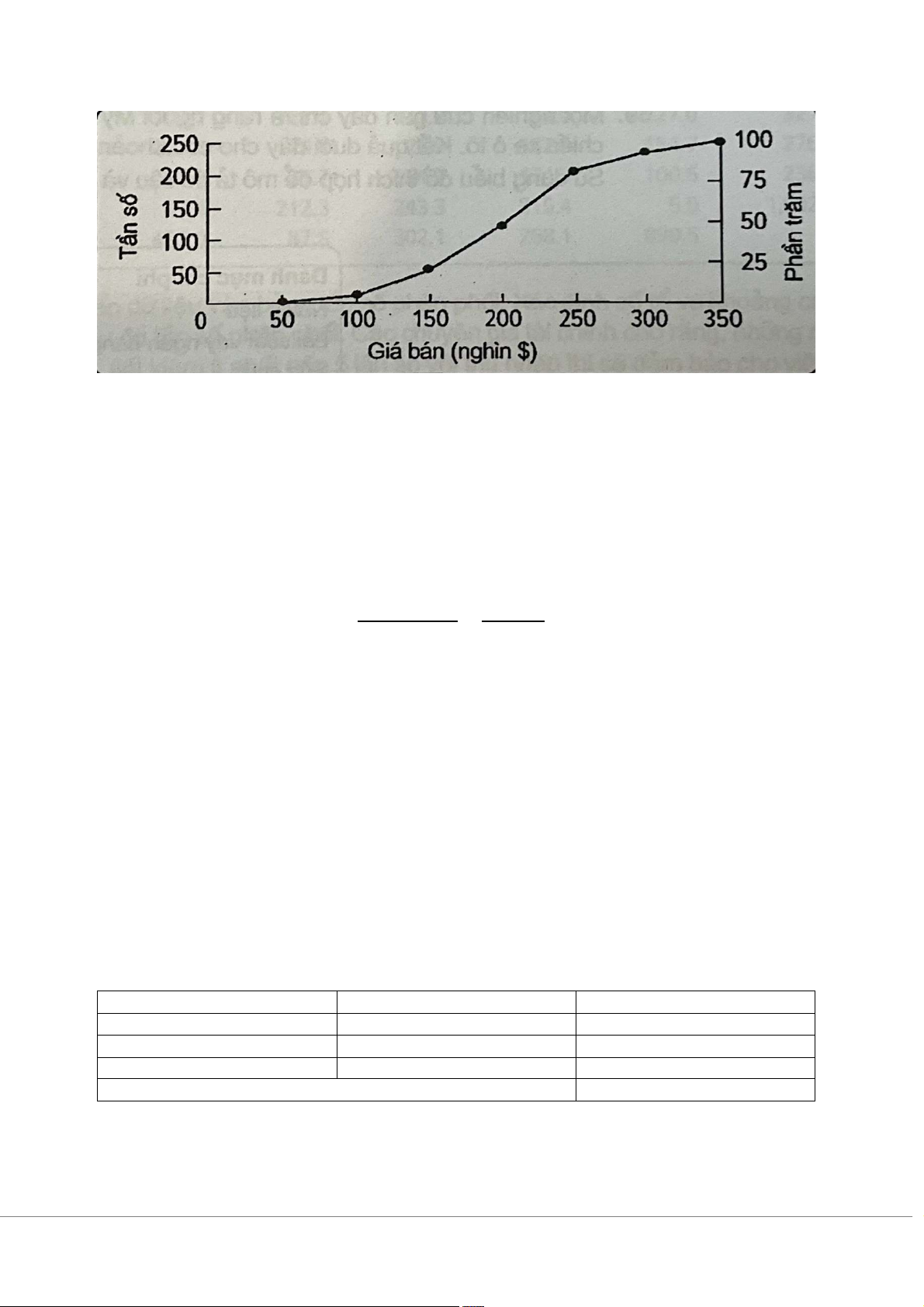
Bài 36/tr45: Biểu đồ dưới đây thể hện giá bán nhà trong tháng trước ở Sarasota, Florida
a/ Biểu đồ trên được được gọi là gì?
b/ Có bao nhiêu ngôi nhà được bán trong tháng qua
c/ Khoảng cách tổ bằng bao nhiêu?
d/ Khoảng 75% ngôi nhà được bán với giá nhỏ hơn bao nhiêu?
e/ 175 ngôi nhà được bán với giá nhỏ hơn bao nhiêu? 5 BÀI LÀM
a/ Biểu đồ trên được gọi là biểu đồ tần số tích lũy
b/ Có tần số cao nhất trên biểu đồ là 250 ứng mới giá bán là 350 nghìn đô ứng với + tổng số
ngôi nhà được bán là 250 ngôi nhà
Vậy có 250 ngôi nhà được bán trong tháng qua.
c/ Có 5 tổ là (0 đến 50; 50 đến 100; 100 đến 150; 150 đến 200; 200 đến 250) + ( , ' . , 3"*+4(3" , #$ !'5 4 5 ', '5
Vậy khoảng cách tổ bằng 50
d/ Khoảng 75% căn nhà được bán với giá dưới 250 nghìn $
e/ có 175 ngôi nhà nằm giữa 150 và 200. Đối chiếu xuống tương ứng với giá là 225 nghìn đô la
Vậy 175 ngôi nhà được bán với giá dưới 225 nghìn đô la PHẦN MỨC ĐỘ:
Bài 69/tr89: Công ty Split-A-Rail Fence chuyên cung cấp ba loại hàng rào cho các hộ gia đình ở
ngoại ô Seattle, Washington. Loại A có giá $5.00 mỗi foot, loại B có giá $6.50 mỗi foot, và loại C
(loại tốt nhất) giá $8.00 mỗi foot. Hôm qua, Split-A-Rail đã lắp đặt 270 feet của loại A, 300 feet
loại B và 100 feet loại C. Chi phí trung bình cho mỗi foot hàng rào được tính bằng bao nhiêu. BÀI LÀM Loại hàng rào Giá ($/foot)
Lắp đặt (foot) -Tần số A 5.00 270 B 6.50 300 C 8.00 100 n 670 6
67 , 86##9#,:';55 < =!5>?:-;'5 < @55>? :A;55 ? 255> -=5, -)2!B
Vậy chi phí trung bình cho mỗi foot hàng rào là $6,12
---------------------------------------------------------------------------------------------------------------------
Bài 70/tr89: Rolland Poust là sinh viên năm thứ hai của Trường Cao đẳng Kinh doanh tại Scandia
Tech. Học kỳ trước, Rolland đã tham gia các khóa học về thống kê và kế toán, mỗi khóa học 3 giờ
và đạt điểm A trong cả 2 khóa học. anh đã giành được điểm B trong khóa học lịch sử 5 giờ và điểm
B trong khóa học lịch sử dài 2 giờ về nhạc jazz. Ngoài ra, anh tham gia một khóa học kéo dài 1
giờ về các quy tắc của bóng rổ và đạt điểm A. Điểm trung bình của anh học kỳ là bao nhiêu? Giả
sử rằng anh ta nhận được 4 điểm cho điểm A, 3 điểm cho điểm B. Nên sử dụng mức độ trung tâm
nào trong trường hợp này? Công thức tính là gì? BÀI LÀM Khóa học Điểm Quy đổi Số giờ
Khóa học lịch sử dài 2 giờ về nhạc jazz B 3 2
Khoa học lịch sử dài 5 giờ B 3 5
Khoa học quy tắc của bóng rổ dài 1 giờ A 4 1
Khóa học thống kê dài 3 giờ A 4 3
Khóa học kế toán dài 3 giờ A 4 3 n 14
Điểm trung bình của Rolland Poust được tính bằng xông thức:
67 ,$ 86#$CD1$ E6#F G1HI$JKL$IM1$(.NL$.OJ #9# 9#:$PQ$R1S$JKL$IM1$(.NL$.OJ
#F TU#R$PQ$R1S$JKL$JVJ$(.NL$.OJ
% 67 , :@ < !>?:@ < '>?:& < 2> 2&? ,:&
= < @>? :& < @> !, @)'
Vậy điểm trung bình của Rolland Poust học kỳ này là 3,5 điểm
Mức độ trung tâm được sử dụng trong trường hợp này là: trung bình có trọng số, vì mỗi khóa học
có số giờ khác nhau, ảnh hưởng đến mức độ đóng góp vào điểm trung bình chung.
PHẦN ƯỚC LƯỢNG:
Bài 38/tr306: Phòng nhân sự của Electronics inc muốn sử dụng chương trình nha khoa như một
phần của gói phúc lợi. Câu hỏi đặt ra là số tiền trung bình mà một nhân viên và gia đình của họ 7
chi cho nha khoa trong một năm là bao nhiêu? Khảo sát gồm 45 nhân viên cho thấy số tiền trung
bình họ chi cho nha khoa trong năm trước là $1.820 với độ lệch chuẩn là $660
a/ Hãy xác định khoảng tin cậy 95% về số tiền trung bình chi cho nha khoa trong một năm của các gia đình.
b/ Từ kết quả khoảng tin cậy ở ý (a), chủ tịch Electronics inc cho biết có thể trả chi phí nha khoa
cho mỗi nhân viên là $1.700. Trung bình của tổng thể có thể có thể là $1.700 không? Vì sao? BÀI LÀM a/
- Khảo sát gồm 45 nhân viên -> # , &'
- Số tiền trung bình chi cho nha khoa trong năm trước là $1.820 -> 67 , 2A!5
- Độ lệch chuẩn là $660 -> W , --5
- Xác suất tin cậy là 95% % 2 4 X , 5)*' + Y-. /, 2)*-$
- 67 4 Y-0 √$Z [ Z 67 ? Y-0√$ % 2A!5 4 2)*- --5 \&' Z [ Z 2A!5$ ? 2)*- --5 \&' % 2-!=)2- Z [ Z !52!)A&
Vậy khoảng tin cậy 95% về số tiền trung bình chi cho nha khoa trong một năm của các gia đình là :2-!=)2-] !52!)A&> b/
Khoảng tin cậy 95% là :2-!=)2-] !52!)A&>
Ta thấy $1.700 nằm trong khoảng tin cậy này
Kết luận: Có thể có khả năng trung bình tổng thể là $1.700, vì nó thuộc khoảng tin cậy 95%. Điều
này có nghĩa là với 95% độ tin cậy mức $1.700 không bị loại trừ là giá trị trung bình thực sự.
---------------------------------------------------------------------------------------------------------------------
Bài 62/tr309: Bạn dự định tiến hánh một cuộc khảo sát để ước lượng tỷ lệ lao động có từ 2 công
việc trở lên. Bạn chọn độ tin cây 95% và chấp nhận phạm vi sai số là 2%. Một cuộc khảo sát thí
điểm cho thấy 5 trong số 50 người được hỏi có từ 2 công việc trở lên. Hãy xác định cỡ mẫu để ước
lượng tỷ lệ lao động có từ 2 công việc chở lên. BÀI LÀM
Độ tin cậy 95% % 2 4 X , 5)*' % X , 5)5'$ + $Y-./, $2)*-
Phạm vi sai số là 2% % ^2, 5)5! 8
Có 5 người trong tổng số 50 người được hỏi có từ 2 công việc trở lên % _ , 33(, 5)2 # , $Y-./._:2 4. _ , > 2) )*-.< 5)2:2 4 5)2> 5)5! ^ ., A-&)@- 2
Vì cỡ mẫu phải là số nguyên, nên n = 865
Vậy cần chọn mẫu gồm ít nhất 865 người để ước lượng tỷ lệ lao động có từ 2 công việc trở lên,
với độ tin cậy 95% và sai số không vượt quá 2% PHẦN KIỂM ĐỊNH
Bài 39/tr344: Tập đoàn đồng hồ Thụy Sỹ tuyên bố đồng hồ của họ không bao giờ chạy nhanh hay
chậm trong suốt một tuần. Nghiên cứu một mẫu gồm 18 đồng hồ đưa ra số liệu về thời gian đồng
hồ chạy nhanh hơn (+) hay chậm hơn (-) trong một tuần, tính bằng giây: -0,38 -0,20 -0,38 -0,32 +0,32 -0,23 +0,30 +0,25 -0,10 -0,37 -0,61 -0,48 -0,47 -0,64 -0,04 -0,20 -0,68 +0,05
Vậy mức ý nghĩa 0,05, có thể kết luận thời gian trung bình đồng hồ chạy nhanh hay chậm hơn 0
không? Hãy xác đinh p-value BÀI LÀM
Bước 1: Xác định vấn đề
`a4F [ , 5$:b$(1c#$Gd$ef1>4 T.S1$R1L#$T0g#R$eh#.$J.ij$#.L#.$.Lj$J.kI , 5 a':[$ l 5 Bước 2: Mức ý nghĩa + X , 5)5'
Nghiên cứu một mẫu gồm 18 đồng hồ + # , 2A
Độ lệch chuẩn mẫu (s) P , m∑(+"&+7)& $&', 5)@2!
Trung bình mẫu 67 , $∑+"2" $, 45)!@! n9:,$ 67 4 [ o ( ,45)!@! 4 5 P\# 5)@2! \ o 2A p 4@)2'A
Bước 3: Điều kiện bác bỏ a( qn9:q r T-. ($&') / Có: T-(.$&'), T(,'(<3. &', $ T(,(. ' 3 = / / 9
Tra bảng phân phối t với 17 bậc tự do T(,'(=.$3p !)225 vì T s !)225 nên nằm trong vùng bác bỏ
Có p-value , ! < t:n'=s @)2'A>
Vì uTu, @)2'A nằm giữa 2,898 và 3,646 nên p-value nằm giữa 0,005 và 0,001
+ t:n s 4@)2'A>p(,((3>(,.(( ,'5)55@
+ _ 4 CLvgw$ p ! < 5)55@ , 5)55-
Vì 0,006 < 0,05 nên ta bác bỏ a(
Kết luận: Với mức ý nghĩa là 5% có đủ bằng chứng để kết luận thời gian trung bình đồng hồ
chạy nhanh hoặc chậm khác không PHẦN XÁC SUẤT
Bài 22/tr225: Trong số 30 thành phố lớn nhất của Mỹ, thời gian đi làm một chiều trung bình đến
nơi làm việc là 25,8 phút. Thời gian đi làm một chiều dài nhất ở New York, với trung bình là 39,7
phút. Giả sử phân phối thời gian đi làm ở New York tuân theo phân phối chuẩn với độ lệch chuẩn là 7,5 phút
a/ Phần trăm thời gian đi làm ở thành phố New York ít hớn 30 phút là bao nhiêu?
b/ Phần trăm thời gian nằm trong khoảng từ 30 đến 35 phút là bao nhiêu?
c/ Phần trăm thời gian nằm trong khoảng từ 30 đến 50 phút là bao nhiêu? BÀI LÀM
Trong số 30 thành phố lớn nhất tại Mỹ + # , @5
Thời gian đi làm một chiều dài nhất ở New York với tung bình là 39,7 phút + [ , @*)=
Thời gian đi làm một chiều trung bình đến nơi làm việc là 25,8 phút + $[ , !')A Độ lệch chuẩn W , =)'$
a/ X là thời gian; 3xy:[ , @*)=] W., '-)!'> t:3 s @5>, t zY s @5 4 @*)=
=)'{ , t:Y s 42)!*@>, 2 4 t:Y r 2)!*@>, 2 4 5)*52' , 5)5*A' , *)A'|
Vậy phần trăm thời gian đi làm ở thành phố New York ít hơn 30 phút là 9,85%
b/ X là thời gian; 3xy:[ , @*)=] W , =)'> 10
t:@5 s 3 s @'>, t zL 4W[s 3 s e 4 [W{ , t z@5 4 @*)= =)'s Y s @' 4 @*)= =)'{
, t:42)!* s Y s 45)-@>, t:Y s 45)-@>4 t:Y s 42)!*>
, 2 4 t:Y s 5)-@>4 }2 4 t:Y s 2)!*>~ , 2 4 5)=@'= 4 2 ? 5)*52' , 5)2-'A , 2-)'A|
Vậy phần trăm thời gian đi làm nằm trong khoảng từ 30 đến 35 phút là 16,58%
c/ X là thời gian, 3xy:[ , @*)=] $W , =)'>
t:@5 s 3 s '5>, t zL 4W[s 3 s e 4 [W{ , t z@5 4 @*)= =)'s Y s '5 4 @*)= =)'{$$$$$$$$$$$
, t:42)!* s Y s 2)@=>, t:Y s 2)@=>4 t:Y s 42)!*>
, t:Y s 2)@=>4•2 4 t:Y s 2)!*>€, 5)*2&= 4 2 ? 5)*52' , 5)A2-! , A2)-!|
Vậy phần trăm thời gian đi làm nằm trong khoảng từ 30 đến 50 phút là 81,62% PHẦN MẪU:
Bài 21/tr272: Một tổng thể gồm 3 đơn vị: 1, 2 và 3.
a/ Sử dụng cách chọn hoàn lại, liệt kê tất cả các mẫu có thể với cỡ mẫu bằng 2 và tính trung bình của tất cả các mẫu.
b/ Tính trung bình của tổng thể và trung bình của các trung bình mẫu. Hãy so sánh 2 giá trị này.
c/ So sánh độ phân tán của phân phối của tổng thể và phân phối của các trung bình mẫu.
Mô tả hình dạng của 2 phân phối trên BÀI LÀM
a/ Sử dụng cạch chọn hoàn lại -> có @ < @ , *$mẫu
Tất cả các mẫu có thể với cơ mẫu = 2 (1;1) (1;2) (1;3) (2;1) (2;2) (2;3) (3;1) (3;2) (3;3) b/ Trung bình mỗi mẫu: (1;1) = 1 (1;2) = 1,5 (1;3) = 2 (2;1) = 1,5 (2;2) = 2 (2;3) = 2,5 (3;1) = 2 (3;2) = 2,5 (3;3) = 3
Tổng bình quân tổng thể [ , ∑+ ?,'>.>@, ! 11
Trung bình mẫu: [+7,∑+$,(',3×.)>(.×@)>B(. ,,3× ! .)>@>'
Vậy trung bình mẫu = trung bình tổng c/ So sánh độ phân tán:
Độ lệch chuẩn tổng thể W , m'?8:6 ? # # C 4 ' [ , >. m' @8:6 ? # # C 4 ',!>. 5)A2-'
Độ lệch chuẩn mẫu W+7,0 √$,(,<')√3., 5)'==&
Vậy trung bình mẫu có độ phát tán nhỏ hơn tổng thể
---------------------------------------------------------------------------------------------------------------------
Bài 22/tr272: Theo thông tin lưu trữ của Đại học Camford, sinh viên dành trung bình 5,5 giờ mỗi
tuần để chơi các môn thể thao. Độ lệch chuẩn của tổng thể là 2,2 giờ. Dựa trên một mẫu gồm 121
sinh viên, Healthy Lifestyles Incorpo (HLI) muốn áp dụng Định lý giới hạn trung tâm để đưa ra
các ước lượng khác nhau. Tính:
a/ Sai số trung bình chọn mẫu.
b/ Xác suất để HL lấy được một mẫu có giá trị trung bình từ 5 đến 6 giờ.
c/ Xác suất để lấy được một mẫu có giá trị trung bình từ 5,3 đến 5,7 giờ.
d/ Xác suất để lấy được một mẫu có giá trị trung bình lớn hơn 6,5 giờ. BÀI LÀM
Sinh viên dành trung bình 5,5 giờ mỗi tuần để chơi các môn thể thao + 67 , ')'
Độ lệch chuẩn tổng thể là 2,2 giờ + $W , !)!$
Dựa trên một mẫu gồm 121 sinh viên + # , 2!2
a/ Sai số trung bình chọn mẫu , W+7,m0&$,m.,.&'.', 5)!
Vậy sai số trung bình (bình quân) chọn mẫu là 0,2
b/ Gọi X là thời gian; 3xy:[ , ')'] $W , !)!>
+$ 3 là thời gian trung bình 3•xy ‚[ , ')']$W.,0& $,.,.&'.'ƒ
t:' s 3•s ->, t „… ' 4 ')' os Y s- 4 ')' ‡ , t:4!)' s Y s !)'> m!)!.2!2 m!)!.2!2 o†
, t:Y s !)'>4 t:Y s 4!)'>, t:Y s !)'>4}2 4 t:Y s !)'>~
, 5)**@A 4 :2 4 5)**@A>, 5)*A=- , *A)=-| 12
Vậy xác suất để HL lấy được một mẫu có giá trị trung bình từ 5 đến 6 giờ là 98,76%
c/ Gọi X là thời gian; 3xy:[ , ')'] $W , !)!>
+$ 3 là thời gian trung bình 3•xy ‚[ , ')']$W.,0& $,.,.&'.'ƒ
t:')@ s 3•s ')=>, t „… ')@ 4 ')' os Y s')= 4 ')' ‡ , t:42 s Y s 2> m!)!.2!2 m!)!.2!2 o†
, t:Y s 2>4 t:Y s 42>, t:Y s 2>4}2 4 t:Y s 2>~
, 5)A&2@ 4 :2 4 5)A&2@>, 5)-A!- , -A)!-|
Vậy xác suất để lấy được một mẫu có giá trị trung bình từ 5,3 đến 5,7 giờ là 68,26%
d// Gọi X là thời gian; 3xy:[ , ')'] $W , !)!>
+$ 3 là thời gian trung bình 3•xy ‚[ , ')']$W.,0& $,.,.&'.'ƒ
t:3•r -)'>, t „…Y r-)' 4 ')' ‡ , t:Y r '>, 5 , 5| m!)!.2!2 o†
Vậy xác suất để lấy được một mẫu có giá trị trung bình lớn hơn 6,5 giờ là 0%
---------------------------------------------------------------------------------------------------------------------
Bài 23/tr272: Công ty eComputers Inc. vừa mới thiết kế một mẫu máy tính xách tay mới. Quản
lý của công ty muốn định giá cho mẫu mới này. Hai công ty nghiên cứu thị trường đã được liên hệ
và yêu cầu chuẩn bị một chiến lược định giá. Công ty nghiên cứu thị trường thứ nhất, Marketing-
Gets-Results đã thử nghiệm máy tính xách tay bằng cách chọn ngẫu nhiên 50 khách hàng từ tổng
thể người tiêu dùng có kế hoạch mua máy tính mới này trong năm tới. Công ty nghiên cứu thị
trường thứ hai, Marketing-Reaps-Profits, thử nghiệm máy tính mới với 200 khách hàng đã từng
dùng máy tính xách tay. Kết quả nghiên cứu của công ty nào hữu ích hơn? Giải thích tại sao? BÀI LÀM Công ty thứ nhất:
- Mẫu khảo sát: 50 người có kế hoạch mua máy tính xách tay trong năm tới. - Ưu điểm:
o Đây là đối tượng khách hàng tiềm năng trực tiếp — những người sẽ đưa ra quyết
định mua trong tương lai gần.
o Phù hợp với mục tiêu định giá sản phẩm để tối ưu khả năng tiếp cận thị trường.
- Hạn chế: Mẫu nhỏ (50 người), có thể ảnh hưởng đến độ tin cậy thống kê nếu không đại diện tốt. Công ty thứ hai: 13
- Mẫu khảo sát: 200 người đã từng sử dụng máy tính xách tay (không rõ có còn nhu cầu mua hay không). - Ưu điểm:
o Mẫu lớn hơn (200 người), có thể có nhiều trải nghiệm về sản phẩm, đưa ra ý kiến
chi tiết hơn về tính năng, giá trị. - Hạn chế:
o Không nhất thiết là người có nhu cầu mua máy tính trong thời gian tới → ít liên
quan hơn đến việc xác định mức giá phù hợp với thị trường hiện tại. Kết luận:
- Nghiên cứu của công ty thứ nhất hữu ích hơn cho việc định giá mẫu máy tính mới, vì họ
khảo sát đúng đối tượng mục tiêu: những người có kế hoạch mua máy tính trong tương lai gần.
- Mặc dù công ty thứ hai có mẫu lớn hơn, nhưng không tập trung đúng vào nhu cầu thực tế
hiện tại, nên ít phù hợp hơn với mục tiêu định giá thị trường. PHẦN CS:
Bài 53/tr521: Ban quản lý các cửa hàng của Ingalls Super Discount, với một số cửa hàng ở khu
vực thành phố Oklahoma, muốn xây dựng một chỉ số hoạt động kinh tế cho khu vực đô thị. Họ
cho rằng, nếu chỉ số cho thấy nền kinh tế đang tăng trưởng chậm lại, hàng tồn kho nên được giữ ở mức thấp.
Ba chuỗi dữ liệu được xem là những yếu tố dự báo phù hợp cho hoạt động kinh tế gồm: doanh số
bán lẻ trong khu vực, tiền gửi ngân hàng và việc làm. Các sữ liệu này có thể được thu thập hằng
tháng bởi Chính phủ Mỹ. Doanh số bán lẻ sẽ được tính quyền số là 40%, tiền gửi ngân hàng là
35% và việc làm là 25%. Số liệu điều chỉnh theo mùa trong 3 tháng đầu năm là: Tháng Doanh số bán lẻ Tiền gửi ngân hàng Việc làm (triệu $) (tỷ $) (nghìn người) Tháng 1 8,0 20 300 Tháng 2 6,8 23 303 Tháng 3 6,4 21 297
Tính chỉ số hoạt động kinh tế cho mỗi tháng, sử dụng tháng 1 làm kỳ gốc BÀI LÀM
Doanh số bán lẻ: quyền số 40%
Tiền gửi ngân hàng: quyền số 35% Việc làm: quyền số 25%
- Tính chỉ số từng tháng (lấy tháng 1 làm mốc bằng 100):
+ Tháng 2: Doanh số bán lẻ: (6,8/8,0) x 100 = 85 14
Tiền gửi ngân hàng; (3/20) x 100 = 115
Việc làm: (303/300) x 100 = 101
+ Tháng 3: Doanh số bán lẻ: (6,4/8,0) x 100 = 80
Tiền gửi ngân hang: (21/20) x 100 = 105
Việc làm: (297/300) x 100 = 99 - Tính chỉ số kinh tế:
+ Tháng 1: (100 x 0,4) + (100 x 0,35) + (100 x 0,25) = 100
+ Tháng 2: (85 x 0,4) + (115 x 0,35) + (101 x 0,25) = 99,5
+ Tháng 3: (80x 0,4) + (105 x 0,35) + (99 x 0,25) = 93,5 Kết quả: Tháng Chỉ số kinh tế 1 100 2 99,5 3 93,5
---------------------------------------------------------------------------------------------------------------------
Bài 54/tr521: Bảng sau đây cung cấp thông tin về chỉ số giá tiêu dùng (kỳ gốc là giai đoạn 1982
– 1984) và mức lương thực lĩnh hằng thàng của Bill Martin, một nhân viên của Ford Motor Corporation. Chỉ số giá tiêu dùng
Lương thực lĩnh hằng tháng Năm (1982 – 1984 =100) của Bill Martin ($) 1982 - 1984 100,0 600 2018 251,107 7000
a/Sức mua của đồng đô la năm 2018 là bao nhiêu, dựa trên kỳ gốc là giai đoạn 1982 – 1984
b/ Xác định thu thập “thực tế” hằng tháng của ông Martin trong năm 2018 BÀI LÀM
a/ Khi chỉ số giá tiêu dùng tẳng thì người người tiêu dùng sẽ phải chi trả nhiều hơn cho cùng một
lượng hàng hóa nên sức mua sẽ giảm
+ Sức mua năm 2018 ,DEỉG:ốGDIE#ỉGáG:KốG#êIM#GáGNK#ùê$MIGGN'ùB$<. IG & $ 'B ă"< G P . G (( 'D G R'()&*'()+ (DQR&,')) )
< $ˆ‰J$IgL$#ŠI$2*A! 4 2*A& 15 ,$255)5 !'2)25= < 2 , 5)@*A
Vậy sức mua của 1 đô-la năm 2018 xấp xỉ bằng 0,398 đô la của năm 1982 -1984
b/ Thu nhập thực tế là thu nhập đã được điều chỉnh theo lạm phát, cho biết sức mua thực sự của
đồng tiền. Để tính thu nhập thực tế thì cần điều chỉnh thu nhập danh nghĩa theo sự thay đổi chỉ số giá tiêu dùng
+ Thu nhập thực tế của Martin năm 2018 ,$ TETỉGE:ỉôG:GI ốG #áG I# K áG#ê K# M ê GN MG ù N $ ù I $ G' IG B $<.& ă"G ' . B ( < ' P
<< $n.g$#.k_$‹L#.$#R.ŒL$#ŠI$$!52A ,$255)5
!'2)25= < =555 , !=A=)-'$:B>
Vậy thu nhập “thực tế” của ôn Martin trong năm 2018 là khoảng 2787,65 $
---------------------------------------------------------------------------------------------------------------------
Bài 55/tr521: Giả sử chỉ số giá sản xuất và doanh số của các nhà phân phối bán buôn của Hoskin năm 2006 và 2018 là: Năm Chỉ số giá sản xuất Doanh số ($) 2006 160,5 2400000 2018 204,0 3500000
Doanh số thực tế (còn gọi là doanh số giảm phát) của Hoskin trong hai năm là bao nhiêu? BÀI LÀM Năm 2006:
Doanh số thực tế năm 2006 ,.P('()((,(
3< 255 , 2;&*';@!A)-! ($) Năm 2018:
Doanh số thực tế năm 2018 = ,@3(.((P(,( (< 255 , 2;=2';-A-)!= ($)
Vậy doanh số thực tế năm 2006 và năm 2018 lần lượt là 2;&*';@!A)-! ($); 2;=2';-A-)!= ($) 16 PHẦN DSTG:
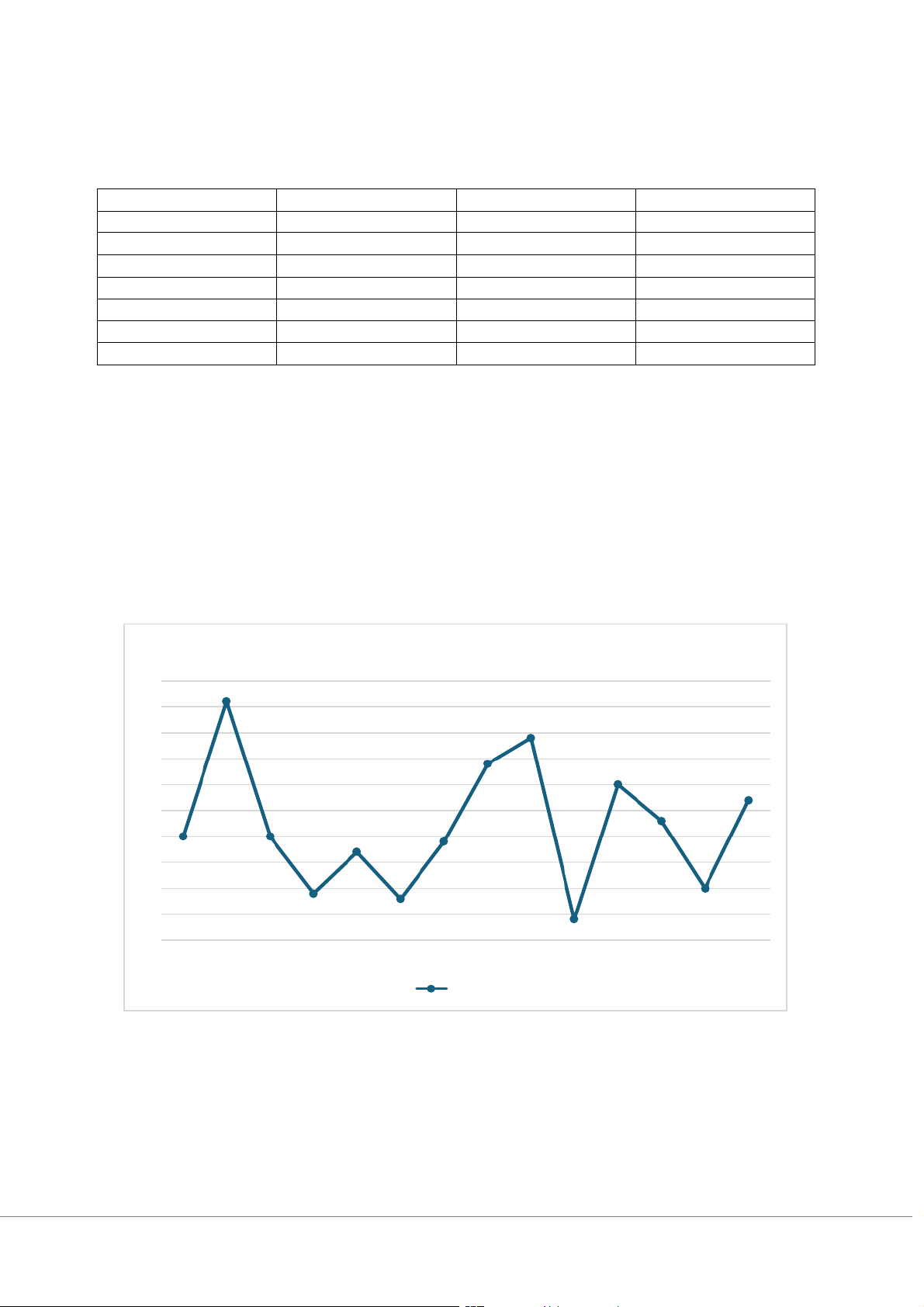
Bài 30/tr566: Sử dụng chuỗi thời gian dưới đây, trả lời các câu hỏi sau: Thời kỳ Nhu cầu Thời kỳ Nhu cầu 1 20 8 34 2 46 9 39 3 20 10 4 4 9 11 30 5 17 12 23 6 8 13 10 7 19 14 27
a/ Vẽ đồ thị chuỗi thời gian. Bạn quan sát thấy điều gì?
b/ Tính các giá trị dự báo có thể bằng san bằng mũ với hệ số san bằng mũ :X> là 0,3
c/ Tính các giá trị dự báo có thể bằng san bằng mũ với hệ số san bằng mũ :X> là 0,7
d/ Tính MAD cho mỗi mô hình dự báo trên
e/ Bạn chọn mô hình dự báo nào? Tại sao? BÀI LÀM a/ Vẽ đồ thị Nhu cầu 50 45 40 35 30 25 20 15 10 5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Nhu cầu
Điều mà nhận ra khi quan sát đồ thị: 17
Biểu đồ cho thấy nhu cầu thay đổi khá thất thường qua các thời kỳ — có những giai đoạn tăng
mạnh và giảm mạnh đột ngột, không theo một xu hướng rõ ràng. Điều này cho thấy dữ liệu có
biến động mạnh, không có xu hướng tuyến tính rõ ràng (tăng hoặc giảm đều). b/
Giá trị dự báot+1 = Giá trị dự báot + α(sai số dự báot)
Sai số dự báo = Giá trị thực tế - Giá trị dự báo
Với hệ số san bằng mũ 0,3
Giả sử giá trị dự báo thời kì 2 là 20
-> sai số dự báo thời kì 2 = Giá trị thực tế - Giá trị dự báo = 46 – 20 = 26
thời kì nhu cầu giá trị dự báo sai số dự báo 1 20 2 46 20 26 3 20 27,8 -7,8 4 9 25,46 -16,46 5 17 20,522 -3,522 6 8 19,465 -11,465 7 19 16,026 2,974 8 34 16,918 17,082 9 39 22,043 16,957 10 4 27,13 -23,13 11 30 20,191 9,809 12 23 23,134 -0,134 13 10 23,094 -13,094 14 27 19,165 7,835 c/
Với hệ số san bằng mũ 0,7
Giả sử giá trị dự báo thời kì 2 là 20
-> sai số dự báo thời kì 2 = Giá trị thực tế - Giá trị dự báo = 46 – 20 = 26 18
thời kì nhu cầu giá trị dự báo sai số dự báo 1 20 2 46 20 26 3 20 38,2 -18,2 4 9 25,46 -16,46 5 17 13,938 3,062 6 8 16,081 -8,081 7 19 10,424 8,576 8 34 16,427 17,573 9 39 28,728 10,272 10 4 35,918 -31,918 11 30 13,576 16,424 12 23 25,073 -2,073 13 10 23,622 -13,622 14 27 14,087 12,913
d/ Với hệ số san bằng mũ 0,3 MAD = ∑|#$%ố| (
MAD = )*+,,.+/*,0*+1,2))+//,0*2+),3,0+/,,4.)+/*,32,+)1,/1+3,.43+4,/10+/1,430+,,.12 /1 MAD = 12,02
- Với hệ số san bằng mũ 0,7 MAD = ∑|#$%ố| ( MAD =
)*+/.,)+/*,0*+1,4*)+.,4./+.,2,*+/,,2,1+/4,),)+1/,3/.+/*,0)0+),4,1+/1,*))+/),3/1 /1 MAD = 14,244
e/ Chọn mô hình với X , 5)@ vì:
- MAD thấp hơn • sai số trung bình nhỏ hơn
- Dữ liệu dao động mạnh, nên α\alphaα nhỏ giúp làm mượt biến động, tránh phản ứng quá
mức với dao động bất thường.
---------------------------------------------------------------------------------------------------------------------
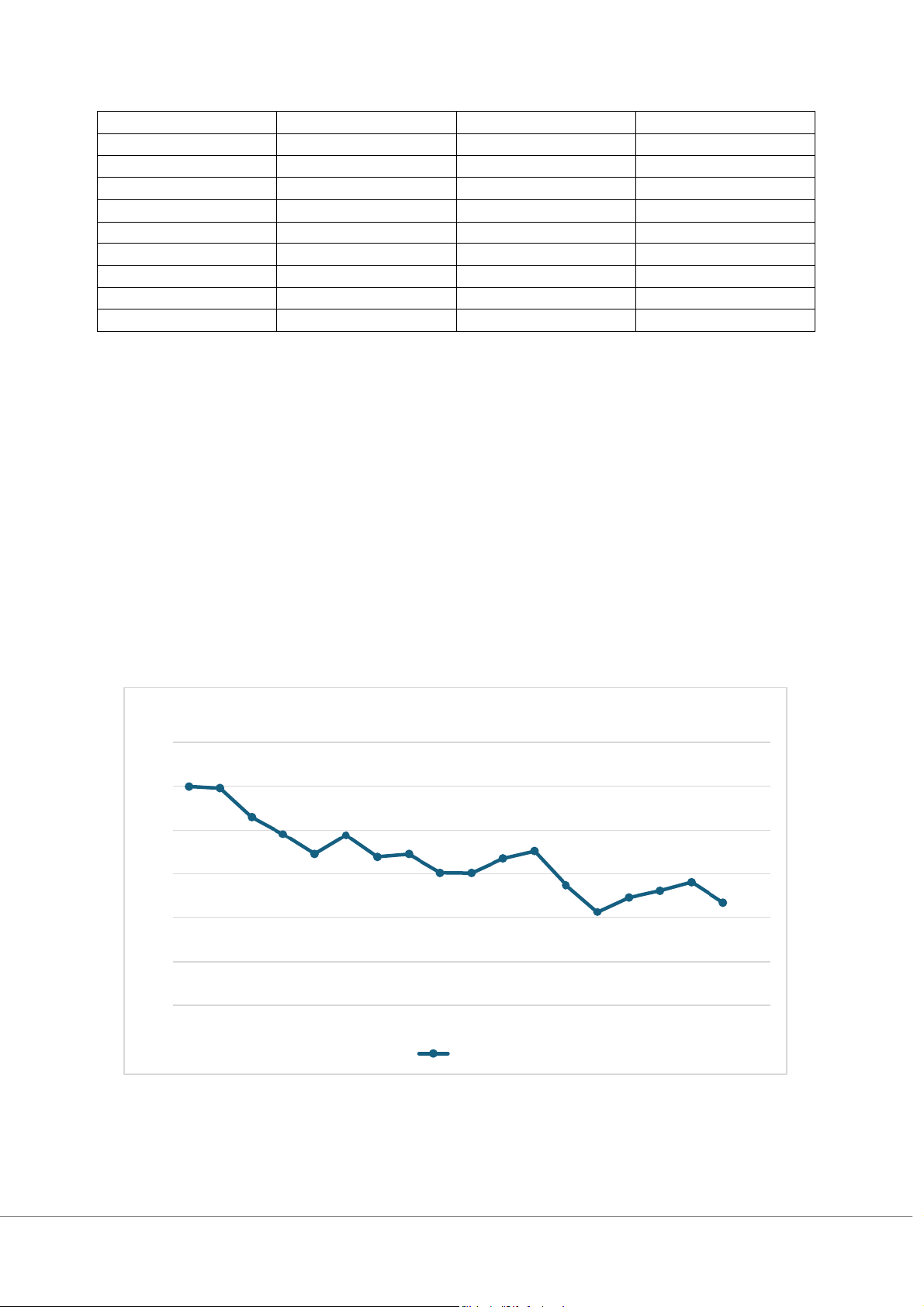
Bài 31/tr566: Sử dụng chuỗi thời gian dưới đây, trả lời các câu hỏi sau: 19 Thời kỳ :T> Nhu cầu :j#> Thời kỳ :T> Nhu cầu :j#> 1 998 10 604 2 990 11 670 3 859 12 703 4 781 13 550 5 691 14 427 6 776 15 493 7 677 16 524 8 690 17 563 9 605 18 471
a/ Vẽ đồ thị với dữ liệu trên.
b/ Dựa vào đồ thị, hãy mô tả thành phần của chuỗi thời gian.
c/ Với chuỗi thời gian này, tại sao dự báo bằng mô hình xu thế là phù hợp?
d/ Đánh giá mô hình dự báo xu thế bằng quy hồi tuyến tính đơn. Tính MAD.
e/ Mức thay đổi hằng năm về doanh số được dự báo là bao nhiêu.
f/ Dự báo doanh số cho ba thời kỳ tiếp theo.
g/ Theo nhận định của bạn, các dự báo có “tốt” không? Bạn sẽ đưa ra giả định nào cùng với dự báo của mình? BÀI LÀM a/ Vẽ đồ thị:
Nhu cầu qua các thời kì (1-18) 1200 1000 800 600 400 200 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Nhu cầu 20