Bài tập nhóm 3 môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐẠI HỌC KINH TẾ QUỐC DÂN BÀI TẬP NHÓM
MÔN: THỐNG KÊ TRONG KINH TẾ KINH DOANH NHÓM 3
LỚP HỌC PHẦN: TKKD1129(224) – 08
GIẢNG VIÊN: TS. CHU THỊ BÍCH NGỌC HÀ NÔI, NĂM 2025 DANH SÁCH SINH VIÊN STT Họ và tên Mã sinh viên 1Bùi Bích Ngọc 11243125 2Hà Hoàng Nhi 11243131
3Ngô Thị Bích Ngọc 11243126 4Trần Đỗ Trà My 11243121 5Nguyễn Trung Kiên 11243086
6Nguyễn Đức Trí Kiên 11243085 I. Bài 1 Bài 14/ trang 15: BÀI LÀM
- Thang đo định danh ví dụ như màu sắc xe ô tô ( đỏ, xanh, trắng ) - Nguồn: MarkLines
- Thang đo thứ bậc ví dụ như xếp hạng khách sạn ( 1 sao đến 5 sao ) – Nguồn Forbes
- Thang đo khoảng ví dụ như nhiệt dộ ( 20°C, 30°C )
- Thang đo tỷ lệ ví dụ như lương hàng tháng ( 3000$, 5000$ ) – Nguồn BLS
II. Phân tổ thống kê Bài 32/ trang 44: BÀI LÀM
a. Ta có: 25≤36≤26
⇒ Nên chọn số tổ là 6 b. Ta có: I≥15−3 6=¿ 2
Vậy ta nên chọn khoảng cách tổ là 2 c. Ta có: 2×6=12 15−3=12
Từ đó ta thấy không có phần chênh lệch nên ta nên chọn giới hạn dưới của tổ đầu tiên là 3 d. Thời gian nắm cổ phiếu Tần số Từ 3→ dưới 5 2 5→ 7 7 7→ 9 11 9→ 11 7 11→ 13 7 13→ 15 2 e. Ta có: Me = 8 Mo = 2 x = 8,42 Ta thấy Mo = Me ¿ x
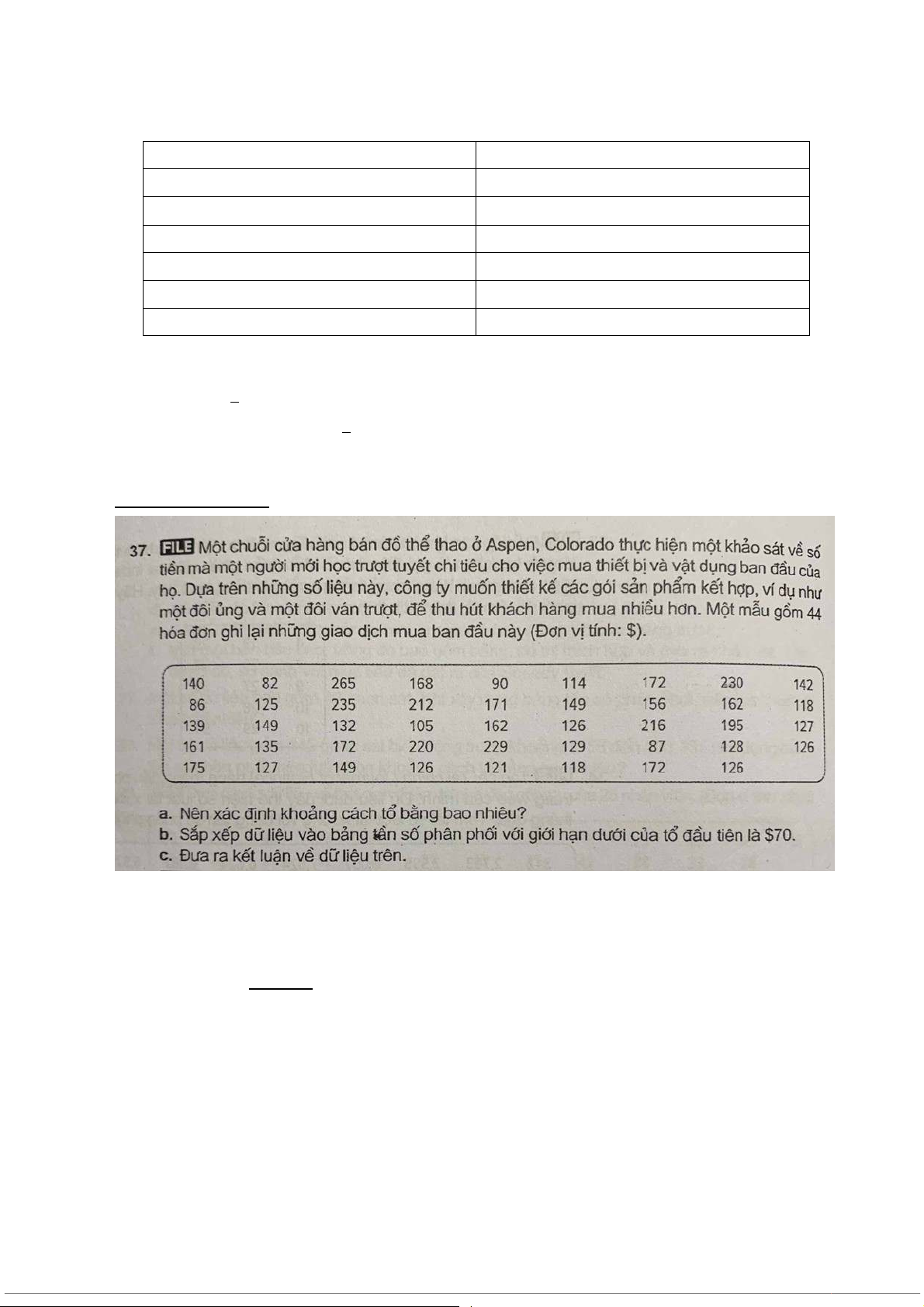
⇒ Phân phối dãy số lệch phải nhẹ Bài 37/ trang 46: BÀI LÀM
a. Ta có: 25≤36≤26
⇒ Nên chọn số tổ là 6 − Ta có: I≥265 82 6≈ 30,5
Vậy ta nên chọn khoảng cách tổ là 35
b. Với giới hạn dưới tổ đầu tiên là 70 ta có bảng: Số tiền chi tiêu Tần số Từ 70 → dưới 105 4 105→140 17 140 →175 14 175→210 2 210→245 6 245→280 1 c.
- Phần lớn khách hang chi tiêu trong khoảng từ 105→dưới 140 đô và có ít
khách tiêu 245 đô trở lên
- Nên thiết kế các gói sản phẩm có giá từ 105→140 đô III. Mức độ Bài 77/ trang 90: BÀI LÀM
a. Vì đó là danh sách tất cả các trường đại học công lập ở bang nên đó là thông tin của tổng thể
b. Số lượng hồ sơ đăng kí là ≈ 25097
c. Sắp xếp lại dự liệu:
1178 3600 12605 16607 16961 19423 20491
22101 24283 36287 39598 44969 67524 ⇒ Trung vị là 20491
d. Mỗi số chỉ xuất hiện 1 lần ⇒ không có mốt
e. Nên sử dụng trung vị vì nó ít bị ảnh hưởng bởi các giá trị cực đại, cực
tiểu hơn so với trung bình
f. σ= √σ2= √∑(xi−x ) N=¿ 17088 hồ sơ Bài 78/ trang 90: BÀI LÀM
- Trung bình số cân các giám đốc bị thừa là:
x=3×14+9×42+15×58+21×28+27×8 150=13,96 - Độ lệch chuẩn: √ 9−13,96 2×42
15−13,96 2×58+(21−13,96)2×28+(27−13,96)2×8
S2=√(3−13,96)2×14+( ) +( ) 150−1 = 6,07 IV. Ước lượng Bài 39/ trang 307: BÀI LÀM
- Theo đề bài ta có: 46≤ μ ≤54
Mà trung bình của mẫu là x = 50 ⇒ εx=4 Khoảng tin cậy 95% z ⇒ α = 1,96 2 √σ2
⇒εx=zα √n 2
⇔4=1,96×16√n ⇔ n ≈ 61,47 Vậy cỡ mẫu là 62 Bài 63/ trang 309: BÀI LÀM
a. Cỡ mẫu ước lượng khi tỷ lệ kế toán viên thay đổi chỗ làm việc trong vòng 3 năm: ¿
n 1,962×0,21× (1−0,21 ) 0,032≈ 708,13
n nguyên nên cỡ mẫu là 709
b. Nếu không có ước lượng của nghiên cứu trước thì ta sẽ chọn tỉ lệ ước lượng là 0,5 Khi đó ta có:
n¿1,962×0,5×(1−0,5) 0,032≈ 1067,11
n là số nguyên nên cỡ mẫu là 1068 V. Kiểm định Bài 40/ trang 344 BÀI LÀM
Giả thuyết tỷ lệ vốn trung bình có cao hơn 4,5% không? ⇒ H0: u¿4,5 H1: u¿4,5 Trung bình:
x=4,63+4,15+4,76+4,7×2+4,65+4,52×2+5,06+4,42+4,51+4,24 12 ≈4,57 Độ lệch chuẩn:
Tqs=4,57−4,5 ≈ Ta có: 0,24 1,01 √12
Với mức ý nghĩa là 0,05 ⇒ tαn−1=1,796 Ta có: n−1 Tqs<tα
⇒ Không thoả mãn điều kiện bác bỏ H0 nên H0 đúng, H1 sai VI. Xác suất Bài 15/ trang 23: BÀI LÀM ¿ − a. z 35 29,81 9,31≈ 0,557
Tra bảng ở phụ lục B_3 ta thấy xác suất người có mức lương từ trung
bình đến 35$ một giờ là 21,23%
b. Từ phần a ⇒ Người có mức lương cao hơn 35$ một giờ là 50%−21,23%=28,77% c. z=20−29,81 9,31=−1,05
⇒ Xác suất người đó có mức lương từ trung bình tới 20$ một giờ là 35,31%
⇒ Xác suất người có lương thấp hơn 20$ một giờ là 50%−35,31%=14,69% VII. Mẫu Bài 27/ trang 273: BÀI LÀM a. Trung bình tổng thể: μ=79+64+84+82+92+77 6=¿ 79,67
b. Có thể lấy được số mẫu là: k=6! 2! ×(6−2)!=15
c. Liệt kê các mẫu và tình trung bình từng mẫu Mẫu Giá trị trung bình mẫu 79, 64 71,5 79, 84 81,5 79, 82 80,5 79, 92 85,5 79, 77 78 64, 84 74 64, 82 73 64, 92 78 64, 77 70,5 84, 82 83 84, 92 88 84, 77 80,5 82, 92 87 82, 77 79,5 92, 77 84,5
d. Trung bình của các trung bình mẫu
x=71,5+81,5+80,5+85,5+78+74+73+78+70,5+83+88+80,5+87+79,5+84,5 15 = 79,67
Ta thấy được trung bình của các trung bình mẫu bằng với trung bình tổng thể e.
- Cách tính điểm này công bằng nếu được chọn ngẫu nhiên
- Nếu loại bỏ điểm thấp mhất là 64 ra khỏi tổng thể thì trung bình tổng thể sẽ là μ=82,2
→ Phương pháp này có thể gây sai lệch nếu tổng thể bị thay đổi. Nên giữ
nguyên tổng thể để đảm bảo tính đại diện Bài 28/ Trang 273: BÀI LÀM
a. Có thể lấy được số mẫu gồm 2 giao dịch viên từ tổng thể có 5 giao dịch viên là: C(5,2) =10 Mẫu Giá trị trung bình mẫu 2, 3 2,5 2, 5 3,5 3, 5 4 3, 3 3 5, 5 5 2, 3 2,5 2, 5 3,5 3, 5 4 5, 3 4 3, 5 4
b. Trung bình của tổng thể: μ=2+3+5+3+5 5=¿ 3,6
Trung bình các trung bình mẫu: x=2,5+3,5+4+3+5 5=¿ 3,6
Vậy trung bình của các trung bình mẫu bằng trung bình tổng thể Bài 29/ trang 273: BÀI LÀM a.
Có thể rút ra được số mẫu gồm 2 kỹ thuật viên từ tổng thể có 5 kỹ thuật viên là: C(5,2)=10 b. Mẫu Giá trị trung bình 4, 3 3,5 4, 5 4,5 4, 3 3,5 4, 2 3 3, 5 4 3, 3 3 3, 2 2,5 5, 3 4 5, 2 3,5 3, 2 2,5 + + + + + + c.
Trung bình của tổng thể: μ=3.5+4.5 3.5 3 4 3+2.5 4+3.5 2.5 10=¿ 3,4
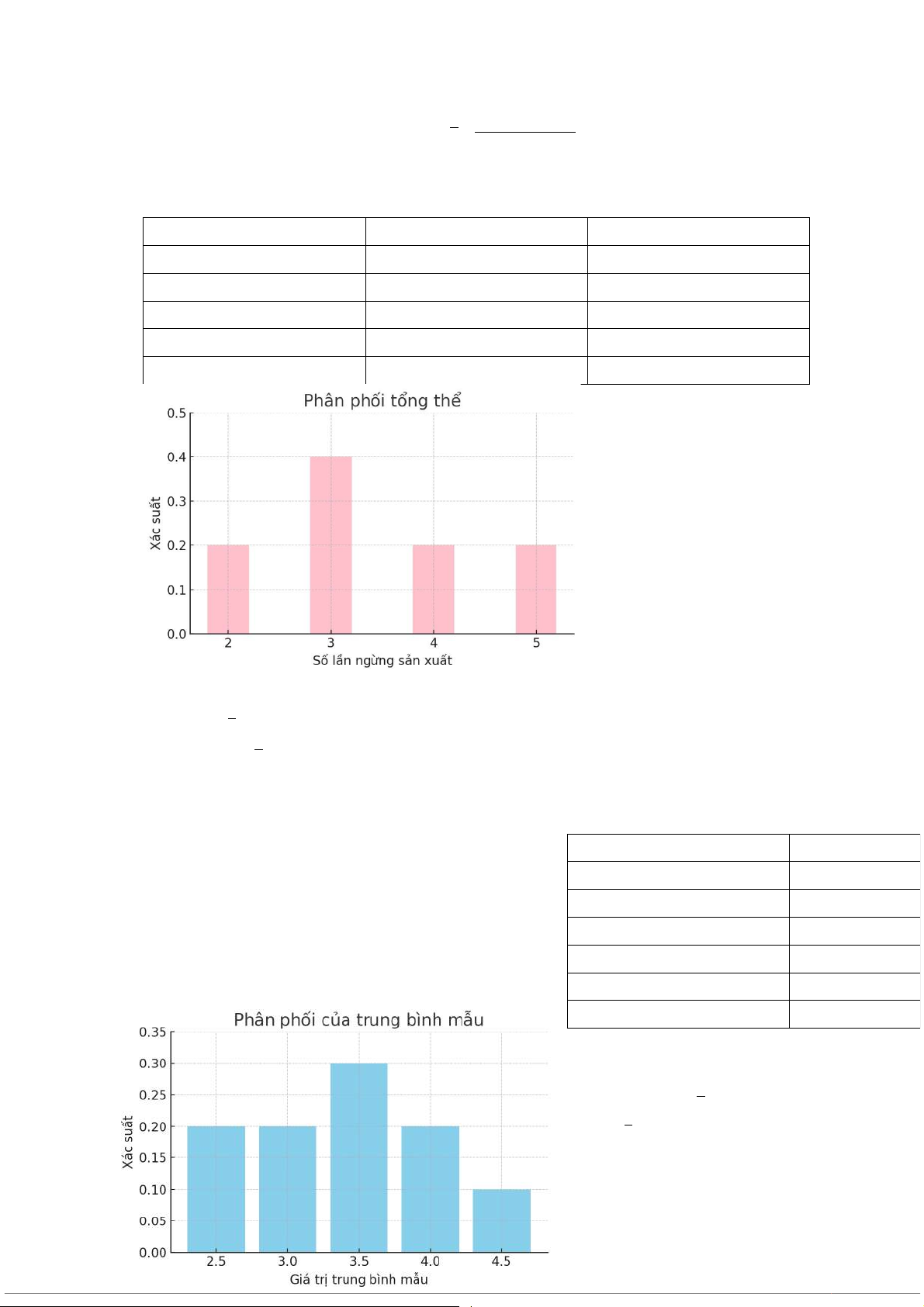
Trung bình các trung bình mẫu: x=4+3+5+3+2 5=¿ 3,4 d. - Phân phối tổng thể
Số lần ngừng sản xuất Tần số Xác suất 2 1 0,2 3 2 0,4 4 1 0,2 5 1 0,4 5 1 Mo=3 Me=3 x=3,4 Mo=Me< x
Biểu đồ lệch phải nhẹ
- Phân phối trung bình mẫu Trung bình mẫu Số lượng 2,5 2 3 2 3,5 3 4 2 4,5 1 10 Mo=3,5 Me=3,5 x=3,4
 x<Mo=Me
Biểu đồ phân phối lệch trái nhẹ VIII. Chỉ số Bài 17/ trang 518: BÀI LÀM
2010 làm gốc → p0=¿ 29,437
Công thức chỉ số đơn: p=pt × 100 p0 Năm
Doanh số nội địa (triệu Chỉ số đơn $) 2011 12,907 43,8 2012 29,830 101,3 2013 31,910 108,4 2014 34,782 118,2 2015 35,687 121,2 2016 37,811 128,4 2017 39,863 135,4 2018 41,884 142,3
→ Doanh số bán hàng nội địa có xu hướng tăng trưởng ổn định từ 2010 đến
2018, trừ năm 2011 có sự sụt giảm đáng kể, từ sau 2011 doanh số tăng trưởng liên tục Bài 18/ trang 518: BÀI LÀM
Sử dụng giai đoạn 2010-2012 làm kì gốc → p0=∑p 3 i =29,437+12,907+29,830 3=24,058 Năm
Doanh số nội địa (triệu Chỉ số đơn $) 2013 31,910 132,6 2014 34,782 144,6 2015 35,687 148,3 2016 37,811 157,2 2017 39,863 165,7 2018 41,884 174,1 Bài 19/ trang 518: BÀI LÀM
2010 làm gốc→ p0=32,124
Công thức tính chỉ số đơn: p=pt × 100 p0 Năm
Doanh số quốc tế (triệu Chỉ số đơn $) 2011 36,107 112,4 2012 37,394 116,4 2013 39,402 122,7 2014 39,584 123,1 2015 34,387 107,0 2016 34,079 106,1 2017 36,587 113,9 2018 39,697 123,6
→ Doanh số bán hàng quốc tế tăng trưởng không đồng đều từ năm 2010 đến
năm 2018. Từ 2011→ 2014 có sự tang nhẹ sau đó giảm đáng kể đến 2016, từ
sau 2016 d0anh số tăng mạnh đáng kể Bài 20/ trang 518: BÀI LÀM
Sử dụng giai đoạn 2010-2012 làm kỳ gốc: → p0=∑p 3 i =32,124+36,107+37,394 3=35,208 Năm
Doanh số quốc tế (triệu Chỉ số đơn $) 2013 39,402 111,9 2014 39,548 112,3 2015 34,387 97,7 2016 34,079 96,8 2017 36,587 103,9 2018 39,697 112,7 Bài 22/ trang 518: BÀI LÀM
Sử dụng giai đoạn 2010-2012 làm gốc → p0=∑p 3 i
=114×0+117×9+127×6 3=119,8 Năm Số lao động (nghìn Chỉ số đơn người) 2013 128.1 106,9 2014 126.5 105,6 2015 127.1 106,1 2016 126.4 105,5 2017 134.0 111,9 2018 135.1 112,8
IX. Dãy số thời gian Bài 27/ trang 565: BÀI LÀM a.
Từ đồ thị ta thấy, chuỗi thời gian thể hiện sự dao động rõ rệt theo từng thời kỳ
của nhu cầu. Có 1 xu hướng tăng nhẹ giai đoạn đầu ( từ kỳ 1→6 ), sau đó giao
động mạnh không theo quy luật rõ rang, không có xu hướng tăng hoặc giảm dài hạn rõ rệt.
b. Trung bình trượt 5 mức độ nên có thể tính các giái trị dự báo từ thời kỳ 6 →16 Thời kỳ Giá trị dự báo 6 104+132+117+120+104 5=115,5 7 132+117+120+104+141 5=122,8 8 117+120+104+141+120 5=120,4 9 120+104+141+120+136 5=124,2 10 104+141+120+136+109 5=122 11 141+120+136+109+143 5=129,8 12 120+136+109+143+142 5=130 13 136+109+143+142+109 5=127,8 14 109+143+142+109+113 5=123,2 15 143+142+109+113+124 5=126,2 16 142+109+113+124+113 5=120,2 |
c. Công thức tính MAD: MAD¿∑ |sai s ố d ự b á o n
Công thức: Sai số dự báo = Giá trị thực tế - Giá trị dự báo Thời kỳ Sai số dự báo 6 141−115,4=25,6 7 120−122,8=−2,8 8 136−120,4=15,6 9 109−124,2=−15,2 10 143−122=21 11 142−129,8=12,2 12 109−130=−21 13 113−127,8=−14,8 14 124−123,2=0,8 15 113−126,2=−13,2 16 104−120,2=−16,2 |
MAD ¿∑ |sai s ố d ự b á o 11=¿ 14,4
d. Dự báo nhu cầu của thời kỳ thứ 17:
e. Nhu cầu của thời kỳ thứ 17¿109+113+124+113+104 5=¿ 112,6
Khoảng dự báo cho nhu cầu của thời kỳ thứ 17 là từ 112,6−14,4=98,2 đến 112,6+14,4=127 Bài 28/ trang 565: BÀI LÀM a.
→ Từ đồ thị ta thấy chuỗi thời gian dao động rất mạnh và không đều, không
có xu hướng tăng/giảm rõ rệt.
Nhu cầu tăng vọt ở các kỳ 3,9,13,14
Nhu cầu giảm mạnh ở các kỳ 7,10,15,16
a. Trung bình trượt 3 mức độ Thời kỳ Giá trị dự báo Sai số dự báo 4 104+207+383 183−231,3=−48,3 3=231,3 5 207+383+183 181−257,7=−76,7 3=257,7 6 383+183+181 212−249=−37 3=249 7 183+181+212 167−192=−25 3=192 8 181+212+167 262−187,6=75,3 3=186,7 9 212+167+262 329−213,7=115,3 3=213,7 10 167+262+329 143−252,7=−109,7 3=252,7 11 262+329+143 285−244,7=40,3 3=244,7 12 329+143+285 188−252,3=−64,3 3=252,3 13 143+285+188 378−205,3=172,7 3=205,3 14 285+188+378 373−283,7=89,3 3=283,7 15 188+378+373 101−313=−212 3=313 16 378+373+101 103−284=−181 3=284
→ MAD ¿∑ |Sai s ố d ự b á o | 13=¿ 95,9 b. Trung bình trượt 6: Thời kỳ Giá trị dự báo Sai số dự báo 7 104+207+383+183+181+212 167+211,7=−44,7 6=211,7 8 207+383+183+181+212+167 262−222,2=39,8 6=222,2 9 383+183+181+212+167+262 329−231,3=97,7 6=231,3 10 183+181+212+167+262+329 143−222,3=−79,3 6=222,3 11 181+212+167+262+329+143 285−215,7=69,3 6=215,7 12 212+167+262+329+143+285 188−233=−45 6=233 13 167+262+329+143+285+188 378−229=149 6=229 14 262+329+143+285+188+378 373−264,2=108,8 6=264,2 15 329+143+285+188+378+373 101−282,7=−181,7 6=282,7 16 143+285+188+378+373+101 103−244,7=−141,7 6=244,7
→ MAD ¿∑ |Sai s ố d ự b á o | 10=¿ 95,7 c.
- Theo mô hình trung bình trượt 3:
Giá trị dự báo nhu cầu của thời kỳ 17¿373+101+103 3=¿ 192,3