Bài Tập Nhóm 4: Hồi Quy Trong Kinh Tế môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

ĐẠI HỌC KINH TẾ QUỐC DÂN
BÀI TẬP NHÓM
HỌC PHẦN: THỐNG KÊ T RONG KINH TẾ VÀ KINH DOANH
NHÓM THỰC HIỆN: NHÓM 4
Lớp học phần: TKKD1129(224) - 08
Giảng viên: TS. Chu Thị Bích Ngọc
Hà Nội, tháng 4 năm 2025
10. HỒI QUY ĐƠN 53. (Tr429) Bài làm
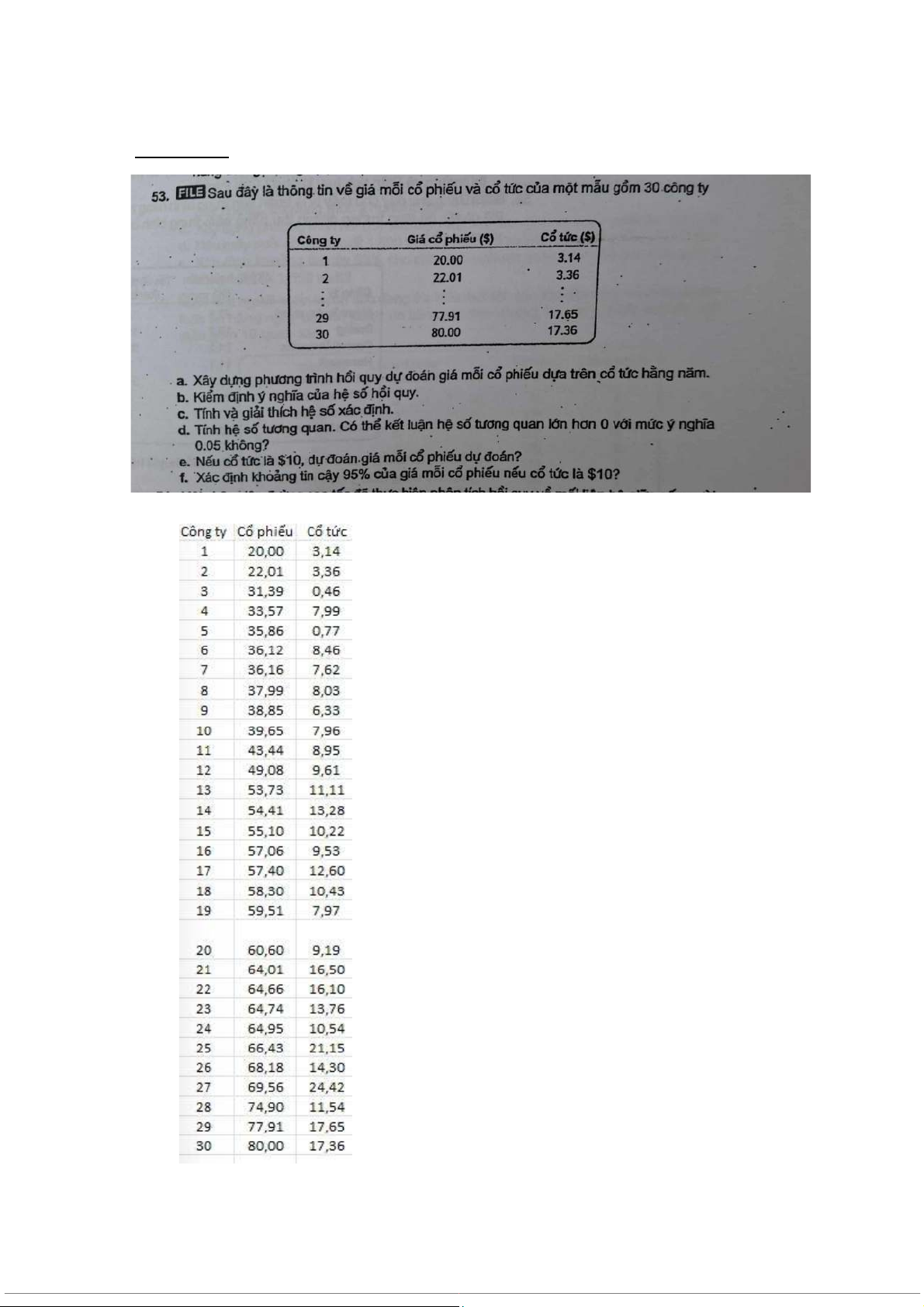
Biến độc lập x là cổ tức, biến phụ thuộc y là cổ phiếu. Ta tính được: 𝑦!=52.52 , 𝑆"=16.28 𝑥!=10.68 , 𝑆#=5.48
Thực hiện phân tích hồi quy trong Excel, ta có bảng sau:
a. Xây dựng phương trình hồi quy dự đoán giá mỗi cổ phiếu dựa trên cổ tức hàng năm.
Phương trình hồi quy tuyến tính dạng tổng quát: 𝑦^= 𝑎 +𝑏𝑥 Trong đó:
a: hệ số tự do ( hệ số chặn), giá trị y khi x = 0
b: hệ số hồi quy (hệ số góc, độ dốc) thể hiện sự thay đổi của y khi x tăng thêm 1 đơn vị.
Từ kết quả của excel , phương trình hồi quy như sau:
Giá mỗi cổ phiếu = 26.805 + 2.408 × cổ tức ($)
b. Kiểm định ý nghĩa của hệ số hồi quy Cặp giả thuyết Ho: β ≤ 0 H1: β > 0
So sánh p-value với mức ý nghĩa.
Giá trị p-value trong bảng là 0.000000<0.05 vì vậy bác bỏ giả thuyết không.
Kết luận: Vì giả thuyết không bị bác bỏ và chấp nhận giả thuyết đối, tức là hệ số hồi quy
của phương trình hồi quy tổng thể lớn hơn 0. Do đó, biến độc lập có ý nghĩa trong việc
dự đoán biến phụ thuộc. Cụ thể, nếu biết số cổ tức thì sẽ dự báo được số cổ phiếu của
công ty và hệ số hồi quy dương có nghĩa là nếu số cổ tức càng lớn thì số cổ phiếu sẽ có thể càng cao hơn.
c. Tính và giải thích hệ số xác định
Hệ số xác định là bình phương của hệ số tương quan.
è Hệ số xác định là r^2=65.83%
è Hệ số xác định cho biết sự thay đổi của biến độc lập x giải thích được bao nhiêu phần
trăm sự thay đổi của biến phụ thuộc y, nghĩa là sự thay đổi của cổ tức giải thích được
65.83% sự thay đổi của giá cổ phiếu.
d. Tính hệ số tương quan. Có thể kết luận hệ số tương quan lớn hơn 0 với mức ý nghĩa 0.05 không?
Hệ số tương quan là 0.811
Để kết luận hệ số tương quan lớn hơn 0 với mức ý nghĩa 0.05, thực hiện kiểm định cho hệ số tương quan. Cặp giả thuyết: Ho: 𝑟 ≤0 H1: 𝑟 >0
Công thức tiêu chuẩn kiểm định t cho hệ số tương quan với n-2=28 bậc tự do 𝑡 =𝑟 ×√𝑛 −2 √1−𝑟%= 7.335
Tiêu chuẩn kiểm định là phân phối t tại 28 bậc tự do (n – 2 = 30 – 2 = 28) và mức ý
nghĩa 0,05, giá trị tới hạn 2.048.
Vì 7.335>2.048 nên bác bỏ giả thuyết Ho
Kết luận: có thể kết luận hệ số tương quan lớn hơn 0 với mức ý nghĩa 0.05.
e. Nếu cổ tức là $10, dự báo giá mỗi cổ phiếu
Sử dụng phương trình hồi quy dự đoán giá mỗi cổ phiếu dựa trên cổ tức hàng năm câu
a, có x=$10 è 𝑦!=50.885 ($)
Kết luận: Nếu giá cổ phiếu $10, dự báo giá mỗi cổ phiếu là $50.88.
f. Xác định khoảng tin cậy 95% của giá mỗi cổ phiếu nếu cổ tức là $10 è x=10
Công thức khoảng tin cậy của giá mỗi cổ phiếu cho giá trị trung bình biết s là: !± × 𝑆"√𝑛
Tra bảng t tại mức ý nghĩa 0.05 và bậc tự do n-1=29 èt=2.045
è Khoảng tin cậy : 52.52±2.045×16.28 = 52.52±33.293
Kết luận: khoảng tin cậy 95% của giá mỗi cổ phiếu nếu cổ tức là $10 là khoảng từ $19.227 đến $85.813
11. HỒI QUY BỘI 27. (Tr483) Bài làm
a. Tính và giải thích ma trận tương quan, có hiện tượng đa cộng tuyến không?
Từ phân tích hồi quy trên Excel, ta có ma trận tương quan: Nhận xét: -
Hàng chéo thể hiện các biến có tương quan chặt chẽ với chính nó (bởi vì các giá
trị hệ số tương quan theo hàng chéo đều là 1). -
Cột đầu tiên có biến phụ thuộc là P/E, P/E có mối liên hệ nghịch khá mạnh với
EPS khi có hệ số tương quan là -0,602 và gần như không có mối liên hệ với Lợi tức khi
chỉ có hệ số tương quan thấp 0,053. Tiếp đó, từ ma trận, ta quan sát thấy mối tương quan
giữa biến phụ thuộc EPS và biến độc lập Lợi tức có vẻ khá yếu với hệ số tương quan đạt 0,162. -
So sánh với các giá trị này với +0,700 và -0,700, ta có thể kết luận rằng không có
hiện tượng đa cộng tuyến xảy ra ở đây. Vì giá trị lớn nhất hay hệ số tương quan lớn nhất
trong bảng là -0,602 và các giá trị còn lại hầu hết rất nhỏ, không lớn hơn +0,2 và -0,2.
Từ đó ta kết luận là bảng không có hiện tượng đa cộng tuyến xảy ra.
b. Xây dựng và giải thích phương trình hồi quy bội với P/E là biến phụ thuộc
Chạy phân tích hồi quy bội trên excel, ta có: 𝑃
𝐸= 29.913−5.324×𝐸𝑃𝑆 +1.449× ợ𝑖 ứ𝑐
c. Áp dụng quy tắc hồi quy từng bước để loại bỏ các biến độc lập không có ý nghĩa.
Xác định lại phương trình hồi quy. Sử dụng mức ý nghĩa 0.05.
P-value của biến lợi tức >0.05 è loại khỏi phương trình và phân tích được:
Ta thấy p-value liên quan đến biến độc lập còn lại EPS 0.005<0.05. Như vậy EPS có ý nghĩa với P/E.
Phương trình hồi quy: P/E = 33.569 - 5.111 × EPS
d. Giải thích mối liên hệ giữa biến phụ thuộc và biến độc lập trong phần c
è Giải thích mối quan hệ giữa P/E và EPS
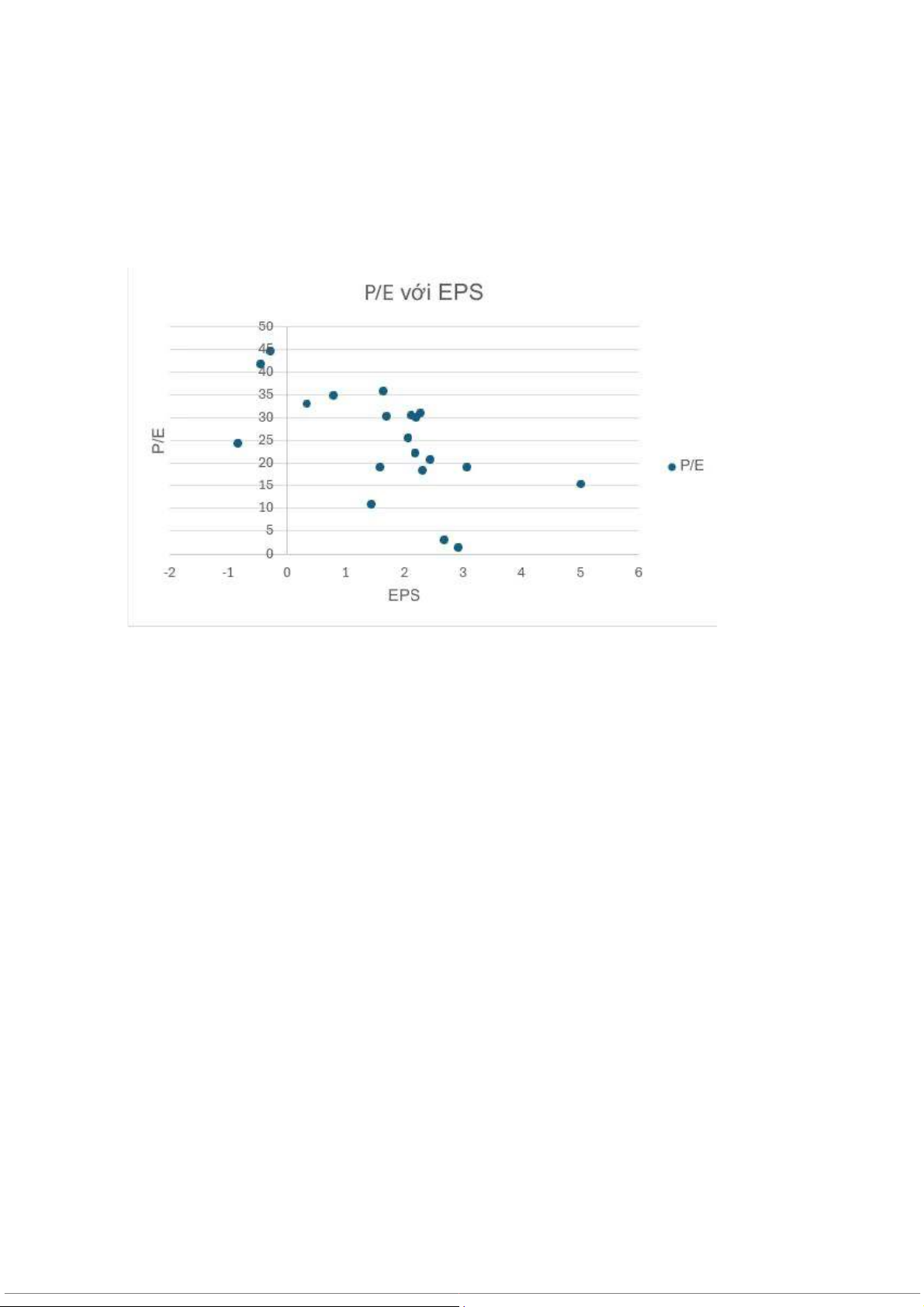
Biểu đồ phân tán P/E và EPS
P/E và EPS tỷ lệ nghịch, EPS tăng thì P/E giảm
Các quan sát có xu hướng thể hiện đường tuyến tính , mối liên hệ tuyến tính khá chặt chẽ.
e. Vẽ biểu đồ của các giá trị ước lượng và phần dư. Nhận xét về giả thiết phương
sai sai số không đổi qua đồ thị này.
*Vẽ biểu đồ của các giá trị ước lượng và phần dư.
Phương trình hồi quy cuối cùng ở trên là P/E = 33.569 – 5.111 × EPS
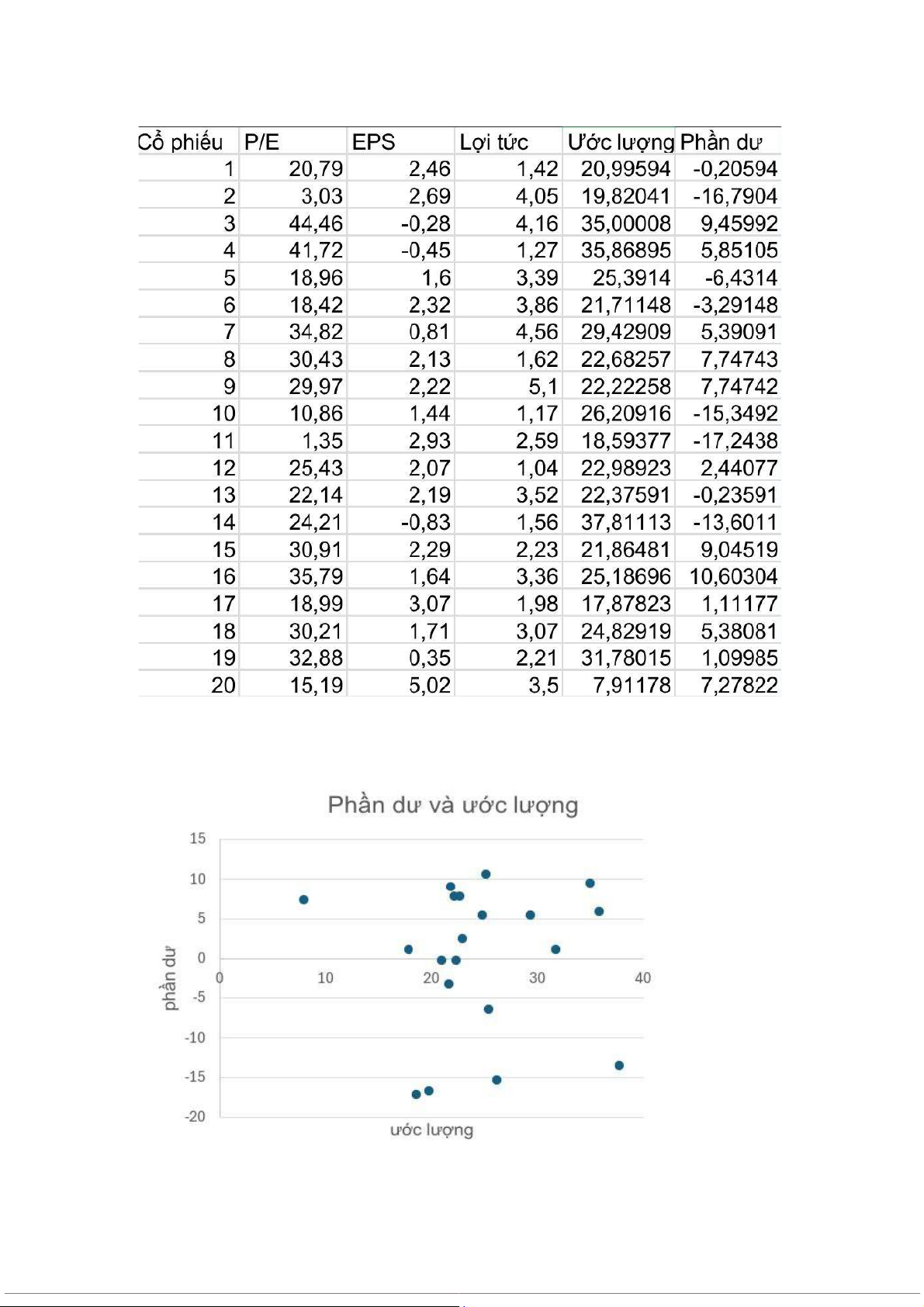
Tính giá trị ướng lượng và phần dư (thực tế - ước lượng) ta được dữ liệu:
Dùng dữ liệu ước lượng và phần dư vừa tính ta vẽ được biểu đồ:
*Dựa trên quan sát biểu đồ, ta có thể nhận xét như sau:
Trên đồ thị phân tán của phần dư so với giá trị P/E ước lượng, các điểm phần dư có vẻ
phân tán ngẫu nhiên xung quanh đường ngang 0. Mặc dù có một vài điểm phần dư có
giá trị tuyệt đối khá lớn (nằm xa đường 0), nhưng không có một hình dạng rõ ràng hay
xu hướng hệ thống nào (như hình nón mở rộng, hình nón thu hẹp, hoặc đường cong) cho
thấy sự thay đổi của độ phân tán của phần dư khi giá trị ước lượng tăng lên.
Do đó, dựa trên quan sát đồ thị này, chúng ta có thể giả định rằng giả thiết phương sai
sai số không đổi có thể được chấp nhận. Điều này có nghĩa là phương sai của sai số được
giả định là đồng nhất trên tất cả các mức của biến độc lập (hay giá trị ước lượng của biến phụ thuộc)
f. Có thể sử dụng phương trình hồi quy này để dự đoán tỷ lệ giá trên thu nhập không? Tại sao? Cặp giả thuyết Ho: không thể H1: có thể
Từ dữ liệu excel mô hình cuối cùng, ta có P-value (Significance F) =0.005
So sánh với mức ý nghĩa 0.05: 0.005<0.05 èphương trình hồi quy này có ý nghĩa thông kê.
Như vậy kết luận phương trình hồi quy để dự đoán tỷ lệ giá trên thu nhập .