Bài Tập Nhóm 8 - Phân Tích Dữ Liệu Cuộc Đua và Khảo Sát Cử Tri môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 82 trang 91
82. Trận Derby Kentucky được tổ chức vào thứ Bảy đầu tiên của tháng Năm
tại Churchill Downs ở Louisville, Kentucky. Cuộc đua được chia theo hai cự
ly: 1 mile và 1/4 mile. Bảng kết quả dưới đây cho biết thông tin về những
người thắng cuộc, cách biệt tỷ số, thời gian thắng của họ và tiền thưởng khi
đặt cược $2. Bảng trang 91
a. Tính trung bình và trung vị đối với “thời gian thắng” và “tiền thưởng”.
b. Xác định khoảng biến thiên và độ lệch chuẩn đối với biến “thời gian thắng”
và “tiền thưởng”.
c. Xét biến “cách biệt tỷ số”, thang đo nào đã được sử dụng? Mức độ trung
tâm nào là phù hợp nhất với biến này? a. Thời gian thắng:
Trung bình: (2.02000 + 1.99950 + 2.01883 + 2.01983 + 2.06767 + 2.04583 +
2.02267 + 2.03617 + 2.03033 + 2.04433 + 2.07417 + 2.03400 + 2.03050 +
2.04817 + 2.06100 + 2.05033 + 2.01517 + 2.03983 + 2.04333) / 19 = 2.03715
Trung vị: Sắp xếp dữ liệu theo thứ tự tăng dần, giá trị ở giữa là 2.03617. Tiền thưởng:
Trung bình: (2.30 + 10.50 + 20.50 + 12.80 + 4.10 + 50.30 + 6.10 + 4.90 + 6.80 +
103.20 + 18.00 + 43.80 + 32.60 + 12.80 + 7.00 + 7.80 + 6.60 + 11.40 + 7.80) / 19 = 22.85
Trung vị: Sắp xếp dữ liệu theo thứ tự tăng dần, giá trị ở giữa là 11.40. b. Thời gian thắng:
Khoảng biến thiên: 2.07417 - 1.99950 = 0.07467 Độ lệch chuẩn: 0.0172 Tiền thưởng:
Khoảng biến thiên: 103.20 - 2.30 = 100.90 Độ lệch chuẩn: 25.50 c. Thang đo: Tỷ lệ
Mức độ trung tâm phù hợp nhất: Trung bình
Bài 29 tr 228: Theo lý thuyết kinh tế, “ngưỡng thu hồi vốn” là lợi tức tối thiểu
mà một người yêu cầu trước khi họ thực hiện đầu tư. Một báo cáo nghiên cứu
nói rằng, lợi nhuận hàng năm của một nhóm cổ phiếu phổ thông cụ thể có
phân phối chuẩn với trung bình là 12% và độ lệch chuẩn là 18%. Một công cụ
sàng lọc cổ phiếu muốn xác định ngưỡng thu hồi vốn sao cho chỉ có một trong
20 cổ phiếu là cao hơn giá trị đó. Vậy ngưỡng thu hồi vốn nên được đặt là bao nhiêu? X ~ N (µ= 0,12, = ) P(X>a)= = 0,05= P(Z> ) =>1- P(Z< )=0,05 => P(Z< )=0,95 => => a=0,4161
Bài 30 tr 228: Nhà sản xuất máy in laser báo cáo số trang trung bình mà một
hộp mực in được trước khi cần thay thế là 12,200 trang. Số trang được in trên
mỗi hộp mực tuân theo phân phối xác suất chuẩn và có độ lệch chuẩn là 820
trang. Nhà sản xuất muốn đưa ra hướng dẫn cho các khách hàng tiềm năng về
thời gian sử dụng dự kiến của một hộp mực. Vậy nhà sản xuất nên quảng cáo
một hộp mực sẽ in được bao nhiêu trang nếu muốn chính xác 99%? X ~ N (µ= 12200, = ) P(X) => => a=14107,32
38. (Tr275) Số tiền trung bình của một khách hàng tại cửa hàng tạp hóa của
Churchill là $23.50 với độ lệch chuẩn lad $5. Giả sử số tiền này tuân theo quy
luật phân phối chuẩn. Với cỡ mẫu gồm 50 khách hàng hãy trả lời câu hỏi sau:
Xác suất để trung bình mẫu lớn hơn hoặc bằng $25.00 a.
b. Xác suất để trung bình mẫu lớn hơn $22.50 và nhỏ hơn $25.00
C. 90% rút ra từ tổng thể có giá trị trung bình nằm trong khoảng nào ?
39. (Tr275) Điểm trung bình cho bài kiểm tra thê lực dành cho vận động viên
khối 1 là 947 với độ lệch chuẩn là 205. Chọn một mẫu ngẫu nhiên gồm 60 vận
động viên. Tỉnh xác suất để giá trị trung bình của mẫu nhỏ hơn 9002
Bài 50 trang 308
Trong một thăm dò để ước lượng mức độ tin tưởng của người dân đối với
Tổng thống, tiến hành khảo sát ngẫu nhiên 1,000 cử tri, trong đó mỗi người
được lựa chọn 1 trong 3 phương án sau:
1. Tổng thống đang làm tốt công việc.
2. Tổng thống làm không tốt công việc.
3. Không có ý kiến
Có 560 người cho rằng Tổng thống đang làm tốt công việc
a. Xác định khoảng tin cậy 95% về tỷ lệ cử tri cho rằng Tổng thống đang làm
tốt công việc.
b. Dựa vào kết quả của ý (a), có thể kết luận rằng đa số (trên 50%) cử tri tin
rằng Tổng thống đang làm tốt công việc không? -Kích thước mẫu (n): 1000 -Số người
cho rằng Tổng thống đang làm tốt công việc (x): 560 -Mức độ tin cậy: 95% Tỷ lệ mẫu: = px/n = 560/1000 = 0.56
Sai số tiêu chuẩn (SE).SE = √( p (1- )/n) p = √(0.56 * 0.44 / 1000) = √(0.0002464) ≈ 0.0157
Giá trị z tương ứng với mức độ tin cậy 95% là 1.96
Biên độ sai số (ME).ME = z * SE = 1.96 * 0.0157 ≈ 0.0308
Khoảng tin cậy = ± pME = 0.56 ± 0.0308
Khoảng tin cậy dưới = 0.56 - 0.0308 = 0.5292
Khoảng tin cậy trên = 0.56 + 0.0308 = 0.5908
Đáp án a: Khoảng tin cậy 95% về tỷ lệ cử tri cho rằng Tổng thống đang làm tốt
công việc là (0.5292, 0.5908)
Vì cả hai giới hạn của khoảng tin cậy (0.5292 và 0.5908) đều lớn hơn 0.50
=> có thể kết luận rằng với độ tin cậy 95%, đa số cử tri (trên 50%) tin rằng
Tổng thống đang làm tốt công việc.
Đáp án b: Có, có thể kết luận rằng đa số cử tri tin rằng Tổng thống đang làm tốt công việc. Bài
1 (Trang 311): Một nghiên
cứ gần đây cho thấy thời gian nghỉ việc không
lương trung bình của phụ nữ khi sinh con là 8.6 tuần. Giả sử phân phối của
dữ liệu có phân phối chuẩn với độ lệch chuẩn là 2.0 tuần. Chọn mẫu 35 phụ
nữ mới quay trở lại làm việc sau khi sinh con. Xác định xác suất để thời gian
nghỉ việc không lương trung bình của mẫu này tối thiểu là 8.8 tuần? BÀI GIẢI
Sai số chuẩn của trung bình mẫu cần tìm: = ≈ 0.338
Chuẩn hóa giá trị trung bình mẫu: Z = = ≈ 0.59 Ta cần tính P(
) tương đương P(Z ≥ 0.59): P(Z ≥ 0.59) = 1 - P(Z < 0.59) = 1 – 0.7224 ≈ 0.2776 Đáp số: 0.2776
Câu 33tr 519: Tính chỉ số đơn về giá của mỗi mặt hàng. Sử dụng năm 2010 làm gốc.
Chỉ số đơn về giá của RC-33: = .100= 120
Chỉ số đơn về giá của SM-14: = .100= 75
Chỉ số đơn về giá của WC50: = .100=117,65
Bài 34 tr 519: Tính chỉ số tổng hợp giản đơn về giá năm 2018. Sử dụng năm
2010 làm gốc.
Chỉ số tổng hợp về giá: = .100 = . 100= 98,04
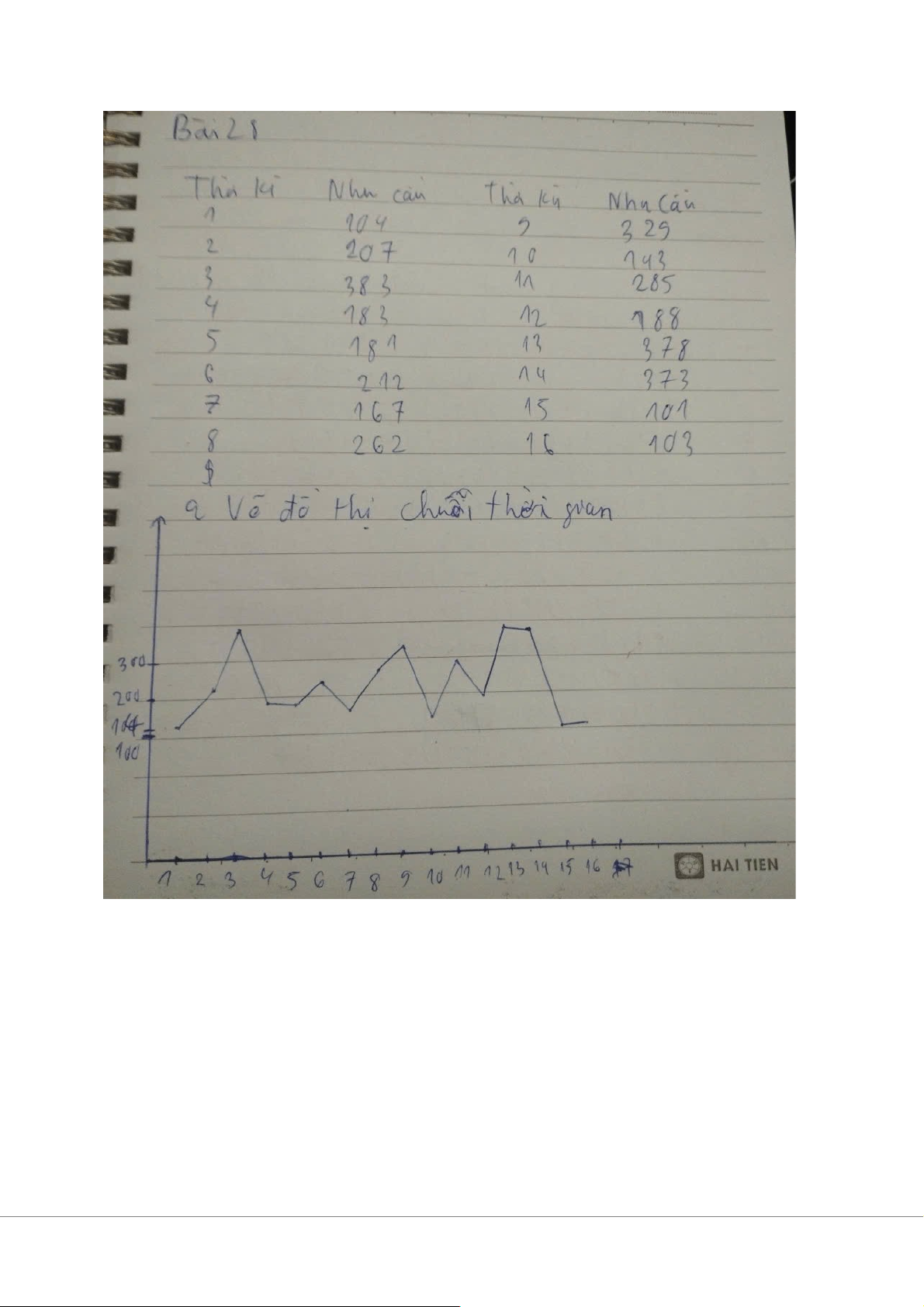
Bài 27 trang 565
a. Khi vẽ đồ thị, ta thấy nhu cầu biến động không đều, không có xu hướng rõ ràng hoặc tính mùa vụ. b. -Dự báo
cho kì 6: (104+132+117+120+104)/5= 115.4 -Dự báo
cho kì 7: (132+117+120+104+141)/5= 122.8 -Dự báo
cho kì 8: (117+120+104+141+120)/5= 120.4 -Dự báo
cho kì 9: (120+104+141+120+136)/5 = 124.2 -Dự báo
cho kì 10: (104+141+120+136+109)/5 = 122 -Dự báo
cho kì 11: (141+120+136+109+143)/5 = 129.8 -Dự báo
cho kì 12: (120+136+109+143+142)/5 = 130 -Dự báo
cho kì 13: (136+109+143+142+109)/5 = 127.8 -Dự báo
cho kì 14: (109+143+142+109+113)/5 = 123.2 -Dự báo
cho kì 15: (143+142+109+113+124)/5 = 126.2 -Dự báo
cho kì 16: (142+109+113+124+113)/5 = 120.2 c.
Sai cố tuyệt đối của mỗi kì là: -Kì 6: 25.6 -Kì 7: 2.8 -Kì 8: 15.6 -Kì 9: 15.2