Bài tập nhóm môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
HỌC PHẦN: THỐNG KÊ TRONG KINH TẾ VÀ KINH DOANH
GIẢNG VIÊN HƯỚNG DẪN: CHU BÍCH NGỌC BÀI TẬP NHÓM - NHÓM 8
LỚP HỌC PHẦN: TKKD1129(124)_05 Thành viên nhóm: Họ và tên Mã sinh viên Nguyễn Thị Minh Anh 11234252 Trần Minh Anh 11234260 Phạm Quỳnh Chi 11234283 Hoàng Thị La Dung 11234292 Nguyễn Xuân Hoa 11234348 Nguyễn Thị Tú Trân 11234527 PHÂN TỔ THỐNG KÊ Bài 37 (trang 46): Bài làm
a. Xác định khoảng cách tổ:
●Xác định số tổ (k): Ta áp dụng quy tắc 2^k
○Quy tắc 2^k: Số tổ k được xác định khi 2^k lớn hơn bằng bằng số quan sát n
Ta có: 44 quan sát => n=44 => 2^k ≥ 44 k ≥ 5,46 => k = 6 Vậy số tổ sẽ là 6
●Xác định khoảng cách tổ (i): Ta có:
+ Giá trị hoá đơn lớn nhất trong dữ liệu: 265
+ Giá trị hoá đơn nhỏ nhất trong dữ liệu: 82
+ Khoảng biến thiên: 265 - 82 = 183.
=> Khoảng cách tổ: i ≥ Khoảng biến thiên/Số tổ i ≥ 183/6=30,5 i = 35 (làm tròn)
Vậy, khoảng cách tổ phù hợp là 35.
b. Sắp xếp dữ liệu vào bảng tần số: Khoảng giá trị
Tần số (số lượng hoá đơn) Từ 70 đến dưới 105 4 Từ 105 đến dưới 140 17 Từ 140 đến dưới 175 14 Từ 175 đến dưới 210 2 Từ 210 đến dưới 245 6 Từ 245 đến dưới 280 1 Tổng 44
c. Kết luận về dữ liệu:
Sau khi hoàn thành bảng tần số, ta có thể đưa ra một số kết luận như:
●Khoảng giá trị chi tiêu phổ biến nhất: Khoảng giá trị có tần số lớn nhất:
$105-$175 (đa số khách hàng chi tiêu trong khoảng này để mua sắm đồ dùng thể thao.)
●Khoảng giá trị chi tiêu ít phổ biến nhất: Khoảng giá trị có tần số nhỏ nhất: $245-$280.
●Phạm vi chi tiêu: Từ giá trị nhỏ nhất đến giá trị lớn nhất: $265 (lớn nhất) và $82 (nhỏ nhất) Bài 40 (trang 47) Bài làm
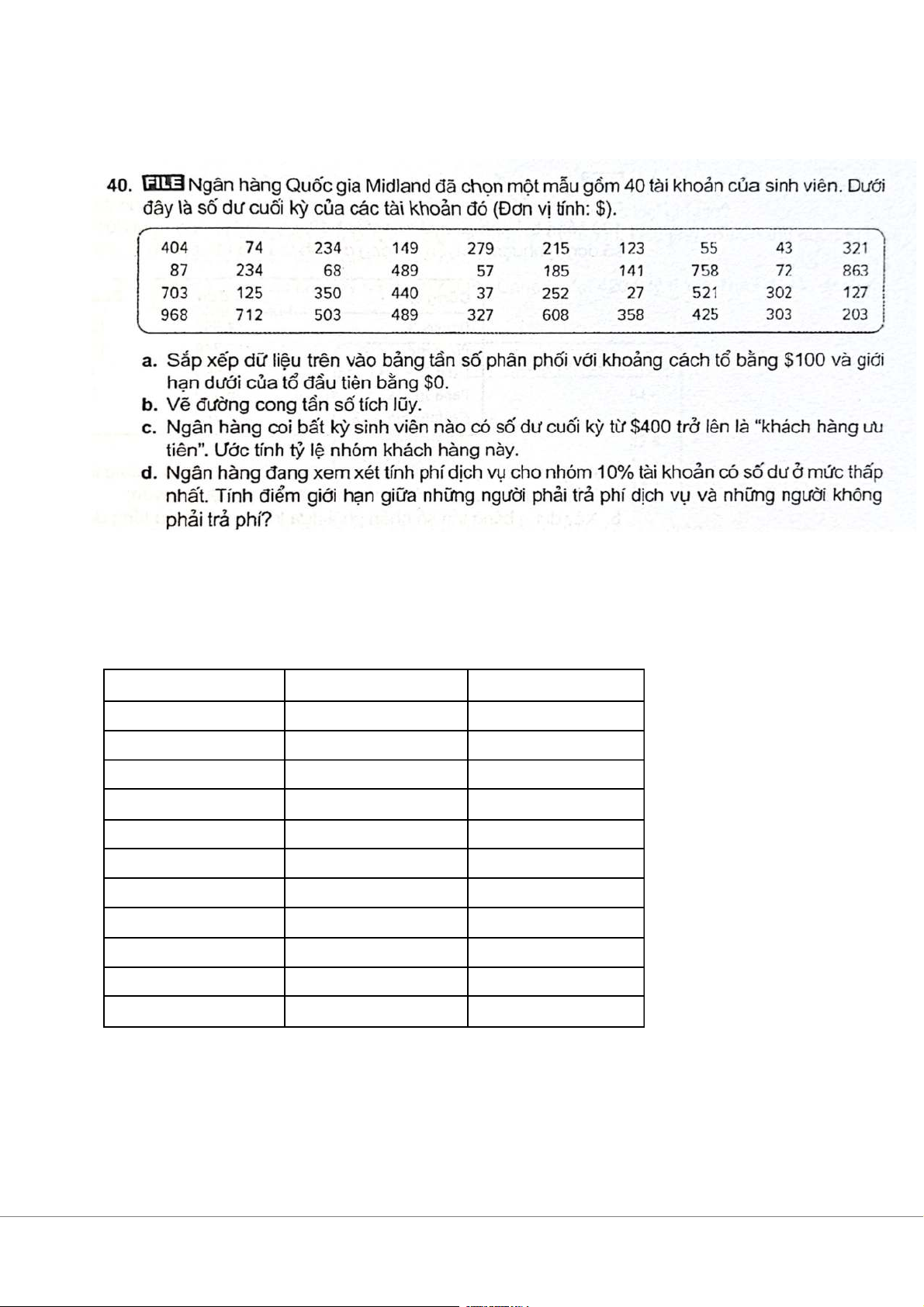
a. Bảng tần số phân phối GHD GHT fi 0 100 9 100 200 6 200 300 6 300 400 6 400 500 5 500 600 2 600 700 1 700 800 3 800 900 1 900 1000 1 N = 40
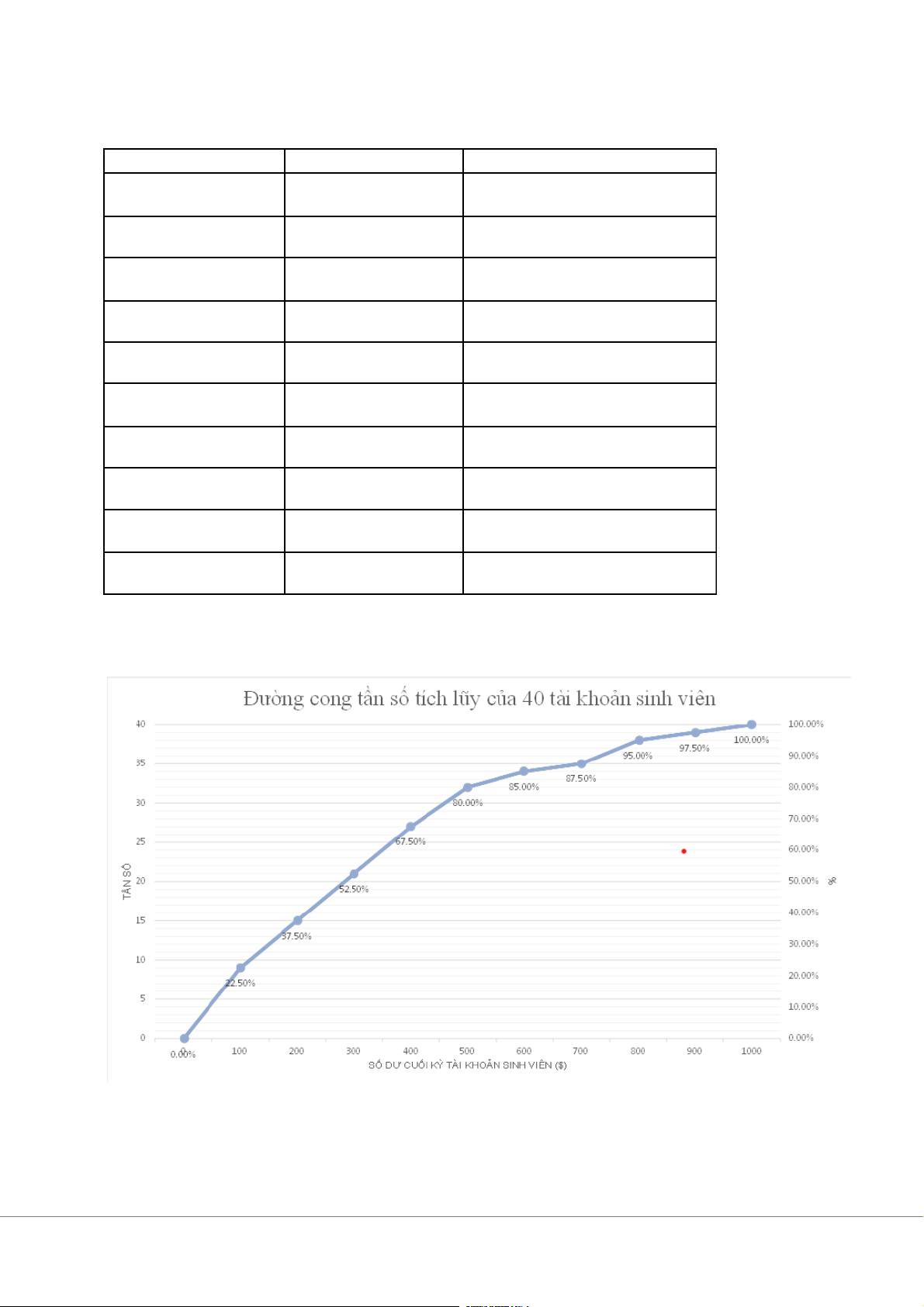
b. Đường cong tần số tích lũy
Từ bảng tần số phân phối, ta lập bảng tần suất tích lũy như sau: Số dư ($) Tần số tích lũy Tần suất tích lũy (%) < 100 9 22.50% < 200 15 37.50% < 300 21 52.50% < 400 27 67.50% < 500 32 80.00% < 600 34 85.00% < 700 35 87.50% < 800 38 95.00% < 900 39 97.50% < 1000 40 100.00%
Từ bảng trên ta lập đường cong tần số tích lũy:
c. Tính tỷ lệ nhóm sinh viên có số dư tài khoản từ $400 trở lên
Xét đường cong tần số tích lũy (hoặc bảng tần suất tích lũy), ta thấy có 67.5% sinh
viên có số dư tài khoản cuối kỳ dưới $400.
Do đó, tỷ lệ sinh viên có số dư cuối kỳ từ $400 trở lên là: 100 – 67.5 = 32.5 (%)
Kết luận: tỷ lệ nhóm “khách hàng ưu tiên” là 32.5%. d. Tính điểm giới hạn
Cách 1: Dựa vào đường cong tần số tích lũy
Xét đường cong tần số tích lũy, có thể thấy 10% tài khoản có số dư ở mức thấp
nhất sẽ có số dư khoảng dưới $55. Vậy có thể lấy $55 là điểm giới hạn giữa những
người phải trả phí và những người không phải trả phí. Cách 2: Tính toán
Số tài khoản thuộc nhóm 10% tài khoản có số dư thấp nhất là: 40 𝑥 10% = 4
Sắp xếp dữ liệu từ bé nhất đến lớn nhất, ta có số dư của 4 tài khoản có số dư thấp
nhất lần lượt là: 27, 37, 43, 55. Vậy có thể lấy $55 là điểm giới hạn giữa những
người phải trả phí và những người không phải trả phí.
MỨC ĐỘ HIỆN TƯỢNG KTXH Bài 24 (trang 67) Bài làm xi wi 1 40 3.5 10 Đơn vị: $
Để tính giá trung bình của một cuốn sách, ta dùng công thức tính trung bình cộng gia quyền:
Vậy giá trung bình của một cuốn sách là $1.5. Bài 72 (trang 89) Bài làm Bảng tần số
96 98 103 106 107 108 109 111 112 115 116 118 121 122 123 124 127 1 1 1 3 1 1 2 1 4 2 4 1 1 1 1 2 1
a. Chỉ số đường huyết trung bình: ∑𝑥𝑖𝑓𝑖 𝑥=
=96×1+98×1+103×1+106×3+...+127×1 28 = 112, 86 ∑𝑓𝑖
Vậy, chỉ số đường huyết trung bình của bệnh nhân trong tháng Hai là khoảng 112,86. b. Xác định trung vị:
●Sắp xếp dữ liệu theo thứ tự tăng dần: 96, 98, 103, 106, 106, 106, 107,
108, 109, 109, 111, 112, 112, 112, 112, 115, 115, 116, 116, 116, 116, 118, 121, 122, 123, 124, 124, 127
●Vì có 28 số (số chẵn), trung vị sẽ là trung bình cộng của hai số ở giữa (số vị trí 14 và 15): ○Số ở vị trí 14: 112 ○Số ở vị trí 15: 112
○Trung vị: 𝑀𝑒=112+112 2= 112
Vậy, trung vị của chỉ số đường huyết là 112. c. Xác định mốt:
●Giá trị xuất hiện nhiều nhất: 112, 116 (xuất hiện 4 lần)
Vậy, mốt của chỉ số đường huyết là 112, 116. Bài 32 (trang 122) Bài làm
Hệ số tương quan r giữa hai biến X và Y( lấy các giá trị x1, x2,....,xn và y1, y2…,
yn) được tính theo công thức sau:
Nếu hệ số dương thì có mối quan hệ trực tiếp giữa 2 biến. Nếu hệ số âm, mối quan hệ sẽ là nghịch đảo.
- Để có được hệ số tương quan, ta cần tính tổng các tích xy:
Tiếp theo tính tổng riêng lẻ:
Sau đó ta tính được tích các tổng và bình phương các tổng:
Sau đó ta tính được tổng bình phương x và y: Từ trên ta có thể tính:
=> Hệ số tương quan là dương cho thấy mối quan hệ thuận giữa hai biến, nếu một
biến tăng thì biến kia cũng tăng theo. Điều này có lý vì có thể mong rằng chi phí
bảo trì cho các máy cũ lớn hơn so với máy mới, nhưng mối quan hệ này không quá chặt chẽ. ĐIỀU TRA CHỌN MẪU Bài 22 (trang 225) Bài làm
a) Gọi X là thời gian đi làm ở New York P(X<30) = Φ ( 30−39,7 7,5 ) = Φ (-1,29) = 0,0985
Vậy phần trăm thời gian đi làm ở thành phố New York ít hơn 30 phút là 9,85
b) Gọi Y là thời gian đi làm ở 30 thành phố P(3035−3 7,9 5,7 ) − 3 Φ 0−39(,77,5 ) = Φ (-0,63) - Φ (-1,29) = 0,2643 - 0,0985 =0,1658
Vậy phần trăm thời gian nằm trong khoảng từ 30 đến 35 phút là 16,58% c) P(305 −3 ) 9,7 − Φ ( 30−39,77,5 ) = Φ (1,37) - Φ (-1,29) = 0,9147 - 0,0985 =0,8162
Vậy phần trăm thời gian nằm trong khoảng từ 30 đến 50 phút là 81,62% ƯỚC LƯỢNG Bài 39 (trang 307) Bài làm 1 - ⍺= 95% => ⍺= 5%
- Ước lượng trung bình μ:
𝑥− ε𝑥 < µ < 𝑥 + ε𝑥 𝑥 Thay = 50 vào:
=> 50 − ε𝑥< µ < 50 + ε𝑥 Mà 46 < µ < 54 => ε𝑥= 4
- Áp dụng công thức xác định số đơn vị mẫu điều tra để ước lượng trung bình:
Chọn nhiều lần (chọn có hoàn lại): 𝑛 = 2 × σ2 𝑧α/2 2 ε𝑥 => 𝑛 = 1,9602 × 162 42 => 𝑛 = 61, 4656
=> 𝑛 = 62 (TMĐK:𝑛 ≥ 30 ,𝑛)∈ ℤ+
Vậy cỡ mẫu mà sinh viên này đã khảo sát là 62 Bài 50 (trang 308) Bài làm a) =𝑓560 1000 = 0, 56
Độ tin cậy 1 - ⍺= 95% => ⍺= 5% Zα/2 =Z0,05/2 = 1,96 - Chọn nhiều lần σ 𝑓 ( 1− 𝑓 ) 0,56 ( 1− 0,56 ) 𝑓 = = = 0,0157 𝑛 1000
ε𝑓 = σ𝑓× 𝑍α/2 = 1, 96 × 0, 0157 = 0, 0308 Ước lượng tỉ lệ : 𝑓
𝑓 -ε𝑓 < p <𝑓 ε + 𝑓
=> 0,56 - 0,0308 < p < 0,56 + 0,0308 => 0,5292 < p < 0,5908
Vậy với khoảng tin cậy 95% về tỷ lệ cử tri cho rằng Tổng thống đang làm tốt công
việc là từ 0,5292 đến 0,5908
b) Dựa vào kết quả ở câu a, ta tìm được khoảng tin cậy (0,5292; 0,5908)
Vì khoảng tin cậy phản ánh bao gồm các giá trị lớn hơn 0,50 hay 50% nên có thể
kết luận rằng Tổng thống đang làm tốt công việc KIỂM ĐỊNH Bài 45 (trang 345) Bài làm Chi phí trung bình Sample size 8 Sample mean 29,7875 Sample S.D 0,917 Significant 0,05 Test mean with 30 Cost T-stat Critical value P-value Conclusion 29,7 H0 μ = 30 -0,655 29,4 H1 μ < 30 -1,894578605
0,2682448811 Chưa bác bỏ H0 31,7 29,0 29,1 30,5 29,1 29,8
=> Chưa đủ cơ sở bác bỏ H0
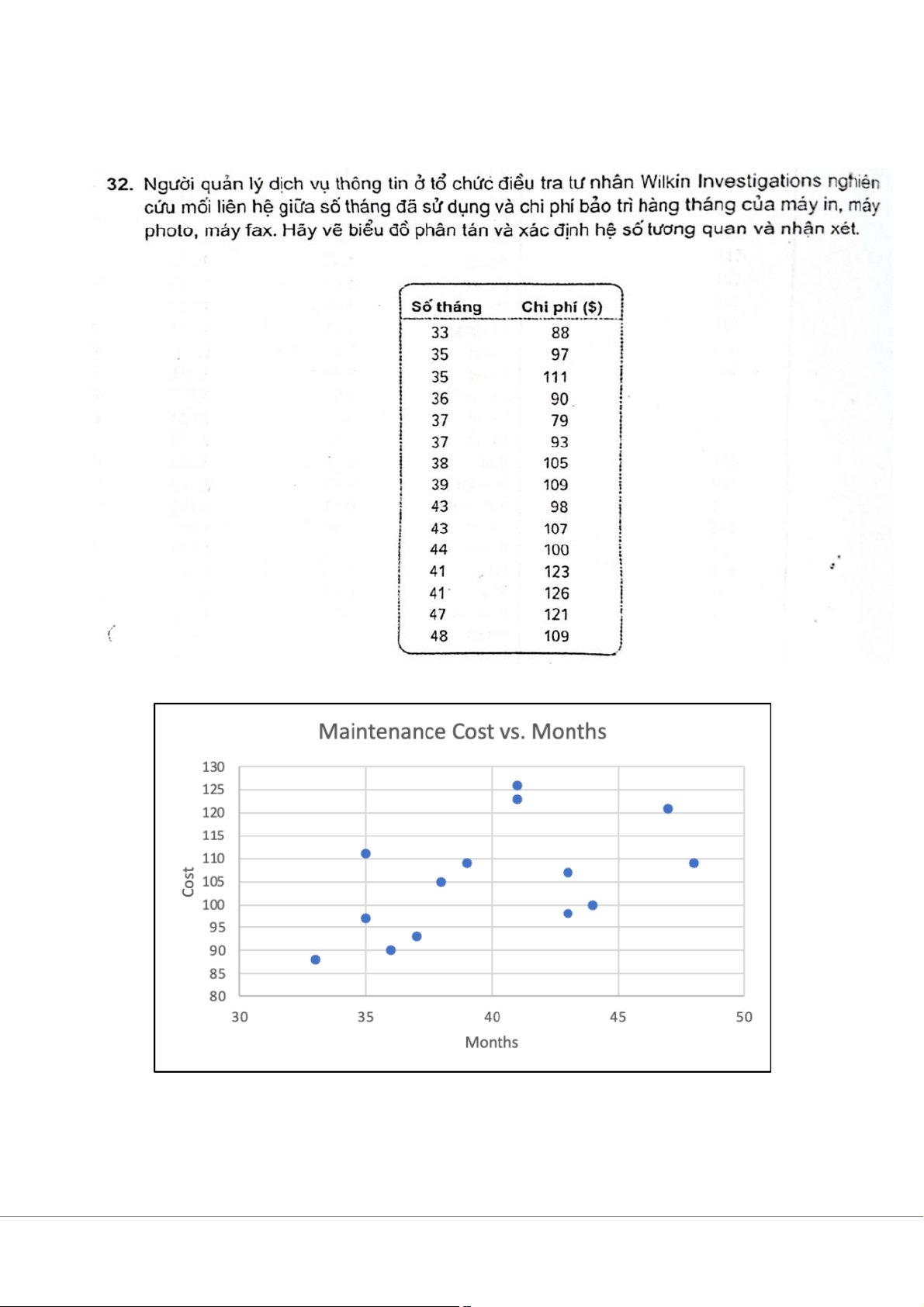
Kết luận: Chi phí trung bình của đám cưới không dưới $30.000 HỒI QUY TƯƠNG QUAN Bài 47 (trang 426) Bài làm a. Biểu đồ phân tán
Nhận xét về mối liên hệ giữa hai biến: hai biến có mối liên hệ tương quan lỏng, có sự phân tán đáng kể
b. Tính hệ số tương quan (𝑟) ∑(𝑋−𝑋)2 ∑(𝑌−𝑌)2 𝑠 (𝑛−1) =43,843 (𝑛−1) =15,924 𝑥= 10−1 = 2, 207 ;𝑠𝑦= 10−1 = 1, 33 ∑(𝑋−𝑋)(𝑌−𝑌) Hệ số tương quan: 𝑟 = =11,93418 (10−1)×2,207×1,33 = 0, 452 (𝑛−1)𝑠𝑋𝑠𝑌
- Nhận xét: trung vị về tuổi và dân số có tương quan lỏng c. Hệ số xác định
=> 𝑅2=𝑆𝑆𝑅𝑆𝑆𝑇 =8,944 43,843 = 0, 204
Hệ số xác định trên cho biết sự thay đổi của biến độc lập “dân số” giải thích được
20,4% sự thay đổi của biến phụ thuộc “trung vị về tuổi”
d. Phương trình hồi quy mẫu có dạng: 𝑌= 𝑏0+ 𝑏1𝑋 Xét hệ:
∑ 𝑌 = 𝑛𝑏0+ 𝑏1∑ 𝑋 320, 4 = 10𝑏0+ 24, 718𝑏1
∑ 𝑋𝑌 = 𝑏0∑ 𝑋 + 𝑏1∑ 𝑋2803, 9 = 24, 718𝑏0+ 104, 94𝑏1
=> 𝑏0= 31, 367; 𝑏1= 0, 272
=> Phương trình hồi quy mẫu: 𝑌= 31, 367 + 0, 272𝑋
Với tổng số dân là 24,718 triệu người thì trung vị về tuổi là
31, 367 + 0, 272 × 24, 781 = 38, 107
e. Kiểm định hệ số hồi quy tổng thể, với mức ý nghĩa 5% - Xét cặp giả thuyết: 𝐻0: β = 0 𝐻1: β ≠ 0 - ; =0,75−0 𝑛−𝑘−1 = 𝑡0,0 8 25 = 2, 306 0,523 = 1, 434 𝑡α/2 𝑠𝑏 => 𝑡 8 𝑞𝑠 | | < 𝑡0,025
=> Chưa đủ cơ sở bác bỏ 𝐻0
Vậy hệ số hồi quy tổng thể bằng 0
f. Kết quả cho thấy không có mối liên hệ tuyến tính giữa dân số và trung vị về tuổi