Bài tập nhóm môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN KHOA THỐNG KÊ
------------------------------------------ BÀI TẬP NHÓM
Môn học: Thống kê trong kinh tế và kinh doanh
Giảng viên hướng dẫn : TS. Chu Thị Bích Ngọc Nhóm sinh viên : 04 Lớp học phần : TKKD1129(124)_06
Danh sách sinh viên : Nguyễn Thị Minh Hằng Nguyễn Khánh Huyền Ngô Thị Yến Chi Mai Ngọc Kiều Vũ Mỹ Huyền Bùi Hải Hà
Hà Nội, NĂM 2024 1 1 MỤC LỤC
MỤC LỤC ......................................................................................................... 2
NỘI DUNG ....................................................................................................... 3
I. Phân tổ thống kê ........................................................................................... 3
1. Bài 17 trang 37 ............................................................................................... 3
2. Bài 29 trang 44 ............................................................................................... 5
II. Mức độ hiện tượng kinh tế - xã hội ........................................................... 6
1. Bài 68 trang 89 ............................................................................................... 6
2. Bài 85 trang 92 ............................................................................................... 7
3. Bài 31 trang 122 ............................................................................................. 8
III. Điều tra chọn mẫu ..................................................................................... 9
1. Bài 31 trang 274 ............................................................................................. 9
IV. Ước lượng ................................................................................................. 10
1. Bài 57 trang 309 ........................................................................................... 10
2. Bài 14 trang 294 ........................................................................................... 12
V. Kiểm định ................................................................................................... 12
1. Bài 48 trang 345 ........................................................................................... 12
VI. Hồi quy tương quan ................................................................................. 14
1. Bài 12 trang 396 ........................................................................................... 14
2. Bài 24 trang 482 ........................................................................................... 17
VII. Chỉ số ....................................................................................................... 22
1. Bài 12 trang 510 ........................................................................................... 22
2. Bài 27 trang 519 ........................................................................................... 23
3. Bài 28 trang 519 ........................................................................................... 24
4. Bài 29 trang 519 ........................................................................................... 24
VIII. Dãy số thời gian .................................................................................... 25
1. Bài 10 trang 539 ........................................................................................... 25
2. Bài 30 trang 566 ........................................................................................... 27 2 2 NỘI DUNG
I. Phân tổ thống kê 1. Bài 17 trang 37
Bảng tần số phân phối dưới đây ghi lại quãng đường bay của các nhân viên ở
Brumley Statistical Consulting Inc. khi đi công tác trong quý gần đây (Đơn vị tính: nghìn mile). Quãng đường bay Số nhân viên (nghìn mile) (người) Từ 0 đến dưới 3 5 Từ 3 đến dưới 6 12 Từ 6 đến dưới 9 23 Từ 9 đến dưới 12 8 Từ 12 đến dưới 15 2 Tổng 50
a. Có bao nhiêu nhân viên đi công tác trong quý?
b. Trị số giữa của tổ đầu tiên là bao nhiêu?
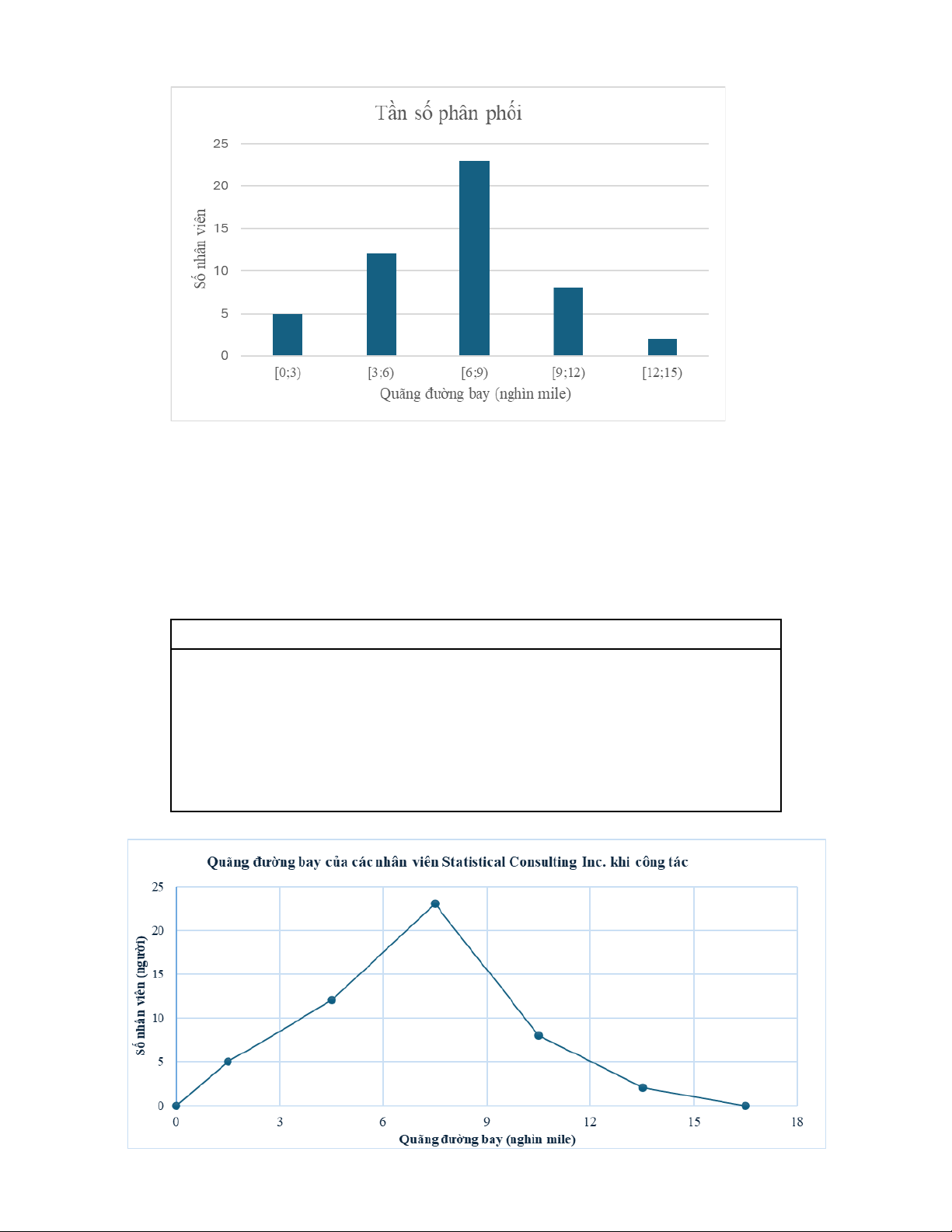
c. Vẽ biểu đồ tần số phân phối.
d. Trong đa giác tần số, toạ độ của điểm đầu tiên là bao nhiêu? e. Vẽ đa giác tần số.
f. Nhận xét về quãng đường bay dựa vào hai biểu đồ trên. Lời giải
a. Có bao nhiêu nhân viên đi công tác trong quý?
Có 50 người đi công tác trong quý
b. Trị số giữa của tổ đầu tiên là bao nhiêu?
Trị số giữa của tổ đầu tiên là: 0 + 3 2= 1.5 (nghìn mile)
c. Vẽ biểu đồ tần số phân phối. 3
d. Trong đa giác tần số, toạ độ của điểm đầu tiên là bao nhiêu?
Trong đa giác tần số, tọa độ của điểm đầu tiên có:
- Hoành độ (quãng đường bay) là trị số giữa của tổ đầu tiên: 𝑥 = 1.5
- Tung độ (số nhân viên): 𝑦 = 5
e. Vẽ đa giác tần số.
Quãng đường bay (nghìn mile)
Trị số giữa Số nhân viên (người) Từ 0 đến dưới 3 1.5 5 Từ 3 đến dưới 6 4.5 12 Từ 6 đến dưới 9 7.5 23 Từ 9 đến dưới 12 10.5 8 Từ 12 đến dưới 15 13.5 2 Tổng 50
f. Nhận xét về quãng đường bay dựa vào hai biểu đồ trên. 4
Khi đi công tác trong quý gần đây, trong 50 nhân viên ở Brumley Statistical
Consulting Inc. Có gần một nửa số nhân viên bay được quãng đường nằm trong khoảng
6,000 đến 9,000 miles. Có 5 nhân viên bay quãng đường ít hơn 3,000 miles và 2 nhân
viên bay quãng đường nhiều hơn 12,000 miles. 2. Bài 29 trang 44
Dưới đây là dữ liệu về thời gian đi làm từ nhà đến công ty của 25 nhân viên (Đơn vị tính: phút) 28 25 48 37 41 19 32 26 16 23 23 29 36 31 26 21 32 25 31 43 35 42 38 33 28
a. Khi xây dựng bảng tần số phân phối, nên lựa chọn số tổ là bao nhiêu?
b. Nên lựa chọn khoảng cách tổ bằng bao nhiêu?
c. Giới hạn dưới của tổ đầu tiên có giá trị bằng bao nhiêu?
d. Xây dựng bảng tần số phân phối.
e. Nhận xét về hình dáng phân phối của dãy số. Lời giải
a. Khi xây dựng bảng tần số phân phối, nên lựa chọn số tổ là bao nhiêu?
Ta có số quan sát n = 25, áp dụng quy tắc 2k> 𝑛, ta có: 2k>25
⇒ Số tổ k = 5 (vì 16 < 25 và 25 =32 >25)
b. Nên lựa chọn khoảng cách tổ bằng bao nhiêu? h = xmax −k x =m 4 i8n−16 5=32 5= 6.4 ≈ 7
c. Giới hạn dưới của tổ đầu tiên có giá trị bằng bao nhiêu? Đáp án: 15
d. Bảng tần số phân phối
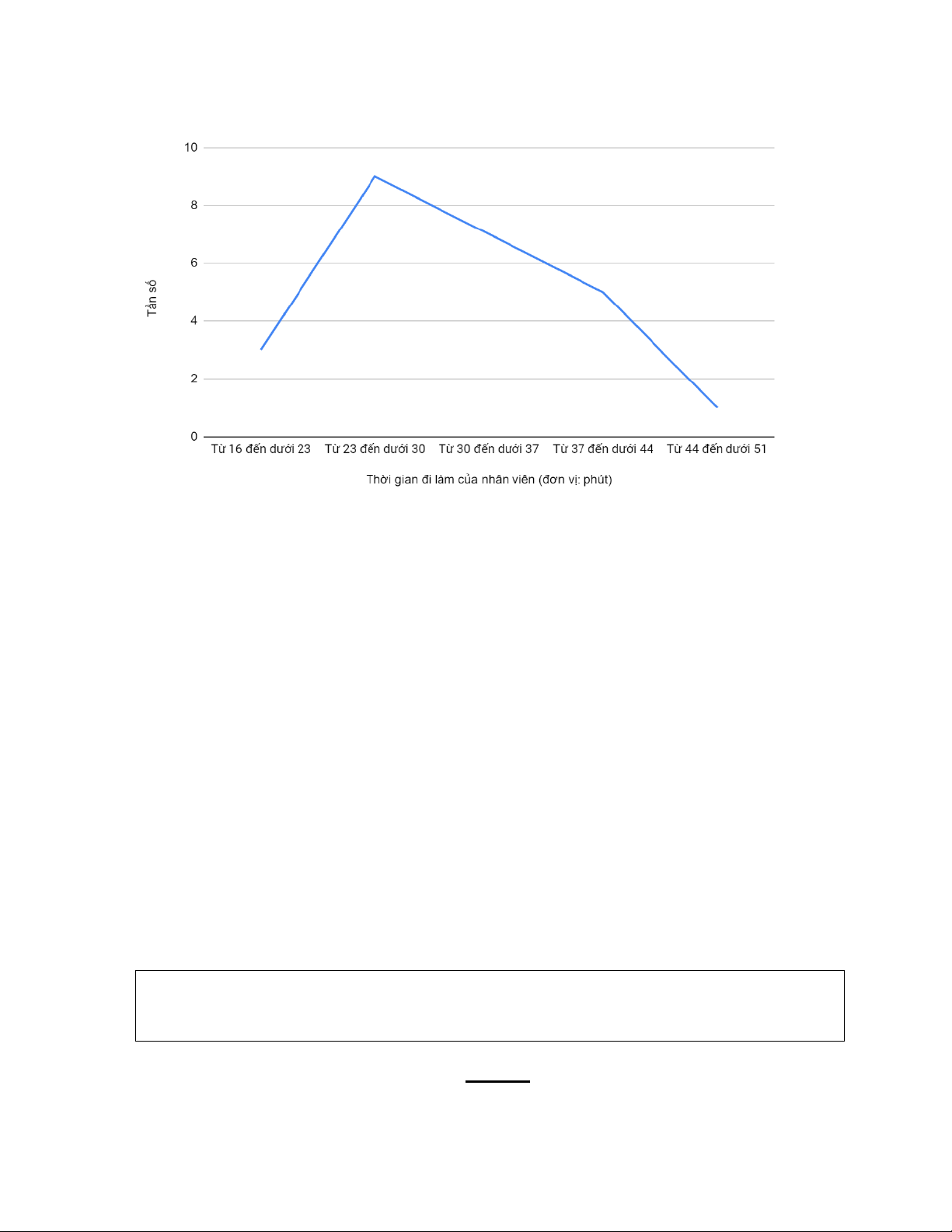
Thời gian đi làm của nhân viên (đơn vị: phút) Tần số Từ 15 đến 22 3 Từ 22 đến 29 8 Từ 29 đến 36 7 Từ 36 đến 43 5 Từ 43 đến 50 2 5
e. Nhận xét về hình dáng phân phối của dãy số
Dựa trên đồ thị, ta có thể rút ra một số nhận xét sau:
- Hình dạng phân phối: Đồ thị cho thấy một phân phối lệch trái. Điều này có nghĩa là
phần lớn nhân viên có thời gian đi làm tương đối ngắn (dưới 30 phút), và chỉ có một số
ít nhân viên có thời gian đi làm dài hơn.
- Giá trị trung bình: Giá trị trung bình của thời gian đi làm có thể ước tính nằm ở khoảng
từ 22 đến 29 phút, dựa vào vị trí đỉnh của đồ thị.
II. Mức độ hiện tượng kinh tế - xã hội 1. Bài 68 trang 89
Trudy Green là nhân viên của True-Green Lawn Company, chịu trách nhiệm giới
thiệu dịch vụ chăm sóc cỏ qua điện thoại. Dữ liệu dưới đây là số cuộc hẹn mà cô ấy đã
thực hiện trong 25 giờ qua. Tính trung bình và trung vị về số cuộc hẹn mà cô ấy đã thực
hiện mỗi giờ. Viết một báo cáo tóm tắt những kết quả thu được từ phân tích trên. 9 5 2 6 5 6 4 4 7 2 3 6 3 4 4 7 8 4 4 5 5 4 8 3 3 Lời giải (1) Tính trung bình
Sử dụng công thức tính trung bình, ta có: 6 x = ∑x n=10525= 4.2
(2) Tính trung vị
Ta có bảng sắp xếp 2 2 3 3 3 3 4 4 4 4 4 4 4 5 5 5 5 6 6 6 7 7 8 8 9
Vì số đơn vị = 25, là số lẻ nên ta có:
Vị trí trung vị =n+12= 13 ⇒ Me = 4
(3) Viết báo cáo tóm tắt kết quả trên
Tổng số cuộc hẹn: 105 cuộc hẹn
Trung bình mỗi giờ Trudy Green thực hiện 4.2 cuộc gọi 2. Bài 85 trang 92
Gần đây, Bidwell Electronics Inc. đã khảo sát một mẫu gồm các nhân viên về
quãng đường họ đi làm hàng ngày. Tính trung bình và độ lệch chuẩn dựa vào thông tin trong bảng dưới đây.
Quãng đường (mile) Tần số M Từ 0 đến dưới 5 4 2.5 Từ 5 đến dưới 10 15 7.5 Từ 10 đến dưới 15 27 12.5 Từ 15 đến dưới 20 18 17.5 Từ 20 đến dưới 25 6 22.5 Lời giải Quãng đường Tần số M fM Từ 0 đến dưới 5 4 2.5 10 Từ 5 đến dưới 10 15 7.5 112.5 Từ 10 đến dưới 15 27 12.5 337.5 Từ 15 đến dưới 20 18 17.5 315 Từ 20 dến dưới 25 6 22.5 135 Tổng 70 910 7
Sử dụng công thức tính trung bình (3 – 11), ta có: x = ∑f M n=91070=13
Vậy trung bình một nhân viên đi làm là 13 miles. Quãng đường Tần số M fM
M - 𝑥 (𝑀 − 𝑥 )2 𝑓(𝑀 − 𝑥 )2 Từ 0 đến dưới 5 4 2.5 10 -10.5 110.25 441 Từ 5 đến dưới 10 15 7.5 112.5 -5.5 30.25 453.75 Từ 10 đến dưới 15 27 12.5 337.5 -0.5 0.25 6.75 Từ 15 đến dưới 20 18 17.5 315 4.5 20.25 364.5 Từ 20 dến dưới 25 6 22.5 135 9.5 90.25 541.5 Tổng 70 910 -2.5 251.25 1807.5
Sử dụng công thức độ lệch chuẩn (3-12), ta có: s = √∑ f( n M − − 1 x =)2 √1807.570−1 = 5.12 3. Bài 31 trang 122
Sau đây là số vụ trộm xe hơi trong 1 tuần ở một thành phố lớn. Hãy xác định hệ số
Skewness bằng hai phương pháp. 3 12 13 7 8 3 8 Lời giải n = 7 - Giá trị trung bình: x = ∑x n=54 7= 7.71 - Trung vị: Me = 8
- Độ lệch chuẩn của mẫu: s = √∑ (x n − − x 1 )2 = 3.9 Từ đó, ta có:
- Hệ số Skewness của Pearson sk = 3( x −s M = e 3 ) (7.71 − 8)3.9= − 0.22 8
- Hệ số Skewness từ phần mềm Excel:
III. Điều tra chọn mẫu 1. Bài 31 trang 274
Công ty Power + Inc. sản xuất pin AA dùng cho điều khiển ô tô đồ chơi từ xa. Tuổi
thọ trung bình của loại pin này tuân theo quy luật phân phối chuẩn với giá trị trung bình
là 35.0 giờ và độ lệch chuẩn là 5.5 giờ. Để kiểm tra chất lượng sản phẩm, Power + Inc. đã lấy mẫu 25 pin.
a. Hãy cho biết hình dạng phân phối của các trung bình mẫu.
b. Tính sai số trung bình chọn mẫu.
c. Tính tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 36 giờ trở lên.
d. Tính tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34.5 giờ trở lên.
e. Tính tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34.5 đến 36 giờ.
f. Tính xác suất để sai số chọn mẫu lớn hơn 1 giờ. Lời giải Tóm tắt n = 25 μ = 35 σ = 5.5
a. Hãy cho biết hình dạng phân phối của các trung bình mẫu.
Vì tuổi thọ trung bình của loại pin này tuân theo quy luật phân phối chuẩn nên các trung
bình mẫu (x) cũng được phân phối chuẩn.
b. Tính sai số trung bình chọn mẫu.
Sử dụng công thức sai số trung bình chọn mẫu, ta có: √25 = 5.5 σ= σ√n= 5.5 x 5= 1.1
c. Tính tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 36 giờ trở lên. 9
Sử dụng công thức tính giá trị z, ta có: z = xσ− / √μn= 36 −35 1.1 = 0.91
Dựa vào bảng “Xác suất phân phối chuẩn hoá”, xác suất của giá trị z < 0.91 là 0.3186
⇒ Tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 36 giờ trở lên là:
p = 0.5000 − 0.3186 = 0.1814
d. Tính tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34.5 giờ trở lên.
Sử dụng công thức tính giá trị z, ta có: z = xσ− / √μn= 34.5 − 35 1.1 = −0.45
Dựa vào bảng “Xác suất phân phối chuẩn hoá”, xác suất của giá trị z < 0.45 là 0.1736
⇒ Tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34.5 giờ trở lên là: p = 0.5000 + 0.1736 = 0.6736
e. Tính tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34.5 đến 36 giờ.
Tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34.5 đến 36 giờ là: p = 0.3186 + 0.1736 = 0.4922
f. Tính xác suất để sai số chọn mẫu lớn hơn 1 giờ.
Sai số chọn mẫu lớn hơn 1 giờ tương ứng với tuổi thọ trung bình của pin nhỏ hơn 34
giờ hoặc lớn hơn 36 giờ.
Sử dụng công thức tính giá trị z, ta có: z1= x1σ − /√ μ n= 36 −35 1.1 = 0.91 z2= x2σ − /√ μ n= 34 −35 1.1 = −0.91
Như phần (c) ta có: Tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 36 giờ trở lên là: p1= 0.1814
Tương tự, ta có: Tỷ lệ các mẫu có tuổi thọ trung bình của pin từ 34 giờ trở xuống là: p2= 0.1814
⇒ Xác suất để sai số chọn mẫu lớn hơn 1 giờ là:
p1+ p2= 0.1814 + 0.1814 = 0.3628 IV. Ước lượng 1. Bài 57 trang 309
Áp suất trong khoang máy bay ảnh hưởng đến sự thoải mái của khách hàng. Mức 10