Bài tập nhóm môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

Bài 14 Trang 32: Bộ phận dịch vụ ăn uống của Công viên giải trí Cedar River
đang thực hiện khảo sát về số tiền chi tiêu cho đồ ăn uống mỗi ngày của các gia
đình khi đến công viên. Một mẫu khảo sát gồm 40 gia đình đã đến công viên
ngày hôm qua với các những khoản chi lần lượt như sau: (Đơn vị tính: $)
77 18 63 84 38 54 50 59 54 56 36 26 50 34 44
41 58 58 53 51 62 43 52 53 63 62 62 65 34 52 60 60 45 66 53 71 63 58 61 71
a. Sắp xếp dữ liệu vào bảng tần số phân phối với số tổ là 7 và giới hạn dưới
của tố đầu tiên bằng 15, nên lựa chọn khoảng cách tổ bằng bao nhiêu?
b. Dữ liệu có xu hướng tập trung quanh giá trị nào?
c. Mô tả về phân phối của dãy số.
d. Xây dựng bảng tần suất phân phối. Bài làm a. Khoảng cách tổ là:
= 𝑚𝑎𝑥−𝑚𝑖𝑛 = 84−18 = 9,43 ≈ 10 𝑘 7
b. Trung vị của dữ liệu là 58
Trung bình của dữ liệu là 56,5 Mode của dữ liệu là 63
Vậy dữ liệu có xu hướng tập trung quanh khoảng 58 đến 63
c. Do dữ liệu có Mean < Median < Mode nên đây là dữ liệu phân phối lệch
trái nhẹ nhưng không mạnh d. Khoản chi ở công viên Tần số Tần suất (%) ($) 15 đến 24 1 2,5 25 đến 34 2 5 35 đến 44 5 12,5 45 đến 54 10 25 55 đến 64 15 37,5 65 đến 74 4 10 75 đến 84 3 7,5 Bài 36 trang 45: Bài làm
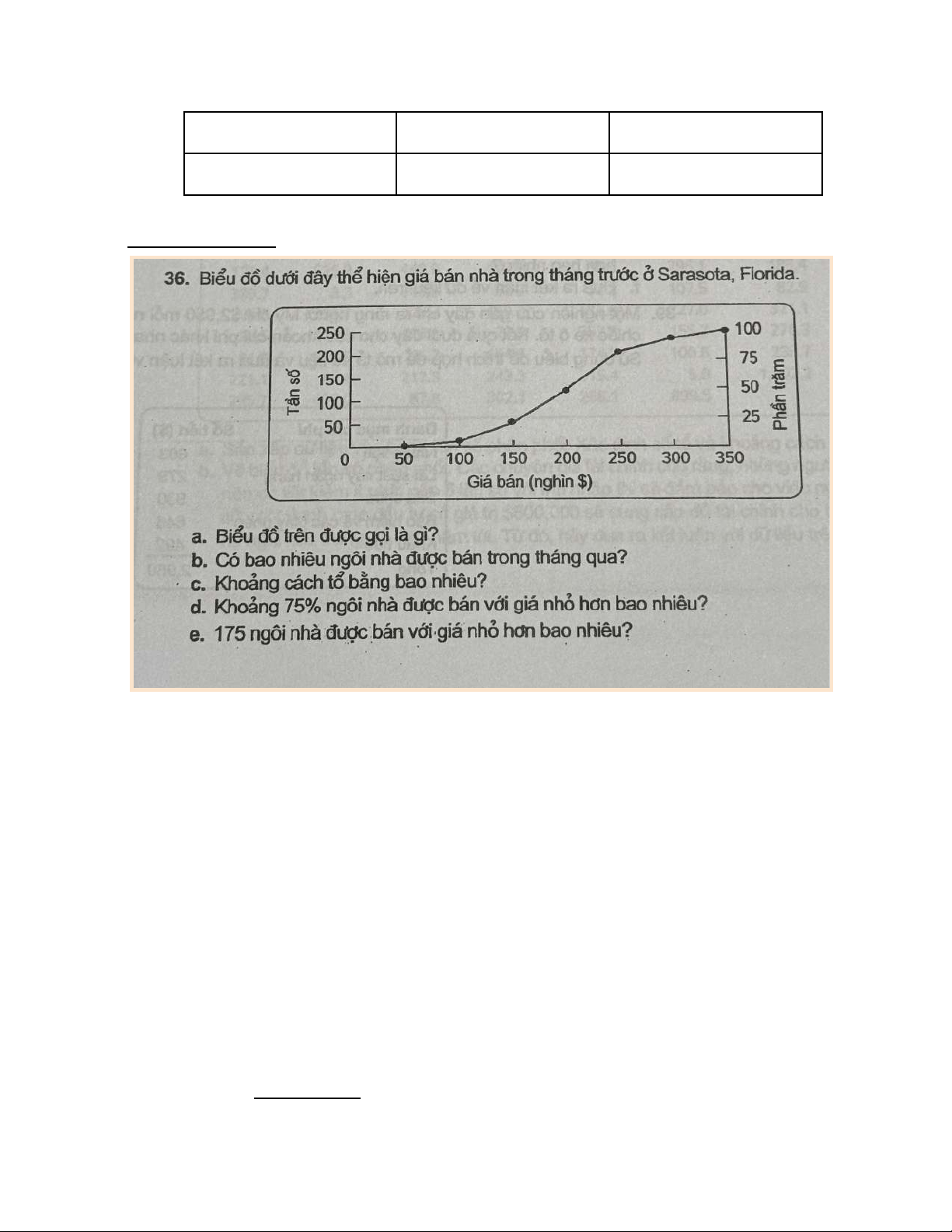
a. Biểu đồ tần số tích lũy (đường cong Ogive)
b. Số nhà tổng cộng = giá trị tích lũy lớn nhất (điểm cuối trục tung) = 250 ngôi nhà
c. Trục giá bán chia theo mốc 0, 50, 100, 150, 200,...,350 (nghìn $). Mỗi tổ
tương ứng một đoạn dài 50 (nghìn $) => Khoảng cách tổ = 50 nghìn $
d. Khoảng 240 nghìn $. (235 - 240 nghìn $).Từ số 75 ở trục Phần trăm
gióng sang trái cho đến khi cắt đường cong, từ đó gióng xuống vuông góc
với trục Giá bán. Điểm rơi nằm gần 250.
Xác định Tần số: 75% của tổng số 250 ngôi nhà là 187,5 nhà. Nội suy Tuyến
tính: Giá trị này nằm trong khoảng tổ [200;250] nghìn $, với tần số tích lũy từ 125 đến 212,5 Giá = 200 + (187,5 − 125) (212,5 − 125) × 50 ≈ 235, 7
e. Dùng nội suy tuyến tính trong khoảng giá [200;250] (tần số tích lũy [125;212.5]). Giá = 200 + (175 − 125)
(212,5 − 125) × 50 ≈ 200 + 28, 6 ≈ 228, 6
=> 175 ngôi nhà được bán với giá nhỏ hơn khoảng 228,6 nghìn $
Bài 81 trang 91: Số liệu về chi phí của 25 sinh viên chưa tốt nghiệp đại học trong năm ngoái
684 710 688 711 722 698 723 743 738 722 696 721 685
763 681 731 736 771 693 701 737 717 752 710 697 Đơn vị tính: $
a) Tính trung bình, trung vị, mốt của dữ liệu
- Trung bình (mean) = 𝚺(25 số liệu) / 25 = 717,2
- Trung vị (medium): sắp xếp các số liệu theo thứ tự từ bé đến lớn: 681,
684, 685, 688, 693, 696, 697, 698, 701, 710, 710, 711, 717, 721, 722,
722, 723, 731, 736, 737, 738, 743, 752, 763, 771
⇒ trung vị là giá trị thứ 13 = 717
- Mốt là 710 và 722 (nhị mốt) do xuất hiện 2 lần
b) Xác định khoảng biến thiên, độ lệch chuẩn
- Khoảng biến thiên = 771 - 681 = 90
- Độ lệch chuẩn của mẫu: s = 24,875
c) Sử dụng quy tắc 3 Sigma để thiết lập 1 khoảng gồm 95% các quan sát
- Quy tắc 3 Sigma: khoảng 95% các quan sát sẽ nằm trong phạm vi (+) và
(-) 2 lần độ lệch chuẩn so với trung bình
⇒ khoảng 95% chi phí của sinh viên chưa tốt nghiệp đại học trong năm
ngoái nằm trong khoảng từ 667.45 đến 766.95 được tính bằng: 717,2 ± 2s = 717,2 + (2 x 24,875)
Bài 14 trang 223: Một phân phối chuẩn có trung bình là 12,2 và độ lệch chuẩn là 2,5
a) Tính giá trị z tương ứng với giá trị 14.3
- z là khoảng cách giữa 14,3 và trung bình, chia cho độ lệch chuẩn
z = (14,3 - 12,2) / 2,5 = 0,84
b) Tỷ lệ trong tổng thể có giá trị nằm trong khoảng từ 12,2 → 14,3 là bao nhiêu?
- Tra bảng phân phối chuẩn hoá, với giá trị 14,3 ta có z = 0,84, xác suất giá
trị nằm trong khoảng từ đuôi trái đến 14,3 là 0,7995. Với giá trị 12,2
tương ứng với z = 0, xác suất giá trị nằm trong khoảng từ đuôi trái đến
12,2 là 50% (vì 12,2 là trung bình)
- Vậy tỷ lệ trong tổng thể có giá trị nằm trong khoảng từ 12,2 → 14,3 là:
0,7995 - 0,5 = 0,2995, tương đương với xấp xỉ 30%
c) Tỷ lệ trong tổng thể có giá trị nhỏ hơn 10.0 là bao nhiêu?
- Giá trị z tương ứng với 10.0 là: z = (10 - 12,2) / 2,5 = -0,88.
⇒ Ta cần tính xác suất P(z < -0,88), nhưng vì bảng xác suất phân phối
chuẩn hoá z chỉ cho giá trị từ 0 → z, ta quy đổi: P(z < -0,88) = 1 - P(z < 0,88) = 1 - 0,8106 = 0,1894
- Vậy tỷ lệ trong tổng thể có giá trị nhỏ hơn 10.0 là 18,94% Bài 38 trang 275
Số tiền trung bình mà một khách hàng chi tại cửa hàng tạp hóa của Churchill là
$23.50, với độ lệch chuẩn là $5. Giả sử số tiền này tuân theo quy luật phân phối
chuẩn. Với cỡ mẫu gồm 50 khách hàng, hãy trả lời các câu hỏi sau:
a, Xác suất để trung bình mẫu lớn hơn hoặc bằng $25.00.
b, Xác suất để trung bình mẫu lớn hơn $22.50 và nhỏ hơn $25.00.
c, 90% mẫu rút ra từ tổng thể có giá trị trung bình nằm trong khoảng nào? Bài làm
a. Xác suất để trung bình mẫu lớn hơn hoặc bằng $25.00 Tìm P( 𝑋 ≥ 25.00)
Tính Z-scrore bằng cách lấy giá trị trừ đi trung bình và chia độ lệch chuẩn (sai số chuẩn) Z = 25.00 − 23.00 0.7071 = 1.50 0.7071 ≈ 2. 12
Tính xác suất P(Z ≥ 2.12) thì cần tìm diện tích bên phải của Z = 2.12 trên
đường cong phân phối chuẩn
Tra bảng Z, P(Z ≤ 2.12) ≈ 0.983 => P(Z 2.12) = 1 - P(Z ≥ ≤ 2.12) = 1 - 0.983 = 0.017
=> Xác suất để trung bình mẫu lớn hơn hoặc bằng $25.00 là 1.70%
- Giải thích: vì σ𝑋 nhỏ hơn rất nhiều so với σ
ban đầu (0.71 so với 5), nên
trung bình của 50 khách hàng sẽ biến động rất ít và luôn có xu hướng gần
$23.50.Xác suất để trung bình chi tiêu của 50 khách hàng đạt $25.00 trở
lên là 1.70%. Đây là một xác suất rất thấp, cho thấy việc trung bình mẫu
sai lệch quá $1.50 so với trung bình tổng thể là điều hiếm gặp.
b. Xác suất để trung bình mẫu lớn hơn $22.00 và nhỏ hơn $25.00 Tìm P(22.50 < < 25.00) 𝑋 Chuẩn hoá về Z-score 𝑋
Giới hạn trên 𝑍𝑢𝑝𝑝𝑒 𝑟 ≈ 2.12 (cho 𝑋 = 25.00) Giới hạn dưới 𝑍 22.50 − 23.50 𝑙𝑜𝑤𝑒 = 𝑟 0.7071 = −10.7071 ≈ − 1. 41
Tìm P(-1.41 < Z < 2.12) = P(Z<2.12) - P(Z< -1.41) P(Z < 2.12) ≈ 0.9830
Tra bảng Z, P(Z < -1.41) 0.0793 ≈ P = 0.9830 - 0.0793 = 0.9037
=> Xác suất để trung bình mẫu nằm trong khoảng $22.00 đến $25.00 là 90.37%
- Giải thích: Khoảng này bao phủ trung bình $23.50 và kéo dài cả hai phía.
Vì phân phối hẹp lại quanh $23.50, nên một phần rất lớn (hơn 90%) của
các trung bình nhóm có khả năng nằm gọn trong khu vực này.
c. 90% mẫu rút ra từ tổng thể có giá trị trung bình nằm trong khoảng nào.
Tìm Z-score cho 90% ở giữa
- Nếu 90% nằm ở giữa, thì 10% còn lại (100%−90%) được chia đều cho hai đuôi
- Mỗi đuôi (trái và phải) sẽ có diện tích là 10%/2=5%
- Tìm giá trị Z sao cho P(Ztra bảng Z, giá trị Z tương ứng với 0.95 (hoặc 0.05 ở đuôi) là Z = ±1.645
Chuyển Z-score về giá trị : 𝑋
𝑋 = µ𝑋± (𝑍 × σ𝑋)
Biên độ dao động: ME = 1.645 × 0.7071 ≈ 1.1632
Giới hạn dưới: 𝑍𝑙𝑜𝑤𝑒𝑟 = 23.50 − 1.1632 = 22.3368
Giới hạn trên: 𝑍𝑢𝑝𝑝𝑒 = 23.50 + 1.1632 = 24.6632 𝑟
=> 90% các mẫu rút ra từ tổng thể sẽ có giá trị trung bình nằm trong khoảng ($22.34, $24.66)
- Giải thích: Khoảng này cho biết nếu bạn ngẫu nhiên 100 mẫu gồm 50
khách hàng, thì 90 trong số 100 giá trị trung bình đó sẽ nằm trong khoảng từ $22.34 đến $24.66. Bài 39 trang 275
Điểm trung bình cho bài kiểm tra thể lực dành cho vận động viên khối I là 947
với độ lệch chuẩn là 205. Chọn một mẫu ngẫu nhiên gồm 60 vận động viên.
Tính xác suất để giá trị trung bình của mẫu nhỏ hơn 900? Dữ liệu:
Giả thiết: µ = 947, σ = 205, n = 60
Ta dùng phân phối chuẩn cho trung bình mẫu vì n lớn (n=60). Tính toán:
Sai số chuẩn: SE = σ / √n = 205 / √60 = 26.4654
Thống kê z = (x - µ) / SE = (900 - 947) / 26.4654 = -1.7759
Xác suất P(x < 900) = Φ(z) = Φ(-1.7759) = 0.037874
Kết luận: Xác suất để giá trị trung bình mẫu nhỏ hơn 900 là 3.7874%. Bài 42. Trang 307 1. Tính snn s Ta có: - s=5s=5 - n=15n=15
Thay vì viết 1515 , ta tính ra số: - 15≈3.87315 ≈3.873 → sn=53.873n s =3.8735 Thực hiện phép chia: 53.873≈1.2913.8735 ≈1.291 2. Tính phạm vi sai số E=t×snE=t×n s
Với t=2.624t=2.624 và sn=1.291n s =1.291: E=2.624×1.291E=2.624×1.291 Thực hiện nhân: E≈3.39E≈3.39
3. Tính khoảng tin cậy 98%
xˉ±E=24±3.39xˉ±E=24±3.39
Hai phép tính bình thường:
- 24−3.39=20.6124−3.39=20.61 - 24+3.39=27.3924+3.39=27.39 Vậy:
CI=(20.61, 27.39)CI=(20.61,27.39) Bài 47. Trang 308
HighTech Inc kiểm tra nhân viên về các chính sách của công ty. Một cuộc khảo
sát ngẫu nhiên 400 nhân viên vào năm ngoái cho thấy có 14 nhân viên bị trượt trong kỳ kiểm tra.
a. Xác định ước lượng điểm về tỷ lệ nhân viên bị trượt trong kỳ kiểm tra.
b. Xác định phạm vi sai số khi ước lượng khoảng tin cậy 99% về tỷ lệ nhân viên bị trượt.
c. Xác định khoảng tin cậy 99% về tỷ lệ nhân viên bị trượt trong kỳ kiểm tra.
d. Có cơ sở để kết luận rằng 5% số nhân viên bị trượt trong kỳ kiểm tra không? Vì sao? Bài làm
a. Ước lượng điểm về tỷ lệ nhân viên bị trượt trong kỳ kiểm tra: 14 400 x100 = 3,5%
b. Với khoảng tin cậy 99%: 𝑍0,00 = 2,576 5 ≈ 2,58 Tính độ lệch chuẩn:
0,035(1−0,035) = 0,035 𝑥 0,965 = 0,033775 = 400 400 400 0, 0000844375 ≈ 0.00919
Phạm vi sai số: 2,58 x 0.00919 ≈ 0,0237
→ Phạm vi sai số ≈ 2,37% c.
● Cận dưới: 0.035−0.0237 = 0.01130.035 - 0.0237 = 0.01130.035−0.0237 = 0.0113
● Cận trên: 0.035+0.0237 = 0.05870.035 + 0.0237 = 0.05870.035+0.0237 = 0.0587
→ Khoảng tin cậy 99%: (0.0113, 0.0587) hay: 1.13% đến 5.87%
d. So sánh 5% (0.05) với khoảng tin cậy 99%: 0.0113≤0.05≤0.05870.0113
Giá trị 0.05 nằm trong khoảng tin cậy 99%.
→ Tỷ lệ trượt 5% là có cơ sở để kết luận. Bài 42 trang 307 Dữ liệu - (n = 15) - (\bar{x} = 24) - (s = 5)
- Mức tin cậy: 98% → (\alpha = 0.02) → tra bảng (t_{0.99, , df=14} \approx 2.624)
a. Phạm vi sai số (margin of error)
[E = t \cdot \frac{s}{\sqrt{n}}] Tính:
[\frac{s}{\sqrt{n}} = \frac{5}{\sqrt{15}} \approx \frac{5}{3.873} \approx 1.291]
[E = 2.624 \times 1.291 \approx 3.39]
Phạm vi sai số ≈ 3.39 lần rao bán
b. Khoảng tin cậy 98% cho số lần rao bán trung bình [\bar{x} \pm E = 24 \pm 3.39] → CI = (20.61 , 27.39) Kết quả
a. Phạm vi sai số: ≈ 3.39
b. Khoảng tin cậy 98%: (20.61 ; 27.39) Bài 29 trang 343:
(Kiểm định trung bình mẫu nhỏ hơn 7):
- Giả thuyết: H0:μ=7H0 :μ=7 (trung bình dân số là 7 giờ) và Ha:μ<7Ha :μ<7.
- Dữ liệu: xˉ=6.8, s=0.9, n=50, α=0.05.xˉ=6.8,s=0.9,n=50,α=0.05.